Prerpints.org logo
Preprint
Article

Evaluation of Power Consumption Efficiency of Encryption Schemes for RFID Systems

Altmetrics

Downloads

84

Views

67

Comments

0

Submitted:

16 February 2024

Posted:

16 February 2024

You are already at the latest version

Alerts
Abstract
This paper provides a comparative analysis of AES (Advanced Encryption Standard) and Salsa20 algorithm implementations, focusing on power consumption efficiency in passive RFID (Radio Frequency Identification) tags and ultra-low-power devices. The main objective of this work is to determine which of these algorithms is more suitable to operate in these types of devices. For this purpose, ASIC (Application-Specific Integrated Circuit) implementations of AES and Salsa20 based on low-power approaches were developed and their power consumption was evaluated. Results demonstrate that Salsa20 power consumption is lower than AES (2.82μW and 4.01μW, respectively - both in 0.18μm), indicating that Salsa20 is a better choice than AES for passive RFID tags.
Keywords: 
Subject: Engineering  -   Electrical and Electronic Engineering

1. Introduction

The range of applications for RFID (Radio Frequency Identification) systems is vast, spanning areas such as logistics, healthcare, access control, ubiquitous computing and supply chain management, as well as applications in the context of IoT (Internet of Things) systems [1]. Among the different types of RFID tags, passive tags are the simplest, cheapest and most ubiquitous [2]. Passive RFID tags operate without an internal board power source, relying on energy received from the RFID reader for its operation. RFID systems are even being proposed for applications commonly covered by conventional battery-powered wireless sensor network (WSN) devices, through the emerging field of RFID sensors [3], which raise even more challenges for the severely energy-constrained passive RFID tags.
Driven by its increasing demand, the use of ultra-low-power RFID tags in commercial products has brought risks related to information security, industrial espionage and individual privacy. Inventory information or personal identification without cryptography can be easily monitored without a trace of who did it. Therefore, most digital ID and tracking applications must have security and privacy addressed in their project architectures, just like credit card applications have.
To meet the growing demand for product tracking via RFID tags, there is a trend toward lowering the cost and power consumption of these devices. Consequently, their computational capabilities tend to be very low, which poses challenges in the implementation of encryption schemes for these devices.
The design of low-power devices should take into account three main fundamental aspects: chip area, power consumption and latency (clock cycles). This work focuses primarily on the issue of power consumption, which may also contribute to improvements regarding other relevant aspects, such as chip area.
The power provided by the RFID reader over the air interface decreases linearly with the operating distance to UHF (Ultra High Frequency) tags. In order to allow cryptographic operations in the whole operating range of a tag, which, in the case of UHF tags, typically ranges up to seven meters, a limit on the power budget of approximately 20 μ W should not be exceeded [4].
In this paper, we present a comparative analysis of the power consumption efficiency of AES (Advanced Encryption Standard) and Salsa20 ASIC implementations (both designed by us) optimized for use in passive RFID tags in order to determine which algorithm is more suitable to operate in low-power devices. In this sense, the main contributions of this work are the design, implementation and evaluation of these algorithms with the goal to provide security to low-power devices for digital identification applications.
The remainder of this paper is organized as follows: Section 2 presents related work while Section 3 and Section 4 presents the algorithm descriptions and implementations respectively, and finally Section 5 presents the results and discussions.

2. Background and Related Work

2.1. Security Level

A deep analysis of the security level of AES and Salsa20 ciphers is out of the scope of this paper, but these two ciphers appear to have similar security levels, according to related cryptanalytic studies presented below.
AES, also known by the name Rijndael, was announced as a standard by the U.S. National Institute of Standards and Technology (NIST) in 2001 [5]. Cryptanalytic papers in the next years culminated in attacks taking [6,7]:
  • 2 140 operations to break 7 rounds of 256-bit AES;
  • 2 204 operations to break 8 rounds of 256-bit AES.
Salsa20 was published in 2005 [8]. Refereed cryptanalytic papers by Fischer et al. [9] and Tsunoo et al. [10] have culminated in attacks taking:
  • 2 151 operations to break 7 rounds of 256-bit Salsa20;
  • 2 251 operations to break 8 rounds of 256-bit Salsa20.
These results indicate that AES and Salsa20 present similar security performance for the same number of rounds.

2.2. AES and Salsa20 Implementations

Over the years, RFID tags have been designed with the goal of reducing their power consumption in order to meet the demand for passive chip applications and lower cost.
Experimental results from L. Fu et al. [11] show that a RFID dedicated AES module can achieve low power operation, down to 4.05 μ W @ 1.8 V and latency of 204 cycles.
The low cost demanded for RFID tags forces them to be very resource-limited. Typically, they can only store a few hundred bits, have 5-10k logic gates and offer a maximum communication range of a few meters. Within this gate counting limitation, only between 250 and 3000 gates can be devoted to security functions [12].
Several papers have presented low-power implementations of the AES suitable for RFID tags applications in terms of power consumption and die size [4,13,14], where the best results are about 4.5 μ W on 0.35 μ m at 100 kHz [15].
There are several implementations of Salsa20 [16] for FPGA (Field Programmable Gate Array) and ASIC (Application-Specific Integrated Circuit) simulation, all of them optimized for speed. However, these implementations are not concerned about low-power constraints.
Some software-based papers combine both ciphers by using Salsa20 for encryption and AES for authentication [17], but we still lack of hardware-based papers as noted in a recent review that excludes a salsa20 implementation on chip for proper comparison [18].

3. Algorithm Descriptions

3.1. The AES Algorithm

An official description of the AES is detailed in the NIST FIPS (Federal Information Processing Standards) PUB 197 [5]. For the sake of clarity, a brief outline of the AES’s structure is explained in this section. The AES algorithm is a block cipher that was published in the FIPS 197, in 2001. It was adopted by the U.S. government when the National Security Agency (NSA) approved AES as a cipher for top-secret information in 2002.
The AES is capable of using cryptographic keys of 128, 192, and 256 bits to encrypt or decrypt data in blocks of 128 bits. The data to be processed is usually expressed as an array of bytes organized as a 4 by 4 matrix and called ’State’.
The design principle is based on a Substitution permutation network and it is specified to convert an input block into a final output block by a number of repetitive transformation rounds [5]. Each round consists of up to four processing steps, which are performed at the byte or bit level of the State. The transformations that describe a round of AES and the respective processing steps are:
  • AddroundKey transformation: this is simply the XOR between each bit of the State to each bit of the round key. This is the operation that depends on the cryptography key.
  • SubByte transformation: this is a non-linear byte substitution. It has two steps, of which the first one is a multiplicative inverse and the other is an affine transformation.
  • ShiftRow transformation: this is a byte-wise operation. The first row of the State is not shifted, but the last three rows of the State are rotated over 1, 2 and 3 bytes, respectively. This operation adds linear diffusion.
  • MixColumn transformation adds linear diffusion into the cryptography. Each column of the State is combined using an invertible linear transformation. Each column is treated as a polynomial over GF (Galois Field) 2 8 and it is then multiplied by a fixed polynomial c ( x ) modulo x 4 + 1 , given by:
(Equation (1))
C ( x ) = 03 x 3 + 01 x 2 + 01 x + 02
During the InvMixColumn operation, each column is treated as a polynomial over GF 2 8 and then multiplied by a fixed polynomial C − 1 ( x ) module x 4 + 1 , given by:
(Equation (2))
C − 1 ( x ) = 0 b x 3 + 0 d x 2 + 09 x + 0 e

3.2. The Salsa20 Algorithm

Salsa20 is a stream cipher that works in counter mode. It generates a sequence of keystream blocks Z, which are then XORed with the input message (plaintext) to produce the encrypted message (ciphertext). The internal keystream generation function of Salsa20 takes as input a 256-bit secret key k = k 0 , k 1 , … , k 7 and a 64 -bit nonce n = n 0 , n 1 , i.e., a unique message number, to produce a sequence of 512-bit keystream blocks. The inputs are configured as a 4 by 4 matrix of 32-bit words:
X = x 0 x 1 x 2 x 3 x 4 x 5 x 6 x 7 x 8 x 9 x 10 x 11 x 12 x 13 x 14 x 15 = ϕ 0 k 0 k 1 k 2 k 3 ϕ 1 n 0 n 1 t 0 t 1 ϕ 2 k 4 k 5 k 6 k 7 ϕ 3
where the 64 -bit counter t = ( t 0 , t 1 ) corresponds to the message block index and the ϕ i are predefined constants. The keystream block Z is then defined as:
(Equation (3))
Z = X + D R ( X )
The double-round function DR ( ) consists of the double computation of four QUARTERROUND functions QR ( ) over the rotated columns and rows of X. DR ( ) is divided into the column step, which applies four QR ( ) functions on the columns of X, and the row step, for the rows of X:
Q R x 0 , x 4 , x 8 , x 12 Q R x 5 , x 9 , x 13 , x 1 Q R x 10 , x 14 , x 2 , x 6 Q R x 15 , x 3 , x 7 , x 11 ; Q R x 0 , x 1 , x 2 , x 3 Q R x 5 , x 6 , x 7 , x 4 Q R x 10 , x 11 , x 8 , x 9 Q R x 15 , x 12 , x 13 , x 14
The Q R ( a , b , c , d ) transformation updates four 32-bit words of the matrix X . It sequentially computes per line over the tuple ( a , b , c , d ) :
(Equation (4))
b = b ⊕ [ ( a + d ) < < < 7 ] , c = c ⊕ [ ( b + a ) < < < 9 ] , d = d ⊕ [ ( c + b ) < < < 13 ] , a = a ⊕ [ ( d + c ) < < < 18 ]
Considering equations 4 , r double-rounds are executed over the input matrix X. Finally, the updated matrix X is added to the original input matrix. Salsa20 has been presented as a r = 10 rounds stream cipher [16].

4. Algorithm Implementations

4.1. AES Implementation

Since the AES algorithm is iterative, a minimum set of processing blocks is used and a simple finite state machine controls the many rounds that repetitively reuse these processing blocks.
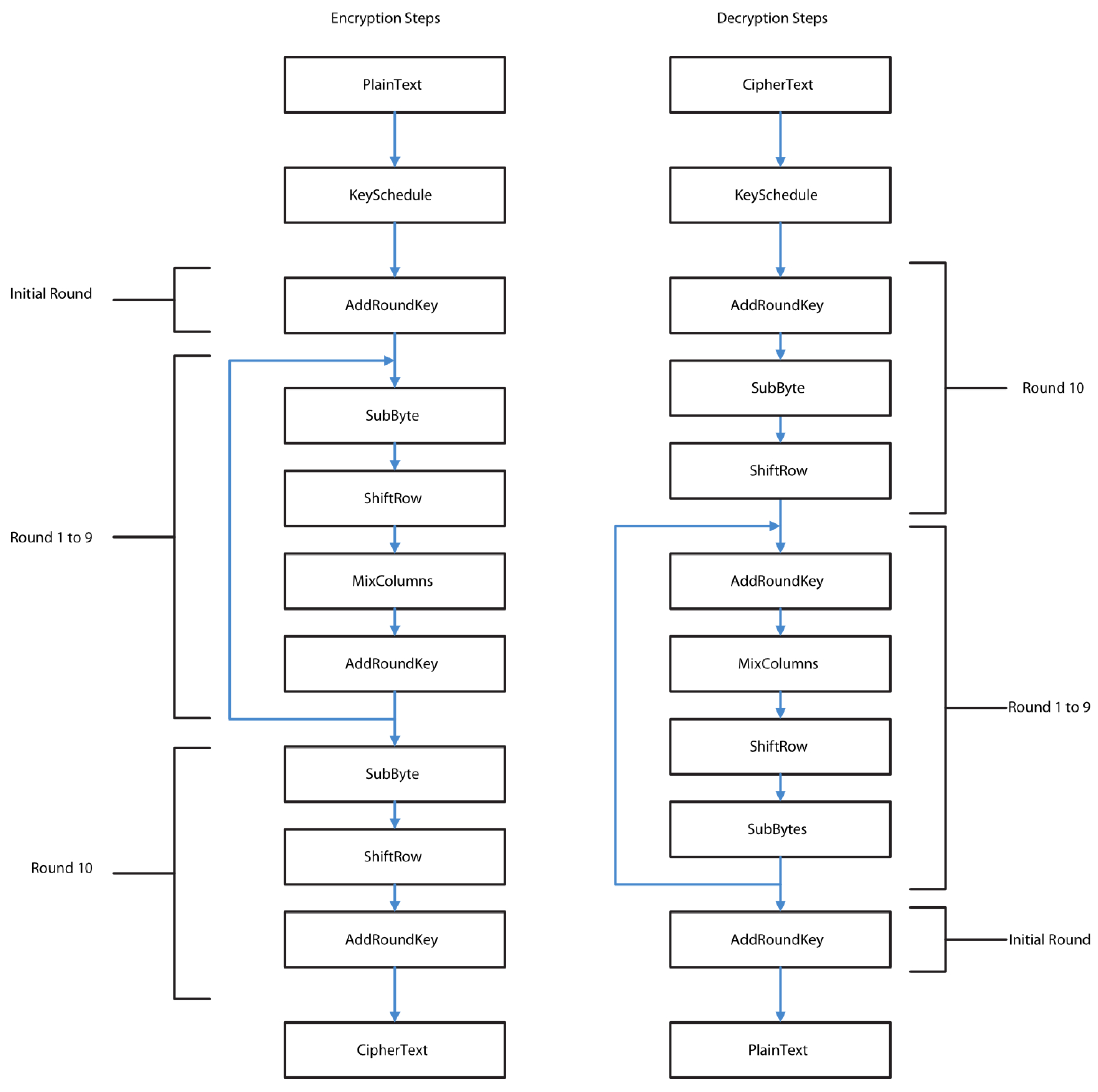
The current implementation has three main processing blocks:KeySchedule, MixColumn and SubByte, where the latter includes also the ShiftRow operation, with both areas being executed by the same processing block. The encryption and decryption steps of the simple finite state machine are described in Figure 1.
In order to save any redundant processing during key expansion for decryption, the ten round keys are saved in registers before any data processing.
As you can see from the implementation flowchart, the first step during cryptography is to derive its ten round keys and to save each round key in a bank of registers. This approach provides a latency improvement of 135 cycles with the area addition of nine 128-bit registers.
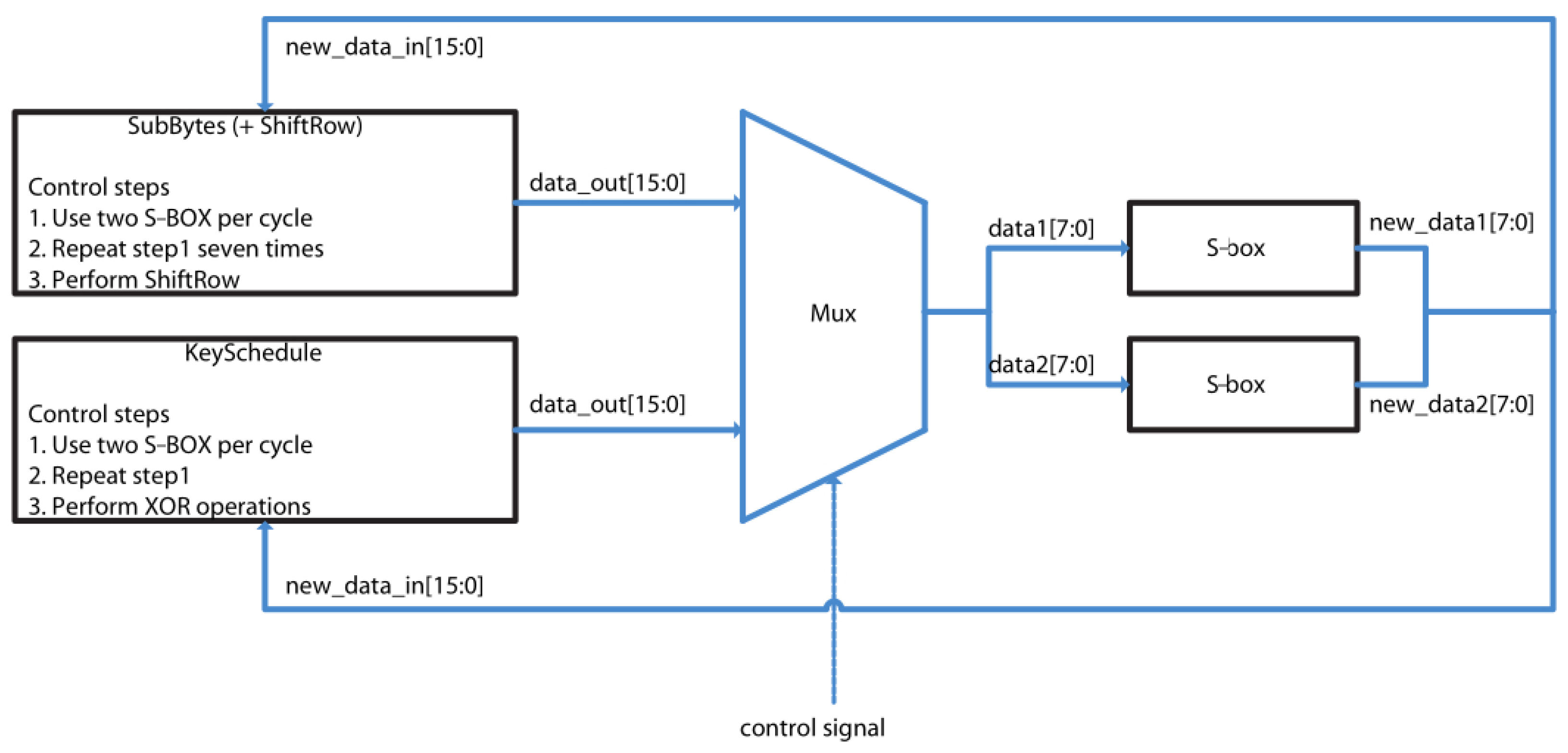
Both SubByte and KeySchedule transformations use a S-box. Since the control unit does not request the SubByte and KeySchedule to operate at the same time, they can share the same S-box logic to minimize area. In this implementation, in order to speed up the S-box tasks, there are two identical instances that function in parallel, as shown in Figure 2.
The first step for the S-box comprises finding the multiplicative inverse of a byte from the AES’s state. The second step S-box comprises an affine Transformation. The element of inversion is performed in G F 2 4 2 by means of mathematical manipulation.
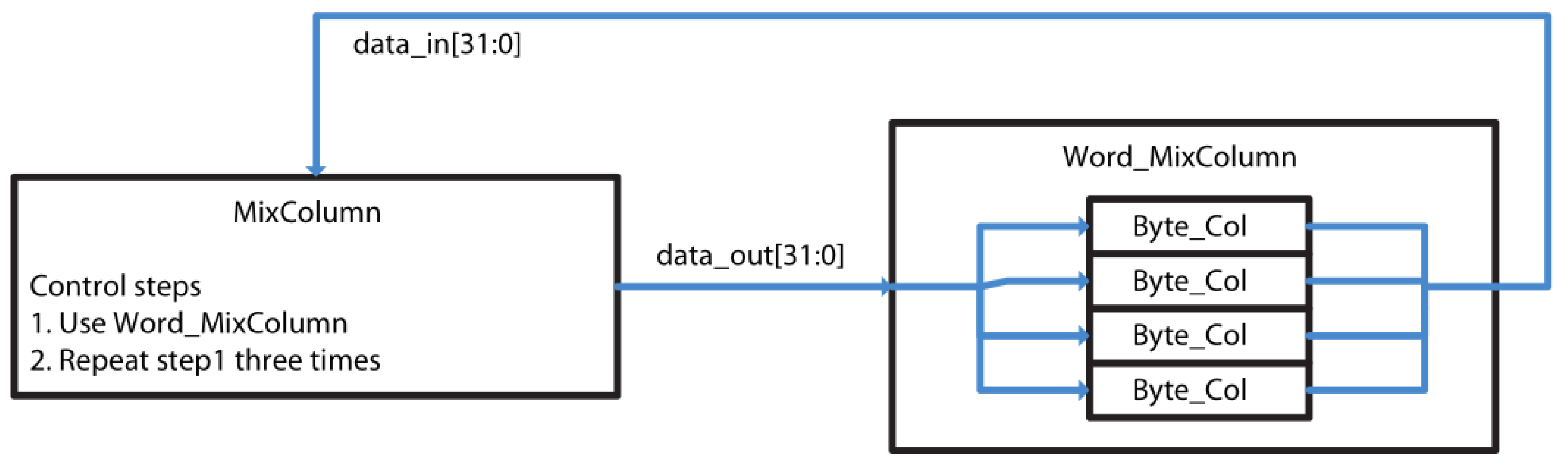
The MixColumn controller sends a 32-bit input to a multiplier block, namely, Word_MixColumn. Each input stream sent from the MixColumn controller is a column of the AES State. Thus, MixColumn operation is performed in four cycles (Figure 3), since each column of the State is processed per cycle. The 32-bit column is processed by four multipliers block. We reused common constant multipliers in the data path between the MixColumn and InvMixColumn operations to reduce the hardware area.

4.2. Salsa20 Implementation

The Salsa20 implementation prioritizes a low-power approach over execution time. Each step of the QUARTERROUND function is executed in a clock cycle for power-saving purposes. In this case, the QUARTERROUND function is executed in four clock cycles. For timing purposes, the double-round function control state machine uses two QUARTERROUND modules at the same time.
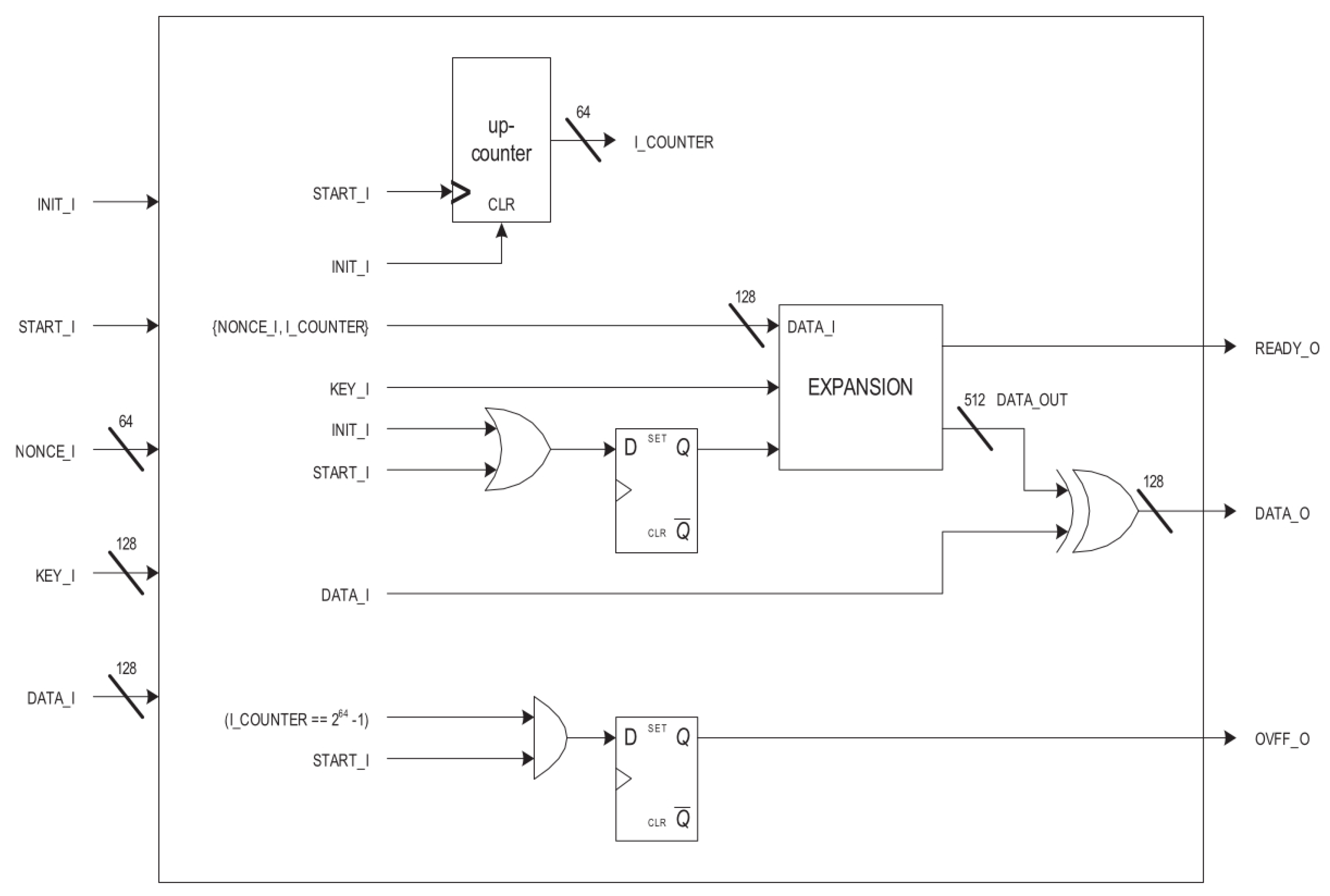
The basic operation of Salsa20 is the QUARTERROUND function. It is executed 80 times in the Salsa20 algorithm, so it is the most obvious choice for optimizing in terms of power. Figure 4 shows the Salsa20 encryption hardware implementation. It includes a 64-bit counter to generate the data input to the Salsa20 expansion module, as described in the Salsa20 specification [8]. It also evaluates the XOR for the encrypted output. The key and data input are 128 bits, for better comparison of the Salsa20 implementation with the AES-128 implementation.
The ’Salsa20 expansion’ module is a simple wire concatenation in the input of the Salsa20 core module as shown in Figure 5. The T0, T1, T2, T3 constants are described in the Salsa20 specification [8].
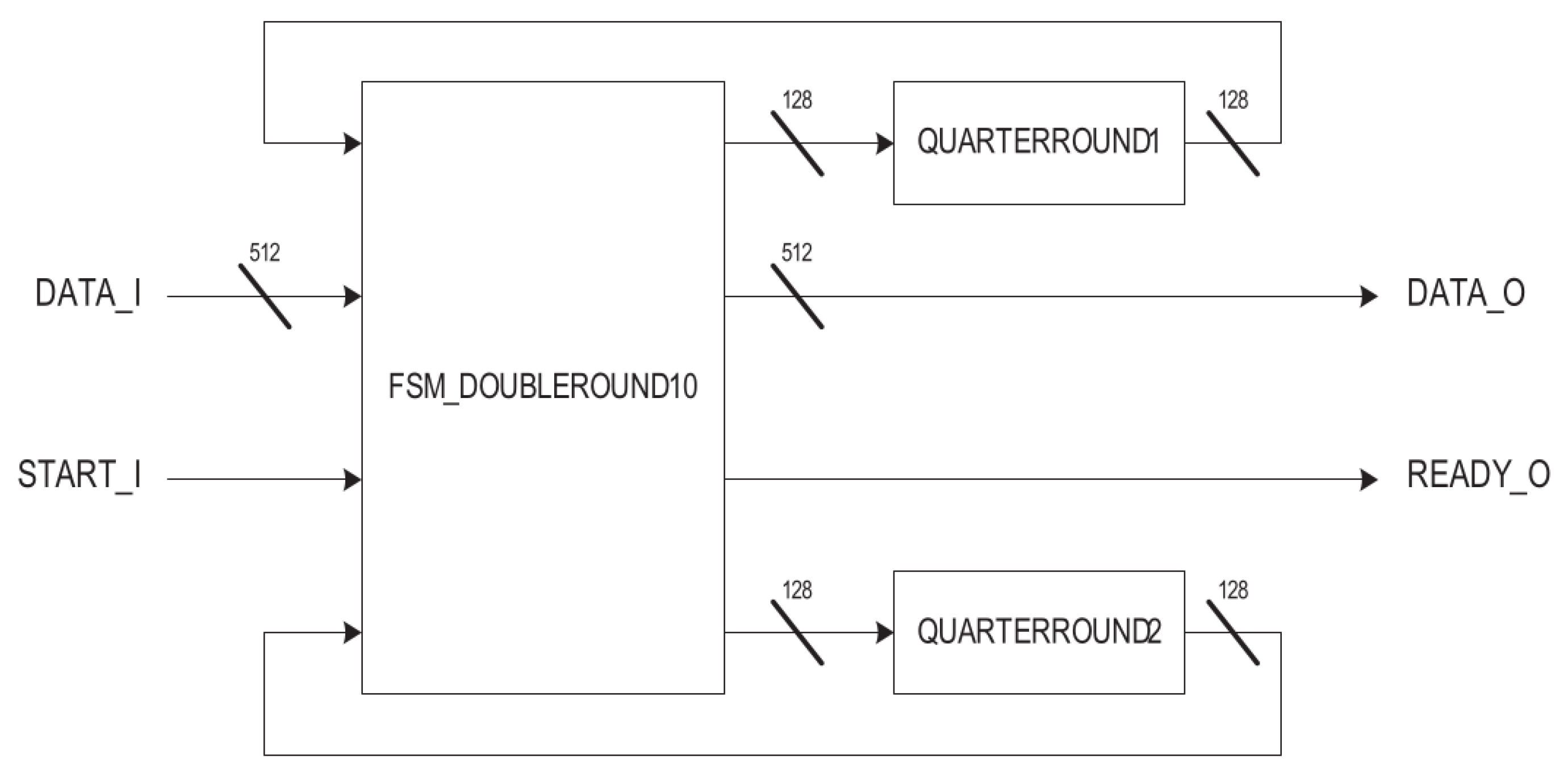
The Salsa20 core module (Figure 6) is composed of the Salsa20 DOUBLEROUND10 module with LITTLE_ENDIAN functions at the input and output. The LITTLE_ENDIAN function changes the endianness using a byte as the minimal block.
Figure 7 shows the Salsa20 DOUBLEROUND10 module implementation. It is composed of a control state machine and two QUARTERROUND modules. The double-round function is a column-round function followed by a row-round function.
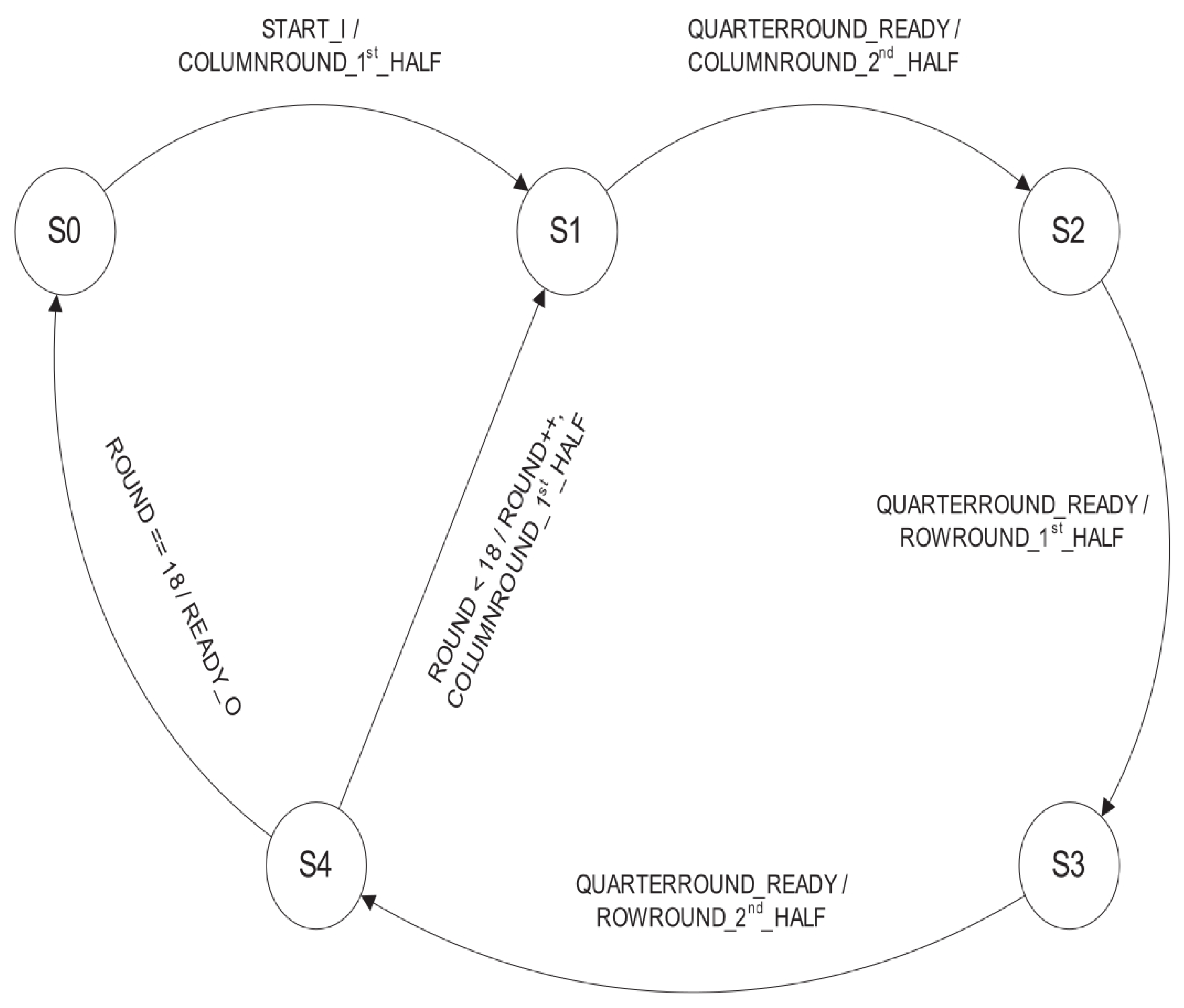
The Salsa20 DOUBLEROUND10 control state machine (Figure 8) controls the data flow to and from the QUARTERROUND modules. This control state machine executes two QUARTERROUND functions at the same time for each half-round of the double-round (the first half of column-round, the second half of column-round, the first half of row-round and the second half of row-round).
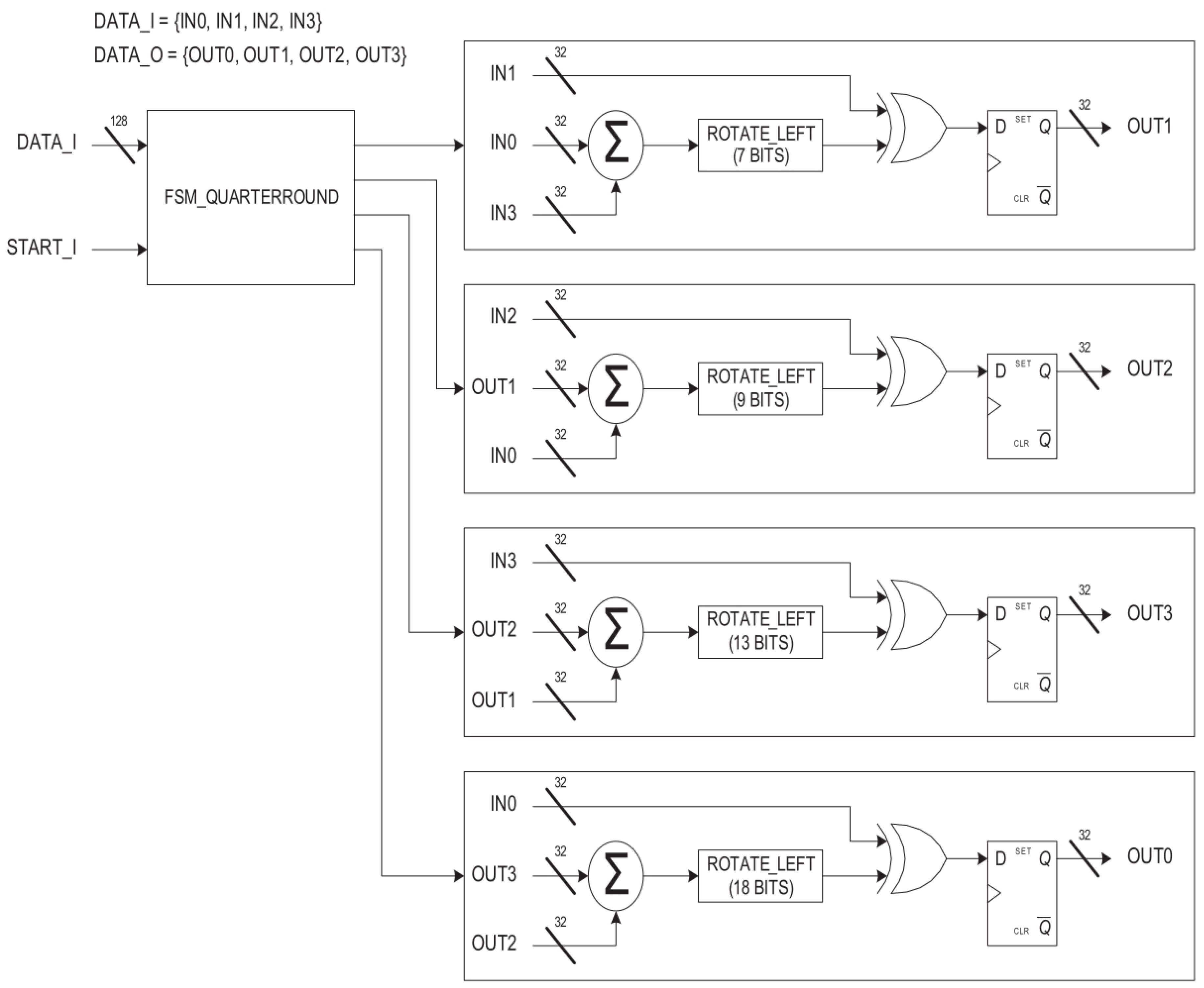
Figure 9 shows the Salsa20 QUARTERROUND, where four words (32 bits each) are evaluated one at a time. The QUARTERROUND is optimized for power: each word takes a clock cycle in the QUARTERROUND execution, so each QUARTERROUND execution takes 4 cycles to complete.
The Salsa20 QUARTERROUND control state machine (Figure 10) controls the clock gating of the four-word evaluation sub-blocks.

5. Results and Discussion

5.1. AES Design

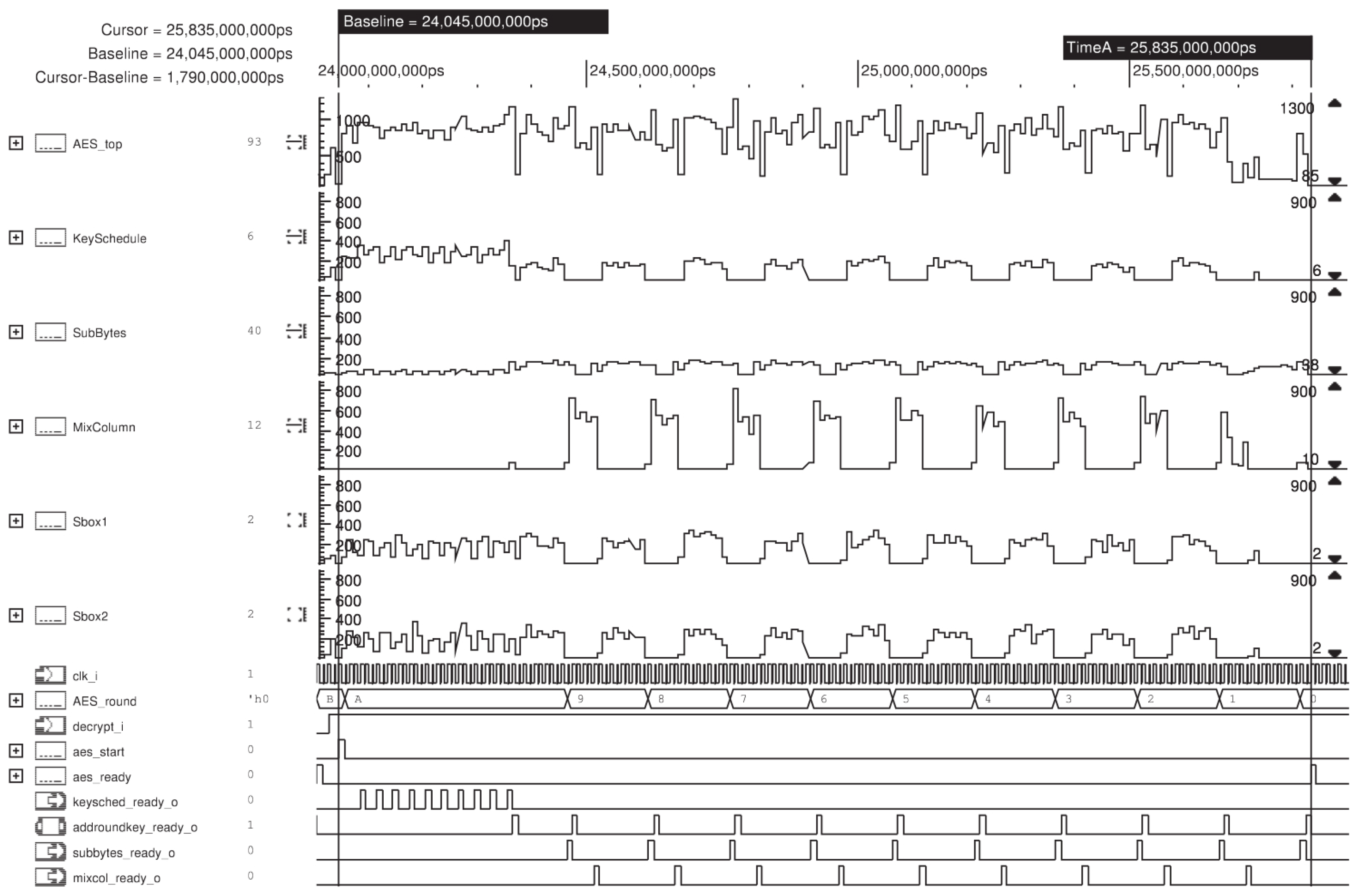
The toggle count of each processing block during the simulation of an AES decryption can be observed in Figure 11. Since the technology node is 0.18 μ m , dynamic power is the dominant factor in our power analysis. Based on the toggle counts of encryption and decryption simulations, one can conclude that the peak power consumption occurs during the MixColumn transformation. Therefore, the decision to add two S-boxes does not affect peak power. We have concluded that the peak power of this AES implementation with two S-boxes is not affected. Moreover, the S-box implementation uses very little area, and the addition of a second S-box does not represent a considerable cost to the overall system.
Table 1 shows a summary of the main simulation results generated from the toggle waveform (that represents the number of transitions in a circuit in a given period, which is a good approximation for the power). The AES design has an average power consumption of 4.01 μ W with a clock of 100 kHz . The encryption or decryption latency is 180 cycles and its critical path takes 19 , 045 p s (we basically achieved the same characteristics obtained by L. Fu et al. [11]). The reduced and balanced latency of both decryption and encryption is achieved at the cost of the nine 128-bit registers used by the KeySchedule block. These extra registers avoided redundant processing but had an impact on the overall area. This AES design has 4,303 cells and a total area of 217 , 250 μ m 2 .

5.2. Salsa20 Design

The toggle count of each processing block of the Salsa20 simulation can be observed in Figure 12. As expected, the peaks of the toggle are concentrated in the QUARTERROUND function. Two QUARTERROUND blocks were used instead of only one to make the timing close to the AES implementation.
Table 2 shows the summary report generated by the simulation-based toggle waveform. The Salsa20 has an average power consumption of 2.82 μ W with a clock of 100 kHz and a 0.18 μ m , 1.8 V cell library. The encryption and decryption latency is 202 clock cycles and its critical path takes 17 , 561 p s .

5.3. Layout Comparison

The layout of both designs used the X-FAB 0.18 μ m and 1.8 V library. The AES and Salsa20 modules have the same utilization area of 75 % .
The AES layout, depicted in Figure 13, includes the AES module and a testing control logic. The layout of the AES module is colored in red and it is 395 μ m × 550 μ m 217 , 250 μ m 2 which is very close to the estimation from Table 1.
The Salsa20 layout (Figure 14) includes the Salsa20 module and the same testing control logic. The layout of the Salsa20 module is colored in red and it is 255 μ m × 530 μ m 135 , 150 μ m 2 which is also very close to the estimation from Table 2. The AES layout has two more filler pads than the Salsa20 layout because of its bigger area.

6. Conclusions

In this paper, low-power implementations of the AES and Salsa20 were proposed and their results were compared. In order to fairly compare the cost and power consumption of those two cryptographic algorithms without any trade-off compromise, the same synthesis and simulation parameters, such as clock, test vectors and tech library, were used on both of them. In addition, both have been designed to have similar latencies.
Our work shows that Salsa20 power consumption is considerably lower than the AES power consumption, suggesting the former is a better choice for low-power devices. Moreover, the area of Salsa20 implementation is also considerably lower than that of the AES one, presenting also a lower fabrication cost. Therefore, Salsa20 is a very attractive cryptographic algorithm for secure RFID applications.

Author Contributions

Mario Gazziro and João Carmo work on the digital implementation of Salsa and AES, respectively. Marco Cavallari and Oswaldo Hideo works on digital verification. José Afonso wrote the article.

Funding

This research received no external funding.

Data Availability Statement

The data presented in this study are available on request from the corresponding author

Acknowledgments

This work was supported by the Wernher von Braun Center for Advanced Research. The authors also want to thank Nelson Guimaraes, Paulo Matias, Henrique Okada, Alexander Sieh, Andre Costa, Dario Thober and Jecel Mattos.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Munoz-Ausecha, C., Ruiz-Rosero, J., & Ramirez-Gonzalez, G. (2021). RFID applications and security review. Computation, 9(6), 69. [CrossRef]
  2. Casella, G., Bigliardi, B., & Bottani, E. (2022). The evolution of RFID technology in the logistics field: a review. Procedia Computer Science, 200, 1582-1592. [CrossRef]
  3. Costa, F., Genovesi, S., Borgese, M., Michel, A., Dicandia, F. A., & Manara, G. (2021). A review of RFID sensors, the new frontier of internet of things. Sensors, 21(9), 3138. [CrossRef]
  4. Oren, Y., & Feldhofer, M. (2009). A low-resource public-key identification scheme for RFID tags and sensor nodes. In Proceedings of the second ACM conference on Wireless network security (WiSec ’09). Association for Computing Machinery, New York, NY, USA, 59–68.
  5. National Institute of Standards and Technology (NIST). ’FIPS-197: advanced encryption standard, November 2001.
  6. Piret, G., & Quisquater, JJ. (2003). A Differential Fault Attack Technique against SPN Structures, with Application to the AES and KHAZAD. In: Walter, C.D., Koç, Ç.K., Paar, C. (eds) Cryptographic Hardware and Embedded Systems - CHES 2003. CHES 2003. Lecture Notes in Computer Science, vol 2779. Springer, Berlin, Heidelberg.
  7. Mangard, S. (2003). A Simple Power-Analysis (SPA) Attack on Implementations of the AES Key Expansion. In: Lee, P.J., Lim, C.H. (eds) Information Security and Cryptology — ICISC 2002. ICISC 2002. Lecture Notes in Computer Science, vol 2587. Springer, Berlin, Heidelberg.
  8. Bernstein, D.J. ‘The salsa20 family of stream ciphers’ eSTREAM, ECRYPT Stream Cipher Project, Report 2005/025, http://www.ecrypt.eu.org/stream, (2005).
  9. Fischer, S., Meier, W., Berbain, C., Biasse, JF., & Robshaw, M.J.B. (2006). Non-randomness in eSTREAM Candidates Salsa20 and TSC-4. In: Barua, R., Lange, T. (eds) Progress in Cryptology - INDOCRYPT 2006. INDOCRYPT 2006. Lecture Notes in Computer Science, vol 4329. Springer, Berlin, Heidelberg.
  10. Tsunoo, Y., Saito, T., Kubo, H., Suzaki, T., & Nakashima, H. (2007). Differential cryptanalysis of Salsa20/8. In: SASC2007. [S.l.: s.n.], pp. 10-22.
  11. Fu, L., Shen, X., Zhu, L., & Wang, J. (2014). A low-cost UHF RFID tag chip with AES cryptography engine. Security Comm. Networks, 7: 365-375. [CrossRef]
  12. Peris-Lopez, P., Hernandez-Castro, J.C., Estevez-Tapiador, J.M., Ribagorda, A. (2006). M2AP: A Minimalist Mutual-Authentication Protocol for Low-Cost RFID Tags. In: Ma, J., Jin, H., Yang, L.T., Tsai, J.JP. (eds) Ubiquitous Intelligence and Computing. UIC 2006. Lecture Notes in Computer Science, vol 4159. Springer, Berlin, Heidelberg.
  13. Satoh, A., Morioka, S., Takano, K., & Munetoh, S. (2001). A Compact Rijndael Hardware Architecture with S-Box Optimization. In: Boyd, C. (eds) Advances in Cryptology — ASIACRYPT 2001. ASIACRYPT 2001. Lecture Notes in Computer Science, vol 2248. Springer, Berlin, Heidelberg.
  14. Mangard, S., Aigner, M., & Dominikus, S. (2003). A highly regular and scalable AES hardware architecture. In IEEE Transactions on Computers, vol. 52, no. 4, pp. 483-491. [CrossRef]
  15. Feldhofer, M., Wolkerstorfer, J., & Rijmen, V. (2005). AES implementation on a grain of sand. IEE Proceedings Information Security, Vol. 152, pp. 13-20. [CrossRef]
  16. Henzen, L., Carbognani, F., Felber N. and Fichtner, W. (2008). VLSI hardware evaluation of the stream ciphers Salsa20 and ChaCha, and the compression function Rumba. In: 2nd International Conference on Signals, Circuits and Systems, Nabeul, Tunisia, 2008, pp. 1-5.
  17. Nikitha, G., Kathrine, G., Duthie, C., Ebenezer, V., & Silas, S. (2023). Hybrid Cryptographic Algorithm to Secure Internet of Things. In: 7th International Conference on Intelligent Computing and Control Systems (ICICCS), Madurai, India, pp. 1556-1562.
  18. Bokhari, M., & Afzal, S. (2023). Performance of Software and Hardware Oriented Lightweight Stream Cipher in Constraint Environment: A Review. In: 10th International Conference on Computing for Sustainable Global Development (INDIACom), New Delhi, India, 2023, pp. 1667-1672.
Preprints 99032 g001
Figure 1. Encryption and decryption flowcharts.
Figure 1. Encryption and decryption flowcharts.
Preprints 99032 g001
Preprints 99032 g002
Figure 2. KeySchedule and SubByte+ShiftRow blocks using two S-boxes.
Figure 2. KeySchedule and SubByte+ShiftRow blocks using two S-boxes.
Preprints 99032 g002
Preprints 99032 g003
Figure 3. MixColumn block.
Figure 3. MixColumn block.
Preprints 99032 g003
Preprints 99032 g004
Figure 4. Salsa20 encryption hardware implementation.
Figure 4. Salsa20 encryption hardware implementation.
Preprints 99032 g004
Preprints 99032 g005
Figure 5. Salsa20 expansion module.
Figure 5. Salsa20 expansion module.
Preprints 99032 g005
Preprints 99032 g006
Figure 6. Salsa20 core module.
Figure 6. Salsa20 core module.
Preprints 99032 g006
Preprints 99032 g007
Figure 7. Salsa20 DOUBLEROUND10 module.
Figure 7. Salsa20 DOUBLEROUND10 module.
Preprints 99032 g007
Preprints 99032 g008
Figure 8. Salsa20 DOUBLEROUND10 control state machine.
Figure 8. Salsa20 DOUBLEROUND10 control state machine.
Preprints 99032 g008
Preprints 99032 g009
Figure 9. Salsa20 QUARTERROUND.
Figure 9. Salsa20 QUARTERROUND.
Preprints 99032 g009
Preprints 99032 g010
Figure 10. Salsa20 QUARTERROUND control state machine.
Figure 10. Salsa20 QUARTERROUND control state machine.
Preprints 99032 g010
Preprints 99032 g011
Figure 11. Toggle waveform of an AES decryption.
Figure 11. Toggle waveform of an AES decryption.
Preprints 99032 g011
Preprints 99032 g012
Figure 12. Toggle waveform of a Salsa20 decryption.
Figure 12. Toggle waveform of a Salsa20 decryption.
Preprints 99032 g012
Preprints 99032 g013
Figure 13. AES layout.
Figure 13. AES layout.
Preprints 99032 g013
Preprints 99032 g014
Figure 14. Salsa20 layout.
Figure 14. Salsa20 layout.
Preprints 99032 g014
Table 1. Summary of the AES results.
Table 1. Summary of the AES results.
average power ( μ W ) encryption ( # cycles ) decryption ( # cycles ) cells ( # ) total area μ m 2
4.01 180 180 4,303 217,250
Table 2. Summary of the Salsa20 results.
Table 2. Summary of the Salsa20 results.
average power ( μ W ) encryption ( # cycles ) decryption ( # cycles ) cells ( # ) total area μ m 2
2.82 202 202 3,468 135,150
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated