Prerpints.org logo
Preprint
Article

Logistics Center Selection and Logistics Network Construction from the Perspective of Urban Geographic Information Fusion

Altmetrics

Downloads

95

Views

34

Comments

0

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

18 February 2024

Posted:

19 February 2024

You are already at the latest version

Alerts
Abstract
The last-mile logistics in cities have become an indispensable part of the urban logistics system. This study aims to explore the effective selection of last-mile logistics nodes to enhance the efficiency of logistics distribution, strengthen the corporate distribution image, and further reduce corporate operating costs and alleviate urban traffic congestion. This paper proposes a clustering-based approach to identify urban logistics nodes from the perspective of geographic information fusion. This method comprehensively considers several key indicators, including the coverage, balance, and urban traffic conditions of logistics distribution. Additionally, we employed a greedy algorithm to identify secondary nodes around primary nodes, thus constructing an effective nodal network. To verify the practicality of this model, we conducted an empirical simulation study using the logistics demand and traffic conditions in the Xianlin District of Nanjing. This research not only identified the locations of primary and secondary logistics nodes but also provided a new perspective for constructing the urban last-mile logistics system, enriching the academic research related to logistics node construction. The results of this study are of significant theoretical and practical importance for optimizing urban logistics networks, enhancing logistics efficiency, and promoting the improvement of urban traffic conditions.
Keywords: 
Subject: Business, Economics and Management  -   Business and Management

1. Introduction

Logistics centers play a crucial role in the urban logistics structure. With the transformation of modern business models, logistics centers have evolved from traditional urban freight distribution centers to urban area freight hubs, becoming a key link in supporting last-mile logistics. This shift has enhanced the service capability and social image of enterprises. For last-mile community logistics centers, the freight dispatch support from advanced logistics centers is of paramount importance. These centers not only support the freight dispatching of multiple community centers but also handle the goods dispatching among large centers. The collaborative work of both types of center nodes is crucial for enhancing the urban logistics service capability of enterprises, making the site selection decision for logistics centers of significant strategic importance.

1.1. Logistics Center Site Selection

Researchers both domestically and internationally have conducted in-depth studies on the location of logistics centers and proposed a range of theoretical and practically valuable optimization models and algorithms. The reasonable site selection of urban logistics centers not only affects the operational efficiency of logistics activities but is also a key factor in constituting logistics costs. Considering that logistics costs are an important part of enterprise profits, researchers have paid special attention to transportation costs in logistics optimization. Emre and other researchers [1] combined Geographic Information Systems (GIS) and Binary Particle Swarm Optimization (BPSO) algorithms, proposing a comprehensive solution for the site selection of urban logistics centers. GIS is used to generate spatial information required for the p-median model, while BPSO is utilized to determine the optimal result considering logistics costs. However, in the urban logistics industry, it often becomes necessary to consider the locations of multiple logistics centers. To address this issue, Ismail and Fahrettin [2] adopted a spatial multi-criteria decision-making method that combines complex problem structures, expert opinions, geographical features, and mathematical modeling methods, aimed at analyzing the locations of multiple logistics centers and minimizing logistics costs. Additionally, Jun and other researchers [3] introduced three socio-economic indicators – economic development, traffic congestion levels, and total logistics demand – and constructed a two-stage model that improved clustering algorithms and the centroid method, to deal with multi-facility issues in real cases. Maryam and Hyunsoo [4] aimed to minimize transportation costs between nodes and applied an integrated meta-heuristic algorithm combining Particle Swarm Optimization (PSO) and Genetic Algorithm (GA) to construct a model for solving the optimal site selection problem of logistics centers. Yingyi and others [5] improved the existing one-dimensional target constraint location model, proposing a multi-factor constrained P-median model that considers operating costs, and used Particle Swarm Algorithm and Immune Genetic Algorithm to determine the optimal location. However, with rapid economic development and constantly changing customer demands, the optimality of the initial location of logistics centers may be affected. To address this challenge, Liying and others [6] introduced transportation costs between adjacent stages, establishing a multi-stage dynamic location model. Meanwhile, Juan and others [7] introduced a balanced learning strategy, improving the Cuckoo Search Algorithm, and Jeng-Shyang and others [8] proposed an intelligent evolutionary algorithm based on the living habits of the Rafflesia – the Rafflesia Optimization Algorithm – to solve the site selection problem of logistics distribution centers.
In the modern urban logistics system, logistics costs are no longer the sole major factor for consideration. With the promotion of the concept of coordinated development of natural environment, technology, economy, and society, sustainability has become one of the important goals for the site selection of logistics centers. Therefore, traditional methods of constructing logistics centers are insufficient for the development of urban community logistics centers. Rémy and others [9] employed a two-level multi-commodity network flow model to solve the urban center parcel distribution problem and assessed its impact on sustainable development by focusing on carbon emissions. Congjun and others [10], considering sustainability, optimized the site selection of logistics centers based on the 2-tuple linguistic representation model decision method. Moreover, with greenhouse gas emissions as a key factor, Hongzan and others [11] used truck trajectory data combined with DBSCAN clustering and an improved P-median model to determine the best location for urban logistics centers to reduce emissions. As an integral part of urban logistics, cold chain logistics by Siying and others [12] was modeled using a two-level programming approach, and Xinguang and Kang [13] employed a multi-objective location model to solve the site selection problem of cold chain logistics distribution centers considering carbon emissions.
In scenarios like natural disasters, the critical time window makes transportation efficiency a core consideration. Xenofon and Christos [14] combined classic heuristic algorithms and forecasting models, as well as deep neural networks, to select distribution center locations to quickly distribute aid materials to disaster areas. Kuo-Hao and others [15] proposed a two-stage stochastic programming model to ensure that logistics operations of relief materials could function most effectively at critical moments. Meanwhile, Zengxi and others [16] combined Multi-Criteria Decision Making (MCDM) with Geographic Information Systems (GIS) to address the site selection problem for Emergency Logistics Centers (ELC), accelerating the delivery of relief materials.
Although current research primarily focuses on reducing costs, minimizing carbon emissions, and improving efficiency through reasonable site selection, the rapid development of urban logistics and the ongoing changes in urban distribution indicators mean that finding optimal solutions among multiple objectives may not be sufficient to meet new challenges. Therefore, this paper proposes the introduction of the concept of multi-data fusion, considering diverse data information, to construct a new logistics planning and design system.

1.2. Multi-data fusion

Multi-data fusion technology involves integrating datasets from different distributions, sources, and types into a unified global space to form a more consistent expression. This technology occupies an important position in modern information processing and has been widely applied in multiple fields. Compared to the independent processing of a single data source, the advantages of multi-data fusion are significant: it not only improves the detectability and credibility of targets but also broadens the spatio-temporal perception range, reduces the ambiguity of inference, and enhances detection accuracy. Additionally, it increases the dimensional complexity of target features, improves spatial resolution, and enhances the system's fault tolerance.
In practical applications, multi-sensor systems can obtain comprehensive information about experimental subjects from various information sources for real-time monitoring purposes. For example, Bai and others [17] used a multi-data fusion method combining near-infrared spectroscopy and machine vision to analyze and assess the fermentation level of black tea. Addressing the issue of estimating the concentration of chlorophyll-a in eutrophic lakes, Cheng and others [18] proposed a multi-source data fusion method based on Bayesian Inference (BIF), effectively combining the advantages of in-situ observations and remote sensing data. Similarly, Yongyun and others [19], for real-time monitoring of dissolved oxygen changes in microbial fuel cell biosensors, constructed a low-cost, high-accuracy real-time dissolved oxygen biosensor based on iMFC and enhanced its performance through a multi-source data fusion strategy predictive model using multiple environmental indicators. Furthermore, Hui and others [20] implemented online monitoring of the simultaneous saccharification and fermentation process of ethanol by merging a convolutional neural network (CNN) with a recurrent neural network (RNN) in a novel cross-perception multi-source data deep fusion model. Zhang Yi and others [21] proposed an interactive platform architecture for provincial power grid voltage dips based on multi-source data fusion, addressing issues such as excessive monitoring, limited application, and lack of interaction in voltage dip-related systems. Lastly, Qilin and others [22] proposed a multi-data fusion calibration method for all parameters of the Orbital Multi-View Dynamic Photogrammetry System (OMDPS), providing a more accurate spatial reference for spacecraft attitude measurement.
Due to environmental complexity, noise interference, instability of recognition systems, and the use of different identification algorithms, the feature information extracted during experiments often lacks precision, completeness, and reliability. To address these challenges, Yan and others [23] proposed a collaborative strategy combining deep learning with machine learning theory for tracking quality differences in rice, aiming to improve the detection performance of the fusion system. Junyi and others [24] developed a real-time target detection system for intelligent vehicles with enhanced real-time and accuracy, using a multi-source fusion method based on the ROS Melody software development environment and the NVIDIA Xavier hardware platform. Huice and others [25], aiming to improve the prediction accuracy and efficiency of coal mine gas generation patterns, proposed a prediction method based on multi-source data fusion. Additionally, Yajie and others [26] combined GNSS-IR technology with optical remote sensing and used a multi-data fusion method based on the Genetic Algorithm-Back Propagation Neural Network (GAP-NN) to improve the accuracy of soil moisture measurements.
Apart from real-time monitoring of target objects, Xueying and others [27] proposed a multi-source data feature fusion method based on deep learning, aimed at solving the multi-feature contribution differential analysis problem in soil carbon content prediction using VNIR and HIS technologies. Given the complexity of vehicle driving conditions, Jihao and others [28] constructed a slope estimation algorithm based on multi-model and multi-data fusion to enhance the vehicle's ability to real-time track actual road slope changes. In the context of maritime activities, Ye and others [29] proposed an Adaptive Data Fusion (ADF) model based on multi-source AIS data for predicting ship trajectories in maritime traffic. In complex industrial processes such as sintering, Yuxuan and others [30] proposed a sintering quality prediction model based on the fusion of industrial camera video data and process parameters. Additionally, for predicting water quality in urban sewer networks, Yiqi and others [31] established a deep learning method based on multi-data fusion, considering environmental, social, water quantity indicators, and monitorable water quality standard indicators.
The development of multi-data fusion technology continues to evolve. For instance, Bo and others [32] proposed a Digital Twin Model (DTM) based on Transfer Learning and Multi-Source Data Fusion (DTM-TL-MSDF). This method effectively integrates experimental and simulation data, aiming to construct an accurate digital twin model for real-time monitoring of structural strength. Sizhe and others [33] developed a novel GeoAI research method that performs deep machine learning from multi-source geospatial data to effectively detect natural features. Moreover, Nan and others [34] proposed a new architecture for a Trusted Execution Environment with integrated blockchain capabilities, aimed at improving the efficiency of multi-source data fusion processing under business scenario constraints.
In recent years, although the research on multi-data fusion mainly focuses on data monitoring or prediction under dynamic changes, there are relatively few discussions on the location of logistics centers. However, in the context of the rapid development of urban logistics industry, a single factor is no longer sufficient to meet the demand for the optimality of logistics center location. Therefore, in the complex solution environment structure of urban logistics center location analysis process, in order to make a reasonable logistics center location decision, it is necessary to evaluate different decision-making factors, especially geographic information data. Because geographic information is a technical means of acquiring, processing, and analyzing spatial data, it can be used to collect, analyze, and apply data on the location of logistics centers. Further, this paper adopts a multidimensional data fusion approach from the perspective of geographic information fusion in the study of logistics center location, focusing on geographically relevant indicators around the logistics nodes, such as logistics and distribution coverage, equilibrium, and urban congestion, in order to construct a more accurate logistics location model.
Moreover, when constructing logistics nodes, this paper also gives special consideration to transportation fluency. To this end, five selection objectives are determined: low operation rate, low rate of change of traffic congestion, high coverage rate of nodes at 3 kilometers, short distance between logistics parks and the nearest city-level nodes and high efficiency of cargo transportation. Meanwhile, from the perspective of the overall logistics system, focusing on the balance and rationality of the system operation, the decentralization of primary nodes and the aggregation of secondary nodes are established as the selection objectives. This study proceeds to establish a multi-objective node selection model and applies cluster analysis to simply cluster the entire region into small regions of similar size. Within each small region, a clustering center, i.e., the initially identified primary node, is identified. Then, the clustering center is dynamically adjusted by the K-mean algorithm, and the distance, i.e., the similarity, between the other nodes within each small region and the initially determined first-level node is calculated. The clustering results are optimized through repeated iterations to minimize the sum of squares of the distances of all categories to their respective category centers, thus determining the final first-level nodes and their jurisdictional areas within 3 km. Compared with other models, this model not only obtains the optimal solution faster, but also performs better in balancing the optimal distribution and coverage of logistics centers, which leads to a more reasonable site selection scheme.

2. Modeling multi-objective node selection

To facilitate understanding and model construction, we have defined the parameters of the model as follows:
Let the total number of nodes be N , then the coordinates of each node are represented as X i , Y i , where i = 1,2 … … N . Define the coordinates of primary node F i as X F i , Y F i , the coordinates of secondary node S i as X S i , Y S i , and the coordinates of the logistics park W i as X W i , Y W i . Assume there are W k logistics parks, where k = 1,2 , 3,4 ; and each logistics park W k corresponds to a primary node F W k .
Let the total number of primary nodes be N F , and define the set of secondary nodes belonging to primary node F i as:
S F i = S i 1 , S i 2 , S i 3 , … … S i N F i ,
Where N F i represents the number of secondary nodes contained in primary node F i . Assuming the total number of secondary nodes is N E , then N E = ∑ i = 1 N F N F i .
Let A i j be the total freight in and out volume between nodes i and j ; let I i j be the inbound freight volume from the area corresponding to node i to the area corresponding to node j ; let A H i be the actual total ground freight in and out volume of node i before the establishment of the underground logistics system, and Y H i be the actual total ground freight in and out volume of the node after the establishment of the underground logistics system.
Finally, define the set G T i as the set of nodes covered by node i within a 3-kilometer range:
G T i = G i 1 , G i 2 , G i 3 , … … G i T i ,
where T i is the number of elements in the set G T i .

2.1. Multi-objective node selection model

The primary goal of developing urban underground logistics networks is to alleviate or even eliminate traffic congestion, achieving at least basic traffic flow. Starting from this main goal, we analyzed various specific factors that might affect urban traffic and established the following five main selection objectives: low turnover rate, low traffic congestion change rate, high node 3-kilometer coverage rate, short distance between logistics parks and the nearest primary node, and high goods transportation efficiency. Additionally, considering the overall logistics system's balance and rationality, we also determined the dispersion of primary nodes and the aggregation of secondary nodes as selection objectives.
Objective 1: Minimize Turnover Rate
Define the total transport volume from logistics park W k to its corresponding primary node F W k as I T k , and the total transport volume from primary node F W k to other primary nodes as O T k . Therefore, the turnover rate of primary node F W k , i.e., the ratio of total output to total input of goods, is defined as:
min ⁡ R T k = O T k I T k
Objective 2: Maximize Node 3-Kilometer Coverage Rate
Define G T i as the set of nodes covered by node i within a 3-kilometer range, and # ⋃ i = 1 N G T i represents the number of nodes covered by node i within a 3-kilometer range. Thus, the 3-kilometer coverage rate of node i , i.e., the ratio of the number of covered nodes to the total number of nodes, is defined as:
max ⁡ R F G = # ⋃ i = 1 N G T i N ,
where # {   } represents the number of elements in the set.
Objective 3: Minimize Traffic Congestion Change Rate
Define f as the functional relationship between logistics volume and traffic congestion. f A H i − f Y H i represents the change in ground traffic congestion before and after the construction of the underground logistics system. Therefore, the traffic congestion change rate is defined as:
R J i = f A H i − f Y H i f A H i × 100 %
min ⁡ R J = ∑ i = 1 N R J i N
Objective 4: Minimize Distance Between Logistics Park and Nearest Primary Node
Define W S i = W i 1 , W i 2 , … … W i W N i as the set of primary node numbers corresponding to logistics park W S i , with a count of W N i . Thus, the distance between the logistics park and the nearest primary node is defined as:
min ⁡ W F D = ∑ i = 1 4 ∑ j ∈ W S i X W i − X j 2 + Y W i − Y j 2 ∑ i = 1 4 W N i
Objective Five: Maximize Goods Transportation Efficiency
Considering the stability of the underground logistics system operation, maximizing goods transportation efficiency is crucial. Transportation efficiency can be measured by the ratio of goods transport volume to the total transportation time (including waiting time at nodes and time spent in transit). Hence, we define Objective Five as follows:
max ⁡ T R i j = N J × M N N F i j × 12 + D i j V
where T R i j represents the maximum volume of goods transported from node i to node j per unit of time; N N F i j is the number of primary nodes passed during the transport of goods from node i to node j ; V is the speed of shuttle transportation; N J is the maximum number of vehicles per shuttle; D i j is the total distance from node i to node j ; M is the volume of goods transported per shuttle, for example, 5 tons or 10 tons.
Objective Six: Maximize Dispersion of Primary Nodes
Let X F , Y F be the central point of all primary nodes. The dispersion of primary nodes can be measured by the standard deviation of the distances from each primary node to the central point of primary nodes, defined as follows:
max ⁡ C F = ∑ k = 1 N F X F k − X F ¯ 2 + Y F k − Y F ¯ 2
Objective Seven: Maximize Aggregation of Secondary Nodes
To enhance the transportation efficiency among secondary nodes covered by each regional primary node, we use the aggregation of secondary nodes to measure this efficiency. The aggregation of secondary nodes is defined as the standard deviation of the distances between each primary node and its covered secondary nodes, as follows:
max ⁡ C C E = ∑ k = 1 N F ∑ S i ∈ S F i X F k − X S i 2 + Y F k − Y S i 2

2.2. Restrictive condition

Constraint One: Ensure Underground Goods Transportation Meets Actual Demand
To ensure the underground logistics system can meet actual freight demands, we set a constraint that the underground goods transportation volume at each node must be greater than a certain percentage θ of the actual freight demand, while also limiting the total amount of goods entering and exiting each node on the ground. The specific expression is as follows:
∑ i = 1 N F i I O i ≥ ∑ j = 1 N E ∑ i = 1 N F A i j × θ
I O i ≤ I O m a x when i is a primary node ,   I O m a x = 4000 t when i is a secondary node , I O m a x = 3000 t
Constraint Two: Promote Traffic Flow
To alleviate traffic congestion and ensure basic road traffic flow, the construction of the underground logistics system needs to satisfy the following constraint:
f Y H i ≤ 4
f = k × Y H i
Constraint Three: Control Ground Goods Volume Change
The difference in ground goods volume Y H i before and after the construction of the underground logistics system must be controlled within a certain range ζ to maintain the overall stability of the logistics system:
Y H i = A H i − M T i , w h e n   A H i ≥ M T i                   0                 , w h e n   A H i < M T i
Y H i ≤ ζ
Dimensionless Treatment: To facilitate solving the multi-objective programming problem, different dimensioned objective functions are normalized. For the objective f i , if smaller is better, find the minimum (best) and maximum (worst) values among n choices; if larger is better, vice versa. The dimensionless value can be obtained by linear interpolation, i.e.:
f x − f m i n f m a x − f m i n
In summary, we established a multi-objective programming node selection model:
max ⁡ R F G ′ + T R i j ′ + C F ′ + C C E ′ − R T k ′ − R J ′ − W F D ′
s . t . ∑ i = 1 N F i I O i ≥ ∑ j = 1 N E ∑ i = 1 N F A i j × θ f Y H i ≤ 4 f = k × Y H i Y H i ≤ ζ ,   Y H i = A H i − M T i , w h e n   A H i ≥ M T i                   0                 , w h e n   A H i < M T i I O i ≤ I O m a x when i is a primary node ,   I O m a x = 4000 t when i is a secondary node , I O m a x = 3000 t

3. Preferred first-level node identification based on cluster analysis

3.1. Cluster analysis algorithms

Cluster analysis algorithm is a learning process aimed at identifying clustering characteristics within a dataset. Based on clustering criteria, namely threshold criteria and function criteria, the algorithm groups the nodes of each region into a major category by analyzing the similarity between different categories and the threshold of their similarity measure. It further selects primary nodes for each region.
The threshold criterion is a criterion for classification based on a distance threshold. Based on past practical experience, we have defined a similarity measure threshold and used the nearest neighbor rule to determine if certain pattern samples belong to a specific cluster category.
In cluster analysis, the function used to represent the similarity or dissimilarity between patterns is known as the cluster criterion function. This function is a function of the pattern sample set X and pattern categories S j , j = 1,2 , L , m , where m is the number of categories. A common function criterion is the sum of squared errors, also known as the minimum variance partition function, defined as:
J = ∑ j = 1 m ∑ X ∈ S i X − M j 2
Where m represents the number of pattern categories, M j = 1 N j ∑ X = S i X is the mean vector of the sample set S j , and N j is the number of samples in S j . When the value of J reaches a minimum, it indicates that the classification result is satisfactory, thus the minimal value of J can be used as the objective function.
In the process of cluster analysis, nodes in different regions show dynamic changes as the clustering becomes progressively refined. To accurately classify nodes in different regions, one of the dynamic clustering methods, the K-means algorithm, is used. This algorithm uses the sum of squared errors as the clustering criterion and iteratively optimizes the clustering results, minimizing the sum of squared distances of all samples to the centers of their respective categories, thus maximizing similarity and enabling samples to be classified into the same category.
The main steps of the K-means algorithm are as follows:
Step1: Initialization: Randomly select K initial clustering centers.
Step2: Calculate Distance: Calculate the distance between samples and each clustering center, and allocate samples based on the principle of minimum distance.
Step3: Assignment: Find the nearest clustering center for each sample and calculate the new clustering center.
Step4: Revise Clustering Center: Recalculate cluster centers based on newly assigned samples.
Step5: Compute Deviation: Calculate clustering deviation.
Step6: Convergence Judgment: If the clustering centers no longer change, the algorithm terminates; otherwise, return to Step 2.
For the flowchart of the K-means algorithm, see Figure 5-1.
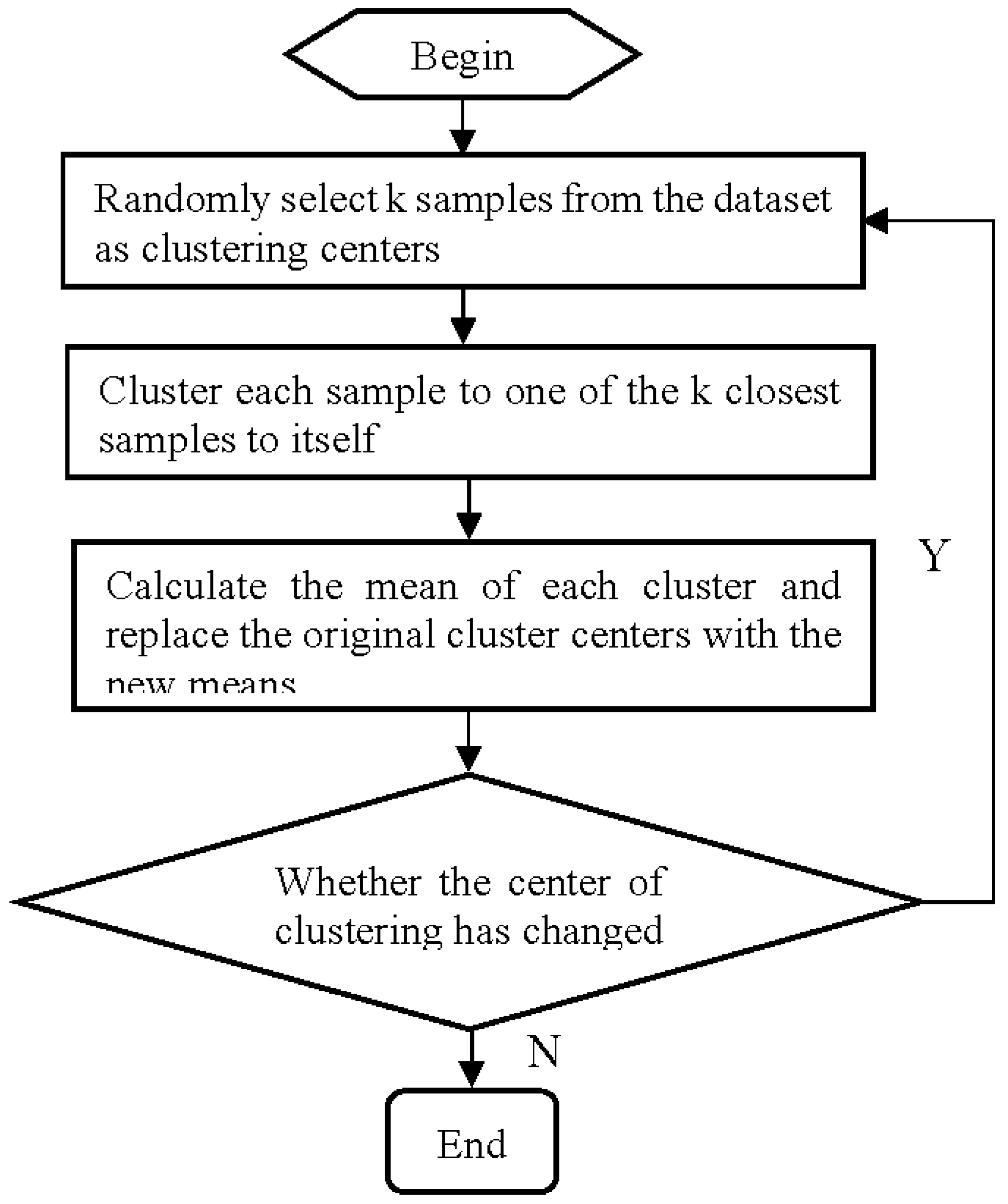
Preprints 99192 g001
Figure 1. Algorithmic flowchart for dynamic clustering method-K-means.
Figure 1. Algorithmic flowchart for dynamic clustering method-K-means.
Preprints 99192 g001
Given the complexity of the freight area division and the corresponding freight Origin-Destination (OD) flow matrix in the Xianlin area of Nanjing City, we took a series of steps to conduct cluster analysis. Initially, based on the freight volume and distance data of various regional nodes, the entire area was simply clustered into small regions of similar size. Next, a clustering center was determined in each small region, associated with other nodes in the region, serving as the preliminarily determined primary node. Then, the distances, i.e., similarity, between other nodes within each small region and the preliminarily determined primary nodes were calculated, ensuring that this similarity was greater than or equal to the set similarity measure threshold. Subsequently, the deviation of the cluster centers was calculated and corrected to determine the cluster center, which is the primary node. Finally, by iteratively optimizing the clustering results, the sum of squared distances of all categories to their respective category centers was minimized, achieving maximum similarity and classifying them into the same category. Through this dynamic clustering process, we determined the primary nodes and their 3-kilometer jurisdiction areas.

3.2. Cluster analysis results test

After clustering the regional nodes using the k-means clustering algorithm, we calculated the sum of average distances of each node to the cluster center in each category and normalized it. If this sum of average distances fell within the set mean threshold range, the clustering result could be considered accurate. For different regional nodes, we defined their mean as:
n ¯ = ∑ i = 1 N n i
and performed the following normalization:
n i ~ = n i − n ¯ ∑ i = 1 N n i − n N
The center value of each preliminarily classified category i is calculated as:
C j = ∑ i = 1 N j n i j                         j = 1,2 , … … , M j
where n i represents the distance from the nodes within the i area to the clustering center, N is the total number of nodes in the entire region, N j is the total number of nodes in the i area, and M j is the total number of nodes in the j area. The average distance from different categories to their respective cluster centers is defined as:
D ¯ = ∑ i = 1 N j ∑ j = 1 M j n i j ~ − C j 2 N

4. Selection of secondary node identification based on greedy algorithm

From the perspective of graph theory, an underground logistics area can be abstracted as a graph G = ( V ,   E ) , where V i represents a connecting node, and E i j = V i , V j represents the edge connecting nodes V i and V j . Each edge is assigned a non-negative weight Q E i j = Q i j , which is determined by both the freight volume and distance between the two nodes. Thus, the process of determining secondary nodes can be viewed as solving the minimum spanning tree problem.
As shown in the diagram, suppose an undirected graph G represents a logistics network, where V 0 , V 1 , V 2 , V 3 … … V 9 represent 10 connecting nodes, and E 01 , E 02 , E 25 , etc., represent paths between nodes.
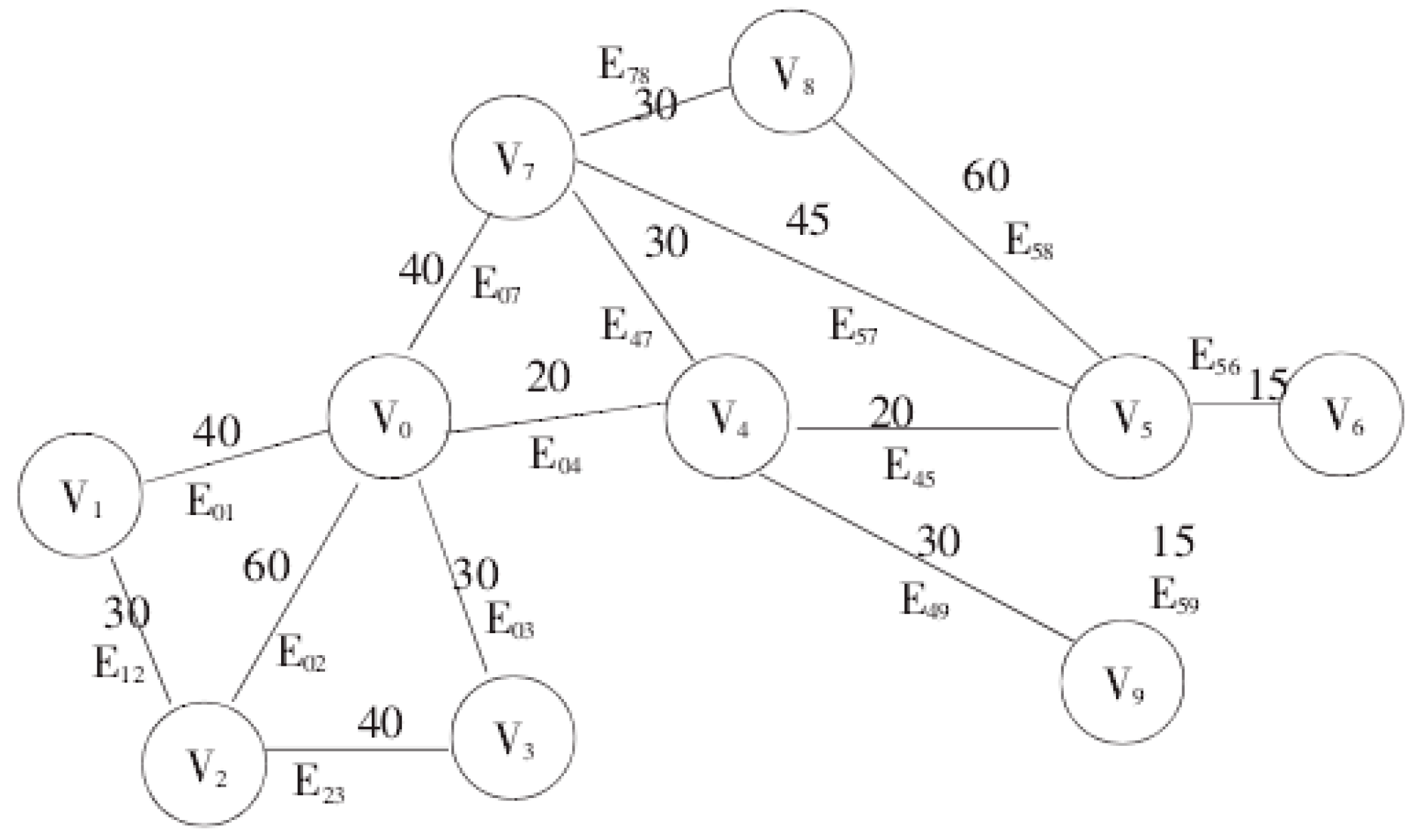
Preprints 99192 g002
Figure 2. Undirected connectivity map.
Figure 2. Undirected connectivity map.
Preprints 99192 g002
The Dijkstra algorithm was invented by the renowned Dutch computer scientist Edsger W. Dijkstra in the mid-1950s. This algorithm is used to solve the single-source shortest path problem, i.e., finding a series of shortest paths from a given starting point to all other vertices in a weighted connected graph. Unlike other algorithms, Dijkstra's algorithm does not require visiting the single shortest path of all vertices. Instead, it generates a set of paths from the starting point to different vertices in the graph, some of which may share common edges.
The specific process of the Dijkstra algorithm is as follows:
Step1: Find the weight of the shortest edge between the starting point and the nearest vertex to that starting point.
Step2: Continue to find the second nearest edge. Before the i iteration, the algorithm has already determined i -1 shortest paths connecting the starting point and its nearest vertices.
Step3: Determine the last required node, and stop when all freight volume demands within the region are met.
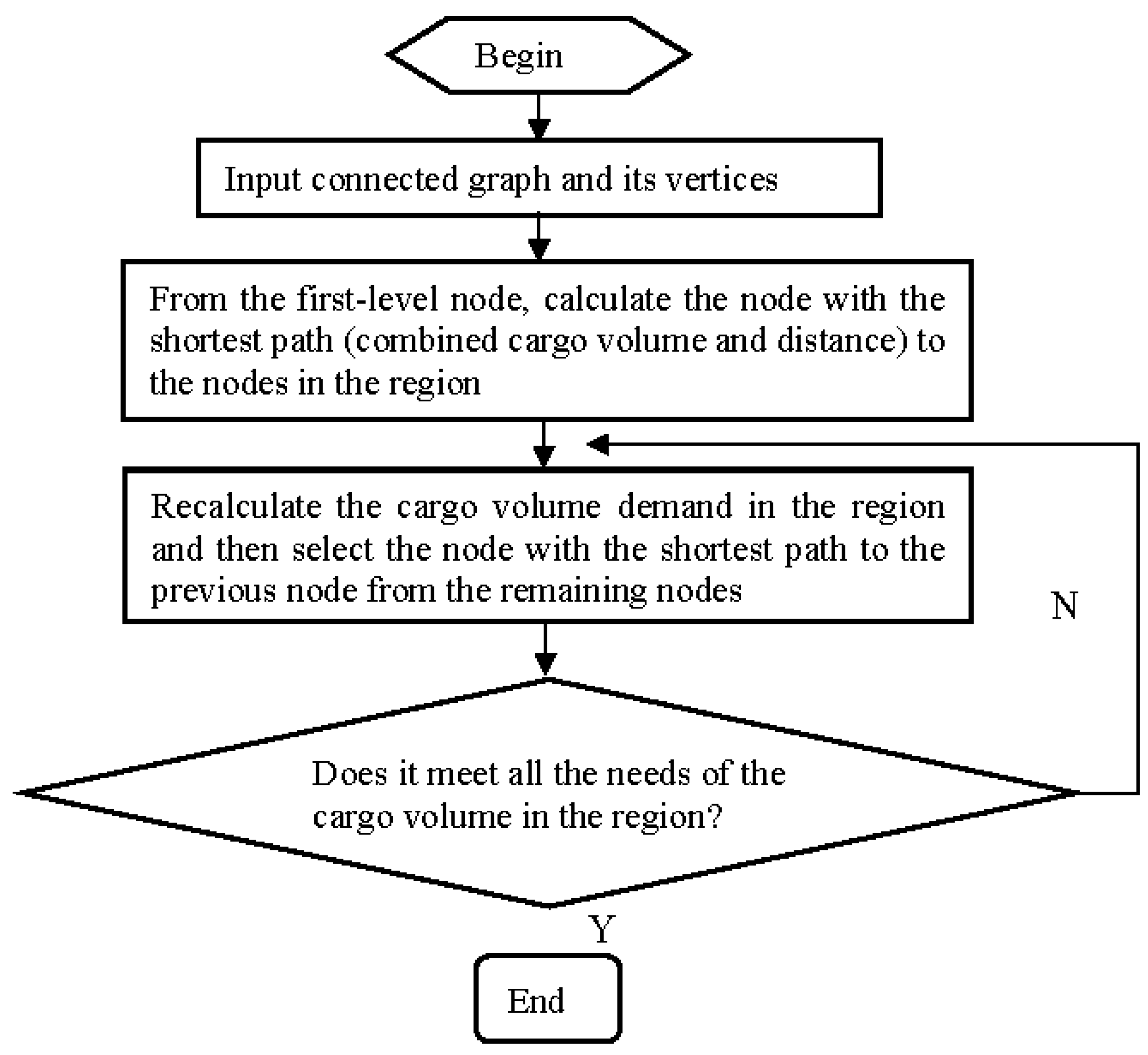
Preprints 99192 g003
Figure 3. Flowchart of the greedy algorithm for selecting secondary nodes.
Figure 3. Flowchart of the greedy algorithm for selecting secondary nodes.
Preprints 99192 g003

5. Example and result analysis

5.1. Selection of underground logistics nodes

By applying dynamic cluster analysis algorithms, we conducted a detailed analysis of the traffic freight area in the Xianlin district of Nanjing City. Based on this method, we successfully selected 7 primary nodes and their jurisdiction areas (see Table 1 for details). Further, using the greedy algorithm, we determined 55 secondary nodes within these primary node categories (see Table 5.2), and analyzed the freight volume for transshipment at the primary nodes. Through MATLAB programming, we calculated the turnover rates for each primary node.
Table 1. Table of information related to the 7 first-level nodes.
Table 1. Table of information related to the 7 first-level nodes.
Level 1 node number Freight volume/t Transit rate Position coordinate
X Y
I-1 44549.12 0.1949 142746.9 152213.7
I-2 13254.41 0.189 164769.5 165451.4
I-3 31508.57 0.1888 148832.7 158220.1
I-4 31094.69 0.1888 138800.1 156621.5
I-5 28393.75 0.1818 156051.9 162385.7
I-6 29472.58 0.1802 148284.2 152085.8
I-7 19674.26 0.1759 144477.2 158718.5
Table 2. Table of information related to 55 secondary nodes.
Table 2. Table of information related to 55 secondary nodes.
Node number Approaching node Freight volume/t Position coordinate Node number Approaching node Freight volume/t Position coordinate
X Y X Y
II-1 811 500.95 143105.67 152346.13 II-29 859 237.997 139712.38 158196.62
II-2 811 499.3 143005.54 152357.19 II-30 869 231.447 137403.37 160390.60
II-3 819 478.205 142735.81 153102.05 II-31 868 278.97 139355.42 160403.74
II-4 819 412.385 142734.58 153100.82 II-32 869 227.177 145960.34 157813.24
II-5 819 392.17 142733.35 153099.59 II-33 845 226.562 139062.69 155216.00
II-6 819 337.825 142730.59 153096.83 II-34 859 211.112 139712.38 158196.62
II-7 819 336.925 142727.83 153094.07 II-35 887 204.432 155779.18 161153.63
II-8 817 328.8 142147.44 152788.09 II-36 887 204.202 155972.26 161519.38
II-9 817 311.925 143839.80 153020.83 II-37 894 202.802 158485.91 164411.95
II-10 807 299.115 142199.94 151897.77 II-38 894 196.537 154679.32 164648.90
II-11 817 286.42 142733.35 153099.59 II-39 886 194.062 154828.66 160253.62
II-12 811 279.64 143106.67 152356.13 II-40 894 191.002 158429.82 162320.97
II-13 811 272.69 143146.67 151356.13 II-41 886 182.712 156649.10 160401.30
II-14 899 265.59 165295.96 166307.48 II-42 894 173.282 155475.94 162649.70
II-15 899 262.93 157354.70 166956.66 II-43 826 173.012 136654.80 157552.12
II-16 899 258.065 163428.02 166293.35 II-44 826 171.227 139712.38 158196.62
II-17 872 256.29 145961.77 157814.67 II-45 805 168.927 142526.33 158311.54
II-18 872 243.59 147221.06 157904.41 II-46 826 167.215 144511.24 158818.60
II-19 872 263.135 149007.88 158255.23 II-47 826 165.815 135605.67 159147.49
II-20 872 250.325 147900.64 158283.67 II-48 805 159.55 142989.12 159395.66
II-21 872 237.63 150211.94 158547.64 II-49 822 157.075 144347.43 159827.39
II-22 872 230.85 145488.59 158833.25 II-50 826 154.015 143383.79 160462.05
II-23 872 223.9 148375.72 159294.26 II-51 856 145.725 141628.28 160162.22
II-24 872 216.8 149100.78 159241.67 II-52 864 279.56 140521.56 160395.32
II-25 872 245.78 140522.99 160396.75 II-53 864 338.67 137403.37 160390.60
II-26 848 345.47 138792.09 155636.76 II-54 864 217.89 139355.42 160403.74
II-27 848 217.65 139841.39 155777.27 II-55 856 457.32 145960.34 157813.24
II-28 857 407.68 137888.25 157780.23
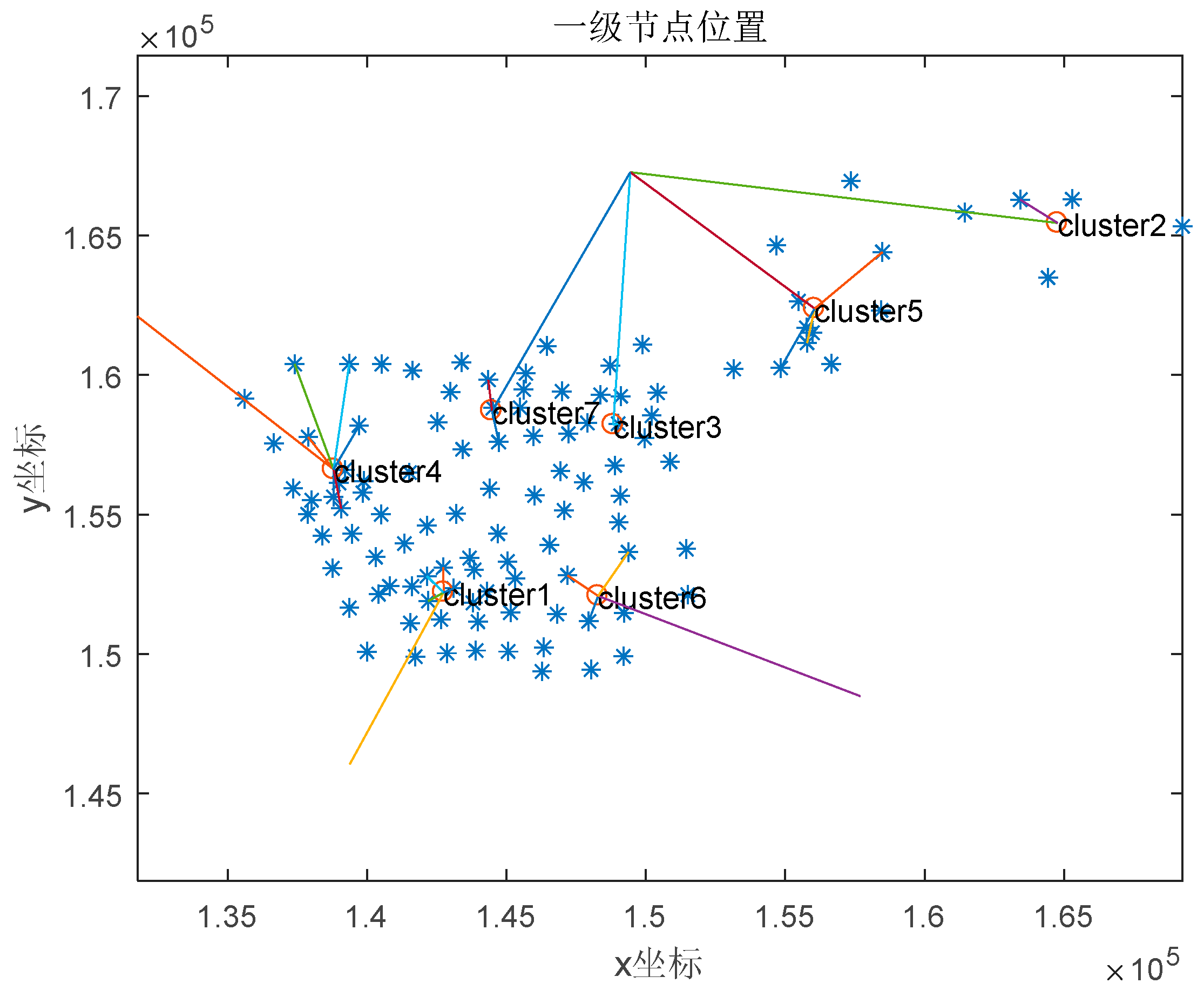
Preprints 99192 g004
Figure 4. Node Location Distribution Schematic.
Figure 4. Node Location Distribution Schematic.
Preprints 99192 g004

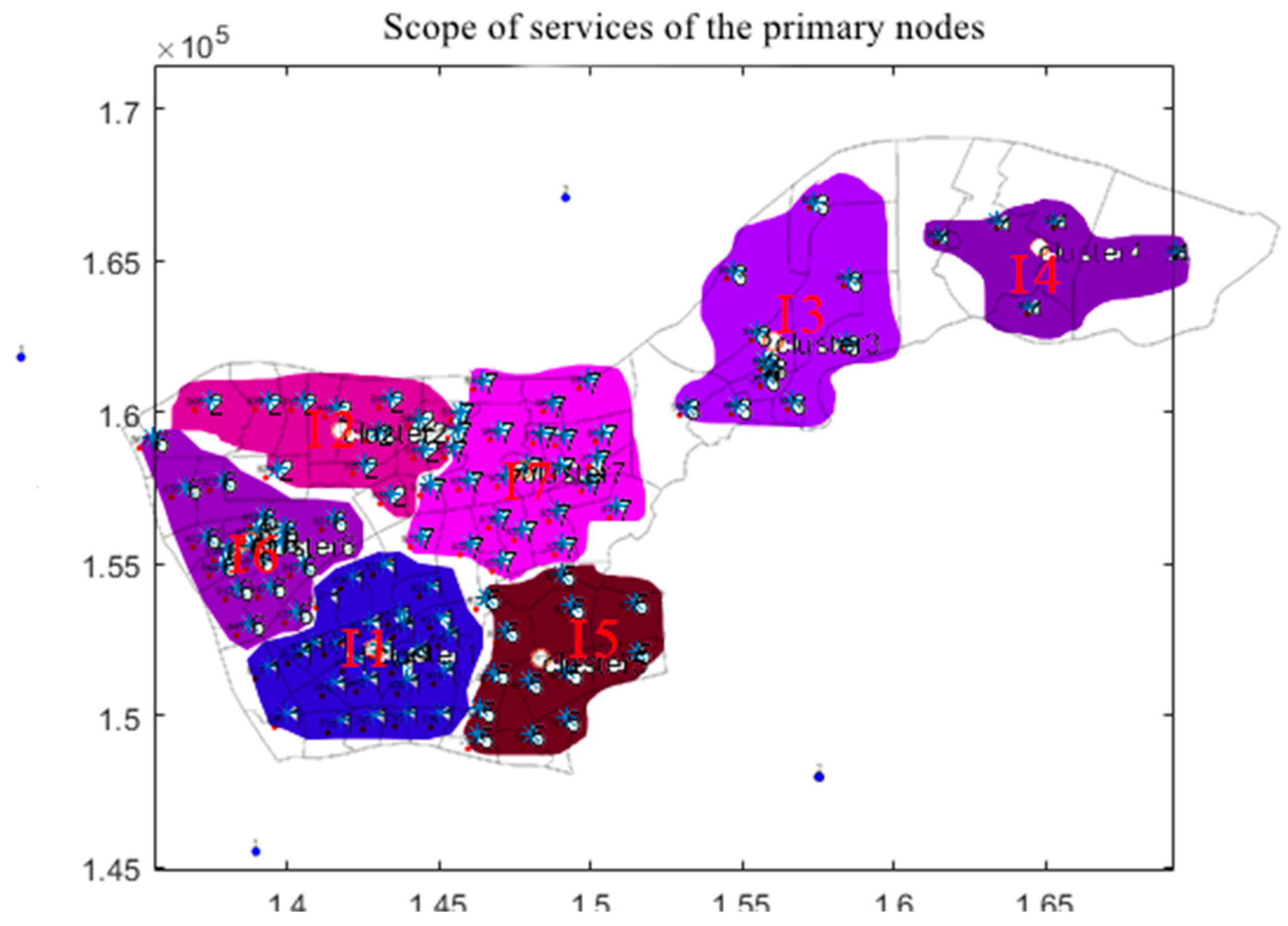
5.2. Scope of nodal services

To represent the service range of each node more intuitively, we analyzed the area within a 3-kilometer radius centered on each node. Taking into account the overall freight volume and transshipment situation of the nodes, we ran MATLAB programs to graphically display the actual service areas of each node (see Figure 5.2), thereby clearly reflecting the operational status of each node.
Table 3. Scope of services for primary nodes.
Table 3. Scope of services for primary nodes.
primary node Contains secondary nodes Includes service area centers
I-1 II-1~II-13 793、795、796、797、798、800、801、802、804、806、807、809、810、811、813、814、815、816、817、818、819、820、821、823、827、828、830、833
I-2 II-14~II-16 892、896、897、899、900
I-3 II-17~II25 832、836、837、838、839、840、871、872、873、874、876、877、879、880、882、884
I-4 II-25~II-32 841、842、843、844、845、846、847、848、849、850、851
852、853、854、857、858、859、862、867、868、869
I-5 II-33~II-40 885、886、887、888、889、890、891、893、894、895、898
I-6 II-41~II-48 791、792、794、799、803、805、808、812、822、824、825、826、829、831
I-7 II-48~II-55 834、835、855、856、860、861、863、864、865、866、870、875、878、881、883

5.3. Analysis of results

The Xianlin district in Nanjing City, serving as a sub-center of the city, includes the Xianhe area, a hub of higher education industry. This region features a combination of multiple universities and residential areas, forming a comprehensive community. Driven by the university industry chain, various small logistics industries have developed rapidly. According to the freight OD data, the typical daily freight volume reached 327,000 tons. Therefore, 15 primary nodes were set up around the Xianlin University Town to accelerate the efficiency of freight transportation.
In the Bai Xiang area of the Xianlin district, an important science and technology industrial park in Nanjing, the development of economic and high-tech industrial parks has led to a relatively high demand for logistics and freight. We established logistics nodes at key transportation hubs and commercial areas such as the Presidential Palace, Jianye Wanda Plaza (Node number 857), and Andemen (Node number 807), to meet the logistics network needs of the region.
The entire logistics network service range reached 289.50 square kilometers, while the total area of Xianlin district is 308.29 square kilometers, achieving a coverage rate as high as 93.91%. This coverage rate satisfies the freight needs of the overall logistics network, enabling the highest turnover rate to reach 0.949.

6. Conclusions

In this paper, based on the background of logistics operation enterprises, we study how enterprises can select logistics nodes according to the freight demand and urban traffic conditions in each region from the perspective of geographic information integration. We comprehensively consider the key indicators for geographic information around logistics centers under meeting the business needs of enterprises, such as operation rate, traffic congestion change rate, node 3km coverage, distance between logistics parks and the nearest first-level nodes, cargo transportation efficiency, dispersion of first-level nodes, and clustering of second-level nodes, and take them as the objectives of node selection. In this study, the cluster analysis method was used to construct the first-level node clustering identification model, and the optimization objective and greedy algorithm were applied to identify and analyze the second-level nodes according to the characteristics of the first-level nodes. Finally, by collecting the freight traffic data of Xianlin District in Nanjing, and carefully dividing and analyzing its traffic and freight coverage area, we implemented a simulation analysis. The analysis results show that the proposed model is able to cover most of the logistics network service area in Xianlin District, Nanjing and meet the freight transportation demand of the overall logistics network.
The model constructed in this study covers a broader scope than existing studies. Previous studies usually focus on the optimal solution to achieve the overall objectives such as minimization of logistics costs, maximization of transport efficiency and reduction of carbon emissions. However, these studies are often limited in their consideration of factors. In contrast, this paper not only focuses on these objectives, but also proposes a multi-dimensional data fusion method from the perspective of geographic information fusion, comprehensively analyzes multiple indicators such as logistics and distribution coverage, equilibrium, urban congestion, etc., and combines the complex problem structure, geographic features, and mathematical modeling methods to provide multi-objective optimization of urban logistics center siting analysis, and constructs a new type of logistics planning and design system. Therefore, this paper differs from the existing literature in terms of node identification of logistics centers and provides new insights into the research field of logistics center siting.
Future research will focus on combining multi-data fusion with logistics center site selection model construction to further enhance the accuracy of site selection. To this end, we will consider not only enterprise-related factors and urban traffic conditions but also include diverse indicators such as the residential situation around logistics nodes in the model.

References

  1. ÇAKMAK E, ÖNDEN İ, ACAR A Z, et al. Analyzing the location of city logistics centers in Istanbul by integrating Geographic Information Systems with Binary Particle Swarm Optimization algorithm[J/OL]. Case Studies on Transport Policy, 2021: 59-67. [CrossRef]
  2. ÖNDEN İ, ELDEMIR F. A multi-criteria spatial approach for determination of the logistics center locations in metropolitan areas[J/OL]. Research in Transportation Business & Management, 2022: 100734. [CrossRef]
  3. WU J, LIU X, LI Y, et al. A Two-Stage Model with an Improved Clustering Algorithm for a Distribution Center Location Problem under Uncertainty[J/OL]. Mathematics, 2022, 10(14): 2519. [CrossRef]
  4. KHAIRUNISSA M, LEE H. Hybrid Metaheuristic-Based Spatial Modeling and Analysis of Logistics Distribution Center[J/OL]. ISPRS International Journal of Geo-Information, 2021: 5. [CrossRef]
  5. HUANG Y, WANG X, CHEN H. Location Selection for Regional Logistics Center Based on Particle Swarm Optimization[J/OL]. Sustainability, 2022: 16409. [CrossRef]
  6. YAN L, GRIFOLL M, FENG H, et al. Optimization of Urban Distribution Centres: A Multi-Stage Dynamic Location Approach[J/OL]. Sustainability, 2022: 4135. [CrossRef]
  7. LI J, YANG Y H, LEI H, et al. Solving Logistics Distribution Center Location with Improved Cuckoo Search Algorithm[J/OL]. International Journal of Computational Intelligence Systems, 2020: 676. [CrossRef]
  8. JENG-SHYANG PAN J S P, JENG-SHYANG PAN Z F, ZONGLIN FU C C H, et al. Rafflesia Optimization Algorithm Applied in the Logistics Distribution Centers Location Problem[J/OL]. Internet Technology Journal, 2022: 1541-1555.
  9. DUPAS R, DESCHAMPS J C, TANIGUCHI E, et al. Optimizing the location selection of urban consolidation centers with sustainability considerations in the city of Bordeaux[J/OL]. Research in Transportation Business & Management, 2023: 100943. [CrossRef]
  10. RAO C, GOH M, ZHAO Y, et al. Location selection of city logistics centers under sustainability[J/OL]. Transportation Research Part D: Transport and Environment, 2015: 29-44. [CrossRef]
  11. KAINZ W, HOCHMAIR H, JIAO H, et al. Using Large-Scale Truck Trajectory Data to Explore the Location of Sustainable Urban Logistics Centres—The Case of Wuhan[J]. [CrossRef]
  12. ZHANG S, CHEN N, SHE N, et al. Location optimization of a competitive distribution center for urban cold chain logistics in terms of low-carbon emissions[J/OL]. Computers & Industrial Engineering, 2021: 107120. arXiv:10.1016/j.cie.2021.107120.
  13. LI X, ZHOU K. Multi-objective cold chain logistic distribution center location based on carbon emission.[J/OL]. Environmental Science and Pollution Research, 2021: 32396-32404. [CrossRef]
  14. TAOUKTSIS X, ZIKOPOULOS C. A decision-making tool for the determination of the distribution center location in a humanitarian logistics network[J].
  15. CHANG K H, CHIANG Y C, CHANG T Y. Simultaneous Location and Vehicle Fleet Sizing of Relief Goods Distribution Centers and Vehicle Routing for Post-Disaster Logistics[J/OL]. SSRN Electronic Journal, 2022. [CrossRef]
  16. Zengxi Feng, Gangting Li, Wenjing Wang, Lutong Zhang, Weipeng Xiang, Xin He, Maoqiang Zhang, Na Wei. Emergency logistics centers site selection by multi-criteria decision-making and GIS[J]. International Journal of Disaster Risk Reduction, Volume 96, 2023:103921. [CrossRef]
  17. ZHANG B, LI Z, SONG F, et al. Discrimination of black tea fermentation degree based on multi-data fusion of near-infrared spectroscopy and machine vision[J/OL]. Journal of Food Measurement and Characterization, 2023: 4149-4160.
  18. CHEN C, CHEN Q, LI G, et al. A novel multi-source data fusion method based on Bayesian inference for accurate estimation of chlorophyll-a concentration over eutrophic lakes[J/OL]. Environmental Modelling & Software, 2021: 105057.
  19. LI Y, CHEN Y, CHEN Y, et al. Fast Deployable Real-Time Bioelectric Dissolved Oxygen Sensor Based on a Multi-Source Data Fusion Approach[Z/OL]. (2023-06). [CrossRef]
  20. JIANG H, DENG J, CHEN Q. Monitoring of simultaneous saccharification and fermentation of ethanol by multi-source data deep fusion strategy based on near-infrared spectra and electronic nose signals[J]. [CrossRef]
  21. ZHANG Yi, HUANG Jiaming, LIN Hongwei, et al. Voltage sag interactive platform of provincial power grid based on multi-source data fusion [J]. Electric Power Automation Equipment, 2023,43(03):196-203.
  22. LIU Q, DONG M, SUN P, et al. All-parameter Calibration Method of On-orbit Multi-view Dynamic Photogrammetry System[J/OL]. Optics Express, 2023: 11471.
  23. SHI Y, YUAN H, XIONG C, et al. Improving performance: A collaborative strategy for the multi-data fusion of electronic nose and hyperspectral to track the quality difference of rice[J/OL]. Sensors and Actuators B: Chemical, 2021: 129546. [CrossRef]
  24. ZOU J, ZHENG H, WANG F. Real-Time Target Detection System for Intelligent Vehicles Based on Multi-Source Data Fusion[J/OL]. Sensors, 2023: 1823. [CrossRef]
  25. JIAO H, SONG W, CAO P, et al. Prediction method of coal mine gas occurrence law based on multi-source data fusion[J/OL]. Heliyon, 2023: e17117.
  26. SHI Y, REN C, YAN Z, et al. Improving soil moisture retrieval from GNSS-interferometric reflectometry: parameters optimization and data fusion via neural network[J/OL]. International Journal of Remote Sensing, 2021: 9085-9108. [CrossRef]
  27. LI X, LI Z, QIU H, et al. Soil carbon content prediction using multi-source data feature fusion of deep learning based on spectral and hyperspectral images[J/OL]. Chemosphere, 2023: 139161.
  28. FENG J, QIN D, LIU Y, et al. Real-time estimation of road slope based on multiple models and multiple data fusion[J/OL]. Measurement, 2021: 109609.
  29. Ye Xiao, Xingchen Li, Jiangjin Yin, Wei Liang, Yupeng Hu. Adaptive multi-source data fusion vessel trajectory prediction model for intelligent maritime traffic[J/OL]. Knowledge-Based Systems, 2023:110799.
  30. LI Y, JIANG W, SHI Z, et al. A Soft Sensor Model of Sintering Process Quality Index Based on Multi-Source Data Fusion[J]. [CrossRef]
  31. JIANG Y, LI C, SUN L, et al. A deep learning algorithm for multi-source data fusion to predict water quality of urban sewer networks[J/OL]. Journal of Cleaner Production, 2021: 128533. [CrossRef]
  32. WANG B, LI Z, XU Z, et al. Digital twin modeling for structural strength monitoring via transfer learning-based multi-source data fusion[J].
  33. WANG S, LI W. GeoAI in terrain analysis: Enabling multi-source deep learning and data fusion for natural feature detection[J/OL]. Computers, Environment and Urban Systems, 2021: 101715.
  34. YANG N, YANG L, DU X, et al. Blockchain based Trusted Execution Environment Architecture Analysis for Multi - source Data Fusion Scenario[Z/OL]//Research Square - Research Square,Research Square - Research Square. (2023-04).
Preprints 99192 g005
Figure 5. Scope of services map of the 7 tier-1 nodes.
Figure 5. Scope of services map of the 7 tier-1 nodes.
Preprints 99192 g005
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated