Prerpints.org logo
Preprint
Article

Advanced Deep Learning Model for Predicting Academic Performance in Students at Educational Institutions

Altmetrics

Downloads

73

Views

35

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

18 February 2024

Posted:

19 February 2024

You are already at the latest version

Alerts
Abstract
Educational institutions must identify students who are academically struggling to provide them with necessary support to improve their performance. In this context, recommendation systems powered by deep learning techniques are vital for detecting and categorizing such students. These systems help students plan their future by uncovering patterns in their historical academic data. This study introduces a new deep learning model designed to classify academically underperforming students in educational settings. The model incorporates a Gated Recurrent Neural Network (GRU) and includes specific neural network features like a dense layer, max-pooling layer, and the ADAM optimization algorithm. The model's training and evaluation were conducted using a dataset comprising 15,165 student assessment records from various academic institutions. The performance of the developed GRU model was benchmarked against other educational recommendation systems, including Recurrent Neural Network models, AdaBoost, and the Artificial Immune Recognition System v2. The proposed GRU model demonstrated remarkable accuracy, achieving an overall rate of 99.70%.
Keywords: 
Subject: Computer Science and Mathematics  -   Artificial Intelligence and Machine Learning

1. Introduction

Educational institutions are treasure troves of data, comprising detailed information about the institutions and their student body, notably academic performances. Harnessing this wealth of data is pivotal for these institutions, as it holds the key to unlocking actionable insights. For instance, a sophisticated predictive model that can accurately interpret this data is indispensable for fostering students' academic success. The goal is to leverage the rich data on student performance [1] to drive educational improvements. It's important to recognize that student performance is influenced by a myriad of factors, a concept visually represented in Figure 1 [2]. The objectives of learning analysis are multifaceted, as thoroughly detailed by [3]. Central to these objectives is the role of educational institutions in monitoring and evaluating the learning process. This encompasses predicting student outcomes, providing effective mentorship, and overseeing advisory services. A paramount goal is to offer meaningful feedback to both educators and learners, gauging the efficacy and impact of the learning process. Based on these insights, strategic alterations to the educational framework are advised. Empowering students with autonomy in their learning endeavors is highly recommended, as is encouraging self-reflection based on previous experiences and accomplishments.
As time progresses, the data repositories of educational organizations have expanded, transforming into massive pools of latent knowledge. This hidden information is brimming with potential yet poses significant challenges in terms of storage, capture, analysis, and representation. These complexities have necessitated the reclassification of these databases as Big Data [4,5,6]. Faced with this paradigm shift, educational institutions are now seeking advanced analytical tools capable of deciphering both student and institutional performance [7]. Data centers in educational settings often exhibit big data characteristics and apply specific data mining methods to extract hidden insights. The synergy between data mining and educational systems, as illustrated in Figure 2, reveals the advantageous impact these insights can have on students, enriching their educational experience with knowledge gleaned from expansive and complex datasets.
This research contributes significantly by employing the Gated Recurrent Neural Network (GRU). The GRU model excels in identifying crucial hidden patterns – the key features within learner records at educational institutions. Given the typically large and intricate nature of these datasets, the GRU model serves as an ideal foundation for learning recommendation systems, which aim to boost student performance through in-depth internal assessments, moving beyond the scope of conventional statistical models. The GRU is particularly proficient in handling non-stationary sequences and effectively assessing student performance. Its comparative advantage over other deep learning models, such as RNNs, and various machine learning algorithms lies in its ability to bypass long-term dependency challenges and offer superior interpretability.
This structure of this research paper is organized into various sections. Section 2, outlines the related works. This is followed by section 3, which details the methods used in this research. Section 4 delves into the datasets utilized and the classification methods employed. Section 5 is dedicated to presenting the experimental results. Finally, section 6 concludes the paper and discusses potential future work.

2. Related Works

Deep learning algorithms have recently become prevalent in solving problems across various domains. They have found applications in the medical sector for disease prediction [8,9], in understanding complex behaviors in systems like biology [10], and in many other areas impacting daily life [11], including customer service, sports forecasting, autonomous vehicles, and weather prediction [12]. This research aims to explore the application of deep learning methods to datasets in educational institutions. With students increasingly engaging in online learning through specialized educational software, there is a rise in educational big data [13]. To extract meaningful patterns from this data, a variety of techniques are employed. Educational machine learning and deep learning tools are utilized in data mining to uncover hidden insights and patterns within educational settings [14]. Additionally, these techniques are applied to assess the effectiveness of learning systems, such as Moodle [15]. Machine learning (ML) and deep learning (DL) are also employed for classification and analysis of useful patterns that can be pivotal in predicting various educational outcomes [16]. These methods are instrumental in shaping a framework to optimize the learning process of students, ensuring a more effective educational journey [17]. The study by [18] explores how students' approaches to learning correlate with measurable learning outcomes, focusing on problem-solving skills evaluated through multiple-choice exams. It delves into the cognitive aspects of problem-solving to better understand processes and principles. Machine learning has been crucial in identifying learners' styles and pinpointing areas where students may face difficulties [19], as well as in organizing educational content effectively and suggesting learning pathways [20]. In the realm of educational institutions, machine learning algorithms have been instrumental in categorizing students. For example, [21] examines several machine learning algorithms, including J48, Random Forest, PART, and Bayes Network, for classification purposes. The primary objective of this research is to boost students' academic performance and reduce course dropout rates. The findings from [21] indicate that the Random Forest algorithm outperforms others in achieving these goals.
[22] employed data log files from Moodle to create a model capable of predicting final course grades in an educational institution. [23] developed a recommendation system for a programming tutoring system, designed to automatically adjust to students' interests and knowledge levels. Additionally, [24] used machine learning (ML) techniques to study students' learning behaviors, focusing on insights derived from the educational environment, particularly from mid-term and final exams. Their model aims to help teachers reduce dropout rates and improve student performance. [25] suggested a model for categorizing learners based on demographics and average course attendance. [26] applied artificial intelligence and machine learning algorithms to track students in e-learning environments. They created a model to gather and process data related to e-learning courses on the Moodle platform. Finally, [27] introduced a framework to analyze the characteristics of learning behavior, particularly during problem-solving activities on online learning platforms. This framework is designed to function effectively while students are actively engaged in these online environments.
Preprints 99186 g001
Figure 1. Student Performance Factors.
Figure 1. Student Performance Factors.
Preprints 99186 g001
Preprints 99186 g002
Figure 2. The relationship between educational system and data mining techniques.
Figure 2. The relationship between educational system and data mining techniques.
Preprints 99186 g002

3. Background

3.1. Artificial Immune Recognition system v2.0

Numerous studies have been inspired by the capabilities of the Artificial Immune Recognition System (AIRS), with several applications successfully incorporating this method. AIRS2, in particular, has garnered significant attention from researchers aiming to develop models based on immune system methodologies to provide solutions to complex problems [36]. The fundamental principle of AIRS2 is to create a central data point that forms a tailored space for each distinct class, thereby clarifying and enriching the learning process. This method primarily focuses on primary data points selectively identified by the AIS system. While AIS is known for generating memory cells, AIRS2 and other similar methods use these points primarily for making predictive configurations. AIRS2 is commonly used in supervised learning for classification tasks. AIRS2 is an adaptive technique inspired by the biological immune system, deemed effective for challenging tasks such as classification [37]. A key advantage of AIRS2 is its ability to reduce the memory cell pool, addressing the challenges of assigning class membership to each cell. As a supervised learning algorithm, AIRS2 incorporates mechanisms like resource competition, affinity maturation, clonal selection, and memory cell generation [37]. These features make AIRS2 a robust tool in the realm of artificial immune systems, offering efficient solutions in various supervised learning scenarios.

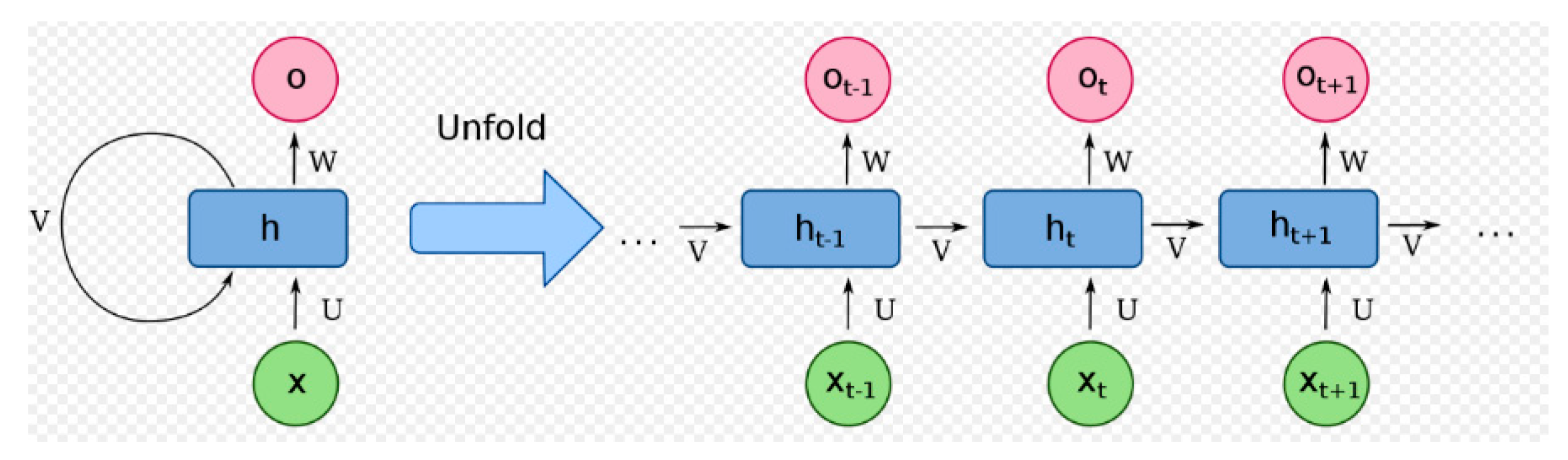
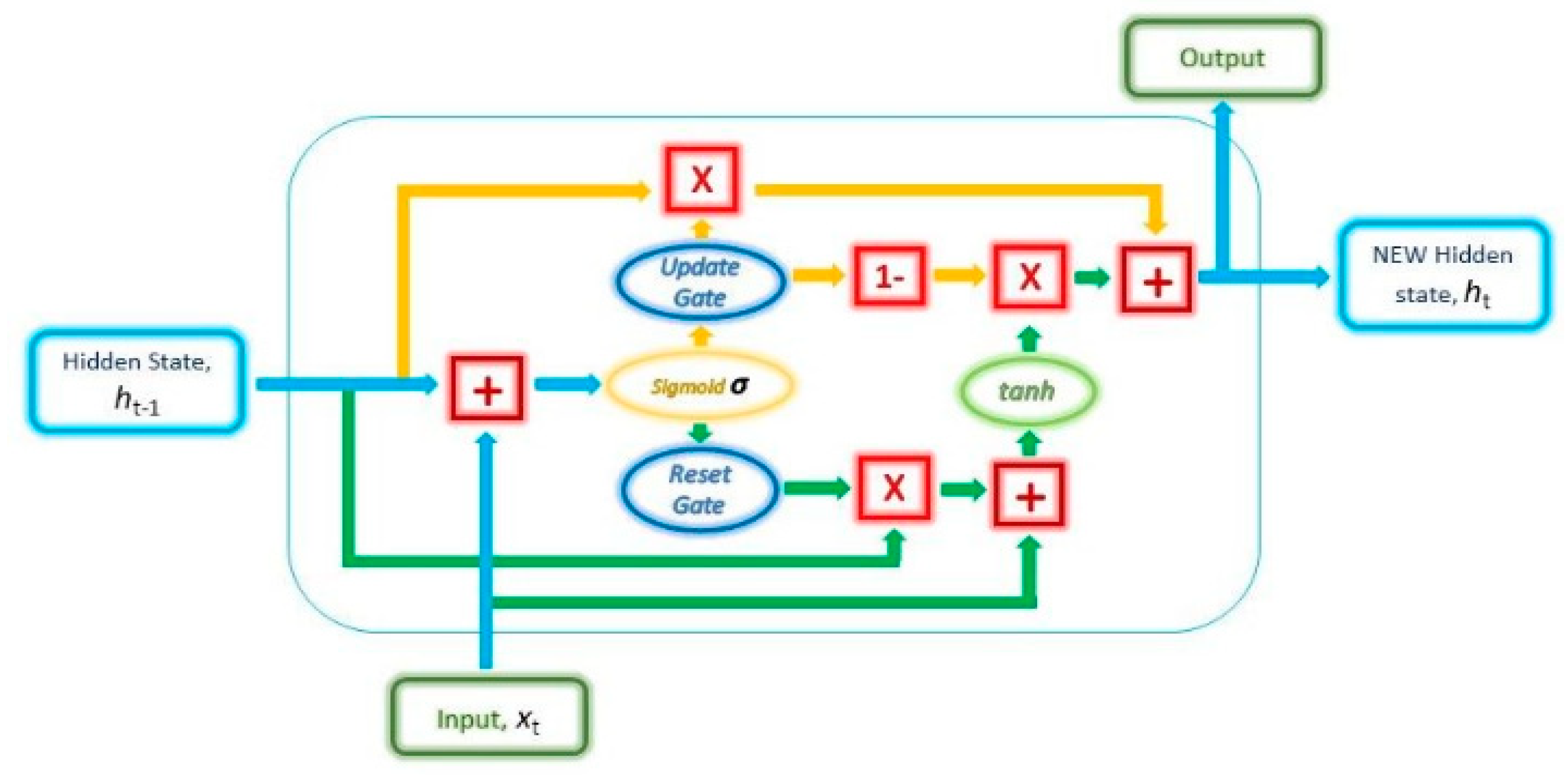
3.2. Recurrent Neural Netwrk (RNN)

Recurrent Neural Networks (RNNs) are a sophisticated class of artificial neural networks uniquely designed to process sequences of data by leveraging their inherent ability to maintain a 'memory' of previous inputs. This capability distinguishes RNNs from traditional neural networks, which treat each input independently, without regard for order or sequence. The core idea behind RNNs is their internal state, or memory, which captures information about what has been processed so far, allowing them to exhibit dynamic temporal behavior. This makes them exceptionally well-suited for applications involving sequential data, such as natural language processing, speech recognition, and time series prediction. RNNs operate by looping through each element in a sequence, updating their internal state based on both the current input and the previously acquired knowledge. This process enables them to make informed predictions about future elements in the sequence, essentially learning patterns and dependencies within the data. For instance, in language modeling, an RNN can predict the next word in a sentence based on the words it has seen so far, capturing the grammatical and contextual nuances of the language.
Despite their powerful capabilities, RNNs are not without challenges. One of the main issues they encounter is the difficulty in learning long-term dependencies, known as the vanishing and exploding gradient problems. These problems arise due to the nature of backpropagation through time (BPTT), the algorithm used for training RNNs, which can lead to gradients becoming too small or too large, making it hard for the RNN to learn correlations between distant elements in a sequence. To overcome these challenges, several variants of RNNs have been developed, including Long Short-Term Memory (LSTM) networks and Gated Recurrent Units (GRU). These architectures introduce mechanisms to better control the flow of information, allowing them to retain important long-term dependencies while forgetting irrelevant data, thereby mitigating the issues of vanishing and exploding gradients. LSTMs, for example, incorporate gates that regulate the addition and removal of information to the cell state, making them highly effective for tasks requiring the understanding of long-range temporal dependencies. In recent years, RNNs and their variants have been at the heart of numerous breakthroughs in fields requiring the analysis of sequential data. From generating coherent text in natural language generation tasks to providing real-time translations in machine translation systems, and even enabling sophisticated voice recognition and synthesis in virtual assistants, RNNs have demonstrated their versatility and power. As research continues to evolve, it is likely that we will see further advancements in RNN architectures and their applications, solidifying their role as a cornerstone of sequential data analysis in artificial intelligence.
Preprints 99186 g003
Figure 6. Recurrent Neural network (RNN).
Figure 6. Recurrent Neural network (RNN).
Preprints 99186 g003

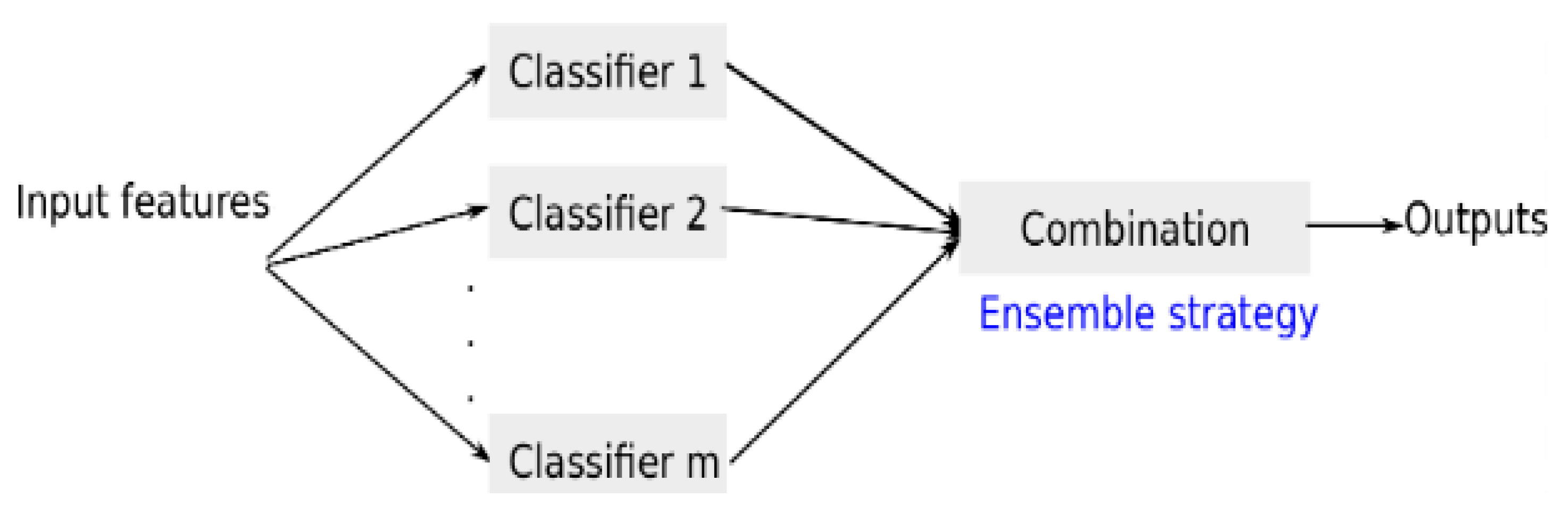
3.3. Adaboost classification techniques

The AdaBoost classifier is a type of Ensemble classifier, a method that amalgamates multiple classifiers to create a more effective one. Known also as a Meta learning approach, it operates by integrating various weak classifiers—each with limited accuracy—to construct a collective of classifiers aiming for stronger predictive performance. Essentially, AdaBoost works by evolving a composite strong classifier out of an assembly of weaker ones. It achieves this by continuously learning from the outcomes of previous classifications and adjusting the weights of individual classifiers based on this feedback. The strength of AdaBoost lies in its ability to progressively diminish the training errors and enhance the overall model performance through several iterations. This process has garnered recognition for its effectiveness in reducing errors and improving results across various domains, including learning analytics. Learning analytics involves the collection, analysis, and interpretation of data about learners and their contexts, with the goal of understanding and optimizing learning and the environments in which it occurs.
Preprints 99186 g004
Figure 5. Adaboost Classification techniques- AdaBoost Classifier.
Figure 5. Adaboost Classification techniques- AdaBoost Classifier.
Preprints 99186 g004

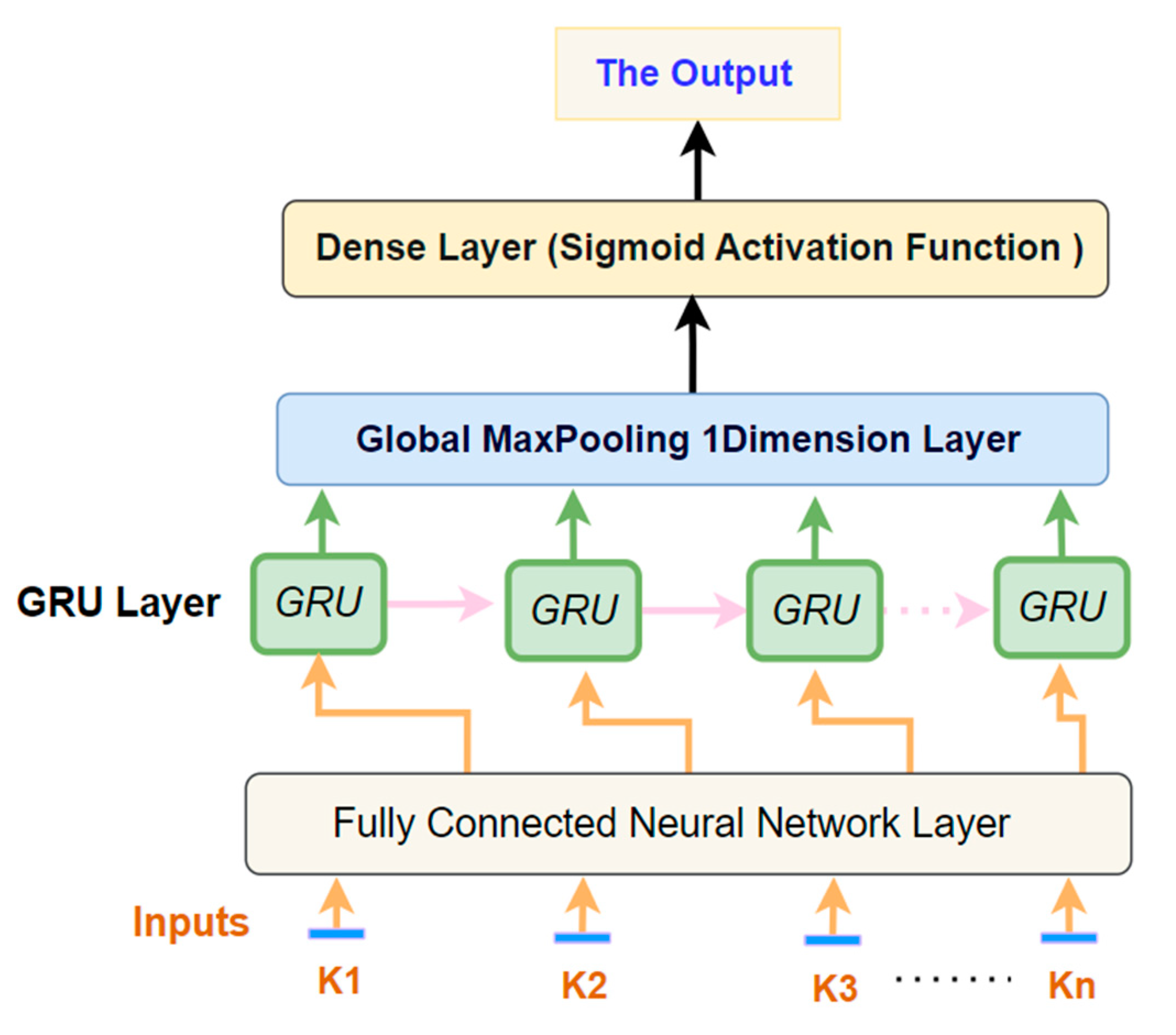
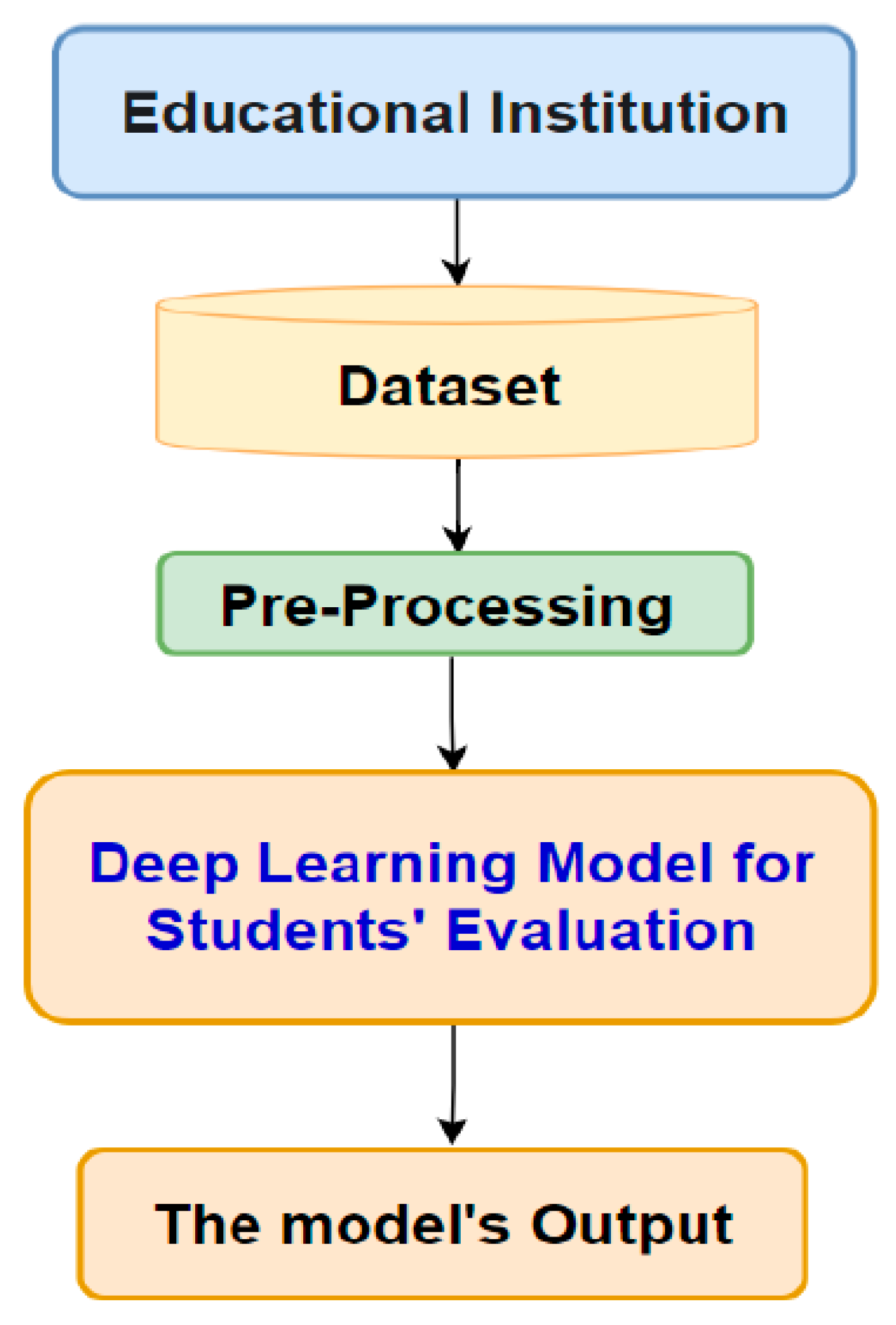
3. The Architecture of the Proposed Deep Learning Model for the Prediction of Students' Performance in Educational Institutions

In our discussion, we elaborate on the key methodologies implemented in our proposed model, specifically focusing on the configurations of the proposed Gated Recurrent Unit (GRU) model. Additionally, we compare the GRU model with other techniques to highlight its effectiveness. Thus, this section also introduces the fundamental concepts of other classifiers, including the Artificial Immune Recognition System v2, Recurrent Neural Network (RNN), and AdaBoost. These classifiers have been utilized in creating a predictive model for educational institutions. Educational institutions have recently begun utilizing deep neural network (NN) algorithms on their datasets for purposes such as making future predictions [28]. Deep neural networks function similarly to the human brain in terms of thinking and problem-solving capabilities. As such, NNs can interpret complex patterns that might be challenging for human analysis or conventional learning algorithms. The architecture of NNs varies, with nodes supporting different processes like forward or backward sequencing, often referred to as sequential or convolutional operations. The Gated Recurrent Neural Network (GRU) is a variant of neural network algorithms, akin to the Recurrent Neural Network (RNN). It plays a critical role in managing information flow between nodes [29]. GRU, an advanced form of the standard RNN, features update and reset gates. These gates, as illustrated in Figure 3, decide which information (vectors) should be passed to the output [30]. During training, these gates have the capability to learn which crucial information should be retained or disregarded for effective prediction [31].
Preprints 99186 g005
Figure 5. The Architecture Gated Recurrent Unit (GRU).
Figure 5. The Architecture Gated Recurrent Unit (GRU).
Preprints 99186 g005
Additionally, Equations 1-4 govern the operations of the gates mentioned earlier. Specifically, Equation 1 demonstrates how vectors for the Update and Reset gates are formulated. In this process, distinct weights (denoted as W_) are applied to both the input and the hidden state, resulting in unique vectors for each gate. This differentiation enables the gates to perform their specific roles effectively.
g a t e u p d a t e = σ ( W i n p u t u p d a t e .   x t + W h i d d e n u p d a t e .   h t − 1 )
g a t e r e s e t = σ ( W i n p u t u p d a t e .   x t + W h i d d e n r e s e t .   h t − 1
Equation 2 describes the process in which the sigmoid function takes the previous hidden state and the current input x t , along with their respective weights, and performs a summation of these values. The sigmoid function then converts these values into a range between 0 and 1. This transformation allows the gate to filter information, distinguishing between less important and more critical information for future steps. Equation 3 represents the current memory content during the training process, whereas Equation 4 depicts the final output in the memory at the current time step.
h t ' = t a n t   ( W x t + r t   ⨀   U h t − 1
h t = r   ⨀   1 − g a t e u p d a t e + u
The proposed GRU model simplifies the understanding of how sequential data inputs impact the final sequence generated as the model's output. This capability is key in unraveling the internal operational mechanisms of the model and fine-tuning specific input-output correlations. Additionally, experimental evaluations using students’ internal assessment datasets have demonstrated that the GRU model surpasses the performance of traditional models. Deep Learning models often train with noisy data, necessitating the use of specialized stochastic optimization methods like the ADAM algorithm [32]. Renowned for its effectiveness in deep learning contexts, the ADAM algorithm is favored for its ease of implementation and low memory requirements, contributing to computational efficiency. It is particularly adept at handling large datasets and numerous parameters. The ADAM algorithm combines elements of stochastic gradient descent and root mean square propagation, incorporating adaptive gradients. During training, it utilizes a randomly selected data subset, rather than the entire dataset, to calculate the actual gradient. This approach is reflected in the workings of the algorithm, as detailed in Equations 5 and 6 [33].
𝑚t = 𝛽1 𝑚t-1 + (1 – 𝛽1)t
𝑣t = 𝛽2/𝑣t-1 + (1 – 𝛽2)t2
m t and v t must approximation of the instant of the gradients, where they adjusted as vectors of 0's, β1, β2 closed to zero. These biases are emulated through the computation of bias-adjusted moment estimations, as delineated in Equations 7, 8, and 9.
m t = m t 1 − β 1 t
v t = v t 1 − β 2 t
Subsequently, the update rule is applied.
θ t + 1 = θ t − h v t + ∈ m t
The Default values of 𝛽1 = 0.9 and 𝛽2 = 0.999, ∈ = 10 -8. The proposed model includes a max-pooling layer, which serves to reduce the number of coefficients in the feature map for processing. This layer facilitates the development of spatial filter hierarchies by generating successive convolution layers with increasingly larger windows relative to the original input's proportion [34]. Furthermore, the proposed GRU model incorporates a Dense layer. This layer is fully connected to its preceding layer, meaning every neuron in the Dense layer is linked to every neuron in the layer before it. The Dense layer receives outputs from all neurons of its preceding layer and performs matrix-vector multiplication. In this context, the matrix's row vector, representing the output from the preceding layer, corresponds to the column vector of the Dense layer [35].Figure 4 visually presents the primary configurations of the proposed GRU model, while Figure 5 depicts the model's development process.

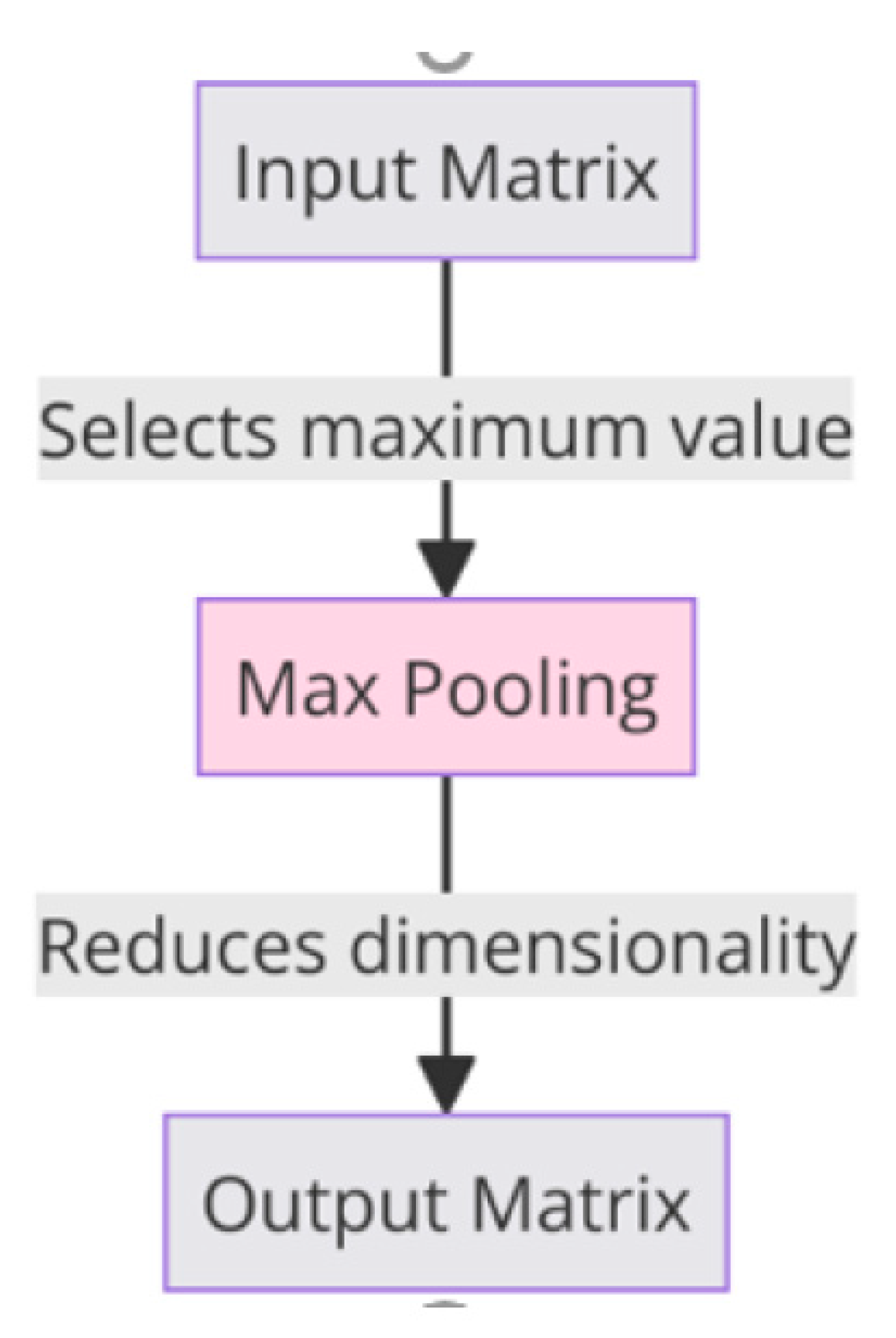
3.1. Maxpooling:

Max pooling is a significant technique in deep learning models, particularly in the realm of convolutional neural networks (CNNs). It functions as a down-sampling strategy, effectively reducing the spatial dimensions of input feature maps. The process involves scanning the input with a fixed-size window, typically 2x2, and outputting the maximum value within each window. This approach not only reduces the computational load for the network by decreasing the number of parameters but also helps in extracting robust features by retaining the most prominent elements within each window. Max pooling contributes to the model's translational invariance, meaning the network becomes less sensitive to the exact location of features in the input space. This property is particularly useful in tasks like image and speech recognition, where the precise location of a feature is less important than its presence. By simplifying the input data and focusing on key features, max pooling enhances the efficiency and performance of deep learning models, making them more effective in recognizing patterns and identifying key characteristics in complex datasets. Max pooling plays a crucial role in predicting student performance, especially when these models process complex input data like patterns in student interaction, engagement metrics, and learning behaviors. In the context of educational data analysis, max pooling helps in effectively reducing the dimensionality of input features, which might include various student performance indicators. By segmenting these indicators into non-overlapping sets and extracting the maximum value from each, max pooling focuses on the most prominent features that are indicative of student performance trends. This process not only simplifies the computational demands of the model but also accentuates key features that are crucial for accurate predictions. For instance, in a model analyzing students' online learning patterns, max pooling can help highlight the most significant engagement metrics while discarding redundant or less informative data. This aids in creating a more efficient and focused predictive model, enabling educational institutions to derive meaningful insights into student performance and potentially identify areas requiring intervention or support.
Preprints 99186 g006
Figure 5. The Architecture of the Proposed GRU Model.
Figure 5. The Architecture of the Proposed GRU Model.
Preprints 99186 g006
Preprints 99186 g007
Figure 5. The Process for the GRU Mode.
Figure 5. The Process for the GRU Mode.
Preprints 99186 g007
Preprints 99186 g008
Figure 5. Max-Pooling Ope.
Figure 5. Max-Pooling Ope.
Preprints 99186 g008

3. Experiments

3.1. Datasets

The GRU model in question was developed using a specific educational dataset, cited in reference [40], which was compiled from three distinct educational institutions in India: Duliajan College, Digboi College, and Doomdooma College. This dataset is large and complex, encompassing internal assessment records of 15,165 students across 10 different attributes. Despite its extensive size, the dataset did present challenges, notably in the form of missing data entries. These missing values were ultimately excluded from consideration in the analysis. Table 1 provides a detailed breakdown of the dataset's attributes, including the range and nature of the data collected. Additionally, Figures 5 and 6 offer a visual representation of the dataset, highlighting the diversity and scale of the educational data gathered from these institutions.
Table 1. Features’ explanation with their values.
Table 1. Features’ explanation with their values.
Feature Explanation Values
Exam The Three Year Degree Six semester Examinations {'BA', ‘BSC’ }
Two tests are occupied into account, i.e. BA and BSc
IN_Sem1 Major/Honours Topics
Of Bachelor and Master Programs		 {'ENGM','PHYM', etc.}
ENGM- Major/Honours in English
PHYM- Major/Honours in Physics
IN_Sem2 Internal evaluation Grades
acquired in the BA/BSc 1st
Semester Examination		 Maximum marks 20
Marks achieved by the students in the range 1 to 20.
Mean: 15.66257
Standard Deviation SD: 2.593816
IN_Sem3 Internal evaluation Grades
obtained in the BA/BSc 3rd
Semester Examination		 Maximum marks 40
Marks achieved by the students in the range 1 to 40.
Mean: 31.95765
Standard Deviation SD: 5.101312
IN_Sem4 Internal evaluation Grades
obtained in the BA/BSc 4th
Semester Examination		 Maximum marks 40
Marks achieved by the students in the range 1 to 40.
Mean: 30.80859
Standard Deviation: 5.43647
IN_Sem5 Internal evaluation Grades
obtained in the BA/BSc 5th
Semester Examination		 Maximum marks 80
Marks achieved by the students in the range 1 to 80.
Mean: 64.71536
Standard Deviation: 10.18944
IN_Sem6 Internal evaluation Grades
obtained in the BA/BSc 6th
Semester Examination		 Maximum marks 80
Marks achieved by the students in the range 1 to 80.
Mean: 64.79921
Standard Deviation: 10.3252
InPc The overall percentage secured
by the candidate in all
the six semesters in the internalassessments		 Mean: 80.44676
Standard Deviation: 11.01706
Result The overall result of the
applicant established the all the six
semesters theory and interior
assessment		 {‘Pass’, ‘Fail’}
If a student secures 40% or overhead, he is termed as ‘Pass’
Else ‘Fail’

3.2. Evaluation Metrics

The evaluation of the GRU Model's effectiveness was conducted using a variety of widely recognized evaluation techniques. These included the use of a Confusion Matrix, as well as metrics such as Accuracy, Recall, Precision, and F-score, as referenced in [42]. The Confusion Matrix, also known as an error matrix, serves as a tool for statistical classification, visually representing the model's performance as shown in Figure 8. This figure illustrates a binary classification scenario, distinguishing between two categories: a positive (P) class and a negative (N) class. The matrix is structured to highlight several key outcomes: True Positive (TP), which indicates accurate predictions of positive instances, meaning the predictions and actual values both are positive. False Positive (FP) refers to instances falsely identified as positive when they are actually negative. True Negative (TN) points to correct predictions of negative instances, where both predicted and actual values are negative. Lastly, False Negative (FN) describes instances where positive values are mistakenly identified as negative[43]. In addition, The Accuracy for the model stands for the ratio among the numbers of corrected predicted samples to the total number of input samples. This is explained by Equation 10.
Accuracy = Sum of TruePositive + Sum of True Negative / Total population
The Recall represents the amount of right positive results divided by the amount of all relevant samples. This is represented in Equation 11.
Recall = TruePositives / (TruePositives + FalseNegatives)
The precession metric estimates the amount of accurate positive results divided by the amount of positive results expected through the classifier. This represented in Equation 12.
Precision = TruePositives / (TruePositives + FalsePositives)
Finally, the F-score measured by equation 9. This equation illustrations just one score that equilibrium\composed the concerns of recall and precision in single value. F-score makes a balance between two metrics; recall and precision. It is a balanced mean of two different scores, product with 2 to get a score of 1 when both of recall and precision equal to 1.
F-Measure = 2 *[(Precision * Recall) / (Precision + Recall)]
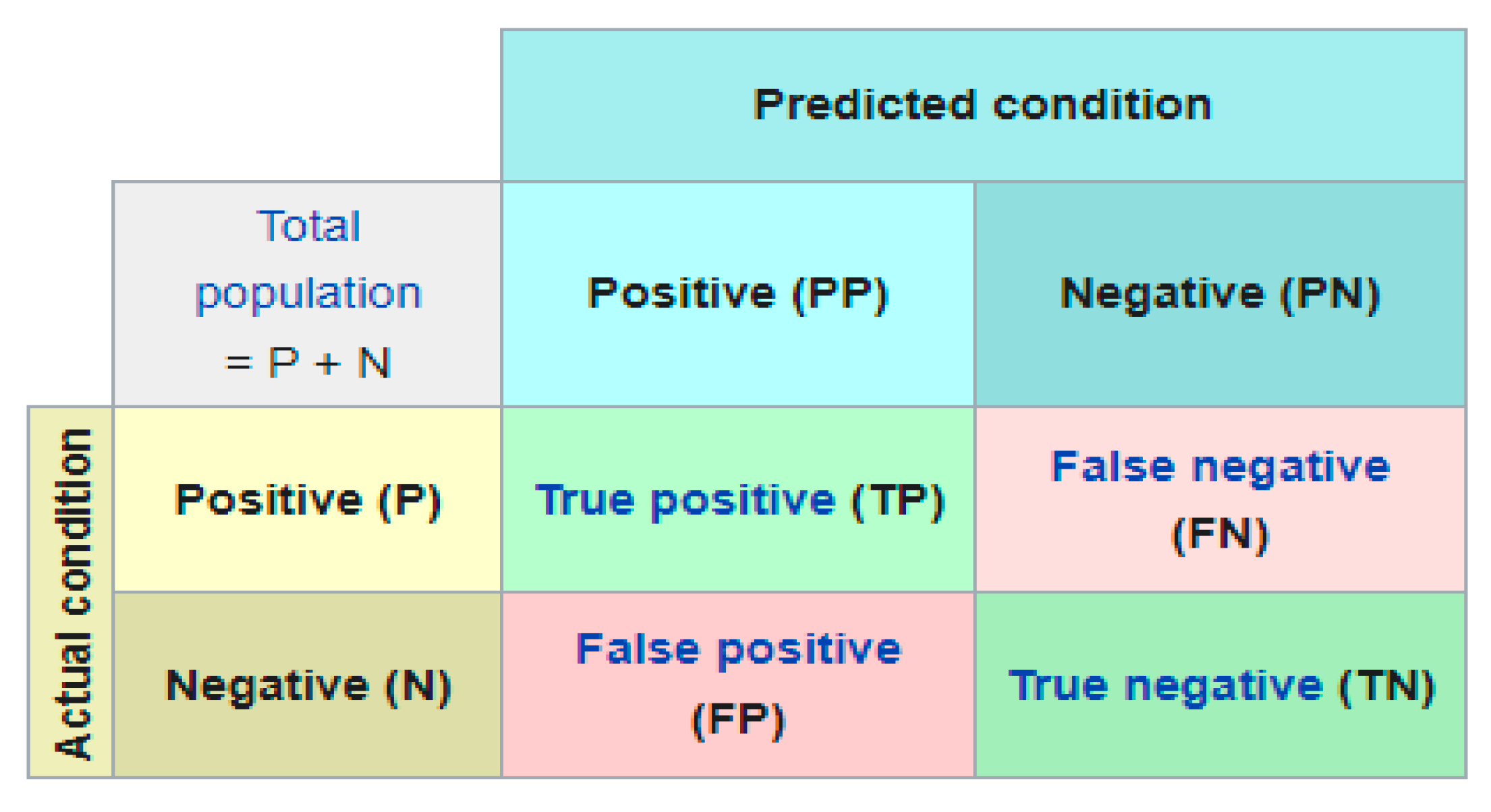
Preprints 99186 g009
Figure 11. General Structure of Confusion Matrix.
Figure 11. General Structure of Confusion Matrix.
Preprints 99186 g009

3.2. Results and the Proposed Model Hyperparameters

The GRU Classifier model was developed using an educational dataset for both its training and testing phases. This model incorporated a sequential architecture featuring a max-pooling layer, a dense layer, and utilized the Adam optimizer for enhancing its performance. The chosen loss function for the model was binary_crossentropy, suitable for binary classification tasks. For validating the model's effectiveness, the K-fold cross-validation method was employed, specifically with a single fold (k = 1), effectively creating a straightforward train/test split. The model's architecture included a fully connected neural network (FCNN) layer with 100 neurons and nine input variables, adopting the ReLU activation function for non-linear processing. The design also incorporated two hidden layers: the initial layer being a GRU layer equipped with 256 units and a recurrent dropout of 0.23 to mitigate overfitting, and the subsequent layer, a one-dimensional Global Max-Pooling layer for feature down-sampling. The output layer activated by a sigmoid function, reflects the binary nature of the dataset's classification challenge. The implementation was carried out using Keras and Python, harnessing the Adam optimizer's capabilities with a learning rate set at 0.01 and a momentum of 0.0, aiming for efficient training dynamics. The model's training was configured with a batch size of 90 and planned for 300 epochs, although an early stopping mechanism was introduced after just 7 epochs to prevent overfitting, with a patience setting of 2 epochs. Initially, the model comprised 275,658 parameters, highlighting its complexity and capacity for learning. Regarding the classification task, the model demonstrated a requirement of approximately 16 seconds per epoch, with each epoch involving a random shuffle of the training data to ensure varied exposure. The overarching goal in training this model was to minimize validation loss as measured by binary_crossentropy, indicating a focused effort on enhancing predictive accuracy for student assessments.
Extensive testing and experimentation were conducted to fine-tune the proposed model, involving various configurations and hyper_parameter adjustments to achieve optimal performance. This effort was aimed at accurately predicting student assessments within educational settings. The effectiveness of the model, as detailed in Figure 9, is evidenced by its high accuracy scores for the prediction task. The data presented in Figure 9 highlights the model's capability in accurately forecasting student assessments, particularly noting the significant impact of integrating the GRU layer and a fully connected neural network. Specifically, the model attained an impressive accuracy rate of 99.70%, showcasing its precision in evaluation predictions. The inclusion of a global Max-Pooling layer played a crucial role in bolstering the model's predictive accuracy concerning student evaluations. When compared to existing models documented in the literature, this model demonstrated superior performance. For example, it outpaced an RNN model, which recorded an accuracy rate of 95.34%, a discrepancy attributed to the RNN's challenges with vanishing gradients, as indicated in Table 2. Additionally, the model showcased enhanced performance over the ARD V.2 and AdaBoost models, which achieved accuracy rates of 93.18% and 94.57% respectively. The successful application of GRU alongside Max-Pooling layers over the neural network layer underscored the model's comprehensive capability and effectiveness in autonomously predicting student assessments. Figure 9 offers a glimpse into the model's experimental evaluation for predicting student performance, while Table 2 consolidates the advantages offered by the GRU model in this context.
Table 2. The Summary of the Proposed GRU model.
Table 2. The Summary of the Proposed GRU model.
Layer (Type) Output Shape Parameters No.
Input_1 (inputLayer) (None, 10, 1) 0
Word_dense (Dense) (None, 10, 100) 200
Gru (GRU) (None, 10, 256) 274944
Global_max_pooling (Global MaxpoolingID (None, 256) 0
Dense (None, 2) 514
Total Parameters: 275,658
Trainable Parameters: 275,658
Non-Trainable Parameters: 275,658
Figure 10 illustrates the prediction model's error rates throughout the simulation process, demonstrating a consistent decrease in error for both the training and actual validation datasets as the learning progressed. This simultaneous reduction in error rates during training indicates that the GRU model effectively avoids the issue of overfitting, showcasing its ability to generalize well to new, unseen data while improving its accuracy on the training data over time.
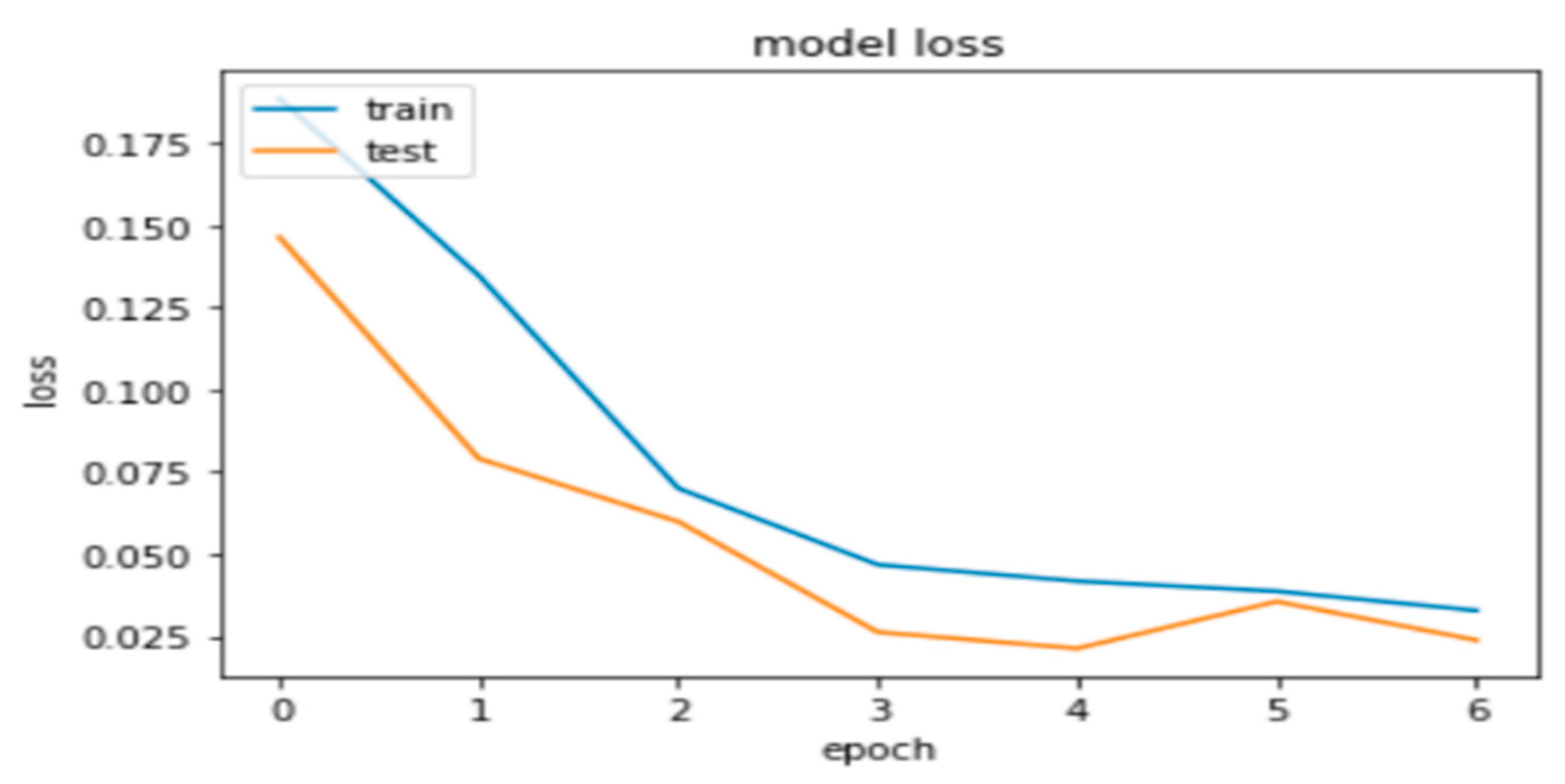
Preprints 99186 g010
Figure 10. relation between model loss (error) with epoch during training and testing the model using the educational dataset.
Figure 10. relation between model loss (error) with epoch during training and testing the model using the educational dataset.
Preprints 99186 g010
Additionally, the accuracy of student performance predictions is graphically depicted in Figure 11. This demonstrates that the proposed GRU model has been effectively trained. There is a noticeable increase in accuracy for both the training and testing phases within educational datasets, starting from epoch number 1 and continuing up to epoch number 4. This upward trend in accuracy highlights the GRU model's ability to perform and classify with precision.
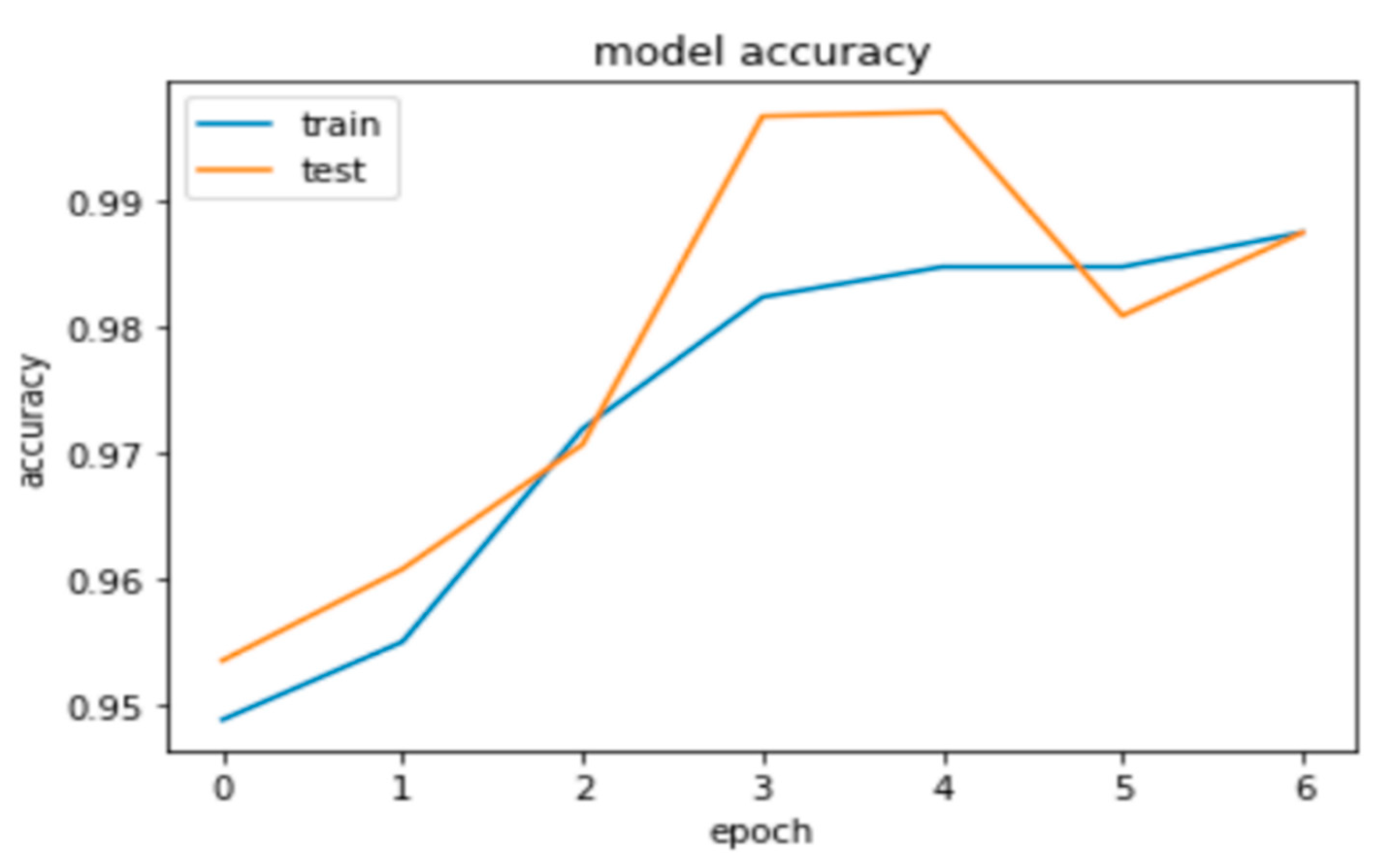
Preprints 99186 g011
Figure 11. Accuracy Analysis for the proposed GRU model.
Figure 11. Accuracy Analysis for the proposed GRU model.
Preprints 99186 g011
Moreover, an additional metric was employed to evaluate the performance of the proposed GRU model, as depicted in Figure 12 through the confusion matrix. This matrix effectively highlights the number of true positives, accurately predicted and correctly classified samples, alongside true negatives, which are correctly identified as belonging to the alternate class in the context of student performance classification. According to Figure 12, the model successfully identified 2885 samples as true positives and 110 samples as true negatives. Conversely, the confusion matrix also reveals instances of incorrect predictions, classified as false positives and false negatives. Specifically, the model incorrectly classified 38 samples as false positives, while no instances were recorded as false negatives. The data presented in Figure 12 underscores the model's high accuracy and proficiency in predicting student assessments, with a minimal error margin.
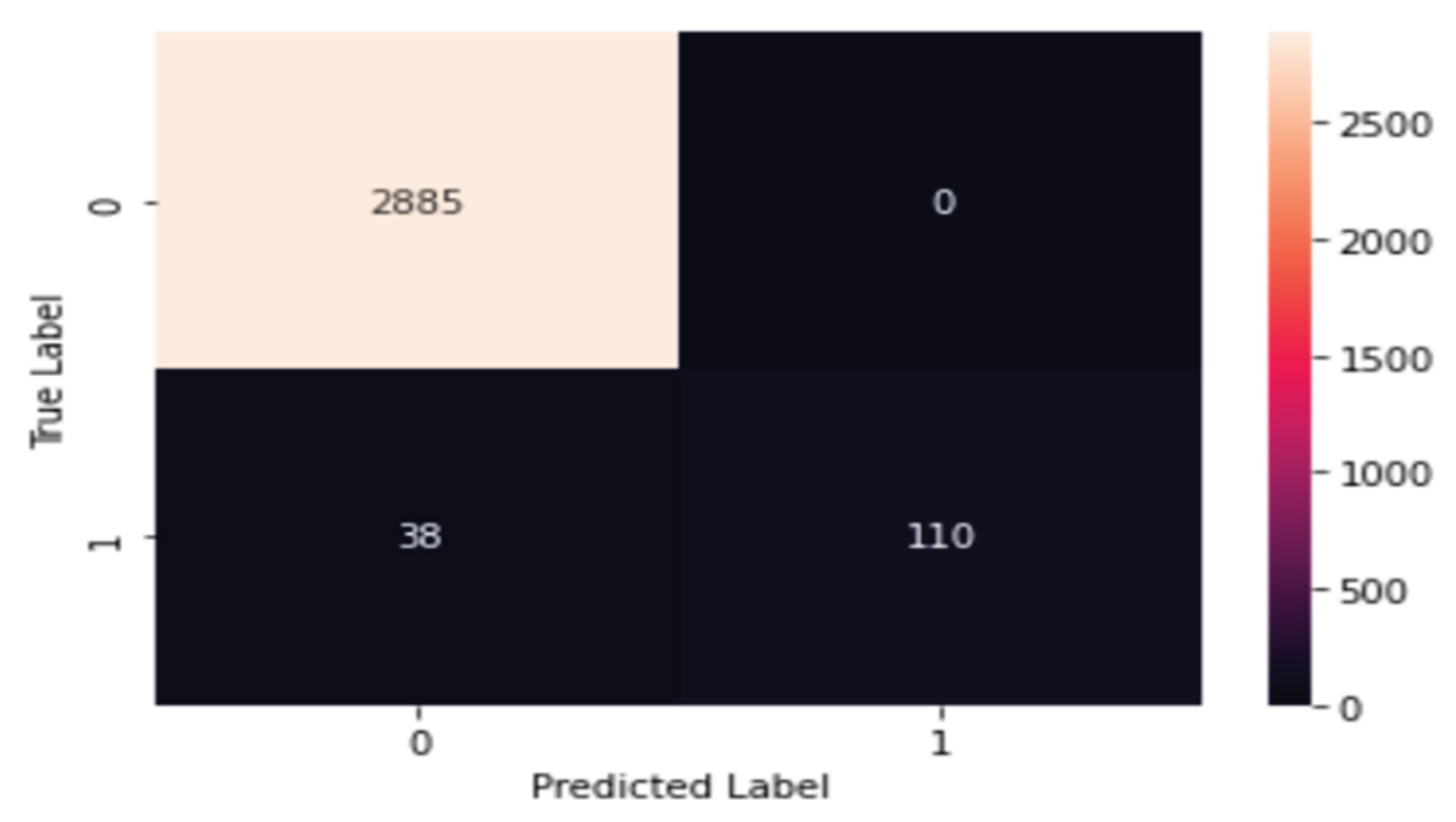
Preprints 99186 g012
Figure 11. Confusion Matrix for the GRU Model.
Figure 11. Confusion Matrix for the GRU Model.
Preprints 99186 g012
Furthermore, the GRU model offers deeper analysis and insights into the educational dataset. For example, Figure 13 showcases the model's capability to discern and illustrate the relationship between two critical variables: the internal evaluation grades from the BA/BSc 5th Semester Examination (IN_Sem5) and those from the BA/BSc 6th Semester Examination (IN_Sem6). This demonstrates the model's effectiveness in identifying significant correlations within the educational data. Additionally, Table 3 presents a comparative analysis of various techniques, including ARD V.2, the RNN model, and AdaBoost, in their ability to classify student performance. It is evident from this comparison that the GRU model outperforms the other methodologies, indicating its superior accuracy and effectiveness in predicting student outcomes.
Preprints 99186 g013
Figure 11. the Correlation between the BA/BSc 5th Semester Examination (IN_Sem5) and the internal evaluation Grades obtained in the BA/BSc 6th Semester Examination (IN_Sem6).
Figure 11. the Correlation between the BA/BSc 5th Semester Examination (IN_Sem5) and the internal evaluation Grades obtained in the BA/BSc 6th Semester Examination (IN_Sem6).
Preprints 99186 g013
Table 3. Comparison Between Diverse Classification Approaches.
Table 3. Comparison Between Diverse Classification Approaches.
The Classifier Precision Recall F-Score Accuracy
RNN Model 0.96 0.99 0.98 95.34
ARD V.2 0.926 0.932 0.939 93.18
AdaBoost 0.934 0.946 0.939 94.57
The Proposed model 0.986 0.963 0.974 99.70

5. Conclusion

Advancing research within higher education systems can significantly boost both the performance and the prestige of educational institutions. Implementing advanced predictive techniques to forecast student success enables these institutions to accurately assess student performance, thereby enhancing the institution's own effectiveness based on empirical evidence. Through the strategic use of internal assessment data, institutions can predict future student outcomes. This study introduces an innovative GRU-based prediction model tailored to educational data gathered from various institutions, demonstrating significantly more precise outcomes compared to established models used on the same dataset. The GRU model specifically utilizes data from students' previous semester assessments to provide targeted support for those identified as at risk. Consequently, students with lower internal assessment scores can be given additional opportunities to enhance their performance before final exams, and potentially be grouped into categories for focused support. This predictive approach enables timely communication with both parents and students, ensuring awareness and facilitating opportunities for academic improvement. Moreover, the GRU model allows educators to intervene proactively, using early semester assessment data to extend extra support to students who need it most. Such early intervention strategies empower instructors to make informed decisions that can positively impact students' academic trajectories, particularly those who are at risk, by offering tailored assistance and support mechanisms.

Author Contributions

L.H.B., S.K. conceived and designed the methodology and experiments; L.H.B. performed the experiments; L.H.B. analyzed the results; L.H.B., S.K. analyzed the data; L.H.B. wrote the paper. S.K. reviewed the manuscript. All authors have read and agreed to the published version of the manuscript.

Funding

This work was supported by the Basic Science Research Program through the National Research Foundation of Korea (NRF), funded by the Ministry of Science and ICT under Grant NRF-2022R1A2C1005316.

Data Availability Statement

The dataset generated during the current study is available in the [ADL-PSF-EI] repository (https://github.come/laith85).

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Agrawal, R.S; Pandya, M.H. Survey of papers for Data Mining with Neural Networksto Predict the Student's Academic Achievements. Intern Journal of Comp Scie Trends and Techn (IJCST) 2015, 3, 15. [Google Scholar]
  2. Beikzadeh, M. R.; Delavari. N. A New Analysis Model for Data Mining Processes in Higher Educational Systems. In Proceedings of the 6th Information Technology Based Higher Education and Training, 7-9 July 2005.
  3. Steiner, C.; Kickmeier-Rust, M.; Albert, D. Learning Analytics and Educational Data Mining: An Overview of Recent Techniques. Learning analytics for and in serious games 2014, 6–15. [Google Scholar]
  4. Khan, S.; Alqahtani, S. Big Data Application and its Impact on Education. Inter Journ of Emer Techno in Learning (iJET0) 2020, 15, 36–46. [Google Scholar] [CrossRef]
  5. Ouatik, F.; Erritali, M.; Ouatik, F.; Jourhmane, M. Predicting Student Success Using Big Data and Machine Learning Algorithms. Intern Journal of Eme Technol in Learn (iJET) 2022, 17. [Google Scholar] [CrossRef]
  6. Philip Chen, C.L.; Zhang, C.-Y. Data-intensive applications, challenges, techniques, and technologies: A survey on Big Data Inform. Sci 2014. [CrossRef]
  7. H, Shuliang.; Cuibi, Y. Learners' Autonomous Learning Behavior in Distance Reading Based on Big Data. Intern Jour of Emer Techn in Learning (iJET) 2022. [CrossRef]
  8. ALSHARAIAH, M A.; BANIATA, L.H.; ALADWAN, O.; AbuaAlghanam, O.; Abushareha, A.A.; Abuaalhaj, M.; Sharayah, Q.; Baniata, M. SOFT VOTING MACHINE LEARNING CLASSIFICATION MODEL TO PREDICT AND EXPOSE LIVER DISORDER FOR HUMAN PATIENTS. Journal of Theor and Applied Information Technology 2022, ,100, 4554 – 4564.
  9. Alsharaiah, M A.; Baniata, L.H.; Adwan, O; Abu-Shareha, A. A ; Abuaalhaj, M.; Kharma, Q.; Hussein, A.; Abualghanam, O.; Alassaf, N.; Baniata, M. Attention-based Long Short Term Memory Model for DNA Damage Prediction in Mammalian Cells. International Journal of Advanced Computer Science and Applications 2022, 13, 91–99.
  10. Alsharaiah, M.A.; Baniata, L.H.; Al Adwan, O.; Abuaalghanam, O.; Abu-Shareha, A.A; Alzboon, L.; Mustafa, N; Baniata, M. Neural Network Prediction Model to Explore Complex Nonlinear Behavior in Dynamic Biological Network. Neural Network Prediction Model to Explore Complex Nonlinear Behavior in Dynamic Biological Network. International Journal of Interactive Mobile Technologies 2022, 16, 32–51.
  11. Krish, K.Data-Driven Architecture for Big Data. Data Warehousing in the Age of BigData.," MK of BigData.-MK Series on Business Intelligence,2013.
  12. Kastranis, A. Artificial Intelligence for People and Business," O’ Reily Media Inc.: Sebastopol, CA, USA, 2019.
  13. Siemens, G.; Baker, R.S. Learning analytics and educational data mining: towards communication and collaboration. 2012. [CrossRef]
  14. Aher, S.B. Data Mining in Educational System using WEKA, 2011.
  15. Sunita, B.; Aher.; Lobo, L.; M, R.J. Mining Association Rule in Classified Data for Course Recommender System in E-Learning. International Journal of Computer Applications 39, 1–7. [CrossRef]
  16. Felix, I.M.; Ambrosio, A.P.; Neves, P.S.; Siqueira, J.; Brancher, J.D. Moodle Predicta: A Data Mining Tool for Student Follow Up. CSEDU 2017. [CrossRef]
  17. International Educational Data Mining Society, [Online]. Available: www.educationaldatamining.org.
  18. Gijbels, D.; Van de Watering, G.; Dochy, F.; Van den Bossche, P. The relationship between students' approaches to learning and the assessment of learning outcomes. European Journal of Psychology of Education, 20, 327-341. [CrossRef]
  19. Elhaj, M.A.E.; Bashir, S.G; Abdullahi, I.; Onyema, E.M.; Hauw. Evaluation of the Performance of K-Nearest Neighbor Algorithm in Determining Student Learning Style. Evaluation of the Performance of K-Nearest Neighbor Algorithm in Determining Student Learning Style. Intern Jour of Innov Sci, Engine. & Techogy 2020, 7, 2348–7968.
  20. Anjali J.; A REVIEW OF MACHINE LEARNING IN EDUCATION," Journal of Emerging Technologies and Innovative Research (JETIR), 6 ,2019.
  21. Hussain, S.; Dahan N. A., Ba-Alwib F. M., Najoua R. Educational Data Mining and Analysis of Students' Academic Performance Using WEKA. Indonesian Journal of Electrical Engineering and Computer Science 2018, 9. [CrossRef]
  22. López, M. Classification via clustering for predicting final marks based on student participation in forums, In the Proceedings of the 5th International Conference on Educational Data Mining, 2012.
  23. Klašnja-Milićević, A. E-Learning personalization based on hybrid recommen recommendation strategy and learning style identification. Computers & Education, 56, 2011. [CrossRef]
  24. Ayesha, S. Data Mining Model for Higher Education System.European Journal of Scientific Research. 43, 1, 24 – 29, 2010.
  25. Permata Alfiani, A.; Ayu Wulandari, F. Mapping Student's Performance Based on the Data Mining Approach (A Case Study)," Agriculture and Agricultural Science Procedia 2015, 173–177, 2015. [CrossRef]
  26. Bovo, A. Clustering moodles data as a tool for profiling students. In the proceedings of International Conference on E-Learning and E-Technologies in Education (ICEEE) 2013, 121-126. [CrossRef]
  27. Antonenko, P.D.; Toy, S.; Niederhauser, D.S. Using cluster analysis for data mining in educational technology research. Educational Technology Research and Development 2012, 60, 383–398. [Google Scholar] [CrossRef]
  28. Bendangnuksung , Prabu P. Students' Performance Prediction Using Deep Neural Network. International Journal of Applied Engineering Research, 13, 2018.
  29. Dey, R.; Salem, F.M. Gate-Variants of Gated Recurrent Unit (GRU) Neural Networks, 2017.
  30. Cho, Kyunghyun; van Merrienboer, Bart; Bahdanau, DZmitry; Bengio, Yoshua. On the Properties of Neural Machine Translation: Encoder-Decoder Approaches, 2014.
  31. Ravanelli, M; Brakel, P; Omologo, M; Bengio, Y. Light Gated Recurrent Units for Speech Recognition. IEEE Transactions on Emerging Topics in Computational Intelligence 2018. [CrossRef]
  32. John Pomerat, Aviv Segev, and Rituparna Datta, On Neural Network Activation Functions and Optimizers in Relation to Polynomial Regression," IEEE International Conference on Big Data (Big Data)., 2019. [CrossRef]
  33. Zijun Zhang, improved Adam Optimizer for Deep Neural Networks, IEEE, 2018. [CrossRef]
  34. k. document. [Online]. Available: https://keras.io/search.html?query=maxpooling.
  35. D. l. :. Keras. [Online]. Available: https://keras.io/api/layers/core_layers/dense/.
  36. Peng, Y., & Lu, B., "Hybrid learning clonal selection algorithm.," Inf. Sci., pp. 296, 128, 2015. [CrossRef]
  37. Saidi, M., Chikh, A., Settouti, N . Automatic Identification of Diabetes Diseases using an Artificial Immune Recognition System2 AIRS2) with a Fuzzy K-Nearest Neighbor," CIIA, 2011.
  38. Abiodun, O. I.; Jantan, A.; Omolara, A. E.; Dada, K.V.; Mohamed, N. A.; Arshad, H. State-of-the-art in artificial neural network applications: A survey. Heliyon 2018. [CrossRef]
  39. Tealab, A. Time series forecasting using artificial neural networks methodologies: A systematic review. Future Computing and Informatics Journal 2018. [CrossRef]
  40. Sadiq. H.; Zahraa, F.M.; Yass, K. S. Prediction Model on Student Performance based on Internal Assessment using Deep Learning. S. Prediction Model on Student Performance based on Internal Assessment using Deep Learning. International Journal of Emerging Technologies in Learning 2019, 14. [CrossRef]
  41. Mukherjee, C.; Rudin.; R. Schapire, The rate of convergence of AdaBoost. Journal of Machine Learning Research 2013,14, 315-2347.
  42. Tharwat, A. Classification assessment methods. Applied Computing and Informatics 2018. [CrossRef]
  43. Powers, D.MW. Evaluation: From Precision, Recall and F-Measure to ROC, Informedness, Markedness & Correlation. Journal of Machine Learning Technologies 2011, 2, 37–63. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated