Best BiCubic Method to Compute the Planimetric Misregistration between Images with Sub-pixel Accuracy: Application to Digital Elevation Models

Preprint

Article

Best BiCubic Method to Compute the Planimetric Misregistration between Images with Sub-pixel Accuracy: Application to Digital Elevation Models

Altmetrics

Downloads

Views

Comments

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

16 February 2024

Posted:

19 February 2024

You are already at the latest version

Alerts

Abstract

Over the last decades, an important number of regional and global Digital Elevation Models (DEMs) have been released publicly. As a consequence, researchers need to choose between several of these models to perform their studies and to use these DEMs as third-party data to compute derived products (e.g., for orthorectification). However, the comparison of DEMs is not trivial. For most quantitative comparisons, DEMs require to be expressed in the same Coordinate Reference System (CRS), sampled over the same grid (i.e., be at the same ground sampling distance with the same pixel-is-area or pixel-is-point convention), and with heights relative to the same Vertical Reference System (VRS). Thankfully, many open tools allow us to perform these transformations precisely and easily. Despite these rigorous transformations, local or global planimetric displacements may still be observed from one DEM to another. These displacements, or disparities, may lead to significant biases in comparisons of DEM elevations or derived products such as slope, aspect or curvature. Therefore, the control of DEM planimetric accuracy is certainly the most important task to perform at first before any comparison. This paper presents the disparity analysis method enhanced to achieve a sub-pixel accuracy, by interpolating the linear regression coefficients computed within an exploration window. This new method is significantly faster than oversampling the input data because it uses the correlation coefficients that have been already computed in the disparity analysis. To demonstrate the robustness of this algorithm, artificial displacements have been performed in a 11x11 grid with a 0.1-pixel step in both directions. The Copernicus DEM GLO-30 has been interpolated by a “classical” bicubic to achieve these 11x11 displacements. This validation method has been applied in four 10 km x 10 km DEMIX tiles showing different height distributions. Globally, this new sub-pixel accuracy method is robust. Artificial displacements have been retrieved with with typical errors (e_b) ranging from 12 to 20 % of the pixel size (worst case in Croatia).These errors in displacement retrievals are not constant in the 11x11 grid and the overall error E_b depends on the roughness (altimetry variations) encountered in the different tiles. The second idea of this paper is to assess the impact of the bicubic parameter (slope of the weight function at a distance d=1 of the interpolated point) on the accuracy of the displacement retrieval. By considering E_b as a quality indicator, tests have been performed in the four DEMIX tiles making the bicubic parameter vary between -1.5 and 0.0 by step of 0.1. For each DEMIX tile, the best bicubic (BBC) parameter b* is interpolated from the four E_b minimal values. This BBC parameter b* is low for flat areas (around -0.95) and higher in mountainous areas (around -0.75). The roughness indicator is the standard deviation of the slope norms computed from all the pixels of a tile. A logarithmic regression analysis performed between the roughness indicator and the BBC parameter b* computed in 67 DEMIX tiles shows a high correlation (r=0.717). The logarithmic regression formula estimating the BBC parameter from the roughness indicator is generic and may be applied to estimate the displacements between two different DEMs. This formula may also be used to set up a future Adaptative Best BiCubic (ABBC) that will estimate the local roughness in a sliding window to compute a local BBC.

Keywords:

Subject: Environmental and Earth Sciences - Remote Sensing

1. Introduction

1.1. Context

This article has been carried out in the framework of the Earthnet Data Assessment Project (EDAP) funded by the European Space Agency (ESA). This project is responsible for “assessing the quality and suitability of missions being considered for ESA’s Earthnet Programme as Third-Party Missions (TPM)”. Studies performed in this article follow the standards of the Digital Elevation Model Intercomparison eXercise (DEMIX), originated by the Committee on Earth Observation Satellites (CEOS). DEMIX is a community-based approach aiming for the harmonisation of terminology [1] and methods used in global DEM comparisons [2]. DEMIX assessments rely on the DEMIX grid, which divides the world into areas of approximately 10 x 10 km called DEMIX tiles [3]. These tiles are the unit of computation of all the tests performed within DEMIX.

One crucial subject tackled by DEMIX is the comparability of DEMs. Prior to any comparison, it must be ensured that the DEMs are relative to the same Coordinate Reference System (CRS), Vertical Reference System (VRS) and are co-gridded. These first requirements can be fulfilled by applying the correct transformations to the input DEM(s). Unfortunately, these transformations are necessary but not sufficient to ensure two DEMs are comparable. Due to different acquisition methods and processing chains, dissimilarities could be observed from one DEM to another. One of the most common and important sources of biases is the planimetric misregistration. Planimetric misregistrations lead to important errors in DEM derived products, such as inaccuracies in hydrographical networks, orthorectification or even discontinuities between adjacent local DEMs. Moreover, these misregistrations also affect DEM comparisons: if two DEMs are not strictly superimposable, all DEM comparisons will be altered (height, slopes, azimuth, curvature pixel differences). This last observation is crucial for DEMIX, and motivated the development of a method allowing to quantify these misregistrations. If these misregistrations are large, some systematic errors are still there and should be corrected before continuing. If they are small enough, we can proceed with confidence because both DEMs are comparable.

The main goal of this paper is to present a novel method allowing to estimate sub-pixel planimetric displacements between two DEMs. This method would greatly benefit DEMIX for two major use-cases. The first use-case would be to run this method prior to any DEM comparison to ensure no planimetric displacement could bias difference statistics, even without considering one of the input DEMs as a reference. The second use-case would be to improve the absolute location accuracy (planimetric bias) and the internal geometry (distortions) of a tested DEM with regard to a reference DEM of higher accuracy.

As this method requires the input DEMs to be in the same geometry (same Coordinate Reference System, Vertical Reference System and also grid), at least one of the input DEMs must be resampled before running the planimetric misregistration analysis. However, many resampling methods exist, and naturally, all of these methods have advantages and downsides which have an effect on the DEM resampling, and thus on subsequent analyses. Therefore, a particular attention should be given to the resampling method used for any specific application. Consequently, the second goal of this study is to provide a methodology allowing to find the best resampling method for the specific use of retrieving accurate planimetric displacements between DEMs.

The next section 1.2 provides an introduction to the effects of planimetric misregistrations in DEM comparisons. Then, the classical “disparity analysis” pairing algorithm and its application to DEMs are presented in section 1.3, with a novel enhancement allowing to retrieve sub-pixel planimetric displacements between DEMs. Section 2 describes in details the methods used to compute the disparity analysis and its enhancement, including the equations and the choice of the algorithm parameters. The methods and results validation of this algorithm are presented in section 3. As this algorithm usually requires the resampling of one of the input DEMs, section 4 proposes a method to retrieve the best resampling method for retrieving accurate planimetric displacements between two DEMs. For this specific case, it has been discovered that the best resampling method is dependent on the study area. As a consequence, the correlation between a roughness indicator and the best resampling method is described in section 5.

1.2. Effect of planimetric misregistration

Ideally, for two DEMs covering the same study area, any land feature depicted in the first DEM (tree, building, ridge, talweg…) should be found at the same location in the second DEM. In reality, planimetric misregistrations are usually observed from one DEM to another. These misregistrations lead to important biases in quantitative DEM comparisons, even when only sub-pixel displacements are observed [4]. In the simplest cases, the displacements are homogenous (i.e., share the same direction and magnitude for every pixel). These displacements are easily observed on DEM height differences images, as they produce patterns of alternating negative and positive differences. Such height differences are depicted in Figure 1, computed between EU-DEM v1.1 (25 m of Ground Sampling Distance, or GSD) and Copernicus DEM EEA-10 v2022_1 (≈10 m of GSD at equator) over Malta. Both DEMs have been reprojected and resampled at a common GSD of 20 metres and in the same CRS.

In most cases, shifts direction and magnitude are varying within a study area. Such variations cannot be precisely described by a visual analysis. Fortunately, planimetric misregistrations can be quantified using pairing methods. These methods may rely on external data, such as reference points [5] or reference surfaces [6]. In the present study, the goal is to measure the displacements between two co-gridded DEMs for every pixel of their overlapping area. For this purpose, the disparity analysis algorithm has been chosen, as it is designed to perform such pairings.

1.3. Disparity analysis

The disparity analysis is based on a generic algorithm which determines displacements by means of correlation computations [7]. This algorithm is generally applied to images [8] and we will use it with the specific case of DEMs. Given two input DEM images, the disparity analysis produces displacement fields giving for any pixel of the first DEM the planimetric displacement required to find its homologous pixel in the second DEM. Two images are produced by this method: one for the pixel displacements in the x-axis (dP) and one for the displacements in the y-axis (dL). Both dP and dL maps can be used, for instance, to compute vectors of planimetric displacements (Figure 2). The classical disparity analysis method only allows to retrieve displacements at a pixel level. Sub-pixel image pairing methods and tools exist, and have already been used on DEMs (see [9]). However, these methods usually suffer from a high computational cost. The sub-pixel displacement retrieval method proposed in this paper is an addition to the disparity analysis method. It is much faster to compute than other methods, as it is interpolated based on coefficients already computed at pixel level.

2. Methods

2.1. Principles

In order to apply this algorithm, input DEMs are assumed to be comparable, i.e., in the same coordinate reference system (CRS), vertical reference system (VRS) and co-gridded. Generally, transformations must be performed on one of the input DEM(s) to comply with these requirements.

The disparity analysis is applied on two DEMs (DEM₁ and DEM₂), and must be parameterized by an exploration window size (e_x,e_y) and a correlation window size (c_x,c_y). The exploration window size sets the extent of the search for homologous pixels. A greater exploration window allows the retrieval of larger displacements. The correlation window size corresponds to the context used to match both DEMs. The size of the correlation window impacts the accuracy and the stability of the displacement retrieval (further discussed in 2.4). Given these inputs and parameters, the disparity analysis produces two images of displacements expressed in pixels (dP for the x-axis, dL for the y-axis). The displacements applied to DEM₁ should fit DEM₂.

For each pixel of DEM₁, a homologous pixel is defined as the one presenting the most similar local configuration in DEM₂. The search is processed in an exploration window centered on the pixel of same location (same geodetic or projected coordinates) than the pixel of DEM₁. The local similarity between DEMs is computed by Normalized Cross-Correlation (NCC, see section 2 for details) between two correlation windows: one centered on the current processed pixel in DEM₁, and one sliding over all the potential homologous pixels of the exploration window in DEM₂. The planimetric displacement is computed as the distance (in pixels, or equivalent in metres) between the centre of the exploration window (same physical location as the current pixel of the first DEM) and the centre of the homologous pixel. By iterating over all the first DEM pixels.

As previously stated (see section 1.3), matchings from DEM₁ to DEM₂ are quantified using NCC coefficients. Other methods could also have been considered, such as retrieving the local lowest height differences between the two DEMs to find a local matching. However, considering that elevation of DEM₂ could be considered as a linear combination of DEM₁ (DEM₂ ≈ A x DEM₁ + B), NCC has the advantage of being robust to systematic biases (B) and gain (A). Systematic biases match many cases where DEM₁ and DEM₂ are not expressed in the same Vertical Reference System (VRS) because of bad ellipsoid or geoid in input DEMs. Gain robustness (A) allows for further flexibility in case of Ground Sampling Distance (GSD) or pixel type (integer or floating-point data) differences between input DEMs, which potentially lead to amplitude differences in retrieved terrain features.

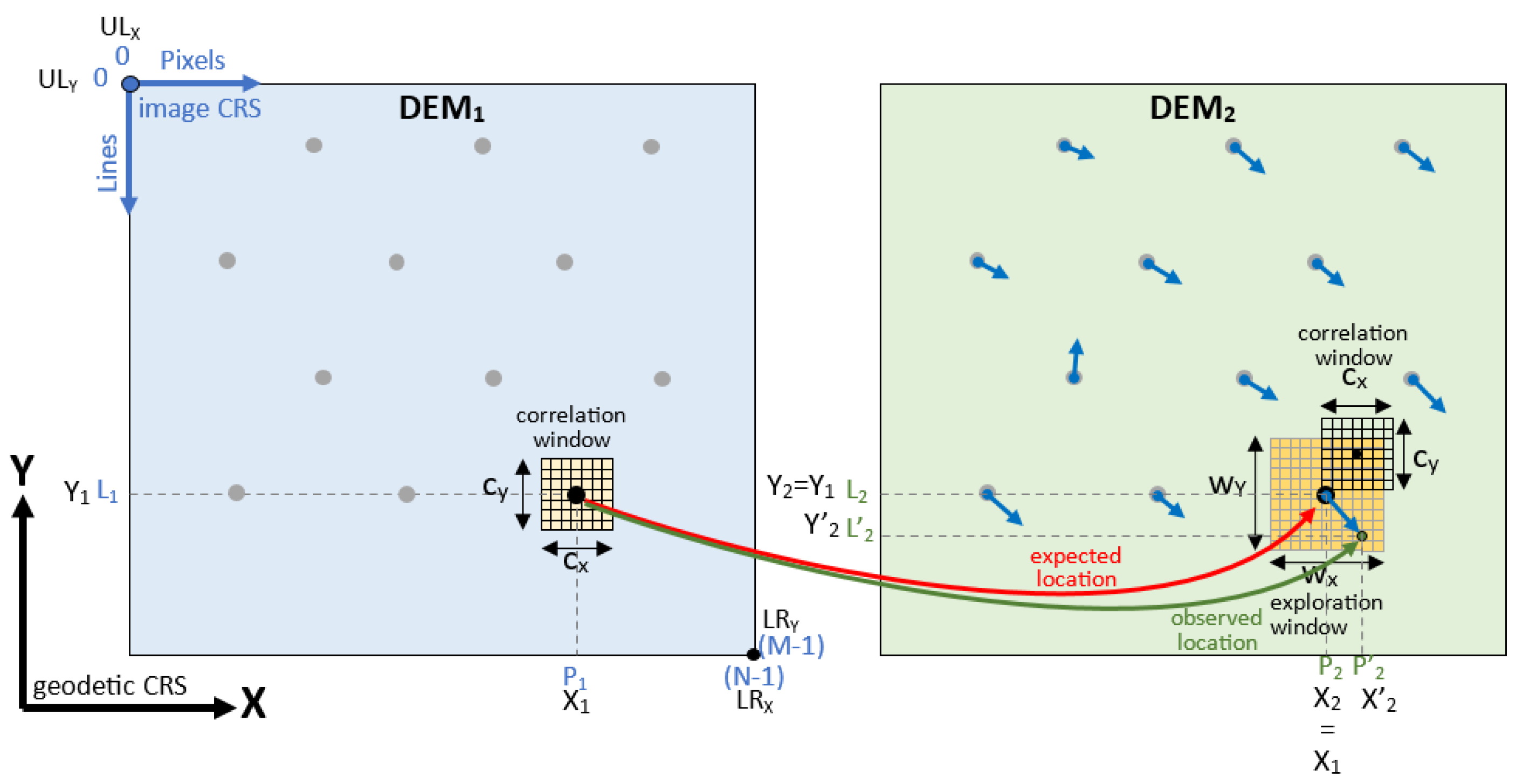
2.2. Pixel matching

For each pixel (L₁,P₁) to be processed in DEM₁, the pixel (L₂,P₂) of same location is retrieved in DEM₂ (red arrow in Figure 3). The real homologous pixel (L’₂,P’₂) (green arrow in Figure 3) is searched for in an exploration window (w_X x w_Y) centered on (L₂,P₂) in DEM₂. For each possible pixel displacement (dL,dP) relative to the centre of this window, a Normalized Cross-Correlation (NCC) coefficient, also called Pearson coefficient, r(dL,dP) is calculated between two correlation windows of size (c_x x c_y): one centred on (L₁,P₁) in DEM₁, the other centred on (L₂ + dL, P₂ + dP) in DEM₂ (1). The displacement (dL,dP) for which the highest correlation has been found is denoted as [dL(L₁,P₁),dP(L₁,P₁)], and corresponds to the planimetric misregistration retrieved by the disparity analysis at pixel level (5).

r (d L, d P) = \frac{C o v ({D E M}_{1} (L_{1}, P_{1}), {D E M}_{2} (L_{2} + d L, P_{2} + d P))}{σ_{1} (L_{1}, P_{1}) \times σ_{2} (L_{2} + d L, P_{2} + d P)}

(1)

C o v ({D E M}_{1} (L_{1}, P_{1}), {D E M}_{2} (L_{2} + d L, P_{2} + d P)) = \sum_{k = - c_{Y} / 2}^{+ c_{Y} / 2} \sum_{l = - c_{X} / 2}^{+ c_{X} / 2} [{D E M}_{1} (L_{1} + k, P_{1} + l) \times {D E M}_{2} (L_{2} + d L + k, P_{2} + d P + l)]

(2)

σ_{1} (L_{1}, P_{1}) = \sqrt{\frac{1}{c_{X} \times c_{Y}} \sum_{k = - c_{Y} / 2}^{+ c_{Y} / 2} \sum_{l = - c_{X} / 2}^{+ c_{X} / 2} {[{D E M}_{1} (L_{1} + k, P_{1} + l)]}^{2} - {[\frac{1}{c_{X} \times c_{Y}} \sum_{k = - c_{Y} / 2}^{+ c_{Y} / 2} \sum_{l = - c_{X} / 2}^{+ c_{X} / 2} {D E M}_{1} (L_{1} + k, P_{1} + l)]}^{2}}

(3)

σ_{2} (L_{2} + d L, P_{2} + d P) = \sqrt{\frac{1}{c_{X} \times c_{Y}} \sum_{k = - c_{Y} / 2}^{+ c_{Y} / 2} \sum_{l = - c_{X} / 2}^{+ c_{X} / 2} {[{D E M}_{2} (L_{2} + d L + k, P_{2} + d P + l)]}^{2} - {[\frac{1}{s_{X} \times s_{Y}} \sum_{k = - c_{Y} / 2}^{+ c_{Y} / 2} \sum_{l = - c_{X} / 2}^{+ c_{X} / 2} {D E M}_{2} (L_{2} + d L + k, P_{2} + d P + l)]}^{2}}

(4)

[d L (L_{1}, P_{1}); d P (L_{1}, P_{1})] = {A r g}_{\begin{matrix} d L = - \frac{w_{X}}{2} \dots + \frac{w_{X}}{2} \\ d P = - \frac{w_{Y}}{2} \dots + \frac{w_{Y}}{2} \end{matrix}} [M a x \{r (d L, d P)\}]

(5)

Where:

$r (d L, d P)$ is the linear regression coefficient computed at position (dL,dP) in the exploration window, i.e., between the correlation window around (L1,P1) of DEM1 and the correlation window around (L2+dL,P2+dP) of DEM2,
$C o v ({D E M}_{1} (L_{1}, P_{1}), {D E M}_{2} (L_{2} + d L, P_{2} + d P))$ is the covariance computed between (L1,P1) of DEM1 and (L2+dL,P2+dP) of DEM2,
$σ_{1} (L_{1}, P_{1})$ is the standard deviation computed within a correlation window (cX x cY) centred on (L1,P1) in DEM1,
$σ_{2} (L_{2} + d L, P_{2} + d P)$ is the standard deviation computed within a correlation window (cX x cY) centred on (L2+dL,P2+dP) in DEM2.

These displacements are computed for all the pixels included in the overlay area of the two DEMs, leading to an “error vector field” (blue arrows in Figure 3).

Figure 3. Principle of the disparity analysis – Pixel level displacement retrieval.

2.3. Sub-pixel matching

Figure 4. Interpolation of the highest correlation – Sub-pixel level displacement retrieval.

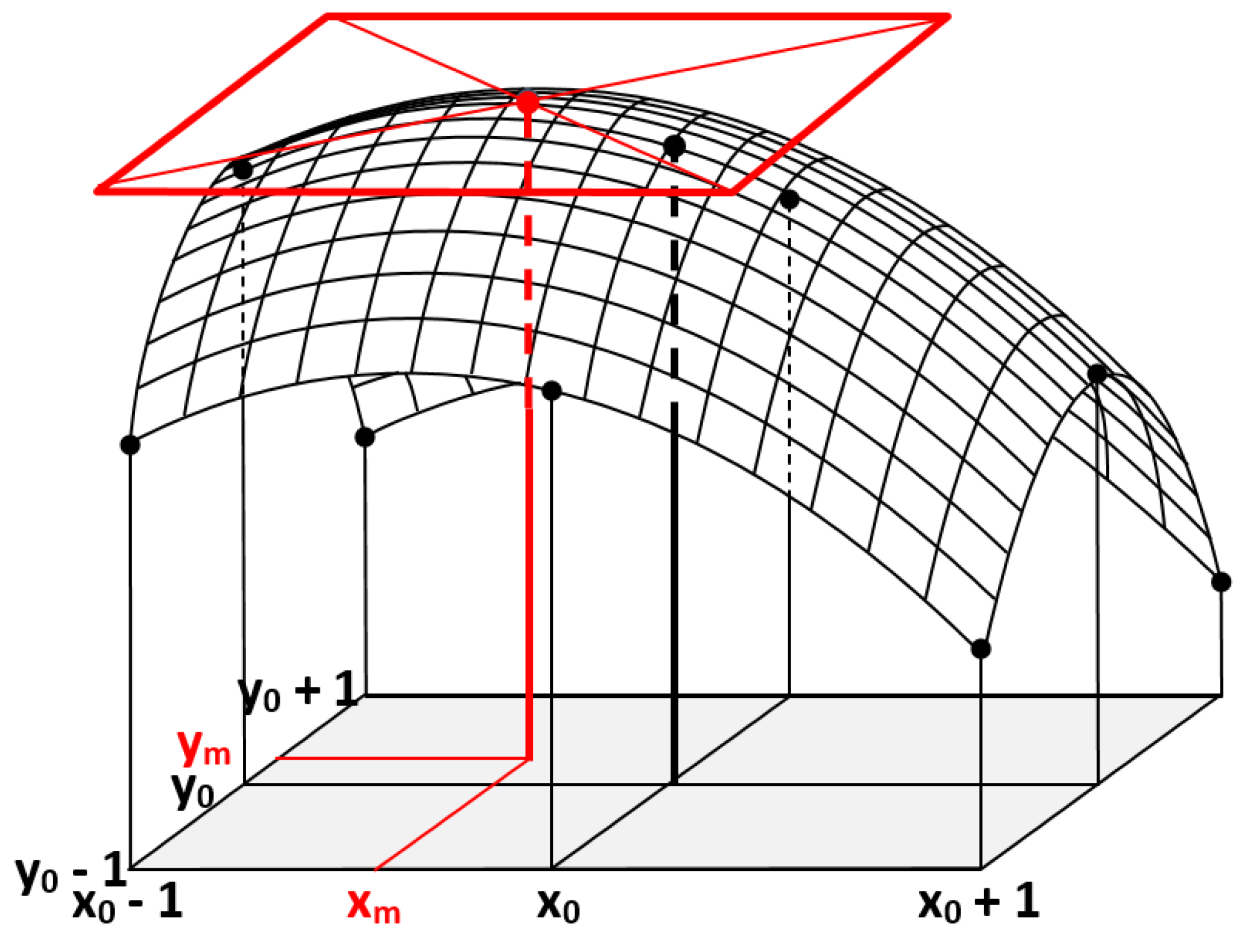
The sub-pixel displacement is estimated based on the NCC coefficients computed for each pixel of the exploration window. A 3 x 3 window of NCC coefficients is extracted from the exploration window, centred on the pixel [dL(L₁,P₁),dP(L₁,P₁)] which has given the maximum of correlation with (L₁,P₁) at pixel level. A paraboloid surface (6) is modelled over this window of coefficients, minimizing the vertical distances between the 9 linear coefficients and this surface according to the least squares method.

r (x, y) = a \cdot x^{2} + b \cdot y^{2} + c \cdot x y + d \cdot x + e \cdot y + f

(6)

Where:

x is the horizontal coordinate (longitude or easting) in the geodetic coordinates reference system. For geocoded images, this coordinate is given by x = ULX+PxGSDw (pixel width).
y is the vertical coordinate (latitude or northing) in the geodetic coordinates reference system. For geocoded images, this coordinate is given by y = ULY-LxGSDh (pixel height).
r(x,y) is the linear regression coefficient computed (for integer values as shown in previous section) or estimated using the paraboloidal interpolation (for sub-pixel floating values).
R(X,Y) represents one of the 3x3 linear regression coefficients computed at pixel level, X=X0-1,X0,X0+1, Y=Y0-1,Y0,Y0+1.
a,b,c,d,e,f are the 6 coefficients estimated from the 3x3 linear regression coefficients R(X,Y).

The goal is to minimize the difference

\bar{D} = \sum_{X = X_{0} - 1}^{X_{0} + 1} \sum_{Y = Y_{0} - 1}^{Y_{0} + 1} {[r (X, Y) - R (X, Y)]}^{2}

(i.e., the difference between the r(x,y) paraboloid and the R(X,Y) coefficients computed at pixel level). This leads to compute the partial derivatives of equation (6) with regard to the unknowns a, b, c, d, e and f. These derivatives result in a system of 6 linear equations, which should have a null value at the best fit. The system of 6 linear equations is solved by inverting the corresponding matrix at equation (7).

(7)

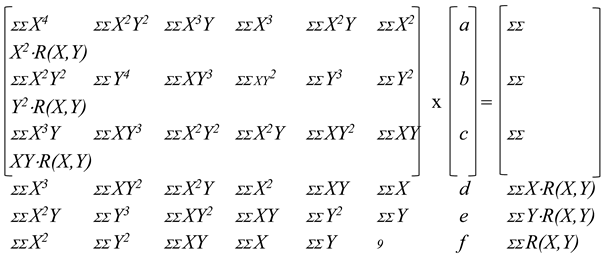
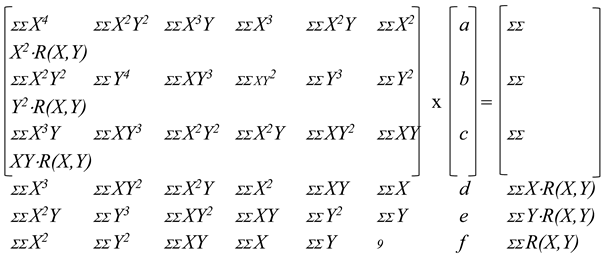
Then, the floating coordinates (x_m,y_m) of the highest points of this surface are retrieved by deriving the surface r(x,y) and by searching for the horizontal tangent (8).

\{\begin{matrix} \frac{\partial (r (x, y))}{\partial x} & = & 2 a \cdot x_{m} + c \cdot y_{m} + d = 0 \\ \frac{\partial (r (x, y))}{\partial y} & = & c \cdot x_{m} + 2 b \cdot y_{m} + e = 0 \end{matrix}

(8)

The (x_m,y_m) coordinates correspond to the location of the maximum of correlation at sub-pixel level.

2.4. Choice of the exploration and correlation window sizes

In order to use the disparity analysis, two parameters must be set: the exploration window size (w_x,w_y) and the correlation window size (c_x,c_y). For simplicity, only square windows are considered for both parameters. The exploration window size can be set according to the magnitude of the shifts observed from one DEM to another. The correlation window size corresponds to the context used to perform a matching from DEM₁ to DEM₂. This last parameter has an important impact on the magnitude of the retrieved displacements (see Figure 5).

Both window sizes have been set by comparing Copernicus DEM GLO-30 to ALOS World 3D over Trentino, Italy (DEMIX tile N46PE010J). This location features both mountains and flat areas, in which local displacements have been observed from one DEM to another. As the shifts observed in this study are low on both x and y axes, an exploration window size of (w_x,w_y) = (7,7) would be sufficient in this case. However, during the testing phase, a large exploration window of (w_x,w_y) = (25,25) has been considered for assessing the robustness of the matching. Small correlation window sizes of (c_x,c_y) = (3,3) and (c_x,c_y) = (5,5) should be avoided, as they do not provide enough context for stable matchings and are sensible to high frequency details in DEMs. In particular, over this area, Copernicus DEM GLO-30 shows different high-frequency details than the ones present in ALOS World 3D (see Figure 6).

Despite assessing the root cause is outside our scope, we can speculate that these dissimilarities could be due to the different methods of acquisition (photogrammetry for ALOS World 3D, interferometry for Copernicus DEM) and DEM generation methods.

Noise and an important number of outlier displacement norms (3 pixels or more, vivid red) can be observed with (c_x,c_y) = (3,3) and (c_x,c_y) = (5,5), which progressively disappear at larger correlation window sizes. Visually and statistically, the displacement norms stabilize starting from correlation window sizes of (c_x,c_y) = (11,11) or (13,13) pixels. For this reason, and as the following studies are complex multivariate problems with a high computational cost, a correlation window size of (c_x,c_y) = (11,11) has been chosen. Experiments of Guan et al. [9] also leaded to use a correlation window of 11x11 pixels in order to compute planimetric misregistrations between DEMs. It is worth mentioning that higher correlation window sizes lead to even better accuracies (further discussed in section 6), and should be considered for simpler analyses than the ones described in this article.

3. Validation of the sub-pixel displacement retrieval

3.1. Principle

To assess the accuracy of the sub-pixel method, displacements are retrieved between a DEM (in this case, Copernicus DEM GLO-30 DGED v2022_1) and its replicas artificially shifted at a sub-pixel level. A homogeneous shift is applied to each replica (i.e, with the same direction and magnitude for all pixels) ranging from 0.0 to 1.0 pixels, with a step of 0.1 pixels on both axes (x and y). As a result, (11x11) replicas shifted DEMs are retrieved for each area, which are used to assess the accuracy of the sub-pixel displacement retrieval.

Shifting DEMs at sub-pixel level require the use of a resampling method. Recent studies show that the bicubic interpolation is accurate for the resampling of DEMs [10]. As a consequence, this resampling method has been chosen to perform this study.

3.2. Study areas

Figure 7. Study areas considered for the validation of the sub-pixel displacement retrieval.

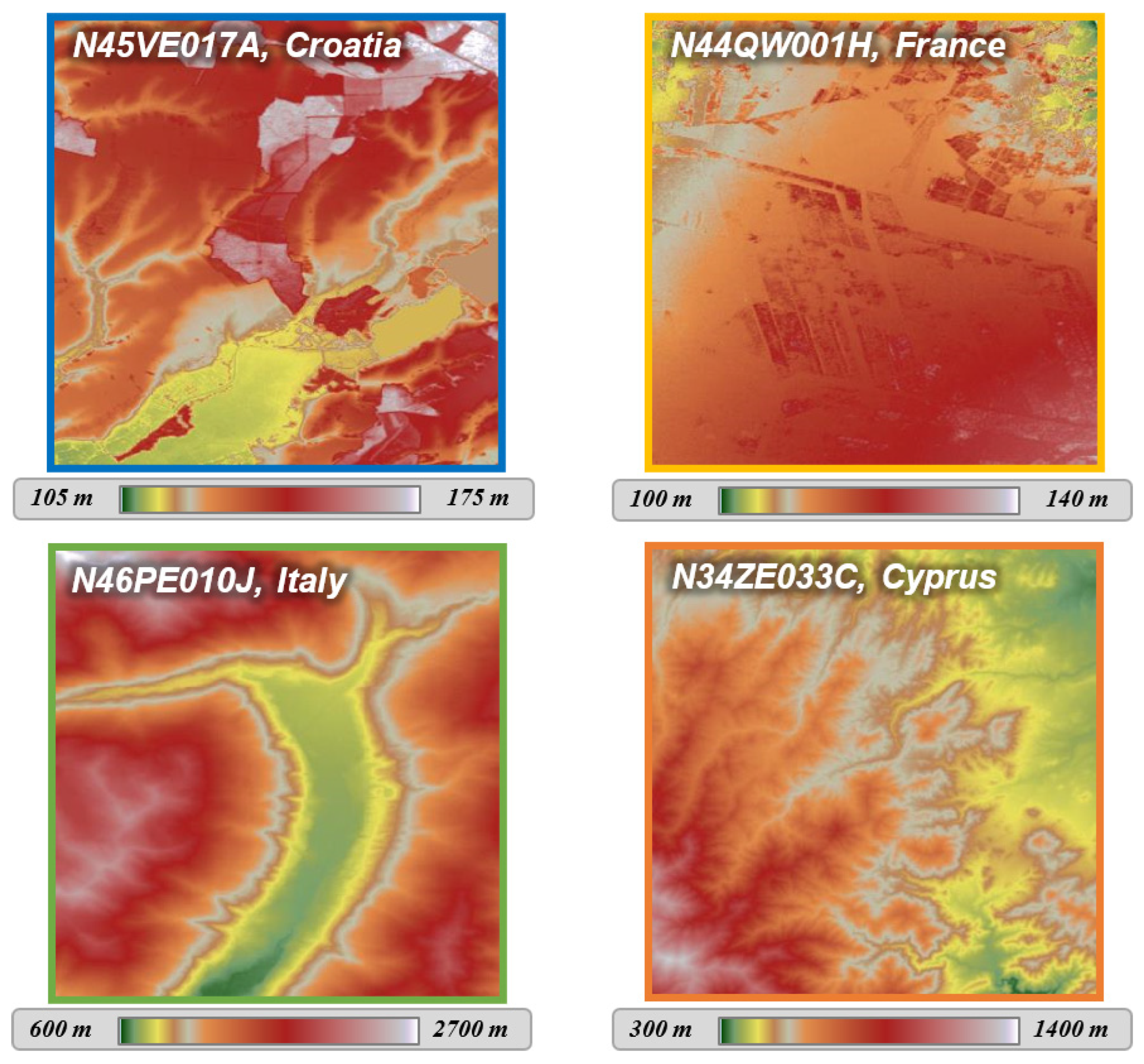
The study areas correspond to four DEMIX tiles (10km per 10km areas) whose identifiers are N46PE010J (Italy), N34ZE033C (Cyprus), N45VE017A (Croatia) and N44QW001H (France). These areas feature both mountainous (Val Redena of Trentino in Italy and Cyprus) and relatively flat (Croatia and Landes in France) landscapes.

3.3. Bicubic formula

The bicubic resampling method is the two-dimensional extension of the cubic interpolation [11]. It considers a 4x4 window of pixels around the coordinates of interpolation. The values of these pixels are weighted according to their position (d_x, d_y) relative to the input point (Figure 8 and Figure 9).

O (I, J) = \frac{\sum_{k = - 1}^{+ 2} w ({d x}_{k}) \times [\sum_{k = - 1}^{+ 2} [w ({d y}_{l}) \times O (i_{0} + k, j_{0} + l)]]}{\sum_{k = - 1}^{+ 2} [w ({d x}_{k})] \times \sum_{l = - 1}^{+ 2} [w ({d y}_{l})]}

(9)

w_{b} (d) = \{\begin{matrix} 1 - (b + 3) \times d^{2} + (b + 2) \times |d^{3}| \\ - 4 b + 8 b \times |d| - 5 b \times d^{2} + b \times |d^{3}| \\ 0 \end{matrix} \begin{matrix} 0 \leq |d| \leq 1 \\ 1 \leq |d| \leq 2 \\ 2 \leq |d| \end{matrix}

(10)

The weights of any pixel are given by the function w of equation (10), tuned by a parameter b. This free parameter corresponds to the slope of the function w at d = 1.

Figure 9 and Figure 10 show the effect of the bicubic parameter b while oversampling the DEM along cross-sections. These cross-sections are located perpendicular to one ridge (case of mountainous area in Trentino, Figure 9) and a boundary between ground and canopy (case of flat area in Croatia, Figure 10). In each figure, the upper-left image shows the entire DEMIX tile and the footprint location of the second zoomed image. The yellow vector gives the location of the full cross-section which has been oversampled with 1000 samples. The limits A and B are located from each side of the slope break.

The impact of the bicubic parameter b can be clearly observed on DEM slope discontinuities, such as mountain ridges (Trentino, Italy, Figure 9) or land-use changes (Croatia, Figure 10). In such areas, the lowest values of the bicubic parameter (close to b=-1.5) increase the maximum of elevation whereas the highest parameters do the opposite (close to b=0.0). Moreover, the maximum elevation is retrieved at different curvilinear distances depending on the bicubic parameter (green points in Figure 8). Both effects are caused by the overshoots (or undershoots) of the bicubic resampling method, which are minimised for the “optimal” bicubic parameter b=-1/2 [12]. However, this optimal parameter may differ depending on the application. As a consequence, the same analysis has been performed with sixteen different values of the bicubic parameter (ranging from -1.5 to 0.0, with a step of 0.1) to ascertain its optimum value.

3.4. Shift validation

Over each area, the first DEM is matched with artificially shifted replicas (Figure 11). These replicas are shifted on both x and y axes and range from 0.0 to 1.0 pixels, with a step of 0.1 pixel.

For each DEM₂ replica shifted by (

s_{λ}

s_{φ}

), the error for each one of the (l,p) pixels is computed by subtracting the artificial shift to the observed one (11). This error is expressed in radians because of the geographic CRS.

\begin{matrix} e_{λ} (l, p) = d_{λ} (l, p) - s_{λ} \\ e_{φ} (l, p) = d_{φ} (l, p) - s_{φ} \end{matrix}

(11)

Then, the error is converted in metres (12) by considering the radius of the WGS84 ellipsoid at given latitude φ (13) and (14).

\begin{matrix} e_{x} (l, p) = e_{λ} (l, p) \times R (φ) \times c o s φ \\ e_{y} (l, p) = e_{φ} (l, p) \times R (φ) \end{matrix}

(12)

R (φ) = \sqrt{\frac{{{(a}^{2} \times \cos φ)}^{2} + {{(b}^{2} \times \sin φ)}^{2}}{{(a \times \cos φ)}^{2} + {(b \times \sin φ)}^{2}}}

(13)

(\begin{matrix} a = 6 378 137.0 m \\ b \approx 6 356 752.3 m \end{matrix}) f o r W G S 84

(14)

Error norm is computed as a geodetic arc between the expected and observed positions (15).

e (l, p) = \sqrt{e_{x}^{2} (l, p) + e_{y}^{2} (l, p)}

(15)

For a given (

s_{λ}

s_{φ}

) shifted image, the “image error” e_b from all the pixels of the image is computed as the quadratic mean of all

e (l, p)

errors (16).

e_{b} (s_{λ}, s_{φ}) = \sqrt{\frac{1}{M \times N} \sum_{l = 0}^{M - 1} \sum_{p = 0}^{N - 1} e^{2} (l, p)}

(16)

For a given bicubic parameter b, the “full error” E_b is the root of the quadratic mean of the “image errors” e_b found for each one of the shifts (

s_{λ}

s_{φ}

) considered (17). These shifts are expressed in 1/10th of the DEM Ground Sampling Distance in both longitudinal (

{G S D}_{λ}

) and latitudinal (

{G S D}_{φ}

) directions.

E_{b} = \sqrt{\frac{1}{11 \times 11} \sum_{i = 0}^{10} \sum_{j = 0}^{10} e_{b}^{2} (s_{λ} = \frac{i}{10} \times {G S D}_{λ}, s_{φ} = \frac{j}{10} \times {G S D}_{φ})}

(17)

3.5. Error matrices and surfaces

For each value of the bicubic parameter b, an error matrix is established. This matrix contains the error

e_{b} (s_{λ}, s_{φ})

retrieved for each

(s_{λ}, s_{φ})

shift considered or,

(s_{p}, s_{l})

the equivalent shift in pixels (Figure 12, left).

Each shift is expressed in tenth of pixels, starting from 0.0 in the upper-left corner, and ending at 1.0 pixel in both directions (in last column for S_p, last line for S_l). The different errors

e_{b} (s_{p}, s_{l})

are also given in the form of a 3D surface, whose vertices heights are proportional to the magnitude of the retrieved errors (Figure 12, right).

3.6. Results

Overall, the results show that the accuracy of the displacement retrieval depends on two parameters: the shift

(s_{p}, s_{l})

introduced and the bicubic parameter b chosen to resample the input DEM.

Over Trentino (Figure 13), the highest errors seem to be found for the displacements close to ¼ and ¾ pixels of displacement on both axes.The best results are obtained with intermediate bicubic parameters (between -1.0 and -0.5), whereas the lowest (-1.5) and highest (0.0) parameters lead to higher errors. The lowest error e_b (4.112 m) is retrieved for a bicubic parameter of b=-1.0, with a shift (s_p,s_l) of (0.1 px, 0.5 px). For other areas, please refer to Appendix A.

The observed error variations in the matrices of Figure 13 are due to the systematic oscillations of the sum of squared differences which are well explained in the frequency domain [13].

These results highlight the importance of choosing the right bicubic parameter for the displacement retrieval.

4. Finding the Best BiCubic (BBC) parameter for disparity analysis

4.1. Principle

As previously observed, the bicubic resampling parameter b used to resample the input DEM(s) has an impact on the accuracy of the displacement retrieval. This second study aims to determine the “Best BiCubic” (BBC) parameter b* for retrieving displacements accurately. The BBC parameter is computed over the same four study areas, including mountainous (Trentino in Italy and Cyprus) and flat (Croatia and Landes in France) areas.

4.2. Displacement error graphs

Over each area, an error E_b is computed for bicubic parameters ranging from -1.5 to 0.0, with a step of 0.1. A plot of the E_b errors allows to get a first approximation of the Best BiCubic (BBC) parameter b*, whose error E_b* is the minimum of the curve.

As the errors E_b consist of discrete values, the BBC parameter b* is interpolated at the minimum of error E_b*.

4.3. Interpolation of the BBC

For any displacement error graph, the BBC parameter b* is interpolated from the local minimum of a third order polynomial fitting the samples of lowest error (18).

\tilde{E} (b) = α + β \cdot b + γ {\cdot b}^{2} + δ \cdot b^{3}

(18)

The α, β, γ and δ parameters of the model are found using a least squares method, given the four bicubic parameter values (b₀, b₁, b₂, b₃) for which the minimal errors (E₀, E₁, E₂, E₃) have been retrieved (see the blue part of the graph in Figure 14).

As the parameters are known, the error model

\tilde{E} (b)

is defined. Then, the local minimum of the error must be found. This minimum is located in the range [b₀;b₃] where the first derivative is equal to 0 (19).

\frac{d \tilde{E}}{d b} = β + 2 γ b + 3 δ b^{2} = 0

(19)

This derivative is a second-degree polynomial, for which two solutions

b_{0}^{*}

and

b_{1}^{*}

can be found (20).

∆ = 4 γ^{2} - 12 β δ \sqrt{∆} = 2 \sqrt{γ^{2} - 3 β δ} b_{0}^{*} = \frac{- 2 γ - \sqrt{∆}}{6 δ} b_{1}^{*} = \frac{- 2 γ - \sqrt{∆}}{6 δ}

(20)

Among

b_{0}^{*}

and

b_{1}^{*}

, the b* value included in the [b₀, b₃] interval is kept, as this interval contains the minimum error value. Then, the error value is simply computed by applying equation (18) on the retrieved value

b^{*}

(21).

\tilde{E} (b^{*}) = α + β \cdot b^{*} + γ \cdot {b^{*}}^{2} + δ \cdot {b^{*}}^{3}

(21)

4.4. Results

By applying the method described in the previous section, the interpolated BBC parameter b* is computed for each one of the four DEMIX tiles.

Figure 15. Displacement error graphs over the four study areas.

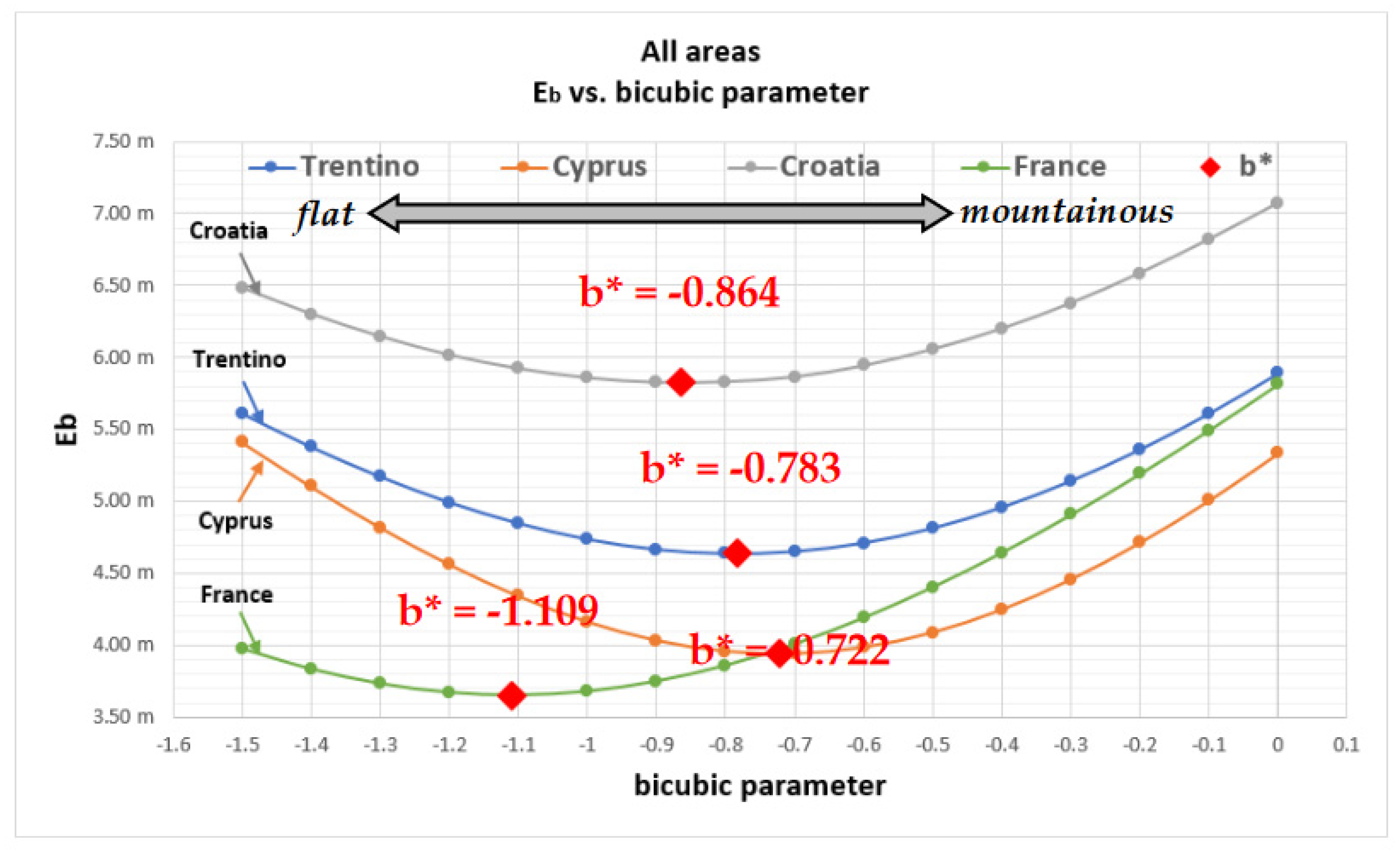
By considering the analysis restricted to the range [-1.5;0.0], an optimal bicubic parameter b* can be found in all the study areas. One can see that b* is progressively getting lower, from the two mountainous areas of Italy (b*=-0.783) and Cyprus (b*=-0.722) followed by the flat areas of Croatia (b*=-0.864) and France (b*=-1.109). A recent study highlights similar results for the Inverse Distance-Weighted interpolation, whose optimum parameters depend on the study area [14].

5. Relation between BBC and DEM slope variations

5.1. Principle

As different BBC parameters have been observed on mountainous and flat areas, the relation between the BBC parameter b* and the DEM roughness is furthermore studied. Similar studies have found links between roughness and the accuracy of interpolation on terrain models [15] as well as bathymetric models [16]. For this study, roughness is defined as the standard deviation of the slope (σ_slope)computed over all the pixels of a DEMIX tile. .. Then, the correlation between this roughness indicator and the BBC parameter is studied.

5.2. Study areas

In order to study the relation between the BBC parameter b* and roughness, a set of 67 European DEMIX tiles have been chosen as study areas. This comprises a first set of tiles over Europe, for which different types of landscape have been chosen (forests, plains, mountains). However, this selection only allowed to retrieve low to intermediate slopes (Figure 16a). As a consequence, a second set of tiles has been selected in the Alps, where higher values of slopes are retrieved (Figure 16b). This selection ensures an almost even distribution of the slope values.

5.3. Slopes computation and statistics

Over each DEMIX tile, the roughness is computed according to (22) and (23). This roughness is based on slope, which have been estimated using the method of Zevenbergen and Thorne [17].

σ_{s l o p e} = \sqrt{\frac{1}{N \times M} \sum_{l = 0}^{M} \sum_{p = 0}^{N} s l o p e {(l, p)}^{2} + {[\frac{1}{N \times M} \sum_{l = 0}^{M} \sum_{p = 0}^{N} s l o p e (l, p)]}^{2}}

(22)

\begin{matrix} s l o p e (l, p) = \sqrt{{(\frac{\partial z}{\partial x})}^{2} + {(\frac{\partial z}{\partial y})}^{2}} \\ = \sqrt{{(\frac{D E M [l, p + 1] - D E M [l, p - 1]}{{2 \times G S D}_{x} (φ)})}^{2} + {(\frac{D E M [l + 1, p] - D E M [l - 1, p]}{{2 \times G S D}_{y}})}^{2}} \end{matrix}

(23)

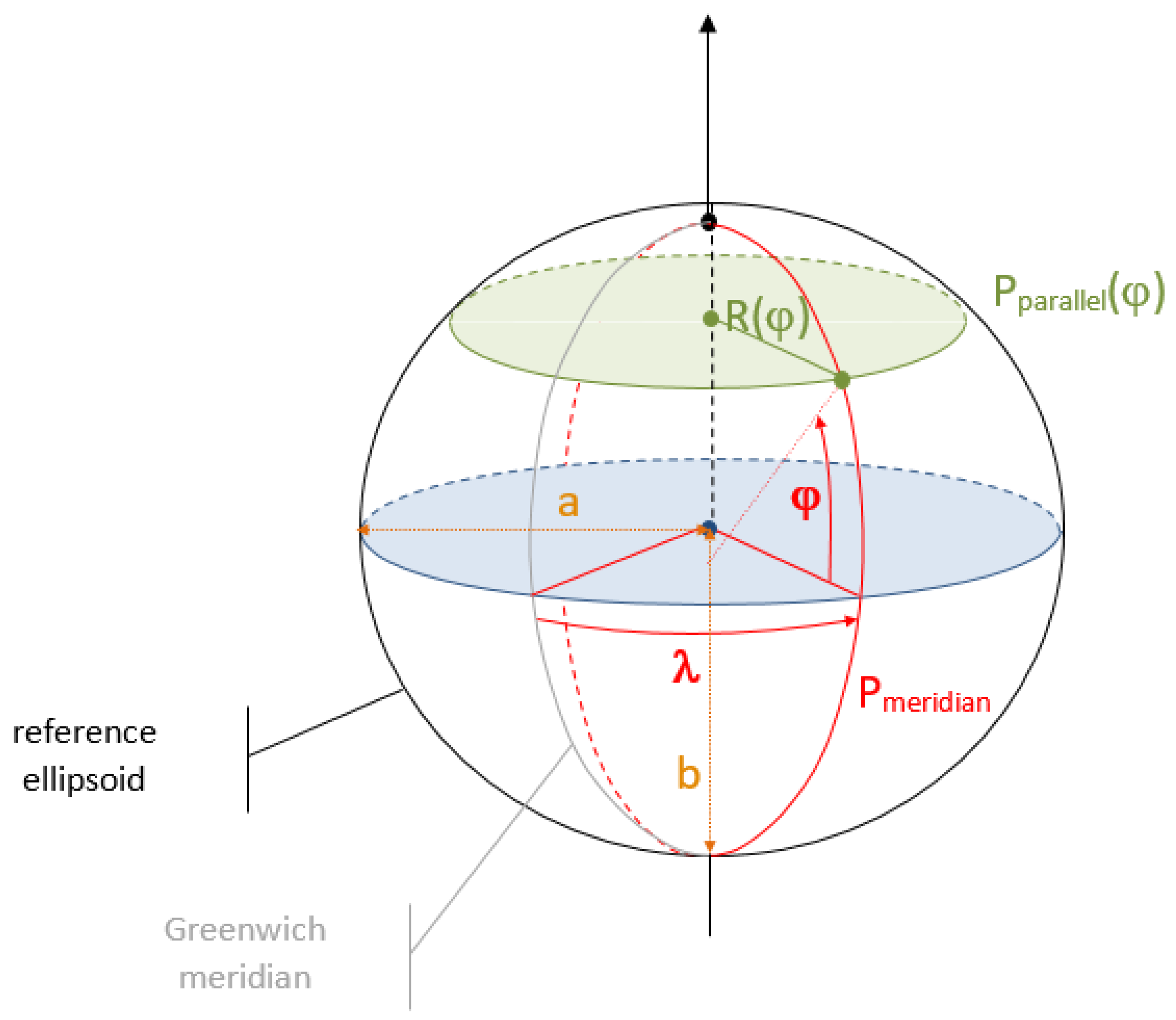
As the slopes are calculated based on distances between elevations, the convergence of meridians should be taken into account for geographic CRS (such as the EPSG:4326, see Figure 17). Due to this phenomenon, the distance along longitudes between two neighbour elevations depends on the latitude of computation (equations (24) and (25)). However, the distance along latitudes between two neighbour elevations is constant, no matter the location (26).

{G S D}_{x} (φ) = \frac{∆_{x}}{2 π} \times P_{p a r a l l e l} (φ)

(24)

P_{p a r a l l e l} (φ) = 2 π \times R (φ) \times \cos φ

(25)

{G S D}_{y} = \frac{∆_{y}}{2 π} \times P_{m e r i d i a n}

(26)

P_{m e r i d i a n} = 4 a \int_{0}^{π / 2} \sqrt{1 - e^{2} \sin^{2} θ} d θ

(27)

e = \sqrt{\frac{a^{2} - b^{2}}{a^{2}}}

(28)

Where:

DEM[l,p] is the elevation in the DEM in line l column p (in metres)
ϕ is the latitude
a is the semi-major axis of the ellipsoid
b is the semi-minor axis of the ellipsoid
GSDx is the horizontal Ground Sampling Distance (in metres)(1)
GSDy is the vertical Ground Sampling Distance (in metres)(1)
$∆_{x}$ is the horizontal angular resolution (in radians)(2)
$∆_{y}$ is the vertical angular resolution (in radians)(2)
Pparallel is the horizontal circumference of the ellipsoid at latitude φ
Pmeridian is the vertical circumference of the ellipsoid passing through the poles, approximately equal to 40 007.863 km for WGS84 $(\begin{matrix} a = 6 378 137.0 m \\ b \approx 6 356 752.3 m \end{matrix})$ ,
e is the eccentricity of the ellipsoid.

(1): Case of DEM expressed in a projected CRS where x matches the Easting and y the Northing expressed in metres. In this case, equations (24) to (28) are not needed.
(2): Case of DEM expressed in the Geographic CRS (EPSG:4326) where x matches the longitude and y the latitude expressed in radians

Figure 17. Reference angles and distances of the ellipsoid.

5.4. Logarithmic correlation

For each tile, a roughness

σ_{s l o p e}

and a best bicubic parameter b* are computed. After having tested different functions, the logarithm expressed by (29) is the regression function showing the highest regression coefficient according to the least squares method.

\tilde{b} (σ_{s l o p e}) = A \times L o g (σ_{s l o p e} + C) + B

(29)

where:

$\tilde{b}$ is the function predicting the best bicubic parameter
$σ_{s l o p e}$ is the standard deviation of slope norm computed within the DEMIX tile

Unknown values A, B and C are estimated by minimizing the mean square error (MSE) between the predicted value

{\tilde{b} (σ}_{s l o p e}

) and the N observed values (

{σ_{s l o p e}}_{i}

b_{i}^{*}

5.5. Results

Over the 67 DEMIX tiles, a logarithmic correlation coefficient of r=0.717 has been computed (Figure 18). The best-fitting parameters A, B and C found for this logarithmic model are 0.0562, 0.0210 and 0.6800, respectively.

By using this model, a BBC parameter can be estimated from roughness rather than relying on expensive error computations.

6. Discussion

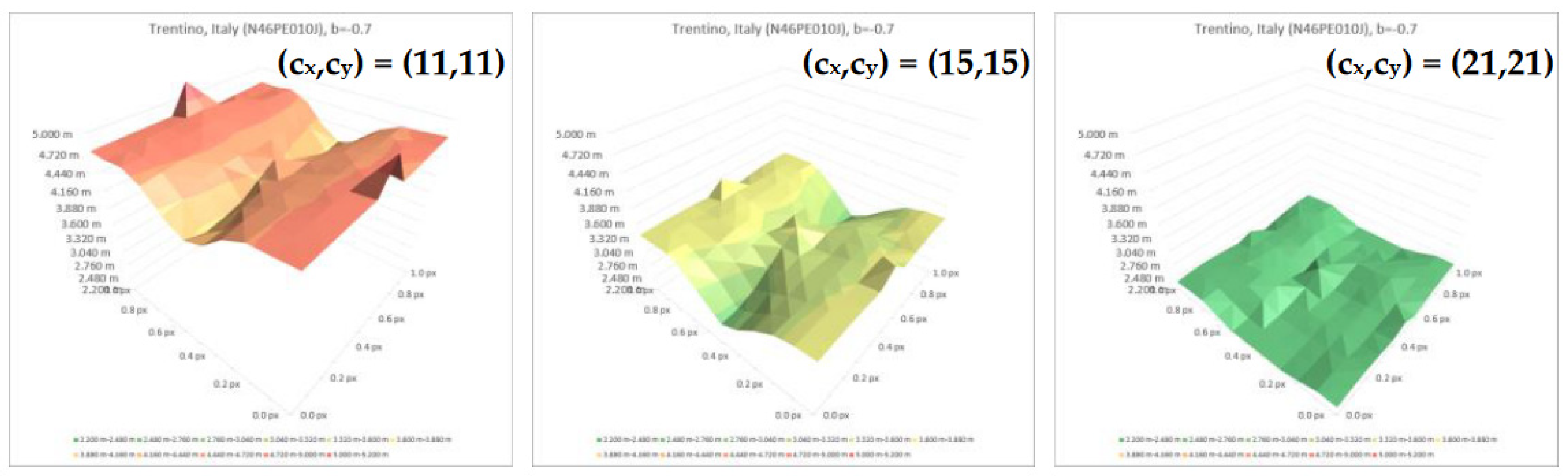
In the first step of this study, a correlation window size of 11x11 has been considered, as smaller correlation windows leaded to a high number of outliers, and larger ones increased the computation cost. In later stages of analysis, it has been observed that a larger correlation window leads to an important increase of the accuracy of the sub-pixel displacement retrieval (see Figure 19).

Over the DEMIX tile of Italy, the maximum retrieval error reaches 5.30 m with a correlation window size of (c_x,c_y) = (11,11). This maximum retrieval error progressively lowers to 3.58 m with (c_x,c_y) = (15,15), and reaches 2.49 m with (c_x,c_y) = (21,21), which is less than 1/10th of the pixel size of Copernicus DEM GLO-30 at equator (≈30 metres). Further studies could be performed on this issue, potentially resulting in an estimation of the optimal correlation window size.While the proposed methodology allows to quantify the accuracy of the sub-pixel displacement retrieval, it must be noted that in our experiment all the input images are derived from the same DEM (i.e., Copernicus DEM GLO-30). This test case is ideal, and does not encompass the high frequency differences which may be observed between two different DEMs. In such real use-cases, these roughness differences could have an impact on the quality of the displacement retrieval, which has not been assessed in the present study. However, this problem is likely to be less important with large correlation windows. Moreover, the methodology used to retrieve the BBC is perfectly applicable to the case of different input DEMs, provided they have been transformed to be in the same geometry (same CRS, VRS and pixel grid).

The methodology described in this paper could be used to produce an “Adaptative Best BiCubic”(ABBC), which would enhance or reduce the acutance to locally retrieve displacements as accurately as possible. Such adaptative interpolators already exist for generic image processing [18] as well as for the generation of DEMs [19].

7. Conclusion

Overall, validation activities have shown that sub-pixel displacements are accurately retrieved by this novel method. This accuracy is not only determined by the implicit parameters of the disparity analysis (i.e., the exploration and correlation window sizes), but also by the resampling method used to retrieve co-gridded input DEMs, which is a pre-processing required by this method. For this purpose, the bicubic resampling method has been used, whose parameter allows to adjust the stretching of heights over slope breaks. In every area, the described methodology allows to interpolate the Best BiCubic (BBC) parameter (i.e., for which the minimal error of displacement retrieval has been computed). Considering these BBC parameters, the quadratic mean of errors of displacement retrieval is comprised between 3.653 m (France) and 5.825 m (Croatia), which is much lower than the pixel size of Copernicus DEM GLO-30 (≈30 metres at equator). Higher accuracy results have been obtained by increasing the size of the correlation window, allowing to lower the maximum retrieval error e_b from 5.30 m (correlation window of 11x11) to only 2.49 m (correlation window of 21x21) in the mountainous area of Trentino, which is below 1/10^th of the input DEM resolution at equator. Beyond the good validation results, the BBC parameter has shown to be different depending on the nature of the area considered. In the mountainous areas of Italy and Cyprus, higher BBC parameters have been retrieved (-0.783 and -0.722, respectively) than in relatively flat areas such as Croatia and France (-0.864 and -1.109). A subsequent study has been performed to assess the correlation between terrain roughness and the BBC. Over 67 European areas, a logarithmic correlation coefficient of 0.717 has been computed between the standard deviation of slope norms and the BBC parameter. Considering the results of these studies, this new pairing method fits its main purpose of retrieving accurate sub-pixel displacements between two DEMs. This method will be used in the framework of the DEM Intercomparison eXercise (DEMIX) to ensure any DEM comparison is not biased by planimetric misregistrations. In the future, this method could not only be used to detect and quantify these misregistrations, but also to correct them. This specific use would require a set of reference DEMs of higher accuracy than the tested ones. The recent emergence of open Very-High Resolution (VHR) DEMs of cities, regions and countries of the world could be beneficial to this use, by providing a set of high accuracy reference DEMs.

Author Contributions

Conceptualization, S. Riazanoff, A. Corseaux, C. Albinet, P.A. Strobl, , C. López-Vázquez, P.L. Guth, T. Tadono; methodology, S. Riazanoff, A. Corseaux, C. Albinet, P.A. Strobl, C. López-Vázquez, P.L. Guth, T. Tadono; software, S. Riazanoff and A. Corseaux; validation, S. Riazanoff and A. Corseaux; formal analysis, S. Riazanoff and A. Corseaux; investigation, S. Riazanoff and A. Corseaux; resources, S. Riazanoff and A. Corseaux; data curation, S. Riazanoff and A. Corseaux; writing—original draft preparation, S. Riazanoff and A. Corseaux; writing—review & editing, S. Riazanoff, A. Corseaux, C. Albinet, P.A. Strobl, C. López-Vázquez, P. L. Guth, T.Tadono; visualization, S. Riazanoff and A. Corseaux; supervision, S. Riazanoff; project administration, S. Riazanoff and A. Corseaux; funding acquisition, C. Albinet. All authors have read and agreed to the published version of the manuscript.

Funding

This work was supported by the European Space Agency (ESA), through the Earthnet Data Assessment Project (EDAP).

Acknowledgments

The authors gratefully acknowledge the European Space Agency for their financial support provided through the EDAP project, and the members of the Digital Elevation Model Intercomparison eXercise (DEMIX) working groups for their support throughout all the stages of this study. The DEMIX members actively discussed and advised about the methodology and results of the studies.

Conflicts of Interest

The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.

Appendix A. Matrices and surfaces of the displacement retrieval errors

Hereafter are given the error matrices and surfaces for the DEMIX tiles of Cyprus, Croatia and France. The computation of these results is further detailed in the validation of the sub-pixel displacement retrieval study (see section 3).

Figure A1. Error matrices and surfaces – Case of Cyprus (N34ZE033C).

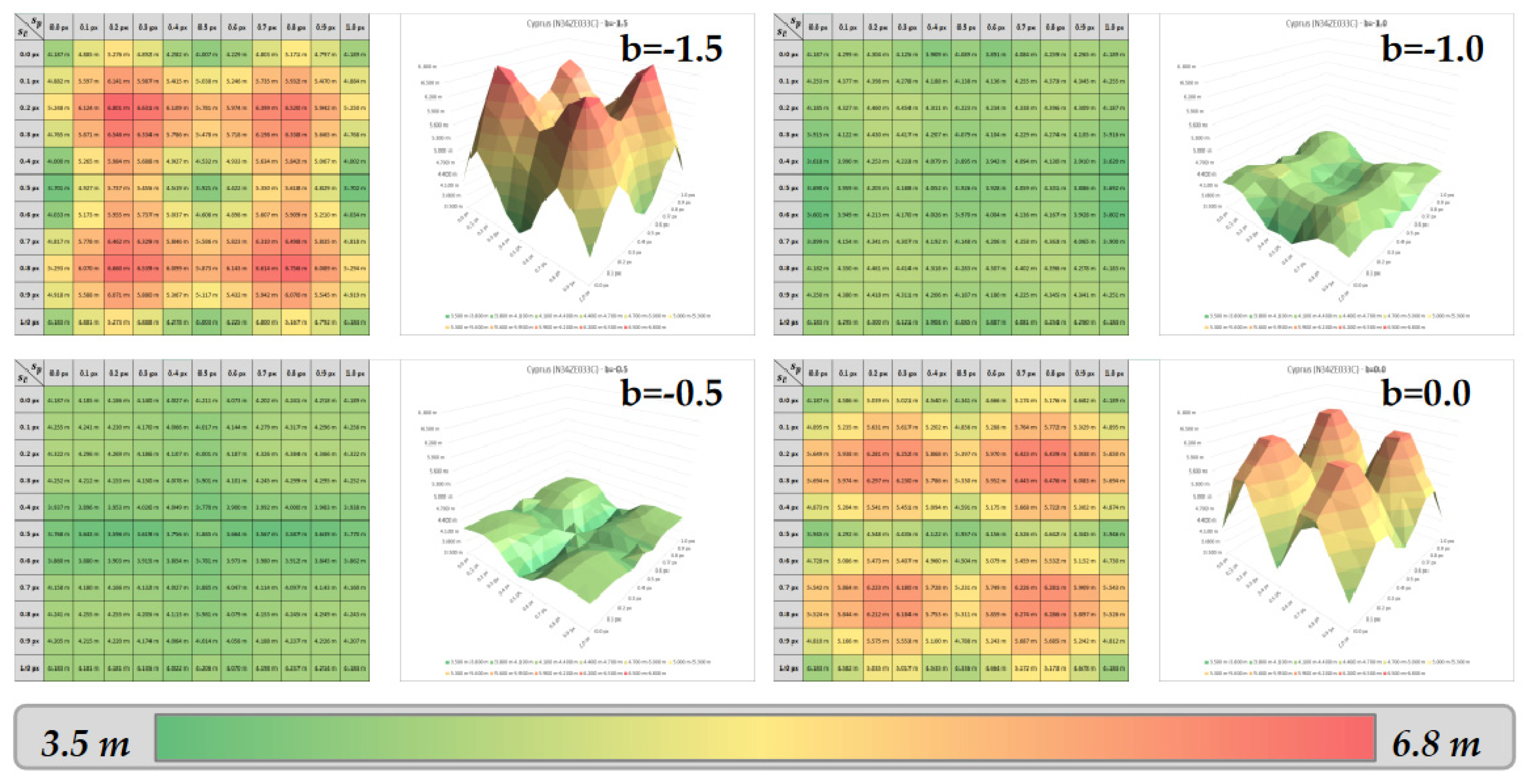
Figure A2. Error matrices and surfaces – Case of Croatia (N45VE017A).

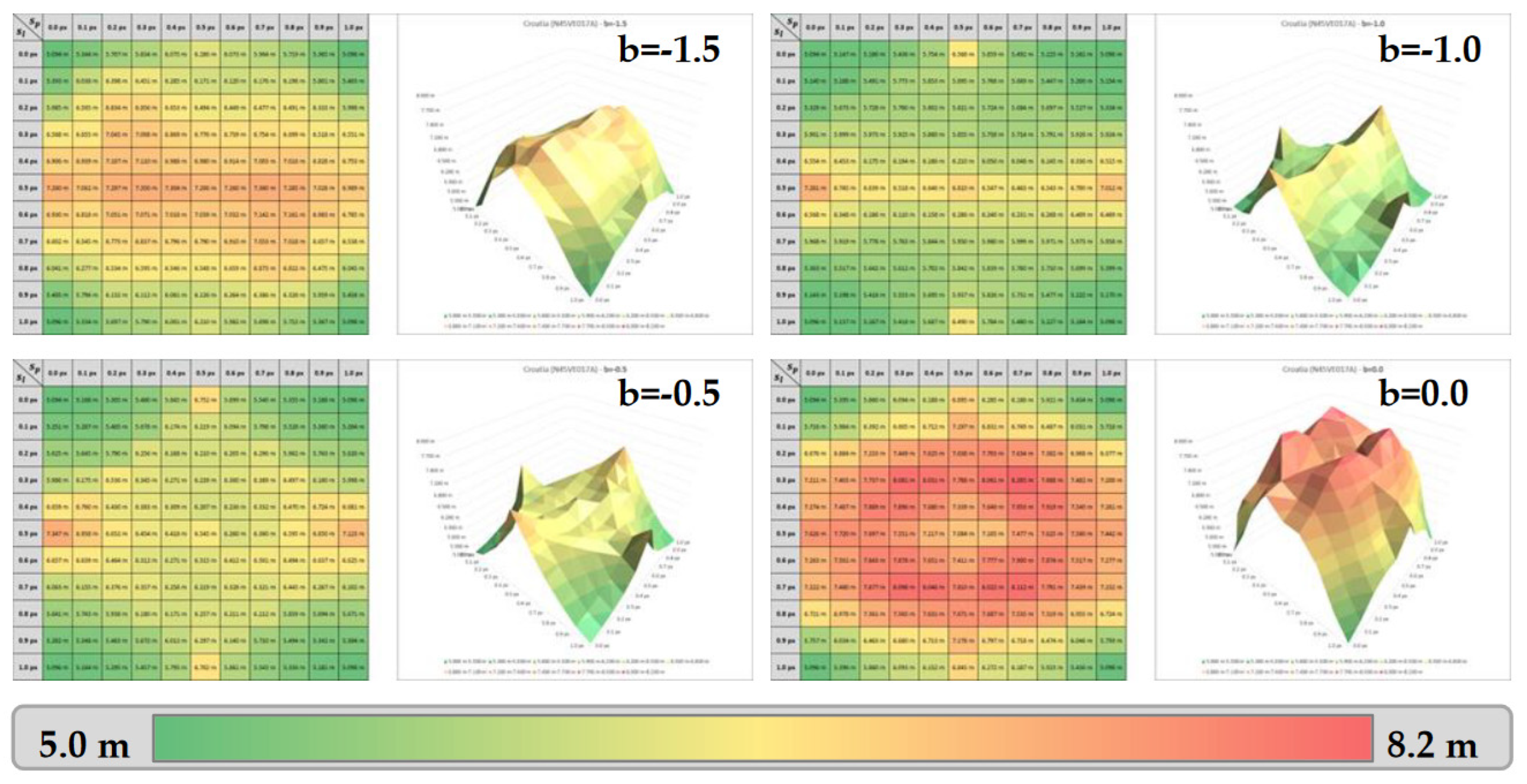
Figure A3. Error matrices and surfaces – Case of France (N44QW001H).

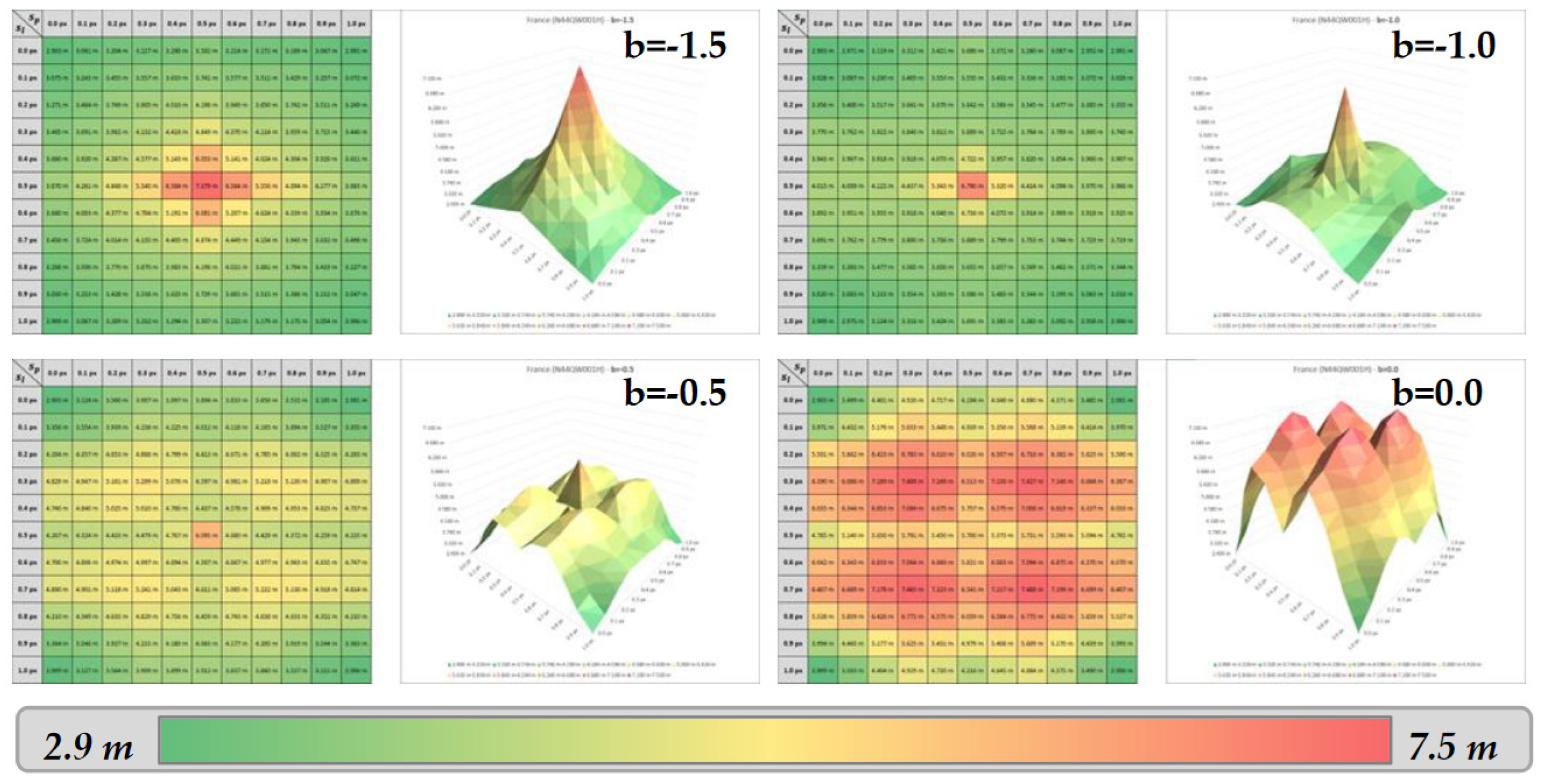
As previously observed for Trentino (see section 3.6), the highest errors seem to be found for the displacements close to ¼ and ¾ pixels on both axes, especially over Cyprus (figure A.1). Flat areas of Croatia (figure A.2) and France (figure A.3) lead to different error patterns, but the same phenomenon on ¼ and ¾ of pixel displacements is observed for bicubic parameters close to 0.0.

References

P. Guth, A. Van Niekerk, C. Grohmann, J.-P. Muller, L. Hawker, I. Florinsky, D. Gesch, H. Reuter, V. Herrera, S. Riazanoff, C. Lopez-Vazquez, C. Carabajal, C. Albinet and P. Strobl, "Digital Elevation Models: Terminology and Definitions," Remote Sensing, vol. 13, September 2021. [CrossRef]
P. A. Strobl, C. Bielski, P. L. Guth, C. H. Grohmann, J.-P. Muller, C. López-Vázquez, D. B. Gesch, G. Amatulli, S. Riazanoff and C. Carabajal, "THE DIGITAL ELEVATION MODEL INTERCOMPARISON EXPERIMENT DEMIX, A COMMUNITY-BASED APPROACH AT GLOBAL DEM BENCHMARKING," The International Archives of the Photogrammetry, Remote Sensing and Spatial Information Sciences, Vols. XLIII-B4-2021, p. 395–400, 2021. [CrossRef]
P. L. Guth, P. Strobl, K. Gross and S. Riazanoff, "DEMIX 10k Tile Data Set," January 2023. [CrossRef]
T. Van Niel, T. McVicar, L. Li, J. Gallant and Q. Yang, "The impact of misregistration on SRTM and DEM image differences," Remote Sensing of Environment, vol. 112, pp. 2430-2442, May 2008. [CrossRef]
M. Hawwa, T. Knudsen, S. Kokkendorff, B. Olsen and B. Rosenkranz, "Horizontal Accuracy of Digital Elevation Models," January 2011. [CrossRef]
A. T. Mozas-Calvache, "Positional Accuracy Assessment of Digital Elevation Models and 3D Vector Datasets Using Check-Surfaces," ISPRS International Journal of Geo-Information, vol. 12, 2023. [CrossRef]
M. A. Sutton, W. J. Wolters, W. H. Peters, W. F. Ranson and S. R. McNeill, "Determination of displacements using an improved digital correlation method," Image and Vision Computing, vol. 1, pp. 133-139, 1983. [CrossRef]
S. Barnard and W. Thompson, "Disparity Analysis of Images," Pattern Analysis and Machine Intelligence, IEEE Transactions on, Vols. PAMI-2, pp. 333-340, August 1980. [CrossRef]
L. Guan, H. Pan, S. Zou, J. Hu, X. Zhu and P. Zhou, "The impact of horizontal errors on the accuracy of freely available Digital Elevation Models (DEMs)," International Journal of Remote Sensing, vol. 41, no. 19, pp. 7383-7399, 2020. [CrossRef]
M. Ghandehari, B. Buttenfield and C. Farmer, "Comparing the accuracy of estimated terrain elevations across spatial resolution," International Journal of Remote Sensing, vol. 40, pp. 1-25, February 2019. [CrossRef]
R. Keys, "Cubic convolution interpolation for digital image processing. IEEE Trans Acoust Speech Signal Process," Acoustics, Speech and Signal Processing, IEEE Transactions on, vol. 29, pp. 1153-1160, January 1982. [CrossRef]
P. Thevenaz, T. Blu and M. Unser, "Interpolation revisited [medical images application]," IEEE Transactions on Medical Imaging, vol. 19, pp. 739-758, 2000. [CrossRef]
Aganj, B. Yeo, M. Sabuncu and B. Fischl, "On Removing Interpolation and Resampling Artifacts in Rigid Image Registration," IEEE Transactions on Image Processing, vol. 22, no. 2, pp. 816-827, 2013. [CrossRef]
H. Lv, Z. Liu, B. Xu, B. Cheng and X. Hu, "Interpolation Parameters in Inverse Distance-Weighted Interpolation Algorithm on DEM Interpolation Error," Journal of Sensors, vol. 2021, p. 3535195, 2021. [CrossRef]
W. Shi, B. Wang and Y. Tian, "Accuracy Analysis of Digital Elevation Model Relating to Spatial Resolution and Terrain Slope by Bilinear Interpolation," Mathematical Geosciences, vol. 46, pp. 445-481, May 2014. [CrossRef]
C. Amante, "Accuracy of Interpolated Bathymetric Digital Elevation Models," January 2012.
L. W. Zevenbergen and C. R. Thorne, "Quantitative analysis of land surface topography," Earth Surface Processes and Landforms, vol. 12, no. 1, pp. 47-56, 1987. [CrossRef]
S. Ousguine, F. Essannouni, L. Essannouni, M. Abbad and D. Aboutajdine, "A New Image Interpolation Using Laplacian Operator," vol. 366, pp. 403-413, February 2016. [CrossRef]
X. Li, H. Jiapei, X. Liu, J. Yu and C. Feng, "Adaptive digital elevation models construction method based on nonparametric regression," Transactions in GIS, vol. 26, May 2022. [CrossRef]

Figure 1. EU-DEM vs. EEA-10 - Height differences highlighting a planimetric misregistration – Case of Malta.

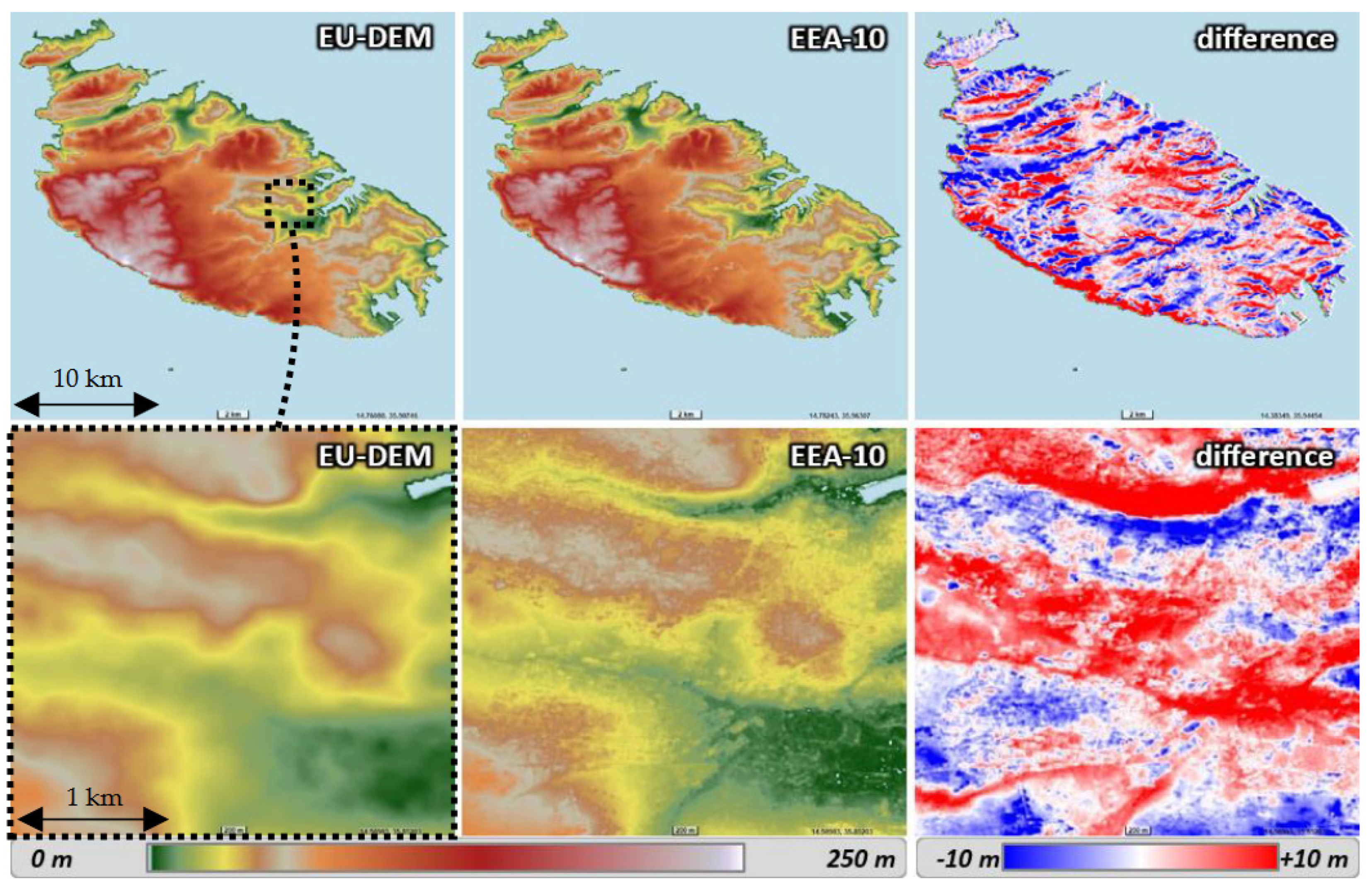
Figure 2. Disparity analysis between EU-DEM and EEA-10 - Case of Malta.

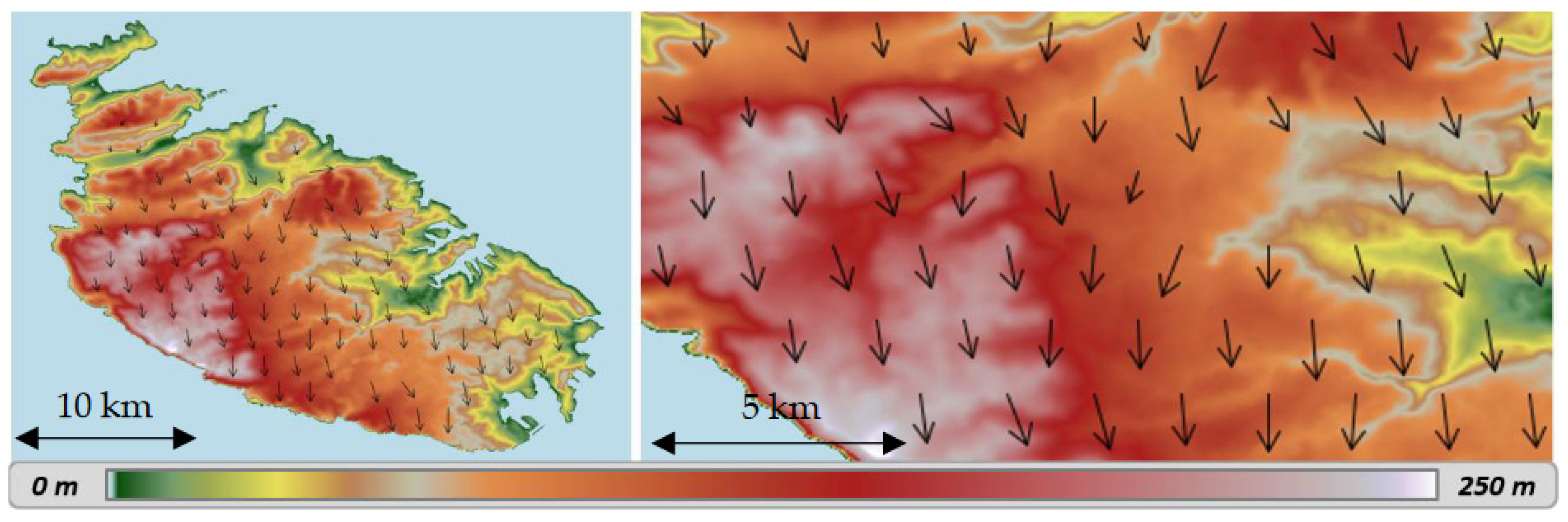
Figure 5. GLO-30 vs. AW3D – Displacement norms vs. correlation window size, images from (3,3) to (21,21), mean of displacements norms (curve a) and its first and second derivatives (maximum of variation in red dashes, selected window size in yellow).

Figure 6. GLO-30 vs. AW3D – Comparison of high frequencies in elevations.

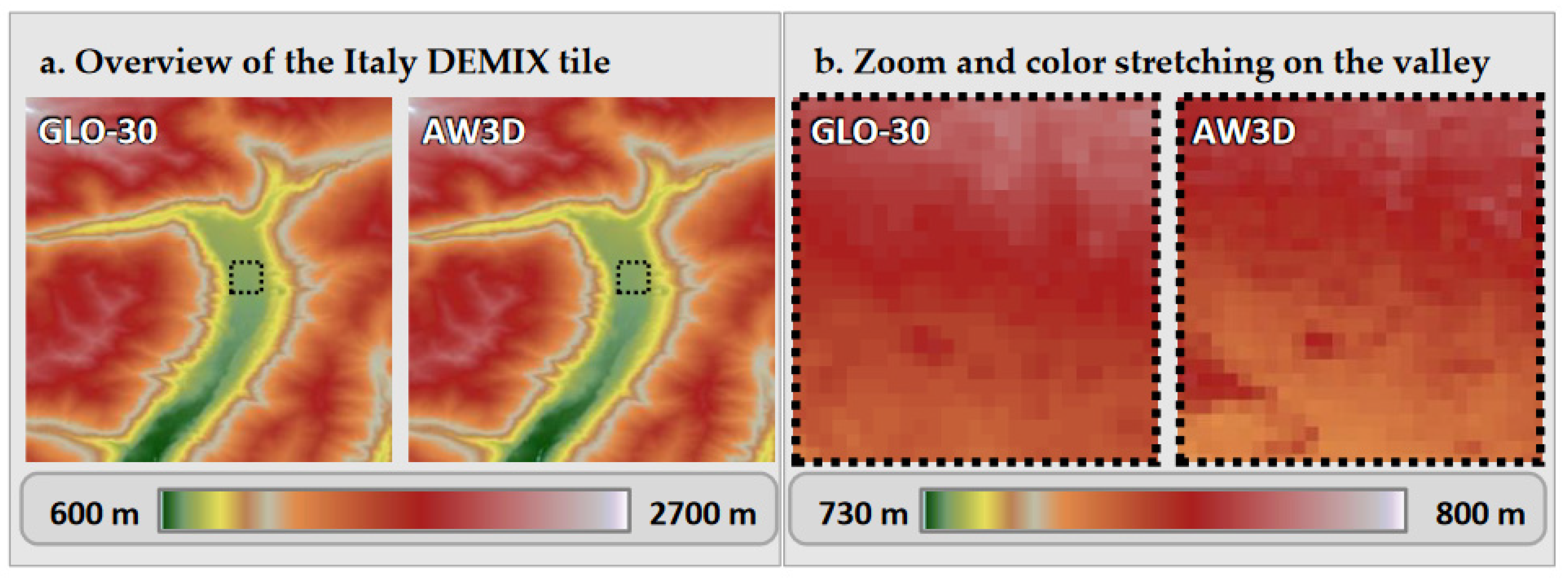
Figure 8. Bicubic resampling principle – Samples considered (left) and weight functions (right). .

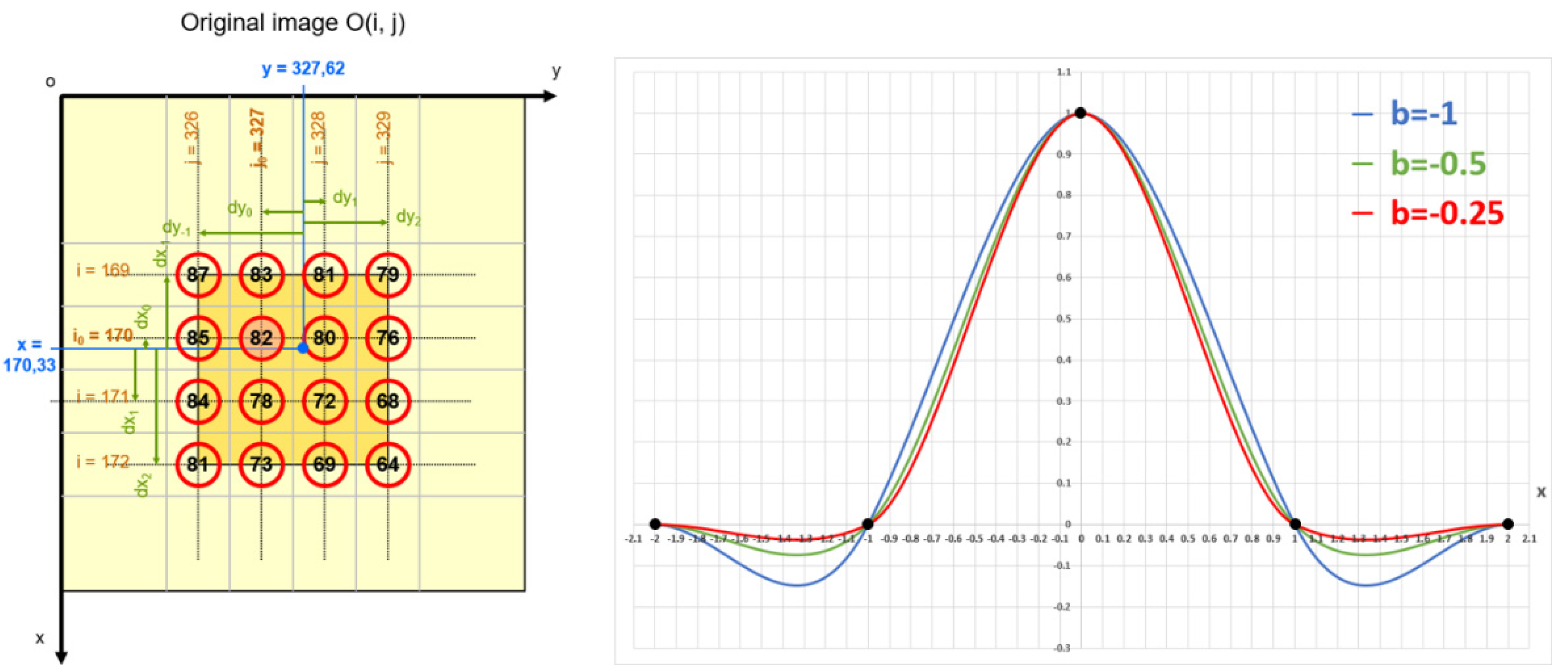
Figure 9. Effect of the bicubic parameter on DEM resampling – Case of Trentino (DEMIX tile N46PE010J).

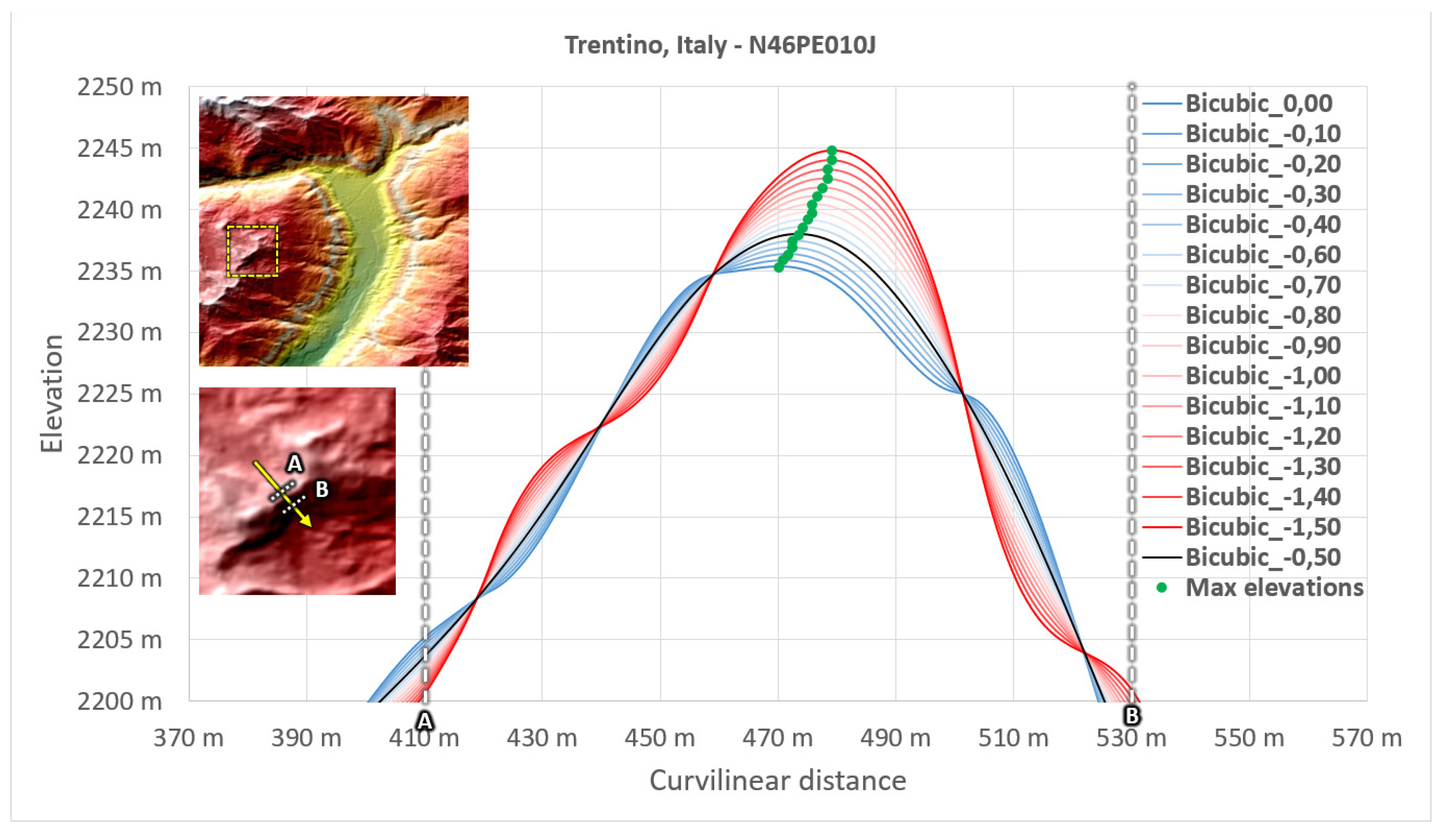
Figure 10. Effect of the bicubic parameter on DEM resampling – Case of Croatia (DEMIX tile N45VE017A).

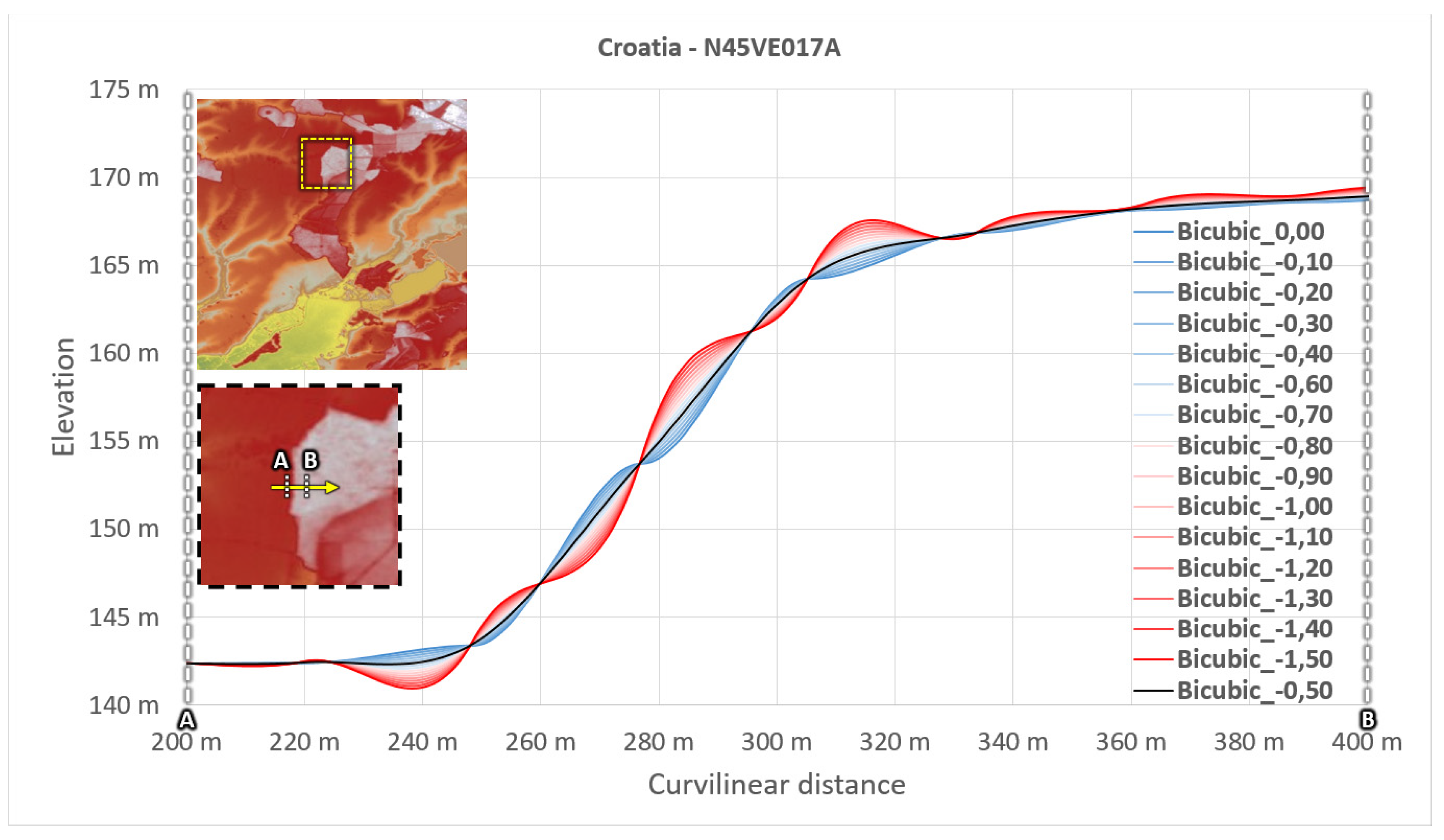
Figure 11. Principle of validation of the sub-pixel displacement retrieval.

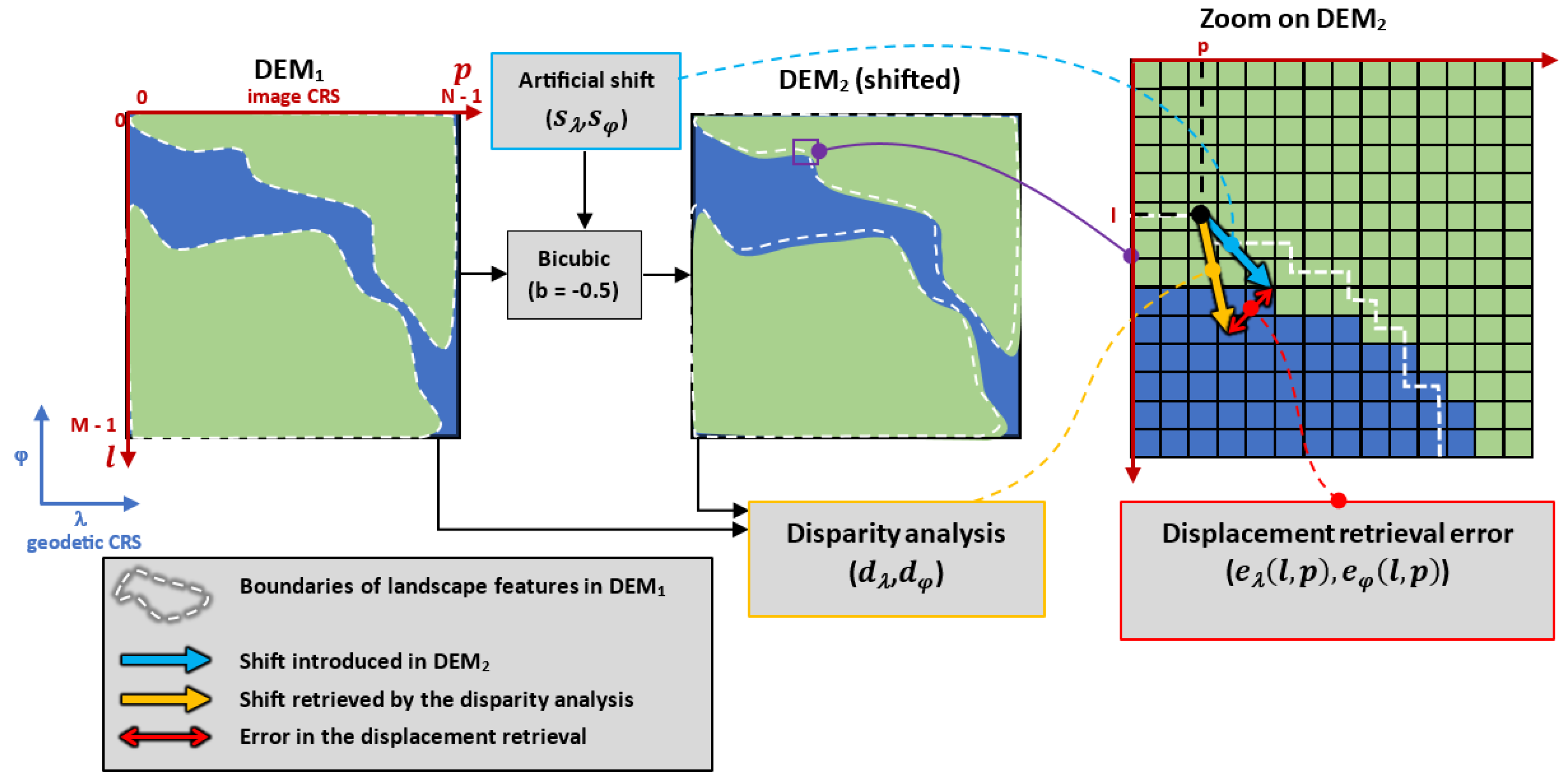
Figure 12. 11x11 matrix showing the “image error” values (left) and the associated surface representation (right).

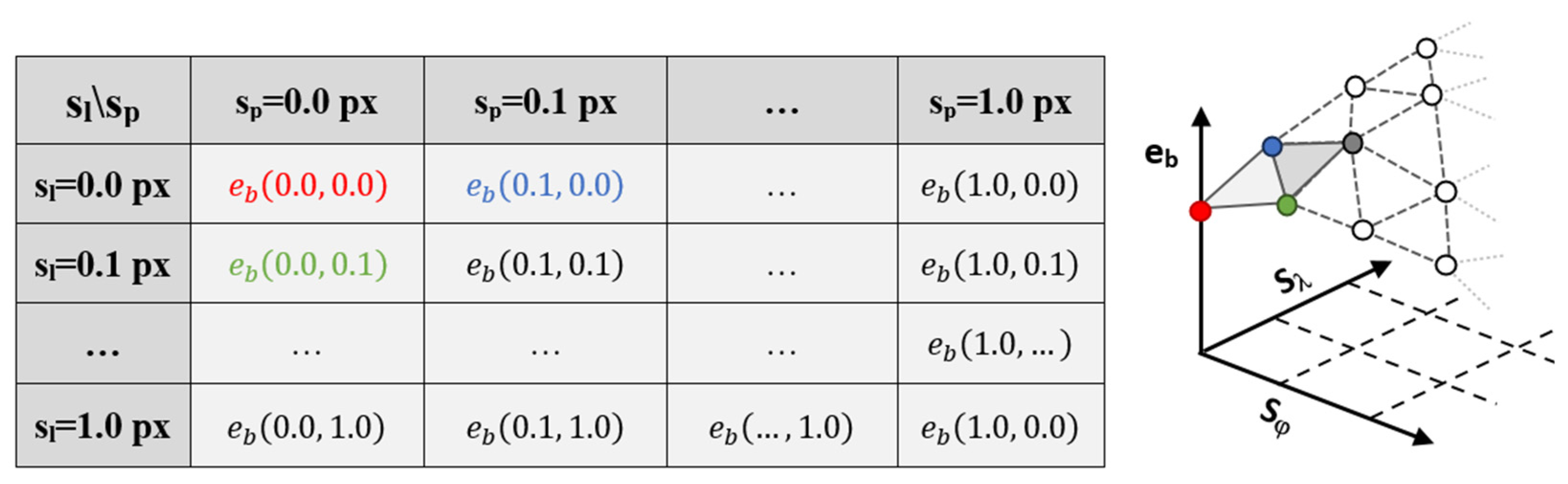
Figure 13. Error matrices and surfaces – Case of Trentino, Italy.

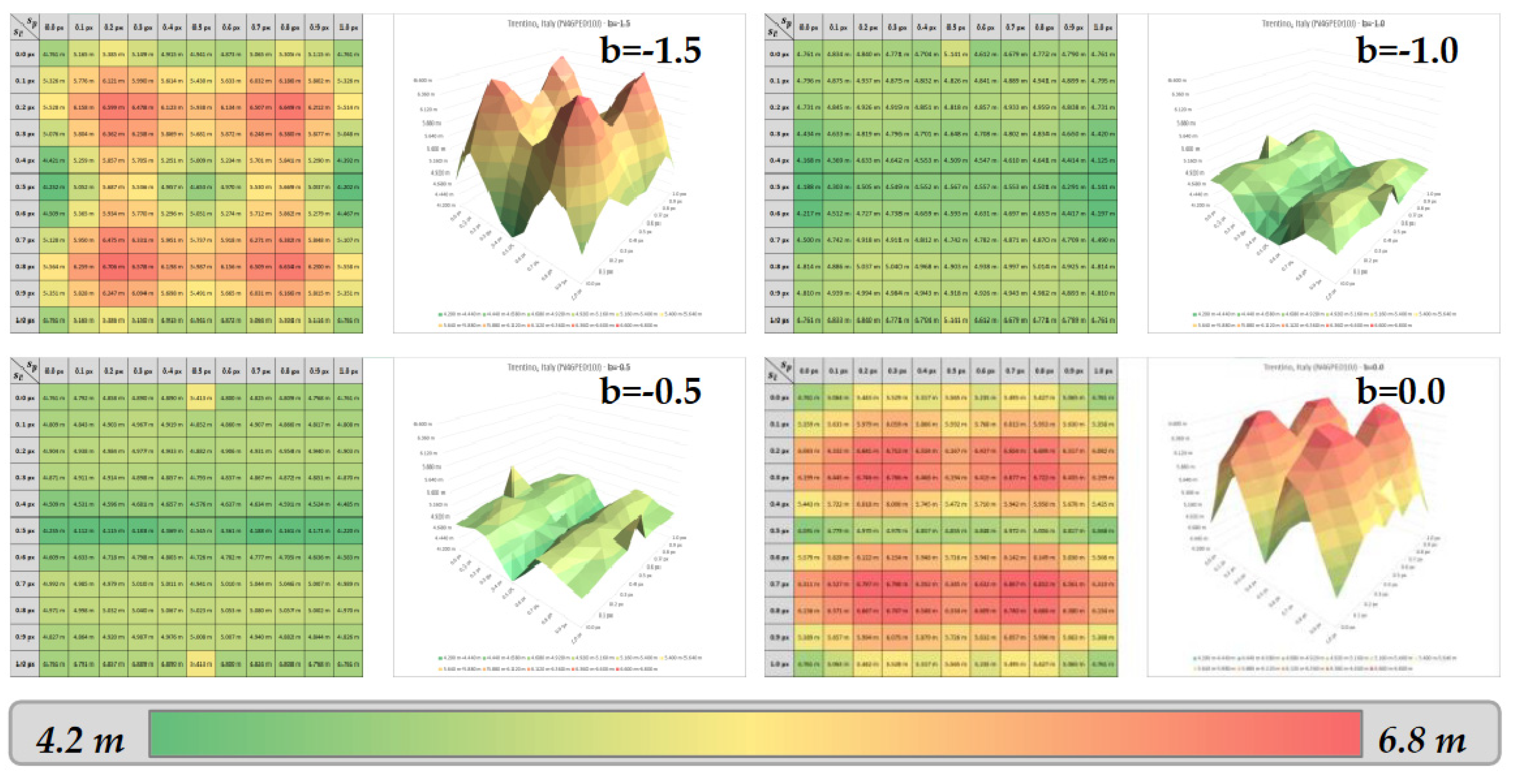
Figure 14. Principle of computation of the displacement error graphs.

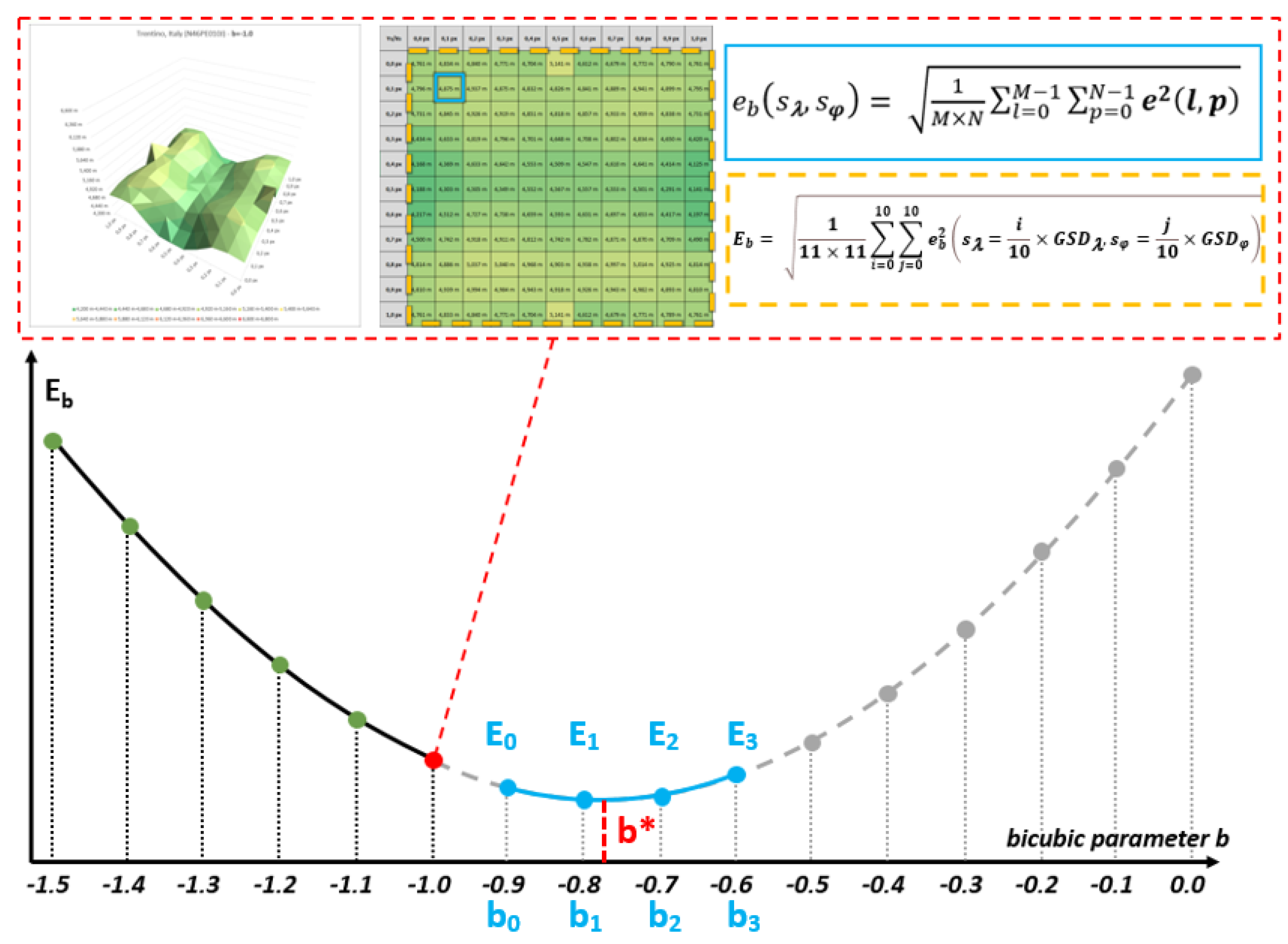
Figure 16. Repartition of the 67 European DEMIX tiles chosen as study areas – Low to moderate slopes European tiles (a), high slope tiles in the Alps (b).

Figure 18. Logarithmic correlation between

σ_{s l o p e}

.and BBC b* over the 67 DEMIX tiles.

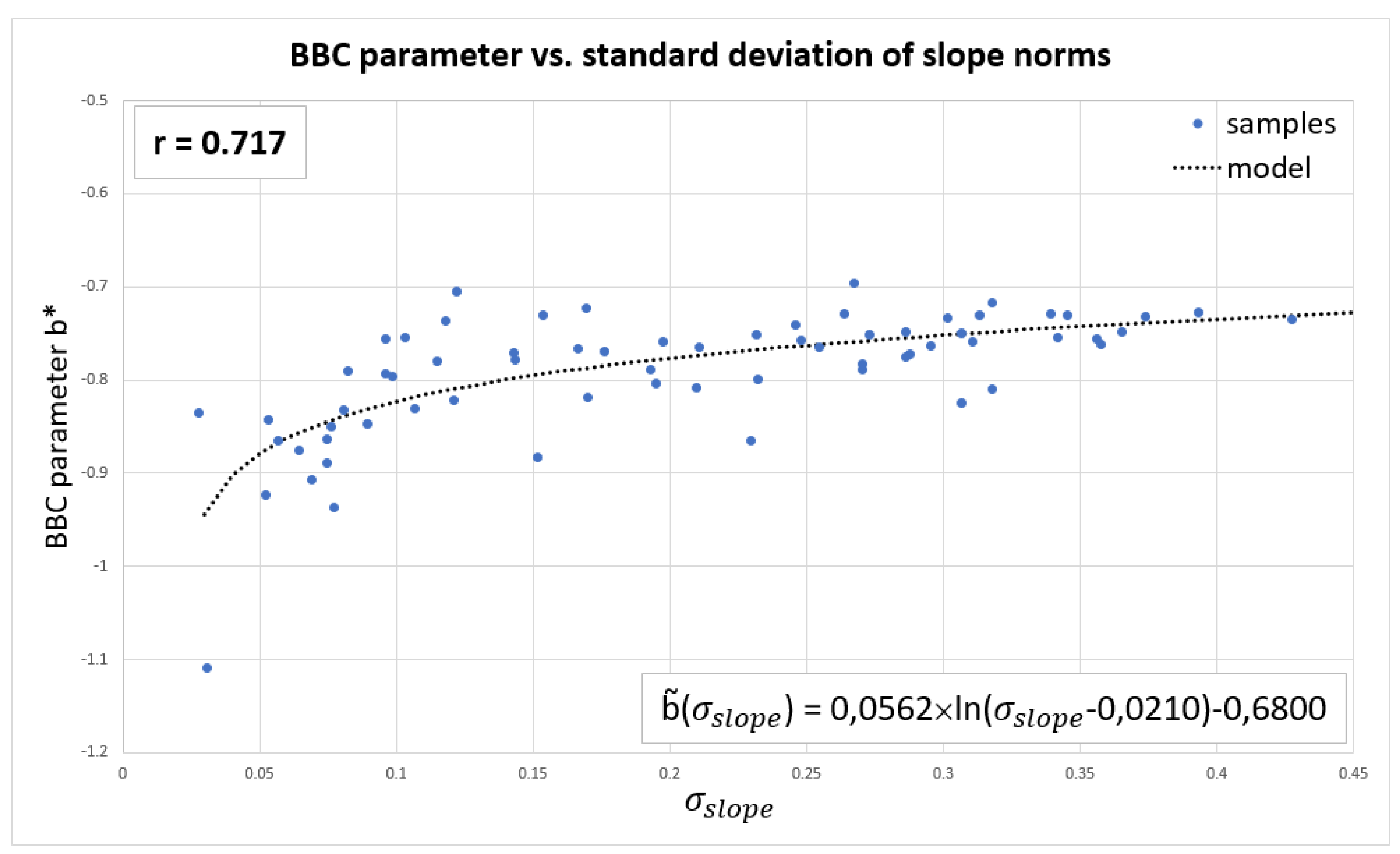
Figure 18. Logarithmic correlation between

σ_{s l o p e}

.and BBC b* over the 67 DEMIX tiles.

Figure 19. Influence of the correlation window size on the sub-pixel retrieval accuracy – Case of Italy (N46PE010J).

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Best BiCubic Method to Compute the Planimetric Misregistration between Images with Sub-pixel Accuracy: Application to Digital Elevation Models

Abstract

1. Introduction

1.1. Context

1.2. Effect of planimetric misregistration

1.3. Disparity analysis

2. Methods

2.1. Principles

2.2. Pixel matching

2.3. Sub-pixel matching

2.4. Choice of the exploration and correlation window sizes

3. Validation of the sub-pixel displacement retrieval

3.1. Principle

3.2. Study areas

3.3. Bicubic formula

3.4. Shift validation

3.5. Error matrices and surfaces

3.6. Results

4. Finding the Best BiCubic (BBC) parameter for disparity analysis

4.1. Principle

4.2. Displacement error graphs

4.3. Interpolation of the BBC

4.4. Results

5. Relation between BBC and DEM slope variations

5.1. Principle

5.2. Study areas

5.3. Slopes computation and statistics

5.4. Logarithmic correlation

5.5. Results

6. Discussion

7. Conclusion

Author Contributions

Funding

Acknowledgments

Conflicts of Interest

Appendix A. Matrices and surfaces of the displacement retrieval errors

References

MDPI Initiatives

Important Links

Subscribe