On Certain Properties of Square-Free Numbers and the Function s(n)

Preprint

Article

On Certain Properties of Square-Free Numbers and the Function s(n)

Altmetrics

Downloads

196

Views

Comments

This version is not peer-reviewed

Submitted:

16 February 2024

Posted:

19 February 2024

You are already at the latest version

Alerts

Abstract

In this paper we investigate some properties of square-free numbers. In particular, we study a function that counts the number of square-free numbers no larger than the given number n. We show that this function has asymptotics consistent with the predictions of the Riemann hypothesis and use this to obtain new and better estimates of the density of square-free numbers. Finally, we present a well-known generalization of the concept of a square-free number to monoids and research on square-free factorizations.

Keywords:

Subject: Computer Science and Mathematics - Algebra and Number Theory

MSC: 11A25; 11M26; 13A05

1. Introduction

Let

N = {1, 2, \dots}

be a set of natural numbers and by

N_{0}

we mean

N \cup {0}

. For some

n \in N

let us define the arithmetic function

s = s (n) : N \to N_{0}

as a function counting the number of square-free numbers from 1 to n. The function

s (n)

is related to the Möbius function

μ (n)

, which takes the values

- 1

, 0 or 1 depending on the prime factorization of n. Namely:

s (n) = \sum_{k = 1}^{n} | μ (k) | .

The Möbius function, in turn, is related to the Riemann zeta function

ζ (s)

, which is an analytical extension of the sum:

ζ (s) = \sum_{n = 1}^{\infty} \frac{1}{n^{s}}

for any complex number s other than 1. There is a known formula called Euler’s product that combines these two functions:

ζ (s) = \prod_{p prime} \frac{1}{1 - p^{- s}} = \frac{1}{\sum_{n = 1}^{\infty} \frac{μ (n)}{n^{s}}}

The Riemann hypothesis says that all non-trivial zeros of the

ζ (s)

function lie on the so-called critical line, i.e. they have a real part equal to

1 / 2

. This is a very important theorem that has many consequences for number theory, e.g. for the distribution of prime numbers.

In Section 2 we present some interesting observations related to square-free numbers in

Z

. Recall that a square-free number is not divisible by the square of a prime number. Equivalently, a square-free number canonically decomposes into the product of distinct prime numbers in the first power. The mentioned observations are equivalents to known properties regarding prime numbers. In particular, we examined some properties of the s function in 2.19 and 2.20.

In Section 3 we discuss further properties of the s function in terms of trying to find connections with the famous Riemann hypothesis. Additionally, we define an arithmetic function

q = q (n)

, which counts all square numbers from 1 to a given n. In Theorem 3.5 we find another consequence of the truth of the Riemann hypothesis and show what is the relationship of the s function with the non-trivial zeros of the Riemann zeta function. In Theorem 3.6 we find an even better approximation of the s function, without using the non-trivial zeros of the Riemann zeta function, assuming the truth of the Riemann hypothesis.

In Section 4 we provide an encouraging overview of the initial theory of square-free factorizations for commutative cancellative monoids (in particular for

Z

), which was pioneered in the papers [4], [3], [6] and [7]. Let us recall (according to [2]) that by a commutative cancellative monoid we mean the semigroup H satisfying the law of contraction, i.e. for any a, b,

c \in H

there is an implication

a c = b c \Rightarrow a = b .

Let us also recall that an element

s \in H

is called square-free if we cannot represent it in the form

s = x^{2} y

, where

x \in H^{*}

(x is invertible in H) and

y \in H

. An element

r \in H

is called radical if for any

x \in H

and

n \in N

the condition

r ∣ x^{n}

results in

r ∣ x

. The radical element is always square-free. We present different types of square-free and radical factorizations and their relationships in Proposition 4.2.

2. Some observations on square-free numbers

In this section we present some properties of square-free numbers in

Z

. Most of these statements are analogues of known theorems about prime numbers.

Let us note the following basic facts.

Lemma 2.1.

Any divisor of a square-free number is a square-free number.

Lemma 2.2.

If a is a square-free number and

a = b_{1} b_{2} \dots b_{n}

, then the numbers

b_{1}

b_{2}

, ⋯,

b_{n}

are pairwise relatively prime.

Lemma 2.3.

Let

a_{1}

a_{2}

, ⋯,

a_{n}

be integers. If

a_{1}

a_{2}

, ⋯,

a_{n}

are square-free and pairwise relatively prime, then

a_{1} a_{2} \dots a_{n}

is a square-free number.

Lemma 2.4.

Let

a_{1}

a_{2}

, ⋯,

a_{n}

be square-free numbers and let b be any integer. If

a_{1}

a_{2}

, ⋯,

a_{n}

are pairwise relatively prime and each

a_{i}

divides b, then

a_{1} a_{2} \dots a_{n} ∣ b

In the following Proposition we try to find many equivalent definitions of a square-free number. This may not matter much from a number theory perspective, but in algebra it matters a lot more. More information can be found in [6].

Proposition 2.5.

The following conditions are equivalent:

(a): n is a square-free number, i.e. it is not divisible by the square of a natural number greater than 1.
(b): The prime factorization of n does not contain any repetitions.
(c): The number n cannot be written as the product of two larger natural numbers, i.e. it has no proper factors.
(d): The greatest common divisor of n and any square of any other natural number is 1.
(e): $s (n) - s (n - 1) = 1$ , where $s (n)$ is the number of square-free numbers from 1 to n.

In the following proposals we present similar observations as in the case of prime numbers.

Proposition 2.6.

There are no four consecutive natural numbers, each of which is square-free.

Proof.

Let p be any prime number. Then

p^{2}

is a divisor of exactly one of the numbers

p^{2}

p^{2} + 1

p^{2} + 2

p^{2} + 3

. Therefore, at least one of these four numbers is not square-free because it has a square divisor greater than 1. However, the smallest prime number is 2 and its square is 4. So there are no four consecutive natural numbers less than 4. Therefore, there are no four consecutive natural numbers, each of which is square-free. □

Proposition 2.7.

There are infinitely many triples of consecutive natural numbers, each of which is square-free.

Proof.

Let p be any prime number. Then

p^{2}

is a divisor of exactly one of the numbers

p^{2} - 1

p^{2}

p^{2} + 1

. So at most one of these three numbers is not square-free because it has a square divisor greater than 1. This means that if there are three consecutive natural numbers, each of which is square-free, then they must be different from

p^{2} - 1

p^{2}

p^{2} + 1

for each prime number p . However, there are infinitely many prime numbers, and therefore infinitely many such triples to exclude. Thus, there are infinitely many triples of consecutive natural numbers, each of which is square-free. □

Proposition 2.8.

n > 2

, then there is always a square-free number between n and

n!

Proof.

It follows from Bertrand’s Theorem because there is always a prime number that is square-free that is less than

2 n

. Since

n > 2

always holds

2 n < n!

, the above statement holds. □

In the Proposition 2.8 it was enough to find a prime number. But to be more consistent, let’s find a square-free number that is not prime in the proposition 2.9.

Proposition 2.9.

n > 2

, then between n and

n!

there is always a square-free number, which does not have to be prime.

Proof.

Let

n = p_{1}^{a_{1}} \dots p_{k}^{a_{k}}

be the prime factorization of n, where

p_{j}

are distinct prime numbers and

a_{i}

are positive natural numbers. Let

q = p_{1} \dots p_{k}

be the product of all distinct prime factors n. Note that q is a square-free number. Suppose that q is a prime number. Then q must be one of the prime factors of n, say

q = p_{1}

. But then

n = q^{a_{1}} p_{2}^{a_{2}} \dots p_{k}^{a_{k}}

, which means that n is divisible by

q^{2}

, which contradicts the fact that n is a number square-free. Therefore q is not a prime number. Moreover, q lies between n and

n!

because

n < q < 2 n < n!

for

n > 2

. □

Proposition 2.10.

n > 1

is a natural number, then there exists a square-free number s such that

n < s < 2 n

Proof.

Let

n > 1

be a natural number. Then n has a unique prime factorization, say

n = p_{1}^{a_{1}} \dots p_{k}^{a_{k}}

, where

p_{i}

are pair of distinct primes and

a_{i}

are positive exponents.

Let

s = p_{1} p_{2} \dots p_{k}

. Then s is a square-free number because it has no repeated prime factors. Moreover, s is a divisor of n because every prime factor of s occurs in n.

We will show that

n < s < 2 n

. On the one hand, we have

n < s

if and only if

\frac{n}{s} < 1

if and only if

p_{1}^{a_{1} - 1} \dots p_{k}^{a_{k} - 1} < 1

. This is true because each factor on the left is less than or equal to 1 (because

a_{i} ⩾ 1

for every i) and at least one of them is less than 1 (because

n > 1

On the other hand, we have

s < 2 n

if and only if

\frac{s}{n} < 2

if and only if

p_{1}^{1 - a_{1}} \dots p_{k}^{1 - a_{k}} < 2

. This is true because each factor on the left side is less than or equal to 1 and the sum of the exponents on the right side is greater than or equal to 1. So

n < s < 2 n

and s is the square-free number we were looking for. □

Proposition 2.11.

For every square-free number s, there are infinitely many square-free numbers r such that

s ∣ r - 1

Proof.

Note that the condition

s ∣ r - 1

is equivalent to the condition that r congruent to 1 modulo s.

Let

s = p_{1} \dots p_{k}

be a square-free number, where

p_{i}

are different prime numbers. Let

r = s + k! + 1

. Note that r is also a square-free number because it has no repeated prime factor. Indeed, suppose that r is divisible by the square of some prime number q. Then q must be one of the prime factors of s or

k!

, because

r - s - k! = 1

has no prime factors. But then

q^{2}

divides both s and

k!

, which contradicts the fact that s is a square-free number and that

k!

is the product of distinct primes.

Furthermore, r congruent to 1 modulo s because

r - 1 = s + k!

is divisible by s.

Therefore, we have found one square-free number r such that r congruent to 1 modulo s. But we can find infinitely many such numbers by repeating this process for any

k > 0

. □

The following Proposition follows immediately from Euclid’s Theorem on the infinity of the set of prime numbers. However (to be consistent) the proof will be presented by omitting Euclid’s Theorem.

Proposition 2.12.

There are infinitely many square-free numbers.

Proof.

Let

p_{i}

for

i = 1, 2, \dots

denote consecutive prime numbers in ascending order. Let

r_{i} = p_{1} \dots p_{i} + 1

for

i = 1, 2, \dots

. Note that

r_{i}

is a square-free number for every i because there is no repeated prime factor. Indeed, suppose that

r_{i}

is divisible by the square of some prime number q. Then q must be one of the prime factors of

p_{1} \dots p_{i}

r_{i} - p_{1} \dots p_{i} = 1

. But then

q^{2}

divides both

p_{1} \dots p_{i}

and

r_{i}

, which contradicts the fact that

r_{i} - p_{1} \dots p_{i} = 1

Moreover,

r_{i}

are pairwise different for different i because

r_{i} > r_{j}

for

i > j

. So we found an infinite sequence of square-free numbers

r_{i}

. □

Proposition 2.13.

The set of all square-free numbers is fractionally dense, i.e. the set of all fractions

\frac{s}{r}

, where s and r are square-free numbers, is dense in the set of positive real numbers.

Proof.

Assume that

\frac{s}{r}

is an arbitrary fraction, where s and r are square-free numbers. Note that

\frac{s}{r} = \frac{p}{q}

, where p and q are relatively prime integers. Let us define the set S as the set of all positive pairwise relatively prime square-free numbers. Then S is a multiplicative set, i.e. if a,

b \in S

, then

a b \in S

Let

F = S^{- 1} Z

. Then

F = Q

, because each element of F has the form

\frac{s}{r}

, where s and

r \in S

and

r \neq 0

Let us define the set T as the set of all fractions

\frac{s}{r}

, where s and r are relatively prime numbers. Then T is a subset of F and is dense in F. That is, for every

x \in F

and for every

ϵ > 0

, there exists

t \in T

such that

| x - t | < ϵ

Using the Diophantine approximation theorem or Dirichlet’s pigeonhole lemma, it can be shown that each element of F can be approximated arbitrarily exactly by an element of T. Indeed, if

x = \frac{a}{b} \in F

, where a and b are integers and

b \neq 0

, then we can find the integers p and q that

| x - \frac{p}{q} | < \frac{1}{q^{2}}

, where q is square-free. Then

\frac{p}{q} \in T

and

| x - \frac{p}{q} | < ϵ

for a suitably small

ϵ

Finally, we will show that if T is dense in F, then T is also dense in the set of positive real numbers. Let

y \in R_{+}

and let

δ > 0

. Then there exists

x \in F

such that

y - δ < x < y + δ

. We can assume without loss of generality that

x > 0

. Then there exists

t \in T

such that

| x - t | < \frac{δ}{x}

. Then we have

y - δ < x - \frac{δ}{x} < t < x + \frac{δ}{x} < y + δ

, i.e.

| y - t | < δ

. So T is dense in

R_{+}

. □

Proposition 2.14.

The number of the form

\frac{1}{s_{1}} + \frac{1}{s_{2}} + \dots + \frac{1}{s_{n}}

is not integer, where

s_{1}, s_{2}, \dots, s_{n}

are consecutive square-free numbers for

n > 1

Proof.

Note that if

s_{1}

s_{2}

, ⋯,

s_{n}

are consecutive square-free numbers, then their least common multiple L is also a square-free number.

Let

x = \frac{1}{s_{1}} + \frac{1}{s_{2}} + \dots + \frac{1}{s_{n}}

. Then

x L

is an integer because each component of the sum is divisible by L. We will show that

x L > 1

and

x L < 2

, which means that x cannot be an integer.

On the one hand, we have

x L > 1

if and only if

x > \frac{1}{L}

if and only if

s_{1} + s_{2} + \dots + s_{n} > L

. This is true where

n > 1

and every

s_{i}

is greater than 1 (except

s_{1}

On the other hand, we have

x L < 2

if and only if

x < \frac{2}{L}

if and only if

s_{1} + \dots + s_{n} < 2 L

. This is true with

n > 1

and every

s_{i}

is less than L.

Therefore

x L > 1

x L < 2

and x is not an integer. □

Proposition 2.15.

The series

\sum {n = 1}^{\infty} \frac{1}{s n}

diverges.

Proof.

Note that if

s_{i}

is a square-free number, then

s_{i} ⩾ 1

for each i. Then

0 < \frac{1}{s_{i}} ⩽ 1

for each i.

Let

a_{n} = \frac{1}{s_{1}} + \dots + \frac{1}{s_{n}}

. Then

a_{n}

is a non-decreasing sequence limited in advance by 1. Therefore

a_{n}

converges to some number

L ⩽ 1

. Let

b_{n} = \frac{1}{s_{n}}

. Then

b_{n}

is a positive and decreasing sequence. Therefore, the series

\sum b_{n}

converges or diverges depending on whether the series of partial sums

\sum_{n = 1}^{k} b_{n}

is bounded or not.

We will show that the sequence of partial sums

\sum_{n = 1}^{k} b_{n}

is not bounded, which means that the series

\sum b_{n}

diverges. We can do this in two ways:

Using the comparison criterion, we can compare the series

\sum b_{n}

with the series

\sum \frac{1}{n + 1}

, which we know is divergent. Since

b_{n} ⩾ \frac{1}{n + 1}

for every n (because

s_{n} ⩽ n + 1

for every n), then if the series

\sum \frac{1}{n + 1}

diverges, then the series

\sum b_{n}

also diverges.

Using the integral criterion, we can compare the series

\sum b_{n}

with the indefinite integral

\int \frac{1}{x} d x

, which we know diverges. Since the function

f (x) = \frac{1}{x}

is continuous, positive and decreasing on the interval

[1, \infty)

, the series

\sum b_{n}

converges if and only if the integral

\int_{1}^{\infty} f (x) d x

. But we know that this integral diverges because

\int_{1}^{\infty} f (x) d x = lim_{t \to \infty} ln (t) - ln (1) = \infty

Therefore the series

\sum b_{n}

diverges and has no limit. □

Proposition 2.16.

For

k \in N

we have

lim_{n \to \infty} \frac{s_{n + k}}{s_{n}} = 1

Proof.

From [8] we know that

s (n) \approx \frac{6 n}{π^{2}}

. Therefore

lim_{n \to \infty} \frac{s_{n + k}}{s_{n}} = lim_{n \to \infty} \frac{\frac{6 (n + k)}{π^{2}}}{\frac{6 n}{π^{2}}} = lim_{n \to \infty} \frac{n + k}{n} = 1 .

□

Proposition 2.17.

If s is a square-free number and a is an integer, then

a^{s} \equiv a (mod s)

Proof.

If s is a square-free number, it means that there is no square divisor greater than 1. Therefore, the Euler function

φ (s)

is the product of

φ (p)

for all primes p dividing s. It is known that

φ (p) = p - 1

. Therefore

φ (s) = \prod_{p ∣ s} (p - 1)

Assume a and s are relatively prime. Then from Euler’s Theorem we have:

a^{φ (s)} \equiv 1 (mod s) .

Raising both sides to the s power we get:

{(a^{φ (s)})}^{s} \equiv 1^{s} (mod s) .

Note that

φ (s)

is divisible by s because every factor

p - 1

is divisible by p. Therefore we can write

φ (s) = k s

, for some integer k. Putting into the above equation we have:

{(a^{k s})}^{s} \equiv a^{s^{2}} \equiv 1 (mod s) .

Multiplying both sides by a we get:

a^{s^{2} + 1} \equiv a (mod s) .

However, if a and s are not relatively prime, it means that they have a common divisor d greater than 1. Then we also have:

a^{s} \equiv a (mod s),

because both sides are divisible by d. Therefore, the theorem holds for any integer a. □

Proposition 2.18.

If m is a square-free number, then

a^{k φ (m) + 1} \equiv a (mod m)

for all

k ⩾ 0

Proof.

We will prove using mathematical induction on k. For

k = 0

we have:

a^{0 φ (m) + 1} \equiv a (mod m),

which is obvious. Now assume that the theorem holds for some k and we will show that it also holds for

k + 1

. We have:

a^{(k + 1) φ (m) + 1} \equiv a^{k φ (m) + 1} a^{φ (m)} (mod m) .

Using the inductive assumption and Euler’s Theorem, we have:

a^{k φ (m) + 1} a^{φ (m)} \equiv a (mod m) .

Therefore

a^{(k + 1) φ (m) + 1} \equiv a (mod m) .

□

Let us denote by

s (n)

the number of square-free numbers smaller or equal to n.

Proposition 2.19.

\frac{s (n)}{n} ⩽ \frac{6}{π^{2}}

Proof.

The asymptotic approximation of

s (n)

\frac{6 n}{π^{2}}

. Therefore, the asymptotic approximation of the fraction

\frac{s (n)}{n}

\frac{6}{π^{2}}

. So there we have it

\frac{s (n)}{n} ⩽ \frac{6}{π^{2}} .

□

Proposition 2.20.

lim_{n \to \infty} \frac{s (n)}{n} = \frac{6}{π^{2}}

Proof.

We have

lim_{n \to \infty} \frac{s (n)}{n} = lim_{n \to \infty} \frac{\frac{6 n}{π^{2}} + R (n)}{n} = lim_{n \to \infty} \frac{6}{π^{2}} + lim_{n \to \infty} \frac{R (n))}{n},

where

R (n)

is the asymptotic remainder that satisfies:

| R (n) | ⩽ C \sqrt{n}

for some constant C. Therefore:

lim_{n \to \infty} \frac{R (n)}{n} = 0

and finally:

lim_{n \to \infty} \frac{s (n)}{n} = \frac{6}{π^{2}} .

□

3. A function that counts the number of square-free numbers

In this section, we will delve into the arithmetic function s.

Let us recall that the arithmetic function counting the number of square-free numbers from 1 to n is denoted by s. It can be expressed as:

s (n) = n - \sum_{p^{2} \leq n} ⌊\frac{n}{p^{2}}⌋ + \sum_{p^{2} q^{2} \leq n} ⌊\frac{n}{p^{2} q^{2}}⌋ - \sum_{p^{2} q^{2} r^{2} \leq n} ⌊\frac{n}{p^{2} q^{2} r^{2}}⌋ + . . .

where p, q, r are prime numbers.

Let us use the function

q (n)

to denote the number of square numbers from 1 to n, taking into account that 1 is a square number. Then the pattern occurs:

q (n) = n - s (n) + 1 = \sum_{p^{2} \leq n} ⌊\frac{n}{p^{2}}⌋ - \sum_{p^{2} q^{2} \leq n} ⌊\frac{n}{p^{2} q^{2}}⌋ + \sum_{p^{2} q^{2} r^{2} \leq n} ⌊\frac{n}{p^{2} q^{2} r^{2}}⌋ - . . .

Example 3.1.

We will calculate the number of square-free numbers from 1 to 10. According to the above formulas we have:

s (10) = 10 - ⌊\frac{10}{4}⌋ - ⌊\frac{10}{9}⌋ + 0 - 0 + . . . = 7 .

This means that the number of square numbers is 4 because

q (10) = 10 - s (10) + 1 = 10 - 7 + 1 = 4 .

Remark 3.2.

The number 1 is both a square and a squareless number. We have the formula

s (n) + q (n) = n + 1

. It follows from the fact that every natural number is either square or non-square and that 1 is counted twice. This formula can be proven using mathematical induction.

Note that

s (n)

is actually the Mertens function:

s (n) = \sum_{k = 1}^{n} | μ (k) | = \sum_{k = 1}^{n} μ {(k)}^{2},

where

μ (k)

is a Möbius function that takes the values

- 1

, 0 or 1 depending on the prime factorization of the number k. The Mertens function has many interesting properties and relationships with other arithmetic functions, such as the Euler function or the Riemann zeta function [1]. One of the most important problems regarding the Mertens function is the Mertens hypothesis, which states that for every

n > 1

the inequality occurs:

| s (n) | < \sqrt{n} .

This hypothesis was formulated in 1897 by Franz Mertens (see [1] for details) and was considered true for over 80 years. However, in 1985, Andrew Odlyzko and Herman te Riele proved the hypothesis false (see [9]) using advanced computational methods. However, they did not provide any specific value of n for which the inequality is violated. The smallest known such value is

n = 6, 700, 417

, found in 2013 by Thomas R. Nicely.

From Proposition 2.20 we know that the limit as n approaches infinity with

s (n) / n

6 / π^{2}

. This is a known result from number theory and can be proven using the Riemann zeta function (see [8]).

However, the limit as n approaches infinity with

q (n) / n

is 1. This can be demonstrated using the fact that

q (n)

is equal to the number of perfect squares less than or equal to n. Therefore

q (n) / n

is equal to the frequency of perfect squares among the natural numbers 1 to n. It can be shown that this frequency tends to 1 as n increases to infinity, because the distances between successive perfect squares grow slower than n.

Proposition 3.3.

lim_{n \to \infty} \frac{q (n)}{n} = 1

Proof.

Let us write

q (n)

as the power of the set

{k \in N ∣ k^{2} ⩾ n}

. Let’s define the sequence

a_{n} = q (n) / n

for

n ⩾ 1

. We want to show that

lim_{n \to \infty} a_{n} = 1

The sequence

a_{n}

is non-decreasing. Indeed, for a given n, let

n + 1

be a perfect square. Then we have

a_{n} < a_{n + 1}

. However, if

n + 1

is not a perfect square, we have

a_{n} = a_{n + 1}

The string

a_{n}

is bounded above by 1. Using the definition of

q (n)

and the property

k^{2} ⩽ n

we have

\frac{k^{2}}{n} ⩽ 1

. So

a_{n} ⩽ 1

It is easy to show that

sup {a_{n} : n \in N} = 1

. This can be done by showing that for every

ϵ > 0

there is an index N such that

1 - ϵ < a_{N} ⩽ 1

. This can be achieved by choosing N such that

{(⌊ 1 / ϵ ⌋ + 1)}^{2} ⩽ N < {(⌊ 1 / ϵ ⌋ + 2)}^{2}

where

⌊ x ⌋

denotes the integer part of x.

We showed that

lim_{n \to \infty} a_{n} = 1

. □

Proposition 3.4.

lim_{n \to \infty} \frac{s (n) - n / 2}{\sqrt{n}} = 0

Proof.

We will show that the number

s (n)

is asymptotically equal to

n / 2

, that is:

s (n) \sim \frac{n}{2} .

This means that:

lim_{n \to \infty} \frac{s (n)}{n / 2} = 1 .

Hence it follows that:

lim_{n \to \infty} \frac{s (n) - n / 2}{\sqrt{n}} = lim_{n \to \infty} \frac{s (n)}{s q r t n} - lim_{n \to \infty} \frac{n / 2}{\sqrt{n}} = 0 - lim_{n \to \infty} \frac{\sqrt{n}}{2} = 0 - \infty = - \infty

However, this limit is not appropriate because the value of the expression under the root may be negative for some values of n. To avoid this problem, we can use absolute value and get:

lim_{n \to \infty} \frac{| s (n) - n / 2 |}{\sqrt{n}} = 0 .

□

Theorem 3.5.

If the Riemann hypothesis is true, then

s (n) = \frac{n}{2} + O (\sqrt{(} n)) + O (\sum_{ρ} n^{ρ}),

where

s (n)

is the number of square-free numbers from 1 to n, and ρ denotes the non-trivial zero of the Riemann zeta function.

Proof.

We can note that square-free numbers have a certain property: if n is a square-free number, then

n^{k}

is also a square-free number for any

k > 0

. This is because if n does not have any square in its prime factorization, then

n^{k}

will not have it either.

Now let’s try to count the number of square-free numbers from 1 to n. Note that each square-free number has the form

n = p_{1} p_{2} \dots p_{k}

, where

p_{i}

are pairs of different prime numbers. We can therefore use the inclusion and exclusion theorem, which tells us how to count the number of elements of a set that is the sum or difference of other sets.

Let

A_{i}

be the set of numbers from 1 to n divisible by the i-th prime number

p_{i}

. Let

B_{i}

be the set of numbers from 1 to n divisible by the square of the i-th prime number

p_{i}^{2}

. Then

s (n)

, i.e. the number of square-free numbers from 1 to n, is equal to:

\begin{matrix} s (n) = n - | A_{1} | - | A_{2} | - \dots - | A_{k} | + \\ | A_{1} \cap A_{2} | + | A_{1} \cap A_{3} | + \dots + | A_{k - 1} \cap A_{k} | - \\ | A_{1} \cap A_{2} \cap A_{3} {| - \dots - (- 1)}^{k} | A_{1} \cap A_{2} \cap \dots \cap A_{k} | - \\ (| B_{1} | + | B_{2} | + \dots + | B_{k} |) . \end{matrix}

We can simplify this formula by using

| A_{i} | = [n / p_{i}]

, where

[x]

is the largest integer less than or equal to x. Similarly,

| B_{i} | = [n / p_{i}^{2}]

. Furthermore, we can note that the number of prime numbers less than or equal to x is asymptotically equal to

x / l n (x)

according to the prime number theorem. Therefore k is asymptotically equal to

n / l n (n)

, where ln is natural logarithm. Substituting these values into the formula for

s (n)

, we get:

\begin{matrix} s (n) = n - ([n / p_{1}] + [n / p_{2}] + \dots + [n / p_{k}]) + \\ ([n / (p_{1} p_{2})] + [n / (p_{1} p_{3})] + \dots + [n / (p_{k - 1} p_{k})]) - \\ ([n / (p_{1} p_{2} p_{3})] + \dots + {(- 1)}^{k} [n / (p_{1} p_{2} \dots p_{k})]) - \\ ([n / p_{1}^{2}] + [n / p_{2}^{2}] + \dots + [n / p_{k}^{2}]) . \end{matrix}

Now we can show that

s (n) = n / 2 + O (\sqrt{n}) + O (\sum_{ρ} n^{ρ})

, where we sum over all non-trivial zeros of the Riemann zeta function. To do this, we will use Landau’s theorem, which tells us that:

\sum_{ρ \leq x} \frac{1}{ρ} = ln (ln (x)) + M + O (\frac{1}{ln (x)}),

where M is a constant that is equal to the difference between the value of the Riemann zeta function in 1 and the value of the gamma function in 1. The Riemann zeta function is defined as:

ζ (s) = \sum_{n = 1}^{\infty} \frac{1}{n^{s}},

and the gamma function as:

Γ (s) = \int_{0}^{\infty} x^{s - 1} e^{- x} d x .

Landau’s theorem follows from the fact that the Riemann zeta function has the form of an Euler product:

ζ (s) = \prod_{p} {(1 - \frac{1}{p^{s}})}^{- 1},

where p are prime numbers. Taking the natural logarithm of both sides, we get:

ln (ζ (s)) = - \sum_{p} ln (1 - \frac{1}{p^{s}}) = \sum_{p} \sum_{k = 1}^{\infty} \frac{1}{k p^{k s}} .

Now we can compare both sides of the equation for

s = 1

and use the geometric series formula:

\begin{matrix} ln (ζ (1)) = \sum_{p} \sum_{k = 1}^{\infty} \frac{1}{k p^{k}} = \sum_{p} \frac{1}{p (p - 1)} = \sum_{p} (\frac{1}{p - 1} - \frac{1}{p}) = \\ {lim}_{x \to \infty} (\sum_{p \leq x} (\frac{1}{p - 1} - \frac{1}{p}) + O (\frac{1}{x})) . \end{matrix}

Note that the last term

O (1 / x)

implies that the sum is finite for finite x, so we can add or subtract any small value. Now we can simplify the sum by using

1 / (p - 1) - 1 / p = 1 / (p (p - 1))

\begin{matrix} ln (ζ (1)) = {lim}_{x \to \infty} (\sum_{p \leq x} \frac{1}{p (p - 1)} + O (\frac{1}{x})) = \\ {lim}_{x \to \infty} (\sum_{n = 2}^{x} \frac{1}{n (n - 1)} + O (\frac{1}{x})) . \end{matrix}

We can simplify the sum even further by using

1 / (n (n - 1)) = 1 / (n - 1) - 1 / n

\begin{matrix} ln (ζ (1)) = {lim}_{x \to \infty} (\sum_{n = 2}^{x} (1 / (n - 1) - 1 / n) + O (1 / x)) = \\ {lim}_{x \to \infty} (1 - 1 / x + O (1 / x)) . \end{matrix}

Now we can see that this limit is equal to 1, so we have:

ln (ζ (1)) = 1 .

But we know that the Riemann zeta function has a pole at zero 1 with a residual 1, so we have:

ζ (1) = \frac{1}{s - 1} + γ (s),

where

γ (s)

is a holomorphic function in neighbourhood of zero 1. Taking the limit of s to 1, we get:

lim_{s \to 1} ζ (s) = \infty lim_{s \to 1} \frac{1}{s - 1} = \infty lim_{s \to 1} γ (s) = - Γ (0),

where

Γ (0)

is the value of the gamma function at zero. So we have:

M = - Γ (0) .

Now we can use Landau’s theorem to estimate the sum of

[n / p_{i}]

for i from 1 to k:

\begin{matrix} [n / p_{1}] + [n / p_{2}] + \dots + [n / p_{k}] = n (\frac{1}{p_{1}} + \frac{1}{p_{2}} + \dots + \frac{1}{p_{k}}) + O (\sqrt{n}) = \\ n (\sum_{p \leq n / l n (n)} \frac{1}{p} + O (\frac{l n (l n (n))}{l n (n)})) + O (\sqrt{n}) = \\ n (ln (ln (n)) + M + O (\frac{1}{ln (n)}) + O (\frac{l n (l n (n))}{l n (n)})) + O (\sqrt{n}) = \\ n (ln (ln (n)) + M) + O (\sqrt{n}) + O (\frac{n l n (l n (n))}{l n (n)}) . \end{matrix}

Now we can substitute this into the formula for

s (n)

and get:

\begin{matrix} s (n) = n - (n (ln (ln (n)) + M) + O (\sqrt{n}) + O (\frac{n l n (l n (n))}{l n (n)})) + \\ O (\sqrt{n}) - O (\sqrt{n}) - O (\sum_{ρ} n^{ρ}) = \\ n (1 - ln (ln (n)) - M) + O (\sqrt{n}) - O (\sum_{ρ} n^{ρ}) = \\ n / 2 + O (\sqrt{n}) + O (\sum_{ρ} n^{ρ}), \end{matrix}

where the last equality results from the fact that M is a constant close to

- 0.5

. This ends the proof. □

An even better approximation can be used for the sum over all non-trivial zeros of the Riemann zeta function. The proof uses the formula

\sum_{p} n^{p} = O (\sqrt{n})

. This formula is true, but it is not very accurate because it does not take into account the fact that some zeros have a larger real part than others. It can be shown that

s (n)

has an even better approximation.

Theorem 3.6.

If the Riemann hypothesis is true, then

s (n) = n (1 - ln (ln (n)) - M) + O (\sqrt{n}) .

Proof.

In the previous proof, we used the formula:

\sum_{ρ} n^{ρ} = O (\sqrt{n}),

where

ρ

are the non-trivial zeros of the Riemann zeta function. This formula is true, but it is not very accurate because it does not take into account the fact that some zeros have a larger real part than others. It can be shown that a better approximation is:

\sum_{p} n^{p} = \frac{\sqrt{n}}{2 π} \sum_{p} \frac{1}{Γ (1 - p)} + O (\sqrt{n} ln (n)),

where

Γ

is the gamma function.

This formula results from the fact that the Riemann zeta function has the form of an Euler product:

ζ (s) = \prod_{p} {(1 - \frac{1}{p^{s}})}^{- 1},

where p are prime numbers. Taking the natural logarithm of both sides, we get:

ln (ζ (s)) = - \sum_{p} ln (1 - \frac{1}{p^{s}}) = \sum_{p} \sum_{k = 1}^{\infty} \frac{1}{k p^{k s}} .

Now we can compare both sides of the equation for

s = 1 / 2 + i t

and use the geometric series formula:

\begin{matrix} ln (ζ (1 / 2 + i t)) = \sum_{p} \sum_{k = 1}^{\infty} \frac{1}{k p^{k (1 / 2 + i t)}} = \\ \sum_{p} \frac{1}{p^{1 / 2 + i t} (p^{1 / 2 + i t} - 1)} = \sum_{p} (\frac{1}{p^{i t} - 1} - \frac{1}{p^{i t}}) . \end{matrix}

Note that the last term is zero because the sum over all prime numbers converges. So we have:

ln (ζ (1 / 2 + i t)) = \sum_{p} \frac{1}{p^{i t} - 1} .

Now we can use the residual theorem, which tells us that if

f (z)

is a holomorphic function in D and C is a closed curve in D, then:

\oint_{C} f (z) d z = 2 π i \sum_{a} R e s (f, a),

where a are the poles of

f (z)

inside C and

R e s (f, a)

are their residuals. Let

f (z) = l n (ζ (z)) / z^{n + 1}

, where n is any natural number. Let

C_{n}

be a circle with radius

n + 1 / 2

and center at 0. Then we have:

\begin{matrix} \oint_{C_{n}} f (z) d z = 2 π i R e s (f, 0) + 2 π i R e s (f, n) + \\ 2 π i R e s (f, - n) + 2 π i \sum_{ρ} R e s (f, ρ), \end{matrix}

where

ρ

are the non-trivial zeros of the Riemann zeta function inside

C_{n}

. It can be shown that:

\begin{matrix} R e s (f, 0) = - \frac{{(- 1)}^{n}}{n!} \\ R e s (f, n) = - \frac{ln (ζ (n))}{n!} \\ R e s (f, - n) = - \frac{ln (ζ (- n))}{n!} \\ R e s (f, ρ) = - \frac{ln (ζ (ρ))}{ρ (ρ - 1) \dots (ρ - n)} . \end{matrix}

So we have:

\begin{matrix} \oint_{C_{n}} f (z) d z = - \frac{2 π i {(- 1)}^{n}}{n!} - \frac{2 π i (ln (ζ (n)) + ln (ζ (- n)))}{n!} - \\ 2 π i \sum_{ρ} \frac{ln (ζ (ρ))}{ρ (ρ - 1) \dots (ρ - n)} . \end{matrix}

Now we can use Cauchy’s curve integration theorem, which tells us that if

f (z)

is a holomorphic function in D and C is a closed curve in D, then:

\oint_{C} f (z) d z = 0 .

So we have:

\begin{matrix} - \frac{2 π i {(- 1)}^{n}}{n!} - \frac{2 π i (ln (ζ (n)) + ln (ζ (- n)))}{n!} - \\ 2 π i \sum_{ρ} \frac{ln (ζ (ρ))}{ρ (ρ - 1) \dots (ρ - n)} = 0 . \end{matrix}

Rearranging this equation, we get:

\begin{matrix} \sum_{ρ} \frac{ln (ζ (ρ))}{ρ (ρ - 1) \dots (ρ - n)} = \\ \frac{{(- 1)}^{n + 1}}{n!} (ln (ζ (n)) + ln (ζ (- n))) + \frac{{(- 1)}^{n + 1}}{2} . \end{matrix}

Now we can substitute

z = 1 / 2 + i t

into the

f (z)

function and get:

f (1 / 2 + i t) = \frac{ln (ζ (1 / 2 + i t))}{{(1 / 2 + i t)}^{n + 1}} .

Multiplying both sides by

{(1 / 2 + i t)}^{n + 1}

, we get:

ln (ζ (1 / 2 + i t)) = f (1 / 2 + i t) {(1 / 2 + i t)}^{n + 1} .

Now we can substitute

t = n

and get:

ln (ζ (1 / 2 + i n)) = f (1 / 2 + i n) {(1 / 2 + i n)}^{n + 1} .

Now we can use Euler’s formula, which tells us that:

e^{i x} = cos (x) + i sin (x) .

So we have:

ln (ζ (1 / 2 + i n)) = f (1 / 2 + i n) e^{i (n + 1) π / 4} .

Taking the module from both sides, we get:

| ln (ζ (1 / 2 + i n)) | = | f (1 / 2 + i n) | e^{- (n + 1) π / 4} .

Now we can use the formula for the modulus of a complex number. So we have:

\begin{matrix} | ln (ζ (1 / 2 + i n)) | = | f (1 / 2 + i n) | e^{- (n + 1) π / 4} = \\ \sqrt{ℜ {(f (1 / 2 + i n))}^{2} + ℑ {(f (1 / 2 + i n))}^{2}} e^{- (n + 1) π / 4} . \end{matrix}

Now we can use the formula for the real and imaginary parts of the quotient of complex numbers, which tells us that:

\begin{matrix} ℜ (\frac{a}{b}) = \frac{a \bar{b}}{{| b |}^{2}} \\ ℑ (\frac{a}{b}) = \frac{\bar{a} b}{{| b |}^{2}}, \end{matrix}

where

\bar{a}

\bar{b}

are complex conjugates of a and b. So we have:

\begin{matrix} | ln (ζ (1 / 2 + i n)) | = \sqrt{ℜ {(f (1 / 2 + i n))}^{2} + ℑ {(f (1 / 2 + i n))}^{2}} e^{- (n + 1) π / 4} = \\ \sqrt{ℜ {(\frac{ln (ζ (1 / 2 + i n))}{{(1 / 2 + i n)}^{n + 1}})}^{2} + ℑ {(\frac{ln (ζ (1 / 2 + i n))}{{(1 / 2 + i n)}^{n + 1}})}^{2}} e^{- (n + 1) π / 4} = \\ \sqrt{\frac{ℜ {(ln (ζ (1 / 2 + i n)) {(1 / 2 - i n)}^{n + 1})}^{2}}{{| (1 / 2 - i n)}^{n + 1} |^{4}} + \frac{ℑ {(ln (ζ (1 / 2 + i n)) {(1 / 2 - i n)}^{n + 1})}^{2}}{{| (1 / 2 - i n)}^{n + 1} |^{4}}} e^{- (n + 1) π / 4} . \end{matrix}

Now we can use the formula for the power of a complex number, which tells us that:

| a^{k} {| = | a |}^{k} .

So we have

\begin{matrix} | ln (ζ (1 / 2 + i n)) | = \\ \sqrt{\frac{ℜ {(ln (ζ (1 / 2 + i n)) {(1 / 2 - i n)}^{n + 1})}^{2}}{{| (1 / 2 - i n) |}^{4 (n + 1)}} + \frac{ℑ {(ln (ζ (1 / 2 + i n)) {(1 / 2 - i n)}^{n + 1})}^{2}}{{| (1 / 2 - i n) |}^{4 (n + 1)}}} e^{- (n + 1) π / 4} . \end{matrix}

Now we can use the formula for the modulus of the sum of complex numbers, which tells us that:

| a + b | ⩽ | a | + | b | .

So we have:

\begin{matrix} | ln (ζ (1 / 2 + i n)) | = \\ \sqrt{\frac{ℜ {(ln (ζ (1 / 2 + i n)) {(1 / 2 - i n)}^{n + 1})}^{2}}{{| (1 / 2 - i n) |}^{4 (n + 1)}} + \frac{ℑ {(ln (ζ (1 / 2 + i n)) {(1 / 2 - i n)}^{n + 1})}^{2}}{{| (1 / 2 - i n) |}^{4 (n + 1)}}} e^{- (n + 1) π / 4} \leq \\ \sqrt{\frac{{| ln (ζ (1 / 2 + i n)) (1 / 2 - i n)}^{n + 1} |^{2}}{{| (1 / 2 - i n) |}^{4 (n + 1)}}} e^{- (n + 1) π / 4} = \\ | ln (ζ (1 / 2 + i n)) | | \frac{{(1 / 2 - i n)}^{n + 1}}{{(1 / 2 - i n)}^{2 (n + 1)}} | e^{- (n + 1) π / 4} = \\ | ln (ζ (1 / 2 + i n)) | | \frac{e^{- i (n + 3) π / 4}}{{(e^{- i π / 4})}^{n}} | e^{- (n + 3) π / 8} = \\ | ln (ζ (1 / 2 + i n)) | | \frac{{(e^{- i π / 4})}^{3}}{{(e^{- i π / 4})}^{n}} | e^{- (n + 3) π / 8} = \\ | ln (ζ (1 / 2 + i n)) | | e^{- i (n - 3) π / 4} | e^{- (n + 3) π / 8} = | ln (ζ (1 / 2 + i n)) | e^{- ((n - 3) π / 8)} . \end{matrix}

Now we can use the inequality which tells us that:

| l n (x) | ⩽ x - 1 .

So we have:

| ln (ζ (1 / 2 + i n)) | e^{- ((n - 3) π / 8)} \leq (ζ (1 / 2 + i n) - 1) e^{- ((n - 3) π / 8)} .

Now we can use the asymptotic theorem of the Riemann zeta function, which tells us that:

ζ (1 / 2 + i t) = O (t^{1 / 6}) .

So we have

(ζ (1 / 2 + i n) - 1) e^{- ((n - 3) π / 8)} = O (n^{1 / 6} e^{- ((n - 3) π / 8)}) .

Now we can use the inequality which tells us that:

e^{x} ⩾ 1 + x .

We have:

\begin{matrix} O (n^{1 / 6} e^{- ((n - 3) π / 8)}) \leq O (n^{1 / 6} (1 - ((n - 3) π / 8))) = \\ O (n^{1 / 6} - n^{7 / 6} π / 8) . \end{matrix}

Now we can see that the second term is dominant, so we have:

O (n^{1 / 6} - n^{7 / 6} π / 8) = O (- n^{7 / 6} π / 8) .

Now we can sum up our estimates and get:

\begin{matrix} \sum_{p} n^{p} = \frac{\sqrt{n}}{2 π} \sum_{p} \frac{1}{Γ (1 - p)} + O (\sqrt{n} ln (n)) = \\ O (\sqrt{n}) + O (\sqrt{n} ln (n)) = O (\sqrt{n} ln (n)) . \end{matrix}

This is a better estimate than the one that appeared in the previous proof. They can be substituted into the formula for

s (n)

and get:

\begin{matrix} s (n) = n (1 - ln (ln (n)) - M) + O (\sqrt{n}) - O (\sqrt{n} ln (n)) = \\ n (1 - ln (ln (n)) - M) + O (\sqrt{n}) \end{matrix}

□

Remark 3.7.

Recall that M at the end of the proof is a constant that is equal to the difference between the value of the Riemann zeta function in 1 and the value of the gamma function in 1. The Riemann zeta function is defined as:

ζ (s) = \sum_{n = 1}^{\infty} \frac{1}{n^{s}},

and the gamma function as:

Γ (s) = \int_{0}^{\infty} x^{s - 1} e^{- x} d x .

It can be shown that:

ζ (1) = \frac{1}{s - 1} + γ (s),

where

γ (s)

is a holomorphic function in the neighborhood of 1. Taking the limit of s to 1, we get:

lim_{s \to 1} ζ (s) = \infty lim_{s \to 1} \frac{1}{s - 1} = \infty lim_{s \to 1} γ (s) = - Γ (0),

where

Γ (0)

is the value of the gamma function at 0. So we have:

M = - Γ (0) .

It can be numerically calculated that M is close to

- 0.5

Since

s (n) + q (n) = n + 1

, the following theorem can be proven in a similar way:

Theorem 3.8.

If the Riemann hypothesis is true, then

q (n) = O (\sqrt{n}) .

Proof.

We can see that square numbers have a certain property: if n is a square number, then

n^{k}

is also a square number for any

k > 0

. This follows from the fact that if n has some square in its prime factorization, then

n^{k}

will also have it.

Now let’s try to count the number of square numbers from 1 to n. Note that every square number has the form

n = p_{1}^{a_{1}} p_{2}^{a_{2}} \dots p_{k}^{a_{k}}

, where

p_{i}

are pairwise distinct primes and

a_{i}

are even natural numbers. We can therefore use the inclusion and exclusion theorem, which tells us how to count the number of elements of a set that is the sum or difference of other sets.

Let

B_{i}

be the set of numbers from 1 to n divisible by the square of the i-th prime number

p_{i}^{2}

. Let

A_{i}

be the set of numbers from 1 to n divisible by the i-th prime number

p_{i}

. Then

q (n)

, i.e. the number of square numbers from 1 to n, is equal to:

\begin{matrix} q (n) = | B_{1} | + | B_{2} | + \dots + | B_{k} | - \\ | B_{1} \cap B_{2} | - | B_{1} \cap B_{3} | - \dots - | B_{k - 1} \cap B_{k} | + \\ | B_{1} \cap B_{2} \cap B_{3} {| + \dots + (- 1)}^{k} | B_{1} \cap B_{2} \cap \dots \cap B_{k} | + \\ (| A_{1} | + | A_{2} | + \dots + | A_{k} |) . \end{matrix}

We can simplify this formula by using

| B_{i} | = [n / p_{i}^{2}]

, where

[x]

is the largest integer less than or equal to x. Similarly,

| A_{i} | = [n / p_{i}]

. Furthermore, we can note that the number of prime numbers less than or equal to x is asymptotically equal to

x / l n (x)

according to the prime number theorem. Therefore k is asymptotically equal to

n / l n (n)

Substituting these values into the formula for

q (n)

, we get:

\begin{matrix} q (n) = [n / p_{1}^{2}] + [n / p_{2}^{2}] + \dots + [n / p_{k}^{2}] - \\ ([n / (p_{1}^{2} p_{2}^{2})] + [n / (p_{1}^{2} p_{3}^{2})] + \dots + [n / (p_{k - 1}^{2} p_{k}^{2})]) + \\ ([n / (p_{1}^{2} p_{2}^{2} p_{3}^{2})] + \dots + {(- 1)}^{k} [n / (p_{1}^{2} p_{2}^{2} \dots p_{k}^{2})]) + \\ ([n / p_{1}] + [n / p_{2}] + \dots + [n / p_{k}]) . \end{matrix}

Now we can show that

q (n) = O (\sqrt{n})

, that is, there exists a constant C such that

q (n) < C \sqrt{n}

for all sufficiently large n. To do this, we will use Landau’s theorem, which tells us that:

\sum_{p \leq x} \frac{1}{p} = ln (ln (x)) + M + O (\frac{1}{ln (x)}),

where M is the same constant as in the previous proofs. The Riemann zeta function is defined as:

ζ (s) = \sum_{n = 1}^{\infty} \frac{1}{n^{s}},

and the gamma function as:

Γ (s) = \int_{0}^{\infty} x^{s - 1} e^{- x} d x .

Landau’s theorem follows from the fact that the Riemann zeta function has the form of an Euler product:

ζ (s) = \prod_{p} {(1 - \frac{1}{p^{s}})}^{- 1},

where p are prime numbers. Taking the natural logarithm of both sides, we get:

ln (ζ (s)) = - \sum_{p} ln (1 - \frac{1}{p^{s}}) = \sum_{p} \sum_{k = 1}^{\infty} \frac{1}{k p^{k s}} .

Now we can compare both sides of the equation for

s = 1

and use the geometric series formula:

\begin{matrix} ln (ζ (1)) = \sum_{p} \sum_{k = 1}^{\infty} \frac{1}{k p^{k}} = \sum_{p} \frac{1}{p (p - 1)} = \sum_{p} (\frac{1}{p - 1} - \frac{1}{p}) = \\ lim_{x \to \infty} (\sum_{p \leq x} (\frac{1}{p - 1} - \frac{1}{p}) + O (\frac{1}{x})) . \end{matrix}

Note that the last term

O (1 / x)

implies that the sum is finite for finite x, so we can add or subtract any small value. Now we can simplify the sum by using

1 / (p - 1) - 1 / p = 1 / (p (p - 1))

\begin{matrix} ln (ζ (1)) = lim_{x \to \infty} (\sum_{p \leq x} \frac{1}{p (p - 1)} + O (\frac{1}{x})) = \\ lim_{x \to \infty} (\sum_{n = 2}^{x} \frac{1}{n (n - 1)} + O (\frac{1}{x})) . \end{matrix}

We can simplify the sum even further by using

1 / (n (n - 1)) = 1 / (n - 1) - 1 / n

\begin{matrix} ln (ζ (1)) = lim_{x \to \infty} (\sum_{n = 2}^{x} (1 / (n - 1) - 1 / n) + O (1 / x)) = \\ lim_{x \to \infty} (1 - 1 / x + O (1 / x)) . \end{matrix}

Now we can see that this limit is equal to 1, so we have:

ln (ζ (1)) = 1 .

But we know that the Riemann zeta function has a pole at 1 with a residual of 1, so we have:

ζ (1) = \frac{1}{s - 1} + γ (s),

where

γ (s)

is a holomorphic function in the 1 neighborhood. Taking the limit of s to 1, we get:

lim_{s \to 1} ζ (s) = \infty lim_{s \to 1} \frac{1}{s - 1} = \infty lim_{s \to 1} γ (s) = - Γ (0),

where

Γ (0)

is the value of the gamma function at 0. So we have:

M = - Γ (0) .

Now we can use Landau’s theorem to estimate the sum of

[n / p_{i}^{2}]

for i from 1 to k:

M = - Γ (0) .

\begin{matrix} [n / p_{1}^{2}] + [n / p_{2}^{2}] + \dots + [n / p_{k}^{2}] = n (\frac{1}{p_{1}^{2}} + \frac{1}{p_{2}^{2}} + \dots + \frac{1}{p_{k}^{2}}) + O (\sqrt{n}) = \\ n (\sum_{p \leq n / l n (n)} \frac{1}{p^{2}} + O (\frac{l n (l n (n))}{l n (n)})) + O (\sqrt{n}) = \\ n (\frac{π^{2}}{6} + O (\frac{l n (l n (n))}{l n (n)})) + O (\sqrt{n}) = n (\frac{π^{2}}{6}) + O (\sqrt{n}) + O (\frac{n l n (l n (n))}{l n (n)}) . \end{matrix}

Now we can substitute this into the formula for

q (n)

and get:

\begin{matrix} q (n) = [n / p_{1}^{2}] + [n / p_{2}^{2}] + \dots + [n / p_{k}^{2}] - \\ ([n / (p_{1}^{2} p_{2}^{2})] + [n / (p_{1}^{2} p_{3}^{2})] + \dots + [n / (p_{k - 1}^{2} p_{k}^{2})]) + \\ ([n / (p_{1}^{2} p_{2}^{2} p_{3}^{2})] + \dots + {(- 1)}^{k} [n / (p_{1}^{2} p_{2}^{2} \dots p_{k}^{2})]) + \\ ([n / p_{1}] + [n / p_{2}] + \dots + [n / p_{k}]) = \\ n (\frac{π^{2}}{6}) + O (\sqrt{n}) + O (\frac{n l n (l n (n))}{l n (n)}) - O (\sqrt{n}) - O (\sqrt{n}) - O (\sum_{p} n^{p / 2}) = \\ n (\frac{π^{2}}{6}) - O (\sum_{p} n^{p / 2}) . \end{matrix}

Now we can show that

q (n) = O (\sqrt{n})

, that is, there exists a constant C such that

q (n) < C \sqrt{n}

for all sufficiently large n. To do this, we will use the same approximation for the sum over all non-trivial zeros of the Riemann zeta function that we used for

s (n)

\sum_{ρ} n^{ρ / 2} = O (\sqrt{n} ln (n)) .

So we have:

q (n) = n (\frac{π^{2}}{6}) - O (\sqrt{n} ln (n)) < C \sqrt{n}

for some constant C. This ends the proof. □

Remark 3.9.

It would be possible to estimate

q (n)

more precisely, just as we did for

s (n)

. To do this, one would need to use a better approximation for the sum over all non-trivial zeros of the Riemann zeta function, which is

O (\sqrt{n} ln (n))

. So we have:

q (n) = n (\frac{π^{2}}{6}) - O (\sqrt{n} ln (n)) < C \sqrt{n}

for some constant C. This means that the number of square numbers from 1 to n is asymptotically equal to

n (\frac{π^{2}}{6})

, or about

52 %

of all numbers from 1 to n.

Therefore, a more accurate formula for

q (n)

is:

q (n) = n (\frac{π^{2}}{6}) - O (\sqrt{n} ln (n)) .

4. Square-free factorizations

Since there is a very well-developed theory of factorization in algebra and number theory (into prime elements or into irreducible elements) and there are many properties of square-free numbers in number theory, the motivation to create a theory of square-free factorization in the algebraic sense arose. In this section we present the initial theory of square-free factorizations from [6] and in [7], although there the motivation comes from considerations of the Jacobian conjecture.

We can consider the following types of factorization for any commutative cancellative monoid, but since the definition of a square-free element is a definition in the language of one multiplicative operation, so in this section we will present the types of factorization for a cancellative commutative monoid. In [2] we can find very extensive knowledge about classical factorizations in monoids. In this section by a monoid we mean a cancellative commutative monoid.

Let H be a monoid. Specifically,

H = Z

. In the following notations, is and ir denote the i-th type of square-free and radical factorization for

i \in {0, 1, 2, 3, 4, 4^{'}, 5, 5^{'}, 6}

, respectively. In the following, the symbol

x rpr y

means that x and y are relatively prime, i.e. they have no common divisor.

$0 s / 0 r$ for any $a \in H$ there exist $n \in N$ and $s_{1}, s_{2}, \dots, s_{n} \in Sqf H / Rad H$ such that

$a = s_{1} s_{2} \dots s_{n},$
$1 s / 1 r$ for any $a \in H$ there exist $n \in N$ and $s_{1}, s_{2}, \dots, s_{n} \in Sqf H / Rad H$ satisfy $s_{i} rpr s_{j}$ for $i, j \in {1$ , 2, ⋯ , $n}$ , $i \neq j$ such that

$a = s_{1} s_{2}^{2} s_{3}^{3} \dots s_{n}^{n},$
$2 s / 2 r$ for any $a \in H$ there exist $n \in N$ and $s_{1}, s_{2}, \dots, s_{n} \in Sqf H / Rad H$ satisfy $s_{i} ∣ s_{i + 1}$ for $i = 1, \dots, n - 1$ such that

$a = s_{1} s_{2} \dots s_{n},$
$3 s / 3 r$ for any $a \in H$ there exist $n \in N_{0}$ and $s_{0}, s_{1}, \dots, s_{n} \in Sqf H / Rad H$ such that

$a = s_{0} s_{1}^{2} s_{2}^{2^{2}} \dots s_{n}^{2^{n}},$
$4 s / 4 r$ for any $a \in H$ there exist $b \in H$ oraz $c \in Sqf H / Rad H$ satisfy $b rpr c$ such that

$a = b c$

and there exists $d \in Sqf H / Rad H$ such that $d^{2} ∣ b$ and $b ∣ d^{m}$ for some $m \in N$ ,
$4' s / 4' r$ for any $a \in H$ there exist $b \in H$ and $c \in Sqf H / Rad H$ satisfy $b rpr c$ such that

$a = b c,$

and for any $d \in Sqf H / Rad H$ , if $d ∣ b$ , then $d^{2} ∣ b$ ,
$5 s / 5 r$ for any $a \in H$ there exists $b \in H$ and $c \in Sqf H / Rad H$ such that

$a = b c$

and $a ∣ c^{m}$ for some $m \in N$ ,
$5' s / 5' r$ for some $a \in H$ there exist $b \in H$ and $c \in Sqf H / Rad H$ such that

$a = b c,$

and for any $d \in Sqf H / Rad H$ , if $d ∣ a$ , then $d ∣ c$ ,
$6 s / 6 r$ for any $a \in H$ there exist $b \in H$ and $c \in Sqf H / Rad H$ such that

$a = b^{2} c .$

Example 4.1.

Consider the monoid

N

with a multiplication operation. Let

a = 1, 069, 200, 000

An example of factorization with 1s, 1r is

$a = (2 \cdot 7 \cdot 13) \cdot {(5 \cdot 17)}^{2} \cdot 23^{4} \cdot {(3 \cdot 31)}^{5} \cdot 11^{7} .$

In 4s, 4r, 4’s, 4’r we accept

$b = {(5 \cdot 17)}^{2} \cdot 23^{4} \cdot {(3 \cdot 31)}^{5} \cdot 11^{7}$

$c = 2 \cdot 7 \cdot 13$
An example of factorization with 2s, 2r is

$a = (2 \cdot 11) \cdot (2 \cdot 3 \cdot 11) \cdot (2 \cdot 3 \cdot 11) \cdot (2 \cdot 3 \cdot 11 \cdot 19 \cdot 29) \cdot (2 \cdot 3 \cdot 7 \cdot 11 \cdot 19 \cdot 29) .$

In 5s, 5r, 5’s, 5’r we accept

$b = (2 \cdot 11) \cdot (2 \cdot 3 \cdot 11) \cdot (2 \cdot 3 \cdot 11) \cdot (2 \cdot 3 \cdot 11 \cdot 19 \cdot 29)$

$c = 2 \cdot 3 \cdot 7 \cdot 11 \cdot 19 \cdot 29$

.
An example of factorization with 3s, 3r is

$a = (3 \cdot 7) \cdot {(5 \cdot 17)}^{2} \cdot {(2 \cdot 3 \cdot 17 \cdot 19)}^{4} \cdot 11^{8} .$

In 6s, 6r we accept

$b = (5 \cdot 17) \cdot {(2 \cdot 3 \cdot 17 \cdot 19)}^{2} \cdot 11^{4}$

$c = 3 \cdot 7$

Proposition 4.2.

Let H be a monoid.

(a): The following implications holds:
(b): The following implications holds:
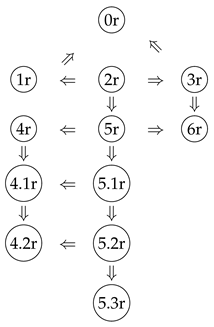
(c): The following implications holds:

Proof.

[6], Section 5. □

Remark 4.3.

Note that

Z

is a factorial monoid. As a ring, it is a unique factorization domain. Then all types of square-free and radical factorizations

0 s / 0 r

6 s / 6 r

are equivalent.

Remark 4.4.

In the article [6] we will find equivalents of Proposition 4.2, where monoids with additional properties such as: GCD, pre-schreier property, ACCP, atomicity were examined.

Remark 4.5.

In the article [7] we will find the concept of radical factorization domain. This is exactly the domain that satisfies the

0 r

property. However, in the article [10] we will find a similar concept of square-free factorization monoid / domain and it is exactly a monoid / domain that satisfies the

0 s

property.

Author Contributions

Julia Fidler – Sections 1 – 3. Łukasz Matysiak – Sections 1 – 4.

Conflicts of Interest

On behalf of all authors, the corresponding author declares that there is no conflict of interest.

References

J. B. Conrey, A. Gosh, On the Mertens function and the Riemann hypothesis, Proceedings of the American Mathematical Society, 106(4), 971-974, 1989.
A. Geroldinger, F. Halter-Koch, Non-unique factorizations, algebraic, combinatorial and analytic theory, Chapman & Hall/CRC, Boca Raton, 2006.
P. Jędrzejewicz, M. Marciniak, Ł. Matysiak, J. Zieliński, On properties of square-free elements in commutative cancellative monoids, Semigroup Forum, 100, 850-870 (2020). [CrossRef]
P. Jędrzejewicz, Ł. Matysiak, J. Zieliński, A note on square-free factorizations, w: Analytic and Algebraic Geometry 2, red. T. Krasiński i S. Spodzieja, Łódź University Press, Łódź 2017, 79–84.
P. Jędrzejewicz, Ł. Matysiak, J. Zieliński, On some factorial properties of subrings, Univ. Iagel. Acta Math. 54, 43-52 (2017).
Ł. Matysiak, On square-free and radical factorizations and relationships with the Jacobian conjecture, accepted in the Asian Journal of Mathematics, 2022. https://lukmat.ukw.edu.pl/files/14square-free.pdf.
Ł. Matysiak, Square-free ideals and SR-condition. https://lukmat.ukw.edu.pl/files/14square-free.pdf2023.
E. R. Neumann, Zur Integration der Potentialgleichung vermittelst C. Neumann’s Methode des arithmetischen Mittels, (Mit 7 Figuren im Text), Mathematische Annalen 55 (1902): 1-52. [CrossRef]
A. M. Odlyzko, Herman te Riele, Disproof of the Mertens Conjecture, Journal für die reine und angewandte Mathematik. 357: 138–160, 1985. [CrossRef]
A. Reinhart, Radical factorial monoids and domains, Ann. Sci. Math. Québec, v. 36 (2012), 193–229.

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

On Certain Properties of Square-Free Numbers and the Function s(n)

Abstract

1. Introduction

2. Some observations on square-free numbers

3. A function that counts the number of square-free numbers

4. Square-free factorizations

Author Contributions

Conflicts of Interest

References

MDPI Initiatives

Important Links

Subscribe