Submitted:
17 February 2024
Posted:
19 February 2024
You are already at the latest version
Abstract
Keywords:
1. Introduction
2. Materials and Methods
2.1. Outputs of GCMs
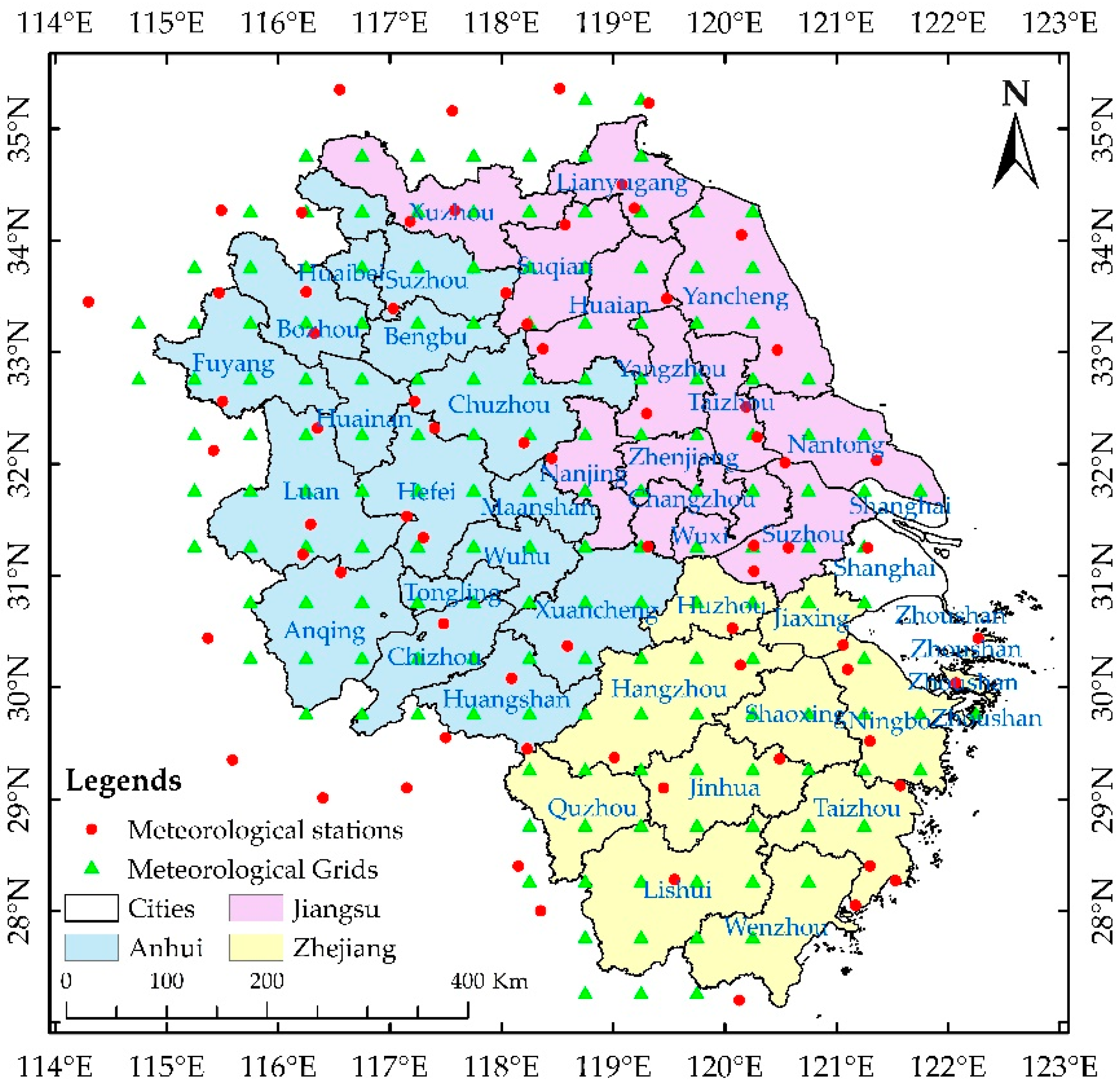
2.2. Observed Meteorological Datasets
2.3. Bias Correction
2.4. Etp Calculation
2.5. Uncertainty Estimation and Decomposition
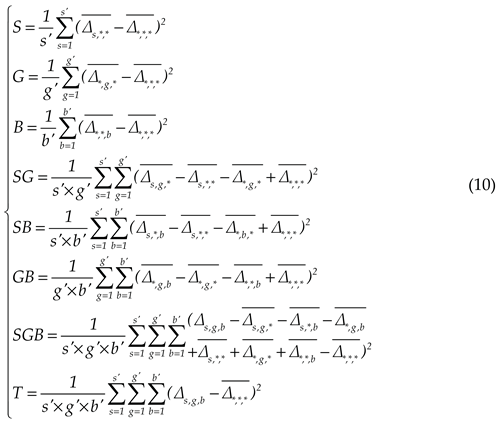
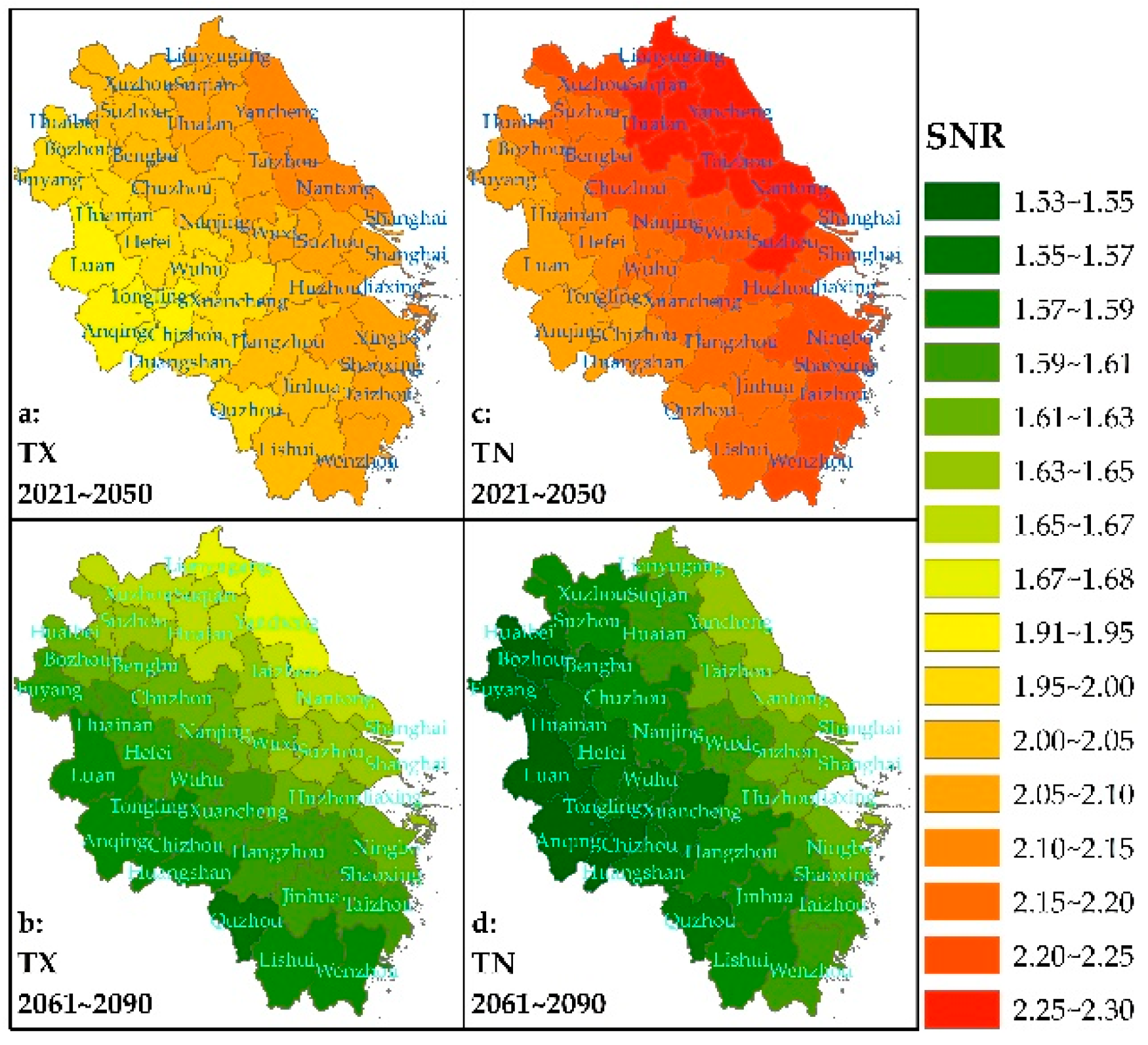
2.6. SNR
2.7. Studying Route
3. Results
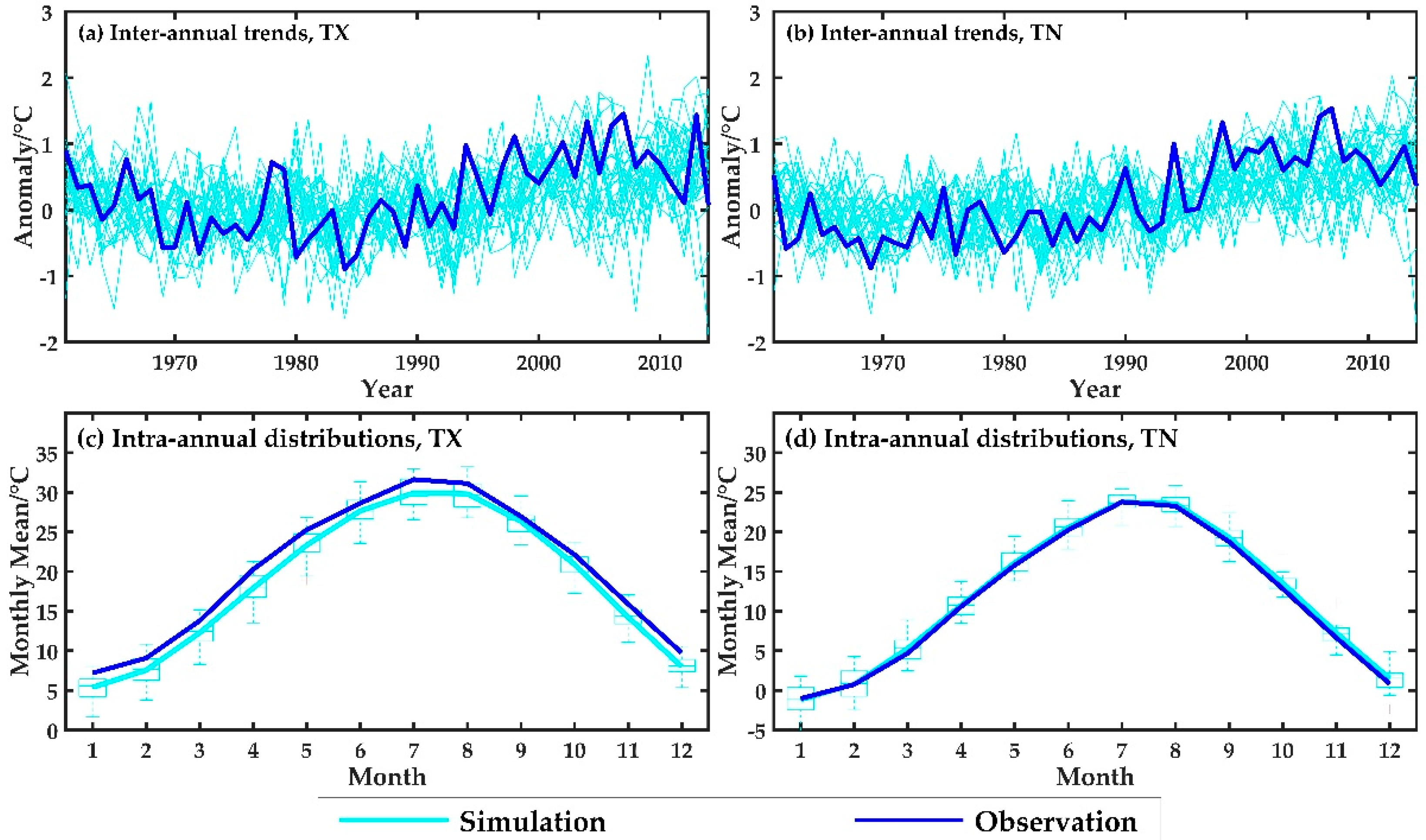
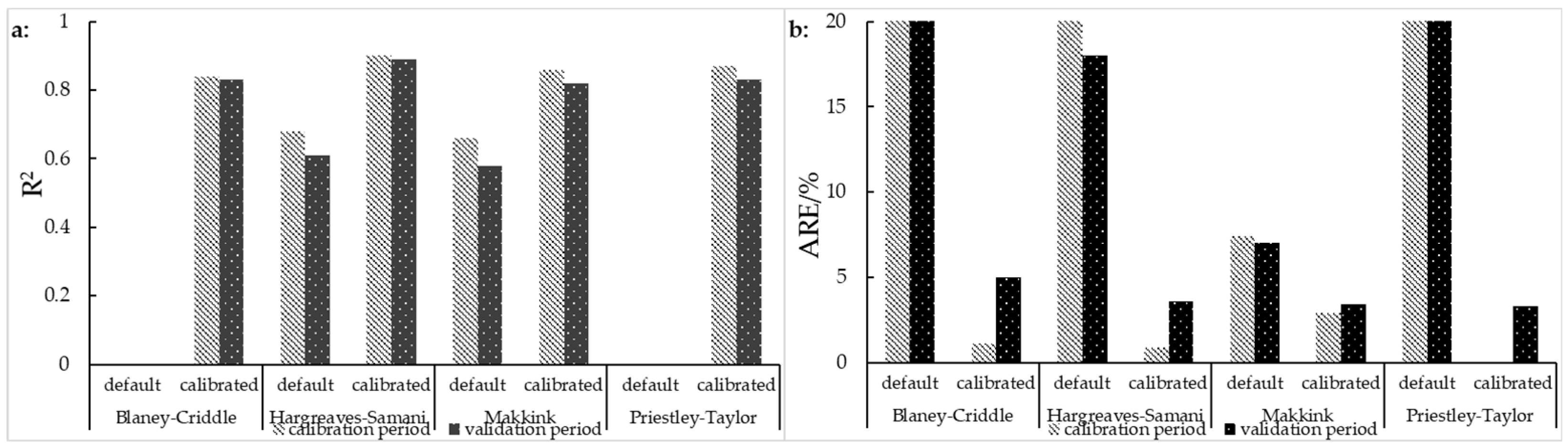
3.1. Performance of GCMs
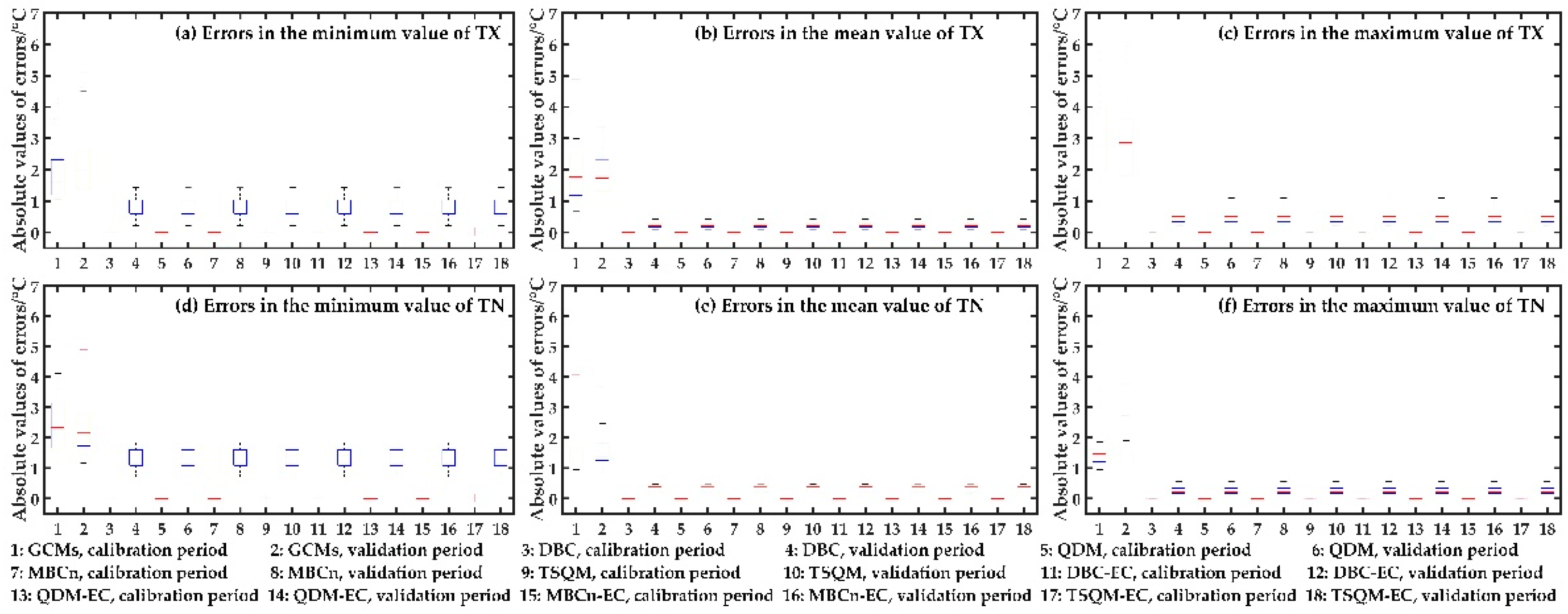
3.2. Performance of Bias Correction Methods
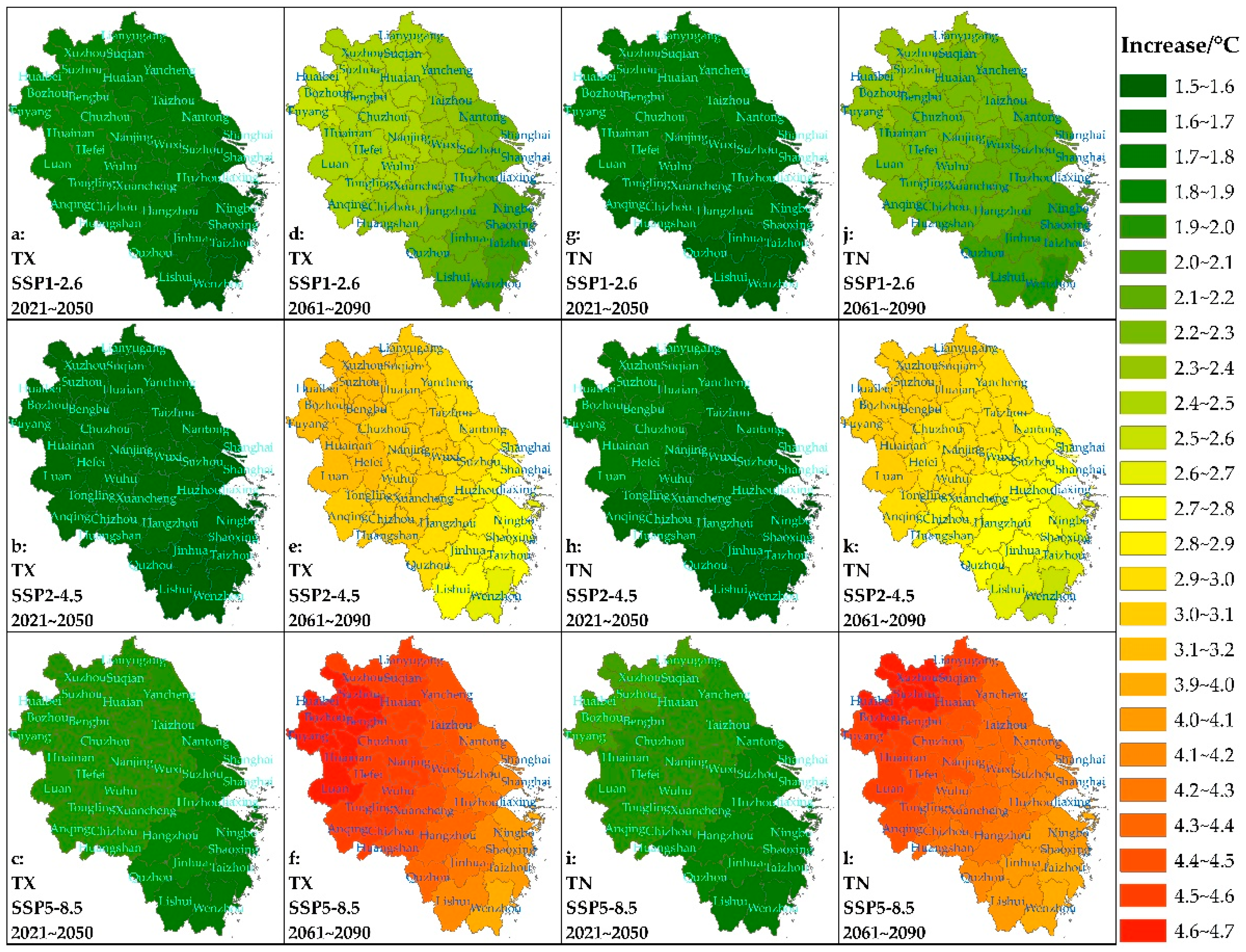
3.3. Temperature Projections
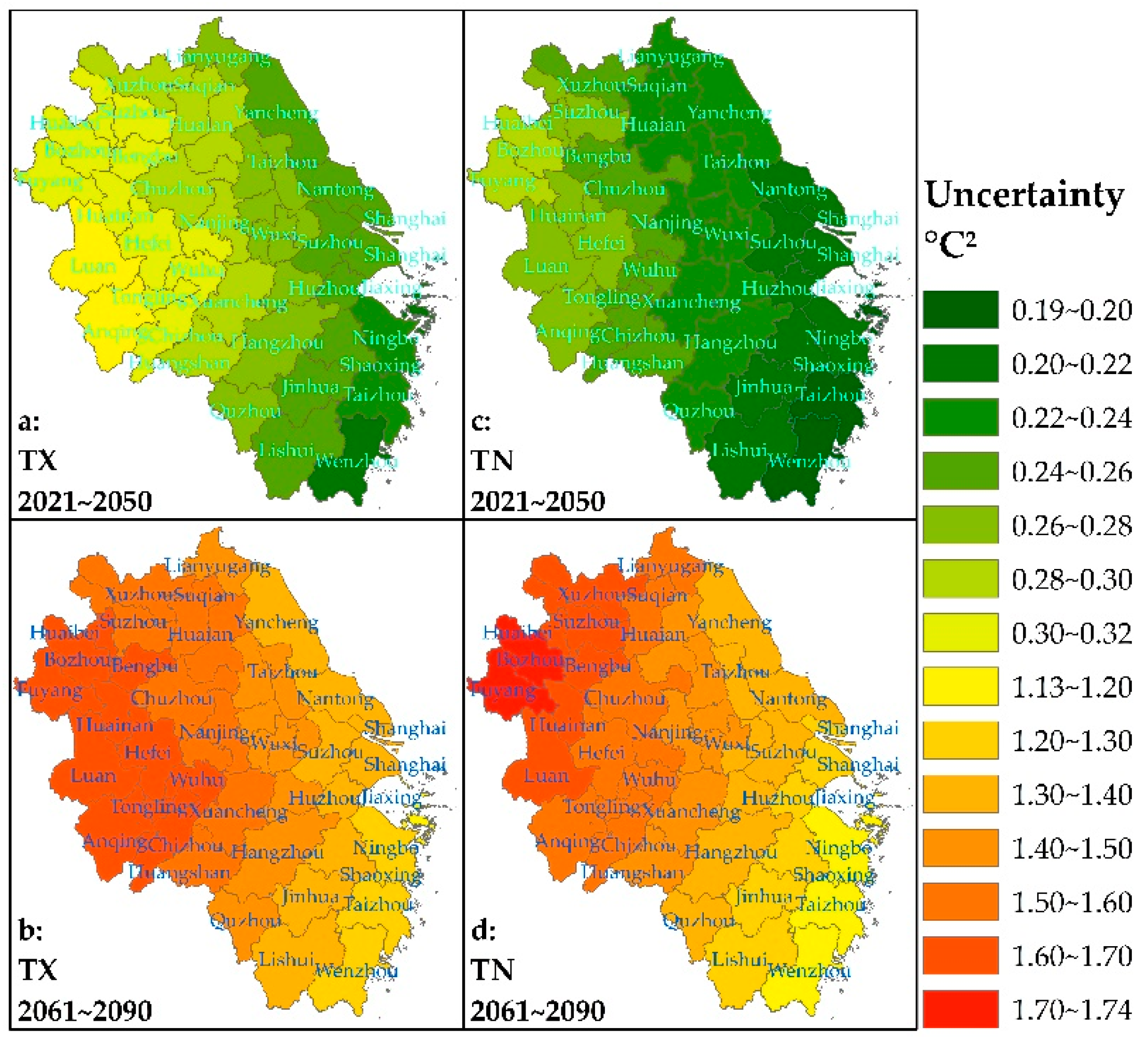
3.4. Uncertainty of Temperature Projections
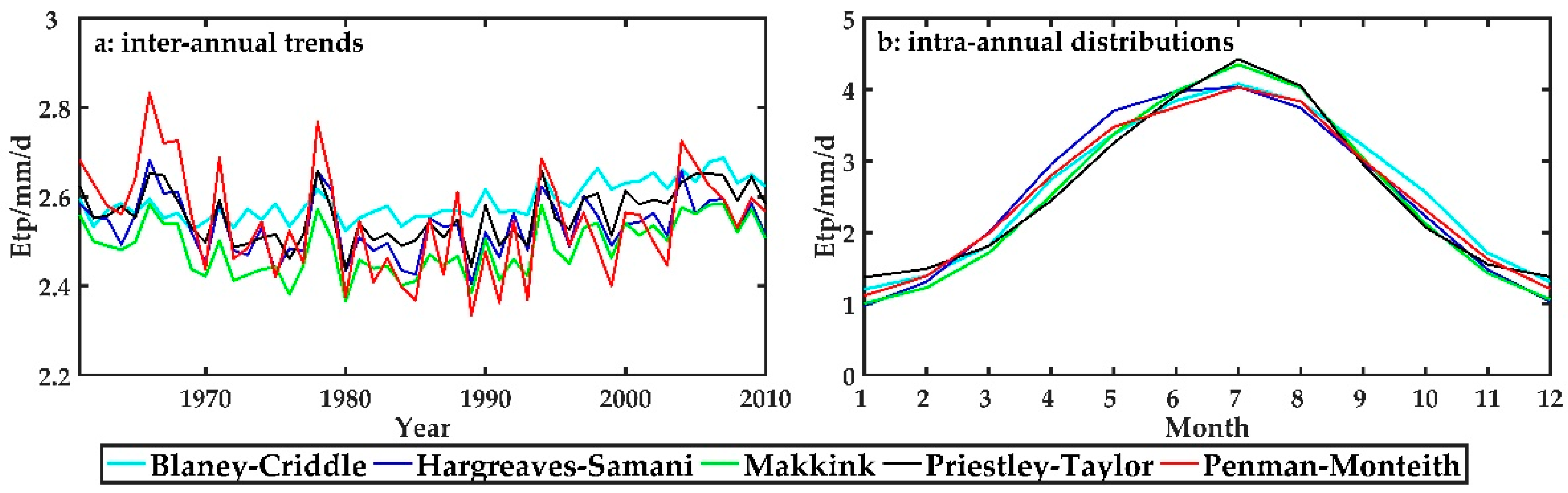
3.5. Performance of the Empirical Etp Calculation Formulas
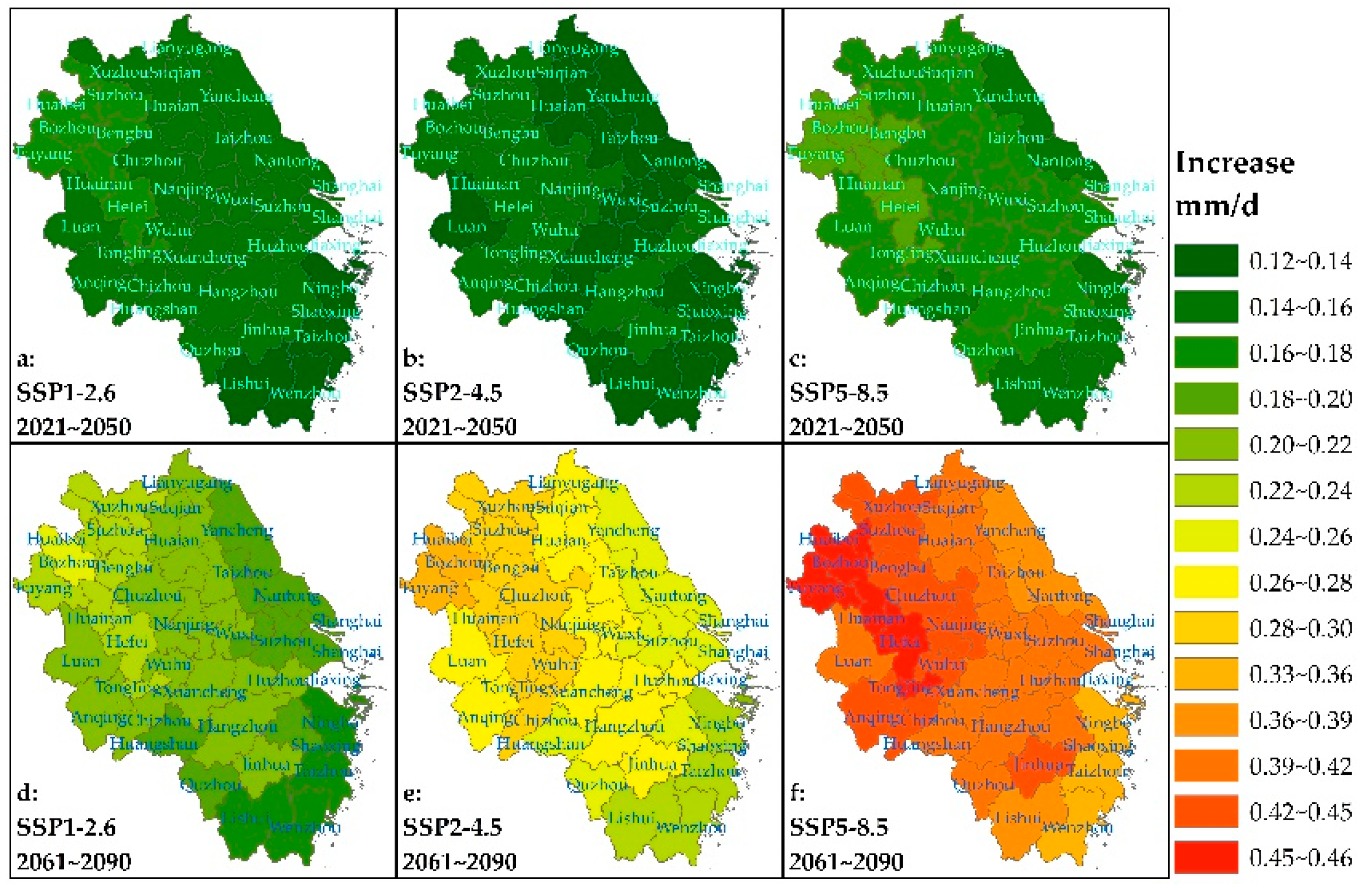
3.6. Etp Projections
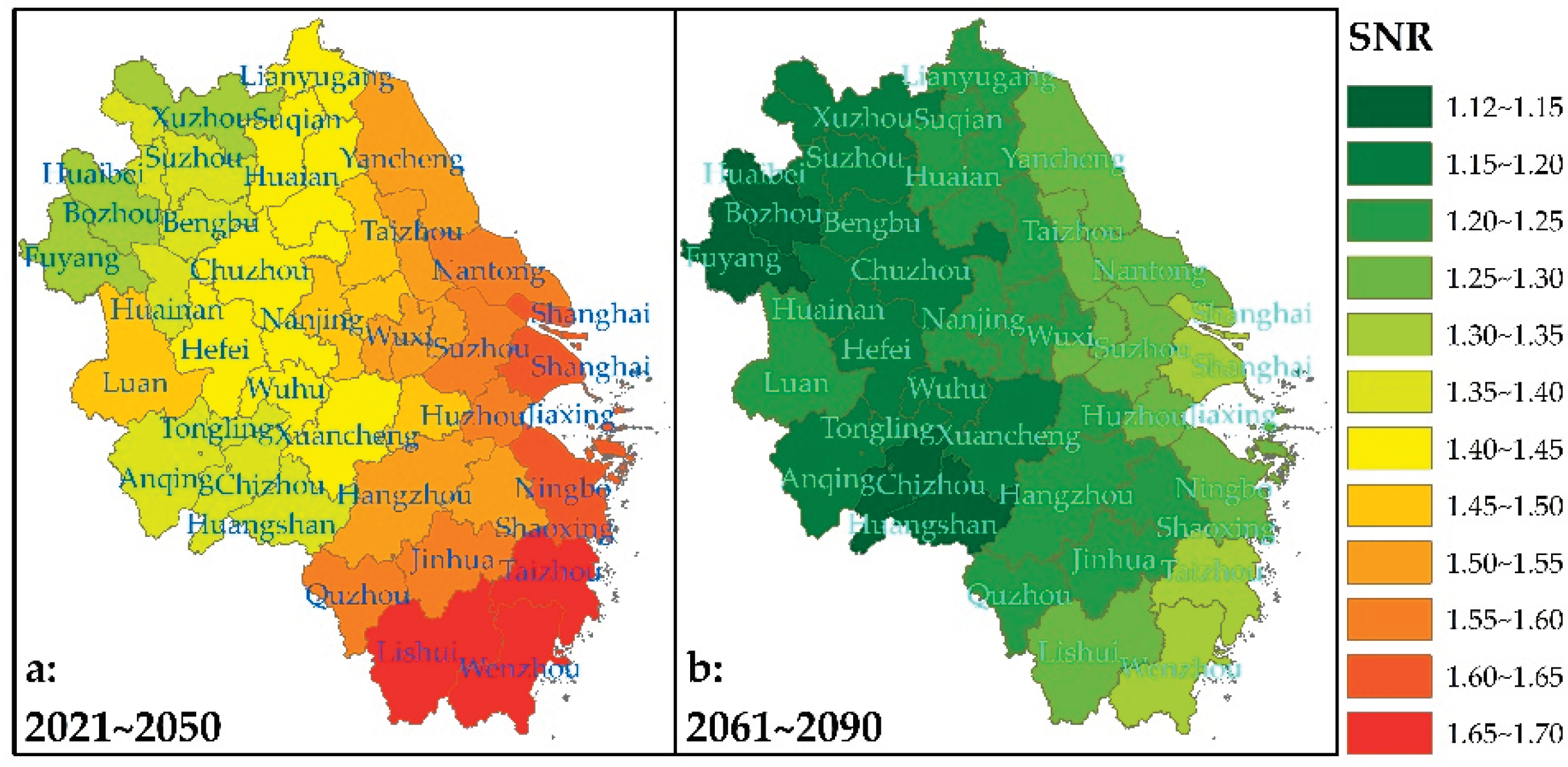
3.7. Uncertainty of Etp Projections
3.8. Discussion
4. Conclusion
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Lu, G.; Wu, Z.; He, H. Hydrological cycle processes and quantitative forecasting; Science Press: Beijing, 2010. [Google Scholar]
- Kirkham, M.B. 26 - Potential Evapotranspiration. In Principles of Soil and Plant Water Relations, Kirkham, M.B., Ed.; Academic Press: Burlington, 2005; pp. 455–468. [Google Scholar]
- Makkink, G. Testing the Penman Formula by Means of Lysimeters. Journal of the Institution of Water Engineers 1957, 11, 277–288. [Google Scholar]
- Monteith, J.L. Evaporation and surface temperature. Quarterly Journal of the Royal Meteorological Society 1981, 107, 1–27. [Google Scholar] [CrossRef]
- Allen, R.G.; Pereira, L.S.; Raes, D.; Smith, M. Crop evapotranspiration-Guidelines for computing crop water requirements. FAO Irrigation and Drainage Paper No. 56; Food and Agriculture Organization of the UN: Rome, Italy, 1998; p. 301. [Google Scholar]
- Oudin, L.; Hervieu, F.; Michel, C.; Perrin, C.; Andréassian, V.; Anctil, F.; Loumagne, C. Which potential evapotranspiration input for a lumped rainfall–runoff model?: Part 2—Towards a simple and efficient potential evapotranspiration model for rainfall–runoff modelling. Journal of Hydrology 2005, 303, 290–306. [Google Scholar] [CrossRef]
- Trajkovic, S. Hargreaves versus Penman-Monteith under Humid Conditions. Journal of Irrigation and Drainage Engineering 2007, 133, 38–42. [Google Scholar] [CrossRef]
- IPCC. Summary for Policymakers. In Climate Change 2021: The Physical Science Basis. Contribution of Working Group I to the Sixth Assessment Report of the Intergovernmental Panel on Climate Change, Masson-Delmotte, V., P. Zhai, A. Pirani, S. L. Connors, C. Péan, S. Berger, N. Caud, Y. Chen, L. Goldfarb, M. I. Gomis, M. Huang, K. Leitzell, E. Lonnoy, J.B.R. Matthews, T. K. Maycock, T. Waterfield, O. Yelek?i, R. Yu and B. Zhou (eds.), Ed.; Cambridge University Press: Cambridge, 2021; pp. 4–5. [Google Scholar]
- Stocker, T. Climate change 2013: the physical science basis: Working Group I contribution to the Fifth assessment report of the Intergovernmental Panel on Climate Change; Cambridge University Press: 2013.
- Shi, L.; Feng, P.; Wang, B.; Li Liu, D.; Cleverly, J.; Fang, Q.; Yu, Q. Projecting potential evapotranspiration change and quantifying its uncertainty under future climate scenarios: A case study in southeastern Australia. Journal of Hydrology 2020, 584, 124756. [Google Scholar] [CrossRef]
- Eyring, V.; Bony, S.; Meehl, G.A.; Senior, C.A.; Stevens, B.; Stouffer, R.J.; Taylor, K.E. Overview of the Coupled Model Intercomparison Project Phase 6 (CMIP6) experimental design and organization. Geoscientific Model Development 2016, 9, 1937–1958. [Google Scholar] [CrossRef]
- O’Neill, B.; Kriegler, E.; Ebi, K.; Kemp-Benedict, E.; Riahi, K.; Rothman, D.; van Ruijven, B.; Vuuren, D.; Birkmann, J.; Kok, K.; et al. The roads ahead: Narratives for shared socioeconomic pathways describing world futures in the 21st century. Global Environmental Change 2015, 42, 169–180. [Google Scholar] [CrossRef]
- Chen, J.; Brissette, F.P.; Leconte, R. Uncertainty of downscaling method in quantifying the impact of climate change on hydrology. Journal of Hydrology 2011, 401, 190–202. [Google Scholar] [CrossRef]
- Cannon, A.; Sobie, S.; Murdock, T. Bias Correction of GCM Precipitation by Quantile Mapping: How Well Do Methods Preserve Changes in Quantiles and Extremes? Journal of Climate 2015, 28, 150722131126009. [Google Scholar] [CrossRef]
- Cannon, A.J. Multivariate quantile mapping bias correction: an N-dimensional probability density function transform for climate model simulations of multiple variables. Climate Dynamics 2018, 50, 31–49. [Google Scholar] [CrossRef]
- Guo, Q.; Chen, J.; Zhang, X.; Shen, M.; Chen, H.; Guo, S. A new two-stage multivariate quantile mapping method for bias correcting climate model outputs. Climate Dynamics 2019, 53, 3603–3623. [Google Scholar] [CrossRef]
- Bárdossy, A.; Pegram, G.G.S. Copula based multisite model for daily precipitation simulation. Hydrology and Earth System Sciences 2009, 13, 2299–2314. [Google Scholar] [CrossRef]
- Rüschendorf, L. On the distributional transform, Sklar's theorem, and the empirical copula process. Journal of Statistical Planning and Inference 2009, 139, 3921–3927. [Google Scholar] [CrossRef]
- Li, X.; Babovic, V. Multi-site multivariate downscaling of global climate model outputs: an integrated framework combining quantile mapping, stochastic weather generator and Empirical Copula approaches. Climate Dynamics 2019, 52, 5775–5799. [Google Scholar] [CrossRef]
- Li, X.; Babovic, V. A new scheme for multivariate, multisite weather generator with inter-variable, inter-site dependence and inter-annual variability based on empirical copula approach. Climate Dynamics 2019, 52, 2247–2267. [Google Scholar] [CrossRef]
- Fan, X.; Miao, C.; Duan, Q.; Shen, C.; Wu, Y. The Performance of CMIP6 Versus CMIP5 in Simulating Temperature Extremes Over the Global Land Surface. Journal of Geophysical Research: Atmospheres 2020, 125, e2020JD033031. [Google Scholar] [CrossRef]
- Tokarska, K.B.; Stolpe, M.B.; Sippel, S.; Fischer, E.M.; Smith, C.J.; Lehner, F.; Knutti, R. Past warming trend constrains future warming in CMIP6 models. Science advances 2020, 6, eaaz9549. [Google Scholar] [CrossRef] [PubMed]
- Zelinka, M.D.; Myers, T.A.; McCoy, D.T.; Po-Chedley, S.; Caldwell, P.M.; Ceppi, P.; Klein, S.A.; Taylor, K.E. Causes of Higher Climate Sensitivity in CMIP6 Models. Geophysical Research Letters 2020, 47, e2019GL085782. [Google Scholar] [CrossRef]
- Kay, A.L.; Davies, H.N. Calculating potential evaporation from climate model data: A source of uncertainty for hydrological climate change impacts. Journal of Hydrology 2008, 358, 221–239. [Google Scholar] [CrossRef]
- Hargreaves, G.H.; Samani, Z.H. Reference Crop Evapotranspiration from Temperature. Applied Engineering in Agriculture 1985, 1, 96–99. [Google Scholar] [CrossRef]
- DehghaniSanij, H.; Yamamoto, T.; Rasiah, V. Assessment of evapotranspiration estimation models for use in semi-arid environments. Agricultural Water Management 2004, 64, 91–106. [Google Scholar] [CrossRef]
- Lu, J.; Sun, G.; McNulty, S.G.; Amatya, D.M. A COMPARISON OF SIX POTENTIAL EVAPOTRANSPIRATION METHODS FOR REGIONAL USE IN THE SOUTHEASTERN UNITED STATES1. JAWRA Journal of the American Water Resources Association 2005, 41, 621–633. [Google Scholar] [CrossRef]
- Vicente-Serrano, S.M.; Beguería, S.; López-Moreno, J.I. A Multiscalar Drought Index Sensitive to Global Warming: The Standardized Precipitation Evapotranspiration Index. Journal of Climate 2010, 23, 1696–1718. [Google Scholar] [CrossRef]
- Beguería, S.; Vicente-Serrano, S.M.; Reig, F.; Latorre, B. Standardized precipitation evapotranspiration index (SPEI) revisited: parameter fitting, evapotranspiration models, tools, datasets and drought monitoring. International Journal of Climatology 2014, 34, 3001–3023. [Google Scholar] [CrossRef]
- Thompson, J.R.; Green, A.J.; Kingston, D.G. Potential evapotranspiration-related uncertainty in climate change impacts on river flow: An assessment for the Mekong River basin. Journal of Hydrology 2014, 510, 259–279. [Google Scholar] [CrossRef]
- Xu, C.Y.; Singh, V.P. Cross Comparison of Empirical Equations for Calculating Potential Evapotranspiration with Data from Switzerland. Water Resources Management 2002, 16, 197–219. [Google Scholar] [CrossRef]
- Xu, C.Y.; Singh, V.P. Evaluation and generalization of radiation-based methods for calculating evaporation. Hydrological Processes 2000, 14, 339–349. [Google Scholar] [CrossRef]
- Xu, C.Y.; Singh, V.P. Evaluation and generalization of temperature-based methods for calculating evaporation. Hydrological Processes 2001, 15, 305–319. [Google Scholar] [CrossRef]
- Roberts, J.; Snelgrove, K. Uncertainty in Regional Climate Model Mean Runoff Projections under Climate Change: Case Study of Labrador's Churchill River Basin. Atmosphere-Ocean 2015, 53, 1–13. [Google Scholar] [CrossRef]
- Troin, M.; Arsenault, R.; Martel, J.-L.; Brissette, F. Uncertainty of Hydrological Model Components in Climate Change Studies over Two Nordic Quebec Catchments. Journal of Hydrometeorology 2017, 19, 27–46. [Google Scholar] [CrossRef]
- Chegwidden, O.S.; Nijssen, B.; Rupp, D.E.; Arnold, J.R.; Clark, M.P.; Hamman, J.J.; Kao, S.-C.; Mao, Y.; Mizukami, N.; Mote, P.W.; et al. How Do Modeling Decisions Affect the Spread Among Hydrologic Climate Change Projections? Exploring a Large Ensemble of Simulations Across a Diversity of Hydroclimates. Earth's Future 2019, 7, 623–637. [Google Scholar] [CrossRef]
- Fisher, R.A. The correlation between relatives on the supposition of Mendelian inheritance. Earth and Environmental Science Transactions of the Royal Society of Edinburgh 1918, 52, 399–433. [Google Scholar] [CrossRef]
- Hawkins, E.; Sutton, R. The potential to narrow uncertainty in regional climate predictions. Bulletin of the American Meteorological Society 2009, 90, 1095–1108. [Google Scholar] [CrossRef]
- Chen, J.; Brissette, F.; Lucas-Picher, P. Assessing the limits of bias correcting climate model outputs for climate change impact studies. Journal of Geophysical Research: Atmospheres 2015, 120, 1123–1136. [Google Scholar] [CrossRef]
- Hui, Y.; Chen, J.; Xu, C.-Y.; Xiong, L.; Chen, H. Bias nonstationarity of global climate model outputs: The role of internal climate variability and climate model sensitivity. International Journal of Climatology 2019, 39, 2278–2294. [Google Scholar] [CrossRef]
- Matthews, J.B.R. ; V. Möller; R. van Diemen; J.S. Fuglestvedt; V. Masson-Delmotte; C. Méndez; S. Semenov; Reisinger, A.; (eds.). Annex VII: Glossary In Climate Change 2021: The Physical Science Basis. Contribution of Working Group I to the Sixth Assessment Report of the Intergovernmental Panel on Climate Change, 2021. [Google Scholar]
- Wang, W.; Xing, W.; Shao, Q. How large are uncertainties in future projection of reference evapotranspiration through different approaches? Journal of Hydrology 2015, 524, 696–700. [Google Scholar] [CrossRef]
- Bosshard, T.; Carambia, M.; Goergen, K.; Kotlarski, S.; Krahe, P.; Zappa, M.; Schär, C. Quantifying uncertainty sources in an ensemble of hydrological climate-impact projections. Water Resources Research 2013, 49, 1523–1536. [Google Scholar] [CrossRef]
- Wang, H.-M.; Chen, J.; Xu, C.-Y.; Zhang, J.; Chen, H. A Framework to Quantify the Uncertainty Contribution of GCMs Over Multiple Sources in Hydrological Impacts of Climate Change. Earth's Future 2020, 8, e2020EF001602. [Google Scholar] [CrossRef]
- Zhang, S.; Chen, J.; Gu, L. Overall uncertainty of climate change impacts on watershed hydrology in China. International Journal of Climatology 2021, 42, 1–14. [Google Scholar] [CrossRef]
- Kingston, D.G.; Todd, M.C.; Taylor, R.G.; Thompson, J.R.; Arnell, N.W. Uncertainty in the estimation of potential evapotranspiration under climate change. Geophysical Research Letters 2009, 36, 1–6. [Google Scholar] [CrossRef]

| Number | Name | Horizontal resolution | Organization/country (region) |
|---|---|---|---|
| Longitude × Latitude | |||
| 1 | ACCESS-CM2 | 1.8750° × 1.25° | CSIRO-ARCCSS/ Australia |
| 2 | ACCESS-ESM1-5 | 1.8750° × 1.25° | CSIRO/ Australia |
| 3 | BCC-CSM2-MR | 1.125° × 1.1213° | BCC/China |
| 4 | CanESM5 | 2.8125° × 2.7893° | CCCma/Canada |
| 5 | CMCC-CM2-SR5 | 1.25° × 0.9424° | CMCC/ Italy |
| 6 | CNRM-CM6-1 | 1.4063° × 1.4004° | CNRM-CERFACS/ France |
| 7 | CNRM-ESM2-1 | 1.4063° × 1.4004° | CNRM-CERFACS/ France |
| 8 | EC-Earth3 | 0.7031° × 0.7017° | EC-Earth-Consortium/ European Union |
| 9 | EC-Earth3-Veg | 0.7031° × 0.7017° | EC-Earth-Consortium/ European Union |
| 10 | FGOALS-g3 | 2° × 2.2785° | CAS/China |
| 11 | GFDL-ESM4 | 1.25° × 1° | NOAA-GFDL/America |
| 12 | HadGEM3-GC31-LL | 1.8750° × 1.25° | MOHC/England |
| 13 | INM-CM4-8 | 2° × 1.5° | INM/Russia |
| 14 | INM-CM5-0 | 2° × 1.5° | INM/Russia |
| 15 | IPSL-CM6A-LR | 2.5° × 1.2676° | IPSL/France |
| 16 | MIROC6 | 1.4063° × 1.4004° | MIROC/Japan |
| 17 | MIROC-ES2L | 2.8125° × 2.7893° | MIROC/Japan |
| 18 | MPI-ESM1-2-HR | 0.9375° × 0.9349° | MPI-M/ Germany |
| 19 | MPI-ESM1-2-LR | 1.875° × 1.8647° | MPI-M/ Germany |
| 20 | MRI-ESM2-0 | 1.1250° × 1.1213° | MRI/Japan |
| 21 | NESM3 | 1.875° × 1.8647° | NUIST/China |
| 22 | NorESM2-LM | 2.5° × 1.8947° | NCC/ Norway |
| 23 | NorESM2-MM | 1.25° × 0.9424° | NCC/ Norway |
| 24 | UKESM1-0-LL | 1.875° × 1.25° | MOHC/England |
| Period | 2021~2050 | ||||||
|---|---|---|---|---|---|---|---|
| Effect | S | G | B | SG | SB | GB | SGB |
| TX/Magnitude/°C2 | 0.01 | 0.25 | 0.00 | 0.01 | 0.00 | 0.00 | 0.00 |
| TN/Magnitude/°C2 | 0.01 | 0.21 | 0.00 | 0.01 | 0.00 | 0.00 | 0.00 |
| TX/Relative contribution/% | 4.93 | 90.76 | 0.00 | 4.31 | 0.00 | 0.00 | 0.00 |
| TN/Relative contribution/% | 5.58 | 89.68 | 0.00 | 4.75 | 0.00 | 0.00 | 0.00 |
| Period | 2061~2090 | ||||||
| Effect | S | G | B | SG | SB | GB | SGB |
| TX/Magnitude/°C2 | 0.75 | 0.66 | 0.00 | 0.07 | 0.00 | 0.00 | 0.00 |
| TN/Magnitude/°C2 | 0.79 | 0.60 | 0.00 | 0.05 | 0.00 | 0.00 | 0.00 |
| TX/Relative contribution/% | 50.79 | 44.31 | 0.00 | 4.90 | 0.00 | 0.00 | 0.00 |
| TN/Relative contribution/% | 55.06 | 41.30 | 0.00 | 3.64 | 0.00 | 0.00 | 0.00 |
| Type | Period | S | G | B | E | SG | SB | SE | GB |
|---|---|---|---|---|---|---|---|---|---|
| Magnitude/(mm/d)2 | 2021~2050 | 0.0001 | 0.0025 | 0.0000 | 0.0010 | 0.0001 | 0.0000 | 0.0000 | 0.0000 |
| 2061~2090 | 0.0071 | 0.0077 | 0.0000 | 0.0042 | 0.0011 | 0.0000 | 0.0006 | 0.0000 | |
| Relative contribution/% | 2021~2050 | 3.24 | 62.54 | 0.05 | 24.24 | 2.86 | 0.00 | 0.37 | 0.08 |
| 2061~2090 | 33.76 | 35.59 | 0.04 | 18.26 | 4.76 | 0.01 | 2.81 | 0.03 | |
| Type | Period | GE | BE | SGB | SGE | SBE | GBE | SGBE | |
| Magnitude/(mm/d)2 | 2021~2050 | 0.0002 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | |
| 2061~2090 | 0.0009 | 0.0000 | 0.0000 | 0.0002 | 0.0000 | 0.0000 | 0.0000 | ||
| Relative contribution/% | 2021~2050 | 5.93 | 0.05 | 0.02 | 0.51 | 0.00 | 0.09 | 0.02 | |
| 2061~2090 | 3.93 | 0.04 | 0.01 | 0.70 | 0.00 | 0.05 | 0.01 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).




