Prerpints.org logo
Preprint
Article

Characterization of Orbital Angular Momentum Beams by Polar Mapping and Fourier Transform

Altmetrics

Downloads

121

Views

44

Comments

0

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

16 February 2024

Posted:

19 February 2024

You are already at the latest version

Alerts
Abstract
Recognition, decoding and tracking of vortex patterns is of increasing importance in many fields reaching from astronomical observation of distant galaxies to turbulence phenomena in liquids or gases. Currently, coherent light beams with orbital angular momentum (OAM) are of particular interest for optical communication, metrology, micro-machining or particle manipulation. One common task is to identify characteristic spiral patterns in pixelated intensity maps at real-world signal-to-noise ratios. Recently, Fast Fourier Transform (FFT) was applied to the quantitative analysis of spiral interference patterns of OAM beams. Our study considers this approach in more detail. It is demonstrated that specific information can be extracted by combining conformal mapping by polar transform with determining one- or two-dimensional angular frequency spectra either in spatially fixed or scanning mode. Results of proof-of-principle experiments are presented.
Keywords: 
Subject: Physical Sciences  -   Optics and Photonics

1. Introduction

Vortex patterns appear on many scales in nature from spiral galaxies [1] and sunspots [2] over hurricanes [3], shells [4], or flower architectures to spiral waves in chemistry [5], double-helix molecules and magnetic skyrmions [6], to mention only a few. Their fast and reliable recognition and tracking at low intensity and/or in the presence of noise is a challenging task. Currently, optical communication systems on the basis of orbital angular momentum (OAM) [7,8,9] or polarization singularities are of rapidly increasing interest because of exploiting additional degrees of freedom and promising robust free-space [10,11] or fiber-based [12,13] data transfer. Such techniques require efficient methods not only for the adaptive generation, encoding, multiplexing, and propagation of OAM modes but also for the detection and decoding of two-dimensional optical vortex patterns even in the case of turbulence, scattering or absorption in atmosphere, ocean, waveguides or fibers. Simulations of the evolution of spiral spectra during the propagation in turbulent suggest the existence of optimum parameters for minimum distortion of data transfer via OAM encoding [14]. The experimental verification of such theoretical predictions, however, requires appropriate, structural selective detection techniques.
OAM beams are, in the simplest case, characterized by helical wavefronts twisted around a central singularity [7,8,9]. In particular, Laguerre-Gauss beams with non-zero topological charges l represent beams of helical structure. The topological charge counts the number of intertwined rotated wavefronts and is thus a measure for the OAM density. The direction of wavefront rotation is indicated by the sign of l. Circular OAM beams of ring shape can be sorted by their diameter [15] which increases depending on l. In general, the reliability of the method is rather limited because of the geometrical similarity of rings. The interference of an OAM beam with a reference phase leads to characteristic spiral patterns which unambiguously can be distinguished [16]. Therefore, the recognition of spiral shapes and counting the number of spiral arms is an alternative approach for tracking, sorting and decoding OAM beams [17,18].
The task of spiral analysis is well known from various areas. In fluid dynamics, complex vector fields are described on the basis of the Helmholtz-Hodge decomposition which separates divergence-free and rotation-free components [19,20]. Moreover, vortex cores are located and tracked on the basis of the Navier-Stokes equation [21]. Software for fluid vortex fitting and tracking based on the Lamb-Oseen vortex model for the flow velocity distribution was developed [22].
In astronomy, distant spiral galaxies have to be identified and classified while often detecting only a few photons. The large number of objects requires automated alogorithms for spiral arm analysis, e.g. based on random forests [23]. Among the mathematical methods applied to this field, Fourier transform was one of the most promising approaches [24,25,26]. The capability of Fourier transform to extract specific spirality information and to distinguish between parabolic, Archimedian and logarithmic spirals from spiral lattices in selected botanical specimens was successfully demonstrated [27]. Because of the pixelated geometry of matrix detectors and digital phase shapers, studies of discrete spiral analysis are of relevance.
With the fast development of OAM-based optical communication, appropriate mathematical methods for reliably recognizing spiral features became especially important. To select characteristic rotational features, intensity maps have to be processed by appropriate transformations. For example, Laguerre-Gaussian transform analysis [28] was applied to the optical vortex tracking [29]. With generalized log-polar transformation, high-resolution OAM mode sorting was realized by conformally mapping logarithmic spirals to parallel lines [30,31]. Hough transform algorithms also enable to identify spiral shapes [32]. Further common techniques for OAM mode sorting are rotational Doppler measurements [33], holography [34,35,36], or Shack-Hartmann wavefront sensing [37,38,39].
Recently, the authors proposed a method for determining the topological charge of OAM beams based on rotational cuts and one-dimensional Fourier transform (1DFFT) [17]. In this case, background scattering of a Gaussian beam at a spatial light modulator (SLM) was used as a coherent reference wave to generate spiral-shaped interference patterns. A similar mathematical approach based on Fourier transform along circles was utilized by other authors [40]. The extraction of radial and azimuthal information on modal oscillations was demonstrated [41]. With extended Fourier methods like Kramers-Kronig interferometry [42], even a single-shot spectrum analysis of OAM beams with full amplitude and phase retrieval can be obtained.
Here we report on two different techniques which represent extensions of previously reported FFT along circular cuts [17]. In the following, these methods will be referred to as Fixed Circle Fourier Transform (FCFT) and Scanning Circle Fourier Transform (SCFT), depending on a static or scanning operation mode. The application of both methods to coherent OAM beams shaped by a high-resolution spatial light modulator will be discussed. Specific capabilities, advantages and disadvantages of the different approaches will be addressed.

2. Principle of Fixed Circle and Scanning Circle Fourier Transform Methods

Both methods extract specific information on spatial modes of structured beams, in particular the topological charge (TC) of OAM beams, via Fourier Transform of spiral-shaped two-dimensional intensity maps detected by a matrix camera. Distinct spiral geometries can be obtained by interference of OAM beams with reference beams. For sufficiently extended Gaussian beams, the interference can approximately be described by interference with a plane reference wave. At normal incidence, the resulting intensity pattern has a circular structure with a number of l spiral arms [43,44,45,46]. The intensity variation with the azimuthal angle θ can be described for the ideal case [45] by the theoretical dependence
1 + e i l θ 2 ~ 4 cos 2 ( i l θ 2 )
where l denotes the topological charge. Similar interference patterns are generated with spherical reference waves [45].
For a Fourier analysis of interference maps, different strategies are pursued:
(i) The FCFT method determines the angular frequency spectrum of interference patterns of interest along concentric circles around their center of gravity (COG) and calculating the Fourier Transform of this discrete data set. The COG is typically identical to a singularity position. For an optimum performance, the radius of the circle has to be varied until the number of intensity lobes and the corresponding frequency peaks (modes) converge. Thus, the main free parameter is the circle radius r.
(ii) The SCFT method extends the FCFT method by additionally scanning the signal map by shifting the centers of the circles and again calculating the Fourier Transform along circles as for FCFT. The variable parameters are the coordinates (x,y) for the centers of circles and circle radii r.
For keeping the comparability of circular cuts of different length caused by different radii, equal angular steps are chosen within each set of measurements.
The geometric situations of both methods are schematically depicted in Figure 1. As realistic example, the spiral-shaped interference pattern of an OAM beam of a TC of l = +10 with a coherent, slightly distorted Gaussian background was chosen (Figure 1a).
Fourier Transform is performed along concentric circular cuts for FCFT (Figure 1b) or by sampling a detector plane by a matrix of circular cuts around variable (x,y)-coordinates (SCFT, Figure 1c). The advantage of the SCFT approach is to cover more image information, however for the price of enhancing the number of steps. The maximum radius of the circles determines the maximum possible scan area for full uncut 360° circles. FCFT requires a high accuracy in predefining the singularity position. SCTF works in sequential operation mode and needs to be fast enough to tolerate typical distortions in real-world applications, e.g. by turbulence. For a reliable identification of the sign of the TC by recognizing the rotational orientation of spiral patterns, two or more circular cuts with different radii are required for each singularity position if shape distortions can be tolerated.
For the detection with a pixelated detector, the minimum step widths of radius and position are physically limited by the pixel pitch. In case of SCFT, the usable area for complete circular cuts depends on the radius of the sampling circles. For areas closer to the rim, different strategies can be applied, e.g. by analyzing incomplete or adaptively reducing the radius.
SCFT provides more detailed information as FCFT and enables to extract the coordinates of singularities. Therefore, it is particularly interesting for characterizing or decoding arrays of OAM beams and mode sorting. Compared to the quasi stationary analysis with FCFT, the effort for programming is higher. If FCFT is combined with standard software to determine centers of gravity of spiral patterns (as available from Shack-Hartmann sensors), the method should also be applicable to the characterization of arrays of OAM beams.

3. Experimental Techniques

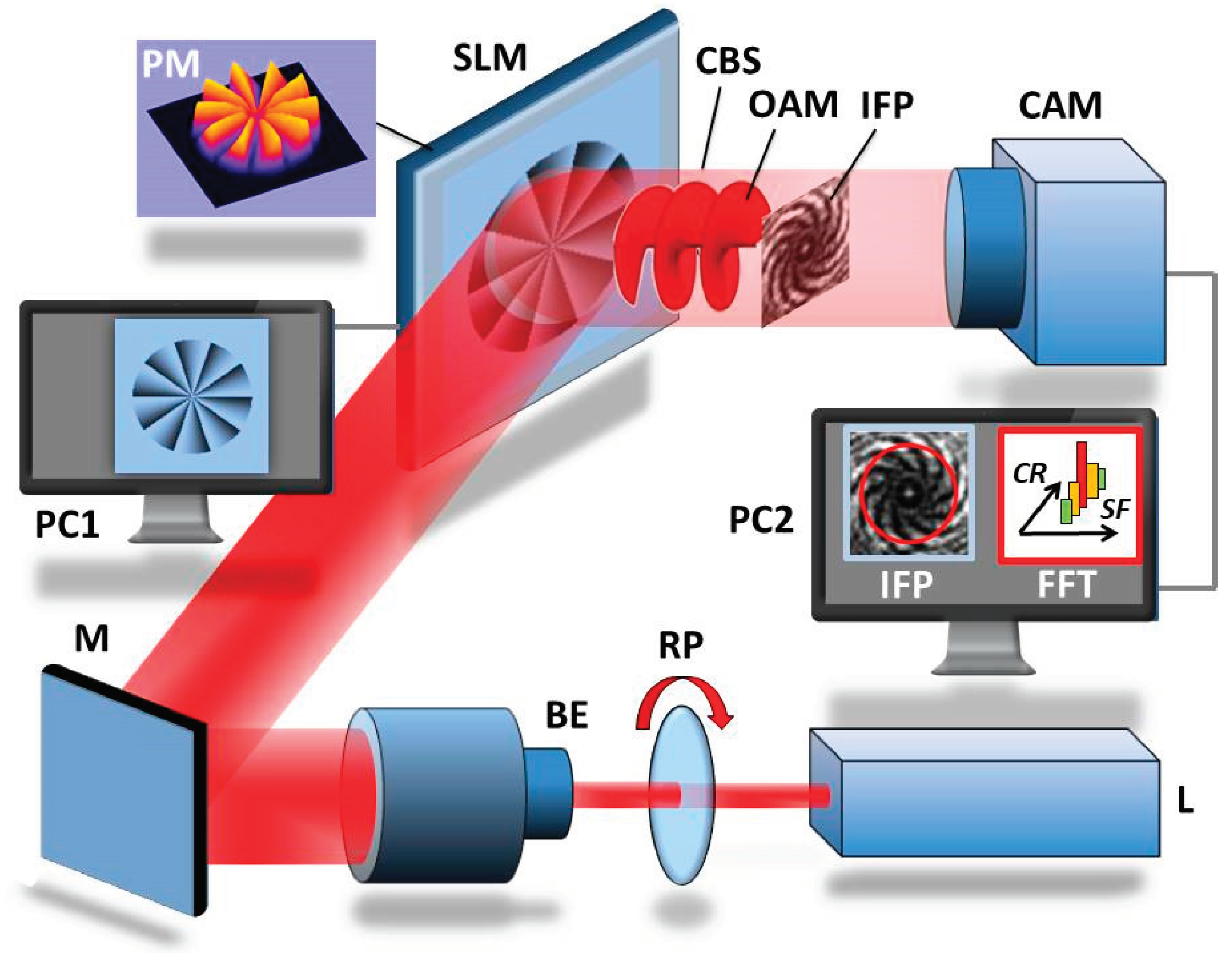
Single and array-shaped OAM-beams were generated by programming helical phase distributions in calibrated grey-scale maps of a 10-Megapixel phase-only, reflective liquid-crystal-on-silicon (LCoS-) SLM (GAEA, HOLOEYE Photonics) with parallel-aligned liquid crystals which was illuminated by the 5x expanded beam of a linearly polarized Ti:sapphire laser oscillator (center wavelength about 800 nm) [17]. The structured beams were detected by a highly sensitive, near-infrared-enhanced, black-and-white CMOS camera (Thorlabs, DCC 324ONN, 1280 x 1024 pixels, 60 fps). A rotatable polarizer in front of the SLM and additional filters in front of the camera were used for a fine-tuning of the intensity to avoid saturation effects. Because of the interference of the OAM beams with the background signal resulting from the limited fill factor of the SLM, the characteristic spiral patterns appeared as theoretically predicted. Programming of the SLM and the analysis of the image data were performed by two separated computers. The setup is depicted schematically in Figure 2.
The subsequent steps of image processing for the different approaches are presented in the following.

4. Results and Discussion

4.1. Fixed Circle Fourier Transform

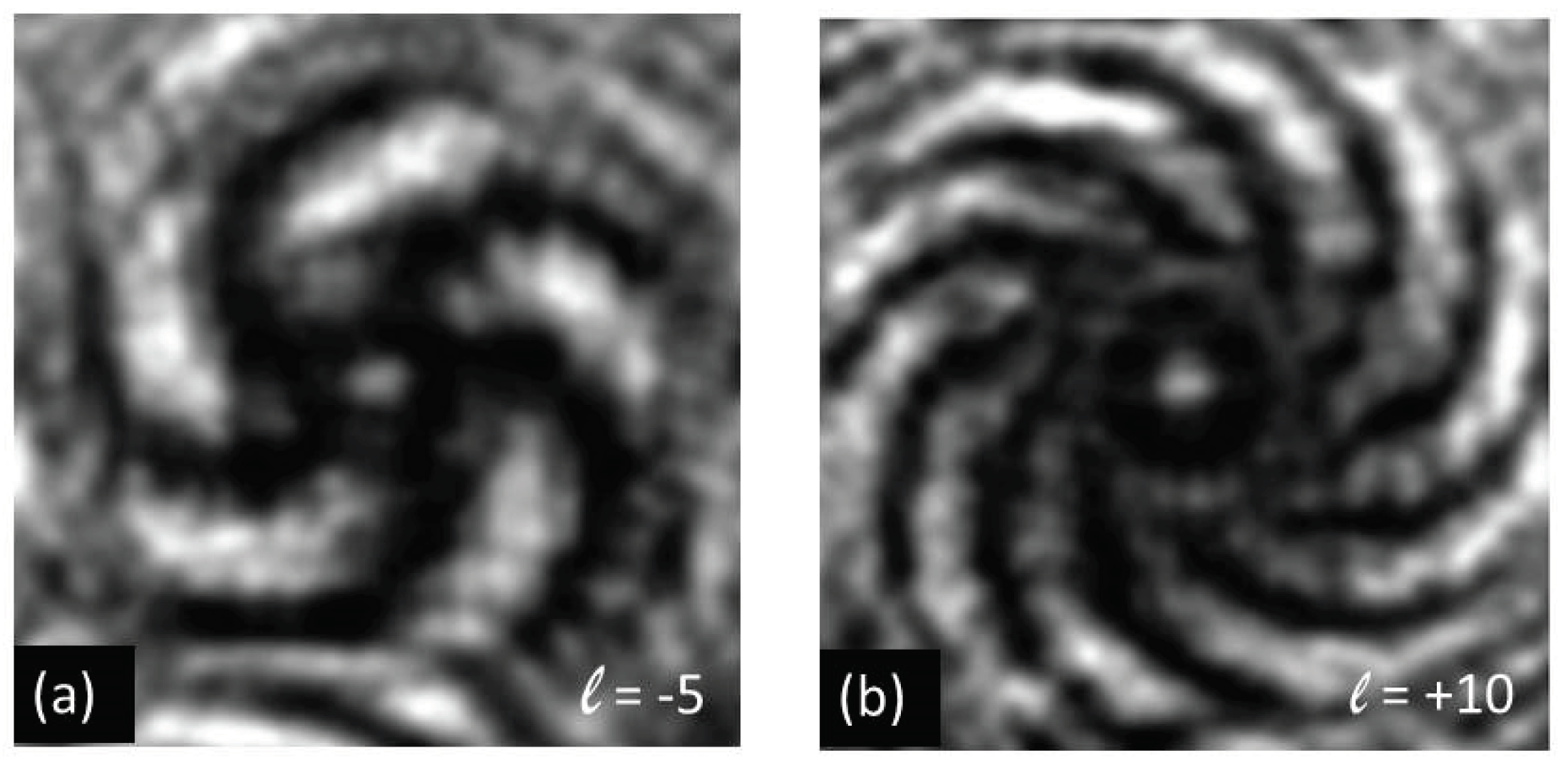
The first step in FCFT is the rotation of a radial cut of a given length at a given rotational direction around a predefined (or automatically determined) center of gravity in discrete angular steps and the transformation of polar data into a 2D matrix [17]. This data matrix contains the radius (from zero to a maximum value) and the rotation angle as parameters. For a complete rotation cycle over 360° it visualizes the number of interference fringes which directly yields information on the topological charge, its sign and possible radial changes of the slope, indicating radial variations of propagation angles (analogous to a thread pitch). In Figure 3a,b, two selected measured interference patterns for OAM beams with topological charges of TC = -5 and TC = +10 are plotted. Corresponding 2D maps from full-circle rotational cuts are compared with each other in Figure 4a,b. Visible distortions were caused by speckles and further interference effects in the optical system.
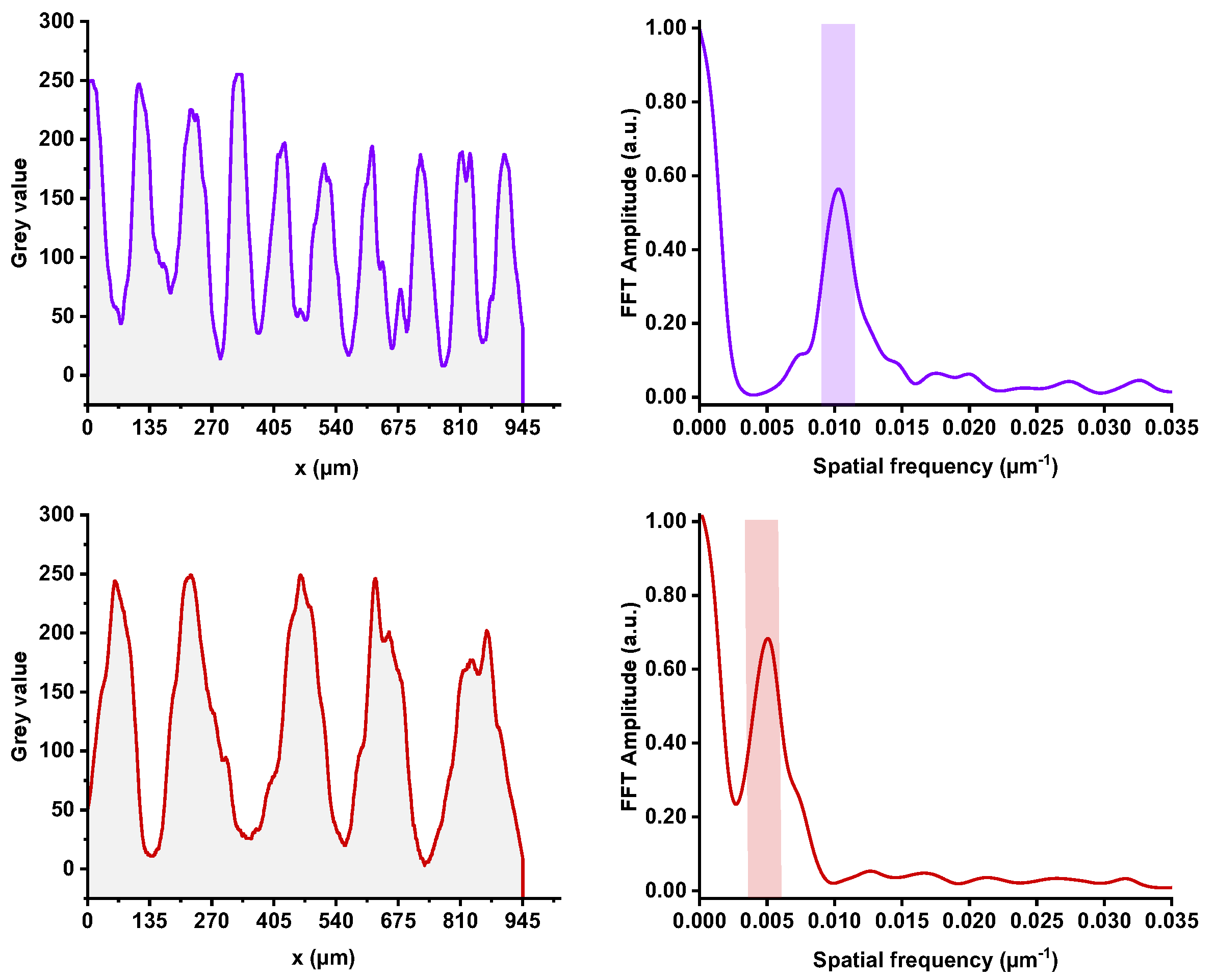
Cartesian representation of rotational cuts indicates TC and sign. Further data processing is enabled by Fourier transform along linear cuts (grey lines in Figure 4a,b) which corresponds to FFT along circles in unprocessed original data space. The transformed maps show radial variations of the fringe contrast. A selection of appropriate radii can be automated by setting threshold levels for the intensity (if the detector works in non-saturated operation mode) and placing cuts in the center of encircled areas. Intensity profiles and related spatial frequency amplitudes from FFT are shown in Figure 5a–d.
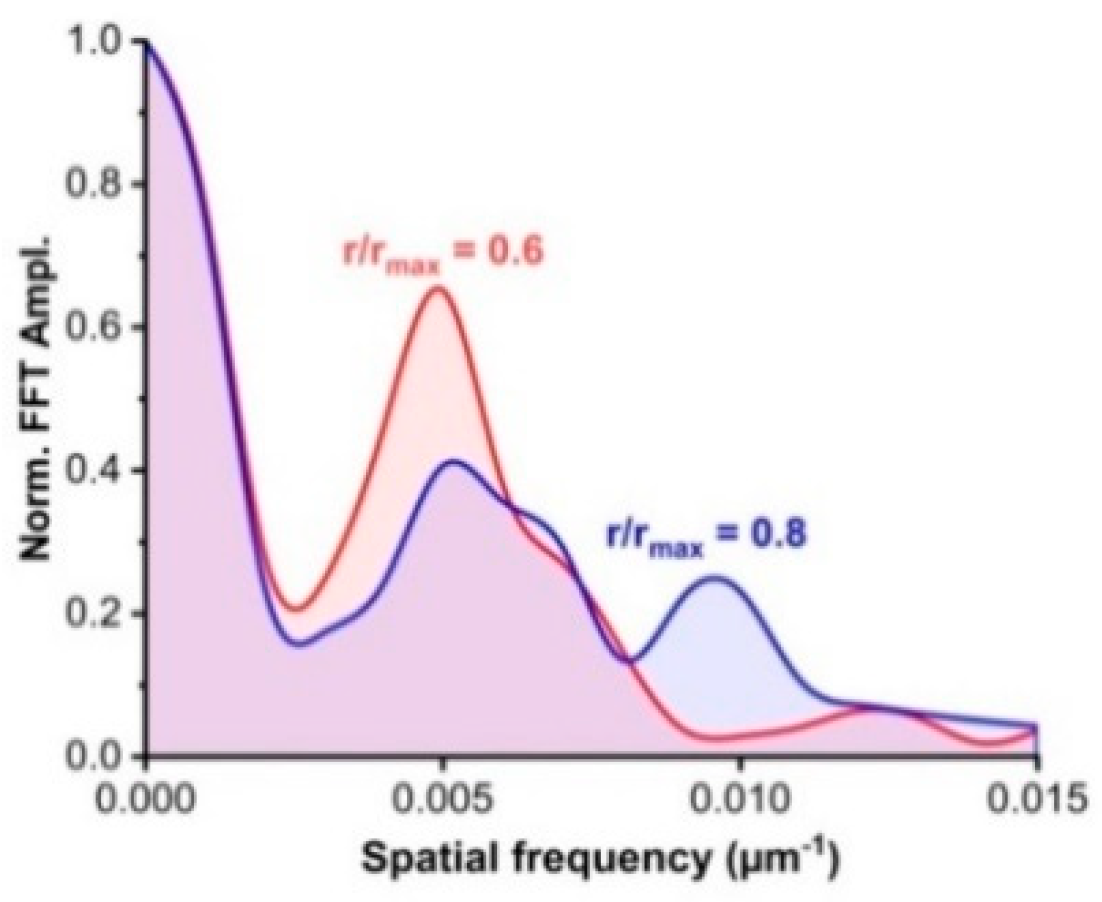
A variation of the radius of the circle of interest delivers additional information about the radial non-uniformity of the spiral shape which either results from the limited quality of reference and structured wavefront, or from subtle spatial encoding. The breakdown of the clear spatial frequency signature at increasing radius for TC = -5 is indicated by the FFT spectra in Figure 6. In this case, the interference pattern was significantly distorted by neighboring sub-beams in an OAM array.
Another measure for radial non-uniformity is a possible nonlinear change of the twist phase with the radius. As Figure 7 shows by comparing the angular positions of fringe centers for an OAM beam with TC = +10, this effect was relatively small for this example.
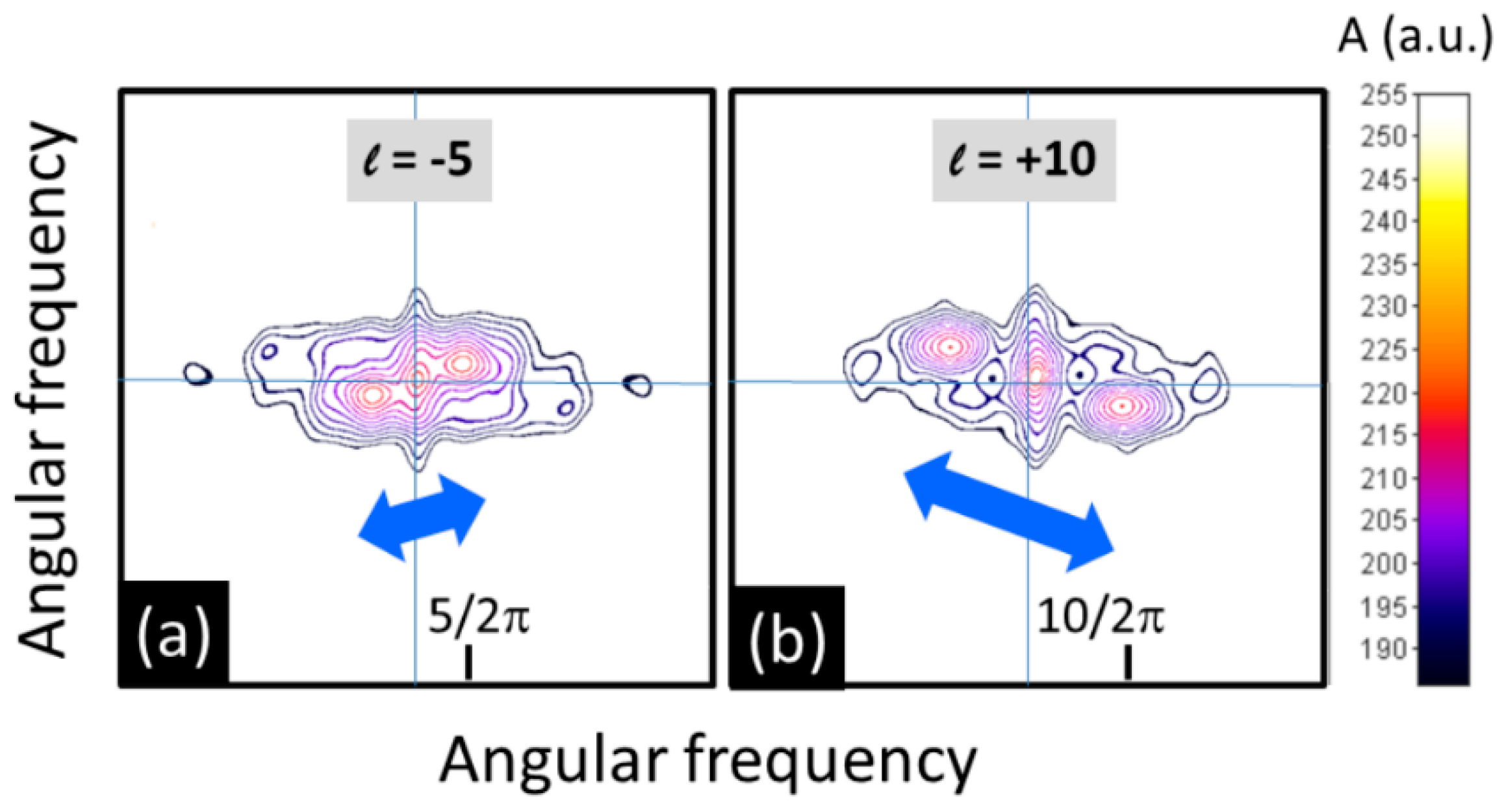
More detailed information can be extracted from radial cut maps by two-dimensional Fourier transform (2DFFT) which directly indicates the sense and slope of rotation, as demonstrated in Figure 8a,b.
Figure 8. Two-dimensional FFT of the radial cut maps for (a) TC = -5 and (b) TC = +10 as contour plot (for sake of better visualization, amplitude A was filtered to suppress lower values). The two-step transformation reveals the orientation of the spirals as well as the angular frequency which directly provides the topological charge. (Both 2DFFT maps were calculated with ImageJ).
The contour lines were generated by filtering the amplitude maps by setting appropriate thresholds to suppress noise and parasitic frequencies.

4.2. Scanning Circle Fourier Transform

For the analysis of beam structures with unknown COG positions and/or multiple spiral patterns, in particular for analyzing spatially encoded OAM beam arrays, the application of SCFT is favorable. At well-adapted step-widths and ranges of radii, the maps of circular cuts and FFT amplitudes enable to determine the singularity positions in good approximation. This will be demonstrated by analyzing an array of OAM beams of alternating TC (-5, +10) arranged around a central reference needle beam (i.e. a single-lobe Bessel-like beam [49]) as shown in Figure 9.
The influence of the displacement of the center of rotating cuts from the real beam center for a selected sub-beam of the array shown in Figure 9b with TC = +10 is demonstrated in Figure 10 and Figure 11. Concatenated, linearized and normalized circular cuts at horizontal and vertical displacements (Δx,Δy) in the detector plane are plotted in Figure 10.
The distributions generated by this specific transformation via circular cuts exhibit characteristic features. In a second step, these intensity maps were analyzed by 2DFFT. The amplitude maps of corresponding angular frequencies Ω = 1/φ for the same data set (Figure 11) enable to extract parameters for a classification and sorting, e.g. on the basis of adapted contrast and fragmentation operators.
In general, the analysis of extended spiral shaped arrays is a complex optimization problem and requires sophisticated image recognition techniques. Results of a scanning circle analysis of the beam array structure according to Figure 9b are presented in Figure 12a–d for four parts of the sampled area each covering 7 x 8 center positions.
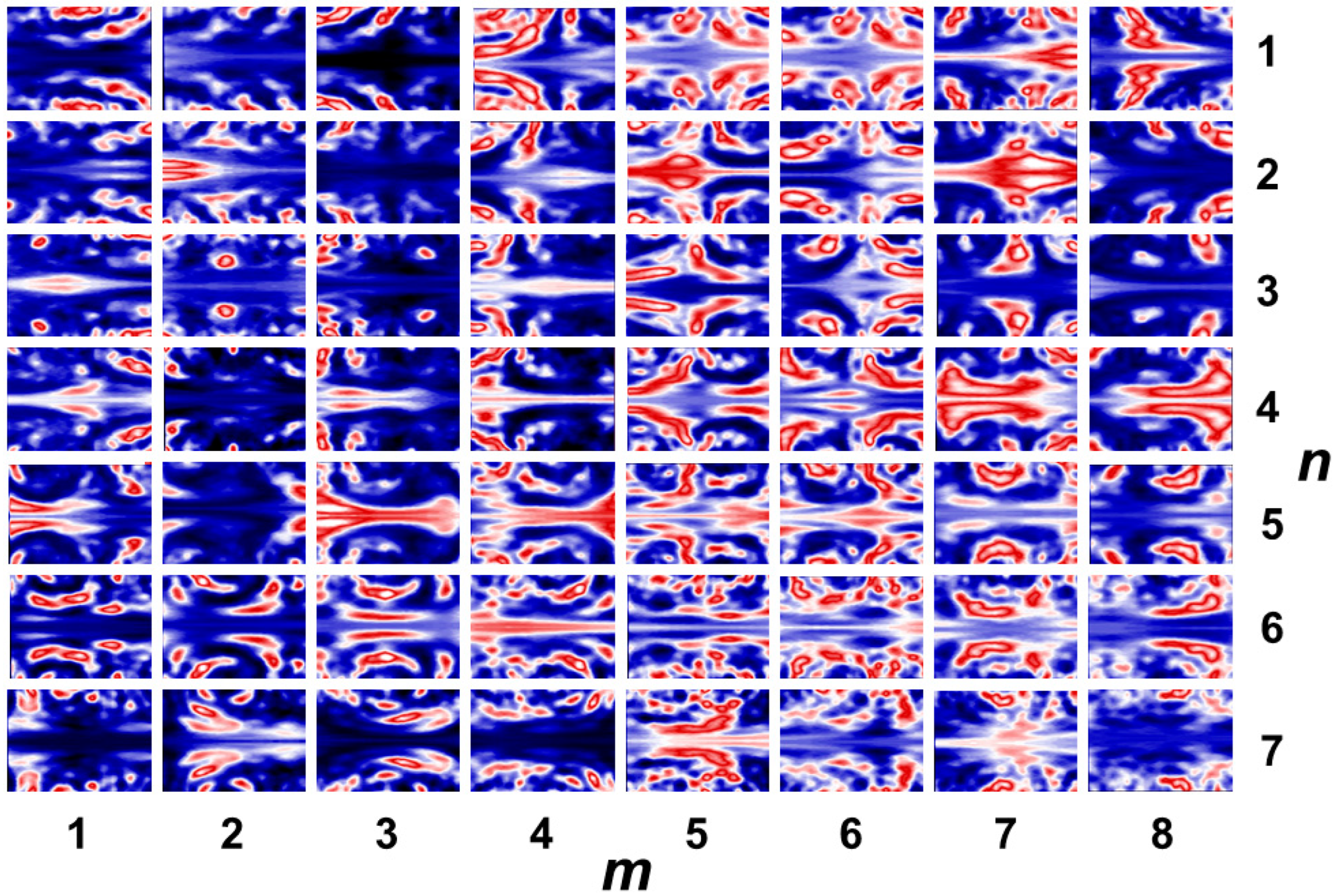
Preprints 99078 g012
Figure 12. a. First quarter of a map of local polar plots for the OAM beam array in Figure 9b (upper left part, mirrored half-circle cuts, horizontal and vertical axes: rotation angle from 0 to π and cut radii from 0 to 100 pixels, respectively). The image (total size: 1024 x 1024 pixels) was partially sampled in steps of 50 pixels, from starting point (91,90) in a coordinate system with origin (0,0) at the upper left corner (number of rotation centers: 14 x 16 = 224).
Figure 12. a. First quarter of a map of local polar plots for the OAM beam array in Figure 9b (upper left part, mirrored half-circle cuts, horizontal and vertical axes: rotation angle from 0 to π and cut radii from 0 to 100 pixels, respectively). The image (total size: 1024 x 1024 pixels) was partially sampled in steps of 50 pixels, from starting point (91,90) in a coordinate system with origin (0,0) at the upper left corner (number of rotation centers: 14 x 16 = 224).
Preprints 99078 g012
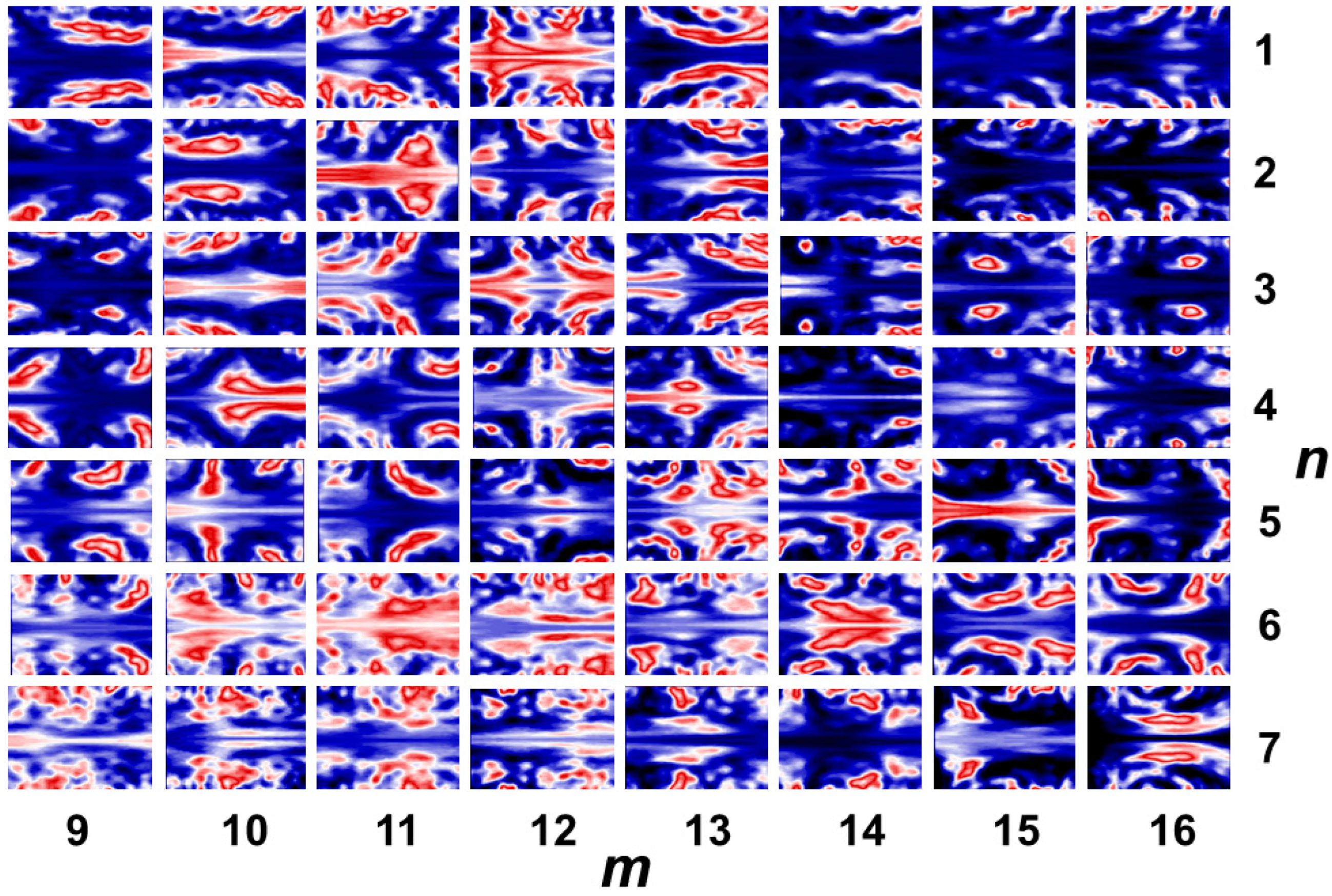
Preprints 99078 g013
Figure 12. b. Second quarter of the scanned area of the OAM beam array (upper right part).
Figure 12. b. Second quarter of the scanned area of the OAM beam array (upper right part).
Preprints 99078 g013
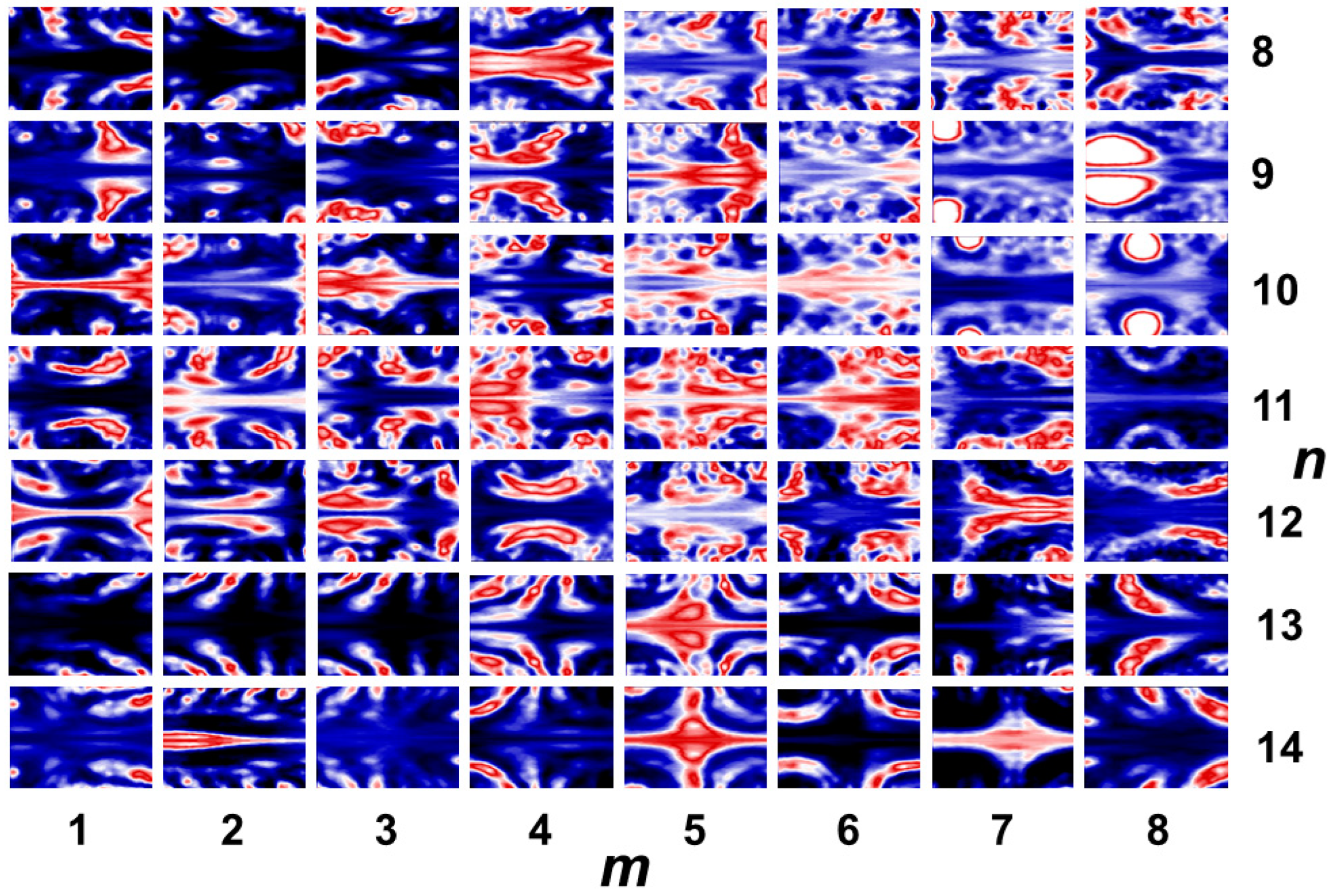
Preprints 99078 g014
Figure 12. c. Third quarter of the scanned area of the OAM beam array (lower left part).
Figure 12. c. Third quarter of the scanned area of the OAM beam array (lower left part).
Preprints 99078 g014
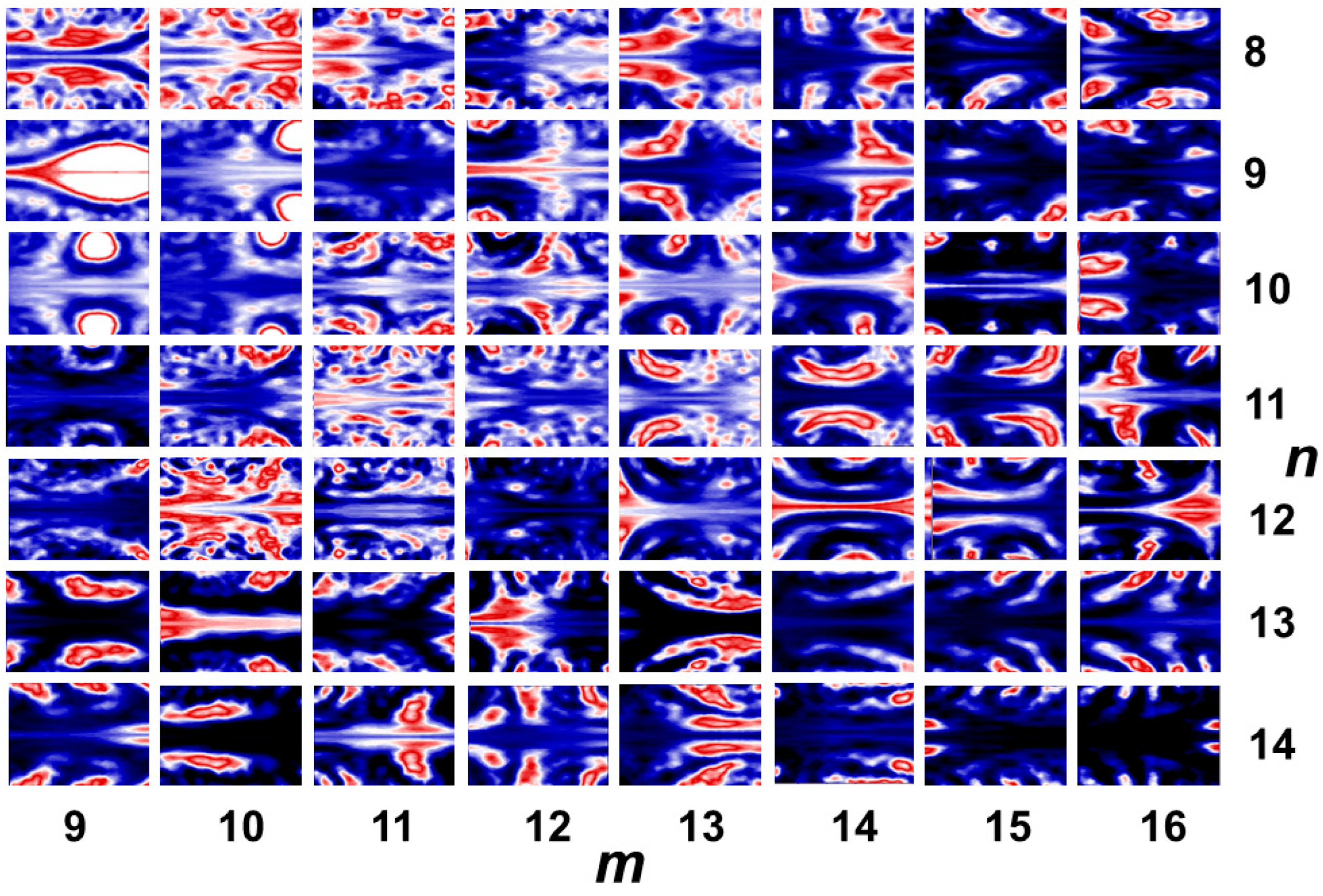
Preprints 99078 g015
Figure 12. d. Fourth quarter of the scanned area of the OAM beam array (lower right part).
Figure 12. d. Fourth quarter of the scanned area of the OAM beam array (lower right part).
Preprints 99078 g015
To minimize computing effort, polar transformation was performed in spatial sampling steps of about r/P = 0.16 at 50 cut radii between zero and a maximum radius of 100 pixels or r/P = 0.32. In contrast to Figure 10, the images correspond to mirrored half circles (angle interval from 0 to π) to facilitate a visual assessment. The resulting matrix of concatenated cuts looks very complex but already indicates the positions of OAM beams. By subsequent 1DFFT or 2DFFT, the rearranged intensity maps can further be processed. For the sake of simplicity, we selected cuts at a radial distance of 4/5 of the maximum cut radius (corresponding to horizontal lines in Figure 12a–d) and calculated related angular frequency amplitudes by FFT for all 224 positions. By filtering out theoreticaly expected frequencies for TC = 10 and TC = -5, a spatial map of the array topology was obtained (Figure 13).
In this proof-of-principle experiment, the resolution was limited by the relative large step width. In a fully automated procedure, resolution and recognition accuracy could be significantly improved. Furthermore, the sign of local topological charges could also be extracted as shown for FCFT. In general, the direct visual representation of three- or four-dimensional FFT data is not trivial. One strategy could be the introduction of statistical meta-moments as recently demonstrated for the spatio-spectral analysis of ultrashort-pulsed OAM beams [48]. Such algorithms for an appropriate quantitative characterization are currently still under development. The high complexity of extended polar and SCFT maps promises to be an interesting field for the application of learning algorithms.

5. Conclusions

To summarize, different approaches for spatially analyzing OAM beams based on a combination of conformal mapping [49] and Fourier transform procedures were studied. Fixed Circle Fourier Transform (FCFT) performs a polar transformation by rotating cuts at angles φ and variable radii r such providing two-dimensional (r,φ) maps which are further processed by one- or two-dimensional FFT. Rotational orientation and angular frequency spectrum can directly be extracted by 2DFFT.
Contrary to single-shot capable FCFT, Scanning Circle Fourier Transform (SCFT) requires to spatially scan the interference patterns. This not only enables to sort OAM modes, to identify topological charges and to determine the rotational orientation of single or multiple OAM beams but also can read out further encoded spatial information, e.g. adjustment markings for centering and scaling. Because of scanning the completed intensity map, image processing does not require a priori knowledge on centers of gravity and is not limited to rotational symmetric mode patterns. The sequential SCFT procedure is more time consuming but extends the field of applications to structured beams of even higher complexity. Particular SCFT applications could be the characterization and decoding of OAM beam arrays, Talbot experiments, or wavefront sensing with OAM encoded beams [17].
Image based Fourier techniques surpass the limited spatial resolution of wavefront sensors but could be completed by the capability to directly determine temporal wavefront autocorrelation in advanced configurations [39,50]. Digital-holographic single-shot detection methods [51] which also work with reference beams could be combined with our approaches. It has to be expected that learning algorithms will contribute to the development of appropriate analysis software and advanced data visualization. We like to mention that adaptive techniques [52] and the combination of the Gerchberg-Saxton approach with neural network recognition [53] are further options.
At the current stage, our calculations were performed on the basis of modular software building blocks. The integration and the extension to AI algorithms will be an important task for the future. Because of the universal appearance of spiral patterns, the developed methods may find further applications beyond advanced optical communication systems.

Author Contributions

Conceptualization and methodology, R.G., M.B., experiments R.G.; software M.B.; data analysis, R.G., M.B., writing—original draft preparation, R.G.; writing—review and editing, R.G. and M.B.; visualization, R.G. and M.B.; project administration and funding acquisition, R.G.; All authors have read and agreed to the published version of the manuscript. The authors declare that no support by AI was used.

Funding

This research was funded in parts by Research Foundation (DFG), project MAXWELL III, grant number GR1782/16-2.

Acknowledgments

Experimental resources including lab space and laser systems were kindly provided by Prof. Elsaesser and Dr. Erik Nibbering (MBI). The authors thank Prof. Jahns (FernUniversity, Hagen) for stimulating discussions. Mathias Jurke (MBI) was involved in previous experiments on the digital generation of OAM patterns.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Hubble, E. P. The realm of nebulae, Mrs. Hepsa Ely Silliman memorial lectures, 25, Yale University Press (New Haven) 1936, 124–151.
  2. Kang, J.; Chae, J.; Nakariakov, V. M.; Cho, K.; Kwak, H.; Lee, K. The physical nature of spiral wave patterns in sunspots, Astrophys. J. Lett. 2019, 877, L9. [Google Scholar] [CrossRef]
  3. Montgomery, M.T.; Kallenbach, R.J. A theory for vortex Rossby-waves and its application to spiral bands and intensity changes in hurricanes, Q. J. R. Meteorol. Soc. 1997, 123, 435–465. [CrossRef]
  4. Clark, J.V.; Aldridge, A.E.; Reolid, M.; Endo, K.; Pérez-Huerta, A. Application of shell spiral deviation methodology to fossil brachiopods: implications for obtaining specimen ontogenetic ages, Palaeontologia Electronica, 2015, 18.3.54A, 1–39. [CrossRef]
  5. Epstein, I.R. Spiral waves in chemistry and biology, Science 1991, 252, 67. [CrossRef]
  6. Everschor-Sitte, K.; Masell, J.; Reeve, R.M.; Kläui, M. Perspective: magnetic skyrmions–overview of recent progress in an active research field. J. Appl. Phys. 2018, 124, 240901. [Google Scholar] [CrossRef]
  7. Allen, L.; Beijersbergen, M.W.; Spreeuw, R.J.C.; Woerdman, J.P. Orbital angular-momentum of light and the transformation of Laguerre-Gaussian laser modes, Phys. Rev. A 1992, 45, 8185–8189. [Google Scholar] [CrossRef]
  8. Yao, A.M.; Padgett, M.J. Orbital angular momentum: origins, behavior and applications. Adv. Opt. Photon. 2011, 3, 161–204. [Google Scholar] [CrossRef]
  9. Padgett, M.; Courtial, J.; Allen, L. Advances in optical angular momentum. Phys. Today 2004, 57, 35–40. [Google Scholar] [CrossRef]
  10. Willner, A. E; Huang, H.; Yan, Y.; Ren, Y.; Ahmed, N.; Xie, G.; Bao, C.; Li, L.; Cao, Y.; Zhao, Z.; Wang, J.; Lavery, M. P. J.; Tur, M.; Ramachandran, S.; Molisch, A. F.; Ashrafi, N.; Ashrafi, S. Optical communications using orbital angular momentum beams, Adv. Opt. Photon., 2015, 7, 66–106. [CrossRef]
  11. Wang, J.; Liu, J.; Zhao, Y.; Du, J.; Long, Z. Orbital angular momentum and beyond in free-space optical communications, Nanophoton. 2022, 11, 645–680. [CrossRef]
  12. Yue, Y.; Yan, Y.; Ahmed, N.; Yang, J. Y.; Zhang, L.; Ren, Y. Huang, H.; Birnbaum, K. M., Erkmen, B. I.; Dolinar, S.; Tur, M.; Willner, A. E. Mode properties and propagation effects of optical orbital angular momentum (OAM) modes in a ring fiber, IEEE Photonics J. 2012, 4, 535–543. [CrossRef]
  13. Ma, M.; Lian, Y.; Lu, Z. Generation, Transmission and Application of orbital angular momentum in optical fiber; a review, Front. in Phys. 2021, 9, 773505. 9. [CrossRef]
  14. Zeng, J.; Liu, X.; Zhao, C.; Wang, F.; Gbur, G.; Cai, Y. Spiral spectrum of a Laguerre-Gaussian beam propagating in anisotropic non-Kolmogorov turbulent atmosphere along horizontal path. Opt. Express 2019, 27, 25342–25355. [Google Scholar] [CrossRef] [PubMed]
  15. Harm, W.; Bernet, S.; Ritsch-Marte, M.; Harder, I.; Lindlein, N. Adjustable diffractive spiral phase plates. Opt. Express. 2015, 23, 413–421. [Google Scholar] [CrossRef]
  16. Vickers, J.; Burch, M.; Vyas, R.; Singh, S. Phase and interference properties of optical vortex beams, J. Opt. Soc. Am. A, 2008, 25, 823–827. [CrossRef]
  17. Grunwald, R.; Jurke, M.; Liebmann, M.; Bock, M. Orbital angular momentum encoded beam tracking and wavefront sensing. IEEE J. Lightwave Technol. 2023, 41, 2017–2024. [Google Scholar] [CrossRef]
  18. Huang, H.; Ren, Y.; Yan, Y.; Ahmed, N.; Yue, Y.; Bozovich, A.; Erkmen, B.I.; Birnbaum, K.; Dolinar, S.; Tur, M.; Wilner, A.E. Phase-shift interference-based wavefront characterization for orbital angular momentum modes. Opt. Lett. 2013, 38, 2348–2350. [Google Scholar] [CrossRef]
  19. Bhatia, H.; Norgard, G.; Pascucci, V.; Bremener, P.-T. The Helmholtz-Hodge decomposition–a survey, IEEE Transact. Visual. Comp. Graph. 2013, 19, 1386–1404. [CrossRef]
  20. Haufe, D.; Gürtler, J.; Schulz, A.; Bake, F.; Enghardt, L.; Czarske, J. Aeroacoustic analysis using natural Helmholtz-Hodge decomposition. J. Sens. Sens. Syst. 2018, 7, 113–122. [Google Scholar] [CrossRef]
  21. Finn, L.I.; Boghosian, B.M.; Kottke, C.N. Vortex core identification in viscous hydrodynamics, Philos. Trans. A Math. Phys. Eng. Sci. 2005, 363, 1937–48. [Google Scholar] [CrossRef]
  22. Lindner, G.; Devaux, Y.; Miskovic, S. VortexFitting: A post-processing fluid mechanics tool for vortex identification, SoftwareX 2020, 12, 100604. [CrossRef]
  23. Silva, P.; Cao, L.T.; Hayes, W.B. SpArcFiRe: Enhancing spiral galaxy recognition using arm analysis and random forests, Galaxies 2018, 695 (2018). [CrossRef]
  24. Puerari, I.; Dottori, H.A. Fourier analysis of structure in spiral galaxies, Astron. Astrophys. Suppl. Ser. 1992, 93, 469–493.
  25. Puerari, I.; Dottori, H.A. A morphological method to determine corotation radii in spiral galaxies, Astrophys. J. 1997, 476: L73–L75. [CrossRef]
  26. Davis, B.L.; Berrier, J.C.; Shields, D.W.; Kennefick, J.; Kennefick, D.; Seigar, M.S.; Lacy, C.H.S.; Puerari, I. Measurement of galactic logarithmic spiral arm pitch angle using two-dimensional Fast Fourier Transform decomposition, Astrophys. J. Suppl. Ser. 2012, 199:33. [CrossRef]
  27. Xudong, F.; Bursill, L.A.; Lin, P.J. Fourier transforms and structural analysis of spiral lattices, Int. J. Mod. Phys. B, 1988, 2, 131–146. [CrossRef]
  28. Wei, D.; Ma, J.; Wang, T.; Xu, C.; Zhu, S.; Xiao, M.; Zhang, Y. Laguerre-Gaussian transform for rotating image processing. Opt. Express 2020, 28, 26898–26907. [Google Scholar] [CrossRef]
  29. Szatkowski, M.; Burnecka, E.; Dyła, H.; Masajada, J. Optical vortex tracking algorithm based on the Laguerre-Gaussian transform. Opt. Express 2022, 10, 17451–17464. [Google Scholar] [CrossRef]
  30. Wen, Y.; Chremmos, I.; Chen, Y.; Zhu, J.; Zhang, J.; Zhang, Y.; Yu, S. Spiral transformation for high-resolution and efficient sorting of optical vortex modes. Phys. Rev. Lett. 2018, 120, 193904. [Google Scholar] [CrossRef] [PubMed]
  31. Berkhout, C.G.; Lavery, M.P.J.; Courtial, J.; Beijersbergen, M.W.; Padgett, M.W. Phys. Rev. Lett. 2010, 105, 153601. [CrossRef]
  32. Torrente, M.-L.; Biasotti, S.; Falcidien, B. Recognition of feature curves on 3D shapes using an algebraic approach to Hough transforms, Pattern Recognition 2018, 73, 111–130. [CrossRef]
  33. Zhou, H.-L.; Fu, D.-Z.; Dong, J.-J.; Zhang, P.; Chen, D.-X.; Cai, X.-L.; Li, F.-L.; Zhang, X.-L. Orbital angular momentum complex spectrum analyzer for vortex light based on the rotational Doppler effect. Light Sci. Appl. 2017, 6, e16251. [Google Scholar] [CrossRef]
  34. Flamm, D.; Schulze, C.; Naidoo, D.; Schröter, S.; Forbes, A. Duparré All-digital holographic tool for mode excitation and analysis in optical fibers. J. Lightwave Technol. 2013, 31, 1023–2032. [Google Scholar] [CrossRef]
  35. Andersen, J.M.; Alperin, S.N.; Voitiv, A.A.; Holtzmann, W.G.; Gopinath, J.T.; Siemens, M.E. Characterizing vortex beams from a spatial light modulator with collinear phase-shifting holography, Appl. Opt. 2019, 58, 404–409. [Google Scholar] [CrossRef]
  36. Pinnell, J.; Nape, I.; Sephton, B.; Cox, M.A.; Rodríguez-Fajardo, V.; Forbes, A. Modal analysis of structured light with spatial light modulators: a practical tutorial. J. Opt. Soc. Am. A 2020, 37, C146–C160. [Google Scholar] [CrossRef]
  37. Leach, J.; Keen, S.; Padgett, M.J.; Saunter, C.; Love, G.D. Direct measurement of the skew angle of the Poynting vector in a helically phased beam, Opt. Express 2006, 14, 11919–11924. [Google Scholar] [CrossRef] [PubMed]
  38. Bowman, R. W.; Wright; A. J.; Padgett, M. J. An SLM-based Shack–Hartmann wavefront sensor for aberration correction in optical tweezers, J. Opt. 2010, 12, 124004. [CrossRef]
  39. Grunwald, R.; Elsaesser, T.; Bock, M. Spatio-temporal coherence mapping of few-cycle vortex pulses. Sci. Rep. 2014, 07148. [Google Scholar] [CrossRef] [PubMed]
  40. Zhu, J.; Wu, Y.; Zhou, H.; Zhao, S. Measuring the orbital momentum complex spectrum of light with the Fast Fourier Transform. Phys. Rev. Appl. 2023, 20, 014010. [Google Scholar] [CrossRef]
  41. D’Errico, A.; D’Amelio, R.; Piccirillo, B.; Cardano, F.; Marrucci, L. Measuring the complex orbital angular momentum spectrum and spatial mode decomposition of structured light beams, Optica 2017, 4, 1350–1357. [CrossRef]
  42. Lin, Z.; Hu, J.; Chen, Y.; Brès, C.-S.; Yu, S. Single-shot Kramers–Kronig complex orbital angular momentum spectrum retrieval. Adv. Photon. 2023, 5, 036006. [Google Scholar] [CrossRef]
  43. Bazhenov, V.Y.; Soskin, M.S.; Vasnetsov, M.V. Screw Dislocations in Light wavefronts. J. Mod. Opt. 1992, 39, 985–990. [Google Scholar] [CrossRef]
  44. Soskin, M.S.; Gorshkov, V.N.; Vasnetsov, M.V.; Malos, J.T.; Heckenberg, N.R. Topological charge and angular momentum of light beams carrying optical vortices. Phys. Rev. A 1997, 56, 4064–40075. [Google Scholar] [CrossRef]
  45. Emile, O.; Emile, J.; Brousseau, C. Detection of the orbital angular momentum in optics, HAL open science 2019, hal-02162140.
  46. Vickers, J.; Burch, M.; Vyas, R.; Singh, S. Phase and interference properties of optical vortex beams. J. Opt. Soc. Am. A 2008, 25, 823–827. [Google Scholar] [CrossRef]
  47. Senthilkumaran, P.; Masajada, J.; Sato, S. Interferometry with vortices. Int. J. Opt. 2012, 517591. [Google Scholar] [CrossRef]
  48. Liebmann, M.; Treffer, A.; Bock, M.; Seiler, T.; Jahns, J.; Elsaesser, T.; Grunwald, R. Spectral meta-moments reveal hidden signatures of vortex pulses, EPJ Web of Conferences 2019, 205, 01005. [CrossRef]
  49. Bryngdahl, O. Geometrical transformations in optics. J. Opt. Soc. Am. 1974, 64, 1092–1099. [Google Scholar] [CrossRef]
  50. Grunwald, R.; Bock, M. Needle beams: A review, Adv. Phys. X 2020, 5, 1736950. [CrossRef]
  51. Otte, E.; Bobkova, V.; Trinschek, S.; Rosales-Guzmán, C.; Denz, C. Single-shot all-digital approach for measuring the orbital angular momentum spectrum of light, APL Photon. 2022, 7, 086105.
  52. Yu, H.; Chen, C; Hu, X.; Yang, H. An Efficient Recognition Method for Orbital Angular Momentum via Adaptive Deep ELM, sensors 2023, 23, 8737. [CrossRef]
  53. Fan, W.-Q.; Gao, F.-L.; Xue, F.-C.; Guo, J.-J.; Xiao, Y.; Gu, Y.-J. Experimental recognition of vortex beams in oceanic turbulence combining the Gerchberg–Saxton algorithm and convolutional neural network, Appl. Opt. 2024, 63, 982–929. [CrossRef]
Preprints 99078 g001
Figure 1. Geometrical conditions for OAM beam analysis with Fourier Transform (schematically): (a) interference pattern (example: topological charge l = +10), (b) Fixed Circle Fourier Transform (FCFT), (c) Scannning Circle Fourier Transform (SCFT) mapping a plane of interest. Fourier Transform is performed along single or multiple circular cuts, respectively. Concentric circles (solid, dashed, dotted) in (b) indicate the variation of the radius for three values r1, r2, r3, respectively. The circles in (c) provide a 2D matrix of circular cuts for variable (x,y)-coordinates (schematically shown for three sequences 1,2,3).
Figure 1. Geometrical conditions for OAM beam analysis with Fourier Transform (schematically): (a) interference pattern (example: topological charge l = +10), (b) Fixed Circle Fourier Transform (FCFT), (c) Scannning Circle Fourier Transform (SCFT) mapping a plane of interest. Fourier Transform is performed along single or multiple circular cuts, respectively. Concentric circles (solid, dashed, dotted) in (b) indicate the variation of the radius for three values r1, r2, r3, respectively. The circles in (c) provide a 2D matrix of circular cuts for variable (x,y)-coordinates (schematically shown for three sequences 1,2,3).
Preprints 99078 g001
Preprints 99078 g002
Figure 2. Experimental setup for generation and analysis of OAM beams (schematically) (L = Laser, BE = beam expander, RP = rotatable broadband polarizer, BE = beam expander, M = high-reflectance mirror, SLM = spatial light modulator, PC1 = computer for programming SLM, PM = phase map, CBS = coherent background signal, OAM = orbital angular moment beam, IFP = interference pattern, CAM = CMOS camera, PC2 = computer for data processing, FFT = Fast Fourier Transform, CR = cut radius, SF = spatial frequency).
Figure 2. Experimental setup for generation and analysis of OAM beams (schematically) (L = Laser, BE = beam expander, RP = rotatable broadband polarizer, BE = beam expander, M = high-reflectance mirror, SLM = spatial light modulator, PC1 = computer for programming SLM, PM = phase map, CBS = coherent background signal, OAM = orbital angular moment beam, IFP = interference pattern, CAM = CMOS camera, PC2 = computer for data processing, FFT = Fast Fourier Transform, CR = cut radius, SF = spatial frequency).
Preprints 99078 g002
Preprints 99078 g003
Figure 3. Detected free-space interference patterns for sub-beams of an OAM array with TC = - 5 and TC = +10 (analyzed image areas on camera chip: 180 x 172 pixels or 990 x 946 µm2, axial measuring distance z = 3.3 cm, contrast enhanced).
Figure 3. Detected free-space interference patterns for sub-beams of an OAM array with TC = - 5 and TC = +10 (analyzed image areas on camera chip: 180 x 172 pixels or 990 x 946 µm2, axial measuring distance z = 3.3 cm, contrast enhanced).
Preprints 99078 g003
Preprints 99078 g004
Figure 4. Analysis of interference patterns corresponding to Figure 3a,b, respectively. Intensity values along circular cuts at increasing radii were linearly concatenated (360 angular steps, counterclockwise sampling). The maps represent the transformation from polar to Cartesian system.
Figure 4. Analysis of interference patterns corresponding to Figure 3a,b, respectively. Intensity values along circular cuts at increasing radii were linearly concatenated (360 angular steps, counterclockwise sampling). The maps represent the transformation from polar to Cartesian system.
Preprints 99078 g004
Preprints 99078 g005
Figure 5. Intensity profiles along circular cuts (a,c) and corresponding spatial frequency spectra (b,d) for both examples with TC = +10 and TC = -5, respectively (slightly smoothened by B-Spline function, data corresponding to linear cuts in Figure 4a,b).
Figure 5. Intensity profiles along circular cuts (a,c) and corresponding spatial frequency spectra (b,d) for both examples with TC = +10 and TC = -5, respectively (slightly smoothened by B-Spline function, data corresponding to linear cuts in Figure 4a,b).
Preprints 99078 g005
Preprints 99078 g006
Figure 6. Non-uniformity of spiral geometry at TC = -5 indicated by FFT for two concentric circular cuts at different radii. The larger radius corresponds to an imperfect interference pattern containing distortions from neighboring beams.
Figure 6. Non-uniformity of spiral geometry at TC = -5 indicated by FFT for two concentric circular cuts at different radii. The larger radius corresponds to an imperfect interference pattern containing distortions from neighboring beams.
Preprints 99078 g006
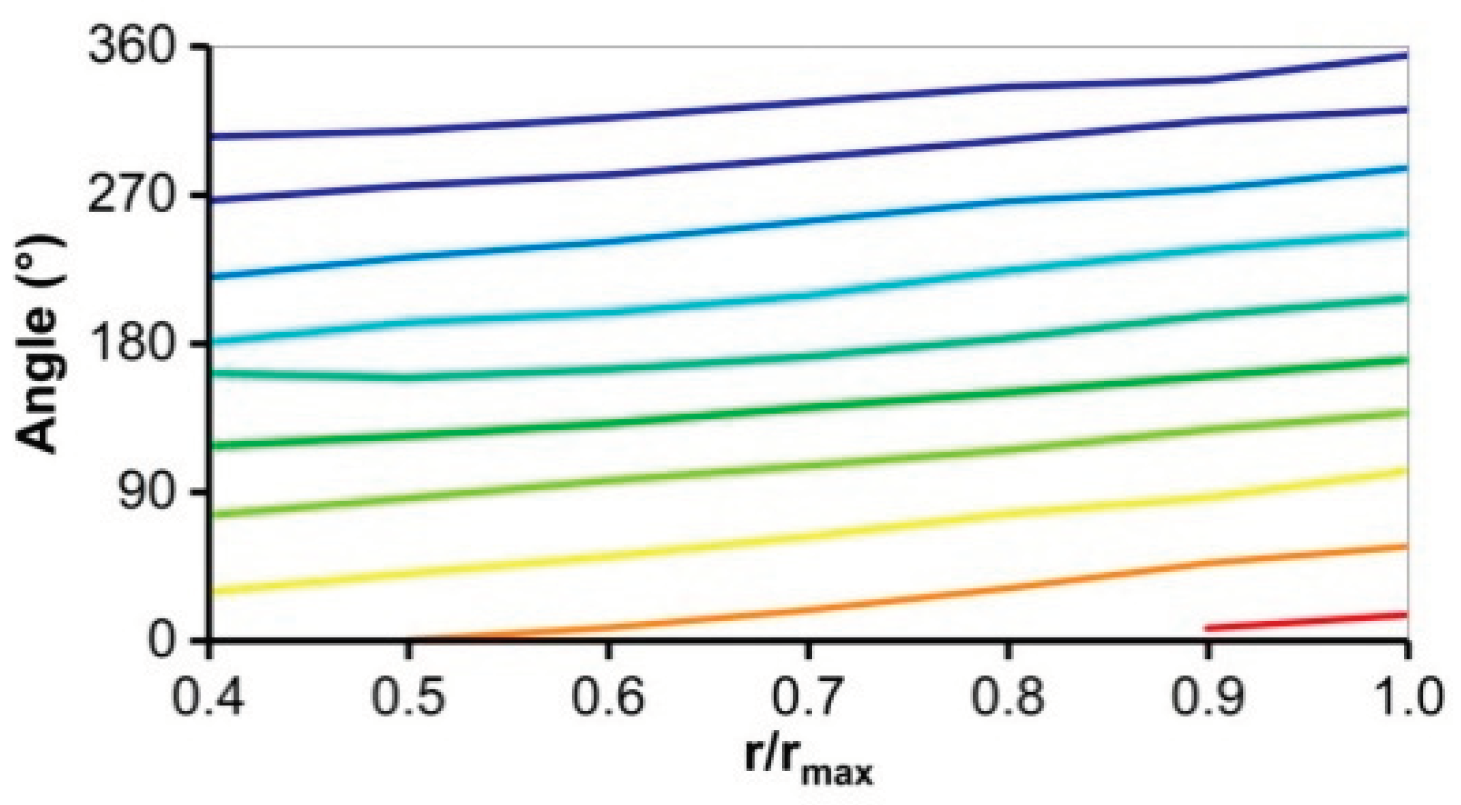
Preprints 99078 g007
Figure 7. Twist uniformity. Changing angular positions of 10 fringe centers of gravity of an OAM beam with TC = +10 as a function of normalized cut radii. Slightly radially dependent distortions are mainly caused by interference effects.
Figure 7. Twist uniformity. Changing angular positions of 10 fringe centers of gravity of an OAM beam with TC = +10 as a function of normalized cut radii. Slightly radially dependent distortions are mainly caused by interference effects.
Preprints 99078 g007
Preprints 99078 g008
Figure 8. Twist uniformity.
Figure 8. Twist uniformity.
Preprints 99078 g008
Preprints 99078 g009
Figure 9. Orthogonal array of OAM beams arranged around a central reference beam: (a) generating SLM phase map (color code from blue to red: phase from 0 to π for a wavelength of 800 nm), (b) detected intensity distribution, (c) post-processed image (enhanced visibility). Periods in the SLM and detector planes are p and P (FOV on the detector: 1024 x 1024 pixels, pixel size 5.5 x 5.5 µm2).
Figure 9. Orthogonal array of OAM beams arranged around a central reference beam: (a) generating SLM phase map (color code from blue to red: phase from 0 to π for a wavelength of 800 nm), (b) detected intensity distribution, (c) post-processed image (enhanced visibility). Periods in the SLM and detector planes are p and P (FOV on the detector: 1024 x 1024 pixels, pixel size 5.5 x 5.5 µm2).
Preprints 99078 g009
Preprints 99078 g010
Figure 10. Concatenated, linearized and normalized circular cuts for a sub-beam of TC = +10 at horizontal and vertical displacements (Δx,Δy) in steps of P/5 (P = 340 pixels = period at the detector plane; 50 cuts, horizontal axes: rotation angle φ from 0 to 2π, vertical axes: radii of cuts from rmin = 0 to rmax = 90 pixels corresponding to 0.265 P, central image: position with zero displacement).
Figure 10. Concatenated, linearized and normalized circular cuts for a sub-beam of TC = +10 at horizontal and vertical displacements (Δx,Δy) in steps of P/5 (P = 340 pixels = period at the detector plane; 50 cuts, horizontal axes: rotation angle φ from 0 to 2π, vertical axes: radii of cuts from rmin = 0 to rmax = 90 pixels corresponding to 0.265 P, central image: position with zero displacement).
Preprints 99078 g010
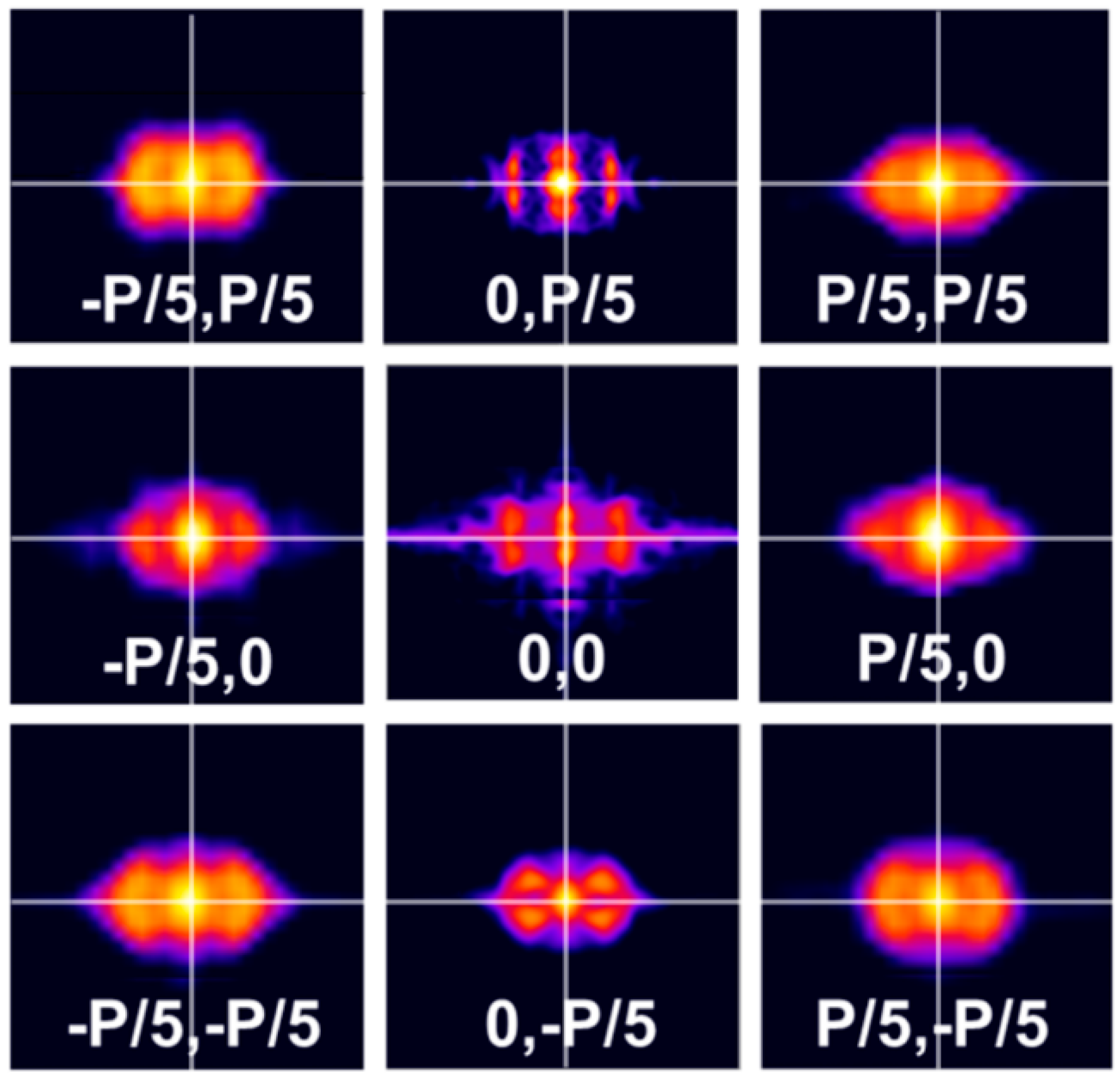
Preprints 99078 g011
Figure 11. 2DFFT amplitudes corresponding to the data set used for Figure 10. The angular frequency axes cover a range between 0 (centers) and 32 x (1/2π).
Figure 11. 2DFFT amplitudes corresponding to the data set used for Figure 10. The angular frequency axes cover a range between 0 (centers) and 32 x (1/2π).
Preprints 99078 g011
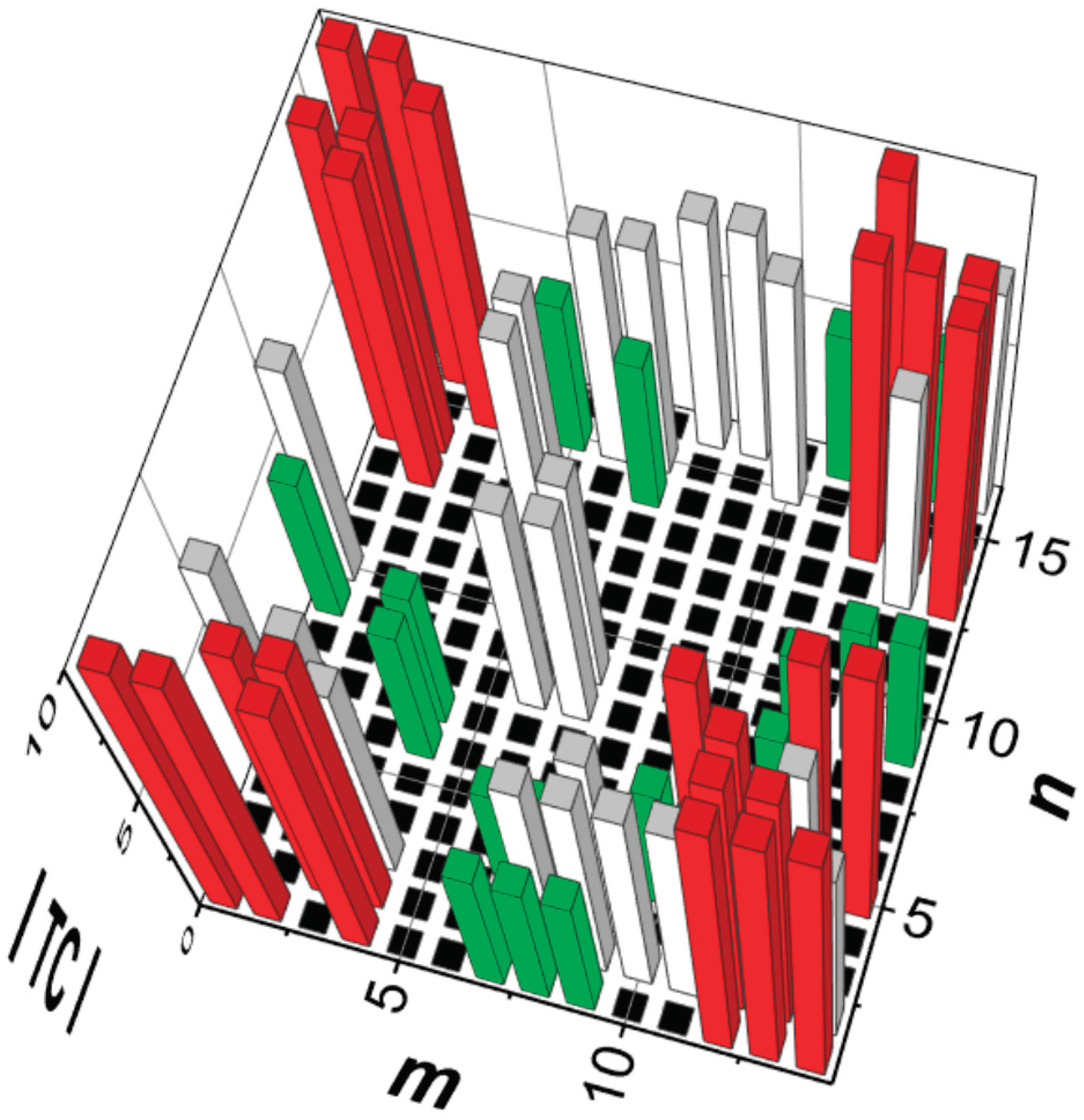
Preprints 99078 g016
Figure 13. Map of absolute values of topological charges corresponding to array data from Figure 12a–d reconstructed by SCFT on the basis of single cuts through the polar plots and 1DFFT for each COG coordinate. The arrangement of alternating sub-beams with |TC| = 10 (red bars) and |TC| = 5 (green bars) is clearly indicated. White bars stand for ambiguous frequency spectra (for convenience only set to TC = 7.5).
Figure 13. Map of absolute values of topological charges corresponding to array data from Figure 12a–d reconstructed by SCFT on the basis of single cuts through the polar plots and 1DFFT for each COG coordinate. The arrangement of alternating sub-beams with |TC| = 10 (red bars) and |TC| = 5 (green bars) is clearly indicated. White bars stand for ambiguous frequency spectra (for convenience only set to TC = 7.5).
Preprints 99078 g016
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated