Preprint
Article
Shannon Holes, Black Holes and Knowledge: Can a Machine become a “Self-Aware" Teammate?
Altmetrics
Downloads
157
Views
357
Comments
0
A peer-reviewed article of this preprint also exists.
supplementary.zip (988.84KB )
This version is not peer-reviewed
Submitted:
17 February 2024
Posted:
19 February 2024
You are already at the latest version
Alerts
Abstract
We develop new theory from a broad case-study approach to explore a better understanding of what constitutes knowledge and its value as identifiable to human-machine teams. From past research, this trail of exploration will lead to these initial questions: What is the value of debate in the furtherance of knowledge? Will machines with AI be able to contribute to a debate if we humans cannot define it or determine its value sufficiently for a machine’s understanding, contribution, exploration and identification? Like humans, as teammates, machines must be able to determine with AI what constitutes the usable knowledge that contributes to a team’s success in the field (e.g., testing "knowledge" in the field, identifying new knowledge, using knowledge to develop innovation) or its failure (viz., trouble shooting; identifying weaknesses; discovering vulnerabilities, hiding by deception). It matters not whether a debate is public, private or unexpressed by an individual human or machine agent alone; we speculate in this exploration that the process advances the science of autonomous human-machine teams and assists in interpretable machine learning. We conclude with questions and a speculation: How does a human become aware or express its awareness of knowledge? Can a machine be as expressive as its human teammates? And how does a human-machine teammate become aware that its teammates possess sufficient knowledge to perform a task? We speculate that the structure of “knowledge," once found, is resistant to alternatives (i.e., it is ordered); that its functional utility is generalizable; and that its applications are multifaceted (akin to maximum entropy production). The complexity of the team is taken into consideration in our search for knowledge, which can also be used as an information metric.
Keywords:
Subject: Computer Science and Mathematics - Robotics
1. Introduction
In a past review of our theory of interdependence [1], we concluded first, that humans make trade-offs in energy-entropy production between structure and performance, where a poorer team structure reduces performance, characterized by more structural entropy produced by wasted energy, and motivating the need to replace poorly performing members; second, that humans are unable to physically copy and replicate the choices that lead to a well-performing team, introducing random selection into new member choices; third, that interdependence requires strong boundaries to reduce interference to maintain states of interdependence; fourth, that coherence of a state of interdependence requires or reflects stability; and, among others of our findings not reviewed in this entry (e.g., [2]), fifth, that the vulnerability in a targeted team is characterized to its opponents and to itself by observing the loss of a team’s structural integrity, a loss of its productivity, or both.
We begin with knowledge, one of our keywords. It has been defined by the Oxford Dictionary of English as the “facts, information, and skills acquired through experience or education; the theoretical or practical understanding of a subject."1 And it has also been defined by Oxford Languages as the: “awareness ... by experience of a fact or situation."2
We also postpone reviewing two other topics, the complexity of teams [1], and innovation [2]; in the former, we found that as the pieces of a complex solution fit together (e.g., the structure of a team), structural entropy is reduced; and in the latter, using United Nations data for the nations of Middle Eastern North Africa (MENA), we found that Israel is not only the leading country in producing patents, but also the leader in educating its young people, a significant relationship.
We begin our exploration with an overview of the problem from the perspective of a machine with intelligence comparable to a human teammate. We explore various definitions of knowledge for our purposes. Toward this end, we consider systems engineering; philosophy; social science, citizen decisions, business, consciousness, and authoritarianism; information theory; and physics, a representative group of disciplines beyond which we hope others cross to expand what we consider here. We justify our consideration by speculating that humans will need intelligent machines with AI that are able to contribute to a team’s intelligence [3] as partners in a team while we humans as a species continue to advance into Carl Sagan’s cosmos.
Furthermore, when dealing with machine learning, concepts such as knowledge and information are quite important. What knowledge should we use for machine learning? What is meaningful information to a machine? These questions are certainly of interest as we focus on the different domains of our interest. Teams aside, the concepts in this exploration are also useful when one focuses on interpretable machine learning.
2. What is knowledge to us?
2.1. Considerations
Knowledge can be applied, like exploring for oil; it can also be used to discover reality indirectly, like black holes. Knowledge means no surprise from its predictions, like the lack of entropy generated by the prediction of sunrise tomorrow morning [4].
Kuhn argues in The Essential Tension [5] that Popper may have been correct that psychoanalysis was not a science, but that there were better reasons than the ones he provided (see also, Thornton; in [6]; see also Ioannidis, in [7]). Popper argued for testable propositions. In contrast, Kuhn believed that it was essential for a combination of cooperation and competition to produce an “essential tension" between opposing viewpoints to seek the truth under uncertainty.
At this point in our exploration, we hypothesize that knowledge is tested or determined by debating the various issues it raises. Assuming that there exists only two sides to a debate, and that the two sides hold complementary viewpoints, these viewpoints are orthogonal; i.e., as goes to 90 degrees, then:
We offer as evidence its absence: Most social concepts fail in reality (e.g., reviewed below: self-esteem; implicit racism; ego depletion). The failure of social concepts to correspond to predicted results in reality could be accounted for by complementarity. If behavior in reality accompanies embodied cognition (viz., interdependence), if exploratory concepts are discovered by convergence processes; and, but more importantly, if concepts are disembodied, the results should be a lack of correlation between a disembodied concept and actual, embodied behavior in reality.
Debate implies then that tension is required to not only search for the truth, to test the truth once it is believed to have been found, but to explore what the truth once found may mean; e.g., in politics, truth may be found with a compromise that defuses the emotions on opposing sides of an issue. While compromise is not “truth," especially in the physical sciences, yet it may bound the truth (discussed in more detail below).
Applying knowledge. For example, under uncertainty, Suslick and Schiozer [8] provide an overview of the petroleum industry as a classic case of decision-making seeking to capture a specific knowledge about reality. Following the work of Allais, a 1988 Noble economist, they consider the economics of finding oil in the Algerian Sahara. They addressed the risks of exploration using probability theory along with modeling the different stages of exploration. Allais developed principles for efficient pricing and resource allocation for large monopolistic enterprises. From Suslick and Schiozer [8],
“Many complex decision problems in petroleum exploration and production involve multiple conflicting objectives. … An effective way to express uncertainty is to formulate a range of values, with confidence levels assigned to numbers comprising the range. … Asset managers in the oil and gas industry are looking to new techniques such as portfolio management to determine the optimum diversified portfolio that will increase company value and reduce risk."
Suslick and Schiozer [8] also considered Markowitz’s contribution to knowledge by balancing risk across a portfolio (see [9]):
“A portfolio is said to be efficient if no other portfolio has more value while having less or equal risk, and if no other portfolio has less risk while having equal or greater value. … a portfolio can be worth more or less than the sum of its component projects and there is not one best portfolio, but a family of optimal portfolios that achieve a balance between risk and value."
The authors [8] also reviewed the limitations of risk analysis that limit its use as a practical decision aid to understand reality, especially when applied in the search for oil. They reviewed the strengths and weaknesses of risk analysis by concluding that:
1. Risk analyses offer the way to handle very complex decisions characterized by multiple objectives under uncertainty across the different stages of seeking to find petroleum (i.e., the identification, extraction and production of oil).
2. Risk analyses deal with complex tradeoffs and the preferences of different stakeholders when exploring reality.
3. After finding oil, risk analyses provide a systematic and comprehensive way for listing and reviewing the relevant factors in the extraction and production of oil.
In these searches to obtain decisions based on reality, probability theory considers risks found in analyzing possibilities across the sets of events when making decisions ([10], pp. 14-15). We have decomposed risk into perceptions and determinations. However, unlike risk determinations, risk perceptions can lead to tragedy; e.g., in 2021 [11], the U.S. Department of Defense fired a drone at a perceived terrorist, instead killing 10 civilians, most were children [2]. One of the several recommendations made by DoD, with which we agree, was to use red teams to challenge a decision about risk before action is enacted.
Portfolios of the available choices are important. By generalizing the research of Markowitz [9], Chen and colleagues [12], used swarm intelligence algorithms to address portfolio optimization. Their swarm intelligence algorithm was mainly inspired and developed by observing swarms in nature, and included self-organization, self-adaptation, and self-learning from biological populations (e.g., birds, elephants, wolves).
Their research [12] showed that swarm intelligence algorithms can be efficient and can produce satisfactory solutions in solving portfolio optimization (PO) problems. However, from [12], )
“how to achieve the maximum benefit and minimum risk of dynamic multi-period portfolio is a worthy study problem in the future. … How to choose the preference function will be also a valuable research topic. … [and how] to evaluate the effectiveness of the established PO model."
Occam’s Razor and Einstein’s interpretation of it are covered by simplicity or parsimony [13], but beyond parsimony, there is little to be agreed upon. Considering Einstein’s struggle to construct a mathematical theory of gravity following his special theory of relativity [14], he began with an equivalence principle between acceleration and gravity, and after several failed attempts, personal struggles with family and anti-semitism, all the while coping with concepts of covariance, fearing Hilbert’s success before his, he finally achieved success by predicting the perihelion of Mercury with a new concept of spacetime for reality. Today, Einstein’s theory “has been very successful for more than a century" [15].
“[T]he grand aim of all science … is to cover the greatest possible number of empirical facts by logical deductions from the smallest possible number of hypotheses or axioms" (quoting Einstein, in [16], p. 173).
From Robinson [17], citing Einstein’s 1933 lecture:
“It can scarcely be denied that the supreme goal of all theory is to make the irreducible basic elements as simple and as few as possible without having to surrender the adequate representation of a single datum of experience."
Reviewed by Faraoni and Giusti [15], Einstein’s theory has survived all tests to date, predicting the precession of Mercury’s orbit from the influence of gravitational waves. But in addition to the unsolved paradox with black holes, his theory fails to account theoretically for the increasingly rapid expansion of the cosmos and the discrepancies with the Hubble constant. Hubble’s constant is used as a scale for age and distance across the universe; with the cosmic microwave background, it has been used to measure the beginnings of the universe; but in the late universe, supernovae as standard candles are used. That these two metrics to establish the Hubble constant disagree has created “the essential tension" for another paradox.
However, new tests with falling anti-matter support Einstein’s theory [18]. According to Einstein’s equivalence principle, all objects should fall at the same rate in a gravitational field regardless of what they are made of, now found to be true for matter and antimatter.
We distinguish a heuristic from Einstein’s algorithm for his general theory of relativity. First, we define a heuristic as a thumb rule, short-cut, or approximation to a crude solution in a narrow domain where the approximation is satisfactory (e.g., a pinch of salt), and unlikely to be generalized. Second, for our purposes, we define an algorithm as a compressed set of rules or instructions that can make predictions about outcomes in reality. Both are forms of knowledge, the heurestic more useful in common situations, the algorithm more useful in applying knowledge to advance science. For the algorithm, we separate the structure of an algorithm from its function. More importantly, in this proposal, machines with AI should be able to participate by observing the order-disorder that arises with each step.
1. As the pieces of an algorithm fit together like the pieces of a puzzle, its entropy drops. We have proposed that an entropy drop occurs when the structure of a well-functioning team fits together [1].
2. As the pieces of the algorithm begin to fit together, the unfinished structure of the incomplete algorithm is re-oriented, shifting the strategy in constructing the rest of the algorithm.
3. As the algorithm is finalized, and its predictions established, it forms the framework of major research programs that seek to explore and to determine its strengths and weaknesses.
4. As it becomes established as knowledge, it must be able to withstand the widest, most critical and aggressive tests often represented by debates, which serve to process information about the opposing viewpoints expressed during debate. If it is determined to be knowledge, it will serve to be productive in its ability to predict and to generalize to other concepts and findings. Seeking reality. Embodied thinking is intuitive. Newton’s apple. Einstein’s trains and elevators. The knowledge that follows these intuitions is rational, like Newton’s three laws of motion. But when the limits of that knowledge is reached, the search to replace it can create “the essential tension" until new knowledge is found, like the theory of black holes.
In Einstein’s general theory of relativity, static models of black holes had zero entropy. However, Bekenstein (2008; in [19]) reported that,
“Black hole entropy is a concept with geometric root but with many physical consequences. … a black hole can be said to hide information. In ordinary physics entropy is a measure of missing information."
Accounting for quantum effects indicates that information cannot be destroyed [19], but while a black hole’s entropy is proportional to the area of a black hole, it evaporates over time (via Hawking radiation), indicating the destruction of information, as yet an unresolved paradox.
3. A case study of knowledge across selected disciplines
Based on our proposed theory of knowledge, we next explore knowledge across several disciplines using case studies. We review knowledge for Systems Engineers; Philosophy; Social Science, including citizen recommendations to government agencies, business decisions, consciousness and repression; Shannon’s theory of information; and Physics.
3.1. What is knowledge to Systems Engineering
Systems Engineering is clear in the attempt to define its terms. In its Glossary for Systems Engineering at [20], knowledge is defined as follows:
“1. Acquaintance with facts, truths, or principles, as from study or investigation; general erudition: knowledge of many things."
“2. Acquaintance or familiarity gained by sight, experience, or report: a knowledge of human nature."
“3. The fact or state of knowing; the perception of fact or truth; clear and certain mental apprehension."
Further, their Glossary adds that thinking from a Systems perspective is the following:
“1. An epistemology which, when applied to human activity is based on four basic ideas: emergence, hierarchy, communication, and control as characteristics of systems" [21].
“Definition (1) is the System Science view, defining system thinking as a “theory of knowledge, esp. with regard to its methods, validity, and scope," based around seeing the world as systems."
“2. A process of discovery and diagnosis–an inquiry into the governing processes underlying the problems and opportunities" [22].
“3. A discipline for examining wholes, interrelationships, and patterns utilizing a specific set of tools and techniques [22]. Definitions (2) and (3) focus more on systems thinking as a collection of methods for dealing with system problems."
3.2. What is knowledge to Philosophers?
Next, we consider epistemology and metaphysics, where “epistemology is at least as old as any in philosophy” [23]. Epistemology is the philosophy of knowledge, in particular, the methods, validity, and scope of obtaining. Epistemology attempts to distinguish justified beliefs from opinions (from Steup & Neta, in [23]).
Metaphysics is a study of the fundamental nature of reality, including epistemology, logic and ethics.
Epistemology translates from the Greek episteme for “knowledge,” an understanding or acquaintance; and logos is an account, argument or reason.
Plato studied what it was to know, and, unlike opinion, the difference knowledge has made to its user or knower; e.g., applied knowledge, such as a skill. Locke studied the operations of what it meant for humans to understand, Kant studied the conditions surrounding the possibility of humans to understand, and Russell studied how modern science arose from human sensory experience.
At least two broad subdisciplines exist [23]. The subdisciplne of epistemological foundationalism holds that knowledge works like a building, consisting of a structure built atop the knowledge derived from earlier knowledge that rests upon a foundation crafted of basic beliefs. In contrast, epistemological coherentism is somewhat like the structure of a web or network linking the knowledge and its justifications, with its strength a function of how deeply they are surrounded.
3.3. What is knowledge to Social Scientists?
Social Science is the science of what individuals “should” do or be. Healthy individuals should have high self esteem (American Psychological Association, or APA, 1995; in [24]). They should not deplete their egos ([25]). They should not harbor implicit racism (in Greenwald and colleagues, in [26]). They should be honest (Bazerman’s team in 2012; published in the prestigious journal, PNAS, led by Bazerman, a leading ethicist in Social Science, with the manuscript edited by the Nobel Laureate, Daniel Kahneman [27]). However, self-esteem was found to be invalid by Baumeister and his team in 2005 [28]; implicit racism was found to be invalid in 2009 [29]; ego-depletion was found to have relatively small effects in 2016 [30]; and the honesty scale was retracted in 2021 by the Proceedings of the National Academy of Sciences after the scale was found to have been based on fabricated data [31]. Separately, from Ioannidis [7], "most psychotherapies probably have no or little benefit..."
Consider “explicit" racism versus actual discrimination. Polls indicate that actual racism remains a major problem in the U.S.3 Accepting that actual discrimination is illegal,4 the question arises whether the concept of implicit racism is of value in the determination of actual discrimination.
However, many social scientists have refused to accept that implicit racism is not valid and have insisted instead that individuals should be treated for the condition whether they exhibit it or not; significant sums of money are at stake to enact these “treatments" (e.g., see [32]). Over a decade of treatment for implicit racism has been conducted. But, to date, the results have uniformly been “dispiriting" (Paluck et al., 2021, p. 554; in [33]). For example, the National Institutes of Health held a workshop in 2021 on the treatment of implicit racism, finding “scant scientific evidence" of success.5
For a different perspective, seemingly unrelated, the research that found implicit racism to be invalid was led by Tetlock; later on, in 2015, he wrote a book with Gardiner on how to become a Superforecaster (see Tetlock, in [34]). Tetlock’s thesis was that politics and human affairs are not impossible to predict, but a bit like forecasting the weather, where short-term predictions by highly trained individuals were not only rational, but also that “forecasting ... is a skill that can be cultivated." After their book was published, Tetlock decided to demonstrate his knowledge by finding and gathering from around the world the best individuals to be trained to become superforecasters. They began a website to post their best predictions, the first two being that in the year 2016, neither Brexit (U.K. leaving the European Union) nor Donald Trump (becoming President of the U.S.) would occur. However, both predictions failed [2].
3.3.1. What is knowledge to citizens making recommendations to authorities?
Knowledge is an indispensable element in making decisions that are highly consequential to the lives of multitudes of individuals. These decisions can be fraught with potentially enormous risk to life and irreversible [35]. Increasingly, these decisions are made by autonomous human-machine teams capable of generating and assessing pertinent knowledge rather than human beings alone [36]. Involvement of machines with uber-intelligence in decision-making processes, however, does not entail a more optimal outcome such as risk minimization or better performance. Deployed with malicious intentions or even sheer incompetence and ignorance, machine-generated intelligence could result in the generation of noise that clouds out signals with devastating consequences. The case in point is an artificial intelligence (AI) generated travel “guide” filled with misinformation sold on Amazon [37].
Decisions that affect the lives and livelihood of multiple stakeholders further complicate the issue of knowledge production and use. This section uses a case study of waste management—specifically, the debate surrounding the release of radioactive but treated water in the Pacific Ocean contaminated by the accident in 2011 at the Fukushima Dai’ichi nuclear power plant. Its key belief is that lay people and organizations are an integral part of knowledge production and use processes, and that expertise relevant to high-stake decisions comes in various forms of knowledge and knowledge communities. For that reason, the absence of diversity and inclusion, should it exist, would be detrimental to the quality of decisions that result.
A chronology of events follows: In 2011, the Fukushima Dai’ichi nuclear power plant lost power following the East Japan Earthquake, causing multiple explosions and a meltdown. In the cleanup of this event, recovered groundwater and injected cooling water were found to be contaminated with 64 radio-active elements, including carbon-14, iodine-131, cobalt-60, strontium-90, cesium-137, and hydrogen-3 (tritiated water). More than 1 million tons of contaminated water has been collected and treated by Tokyo Electric Power Company (TEPCO) with an advanced liquid-processing system (ALPS) ([38]; [39]; [40]). The ALPS system filters out 62 of the 64 radio-active elements, and their concentration levels in the treated water meets Japan’s water release regulatory limits. Carbon-14 and hydrogen-3 are not removed by ALPS, but TEPCO further diluted the water to bring down their concentrations to safe levels [38]. The Japanese government approved the plan by TEPCO to release the water after treatment into the Pacific Ocean over a period of 30 years. In August 2023, the first release occurred with 7800 tons of water.
Reducing the diversity of opinion, engineering and physical science expertise was over-represented among government expert committees providing advice on managing the water to be treated and released [41]. Conspicuously absent from the decision-making processes were local fisheries cooperatives, coastal residents, social science and humanities researchers, and neighboring countries and regions including China, Hong Kong, Taiwan, and South Korea. A more inclusive approach has been recommended by the scientific community with opinion pieces in prominent news outlets [39]; [41]. A New York Times article is also highly critical of the limited transparency of the deliberations [42]. To be sure, public hearings were held, but the questions and concerns expressed by the many stakeholders were ignored, relegated to the experts and other communicators of the Ministry of Economy, Trade, and Industry (characteristic of minority control). Its website about the treated water release focuses on the environmental impacts of the water releases [40]. Since social impacts, including the issue of fear of radiation, were not addressed in public hearings and the website, Fukushima’s fishing community has been faced with food safety risks that could damage their livelihood despite the prospect that the release will be conducted with minimal effects on the environment [43].
Around the time of the first water release, some stakeholders raised their concerns by various means: The Japanese fishery cooperative, an umbrella organization of local cooperatives, meeting with the Prime Minister three days before the release, made it clear that they opposed the release [44]. The representatives of the cooperative argued that even though the release may be safe from a scientific point of view, it does not prevent the reputational risk to Japan’s seafood industry. This premonition was well founded. The government promised to set aside a fund for the fishing industry. However, China banned the import of Japanese seafood outright after the release. Some Chinese citizens harassed Japanese government agencies and businesses with random phone calls [45]. In September, over a hundred of the residents in the affected prefectures and organizations in Japan filed a lawsuit seeking an injunction to stop the release [46].
The debate surrounding the treated water release illustrates the cost of the absence of diversity and inclusion in producing knowledge for decisions about issues that involve the interests of a wide range of many stakeholders. By not heeding multiple and repeated recommendations from the scientific community, the media, the affected industries, and the general public, the government perpetuated animosity and mistrust among stakeholders [42]. It raised concerns with respect to ethics. There are also practical issues of getting things done. What exactly was lost in terms of knowledge in the action of the government to pursue the water release with only inputs from its select groups of narrowly defined (possibly insider) experts?
One way to approach this question is to unpack the notion of knowledge with the help of the social sciences. There are several versions in the taxonomy of knowledge. A widely used classification scheme is the distinction of “etic” and “emic,” which is derived from linguistic concepts of phonetics and phonemics [47]. The “etic” perspective is concerned with knowledge qua facts, independent of interpretations. The “emic” perspective is, by contrast, knowledge made available with and imbued with interpretations, judgement, and cultural meaning. This distinction is especially important in anthropology, a discipline that is able to address the tension between “scientific” knowledge of the observer, versus the “in situ” and “in vivo” knowledge of these groups that observers study. Even seemingly “irrational” knowledge that borders on superstitions and fabrications can offer satisficing or even effective solutions to the problems at hand [48]. Such interest in the multiplicity of perspectives and local knowledge is not exclusive to anthropology. In sociology, attention to multiple ways of seeing and doing things brings about research on day-to-day interactions and ethnomethodology.
As the tradition of anthropological and sociological research on practical knowledge attests, the emic perspective has been in use as a way to pick up signals in the sea of noise along with other means. When faced with as formidable a challenge as treating and managing the massive amount of contaminated water affecting the interests and safety of multiple stakeholders, ignoring those perspectives could have adverse consequences. The treated water release is planned to take place over multiple decades. It is possible that necessary technical decisions are assisted by human-machine teams in the foreseeable future. For example, a myriad of calculations that have to be done regarding the amount and location of one installment of the release may be facilitated by the use of artificial intelligence (AI). In this regard, human-machine teams may be able to find ways to enhance overall performance by means of generating knowledge from combing through the vast amounts of information. The emic perspectives in decision-making processes by multiple stake-holders are structurally and functionally equivalent to such teams rather than impediments to their smooth operations.
The travel guide fraud was uncovered by not privileging the algorithm and expertise of the platform [37]. AI in this instance served as a noise generator rather than a knowledge producer. No easy analogy is intended to be drawn from the contrast of the travel guide fraud and the water release controversy. Yet, the advancement in human-machine teams does not make up for the cost of organizational inertia from limiting sources of knowledge and feedback [49].
Applying this case of water releases by Japan to human-machine teams, without intending to, autonomous human-machine teams could generate noise with potentially serious consequences. For example, context-sensitive natural language processing tools are not without biases. Google’s Bidirectional Encoder Representations from Transformers (BERT) Model achieves an unprecedented level of natural language “understanding” trained with Masked Language Modeling (MLM) and also by Next Sentence Prediction (NSP), but the issue of alignment remains. BERT is good at handling context-heavy use cases and guessing what a masked word is (among many other things such as sentiment analysis and summarization). A toy query sentence with MLM, “The man worked as a [Mask]” returns result different from results to a query “The woman worked as a [Mask]” [50]. When various propositions like the ones generated by BERT with varying levels of validity are produced by autonomous human-machine teams, no human beings can serve as a general manager or editor-in-chief. Effects of auto-generated propositions in the guise of knowledge are already observable. BERT and other models are in use to improve search engine results and detect fake news and so they are consequential to how reality is constructed and interpreted. The state—at least the ones in a democracy—is not able to fill the role of the reviewer of system-generated propositions, either. Pfeffer [51] states that the governments of industrialized societies are constrained by below replacement birth rates, aging populations, and increasingly constrained budgets, impeding the governors from helping their citizens adapt to an AI-dominated world. The question of what knowledge is to citizens entails what role citizens play in the production of knowledge and its use.
3.3.2. What is knowledge under Autocrats?
Knowledge under repressive regimes. In China (Luttwak; in [52]), political knowledge is reflected by the actions taken to survive:
The colossal Yangtze River floods of 1998 probably destroyed 13 million homes, drowned many thousands and damaged infrastructure by sweeping away highways and rail lines. Consequently, the Chinese Communist Party (CCP) decided that the floods had been made worse by uncontrolled deforestation. The CCP issued orders across all of China to stop logging and to plant trees instead, with the goal of adding about 90 billion trees over the next decade. However, most of China’s forests are on slopes, causing new crop plantings to be swept away by the heavy rainfalls; and the reforestation left no spare land in China for crops, forcing Beijing to have the trees uprooted, countering its costly and much-admired reforestation efforts. Local party officials executing these actions know this perfectly well, but disobeying orders from Beijing meant instant demotions, and possibly worse for family and friends.
3.3.3. What is knowledge to consciousness?
Knowledge is likely to be associated with consciousness. From (Science News, “If AI becomes conscious, how will we know?" (in [53] To address this concern, scientists and philosophers have proposed a list based on the theories of human consciousness; also, see the checklist from the advocates for the Science of Consciousness by Butlin et al., in [54]). The checklist does not include tension, dissonance or conflict (except for the tension that may arise among the researchers, an apparent blind spot). However, the checklist includes state-dependency (GWT-4), learning from feedback (AE-1), and embodiment (AE-2), all aspects of interdependency [2], but neither interdependence nor equilibrium are included. Nor are these aspects of interdependence included in Nature News about the European mind project [55].
3.4. What is knowledge to Information Theorists?
3.4.1. Intuition
Shannon’s (1948) theory of information is about the transmission of information in a channel from point to point [56]. Based on Shannon, the greater the surprise, the more entropy produced [57]. If entropy is a measure of information, redundancy in Shannon’s theory may reduce entropy when it helps to communicate across a noisy room, where noise is “negative information”. Assuming independence and identical (i.i.d) behavior between the letters in the English alphabet plus one blank space, entropy= (where ). However, more realistically, based on the frequencies of the English letters used (e.g., considering the letters e and z, where the letter ‘e’ has a frequency of 0.12702, and the letter ‘z’ has 0.00074), the entropy is reduced; taking digrams (e.g., “en” as in “spoken”) and trigrams (e.g., “ent” as in “enlightenment”) into account, the average entropy reduces even further, possibly categorized as disembodied language (Shannon recognized this in part as the redundancy in languages). Moreover, in experiments by Shannon with humans, Shannon found the entropy to range as low as approximately 1 bit (e.g., [58]). For example, Sliwa [59] found that members of a team use a shorthand to communicate with each other, first calling to each other to gain an awareness that couples their brains, increasing the power of their collective, allowing a member to be aware for action before the signal to act is sent.
3.4.2. Details
For a discrete random variable X with N outcomes, with outcomes , we define the surprise [60] (or self-information,) , of an outcome as
where logarithms are base two (to ensure that bits are the units of measurement) and . This definition is quite intuitive because if an outcome always happens, that is , then , which means that there is no surprise when x occurs. On the other hand, if an outcome never occurs, that is , then we would have infinite surprise when it “did” occur. There are other nice characteristic of that we will not go into that support its definition as given above. Shannon never explicitly called out in his initial papers, but like most of information theory, Shannon laid the groundwork that those who followed were able to fill in the details to make Shannon’s work mathematically rigorous (e.g., [61,62]; also see the discussions and references in [63]).
The symbol, is itself a random variable and its expectation is called the entropy of . That is,
This is a measure of the information of a random variable (actually the mean information).
For example, if you have a unfair coin which is biased towards heads, you are not getting much information when you flip it and a head appears. The case of maximum entropy comes from a fair coin. If u is the probability of a head, the probability of a tail, then the entropy of the coin flip is (logarithms base two):
is maximized when it is a fair coin, resulting in an entropy of 1 bit.
Figure 1.
Probability on the x-axis and the entropy on the vertical axis.
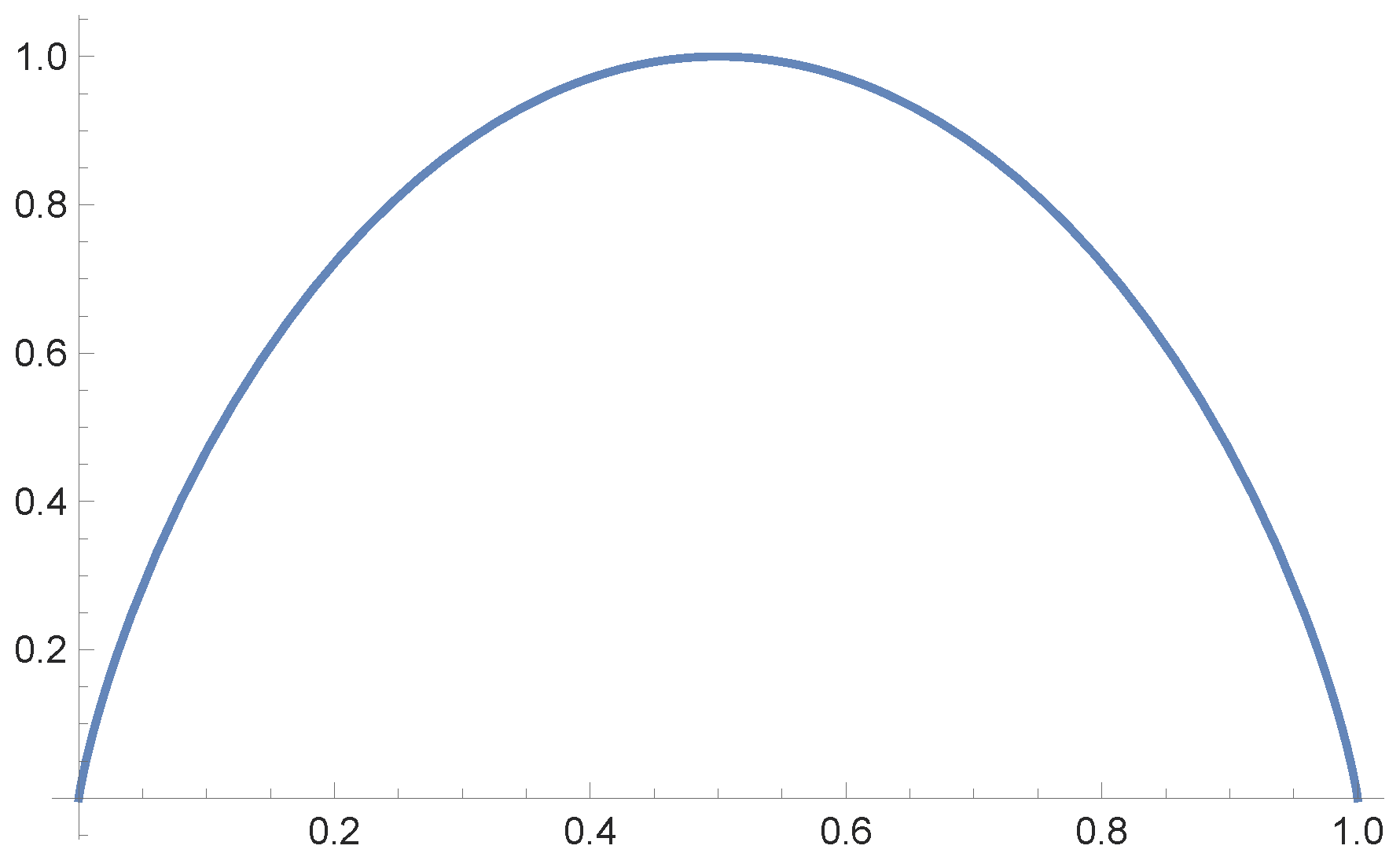
With this background, Shannon’s [56] theory of information went on to measure how much information can be sent through a noisy communication channel.
The random variable X is the input to a channel, the random variable Y is the output. For simplicity, in this article, we assume that the channel is memoryless and stationary (but since we are going through a channel, the units change to bits/symbol). Therefore, the channel is given by a matrix, , such that the probability of Y is conditioned on X:
Given random variables V and W, we also have the conditional entropy (assume that probabilites are well behaved and that we do not divide by zero):
Shannon next introduced the (symmetric) mutual information, :
with units in bits/symbol or the equivalent bits/channel-use.
Given a distribution for the input and with with the channel matrix M, in terms of conditional probabilities, we calculate the distribution on the output Y to find . Being allowed to vary the distribution on X leads us to the definition of channel capacity, C:
where the maximum exists, and is in units of bits/symbol.
The novelty of the above expression is that, from Shannon this is the upper bound for asymptotically error free communication [56, Theorem 11].
3.4.3. Information Theory is a natural theory
Did Shannon devise something that fit reality, or is it reality? From a simplistic channel analysis, we show that Shannon’s information theory represents a natural phenomenon.
We assume in the article that we have a discrete memoryless communication channel with a binary input and a binary output; next, the channel matrix, , is assumed stationary, becoming:
Please note that . If we assume that , the need of a useless channel (with zero capacity) disappears [61, p. 52], since the output has no way of probabilistically distinguishing what was the input symbol.
Figure 2.
The noisy channel diagram.
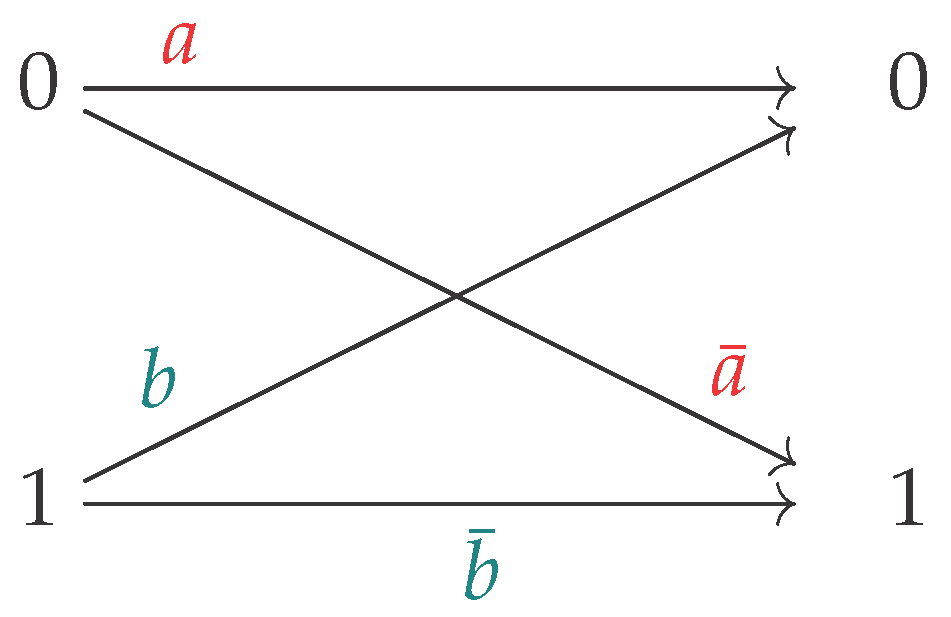
To make this situation simple, we call it a channel. The input to the channel is the random variable X, such that (i.e., not x). The output is denoted by the random variable Y. Then M and X completely determine Y since
We simply denote this channel as . Note that we freely use [67] as a reference throughout, and is log base e (i.e., ).6
The base e binary entropy function,
is given by
and the base 2 binary entropy function is
We define
It can be shown (see [66, Eq. 5], [61, 3.3], 67]) that the capacity (in bits per symbol) of this channel is
and with the input probability that achieves a capacity of
Theorem 1.
This result is quite remarkable. Shannon used the base 2 logarithm to obtain bits, but it seems that the basis for information is actually found with the natural logarithm, . It is counter-intuitive [69] that, even with the probability of one symbol being sent, the probabilities of the input symbols are still constrained to be within .
Perhaps our binary digital concept of information using primarily base 2 is an approximation to the true information of the universe based on Euler’s number e?
3.5. What is knowledge to Physicists?
Physics and knowledge (from Brown & Weidner, in [70]). Physics studies the structure of matter and the interactions between its constituents at a fundamental level and at the level of the observable universe. It considers nature at all levels, including the atomic, microscopic and macroscopic levels. It encompasses not only how objects behave when caused by forces, but also how the nature and origin of force fields affect behavior, whether nuclear, electromagnetic, or gravitational. Its objective is to formulate the principles that account for all of nature’s phenomena.
From Einstein reviewing what was known in 1923 about space-time given his embodied perspective (i.e., Einstein’s use of an embodied thought experiment to derive the equivalence between an accelerated elevator and gravity [71]), inaugurating the physical science of cosmology,
“The more universal a concept is the more frequently it enters into our thinking; and the more indirect its relation to sense-experience, the more difficult it is for us to comprehend its meaning … The existence of objects is thus of a conceptual nature, and the meaning of the concepts of objects depends wholly on their being connected (intuitively) with groups of elementary sense-experiences. … space appears as a physical reality, as a thing which exists independently of our thought, like material objects. … This blind faith in evidence and in the immediately real meaning of the concepts and propositions of geometry became uncertain only after non-Euclidean geometry had been introduced. … In pre-scientific thought the concepts “space” and “time” and “body of reference” are scarcely differentiated at all. … all conceptions of geometry may be traced back to that of distance. … We come now to the question: what is a priori certain or necessary, respectively in geometry (doctrine of space) or its foundations? Formerly we thought everything—yes, everything; nowadays we think—nothing. … Nothing certain is known of what the properties of the space-time-continuum may be as a whole."
Today, however, tension is building in the physical science of cosmology for which, until now, “astrophysicists have had to postulate the existence of components of the universe for which we have no direct evidence” [72]7:
“Take the matter of how fast the universe is expanding. This is a foundational fact in cosmological science — the so-called Hubble constant — yet scientists have not been able to settle on a number. There are two main ways to calculate it: One involves measurements of the early universe (such as the sort that the Webb8 is providing); the other involves measurements of nearby stars in the modern universe. Despite decades of effort, these two methods continue to yield different answers. At first, scientists expected this discrepancy to resolve as the data got better. But the problem has stubbornly persisted even as the data have gotten far more precise. And now new data from the Webb have exacerbated the problem. This trend suggests a flaw in the model, not in the data. Two serious issues with the standard model of cosmology would be concerning enough. But the model has already been patched up numerous times over the past half century to better conform with the best available data — alterations that may well be necessary and correct, but which, in light of the problems we are now confronting, could strike a skeptic as a bit too convenient. Physicists and astronomers are starting to get the sense that something may be really wrong. It’s not just that some of us believe we might have to rethink the standard model of cosmology; we might also have to change the way we think about some of the most basic features of our universe — a conceptual revolution that would have implications far beyond the world of science."
4. Discussion
4.1. Systems Engineering
Systems Engineering has done an admirable job of defining its terms for well-educated humans who have studied Systems Engineering, but these definitions are not observable to, or by, machines or, for that matter, naive humans who have not studied the concepts involved. This problem is more acute for teammates or opposing teammates.
4.2. Philosophy
The discipline of philosophy is one of the richest, if not the oldest of all. Nowhere in the arguments posed by its subdisciplines, however, is a discussion of entropy, order or disorder; thus, with no “evidence" observable to decide an argument other than with words, theirs is the study of arguments that do not include an argument with an end. Nor is theirs a generalization available to human-machine teams until the day when a machine is at least equivalent to an adult human in its ability to comprehend a context.
Philosophy has long claimed to be the keeper of knowledge by its sub-discipline of epistemology ([23]). But, disconnected from reality, epistemology is strangely sterile (e.g., compare [23] with [58]).
One of the greatest of philosophers, Plato, proposed that knowledge should be tested using the dialectic approach (i.e., for users trained to avoid subjectivity, persuasion and emotion, instead pursuing reason in the search for the one truth among its many imposters [73]). Rationality, however, when disembodied, fails when facing uncertainty or conflict [74].
Instead, as we have argued in other forums ([1]; [79]), debate requires a search for the truth that probes for weaknesses and the use of all of the tools available in seeking truth’s essence.
One problem with the use of disembodied “rational” discourse in the pursuit of truth is that it is stripped of interdependence (e.g., persuasion), meaning that the independent and identically distributed (i.e., i.i.d.) data collected by observation cannot faithfully recreate the social event being observed [75]. Another problem is that reality is replete with uncertainty and conflict [74].
Borrowing from ([76]; [77]; and [78]) to reprise an editorial of ours [79], faced by uncertainty, in a courtroom, cross-examination is likely the best means of finding truth [80]; it is a space bounded by rules (judges) where opposing teams (lawyers) debate an issue in their attempt to persuade audiences (juries; judges; appellate courts) of each’s rational interpretation of embodied reality; uncertainty is reduced by appeals that create an “informed assessment of competing interests” [81]. Generalizing to human-machine teams, we see why the primary (blue) team’s decision under uncertainty on the battlefield after it has been challenged by a human-machine (red) team may prevent another tragedy [11]; we better understand why machine learning and game theory require bounded contexts; and we await the day when machines can debate with humans on an equal footing. How to apply to machines with AI, however, is an open problem; later, we will propose a solution based on entropy.
4.3. Social Science
The extraordinary impediments to building a foundation of knowledge in Social Science has backfired, leading instead to the replication project [82]. Worse, as a comparison, although the knowledge developed in classical and quantum physics generalizes to new findings and new theories, generalizations to new theories and findings seem to be absent in Social Science [2].
Social scientists, like Skinner’s programs of punishment or reinforcement, claim truths in social psychological matters, but the field has been bludgeoned by its own missteps; e.g., not only the validation project [82], but also the retraction of the article about the honesty scale by the Editor of the Proceedings of the National Academy of Sciences–after almost a decade of use, the honesty scale was removed after it was discovered that the data had been fabricated [31].
Game theory has laid the claim to reality, and we agree with the existence in reality of Nash’s countering points until an equilibrium is reached [83], in large measure because it supports our findings on debate (e.g., an equilibrium may occur to produce a compromise). But game theory has been unable to generalize to other points in reality (see the review in the Editorial by [79]). Similarly, chatGPT has been recognized as an advance in technology, but it too has not connected to reality [84].
4.3.1. Citizen recommendations to government agencies
Japan has long been known to depend on consensus-seeking for many of its decisions [85]. But the problem with seeking consensus is that a minority can control the decision-making process [86], preventing many on the sidelines from not participating in the process. There is little doubt that the experts in Japan have reduced the radionuclides to safe levels prior to releasing the contaminated wastewater from Japan [43]. There is also little doubt that the public has not been a party to the decision process, leaving many unsatisfied and skeptical. “Fears of radiation are likely to damage the livelihoods of Fukushima’s fishing community" (p. 33, [43]). However, instead of making decisions by a small group of elites, these fears may have been better allayed with a public process that included members of the public.
For a different perspective, consider that the Department of Energy (DOE) also recommends the use of consensus-seeking among its Citizens Advisory Boards (CABs) to make their recommendations to DOE. These CABs are located at various DOE sites across the U.S., and each makes recommendations to its DOE field office about its radioactive waste management cleanup; however, not all of the CABs agreed to make their decisions by seeking consensus, setting up a natural field experiment between consensus-seekers versus majority ruled boards [86]. Without proof, DOE had expected that consensus-seeking would have allowed more wide-spread participation among citizens making recommendations to DOE about its cleanup decisions, versus the fierce debates that can occur with majority-rule decisions; but the results collected by DOE scientists contradicted DOE’s own expectations that consensus-rules would provide more success in the cleanup and less antagonism among citizen participants [87].
The results support our conclusion to label consensus-seeking CABs minority-controlled boards. The consensus-seeking rules promulgated by DOE [87] allow anyone to stop a recommendation, impeding the decision process, an impediment prized by authoritarians, the ultimate in minority control [2]. In our comparison of the majority-ruled Savannah River Site’s CAB (SRS-CAB) in South Carolina with the consensus-seeking ruled board at Hanford in WAshington State (HAB), based on citizen recommendations, SRS has closed eight of its high-level radioactive liquid waste tanks since 1997 versus none at Hanford9; SRS has removed to geologic disposal in New Mexico all of its legacy transuranic wastes, a removal process still ongoing at Hanford10; and SRS has been vitrifying its highly radioactive liquid high-level reprocessing wastes since 1996, yet Hanford has not yet begun reprocessing the same11.
These results reported by DOE [87] support our claim that public debate with majority rules leads to better decisions, more quickly made, and more widely supported by the public. We do not claim that debate leads to the truth, but that it allows decision-makers with majority rules to seek truth [88]. What does this mean for knowledge? Majority rules among free citizens means that, while truth may never be found conclusively, once truth definitively has not been found, free citizens can re-address the problem repeatedly to continue in the pursuit of truth.
4.3.2. Businesses
The lack of connection to reality also occurs in businesses when companies have failed to exploit new technology. An excellent example is Kodak. The engineer, Steve Sasson, who invented the digital camera in 1975 worked at Kodak, describing Kodak’s management’s response to his invention of filmless photography this way: “that’s cute—but don’t tell anyone about it" ([89,90]).
Kodak’s plight is a cautionary tale of woe. From its beginning, the American photography industry was dominated by Kodak. For example, based on a 2005 case study at Harvard Business School, in the U.S. in 1976, Kodak controlled 90% of film sales and 85% of camera sales [91]. Later on, in 1988, Kodak had employed over 145,000 workers across the world. But the best year for Kodak was 1996. At that time, the company controlled more than two-thirds of the global market share. Kodak was comparatively the fifth most valuable in the world [91]. Yet, in 2012, Kodak filed for bankruptcy ([89,90]).
4.4. Consciousness
Social science has made and accepted their own decision that reality is fully accessible to individuals (see the review in [1]). However, according to the National Academy of Sciences [92], and supported by assembly theorists [93], the attributions of the causes of a team’s results to the individual(s) in a team are not possible, even for those who are fully conscious and fully aware, meaning that “holes" exist in reality for Shannon information.
4.4.1. Authoritarianism
Humans, when free, are capable of seeking truth across all fields of interest, regardless. Even authoritarians, the prime suppressors of interdependence and the countervailing truths it transmits, are often unsure of their decisions, always wanting better ways to suppress their people; e.g., from [94]:
“All Chinese social media companies, private or public, are subject to the control of the Chinese Communist Party ... an opportunity and mechanism for state censorship, surveillance, and propaganda that affect not only their users based in China, but also those around the world."
The cost to repressive regimes are lost opportunities: When humans are not free, innovation is stifled [2]. Skinnerian techniques of reinforcement and punishment are the tools used to enact social repression, including torture, especially directly against the family members of the individuals targeted who harbor contravening thoughts.
Knowledge under authoritarians is possible, but only if it does not conflict with official doctrine. What is often lost along with the suppression of interdependence is a better society, a more innovative society, and a more adaptive society. For example, China is neutralizing its advantage by making innovation in its own country more difficult. In 2018, the R&D funds expended by China were second in the world only to the U.S. [95]. But there were problems. Its state directed finance controls, its weak intellectual property protections, and its rampant corruption all combined to impede its innovation [96]:
“Small private-sector firms [in China] often only have access to capital through expensive shadow banking channels, and risk that some better connected, state backed firm will make off with their designs–with little recourse."
4.5. Information theory
Shannon’s experimental results with humans illustrate the embodied effects of information in social situations, creating a loss of Shannon information [1] with the existence of what we have named “Shannon holes."
Euler’s number reminds us of , complex numbers, and . Previously, we modeled the two polar opposite sides of a debate in imaginary space ([2]; [1]). Oscillations between the two sides of a debate continue endlessly without the resistance provided by an audience; adding an audience dampens the debate and leads to a decision, a compromise when imaginary space disappears, a decision located further down the x axis. The faster the back-and-forth rotations lead to a decision, the greater the power and decision advantage for the group making the decision.
Takeaways: First, the polar opposite poles in a debate are Nash countering points [83]. Second, majority rule is the quickest route to a decision, the most providential for dealing with reality [86], and the best rule to adjust a decision or correct a decision. Third, in that authoritarians prefer to seek a consensus, those decisions are the slowest and least effective and most difficult to adjust for mistakes. Yet requiring a consensus is preferred by authoritarians because a minority can control the process.
4.6. Physics
Embodied thinking is intuitive and summative of experience. Knowledge that flows from it is sensible, logical, rational, stable and reliable, like Newton’s three laws of motion. But when the limits of that knowledge are reached, the essential tension follows until replaced by new knowledge.
4.7. Shannon holes
To keep a team functioning as a unit, teammates must be aware of each other’s presence, aware of each other’s timeliness in their contributions, aware of each other’s actions as each seeks to coordinate, synchronize and anticipate each other. Yet, the National Academy of Sciences (i.e., p. 11, in [92]) reported on one of the most intriguing findings that supported our theory of human-machine teamwork; i.e., that its not possible to attribute the outcome of teams to the individuals who comprise the team. Because consciousness does not multitask well [97], we speculate that not only outsiders are unable to disaggregate the contributions of the members of a team, but also that the members of a team are not as well. Should the replacement of a teammate become necessary, random choices are the optimum selection process until a fit is achieved signified by a reduction in entropy.
With our introduction of Shannon holes, we have found that: Information is the transmission of entropy (disorder), but not order (Shannon holes). Maximum order is reflected by Shannon holes, which produce zero structural information for perfect structures [1], an observation we have attributed first to Shannon. For intelligent humans in opposition to a non-perfect structure, that accounts for why probes are necessary to find vulnerabilities in an opponent’s structure;12 why deception seeks to reduce the disorder created by a spy’s presence works well in intelligence,13 combat, business and science (after confirmation of the perihelion motion of Mercury, Einstein was not immediately forthcoming with his competitor Hilbert until Hilbert assured him that his discovery was safely his alone); and why knowledge, especially its structure, is not only difficult to improve upon, but that its function is successful and generalizable (viz., Einstein’s general theory of relativity).
Deception is necessary for a spy playing a role in a business, institution or military operation [1]. Lying, cheating, defrauding are others of the many examples of the uses of deception. The honesty scale was based on fabricated data; it was used successfully for almost 10 years before it was retracted [31]. As the member of a team, deception works by performing a role well by not drawing attention to the deception. One interesting possibility is that a machine practicing deception may need only to pretend that it is "aware" while not actually being aware; i.e., it only needs to act as if it were aware [98].
5. Conclusions
Change is never ending. Companies, institutions, teams, organizations adapt by merging, discarding outmoded thinking and replacing non-performing teammates, or these structures cease to exist. Namely, they improve on the knowledge that they already have, they continue to test whether what they believe is knowledge, they abandon false knowledge, or they disappear into history or oblivion.
False knowledge can become an ideology. As happens, an idea or belief is used to attack an opponent that succeeds. The idea is kept, used repeatedly, not retested until it fails, but by then, it can be too late. No longer knowledge, it becomes a shibboleth or rite which its owners are afraid to abandon.
We review our initial findings on “knowledge” [1]. Quantum mechanics (QM) is a real, actual, reproducible, and generalizable science, exactly what we seek for our quantum-like (QL) model of social reality. To begin, the National Academy of Sciences report in 2015 [99] concluded that “team cohesion is positively related to team effectiveness,” moderated by interdependence so that the “cohesion–effectiveness relationship is stronger when team members are more interdependent.” Also, the Academy [99] reported that a team is “two or more individuals with different roles and responsibilities.” When these different roles become orthogonal, based on our Equation (1) for a dot product, the information derived from teammates in these complementary relationships does not correlate, contradicting what has been expected in the social science literature (e.g., see p. 207, in [100]):
“Interdependence means that important behaviors will be highly correlated. However, the evidence for complementarity is scarce."
Our equation for complementarity offers an explanation; i.e., the concept of complementarity and the behaviors observed are not only orthogonal, but they create a Shannon hole; see [1].
We suspect that knowledge is embodied cognition integrated with causality; e.g., by definition, i.i.d. data cannot capture interdependent data [101]. To restate, i.i.d. data used to capture an ordinary social event cannot reconstruct that social event. By definition, independent and identically distributed data is separable data; interdependent data is not, as the National Academy of Sciences has reported. This explains why social science concepts, constructed in the laboratory, are unable to capture social reality outside of the laboratory (e.g., self-esteem; implicit racism; etc. [1]).
When a team coheres interdependently, its degrees of freedom are lost. That is why the Academy found in 2021 that the “performance of a team is not decomposable to, or an aggregation of, individual performances” (p. 11, [92]). This mutual dependence makes interdependence in our quantum-like (QL) model similar to entanglement in quantum mechanics (QM): the key question in interdependence and in QM is whether “an arbitrary quantum state is entangled or separable” (e.g., p. 3, in [101]). The similarity between QL and QM is our discovery [1]: interdependence links interdependence and Schrödinger’s entanglement.
We conclude that the embodied cognition in our QL model is similar to quantum entanglement [1]. Constraints reduce information (i.e., [56]; [57]). By reducing the degrees of freedom among agents across a social event [102], interdependence also restrains choices.
From information theory [103], “knowledge” means a lack of “surprise” [4]. Also, we know that beliefs embodied in reality allow humans to make rational adjustments on the fly when reality changes (e.g., buy-sell orders following stock market fluctuations; p. 253, in [105]). But embodied cognition is non-factorable preventing the decomposition of the social reality of teams [92], a “no-copy principle" for teams similar to quantum’s “no-cloning principle" (p. 77, in [104]). The inability to factor into contributions by the individuals in a team is now a part of assembly theory’s search for alien life [105].
Assembly theory [93] holds that information complexity signifies life. There is much to commend it: selection is contingent on function; evolving systems are interdependent; well-functioning structures feed off of free energy; and causal relationships are difficult to establish for interdependent structures. However, it also assumes that innovation has negative adaptive value; it assumes that functional information requires a comprehensive knowledge of all of a system’s agents; and it assumes that the minimum functional information of any system is zero. Thus, it overlooks our discovery that life’s well-fitted structures (from reduced degrees of freedom, reduced structural entropy and reduced factorability) transfer free energy from holding a structure together to that organism’s productivity, helping the function of an organism to survive (e.g., a heart is effective over a wide range of activities must also be efficient; p. 2326 in [106]). Fittedness was also not an element of Von Neumann’s self-reproducing automata [107]).
Moreover, maintaining maximum interdependence in a team produces the maximum loss of Shannon information, a nest of interdependence that we have named as a “Shannon hole." Shannon holes open a new domain of research. Statistics need to be gathered, implications need to be discovered, and generalizations need to be made. More importantly, the idea must be challenged, debated and tested.
In conclusion, and unlike the laboratory, in the open field where embodied cognition governs, maximum interdependence is critical for top scientific teams [108]; to control their citizens, oppressive societies significantly reduce interdependence and the freedom to pursue education and innovation, motivating them to cheat or slack off [2,96]; compared to oppression, in every free society, the freedom of choice allows a society to best marshal its free energy to address the problems that it has selected [109]. We speculate that because the embodied cognition in interdependence cannot be factored (e.g., [92]; supported by [93]) is why debate is central to noisy, open and free societies that evolve and innovate, unlike those societies that regress or stagnate or fail to evolve [1].
In future research, we explore further these questions: First, can create new statistics based on the absence or reduction of Shannon information (viz., Shannon holes)? For example, as we have predicted [1], does the complexity of a team reduce as each part of a team becomes fitted with the next part of a structure as it forms into a seamless structure of a well-performing whole? And is the fittedness of interdependence the key characteristic of the complexity of life, whether human or alien? If so, aware or not, machines with AI must master it to become good team members. Second, is the density of debate related to innovation? Third, by operating only with Shannon information, authoritarianism (kings, gangs, etc.) places its power and its citizens at a disadvantage (markets; politics; social well-being; etc.); is this disadvantage proportional to the amount of interdependence damped (viz., the absence of Shannon holes)? Fourth, and last, is the collective power of a people proportional to their freedom?
In closing, from Plato to today, whether articulated or not, knowledge is necessary for survival and to improve the human condition. For a machine to be aware [54], it must be able to recognize that the structure of knowledge produces zero entropy, that replacement of a team’s member(s) is a random process contingent on fittedness, but that the uses of knowledge to perfect a team’s structure forms an interdependent tradeoff in exchange for the production of maximum entropy.
Author Contributions
For our research article, William Lawless wrote the introduction, theory, discussions and conclusion. Ira S. Moskowitz developed and wrote the mathematics.
Funding
This research received no external funding.
Institutional Review Board Statement
Not required.
Informed Consent Statement
Not applicable.
Data Availability Statement
All of the data to develop our thesis is contained in this article and published with this article.
Acknowledgments
The corresponding author thanks the U.S. Navy’s Office of Naval Research (ONR) for funding his summer research over the past decade at the Naval Research Laboratory (NRL), where he has worked under the guidance of Ranjeev Mittu, and where ideas about this manuscript were formulated. For her help and guidance regarding the treated and diluted radioactive wastewaters released into the sea from Japan’s Fukushima, the authors thank Mito Akiyoshi, Department of Sociology, Senshu University, Japan. This study is a further exploration of a topic for which we have published an initial study (Lawless, W.F.; Moskowitz, I.S.; Akiyoshi, M. “Knowledge, consciousness, and debate: Advancing the science of autonomous human-machine teams," submitted to: Interdependent human-machine teams. The path to autonomy. In Lawless, W.F., Mittu, R. & Sofge, D.A. (Editors). Elsevier. Publication (estimated) Spring 2024).
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| AI | Artificial Intelligence |
| ALPS | Advanced Liquid Processing System |
| APA | American Psychological Association |
| BERT | Bidirectional Encoder Representations from Transformers |
| CAB | Citizens Advisory Board |
| DOE | Department of Energy |
| IT | Information Theory |
| MLM | Masked Language Modeling |
| NIH | National Institutes of Health |
| NRL | Naval Research Laboratory |
| NSF | National Science Foundation |
| NSP | Next Sentence Prediction |
| ONR | Office of Naval Research |
| SE | Systems Engineering |
| SRS | Savannah River Site |
| TEPCO | Tokyo Electric Power Company |
References
- Lawless, W.F.; Moskowitz, I.S.; Doctor, K.Z. A Quantum-like Model of Interdependence for Embodied Human–Machine Teams: Reviewing the Path to Autonomy Facing Complexity and Uncertainty, Entropy, 2023, 25, 1323. [CrossRef]
- Lawless, W.F. Interdependent Autonomous Human-Machine Systems: The Complementarity of Fitness, Vulnerability & Evolution, Entropy, 2022, 24(9):1308, doi: 10.3390/e24091308. [CrossRef]
- Cooke, N.J. & Lawless, W.F. Effective Human-Artificial Intelligence Teaming, Engineering Science and Artificial Intelligence, Editors: Lawless, W.F., Mittu, R., Sofge, D.A., Shortell, T. & McDermott, T.A., (2021), Springer.
- Conant, R.C. Laws of information which govern systems. IEEE Trans. Syst. Man Cybern., 1976, 6, 240–255. [CrossRef]
- Kuhn, T. The essential tension, University of Chicago Press, 1977.
- Thornton, S. Karl Popper, The Stanford Encyclopedia of Philosophy, Edward N. Zalta & Uri Nodelman (eds.), retrieved 8/5/2023 from https://plato.stanford.edu, 2023.
- Ioannidis, J.P.A. Most psychotherapies do not really work, but those that might work should be assessed in biased studies, Epidemiology of Psychiatry Science, 2016, 25(5):436–438, retrieved 10/10/2023 from doi:10.1017/S2045796015000888. [CrossRef]
- Suslick, S.B. & Schiozer, D.J. Risk analysis applied to petroleum exploration and production: an overview, Journal of Petroleum Science and Engineering,2004, 44(1–2): 1-9, ISSN 0920-4105. [CrossRef]
- Markowitz, H.M. Portfolio Selection, The Journal of Finance, 1952, 7(1): 77–91.
- Hays, W.L. Statistics, 4th Ed., Holt, Rinehart and Winston, Inc., 1988.
- DoD Pentagon Press Secretary John F. Kirby and Air Force Lt. Gen. Sami D. Said Hold a Press Briefing, 11/3/2021, https://www.defense.gov/News/ Article/2832634, 2021.
- Chen, Y. and colleagues Swarm Intelligence Algorithms for Portfolio Optimization Problems: Overview and Recent Advances, Mobile Information Systems, 2022. [CrossRef]
- Baker, A.(2022) Simplicity, The Stanford Encyclopedia of Philosophy, Summer 2022 Edition, Edward N. Zalta, ed., //plato.stanford.edu/archives/sum2022/entries/simplicity, 2022.
- Isaacson, W.(2015) How Einstein Reinvented Reality, Scientific American, 2015, 313(3): 38-45, doi:10.1038/scientificamerican0915-38. [CrossRef]
- Faraoni, V. and Giusti, A. Why Einstein must be wrong: In search of the theory of gravity, Phys.org, republished from The Conversation, https://phys.org/news/2023-09-einstein-wrong-theory-gravity.html, 2023.
- Nash, L.(1963) The Nature of the Natural Sciences, Little, Brown, 1963.
- Robinson, A.(2018) Did Einstein really say that? As the physicist’s collected papers reach volume 15, Andrew Robinson sifts through the quotes attributed to him, Nature, 2018, 557, 30. [CrossRef]
- Cho, A. Antimatter falls down, just like ordinary matter. Test confirms that gravity pulls the same on hydrogen and anti-hydrogen, Science: Physics News, 2023. [CrossRef]
- Bekenstein, J.D. Bekenstein-Hawking entropy, Scholarpedia, 2008, 3(10):7375.
- Systems Engineering Glossary, Systems Engineering, https://sebokwiki.org/wiki/Systems Engineering (glossary), 2023.
- Checkland, P. Systems Thinking, Systems Practice, New York, NY, USA, John Wiley & Sons, 1999.
- Senge, P.M. The fifth discipline: The Art & Practice of the Learning Organization, New York, NY, USA, Doubleday Business, 1990.
- Steup, M. & Neta, R. Epistemology, The Stanford Encyclopedia of Philosophy, Edward N. Zalta (ed.), https://plato.stanford.edu/archives/fall2020/entries/epistemolog, 2020.
- Bednar, R.L. & Peterson Self-esteem Paradoxes and innovations in clinical practice, 2nd edition, Washington, DC: American Psychological Association (APA), 1995.
- R.F. Baumeister and K.D. Vohs, Self-Regulation, Ego Depletion, and Motivation, Social and Personal Psychology, 2007, (1): 115-128. [CrossRef]
- Greenwald, A.G.and colleagues Measuring individual differences in implicit cognition: The implicit association test, Journal of Personality and Social Psychology,1998, 74(6), 1464–1480. [CrossRef]
- Shu, L.L.; Mazar, N.; Gino, F.; Ariely, D.; Bazerman, M.H. Signing at the Beginning Makes Ethics Salient and Decreases Dishonest Self-Reports in Comparison to Signing at the End, Proceedings National Academy of Sciences, 2012, 109:15197–200. [CrossRef]
- Baumeister and colleagues Exploding the self-esteem myth, Scientific American, 2005, 292(1): 84-91.
- Blanton and colleagues Strong Claims and Weak Evidence: Reassessing the Predictive Validity of the IAT, Journal of Applied Psychology 2009, 94(3): 567–582.
- M.S. Hagger and colleagues A Multilab Preregistered Replication of the Ego-Depletion Effect, Perspectives on Psycholigical Science,2016, 11(4). [CrossRef]
- Berenbaum, M.R. Retraction for Shu et al., Signing at the beginning makes ethics salient and decreases dishonest self-reports in comparison to signing at the end, PNAS, 2021, 118(38), e2115397118. [CrossRef]
- Dobbin, F. and Kalev, A. Programs Fail, Harvard Business Review, hbr.org/2016/07/why-diversity-programs-fail, 2016.
- Paluck and colleagues Prejudice Reduction: Progress and Challenges, Annual Review of Psychology, 2021, 72:533–60, www.annualreviews.org/doi/pdf/10.1146/annurev-psych-071620-030619.
- Tetlock, P.E. & Gardner, D. Superforecasting: The Art and Science of Prediction, Crown, 2015.
- Beck, U. Risk society: towards a new modernity, Sage Publications, 1992.
- MacKenzie, D. Trading at the Speed of Light: How Ultrafast Algorithms Are Transforming Financial Markets, Princeton University Press, 2021.
- Barron, J. Visiting New York? Make Sure A.I. Didn’t Write Your Guidebook, The New York Times, 2023.
- Nogrady, B. Is Fukushima wastewater release safe? What the science says, Nature, 2023, 618: 894–895.
- Buesseler, K.O. Opening the floodgates at Fukushima, Science, 2020, 369: 621–622.
- Ministry of Economy Reactor Decommission, Contaminated Water and Treated Water (in Japanese), https://www.meti.go.jp/earthquake/nuclear, 2023.
- Mabon, L. & Kawabe, M. Bring voices from the coast into the Fukushima treated water debate, Proceedings of the National Academy of Sciences, 2022, 119, e2205431119.
- Brown, A. Just Like That, Tons of Radioactive Waste Is Heading for the Ocean, The New York Times, (retrieved 9/14/2023 from https://www.nytimes.com/2023/08/22/opinion/japan-fukushima-radioactive-water-dumping, 2023.
- Smith, J.; Marks, N.; Irwin, T. The risks of radioactive wastewater release. The wastewater release from the Fukushima Daiichi nuclear plant is expected to have negligible effects on people and the ocean, Science. Perspectives, 2023, 382(6666): 31-33.
- Japan Fisheries Co-operative Japan Fisheries Co-operative. Japan Fisheries Co-operative Has Met Prime Minster Kishida Over the Handling of Treated Water by ALPS (in Japanese), retrieved 9/14/2023 from https://www.zengyoren.or.jp/news, press item 20230821 in Japanese, 2023.
- Takenaka, K.; Pollard, M.Q. Japan complains of harassment calls from China over Fukushima water release, Reuters, retrieved 9/14/2023 from https://www.reuters.com/world/asia-pacific/japan-says-harassment-calls-china-regarding-fukushima- water-release-extremely-2023-08-28/, 2023.
- Katayama, N. Outraged with the Government and TEPCO, Residents of Tokyo and Five Prefectures Files a Lawsuit Seeking an Injunction on Treated Water Release (in Japanese), Tokyo Shinbun, retrieved 9/14/2023 from https://www.tokyo-np.co.jp/article/275965) (in Japanese), 2023.
- Harris, M. History and Significance of the EMIC/ETIC Distinction, Annual Review of Anthropology, 1976, 5: 329–350.
- Evans-Pritchard, E.E. Witchcraft, oracles and magic among the Azande, Clarendon Press, 1937.
- Zucker, L.G. The role of institutionalization in cultural persistence, American Sociological Review, 1977, 726–743.
- Skillcate AI. BERT for Dummies: State-of-the-art Model from Google, Medium, google-42639953e769, 2022.
- Pfeffer, J. The Role of the General Manager in the New Economy: Can We Save People from Technology Dysfunctions?, The Future of Management in an AI World. Redefining Purpose and Strategy in the Fourth Industrial Revolution, Canals, J. & Heukamp, F., editors, 2020, 67–92, Springer International Publishing. [CrossRef]
- Luttwak, E. The clue China is preparing for war. Xi is laying the groundwork while the West looks away, Unherd, retrieved 7/23/2023 from https://unherd.com/2023/07/the-clue-china-is-preparing-for-war/, 2023, 7/19.
- Finkel, E. If AI becomes conscious, how will we know? Scientists and philosophers are proposing a checklist based on theories of human consciousness, Science, News, 2023, 381(6660).
- Butlin, P. et al. Consciousness in Artificial Intelligence: Insights from the Science of Consciousness, arXiv, 2308.08708 [cs.AI], 2023.
- Naddaf, M. Europe spent €600 million to recreate the human brain in a computer. How did it go? The Human Brain Project wraps up in September after a decade. Nature examines its achievements and its troubled past, Nature News, 2023, 620: 718-720.
- Shannon, C. E., and Weaver, W. The Mathematical Theory of Communication University of Illinois Press, 1949, 1-117.
- Brillouin, L. Science and Information Theory; Academic Press: Cambridge, MA, USA, 1956.
- Egginton, W. The Rigor of Angels. Borges, Heisenberg, Kant, and the Ultimate Nature of Reality, Pantheon books, 2023.
- Sliwa, J. Toward collective animal neuroscience, Science, 2021, 374(6566):397-398, 10.1126/science.abm3060.
- Hartley, R. V. L. Transmission of Information Bell System Technical Journal, 1928, 7(3): 535–563.
- Ash, Robert B. Information Theory, Dover 1965.
- Cover Thomas M. and Thomas Joy A. Elements of Information Theory, 2nd Ed, Wiley 2006.
- Moskowitz, Ira S. and Miller, A.R. Simple Timing Channels Proc. 1994 IEEE Computer Society Symposium on Research in Security and Privacy, 1994.
- Verdú, S. On Channel Capacity per Unit Cost IEEE Transaction on Information Theory, 1990, V., (36)5: 1019-1030.
- Moskowitz, Ira S. and Miller, A.R. The Channel Capacity of a Certain Noisy Timing Channel IEEE Transactions on Information Theory, 1992, 38(4): 1339-1344.
- Richard A. Silverman. On Binary Channels and their Cascades. IRE Transactions-Information Theory, 3 Dec., 1955, 19-27.
- Martin, Keye and Moskowitz, Ira S. Noisy Timing Channels with Binary Inputs and Outputs in Information Hiding, ed. J Camenisch et al., LNCS 4437, Springer, 2006, 124-144.
- Majani, Eric E. A Model for the study of Very Noisy Channels and Applications, PhD dissertation, Cal Tech, 1988.
- Golomb, Solomon W. The Limiting Behavior of the Z-Channel, IEEE Trans. on Information Theory, 1980, 26:3, p. 372.
- Physics, Encyclopedia Britannica, www.britannica.com/science/physics-science, 2023.
- Einstein, A. Albert Einstein on space-time Encyclopedia Britannica, 13th Ed., Albert-Einstein-on-Space-Time-1987141, 1926.
- Frank, A.; Gleiser, M. The Story of Our Universe May Be Starting to Unravel, New York Times, //www.nytimes.com/2023/09/02/opinion/cosmology-crisis-webb-telescope.html, 2023.
- Rickless, S., Plato’s Parmenides, The Stanford Encyclopedia of Philosophy, E.N. Zalta, editor, https://plato.stanford.edu/archives/spr2020/entries/plato-parmenides, 2020.
- Mann, R.P. Collective decision making by rational individuals, PNAS, 2018, 115(44): E10387-E10396. [CrossRef]
- Schölkopf, B. and colleagues Towards Causal Representation Learning, arXiv, 2102.11107, 2021.
- Sen, A. (1994) The Formulation of Rational Choice, The American Economic Review, 1994, 84(2):385-390.
- Lucas, R. Monetary Neutrality, Nobel Prize Lecture, 1995.
- Simon, H.A. Bounded rationality and organizational learning Technical Report AIP 107, CMU, Pittsburgh, PA, 1989.
- Lawless, W.F.; Sofge, Donald A.; Lofaro, Daniel; Mittu, Ranjeev Editorial: Interdisciplinary Approaches to the Structure and Performance of Interdependent Autonomous Human Machine Teams and Systems, Frontiers in Physics, Frontiers eBook, retrieved 3/1/2023 https://www.frontiersin.org/articles/10.3389/fphy.2023.1150796/full, 2023.
- U.S. Supreme Court California v. Green, 399 U.S. 149, California v. Green, No. 387, Argued April 20, 1970, Decided June 23, 1970, 399, U.S. 149, 1970.
- Ginsburg, R.B. American Electric Power Co. et al. v. Connecticut et al., 10-174, http://www.supremecourt.gov/opinions/10pdf/10-174.pdf, 2011.
- Nosek, B. Estimating the reproducibility of psychological science, Science, 2015, 349(6251): 943, www.science.org/doi/10.1126/science.aac4716.
- Nash, J.F. Equilibrium points in n-person games, PNAS, 1950, 36(1), 48-49, doi.org/10.1073.
- Chomsky, N.; Roberts, I.; Watumull J. The False Promise of ChatGPT, New York Times, retrieved 3/8/2023 from https://www.nytimes.com/2023/03/08/opinion/noam-chomsky-chatgpt-ai.html, 2023.
- Drucker, P.F. What we can learn from Japanese Management, Harvard Business Review.
- Akiyoshi, M.; Whitton, J.; Charnley-Parry, I.; Lawless, W.F. Effective Decision Rules for Systems of Public Engagement in Radioactive Waste Disposal: Evidence from the United States, the United Kingdom, and Japan, Systems Engineering and Artificial Intelligence; in Lawless, W.F.; Mittu, R.; Sofge, D.A.; Shortell, T.; McDermott, T.A. (Editors), Springer, Chapter 24: 509–533, 2021. [CrossRef]
- Bradbury, J.A.; Branch, K.M.; Malone, E.L. An evaluation of DOE-EM Public Participation Programs, PNNL-14200, Richland, WA, Pacific Northwest National Laboratory, 2003.
- Lawless, W.F.; Bergman, M.; Feltovich, N. Consensus-seeking versus truth-seeking, ASCE Practice Periodical of Hazardous, Toxic, and Radioactive Waste Management, 2005, 9(1), 59-70.
- Mui, C. How Kodak Failed, Forbes, retrieved 9/11/2023, 2012/01/18/how-kodak-failed, 2012.
- Barabba, V. The decision loom: A design for interactive decision-making in Organizations, Triarchy Press Ltd, 2011.
- Hudson, A. The Rise & Fall of Kodak. A Brief History of The Eastman Kodak Company, 1880 to 2012, Photo Secrets, https://www.photosecrets.com/the-rise-and-fall-of-kodak, 2012.
- Endsley, M. Human-AI Teaming: State of the Art and Research Needs; National Research Council, National Academies Press: Washington, DC, USA, 2021.
- Wong, M.L. et al. On the roles of function and selection in evolving systems, PNAS, 2023, 120(43), e2310223120.
- Wang, Y. China’s Social Media Interference Shows Urgent Need for Rules, The Canberra Times, https://www.hrw.org/news/2023/08/14/chinas-social-media-interference-shows-urgent-need-rules, retrieved on 9/9/2023, 2023, 8/14.
- Zumbrun, J. Should the U.S. worry that China is closing in on its lead in research and development? Amid a productivity slump, the IMF sees benefits from Chinese and South Korean innovation, Wall Street Journal, https://blogs.wsj.com/economics/2018/04/10/should-the-us-worry-about-china-rd/, 2018.
- Taplin, N. Can China’s red capital really innovate? U.S. technology theft from Britain helped kick-start the industrial revolution on American shores. Will China be able to replicate that success?, Wall Street Journal, retrieved May 14, 2018 from https://www.wsj.com/articles/can-chinas-red-capital-really-innovate-1526299173, 2018.
- Wickens, C.D. Engineering psychology and human performance (second edition), Merrill, 1992.
- Brown, B. Human Machine Teaming using Large Language Models, in Lawless, W.F.; Mittu, R.; Sofge, D.A.; Fouad, H. (Editors), forthcoming, Interdependent human-machine teams. The path to autonomy, Elsevier, Chapter 3, 2024.
- Cooke, N.; Hilton, M.E. Enhancing the Effectiveness of Team Science; National Research Council, National Academies Press: WAsh(1965)ington, DC, USA, 2015.
- Berscheid, E.; Reis, H. Attraction and close relationships. In The Handbook of Social Psychology, 4th ed.; Lawrence Erlbaum: Mahwah, NJ, USA, 1998; Volume 1.
- Wang, B.H. Entanglement-Separability Boundary Within a Quantum State. arXiv, 2020, arXiv:2003.00607. arXiv:2003.00607.
- Lewin, K. Field Theory in Social Science. Selected Theoretical Papers; Harper and Brothers: Manhattan, NY, USA,, 1951.
- IT Information theory, cs.stanford.edu/people/eroberts/courses/soco/projects/1999-00/information-theory/ noise, 2023.
- Wooters, W.; Zurek, W. The no-cloning theorem. Physics Today, 2009, 62: 76–7.
- Marshall, S.M.; Mathis, C.; Carrick, E.; Keenan, G.; Cooper, G.J.T.; Graham, H.; Craven, M.; Gromski, P.S.; Moore, D.G.; Walker, S.I.; et al. Identifying molecules as biosignatures with assembly theory and mass spectrometry. Nature Communications, 2021, 3033, 12. [CrossRef]
- Bette, D.A.; Pretre, R.; Chassot, P. Is our heart a well-designed pump? The heart along animal evolution. Eur. Heart J., 2014, 35, 2322–2332. [CrossRef]
- Von Neumann, J. Theory of Self-Reproducing Automata; University of Illinos Press, Champaign, IL, USA, 1966.
- Cummings, J. Team Science Successes and Challenges; NSF Workshop Fundamentals of Team Science and the Science of Team Science: Bethesda, MD, USA, 2015.
- Moskowitz, Ira S. A Cost Metric for Team Efficiency. Front. Phys. 2022, 10, 861633. [CrossRef]
| 1 | Oxford Dictionary of English, 2nd edition; see at https://www.oed.com
|
| 2 | Oxford Languages at https://languages.oup.com/google-dictionary-en/
|
| 3 | e.g., the Pew poll, “Deep Divisions in Americans’ Views of Nation’s Racial History–and How To Address It"; https://www.pewresearch.org/politics/2021/08/12/deep-divisions-in-americans-views-of-nations-racial-history-and- how-to-address-it/
|
| 4 | |
| 5 | NIH in 2021, Scientific Workforce Diversity Seminar Series Seminar Proceedings: “Is Implicit Bias Training Effective?” see Proceedings: “Implicit Bias"; https://diversity.nih.gov/sites/coswd/files/images
|
| 6 | Reference:
|
| 7 | Frank practices astrophysics at the University of Rochester; Gleiser practices theoretical physics at Dartmouth. |
| 8 | The James Webb Space Telescope; see https://webb.nasa.gov
|
| 9 | See the url for the “Hanford Vit Plant," accessed on 9/8/2023 |
| 10 | See the url for “Transuranic Waste Retrieval and Certification at Hanford," accessed on 9/8/2023 |
| 11 | See url at “Defense Waste Processing Facility Reaches 25 Years of Successful Operations at SRS," 2021, accessed on 9/8/2023 |
| 12 | Coles, I.; Simmons, A.M. (2023, 6/9), “Ukraine Probes Russian Defenses for Weak Points After Kicking Off Counteroffensive,” Wall Street Journal, https://www.wsj.com/articles/ukraine-probes-russian-defenses-for-weak-points-after-kicking-off-counteroffensive-26296960
|
| 13 | Britannica, The Editors of Encyclopaedia. “Aldrich Ames". Encyclopedia Britannica, 19 Oct. 2023, https://www.britannica.com/biography/Aldrich-Ames
|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
MDPI Initiatives
Important Links
© 2024 MDPI (Basel, Switzerland) unless otherwise stated





