Threshold and Upper Bound for the Controller’s Designed Parameter of Fokker Planck Kolmogorov Probability Density Function with Applications to Cryptocurrency

Preprint

Article

Threshold and Upper Bound for the Controller’s Designed Parameter of Fokker Planck Kolmogorov Probability Density Function with Applications to Cryptocurrency

Altmetrics

Downloads

Views

Comments

Ismail A. Mageed^*

This version is not peer-reviewed

This preprints belongs to the Topic

Advances on Automatic Control and Soft Computing from 15th APCA International Conference CONTROLO’2022

Submitted:

17 February 2024

Posted:

20 February 2024

You are already at the latest version

Alerts

Abstract

This work is the first in literature to tackle the difficult open problem of determining the upper bound and threshold theorem for the TDCDP (time-dependent controller parameter) of the (Fokker Planck Kolmogorov) probability density function. This revolutionary exposition will put control theory and other related inter-disciplinary fields to a higher level towards contemporary control theory. Notably, based on the influential role of control theory in both engineering and industry, this paper will be of great value to all engineering and industry professionals who seek to know more about advanced trends within control theory settings. On the other remit of the spectrum, Fokker Planck Kolmogorov(FPK) equations are of high importance to physicists as well as mathematicians, based on their multiple applicability to information theory, graph theory, data science, finance, economics, and beyond. So, this by default adds more taste and credibility to this study. This leads by nature to introducing a different flavor to this ground-breaking research by highlighting the impact of Fokker Planck Kolmogorov(FPK) to revolutionize crypocurrency,which have received its name because it uses encryption to verify transactions, a new debatable digital payment system that doesn't rely on banks to verify transactions. It’s a peer-to-peer system that can enable anyone anywhere to send and receive payments. The paper ends with closing remarks combined with some challenging open problems and the next phase of research.

Keywords:

Subject: Computer Science and Mathematics - Applied Mathematics

Abstract. This work is the first in literature to tackle the difficult open problem of determining the upper bound and threshold theorem for the TDCDP (time-dependent controller parameter) of the (Fokker Planck Kolmogorov) probability density function. This revolutionary exposition will put control theory and other related inter-disciplinary fields to a higher level towards contemporary control theory. Notably, based on the influential role of control theory in both engineering and industry, this paper will be of great value to all engineering and industry professionals who seek to know more about advanced trends within control theory settings. On the other remit of the spectrum, Fokker Planck Kolmogorov(FPK) equations are of high importance to physicists as well as mathematicians, based on their multiple applicability to information theory, graph theory, data science, finance, economics, and beyond. So, this by default adds more taste and credibility to this study. This leads by nature to introducing a different flavor to this ground-breaking research by highlighting the impact of Fokker Planck Kolmogorov(FPK) to revolutionize crypocurrency,which have received its name because it uses encryption to verify transactions, a new debatable digital payment system that doesn’t rely on banks to verify transactions. It’s a peer-to-peer system that can enable anyone anywhere to send and receive payments. The paper ends with closing remarks combined with some challenging open problems and the next phase of research.

Introduction

Because complex stochastic systems are highly unpredictable and random, they are difficult to manage. Gaussian stochastic systems are controlled for unpredictability using a statistical measure called variance [1,2,3,4].

Variance control techniques cannot be directly applied to stochastic systems with nonlinearities. This is since non-Gaussian distributions of system variables are possible even in the case of Gaussian noise in the system [5].

Gaussian processes may not be sufficient to capture the randomness and uncertainty of certain nonlinear systems. Variance control techniques are ineffective in these situations [6].

Discrete-time stochastic nonlinear systems (SNSs) frequently use PDF control techniques. However, it is challenging to develop an analytical solution for the FPK equation for continuous-time SNSs [7].

With the specified control method, the closed-loop system may be seen [7] as an Ornstein-Uhlenbeck process.

d x_{t} = - φ x_{t} d t + σ d W_{t}

(1)

Here

x_{t}

is the system’s state,

φ

> 0

defines the controller’s designed parameter,

W_{t}

defines the Weiner process and

σ

is a positive real constant.

The FPK reads as follows:

p (x, t)

serves as the PDF with

x

to define the random variable of

x_{t} .

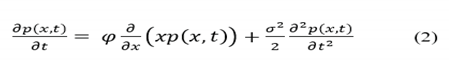
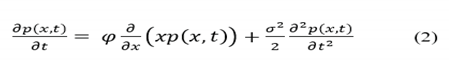
The PDF provides the closed form solution for equation (2) Preprints 99164 i001

p (x, t) = \sqrt (\frac{φ}{π σ^{2} (1 - e^{- 2 φ t})}) e^{(- \frac{φ {(x - x_{0} e^{- φ t})}^{2}}{π σ^{2} (1 - e^{- 2 φ t})})}

(3)

x_{0}

x_{t} (t = 0) a n d φ

reads as:

φ (t) = \frac{W_{0} (- \frac{t σ^{2}}{r (t)} e^{- \frac{t σ^{2}}{r (t)}})}{2 t} + \frac{t σ^{2}}{2 r (t)}

(4)

Provided that

W_{0}

is the Lambert W function [8] and

r (t)

serves as a variance function that depends on time. Figure 1 [7] shows a simulation of the outcomes, discretizing the undertaken model with a sampling time of 0.1. Figure 1 depicts the system’s trajectory in relation to state

x_{t}

and offers compelling evidence that the system’s variable stabilization was attained.

On another important note, the Lamber W function,

W_{0}

(c.f., (4)) reads (c.f., [8])

W_{0} (z) = \sum_{n = 1}^{\infty} \frac{{(- n)}^{n - 1} z^{n}}{n!}

(5)

Where

z

is any complex number and it is satisfied when

z

is real. Also, for real values of

z

W_{0} (z)

satisfies:

\frac{d W_{0} (z)}{d z} = \frac{W_{0} (z)}{z (1 + W_{0} (z))}

(6)

The following theorem is essential to obtain the main results of section two.

Preliminary Theorem (PT) [9]

Let f be a function that is defined and differentiable on an open interval (c,d).

f^{'} (x) > (<) 0

\forall x \in (c, d)

, then f increases(decreases) on

(c, d)

(7)

This current paper contributes to:

Finding the TDCDP’s threshold.
Finding for the first time ever, the TDCDP’s upper bound.
The provision of some FPK equations applications to cryptocurrency.
The provision of new emerging open problems.

This paper’s roadmap reads as: Section two is concerned with the methodology. Section three provides results and discussion. A summary of some influential applications of the FPK equations to cryptocurrencies is given in section four. Section five concludes with tough open problems and offers suggestions for further investigation.

Methodology

Notably, a mathematical approach is undertaken to calculate the threshold based on the preliminary theorem(see Equation (7)). More potentially, calculus and more advanced algebraic forms are utilized to uncover the upper bound of the time-dependent controller’s designed parameter. Looking at the bigger picture, this discovery will lead to a contemporary control theory rather than being limited within the traditional classical frames.

From another perspective, one might wonder about the possibility of employing Fokker Planck Kolmogorov Probability Density Function to revolutionize the most advaocated hot topic, namely cryptocurrency. Is this posible or not?

This current paper provides the full answer, by providing some potential applications of Fokker Planck Kolmogorov Probability Density Function to crypotcurrency, but yet there are still numerous unexplored applications. This will put the research community into more spacious frontiers of thoughtful innovation.

Results and Discussion

Theorem 1.

For

φ

(c.f., (4)-(7)), it holds that:

φ

is forever(increasing)(decreasing) in

σ

if and only if

\frac{t σ}{r (t)} (1 - \frac{W_{0} (z)}{z t (1 + W_{0} (z))} e^{- \frac{t σ^{2}}{r (t)}}) (1 - \frac{t σ^{2}}{r (t)}) > (< 0), z = - \frac{t σ^{2}}{r (t)} e^{- \frac{t σ^{2}}{r (t)}}

(8)

ii)

φ

is forever(increasing)(decreasing) in

t

if and only if

\frac{t σ^{2}}{2 r (t)} - \frac{t σ^{2}}{2 (r (t))^{2}} - \frac{W_{0} (z)}{2 t^{2}} - (\frac{W_{0} (z)}{2 t z (1 + W_{0} (z))}) \frac{σ^{2}}{(r (t))^{2}} e^{- \frac{t σ^{2}}{r (t)}} (1 - t σ^{2} + t \frac{d r (t)}{d t} (\frac{σ^{2}}{2 r (t)} - 1)) > (< 0)

(9)

iii)

φ

is forever(increasing)(decreasing) in

r (t)

if and only if

\frac{t σ^{2}}{({r (t))}^{2}} (1 + \frac{W_{0} (z)}{2 t z (1 + W_{0} (z))}) (\frac{t σ^{2}}{({r (t))}^{2}} - 1) > (< 0)

(10)

Proof

We have

\frac{\partial φ}{\partial σ} = \frac{t σ}{r (t)} + \frac{1}{2} \frac{\partial W_{0} (z)}{\partial z} (\frac{\partial z}{\partial σ}), z = - \frac{t σ^{2}}{r (t)} e^{- \frac{t σ^{2}}{r (t)}}

(11)

Following (6), it is implied that:

\frac{\partial φ}{\partial σ} = \frac{t σ}{r (t)} (1 - \frac{W_{0} (z)}{z t (1 + W_{0} (z))} e^{- \frac{t σ^{2}}{r (t)}}) (1 - \frac{t σ^{2}}{r (t)})

(12)

By (7) and (12), the proof of part i) is immediate.

ii)

\frac{d φ}{d t} = \frac{t σ^{2}}{2 r (t)} - \frac{t σ^{2}}{2 (r (t))^{2}} - \frac{W_{0} (z)}{2 t^{2}} + + \frac{1}{2} \frac{d W_{0} (z)}{d z} (\frac{d z}{d t})

= \frac{t σ^{2}}{2 r (t)} - \frac{t σ^{2}}{2 (r (t))^{2}} - \frac{W_{0} (z)}{2 t^{2}} + (\frac{W_{0} (z)}{2 t z (1 + W_{0} (z))}) (\frac{d z}{d t})

(13)

Computing

(\frac{d z}{d t})

and plugging it back in (13), yields

\frac{d φ}{d t} = (\frac{t σ^{2}}{2 r (t)} - \frac{t σ^{2}}{2 (r (t))^{2}} - \frac{W_{0} (z)}{2 t^{2}})

- (\frac{W_{0} (z)}{2 t z (1 + W_{0} (z))}) \frac{σ^{2}}{(r (t))^{2}} e^{- \frac{t σ^{2}}{r (t)}} (1 - t σ^{2} + t \frac{d r (t)}{d t} (\frac{σ^{2}}{2 r (t)} - 1))

(14)

Combining (7) with (4), ii) follows.

iii) Engaging the same procedure, the proof follows.

Theorem 2.

For

φ

(c.f., (4) and (5)), it holds that

φ (t) <

\frac{1}{t} \sum_{n = 1}^{\infty} \frac{{(\frac{n t σ^{2}}{r (t)})}^{n}}{n!} +

\frac{t σ^{2}}{2 r (t)}

(11)

Proof

Following (4) and (6),

φ (t) = \frac{\sum_{n = 1}^{\infty} \frac{{(- n)}^{n - 1} z^{n}}{n!}}{2 t} + \frac{t σ^{2}}{2 r (t)}

z = - \frac{t σ^{2}}{r (t)} e^{- \frac{t σ^{2}}{r (t)}}

<

\frac{\sum_{n = 1}^{\infty} \frac{{(n)}^{n} z^{n}}{n!}}{2 t} + \frac{t σ^{2}}{2 r (t)}

<

\frac{\sum_{n = 1}^{\infty} \frac{{(n)}^{n} {(\frac{t σ^{2}}{r (t)})}^{n}}{n!}}{2 t} +

\frac{t σ^{2}}{2 r (t)}

(Since,

e^{- \frac{n t σ^{2}}{r (t)}} < 1

)

< \frac{1}{t} \sum_{n = 1}^{\infty} \frac{{(\frac{n t σ^{2}}{r (t)})}^{n}}{n!} +

\frac{t σ^{2}}{2 r (t)}

(c.f., (15))

Notably, the obtained upper bound (c.f., (15)) is time dependent.

DCP Applications to Cryptocurrency

The mean-variance paradigm, or Markowitz paradigm [10], is frequently linked to expected return and portfolio risk. When there are several decision-making bodies active in online markets, including digital and cryptocurrency markets, variance reduction issues can occur. These interactive decision-making issues, sometimes known as “game problems,” can be represented as linear-quadratic Gaussian (LQG) games, in which the cost functional in the state and control variables is quadratic and the state dynamics are a linear stochastic system.

If the cost functional and/or state dynamics involve an average or expected value of the state and/or the control actions, the game is referred to as a mean-field LQG game, or MFT-LQG [10,11,12,13,14,15]. These kinds of game problems have been solved using a variety of techniques, including the FPK equation, the Hamilton-Jacobi-Bellman-Isaacs equation, and the Stochastic Maximum Principle [10,11,12,13,14,15].

The creation of a probabilistic master equation method to identify the best course of action for decision-makers was discussed in [10,11,12]. Prior research in this field has employed a master equation incorporating a stochastic FPK or a maximal principle. Assuming indistinguishability within classes, most studies [11,12,13,14,15,16] have concentrated on mean-field game methods in linear-quadratic games with an infinite number of decision-makers. This assumption, however, might not apply in circumstances like variance reduction or risk quantification issues where decision-makers have varying levels of sensitivity to risk.

The term “Direct method” describes a particular method or methodology applied in a matrix-valued linear jump-diffusion-regime switching system of mean-field type mathematical framework. Therefore, to analyze and solve this system, the “Direct method” entails a few crucial phases or procedures [10]. Figure 2 provides a schematic (c.f., [10]).

While macroeconomics has not directly influenced financial mathematics or financial engineering, certain contributions are influential to develop stochastic optimization and stochastic differential game theory [17]. One such example is the work of Krusell and Smith, whose numerical algorithm for approximating equilibrium closely resembles the mean field game strategy, which is used to solve equations and search for Nash equilibria in the context of generic agents and FPK equations, by which this connection suggests a potential link between macroeconomic models and mean field games in economic theory [17].

In the context of cryptocurrency mining, [17] presented a dynamic competitive mining game in which miners compete by putting up computational effort to gain mining rewards, balancing the reward associated with block production with the cost of computing (such as power). The explicit determination of the game’s equilibrium under specific utility functions exposes the impact of model parameters on the equilibrium and draws attention to elements like risk aversion and wealth distribution that may contribute to a greater concentration of mining power [17].

In a Markovian setting, when considering the behavior of a population average, the best response of individual players can be expressed as a function of their own state. By simultaneously solving for the response of all players, we can determine the best response [17]. The temporal variations in the miners’ wealth distribution in the Bitcoin network are depicted in Figure 3. As time progresses, most miners experience a decrease in wealth, resulting in a concentration of wealth towards the lower end of the distribution. However, a small portion of miners who initially had more money accumulated wealth over time, leading to a spike in their wealth. This observation aligns with the empirical findings and supports the notion of preferential attachment effects in the Bitcoin network.

Conclusions and Future Research

In this exposition, the TDCDP’s threshold theorem and upper bound are determined. More potentially, this study has highlighted how FPK equations can advance cryptocurrency.

Here are some proposed open problems:

Open Problem 1

Is it mathematically doable to unlock the challenging open problem of finding the lower bound of

φ

(c.f., (4) and (5))? If yes, will it be time-dependent?

Open Problem 2

Is it possible mathematically wise to unlock the most challenging open problem ever in finding the threshold values governing the increasability(decreasability) regions for Lamber W function,

W_{0}

W_{0} (z) = \sum_{n = 1}^{\infty} \frac{{(- n)}^{n - 1} z^{n}}{n!}

(c.f., (5))

with

z = - \frac{t σ^{2}}{r (t)} e^{- \frac{t σ^{2}}{r (t)}}

Open Problem 3

Is it possible to unlock more FPK applications to Satellite Technology?

Open Problem 4

It is still a mathematical challenge to solve higher-dimensional FPK equations, will it be viable to find such an analytic solution to them, if there is any?

The next phase of research includes searching for solutions to the proposed open problems and investigating more extensions to FPK theory to other multi-interdisciplinary fields of human knowledge.

References

P. R. Kumar, P. Varaiya, Stochastic Systems: Estimation, Identification, and Adaptive Control, ; SIAM: Philadelphia, PA, USA, (2015).
A. Hotz, R. E. Skelton, Covariance control theory, Int. J. Control, (1987)13–32.
K. J. Åström, Introduction to Stochastic Control Theory, Courier Corporation: North Chelmsford, MA, USA, (2012).
M. Ren, et al., An introductory survey of probability density function control, Syst. Sci. Control Eng.,(2019)158–170.
H. Wang, Bounded Dynamic Stochastic Systems: Modelling and Control, Springer Science & Business Media: Berlin/Heidelberg, Germany, (2012).
S.M. Ross, et al., “Stochastic Processes, ”Wiley: New York, NY, USA, (1996).
I.A. Mageed, et al., Towards a Revolutionary Info-Geometric Control Theory with Potential Applications of Fokker Planck Kolmogorov (FPK) Equation to System Control, Modelling and Simulation. In2023 28th International Conference on Automation and Computing (ICAC) (2023)1-6.
I. Mezo, Lambert W Function: Its Generalizations and Applications, Chapman and Hall/CRC: London, UK, (2022).
P. V. Gapeev , et al., Optimal double-stopping problems for maxima and minima of geometric Brownian motions, Methodology and Computing in Applied Probability, (2022)789-813.
I. A. Mageed, D.D. Kouvatsos, The Impact of Information Geometry on the Analysis of the Stable M/G/1 Queue Manifold, In ICORES (2021)153-160.
I.A. Mageed, Q.Zhang, Information Geometry? Exercises de Styles. electronic Journal of Computer Science and Information Technology, (2022) 9-14.
J. Barreiro-Gomez, T. E. Duncan, H. Tembine, “Mean-field-type Games for Engineers, 2021, CRC Press.
T. Elsaesser, The mind-game film, In The Mind-Game Film, Routledge, (2021) 89-112.
C. Li, et al., “Off-Policy Risk-Sensitive Reinforcement Learning-Based Constrained Robust Optimal Control, IEEE Transactions on Systems, Man, and Cybernetics: Systems, (2022)2478-2491.
J. Huang, et al., A Unified Relation Analysis of Linear-Quadratic Mean-Field Game, Team and Control, IEEE Transactions on Automatic Control, (2023).
R. Carmona, The influence of economic research on financial mathematics: Evidence from the last 25 years, Finance and Stochastics, (2022)85-101.
Z. Li, A. M. Reppen, R. Sircar, A mean field games model for cryptocurrency mining, Management Science, (2023).

Figure 1. The system’s trajectory state

x_{t}

[7].

Figure 1. The system’s trajectory state

x_{t}

[7].

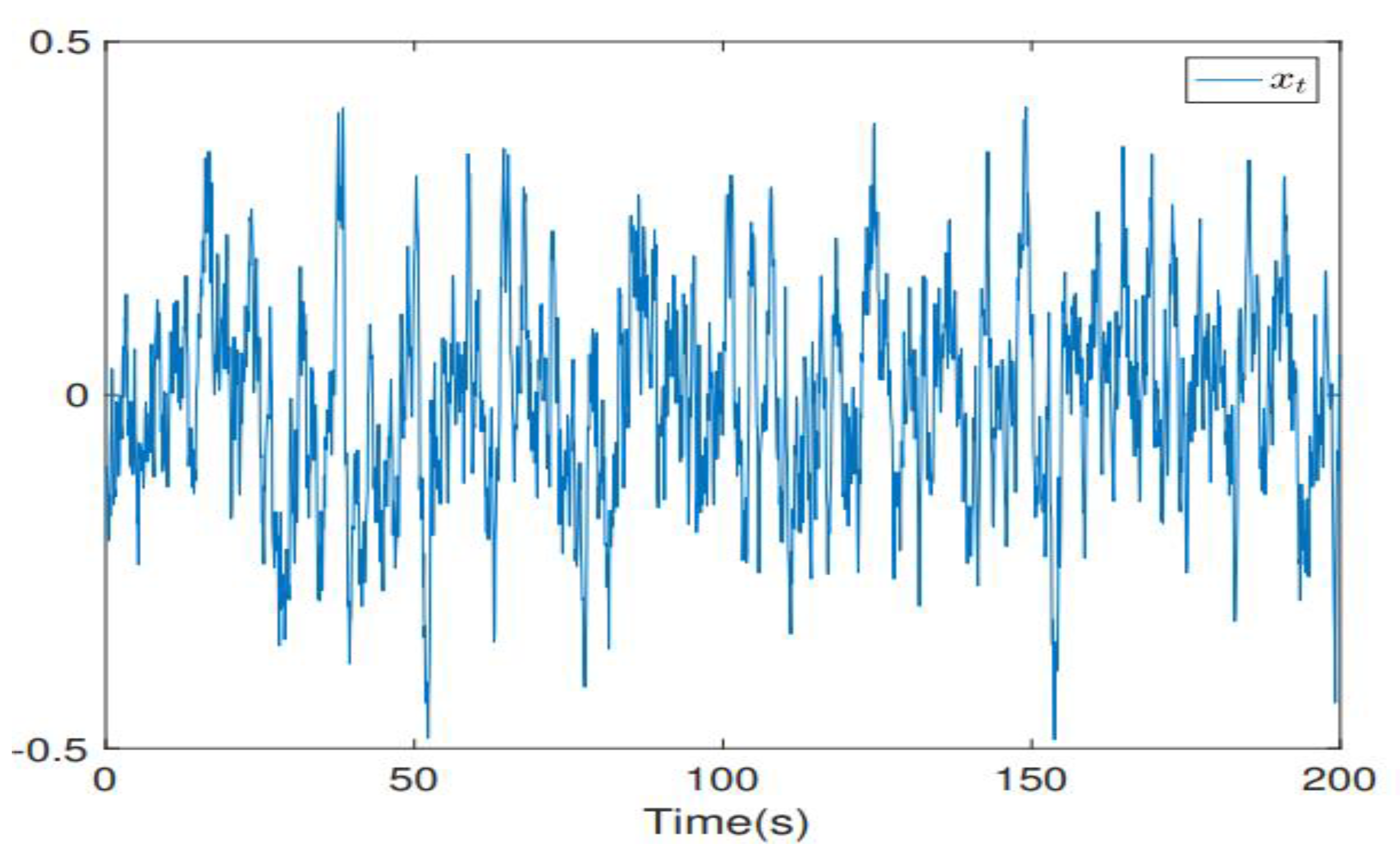
Figure 2. A schematic for the direct method’s key steps [10].

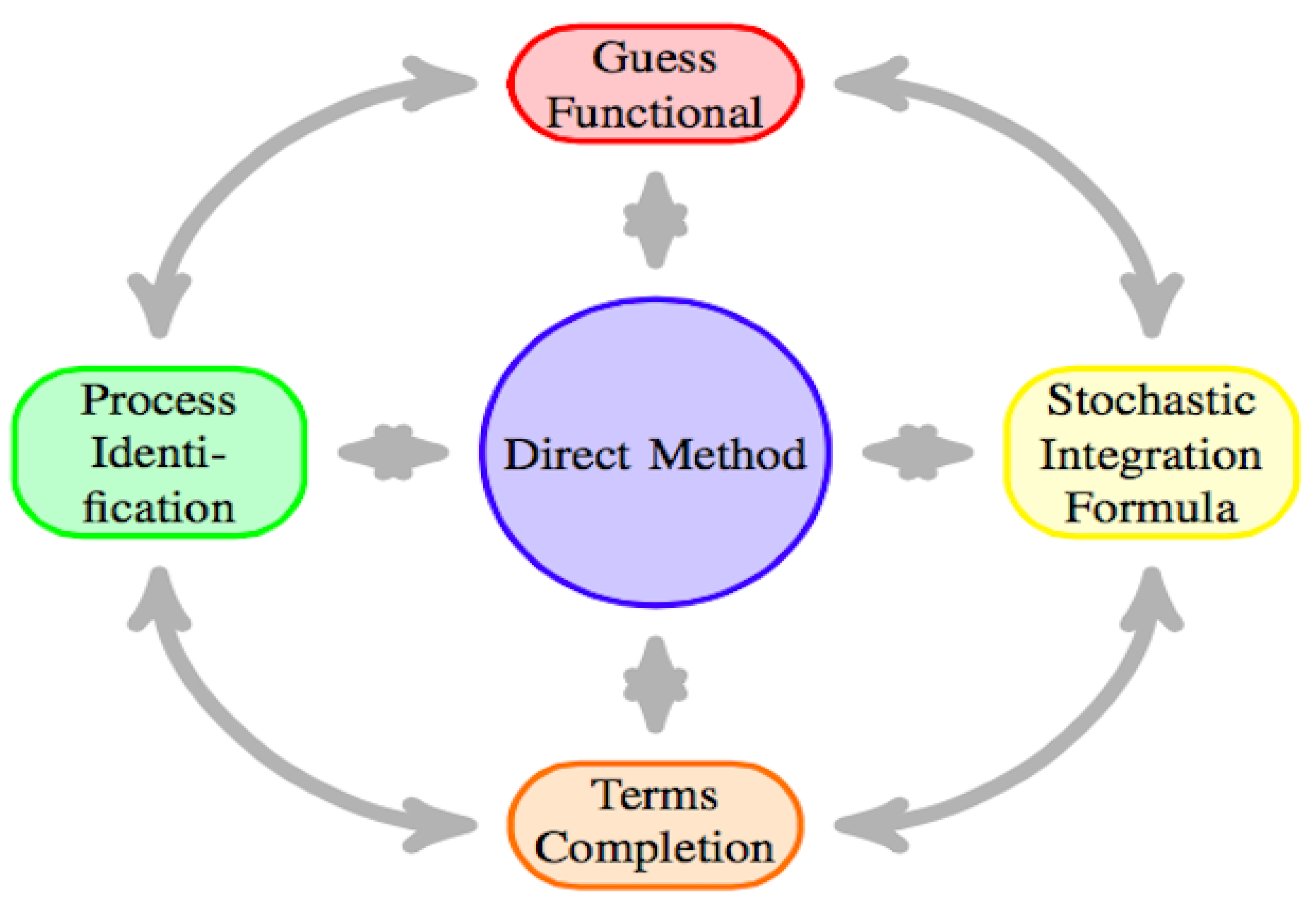
Figure 3. As time passes, the wealth concentration shifts towards the left side of a peak value, indicating that miners with higher initial wealth accumulate more wealth over time [17].

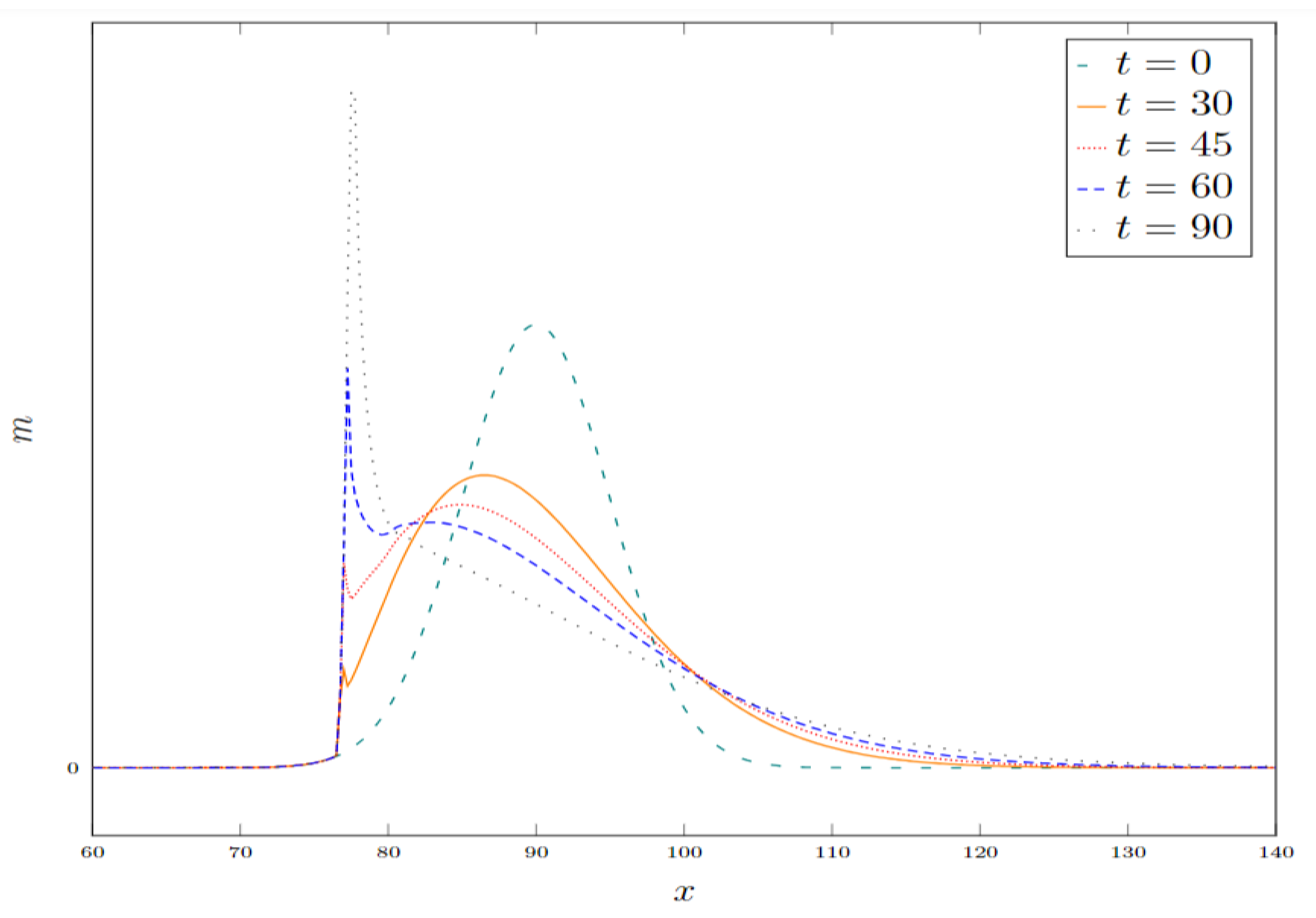
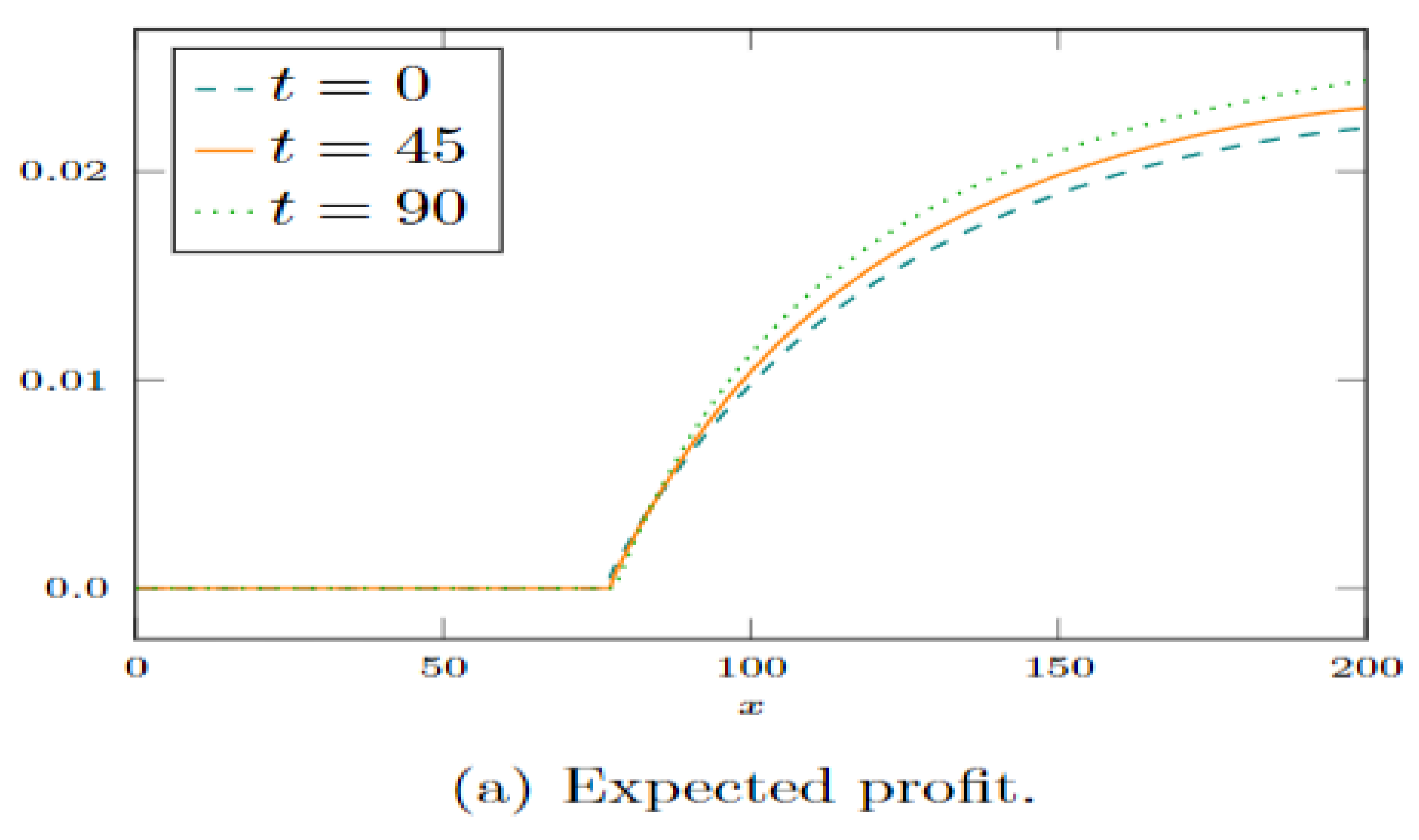
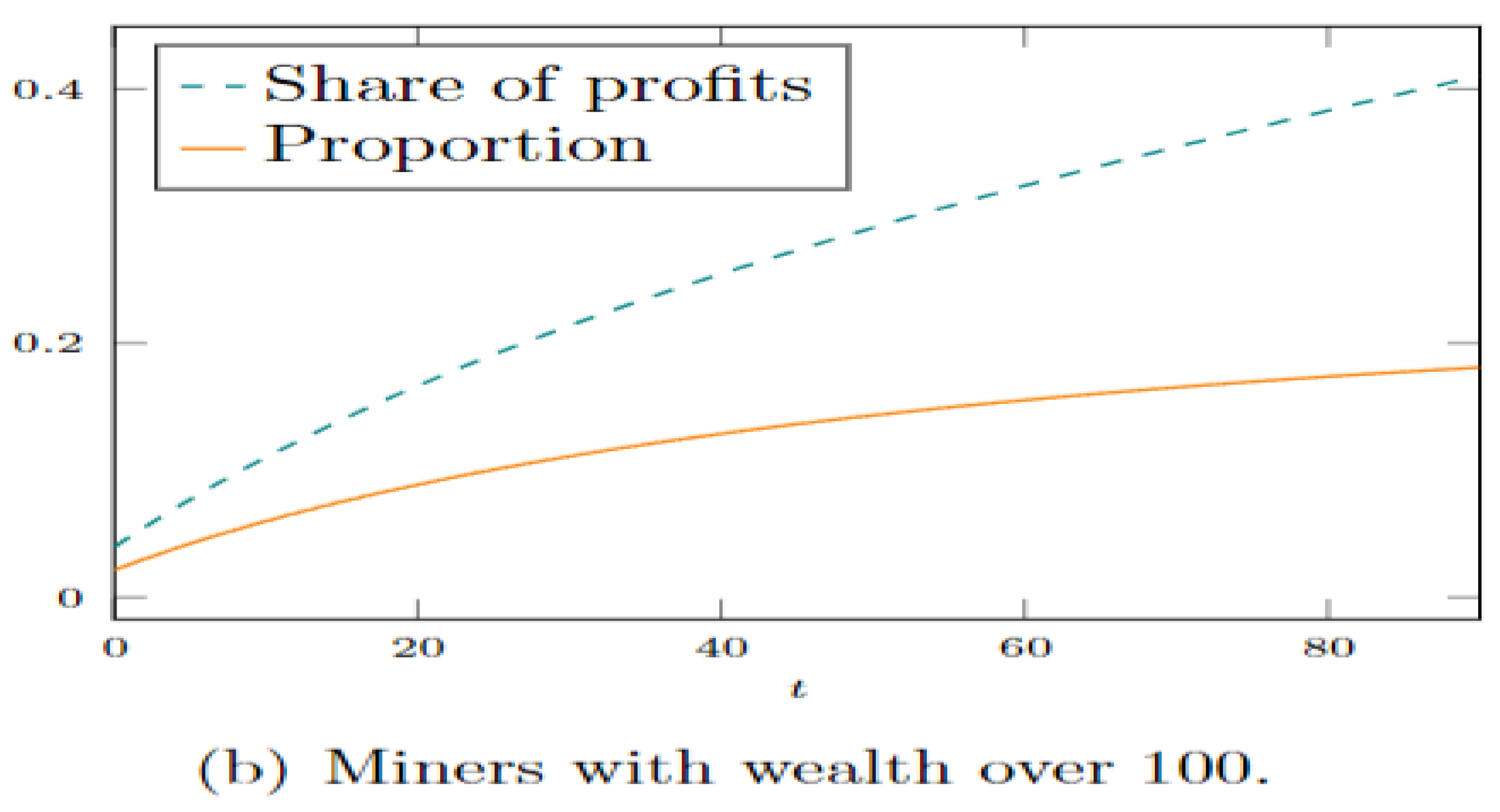
Figure 4. The estimated instantaneous profit for miners at various wealth levels and times is displayed in Figure (a). It demonstrates that miners with greater wealth typically anticipate higher rates of profit. The percentage of miners with wealth over 100 and their share of the total instantaneous earnings are shown in Figure (b), which shows that as time goes on, a bigger percentage of profits flow to wealthier miners. The parameters of Figure (b) are the same as those in Figure 3 [17].

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Threshold and Upper Bound for the Controller’s Designed Parameter of Fokker Planck Kolmogorov Probability Density Function with Applications to Cryptocurrency

Abstract

Introduction

Preliminary Theorem (PT) [9]

Methodology

Results and Discussion

DCP Applications to Cryptocurrency

Conclusions and Future Research

References

MDPI Initiatives

Important Links

Subscribe