Preprint
Article
Introducing Novel Geometric Insights and Three-Dimensional Depictions of the Pythagorean Theorem for Any Triangles
Altmetrics
Downloads
199
Views
84
Comments
0
This version is not peer-reviewed
Submitted:
07 April 2024
Posted:
09 April 2024
You are already at the latest version
Alerts
Abstract
The paper primarily demonstrates that the three internal triangles formed by connecting any point on a midsegment with the vertices of a generic triangle satisfy the geometric Proof of the Pythagorean theorem in Euclidean geometry. Moreover, this study elucidates the Pythagorean relationships inherent within three-dimensional geometric constructs resulting from the arrangement of three-dimensional spatial triangles. This geometric relationship, akin to a generalized extension of the Pythagorean theorem, unveils a unique spatial region characterized by this harmonious area interrelation among triangles.
Keywords:
Subject: Computer Science and Mathematics - Mathematics
1. Introduction
The Pythagorean theorem stands as a cornerstone of elementary mathematics, its significance echoing across centuries of mathematical inquiry and practical applications. Despite its seemingly simple statement, its ramifications are profound and far-reaching. The body of literature dedicated to the Pythagorean theorem is vast, spanning numerous proofs, historical investigations, and practical applications. However, the scope of this discussion merely scratches the surface of this rich tapestry. To embark on our exploration, we turn our attention to a seminal work, referenced as [1]. Within its pages lies a comprehensive examination of the historical evolution of the Pythagorean theorem, a journey that traverses the annals of diverse cultures and civilizations. This scholarly endeavor illuminates not only the theorem’s mathematical essence but also its cultural and historical significance, revealing how its understanding has evolved over time. One of the most compelling aspects of [1] is its exhaustive compilation of over 370 proofs of the Pythagorean theorem. Each proof represents a unique perspective, employing distinct methodologies and mathematical techniques to unveil the truth behind this fundamental theorem. From elegant geometric constructions to sophisticated algebraic manipulations, these proofs offer a kaleidoscopic view of mathematical creativity and ingenuity. Beyond its mathematical elegance, the Pythagorean theorem finds resonance in various domains beyond the confines of pure mathematics. [1] delves into the practical implications of the theorem, exploring its applications in geometry, physics, engineering, and beyond. Its versatility becomes apparent as it serves as a cornerstone for solving practical problems, ranging from architectural design to celestial navigation. Moreover, the book ventures into the realm of non-right triangles, transcending the traditional boundaries of the theorem. Through the lens of trigonometry and advanced geometric concepts, it elucidates how the Pythagorean framework can be extended to encompass triangles of all shapes and sizes, including acute and obtuse triangles. This extension broadens the theorem’s utility, unlocking new vistas of mathematical exploration and problem-solving. In essence, [1] serves as a beacon illuminating the multifaceted nature of the Pythagorean theorem.
Kassie Smith in reference [2] inquires about a more geometric proof for these concepts. Consequently, starting with the equation, they deduce that the combined area of two regular n-gons with side lengths a and b respectively, equates to the area of a regular n-gon with side length c. This can be shown by multiplying both sides of the equation by a specific constant, which is essentially the area of a regular n-gon with a side length of 1. Interestingly, for any given , this assertion also serves as a way to derive Pythagorean theorem in reverse. Within this context, the Wallace-Bolyai-Gerwien decomposition theorem ([3]) becomes applicable. This theorem suggests the existence of a decomposition of the smaller n-gons into polygonal components, which can be rearranged to form the larger n-gon. However, it’s important to note that the number of individual pieces involved in this process might be extensive. The reference [4] proposes still another proof which is nonstandard as he does not use neither squares nor similarity of triangles. The author introduces a geometric demonstration of the aforementioned assertion concerning equilateral triangles employing arithmetical operations of triangular shapes.
The interesting premise posited by [6] suggests that when x equals y, the particular instance of the three-dimensional iteration of the Pythagorean geometric gear can be assembled from multiple instances of its two-dimensional counterparts arranged along the three orthogonal planes. Consequently, it is demonstrated that akin to how two perpendicular lines delineate a hypotenuse, forming a right-angled triangle, aligning three triangles across orthogonal planes with a shared central point establishes a novel three-dimensional ’hypotenuse,’ constituting a hexagon, and collectively shaping a truncated tetrahedron. Just as the hexagon emerges from three diagonal hypotenuses, the truncated tetrahedron arises from three isosceles right triangles. Thus, the truncated tetrahedron represents the three-dimensional counterpart of the two-dimensional isosceles right triangle. The Pythagorean gear amalgamates one-, two-, and three-dimensional theorems, epitomizing a harmonious equilibrium between lengths, areas, and volumes. This equilibrium is delineated through orthogonal and diagonal orientations, forming distinct grids. This discourse holds practical implications, notably in the modern aerospace sector, particularly within computational fluid dynamics, where a grid composed of geometric elements, such as tetrahedra and prisms, termed ’cells,’ facilitates the analysis of fluid behavior in proximity to or within a structure, such as an aircraft. Analogously, the Pythagorean gear embodies a similar concept, wherein a gear can represent an individual balance or contribute to a network of balances when interconnected truncated octahedrons fill space. The Pythagorean constant 2 operates as a fractal intermediary, facilitating the conversion of information—lengths, areas, and volumes—between orthogonal and diagonal grids.
The comprehensive analysis conducted by [7] delves deeply into the multifaceted nature of the direct product group C2C2C2. By meticulously examining its foundational principles within the realm of Pythagorean arithmetic, the study offers a succinct yet thorough overview of the group’s intricate structure. Moreover, the exploration extends beyond theoretical frameworks to visually demonstrate the group’s manifestation in three-dimensional space. Through compelling visual representations, the study elucidates the geometric properties inherent in the group, shedding light on its potential implications in various fields, including music notation. Of particular note is the examination’s focus on four distinct decompositions of the group. Through meticulous enumeration and vivid illustration of all subsets, the study provides a comprehensive understanding of the group’s compositional elements. Furthermore, the text doesn’t merely stop at theoretical analysis but also suggests diverse practical applications of this structure. It encourages further systematic exploration in areas such as architectural design, where the insights gained from analyzing and synthesizing architectural forms using the principles of the C2C2C2 group could lead to innovative and aesthetically compelling designs. Overall, this study contributes significantly to our understanding of the C2C2C2 group, paving the way for both theoretical advancements and practical applications in various domains.
The author of the paper [8], Chetansing Rajput, presents an intricate interplay between the 3-4-5 Pythagorean triangle and the 1:2 right-angled triangle, highlighting their perfect complementary nature. This classical geometric harmony not only validates the Golden Ratio but also uncovers a precise correlation between and , rooted deeply in classical geometric principles. It showcased the distinctive characteristics of the triangle, establishing it as the true embodiment of the Golden Ratio Triangle. Through meticulous examination, it became evident that the Golden Ratio permeates every aspect of this particular right triangle’s geometry. This unique triangle, inherently imbued with the Golden Proportion, exhibits a close relationship with the regular pentagon. Not only does it offer a novel method for constructing a regular pentagon, but the pentagon itself reflects the proportions of within its geometry. Moreover, just as the triangle embodies the Golden Ratio, this research introduces a concept of specialized right triangles accurately representing each Metallic Mean. These Metallic Ratios find perfect representation within the generalized right triangle described herein. Additionally, this study unveils a hidden geometric connection: the precise complementary relationship between the triangle and the 3-4-5 Pythagorean triple. Remarkably, these two right triangles not only emerge together through various geometric constructions but also complement each other perfectly. Through their interaction, they uniquely manifest the Golden Ratio. Combining equivalent-sized triangles and 3-4-5 triples along their common hypotenuse reveals the exact value of the Golden Ratio. Connecting them along their shorter or longer legs also unveils the precise Pi:Phi Correlation, demonstrating the profound connection between these two triangles. Thus, the Golden Triangle, both individually and in conjunction with the 3-4-5 Pythagorean triple, not only serves as the ultimate geometric proof of the Golden Ratio but also elucidates the Golden Link in Geometry—a : correlation rooted in classical geometric principles with unparalleled precision.
In his paper [9], Ayushmaan Gupta has meticulously explored several distinct methods for proving the Pythagorean Theorem. These varied approaches shed light on the depth and versatility of this fundamental geometric principle. One of the most renowned proofs discussed is the Windmill proof, also referred to as the bride’s chair proof, famously attributed to Euclid, the esteemed Greek mathematician whose contributions have profoundly shaped the geometric landscape. This elegant proof method ingeniously demonstrates the theorem’s validity through a series of rotations resembling the blades of a windmill, showcasing the timeless ingenuity of ancient mathematical thought. Another compelling approach examined in this paper involves drawing altitudes within the geometric configuration and leveraging the properties of similarity, commonly referred to as the proof by similar triangles. This method highlights the inherent geometric relationships that underpin the Pythagorean Theorem, emphasizing the significance of geometric congruence and proportionality in its proof. Furthermore, the research delves into Garfield’s proof, attributed to James Garfield, the 20th President of the United States, who was not only a statesman but also a scholar with a keen interest in mathematics. Garfield’s proof offers a unique perspective on the theorem, showcasing the interdisciplinary nature of mathematical inquiry and its intersection with historical figures and events. Additionally, the paper explores a modern approach to proving the Pythagorean Theorem utilizing differentials, a technique that was once considered challenging to demonstrate rigorously. By leveraging concepts from calculus and differential geometry, this method offers a novel perspective on the theorem’s underlying principles, illustrating the evolving nature of mathematical reasoning and its applications across diverse domains. Through the examination of these varied proof methods, this research underscores the richness and complexity inherent in the Pythagorean Theorem, showcasing its enduring relevance and profound implications across mathematical disciplines. Each proof method offers a unique lens through which to appreciate the elegance and universality of this fundamental geometric principle, highlighting the dynamic interplay between historical insights, contemporary scholarship, and mathematical innovation.
In the ensuing discourse, we aim to elucidate two fundamental theorems pertaining to the utilization of the Geometric Pythagorean relationship. The initial theorem delves into the examination of triangles fashioned by linking a point within the midsegment to the vertices of the triangle. This theorem scrutinizes the geometric configurations arising from such constructions and delineates their inherent properties and characteristics.
The second theorem ventures into the realm of non-coplanar triangles, where connections are established between the sides of the original triangle and a point situated in the spatial domain. This theorem explores the intricate interplay between geometric elements in three-dimensional space, elucidating the geometric implications and ramifications of these non-coplanar configurations. Through rigorous analysis and mathematical reasoning, we seek to unveil the underlying principles governing these geometric arrangements and their relevance in geometric theory and practice.
2. Pythagorean concept for coplanar triangles formed from a point in the midsegment and the vertices of a triangle
Theorem 1
(Geometric Pythagorean Relationships within Triangular Midsegment Compositions). In Euclidean geometry, for any triangle and a point M lying on the midsegment connecting the midpoints of sides and , as depicted in Figure 1, the relationship between the areas of the three triangles , , and , is governed by the Geometric Proof of the Pythagorean theorem. Specifically, the sum of the areas of the triangles and is equal to the area of the triangle .
2.1. Definitions and Proof
Consider a generic triangle , where is the base, and is the midsegment connecting the midpoints of sides and , as illustrated in Figure 1.
The Triangle Midsegment Theorem is a fundamental principle in geometry that sheds light on the intricate properties of triangles and the fascinating interplay between their constituent parts. Essentially, this theorem posits that connecting the midpoints of the sides of any given triangle results in the formation of four smaller triangles, each possessing identical characteristics.
These smaller triangles, derived from the original triangle through the connection of its midpoints, exhibit remarkable symmetry and congruence. Notably, they share proportional sides and angles, mirroring the geometric intricacies inherent in the larger triangle. This revelation offers valuable insights into the underlying structure of triangles and unveils the hidden symmetries encoded within their configurations.
Furthermore, the Triangle Midsegment Theorem serves as a foundational tool in geometric analysis, providing a systematic approach to understanding the relationships between various components of a triangle. By dissecting the triangle into smaller, more manageable components, mathematicians and geometers can unravel the complexities of its geometry and derive meaningful conclusions about its properties and behavior.
In essence, the Triangle Midsegment Theorem stands as a testament to the elegance and sophistication of geometric principles, illuminating the inherent beauty and orderliness embedded within the realm of mathematics. Through its elucidation of the relationships between midpoints and triangles, this theorem enriches our understanding of geometry and empowers us to explore the intricate tapestry of shapes and forms that populate the mathematical landscape.
Let M denote any point situated on the midsegment of triangle . The midsegment theorem states that the midsegment of a triangle is parallel to its third side and is half its length. If the area of each triangle formed by connecting the midpoints of the sides of triangle is one-fourth the area of the original triangle, it indicates that these internally constructed triangles are precisely one-fourth the area of the larger triangle . This observation aligns with the fundamental principles of the Triangle Midsegment Theorem.
Expanding on this concept, it can be asserted that when any point M lies on the midsegment , the triangles formed by connecting the midpoints of the sides of share an intrinsic relationship with the midsegment . This relationship underscores the theorem’s implications, illustrating that the areas of these internally constructed triangles are proportional to the area of the original triangle .
Furthermore, this alignment with the Triangle Midsegment Theorem underscores the significance of the midsegment in partitioning the triangle into smaller triangles with specific area relationships.
The summation of the areas of the triangles and is given by Eq. 5
Since
It can be demonstrated that irrespective of the size or configuration of a triangle, and regardless of the placement of any point along its midsegment, the relationship between the areas of the three resulting internal triangles adheres to the principles outlined in the Geometric Proof of the Pythagorean theorem. This means that the combined areas of the two smaller internal triangles, as defined by Equation 5, will always equal the area of the larger internal triangle, as defined by Equation 6. This fundamental relationship underscores the inherent geometric harmony within triangles, showcasing the timeless validity of the Pythagorean theorem across various geometrical contexts. Thus, regardless of the specific attributes of the triangle or the position of the point along its midsegment, this principle remains steadfast, providing a reliable framework for understanding and exploring geometric relationships within triangles.
2.2. Theorem special case for
For the case shown in Figure 2 where , it holds true that
It is not unexpected that the connection between the internal triangle persists, upholding the assertion of Eq. 9. This enduring relationship underscores the stability and consistency of the mathematical framework being discussed. As we delve deeper into the analysis, we find that this connection serves as a foundational element, guiding our understanding and interpretation of the mathematical expressions at hand. Moreover, this ongoing correlation reaffirms the validity of the principles established earlier, lending further credence to the conclusions drawn from the mathematical model under scrutiny.
2.3. Theorem special case for
In the situation depicted in Figure 3, where M is not inside the , the Pythagorean structure undergoes a transformation such that the Eq. 7 becomes the relationship shown in Eq. 10.
Certainly, the triangle has been meticulously enlarged to assert its dominance as the largest among the trio of triangles under consideration. This deliberate augmentation is executed with utmost precision, meticulously ensuring that the fundamental Pythagorean composition remains intact throughout the transformation process. By enlarging to its maximal extent within the given context, every effort is made to maintain the geometric integrity and inherent relationships that characterize the original configuration. This strategic enlargement serves to accentuate the significance and prominence of within the geometric framework, emphasizing its pivotal role in the analysis or application at hand. Through this deliberate action, the integrity of the underlying Pythagorean structure is preserved, while simultaneously amplifying the visual and analytical impact of within the broader geometric context.
3. Extrapolating the Pythagorean structure into the 3D Space
Theorem 2
(Pythagorean Relationships in Three-Dimensional Geometric Structures Formed by Three-Dimensional Spatial Triangular Compositions). In a specific curvature-domain shape within three-dimensional space, a geometric configuration is established wherein the summation of the areas of two constituent triangles created by connecting the vertices of a generic triangle with a point in 3D space, specifically triangle and triangle , is invariably equivalent to the area of the encompassing triangle for any selection of points A, B, and C that form said triangles, equivalent to the geometric demonstration of the Pythagorean Theorem.
3.1. Definitions and Proof
Now, let’s delve into the intricate details of the general triangle as illustrated in Figure 4. Within this geometric framework, the sides , , and symbolize the foundational elements of the triangle.
Expanding our exploration further, consider the formation of three distinct triangles: , , and . These triangles emerge through the connection of a generic point situated within three-dimensional space with the sides , , and of the main triangle .
In essence, by introducing this additional point P, we extend our analysis beyond the two-dimensional plane, allowing for a comprehensive examination of the geometric relationships within the spatial context. This expansion broadens the scope of our investigation, offering insights into the dynamic interplay between points and lines within a three-dimensional geometric framework.
Through the exploration of these supplementary triangles, we aim to uncover deeper insights into the structural properties and geometric configurations present within the general triangle .
The altitude h of triangle and the distance l from its altitude to the y-axis are both established based on the triangle’s area, which is calculated utilizing the concise Heron’s formula, providing a streamlined method for determining these geometric properties with accuracy and efficiency.
Hence, h and l may be expressed in the following manner:
In order to illustrate the concept efficiently, we employ a computationally streamlined equation requiring only one square root operation. This equation facilitates the calculation of the area of a triangle in coordinate geometry. The formula, denoted as Eq. 17, operates as follows: it utilizes the coordinates of the vertices , , and to determine the area of the triangle situated within three-dimensional space.
In the subsequent iterations of our analysis, we employ Equation 17 to compute the areas of the triangles , , and individually. For the specific case of , let’s denote the coordinates of its vertices as follows: , , , , , , , , and .
This setup allows us to precisely delineate the spatial configuration of within the coordinate system. The vertex A is anchored at the origin , while B is positioned at along the positive x-axis. The third vertex, P, holds the coordinates , allowing for flexibility in the placement of this point within the spatial domain.
With these coordinate specifications in place, we proceed to apply Equation 17 to calculate the area of . This area computation involves the determination of the magnitude of the cross-product of the vectors and . Through this method, we derive the precise numerical value representing the area enclosed by the vertices A, P, and B.
Similarly, we extend this computational procedure to ascertain the areas of and . Each triangle’s unique configuration, defined by the specified coordinates of its vertices, allows us to systematically evaluate its area utilizing the established mathematical framework.
Regarding the triangle where
with
Concerning the triangle where
Utilizing the Pythagorean geometric proof concept within the context of the irregular tetrahedron not only offers a profound insight into its structural intricacies but also reveals a plethora of mathematical solutions. The application of this concept leads to the derivation of three distinct solutions, each shedding light on different aspects of the tetrahedron’s geometry and relationships among its vertices.
Equation 23 serves as a crucial tool in elucidating these solutions, providing a mathematical framework through which the Pythagorean theorem can be applied to analyze the relationships between the lengths of the sides and diagonals of the tetrahedron. Through this equation, we can explore the various configurations and arrangements of the vertices A, B, C, and P, uncovering the intricate interplay between their spatial coordinates and distances.
Each solution derived from Equation 23 offers valuable insights into the geometric properties of the irregular tetrahedron . By leveraging the Pythagorean geometric proof concept, we can unravel the mysteries hidden within the complex geometry of tetrahedra.
By substituting the terms from equations 18, 19, and 22 into equation 23, we derive three respective implicit solutions for the hypothesized theorem, which are tailored specifically to tetrahedrons. We hereby denote these tetrahedrons as the Pythagorean Tetrahedron. These solutions encapsulate the geometric relationships and properties inherent to these specially defined tetrahedrons, thus providing a framework for understanding their structural characteristics and mathematical properties in the context of Pythagorean principles.
Expanding upon this, we can delve into the intricate interplay between the constituent elements of the Pythagorean Tetrahedron and how they contribute to its overall geometry and symmetry. Through rigorous analysis and mathematical manipulation, we elucidate the fundamental principles governing these tetrahedrons and establish their significance within the broader realm of geometric theory.
Furthermore, these implicit solutions offer insights into the spatial configurations and dimensional constraints of Pythagorean Tetrahedrons, shedding light on their unique structural attributes and potential applications in various mathematical and scientific disciplines.
It is imperative to clarify that the concepts elucidated in this discussion should not be conflated with the notion of the Trirectangular Tetrahedron or with De Gua’s theorem [5]. De Gua’s theorem posits a relationship within a tetrahedron that contains a right-angle corner akin to a corner on a cube. According to De Gua’s theorem, the sum of the squares of the areas of the three faces adjoining the right-angle corner equals the square of the area of the face opposite that corner. This theorem provides valuable insights into the geometric properties of such tetrahedra, shedding light on the intricate interplay between their constituent faces and angles.
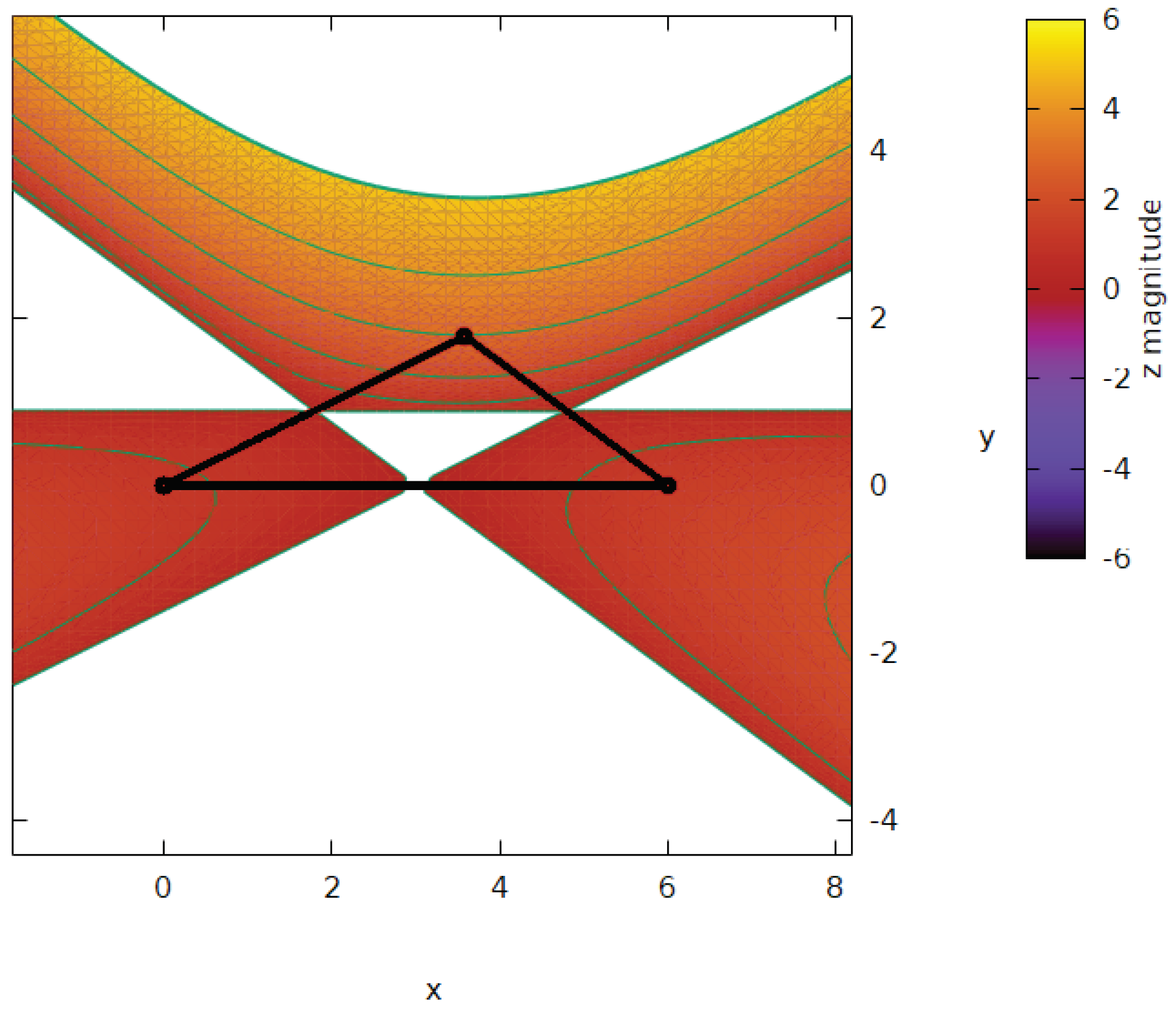
3.2. Graphic representation of the resultant curvature
In this section, we offer a visual exploration of the solution space provided by the implicit equations labeled as Eq.24,25, and 26, which directly relate to the conjectured theorem discussed in Section 3. Leveraging the computational capabilities of a computer algebra system (CAS), we present three-dimensional graphical representations that vividly depict the solutions to these equations. Through these visualizations, we aim to provide intuitive insights into the geometric relationships and patterns embedded within the theorem under consideration. We commence the visual exploration of resultant curvature by utilizing the classic 3-4-5 right triangle as our foundation. Through graphical representation of equations 24, 25, and 26, we unveil the emergence of three distinct bell-shaped tri-dimensional curvatures extending outward from the midsegments of triangle . This depiction is vividly illustrated in Figure 5. Foreseen is the indefinite expansion of these bell-curvatures, suggesting their potential for perpetual growth. The void spaces within this geometric configuration encompass not only the internal triangle enclosed by the midsegments but also three supplementary regions generated by extending these midsegments in a manner that circumvents intersection with the vertices of the prototypical triangle. Figure 6, Figure 7, and Figure 8 provide visual representations of the projection of the resultant surface onto the -plane. In these figures, the original triangle is highlighted using bold black lines, while the contour levels are delineated by green lines for 3-4-5 right triangles, 3-3-3 isosceles triangles, and 3-4-6 scalene triangles. The conjectured Theorem 1, elucidated in Section 2, can be easily substantiated by examining the midsegments of these triangles. Expanding further, the projections offer a comprehensive view of how the resulting surface interacts with the -plane, showcasing the intricate relationships between the original triangle and its transformed counterparts. The use of bold black lines emphasizes the foundational structure of the original triangle, serving as a reference point for comparison. Meanwhile, the varying contour levels, depicted by green lines, highlight the distinct characteristics of each triangle type, facilitating a nuanced analysis of their geometric properties. By scrutinizing the midsegments within these projections, one can discern patterns and relationships that affirm the conjectured Theorem 1. The alignment and distribution of midsegments provide compelling evidence of the underlying geometrical principles at play, further reinforcing the validity of the theorem as proposed in Section 2. Overall, the visualizations presented in Figure 6, Figure 7, and Figure 8 offer valuable insights into the geometric transformations and relationships explored within this study. Thus, as posited, our demonstration has elucidated that the trio of inner triangles formed by joining a point on a midsegment with the vertices of the triangle adheres rigorously to the geometric validation of the Pythagorean theorem. This discovery not only reinforces the timeless relevance of the Pythagorean theorem but also sheds light on a deeper geometric connection. This connection, reminiscent of an expanded interpretation of the Pythagorean theorem, unveils a distinct spatial configuration defined by the intricate interplay of triangle areas within any given triangle. Moving forward, it becomes imperative for future endeavors to focus on the refinement and development of explicit formulas corresponding to the newly introduced concepts within our current framework. By pursuing this avenue of research, we can delve deeper into the mathematical intricacies and unveil further insights into the fundamental relationships that govern geometric structures. Such endeavors promise to enrich our understanding of geometry and pave the way for new avenues of exploration within the realm of mathematical theory and application.
Acknowledgments
Posthumous tributes are extended to Professor Dr. Pérides Silva for his pioneering insights into these conceptions.
References
- Loomi, E. S.,The Pythagorean Proposition: Its Demonstrations Analyzed and Classified, and Bibliography of Sources for Data of the Four Kinds of Proofs, Washington, National Council of Teachers of Mathematics, 1968. I: Pythagorean Proposition.
- Smith, K., Pythagorean Theorem, http://jwilson.coe.uga.edu/EMAT6680Fa2012/Smith/6690/pythagorean%20theorem/KLS_Pythagorean_Theorem.html (Accessed: August 18, 2023).
- Wallace–Bolyai–Gerwien theorem, Wallace–Bolyai–Gerwien theorem — Wikipedia, The Free Encyclopedia, https://en.wikipedia.org/wiki/WallaceâĂȘBolyaiâĂȘGerwien_theorem (Accessed: August 18, 2023).
- Navas A., The Pythagorean Theorem Via Equilateral Triangles, Math. Mag., vol. 93, no. 5, pp. 343–346, Oct. 2020. [CrossRef]
- Gua de Malves, J.P. de. 1740. Usages de l’analyse de Descartes Pour Découvrir, sans Le Secours Du Calcul Differentiel, Les Propriétés, Ou Affections Principales Des Lignes Géometriques de Tous Les Ordres. Chez Briasson, libraire, ruë S. Jacques, à la science.
- Luis Teia. Special Case of the Three-Dimensional Pythagorean Gear. Journal of the Australian Mathematical Society, vol. 32, pp. 36-49, Dec. 2018.
- Economou, Athanassios. C2C2C2: Pythagorean structures in design. Digital Hand Eye Ear Mind: Proceedings of the Third International Conference on Mathematics and Design (M&D), Deakin University, Geelong, Australia, pp. 128-138, Jan. 2001.
- Chetansing Rajput. A Classical Geometric Relationship That Reveals The Golden Link in Nature, Journal of Advances in Mathamatics, Vol. 17, pp. 400-413, 2019. [CrossRef]
- Ayushmaan Gupta, Pythagorean Theorem Research Paper, Journal of Research in Applied Mathematics, Vol. 7, Issue 7, pp: 13-18, 2021.
Figure 1.
Generic triangle .
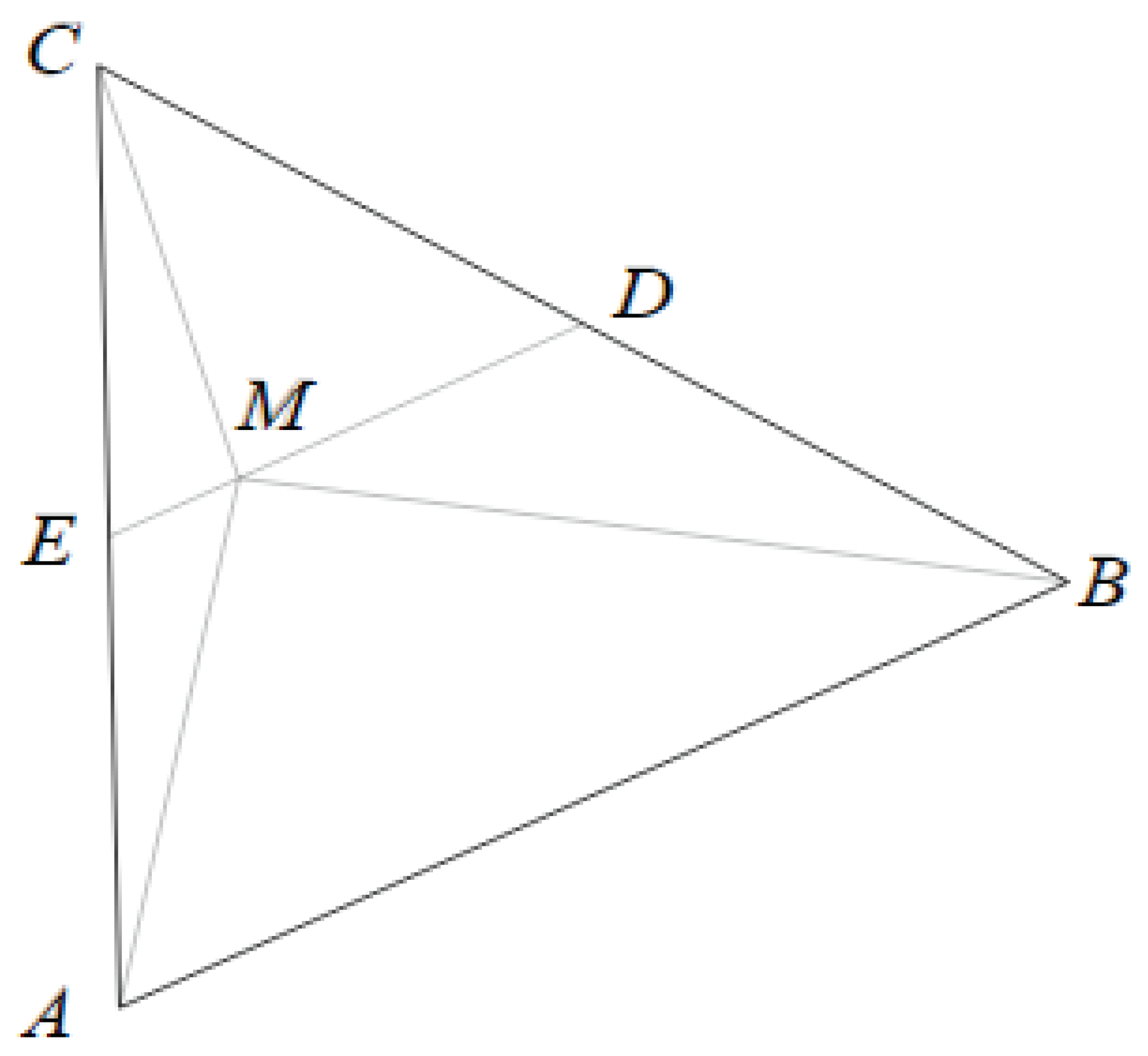
Figure 2.
Theorem special case for .
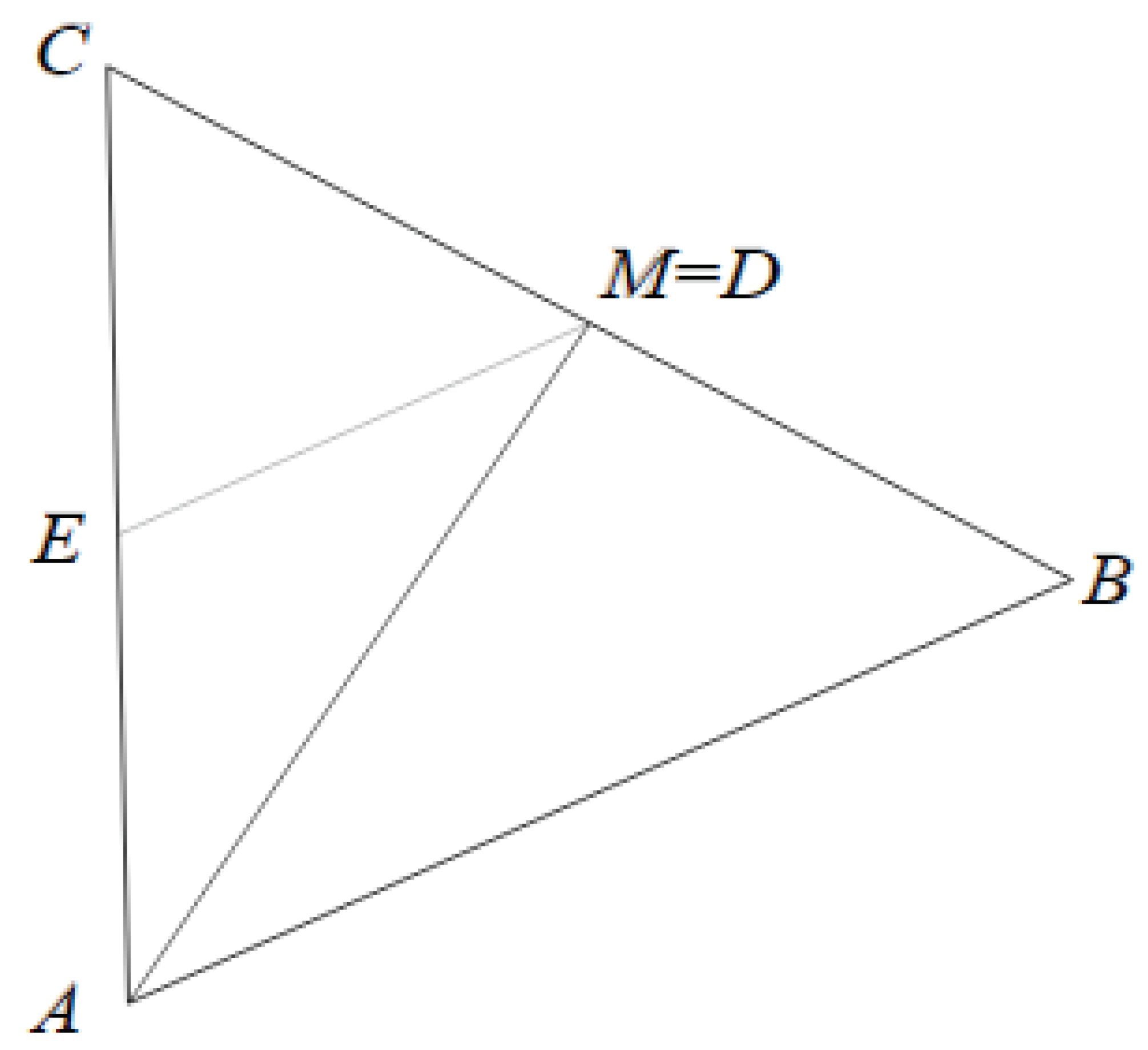
Figure 3.
Theorem special case for .
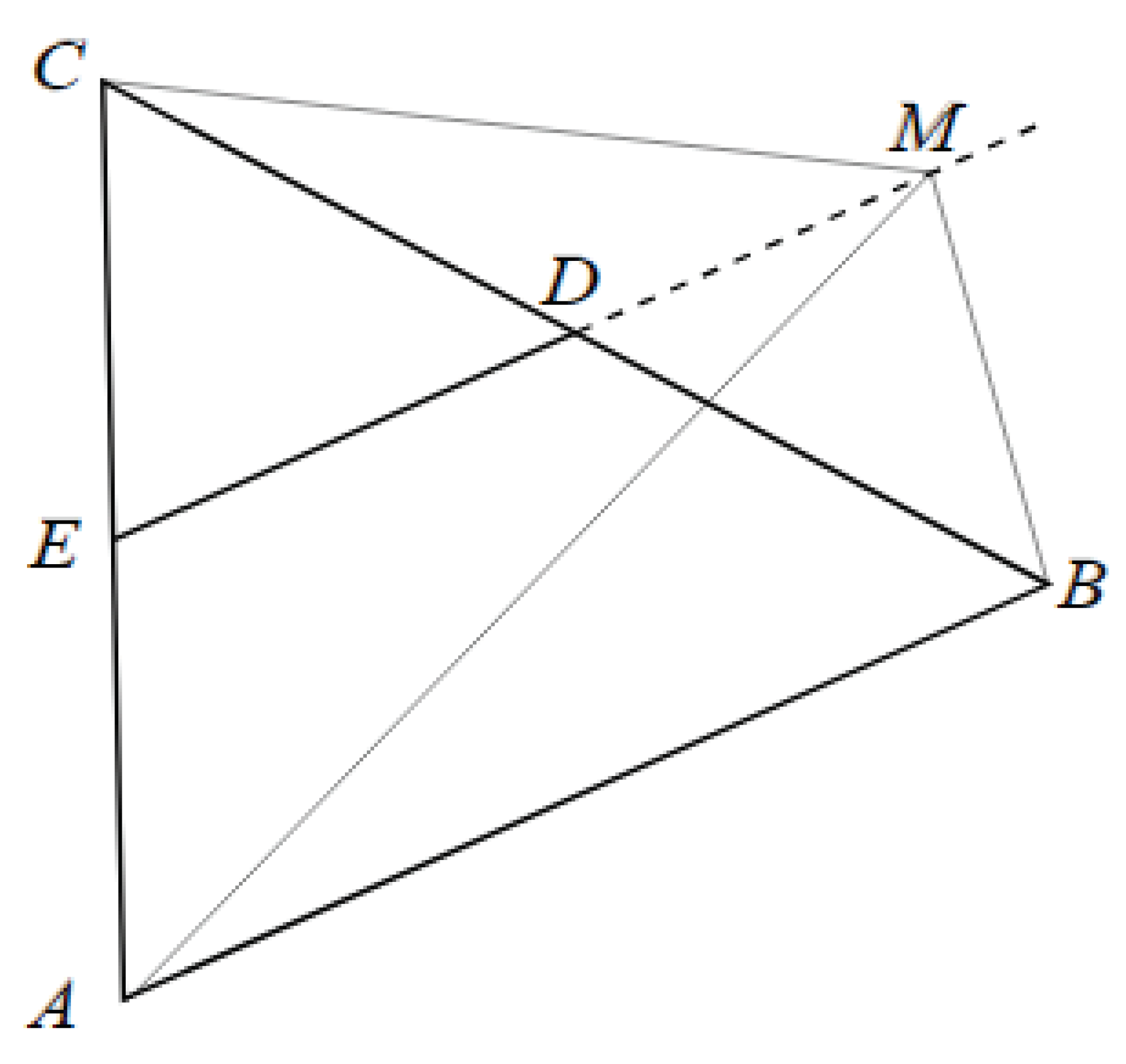
Figure 4.
3D Pythagorean composition from .
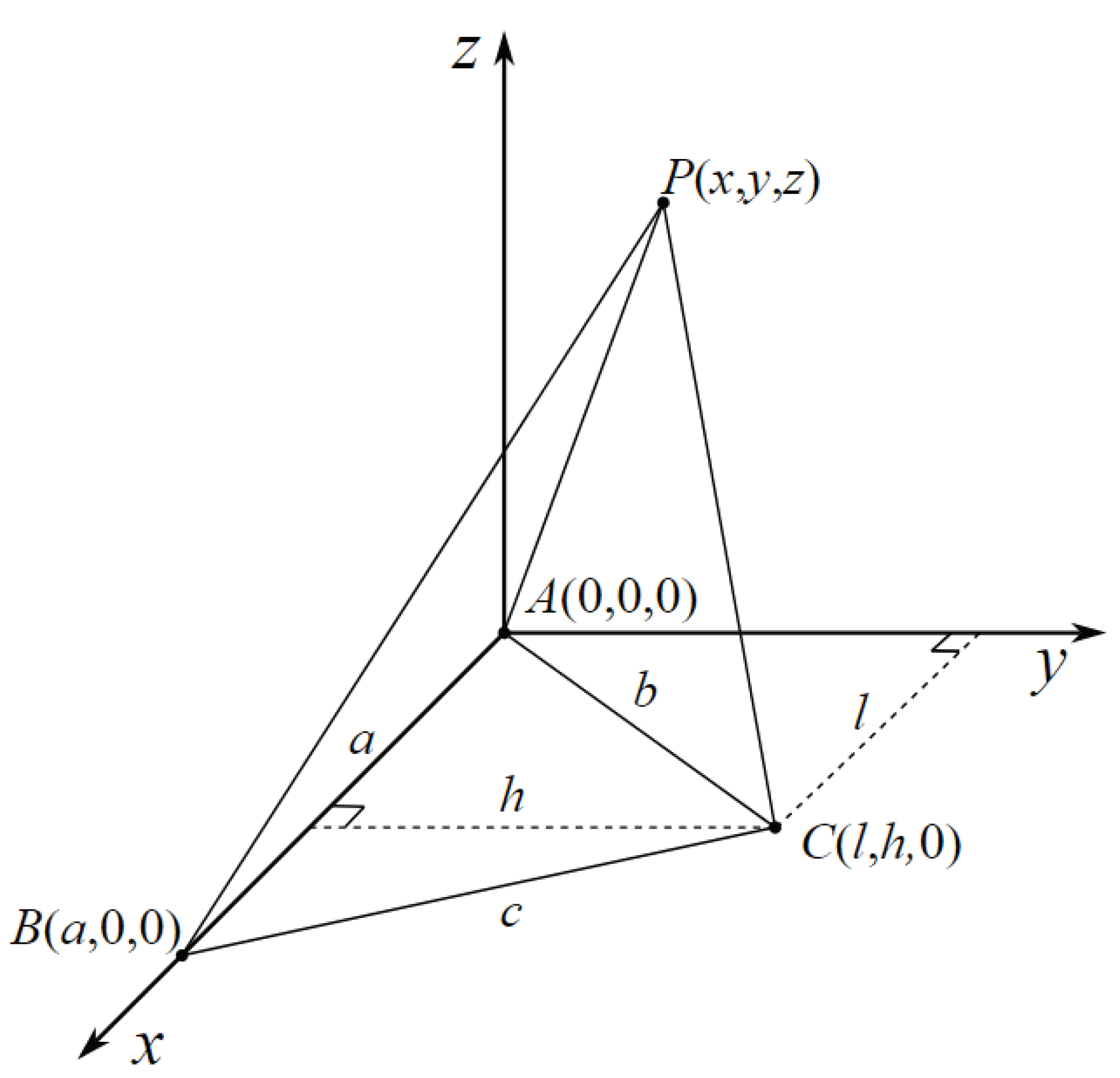
Figure 5.
Visual representation of the resulting curvature and contour levels for a 3-4-5 right triangle.
Figure 5.
Visual representation of the resulting curvature and contour levels for a 3-4-5 right triangle.
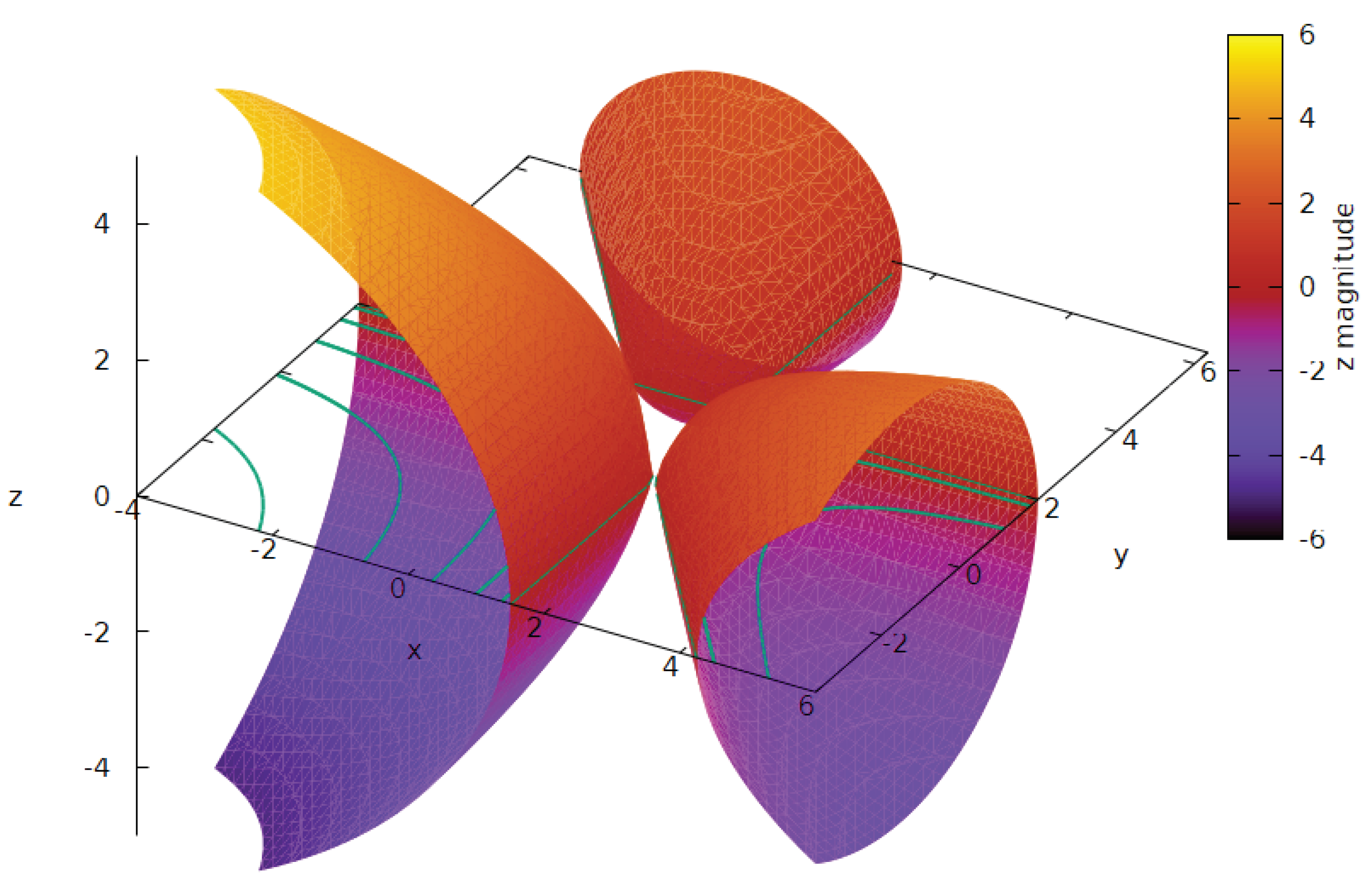
Figure 6.
The 3-4-5 right triangle and the -plane view of its resulting curvature and contour levels.
Figure 6.
The 3-4-5 right triangle and the -plane view of its resulting curvature and contour levels.
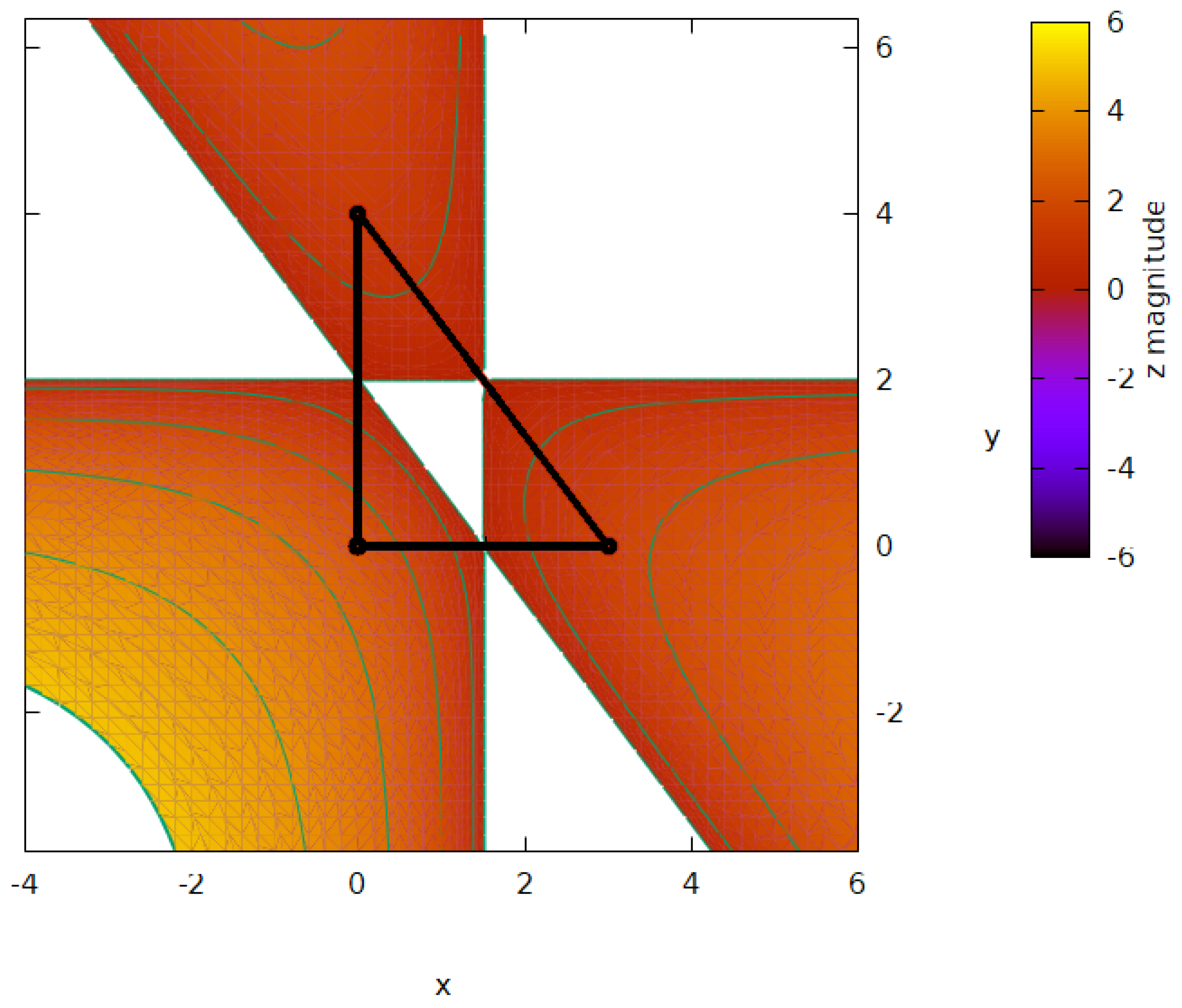
Figure 7.
A 3-3-3 isosceles triangle and the -plane view of its resulting curvature and contour levels.
Figure 7.
A 3-3-3 isosceles triangle and the -plane view of its resulting curvature and contour levels.
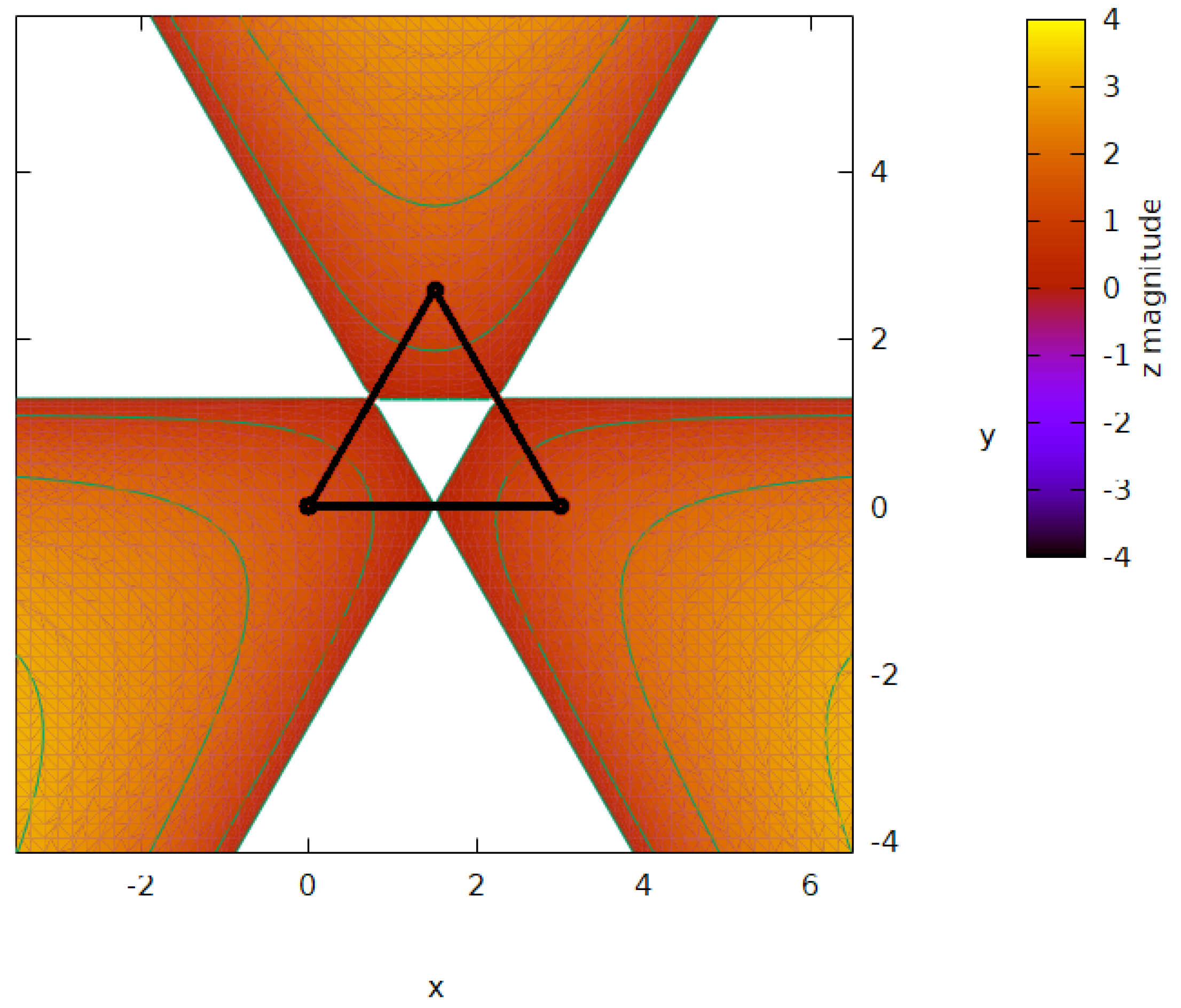
Figure 8.
A 3-4-6 scalene triangle and the -plane view of its resulting curvature and contour levels.
Figure 8.
A 3-4-6 scalene triangle and the -plane view of its resulting curvature and contour levels.
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
MDPI Initiatives
Important Links
© 2024 MDPI (Basel, Switzerland) unless otherwise stated





