Preprint
Article
Deterministic Shaping of Quantum Light
Altmetrics
Downloads
138
Views
70
Comments
0
A peer-reviewed article of this preprint also exists.
This version is not peer-reviewed
Submitted:
19 February 2024
Posted:
20 February 2024
You are already at the latest version
Alerts
Abstract
We propose a theoretical method for the deterministic shaping of quantum light via photon number state selective interactions. Nonclassical states of light are an essential resource for high precision optical techniques that rely on photon correlations and noise reshaping. Notable techniques include quantum enhanced interferometry, ghost imaging, and generating fault tolerant codes for continuous variable optical quantum computing. We show that a class of nonlinear-optical resonators can transform many-photon wavefunctions to produce structured states of light with nonclassical noise statistics. The devices, based on parametric down conversion, utilize the Kerr effect to tune photon number dependent frequency matching, inducing photon number selective interactions. With a high amplitude coherent pump, the number selective interaction shapes the noise of a two-mode squeezed cavity state with minimal dephasing, illustrated with simulations. We specify the requisite material properties to build the device and highlight the remaining material degrees of freedom which offer flexible material design.
Keywords:
Subject: Physical Sciences - Optics and Photonics
1. Introduction
Systems that utilize quantum information resources generally take advantage of coherent macroscopic superposition and/or entanglement. The increased information density and sensitivity to measurements of such quantum states, compared to their classical counter parts, is central to their application in modern quantum information technologies like quantum key distribution[1,2], quantum computing [3,4,5], and metrology at the fundamental noise limit[6,7,8]. This article focuses on the generation of quantum states of light for such applications. Both macroscopic superposition and entanglement are generically found in states supported by nonlinear systems [9,10]. However, optical nonlinearities are typically weak for closed systems. Much attention has therefore been paid to developing methods for generating quantum states of light which utilize wavefunction collapse as a source of nonlinear evolution, where a particular measurement outcome heralds the desired quantum state. Though hugely successful, measurement based state preparation is inherently non-deterministic making sequential preparations low probability events[11,12,13,14].
To overcome low heralding success rates, we return to the paradigm of deterministic generation of quantum states via strong coherent nonlinear interactions. With the advent of epsilon-near-zero materials [15] and polariton enhanced scattering, commonly facilitated by electronically induced transparency, [16,17,18,19], large effective nonlinearities become increasingly realistic. When realized in a high-Q optical resonator, strong optical nonlinearities with relatively long evolution time and low loss facilitate deterministic quantum optical state engineering. Trapped atom and single quantum emitter systems show great promise for this application [20,21,22,23]. In these systems, the quantum information content of a state of interest is first written onto an array of quantum emitters, typically in a decoherence free subspace, then mapped to super-radiant light-matter states which couple to an optical waveguide.
This work introduces an alternative technique for precision shaping of quantum noise statistics without the need for precise emitter engineering. For simplicity we consider a material with only second and third order nonlinearities in the photon field interaction, though this analysis generalizes to a large class of interactions which will be discussed in future work. The key step is to separate the phase rotating interactions from the mode mixing interactions. In the present case, we solve the combined first and third order system exactly, then investigate the second order mode mixing in the interaction picture. We show that, when second and third order nonlinearities are comparable in strength, the optical Kerr effect alters the frequency matching condition for optical parametric oscillation such that the interaction between field states is strongly photon number dependent. We illustrate the general characteristics of this effect and demonstrate a procedure for deterministically generating approximate Fock states. General material constraints are highlighted and developed into figures of merit to guide experimental realizations of this method.
2. Background
Let us begin with a brief discussion of electromagnetic field quantization. Dirac recognized that Hamiltonian mechanics has simple rules for canonical quantization, that Lagrangian mechanics is well suited for relativistic gauge invariant classical field theories, and that they both poorly handle what the other does well. So, to formulate relativistic quantum theory, he generalized Hamiltonian mechanics to handle systems with constraints[24]. His mechanics encodes symmetries that are simple to write into a Lagrangian, into constraints on a Hamiltonian, recovering Hamilton’s equations of motion with a generalized Poisson bracket called the Dirac bracket. Canonical quantization of Dirac’s bracket reveals, in part, Dirac’s relativistic theory of quantum mechanics. Born and Infeld adopted Dirac’s procedure to show that Maxwell’s equations in the Coulomb gauge assume a Hamiltonian formulation [25,26] where the Hamiltonian is the classical field energy
and the fields obey a version of the canonical Dirac bracket relations,
with the second equation defining the transverse delta function . 1According to Dirac’s canonical quantization, the field amplitudes are promoted to operators, and the Dirac brackets become commutators
Quesada et al. [27] later showed that, to correctly recover Maxwell’s equations in nonlinear dielectric media from the Born-Infeld Dirac brackets, it is imperative to consider the displacement field and magnetic flux density to be the fundamental dynamical variables. Here ’fundamental’ indicates that D and B are Hermitian linear combinations of Bose operators, i.e. they are Boson fields, whereas the electric and magnetic fields E and H are generally higher polynomials of Bose operators2. For modern derivations and perspectives of quantum field theory in linear dielectric media, see [28,29,30,31].
For a finite linear cavity, the eigenstates of the system are enforced by the dielectric structure and boundary conditions of the cavity. Let us restrict ourselves to one effective spatial dimension, scalar susceptibilities, and a single polarization of the field modes without loss of generality3 This amounts to a single parameter family of eigenstates. Consider a uniform cavity of length L with periodic boundary conditions, as is the case for a microring resonator [32]. The allowed wavenumbers, k, within the cavity are integer multiples of . The fields D and B are physical, therefore real valued. Each may then be expanded with respect to the basis of eigenmodes in the following form,
where A represents the transverse cross sectional area of the modes in the cavity4.
The field amplitudes of a single photon, – defined later, are determined such that the energy of a photon with well defined momentum agrees with the Einstein energy of a photon, . Suppose a dispersive permitivity such that the Fourier components of the linear electric field and displacement field are related by . If the medium is dispersive, each frequency mode solves a different eigenvalue equation, so normalization requires special care [29]. We rescale the amplitude by the single photon amplitude, , and promote the amplitude variable to a Bose operator obeying the canonical commutation relations
The displacement field operator becomes
where we have adopted a common quantum optics phase convention of initial phase , is the group velocity and the refractive index of the mode with wave-vector k. The magnetic flux field operator obtains a similar form[29].
Having properly dealt with linear dispersion, the Hamiltonian for linear quantum optics takes the form of an infinite set of harmonic oscillators
2.1. Nonlinear Quantum Optics
We introduce nonlinear optics assuming that the dispersion of nonlinear susceptibilities is negligible for frequency bands we are interested in. The electric field is related to the displacement field and polarization field, P, via [33]
Recall from equation (1) the electric field contribution to the field energy, . The energy term is handled in the linear part of the Hamiltonian upon quantization. The remaining interaction relays the effect of the nonlinear polarization .
We assume that the polarization at a point in space depends on the displacement field at that point, i.e. the response function is local. Expanding the nonlinear polarization in a power series of the displacement field amplitudes up to third order, the part of the Hamiltonian associated with classical nonlinear dynamics is
where is the second order displacement field susceptibility that is responsible for optical parametric oscillation (OPO) – often referred to as parametric down conversion. is the third order displacement field susceptibility responsible for four effects: the two optical Kerr effects called self phase modulation (SPM) and cross phase modulation (XPM), a mode mixing process called four wave mixing (FWM), and a static field induced OPO. Both are defined by the power series expansion of the polarization field in terms of displacement field [32].
3. Approach
We aim to show how strong Kerr nonlinearities affect OPO. The essential result is that photon number dependent frequency shifts from the Kerr effect generate a photon number dependent detuning in OPO. The number dependent detuning is exploited for coherent deterministic number selective shaping of noise statistics in select modes. To make this effect clear, we constrain our view to the subspace of three optical modes engaging in OPO, called signal, idler, and sum. We first solve the system exactly under the action of the sum of Hamiltonian terms that preserve photon number in each mode. Evolution under this Hamiltonian gives nontrivial structure to the time dependent displacement field operator; it is scaled by a diagonal unitary operator with a frequency that is a function of the photon number operators. OPO is analyzed in the interaction picture, exhibiting photon number selective behaviour. The nature of this behaviour is discussed, and explored numerically in Section 4.1.
3.1. Eigenstates of Kerr Hamiltonian
The Hamiltonian from (9) is responsible for two distinct photon number density preserving processes, SPM and XPM, and a mode mixing process, FWM. FWM is a rich effect, leading to optical frequency combs and soliton propagation in micro-resonators [35]. However, our aim is to study an entirely different phenomenon in the same environment, so we do not wish to handle these complications presently. We will suppose the dispersion relation of our system is specified such that no FWM is phase matched for the active modes.
Unlike FWM, SPM and XPM are always phase matched. These effects, together with the linear Hamiltonian, dominate the phase dynamics of the system. The corresponding Hamiltonian is diagonal in the Fock basis and, equivalently, conserves photon number for each mode. Our present objective is to solve for the time evolution of the field operator under photon number density preserving Hamiltonian such that , where , , are defined in (7) and (9). We later show how this time evolution affects , producing a photon number selective interaction under the right conditions. We will consider the dynamics of three modes interacting in the cavity; a sum, signal, and idler mode with frequencies respectively.
We assume permutation invariance of all susceptibilities5 and abbreviate the frequency dependence of Kerr susceptibilities . Furthermore, we uphold the rotating wave approximation6 and assume spatially constant third order susceptibility. After ordering all permutations of the creation and annihilation operators to be simple powers of the mode number operators , the Hamiltonian pertaining to the sum, signal, and idler modes is
Heisenberg’s equation of motion, , tells us the time evolution for the field annihilation operators .
To condense our notation, let us define the Kerr frequencies
where are the frequencies of self phase modulation and are the frequencies of cross phase modulation. These frequencies are proportional to the classical Kerr frequency shifts in accordance with the relation where I is the classical intensity and is the mean photon number. The time evolution of each field annihilation operator under is
Note that the exponentials above do not commute with the field annihilation operators. To further simplify our notation we call , and use to represent the exponential operators on the right hand side of equation (14) such that
Substituting these operators into equation (6) yields the time dependent displacement field operator for the nonlinear field described by ,
The operators neatly quantify the photon blockade effect, reviewed in [19]. Consider a cavity pumped by a near monochromatic beam that is near resonance to a mode with wavenumber . As the photon number in the cavity increases from to , the frequency shifts by . If the frequency of the next excitation shifts out of the pump line width, the cavity will no longer be excited, i.e. additional photons are blockaded from entering by the photons already in the cavity. Consequently, obtaining a high cavity intensity requires a pump beam with a wide linewidth for very strong Kerr nonlinearities.
Note that self phase modulation by a positive susceptibility red shifts the frequency by . If , the largest photon number achievable in the cavity pumped by a beam with a spectral edge at some fraction f of is
When considering optical parametric oscillation in the next sections, we drive the sum frequency cavity mode with an external pump. It is important that the external pump spectrum does not overlap with the signal and idler modes to avoid unwanted excitation. Therefore it is necessary that and preferable that . We discuss later in Section 4.3, and simply note now, that a large coherent state for the sum mode minimizes dephasing and enhances OPO efficiency. Because unwanted excitations and high pump intensity are coincident, it is best for the Kerr nonlinearities involving the pump frequency to be small or negative.
3.2. Number Selective Optical Parametric Oscillation
With an exact time evolution for the Kerr photons in hand, we construct the Hamiltonian for number selective optical parametric oscillation (NSOPO). In the interaction picture, the OPO Hamiltonian evolves via the photon number preserving propagator, . From equation (9) we obtain the time dependent OPO Hamiltonian in the interaction picture,
We assume the susceptibility is spatially local, spatially constant, and frequency permutation invariant7. The time dependent displacement field operators, (16), are substituted into (18). Terms of the form and are neglected by assuming the rotating wave approximation for the three modes, but the time dependence from the Kerr induced frequency mismatch is preserved. All possible permutations of the three relevant mode contributions to the field operators are reordered to a common tractable form, accounting for the noncommutativity of a and . The simplified interaction Hamiltonian is thus
where h.c. denotes hermitian conjugate.
Suppose the sum frequency mode is a high amplitude coherent state such that . Then we can reasonably replace the operator with the c-number without worrying much about dephasing effects. For example, if shaping of signal and idler modes is done in a range of m photons, the purity of the manipulated quantum state is on the order of 8.
To simplify notation we define the NSOPO complex squeezing parameter and OPO resonance detuning frequency such that
where
and
are the set of detuning weights for each photon number, as well as a static detuning .
The interaction Hamiltonian is now expressed compactly as
Without Kerr nonlinearities, non-degenerate parametric down conversion generates 2-mode squeezing between the signal and idler modes [36]. With Kerr nonlinearities, the squeezing parameter hosts a detuning oscillation with photon number dependent frequency, making two mode squeezing amplitude dependent. Let us explore precisely how this feature affects the interaction.
The OPO detuning governs how number states experience 2-mode squeezing. A simple, and very useful case to study is when a large- coherent state is injected into the nonlinear cavity in the presence of a 2-mode squeezed state of signal and idler frequencies. Experimentally this would require a method for coherently injecting a 2-mode squeezed state into the nonlinear cavity initially in the vacuum state. Acknowledging the technological challenge9, we will assume it is possible and investigate its consequences10.
So we start assuming an initial 2-mode squeezed state – the state which is a superposition of all equal populations of signal and idler photons. Evident from the interaction operator , the difference in signal and idler photon numbers is a conserved quantity, so the state remains a superposition of equal photon numbers for all times much less than the cavity decay time. When , the OPO detuning is independent of the sum frequency photon number and NSOPO is coherently driven by the sum frequency beam. Each OPO interaction event will decrement or increment the signal and idler photon numbers by one, transporting probability amplitude along the space of states. Adjacent states see a difference in detuning of
Suppose there is a photon number, such that the detuning is minimal. We call this the shape center. Then the OPO Hamiltonian in Dirac notation takes the form
This Hamiltonian generates particularly interesting evolution when and are of similar magnitude, however challenging to describe analytically. We explore this behavior in the following section.
4. Results and Discussions
In the previous section we developed a theoretical method for directly targeting photon number states to coherently shape the quantum statistics of an optical field in a cavity. In the following we numerically simulate the model and illustrate how the parameters can be controlled to generate quantum states with useful structure. The constraints established here and in Section 3 are elaborated on and brought together to determine what regions of parameter space are viable for experimental realization.
4.1. Simulations
The time dependent Schrödinger equation corresponding to the interaction Hamiltonian, equation (26), is numerically evolved with a Crank-Nicolson method, which preserves unitarity. Numerical simulation reveals characteristic behavior in NSOPO. Figure 1 shows that probability amplitude tends to coalesce around number states separated by a spacing
where states see constructive interference from two mode squeezing. These peaks rapidly fall off in amplitude from the shape center when near the shape center, but fall off more slowly when away from the shape center maintaining a wide tail in their height distribution. The peak nearest the shape center deviates from this pattern, consequently shifting the pattern for states with higher photon number. The location of the central peak depends on the phase of the NSOPO squeezing parameter . For , the peak is centered on the shape center. For , there is a deep trough at the shape center with nearest peaks equidistant to the left and right. For , the nearest peak and trough are to the right and left (left and right) of the shape center. The plots in Figure 1 overlay the function
which approximately replicate the height and location of each peak, breaking accuracy at the central peak. This function is obtained by integrating the Hamiltonian over time and acts as a more tractable guideline for engineering states with shaping.
These shaping principles can be applied in several ways. Setting the shape center to be aligned with the peak of a state, , and the peak spacing s to be greater than the width of the state, the photon number probability will coalesce into an approximate Fock state. Plot (a) in Figure 2 illustrates this process, generating a state with signal photon number probabilities , . Alternatively, if the shape center is set far from the concentration of initial state probabilities, clean periodic oscillations in photon number probabilities, with period s, are introduced into the state. Plots (b-d) in Figure 2 illustrate this process. (b) shows precision shaping of a coherent state with . (c) is the same as (b) but acting on a two-mode squeezed vacuum. (d) shows shaping with .
In tandem with photon number probabilities, NSOPO offers control over states in optical phase space. The following demonstrates an interesting case of this control. Recall that, in the Schrödinger picture, the modes experience self phase modulation and cross phase modulation via the Kerr effect. Introducing the condition into equation (12), we see that the term of the Hamiltonian
generates non-linear dynamics for the signal and idler modes. Noting that N is an integer, we see that states of a single mode are periodic in time when the sum of Kerr frequency satisfies , with m an integer. For simple rational values of m, the evolution maps coherent states to generalized coherent states [9].
We extend this argument to the two mode squeezed state, recalling . We choose a preferred final state by selecting m to satisfy
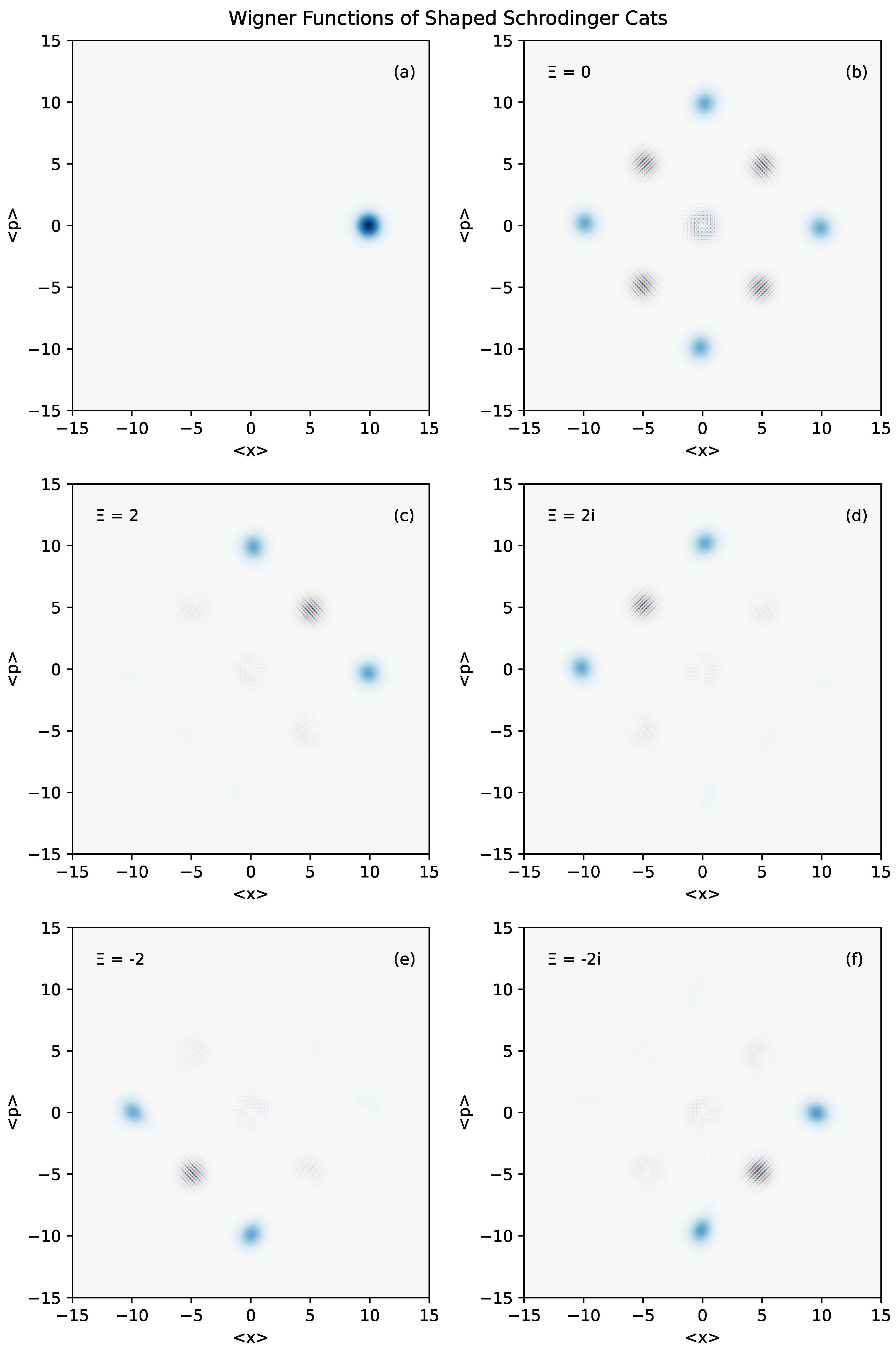
Equation (27) provides a similar constraint. Recall the adjacent state detuning difference (25). If we suppose , then making equation (30) and equation (27) the same constraint with . Setting we obtain a four-phase Schrödinger cat state. Figure 3 shows the action of NSOPO on a coherent state, (a), that is split into a generalized four-phase Schrödinger cat state, (b). Depending on the phase , NSOPO restricts the amplitude of the cat to two of four phases, shown in (c-f). The axes in each plot are independent phase space quadratures of the displacement field. Not shown in Figure 3, shifting the shape center by one rotates the action of NSOPO among the operations shown in (c-f). Namely, under , the plots map to each other according to . This behavior alludes quantum logic gates for macroscopic quantum states, though further investigation is needed to understand the range of this capability.
4.2. Solving the Time Constraints
To apply the theory developed in this paper, all shaping should occur on a time scale faster than the cavity decay time. Otherwise correlations in two mode squeezed states will be lost. Shaping a single mode state ought to be more robust to loss, but an alternative analysis will be needed to consider interplay between loss and shaping. The cavity decay time constant is related to the cavity quality factor Q by
Let us assume a typical Q factor for a high quality cavity . For UV light, . As mentioned previously, shaping of a state is determined by the quantities , , and . Numerical simulations show the quantity is useful around the order . Thus, to shape the state with minimal decay, .
4.3. State Purity
A key challenge to overcome for preserving the quantum coherence of noise shaped states of light is to mitigate the dephasing effects of the pump beam. The two criteria to satisfy are a strong pump beam, quantified below, and a vanishing detuning weight (23) for the pump frequency, in this case for the sum frequency, . Specifically, we demand
A vanishing pump detuning weight ensures that the desired OPO detuning is independent of pump photon number, rendering NSOPO not number selective for the pump field. This condition is important because a pump photon number selective process implies that far fewer states in the entire Hilbert space contribute to OPO, dramatically decreasing the efficiency of the process. Furthermore, if the interaction were number selective for the pump, the state of the pump field would vary dramatically for different possible interaction histories, resulting in strong detuning.
When NSOPO is not number selective for the pump, the OPO interaction is simply a displacement operation, which minimally disturbs the structure of the pump field. To illustrate, consider the state time evolved under the OPO interaction with . The result is a superposition of products of shifted coherent states in the sum frequency and incremented number states in the signal and idler. The coherent states are at most shifted by a displacement corresponding to the maximum photon number change of the signal and idler. For large amplitude coherent states, shifts in the coherent states on the scale of shifts in the signal and idler yield minimal deviations in the overlap between the coherent pump states.
To obtain a generic measure of state purity, we note that photon number probabilities are primarily shifted between adjacent NSOPO peaks. The pump beam coherent states that are entangled with either peak have a relative shift in photon number equal to the peak spacing. This entanglement between the pump, signal, and idler contributes a dephasing in the signal and idler density matrix. Where the signal/idler is split into two peaks of equal height, the purity of the signal/idler density matrix, , is well approximated by the squared overlap of the pump beam states. Thus, for a pump beam in a coherent state and spacin s, the purity measure is
4.4. Summary of Constraints and Figures of Merit
Five conditions must be met in order to realize coherent NSOPO. The following subsections summarize each.
- In the presence of strong Kerr nonlinearities, exciting a cavity pump field to high intensity requires a broad external pump linewidth. However, a broad external pump will excite superfluous modes in the system. Suppose the pump beam is a broad spectrum coherent state . To mitigate unintended interactions from modes above the signal and idler frequency, we restrict the magnitude of the sum mode self phase modulation frequency by equation (17) to obtain
- The purity measure (34) indicates the constraintThis constraint limits the scale of noise shaping, i.e. the NSOPO peak spacing, to be much less than the pump field strength. Using Equation (35), we constrain the spacing by the pump frequency and pump Kerr frequency,This relation reinforces the desirability for small .
- As discussed in SubSection 4.3 above, shaping maintains quantum coherence if the pump field detuning weight vanishes, . Equation (33) provides a qualitative expression of the requisite smallness of . The upshot is that greater pump power requires higher precision in the proximity of to zero.
- Numerical simulations place useful values of in the range to 10. For an order of magnitude estimate of this constraint, consider a case where and . Using the definitions of , ,and g, (25), (21), (13), (6),The quantity is the single photon displacement field amplitude in equation (6). Expanding the ratio with the definitions of each frequency yieldsCareful use of equation (11) relates the displacement field susceptibilities to the more commonly measured electric field susceptibilities. We see that epsilon near zero (ENZ) materials limit the burden of strength on the nonlinear susceptibilities so long as the effects on group velocities are carefully considered as well.
- The lower bound on the Kerr frequencies is constrained by the cavity lifetime, (32). Recalling the definitions of the Kerr frequencies (13) and cavity lifetime (31) and substituting them into the constraint above we obtainSubstituting the form of from (6) and relating to with (11), we find the relationconstrains the signal and idler modes. Consistent with constraint (39), ENZ materials with high group velocity are centrally important to realizing NSOPO. Furthermore, materials in a state of electronically induced transparency allow for simultaneously high quality in factors and high-nonlinear susceptibilities, though typically reduce the group velocity heavily. Some of the burden of constraint (41) can be reduced with a small quantization volume as well. The quantityis a figure of merit for realizing NSOPO. Candidate systems will have large F at the signal and idler frequencies and small F at the sum frequency.
4.5. Control Parameters
The shape center is controlled by modulating the linear refractive index of the material, therefore the static detuning parameter , in time. To understand the extent of modulation we may ask, what are the possible rates of change for the shape center with respect to refractive index shifts? Recall the expression for , (23), contains the frequency difference . In the simplest case, the frequencies are related to the fixed wavenumbers of each mode by
where is maximal, so is . Therefore it is desirable for the refractive index of each mode to be near zero. This conclusion is agreeable with the figures of merit derived above. One can change the refractive index of the material by, for example, introducing a static field, or by utilizing acoustic oscillations in the cavity material.
The NSOPO squeezing parameter, (21), is primarily controlled by modulating the amplitude and phase of the pump beam. In practice one should be aware that changing the shape center affects the strength of NSOPO in three ways.
- Equation (26) shows that OPO strength is scaled by , where m is the signal photon number of the state being acting upon. Thus the OPO strength is scaled by the shape center.
- In some materials, e.g. organic materials, changing a static field to modulate the refractive index will reorient molecules affecting .
- Static fields will also introduce a contribution to OPO strength .
Ultimately, determining the parameters for preparing a particular state will be a matter of empirical tuning guided by rough numerical estimates.
A final note on state control: if the static field can be modulated on a time scale faster than the state preparation time , more complicated shaping of the field noise statistics can be accomplished, beyond fixed shaping parameters.
5. Conclusions
We have proposed a novel method for the deterministic manipulation of quantum states of light. The underlying theoretical tools required for its implementation are developed and the physical constraints for its practical implementation described. The method utilizes strong Kerr nonlinearities to introduce photon number dependence into the frequency matching condition for optical parametric oscillation, rendering the OPO interaction photon number selective. Number selective interactions expand the capabilities of current CV quantum optical state control and preparation techniques by introducing targeted deterministic manipulations to subspaces of a light field’s Fock space.
Simulations indicate the generation of highly nonclassical quantum states of light. We establish five necessary conditions to realize NSOPO in practice, which will aid the search for candidate materials and optical configurations. The constraints are consistent with a common figure of merit, F, expressed in Equation (42). The best materials for NSOPO will have large F at the signal and idler frequencies, and small F at the sum frequency. Each constraint alone can be satisfied by modern materials, but it remains to be seen if they can all be realized within the same system.
Future research will aim to realize the requisite constraints in detailed models of highly resonant cavity light coupled with matter systems, with special attention paid to dark resonances. From specific models, the approach derived in this paper will be adapted to accommodate Hamiltonians beyond the simple cubic and quartic interactions treated above. These new models will be used to guide experimental design and to search for novel sculpted states. Future research will also investigate generation of entanglement between two uncorrelated signal and idler states, and study how noise shaping can be generalized to pulses of light, in particular to solitons in optical resonators with attention paid to mitigating the dephasing effects of quantum soliton propagation.
Author Contributions
Conceptualization, Garrett Compton and Mark Kuzyk; Data curation, Garrett Compton; Formal analysis, Garrett Compton and Mark Kuzyk; Funding acquisition, Mark Kuzyk; Investigation, Garrett Compton and Mark Kuzyk; Methodology, Garrett Compton and Mark Kuzyk; Project administration, Mark Kuzyk; Resources, Mark Kuzyk; Software, Garrett Compton; Supervision, Mark Kuzyk; Validation, Garrett Compton; Visualization, Garrett Compton; Writing original draft, Garrett Compton; Writing review & editing, Garrett Compton and Mark Kuzyk.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
We encourage all authors of articles published in MDPI journals to share their research data. In this section, please provide details regarding where data supporting reported results can be found, including links to publicly archived datasets analyzed or generated during the study. Where no new data were created, or where data is unavailable due to privacy or ethical restrictions, a statement is still required. Suggested Data Availability Statements are available in section “MDPI Research Data Policies” at https://www.mdpi.com/ethics.
Acknowledgments
We thank Ned and Nancy Wogman for the Wogman fellowship, the WSU CAS Graduate Research Scholarship, and the donors to the Innovative Physics Fund and the Department of Physics for support.
Conflicts of Interest
The authors declare no conflicts of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.
Abbreviations
The following abbreviations are used in this manuscript:
| OPO | Optical parametric oscillation |
| SPM | Self phase modulation |
| XPM | Cross phase modulation |
| FWM | four wave mixing |
| NSOPO | Number selective optical parametric oscillation |
| TMSV | Two mode squeezed vacuum |
| ENZ | Electronically induced transparency |
| CV | Continuous variable |
References
- Sangouard, N.; Simon, C.; Gisin, N.; Laurat, J.; Tualle-Brouri, R.; Grangier, P. Quantum repeaters with entangled coherent states. J. Opt. Soc. Am. B 2010, 27, A137. [Google Scholar] [CrossRef]
- Brask, J.B.; Rigas, I.; Polzik, E.S.; Andersen, U.L.; Sørensen, A.S. Hybrid Long-Distance Entanglement Distribution Protocol. Phys. Rev. Lett. 2010, 105, 160501. [Google Scholar] [CrossRef] [PubMed]
- Sakaguchi, A.; Konno, S.; Hanamura, F.; Asavanant, W.; Takase, K.; Ogawa, H.; Marek, P.; Filip, R.; Yoshikawa, J.I.; Huntington, E.; Yonezawa, H.; Furusawa, A. Nonlinear feedforward enabling quantum computation. Nat. Commun. 2023, 14, 3817. [Google Scholar] [CrossRef] [PubMed]
- Gottesman, D.; Kitaev, A.; Preskill, J. Encoding a qubit in an oscillator. Phys. Rev. A 2001, 64. [Google Scholar] [CrossRef]
- Lidar, D.A.; Chuang, I.L.; Whaley, K.B. Decoherence-Free Subspaces for Quantum Computation. Phys. Rev. Lett. 1998, 81, 2594–2597. [Google Scholar] [CrossRef]
- Polino, E.; Valeri, M.; Spagnolo, N.; Sciarrino, F. Photonic quantum metrology. AVS Quantum Sci. 2020, 2, 024703. [Google Scholar] [CrossRef]
- Oszmaniec, M.; Augusiak, R.; Gogolin, C.; Kołodyński, J.; Acín, A.; Lewenstein, M. Random Bosonic States for Robust Quantum Metrology. Phys. Rev. X 2016, 6, 041044. [Google Scholar] [CrossRef]
- Unternährer, M.; Bessire, B.; Gasparini, L.; Perenzoni, M.; Stefanov, A. Super-resolution quantum imaging at the Heisenberg limit. Optica 2018, 5, 1150–1154. [Google Scholar] [CrossRef]
- Yurke, B.; Stoler, D. Generating quantum mechanical superpositions of macroscopically distinguishable states via amplitude dispersion. Phys. Rev. Lett. 1986, 57, 13–16. [Google Scholar] [CrossRef] [PubMed]
- Kolesnikow, X.C.; Bomantara, R.W.; Doherty, A.C.; Grimsmo, A.L. Gottesman-Kitaev-Preskill state preparation using periodic driving. 2023.
- Asavanant, W.; Nakashima, K.; Shiozawa, Y.; Yoshikawa, J.I.; Furusawa, A. Generation of highly pure Schrödinger’s cat states and real-time quadrature measurements via optical filtering. Opt. Express 2017, 25, 32227. [Google Scholar] [CrossRef]
- Takase, K.; Yoshikawa, J.I.; Asavanant, W.; Endo, M.; Furusawa, A. Generation of optical Schrödinger cat states by generalized photon subtraction. Phys. Rev. A (Coll. Park.) 2021, 103. [Google Scholar] [CrossRef]
- Chen, Y.R.; Hsieh, H.Y.; Ning, J.; Wu, H.C.; Chen, H.L.; Shi, Z.H.; Yang, P.; Steuernagel, O.; Wu, C.M.; Lee, R.K. Generation of heralded optical `Schroedinger cat’ states by photon-addition 2023.
- Fukui, K.; Endo, M.; Asavanant, W.; Sakaguchi, A.; Yoshikawa, J.I.; Furusawa, A. Generating the Gottesman-Kitaev-Preskill qubit using a cross-Kerr interaction between squeezed light and Fock states in optics. Phys. Rev. A (Coll. Park.) 2022, 105. [Google Scholar] [CrossRef]
- Vertchenko, L.; Nikitin, M.; Lavrinenko, A. Near-zero-index platform in photonics: tutorial. J. Opt. Soc. Am. B 2023, 40, 1467. [Google Scholar] [CrossRef]
- Camacho-Guardian, A.; Bastarrachea-Magnani, M.; Pohl, T.; Bruun, G.M. Strong photon interactions from weakly interacting particles. Phys. Rev. B. 2022, 106. [Google Scholar] [CrossRef]
- Ribeiro, R.F.; Campos-Gonzalez-Angulo, J.A.; Giebink, N.C.; Xiong, W.; Yuen-Zhou, J. Enhanced optical nonlinearities under collective strong light-matter coupling. Phys. Rev. A (Coll. Park.) 2021, 103. [Google Scholar] [CrossRef]
- Hu, X.X.; Zhao, C.L.; Wang, Z.B.; Zhang, Y.L.; Zou, X.B.; Dong, C.H.; Tang, H.X.; Guo, G.C.; Zou, C.L. Cavity-enhanced optical controlling based on three-wave mixing in cavity-atom ensemble system. Opt. Express 2019, 27, 6660–6671. [Google Scholar] [CrossRef] [PubMed]
- Imamoḡlu, A.; Schmidt, H.; Woods, G.; Deutsch, M. Strongly interacting photons in a nonlinear cavity. Phys. Rev. Lett. 1997, 79, 1467–1470. [Google Scholar] [CrossRef]
- González-Tudela, A.; Paulisch, V.; Chang, D.E.; Kimble, H.J.; Cirac, J.I. Deterministic Generation of Arbitrary Photonic States Assisted by Dissipation. Phys. Rev. Lett. 2015, 115, 163603. [Google Scholar] [CrossRef]
- Porras, D.; Cirac, J.I. Collective generation of quantum states of light by entangled atoms. Phys. Rev. A 2008, 78, 053816. [Google Scholar] [CrossRef]
- Perarnau-Llobet, M.; González-Tudela, A.; Cirac, J.I. Multimode Fock states with large photon number: effective descriptions and applications in quantum metrology. Quantum Science and Technology 2020, 5, 025003. [Google Scholar] [CrossRef]
- Verstraete, F.; Wolf, M.M.; Ignacio Cirac, J. Quantum computation and quantum-state engineering driven by dissipation. Nat. Phys. 2009, 5, 633–636. [Google Scholar] [CrossRef]
- Dirac, P.A.M. Generalized Hamiltonian Dynamics. Canadian Journal of Mathematics 1950, 2, 129–148. [Google Scholar] [CrossRef]
- Born, M.; Infeld, L. On the quantization of the new field equations I. Proc. R. Soc. Lond. 1934, 147, 522–546. [Google Scholar]
- Born, M.; Infeld, L. Foundations of the new field theory. Proc. R. Soc. Lond. A Math. Phys. Sci. 1934, 144, 425–451. [Google Scholar] [CrossRef]
- Quesada, N.; Sipe, J.E. Why you should not use the electric field to quantize in nonlinear optics. Opt. Lett. 2017, 42, 3443. [Google Scholar] [CrossRef]
- Bhat, N.A.R.; Sipe, J.E. Hamiltonian treatment of the electromagnetic field in dispersive and absorptive structured media. Phys. Rev. A 2006, 73, 063808. [Google Scholar] [CrossRef]
- Raymer, M.G. Quantum theory of light in a dispersive structured linear dielectric: a macroscopic Hamiltonian tutorial treatment. J. Mod. Opt. 2020, 67, 196–212. [Google Scholar] [CrossRef]
- Hillery, M.; Mlodinow, L.D. Quantization of electrodynamics in nonlinear dielectric media. Phys. Rev. A Gen. Phys. 1984, 30, 1860–1865. [Google Scholar] [CrossRef]
- Drummond, P.D.; Hillery, M. The quantum theory of nonlinear optics; Cambridge University Press: Cambridge, England, 2014. [Google Scholar]
- Quesada, N.; Helt, L.; Menotti, M.; Liscidini, M.; Sipe, J. Beyond photon pairs: Nonlinear quantum photonics in the high-gain regime. Adv. Opt. Photonics 2022. [Google Scholar] [CrossRef]
- Jackson, J.D. lectrodynamics, Classical. In digital Encyclopedia of Applied Physics; Wiley-VCH Verlag GmbH & Co. KGaA: Weinheim, Germany, 2003. [Google Scholar]
- Boyd, R.W. Nonlinear optics, 4 ed.; Academic Press: San Diego, CA, 2020. [Google Scholar]
- Pasquazi, A.; Peccianti, M.; Razzari, L.; Moss, D.J.; Coen, S.; Erkintalo, M.; Chembo, Y.K.; Hansson, T.; Wabnitz, S.; Del’Haye, P.; Xue, X.; Weiner, A.M.; Morandotti, R. Micro-combs: A novel generation of optical sources. Phys. Rep. 2018, 729, 1–81. [Google Scholar] [CrossRef]
- Alam, M.; Mandal, S.; Wahiddin, M.R. Squeezing, mixed mode squeezing, amplitude squared squeezing and principal squeezing in a non-degenerate parametric oscillator. Optik 2018, 157, 1035–1052. [Google Scholar] [CrossRef]
| 1 | The transverse delta function captures the constraints on the field enforced by the Coulomb gauge. In particular, note that in a medium without free charges or free currents, Maxwell’s equations ensure D and B are always transverse to the direction of radiation propagation, unlike E and H. Furthermore, since both D and B are divergenceless, so must be their commutator. The transverse delta function is consistent with these two properties. It has no divergence and acts as an ordinary delta function on transverse fields. |
| 2 | For a rigorous discussion see [27]. Quesada provides the following intuitive argument for why neither E nor H can be fundamental: Suppose the Hamiltonian is order in Bose operators. If E is fundamental, it is of order 1. If B is order 1, then is order N. Thus E is order N, a contradiction. A similar argument holds for H. No contradiction occurs with D and B as fundamental. |
| 3 | Our analysis depends only on the algebraic structure of the Hilbert space and the dynamics generated by the Hamiltonian, so is easily generalized to richer mode structures. |
| 4 | If the refractive index is not isotropic, A defines an effective cross sectional area, discussed in [32]. |
| 5 | Permutation invariance typically does not hold near resonance, where we expect our system to reside given the constraints derived later. However, accounting for variability in simply amounts to substituting the average in place of and does not change the results. |
| 6 | The rotating wave approximation is synonymous with the secular approximation. |
| 7 | As is the case for , permutation invariance is not valid for the strong nonlinearities required of NSOPO. However, accounting for variability simply amounts to substituting the average in place of and does not change the result. |
| 8 | See Section 4.3
|
| 9 | This may be realized, for example, with an acousto-optic modulator. |
| 10 | This example also captures the behavior of NSOPO via degenerate parametric down conversion and second harmonic generation. In these cases, the fundamental mode and second harmonic are entirely uncorrelated and coupled into the cavity without a need to preserve correlations. We choose to study NSOPO on a two mode squeezed state rather than a single mode state to highlight how noise shaping is identically present in the entangled signal and idler modes. |
Figure 1.
General characteristics of NSOPO. In each plot the state is initially a uniform real valued distribution. The plots differ only in the phase of the NSOPO complex squeezing parameters . Orange dots are spaced by and aligned with the shaping center. The green curve shows a first order approximation of shaping that follows the peak positions and magnitude closely. The blue curve is the shaped uniform distribution with shaping parameters shown in each plot legend.
Figure 1.
General characteristics of NSOPO. In each plot the state is initially a uniform real valued distribution. The plots differ only in the phase of the NSOPO complex squeezing parameters . Orange dots are spaced by and aligned with the shaping center. The green curve shows a first order approximation of shaping that follows the peak positions and magnitude closely. The blue curve is the shaped uniform distribution with shaping parameters shown in each plot legend.
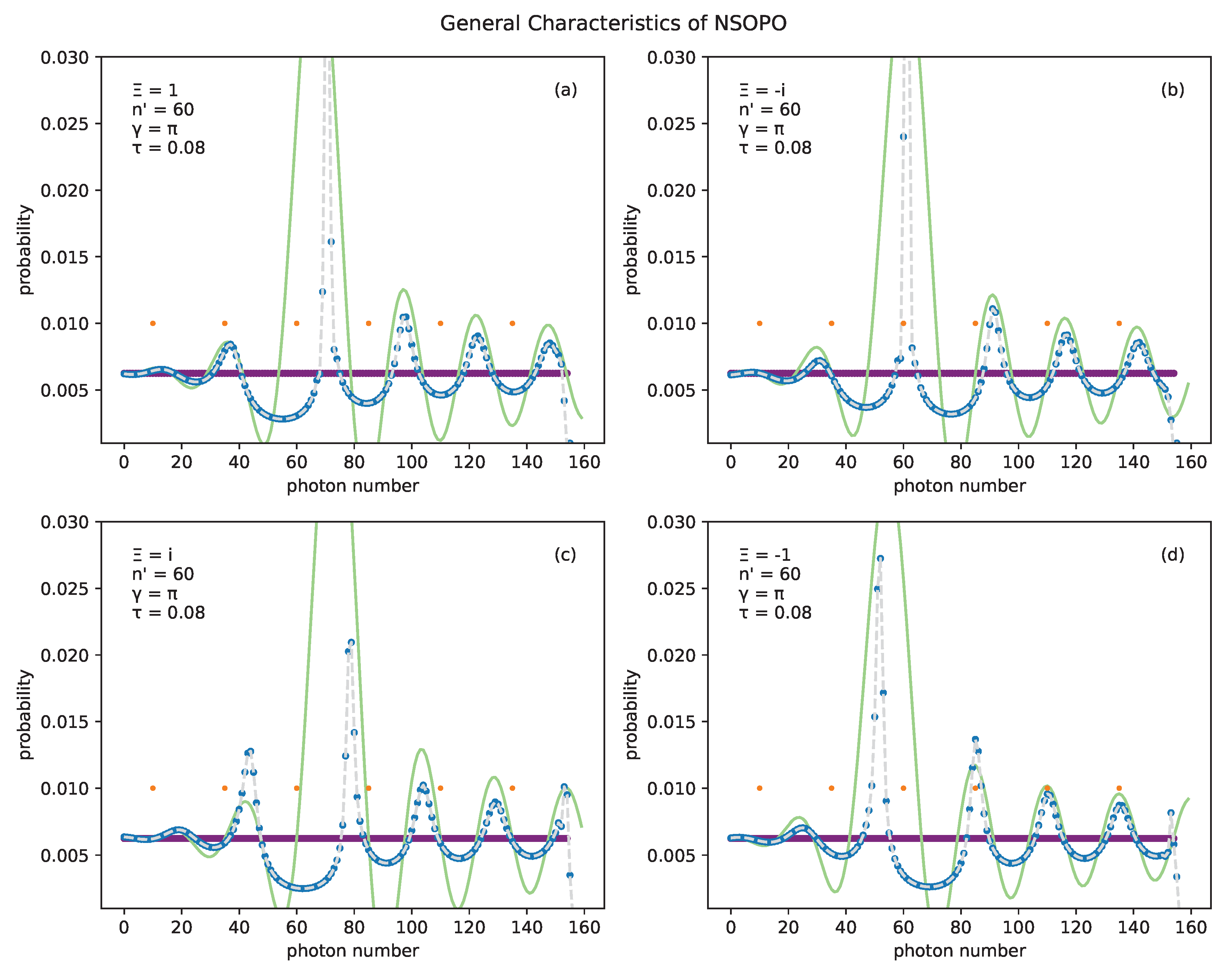
Figure 2.
Examples of photon probability shaping offered by NSPO. (a) An approximate Fock state of accomplished by placing the shaping center on the peak of an initial coherent state with amplitude 7. (b) A precision shaping of the same coherent state. Parameter is chosen such that peak spacing s is two photons. (c) A two mode squeezed vacuum state with . (d) A two mode squeezed vacuum with .
Figure 2.
Examples of photon probability shaping offered by NSPO. (a) An approximate Fock state of accomplished by placing the shaping center on the peak of an initial coherent state with amplitude 7. (b) A precision shaping of the same coherent state. Parameter is chosen such that peak spacing s is two photons. (c) A two mode squeezed vacuum state with . (d) A two mode squeezed vacuum with .
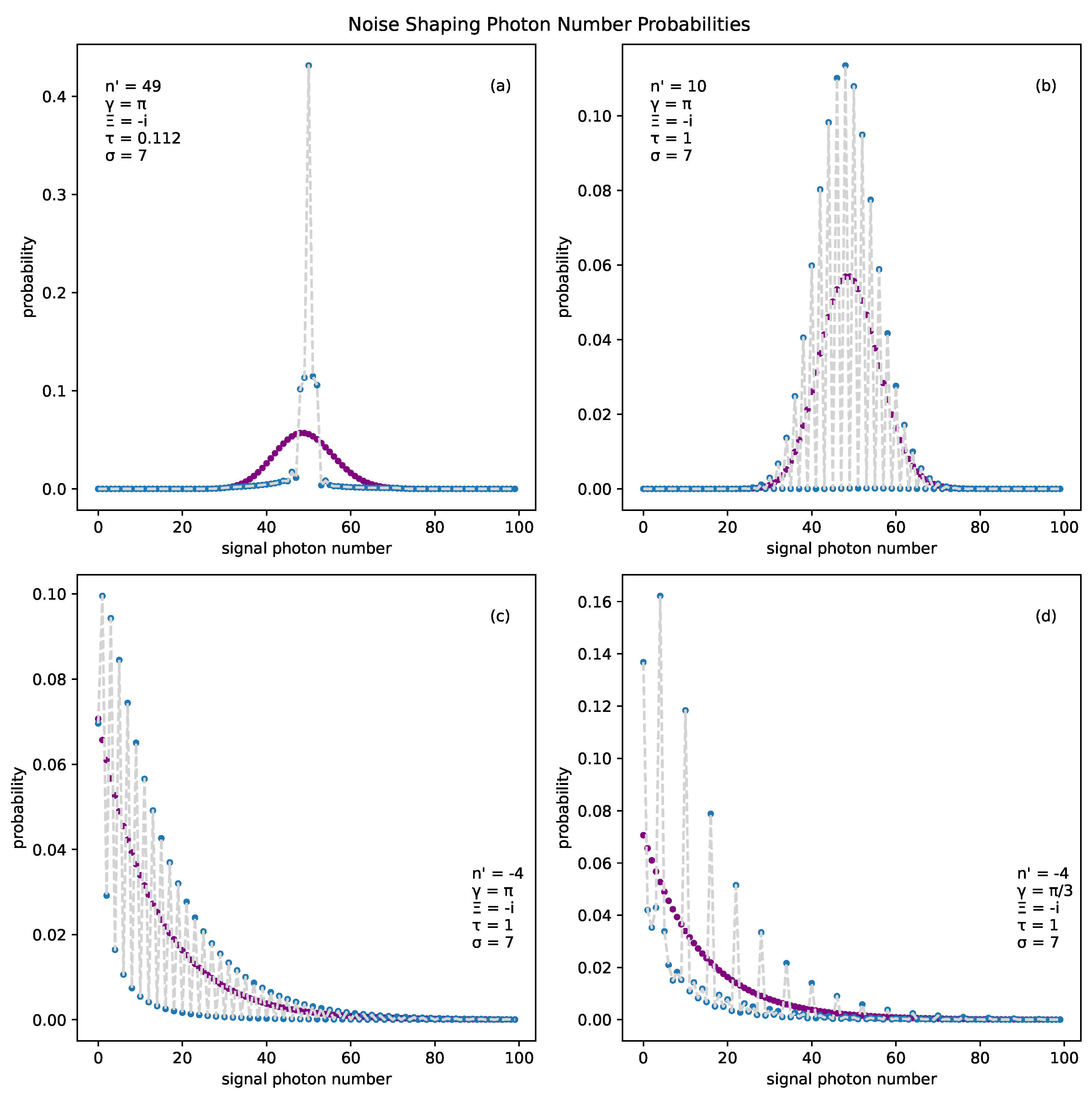
Figure 3.
(a) Wigner function of an initial coherent state of amplitude . (b) The coherent state subject to Kerr rotation without any NSPO. (c-f) The state shaped with NSPO complex squeezing parameter . In all plots, blue regions are positive valued and red regions are negative. Every state is shaped with parameters . As the phase of is varied by increments of , number selective shaping changes predictably.
Figure 3.
(a) Wigner function of an initial coherent state of amplitude . (b) The coherent state subject to Kerr rotation without any NSPO. (c-f) The state shaped with NSPO complex squeezing parameter . In all plots, blue regions are positive valued and red regions are negative. Every state is shaped with parameters . As the phase of is varied by increments of , number selective shaping changes predictably.
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
MDPI Initiatives
Important Links
© 2024 MDPI (Basel, Switzerland) unless otherwise stated






