Division by Zero: Using Semi-structured Complex Numbers to Find the Inverse of a Singular Matrix and Show Its Applications

Preprint

Article

Division by Zero: Using Semi-structured Complex Numbers to Find the Inverse of a Singular Matrix and Show Its Applications

Altmetrics

Downloads

Views

Comments

Peter Jean Paul^*,Shanaz Wahid

This version is not peer-reviewed

Submitted:

18 February 2024

Posted:

21 February 2024

You are already at the latest version

Alerts

Abstract

Matrices and their inverses allow accurate calculations to be produced quickly and compactly and can be used to control any process represented by a system of equations. Singular matrices require extensive workarounds (costing time and money) to solve these systems of equations because they have no inverse. Finding their inverse involves division by zero. Nevertheless, recently a new number set called semi-structured complex numbers was developed to enable division by zero in algebraic equations. The aim of this research was to demonstrate that the inverse of a singular matrix can be found using semi-structured complex numbers. This research reveals (1) Singular matrices and their inverses can be used to find a unique solution to a pair of simultaneous equations that appear to have infinitely many solutions or appear to have no solution; (2) Singular matrices map coordinates in projective space to coordinates in Euclidean space and their inverse maps coordinates in Euclidean space to coordinates in projective space; (3) the inverse of a singular matrix proves that parallel lines in Euclidean space do not intersect but in projective space intersect at a “point at infinity” and (4) collinear lines that intersect at infinitely many points in Euclidean space only intersect at one point in projective space.

Keywords:

Subject: Computer Science and Mathematics - Mathematics

1. Introduction

1.1. Matrices and Their Determinants

Matrices are the ordered rectangular array of numbers, which are used to express linear equations. A matrix can be used to perform mathematical operations such as addition, subtraction and multiplication. A matrix consisting of

m

rows and

n

columns is called a

m \times n

matrix. Matrices and their inverse allow accurate calculations to be produced quickly and compactly, which can be used to better control a mechanical device, industrial process or any process that can be presented as a system of equations.

Inverse of a matrix is defined usually for square matrices. For every

m \times m

square matrix

A

, there exists an inverse matrix

A^{- 1}

such that:

A^{- 1} = \frac{1}{|A|} \times a d j (A)

A \times A^{- 1} = I

where

$\|A\|$	Determinant of A
$a d j (A)$	Adjoint matrix of A
$I$	Identity matrix

The inverse of a matrix depends on the determinant of the matrix. Important properties of the determinant of a matrix are given in Appendix A. According to standard definition, the determinant of a matrix should not be equal to zero. If the determinant is equal to zero, then this would mean that the matrix has no inverse because finding the inverse would involve division by zero. Matrices with determinant equal to zero are called singular matrices because they do not have inverses. Singular matrices have several disadvantages. These are listed in Table 1.

It is clear from Table 1 that if the inverse of a singular matrix can be found this would resolve a large number of problems in mathematics, science, engineering and any mathematically based subject where matrices are used.

Usually, when investigating potentially new insights into matrices

2 \times 2

matrices are used. This is because (1) they are one of the simplest types of matrices where matrix calculations can be done very easily and (2) finding the inverse of higher order square matrices comes down to finding the determinant of all the

2 \times 2

submatrices within it.

In this regard, when looking at a new method to find the inverse of a singular matrix,

2 \times 2

matrices can be investigated. However, additional tools are needed since finding the inverse of a singular matrix hinges on the ability to solve division by zero and the ability to provide an adequate geometric interpretation to this inverse.

Fortunately, a new number set called semi-structured complex numbers was recently created to solve the problem of division by zero in algebraic equations. Moreover, if a proper geometric interpretation is to be given geometries beyond standard Euclidean geometry needs to be considered. One such geometry that was found to be useful is projective geometry. It is instructive to understand what these tools are and how they are used to find and provide an interpretation to the inverse of a singular matrix.

1.2. Semi-Structured Complex Numbers: Enabling Division by Zero

Recently there has been a range of research involving division by zero. The problem of division by zero can simply be stated as: What is

\frac{a}{0}

where “a” is any complex number. Table A1, Appendix B, shows sample research conducted on “division by zero”.

There have been several solutions to the problem the most recent being the invention of the semi-structured complex number set

H

[1]. The first attempt at creating this number set was riddled with issues [1], however, a second paper [2], written to reformulate and strengthen the theory of semi-structured complex numbers, produced several grounded and profound results. Table A2 in Appendix C, shows the major results developed in paper [2].

According to the first three results shown in Table A2 (Appendix C), Semi-structured complex number set can be defined as follows:

A semi-structured complex number is a three-dimensional number of the general form h = x + yi + zp; that is a linear combination of real (1), imaginary (i) and unstructured (p) units whose coefficients, x, y, z are real numbers.

The number

h

is called semi-structured complex because it contains a structured complex part

(x + y i)

and an unstructured component

(z p)

. The unstructured unit

p

was redefined as:

p^{n} = \frac{\sqrt{2} \times \cos (\frac{π}{2} n - \frac{π}{4})}{f^{n} (1)}

(1)

where

f^{n} (c)

is a composite function such that

f (c) = 1 - c

. Integer powers of

p

yield the following cyclic results:

p^{1} = \frac{1}{0}, p^{2} = - 1, p^{3} = - p, p^{4} = 1, p^{5} = \frac{1}{0}, p^{6} = - 1, p^{7} = - p \dots

(2)

p

does not belong to the set of complex numbers

C

(that is,

p \notin C

), but belongs to a higher order number set

H

called the set of semi-structured complex numbers such that the set of complex numbers is a subset of

H

(that is,

C \subset H

Clearly from Table A2 (Appendix C), very little work has been done on the inverse of singular matrices. Moreover, very little has been done to show what the interpretation of such a result would be and where such a result would be useful.

1.3. Projective Geometry

Projective geometry is the study of geometric properties that remain unchanged by a projective transformation. A projective transformation is one that occurs when: points on one line are projected onto another line; points in a plane are projected onto another plane; or points in space are projected onto a plane.

Projections can be parallel or central. For example, the sun shining behind a person projects his or her shadow onto the ground. Since the sun’s rays are for all practical purposes parallel, it is a parallel projection.

A slide projector projects a picture onto a screen. Since the rays of light pass through a lens and the lens acts like a point through which all the rays pass, the projection is called a central projection (that is, the lens is the centre of the projection).

Some properties that remain unchanged by a projection are collinearity, intersection, and order. If three points are collinear, then when projected they will remain collinear. If two lines intersect then when projected their projections will remain intersected. If an object exists between two others, then their order will remain the same when they are projected onto a plane. Properties that can change during a projection are size and angles.

An ordinary Euclidean plane in which points are addressed with Cartesian coordinates,

(x, y)

, this plane can be converted to a projective plane by adding a line at infinity. The original visualization for this line at infinity is shown in Figure 1.

However, the visualization shown in Figure 1 was difficult to translate into mathematics and so a new way to visualize projective geometry was developed and is shown in Figure 2.

The Cartesian plane is represented as the plane

z = 1

and the “line at infinity” is now represented as a plane

z = 0

. Hence a point on the Cartesian plane is give as

(x, y, 1)

or simply as

(x, y)

and “points at infinity” have coordinates

(x, y, 0)

or simply as

(\frac{x}{0}, \frac{y}{0})

(in semi-structured complex form

(x p, y p)

since

\frac{1}{0} = p

The three-coordinate system

(x, y, z)

is called the homogeneous coordinate system whilst the two-coordinate system

(x, y)

is called Cartesian coordinate system. Both coordinate systems are essential in dealing with projective geometry calculations.

If a point has homogeneous coordinates

(x_{1}, x_{2}, x_{3})

, then these homogeneous coordinates can be converted to Cartesian coordinates

(x, y)

where

x = \frac{x_{1}}{x_{3}}

and

y = \frac{x_{2}}{x_{3}}

. This enables Cartesian coordinates to be converted to homogeneous coordinates and vice-versa. For example, if a point has homogeneous coordinates

(7, 3, 5)

, these coordinates can be converted to Cartesian coordinates

(\frac{7}{5}, \frac{3}{5})

. Conversely if a point has Cartesian coordinates

(4, 1)

, these coordinates can be converted to homogeneous coordinates

(4, 1, 1)

(or any multiple, such as

(12, 3, 3)

(8, 2, 2)

The motivation for having homogeneous coordinates is very practical. Homogeneous coordinates are extensively used in computer graphics for computing transformations such as projection of a 3D scene (consisting of a set of 3D coordinates

(x_{1}, x_{2}, x_{3})

) onto a viewing plane (with a set of coordinates

(x, y)

such as a computer display).

Projective geometry theory can be applied to solving linear equations. For example, in the Euclidean plane

3 x - y + 4 = 0

is the equation of a line. Written with homogeneous coordinates the equation of the line becomes

3 \frac{x_{1}}{x_{3}} - \frac{x_{2}}{x_{3}} + 4 = 0

. If this equation is multiplied through by

x_{3}

, the equation becomes

3 x_{1} - x_{2} + 4 x_{3} = 0

. The point

(1, 7)

satisfied the original equation; the point

(1, 7, 1)

satisfies the homogeneous equation. So, do

(0, 4)

and

(0,4, 1)

and so on.

As another example, in the Euclidean plane, the lines

3 x - y + 4 = 0

and

3 x - y + 10 = 0

are parallel and have no point in common. In homogeneous coordinates, they do. In homogeneous coordinates the system

3 x_{1} - x_{2} + 4 x_{3} = 0

and

3 x_{1} - x_{2} + 10 x_{3} = 0

does have a solution. It is

(1, 3, 0)

or any multiple of

(1, 3, 0)

. Since the third coordinate is zero, this is a point at infinity. In the Euclidean plane, the lines are parallel and do not intersect. In the projective plane, they intersect at infinity.

For the purposes of this paper, Cartesian coordinates and homogeneous coordinates are considered coordinates in projective space, whilst Euclidean coordinates are considered coordinates in Euclidean space. Note, however, that Cartesian coordinates and Euclidian coordinates are numerically the same.

Using these basic concepts of projective geometry and the semi-structured complex number set, the inverse of a singular matrix can be found and its geometric interpretation given.

1.4. Major Contributions

Given the potential importance of the inverse of singular matrices, the aim of this paper was:

Use semi-structured complex numbers and projective geometry to find the inverse of a general singular 2 × 2 matrix, give its geometric interpretation and its potential applications.

In the process of fulfilling the stated aim, this paper makes four major contributions:

The inverse of a 2 ×2 matrix $A = (\begin{matrix} a & b \\ c & d \end{matrix})$ is given by the equation:

$A^{- 1} = \frac{p}{2 a d} (\begin{matrix} d & - b \\ - c & a \end{matrix})$

(3)

where $p$ is the unstructured unit.
Singular matrices and their inverses can be used to find a unique solution to a pair of simultaneous equations that appear to have infinitely many solutions and a pair of simultaneous equations that appear to have no solution. This unique solution is called the principle inverse solution.
Singular matrices map coordinates in projective space to coordinates in Euclidean space and their inverse maps coordinates in Euclidean space to coordinates in projective space.
The inverse of a singular matrix proves that parallel lines in Euclidean space do not intersect but in projective space intersect at a “point at infinity”.
The inverse of a singular matrix proves that collinear lines that intersect at infinitely many points in Euclidean space only intersect at one point in projective space.

The rest of this paper is devoted to showing how achieving the main aim of the paper led to these major contributions.

2. Inverse of a Singular Matrix

The inverse of a

2 \times 2

matrix

A = (\begin{matrix} a & b \\ c & d \end{matrix})

is given by the equation:

A^{- 1} = \frac{p}{2 a d} (\begin{matrix} d & - b \\ - c & a \end{matrix})

(4)

where

p

is the unstructured unit.

Proof of Equation (4) is given in Appendix D. Essentially the inverse of a singular matrix consists of the adjoint matrix

a d j (A) = (\begin{matrix} d & - b \\ - c & a \end{matrix})

, the determinant

\frac{1}{|A|} = \frac{p}{2 a d}

3. Solving Simultaneous Equations Represented by a Singular Matrix

3.1. Solving Simultaneous Equations Which Appear to Have Infinitely Many Solutions

Suppose there is a pair of simultaneous equations with the form given by Equation (5). Here

m

is a scalar.

\begin{matrix} a x + b y = f \\ m a x + m b y = m f \end{matrix}

(5)

In terms of linear algebra Equations (5) represents the general equations of two collinear lines. The solution to these equations is the point of intersection of these two lines. Recall that collinear lines intersect at an infinitely many points in ordinary Euclidean space since the lines essentially rest on top of each other. This implies that simultaneous Equations (5) have infinitely many solutions. So, any method used to solve these equations must resolve this fact.

Suppose the matrix method is used to solve these equations. The matrix method for solving simultaneous equations involves converting the system of equations into the matrix form

A X = B

(where

A

is the matrix of coefficients,

X

the matrix of variables and

B

the matrix of constants) and then solving for

X

using the expression

X = A^{- 1} B

(where

A^{- 1}

is the inverse of the matrix

A

Using this idea, Equations (5) can be represented in matrix form as shown in Equation (6).

(\begin{matrix} a & b \\ m a & m b \end{matrix}) (\begin{matrix} x \\ y \end{matrix}) = (\begin{matrix} f \\ m f \end{matrix})

(6)

Here

A = (\begin{matrix} a & b \\ m a & m b \end{matrix})

is a singular coefficient matrix,

X = (\begin{matrix} x \\ y \end{matrix})

is the variable matrix and

B = (\begin{matrix} f \\ m f \end{matrix})

is the matrix of constants. This system of equations that appear to have infinitely many solutions (according to standard algebra). However, using the inverse of a

2 \times 2

singular matrix given by Equation (4), a unique solution can be found for this system of equations. This solution is given by Equation (7).

(\begin{matrix} x \\ y \end{matrix}) = \frac{p}{2 (m a b)} (\begin{matrix} m b & - b \\ - m a & a \end{matrix}) (\begin{matrix} f \\ m f \end{matrix})

(7)

where

A^{- 1} = \frac{p}{2 (m a b)} (\begin{matrix} m b & - b \\ - m a & a \end{matrix})

Hence solving for the Equations given by (5) gives:

(\begin{matrix} x \\ y \end{matrix}) = \frac{p}{2 (m a b)} (\begin{matrix} m b & - b \\ - m a & a \end{matrix}) (\begin{matrix} f \\ m f \end{matrix}) (\begin{matrix} x \\ y \end{matrix}) = \frac{p}{2 (m a b)} (\begin{matrix} m b f - m b f \\ - m a f + m a f \end{matrix}) (\begin{matrix} x \\ y \end{matrix}) = \frac{p}{2 (m a b)} (\begin{matrix} m b f (1 - 1) \\ m a f (- 1 + 1) \end{matrix}) (\begin{matrix} x \\ y \end{matrix}) = \frac{p}{2 (m a b)} (\begin{matrix} m b f (0) \\ m a f (0) \end{matrix}) (\begin{matrix} x \\ y \end{matrix}) = (\begin{matrix} \frac{p}{2 (m a b)} \times m b f (0) \\ \frac{p}{2 (m a b)} \times m a f (0) \end{matrix}) (\begin{matrix} x \\ y \end{matrix}) = (\begin{matrix} \frac{m b f (0 p)}{2 (m a b)} \\ \frac{m a f (0 p)}{2 (m a b)} \end{matrix})

According to semi-structured complex numbers

0 p = 1

. Hence:

(\begin{matrix} x \\ y \end{matrix}) = (\begin{matrix} \frac{f}{(2 a)} \\ \frac{f}{(2 b)} \end{matrix})

(8)

Result (8) if substituted into Equations (5) yields the correct output. Hence, the inverse of a singular matrix was used to find a unique solution to a pair of simultaneous equations that represent collinear lines. The unique solution given by Result (8) is called the principle inverse solution.

The principle inverse solution found from Result (8) represents Cartesian coordinates in projective space. These coordinates can be converted to homogeneous coordinates

(x_{1}, x_{2}, x_{3})

in projective space using the conversion

(x, y) = (\frac{x_{1}}{x_{3}}, \frac{x_{2}}{x_{3}})

. Hence:

(\begin{matrix} x \\ y \end{matrix}) = (\begin{matrix} \frac{f}{(2 a)} \\ \frac{f}{(2 b)} \end{matrix}) = (\begin{matrix} \frac{x_{1}}{x_{3}} \\ \frac{x_{2}}{x_{3}} \end{matrix}) This implies that x_{1} = \frac{f}{(2 a)}, x_{2} = \frac{f}{(2 b)} and x_{3} = 1 .

Therefore, the solution to Equations (5) is the Cartesian coordinates

(\frac{f}{(2 a)}, \frac{f}{(2 b)})

or the homogeneous coordinates

(\frac{f}{(2 a)}, \frac{f}{(2 b)}, 1)

in projective space. Substituting the homogeneous coordinates into Equation (5) yields Result (9) (the correct output).

\begin{matrix} a (\frac{f}{2 a}) + b (\frac{f}{2 b}) = (1) f \\ m a (\frac{f}{2 a}) + m b (\frac{f}{2 b}) = (1) f \end{matrix}

(9)

A numerical example of solving simultaneous equations which appear to have infinitely many solutions is given in Appendix E PART 1.

3.2. Solving Simultaneous Equations Which Appear to Have No Solutions

Suppose there is a pair of simultaneous equations with the form given by Equation (10).

\begin{matrix} a x + b y = f_{1} \\ a x + b y = f_{2} \end{matrix}

(10)

In terms of linear algebra Equations (10) represents the general equations of two parallel lines. The solution to these equations is the point of intersection of these two lines. Recall that parallel lines do not intersect in ordinary Euclidean space. However, they do intersect at a “point at infinity” in projective space. So, any method used to solve these equations must demonstrate these two facts.

Suppose the matrix method is used to solve these equations. The matrix method for solving simultaneous equations involves converting the system of equations in the matrix form

A X = B

(where

A

is the matrix of coefficients,

X

the matrix of variables and

B

the matrix of constants) and then solving for

X

using the expression

X = A^{- 1} B

(where

A^{- 1}

is the inverse of the matrix

A

Using this idea, Equations (10) can be represented in matrix form as shown in Equation (11).

(\begin{matrix} a & b \\ a & b \end{matrix}) (\begin{matrix} x \\ y \end{matrix}) = (\begin{matrix} f_{1} \\ f_{2} \end{matrix})

(11)

Here

A = (\begin{matrix} a & b \\ a & b \end{matrix})

is a singular coefficient matrix,

X = (\begin{matrix} x \\ y \end{matrix})

is the variable matrix and

B = (\begin{matrix} f_{1} \\ f_{2} \end{matrix})

is the matrix of constants. This system of equations that appear to have no solution (according to standard algebra). However, using the inverse of a

2 \times 2

matrix given by Equation (4), these systems of equations has a unique solution given by Equation (12).

(\begin{matrix} x \\ y \end{matrix}) = \frac{p}{2 (a b)} (\begin{matrix} b & - b \\ - a & a \end{matrix}) (\begin{matrix} f_{1} \\ f_{2} \end{matrix})

(12)

where

A^{- 1} = \frac{p}{2 (m a b)} (\begin{matrix} b & - b \\ - a & a \end{matrix})

. Hence solving for Equation (11) gives:

(\begin{matrix} x \\ y \end{matrix}) = \frac{p}{2 (a b)} (\begin{matrix} b & - b \\ - a & a \end{matrix}) (\begin{matrix} f_{1} \\ f_{2} \end{matrix}) (\begin{matrix} x \\ y \end{matrix}) = \frac{p}{2 (a b)} (\begin{matrix} b f_{1} - b f_{2} \\ - a f_{1} + a f_{2} \end{matrix}) (\begin{matrix} x \\ y \end{matrix}) = \frac{p}{2 (a b)} (\begin{matrix} b (f_{1} - f_{2}) \\ a (- f_{1} + f_{2}) \end{matrix}) (\begin{matrix} x \\ y \end{matrix}) = (\begin{matrix} \frac{p}{2 (a b)} \times b (f_{1} - f_{2}) \\ \frac{p}{2 (a b)} \times a (f_{2} - f_{1}) \end{matrix}) (\begin{matrix} x \\ y \end{matrix}) = (\begin{matrix} \frac{p (f_{1} - f_{2})}{2 a} \\ \frac{p (f_{2} - f_{1})}{2 b} \end{matrix})

Hence:

(\begin{matrix} x \\ y \end{matrix}) = (\begin{matrix} \frac{(f_{1} - f_{2})}{2 a} p \\ \frac{(f_{2} - f_{1})}{2 b} p \end{matrix})

(13)

The result shown in Result (13) if substituted into Equation (10) yields the correct output. Hence, the inverse of a singular matrix was used to find a unique solution to a pair of simultaneous equations that represent parallel lines. The unique solution given by Result (13) is called the principle inverse solution.

The principle inverse solution found from Result (13) represents the Cartesian coordinates in Euclidean space (governed by Euclidean geometry). These coordinates can be converted to homogeneous coordinates in projective space (governed by projective geometry) coordinates using the conversion

(x, y) = (\frac{x_{1}}{x_{3}}, \frac{x_{2}}{x_{3}})

where

(x_{1}, x_{2}, x_{3})

are homogeneous coordinates in the projective space. Hence:

(\begin{matrix} x \\ y \end{matrix}) = (\begin{matrix} \frac{(f_{1} - f_{2})}{2 a} p \\ \frac{(f_{2} - f_{1})}{2 b} p \end{matrix}) = (\begin{matrix} \frac{(f_{1} - f_{2})}{(2 a) (0)} \\ \frac{(f_{2} - f_{1})}{(2 b) (0)} \end{matrix}) = (\begin{matrix} \frac{x_{1}}{x_{3}} \\ \frac{x_{2}}{x_{3}} \end{matrix}) This implies that x_{1} = \frac{(f_{1} - f_{2})}{2 a}, x_{2} = \frac{(f_{2} - f_{1})}{2 b} and x_{3} = 0 .

Therefore, the solution to Equations (5) is the Cartesian coordinates

(\frac{(f_{1} - f_{2})}{2 a} p, \frac{(f_{2} - f_{1})}{2 b} p)

or the homogeneous coordinates

(\frac{(f_{1} - f_{2})}{2 a}, \frac{(f_{2} - f_{1})}{2 b}, 0)

in projective space. Substituting the homogeneous coordinates into Equation (10) yields Result (14) (the correct output).

\begin{matrix} a (\frac{(f_{1} - f_{2})}{2 a}) + b (\frac{(f_{2} - f_{1})}{2 b}) = (0) f_{1} \\ a (\frac{(f_{1} - f_{2})}{2 a}) + b (\frac{(f_{2} - f_{1})}{2 b}) = (0) f_{2} \end{matrix}

(14)

Any point in projective space that has homogeneous coordinate

x_{3} = 0

represents a “point at infinity” in projective space. This implies that solution of the equation using the inverse of a singular matrix lead to the fact that parallel lines intersect at a “point at infinity” in projective space. This agrees with currently established mathematics of projective geometry. A numerical example of solving simultaneous equations which appear to have no solutions is given in Appendix E PART 2.

Based on the examples given in Section 3.1 and Section 3.2 it is clear that there is a relationship between Euclidean space and coordinates in projective space. The simultaneous equations shown in Equations (5) and Equations (10) are collinear and parallel lines respectively in Euclidean space. These equations when put in matrix form result in singular matrices. The solution to these equations (found by using the inverse singular matrix) results in points that rest in projective space. This implies that singular matrices and their inverses results in transformations move objectives from Euclidean space to projective space and vice versa. Therefore, singular matrices and their inverse establish a strong relationship between these two geometries.

4. Discussion

It is clear from Section 3 that semi-structured complex numbers can be used to find the inverse of a singular matrix and this inverse can be used to find unique solutions to a pair of simultaneous equations that appear to have infinitely many solutions and a pair of simultaneous equations that appear to have no solution. The unique solution is called the principle inverse solution.

Projective geometry was used to clarify the meaning of the principle inverse solutions. Using projective geometry, it was clear that singular matrices map coordinates in projective space to coordinates in Euclidean space and the inverse of a singular matrix maps coordinates in Euclidean space to coordinates in projective space.

It is also important to note that the inverse of a singular matrix proves that parallel lines in Euclidean space do intersect at a “point at infinity” in projective space. Additionally, collinear lines that intersect at an infinitely many points in Euclidean space only intersect at one point in projective space.

These results are useful in producing time and cost savings in processes that are analysed using matrices and often require extensive workarounds when singular matrices are encountered. Additionally, the fact that the inverse of a singular matrix can be found implies that these matrices can now be used in areas of mathematics such as cryptography, graph theory and any other area of science and engineering where singular matrices may pose a problem.

5. Conclusion

Matrices and their inverses allow accurate calculations to be produced quickly and compactly, which can be used to better control any process that is represented by a system of equations. In cases where singular matrices are encountered, this may require extensive workaround to solve these systems of equations. This workaround often cost time and money.

Singular matrices have no inverse because finding their inverse involves division by zero. However, recently a new number set called semi-structured complex numbers has been developed to enable division by zero in regular algebraic equations. The aim of this research is to demonstrate that the inverse of a singular matrix can be found using semi-structured complex numbers.

The results reveal (1) Singular matrices and their inverses can be used to find a unique solution to a pair of simultaneous equations that appear to have infinitely many solutions and a pair of simultaneous equations that appear to have no solution; (2) Singular matrices map coordinates in projective space to coordinates in Euclidean space and their inverse maps coordinates in Euclidean space to coordinates in projective space; (3) the inverse of a singular matrix proves that parallel lines in Euclidean space do intersect but in projective space intersect at a “point at infinity” and collinear lines that intersect at infinitely many points in Euclidean space only intersect at one point in projective space.

These results provide a firm foundation for the use of semi-structured complex numbers in mathematics.

Appendix A. Other Important Properties of the Determinant of a Square Matrix

The following is a list of important properties of a square a matrix.

If $I_{n}$ is the identity matrix of the order $n \times n$ , then the $d e t (I_{n}) = 1$
If the matrix $M^{T}$ is the transpose of matrix M, then $d e t (M) = d e t (M^{T})$
If the matrix $M^{- 1}$ is the inverse of matrix M, then $d e t (M^{- 1}) = \frac{1}{d e t (M)} = {d e t (M)}^{- 1}$
If two square matrices M and N have the same size, then $d e t (M N) = d e t (M) \times d e t (N)$
If matrix M has a size $n \times n$ and C is a constant, then $d e t (C M) = C^{n} \times d e t (M)$
If X, Y and Z are three positive semidefinite matrices of equal size, then the following holds true along with the corollary $d e t (X + Y) \geq \det (X) + d e t (Y)$ for $X, Y, Z \geq 0$ . Additionally, $d e t (X + Y + Z) \geq \det (X + Y) + d e t (Y + Z)$
In a triangular matrix, the determinant is equal to the product of the diagonal elements.
The determinant of a matrix is zero if all the elements of the matrix are zero.
The determinant of a matrix can be calculated using the Laplace formula for Determinant of a matrix A with dimensions $n \times n$ . This formula is given below:

$\det (A) = \sum_{i = 1}^{n} [{(- 1)}^{i + j} a_{i j} M_{i j}]$

where 𝑎𝑖𝑗 is the entry of the 𝑖 𝑡ℎ row and 𝑗 𝑡ℎ column of A, and 𝑀𝑖𝑗 is the determinant of the submatrix 𝑀 obtained by removing the 𝑖 𝑡ℎ row and the 𝑗 𝑡ℎ column of A.

Appendix B. Research Conducted on Division by Zero

Table A1. Research conducted on division by zero from 2018 to 2022.

Research	Research Aim
[3,4,5]	Explores the application of division by zero in calculus and differentiation
[6]	Uses classical logic and Boolean algebra to show the problem of division by zero can be solved using today’s mathematics
[7]	Develops an analogue to Pappus Chain theorem with Division by Zero
[8]	This paper proposes that the quantum computation being performed by the cancer cell at its most fundamental level is the division by zero. This is the reason for the insane multiplication of cancer cells at its most fundamental scale.
[9]	Explores evidence to suggest zero does divide zero
[10]	Considered using division by zero to compare incomparable abstract objects taken from two distinct algebraic spaces
[11]	Show recent attempts to divide by zero
[12]	Generalize a problem involving four circles and a triangle and consider some limiting cases of the problem by division by zero.
[13]	Paper considers computing probabilities from zero divided by itself
[14,15]	Considers how division by zero is taught on an elementary level
[16]	Develops a method to avoid division by zero in Newton’s Method
[17]	This work attempts to solve division by zero using a new form of optimization called Different-level quadratic minimization (DLQM)

Appendix C. Major Results of Semi-Structured Complex Numbers from Paper [2]

Table A2. Major results from paper.

Result 1	Semi-structured complex number set can be defined as follows: A semi-structured complex number is a three-dimensional number of the general form h = x + yi +zp; that is, a linear combination of real (1), imaginary (i) and unstructured (p) units whose coefficients x, y, z are real numbers. The number h is called semi-structured complex because it contains a structured complex part $(x + y i)$ and an unstructured part $(z p)$ .
Result 2	The unstructured number $p$ was redefined as: $p^{n} = \frac{\sqrt{2} \times \cos (\frac{π}{2} n - \frac{π}{4})}{f^{n} (1)}$ (A1) where $f^{n} (c)$ is a composite function such that $f (c) = 1 - c$ . Integer powers of $p$ yield the following cyclic results: $p^{1} = \frac{1}{0}, p^{2} = - 1, p^{3} = - p, p^{4} = 1, p^{5} = \frac{1}{0}, p^{6} = - 1, p^{7} = - p, \dots$
Result 3	$p$ does not belong to the set of complex numbers $C$ (that is, $p \notin C$ ), but belongs to a higher order number set $H$ called the set of semi-structured complex numbers such that the set of complex numbers is a subset of $H$ (that is, $C \subset H$ ).
Result 4	The field of semi-structured complex numbers was defined, and proof was given that this field obeys the field axioms. This implies (1) the number set can easily be used in everyday algebraic expressions and can be used to solve algebraic problems, (2) the number set can be used to form more complicated structures such as vector spaces and hence solve more complex problems that may involve “division by zero”.
Result 5	Semi-structured complex number set $H$ does not form an ordered field. For the objects in a field to have an order, operations such as greater than or less than can be applied to these objects. This is because in an ordered field the square of any non-zero number is greater than 0; this is not the case with semi-structured complex numbers.
Result 6	Semi-structured complex numbers can be represented by points in a 3-dimensional Euclidean $x y z$ -space. The xyz-space consist of three perpendicular axes: the real $x$ -axis, the imaginary y-axis, and the unstructured $z$ -axis. These axes form three perpendicular planes: the real-imaginary $x y$ -plane, the real-unstructured $x z$ -plane, and the imaginary-unstructured $y z$ -plane.
Result 7	The unit $p$ was used to find a viable solution to the logarithm of zero. The logarithm of zero was found to be: $\log 0 = - p (\frac{π}{2} + 2 k π)$ (A2) where k is some integer value.
Result 8	The new definition of $p$ provided an unambiguous understanding that $\frac{0}{0} = n$ simply represents $90^{°}$ clockwise rotation of the vector $n p$ from the positive unstructured z-axis to $n$ on the positive real x-axis along the real-unstructured $x z$ -plane. Note that $n$ is any real number.
Result 9	Semi-structured complex numbers have both a 3D and 4D representation in the form: $h = x + y i + z p$ (3D form) $h = A + B i + C p + D i p$ (4D form) where: $x, y, z, A, B, C, D$ are real numbered scalars and $i, p$ are semi-structured basis units.
Result 10	Two new Euler formulas were developed. 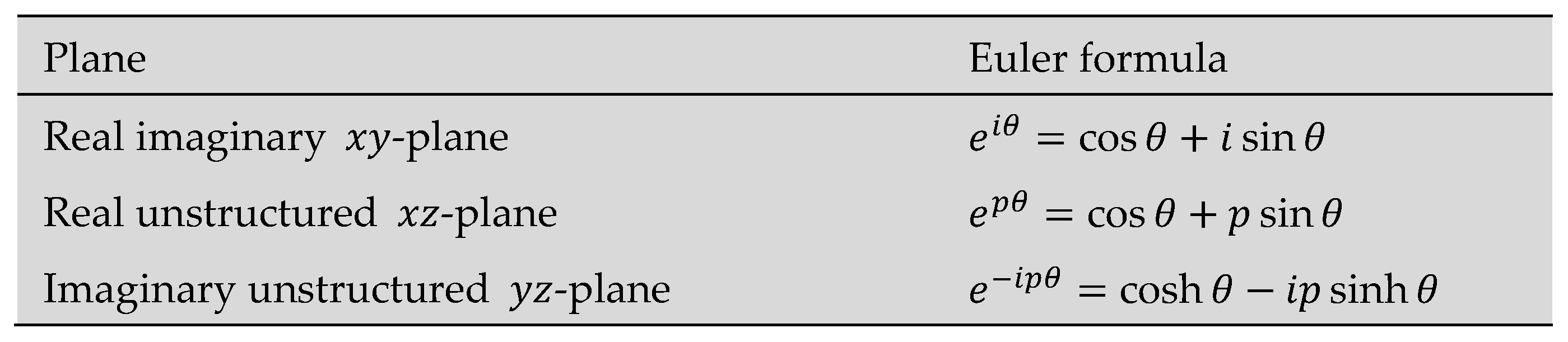When combined with the original Euler formula describes the relationship between trigonometric, hyperbolic, and exponential functions for the entire semi-structured complex Euclidean
Result 11	Semi-structured complex numbers can be used to resolve singularities that may arise in engineering and science equations (because of division by zero) to develop reasonable conclusions in the absence of experimental data.
Result 12	From Result 10 semi-structured complex numbers can present in four forms as given below:
Result 13	The zeroth root of a number h can be found using the equation $\sqrt[0]{h} = h^{p} = e^{p \ln h} = \cos (\ln h) + p \sin (\ln h)$
Result 14	Since $p^{1} = \frac{1}{0}$ this implies that $\frac{1}{p} = 0$ which further implies that $- p = 0$
Result 15	Any real number with the semi-structured unit $p$ attached to it is not a physically measurable quantity. That is, $k p$ where $k$ is a real number is not physically measurable (however, $k$ can be calculated given enough information)
Result 16	If $a$ and $b$ measure different (but quantitatively related) aspects of the same object, where $a$ is physically measurable but $b$ is not, then $a$ and $b$ can be combined into one equation in the form $a + b p$

Appendix D. Proof of Inverse of Singular Matrix

Suppose we have a singular matrix

A = (\begin{matrix} a & b \\ c & d \end{matrix})

. The inverse of this matrix can be found as follows:

Inverse of matrix

A = (\begin{matrix} a & b \\ c & d \end{matrix})

is given as:

A^{- 1} = \frac{1}{|A|} \times a d j (A) A^{- 1} = \frac{1}{a d - b c} \times (\begin{matrix} d & - b \\ - c & a \end{matrix})

But since A is singular

a d = b c

. Therefore,

a d - b c = 0

. Hence:

A^{- 1} = \frac{1}{a d - b c} \times (\begin{matrix} d & - b \\ - c & a \end{matrix}) A^{- 1} = \frac{1}{(a d - a d)} \times (\begin{matrix} d & - b \\ - c & a \end{matrix})

Now

(a d - a d)

can be treated as a difference of squares. This would imply that

a d - a d = (\sqrt{a d} + \sqrt{a d}) (\sqrt{a d} - \sqrt{a d})

. Hence:

A^{- 1} = \frac{1}{(\sqrt{a d} + \sqrt{a d}) (\sqrt{a d} - \sqrt{a d})} \times (\begin{matrix} d & - b \\ - c & a \end{matrix}) A^{- 1} = \frac{1}{(2 \sqrt{a d}) (\sqrt{a d}) (1 - 1)} \times (\begin{matrix} d & - b \\ - c & a \end{matrix}) A^{- 1} = \frac{1}{(2 \sqrt{a d}) (\sqrt{a d}) (0)} \times (\begin{matrix} d & - b \\ - c & a \end{matrix}) A^{- 1} = \frac{1}{(2) (\sqrt{a d} \times \sqrt{a d}) (0)} \times (\begin{matrix} d & - b \\ - c & a \end{matrix}) A^{- 1} = \frac{1}{(2) (a d) (0)} \times (\begin{matrix} d & - b \\ - c & a \end{matrix}) A^{- 1} = \frac{1}{(2) (a d)} \times \frac{1}{(0)} \times (\begin{matrix} d & - b \\ - c & a \end{matrix}) A^{- 1} = \frac{1}{(2) (a d)} \times p \times (\begin{matrix} d & - b \\ - c & a \end{matrix}) A^{- 1} = \frac{p}{(2) (a d)} \times (\begin{matrix} d & - b \\ - c & a \end{matrix})

Hence the inverse of a singular

2 \times 2

matrix is given by:

A^{- 1} = \frac{p}{2 a d} \times (\begin{matrix} d & - b \\ - c & a \end{matrix})

To show that

A^{- 1} = \frac{p}{2 a d} \times (\begin{matrix} d & - b \\ - c & a \end{matrix})

is the true inverse of a singular

2 \times 2

matrix

A = (\begin{matrix} a & b \\ c & d \end{matrix})

, it is necessary to show that:

A^{- 1} A = I

Hence:

A^{- 1} A = \frac{p}{2 a d} \times (\begin{matrix} d & - b \\ - c & a \end{matrix}) (\begin{matrix} a & b \\ c & d \end{matrix}) A^{- 1} A = \frac{p}{2 a d} \times (\begin{matrix} d a - b c & b d - b d \\ - c a + a c & - b c + a d \end{matrix})

Recall

a d = b c

and

b d - b d = \frac{1}{2} (b - b) (d - d)

. Hence the equation becomes:

A^{- 1} A = \frac{p}{2 a d} \times (\begin{matrix} a d (1 - 1) & \frac{1}{2} (b - b) (d - d) \\ \frac{1}{2} (a - a) (c - c) & a d (1 - 1) \end{matrix}) A^{- 1} A = \frac{p}{2 a d} \times (\begin{matrix} a d (0) & \frac{1}{2} (0) (0) \\ \frac{1}{2} (0) (0) & a d (0) \end{matrix}) A^{- 1} A = p \times (\begin{matrix} \frac{a d (0)}{a d (2)} & \frac{(0) (0)}{a d (2) (2)} \\ \frac{(0) (0)}{a d (2) (2)} & \frac{a d (0)}{a d (2)} \end{matrix}) A^{- 1} A = (\begin{matrix} \frac{p (0)}{(2)} & \frac{p (0) (0)}{a d (4)} \\ \frac{p (0) (0)}{a d (4)} & \frac{p (0)}{(2)} \end{matrix})

Since

p (0) = 1

and

p = \frac{1}{0}

(according to the algebra of semi-structured complex numbers)

A^{- 1} A = (\begin{matrix} \frac{1}{0} \times \frac{(0)}{(2)} & \frac{(1) (0)}{a d (4)} \\ \frac{(1) (0)}{a d (4)} & \frac{1}{0} \times \frac{(0)}{(2)} \end{matrix}) A^{- 1} A = (\begin{matrix} \frac{(0)}{(0)} & \frac{(1) (0)}{a d (4)} \\ \frac{(1) (0)}{a d (4)} & \frac{(0)}{(0)} \end{matrix}) A^{- 1} A = (\begin{matrix} \frac{(0)}{(0)} & \frac{(0)}{a d (4)} \\ \frac{(0)}{a d (4)} & \frac{(0)}{(0)} \end{matrix}) A^{- 1} A = (\begin{matrix} 1 & 0 \\ 0 & 1 \end{matrix})

Appendix E. Numerical Examples of Solving Simultaneous Equations That Can Be Represented by Singular Matrices

PART 1: Example of solving simultaneous equations which appear to have infinitely many solutions

Solve the following simultaneous Equations:

\begin{matrix} 2 x + 3 y = 23 \\ 8 x + 12 y = 92 \end{matrix}

(A3)

(\begin{matrix} x \\ y \end{matrix}) = \frac{p}{(24) (2)} (\begin{matrix} 12 & - 3 \\ - 8 & 2 \end{matrix}) (\begin{matrix} 23 \\ 92 \end{matrix}) (\begin{matrix} x \\ y \end{matrix}) = \frac{p}{(24) (2)} (\begin{matrix} 12 \times 23 - 3 \times 92 \\ - 8 \times 23 + 2 \times 92 \end{matrix}) (\begin{matrix} x \\ y \end{matrix}) = \frac{p}{(24) (2)} (\begin{matrix} 276 (1 - 1) \\ 184 (- 1 + 1) \end{matrix}) (\begin{matrix} x \\ y \end{matrix}) = \frac{p}{(24) (2)} (\begin{matrix} 276 (0) \\ 184 (0) \end{matrix}) (\begin{matrix} x \\ y \end{matrix}) = (\begin{matrix} \frac{p}{(24) (2)} \times 276 (0) \\ \frac{p}{(24) (2)} \times 184 (0) \end{matrix}) (\begin{matrix} x \\ y \end{matrix}) = (\begin{matrix} \frac{276 (0 p)}{(24) (2)} \\ \frac{184 (0 p)}{(24) (2)} \end{matrix})

According to semi-structured complex numbers

0 p = 1

. Hence the solution to Equation (A3) is given in Result (A4).

(\begin{matrix} x \\ y \end{matrix}) = (\begin{matrix} \frac{23}{4} \\ \frac{23}{6} \end{matrix})

(A4)

PART 2: Example of solving simultaneous equations which appear to have no solution

Solve the following simultaneous Equations representing parallel lines:

\begin{matrix} 5 x + 7 y = 17 \\ 5 x + 7 y = 19 \end{matrix}

(A5)

(\begin{matrix} x \\ y \end{matrix}) = \frac{p}{2 (a b)} (\begin{matrix} b & - b \\ - a & a \end{matrix}) (\begin{matrix} f_{1} \\ f_{2} \end{matrix})

Hence:

(\begin{matrix} x \\ y \end{matrix}) = \frac{p}{(5 \times 7) (2)} (\begin{matrix} 7 & - 7 \\ - 5 & 5 \end{matrix}) (\begin{matrix} 17 \\ 19 \end{matrix}) (\begin{matrix} x \\ y \end{matrix}) = \frac{p}{(35) (2)} (\begin{matrix} 7 \times 17 - 7 \times 19 \\ - 5 \times 17 + 5 \times 19 \end{matrix}) (\begin{matrix} x \\ y \end{matrix}) = \frac{p}{(35) (2)} (\begin{matrix} 7 \times (17 - 19) \\ 5 \times (- 17 + 19) \end{matrix}) (\begin{matrix} x \\ y \end{matrix}) = (\begin{matrix} \frac{p}{(35) (2)} \times 7 \times (17 - 19) \\ \frac{p}{(35) (2)} \times 5 \times (19 - 17) \end{matrix}) (\begin{matrix} x \\ y \end{matrix}) = (\begin{matrix} \frac{p (17 - 19)}{10} \\ \frac{p (19 - 17)}{14} \end{matrix}) (\begin{matrix} x \\ y \end{matrix}) = (\begin{matrix} \frac{- 2}{10} p \\ \frac{2}{14} p \end{matrix})

Hence the solution to Equation (A5) is given in Result (A6).

(\begin{matrix} x \\ y \end{matrix}) = (\begin{matrix} \frac{- 1}{5} p \\ \frac{1}{7} p \end{matrix})

(A6)

If simultaneous Equation (A5) is converted to a homogeneous equation and Result (A6) is converted to homogeneous coordinates, then it becomes more clear by Result (A6) is correct. This is shown below:

(\begin{matrix} x \\ y \end{matrix}) = (\begin{matrix} \frac{- 1}{5} p \\ \frac{1}{7} p \end{matrix}) = (\begin{matrix} \frac{- 1}{(5) (0)} \\ \frac{1}{(7) (0)} \end{matrix}) = (\begin{matrix} \frac{x_{1}}{x_{3}} \\ \frac{x_{2}}{x_{3}} \end{matrix})

This implies that

x_{1} = \frac{- 1}{5}

x_{2} = \frac{1}{7}

and

x_{3} = 0

Substituting the

(x_{1} . x_{2} . x_{3})

coordinates into simultaneous Equation (A5) yields Result (A7) (the correct output).

\begin{matrix} 5 (\frac{- 1}{5}) + 7 (\frac{1}{7}) = 17 (0) \\ 5 (\frac{- 1}{5}) + 7 (\frac{1}{7}) = 19 (0) \end{matrix}

(A7)

References

P. Jean Paul and S. Wahid, "Unstructured and Semi-structured Complex Numbers: A Solution to Division by Zero.," Pure and Applied Mathematics Journal,, vol. 10, no. 2, p. 49-61, 2021.
Paul, P. J., & Wahid, S. (2022). Reformulating and Strengthening the theory of Semi-strucutred Complex Numbers. International Journal of Applied Physics and Mathematics, 12(4), 34-58.
S. Pinelas and S. Saitoh, "Division by Zero Calculus and Differential Equations," in Differential and Difference Equations with Applications: ICDDEA, Amadora, Portugal, 2018.
S. Saitoh, "Introduction to the division by zero calculus," in Scientific Research Publishing, Inc, USA, 2021.
H. Okumura, "The arbelos in Wasan geometry: Atsumi’s problem with division by zero calculus," Sangaku Journal of Mathematics, vol. 5, pp. 32-38, 2021.
Barukčić, "Classical logic and the division by zero," International Journal of Mathematics Trends and Technology IJMTT, vol. 65, no. 7, pp. 31-73, 2019.
H. Okumura, "An Analogue to Pappus Chain theorem with Division by Zero," In Forum Geom, vol. 18, pp. 409-412, 2018.
M. P. Lobo, "Cancer: Division by Zero," Open Journal of Mathematics and Physics, vol. 2, no. 73, p. 5, 2020.
M. P. Lobo, "Does zero divide zero," Open Journal of Mathematics and Physics, vol. 2, no. 69, p. 3, 2020.
J. Czajko, "On unconventional division by zero," World Scientific News, vol. 99, pp. 133-147, 2018.
H. Okumura, "Is It Really Impossible To Divide By Zero," J Appl Math, vol. 27, no. 2, pp. 191-198, 2018.
H. Okumura, "A four circle problem and division by zero," Sangaku Journal of Mathematics, vol. 4, pp. 1-8, 2020.
W. Mwangi, "Definite Probabilities from Division of Zero by Itself Perspective," Asian Journal of Probability and Statistics, vol. 6, no. 2, pp. 1-26, 2020.
J. Dimmel and E. Pandiscio, "When it’s on zero, the lines become parallel: Preservice elementary teachers’ diagrammatic encounters with division by zero," The Journal of Mathematical Behavior, vol. 58, pp. 1-27, 2020.
F. Karakus and B. Aydin, "Elementary Mathematics Teachers’specialized Content Knowledge Related To Division By Zero," Malaysian Online Journal of Educational Sciences, vol. 7, no. 2, pp. 25-40, 2019.
Abdulrahman, "A Method to Avoid the Division-by-Zero or Near-Zero in Newton-Raphson Method," Feburary 2022. Available online: https://www.researchgate.net/publication/358857049_A_Method_to_Avoid_the_Division-by-Zero_or_Near-Zero_in_Newton-Raphson_Method (accessed on 28 April 2022).
Y. Zhang, Y. Ling, M. Yang and M. Mao, "Exemplar Different-Level Quadratic Minimization,," in The 2018 5th International Conference on Systems and Informatics, 2018.
Hasoun, R. K., Khlebus, S. F., & Tayyeh, H. K., "A new approach of classical Hill Cipher in public key cryptography.," International Journal of Nonlinear Analysis and Applications, vol. 12, no. 2, pp. 1071-1082, 2021.
Paragas, J. R., Sison, A. M., & Medina, R. P., "Hill cipher modification: A simplified approach.," 2019 IEEE 11th International Conference on Communication Software and Networks (ICCSN), pp. pp. 821-825, 2019.
Hraoui, S., Gmira, F., Abbou, M. F., Oulidi, A. J., "A new cryptosystem of color image using a dynamic-chaos hill cipher algorithm," Procedia computer science, vol. 148, pp. 399-408, 2019.

Figure 1. Initial visualization of the projective plane and line at infinity.

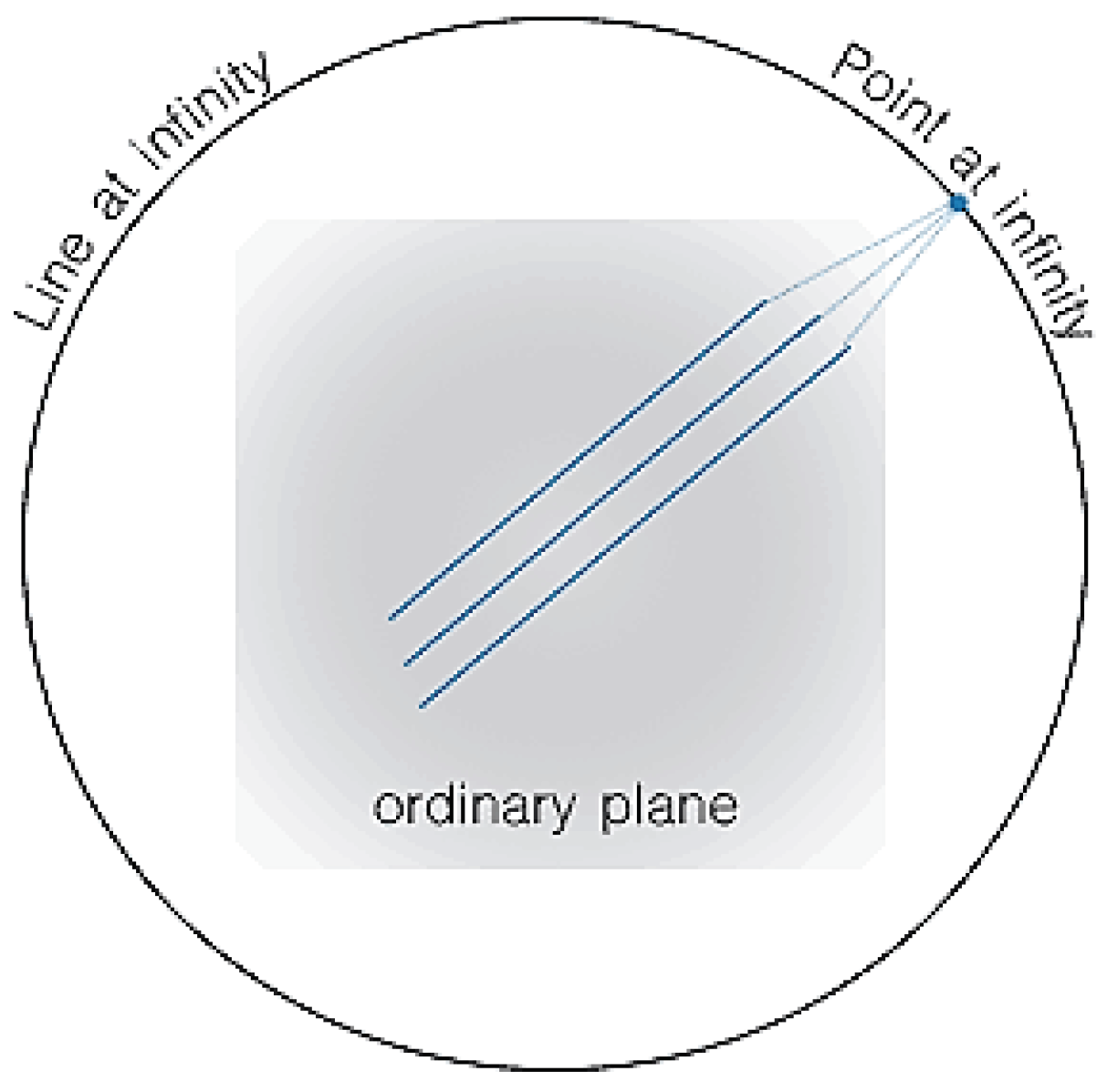
Figure 2. Adjusted visualization of the projective plane and line at infinity.

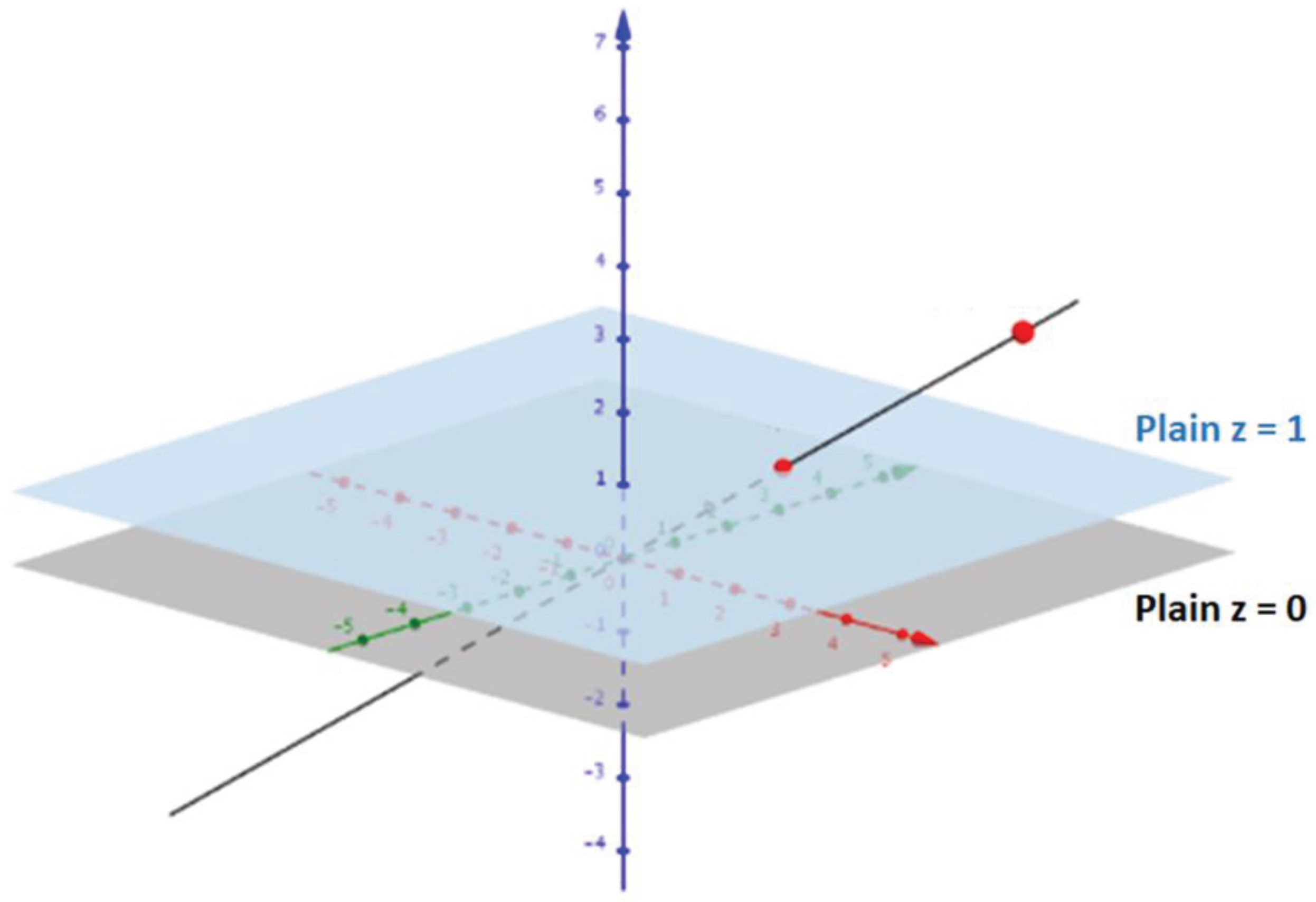
Table 1. Disadvantages of Singular Matrices.

Disadvantage	Explanation
Non-existence of inverse	Singular matrices do not have an inverse. The inverse of a matrix is essential for various mathematical operations, such as solving linear systems of equations or performing certain transformations. Without an inverse, these operations become impossible or highly constrained. In practical terms this would mean that singular matrices cannot be used to represent processes and in cases where they do end up representing practical processes expensive workarounds are often employed to avoid or overcome them. This results in wasted time and money.
Limited applicability in solving equations	Singular matrices cannot be used to uniquely solve systems of linear equations. In a non-singular matrix, each equation in the system corresponds to a unique solution. However, in the case of a singular matrix, the system of equations may have either no solution or infinitely many solutions. This limitation restricts their use in many practical applications represented by a system of linear equations.
Numerical instability	The lack of an inverse can introduce significant errors or inaccuracies, especially when solving equations or performing matrix operations. Small changes in the matrix elements can result in large changes in the computed solutions, making the results unreliable.
Ambiguity in interpretation	Singular matrices can lead to ambiguity in interpreting the data or model they represent. In some cases, a singular matrix may indicate redundancy or collinearity in the data, where certain variables or observations are perfectly correlated. This can make it challenging to draw meaningful conclusions or make accurate predictions based on the matrix representation alone.
Limitations in matrix factorization techniques	Many matrix factorization techniques, such as lower–upper (LU) decomposition or Eigen decomposition, rely on the existence of an inverse matrix. Singular matrices may not be amenable to these factorization methods, limiting their applicability in various computational algorithms and numerical techniques.
Reduced rank and dimensionality	Singular matrices have a reduced rank compared to non-singular matrices. The rank of a matrix represents the maximum number of linearly independent rows or columns. A singular matrix has at least one row or column that can be expressed as a linear combination of the other rows or columns, which reduces the effective dimensionality of the matrix.

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Division by Zero: Using Semi-structured Complex Numbers to Find the Inverse of a Singular Matrix and Show Its Applications

Abstract

1. Introduction

1.1. Matrices and Their Determinants

1.2. Semi-Structured Complex Numbers: Enabling Division by Zero

1.3. Projective Geometry

1.4. Major Contributions

2. Inverse of a Singular Matrix

3. Solving Simultaneous Equations Represented by a Singular Matrix

3.1. Solving Simultaneous Equations Which Appear to Have Infinitely Many Solutions

3.2. Solving Simultaneous Equations Which Appear to Have No Solutions

4. Discussion

5. Conclusion

Appendix A. Other Important Properties of the Determinant of a Square Matrix

Appendix B. Research Conducted on Division by Zero

Appendix C. Major Results of Semi-Structured Complex Numbers from Paper [2]

Appendix D. Proof of Inverse of Singular Matrix

Appendix E. Numerical Examples of Solving Simultaneous Equations That Can Be Represented by Singular Matrices

References

MDPI Initiatives

Important Links

Subscribe