Assessing the Performance of a Hand-held Laser Scanning for Individual Tree Mapping in an Urban Area

Precise individual tree or sample-based inventories derived from 3D point cloud data of mobile laser scanning can improve our comprehensive understanding of the structure, function, resilience, biodiversity, and ecosystem services of urban forests. This study assessed the performance of a hand-held laser scanning system for the extraction of tree position, diameter at breast height (DBH) and tree height (H) in an urban area. A total of 2083 trees of 13 species from 34 plots were analyzed. The results showed that the registration of tree positions using ground control points (GCPs) demonstrated high accuracy, with errors consistently below 0.4 m, except for a few instances. The extraction accuracy of DBH for all trees and individual species remained consistently high, with a total root mean square error (RMSE) of 2.06 cm (6.89%) and a bias of 0.62 cm (2.07%). Notably, broad-leaved trees outperformed coniferous trees, with RMSE and bias values of 1.86 cm (6%) and 0.76 cm (2.46%) compared to 2.54 cm (9.46%) and 0.23 cm (0.84%). Tree height extraction accuracy varied significantly among different species, with R2 values ranging from 0.65 to 0.92. Generally, both DBH and height were underestimated. Linear mixed effects models (LME) were applied to evaluate factors affecting the performance of HLS with the plot as a random factor. LME analysis revealed that plant type and terrain significantly influenced the accuracy of DBH and H derived from HLS data. Other fixed factors of plot area, tree density and trajectory length didn’t have significance. With a large sample size, we concluded that the HLS demonstrated sufficient accuracy in extracting individual tree parameters in urban forests.

Keywords:

Subject: Biology and Life Sciences - Forestry

1. Introduction

Urban forests, with their minimal spatial footprint, provide significant ecosystem services for urban residents and wildlife by promoting health and social well-being, enhancing children’s cognitive development and educational success rate, providing a strong economy and numerous resources, mitigating urban heat island effect and storing and sequester carbon, providing habitat and food for animals, and managing stormwater in the form of green infrastructure [1,2]. Precise individual tree or sample-based inventories are fundamental to a comprehensive understanding of the structure, function, resilience, biodiversity, and ecosystem services of urban forests [3,4]. In traditional plot-based forest inventories, the most frequently measured individual attributes are tree species, diameter at breast height (DBH), and tree height [5,6]. These tree attributes, either individually or in combination and utilizing species-specific equations (allometric models), are employed to compute and estimate a range of characteristics at the tree, plot, and stand levels, including basal area, volume, biomass, carbon stock, and others [7,8,9,10]. However, The diversity of urban forests, the nuanced impacts of urban trees at a small scale, and the pronounced spatial variations in urban areas create unique site-specific differences that must be taken into account to obtain highly accurate measurements [11]. To address these site-specific variations, comprehensive and high-resolution data at local scales are essential [12].

In recent decades, close-range remote sensing has undergone rapid development, fundamentally altering the landscape of in situ forest inventories [8]. Three-dimensional point cloud data obtained through Light Detection and Ranging (LiDAR) technology is currently being utilized for the precise extraction of forest characteristics, such as individual tree position, Diameter at breast height (DBH), tree height and forest biomass [7,13,14,15,16,17,18].

Among all LiDAR sensors and platforms, the static terrestrial laser scanning (TLS) system has the highest geometric data quality at the plot level[8]. It can capture high-quality point clouds that provide detailed information at the millimeter level [19]. Over the past decade, TLS has gained global recognition as an alternative to traditional methods for forest resource surveys [5,20,21,22]. However, the TLS lacks mobility and is unable to capture the complete profile of a tree from a single viewpoint. And, it is well known that artificial reference targets are needed to combine multiple scans into a single point cloud in order to cover the entire area of interest [19,23]. This inconvenience in data acquisition and processing has become a major obstacle to the widespread adoption of TLS. Recent studies have explored marker-free automated registration[5,6] to enhance the applicability of TLS in forest conditions. However, the results indicated that these methods do not achieve the same level of reliability as traditional approaches using artificial reference targets.

Mobile and portable systems greatly enhance the efficiency of data collection and have the potential to be embraced as next-generation operational tools in studying forest spatial characteristics when they achieve geometric accuracy comparable to TLS systems [8]. Its platform can be a vehicle [6,24] or a person, and the latter is also known as personal laser scanning (PLS) [25,26] or wearable laser scanning [27]. According to the system it mounted, PLS can be further divided into backpack laser scanning (BPLS) [5,28,29] or handheld laser scanning (HLS) [4,26,30,31,32]. A mobile laser scanning (MLS) system usually comprises a LiDAR sensor, a global navigation satellite system (GNSS) receiver and an inertial measurement unit (IMU)[33]. Due to weak or absent GNSS signals beneath the forest canopy, there are limitations for GNSS MLS in positioning. The introduction of simultaneous localization and mapping (SLAM) has empowered the latest MLS systems, particularly HLS devices, with the capability to capture detailed 3D scenarios while in motion without GNSS. By providing spatial data in a local coordinate system, the SLAM software enables raw data to be quickly pre-processed and exported to various point cloud formats even on a modest laptop [4]. Thus, PLS exhibits superior mobility compared to MLS, providing adaptability in the data collection to reduce object occlusion and enhance data coverage. This flexibility is particularly advantageous in forest inventory in challenging terrain and structural complexity forest environments[8]. For example, [5] reported that, the efficiency of backpack PLS is 2.8 times greater than that of TLS when considering the time required to complete all indoor and outdoor tasks.

The state of the art in HLS has exhibited time-efficiency and good performance in tree mapping [31,34,35]. Individual tree attributes such as tree position, DBH and tree height are the primary focus of researchers [26] investigated up to 2466 trees from 20 sample plots with different sizes distributed across various forest types, stand structures, and terrain characteristics in Austria. The root mean square error (RMSE) of the best DBH was 2.32 cm (12%) and the highest precision of relative bias was approximately 1%, which can be considered satisfactory for operational forest inventories (FI). However, most of the studies often lack sufficient data at the tree or plot levels, which may do not have strong statistical robustness [36] reviewed all studies involving HLS in FI. They reported that the limited number of conducted studies prohibits a definitive conclusion on the current suitability of HLS systems for operational FI. After an overview of the current status and advancements in close-range remote sensing for forest observations, [8] also stated that although promising results have been shown, some challenges are still ahead. For practical applications in forests, additional studies with sufficient test data are needed to offer statistically reliable conclusions, including insights into the quantity, variability, and complexity of the test data. Furthermore, most studies only consider a few tree species and do not account for the influence of tree species on the accuracy of LiDAR scanning.

On the other hand, the barrier to entry for LiDAR measurements remains relatively high. While data acquisition has become more efficient, the absence of standardized procedures for post-processing and parameter extraction hampers the practical application of this technology. Meanwhile, user-friendly data acquisition protocols are lack for most systems, which are urgently required to facilitate data collection with high levels of completeness and accuracy [8].

The main objectives of this study are to (1) obtain sufficient single tree attributes in an urban area using an HLS system and a standardized workflow in data acquisition and parameter extraction; (2) investigate the accuracy of tree position, DBH and tree height estimation with reference data; and (3) assess the impact of terrain, tree species, and other factors on the accuracy of tree parameter extraction.

2. Materials and Methods

2.1. Study Area and Tree Mensuration

The area for PLS performance assessment in this study is located on the campus of Qingdao Agricultural University (QAU), Chengyang, Qingdao, Shandong, China. As a coastal and mid-latitude city, Qingdao has a typical maritime climate with four distinctive seasons. The average annual temperature is 12.6 ℃ with a cold winter of 0.9 ℃ mean temperature from December to February and a mild summer of 23.3 ℃ mean temperature from June to August. The average annual precipitation is about 662 mm and is mainly distributed in summer[37,38]. The Chengyang campus of QAU was constructed in July 2001 on agricultural lands. Therefore, nearly all of the trees on the campus were planted or transplanted during the last twenty years with a heterogeneous nature in species type, age and height.

Different from natural forests, urban trees are distributed in diverse forms of vegetated areas within built-up regions which consist of natural surfaces, such as streets, open fields in parks, affiliated areas or residential areas[9]. The characters of small forest patches and heterogeneous tree distribution determine that the sample size, shape and location will greatly influence the estimated parameters e.g. number of trees per hectare, mean DBH or tree height. Therefore, some greenness areas in the campus of QAU were selected and no plot size was designed. Instead, all trees with DBH greater than 5 cm in these areas were surveyed except those economic tree species which usually have several branches below 1.3 m.

The tree measurement took place in December 2023. DBH was measured using a diameter tape to 1 mm precision. Tree height was mainly measured by a Blume Leiss (CGQ-1, Harbin Optical Instrument Factory Ltd, Harbin, China) which was developed to measure slope and tree height by the trigonometric principle. Before measuring, a distance of 15 m or 20 m between the surveyor and the tree was first ranged by a measuring tape according to the estimated tree height. Then, the operator observed the treetop through the eyepiece of the device and triggered. Finally, the tree height can be obtained by adding the value directly read from the device depending on the fixed distance and the operator’s eye height. For small trees below 10 m, height was measured directly by a tower ruler. Tree position was measured with a real-time kinematic (RTK) system (QianXun Xingyao X Plus, Qianxun SI, Shanghai, China) under the projected China Geodetic Coordinate System 2000 (CGCS 2000). Based on real-time network calculating, the system can provide a 1-3 cm positional accuracy.

The tree species were also recorded during the measurement work. Finally, a total of 2227 trees from 34 tree species were surveyed. However, many species had insufficient sample sizes, with some species even having only one single tree. To ensure robust statistical analysis, tree species with fewer than 20 samples were excluded. Consequently, 2083 trees from 13 species were retained. The summary information of the measured plots and the parameters of tree species are shown in Table 1 and Table 2.

Figure 1. The location of the study area in Qingdao city, Shandong, China (a), and the PLS trajectories and tree positions of each plot (b). The pink labels indicate the number of plots.

Figure 2. The workflow executed in this study.

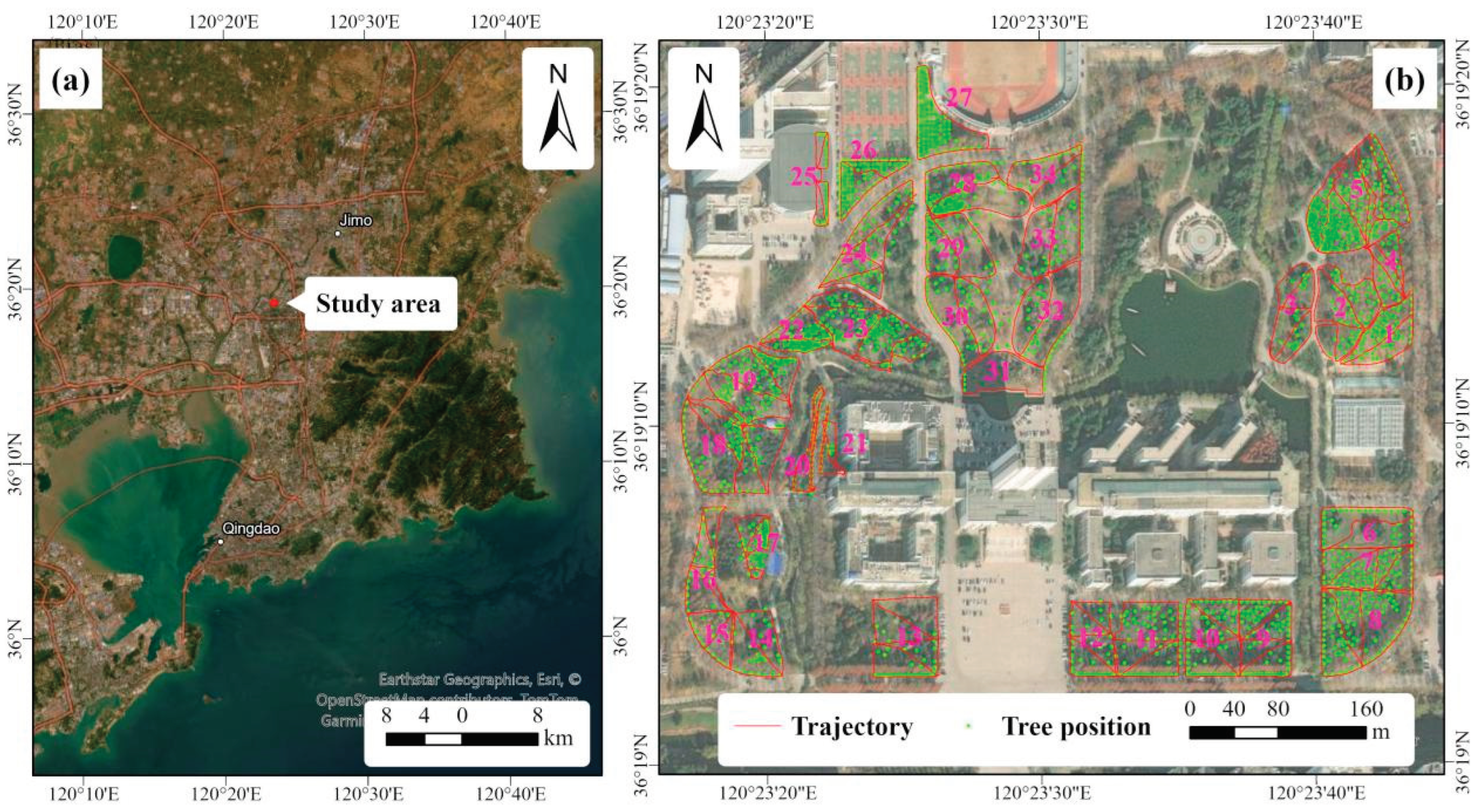
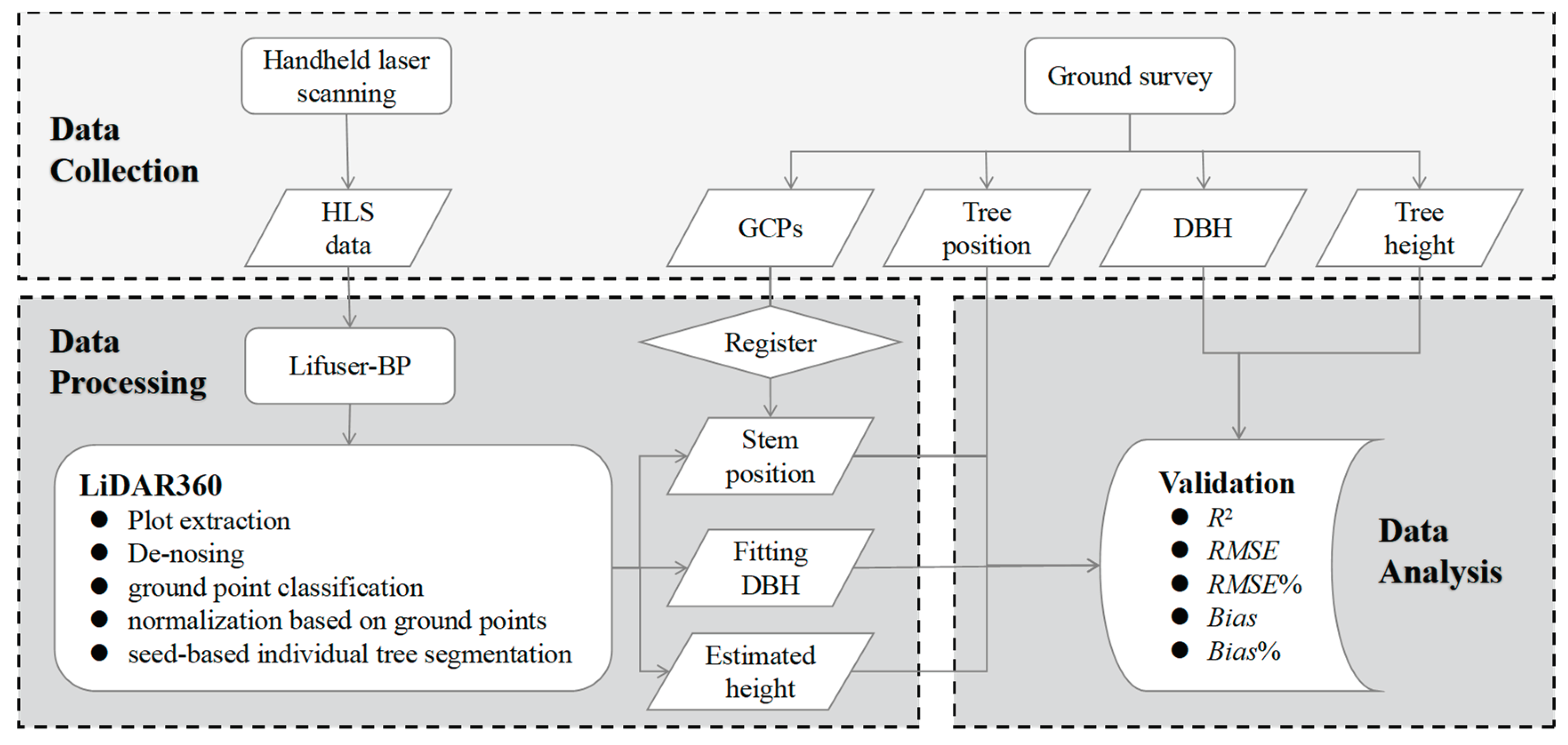
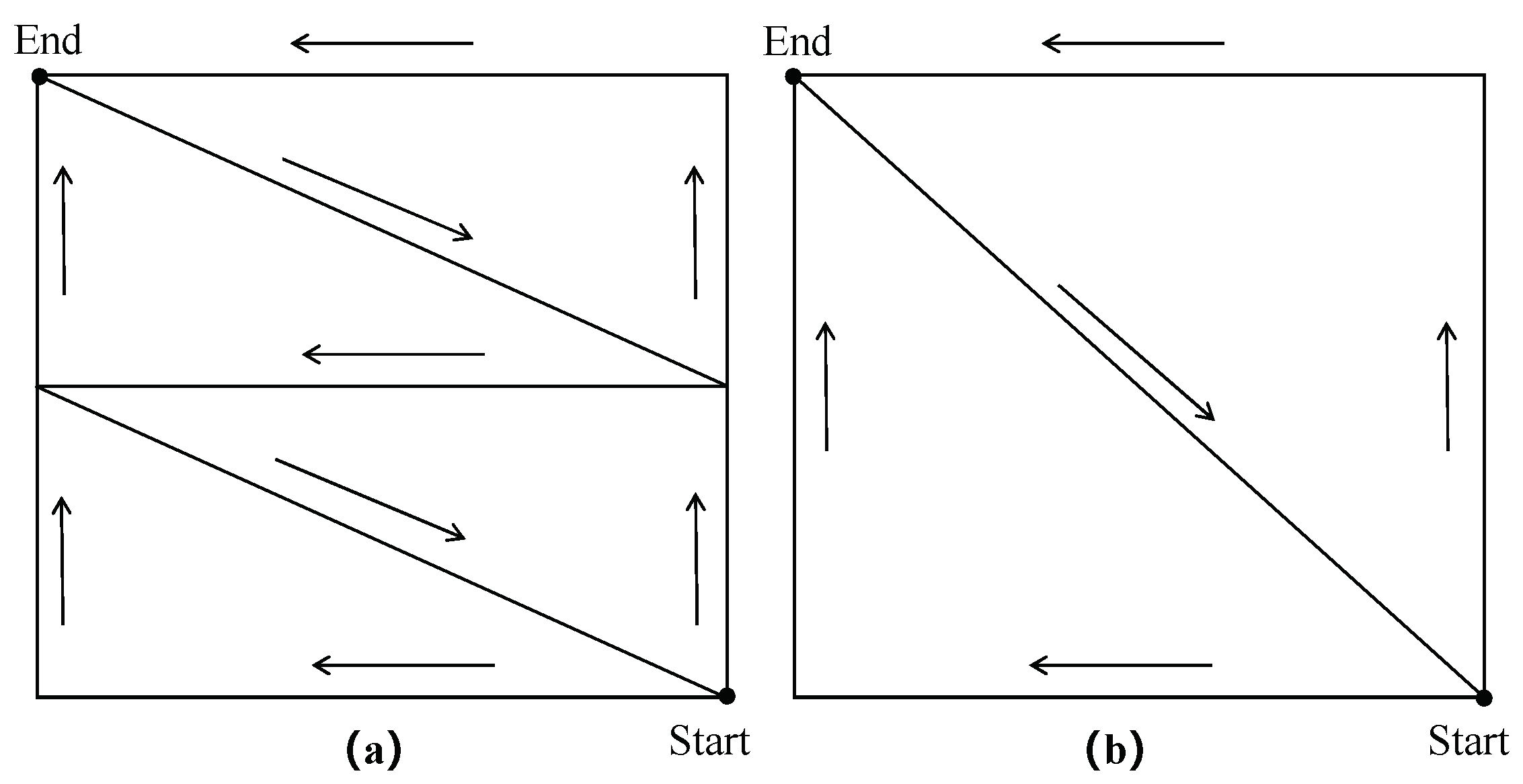
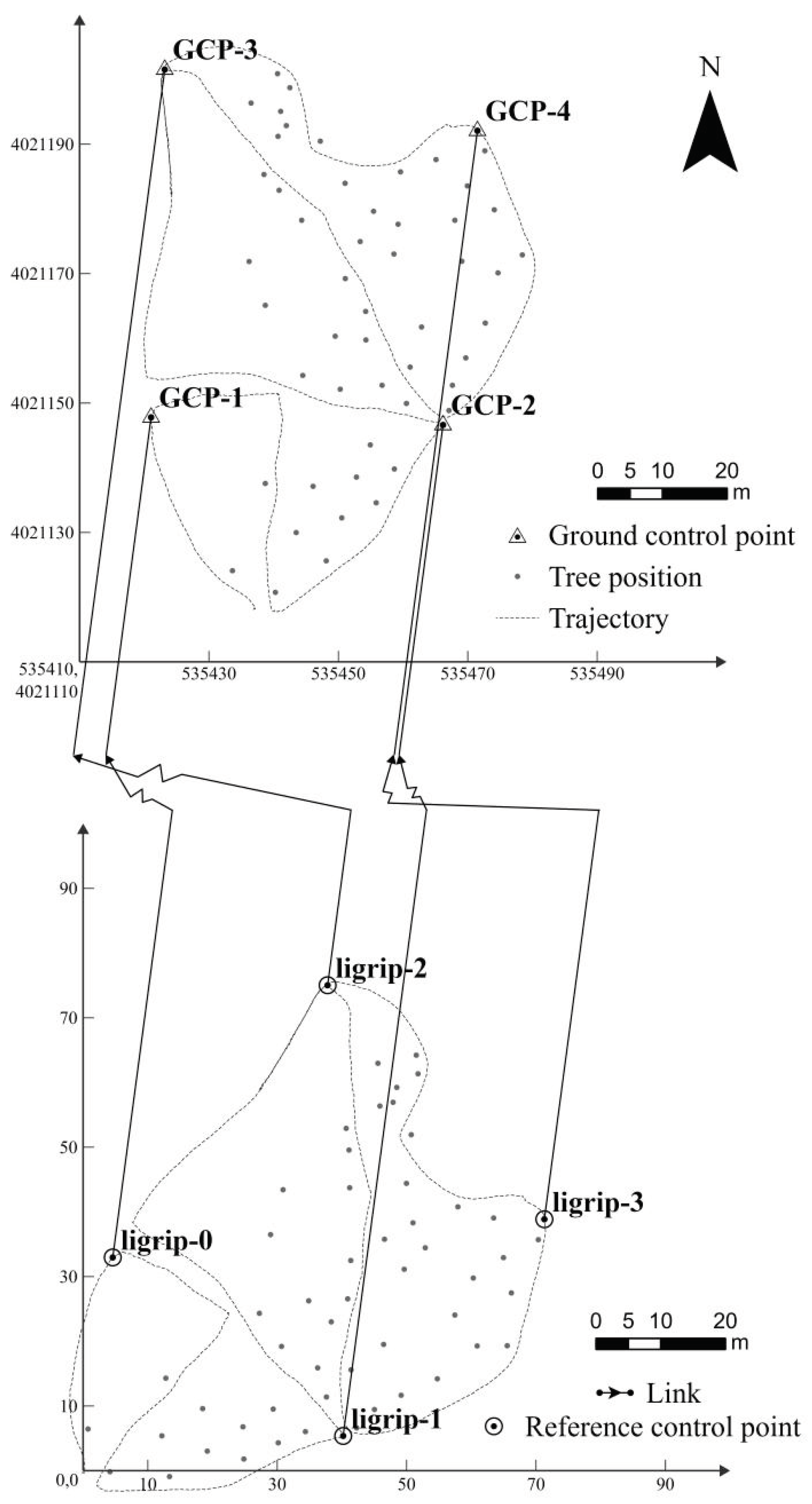
2.2. HLS Data Acquisition

The HLS data was collected on 6-9 April 2023 using the LiGrip H120 from Beijing Green Valley Technology Co., Ltd, Beijing, China (www.lidar360.com/archives/portfolio/ligrip-h120). This system also mounted a video camera with 360° panoramic lens combination. The PLS sensor can capture 320,000 pts/s in a single return and the scan range is120 m with an accuracy of ±3 cm in a field view of 280° × 360°. Based on the Simultaneous Localization and Mapping (SLAM) and Inertial Measurement Unit (IMU) techniques, the PLS system can automatically match and calibrate of data reiterations. However, the performance is decided by weather conditions (mainly wind) and obstacles from tree canopy and low shrubs.

APP installed on a smartphone or tablet is recommended for data collection. The advantage is that the operator can view current scanning data, coverage, trajectory of the measured area, and other details in real time. The device was first placed on a stationary surface or platform without high pedestrian or vehicular traffic to complete the initialization. This entire process takes approximately 75 seconds. Subsequently, the operator handheld the laser device to walk through the sample plot with a stable speed of 1 m/s along the pre-designed route to collect point data and record video. Effective path planning is able to collect all information about the trees while reducing data redundancy. In this study, the size and shape of the measured forest area were not specified. We conducted data collection following the recommended path outlined in the equipment manual (Figure 3). If the trees are densely packed, the path would follow the pattern (a) in Figure 3, otherwise the pattern (b) when the trees are sparse. The size of the sampled area was determined based on the requirement that the collection time does not exceed 30 minutes. A closed loop can significantly enhance the reliability and precision of data. Therefore, an additional distance of 5-10 meters was traversed to cover the former trajectories to ensure the accurate loop closure was recognized by the program.

Due to the absence of a GNSS module in the device we used, at least three ground control points (GCP) were set up along each trajectory, to compare estimated tree parameters with measurement results through absolute tree position matching. During walking, the operator aligned the "cross" hole of the marking base with the ground control point and stabilized the device to record the GCP’s local coordinates in the point cloud. After completing handheld marking, the marked positions were measured using GNSS-RTK. This method is also suitable for areas with poor GNSS signals, such as dense forests in natural environments. After all, as long as a few control points with GNSS signals are identified, it is possible to correct tree positions from the point cloud.

2.3. Point Cloud Processing

The raw collected data was first fused using LiFuser-BP (Beijing Green Valley Technology Co., Ltd, Beijing, China) software. Point clouds and their corresponding trajectories were generated separately from the raw data for each data acquisition. The processed output consisted of point clouds exported in LiData files and the corresponding calculated trajectories and marked GCPs exported as text files. Figure 4 gives an example of point cloud profiles from two sample plots.

After data fusion, the LiData files and trajectories were imported into the LiDAR360 software for further processing to extract tree parameters. At the beginning, the area enclosed by the trajectory is clipped ensuring that all trees can be observed from various directions. Subsequently, a standardized procedure with fixed parameters setting was executed. The procedure consists of de-noising, ground point classification, normalization based on ground points and seed-based individual tree segmentation (Figure 2). First, the outliers result from multi-path errors or inaccuracies in the laser rangefinder during the measurement process to enhance data quality. The default parameters of neighborhood size 10 and standard deviation multiplier 5 were adopted. Second, the Improved Progressive TIN Densification (IPTD) algorithm[11] was employed for ground point classification. This algorithm initially generates a sparse triangular network using seed points and iteratively densifies it layer by layer until all ground points are classified. Third, the elevation value Z of the nearest ground point was subtracted from each point in the procedure of normalization to eliminate the influence of terrain undulations on the elevation values of point cloud data. Finally, the point cloud of each individual tree was subsequently extracted based on stem seeds to identify the tree’s position and estimate both its DBH and height. The stem seeds were obtained through the batch extraction tool in the HLS editing section for DBH. DBH was determined by cylinder fitting in the slice at the 1.2–1.4 m height.

The tree position derived from the point cloud refers to the center point coordinate of the trunk at a height of 1.3 m. It was registered to the CGCS 2000 coordinate system using the affine transformation method based on GCPs to match the position of measured trees. This process was operated through a spatial adjustment tool in the ArcGIS 10.4 software (Environmental Systems Research Institute, Redlands, CA, USA). Figure 5 gives an example to register the tree position and trajectory using the affine transformation method.

2.4. Evaluation

In order to assess the accuracy of DBH and tree height derived from HLS point clouds for different species and plots, the total explained variance (R²), root mean squared error (RMSE), relative RMSE (RMSE%), absolute bias (Bias) and relative bias (Bias%) were calculated using Eqs (1)-(5):

R^{2} = 1 - \frac{\sum_{i = 1}^{n} {(y_{i} - {\hat{y}}_{i})}^{2}}{\sum_{i = 1}^{n} {(y_{i} - \bar{y})}^{2}}

(1)

R M S E = \sqrt{\frac{\sum_{i = 1}^{n} {(y_{i} - {\hat{y}}_{i})}^{2}}{n}}

(2)

R M S E % = \frac{R M S E}{\bar{y}} \times 100 %

(3)

B i a s = \frac{\sum_{i = 1}^{n} (y_{i} - {\hat{y}}_{i})}{n}

(4)

B i a s % = \frac{B i a s}{\bar{y}} \times 100 %

(5)

where n is the number of individuals of a tree species, plot or the whole detected trees;

y_{i}

is the field-measured DBH or tree height of tree i;

{\hat{y}}_{i}

indicate the estimated DBH or tree height value of tree i from HLS point clouds;

\bar{y}

denotes the mean DBH or tree height value of n.

2.5. Statistical Analysis

In order to assess the factors affecting the performance of HLS in tree mapping, linear mixed-effects models (LME) analysis was applied (Eq. (6)).

Y_{i} = β_{0} + β_{1} \times area + β_{2} \times tree density + β_{3} \times trajectory length + β_{4} \times plant type + β_{5} \times terrain + β_{6} \times plot + ε_{i}

(6)

where Y_i is the ith response variable of RMSE, RMSE%, Bias or Bias% for DBH and H; area is the scanning area of each plot (m²); tree density is the number of trees per hectare; trajectory length is the total length of trajectory for each plot (m); plant type indicates whether the tree species is coniferous or broad-leaved; terrain indicates the topography of plot;

ε_{i}

is the error. We considered area, tree density, trajectory length, plant type and terrain as fixed factors and the plot as a random factor to address the repeated measurements within the plot.

The statistical analysis was conducted with R 4.2.3[39]. The lmer() function of the lme4 package [40] was used to execute the linear mixed-effects models. We tested all linear mixed-effects models with a random intercept to assess the significance of candidate factors on HLS performance. If the interaction effects were deemed non-significant, they were excluded to simplify the statistical model. The model with the lowest Akaike’s Information Criteria (AIC) was selected, and the estimated p-values were computed. The r.squaredGLMM() function of the MuMIn package [41] was used to compare the R² in models. The significance threshold for all tests was set at 5%.

The workflow of the methods executed in this study is shown in Figure 2.

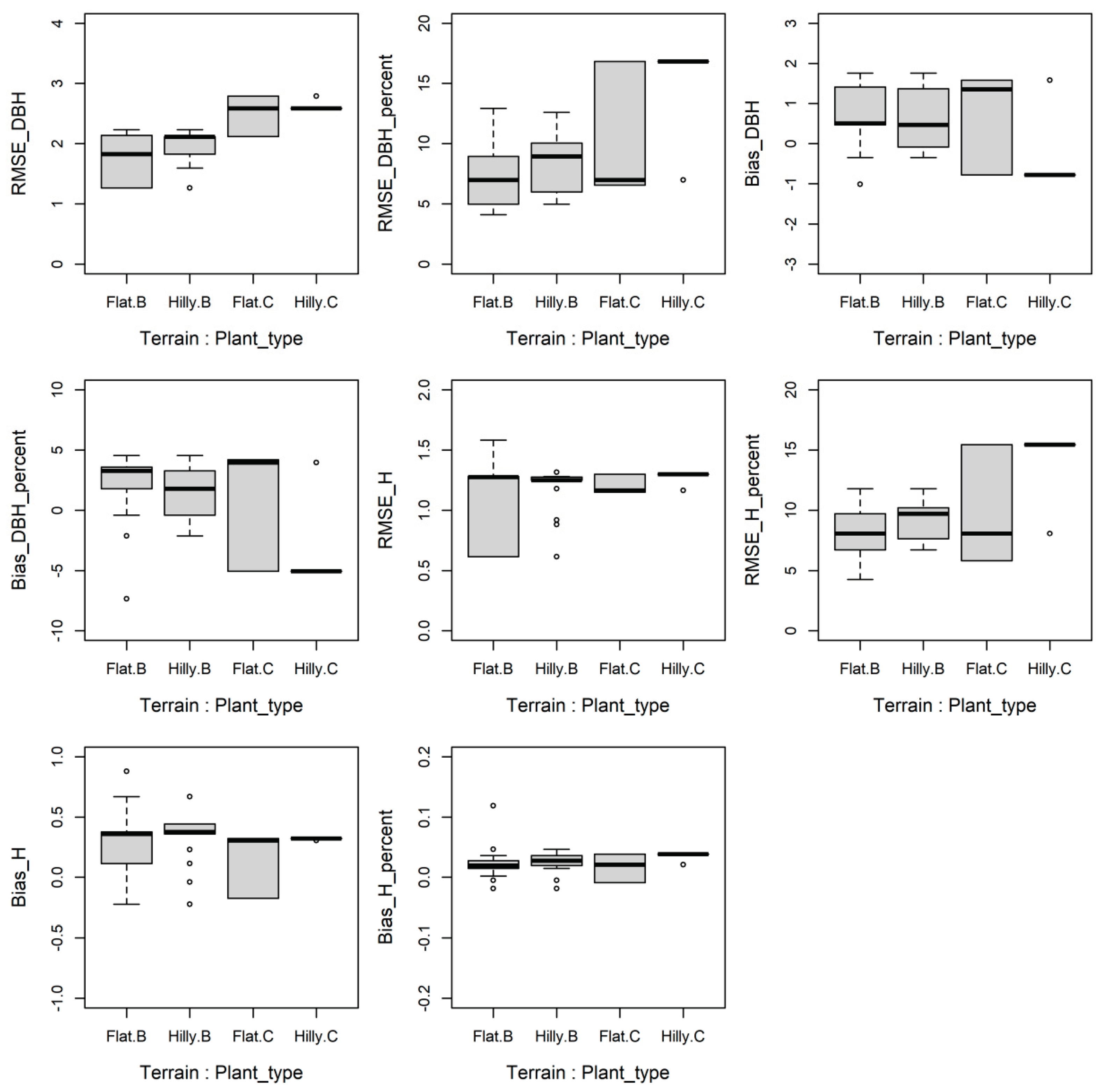
3. Results

3.1. Tree Position

The tree positions obtained through the registration of HLS using ground control points showed high consistency with those obtained through RTK measurements, with a maximum error is 0.39 m shown in the box plot in Figure 6. No significant differences were exhibited in tree position accuracy between different plots, with some outliers distributed across various plots.

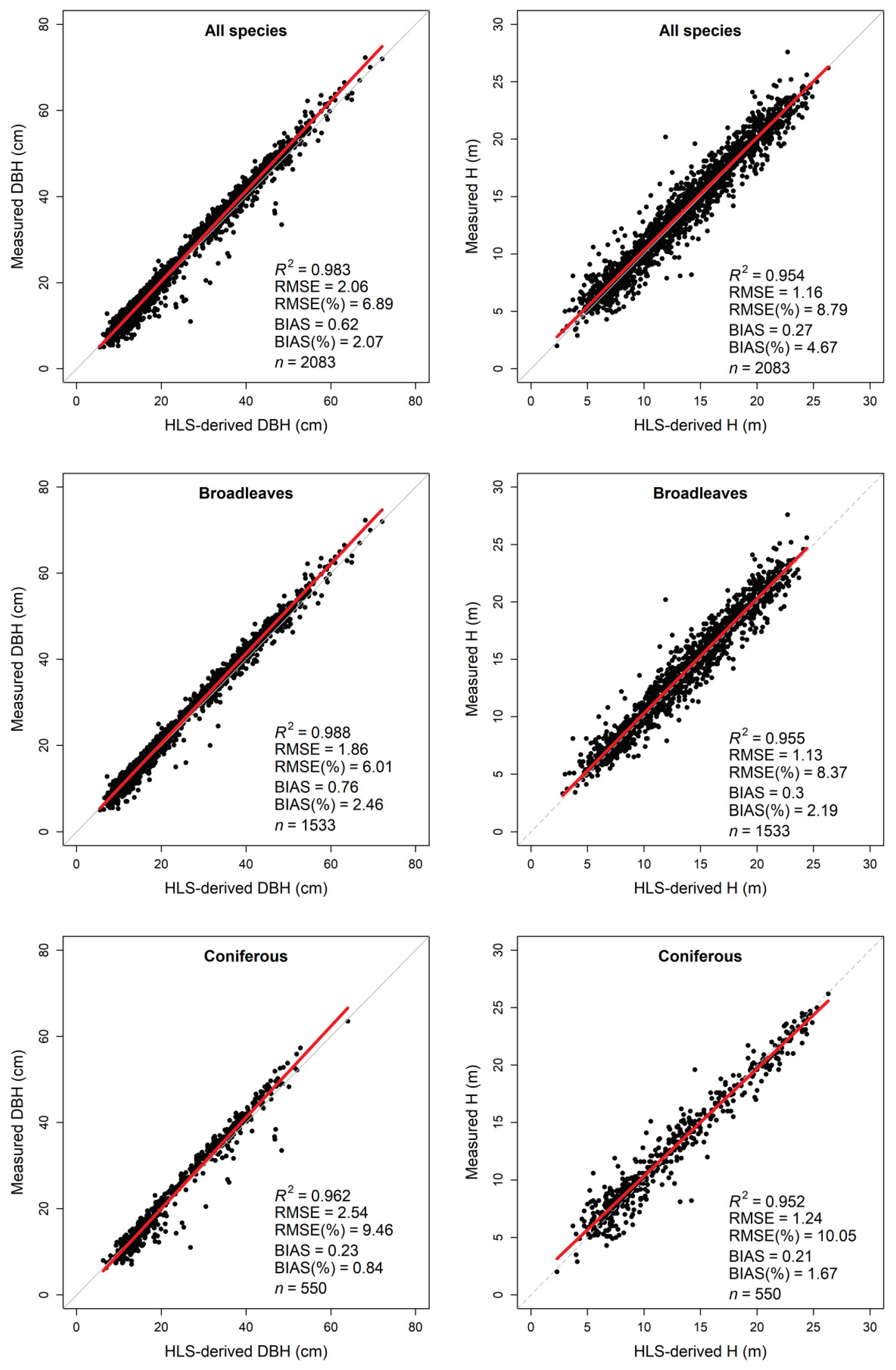
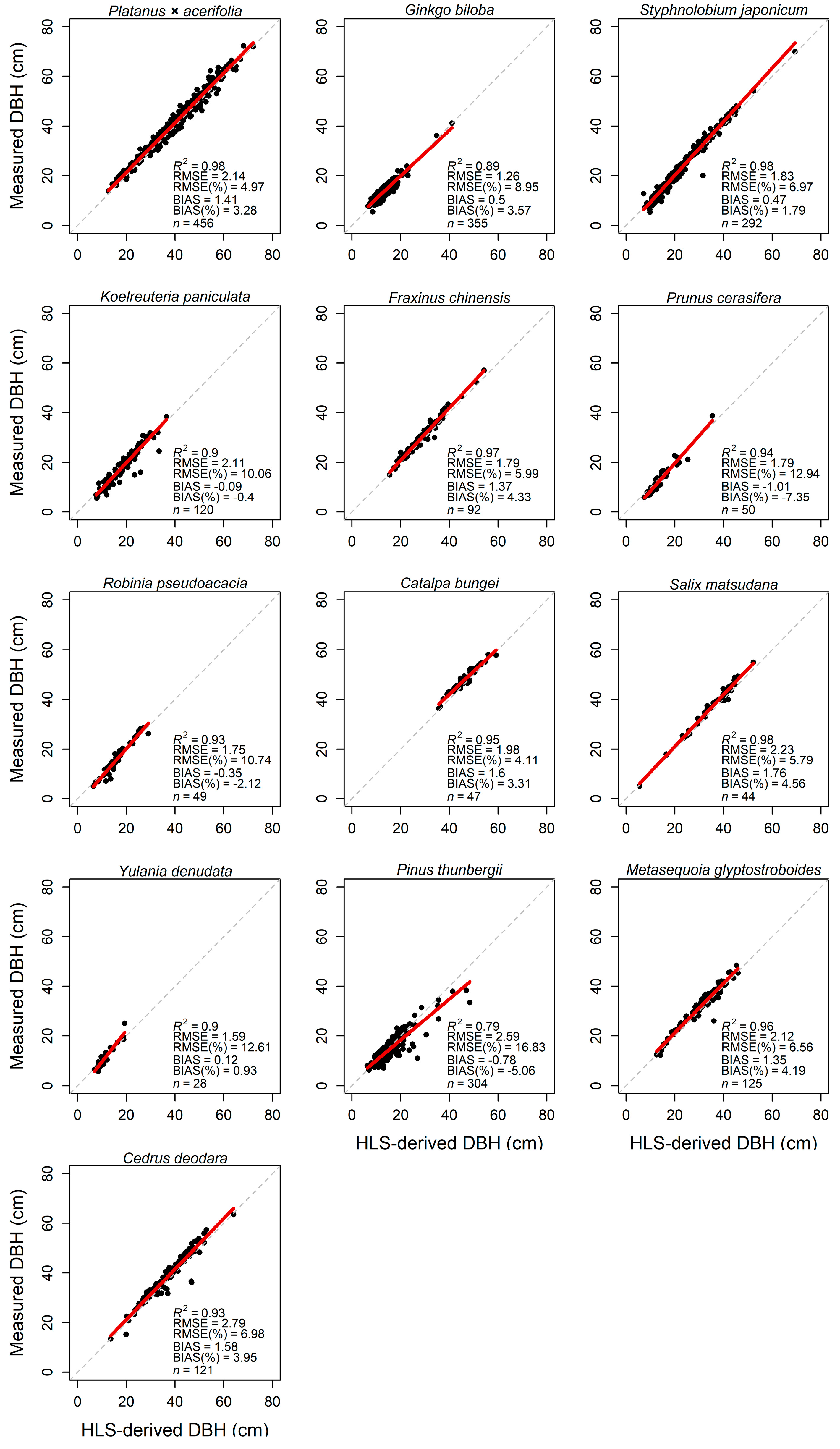
3.2. Estimation of DBH

The comparison between estimated DBH using HLS and measured DBH is shown in Figure 7. The result showed a high precision with the overall interpretive capability (R²) is 0.98, and the RMSE was only 2.06 cm which was below 7 percent of quadratic mean diameter. Additionally, a slight underestimation (the bias was 0.62, and the percent was about 2%) was detected for the total of 2083 trees. Further analysis was conducted based on coniferous and broad-leaved trees. In general, the HLS-derived DBH accuracy was better for broad-leaved trees than for coniferous trees, with the RMSE being 1.86 cm (6.01%) and 2.54 cm (9.46%), respectively. However, in terms of bias, the broad-leaved trees were subject to much more underestimation than the coniferous trees.

For visual interpretation, the performance of specifically 13 tree species was plotted in Figure 8. Generally, high accuracy was achieved for all tree species regarding different ranges of DBH. Except for Pinus thunbergii, R² ranged from 0.90 to 0.98. Additionally, RMSE varied from 1.26 to 2.79 cm, which was not consistent with its percent due to differences in DBH range. The tree species with relative RMSE greater than 10% usually were those with smaller DBH. In terms of bias and relative bias, the HLS technique tended to overestimate DBH for Koelreuteria paniculata, Prunus cerasifera, Robinia pseudoacacia, and Pinus thunbergii, while it slightly underestimated other tree species. Specifically, the relative bias of Prunus cerasifera was notably high at 7.35%. In contrast, Koelreuteria paniculata was one of the most accurately estimated species, with a relative bias of only 0.4%. For most tree species, the relative bias ranged between 1% and 5%.

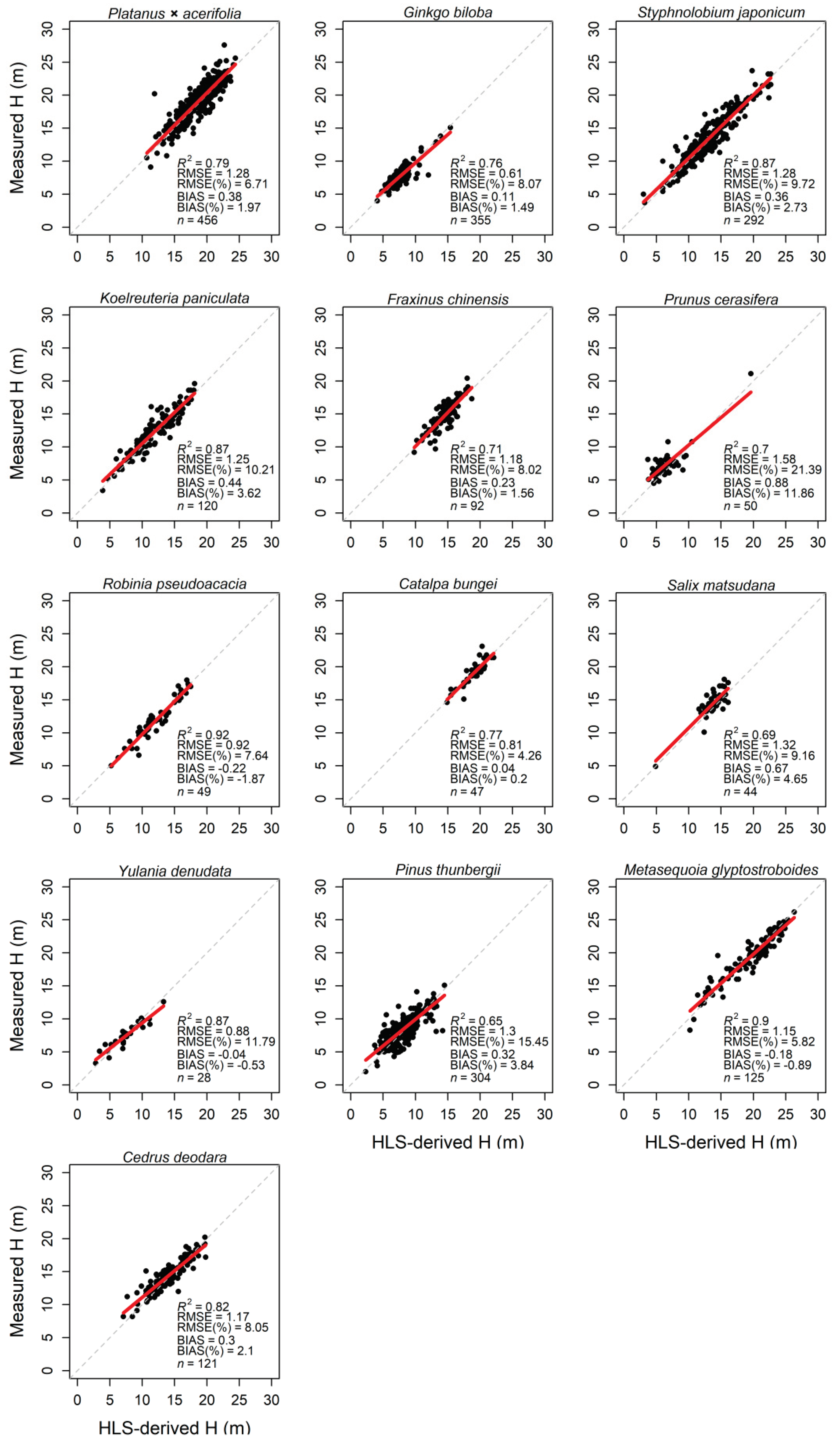
3.3. Estimation of Tree Height

Similar to DBH, the relationship between HLS-derived and measured tree height also resulted in a high R² value of 0.95 for all species of trees. As depicted in Figure 7, the RMSE reached 1.16 m, which was less than 9% of the mean height. Meanwhile, slight underestimation in H was also observed with a bias of 0.27 m (4.67%). There was no significant difference between broad-leaved and coniferous trees.

However, when it came to each specific tree species, the differences among them were significant. Firstly, the explanatory power for individual tree species’ height was much lower, ranging from a maximum of 0.92 to a minimum of 0.69 which was 25% lower than the explanatory power for all trees (R² = 0.95). Secondly, the RMSE values ranged from 0.61 to 1.58 m, its relative values spanning from 4% to 21.4%, indicating a significant difference between species. Finally, the heights of three species (Robinia pseudoacacia, Yulia deudata and Metasequoia glyphostroboides) exhibited a tendency of overestimation, while for other species, the trend was the opposite. Additionally, these evidences also suggested that the precision of DBH values was higher than that of tree height values.

3.4. LME Results

In general, handheld laser scanning tends to exhibit higher accuracy in DBH and H extraction for broadleaved trees and trees situated in flat terrain (Figure 10). The linear mixed-effects model (LME) analysis revealed a significant of plant type and terrain on the accuracy of HLS-derived DBH for individual trees. However, the influence of terrain on tree height accuracy was relatively weaker, with only terrain showing a significant effect on RMSE% of H (Table 4). Additionally, no significant interaction effect of plot size, tree density and trajectory length was observed (Table 3).

4. Discussion

The registration of tree positions using HLS and GCPs achieved satisfactory accuracy in this study except for some tilted trees with stem position at 1.3 m from point clouds versus the base position measured. There are typically two approaches to obtain absolute positions in forests by MLS. One is to utilize GNSS receivers and IMUs which are commonly tightly coupled to create positioning subsystems. These subsystems capture platform movements and sensor orientation data, providing the system’s position and sensor orientation at discrete time intervals. This information enables direct georeferencing of collected data [8,42]. With a tactical-grade GNSS IMU, the absolute accuracy can be reached 0.2-0.7 m after post-processed positioning in boreal forests [24,43]. However, this accuracy may degrade with low-cost IMUs due to high positional drift in low GNSS visibility conditions and increased angular uncertainty. The other approach involves registering point cloud data using GCPs. Total station is commonly used to provide high-precision coordinates of GCPs [44,45]. However, different transformation modes (e.g. the rigid and non-rigid modes) for generating 3D point clouds with absolute positions could result in different performances of MLS [33]. Meanwhile, setting up and using the total station is time-consuming and a known control point is required to initiate the measurement. In our study, GCPs were not used for point cloud registration but rather for the correction of tree position derived from data processing. It does not affect the quality of the point cloud, therefore, the precision of GCPs does not require exceptionally high levels. We utilized a real-time kinematic (RTK) for measuring the GCPs, and the accuracy attained in correcting tree positions adequately fulfills the demands of forestry inventories.

In terms of DBH estimation, our study indicated a high accuracy using HLS in an urban area with RMSE ranging from 1.26 to 2.79 cm. Consistently, studies from human-altered environments, such as city parks, urban streets, plantation sites, regular and pure stands, and so on [25,46,47,48] also had a good performance in estimating DBH by HLS, thanks to the clean and unobstructed understory [27] employed multiple LiDARs to assess the DBH and tree height across various tree density plots within urban forests. Their investigation revealed minimal occlusion at 1.3 m, contributing significantly to the high accuracy observed in DBH measurements. Although it is easier for an operator to walk on those flat plots while handed an MLS device, obstacles such as pedestrians, moving or parking cars, and landscape shrubs would also affect the accuracy of LiDAR scanning. For example, in the study of [49], the RMSE value of DBH for the park trees was 8.95 cm due to irregular trunk shapes and incomplete scanning data of the trunk. In our study, factors affecting the accuracy of DBH mainly included inclined tree trunks, cross-section irregularities (e.g. forked, scarred, non-circular) and occlusion, which was more likely to exist in coniferous trees, leading to higher accuracy values for the broad-leaved trees than coniferous trees. This was following some studies in difficult forest plots [4,34].

Meanwhile, most of the previous studies were conducted based on limited samples, lacking sufficient robustness in their results, especially in urban areas. With a total of 2466 trees from 20 sample plots of various sizes distributed across diverse forest types, stand structures, and terrain characteristics in Austria, [26] reported an RMSE of 2.32 cm (12%) with a relative bias of approximately 1%. Our study provided 2083 trees of 34 plots in an urban area, which was a sufficient sample size to assess the capability of HLS in extracting tree parameters [34] demonstrated that the RMSE for DBH derived from LiDAR data exhibited significant variability depending on the complexity of the forest plots. Consequently, more studies should be carried out in different circumstances to provide statistically reliable conclusions [8].

In comparison to DBH, tree height were relatively inaccurate with lower R² and higher RMSE values, especially when considering individual tree species. Similarly, in a study by [27], tree heights were compared using a TLS and a portable laser scanner (PLS) in two plots with different tree densities in Spain. The results showed that the RMSE difference between the two devices was 1.34 m in the plot with lower density and 9.44 m in the plot with higher density. These variations were attributed to differences between the devices and the environmental conditions of the plots. Difficulty environments not only influence the HLS device’s performance but also affect the accuracy of TLS. For example, [50] classified three forests into categories of Easy, Moderate, and Hard based on tree density and vegetation cover to evaluate the accuracy of measuring tree parameters using a TLS multi-scan approach. They reported lower average accuracy compared to our study, with RMSE and RMSE% values for height measurements ranging from 2.4 to 4.5 m and 12 to 23% for Easy conditions, and 4.0 to 7.7 m and 28 to 57% for Hard conditions.

In general, the tree height was underestimated in this study, which is consistent with previous studies [34,51,52,53,54]. For instance, [55] reported an underestimation of tree heights with a bias of -4.61 m and an RMSE of 2.15 m compared to field reference data using the HLS method. On the contrary, HLS tree heights were slightly overestimated in the study of [56]. However, it’s essential to consider that indirect field measurements of tree height were complex [57]. Its accuracy can be influenced by various potential sources of error, such as forest structure and complexity, tree species and crown shape, leaning trees, tree height, measuring distance, tree height, instrument, and human errors. Therefore, the errors in tree height accuracy from HLS encompass both errors associated with HLS itself and those related to the reference field-measured tree heights.

Most of the previous studies using LiDAR for extracting tree parameters had limited sample sizes, allowing only for qualitative analysis of the impacts of forest structure, topography, etc,, on the accuracy of extraction. In our study, 34 sample plots and linear mixed-effects models were employed to quantitatively analyze the effects of forest structure and other factors on the accuracy of DBH and tree height extraction. The result revealed that the plant type (broad-leaved or coniferous) and terrain were two significant factors leading to decreased accuracy of DBH and H. As stated in a study by [58], detecting spruce trees via terrestrial-based remote sensing posed considerable challenges. The dense branching and limited visibility of the lower part, especially at breast height, make it difficult for sensors to capture their entire stems. Similarly, [4] analyzed the influence of stand characteristics (such as the number of trees, stand basal area, dominant height, understorey cover, slope, etc.) on HLS data accuracy using datasets from 39 sample plots. Concerning site conditions, errors in the estimation of all forest attributes showed a positive correlation with both ground slope and understorey cover. The errors in arithmetic mean diameter and stand basal area estimations exhibited a significant increase with understorey coverage, while the errors in stand volume estimations significantly increased with slope gradient.

Finally, handheld LiDAR devices are undergoing rapid updates. During our study, a new generation product, the LiGrip H300 of the LiGrip handheld series from Beijing Green Valley Technology Co., Ltd, was released. Compared to its predecessor LiGrip H120, it boasted an increased maximum measurement range from 100 m to 300 m, a scanning frequency from 320, 000 to 640, 000 pts/s, and enhanced LiDAR accuracy to 1 cm. Recently, consumer-grade laser sensors have been integrated into smartphones. These affordable sensors are anticipated to proliferate in the future, offering more handheld laser scanning technology that is user-friendly [59]. Therefore, we believe that mobile and portable laser scanning systems hold the potential to be embraced as next-generation operational tools.

5. Conclusions

This study evaluated the applicability of a hand-held laser scanning system (HLS) for the examination of urban forest resource inventories and their performance in mapping individual trees. Tree position, DBH and height were estimated by HLS from 34 different plots in QAU, and its results were compared with field measurements.

The registration of tree position using GCPs showed high accuracy with errors under 0.4 m, except for some outlets. The extraction accuracy of DBH for all trees and individual tree species was consistently high, with a total RMSE was 2.06 cm (6.89%) and a bias was 0.62 cm (%2.07). Broad-leaved trees exhibited better performance than coniferous trees, with RMSE and bias were 1.86 cm (6%) and 0.76 cm (2.46%) vs. 2.54 cm (9.46%) and 0.23 cm (0.84%). The accuracy of tree height extraction varied significantly among different tree species. The R² ranged from 0.65 to 0.92. Both DBH and H were generally underestimated. LME results revealed that plant type and terrain were the significant factors influencing the accuracy of HLS-derived DBH and H.

Author Contributions

Conceptualization, J.Y.; methodology, J.Y.; investigation, W.Y., Y.L., Y.W. and L.S.; data curation, W.Y. and H.L.; writing—original draft preparation, J.Y. and W.Y.; writing—review and editing, J.Y. and H.L.; funding acquisition, H.L., S.L. and H.L. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by Qingdao Science and Technology Foundation for Public Wellbeing, grant number 23-2-8-cspz-10-nsh, National Natural Science Foundation of China, grant number 31800374 and Horizontal project of Shandong Provincial Institute of Land and Space Planning, grant number 6602422217 and 6602422218.

Data Availability Statement

The raw data supporting the conclusions of this article will be made available by the authors on request.

Acknowledgments

We thank several students from Qingdao Agricultural University for data collection and compiling. The manuscript also benefited from the constructive comments and suggestions by three anonymous reviewers.

Conflicts of Interest

The authors declare no conflicts of interest.

References

Guo, W.; Serra-Diaz, J.; Eiserhardt, W.; Maitner, B.; Merow, C.; Violle, C.; Pound, M.; Sun, M.; Silk, F.; Blach-Overgaard, A.; et al. Climate Change and Land Use Threaten Global Hotspots of Phylogenetic Endemism for Trees. Nature Communications. 2023, 14, 6950. [Google Scholar] [CrossRef]
Turner-Skoff, J.; Cavender, N. The Benefits of Trees for Livable and Sustainable Communities. PLANTS, PEOPLE, PLANET. 2019, 4, 323–335. [Google Scholar] [CrossRef]
Derkzen, M.; van Teeffelen, A.; Verburg, P. Review: Quantifying Urban Ecosystem Services Based on High-Resolution Data of Urban Green Space: An Assessment for Rotterdam, the Netherlands. Journal of Applied Ecology. 2015, 52, 1020–1032. [Google Scholar] [CrossRef]
Vatandaşlar, C.; Seki, M.; Zeybek, M. Assessing the Potential of Mobile Laser Scanning for Stand-Level Forest Inventories in near-Natural Forests. Forestry: An International Journal of Forest Research. 2023, 96, 448–464. [Google Scholar] [CrossRef]
Ko, C.; Lee, J.; Kim, D.; Kang, J. The Application of Terrestrial Light Detection and Ranging to Forest Resource Inventories for Timber Yield and Carbon Sink Estimation. Forests. 2022, 13, 2087. [Google Scholar] [CrossRef]
Liu, J.; Feng, Z.; Yang, L.; Mannan, A.; Khan, T.; Zhao, Z.; Cheng, Z. Extraction of Sample Plot Parameters from 3d Point Cloud Reconstruction Based on Combined RTK and CCD Continuous Photography. Remote Sensing. 2018, 10, 1299. [Google Scholar] [CrossRef]
Brede, B.; Terryn, L.; Barbier, N.; Bartholomeus, H.; Bartolo, R.; Calders, K.; Derroire, G.; Krishna Moorthy, S.; Lau, A.; Levick, S.; et al. Non-Destructive Estimation of Individual Tree Biomass: Allometric Models, Terrestrial and Uav Laser Scanning. Remote Sensing of Environment. 2022, 280, 113180. [Google Scholar] [CrossRef]
Liang, X.; Kukko, A.; Balenovic, I.; Saarinen, N.; Junttila, S.; Kankare, V.; Holopainen, M.; Mokros, M.; Surovy, P.; Kaartinen, H.; et al. Close-Range Remote Sensing of Forests: The State of the Art, Challenges, and Opportunities for Systems and Data Acquisitions. IEEE Geoscience and Remote Sensing Magazine. 2022, 10, 32–71. [Google Scholar] [CrossRef]
Schick, M.; Griffin, R.; Cherrington, E.; Sever, T. Utilizing Lidar to Quantify Aboveground Tree Biomass within an Urban University. Urban Forestry & Urban Greening. 2023, 89, 128098. [Google Scholar] [CrossRef]
Yang, J.; Zhang, M.; Zhang, J.; Lu, H.; Richard, J. Allometric Growth of Common Urban Tree Species in Qingdao City of Eastern China. Forests. 2023, 14, 472. [Google Scholar] [CrossRef]
Zhao, C.; Sander, H. Assessing the Sensitivity of Urban Ecosystem Service Maps to Input Spatial Data Resolution and Method Choice. Landscape and Urban Planning. 2018, 175, 11–22. [Google Scholar] [CrossRef]
Brzoska, P.; Spāģe, A. From City- to Site-Dimension: Assessing the Urban Ecosystem Services of Different Types of Green Infrastructure. Land. 2020, 9, 150. [Google Scholar] [CrossRef]
Brede, B.; Calders, K.; Lau, A.; Raumonen, P.; Bartholomeus, H.; Herold, M.; Kooistra, L. Non-Destructive Tree Volume Estimation through Quantitative Structure Modelling: Comparing UAV Laser Scanning with Terrestrial LiDAR. Remote Sensing of Environment. 2019, 233, 111355. [Google Scholar] [CrossRef]
Kuželka, K.; Marušák, R.; Surový, P. Inventory of Close-to-Nature Forest Stands Using Terrestrial Mobile Laser Scanning. International Journal of Applied Earth Observation and Geoinformation. 2022, 115, 103104. [Google Scholar] [CrossRef]
Liang, X.; Wang, Y.; Jaakkola, A.; Kukko, A.; Kaartinen, H.; Hyyppa, J.; Honkavaara, E.; Liu, J. Forest Data Collection Using Terrestrial Image-Based Point Clouds from a Handheld Camera Compared to Terrestrial and Personal Laser Scanning. IEEE Transactions on Geoscience and Remote Sensing. 2015, 53, 5117–5132. [Google Scholar] [CrossRef]
Münzinger, M.; Prechtel, N.; Behnisch, M. Mapping the Urban Forest in Detail: From LiDAR Point Clouds to 3D Tree Models. Urban Forestry & Urban Greening. 2022, 74, 127637. [Google Scholar] [CrossRef]
Su, Y.; Guo, Q.; Xue, B.; Hu, T.; Alvarez, O.; Tao, S.; Fang, J. Spatial Distribution of Forest Aboveground Biomass in China: Estimation through Combination of Spaceborne Lidar, Optical Imagery, and Forest Inventory Data. Remote Sensing of Environment. 2016, 173, 187–199. [Google Scholar] [CrossRef]
Tupinambá-Simões, F.; Pascual, A.; Guerra-Hernández, J.; Ordóñez, C.; de Conto, T.; Bravo, F. Assessing the Performance of a Handheld Laser Scanning System for Individual Tree Mapping—a Mixed Forests Showcase in Spain. Remote Sensing. 2023, 15, 1169. [Google Scholar] [CrossRef]
Liang, X.; Kankare, V.; Hyyppä, J.; Wang, Y.; Kukko, A.; Haggrén, H.; Yu, X.; Kaartinen, H.; Jaakkola, A.; Guan, F.; et al. Terrestrial Laser Scanning in Forest Inventories. ISPRS Journal of Photogrammetry and Remote Sensing. 2016, 115, 63–77. [Google Scholar] [CrossRef]
Guan, H.; Su, Y.; Sun, X.; Xu, G.; Li, W.; Ma, Q.; Wu, X.; Wu, J.; Liu, L.; Guo, Q. A Marker-Free Method for Registering Multi-Scan Terrestrial Laser Scanning Data in Forest Environments. ISPRS Journal of Photogrammetry and Remote Sensing. 2020, 166, 82–94. [Google Scholar] [CrossRef]
Moskal, L.; Zheng, G. Retrieving Forest Inventory Variables with Terrestrial Laser Scanning (TLS) in Urban Heterogeneous Forest. Remote Sensing. 2011, 4, 1–20. [Google Scholar] [CrossRef]
Watt, P.; Donoghue, D. Measuring Forest Structure with Terrestrial Laser Scanning. International Journal of Remote Sensing. 2005, 26, 1437–46. [Google Scholar] [CrossRef]
Wilkes, P.; Lau, A.; Disney, M.; Calders, K.; Burt, A.; Gonzalez de Tanago, J.; Bartholomeus, H.; Brede, B.; Herold, M. Data Acquisition Considerations for Terrestrial Laser Scanning of Forest Plots. Remote Sensing of Environment. 2017, 196, 140–153. [Google Scholar] [CrossRef]
Kukko, A.; Kaijaluoto, R.; Kaartinen, H.; Lehtola, V.; Jaakkola, A.; Hyyppä, J. Graph Slam Correction for Single Scanner MLS Forest Data under Boreal Forest Canopy. ISPRS Journal of Photogrammetry and Remote Sensing. 2017, 132, 199–209. [Google Scholar] [CrossRef]
Chen, S.; Liu, H.; Feng, Z.; Shen, C.; Chen, P. Applicability of Personal Laser Scanning in Forestry Inventory. PLOS ONE. 2019, 14, e0211392. [Google Scholar] [CrossRef]
Gollob, C.; Ritter, T.; Nothdurft, A. Forest Inventory with Long Range and High-Speed Personal Laser Scanning (PLS) and Simultaneous Localization and Mapping (Slam) Technology. Remote Sensing. 2020, 12, 1509. [Google Scholar] [CrossRef]
Cabo, C.; Del Pozo, S.; Rodríguez-Gonzálvez, P.; Ordóñez, C.; González-Aguilera, D. Comparing Terrestrial Laser Scanning (TLS) and Wearable Laser Scanning (WLS) for Individual Tree Modeling at Plot Level. Remote Sensing. 2018, 10, 540. [Google Scholar] [CrossRef]
Liu, L.; Zhang, A.; Xiao, S.; Hu, S.; He, N.; Pang, H.; Zhang, X.; Yang, S. Single Tree Segmentation and Diameter at Breast Height Estimation with Mobile LiDAR. IEEE Access. 2021, 9, 24314–24325. [Google Scholar] [CrossRef]
Oveland, I.; Hauglin, M.; Giannetti, F.; Kjørsvik, N.; Gobakken, T. Comparing Three Different Ground Based Laser Scanning Methods for Tree Stem Detection. Remote Sensing. 2018, 10, 538. [Google Scholar] [CrossRef]
Balenovic, I.; Liang, X.; Jurjevic, L.; Hyyppä, J.; Seletković, A.; Kukko, A. Hand-Held Personal Laser Scanning. Croatian journal of forest engineering. 2021, 42, 165–183. [Google Scholar] [CrossRef]
Bauwens, S.; Bartholomeus, H.; Calders, K.; Lejeune, P. Forest Inventory with Terrestrial LiDAR: A Comparison of Static and Hand-Held Mobile Laser Scanning. Forests. 2016, 7, 127. [Google Scholar] [CrossRef]
Ryding, J.; Williams, E.; Smith, M.; Eichhorn, M. Assessing Handheld Mobile Laser Scanners for Forest Surveys. Remote Sensing. 2015, 7, 1095–111. [Google Scholar] [CrossRef]
Tupinambá-Simões, F.; Pascual, A.; Guerra-Hernández, J.; Ordóñez, C.; de Conto, T.; Bravo, F. Assessing the Performance of a Handheld Laser Scanning System for Individual Tree Mapping—a Mixed Forests Showcase in Spain. Remote Sensing. 2023, 15, 1169. [Google Scholar] [CrossRef]
Hyyppä, E.; Yu, X.; Kaartinen, H.; Hakala, T.; Kukko, A.; Vastaranta, M.; Hyyppä, J. Comparison of Backpack, Handheld, under-Canopy UAV, and above-Canopy UAV Laser Scanning for Field Reference Data Collection in Boreal Forests. Remote Sensing. 2020, 12, 3327. [Google Scholar] [CrossRef]
Perugia, B.; Giannetti, F.; Chirici, G.; Travaglini, D. Influence of Scan Density on the Estimation of Single-Tree Attributes by Hand-Held Mobile Laser Scanning. Forests. 2019, 10, 277. [Google Scholar] [CrossRef]
Balenović, I.; Liang, X.; Jurjević, L.; Hyyppä, J.; Seletković, A.; Kukko, A. Hand-Held Personal Laser Scanning. Croatian journal of forest engineering. 2021, 42, 165–83. [Google Scholar] [CrossRef]
Yang, J.; Li, X.; Li, S.; Liang, H.; Lu, H. The Woody Plant Diversity and Landscape Pattern of Fine-Resolution Urban Forest Along a Distance Gradient from Points of Interest in Qingdao. Ecological Indicators. 2021, 122, 107326. [Google Scholar] [CrossRef]
Yang, J.; Li, S.; Lu, H. Quantitative Influence of Land-Use Changes and Urban Expansion Intensity on Landscape Pattern in Qingdao, China: Implications for Urban Sustainability. Sustainability. 2019, 11, 6174. [Google Scholar] [CrossRef]
Team, R Core. R: A Language and Environment for Statistical Computing. R Foundation for Statistical Computing, Vienna, Austria. 2018. Available online at https://www.R-project.org/.
Bates, D.; Maechler, M.; Bolker, B.; Walker, S. Lme4: Mixed-Effects Models in R. 2013. Available online at https://github.com/lme4/lme4/.
Barton, K. Mumin: Multi-Model Inference. R package version 1.47.5. 2013. Available online at http://cran.r-project.org/package=MuMIn.
Puente, I.; González-Jorge, H.; Martínez-Sánchez, J.; Arias, P. Review of Mobile Mapping and Surveying Technologies. Measurement. 2013, 46, 2127–2145. [Google Scholar] [CrossRef]
Kaartinen, H.; Hyyppä, J.; Vastaranta, M.; Kukko, A.; Jaakkola, A.; Yu, X.; Pyörälä, J.; Liang, X.; Liu, J.; Wang, Y.; et al. Accuracy of Kinematic Positioning Using Global Satellite Navigation Systems under Forest Canopies. Forests. 2015, 6, 3218–3236. [Google Scholar] [CrossRef]
Piermattei, L.; Karel, W.; Wang, D.; Wieser, M.; Mokroš, M.; Surový, P.; Koreň, M.; Tomaštík, J.; Pfeifer, N.; Hollaus, M. Terrestrial Structure from Motion Photogrammetry for Deriving Forest Inventory Data. Remote Sensing. 2019, 11, 950. [Google Scholar] [CrossRef]
Mikita, T.; Janata, P.; Surový, P. Forest Stand Inventory Based on Combined Aerial and Terrestrial Close-Range Photogrammetry. Forests. 2016, 7, 165. [Google Scholar] [CrossRef]
Guo, Q.; Su, Y.; Hu, T.; Guan, H.; Jin, S.; Zhang, J.; Zhao, X.; Xu, K.; Wei, D.; Kelly, M.; et al. Lidar Boosts 3D Ecological Observations and Modelings: A Review and Perspective. IEEE Geoscience and Remote Sensing Magazine. 2021, 9, 232–257. [Google Scholar] [CrossRef]
Jurjević, L.; Liang, X.; Gašparović, M.; Balenović, I. Is Field-Measured Tree Height as Reliable as Believed - Part II, a Comparison Study of Tree Height Estimates from Conventional Field Measurement and Low-Cost Close-Range Remote Sensing in a Deciduous Forest. ISPRS Journal of Photogrammetry and Remote Sensing. 2020, 169, 227–241. [Google Scholar] [CrossRef]
Zhou, S. , Kang, F.; Li, W.; Kan, J.; Zheng, Y.; He, G. Extracting Diameter at Breast Height with a Handheld Mobile LiDAR System in an Outdoor Environment. Sensors (Basel). 2019, 19, 3212. [Google Scholar] [CrossRef] [PubMed]
Heo, H.; Lee, D.; Park, J.; Thorne, J. Estimating the Heights and Diameters at Breast Height of Trees in an Urban Park and Along a Street Using Mobile LiDAR. Landscape and Ecological Engineering. 2019, 15, 253–263. [Google Scholar] [CrossRef]
Liang, X.; Hyyppä, J.; Kaartinen, H.; Lehtomäki, M.; Pyörälä, J.; Pfeifer, N.; Holopainen, M.; Brolly, G.; Francesco, P.; Hackenberg, J.; et al. International Benchmarking of Terrestrial Laser Scanning Approaches for Forest Inventories. ISPRS Journal of Photogrammetry and Remote Sensing. 2018, 144, 137–179. [Google Scholar] [CrossRef]
Bienert, A.; Georgi, L.; Kunz, M.; Maas, H.; Oheimb, G. Comparison and Combination of Mobile and Terrestrial Laser Scanning for Natural Forest Inventories. Forests. 2018, 9, 395. [Google Scholar] [CrossRef]
Sofia, S.; Maetzke, F.; Crescimanno, M.; Coticchio, A.; La Mela Veca, D.; Galati, A. The Efficiency of Lidar Hmls Scanning in Monitoring Forest Structure Parameters: Implications for Sustainable Forest Management. EuroMed Journal of Business. 2022, 17, 350–373. [Google Scholar] [CrossRef]
Chiappini, S.; Pierdicca, R.; Malandra, F.; Tonelli, E.; Malinverni, E.; Urbinati, C.; Vitali, A. Comparing Mobile Laser Scanner and Manual Measurements for Dendrometric Variables Estimation in a Black Pine (Pinus Nigra Arn.) Plantation. Computers and Electronics in Agriculture. 2022, 198, 107069. [Google Scholar] [CrossRef]
Donager, J.; Sánchez Meador, A.; Blackburn, R. Adjudicating Perspectives on Forest Structure: How Do Airborne, Terrestrial, and Mobile Lidar-Derived Estimates Compare? Remote Sensing. 2021, 13, 2297. [Google Scholar] [CrossRef]
Giannetti, F.; Puletti, N.; Quatrini, V.; Travaglini, D.; Bottalico, F.; Corona, P.; Chirici, G. Integrating Terrestrial and Airborne Laser Scanning for the Assessment of Single-Tree Attributes in Mediterranean Forest Stands. European Journal of Remote Sensing. 2018, 51, 795–807. [Google Scholar] [CrossRef]
Jurjević, L.; Gašparović, M.; Liang, X.; Balenović, I. Assessment of Close-Range Remote Sensing Methods for DTM Estimation in a Lowland Deciduous Forest. Remote Sensing. 2021, 13, 2063. [Google Scholar] [CrossRef]
Persson, H.; Olofsson, K. , Holmgren, J. Two-Phase Forest Inventory Using Very-High-Resolution Laser Scanning. Remote Sensing of Environment. 2022, 271, 112909. [Google Scholar] [CrossRef]
Liang, X.; Wang, Y.; Pyörälä, J.; Lehtomäki, M.; Yu, X.; Kaartinen, H.; Kukko, A.; Honkavaara, E.; Issaoui, A.; Nevalainen, O.; et al. Forest in Situ Observations Using Unmanned Aerial Vehicle as an Alternative of Terrestrial Measurements. Forest Ecosystems. 2019, 6, 20. [Google Scholar] [CrossRef]
Mokroš, M.; Mikita, T.; Singh, A.; Tomaštík, J.; Chudá, J.; Wężyk, P. , Kuželka, K.; Surový, P.; Klimánek, M.; Zięba-Kulawik, K.; et al. Novel Low-Cost Mobile Mapping Systems for Forest Inventories as Terrestrial Laser Scanning Alternatives. International Journal of Applied Earth Observation and Geoinformation. 2021, 104, 102512. [Google Scholar] [CrossRef]

Figure 3. Path planning for dense trees (a) and sparse trees (b) conditions.

Figure 4. An example of point cloud profiles from two sample plots. The top image depicts the profile of a flat ground, while the bottom one illustrates the profile of a hilly area.

Figure 5. An example of register tree position and trajectory using the affine transformation method. GCP-1 indicates the Ground Control Point and ligrip-0 refers to its corresponding local coordinates in the point cloud marked with the HLS device.

Figure 6. The accuracy of registration for tree position.

Figure 7. HLS-derived versus observed DBH (diameter at breast height) and H (tree height) for all species, broad-leaved and coniferous trees. The red lines represent the linear regressions, while the dashed lines are the 1:1.

Figure 8. Comparison of the performance of HLS in estimating DBH (diameter at breast height) between 13 tree species. The red lines represent the linear regressions, while the dashed lines are the 1:1.

Figure 9. Comparison of the performance of HLS in estimating H (tree height) between 13 species. The red lines represent the linear regressions between measured H and HLS-derived H, while the dashed lines are the 1:1.

Figure 10. Boxplot with the accuracy of DBH (diameter at breast height) and H (tree height) for different plant types (broadleaf or conifer) and terrain (flat or hilly) of the plot. Where Flat.B and Hilly.C indicate broadleaved tree species on flat ground and conifer tree species on a hilly terrain, respectively.

Table 1. The summary information of the 34 measured plots on the campus of QAU.

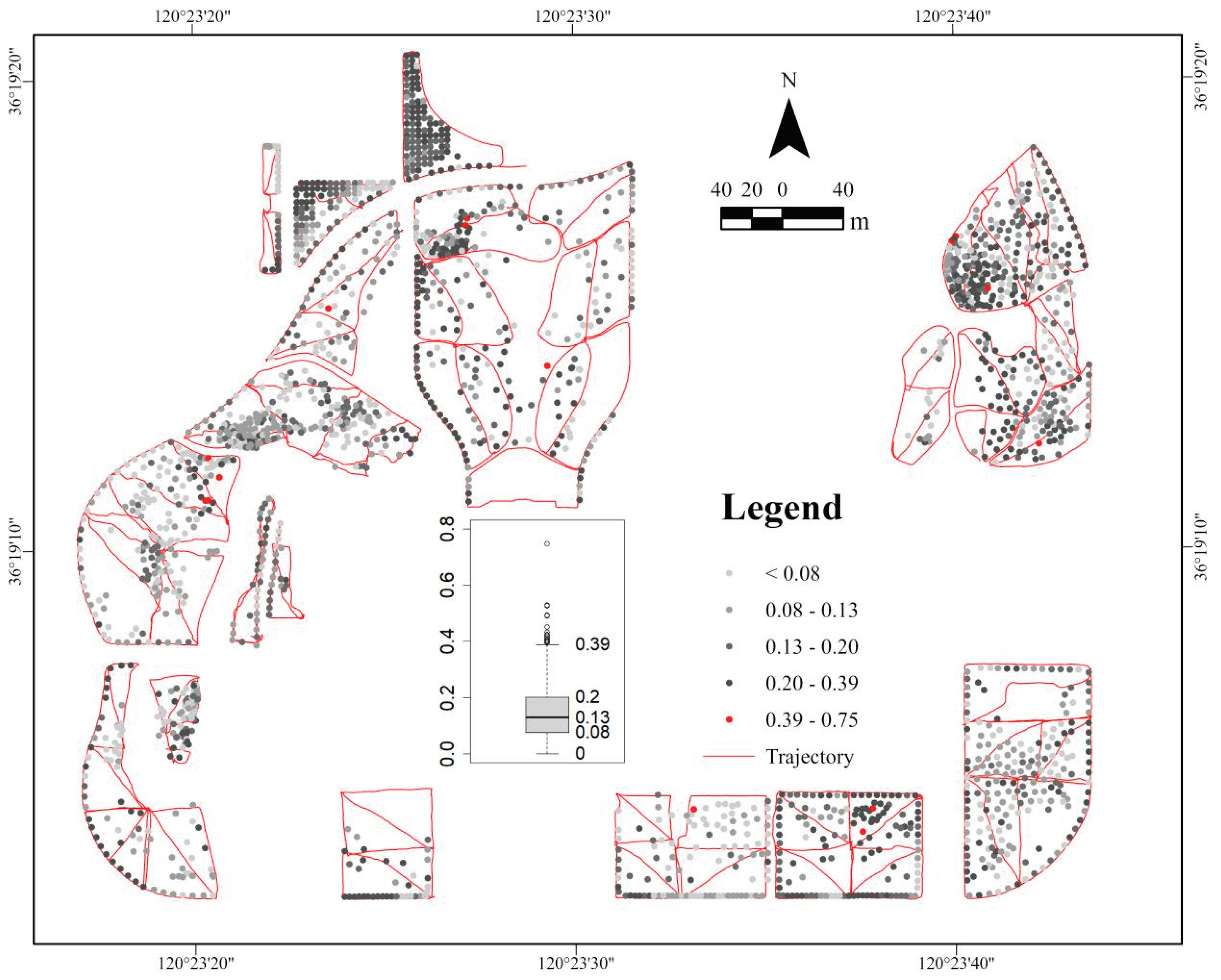
Plot ID	n	DBH range (cm)	Mean DBH (cm)	H range (m)	Mean H (m)	Area (m2)	Tree density (tree/hectares)	Trajectory length (m)	Scanning time (min)	Terrain
Plot 1	67	16.1-62.9	33.7	11.2-22.7	19.1	2230	300	330	7.5	Flat
Plot 2	50	21.0-59.5	36.6	10.8-25.2	19.0	3465	144	446	11.3	Flat
Plot 3	20	10.3-41.3	21.8	5.6-14.5	9.6	2533	237	382	9.0	Flat
Plot 4	29	20.8-45.4	35.7	15.1-22.6	19.9	1566	230	335	10.1	Flat
Plot 5	259	5.1-62.5	25.2	5.0-23.7	14.4	6096	428	843	24.3	Flat
Plot 6	31	14.4-55.2	37.5	7.0-20.6	15.1	3060	101	361	9.1	Flat
Plot 7	73	11.0-57.1	22.2	6.5-21.6	9.6	3211	230	440	12.3	Flat
Plot 8	95	5.0-72.3	31.7	4.9-24.6	12.3	4995	228	475	12.6	Flat
Plot 9	69	12.7-70	33.4	8.3-23.8	16.7	3245	213	446	12.7	Flat
Plot 10	61	12.4-53.8	37.5	12.4-26.2	19.1	3444	177	446	13.1	Flat
Plot 11	66	14.3-52.7	35.5	8.4-24.0	17.6	3700	181	394	11.7	Flat
Plot 12	38	23.8-58.1	41.5	12.9-22.5	18.6	2539	161	401	12.8	Flat
Plot 13	36	12.3-63.5	43.2	8.3-23.6	19.4	4121	87	485	12.1	Flat
Plot 14	28	10.8-67.0	41.0	6.0-24.1	17.1	2443	115	287	7.2	Flat
Plot 15	19	10.3-66.5	46.6	7.7-25.6	19.5	1484	128	221	6.2	Flat
Plot 16	35	5.7-63.8	34.2	3.3-23.6	13.1	2160	204	414	9.1	Flat
Plot 17	81	5.5-43.5	18.9	3.4-18.0	12.2	936	865	237	7.4	Hilly
Plot 18	81	5.5-63.5	30.7	4.0-27.6	13.0	5943	138	611	16.8	Hilly
Plot 19	103	9.1-62.2	25.4	5.4-19.6	10.9	4865	245	557	16.5	Hilly
Plot 20	34	15.0-55.0	35.0	10.1-18.1	14.3	770	455	471	9.6	Flat
Plot 21	19	6.3-36.0	26.4	2-17.5	13.2	656	488	295	8.0	Flat
Plot 22	94	7.4-55.0	20.2	4.9-18.2	8.7	1581	626	262	7.2	Hilly
Plot 23	116	7.4-57.0	20.8	2.9-19.2	9.0	4606	280	571	17.9	Hilly
Plot 24	68	8.2-61.4	36.5	3.7-19.6	13.2	3434	198	531	14.7	Flat
Plot 25	23	9.7-18.2	14.7	6.3-8.9	7.6	808	285	303	8.6	Flat
Plot 26	95	9.1-61.2	21.2	4.9-24.6	9.0	1484	640	263	6.3	Flat
Plot 27	108	7.7-62.4	18.3	5.4-22.6	8.1	2402	450	288	5.9	Flat
Plot 28	85	5.9-62.9	28.4	4.5-21.8	11.4	3523	250	384	7.4	Flat
Plot 29	48	13.1-54.7	30.6	6.7-21.3	11.9	2880	167	312	6.5	Flat
Plot 30	50	10.0-64.0	38.0	6.1-22.4	13.8	3375	148	327	7.1	Flat
Plot 31	12	12.9-49.4	30.5	7.1-18.8	12.2	2116	57	217	5.1	Flat
Plot 32	32	13.6-72.0	42.3	8.2-21.4	16.6	3643	88	348	7.4	Flat
Plot 33	35	9.5-49.3	33.3	6.6-18.3	13.1	3211	118	326	8.5	Flat
Plot 34	23	24.9-52.7	39.3	12-18.7	15.1	2337	128	293	7.6	Flat

where n is the number of trees, DBH indicates Diameter at Breast Height, H is tree height and mean DBH refers to the quadratic mean of DBH values.

Table 2. Summary statistics of tree species collected from 34 plots.

Plant type	Species	n	DBH				Tree height
Plant type	Species	n	Min	Max	Mean	Sd	Min	Max	Mean	Sd
Broadleaf	Catalpa bungei	47	36.4	58.1	48.3	4.9	14.6	23.1	19.2	1.7
	Fraxinus chinensis	92	15.0	57.0	31.6	7.4	9.2	20.4	14.9	2.2
	Ginkgo biloba	355	5.5	41.2	14.1	3.3	4.0	15.1	7.7	1.2
	Koelreuteria paniculata	120	5.5	38.4	21.0	6.6	3.4	19.6	12.6	3.2
	Platanus acerifolia	456	13.8	72.3	43.0	10.6	9.1	27.6	19.3	2.6
	Prunus cerasifera' Atropurpurea'	50	5.9	38.7	13.8	5.6	4.5	21.1	7.8	2.4
	Robinia pseudoacacia	49	5.1	28.5	16.3	6.1	5.0	18.0	12.4	3.1
	Salix babylonica	44	5.0	55.0	38.6	9.6	4.9	18.1	14.5	2.1
	Styphnolobium japonicum	292	5.3	70.0	26.2	11.3	3.7	23.7	13.6	3.4
	Yulania denudata	28	5.7	25.0	12.6	4.4	3.3	12.6	7.7	2.0
	Total	1533	5.0	72.3	30.9	14.7	3.3	27.6	14.1	5.2
Coniferous	Cedrus deodara	121	13.5	63.5	40.0	8.8	8.2	20.2	14.7	2.4
	Metasequoia glyptostroboides	125	12.3	48.4	32.3	8.4	8.3	26.2	20.0	3.4
	Pinus thunbergii	304	6.3	38.4	15.4	5.0	2.0	15.1	8.7	2.0
	Total	550	6.3	63.5	26.8	12.6	2.0	26.2	13.4	5.3

where n is the number of trees, DBH indicates the Diameter at Breast Height, mean DBH refers to the quadratic mean of DBH values, and Sd indicates the standard deviation.

Table 3. The coefficients (Coef.), standard errors (Std.Error) and P-values (P) of linear mixed-effects models between the accuracy (RMSE, RMSE%, Bias, Bias% for DBH and H) and its candidate influence factors (tree density, trajectory length, scanning time, terrain of plot and plant type).

Fixed effects	RMSE_DBH			RMSE%_DBH			Bias_DBH			Bias%_DBH
Fixed effects	Coef.	Std.Error	P	Coef.	Std.Error	P	Coef.	Std.Error	P	Coef.	Std.Error	P
Area	-0.00007	0.00005	0.2222	0.0003	0.0004	0.509	-0.0001	0.2533	0.1471	-0.0003	0.0004	0.4125
Tree density	-0.0005	0.0003	0.1188	0.0054	0.0022	0.0186	-0.0015	0.0005	0.0047	-0.0034	0.002	0.0997
Trajectory length	0.0006	0.0005	0.2230	-0.0027	0.0038	0.4916	0.0009	0.0008	0.3034	0.0016	0.0036	0.6589
Plant type/Conifer	0.6519	0.01556	<10-3	4.9848	0.1661	<10-3	-0.5108	0.0418	<10-3	-2.9707	0.1521	<10-3
Terrain/Hilly	0.2430	0.1260	0.0636	2.0013	0.9630	0.0467	-0.4746	0.2167	0.0367	-2.3887	0.8988	0.0127
Random effects	variance	Std.Dev.		variance	Std.Dev.		variance	Std.Dev.		variance	Std.Dev.
Plot (intercept)	0.0438	0.2094		2.516	1.5862		0.1264	0.3555		2.1942	1.4813
Residual	0.0551	0.2348		6.3388	2.5177		0.4031	0.6349		5.3126	2.3049
Fixed effects	RMSE_H			RMSE%_H			Bias_H			Bias%_H
Fixed effects	Coef.	Std.Error	P	Coef.	Std.Error	P	Coef.	Std.Error	P	Coef.	Std.Error	P
Area	-0.00004	0.00004	0.4026	0.0002	0.0005	0.7394	-0.000007	0.00003	0.8172	0.000002	0.0086	0.6041
Tree density	-0.0003	0.0002	0.1759	0.0032	0.0026	0.2201	-0.00004	0.0002	0.8138	0.00001	0.00002	0.4319
Trajectory length	0.0005	0.0004	0.2394	-0.0005	0.0045	0.9045	0.0001	0.0003	0.7024	-0.000008	0.00003	0.7829
Plant type/Conifer	0.0989	0.0111	<10-3	3.0512	0.1603	<10-3	-0.0799	0.0104	<10-3	0.0026	0.001	0.0106
Terrain/Hilly	0.1655	0.1017	0.1146	1.7915	1.1351	0.1253	0.0909	0.0745	0.2327	0.0055	0.0075	0.4708
Random effects	variance	Std.Dev.		variance	Std.Dev.		variance	Std.Dev.		variance	Std.Dev.
Plot (intercept)	0.0286	0.1691		3.5325	1.8795		0.0153	0.1235		0.0002	0.0124
Residual	0.0282	0.168		5.8574	2.4202		0.0248	0.1576		0.0002	0.0151

Table 4. The coefficients (Coef.), standard errors (Std.Error) and P-values (P) of final models between the accuracy (RMSE, RMSE%, Bias, Bias% for DBH and H) and its candidate influence factors (tree density, trajectory length, scanning time, terrain of plot and plant type).

Fixed effects	RMSE_DBH			RMSE%_DBH			Bias_DBH			Bias_DBH
Fixed effects	Coef.	Std.Error	P	Coef.	Std.Error	P	Coef.	Std.Error	P	Coef.	Std.Error	P
Plant type/Conifer	0.6534	0.01554	<10^-3	4.9785	0.1663	<10^-3	-0.5087	0.0419	<10^-3	-2.9649	0.1521	<10^-3
Terrain/Hilly	-	-	-	3.1313	0.9009	0.0015	-0.8248	0.2074	<10^-3	-3.2282	0.7856	<10^-3
Random effects	variance	Std.Dev.		variance	Std.Dev.		variance	Std.Dev.		variance	Std.Dev.
Plot (intercept)	0.0453	0.2129		3.369	1.835		0.1776	0.4214		2.555	1.598
Residual	0.0551	0.2348		6.342	2.518		0.4033	0.635		5.315	2.305
Fixed effects	RMSE_H			RMSE%_H			Bias_H			Bias%_H
Fixed effects	Coef.	Std.Error	P	Coef.	Std.Error	P	Coef.	Std.Error	P	Coef.	Std.Error	P
Plant type/Conifer	0.0997	0.032	<10^-3	3.0477	0.1602	<10^-3	-0.079	0.0104	<10^-3	0.0206	0.0023	0.0087
Terrain/Hilly	-	-	-	2.5277	0.9752	0.0144	-	-	-	-	-	-
Random effects	variance	Std.Dev.		variance	Std.Dev.		variance	Std.Dev.		variance	Std.Dev.
Plot (intercept)	0.0338	0.1839		3.971	1.993		0.0168	0.1296		0.0002	0.0131
Residual	0.0283	0.1681		5.86	2.421		0.0249	0.1577		0.0002	0.0151

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer