Preprint
Article
Solvent Extraction of Au(III) by 2-ethylhexanol and Kinetic Modelling of the Facilitated Transport Across a Liquid Membrane
Altmetrics
Downloads
92
Views
26
Comments
0
This version is not peer-reviewed
Submitted:
20 February 2024
Posted:
20 February 2024
You are already at the latest version
Alerts
Abstract
The solvent extraction of gold(III) by undiluted 2-ethylhexanol or dissolved in toluene from HCl solution has been investigated. The numerical analysis of gold distribution data suggests the formation of HAuCl4·L and HAuCl4·2L (L= 2-ethylhexanol) species in the organic phase with formation constants K11= 38 and K12= 309, respectively. The results derived from gold(III) distribution have been implemented in a solid-supported liquid membrane system. The influence of several variables on gold transport was considered: feed and receiving phases stirring speeds, HCl and gold concentrations in the feed phase and carrier concentration in the membrane phase as well as the presence of base metals (Fe,Cu,Ni) and PGMs in the feed phase. Also, diffusional resistances to mass transfer are estimated. Gold is recovered as zero valent nanoparticles.
Keywords:
Subject: Chemistry and Materials Science - Applied Chemistry
1. Introduction
Over the last years, there were an increasing interest in the recovery and utilization of the so-named strategic metals (rare earth elements, lithium, neodymium and tantalum, etc.), less mentioned was the recovery, from secondary materials or wastes, of gold and platinum group metals which always were of interest.
The recovery of gold has two main tendencies: i) recovery from raw materials, which is dominated by cyanidation and gold adsorption, and ii) recovery from secondary materials or wastes (printed circuit boards, jewelry scraps, e-wastes, etc.), in which the precious metal is usually dissolved in non-cyanide medium i.e. aqua regia, thiourea, tiosulphate, etc, From the leachates, gold is purified and recovered by the use of different options.
Though yet with not any apparent or definitive practical application, the scientific community considered of importance the recovery of gold from these various non-cyanide media, importance which is reflected by the series of publications that every year appeared in journals. In the case of gold adsorption onto different materials recent several approaches are considered by the use of metal organic frameworks [1], metal sulphides microspheres [2] or Aliquat 336 (quaternary ammonium salt) impregnating Nitrolite adsorbent [3].
It is well known the recovery of metals by solvent extraction processing, this is also demonstrated by the number of publications produced over the years. Gold (III) solvent extraction has attracted interest, with recent publications involving the use of ionic liquids [4] or pseudo-protic ionic liquids [5] as extractants for this precious metal.
Due to some environmental concerns, liquid membranes emerged as an alternative to solvent extraction, however, it must say here that at the present time still there is not any plant using any of the different liquid membranes operational variations. Indeed, the interest of scientists for the utilization of these membranes technologies on the recovery of metals or other pollutants still is alive as some recent publications also demonstrated. Several reviews about the general use of liquid membranes included: the transport of actinide elements using diglycolamides as carriers [6] and the application of membranes on the recovery of various elements [7-10], with mention to the use of polymer-inclusion membranes (PIMs) [11]. Experimental papers were devoted to investigate the transport of both, inorganic and organic solutes or harmful species of potential appearance in liquid wastes. As organic compounds, it was investigated the transport of diclofenac and iboprufene by supported liquid membrane technology and using Cyanex 923 (mixture of tri-alkylphosphine oxides) dissolved in kerosene as carrier phase [12,13]. By the use of flat-sheet supported liquid membrane operational mode, the transport of chromium(VI), indium(III) and the separation of Nd(III) and Er(III) were investigated [14-16]; a variation of the above operation was the investigation of the transport process (copper, zinc or cobalt) using electromembranes [17-19].
The utilization of a more dynamic supported liquid membrane procedure as is the operation in hollow fiber modules, found applications in the simultaneous removal of arsenic and mercury [20] or only mercury [21]. A yet more advanced hollow fiber operation, as it is the so-called (though other names are using) pseudo-emulsion based hollow fiber membrane with strip dispersion technology (PEHFMSD), in which, differently to conventional hollow fiber operation using two modules (one for extraction and other for stripping), just one module was used for extraction and stripping. Moreover, in this PEHFMSD operation the organic and the receiving or stripping phase were mixed in one tank, and continuously pumped to the module, to improve the transport and the removal of the solute from the feed to the organic and from the organic to the receiving phases. This PEHFMSD operation was recently used in the removal of iron(III) [22] and in the treatment of stainless steel rinse waters [23]. It is worth to note that against all the literature favoring the use of liquid membranes in the treatment of wastewaters, these technologies seemed to be unpopular in the case of acid mine wastewater treatment [24].
In these membranes operations is of the utmost importance gain knowledge on interfacial phenomena associated to metal-carrier (extractant) chemical reactions occurring in the feed phase and the membrane interfaces when the metal (solute) is transported against its concentration gradient. Before scaling up the flat-sheet supported liquid membrane operation (the most simple form of supported liquid membranes), in spiral wound or hollow fiber modules operational modes, a theoretical model of the membrane system is welcomed in order to design an efficient and stable process.
The present work implemented solvent extraction investigations in a solid-supported liquid membrane configuration. Firstly, a quantitative characterization of the solvent extraction of gold(III) by 2-ethylhexanol was undertaken. Further, a liquid membrane system was designed by using the extraction process mentioned above, and the parameters affecting the liquid membrane: stirring speeds applied on both feed and receiving phases, compositions of the feed and organic phases, etc. were investigated. A model was developed to estimate the mass transfer coefficients relative to the transport of gold across the 2-ethylhexanol-immobilized supported liquid membrane.
2. Materials and Methods
2.1. Materials
A stock solution of gold(III) was prepared by dissolving HAuCl4 (Fluka) in HCl. The aqueous solutions for solvent extraction or membrane transport experiments were prepared by dilution of this stock solution. The extractant 2-ethylhexanol (Merck) was used without further purification. The PGMs stock solution was a commercially available standard solution for ICP analysis. All other reagents used in the investigation were of AR grade.
The support for the liquid membrane was a polydifluoroethylene film (Millipore GVHP4700) with thickness of 125·10-4 cm, porosity 75%, tortuosity 1.67, and 0.22 µm average pore size.
2.2. Methods
2.2.1. Liquid-liquid extraction experiments
Before experimentation, undiluted 2-ethylhexanol was pre-saturated with 6 M HCl in order to avoid change in the organic and aqueous phases volume after gold extraction, and from this pre-saturated alcoholic solution all the organic phases used in the investigation were prepared. Distribution ratio experiments were performed at 20º C by shaking (800 min-1) equal volumes (25 cm3) of the aqueous and organic phases in glass separatory funnels for the required time. After phase separation, the metal remaining in the raffinate was analysed by AAS using a Perkin Elmer 1100B spectrophotometer. The amount of metals extracted in the organic phase was calculated by difference with the initial concentration in the aqueous phase. The percentage of extraction was calculated as:
where [M]aq,0 and [M]aq,t were the metal concentrations in the initial aqueous phase and in the raffinate, respectively.
2.2.2. Liquid membrane experiments
The batch transport experiments were carried out in a methacrylate permeation cell having two (200 cm3 each) compartments separated by the solid support. One compartment was for the feed phase and the other for the receiving or stripping phase. The liquid membrane was prepared by impregnation of the laminar microporous support by the carrier phase during 24 hours, and then leaving it to drip during twenty seconds, before placing in the cell. Metal contents in the feed and receiving phases were periodically analyzed by AAS or ICP (Platinum Group Metals), whereas the overall mass transfer coefficient (K0) was calculated from:
where [M]f,0 and [M]f,t were the metal concentrations in the feed at time zero at an elapsed time, respectively, A was the effective membrane area 11.3 cm2, V the volume of the feed phase (200 cm3), and t the elapsed time.
3. Results and discussion
3.1. Solvent extraction experiments
Firstly, it was studied the influence of equilibration time on attachement gold(III) extraction equilibrium. In these series of experiments the aqueous phase contained 35 g/L Au(III) in 6 M HCl, whereas the organic phase was of 75% v/v 2-ethylhexanol in toluene. From results showed in Table 1 it can be concluded that equilibrium was almost reached within 2 minutes of contact between both phases, and the same conclusion was reached when the aqueous phase contained other (15-100 g/L) gold concentrations.
In this Table 1, the fractional attachment to equilibrium (F) was calculated as:
where [Au]org,t and [Au]org,e were the gold concentrations in the organic phase at an elapsed time and at the equilibrium, respectively. According with these experimental data, all subsequent experiments were carried out using 5 minutes of contact between the respective organic and aqueous phases.
The variation of the initial gold concentration on the extraction of this precious metal from 6 M HCl medium was also investigated. In these cases, the initial aqueous solutions contained varying gold concentrations in the 5-200 g/L range, and the organic phases were of undiluted 2-ethylhexanol. The results from this set of experiments were shown in Table 2.
These results concluded that in the 5-100 g/L gold concentrations range the variation in the percentage of gold extraction in the organic phase was almost negligible (96-98%), whereas at higher initial gold concentrations in the aqueous solutions these percentages decreased from 93% at 100 g/L gold to 87% at 200 g/L gold. This decrease in the percentage of gold extraction with the increase of the initial metal concentration was not rare [25-28], and it can be due to polymerization of the metal in the aqueous phase and also to the common ion effect, in which the organic phase was dominated by the metal anion (AuCl4- in this work) and the aqueous phase by the halide ions (Cl- in this case) [29].
The influence of the variation of the initial extractant concentration on gold extraction was also investigated using organic phases containing 25-90% v/v 2-ethylhexanol in toluene or undiluted extractant. The aqueous phase were of 35 g/L Au(III) in a 6 M HCl medium, showing Table 3 the results from the experiments.
These results indicated that there was an increase of the percentage of gold extraction with the increase of the extractant concentration in the organic phase from 25 to 60% v/v, though for extractant concentrations higher than 70% v/v the variation in gold extraction did not exceed 5%.
The stoichiometry of the extracted species and their equilibrium constants were determined by the treatment of the experimental data by a numerical program, which minimized the U function defined as:
being Dcal and Dexp the respective distribution ratios calculated from the mass balance equations for the various models and experimentally calculated as:
The results of the numerical treatment indicated that the extraction of gold(III) can be explained (U= 0.009) by formation of HAuCl4·L (log Kext= 1.58±0.09) and HAuCl4·2L (log Kext= 2.49±0.26) species in the gold-loaded organic phases. In the above formulations, L represented 2-ethylhexanol molecules.
Once gold was extracted into the organic phase, the stripping operation was performed using water as strippant. In this case from an organic phase of undiluted 2-ethylhexanol containing 34 g/L gold and using the same volume of water (Org/Aq= 1), near 89% gold was recovered at 20º C in one step. From these solutions, gold can be recovered by precipitation with sodium borohydride, oxalic acid, etc., however, this last step was not investigated here but it was in the case of solutions derived from the supported liquid membrane experimentation (see further).
The selectivity of the present system against the presence of Cu(II), Zn(II) and Ni(II) in the aqueous phase was also investigated. These experiments used organic phases of undiluted 2-ethylhexanol and aqueous phases containing separately 0.18 M of the element in 6 M HCl. The results from these set of experiments were summarized in Table 4.
The Separation Factor (SF) values showed the extreme selectivity of the system; these separation factors were calculated within the next relationship:
Further experiments had been performed to elucidate the separation Au(III)/Cu(II) using this same organic phase, and aqueous phase containing both elements in 6 M HCl and using various Au(III):Cu(II) molar concentration relationships. Table 5 summarized these results.
These results that in mixed Au(III)-Cu(II) solutions, the extraction of this last element decreased with respect to the results obtained from the use of single metal-bearing solutions. This is why the SF values resulted in the 1400-1500 order, though the variation in the [Au(III)]0:[Cu(II)]0 relationships seemed not to influence greatly on this separation.
3.2. Supported liquid membrane experiments
In these membrane systems, the extraction (transport) of a given metal-species depends not only of the equilibrium parameters but also the kinetics parameters.
The influence of the variation (600-1600 min-1) of the stirring speed of the feed phase on gold transport was investigated. The results from these experiments were shown in Table 6, and it can be observed that the overall mass transfer coefficient value (KO) increased with the increase of the stirring speed from 600 to 1000 min-1, and beyond that not increase in gold transport was observed. In fact, there was a decrease of the transport from 1400 min-1 due to membrane instability probably attributable to the displacement of the organic phase from the membrane pores caused by the turbulence due to these higher stirring speeds.
In supported liquid membranes experimentation, two types of diffusional resistances are usually found: i) one due to the feed phase boundary layer, and ii) another in relation with the membrane support. Many times the magnitude of the values of both resistances competed between them [30]. These experimental results show that, in the 1000-1200 min-1 range, the feed phase boundary layer reached a minimum and the aqueous resistance to mass transfer are minimized, thus, the diffusion contribution of the aqueous species to the mass transfer phenomena is constant [31].
The influence of the variation (800-1200 min-1) of the stirring speed of the receiving phase on gold transport was also investigated using the very same experimental conditions as in Table 4, but using a stirring speed of 1000min-1 in the feed phase. The results from these experiments showed that the variation of the stirring speed applied to the receiving phase had a negligible influence on gold transport. In the case of the receiving phase, and if the stirrer in the receiving compartment was close to the support, the thickness of the boundary layer was minimized and the resistance in the receiving side was neglected [32]. Thus, subsequent experiments were performed using stirring speeds of 1000 min-1 for both feed and receiving phases.
Another variable investigated was the variation (0.5-6 M) of the HCl concentration in the feed phase on gold transport, keeping the carrier concentration in the membrane support constant. The results were shown in Table 7. It can be seen that gold permeation increased when the acid concentration in the feed solution was increased up to 1 M, being metal permeation independent of the HCl concentration in the 3-6 M range due to that the equilibrium:
was shifted completely to the left, and HAuCl4 was the predominant species in the feed solution.
The influence of the variation of the carrier concentration on gold transport was next investigated. In these experiments, the feed phase was of 0.01 g/l Au(III) in 6 M HCl, whereas the organic phase contained 10-75% v/v 2-ethylhexanol in toluene or undiluted extractant. Table 8 showed the variation of the overall mass transfer coefficient with the variation of the carrier concentration in the membrane phase.
These results demonstrated that gold transport increased from 10 to 50% v/v carrier concentration in the membrane phase, then levels off and after decreased at the highest carrier concentrations. These phenomena can be attributable to that at low carrier concentrations, metal transport was dominated by membrane diffusion, whereas in the 50% v/v range the contribution of membrane diffusion was negligible and gold transport was controlled by diffusion in the stagnant film of the feed phase. At this maximum KO value [33]:
where Daq represented the average aqueous diffusion coefficient (10-5 cm2/s) of metal species in the feed phase [34], and daq was the minimum thickness of the feed phase boundary layer, thus, daq for the present system was estimated as 1.8·10-3 cm. The decrease of gold transport at the highest carrier concentration was due to the increase of the organic phase viscosity, which decreased the Au(III)-2-ethylhexanol complexes diffusion coefficients values [35].
Investigation about the effect of the initial concentration (0.01-0.1 g/l) of gold, in the feed phase, on metal transport (Table 9), it was observed that the increase of the initial gold concentration was accompanied by a continuous decrease of metal transport, whereas the initial metal flux (J) defined as:
initially increased from 0.005-0.04 g/L initial gold concentrations, and beyond this concentrations range, J became almost independent of the initial gold concentration in the feed phase.
According with these results, at low metal concentrations (0.01-0.04 g/L), the transport process was controlled by diffusion of gold species, whereas in the highest metal concentrations range, the near constant metal flux values were due to a change in the rate- determining step for the transport process. At these higher gold concentrations, membrane became saturate by metal-carrier species on the feed-membrane interface, resulting in a lower effective membrane area, which led to a near constant initial flux value.
Following the same considerations described in the literature [36], it can be concluded that the gold transport rate was determined by the rate of diffusion of the HAuCl4 species across the feed phase diffusion layer and the rate of diffusion of the gold species eq. () and () through the liquid membrane. Thus, taking the same assumptions that in [37,38], a final expression for the overall mass transfer coefficient can be derived as:
where ∆org and ∆f were the transport resistances due to diffusion across the membrane and the aqueous feed boundary layer, respectively. The above equation combined in one expression both equilibrium and diffusional parameters involved in the gold(III) transport process from the feed phase, across supported liquid membranes using 2-ethylhexanol as carrier.
To estimate the values of the resistance to the mass transfer, the above equation was linearized, resulting in:
and a plot of 1/KO versus 1/ might result in a straight line with slope ∆org and intercept ∆f. From the plot, it resulted that ∆org and ∆f were found to be 2580 s/cm and 147 s/cm, respectively, with r2= 0.9895. The utility of eq.(11) to describe gold transport across the supported liquid membrane by 2-ethylhexanol was shown in Figure 1, where the experimental and calculated values using this equation have been represented versus the initial carrier concentration.
Whereas the first term (1/KO) of eq. (11) represented the value of the total resistance (RT), and being this resistance the sum of the mass transfer resistances due to the feed and the membrane phase, eq. (11) can be expressed as:
The total resistance calculated from experiments in Table 6 presented values in the 175-1052 s/cm range, in comparison the total resistance calculated by the model is 206 s/cm, which indicated that the resistance due to the membrane is dominant at low stirring speeds.
The contribution of the fractional resistances due to each step of the total transport process, Rfo and Rmo can be expressed by equations:
Under various experimental conditions, the values of %Rfo and %Rmo are summarized in Table 10.
Taking into account that:
where Dorg represented the diffusion coefficient of the gold-containing species in the organic phase immobilized on the solid support and dm was the membrane thickness, then, Dorg was found to be 4.8·10-6 cm2/s. The diffusion coefficient of the gold transported species in the bulk organic phase can be estimated by the next expression [39]:
where τ and ε were the membrane tortuosity and porosity values, respectively. The above resulted in Dorg,b calculated as 1.8·10-5 cm2/s. Comparison of Dorg and Dorg,b values showed that Dorg was lower than Dorg,b, which can be attributed to the diffusional resistance caused by the solid support separating the feed and receiving phases.
The selectivity of the present system against the presence of other metals in the feed phase was investigated. In this case, the feed phase contained 0.01 g/L each of Au(III), Ni(II), Cu(II), Fe(III) and PGMs (Ir, Os, Pd, Pt, Re, Rh, Ru) in 6 M HCl medium, being the organic phase of 50% v/v 2-ethylhexanol in toluene immobilized on Durapore GVHP4700 support. Like all the previous experimentation, water was used as receiving phase. The results indicated that PGMs were not transported under the present experimental conditions, whereas the transport of gold and the base metals followed the Au(III)>Fe(III)>Cu(II)=Ni(III) order, with separation factors Au/Fe, Au/Ni and Au/Cu of 1.3, 4.5 and 4,7, respectively. In these transport experiments the separation factors were calculated as:
However, the presence of all these elements in the feed phase produced a decrease of the gold overall mass transfer coefficient from 5.7·10-3 cm/s to 2.3·10-3 cm/s. This behavior is not rare in supported liquid membrane operations and it is attributable to the multi-ion competition or crowding effect [40].
Once gold was transported from the feed solution to the membrane phase and finally to the receiving phase, it can be recovered from this last solution by precipitation as zero valent gold nanoparticles by the use of sodium borohydride. This procedure was used by one of us from years ago [41], otherwise the importance about the recovery of this precious metal as nanoparticles was also demonstrated [42], and uses of these nanoparticles in different fields (catalysis, medicine, sensors, etc,) regularly appeared in the literature [43-46]. In the present work, the receiving solution containing 0.009 g/L was precipitated by the direct action of solid sodium borohydride, after the reaction stopped, the dark solid was filtered. From this dry solid the next images were obtained.
Figure 2.
Gold nanoparticles under magnifier.

Figure 3.
TEM image of gold nanoparticles. Some degree of agglomeration is observed.

Conclusions
2-ethylhexanol was used to extract gold(III) from macro amounts from 6 M HCl medium. The extraction process reached equilibrium within few minutes, being metal extraction dependent on gold and extractant concentrations. On the basis of numerical simulation, gold(III) extraction by 2-ethylhexanol can be explained by formation of HAuCl4·L and HAuCl4·2L, with extraction constants of 38 and 309, respectively, and where L represented the extractant molecule. The extraction process is highly selective with respect to gold(III) in the presence of copper(II), nickel(II) and zinc(II). Gold can be stripped from the metal-loaded organic phase with water.
The extraction system was implemented in a solid supported liquid membrane system in which the metal flux was dependent on the initial gold concentration (up to 0.04 g/L) but almost independent of this variable above this concentration. The metal transport was also dependent on extractant concentration but for 2-ethylhexanol concentrations in the 50% v/v range in toluene, a limiting value for the overall mass transfer coefficient was obtained. Mass transfer coefficients in the feed and in the membrane phases were calculated as 6.8·10-3 cm/s and 3.9·10-4 cm/s, respectively. The minimum thickness of the feed boundary layer was calculated to be 1.8·10-3 cm. The transport process was controlled by mixed diffusion of gold across the feed phase and the diffusion of the gold-2-ethylhexanol complexes in the liquid membrane phase. The system was highly selective respect to Au(III) in the presence of Platinum Group Metals and Cu(II), Ni(II) and Fe(III) in the aqueous feed phase. From the water-receiving phase, gold was recovered as zero valent gold nanoparticles by the use of sodium borohydride.
Author Contributions
Conceptualization, F.J.A.; methodology, F.J.A.; formal analysis, F.J.A.; investigation, F.J.A. and J.I.R.; writing—original draft preparation, F.J.A.; writing—review and editing, F.J.A. and J.I.R.; funding acquisition, J.I.R. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by CSIC-Project 202250E019 and the APC was kindly funded by Processes Editorial Office.
Data Availability Statement
Not applicable.
Acknowledgments
To the CSIC (Spain) for support. To Mr. M.I. Maher for checking English.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Hu, G. Wang, Z.; Zhang, W.; He, H.; Zhang, Y.; Deng, X.; Li, W. MIL-161 metal–organic framework for efficient Au(III) recovery from secondary resources: performance, mechanism, and DFT calculations. Molecules 2023, 28, 5459. [Google Scholar] [CrossRef] [PubMed]
- Zhao, L.; Zhou, Q.; Yang, Y.; Zhang, Y.; Qiu, Y.; Chen, Y.; Jin, X.; Yang, X.; Wang, S. Ultra-high adsorption capacity and selectivity of photo-enhanced sulfur-rich M2S3 (M[dbnd]Bi and Sb) for gold recovery from electronic wastewater. J. Water Proc. Eng. 2024, 57, 104572. [Google Scholar] [CrossRef]
- Hubicki, Z.; Zinkowska, K.; Wójcik, G. A new impregnated adsorbent for noble metal ion sorption. Molecules 2023, 28, 6040. [Google Scholar] [CrossRef]
- Thombre, A.V.; Kundu, D. Ionic liquid promoted extraction of gold(III) from electronic waste: a modeling study. Sep. Sci. Technol. 2023, 58, 2641–2654. [Google Scholar] [CrossRef]
- Alguacil, F.J.; Robla, J.I. On the use of pseudo-protic ionic liquids to extract gold(III) from HCl solutions. Int. J. Molec. Sci. 2023, 24, 6305. [Google Scholar] [CrossRef]
- Ansari, S.A. ; Mohapatra, P,K. Diglycolamides as highly efficient carrier ligands for actinide transport in supported liquid membranes. Desalin. Water Treat. 2023. [Google Scholar] [CrossRef]
- Botelho Junior, A.B.; Tenório, J.A.S.; Espinosa, D.C.R. Separation of critical metals by membrane technology under a circular economy framework: a review of the state-of-the-art. Processes 2023, 11, 1256. [Google Scholar] [CrossRef]
- Kaczorowska, M.A. The latest achievements of liquid membranes for rare earth elements recovery from aqueous solutions—a mini review. Membranes 2023, 13, 839. [Google Scholar] [CrossRef] [PubMed]
- Kostanyan, A.E.; Voshkin, A.A.; Belova, V.V.; Zakhodyaeva, Y.A. Modelling and comparative analysis of different methods of liquid membrane separations. Membranes 2023, 13, 554. [Google Scholar] [CrossRef] [PubMed]
- Rzelewska-Piekut, M.; Regel-Rosocka, M. Liquid membranes for separation of metal ions from wastewaters. Phys. Sci. Rev. 2023, 8, 937–982. [Google Scholar] [CrossRef]
- Wang, B.; Wang, H.; Yan, J.; Wang, Y.; Xu, T. Research progress of polymer inclusion membrane in metal separation and recovery. Huagong Jinzhan/Chem. Ind. Eng. Prog. 3990. [Google Scholar] [CrossRef]
- Farah, M.; Giralt, J.; Stüber, F.; Font, J.; Fabregat, A.; Fortuny, A. Hollow fiber liquid membrane: a promising approach for elimination of pharmaceutical compounds from wastewater. J. Environ. Chem. Eng. 2023, 11, 111544. [Google Scholar] [CrossRef]
- Farah, M.; Giralt, J.; Stüber, F.; Font, J.; Fabregat,A. ; Fortuny, A. Intensification of diclofenac removal through supported liquid membrane and ozonation. Environ. Technol. Innov. 2024, 33, 103469. [Google Scholar] [CrossRef]
- Alguacil, F.J.; Robla, J.I. Transport of chromium(VI) across a aupported liquid membrane containing Cyanex 921 or Cyanex 923 dissolved in Solvesso 100 as carrier phase: estimation of diffusional parameters. Membranes 2023, 13, 177. [Google Scholar] [CrossRef] [PubMed]
- Kumar, R.; Dhiman, S.; Gupta, H. . Indium extraction from nitrate medium using Cyphos ionic liquid 104 and its mathematical modeling. Environ. Sci. Pollut. Res. 1073. [Google Scholar] [CrossRef]
- Middleton, A.; Hsu-Kim, H. Separation of rare-earth elements by supported liquid membranes: impacts of soluble iron, aluminum, and pH in low-grade feedstocks. ACS ES T Eng. 2023, 3, 1197–1204. [Google Scholar] [CrossRef]
- Kadhim, N.R.; Abbar, A.H.; Flayeh, H.M. Removal of copper from a simulated wastewater by electromembrane extraction technique using a novel electrolytic cell provided with a flat polypropylene membrane infused with 1-octanol and DEHP as a carrier. Case Stud. Chem. Environ. Eng. 2023, 8, 100430. [Google Scholar] [CrossRef]
- Kadhim, N.R.; Flayeh, H.M.; Abbar, A.H. Zinc (II) removal from simulated wastewater by electro-membrane extraction approach: adopting an electrolysis cell with a flat sheet supported liquid membrane. J. Electrochem. Sci. Eng. 2023, 13, 1097–1112. [Google Scholar] [CrossRef]
- Kadhim, N.R.; Flayeh, H.M.; Abbar, A.H. A new approach for cobalt (II) removal from simulated wastewater using electro membrane extraction with a flat sheet supported liquid membrane. Heliyon 2023, 9, e22343. [Google Scholar] [CrossRef]
- Suren, S.; Punyain, W.; Maneeintr, K.; Nootong, K.; Pancharoen, U. The simultaneous elimination of arsenic and mercury ions via hollow fiber supported liquid membrane and their reaction mechanisms: experimental and modeling based on DFT and generating function. Arabian J. Chem. 2023, 16, 104501. [Google Scholar] [CrossRef]
- Traiwongsa, N.; Suren, S.; Pancharoen, U.; Nootong, K.; Maneeintr, K.; Punyain, W.; Lothongkum, A.W. Mechanisms of mercury ions separation by non-toxic organic liquid membrane via DFT, thermodynamics, kinetics and mass transfer model. J. Ind. Eng. Chem. 2023, 117, 522–537. [Google Scholar] [CrossRef]
- Alguacil, F.J.; Robla, J.I. Iron control in liquid effluents: pseudo-emulsion based hollow fiber membrane with strip dispersion technology with pseudo-protic ionic liquid (RNH3+HSO4−) as mobile carrier. Membranes 2023, 13, 723. [Google Scholar] [CrossRef] [PubMed]
- Alguacil, F.J.; Robla, J.I. Treatment of stainless steel rinse waters using non-dispersive extraction and strip dispersion membrane technology. Membranes 2023, 13, 902. [Google Scholar] [CrossRef]
- Wang, Y.; Cao, J.; Biswas, A.; Fang, W.; Chen, L. Acid mine wastewater treatment: a scientometrics review. J. Water Proc. Eng. 2024, 57, 104713. [Google Scholar] [CrossRef]
- Pacary, V.; Burdet, F.; Duchesne, M.T. Experimental and modeling of extraction of lanthanides in system HNO3-TEDGA-{DMDOHEMA-HDEHP}. Proc. Chem. 2012, 7, 328–333. [Google Scholar] [CrossRef]
- Zhang, J.; Liu, R.; Liu, X.; Li, J.; Wu, R.; Yang, Y. Study on extraction of Rh(III) by DABCO-based ionic liquid from hydrochloric acid medium. Sep. Purif. Technol. 2023, 324, 124578. [Google Scholar] [CrossRef]
- Li, H.; Mabhiza, T.; Ning, Y.; Yu, Z.; Lv, C.; Shen, X.; Wei, G.; Qu, J. Solvent extraction and recovery of beryllium from hydrochloric acid solution with naphthenic acid. Sep. Purif. Technol. 2024, 331, 125594. [Google Scholar] [CrossRef]
- Dong, H.; Ci, E.; Zhao, T.; Chen, P.; Liu, F.; Hu, G.; Yang, L. Hydrophobic deep eutectic solvents as the green media for highly efficient extraction of Cr(VI) over a broad pH range and low oil-water ratio. Sep. Purif. Technol. 2024, 334, 126104. [Google Scholar] [CrossRef]
- Diamond, R.M. The solvent extraction behavior of inorganic compounds. III. Variation of the distribution quotient with metal ion concentration. J. Phys. Chem. 1957, 61, 75–81. [Google Scholar] [CrossRef]
- Bohrer, M. P. Diffusional boundary layer resistance for membrane transport. Ind. Eng. Chem. Fundam. 1983, 22, 72–78. [Google Scholar] [CrossRef]
- Alguacil, F.J.; Martinez, S. Permeation of iron(III) by an immobilised liquid membrane using Cyanex 923 as mobile carrier. J. Membr. Sci. 2000, 176, 249–255. [Google Scholar] [CrossRef]
- Pavón, S.; Fortuny, A.; Coll, M. T.; Bertau, M.; Sastre, A. M. Permeability dependencies on the carrier concentration and membrane viscosity for Y(III) and Eu(III) transport by using liquid membranes. Sep. Purif. Technol. 2020, 239, 116573. [Google Scholar] [CrossRef]
- Alguacil, F.J.; Alonso, M.; Lopez, F.; Lopez-Delgado, A. Uphill permeation of Cr(VI) using Hostarex A327 as ionophore by membrane-solvent extraction processing. Chemosphere 2008, 72, 684–689. [Google Scholar] [CrossRef] [PubMed]
- El Aamrani, F.Z.; Kumar, A.; Beyer, L.; Cortina, J.L.; Sastre, A.M. Uphill permeation model of gold(III) and its separation from base metals using thioures derivatives as ionophores across a liquid membrane. Hydrometallurgy 1998, 50, 315–330. [Google Scholar] [CrossRef]
- Gupta, S.K.; Rathore, N.S.; Sonawane, J.V.; Pabby, A.K.; Janardan, P.; Changrani, R.D.; Dey, P.K. Dispersion-free solvent extraction of U(VI) in macro amount from nitric acid solutions using hollow fiber contactors. J. Membr. Sci. 2007, 300, 131–136. [Google Scholar] [CrossRef]
- Sastre, A.M.; Madi, A. , Cortina, J.L.; Miralles, N. Modelling of mass transfer in facilitated supported liquid membrane transport of gold(III) using phospholene derivatives a s carriers. J. Membr. Sci. [CrossRef]
- Haghighi, H.K.; Irannajad, M. ; Fortuny, A,; Sastre, A.M. Mathematical modeling on non-dispersive extraction of germanium from aqueous solutions using Aliquat 336. Water Sci. Technol. 2489. [Google Scholar] [CrossRef]
- Alguacil, F.J. Mechanistic investigation of facilitated transport of gold(III) from HCl media using ionic liquid Cyphos IL102 as carrier across a supported liquid membrane. Gold Bull. 2019, 52, 145–151. [Google Scholar] [CrossRef]
- Huang, T.-C.; Juang, R.-S. Rate and mechanism of divalent metal transport through supported liquid membrane containing di(2-ethylhexyl) phosphoric acid as a mobile carrier. J. Chem. Technol. Biotechnol. 1998, 42, 3–17. [Google Scholar] [CrossRef]
- De Gyves, J.; De San Miguel, E.R. Metals separations by supported liquid membranes, Ind. Eng. Chem. Res. 1999, 38, 2182–2202–2202. [Google Scholar] [CrossRef]
- Alguacil, F.J.; Adeva, P.; Alonso, M. Processing of residual gold(III) solutions via ion exchange. Gold. Bull. 2005, 38, 9–13. [Google Scholar] [CrossRef]
- Oestreicher, V.; García, C.S.; Soler-Illia, G.J.A.A.; Angelomé, P.C. Gold recycling at laboratory scale: from nanowaste to nanospheres. ChemSusChem 2019, 12, 4882–4888. [Google Scholar] [CrossRef] [PubMed]
- Layek, K. Hydroxyapatite supported gold nanoparticles catalyzed efficient catalysis for the reduction of nitroarenes and degradation of azo dyes. Catal. Surv. Asia 2024, 27, 349–362. [Google Scholar] [CrossRef]
- Cheng, C.-W.; Lee, S.-Y.; Zhan, S.-Q.; Huang, C.-L.; Chen, T.-Y.; Yuan, J.-M.P.; Huang, S.-T. Chiu, C.-M-: Liang, J.-Y. The effect of photolysis of sodium citrate treated with gold chloride using coloured light on the generation of gold nanoparticles and the repression of WiDr colon cancer cells. J. Photochem. Photobiol. B: Biology 2024, 251, 112844. 251,. [CrossRef]
- Hiral, V.; Kokila, P.; Jyotindra, M. Biogenic synthesis of gold nanoparticles using bark extract of Bauhinia variegata: antibacterial and in vitro anticancer study. Res. J. Chem. Environ. [CrossRef]
- Ajayi, R.F.; Nqunqa, S.; Ngema, N.P.P.; Barry, S.C.L.; Feleni, U.; Mulaudzi, T. UV–Vis detection of E. coli 0157:H7 using Vitis vinifera and Musa paradaisica modified Au-NPs. MethodsX, 1025. [Google Scholar] [CrossRef]
Figure 1.
Plot of 1/KO versus [2-ethylexanol]. Feed phase: 0.01 g/L Au(III) in 6 M HCl. Membrane phase: 10-50% v/v 2-ethylhexanol in toluene immobilized on GVHP4700. Receiving phase: water. .
Figure 1.
Plot of 1/KO versus [2-ethylexanol]. Feed phase: 0.01 g/L Au(III) in 6 M HCl. Membrane phase: 10-50% v/v 2-ethylhexanol in toluene immobilized on GVHP4700. Receiving phase: water. .
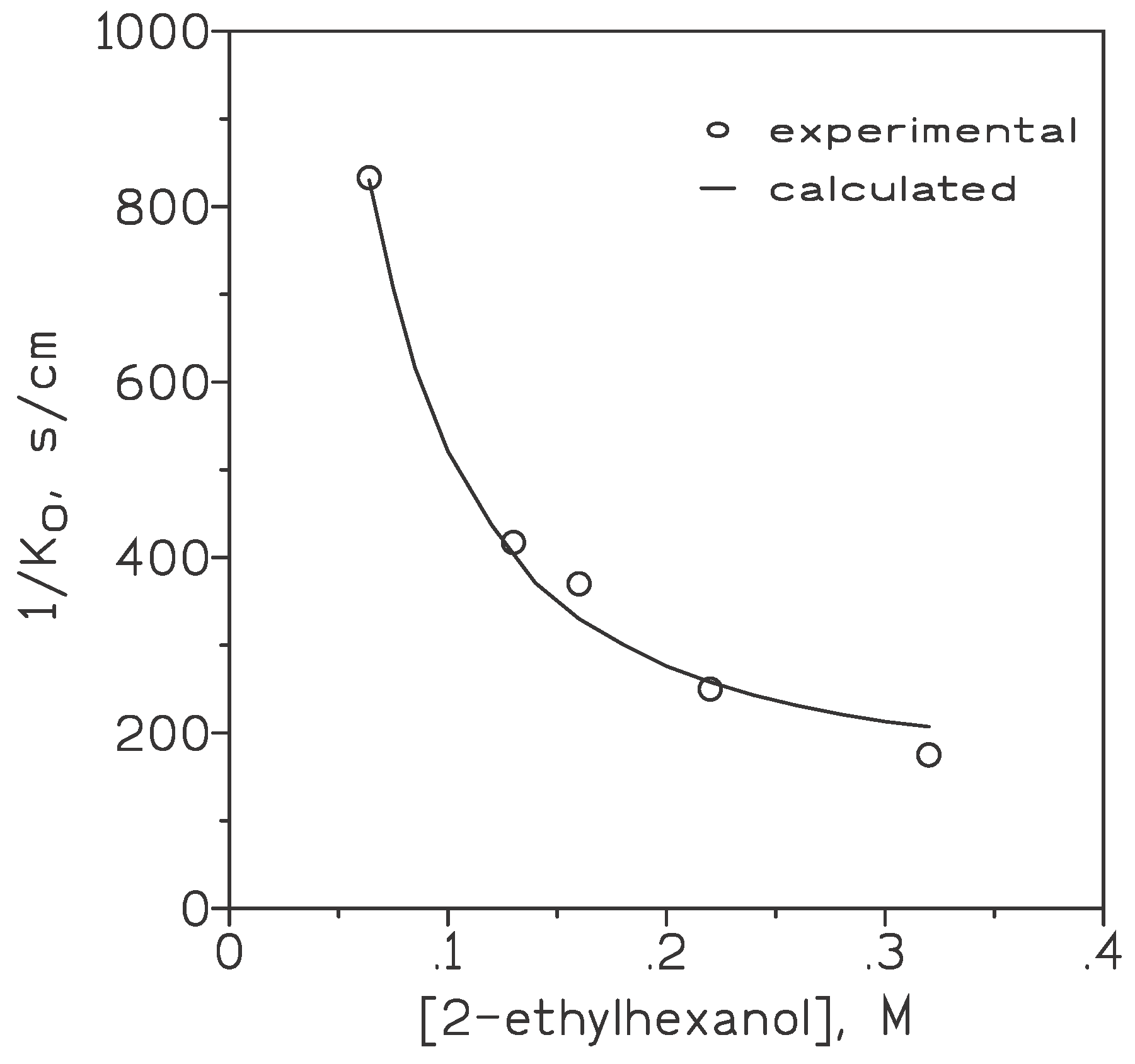
Table 1.
Influence of equilibration time on the fractional attachment to equilibrium.
| Time, min | F |
|---|---|
| 1 2 5 10 15 |
0.71 0.98 1 1 1 |
Temperature: 20º C. Org/Aq volume ratio: 1.
Table 2.
Percentages of gold extraction at various initial metal concentrations in the aqueous phase.
Table 2.
Percentages of gold extraction at various initial metal concentrations in the aqueous phase.
| [Au]0, g/L | % Extraction |
|---|---|
| 5 15 25 35 50 75 100 150 200 |
98 98 98 98 98 97 96 93 87 |
Temperature: 20º C. Org/Aq volume ratio: 1.
Table 3.
Percentages of gold extraction at various extractant concentrations in the organic phase.
| [2-ethylhexanol], % v/v | % Extraction |
|---|---|
| 25 35 50 60 70 75 80 90 undiluted |
57 75 88 92 94 95 96 98 98 |
Temperature: 20º C. Org/Aq volume ratio: 1.
Table 4.
Extraction of Au(III), Cu(II), Fe(III) and Ni(II).
| Element | % Extraction | D | SF |
|---|---|---|---|
| Au(III) Cu(II) Zn(II) Ni(II) |
98 21 11 12 |
69 0.25 0.12 0.13 |
276 575 530 |
Temperature: 20º C. Org/Aq volume ratio: 1.
Table 5.
Extraction and separation of Au(III) and Cu(II) at various molar concentration relationships.
Table 5.
Extraction and separation of Au(III) and Cu(II) at various molar concentration relationships.
| [Au]0:[Cu]0 | DAu | DCu | SF |
|---|---|---|---|
| 2:1 3:1 6:1 18:1 |
69 69 69 69 |
0.045 0.047 0.044 0.049 |
1533 1468 1568 1408 |
[Au]0: 0.18 M. temperature: 20º C. Org/Aq volume ratio: 1.
Table 6.
Influence of the feed phase stirring speed on gold transport.
| Stirring speed, min-1 | KO·103, cm/s |
|---|---|
| 600 800 1000 1200 1400 1600 |
0.95 2.6 5.7 5.7 5.5 4.9 |
Feed phase: 0.01 g/L Au(III) in 6 M HCl. Membrane phase: 50% v/v 2-ethylhexanol in toluene immobilized on GVHP4700 support. Receiving phase: water. Receiving phase stirring speed: 1200 min-1. Temperature: 20º C.
Table 7.
Gold(III) permeation at various HCl concentrations in the feed phase.
| [HCl], M | KO·103 , cm/s |
| 0.5 1 3 6 |
3.8 4.7 5.7 5.7 |
Feed phase: 0.01 g/L Au(III) and HCl. Membrane phase: 50% v/v 2-ethylhexanol in toluene immobilized on GVHP4700 support. Receiving phase: water. Temperature: 20º C.
Table 8.
Gold transport at various carrier concentrations.
| [carrier], % v/v | KO·103, cm/s | a% Gold recovery |
|---|---|---|
| 10 25 35 45 50 65 75 undiluted |
1.2 2.7 4.0 5.6 5.7 5.5 3.0 1.2 |
95 95 94 93 92 93 90 89 |
Membrane support: GVHP4700. Receiving phase: water. aIn the receiving phase after 3 hours.
Table 9.
Variation in gold transport and initial flux at various metal concentrations.
| [Au]0, g/L | KO·103, cm/s | J, mol/cm2s | a% Gold recovery |
|---|---|---|---|
| 0.01 0.02 0.04 0.06 0.08 0.1 |
5.7 4.5 3.0 2.2 1.7 1.4 |
2.9 4.6 6.0 6.6 6.8 7.0 |
95 93 94 93 94 95 |
Feed phase: gold(III) in 6 M HCl. Membrane phase: 50% v/v 2-ethylhexanol in toluene immobilized on GVHP4700 support. Receiving phase: water. aIn the receiving phase after 3 hours.
Table 10.
Contribution of the mass transfer resistances to gold(III) transport process.
| Experimental condition | RT, s/cm | aRT, s/cm | %Rfo | %Rmo |
|---|---|---|---|---|
| Carrier 10-50% v/v Gold: 0.01-0.1 g/L HCl 6 M |
370-175 175-714 175 |
147 147 147 |
40-84 84-21 84 |
60-16 16-79 16 |
aValue from the theoretical model (eq. (11)).
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
MDPI Initiatives
Important Links
© 2024 MDPI (Basel, Switzerland) unless otherwise stated







