Prerpints.org logo
Preprint
Article

Best Practices to Train Accurate Deep Learning Models: A General Methodology

Altmetrics

Downloads

156

Views

103

Comments

0

Submitted:

19 February 2024

Posted:

20 February 2024

You are already at the latest version

Alerts
Abstract
In recent years the field of computer science has experienced great changes, due to the incredible advances in the field of artificial intelligence. Deep Learning models are responsible for most of them since the biggest milestones occurred in 2012 when AlexNet won the image classification challenge called ImageNet. These models have demonstrated great performances in different types of complex tasks like image restoration, medical diagnosis or object recognition. Their disadvantages are related to their high data dependency, which forces experts in the field to follow a precise methodology to obtain accurate models. In this paper, we describe a complete workflow that begins with the management of the raw data until the in-depth interpretation of the performance of the models. This should be taken as a high-level consultation document describing good practices that should be applied. Apart from the step-by-step methodology, we present different use cases that correspond to the two main problems of the field: classification and regression.
Keywords: 
Subject: Computer Science and Mathematics  -   Artificial Intelligence and Machine Learning

1. Introduction

If we talk about what has been one of the biggest advances in recent history, we have to talk about the revolution of Artificial Intelligence (AI). AI is the domain within computer science which analyzes and interprets the processes underlying intelligent actions in humans, aiming to replicate these actions in machines, not always employing the same mechanisms, (Russell and Norvig 2016). These advancements have been fostered by two main factors. First, the creation and availability of big amounts of data never seen before. Second, the affordable price of hardware to compute this data and train the AI models.
But if we must talk about the milestone in the modern AI era, we have to talk about Deep Learning (DL) models. This is a family of models whose term was coined in 2006 by Hinton. They are defined as multiple-layer models using hierarchical Artificial Neural Networks (ANNs) with the capacity to progressively learn data representations, beginning with the input data and advancing to higher levels of abstraction, (LeCun, Bengio, and Hinton 2015). Its biggest milestone occurred in 2012 when AlexNet was the first DL model that won an image classification challenge called ImageNet, (Krizhevsky, Sutskever, and Hinton 2012).
Deep Learning models have been demonstrated to have a high performance in solving many different complex tasks. Nevertheless, some weaknesses face constantly any expert in the field such as poor interpretability, data dependency or overfitting. The last two, apart from being interrelated, are common to all the implementation workflows of these models. Normally, large amounts of data are needed to train accurate models but there is, also, a need to avoid overfitting. This is described in (Sammut and Webb 2011) as the situation in which the model learns characteristics associated with noise or variability within the data, rather than the fundamental distribution from the training data. So, avoiding overfitting is the main condition to obtain a model that performs well.
Overfitting is tested at the end of a process of models’ training. At the end of this process different measures of a metric are compared, corresponding these values to the different sets into which the data in origin is split. The success of the training process depends on different decisions to be taken which are related to the type of problem to be solved, the nature of data and other conditions. The large number of decisions to take and the lack of knowledge about what they depend on, have allowed the publication of papers where the overfit of the models is noticeable. The motivation of this paper is to compile and explain step by step how to do accurate processes to train deep learning models.
The work aims to provide resource information for researchers so they can know which steps to apply and understand them. This will be very useful for scientists without a deep understanding of deep learning terms, In the case of experts in the field, they could have a guide of best practices to follow. In this sense, the main contribution is to compile in a single document the explanation of each step. It will not only describe the method step by step, but we will also provide why each step is necessary and how to apply it depending on several conditions such as use case to solve or type of data. As we want this paper to be accessible to any researcher interested in the field no mathematical formalization is provided, we are providing a high-level explanation of terms, strategies, etc.
The rest of the paper is organized as follows. Section 2 describes all the antecedents of the DL field so a general idea of different terms could be obtained with the possible applications DL could have. Section 3 explains step by step the proposed methodology to obtain accurate models. Section 4 shows different use cases where the methodology is applied. Finally, section 5 compiles different conclusions related to what has been explained in the work.

2. Antecedents

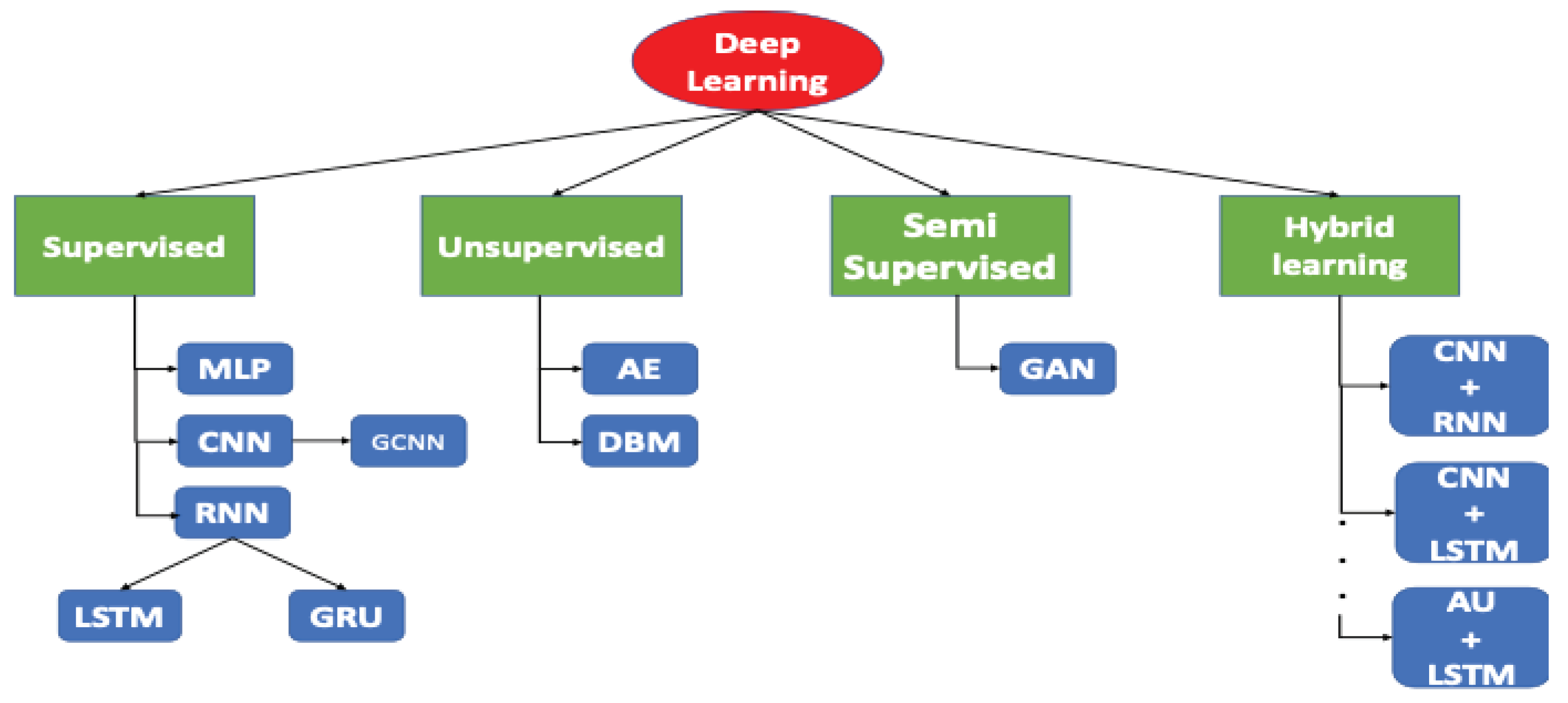
DL models are very diverse, being their performance tied to the nature and quality of the training data. This section explores the different models used in the field. Figure 1 shows the hierarchical organization of these models depending on the way they learn. An in-depth description of the models will be given later on.
DL models are first categorized based on their approach to learning from data (training stage), which includes supervised, unsupervised, and semi-supervised methods. The first category corresponds to those using labelled data for training, where the model understands the relationship between input data and expected output, which is a classification task.
The Multilayer Perceptron (MLP) represents the most basic form of a DL model. Its architecture consists of an input layer, multiple hidden layers, and an output layer. It is typically used to predict a particular numeric value, but classification problems can also be solved. For example, (Li and Baghban 2024) take the benefit of using MLPs to predict the density of 48 refrigerant systems.
Convolutional Neural Networks (CNNs) stand out as one of the most used models, particularly in computer vision applications. Their primary strength lies in their capability to detect patterns in a spatially invariant manner. This characteristic enables them to recognize specific patterns in an image, regardless of their location. More recently, there has been a development of a specialized type of CNN known as Graph Convolutional Neural Networks (GCNNs). Introduced by (Kipf and Welling 2016), GCNNs are designed to process graph-structured data. This model encodes both the structure of a graph and the features of its nodes. Examples of the application of these models can be found in the following papers. (Ehtisham et al. 2024) where CNNs are used for automated assessment of damage type and severity in wooden structures. (Hu et al. 2024) use a GCNN model for identifying essential genes in organisms.
The other prominent set of models falls under the unsupervised training category. In this scenario, the data has no labels, and there exists no prior knowledge regarding the results, (Sathya, Abraham, and others 2013).
Recurrent Neural Networks (RNNs), as defined by (Elman 1990), employ an input vector of variable length and recursively apply a transition function to their internal hidden state vector ht. They are particularly useful for time series data structures. Within the family of RNNs, there is a specific subtype known as Long Short-Term Memory (LSTMs) and another called Gated Recurrent Units (GRUs). LSTMs, introduced by (Hochreiter and Schmidhuber 1997), were devised to effectively handle noisy or ambiguous input data. (Lu and Xu 2024) is an example where RNNs are used for the particular task of stock prediction.
Deep Autoencoders (DAEs) apply unsupervised learning. First described by (Ballard 1987), they are characterized by having input and output layers of the same or similar size, along with two processing modules. The first structure, the encoder, takes the input data and compresses it to a smaller representation containing its essential features. The second structure, the decoder, aims to reconstruct the original input data by upsampling the compressed representation until it reaches the size of the input data.
Restricted Boltzmann Machines (RBMs) are regarded as a specific form of Autoencoder, initially proposed by (Smolensky 1985), capable of learning probability distributions. RBMs have been employed to construct Deep Boltzmann Machines (DBMs), as stated by (Salakhutdinov and Hinton 2009). In (Almalki and Latecki 2024), Autoencoders are used for segmenting teeth in Intra-Oral 3D Scans.
Transformer is a model that avoids recurrence and exclusively relies on an attention mechanism to establish global dependencies between input and output, (Vaswani et al. 2017). This type of model is used by (Z. U. Rahman et al. 2022) for the prediction of risk in cardiovascular diseases.
By combining the previous learning types, it creates a new category known as semi-supervised learning. Within this classification falls Generative Adversarial Networks (GANs). GANs comprise two neural models: the generator and the discriminator, operating in an adversarial training paradigm (Goodfellow et al. 2014). This architecture aims to understand and replicate a given data distribution. The generative model tries to generate synthetic instances of the input data, while the discriminator assesses these instances to determine their similarity to the input data. This adversarial process provides a probability of authenticity for each instance, distinguishing between input (authentic) and synthetic (generated) data. Through iterative refinement, the generator learns to produce data that increasingly resembles the input data. (Boroujeni and Razi 2024) implements a GAN model to translate RGB images into IR ones for fire forest monitoring.
In recent years, a trend has emerged within the field of deep learning, the development of hybrid models. These models are considered important for future advancements in DL. They combine two or more distinct architectures, such as CNN-LSTM or Autoencoder-LSTM, (Ding et al. 2024) and (Zhou et al. 2024).

3. Methodology to train deep learning models

In this section, the methodology to obtain accurate DL models is described in-depth. The process has been divided into different steps adding the best practices and an explanation about how they should be applied. It goes from having the dataset raw with a use case to solving it. Then, deciding which DL model fits better util to the obtention of a set of accurate metrics that avoid overfitting and ending with an interpretation of the models using other metrics and making a comparison with some baselines.

3.1. Deciding what Deep Learning model to use

The first decision to be taken when solving a DL problem corresponds to choosing a suitable model. Considering what has been described in Section 2, the different DL models that can be applied depend on the nature of the data and the use case to be solved. If we talk about the different use cases, there are also many applications but all of them can be classified into two main types: classification and regression. Belonging to one group or the other will have consequences, as will be described later, in the metrics used to measure the performance of the model. Classification problems consist of building a model that links the attributes of the instances, typically represented as attribute-value pairs, to the corresponding class labels, (Sammut and Webb 2011). Regression problems aim to predict the value of a dependent variable based on one or more independent variables, (Sammut and Webb 2011). Typical classification problems in DL are image classification or disease diagnosis. Within the regression problems group, we have text generation, time series prediction or object detection.
Due to the wide range of models and use cases, this decision has multiple solutions, we provide a general vision about how to choose the proper DL model. Table 1 compiles information on the different models, the type of data used to train them and the typical use cases to solve.

3.2. Splitting the dataset into train, validation, and test

As has been said before, to obtain a Deep Learning model that performs well, we need to avoid overfitting. Model validation which consists of checking how a trained model performs with new data never seen before is the way to prevent it. For this purpose, first of all, there is a need to split the data into three sets: training, validation and test.
The training set shows instances of the model so it can be adjusted to generalize its distribution. The validation set measures the accuracy of the model based on the errors obtained. The test set is used to check the capacity of the model to generalize by using data never seen before.
So, the first decision to be taken is the percentages used to create the three sets. A typical criterion is based on the Pareto principle which states that for many phenomena in nature, about 80% of the consequences are produced by 20% of the causes, (Dunford, Su, and Tamang 2014). In this way, a good choice is to split training and test by 80% and 20% respectively. Then, split training set into 80-20 for training and validation. Anyway, this is not an exact rule and depending on the size of the original dataset these percentages could vary. For small datasets it could be 70-30 and for big datasets 90-10, as done in (Maray et al. 2023) and (Kehnkar et al. 2023) respectively.
The second decision to take related to the training, validation and test sets is the strategy to follow during the split. Typically, a randomize is applied to avoid patterns depending on the order of the data. This prevents potential biases by ensuring that there is enough diversity representing the complete dataset in the three subsets. However, depending on the type of data and its organization, randomizing it is not always the best option. It is very important to avoid instances from the test set being introduced during training which is called data leakage. A typical data leakage case occurs when using frames of videos in a model. If we split randomly the sets of subsequent frames, almost equal frames could be part of the training and test set. To avoid this, it is better to split the dataset into full sequences.
Finally, a problem could occur in classification problems with imbalanced classes. This could lead to a training or test set where a class has more presence compared to the other. The strategy that is applied to avoid this is called stratification. This will ensure that each subset maintains an identical class distribution.

3.3. Feature scaling

Apart from the obvious transformation of data into continuous values as input data in DL models is always numeric data, feature scaling is a best practice to apply just before starting to train the models. This term is defined in (Protić et al. 2023) as transforming all features to a uniform range avoiding the influence of large-scale features on classification models or other feature-dependent processes. Feature scaling has also different benefits. For example, they can accelerate the process of gradient-based optimization algorithms, as in DL models, which leads to faster training times. Also, by avoiding the influence of features over the rest, the model performance tends to be improved. Finally, calculating distances is more accurate after feature scaling, being this process is part of algorithms used in DL, for example, L1 regularization.
In this sense, there are two main strategies scaling and normalization. The former transforms features to have a mean of zero and a standard deviation of one which prevents certain features from dominating others during training. The latter scales features to a range between 0 and 1 or -1 and 1 which is particularly useful for algorithms sensitive to the magnitude of features, such as distance-based algorithms. There are many different strategies to apply scaling and normalization but the following should be highlighted.
In the case of scaling most well-known is Min-Max. This strategy rescales the features to a fixed range, typically [0, 1], by subtracting the minimum value from each feature and then dividing by the range (the maximum value minus the minimum value). Equation 1 formalizes this process.
X M i n M a x = X − X m i n X m a x − X m i n
The main strategies in normalization are Euclidean Norm and Z-Score. Z-Score transforms the features to have a mean of 0 and a standard deviation of 1. This strategy is depicted by Equation 2.
Z S c o r e = X − µ δ
In the equation, µ is the mean and δ is the standard deviation.

3.4. Choosing the metrics depends on the problem to solve

The way to measure the performance of a DL model is by using metrics. The aim is to obtain the values that ensure that the model is well-trained. As a first step, we have to choose which generic metric to use depending on the problem to solve. As we have said before, DL problems can be framed into two big classes: classification and regression.
In classification problems, the main metric is called accuracy. This is defined as the proportion of the samples that the model has predicted correctly among the total number of instances. Equation 3 describes this metric.
Accuracy = T P + T N T P + F N + F P + T N
In the Equation above. True Positive (TP) refers to cases where the actual sample class is positive, and the model's prediction is also positive. True Negative (TN) denotes instances where the actual sample class is negative, and the model's prediction is also negative. False Positive (FP) signifies scenarios where the actual sample class is positive, yet the model predicts a negative outcome. False Negative (FN) represents situations where the actual sample class is negative, but the model predicts a positive result. The accuracy measures a percentage in ranges of 1, so the best value is the nearest to this one.
For regression problems, it is usually used the Mean Squared Error (MSE). It is defined in (Jadon, Patil, and Jadon 2022) as the mean of the squared differences between the predictions and the actual values. The following Equation describes this metric.
MSE = 1 N ∑ i = 1 N ( y i − y ^ i ) 2
In the previous Equation, N corresponds to the number of instances of the dataset, y i is the real value and y ^ i is the prediction made by the model. When using the MSE, the aim is to obtain a value as close to 0 as possible.
These metrics will be used as a first step to measure the performance of the model during training, validation and test or check if underfitting or overfitting is happening. For a deeper analysis of how models work, we will use other metrics that will be introduced in subsection 3.7.

3.5. Using k-fold validation during the training stage

K-fold validation is a typical strategy used when data is scarce. Apart from that it should be used as a way to validate the models more exhaustively. As DL models are initialized by randomization of their weights, this initialization could benefit alongside the data split in how the model performs. To mitigate this issue, k-fold cross-validation is employed.
In this strategy, the training set is divided into k smaller subsets or "folds." Subsequently, a loop is executed for each of the k folds. Then, the model is trained using k-1 folds as the training data and validated (evaluated for its performance) using the remaining fold. The numeric measure reported by k-fold cross-validation is the average of the values calculated across the entire loop. Also, a standard deviation is given that will be useful to know if the performance is worse in any of the folds.
Considering these factors, a good practice is using k-fold cross-validation with k values set to either 5 or 10. Empirical studies have demonstrated that these values provide test error rate estimates that strike a balance, avoiding typical DL problems as discussed by (Kuhn et al. 2013).

3.6. Avoiding underfitting and overfitting

As we have said before the main aim when training a DL model is avoiding overfitting/underfitting. Apart from that it is also important that it could perform better than a human doing the specific task for which we are training it. To accomplish this, we will introduce the concept of trade-off between bias and variance, (Belkin et al. 2019). This term addresses the balance between model complexity and its ability to generalize to unseen data (test set). In DL models, this tradeoff plays a crucial role in determining model performance and robustness. The bias of a model refers to its ability to capture the underlying patterns in the input data, while variance refers to its sensitivity to small fluctuations during training.
The aim of the bias is accomplished when the metric at the training stage improves how the human performs this task. For example, if we are training a model for the diagnosis of Parkinson's Disease with Magnetic Resonances, we have to obtain a better accuracy than the one obtained by a physician. A model with low bias may simplify the underlying patterns in the data, leading to underfitting and poor performance on both the training and test sets. Apart from the bias, we use the concept of variance which is the difference between the metrics of at training and test stage. A model with high variance may capture noise or irrelevant patterns in the training data, leading to overfitting and poor generalization of unseen data. There is no exact value for this but having a difference greater than 10% of the value at the training stage seems too much. In the case of underfitting, the metrics during the training stage are higher than during the test. When overfitting occurs, training is lower than the test. In conclusion, the aim is to obtain a high bias and low variance.
To avoid underfitting in DL models, several strategies can be employed. Firstly, increasing model complexity by adding more layers, neurons, or parameters can help capture underlying patterns in the data. Additionally, experimenting with more complex architectures such as CNNs, RNNs, or Transformers tailored to the nature of the data and task can enhance model performance. Another option is training for longer by increasing the number of epochs or iterations which allows the model to learn intricate patterns for more time.
To prevent overfitting in DL models, several strategies can be employed. Firstly, regularization techniques like dropout, and batch normalization. The former consists of temporarily disconnecting several neurons from the network, including all its incoming and outgoing connections, (Srivastava et al. 2014). The latter normalizes the inputs of the layers. Another technique is early stopping, where training is stopped when the validation metric stops to improve. We also can use data augmentation techniques, such as rotation, translation, scaling, and adding noise, to enhance training diversity. Finally, increasing the size of the training dataset or simplifying the model by reducing layers, neurons, or parameters can also mitigate overfitting.

3.7. Adding new metrics for an in-depth interpretation of the model

In subsection 3.4 we talked about the main metrics that could be used for classification and regression problems. These metrics have been used as a way to measure the performance of the model to find a bias-variance trade-off. As a first approach, these metrics are enough, but in some cases, more complex metrics should be used. For example, if the developed model is used in the field of medicine metrics considering FP and FN should be used. This will let us interpret the models more deeply. Let’s consider a model for cancer diagnosis, it is not the same in that it has problems with FN (healthy people diagnosed with cancer) than FP (people with cancer that have been considered as healthy). In the last case, this is a problem that a model should minimize. So, considering all these points we are introducing more metrics.
In the case of classification problems, metrics like specificity and sensitivity (sometimes called recall) are very useful. Specificity calculates the ratio of true negatives to the sum of true negatives and false positives, while sensitivity performs a similar calculation, changing true negatives for true positives and false positives for false negatives. Finally, precision is computed by dividing the number of true positives by the sum of true positives and false positives. These 3 Equations are formalized following.
Specificity = T N T N + F P
Sensitivity = T P T P + F N
Precision = T P T P + F P
The interpretation of the metrics above can be done as follows. Specificity is used so the model can distinguish healthy individuals from those without cancer, crucial for minimizing unnecessary treatments or interventions. In the case of sensitivity, the model can identify most cases of cancer, reducing the risk of treating cases of disease and applying an accurate intervention and treatment minimised unnecessary stress for patients. Finally, with precision, we ensured to identify cases of cancer and applying an accurate intervention and treatment. Apart from that there are other more complex metrics like F1-Score, Area Under the Curve (AUC) and Receiver Operating Characteristic (ROC) Curve.
If we talk about regression problems with DL models some points should be considered. If the use case consists of predicting a particular value like a time series problem for predicting the value of a company´s stock, the concepts of FN and FP do not apply. Anyway, there are more metrics similar to MSE such as Mean Absolute Error (MAE), Root Mean Squared Error (RMSE), Mean Absolute Percentage Error (MAPE) or R-squared (also Coefficient of Determination) that can be used similarly. But this is not the only case of regression problems that can be solved with DL models, we also have object detection, audio restoration and others. In these cases, the concepts of FP and FN can be used. Therefore, there exists metrics for this purpose, for example, Intersection over Union (IoU) and Dice score.
IoU computes the ratio of the overlapping area between the predicted (output image of the model) and ground truth (image used in the output layer during training) regions to the total area covered by both regions, (M. A. Rahman and Wang 2016). It ranges from 0 to 1, where 0 signifies no overlap and 1 denotes perfect spatial alignment between the regions. So, it is defined as the ratio of the area of intersection between the predicted image and ground truth to the area of their union. Equation 7 formalizes it mathematically.
IoU = P r e d i c t e d   ∩   G r o u n d   T r u t h P r e d i c t e d   ∪   G r o u n d   T r u t h
In the equation above ∣Predicted ∩ Ground Truth∣ represents the area of intersection between the predicted and ground truth regions. Then, ∣Predicted ∪ Ground Truth∣ represents the area of union between the predicted and ground truth regions.
Dice score is a metric based on IoU and calculates the ratio of twice the overlapping area to the sum of the sizes of the predicted and ground truth regions, (Chegraoui et al. 2021). It also ranges from 0 to 1 having the same interpretation as IoU. Equation 8 describes it.
IoU = 2 × P r e d i c t e d   ∩   G r o u n d   T r u t h P r e d i c t e d + P r e d i c t e d
Regarding the Equation above, the numerator is the same as in IoU. Then, ∣Predicted∣ represents the size of the predicted region and ∣Ground Truth∣ represents the size of the ground truth region.

3.8. Making a comparison with a baseline

Using a baseline is essential for evaluating the performance of a Deep Learning model for several reasons. Firstly, it provides a point of reference against which the model's performance can be compared. This is crucial in understanding whether the model is learning meaningful patterns in the data or if its performance is merely a matter of luck. Secondly, baselines help in setting realistic expectations for the model's performance. By comparing against a simple baseline, we can measure how much improvement DL techniques offer over simpler approaches. This helps in assessing whether the additional complexity of applying DL techniques is justified. Moreover, using a baseline can also highlight potential shortcomings or biases in the dataset. If a DL model struggles to outperform a simple baseline, it may indicate issues with the quality or representativeness of the data, prompting further investigation and data preprocessing. Overall, employing a baseline is a fundamental step in the evaluation process of Deep Learning models, providing context, and insights that are essential for making informed decisions about model performance and deployment.

4. Use cases

In this section, we are exploring some use cases where the methodology explained above has been explained in detail step by step. These examples try to cover most of the situations that could happen during the implementation of a DL model considering the decisions to take. The first use case is a model that could diagnose breast cancer using thermographic images. In the second use case, a brain tumour detection model is trained with MRs. Finally, the third use case solves the problem of background audio suppression in conversational audio. In the following Tables (one for each use case), we summarize each step of the methodology adding the decision taken and its explanation.
Table 2. Methodology applied to breast cancer diagnosis.
Table 2. Methodology applied to breast cancer diagnosis.
Step Decision Explanation
3.1. Classification problem with coloured images solved with CNNs The dataset consists of thermographic images of healthy people and people with breast cancer.
3.2. Randomize 80-20 split The number of images is enough and images between patients are very different.
3.3. Scaling: Min-Max Typical decision when working with images.
3.4. Accuracy metrics In a diagnosed problem, we need to measure the number of hits.
3.5. K-fold validation with k=5 Usual decision
3.6. Bias-variance trade-off. Train: 87.67%±6.65, Val: 86.67%±12.47, Test: 89.23%±5.85 Bias is correct as human performance accuracy, assisted by a CAD, is near 83%, (Keyserlingk et al. 2020). The variance is also correct.
3.7. Other metrics. Specificity: 88%, Sensitivity: 90.53% and Precision: 88.91% These metrics are around the same values which means the model is very stable
3.8. Baselines. VGG16: 68%. VGG19: 51.33%, Inception 84% The proposed model performs better than the baseline
Table 3. The methodology applied to EEGs classification.
Table 3. The methodology applied to EEGs classification.
Step Decision Explanation
3.1. Classifying chunks of an EEG using a CNN The dataset is chunked into timestamps that are model as graphs represented in images. The CNN model discriminates between stages of a seizure.
3.2. 80-20 split between patients As brain states in a person does not change a lot from a particular moment and the following, the split is done considering the EEGs of the patients.
3.3. Scaling: does not apply As images are in greyscale, they are in the same ranges.
3.4. Accuracy metrics For a classification problem, accuracy should be used.
3.5. K-fold validation with k=5 Usual decision
3.6. Bias-variance trade-off. Model 1: 93.6%, 88.2%, 87.2%. Model 2: 91.9%, 86.8%, 81.3% Bias can not be measured as there are no official studies about the performance of physicians distinguishing seizure’s states. The variance is correct.
3.7. Other metrics. Specificity: 94%, Sensitivity: 94.1% and Precision: 93.2% These metrics are around the same values which means the model is very stable.
3.8. Baselines: nothing. There is no baseline for being a very specific use case.
Table 4. The methodology applied to tumor detection.
Table 4. The methodology applied to tumor detection.
Step Decision Explanation
3.1. Small brain tumor detection in MR using a U-Net The dataset is pairs of MRs of the brain and the mask that isolates the brain tumor in this MR
3.2. Randomize 80-20 split The number of MRs is enough and are very different between them.
3.3. Scaling: Not needed The images are in greyscale.
3.4. Loss metrics: MSE In an object detection, we need to know how the predicted mask resembles the ground truth image that represents the mask.
3.5. K-fold validation with k=5 Usual decision.
3.6. Bias-variance trade-off. Train:10% ± 0.5%, Validation: 11.1% ± 0.5%, Test: 14% Human performance goes from 28 and 44% error (the model performs better) and variance is not high.
3.7. Other metrics: Dice score. Train: 96.3% ± 0.8%. Validation: 92% ± 1%. Test: 91.6%. Dice score considers FP and FN.
3.8. Baselines. Dice score: 45% The proposed model performs better than the baseline.

5. Conclusions

This paper presents a step-by-step methodology to train accurately DL models. Apart from that, it presents the best practices to do so a complete information is provided during the process. The manuscript should be taken as an information resource for researchers that are not experts in DL and want to use these techniques in their field, so they could understand the main terms and strategies to apply and why. In case of having a deeper understanding of DL models, this could be used as a guide of best practices.
The methodology is divided into 8 steps. First tries to explain which DL models should be used depending on the nature of the data and use case to solve. Second describe how to split training, validation and test sets considering the distribution of the dataset and its similarities. Third compiles different strategies to apply feature scaling which is related to the value ranges of the different features of the data. Fourth shows which general metrics should be used depending on if the problem to solve is regression or classification. Fifth describes the validation strategy called k-fold cross. Sixth, introduces the concept of bias-variance trade-off that shows if there is any underfitting or overfitting. Seventh tries to understand in-depth how the model performs by introducing metrics that consider false positives or false negatives. Eighth evaluates the proposed model against a baseline, so it can be demonstrated that it is better that what can be found in the scientific literature.
Finally, three different use case have been compiled where we have provided information for each step of the method pointing out the decision that has be taken and an explanation about it, if possible.

References

  1. Almalki, Amani, and Longin Jan Latecki. 2024. “Self-Supervised Learning With Masked Autoencoders for Teeth Segmentation From Intra-Oral 3D Scans.” In Proceedings of the IEEE/CVF Winter Conference on Applications of Computer Vision, , 7820–30.
  2. Ballard, Dana H. 1987. “Modular Learning in Neural Networks.” In AAAI, , 279–84.
  3. Belkin, Mikhail, Daniel Hsu, Siyuan Ma, and Soumik Mandal. 2019. “Reconciling Modern Machine-Learning Practice and the Classical Bias--Variance Trade-Off.” Proceedings of the National Academy of Sciences 116(32): 15849–54. [CrossRef]
  4. Boroujeni, Sayed Pedram Haeri, and Abolfazl Razi. 2024. “IC-GAN: An Improved Conditional Generative Adversarial Network for RGB-to-IR Image Translation with Applications to Forest Fire Monitoring.” Expert Systems with Applications 238: 121962. [CrossRef]
  5. Chegraoui, Hamza et al. 2021. “Object Detection Improves Tumour Segmentation in MR Images of Rare Brain Tumours.” Cancers 13(23): 6113. [CrossRef]
  6. Ding, Dan et al. 2024. “A Tunable Diode Laser Absorption Spectroscopy (TDLAS) Signal Denoising Method Based on LSTM-DAE.” Optics Communications: 130327. [CrossRef]
  7. Dunford, Rosie, Quanrong Su, and Ekraj Tamang. 2014. “The Pareto Principle.”.
  8. Ehtisham, Rana et al. 2024. “Computing the Characteristics of Defects in Wooden Structures Using Image Processing and CNN.” Automation in Construction 158: 105211. [CrossRef]
  9. Elman, Jeffrey L. 1990. “Finding Structure in Time.” Cognitive science 14(2): 179–211.
  10. Goodfellow, Ian et al. 2014. “Generative Adversarial Nets.” Advances in neural information processing systems 27.
  11. Hochreiter, Sepp, and Jürgen Schmidhuber. 1997. “Long Short-Term Memory.” Neural computation 9(8): 1735–80.
  12. Hu, Wenxing, Mengshan Li, Haiyang Xiao, and Lixin Guan. 2024. “Essential Genes Identification Model Based on Sequence Feature Map and Graph Convolutional Neural Network.” BMC genomics 25(1): 47. [CrossRef]
  13. Jadon, Aryan, Avinash Patil, and Shruti Jadon. 2022. “A Comprehensive Survey of Regression Based Loss Functions for Time Series Forecasting.” arXiv preprint arXiv:2211.02989.
  14. Keyserlingk, J. R., Ahlgren, P. D., Yu, E., Belliveau, N., & Yassa, M. (2000). Functional infrared imaging of the breast. IEEE Engineering in Medicine and Biology Magazine,19(3), 30–41.
  15. Kipf, Thomas N, and Max Welling. 2016. “Semi-Supervised Classification with Graph Convolutional Networks.” arXiv preprint arXiv:1609.02907.
  16. Khenkar, S. G., Jarraya, S. K., Allinjawi, A., Alkhuraiji, S., Abuzinadah, N., & Kateb, F. A. (2023). Deep Analysis of Student Body Activities to Detect Engagement State in E-Learning Sessions. Applied Sciences, 13(4), 2591. [CrossRef]
  17. Krizhevsky, Alex, Ilya Sutskever, and Geoffrey E Hinton. 2012. “Imagenet Classification with Deep Convolutional Neural Networks.” Advances in neural information processing systems 25: 1097–1105.
  18. Kuhn, Max, Kjell Johnson, Max Kuhn, and Kjell Johnson. 2013. “Over-Fitting and Model Tuning.” Applied predictive modeling: 61–92.
  19. LeCun, Yann, Yoshua Bengio, and Geoffrey Hinton. 2015. “Deep Learning.” nature 521(7553): 436–44.
  20. Li, Huaguang, and Alireza Baghban. 2024. “Insights into the Prediction of the Liquid Density of Refrigerant Systems by Artificial Intelligent Approaches.” Scientific Reports 14(1): 2343. [CrossRef]
  21. Lu, Minrong, and Xuerong Xu. 2024. “TRNN: An Efficient Time-Series Recurrent Neural Network for Stock Price Prediction.” Information Sciences 657: 119951. [CrossRef]
  22. Maray, Nader et al. 2023. “Transfer Learning on Small Datasets for Improved Fall Detection.” Sensors 23(3): 1105. [CrossRef]
  23. Protić, Danijela et al. 2023. “Numerical Feature Selection and Hyperbolic Tangent Feature Scaling in Machine Learning-Based Detection of Anomalies in the Computer Network Behavior.” Electronics 12(19): 4158. [CrossRef]
  24. Rahman, Md Atiqur, and Yang Wang. 2016. “Optimizing Intersection-over-Union in Deep Neural Networks for Image Segmentation.” In International Symposium on Visual Computing, , 234–44.
  25. Rahman, Zia Ur et al. 2022. “Automated Detection of Rehabilitation Exercise by Stroke Patients Using 3-Layer CNN-LSTM Model.” Journal of Healthcare Engineering 2022. [CrossRef]
  26. Russell, Stuart J, and Peter Norvig. 2016. “Artificial Intelligence: A Modern Approach. Malaysia.”.
  27. Salakhutdinov, Ruslan, and Geoffrey Hinton. 2009. “Deep Boltzmann Machines.” In Proceedings of the Twelth International Conference on Artificial Intelligence and Statistics, Proceedings of Machine Learning Research, eds. David van Dyk and Max Welling. Hilton Clearwater Beach Resort, Clearwater Beach, Florida USA: PMLR, 448–55. https://proceedings.mlr.press/v5/salakhutdinov09a.html.
  28. Sammut, Claude, and Geoffrey I Webb. 2011. Encyclopedia of Machine Learning. Springer Science \& Business Media.
  29. Sathya, Ramadass, Annamma Abraham, and others. 2013. “Comparison of Supervised and Unsupervised Learning Algorithms for Pattern Classification.” International Journal of Advanced Research in Artificial Intelligence 2(2): 34–38. [CrossRef]
  30. Smolensky, Paul. 1985. “Chapter 6: Information Processing in Dynamical Systems: Foundations of Harmony Theory.” Parallel distributed processing: explorations in the microstructure of cognition 1.
  31. Srivastava, Nitish et al. 2014. “Dropout: A Simple Way to Prevent Neural Networks from Overfitting.” The journal of machine learning research 15(1): 1929–58.
  32. Vaswani, Ashish et al. 2017. “Attention Is All You Need.” Advances in neural information processing systems 30.
  33. Zhou, Fangzheng et al. 2024. “Unified CNN-LSTM for Keyhole Status Prediction in PAW Based on Spatial-Temporal Features.” Expert Systems with Applications 237: 121425. [CrossRef]
Preprints 99353 g001
Figure 1. Classification of Deep Learning models based on their different training strategies.
Figure 1. Classification of Deep Learning models based on their different training strategies.
Preprints 99353 g001
Table 1. Summary of DL models used type of data and applications.
Table 1. Summary of DL models used type of data and applications.
Model type Nature of data Use case
MLP Tabular data Prediction of a continuous value
CNNs Image data with spatial relationships Image Classification, Object Detection, Segmentation
GCNNs Data represented as graphs or networks Graph-structured Data, Social Network Analysis
RNNs Temporal sequences, sequential data Sequential Data Modeling, Time Series Prediction
Autoencoders Unlabeled images Data Compression, Denoising, Anomaly Detection
Transformers Sequential data, particularly text data Language Translation, Text Generation
GANs Often images, but can be applied to other domains Image Generation, Style Transfer, Data Augmentation
DRL Sequential decision-making tasks with rewards Game Playing, Robotics, Autonomous Systems
Hybrid models Mixed data types or tasks Multiple types of data/modalities or tasks
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated