Prerpints.org logo
Preprint
Article

Unveiling Influence in Networks: A Novel Centrality Metric and Comparative Analysis through Graph-Based Models

Altmetrics

Downloads

115

Views

28

Comments

0

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

20 February 2024

Posted:

20 February 2024

You are already at the latest version

Alerts
Abstract
Identifying influential actors within social networks is pivotal for optimizing information flow and mitigating the spread of both rumors and diseases. Several methods have emerged to pinpoint these influential entities in networks that are represented as graphs. In these graphs, nodes corre-spond to individuals and edges indicate their connections. This study focuses on centrality measures, prized for their straightforwardness and effectiveness. We categorize structural central-ity into two: local, considering a node's immediate vicinity, and global, accounting for overarching path structures. Some techniques blend both centralities to highlight nodes influential at both mi-cro and macro levels. Our paper presents a novel centrality measure, accentuating node degree and incorporating the network's broader features, especially paths of different lengths. Through Spearman and Pearson's correlations tested on seven standard datasets, our method proves its merit against traditional centrality measures. Additionally, we employ the SIR model, portraying disease spread, to further validate our approach. The ultimate influential node is gauged by its capacity to infect the most nodes during the SIR model's progression. Our results indicate a nota-ble correlative efficacy across various real-world networks relative to other centrality metrics.
Keywords: 
Subject: Computer Science and Mathematics  -   Computer Science

1. Introduction

In the dynamically evolving landscape of digital interconnectedness, social network analysis (SNA) emerges as a crucial disciplinary field, positioned at the intersection of graph theory and sociology. This unique discipline offers a deep understanding of complex interactions among diverse entities such as individuals, organizations, or even URLs [1]. Utilizing nodes to represent entities and links to symbolize their interactions, SNA provides both a visual and mathematical perspective on human interconnections. This analytical approach reveals insights into community dynamics, market trends, and political movements, and finds practical applications in varied areas, ranging from influence marketing to crisis management and public health surveillance. The primary objectives of this analysis include the detection of communities [2,47], the prediction of potential links [3,45,46], and crucially, the identification of influential actors [8], thus demonstrating its versatility and relevance in contemporary society.
The significance of identifying these influencers or opinion leaders cannot be understated. These are unique individuals who, even though a minority, can cast vast influence over a majority [4]. Their role becomes even more critical when considering the implications of their influence, such as mitigating rumor spread, disease control [5,6], optimizing energy dissemination [7], and fortifying crucial zones against deliberate threats [8,9,10]. Over time, a rich tapestry of methodologies has evolved to identify influential figures within social networks, each leveraging distinct features such as content and network structure [11]. Content-based detection methods focus on the impact of textual content, considering both linguistic criteria, like the nature of arguments or agreement/disagreement between users, and numerical criteria, such as response frequency, message size, or the extent of relationships. For example, empirical studies have compared messages from influencers with those from non-influencers to discern patterns [12]. Another content-based approach involves analyzing how influencers affect the themes and directions of conversations [13]. Simultaneously, approaches focusing on network structure harness various structural components, with centrality-based methods being particularly prominent [14]. In these approaches, social networks are typically represented as simple undirected graphs, G=(V,E), where V symbolizes the set of vertices (network users), and E denotes the interconnections between users. We employ centrality measures to capture the structural properties of these nodes. These measures assign real values to nodes, ranking them based on their significance within the network. Structural centrality encompasses two core types: local centrality measures, which are based on the immediate neighborhood of a node [15], and global centrality measures, taking into account a node's broader membership paths within the network. Local centrality measures include degree centrality [15], local rank [16], and K-shell [17], while global measures feature metrics like eccentricity [18], closeness centrality [15], betweenness centrality [15], and Katz centrality [19]. However, it is crucial to note that despite their utility in understanding network structure, centrality-based methods may exhibit instability in large-scale networks. This is particularly evident in methods like degree centrality, which, while valuable, may overlook nodes with fewer direct connections yet substantial influence within the network's broader context. This highlights the need for a more nuanced approach to effectively balance both content-based and structural insights to accurately map out the influence landscape within social networks.
This paper introduces a novel methodological approach in the field of social network analysis (SNA), standing out for its integration of innovative and unconventional elements. This approach emphasizes the importance of node degree while also considering the broader network context, grounded in a solid theoretical foundation. Based on the premise that direct connections (node degree) are significant, our study acknowledges that the true essence of a node's influence often lies in its broader relationships within the network, including indirect paths of varying lengths. Therefore, rather than solely focusing on the degree of connectivity, we have incorporated the concept of paths of different lengths, aiming for a more nuanced understanding of influence within the network. This innovative approach highlights the importance of indirect paths and their variability in length for a more comprehensive analysis of influence in social networks.
The experimental framework of our study is carefully structured to test the effectiveness of our approach. We have selected a variety of real-world social networks for our analysis, each chosen for its unique characteristics and relevance to our research objectives. Our methodology integrates specific tools and techniques, including advanced statistical methods and computational algorithms, to evaluate the proposed centrality measure. To attest to the viability of our proposed methodology, we subjected it to rigorous testing using Spearman and Pearson correlations across selected real-world social networks. The initial results are promising, with our metric effectively highlighting influential nodes. Continuing our exploration, a cornerstone of our experimental analysis is the application of the Susceptible-Infectious-Recovered (SIR) model, traditionally used in epidemiology and adapted in our study to simulate the spread of information and influence within social networks. The adaptability of the SIR model to our context demonstrates its utility beyond traditional public health applications, providing valuable insights into the dynamics of information flow and influence propagation in social networks.
The structure of this paper is as follows: Section 2 touches upon prior research, Section 3 details the proposed method, Section 4 offers a deep dive into our findings, and Section 5 wraps up with concluding remarks.

2. Related Work

Over the years, social network analysis has continuously evolved, consistently emphasizing understanding the roles and significance of entities within a network. Among the various aspects studied, centrality computation has stood out as an essential component, having been at the forefront for several decades [20]. This importance stems from the underlying quest to discern and quantify the prominence or influence of individual actors within a broader collective or network. The centrality concept not only gauges the immediate impact of an actor but also reflects its broader implications on the network's dynamics and flow. As we navigate this section, we will elucidate three fundamental definitions that have been instrumental in shaping the understanding of centrality: degree centrality, betweenness centrality, and PageRank [21]. Each of these metrics offers a unique perspective on the role and influence of nodes within a network, contributing to the comprehensive landscape of social network analysis.

2.1. Degree Centrality

Degree Centrality (DC) is foundational in centrality metrics. It quantitatively assesses of a node's importance based on its direct connections within the network. This metric's intuitive nature correlates increased connections with enhanced influence. Mathematically, using the adjacency matrix A = ( a i , j ) of an undirected graph G with N representing the total number of nodes, the degree centrality for a node v i ∈ V is defined as:
C d e g v i = 1 N − 1 ∑ j = 1 N a i j
However, while DC offers valuable insights [35], it may have limitations, mainly when employed in complex scenarios such as web page graph analyses. Building on this, a study by Kitsak et al. [24] highlighted an intriguing observation: the most influential nodes are not necessarily the ones with the most connections. Their research led them to explore k-core decomposition, an iterative process that segregates nodes based on their minimum degrees [25,26]. A node's coreness, indicating its rank in the decomposition hierarchy, is directly tied to its capacity to influence network dynamics [27]. In contrast to coreness, the H-index is a local centrality measure that utilizes only partial information, specifically the degrees of the neighbors of the nodes [28]. This emphasizes that, while degree centrality offers a foundational understanding, capturing the nuances of influence in complex networks often necessitates a more multifaceted approach.

2.2. Betweenness Centrality

Betweenness Centrality (BC) quantifies how often an agent acts as a conduit on the most direct path between two other nodes. Crucial for discerning power dynamics in communication networks, BC measures an entity's control over information flow. Conceptually, BC offers a probabilistic perspective: it quantifies the likelihood that information traveling between two distinct nodes will traverse through a given node [29]. Formally, the betweenness centrality for any node v i ∈ V can be articulated as
C v i = ∑ j = 1 N ∑ k = 1 N g j k ( v i ) g j k
Herein, g j k ( v i ) denotes the ensemble of shortest paths linking nodes v j and v k that incorporate node v i , while g j k is the total number of geodesic paths between nodes v j and v k . This concept of node betweenness centrality, a brainchild of Freeman, has evolved over time, accommodating nuances like link betweenness centrality or edge betweenness [30,31]. Broadening the horizon further, Katz [19] introduced an innovative methodology, prioritizing all potential paths within a network but assigning diminishing significance to increasingly longer paths, thereby capturing both the direct and indirect influences within the system.

2.3. Page Rank

Page Rank, pioneered by Larry Page and Sergey Brin [21], revolutionized web search optimization. It ranks each node based on its connections and affiliations with significant nodes. The foundation of PageRank lies in the "Random Surfer" model, reflecting typical Internet navigation patterns. The page rank formula is given by:
P R v i = 1 − α + α ∑ v j ϵ I n ( v i ) P R ( v j ) O u t ( v j )
Herein, l n ⁡ ( v i ) is the set of nodes for which there is a link to v i (i.e., v j ∈ V , v i , v j ∈ E ), o u t ( v j ) is the outgoing degree of u j , α is a damping factor. The computational complexity of the Page Rank algorithm mainly arises from the matrix multiplication step, which has a time complexity of O(nm), where m represents the number of iterations and n represents the number of nodes in the network.
However, another study has led to the development of the "Bridging Centrality" metric [32], gaining increasing recognition for its proficiency in the analysis of complex networks. It is crucial to emphasize that the effort to combine basic degree metrics with advanced structural determinants introduces its own complexities, making the quest for a universally effective method a formidable challenge. Utilizing various structural properties to identify the most influential nodes in a network indeed proves to be an effective approach. Nevertheless, the selection of these properties for combination remains a challenging task.

3. The Proposed CDP Measure

In the vast field of network analysis, a variety of metrics have been introduced over the years. These measures, while insightful, often operate in isolation, focusing mainly on specific facets of node importance. This section introduces the CDP measure, a holistic approach that integrates multiple aspects of node influence, in recognition of this limitation. In the subsequent sections, we delve into the intricacies of this innovative approach.

3.1. Problem Context

In this research, we delve into the structural analysis of an undirected and unweighted graph, representing a complex social network. Our primary objective is to pinpoint nodes that wield significant influence within this network. This task transcends the simple evaluation of nodes' degrees, extending to a meticulous examination of paths of varied lengths. Such an approach is critical for encapsulating both direct and indirect interactions between nodes.
The impetus for identifying influential nodes is rooted in the need to comprehend the dynamics of information dissemination, the spread of trends, and the propagation of behaviors across the network. This understanding is pivotal for various applications, ranging from marketing strategies and public health campaigns to the analysis of social movements and the spread of misinformation.
To tackle this challenge effectively, we propose a multi-faceted approach. This involves assessing not only the immediate reach of each node, represented by its degree, but also its extended influence, reflected in the network pathways it influences or controls. By examining both direct and indirect connections, our method aims to provide a comprehensive view of a node's influence.
The complexity of social networks, with their inherent unpredictability and non-linear interactions, necessitates a methodology, both simple and robust, capable of capturing the nuances of these networks. Our approach, therefore, focuses on developing a more sophisticated model that considers various factors contributing to a node's influence. This includes examining network topology, node centrality, and the role of clusters within the network.

3.2. CDP Measure

Traditional local and global centrality metrics, while insightful, have inherent limitations, particularly when applied to specific network typologies. The amalgamation of multiple measures can provide enriched insights. In this research, we introduce the CDP (Centrality Degree Paths) score, a composite measure that accentuates degree centrality while incorporating the number of paths. Solely relying on degrees may result in potentially overlooking crucial network dynamics; the proposed approach enhances node importance using squared degrees and concurrently considers the number of simple paths. Let G = ( V , E ) represent an undirected simple graph. The CDP centrality score of a node x ∈ V is defined as follows:
C D P ( x ) = deg ( x ) ⁡ 2 P ( x , y ) l ≤ d
Here P ( x , y ) l ≤ d denotes the number of simple paths from node x to node y, where d is the length of the path and deg(x) indicates the number of neighbors of node x.
To derive the CDP centrality score for nodes in a graph, the methodology below is proposed:
  • Squared Degree of a Node ( deg ( x ) ) ⁡ 2 : The degree of a node in a network graph denotes the count of edges connected to that node. Squaring this value accentuates the impact of nodes with heightened degrees over those with lesser degrees. This approach proves beneficial in networks where nodes with substantially augmented connections wield disproportionate influence vis-à-vis those with fewer connections. By squaring the degree, the formula magnifies the significance of highly interconnected nodes.
  • Path Count ( P ( x , y ) l ≤ d ): This facet of the formula entails tallying the number of paths between nodes x and y, constrained by a predefined distance threshold (denoted as l≤d). This aspect acknowledges not only the direct influence exerted by a node (as denoted by its degree) but also its indirect influence through network connections within a specific proximity. This contributes to a holistic understanding of a node's influence diffusion within the network.
  • Division of the Two Components: The division of the squared degree of a node by the count of paths within a stipulated distance appears to standardize the influence exerted by a node. This serves to mitigate the potential distortion caused by nodes with exceptionally high degrees, particularly in extensive or dense networks.
Collectively, the choice to square the degree underscores nodes that are not merely connected but highly interconnected, conceivably serving as hubs or pivotal influencers in the network. The incorporation of path count introduces a layer of intricacy to the analysis, acknowledging that influence within a network extends beyond direct connections to encompass the dissemination of these connections throughout the network. Such methodological deliberations enhance the scholarly rigor of the manuscript by furnishing a nuanced and comprehensive measure of node influence in network analysis.
This procedural approach facilitates the identification of pivotal nodes, which can be visualized and verified as illustrated in Figure 1.

3.3. Example

To illustrate the application of the CDP score, we consider Figure 1. For this analysis, a specific choice of l=2 has been made, focusing on direct neighbors and those of second-degree proximity. This parameter choice provides a balance between depth and computational feasibility.
The CDP score in Table 1 displays the influence of each node. As depicted, node 3 stands out as the most influential despite its degree, underscoring the advantage of the CDP measure.
To underscore the added value of the proposed metric, we turn our attention to the network depicted in Figure 1. When relying solely on degree centrality, node 5 stands out as the most influential with a degree of 4, followed by nodes 1, 3, 8 and 11, each having a degree of 3. However, when applying the CDP metric, node 3 emerges as the predominant node with a score close to 1.8. It is followed by node 5 with a score of 1.77 and node 8 with 1.5. Even though node 3 has a lower degree than node 5, its position within the network makes it more influential. In summation, this innovative metric elevates accuracy in ranking by assimilating not just the degree centrality but also the abundance of simple paths throughout the network.

4. Experiments

In the previous section, we introduced and discussed the conceptual framework of our novel CDP method. Building on that foundation, this section is devoted to an empirical evaluation of the proposed method. We employ seven distinct real-world networks for this purpose: Karate Club Network, Dolphin Network, Les Misérables Network, Books about US Politics Network, American College Football, USair97, and Mouse-Kasthuri Network. Our primary objective is to ascertain the correlation between traditional centrality measures and the results derived from the proposed CDP method. To rigorously evaluate this association, both Pearson's and Spearman's correlation metrics have been employed, offering a comprehensive understanding of the statistical interdependence between the centrality metrics and the scores generated by the CDP approach. Furthermore, the propagation dynamics within these networks are examined using the Susceptible-Infective-Recovered (SIR) model, enabling us to gauge the spreading efficiency associated with each node. The performance of the CDP method, in conjunction with the SIR model, is further scrutinized using the Kendall tau and Overlap coefficients.

4.1. Dataset

To critically assess our proposed metric, we engage with an array of networks originating from varied disciplines. Our scrutiny is meticulously confined to undirected simple graphs, thus ensuring an unambiguous omission of loops and duplicate edges. An outline of the datasets marshalled for this exploration is presented subsequently. In Table 2, we utilized the dataset previously introduced in [49] and incorporated two additional large datasets (USair97 and Mouse-Kasthuri) to further validate the performance of the proposed CDP metric.
  • Zachary’s Karate Club: A representation of social interactions among 34 members of a karate club at a US-based university during the 1970s.
  • Dolphin Social Network: A depiction of regular interactions among 62 dolphins in a community near Doubtful Sound, New Zealand.
  • Les Misérables: A network delineating the coappearances of characters in Victor Hugo's celebrated novel, "Les Misérables".
  • Books about US Politics: This network visualizes the co-purchasing patterns of political books around the 2004 US presidential election, as recorded by Amazon.com.
  • American College Football: A matrix of football games amongst Division IA colleges during the Fall 2000 season.
  • USair97: A topological representation of the US air travel landscape in 1997, with nodes as airports and edges as direct flight connections.
  • Mouse-Kasthuri: A dataset from the Neurodata repository, representing unweighted fiber tracts connecting vertices in brain networks.

4.2. Evaluation Metrics

4.2.1. Pearson's Correlation

Denoted by ρ , quantifies the linear association between two variables. This coefficient, often used in linear regression analysis, ranges from -1 to +1. A coefficient of +1 implies a perfect positive linear relationship, -1 denotes a perfect negative linear relationship, and a value of 0 suggests no linear correlation. The formula for calculating Pearson's correlation for variables x and y is:
ρ x , y = c o v ( x , y ) σ x σ y
Here, cov(x,y) represents the covariance between x and y, while σ x and σ y denote the standard deviations of x and y, respectively.

4.2.2. Spearman's Correlation

A nonparametric measure assesses the strength and direction of the monotonic relationship between two variables. Distinct from Pearson's correlation, which evaluates linear relationships, Spearman's correlation captures both linear and nonlinear monotonic associations. It computes the correlation based on the rank values of the variables rather than their actual values. A coefficient value of +1 or -1 reflects a perfect monotonic relationship. The formula for Spearman's correlation is given by:
ρ R x , R ( y ) = c o v ( R x , R y ) σ R ( x ) σ R ( y )
In this equation, ρ signifies the Pearson correlation coefficient when applied to rank variables. cov(R(x),R(y)) is the covariance of the rank variables, and σ R ( x ) and σ R ( y ) represent their respective standard deviations.

4.2.3. SIR Model

The Susceptible, Infected, Recovered (SIR) model is a well-known method for evaluating centrality measures in network analysis. This epidemiological model simulates the spread of a virus within a network, categorizing nodes into three distinct states: Susceptible (S), Infected (I), and Recovered (R) [40].
  • Susceptible (S): A susceptible node is one that is unaware of the information spreading within the network. These nodes are healthy but not immune and can be infected by adjacent infected nodes. Initially, all nodes are considered susceptible except for the source node.
  • Infected (I): An infected node has received and is aware of the information propagating through the network. It actively transmits this information to its neighbors. An infected node transitions to the recovered state after a certain period, dictated by an infection probability β at each time step and a recovery probability λdt in any time interval dt. The average duration of a node being infected is represented by D.
  • Recovered (R): Recovered nodes have lost interest in the information and no longer spread it. They also become immune to further infection. At the end of the process, only susceptible and recovered nodes remain in the network.
The dynamics of the SIR model are governed by a set of ordinary differential equations, describing the transitions between these states. The total population in the network is denoted by N, and at any time t, the sum of susceptible, infected, and recovered nodes equals N. The SIR system can be described by the following system of ordinary differential equations:
d S d t = β I S N
d I d t = β I S N − λ I
d R d t = λ I
S(t) + I(t) + R(t) = N
The SIR model's utility extends beyond traditional epidemiological contexts to the analysis of information spread in social networks, providing insights into the influence exerted by various nodes based on their centrality measures.

4.2.4. Kendall's Tau

Denoted by τ, Kendall's tau is a statistic that measures the rank correlation between two variables, assessing the association based on their ranks. It is particularly useful for non-linear relationships. The pairs of observations ( x i , y i ) and ( x j , y j ) are concordant if both x i and x j or y i and y j are either both increasing or both decreasing. They are discordant if one is increasing and the other is decreasing. Kendall's tau is calculated as the difference between the probability of concordant pairs and discordant pairs. The value of τ ranges from -1 (perfect disagreement) to +1 (perfect agreement), with 0 indicating no correlation. Kendall's tau is given by
τ = n u m b e r   o f   c o n c o r d a n t   p a i r s − n u m b e r   o f   d i s c o r d a n t   p a i r s 1 2 n ( n − 1 )
where n is the number of observations.

4.2.5. Overlap Coefficient

This similarity measure, related to the Jaccard index, quantifies the overlap between two finite sets. Represented as the size of the intersection divided by the smaller sizes of the two sets, the Overlap coefficient is a valuable tool for comparing different sets. It is particularly useful for assessing the correlation of the most influential node sets obtained from ranking scores and the SIR model. The Overlap coefficient ranges from 0 (no overlap) to 1 (complete overlap), with higher values indicating more significant overlap. The formula for calculating the Overlap coefficient between two sets X and Y is given by:
o v e r l a p X , Y = X ∩ Y min ⁡ ( X , Y )
In this context, a higher Overlap coefficient value indicates a greater reliability of the ranking score in identifying influential nodes within the network.

4.3. Experimental Results

4.3.1. Top-Ranked Nodes

In Table 3, we delineate the results of the CDP in comparison with Degree Centrality, Betweenness Centrality, and PageRank Centrality for six pivotal nodes across seven real-world networks. We leverage the findings and results from our previous work [49]. Additionally, we present new results from two additional datasets, USAir97 and Mouse-Kasthuri, providing further insights into the proposed CDP score. In networks like Dolphin and Karate Club, the highly influential nodes identified by the CDP score closely resemble those obtained through methods such as Degree Centrality and PageRank.
Turning our gaze to more complex networks like USAir97 and Mouse-Kasthuri, the CDP method's adaptability is underscored. In the USAir97 network, the nodes highlighted by CDP exhibit a significant overlap with those identified by PageRank, showcasing the method's consistent performance across varying network topologies. The Mouse-Kasthuri dataset further accentuates the CDP's precision, as it harmoniously aligns with both the PageRank and Degree Centrality measures, indicating its capability to adeptly navigate intricate neural networks. Collectively, the findings amplify the versatility and robustness of the CDP method. It not only aligns with established measures but also offers unique insights.

4.3.2. Pearson and Spearman Results

In our quest to validate the efficacy of the newly proposed CDP score, comprehensive evaluations were undertaken, juxtaposing it with prevailing centrality metrics—Degree Centrality (DC), Betweenness Centrality (BC), and PageRank—across a diverse spectrum of benchmark networks. The ensuing correlations, both Pearson and Spearman, have been meticulously delineated in Table 4 and Table 5. Additionally, to further substantiate our findings and enhance the robustness of our analysis, we incorporated results from our previous work [49]. Moreover, we introduced new results derived from two additional large datasets (USAir97 and Mouse-Kasthuri), aiming to confirm the effectiveness of the CDP score in diverse network scenarios. This comprehensive approach provides a more holistic understanding of the proposed metric's performance and applicability.
When we delve into the intricacies of these correlations, certain observations emerge saliently. First and foremost, a compelling correlation between the CDP score and the DC method can be discerned. Such an association intimates that the CDP score, in its essence, is adept at echoing similar facets of node centrality as that evoked by degree centrality. Furthermore, our results exhibit a heightened reliability when correlated with the PageRank method. This can be attributed to their shared foundational principles, specifically the emphasis on node degree and the intricate interplay of links between origin and terminal nodes, operationalized through the count of paths spanning a length of two. However, when juxtaposed with the BC method, the correlation is relatively attenuated. This stems from the intrinsic nature of the BC method, which inherently skews towards nodes that find themselves integral to a more extensive gamut of paths within the network. “Contrarily, the CDP method has been conceived to mediate harmoniously between node degree and betweenness centrality, ensuring neither is disproportionately favored.

4.3.3. The Influence of Parameter l

The proposed CDP measure's performance, when adjusted against varied path length ’l’ values, the performance of the proposed CDP measure presents compelling insights. Using an expansive dataset set that comprises Dolphins, Les Miserables, US Books about Politics, American College Football, USair97, and Mouse-Kasthuri, we juxtaposed the correlation against mainstream metrics, with 'l' spanning from 2 to 4 using the Pearson coefficient.
We incorporated insights from our previous work to further enrich our analysis [49]. We augmented our analysis by including the performance of the CDP score with the variation of path length for the networks usair97 and Mouse-Kasthuri. This addition provides a more comprehensive understanding of how the CDP measure behaves in diverse network structures, further enriching our insights into its adaptability and effectiveness.
Upon assessing the Page Rank metric, a clear pattern emerges: the 'l' value predominantly shines at 2 for most datasets, echoing our foundational findings. For instance, networks like Dolphins, US Books about Politics, American College Football, and Mouse-Kasthuri showcase correlation values of 0.976, 0.97, 0.966, and 0.983, respectively, when "l=2". Conversely, Les Misérables dataset and USair97 stand out, with the former reaching its zenith at 0.96 for "l=3" and the latter peaking at 0.893 for "l=2". A parallel trend is discernible in the Degree Centrality metric. With Dolphins, US Books about Politics, and Mouse-Kasthuri, the optimal 'l' gravitates towards 2, exhibiting values of 0.966, 0.94, and 0.964, respectively. However, Les Misérables veers off this course, registering an optimal correlation of 0.864 at "l=3". Usair97's best result of 0.901 is also at "l=2", fitting the broader trajectory. The Betweenness metric further enriches this narrative. With Dolphins, a peak correlation of 0.914 is noted at "l=2", in sync with prior revelations. However, the best correlations for datasets like American College Football, Les Misérables, USAir97, and Mouse-Kasthuri are 0.327, 0.914, 0.818, and 0.666, respectively.
Interestingly, while "l=2" maintains its dominance, Les Misérables diverges from the trend, solidifying its optimal "l" value at 3. On the other hand, the Karate Club network stands out with its unique optimal "l" values, which are exclusively 3 and 4. A salient aspect underpinning this analysis is the conceptual depth offered by paths of "l=2", which unveils information about secondary neighbors (as illustrated in Figure 2). Such granularity ensures that the CDP measure adeptly captures the nuances of node influence within the networks.
To summarize, the prevailing consensus advocates for "l=2" as the premier path length for the CDP measure. across various networks. Nonetheless, datasets such as Les Misérables and Karate club necessitate a nuanced approach, hinting at "l=3" or "l=4" for optimal efficacy.

4.3.4. SIR Model Results

In our quest to highlight the efficacy of the newly introduced CDP score, we leverage the Susceptible-Infected-Recovered (SIR) model—a paradigm simulating viral dissemination across networks. Our procedure entails determining the spreading efficiency for every network node. The ultimate goal is a side-by-side comparison of the CDP metric with benchmark centralities to rank node spreading efficiencies, subsequently spotlighting influential propagators. In this experimentation phase, an initial ranking of nodes within each network was orchestrated using established metrics: Degree Centrality (DC), Betweenness Centrality (BC), PageRank, and the proposed CDP metric. We then employed the SIR model, treating each node as an information fountainhead (akin to an infection source within the SIR framework). This method calculates the resultant infected nodes post-process. We fixed the number of iterations for our study’s parameters at 50. The specific beta value for every real-world network is enumerated in Table 3, with λ set at 1.
Subsequently, we assessed the Kendall’s tau correlation juxtaposing the node ranking, as determined by centrality measures, against the infected node count from the SIR model. The results are tabulated in Table 6.
Upon inspecting Table 6, it is palpable that the CDP metric's performance is consistently formidable across many network data sets. The CDP score remains competitive across all datasets, displaying minimal fluctuations. This is a testament to its robustness and adaptability to diverse network structures. In networks like Football, Les Misérables, and US Politics Books, CDP slightly edges out the PageRank algorithm. While the margins are nuanced, this demonstrates the potency of the CDP method in certain contexts, indicating its potential utility for researchers and practitioners alike. For datasets like USair97 and Mouse-Kasthurie, which are arguably representative of more intricate real-world systems, CDP exhibits a close alignment with other well-regarded metrics like Betweenness and Degree Centrality. This parallelism is especially commendable given the complexity inherent in such networks.
One of the hallmarks of an effective metric is its stability across a variety of scenarios. The CDP's performance in networks like Dolphin, Karate, and Les Misérables highlights its capability to maintain a steady ranking, which is crucial for accurate node assessments. While Degree and Betweenness Centralities have peaks in specific networks, their performance is inconsistent with the CDP method. PageRank, a widely-recognized algorithm, is at times outperformed by CDP, emphasizing the latter's potential as a primary tool in network analysis.
In Table 7, we engage the overlap coefficient as an analytical lens to evaluate the congruence between the ranking scores and the top 10 influential nodes delineated by the SIR Model. This methodological approach is particularly germane, as it gives us a tangible metric to quantify the intersection of results between different methods. A cursory observation of Table 7 reveals a rather compelling narrative in favor of the CDP metric: The CDP metric distinctly differentiates itself in networks such as the Football and Zakary karate club. In the Football network, it is noteworthy that while other metrics hover at a 0.7 or lower overlap coefficient, CDP boasts a perfect 1. “This indicates that CDP has flawlessly identified the top 10 influential spreaders in this network as per the SIR Model, a feat unparalleled by other metrics. In networks like the US Politics books, Les Misérables, and Dolphin, the CDP metric holds its ground, paralleling the performance of established centrality measures such as PageRank, DC, and BC. This is an attestation of CDP's generalizability and robustness across diverse networks. The Karate network offers an illustrative case study. While Degree, Betweenness, and PageRank all score a 0.3 overlap coefficient, CDP marginally advances with a 0.4. This incremental advantage might appear subtle but signifies CDP's nuanced capabilities that the other metrics might overlook.
Synthesizing the information, it is clear that the CDP method is not merely an addition to the suite of centrality measures available to analysts —it is a significant enhancement. Its remarkable performance across diverse networks and consistent ranking ability underscores its potential as a vital tool for future network analyses. It effectively bridges the gap between established methods and the ever-evolving complexities of real-world networks, showcasing promise as an influential spreader identifier. The CDP method exemplifies the vanguard of centrality measures, bringing with it a refined precision and an adeptness that, in certain networks, even surpasses time-tested metrics. The data underscores its prowess in ranking nodes with high fidelity and spotlighting influential spreaders with a commendable degree of accuracy.

5. Conclusion

In the intricate tapestry of network analysis, the study presented herein sought to unveil a novel approach, the CDP method, to identify influential nodes within varied real-world networks. Our comprehensive assessment and juxtaposition with established centrality measures — Degree Centrality, Betweenness Centrality, and PageRank — illuminate the adeptness and precision of the CDP technique. The CDP method consistently showcased its versatility from simpler networks like the Dolphin and Karate Club to the more complex of USAir97 and Mouse-Kasthuri. This ability to adapt and maintain precision, especially in complex structures, underscores its potential as a pivotal tool for future network investigations. Moreover, the convergences and occasional divergences with traditional methods provide a fresh perspective, reminding us of the continual evolution of network analysis paradigms. As we stand at the cusp of expanding digital interconnectedness, The CDP method presents a valuable methodology for achieving deeper, more nuanced insights. In conclusion, while this study has paved the way for a more holistic understanding of network structures, it also beckons further exploration. We remain hopeful that the CDP method will be instrumental in unraveling the myriad mysteries of networks, driving both academic and practical advancements in the domain.

Author Contributions

Nada Bendahman and Dounia Lotfi contributed equally to the conceptualization and design of the study, conducted data analysis and contributed to the interpretation of results and manuscript writing.

Funding

No funding.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Osman, I. H. (Ed.). (2013). Handbook of research on strategic performance management and measurement using data envelopment analysis. IGI global.
  2. Asmi, K., Lotfi, D., & Abarda, A. (2022). The greedy coupled-seeds expansion method for the overlapping community detection in social networks. Computing, 104(2), 295-313. [CrossRef]
  3. Jibouni, L., Lotfi, D., & Hammouch, A. (2022). Mean received resources meet machine learning algorithms to improve link prediction methods. Information, 13(1), 35. 1. [CrossRef]
  4. Watts, D. J., & Dodds, P. S. (2007). Influentials, networks, and public opinion formation. Journal of consumer research, 34(4), 441-458. 4. [CrossRef]
  5. Newman, M. E. (2003). The structure and function of complex networks. SIAM review, 45(2), 167-256. [CrossRef]
  6. Duanbing C., Linyuan L., Ming-Sheng S., Yi-Cheng Z., and Tao Z. (2012). Identifying influential nodes in complex networks. Physica A, 391(4), 1777-1787. 4. [CrossRef]
  7. Reka A., Istvan A., and Gary L. N. (2004). Structural vulnerability of the North American power grid. PHYSICAL REVIEW E, 69(2). [CrossRef]
  8. Wuellner, Daniel R., Soumen R., and Raissa M. D. (2010). Resilience and rewiring of the passenger airline networks in the United States. Physical Review E, 82(5), 056101. [CrossRef]
  9. Albert R., Jeong H., and Barab´asi A.-L. (2000). Error and attack tolerance of complex networks. Nature, 406(6794), 378-382. [CrossRef]
  10. Hou B., Yao Y., and Liao D. (2012). Identifying all-around nodes for spreading dynamics in complex network. Physica A: Statistical Mechanics and its Applications, 391(15), 4012-4017. [CrossRef]
  11. Hafiene, N., Wafa K., and Lotfi B. (2020). Influential nodes detection in dynamic social networks: A survey. Expert Systems with Applications, 159, 113642. [CrossRef]
  12. Quercia D., Ellis J., Capra L., and Crowcroft J. (2011). In the mood being influential on twitter mood. IEEE International Conference on Privacy, Security, Risk and Trust and IEEE International Conference on Social Computing PASSAT/SocialCom, 307–314.
  13. Nguyen V., Boyd-Graber J., Resnik P., Cai D. A., Midberry J. E., and Wang Y. (2014). Modeling topic control to detect influence in conversations using nonparametric topic models. Machine Learning, 95(3), 381–421. 3. [CrossRef]
  14. Hafiene N., Karaoui W., and Ben Romdhane L. (2020). Influential nodes detection in dynamic social networks: A Survey. Expert Systems with Applications, 159, 113642. [CrossRef]
  15. Freeman L. C. (1978). Centrality in social networks conceptual clarification. Social Networks, 1(3), 215-239. [CrossRef]
  16. Chen, D., Lu, L., Shang, M.-S., Zhang, Y.-C., & Zhou, T. (2012). Identifying influential nodes in complex networks. Physica A: Statistical Mechanics and its Applications, 391(4), 1777-1787. [CrossRef]
  17. Seidman, S. B. (1983). Network structure and minimum degree. Social Networks, 5(3), 269-287. [CrossRef]
  18. Hage, P., & Harary, F. (1995). Eccentricity and centrality in networks. Social Networks, 17(1), 57-63. 1. [CrossRef]
  19. Katz, L. (1953). A new status index derived from sociometric analysis. Psychometrika, 18(1), 39–43. [CrossRef]
  20. Wasserman, S., & Faust, K. (1994). Social Network Analysis: Methods and Applications. Cambridge: Cambridge University Press.
  21. Lawrence, P., & Brin, S. (1999). The PageRank Citation Ranking: Bringing Order to the Web. Technical Report. Stanford InfoLab.
  22. Scott, J. (2000). Social Network Analysis: A Handbook. 2nd Edition, Sage Publications.
  23. Kleinberg, J. M. (1999). Authoritative Sources in a Hyperlinked Environment. J. ACM, 46(5), 604-632. [CrossRef]
  24. Kitsak, M., Gallos, L. K., Havlin, S., Liljeros, F., Muchnik, L., Stanley, H. E., & Makse, H. A. (2010). Identification of influential spreaders in complex networks. Nature Physics, 6, 888–893. [CrossRef]
  25. Dorogovtsev, S. N., Goltsev, A. V., & Mendes, J. F. F. (2006). K-core organization of complex networks. Physical review letters, 96(4). [CrossRef]
  26. Liu, J.-G., Ren, Z.-M., & Guo, Q. (2013). Ranking the spreading influence in complex networks. Physica A: Statistical Mechanics and its Applications, 392(18), 4154-4159. [CrossRef]
  27. Vitali, S., Glattfelder, J. B., & Battiston, S. (2011). The Network of Global Corporate Control. PLOS ONE, 6(10). [CrossRef]
  28. Lu, L., Chen, D., Ren, X.-L., Zhang, Q.-M., Zhang, Y.-C., & Zhou, T. (2016). Vital nodes identification in complex networks. Physics Reports, 650, 1-63. [CrossRef]
  29. Borgatti, S. P., & Everett, G. M. (2006). A Graph-Theoretic Perspective on Centrality. Social Networks, 28(4), 466-484. [CrossRef]
  30. Girvan, M., & Newman, M. E. J. (2002). Community structure in social and biological networks. Proceedings of the National Academy of Sciences, 99(12), 7821-7826. 12. [CrossRef]
  31. Newman, M. E., & Girvan, M. (2004). Finding and Evaluating Community Structure in Networks. Physical Review E, 69(2). [CrossRef]
  32. Liu, W., PELLEGRINI, M., & WU, A. (2019). Identification of Bridging Centrality in Complex Networks. IEEE Access. [CrossRef]
  33. Opsahl, T., Agneessens, F., & Skvoretz, J. (2010). Node centrality in weighted networks: Generalizing degree and shortest paths. Social Networks, 32(3), 245–251. [CrossRef]
  34. Zachary, W. (1977). An information flow model for conflict and fission in small groups. Journal of Anthropological Research, 33, 452-473. [CrossRef]
  35. Lusseau, D., Schneider, K., Boisseau, O. J., Haase, P., Slooten, E., & Dawson, S. M. (2003). The bottlenose dolphin community of Doubtful Sound features a large proportion of long-lasting associations - Can geographic isolation explain this unique trait? Behavioral Ecology and Sociobiology, 54, 396-405. [CrossRef]
  36. Knuth, D. E. (1993). The Stanford GraphBase: A Platform for Combinatorial Computing. Addison-Wesley, Reading, MA.
  37. Orgnet. (n.d.). Books about US politics database. Available online: http://www.orgnet.com/.
  38. Benesty, J., Chen, J., Huang, Y., & Cohen, I. (2009). Pearson correlation coefficient. In Noise reduction in speech processing (p. 1–4). Springer.
  39. Zar, J. H. (1972). Significance testing of the Spearman rank correlation coefficient. Journal of the American Statistical Association, 67(339), 578–580. [CrossRef]
  40. Smith, D., & Moore, L. (2004). The SIR Model for Spread of Disease - The Differential Equation Model. Convergence.
  41. Nelsen, R. (2001). Kendall tau metric. In Encyclopedia of Mathematics. EMS Press.
  42. Vijaymeena, M. K., & Kavitha, K. (2016). A survey on similarity measures in text mining. Machine Learning and Applications: An International Journal, 3(2), 19-28. [CrossRef]
  43. Jibouni, A., Lotfi, D., El Marraki, M., & Hammouch, A. (2018, October). A novel parameter free approach for link prediction. In 2018 6th International Conference on Wireless Networks and Mobile Communications (WINCOM) (pp. 1-6). IEEE.
  44. Ayoub, J., Lotfi, D., & Hammouch, A. (2022). Link prediction using betweenness centrality and graph neural networks. Social Network Analysis and Mining, 13(1), 5. 1. [CrossRef]
  45. Asmi, K., Lotfi, D., & El Marraki, M. (2020). Overlapping community detection based on the union of all maximum spanning trees. Library Hi Tech, 38(2), 276-292. 2. [CrossRef]
  46. Amunts, K., Lepage, C., Borgeat, L., Mohlberg, H., Dickscheid, T., Rousseau, M., Bludau, S., Bazin, P., Lewis, L. B., Oros-Peusquens, A., Shah, N. J., Lippert, T., Zilles, K., & Evans, A. C. (2013). BigBrain: An Ultrahigh-Resolution 3D Human Brain Model. Science, 340(6139), 1472–1475. [CrossRef]
  47. Ryan, A. R., & Nesreen, K. A. (2015). The Network Data Repository with Interactive Graph Analytics and Visualization. Available online: https://networkrepository.com.
  48. Rossi, R., & Ahmed, N. (2015, March). The network data repository with interactive graph analytics and visualization. In Proceedings of the AAAI conference on artificial intelligence (Vol. 29, No. 1). [CrossRef]
  49. Bendahman, N., & Lotfi, D. (2023). A Novel Centrality based Measure for Influential Nodes Detection in Social Networks, 10th International Conference on Wireless Networks and Mobile Communications (WINCOM), Istanbul, Turkiye, 2023, pp. 1-7.
Preprints 99414 g001
Figure 1. A graph G.
Figure 1. A graph G.
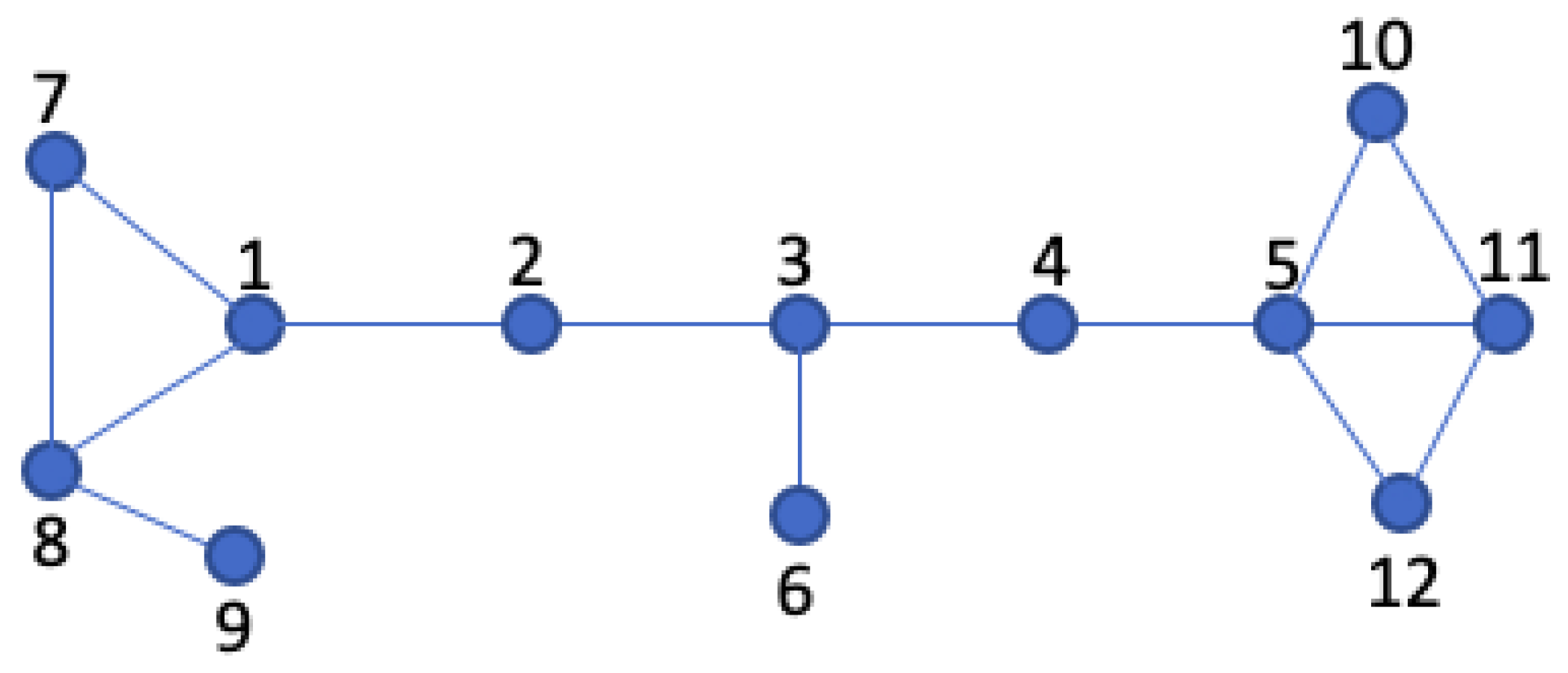
Preprints 99414 g001
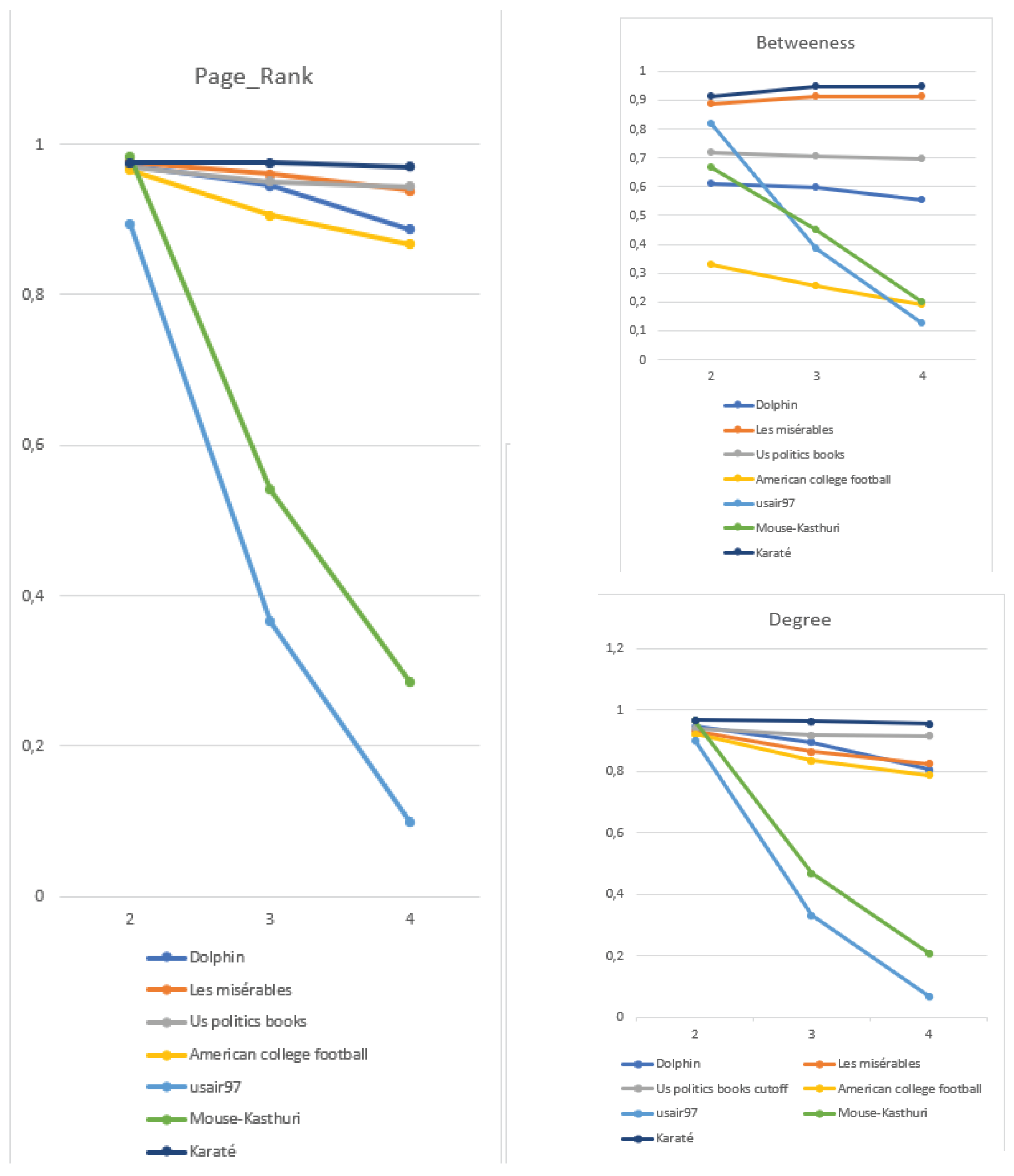
Preprints 99414 g002
Figure 2. Performance of CDP using different values of length l in the range from 2 to 4 .
Figure 2. Performance of CDP using different values of length l in the range from 2 to 4 .
Preprints 99414 g002
Table 1. CDP and Degree Scores.
Table 1. CDP and Degree Scores.
x 1 2 3 4 5 6 7 8 9 10 11 12
CDP 1.28 0.66 1.8 0.57 1.77 0.33 0.66 1.5 0.33 0.57 1.12 0.57
Degree 3 2 3 2 4 1 2 3 1 2 3 2
Table 2. Fundamental topological features of benchmark real-world networks. Within this framework, |V| represents the total count of nodes, |E| indicates the total number of edges, k stands for the average degree, C encapsulates the clustering coefficient, r signifies the assortative coefficient, and β denotes the infection probability.
Table 2. Fundamental topological features of benchmark real-world networks. Within this framework, |V| represents the total count of nodes, |E| indicates the total number of edges, k stands for the average degree, C encapsulates the clustering coefficient, r signifies the assortative coefficient, and β denotes the infection probability.
Network |V| |E| C r k β
Karate [34] 34 78 0,5706 -0.475 4.588 0.12
Dolphin [35] 62 159 0.258 -0.0435 5.129 0.14
Les Misérables [36] 77 254 0.74 −0.165 3.3 0.082
Books about US Politics [37] 105 441 0.48 -0.12 8.4 0.083
American College Football [30] 115 613 0.40 -0.162 10.66 0.093
USair97 [47] 332 2126 0.625217 -0.207876 12.8072 0.022
Mouse-Kasthuri [48] 1000 1700 0 -0.215013 3 0.023
Table 3. The top six nodes ranked using CDP, DC, BC, and PageRank methods.
Table 3. The top six nodes ranked using CDP, DC, BC, and PageRank methods.
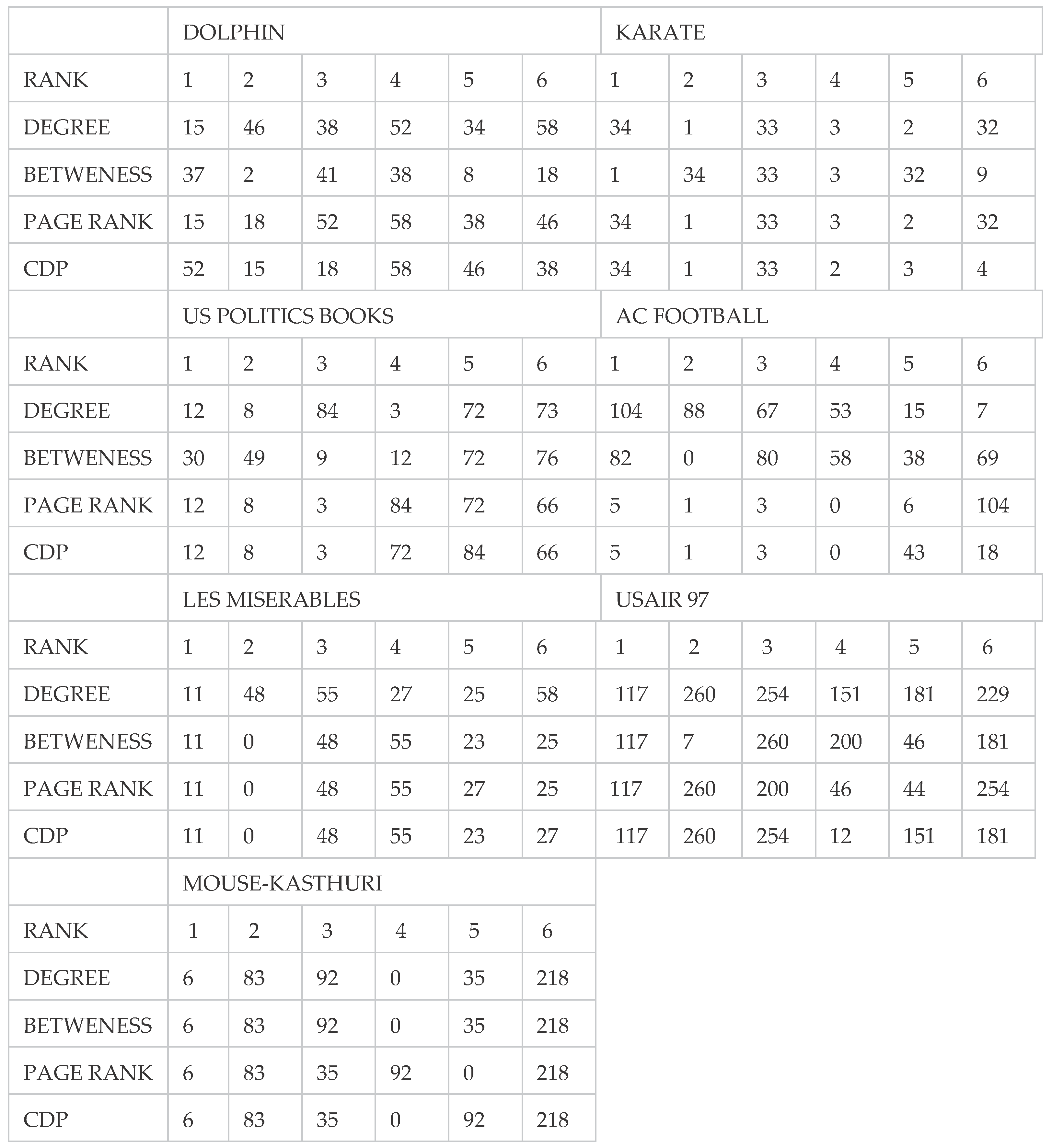
Preprints 99414 i001
Table 4. Pearson correlation comparing established centrality measures with CDP.
Table 4. Pearson correlation comparing established centrality measures with CDP.
Score Karate Dolphin Les Misérable Us politics books American college football USair97 Mouse-Kasthuri
Degree 0.966 0.948 0.931 0.940 0.922 0.901 0.964
Betweenness 0.914 0.61 0.887 0.716 0.327 0.818 0.90
PageRank 0.976 0.971 0.977 0.970 0.966 0.893 0.983
Table 5. Spearman correlation comparing established centrality measures with CDP.
Table 5. Spearman correlation comparing established centrality measures with CDP.
Score Karate Dolphin Les Misérable Us politics books American college football USair97 Mouse-Kasthuri
Degree 0.86 0.94 0.93 0.81 0.87 0.811 0.458
Betweenness 0.80 0.81 0.70 0.74 0.33 0.774 0.39
PageRank 0.91 0.96 0.94 0.87 0.98 0.845 0.69
Table 6. Kendall’s correlation of centrality methods and spreading efficiency.
Table 6. Kendall’s correlation of centrality methods and spreading efficiency.
Degree Betweenness Page rank CDP
Dolphin 0.783 0.784 0.778 0.775
Karate 0.746 0.759 0.729 0.701
Football 0.83 0.79 0.78 0.79
Les Misérables 0,74 0,77 0,73 0,74
US Politics books 0.731 0.744 0.725 0.736
USair97 0.75 0.77 0.743 0.743
Mouse-Kasthuri 0.706 0.699 0.644 0.644
Table 7. Overlap coefficient of the top 10 influential spreaders.
Table 7. Overlap coefficient of the top 10 influential spreaders.
Degree Betweenness Page rank CDP
Dolphin 0.2 0.2 0.2 0.2
Karate 0.3 0.3 0.3 0.4
Football 0.7 0.2 0.7 1
Les Misérables 0.2 0.2 0.2 0.2
US Politics books 0.2 0.2 0.2 0.2
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated