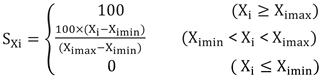1. Introduction

2. Materials and Methods

2.1. Constructing a health evaluation index system for drainage network

2.1.1. Purpose and significance of constructing indicator system

The health status of drainage networks is influenced by many factors and is dynamically changing, which is difficult to describe through precise mathematical expressions. The health condition of the drainage network has a significant impact on the ability to perform predetermined functions and the surrounding environment. Traditional single evaluation indicators can only reflect the operational status of drainage pipelines from a certain aspect, and the results have a certain degree of one-sidedness. However, by constructing an indicator system, the health status of drainage pipelines can be comprehensively evaluated from multiple perspectives and all aspects, enabling construction units, maintenance units, and industry regulatory departments to have a clearer understanding of the operational status of drainage pipelines. At the same time, it can provide a basis for the inspection, rectification, and maintenance of drainage networks, point out the direction, and promote the improvement of quality and efficiency in sewage collection and treatment.

2.1.2. Theoretical basis and principles of indicator system architecture

The establishment of an indicator system is a prerequisite for evaluating the health status of drainage networks. There are many factors that affect the health of drainage networks, and they are interrelated. There are many factors that need to be considered. To ensure that the selected indicators can comprehensively reflect the health status of drainage networks, the following principles need to be noted:

1. Systematic principle

The health status of the drainage network involves a wide range of aspects. When evaluating, it is important to not only pay attention to the characteristics of the pipeline itself, but also to the current operation status, social environment, and maintenance of the network. Therefore, when selecting indicators, it is necessary to consider all aspects in a balanced manner, and each indicator should be independent of each other and have inherent connections, which can comprehensively reflect the health status of the drainage network.

2. Objectivity principle

The evaluation indicators selected for evaluating the health status of drainage networks should be able to be qualitatively or quantitatively described, that is, the evaluation results of the indicators can be objectively measured by objective data, avoiding the influence of subjective factors on the evaluation results as much as possible, making the evaluation results more accurate and authentic.

3. Principle of scientificity

The main purpose of evaluating the health status of drainage networks is to comprehensively evaluate the health status of drainage networks, providing a basis for later pipeline inspection, rectification, and maintenance. Therefore, comprehensive analysis should be conducted on the basis of fully considering the operational requirements of the pipeline network, scientifically and reasonably selecting indicators, constructing an indicator system, and ensuring that the selected indicators can truly reflect the actual health status of the drainage network.

4. Principle of representativeness

The evaluation indicators for the health status of drainage networks should be representative, which means reducing the number of indicators as much as possible while fully reflecting the health status, ensuring that there is no overlap between indicators, and the content should be as independent as possible to avoid complexity.

5. Feasibility principle

When selecting indicators, special attention should be paid to the availability and difficulty of obtaining indicator data. The selected indicators should not only be easy for researchers to analyze and calculate, but also for construction units, maintenance units, administrative authorities, and even the public to understand and master. The original data of indicators should be as easily accessible from existing data as possible to ensure the practicality of evaluation.

2.1.3. Indicator screening and system construction

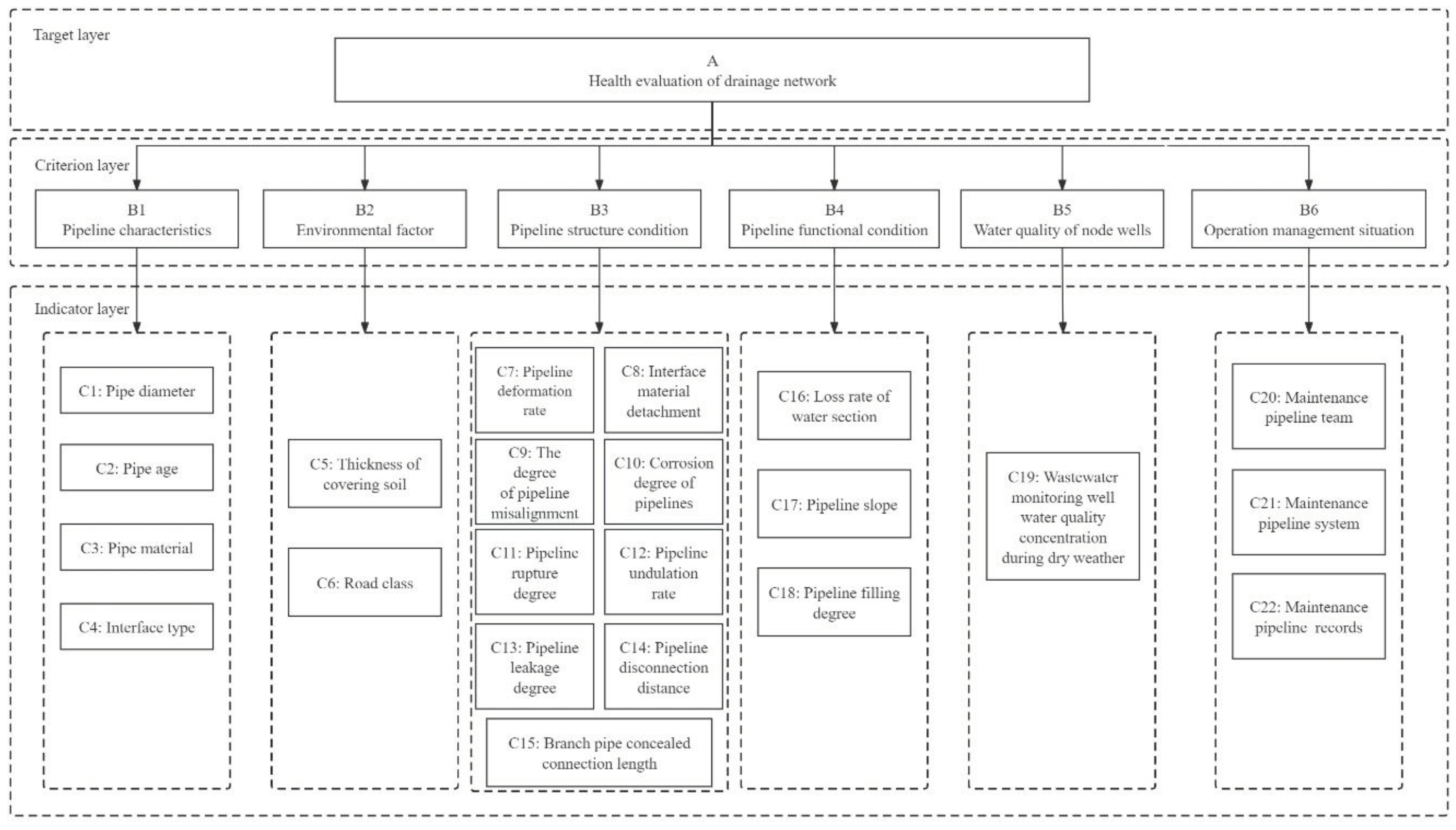
Selecting scientifically reasonable evaluation indicators is a necessary prerequisite to ensure the accuracy and reliability of evaluation results. Based on the requirements of evaluating the health status of drainage networks and the feasibility of obtaining indicator data, this article takes the evaluation of the health status of drainage networks as the target layer. Based on the investigation, rectification, and later operation and maintenance of the pipeline network, select the criteria layer and indicator layer indicators in sequence. From the perspective of the hierarchical structure characteristics of health evaluation indicators for drainage networks, the indicator system includes bottom level diagnostic indicators and intermediate transition indicators. The health status of the drainage network can be comprehensively reflected through the evaluation results of various levels of indicators.

This article selects six criteria layer indicators: pipeline characteristics, environmental factors, pipeline structure condition, pipeline function condition, water quality of node wells, and operation management situation, and selects appropriate indicators as the indicator layer indicators.

1. Pipeline characteristics

The diameter, age, pipe material, and interface form of the drainage network are the basis for the health status of the drainage network. The size of the pipe diameter in the drainage network plays a decisive role in the water flow velocity and head loss within the network. The smaller the pipe diameter, the thinner the pipe wall, and the poorer the impact resistance. The pipe age refers to the service life of the drainage network, and the longer the pipe age, the greater the possibility of defects. The construction methods of different pipes are different, and their material characteristics determine their advantages and disadvantages. For example, plastic pipes such as HDPE have lower roughness coefficient, faster water flow rate, and stronger corrosion resistance compared to reinforced concrete pipes. However, they also have the disadvantage of poor external pressure resistance. The interface is the midpoint at which the pipeline bears stress. Once it is misaligned or disconnected, it can lead to external water intrusion, which is also an important factor affecting the health of the pipeline network.

2. Environmental factors

The drainage pipeline is buried underground and has openness, which is influenced by various natural conditions and human factors. The thickness of soil cover and road grade are two important environmental factors. The distance from the top of the outer wall of the pipeline to the ground is the thickness of the pipeline’s soil cover. According to the "Outdoor Drainage Design Standard (GB50014-2021)", the burial depth of the pipeline is determined by factors such as pipe strength, external loads, soil freezing depth, and soil properties. The minimum soil cover depth under sidewalks should be 0.6m, and under roadways it should be 0.7m. For existing pipelines, the deeper they are buried, the less they are affected by external factors, the higher their safety, but the higher their construction costs. The health condition of buried drainage pipes is closely related to external ground loads. Generally speaking, the higher the road level, the greater the traffic flow, the greater the ground load, and the higher the likelihood of pipeline damage. However, the ground load on drainage pipelines is generally difficult to calculate, so road grades are used to classify the external load on pipelines [5].

3. Pipeline structure condition

The health of pipeline structure is based on the relative concept of pipeline structural defects, indicating the integrity of the internal structure of the pipeline. It has a decisive impact on the infiltration of external water and is also a decisive factor in whether the drainage network needs to be repaired. The indicators for measuring the structural condition of pipelines include pipeline deformation rate, interface material detachment, degree of pipeline misalignment, degree of pipeline corrosion, degree of pipeline rupture, pipeline undulation rate, degree of pipeline leakage, pipeline disconnection distance, and concealed connection length of branch pipes, totaling 9 items.

4. Pipeline functional condition

Pipeline functional health is based on the relative concept of pipeline functional defects, expressing the water transmission capacity of pipelines. It is mainly divided into three indicators: pipeline water loss rate, pipeline slope, and pipeline fullness. The loss rate of pipeline water section refers to the loss ratio of the current water section compared to the intact state caused by sedimentation, residual walls, dam roots, hard scaling, obstacles, tree roots and foreign objects that affect the flow in the pipeline. The slope of a pipeline refers to the ratio of the height difference between the starting and ending ends to the length of the pipeline. The drainage pipe is mainly gravity flow, and the slope of the pipeline is an important factor affecting the flow velocity and sedimentation conditions inside the pipe. The pipeline filling degree refers to the ratio of the water depth inside the pipeline to the pipe diameter, which has a certain impact on the pipeline load.

5. Water quality of node wells

The water quality of the node well is mainly determined by the water concentration of the sewage monitoring well during dry days, in order to determine the collection effect of the sewage pipeline network and the situation of external water intrusion.

6. Operation management situation

The operation and management of the drainage network includes three indicators: management team, management system, and management records.

The evaluation index system for the health status of the drainage network is shown in Figure 1.

2.1.4. Index scoring method construction

This article combines the evaluation methods of domestic and foreign scholars on the standardized performance indicators of drainage networks [80–82], existing standards in China, such as the Technical Regulations for Testing and Evaluation of Urban Drainage Pipelines (CJJ181-2012), and quantitative scoring suggestions from relevant experts in the field for qualitative indicators in health condition evaluation, to develop a scoring method. The maximum score for the health evaluation index layer of the drainage network is 100 points. The scoring method for the 22 evaluation indicators is as follows:

1. Pipe diameter: According to the drainage design specifications, the minimum pipe diameter for outdoor sewage pipe networks is DN300. As the amount of sewage increases and the pipe diameter increases, the probability of pipe damage gradually decreases. This article selects DN300 and DN800 as the dividing lines for pipe diameters. A pipe diameter not less than DN800 is defined as 90, DN600 ≤ pipe diameter<DN800 is defined as 80, DN400 ≤ pipe diameter<DN600 is defined as 70, DN300 ≤ pipe diameter<DN400 is defined as 60, and a pipe diameter less than DN300 is defined as 0.

2. Pipe age: The water delivery performance of the pipeline decreases with the increase of pipe age. At present, about 10% of the total length of urban sewage pipelines in China are over 30 years old, and the damage rate of such pipelines is extremely high [83]. This article selects 5 years and 30 years as the dividing line for pipe age, with 90 points for pipes less than 5 years, 80 points for pipes less than 5 years ≤ pipe age<10 years, 70 points for pipes less than 10 years ≤ pipe age<20 years, 60 points for pipes less than 20 years ≤ pipe age<30 years, and 0 points for pipes greater than or equal to 30 years.

3. Pipes: Taking into account the corrosion resistance, compressive and seismic resistance of pipes, steel plastic pipes are defined as 90 points, ductile iron pipes are defined as 80 points, plastic pipes such as HDPE are defined as 70 points, and concrete pipes are defined as 60 points.

4. Interface form: Based on the adaptive performance of different interface forms in geological settlement, flexible interfaces such as plug-in rubber rings are defined as 90 points, prefabricated sleeve asbestos cement (or asphalt mortar) interfaces are defined as 80 points, cement mortar plastering interfaces are defined as 70 points, and cast-in-place concrete sleeve interfaces are defined as 60 points.

5. Soil cover thickness: If the minimum burial depth thickness recommended by the specifications is met, 100 points will be given, otherwise 0 points will be given.

6. Road level: Based on traffic type, capacity, and volume, the impact of roads on pipelines is divided into four levels. Pipelines laid under green belts and sidewalks are defined as 90 points, pipelines laid under branch roads are defined as 80 points, pipelines laid under secondary roads and slow lanes are defined as 70 points, pipelines laid on main roads and under fast lanes are defined as 60 points.

7. Pipeline deformation rate: Full score for no deformation, defined as 80 points for deformation not exceeding 5% of pipeline diameter, 60 points for deformation ranging from 5% to 15% of pipeline diameter, 40 points for deformation ranging from 15% to 25% of pipeline diameter, and 0 points for deformation greater than 25% of pipeline diameter.

8. Interface material detachment: If the interface material does not detach, it will receive a full score. If the interface material is visible above the horizontal centerline in the pipeline, it will receive a score of 60 points. If the interface material is visible below the horizontal centerline in the pipeline, it will receive a score of 0 points.

9. Degree of pipeline misalignment: If no misalignment occurs, the score is full. If the deviation between the two adjacent pipe orifices is not more than 0.5 times the thickness of the pipe wall, it is defined as 90 points. If the deviation is 0.5-1 times the thickness of the pipe wall, it is defined as 60 points. If the deviation is 1-2 times the thickness of the pipe wall, it is defined as 40 points. If the deviation is more than 2 times the thickness of the pipe wall, it is defined as 0 points.

10. Degree of pipeline corrosion: Full score for no corrosion, defined as slight surface peeling, and defined as concave and convex surfaces on the pipe wall as 90 points. Surface peeling exposing coarse aggregate or steel bars is defined as 60 points, and complete exposure of coarse aggregate or steel bars is defined as 0 points.

11. Degree of pipeline rupture: No rupture is given a full score. According to the level of pipeline structural rupture, slight fine cracks or peeling on the pipeline wall are defined as 90 points. Cracks on the pipeline wall that are not affected by the shape of the pipeline and do not fall off are defined as 60 points. The circumferential coverage range of fragments left at the location where the pipeline wall ruptures or falls off is defined as 40 points, with an arc length of 60 ° or less. Collapse with a circumferential coverage range greater than 60 ° at the location of pipeline rupture is defined as 0 points.

12. Pipeline undulation rate: If there is no undulation, it is a full score. The undulation rate is the ratio of the pipeline undulation height to the pipe diameter. A undulation rate of less than or equal to 20% is defined as 90 points, 20% ＜ undulation rate ≤ 35% is 60 points, 35% ＜ undulation rate ≤ 50% is 40 points, and a undulation rate greater than 50% is 0 points.

13. Pipeline leakage degree: Full score for no leakage, 90 points for drip leakage, 60 points for line leakage, 40 points for water surface area less than or equal to 1/3 of the pipeline cross-section when leakage occurs, and 0 points for water surface area greater than 1/3 of the pipeline cross-section when leakage occurs.

14. Pipeline disconnection distance: If there is no disconnection, the score is full. When there is a small amount of soil squeezed into the end of the pipeline, it is defined as 80 points. If the disconnection distance is not greater than 2cm, it is 60 points. If the disconnection distance is 2-5cm, it is 40 points. If the disconnection distance is greater than 5cm, it is 0 points.

15. Branch pipe concealed connection length: If there is no branch pipe concealed connection, it is full score. When the distance between the concealed connection branch and the main pipe is not more than 10% of the diameter of the main pipe, it is defined as 90 points. When the distance between the concealed connection branch and the main pipe is 10% to 20%, it is defined as 60 points. When the distance between the concealed connection branch and the main pipe is greater than 20%, it is defined as 40 points.

16. Loss rate of water flow section: Full score for intact water flow section. When the water flow loss rate of the pipeline is less than 15%, it is defined as 80 points. When the loss rate is between 15% and 25%, it is 60 points. When the loss rate is between 25% and 50%, it is 40 points. When the loss rate is greater than 50%, it is 0 points.

17. Pipeline Slope: When the pipeline slope meets the minimum slope requirements in the outdoor drainage design specifications, it is considered full score. Otherwise, it is considered 0 point.

18. Pipeline filling degree: When the filling degree is not greater than the maximum design filling degree in the outdoor drainage design specification, it is full score; otherwise, it is 0 point.

19. Sewage monitoring well dry day water quality concentration: Set up a high line Ximax and a low line Ximin for evaluating the dry day water quality concentration of the sewage monitoring well. The scoring method is as follows: Xi represents the measured values of various water quality indicators in the sewage monitoring well during dry days, SXi represents the scores of each water quality indicator, and SW represents the scores of the sewage monitoring well during dry days.

(1)

$${\mathrm{S}}_{\mathrm{W}}=\frac{1}{\mathrm{n}}{{{\displaystyle \sum }}^{ }}_{\mathrm{i}=1}^{\mathrm{n}}{\mathrm{S}}_{\mathrm{Xi}}$$

(2)

(n represents the number of water quality indicators, i represents different water quality indicators) (2.4)

20. Operation and Maintenance Status: The indicators of operation and maintenance status include the management team, management system, and management records. If the regional requirements are met, a full score will be given for each item. If there is no corresponding content, it will be 0 points.

This article aims to evaluate the health status of the entire regional sewage pipeline network, not limited to individual sewage pipe sections. Therefore, sewage pipelines are divided based on roads for evaluation, and the overall pipeline score is obtained by weighting the average length of individual pipe sections.

The score of the evaluation criteria for the health status of the drainage network is the sum of the corresponding indicator scores and their weights, and the total score is the sum of the product of the indicator scores and their weights for each criterion layer.

2.2. Determination of Evaluation Index Weights

2.2.1. Analytic Hierarchy Process (AHP)

This article takes into full consideration the feasibility of the data and selects the evaluation indicators as the content, combined with expert consultation and Analytic Hierarchy Process (AHP) to calculate the weights of each level of evaluation indicators. The specific steps are as follows:

1. Construct a judgment matrix

Through a questionnaire survey, experts determined the importance of each layer of indicators relative to the previous layer of indicators through pairwise comparison, and quantified them into numerical values using the scaling rule shown in Table 1 to obtain the judgment matrix of each expert for each evaluation indicator, as shown in Table 2.

2. Weight calculation

Calculate the eigenvectors of each expert’s judgment matrix separately, and then calculate their weights. To determine the matrix Cn × Taking n as an example, if its feature vector is W, then W is the allocation of weights for each indicator in level C.

(1) Normalize the judgment matrix

$${\mathrm{d}}_{\mathrm{ij}}=\frac{{\mathrm{c}}_{\mathrm{ij}}}{{{{\displaystyle \sum }}^{ }}_1^{\mathrm{n}}{\mathrm{c}}_{\mathrm{ij}}}\left(\mathrm{i},\mathrm{j}=1,2,3\dots \mathrm{n}\right)$$

(3)

(2) Add normalized matrices by row

$${\mathrm{w}}_{\mathrm{i}}^{\prime }={{{\displaystyle \sum }}^{ }}_{\mathrm{j}=1}^{\mathrm{n}}{\mathrm{d}}_{\mathrm{ij}} \left(\mathrm{i}=1,2,3\dots \mathrm{n}\right)$$

(4)

(3) Calculate weight vectors

Normalize the vector to obtain an approximate solution for the weight vector.

$${\mathrm{w}}_{\mathrm{i}}=\frac{{\mathrm{w}}_{\mathrm{i}}^{\prime }}{{{{\displaystyle \sum }}^{ }}_{\mathrm{i}=1}^{\mathrm{n}}{\mathrm{w}}_{\mathrm{i}}^{\prime }} \left(\mathrm{i}=1,2,3\dots \mathrm{n}\right)$$

(5)

The vector w=(w1, w2,..., wn) is the desired vector.

3. Consistency judgment and error analysis

Consistency testing can be used to determine whether the error of the weight approximation solution is within the allowable range.

(1) Calculate the maximum eigenvalue of a matrix

Let the maximum eigenvalue of the judgment matrix be λ Max, then:

$${\mathsf{\lambda }}_{\max }={{{\displaystyle \sum }}^{ }}_{\mathrm{i}=1}^{\mathrm{n}}\frac{{\left(\mathrm{Cw}\right)}_{\mathrm{i}}}{{\mathrm{nw}}_{\mathrm{i}}}$$

(6)

Where (Cw) i represents the product of the i-th element of the judgment matrix C and its weight, and n represents the order of the matrix.

(2) Consistency indicators

$$\mathrm{CI}=\frac{{\mathsf{\lambda }}_{\max }-\mathrm{n}}{\mathrm{n}-1}$$

(7)

(3) The average random consistency index can be obtained by looking up the Table 3:

(4) Consistency ratio

$$\mathrm{CR}=\frac{\mathrm{CI}}{\mathrm{RI}}$$

(8)

When CR ≤ 0.1, it is considered that the judgment matrix has satisfactory consistency; When CR>0.1, the judgment matrix must be reconstructed.

4. Hierarchy combination weight

By the above calculation, the weight of each indicator relative to the previous level can be obtained, and the weight of each indicator relative to the target layer can be obtained through hierarchical combination. Let the first level indicator layer be A, and the next level B has B1, B2,..., Bm. The indicator weight vector of B has w1={b1, b2,..., bm}; The next layer of layer B is layer C, which has C1, C2,..., and Cn specific indicators. The weight vector of C has w2={c1, c2,..., cn}, so the weight of the i-th element in layer C relative to the target layer is:

$${\mathrm{W}}_{{\mathrm{C}}_{\mathrm{i}}}={\mathrm{a}}_{\mathrm{k}}\times {\mathrm{b}}_{\mathrm{m}}\times {\mathrm{c}}_{\mathrm{i}}$$

(9)

Among them, bm is the weight of the second level indicator (Bm) to which the third level indicator Ci belongs; Ak is the weight of the primary indicator Ak to which the secondary indicator Bj belongs.

2.2.2. Entropy weight method

Entropy was originally a thermodynamic concept, but later passed down by C E. Shannon introduced information theory, which is now widely used in engineering technology and social work. Usually, entropy is used to represent weights. When the values of the evaluation object on a certain indicator differ significantly, the entropy value is small, indicating that the indicator provides more effective information and occupies a larger weight; On the contrary, if the value difference of a certain indicator is small and the entropy value is large, the weight of the indicator is small [6,7]. This article attempts to use the entropy weight method to weight and analyze some indicators in the health evaluation system of drainage networks. The entropy weight method involves the following three steps in determining weights:

1. Calculate the proportion pij of the i-th item's indicator value under the j-th indicator;

$${\mathrm{p}}_{\mathrm{ij}}=\frac{{\mathrm{r}}_{\mathrm{ij}}}{{{\displaystyle \sum }}_{\mathrm{i}=1}^{\mathrm{m}}{\mathrm{r}}_{\mathrm{ij}}}$$

(10)

2. Calculate the entropy value ej of the jth indicator:

$${\mathrm{e}}_{\mathrm{j}}=-\mathrm{k}{{\displaystyle \sum }}_{\mathrm{i}=1}^{\mathrm{m}}{\mathrm{p}}_{\mathrm{ij}}\ln {\mathrm{p}}_{\mathrm{ij}}\text{，}\mathrm{Among}\mathrm{them}\mathrm{k}=\frac{1}{\mathrm{lnm}}$$

(11)

3. Calculate the entropy weight wj for the jth indicator:

$${\mathrm{w}}_{\mathrm{j}}=\frac{\left(1-{\mathrm{e}}_{\mathrm{j}}\right)}{{{\displaystyle \sum }}_{\mathrm{j}=1}^{\mathrm{n}}\left(1-{\mathrm{e}}_{\mathrm{j}}\right)}$$

(12)

2.2.3. Evaluation Index Weight Fusion

In the previous text, the subjective AHP method was used to determine the relative weights of each level in the health evaluation system of the drainage network; The entropy weight method was used to determine the initial weight values of some quantitative indicators relative to the previous layer of indicators. Taking into account the advantages of both weight assignment methods, the game theory combination weighting method is adopted to determine the optimal weight of the indicators [8]. The indicator weight obtained by AHP method is W1=w1i, (i=1, 2,..., n), while the indicator weight obtained by entropy weight method is W2=w2i, (i=1, 2,..., n). Consider the weights of the two as the two sides of the game, and the optimal combination weight is when the two reach an equilibrium state. In a balanced state, the sum of the deviations between the weights of the combination of w1 and w2 indicators should be minimized, and its calculation method is as follows:

1. The weight vector W of the indicator combination expressed by the linear combination of W1 and W2 is denoted as

$$\mathrm{W}=\left(\begin{array}{c}{\mathsf{\lambda }}_1{\mathrm{w}}_{11}+{\mathsf{\lambda }}_2{\mathrm{w}}_{21}\\ {\mathsf{\lambda }}_1{\mathrm{w}}_{12}+{\mathsf{\lambda }}_2{\mathrm{w}}_{22}\\ ·\\ ·\\ ·\\ {\mathsf{\lambda }}_1{\mathrm{w}}_{1\mathrm{n}}+{\mathsf{\lambda }}_2{\mathrm{w}}_{2\mathrm{n}}\end{array}\right)=\left(\begin{array}{cc}{\mathrm{w}}_{11}& {\mathrm{w}}_{21}\\ {\mathrm{w}}_{12}& {\mathrm{w}}_{22}\\ ·& ·\\ ·& ·\\ ·& ·\\ {\mathrm{w}}_{1\mathrm{n}}& {\mathrm{w}}_{2\mathrm{n}}\end{array}\right)\left(\begin{array}{c}{\mathsf{\lambda }}_1\\ {\mathsf{\lambda }}_2\end{array}\right)={\mathsf{\lambda }}_1{\mathrm{W}}_1+{\mathsf{\lambda }}_2{\mathrm{W}}_2$$

(13)

λ 1 and λ 2 is the linear combination coefficient.

2. Based on the ideas of game theory, establish an objective function with the goal of minimizing the sum of deviations between indicator combination weights W and W1 and W2, and seek the optimal linear combination coefficient λ 1 * and λ 2 *, the weight of the indicator combination at this time is the optimal combination weight W *. The objective function and constraints are as follows:

$$\min \left({\begin{array}{c}\Vert \mathrm{W}-{\mathrm{W}}_1\Vert \end{array}}_2+{\begin{array}{c}\Vert \mathrm{W}-{\mathrm{W}}_2\Vert \end{array}}_2\right)=\min ({\begin{array}{c}\Vert {\mathsf{\lambda }}_1{\mathrm{W}}_1+{\mathsf{\lambda }}_2{\mathrm{W}}_2-{\mathrm{W}}_1\Vert \end{array}}_2+{\begin{array}{c}\Vert {\mathsf{\lambda }}_1{\mathrm{W}}_1+{\mathsf{\lambda }}_2{\mathrm{W}}_2-{\mathrm{W}}_2\Vert \end{array}}_2)$$

(14)

s.t. λ1+λ2=1，λ1，λ2＞0

According to the principle of differentiation, the first derivative condition for obtaining the minimum value of model is:

(15)

4. Normalize the linear combination coefficients obtained from the above equation:

$$\{\begin{array}{c}{\mathsf{\lambda }}_1^{*}=\frac{\left|{\mathsf{\lambda }}_1\right|}{\left|{\mathsf{\lambda }}_1\right|+\left|{\mathsf{\lambda }}_2\right|}\\ {\mathsf{\lambda }}_2^{*}=\frac{\left|{\mathsf{\lambda }}_2\right|}{\left|{\mathsf{\lambda }}_1\right|+\left|{\mathsf{\lambda }}_2\right|}\end{array}$$

(16)

The optimal combination weight of evaluation indicators can be obtained as

$${\mathrm{W}}^{*}={\mathsf{\lambda }}_1^{*}{\mathrm{W}}_1+{\mathsf{\lambda }}_2^{*}{\mathrm{W}}_2$$

(17)

3. Results

3.1. Calculation results of indicator weights

3.1.1. Calculation of AHP Index Weights

Based on the selected evaluation indicators, establish a hierarchical structure of indicators. Through a questionnaire survey (see appendix), compare the criteria layer and indicator layer indicators for evaluating the health status of the drainage network pairwise. Invite 5 experts who have a detailed understanding of the construction, operation, inspection, and maintenance process of the drainage network to judge the importance of each layer indicator based on the scale rules of 1-9 (Table 1), Then obtain the weight judgment matrix of the criterion layer (B) indicator and the indicator layer (C) indicator. For each expert’s judgment matrix, use SPSSPRO weight calculation software to calculate the weights of each indicator and conduct consistency checks.

1. Calculation of criterion layer weights

The judgment matrices corresponding to the criteria layer indicators constructed by experts, including pipeline characteristics, environmental factors, pipeline structure conditions, pipeline function conditions, water quality conditions of node wells, and operational management conditions, are as follows:

The weights corresponding to each judgment matrix can be calculated as shown in Table 4.

The consistency ratio CR of each judgment matrix is less than 0.1, which meets the consistency test, and the weight calculation results are all valid. By calculating the arithmetic mean of the criterion layer indicators, the weights W1, W2, W3, W4, W5, and W6 for pipeline characteristics B1, environmental factor B2, pipeline structure condition B3, pipeline function condition B4, node well water quality condition B5, and operation management condition B6 are obtained as 0.0533, 0.0577, 0.3014, 0.2884, 0.1998, 0.0994, and the sum of weights is 1.

2. Calculation of indicator layer weights

(1) Pipeline characteristics

The judgment matrix for the four indicator layers under the pipeline characteristic indicators relative to the pipeline characteristic indicators is:

$$\left[\begin{array}{cccc}1& \frac{1}{5}& \frac{1}{3}& 1\\ 5& 1& 2& 5\\ 3& \frac{1}{2}& 1& 4\\ 1& \frac{1}{5}& \frac{1}{4}& 1\end{array}\right]\left[\begin{array}{cccc}1& \frac{1}{3}& \frac{1}{3}& \frac{1}{2}\\ 3& 1& 1& 2\\ 3& 1& 1& 2\\ 2& \frac{1}{2}& \frac{1}{2}& 1\end{array}\right]\left[\begin{array}{cccc}1& \frac{1}{5}& \frac{1}{3}& \frac{1}{2}\\ 5& 1& 3& 5\\ 3& \frac{1}{3}& 1& 4\\ 2& \frac{1}{5}& \frac{1}{4}& 1\end{array}\right]\left[\begin{array}{cccc}1& \frac{1}{5}& \frac{1}{5}& \frac{1}{2}\\ 5& 1& 2& 4\\ 5& \frac{1}{2}& 1& 4\\ 2& \frac{1}{4}& \frac{1}{4}& 1\end{array}\right]\left[\begin{array}{cccc}1& \frac{1}{4}& \frac{1}{4}& 1\\ 4& 1& 3& 5\\ 4& \frac{1}{3}& 1& 4\\ 1& \frac{1}{5}& \frac{1}{4}& 1\end{array}\right]$$

The weight of each indicator relative to the pipeline characteristic indicator can be calculated as shown in Table 5.

The consistency ratio CR of each judgment matrix is less than 0.1, which meets the consistency test, and the weight calculation results are all valid. Through calculation, the weights w1-w4 of indicators C1-C4 under pipeline characteristics are 0.0905, 0.4835, 0.3085, and 0.1175, respectively.

(2) Environmental factors

The judgment matrix for indicator layer indicators under environmental factors, including soil cover thickness and road grade, is:

$$\left[\begin{array}{cc}1& 3\\ \frac{1}{3}& 1\end{array}\right]\left[\begin{array}{cc}1& 1\\ 1& 1\end{array}\right]\left[\begin{array}{cc}1& 1\\ 1& 1\end{array}\right]\left[\begin{array}{cc}1& 2\\ \frac{1}{2}& 1\end{array}\right]\left[\begin{array}{cc}1& 1\\ 1& 1\end{array}\right]$$

The weight of each indicator relative to environmental factors can be calculated as:

The consistency ratio CR of each judgment matrix is less than 0.1, which meets the consistency test, and the weight calculation results are all valid. By calculation, the weights w5 and w6 of indicators C5 and C6 under environmental factors are 0.4167 and 0.5833, respectively.

(3) Pipeline structure condition

The judgment matrix for the 9 indicators of the pipeline structure relative to the pipeline structure condition is:

The weight of each indicator relative to the pipeline structure condition indicator can be calculated as shown in Table 7.

The consistency ratio CR of each judgment matrix is less than 0.1, which meets the consistency test, and the weight calculation results are all valid. Through calculation, the weights w7-w15 of indicator C7-C15 under pipeline structure conditions are 0.1273, 0.0534, 0.1196, 0.0662, 0.1062, 0.1272, 0.1560, 0.1995, and 0.0446, respectively.

(4) Pipeline functional condition

The judgment matrix for the indicator layer indicators under pipeline functional conditions, including the loss rate of water flow section, pipeline slope, and pipeline fullness, is:

$$\left[\begin{array}{ccc}1& 3& 3\\ \frac{1}{3}& 1& 1\\ \frac{1}{3}& 1& 1\end{array}\right]\left[\begin{array}{ccc}1& 4& 5\\ \frac{1}{4}& 1& 3\\ \frac{1}{5}& \frac{1}{3}& 1\end{array}\right]\left[\begin{array}{ccc}1& 5& 4\\ \frac{1}{5}& 1& \frac{1}{2}\\ \frac{1}{4}& 2& 1\end{array}\right]\left[\begin{array}{ccc}1& 1& 1\\ 1& 1& 1\\ 1& 1& 1\end{array}\right]\left[\begin{array}{ccc}1& 5& 3\\ \frac{1}{5}& 1& \frac{1}{2}\\ \frac{1}{3}& 2& 1\end{array}\right]$$

The weight of each indicator relative to the pipeline functional condition indicator can be calculated as shown in Table 8.

The consistency ratio CR of each judgment matrix is less than 0.1, which meets the consistency test, and the weight calculation results are all valid. By calculation, the weights w16, w17, and w18 of indicators C16, C17, and C18 under pipeline functional conditions are 0.5878, 0.1995, and 0.2127, respectively.

(5) Water quality of node wells

Under the water quality situation of the node well, the indicator layer only has the dry day water quality concentration of the sewage monitoring well, so its weight is 1.

(6) Operation management situation

The judgment matrix for the indicator layer indicators under operational management, including the management team, management system, and management records, is:

The weight of each indicator relative to the operational management indicators can be calculated as:

The consistency ratio CR of each judgment matrix is less than 0.1, which meets the consistency test and the weight calculation results are all valid. By calculation, the weights of indicators C20, C21, and C22 under operational management are 0.3167, 0.3666, and 0.3160, respectively.

3.1.2. Entropy Weight Method Index Weight Calculation

Due to the suitability of entropy weight method for weight analysis of quantitative indicators, combined with the characteristics of health evaluation indicators for drainage network, the determination of positive and negative indicators, and the determination of combined weights, it is used for the analysis of relative weights of indicator layer indicators C7-C15 under pipeline structural conditions (quantified based on structural defects level I, II, III, and IV). The calculation results are shown in Table 10.

3.1.3. Evaluation index weight fusion calculation

After calculating the comprehensive weight of the pipeline structure condition indicator layer, $W^{*}=0.4106W_1+0.5894W_2$

The relative weight values of the integrated pipeline structure condition indicator layer are shown in Table 11.

3.1.4. Index weight results of the health evaluation system for drainage network

The comprehensive weight of each indicator layer is the product of its weight in the criterion layer indicator and the corresponding criterion layer indicator weight. The weight allocation of indicators for the health evaluation system of drainage network is shown in Table 12.

4. Analysis and evaluation of the sewage pipeline network in Zone A of Zhenjiang

4.1. Evaluation Index Score

4.1.1. Determination of water quality assessment line

The determination of the water quality assessment line in this study is mainly based on the three-year action plan for improving the quality and efficiency of urban sewage treatment issued by the country, Jiangsu Province, and Zhenjiang City, as well as the actual carbon nitrogen ratio of the water quality in the sewage pipeline network in the region. The high and low evaluation lines for water quality concentration in sewage monitoring wells during dry weather are shown in Table 13:

4.1.2. Calculation of indicator scores

Table 14. Scores of WS77004-WS272098.

Table 14. Scores of WS77004-WS272098.

Target layer	Criterion layer	Indicator layer	Score
	Indicator name	Indicator name
Health evaluation of drainage network	Pipeline characteristics	pipe diameter	70.00
		Age of management	70.00
		tubing	70.00
		Interface form	90.00
	environmental factor	Cover soil thickness	100.00
		Road grade	70.00
	Pipeline structure condition	Pipeline deformation rate	84.62
		Interface material detachment	99.28
		The degree of pipeline misalignment	100.00
		Corrosion degree of pipelines	100.00
		Pipeline rupture degree	91.13
		Pipeline undulation rate	98.73
		Pipeline leakage degree	92.92
		Pipeline disconnection distance	100.00
		Branch pipe concealed connection length	100.00
	Pipeline functional condition	Loss rate of water section	80.00
		Pipeline slope	100.00
		Pipeline filling degree	100.00
	Water quality of node wells	Wastewater monitoring well water quality concentration during dry weather	0.00
	Operation management situation	Management and maintenance team	100.00
		Management and maintenance system	100.00
		Maintenance records	100.00

4.2. Health status evaluation of sewage pipeline network in Zone A

4.2.1. Determination of indicator membership degree

According to the calculation method of indicator membership degree in 2.3.2, the following results can be obtained:

Table 15. WS77004-WS272098 Health status evaluation index layer membership matrix.

Table 15. WS77004-WS272098 Health status evaluation index layer membership matrix.

Criterion layer B	Indicator layer C	Membership matrix
		1	2	3	4	5
Pipeline characteristics	pipe diameter C1	0	1	0	0	0
	Age of management C2	0	1	0	0	0
	tubing C3	0	1	0	0	0
	Interface form C4	0	0	0	1	0
environmental factor	Cover soil thickness C5	0	0	0	0	1
	Road grade C6	0	1	0	0	0
Pipeline structure condition	Pipeline deformation rate C7	0	0	0.538	0.462	0
	Interface material detachment C8	0	0	0	0.072	0.928
	The degree of pipeline misalignment C9	0	0	0	0	1
	Corrosion degree of pipelines C10	0	0	0	0	1
	Pipeline rupture degree C11	0	0	0	0.887	0.113
	Pipeline undulation rate C12	0	0	0	0.873	0.127
	Pipeline leakage degree C13	0	0	0	0.292	0.708
	Pipeline disconnection distance C14	0	0	0	0	1
	Branch pipe concealed connection length C15	0	0	0	0	1
Pipeline functional condition	Loss rate of water section C16	0	0	1	0	0
	Pipeline slope C17	0	0	0	0	1
	Pipeline filling degree C18	0	0	0	0	1
Water quality of node wells	Wastewater monitoring well water quality concentration during dry weather C19	1	0	0	0	0
Operation management situation	Management and maintenance team C20	0	0	0	0	1
	Management and maintenance system C21	0	0	0	0	1
	Maintenance records C22	0	0	0	0	1

4.2.2. Multi level fuzzy comprehensive evaluation

(1) Fuzzy comprehensive evaluation of criterion layer

According to the multi-level fuzzy evaluation method in 2.3.2, calculate the membership degree of the criterion layer based on the weight vectors and their membership matrices of each indicator layer.

Membership degree B1 of pipeline characteristics=$\left(\begin{array}{ccccc}0& 0.8825& 0& 0.1175& 0\end{array}\right)$

Membership degree B2 of environmental factors =$\left(\begin{array}{ccccc}0& 0.5833& 0& 0& 0.4167\end{array}\right)$

Membership degree B3 of pipeline structure condition = $\left(\begin{array}{ccccc}0& 0& 0.0382& 0.3253& 0.6365\end{array}\right)$

Membership degree B4 of pipeline function status =$\left(\begin{array}{ccccc}0& 0& 0.5878& 0& 0.4122\end{array}\right)$

Membership degree B5 of node water quality situation=$\left(\begin{array}{ccccc}1& 0& 0& 0& 0\end{array}\right)$

Membership degree B6 of operation management situation==$\left(\begin{array}{ccccc}0& 0& 0& 0& 1\end{array}\right)$

In summary, the membership matrix of criterion layer is:

Table 16. WS77004-WS272098 Criterion layer membership matrix.

Table 16. WS77004-WS272098 Criterion layer membership matrix.

Criterion layer B	Membership matrix
	Critical illness	Moderate illness	General illness	Sub health	Overall health
Pipeline characteristics	0	0.8825	0	0.1175	0
environmental factor	0	0.5833	0	0	0.4167
Pipeline structure condition	0	0	0.0382	0.3253	0.6365
Pipeline functional condition	0	0	0.5878	0	0.4122
Water quality of node wells	1	0	0	0	0
Operation management situation	0	0	0	0	1

The construction of the sewage pipeline network in Zone A is composed of multiple sewage pipelines. After solving the membership matrix of the criterion layers (B1~B6) of each pipeline, it is necessary to induce each pipeline to obtain the overall membership vector of the criterion layer of the constructed sewage pipeline network in Zone A. Taking pipelines as an example, their inductive function form is as follows:

$${\mathrm{B}}_{\mathrm{m}}={{\displaystyle \sum }}_{\mathrm{i}=1}^{\mathrm{n}}{\mathrm{W}}_{\mathrm{i}}·{\mathrm{B}}_{\mathrm{m}}^{\mathrm{i}}\left(\mathrm{m}=1、2\dots 、6\right)$$

(32)

$${\mathrm{W}}_{\mathrm{i}}=\frac{{\mathrm{Q}}_{\mathrm{i}}}{{{\displaystyle \sum }}_{\mathrm{i}=1}^{\mathrm{n}}{\mathrm{Q}}_{\mathrm{i}}}$$

(33)

In the formula,

Bm——The membership degree vector of the overall criterion layer for the construction of the sewage pipeline network in Zone A

Bmi——The membership vector of the criterion layer for pipeline i

Wi—— Weight of pipeline i

N —— Number of sewage pipeline networks built in Zone A

Qi—— flow rate in pipeline i

M—— Number of items in the criterion layer

According to equations 5.29 and 5.30, based on the membership matrix of each pipeline criterion layer, the membership matrix of the health status evaluation criterion layer of the constructed sewage pipeline network in Zone A is obtained as shown in Table 17:

(2) Fuzzy comprehensive evaluation of the target layer

The fuzzy evaluation result of the target layer can be obtained by multiplying the weight vectors of each indicator in the criterion layer relative to the target layer by the membership matrix of the criterion layer.

$$\mathrm{A}=\left(\begin{array}{ccccc}0.0913& 0.1530& 0.2259& 0.2301& 0.2997\end{array}\right)$$

The health status evaluation results of the sewage pipeline network in Zone A are shown in Table 18.

By analyzing the membership degree of each health level in the evaluation results and using the confidence criterion method, it is determined that the health status of the sewage pipeline network in Zone A is generally pathological. When the health level is higher than the general pathological state, the sewage pipe network system operates relatively normally, with a healthy and sub healthy state accounting for 52.98%. However, there are still many unhealthy factors, with critically ill and moderately ill states accounting for 24.43%. Based on the above conclusions, it can be basically concluded that the overall health status of the sewage pipeline network in Zone A is in a generally pathological state, and rectification and maintenance are needed to improve the health status of the pipeline network.

5. Discussion

6. Conclusions

References

1. Xu, Z.; Xu, J.; Jin, W.; et al. The challenges and opportunities faced by the treatment of black and odorous water bodies in Chinese cities [J]. Water supply and drainage 2019, 55, 1–5. [Google Scholar]
2. China Urban Water Supply and Drainage Association Urban Drainage Statistical Yearbook 2017 [J]. Beijing: China Statistical Publishing House, 2017.
3. Cao, Y.S.; Tang, J.G.; Henze, M.; et al. The leakage of sewer systems and the impact on the ‘black and odorous water bodies’ and WWTPs in China [J]. Water Science and Technology 2019, 79, 334–341. [Google Scholar] [CrossRef] [PubMed]
4. Dai, Y.; Luo, F.; Wen, Q. Analysis of the Potential for Improving Quality and Efficiency of Urban Sewage Treatment in Dongguan City [J]. China Water Supply and Drainage 2020, 36(04), 1–5. [Google Scholar]
5. Zhang, Y. Research and Application of Health Diagnosis Methods for Urban Water Supply Network [D]. Master’s Thesis, Harbin Institute of Technology, Harbin, 2013. [Google Scholar]
6. Zou, Z.; Sun, J.; Ren, G. The entropy weighting method for fuzzy evaluation factors and its application in water quality evaluation [J]. Journal of Environmental Science 2005, (04), 552–556. [Google Scholar]
7. Cheng, Q. The Structural Entropy Weight Method for Determining the Weights of Evaluation Indicators [J]. Systems Engineering Theory and Practice 2010, 30, 1225–1228. [Google Scholar]
8. Tu, S.; Zhao, Z.; Deng, M.; et al. Overall risk assessment of urban comprehensive pipe gallery operation and maintenance based on combination weighting regret theory [J]. Safety and Environmental Engineering 2020, 27, 160–167. [Google Scholar]
9. Liang, H. Research on Comprehensive Benefit Evaluation of Cultural and Tourism Characteristic Towns Based on AHP Fuzzy Comprehensive Evaluation Method [D]. Master’s Thesis, Guangxi University, Guangxi, 2019. [Google Scholar]
10. Zhao, W.B.; Xiao, C.L.; Chai, Y.X.; et al. Application of a new improved weighting method, ESO method combined with fuzzy synthetic method, in water quality evaluation of Chagan Lake [J]. Water 2021, 13(10), 1424. [Google Scholar] [CrossRef]
11. Liu, L.; Zhou, J.Z.; An, X.L.; et al. Using fuzzy theory and information entropy for water quality assessment in Three Gorges region, China [J]. Expert Systems with Applications 2010, 37, 2517–2521. [Google Scholar] [CrossRef]
12. He, Y.; Dai, B.; Tao, X. Fuzzy comprehensive evaluation of surface water quality based on confidence criteria [J]. China Water Supply and Drainage 2011, 27, 52–55. [Google Scholar]