Whole Genome Alignment: Methods, Challenges, and Future Directions

Whole genome alignment (WGA) is a critical process in comparative genomics, facilitating the detection of genetic variants and aiding our understanding of evolution. This paper offers a detailed overview and categorization of WGA techniques, encompassing suffix tree-based, anchors-based, and graph-based methods. It elaborates on the algorithmic properties of these tools, focusing on performance and methodological aspects. The paper underscores the latest progress in WGA, emphasizing the increasing capacity to manage the growing intricacy and volume of genomic data. However, the field still grapples with computational and biological hurdles affecting the precision and speed of WGA. We explored these challenges and potential future solutions. This paper aims to provide a comprehensive resource for researchers, deepening our understanding of WGA tools and their applications, constraints, and prospects.

Keywords:

Subject: Biology and Life Sciences - Biology and Biotechnology

1. Introduction

The genomics era, heralded by the availability of whole genome sequences for a wide range of organisms, has created unprecedented opportunities for researchers to understand evolutionary relationships, genetic variation, and functional elements of genomes [1]. A critical step towards this understanding is Whole Genome Alignment (WGA), a cornerstone of bioinformatics that aligns entire genomes from different species or individuals within the same species [2,3]. WGAs provide a global perspective on genomic similarity and variation, yielding insights into species' evolution, gene function, and genetic diseases [4].

Despite the importance of WGA, the task of aligning whole genome is non-trivial due to the sheer size of genomes, their complex evolutionary histories, and the computational demands of alignment algorithms [5]. For instance, the human genome consists of approximately 3 billion base pairs, and aligning such extensive sequences poses significant computational challenges, including execution time, memory usage, and management of genomic rearrangements [6].

A multitude of algorithms have been developed over the years to address these challenges [7]. Each algorithm offers a unique approach to WGA and has its specific strengths and weaknesses in terms of computational efficiency, scalability, and alignment accuracy [8]. Therefore, a comprehensive understanding of these algorithms is crucial for researchers to choose the most suitable tool for their specific tasks [9].

This study aims to provide a comprehensive review of the most prevalent WGA algorithms, highlighting their algorithmic aspects, methodological underpinnings, and the current challenges faced with them. We focused on three primary classes of algorithms: Suffix tree-based methods, Anchors-based methods, and Graph-based methods, with an emphasis on recent advancements in the field, including algorithms developed such as SibeliaZ, BubbZ, [10], and the innovative methods like PlusV [11] and MAGOT [12].

Our goal is to offer a balanced, comprehensive, and critical view of the current landscape of WGA algorithms, assisting researchers in their choice of suitable algorithms for specific applications.

In the following sections, we will delve into the classification of WGA algorithms, their algorithmic aspects, recent advancements, and the challenges in Whole Genome Alignment. We hope that this review will serve as a valuable guide for researchers and practitioners in the field of bioinformatics, genomics, and computational biology [13].

2. Classification of Whole Genome Alignment Algorithms

Whole genome alignment, a foundational task in genomics, relies on a variety of sophisticated algorithms to compare and contrast entire genomes. These algorithms can be broadly classified into three categories: Suffix Tree-Based Methods, Anchors-Based Methods, and Graph-Based Methods. Each of these categories embodies different alignment strategies, offering unique advantages and facing distinct challenges.

2.1. Suffix tree-based alignment methods

2.1.1. Suffix tree

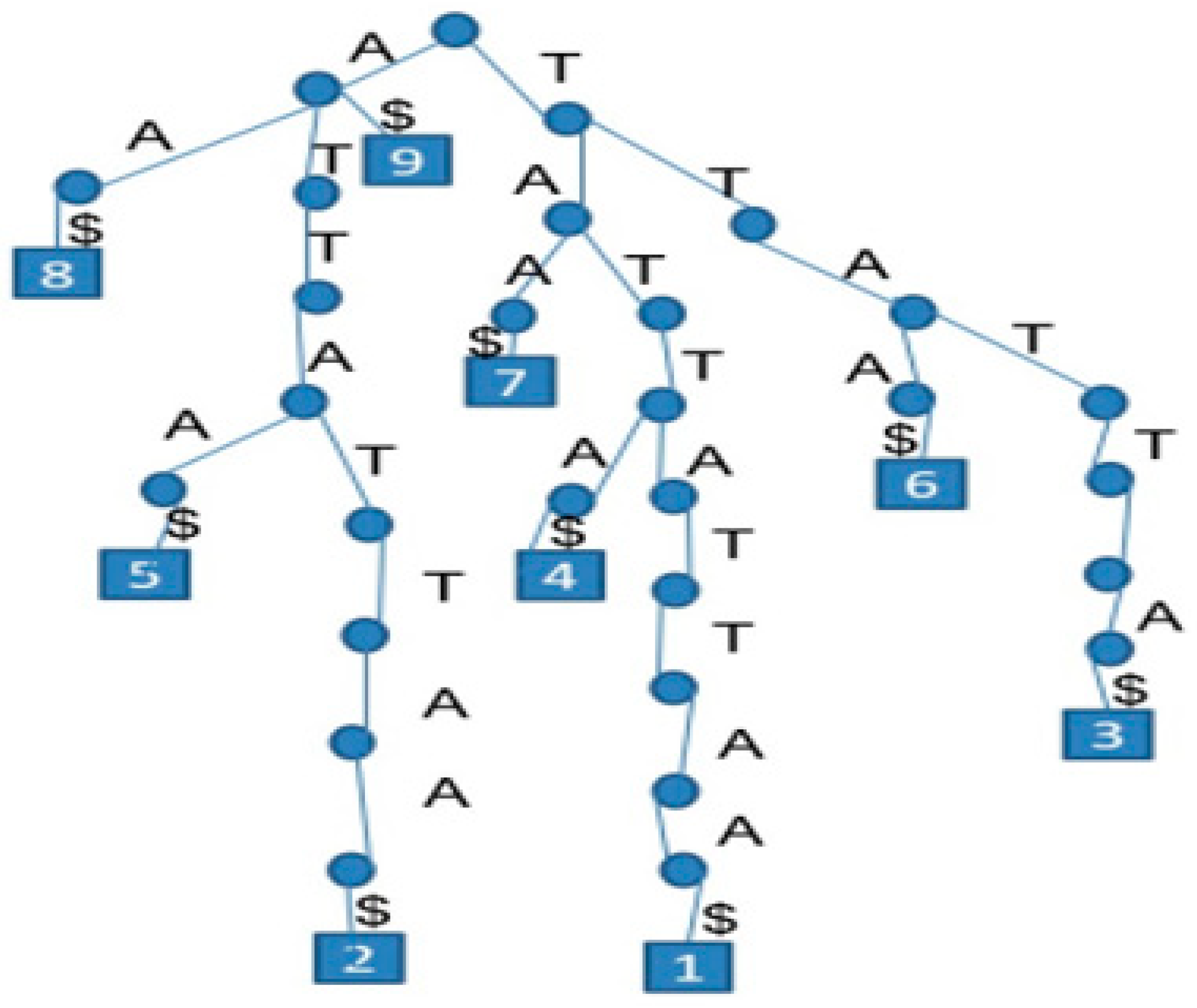
A suffix tree is a compressed tree containing all the suffixes of a given text (Figure 1). The tree saves their positions in the text as well as their values. This data structure provides a fast implementation for string operations. The main advantage is the fast computational time to detect an exact match with user-defined inputs [13].

2.1.2. MUMmer technique

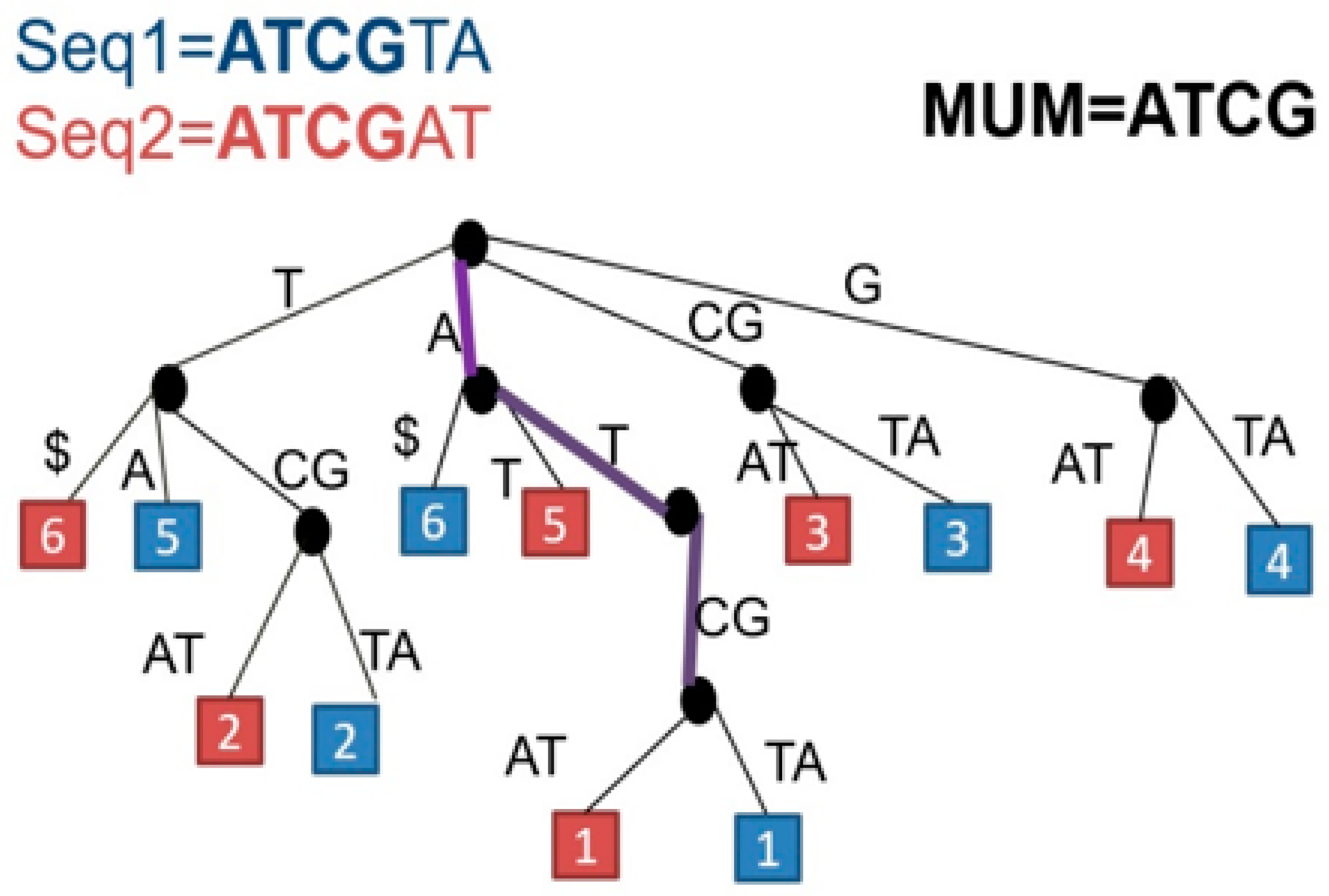
MUMmer is an alignment algorithm based on suffix tree representation [14]. The main idea of this algorithm is to find all distinct matches for two given genomes [15]. To better align the two given genomes, we assume that they are closely homologous.

MUMmer algorithm is based on four main steps:

(i): Perform a maximal unique match (MUM) decomposition of the two genomes. A MUM is a subsequence that occurs exactly once in genome A and once in genome B. This decomposition identifies all maximal unique matches between the two genomes. To detect those MUMs, the two genomes are represented by a suffix tree. The common substrings detected on the tree will represent all the MUMs between the two genomes (Figure 2).
(ii): Sort the MUMs and extract the longest possible set of matches that occur in the same order in both genomes.
(iii): Close the gaps in the alignment by performing an identification of large inserts, repeats, mutated regions and single nucleotide variation (SNV).

Perform a Smith-Waterman alignment for the regions between the MUMs and construct the final alignment.

2.1.3. MUMmer 2.1

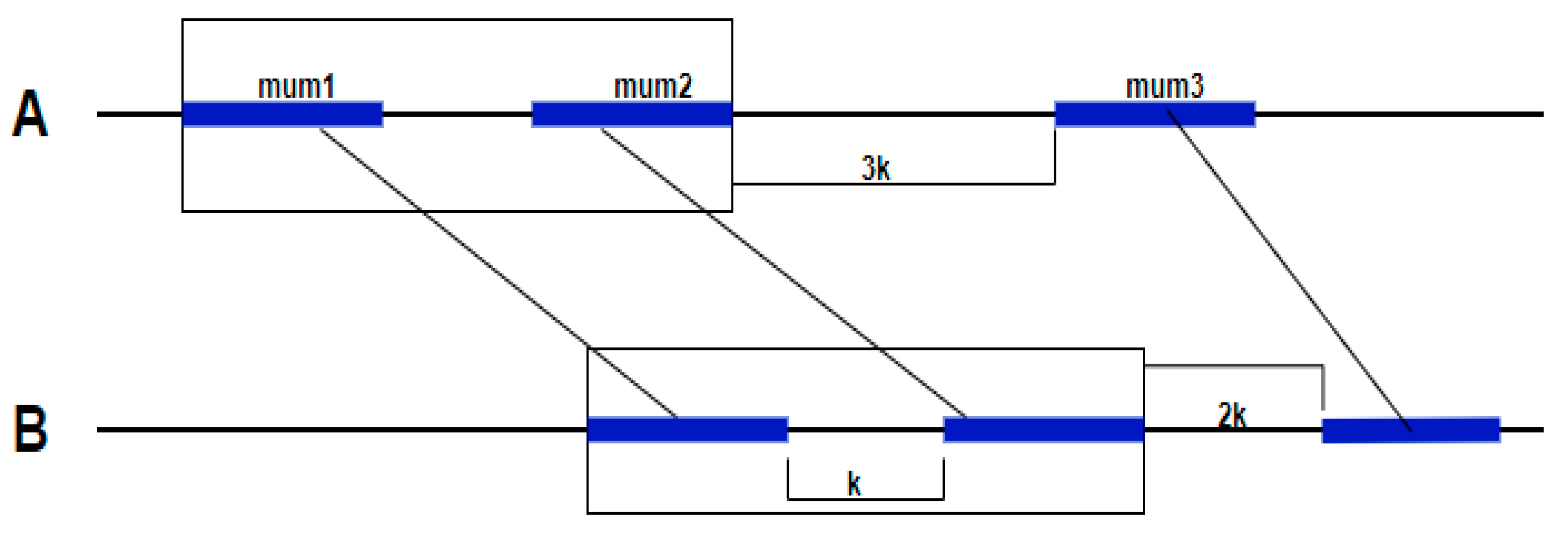
MUMmer 1.0 was first used to detect large-scale inversions in bacterial genomes. The bacterial genomes’ sizes don’t exceed few Mbp. It means that MUMmer 1.0 would require powerful computational resources to align genomes having billions of nucleotides. In addition, when the human genome was sequenced, it was necessary to implement a new algorithm able to align entire human chromosomes rapidly and accurately.

For that reason, the authors proposed a new method that requires less memory and runs the four steps faster [12]. In addition, a new parameter k was introduced. This parameter represents a maximum gap length allowed between MUMs. If the gap is lower than k, the two adjacent MUMs are regrouped in the same cluster (Figure 3).

2.1.4. MUMmer 3.0

Unique MUMs occur exactly once in both genomes. However, in certain cases, the exact match may be duplicated within the subject genome. To overcome this problem, the new MUMmer 3.0 uses the all-maximal matches including non-unique ones to align the two genomes [16]. In addition, the execution time of MUMmer 3.0 and the memory usage has been improved. While using MUMmer 3.0, the query time for a whole genome alignment of Comparison between Humans and Human Chromosomes is about 300 minutes and can reach 600 minutes depending on the sizes of the chromosomes used for the alignment.

2.1.5. MUMmer 4.0

With the large genomic data, MUMmer 3.0 has limitations and fails to perform whole genome alignments. In 2018, the new version MUMmer 4.0, which includes an improved version of MUMmer algorithm, uses a 48-bit suffix array for the genome size constraints. In addition, MUMmer 4.0 introduces an improved speed and memory usage through parallel processing of input query sequences [17]. With this improvement, a whole genome alignment of Human/Chimpanzee genomes can be performed in 2,897 minutes. This operation cannot be performed using MUMmer 3.0. Furthermore, with a theoretical limit on the input size of 141 Tbp, MUMmer 4.0 would perform alignment with input sequences of any biologically realistic length.

2.1.6. Other sequence comparison approaches based on suffix tree method

Suffix tree approaches provide fast computational time to detect exact matches between sequences. Different algorithms rely on the construction of suffix tree between the two sequences to detect similar regions (words). SuffixTree & Lwords algorithm is a sequence comparison alignment-free approach based on the construction of a generalized suffix tree of all sequences [18]. Following the construction of the suffix tree, the frequency of all possible words with a length L, provided as a parameter, is calculated. Then, based on the L-words frequency profile on each sequence, a pairwise Euclidean distance is computed producing a symmetric genetic distance matrix between the sequences.

The execution time of SuffixTree & Lwords algorithm is satisfactory when the algorithm is applied to complete intra/inter mitochondrial species’ genomes. It can perform its sequence comparison alignment-free approach for 29 primates’ genomes (ranging from 14 to 25 Mbp) in just 66 seconds.

Another algorithm based on suffix tree method is Multiple Sequence Alignment algorithm (MSA) [19]. MSA algorithm starts by detecting the similar substrings between the sequences. Then, it uses an approach called the Center Star Strategy in order to calculate a pairwise optimal alignment distance between the set of inputs and select a central sequence which has the highest degree of similarity with other sequences in the set [20]. Finally, the algorithm runs a pairwise alignment between aligned center and the other sequences to construct the final multiple alignment. This algorithm can perform an alignment of 67,200 strains, all longer than 10,000 bps, in 9 minutes.

2.2. Anchors based methods

An anchor is a similar region of two or more genomes. Some algorithms perform local alignments on each consecutive pair of anchors that are separated by a non-similar region smaller than a given length k. The algorithms join all the anchors and the non-similar regions together. Different algorithms use this method either to perform a local alignment on chromosomes or a specific DNA sequence or to perform a global genomic alignment. In this section, we will enumerate some of the most commonly used algorithms that use anchor-based methods and explain their computational steps.

2.2.1. Lagan

Lagan algorithm is based on dynamic programming as it uses anchoring to subdivide the alignment into small anchors [21]. Lagan also assumes that the two sequences are relatively close. It starts by detecting the anchors and then performs a dynamic programming alignment algorithm on the limited area around the anchors.

Steps:

(i): Generation of Local Alignments

Lagan uses CHAOS method [22] to detect local homologies between the two genomes and chains them into a rough global map.

The first step of CHAOS is chaining short exact matches (seeds) which match between the two genomes. The seeds, that are close, are regrouped to same anchors. The gaps between the seeds are aligned using a dynamic programming alignment method.
(ii): Construction of a Rough Global Map

Lagan uses local alignments to perform a rough global map. Each local alignment has a score of similarity. The optimal rough global map has the highest-scoring chain, which can be computed using Sparse Dynamic Programming [23].
(iii): Computation of Global Alignment

To compute the final global alignment, Lagan uses Needleman-Wunsch algorithm to perform an alignment of the limited-area between the anchors.

2.2.2. Multi-LAGAN

Multi-LAGAN aligns a set of genomes progressively. An alignment of n sequences is constructed after n–1 pairwise alignment operation. Multi-Lagan uses a phylogenetic tree of the sequence to choose, on each step, which genome will be used for the alignment. This, on similarity-based method, will perform an alignment with a high similarity between sequences and can detect orthologous genomic regions between them. Multi-LAGAN uses two main steps to align N genomes having a phylogenetic binary tree between them:

STEP 1: Generation of rough global maps. Find the rough global map between each pair of sequences using Lagan.

STEP 2: Progressive multiple alignment with anchors:

1) Perform an alignment between the two closest sequences according to the binary phylogenetic tree using LAGAN.

2) Each alignment is a new multi-sequence. Find the rough global maps of this multi-sequence to the closest sequence; 3) Iterate Steps 2.1 and 2.2, perform a global alignment between the multi-sequences and the closest sequence; 4) Repeat Step 2 until performing a multiple alignment of all the set of sequences (Figure 4).

2.2.3. Mauve

Mauve is a genome alignment method which is able to identify entire similar regions between a set of genomes such as rearrangements, translocation and inversions, and the exact breakpoints of each rearrangement across multiple genomes [24].

Mauve uses anchoring as a heuristic to detect similar regions. However, the main originality of this algorithm is that unlike the other multiple genomes’ alignment methods. Mauve uses a heuristic approach to predict if the anchors represent a similar region between the genomes or if it is only a similar region caused by random mutations.

2.2.3.1. Steps

a. Finding Multi-MUMs

While the algorithm detects anchors across multiple genomes comparison, some repetitive regions can occur several times in each genome as a duplication of those regions. The more there are aligned genomes, the more difficult it becomes to place each anchor in the correct place of the global alignment. To resolve this problem, Lagan uses Multiple Maximal Unique Matches (multi-MUMs) with a minimal length k as anchors. Those multi-MUMs are the exact matching sub chains shared by two or more genomes that occur only once in each genome and that are bounded on either side by mismatched nucleotides.

In addition, to detect other anchors of a length less than k, Mauve uses an anchoring technique that reduces k while looking for smaller anchors in the remaining unmatched regions.

b. Calculating a Phylogenic Guide Tree

Mauve uses the genomes similarity regions provided by the subset of multi-MUMs as a binary distance metric to build a phylogenetic guide tree using Neighbor Joining [25].

c. Selecting a Set of Anchors

This step consists in the detection of homologous subsequences. Those regions are called locally collinear blocks (LCBs). Each locally collinear block is a homologous region shared by two or more genomes and does not contain any rearrangement of similar blocks.

d. Recursive Anchoring and Gapped Alignment

The previous step may not detect all the regions of homology between the genomes, as a minimum length k is required to consider a region as an LCB. To resolve this problem, two techniques of recursive anchoring are performed. The first technique consists in the detection of similar regions outside of LCBs to extend the number of LCBs and identify new ones. The second technique consists in detecting unanchored regions within LCBs.

Regions that are not unique in the entire genome may be unique in regions outside LCBs. For that reason, new LCBs having the minimum length k may be identified as outside LCBs regions.

Finally, Mauve performs a CLUSTAL-W alignment using the set of anchors as well as the genome guide tree generated on step 2 [26]. The progressive alignment algorithm is executed once for each adjacent anchors’ pairs in every LCB and performs a global alignment for each LCB.

2.2.3.2 Alignment visualization tool

In addition to the Mauve alignment algorithm, a visualization tool has been developed to display the whole genome alignment that shows the rearrangement between the genomes.

2.2.3.3 Progressive Mauve

Content and rearrangement are the two main techniques that are used in this method to better detect variable genes. The first scores all possible configurations of alignment anchors across the set of genomes [27]. The second applies the homology hidden Markov model (HMM) to predict similar subsequences caused by random mutations and reject them.

The experimental results made using Progressive Mauve method shows that the algorithm was able to detect the pan-genome and the core-genome of species from Enterobacteriaceae family.

2.2.4. BLASTZ

Many research projects analyze similarities between the human and the mouse genome. They implemented many programs to align the mouse and human chromosomes, such as Blast2sequences [28] and Pattern Hunter [29]. The high percentage of similarity between the two genomes has led researchers to implement a new algorithm that is able to detect chromosomes synteny and orthologous regions between them.

2.2.4.1 Main steps

First, the algorithm started by detecting similar regions between the two genomes that occur in the same order and orientation. By using this approach, it is possible to detect exact orthologous regions [30].

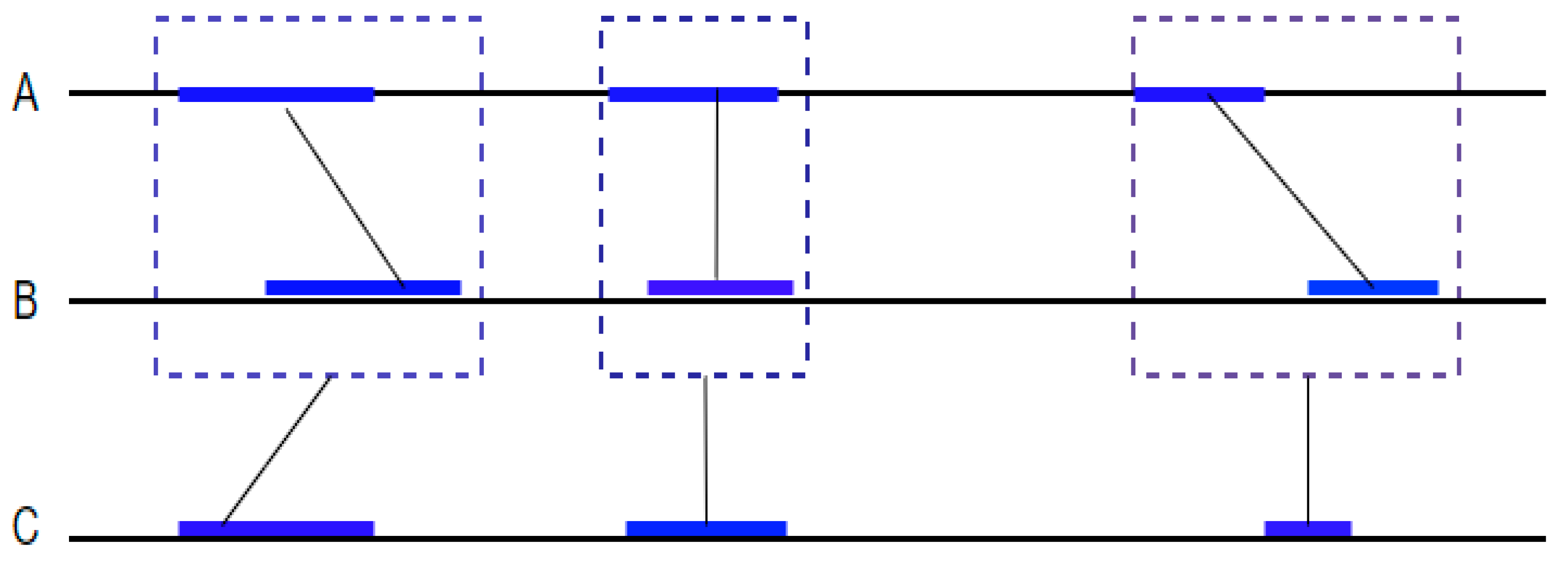
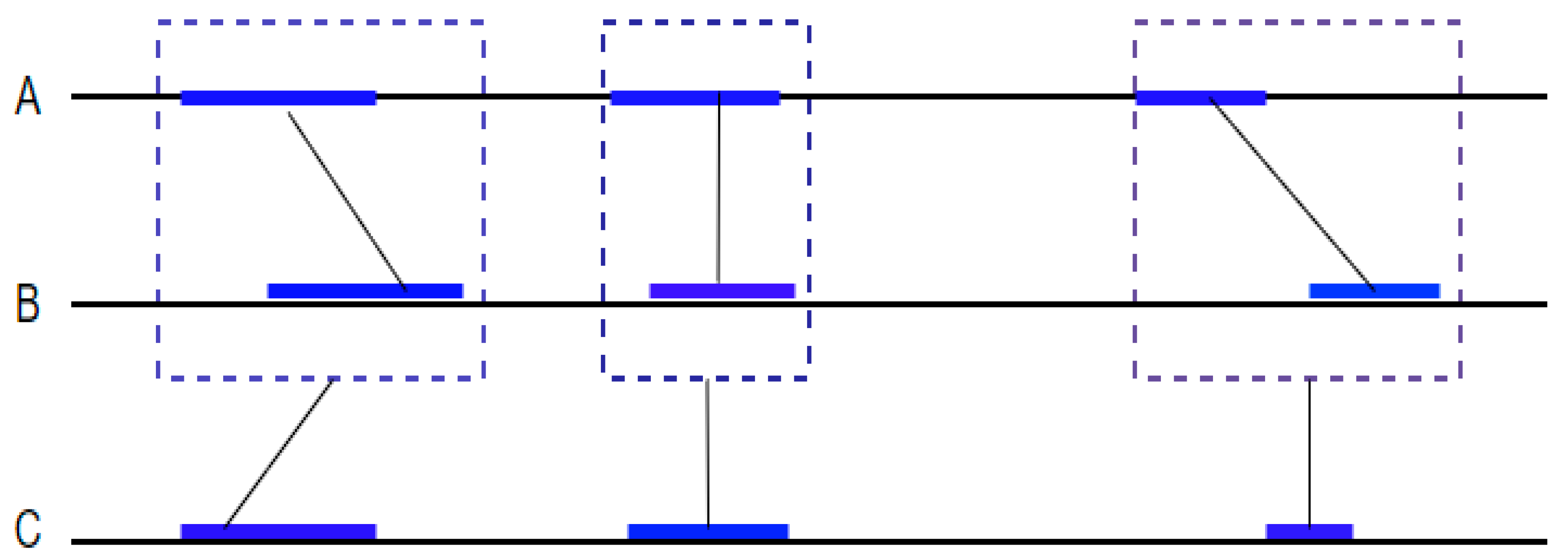
Second, BLASTZ aligns the other regions to detect small matching subsequences (seeds) and extend them while limiting the gap length to k (Figure 5). This step is based on looking for identical words of eight or nineteen consecutive nucleotides in each sequence. To increase sensitivity, the algorithm allows transitions between the nucleotides.

Figure 4. Multi-sequences alignment using Lagan. Lagan performs a pairwise alignment between the closest sequence. Each alignment will be considered as new multi-sequence to be compared with another sequence in the set.

2.2.4.2 Main use

The first use of the algorithm was for the conservation of synteny between human and mouse chromosomes. The experimental results showed that the Human Chromosome 20 is partially homologous to the mouse’s Chromosome 2. In addition, only 3.3% of the human Chromosome 20 nucleotides align outside of the mouse chromosome 2.

2.2.5. STELLAR

STELLAR enumerates all local alignments of a given minimal length k [31]. It starts by detecting matches having few dissimilarities then attempts to identify maximal matches with minimal mismatches (errors). These matches are then filtered by the SWIFT algorithm [32] because false positive matches between the sequences could be generated.

This step also removes any overlapping matches. Compared to heuristic tools such as BLAST, STELLAR can detect more significant local alignments.

2.2.6. LASTZ

LASTZ is mainly used to perform alignment of complete chromosomes [33]. This algorithm starts by detecting short near matches (seeds) between target and query sequences. Next, an adaptive score threshold is calculated to extend these seeds based on a match, mismatch, and gap scores. Like Lagan, LASTZ performs a dynamic programming approach to align the non-extended blocks and construct the final alignment result.

2.2.7. DIALLGN

DIALING was designed for multiple sequence alignment and is particularly useful to detect local homologies in sequences with low overall similarities [34]. This algorithm’s various versions have been implemented and their main innovation consists of the insertion of user-specified external information. The user can insert the two sequences’ anchors’ details, including the length of the anchor and its starting position in sequence 1 and in sequence.

2.2.8. AnchorWave

AnchorWave performs whole-genome duplication–informed collinear anchor identification between genomes and performs base pair–resolved global alignment for collinear blocks using a two-piece affine gap cost strategy [35]. It precisely aligns up to three times more of the genome as position matches or indels than the closest competitive approach when comparing diverse genomes.

The algorithm starts by aligning the query genome with a reference genome annotation. Then, it uses a dynamic programming algorithm to find the collinear blocks between the two genomes. It may use the longest path to define these similar regions. The user can also decide to include paths containing inversions, rearrangements, and whole genome duplication. The next step of the algorithm is optional. In order to reduce the size of the non-similar blocks (inter-anchors blocks), the user can decide to try to identify new additional anchors. Finally, AnchorWave performs a base pair alignment using the two-piece affine gap cost strategy [36]. This pairwise alignment method reduces the error rate and assemble similar genomes up to 30 faster than existing alignment tools [37].

2.2.9. Minimap-2

Minimap2 uses a method based on hashing and chaining, which is an anchor-based approach. This technique involves identifying "anchors" (similar or identical sequence regions) between the sequences being compared, and then chaining these anchors together to create an alignment. The efficiency and speed of Minimap2 largely stem from its ability to quickly identify and utilize these anchors for alignment [37].

2.3. Graph-based homology mapping methods

The previous alignment methods are mainly used for the detection of similarities at the DNA level. A new class of alignment methods has emerged to perform genome comparison in terms of gene composition and interspecies evolutionary relationship. These methods are graph-based methods that map the DNA/genes composition of the genomes and, thus, highlight the evolutionary relationship between species, including syntenic, homologous, orthologous, and paralogous regions.

Mercator is a multiple whole genome orthologous map construction algorithm. It is mainly used to identify the evolutionary relationships between multiple genomes [38]. The algorithm takes a set of exon annotation for each genome. Second, it compares all exons of all genomes and builds an alignment between them. Third, the algorithm builds a graph where each vertex represents an exon and edges between vertexes represent the alignment score between exons. Finally, the algorithm identifies cliques in this graph and performs a join neighboring cliques together to form similar anchors between the genomes. The cliques formed in each genome are used to highlight the orthologous blocks between them (Figure 6).

2.3.1. Mugsy

Mugsy is a graph-based algorithm that is mainly used for whole bacterial genomes alignment and multiple human chromosomes alignment [39]. It first performs a pairwise local alignment between the sequences. Then it constructs and uses an alignment graph to identify LCBs.

The main advantage of this algorithm is that it identifies genomic regions that are homologous, collinear, free of rearrangements and suitable for multiple alignment. In addition, Mugsy can align 57 E. coli genomes (299 Mb) in <1 day on a single CPU. It also performs an alignment of four assembled human chromosomes, completing the LCB identification and multiple alignment in <1 h.

2.3.2. BubbZ

BubbZ is a fast whole-genome homology mapper which detects pairwise chains in the homologous blocks using De Bruijn graph [40]. The algorithm was recently tested on closely related mammalian genomes and a large collection of bacterial genomes.

2.3.3. SibeliaZ

SibeliaZ-LCB algorithm is used to identify collinear blocks in closely related genomes based on the construction of a De Bruijn graph [41] to build collinear blocks. It globally aligns the collinear blocks to generate the whole-genome alignment. On sixteen recently assembled mice genomes, SibeliaZ ran in less than 16 hours on a single machine, while other tools did not run to completion for eight mice within a week. It also provided better performance, in terms of time of execution, compared to Mercator tool.

3. Algorithmic aspects of WGA algorithms

3.1. Performance characteristics

The performance of Whole Genome Alignment (WGA) algorithms is often evaluated based on their speed, memory usage, scalability, and accuracy [37]. The speed at which an algorithm can process and align genomes is crucial in handling the ever-increasing size of genomic data. The memory usage determines on how large genomes or datasets the algorithm can handle at once [38].

Scalability, in the context of WGA algorithms, refers to the ability of an algorithm to handle increasing volumes of data without a proportional increase in computational resources. This is a critical characteristic, especially when dealing with larger and more complex genomes [39].

The accuracy of WGA algorithms is usually assessed by comparing the generated alignment with a reference alignment or by evaluating the biological relevance of the alignment. Accuracy is influenced by the algorithm's ability to correctly identify homologous regions, handle genomic rearrangements, and align divergent sequences [40,41].

3.2. Methodological Underpinnings

The methodological underpinnings of WGA algorithms can be broadly categorized into heuristic and exact methods. Heuristic methods, such as MUMmer and BLASTZ, generate approximate alignments rapidly but may not always produce the optimal alignment [42,43]. These methods are often used for the initial stage of alignment to identify regions of similarity, which are then refined using more accurate methods [44].

Exact methods, on the other hand, guarantee to find the optimal alignment but are typically slower and require more computational resources. These methods, such as those based on dynamic programming, are often used for refining alignments or for aligning smaller regions of the genome [45,46].

Recent advancements in WGA algorithms have seen the development of methods that strike a balance between speed and accuracy. For instance, tools like Cactus and Progressive Cactus, utilize a combination of heuristic and exact methods to generate accurate alignments quickly [47,48]. These tools use heuristic methods for the initial alignment and then apply exact methods to refine the alignment, resulting in a balance of speed and accuracy [49].

WGA algorithms also vary in their ability to handle genomic rearrangements, such as inversions, duplications, and translocations. Some algorithms, like Mauve and Progressive Cactus, have built-in features for handling these rearrangements [24]. Other algorithms may require additional steps or tools to correctly align regions with genomic rearrangements [24].

Finally, the choice of a suitable WGA algorithm often depends on the specific requirements of the research question. For instance, studies focusing on closely related species may benefit from algorithms that excel at aligning highly similar sequences, while studies on divergent species may require algorithms that can handle high levels of sequence divergence [50,51].

In summary, the algorithmic aspects of WGA algorithms, from their performance characteristics to their methodological underpinnings, are key factors influencing their suitability for different research applications. Continued advancements in these aspects will undoubtedly contribute to the ongoing evolution of the field of whole-genome alignment [52,53].

4. Recent advancements in WGA algorithms

The field of whole-genome alignment has seen significant progress over the years. With the rapid advancements in sequencing technologies and the ever-increasing amount of genomic data, the development of efficient and accurate WGA algorithms has become more critical than ever [54].

One of the major advancements in WGA algorithms is the development of methods that can handle large-scale genomic rearrangements. While traditional alignment algorithms often struggle with these rearrangements, newer tools like Cactus and Progressive Cactus have incorporated mechanisms to accurately align regions with inversions, duplications, and translocations [48]. These tools use a graph-based approach, which allows them to model and align complex genomic structures [55] (table 1).

Another significant advancement is the development of algorithms that can align divergent genomes. Traditionally, aligning divergent genomes has been challenging due to the high levels of sequence divergence and the presence of unique genomic elements. However, tools like LASTZ and MULTIZ have been designed to tackle these challenges, enabling the alignment of divergent genomes [56,57].

The advent of cloud computing and parallel processing has also influenced the development of WGA algorithms. Tools like Cloud Aligner and ParaGraph have leveraged these technologies to perform alignments on a massive scale, handling large volumes of data and multiple genomes simultaneously [58,59]. This has significantly improved the speed and scalability of WGA algorithms, allowing researchers to undertake more ambitious projects.

Incorporating machine learning techniques into WGA algorithms is another promising direction. By learning from existing alignments, these algorithms can potentially improve their accuracy and efficiency. For instance, tools like Deep Align have demonstrated the potential of machine learning in improving the accuracy of sequence alignments [60].

Furthermore, the integration of WGA algorithms with other bioinformatics tools has also seen notable progress. For example, pipelines like EAGER2 integrate WGA tools with other bioinformatics software, providing a comprehensive solution for genomic analysis [61]. This not only simplifies the analysis process but also enhances the utility of WGA algorithms in research.

In conclusion, the recent advancements in WGA algorithms have significantly improved their performance and versatility, catering to a wider range of research applications. As the field continues to progress, it will be exciting to see how these advancements will shape the future of whole-genome alignment [62].

5. Comprehensive Analysis of Genomic Comparison Tools: Human and Diverse Genomes

To evaluate the effectiveness of genomic alignment tools under varies conditions, we conducted a study using MUMmer4, Sibeliaz, Dialign2, and Minimap2. The analyses involved two sets of genomes: human genomes (exhibiting high similarity) and those of Caenorhabditis elegans (C. elegans) and Saccharomyces cerevisiae (Baker's yeast), representing species with considerable evolutionary divergence. Our analyses were conducted on a server equipped with dual E5-2699 v4 processors and 512GB of RAM which is running on CentOS 7.

5.1. Analyses of Human Genomes

The initial phase of our study used MUMmer4, Sibeliaz, Dialign2, and Minimap2 for analyzing two human genomes. The contrasting results from these tools provided insights into their specific functionalities and limitations:

• MUMmer4: Demonstrated a remarkable ability to detect near-identical sequences in human genomes, reporting a similarity of almost 100%. This high similarity index indicates that MUMmer4 is particularly efficient at aligning genomes with minimal genetic variations, making it an ideal tool for studies where the genomes are closely related.

• Sibeliaz: Presented a different perspective, reporting a much lower similarity percentage (9% of coverage). Sibeliaz's methodology, which focuses on k-mer pattern analysis, allows it to uncover subtle variations that direct sequence comparison methods might miss. This attribute is particularly beneficial for research that delves into genomic diversity, mutation analysis, and evolutionary biology.

• Dialign2: Encountered limitations with the human genomes, primarily due to their size. This outcome underscores the necessity of considering genomic data scale when selecting analytical tools, particularly for large and complex genomes.

• Minimap2: Mirroring MUMmer4 in effectiveness, Minimap2 showed a 100% mapping rate, aligning the human genomes completely. It demonstrated additional capabilities in managing complex mapping situations, indicated by the presence of secondary and supplementary alignments, thus offering a broader scope in genomic analysis.

5.2. Analysis of C. elegans and Baker's Yeast Genomes

The study then extended to a comparison of C. elegans and Baker's yeast genomes to evaluate the tools under significantly different genomic conditions:

• MUMmer4: In stark contrast to its performance with human genomes, MUMmer4 yielded no output for the C. elegans and Baker's yeast genomes. This indicates MUMmer4’s limitations in aligning genomes that are not closely related, thereby suggesting its niche application in genomic studies.

• Sibeliaz: Revealed only 12% coverage in conserved regions between C. elegans and Baker's yeast, identifying 21,816 distinct blocks. This low coverage identifies a substantial evolutionary distance between these species. Sibeliaz's strength lies in its ability to analyze and compare genomes with significant structural and evolutionary variations, making it a versatile tool for comparative genomics across diverse species.

• Dialign2: Like its performance with human genomes, Dialign2 was unsuccessful in processing the data from C. elegans and Baker's yeast, further highlighting its limitations in handling diverse genomic data.

• Minimap2: Unlike its effective mapping of human genomes, Minimap2 failed to map the C. elegans and Baker's yeast genomes, indicating challenges in aligning significantly divergent genomes.

5.3. Execution Times and Tool Complexity

In our comparative analysis of genomic alignment tools applied to human genomes, we observed significant variations in execution times, reflecting each tool's computational approach and efficiency. MUMmer4 took approximately 15 hours and 34 minutes, indicating its intensive computational process, especially effective for aligning highly similar sequences. Sibeliaz completed its analysis in about 6 hours and 19 minutes, showcasing its efficiency in handling complex k-mer pattern analysis despite the large data size. Dialign2 faced challenges with the human genome size, leading to a crash and underscoring the need for more scalable solutions in genomic analysis tools. Minimap2 stood out for its speed, completing the mapping in just 44 minutes, demonstrating its capability for rapid and efficient genomic alignment. These varying execution times are indicative of the underlying algorithms and computational strategies employed by each tool, highlighting the importance of considering both accuracy and efficiency when selecting genomic analysis tools for large-scale studies.

5.4. Methodological insights

Our study revealed distinct strengths and challenges for each tool. MUMmer4 and Minimap2, effective for similar genomes, struggle with significant genomic divergence. Sibeliaz excels in analyzing complex and varied genomic data. Dialign2's limitations underscore the necessity for robust, scalable tools in modern genomic research.

This comparative analysis emphasizes the importance of tool selection based on genomic data characteristics. The choice of tools, influenced by their methodologies – suffix trees, k-mer analysis, or hashing and chaining algorithms – significantly impacts genomic data interpretation. Furthermore, computational time, a critical factor in genomic research, ranged from 44 minutes (Minimap2) to over 15 hours (MUMmer4), underscoring the need to balance accuracy and efficiency in tool selection (table 3).

Table 2. WGA mapped alignment Coverage.

Whole Genome Alignment Tools	Human Vs Human	C. elegans Vs Baker’s Yeast
SibeliaZ	9%	12%
MUMmer 4.0	99%	0%
Minimap2	100%	0%

Table 3. Human vs. Human WGA execution time performed by each software.

Whole Genome Alignment Tools	Alignment Time
SibeliaZ	6 hours and 19 minutes
MUMmer 4.0	15 hours and 34 minutes
Diaalign-2	Fail
Minimap2	44 minutes

6. Challenges in whole genome alignment

Whole genome alignment (WGA) has been a tremendous asset to the scientific community, enabling insights into evolutionary biology, comparative genomics, and disease pathology, among other fields. However, the complex nature of genomic data and the increasing demands for accurate and efficient analysis present several challenges that need to be addressed. Additionally, the dynamic nature of this field also opens up new directions for future research and development [63].

6.1. Computational challenges

Computational challenges in WGA span from the handling of large and complex datasets to the efficiency of alignment algorithms. The exponential increase in the volume of genomic data due to advancements in sequencing technologies necessitates WGA algorithms that can handle large datasets efficiently and accurately [64].

Time and space complexities are significant challenges. As the size of the genomes increase, the time taken for alignment and the memory required for processing also increase exponentially [65]. Even with advancements in algorithmic design and computational power, dealing with large genomes or multiple alignments simultaneously remains a daunting task [66].

The implementation of parallel and distributed computing strategies can help mitigate these challenges to some extent. However, these approaches also require specialized knowledge, resources, and can be associated with significant costs [67].

6.2. Biological relevance

Ensuring biological relevance in the results produced by WGA algorithms is paramount. The complexity of genomes, including structural variations and non-coding regions, present a significant challenge for alignment [68]. Misinterpretation or oversights can lead to inaccurate biological conclusions, highlighting the importance of precision in WGA algorithms [69].

Understanding the biological significance of alignment results is another challenge. This often involves complex bioinformatics analyses, requiring a wide array of skills and expertise [70].

6.3. Future directions

There are several promising directions for future research in WGA. The development of more efficient and scalable algorithms remains a top priority. This includes methods that can handle large genomes and multiple alignments more efficiently, as well as algorithms that can better account for structural variations and non-coding regions [71].

Further, there is a need for user-friendly and accessible WGA tools. This would make WGA more accessible to researchers from various backgrounds, promoting interdisciplinary research and broadening the applications of WGA [72].

The integration of machine learning and artificial intelligence techniques in WGA also presents a promising direction. These techniques could potentially enhance the accuracy, efficiency, and scalability of WGA algorithms, and offer new ways to interpret and visualize alignment results [73].

In summary, the field of WGA continues to evolve, with numerous challenges to address and exciting avenues for future research. The collaboration between bioinformaticians, computer scientists, biologists, and other stakeholders will be critical in pushing the boundaries of what can be achieved with WGA [74].

7. Discussion

The advancements in whole genome alignment (WGA) over the past few decades have been remarkable, providing critical insights into the genetic underpinnings of life. However, as we have discussed in the preceding sections, there are still significant challenges and opportunities that lie ahead [63].

The computational challenges in WGA, particularly those associated with handling large and complex genomic datasets, remain a key obstacle. Despite the significant strides made in improving the computational efficiency of WGA algorithms, the exponential growth of genomic data continues to pose challenges [71]. This necessitates the development of even more scalable and efficient algorithms that can cope with the volume and complexity of modern genomic datasets. Also, the potential of parallel and distributed computing in enhancing the efficiency of WGA has been recognized, but the cost, resources, and expertise required for these approaches limit their adoption [75].

Ensuring the biological relevance of WGA results is another critical challenge. The complexity of genomes, including the presence of structural variations and non-coding regions, increases the difficulty of producing biologically accurate alignments. It also amplifies the need for precise and sophisticated WGA algorithms. Even with accurate alignments, understanding the biological significance of the results requires complex bioinformatic analyses, highlighting the need for interdisciplinary collaboration in the field [76].

The integration of machine learning and artificial intelligence techniques in WGA could potentially enhance the accuracy, efficiency, and scalability of WGA algorithms, and offer innovative ways to interpret and visualize alignment results [77]. Additionally, developing user-friendly and accessible WGA tools would not only make WGA more accessible to a broader range of researchers but also promote interdisciplinary research, ultimately expanding the applications of WGA [60].

Therefore, there are significant challenges to overcome, the future of WGA is undoubtedly promising. Through continued research, collaboration, and innovation, we can look forward to new breakthroughs that will further our understanding of genomes and fuel discoveries in various fields of biology [74].

8. Conclusion

Whole genome alignment (WGA) stands as a cornerstone in comparative genomics, illuminating insights into evolutionary processes, species relationships, and functional genomics. As we have reviewed, the field has seen substantial advancement in terms of algorithmic development, with diverse methodologies introduced and continually refined to tackle the inherent complexity of genomic data.

However, as we have also highlighted that this field continues to face significant computational and biological challenges. The sheer scale of genomic data, coupled with its complexity, calls for increasingly efficient and scalable algorithms. The need for biological relevance further underscores the necessity for sophisticated and precise WGA methodologies. Moreover, the effective interpretation of WGA results requires deep bioinformatic analyses, thus emphasizing the need for interdisciplinary collaboration.

There is considerable potential for this field. The incorporation of machine learning and artificial intelligence techniques into WGA methodologies offers exciting prospects for enhancing accuracy and scalability. However, efforts towards making WGA tools more user-friendly and accessible will democratize the use of these tools, promoting interdisciplinary research, and expanding the applications of WGA.

In conclusion, the challenges faced by the WGA field are significant, but they are outweighed by the potential for growth and discovery. As we continue to refine and innovate WGA methodologies, we can anticipate new insights into genomic organization and function, further driving the fields of evolutionary biology, genomics, and beyond.

Author Contributions

BS wrote the initial draft of the review. ES updated various sections and revised the references. JZ, MMMM, and TCZ thoroughly revised the manuscript. All authors approved the final manuscript.

Funding

This research was supported by: (1) 2020-2022 National Natural Science Foundation of China under Grand No. 52001039 (2) 2020-2022 Shandong Natural Science Foundation in China No. ZR2019LZH005 (3) 2022-2025 National Natural Science Foundation of China under Grand, No.52171310 (4) Science and Technology on Underwater Vehicle Technology Laboratory under Grant 2021JCJQ-SYSJJ-LB06903

Data and Scripts Availability

The genomic datasets used in our analysis are available in the NCBI database. For the human genome, we accessed the primary human reference genome (GRCh38) and the mitochondrial genome (GRCh38 mitochondrial assembly). For the comparative analysis involving different species, the genome of Caenorhabditis elegans (accession GCF_000002985.6) was used, and for the baker's yeast, Saccharomyces cerevisiae, we utilized the genome with the accession GCA_000146045.2. The source code used for these analyses can be downloaded from the Github repository: https://github.com/BacemDataScience/WholeGenomeAlignment

Acknowledgments

We would like to thank all the organizers of the 2017 Bioinformatics and Genome Analyses course which was held at Pasteur Institute in Tunisia. The participation of Dr. Bacem Saada in this training inspired him to write this review.

References

Guerfali, F.; Laouini, D.; Boudabous, A.; Tekaia, F. Designing and running an advanced Bioinformatics and genome analyses course in Tunisia. PLoS Computational Biology 2019, 15, e1006373. [Google Scholar] [CrossRef] [PubMed]
Saada Bacem and Z. Jing. DNA sequences compression algorithms based on the two bits codation method. in 2015 IEEE International Conference on Bioinformatics and Biomedicine (BIBM). 2015. IEEE.
Venter JC, A.M.D. , Myers EW, Li PW, Mural RJ, Sutton GG., The sequence of the human genome. science 2001, 291, 1304–51. [Google Scholar]
Goldfeder, R.L.; et al. Human Genome Sequencing at the Population Scale: A Primer on High-Throughput DNA Sequencing and Analysis. American Journal of Epidemiology 2017, 186, 1000–1009. [Google Scholar] [CrossRef] [PubMed]
Pinese, M.; et al. The Medical Genome Reference Bank contains whole genome and phenotype data of 2570 healthy elderly. Nature Communications 2020, 11, 435. [Google Scholar] [CrossRef] [PubMed]
Anderson, W.; et al. International network of cancer genome projects. Nature 2010, 464. [Google Scholar]
Blake, J.A.; et al. Mouse Genome Database (MGD): Knowledgebase for mouse–human comparative biology. Nucleic Acids Research 2021, 49, D981–D987. [Google Scholar] [CrossRef] [PubMed]
Abascal, F.; et al. Expanded encyclopaedias of DNA elements in the human and mouse genomes. Nature 2020, 583, 699–710. [Google Scholar]
Needleman, S.B.; Wunsch, C.D. A general method applicable to the search for similarities in the amino acid sequence of two proteins. Journal of Molecular Biology 1970, 48, 443–453. [Google Scholar] [CrossRef]
Smith, T.F.; Waterman, M.S. Identification of common molecular subsequences. Journal of molecular biology 1981, 147, 195–197. [Google Scholar] [CrossRef]
Morgenstern, B. DIALIGN 2: improvement of the segment-to-segment approach to multiple sequence alignment. Bioinformatics 1999, 15, 211–218. [Google Scholar] [CrossRef]
Delcher, A.L.; et al. Fast algorithms for large-scale genome alignment and comparison. Nucleic Acids Research 2002, 30, 2478–2483. [Google Scholar] [CrossRef] [PubMed]
Gusfield, D. Algorithms on stings, trees, and sequences: Computer science and computational biology. Acm Sigact News 1997, 28, 41–60. [Google Scholar] [CrossRef]
Tian, Y.; et al. Practical methods for constructing suffix trees. The VLDB Journal 2005, 14, 281–299. [Google Scholar] [CrossRef]
Delcher, A.L.; et al. Alignment of whole genomes. Nucleic Acids Research 1999, 27, 2369–2376. [Google Scholar] [CrossRef] [PubMed]
Kurtz, S.; et al. Versatile and open software for comparing large genomes. Genome Biology 2004, 5, R12. [Google Scholar] [CrossRef]
Marçais, G.; et al. MUMmer4: A fast and versatile genome alignment system. PLoS computational biology 2018, 14, e1005944. [Google Scholar] [CrossRef]
Soares, I.; Goios, A.; Amorim, A. Sequence Comparison Alignment-Free Approach Based on Suffix Tree and <i>L-Words</i> Frequency. The Scientific World Journal 2012, 2012, 450124. [Google Scholar]
Su, W.; et al. Multiple sequence alignment based on a suffix tree and center-star strategy: a linear method for multiple nucleotide sequence alignment on spark parallel framework. Journal of Computational Biology 2017, 24, 1230–1242. [Google Scholar] [CrossRef]
Quan, Z.O.U.; et al. An Algorithm for DNA Multiple Sequence Alignment Based on Center Star Method and Keyword Tree. ACTA ELECTONICA SINICA 2009, 37, 1746–1750. [Google Scholar]
Brudno, M.; et al. LAGAN and Multi-LAGAN: efficient tools for large-scale multiple alignment of genomic DNA. Genome research 2003, 13, 721–731. [Google Scholar] [CrossRef]
Wan, X.; Karniadakis, G.E. An adaptive multi-element generalized polynomial chaos method for stochastic differential equations. Journal of Computational Physics 2005, 209, 617–642. [Google Scholar] [CrossRef]
Eppstein, D.; et al. Sparse dynamic programming I: linear cost functions. Journal of the ACM (JACM) 1992, 39, 519–545. [Google Scholar] [CrossRef]
Darling, A.C.; et al. Mauve: multiple alignment of conserved genomic sequence with rearrangements. Genome research 2004, 14, 1394–1403. [Google Scholar] [CrossRef]
Saitou, N.; Nei, M. The neighbor-joining method: a new method for reconstructing phylogenetic trees. Molecular Biology and Evolution 1987, 4, 406–425. [Google Scholar] [PubMed]
Thompson, J.D.; Higgins, D.G.; Gibson, T.J. CLUSTAL W: improving the sensitivity of progressive multiple sequence alignment through sequence weighting, position-specific gap penalties and weight matrix choice. Nucleic Acids Research 1994, 22, 4673–4680. [Google Scholar] [CrossRef] [PubMed]
Darling, A.E.; Mau, B.; Perna, N.T. progressiveMauve: multiple genome alignment with gene gain, loss and rearrangement. PloS one 2010, 5, e11147. [Google Scholar] [CrossRef] [PubMed]
Tatusova, T.A.; Madden, T.L. BLAST 2 Sequences, a new tool for comparing protein and nucleotide sequences. FEMS Microbiology Letters 1999, 174, 247–250. [Google Scholar] [CrossRef] [PubMed]
Ma, B.; Tromp, J.; Li, M. PatternHunter: faster and more sensitive homology search. Bioinformatics 2002, 18, 440–445. [Google Scholar] [CrossRef] [PubMed]
Schwartz, S.; et al. Human–mouse alignments with BLASTZ. Genome research 2003, 13, 103–107. [Google Scholar] [CrossRef]
Kehr, B.; Weese, D.; Reinert, K. STELLAR: fast and exact local alignments. BMC Bioinformatics 2011, 12, S15. [Google Scholar] [CrossRef]
Rasmussen, K.R.; Stoye, J.; Myers, E.W. Efficient q-Gram Filters for Finding All ε-Matches over a Given Length. In Research in Computational Molecular Biology; Springer: Berlin/Heidelberg, Germany, 2005. [Google Scholar]
Harris, R.S. Improved pairwise alignment of genomic DNA. 2007: The Pennsylvania State University.
Al Ait, L.; Yamak, Z.; Morgenstern, B. DIALIGN at GOBICS—multiple sequence alignment using various sources of external information. Nucleic Acids Research 2013, 41, W3–W7. [Google Scholar] [CrossRef]
Song, B.; et al. AnchorWave: Sensitive alignment of genomes with high sequence diversity, extensive structural polymorphism, and whole-genome duplication. Proceedings of the National Academy of Sciences 2022, 119, e2113075119. [Google Scholar] [CrossRef]
Li, H. New strategies to improve minimap2 alignment accuracy. Bioinformatics 2021, 37, 4572–4574. [Google Scholar] [CrossRef]
Li, H. Minimap2: pairwise alignment for nucleotide sequences. Bioinformatics 2018, 34, 3094–3100. [Google Scholar] [CrossRef] [PubMed]
Dewey, C.N. Aligning multiple whole genomes with Mercator and MAVID. Comparative genomics 2008, 221–235. [Google Scholar]
Angiuoli, S.V.; Salzberg, S.L. Mugsy: fast multiple alignment of closely related whole genomes. Bioinformatics 2010, 27, 334–342. [Google Scholar] [CrossRef] [PubMed]
Minkin, I.; Medvedev, P. Scalable pairwise whole-genome homology mapping of long genomes with BubbZ. IScience 2020, 23. [Google Scholar] [CrossRef] [PubMed]
Minkin, I.; Medvedev, P. Scalable multiple whole-genome alignment and locally collinear block construction with SibeliaZ. Nature Communications 2020, 11, 6327. [Google Scholar] [CrossRef] [PubMed]
Saada, B.; Zhang, J. DNA sequences compression algorithm based on extended-ASCII representation. in Proceedings of the world congress on engineering and computer science. 2015.
Silva, M.; Pratas, D.; Pinho, A.J. Efficient DNA sequence compression with neural networks. GigaScience 2020, 9. [Google Scholar] [CrossRef]
Corbett, R.D.; et al. A distributed whole genome sequencing benchmark study. Frontiers in genetics 2020, 11, 612515. [Google Scholar] [CrossRef]
Marco-Sola, S.; et al. Optimal gap-affine alignment in O(s) space. Bioinformatics 2023, 39. [Google Scholar] [CrossRef]
Alser, M.; et al. Technology dictates algorithms: recent developments in read alignment. Genome Biology 2021, 22, 249. [Google Scholar] [CrossRef]
Armstrong, J.; et al. Progressive Cactus is a multiple-genome aligner for the thousand-genome era. Nature 2020, 587, 246–251. [Google Scholar] [CrossRef] [PubMed]
Armstrong, J.; et al. Progressive Cactus is a multiple-genome aligner for the thousand-genome era. Nature 2020, 587, 246–251. [Google Scholar] [CrossRef] [PubMed]
Armstrong, J.; et al. Progressive alignment with Cactus: a multiple-genome aligner for the thousand-genome era. BioRxiv, 2019: p. 730531. [CrossRef]
Zhou, Y.; et al. A completeness-independent method for pre-selection of closely related genomes for species delineation in prokaryotes. BMC Genomics 2020, 21, 183. [Google Scholar] [CrossRef] [PubMed]
Gardner, S.N.; et al. Multiplex primer prediction software for divergent targets. Nucleic Acids Research 2009, 37, 6291–6304. [Google Scholar] [CrossRef] [PubMed]
Dewey, C.N. Whole-Genome Alignment. In Evolutionary Genomics: Statistical and Computational Methods; Volume, 1, Anisimova, M., Eds.; Humana Press: Totowa, NJ, 2012; pp. 237–257. [Google Scholar]
Löytynoja, A. Alignment methods: strategies, challenges, benchmarking, and comparative overview. Evolutionary Genomics: Statistical and Computational Methods, Volume 1, 2012: p. 203-235.
Couronne, O.; et al. Strategies and tools for whole-genome alignments. Genome research 2003, 13, 73–80. [Google Scholar] [CrossRef] [PubMed]
Govek, K.W.; Yamajala, V.S.; Camara, P.G. Clustering-independent analysis of genomic data using spectral simplicial theory. PLoS computational biology 2019, 15, e1007509. [Google Scholar] [CrossRef] [PubMed]
Wu, Y.; et al. A multiple alignment workflow shows the effect of repeat masking and parameter tuning on alignment in plants. The Plant Genome 2022, 15, e20204. [Google Scholar] [CrossRef]
Dewey, C.N. Aligning Multiple Whole Genomes with Mercator and MAVID. In Comparative Genomics; N.H. Bergman, Editor; Humana Press: Totowa, NJ, 2008; pp. 221–235. [Google Scholar]
Dewey, C.N. Whole-genome alignment. Evolutionary Genomics: Statistical and Computational Methods, 2019: p. 121-147.
Huang, C.; Li, R.; Li, A. Parallel Implementation of Key Algorithms for Intelligent Processing of Graphic Signal Data of Consumer Digital Equipment. Mobile Networks and Applications 2023. [Google Scholar] [CrossRef]
Nolle, T.; et al. DeepAlign: alignment-based process anomaly correction using recurrent neural networks. in International conference on advanced information systems engineering. 2020. Springer.
Peltzer, A.; et al. EAGER: efficient ancient genome reconstruction. Genome Biology 2016, 17, 60. [Google Scholar] [CrossRef] [PubMed]
Song, B.; Buckler, E.S.; Stitzer, M.C. New whole-genome alignment tools are needed for tapping into plant diversity. Trends in Plant Science 2023. [Google Scholar] [CrossRef] [PubMed]
Earl, D.; et al. Alignathon: a competitive assessment of whole-genome alignment methods. Genome research 2014, 24, 2077–2089. [Google Scholar] [CrossRef] [PubMed]
Schadt, E.E.; et al. Computational solutions to large-scale data management and analysis. Nature Reviews Genetics 2010, 11, 647–657. [Google Scholar] [CrossRef] [PubMed]
Dewey, C. Whole-Genome Alignment. 2019. pp. 121–147.
Ye, C.; et al. DBG2OLC: Efficient Assembly of Large Genomes Using Long Erroneous Reads of the Third Generation Sequencing Technologies. Scientific Reports 2016, 6, 31900. [Google Scholar] [CrossRef] [PubMed]
Kshemkalyani, A.D.; Singhal, M. Distributed computing: principles, algorithms, and systems. 2011: Cambridge University Press.
Volozonoka, L.; Miskova, A.; Gailite, L. Whole genome amplification in preimplantation genetic testing in the era of massively parallel sequencing. International Journal of Molecular Sciences 2022, 23, 4819. [Google Scholar] [CrossRef] [PubMed]
Uffelmann, E.; et al. Genome-wide association studies. Nature Reviews Methods Primers 2021, 1, 59. [Google Scholar] [CrossRef]
Girisha, M.N.; Badiger, V.P.; Pattar, S. A comprehensive review of global alignment of multiple biological networks: background, applications and open issues. Network Modeling Analysis in Health Informatics and Bioinformatics 2022, 11, 9. [Google Scholar] [CrossRef]
Hennig, A.; Nieselt, K. Efficient merging of genome profile alignments. Bioinformatics 2019, 35, i71–i80. [Google Scholar] [CrossRef]
Armstrong, J.; et al. Whole-genome alignment and comparative annotation. Annual review of animal biosciences 2019, 7, 41–64. [Google Scholar] [CrossRef]
Kille, B.; et al. Multiple genome alignment in the telomere-to-telomere assembly era. Genome Biology 2022, 23, 182. [Google Scholar] [CrossRef] [PubMed]
Macaulay, I.C.; Voet, T. Single cell genomics: advances and future perspectives. PLoS genetics 2014, 10, e1004126. [Google Scholar] [CrossRef] [PubMed]
Shi, L.; Wang, Z. Computational strategies for scalable genomics analysis. Genes 2019, 10, 1017. [Google Scholar] [CrossRef] [PubMed]
Ryva, B.; et al. Wheat germ agglutinin as a potential therapeutic agent for leukemia. Frontiers in oncology 2019, 9, 100. [Google Scholar] [CrossRef]
Taylor, J.; et al. Alignment for advanced machine learning systems. Ethics of Artificial Intelligence 2016, 342–382. [Google Scholar]

Figure 1. Suffix Tree for the sequence TATTATTAA.

Figure 2. MUMs detected between Seq1 and Seq2. The maximal exact match is ATCG.

Figure 3. Cluster detected with MUMmer 2.1. The algorithm detects the adjacent MUMs. If a gap between these MUMs is lower than a parameter k, the two adjacent MUMs are regrouped in the same cluster.

Figure 6. Mercator orthologous genes detection. Mercator builds a graph where each vertex represents an exon and edges between vertexes represent the alignment score between exons. The cliques formed are used to highlight the orthologous blocks between them.

Table 1. WGA algorithm classification based on approach of alignment.

Approach	Method	Type
Suffix tree based methods	MUMmer	Local alignment
	MUMmer 4.0	Global multiple genome alignment
	Suffix tree & Lword	Global multiple genome alignment
	Multiple Sequence Alignment (MSA)	Local Alignment
Anchor based methods	LAGAN/ Multi-LAGAN	Global multiple genome alignment
	ProgressiveMauve	Hierarchical WGA mapping
	BlastZ	Local alignment
	STELLAR	Local alignment
	LASTZ	Local alignment
	DIALIGN	Global multiple genome alignment
Graph based methods	AnchorWave	Global alignment
	MERCATOR	Homology mapping
	Mugsy	Hierarchical WGA mapping
	BubbZ	Homology mapping
	SibeliaZ	Hierarchical WGA mapping

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer