A Review on Sheet Metal Forming Evaluation of Advanced High Strength Steels (AHSS)

Preprint

Review

A Review on Sheet Metal Forming Evaluation of Advanced High Strength Steels (AHSS)

Altmetrics

Downloads

155

Views

Comments

A peer-reviewed article of this preprint also exists.

Rui Pereira^*

Nuno Peixinho,Sérgio Luís Costa

Rui Pereira^*

Nuno Peixinho,Sérgio Luís Costa

This version is not peer-reviewed

Submitted:

20 February 2024

Posted:

22 February 2024

You are already at the latest version

Alerts

Abstract

This paper presents a review on numerical and experimental methods to predict fracture of ad-vanced high strength steels (AHSS). AHSS are widely processed through sheet metal forming processes. Although being an excellent choice when lightweight, high strength and ductility are critical factors, their multi-phase microstructure accentuates forming challenges. To accurately model forming behavior, necking based failure criteria as well as direct fracture models require improvements. As a necking based failure model, the conventional forming limit diagram/curve (FLD/FLC) presents limitations such as in estimating direct fracture (surface cracks, edge cracks, shear cracks), as well as deformation histories under nonlinear strain paths. Thus, significant re-search efforts are being made towards the needs of advanced fracture constitutive models capa-ble of predicting fracture scenarios without necking, more frequently observed in the realm of AHSS. Scientific community research is divided into several directions aiming at improving the forming and fracture behavior accuracy of parts subjected to sheet metal forming operations. In this review paper, a comprehensive overview on ductile fracture modeling is presented. Firstly, the FLD/FLC limitations modeling fracture behavior in sheet metal forming operations are stud-ied. Followed by the recent trends in constitutive material modeling. Afterwards, material char-acterization methods advancements to cover a broad range of stress states are comprised. Final-ly, damage and fracture models predicting failure in AHSS are investigated. This review paper supplies relevant information on the current issues the sheet metal forming community is chal-lenged with due to the trend towards AHSS employment in the automotive industry.

Keywords:

Subject: Engineering - Mechanical Engineering

1. Introduction

The 2023 report from the European Environmental Agency on climate change underscores that the transportation sector constituted a substantial contributor to greenhouse gas emissions, comprising nearly 25% of the total emissions across European Union member states in the year 2021 [1]. European Union government policies are committed to achieve a 23% reduction in greenhouse gas emissions from the transport sector in 2030, compared to 2005. In vehicles, a 10% weight reduction corresponds to fuel consumption saving of 6.5% [2]. The ultimate goal of mitigating CO2 gas emissions through the reduction of fossil fuel emissions in vehicles has prompted automobile manufacturers to prioritize lightweight construction as a main concern [3,4,5]. The CO2 emissions of newly registered cars are substantially decreasing, with noteworthy year-on-year declines of 12% for both 2020 and 2021. This trend is partially attributed to the reductions of Body in White (BiW) components overall weight, which are the main contributors of the overall weight of vehicles [6]. Along with environmental concerns, passenger safety may never be compromised. In order to comprise lightweight construction, safety, and structural performance, vehicle’s material list have been continuously shifting through the employment of a higher variety of materials, e.g., through the usage of aluminum alloys and Advanced High Strength Steels (AHSS).

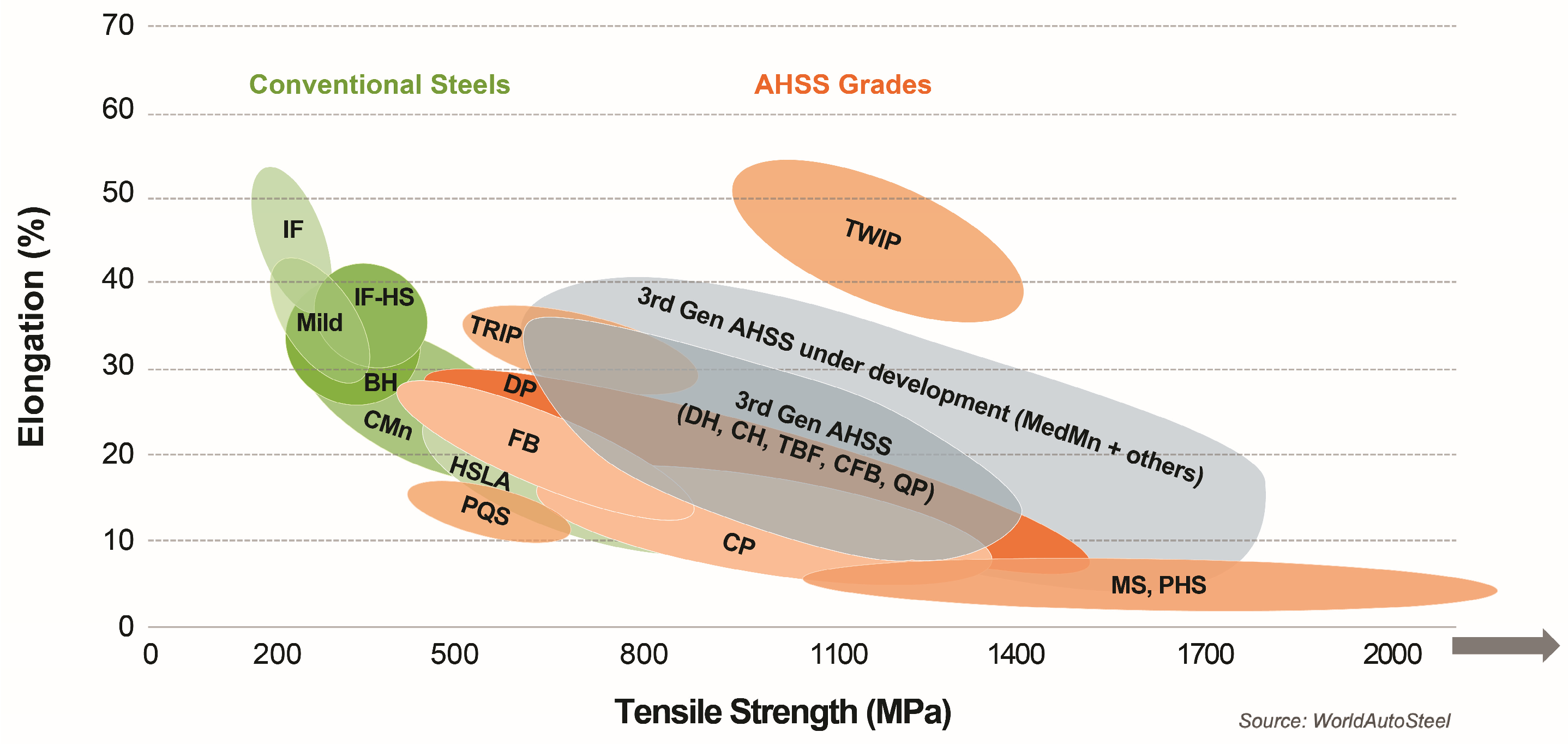
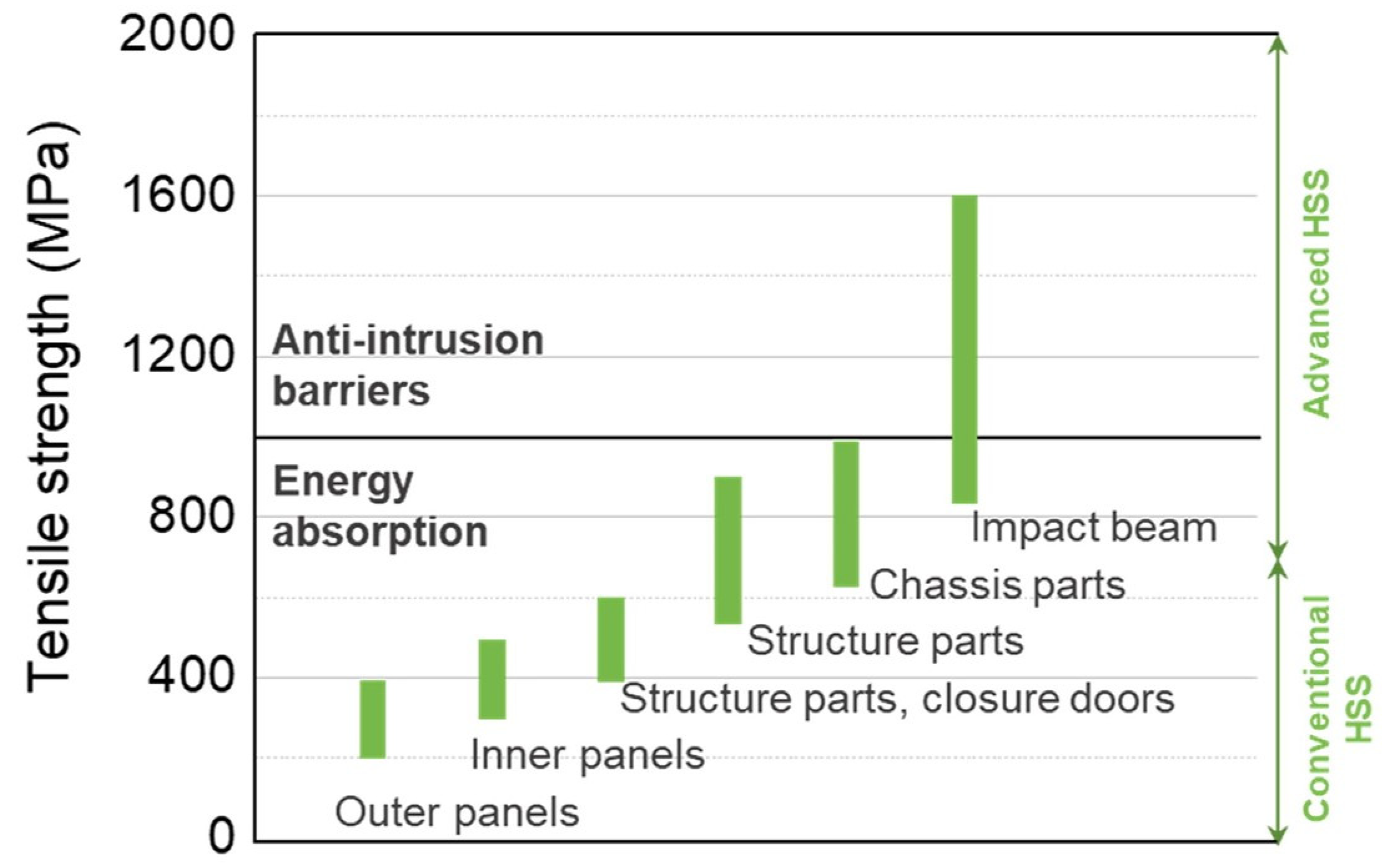
The use of AHSS have become increasingly popular in the automotive industry, due to their appropriate mechanical properties, namely: high structural strength, high stiffness, high work hardening capacity, low cost, high performance and mass optimization capacity [7], while maintaining good levels of ductility [8,9]. Figure 1 presents the relationship between Ultimate Tensile Strength (UTS) and Total Elongation of AHSS compared to conventional steels. The enhanced high strength to density ratio of these materials renders them a competitive contender of aluminum and magnesium alloys, as thinner sheets can be used. Based on the material requirements of different automotive components conventional High Strength Steels are typically applied to panels (both outer and inner) and structural parts, while AHSSs are engineered for anti-intrusion barriers such as bumpers and impact beams [4], as illustrated in Figure 2.

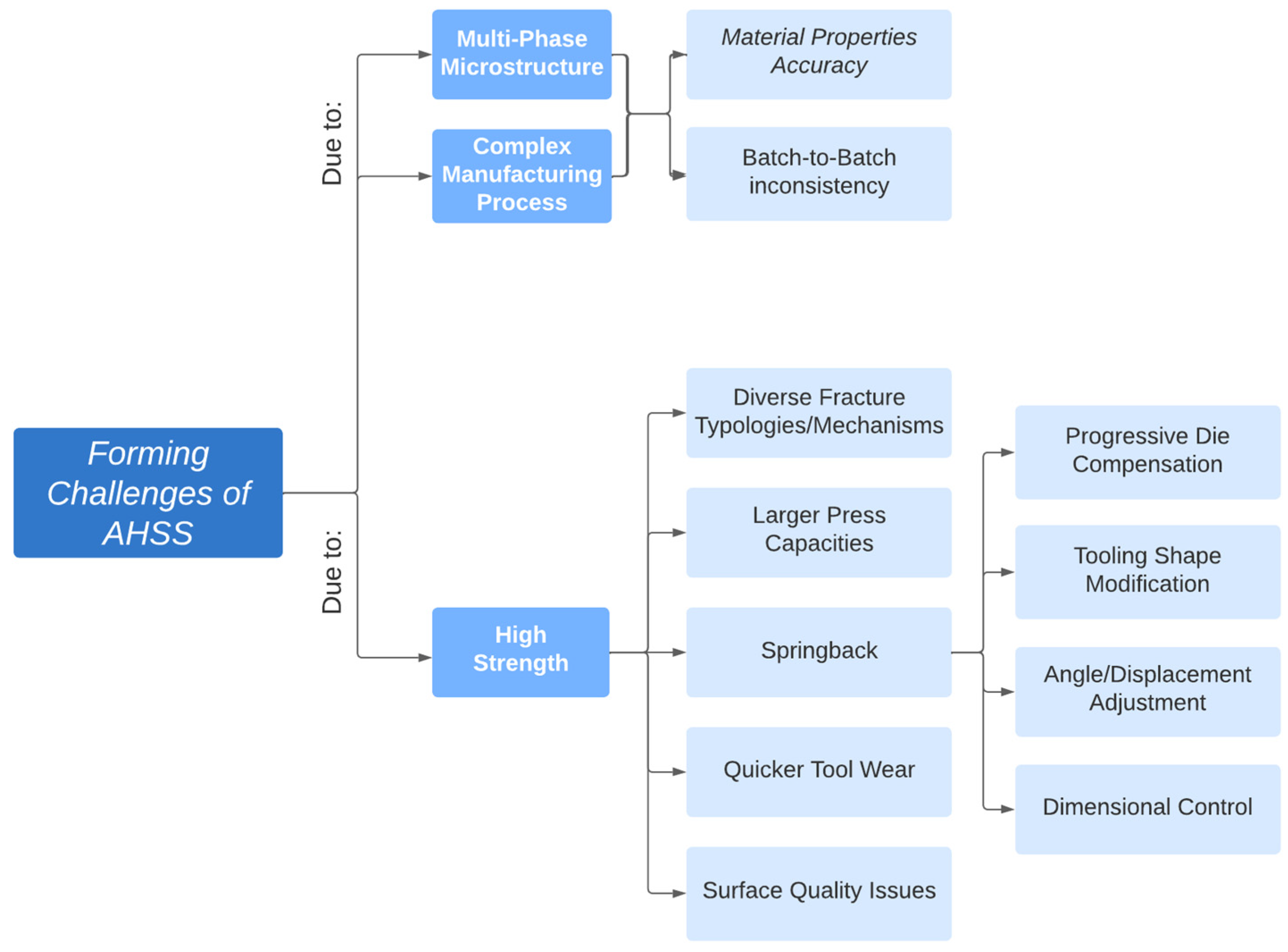
Sheet metal forming operations are widely employed in the automotive 2nd tier [12,13]. Table 1 summarized AHSS types, characteristics and common applications in the field of automotive industry. The manufacturing of Body in White components heavily relies on various sheet metal forming processes such as stamping and deep drawing. Although the major advantages of AHSS employment, the forming process of such materials is increasingly complex. This can be attributed to their multiphase microstructural composition, high yield strength as well as the thinner sheet thickness considered. Thus, the usage of AHSS intensified and introduces forming challenges almost never encountered before. These forming challenges are depicted in Figure 3. The significant yield strength leads to higher forming forces, energy consumption and higher stresses [14,15]. Thus, requiring the selection of appropriate press machines. Moreover, AHSS exhibit greater tendency to wrinkle due to the lack of adequate hold-down and a reduction of sheet thickness is frequently observed. Springback and dimensional control inconsistencies are accentuated, requiring the need of tooling shape modification and/or adoption of progressive die compensation techniques [16,17,18,19]. On the other hand, the multi-phase microstructure of AHSS leads to batch-to-batch inconsistencies. Simultaneously, die designs are getting increasingly complex. Sharp edges and quick curvature changes are frequently introduced to meet aesthetic concerns [20].

In accordance with the aforementioned forming challenges associated with manufacturing AHSS, the evaluation of the sheet metal forming process solemnly through the analysis of the traditional forming limit diagrams (FLD) can lead to inadequate and misleading interpretations. The material susceptibility to different fracture typologies increased with the employment of AHSS. Thereby justifying the need for more accurate fracture modeling of sheet metal forming operations [22]. Once the factors affecting failure are understood, engineers can minimize the risk of failure. This, in turn can improve product quality and efficiency, reduce scrap rates and the number of experimental tryouts [23].

This review paper introduces an assessment of the applicability of the Forming Limit Diagram (FLD) in the post-processing of Advanced High-Strength Steel (AHSS) forming processes. Following this introduction, the limitations of the FLD are discussed. The subsequent discourse emphasizes the critical necessity for advanced and precise fracture/damage models within the realm of AHSS forming processes, thereby accentuating their significance in the contemporary analysis of post-processing results for AHSS.

Table 1. Summary of different types of 1st generation of AHSS: microstructure, mechanical properties and typical applications. Adapted from [4,7,14,24,25,26,27].

AHSS	Microstructure	Mechanical Properties							Characteristics	Typical Applications
AHSS	Microstructure	$R_{P 0.2}$ (MPa)		$R_{m}$ (MPa)		A80 %		$t$ (mm)	Characteristics	Typical Applications
Dual Phase (DP)	Ferrite + Martensite	Docol DP500							Conventional: Lower Yield Strength Low Yield-to-Tensile Strength Ratios High Initial Work Hardening No Yield Point Elongation Significant Bake Hardening Good Uniform Elongation High Energy Absorption Good Cold Formability	Body Panels; Front and Rear Longitudinal Rails; Supporting Structure
		290-380		490-600		24		0.5-2.1
		Docol DP600
		330-430		590-700		20		0.5-2.1
		Docol DP800
		440-550		780-900		14		0.5-2.1
		Docol DP1000
		590-900		980-1130		8		0.5-2.1
		590-900		980-1130		8		0.5-2.1	Higher Yield Strength Grades:High Yield-to-Tensile Strength RatiosSome Yield Point ElongationLower Bake HardeningReasonable Uniform ElongationGood Energy Absorption	Passenger Safety Cage Components (limited by axial or transverseBending): Rockers, Pillars, Pillar Reinforcements,Roof Rails and Cross Members

Transformation Induced Plasticity (TRIP)	Ferrite Matrix + Retained Austenite Hard phase of Bainite and/or Martensite	TRIP700							Excellent Combination of Strength and Ductility High Total Elongation Considerable Strain Hardening Capacity High Energy Absorption Excellent Formability High Fatigue Endurance Resistance	Cross Members; Longitudinal Beams; B-Pillar Reinforcements; Sills; Bumper Reinforcements
		400-520	690-800		24		1
		TRIP800
		450-570	780-910		21		1
Martensitic Steel (MS)	Martensitic Matrix + Small Amounts of Ferrite and/or Bainite	Docol 900M							High Yield Strength High Tensile Strength Good Hardness High Toughness	EV Battery Protection; Sill (Rocker) Reinforcements; Roof Reinforcements; Door Beams; Bumper Beams; Seat Structures; Rocker Panel Inners
		700-1000	900-1100		3		0.5-2.1
		Docol 1100M
		860-1100	1100-1300		3		0.5-2.0
		Docol 1500M
		1220-1520	1500-1750		3		0.5-2.1
		Docol 1700M
		1350-1700	1700-2000		3		1-2.1
Complex Phase Steel (CP)	Ferrite/Bainite Matrix + Small Amounts of Martensite; Retained Austenite and Pearlite	Docol 600CP							High Yield Strength Very High Ultimate Tensile Strength Excellent Uniform Ductility High Energy Absorption Excellent True Fracture Strain High Fatigue Strength Good Impact Strength High Residual Deformation Capacity Good Bendability	Seat Flange; Door Bar; Tunnel Stiffener; Rear suspension Bracket; Fender Beam; Seat Tracks; Seat Recliners
		350-500	600-740		16		0.7-2.5
		Docol 800CP
		780-950	980-1140		6		0.5-2-1
		Docol 1200CP
		900-1100	1180-1350		5		0.5-2.1

2. Failure, damage and fracture in sheet metal forming

Failure and fracture are two distinct terms that are often used interchangeably, although having different meanings. In the realm of sheet metal forming community, failure refers to the point at which the material can no longer withstand the applied stress and loses its ability to maintain its shape, due to the loss of load-carrying capacity [28]. Thickness instability is typically referred to as failure. Fracture, on the other hand, relates to the point at which material separation occurs, due to excessive stress. Damage is defined as an intermediate state, a product property that accumulates between processes. It represents the undesired evolution of one or more structural characteristics, e.g., micro voids, that hinder an engineering capability [29].

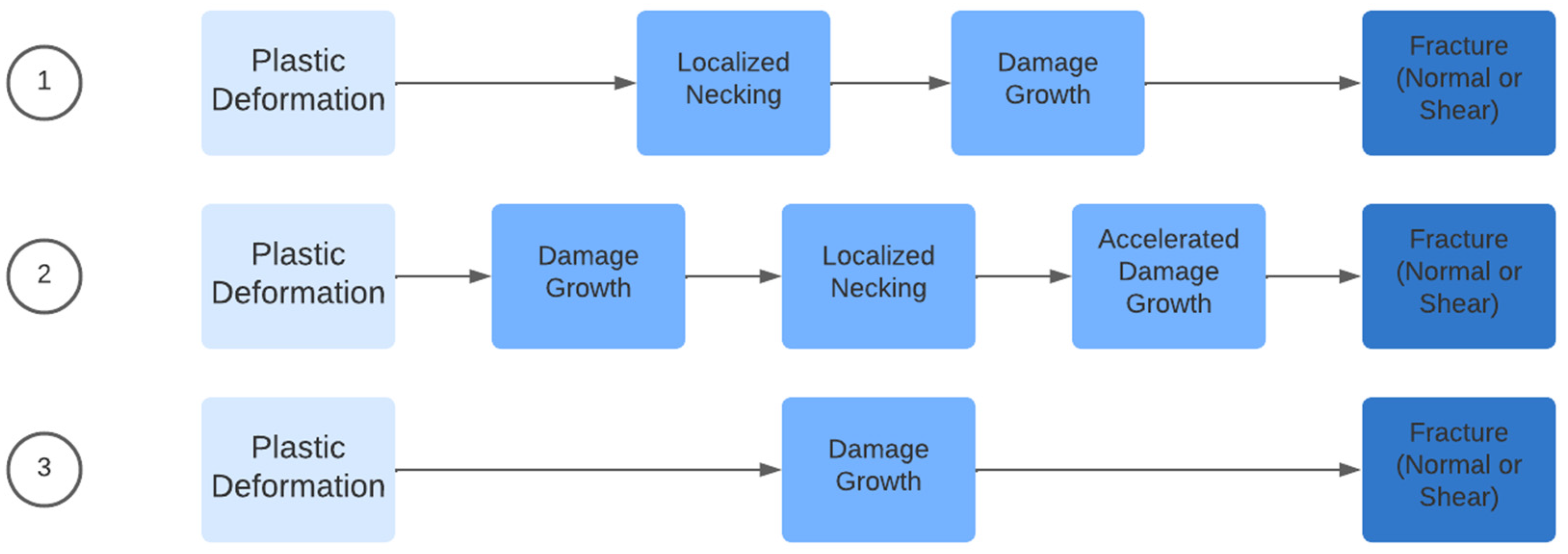
The ductile fracture phenomenon can be divided into two modes: (i) Ductile Normal Fracture; (ii) Ductile Shear Fracture [30]. The former is caused by void nucleation, growth and coalescence leading to damage growth, eventually fracture where a crack appears. The latter is a result of shear band localization which may occur through the thickness or in the plane. According to Mattiasson et al. [30], there are types of fracture scenarios, as illustrated in Figure 4. The first one addresses the commonly observed outcome in sheet metal forming operations. Constitutive failure models are adequate to provide proper results in this scenario. However, for the other two scenarios, a fracture constitutive model is required to accurately capture fracture occurrence.

Formability is defined as the ability of sheet metal to be formed into the desired shape without necking or cracking [31]. Thus, formability evaluation should comprise failure mechanisms on account of localized necking and fracture mechanisms not preceded by necking. The FLD lies under the assumption that localized necking precedes damage growth and failure. In this context, necking instability defines the process limits [22]. AHSS require the need of modelling fracture occurrence without necking. Such eventualities can arise under specific stress states such as in-plane shear deformation and nearly pure bending loading [20].

3. Traditional forming limit diagram (FLD)

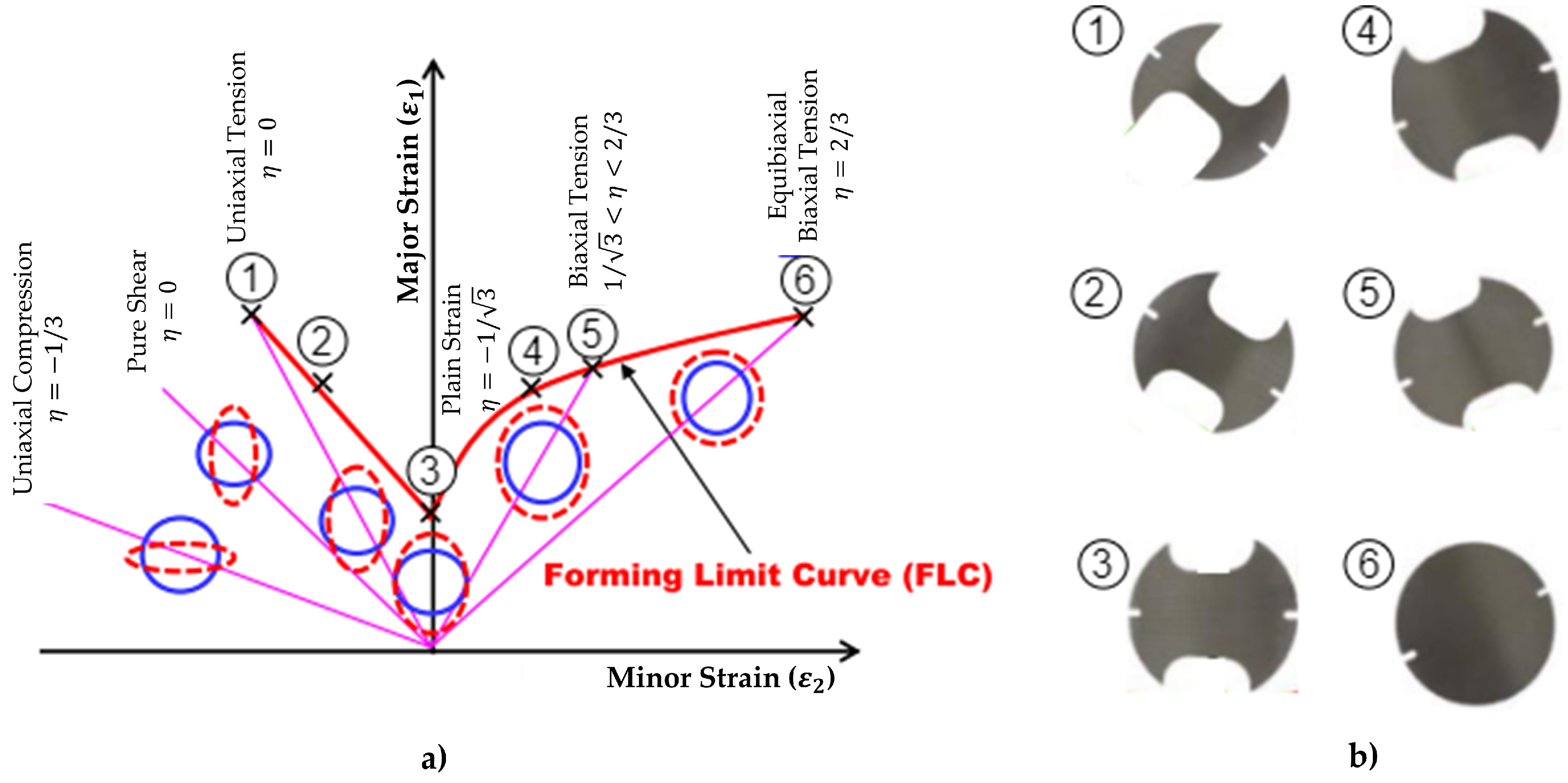
Formability evaluation is usually performed through the FLD. The simplicity of representing the principal strains,

ε_{1}

and

ε_{2}

, in a graphical way is of great interest for industry. The critical feature of the FLD is the FLC, which describes the strain limits at the onset of necking: the strains located above the FLC fail in a critical state, where necking instability has occurred; the strains behind the FLC are in a safe region, characterized by remaining formability. Therefore, the failure locus for necking instability under various loading conditions, ranging from uniaxial tension to biaxial tension, is depicted by the FLC.

The FLC is affected by different factors. Even for the same material grade, variations in the FLC can be noticed. The reason for that lies in the dependency of factors such as forming temperature [32], material thickness [33], forming speed [33], strain rate [32] and friction conditions [34]. Liu et al. [35] investigated the strain rate effect through a comparison between AHSS and three different kinds of conventional steels. They concluded that the AHSS are much more dependent on strain rate variations rather than the conventional steels.

3.1. FLC experimental determination

The FLC is determined in accordance with the ISO 12004-2_2008 standard [36] using either Nakazima [37] or Marciniak [38] test procedures.

The Nakazima testing method involves the use of specimens with varying cutout widths which are clamped using a circular blank-holder. Subsequently, the specimens are drawn until fracture through a drawing die by the rectilinear movement of a hemispherical punch. Draw beads in tools are used to restrain the blank between the die and blank-holder and also to avoid stress concentration at the transition from strip section to the blank [39]. Nakazima tests should be executed in frictionless conditions between the contact zone of the punch and specimen pair [40]. As an out-of-plane stretching method, Nakazima test is dependent on the tool geometries, through-thickness pressure and lubrification conditions [22].

On the other hand, the Marciniak in-plane test involves the deformation of specimens under balanced biaxial conditions. By modifying the washer and specimen geometries, the FLC can be generated [22]. An adapted design of the punch geometry is adopted in order to minimize the friction in the specimen central region.

Irrespective of the performed method, a wide range of deformation modes can be achieved by modifying the specimen geometry. Figure 5 portrays the influence of specimen geometry on deformation modes. To cover a broad range of deformation modes, at least five different specimen widths must be tested [36]. The FLC shape is strongly dependent on strain path, hence on specimen geometry. The more the specimen tested, the more accurate the FLC formability prediction.

The experimental methods to determine the DLC are usually time-consuming, low cost-effective and limited by experimental conditions, even though they are more trustable than other approaches [43]. Many researchers select the Nakazima test procedure due to the simplicity of tools required [44].

3.2. Limit strains determination methods

The accurate assessment of the limit strains consists of a major step for the experimental determination of the FLC. The onset of localized necking is an instantaneous moment, difficult to detect and, even more, to measure. Frequently, the limit strain methods calculations are divided into: (i) position-dependent methods; (ii) time-dependent methods; (iii) time-position-dependent methods.

The position-dependent methods are characterized by the individual, well established single and unique evaluation of the onset of necking. ISO 12004-2:2008 [36] recommends a position-dependent approach. As a standard, it is intended to provide practices and unify test condition procedures in order to gather consensus between different laboratories. According to this method, the strain variations are analyzed prior to the occurrence of a crack. The procedure for limit strains determination in accordance with ISO standard are provided by Martínez-Donaire et al. [45]. An alternative position-dependent method was proposed by Zhang et al. [46] to provide more stable and precise FLC determination.

The time-dependent methods rely on the analyses of the strain, strain rate or strain acceleration to determine the onset of through-thickness necking. In the work developed by Merklein et al. [47] the necking initiation occurs in the highest value of a linear regression coefficient curve, selected based on the rate of change of strain rate. Iquilio et al. [48] developed a more realistic method to precisely calculate the limit strains of a stainless steel with an heterogeneous strain distribution. Another time-dependent methods were proposed by Huang and Shi [49], Volk and Hora [50] and Hotz et al. [51]. Overall, these techniques rely on mathematical manipulation of strain rate rather than physical behavior of materials, which can be unreliable due to noise in data signals and may not be applied to all sheet metals [52].

Time-position-dependent methods are hybrid approaches which consider either the temporal evolution of strain, position or displacement of points on a line drawn perpendicular to the fracture direction [52]. Martínez-Donaire et al. [53] inferred the initiation of necking when the slope in the first special derivative of the vertical displacement remained constant within the necking region. Furthermore, Min et al. [52] established a time—position-dependent method to identify the onset of localized necking under in-plane deformation based on the measured surface geometry of the test specimen.

Although the availability of a wide number of limit strain methods there is no consensus about the method to be chosen, since the overall methods possesses their specific applications. Therefore, a continuous search for more accurate, innovative methods to incorporate specific loading conditions, typology of fracture is ongoing to handle with ISO standard limitations, namely: (i) unfit for significant strain gradients across the sheet thickness, e.g., when using small punch radii or corner radii in forming dies; (ii) unsuitable in stretch-bending operations; (iii) inapt for multiple necking implying variable strain distribution; (iv) inappropriate for sudden fracture leading to limit strain imprecisions particularly under plane strain or biaxial testing conditions.

3.3. Grid marking and deformation determination methods

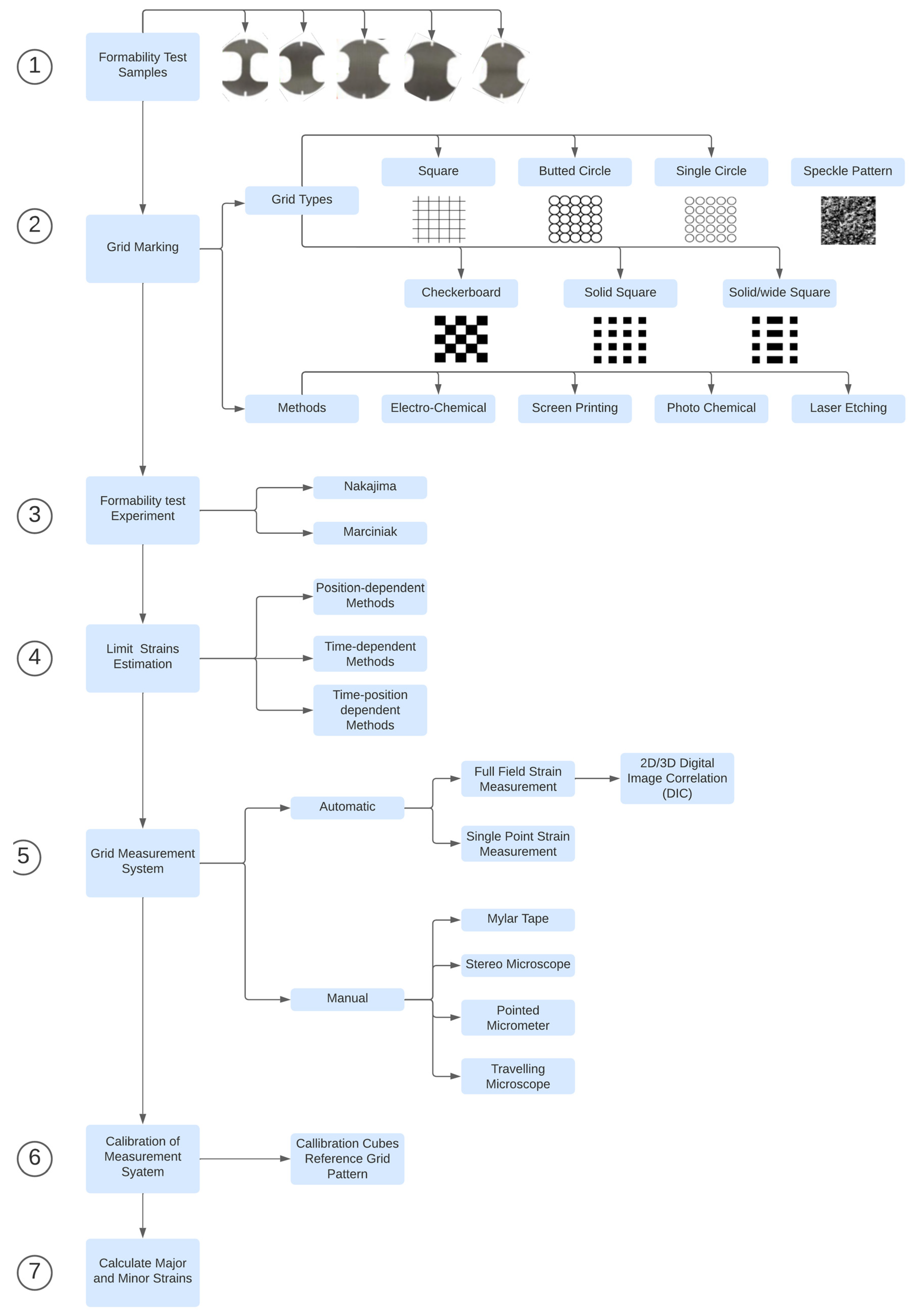
Materials employed in sheet metal forming operations have a reduced sheet thickness, particularly the AHSS where the sheet thickness commonly used is less than 1.5 mm. As a result, surface strain sensitivity significantly increases and requires more advanced strain measurements methods for an accurate formability evaluation. The FLC determination is influenced by the strain measurement technique employed, implying concerns regarding grid marking type and method, which also plays a key role in addressing major and minor strain calculations. Grid marking is performed prior to the formability test experiment and followed by strain measurement. Figure 6 displays the main tasks involved in the FLC determination.

Grid marking is defined as the process of printing line patterns on the surface of the area of interest on the sheet sample [54]. There are mainly four grid methods for creating grid patterns. Circular or square grid types are the most commonly used for assessing formability. The choice between the available methods must take into considerations parameters such as durability, quality, resolution, contrast, pattern accuracy and cost. Nevertheless, one must guarantee the independence of process and forming conditions, such as lubrification and friction, from grid marking [54]. Ozturk et al. [54] introduced the main differences between the overall grid marking methods and a qualitative comparison of the grid marking methods was appointed. Laser etching process require the study of power speed, focus and width parameters [55]. Guk et al. [56] utilized a diode laser marking system to generate grid patterns on multiphase steels: the scanning speed and laser power influence on the mark depth was investigated. Furthermore, Yildiz and Yilmaz [57] after applying four different grid marking methods, namely: serigraphy, electro-chemical etching, photo-chemical etching and laser concluded that laser is best suited due to ease of application and stability.

The circular or square patterns are printed before deformation and transform into ellipses or quadrilaterals after forming operation, respectively. The major and minor strains are determined by comparing previous and subsequent patterns dimensions [58]. ISO 12004-2:2008 [36] stipulates that the dimensions of the grids are related to the thickness of the material, e.g., the circle diameter on circular patterns has a significant impact on strain calculation [59]. Speckle patterns are required to be used simultaneously with Digital Image Correlation (DIC) systems for strain measurement. Li et al. [60] sprayed speckle pattern on the top surface of the sample and one must guarantee the adhesion of the paint to the surface before and after deformation.

The most practical method of measuring the strains in a formed part is to utilize measuring grid pattern on the part surface. This can be done either manually or by use of an automatic method [55]. Manual techniques are characterized by several drawbacks such as high measurement time requirements, less accuracy and low resolution. Even though, Bandyopadhyayet et al. [61] adopted a manual strain measurement method to build the stress based forming limit diagram of a tailor welded blank material. Additionally, the deformed grids of a Inconel 718 was assessed by means of a stereo microscope [62].

The alternative automatic methods are the Single Point Strain Measurement as well as the Full Field Strain Measurement [43]. Both techniques require less time, and have better resolution, hence contributing with more reliable results. The main components in the automatic strain measurement system are the image acquisition hardware and image processing software [63]. ASTM E2218-02 standard [64] provides guidelines for strain measurement.

Single Point Strain Measurement is characterized by the measurement of one grid element separately. Grid Pattern Analyser (GPA) and Forming Measurement Tool Innovations (FMTI) are two available commercial software for automatic single-point strain analysis built on image processing. The image acquisition demands machine vision cameras to capture the deformed grids after forming and specialized lenses. Afterwards, the software fits the ellipse to the deformed grids and calculates major and minor principal strains [59].

Full Field Strain Measurement methods such as Digital Image Correlation (DIC) possess the advantage of measuring larger areas considerably quicker. This method, applicable either in two or three dimensions, require a significant amount of material images prior and after forming operation with a geometrical relationship between them to derive gradients and correlate them in order to calculate the major and minor strains [65]. As previously mentioned, DIC system must be used in association with image processing software. The commonly used are namely: German Argus or ARAMIS system of GOM company, the American Grid Analyser Model 100U of the FMTI system Inc., the VIC-2D(3D) from the Correlated Solutions Inc., the Dante Dynamics as well as the ICASOF [59,63]. In spite of the high measurement accuracy provided by these systems, they are characterized by an expensive cost [66]. Open source DIC alternatives are a cost effective solution such as: Ncorr [67], ALDIC [68], py2DIC [69], µDIC [70] and Multi-DIC [71]. Commonly these alternatives require a huge memory of images taken from a high-speed image acquisition system [59]. The DIC Full Field Strain Measurement Systems have been broadly used to build the FLC [72,73]. Min et al. [74] and Huang and Shi [49] compared standard, spatial and temporal methods to determine the onset of localized necking by the use of DIC data. The introduction of these systems able to record and memorize the whole forming process has shifted research attention towards time-dependent methods as alternatives to position-dependent methods.

Additionally, DIC may be used to calibrate ductile damage models, evaluation of anisotropic materials as well as to obtain strain distribution either in tensile tests or in a forming operation. In the work conducted by Gkolfinopoulos and Chijiwa [75], DIC analysis alongside GOM commercial software and a full frame CMOS camera enabled to investigate strain concentration in the tensile specimen necking region before fracture. The damage model parameters were numerically validated with the aid of DIC analyses.

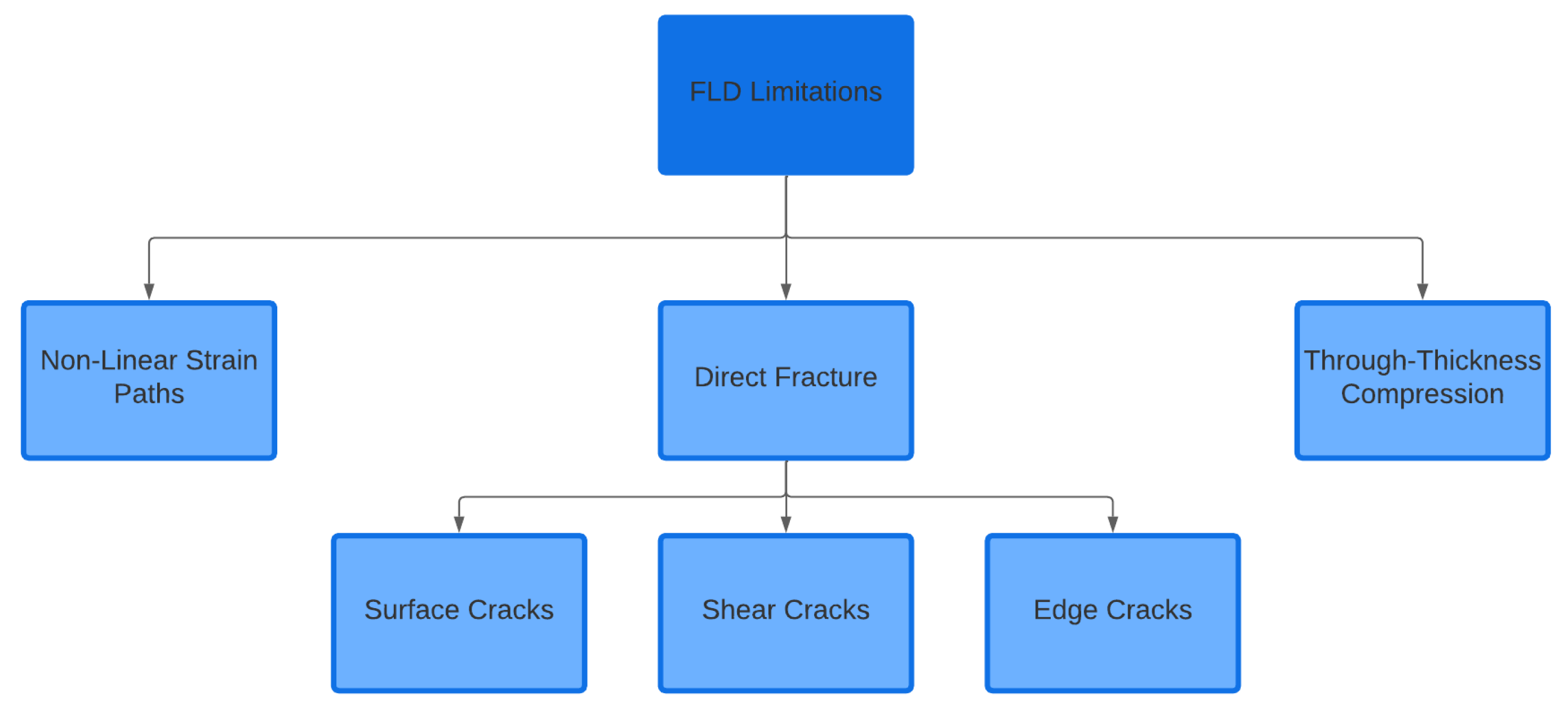
4. Limitations of FLD

Forming limit diagrams play a crucial role in assessing the formability of metal sheets by defining the maximum strain to failure in terms of major and minor strains. The primary objective is to identify the onset of necking in limited regions of the examined sheet metals [76]. Industrial sheet metal forming manufacturers are interested in the phenomenological outcome observed, as such the FLD is well established as a failure criterion. However, FLD has some limitations with respect to forming behavior modelling accuracy. Those limitations are depicted in Figure 7.

On one hand, the FLD as a necking based failure criterion is intended to detect through-thickness necks and splits which lead to a global loss of carrying capacity of the material. Moreover, the range of study of the traditional FLD is limited to the deformation paths illustrated previously in Figure 5. Therefore, the points below the left diagonal are not covered. On the other hand, local instabilities as well as direct fracture on material surface are not covered by the FLD analysis. The forming industry trend towards high strength/low density alongside with sharp geometrical features accentuates forming challenges. Thus, the need for more advanced models able to model forming behavior, failure and fracture is a current demand. The AHSS tend to exacerbate these forming challenges in comparison to the conventional mild steels, as such direct fracture on material surface is more likely to occur.

To overcome FLD limitations, the special characteristics of the AHSS must be taken into consideration. On accordance, more advance fracture and damage models have been developed to meet the special characteristics of these kind of materials. Usually, these models require experimental characterization at different stress states [77]. Different specimen geometries and loading conditions are adopted. Section 6 presents the state of the art of the testing methods employed for a fully material characterization. Section 7 addresses the current trends in failure and damage models.

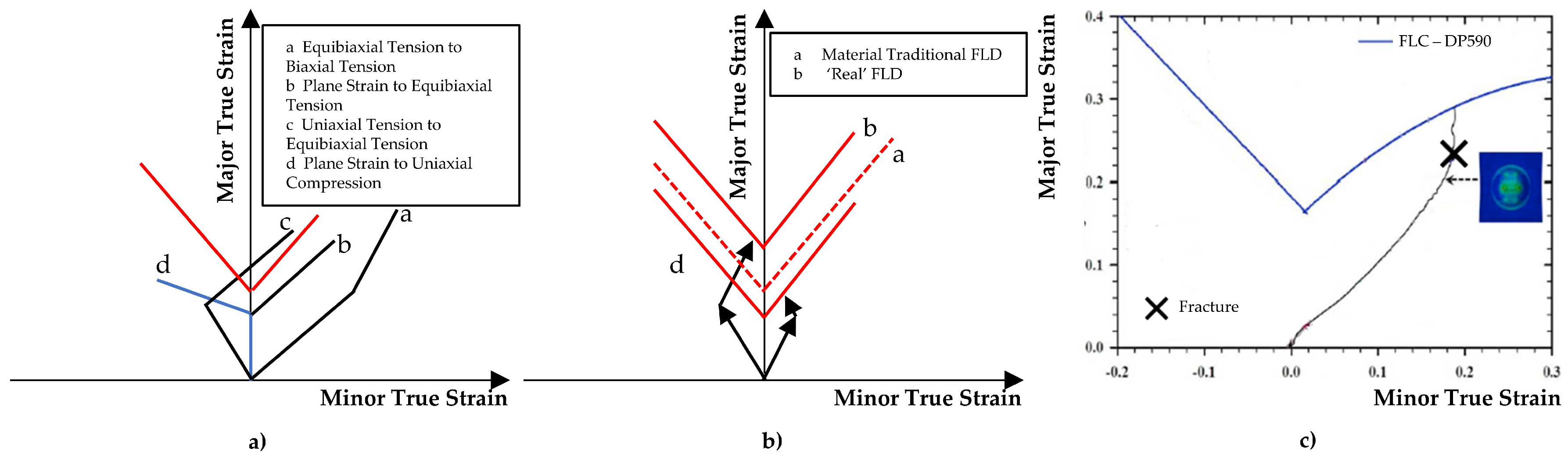
4.1. Non-linear strain paths

The main disadvantage of the traditional FLD is that the different experimental points in the standard FLC are all determined under the assumption of simple proportional loading states. Therefore, it fails to provide proper results for non-linear strain paths histories in sheet metal forming processes [78]. In multi-stage forming processes, or even at deep drawing operations under complex loading conditions, the probability of loading paths deviation from linearity is more commonly observed [79]. Furthermore, the traditional LD can also fail to provide adequate precision of the forming process because the material exhibits a different strain hardening behavior when a strain path change occurs compared to monotonic loading [80]. Figure 8a) illustrates some possible non-linear strain paths observed in sheet metal forming operations. Da Rocha and Jalinier [81] stated that a biaxial solicitation preceded by a uniaxial loading leads to an increased formability, as opposed to a biaxial solicitation followed by a uniaxial loading, as illustrated by Figure 8b). Thus, the disregard for this shift in loading may result in both conservative and optimistic outcomes with respect to the traditional FLD. Figure 8c) presents a deformation path exhibiting high non-linearity leading to failure before the forming limit is reached under the standard FLC.

Manopulo et al. [83] used a theoretical approach based on an extended Modified Maximum Force (eMMF) criterion to account non-proportional loading. Stress-based models are effective in modelling fracture occurrences in multi-forming operations that are characterized by non-linear strain paths [82]. However, these models may be limited to deformation histories within the Nakazima range. Non-linearities that arise from predeformation in shear or compression can be effectively modeled by damage accumulation models [20]. Furthermore, the Generalized Forming Limit Curve (GFLC) offers advantages such as its independence from the material model and its ability to represent multilinear strain paths. The GLFC was developed by Volk et al. [84] and it is currently implemented in AutoForm R10. Section 6.2 presents experimental techniques specially designed to address non-linear strain paths generation.

4.2. 3D stress states

Typically, the process of thin sheet forming operates under the plane stress mode [85]. Under this context, as deformation leads to thinning, the traditional FLD predicts accurately the forming behavior. However, when strain states occur below and within the left diagonal (

ε_{1}

ε_{2}

), the presence of a compressive hydrostatic stress component in the thickness direction mitigates the risk of necking. Thus, even under severe thinning, necking will not occur, and the material will deform until the fracture limit is reached. For an accurate prediction of the forming behavior in ironing and coining operations, in-plane shear deformation modes as well as surface defects, the consideration of 3D stress states under the left diagonal of the FLD diagram is required.

The strain increments generated in this region can be analyzed by means of the stress triaxiality. The stress triaxiality is a reliable indicator to determine whether a material is subjected to volumetric tension or a compressive stress state. Hence, failure models considering stress triaxiality have garnered attention as they can identify strain increments arising from a compressive stress state, thereby not contributing to the risk of necking.

4.3. Shear fracture

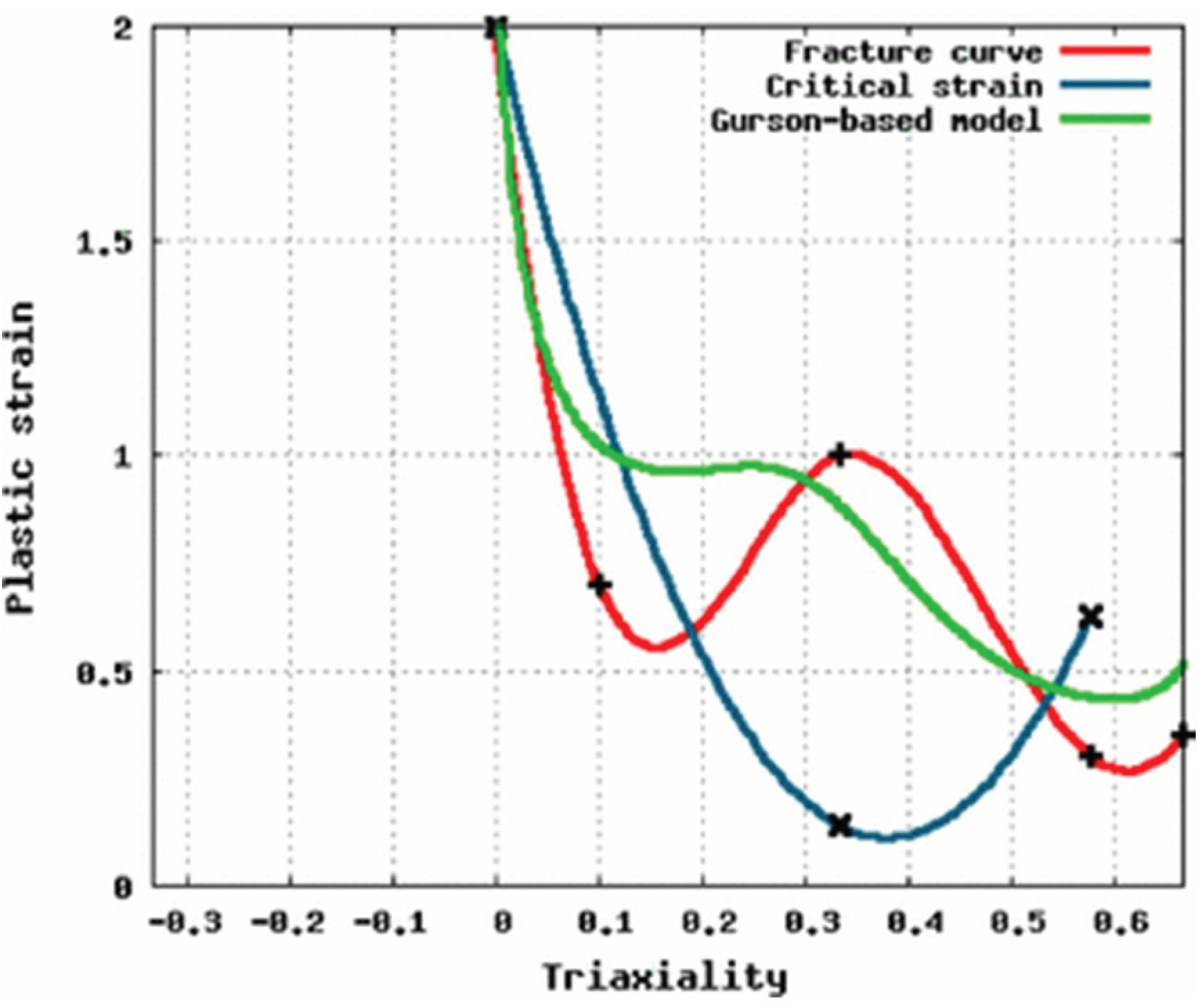
Within the realm of AHSS, there is a heightened frequency of shear fracture occurrence on tight radii [86,87,88]. Shear deformation inherently maintains the thickness of the sheet [20] and the FLD fails to encompass the second quadrant beyond pure shear conditions [89]. The fracture limit in the low triaxiality regime exhibits a greater sensitivity to the Lode angle [20]. In fact, the pure shear fracture limit can be significantly lower than the ductile fracture limit [90]. Li et al. [89] have effectively showcased the limitations of the FLD in accurately predicting shear fracture, particularly due to the relatively lower pure shear fracture limit when compared to the uniaxial tension limit, as depicted in Figure 9.

The determination of fracture limits in pure in-plane shear remains an area of ongoing investigation, as there is currently no established standardized experimental method for characterizing shear fracture modes. The main difficulty associated with the achievement of pure shear fracture limits regards with the crack opening modes which generally occurs near the transition region between uniaxial tension and in-plane shear conditions [91]. Furthermore, the double-notched shear (DNS) test is commonly used to determine fracture strains induced by crack opening through in-plane shear. It should be noted that this test does not strictly fulfill the conditions of pure shear due to the presence of bending effects and the development of localized necking at the end of the testing process [92]. Roth and Mohr [93] proposed 600 distinct specimen geometries and demonstrated the value of using three instead of one type of shear specimen. Further insights on specimens implying shear fracture are given in section 6.1.1.

4.4. Edge cracks

The FLD is also not reliable in accurately predicting edge cracks on shear cut surfaces during component forming. The preparation of blank edges presents a wide range of possibilities, making it challenging to describe the reduced formability on the edge [20]. The stress state experienced at the blank edge is typically uniaxial, implying that it should undergo necking before fracturing under tension. However, due to the shearing process, the material properties and surface characteristics of blank edges are significantly altered. Consequently, the occurrence of fracture at the edge can vary depending on microscopic features or defects before the material reaches its actual necking limit [94]. Pre-forming is an important forming process in the prevention of edge cracking in flanging and edge stretching processes. Various process parameters in shear cutting have been identified to impact the residual formability of metallic materials. Nasheralahkami et al. [95] investigated the influence of die clearance on sheared edge quality, while Matsuno et al. [96]examined the impact of cutting edge geometry on residual forming capacity. Shih et al. [97] explored the effect of shear rake angle. Standardized experimental approaches are still necessary for a successful inclusion of this effect into the modelling [20].

Frómeta et al. [98] demonstrated the reliability of the Essential Work of Fracture (EWF) methodology in assessing the fracture toughness of CP and DP steel grades to properly address issues associated with edge cracking. More recently, Feistle et al. [99] stated that it is imperative to use the GFLC to correctly take into account the introduced pre-forming in the formation of the Edge-Crack-Sensitivity-Factor and to be able to use it in the finite element simulation. The pre-deformation should not be considered as pre-damage, which would increase the edge crack sensitivity when using multi-phase steels [99].

4.5. Bending influence

The traditional FLD determination is based on in plane deformation without taking a bending component into account [100,101]. Hence, in situations where the strains on the outer layer surpass those of the membrane layers, the FLD fails to provide proper forming behavior results [20,102]. Although known and not being a concern for many years, the advances towards materials with higher strength/lower ductility as well as lower post-necking plasticity such as the AHSS accentuates the impact of bending on forming behavior.

Under superimposed bending, the FLD usually gives conservative results. This behavior arises from the fact that bending introduces a partially compressive stress state throughout the material thickness, which stabilizes the sheet and delays or prevents the onset of necking. When a material is subjected to bending in addition to other loading conditions, the conventional FLD often provides inaccurate results. In these contexts, the materials exhibit a higher deformation capacity than indicated by the FLD, as major strain values located above the safety limit, are in reality, below the failure limit [20,103]. Research conducted by Kitting et al. [104] involved stretch-bending tests conducted on DP800 and CP800 steels under plane-strain and biaxial stretching conditions. The results revealed a significant underestimation of the forming potential of these materials by the traditional FLD in combined stretching and bending operations. However, it should be noted that under severe stretch bending conditions, materials may experience surface failure, even if the strains remain below the FLC [20].

Kitting et al. [103] proposed a phenomenological approach that offers the ability to predict stretch-bending formability by using the conventional FLC prediction method. Neuhauser et al. [101] conducted angular stretch bending tests on DP600 steel and presented a methodology for quantitatively assess the formability of steel sheets subjected to stretching with superimposed bending. They also demonstrated how to integrate these findings into the existing FLD framework. Despite the well-known relationship between instability and bending radius, this area of research has not yet reached full industrial maturity. Its development is crucial for achieving a comprehensive analysis of formability [20].

4.6. Ironing and coining

Through thickness compression in negative hydrostatic stress states is encountered during ironing and coining operations. As a result, the FLD is unable to correctly predict the component criticality, indicating premature failure [94]. Borrego et al. [105] evaluated the hole flanging operation through the traditional FLD analysis. Their findings revealed that strain path curves for successful hole flanged parts near the formability limit exceeded the limits defined by the FLC, yet no failure was observed. Alternatively, the Limiting Forming Ratio (LFR) is a more suitable measure of formability in conventional hole flanging operations. This parameter directly quantifies the maximum stretching of the material at the hole tip [105].

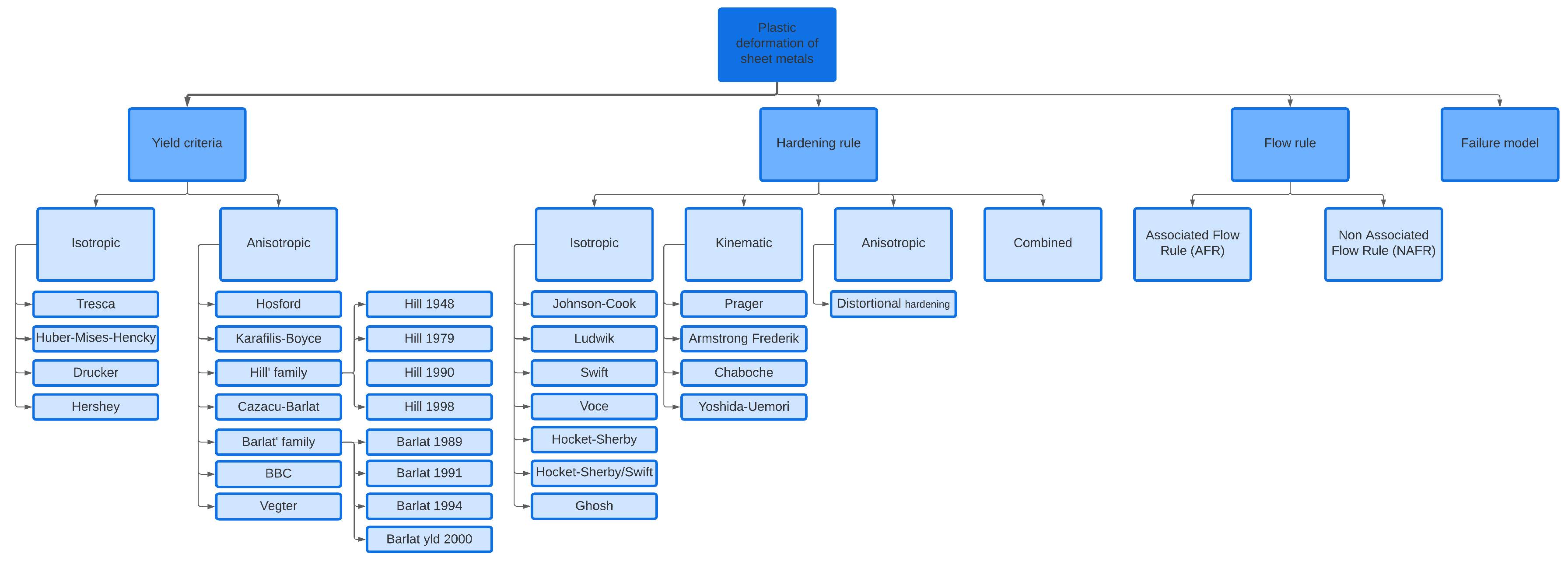
5. Constitutive Material Models

In sheet metal forming applications, an accurate representation of the material’s plastic behavior is crucial for obtaining reliable results in finite element simulations [106]. The accuracy of finite element simulation strongly depends on the extent to which a material constitutive model can characterize the real material properties [107]. The plastic behavior of a material in a general stress state is described by three elements [108]:

Yield Criterion;
Associated Flow Rule;
Hardening Rule.

Figure 10 presents an overview of the required material model parameterization concerning sheet metal forming simulation. Currently, constitutive models with anisotropic yield criteria based on associated flow rule and isotropic hardening rule are extensively used in this field. However, the increased adoption of lightweight materials like AHSS and the growing demand for accurate simulation of forming behavior necessitate the development of more accurate constitutive material models. The selection of appropriate yield criteria and hardening rules as well as the fitting of these models through suitable material testing procedures is of significant importance in sheet forming simulations. Even though, the adoption of most advanced and comprehensive material model formulations is not always favored for predicting forming behavior. Factors such as cost, ease of implementation and accuracy must be considered. Cost concerns mainly pertain to the mechanical testing required for model calibration which explains the widespread utilization of Hill’s 1948 model. Furthermore, the chosen model should gain industrial acceptance, with emphasis on computational efficiency, ease of implementation in numerical simulation codes and user-friendliness. Ultimately, the accuracy of the model’s predictions concerning yield locus, uniaxial yield stress and the coefficient of plastic anisotropy in uniaxial conditions must be guaranteed. Banabic [108] offers a comprehensive and historically detailed analysis of various material models, while a recent review paper written by Hou et al. [43] outlines the latest trends in material models addressing sheet metal forming applications.

5.1. Yield criterion

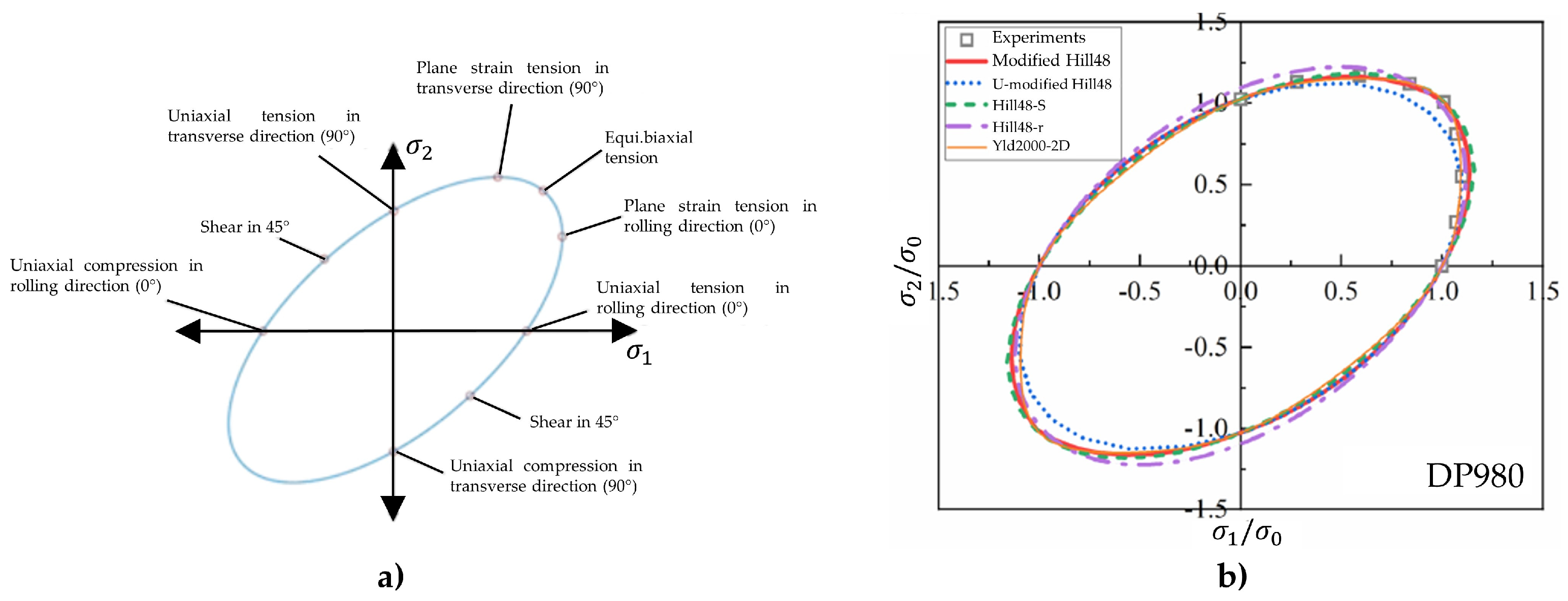
A yield criterion serves as a defining boundary that marks the transition from elasticity to plastic flow in response to various stress combinations [109]. Thus, accurately characterizing the yield surface is of significance, as sheet metal forming processes typically operate within the plastic region. Although high-strength sheets generally exhibit average r-values of 0.8-1.0, certain steels exhibit significant planar anisotropy r-value [110]. Anisotropic yield criteria are favored in material models for sheet metal forming operations during the production stage. The yield locus depicted in Figure 11a) represents different forming states. The precision of the yield locus is a key indicator of the accuracy of failure/fracture prediction, making it vital for the sheet metal forming community to establish highly precise yield criteria. This precision is essential for effectively anticipating failures/fractures and preventing costly production mishaps [111].

Isotropic yield functions such as the Tresca [114], the Huber-Mises-Hencky [115,116,117], the Drucker [118] and the Hershey [119] yield criteria are not commonly employed in the forming industry. The Hill 1948 [120] anisotropic quadratic function remains widely used due to its ease of parameter determination from uniaxial tension experiments in three directions. However, it exhibits limited capability in accurately predicting anisotropy in sheet metals [110]. Several studies have concluded that only non-quadratic functions can accurately capture the influence of anisotropy on the yield surface [108]. Therefore, the non-quadratic Hill 1979 [121] yield function was proposed, even though it is applicable only when the principal stress directions align with the orthotropic axes [108]. In 1990, Hill 1990 [122] provided an excellent description of the anisotropy coefficient and uniaxial yield stress variation within the sheet plane. Afterwards, Hill 1993 [123] offered a more user friendly expression, albeit with limited applicability. The emergence of lightweight materials, such as AHSS has shifted the anisotropic yield criteria towards more advanced formulations in the 21st century. Noteworthy examples include Barlat [124,125,126,127], Banabic-Balan-Comsa (BBC) [128,129], Cazacu-Barlat [130] and Vegter [131,132] which offer improved descriptions of the yield surface and closely track the planar variation of uniaxial yield stress and the coefficient of plastic anisotropy [108]. Figure 11b) depicts the yield locus of various yield criteria for a DP980 steel. The Barlat yld2000 model was used by Gutierrez et al. [133] for the analytical determination of forming limit curves in two third generation steels. While these yield criteria successfully accounted steels anisotropy, they underestimated the yield stress under shear conditions. Yoshida et al. [110] developed a more advanced yield function that provides a more accurate description of anisotropy influence.

Table 2 summarizes the most commonly used yield criteria for sheet metal forming simulations and the corresponding mechanical property parameters. All models require measurement of the material’s plastic anisotropy, serving as an indicator of sheet metal formability. Hill 1948 only requires standardized uniaxial tension along the rolling, diagonal and transverse direction. Additionally, Barlat yld2000 and BBC2005 require biaxial tension. In its initial formulation the Vegter material model also necessitated plane strain and shear tests in order to calibrate 17 parameters. However, Vegter 2017 [131] only requires standardized tensile tests.

The research conducted by Gösling [134] demonstrated that Barlat yld2000 exhibits superior accuracy in predicting erring compared to the Hill 1948 material model, which is influenced by the yield strength in the diagonal direction. A comparative analyses of three different yield criterion, namely Hill 1948, Barlat yld2000 and Barlat yld2000-Var [135] was performed by Cheng et al. [136]. Among these, the third mentioned model provided more precise results addressing the hardening behavior, the forming limit curve, especially under biaxial tension stress state, and the stretch formability.

Regarding the future trends in yield criteria for sheet metal forming applications of AHSS, several directions can be identified. Firstly, there is a need for the development of new yield criteria aimed at improving flexibility and reducing the number of parameters and the required experimental tests [107]. Secondly, standardized shear and plane strain experimental tests need to be developed. Lastly, there is a growing interest in the development of crystal plasticity material models. According to Hou et al. [43], crystal plasticity material models are advanced multi-scale modelling approaches that capture the deformation behavior of polycrystalline materials by considering slip, twinning and phase transformation processes.

5.2. Hardening rule

The hardening laws play a crucial role in describing how the yield surface evolves under plastic deformation and various loading conditions. These laws can be categorized in to four main families [137]: (i) isotropic; (ii) kinematic, (iii) anisotropic; for example distortional hardening and (iv) combined. Isotropic hardening implies that the yield surface expands without changing its shape as plastic strain increases. Kinematic hardening maintains the shape of the yield surface while translating it in the direction of strain. Distortional hardening refers to the distortion of the yield surface shape during plastic deformation [138]. Combined hardening models, such as kinematic + isotropic or kinematic + distortional hardening have also been proposed. 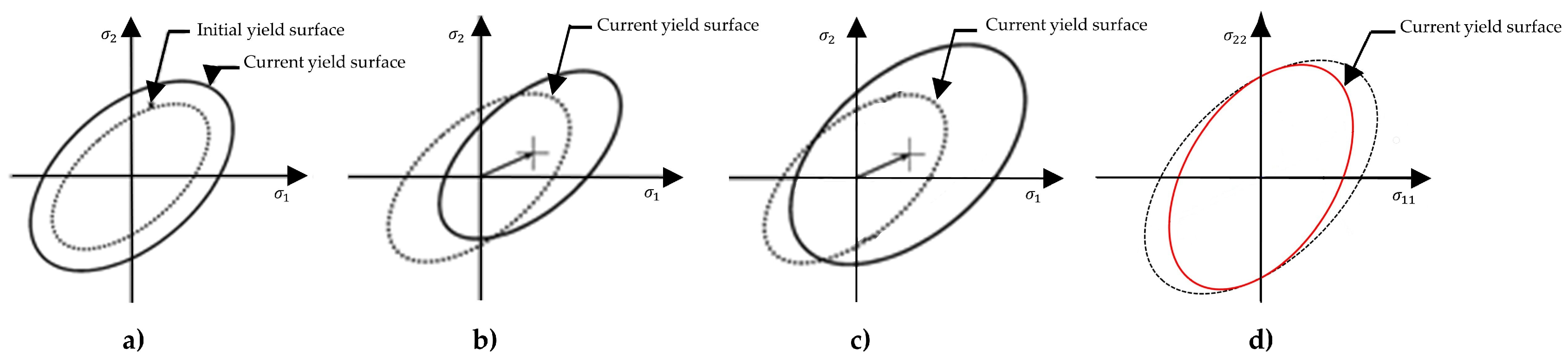Figure 12 illustrates the representation of the yield locus for these four different families of hardening rules.

Typically, the isotropic hardening is selected to reproduce the hardening behavior of metals in sheet metal forming processes, due to its simplicity. Commonly used isotropic hardening models include Ludwik [141], Swift law [142] and the Voce law [143]. However, experimental observations indicate that the hardening behavior differs under various loading conditions and directions, even under proportional loading conditions [43,141,144,145]. Therefore, the anisotropic hardening behavior can not be described by the anisotropic yield functions under isotropic hardening [145]. Moreover, cyclic loading and unloading occur frequently during sheet flow through draw beads and die radii. Under such loading and continuous reverse loading conditions, the stress-strain relationship is significantly influenced by the Bauschinger effect [107], which refers to a material property of stress/strain characteristics under non-proportional loadings [43]. Isotropic hardening laws fail to accurately capture the Bauschinger effect. The aforementioned limitations result in inaccuracies representing the forming behavior, particularly in cases where springback, tearing and earing occur. Kinematic hardening models have been proposed to address the Bauschinger effect, including Prager’s model [146], Armstrong and Frederick model [147], Chaboche’s model [148] and the model of Yoshida and Uemori [149]. Rosenschon and Merklein [150] have stated that a kinematic hardening law leads to a significantly better approximation of the cyclic hardening behavior rather than a pure isotropic formulation. Distortional hardening models such as the Homogeneous Yield Function-based Anisotropic Hardening model (HAH) offer an advantage in that the expression and parameter calibration of isotropic and anisotropic hardening terms are independent from each other [43]. Zhu et al. [139] demonstrated that the HAH-2d model reasonably captures the Bauschinger effect, permanent softening effect in reverse loading and latent hardening effect in cross loading., while the predictive accuracy for cross-loading softening requires further improvement. Additionally, combined kinematic + distortional hardening models have been proposed to study the material response under non-proportional loadings [151,152,153].

Butuc et al. [154] performed a comparative analysis of different hardening models in predicting the FLC of a DC06 steel. The right-hand side was well predicted by all evaluated models. The left-hand side was overestimated by the Swift law and combined Swift/Armstrong-Frederik law. Dizaji et al. [155] adopted a similar approach but focused on the influence of different hardening models on ductile fracture criteria. Their results showed that the combined Chaboche-Zeigler hardening model [156] and the kinematic Zeigler-Prager equation [146] provided more accurate predictions for the fracture location in square cup drawing using the Brozzo et al. [157] and Cockcroft and Latham [158] ductile fracture criterion, respectively. Nevertheless, the isotropic hardening model delivered best results than the kinematic hardening model for the Ayada et al. [159] ductile fracture criterion.

5.3. Flow rule

Yield criteria can be formulated with associated flow rule (AFR) and non-associated flow rule (NAFR). AFR models such as Barlat yld2000 capture yield stress and strain rate ratio using a linear combination of two functions, suitable for high-strength steels. However, third generation AHSS such as Q&P steels, exhibit a strength differential effect that requires more advanced AFR yield functions leading to higher complex formulations and computational costs [43]. NAFR offers a simpler approach for modelling anisotropic yield and plastic flow in metallic materials. It uses separate yield and plastic potential functions with simpler forms and analytical parameter calibration. Stoughton’s non-associative flow model [160], based on Hill 1948 function, accurately predicts yield stress in strongly anisotropic materials. NAFR’s usage and applications are increasing as more research investigates its effectiveness [161,162,163,164,165].

6. Material characterization methods

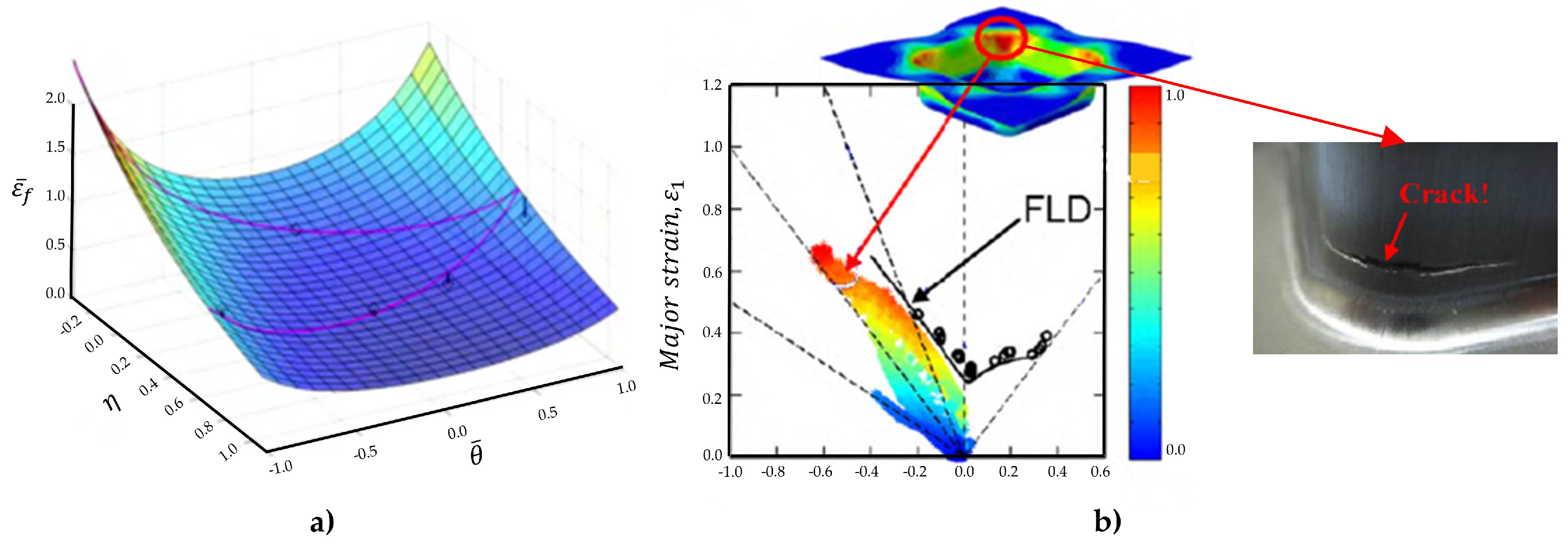
In the realm of sheet metal forming processes, the material undergoes various types of loading. Accurate experimentation plays a significant role in accurately calibrating models which predict crack initiation on macroscopic features. The fracture models rely on the correct assessment of the fracture strain. These fracture models require experimental testing under different stress states to fully characterize fracture occurrence. Different sample geometries, test configurations and/or loading paths generate different levels of stress states which significant influence the fracture typology. In order to represent any stress state, two dimensionless parameters, namely the Lode Angle and the Stress Triaxiality need to be represented. The loading path leading to fracture, represented in terms of the equivalent plastic strain evolution as a function of the Stress Triaxiality,

η

and Lode Angle parameter,

θ

significantly influences the precise assessment of fracture initiation location. Therefore, a wide range of stress states need to be covered by employing diverse experimental tests. Lian et al. [166] proposed a hybrid ductile damage modelling with a hybrid ductile experimental-numerical parameters calibration procedure specifically tailored to account for the damage characteristics of modern high-strength steels. 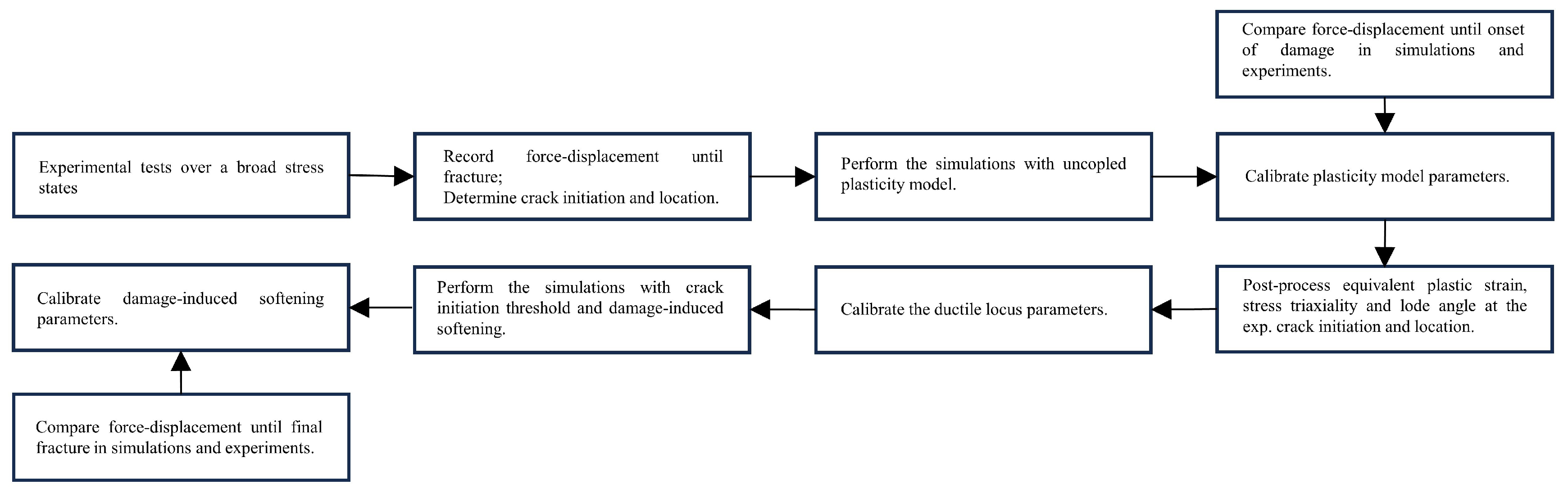Figure 13 presents the methodology followed by the authors in order to calibrate material and fracture parameters based on experimental tests. Although the knowledge of the strain to fracture is the main ingredient of damage models [167], they used a phenomenological model to characterize the onset of damage: the crack initiation strain, rather than the fracture strain.

Currently, most material characterization methods are based under the assumption of proportional loading histories. Figure 14 presents some conventional experimental techniques employed for the assessment of relevant data such as fracture strain,

η

and

θ

. However, the achievement of proportional loading conditions at the specific material point where fracture initiates proves to be challenging. Thes sample geometry and test configuration often induce a certain level of deviation from linearity during ductile fracture. Furthermore, non-linear deformation paths commonly arise in multi-forming operations. As such, method able to characterize the stress state under non-proportional loading are needed. The current trends on behalf of material characterization methods rely on industrial standardization of fracture limits determination and the enhancement of material assessment techniques for both proportional and non-proportional loading histories. Table 3 provides a review on the material characterization methods employed to calibrate fracture/damage models parameters.

6.1. Proportional loading

6.1.1. Pure shear ( $η = 0; \bar{θ} = 0$ )

The accurate assessment of the shear fracture limit is currently one of the most questioned subjects in sheet metal fracture modelling. Over the years, a large amount of sample geometries and methods have been proposed to address this issue. One hand, the ability of metallic materials to undergo shear deformation facilitates the attainment of elevated levels of plastic strains. On the other hand, makes it more difficult to achieve pure shear deformation paths at the crack initiation location.

Miyauchi [179] introduced the initial planar shear test documented in literature. The specimen comprises two symmetrically sheared regions and it is subjected to an axial load [180]. Rauch and G’Sell [181] adopted a modified version of this test, which was further refined by Genevois [182]. In Genevois’s test, the rotation of the specimen under the influence of shearing forces is impeded by a highly rigid frame. The specimens employed in this test possess a simple rectangular shape which deforms into a parallelogram. Bouvier et al. [180] conducted an optimization of the mechanical test, focusing on the impact of sample geometry and setup configuration on stress and strain uniformity. Subsequently, the ASTM-B831 [183] standard test method was established for shear testing, proposing a novel sample geometry and loading conditions. Alternative shear specimen designs have also been proposed such as the symmetric double-shear specimen with two identical gage sections [184]. However, the application of these specimens is limited due to the interference of edge effects when calculating shear stress [43]. It is important to note that the aforementioned approaches were originally devised for the determination of plastic hardening and are not generally suitable for characterizing formability limits caused by fracture [185]. Furthermore, they are affected by fracture occurrence at the free edges.

The primary prerequisite for determining the fracture limit strain in shear tests is the ability to achieve pure shear deformation paths, thereby ensuring a consistent zero triaxiality throughout the entirety of the experiment. To achieve this goal, it is essential to assure homogeneous stress and strain distribution while also preventing crack initiation at free edges, which can prove to be challenging, as most of the materials exhibit higher strain to fracture under uniaxial tension rather than pure shear. The importance of it relies on the crack initiation likelihood occurrence on higher stress triaxialities. Iosipescu [186] was among the first to endeavour the development of a pure shear test with constant triaxiality evolution. The subsequent ASTM D5379 [187] standard was formulated based on Iosipescu’s work and it is predominantly employed for composite materials. However, both approaches fail to adequately address the issue of edge cracking, similar to the specimens proposed by Bao and Wierzbicki [188] and Shouler and Allwood [189]. Dunand and Mohr [190] introduced a novel specimen incorporating localized sheet thickness reduction. Nevertheless, the initiation of fracture in this specimen could be reliably guaranteed to commence precisely at the centre of the sheared zone, thus compromising the achievement of triaxiality constancy. Figure 15 illustrates the four aforementioned proposed specimens.

Significant developments have been made in addressing the need for more accurate pure shear strain deformation paths through adapted in-plane torsion tests. These tests offer the capacity to achieve maximum strains up to 1.0 [191]. In the context of in-plane torsion testing, a circular sheet sample is clamped at both the outer rim and in the centre. By inducing planar rotation of the outer fixture, a simple shear is applied to the circular region situated between the clamps [192]. Yin et al. [185] determined the fracture strains for DP1000 using an in-plane torsion test, with a grooved specimen free of slits. This test configuration facilitated fracture propagation under constant zero triaxiality and effectively mitigated incipient cracking arising from edge effects. Grolleau et al. [193] proposed an alternative clamping system featuring a highly rigid device for in-plane torsion testing using grooved specimens. The system allowed for full optical access to the specimen’s gage section, enabling DIC measurements. It provided an almost perfectly proportional loading path for simple shear loading making it suitable for cyclic loading as well as testing ultra-high strength steels. 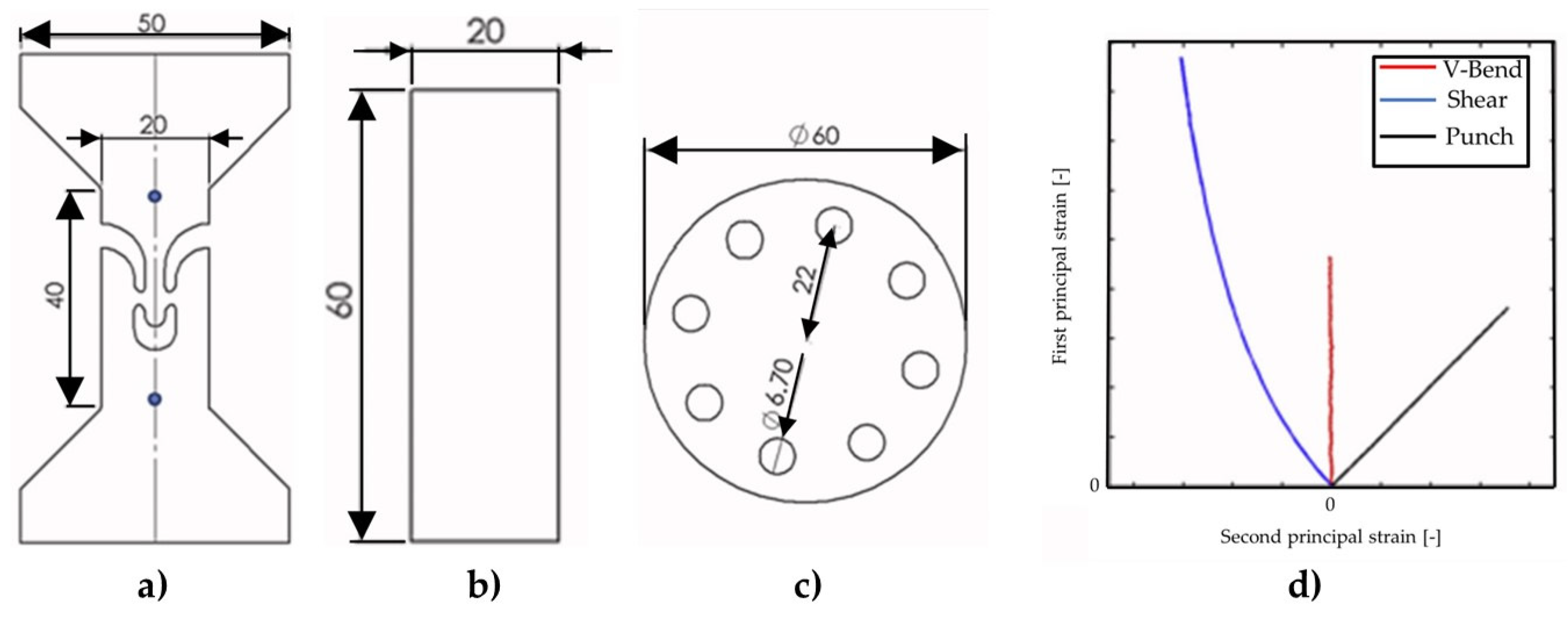Moreover, Roth and Mohr [170] recently reported a geometry shape optimization procedure which effectively addressed the strain to fracture under pure shear. The smiley shear specimen, depicted in Figure 16a), is distinguished by a series of notches that define the contours of the shear gage sections. As observed in Figure 16d) a more linear strain path evolution is achieved.

6.1.2. Uniaxial tension ( $η = 1 / 3; \bar{θ} = 1$ )

ASTME-8 outlines the procedure for conducting uniaxial tensile tests on metals at room temperature, enabling the determination of mechanical properties [194]. The amount of plastic deformation achievable through the uniaxial tensile test is typically limited to around 20-30%, which is noticeably lower when compared to other stress states such as shear. Uniaxial tensile tests are usually performed in three directions: rolling, transverse and diagonal, to investigate material anisotropy. The mechanical properties obtained from uniaxial tensile testing include Young Modulus, Yield Strength, Tensile Strength, Uniform and Total Elongation and r-values. When measuring the fracture strain under uniaxial tension using the conventional flat dog-bone specimen, the stress state undergoes changes during the loading process. To measure the limit strains under uniaxial tension, a tensile specimen with a central hole can be used instead, which offer the advantage of maintaining a more constant linear strain path until fracture occurs near the hole boundary [195]. However, careful selection of the hole manufacturing process as well as hole diameter dimension is relevant, as inadequate choices can lead to significant errors in the estimated strains to fracture for uniaxial tension [170]. Conversely, the work conducted by Behrens et al. [77] reveals that the central hole specimen yields non-linear strain path histories.

6.1.3. Notch tension

In order to encompass a wider spectrum of stress triaxiality values along the fracture locus, the utilization of notch tension is frequently employed. By adjusting the notch angle and size on notched flat specimens, a diverse range of stress triaxiality conditions can be attained [196]. The presence of notches ensures the development of a localized neck at the centre of the specimen, perpendicular to the loading axis [195]. For instance, notch tension tests have been proposed to calibrate the parameters of the extended Modified Mohr Coulomb model (eMMC) [171,173].

6.1.4. Plane strain tension ( $η = 1 / \sqrt{3}; \bar{θ} = 0$ )

Fracture occurrence during plane strain tension is primarily attributed to the load carrying capacity in the out-of-plane shear direction. Various approaches have been employed to determine the strain limits under plane strain tension. Jia and Bai [173] utilized uniform plane strain specimens as well as butterfly-shaped specimens. Santos et al. [197], on the other hand, employed double-notched specimens to assess the deformation mode under plane strain tension. However, it should be noted that with these test configurations, the stress state leading to fracture may not remain constant. The point at which plane strain tension limit is typically reached is on the material surface during bending operations. To address this, Roth and Mohr [170] introduced a modified plane strain bending configuration able to deliver proportional loading histories (Figure 16d). Their V-bending experiment involves placing a rectangular sheet material coupon (Figure 16b) on top of two parallel rollers. The sheet specimen is then subjected to loading by the two parallel rollers through a thin, knife-like tool which remains stationary, resulting in the formation of a shar V-bend.

6.1.5. Equi-biaxial tension ( $η = \frac{2}{3}; \bar{θ} = - 1$ )

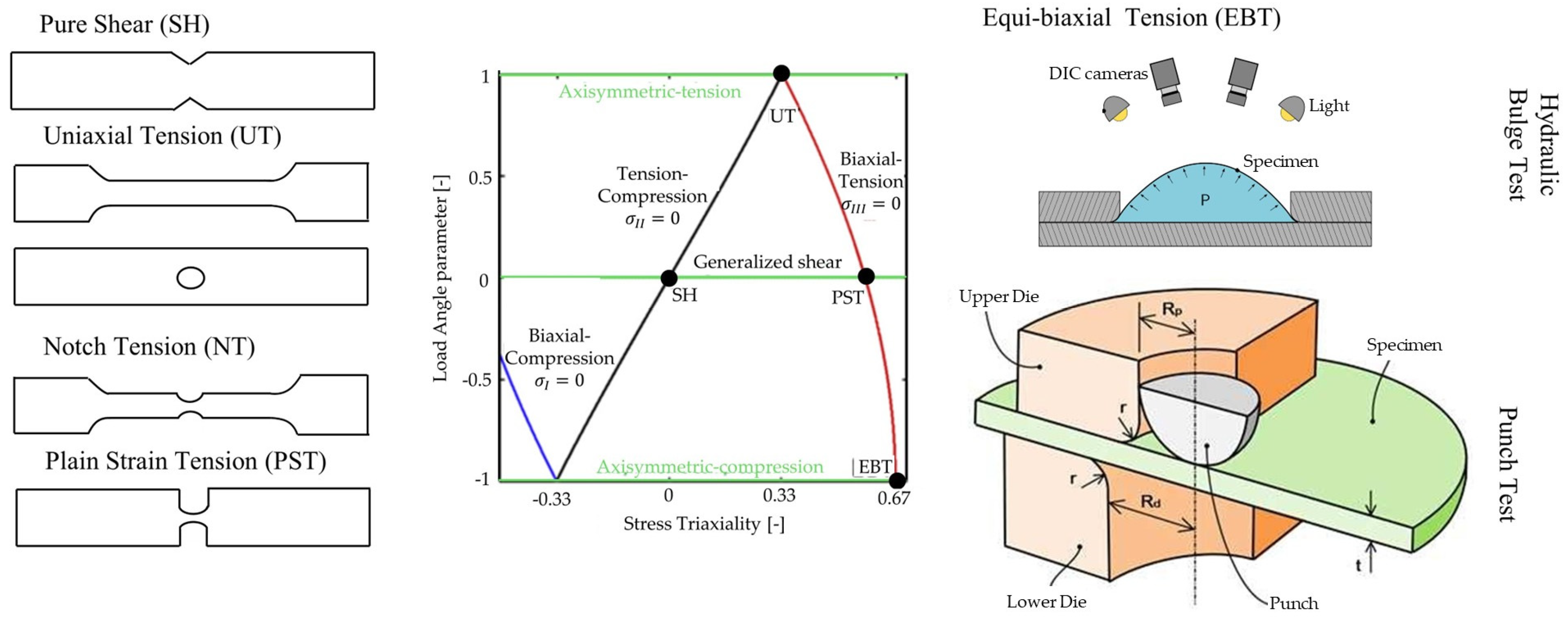
Fracture testing of sheet materials under equi-biaxial tension is well standardized [170]. Usually either bulge test or punch test is used. The hydraulic bulge test involves the deformation of a flat specimen through the application of hydraulic pressure. The outer edge of the sample is firmly clamped with a circular die, while the internal area is subjected to increasing fluid pressure during the test, causing deformation until fracture occurs [168]. The ISO 16808 standard [198] specifies a method for determining the biaxial stress-strain curve using an optical measuring system. The bulge test allows for a much larger achievable strain prior to necking, owing to the nearly equi-biaxial stress state, compared to the uniaxial tensile test. The punch test, on the other hand, utilizes a miniature disc sample subjected to compressive force applied through a hemispherical punch indenter on the upper surface of the disc [199]. The small punch deformation test procedure for metallic materials is covered by the standard ASTM E3205-20 [200]. The configuration used to perform both tests is schematically presented in Figure 14. The punch test offers the advantage of avoiding the evacuation of excess fluid after fracture, although the presence of tool friction can influence the experimental results. Roth and Mohr [170] proposed an adaptive punch testing procedure, wherein the distinctive feature is that the punch remains stationary throughout the experiment while the die and clamping plate move downwards. The specimen geometry is presented in Figure 16c). This approach reduces the required focal depth of the DIC camera system, enabling shorter object distances and ultimately enhancing the spatial resolution of the acquired surface strain fields. Furthermore, the location of fracture initiation remains fixed throughout the entire experiment.

6.1.6. Butterfly test

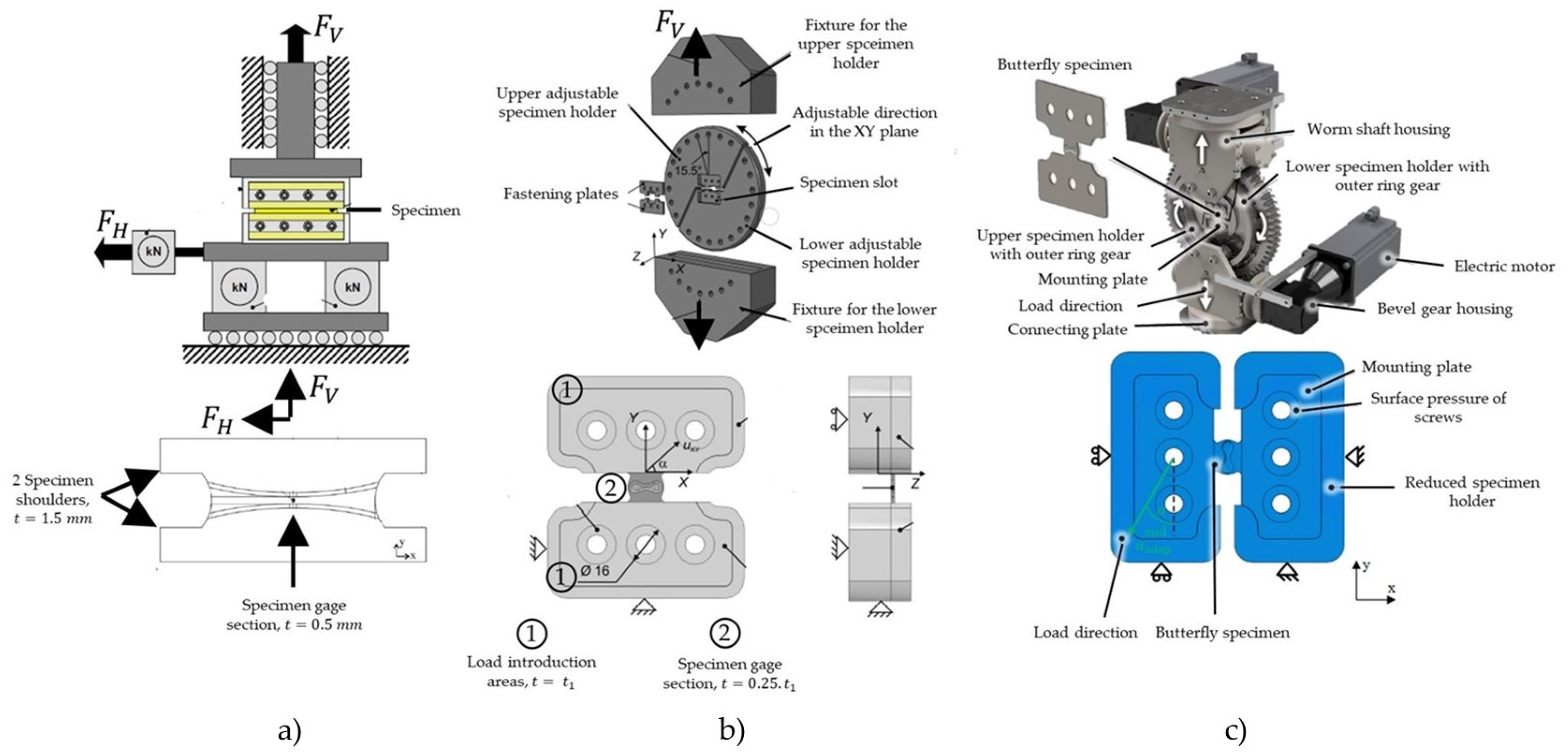
Mohr and Henn [201] devised a butterfly-shaped specimen that facilitated the examination of fracture behaviour under low and intermediate stress triaxialities, ranging from 0.0 and 0.6. The generation of different stress triaxialities can be accomplished without altering the design or dimensions of the specimen, but rather by adjusting its orientation. The experimental procedure is conducted using a biaxial testing apparatus comprising a fixed portion, a vertically movable portion and the corresponding specimen. By adjusting the angle between the specimen axis and the vertical axis, different stress triaxialities can be achieved. The gage section of the specimen exhibits a uniformly reduced sheet thickness compared to its boundaries and it is designed to induce crack formation at the centre of the specimen. Bai [202] introduced modifications to the design of the gage section, resulting in a non-uniform sheet thickness within the gage section.

Dunand and Mohr [190] further improved the initial specimen design attempting to increase homogeneity of the stress state and strain fields at the specimen centre. Additionally, the configuration of the testing setup enabled the application of combined normal and shear loads, as illustrated in Figure 17a). The experimental investigation focused on TRIP780 steel, encompassing a range of loads from pure shear to transverse plane strain tension. The findings revealed that under shear loading, both stress triaxiality and lode angle parameter exhibited relative constancy. However, a linear increase in stress triaxiality after the onset of through-thickness necking was observed for tension loading. Moreover, it was noticed the highly sensitivity to imperfections in the specimen geometry.

Despite the improvements made to the initial butterfly specimen design proposed by Mohr and Henn [201], achieving uniform stress and strain distribution throughout the entire experiment, especially under shear-dominated loading conditions, remained challenging. Therefore, Peshekhodov [203] further enhanced the butterfly design with the aim of ensuring strain localization at the specimen’s gage section regardless of the applied load direction. The new specimen geometry was divided was divided into three areas, as illustrated in Figure 17b). The comparative FEM analysis between this new geometry and the one proposed by Bai [202] demonstrated an increased likelihood of fracture initiation at the desired central area under arbitrary stress states. Furthermore, a more precise definition of the stress state could be achieved by specifying the load application angle. The implemented apparatus, based on a single material characterization technique, facilitated the generation of a wide range of stress triaxialities, from pure shear to plane strain tension. This approach accurately modelled the fracture behaviour of a DP600 steel using the CrachFEM and MMC fracture models.

Behrens et al. [77] adopted a similar experimental and numerical approach to obtain fracture data for a CP800 steel and calibrate the MMC fracture model. Similarly, the butterfly specimen developed by Peshekhodov [203] demonstrated fracture initiation at the specimen centre under various stress triaxialities, ranging from shear to uniaxial tension. Even though, the butterfly specimen did not deliver entirely proportional strain paths, improvements compared to other experimental tests are undeniable. In order to solve the problem of non-linear strain path evolution, Stockburger et al. [204] proposed an innovative adaptive experimental configuration, as shown in Figure 17c). The key feature if this setup was the continuous real-time adjustment of the loading angle to maintain constant stress states. To achieve this, a Phyton script was incorporated into the numerical simulation, compensating for deviations in stress triaxiality exceeding 0.03. A comparative analysis between the calibration of the MMC fracture model using the new adaptive test methodology and the fixed loading angle approach revealed significant enhancements in achieving linear strain paths. Furthermore, as the strain paths became more consistent, the equivalent plastic strain at fracture increased.

6.2. Non-proportional loading

In the context of sheet metal forming operations, the presence of non-linear strain path histories at fracture initiation sites has been a frequent phenomenon. Hence, attention within the sheet metal forming research community has also been directed towards enhancing experimental methodologies able of generating controlled non-linear strain paths, further improving the accuracy of material fracture and failure modelling. Aisvaran [205] identified the main test procedures to generate non-linear strain paths: (i) Nakazima test with modified punch geometry; (ii) two step drawing; (iii) in-plane biaxial test with cruciform specimen; (iv) Bulge test with stepped dies; (v) cruciform specimen in conventional Nakazima test setup. Table 4 summarizes the main approaches for generating NLSPs tested on AHSS.

The Nakazima test with modified punch geometry offers the advantage of achieving non-linear strain paths in a single step procedure. Saxena et al. [78] designed five novel punch geometries to replace the conventional hemispherical punch in order to change the strain path during deformation in the necking initiation site. The Nakazima test, employing a cruciform specimen serves as an alternative technique to generate NLSPs. An innovative procedure proposed by Jocham et al. [210] incorporates a modified blank-holder with adjustable draw bead height, simplifying the need for a single specimen geometry to produce the FLC [210], as opposed to the two step drawing approach requiring varying specimen geometry [206]. He et al. [211] introduced an innovative test procedure designed to facilitate continuous non-linear biaxial tensile deformations of sheet metals via bulging with stepped dies. This bulging process lead into a distinctive change in curvature radius relative to the bulging height and as the difference between successive elliptical sections increases, the presence of NLSPs becomes more pronounced [111]. The main distinctive feature of the in-plane biaxial test with cruciform specimen is that it provides a frictionless way of investigating the strain path change in a cruciform specimen. The design of this specimen continues to undergo refinement within the scientific community, yet standardization has not been established.

7. Damage and fracture models

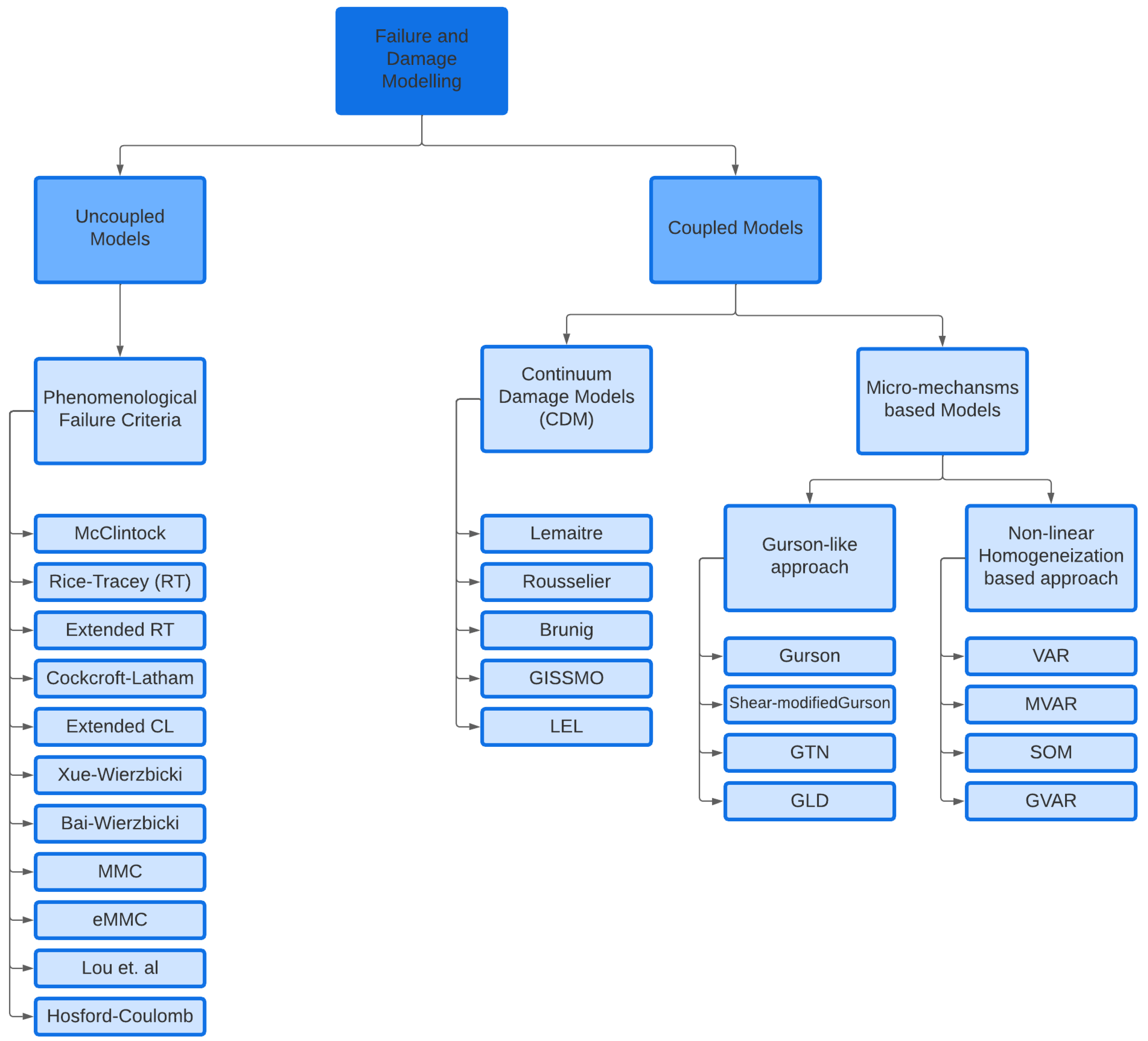
The incorporation of damage or fracture models holds substantial significance within the realm of sheet metal forming simulation, enabling the anticipation of fracture occurrences in industrial contexts as well as facilitating a comprehensive understanding of damage behaviour. These models can be systematically classified into two principal categories, namely coupled and uncoupled, each grounded either in micromechanical or phenomenological foundations. Figure 18 provides an overview of the classification of ductile fracture models and showcases various models within their respective family backgrounds. The fundamental divergence between coupled and uncoupled models resides in the former’s integration of damage mechanisms alongside elastic and/or plastic responses, as opposed to the latter, which distinctly segregates damage evolution from material behaviour. Furthermore, the domain of coupled models can be further bifurcated into micro-mechanical based models and continuum damage models (CDM). The former considers the deterioration of material during the loading process, attributed to damage propagation, while the later finds its underpinning in a thermodynamic framework and is formulated upon a phenomenological basis.

Damage and fracture model or fracture criteria operate by employing an accumulating damage parameter, which serves as a fundamental basis for assessing fracture. By using equation (1), a general fracture model can be expressed.

D \int_{0}^{ε_{f}} f (σ, ε, \dot{ε}, T, \dots) \bar{{d ε}^{p}} \leq 1

(1)

where

ε_{f}

is the equivalent plastic strain at fracture,

\bar{{d ε}^{p}}

is the equivalent plastic strain increment, and

f

is a scaling function which depends on internal variables such as stress state

σ

, strain rate

\dot{ε}

, and temperature

T

D

is seen as a damage indicator [28].

In order to accurately depict the normalized stress state, it is necessary to consider both stress triaxiality

η

, as well as lode angle parameter

\bar{θ}

. It is well established that the strain to localization decreases when the stress triaxiality increases. Conversely, a lower stress triaxiality value results in an increased sensitivity to the lode angle parameter [212]. The stress triaxiality is very important to characterize the stress state of metallic materials and consists in the relative degree of hydrostatic stress in a given stress state which is defined according to equation (2).

η = \frac{σ_{m}}{σ_{e q}} = \frac{\frac{1}{3} (σ_{1} + σ_{2} + σ_{3})}{\sqrt{\frac{{(σ_{1} - σ_{2})}^{2} + {(σ_{2} - σ_{3})}^{2} + {(σ_{1} - σ_{3})}^{2}}{2}}}

(2)

where

σ_{m}

corresponds to the hydrostatic stress, while

σ_{e q}

refers to the Von Mises equivalent stress.

σ_{1}

σ_{2}

and

σ_{3}

are the principal normal stresses.

η

controls physically the size of a given void, i.e., controls the micro-void growth during ductile fracture. For isotropic materials under plane stress, the triaxiality alone is enough to define any possible stress state relevant for fracture characterization [213]. On the other hand,

\bar{θ}

controls the shape of a given void [29] and is required to model three dimensional stress states. To determine the lode angle parameter, it is worth mentioning the lode angle,

θ

which is defined through the normalized third stress invariant,

ξ

θ = \frac{1}{3} \arccos (ξ) = \frac{1}{3} \arccos {(\frac{r}{q})}^{3} = \frac{1}{3} \arccos {(\frac{{(\frac{27}{2} . J_{3})}^{1 / 3}}{\sqrt{3 J_{2}}})}^{3}

(3)

where

r

and

q

are two stress state parameters and

J_{2}

as well as

J_{3}

are the second and third deviatoric stress invariants, respectively. Therefore,

\bar{θ}

is defined on account of the given transformation:

\bar{θ} = 1 - \frac{6 θ}{π}, w i t h \bar{θ} ϵ [- 1; 1]

(4)

This section presents a brief historical review on ductile fracture and damage models. For a more comprehensive overview, the reader should refer to the work conducted by Cao [212] as well as Tekkaya et al. [29].

7.1. Comparison between different fracture and damage models

There are a large number of ductile fracture models. Therefore, it can be difficult to choose the most appropriate one to employ in a particular sheet metal forming process. Table 5 presents a brief and simplified qualitative comparison between the three main families of ductile fracture models.

For the fracture or damage model to garner acceptance within real industrial forming applications, a wise equilibrium must be attained between ease of implementation and forming behavior accuracy. In this realm, the investment time in both model formulation as well as its implementation in finite element software must be as low as possible. On the other hand, the accuracy of the model should be as high as feasible to correctly predict the component forming behavior. Generally, these parameters work in an inverse manner.

In these contexts, phenomenological uncoupled models are commonly preferred, e.g., where the components exhibit relatively straightforward geometries, characterized predominantly by linear strain paths. These models suit to optimize process parameters aiming of minimizing damage occurrence. The major advantage of such models consists on their ease of implementation and use. The simpler calibration procedure as well as the comparatively less number of parameters contribute to their quicker implementation. Additionally, since damage softening effects are not considered, mesh dependency is avoided, facilitating the simulation process: less CPU time and more convergence stability. However, it is imperative to acknowledge that the principal limitation of this category of models pertains to their applicability in scenarios involving complex loading paths outside the identification zone, as well as those relating to large plastic deformation. Thus, special care should be taken for their application outside the identification domain, due to their phenomenological foundation [212].

In many industrial applications, the loading path frequently exhibits intricate characteristics. Therefore, coupled models may be seen as an appropriate choice, since they account for softening effect due to damage accumulation, as opposed to uncoupled models. Indeed, the coupled models predictive damage accuracy is significantly higher. These models can capture continuous degradation due to damage. Although important when the material experiences very large plastic deformation in multi-step forming processes, the complexity of the simulation process is unavoidably raised, i.e., softening effect introduces mesh dependency. As a result, finer mesh induces faster damage accumulation. In order to mitigate mesh dependency, two validated approaches can be pursued: (i) integration of non-local methodologies, which may be grounded in either integral formulations or implicit/explicit formulations, requiring careful calibration; (ii) delineation of damage model parameters tailored to specific element dimensions, ensuring that during computations, the element sizes remain beneath this predetermined threshold [29]. This mesh dependency results in an increased CPU time in comparison to uncoupled models. However, to handle the complex strain path the material may undergoes, it is required the use of phenomenological models [29]. No purely micro-mechanical model has been shown to be able of capturing both damage mechanisms at high and low stress triaxialities in real multi-forming operations, due to their construction and current computational efficiency [212]. Thus, the micro-mechanical based models are discarded for industrial forming processes implementation. With a significantly high physical background, their complexity is high. The CPU time as well as the calibration procedure dissuades its implementation. Conversely, the CDM models require comparatively less effort in the calibration process as a smaller number of damage parameters are used. Additionally, these models couple elasticity with damage evolution.

Therefore, each family of models has their own advantages and drawbacks. The effort one is willing to take in model accuracy, neglecting simplicity, or vice versa, is the main factor in model selection. In this context, the advanced uncoupled phenomenological models are very popular in the sheet forming industry. Even though, their comparatively diminished damage prediction accuracy, they have been used and demonstrated satisfactory results even for applications involving complex stress states. Moreover, these ductile fracture models facilitate the incorporation of strain rate dependencies through accurately constructed strain-rate dependent terms. Among all phenomenological fracture models, it is worth mentioning the modified Mohr-Coulomb (MMC) [214], the all-strain based MMC (eMMC) [173] and the Hosford-Coulomb model (HC) [175]. All of them showed good performance modelling sheet metal forming fracture of AHSS. Table 6 summarizes the implementation of ductile fracture models in some representative studies reported in literature.

Alternatively, the adoption of ‘modular’ models has been progressively gaining attention. Even though coupled models generally exhibit better predictive accuracy, they encounter limitations in addressing conditions characterized by low stress triaxialities and notably shear-dominated loading conditions. Therefore, the conceptual framework of the ‘modular’ models is to upgrade these models by adding terms which increase the predictive accuracy for specific situation (e.g., the Lode dependent term; a strain threshold for damage accumulation which depends on the stress triaxiality). When thoughtfully formulated, these diverse models may converge towards consistent predictions concerning damage location [212].

7.2. Phenomenological fracture models

In these models, fracture is assumed to occur when a critical stress or strain rate is reached. Damage variable is just a ‘warning’ for the approach of fracture [212]. Although most of the uncoupled models encountered in the literature have a phenomenological background, the first developed fracture models were rooted in physical principles, incorporating considerations of void growth. Examples of such models are the McClintock [220] and Rice-Tracey [221] models.

In the realm of phenomenological fracture criteria, the concept of damage is approached as an integration of a stress-based function along the loading trajectory. Initially, early research effort solely focused on considering either stress triaxiality, e.g., the Oyane model [222], or principal stress, e.g., Cockcroft-Latham model [158]. However, it was observed that when subjected to complex loading paths, the predictive accuracy of these models in simulating forming behavior is diminished. The primarily stems from the fact that the critical damage threshold is contingent upon the specific loading trajectory. Recognizing this limitation, Bao and Wierzbicki [223] highlighted the necessity of incorporating the lode angle parameter dependence into these criteria to establish a unique definition of the normalized stress state. Thus, the recently proposed models, named advanced uncoupled phenomenological models comprehensively account for both stress triaxiality and lode angle influence. These criteria usually define a fracture locus where the strain to fracture is a function of stress triaxiality and lode angle [29]. Nevertheless, it is prudent to acknowledge that while such models enhance predictive accuracy within complex stress states, further refinements are necessary to address non-linear strain paths. In such cases, the equivalent strain to fracture no longer represents the actual strain at fracture, but rather serves as a weighting function which accounts for the stress state [212].

7.2.1. Modified Mohr-Coulomb model (MMC)

The Modified Mohr-Coulomb model [171] was proposed by Bai and Wierzbicki. The model was formulated by the transformation of the stress-based Mohr-Coulomb (MC) criterion to the corresponding strain-based model, where the spherical coordinate system is derived in terms of

\bar{ε_{f}}

η

and

\bar{θ}

. The damage indicator can be formulated as in equation (5).

D ({\bar{ε}}_{f}) = \int_{0}^{{\bar{ε}}_{p}} \frac{d {\bar{ε}}_{p}}{f (η \bar{θ})}

(5)

The fracture locus is calculated according to:

{\bar{ε_{f}} = \{\frac{A}{c_{2}} [c_{θ}^{S} + \frac{\sqrt{3}}{2 - \sqrt{3}} (c_{θ}^{a x} - c_{θ}^{S}) (\sec (\frac{θ π}{6}) - 1)] [\sqrt{\frac{1 + c_{1}^{2}}{3}} . \cos (\frac{θ π}{6}) + c_{1} (η + \frac{1}{3} s e n (\frac{θ π}{6}))]\}}^{\frac{- 1}{n}}

(6)

There are a total of six parameters (

A

n

c_{1}

c_{2}

c_{θ}^{s}

c_{θ}^{c}

)that need to be determined. Parameter

A

and

n

represent the Swift hardening law parameters, while the remaining parameters are material constants. These constants are determined through a minimum of three fracture experimental tests conducted at different stress triaxiality ranges.

The engineering applicability of the MMC fracture model for a TRIP690 steel was demonstrated by Li et al. [89]. They accurately predicted the fracture location and magnitude of punch travel for two deep-drawing operation setups: square punch and circular punch. Furthermore, the results indicated that the MMC model outperformed the FLC criterion in dealing with NLSPs and shear-induced fracture. Nevertheless, Behrens et al. [216] highlighted the significance of considering no damage accumulation effects for stress triaxialities below -0.33 in the MMC formulation. Their study detected premature shear fracture initiation of a DP600 steel workpiece in a deep drawing operation without the aforementioned condition. Luo and Wierzbicki [215] investigated the accuracy of the MMC model in predicting fracture behavior in stretch forming simulator tests. The comparative evaluation between different element types revealed that both 3D and shell elements are sufficiently adequate to fit the experimental fracture data. The fracture location/mode, fracture wall stress and fracture wrap angle are particularly well predicted by the 3D element type. Moreover, the MMC model can detect variations in experimental friction conditions. More recently, Fu et al. [224] also proved the effectiveness of the MMC model for predicting ductile fracture both in stretch-bending and Nakazima tests for DP980 and DP1180 steels.

7.2.2. Strain based Modified Mohr-Coulomb (eMMC)

The eMMC model is derived by converting the stress state variables:

η

and

\bar{θ}

from the MMC model to the strain state. By considering the stress ratio,

β

and the strain ratio,

α

of in-plane principal strain increments, the model can be expressed in a space based solely on strain. In this space, the fracture strain is affected by either the strain ratio or a new plastic strain based parameter,

ϕ

[173].

α = \frac{{d ε}_{2}}{{d ε}_{1}}, β = \frac{σ_{2}}{σ_{1}}

(7)

The eMMC formulation is based on the premise of monotonic loading and the plastic flow rule of Mises-Levy. This formulation enables the establishment of a correlation between

α

and

β

α = \frac{2 β - 1}{2 - β}, β = \frac{2 α + 1}{2 + α}

(8)

One significant benefit of transforming the MMC into the eMMC lies in the decoupling of the fracture model from plasticity, allowing for the study of fracture independent of plasticity [173]. This is achieved by the introduction of the

ϕ

parameter, denoted as:

ϕ = \frac{180 °}{π} a t a n 2 (- \dot{ε_{2}^{p},} \dot{ε_{1}^{p}) + 90 °}

(9)

The

ϕ

parameter represents the effect of in-plane anisotropy under all possible loading conditions. Furthermore, it denotes the angle to the positive minor strain direction in the forming fracture limit diagram (FFLD) under proportional loading.

A calibration study conducted by Jia and Bai [173] demonstrated good accuracy in predicting the eMMC fracture locus for a TRIP780 steel. Their study combined experimental and numerical methods and produced precise estimates for material strength, plastic flow behaviour, fracture initiation location and fracture propagation modes.

7.2.3. Hosford-Coulomb (HC)

Mohr and Marcadet [175] proposed the Hosford-Coulomb phenomenological model, which is motivated by micromechanics and assumes that fracture onset is closely linked to the formation of a primary of secondary band of localization. Despite being a phenomenological model, the underlying physical significance of the stress-based localization criteria is preserved. The HC model converts the stress space of the localization criterion into a mixed strain-stress space, incorporating the equivalent plastic strain, stress triaxiality and lode angle parameter. The HC model was specifically developed by Mohr and Marcadet to cater to the distinctive characteristics of AHSS. The accuracy of the model was confirmed by these authors under proportional loading and at low strain rates for three AHSS materials (DP590, DP780, TRIP780).

According to the HC model, fracture occurs when the following conditions are met:

\int_{0}^{{\bar{ε}}_{f}} \frac{d {\bar{ε}}_{p l}}{{\bar{ε}}_{f}^{p r} [η, \bar{θ}]} = 1

(10)

In the mixed strain-space, the criterion is defined as in equation (11)

{\bar{ε}}_{f}^{p r} = k^{- 1} [σ_{f} [η \bar{θ}]]

(11)

where in the Modified Haigh-Westergaard stress space,

\bar{σ}

takes the form of:

\bar{σ} = {\bar{σ}}_{f} [η, \bar{θ}] = \frac{b}{{\{\frac{1}{2} ({(f_{1} - f_{2})}^{a} + {(f_{2} - f_{3})}^{b} + {(f_{1} - f_{3})}^{a})\}}^{\frac{1}{a}} + c (2 η + f_{1} + f_{3})}

(12)

The model parameters are referred as

a

b

and

c

Compared to the MC criterion, the HC model exhibits greater suitability for handling biaxial loading [175]. Roth and Mohr [225] proposed an empirical extension to the HC model which considers the influence of strain rate on fracture initiation in two AHSS materials (DP590 and TRIP780). This extension introduces an additional scalar parameter to the model formulation to account for strain rate effects. A similar approach was adopted by Erice et al. [176] who verified that the HC model provides a satisfactory approximation of the impact the stress triaxiality and lode angle parameter on three other AHSS (DP980, CP980 and CP1180).

The calibration procedure of the aforementioned studies was addressed through numerical simulations using solid elements. However, when it comes to calibrating the HC using shell elements, it becomes necessary to establish the Domain of Shell-to-Solid Equivalence (DSSE) in order to achieve convergence in the initiation of ductile fracture relative to the mesh size [178]. To address this issue, Pack and Mohr [217] introduced the DSSE-HC model, which combines the DSSE concept with the Hosford-Coulomb model. The DSSSE-HC model can capture fracture initiation without prior necking, as well as through-thickness necking failure. Notably, the DSSE approach offers the advantage of distinguishing between membrane and bending loading conditions, setting it apart from the FLD/FLC criterion. Fracture is assumed to occur when the loading path in a shell element either departs from the DSSE boundary or satisfies the HC fracture criterion. The DSSE-HC model was successfully calibrated for a DP780 steel and applied to accurately predict the displacement to fracture in both stretch bending and ‘V-bending’ operations. However, as highlighted by Pack et al. [178], further enhancements are necessary to mitigate the pronounced mesh size dependence of fracture predictions when employing a combined ductile fracture model and a necking based forming limit criterion.

Furthermore, the efficacy of the HC model in investigating the impact of interrupted loading conditions, as often encountered in servo press forming operations, has been demonstrated by Prasad et al. [177].

7.3. Continuum damage models (CDM)

CDM models are classified as phenomenological due to their foundational development hinging upon a rigorous thermodynamic framework, thereby ensuring a non-negative dissipation [212]. The degradation of material stiffness is addressed through the introduction of an internal scalar damage variable, which interacts with the stress tensor to account for isotropic damage phenomena. To impart the macroscopic response with damage effects, the concept of effective stress is introduced based on the principle of strain equivalence. This notion of effective stress allows a unified integration of damage evolution with the material behavior law, enabling the consideration of damage effects on both elasticity and plasticity [29].

The first contributor towards the formulation of models grounded in thermodynamical assumptions was Kachanov [226]. Subsequent improvements in this theoretical domain were introduced by Chaboche [227] and Lemaitre [228]. Indeed, among CDM models, the Lemaitre damage model is widely used, wherein stress triaxiality and equivalent stress are the pivotal factors governing damage propagation. Notably, Lemaitre’s model underwent enhancements, aiming to tailor their applicability to metal forming applications. These adaptations encompassed the augmentation of the damage dissipation potential, with Lemaitre and Desmorat [229] introducing a strain threshold beyond which damage remain constant [29]. To further enhance model accuracy, particularly at low stress triaxialities, Cao et al. [230] devised the Lemaitre Enhanced Model (LEL) by including a parabolic lode dependent term. The main modifications focused on [212]: (i) accounting for the influence of the Lode Angle parameter on damage evolution; (ii) improving the influence of stress triaxiality on damage threshold; (iii) enhancing the weakening function at low stress triaxialities.

Another notable CDM model is the Generalized Incremental Stress State Dependent Damage Model (GISSMO) [213]. In this model, beside the damage variable, D an instability function, F dependent of the critical strain,

ε_{c r i t} (η)

is introduced. Once F reaches 1, the coupling between damage and the stress tensor is activated [29].

7.3.1. GISSMO model

Andrade et al. [213] formulated the GISSMO model. The model aims to predict fracture of ductile materials by depicting a fracture curve dependent on the stress triaxiality ratio. The incorporation of a damage accumulative parameter, which is dependent on the plastic strain increment allows the accurate modelling of non-proportional loading histories. In this context, the damage variable with respect to time is given by equation (13)

\dot{D} = \frac{n}{ε_{f} (η)} . D^{(1 - \frac{1}{n})} . {\dot{ε}}^{p}

(13)

This expression serves as an evolutionary equation which effectively addresses non-proportional loading histories. Additionally, the authors have introduced an instability function denoted as F able to understand when a strain localization arises, and therefore to accelerate material degradation when those situations occur. Using this approach, the eventual non-linearity affecting the onset fracture behavior is taken into consideration. To deal with mesh dependency, a triaxiality-dependent regularization strategy is adopted adjusting the fracture curve to the corresponding element size.

One of the main advantages of the GISSMO model lies in its ease of numerical implementation in comparison to other CDM models. Its feature of allowing coupling with any plastic material model ensures high flexibility. The resulting curves from the GISSMO model are presented in Figure 19. The calibration procedure involves the determination of several parameters, including the fracture curve as a function of stress triaxiality,

ε_{f} (η)

, the damage exponent,

n

, the curve for critical strain,

ε_{c r i t .} (η)

and the fading exponent,

m

. The GISSMO model is implemented in the commercial finite element code LS-DYNA.

7.4. Micro-mechanics based models

The micro-mechanics based models consider the underlying physical meaning attained to the damage. Hence, the macroscopic feature is a result of micro-mechanical void, void growth and coalescence of neighboring voids. The material deterioration is linked with the fracture occurrence. The micro-mechanics based models can be subdivided into: (i) Gurson-like approach, (ii) non-linear homogenization based approach.

The effect of void growth on material degradation was introduced by Gurson [231]. The widely recognized Gurson-Tvergaard-Needleman (GTN) model [232] represents a further advancement of the Gurson framework. The GTN is a porous plasticity theory, accounting for the evolution of the void volume fraction: interaction, nucleation and final coalescence of voids, where the void growth depends on the trace of the plastic strain rate [29]. Multiple extensions have been proposed to enhance the GTN model’s accuracy, exemplified by the development of the GLD model which accounts for void shape effects. Stress triaxiality and lode angle dependent terms can be integrated into these models. As the main drawback of the micro-mechanics based models, particularly the GTN model is the low accuracy predicting shear-dominated loading cases, the incorporation of these stress state parameters increases the model’s accuracy. The stress triaxiality allows the void nucleation process to take place earlier at high stress triaxialities [212]. Xue [233] and Nahshon and Hutchinson [234] added a lode-dependent term in order to more accurately model the void growth [29]. However, these modifications are purely phenomenological.

The non-linear homogenization based approach models can describe the change of void shape and orientation, which have been showed important at low stress triaxialities [212].

7.4.1. Gurson-Tvergaard-Needleman (GTN) model

The GTN model postulates that damage growth is an outcome of material degradation occurring as the loading process takes place. Void evolution plays a crucial role in shaping the yielding behaviour, and is appropriately incorporated into the GTN model through a modification of the Von Mises yield potential [235]:

ϕ = {(\frac{σ_{v}}{σ_{Y}})}^{2} + 2 q_{1} f^{*} \cosh (\frac{3}{2} q_{2} \frac{σ_{H}}{σ_{Y}}) - (1 + q_{3} f^{*^{2}}) = 0

(14)

where

σ_{v}

represents the Von Mises equivalent stress,

σ_{Y}

denotes the matrix material yield stress, and

σ_{H}

refers to the hydrostatic component.

q_{1}

q_{2}

and

q_{3}

are material constants.

f^{*}

represents the effective volume void fraction, capturing the effects of void coalescence.

The evolution of voids is mathematically defined as follows:

{\dot{f} = \dot{f}}_{g r o w t h} + {\dot{f}}_{n u c l e a t i o n}

(15)

where

{\dot{f}}_{g r o w t h}

and

{\dot{f}}_{n u c l e a t i o n}

are determined through equations (16) and (17).

{\dot{f}}_{g r o w t h} = (1 - f) {\dot{ε}}_{k k}^{p l}

(16)

{\dot{f}}_{n u c l e a t i o n} = \frac{f_{N}}{S_{N} \sqrt{2 π}} {\dot{\bar{ε}}}^{p l} e^{{(- \frac{1}{2} \frac{{\bar{ε}}^{p l} ε_{N}}{S_{N}})}^{2}}

(17)

The volume dilatation rate is denoted by

{\dot{ε}}_{k k}^{p l}

, whereas

{\bar{ε}}^{p l}

represents the equivalent plastic strain, and

{\dot{\bar{ε}}}^{p l}

is the rate of equivalent plastic strain. The standard deviation is represented by

S_{N}

The effective volume void fraction,

f^{*}

accounts for the micro-mechanics at work, including the presence of micro-voids the growth of voids, and the coalescence of neighboring voids leading up to the fracture at the macroscopic level [111].

f^{*}

is determined as per the equation (18):

f^{*} (f) = \{\begin{matrix} f \\ f_{C} + K (f - f_{C}) \end{matrix}\} \begin{matrix} f \leq f_{C} \\ f > f_{C} \end{matrix}

(18)

where

K = \frac{f_{u - f_{C}}^{*}}{f_{f} - f_{C}}

In this context, the void volume fraction, critical void volume fraction and void volume fraction at macroscopic failure are denoted by

f

f_{c}

and

f_{f}

, respectively. The modified void volume fraction at macroscopic failure is represented by

f_{u}^{*} = f^{*} (f_{f})

. The calibration process for the GTN model requires determination of a total of eight parameters, where a few parameters can be found in existing literature (

q_{1}

q_{2}

and

S_{N}

) [218]. Moreover,

f_{f}

is frequently assumed as 10% [236]. In the study conducted by Cui et al.[237],

f_{f}

was computed through observations of the fracture morphology using SEM technology. Employing response surface methodology, five other parameters (

f_{0}

f_{N}

f_{c}

ε_{N}

S_{N}

) were determined. In addition, Achineethongkham and Uthaisangsuk [238] identified damage model parameters through the use of metallographic analyses, local strain measurement and representative volume element (RVE) simulations.

The analysis of local crack initiation in Nakazima forming process on DP600 and TRIP600 steel was carried out by Uthaisangsuk et al. [235] through the application of the GTN damage model. Their findings indicated that this microstructure-based damage model provided satisfactory predictions of the fracture behavior of both multiphase steels in Nakazima stretching tests. Nevertheless, the influence of stress triaxiality on the fracture behavior has to be taken into account due to the void formation mechanism, which might be described by modifying model parameters [235]. Doig and Roll [218] stated that the GTN model is appropriate to treat real industrial cases. In their study, the GTN model accurately predicted the localization of cracks in a cross die part. However, similar to the FLD criterion, the coupled model overestimated the drawing depth. As opposed to the work conducted by Cui et al. [237], whom observed that the fracture position and limit strains in various loading conditions of a bulge test were almost identical between experimental and numerical simulation results of a DP590 steel. Furthermore, the GTN model was employed for evaluating the forming behavior in two-stage forming processes, as concluded by Achineethongkham et al. [238]. The authors concluded that the GTN model provided reliable predictions for the fracture states of samples subjected to NLSPs.

8. Conclusions

The shift towards the employment of AHSS in BiW components has been leading to forming challenges almost never encountered when forming conventional mild steels. Shear cracks, edge cracks and surface cracks are more frequently noticed within sheet metal forming industrial operations. The conventional FLD is unable to accurately model and account for these fracture occurrences.

The state of the art presented in this paper addresses the current trends to improve the forming behavior and fracture modelling accuracy of sheet metal forming processes. The FLD limitations and main drawbacks dealing with fracture occurrences are analyzed as well as the academic directions followed to overcome those limitations. The GFLC is an upgrade to the conventional FLD, currently implemented in AutoForm R10, aiming to improve non-linear strain paths modeling accuracy. However, further enhancements are required to deal with fracture modelling. Material modelling is significant for the forming behavior accuracy. Thus, a comprehensive review on material modelling is given. The directions followed by academic community with respect to material characterization methods and techniques is presented. Further improvements particularly for pure shear stress state are required in order to develop a standardized specimen. Furthermore, damage and fracture models are subjected to analysis.

The formability evaluation should be attained by the analysis of failure on account of through-thickness necks and splits as well as direct fracture. The consideration of a central framework is necessary to account for all relevant phenomenological outcomes. In this context, the advanced uncoupled phenomenological models are a promising approach. In order to garner industrial acceptance, the simplicity of use and implementation are favored. GISSMO model as well as ‘modular’ models have also been shown to provide accurate results. Even though, the analysis of relevant case studies, covering a wide range of stress states and complex strain paths is required to further enhance fracture modelling accuracy of such models when applied on AHSS in real industrial applications.

Funding

This research was funded by Fundação para a Ciência e a Tecnologia (FCT), grant number 2022.13884.BDANA.

Data Availability Statement

Not applicable.

Acknowledgments

Rui Pereira is grateful to the FCT for the Ph.D. grant 2022.13884.BDANA.

Conflicts of Interest

The authors declare no conflict of interest.

References

European Environment Agency., Trends and projections in Europe 2023. LU: Publications Office, 2023. Accessed: Feb. 12, 2024. [Online]. Available: https://data.europa.eu/doi/10.2800/595102.
“Environmental Issues Facing Future Of European Car Industry Marketing Essay.” Accessed: Mar. 23, 2023. [Online]. Available: https://www.ukessays.com/essays/marketing/environmental-issues-facing-future-of-european-car-industry-marketing-essay.php.
J. C. Kelly, J. L. Sullivan, A. Burnham, and A. Elgowainy, “Impacts of Vehicle Weight Reduction via Material Substitution on Life-Cycle Greenhouse Gas Emissions,” Environ. Sci. Technol., vol. 49, no. 20, pp. 12535–12542, Oct. 2015. [CrossRef]
W. Zhang and J. Xu, “Advanced lightweight materials for Automobiles: A review,” Materials & Design, vol. 221, p. 110994, Sep. 2022. [CrossRef]
A. Giampieri, J. Ling-Chin, Z. Ma, A. Smallbone, and A. P. Roskilly, “A review of the current automotive manufacturing practice from an energy perspective,” Applied Energy, vol. 261, p. 114074, Mar. 2020. [CrossRef]
M. Tisza and I. Czinege, “Comparative study of the application of steels and aluminium in lightweight production of automotive parts,” International Journal of Lightweight Materials and Manufacture, vol. 1, no. 4, pp. 229–238, Dec. 2018. [CrossRef]
P. Khedkar, R. Motagi, P. Mahajan, and G. Makwana, “A Review on Advance High Strength Steels,” Int. J. Curr. Eng., vol. 6, pp. 240–243, Oct. 2016.
J.-H. Schmitt and T. Iung, “New developments of advanced high-strength steels for automotive applications,” Comptes Rendus Physique, vol. 19, no. 8, pp. 641–656, Dec. 2018. [CrossRef]
R. Kuziak, R. Kawalla, and S. Waengler, “Advanced high strength steels for automotive industry,” Archives of Civil and Mechanical Engineering, vol. 8, no. 2, pp. 103–117, Jan. 2008. [CrossRef]
“banana diagram Archives,” AHSS Guidelines. Accessed: Feb. 12, 2024. [Online]. Available: https://ahssinsights.org/tag/banana-diagram/.
“WorldAutoSteel,” WorldAutoSteel. Accessed: Feb. 12, 2024. [Online]. Available: https://www.worldautosteel.org/.
L. Marretta, “Sheet Stamping Processes Design: Optimization Methodologies for Robust and Environmental Conscious Decisions.,” PhD Thesis, Università Degli Studi di Palermo, Palermo, 2011. [Online]. Available: https://core.ac.uk/download/pdf/53296994.pdf.
“A Meaningful Review of Metal Stamping and Safety | MCR Safety Info Blog.” Accessed: Mar. 23, 2023. [Online]. Available: https://www.mcrsafety.com/en/blog/2019/august/metal-stamping.
J. R. Fekete, “Manufacturing Challenges in Stamping and Fabrication of Components from Advanced High Strength Steel,” Int. Symposium Niobum Microalloyed Sheet Steel Aut. Appl., pp. 107–115, 2006.
T. Gomes, F. J. G. Silva, and R. D. G. S. Campilho, “Reducing the Simulation Cost on Dual-phase Steel Stamping Process,” Procedia Manufacturing, vol. 11, pp. 474–481, 2017. [CrossRef]
E.-M. Lee, D.-S. Shim, J.-Y. Son, G.-Y. Baek, H.-S. Yoon, and K.-B. Ro, “Study on design of progressive dies for manufacture of automobile structural member using DP980 advanced high strength steel,” J Mech Sci Technol, vol. 30, no. 2, pp. 853–864, Feb. 2016. [CrossRef]
H. Shawn Cheng, J. Cao, and Z. C. Xia, “An accelerated springback compensation method,” International Journal of Mechanical Sciences, vol. 49, no. 3, pp. 267–279, Mar. 2007. [CrossRef]
W. Gan and R. H. Wagoner, “Die design method for sheet springback,” International Journal of Mechanical Sciences, vol. 46, no. 7, pp. 1097–1113, Jul. 2004. [CrossRef]
C. Jiao-Jiao, C. Jian-Guo, Z. Qiu-Fang, L. Jiang, Y. Ning, and Z. Rong-guo, “A novel approach to springback control of high-strength steel in cold roll forming,” Int J Adv Manuf Technol, vol. 107, no. 3–4, pp. 1793–1804, Mar. 2020. [CrossRef]
N. Manopulo and B. Carleer, “On the way towards a comprehensive failure modelling for industrial sheet metal stamping processes,” IOP Conf. Ser.: Mater. Sci. Eng., vol. 651, no. 1, p. 012004, Nov. 2019. [CrossRef]
E. Billur, “Challenges in Forming Advanced High Strength Steels,” 2010. Accessed: Mar. 23, 2023. [Online]. Available: https://www.semanticscholar.org/paper/Challenges-in-Forming-Advanced-High-Strength-Steels-Billur/cacd2133b77c30a7a0722336018a2313bd5883bf.
Q. Hu, F. Zhang, X. Li, and J. Chen, “Overview on the Prediction Models for Sheet Metal Forming Failure: Necking and Ductile Fracture,” Acta Mech. Solida Sin., vol. 31, no. 3, pp. 259–289, Jun. 2018. [CrossRef]
V. Lakkannavar and K. Kattimani, “Modelling and Failure Analysis In Sheet Metal Forming Process using Cae,” International Journal of Engineering Research & Technology, vol. 3, no. 7, Jul. 2014. [CrossRef]
“Complex phase (CP) steels for the highest hole expansion ratios,” SSAB. Accessed: Apr. 04, 2023. [Online]. Available: https://www.ssab.com/en/brands-and-products/docol/automotive-steel-grades/complex-phase-steel.
“Dual phase (DP) steel: excellent ductility and energy absorption,” SSAB. Accessed: Apr. 04, 2023. [Online]. Available: https://www.ssab.com/en/brands-and-products/docol/automotive-steel-grades/dual-phase-steel.
“Martensitic steel: excellent formability-to-strength ratio,” SSAB. Accessed: Apr. 04, 2023. [Online]. Available: https://www.ssab.com/en/brands-and-products/docol/automotive-steel-grades/martensitic-steel.
“TRIP steels.” Accessed: Apr. 04, 2023. [Online]. Available: https://automotive.arcelormittal.com/products/flat/first_gen_AHSS/TRIP.
O. Björklund, A. Govik, and L. Nilsson, “Prediction of fracture in a dual-phase steel subjected to non-linear straining,” Journal of Materials Processing Technology, vol. 214, no. 11, pp. 2748–2758, Nov. 2014. [CrossRef]
A. E. Tekkaya, P.-O. Bouchard, S. Bruschi, and C. C. Tasan, “Damage in metal forming,” CIRP Annals, vol. 69, no. 2, pp. 600–623, 2020. [CrossRef]
K. Mattiasson, J. Jergéus, and P. DuBois, “On the prediction of failure in metal sheets with special reference to strain path dependence,” International Journal of Mechanical Sciences, vol. 88, pp. 175–191, Nov. 2014. [CrossRef]
S. P. S. S. Sivam, K. Saravanan, N. Pradeep, A. S. Jain, and S. G. S. and N. Vishaal, “OVERVIEW AND ASSESSMENT OF FORMABILITY EFFECT OF MATERIAL PROPERTIES OF SHEET METAL - A SHORT COMMUNICATION,” Journal of Industrial Pollution Control, pp. 1732–1738, Dec. 2017.
B. Hou, Y. Huang, M. Ding, and H. Dong, “Effect of temperature and strain rate fluctuation on forming limit curve of 5083 Al-Mg alloy sheet,” Advances in Mechanical Engineering, vol. 14, no. 6, p. 168781322211074, Jun. 2022. [CrossRef]
S. Sattarpanah Karganroudi et al., “Insight into the Influence of Punch Velocity and Thickness on Forming Limit Diagrams of AA 6061 Sheets—Numerical and Experimental Analyses,” Metals, vol. 11, no. 12, p. 2010, Dec. 2021. [CrossRef]
M. M. Kasaei and M. C. Oliveira, “Influence of the contact with friction on the deformation behavior of advanced high strength steels in the Nakajima test,” The Journal of Strain Analysis for Engineering Design, vol. 57, no. 3, pp. 193–207, Apr. 2022. [CrossRef]
R. Liu, L. Sun, X. Wang, L. Lin, L. Zhang, and J. Lin, “Strain Rate Effect on Forming Limit Diagram for Advanced High Strength Steels,” SAE Int. J. Mater. Manf., vol. 7, no. 3, pp. 583–587, Apr. 2014. [CrossRef]
14:00-17:00, “ISO 12004-2:2008,” ISO. Accessed: Mar. 23, 2023. [Online]. Available: https://www.iso.org/standard/43621.html.
K. Nakazima, T. Kikuma, and K. Hasuka, “Study on the Formability of Steel Sheets,” Technical Research Institute, Yawata Works, 264, 1968.
Z. Marciniak and K. Kuczyński, “Limit strains in the processes of stretch-forming sheet metal,” International Journal of Mechanical Sciences, vol. 9, no. 9, pp. 609–620, Sep. 1967. [CrossRef]
R. Amaral, A. D. Santos, C. de S. José, and S. Miranda, “Formability prediction for AHSS materials using damage models,” J. Phys.: Conf. Ser., vol. 843, p. 012018, May 2017. [CrossRef]
T. Bergs, M. Nick, D. Trauth, and F. Klocke, “Damage Evolution in Nakajima Tests of DP800 Dual Phase Steel,” IOP Conf. Ser.: Mater. Sci. Eng., vol. 418, p. 012048, Sep. 2018. [CrossRef]
Z. Shao et al., “Experimental investigation of forming limit curves and deformation features in warm forming of an aluminium alloy,” Proceedings of the Institution of Mechanical Engineers, Part B: Journal of Engineering Manufacture, vol. 232, no. 3, pp. 465–474, Feb. 2018. [CrossRef]
S. K. Paul, “Controlling factors of forming limit curve: A review,” Advances in Industrial and Manufacturing Engineering, vol. 2, p. 100033, May 2021. [CrossRef]
Y. Hou et al., “A Review of Characterization and Modelling Approaches for Sheet Metal Forming of Lightweight Metallic Materials,” Materials, vol. 16, no. 2, p. 836, Jan. 2023. [CrossRef]
S. D. Kumar, T. R. Amjith, and C. Anjaneyulu, “Forming Limit Diagram Generation of Aluminum Alloy AA2014 Using Nakazima Test Simulation Tool,” Procedia Technology, vol. 24, pp. 386–393, 2016. [CrossRef]
A. Martínez-Donaire, C. Vallellano, D. Morales-Palma, and F. J. García-Lomas, “Experimental Detection of Necking in Stretch-Bending Conditions: A Critical Review and New Methodology,” Steel Research International, vol. 81, pp. 785–788, Sep. 2010.
L. Zhang, J. Lin, L. Sun, C. Wang, and L. Wang, “A New Method for Determination of Forming Limit Diagram Based on Digital Image Correlation,” presented at the SAE 2013 World Congress & Exhibition, Apr. 2013, pp. 2013-01–1421. [CrossRef]
M. Merklein, A. Kuppert, and M. Geiger, “Time dependent determination of forming limit diagrams,” CIRP Annals, vol. 59, no. 1, pp. 295–298, 2010. [CrossRef]
R. A. Iquilio et al., “Novel experimental method to determine the limit strain by means of thickness variation,” International Journal of Mechanical Sciences, vol. 153–154, pp. 208–218, Apr. 2019. [CrossRef]
L. Huang and M. Shi, “Determination of the Forming Limit Curve Using Digital Image Correlation - Comparison of Different Approaches to Pinpoint the Onset of Localized Necking,” presented at the WCXTM 17: SAE World Congress Experience, Mar. 2017, pp. 2017-01–0301. [CrossRef]
W. Volk and P. Hora, “New algorithm for a robust user-independent evaluation of beginning instability for the experimental FLC determination,” Int J Mater Form, vol. 4, no. 3, pp. 339–346, Sep. 2011. [CrossRef]
W. Hotz, M. Merklein, A. Kuppert, H. Friebe, and M. Klein, “Time Dependent FLC Determination Comparison of Different Algorithms to Detect the Onset of Unstable Necking before Fracture,” KEM, vol. 549, pp. 397–404, Apr. 2013. [CrossRef]
J. Min, T. B. Stoughton, J. E. Carsley, and J. Lin, “A Method of Detecting the Onset of Localized Necking Based on Surface Geometry Measurements,” Exp Mech, vol. 57, no. 4, pp. 521–535, Apr. 2017. [CrossRef]
A. J. Martínez-Donaire, F. J. García-Lomas, and C. Vallellano, “New approaches to detect the onset of localised necking in sheets under through-thickness strain gradients,” Materials & Design, vol. 57, pp. 135–145, May 2014. [CrossRef]
F. Ozturk, M. Dilmec, M. Turkoz, R. E. Ece, and H. S. Halkaci, “Grid Marking and Measurement Methods for Sheet Metal Formability,” presented at the 5th International Conference and Exhibition on Design and Production of MACHINES and DIES/MOLDS, Kusadasi, Turkey, Jun. 2009, pp. 41–49. Accessed: Mar. 29, 2023. [Online]. Available: https://www.researchgate.net/publication/265982204_Grid_Marking_and_Measurement_Methods_for_Sheet_Metal_Formability.
K. Mäntyjärvi, J. Tulonen, T. Saarnivuo, J. Porter, and J. A. Karjalainen, “Grid patterns by laser for forming strain analysis,” Int J Mater Form, vol. 1, no. S1, pp. 249–252, Apr. 2008. [CrossRef]
S. Guk, M. Preiß, and R. Kawalla, “Metal Formability Interactions in Laser Marking for Creating of Grid Patterns for Forming Strain Analysis of High Strength Steels,” KEM, vol. 746, pp. 92–98, Jul. 2017. [CrossRef]
R. A. Yildiz and S. Yilmaz, “The verification of strains obtained by grid measurements using digital image processing for sheet metal formability,” The Journal of Strain Analysis for Engineering Design, vol. 52, no. 8, pp. 506–514, Nov. 2017. [CrossRef]
D. C. Li, J. Liang, H. Hu, Z. Z. Tang, X. Guo, and L. G. Li, “Strain Measurement for Sheet Metal Forming Based on Close Range Photogrammetry,” AMM, vol. 475–476, pp. 148–155, Dec. 2013. [CrossRef]
P. Wankhede and K. Suresh, “A review on the evaluation of formability in sheet metal forming,” Advances in Materials and Processing Technologies, vol. 6, no. 2, pp. 458–485, Apr. 2020. [CrossRef]
H. Li, G. Li, G. Gao, W. Zhang, and X. Wu, “A formability evaluation method for sheet metal forming with non-linear strain path change,” Int J Mater Form, vol. 11, no. 2, pp. 199–211, Mar. 2018. [CrossRef]
K. Bandyopadhyay, S. Basak, S. K. Panda, and P. Saha, “Use of stress based forming limit diagram to predict formability in two-stage forming of tailor welded blanks,” Materials & Design, vol. 67, pp. 558–570, Feb. 2015. [CrossRef]
K. Sajun Prasad, S. K. Panda, S. K. Kar, M. Sen, S. V. S. N. Murty, and S. C. Sharma, “Microstructures, Forming Limit and Failure Analyses of Inconel 718 Sheets for Fabrication of Aerospace Components,” J. of Materi Eng and Perform, vol. 26, no. 4, pp. 1513–1530, Apr. 2017. [CrossRef]
P. Wankhede, N. G. Narayanaswamy, S. Kurra, and A. Priyadarshini, “A portable device for single point strain analysis in sheet metal forming processes,” HardwareX, vol. 12, p. e00371, Oct. 2022. [CrossRef]
E28 Committee, “Test Method for Determining Forming Limit Curves,” ASTM International. [CrossRef]
M. A. Iadicola, “Augmented use of standard mechanical testing measurements for sheet metal forming: Digital image correlation for localized necking,” presented at the NUMISHEET 2014: The 9th International Conference and Workshop on Numerical Simulation of 3D Sheet Metal Forming Processes: Part A Benchmark Problems and Results and Part B General Papers, Melbourne, Australia, 2013, pp. 614–619. [CrossRef]
B.-Q. Shi and J. Liang, “Circular grid pattern based surface strain measurement system for sheet metal forming,” Optics and Lasers in Engineering, vol. 50, no. 9, pp. 1186–1195, Sep. 2012. [CrossRef]
J. Blaber, B. Adair, and A. Antoniou, “Ncorr: Open-Source 2D Digital Image Correlation Matlab Software,” Exp Mech, vol. 55, no. 6, pp. 1105–1122, Jul. 2015. [CrossRef]
J. Yang and K. Bhattacharya, “Augmented Lagrangian Digital Image Correlation,” Exp Mech, vol. 59, no. 2, pp. 187–205, Feb. 2019. [CrossRef]
V. Belloni, R. Ravanelli, A. Nascetti, M. Di Rita, D. Mattei, and M. Crespi, “py2DIC: A New Free and Open Source Software for Displacement and Strain Measurements in the Field of Experimental Mechanics,” Sensors, vol. 19, no. 18, p. 3832, Sep. 2019. [CrossRef]
S. N. Olufsen, M. E. Andersen, and E. Fagerholt, “μ DIC: An open-source toolkit for digital image correlation,” SoftwareX, vol. 11, p. 100391, Jan. 2020. [CrossRef]
D. Solav, K. M. Moerman, A. M. Jaeger, K. Genovese, and H. M. Herr, “MultiDIC: An Open-Source Toolbox for Multi-View 3D Digital Image Correlation,” IEEE Access, vol. 6, pp. 30520–30535, 2018. [CrossRef]
P. Farahnak, M. Urbánek, P. Konopík, and J. Džugan, “Influence of thickness reduction on forming limits of mild steel DC01,” Int J Mater Form, vol. 13, no. 3, pp. 371–381, May 2020. [CrossRef]
P. Farahnak, M. Urbanek, and J. Džugan, “Investigation Study on Determination of Fracture Strain and Fracture Forming Limit Curve Using Different Experimental and Numerical Methods,” J. Phys.: Conf. Ser., vol. 896, p. 012082, Sep. 2017. [CrossRef]
J. Min, T. B. Stoughton, J. E. Carsley, and J. Lin, “Comparison of DIC Methods of Determining Forming Limit Strains,” Procedia Manufacturing, vol. 7, pp. 668–674, 2017. [CrossRef]
I. Gkolfinopoulos and N. Chijiwa, “Determination of Johnson–Cook Material and Failure Model Constants for High-Tensile-Strength Tendon Steel in Post-Tensioned Concrete Members,” Applied Sciences, vol. 12, no. 15, p. 7774, Aug. 2022. [CrossRef]
C. Jaremenko, X. Huang, E. Affronti, M. Merklein, and A. Maier, “Sheet metal forming limits as classification problem,” in 2017 Fifteenth IAPR International Conference on Machine Vision Applications (MVA), Nagoya, Japan: IEEE, May 2017, pp. 113–116. [CrossRef]
B.-A. Behrens, D. Rosenbusch, H. Wester, and M. Dykiert, “Comparison of different testing approaches to describe the fracture behaviour of AHSS sheets using experimental and numerical investigations,” IOP Conf. Ser.: Mater. Sci. Eng., vol. 1157, no. 1, p. 012059, Jun. 2021. [CrossRef]
K. Saxena, K. Drotleff, and J. Mukhopadhyay, “Design of New Punch Geometries for Generation of Non-Linear Strain Paths and Formability Evaluation,” Light Metal Age, vol. December, p. 24, Dec. 2015.
J. He, D. Zeng, X. Zhu, Z. Cedric Xia, and S. Li, “Effect of nonlinear strain paths on forming limits under isotropic and anisotropic hardening,” International Journal of Solids and Structures, vol. 51, no. 2, pp. 402–415, Jan. 2014. [CrossRef]
M. S. Wi, S. Y. Lee, and F. Barlat, “Non-linear strain path experiment and modeling for very high strength material,” IOP Conf. Ser.: Mater. Sci. Eng., vol. 651, no. 1, p. 012005, Nov. 2019. [CrossRef]
A. B. D. Rocha and J. M. Jalinier, “Plastic instability of sheet metals under simple and complex strain paths.,” ISIJ Int., vol. 24, no. 2, pp. 132–140, 1984. [CrossRef]
S. Panich, K. Chongbunwatana, and M. Kamonrattanapisud, “Formability prediction of advanced high-strength steel sheets by means of combined experimental and numerical approaches,” Procedia Manufacturing, vol. 29, pp. 528–535, 2019. [CrossRef]
N. Manopulo, P. Hora, P. Peters, M. Gorji, and F. Barlat, “An extended Modified Maximum Force Criterion for the prediction of localized necking under non-proportional loading,” International Journal of Plasticity, vol. 75, pp. 189–203, Dec. 2015. [CrossRef]
W. Volk, H. Hoffmann, J. Suh, and J. Kim, “Failure prediction for nonlinear strain paths in sheet metal forming,” CIRP Annals, vol. 61, no. 1, pp. 259–262, 2012. [CrossRef]
K. Chung, H. Kim, and C. Lee, “Forming limit criterion for ductile anisotropic sheets as a material property and its deformation path insensitivity. Part I: Deformation path insensitive formula based on theoretical models,” International Journal of Plasticity, vol. 58, pp. 3–34, Jul. 2014. [CrossRef]
K. Hickey, “Shear Fracture,” AHSS Guidelines. Accessed: Jun. 05, 2023. [Online]. Available: https://ahssinsights.org/forming/formability/shear-fracture/.
M. Luo et al., “Numerical Analysis of AHSS Fracture in a Stretch-bending Test,” presented at the NUMIFORM 2010: Proceedings of the 10th International Conference on Numerical Methods in Industrial Forming Processes Dedicated to Professor O. C. Zienkiewicz (1921–2009), Pohang (Republic of Korea), 2010, pp. 455–463. [CrossRef]
S. Huang, Y. Zhao, and C. He, “Stamping failure analysis of advanced high strength steel sheet based on non-uniform local deformation through thickness,” presented at the NUMISHEET 2014: The 9th International Conference and Workshop on Numerical Simulation of 3D Sheet Metal Forming Processes: Part A Benchmark Problems and Results and Part B General Papers, Melbourne, Australia, 2013, pp. 583–586. [CrossRef]
Y. Li, M. Luo, J. Gerlach, and T. Wierzbicki, “Prediction of shear-induced fracture in sheet metal forming,” Journal of Materials Processing Technology, vol. 210, no. 14, pp. 1858–1869, Nov. 2010. [CrossRef]
T. Wierzbicki, Y. Bao, Y.-W. Lee, and Y. Bai, “Calibration and evaluation of seven fracture models,” International Journal of Mechanical Sciences, vol. 47, no. 4–5, pp. 719–743, Apr. 2005. [CrossRef]
J. P. Magrinho, M. B. Silva, L. Reis, and P. A. F. Martins, “Formability Limits, Fractography and Fracture Toughness in Sheet Metal Forming,” Materials, vol. 12, no. 9, p. 1493, May 2019. [CrossRef]
J. P. Magrinho, M. B. Silva, and P. A. F. Martins, “Experimental determination of the fracture forming limits in metal forming,” Discov Mechanical Engineering, vol. 2, no. 1, p. 7, May 2023. [CrossRef]
C. C. Roth and D. Mohr, “Determining the strain to fracture for simple shear for a wide range of sheet metals,” International Journal of Mechanical Sciences, vol. 149, pp. 224–240, Dec. 2018. [CrossRef]
D. N. Manopulo and AutoForm, “Advanced Formability Analysis: Moving Beyond the Limitations of the Traditional FLD for an Accurate and Streamlined Formability Analysis - FormingWorld.” Accessed: Mar. 28, 2023. [Online]. Available: https://formingworld.com/advanced-formability-analysis-fld/.
S. Nasheralahkami, W. Zhou, and S. Golovashchenko, “Study of Sheared Edge Formability of Ultra-High Strength DP980 Sheet Metal Blanks,” Journal of Manufacturing Science and Engineering, vol. 141, no. 9, p. 091009, Sep. 2019. [CrossRef]
T. Matsuno, M. Mizumura, A. Seto, and M. Suehiro, “Improvement in Hole Expansion Ratio by Chamfered Die Edge,” Journal of the JSTP, vol. 54, no. 627, pp. 353–357, 2013. [CrossRef]
H.-C. Shih, C.-K. Hsiung, and B. Wendt, “Optimal Production Trimming Process for AHSS Sheared Edge Stretchability Improvement,” presented at the SAE 2014 World Congress & Exhibition, Apr. 2014, pp. 2014-01–0994. [CrossRef]
D. Frómeta, M. Tedesco, J. Calvo, A. Lara, S. Molas, and D. Casellas, “Assessing edge cracking resistance in AHSS automotive parts by the Essential Work of Fracture methodology,” J. Phys.: Conf. Ser., vol. 896, p. 012102, Sep. 2017. [CrossRef]
M. Feistle, A. Kindsmüller, I. Pätzold, R. Golle, and W. Volk, “Influence of Sheet Metal Pre-forming on Edge Crack Sensitivity using an AHSS Steel Grade,” Int J Mater Form, vol. 15, no. 4, p. 50, Jul. 2022. [CrossRef]
F. M. Neuhauser, O. R. Terrazas, N. Manopulo, P. Hora, and C. J. Van Tyne, “Stretch bending - the plane within the sheet where strains reach the forming limit curve,” IOP Conf. Ser.: Mater. Sci. Eng., vol. 159, p. 012011, Nov. 2016. [CrossRef]
F. M. Neuhauser, O. Terrazas, N. Manopulo, P. Hora, and C. Van Tyne, “The bending dependency of forming limit diagrams,” Int J Mater Form, vol. 12, no. 5, pp. 815–825, Sep. 2019. [CrossRef]
B. S. Levy and C. J. Van Tyne, “Predicting breakage on a die radius with a straight bend axis during sheet forming,” Journal of Materials Processing Technology, vol. 209, no. 4, pp. 2038–2046, Feb. 2009. [CrossRef]
D. Kitting, A. Ofenheimer, H. Pauli, and E. T. Till, “A Phenomenological Concept to Predict Formability in Stretch-Bending Forming Operations,” Int J Mater Form, vol. 3, no. S1, pp. 1163–1166, Apr. 2010. [CrossRef]
D. Kitting, A. Ofenheimer, H. Pauli, and E. T. Till, “Experimental Characterization of Stretch-Bending Formability of AHSS Sheets,” presented at the THE 14TH INTERNATIONAL ESAFORM CONFERENCE ON MATERIAL FORMING: ESAFORM 2011, Belfast, (United Kingdom), 2011, pp. 1589–1594. [CrossRef]
M. Borrego, D. Morales-Palma, A. J. Martínez-Donaire, G. Centeno, and C. Vallellano, “Analysis of formability in conventional hole flanging of AA7075-O sheets: punch edge radius effect and limitations of the FLC,” Int J Mater Form, vol. 13, no. 2, pp. 303–316, Mar. 2020. [CrossRef]
S. Jadhav, M. Schoiswohl, and B. Buchmayr, “Applications of Finite Element Simulation in the Development of Advanced Sheet Metal Forming Processes,” Berg Huettenmaenn Monatsh, vol. 163, no. 3, pp. 109–118, Mar. 2018. [CrossRef]
K. Chen and J. P. Lin, “Material Modeling and Correlative Mechanical Testing on AHSS Sheet Forming Simulation,” AMR, vol. 337, pp. 198–202, Sep. 2011. [CrossRef]
D. Banabic, “Yield criteria for isotropic materials,” in Sheet Metal Forming Processes, Berlin, Heidelberg: Springer Berlin Heidelberg, 2010. [CrossRef]
CIRP - The International Academy for Production Engineering and L. Laperrière, Eds., CIRP Encyclopedia of production engineering. Volume 1: A-H, Second edition. Berlin [Heidelberg]: Springer, 2019.
F. Yoshida, H. Hamasaki, and T. Uemori, “A user-friendly 3D yield function to describe anisotropy of steel sheets,” International Journal of Plasticity, vol. 45, pp. 119–139, Jun. 2013. [CrossRef]
A. Eriksson, “Non-linear strain paths in sheet metal forming,” masterThesis, Blekinge Institute of Technology, Karlskrona, 2021. [Online]. Available: https://www.diva-portal.org/smash/get/diva2:1576277/FULLTEXT01.pdf.
D. A. Güner and T. P. M. AutoForm, “Material Matters: Sheet metal plasticity visualized (part 1 of 2) - FormingWorld.” Accessed: Mar. 23, 2023. [Online]. Available: https://formingworld.com/sheet-metal-plasticity-visualized-part-1-of-2/.
Z. Mu, J. Zhao, Q. Meng, Y. Zhang, and G. Yu, “Limitation analysis of the Hill48 yield model and establishment of its modified model for planar plastic anisotropy,” Journal of Materials Processing Technology, vol. 299, p. 117380, Jan. 2022. [CrossRef]
H. Tresca, “On the yield of solids at high pressures,” Comptes Rendus Academie des Sciences, vol. 59, p. 754, 1864.
M. Huber, “Przyczynek do podstaw wytorymalosci,” Czasop Techn, vol. 22, p. 81, 1904.
H. Hencky, “Zur Theorie plastischer Deformationen und der hierdurch im Material hervorgerufenen Nachspannungen,” Z. angew. Math. Mech., vol. 4, no. 4, pp. 323–334, 1924. [CrossRef]
R. Mises, “Mechanics of solids in plastic state (Almanca), Göttinger Nachrichten Math,” Phys. Klasse, p. 582, 1913.
D. C. Drucker, “Relation of Experiments to Mathematical Theories of Plasticity,” Journal of Applied Mechanics, vol. 16, no. 4, pp. 349–357, Dec. 1949. [CrossRef]
A. V. Hershey, “The Plasticity of an Isotropic Aggregate of Anisotropic Face-Centered Cubic Crystals,” Journal of Applied Mechanics, vol. 21, no. 3, pp. 241–249, Sep. 1954. [CrossRef]
R. Hill, “A theory of the yielding and plastic flow of anisotropic metals,” Proc. R. Soc. Lond. A, vol. 193, no. 1033, pp. 281–297, May 1948. [CrossRef]
R. Hill, “Theoretical plasticity of textured aggregates,” Math. Proc. Camb. Phil. Soc., vol. 85, no. 1, pp. 179–191, Jan. 1979. [CrossRef]
R. Hill, “Constitutive modelling of orthotropic plasticity in sheet metals,” Journal of the Mechanics and Physics of Solids, vol. 38, no. 3, pp. 405–417, Jan. 1990. [CrossRef]
R. Hill, “A user-friendly theory of orthotropic plasticity in sheet metals,” International Journal of Mechanical Sciences, vol. 35, no. 1, pp. 19–25, Jan. 1993. [CrossRef]
F. Barlat et al., “Plane stress yield function for aluminum alloy sheets—part 1: theory,” International Journal of Plasticity, vol. 19, no. 9, pp. 1297–1319, Sep. 2003. [CrossRef]
H. Aretz, “General Orthotropic Yield Functions Based on Linear Stress Deviator Transformations,” in AIP Conference Proceedings, Columbus, Ohio (USA): AIP, 2004, pp. 147–156. [CrossRef]
F. Barlat et al., “Constitutive modeling for aluminium sheet forming simulations,” presented at the Plastic and Viscoplastic Response of Materials and Metal Forming, Proc. 8th Intern. Symposium on Plasticity and its Current Applications, Whistler, Canada, 2000, pp. 591–593.
F. Barlat, H. Aretz, J. W. Yoon, M. E. Karabin, J. C. Brem, and R. E. Dick, “Linear transfomation-based anisotropic yield functions,” International Journal of Plasticity, vol. 21, no. 5, pp. 1009–1039, May 2005. [CrossRef]
D. Banabic, “An improved analytical description of orthotropy in metallic sheets,” International Journal of Plasticity, vol. 21, no. 3, pp. 493–512, Mar. 2005. [CrossRef]
D. Banabic, “Yield criterion for orthotropic sheet metals,” presented at the Proc. 8th Intern. Conf. Metal Working-Metal Working 2000, 2000, pp. 755–761.
O. Cazacu and F. Barlat, “Generalization of Drucker’s yield criterion to orthotropy,” Mathematics and Mechanics of Solids, vol. 6, no. 6, pp. 613–630, 2001.
M. Abspoel, M. E. Scholting, M. Lansbergen, Y. An, and H. Vegter, “A new method for predicting advanced yield criteria input parameters from mechanical properties,” Journal of Materials Processing Technology, vol. 248, pp. 161–177, Oct. 2017. [CrossRef]
H. Vegter and A. H. Van Den Boogaard, “A plane stress yield function for anisotropic sheet material by interpolation of biaxial stress states,” International Journal of Plasticity, vol. 22, no. 3, pp. 557–580, Mar. 2006. [CrossRef]
J. E. Gutierrez, J. Noder, and C. Butcher, “Experimental Characterization and Deterministic Prediction of In-Plane Formability of 3rd Generation Advanced High Strength Steels,” Metals, vol. 10, no. 7, p. 902, Jul. 2020. [CrossRef]
M. Gösling, “Influence of Yield Condition on the Accuracy of Earing Prediction for Steel Sheets,” J. Phys.: Conf. Ser., vol. 734, p. 032045, Aug. 2016. [CrossRef]
Z. Cai, K. Diao, X. Wu, and M. Wan, “Constitutive modeling of evolving plasticity in high strength steel sheets,” International Journal of Mechanical Sciences, vol. 107, pp. 43–57, Mar. 2016. [CrossRef]
C. Cheng, M. Wan, X. D. Wu, Z. Y. Cai, R. Zhao, and B. Meng, “Effect of yield criteria on the formability prediction of dual-phase steel sheets,” International Journal of Mechanical Sciences, vol. 133, pp. 28–41, Nov. 2017. [CrossRef]
D. Britez, S. Werda, R. Laheurte, P. Darnis, and O. Cahuc, “A comparison of different hardening rules on a multi-step global manufacturing process modeling,” ESAFORM 2021, Apr. 2021. [CrossRef]
H. P. Feigenbaum and Y. F. Dafalias, “Directional distortional hardening in metal plasticity within thermodynamics,” International Journal of Solids and Structures, vol. 44, no. 22–23, pp. 7526–7542, Nov. 2007. [CrossRef]
H. Zhu, Y. Lin, K. Chen, Z. He, and S. Yuan, “A Homogeneous Anisotropic Hardening Model in Plane Stress State for Sheet Metal under Nonlinear Loading Paths,” Materials, vol. 16, no. 3, p. 1151, Jan. 2023. [CrossRef]
“Cyclic Hardening.” Accessed: Jun. 08, 2023. [Online]. Available: https://2021.help.altair.com/2021.0.1/form/en_us/topics/form/reference/cyclic_hardening_r.htm.
P. Ludwik, Elemente der technologischen Mechanik. Springer, 1909.
H. W. Swift, “Plastic instability under plane stress,” Journal of the Mechanics and Physics of Solids, vol. 1, no. 1, pp. 1–18, Oct. 1952. [CrossRef]
E. Voce, “The relationship between stress and strain for homogeneous deformation,” Journal of the Institute of Metals, vol. 74, pp. 537–562, 1948.
T. B. Stoughton and J. W. Yoon, “Anisotropic hardening and non-associated flow in proportional loading of sheet metals,” International Journal of Plasticity, vol. 25, no. 9, pp. 1777–1817, Sep. 2009. [CrossRef]
Z. Chen, Y. Wang, and Y. Lou, “User-friendly anisotropic hardening function with non-associated flow rule under the proportional loadings for BCC and FCC metals,” Mechanics of Materials, vol. 165, p. 104190, Feb. 2022. [CrossRef]
W. Prager, “A New Method of Analyzing Stresses and Strains in Work-Hardening Plastic Solids,” Journal of Applied Mechanics, vol. 23, no. 4, pp. 493–496, Dec. 1956. [CrossRef]
P. J. Armstrong and C. Frederick, A mathematical representation of the multiaxial Bauschinger effect, vol. 731. Berkeley Nuclear Laboratories Berkeley, CA, 1966.
J. L. Chaboche, “Time-independent constitutive theories for cyclic plasticity,” International Journal of Plasticity, vol. 2, no. 2, pp. 149–188, Jan. 1986. [CrossRef]
F. Yoshida and T. Uemori, “A model of large-strain cyclic plasticity describing the Bauschinger effect and workhardening stagnation,” International Journal of Plasticity, vol. 18, no. 5–6, pp. 661–686, Oct. 2002. [CrossRef]
M. Rosenschon and M. Merklein, “Analysis of the stress and directional dependent Bauschinger-effect of sheet metals,” IOP Conf. Ser.: Mater. Sci. Eng., vol. 418, p. 012084, Sep. 2018. [CrossRef]
H. Rokhgireh, A. Nayebi, and J. L. Chaboche, “Application of a new distortional yield surface model in cyclic uniaxial and multiaxial loading,” International Journal of Solids and Structures, vol. 110–111, pp. 219–238, Apr. 2017. [CrossRef]
J. Qin, B. Holmedal, and O. S. Hopperstad, “A combined isotropic, kinematic and distortional hardening model for aluminum and steels under complex strain-path changes,” International Journal of Plasticity, vol. 101, pp. 156–169, Feb. 2018. [CrossRef]
B. Holmedal, “Bauschinger effect modelled by yield surface distortions,” International Journal of Plasticity, vol. 123, pp. 86–100, Dec. 2019. [CrossRef]
M. C. Butuc, C. Teodosiu, F. Barlat, and J. J. Gracio, “Analysis of sheet metal formability through isotropic and kinematic hardening models,” European Journal of Mechanics - A/Solids, vol. 30, no. 4, pp. 532–546, Jul. 2011. [CrossRef]
S. Abbasnejad Dizaji, H. Darendeliler, and B. Kaftanoğlu, “Effect of hardening models on different ductile fracture criteria in sheet metal forming,” Int J Mater Form, vol. 9, no. 3, pp. 261–267, Jul. 2016. [CrossRef]
J. Lemaitre and J.-L. Chaboche, Mechanics of Solid Materials, 1st ed. Cambridge University Press, 1990. [CrossRef]
P. Brozzo, Deluca, and R. Rendina, “A new method for the prediction of formability limits of metal sheets,” presented at the Sheet Metal Forming and Formability, Proceedings of the Seventh Biennial Congress of International Deep Drawing Research Group, Amesterdam, Netherlands, 1972.
M. Cockcroft, “Ductility and workability of metals,” J. of Metals, vol. 96, p. 2444, 1968.
M. Ayada, “Central bursting in extrusion of inhomogeneous materials,” presented at the roc 2nd Int Conf on Technol for Plasticity, Stuttgart, Germany, 1987, pp. 553–558.
T. B. Stoughton, “A non-associated flow rule for sheet metal forming,” International Journal of Plasticity, vol. 18, no. 5–6, pp. 687–714, Oct. 2002. [CrossRef]
J. Min, J. E. Carsley, J. Lin, Y. Wen, and B. Kuhlenkötter, “A non-quadratic constitutive model under non-associated flow rule of sheet metals with anisotropic hardening: Modeling and experimental validation,” International Journal of Mechanical Sciences, vol. 119, pp. 343–359, Dec. 2016. [CrossRef]
E.-H. Lee, T. B. Stoughton, and J. W. Yoon, “A yield criterion through coupling of quadratic and non-quadratic functions for anisotropic hardening with non-associated flow rule,” International Journal of Plasticity, vol. 99, pp. 120–143, Dec. 2017. [CrossRef]
N. Park, T. B. Stoughton, and J. W. Yoon, “A criterion for general description of anisotropic hardening considering strength differential effect with non-associated flow rule,” International Journal of Plasticity, vol. 121, pp. 76–100, Oct. 2019. [CrossRef]
Y. Hou, K. Du, A. A. El-Aty, M.-G. Lee, and J. Min, “Plastic anisotropy of sheet metals under plane strain loading: A novel non-associated constitutive model based on fourth-order polynomial functions,” Materials & Design, vol. 223, p. 111187, Nov. 2022. [CrossRef]
Y. Lou, C. Zhang, S. Zhang, and J. W. Yoon, “A general yield function with differential and anisotropic hardening for strength modelling under various stress states with non-associated flow rule,” International Journal of Plasticity, vol. 158, p. 103414, Nov. 2022. [CrossRef]
J. Lian, M. Sharaf, F. Archie, and S. Münstermann, “A hybrid approach for modelling of plasticity and failure behaviour of advanced high-strength steel sheets,” International Journal of Damage Mechanics, vol. 22, no. 2, pp. 188–218, Mar. 2013. [CrossRef]
Q. T. Fu, D. Li, H. Song, X. F. Liu, J. C. Xu, and N. Jiang, “Shear Fracture Criterion of Advanced High-Strength Steel Based on Stress Triaxiality and Equivalent Strain,” Journal of Engineering Materials and Technology, vol. 145, no. 1, p. 011002, Jan. 2023. [CrossRef]
M. Rossi et al., “Testing methodologies for the calibration of advanced plasticity models for sheet metals: A review,” Strain, vol. 58, no. 6, Dec. 2022. [CrossRef]
J. C. Chica, P. M. Bravo Díez, and M. Preciado Calzada, “Improved correlation for elastic modulus prediction of metallic materials in the Small Punch Test,” International Journal of Mechanical Sciences, vol. 134, pp. 112–122, Dec. 2017. [CrossRef]
C. C. Roth and D. Mohr, “Ductile fracture experiments with locally proportional loading histories,” International Journal of Plasticity, vol. 79, pp. 328–354, Apr. 2016. [CrossRef]
Y. Bai and T. Wierzbicki, “Application of extended Mohr–Coulomb criterion to ductile fracture,” Int J Fract, vol. 161, no. 1, pp. 1–20, Jan. 2010. [CrossRef]
M. Dunand and D. Mohr, “Ductile Fracture of AHSS Sheets under Multi-axial Loading: Experiments and Modeling,” presented at the THE 8TH INTERNATIONAL CONFERENCE AND WORKSHOP ON NUMERICAL SIMULATION OF 3D SHEET METAL FORMING PROCESSES (NUMISHEET 2011), Seoul, (Republic of Korea), 2011, pp. 484–491. [CrossRef]
Y. Jia and Y. Bai, “Ductile fracture prediction for metal sheets using all-strain-based anisotropic eMMC model,” International Journal of Mechanical Sciences, vol. 115–116, pp. 516–531, Sep. 2016. [CrossRef]
Y. Jia, Y. Qiao, H. Pan, E. Chu, and Y. Bai, “A Comprehensive Plasticity and Fracture Model for Metal Sheets under Multi-axial Stress and Non-Linear Strain Path,” SAE Int. J. Engines, vol. 10, no. 2, pp. 266–273, Mar. 2017. [CrossRef]
D. Mohr and S. J. Marcadet, “Micromechanically-motivated phenomenological Hosford–Coulomb model for predicting ductile fracture initiation at low stress triaxialities,” International Journal of Solids and Structures, vol. 67–68, pp. 40–55, Aug. 2015. [CrossRef]
B. Erice, C. C. Roth, and D. Mohr, “Stress-state and strain-rate dependent ductile fracture of dual and complex phase steel,” Mechanics of Materials, vol. 116, pp. 11–32, Jan. 2018. [CrossRef]
K. Prasad, A. Gupta, H. Krishnaswamy, U. Chakkingal, D. K. Banerjee, and M.-G. Lee, “Does friction contribute to formability improvement using servo press?,” Friction, vol. 11, no. 5, pp. 820–835, May 2023. [CrossRef]
K. Pack, T. Tancogne-Dejean, M. B. Gorji, and D. Mohr, “Hosford-Coulomb ductile failure model for shell elements: Experimental identification and validation for DP980 steel and aluminum 6016-T4,” International Journal of Solids and Structures, vol. 151, pp. 214–232, Oct. 2018. [CrossRef]
M. Miyauchi, “A proposal of a planar simple shear test in sheet metals.,” Scientific Papers of the Institute of Physical and Chemical Research, vol. 78, no. 3, pp. 27–40, 1984.
S. Bouvier, H. Haddadi, P. Levée, and C. Teodosiu, “Simple shear tests: Experimental techniques and characterization of the plastic anisotropy of rolled sheets at large strains,” Journal of Materials Processing Technology, vol. 172, no. 1, pp. 96–103, Feb. 2006. [CrossRef]
E. F. Rauch and C. G’Sell, “Flow localization induced by a change in strain path in mild steel,” Materials Science and Engineering: A, vol. 111, pp. 71–80, May 1989. [CrossRef]
P. Genevois, “Etude expérimental et modélisation du comportement plastique anisotrope de tôles d’acier en grandes déformations,” PhD Thesis, Institut National Polytechnique de Grenoble, Grenoble, France, 1992. Accessed: Jun. 14, 2023. [Online]. Available: https://www.semanticscholar.org/paper/Etude-exp%C3%A9rimentale-et-mod%C3%A9lisation-du-comportement-Genevois/155b4fe01e39b88202ce2a6a973862645ed83d73.
B07 Committee, “Test Method for Shear Testing of Thin Aluminum Alloy Products,” ASTM International. [CrossRef]
A. M. Beese and D. Mohr, “Effect of stress triaxiality and Lode angle on the kinetics of strain-induced austenite-to-martensite transformation,” Acta Materialia, vol. 59, no. 7, pp. 2589–2600, Apr. 2011. [CrossRef]
Q. Yin, C. Soyarslan, K. Isik, and A. E. Tekkaya, “A grooved in-plane torsion test for the investigation of shear fracture in sheet materials,” International Journal of Solids and Structures, vol. 66, pp. 121–132, Aug. 2015. [CrossRef]
N. Iosipescu, “New accurate procedure for single shear testing of metals,” J Mater, vol. 2, pp. 537–566, 1967.
D30 Committee, “Test Method for Shear Properties of Composite Materials by the V-Notched Beam Method,” ASTM International. [CrossRef]
Y. Bao and T. Wierzbicki, “On fracture locus in the equivalent strain and stress triaxiality space,” International Journal of Mechanical Sciences, vol. 46, no. 1, pp. 81–98, Jan. 2004. [CrossRef]
D. R. Shouler and J. M. Allwood, “Design and use of a novel sample design for formability testing in pure shear,” Journal of Materials Processing Technology, vol. 210, no. 10, pp. 1304–1313, Jul. 2010. [CrossRef]
M. Dunand and D. Mohr, “Optimized butterfly specimen for the fracture testing of sheet materials under combined normal and shear loading,” Engineering Fracture Mechanics, vol. 78, no. 17, pp. 2919–2934, Dec. 2011. [CrossRef]
A. Brosius, Q. Yin, A. Güner, and A. E. Tekkaya, “A New Shear Test for Sheet Metal Characterization,” steel research int., vol. 82, no. 4, pp. 323–328, Apr. 2011. [CrossRef]
Q. Yin, A. E. Tekkaya, and H. Traphöner, “Determining cyclic flow curves using the in-plane torsion test,” CIRP Annals, vol. 64, no. 1, pp. 261–264, 2015. [CrossRef]
V. Grolleau, C. C. Roth, and D. Mohr, “Characterizing plasticity and fracture of sheet metal through a novel in-plane torsion experiment,” IOP Conf. Ser.: Mater. Sci. Eng., vol. 651, p. 012101, Nov. 2019. [CrossRef]
E28 Committee, “Test Methods for Tension Testing of Metallic Materials,” ASTM International. [CrossRef]
S. J. Marcadet and D. Mohr, “Effect of compression–tension loading reversal on the strain to fracture of dual phase steel sheets,” International Journal of Plasticity, vol. 72, pp. 21–43, Sep. 2015. [CrossRef]
J. Peng, P. Zhou, Y. Wang, Q. Dai, D. Knowles, and M. Mostafavi, “Stress Triaxiality and Lode Angle Parameter Characterization of Flat Metal Specimen with Inclined Notch,” Metals, vol. 11, no. 10, p. 1627, Oct. 2021. [CrossRef]
R. O. Santos, L. P. Moreira, M. C. Butuc, G. Vincze, and A. B. Pereira, “Damage Analysis of Third-Generation Advanced High-Strength Steel Based on the Gurson–Tvergaard–Needleman (GTN) Model,” Metals, vol. 12, no. 2, p. 214, Jan. 2022. [CrossRef]
E. ISO, “Metallic materials—sheet and strip—determination of biaxial stress–strain curve by means of bulge test with optical measuring systems,” Standard No. ISO 16808: 2014, 2014.
R. J. Lancaster, S. P. Jeffs, B. J. Haigh, and N. C. Barnard, “Derivation of material properties using small punch and shear punch test methods,” Materials & Design, vol. 215, p. 110473, Mar. 2022. [CrossRef]
E10 Committee, “Standard Test Method for Small Punch Testing of Metallic Materials,” ASTM International. [CrossRef]
D. Mohr and S. Henn, “Calibration of Stress-triaxiality Dependent Crack Formation Criteria: A New Hybrid Experimental–Numerical Method,” Exp Mech, vol. 47, no. 6, pp. 805–820, Dec. 2007. [CrossRef]
Y. Bai, “Effect of loading history in necking and fracture,” Thesis, Massachusetts Institute of Technology, 2008. Accessed: Jun. 16, 2023. [Online]. Available: https://dspace.mit.edu/handle/1721.1/43148.
I. Peshekhodov, S. Jiang, M. Vucetic, A. Bouguecha, and B.-A. Berhens, “Experimental-numerical evaluation of a new butterfly specimen for fracture characterisation of AHSS in a wide range of stress states,” IOP Conf. Ser.: Mater. Sci. Eng., vol. 159, p. 012015, Nov. 2016. [CrossRef]
E. Stockburger, “Improved failure characterisation of high-strength steel using a butterfly test rig with rotation control,” presented at the Material Forming, May 2023, pp. 737–746. [CrossRef]
C. Aisvaran, “Study of non-linear strain path in sheet metal forming,” Faculty of Engineering, Blekinge Institute of Technology, Karlskrona, Sweden, 2021.
C. Gaber, D. Jocham, H. A. Weiss, O. Böttcher, and W. Volk, “Evaluation of non-linear strain paths using Generalized Forming Limit Concept and a modification of the Time Dependent Evaluation Method,” Int J Mater Form, vol. 10, no. 3, pp. 345–351, Jun. 2017. [CrossRef]
X. Song, L. Leotoing, D. Guines, and E. Ragneau, “Identification of forming limits at fracture of DP600 sheet metal under linear and unloaded non-linear strain paths,” Procedia Engineering, vol. 207, pp. 562–567, 2017. [CrossRef]
X. Song, L. Leotoing, D. Guines, and E. Ragneau, “Effect of continuous strain path changes on forming limit strains of DP600,” Strain, vol. 55, no. 6, p. e12329, Dec. 2019. [CrossRef]
K. Saxena, D. Kumar, and J. Mukhopadhyay, “A novel experimental approach for detection of forming limits considering non linear strain paths,” May 2015.
D. Jocham, C. Gaber, O. Böttcher, and W. Volk, “Prediction of formability for multi-linear strain paths,” Jun. 2015.
Z. He, H. Zhu, Y. Lin, D. J. Politis, L. Wang, and S. Yuan, “A novel test method for continuous nonlinear biaxial tensile deformation of sheet metals by bulging with stepped-dies,” International Journal of Mechanical Sciences, vol. 169, p. 105321, Mar. 2020. [CrossRef]
T. S. Cao, “Models for ductile damage and fracture prediction in cold bulk metal forming processes: a review,” Int J Mater Form, vol. 10, no. 2, pp. 139–171, Apr. 2017. [CrossRef]
F. X. C. Andrade, M. Feucht, A. Haufe, and F. Neukamm, “An incremental stress state dependent damage model for ductile failure prediction,” Int J Fract, vol. 200, no. 1–2, pp. 127–150, Jul. 2016. [CrossRef]
Y. Bai and T. Wierzbicki, “A new model of metal plasticity and fracture with pressure and Lode dependence,” International Journal of Plasticity, vol. 24, no. 6, pp. 1071–1096, Jun. 2008. [CrossRef]
M. Luo and T. Wierzbicki, “Numerical failure analysis of a stretch-bending test on dual-phase steel sheets using a phenomenological fracture model,” International Journal of Solids and Structures, vol. 47, no. 22–23, pp. 3084–3102, Nov. 2010. [CrossRef]
B.-A. Behrens, C. Bonk, and I. Peshekhodov, “On modelling of shear fracture in deep drawing of a high-strength dual-phase sheet steel,” J. Phys.: Conf. Ser., vol. 896, p. 012125, Sep. 2017. [CrossRef]
K. Pack and D. Mohr, “Combined necking & fracture model to predict ductile failure with shell finite elements,” Engineering Fracture Mechanics, vol. 182, pp. 32–51, Sep. 2017. [CrossRef]
M. Doig and K. Roll, “Assessment of Damage Models in Sheet Metal Forming for Industrial Applications,” KEM, vol. 473, pp. 482–489, Mar. 2011. [CrossRef]
S. Heibel, W. Nester, T. Clausmeyer, and A. E. Tekkaya, “Failure assessment in sheet metal forming using a phenomenological damage model and fracture criterion: experiments, parameter identification and validation,” Procedia Engineering, vol. 207, pp. 2066–2071, 2017. [CrossRef]
F. McClintock, “Ductile failure,” J. Appl. Mech., vol. 35, p. 363, 1968.
J. R. Rice and D. M. Tracey, “On the ductile enlargement of voids in triaxial stress fields∗,” Journal of the Mechanics and Physics of Solids, vol. 17, no. 3, pp. 201–217, 1969.
M. Oyane, T. Sato, K. Okimoto, and S. Shima, “Criteria for ductile fracture and their applications,” Journal of Mechanical Working Technology, vol. 4, no. 1, pp. 65–81, Apr. 1980. [CrossRef]
Y. Bao and T. Wierzbicki, “A comparative study on various ductile crack formation criteria,” J. Eng. Mater. Technol., vol. 126, no. 3, pp. 314–324, 2004.
Q. Fu, D. Li, H. Song, X. Liu, Z. Lu, and H. Cui, “Research on parameters of MMC fracture criterion for advanced high strength dual-phase steel sheets,” Journal of Theoretical and Applied Mechanics, pp. 253–264, Apr. 2022. [CrossRef]
C. C. Roth and D. Mohr, “Effect of strain rate on ductile fracture initiation in advanced high strength steel sheets: Experiments and modeling,” International Journal of Plasticity, vol. 56, pp. 19–44, May 2014. [CrossRef]
L. Kachanov, “Time of the Rupture Process under Creep Condition [J]. TVZ Akad,” Nauk. SSR Otd. Tech. Nauk, vol. 8, 1958.
J.-L. Chaboche, “Anisotropic creep damage in the framework of continuum damage mechanics,” Nuclear engineering and design, vol. 79, no. 3, pp. 309–319, 1984.
J. Lemaitre, “Local approach of fracture,” Engineering Fracture Mechanics, vol. 25, no. 5–6, pp. 523–537, Jan. 1986. [CrossRef]
J. Lemaitre and R. Desmorat, Engineering damage mechanics: ductile, creep, fatigue and brittle failures. Springer Science & Business Media, 2006.
T.-S. Cao, J.-M. Gachet, P. Montmitonnet, and P.-O. Bouchard, “A Lode-dependent enhanced Lemaitre model for ductile fracture prediction at low stress triaxiality,” Engineering Fracture Mechanics, vol. 124–125, pp. 80–96, Jul. 2014. [CrossRef]
A. L. Gurson, “Continuum Theory of Ductile Rupture by Void Nucleation and Growth: Part I—Yield Criteria and Flow Rules for Porous Ductile Media,” Journal of Engineering Materials and Technology, vol. 99, no. 1, pp. 2–15, Jan. 1977. [CrossRef]
V. Tvergaard and A. Needleman, “Analysis of the cup-cone fracture in a round tensile bar,” Acta Metallurgica, vol. 32, no. 1, pp. 157–169, Jan. 1984. [CrossRef]
L. Xue, “Constitutive modeling of void shearing effect in ductile fracture of porous materials,” Engineering Fracture Mechanics, vol. 75, no. 11, pp. 3343–3366, 2008.
K. Nahshon and J. Hutchinson, “Modification of the Gurson model for shear failure,” European Journal of Mechanics-A/Solids, vol. 27, no. 1, pp. 1–17, 2008.
V. Uthaisangsuk, U. Prahl, and W. Bleck, “Characterisation of formability behaviour of multiphase steels by micromechanical modelling,” Int J Fract, vol. 157, no. 1–2, pp. 55–69, May 2009. [CrossRef]
Z. Zhang, “A complete Gurson Model,” Nonlinear Fracture and Damage Mechanics, Jan. 2001.
X.-L. Cui, W. W. Zhang, Z.-C. Zhang, Y.-Z. Chen, P. Lin, and C.-Z. Chi, “Prediction of Forming Limit of Dual-Phase 500 Steel Sheets Using the GTN Ductile Damage Model in an Innovative Hydraulic Bulging Test,” JOM, vol. 70, no. 8, pp. 1542–1547, Aug. 2018. [CrossRef]
K. Achineethongkham and V. Uthaisangsuk, “Analysis of forming limit behaviour of high strength steels under non-linear strain paths using a micromechanics damage modelling,” International Journal of Mechanical Sciences, vol. 183, p. 105828, Oct. 2020. [CrossRef]

Figure 1. Banana chart of steels used in automotive applications: UTS vs Total Elongation [10]. Courtesy of WorldAutoSteel [11].

Figure 2. Tensile strength specifications for typical automotive parts. Reprinted from Ref. [4] with permission. Copyright Elsevier, 2022.

Figure 3. Forming challenges of AHSS. Adapted from [4,15,21].

Figure 4. The three fracture scenarios. Adapted from [30].

Figure 5. Schematic illustration of FLC in relation to specimen geometries. Adapted from [41,42].

Figure 6. Schematic procedure of the main steps to produce a FLC. Adapted from [43,54].

Figure 7. Forming limit diagram limitations.

Figure 8. a) Non-Linear Strain Paths; b) Non-linearity influence on forming limits; c) Non-Linear strain path during forming of a component by Fukui stretch drawing test and FLC of DP590 (adapted from [82]).

Figure 9. a) 3D fracture locus in the space of equivalent strain to fracture, stress triaxiality and lode angle parameter; b) FLD and fracture mode localization. Reprinted from Ref. [89] with permission. Copyright 2010, Elsevier.

Figure 10. Summary of constitutive material models.

Figure 11. a) Different stress states identified on a yield locus representation [112]; b) comparison of the yield loci proposed by different yield criterion, reprinted from [113] with permission. Copyright 2022, Elsevier.

Figure 12. Schematic representation of the yield locus for: a) isotropic hardening; b) kinematic hardening; c) combined hardening; d) distortional hardening. Adapted from[139,140].

Figure 13. Methodology followed by Lian et al. [166] for material and fracture model parameters calibration.

Figure 14. Load angle parameter as a function of stress triaxiality for plane stress conditions and conventional specimens over a wide range of stress triaxialities: pure shear, uniaxial tension, notch tension, plane strain tension and equi-biaxial tension. Reprinted from: Ref. [168], open access; Ref. [169] with permission, copyright 2017, Elsevier; Ref. [170] with permission, copyright 2016, Elsevier.

Figure 15. Shear test specimens proposed by [185]: a) Iosipescu [186]; b) Shouler and Allwood [189]; c) Bao and Wierzbicki [188]; d) Dunand and Mohr [190]. Reprinted from Ref. [185] with permission. Copyright 2015, Elsevier.

Figure 16. Roth and Mohr [170] novel proposed specimens to address fracture limits under: a) in-plane shear; b) plane strain tension; c) equi-biaxial tension; and d) evolution of the principal strain paths in the major vs minor space. Reprinted from Ref. [170] with permission. Copyright 2016, Elsevier.

Figure 17. Specimen shape and experiment test configuration setup proposed by: a)Dunand and Mohr [190], dual actuator system; reprinted from Ref. [190] with permission, copyright 2011, Elsevier; b) Peshekhodov et al. [203], tensile testing machine; reprinted from Ref. [203], open access; c) Stockburger et al. [204], tensile testing machine; reprinted from Ref. [204], open access.

Figure 18. Ductile fracture models classification and some representative models.

Table 2. Overview of the essential parameters needed for most common material models.

	Uniaxial Tensile Test				Biaxial Tension			FE Software
	Uniaxial Tensile Test				Biaxial Tension			AutoForm	LS-DYNA	Abaqus
	$r_{0}$ , $r_{45}$ , $r_{90}$	$σ_{0}$ , $σ_{45}$ , $σ_{90}$	$R_{m 0}$ , $R_{m 45}$ , $R_{m 90}$	$A_{g 0}$ , $A_{g 45}$ , $A_{g 90}$	$r_{b}$	$σ_{b}$	M	AutoForm	LS-DYNA	Abaqus
Hill 48	X							X	X	X
Barlat Yld2000	X	X			X	X	X	X	*(Barlat2004)
BBC 2005	X	X			X	X	X	X
Vegter 2017	X		X	X				X

Table 3. Overview of stress states covered by different phenomenological uncoupled models.

Model	Material	Pure Shear (PS)		Uniaxial Tension (UT)			NotchTension (NT)	Plane Strain Tension (PST)			Equi-biaxialTension (EBT)
Model	Material	Conventional	Butterfly	Dog-bone	Central Hole	Butterfly	Circular Cuts	Uniform	‘V’ bending	Butterfly	Punch Test
MMC [171]	TRIP690		X	X		X	X				X
MMC [172	DP590 DP780 DP980 DP1180	X		X
MMC [172]	TRIP780		X			X		X		X	X
eMMC [173]	TRIP780			X			X	X		X
eMMC [174]	TRIP780			X			X				X
HC [175]	DP590 DP780 TRIP780		X	X	X		X				X
HC [170]	DP780	X		X	X		X		X		X
HC [176]	DP980 CP980 CP1180	X		X	X		X				X
HC [177]	DP600	X		X	X		X
DSSE-HC [178]	DP980	X							X		X

Table 4. Summary of non-linear strain path generation by different test procedures applied on AHSS.

Authors	Material	Procedure:		Findings:
		Two Step Drawing
Gaber et al. [206]	DP600	Two-step deep-drawing operation: non-linear strains are generated with an axisymmetrical punch attached to the upper die that draws the blank over an elliptical shaped counterpunch located on the lower die.	The strain path is changed by using a different specimen geometry.	The GFLC and TDEM showed good predictive accuracy to model the NLSPs introduced by the experimental two-step drawing setup.
		In-plane biaxial test with cruciform specimen
Song et al. [207] Song et al. [208]	DP600	A circle arc profile is adopted in the thickness direction of the circular reduced zone to generate strain localization at the central point of the cruciform specimen. Six slots are added at each arm and the arrangement of slots is optimized.	The strain path during the test can be directly controlled by the motion of actuators along the two axes, which is sufficient to cover the whole forming limit diagram under linear and nonlinear strain paths. The strain path change in the central area of the cruciform is accomplished simply by changing either independent actuators speed or loading directions, in a single procedure without unloading. Two NLSP are induced: (i) uniaxial tension followed by equi-biaxial stretching; (ii) equi-biaxial stretching followed by plane strain tension.	Strain path changes in the fracture initiation site are experimentally observed. The strain path change has almost no effect on the forming limit strains at fracture. The Oyane ductile fracture criterion predicts the experimental results under different strain paths.
		Nakazima test with modified punch geometry
Saxena et al. [209]	DP600	Nakazima test with modified punch geometry.	The strain path is changed by using an adapted punch geometry with two tailored patterns. The use of different specimens widths allow to cover a wide range of the major vs minor principal strains spectrum.	The experimental biaxial formability test revealed strain path modification: plane strain followed by equi-biaxial. The material formability was reduced by the introduction of strain path deviation. The NLSPs negatively affected the drawability and stretchability of the material.
Panich et al. [82]	DP590	Nakazima test with modified punch geometry.		The generated FLC based on the conducted procedure revealed a decreased material formability. Experimental Fukui stretch drawings tests have shown a better predictive accuracy of the FLC generated by NLSPs rather than the conventional FLC.

Table 5. Qualitative comparison of the different families of ductile fracture models for sheet metal forming applications.

		Uncoupled Models	CDM Models	Micromechanical-based Models
Implementation	Simplicity	+	0	-
	Calibration	+	-	-
	Simulation Convergence	+	-	-
	CPU Time	+	-	-
Accuracy	Damage Softening	-	+	+
	NLSPs Modeling Accuracy	0	+	+
	Physical Interpretation	-	-	+
	Large Plastic Deformation Modeling	-	-	+
	Low Triaxialities Modeling Accuracy	0	-	-

Table 6. Summary of ductile fracture models implemented in finite element software.

Fracture Model	Material Model			Software	Tools	Mesh Type/ Element Type	Testing	Material
Fracture Model	Yield Criterion	Hardening Rule	Flow Rule	Software	Tools	Mesh Type/ Element Type	Testing	Material
Johnson-Cook [39]	Elasto-plastic	Swift	AFR	Abaqus/ Explicit	Analytical Rigid	Shell/S4R	Nakazima	-
MMC [89]	Von Mises	Isotropic	AFR	Abaqus/ Explicit	Discrete Rigid	Shell/S4R	Deep Drawing	TRIP690
MMC [215]	Hill1948	Swift	AFR	Abaqus/ Explicit	Analytical Rigid	3D/C3D8R Shell/S4R Plain Strain/CPE4R
MMC [171]	Hill1948	Swift-Hocket-Sherby	AFR	Abaqus/ Explicit	-	-	Stretch Bending Nakazima	DP590 DP780 DP980 DP1180
Adapted MMC [216]	Hill1948	Swift-Hocket-Sherby	AFR	Abaqus/ Explicit	Analytical Rigid	3D/C3D8R	Deep Drawing	DP600
HC [177]	Von Mises	Swift-Voce	AFR	Abaqus/ Explicit	-	3D/C3D8R	Hole Expansion Test	DP600
DSSE-HC [217]	Von Mises	Swift-Voce	AFR	Abaqus/ Explicit	Analytical Rigid	Shell/S4R	Stretch Bending ‘V’ Bending	DP780
DSSE-HC [178]	Von Mises	Swift-Voce	AFR	Abaqus/ Explicit	Analytical Rigid	Shell/S4R	Stretch Bending	DP980
GTN [39]	Elasto-plastic	Swift	AFR	Abaqus/ Explicit		Shell/S4R	Nakazima	-
GTN [218]	-	-	-	LS-DYNA	-	-	Cross Die Part	TRIP700
GISSMO [219]	Hill1948	Swift-Hocket-Sherby	AFR	LS-DYNA	-	Shell/-	Cross Die Part	DP1000

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

A Review on Sheet Metal Forming Evaluation of Advanced High Strength Steels (AHSS)

Abstract

1. Introduction

2. Failure, damage and fracture in sheet metal forming

3. Traditional forming limit diagram (FLD)

3.1. FLC experimental determination

3.2. Limit strains determination methods

3.3. Grid marking and deformation determination methods

4. Limitations of FLD

4.1. Non-linear strain paths

4.3. Shear fracture

4.4. Edge cracks

4.5. Bending influence

4.6. Ironing and coining

5. Constitutive Material Models

5.1. Yield criterion

5.2. Hardening rule

5.3. Flow rule

6. Material characterization methods

6.1. Proportional loading

6.1.1. Pure shear ( η = 0 ; θ ¯ = 0 )

6.1.2. Uniaxial tension ( η = 1 / 3 ; θ ¯ = 1 )

6.1.3. Notch tension

6.1.4. Plane strain tension ( η = 1 / 3 ; θ ¯ = 0 )

6.1.5. Equi-biaxial tension ( η = 2 3 ; θ ¯ = − 1 )

6.1.6. Butterfly test

6.2. Non-proportional loading

7. Damage and fracture models

7.1. Comparison between different fracture and damage models

7.2. Phenomenological fracture models

7.2.1. Modified Mohr-Coulomb model (MMC)

7.2.2. Strain based Modified Mohr-Coulomb (eMMC)

7.2.3. Hosford-Coulomb (HC)

7.3. Continuum damage models (CDM)

7.3.1. GISSMO model

7.4. Micro-mechanics based models

7.4.1. Gurson-Tvergaard-Needleman (GTN) model

8. Conclusions

Funding

Data Availability Statement

Acknowledgments

Conflicts of Interest

References

MDPI Initiatives

Important Links

Subscribe

6.1.1. Pure shear ( $η = 0; \bar{θ} = 0$ )

6.1.2. Uniaxial tension ( $η = 1 / 3; \bar{θ} = 1$ )

6.1.4. Plane strain tension ( $η = 1 / \sqrt{3}; \bar{θ} = 0$ )

6.1.5. Equi-biaxial tension ( $η = \frac{2}{3}; \bar{θ} = - 1$ )