Exact Renormalization Group Dynamics through Schrödinger-Type Equations

Preprint

Communication

Exact Renormalization Group Dynamics through Schrödinger-Type Equations

Altmetrics

Downloads

116

Views

Comments

Anna Maria Wojtyra,Matthew James Stephenson^*

This version is not peer-reviewed

Submitted:

21 February 2024

Posted:

21 February 2024

You are already at the latest version

Alerts

Abstract

We explore the relationship between the exact renormalization group (RG) equation and quantum mechanics. The central idea is to rewrite the exact Wilsonian RG equation as a Schrödinger-type equation, opening avenues for analysis. By introducing a functional transformation, the RG equation takes on a form analogous to a quantum mechanical Schrödinger equation. The study investigates solutions to this equation and draws parallels with quantum mechanics, paving the way for understanding the infrared behavior of quantum field theories. Furthermore, we extends its insights to a one-dimensional toy model, providing illustrative examples. The discussion encompasses the implications of these findings in multiple dimensions and quantum field theory, with a brief exploration of their relevance in the context of inflationary cosmology.

Keywords:

Subject: Physical Sciences - Mathematical Physics

1. Introduction

Commencing our exploration, we delve into the precise Wilsonian renormalisation group equation, given by

\partial_{t} S = \int_{p} (c + 2 p^{2}) (\frac{δ^{2} S}{δ ϕ_{p} δ ϕ_{- p}} - \frac{δ S}{δ ϕ_{p}} \frac{δ S}{δ ϕ_{- p}} + ϕ_{p} \frac{δ S}{δ ϕ_{p}}),

(1)

where the notation

\int_{p} = \int \frac{d^{d} p}{{(2 π)}^{d}}

is employed for a more concise representation. This equation, governing the action S, manifests as a non-linear entity, featuring terms of quadratic nature within the action. Notably, a transformative insight arises when we shift our focus to the functional

\begin{matrix} ψ = e^{- S}, \end{matrix}

leading to a reformulation of the equation as

\partial_{t} ψ = \int_{p} (c + 2 p^{2}) (\frac{δ^{2} ψ}{δ ϕ_{p} δ ϕ_{- p}} + ϕ_{p} \frac{δ ψ}{δ ϕ_{p}}),

(2)

or equivalently

\partial_{t} ψ = H ψ,

(3)

with

H = \int_{p} (c + 2 p^{2}) (\frac{δ^{2}}{δ ϕ_{p} δ ϕ_{- p}} + ϕ_{p} \frac{δ}{δ ϕ_{p}}) .

(4)

This transformation renders exact RG theory amenable to the solution of a linear differential equation.

In the context of the Wilsonian scenario, a distinctive feature is the constancy of the "Hamiltonian"

H

with respect to the RG-time t. This behavior undergoes a notable deviation in certain functional RG equations, exemplified by the Polchinski equation. However, if the RG-time dependence of

H

allows for a factorization in the form:

H (t) = f (t) \cdot H_{0},

where

H_{0}

remains independent of t, then this departure from the typical RG behavior is observed.

\partial_{\tilde{t}} ψ = H_{0} ψ,

where the new variable

\tilde{t}

is defined by

\frac{d \tilde{t}}{d t} = f (t) .

The pivotal observation lies in the linearity of (3), featuring a t-independent right-hand side, thereby enabling solution through methods akin to those in quantum mechanics. In essence, (3) exhibits a striking resemblance to a Schrödinger-type equation.

2. Functional Quantum Mechanics

Inspired by the form of (3), we embark on the "solution" of this equation, employing methodologies akin to Quantum Mechanics. Let

| ψ_{i} 〉

denote an eigenvector of

H

, expressed as

H | ψ_{i} 〉 = λ_{i} | ψ_{i} 〉,

(5)

adopting the bra-ket notation. We posit a complete set of eigenvectors

{| ψ_{i} 〉}

and introduce an index i to label the functions, emphasizing that i is not necessarily discrete.

Leveraging completeness, any functional

ψ

can be expanded as

ψ = \sum_{i} α_{i} ψ_{i} .

(6)

We further assume the existence of an inner product

(,)

on the space of functionals, transforming it into a Hilbert space. For instance, the path integral

(ψ_{1}, ψ_{2}) = 〈 ψ_{1} | ψ_{2} 〉 = \int D ϕ ψ_{1} [ϕ] {\bar{ψ}}_{2} [ϕ],

can serve as a suitable inner product, allowing for complex-valued functionals. The eigenfunctionals

ψ_{i}

are assumed to be normalized with respect to this inner product, as expressed by

\begin{matrix} \int D ϕ ψ_{i} [ϕ] ψ_{j} [ϕ] = δ_{i j}, \end{matrix}

(7)

where

δ_{i j}

denotes the "Kronecker delta," potentially manifesting as a functional. For example, in the context of a "free" Hamiltonian, where

H \propto \frac{δ^{2}}{δ ϕ δ ϕ} = \int_{x, y} Δ (x, y) \frac{δ^{2}}{δ ϕ_{x} δ ϕ_{y}},

with a introduced "metric"

Δ (x, y)

on the dummy index space

{x, y}

, the eigenfunctionals take the form

ψ_{J} [ϕ] \propto e^{i \int_{x} ϕ_{x} J_{x}} .

This leads to

(ψ_{J}, ψ_{J^{'}}) \propto δ (J - J^{'}),

resembling a functional delta-function. Notably, the currents J behave analogously to conjugates of the fields

ϕ

, analogous to momenta p conjugate to positions x in conventional quantum mechanics. The self-adjoint nature of

H

with respect to the inner product is assumed. Completeness of the set

{| ψ_{n} 〉}

enables the standard decomposition of unity

1 = \sum_{n} | ψ_{n} 〉 〈 ψ_{n} | .

Utilizing this, the spectral theorem for

H

takes the form

H = \sum_{i} λ_{i} | ψ_{i} 〉 〈 ψ_{i} | .

(8)

In principle, one could compute different weights

α_{i}

, given by

(ψ_{i}, ψ) = α_{i} = \int D ϕ ψ_{i} \bar{ψ} .

(9)

This implies that an RG flow of any theory can be represented by a flow of coefficients multiplying different weights of theories. Substituting (6) into (3) yields

\partial_{t} α_{i} (t) = λ_{i} α_{i} (t),

or equivalently

α_{i} (t) = α_{i 0} e^{λ_{i} t} .

The action is then formally expressed as

S = - log [\sum_{i} α_{i 0} e^{λ_{i} t} ψ_{i}] .

(10)

Solving exact RG theory in this manner hinges on the ability to diagonalize the "Hamiltonian"

H

and perform the path integrals (9), which can be challenging. Moreover, after finding the spectrum of

H

and computing the integrals (9), expressing (10) in the conventional form as a spacetime integral is nontrivial. Typically, the final action is expected to contain non-local interaction terms.

In many cases, interest lies not in the full solution but rather in the infrared (IR) behavior of the theory, i.e., when

t \to \infty

. In this scenario, the dominant eigenfunctional(s) in (10) will correspond to those with the highest weight. In the deep IR, the largest

λ_{i}

will exert complete dominance.1 Assuming the original theory aligns with eigenfunctionals of this eigenvalue, which is typically the case, the action takes the form

S = - log [\sum_{m a x} α_{m a x 0} e^{λ_{m a x} t} ψ_{i}],

with the sum now over eigenfunctionals of the maximal eigenvalue

λ_{m a x}

2.1. One-Dimensional Case

To gain a preliminary insight into the situation, we confine ourselves to a simplified model in one dimension, where the problem is encapsulated by the equation

\partial_{t} ψ = \partial_{x}^{2} ψ + x \partial_{x} ψ .

(11)

This equation emerges from a rudimentary form of mean-field approximation, assuming that the field is constant over space-time, neglecting the impact of higher derivative modes. In this context, the associated Hamiltonian reads

H = \partial_{x}^{2} + x \partial_{x} = \partial_{x}^{2} + \frac{1}{2} (x \partial_{x} + \partial_{x} x) - \frac{1}{2} [\partial_{x}, x] = {(\partial_{x} + \frac{1}{2} x)}^{2} - \frac{1}{4} x^{2} - \frac{1}{2} .

Observe that

\partial_{x} + \frac{1}{2} x = e^{- \frac{1}{4} x^{2}} \partial_{x} e^{\frac{1}{4} x^{2}} .

Additionally, let us perform the rescaling

\tilde{ψ} = e^{\frac{1}{4} x^{2}} ψ .

With this transformation, equation (11) can be recast as

\partial_{t} \tilde{ψ} = - [{\hat{p}}^{2} + \frac{1}{4} {\hat{x}}^{2} + \frac{1}{2}] = \hat{H} \tilde{ψ},

where we introduce the customary momentum operator

\hat{p} = - i \partial_{x} .

In particular, note that

\hat{H} = - [{\hat{p}}^{2} + \frac{1}{4} {\hat{x}}^{2} + \frac{1}{2}],

closely resembles the Hamiltonian of a harmonic oscillator. Defining the ladder operators

\begin{matrix} \hat{a} & = \frac{1}{2} \hat{x} + i \hat{p} \\ {\hat{a}}^{†} & = \frac{1}{2} \hat{x} - i \hat{p}, \end{matrix}

the Hamiltonian takes the form

\hat{H} = - ({\hat{a}}^{†} \hat{a} + 1) .

Note the difference from the standard harmonic oscillator in the minus sign and the factor of one instead of one-half within the brackets.

The Hamiltonian

\hat{H}

is negative definite, and the highest eigenvalue is

E_{0} = - 1

, achieved by the vacuum state

ψ_{0}

\begin{matrix} \hat{a} {\tilde{ψ}}_{0} & = 0 \end{matrix}

(12)

\begin{matrix} \hat{H} {\tilde{ψ}}_{0} & = - ψ_{0} . \end{matrix}

(13)

Assuming that the initial state

{\tilde{ψ}}_{I}

overlaps with this vacuum, it becomes the dominant state in the deep infrared (IR) limit as

t \to \infty

. Consequently, we aim to elucidate the characteristics of this vacuum. Equation (13) translates to

\partial_{x}^{2} {\tilde{ψ}}_{0} - \frac{1}{4} x^{2} {\tilde{ψ}}_{0} + \frac{1}{2} {\tilde{ψ}}_{0} = 0,

which admits the general solution

ψ_{0} (x) = e^{- \frac{1}{2} x^{2}} (C_{1} + C_{2} E i (x / \sqrt{2}))

with constants

{C_{1}, C_{2}}

. Here, we reintroduce the original field as

ψ = e^{- \frac{1}{4} x^{2}} \tilde{ψ}

. The function

f (x) = e^{- \frac{1}{2} x^{2}} E i (x / \sqrt{2})

is not a normalizable function, as required in standard quantum mechanics. Nevertheless, it tends to zero as

| x | \to \infty

The corresponding potential is then

V (x) = - log [e^{- \frac{1}{2} x^{2}} (C_{1} + C_{2} E i (x / \sqrt{2}))] = \frac{1}{2} x^{2} - log (C_{1} + C_{2} E i (x / \sqrt{2}))

It consists of the typical Gaussian quadratic part, indicating a free fixed point, and an additional correction. We consider three cases,

\begin{matrix} Case I : & C_{2} = 0 \\ Case II : & C_{1} = 0 \\ Case III : & C_{2} = ϵ, \end{matrix}

where

ϵ

is a small number.

Case I, $C_{2} = 0$

This is the trivial case, where the fixed point corresponds to a usual Gaussian, characterized by the potential

V (x) = \frac{1}{2} x^{2} + C,

where C represents a cosmological constant determined by the pre-factor

C_{1}

, specifically

C = - log (C_{1})

Case II, $C_{1} = 0$

In this case, the fixed point potential takes on a more intriguing form:

V (x) = \frac{1}{2} x^{2} - log (E i (x / \sqrt{2})) + C,

(14)

where

C = - log (C_{2})

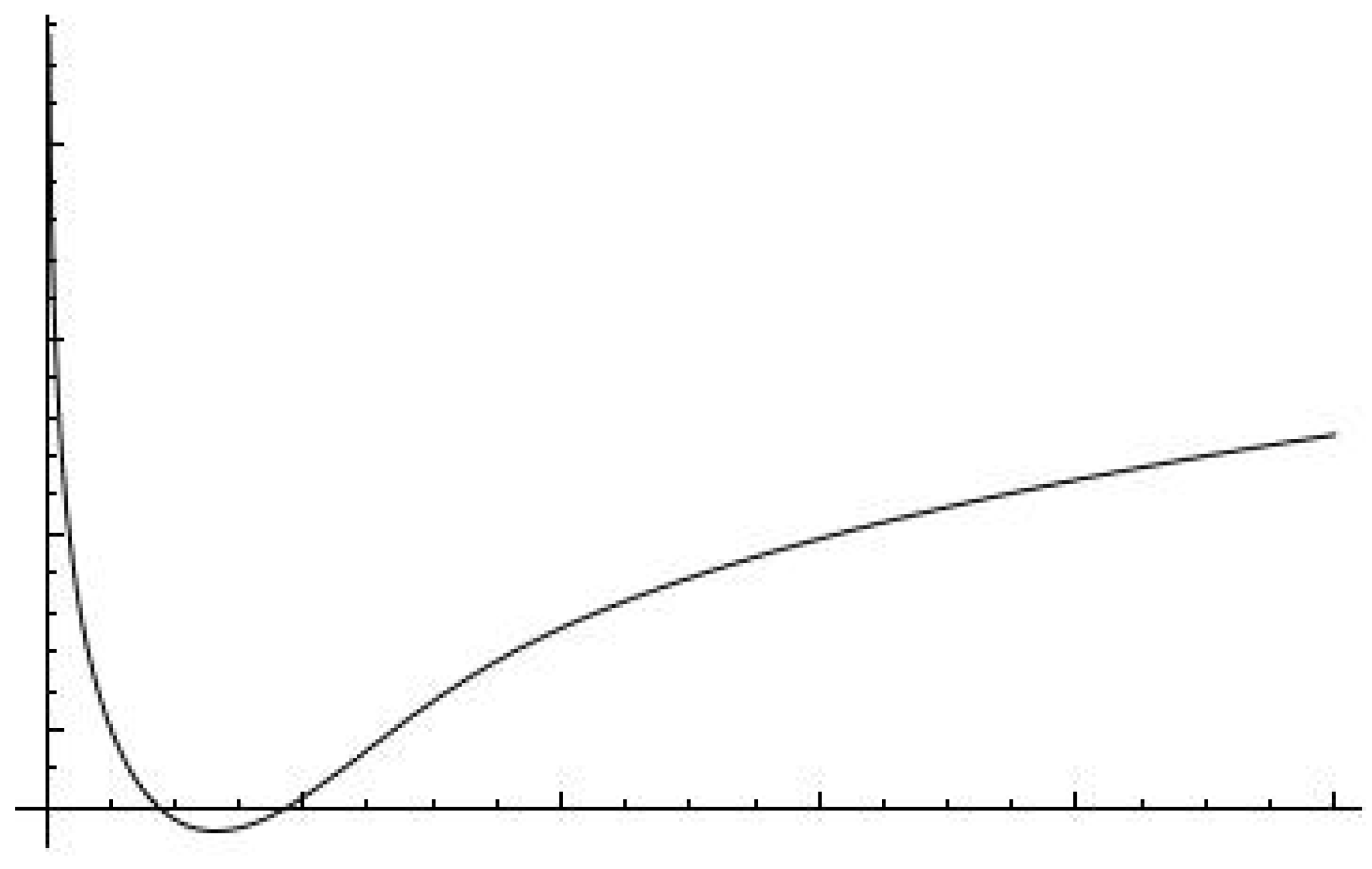
. The general shape of this potential is illustrated in Figure 1. Notably, despite the presence of a Gaussian term, the correction introduced by the error function imparts a distinct non-Gaussian character to the curve.

Case III, $C_{2} = ϵ$

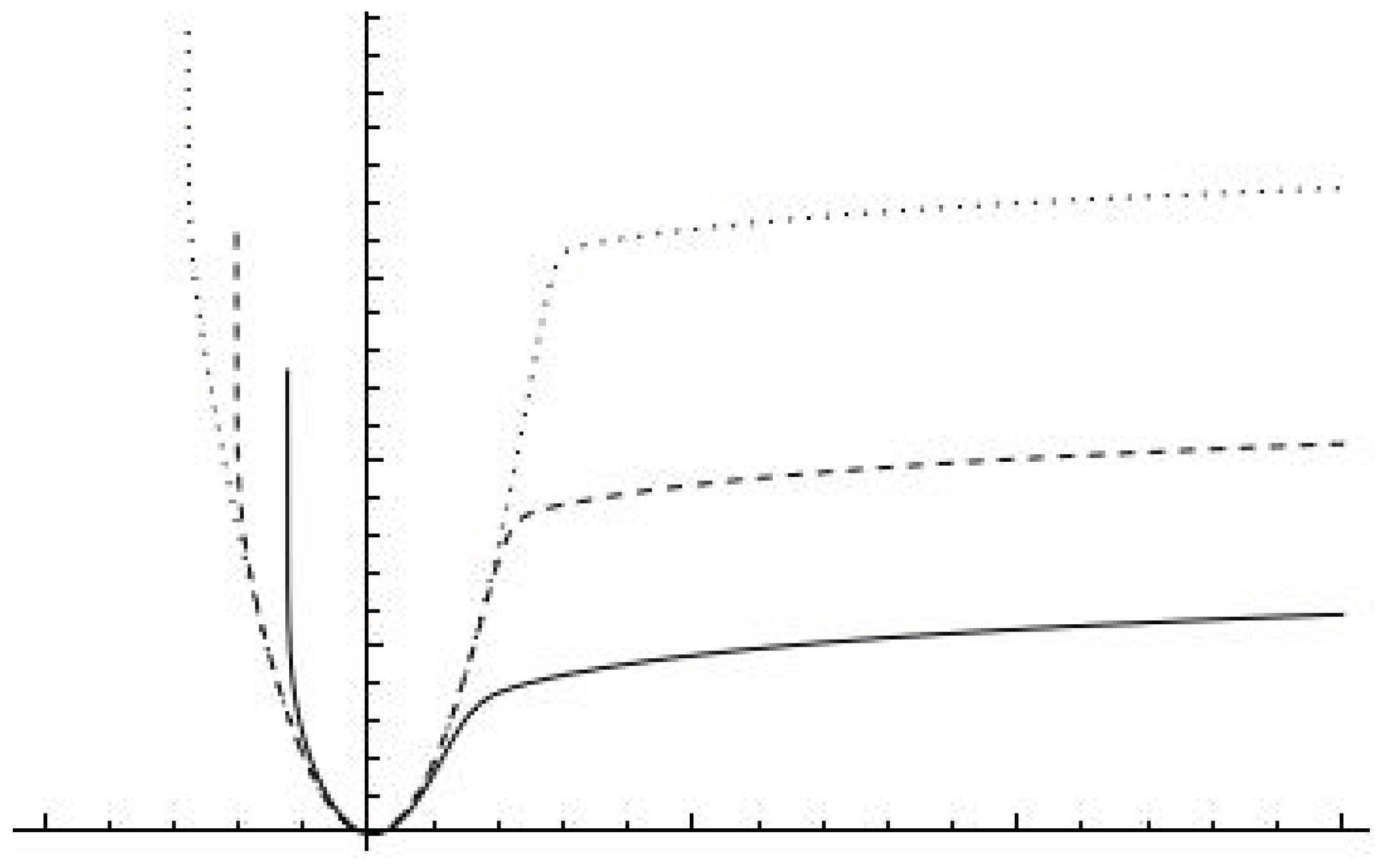
We now explore the most intriguing scenario, where

C_{2}

is non-zero but small compared to

C_{1}

. For specificity, let

C_{1} = 1

and

C_{2} = ϵ

, assuming

ϵ

is small. The resulting potential is given by

V (x) = \frac{1}{2} x^{2} - log (1 + ϵ E i (x / \sqrt{2})) .

(15)

A generic representation of this potential is depicted in Figure 2.

2.2. Analysis of the Schrödinger Equation

Let us proceed by analyzing the Wilsonian Hamiltonian (4). Suppose

H ψ = λ ψ .

Performing the path integral

\int D ϕ

on both sides yields

\int D ϕ \int_{p} (c + 2 p^{2}) (\frac{δ^{2} ψ}{δ ϕ_{p} δ ϕ_{- p}} + ϕ_{p} \frac{δ ψ}{δ ϕ_{p}}) = λ \int D ϕ ψ .

Assuming

ψ [ϕ] = e^{- S [ϕ]}

and that

S [ϕ]

tends to infinity as

ϕ

approaches infinity (ensuring no flat directions), we refer to such theories as bounded. Considering the boundary conditions, the first term vanishes as a total derivative, and the second term is

\int D ϕ \int_{p} (c + 2 p^{2}) ϕ_{p} \frac{δ ψ}{δ ϕ_{p}} = - \int_{p} (c + 2 p^{2}) \int D ϕ ψ,

following an integration by parts. This implies

λ = - \int_{p} (c + 2 p^{2}) .

Notice that

\int_{p} (c + 2 p^{2}) \frac{δ}{δ ϕ_{p}} (\frac{δ ψ}{δ ϕ_{- p}} + ϕ_{p} ψ) = 0,

\int_{p} (c + 2 p^{2}) \frac{δ}{δ ϕ_{p}} [\exp (- \frac{1}{2} \int_{p} ϕ_{- p}^{2}) \frac{δ}{δ ϕ_{- p}} (\exp (\frac{1}{2} \int_{p} ϕ_{- p}^{2}) ψ)] = 0 .

(16)

Let

\tilde{ψ} = \exp (\frac{1}{2} \int_{p} ϕ_{- p}^{2}) ψ,

Multiply (16) by

\tilde{ψ}

and integrate over

ϕ

to obtain

\int D ϕ \exp (- \frac{1}{2} \int_{p} ϕ_{- p}^{2}) \int_{p} (c + 2 p^{2}) \frac{δ \tilde{ψ}}{δ ϕ_{p}} \frac{δ \tilde{ψ}}{δ ϕ_{- p}} = 0,

following a partial integration. In position space, this reads

\int D ϕ \exp (- \frac{1}{2} \int_{x} ϕ_{x}^{2}) \int_{x, y} Δ^{- 1} (x - y) \frac{δ \tilde{ψ}}{δ ϕ_{x}} \frac{δ \tilde{ψ}}{δ ϕ_{y}} = 0,

(17)

where

Δ^{- 1} (x - y) = \int_{p} (c + 2 p^{2}) e^{i p (x - y)}

is the inverse propagator. Notice how the propagator

Δ (x - y)

acts as a metric in the above expression (17). Assuming this metric is positive definite, it follows from (17) that

\frac{δ \tilde{ψ}}{δ ϕ_{y}} = 0,

ψ = C \exp (- \frac{1}{2} \int_{x} ϕ_{x}^{2})

for some constant C. Hence we are dealing with a canonically normalized and non-propagating free theory. Note that

ψ

is not a fixed point of the Wilsonian flow, but it is the only bounded eigenvector of

H

The deduction we endeavor to articulate is as follows: Under the assumption that the ultraviolet (UV) theory manifests a discernible intersection with both infrared (IR) theories, the ensuing infrared state transcends the mere Gaussian fixed point, evolving into a composite fixed point harmonizing the attributes of the two distinct theories. The resultant potential exhibits a captivating character reminiscent of a gradual-roll inflationary profile. Significantly, as the parameter

ϵ

diminishes, the plateau region of the potential assumes a progressively more level disposition. Furthermore, the theoretical framework exhibits Gaussian characteristics until the advent of the plateau, where it undergoes an abrupt transition into a flattened configuration.

3. Multiple Dimensions and QFT

Extending our analysis to multiple dimensions and exploring Quantum Field Theory (QFT) unveils the intricate connections between Quantum Mechanics (QM) and the Renormalization Group (RG), offering deeper insights into fundamental physical phenomena. Generalizing our study to higher dimensions goes beyond one-dimensional considerations. Investigating the interplay between QM and RG in multi-dimensional systems sheds light on the universality or limitations of our observed phenomena. In Quantum Field Theory (QFT), the integration of QM principles with field theory prompts a nuanced exploration of the QM-RG analogy. This mathematical journey examines compatibility boundaries and implications for our understanding of fundamental physical processes. The pursuit of these connections leads us through a precise analysis, unraveling the intricate relationships that bind these theories.

4. Inflation

Consider a scalar field coupled to gravity described by the action

\begin{matrix} S = \frac{1}{2 κ^{2}} \int d^{4} x \sqrt{- g} [R + {(\partial_{μ} ϕ)}^{2} + 2 V (ϕ)], \end{matrix}

(18)

where

κ^{2} = 8 π G_{N}

and

\begin{matrix} V (ϕ) = \frac{1}{2} ϕ^{2} - log C_{0} - log [1 + \frac{C}{C_{0}} \sqrt{\frac{π}{2}} E i (ϕ / \sqrt{2})] . \end{matrix}

(19)

Expanding the potential around

ϕ \approx 0

, we find

\begin{matrix} V (ϕ) = - log (C_{0}) - \frac{C}{C_{0}} ϕ + \frac{1}{2} (1 + \frac{C^{2}}{C_{0}^{2}}) ϕ^{2} + \dots . \end{matrix}

(20)

Identifying

log C_{0} = Λ

, where

Λ

is the cosmological constant, and noting that the mass of the scalar field is

m^{2} = 1 + C^{2} e^{- 2 Λ}

, we have

\begin{matrix} C = \pm e^{Λ} \sqrt{m^{2} - 1} . \end{matrix}

(21)

Rewriting the action as

\begin{matrix} S = \frac{1}{2 κ^{2}} \int d^{4} x \sqrt{- g} [R - 2 Λ + {(\partial_{μ} ϕ)}^{2} + 2 V (ϕ)], \end{matrix}

(22)

where

\begin{matrix} V (ϕ) = \frac{1}{2} ϕ^{2} - log [1 \pm \sqrt{\frac{π (m^{2} - 1)}{2}} E i (ϕ / \sqrt{2})] . \end{matrix}

(23)

In this notation, for small

ϕ ≪ 1

the potential is

\begin{matrix} V (ϕ) \approx \mp \sqrt{m^{2} - 1} ϕ + \frac{m^{2}}{2} ϕ^{2} + \dots, \end{matrix}

(24)

while for large

ϕ ≫ 1

, the potential behaves as

\begin{matrix} V (ϕ) \to log [\pm \frac{ϕ}{\sqrt{m^{2} - 1}}] + \dots . \end{matrix}

(25)

5. Derivation

Let

ϕ^{'} (x) = ϕ (x) + σ Ψ [ϕ]

; then,

\begin{matrix} S [ϕ^{'}] = S [ϕ] + σ \int d^{4} x Ψ [ϕ] \frac{δ S}{δ ϕ (x)} . \end{matrix}

(26)

The measure transformation yields

\begin{matrix} \int D ϕ^{'} = \int D ϕ (1 + σ \int d^{4} y \frac{δ Ψ [ϕ (y)]}{δ ϕ (y)}), \end{matrix}

(27)

resulting in the partition function

\begin{matrix} Z & = \int D ϕ^{'} e^{- S [ϕ^{'}]} \\ = \int D ϕ exp \{- S [ϕ] - σ \int d^{4} x [Ψ \frac{δ S}{δ ϕ (x)} - \frac{δ Ψ}{δ ϕ (x)}]\} . \end{matrix}

(28)

5.1. Polchinski’s Equation

Consider Polchinski’s RG equation

\partial_{t} ψ = - \int_{p} K^{'} (p^{2}) (\frac{δ^{2} ψ}{δ ϕ_{p} δ ϕ_{- p}} + \frac{2 p^{2}}{K (p^{2})} ϕ_{p} \frac{δ ψ}{δ ϕ_{p}}),

(29)

where

K^{'} (p^{2}) = d K (p^{2}) / d p^{2}

. The corresponding "Hamiltonian"

H = - \int_{p} K^{'} (p^{2}) (\frac{δ^{2}}{δ ϕ_{p} δ ϕ_{- p}} + \frac{2 p^{2}}{K (p^{2})} ϕ_{p} \frac{δ}{δ ϕ_{p}})

also has a free theory as its only bounded eigenvector, but in this case we have

ψ = C \exp (- \int_{p} \frac{p^{2}}{K (p^{2})} ϕ_{p}^{2}),

with eigenvalue

λ = \int_{p} K^{'} (p^{2}) \frac{2 p^{2}}{K (p^{2})} .

6. Conclusion

Our exploration of the interplay between Quantum Mechanics (QM) and the Renormalization Group (RG) has provided valuable insights into fundamental physical phenomena. Establishing connections between the Schrödinger equation and the functional RG equation opens avenues for a nuanced understanding of quantum system dynamics. The analysis of the one-dimensional case uncovered distinct fixed points under the RG flow, revealing various scenarios (Cases I, II, and III). Generalizing our study to multiple dimensions demonstrated the adaptability and universality of our findings, while delving into Quantum Field Theory (QFT) unveiled intricate connections between quantum mechanics and field theory. This investigation contributes to a refined comprehension of the QM-RG relationship, with potential applications across diverse physical theories. As we unveil the mathematical intricacies linking these theories, future research promises to unveil novel insights, pushing the boundaries of our understanding of the fundamental principles governing the physical universe.

References

Ji-seong Chae and Jae-Hyuk Oh. Momentum-space Langevin dynamics of holographic Wilsonian RG flow: self-interacting massive scalar field theory. arXiv 2024, arXiv:2402.03841. [Google Scholar] [CrossRef]
Cenk Akyüz, Fatih Erman, and Haydar Uncu. The Harmonic Oscillator Potential Perturbed by a Combination of Linear and Non-linear Dirac Delta Interactions with Application to Bose-Einstein Condensation. arXiv 2024, arXiv:2402.02169. [Google Scholar] [CrossRef]
K. G. Wilson and J. Kogut. The Renormalization Group and the Sigma Expansion. Physics Reports 1974, 12, 75–199. [Google Scholar]
J. Polchinski. Renormalization and Effective Lagrangians. Nuclear Physics B 1984, 231, 269–295. [Google Scholar] [CrossRef]
A. Einstein. On the Electrodynamics of Moving Bodies. Annalen der Physik 1905, 322, 891–921. [Google Scholar]
E. Schrödinger. An Undulatory Theory of the Mechanics of Atoms and Molecules. Physical Review 1926, 28, 1049–1070. [Google Scholar] [CrossRef]
M. Gell-Mann and F. E. Low. Bound States in Quantum Field Theory. Physical Review 1956, 84, 350–354. [Google Scholar] [CrossRef]
J. M. Luttinger and J. C. Ward. Ground-State Energy and Fermi Surface of a System of Interacting Fermions. Physical Review 1960, 118, 1417–1427. [Google Scholar] [CrossRef]

1	We assume $H$ possesses a maximal eigenvalue, differing from quantum mechanics, where a minimal eigenvalue, i.e., the vacuum, is assumed.

Figure 1. Generic plot of the error function potential (14).

Figure 2. Generic plots of the potential (15) for

ϵ = 0.1

(solid),

ϵ = 10^{- 3}

(dashed), and

ϵ = 10^{- 6}

(dotted).

Figure 2. Generic plots of the potential (15) for

ϵ = 0.1

(solid),

ϵ = 10^{- 3}

(dashed), and

ϵ = 10^{- 6}

(dotted).

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Exact Renormalization Group Dynamics through Schrödinger-Type Equations

Abstract

1. Introduction

2. Functional Quantum Mechanics

2.1. One-Dimensional Case

Case I, C 2 = 0

Case II, C 1 = 0

Case III, C 2 = ϵ

2.2. Analysis of the Schrödinger Equation

3. Multiple Dimensions and QFT

4. Inflation

5. Derivation

5.1. Polchinski’s Equation

6. Conclusion

References

MDPI Initiatives

Important Links

Subscribe

Case I, $C_{2} = 0$

Case II, $C_{1} = 0$

Case III, $C_{2} = ϵ$