Preprint
Review
Digital Image Correlation for Assessment of Bridges’ Technical State and Remaining Resource
Altmetrics
Downloads
370
Views
118
Comments
0
A peer-reviewed article of this preprint also exists.
This version is not peer-reviewed
Submitted:
24 August 2024
Posted:
26 August 2024
You are already at the latest version
Alerts
Abstract
Bridges enable communications and transportation of goods nationally and internationally, underpinning economic and social activities, thus they are pylons of our prosperity and mobility. Bridges worldwide are constantly subjected to physical wear, ageing, deterioration, hazards, environmental influences, and increased loading. Loss of performance and functionality of bridge structures would have a crucial impact on overall infrastructural resilience and would cause significant negative economic and social consequences. Monitoring their behaviour for different loading conditions relies on accurate estimations of the stress-strain state of various critical components and remaining capacities. These activities are of high importance for better planning and lifespan prolongation, that is the extension of their service life and prevention of unforeseen collapses, in line with sustainability principles of well-informed maintenance. In many cases, access to the structure is limited or even impossible, which causes the need for the deployment of remote and contactless methods. One such innovative technique, which has recently attracted attention in scientific and practical applications is the digital image correlation (DIC). DIC is a contactless approach applicable for obtaining the full field of strains and deformations of full-scale real structures. Although the DIC approach has been widely used in world engineering practice for monitoring bridges and has proved to be a reliable and accurate method, there is a lack of systematic integral review on previous practical applications, revealing limitations and perspectives. This is the main motivation and novelty of this study, which will describe selected case studies, in which DIC was used on real full-scale bridge structures and propose improvements for the method.
Keywords:
Subject: Engineering - Architecture, Building and Construction
Introduction
The transport infrastructure of any country should be considered as a complex multi-scale system, integrating various sectors of the social, economic, and political life of the region. Bridges, as important components of this system, play a vital role in its functionality, fostering communication and facilitating the transportation of goods both nationally and internationally. Their significance extends beyond mere physical structures; they serve as the backbone of economic and social activities, acting as crucial pylons supporting the prosperity and mobility of societies. In particular, bridge structures connect regions, cities, and even countries, forming essential links for the movement of goods, ensuring international global supply chains, and facilitating the flow of resources, labour, and capital, by reducing transportation costs and improving accessibility to markets. Accessibility and strategic locations of bridges are vital for efficient emergency response and disaster management, as they serve as critical evacuation routes during emergencies and natural disasters; thus, playing a crucial role in sustainability and resilience of the overall infrastructure. Considering the remarkable role of bridges in the lifelines of societies, economic growth, and social cohesion, the task of ensuring their safety and functionality reaches its prevailing importance.
Bridges worldwide face relentless challenges from a multitude of factors, including physical wear, ageing, deterioration, extreme hazards, environmental influences, and increased loading. Thus, long-term operation, associated with progressing wear and ageing of structural components in combination with critical environmental factors such as corrosive substances, extreme weather conditions, and pollution leads to accelerated deterioration of bridge materials. The concentration of the most significant bridges in main cities, industrial hubs, and economic centres marks a pivotal intersection between infrastructural importance and urban development. The ongoing urbanization trend, characterized by a steady increase of residents in major cities, directly correlates with escalated traffic loading and heightening stress on bridge structures. Hence, bridges are subjected to stresses beyond their original design parameters, which could cause increased wear and tear, accelerated deterioration, and heightened risk of structural deficiencies. The cumulative impact of the challenges, mentioned above, poses a threat to the structural integrity of bridges and to the broader infrastructural resilience and operability, which reveals the criticality of establishment of robust monitoring systems and adopting proactive maintenance practices. On-site monitoring of bridges` stress-strain state, deformations, and behaviour under different external impacts is significant for structural health assessment of various critical components and their remaining capacities. Timely and consequent assessment procedures can provide an indispensable basis for reliable planning of proactive measures, lifespan prolongation and prevention of unforeseen collapses.
Active operation of bridges by traffic in most cases causes limited access to them, making it challenging to install and maintain conventional contact/invasive monitoring systems. Traditional load-testing approaches are often attributed to expenses and difficulties, associated with both direct costs for sensor systems purchase and installation and indirect time-dependent losses related to traffic disruptions [1]. Similarly, after the occurrence of extreme natural or human-induced hazards, direct inspection of bridges could be impossible due to safety reasons, or technical inability in difficult-to-reach areas. Consequences and limitations, described above, cause the increased interest in engineering society to contactless monitoring methods, such as laser vibrometry, microwave radar interferometry, optical-based laser systems, digital image correlation, etc [2,3]. Although all these approaches enable accurate and precise monitoring of the structure without road closure and direct access to it, some of them are associated with certain limitations. Thus, the use of laser vibrometry equipment is associated with high costs, long measuring time, reduced signal-to-noise ratio and enables measuring the position of a singular target. Microwave radar interferometry is applicable for multiple targets assessment within a radar image, but the measurements of displacements are confined to the instrument line of sight [3] and necessity to use at least two radars to reach a satisfactory accuracy [4]. Optical-based laser systems, while ensuring long-term measurements with low error, are constrained by a relatively small distance between the receiver and radiation source and a small displacement measurement range [2,5]. In contrast, the digital image correlation approach (DIC) is a completely contactless method, applicable for remote measurements of full-scale structures and enables obtaining the full field of strains and deformations until the latest loading stages. This method, after being developed, improved, and tested in laboratory conditions, has already spread to practical engineering implications worldwide. Among existing works, providing a systematic review of the DIC applications can be noted recent study by Mousa et al in 2023 [6], being focused on laboratory structural tests and applications. However, on-site DIC measurements are associated with the number of specific features and challenges, which require additional attention to existing practices. Although a sufficient number of practical examples of DIC application for real bridges have already been published in recent years, there is still a lack of comprehensive review of these practices, systematization and analysis of existing findings, limitations, and challenges. For today the authors have identified only one detailed review, which consistently focused on DIC application for on-site bridge monitoring [7]. In our study we widen this significant topic, providing more detailed insights on limitations, addressed in the case studies, approaches to overcome challenges during on-site monitoring (e.g. lightning conditions, camera movement, etc). Detailed investigation of DIC errors during on-site monitoring and their possible impact on resolution, accuracy, and repeatability of results is provided, facilitating further development and improvement of the method for on-site applications. Information from relevant papers in international literature is summarized in tabular form to enhance understanding of the key aspects of the DIC methodology.
DIC—The Main Principles of the Method
DIC is a multi-stage technique which enables remote contactless measurement of full-field displacements and strains on the surface of objects. DIC has been widely used in various fields, including materials testing [2,8], structural analysis, biomechanics, and experimental mechanics, providing valuable insights into the mechanical behaviour of materials and structures. Although this method has experienced a long history of development [2] and modifications and could have specific features, which depend on the particular application field, it generally includes several key steps (see Figure 1).
First, high-resolution digital images of the object's surface are captured using a camera, covering the entire area of interest. At the pre-processing stage images are divided into smaller regions or subsets for further tracking throughout the deformation process. The size of the subsets is determined based on the expected deformation and the level of detail required. The initial image, corresponding to an undeformed state should be chosen as the reference image against which subsequent images will be compared. The basic principle of DIC image tracking entails the representation (coding) of it with a matrix of natural numbers (e.g. white areas corresponding to 0, while black, to 100). Thus, the subset of the image (normally a square with a 10–50 pixels side) will contain the group of points with different grey level variations and unique numerical coding [2,9] (see Figure 2).
The centre of a particular subset, as the reference point, serves for its further tracking through the subsequent “deformed” images and coordinates identification. The core principle employed in the DIC method involves aligning a specific pixel's location on the reference image with its corresponding position on the deformed surface images. The region around a given reference point is designated as an arbitrarily shaped area, within which a unique distribution of shades is present. Subsequently, employing a suitable algorithm through specialized software, the region with a matching distribution of pixel shades is identified. Throughout the correlation procedure, sets of numbers are systematically shifted until the pattern on the deformed image aligns optimally with the reference image. This alignment is determined by assessing the overall difference in grey levels for each corresponding point [2,9]. By tracking the movement of features on the material's surface between these images, displacement and strain data can be calculated.
It is obvious, that for effective and precise correlation, the tracked area could have specific features, easily recognised at the processing stage. For this purpose, either the natural speckle pattern on a surface can be used, or the surface should be artificially prepared before the beginning of measurement. The latter approach includes separate printing of the speckle on the paper and application (glueing) to the investigated surface (artificial target) or direct creation of the speckle pattern to the surface. The target-tracking method entails the use of an artificial target as an independent sensor on the structure. Targets with salient features and known parameters should be rigidly attached to the structure surface, preventing any possible movements or rotation. The targets` size is determined by the field of view (FOV) and, therefore, the distance between the structure and camera, the larger FOV corresponds to a bigger target size. Thus, the unique dots configuration on coded targets serves as an analogous of the stochastic pattern marking, facilitating mutual orientation and recognition of the 3D coordinates from subsequent images by software [9]. Creation of the speckle pattern directly on the investigated surface is more effective for obtaining a full field of strains but is more time- and labour-consuming and often associated with on-site limitations for long-term access.
Although the application of artificial targets on a surface can be labour-intensive, especially for large or complex structures, they provide distinct and easily recognizable features. They can be precisely placed, allowing for accurate tracking of displacements in specific regions of interest (ROI). They also facilitate in reduction of ambiguity in matching subsets, especially in areas with low texture or uniform patterns. However, for each particular case study, an artificial speckle pattern should be individually developed, considering the natural behaviour (roughness, coating) of the material or surface to eliminate possible interference. Thus, the choice between natural and artificial, or a combination of both patterns involves a trade-off between precision and ease of application, being an aspect of crucial importance for ensuring the accuracy of results [11,12]. Thus, the artificial speckle pattern, which is a random arrangement of bright and dark spots on a surface, should align with the following requirements [2,11]:
- high contrast;
- 50–70% degree of density;
- isotropy and randomness;
- optimal size of dots;
- consistent speckle size.
Following the flowchart of the DIC process (Figure 1) ensuring the use of optimal speckle pattern, cross-correlation can be performed with high accuracy and low noise level. These principles are usually applied in specialised software, including the following: Vic-2D/3D (Correlated Solutions, Inc., Irmo, SC, USA [13]), StrainMaster (LaVision, Ypsilanti, MI, USA [14]), GOM Correlate Pro, ARAMIS (GOM, Carl Zeiss GOM, Metrology GmbH, Braunschweig, Germany [15]), Solid Mechanics DIC (Dantec Dynamics, Skovlunde, Denmark [16]), MatchID (University of Leuven-Technology campus Ghent, Belgium, [17]), Image Systems (Image Systems AB (HQ), Linköping, Sweden [18]), Imetrum (Imetrum Limited, Bristol, UK [19]), etc. Nowadays, the number of open-access sources for specialized analyses are also available: Ncorr ([20,21,22]), DICe ([23,24]), YaDICs ([25,26]), Py2DIC ([27,28,29,30]), µDIC ([31,32]), ALDIC ([33,34]), Multi-DIC ([35,36]). Based on the subset tracking, the software calculates the displacement field, providing information about how each point on the surface has moved. Next, from the analysis of changes in subset shapes and sizes, strains and deformation gradients are estimated. After the results, including displacement and strain maps, are generated, and visualized to represent the object's deformation, their accuracy and reliability should be validated and adjustments may be made to the analysis parameters or subset sizes, if necessary. Depending on the complexity of the particular application, the process may need to be repeated with finer subsets or different analysis settings.
Among the most crucial concerns associated with the DIC measurements is the effect of out-of-plane motion, which can probably cause data corruption [37,38]. Therefore, in such a context, two approaches can be considered: 2D-DIC (planar measurements) and 3D-DIC (spatial measurements). During 2D planar measurements, one or several time-synchronized cameras enable in-plane full-field deformations` recording in the pre-determined area of interest (AOI). However, the basic prerequisite of this approach is the absence of out-of-plane displacement and normality of the camera lens axis to the AOI plane [39]. During on-site monitoring of real structures, out-of-plane movement of the investigated surface is a widespread issue, resulting in fictive planar displacement and a considerable measurement error, respectively [12,40], On the other hand, spatial measurements with a synchronized stereo camera system (3D-DIC) method enable capturing out-of-plane displacements and, thus, tend to yield more precise results, especially when the experiment is not appropriately arranged. One of the requirements for reliable 3D-DIC measurement is a comprehensive calibration procedure to define the spatial coordinate system and the scale for all-direction displacement [38]. In DIC, camera calibration is a process that involves determining the intrinsic and extrinsic parameters of a camera system to accurately transform from images (pixels) to real-world coordinates in engineering units (e.g. mm). The intrinsic parameters include focal length, lens distortion, and optical centre, while the extrinsic parameters involve the camera's position and orientation in the 3D space. The general scheme, illustrating the main parameters of the 3D-DIC measurement process is illustrated in Figure 3.
In general, the calibration process typically involves capturing images of a known calibration target with features of known dimensions. By analyzing the images and comparing the known dimensions with the measured pixel coordinates, the software can establish the camera parameters. The 3D tracking systems measure distances by capturing a series of images of an object from two cameras, determining their relative positioning based on characteristic common points. Corresponding distances between the camera matrix and the targets are calculated using epipolar geometry and a triangulation process. In such a setup, cameras are assigned with origins OL and OR for left and right positions, respectively. The baseline, which connects the cameras` origins intersects the camera planes at the epipoles (pL and pR, respectively). The principal parameter, determining the relationship between images recorded by pairs of cameras is the epipolar plane, connecting epipoles. Thus, if the pL is observed in the image on the left camera, the pR should be located on the epipolar line in the image on the right camera. If we consider the particular physical point P, its projections for each of the cameras will have coordinates (xi`, yi`, fi`) in the image planes. If the shift from the original pixel coordinate by fi` is taken into account, then the coordinates of the point in the image coordinate system are (xi`, yi`, 0). Thus, at these stages the global coordinates of a target point are transformed to the camera system coordinates and the coordinates are projected into the retinal plane. The final transformation of the coordinates is associated with the introduction of the sensor system (xs, ys), so that the position of the point could be described as pL(xs1, ys1), and pR(xs2, ys2), respectively. Afterwards, by combining these two points with the intrinsic and extrinsic parameters of the two cameras, the triangulation theory can be applied to derive the 3D coordinates of the physical point P [10].
Figure 3 illustrates the main stages of image translation and interdependencies between world coordinate system (WCS), image coordinate systems (ICS) and camera coordinate systems (CCS). Transformation of an object from 3D space to 2D-image is associated with the impact of perspective projection (defined by camera focal length fi), translation (ti) and rotation (ri) components. A more detailed description of the algorithms for 3D-2D transformation usually used in DIC, (e.g. holography) can be found in several recent studies [3,10,41].
It can be summarized, that the digital image approach provides substantial advantages for structural health assessment due to a completely contactless process and suitability for difficult measuring tasks without stable support for conventional sensors. The approach enables full-field monitoring of a high number of points by a single camera sensor, which allows for obtaining complex deformation gradients. In complicated on-site conditions, possible measurement errors due to off-plane motion can be eliminated by the 3D technique, making it applicable to a wider area of practical engineering tasks. However, the specific feature of the image processing approach is a high dependency on external environmental conditions and the necessity of individual system parameters adjustment for each particular case study. Therefore, the most relevant challenges and widespread error sources in on-site DIC applications are discussed in the next section of the paper.
The Most Relevant Challenges in On-Site DIC Application
As was mentioned by [3], if the optimal conditions are ensured, the modern DIC algorithms enable accurate tracking of in-plane movements of targets and displacements on the investigated surface with a precision of less than 0.01 pixels. Although the DIC technique has been developed, improved, and calibrated during wide application for structural health monitoring worldwide, on-site use of image processing is still associated with several challenges, caused by environmental conditions, technical limitations, calibration errors, etc. Each of the possible error sources should be accurately evaluated, considering their possible impact on the overall quality of the measurement data (e.g. resolution, accuracy, and repeatability). Table 1, adopted from [3] summarizes the qualitative evaluation of the possible impact of various error sources in the context of:
(1) resolution, which is the smallest displacement, within the sensitivity of the system, assumed through the standard deviation of measurement noise;
(2) repeatability pertains to the consistency and precision of repeated measurements taken under identical or nearly identical conditions with minimal variability or scatter, quantified using the standard deviation or the coefficient of variation;
(3) accuracy refers to the closeness of the measured value to the truth, indicating the reliability of measurement and the absence of systematic errors.
Accuracy, resolution, and repeatability are interconnected supplementary aspects in measurements, each addressing different facets of the measurement process, contributing to overall system performance (Figure 4).
Thus, resolution is a component of precision, which contributes to accuracy and supports the goal of achieving accurate measurements. However, precision and accuracy should still be considered as two independent important concepts, with supplementary but diverse features. Repeatability is unidirectionally related to the consistency of measurements (precision), as a system with good repeatability is likely to have high precision. Collectively, accuracy, resolution, and repeatability play integral roles in determining the overall effectiveness and dependability of a measurement system. Balancing these elements is essential to achieve measurements that are both precise and trustworthy.
Among the parameters, which should be taken into account during the preparation of the experimental set-up is the quality of the target, either artificial or natural pattern of the surface (see previous section). Thus, the implementation of artificial targets of optimal size and speckle could play a crucial role in facilitating the tracking and analysis of displacements. Qualitative assessment of the speckle parameters is normally based on such features as mean speckle size (dots` size), subset entropy, sum of squares of subset, intensity gradients, subset size, contrast level, etc. The unique and random nature of speckle pattern allows for accurate correlation, subpixel precision, and the ability to capture fine details of deformation and strain in structures. [12]. For instance, in optimal environmental conditions, natural brick and mortar surfaces can have texture applicable for testing without artificial patterns. However, the suitability of the natural pattern is usually evaluated during the postprocessing, by comparing resolution to the required pixel precision, thus, the necessity of repeating measurement is justified [3] (see Figure 1). After the identification of suitable target characteristics, extrinsic parameters of the sensing system should be assessed. Precise metric calibration is essential for accurate transformation between coordinate systems and elimination of substantial errors in displacement measurements. Calibration errors can be mitigated by a thorough geometric survey (e.g. with a laser scanner) to validate metric distances from camera reconstruction. Additionally, the pitch and roll angles of the camera, measured during equipment setup, can be compared with the angles calculated from the calibrated rotation matrix [3]. One of the prevalent sources of poor correlation and low accuracy is low-resolution or high level of noise in recorded images This can be prevented by the use of resolution cameras with adequate parameters, proper lighting, and ensuring clear images without distortions. In particular, cameras with increased resolution are more appropriate for diagnostic measurement tasks, specifically for monitoring crack patterns or strain distribution. On the other hand, cameras with lower resolution, in most cases about 2.3 megapixels, have advantages in dynamic behaviour capturing due to the possibility to increase sampling frequency [4]. Focal length is another critical parameter, which has to be considered for optimum equipment selection and setup. Thus, higher focal lenses ensure higher resolution, while reducing the size of the field of view (FOV). Also, the high focal length of lenses typically increases their weight, which makes them susceptible to oscillations due to wind or traffic loads [4].
Some of the error reasons can be addressed by careful setting of the sensing system. Thus, during the subset tracking resolution and repeatability are highly dependent on exposure settings, as high contrast in each greyscale target is required for better performance [3,42]. Also, if several targets are tracked simultaneously, it can be recommended to use the smallest aperture possible to obtain a large depth of field. Authors [43,44] also report issues due to radial distortions if a wide field of view is captured from the closer range (which necessitates wide-angle lens configurations). However, this factor can be partly eliminated by the introduction of lens distortion coefficients through a lab calibration or postprocessing calibration.
One of the crucial factors determining the efficiency of the DIC technique is the stability of the camera during the measurement. Thus, ground vibration, due to heavy vehicles` passage or wind-caused vibration can be the reason for the camera's slight movements. Being imperceptible to the naked eye, these changes are rather hard to eliminate during the camera set-up, thus, they are mostly corrected during the post-processing. Wind impacts can be also relegated to the group of environmental source errors, which are among the most critical during on-site measurements. In particular, changes in lightning conditions are the common reason for reduced accuracy and repeatability during structure monitoring. One of the recommended mitigation techniques is the utilization of autoexposure, enabling the automatic setting of optimal exposure rate and maintaining the same illumination levels. However, if the particular case entails monitoring of several targets, the efficiency of this method is significantly reduced. In case of lightning changes low-frequency drift from data with a high pass filter or linear baseline can be removed, but the correction of errors is complicated, as lightning deviations usually follow unclear trends [3]. Thus, the general recommendation would be to perform on-site DIC measurements in the shade (or at night) with artificially controlled lightning levels during short periods. In addition, possible mitigation approaches, proposed in the literature, include the introduction of optical bandpass filtering solutions [42] and subpixel tracking techniques, which partly eliminate the impact of ambient light changes [45,46,47,48]. Other ambient error sources, such as traffic-induced vibration, wind, rain, or water wave reflection can be eliminated by positioning the cameras as far as possible from the source or introducing barrier protection [38]. Furthermore, the effects of camera temperature variations can be mitigated to some extent by employing a pre-established temperature-dependent model for displacements determined in the laboratory [49].
Another category of error sources includes structural actions, which are mostly determined by the specific features of the monitoring case and can be addressed at the processing stage. Thus, if rigid body rotations take place, this can cause altering of pixel optical characteristics and challenge efficient tracking of targets. This limitation can be eliminated by the use of high-order shape functions in DIC processing [3,50]. Out-of-plane movement is reported in previous research as one of the critical error sources, particularly at the edges of the image [37]. The impact of out-of-plane movements can be mitigated with the use of alternative parallel measurements to identify its magnitude, or the use of a 3D-DIC approach (especially if the magnitude is likely to be high). 3D-DIC sensing system, utilizing a stereoscopic camera set-up enables tracking of 3 spatial coordinates by 2 cameras simultaneously, eliminating the effect of out-of-plane movement. However, as the 3D-DIC is often associated with several limitations (complicated set-up process on-site, limited observed area and lower resolution, compared to 2D-DIC), the decision on the most optimal measurement technique should be made with consideration of each particular case [3,37]. Potential errors during the processing are mostly associated with improper selection of correlation algorithms and subset size. These errors have a relatively small influence on the overall performance of the sensing system and can be mitigated by introducing advanced algorithms to handle discontinuities, iterative selection of the optimal correlation algorithm and use of smaller subsets in critical areas.
It can be indicated that the digital image correlation approach, either in planar or in spatial coordinates in a complex synergic sensing system, which requires thorough attention to possible error sources to maximize the efficiency of the measurement process. Addressing such challenges during on-site monitoring of full-scale structures requires meticulous planning, adaptation of measurement setups, and continuous monitoring to ensure the reliability and accuracy of DIC measurements in real-world environments. Recent case studies demonstrate various ways the challenges of DIC for assessing bridges' technical state and remaining resource are being addressed and mitigated and this described in more detail in the next section.
Application of the DIC Method for Bridge Monitoring: Selected Case Studies
The application of innovative non-contact technologies such as wireless sensing or vision-based tracking is a sufficient improvement in the current state of practice in structural health monitoring during service and extreme events. Processing of digital images (e.g. DIC method), among other vision-based approaches has provided effective possibilities for measuring the displacement of full-scale bridges. Practical implementations of this sensor system have already confirmed its cost-effectiveness, reliability, and accuracy; it is also easy to implement and offers real-time capabilities to measure dynamic displacements with a high level of resolution [51]. It is important to note the lack in comprehensive systemised review on application of DIC to full scale structures in real-time conditions. Among existing review works can be mentioned studies [6,7,52]. However, study [6] was mostly focused on full-scale structural elements, tested in laboratory conditions, rather than measurement of bridges on site. The paper [52] focused on structural dynamics, summarized research findings before 2010, thus, necessitating more updated review of DIC applied to real structures. For today, the most detailed review in this area was provided by Mousa, et al This paper continues the recent research [7] providing more detailed insights on limitations and challenges, arising during on-site monitoring of bridges and existing methods for their elimination. Additionally, in-depth analysis of DIC errors during on-site monitoring and their possible impact on resolution, accuracy, and repeatability, given in previous section will be addressed with the examples of practical case studies, herein. Hence, Table 2 provides a summary of the selected case studies, demonstrating the DIC application for structural health monitoring of bridges and a brief description of the experimental set-up used.
Application of photogrammetric methods, which are a prototype of the modern image correlation approach, reach back to the 80s years of last century [53,54,55,56,57]. For instance, pilot studies on the photogrammetric method for bridge deformation monitoring were introduced by Mass, et al [58], indicating fast and economic setup, integral approach for full-field measurements of a large number of targets and, thus, high potential for further development. Among the earliest studies, which demonstrated the applicability of digital image processing (DIP) for on-site monitoring of full-scale bridges is the study of Lee & Shinozuka, 2006 [51], who verified the method through a laboratory shaking table test and a field application on a steel box girder Yeondae Bridge with less than 3% error. Another work of these authors [59] presented image processing results for the profile of 3 bridges of different structural types, confirming the versatility of the approach. In this period on-site study of the girder bridge, subjected to loading by a heavy cargo truck at different positions was performed by Yoneyama, et al, 2007 [60], confirming the effectiveness of the DIC for structural integrity evaluation of infrastructures. Results, presented in this early study show good correspondence to parallel transducer measurements and authors claim that the DIC maintains its functionality even without the artificial speckle pattern on the investigated surface [60].
Thus, the emerging technology of vision-based monitoring is currently facilitated mainly by template matching techniques, which stand out as one of the most efficient methods for tracking objects [10]. In particular, the DIC vision-based target-tracking method for bridge monitoring was introduced in several previous studies and field applications [51,60,61,62,63,64,65]. Particular attention should be paid to the study of [10], which, based on previously introduced larger testing and DIC monitoring program [66], demonstrated the capabilities and potential of a non-contact DIC approach for two applications: for assessment of the dynamic response of a large-scale full bridge, subjected to extreme hazards; and for monitoring of bridges natural vibration under pedestrian loads. Target-tracking 3D-DIC approach was used with circular black and white stickers of varying size, depending on the field of view (FOV). The measurements of 3D displacements and bridge deck rotation, validated by conventional instrumentation, corroborated the applicability of the method for seismic and dynamic response monitoring based on very comparable results. Authors noted the outstanding capability of the method for both complex seismic response monitoring (which is normally associated with very limited access for post-event reconnaissance), as well as for walking and jumping pedestrian loading due to high sensitivity to ambient vibrations [10].
A monitoring setup based on 2D and 3D DIC was used in another case study, a pedestrian bridge in the de Porto urban area, subjected to static loading[67]. The investigation demonstrated the good agreement between data obtained from two setups [67], thus confirming the applicability of the approach for urban areas without preparing of investigated surface. Similarly, vibration analysis of the suspension bridge, subjected to pedestrian loadings, performed by Yung-Chiang Lin et al, 2022 [68] has shown satisfactory results for quick remote assessment of the bridge. Similarly, heavy trucks` vehicle loading tests have confirmed the effectiveness of the method, as was reported in several studies [1,69,70,71,72,73]. For instance, the comprehensive investigation of aged railway arch bridges, validated with FE- simulation enabled monitoring of strain variation with the wheel positions with high accuracy [70]. In addition to results, comparable to conventional sensor installations, DIC-based techniques, provide considerable advantages in terms of operational logistics of transport routes and generally show higher accuracy due to a combination of algorithmic differences and additional signal post-processing [1]. Cost-effectiveness, rapidity, and the possibility to maintain the full-service operation of bridges are among the crucial stakeholder`s requirements and are completely ensured by DIC, as an effective tool for infrastructure whole life management [71].
Crack assessment in bridge structures is among the perspective applications of the image correlation technology, enabling full-field plots, investigation of the time of crack detection and monitoring of crack widths, proved by a number of studies [63,74,75,76]. For instance, the effectiveness of 3D-DIC for bridge structural health monitoring has been demonstrated in the study [63] with specific attention to crack and spalling assessment during 4.5 months by using a projected pattern to measure surface geometry. Similarly, the DIC approach confirms its effectiveness for quantitative crack characterization for out-of-plane distortion-induced fatigue cracks, which is a topical problem in operated steel highway bridges [76]. 2D-DIC provides reliable estimations for verification of qualitative and quantitative stop criteria, based on crack identification, in combination with structural response analysis [74].
Cable tension, as a critical cable-stayed bridge serviceability parameter, has become the motivation of another application of digital image processing [41,77]. The vibration of small cables was successfully assessed from a close distance in the early work of Jo et al, 2021 [41], which, however, identified limitations and the need for further development of the technique for large cable-stayed bridges. Thus, a method for evaluating the instantaneous tension in cables was developed [41], integrating extracts of the digital image processing for cable sag assessment and the parabolic cable theory for tension force evaluation. The validation of the proposed approach on the Godeok bridge under construction (from a 300-m distance) has shown deviations from the direct measurements below 0.22 %, providing concise, time- and cost-effective options for structural health monitoring of cable-stayed bridges. The challenging problem in the reliable estimation of cable forces in contact-type sensors and conventional fixed camera-based methods was also addressed in the study of Tian et al, 2021 [78], where authors proposed the combination of UAV technology and computer vision algorithms to overcome existing limitations. The proposed method confirmed its effectiveness for cables having large vibrations if no wind disruption is present, validated with the full-scale bridge case study.
The unique of its kind investigation of the full-scale real bridge, loaded until the failure, was described in the study of Sas et al, 2012 [79], who highlighted the prevalent suitability of photogrammetric methods for full-field strain monitoring at late loading stages. Thus, the authors noted, that the image correlation approach provided a more comprehensive picture of the strains, than conventional contact methods, as the latter were greatly influenced by crack formation and the longitudinal curvature of the bridge.
In the field of modal analysis, the main advantage of digital image correlation is lower influence on lightweight structural components (e.g. cables, frames) and better full-field measurement performance in comparison with conventional methods (e.g. acceleration sensor method). Although accurate measurements of the first natural frequency are ensured, certain noise levels could be caused by longer shooting distances or smaller displacements, easily eliminated by developed filtering techniques [80]. Similarly, on-site research by Adam Hoag et al, 2017 [73] has confirmed, that the DIC technique outperforms conventional accelerometer sensing because the latter was not optimized for low-frequency acceleration measurement, which resulted in occasional large erroneous peaks due to equipment limitations. A considerable increase in the measurement accuracy (errors below 0.2-3%) was reported in a later study stable on cable force measurement [81]. Notably, authors [81] have predicted certain problems in engineering on-site applications, in particular, unstable lightning conditions, which they managed to resolve in their following works [82].
On-site measurements for real bridges are associated with such factors as wind, oscillations, and unstable ground conditions, resulting in slight changes in the position and direction of a camera. In such situations, the measured displacement is affected by the movement of the camera, making it challenging to obtain accurate displacement measurements [46]. The ambient error sources and stability issues like the camera movement due to settlement or the out-of-plane motion phenomenon could become the reason for significant distortion in measurement data. These challenges could be eliminated with an appropriate experimental set-up, choice of calibration methods and compensation techniques, as was demonstrated in the number of practical bridge case studies with different purposes [38]. The group of recent works demonstrated the developments to address these challenges by robust image processing algorithms to filter out noise from environmental conditions and eliminate possible off-axis deviations in camera positioning [3,83,84,85,86,87,88,89,90]. Yoneyama et al [87] propose a method for correcting the effect of camera movement by introducing the equation of perspective transformation. The effectiveness of the proposed correction was validated through both laboratories testing of a wide-flange beam and application to deflection measurement of a real bridge girder [87]. The problem with ensuring camera stability during on-site measurements was addressed also in the study of Liang, et al, 2021 [93], enabling the use non-fixed camera. Challenges in fixing the camera in a stable position and ensuring that the optical axis of the camera is normal to the investigated surface were highlighted also in a previous study by Pan, et al, 2016 [84]. In addition, with the developed video defectometer, authors managed to replace the unpractical artificial targets with the laser range finder and demonstrated the real-time, non-contact targetless and off-axis DIC measurement approach through laboratory testing and a railway bridge field application. Further development of the off-axis DIC method [86] led to a simplified, yet accurate deflection measurements method, based on a special straight-line fitting principle, validated through the indoor cantilever beam experiment and the on-site actual bridge deflection.
Another widespread issue in the long-term monitoring was highlighted by Xie et al, 2023 [82] and Juno et al, 2020 [94] and is associated with the notable challenge due to illumination factors. Throughout the monitoring process, fluctuations in natural light result in variations in light intensity and angle. Deviations in light intensity have an impact on the grayscale value of the image, giving rise to two issues associated with the use of a fixed grayscale threshold for binarization. Thus, authors [82] proposed the improved dual-channel approach, integrating the principle of the dark channel and the maximum interclass variance method. The experimental approbation of the bridge prototype in complex and changing light conditions has shown an error of less than 3 % compared with the traditional displacement meter. This confirms the applicability of the technique for eliminating illumination factors, providing a scientific basis for engineering practice. Specific attention in this direction should be paid to the research paper of [3], providing a detailed evaluation of the errors due to equipment set-up, lighting effects, target quality, camera movements, and metric calibration, influencing the DIC technique performance. The proposed calibration method using vanishing points and a single distance was effectively implemented for on-site multipoint displacement monitoring of Marsh Lane Viaduct, which facilitated to assessment of the complex structural 3D behaviour of the asset. To address lighting and weather variability, the DIC system can also be equipped with adaptive lighting and weather-resistant enclosures for the cameras. This, in addition to robust image processing algorithms developed (e.g. [82,83,84,85,86,87,93,94], etc) will enable to minimize the impact of noise from environmental conditions.
The evolving area on the combined lightweight remotely operated stereovision systems, entailing unmanned aerial vehicle (UAV) and 3D-DIC quantified their applicability to acquire data for DIC analysis, but are still associated with significant limitations due to system instability. Thus, while enabling displacement evolution measurements and assessment of the joint state in limited access conditions, the approach is influenced by the effect of lighting, drone unwanted oscillations, challenges in GPS-denied environments positioning, etc [88,89]. Although, this approach enables to minimise the resources for timely on-site inspections, further developments are still required to address all the limitations.
The issues arising during efforts to monitor cracking patterns in real-life conditions were analysed in the disparate group of studies [95,96,97]. The challenges in ensuring stationary fixing of cameras during long-term monitoring inspired the development of techniques for processing images collected with no fixed camera positions. Hence, works [96,97] describe application of reflective targets and corresponding transformation algorithms to the obtained cracks images. In contrast, in the study [95] novel methodologies, integrating Convolutional Neural Networks and photogrammetry were used, without additional targets required. These works have efficiently proven that implementation of robust image processing algorithms and integration of disparate techniques enable processing images collected with non-fixed cameras, thus overcoming the limitations of standard DIC.
Recent years, specific attention was also paid to DIC for experimental investigation of local dynamics and nonlinear response in multi-component structures [98,99,100,101]. In particular, as the dynamic properties in structures, containing multiply joints and nonlinear interfaces are often complicated to identify correctly with traditional approaches, image correlation reaches the enhanced attention when there is the necessity to study large bridges, subjected to dynamic loads. Issues, arising in practical applications of DIC to large bridge structures and complex structures include the limited field of view, requiring multiple setups to cover extensive areas, as well as ensuring consistent lighting and camera alignment over large distances. Ensuring comprehensive coverage of all critical areas requires meticulous planning and potentially additional equipment. However, creation of scalable DIC system using a network of synchronized cameras positioned at strategic points along the bridge coupled with advanced stitching algorithms is capable to employ and merge data from multiple cameras into a cohesive dataset and capture comprehensive strain data across the entire bridge.
Cost-effectiveness is among the most widely mentioned practical challenges in on-site implementation of DIC measurements due to the cost of high-resolution cameras, specialized lighting, image processing software, and the training required for personnel to effectively use and interpret DIC data. Moreover, regular maintenance and calibration of the equipment are necessary to ensure accurate measurements, contributing to ongoing operational expenses. However, the rapid development of digital cameras in the recent years have made DIC more versatile and cost effective, as was reported in the number of practical works [71,72,81]. The increase in resolution of camera images leads to increased low-cost computing power and this enables more cost effective, rapid monitoring in real practical scenarios. In addition, the availability of open-source software for DIC analysis [20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36] and recent computational targetless approaches ([60,72,77,84],etc) contribute to the reduction in both initial investment and operational costs and facilitates further implementation of the method. The use of non-target techniques using the natural pattern of the surface ([46,67,72,73,84], etc) mentioned above, also help to reduce the time, required for experimental set-up and surface preparation, simplifying the DIC application for on-site scenarios. The time duration can be further decreased by development of an automated DIC system that includes pre-calibrated camera setups and automated speckle pattern generation.
The case studies described in this section illustrate that recent advancements in technology and methodology are effectively addressing and eliminating the traditional challenges associated with DIC. By focusing on cost reduction, time efficiency, scalability, robustness, data interpretation, durability, real-time monitoring, and integration with other technologies, DIC is becoming a more practical and reliable tool for the structural assessment of bridges. These innovations are facilitating more widespread adoption and enhancing the ability to maintain and monitor critical infrastructure effectively.
Table 2.
Selected case studies of DIC method application for bridge monitoring: description and the experimental setup. Post-processing for target coordinates recognition.
Table 2.
Selected case studies of DIC method application for bridge monitoring: description and the experimental setup. Post-processing for target coordinates recognition.
| Investigated structure* | Method, pros | Limitations, cons |
Hardware (H), Software (S)** | Source |
| Street bridge over the Flutgraben in Erfurt, Thuringia (non-reinforced concrete bow bridge, L= 27 m, W= 12.5 m. Vehicle (truck) loading test. Camera at distance 32 m | 2D monocular digital photogrammetric technique and an ellipse operator for image coordinates determination | Necessity to close traffic on the bridge. Need of direct access to the asset to mount targets. Impact of the natural illumination changes and overexposure of the targets on the quality of image data processing. Need in reliable methods to detect possible camera orientation changes. | H: machine vision camera (The Imaging Source, 1024 ×768 pixels, 21 fps, standard deviation- 0.017 pixels (EF), rel. accuracy 1: 60.000); grey level machine vision camera (1300×1030 pixels); Still Video camera (Kodak DCS 660, 3040×2008 pixels, 0.1 (max 3) fps, standard deviation-0.01-0.015 pixel (LSM), rel. accuracy 1: 30.000); image rate 1 Hz | [58] |
|
2D-digital image processing for real-time displacement measurement with a target recognition algorithm. | Need of direct access to the asset to mount targets. Limitation for dynamic response monitoring (frequencies below 3 Hz). Impact of vibrations caused by wind (the wind shield equipment should be employed). Impact of low lightning conditions (light source may be needed) | H: digital camcorder (30× optical zooming capability, 720×480 pixels, 30 fps); telescopic lens (8× optical zooming); laptop (Pentium M 1.6 GHz processor 512 MB RAM); S: MATLAB | [51,59] |
| Continuation of Table 2. Optical flow method for post-processing | ||||
| The cable-stayed pedestrian bridge. Vibration testing of cable (Ø=40 mm). Camcorders at distance 2 and 2.5 m. | 2D-digital image processing novel non-target technique based on the use of an optical flow method. | Approach is applicable to vibration assessment of cables without a noticeable sag effect). The amplitude error and image blurriness increase at higher frequencies (about 3 Hz). Long processing time. Not applicable for real-time measurement. Necessity to ensure camera stationarity. Telescopic lens and a large optical zoom capability needed for long-span bridges. | H: digital camcorder (1/3-in. 1.18-megapixel progressive CCDs, 1280×720 pixels, 29.97 fps); lens of F1.8 (52 mm focal length, 10× optical and 200×digital zoom); total station | [77] |
|
2D-DIC with reprojection of video frames by using a linear homography matrix compared with phase-based optical flow method. | Need of direct access to apply targets. Impact of lighting changes. Challenges in aligning the plane of the imaging sensor with the 2D plane of surface to eliminate perspective distortion effects. Need in post-processing for reprojection of out-of-plane motions. | H: 2 Imetrum cameras (6.3 and 13.4mm sensor diagonals); 2 lenses, (12 and 25 mm), Panasonic GH5 camera (12-mm f1.4 lens, 30 fps in B1 and 60 30 fps in B2). S: Imetrum Video Gauge. | [1] |
| Continuation of Table 2. Post-processing approaches for uneven lightning conditions | ||||
| The Wuhan Yangtze River Bridge (L=1670 m, 8 piers, spaced 128 m and 9 apertures). Static and dynamic load testing. Vehicle (truck) and train loading test. Camera at distance 107.3 m, 134.2 m, 164.2 m, 226.1 m. | 2D-DIC. Video deflectometer for active imaging, combining high-brightness monochromatic LED targets with coupled bandpass filter imaging to eliminate against ambient light changes. | Measuring system should be kept stationary during the whole measurement period. Necessity of measurement at night to avoid the interference of daily traffic. | H: camera (Genie HM1024, Teledyne DALSA, ON, Canada, 1024×768 pixels, 8-bit quantization, max 117 fps); fixed-focal optical lens; laser rangefinder (BOSCH GLM 250VFPro, Robert Bosch GmbH, Power, max distance 250 m, ±1 mm), optical theodolite, laptop (Thinkpad T440p, Lenovo, Beijing, China, Intel(R) Core(TM) i7-4700MQ CPU, 2.40 GHz main frequency and 8 GB RAM). | [85] |
| The 1/70 scale model (L=2.15+4.8+2.15=9.1 m) of the GuanHe Bridge (L=32.9+115.4+340+115.4+32.9=636.6 m). Dynamic response experiments. Camera at distance 0.78 m | 2D DIC with dual-channel and the maximum interclass variance for measurement of bridge displacement under uneven illumination | Complicated post-processing, time consuming for structures with high dimensions. Necessity in additional calibration of method in on-site conditions. | H: android phone (HONOR V30) (3840×2160 pixels, 60 Hz) | [82] |
| Highway bridge. Loading by a heavy lorry (32 tonnes). Camera at distance 15 m. | 2D-DIC under the varying lighting conditions between images, eliminated by NPL DIC code. | Impact of imaging at an angle and repositioning of the camera between digital photographs. | H: PhaseOne camera (39 MPixel); 80 mm lens. S: NPL Grid | [83] |
| Continuation of Table 2. Application of filters to eliminate environmental impacts. | ||||
| The Entre-Águas bridge in Caniçal (Madeira, Portugal). Vehicle loading (30-ton trucks). Camera at distance 70 m | 2D DIC measurements without camera calibration with post-filtering to eliminate the measurements noise due to the changing environmental conditions. | Need of direct access to the surface to apply the target speckle pattern. Challenges of large areas monitoring. Possible impacts of wind or road movement (need to ensure stability of tripod and camera). Necessity to ensure camera is parallel to the image frame. Impact of heat wave, causing motion blur (need in short image exposure). | H: digital camera (4-megapixel iDS UI-3370CP, 70 – 300 mm zoom lens, 1.4× teleconverter, eq. to a 420 mm focal distance lens; CMOSIS CMV4000-3E5M sensor, 80 fps). S: INEGI | [69] |
|
2D-DIC measurements, mapped against the wheel positions obtained from laser data sets coupled with noise reduction using the Savitzky-Golay filter. | Need of direct access to the surface to apply the speckle pattern. Necessity to reduce the data noise and oscillations. | H: digital camera (Sony (Tokyo, Japan) IDS, 2.35 megapixels, 1,936×1,216 pixels, 50 fps, 6 ms exposure time, 5.863 mm/pix); high-resolution lens (Kowa, Torrance, California, 35 mm focal length, f1.4 aperture); Infrared (IR) Light Emitting Diode (LED) model, IR filter - 850 nm. S: Istra4D (Nova Instruments) | [70] |
| Continuation of Table 2. Application of filters to eliminate environmental impacts. | ||||
Docklands Light Railway (DLR):
|
2D DIC with optimizing contrast levels and exact positioning of reference points for the virtual strain gauges. DIC calibration by specifying real-world distances. Fatigue management strategy based on measured data. | Necessity to avoid movement in the third dimension compared to the two being measured. Limited time for measurement to avoid traffic closure. |
H: digital camera (20–40 Hz, 1/50th pixel resolution). | [71] |
| The Halton railroad 26.36 bridge (Canada-USA; 43⁰37‟18.7” N, -79⁰55‟54.9” W; steel Deck Plate Girder; 6 spans×30 m; masonry piers). Train loading testing | 2D-DIC with accuracy optimisation by adjusting the scale factor and filtering using a low low-pass filter. | Impact of camera and tripod vibrations (can be reduced by post-processing). Challenges in long-term monitoring. | High speed camera (Allied Vision Technologies (AVT) GX1050 8 8-bit monochrome 1 megapixel (MP)); 85 mm lenses; 100 Hz, | [73] |
| The Delaware River Bridge (4 span; truss, W14×314 sections). Monitoring of structural behaviour during the repair works | 3D-DIC measurements, post-processed with the median filter for area averaging and the binomial filter for time averaging. Rapid application of the DIC pattern with pressure-activated adhesive tape. | Need of direct access to the surface to apply the speckle pattern. Necessity to reduce the environmental noise by area averaging and time averaging. Susceptiveness of results to out-of-plane bending. | H: 2 cameras (2448×2050 pixels); 12 mm lenses. S: GOM Correlate | [91,92] |
| Continuation of Table 2. Other methods to eliminate environmental impacts. | ||||
|
2D-DIC and 3D-DIC for bridge on-site diagnostics and load testing. Methods for mitigation out-of-plane motion, camera movement and ambient errors minimization. | Need of direct access to the surface to apply the speckle pattern. For 2D-DIC-the effect of out-of-plane motion, which may corrupt the data due to fictive planar displacement. For 3D DIC method, - limited region of measurement. Possible impact of lighting condition and environmental factors. Necessity to use additional reflectors to improve natural lightning conditions. |
H: 2 cameras (Basler acA4096-30μm); lens of focal length f = 35 mm, 75 mm, 50 mm (depending on distance). S: Correlated Solutions Inc and ISI-sys GmbH system, VIC-snap, VIC-2D and VIC-3D. | [4] |
| Continuation of Table 2. Other post-processing and correction approaches | ||||
| Ornskoldsvik Bridge, Sweden (2 spans, 12 +12-m frame, L=36.293 m, H=8.2 m). Loading-to failure testing. Camera at distance 3.1 m. | 2D- DIC with MATLAB post-processing with conversion process based on the Mohr–Coulomb strain/stress transformation theory | Need of direct access to the surface to apply the speckle pattern. Need to ensure fixed independent scaffold to prevent accidental displacement of camera. Limitations to the size of the monitored area by performance of the photographic equipment. Need in camera with a shutter speed higher than the velocity of the object movement to avoid blurring. | H: digital camera (Canon EOS 5D); 90-mm lens. S: tailor-made toolkit in MATLAB | [79] |
| Concrete girder bridge. Usual traffic loading | 2D-DIC with camera movement correction method through perspective transformation. | Need of direct access to the surface to apply the speckle pattern. Need in multiply measurements (unloaded and loaded conditions) | H: single-reflex type digital camera (3008×2000 pixels×24 bits) | [87] |
| Continuation of Table 2. DIC measurements for random pattern effect analysis. | ||||
| Girder bridge (L=15.4 m, W=7 m) Loading by a heavy cargo truck (20 t, various positions) | 2D-DIC for random pattern effect analysis: with random-shaped magnet plates attached on the surface to create random pattern and no random pattern attached. | Need of direct access to the asset to attach plates with pattern. The possibility of incompatibility of deformations of plates and studied surface (e.g. sliding, delamination). Need in additional illumination by high-intensity light sources. | H: 2 single-lens reflex cameras for 2 girders (3072×2048 pixels and 3504×2336 pixels resolution) | [60] |
|
2D-DIC for random pattern effect analysis: with target panel and on an existing surface. Approaches to mitigate ambient light conditions at night: illuminated by a flashlight, using the surface-attached LED lights. | Need of direct access to the surface to attach targets. Need in additional illumination by high-intensity light sources. Impacts of wind induced vibration and lightning changes. Increased errors at long measurement distances. Long-term preparation to install additional lightning sources. | H: monochrome camera (Point Grey/FL3-U3-13Y3M-C, 1280×1024 pixels, 150fps, CMOS sensor, 4.8 μm pixel size, C-mount lens); Kowa/LMVZ990 IR lens (9 to 90 mm focal length, maximum aperture F1.8); Sony /PCG-41216L laptop (Intel(R) Core(TM) i7-2620M CPU, 2.70 GHz, 8192 RAM, 250 HDD, 14.1" Screen), Tripod, USB3.0 type-A to micro-B cable. S: FlyCapture Software Development Kit (SDK) by Point Grey Research | [46] |
| Continuation of Table 2. DIC measurements with natural texture of the surface. | ||||
| Masonry arch railway bridge (4 spans). Train loading testing (weight ca. 45 tonnes per bogie, maximum speed 200 km/h). Camera at distance 10 m. | 2D DIC with the random grey intensity distribution of natural texture of the specimen’s surface. | Need to use shutter remote control to avoid errors due to camera movement and lighting. Impact of vibration, correlation function errors in the region of rough edges, i.e. intersection of the specimen with the background. Difficulties in detecting the correct position of the subset. Demonstration of method, rather than numerical values in the test. | H: digital camera (Nikon D3100 DSLR, 14 MPixel); Nikon AF-S DX Micro NIKKOR 40 mm f/2.8G lens; Photo Video Studio focusable Redhead spotlight. S: MatchID-2D (Mechanical Engineering department of the Catholic University College Ghent) | [72] |
| Pedestrian bridge (campus of the Faculty of Engineering of the University of Porto). Static loading. 3D-Cameras at distance 30 m, separated at 4 m. 2D-Camera at distance 13 m. |
Parallel 3D and 2D-DIC measurements with irregular contrasting pattern of the natural surface. Distortion computing by camera calibration using the Zhang calibration algorithm (2nd and 4th orders) | Necessity in post-processing to compute distortions due to perspective. Substantial level of noise over the whole region of interest for 3D-DIC. No visible gradient on the 2D displacement field due to small field of view. |
H (3D-DIC): 2 cameras (Bosch DINION IP Ultra 8000 MP, 75 mm lens, 4000× 3000 pixels). H (2D-DIC): 1 USB camera (iDS uEye UI-3370CP model, 150 mm lens, 2048×2048 pixels). S: MATLAB. |
[67] |
| Continuation of Table 2. Calibration from the simple pinhole camera model. | ||||
| Shuohuang railway bridge (3 spans, L=60 m). Deflection measurement under freight train travelling with speed of 80 km/h. Camera at distance 22.5-22.8 m. | 2D-DIC. Video deflectometer for off-axis targetless imaging with calibration from the simple pinhole camera model. | Necessity to ensure the system stationarity. Necessity to ensure aperture of the lens, sufficient contrast without overexposure. Possible impact of texture information contained in the subset, ambient vibration, ambient temperature, wind, and light variations. | H: high-speed area scan monochrome camera (Genie HM1024, Teledyne DALSA, Ontario, Canada, max capture rate of 117 fps, 1024×768 pixels, 8-bit quantization); fixed-focal optical lens; laptop (Thinkpad T440, Lengend, Intel(R) Core(TM) i7-4700 MQ CPU,2.40 GHz main frequency and 8GRAM); laser rangefinder (BOSCH, GLM 250VFPro, max distance 200 m, ±1 mm); optical theodolite. | [84] |
|
Target-tracking 3D-DIC for monitoring the vibration frequencies. Camera calibration with pinhole camera model. | Need of direct access to the asset to attach targets. Possible impact of arbitrary excitations like ambient vibrations of bridges due to wind loads. | H: 2 high-speed cameras (IL5QM4, Fastec Imaging, USA, 2560 × 2048 pixels, 8-bit grayscale); FasMotion software. S: TRITOP; GOM photogrammetric. | [10,66] |
| Continuation of Table 2: Other calibration methods. | ||||
| High-speed railway bridge (MS=16 m). Camera at distance 30 m. | 2D-DIC off-axis scheme and a full-field scale factor determination method assisted by a laser rangefinder. | The trade-off between resolution and speed. Challenges due to non-suitable natural texture patterns (need in artificial speckle patterns or LED-illuminated speckle targets). Need in post-processing, mean and median filtering to reduce the measurement noise. Dependency on image resolution, intensity variations, field of view, measurement distance, frame rate, environmental constraints. | H: high-speed video camera (Daheng Imaging, Mer-131-210u3m, 1280 ×1024 pixels, 8-bit grayscale, 210 fps), fixed focal length/ fixed focus lens (F-number according to the actual imaging needs), laser distance measurer/rangefinder (Bosch GLM200, max distance: 200 m, measurement accuracy ± 1 mm); electronic theodolite; tripod; laptop. | [86] |
| Suspension bridge (MS=50 m). Vibration analysis under pedestrian loading. Cameras at distance 54.6 m, separated at 0.644 m. | 3D DIC measurement with new calibration method for large structures (using inertial measurement units (IMU) and laser sensors along with a virtual stereovision tool). | Need of direct access to the surface to apply targets. Need in calibration process prior to measurement. Impact of lighting condition and environmental factors (temperature, humidity, and wind). | H: 2 cameras (Sony, recording period 563s, frequency 0.002Hz.); Nikon total station; IMU-laser sensors | [68] |
| Continuation of Table 2: Dynamic displacement measurements. | ||||
| Marsh Lane Viaduct (brick masonry viaduct; up to 25-ton axles, up to 55 km/h speed; investigated arch with span of 7.7 m, a rise of 2.1 m, W= 8 m). Train loading testing | 2D-DIC and 3D-DIC: multipoint dynamic displacement measurement using vanishing points and a single distance in the image. | Potential errors due to lighting changes, image texture, and camera movements. Need in specific calibration to minimize pixel-metric scaling errors. Possible influence of radial distortions and out of-plane movements on relative displacement (can be eliminated with division and pinhole camera models). | H: 2 video cameras (industrial-grade Allied Vision GigE, 2048×1088 pixels, 11.26 × 5.98-mm-size sensor, 50 Hz). S: Imetrum Video Gauge software; MATLAB | [3] |
| The truss bridge model (28 spans: 0.35×0.35×0.35 m, L=9.8 m; 353 rods connected by 112 bolted balls (Ø50 mm); Q235 steel; simply supported at both ends). Modal Analysis | 2D-DIC for tracking of the dynamic displacement and identification of the natural frequencies and mode shapes of bridges. | Small displacement amplitudes and long shooting distance may result in the low quality of the measured data (can be eliminated by filtering). Impacts of environmental disturbance of the camera and image distortion. | H: digital video camera (D5300, Nikon Corporation, Japan); MA: 2 acquisition systems: JM3840 (Jing-Ming Technology Inc., Yangzhou, China), acceleration sensors with nominal sensitivity of 100 mV/g. S: kit software. | [80] |
| Continuation of Table 2. Cable-force measurements. | ||||
| The 2-pylon concrete cable-stayed Godeok bridge under construction (L=1000 m; MS=540m; H= 165 m). Tension-testing in cables. (Target cable -CRS05R). Camera at distance 300 m. | 2D-digital image processing for the sag-based cable tension force evaluation based on the parabolic cable theory. Post-processing with the perspective transformation approach. | Need of direct access to the surface to apply B/W markers for reference points. Need in post-processing to correct distortion due to the internal factors of the camera, geometric changes and to remove the effect of perspective projection. The method narrowly focused on cable-stayed bridges. | H: digital camera (Canon’s EOS R5; 8192× 5464 pixels); 70–200 mm F2.8 telephoto lens; total station. S: camera calibrator toolbox in MATLAB. | [41] |
| The 1/70 scale model (L=2.15+4.8+2.15=9.1 m) of GuanHe Bridge (L=32.9+115.4+340+115.4+32.9=636.6 m). Dynamic response experiments. Camera at distance 0.78 m. | Combination of 2D-DIC and DIP (digital image processing) for cable force measurement with the vibration frequency method. | Measuring errors due to more complex background changes such as bad weather, changes in light and the emergence of other dynamic backgrounds. Could be eliminated by targets such as LED lights and narrowed region of interest. The method narrowly focused on cable-stayed bridges. | H: digital camera (DSLR Canon 70D, 1280×720 pixels r, 50 frs); Canon STM lens (Focal length: 18–55 mm, manual zoom); acceleration sensor (TST120A500, 100 Hz) | [81] |
| Continuation of Table 2. The use of UAV | ||||
| Bridges in Lowell, Massachusetts (concrete cast-in-place). Assessment of displacements due to the thermal expansion and contraction of the concrete abutments and expansion joint. Cameras at distance 1.75 m, separated at 0.707 m, 25°separation angle. | Unmanned aerial vehicle (UAV) and 3D-DIC full-field displacement monitoring with 3D measurement stitching, and 3D point-tracking techniques. | Need of direct access to the surface to apply the speckle pattern. Challenge of positioning and localization in GPS restricted environments. Problems with stitching the point cloud data sets for large areas monitoring. Impacts of lighting and UAV oscillations. | H: 2 cameras (Basler acA1600-20 series, 2 2-Megapixels employing a (7.16 ×5.44)·10-3m); Sony ICX274 charge coupled device monochrome image sensors (1626×1236 pixels, pixel size of 4.4×4.4 μm); 8.5 mm focal length lenses (Edmund Optics Ltd), Minnowboard MAX dual-core single board computer. UAV: InstantEye®Gen 4 Quadcopter (Physical Science, Inc.);. S: GOM’s TRITOP; ARAMIS. | [88,89,90] |
| Nansha Bridge, Guangdong province, China (twin-tower 1 span suspension bridge, MS= 1200 m, side span =360 m, span ratio= 1:9.5, the center spacing of 2 main cables = 42.1 m, the standard spacing of cables is 12.8 m. H=193.1 m, W= 49.7 m). Cable forces testing | Unmanned aerial vehicle (UAV) and 2D-DIC for noncontact cable force estimation. Post-processing with line segments detector (LSD) and matching algorithm for calculating dynamic displacements of bridge cables without need to adjust predefined parameters. | Challenge of positioning and localization in GPS restricted environments. Impacts of lighting and UAV oscillations. Applicability of method only for large vibrations and under the condition of non-windy region. | H: Digital camera (DJI Zenmuse X4S, 4096×2160 pixels resolution, 60 Hz); UAV: Model Jingwei M200 (DJI). | [78] |
| Continuation of Table 2. Full-field monitoring for structural health assessment. | ||||
| Three bridges near Lowell, Massachusetts. Crack and spalling evaluation. | 3D DIC for measuring full-field displacement, strain, and locating cracks from images recorded at different dates and operating conditions. | Need of direct access to the surface to apply the speckle pattern and (or) targets. Dimensional distortions due to subpar camera calibration, shallow camera angle, lens distortion errors, camera shift. Need in imagining from multiply points. |
H: DIC cameras; high power projector. S: GOMTM’s ARAMIS. |
[63] |
|
2D DIC for monitoring stop criteria in in situ proof-loadings for a systematic reclassification of concrete bridges based on crack detection and monitoring. | Need of direct access to the surface to apply the speckle pattern. Challenges in identification of optimal parameters of the speckle pattern. Possible pseudo deformation from out-of-plane movement and rotation of the surface. Environmental impacts circumstances (humidity, temperature, wind, variation of lighting, contrast pattern detection, reflections). |
H: 2 cameras: Canon 6D with 20 Megapixel (Mpx) with a wide-angle lens (Canon EF 16-35 mm f/2.8L II USM); Canon 550D with 18.7 Mpx with a regular lens (Canon EF-S 18–55 mm f/3.5–5.6 IS). Images were captured every 3 min (on site) and 10 s (lab). S: GOM Correlate. |
[74] |
*W-width; L-length; H-height; MS-main span; translation from ft to m, - approximate by authors. **The hardware and software characteristics are provided upon the availability in the references source
Recommendations and Future Perspective Directions of Research
As was demonstrated in the review of case studies, DIC is a powerful tool for structural assessment, but its full potential is still being explored. Future research in DIC is needed to address current challenges and expand its applicability and effectiveness in on-site technical state assessment. The most critical concerns regarding on-site application of DIC are associated with possible impacts of environmental factors (e.g. ambient light conditions, wind, humidity, and temperature variations, etc), which can significantly impact the accuracy of results. Hence, future perspective directions in DIC development should include enhancements the algorithms to better filter out noise caused by environmental factors and improve signal clarity will increase the reliability of DIC measurements. Recent studies have already demonstrated that the efficient post-processing and filtering techniques can substantially reduce the environment- induced distortions in measured images. Research on improving the robustness of DIC systems in adverse environmental conditions can also include developing durable adaptive lighting and weather-resistant enclosures for the cameras, as well as more resilient speckle patterns. In addition, the further attention to targetless approaches will facilitate the simplification of the preparation process and setup and will eliminate the time-consuming speckle pattern or targets application.
The emerging development of digital cameras and enhancement of their resolution contributed to making the DIC-applications more cost-effective and affordable. It can also be recommended in future developments to focus on open-source software platforms for DIC data interpretation, allowing more researchers and practitioners to contribute to and benefit from advancements in this technology. It can also be assumed, that the further research aims to development of scalable DIC solutions that can efficiently cover large bridge structures. This might involve networked camera systems and synchronized data acquisition methods to ensure comprehensive coverage and eliminate possible issues of scalability in full-field monitoring. Also, research, focused on automation of the setup and calibration processes to reduce the time and expertise required for DIC deployment. This can include the development of intelligent camera positioning systems and automated speckle pattern application methods.
Among other areas and directions for future research can be mentioned integration of the artificial intelligence (AI) and machine learning (ML) algorithms to enhance the speed and accuracy of data processing. AI can help in real-time analysis, pattern recognition, and anomaly detection, reducing the time from data acquisition to actionable insights. In addition, combining DIC with other structural health monitoring technologies, such as acoustic emission sensors, strain gauges, and laser scanning, can provide a multi-faceted view of structural health. Data fusion techniques will be essential to integrate diverse data sources effectively. Considerable gap in research on real-time continuous remote monitoring can be addressed by advancing computational power and data transmission. Developing remote DIC systems that can be operated and monitored wirelessly will enhance accessibility, especially for hard-to-reach or dangerous locations, for instance by integrating with drones or autonomous robots for inspection tasks. This real-time capability is crucial for early detection of potential failures and timely maintenance, introducing high practical potential and relevance for structural health assessment of bridge portfolios.
To summarize, the future of DIC research is geared towards enhancing the technology's efficiency, robustness, and accessibility. By addressing current limitations and exploring new applications, DIC can become an indispensable tool for structural health monitoring and maintenance, contributing to the longevity and safety of critical infrastructure.
Conclusions
The paper is focused on a detailed comprehensive review of existing studies demonstrating practical experience in the application of digital image correlation (DIC) techniques for structural health assessment of bridge structures worldwide. The current review provides evidence of the remarkable potential of DIC for advancing structural and infrastructure health monitoring during service or after extreme events. With the utilization of high-resolution cameras and advanced algorithms, this approach provides essential advances for capturing complex deformations, such as those induced by dynamic loads or environmental factors, providing engineers and researchers with valuable insights into a bridge's performance. The ability to operate in real-world conditions, coupled with its non-contact nature, makes image correlation particularly valuable for on-site measurements. Thus, many practical studies have demonstrated the possibility of implementing the method on existing urban structures, requiring little intervention in the structure being monitored. In particular, from a logistical point of view, the DIC setup significantly outperforms previous conventional methods, minimizing traffic disruption and optimizing the overall monitoring process.
Despite its obvious advantages, careful consideration must be given to calibration procedures, camera selection, and potential error sources to ensure the accuracy and reliability of DIC measurements. The additional complexity of the approach is associated with the camera setup process (e.g. the choice of camera focal length, positioning, and target installation or optimization of speckle pattern) as well as the necessity for sophisticated calibration and data processing. However, ongoing advancements in technology and methodology continue to enhance the capabilities of DIC for bridge assessment, promising even greater accuracy and efficiency in the future.
The evolution of DIC over the recent decades, including the development of digital hardware, software, and computational algorithms, has significantly strengthened and established DIC as a robust technique. It is widely recognized as a groundbreaking method for accurately computing full-field deformations and structural displacements in both static and dynamic conditions. The capability to capture full-field displacement maps provides a holistic understanding of a bridge's behaviour, allowing for the identification of localized structural issues and potential vulnerabilities. Ongoing advancements in optical instrumentation, such as high-definition video recording devices and unmanned autonomous imaging tools, combined with sophisticated matching algorithms for comprehensive analysis of captured images in full-field 2D and 3D, ensure that DIC is likely to retain its position as the most effective and multifaceted tool for deformation measurement in the years ahead.
It can be summarized, that the digital image correlation (DIC) emerges as a powerful and versatile technique in the field of bridge engineering, contributing to the development of sustainable and resilient infrastructure systems. The continuous refinement of this approach, along with interdisciplinary collaboration, enables the precise measurement of deformations, optimizing maintenance strategies, extending the lifespan of bridges, and contributing to the overall safety and resilience of critical infrastructure.
Funding
First author would like to thank the British Academy’s Researchers at Risk Fellowships Programme for provided support [Award Reference: RaR\100770].
Data Availability Statement
Authors confirm that the data supporting the findings of this study are available within the article.
Acknowledgments
First author would like to thank the British Academy’s Researchers at Risk Fellowships Programme for provided support [Award Reference: RaR\100770]. A preprint has previously been published [102].
Conflicts of Interest
Authors declare that there is no conflict of interest regarding the publication of this paper.
References
- M. Ghyabi, L.C. Timber, G. Jahangiri, D. Lattanzi, H. W. Shenton III, M. J. Chajes, M. H. Head. “Vision-Based Measurements to Quantify Bridge Deformations”. Journal of Bridge Engineering, vol. 28, no 1, 05022010, 2023. [CrossRef]
- Y. Blikharskyy, N. Kopiika, R. Khmil, J. Selejdak, Z. Blikharskyy (2022). “Review of development and application of digital image correlation method for study of stress–strain state of RC Structures”. Applied Sciences, vol 12, no 19, 10157, 2022. [CrossRef]
- S. Acikgoz, M. J. DeJong, K. Soga. “Sensing dynamic displacements in masonry rail bridges using 2D digital image correlation”. Structural Control and Health Monitoring, vol 25, no 8, e2187, 2018. [CrossRef]
- V. Stančík, P. Ryjáček. “The application of modern methods for bridge diagnostics and load testing”. ce/papers, vol 6, no 5, pp. 949-958, 2023. [CrossRef]
- Maksymenko, O.M. Sakharuk, Y. L. Ivanytskyi, P.S. Kun. “Multilaser spot tracking technology for bridge structure displacement measuring” Struct. Control Health Monit, vol 28, no 3, e2675, 2021. [CrossRef]
- M. A. Mousa, M. M. Yussof, T. S. Hussein, L. N. Assi, S. Ghahari. “A Digital Image Correlation Technique for Laboratory Structural Tests and Applications: A Systematic Literature Review”. Sensors, vol 23, no 23, 9362, 2023. [CrossRef]
- M. A. Mousa, M. M. Yussof, U. J. Udi, F. M. Nazri, M. K. Kamarudin, G. A. Parke, L. N. Assi, S. A. Ghahari. “Application of digital image correlation in structural health monitoring of bridge infrastructures: A review”. Infrastructures, vol 6, no 12, pp 176-194, 2021. [CrossRef]
- N. Kopiika, J. Selejdak, Y. Blikharskyy. “Specifics of physico-mechanical characteristics of thermally-hardened rebar”. Production Engineering Archives, vol 28, no 1, pp. 73-81, 2022. [CrossRef]
- C. Niezrecki, J. Baqersad, A. Sabato. “Digital Image Correlation Techniques for Non-Destructive Evaluation and Structural Health”. Monitoring. Handb. Adv. Non-Destr. Eval, pp. 1-46, 2018.
- L. Ngeljaratan, M. A. Moustafa. “Structural health monitoring and seismic response assessment of bridge structures using target-tracking digital image correlation”. Engineering Structures, vol 213, 110551, 2020. [CrossRef]
- Y. Blikharskyy, N. Kopiika, R. Khmil, Z. Blikharskyy. “Digital Image Correlation Pattern for Concrete Characteristics—Optimal Speckle”. In International Conference Current Issues of Civil and Environmental Engineering Lviv-Košice–Rzeszów, Cham: Springer Nature Switzerland, pp.22-31, 2023. [CrossRef]
- B. Pan, K. Qian, H. Xie, A. Asundi, “Two-dimensional digital image correlation for in-plane displacement and strain measurement: a review”. Measurement science and technology, vol 20, no 6, 062001, 2009. [CrossRef]
- VIC-2D. Reference Manual. Correlated Solutions, Inc. Knowledgebase-Manuals and Guides. 26p. Available online: https://correlated.kayako.com/article/87-vic-volume-manual (accessed on 30 January 2024).
- StrainMaster. Digital Image Correlation Systems for Full Field Shape, Displacement and Strain. Manual. LaVision. 20 p. Available online: https://www.lavision.de/de/products/strainmaster/index.php (accessed on 13 January 2024).
- GOM Correlate Pro. Electronic Manual. GOM. Available online: https://www.globus.co.il/wp-content/uploads/2022/01/Operating-Instructions-gom-correlate-prof-basic-v8.pdf (accessed on 13 January 2024).
- Solid Mechanics DIC. Dantec Dynamics. Available online: https://www.dantecdynamics.com/solutions/stress-strain-espi-dic/solid-mechanics-dic/measurement-principles-of-dic/#:~:text=Digital%20Image%20Correlation%20(DIC)%20is,mechanic%20applications%20in%20materials%20testing. (accessed on 13 January 2024).
- The MatchID. Compose the software stack that best fits your needs https://www.matchid.eu/en/solutions-overview/software (accessed on 13 April 2024).
- Image Systems https://imagesystems.se/ (accessed on 13 April 2024).
- Imetrum. Measuring the industrial world. https://www.imetrum.com/ (accessed on 13 April 2024).
- Ncorr: 2D Digital Image Correlation Matlab Software. Available online: https://www.ncorr.com/index.php (accessed on 13 April 2024).
- J. Blaber, B. Adair, A. Antoniou. “Ncorr: Open-Source 2D Digital Image Correlation Matlab Software”. Exp Mech, vol 55, pp. 1105–1122, 2015. [CrossRef]
- R. Harilal, M. Ramji. “Adaptation of Open Source 2D DIC Software Ncorr for Solid Mechanics Applications”. 9th International Symposium on Advanced Science and Technology in Experimental Mechanics, New Delhi, India, November 2014. [CrossRef]
- Digital Image Correlation Engine (DICe). Center for Computing Research (CCR). Sandia National Laboratories. https://www.sandia.gov/ccr/software/digital-image-correlation-engine-dice/ (accessed on 13 April 2024).
- D.Z. Turner. “Digital Image Correlation Engine (DICe) Reference Manual”. Sandia Report, SAND2015-10606 O, 2015. https://dicengine.github.io/dice/ (accessed on 10 May 2024).
- YaDICs. https://yadics.univ-lille1.fr/wordpress/index.html (accessed on 13 April 2024).
- R. Seghir, J.F. Witz, S. Coudert. YaDICs - Digital Image Correlation 2/3D software. https://www.yadics.univ-lille1.fr , 2014. (accessed on 10 May 2024).
- Py2DIC: https://github.com/Geod-Geom/py2DIC (accessed on 13 April 2024).
- V. Belloni, R. Ravanelli, A. Nascetti, M. Di Rita, D. Mattei, M. Crespi. “py2dic: A new free and open source software for displacement and strain measurements in the field of experimental mechanics”. Sensors, vol 19, no 18, 3832, 2019. [CrossRef]
- V. Belloni, R. Ravanelli, A. Nascetti, M. Di Rita, D. Mattei, M. Crespi. “Digital Image Correlation from commercial to FOS software: a mature technique for full-field displacement measurements”. The International Archives of the Photogrammetry, Remote Sensing and Spatial Information Sciences, vol XLII-2, pp. 91-95, 2018. [CrossRef]
- R. Ravanelli, A. Nascetti, M. Di Rita, V. Belloni, D. Mattei, N. Nisticò, M.Crespi. “A new Digital Image Correlation software for displacements field measurement in structural applications”. The International Archives of the Photogrammetry, Remote Sensing and Spatial Information Sciences, vol XLII-4/W2, pp. 139-145, 2017. [CrossRef]
- µDIC: A toolkit for digital image correlation. https://mudic.readthedocs.io/en/latest/ (accessed on 13 April 2024).
- S. N. Olufsen, M. E. Andersen, E. Fagerholt, E. “μDIC: An open-source toolkit for digital image correlation”. SoftwareX, vol 11, 100391, 2020. [CrossRef]
- Augmented Lagrangian Digital Image Correlation and Tracking https://www.mathworks.com/matlabcentral/fileexchange/70499-augmented-lagrangian-digital-image-correlation-and-tracking (accessed on 13 April 2024).
- J. Yang, K. Bhattacharya. “Augmented Lagrangian Digital Image Correlation”. Exp.Mech., vol 59, no 187, 2018. [CrossRef]
- MultiDIC: a MATLAB Toolbox for Multi-View 3D Digital Image Correlation https://github.com/MultiDIC/MultiDIC (accessed on 13 April 2024).
- D. Solav, K. M. Moerman, A. M. Jaeger, K. Genovese, H. M. Herr. (2018). “MultiDIC: An open-source toolbox for multi-view 3D digital image correlation”. Ieee Access, vol 6, pp. 30520-30535, 2018. https://ieeexplore.ieee.org/document/8371235/.
- M. Sutton, J. Yan, V. Tiwari, H. Schreier, J. Orteu. “The effect of out-of-plane motion on 2D and 3D digital image correlation measurements”. Optics and Lasers in engineering, vol 46, pp. 746–757, 2008. [CrossRef]
- V. Stančík, P. Ryjáček. “The application of modern methods for bridge diagnostics and load testing”. ce/papers, vol 6, no 5, pp 949-958, 2023. [CrossRef]
- H. Schreier, J-J. Orteu, M.A. Sutton. “Image Correlation for Shape, Motion and Deformation Measurements”. New York: Springer US, 322 p, 2009. [CrossRef]
- J. Zhao, Y. Sang, F. Duan, F. “The state of the art of two-dimensional digital image correlation computational method”. Engineering reports, vol 1, no 2, e12038, 2019. [CrossRef]
- H.C. Jo, S. H. Kim, J. Lee, H. G. Sohn, Y.M. Lim. “Sag-based cable tension force evaluation of cable-stayed bridges using multiple digital images”. Measurement, vol 186, 110053, 2021. [CrossRef]
- B. Pan, D. Wu, Y. Xia. “An active imaging digital image correlation method for deformation measurement insensitive to ambient light”. Opt. Laser Technol. 2012, vol 44, no 1, pp 204-209, 2012. [CrossRef]
- B. Pan, L. Yu, D. Wu, L. Tang. “Systematic errors in two-dimensional digital image correlation due to lens distortion”. Opt. Lasers Eng, vol 51, no 2, pp 140-147, 2013. [CrossRef]
- Y. Xu, J. M. W. Brownjohn, J. “Review of machine-vision based methodologies for displacement measurement in civil structures”. Civil Struct. Health Monit, vol 8, pp 91-110, 2018. [CrossRef]
- T. Khuc, N. Catbas, “Completely contactless structural health monitoring of real-life structures using cameras and computer vision”. Struct. Control Health Monit, vol 24, no 1, e1852, 2017. [CrossRef]
- M. Q. Feng, Y. Fukuda, D. Feng, M. J. Mizuta. “Nontarget Vision Sensor for Remote Measurement of Bridge Dynamic Response”. Bridge Eng, vol 20, no 12, pp 1-12, 2015. [CrossRef]
- J. G. Chen, N. Wadhwa, Y. J. Cha, F. Durand, W. T. Freeman, O. Buyukozturk. “Modal identification of simple structures with high-speed video using motion magnification”. J. Sound Vib., vol 345, pp 58-71, 2015. [CrossRef]
- H. Yoon, H. Elanwar, H. Choi, M. Golparvar-Fard, B. F. Spencer. “Target-free approach for vision-based structural system identification using consumer-grade cameras”. Struct. Control Health Monit., vol 23, no 12, pp 1405-1416, 2016. [CrossRef]
- P. Podbreznik, B. Potočnik. “Influence of temperature variations on calibrates cameras”. International Journal of Computer and Information Engineering, vol 2, no 4, pp. 261-267, 2008.
- C. A. Murray, W. A. Take, N. A. Hoult. “Dynamic measurements using digital image correlation”. International Journal of Physical Modelling in Geotechnics, vol 17, no 1, pp 41-52, 2017. [CrossRef]
- J. J. Lee, M. Shinozuka. “A vision-based system for remote sensing of bridge displacement.” Ndt & E International, vol 39, no 5, pp 425-431, 2006. [CrossRef]
- C. Niezrecki, P. Avitabile, C. Warren, P. Pingle, M. Helfrick. "A review of digital image correlation applied to structural dynamics." In AIP Conference Proceedings, vol. 1253, no. 1, pp. 219-232. American Institute of Physics, 2010.
- R. Jiang, D. V. Jauregui, K. R. White. “Close range photogrammetry applications in bridge measurement: literature review.” Measurement, vol 41, no 8, pp 823–834, 2008. [CrossRef]
- D. V. Jauregui, K. R. White, P. E. Woodward, K. R. Leitch. “Non contact photogrammetric measurement of vertical bridge deflection.” J. Bridge Eng., vol 8, no 4, pp 212–222. 2003. [CrossRef]
- F. B. Bales. “Close-range photogrammetry for bridge measurement.” Transportation Research Record, Washington, DC, vol 950: pp 39–44, 1985.
- J. C. Li, B. Z. Yuan. “Using vision technique for bridge deformation detection.” Proceedings of International Conference on Acoustic, Speech and Signal Processing, New York, pp 912–915, 1988.
- G. W. Johnson. “Digital close-range photogrammetry – a portable measurement tool for public works.” Proceedings of 2001 Coordinate Measurement Systems Committee Conference, Coordinate Measurement Systems Committee, Albuquerque, USA. 2001.
- J. Albert, H. G. Maas, A. Schade, W. Schwarz, W. “Pilot studies on photogrammetric bridge deformation measurement.” In Proceedings of the 2nd IAG Commission IV Symposium on Geodesy for Geotechnical and Structural Engineering, vol. 21, pp 24-31, 2002.
- J. J. Lee, M. Shinozuka. “Real-time displacement measurement of a flexible bridge using digital image processing techniques.” Experimental mechanics, vol 46, pp 105-114. 2006. [CrossRef]
- S. Yoneyama, A. Kitagawa, S. Iwata, K. Tani, H. Kikuta. “Bridge deflection measurement using digital image correlation.” Experimental techniques, vol 31, pp 34-40, 2007. [CrossRef]
- C-H. Chiang, M-H. Shih, W. Chen, C-P. Yu. “Displacement measurements of highway bridges using digital image correlation methods”. In: Seventh international symposium on precision engineering measurements and instrumentation. International Society for Optics and Photonics, vol 8372, 2011. [CrossRef]
- J. Peddle, A. Goudreau, E. Carlson, E. Santini-Bell. “Bridge displacement measurement through digital image correlation”. Bridge Struct, vol 7, no 4, pp 165-173, 2011. [CrossRef]
- C. Nonis, C. Niezrecki, T-Y. Yu, S. Ahmed, C-F. Su, T. Schmidt. “Structural health monitoring of bridges using digital image correlation.” In: Health monitoring of structural and biological systems. International Society for Optics and Photonics, vol 869507, 2013. [CrossRef]
- C. Murray, A. Hoag, N. A. Hoult, W. A. Take. “Field monitoring of a bridge using digital image correlation.” In: Proceedings of the institution of civil engineers-bridge engineering. Thomas Telford Ltd, vol 168, no 1, pp. 3-12, 2015. [CrossRef]
- C. Murray. “Dynamic monitoring of rail and bridge displacements using digital image correlation.” Queen's University (Canada); 2013, 107 p.
- L. Ngeljaratan, M. A. Moustafa. “System identification of large-scale bridge models using target-tracking digital image correlation.” Front Built Environ, vol 5, no 85, 2019. [CrossRef]
- F. Barros, S. Aguiar, P. J. Sousa, A. Cachaço, P. J. Tavares, P.M. Moreira, D. Ranzal, N. Cardoso, N. Fernandes, R. Fernandes, R. Henriques, P.M. Cruz, A. Cannizzaro. “Displacement monitoring of a pedestrian bridge using 3D digital image correlation.” Procedia Structural Integrity, vol 37, pp 880-887, 2022. [CrossRef]
- Y. C. Lin, C. H. Tseng, C. H. Chiang, W. H. Hung. “Vibration Analysis and Digital Image Correlation Techniques for a Suspension Bridge.” NDT-CE 2022 - The International Symposium on Nondestructive Testing in Civil Engineering Zurich, Switzerland, August 16-18, 2022. [CrossRef]
- P. J. Sousa, F. Barros, P. Lobo, P. J. Tavares, P. M. Moreira, P. M. “Experimental measurement of bridge deflection using Digital Image Correlation.” Procedia Structural Integrity, vol 17, pp 806-811, 2019. [CrossRef]
- M. Dhanasekar, P. Prasad, J. Dorji, T. Zahra. “Serviceability assessment of masonry arch bridges using digital image correlation.” Journal of Bridge Engineering, vol 24, no 2, 04018120, 2019. [CrossRef]
- J. Winkler C. Hendy. “Improved Structural Health Monitoring of London’s Docklands Light Railway Bridges Using Digital Image Correlation”. Structural Engineering International, vol 27, no 3, pp 435-440, 2017. [CrossRef]
- I. Koltsida, A. Tomor, C. Booth. “The use of digital image correlation technique for monitoring masonry arch bridges.” In 7th International Conference on Arch Bridges, pp. 681-690, 2013.
- A. Hoag, N. A. Hoult, W. A. Take, F. Moreu, H. Le, V. Tolikonda. V. “Measuring displacements of a railroad bridge using DIC and accelerometers.” Smart Structures and Systems, vol 19, no 2, pp 225-236. 2017. [CrossRef]
- C. O. Christensen, J. W. Schmidt, P. S. Halding, M. Kapoor, P. Goltermann, P. “Digital image correlation for evaluation of cracks in reinforced concrete bridge slabs” Infrastructures, vol 6(7), no 99, 2021. [CrossRef]
- H. Al-Salih, M. Juno, W. Collins, C. Bennett, J. Li, E. J. Sutley. “Evaluation of a digital image correlation bridge inspection methodology on complex distortion-induced fatigue cracking.” Procedia Structural Integrity, vol 17, pp 682-689, 2019. [CrossRef]
- L. Dellenbaugh, X. Kong, H. Al-Salih, W. Collins, C. Bennett, J. Li, E. J. Sutley. “Development of a distortion-induced fatigue crack characterization methodology using digital image correlation.” Journal of Bridge Engineering, vol 25, no 9, 04020063. 2020. [CrossRef]
- Y. F. Ji, C. C. Chang. (2008). “Nontarget image-based technique for small cable vibration measurement.” Journal of Bridge Engineering, vol 13, no 1, pp 34-42, 2008. [CrossRef]
- Y. Tian, C. Zhang, S. Jiang, J. Zhang, W. Duan. “Noncontact cable force estimation with unmanned aerial vehicle and computer vision.” Computer-Aided Civil and Infrastructure Engineering, vol 36, no 1, pp 73-88, 2021. [CrossRef]
- G. Sas, T. Blanksvärd, O. Enochsson, B. Täljsten, L. Elfgren. “Photographic strain monitoring during full-scale failure testing of Örnsköldsvik bridge.” Structural Health Monitoring, vol 11, no 4, pp 489-498, 2012. [CrossRef]
- G. Chen, Z. Wu, C. Gong, J. Zhang, X. Sun. “DIC-based operational modal analysis of bridges.” Advances in Civil Engineering, vol 2021, 6694790, pp 1-13, 2021. [CrossRef]
- W. Du, D. Lei, P. Bai, F. Zhu, Z. Huang. “Dynamic measurement of stay-cable force using digital image techniques.” Measurement, vol 151, 107211, 2020. [CrossRef]
- K. Xie, D. Lei, W. Du, P. Bai, F. Zhu, F. Liu. “The monitoring of bridge under complex illumination based on digital image technology.” Measurement, vol 206, 112219, 2023. [CrossRef]
- N. J. McCormick, J. D. Lord “Practical in situ applications of DIC for large structures”. Applied mechanics and materials, vol 24, pp 161-166, 2010. [CrossRef]
- B. Pan, L. Tian, X. Song. “Real-time, non-contact and targetless measurement of vertical deflection of bridges using off-axis digital image correlation”. Ndt & E International, vol 79, pp 73-80, 2016. [CrossRef]
- L. Tian, B. Pan. “Remote bridge deflection measurement using an advanced video deflectometer and actively illuminated LED targets”. Sensors, vol 16, no 9, 1344, 2016. [CrossRef]
- L. Tian, J. Zhao, B. Pan, Z. Wang. “Full-Field Bridge Deflection Monitoring with Off-Axis Digital Image Correlation”. Sensors, vol 21, no 15, 5058, 2021. [CrossRef]
- S. Yoneyama, H. Ueda. “Bridge deflection measurement using digital image correlation with camera movement correction”. Materials transactions, vol 53, no 2, pp 285-290, 2012. [CrossRef]
- D. Reagan, A. Sabato, C. Niezrecki, T. Yu, R. Wilson. “An autonomous unmanned aerial vehicle sensing system for structural health monitoring of bridges”. In Nondestructive Characterization and Monitoring of Advanced Materials, Aerospace, and Civil Infrastructure, vol 9804, pp. 244-252, 2016. [CrossRef]
- D. Reagan, A. Sabato, C. Niezrecki. “Unmanned aerial vehicle acquisition of three-dimensional digital image correlation measurements for structural health monitoring of bridges”. In Nondestructive Characterization and Monitoring of Advanced Materials, Aerospace, and Civil Infrastructure, vol 10169, pp. 68-77, 2017. [CrossRef]
- D. Reagan, A. Sabato, C. Niezrecki. “Feasibility of using digital image correlation for unmanned aerial vehicle structural health monitoring of bridges”. Structural Health Monitoring, vol 17(5), 1056-1072, 2018. [CrossRef]
- Y. Wang, A. P. Thrall, T. P. Zoli “Delaware river bridge fracture: Repair strategy and monitoring by digital image correlation”. ProcWorld Steel Bridge Symp, vol 2018, pp 1-6, 2018.
- Y Wang, M. D. Tumbeva, A. P. Thrall, T. P. Zoli. “Pressure-activated adhesive tape pattern for monitoring the structural condition of steel bridges via digital image correlation”. Struct Control Health Monit, vol 26, no 8, e2382, 2019. [CrossRef]
- Z. Liang, J. Zhang, L. Qiu, G. Lin, F. Yin. “Studies on deformation measurement with non-fixed camera using digital image correlation method”. Measurement, vol 167, 108139, 2021. [CrossRef]
- M. Juno, H. Al-Salih, W. Collins, C. Bennett, J. Li, E. J. Sutley. Investigating lighting and focus limitations of digital image correlation as a bridge inspection tool. In Structures Congress, 2020, pp. 341-348.
- V. Belloni, A. Sjölander, R. Ravanelli, M. Crespi, A. Nascetti. “Crack Monitoring from Motion (CMfM): Crack detection and measurement using cameras with non-fixed positions”, Automation in Construction, vol 156, 10507, 2023. [CrossRef]
- H.-G. Sohn, Y.-M. Lim, K.-H. Yun, Gi-H. Kim. “Monitoring Crack Changes in Concrete Structures”, Computer-Aided Civil and Infrastructure Engineering, vol 20 pp. 52–61, 2005. [CrossRef]
- S. Nishiyama, N. Minakata, T. Kikuchi, T. Yano. “Improved digital photogrammetry technique for crack monitoring”, Advanced Engineering Informatics, vol 29, pp. 851-858, 2015. [CrossRef]
- M. Brøns, T.A. Kasper, G. Chauda, S.W.B. Klaassen, C.W. Schwingshackl, M.R.W. Brake. “Experimental investigation of local dynamics in a bolted lap joint using digital image correlation” Journal of Vibration and Acoustics, vol 142, no 5, 051114, 2020. [CrossRef]
- W. Chen, D. Jana, A. Singh, M. Jin, M. Cenedese, G. Kosova, M. R.W. Brake, C. W. Schwingshackl, S. Nagarajaiah, K. J. Moore, J.-P. Noël. “Measurement and identification of the nonlinear dynamics of a jointed structure using full-field data, Part I: Measurement of nonlinear dynamics”, Mechanical Systems and Signal Processing, vol 166, 108401, 2022. [CrossRef]
- M. Jin, G. Kosova, M. Cenedese, W. Chen, A. Singh, D. Jana, M. R.W. Brake, C. W. Schwingshackl, S. Nagarajaiah, K. J. Moore, J.-P. Noël. “Measurement and identification of the nonlinear dynamics of a jointed structure using full-field data; Part II-Nonlinear system identification”, Mechanical Systems and Signal Processing, vol 166, 108402, 2022. [CrossRef]
- D. Roettgeni, E. Jones, A. Brinle, P. Reu, D. Rohe, J. Wagner. “Nonlinear System Identification using Digital Image Correlation”. No. SAND2018-5857C. Sandia National Lab.(SNL-NM), Albuquerque, NM (United States), 2018.
- Kopiika, N.; Blikharskyy, Y. Digital Image Correlation for Assessment of Bridges’ Technical State and Remaining Resource. Preprints 2024, 2024021251. [CrossRef]
Figure 1.
General stages of digital image correlation (DIC) approach for displacement and strain measurement.
Figure 1.
General stages of digital image correlation (DIC) approach for displacement and strain measurement.
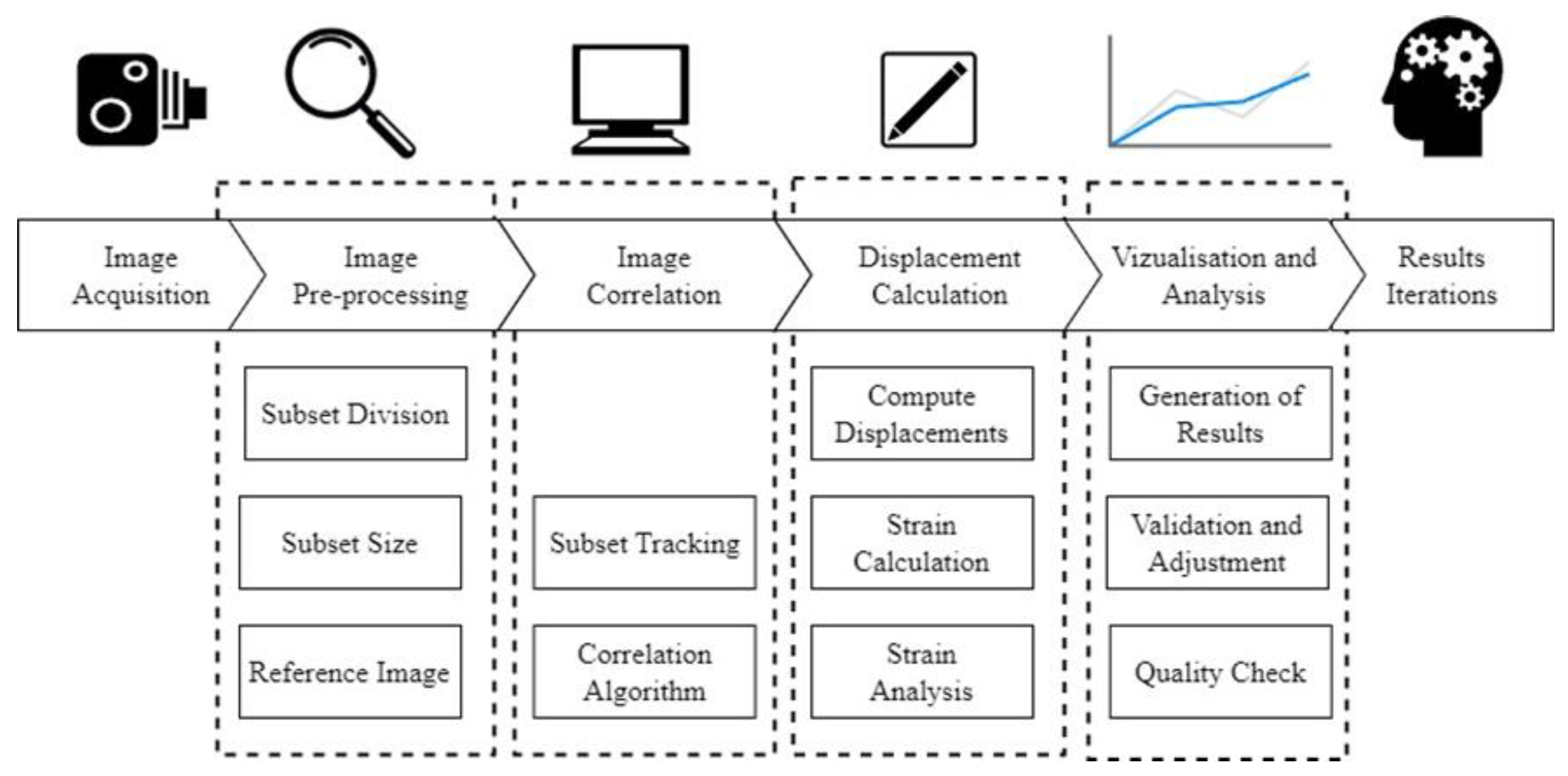
Figure 2.
Principle of grey level coding and subset tracking in the DIC method: P-initial position of a point on the reference (undeformed image), P`-position after deformation; P-P`(dX, dY)- displacement of Point P.
Figure 2.
Principle of grey level coding and subset tracking in the DIC method: P-initial position of a point on the reference (undeformed image), P`-position after deformation; P-P`(dX, dY)- displacement of Point P.
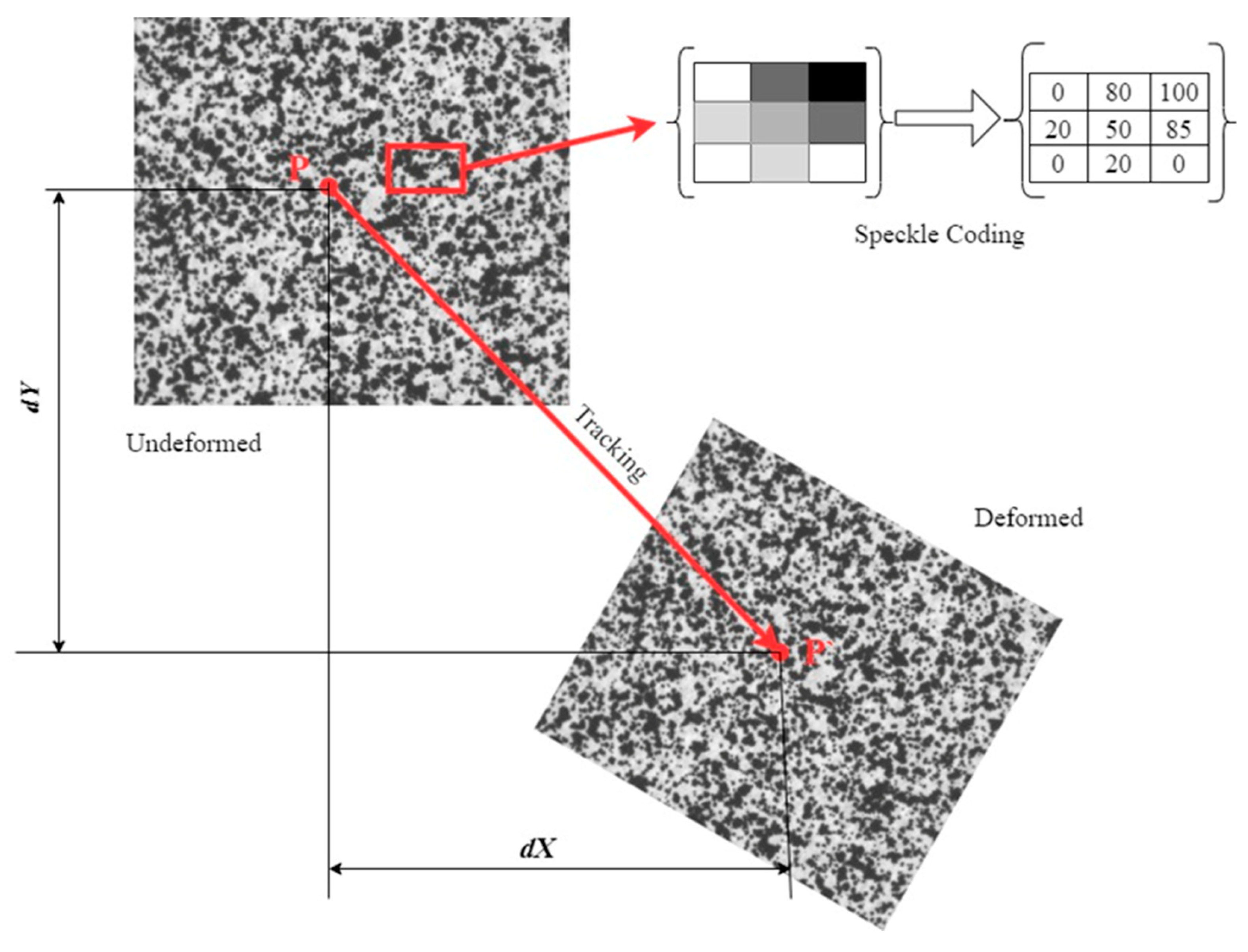
Figure 3.
Scheme of image translation between coordinate systems in DIC approach: WCS-world coordinate system, ICS-image coordinate system, CCS-camera coordinate system, P- point in physical 3D-space, pL(xL,yL,fL) and pR(xR,yR,fR)-its projections for left and right camera, respectively; pL(xs1,ys1) and pR(xs2,ys2)-coordinates in sensor system of left and right camera; OL and OR- origins of left and right cameras; fi-focal length (projection component), ri, ti-rotation and translation components of displacement.
Figure 3.
Scheme of image translation between coordinate systems in DIC approach: WCS-world coordinate system, ICS-image coordinate system, CCS-camera coordinate system, P- point in physical 3D-space, pL(xL,yL,fL) and pR(xR,yR,fR)-its projections for left and right camera, respectively; pL(xs1,ys1) and pR(xs2,ys2)-coordinates in sensor system of left and right camera; OL and OR- origins of left and right cameras; fi-focal length (projection component), ri, ti-rotation and translation components of displacement.
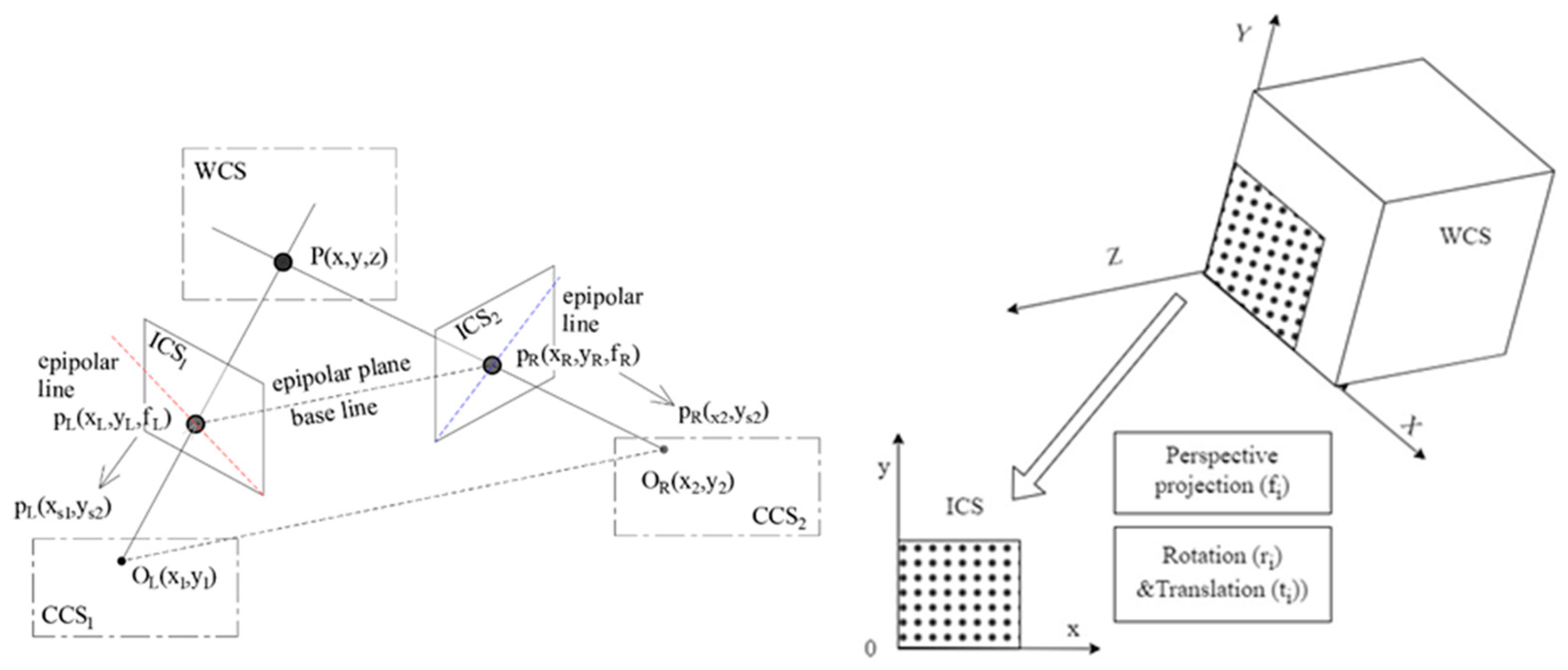
Figure 4.
Accuracy, resolution, and repeatability as constituent parts of measuring system performance.
Figure 4.
Accuracy, resolution, and repeatability as constituent parts of measuring system performance.

Table 1.
Evaluation of DIC errors during on-site monitoring and their possible impact on resolution, accuracy, and repeatability (adopted from Akcitgoz et al, 2018, [3]).
Table 1.
Evaluation of DIC errors during on-site monitoring and their possible impact on resolution, accuracy, and repeatability (adopted from Akcitgoz et al, 2018, [3]).
| Error sources of DIC in on-field measurements | Resolution | Repeatability | Accuracy | Mitigation approaches |
| Preparation of experimental set-up (before measurement) | ||||
| Target/speckle pattern | 3 | 3 | 3 | Implementation of artificial targets; Optimal size and location of targets. Optimal speckle dots` size, contrast level, subpixel precision, intensity gradients, etc |
| Low quality of images | 3 | 1 | 3 | Use of cameras and lenses with appropriate resolution |
| Metric calibration | 1 | 1 | 3 | Detailed geometric survey during the set-up. Assessment of camera extrinsic parameters and reconstructed features. |
| Continuation of Table 1. | ||||
| Image recording | ||||
| Movement of camera | 1 | 3 | 3 | Ensuring the stable position of a camera. Correction during post-processing through comparison with stationary targets. Filtering during postprocessing. |
| Environmental impacts | 1 | 3 | 3 | Autoexposure. Monitoring in shade with artificial lightning control during short periods. Protective barriers. Temperature-displacement models |
| Elastic deformations and rigid body rotations | 1 | 1 | 1 | The use of high-order shape functions in DIC processing. |
| Out-of-plane movement | 1 | 1 | 3 | Alternative parallel measurements. The use of 3D-DIC method. |
| Image processing | ||||
| Correlation algorithms | 1 | 1 | 1 | Iterative choice of the most optimal algorithm |
| Subset selection | 2 | 1 | 1 | Smaller subsets in critical areas. Advanced algorithms to handle discontinuities. |
*The colour-coded rating system is applied to identify the impact of each error on measurement system performance:1-low, 2-medium, 3-high.
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
MDPI Initiatives
Important Links
© 2024 MDPI (Basel, Switzerland) unless otherwise stated






