Preprint
Article
The Environmental and Economic Importance of Mixed and Boundary Lubrication
Altmetrics
Downloads
86
Views
28
Comments
0
This version is not peer-reviewed
Submitted:
21 February 2024
Posted:
22 February 2024
You are already at the latest version
Alerts
Abstract
One route to reducing CO2 emissions is to improve the energy efficiency of machines. For example, conventional combustion engines are being downsized (and down-speeded), are now running on lower viscosity engine lubricants (such as SAE 0W-20 or lower viscosity grades) and often also have stop-start systems fitted (to prevent engine idling when the vehicle is stopped). Some of these changes result in higher levels of mixed and boundary friction, and so accurate estimation of mixed/boundary friction losses is becoming of increased importance, both for estimating friction losses, and also for estimating wear volumes. Traditional approaches to estimating mixed/boundary friction, which employ real area of contact modelling such as the Greenwood-Tripp model [1] are widely used, but recent experimental data suggests that these approaches underestimate mixed/boundary friction losses [2-5]. A new model has been developed, based on experimental data, which estimates the proportion of mixed/boundary lubrication, X, as a function of the value (where is the ratio of the oil film thickness separating the surfaces to the combined root mean square surface roughness of the interface surfaces). The precise equation that describes the way in which X varies with takes the form of a “reverse S-curve”, which makes physical sense since S-curves arise naturally in growth processes, and in mixed/boundary lubrication, the real area of contact of rough surfaces grows as the load (and 1/) increases. Numerical estimates of mixed/boundary lubrication losses in internal combustion engines are presented here and compared with published data [2,6]. In addition, the improved method described here is used to estimate both the financial cost of mixed/boundary lubrication for today’s passenger car fleet, and the CO2 emissions associated with these friction losses.
Keywords:
Subject: Engineering - Mechanical Engineering
1. Introduction
In most internal combustion engines, friction losses in engines and transmissions are primarily due to film shear in hydrodynamic lubrication (in journal bearings, piston assembly), or elastohydrodynamic lubrication (in valve train, gears). However, at high loads, and/or under stop-start conditions, mixed/boundary lubrication can also occur. If the minimum oil film thickness separating the surfaces is hmin (m), and the roughness of each surface is σ1 (m) and σ2 (m), then the combined root mean square roughness is σ (m), where . The λ ratio can then be defined as λ = hmin/σ. (It should be noted that recent interesting work has been published that considers other ways to define the λ ratio [8]). It is generally assumed, in tribology, that moving rough surfaces are fully separated when the λ ratio is greater than about 3 [7]. Mixed lubrication is generally assumed to take place if 1 < λ < 3 and boundary lubrication is assumed to occur if λ < 1. [7]. In many machine elements, it is possible to calculate the minimum oil film thickness in a contact, by solving Reynolds’ equation assuming perfectly flat interface surfaces, and so, if the surface roughnesses are known, it is conventional to then estimate the λ ratio based on the film thickness estimate and the surface roughnesses to determine the likely level of surface contact arising in hydrodynamic, mixed and boundary lubrication.
As an example, consider the piston rings of an internal combustion engine. The piston assembly of an internal combustion engine is often thought to contribute about 50% or so to total engine friction [9] and the piston rings are thought to contribute 50% (or more) to total piston assembly friction [9] so the piston rings themselves (and most engines have three piston rings) could contribute around 25% to total engine friction. Now if F (N) is the friction force of the piston ring, hmin (m) is the minimum oil film thickness under the piston ring, W (N) is the load acting on the piston ring, and η (Pa.s) is the viscosity of the lubricant, then hydrodynamic analysis of piston lubrication [10] finds that:
Similarly, Taylor [11] has reported that the hydrodynamic power loss of highly loaded short journal bearings is proportional to η0.75. Therefore, one obvious way to decrease hydrodynamic friction losses is to reduce lubricant viscosity. Table 1 shows trends in passenger car lubricant viscosity grades over the last 20-30 years demonstrating that viscosities recommended by engine manufacturers have indeed tended to reduce with time (and are still getting lower) to reduce engine friction.
Although reducing lubricant viscosity is an effective way to reduce power loss by viscous shear, and therefore, passenger car engine friction (since such engines are predominantly lubricated hydrodynamically), the minimum oil film thickness separating the moving, rough surfaces is also reduced, leading to increased levels of mixed/boundary lubrication and metal-metal contact (particularly under high load, and/or, stop-start conditions).
When mixed/boundary lubrication occurs, it can be assumed that a portion of the total load, W(N), is carried by the rough asperities, WA (N), and that the remainder of the load, WF (N), is carried by the fluid pressure. If the respective friction coefficients are written as fA and fF and if the total friction force is FTOTAL (N) and the overall friction coefficient is f, then it is possible to write:
If X is defined to be WA/W, then X is a measure of the proportion of mixed/boundary lubrication in a contact. When hydrodynamic conditions hold X = 0 and in this case the rough surfaces are completely separated by a fluid film and so WA=0. In addition, when there is no fluid film separating the surfaces, WF=0 and so X = 1, as expected. The overall friction coefficient, f, can thus be written as:
Such an expression has been previously reported by Olver and Spikes [12].
It is of great interest to know how X varies with the λ ratio. In the next section, it is explained how experimental data has been used to derive an equation for X versus λ, and this equation is compared to other models that have been used in tribology to model mixed/boundary friction.
The derived equation can then also be used to estimate the friction losses due to mixed/boundary lubrication in passenger car internal combustion engines. By then considering the total number of engines in use (in the UK) total friction losses due to mixed/boundary lubrication can be estimated, together with the total cost of such losses, and the equivalent CO2 emissions associated with these friction losses.
2. Models for Mixed/Boundary Lubrication Friction
Numerous well-known models for mixed/boundary friction employ surface contact models which assume that contacting asperities deform elastically [1,13,14,15]. Although at first sight this seems to be a drastic oversimplification, in fact there is much experimental evidence for this being true for most contacts, once “running-in” of the component has completed. It is well known that new components “run-in” and during this process, the highest asperities are truncated by material loss and plastic deformation, and the component, once “run-in” will usually have a lower root mean square surface roughness and higher surface hardness, compared to the new component. It can also be the case that the overall shape (form) of the component can change during “running-in” (for example, a curved piston ring can become flatter [16]) and such changes in shape can result in a higher oil film thicknesses at critical positions (for example, at top dead centre, piston lubrication is primarily due to the “squeeze” effect [17], and at this position, a flatter piston ring will result in a thicker oil film). Any plastic deformation will tend to have occurred during the “running-in” process, which is only a small fraction of a typical machine element’s lifetime, and so, in fact, the assumption of elastic deformation is much more reasonable than appears at first sight. In addition, it was found by a number of researchers that by assuming elastic deformation of rough surfaces, and by assuming a statistical distribution of asperity properties and heights, the real contact area was proportional to the applied load [1,13,14,15], as determined experimentally. As an example of such a model, the Greenwood-Williamson model describes a rough surface in static contact against a flat surface. If the separation of the flat surface from the centre line average of the rough surface is d (whose rms surface roughness is σ), and if the asperity height probability distribution is assumed to be exponential, then the load, W(d) (N), supported by the asperities is reported [14] to be:
On the other hand, when the rough surface was assumed to have a Gaussian distribution of asperity heights, then it was found that W(d) was given by:
Where:
In a later model, due to Greenwood and Tripp [1], where it was assumed both contacting surfaces were rough, it was found that:
The above equations can be recast in terms of the proportion of mixed/boundary lubrication, X, by dividing W(d) by W(0), and so the above equations become (where we have also written d/σ = λ):
A later model, due to Bush et al [15] which assumed paraboloid asperity geometry, gave a different equation for X as below:
Rough surface contact models that assume elastic deformation of asperities strictly only apply when the real area of contact is small (less than a few %). However, rough surface contact models are also available at the opposite limit, where real contact areas are high [18]. These models were originally motivated by the study of rubber surfaces. It is of interest to note that elastic deformation models tend to predict that the pressure in the contact varies with separation of the surfaces, d, according to:
On the other hand, rough surface contact models that assume plastic deformation [18] tend to find that the pressure varies according to:
According to Persson [18] the variation of contact pressure according to the plastic model variation above is generally in better agreement with experimental data.
In practice, however, the Greenwood and Tripp model is still widely used today for predicting the load carried by asperities in rough surface contacts. A comparison of a selection of the above models is shown in Figure 1. When λ=1, the value of X is predicted to be approximately 0.368 for the exponential Greenwood & Williamson model [14], about 0.317 for the Bush et al model [15], and only about 0.131 for the Greenwood & Tripp model [1]. It is clearly of interest, when predicting mixed/boundary friction, to clarify which of these different values of X is the more reliable.
Recently, good quality experimental data has become available that can be used to show explicitly how X varies with λ [3]. Details of the experiment performed can be found in [3], and Figure 2 shows how typical experimental data (obtained from the Mini Traction Machine [3]) can be plotted to explicitly show how X varies with λ, for a range of non-friction modified lubricants, which also includes data from other Mini Traction Machine experiments [19,20].
One of the interesting features of Figure 2 is that, despite the wide range of different lubricants tested, the experimental data fits fairly well on a single “master curve”, and so it is reasonable to attempt to use a single mathematical function to describe this curve. (Clearly there is some scatter in the experimental data, so a single curve passing through the data is not perfect but will still be useful as a guide). In addition, the data plotted in Figure 2 shows that it follows a classic “reverse S-curve”. S-curves tend to arise in growth processes, and in rough surface contacts, the real contact area grows as load (and as 1/λ) increases, and so it is natural that S-curves should appear. If the data in Figure 2 had been plotted against 1/λ, rather than λ, the data would show a classic S-curve shape, as has been reported previously [5].
A suitable mathematical function, which takes the form of a “reverse S-curve” and which provides a good fit to the experimental data shown in Figure 2 is [4,5]:
In the above equation, the values of k and a which ensure a good fit to the data are k ≈ 3/2 and a ≈ 4/3. The above equation predicts that X ≈ 0.397 when λ=1, which suggests that the widely used Greenwood & Tripp model [1] substantially underestimates the amount of mixed and boundary friction in the range 1 < λ < 3. This underestimate arises at least partly because the Greenwood and Tripp model does not incorporate the stress due to the lateral forces which arise in sliding due to friction. It has been demonstrated that lateral forces which oppose friction serve to increase the real contact area in a process often referred to as “junction growth”. This lateral force tends to increase both contact spot size and the number of contact spots increasing the contact area to be sheared [16]. Failing to include this effect in a friction model, therefore, results in an underestimate of the predicted friction force.
3. Mixed/Boundary FRICTION estimates for Internal Combustion Engines
In internal combustion engines, there are a range of components, and they operate in different lubrication regimes. For example, journal bearings are designed to operate primarily in the hydrodynamic lubrication regime, so in normal operation the moving rough surfaces in the bearing would be expected to be fully separated by a fluid film. However, even in journal bearings, mixed/boundary lubrication could potentially occur at high loads (especially if the lubricant temperature is high), under stop-start conditions (where speeds are low) and/or if there is fuel dilution [22,23] of the lubricant (which can result in lower lubricant viscosities). On the other hand, the valve train operates almost entirely in the mixed/boundary lubrication regime, at least when the engine is fully warmed up, since the oil film thickness separating the moving parts is very low (usually less than 0.2 μm) and the λ ratio is usually much less than 3. Under these circumstances, the friction loss of valve trains is often estimated by assuming the valve train is in the mixed lubrication regime, and where a suitable friction coefficient is assumed [24]. Between these extremes lies the piston assembly, which is lubricated hydrodynamically for most of its operation, but it is also known that mixed/boundary friction occurs near top and bottom dead centre positions (positions where the piston speed is zero). Most of the mixed/boundary friction in the piston assembly will occur near to the top dead centre position when combustion occurs, since at this point in the engine cycle, the piston speed is zero, ring to cylinder contact loads are high (due to high combustion chamber pressures) and oil temperatures are also high (leading to low viscosity). This will also lead to higher levels of piston ring and cylinder wear.
Published experimental data on piston assembly friction [6] for a fully warmed up engine shows that the amount of mixed/boundary friction drops off rapidly as engine speeds increase. This is as expected since oil film thickness, and the λ ratio, increase with engine speed. An example of such data is plotted in Figure 3, with the engine in that study being a 1990 2.0 litre gasoline engine. Clearly, the overall amount of mixed/boundary lubrication will depend to a great extent on the driving cycle. “City type” driving, with many stop-starts and low speeds, will tend to have more mixed/boundary lubrication compared to motorway driving (where speeds are steady and relatively high). However, the impact of mixed/boundary friction on vehicle fuel consumption is less than may be expected, since most mixed/boundary lubrication occurs at “low” speeds. (For individual contacting components this means that power loss, the product of friction force and sliding speed is low due to the low speeds). Consequently, under these conditions the fuel consumption is relatively low. This can be illustrated in the older European NEDC driving cycle [25], which was used for vehicle fuel economy evaluations before 2020. In this cycle there is around 25% idling (in which mixed/boundary friction could potentially be responsible for 40-50% or more of total engine friction, most of which would come from the valve train), but this only actually contributed about 10% to the overall fuel consumption figure. In modern cars fitted with stop-start systems, there will be much less engine idling.
Interesting data on piston assembly friction for “new” and “run-in” piston assemblies has also been published [26] in which a significantly higher amount of mixed/boundary friction was measured for “new” piston assemblies, and the amount of mixed/boundary friction measured for the “run-in” piston assembly was found to be lower. This is because in the process of “running-in” the root mean square surface roughness of the surfaces will be reduced, and at the same time, the change in shape of the piston ring/liner contact (due to wear) will result in an effectively flatter contact, which will result in a higher oil film thickness at top dead centre (due to “squeeze” lubrication effects [17]) and so the λ ratio of the “run-in” piston assembly will be substantially greater than that of the “new” piston assembly. It has been reported that estimate piston ring-pack frictional power losses are 10-15% higher for new piston ring-packs, as compared to “run-in” ring-packs [16].
A useful discussion in reference [11] attempted to quantify the fuel consumption that arose from the mixed/boundary lubrication regime. That discussion focused on the older European NEDC driving cycle (Figure 4 below). In that cycle, there was a large proportion (25% of the cycle time) of engine idling, and at that time, engines idled at around 750 rpm. Despite the large amount of idling, it was estimated that only 10% of the overall fuel consumption (measured for the complete cycle) was due to idling. If it is assumed, from Figure 3, that at 750 rpm, approximately 57% of piston assembly friction is due to mixed/boundary friction, and at 750 rpm the piston assembly friction made up 32% of total engine friction, and the valve train friction was 40% of total engine friction [6], and that all the valve train friction is in the mixed/boundary regime, then, at idling, approximately 58% of all the engine friction is in the mixed/boundary regime. (It should be noted that we have assumed no mixed/boundary friction occurs in the journal bearings). If it is assumed that 40% of the total fuel consumption, at idling, is due to engine friction, then the total fuel consumption due to mixed/boundary friction will be (40% x 58% x 10%) which is approximately 2.3%. For the remaining part of the driving cycle, if it is assumed that the average engine speed is 2000 rpm, then, from Figure 3 and reference [6], the proportion of mixed/boundary friction in the piston assembly has dropped to 24%. At this engine speed, the piston assembly friction is roughly 41% of total engine friction, and the valve train friction is 17% of total engine friction. At 2000 rpm, the estimated total percentage of mixed/boundary friction is roughly 27%. If it is assumed that 25% of total fuel consumption is used to overcome engine friction at 2000 rpm, the total fuel consumption due to mixed/boundary friction for the remainder of the driving cycle can be estimated to be (25%*27%*90%) which is approximately 6%. The total estimated fuel consumption to overcome mixed/boundary friction is thus estimated to be roughly 8.3%. This estimate also depends on the lubricants used in the engine. For the above calculation, data from reference [6] based on a friction modified SAE 0W-8 lubricant were used. In reference [6] data was also reported for a non-friction modified SAE 0W-8 lubricant and a more viscous, non-friction modified SAE 15W-40 lubricant. Similar estimates for the approximate amount of fuel needed to overcome mixed/boundary friction can be made for these other two lubricants, and it was found that for the low viscosity, non-friction modified SAE 0W-8 lubricant that the figure is approximately 9.2%, whilst for the non-friction modified viscous SAE 1W-40 lubricant the figure is 7.0%.
The figures above are similar to those reported by Holmberg and Erdemir [27]. It should also be emphasized that fuel economy driving cycles are generally fairly low-load, low stress driving conditions, and more severe driving styles (involving, for example, strong accelerations and harsh braking, driving heavily loaded cars up hills, driving in extremely hot conditions) could result in a higher proportion of fuel used to overcome mixed/boundary friction and so for estimating the financial and environmental impact of mixed/boundary friction, it is proposed to use a figure of 10% for the fuel consumption use, in passenger cars, to overcome mixed/boundary friction.
4. The Financial and ENvironmental impact of Mixed/Boundary FRICTION
In the UK, at the time of writing, a typical realistic fuel consumption figure for a modern gasoline engine vehicle is approximately 7 litres/100 km. If it is assumed that an average UK car is driven 16,000 km per year, then the amount of fuel used per car per year is roughly 1100 litres. Currently, in the UK, there are approximately 19 million gasoline engine vehicles (plus another 12 million passenger cars with diesel engines). If, for the sake of argument, the amount of fuel used to overcome mixed/boundary friction is assumed to be the same for diesel fueled passenger cars, then in total there will be 31 million cars, each with an average annual fuel consumption of 1100 litres. At current UK fuel prices (about £1.50 per litre), the total annual fuel consumption for passenger cars will be around 34 billion litres. Therefore, the amount of fuel used to overcome mixed/boundary friction will be approximately 3.4 billion litres per year, with a total annual cost of £5.1 billion, and these figures are just for the UK.
In terms of CO2 emissions, it has been estimated that 2.4 kg of CO2 is generated from the combustion of one litre of gasoline, and in addition, approximately 0.7 kg of CO2 are generated during the manufacturing of gasoline and transporting it to where it is needed [28]. Therefore, for each litre of gasoline used, approximately 3.1 kg of CO2 are emitted. Since the annual average fuel consumption is 1100 litres, the amount of fuel burnt to overcome mixed/boundary friction will be 110 litres, and so each car will generate, on average 340 kg of CO2 per year, to overcome mixed/boundary friction. By scaling this up to all the cars in the UK (and also assuming the figures for diesel cars will be similar to those for gasoline cars), this means that a total of about 10.5 million tonnes of CO2 are released each year, by the UK passenger car fleet, to overcome mixed/boundary friction.
Worldwide, there are approximately 1 billion passenger cars, so if the UK figures above are typical, then the total amount of fuel used annually worldwide to overcome mixed/boundary friction in passenger cars will be approximately 100 billion litres, with a financial impact of about $200 billion, and in addition there will be CO2 emissions of around 300 million tonnes per year associated with mixed/boundary friction in passenger cars.
It would be instructive to extend the above analysis to other sectors (such as heavy-duty diesel vehicles, ships, trains, etc.) and to other machine elements (such as industrial gears, rolling element bearings etc.) to estimate the importance of mixed/boundary friction in these sectors/machine elements to obtain better estimates of the importance of mixed/boundary friction across all applications.
5. DISCUSSION
Section 4 has highlighted the large financial and environmental impact of mixed/boundary friction in passenger cars. Worldwide, many billions of litres of fuel are consumed annually simply to overcome mixed/boundary friction in passenger cars, at a cost of billions of dollars. In addition, many hundreds of millions of tonnes of CO2 are released.
As lubricant viscosities decrease, to reduce the impact of viscous shear and improve machine energy efficiency, it is likely that mixed/boundary friction will become ever more important, and so measures aimed at reducing mixed/boundary friction will become of greater and greater interest. Examples of some of the measures that have been, or are being taken, to reduce the impact of mixed/boundary friction include:
- The use of friction modifier additives in passenger car lubricants (mainly aimed at reducing friction in valve trains and near the top dead centre of piston ring travel)
- The use of start-stop system to minimize the amount of time engines idle
- The use of coatings to reduce friction and wear (examples include ceramic coatings and diamond-like carbon (DLC) coatings
- Superfinishing of components to reduce surface roughness
There is also much tribology research into superlubricity [29,30,31], where an order of magnitude reduction in friction coefficients could potentially be achieved by a combination of use of novel materials, surface design (potentially using combinations of hydrophobic and/or hydrophilic surfaces), novel lubricants etc. If such step change reductions in friction coefficients could be routinely achieved in standard machine elements, it would result in a massive improvement in energy efficiency, and potentially longer machine lifetimes (due to lower wear). However, the timescales for transferring promising laboratory technologies to industry may take decades to occur in practice.
6. Conclusions
One route to reducing CO2 emissions and energy usage is to improve the energy efficiency of machines, such as internal combustion engines. Lubricant viscosities have been decreasing steadily since the 1990s, in order to reduce engine friction, and this approach has been effective in substantially reducing hydrodynamic friction. However, this approach also leads to a decreased lubricant film thickness separating the rough moving surfaces and will increase the levels of mixed/boundary lubrication where there is interface contact).
It is thus becoming increasingly important to be able to accurately predict the amount of mixed/boundary friction losses. Recent experimental data published by the Imperial College Tribology Group [3] has been used to develop an easy-to-use equation that better predicts the amount of mixed/boundary friction in a tribological contact.
Studies reported here for the amount of mixed/boundary lubrication in a gasoline engine have found that approximately 10% of the fuel used by a passenger car is used to overcome mixed/boundary friction. Since there are approximately one billion passenger cars in use worldwide, it is found that around 100 billion litres of fuel are used annually to overcome mixed/boundary friction, at an approximate cost of $200 billion, and in addition, the CO2 emitted (from combustion of the fuel) equates to around 300 million tonnes per year.
Internal combustion engines will remain in use across many applications for years to come, so to protect the environment, it is imperative to reduce mixed/boundary friction, either by reducing friction coefficient directly (by the use of friction modified lubricants and/or low friction coatings), or by reducing the amount of time the machine spends in mixed/boundary lubrication (such as the use of start-stop systems in cars to reduce the amount of engine idling). More speculative approaches based on superlubricity may result in a step-change reduction in friction coefficient, and a significant improvement in machine energy efficiency and longer lifetimes, if promising tribological technologies from laboratory studies can be successfully transferred to industry.
Funding
This research received funding from the Taiho Kogyo Tribology Research Foundation (TTRF).
Acknowledgments
The authors wish to thank the Taiho Kogyo Tribology Research Foundation (TTRF) for providing funding to support some of the research described in this paper.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Greenwood, J.A.; Tripp, J.H. The Contact of Two Nominally Flat Surfaces. Proc. Instn. Mech. Engrs. 1970, 185, 625–633. [Google Scholar] [CrossRef]
- Leighton, M.; Morris, N.; Rahmani, R.; Rahnejat, H. Surface Specific Asperity Model for Prediction of Friction in Boundary and Mixed Regimes of Lubrication. Meccanica 2017, 52, 21–33. [Google Scholar] [CrossRef]
- Dawczyk, J.; Morgan, N.; Russo, J.; Spikes, H. Film Thickness and Friction of ZDDP Tribofilms. Tribology Letters 2019, 67, 1–15. [Google Scholar] [CrossRef]
- Taylor, R.I. Rough Surface Contact Modelling – A Review. Lubricants 2022, 10:98.
- Taylor, R.I.; Sherrington, I. A Simplified Approach to the Prediction of Mixed and Boundary Friction. Tribology International 2022, 175, 107836. [Google Scholar] [CrossRef]
- Taylor, R.I.; Morgan, N.; Mainwaring, R.; Davenport, T. How Much Mixed/Boundary Friction is there in an Engine – and Where is it? Proc IMechE Part J: J Engineering Tribology 2020, 234(10), 1563–1574. [Google Scholar] [CrossRef]
- Martini, A. Introduction to Tribology for Engineers. 2022, ISBN 9798844576508.
- Hansen, J.; Björling, M.; Larsson, R. A New Film Parameter for Rough Surface EHL Contacts with Anisotropic and Isotropic Structures. Tribology Letters 2021, 69, 37. [Google Scholar] [CrossRef]
- Mufti, R.A.; Priest, M. Effect of Operating Conditions and Lubricant Rheology on the Distribution of Losses in an Internal Combustion Engine. Journal of Tribology 2009, 041101. [Google Scholar] [CrossRef]
- Furuhama, S.; Sasaki, S. Effect of Oil Properties on Piston Frictional Forces. Int J of Vehicle Design 1986, 7(1/2), 133–150. [Google Scholar]
- Taylor, R.I. Tribology and Energy Efficiency: From Molecules to Lubricated Contacts to Complete Machines. Faraday Discussions 2012, 156, 361–382. [Google Scholar] [CrossRef]
- Olver, A.V.; Spikes, H.A. Prediction of Traction in Elastohydrodynamic Lubrication. Proc IMechE Part J: J Engineering Tribology 1998, 212(5), 321–332. [Google Scholar] [CrossRef]
- Archard, J.F. Elastic Deformation and the Laws of Friction. Proc R Soc Lond A 1957, 243, 190–205. [Google Scholar]
- Greenwood, J.A.; Williamson, J.B.P. Contact of Nominally Flat Surfaces. Proc R Soc Lond A 1966, 295, 300–319. [Google Scholar]
- Bush, A.W.; Gibson, R.D.; Thomas, T.R. The Elastic Contact of a Rough Surface. Wear 1975, 35, 87–111. [Google Scholar] [CrossRef]
- Priest, M.; Dowson, D.; Taylor, C.M. Predictive Wear Modelling of Lubricated Piston Rings in a Diesel Engine. Wear 1999, 231(1), 89–101. [Google Scholar] [CrossRef]
- Taylor, R.I. Squeeze Film Lubrication in Piston Rings and Reciprocating Contacts. Proc IMechE Part J: J Engineering Tribology 2015, 229(8), 977–988. [Google Scholar] [CrossRef]
- Persson, B.N.J. Elastoplastic Contact Between Randomly Rough Surfaces. Phys Rev Lett 2001, 87(11), 116101. [Google Scholar] [CrossRef] [PubMed]
- Kanazawa, Y.; Sayles, R.S.; Kadiric, A. Film Formation and Friction in Grease Lubricated Rolling-Sliding Non-Conformal Contacts. Tribology International 2017, 109, 505–518. [Google Scholar] [CrossRef]
- Tabor, D. “Junction Growth in Metalic Friction – The Role of Surface Stresses and Surface Contamination”. Proc Roy Soc. Series A 251 (1266) 378 – 393.
- Taylor, R.I.; Nagatomi, E.; Horswill, N.R; James, D.M. A Screener Test for the Fuel Economy Potential of Engine Lubricants, Proceedings of 13th International Colloquium Tribology, 2002, 1419-1424.
- Taylor, R.I. Fuel-Lubricant Interactions: Critical Review of Recent Work. Lubricants 2021, 9(9), 92. [Google Scholar] [CrossRef]
- Yu, M.; Zhang, J.; Joedicke, A.; Reddyhoff, T. Experimental Investigation into the Effects of Diesel Dilution on Engine Lubrication. Tribology International 2021, 156, 106828. [Google Scholar] [CrossRef]
- Staron, J.T.; Willermet, P.A., An Analysis of Valve Train Friction in Terms of Lubrication Principles. SAE Transactions, 1983, 625-639.
- Barlow, T.J.; Latham, S.; McCrae, I.S.; Boulter, B.G., A Reference Book of Driving Cycles for Use in the Measurement of Road Vehicle Emissions, TRL Published Project Report, 2009.
- Koch, F.; Geiger, U.; Hermsen, F-G. PIFFO – Piston Friction Force Measurements During Engine Operation, SAE Technical Paper Series, 1996, SAE 960306.
- Holmberg, K.; Andersson, P.; Erdemir, A. Global Energy Consumption Due to Friction in Passenger Cars. Tribology International 2012, 47, 221–234. [Google Scholar] [CrossRef]
- Taylor, R.I. A Closer Look at Sustainable Lubricants. Tribology Online 2023, 18(6), 268–274. [Google Scholar] [CrossRef]
- Hod, O.; Meyer, E.; Zheng, Q.; Urbakh, M. Structural Superlubricity and Ultralow Friction Across Length Scales. Nature 2018, 563(7732), 485–492. [Google Scholar] [CrossRef] [PubMed]
- Luo, J.; Liu, M.; Ma, L. Origin of Friction and the New Frictionless Technology – Superlubricity: Advancements and Future Outlook. Nano Energy 2021, 86, 106092. [Google Scholar] [CrossRef]
- Berman, D.; Erdemir, A.; Sumant, A.V. Approaches for Achieving Superlubricity in Two-Dimensional Materials. ACS nano 2018, 12(3), 2122–2137. [Google Scholar] [CrossRef]
Figure 1.
Graph showing the predicted variation of X (the proportion of mixed/boundary lubrication in a contact) versus the λ ratio, for three commonly used rough surface contact models.
Figure 1.
Graph showing the predicted variation of X (the proportion of mixed/boundary lubrication in a contact) versus the λ ratio, for three commonly used rough surface contact models.
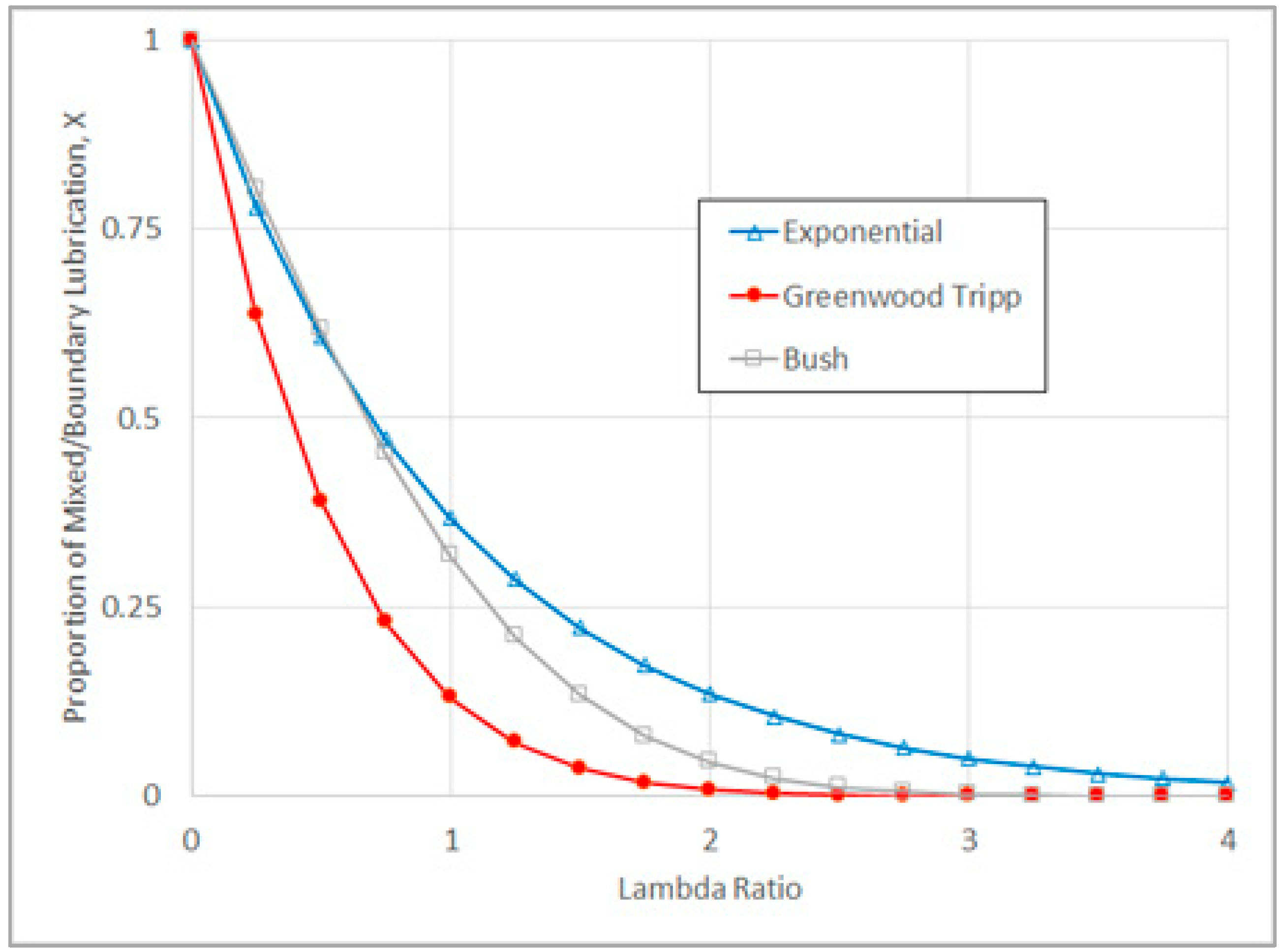
Figure 2.
Experimental data [3,19,20] showing how X, the proportion of mixed/boundary lubrication in a contact varies with λ, for a range of different rough surfaces and lubricants.
Figure 2.
Experimental data [3,19,20] showing how X, the proportion of mixed/boundary lubrication in a contact varies with λ, for a range of different rough surfaces and lubricants.
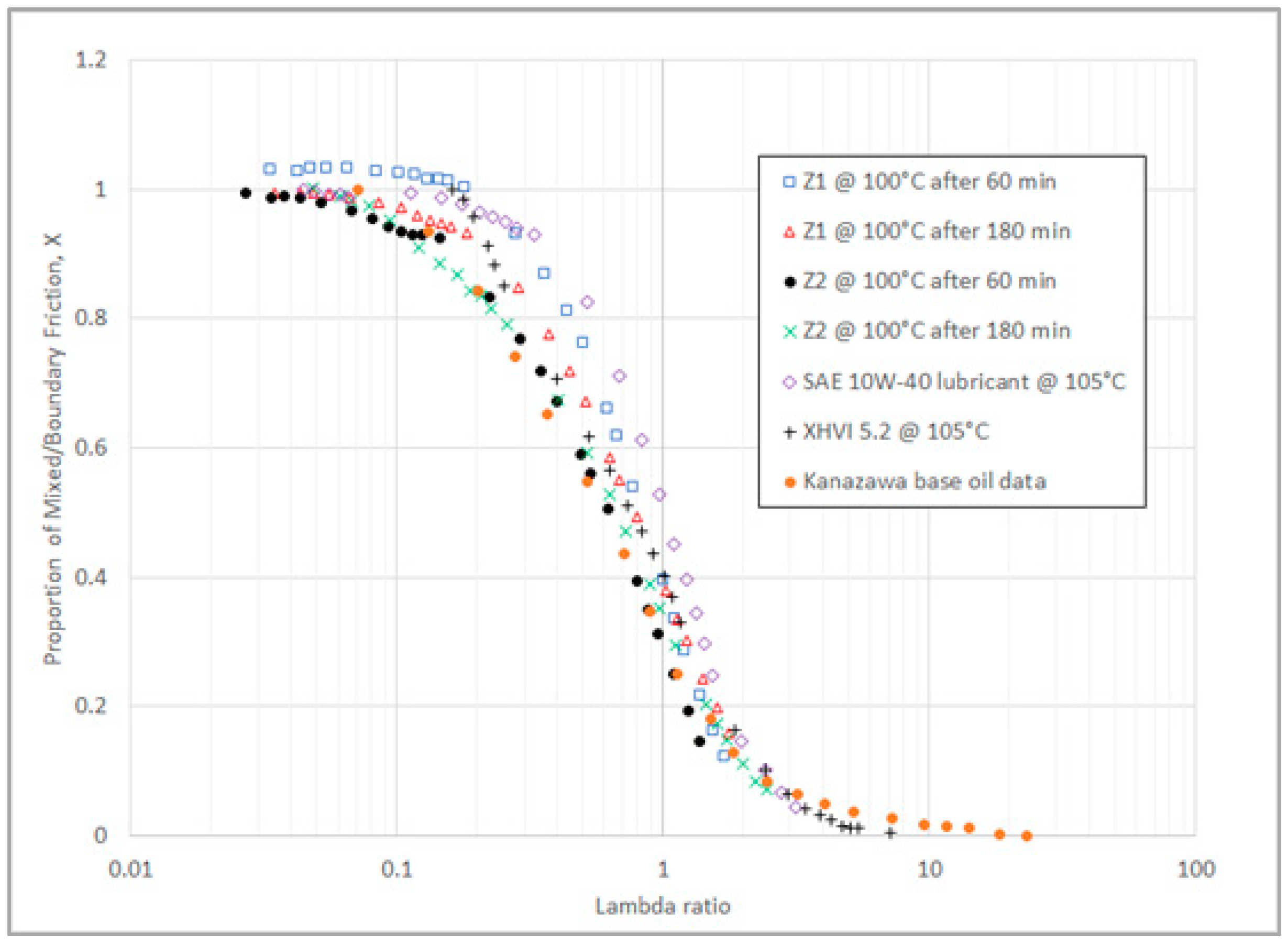
Figure 3.
Experimental data [6] for the measured piston assembly power loss (Watts) versus engine speed, for a low viscosity SAE 0W-8 lubricant, in a 1990’s 2.0 litre gasoline engine.
Figure 3.
Experimental data [6] for the measured piston assembly power loss (Watts) versus engine speed, for a low viscosity SAE 0W-8 lubricant, in a 1990’s 2.0 litre gasoline engine.
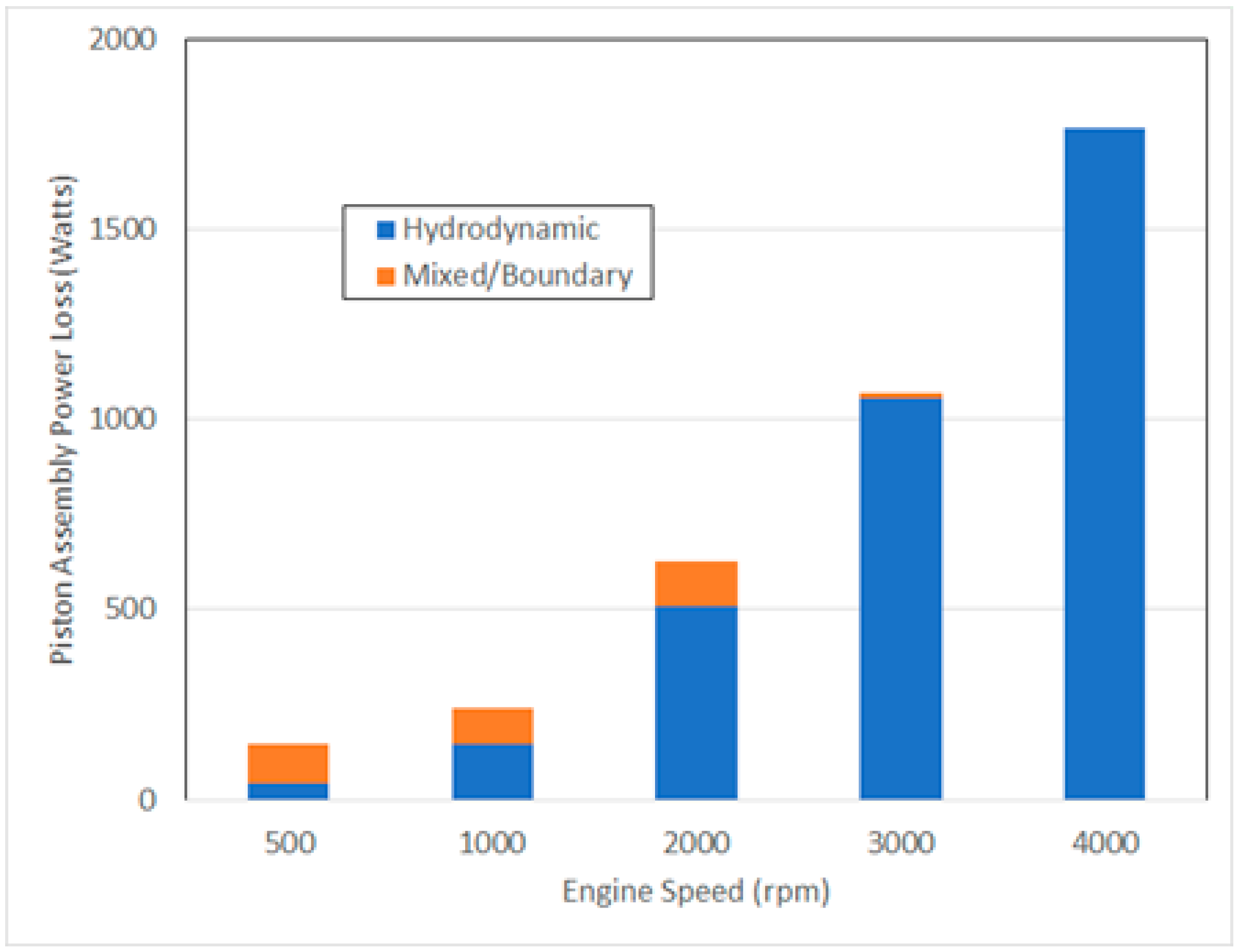
Figure 4.
The older NEDC driving cycle used for vehicle fuel economy tests in Europe up until 2020. The newer driving cycle currently used in Europe (WLTP) is also shown (NEDC stands for “New European Driving Cycle”, and WLTP is the “Worldwide Harmonized Light Vehicle Test Procedure”).
Figure 4.
The older NEDC driving cycle used for vehicle fuel economy tests in Europe up until 2020. The newer driving cycle currently used in Europe (WLTP) is also shown (NEDC stands for “New European Driving Cycle”, and WLTP is the “Worldwide Harmonized Light Vehicle Test Procedure”).
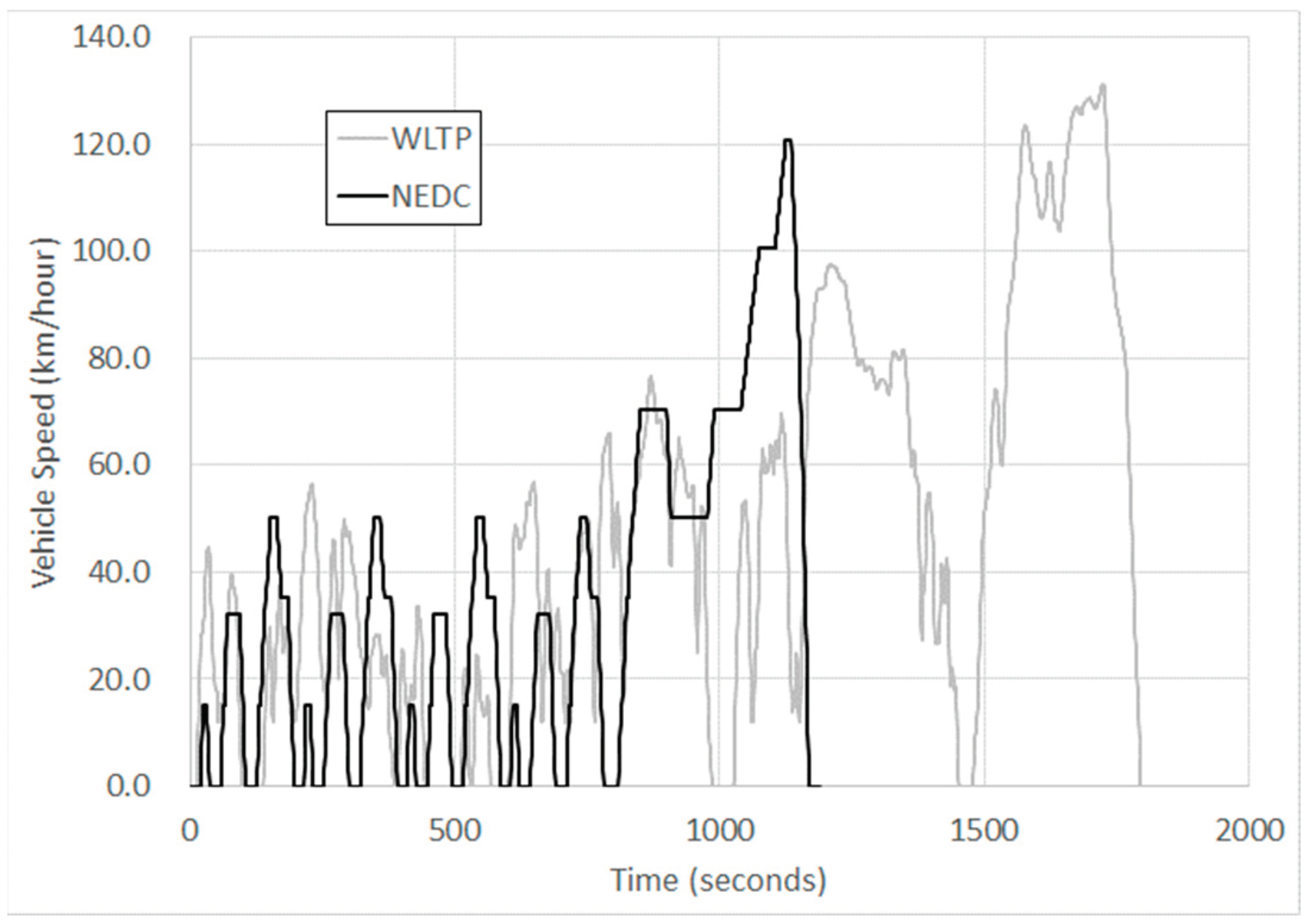
Table 1.
Typical viscosities of different lubricant viscosity grades, showing the decrease in engine oil viscosity over the last 20-30 years (Vk are kinematic viscosities, and HTHS is the High Temperature High Shear Viscosity of a lubricant measured at a temperature of 150°C and a shear rate of 106 s-1).
Table 1.
Typical viscosities of different lubricant viscosity grades, showing the decrease in engine oil viscosity over the last 20-30 years (Vk are kinematic viscosities, and HTHS is the High Temperature High Shear Viscosity of a lubricant measured at a temperature of 150°C and a shear rate of 106 s-1).
| Grade | Typical Vk40 (cSt) | Typical Vk100 (cSt) | Typical HTHS viscosity (mPa.s) | Approx viscosity (mPa.s) at -15°C | ApproxYear |
| SAE 20W-50 | 144.8 | 17.8 | 4.1 | 5,900 | Before 1990 |
| SAE 15W-40 | 114.3 | 14.9 | 3.5 | 2,900 | 1990 |
| SAE 10W-30 | 72.3 | 10.8 | 3.2 | 1,900 | 1995 |
| SAE 5W-30 | 57.4 | 9.9 | 2.9 | 1,100 | 2000 |
| SAE 0W-20 | 44.4 | 8.3 | 2.6 | 700 | 2015 |
| SAE 0W-8 | 26.4 | 5.5 | 1.9 | ≈ 250 | Future |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
MDPI Initiatives
Important Links
© 2024 MDPI (Basel, Switzerland) unless otherwise stated





