Prerpints.org logo
Preprint
Article

Monthly Hydraulic Geometry Relationship Quantification With Environmental LAI by Utilizing Sentinel Data: A Case in Jingjiang Reach of the Yangtze River

Altmetrics

Downloads

117

Views

53

Comments

0

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

22 February 2024

Posted:

22 February 2024

You are already at the latest version

Alerts
Abstract
This study presents a novel approach for quantifying the dynamics of monthly hydraulic geometry relationships in the Jingjiang reach of the Yangtze River by integrating leaf area index (LAI) data as an indicator of riparian vegetation. A comprehensive system of ordinary differential equations (ODEs) couples traditional power-law hydraulic geometry equations with LAI, capturing the influence of erosion control on channel morphology. The periodic delayed response theory and automatic differentiation techniques are employed to enhance the modeling framework's capabilities. Calibration and verification demonstrate the models' effectiveness in capturing overall trends in discharge, width, and depth dynamics, outperforming traditional constant-parameter approaches. However, model predictive abilities are limited under extreme climate conditions due to training on normal climate data. Key assumptions, including the periodic delayed response theory's neglect of peak discharges, simplified representation of artificial cut-offs, and reliance on remotely sensed data with limited local validation, introduce uncertainties. The proposed modeling framework shows potential for broader application to other river systems with appropriate adjustments. Future research could incorporate additional environmental factors, integrate models across scales, couple with advanced simulation techniques, and expand stability assessments beyond the riverbed index. By addressing related challenges, this integrated approach lays a foundation for enhancing understanding of river morphodynamics and channel stability.
Keywords: 
Subject: Environmental and Earth Sciences  -   Water Science and Technology

1. Introduction

River hydraulic geometry and hydrodynamics have long been critical research topics in the field of river management and engineering (Charlton, 2007; Gleason, 2015). Channel morphology, characterized by parameters such as width, depth, and slope, is closely intertwined with discharge, sediment load, and erosion-deposition processes, collectively determining the stability and evolutionary trends of river channels. A profound understanding of this complex dynamic system holds significant implications for flood risk assessment, infrastructure planning, and water resource management.
Traditionally, river hydraulic geometry parameters have been considered to follow power-law relationships, varying with changes in discharge (Eaton et al., 2010; Leopold and Maddock, 1953; Singh, 2003). However, this classical theory overlooks many key factors influencing channel morphological evolution, such as riparian vegetation, sediment transport, and bank boundary conditions (Gran and Paola, 2001). In recent years, the impacts of climate change and human activities have further amplified the uncertainty and complexity of river systems, rendering traditional models inadequate for more refined and comprehensive quantitative analyses of channel dynamics.
Therefore, there is a pressing need to develop novel hydraulic geometry dynamics models that integrate environmental factors into the power-law relationships, enhancing the models’ ability to describe and predict channel morphological evolution and stability (Bridge, 2009). Concurrently, advancements in satellite remote sensing data acquisition and processing techniques have significantly increased the feasibility of accurately estimating channel geometry parameters and related environmental indicators. By leveraging these new data sources and processing methods, coupled with modern mathematical and computational tools, it is possible to establish more advanced hydrodynamic models, deepening our understanding of river morphodynamics (Yue et al., 2021).
The primary objective of this study is to develop an innovative hydraulic geometry dynamics model that integrates environmental factors, particularly leaf area index (LAI), into the traditional power-law relationships. By coupling LAI as an indicator of riparian vegetation with the hydraulic geometry equations, the proposed approach aims to capture the influence of erosion control on channel morphology, a crucial aspect often neglected in existing models. The novelty of this research lies in the formulation of a comprehensive ordinary differential equation (ODE) system that dynamically links discharge, channel width, depth, and LAI data within a unified mathematical framework. Leveraging advancements in remote sensing technologies and computational techniques, the models incorporate high-resolution LAI data derived from Sentinel satellite observations, enabling a spatially explicit representation of vegetation characteristics along the river banks.

2. Study Site

The river stretch from Zhicheng to Chenglingji in the middle Yangtze River is referred to as the Jingjiang River. It holds strategic significance due to its proximity to the Three Gorges Dam and direct influence by the dam’s water-sediment discharge. It is geographically divided into Upper and Lower Jingjiang by the Ouchikou, as illustrated in Figure 1 along with its recent hydrologic history.
The Upper Jingjiang extends approximately 171.5 km, characterized by a meandering course with a relatively minor lateral swing. The region from Zhicheng to Shashi marks a transition zone from low hills to alluvial plains, featuring stable riverbanks. Moving downstream from Shashi to Ouchikou, the landscape transforms into expansive alluvial plains, adorned with lake terraces, erosion hills, river terraces, and river floodplains.
Stretching over 175.7 km, the Lower Jingjiang takes the form of a sinuous river course with pronounced collapses on both sides. Its winding and tortuous nature has earned it the moniker “Nine Bends in a Loop.” Historically, this stretch has experienced instability, characterized by frequent bends and shoal changes (see Figure 1b). Following two artificial cut-offs and one natural cut-off, and continuous efforts in river control and bank protection projects, the lateral swing amplitude of the Lower Jingjiang has significantly diminished. Presently, it has transformed into a meandering river stretch with restricted bends. The right bank exhibits hilly terraces with robust erosion resistance, while the left bank comprises an alluvial plain, with riverbanks composed of lower sand layers and upper sticky soil layers, showcasing lower erosion resistance.
Considering the intrinsic variability of alluvial river systems, our primary focus in this study is on the reach from Shashi to Chenglingji and its surrounding areas.

3. Methodology

3.1. Monthly Hydraulic Geometry Relationship Theory

3.1.1. Model Establishment

We hypothesize that the monthly reach-averaged hydraulic geometries (e.g., river width and depth) adhere to a power-law relationship with the mean inflow discharge:
X t = α Q t η
where Xt and Qt represent monthly average variables in the hydraulic geometry and inflow discharge, respectively, at time t; α and η signify the environmental impact parameters, averaged across the river reach.
Inspired by Wu et al. (2008), we model Qt using a periodic delayed response theory. This theory adjusts the current value towards a potential equilibrium before the major flood and away from this equilibrium value after the major flood within one year, as expressed by Equation (2):
d Q t d t = β cos ω t + φ Q e − Q t
where β, ω and φ represent the amplitude, angular frequency, and phase angle of the equilibrium state approach rate, respectively, which are associated with the magnitude of water flow energy and the mobility of river boundaries; Qe is the equilibrium discharge, determined by a formula dependent on the mean inflow discharge and suspended sediment concentration at the inlet station during the major flood:
Q e = K ξ f b Q f c = K C f Q f b Q f c
where Qf, ξf, and Cf denote the major-flooded mean discharge, incoming sediment coefficient and suspended sediment concentration, respectively; K, b, and c are unknowns.
To incorporate the periodic delayed response theory of discharge into the time-continuous power-law Equation (1), we perform derivation and integration, resulting in Equation (4):
d X t d t = α η Q t η − 1 d Q t d t = η 1 Q t d Q t d t X t = η β cos ω t + φ Q e Q t − 1 X t
Hence, Equations (2) and (4) together form a fundamental Ordinary Differential Equation (ODE) system describing the monthly hydraulic geometry relationship dynamics.

3.1.2. Data Acquisition

Essentially, we gather monthly water and sediment inflow data from the Shashi hydrological station, sourced from the “Bulletin of Sedimentation in Chinese Rivers.” Due to limited large cross-section data, we turn to high-precision Sentinel satellite data for channel geometry characteristics. Comprehensive datasets from Sentinel-1, 2, and 3 have been available since March 2016. Considering that water and sediment data are publicly accessible only until 2022, our study period is set from April 2016 to December 2022.
Leveraging Google Earth Engine (GEE), we extract Sentinel-1 (10m accuracy) synthetic aperture radar (SAR) data. Preprocessing involves applying a Lee Sigma speckle filter (Lee et al., 2008) and slope correction (Vollrath et al., 2020) using the hydrafloods python package and a simple boxcar mean filter. Water extraction utilizes the Water Index (W) and the Otsu thresholding method (Donchyts et al., 2016; Otsu, 1979). In cases of Sentinel-1 data unavailability (specifically, satellite imagery of the Upper Jingjiang in June 2020, 2021 and July 2022), Sentinel-2 (20m accuracy) optical imagery acts as a supplementary dataset, applying a 50% cloud threshold and the Normalized Difference Water Index (NDWI) (McFeeters, 1996) with the Otsu thresholding method.
Subsequently, we process surface water maps to generate monthly spatial representations of water occurrence. The median occurrence is identified as the typical planar state, and both the banklines and centerlines are extracted using the RivMAP tool (Schwenk et al., 2017). The typical characteristic width is quantified by calculating the average channel width at predefined intervals along the channel centerline. Mathematically, the centerline is parameterized using the streamwise distance computed between successive (xi,yi) centerline points, as represented by Equation (5):
d s i = x i + 1 − x i 2 + y i + 1 − y i 2
where i denotes the centerline node number.
The reach-average width of the entire channel mask is then computed as follows:
W r a = P ∑ d s i
where P is the number of pixels in the holes-filled channel mask and the summation of dsi extends over all centerline nodes in the channel mask (Rhoads et al., 2016).
Furthermore, for depth estimation, we employ the Floodwater Depth Estimation algorithm (FwDET 2.0) developed by Cohen et al. (2019). The procedure encompasses several steps: first, the conversion of the inundation polygon into a line layer; second, the creation of a raster layer from the line layer, ensuring consistent grid cell size and alignment with the Digital Elevation Model (DEM); third, the extraction of DEM values (elevation) for these grid cells, identified as boundary grid cells. Following that, the local floodwater elevation for each grid cell within the flooded domain is allocated from its nearest boundary grid cell using the ArcGIS “Cost Allocation” tool. Notably, this tool employs a non-iterative approach to modify the way nearest boundary grid cells are allocated. Finally, floodwater depth is calculated by subtracting the local floodwater elevation from the topographic elevation at each grid cell within the flooded domain.
In this process, we utilize inundation maps derived from processed Synthetic Aperture Radar (SAR) and optical data, complemented by the Shuttle Radar Topography Mission Digital Elevation Model (SRTM DEM) (Smith and Sandwell, 2003). Statistical information derived from the estimated water depth maps is then utilized to determine the time-averaged reach-averaged depth state, representing the typical vertical state. The corresponding depth value is identified as the typical characteristic depth.

3.2. Environmental Leaf Area Index (LAI) Quantification and Clustering

The vegetation along riverbanks plays a crucial role in erosion control, providing essential stability to these areas. In particular, the presence and characteristics of vegetation in riparian zones significantly contribute to erosion resistance, making it a pivotal factor in maintaining the ecological integrity of riverbanks. One key parameter that aids in understanding and quantifying the effectiveness of such vegetation is the leaf area index (LAI).
LAI, a fundamental metric in vegetation research and environmental monitoring, represents the total leaf area per unit ground area within vegetation canopies. It serves as a vital indicator of plant canopy density, health, and photosynthetic capacity. In the context of our study, where various definitions of LAI exist, we specifically adopt the term LAI to refer to green LAI (GAI) (Duveiller et al., 2011). GAI is a highly pertinent variable, particularly crucial for characterizing radiation transfer within vegetated canopies. This nuanced focus on GAI allows us to delve deeper into the specific contribution of green foliage in riparian zones, enhancing our understanding of its role in erosion resistance and overall ecosystem dynamics.

3.2.1. LAI Retrieval Model

The leaf area index (LAI) retrieval model utilized in this study, known as S3-TOA-GPR-1.0, is adapted from the research by Reyes-Muñoz et al. (2022). This machine learning model employs Gaussian process regression (Williams and Rasmussen, 2006) and was pre-trained on a database featuring 2000 coupled leaf-canopy and atmospheric radiative transfer simulations. These simulations, matching Sentinel-3 OLCI bands, utilized SCOPE (Van der Tol et al., 2014) and 6SV (Vermote et al., 1997) models, sampling a broad parameter space of vegetation biophysical and biochemical variables along with atmospheric conditions. This training enables the model to discern nonlinear relationships between OLCI top-of-atmosphere radiances and LAI. To enhance realism, actual OLCI spectra from diverse land cover types in Europe were included in the training dataset. Implemented in Google Earth Engine to harness computational capabilities for continental-scale processing, the S3-TOA-GPR-1.0 model processed Sentinel-3 Analysis Ready data. Preprocessing involved applying quality flags to filter out low-quality observations and masking inland water bodies using bitwise operators.
Monthly LAI composites at 300m resolution were generated by applying the regression model to mean monthly OLCI TOA reflectance radiances. Gaussian process temporal interpolation, utilizing predetermined hyperparameters for smoothing and continuity, filled gaps in the time series. Quantitative validation involved comparing the LAI product against reference LAI maps from MODIS and in-situ LAI measurements across various land cover classes in European areas. Statistical analysis assessed product performance in terms of accuracy, precision, and uncertainty. Spatial consistency and seasonality of the LAI product were analyzed to verify its reliability for spatio-temporal vegetation monitoring based on the operational Sentinel-3 data stream (Reyes-Muñoz et al., 2022).
The Jingjiang River basin, locates only 5° south of Europe’s southern boundary, shares a similar latitude. Acknowledging the correlation between vegetation characteristics and latitude (Whittaker, 1970), we directly apply the S3-TOA-GPR-1.0 model without local ground measurement validation, relying on its prior validation with European data. Moreover, acquiring ample in-situ LAI reference data in our study area proves to be particularly challenging.
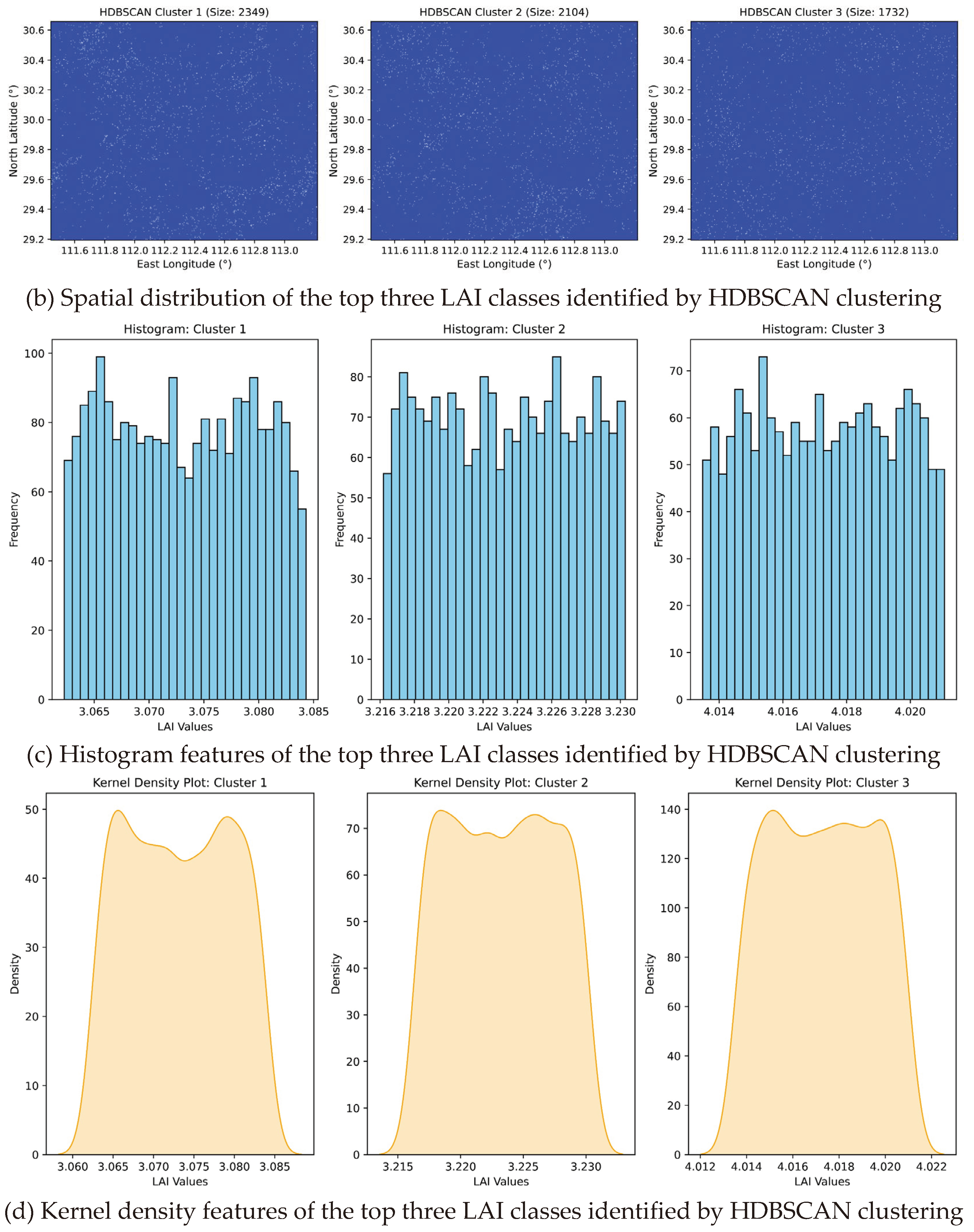
An example illustration of monthly composite LAI maps (July 2019) generated by the S3-TOA-GPR-1.0 model across the study area is presented in Figure 2a. Here, the northern and southern boundaries are deliberately set by the latitudinal lines situated 0.25° north of Shashi and 0.25° south of Chenglingji, respectively.

3.2.2. LAI Spatial Clustering

After generating the LAI distribution maps, spatial clustering analysis of LAI is performed using the Hierarchical Density-Based Spatial Clustering of Applications with Noise (HDBSCAN) (McInnes and Healy, 2017) algorithm from the scikit-learn Python library (Pedregosa et al., 2011). HDBSCAN extends the density-based spatial clustering concepts of DBSCAN (Campello et al., 2013) and OPTICS (Ankerst et al., 1999) algorithms to identify areas of high and low density LAI.
DBSCAN views clusters as areas of high density separated by areas of low density, based on two parameters min_samples (the number of samples in a neighborhood for a point to be considered as a core point) and eps (the maximum distance between two samples for one to be considered as in the neighborhood of the other). Its limitation lies in the assumption that density thresholds are globally homogeneous, which may fail for clusters of varying densities. OPTICS relaxes the single eps value and allows density extraction across a range of values to deal with variable densities. However, it requires manual cutting of its signature “reachability plot” to define clusters.
HDBSCAN builds upon these algorithms and introduces the mutual reachability graph and hierarchical clustering to automatically find clusters across changing density thresholds. It defines “core” and “mutual reachability” distances to construct the graph. An optimization extracts the minimum spanning tree and partitions it by greedy cutting of maximum weight edges. Connected components form clusters, with leftover noise marked points. Algorithm theory and outline details can be found in the original paper (McInnes and Healy, 2017) and the official Scikit-learn python library User Guide (https://scikit-learn.org/stable/modules/clustering.html#hdbscan).
In this study, we set the min_samples = min_cluster_size = 50 based on the LAI value distribution to robustly identify core high density areas and mutual reachability distances (min_cluster_size: the minimum number of samples in a group for that group to be considered a cluster; groupings smaller than this size will be left as noise). The derived HDBSCAN model separates the LAI maps into spatially contiguous high and low density areas representing different land cover types and growth conditions. The clustered regions are analyzed for distribution characteristics. This density-based spatial segmentation overcomes limitations of global density thresholds and provides a data-driven regionalization.
The distributional characteristics of the top three classes identified through HDBSCAN LAI spatial clustering for the example illustrative Figure 2a as representative, along with their histograms and kernel density features, are displayed in Figure 2b–d.

3.3. Monthly Hydraulic Geometry Relationship – LAI Coupled Model

3.3.1. Construction of the Coupled Model

Given the substantial erosion control impact of riparian zone vegetation on the riverine watershed, we establish a functional correlation between the environmental impact coefficient η in Equation (1) and representative LAI characteristics. To achieve this, we leverage the mean values for the top three LAI classes obtained through HDBSCAN clustering to formulate the regional representative LAI, as expressed in Equation (7) below:
η LAI c = η 0 + l 1 LAI 1 + l 2 LAI 2 + l 3 LAI 3
where LAIc, LAI1, LAI2, LAI3 represent the characteristic representative LAI, and mean values for the first, second and third major classes of LAI, respectively; η0, l1, l2 and l3 are unknowns.
Upon specifying the monthly hydraulic geometry variables as the typical characteristic width and depth (Section 3.1.2), we derive the final comprehensive ODE system:
d Q t d t = β cos ω t + φ Q e − Q t d B t d t = η B 0 + l B 1 LAI 1 + l B 2 LAI 2 + l B 3 LAI 3 β cos ω t + φ Q e Q t − 1 B t d H t d t = η H 0 + l H 1 LAI 1 + l H 2 LAI 2 + l H 3 LAI 3 β cos ω t + φ Q e Q t − 1 H t
where ηB0, lB1, lB2, lB3 and ηH0, lH1, lH2, lH3 are unknown parameters corresponding to the width (B) and depth (H) sub-equations, respectively.

3.3.2. ODE Solving and Parameter Estimation

We employ the Tsit5 (Tsitouras 5/4) Runge-Kutta method (Tsitouras, 2011) provided by the Julia package DifferentialEquations.jl (Rackauckas and Nie, 2017), as the solver of our proposed ODE system. This numerical integration technique, recognized for its accuracy and stability, is widely utilized for solving ODEs in diverse scientific and engineering applications. The Tsit5 method, a fourth-order method with five stages, includes an embedded fourth-order method with four stages, and can be expressed mathematically as follows:
Ζ i + 1 = Ζ i + λ 6 Μ 1 + 4 Μ 3 + Μ 4 Μ 1 = Γ t i , Ζ i Μ 2 = Γ t i + λ 2 , Ζ i + λ 2 Μ 1 Μ 3 = Γ t i + 3 λ 4 , Ζ i + 3 λ 4 Μ 2 Μ 4 = Γ t i + λ , Ζ i + λ Μ 3
here, Zi represents the approximate solution at time ti; Γ denotes the ODE function; λ signifies the step size.
To perform parameter estimation for the proposed ODE system, within the DifferentialEquations.jl framework, we initiate the process by utilizing an Automatic Differentiation (AD)-compatible solve function that takes the parameters and an initial condition and returns the solution of the differential equation.
Our objective is to identify parameters that align the ODE solutions with measurements. To achieve this, we formulate a loss function, quantifying the sum of the squared distance from the target value.
Subsequently, we utilize the Optimization.solve function from the Optimation.jl package (a unified optimization package) (Dixit and Rackauckas, 2023). This function employs reverse-mode automatic differentiation through Zygote.jl, allowing efficient computation of gradients and sensitivities required for optimizing the parameters. The ADAM (Kingma and Ba, 2014) optimization algorithm is applied iteratively to adjust parameters, converging towards values that optimize our defined objective. ADAM is known for its efficiency in handling non-stationary objectives and noisy gradients, making it well-suited for parameter optimization tasks. The algorithm maintains per-parameter learning rates and exponentially decaying moving averages of past gradients and squared gradients. This adaptive approach allows ADAM to converge efficiently in scenarios with varying and noisy gradients.

3.3.3. Prediction of the Key Input Data

The prediction of key input data for ODEs-(8) involves critical variables such as yearly major-flooded mean discharge (Qf), incoming sediment coefficient (ξf), and monthly mean values for the top three LAI classes (LAI1, LAI2, LAI3). These variables exhibit complex nonlinear relationships, influenced by interactions among climate change, human activities, and environmental factors like temperature and light.
For the yearly data, we leverage Long Short-Term Memory (LSTM) method using Flux.jl (Innes et al., 2018) for ensemble modeling, owing to their effectiveness in capturing long-term dependencies and mitigating vanishing gradients. This contributes to robust long-term predictions. We further enhance predictions using the AdaBoostRegressor (Drucker, 1997) from scikit-learn (Pedregosa et al., 2011) for its ensemble learning strengths. By combining multiple weak learners, AdaBoost adapts well to diverse data, mitigating overfitting (the combination is abbreviated as AdaBoost_LSTM). Besides, to address potential climate change impacts, particularly drought, statistical features of minima (quartile 0.01) are incorporated into the ensemble computed results of LSTM, abbreviated as Min_LSTM.
For monthly predictions, given greater short-term needs, we employ an ARIMA-LSTM model following Song et al. (2024). AutoRegressive Integrated Moving Average (ARIMA) models, denoted as ARIMA(p, d, q) (‘p’ is the autoregressive order, ‘d’ is the differencing degree and ‘q’ is the moving average order), form the foundation for capturing short-term correlations (as expressed in Equation (10)). We incorporate a constant offset term, fitting using StateSpaceModels.jl (Saavedra et al., 2019). The ARIMA simulation results are integrated with LSTM monthly error predictions for final refined forecasts. That is, the ARIMA models short-term dynamics while LSTM focuses on longer-term nonlinear error patterns.
Y t = Y 0 + ϕ 1 Y t − 1 + ϕ 2 Y t − 2 + ⋯ ϕ p Y t − p + ε t − θ 1 ε t − 1 − θ 2 ε t − 2 − ⋯ − θ q ε t − q
where Yt represents the observed value at time t; Y0 is a constant term; ϕi are autoregressive coefficients; εt is the white noise error term at time t; and θi are moving average coefficients.
By selectively combining time series methods based on their complementary strengths, our framework provides both robust yearly predictions and accurate monthly forecasts critical for decision-making. The integrated modeling approach enhances reliability and adaptability across timescales.

4. Results and Discussions

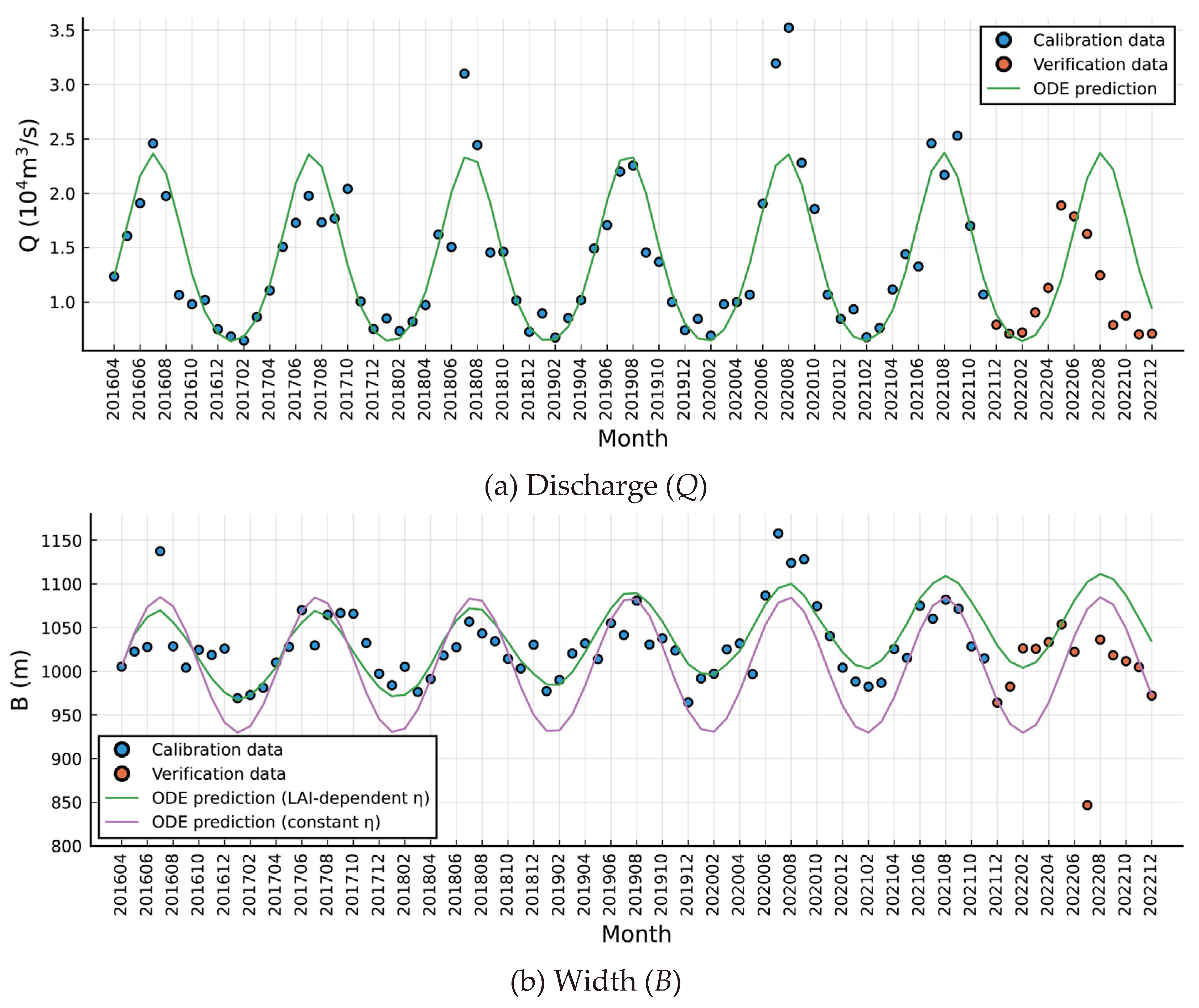
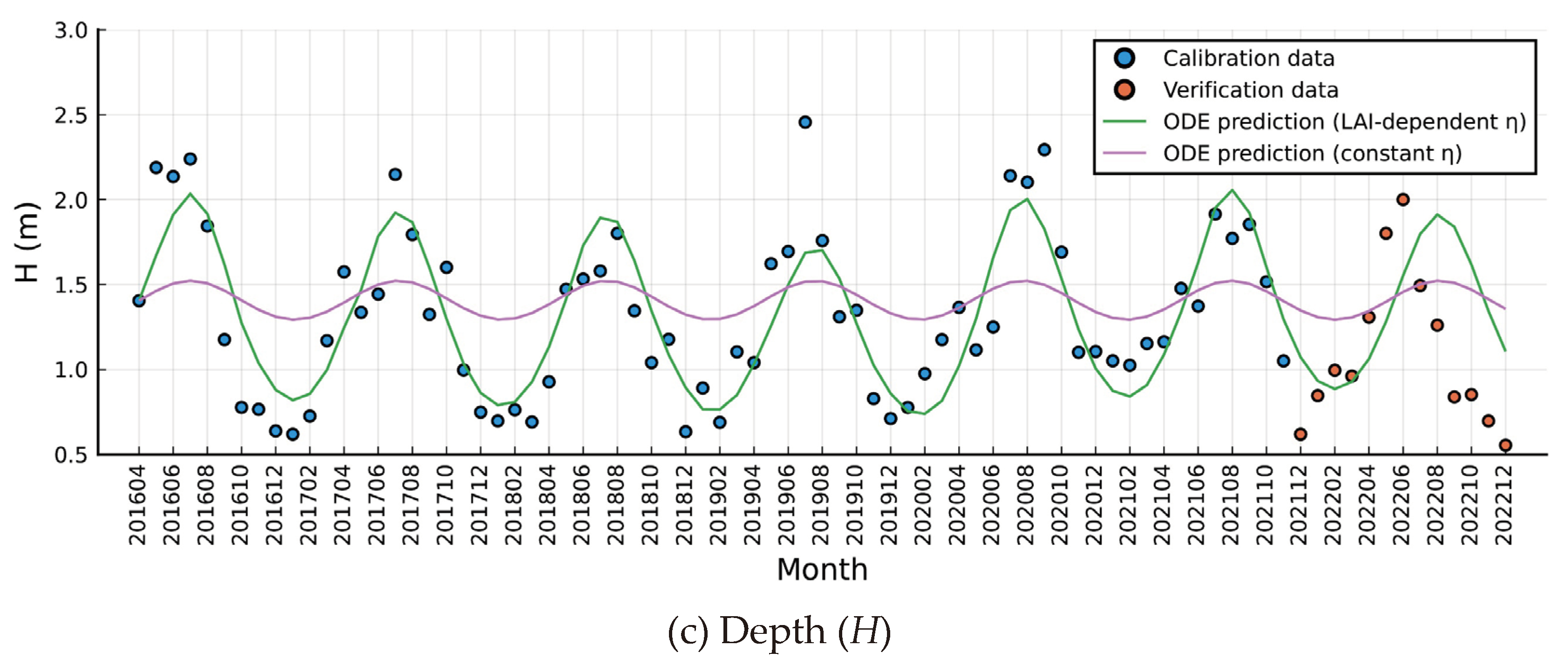
4.1. Calibration, Verification and Forecast

Figure 3 illustrates the calibration and verification of ODEs-(8) in modeling the dynamics of monthly inflow discharge Q and hydraulic geometry variables (i.e., width B and depth H). In the calibration phase, the model effectively captures the Q change process, except for the flood peak discharge in specific years (2018 and 2020) due to the periodic delayed response theory (Equation (2)), which primarily focuses on discharge adjustment around the mean value of the major flood season, neglecting the peak value. Additionally, the model demonstrates significantly improved capabilities in capturing B and H changes when considering the variation of the η parameter as a function of LAIc, as opposed to the traditional constant η case.
During the verification phase, the three sub-models perform well in the first half of 2022; however, in the latter half of the year, errors increase, and actual values are markedly lower than the predicted values. This discrepancy stems from the severe meteorological drought in the Yangtze River Basin during the summer of 2022, the most serious since 1961. Basin-wide drying in the flood season resulted in the lowest water levels recorded at each control station in historical records. The annual sediment discharge at each hydrological control station also reached its historical minimum.
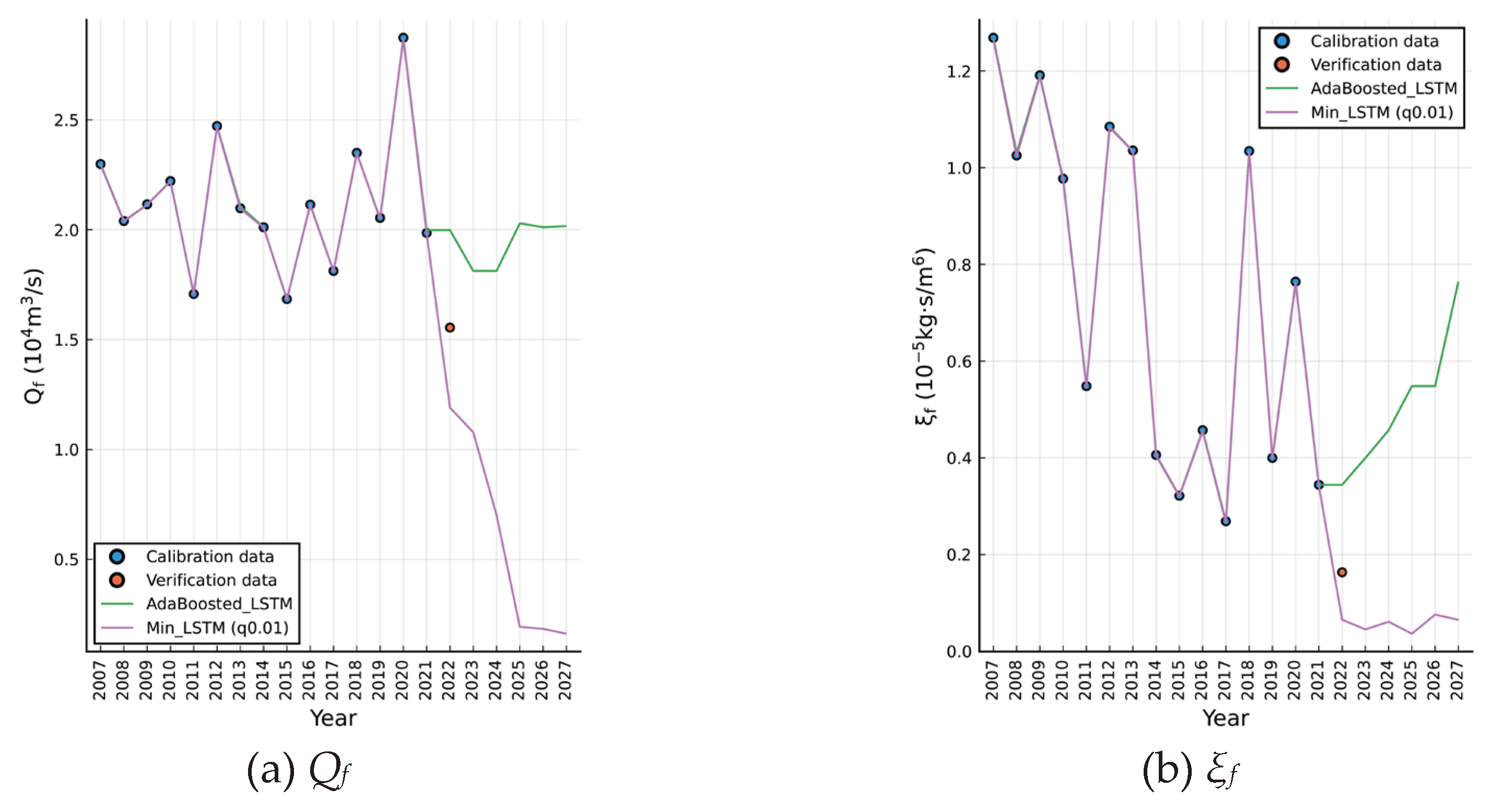
Figure 4 depicts the calibration, verification, and forecast of critical input data for ODEs-(8). For the annual major-flooded incoming water-sediment quantities (Qf, ξf) (Figure 4a,b), we incorporate additional data from 2007 spanning the initial operation period of the Three Gorges Dam up to present for model training, utilizing 1000 ensemble LSTM networks (Table A3). The Min_LSTM projections capture the rare 2022 drought event just right. 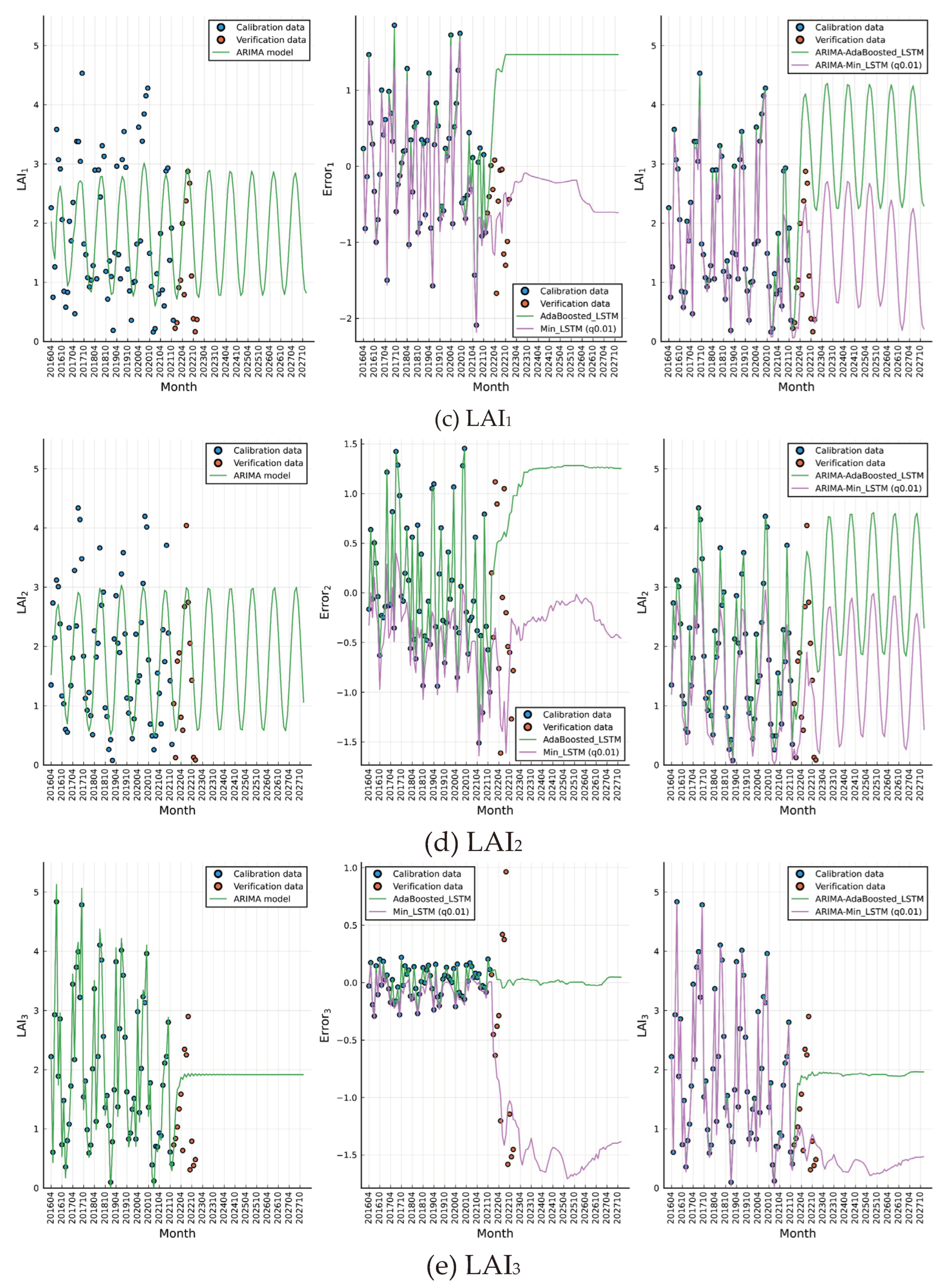Smooth predictions from AdaBoost_LSTM show ξf exhibiting a continuous upward trend over the next five years (Figure 4b). For the monthly LAI indicators (Figure 4c,d), an ARIMA(2,0,2) model is selected as the foundation, with LAI3 demonstrating greater stochasticity in changes per the substantial white noise variance (refer to Table A2 for parameters). Due to this volatility, the integrated ARIMA-AdaBoost_LSTM can only simulate the long-term flat trend for LAI3 (Figure 4e). Model verification indicates the ARIMA-Min_LSTM effectively predicts the extreme 2022 drought impact on LAI, with actual values anticipated to remain within or near the limits forecasted by ARIMA-AdaBoost_LSTM too. The two models are combined to demonstrate reliable prediction capabilities.
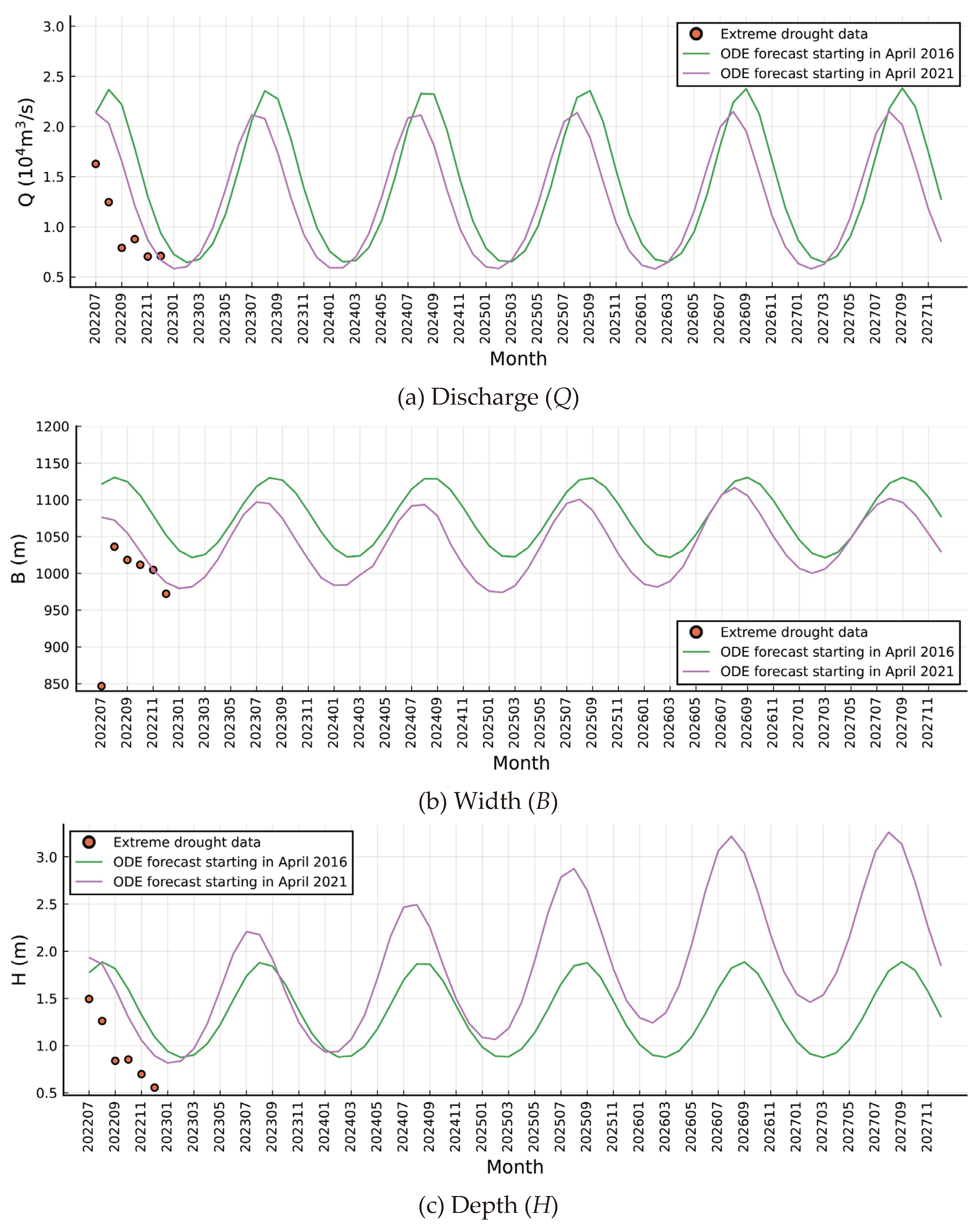
Concluding this section, we attempt to forecast monthly water discharge trends and hydraulic geometry relationship characteristics under submesic and arid climate conditions corresponding to ARIMA-AdaBoost_LSTM and ARIMA-Min_LSTM modeled data respectively, utilizing ODE-(8) and its estimated parameters. However, upon analysis, minimal differences between the two are observed, indicating our models trained on normal climate data cannot simulate inflow discharge and hydraulic geometries under extreme drought influence. Nonetheless, we perform a sensitivity analysis by shifting the initial value from April 2016 to April 2021, as depicted in Figure 5.
Specifically, measured values of Q, B, and H in the latter half of 2022 consistently fall below predictions, averaging 8000 m3/s, 120 m, and 0.63 m less respectively. Provided such extreme drought conditions do not recur, our projections indicate Q, B, and H will exhibit steady, cyclical fluctuations within ranges of 6400-24000 m3/s, 1020-1130 m, and 0.87-1.9 m respectively. We further predict the variables will peak in August before 2024, shifting to September post-2024, aligning with autumn flood patterns in the watershed during 2023 (Yue et al., 2023). Moreover, forwarding the initial values results in small Q and B decreases, alongside a large H increase, indicating strong water depth sensitivity. In addition, this results in the phase shifting forward by one month for all three variables.

4.2. Extended Systematic Evaluation

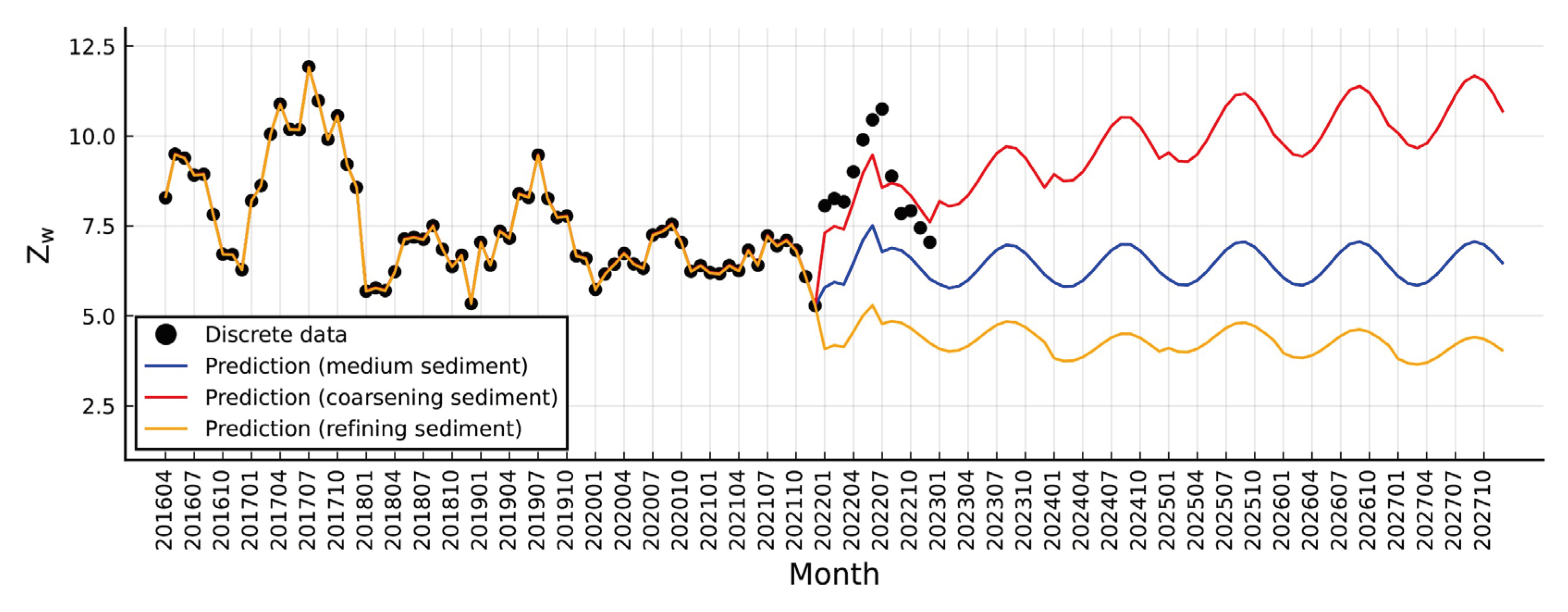
River system stability depends on the balance between discharge and channel morphology regulating flow - width, depth, slope, roughness, sediment, boundaries, etc. As the primary driver, discharge shapes diverse landscapes through nonlinear relations with channel forms due to factors like gravel bars, variable riffles, and dynamic flow resistance. Thus, stability assessment requires examining key process metrics. One useful stability index is the riverbed index (Zw) by Zhang (1995), categorizing planforms into braided (Zw <5), anabranching (5< Zw <15), and meandering (Zw >15) based on width, depth, slope, sediment size/density. The mathematical expression is:
Z w = ρ s − ρ ρ d 50 H 1 / 3 J B 2 / 3
Here we analyze the trend of Zw along the river reach (Figure 6) using previously calculated data supplemented by additional information including multi-year average slope (J) of 0.0459‰, sediment density (ρs) of 2650 kg/m3, and annual median particle size (d50) at Shashi station with yearly LSTM-predicted variations (Figure A1). Notably, as discharge and sediment load increase, coarser sediment results from higher flow energy. However, these trends are not absolute as factors like topography, soil, vegetation also influence sediment sizes. We consider both sediment coarsening and fining scenarios when modeling d50 for Zw calculation.
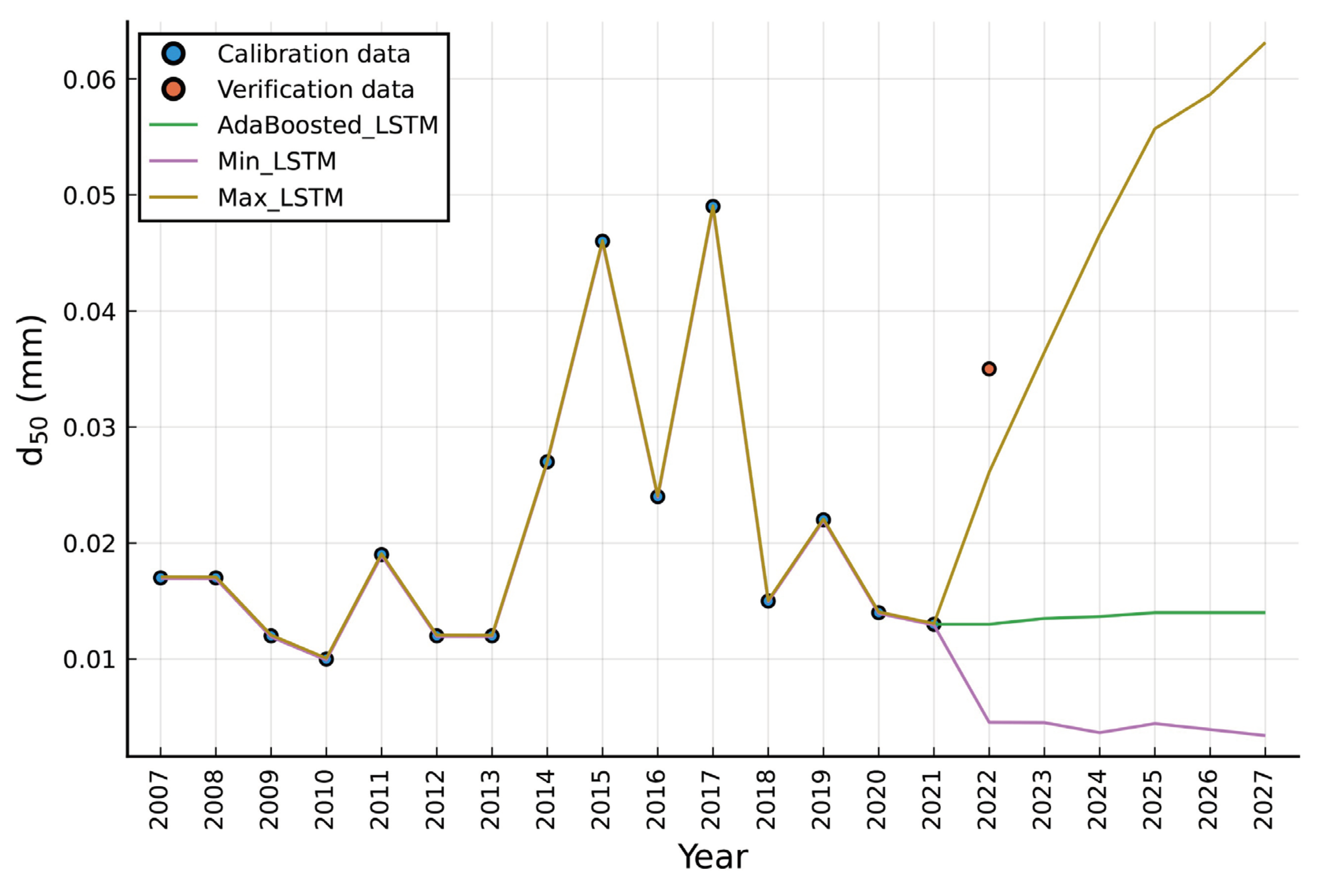
Comparing the three 2022 d50 driven scenarios, the sustained Zw range (still in the 5 to 15 range) indicates the river reach likely maintains its anabranching pattern for an extended period, despite some divergence between the modeled and observed sediment coarsening conditions. This is aligned with the prevailing coarsening phenomenon (Zhou et al., 2023). The discernible coarsening trend temporally increases stability, favoring a meandering planform. Conversely, significant fining decreases stability over time, favoring braiding despite low current probability. We recognize limitations in utilizing annually-aggregated sediment data lacking monthly details, which warrants prudent interpretation of the modeling results.

4.3. Methodological Discussion

The dynamic ODE models proposed in this study offer advantages in capturing time-varying hydraulic geometry relationships by coupling the differentialized power-law equations with leaf area index (LAI) data. Incorporating LAI as an indicator of riparian vegetation enables the models to account for the influence of erosion control on channel morphology. However, the models have certain limitations. A key challenge is accurately simulating extreme weather events, such as the severe drought of 2022, as the models are calibrated on normal climate data. Several assumptions underpin the ODE models, introducing uncertainties. The periodic delayed response theory assumes discharge adjusts around the mean value during major flood seasons, neglecting peak values. While suitable for capturing overall trends, this assumption limits accuracy during high-flow events. Furthermore, the artificial cut-offs along the river are simplified, potentially overlooking complexities in planform changes. Data quality presents another source of uncertainty. The study relies on remotely sensed data from Sentinel satellites, with limited validation against in-situ measurements in the study area. Channel geometry estimates may be impacted by factors like vegetation cover, terrain shadow, and sensor limitations. Additionally, the use of annually-aggregated sediment data lacking monthly details hinders a more nuanced assessment of sediment dynamics and their impact on channel stability.
While the current study focuses on the Jingjiang reach of the Yangtze River, the modeling approach has broader applicability. Integrating remotely sensed LAI data with hydraulic geometry equations could be extended to other river systems, provided appropriate adjustments are made to account for variations in local conditions, such as climate, vegetation types, and sediment regimes. However, specific parameter values and assumptions may require recalibration or adaptation to ensure reliable performance in new contexts.
Building upon this work, several avenues for future research can be explored. Incorporating additional environmental factors, such as temperature, precipitation, and land use changes, may enhance the models’ predictive capabilities and capture a more comprehensive set of drivers influencing channel dynamics. Moreover, integrating models across different spatial and temporal scales could yield insights into the interactions between local and regional processes shaping river morphology. Advances in simulation techniques, such as agent-based modeling and machine learning approaches, offer promising avenues for modeling complex river systems. Coupling the proposed models with these techniques could improve the representation of emergent patterns and nonlinear dynamics, leading to more robust predictions.

5. Conclusions

This pioneering study proposes an innovative approach to quantify the dynamics of monthly hydraulic geometry relationships in the Jingjiang reach of the Yangtze River by formulating a comprehensive ordinary differential equation (ODE) system that dynamically couples discharge, channel geometry, and remotely sensed leaf area index (LAI) data within a unified mathematical framework. Through calibration and validation, the integrated models demonstrate superiority over conventional constant-parameter formulations in capturing overall trends, yet their predictive capabilities are limited under anomalous climatic conditions like the severe 2022 drought due to model training on historical data representing normal climate patterns. Key assumptions inherent to the modeling framework, including the periodic delayed response theory neglecting peak flows, simplified artificial cut-off representation, reliance on remotely sensed data lacking comprehensive local ground-truthing, and lack of monthly sediment data, introduce uncertainties warranting careful consideration. Despite limitations, the proposed approach shows promise for broader applicability across diverse river systems contingent upon appropriate adaptations to local conditions, enhanced data sources, improved validation techniques, and refinement of underlying assumptions. Future research incorporating additional environmental variables, integrating models across scales, and coupling with advanced simulation techniques like agent-based modeling and machine learning could further enrich predictive capabilities, capture emergent patterns, represent nonlinear dynamics and feedback mechanisms, and yield more robust predictions, ultimately contributing to a deeper understanding of the intricate relationships between riparian ecology, erosion processes, and channel stability.

CRediT authorship contribution statement

Hai Huang: Conceptualization, Methodology, Funding acquisition, Resources, Project administration. Xiaolong Song: Conceptualization, Methodology, Investigation, Formal analysis, Writing - original draft, Writing - review and editing, Funding acquisition. Haijue Xu: Conceptualization. Yuchuan Bai: Conceptualization, Supervision.

Acknowledgements

This research was funded by the Significant Science and Technology Project of the Ministry of Water Resources, China (Grant No. SKR-2022055), the Basic Scientific Research Project of the China Institute of Water Resources and Hydropower Research (Grant Nos. SE110145B0022023 and SE0145B042021), and the Open Research Fund of Key Laboratory of Sediment Science and Northern River Training, the Ministry of Water Resources, China Institute of Water Resources and Hydropower Research (Grant No. IWHR-SEDI-2023-02).

Appendix A

Table A1. Estimated parameters of ODEs-(8).
Table A1. Estimated parameters of ODEs-(8).
Parameters ODE (LAI-dependent η) ODE (constant η)
β 0.3393 0.3380
ω 0.5158 0.5157
φ 3.1499 3.1545
K 347.3363 347.5032
b 0.2245 0.2574
c 0.1394 -0.0454
ηB0 0.0630 0.1177
lB1 -0.0040 /
lB2 0.0216 /
lB3 -0.0092 /
ηH0 0.6558 0.1247
lH1 0.1085 /
lH2 -0.0667 /
lH3 -0.0291 /
Note: “/” means no such parameter.
Table A2. Estimated parameters of ARIMA(2,0,2) for the three LAI indicators. ar_L1 and ar_L2 are autoregressive coefficients. ma_L1 and ma_L2 are moving average coefficients. mean represents a constant term and sigma2 represents white noise variance.
Table A2. Estimated parameters of ARIMA(2,0,2) for the three LAI indicators. ar_L1 and ar_L2 are autoregressive coefficients. ma_L1 and ma_L2 are moving average coefficients. mean represents a constant term and sigma2 represents white noise variance.
Parameters LAI1 LAI2 LAI3
ar_L1 1.7213 1.7352 -0.3788
ar_L2 -0.9976 -0.9998 0.4691
ma_L1 -1.6842 -1.7228 0.8738
ma_L2 0.9921 0.9989 -0.1258
mean 1.8268 1.7848 1.9152
sigma2 0.7353 0.4728 1.1240
Note: “/” means no such parameter.
Table A3. LSTM hyperparameters used in simulation of the five key input data of ODEs-(8). num_epochs is the number of epochs. hidden_size is the number of hidden layer neurons. ensemble_size is the number of ensemble LSTM models.
Table A3. LSTM hyperparameters used in simulation of the five key input data of ODEs-(8). num_epochs is the number of epochs. hidden_size is the number of hidden layer neurons. ensemble_size is the number of ensemble LSTM models.
Parameters Qf ξf LAI1 LAI2 LAI3
num_epochs 5000 5000 5000 5000 5000
learning_rate 0.01 0.01 0.01 0.01 0.01
hidden_size 50 50 200 200 200
ensemble_size 1000 1000 720 720 720
Preprints 99590 g0a1
Figure A1. Simulation of the annual variation process of median particle size (d50) at the Shashi station. “Max” represents the 0.99 quantile result, “Min” represents the 0.01 quantile result.
Figure A1. Simulation of the annual variation process of median particle size (d50) at the Shashi station. “Max” represents the 0.99 quantile result, “Min” represents the 0.01 quantile result.
Preprints 99590 g0a1

References

  1. Ankerst, M., Breunig, M.M., Kriegel, H.-P., Sander, J., 1999. OPTICS: Ordering points to identify the clustering structure. ACM Sigmod record, 28(2), 49-60. [CrossRef]
  2. Bridge, J.S., 2009. Rivers and Floodplains: Forms, Processes, and Sedimentary Record. John Wiley & Sons.
  3. Campello, R.J.G.B., Moulavi, D., Sander, J., 2013. Density-Based Clustering Based on Hierarchical Density Estimates. In: J. Pei, V.S. Tseng, L. Cao, H. Motoda, G. Xu (Eds.), Advances in Knowledge Discovery and Data Mining. Springer Berlin Heidelberg, Berlin, Heidelberg, pp. 160-172. [CrossRef]
  4. Charlton, R., 2007. Fundamentals of fluvial geomorphology. Routledge. [CrossRef]
  5. Cohen, S., Raney, A., Munasinghe, D., Loftis, J.D., Molthan, A., Bell, J., Rogers, L., Galantowicz, J., Brakenridge, G.R., Kettner, A.J., Huang, Y.F., Tsang, Y.P., 2019. The Floodwater Depth Estimation Tool (FwDET v2.0) for improved remote sensing analysis of coastal flooding. Nat. Hazards Earth Syst. Sci., 19(9), 2053-2065. [CrossRef]
  6. Dixit, V.K., Rackauckas, C., 2023. Optimization. jl: A unified optimization package. Zenodo.
  7. Donchyts, G., Schellekens, J., Winsemius, H., Eisemann, E., Van de Giesen, N., 2016. A 30 m resolution surface water mask including estimation of positional and thematic differences using landsat 8, srtm and openstreetmap: a case study in the Murray-Darling Basin, Australia. Remote Sensing, 8(5), 386. [CrossRef]
  8. Drucker, H., 1997. Improving regressors using boosting techniques, Icml, pp. e115.
  9. Duveiller, G., Weiss, M., Baret, F., Defourny, P., 2011. Retrieving wheat Green Area Index during the growing season from optical time series measurements based on neural network radiative transfer inversion. Remote Sensing of Environment, 115(3), 887-896. [CrossRef]
  10. Eaton, B., Millar, R.G., Davidson, S., 2010. Channel patterns: Braided, anabranching, and single-thread. Geomorphology, 120(3-4), 353-364. [CrossRef]
  11. Gleason, C.J., 2015. Hydraulic geometry of natural rivers:A review and future directions. Progress in Physical Geography: Earth and Environment, 39(3), 337-360. [CrossRef]
  12. Gran, K., Paola, C., 2001. Riparian vegetation controls on braided stream dynamics. Water Resources Research, 37(12), 3275-3283. [CrossRef]
  13. Innes, M., Saba, E., Fischer, K., Gandhi, D., Rudilosso, M.C., Joy, N.M., Karmali, T., Pal, A., Shah, V., 2018. Fashionable modelling with flux. arXiv preprint arXiv:1811.01457. [CrossRef]
  14. Kingma, D.P., Ba, J., 2014. Adam: A method for stochastic optimization. arXiv preprint arXiv:1412.6980. [CrossRef]
  15. Lee, J.-S., Wen, J.-H., Ainsworth, T.L., Chen, K.-S., Chen, A.J., 2008. Improved sigma filter for speckle filtering of SAR imagery. IEEE Transactions on Geoscience and Remote Sensing, 47(1), 202-213. [CrossRef]
  16. Leopold, L.B., Maddock, T., 1953. The hydraulic geometry of stream channels and some physiographic implications, 252. US Government Printing Office.
  17. McFeeters, S.K., 1996. The use of the Normalized Difference Water Index (NDWI) in the delineation of open water features. International journal of remote sensing, 17(7), 1425-1432. [CrossRef]
  18. McInnes, L., Healy, J., 2017. Accelerated Hierarchical Density Based Clustering, 2017 IEEE International Conference on Data Mining Workshops (ICDMW), pp. 33-42. [CrossRef]
  19. Otsu, N., 1979. A threshold selection method from gray-level histograms. IEEE transactions on systems, man, and cybernetics, 9(1), 62-66.
  20. Pedregosa, F., Varoquaux, G., Gramfort, A., Michel, V., Thirion, B., Grisel, O., Blondel, M., Prettenhofer, P., Weiss, R., Dubourg, V., 2011. Scikit-learn: Machine learning in Python. the Journal of machine Learning research, 12, 2825-2830.
  21. Pekel, J.-F., Cottam, A., Gorelick, N., Belward, A.S., 2016. High-resolution mapping of global surface water and its long-term changes. Nature, 540(7633), 418-422. [CrossRef]
  22. Rackauckas, C., Nie, Q., 2017. DifferentialEquations.jl – A Performant and Feature-Rich Ecosystem for Solving Differential Equations in Julia. Journal of Open Research Software. [CrossRef]
  23. Reyes-Muñoz, P., Pipia, L., Salinero-Delgado, M., Belda, S., Berger, K., Estévez, J., Morata, M., Rivera-Caicedo, J.P., Verrelst, J., 2022. Quantifying Fundamental Vegetation Traits over Europe Using the Sentinel-3 OLCI Catalogue in Google Earth Engine. Remote Sensing, 14(6), 1347. [CrossRef]
  24. Rhoads, B.L., Lewis, Q.W., Andresen, W., 2016. Historical changes in channel network extent and channel planform in an intensively managed landscape: Natural versus human-induced effects. Geomorphology, 252, 17-31. [CrossRef]
  25. Saavedra, R., Bodin, G., Souto, M., 2019. StateSpaceModels. jl: A julia package for time-series analysis in a state-space framework. arXiv preprint arXiv:1908.01757. [CrossRef]
  26. Schwenk, J., Khandelwal, A., Fratkin, M., Kumar, V., Foufoula-Georgiou, E., 2017. High spatiotemporal resolution of river planform dynamics from Landsat: The RivMAP toolbox and results from the Ucayali River. Earth and Space Science, 4(2), 46-75. [CrossRef]
  27. Singh, V.P., 2003. On the theories of hydraulic geometry. International journal of sediment research, 18(3), 196-218.
  28. Smith, B., Sandwell, D., 2003. Accuracy and resolution of shuttle radar topography mission data. Geophysical Research Letters, 30(9).
  29. Song, X., Xu, H., Bai, Y., 2024. An integrated SWJ-LSTM-ETS modeling strategy for investigating upper morphology dynamics of a stochastic laboratory delta with environmental changes. Geomorphology, 445, 108977.
  30. Tsitouras, C., 2011. Runge–Kutta pairs of order 5 (4) satisfying only the first column simplifying assumption. Computers & Mathematics with Applications, 62(2), 770-775.
  31. Van der Tol, C., Berry, J., Campbell, P., Rascher, U., 2014. Models of fluorescence and photosynthesis for interpreting measurements of solar-induced chlorophyll fluorescence. Journal of geophysical research: Biogeosciences, 119(12), 2312-2327.
  32. Vermote, E.F., Tanré, D., Deuze, J.L., Herman, M., Morcette, J.-J., 1997. Second simulation of the satellite signal in the solar spectrum, 6S: An overview. IEEE transactions on geoscience and remote sensing, 35(3), 675-686.
  33. Vollrath, A., Mullissa, A., Reiche, J., 2020. Angular-based radiometric slope correction for Sentinel-1 on google earth engine. Remote Sensing, 12(11), 1867.
  34. Whittaker, R.H., 1970. Communities and ecosystems. Communities and ecosystems.
  35. Williams, C.K., Rasmussen, C.E., 2006. Gaussian processes for machine learning, 2. MIT press Cambridge, MA.
  36. Wu, B., Wang, G., Xia, J., Fu, X., Zhang, Y., 2008. Response of bankfull discharge to discharge and sediment load in the Lower Yellow River. Geomorphology, 100(3-4), 366-376.
  37. Yue, P.Y., Xiao, Z.W., Zhao, Y.T., 2023. Taking “floods” as a command to fight against the storm - a record of the Yangtze River Commission’s full response to the autumn floods of the Han River in 2023. Tencent Network. https://new.qq.com/rain/a/20231016A09R4300. (in Chinese).
  38. Yue, Z., Huang, W., Xiong, L., Wang, Z., Wang, X., Wang, Q., Shen, Q., 2021. A new strategy for environmental flow management by using the remote sensing method. Journal of Cleaner Production, 325, 129226.
  39. Zhang, H.W., 1995. The study of the law of similarity for models of flood flows of the lower reach of the Yellow River, Tsinghua University, Beijing. (in Chinese).
  40. Zhou, M.R., Xia, J.Q., Deng, S.S., Mao, Y., 2023. Longitudinal variation of channel evolution along the middle Yangtze River after the operation of the Three Gorges Project. Journal of Lake Sciences, 35(2), 642-650. (in Chinese).
Preprints 99590 g001
Figure 1. Recent historical changes in the Jingjiang reach of the Yangtze River under study.
Figure 1. Recent historical changes in the Jingjiang reach of the Yangtze River under study.
Preprints 99590 g001
Preprints 99590 g002aPreprints 99590 g002b
Figure 2. Exemplar monthly LAI acquisition and representative HDBSCAN clustering results.
Figure 2. Exemplar monthly LAI acquisition and representative HDBSCAN clustering results.
Preprints 99590 g002aPreprints 99590 g002b
Preprints 99590 g003aPreprints 99590 g003b
Figure 3. Calibration and verification of monthly hydraulic geometry variables versus inflow discharge using the proposed ODEs-(8), with the no-LAI-dependent-η model as a control.
Figure 3. Calibration and verification of monthly hydraulic geometry variables versus inflow discharge using the proposed ODEs-(8), with the no-LAI-dependent-η model as a control.
Preprints 99590 g003aPreprints 99590 g003b
Preprints 99590 g004aPreprints 99590 g004b
Figure 4. Calibration, verification and forecast of key input data using the integrated models based on ARIMA and LSTM.
Figure 4. Calibration, verification and forecast of key input data using the integrated models based on ARIMA and LSTM.
Preprints 99590 g004aPreprints 99590 g004b
Preprints 99590 g005
Figure 5. Forecast of monthly hydraulic geometry variables versus inflow discharge until 2027, using the proposed ODEs-(8) under different initial value conditions.
Figure 5. Forecast of monthly hydraulic geometry variables versus inflow discharge until 2027, using the proposed ODEs-(8) under different initial value conditions.
Preprints 99590 g005
Preprints 99590 g006
Figure 6. Time-varying prediction of system stability assessment indicator Zw in the reach.
Figure 6. Time-varying prediction of system stability assessment indicator Zw in the reach.
Preprints 99590 g006
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated