Prerpints.org logo
Preprint
Article

Causal Meta-Reinforcement Learning for Multimodal Remote Sensing Data Classification

Altmetrics

Downloads

149

Views

59

Comments

0

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

22 February 2024

Posted:

22 February 2024

You are already at the latest version

Alerts
Abstract
Multimodal remote sensing data classification can enhance the model’s ability to distinguish land features through multimodal data fusion. In this context, how to help models understand the relationship between multimodal data and target tasks is the focus of researchers. Inspired by human feedback learning mechanisms, causal reasoning mechanisms, and knowledge induction mechanisms, this paper integrates causal learning, reinforcement learning, and meta learning into a unified remote sensing data classification framework and proposed the causal meta-reinforcement learning (CMRL). First, based on feedback learning mechanisms, we have overcome the limitations of traditional implicit optimization of fusion features and customized a reinforcement learning environment for multimodal remote sensing data classification tasks. Through feedback interactive learning between agents and the environment, we help them understand the complex relationships between multimodal data and labels, thereby achieving full mining of multimodal complementary information. Second, based on the causal inference mechanism we designed causal distribution prediction action, classification reward, and causal intervention reward, capturing pure causal factors in multimodal data and cutting off false statistical associations between non-causal factors and class labels. Finally, based on the knowledge induction mechanism, we designed a bi-layer optimization mechanism based on meta-learning. By constructing a meta training task and meta validation task simulation model in the generalization scenario of unseen data, we helped the model induce cross-task shared knowledge, thereby improving its generalization ability for unseen multimodal data. The experimental results on multiple sets of multimodal datasets show that the proposed method achieved state-of-the-art performance in multimodal remote sensing data classification tasks.
Keywords: 
Subject: Computer Science and Mathematics  -   Artificial Intelligence and Machine Learning

1. Introduction

Remote sensing data classification has important research significance in the fields of urban planning , mining exploration, and agriculture [1,2,3,4,5]. In recent years, with the rapid development of sensor technology, a variety of remote sensing data sources have been provided to support remote sensing data classification tasks. For example, hyperspectral image (HSI) is able to reflect fine spectral information of ground objects [6,7], but is susceptible to factors such as weather and has challenges in distinguishing ground objects with similar spectral reflectance. In contrast, light detection and ranging (LiDAR) is not sensitive to weather conditions, and the elevation information it contains helps the model distinguish between objects with similar spectral information but different heights [8]. Multimodal remote sensing data classification can improve the model’s ability to distinguish ground objects through multimodal data fusion, which has attracted extensive attention from researchers in recent years.
In the process of multimodal data fusion, a key problem is: How to help models understand the relationship between multimodal data and target tasks? The difficulty of solving this problem lies in: On the one hand, the coupling relationship between task-related information and task-unrelated information in multimodal data is often tight and complex, which makes it difficult for the model to accurately distinguish the two above. For example, there may be spectral noise in HSI, and there may also be noise in LiDAR due to the scattering effect of multipath effects. It is frustrating that the noise information is not only difficult to be directly observed and interfered with, but also often brings serious interference to the model learning process. On the other hand, the association pattern between multimodal data and target tasks often changes dynamically with specific context information. Take HSI and LiDAR for example, different classes of ground objects in urban scenes often have inconsistent heights and different spectral reflectance (difference in ground object materials), so multimodal data fusion tends to make comprehensive use of HSI and LiDAR. However, in the forest scene with similar height of trees, attention to LiDAR information can lead to intermodal information interference. The dynamic change of the association pattern requires the model to fully understand the dependency between the context information and the multimodal data fusion, which puts forward higher requirements for its intelligence.
In order to accurately capture task-related information from multimodal data, inspired by the human visual system’s focus on only the key information in the visual scene, researchers have developed a variety of attention mechanisms. These attention mechanisms were designed to adaptively emphasize task-related information and suppress task-unrelated information in model learning. Gao et al. [9] proposed an adaptive feature fusion module to adjust the model’s degree of attention to different modalities through dynamic attention allocation. However, this method only models the global importance of multimodal data, and the noise information contained in the data is also concerned when a certain modality is emphasized. Considering the consistency of multimodal data in describing objects, the mutual supervision between multimodal data can help the model to capture task-related information. To solve this problem, Zhang et al. [10] proposed a mutual guidance attention module, which highlights key task-based information and suppresses useless noise information by establishing mutual supervision between different modal information flows. In order to more fully mine the consistency information among multimodal data, Song et al. [11] developed a cross-modal attention fusion module, which learns the global dependency relationship between multimodal data by establishing deep interaction between them, and then uses this dependency relationship to improve the model’s ability to capture task-related information. However, optimization of attention mechanisms in the above methods often relies on establishing statistical associations between multimodal data and labels, thus minimizing the empirical risk of the model on the training data. It should be noted that overemphasis on statistical dependencies between multimodal data and labels can lead models to falsely establish false statistical associations between non-causal factors (such as spectral noise) and labels. For example, ground objects in a certain region show abnormal spectral responses within a certain band due to weather factors. If the model establishes a statistical correlation between abnormal spectral responses and labels, the model will often mistakenly emphasize abnormal spectral information. In addition, multimodal remote sensing data classification tasks usually face high labeling costs, which makes it difficult to obtain sufficient labeling training data in practical applications. This problem of data sparsity leads to the possibility that the training data may not accurately reflect the real data distribution. In this context, simply minimizing the empirical risk of the model on the training data may make it difficult for the model to achieve satisfactory generalization performance on the unseen multimodal data.
Fortunately, human causal reasoning mechanisms and knowledge induction mechanisms provide solutions to the above problems. On the one hand, humans are able to identify causal associations that are truly related to each other from appearances, rather than through statistical learning. For example, although “fish” is usually found in water and the two show a high statistical dependence, humans can clearly recognize that there is non-causal relationship between “water” and “fish”. Inspired by this, if a causal reasoning mechanism can be built into the model learning process, it can be made to cut off the false statistical association between non-causal factors and labels, and learn the real causal effect between data and labels. On the other hand, humans are able to generalize core knowledge from different tasks, so they can effectively deal with unseen tasks. For example, by practicing addition and subtraction exercises, students can deduce the rules of addition and subtraction operations from them, so that they can perform them correctly when they encounter addition and subtraction exercises that they have not seen in practice. Inspired by this, if a knowledge induction mechanism can be established in the process of model optimization, the model can jump out of the limitations of fitting training data in the learning process, and generalize cross-task shared knowledge from different multimodal remote sensing data classification tasks to improve its generalization ability to unseen multimodal data.
In order to capture complex association patterns among multimodal data, researchers have conducted extensive explorations. Considering that the association modes of multimodal data are often closely related to the above information, Xue et al. [12] proposed a self-calibrated convolution, which captures multi-scale context information of multimodal data. The weight of multi-scale context information is adjusted adaptively by spectral and spatial self-attention. Roy et al. [13] taking into account the differences among multimodal data, customized a personalized feature learning mode for HSI and LiDAR, captured HSI rich spatial-spectral information by convolution, and LiDAR spatial structure information by morphological expansion layer and erosion layer. Finally, multimodal data was integrated by additive operation. However, simple additive operations are difficult to capture complex nonlinear relationships between multimodal data. Therefore, Wang et al. [14] proposed a spatial-spectral mutual guided module to realize cross-modal information fusion of multimodal spatial and spectral information, and to improve the semantic correlation between multimodal spectrum and spatial information by using adaptive, multi-scale and mutual learning technologies. Further, in order to fully capture the local and global associations of multimodal data, Du et al. [15] proposed a spatial-spectral graph network, which uses image block-based convolution to preserve the local structures of multimodal data, and uses the information transfer mechanism of graph neural networks to capture the global associations. The above one-step multimodal data fusion method has significant limitations in the mining of complex association patterns: The multimodal data only goes through one forward process in the fusion process, and cannot evaluate the quality of its current fusion strategy and make adaptive adjustments to it. Such one-step fusion process limits the model’s ability to mine complex association patterns. In addition, the optimization process of multimodal data fusion strategies of these methods is often implicit, and is not directly guided by the gradient of classification loss. It is difficult to ensure that the model truly understands the complex role relationship between multimodal data and labels in feature fusion, which can lead to the model incorrectly suppressing task-related information or emphasizing task-unrelated information.
Fortunately, the human feedback learning mechanism provided a solution to this problem, specifically, humans can understand the complex relationships between things through interactive feedback with the environment. For example, chemists combine different chemicals during experiments and get feedback signals by observing the reaction phenomena between them. Based on the feedback signal, chemists can better understand the interaction between chemical substances and the effect of this interaction relationship on the reaction phenomenon, and then modify their experimental operations to obtain the expected experimental results. Inspired by this, if the task-oriented feedback mechanism can be established in the process of multimodal feature fusion, the model can fully understand how the current multimodal data fusion strategy acts on the target task, and adjust its multimodal data fusion strategy according to its performance in the target task, fully capturing and intelligently adapting to complex association patterns among multimodal data.
In summary, the key issue that this paper aims to address is: How to establish feedback learning mechanisms, causal inference mechanism and knowledge induction mechanisms in multimodal remote sensing data classification tasks?
To address this issue, we integrated reinforcement learning, causal learning, and meta-learning into a unified multimodal remote sensing data classification framework and proposed a causal meta-reinforcement learning framework. Specifically, to establish feedback learning mechanisms and causal reasoning mechanisms, we customized a reinforcement learning environment for multimodal remote sensing data classification tasks and designed causal distribution prediction actions, classification rewards, and causal intervention rewards. Through this approach, on the one hand, intelligent agents can understand the complex relationships between multimodal data and labels in their interaction feedback with the environment. On the other hand, intelligent agents can distinguish causal and non-causal factors in multimodal data under the feedback and driving of reward signals, and accurately capture pure causal factors by mining multimodal complementary information. To establish a knowledge induction mechanism, inspired by meta-learning scenario simulation training, we constructed meta training tasks and meta validation tasks, and based on this, we constructed a bi-layer optimization mechanism. By simulating the generalization scenario of visible multimodal data to unseen multimodal data, we encouraged intelligent entities to induce cross-task shared knowledge, thereby improving their generalization ability on unseen multimodal data. The contributions of this paper are as follows:
1)
A causal meta-reinforcement learning (CMRL) is proposed, which simulates human feedback learning mechanism, causal inference mechanism and knowledge induction mechanism to fully mine multimodal complementary information, accurately capture true causal relationships, and reasonably induce cross-task shared knowledge;
2)
Breaking the limitations of implicit optimization of fusion features, a reinforcement learning environment has been customized for the classification task of multimodal remote sensing data. Through the interaction feedback between intelligent agents and multimodal data, full mining of multimodal complementary information has been achieved;
3)
Breaking through the traditional learning model of establishing statistical associations between data and labels, causal reasoning has been introduced for the first time into multimodal remote sensing data classification tasks. Causal distribution prediction actions, classification rewards, and causal intervention rewards have been designed to encourage intelligent agents to capture pure causal factors and cut off false statistical associations between non-causal factors and labels;
4)
The shortcomings of the optimization mode that minimizes the empirical risk of the model on training data under sparse training samples are revealed, and a targeted bi-layer optimization mechanism based on meta-learning was proposed. By encouraging agents to induce cross-task shared knowledge from scenario simulation, their generalization ability on unseen test data is improved.

2. Relate Work

2.1. Reinforcement Learning

In recent years, reinforcement learning has achieved tremendous success in fields such as game AI [16,17,18], robotics [19,20,21], and autonomous driving [22,23,24]. Particularly, with its integration into large-capacity deep neural networks, reinforcement learning has surpassed expert human performance in certain scenarios, such as Go [25] and StarCraft [26]. Reinforcement learning, inheriting the trial-and-error learning mechanism from psychology and the principles of optimal control [27], [28] can learn optimal strategies through the interaction feedback between an agent and environment under predefined human rules [29]. Early reinforcement learning methods were plagued by the curse of dimensionality, as they typically stored and iterated states in a tabular form, making it difficult to handle tasks with large-scale or continuous actions. Mnih et al. [30] first combined deep learning with Q-learning, introducing the deep Q-network (DQN), which provided a deep learning solution for reinforcement learning and surpassed human expert levels in several classic games. Building on DQN, researchers further explored and proposed solutions like the double DQN [31] to mitigate overestimation issues and deep recurrent Q-network (DRQN) [32] for partially observable Markov decision processes..
However, these methods were unable to handle continuous action scenarios, limiting the application of reinforcement learning in real-world settings. To address this issue, the theory of policy gradients [33] was proposed. Breaking through the limitations of value iteration and policy iteration, this theory directly learns the policy function, mapping states to the probability distribution of actions without the need to discretize the action space. Based on this theory, Lillicrap et al. [34] proposed the deep deterministic policy gradient (DDPG), consisting of an actor network for directly outputting deterministic actions, and a critic network for evaluating future expected returns based on input states. By optimizing these networks, agents can learn action strategies that maximize future expected returns under the motivation of reward function signals. However, as an offline reinforcement learning algorithm, DDPG struggles with the complex dynamic changes and real-time decision-making demands of real-world scenarios. Proximal policy optimization [35], updating through experience trajectories and calculating advantage functions to assess the relative advantage of each action over the average, allows for policy updates using samples obtained from online sampling, effectively resolving this issue.
It’s noteworthy that, despite the promising feedback learning mechanism of reinforcement learning for learning multimodal data fusion strategies, its potential in multimodal data fusion tasks remains underexplored. This paper is the first to utilize the reinforcement learning framework for multimodal remote sensing data classification, learning multimodal remote sensing data fusion strategies through agent interaction and feedback with a customized environment, providing a new reinforcement learning paradigm for multimodal remote sensing data classification.

2.2. Causal Learning

Causal learning focuses on discovering and understanding the true causal relationships between entities rather than statistical dependencies, offering new solutions for enhancing the generality and credibility of deep models [36]. In recent years, researchers have been dedicated to exploring the potential of causal learning in various deep learning tasks. Wang et al. [37] have considered causal factors that have a real causal relationship with labels as cross-domain invariant, transferable knowledge in domain generalization tasks. By intervening in features, they have effectively mined invariant causal factors with strong generalization capabilities. Liu et al. [38] proposed a cross-modal causal conceptual reasoning framework in visual question answering tasks, discovering the underlying causal structure between visual and language modalities through causal intervention. Lin et al. [39] focused on using causal learning to eliminate diagnostic errors induced by task-irrelevant information in data for medical diagnostic tasks, thereby enhancing the model’s credibility and generality in this domain. Zhang et al. [40] constructed a structural causal model (SCM) in person re-identification tasks and intervened in SCM through backdoor adjustment, achieving effective mining of pure causal factors.
Although the causal reasoning mechanism of causal learning holds promise for helping models discover the real causal connections between data and labels, thus enhancing credibility in multimodal data fusion tasks, its potential in this area has not yet been fully explored. This paper is the first to construct a causal inference mechanism in multimodal remote sensing data classification tasks. By combining this mechanism with the feedback learning mechanism of reinforcement learning, it enables agents to capture pure causal factors during their interaction with the environment. This method cuts off the false statistical association between non-causal factors and labels, providing a new causal perspective for multimodal remote sensing data classification.

2.3. Meta-Learning

Meta-learning, as an method for “learning to learn” has garnered widespread attention in recent years due to its unique knowledge induction mechanism, which allows models to induce shared knowledge across tasks from a large number of similar yet different meta-tasks [41,42,43].
Yu et al. [44] created zero-sample face manipulation meta-tasks to simulate unseen external attacks and shared meta-knowledge across tasks within a meta-learning optimization framework. Jia et al. [45] constructed pseudo-classes through data augmentation in an unsupervised setting and based on these, built meta-tasks. They simulated small-sample classification scenarios for unseen classes by reallocating meta-labels in each meta-task, achieving the induction of general knowledge for small-sample classification. Lv et al. [46] used meta-learning for drug discovery tasks to facilitate cross-task knowledge transfer, reducing the model’s dependency on large data volumes. Wang et al. [47] integrated graph learning with meta-learning into a unified framework for cross-domain small-sample hyperspectral image classification, utilizing the knowledge induction mechanism of meta-learning to learn general node aggregation functions.
Despite the potential of the knowledge induction mechanism of meta-learning to help models induce general knowledge for multimodal data fusion from meta-tasks, thereby enhancing their generalization performance on unseen multimodal data, its potential in multimodal data fusion tasks has not been fully explored. This paper establishes meta-training and meta-validation tasks and uses a bi-layer optimization mechanism to induce shared multimodal data fusion knowledge across tasks, providing a new meta-optimization mechanism for multimodal remote sensing data classification.

3. Method

3.1. Framework of CMRL

In this section, we will introduce CMRL from two aspects: Meta-optimization mechanisms and meta-task learning.

3.1.1. Meta-Optimization Mechanisms

The Figure 1 has shown the framework of meta-optimization mechanism. In this section, we will elaborate on the workflow of the meta-optimization mechanism, which is primarily divided into two parts: meta-task construction and bi-level optimization.
1)
Meta-task construction: First, multimodal data is input into the meta-task generation module, where meta-samples are generated based on a class mixing strategy. Then, an equal number of meta-samples from each class are randomly selected to construct meta-training tasks and meta-validation tasks;
2)
Bi-level optimization: First, in the inner optimization, calculate the model’s meta-training loss on meta-training tasks, pseudo-update the model based on this loss, and save the optimization gradients of the meta-training tasks. Then, in the outer optimization, calculate the meta-validation loss of the model after pseudo-updates on meta-validation tasks, and perform meta-updates on the model considering both meta-training and meta-validation losses.

3.1.2. Meta-Training Task Learning

The Figure 2 has shown the framework of meta training task learning. In this section, we will elucidate the workflow within the meta-training task:
1)
Exploration of interaction: First, input multimodal data from the meta-training task into the multimodal state perception module to obtain the state s t , where t represents the time step. Then, input s t into the action module to obtain causal distribution predictions a t , and obtain causal fusion features z F t by sampling from the causal distribution. Next, use the state transition function to update the state to s t + 1 and calculate classification rewards and causal intervention rewards to obtain the total reward r t . Finally, repeat the above process until the predefined number of interactions is reached, obtaining an interaction trajectory;
2)
Meta-training task loss calculation: First, estimate the state values for each time step in the interaction trajectory using a state value network. Then, calculate the value loss by computing the difference between the state value estimate and the future expected rewards. Simultaneously, use the generalized advantage estimation (GAE) algorithm based on the state value estimate to obtain the advantage function. Calculate the policy loss based on the advantage function. Finally, compute the meta-training loss.

3.1.3. Meta-Validation Task Learning

In this section, we will elucidate the workflow within the meta-validation task:
First, the agent predicts the causal distribution of multimodal data in the meta-validation task based on the current action policy. It then obtains causal fusion features by sampling from the causal distribution. Next, it calculates class prototypes based on the causal fusion features of multimodal data from various classes in the meta-validation task. Class predictions are obtained through prototype matching. Finally, the meta-validation loss is calculated based on the class predictions and labels.

3.2. Modeling Multimodal Remote Sensing Data Classification as an MDP

Reinforcement learning can leverage exploration and interaction with the environment to understand the intricate associations between actions and the environment. In the task of classifying multimodal remote sensing data, this characteristic of reinforcement learning holds the potential to assist models in comprehending the complex relationships between multimodal data and labels. This, in turn, allows the model to capture task-related complementary information from multimodal data.
However, there is currently a lack of research customizing a reinforcement learning environment specifically for the task of multimodal remote sensing data classification. This poses a challenge to realizing the full potential of reinforcement learning in this task. Therefore, we model the multimodal remote sensing data classification problem as a markov decision process (MDP) and customize its states, state transition function, actions, and rewards. Below, we will provide a detailed explanation of the modeling process:

3.2.1. State and State Transition Function

The state is a comprehensive description of the environment at any given moment. It not only reflects the current attributes of the environment but also contains key information needed by the agent to make decisions. Therefore, the state is the foundation for an agent to learn and understand its environment, ensuring it can learn effective behavior strategies based on complete information. The state transition reveals how the current state and the actions of the agent together affect the future state of the environment. It defines how the environment responds to the actions of the agent and is the basis for the agent to understand the complex interactions between its actions and the environment. This section will introduce the design of the state and the design of the state transition function:
Firstly, considering the existence of modal heterogeneity, data from different modalities often have inconsistent data dimensions. Therefore, we use a dimension unification module to unify the dimensions of samples from both modalities:
x H = W H x ˜ H x L = W L x ˜ L
where x ˜ H and x ˜ L represent the meta-samples of the two modalities, and their generation methods are described in Section III.D. x H and x L represent the dimensionally unified HSI and LiDAR, respectively, W H and W L are the learnable dimension unification parameters for each modality.
Then, we divide the data from the two modalities into a series of spatial tokens along the spatial dimension, and use encoders to obtain state-aware features for both modalities:
z H = TE x 1 H , … , x O H z L = TE x 1 L , … , x O L
where TE · represents the Transformer encoder. x 1 H and x 1 L are the spatial tokens for the two modalities, O = h ∗ w , h and w are the spatial dimensions of the two-modal data, z H and z L are the state-aware features of the two modalities.
Finally, we define the state as the concatenation of the state-aware features of the two modalities and the causal fusion features, and define the following state transition function:
s t = CONCAT z H , z L , Ω if t = 0 CONCAT z H , z L , z F t - 1 otherwise
where z F t − 1 represents the causal fusion feature at time step t − 1 , which is determined by the agent’s action Ω is the initial causal fusion feature, which can be expressed as Ω = z H + z L .
The advantage of this design lies in the fact that the state transition function replaces the causal fusion feature of the previous time step with that of the current time step at each time step, while retaining the unmerged state-aware features of the two modalities. This helps the agent understand the potential connections between the causal fusion feature and multimodal data, allowing it to optimize and adjust its action strategies accordingly.

3.2.2. Designing Actions and Rewards Based on Causal Intervention

In CMRL, the main goal of the agent is to discover the optimal action strategy that maximizes cumulative rewards through continuous exploration and feedback interactions. The realization of this goal depends on the fine design of actions and the reward mechanism. The design of actions needs to consider the characteristics of the environment and task requirements. Rewards, as the environment’s immediate feedback to specific actions of the agent, quantify the effectiveness of each action in achieving the target task. By imposing rewards and punishment feedback, the agent is guided to learn how to optimize its behavior strategy. In this section, we will elaborate on the design of actions and rewards:
Inspired by human causal reasoning mechanisms, we treat information related to classes in multimodal data as causal factors, while information independent of classes is considered non-causal factors, such as spectral noise caused by weather or collection equipment. Multimodal data is a mix of causal and non-causal factors. Our goal is to capture causal factors to learn the true causal associations between multimodal data and class labels. Causal factors should meet three conditions: 1) Causal factors are mutually independent. 2) They contain sufficient task-relevant information. 3) They are distinct from non-causal factors. Therefore, to enable the agent to intelligently capture causal factors from multimodal data, we have designed the following actions and rewards:
1)
Predicting actions from causal distribution
Inspired by the Variational Autoencoder, we have designed an action module that predicts the causal distribution in multimodal data based on the current state perceived by the agent. To ensure the mutual independence of causal factors, in this paper, the prior distribution of the causal distribution is designed as a multivariate Gaussian distribution with independent components. The output of the action module is the predicted action a t for the causal distribution in the multimodal data, which can be expressed as:
a t = Action s t , a t = u t , σ t 2
where u t and σ t 2 respectively represent the mean and variance of the causal distribution predicted at time step t.
Next, sampling from the causal distribution using reparameterization [48] to obtain causal fusion features:
z F t = u t + ε σ t 2 , ε ∼ N 0 , I
where N 0 , I represents a standard multivariate Gaussian distribution, ∼ denoting the sampling operation.
Finally, we minimize the difference between the causal distribution and the prior distribution (standard multivariate Gaussian distribution) using the following KL divergence constraint:
L KL = 1 T ∑ t = 1 T K L N u t , σ t 2 | | N 0 , I
where T represents the predefined total number of time steps, K L · represents the KL divergence.
2)
Classification rewards
To ensure that the causal fusion features contain sufficient task-relevant information, we have designed a prototype matching reward mechanism that provides reward signals to the agent by comparing the similarity between the causal fusion features and class prototypes.
Specifically, first, we will compute class prototypes based on the collection of classes from the meta-training task, and obtain class predictions for causal fusion features by calculating the distance between causal fusion features and class prototypes. For the causal fusion feature z F t at time step t, its probability prediction for class class c can be represented as:
P y F t = c | z F t = exp − d z F t , P c ∑ c = 1 C exp − d z c F t , P c
where y F t is the class label for z F t , d · is the distance metric, which is the Euclidean distance in this case. P c is the class prototype and can be represented as:
P c = 1 R ∑ r = 1 R z c , r F s
where R is the number of samples in the class set, z c , r F s is the causal fusion feature of the t-th sample in the c-th class.
Finally, we can calculate the cross-entropy between class predictions and the true labels to obtain the classification reward for the t-th time step:
r t p z F t = − λ 1 CrossEntropy y ^ F t , y F t y F t log y ^ F t
where y F t is the true class label, y ^ F t is the class prediction, λ 1 is the reward coefficient.
3)
Causal intervention reward
To ensure a sufficient separation between causal and non-causal factors, we attempt to achieve this goal through causal intervention. If we can intervene on the non-causal factors in multi-modal data, we can disrupt their spurious statistical associations with class labels, thus capturing pure causal factors. However, the effectiveness of this mechanism relies on accurate interventions on non-causal factors, which are often challenging to directly observe and manipulate.
Considering in HSI, the class of objects is typically determined by the trends in their spectral variations, low-frequency information reflecting changes in spectral curves can be considered causal factors, while local subtle variations are often caused by high-frequency noise information, which can be regarded as non-causal factors. Therefore, first, we utilize Fourier transformation to decompose the HIS x H into low-frequency x HL components and high-frequency components x HH :
x HL , x HH = FFT x H
where FFT · represents the Fourier transform.
Then, we perturb the high-frequency components to intervene on the non-causal factors and obtain the counterfactual HSI x HC by performing an inverse Fourier transform:
x HC = = FF T − 1 x HL , x ^ HH
where FF T - 1 · represents the inverse Fourier transform, and x ^ HH represents the high-frequency components obtained after performing the Fourier transform on the randomly selected HSI.
Afterward, the counterfactual state s ^ t is obtained by feeding x HC and the corresponding x L input into the state perception module, and then it is input into the action module to obtain the counterfactual causal fusion features z ^ F t .
Finally, the classification reward is calculated based on z ^ F t , and the causal intervention reward is obtained by calculating the mean squared error between the classification rewards corresponding to z ^ F t and z F t :
r t I z F t , z ^ F t = − r t p z F t − r t p z ^ F t 2
where r t p z ^ F t = − λ 1 y F t log y ¯ F t , y ¯ F t corresponds to class predictions based on counterfactual causal fusion features. Causal intervention reward is obtained by constraining the consistent causal effects between counterfactual causal fusion features and causal fusion features, which can break the causal relationship between non-causal factors and class labels, ensuring a sufficient separation between causal factors and non-causal factors.
4)
Total reward
The total reward can be represented as follows:
r t = r t p + χ r t I
where χ is the weighting coefficient.

3.3. Policy Gradient-based Reinforcement Learning

This section aims to optimize the action strategies of the agent. Specifically, in this paper, the action of the agent is to predict the causal distribution of multimodal data, while the prior distribution of the causal distribution is assumed to be a multivariate Gaussian distribution. Based on this assumption, the actions of the agent are often high-dimensional and continuous. At this time, reinforcement learning schemes based on value iteration or policy iteration are often difficult to apply. Fortunately, policy gradient theory provides a solution for dealing with such situations. Policy gradient theory optimizes the policy by maximizing the expected return, without the need to solve complex value functions. The commonly used policy loss can be expressed as:
L p = − ∫ s ρ π θ s ∫ a π θ a | s A π θ a | s s , a d s d a = − E s ⁡ ˜ ∼ ρ π , a ∼ π θ A π θ a | s s , a .
where ρ π θ s = 1 − γ ∑ t γ t ρ π θ s t = s . ρ π θ s t = s represents the distribution of state s at time step t, and γ is the discount factor. π θ a | s is a parameterized policy network that, based on state s , outputs the corresponding action a , corresponding to the action module in this paper.
A π θ a | s s , a is the advantage function, which is used to quantify how much additional reward the current policy network’s output action, relative to the expected average performance, can bring given the state s . The advantage function can be represented as follows:
A π θ a | s s , a = Q π θ a | s s , a − V π θ a | s s
where Q π θ a | s s , a represents the expected reward of the agent taking action a in state s , and V π θ a | s s is the expected reward of following the current policy in state s . The optimization goal of the model is to improve the current policy by maximizing the advantage function, thereby achieving the maximization of expected rewards.
However, it is often difficult to directly obtain the expected reward for the agent taking action a in a given state s . Therefore, we use generalized advantage estimation (GAE) [49] to fit the advantage function. GAE uses a weighted average of a series of temporal difference residuals to estimate the advantage function. The advantage function at the nth time step t can be represented as:
A t π θ a | s s , a = ∑ l = 0 T − t − 1 γ λ l δ t + l
where δ t + l = V s t − r t + γ V s t + l + 1 − V s t + l , V · is the value module used to assess the expected value of an input state. λ is discount factors.
From the above equation, it can be seen that the optimization of the action module is closely related to the advantage function, and the quality of the advantage function depends on the accuracy of the state value network’s evaluation of state values. Therefore, we optimize it by minimizing the following value loss:
L V = 1 T ∑ t = 1 T V s t − r t + γ V s t + 1 2

3.4. Knowledge Induction Mechanism

The knowledge induction mechanism is designed to help models deduce cross-task shared knowledge from a multitude of tasks by simulating scenarios where the model generalizes on unseen data. This is achieved through the construction of meta-training tasks and meta-validation tasks. Meta-training tasks simulate the available multimodal data to train the model, while meta-validation tasks simulate unseen multimodal data. The model’s performance on these new data is evaluated to validate its generalization capability. The knowledge induction mechanism mainly consists of two parts: Meta-task construction and bi-layer optimization.

3.4.1. Meta-Task Construction

To construct the meta-training and meta-validation tasks, we developed a class-mixing-based meta-task generation module. This module is designed to ensure that the meta-training and meta-validation tasks adequately reflect the diversity of real-world data. Specifically, we employed a class-mixing strategy to generate meta-samples, which are used to expand the original training data and form the meta-training and meta-validation sets. The class-mixing strategy involves combining different modal samples from the same class (for example, HSI and LiDAR) to create new meta-samples. These meta-samples can be represented as:
x ˜ H = ϑ x o H + 1 − ϑ x ⌢ o H , x ˜ L = ϑ x o L + 1 − ϑ x ⌢ o L
where x ˜ H and x ˜ L are the multimodal meta-samples, x ⌢ o H and x ⌢ o L are the original HSI and LiDAR samples randomly selected from the same class sample set, and ϑ is the mixing coefficient, which can be expressed as ϑ ∼ U 0 , 1 . Meta-samples can be considered as interpolations within the real data distribution, allowing them to more comprehensively cover the actual data distribution.
During the construction of the meta-training and meta-validation tasks, we uniformly sample multimodal data from each class of the meta-training and meta-validation sets, ensuring that the model can learn each class in a balanced manner. It’s important to note that in each meta-update process, the samples in both the meta-training and meta-validation tasks will be newly generated meta-samples. This method ensures the diversity of the meta-training tasks and the novelty of the meta-validation tasks.

3.4.2. Bi-Layer Optimization

In the inner optimization, we train the model using meta-training tasks and perform pseudo-updates on the model using gradient descent:
Θ ′ = Θ − α ∇ Θ L T r Θ
where Θ represents the model parameters before the update, α is the learning rate for inner layer optimization, and T r represents the meta-training tasks. L T r Θ denotes the meta-training loss with model parameters Θ . The meta-training loss can be expressed as:
L T r = L p + λ 1 L V + λ 2 L KL
where λ 1 and λ 2 are weight coefficients.
In the outer layer optimization, we calculate the loss of the pseudo-updated model on the meta-validation tasks to assess the model’s generalization ability on new tasks. This process involves combining both meta-training loss and meta-validation loss to perform a meta-update on the model:
Θ = Θ − ∇ ∂ L T r Θ + β L V a Θ ′ ∂ Θ
where β is the meta-learning rate, V a represents the meta-validation tasks. L V a Θ ′ denotes the meta-validation loss corresponding to the model parameters Θ ′ . The meta-validation loss can be expressed as:
L V a = CrossEntropy y ^ V a F t , y V a F t
where y ^ V a F t is the class prediction for the meta-validation task based on causal fusion features, which can be obtained by measuring the similarity between the causal fusion features and the class prototypes. Through this approach, the learning objective of the model is not merely to achieve optimal performance in the meta-training tasks, but rather to learn cross-task shared knowledge that can be generalized to unseen meta-validation tasks. This, in turn, enables the accurate classification of unseen multimodal data.

4. Experiment

4.1. HSI Dataset

We selected three sets of HSI and LiDAR datasets to validate the performance of the algorithm proposed in this paper:
1)
MUUFL Dataset: The MUUFL dataset was collected at the University of Southern Mississippi in Gulfport, covering 11 classes of ground objects. The data was acquired in November 2010 using Gemini LiDAR and CASI-1500 equipment. These devices were synchronized on the same flight platform to collect hyperspectral image data and LiDAR data simultaneously, ensuring spatial and temporal consistency between the two types of data. Both hyperspectral images and LiDAR data consist of 325 × 220 pixels with a spatial resolution of 1 m. The hyperspectral images have 64 bands, and the LiDAR data records precise elevation information of the terrain;
2)
Houston Dataset: Funded by the National Science Foundation of the United States and collected by the Airborne Laser Mapping Center, the Houston dataset covers 15 classes of ground objects in and around the University of Houston campus. This multimodal dataset primarily consists of two parts: hyperspectral data and LiDAR data. Both types of data have the same spatial resolution of 2.5 meters and include 349 × 1905 pixels. The HSI covers 144 spectral bands from 380 nm to 1050 nm. The LiDAR data records precise elevation information of the terrain;
3)
Trento Dataset: The Trento dataset was collected in the rural areas south of Trento, Italy, encompassing 6 classes of ground objects, including various natural features and artificial agricultural structures. This dataset integrates hyperspectral images captured by an airborne hyperspectral imager and LiDAR data obtained from an aerial laser scanning system. Both modalities have a consistent spatial resolution and consist of 166 × 600 pixels. The hyperspectral images include 63 spectral bands, and the LiDAR data records precise elevation information of the terrain.

4.2. Experimental Setting

All experiments were conducted on a computer equipped with a 3.80 GHz Intel Core i7-10700KF CPU, 32GB RAM, and an RTX 3090Ti GPU, with PyTorch as the experimental environment. The comparison methods included unimodal approaches: Convolutional recurrent neural networks(CRNN) [50]; multimodal decision fusion methods: hierarchical random walk network(HRWN) [51]; and multimodal feature fusion methods: two-branch convolution neural network(TBCNN) [52], patch-to-patch convolution neural network(PTPCNN) [53], coupled adversarial learning based classification(CALC) [54], and multimodal fusion transformer(MFT) [55].
To ensure fairness in the comparative experiments, the parameter settings for each method followed their original configurations. For the unimodal methods, we trained the models using 20 HSI samples per class. For multimodal methods, we trained the models using 20 paired HSI and LiDAR samples per class. In all experiments, AdamW was used as the optimizer, with an episode setting of 2000, an inner layer optimization learning rate of 0.001, a meta-learning rate of 0.001, a patch size of 7, a predefined number of time steps set to 5, and an inner layer optimization count of 5. To balance the diversity of samples in the meta-training/meta-validation tasks and computational efficiency, we set the number of samples per class in the meta-task to 20. To eliminate the impact of randomness on the experiments, all experimental results are the average of 10 runs. Three evaluation metrics were chosen, including Overall Accuracy (OA), Average Accuracy (AA) per class, and the Kappa coefficient.

4.3. Comparative Experiments

The experimental results of CMRL and its comparative methods on three datasets are shown in Table 1, Table 2 and Table 3. From these, it can be observed that:
1)
Compared to unimodal methods, multimodal methods exhibit higher classification accuracy. This is because, due to the phenomena of “different objects have the same spectra” and “the same objects have different spectra” in HSI, some samples may have low class distinguishability, making it difficult for unimodal methods that only use HSI to achieve satisfactory performance. In contrast, multimodal methods can combine LiDAR information to enhance the model’s ability to differentiate features when such phenomena occur;
2)
Compared to multimodal decision fusion methods, multimodal feature fusion methods demonstrate higher classification performance. This is because multimodal decision fusion methods integrate the output information of classifiers. When noise exists in multimodal data, the noise interference from different modalities might accumulate during the decision-making process, leading to inaccurate class predictions. On the other hand, multimodal feature fusion methods can establish deep interactions between multimodal data, more effectively mining class-distinguishing information;
3)
CMRL shows the highest classification performance across all three datasets, demonstrating its superiority in multimodal remote sensing data classification tasks. It particularly shows a clear classification advantage in challenging classes like “Mixed ground surface” and “Sidewalk.” The former often contains complex noise information, while the latter is frequently obscured by structures such as buildings and trees, presenting significant intra-class variability and blurred inter-class boundaries. The superior performance of CMRL can be attributed to: On one hand, its feedback learning mechanism and causal inference mechanism allow the agent to fully understand which information in the multimodal data has a causal relationship with the labels. This enables the agent to cut off false statistical associations between non-causal factors (like noise information and obstructed heterogenous ground features) and labels, achieving precise mining of real causal effects. On the other hand, the knowledge induction mechanism of CMRL enables the agent to learn cross-task shared knowledge, which can help it achieve higher generalization performance on unseen multimodal data.

4.4. Visual Analysis

4.4.1. Classification Accuracy Maps

In this section, we visualized the classification accuracy maps of CMRL and its comparative methods on three datasets, as shown in Figure 3, Figure 4 and Figure 5. It can be observed that CMRL exhibits the best continuity in the classification accuracy diagrams across all three datasets, especially in some easily confusable classes. For example, in the Trento dataset, the classes “Buildings” (green) and “Roads” (yellow) are both made of concrete material, hence they have similar spectral curves. However, LiDAR elevation data helps distinguish these two types of features. Benefiting from the feedback learning mechanism of reinforcement learning, CMRL shows the strongest capability among all comparative methods in capturing multimodal complementary information, resulting in the least confusion and misclassification in these two classes.

4.4.2. T-SNE Maps

In this section, using the Trento dataset as an example, we present the t-SNE diagrams of CMRL and its comparative methods, as shown in Figure 6. It can be observed that CMRL demonstrates the highest intra-class consistency and inter-class separability, especially in the easily confusable classes "Buildings" and "Roads". Other methods show a mix of these two classes, while CMRL almost entirely avoids this phenomenon. This indicates that CMRL can effectively capture class-distinguishing information in multimodal data, possessing the best feature learning ability.

4.4.3. Ablation Study

To validate the effectiveness of the components in this paper, we constructed ablation models as shown in Table 4 and Table 5. Below, we will introduce the design principles of these models: Baseline-A: The initial causal fusion features are directly used for multimodal remote sensing data classification tasks through prototype matching, and the model is updated using cross-entropy loss.
Baseline-B: Builds upon Baseline-A by adding a reinforcement learning (RL) feedback learning mechanism, exclusively using classification rewards as the reward signal, and updating the model using value loss and policy loss.
Baseline-C: Enhances Baseline-B by incorporating a causal learning (CL) causal inference mechanism specifically adding causal intervention rewards and constraints on the KL divergence of the causal distribution.
CMRL: Further develops Baseline-C by integrating a meta-learning (ML) knowledge induction mechanism, which involves constructing meta-training tasks and meta-validation tasks, and updating the model using a bi-layer optimization mechanism.
Table 4 and Table 5 show the classification accuracy of each model on three datasets, from which it can be observed:
1)
Compared to Baseline-A, Baseline-B improved classification performance on three datasets by 2.81%, 2.21%, and 2.23%, respectively. This is because the feedback learning mechanism of reinforcement learning allows the agent to interact with a custom environment to understand the complex association mechanisms between its actions (predictions about the causal distribution) and the multimodal remote sensing data classification task. It can adjust and optimize action strategies based on immediate feedback from rewards. This iterative feedback structure enhances the model’s ability to capture task-relevant complementary information in multimodal data. The experimental performance also validates the effectiveness of the feedback learning mechanism of reinforcement learning in multimodal remote sensing data classification tasks;
2)
Compared to Baseline-B, Baseline-C improved classification performance on three datasets by 1.08%, 0.91%, and 1.42%, respectively. This is because the causal reasoning mechanism of causal learning helps the model identify causal and non-causal factors in multimodal data. This mechanism effectively reduces the influence of spectral noise in HSI by disrupting the false statistical association between non-causal factors and labels through causal intervention, helping the model establish a true causal relationship between multimodal data and labels. The experimental performance also validates the effectiveness of the causal reasoning mechanism of causal learning in multimodal remote sensing data classification tasks;
3)
Compared to Baseline-C, CMRL improved classification performance on three datasets by 2.24%, 2.03%, and 1.23%, respectively. This is because the knowledge induction mechanism of meta-learning helps the model induce cross-task shared knowledge applicable to unseen multimodal data from a large number of similar yet different meta-tasks. This effectively alleviates the issue of limited model generalization capability caused by data distribution bias between training and test samples. The experimental performance also validates the effectiveness of the knowledge induction mechanism of meta-learning in multimodal remote sensing data classification tasks.

5. Conclusion

This paper integrates reinforcement learning, causal learning, and meta-learning into a unified framework, inspired by human cognitive mechanisms of feedback learning, causal inference, and knowledge induction. The proposed CMRL addresses key challenges in multimodal remote sensing data classification tasks, such as the difficulty in mining multimodal complementary information, suppressing interference from non-causal factors, and generalizing to unseen data. Firstly, the feedback learning mechanism based on reinforcement learning enables the agent to fully understand the complex associations between multimodal remote sensing data and labels, capturing class-discriminative multimodal complementary information from noisy data. Secondly, the causal inference mechanism based on causal intervention helps the model to establish the true causal connections between multimodal remote sensing data and labels, accurately suppressing interference from non-causal factors. Lastly, the knowledge induction mechanism based on meta-learning assists the model in capturing cross-task shared knowledge from meta-training and meta-validation tasks, enhancing the model’s generalization capabilities on unseen multimodal remote sensing data. Experiments on three multimodal remote sensing datasets demonstrate that CMRL achieves state-of-the-art performance, offering a new paradigm in reinforcement learning, a novel perspective in causal learning, and an innovative meta-optimization mechanism for multimodal remote sensing data classification. However, currently, CMRL focuses only on HSI and LiDAR modalities. In the future, we plan to explore its potential in a broader range of multimodal remote sensing data.

Author Contributions

W. Z., X. W., H. W., Y. C. provided significant contributions to the work. W. Z. and Y. C. provided method ideas for this study; W. Z. and H. W. performed the experiments; X. W. analyzed the data; W. Z., X. W. wrote the original paper; Y. C. reviewed and edited the paper. All authors have read and agreed to the published version of the manuscript.

Funding

This work was funded by the National Natural Science Foundation of China under Grant 62176259, Grant 62373364, Grant 62303468, by the Key Research and Development Program of Jiangsu Province under Grant BE2022095, and by the Natural Science Foundation of Jiangsu Province under Grant BK20221116. (Corresponding author: Yuhu Cheng.)

Data Availability Statement

The locations of these observers are generated by computer simulation. lt is easy to generate the simulation with the method in the manuscript.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Zhang, Y.; Li, W.; Zhang, M.; Wang, S.; Tao, R.; Du, Q. Graph information aggregation cross-domain few-shot learning for hyperspectral image classification. IEEE Trans. Neural Netw. Learn. Syst. 2022, 1–14. [Google Scholar] [CrossRef]
  2. Zhang, T.; Wang, W.; Wang, J.; Cai, Y.; Yang, Z.; Li, J. Hyper-LGNet: Coupling local and global features for hyperspectral image classification. Remote Sens. 2022, 14, 5251. [Google Scholar] [CrossRef]
  3. Datta, D.; Mallick, P.K.; Reddy, A.V.N.; Mohammed, M.A.; Jaber, M.M.; Alghawli, A.S.; Al-qaness, M.A.A. A hybrid classification of imbalanced hyperspectral images using ADASYN and enhanced deep subsampled multi-grained cascaded forest. Remote Sens. 2022, 14, 4853. [Google Scholar] [CrossRef]
  4. Xing, C.; Cong, Y.; Duan, C.; Wang, Z.; Wang, M. Deep network with irregular convolutional kernels and self-expressive property for classification of hyperspectral images. IEEE Trans. Neural Netw. Learn. Syst. 2022, 34, 10747–10761. [Google Scholar] [CrossRef] [PubMed]
  5. Zhu, Q.; Deng, W.; Zheng, Z.; Zhong, Y.; Guan, Q.; Lin, W.; Zhang, L.; Li, D. A spectral-spatial-dependent global learning framework for insufficient and imbalanced hyperspectral image classification. IEEE Trans. Cybern. 2021, 52, 11709–11723. [Google Scholar] [CrossRef] [PubMed]
  6. Ding, Y.; Chong, Y.; Pan, S.; Wang, Y.; Nie, C. Spatial-spectral unified adaptive probability graph convolutional networks for hyperspectral image classification. IEEE Trans. Neural Netw. Learn. Syst. 2021, 34, 3650–3664. [Google Scholar] [CrossRef] [PubMed]
  7. Ren, Q.; Tu, B.; Liao, S.; Chen, S. Hyperspectral image classification with iformer network feature extraction. Remote Sens. 2022, 14, 4866. [Google Scholar] [CrossRef]
  8. Roy, S. K.; Deria, A.; Hong, D.; Ahmad, M.; Plaza, A.; Chanussot, J. Hyperspectral and LiDAR data classification using joint CNNs and morphological feature learning. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–16. [Google Scholar] [CrossRef]
  9. Gao, H.; Feng, H.; Zhang, Y.; Xu, S.; Zhang, B. AMSSE-Net: adaptive multiscale spatial–spectral enhancement network for classification of hyperspectral and LiDAR data. IEEE Trans. Geosci. Remote Sens. 2023, 61, 1–17. [Google Scholar] [CrossRef]
  10. Zhang, T.; Xiao, S.; Dong, W.; Qu, J.; Yang, Y. A mutual guidance attention-based multi-level fusion network for hyperspectral and LiDAR classification. IEEE Geosci. Remote Sens. Lett. 2021, 19, 1–5. [Google Scholar] [CrossRef]
  11. Song, L.; Feng, Z.; Yang, S.; Zhang, X.; Jiao, L. Discrepant bi-directional interaction fusion network for hyperspectral and LiDAR data classification. IEEE Geosci. Remote Sens. Lett. 2023, 20, 1–5. [Google Scholar] [CrossRef]
  12. Dong, W.; Yang, T.; Qu, J.; Zhang, T.; Xiao, S.; Li, Y. Joint contextual representation model-informed interpretable network with dictionary aligning for hyperspectral and LiDAR classification. IEEE Trans. Circuits. Syst. Video Technol. 2023, 33, 6804–6818. [Google Scholar] [CrossRef]
  13. Xue, Z.; Yu, X.; Tan, X.; Liu, B.; Yu, A.; Wei, X. Multiscale deep learning network with self-calibrated convolution for hyperspectral and LiDAR data collaborative classification. IEEE Trans. Geosci. Remote Sens. 2021, 60, 1–16. [Google Scholar] [CrossRef]
  14. Wang, J.; Li, J.; Shi, Y.; Lai, J.; Tan, X. AM³Net: adaptive mutual-learning-based multimodal data fusion network. IEEE Trans. Circuits. Syst. Video Technol. 2022, 32, 5411–5426. [Google Scholar] [CrossRef]
  15. Du, X.; Zheng, X.; Lu, X.; Wang, X. Hyperspectral and LiDAR representation with spectral-spatial graph network. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2023, 16, 9231–9245. [Google Scholar] [CrossRef]
  16. Oh, I.; Rho, S.; Moon, S.; Son, S.; Lee, H.; Chung, J. Creating pro-level AI for a real-time fighting game using deep reinforcement learning. IEEE Trans. Games 2021, 14, 212–220. [Google Scholar] [CrossRef]
  17. Donge, V. S.; Lian, B.; Lewis, F. L.; Davoudi, A. Multi-agent graphical games with inverse reinforcement learning. IEEE Trans. Control Netw. Syst. 2022, 10, 841–852. [Google Scholar] [CrossRef]
  18. Justesen, N.; Bontrager, P.; Togelius, J.; Risi, S. Deep learning for video game playing. IEEE Trans. Games 2019, 12, 1–20. [Google Scholar] [CrossRef]
  19. Matarese, M.; Sciutti, A.; Rea, F.; Rossi, S. Toward robots’ behavioral transparency of temporal difference reinforcement learning with a human teacher. IEEE Trans. Human Mach. Syst. 2021, 51, 578–589. [Google Scholar] [CrossRef]
  20. Zhang, L.; Hou, Z.; Wang, J.; Liu, Z.; Li, W. Robot navigation with reinforcement learned path generation and fine-tuned motion control. IEEE Robot. Autom. 2023, 8, 4489–4496. [Google Scholar] [CrossRef]
  21. Garaffa, L. C.; Basso, M.; Konzen, A. A.; de Freitas, E. P. Reinforcement learning for mobile robotics exploration: A survey. IEEE Trans. Neural Networks Learn. Sys. 2023, 8, 3796–3810. [Google Scholar] [CrossRef]
  22. Wu, J.; Huang, Z.; Lv, C. Uncertainty-aware model-based reinforcement learning: Methodology and application in autonomous driving. IEEE Trans. Intell. Veh. 2022, 8, 194–203. [Google Scholar] [CrossRef]
  23. Shu, H.; Liu, T.; Mu, X.; Cao, D. Driving tasks transfer using deep reinforcement learning for decision-making of autonomous vehicles in unsignalized intersection. IEEE Trans. Veh. Technol. 2021, 71, 41–52. [Google Scholar] [CrossRef]
  24. Zhu, Z.; Zhao, H. A survey of deep RL and IL for autonomous driving policy learning. IEEE Trans. Intell. Transp. Syst. 2021, 23, 14043–14065. [Google Scholar] [CrossRef]
  25. Silver, D.; Huang, A.; Maddison, C. J.; Guez, A.; Sifre, L. ; Van Den Driessche; et al. Mastering the game of Go with deep neural networks and tree search. Nature 2016, 529, 484–489. [Google Scholar] [CrossRef]
  26. Vinyals, O.; Babuschkin, I.; Czarnecki, W. M.; Mathieu, M.; Dudzik, A.; Chung, J.; et al. Grandmaster level in StarCraft II using multi-agent reinforcement learning. Nature 2019, 575, 350–354. [Google Scholar] [CrossRef]
  27. Wang, X.; Gu, Y.; Cheng, Y.; Liu, A.; Chen, C. P. Approximate policy-based accelerated deep reinforcement learning. IEEE Trans. Neural Netw. Learn. Syst. 2019, 31, 1820–1830. [Google Scholar] [CrossRef]
  28. Kaelbling, L. P.; Littman, M. L.; Moore, A. W. Reinforcement learning: A survey. J. Artif. Intell. Res. 1996, 4, 237–285. [Google Scholar] [CrossRef]
  29. Bai, Z.; Hao, P.; Shangguan, W.; Cai, B.; Barth, M. J. Hybrid reinforcement learning-based eco-driving strategy for connected and automated vehicles at signalized intersections. IEEE Trans. Intell. Transp. Syst. 2022, 23, 15850–15863. [Google Scholar] [CrossRef]
  30. Mnih, V.; Kavukcuoglu, K.; Silver, D.; Rusu, A. A.; Veness, J.; Bellemare, M. G.; et al. Human-level control through deep reinforcement learning. Nature 2015, 518, 529–533. [Google Scholar] [CrossRef]
  31. Van Hasselt, H.; Guez, A.; Silver, D. Deep reinforcement learning with double Q-learning. In Proceedings of the AAAI conference on artificial intelligence, United states, 12–17 February 2016; pp. 2094–21003. [Google Scholar]
  32. Baek, J.; Kaddoum, G. Online partial offloading and task scheduling in SDN-fog networks with deep recurrent reinforcement learning. IEEE Internet Things J. 2022, 9, 11578–11589. [Google Scholar] [CrossRef]
  33. Kohl, N.; Stone, P. Policy gradient reinforcement learning for fast quadrupedal locomotion. In IEEE International Conference on Robotics and Automation, United states, 26 April – 1 May 2004; pp. 2619–2624.
  34. Lilicrap, T.; Hunt, J.; Pritzel, A.; Hess, N.; Erez, T.; Silver, D.; Wiestra, D. Continuous control with deep reinforcement learning. In International Conference on Representation Learning, Puerto rico, 2–4 May 2016; pp. 1–14.
  35. Cheng, Y.; Huang, L.; Wang, X. Authentic boundary proximal policy optimization. IEEE Trans. Cybern. 2021, 52, 9428–9438. [Google Scholar] [CrossRef]
  36. Zhang, H.; Xiao, L.; Cao, X.; Foroosh, H. Multiple adverse weather conditions adaptation for object detection via causal intervention. IEEE Trans. Pattern Anal. Mach. Intell. 2022. [Google Scholar] [CrossRef]
  37. Wang, Y.; Liu, F.; Chen, Z.; Wu, Y.-C.; Hao, J.; Chen, G.; Heng, P.-A. Contrastive-ace: domain generalization through alignment of causal mechanisms. IEEE Trans. Image Process. 2023, 32, 235–250. [Google Scholar] [CrossRef]
  38. Liu, Y.; Li, G.; Lin, L. Cross-modal causal relational reasoning for event-level visual question answering. IEEE Trans. Pattern Anal. Mach. Intell. 2023, 45, 11624–11641. [Google Scholar] [CrossRef]
  39. Lin, J.; Wang, K.; Chen, Z.; Liang, X.; Lin, L. Towards causality-aware inferring: a sequential discriminative approach for medical diagnosis. IEEE Trans. Pattern Anal. Mach. Intell. 2023, 45, 13363–13375. [Google Scholar] [CrossRef]
  40. Zhang, Y.-F.; Zhang, Z.; Li, D.; Jia, Z.; Wang, L.; Tan, T. learning domain invariant representations for generalizable person re-identification. IEEE Trans. Image Process. 2023, 32, 509–523. [Google Scholar] [CrossRef]
  41. Nag, S.; Raychaudhuri, D. S.; Paul, S.; Roy-Chowdhury, A. K. Reconstruction Guided Meta-Learning for Few Shot Open Set Recognition. IEEE Trans. Pattern Anal. Mach. Intell. 2023, 45, 15394–15405. [Google Scholar] [CrossRef]
  42. Hospedales, T.; Antoniou, A.; Micaelli, P.; Storkey, A. Meta-learning in neural networks: a survey. IEEE Trans. Pattern Anal. Mach. Intell. 2022, 44, 5149–5169. [Google Scholar] [CrossRef] [PubMed]
  43. Coskun, H.; Zia, M. Z.; Tekin, B.; Bogo, F.; Navab, N.; Tombari, F.; Sawhney, H. S. Domain-specific priors and meta learning for few-shot first-person action recognition. IEEE Trans. Pattern Anal. Mach. Intell. 2023, 45, 6659–6673. [Google Scholar] [CrossRef] [PubMed]
  44. Yu, B.; Li, X.; Li, W.; Zhou, J.; Lu, J. Discrepancy-aware meta-learning for zero-shot face manipulation detection. IEEE Trans. Image Process. 2023, 32, 3759–3773. [Google Scholar] [CrossRef] [PubMed]
  45. Ye, H.-J.; Han, L.; Zhan, D.-C. Revisiting unsupervised meta-learning via the characteristics of few-shot tasks. IEEE Trans. Pattern Anal. Mach. Intell. 2023, 45, 3721–3737. [Google Scholar] [CrossRef] [PubMed]
  46. Lv, Q.; Chen, G.; Yang, Z.; Zhong, W.; Chen, C. Y.-C. Meta learning with graph attention networks for low-data drug discovery. IEEE Trans. Neural Networks Learn. Sys. 2023, 1–13. [Google Scholar] [CrossRef] [PubMed]
  47. Wang, H.; Wang, X.; Cheng, Y. Graph meta transfer network for heterogeneous few-shot hyperspectral image classification. IEEE Trans. Geosci. Remote Sens. 2023, 61, 1–12. [Google Scholar] [CrossRef]
  48. Jiao, P.; Guo, X.; Jing, X.; He, D.; Wu, H.; Pan, S.; Gong, M.; Wang, W. Temporal network embedding for link prediction via vae joint attention mechanism. IEEE Trans. Neural Networks Learn. Sys. 2022, 33, 7400–7413. [Google Scholar] [CrossRef] [PubMed]
  49. Schulman, J.; Moritz, P.; Levine, S.; Jordan, M.I.; Abbeel, P. High-dimensional continuous control using generalized advantage estimation. Computer Science 2015. [Google Scholar] [CrossRef]
  50. Wu, H.; Prasad, S. Convolutional recurrent neural networks for hyperspectral data classification. Remote Sens. 2017, 9, 298. [Google Scholar] [CrossRef]
  51. Zhao, X.; Tao, R.; Li, W.; Li, H.-C.; Du, Q.; Liao, W.; Philips, W. Joint classification of hyperspectral and LiDAR data using hierarchical random walk and deep CNN architecture. IEEE Trans. Geosci. Remote Sens. 2020, 58, 7355–7370. [Google Scholar] [CrossRef]
  52. Xu, X.; Li, W.; Ran, Q.; Du, Q.; Gao, L.; Zhang, B. Multisource remote sensing data classification based on convolutional neural network. IEEE Trans. Geosci. Remote Sens. 2018, 56, 937–949. [Google Scholar] [CrossRef]
  53. Zhang, M.; Li, W.; Du, Q.; Gao, L.; Zhang, B. Feature extraction for classification of hyperspectral and LiDAR data using patch-to-patch CNN. IEEE Trans. Cybern. 2020, 50, 100–111. [Google Scholar] [CrossRef]
  54. Lu, T.; Ding, K.; Fu, W.; Li, S.; Guo, A. Coupled adversarial learning for fusion classification of hyperspectral and LiDAR data. Inf. Fusion 2023, 93, 118–131. [Google Scholar] [CrossRef]
  55. Roy, S.K.; Deria, A.; Hong, D.; Rasti, B.; Plaza, A.J.; Chanussot, J. Multimodal fusion transformer for remote sensing image classification. IEEE Trans. Geosci. Remote Sens. 2023, 63, 1–20. [Google Scholar] [CrossRef]
Preprints 99587 g001
Figure 1. Framework of meta-optimization mechanism.
Figure 1. Framework of meta-optimization mechanism.
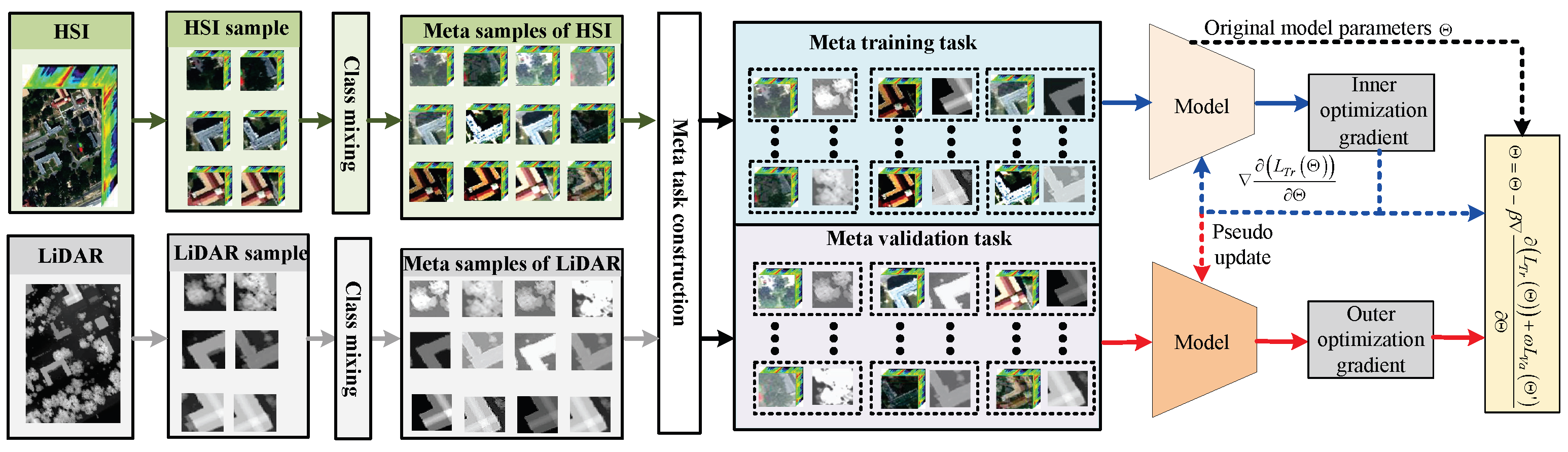
Preprints 99587 g001
Preprints 99587 g002
Figure 2. Framework of meta training task learning.
Figure 2. Framework of meta training task learning.
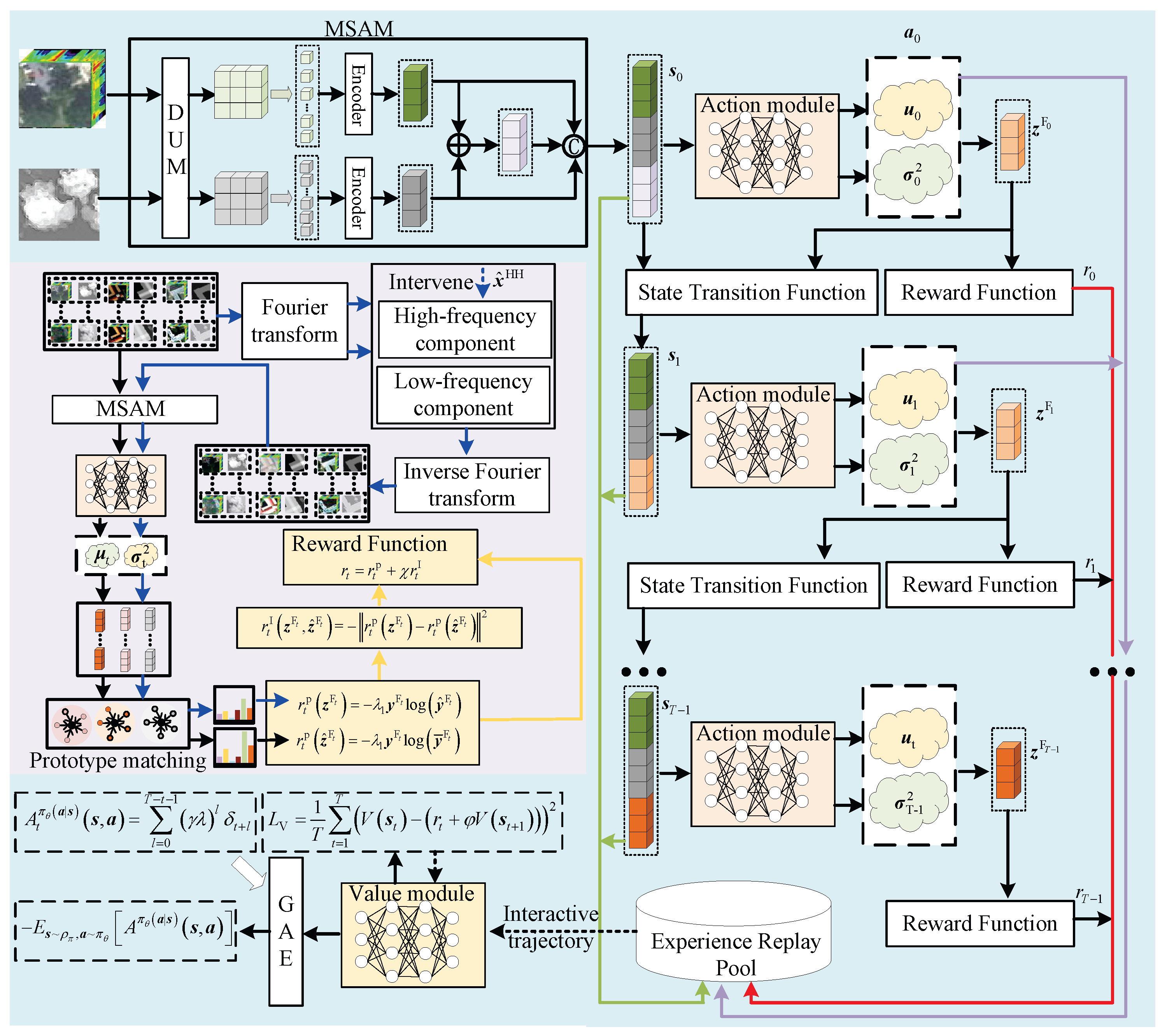
Preprints 99587 g002
Preprints 99587 g003
Figure 3. Classification accuracy map on MUUFL dataset. (a) Label map (b) CRNN (c) HRWN (d) TBCNN (e) PTPCNN (f) CALC (g) MFT (h) CMRL.
Figure 3. Classification accuracy map on MUUFL dataset. (a) Label map (b) CRNN (c) HRWN (d) TBCNN (e) PTPCNN (f) CALC (g) MFT (h) CMRL.
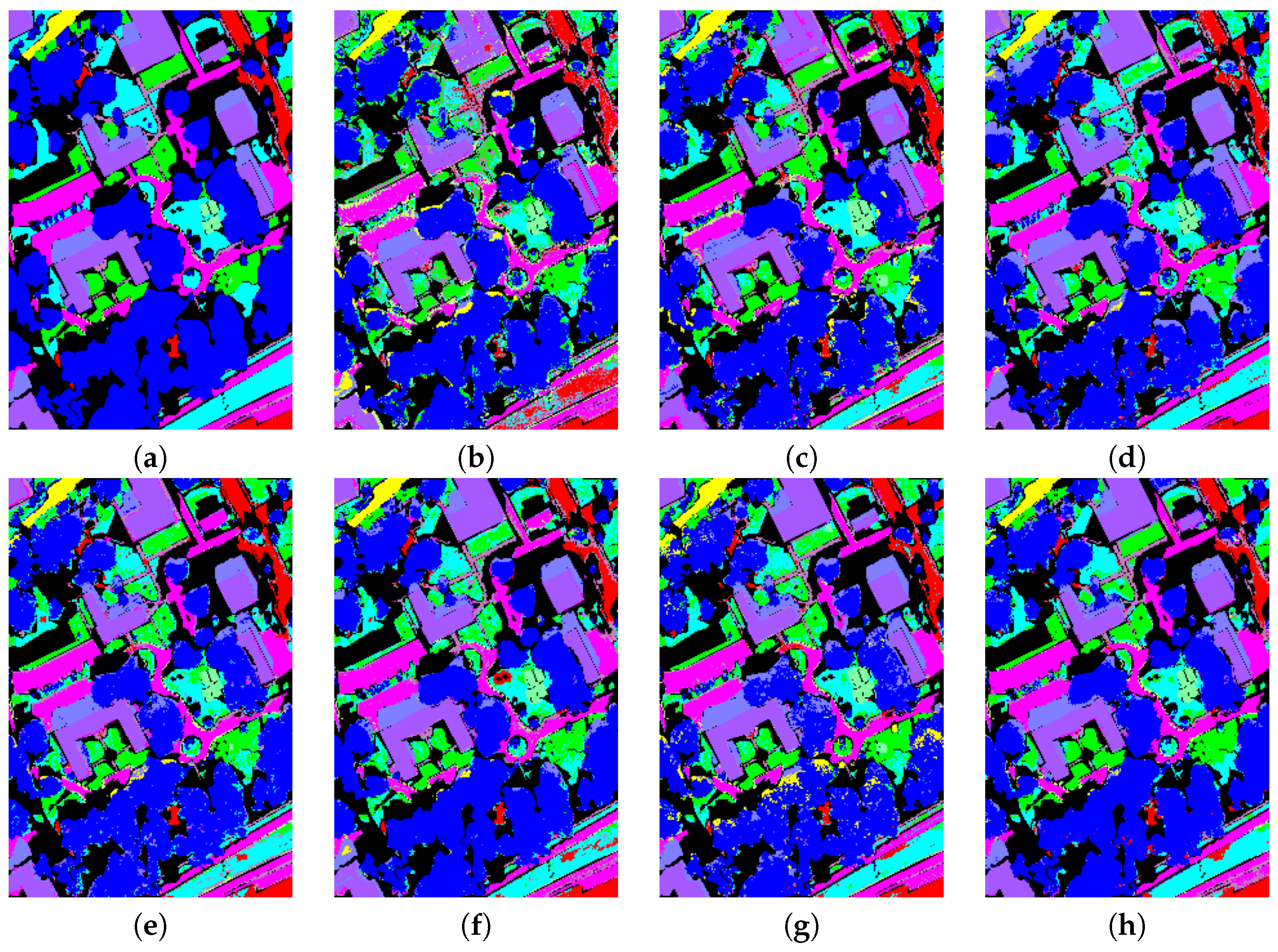
Preprints 99587 g003
Preprints 99587 g004
Figure 4. Classification accuracy map on Houston dataset. (a) Label map (b) CRNN (c) HRWN (d) TBCNN (e) PTPCNN (f) CALC (g) MFT (h) CMRL.
Figure 4. Classification accuracy map on Houston dataset. (a) Label map (b) CRNN (c) HRWN (d) TBCNN (e) PTPCNN (f) CALC (g) MFT (h) CMRL.
Preprints 99587 g004
Preprints 99587 g005
Figure 5. Classification accuracy map on Trento dataset. (a) Label map (b) CRNN (c) HRWN (d) TBCNN (e) PTPCNN (f) CALC (g) MFT (h) CMRL.
Figure 5. Classification accuracy map on Trento dataset. (a) Label map (b) CRNN (c) HRWN (d) TBCNN (e) PTPCNN (f) CALC (g) MFT (h) CMRL.
Preprints 99587 g005
Preprints 99587 g006
Figure 6. T-SNE map on Trento dataset. (a) CRNN (b) TBCNN (c) PTPCNN (d) CALC (e) MFT (f) CMRL.
Figure 6. T-SNE map on Trento dataset. (a) CRNN (b) TBCNN (c) PTPCNN (d) CALC (e) MFT (f) CMRL.
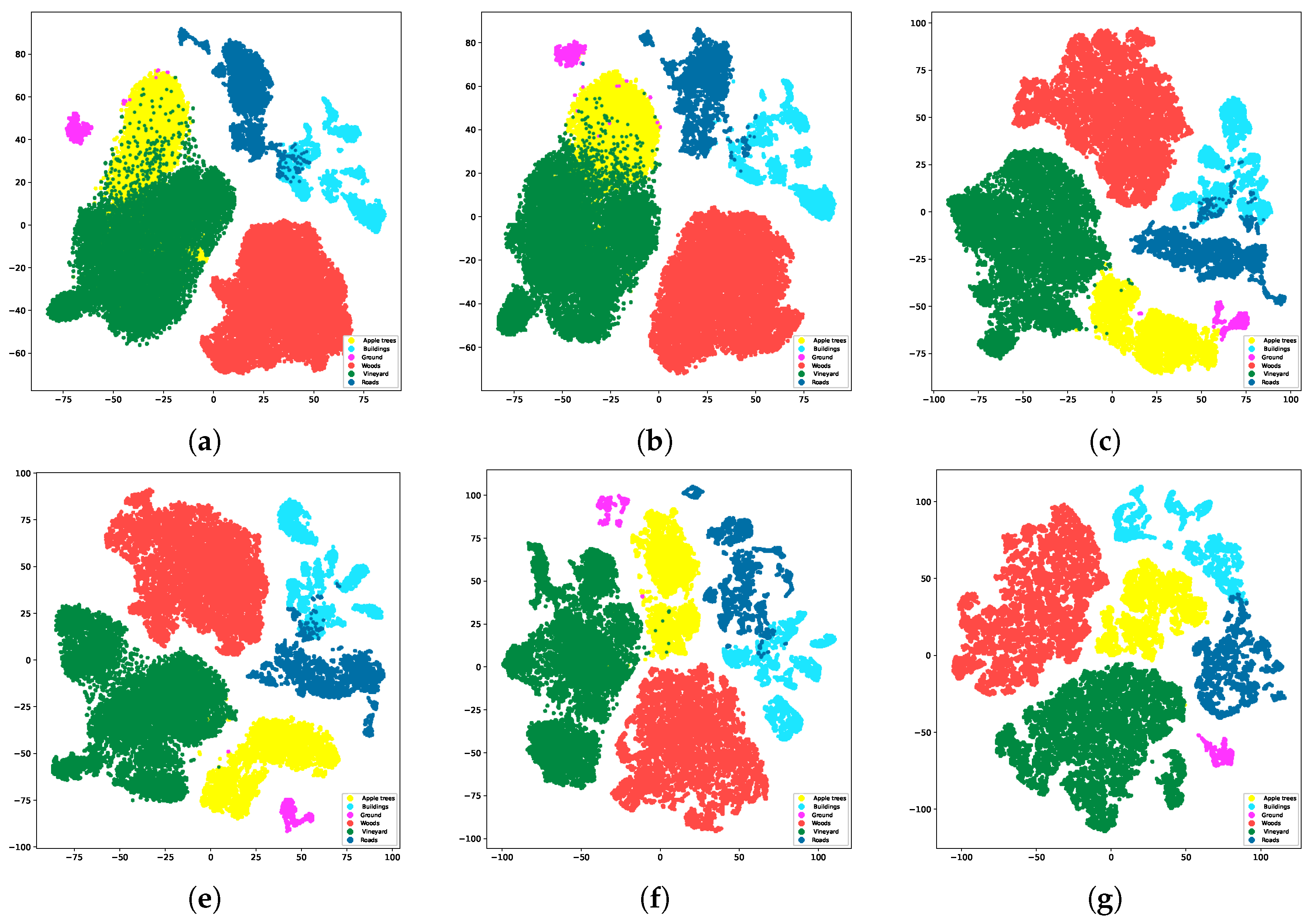
Preprints 99587 g006
Table 1. Classification accuracy of the MUUFL dataset.
Table 1. Classification accuracy of the MUUFL dataset.
Class CRNN HRWN TBCNN PTPCNN CALC MFT CMRL
Trees (20/23246) 76.65 77.25 81.90 84.06 85.50 84.74 89.78
Mostly grass (20/4270) 71.15 74.94 76.07 81.08 80.12 79.60 85.34
Mixed ground surface (20/6882) 51.68 64.60 66.05 53.29 70.75 60.52 67.36
Dirt and sand (20/1826) 71.43 88.48 78.41 84.22 92.25 82.56 83.44
Road (20/6687) 76.36 84.43 87.15 89.46 77.53 80.32 89.88
Water (20/466) 99.78 99.78 99.10 97.31 95.96 100 98.66
Building shadow (20/2233) 80.98 89.20 91.32 87.75 94.80 91.59 87.30
Building (20/6240) 90.42 85.02 91.46 90.90 89.84 90.69 92.09
Sidewalk (20/1385) 56.56 68.13 72.89 61.98 74.14 67.18 75.60
Yellow curb (20/183) 66.87 86.50 90.80 91.41 90.18 93.87 95.09
Cloth panels (20/269) 94.78 95.58 95.18 92.77 97.99 97.19 95.98
OA(%) 74.31 78.19 81.44 82.39 83.17 81.34 86.27
AA(%) 76.06 83.08 84.58 84.02 86.28 84.39 87.32
Kappa(%) 67.87 72.54 76.44 77.54 78.44 76.25 82.20
Table 2. Classification accuracy of the Houston dataset.
Table 2. Classification accuracy of the Houston dataset.
Class CRNN HRWN TBCNN PTPCNN CALC MFT CMRL
Healthy grass (20/1251) 87.41 84.08 94.96 93.50 96.18 97.40 96.91
Stressed grass (20/1254) 87.93 77.07 80.63 93.03 96.35 95.38 98.46
Synthetic grass (20/697) 94.39 100 99.71 100 100 100 99.85
Trees (20/1244) 91.75 93.87 95.92 92.89 95.10 96.65 98.53
Soil (20/1242) 98.61 97.55 99.26 95.91 96.56 94.11 96.24
Water (20/325) 89.18 97.71 100 96.39 99.02 100 100
Residential (20/1268) 84.06 84.86 83.33 91.27 94.23 94.23 94.55
Commercial (20/1244) 88.07 85.87 84.56 86.93 86.60 93.55 93.30
Road (20/1252) 72.16 75.73 75.89 79.30 85.63 78.25 90.26
Highway (20/1227) 63.22 74.48 88.73 77.71 94.86 96.27 92.46
Railway (20/1235) 62.39 94.73 85.35 92.76 99.34 88.48 97.61
Parking lot 1 (20/1233) 85.41 90.03 87.88 90.68 88.54 94.64 87.80
Parking lot 2 (20/469) 81.74 94.21 95.77 99.11 97.55 99.33 99.55
Tennis court (20/428) 99.76 100 98.28 99.51 100 100 100
Running track (20/660) 97.03 95.63 98.59 100 99.69 99.22 100
OA(%) 83.97 87.79 89.46 91.08 94.50 94.03 95.51
AA(%) 85.54 89.72 91.26 92.60 95.17 95.17 96.37
Kappa(%) 82.68 86.80 88.61 90.36 94.01 93.55 95.14
Table 3. Classification accuracy of the Trento dataset.
Table 3. Classification accuracy of the Trento dataset.
Class CRNN HRWN TBCNN PTPCNN CALC MFT CMRL
Apple trees (20/4034) 77.03 96.61 96.21 97.29 98.73 96.56 99.10
Buildings (20/2903) 95.42 92.09 96.07 96.01 96.29 93.65 97.50
Ground (20/479) 93.25 97.82 99.78 97.60 98.48 100 99.35
Woods (20/9123) 99.45 100 97.10 99.82 99.99 99.99 99.35
Vineyard (20/10501) 77.45 80.20 84.50 99.35 99.64 99.31 99.05
Roads (20/3174) 89.09 88.62 92.42 94.20 97.53 97.97 98.35
OA(%) 87.23 90.67 92.05 98.33 99.06 98.48 99.41
AA(%) 88.62 92.56 94.35 97.38 98.44 97.92 99.02
Kappa(%) 83.22 87.76 89.55 97.78 98.75 97.97 99.21
Table 4. Baseline models.
Table 4. Baseline models.
Component Baseline-A Baseline-B Baseline-C CMRL
RL ✓ ✓ ✓ ✓
CL x x ✓ ✓
ML x x x ✓
Table 5. Impact of different components on OA (%).
Table 5. Impact of different components on OA (%).
Dataset Baseline-A Baseline-B Baseline-C CMRL
MUUFL 80.14 82.95 84.03 86.27
Houston 90.36 92.57 93.48 95.51
Trento 94.53 96.76 98.18 99.41
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated