Preprint
Article
An Optimization Model for Flight Rescheduling from an Airport’s Centralized Perspective for Better Management of Demand and Capacity Utilization
This version is not peer-reviewed.
Submitted:
19 February 2024
Posted:
22 February 2024
You are already at the latest version
A peer-reviewed article of this preprint also exists.
Abstract
Over-capacity flight scheduling by commercial airlines due to the surging demand in recent years creates congestion and significant delays at major airports. This maximizing throughput attitude calls for tactical flight rescheduling to comply with airports’ capacity limitations and distribute the peak hour demand over the course of a day. Such displacements of flights may cause significant problems and costs for airlines and some cancellations or missed connections for the passengers. This paper presents an optimization model for flight rescheduling at a schedule-coordinated airport to minimize congestion and flight delays. The optimization model is used to make better scheduling intervention decisions considering the airport resource constraints and safety of operation. We have also developed a simulation method to replicate arrival and departure processes in such an airport. The simulation adheres to a first come first served (FCFS) discipline and enforces runway capacity constraints and minimum turnaround times. We compare the delays caused by an ad hoc FCFS operation with those obtained by the optimization model. Computational results from a case study demonstrate that a reduction of 40.7% and 61.6% in total delay times for the arrival and departure flights can be achieved by the optimization model. It also facilitates implementing a collaborative decision-making system for better coordination with commercial airlines.
Keywords:
Subject:
Engineering - Transportation Science and Technology1. Introduction
Management of airport demand and capacity has complex challenges due to the existence of multiple stakeholders’ incentives and performance objectives in the face of scarcity of resources [1]. The unprecedented growth in demand in the aviation industry in recent years has been associated with over-capacity flight scheduling by most commercial airlines. A direct consequence of such developments is increasing congestion at airports, flight delays, and discomfort for passengers, especially when a major disruption occurs. Because of the connectivity of an airline’s resources (aircraft, crews, and passengers) in a flight network, the delay of an upstream flight can propagate across multiple downstream flights. Statistics show that about 20% of flights in the USA were delayed in 2015, out of which 26.3% of the delays occurred due to circumstances within the airline’s control; 30.9% due to the late arrival of aircraft, and 36.5% could be attributed to airport operations, heavy traffic volume, and air traffic control [2].
Despite the significant effort that airlines put into flight schedules, the execution of their operations often deviate from the original schedules due to airport capacity limitations and unexpected disruptions such as aircraft breakdowns, crew sickness, or severe weather conditions. That is why more researchers have worked on tactical rescheduling of inbound and outbound flights based on available runway slots and other resources in a schedule-facilitated or fully coordinated airport. A schedule-coordinated airport requires a level of coordination to manage demand because airlines’ demands significantly exceed the capacity of the airport. Thus, planned flight times need to be adjusted to satisfy airline and passenger service level expectations [3]. However, an optimal schedule from an airport’s centralized perspective may not be optimal from airlines’ perspectives and impose higher costs on the airlines. At the tactical level, when flight schedules need to change due to airports’ limitations, commercial airlines would have to adjust their schedules based on slot limitations at schedule-coordinated airports. The airline operation control center is responsible for handling resource violations that might occur during operation. When this information is analyzed to evaluate the impact of flight displacements on other downline flights, an updated schedule is proposed. This process may take several iterations before they can reach an agreement on the final schedule, which is a time-consuming process. In recent years, many airports have tried to implement a collaborative decision-making (CDM) framework to facilitate this process while enforcing safety regulations. In a CDM environment, airline flight scheduling and airport operations are becoming more synchronized [4]. This is a complicated process and needs analytical models and tools to facilitate communication. CDM is a truly fundamental innovation, but the benefits from this concept are yet to become fully operationalized. This research is motivated by exploring the interdependencies between airline flight scheduling and airport capacity limitations to make better resource allocation. Ideally, such scheduling activities between airlines and airports can be formalized into a CDM system.
Operations research (OR) has contributed significantly to the aviation industry by improving their operations and accommodating their high growth rates [5]. Airline scheduling and airport resource allocation are natural contexts for the application of OR techniques and optimization models. In particular, these applications are well-suited to the use of large-scale, discrete optimization and have motivated the publication of over 1,000 articles over the last 50 years [5]. Despite the long-term development of this field, there are still scientific challenges in developing novel mathematical models and solution approaches to deal with integrated airline scheduling considering airports' resource limitations and slot allocation. Airport slot allocation has been proposed as a short-term measure for dealing with the excessive demand at overly congested (Level 3) airports [6]. Optimal scheduling intervention is another approach to adjusting flight schedules at a busy airport to minimize system-wide delays [7]. It is shown in a case study that by rescheduling 1% of flights up to 15 minutes each, one can reduce expected network-wide delays by 20%–30% [7]. Flight rescheduling at airports without scheduling limits, such as the majority of North American airports, can be used to reduce potential delays through limited interference with airline competitive scheduling. This can lead to a better trade-off between schedule displacement and flight delays. Improving airport capacity utilization is related to air traffic flow management which tries to enhance the efficiency of operations by optimizing the allocation of airport resources to both arriving and departing aircrafts [8]. Many existing optimization models that are concerned with the effective use of runway systems achieve increased utilization through the removal of slack times [8,10]. Although having less slack time may bring more economic benefits, it could lead to less robustness and increased costs in practice [5].
This paper presents an optimization model for flight rescheduling at a schedule-coordinated airport to minimize congestion and flight delays. The optimization model used herein is a modification of the model presented in [8] by explicitly enforcing runway capacity constraints. Given an existing flight schedule to an airport on a particular day that has been created during the strategic planning phase, this optimization model produces a feasible modified schedule considering the runway capacity and the minimum turnaround times without canceling any flights. The outcome of such an optimized schedule is a reduction in potential delays and better distribution of demand on the actual day of operation. The next section describes the mathematical models as well as the simulation algorithm used to verify the results. A case study on Atlanta, Georgia, USA airport operation and the experimental data used therein are also explained in Section 2. The optimization results are presented in Section 3 and compared with simulated and previously scheduled flight data. The discussion of the results is in Section 4 and finally, the conclusion and future research are contained in Section 5.
2. Materials and Methods
Consider the airport at which all the incoming and outgoing flights are to be rescheduled due to overcapacity scheduling or a ground delay program due to poor weather conditions. The method used in this research is a combination of a simulation algorithm and an optimization model to analyze the balance between the demand and capacity and the potential of creating delays in flights. The main inputs to this study include (i) estimates of the airport runway capacity and configurations under various weather conditions; and (ii) the original schedule of flights for a particular day of operation as well as the planned connections between the arrival and departure flights. In this section, we present the optimization model first and then briefly explain the algorithm developed in this project to simulate the arrival and departure processes. The last part describes the case study and data used for computational experiments.
2.1. Mathematical Formulation
The following table defines the notations used throughout this paper.
|
Sets and Parameters |
Description |
| 𝓣 | The set of periods, |
| The set of arrival flights scheduled to land at the airport | |
| The set of departure flights scheduled to take off from the airport | |
| A subset of flight pairs such that flights and are flown by the same aircraft |
|
|
0; otherwise |
|
|
0; otherwise |
|
| / | The minimum/maximum turnaround time between flights and such that |
| Maximum number of allowable arrival flights in period | |
| Maximum number of allowable departure flights in period | |
|
Decision Variables |
Description |
| Positive or negative displacement of arrival flight | |
| A binary array representing the newly scheduled arrival of flight | |
| Maximum of all positive or negative flight displacements |
It is a common practice to discretize the time into 15-minute periods. However, we use 5-minute intervals in the optimization model to avoid unnecessary large schedule displacements. The novelty of this formulation lies in the structure of the scheduling parameters and as defined in [8]. The array (similarly ) is of the form if flight i is originally scheduled to land (take off) no earlier than period t, where the last 1 in the array corresponds to period t.
The parameters and are expressed as numbers of 5-minute periods. If flights i and j are connected by an aircraft, we set the corresponding value of to the minimum turnaround time required to complete the ground operation for the type of aircraft and make it ready for the next flight. The decision variables take the same form as the input parameters and . By convention, we assume that . The displacement variables and are also expressed as numbers of 5-minute periods and allow for positive or negative displacement, i.e., a flight can be rescheduled for a later or earlier time of the day.
The objective function is to minimize the total displacements of arrival and departure flights on a particular day. The maximal displacement of any flight, denoted by , could be considered as the second objective function. However, we restrict it by assigning a fixed value to so that it would not hurt the first objective, based on various initial runs of the model. The optimization model for scheduling interventions at a busy airport can be formulated as follows.
This is a mixed-integer linear programming model. Constraints (2) and (3) ensure that all arriving and departing flights are scheduled. Constraints (4) and (5) define the rescheduled arrival and departure times, respectively, based on the decisions on displacements of the original flight schedules. The combination of constraints (4) and (5) ensures that flight block times are kept unchanged. Constraints (6) and (7) enforce the minimum and maximum connection times. Constraints (8) and (9) ensure that are nonincreasing for each flight, consistently with their definition. Constraints (10) and (11) ensure that the aggregate number of scheduled arrivals and departures in each period t do not exceed the runway capacity limits. Constraints (12) define the maximum of all positive and negative displacements for all incoming and outgoing flights and finally (13) define variables’ type and sign constraints.
2.2. Simulation of Arrival and Departure Processes
We have developed an algorithm to simulate the arrival and departure processes using the first come first served (FCFS) discipline while respecting runway capacity limitations in a schedule-coordinated airport. The capacity is defined as the number of arrival or departure slots that can be safely assigned to the incoming or outgoing flights from the airport in each 15-minute time interval during a day. The number of arrival or departure slots for each 15-minute time interval depends on the minimum separation time between two consecutive landings or take-offs for safe operations. The minimum safe separation interval between successive flights is a critical safety measure that mitigates the risk of in-flight incidents by ensuring a sufficient buffer to prevent the aerodynamic effects of one aircraft from adversely affecting another. We assume 3 minutes minimum safe separation time for arrivals and 2 minutes for departures. After assigning a time for a flight in a certain interval, the value of the delay is calculated, which is the difference between the flight time that we can reschedule after slot allocation and the original scheduled time. The arrival delay, caused by shifting some flights to subsequent time intervals, may get propagated to those departure flights that are connected to the arrival flight by some airline resources (aircraft, crew members, and/or passenger connections). In this study, we consider flight connections only by aircraft since other connection data were not available. We assumed fixed taxi and turnaround times under the assumption that there are no capacity limitations for ground operation resources. The simulation of the departure process is done similarly. However, before starting the allocation of flights to runways, we check the minimum ready time after the execution of ground operations following the aircraft's actual arrival. An arrival delay will result in a departure delay if there is not enough slack between the two connected flights. We ensure that a minimum turnaround time of 35 minutes between each pair of connected arrival and departure flights that are performed by a certain aircraft is maintained. After taking into account the ground operation time, the delay is calculated, which is the difference between scheduled and actual times. The details and flowchart of the simulation algorithm can be found in [9].
2.3. Case Study and Computational Experiments
The data used in our experiments were collected from the FAA website for Hartsfield-Jackson Atlanta International Airport (ATL) on March 24, 2023, which happened to be the busiest day in 2023 [11]. It includes all departure and arrival statistics (scheduled time, actual time, flight delay, etc.) for all the flights going to or departing from the USA airports. The connections between flight pairs were found using the tail numbers of the aircraft performing those flights. ATL is the number two weather-affected airport, largely because of system delays and thunderstorms at ATL [11]. We collected statistics for 881 arrivals and 873 departures as well as for 739 connection flights at ATL on that day.
According to the FAA, the capacity benchmark is defined as the maximum number of flights an airport can routinely handle in an hour, for the most commonly used runway configuration in each specified weather condition. In our research, we analyzed the capacity of the 5 parallel runways in this airport. ATL normally assigns three runways for arrivals and two for departures. We assumed that each runway was designated for either incoming or outgoing flights, but not for both at the same time. To validate the simulation code, we ran the algorithm considering the capacity of 20 arrivals and 20 departures in each 15-minute interval and observed that the simulated data closely matched the actual data [9]. It should be noted that the simulation algorithm enforced runway capacity limitations for safer operation whereas the actual data were the result of ad hoc operation based on FCFS discipline. After validating the simulation code, the algorithm was run with an operational capacity of 15 – 15 flights in each 15-minute interval. This is equivalent to enforcing a 3-minute separation time for arrivals and 2 minutes for departures.
3. Results and Discussion
We implemented the optimization model in GAMS 24.0 and solved it using CPLEX 12.5.1.0 on a personal computer with a 2.5 GHz Intel Core i7 processor and 12 GB of RAM. All the reported solutions to the model are optimal and have been found in less than 5 minutes. The simulation algorithm was implemented in Python 3.12.
Table 1 and Table 2 demonstrate the computational results of this study. We report three measures for arrival flight delays using the actual data, simulated, and optimized schedules in Table 1. Similarly, the results for departure flights are reported in Table 2. The actual data are the same as reported on the FAA website for ATL airport on a particular day [11]. The results under the simulated arrivals column have been obtained by processing the flights in a queue on an FCFS basis while enforcing runway capacity limitations. The optimization results on flight displacements are reported under two scenarios: with and without allowing for negative displacements of the flights from their original schedules. It is noted that such displacements could be implemented in the schedule well ahead of the actual day of operation and should not be considered as delays. In other words, if all the flights were rescheduled ahead of time, based on the optimization results, the same number of arrival/departure flights could be handled in a day without any delay caused by airport capacity limitations. However, in practice, we may still observe some delays even with the optimized schedule due to overlapping some flights within some time intervals. That is why we have simulated again both arrival and departure processes using the optimized schedules (allowing up to 15 minutes of negative displacements) and measured the potential delays, as reported in the last column of Tales 1 and 2.
The results in Table 1 illustrate that simulation of the arrival process with a capacity of 15 flights in each 15-minute interval led to a 25.2% increase in the actual delay times and more than doubled the number of delayed flights. However, the maximum delay that any arrival flight may experience is 45 minutes, which is 77% lower than 196 minutes in the actual operation. This observation was expected since the lower airport capacity used in the simulation experiments exacerbates delays. It can be seen in [9] that our simulation results would closely match the actual data if we assumed the runway capacity of 20 for arrival and 20 for departure flights. The lower actual delay times could also be attributed to the fact that the airport operation control may have utilized some runways for both arrival and departure flights with possibly less separation time whenever possible to achieve higher throughput. Our simulation algorithm assumes designated runways for arrival and departure flights while enforcing a three-minute separation time for consecutive arrivals and two minutes for consecutive departures to ensure safety of operations.
To utilize the full capacity of airport runways during off-peak hours, we ran the optimization model allowing for both positive and negative displacements of flights to happen, and the results turned out to be significantly better for both arrival and departure flights as reported in the last columns of Table 1 and Table 2. For practical reasons, the maximum allowable positive (negative) displacement for a flight was restricted to 60 (15) minutes. The results in Table 1 show that the total flight displacement times in the optimized schedule (with positive displacements only) is 23.3% higher than the actual delay times, which is similar to the simulation results. However, when we allowed negative displacements in the optimization model, the result was 40.7% lower than the actual total delay times for the arrival processes. As mentioned before, such displacements should not be considered as delays and can be accommodated well ahead of the actual operation day. This significant improvement achieved by the optimization model could be attributed to better utilization of airport resources during off-peak hours. Figure 1 demonstrates how the optimization model distributes the arrival flights over the course of a day. It also shows that the number of arriving flights is cut off at 15 in both simulation and optimization results.
The results in Table 2 illustrate that simulation of the departure process with a capacity of 15 flights in each 15-minute interval led to a 2.8% decrease in the actual delay times and more than double increase in the number of delayed flights. This observation was expected since the lower airport capacity used in the simulation experiments exacerbates the number of delayed flights, as explained for the arrival process. However, the maximum delay that any departure flight may experience is 32 minutes, which is 84% lower than 199 minutes in the actual operations. The results in Table 2 show that the total flight displacement times in the optimized schedule (with positive displacements only) is 17.6% lower than the actual delay times, which is much better than the simulation results for the departure process. Yet, when we allowed negative displacements in the optimization model, the result was 61.6% lower than the actual total delay times. Furthermore, the number of displaced flights becomes 308, which is lower than the 341 delayed departure flights by 9.6%. As mentioned before, such displacements should not be considered as delays. We observe that significant improvement in total delay times can be achieved by the optimization model for both arrival and departure flights.
Figure 2 demonstrates how the optimization model distributes the departure flights over the course of a day. It also shows that the number of departing flights is cut off at 15 in both simulation and optimization results.
4. Conclusions
We have developed an optimization model for flight rescheduling at a schedule-coordinated airport. The model demonstrates the potential for a significant reduction of delay and congestion by moderately rescheduling the flight times. Furthermore, by distributing the peak hour demand over the course of the operation day, better utilization of airport resources and less congestion can be achieved. Mitigating flight delays at such a busy airport can significantly reduce propagated delays in the downstream flight network. Computational results show that total displacements or potential delay times could be reduced by 40.7% and 61.6% for the arrival and departure flights, respectively. This is achieved by allowing flights to be rescheduled to a maximum of one hour later or 15 minutes earlier without eliminating any flight or missing connections at ATL airport. However, we realize that scheduling intervention at a selected airport may not be easily accepted by airlines unless their challenges and interests are addressed. Our study to date suggests that this type of airport-wide cross-airline coordination could reduce total delays and the maximum delay times that any flight may experience due to airport capacity limitations by 40-61% and 70%, respectively.
Our future research will focus on extending this optimization model to account for propagated delays at the downstream flight network. We aim to adjust flight schedules considering the airport resource constraints and congestion to reduce the total delay propagations. We will also calculate the total propagated delays on the subsequent connection flights after a tail number departs from the airport until it completes its rotation. This propagated delay calculation will be used as another objective function in the optimization model leading to a multiobjective optimization model. It is expected that the results of such a new schedule intervention paradigm will be more acceptable to the airlines. We believe that the new model could be a good common ground for the successful implementation of a CDM system in the near future.
Author Contributions
A. Seifi conceived and designed the study, developed the simulation and optimization models, analyzed the results, and wrote the paper; K. Ponnambalam contributed to fund acquisitions, design of the study, project administration, conceptualization and supervised the work; A. Kudiakova developed the codes for data extraction and conducted the simulation experiments, helped writing some sections; L. Aultman-Hall contributed to fund acquisitions and resources for the work, advised on the project work and edited the draft. All authors have read and agreed to the published version of the manuscript.
Funding
This research project was financially supported by the Waterloo Institute for Sustainable Aeronautics’ (WISA) Research-for-Impact (RFI) funds provided by FedDev’s Aerospace Regional Recovery Initiative in 2023.
Data Availability Statement
The data analyzed in this study is publicly available and can be found at https://transtats.bts.gov/ONTIME/.
Conflicts of Interest
The authors declare no conflicts of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.
References
- Gillen, D.; Jacquillat, A.; Odoni, A. R. ; Airport demand management: The operations research and economics perspectives and potential synergies. Transportation Research Part A 2016, 94, 495–513. [Google Scholar] [CrossRef]
- US Department of Transportation. Airline on-time statistics and delay cause: Airline service quality performance 234. 2015, http://www.transtats.bts.gov/ot_delay/ot_ delaycause1.asp.
- International Air Transport Association. https://www.iata.org/en/programs/ops-infra/slots/coordinated-airports. (accessed on 20 January 2024).
- Erkan, H.; Erkip, N. K.; Şafak, Ö. Collaborative decision making for air traffic management: A generic mathematical program for the rescheduling problem. Computers & Industrial Engineering 2019, 137, 106016. [Google Scholar]
- Barnhart, C.; Belobaba, P.; Odoni, A. R. , Applications of operations research in the air transport industry. Transportation Science 2023, 37, 368–391. [Google Scholar] [CrossRef]
- F. A. Katsigiannis, K. G. Zografos. Optimising airport slot allocation considering flight-scheduling flexibility and total airport capacity constraints. Transportation Research Part B 2021, 146, 50–87. [Google Scholar] [CrossRef]
- Wang, K.; Jacquillat, A. A stochastic integer programming approach to air traffic scheduling and operations. Operations Research 2020, 68, 1375–1402. [Google Scholar] [CrossRef]
- Jacquillat, A.; Odoni, A. R. An integrated scheduling and operations approach to airport congestion mitigation. Operations Research 2015, 63, 1390–1410. [Google Scholar] [CrossRef]
- Seifi, A.; Kudiakova, A.; Ponnambalam, K.; Aultman-Hall, L. Modeling delay propagation within a network of outbound flights at a hub airport. In Proceedings of the AMMCS2023 Conference, Wilfrid Laurier University, Waterloo, Ontario, Canada, 14-18 August 2023. [Google Scholar]
- AhmadBeygi, S.; Cohn, A.; Lapp, M. , Decreasing airline delay propagation by re-allocating scheduled slack. IIE Transactions 2010, 42, 478–489. [Google Scholar] [CrossRef]
- Federal Aviation Administration (FAA). Airport Capacity Profiles 2022.
Figure 1.
Number of arrival flights based on the actual, simulated, and optimized schedules.

Figure 2.
Number of departure flights based on the actual, simulated, and optimized schedules.
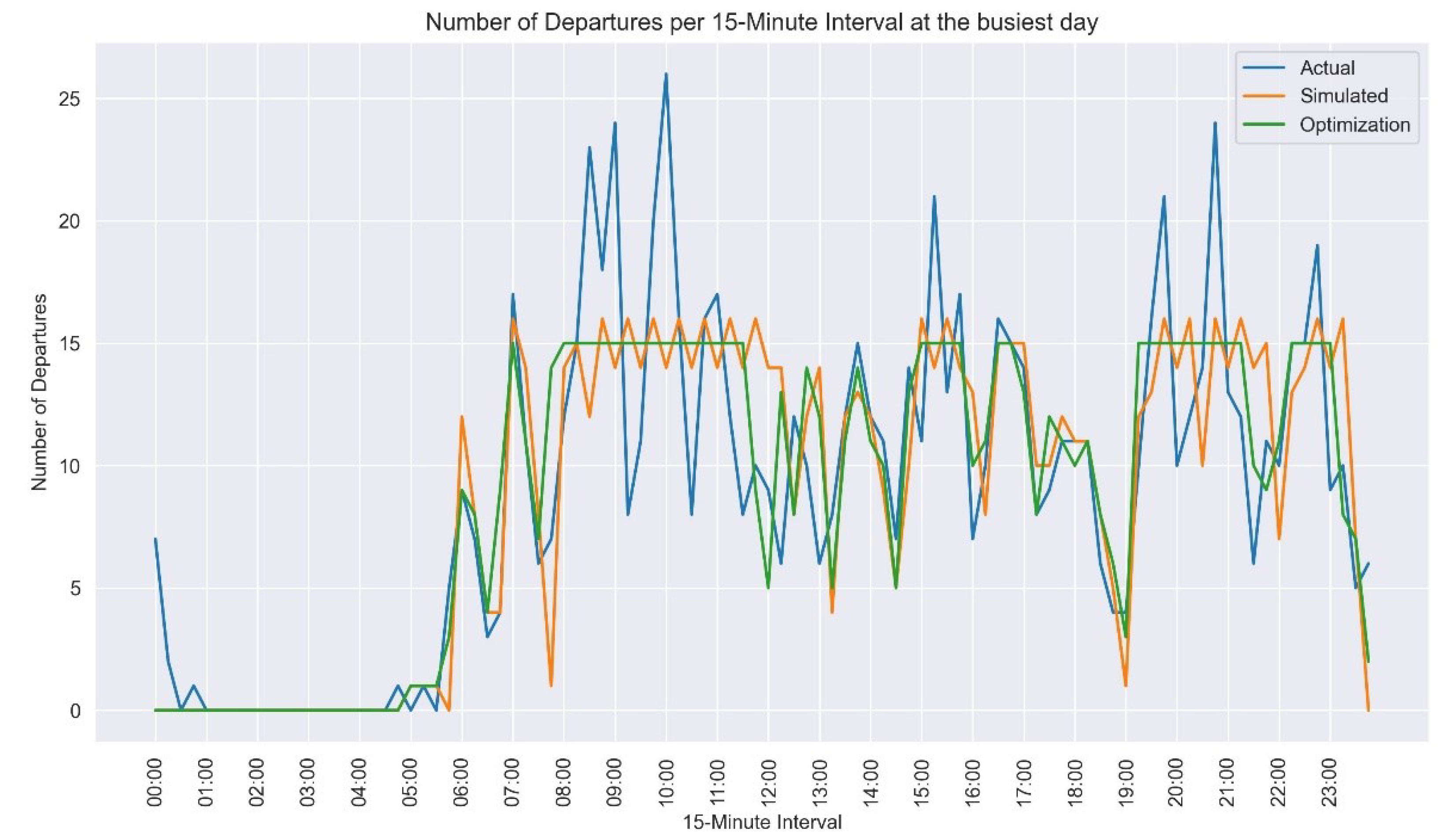
Table 1.
Comparison of actual, simulated, and optimized schedules for arrival flights.
| Actual Arrivals |
Simulated Arrivals (FCFS) |
Optimized Schedule (with positive displacement) |
Optimized Schedule (allowing negative displacements) |
||||
| Total delay or displacement times (min.) | 6279 | 7862 | +25.2% | 7745 | +23.3% | 3725 | - 40.7% |
| Max. delay or displacement of a flight (min.) | 196 | 45 | -77% | 60 | -69.4% | 60 | -69.4% |
| Number of delayed or displaced flights |
285 | 591 | +107% | 338 | +18.6% | 296 | +3.8% |
Table 2.
Comparison of actual, simulated, and optimized schedules for departure flights.
| Actual Departures |
Simulated Departures (FCFS) |
Optimized Schedule (with positive displacement) |
Optimized Schedule (allowing negative displacements) |
||||
| Total delay or displacement times (min.) | 8001 | 7773 | -2.8% | 6590 | -17.6% | 3075 | -61.6% |
| Max. delay or displacement of a flight (min.) | 199 | 32 | -84% | 60 | -70% | 60 | -70% |
| Number of delayed or displaced flights |
341 | 698 | +104% | 334 | +98% | 308 | -9.6% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Alerts
MDPI Initiatives
Important Links
© 2025 MDPI (Basel, Switzerland) unless otherwise stated






