Preprint

Article

Universality and Complexity in Natural Languages: Mechanistic and Emergent

Altmetrics

Downloads

492

Views

857

Comments

Gemma de les Coves^*,

Bernat Corominas Murtra^*

Ricard Sole^*

Gemma de les Coves^*,

Bernat Corominas Murtra^*

Ricard Sole^*

This version is not peer-reviewed

Submitted:

21 February 2024

Posted:

23 February 2024

You are already at the latest version

Alerts

Abstract

Human language is a prime example of a complex system characterized by multiple scales of description. Understanding its origins and distinctiveness has sparked investigations with very different approaches, ranging from the Universal Grammar to statistical analyses of word usage, all of which highlight, from different angles, the potential existence of universal patterns shared by all languages. Yet, a cohesive perspective remains elusive. In this paper we address this challenge. First, we provide a basic structure of universality, and define recursion as a special case thereof. We cast generative grammars of formal languages, the Universal Grammar and the Greenberg Universals in our basic structure of universality, and compare their mathematical properties. We then define universality for writing systems and show that only those using the rebus principle are universal. Finally, we examine Zipf's law for the statistics of word usage, explain its role as a complexity attractor, and explore its relation to universal writing systems as well as its similarities with universal Turing machines. Overall, we find that there are two main kinds of universality, termed {\it mechanistic} and {\it emergent}, and unveil some connections between them.

Keywords:

Subject: Physical Sciences - Other

1. Introduction

The emergence of language is considered one of the major evolutionary transitions [1]. It enables us to connect with others in rich ways, as individuals receive and process information from their surroundings and respond with behavioural changes. It is efficiently propagated among individuals (through its acquisition by children from adults) and is easily learnt, allowing its users to access general conceptualisation [2]. In the evolutionary context, the development of human language is intricately tied to the survival advantages it conferred on early social groups.

If anything characterizes linguistic phenomena is its astonishing ubiquity and diversity, spanning disparate research fields and scales [2,3,4]. 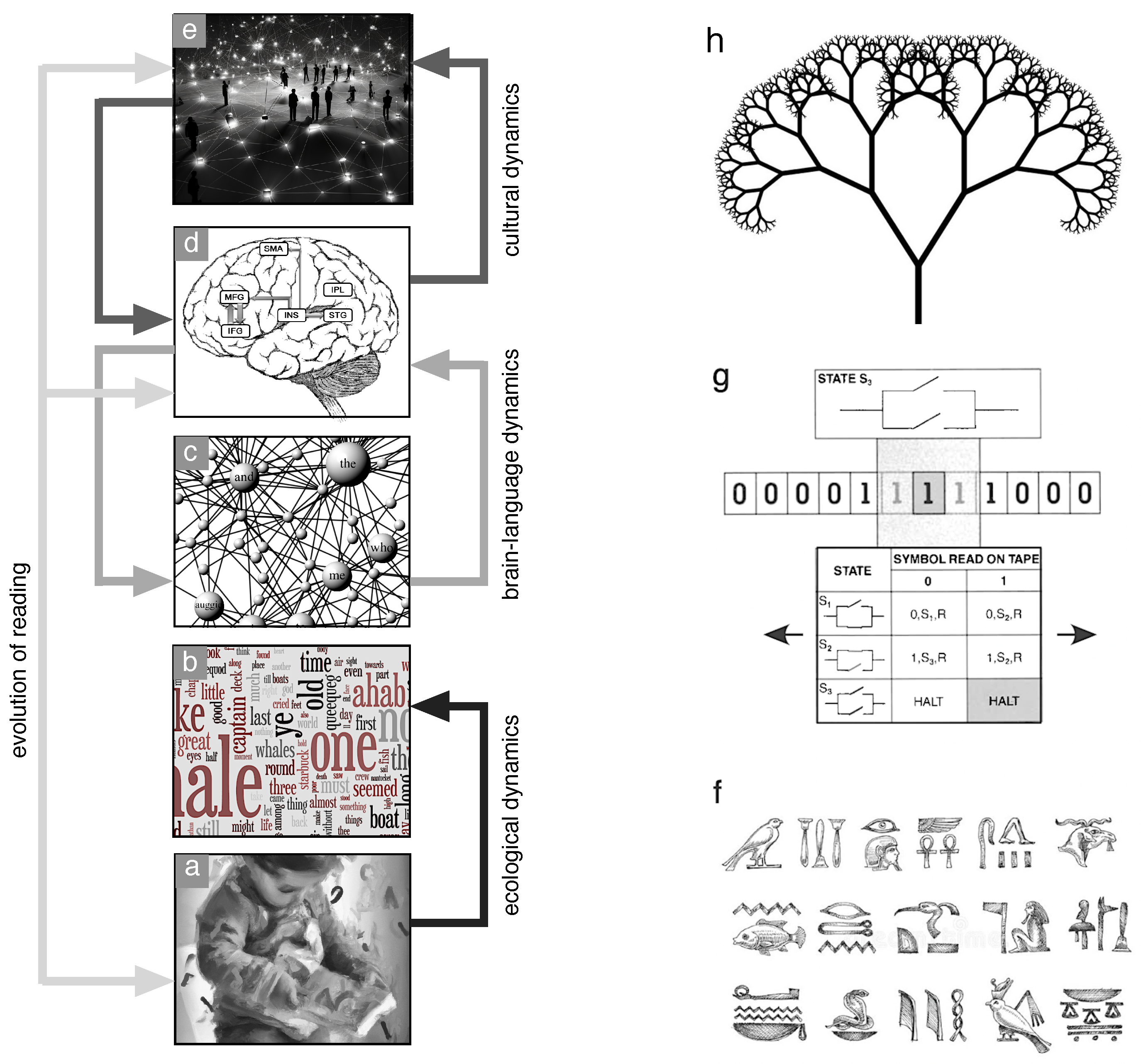Linguistics [5], psychology [6], population dynamics [7,8], population genetics [9], artificial intelligence [10,11,12], network science [13,14,15,16,17], statistical physics [18,19,20,21,22,23], theoretical and evolutionary biology [24,25,26,27] and cognitive science [28,29,30,31] provide different frameworks encompassing some aspect of language complexity. Yet, such explanations are not independent, but their relations give rise to a complex net of relations, as illustrated in Figure 1a-e, exhibiting a hierarchy of such representations ranging from its minimal components to the socio-cultural domain. This complexity is deeply rooted in the evolutionary history of human communication and its coevolution with the brain, which reflects adaptive responses to environmental and social challenges. At the microscale, the arrangement and combination of these units adhere to syntactic and grammatical rules, providing the structural basis for constructing words and sentences. At the mesoscale, language exhibits emergent properties beyond lexicons, as words and sentences interact to convey new meaning. Sentence structures, constrained by grammatical rules, emerge from complex syntactic and semantic rules.

Each scale involves novel features: the properties observed at one scale seem to be emergent, that is, not reducible to the properties of the lower one. Within each scale, scholars have found constraints to the space of the possible: extant languages (written or spoken) seem to share several ‘optimal’ properties, which can often be seen as the result of certain evolutionary dynamics. As a matter of fact, in some respects languages behave like species in ecosystems—originating, coexisting within a great diversity, and potentially becoming extinct. In addition, the scales of description interact in causal loops: language is maintained by the cultural substrate of interacting human groups, but needs human brain architectures to develop within individuals. These features necessitate such diverse models and frameworks that a unified picture seems very challenging.

Despite the disparity of phenomena, the obvious differences among languages, and their ‘accidental’ histories, scholars have intensively explored the possibility of discovering general laws. Behind this effort lies the hypothesis that all languages share fundamental traits that reveal the presence of so-called universal patterns of organization, either at the level of grammar, writing systems or statistical patterns of their usage. This search puts language in a unique position within other scientific disciplines, as universality in language is defined, postulated or identified from many different angles, more than any other phenomena, some of them sketched in (Figure 1f-h). As we shall discuss in this work, the evolution of written languages (Figure 1f) provides a privileged window into the transitions towards universal patterns. The gold standard of universality is that of universal Turing machines (see e.g. [32]; Figure 1g), for its power and beauty. Intimately connected to universality will be the concept of recursion, shown as an example in (Figure 1h), where a tree is generated by a simple algorithm that can be represented as a grammar [33]. Another instance of universality are scaling laws in the usage of words.

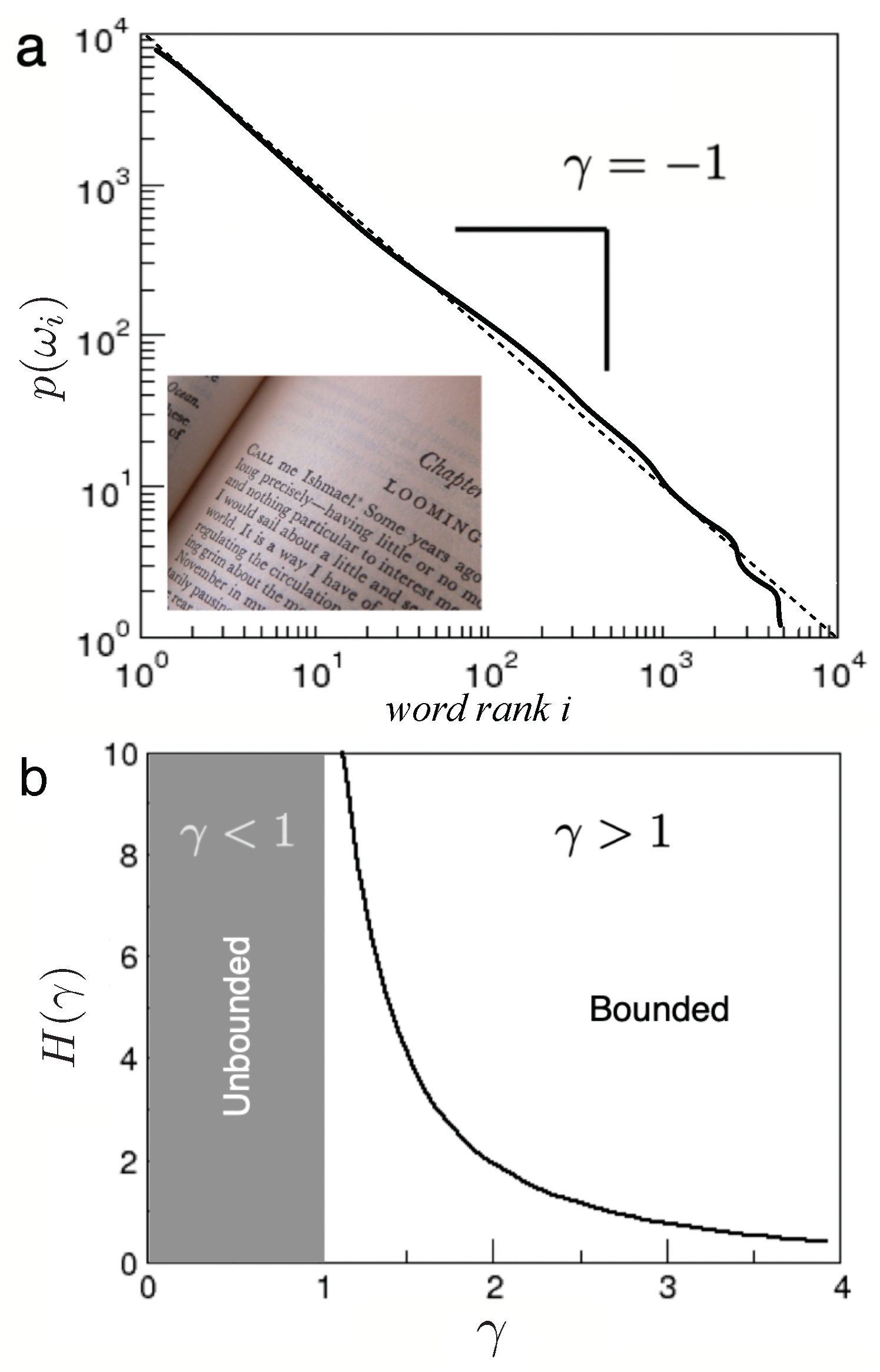
In physics, certain forms of universality plays a crucial role in our understanding of complexity, particularly in relation with phase transitions: very different systems share commonalities close to critical points [34,35]. The conceptual power of this type of universality has percolated deeply within complex systems sciences, as well as evolutionary theory [36,37]. In particular, ‘universal’ statistical patterns have been identified (such as Zipf’s law, which we will consider in Section 5). However, most of these works have largely ignored other important studies on the structure of grammars. This includes the so-called Universal Grammar, which describes an innate knowledge and stems from the rationalist tradition [38,39]. Or the so-called Greenberg Universals [40], which postulate the existence of universal traits in the grammatical structure of any language, a result based only on empirical grounds. As a consequence of the divergent course taken by these studies, there is a knowledge gap that necessitates a theoretical bridge.

In other words: Despite the central role of universality in approaches to linguistic phenomena, no definition has yet been provided that enables to

(i): Identify and characterize the potential universals, and, more importantly,
(ii): Establish relations between them.

The goal of this paper is to bridge this gap by first establishing a minimal definition of universality, termed a ‘basic structure’. We shall then identify this skeleton in various established instances of universality, casting the different examples in this light. This groundwork will enable the exploration of potential connections between them, as well as the study of the transition from non-universal to universal (sometimes called the jump to universality [41]).

To this end, we first present the basic structure of universality, as well as that of recursion. We identify the latter as a special case of universality (where the relation between the universal object and the objects in the collection is of a special kind), and term its universal object a ‘grammar’. We then examine various notions of grammars in this light: we cast generative grammars of formal languages, the Universal Grammar and the Greenberg Universals in these structures, and compare the mathematical properties of the last two. We also define universal writing systems, and show that they are the ones that exclusively use the rebus principle. Lastly, we consider the statistics of word usage, where we encounter Zipf’s law. We explain one mechanism that accounts for its emergence, draw a connection between Zipf’s law and universal writing systems, and compare its properties with those of universal Turing machines.

As it shall become clear soon, to instantiate the basic structure of universality entails, in a certain way, that a plurality be considered a unity. One main conclusion of this work is that, while all notions of universality instantiate the basic structure, universality comes in two main flavours. One is such that when universality is attained, all possibilities of a complexity universe can be explored.1 While the paradigmatic example is a universal Turing machine, we also encounter universal spin models [43], NP-complete problems, the denseness of a subset, the basis of a vector space and others [44]. In this case, the jump to universality is the crossing of a threshold after which no more complexity need be incorporated in the universal object so that it can reach any other object in the collection.

In contrast, in the second flavour of universality, the transition to universality is that by which a collection of objects come to share an attribute. This is a form of emergence: a degree of freedom, capturing that attribute, becomes relevant at the scale where the transition occurs. The paradigmatic example is that of universality classes in statistical mechanics, where many hamiltonians behave similarly close to criticality. This transition often has a more empirical nature than the first one.

If the first flavour is related to an exhaustion of possibilities, the second is linked to a massive reduction of effective degrees of freedom. The first is related to forms of unreachability via Lawvere’s fixed point theorem [44,45,46], which can be seen as limitations—in probability (via Gödel’s theorem), computability (via the uncomputability of the halting problem), the definition of sets (via Russell’s paradox), or the impossibility to define the set of all sets or an ordinal that contains all others (via Cantor’s theorem; see also [47]), to mention a few (see [45] for more). The second is related to the presumed validity of asymptotic reasoning to derive macroscopic behaviours [48], which results in limitations of predictability insofar as the appearance of new effective degrees of freedom was not foreseen from the finite.2 We shall refer to the first flavour of universality as mechanistic and to the second as emergent. Note that we do not have a rigorous definition of either, but only the properties mentioned in the preceding paragraphs. Devising a meaningful definition would be part of the solution.

Broadening the scope, our contribution can be seen as part of a larger endeavour, which seeks to understand:

What is the relation between mechanistic-universality and emergent-univerality?

Does one imply the other? Or are they independent? These questions can only be addressed from a common framework with which to compare them. This is what we (hope to) provide in this work.

This paper is structured as follows. First we present the basic structures of universality and recursion (Section 2). Then, we cast several notions of universality in grammars in these structures (Section 3, and other infinite sets with a finite description in Appendix A). Then we turn to written representations of languages, where we define and characterize universal writing systems (Section 4). Finally, we examine emergent universals in the light of our structures (Section 5, while the details of communication conflicts leading to Zifp’s law are deferred to Appendix B). We conclude and present an outlook in Section 6.

2. The basic structures of universality and recursion

Let us start by defining the basic structure of universality and recursion.

‘Universal’ means ‘relative to the Universe’, and by extension, ‘all-encompassing’.3 More formally (see Figure 2),

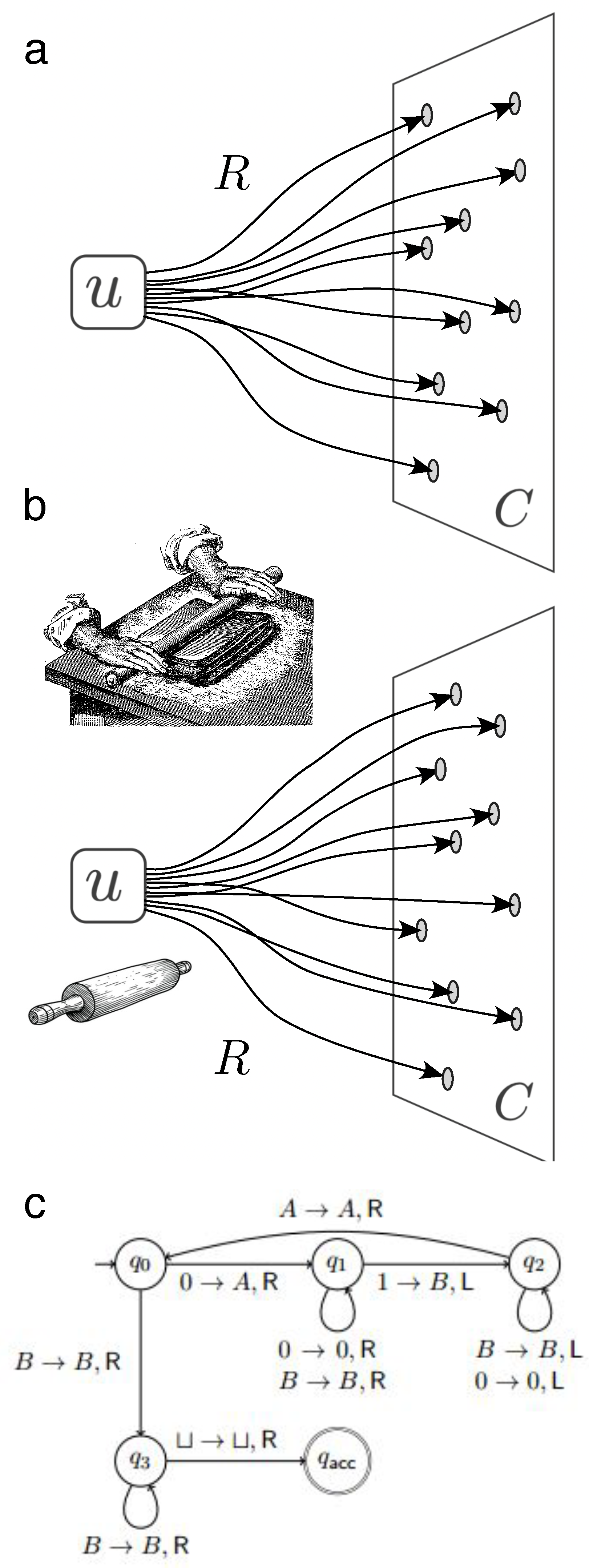
Basic structure of universality

Given a set C and a relation R landing in C,

a finite u is universal if $(u, c) \in R$ for all $c \in C$ .

‘All’ qualifies the set C and ‘encompass’ is captured by the relation R—in this minimal sense, this formalizes the idea that universal stands for all-encompassing. Recall that a relation R is a subset of the Cartesian product of two other sets,

R \subseteq S \times C

, i.e. R is identified with the set of pairs where it is true. We say that Rlands in C if the second component of this product is precisely C. We leave S unspecified, as we do not want to commit to where u belongs. We also require that u have a finite description, because, how could we even present an object that requires an infinite description?4 If C is infinite, the finiteness of u will exclude trivial structures of universality in which R is the identity relation and

u = C

. However, if C is finite (e.g.

G

in Section 3.2), such trivial universality is not excluded by the finiteness of u.

A special kind of universality is given by recursion:

Basic structure of recusion

Let u be universal for set C with relation R. u is recursive if R reads ‘can be applied to a base case a finite but unbounded number of times’. We call such u a grammar.

In this case, R consists of applying a finite set of rules (or ‘mould’) a potentially unbounded number of times to generate the elements of a family. Note that this use of the term ‘grammar’ is broader than the usual one. A paradigmatic example are so-called generative grammars (Section 3.1), such as

S \to A S B

and

S \to 0

, with S the start symbol, A and B terminal symbols and 0 the empty symbol, where these two rules (the ‘mould’) generate the (context-free) language

{A^{n} B^{n} ∣ n \geq 0}

(the set C; see Figure 2c).

Another example of a recursive system is an axiomatic formal system, where a finite number of axioms and transformation rules generate an (infinite) set. For example, in the simplest case and the most naive formulation, the natural numbers (the set C) are generated by the successor function

+ 1

applied to a base case (the number 0)—where the two define the ‘mould’—an unbounded number of times. One of the appeals (if not the main one) of axiomatization is precisely that it purports to trap an infinite wealth of information in a finite, manageable stock of basic (self-evident) principles (see e.g. [50]).

3. Grammars

Let us now consider notions of universality in grammars. We will first examine generative grammars (Section 3.1), which form a paradigmatic framework for a theory of grammar [51,52]. We will then consider two concepts of universality postulated for the grammatical structure of human language(s): the Universal Grammar in Section 3.2, and the Greenberg Universals in Section 3.3, as well as their potential connections in Section 3.4.

Let us start with some general considerations. The two notions of universality originate from two distinct, almost opposed perspectives. First, the potential existence of an innate endowment provided by a Universal Grammar originates from the rationalist tradition [38,39,51]. Rationalism posits that human beings possess a priori knowledge, which exists independently of experience [53,54,55]. This universality, therefore, would be generic and part of the human brain’s capacity for processing complex computations, presumably utilized for communication purposes. Its existence is postulated to be necessary to overcome the lack of comprehensive and systematic linguistic input encountered during the process of language acquistion [56].

In contrast, the Greenberg Universals provide a different, albeit potentially related notion, as they postulate the existence of traits that presumably hold in the grammatical structures of any language—so-called universal traits [40,57]. The conclusion is drawn from a generalization that relies solely on empirical evidence, without any regard to the epistemological issues related to language acquisition.

Throughout the text we pass no judgements on the validity of either approach in exploring the functioning of human language.

3.1. Generative grammars

Given a finite alphabet

Σ

—e.g.

Σ = {0, 1}

for a binary alphabet—and its so-called Kleene star

Σ^{*} ⋃_{n \geq 0} Σ^{n},

where

Σ^{n}

denotes the n-fold Cartesian product of

Σ

, a formal language L is

L \subseteq Σ^{*}

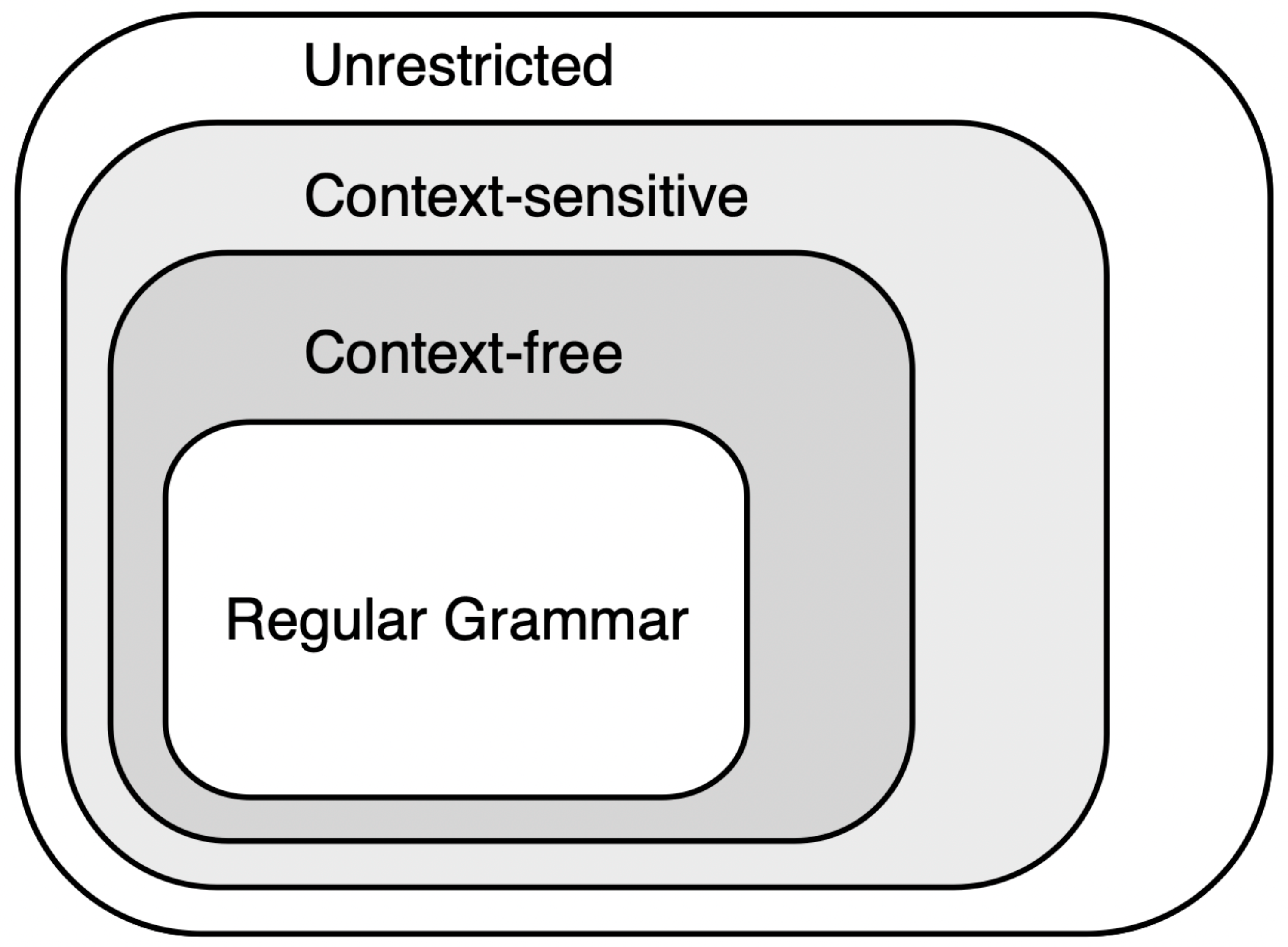
, that is, a subset of the set of finite concatenations of elements of the alphabet. Let a generative grammar G be a finite set of transformation rules which are well-formed, i.e. contain a start symbol, non-terminal and terminal symbols (see e.g. [32] or [58]). Additional constraints lead to the appearance of specific grammars organized in a hierarchy of escalating complexity that begins with regular grammars, progresses through context-free and context-sensitive grammars, and culminates in unrestricted grammars. This classification of grammars is known as the Chomsky hierarchy (Figure 3).

A grammar G is said to generate a formal language L, written

L = L 〈 G 〉

, if for every

x \in L

, there exists a finite sequence of applications of the rules in G resulting in x [58]. This instantiates the basic structure of recursion as follows:

C = L

so that the elements

c \in C

are precisely the strings

x \in L

. Let

S \overset{G}{\to} x

denote ‘there exists a finite application of the grammar rules G from the start symbol S that result in string x’. Then relation R precisely captures this condition, namely

(G, x) \in R \Leftrightarrow S \overset{G}{\to} x .

L = L 〈 G 〉

, we say that ‘G generates L’ or, in this work, that ‘G is universal for L’.

Four remarks are in order. First, another recursive description of L is provided by the Turing machine (TM) T that accepts it, denoted

L = L (T)

. A Turing machine is a finite set of rules (formally it is a 7-tuple specifying some finite alphabets, start and end symbol as well as a finite set of transition rules [32]) such that, if input x is initially written on the tape, T (eventually) accepts it if

x \in L

. In this case, T is said to accept L; if x is accepted if and only if

x \in L

, T is said to decideL. What is important for our discussion is that an infinite collection of strings (namely L) is characterized by a finite mould (namely the transition rules of T). The mould can be unravelled to give rise to the finite but unbounded element, namely any

x \in L

. Depending on the complexity of the grammar, a language is accepted by a finite state automaton, a pushdown automaton, a linear bounded automaton or a Turing machine if and only if it is generated by a regular grammar, context free grammar, context sensitive grammar or unrestricted grammar, respectively (cf. Figure 3). In this sense, the Turing machine T provides an alternative finite description of L than its generative grammar G—that of T can be seen as a passive description, as it accepts the string, whereas that of G as an active description, as it generates the string. Either way, they are both recursive and thus universal according to our definition, only the relation R is slightly different in the two cases.

Second, note that the foregoing definition of universality for Turing machines is different than that of a universal Turing machine, by which a fixed Turing machine can simulate any other Turing machine on any input (see e.g. [44]). Here, that a Turing machine T be universal for a language L means that it accepts it, i.e.

L = L (T)

. A universal Turing machine U accepts the language

L (U) = {d (T) # x ∣ T is a TM, x is accepted by T}

where d is a map from Turing machine to strings, i.e. a description, and # is a special symbol separating the parts of the string.

Third, the vast majority of formal languages do not admit a finite description (either by a generative grammar or a machine), but their only ‘description’ consists of providing each string x in the language—which scarcely qualifies as a description at all. These languages cannot be cast in the basic structure of universality because of the requirement that u be finite. (Without this requirement, they could trivially be cast by identifying

u = C = L

where L is the language, and R with the identity). This mismatch between languages with a finite description (or handle) and generic languages can be seen with a simple counting argument: the number of generative grammars or Turing machines is given by the cardinality of the naturals,

ℵ_{0}

, whereas the number of languages is given by the cardinality of power set of

Σ^{*}

| ℘ (Σ^{*}) |

, which is

2^{ℵ_{0}}

, an infinity of larger cardinality. By Cantor’s Theorem, there does not exist a surjection from the naturals to its power set. It follows that the fact that L have a finite description is extremely informative. Note that having a finite description significantly contributes to making the language L interesting, at least for most notions of ‘interesting’ we can think of (see also the discussion in [41]). As a matter of fact, most languages we ever consider have a grammar, i.e. are recursively enumerable. This situation is parallel to that of other infinite sets with a finite handle (Appendix A).

Finally, these considerations do not only apply to formal languages, but also extend to grammars of natural languages. The latter are usually classified as context free, or mildly context sensitive in certain exceptional cases [58].

3.2. Universal Grammar

The concept of a Universal Grammar (UG) was proposed by Chomsky in 1957 to explain how a child, exposed to only a finite set of sentences, can ‘extract’ the underlying grammar from this sample and then creatively construct new sentences that adhere to correct grammatical rules [51]. This seemingly paradoxical situation is known as the problem of the Poverty of Stimulus [39,56]. Possessing a ‘universal grammar’ in our brain would solve this paradox: The existence of the UG would restrict enormously the search space of the potential grammatical structures, thereby acting both as a guide and a frame for the process of language acquisition. This ‘grammar’ would transform language acquisition into a process of setting the parameters for the specific grammar of the language the child is exposed to. Specifically, the UG—in the Principles & Parameters approach [59,60]—can be seen as a ‘grammar’ with free parameters. As these parameters are set to different values, the UG specializes to the grammar of different natural languages [61], presumably characterized by certain parametrization of the UG. In this regard, the UG can be considered a meta-grammar.

We start by observing that, from a mathematical perspective, the existence of a UG in the Principles & Parameters paradigm is trivial, for the following reason. There is a finite number of natural languages (about six thousand [62]); let us assume that every natural language has its own distinctive grammar. It is a plain fact that every finite set can be parametrized. From a mathematical standpoint, this is precisely what the Universal Grammar represents: a parametrization of the set of grammars for all natural languages. More quantitatively, a set of about six thousand elements can be parametrized with

{log}_{2} 6000 \approx 13

independent binary parameters, which is roughly the number of parameters of

UG

[60]. For example, the value of one parameter would determine if the order of the sentence is Subject-Verb-Object (as in Catalan) or Subject-Object-Verb (as in Japanese), and another would determine whether the subject of the sentence can be omitted (as in Catalan) or not (as in German). (For further parameters, see [60].)

Slightly more formally, let

P {0, 1}^{13}

denote the space of values of 13 binary parameters, and let

G

denote the set of grammars of natural languages. We see the universal grammar

UG

as a map

UG : P \to G,

(1)

so that

UG (p)

corresponds to the grammar of Navajo, Mohawk, Welsh or Basque (to mention some) depending on

p \in P

. The claim of universality corresponds to the statement that, for any

G \in G

, there is a

p \in P

so that

UG (p) = G

. That is,

UG

is surjective. But this holds because

UG

is a parameterization of

G

We can easily cast the Universal Grammar in the basic structure of universality, by identifying

C = G

u = P

and R with

(u, G) \in R \Leftrightarrow \exists p \in u : G = UG (p) .

We would also like to mention that it is often unclear in the literature whether

G

refers to the set of grammars of existing languages, or of languages that could exist. In our view, characterising the latter would be tantamount to achieving a thorough understanding of what is possible in terms of grammars of natural languages—a major achievement (see [63] and [64,65] for considerations on the actual and the possible). For this reason, we assume that

G

refers to the former, and maintain our claims above.

Yet, we highlight the conspicuous fact that the number of parameters in the UG corresponds precisely to the number required to parametrize the set of actual languages (in a binary manner). By ‘actual’ we mean a language that either exists or has existed and there is a record of it. If the aim of the UG endeavour is to characterize the set of possible human languages, then our claims above about the mathematical triviality of the instantiation of the basic structure of universality would no longer hold, as such a set would presumably have a larger cardinality, so it is not trivial that it can be parametrized with 13 binary parameters. This challenge underpins some theoretical extensions, in particular the so-called Minimalist Program [66,67], which puts less emphasis on the structure of parameters but maintains the thesis that a fundamental backbone is shared by all languages.

3.3. Greenberg Universals

A somewhat orthogonal perspective is given by the identification of patterns in grammar that seem to appear throughout all known languages. In this case, the presence of so-called universal traits is the result of a generalization stemming from an empirical approach, in contrast to the rationalistic reasoning underlying the UG considered in Section 3.2. Despite this fact, these ‘Grammar Universals’, also called ‘Greenberg Universals’, aim to be the starting point of a theory of grammar with predictive capacity. In any case, so far this approach makes no statements about the epistemological problem of language acquisition.

We focus on the early proposal made by J. H. Greenberg [40], based on a list of declarative statements with various logical structures. Without the aim of being fully comprehensive, one can classify the universals by their logical structure. Given the set of all natural languages

L

and some grammatical properties P, Q, V, the statements mainly obey one of the two following logical structures:

\begin{matrix} \forall L \in L P (L) \\ \forall L \in L Q (L) \Rightarrow V (L) . \end{matrix}

The first type of statements (supposedly) hold for all natural languages. The second type of statements are implicational, and apply to those languages where the first condition is satisfied. The statements may contain negations, too.

An example of a statement of the first type is:

A language never has more gender categories in nonsingular numbers than in the singular.

An example of a statement of the second type—which are the vast majority—is:

If a language has the category of gender, then it has the category of number.

In standard (classical) logic, an implicational universal of the form

Q \Rightarrow V

can be written as

V \lor \neg Q

. As a consequence, each implicational statement can be interpreted as an assertive statement (i.e. of the first type), that is, an attribute satisfied by all grammars of natural languages.

Let us now cast the Greenberg Universals in our basic structure (cf. Section 2). Let

L

be the set of all natural languages;5 we identify the set C with

L

. Let

u = {u_{1}, \dots, u_{M}}

be the finite set of all logical statements in the list of Greenberg Universals. We write

u_{k} (L)

to denote that statement

u_{k}

is true for language

L \in L

. Relation R between u and

L

, as stated by Greenberg, can be written as

(u, L) \in R \Leftrightarrow u_{1} (L), \dots, u_{M} (L) .

That is, relation R holds if all (potentially infinite) natural languages satisfy the (finite set of) statements provided by the list of Greenberg’s Universals. We observe that, again, the notion of universality is very simple from a mathematical perspective; what is not simple is the identification of these common attributes, and more interestingly, the explanation of the mechanisms giving rise to them.

3.4. On the relation between UG and GU

While the two notions of universality stem from radically different grounds, they should bear, at the very least, a consistency relation: The statements of the two approaches cannot contradict each other. Moreover, despite the fact the UG is not directly accessible as only particular instantiations thereof are manifested—languages—, it is reasonable to assume that it must leave ‘footprints’ in the structure of languages, which should lead to some kind of general phenomenology within the set of actual human languages. One would like to see the Greenberg Universals as consequences, or by-products, of the instantiations of the UG. Let us make this idea more precise and, as a result, sketch the potential relation between the two notions of universality.

Let F be the state space of the truth values of the attributes satisfied by all natural languages. If there are 47 Greenberg Universals, F is isomorphic to

{f, t}^{47}

, where

f

stands for false and

t

for true. The Greenberg Universals can be seen as a map

GU

GU : G \to F

where, for

G \in G

GU (G)

is a string of length 47 specifying whether G satisfies the first attribute (

t

), does not satisfy the second attribute (

f

), etc.

Now, the Universal Grammar

UG

and the Greenberg Universals

GU

can be seen as maps

P \overset{UG}{⟶} G \overset{GU}{⟶} F

where the universality of the Universal Grammar translates to the mathematical statement that

UG

be surjective, while the universality of the Greenberg Universals translates to the statement that the image of

GU

has a single point, namely

{t, t, \dots, t}

, that is, all grammars in

G

have those attributes. In conclusion, mathematically, the two universality statements are opposite: One is to the effect that a given map is a parametrization, whereas the other states that all elements in a set share a set of properties. Note also that, if the goal is to characterize

G

, this corresponds to the co-domain of

UG

and the domain of

GU

. We are aware that such interpretation may be riddled with various issues arising from the different nature of the two approaches.

Finally, we note that it is unclear whether the Universal Grammar or the Greenberg Universals exhibit universality of the mechanistic or emergent type.

4. Writing of languages

The writing of languages was a major technological innovation, which arose independently in various cultures and became a cornerstone of all emerging civilizations. As pointed out by Stanislas Dehaene, writing could be understood as a virus: from its original creation in Mesopotamia, it massively spread to all neighbouring cultures [68]. Writing and reading enabled the storage and transmission of information in time and space.

The emergence of writing required a fortunate combination of already-present brain circuits; similarly, the transition to a reading brain involved a blend of contingency and inevitability. While reading and writing only entered the cognitive scene a few thousand years ago, once this cultural innovation emerged it became widespread [69]. The cultural transmission of these capabilities was not only affected by the still-evolving writing systems, but also by the anatomical and perceptual constraints placed by human brains. For example, written symbols were spatially localized and well-contrasted, exploiting the feature of the human eye by which a reduced area of the retina (the fovea) can capture an item in a single eye fixation. In this process, a revolutionary turn occurred: The transition to alphabetic languages, by which as a small inventory of basic symbols representing sounds can be combined to form syllables and words. As we shall discuss very soon, this transition can be seen as a jump to universality.

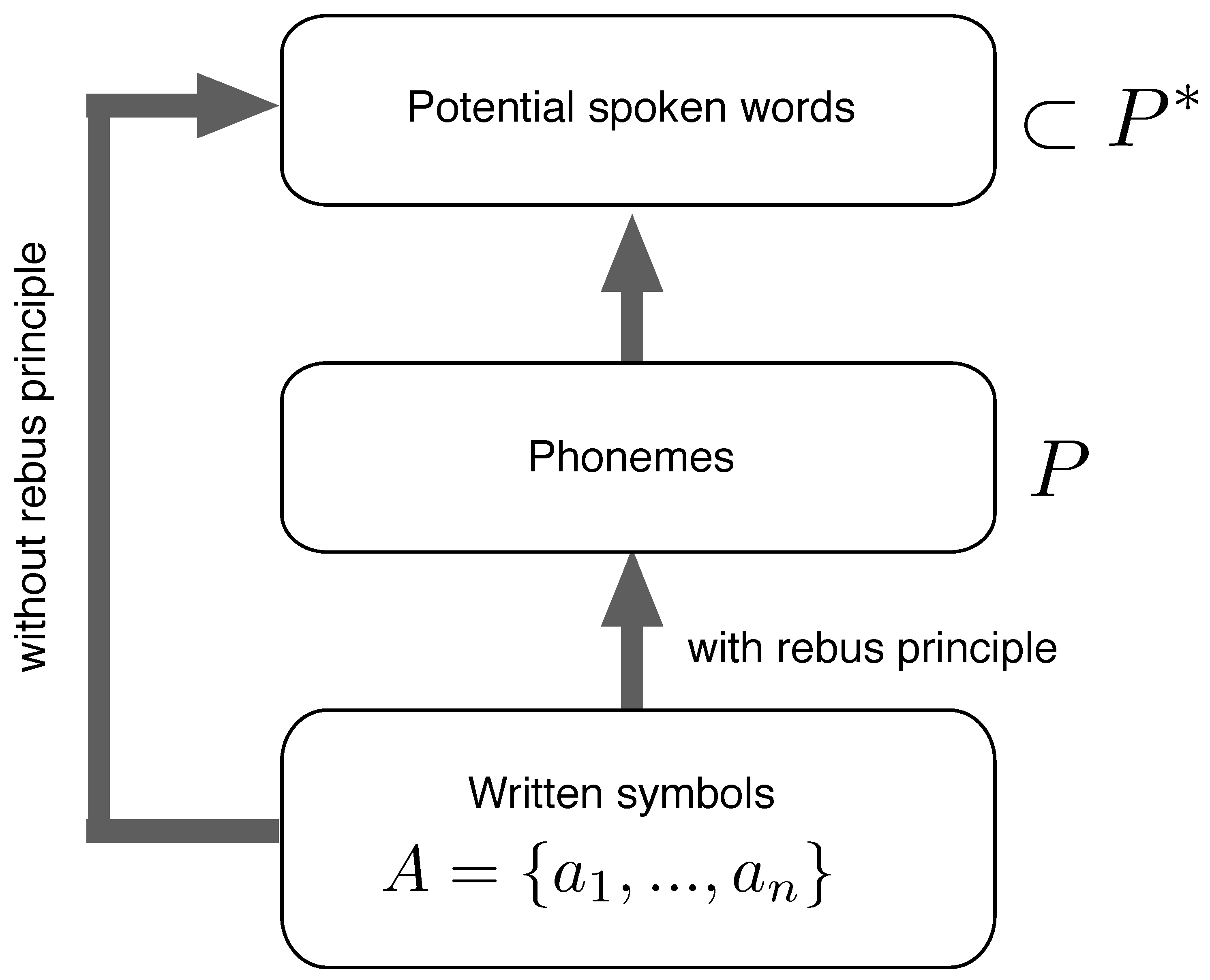
So let us consider notions of universality in the written representation of natural languages. In some writing systems, symbols represent objects or concepts. A prominent example are pictograms such as Preprints 99470 i001

or the ideographic writing system Blissymbolics. These writing systems do not obey the so-called rebus principle, by which symbols represent phonemes, instead of spoken words [70]. Since the phonemes of a language constitute a finite alphabet P, and spoken words can be identified with finite strings of phonemes (i.e. elements of

P^{*}

), it follows that in writing systems using the rebus principle, a finite number of symbols suffices to represent an unbounded number of words. This is in opposition to writing systems that do not (exclusively) use the rebus principle, where a new lexical item6 generally leads to the introduction of a new symbol.

This brings us to our definition of universal writing systems:

A writing system for a natural language is universal if it can represent any possible lexical item with a finite number of symbols.

The basic structure of universality is instantiated by letting C be the set of possible lexical items, R the relation of written representation, and u the finite repertoire of symbols (we shall be more specific below). Note that ‘possible’ is an important qualification in this definition, as every natural language has a finite number of lexical items and hence a finite representation, but not necessarily a finite representation of any possible lexical item. While we cannot characterize (or even grasp) the set of possible lexical items, we posit that it be unbounded, and that suffices for our argument.

More formally, we can model the generation of words as a map. Let

A = {a_{1}, . . ., a_{n}}

denote the alphabet, that is, the finite repertoire of symbols. Let

A^{*}

denote the set of finite and ordered sequences of symbols of A, and let

x \in A^{*}

be one such sequence. Let S denote the set of lexical items of a spoken language. As mentioned above, if S denotes the set of actual spoken lexical items, then S is finite; if it is the set of possible spoken lexical items, then we contend it is unbounded. The following argument holds for either case. Writing such lexical items can be seen as a map r (for ‘representation’),

r : S \to A^{*} .

The basic structure of universality (cf. Section 2) is reproduced by letting

u = A

C = S

, and

(A, s) \in R \Leftrightarrow \exists x \in A^{*} : r (s) = x .

That is, the alphabet A and a spoken word s are in relation R if s can be represented as a string of elements of A. If relation R holds for all

s \in S

, the writing system given by A and r is universal.

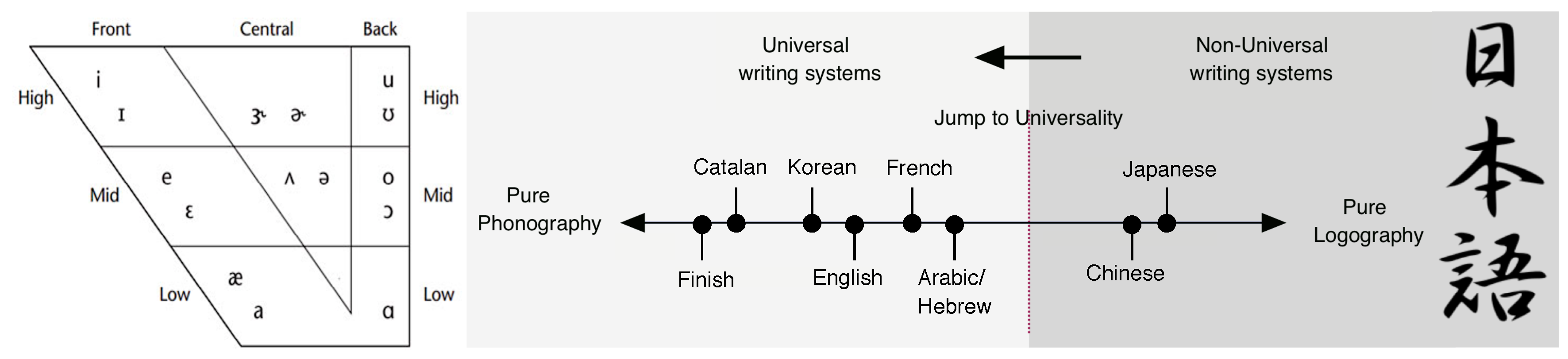
Writing systems using exclusively the rebus principle are finite, and thus universal according to our definition (Figure 4). They exploit the fact that a finite number of phonemes give rise to an unbounded number of spoken words. That is, ultimately they exploit the fact that the phonetic code itself is finite. Examples are the Latin, Cyrillic, Greek or Korean alphabet. The transition from writing systems without the rebus principle to those with it can be seen as a jump to universality (see Figure 5). Note that this universality is of the mechanistic type (cf. Section 1).

We remark that the rebus principle requires that there be a map from sounds to symbols, yet the degree to which this map is one-to-one depends on the orthography of the language. In some languages (e.g. Finnish) this map is quite faithful, i.e. close to a bijection, whereas for others it is far from so (e.g. Arabic and Hebrew generally do not write vowels, and English is well-known for its intrincate and sometimes inconsistent spelling rules). On the other hand, the writing systems of Chinese and Japanese partially employ the rebus principle in the creation of characters (but not only), so generally necessitate an unbounded number of characters to represent an unbounded number of words (Figure 5). In this context, some have suggested that the rebus principle triggered the transition from proto-writing to full-writing (see [70, p.89]).

Finally, we note that precisely because pictograms are detached from phonetics, they can be ‘understood’ by speakers of different languages, provided there is a shared cultural background. This is why they are used in public spaces like airports, on clothing labels, and to indicate facilities such as bathrooms or pharmacies. As a matter of fact, this widespread comprehensibility is often the very reason for their introduction. In this sense, pictographic writing systems are more universal than writing systems with the rebus principle, precisely becuase the former decouple representation from phonetics. This somewhat paradoxical situation can be phrased in terms of a tension between the universality of a pictographic code, accessible to speakers of different languages, and a code with the rebus principle, which systematically encodes an unbounded number of lexical items.

Ultimately, what is at stake in this discussion is Leibniz’ dream of a Characteristica Universalis, an idea borrowed from Ramon Llull [71]. The Characteristica Universalis is supposed to be an artificial formal language that establishes a clear and unambiguous correspondence between symbols and concepts [72, Chapter 2]. Leibniz envisioned the program as consisting of three key steps: (i) to systematically identify simple concepts, (ii) to choose signs or characters to designate these concepts, constituting a kind of universal alphabet for the artificial language, and (iii) to develop a combinatorial method governing the combination of these concepts. Such an artificial formal language should allow to resolve any dispute through calculation.7 It remains uncertain whether the number of simple concepts in (i) should be finite. What is even more uncertain, and of greater significance, is whether a Characteristica Universalis can exist at all. Addressing this question requires facing the challenging question of the extent to which to think is to compute.

5. Emergent language universals

We now turn to universality in language as usually understood in statistical physics. In this section, universality will be of the emergent type (cf. Section 1). As we will see below, the transition to universality occurs when a certain complexity threshold in the linguistic code is overcome. This phenomenon can be studied adopting a strategy involving asymptotic reasoning [48,73], which results in a massive collapse of degrees of freedom, which we (and others) associate with universality. In other words: beyond a certain size/degree of internal complexity, a single parameter suffices to describe the macroscopic behaviour of a system with an a priori gigantic amount of degrees of freedom. As mentioned in the introduction, a paradigmatic example is the scaling exponents around critical points in statistical physics. We will see that the emergence of a remarkably recurrent pattern in the statistics of word counts—the so-called Zipf’s law—seems to be linked to the universality of writing systems of Section 4.

We will first describe the emergence of Zipf’s law when a code breaks the barrier of bounded information content, as well as its role as an attractor for such codes (Section 5.1). Then we will compare Zipf’s law universality to Turing machine universality (Section 5.2).

5.1. Zipf’s law: Statement and origin

Let us start with a set of codewords L sampled from the whole repertoire of codewords defining a language

\tilde{L}

, i.e.

L \subset \tilde{L}

.8 While we think of codewords as finite concatenations of the finite elements of the alphabet in the phonetic writing system, they can also stand for sequences of bits representing sentences. By construction, our set L is finite, with

| L |

codewords.

Given a sample L of a natural language, we consider the statistical distribution of word abundances. Despite the differences between word inventories, a strong statistical regularity is found throughout all studied languages, leading to a sole candidate of universal pattern (in the sense of statistical physics): Zipf’s law [74,75]. To present it, let us label the words

w_{i} \in L

by rank, so that _i is attached to the i-th most common word in the inventory under consideration. Zipf’s law states that the probability to encounter

w_{i}

p (w_{i})

, falls off as

\begin{matrix} p (w_{i}) & = & \frac{1}{Z} i^{- γ}, \end{matrix}

(2)

where Z is a normalisation factor,

Z = \sum_{i \leq | L |} i^{- γ} .

Interestingly,

γ

is very close to one in most human languages and complex communication systems9 [77,78,79], even beyond the communication/information theoretic framework [80,81]. Roughly speaking, Zipf’s law says that the most frequent word will appear twice as often as the second most frequent word, three times as often as the third one, and so on (see Figure 6).

This massive regularity in human languages motivates us to term it (tentatively) universal of the emergent type, as a single scaling exponent characterizes presumably all known languages (provided the sample L is large enough). But there is more: such statistical pattern can be connected with the universality of writing systems, to which we now turn.

Many mechanisms have been postulated to explain the appearance of Zipf’s law [77,78,80,81,82]. For communication systems, most frameworks assume a type of coding/decoding tension that limits the actual configurations of the code [77,78,79]. Without delving into the formal details of these communicative conflicts, the key observation is that the potential informative content of the code is constrained, and hence lower than the maximum entropy configurations found in equilibrium.

Slightly more formally, and following the frame of [79,82,83], let us consider L of page Section 5.1, or rather, a sequence thereof

{L_{n}}

, where each is

L_{n} \subset \tilde{L}

L_{1} \subseteq L_{2} \subseteq \dots \subseteq L_{n} \subseteq L_{n + 1} \dots,

and such that

| L_{n} | \to \infty as n \to \infty .

(3)

That is, the language

\tilde{L}

may point to an unbounded number of referential values. If

\tilde{L}

can be expressed as

\tilde{L} \subseteq A^{*} where A is a finite alphabet

(4)

then A (as a writing system) is universal in the sense of Section 4.10 Let the Shannon entropy H measure the informative content (per signal) of a code. For a language

L_{n}

it is given by

H (L_{n}) = - \sum_{i \leq | L_{n} |} p_{n} (w_{i}) log p_{n} (w_{i}),

where

p_{n} (w_{i})

is the probability of appearance of codeword

w_{i}

in language

L_{n}

[84]. The Shannon entropy measures the amount of information that could be transmitted through the channel if the language sample

L_{n}

is the source of an information system. Crucially, condition (3) does not guarantee that the informative capacity of code

L_{n}

grows unboundedly with n, as the information content depends on the statistical appearance of the codewords. We need, in addition, that

H (L_{n}) \to \infty as n \to \infty .

(5)

If this condition is satisfied, the existence of an

\tilde{L}

such that (4) holds is guaranteed by the finite value of the Shannon entropy for each

L_{n}

. Specifically, within the Shannon–Fano coding strategy, the value of the entropy corresponds to the average length per codeword in a prefix-free coding scheme based on a finite alphabet. The finite value of the entropy, while unbounded, ensures that any codeword of any language sample

L_{n}

will be finite. We observe that whereas

H (L_{n}) \to \infty

implies that

| L_{n} | \to \infty

, the converse need not hold.

We now turn our attention to the consequences of the communicative conflicts/constraints underlying the information-theoretic derivations of Zipf’s law. The functional H reaches its maximum at [84]

H_{\max} (L_{n}) = log | L_{n} | when p_{n} (w_{i}) = \frac{1}{| L_{n} |} for all w_{i} .

The communicative conflicts/constraints entail that such maximum is unattainable.11 Instead, the maximum attainable may be

H (L_{n}) = μ log | L_{n} | for a μ \in (0, 1) .

(6)

This result could be the outcome of the following optimization process (described more formally in Appendix B).

Assume first that

| L_{n + 1} | > | L_{n} |

for all n. We start increasing the sample of the code or, alternatively, we let it grow. The code will change at every step n as new codewords will be incorporated with non-vanishing probability to occur, for otherwise (5) would not be satisfied. However, the system will try to retain its previous structure, which can be seen as an example of the least effort principle in human behaviour [74], or a footprint of the minimization of the action in physical terms. To state this condition, define the mutual information between

L_{n}

and

L_{n + 1}

I (L_{n} : L_{n + 1}) = H (L_{n}) - H (L_{n} | L_{n + 1}),

where

H (L_{n} | L_{n + 1})

is the conditional entropy of

L_{n}

with respect to

L_{n + 1}

[84]. The least effort principle translates to the statement that the mutual information between

L_{n}

and

L_{n + 1}

be maximized, implying that the change between both coding schemes is minimum. Under these conditions, all solutions of the optimization problem converge for large n to

p (w_{i}) \propto i^{- γ} with γ = 1 .

What makes this result remarkable is its independence of the actual value of

H (L_{n})

as soon as this is unbounded and lower than the absolute maximum. Under these conditions, all distributions ‘collapse’ to Zipf’s law [79,82,83].

In summary, if a finite alphabet A is universal in the sense of Section 4, so that (4) holds, and the sequence of languages

{L_{n}}

is such that their codewords, i.e.

w_{i} \in A^{*}

and their probabilities

p_{n} (w_{i})

are such that the information content is unbounded, i.e. (5) holds, then the distribution of codewords at the limiting language,

{p (w_{i})}_{i}

, is expected to display a universal statistical pattern (of the emergent type, i.e. Zipf’s law).

If we consider a writing system not exclusively based on the rebus principle, such as Chinese’s (not pinyin), the relative frequency of words would also follow Zipf’s law. While this writing system would exhibit the form of universality given by Zipf’s law, it would not be universal according to the definition of Section 4.

5.2. On the universality of Zipf’s law and Turing machines

We have seen that the unboundedness of Shannon’s entropy (expressed in equation (5)) leads to Zipf’s law, and we want to emphasize the mildness of this condition. The parameter

μ

in (6) could be very close to 0 or to 1—say, 0.001 or 0.999—representing disparate values of the limiting entropy. Yet, strikingly, the limiting distribution is the same. This suggests that, upon reaching Zipf’s law, there appears to be a complexity threshold that cannot be exceeded. This is reminiscent of Turing machines, where simpler kinds of automata (finite state automata, pushdown automata and linear bounded automata [32]) are such that their computational capabilities increase by the addition of certain features (such as a stack or the capability of the head to overwrite); yet, as soon as Turing machines are reached, the definition is very robust to changes (multiple tapes, nondeterminism of the head, etc).

Crucially, though, Turing machines jump to universality because of their ability to interpret their own source code, from where it follows that there exist certain so-called universal Turing machines capable of computing any computable function—a single Turing machine can do the job of any other. This type of universality is of the mechanistic type (cf. Section 1; see also [44]), as a single machine can explore all complexity of a certain domain (that of computable functions).

Reaching Zipf’s law bears similar features to jumping to computational universality. As long as we are in a constrained scenario with an unbounded information content, it appears both as an attractor and as a boundary, since lower exponents seem to be impossible to reach through a process of code growing. But it also has distinctive features not encountered in the universality of Turing machines, such as the fact that the growing process results in a self-similar behavior, like the Ising model at criticality. The latter explains the phrase ‘life at the edge of chaos’, i.e. right at the border between the ordered and disordered phase [85].

In conclusion, universal Turing machines (the key example of mechanistic universality) and Zipf’s law (a good example of emergent universality) show some similarities and dissimilarities. It is unclear whether there is (or, even, ought to be) any causal relation between the two.

6. Summary and Outlook

In summary, we have (attempted to) establish a common ground to study and compare universalities of different aspects of language. In particular, we have defined the basic structure of universality and recursion, and have identified it in generative grammars, the Universal Grammar, Greenberg Universals, writing systems, and Zipf’s law. On some occasions, we have examined the boundary of universality with regard to the transition from non-universal to universal. We have also posited that there are two ‘flavours’ of universality, termed mechanistic and emergent, which we have identified and compared whenever possible.

Let us now turn to the outlook of this work. On the question of grammars, recent works have seen spin models as formal languages, and consequently physical interactions as grammars [86,87]. It would be interesting to shine the light of universality for natural languages on spin models, and to explore its implications.

Regarding scriptures, our main conclusion was that the universality of writing systems was enabled because the very code of language is universal, that is, the phonetic code is finite. We note that this is consistent with Deutsch’s suggestion [41] that a discrete code is a necessary condition for the jump the universality, as only discrete codes allow for error correction.

Still on the topic of language representations, an interesting question concerns sign languages, as they a priori would not need to draw any connection to phonetics. How would an analogue to the rebus principle for sign languages be defined? In fact, we need not address this question, as sign language do correlate to phonetics, and have a finite repertoire of signs by virtue of the finiteness of phonetical traits. The same is true for tactile languages such as Braille.

Analogously to the representation of language, the representation of music is also discrete and finite, as mentioned in [41]. Despite the fact that frequency is continuous, the representation of music uses a discrete number of notes (C, C^♯, D, D^♯, E, F, F^♯, G, G^♯, A, A^♯, B), because the code is finite.12 The same is true for volume: despite its continuity in the physical world, the dynamic markings in partitures are discrete (ppp, pp, p, mp, mf, f, ff, fff). In this sense, notes play an analogous role to phonemes in language—they are abstract and discrete—and partitures represent music as books represent language.

Returning to language, we may wonder: In what other way could a representation of language be finite? Without stepping on the muddy terrain of the relation between language and thought (see, e.g., [88]), this question brings us back to Leibniz’ quest for an alphabet of thought, the Characteristica Universalis (see e.g. [72, Chapter 2] or [50]), and the many fascinating implications derived from it.

Acknowledgements.— GDLC’s research was funded by the Austrian Science Fund (FWF) [START Prize Y-1261-N]. For open access purposes, the author has applied a CC BY public copyright license to any author accepted manuscript version arising from this submission. B.C.-M. acknowledges the support of the field of excellence ‘Complexity of life in basic research and innovation’ of the University of Graz. RS thanks Luis F. Seoane for so many discussions about language complexity and the Santa Fe Institute, where many of these ideas were explored.

Appendix A. Infinite sets with a finite description

In Section 3.1 we described that the generative grammar of a formal language is universal for the language, and explained that the vast majority of languages do not have a grammar—languages with a grammar are extremely rare. In this appendix, we illustrate that this is not exclusive to languages, but provide a broader perspective of this fact by showing that is also the case for other infinite sets, where having a finite handle is the exception.

Table A1. Equivalences between objects with and without structure, where the object is a formal language L or an attribute

g : S \to 2

. ‘With structure’ means recursive, where recursion is a form of universality (cf. Section 1), where the finite description (second row) is universal for the set of the elements in the top row. ‘Without structure’ means that the only description is the element itself; these objects cannot be cast in the basic structure of recursion.

Table A1. Equivalences between objects with and without structure, where the object is a formal language L or an attribute

g : S \to 2

	Language L	Attribute $g : S \to 2$
With structure	With grammar	Computable
Finite description	Grammar	T’s transition rules
Without structure	Without grammar	Non-computable
Infinite ‘description’	Listing all elements in L	Specifying $g (x)$ for all $x \in S$

To this end, denote by

2 = {0, 1}

the binary alphabet, and let S be the strings of elements of

2

S 2^{*} .

13 S is isomorphic to the set of the natural numbers, so its cardinality is countable infinite,

| S | = ℵ_{0}

. Let us now consider a binary attribute g of S, which we describe as a function

\begin{matrix} g : S \to 2 \end{matrix}

so that

g (x) = 1

if x has that attribute, and

g (x) = 0

if it does not. For example, g could represent the attribute ‘being odd’, in which case

\begin{matrix} g : x \mapsto \{\begin{matrix} 1 & if x is odd \\ 0 & if x is even \end{matrix} \end{matrix}

Or it could represent ‘being prime’, in which case it would map

2, 3, 5, 7, 11, 13, 17, 19, 23, \dots

to 1 and composite numbers to 0. These examples are very simple—as a matter of fact, most examples we can think of are simple, or ‘tidy’ as Moore puts it [50, Chapter 12]. The point is that simple examples are extremely rare: a generic g will not admit any finite description—it has ‘no structure’, it is too ‘untidy’, and the only way of describing it is by giving g itself, i.e. listing all of its elements.

Now, let us identify attribute g with its extension, i.e. the set of elements where it is true,

{x \in S ∣ g (x) = 1} .

Then the set of all attributes corresponds to the power set of S, i.e. the set of all subsets of S. So we may write

℘ (S) = {g : S \to 2} .

Equivalently, each attribute g can be uniquely associated with the language

L_{g}

that contains the graph of g, i.e. the set of pairs

(x, g (x))

, viz.

L_{g} {(x, g (x)) ∣ x \in S} .

The set of all such languages is

L_{S} {L_{g} ∣ g : S \to 2} .

Which attributes of S (equivalently: languages in

L_{S}

) admit a finite description? We have seen in Section 3.1 that a language L admits a finite description precisely when it has a grammar G,

L = L 〈 G 〉

, and that G precisely provides such a finite description. Similarly, an attribute

g : S \to 2

is computable if its extension is the language accepted by a Turing machine T,

{x \in S ∣ g (x) = 1} = L (T) .

In this case, the finite set of transition rules of T serves as the finite description of g. If g is not computable, its only description consists of listing all

x \in S

such that

g (x) = 1

(Table A1).

We note that a similar distinction applies to transcendental versus algebraic reals. A generic

x \in R

is transcendental, i.e. not algebraic, where x is algebraic if it is the solution of a finite set of polynomial equations of finite degree with integer coefficients. For example,

π

or e are transcendental, while

\sqrt{2}

is algebraic. For transcendental x, its only description is x itself, which can be provided as the infinite expansion of x in, say, the binary basis. Again, essentially all reals are transcendental, precisely because algebraic reals are countable, whereas transcendental are not.

As a side note, we remark that the distinction between attributes described in finite and infinite terms can hold philosophical significance. For example, Leibniz relies on this distinction as the foundation for discerning between attributes that are true by necessity (i.e. which follow from the truths of reason, such as the principle of identity) versus attributes that are true by fact (i.e. they follow from the truths of fact, such as the principle of sufficient reason). The first have a finite description, whereas the second have an infinite one. This is a key aspect of his account of contingency [72, Chapter 5].

Appendix B. Communicative conflicts leading to Zipf’s law

Here we provide the optimization problem leading to Zipf’s law for languages with unbounded informative potential described in Section 5.1. We shall provide a simple version of the problem for the sake of readability; proofs can be found in [79,82,83].

Consider the setting and definitions of page 14, including the constrained information content of (6), meaning that the entropy is a constant fraction of the maximum entropy value, which is

log | L_{n} |

for every n. Assume, for now, that the following limit exists for all k:

ϕ_{k} lim_{n \to \infty} \frac{p_{n} (w_{k + 1})}{p_{n} (w_{k})} .

Due to the unboundedness of the Shannon entropy, we consider the so-called normalized entropy

h (L_{n})

h (L_{n}) \frac{H (L_{n})}{log | L_{n} |} .

After these preliminary steps, we are now ready to define the optimization problem:

Start from a given sample $L_{1} \subset \tilde{L}$ with distribution $p_{1}$ . For every $k \geq 1$ , compute $ϕ_{k}$ under the following conditions:

(i): For all n it must hold that $h (L_{n}) = μ$ (where $μ \in (0, 1)$ is fixed);
(ii): $I (L_{n} : L_{n + 1})$ is maximal for all n.

The first condition ensures that the code has an unbounded information content (as the sample size grows

| L_{n} | \to \infty

), albeit lower than the maximum entropy value. The second condition imposes that the code be maximally conserved throughout the growing process.

The optimization problem described above can be informally interpreted as follows. Construct a series of codes

L_{1}, L_{2}, \dots, L_{n}, \dots

whose associated codeword probability distributions are constrained by an entropy of

μ log | L_{n} |

, and such that, as n increases, a specific relation between any two successive codes is imposed, namely, their mutual information be maximized. Note that, without this path-dependence requirement, one would be considering a series of unrelated problems, each bound by a specific entropy value. The critical aspect of our problem is, therefore, the evolutionary nature of the code development process.

Under these conditions, one can prove that there exists a non-increasing sequence

{ϵ_{n} > 0}

with

ϵ_{n} \to 0

n \to \infty

, which for all k

{(\frac{k}{k + 1})}^{1 + ϵ_{n}} < \frac{p_{n} (w_{k + 1})}{p_{n} (w_{k})} < {(\frac{k}{k + 1})}^{1 - ϵ_{n}},

leading to:

ϕ_{k} = \frac{k}{k + 1} for all k .

For very large n, we can approximate the asymptotic behaviour of

p_{n}

constructively by fixing

p_{n} (w_{1})

and exploiting the above result. Namely, let us for now

p_{n} (w_{1})

use as a parameter whose value will be later determined through normalization.

p_{n} (w_{2})

can be approximated by

p_{n} (w_{2}) = \frac{p_{n} (w_{1})}{2} .

Analogously,

p_{n} (w_{3})

can be approximated by

p_{n} (w_{3}) = \frac{2 p_{n} (w_{2})}{3} = \frac{p_{n} (w_{1})}{3},

and, by a similar reasoning,

p_{n} (w_{k})

for any

k < n

p_{n} (w_{k + 1}) = \frac{p_{n} (w_{1})}{k + 1} .

Due to normalization, we find that

p_{n} (w_{1})

is equal to the inverse of the normalization constant

Z_{n}

p_{n} (w_{1}) \sum_{k = 1}^{| L_{n} |} \frac{1}{k} = \frac{1}{Z_{n}} \sum_{k = 1}^{| L_{n} |} \frac{1}{k} .

Since

\sum_{k = 1}^{n} 1 / k \approx log n

for large n, one arrives at

Z_{n} \approx log | L_{n} |

, leading to Zipf’s law,

p_{n} (w_{k}) \approx \frac{1}{Z_{n}} k^{- 1} .

References

Maynard Smith, J.; Szathmáry, E. The Major Transitions in Evolution; Oxford University Press: Oxford, UK, 1995. [Google Scholar]
Hauser, M.D.; Chomsky, N.; Fitch, W.T. The faculty of language: what is it, who has it, and how did it evolve? Science 2002, 298, 1569–1579. [Google Scholar] [CrossRef] [PubMed]
Bickerton, D. Language and species; University of Chicago Press, 1990. [Google Scholar]
Nowak, M.A.; Komarova, N.L.; Niyogi, P. Computational and evolutionary aspects of language. Nature 2002, 417, 611–617. [Google Scholar] [CrossRef]
Jackendoff, R. Précis of foundations of language: Brain, meaning, grammar, evolution. Behav. Brain Sci. 2003, 26, 651–665. [Google Scholar] [CrossRef]
Harley, T.A. The psychology of language: From data to theory; Psychology press, 2013. [Google Scholar]
Zanette, D.H. Analytical approach to bit-string models of language evolution. Int. J. Mod. Phys. C 2008, 19, 569–581. [Google Scholar] [CrossRef]
Solé, R.V.; Corominas-Murtra, B.; Fortuny, J. Diversity, competition, extinction: the ecophysics of language change. J. R. Soc. Interface 2010, 7, 1647–1664. [Google Scholar] [CrossRef] [PubMed]
Cavalli-Sforza, L.L. Genes, peoples, and languages. Proc. Natl. Acad. Sci. USA 1997, 94, 7719–7724. [Google Scholar] [CrossRef] [PubMed]
Steels, L. Evolving grounded communication for robots. Trends in cognitive sciences 2003, 7, 308–312. [Google Scholar] [CrossRef] [PubMed]
Steels, L. The Talking Heads experiment: Origins of words and meanings; Language Science Press, 2015; Volume 1. [Google Scholar]
Lake, B.M.; Ullman, T.D.; Tenenbaum, J.B.; Gershman, S.J. Building machines that learn and think like people. Behav. Brain Sci. 2017, 40, e253. [Google Scholar] [CrossRef] [PubMed]
Solé, R.V.; Corominas-Murtra, B.; Valverde, S.; Steels, L. Language networks: Their structure, function, and evolution. Complexity 2010, 15, 20–26. [Google Scholar] [CrossRef]
Borge-Holthoefer, J.; Arenas, A. Semantic networks: Structure and dynamics. Entropy 2010, 12, 1264–1302. [Google Scholar] [CrossRef]
Cong, J.; Liu, H. Approaching human language with complex networks. Phys. Life Rev. 2014, 11, 598–618. [Google Scholar] [CrossRef]
Stella, M.; Beckage, N.M.; Brede, M.; Domenico, M.D. Multiplex model of mental lexicon reveals explosive learning in humans. Sci. Rep. 2018, 8, 2259. [Google Scholar] [CrossRef]
Seoane, L.F.; Solé, R. The morphospace of language networks. Sci. Rep. 2018, 8, 10465. [Google Scholar] [CrossRef]
Baronchelli, A.; Felici, M.; Loreto, V.; Caglioti, E.; Steels, L. Sharp transition towards shared vocabularies in multi-agent systems. J. Stat. Mech. Theory Exp. 2006, 2006, P06014. [Google Scholar] [CrossRef]
Corominas-Murtra, B.; Fortuny, J.; Solé, R. Emergence of zipf’s law in the evolution of communication. Phys. Rev. E 2011, 83, 036115. [Google Scholar] [CrossRef]
Luque, J.; Luque, B.; Lacasa, L. Scaling and universality in the human voice. J. R. Soc. Interface 2015, 12, 20141344. [Google Scholar] [CrossRef]
Torre, I.G.; Luque, B.; Lacasa, L.; Luque, J.; Hernández-Fernández, A. Emergence of linguistic laws in human voice. Sci. Rep. 2017, 7, 43862. [Google Scholar] [CrossRef]
DeGiuli, E. Random language model. Phys. Rev. Lett. 2019, 122, 128301. [Google Scholar] [CrossRef]
Seoane, L.F.; Solé, R. Criticality in pareto optimal grammars? Entropy 2020, 22, 165. [Google Scholar] [CrossRef]
Nowak, M.A.; Krakauer, D.C. The evolution of language. Proc. Natl. Acad. Sci. USA 1999, 96, 8028–8033. [Google Scholar] [CrossRef]
Pagel, M. Human language as a culturally transmitted replicator. Nat. Rev. Genet. 2009, 10, 405–415. [Google Scholar] [CrossRef]
Számadó, S.; Szathmáry, E. Selective scenarios for the emergence of natural language. Trends Ecol. Evol. 2006, 21, 555–561. [Google Scholar] [CrossRef]
Tomasello, M. Origins of human communication; MIT Press, 2010. [Google Scholar]
Pulvermüller, F. Words in the brain’s language. Behav. Brain Sci. 1999, 22, 253–279. [Google Scholar] [CrossRef]
Christiansen, M.H.; Chater, N. Language as shaped by the brain. Behav. Brain Sci. 2008, 31, 489–509. [Google Scholar] [CrossRef]
Berwick, R.C.; Friederici, A.D.; Chomsky, N.; Bolhuis, J.J. Evolution, brain, and the nature of language. Trends Cogn. Sci. 2013, 17, 89–98. [Google Scholar] [CrossRef]
Dehaene, S.; Roumi, F.A.; Lakretz, Y.; Planton, S.; Sablé-Meyer, M. Symbols and mental programs: a hypothesis about human singularity. Trends Cogn. Sci. 2022. [Google Scholar] [CrossRef]
Kozen, D.C. Automata and Computability; Springer, 1997. [Google Scholar]
Prusinkiewicz, P.; Lindenmayer, A. The algorithmic beauty of plants; Springer Science & Business Media, 2012. [Google Scholar]
Stanley, H.E. Scaling, universality, and renormalization: Three pillars of modern critical phenomena. Rev. Mod. Phys. 1999, 71, S358. [Google Scholar] [CrossRef]
Solé, R.; Manrubia, S.C.; Luque, B.; Delgado, J.; Bascompte, J. Phase transitions and complex systems: Simple, nonlinear models capture complex systems at the edge of chaos. Complexity 1996, 1, 13–26. [Google Scholar] [CrossRef]
Drossel, B. Biological evolution and statistical physics. Adv. Phys. 2001, 50, 209–295. [Google Scholar] [CrossRef]
Szathmáry, E. Toward major evolutionary transitions theory 2.0. Proc. Natl. Acad. Sci. USA 2015, 112, 10104–10111. [Google Scholar] [CrossRef]
Chomsky, N. Cartesian Linguistics: A Chapter in the History of Rationalist Thought; Cambridge University Press: New York, NY, USA; London, UK,, 1966. [Google Scholar]
Chomsky, N. Language and problems of knowledge : the Managua lectures; MIT Press: London, UK, 1988; Old accession number 11728. [Google Scholar]
Greenberg, J.H. Universals of Language; The M.I.T. Press, 1963. [Google Scholar]
Deutsch, D. The beginning of infinity. Begin. Infin. Allen Lane 2011. [Google Scholar]
De las Cuevas, G. Universality everywhere implies undecidability everywhere. FQXi Essay 2020. [Google Scholar]
De las Cuevas, G.; Cubitt, T.S. Simple universal models capture all classical spin physics. Science 2016, 351, 1180–1183. [Google Scholar] [CrossRef]
Gonda, T.; Reinhart, T.; Stengele, S.; De les Coves, G. A Framework for Universality in Physics, Computer Science and Beyond. arXiv 2023, arXiv:2307.06851. [Google Scholar]
Yanofsky, N.S. A universal approach to self-referential paradoxes, incompleteness and fixed points. Bull. Symbolic Logic 2003, 9, 362–386. [Google Scholar] [CrossRef]
Lawvere, F.W. Diagonal arguments and cartesian closed categories. Lect. Notes Math. 1969, 92, 134–145. [Google Scholar]
Priest, G. Beyond the limits of thought; Clarendon Press: Oxford, UK, 2001. [Google Scholar]
Batterman, R.W. The Devil in the Details: Asymptotic Reasoning in Explanation, Reduction, and Emergence; Oxford University Press: New York, NY, USA, 2002. [Google Scholar]
De les Coves, G. Quantum Theory: Ideals, Infinities and Pluralities. In Open Systems: Physics, Metaphysics, and Methodology; Cuffaro, M., Hartmann, S., Eds.; Oxford University Press, 2024. [Google Scholar]
Moore, A.W. The Infinite, 3rd ed.; Routledge, 2019. [Google Scholar]
Chomsky, N. Syntactic Structures; Mouton and Co.: The Hague, The Netherlands, 1957. [Google Scholar]
Hopcroft, J.E.; Ullman, J.D. Introduction to Automata Theory, Languages, and Computation; Addison-Wesley Publishing Company, 1979. [Google Scholar]
Cottingham, J. Rationalism; Paladin: London, UK, 1984. [Google Scholar]
Cottingham, J. The Rationalists; Oxford University Press: New York, NY, USA, 1988. [Google Scholar]
Chomsky, N. Reflections on Language; Temple Smith, 1975. [Google Scholar]
Radford, A. Syntactic theory and the acquisition of English syntax; Blackwell: Oxford, UK, 1990. [Google Scholar]
Christiansen, M.H.; Collins, C.; Edelman, S. Language Universals; Oxford University Press, 2009. [Google Scholar]
Francez, N.; Wintner, S. Unification Grammars; Cambridge University Press, 2011. [Google Scholar]
Chomsky, N. Aspects of the theory of syntax; MIT Press, 1965. [Google Scholar]
Baker, M.C. The atoms of language; Basic Books, 2001. [Google Scholar]
Nowak, M.A. Evolutionary dynamics: exploring the equations of life; Harvard University Press, 2006. [Google Scholar]
Anderson, S.R. Languages: A very short introduction; Oxford University Press, 2012. [Google Scholar]
Moro, A. Impossible languages; MIT Press: 2016.
Solé, R.V. La lógica de los monstruos; Tusquets, 2016. [Google Scholar]
Deutsch, D. Constructor Theory. Synthese 2012, 190, 18. [Google Scholar] [CrossRef]
Chomsky, N. The Minimalist Program; MIT Press: Cambridge, MA, USA, 1995. [Google Scholar]
Adger, D. Core Syntax: A Minimalist Approach; Oxford University Press: Oxford, UK, 2003. [Google Scholar]
Dehaene, S. Reading in the Brain: The Science and Evolution of a Human Invention; Viking, 2009. [Google Scholar]
Tuson, J. Introducció a la lingüística; Aula, 2009. [Google Scholar]
Robinson, A. Writing and script: A very short introduction; Oxford University Press, 2009. [Google Scholar]
Yates, F. The art of memory; The Bodley Head, 1966. [Google Scholar]
Antognazza, M.R. Leibniz: A very short Introduction; Oxford University Press: 2016.
Sklar, L. Physics and Chance: Philosophical Issues in the Foundations of Statistical Mechanics; Cambridge University Press: New York, NY, USA, 1993. [Google Scholar]
Zipf, G.K. Human Behaviour and the Principle of Least Effort; Addison-Wesley, 1949. [Google Scholar]
Piantadosi, S.T. Zipf’s word frequency law in natural language: a critical review and future directions. Psychon. Bull. Rev. 2014, 21, 1112–1130. [Google Scholar] [CrossRef]
Ferrer-i Cancho, R.; Solé, R. Two regimes in the frequency of words and the origins of complex lexicons: Zipf’s law revisited. J. Quant. Linguist. 2001, 8, 165–173. [Google Scholar] [CrossRef]
Harremoes, P.; Topsoe, F. Maximum entropy fundamentals. Entropy 2001, 3, 191–226. [Google Scholar] [CrossRef]
Ferrer i Cancho, R.; Solé, R.V. Least effort and the origins of scaling in human language. PNAS 2003, 10, 788. [Google Scholar] [CrossRef] [PubMed]
Corominas-Murtra, B.; Fortuny, J.; Solé, R. Emergence of zipf’s law in the evolution of communication. Phys. Rev. E 2011, 83, 03611. [Google Scholar] [CrossRef] [PubMed]
Gabaix, X. Zipf’s law for cities: An explanation. Q. J. Econ. 1999, 114, 739–767. [Google Scholar] [CrossRef]
Corominas-Murtra, B.; Hanel, R.; Thurner, S. Understanding scaling through history-dependent processes with collapsing sample space. Proc. Natl. Acad. Sci. USA 2015, 112, 5348–5353. [Google Scholar] [CrossRef] [PubMed]
Corominas-Murtra, B.; Solé, R.V. On the universality of Zipf’s Law. Phys. Rev. E 2010, 82, 011102. [Google Scholar] [CrossRef] [PubMed]
Corominas-Murtra, B.; Seoane, L.F.; Solé, R. Zipf’s Law, unbounded complexity and open-ended evolution. J. R. Soc. Interface 2018, 15, 20180395. [Google Scholar] [CrossRef] [PubMed]
Cover, T.M.; Thomas, J.A. Elements of information theory, 2nd ed.; Wiley, 2006. [Google Scholar]
Solé, R.V.; Goodwin, B. Signs of Life: How complexity pervades biology; Basic Books, 2000. [Google Scholar]
Stengele, S.; Drexel, D.; De las Cuevas, G. Classical spin Hamiltonians are context-sensitive languages. Proc. R. Soc. A 2023, 479, 20220553. [Google Scholar] [CrossRef]
Reinhart, T.; De las Cuevas, G. The grammar of the Ising model: A new complexity hierarchy. arXiv 2022, arXiv:2208.08301. [Google Scholar]
Hinzen, W.; Sheehan, M. The philosophy of universal grammar; Oxford University Press, 2013. [Google Scholar]

1	This is the one implicitly considered in [42].
2	For some perspectives on the role of infinities in physics, as well as the impossibility to conceive of certain pluralities as a unity, see [49].
3	The latter meaning of ‘all-encompassing’ is a frozen metaphor, where ‘frozen metaphor’ is itself a frozen metaphor.
4	The fact that we can conceive of objects that do not admit a finite description is remarkable in itself. However, in all fairness, perhaps we can only conceive their negation. More in Appendix A.
5	The same caveat as for the Universal Grammar applies: Is it the set of actual or possible natural languages? We assume it is the actual, but the aim is to reach the possible.
6	We adopt a broad definition of lexical item as a basic unit of the lexicon of a spoken language. This includes words, morphemes or phrasal verbs, among other basic units.
7	One can only wonder: What would the world be like if such a language were invented?
8	This L is not to be confused with a formal language such as the ones in Section 3.1.
9	There is a regime shift (around rank values of $i \sim O (10^{4})$ ) that defines a crossover between common and infrequent words in human language, where the exponent turns to $γ = 2$ [76].
10	The representation r is implicitly included in the definition of L.
11	Note that instead of imposing constraints on the system to calculate the maximum entropy à la Jaynes, we are saying that the maximum entropy distribution (e.g., the uniform one) is unattainable due to an internal conflict of the system. Consequently, the system experiences a non-equilibrium tension, making this problem distinct from a conventional maximum entropy problem with constraints.
12	We are neglecting the issue of tuning in music systems, a problem stemming from the mathematics of frequency ratios. Depending on the selected approach to the so-called comma, F^♯ may not correspond to the same frequency as G^♭, and the same discrepancy applies to other notes. As a matter of fact, this issue can be viewed as the challenge of establishing a discrete code within a continuum of frequencies, where the code must be compatible with the mathematics of frequency ratios.
13	This S is not to be confused with the set of spoken words of Section 4.

Figure 1. Human language is a multiscale phenomenon with distinct hierarchical levels ranging from phonemes at the microscale, grammar and sentences at the mesoscale, and sociocultural dynamics at the macroscale. These include: (a,b) the symbols required to build the basic units of language (signs or words), (c) the rules required to organise words in sentences (grammar), (d) the neural substrate of these processes, or (e) the role played by cultural change and social networks. While these path-dependent features have been influenced by historical contingencies, there are also universal properties that pervade language complexity. One can approach the presence of universals in natural languages from the perspective of: (f) writing systems, whose history experienced marked transitions, (g) machines and recursion, where the latter is a fundamental trait of human language. An example of a recursive tree is shown in (h).

Figure 2. (a) The basic structure of universality. Given a set C and a relation R landing in C, a finite u is universal if

(u, c) \in R

for all

c \in C

. Note that u need not be in C, that C need not be finite, and that no further property of R is required. (b) The basic structure of recursion is a special case of the basic structure of universality where u consists of a ‘mould’ and R consists of applying this mould to a base case a finite but unbounded number of times. We call such u a grammar. An example from formal language theory is a context-free grammar, such as the one that generates the language

L = {A^{n} B^{n} ∣ n \geq 0}

. Context-free languages can be recognized by pushdown automata [32].

Figure 2. (a) The basic structure of universality. Given a set C and a relation R landing in C, a finite u is universal if

(u, c) \in R

for all

c \in C

L = {A^{n} B^{n} ∣ n \geq 0}

. Context-free languages can be recognized by pushdown automata [32].

Figure 3. The Chomsky hierarchy of generative grammars categorizes them into four distinct levels: regular grammars, context free grammars, context sensitive grammars, and unrestricted grammars. Each level is strictly included in the next. Correspondingly, these grammars generate regular languages, context free languages, context sensitive languages and recursively enumerable languages.

Figure 4. In writing systems with the rebus principle, written symbols represent phonemes. In those without it, they represent spoken words. The former need only finitely many symbols, and are thus universal according to our definition. The latter require an a priori unbounded number of symbols, so are not universal.

Figure 5. Full writing systems mix phonetic symbols with logograms, with varying proportions. The jump to universality for writing systems occurs when exclusively the rebus principle is applied. Adapted from [70, p.65].

Figure 6. The statistical distribution of word frequencies in large word inventories, such as written books (here Moby Dick, inset) follows certain universal patterns such as that displayed in (a). This shows the frequency of words, ranked from the most to the least abundant, which follows a power law

p (w_{i}) \sim i^{- γ}

with a slope given by

γ \approx 1

. (b) The upper bound of the entropy

H (γ)

of a code following a power law with exponent

γ

diverges at

γ = 1

, corresponding to Zipf’s law. While the figure only shows power laws, any other function which describes the information potential will also converge to Zipf’s law.

p (w_{i}) \sim i^{- γ}

with a slope given by

γ \approx 1

. (b) The upper bound of the entropy

H (γ)

of a code following a power law with exponent

γ

diverges at

γ = 1

, corresponding to Zipf’s law. While the figure only shows power laws, any other function which describes the information potential will also converge to Zipf’s law.

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Universality and Complexity in Natural Languages: Mechanistic and Emergent

Abstract

1. Introduction

2. The basic structures of universality and recursion

3. Grammars

3.1. Generative grammars

3.2. Universal Grammar

3.3. Greenberg Universals

3.4. On the relation between UG and GU

4. Writing of languages

5. Emergent language universals

5.1. Zipf’s law: Statement and origin

5.2. On the universality of Zipf’s law and Turing machines

6. Summary and Outlook

Appendix A. Infinite sets with a finite description

Appendix B. Communicative conflicts leading to Zipf’s law

References

MDPI Initiatives

Important Links

Subscribe