Prerpints.org logo
Preprint
Article

Stable Heteroclinic Channel-based Movement Primitives: Tuning Trajectories using Saddle Parameters

Altmetrics

Downloads

91

Views

25

Comments

0

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

22 February 2024

Posted:

23 February 2024

You are already at the latest version

Alerts
Abstract
Dynamic systems which underly controlled systems are expected to increase in complexity as robots, devices, and connected networks become more intelligent. While classical stable systems converge to a stable point (a sink), another type of stability is to consider a stable path rather than a single point. Such stable paths can be made of saddles which draw in trajectories from certain regions, and then push the trajectory toward the next saddle point. These are chains of saddles are called stable heteroclinic channels (SHCs), and can be used in robotic control to represent time sequences. While we have previously shown that each saddle is visualizable as a trajectory waypoint in phase space, how to increase the fidelity of the trajectory was unclear. In this paper, we hypothesized that the waypoints can be individually modified to locally vary fidelity. Specifically, we expected that increasing the saddle value (ratio of saddle eigenvalues) causes the trajectory to slow to more closely approach a particular saddle. Combined with other parameters that control speed and magnitude, a system expressed with an SHC can be modified locally, point by point, without disrupting the rest of the path, supporting their use in motion primitives. However, even more complex trajectory shape modifications are possible. While some combinations can enable a trajectory to better reach into corners, other combinations can rotate, distort and round the trajectory in the region of a corner. In our example, modifying select saddle values produced a 32% decrease in the trajectory error of a complex trajectory produced using this system. This is an effect not visible in previous 1D studies, that can lead to different learnable and tunable representations of dynamic systems.
Keywords: 
Subject: Engineering  -   Control and Systems Engineering

1. Introduction

As we look to broaden the applications of robotic systems, the learnability, robustness and versatility of their controllers becomes critical. A versatile controller enables the robot to complete a range of tasks, robustness maintains the system’s stability through a varied parameter-space, and a learnable controller allows a user to tune the robot’s performance according to some arbitrary criteria. Stable heteroclinic channel-based movement primitives (SMPs) are a user-intuitive, tunable system for robotic control applications [1]. In this work, we explore the versatility of SMPs by using them to tune the trajectory produced by a second-order system.
Movement primitives – a popular approach to robot motion planning – provide a modular framework to build control policies [2,3]. Of these, dynamic movement primitives can produce smooth kinematic control policies for robots with a learnable, stable parameter space. Stable heteroclinic channel-based movement primitives (SMPs) are a framework which uses dynamic movement primitives (DMPs) as a base, and replaces the attractor points that form its mathematical foundation with saddle points structured as stable heteroclinic channels (SHCs) [1]. SHCs are a series of saddle equilibria where the unstable manifold of one equilibrium point leads onto the stable manifold of another; this creates pathways between the saddle points [4,5,6]. The modular components of DMPs, SHCs, or SMPs will be referred to as kernels for the remainder of this article.
Both SHCs and DMPs can be used as robotic control frameworks. DMPs are a more popular framework which uses a series of connected underlying kernels — attractor points or limit cycles — to produce trajectories [2,3,7,8]. The strength, timing and growth/decay of the attractors can be varied to create custom trajectories [9]. SHCs have been used as a model for neural activation patterns in animals [10,11,12]. They have also been used to produce and investigate dynamical state systems [13,14], and apply those systems to robotic movement [5]. Horchler et al described the system parameters alpha α , beta β , and nu ν for SHCs [6]. In their work, they described alpha as the growth rate of a kernel — how fast the kernel grows in its respective dimension. Beta was described as the kernel magnitude — the maximum amplitude of the waveform. Nu was described as the saddle value — a kernel’s insensitivity to input noise. In the SMP system, these variables (and the noise) are varied synchronously to create kernels that remain connected in state space, i.e. the connected kernels create a smooth trajectory in the task space. SMPs expand SHCs into a stable, learnable system with a clear transformation from state space into a robot’s task space, and they offer a unique visualization feature not seen in DMPs.
Mathematical representations of biological systems are commonly used to develop engineering frameworks [2,15,16,17,18,19,20]. These frameworks have value in both biological and engineering applications, and characterizing their parameters increases ease-of-use in either application [21,22,23]. Some transient dynamic systems, like neural networks, have gained a lot of popularity in recent years but the "black-box" nature of these systems reduces their parameterization and their explainability [24,25,26,27]. Like these other frameworks, SMPs have a biological relevance because of their construction from biologically-relevant SHCs. Unlike these frameworks, SMPs are parameterizable because their parameters — from DMPs and from SHCs — have already been described separately in each framework [6,7].
In this work, we show how varying these parameters affects the SMP system itself, and we use the parameters to modify the system results. To show the effect on the results, we use simple trajectory following tasks and evaluate the resulting trajectories quantitatively and visually. We compare the produced trajectories across the range of a single parameter, as well as the produced trajectories across the collective parameter-space. To evaluate the effect on the system, we observe the changes in the system’s state space for a similar range (across a single parameter, and across the collective parameter-space). We hypothesize that we can prescribe parameter changes to modify the waveform frequency, magnitude and shape for single/multiple kernels, resulting in a change to the trajectory’s speed, precision and/or shape. More specifically, we predict that increasing ν — the saddle value — will increase the precision of the trajectory around a saddle without disrupting the rest of the path.

2. Methods

The goal of this work is to demonstrate how SMP system variables modify the system and the trajectory it produces. The trajectory for any variable of interest (e.g. end-effector position or join angle) is produced by controlling a second-order system. The MATLAB code for this formulation can be found at https://github.com/NatRouse/SMP-Characterization.git.

2.1. System Model

The SMP system model is below. Equation (1) is the governing equation. It produces the final trajectory for the system’s variable of interest, y, using a forcing function, f, from the SHC formulation.
τ y ¨ = α y ( β y ( g − y ) − y ˙ ) + f
The forcing function (2) is summed over the number of kernel functions, K, used in the system. K is chosen based on the complexity of the system (e.g. actuatable degrees of freedom), and the desired smoothness of the produced trajectory. SMPs are O ( K 2 t ) at their most complex, where t is the number of timesteps calculated [1]. K=4 in Figure 2, Figure 3 & Figure 4 and K=8 in Figure 5. In this work, the kernels are color-matched to show which state space waveform corresponds to each region of the task space trajectory.
f ( x ) = ∑ i = 1 K x i w i
The canonical state equation (3) is based on competitive Lotka-Volterra (LV) equations [28].
τ d x i = x i α i − ∑ j = 1 K ρ i j x j d t + ∑ j = 1 N C i j z j
Noise is a critical factor in the use of LV kernels; noise, or external perturbation, z j , ensures that the system variable, x, passes close to the SHC saddle point, but not so close that the system remains in static equilibrium [6]. The effect of noise on SHCs has been explored in other work, and for practical uses, we can establish a reasonable noise magnitude compared to the rest of the system [4,5,29,30,31,32].
All of the variables across the SMP system model are defined in the following table.
Variable Definition
y relevant system variable
τ time-scaling term
α y system damping
β y system stiffness
g system’s "goal" position
f controller force (applied to system)
K total number of kernel functions
w i kernel function weight
x i canonical state of the system (for a single kernel)
α i , ρ i system behavior parameters
N number of sensors
C i j coupling matrix
z j noise

2.2. System Parameters

The variables that control SMP behavior are the noise z j , the kernel weights w i , and the parameters that make up the connection matrix ρ i j (seen in 3). In our previous work [1], we observed the effect of the kernel weights on the system, and optimized the weights to make the system follow a desired trajectory. When the system is at unit scale (magnitude, β = 1 ), the kernels can be plotted in the task space using the weights as locations.
In this work, we focus on the connection matrix, ρ i j . The connection matrix is a real, non-symmetric matrix constructed from three saddle characteristics: the growth rate α , the magnitude β , and the saddle value ν [6]. The matrix is constructed as follows:
ρ i j = α i / β i , if i = j α i − α j / ν j β j , if i = j − 1 α i + α j β j , otherwise
Preprints 99659 g001
Figure 1. SMP design flowchart
Figure 1. SMP design flowchart
Preprints 99659 g001
In the SHC system, α i controls how fast the kernel grows in the ith dimension, β i is the maximum amplitude of the waveform, x i , and ν i defines the stability of the ith saddle with respect to input noise. When designed together, these variables and the noise create kernels with smooth, connected pathways [6] which aids in producing a smooth trajectory. In this work, we will observe how α , β , and ν affect SMPs.
The number of inputs N, the noise values z j and the coupling matrix C i j collectively form the final term in 3. These are selected to create a proportionally small input noise in comparison to the rest of the system. As noted in Section 2.1, this noise is necessary to produce a trajectory along the kernel pathways.
To show the effect of each system parameter on the resulting trajectory, we vary each parameter over a spread of values for a single kernel and for all four kernels. The effect on the trajectory is measured as an area error from the original trajectory (the square in Figure 2). Additionally, since SMP kernels are functions of time, we can measure the time it takes for each kernel to grow and decay. A baseline trial (discussed in Section 2.3) is compared to trials with individually and collectively varied parameter values, and the kernel function waveforms (produced by x from 3) show the effects.

2.3. Desired Trajectories

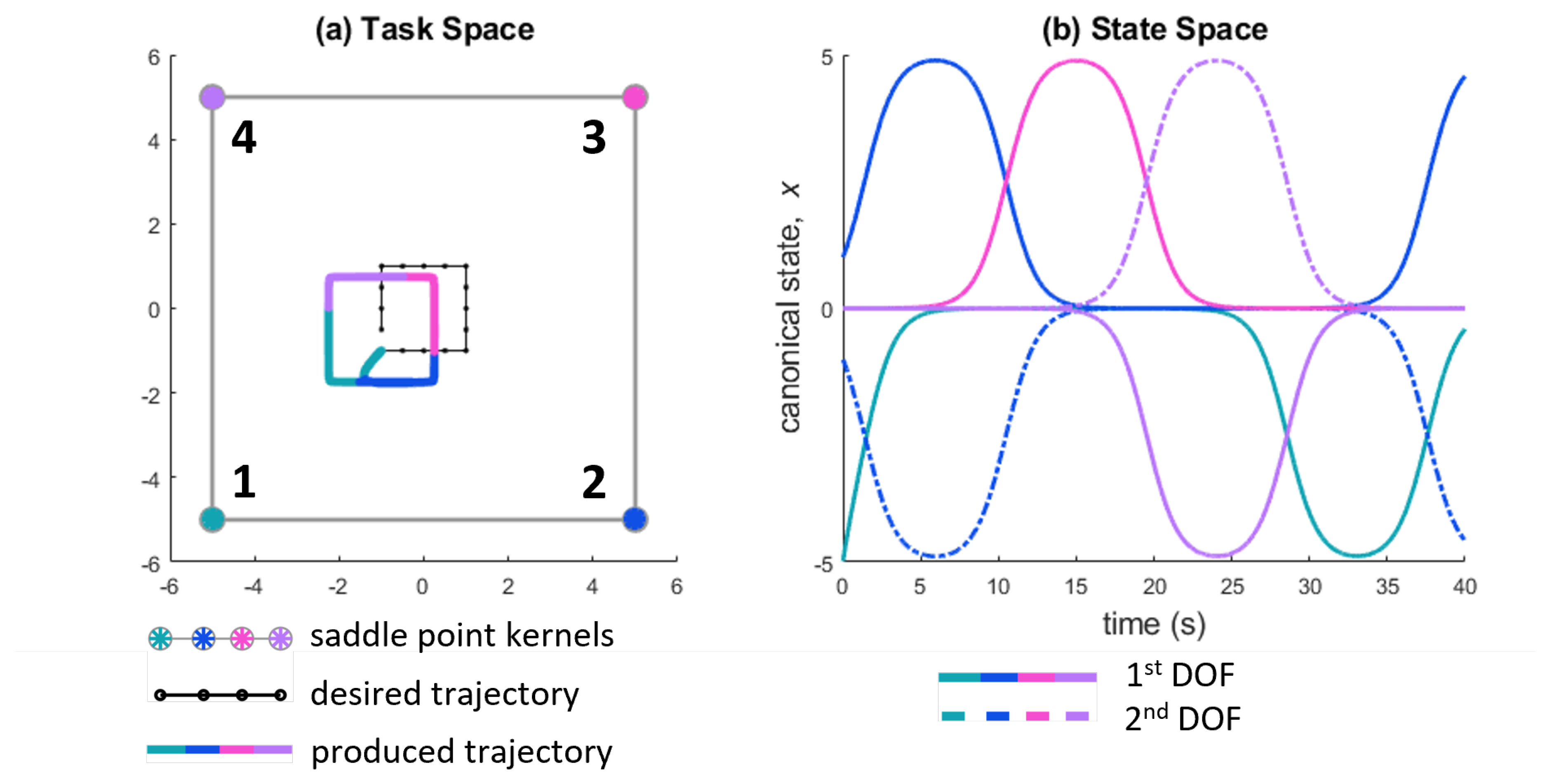
Preprints 99659 g002
Figure 2. (a) Saddle point kernels, desired trajectory and produced trajectory for a square trajectory plotted in the task space. (b) The canonical state waveforms of the weighted kernels. The degrees of freedom are the x and y directions in Cartesian space. The initialization waveform of kernel one (the green waveform at time = 0) contributes to the part of the produced trajectory that deviates from the square. Preliminary investigations into the steady state error (displacement from the desired trajectory) can be found in [33]. For the remainder of this work, the initialization and steady state error will be ignored.
Figure 2. (a) Saddle point kernels, desired trajectory and produced trajectory for a square trajectory plotted in the task space. (b) The canonical state waveforms of the weighted kernels. The degrees of freedom are the x and y directions in Cartesian space. The initialization waveform of kernel one (the green waveform at time = 0) contributes to the part of the produced trajectory that deviates from the square. Preliminary investigations into the steady state error (displacement from the desired trajectory) can be found in [33]. For the remainder of this work, the initialization and steady state error will be ignored.
Preprints 99659 g002

2.3.1. Square

The square trajectory-following task is defined in Figure 2. The trajectory starts at ( − 1 , − 1 ) and moves counterclockwise around a square. The desired trajectory is the first input to the system. Next, the kernel weights are chosen [1]. K = 4 corresponds to each corner of the square. This choice enables each kernel and its associated trajectory region to be visualized separately (see Figure 2).
The baseline SMP system parameters for the square trajectory are α , β , ν = 1 . These baseline parameters produce the square shown in Figure 2(a), which has a runtime of approximately 40 seconds; all the further parameter trials are compared against this baseline square. The variables from the system model that remain the same across all trials are listed below.
  • τ = 1
  • α y = 4
  • N = 4
  • g = ( − 1 , − 0.5 )
  • K = 4
  • β y = 1
  • z j = 10 − 9

2.3.2. “3" Shape

To explore how the system parameters can be used for trajectory tuning, a “number 3" trajectory is reproduced using eight kernels ( K = 8 ). The original system parameters for this trajectory are α = 10 , β = 1 , and ν = 1.2 . These are the same parameters used for the complex trajectories in our previous work [1].

2.4. Evaluating the Produced Trajectories

2.4.1. Square

The parameters that are varied are all α , all β , or all ν (collective parameter change) or a single α , β , or ν (individual parameter change). To evaluate the effects of varying parameters, we measure time and area error.
The system time is measured as the time it takes the system to complete the square trajectory. We determine closure of the square by identifying the first point at which the trajectory crosses itself.
The area error is the difference in area between the baseline produced trajectory (Figure 2) and the modified produced trajectory. The area enclosed (in the task space) by the original produced trajectory and each new produced trajectory is found, and their difference is calculated.
a r e a e r r o r = A baseline − A modified

2.4.2. “3" Shape

The distance error is measured as the sum of the shortest Euclidean distances between the desired and modified “3" shapes. The desired “3" is described using 13 waypoints, and this trajectory is used to select the weights of the 8 kernels that are used to run the system. The weight selection process is described in [1].
d i s t a n c e e r r o r = ∑ D O F ∑ t ( y modified − y desired ) 2

3. Results

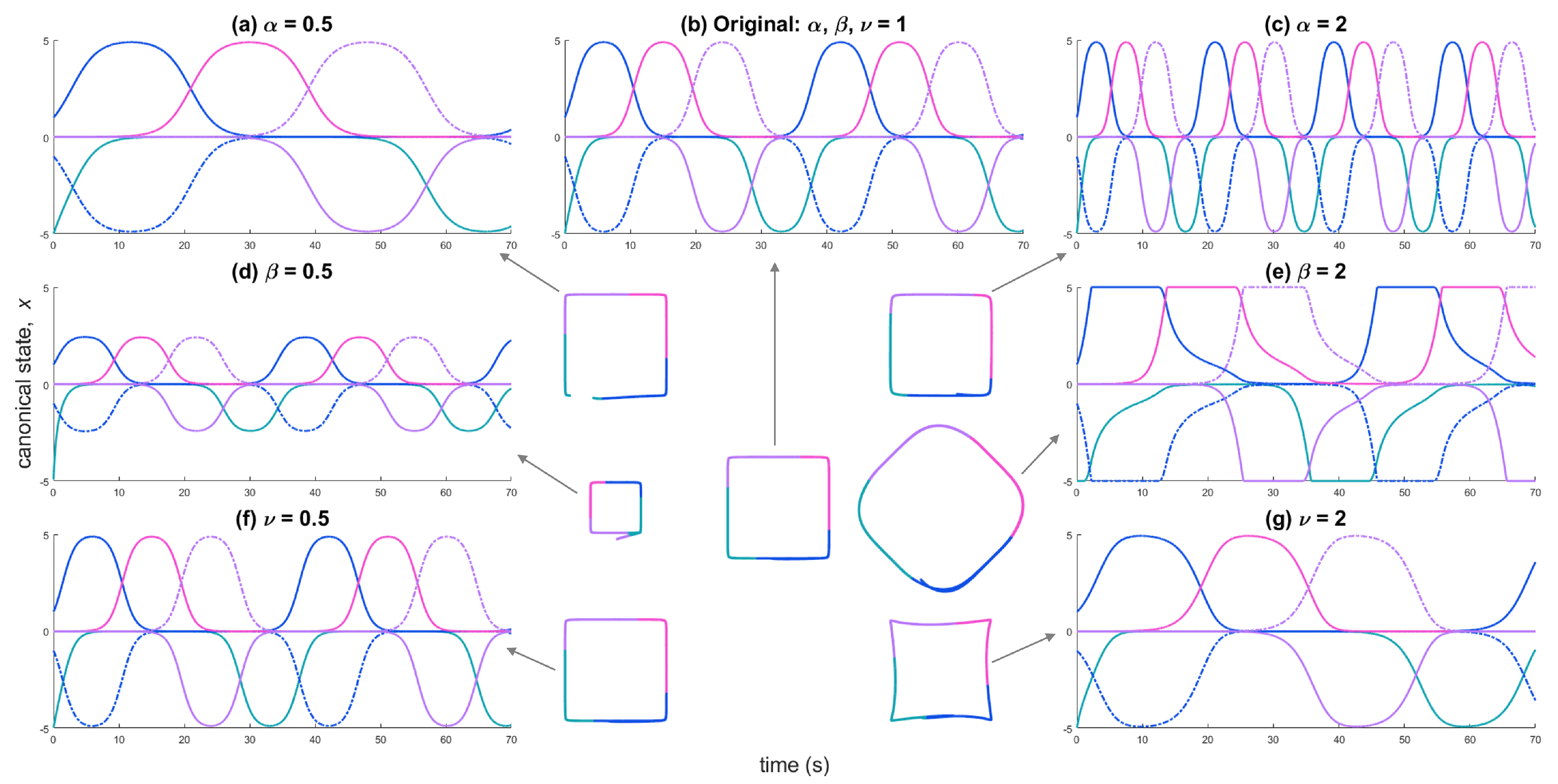
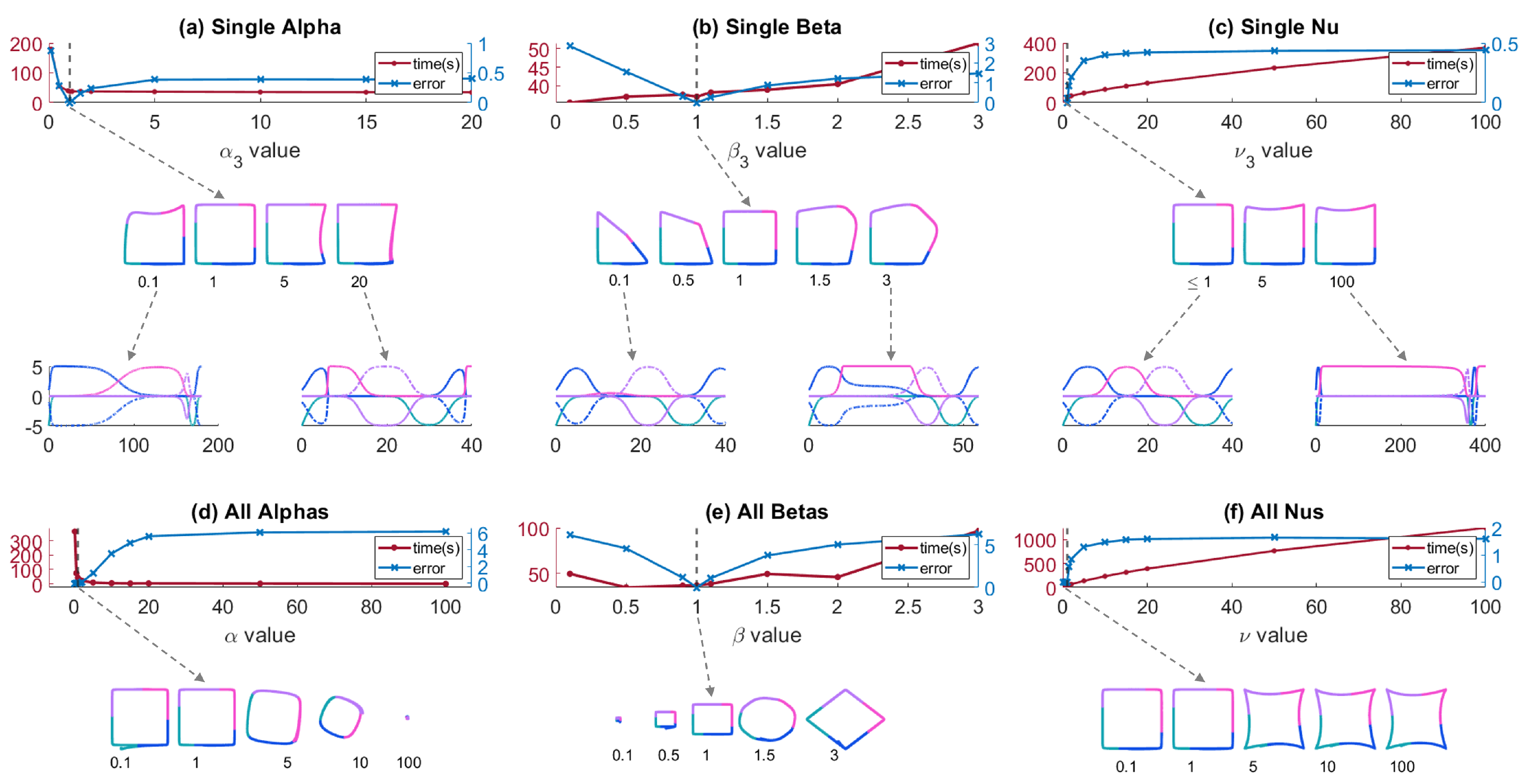
First, each system parameter was halved and doubled from an original value of 1 for all kernels. The effects on the system are summarized in Table 1 and plotted in Figure 3. Next, each system parameter was varied across a range for an individual kernel and collectively for all kernels. The system time and area error were collected for these trials. The results are shown in Figure 4. The results for each parameter are described below. Finally, with the accumulated information on how these variables affect the SMP system and its produced trajectory, we demonstrate that the saddle characteristics can be used to reduce the distance error of the “3" shaped trajectory.

3.1. Alpha: Growth Rate

3.1.1. All Alpha

In the state space, varying α varies the frequency of the canonical state waveform almost proportionally (Figure 3a,c). When α > > 1 , there is a rotation introduced into the produced trajectory and the trajectory decreases in size (Figure 4d). This can be attributed to the increased frequency of the waveforms. Faster waveforms indicates less time for the kernels to affect the system. The kernels grow so quickly that the trajectory does not fall into the saddle points’ neighborhoods in state space. In the task space, this appears as the trajectory passing farther away from the kernels resulting in reduced precision.

3.1.2. Single Alpha

α 3 was varied from 0.1 to 20 (Figure 4a) while α i ≠ 3 = 1 . According to (3) & (4), the prior and subsequent kernels are affected when a single α is changed.
When α 3 < 1 , the third kernel’s pink waveform rises gradually — slowing the kernel down and creating a wider waveform in state space. The second (prior, blue) kernel’s waveform decreases slowly — at a rate similar to the third kernel — while the following kernel’s entire waveform rises and falls quickly. The fourth kernel (purple) activates at a smaller magnitude than the others. In the produced trajectory, this presents itself as a curve away from kernel 4’s corner — the fourth kernel’s trajectory passes farther away from the kernel than in the unit trial ( α a l l = 1 ).
When α 3 > 1 , the pink third kernel waveform rises more sharply than the other kernels. To maintain the LV construction, the previous blue kernel’s waveform must decrease sharply. This translates across the entire kernel 3 waveform, which activates at a smaller magnitude than the other kernels. In the produced trajectory, this means that the trajectory curves away from the kernel 3 corner.

3.2. Beta: Magnitude

3.2.1. All Beta

In the state space, varying β changes the magnitude of the canonical state waveform almost proportionally (Figure 3d,e). When β < 1 the proportional magnitude translates to the size of the produced trajectory, e.g. at a halved β , the square’s sides are halved. When β > 1 , the waveforms are truncated at the system’s maximum — the maximum weight assigned to any kernel. All the waveforms are wider, slower, and decay more slowly than the original trial ( β = 1 ). Slower and wider waveforms indicate more time spent in each kernel’s neighborhood. In the produced trajectory, this translates to a larger, rotated square (Figure 4e). The rotation is likely the truncated tops of the waveforms forming new edges in the produced trajectory.
When a kernel remains activated at its maximum, the trajectory is pulled onto that kernel’s stable eigenvector [1] and remains in the kernel’s neighbourhood for a longer period of time [6]. In the task space, this presents as a straight line where the corners of the square used to be — the trajectory stays in the kernel’s neighborhood instead of approaching and leaving. Each straight line is a new edge in the produced trajectory, thus the entire square appears to rotate.

3.2.2. Single Beta

β 3 was varied from 0.1 to 3 (Figure 4b) while β i ≠ 3 = 1 .
When β 3 < 1 , the third kernel’s waveform magnitude is smaller than the other kernels, but does not affect the others in any other way. In the produced trajectory, the trajectory skips kernel 3’s pink corner, moving almost directly from the kernel 2 corner to the kernel 4 corner.
When β 3 > 1 , the third kernel’s waveform is truncated (as in the collective parameter trial). Similar to the collective parameter trial, the truncated waveform causes the trajectory to be pulled into the third kernel’s neighborhood faster and longer than the other kernels. This presents itself as a new edge tangential to the kernel location (recall the new edges formed when β a l l = 2 in Figure 3e).

3.3. Nu: Insensitivity to Noise

3.3.1. All Nu

Decreasing ν below 1 showed no change in either the state space or the produced trajectory. When ν > 1 , the waveforms become more square; they are not truncated, but they remain near their maximum for an extended period of time before decaying (Figure 3f,g). Unlike the modified β waveform activation at maximum, the modified ν kernels do not remain at their maximum value. Additionally, the rate of both their rise and decay is comparable to the original value ( ν = 1 ). In the produced trajectory, this change presents itself as an increased sharpness in the corners of the square (Figure 4f).

3.3.2. Single Nu

ν 3 was varied from 1 to 100 (Figure 4c) while ν i ≠ 3 = 1 . When ν 3 < 1 , there was no change in the state space or the produced trajectory.
When ν 3 > 1 , the third waveform increases in width, does not remain at its maximum value, and decays quickly. To maintain LV construction, the following kernel’s waveform must rise at a similar rate; kernel 4’s waveforms rises and decays quickly, resulting in a smaller waveform. In the produced trajectory, these waveform characteristics present themselves as an increased precision in the kernel 3 corner, a curve along the top edge, and a decreased precision in the kernel 4 corner.

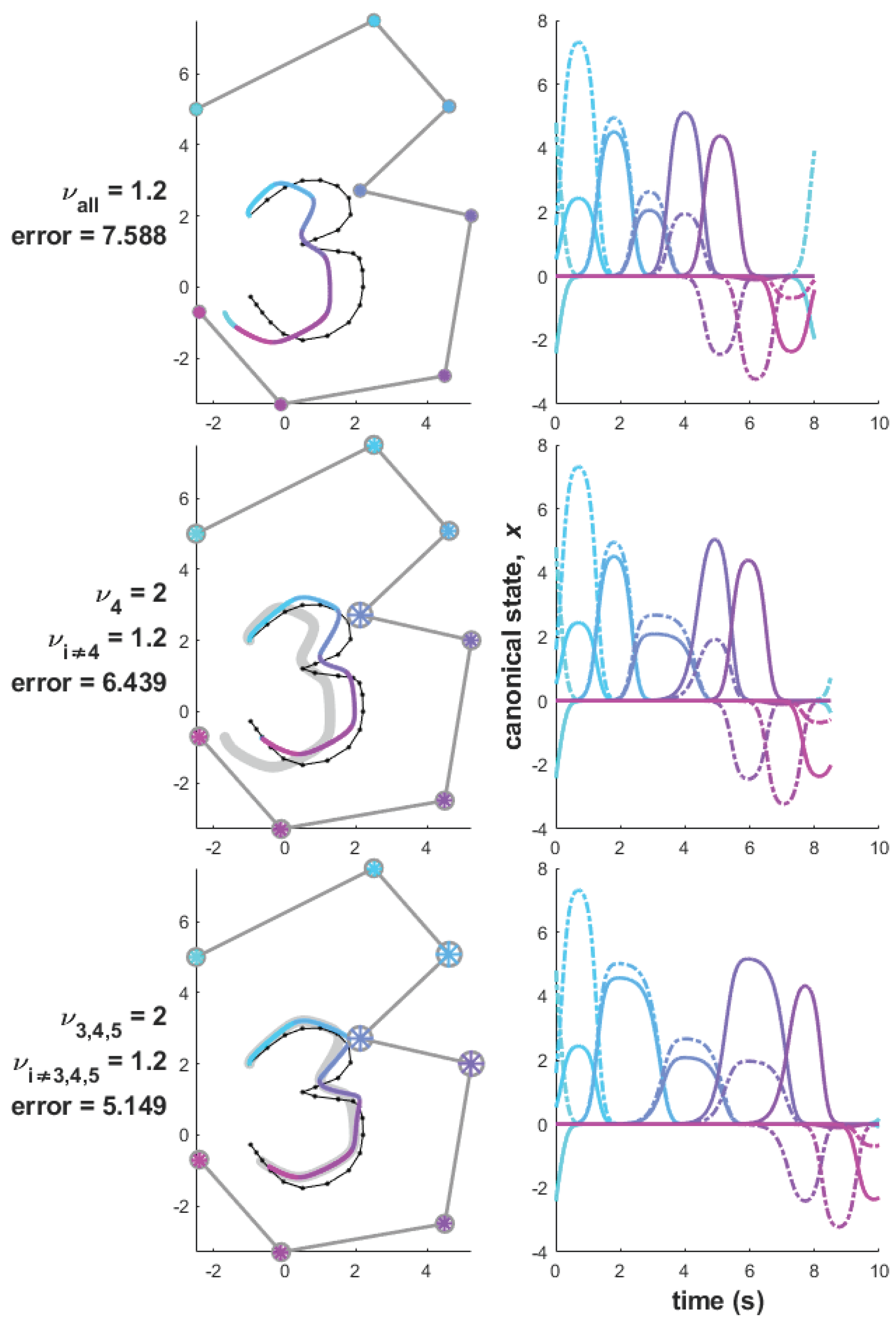
3.4. Complex Trajectory Tuning

With the knowledge of how these parameters affect both the system’s canonical state and the produced trajectory, we can now use them to modify the path precision of a trajectory at key points. In Figure 5, we define the trajectory as a “number three" using thirteen waypoints. We initialize our system with 8 kernel weights sampled from the trajectory and α = 10 , β = 1 , and ν = 1.2 . These variables originate from our previous work [1], but they could be derived via the process outlined in [6] using [34]. With this initialization, we achieve a trajectory that mimics a number three, but could represent the desired shape (Figure 5, top row) by being more precise in the inner point of the shape.
According to the previous sections (3.3), we can use ν to change the time the trajectory spends in a kernel’s neighborhood, thus affecting the precision of that portion of the trajectory. For this new trajectory, we want to match the curves closest to the inner point of the “number three". To do this, we increase those kernels’ ν value to ν = 2 . Now the trajectory more tightly follows the inner point of the shape (Figure 5, bottom row), reducing the distance error of the overall produced trajectory. The error changes as follows:
Modification Error
Baseline 7.588
ν 4 = 2 6.439 (15% ↓)
ν 3 , 4 , 5 = 2 5.149 (32% ↓)

4. Discussion

In this work, we characterized the effect of the SMP system parameters α , β , and ν on both the system and its produced trajectory. Additionally, we used these parameters to tune a more complex trajectory.
Alpha is a frequency (speed) modifier. As α increases, the kernel takes less time to grow and decay. This decreases the effect of that kernel on the trajectory, causing lower precision in the trajectory areas where a kernel’s α value has been increased. In the task space, increasing α increases the trajectory’s speed for that kernel’s activation.
Beta is a magnitude (scale) modifier. As β increases, the magnitude of the kernel’s waveform increases until it would exceed the system’s maximum. At that point, the waveform is truncated and the produced trajectory’s shape around that kernel is changed. In the task space, β can be used to under- or over-direct the trajectory past a kernel by decreasing or increasing it respectively.
Nu is a precision modifier. As ν increases, the kernel takes more time to grow and decay. This increases the “power" of that kernel on the trajectory, causing a higher precision in those areas in the task space.
The amount of time the system takes to grow/decay towards a kernel determines how closely its associated trajectory will be attracted to that kernel’s saddle point. With more time, the trajectory can be executed more closely, e.g. sharper corners for the square trajectory, and a more defined inner point for the “number three" trajectory. With less time, the trajectory will be executed more loosely, potentially skipping a kernel’s associated portion of the trajectory.
We hypothesized that the kernels can be individually modified to vary the trajectory’s fidelity in that location. Specifically, increasing the saddle value ν would increase the trajectory’s precision around that saddle. This was achieved in tuning a number “3" shape. We were able to produce a 32% decrease in the trajectory error by increasing the ν values of the saddles in the inner point of the shape.
In a limited parameter-space, the system variables can be used separately or in tandem to modify the produced trajectory at key points without significantly affecting the surrounding trajectory areas. For example, if a specific kernel becomes higher priority than others, we can increase the activation time for that kernel by increasing its β or ν value, or decreasing its α value. If a kernel becomes lower priority or needs to be avoided, we can decrease its activation time by increasing its α value or decreasing its β value. The variable β shows a unique feature when it is reduced below 1 for all kernels; it acts as a scaling factor for the whole trajectory.
For practical applications there are three main considerations: speed, precision, and scale. There is a trade off between speed and precision in adjusting α & ν , especially when their values are greater than 1. Due to the visualization feature of SMPs, the scale of a trajectory path can be easily adjusted using β , and a new path can be initialized quickly. Since the SMP system is stable and robust for this parameter space, all of the system parameters can be learned via a user’s chosen optimization algorithm according to the desired task specifications.
In addition to predictable changes at small parameter changes, we observed unexpected changes to the produced trajectories at large parameter changes, such as rotations, distortions and roundness in corners and sharp turns. Changes in the task space are implied when we look at the state space representations of these trajectories. The state space plots indicate that each kernel waveform is interdependent on its neighbors, and that interdependence uniquely affects their activation.
Several opportunities arise from this work. First, a full characterization of SMP state space may explain the unexpected trajectory changes illustrated in this paper. Additionally, we have not characterized the effect of noise on the SMP system. The SMP framework depends on perturbation to be functional, so an extended mathematical framework could leverage noise as an input to directly introduce sensory information to the system. In this work, we use SMPs to produce a kinematic trajectory plan. As with other modular activation frameworks, SMPs can be used to encode motor activation for different degrees of freedom on a robot instead. Finally, the spatial definition of SMPs enables more complicated network topologies. Each pathway, cycle or network could encode behaviors — either desired behaviors for a robotic platform or observed behaviors from other, less explainable (less visualizable) control frameworks.

Author Contributions

Conceptualization, Natasha Rouse and Kathryn Daltorio; Data curation, Natasha Rouse; Formal analysis, Natasha Rouse and Kathryn Daltorio; Funding acquisition, Kathryn Daltorio; Investigation, Natasha Rouse; Methodology, Natasha Rouse; Project administration, Kathryn Daltorio; Resources, Kathryn Daltorio; Software, Natasha Rouse; Supervision, Kathryn Daltorio; Validation, Natasha Rouse; Writing – original draft, Natasha Rouse; Writing – review & editing, Natasha Rouse and Kathryn Daltorio.

Funding

This project was funded by NSF Grant #2047330.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

Not applicable.

Conflicts of Interest

The authors declare no conflicts of interest.

Abbreviations

The following abbreviations are used in this manuscript:
SMP Stable heteroclinic channel-based movement primitive
DMP Dynamic movement primitive
SHC Stable heteroclinic channel
DOF Degrees of freedom

References

  1. Rouse, N.A.; Daltorio, K.A. Visualization of Stable Heteroclinic Channel-Based Movement Primitives. IEEE Robotics and Automation Letters 2021, 6, 2343–2348. [Google Scholar] [CrossRef]
  2. Schaal, S.; Kotosaka, S.; Sternad, D. Nonlinear Dynamical Systems as Movement Primitives. International Conference on Humanoid Robotics Cambridge MA 2001, 38, 117–124. [Google Scholar] [CrossRef]
  3. Schaal, S.; Peters, J.; Nakanishi, J. Control, planning, learning, and imitation with dynamic movement primitives. Neuroscience 2003, pp. 1–21.
  4. Rabinovich, M.; Huerta, R.; Laurent, G. Neuroscience: Transient dynamics for neural processing, 2008. [CrossRef]
  5. Daltorio, K.A.; Horchler, A.D.; Shaw, K.M.; Chiel, H.J.; Quinn, R.D. Stable Heteroclinic Channels for Slip Control of a Peristaltic Crawling Robot. Lecture Notes in Computer Science (including subseries Lecture Notes in Artificial Intelligence and Lecture Notes in Bioinformatics); Lepora, N.; Mura, A.; Krapp, H.; Verschure, P.; Prescott, T., Eds. Springer, Berlin, Heidelberg, 2013, Vol. 8064, pp. 59–70. [CrossRef]
  6. Horchler, A.D.; Daltorio, K.A.; Chiel, H.J.; Quinn, R.D. Designing responsive pattern generators: stable heteroclinic channel cycles for modeling and control. Bioinspiration & Biomimetics 2015, 10, 026001. [Google Scholar] [CrossRef]
  7. Schaal, S. Dynamic Movement Primitives -A Framework for Motor Control in Humans and Humanoid Robotics. In Adaptive Motion of Animals and Machines; Springer Tokyo: Tokyo, 2006; pp. 261–280. [Google Scholar] [CrossRef]
  8. Schaal, S.; Peters, J.; Nakanishi, J.; Ijspeert, A. Learning movement primitives. Springer Tracts in Advanced Robotics 2005, 15, 561–572. [Google Scholar] [CrossRef]
  9. Ijspeert, A.J.; Nakanishi, J.; Hoffmann, H.; Pastor, P.; Schaal, S. Dynamical Movement Primitives : Learning Attractor Models for Motor Behaviors. Neural Computation 2013, 25, 328–373. [Google Scholar] [CrossRef] [PubMed]
  10. Laurent, G.; Stopfer, M.; Friedrich, R.W.; Rabinovich, M.I.; Volkovskii, A.; Abarbanel, H.D. Odor Encoding as an Active, Dynamical Process: Experiments, Computation, and Theory. Annual Review of Neuroscience 2001, 24, 263–297. [Google Scholar] [CrossRef] [PubMed]
  11. Rabinovich, M.; Volkovskii, A.; Lecanda, P.; Huerta, R.; Abarbanel, H.D.I.; Laurent, G. Dynamical Encoding by Networks of Competing Neuron Groups: Winnerless Competition. Phys. Rev. Lett. 2001, 87, 068102. [Google Scholar] [CrossRef]
  12. Varona, P.; Rabinovich, M.I.; Selverston, A.I.; Arshavsky, Y.I. Winnerless competition between sensory neurons generates chaos: A possible mechanism for molluscan hunting behavior. Chaos: An Interdisciplinary Journal of Nonlinear Science 2002, 12, 672–677. [Google Scholar] [CrossRef]
  13. Voit, M.; Meyer-Ortmanns, H. Dynamical Inference of Simple Heteroclinic Networks. Frontiers in Applied Mathematics and Statistics 2019, 5, 63. [Google Scholar] [CrossRef]
  14. Shaw, K.M.; Park, Y.M.; Chiel, H.J.; Thomas, P.J. Phase resetting in an asymptotically phaseless system: On the phase response of limit cycles verging on a heteroclinic orbit. SIAM Journal on Applied Dynamical Systems 2012, 11, 350–391. [Google Scholar] [CrossRef]
  15. Nourse, W.; Quinn, R.D.; Szczecinski, N.S. An Adaptive Frequency Central Pattern Generator for Synthetic Nervous Systems. Biomimetic and Biohybrid Systems; Vouloutsi, V., Halloy, J., Mura, A., Mangan, M., Lepora, N., Prescott, T.J., Verschure, P.F., Eds.; Springer International Publishing: Cham, 2018; pp. 361–364. [Google Scholar]
  16. Riddle, S.; Nourse, W.R.P.; Yu, Z.; Thomas, P.J.; Quinn, R.D. A Synthetic Nervous System with Coupled Oscillators Controls Peristaltic Locomotion. Biomimetic and Biohybrid Systems; Hunt, A., Vouloutsi, V., Moses, K., Quinn, R., Mura, A., Prescott, T., Verschure, P.F.M.J., Eds.; Springer International Publishing: Cham, 2022; pp. 249–261. [Google Scholar]
  17. Daltorio, K.A.; Boxerbaum, A.S.; Horchler, A.D.; Shaw, K.M.; Chiel, H.J.; Quinn, R.D. Efficient worm-like locomotion: slip and control of soft-bodied peristaltic robots. Bioinspiration & Biomimetics 2013, 8, 035003. [Google Scholar] [CrossRef]
  18. M. Wensing, P.; Slotine, J.J. Sparse Control for Dynamic Movement Primitives. IFAC-PapersOnLine 2017, 50, 10114 – 10121. 20th IFAC World Congress. [CrossRef]
  19. Maass, W.; Markram, H. On the computational power of circuits of spiking neurons. Journal of Computer and System Sciences 2004, 69, 593–616. [Google Scholar] [CrossRef]
  20. de Azambuja, R.; Klein, F.B.; Adams, S.V.; Stoelen, M.F.; Cangelosi, A. Short-term plasticity in a liquid state machine biomimetic robot arm controller. 2017 International Joint Conference on Neural Networks (IJCNN), 2017, pp. 3399–3408. [CrossRef]
  21. Rico Mesa, E.M.; Hernández-Riveros, J.A. Determination of the Central Pattern Generator Parameters by a Neuro-Fuzzy Evolutionary Algorithm. Advances in Emerging Trends and Technologies; Botto-Tobar, M., León-Acurio, J., Díaz Cadena, A., Montiel Díaz, P., Eds.; Springer International Publishing: Cham, 2020; pp. 518–530. [Google Scholar]
  22. Szczecinski, N.S.; Hunt, A.J.; Quinn, R.D. Design process and tools for dynamic neuromechanical models and robot controllers. Biological Cybernetics 2017, 111, 105–127. [Google Scholar] [CrossRef] [PubMed]
  23. Fitzpatrick, Marshaun N. and Wang, Y.; Thomas, P.J., Quinn, R.D., Szczecinski, N.S. Robotics Application of a Method for Analytically Computing Infinitesimal Phase Response Curves. Biomimetic and Biohybrid Systems, Vouloutsi, V., Mura, A., Tauber, F., Speck, T., Prescott, T.J., Verschure, P.F.M.J., Eds.; Springer International Publishing: Cham, 2020; pp. 104–115. [Google Scholar]
  24. Kuwabara, J.; Nakajima, K.; Kang, R.; Branson, D.T.; Guglielmino, E.; Caldwell, D.G.; Pfeifer, R. Timing-based control via echo state network for soft robotic arm. The 2012 International Joint Conference on Neural Networks (IJCNN), 2012, pp. 1–8. [CrossRef]
  25. Jaeger, H. The "echo state" approach to analysing and training recurrent neural networks-with an erratum note. Technical report, German National Research Center for Information Techology, 2001.
  26. Pastor, P.; Righetti, L.; Kalakrishnan, M.; Schaal, S. Online movement adaptation based on previous sensor experiences. 2011 IEEE/RSJ International Conference on Intelligent Robots and Systems, 2011, pp. 365–371.
  27. Yuan, Y.; Li, Z.; Zhao, T.; Gan, D. DMP-Based Motion Generation for a Walking Exoskeleton Robot Using Reinforcement Learning. IEEE Transactions on Industrial Electronics 2020, 67, 3830–3839. [Google Scholar] [CrossRef]
  28. Bick, C.; Rabinovich, M.I. On the occurrence of stable heteroclinic channels in Lotka–Volterra models. Dynamical Systems 2010, 25, 110–97. [Google Scholar] [CrossRef]
  29. Li, D.; Cross, M.C.; Zhou, C.; Zheng, Z. Quasiperiodic, periodic, and slowing-down states of coupled heteroclinic cycles. Phys. Rev. E 2012, 85, 016215. [Google Scholar] [CrossRef]
  30. Stone, E.; Holmes, P. Random Perturbations of Heteroclinic Attractors. SIAM Journal on Applied Mathematics 1990, 50, 726–743. [Google Scholar] [CrossRef]
  31. Jeong, V.; Postlethwaite, C. Effect of noise on residence times of a heteroclinic cycle. Dynamical Systems 2023, 38, 79–101. [Google Scholar] [CrossRef]
  32. Ashwin, P.; Postlethwaite, C. Quantifying Noisy Attractors: From Heteroclinic to Excitable Networks. https://doi.org/10.1137/16M1061813, 2016; 15, 1989–2016. [Google Scholar] [CrossRef]
  33. Rouse, N.; Daltorio, K. A Convergence Feature of Stable Heteroclinic Channel-based Movement Primitives, 2023.
  34. Horchler, A.D. SHCTools: Matlab toolbox for simulation, analysis, and design ofstable heteroclinic channel networks, 2014.
Preprints 99659 g003
Figure 3. State space waveforms of the square trajectory kernels. The canonical state, x, as described in (3) is plotted against time. An “original" state (b) is set in the middle of the top row. It shows a four kernel system (square) that has two full activations: each kernel is activated twice in time. Each parameter is reduced by half — (a), (d), (f) — or doubled — (c), (e), (g). All of the trials are run for the same amount of time. The effects on the system can be seen in the function waveform frequencies, magnitudes and shapes, and are described in Table 1.
Figure 3. State space waveforms of the square trajectory kernels. The canonical state, x, as described in (3) is plotted against time. An “original" state (b) is set in the middle of the top row. It shows a four kernel system (square) that has two full activations: each kernel is activated twice in time. Each parameter is reduced by half — (a), (d), (f) — or doubled — (c), (e), (g). All of the trials are run for the same amount of time. The effects on the system can be seen in the function waveform frequencies, magnitudes and shapes, and are described in Table 1.
Preprints 99659 g003
Preprints 99659 g004
Figure 4. Plot of time (red) and area error (blue) vs various parameter values: (a) α 3 , (b) β 3 , (c) ν 3 , (d) α a l l , (e) β a l l , & (f) ν a l l . The produced trajectory for various values is pictured below each plot. Each set of produced trajectories is scaled according to the original (value = 1). The individual parameter trials (a, b, c) also have canonical state plots below their produced trajectories. Note that the x-axis, time, varies across the canonical state plots. This agrees with the change in time across the individual parameter trials.
Figure 4. Plot of time (red) and area error (blue) vs various parameter values: (a) α 3 , (b) β 3 , (c) ν 3 , (d) α a l l , (e) β a l l , & (f) ν a l l . The produced trajectory for various values is pictured below each plot. Each set of produced trajectories is scaled according to the original (value = 1). The individual parameter trials (a, b, c) also have canonical state plots below their produced trajectories. Note that the x-axis, time, varies across the canonical state plots. This agrees with the change in time across the individual parameter trials.
Preprints 99659 g004
Preprints 99659 g005
Figure 5. “Number three" trajectory. Left column: the produced trajectory, desired trajectory and kernels in the task space. The kernel weights inform their location in the task space (colored dots, gray lines). The produced trajectory (colored line) is unmodified in the top row, and modified according to the values on the y-axis in the middle and bottom rows. The distance error is listed under each modification. The produced trajectory from each previous trial is shown in gray to show the progression from a unmodified system, to a more modified system. Right column: the kernel waveforms in state space.
Figure 5. “Number three" trajectory. Left column: the produced trajectory, desired trajectory and kernels in the task space. The kernel weights inform their location in the task space (colored dots, gray lines). The produced trajectory (colored line) is unmodified in the top row, and modified according to the values on the y-axis in the middle and bottom rows. The distance error is listed under each modification. The produced trajectory from each previous trial is shown in gray to show the progression from a unmodified system, to a more modified system. Right column: the kernel waveforms in state space.
Preprints 99659 g005
Table 1. The effect on the SMP system (Canonical State Waveform) and the SMP results (Produced Trajectory) for collective parameter changes — all α , β , & ν values.
Table 1. The effect on the SMP system (Canonical State Waveform) and the SMP results (Produced Trajectory) for collective parameter changes — all α , β , & ν values.
Parameter Canonical State Waveform Produced Trajectory
Frequency Magnitude Shape Size
Growth Rate α ( 0 , ∞ ) Increases No effect Rotation Reduces
Magnitude β ( 0 , ∞ ) No effect Increases Rotation Increases
Insensitivity to Noise ν [ 1 , ∞ ) Decreases No effect Increased precision around kernel locations No effect
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated