Feedback Beamforming in the Time Domain

Preprint

Article

Feedback Beamforming in the Time Domain

Altmetrics

Downloads

Views

Comments

A peer-reviewed article of this preprint also exists.

Zvi Aharon Herscovici^*,

Israel Cohen^*

Zvi Aharon Herscovici^*,

Israel Cohen^*

This version is not peer-reviewed

Submitted:

20 February 2024

Posted:

23 February 2024

You are already at the latest version

Alerts

Abstract

This work introduces a new architecture for a time-domain feedback-based beamformer designed to meet real-time processing demands. The primary goal of this design is to locate reflective sources by estimating their direction of arrival (DOA) and signal range. Incorporating a feedback mechanism in this architecture is a unique aspect that refines localization precision. We conduct an in-depth analysis highlighting their respective benefits and limitations to compare the effectiveness of time-domain feedback beamforming against conventional time-domain methods. Our evaluation of the proposed architecture, based on critical performance indicators such as peak-to-sidelobe ratio, mainlobe width, and directivity factor, demonstrates its ability to improve beamformer effectiveness significantly.

Keywords:

Subject: Engineering - Electrical and Electronic Engineering

1. Introduction

Array signal processing has profound applications across radar and sonar systems [1,2,3], smart antennas for satellite and cellular communications [4,5,6], automotive radar [7,8], and medical imaging [9,10]. This work delves into the critical task of source localization in noisy environments, employing sensor arrays to pinpoint a signal’s origin. Source localization is an essential aspect of spatial signal processing. It involves the use of sensor arrays to detect and determine the origin of signals in different environments. This process starts with a reference sensor emitting signals into space, while the sensor array captures reflections from various sources. By analyzing the time delays between the readings of these sensors, it is possible to estimate the exact location of the source accurately.

Beamforming is a technique used in spatial processing that helps detect a signal coming from a specific direction while minimizing the influence of noise and interference from other directions [11]. This technique uses an array of sensors and determines the direction of the signal by weighing the inputs from each sensor. The goal is to enhance the signal from the target direction while reducing interferences. When beamforming is implemented on digital platforms, it requires discretization of the signal, which introduces quantization errors and necessitates a higher sampling rate. Because of these factors, research has focused on frequency domain approaches [12,13], which require lower sampling rates and can benefit from the combined utilization of spectral and spatial data. However, the time domain is still an important area for development [3,10,14,15], particularly for applications that require low latency [15], such as real-time communication [3,10]. In such cases, the time-domain approach can reduce computational complexity and execution time, even with a limited number of sensors.

Sensor arrays are available in different configurations such as uniform linear [16,17,18], circular [19,20,21], and planar arrays [22,23], each having its benefits and challenges. Uniform linear arrays (ULAs) have been a significant area of research due to their simple implementation and easy analysis. The design of a ULA, including the number of elements and their spacing, significantly impacts its performance, affecting the sharpness of the mainlobe and sidelobe levels. Choosing the right weight is crucial to optimizing the beamformer’s performance. Recent advancements have introduced a unique frequency domain feedback beamforming architecture [13], which incorporates a feedback loop to enhance source localization and signal rebroadcasting. Although this approach introduces additional complexity, it offers better system tuning by integrating an infinite-impulse response (IIR) filter. This circumvents the challenges associated with temporal processing while maintaining a low-complexity array.

This paper proposes a new architecture for a time-domain feedback beamformer designed to meet real-time processing demands. This architecture aims to locate a reflective source by estimating its direction of arrival (DOA) and range while incorporating a feedback mechanism to improve accuracy. We have compared this new architecture against established metrics such as peak-to-sidelobe ratio, mainlobe width, and directivity factor, demonstrating its potential to enhance beamformer performance significantly. The contributions of this manuscript are twofold: 1) We develop a theoretical framework and a closed-form solution for a time-domain feedback-based beamformer. 2) We present a comprehensive comparison and analysis of feedback beamforming in the time domain versus traditional time-domain approaches, highlighting their operational advantages and potential drawbacks.

The paper is structured as follows: We start in Section 2 by explaining the signal model for impinging signals on a ULA in the time domain. Next, we delve in Section 3 into the design of the feedback beamformer and elaborate on the signal model within this innovative architecture. In Section 4, we propose a methodology to optimize beamformer weights for precise estimation of the direction of arrival and signal range. In Section 5, we present simulation results, demonstrating significant improvements in spatial performance metrics compared to conventional beamformers. In Section 6, we compare the performances of time-domain and frequency-domain implementations. Finally, we conclude in Section 7 with a discussion of the implications of our findings and suggest future research directions.

Notations: Variables are represented in italics, while matrices and vectors are distinguished by boldfaced type with matrices in uppercase and vectors in lowercase. The superscript ^T denotes the transpose operation for matrices or vectors. Elements within vectors and matrices are referenced as follows:

v_{i}

indicates the ith element within vector

v

, and

A_{i j}

specifies the element located at the ith row and jth column of matrix

A

2. Signal Model

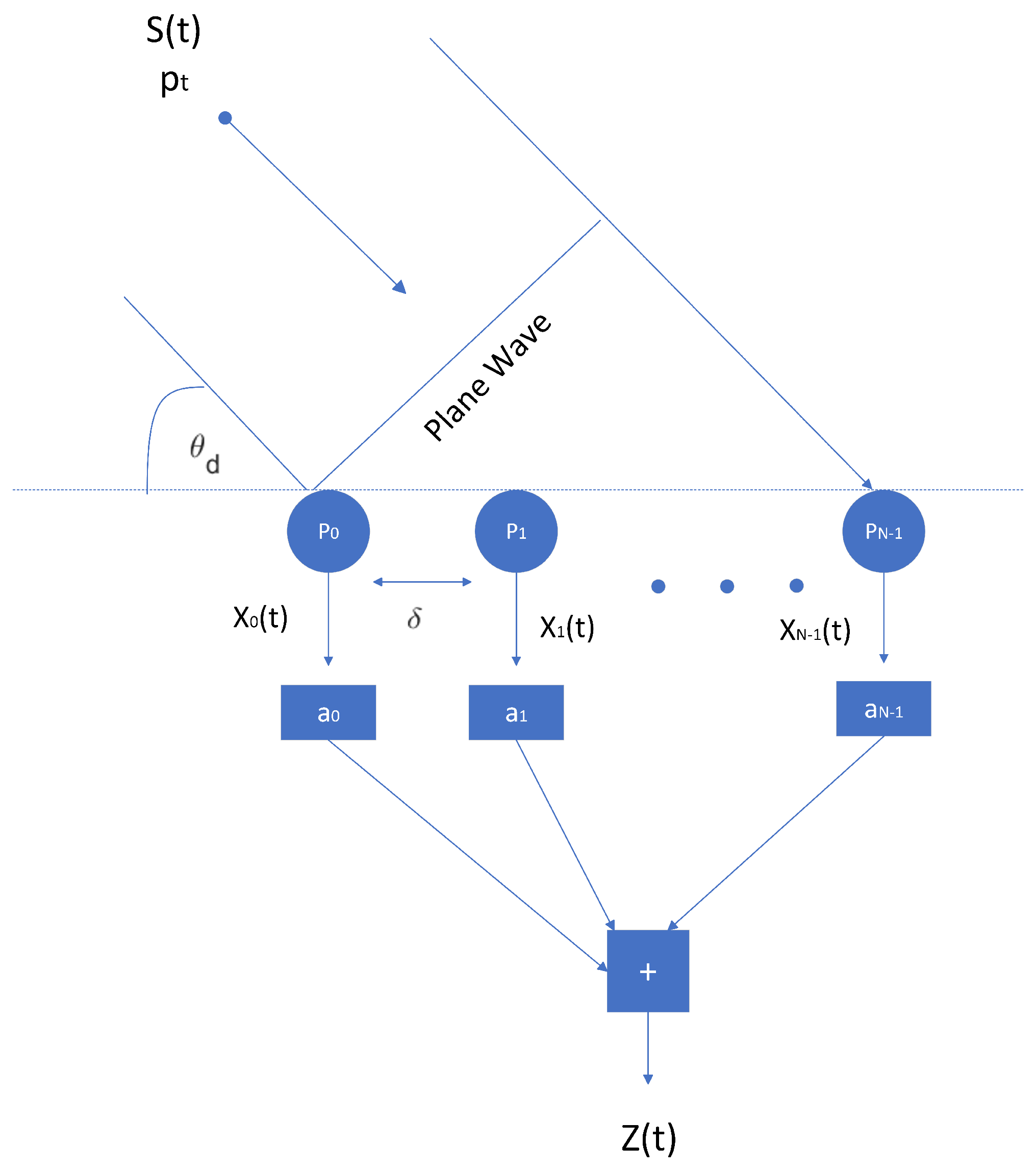
Consider a far-field source signal

s (t)

that propagates in an anechoic environment at the speed of light c. The signal

s (t)

, which can be an impulse or continuous signal, impinges an object and reflects back to the sensor array. A ULA beamformer, functioning analogously to an FIR filter in the time domain, is utilized in the design. Consider the ULA consisting of N omnidirectional elements with inter-element spacing

δ

. The location of the nth sensor is indicated by

p_{n}

for

n = 0, \dots, N - 1

, with

p_{0}

serving as the reference point relative to a stationary target positioned at

p_{t}

. In addressing this as a two-dimensional issue, the DOA of the reflected signal is identified as

θ_{d}

, positioned relative to the broadside of the array. The term

d = |p_{0} - p_{t}|

quantifies the distance from the reference sensor to the target. A depiction of the ULA configuration is provided in Figure 1.

The reflection induces a delay in signal reception at each sensor, contingent on the DOA. The signal captured by each sensor is then sampled, with the collective output being a weighted aggregation of these samples. This analytical approach is conducted entirely within the time domain, ensuring a thorough examination of signal propagation and reception dynamics within a controlled, anechoic environment.

The signal measured at the nth sensor is given by

x_{n} (t) = g_{c} s (t - τ_{pd} - f_{s} τ_{n}) + v_{n} (t),

(1)

where

g_{c}

is the channel gain,

τ_{pd}

is the prorogation delay from the reference sensor to the target and back, given by

τ_{pd} = \frac{2 d}{c}

f_{s}

is the sampling frequency,

τ_{n}

is the time delay between the reference and nth sensor which is represented by

τ_{n} = \frac{n δ cos (θ_{d})}{c}

, and

v_{n}

(t) is the noise in the nth sensor.

Following the framework presented in [24] for the general analysis, and under the assumption of a noiseless environment where

v_{n} (t) = 0

across all sensors, we draw upon Shannon’s sampling theorem to deduce that [25]

\begin{matrix} x_{n} (t) & = g_{c} s (t - τ_{pd} - f_{s} τ_{n}) \\ = g_{c} \sum_{l = - \infty}^{\infty} s (t - l) sinc (l - τ_{pd} - f_{s} τ_{n}) \end{matrix}

(2)

\begin{matrix} \approx g_{c} \sum_{l = - P - L_{h} + 1}^{P} s (t - l) sinc (l - τ_{pd} - f_{s} τ_{n}), \end{matrix}

(3)

where

sinc (x) = \frac{sin (π x)}{π x}

is the Fourier Transform of the rectangular function. The last line holds for

P ≫ f_{s} τ_{n}

and

L_{h}

is the number of successive time samples of the sensor signal. We can formulate (1) as

x_{n} (t) = g_{c} g_{n}^{T} (θ_{d}, d) s (t)

(4)

where

s (t)

contains

L = 2 P + L_{h}

successive samples of the signal

s (t)

and

g_{n} (θ_{d}, d)

is the interpolation coefficients, depending on

θ_{d}

, d and N.

s (t)

is formed as:

s (t) = {[\begin{matrix} s (t + P + L_{h} - 1) & s (t + P + L_{h} - 2) & \dots & s (t - P) \end{matrix}]}^{T} .

(5)

Considering

L_{h}

successive time samples of the nth sensor signal, (4) becomes a vector of length

L_{h}

x_{n} (t) = g_{c} G_{n} (θ_{d}, d) s (t),

(6)

where

G_{n} (θ_{d}, d)

is a Toeplitz matrix of size

L_{h} \times L

with

\begin{matrix} {[G_{n} (θ_{d}, d)]}_{i j} & = sinc (- P - L_{h} + 1 - i + j - f_{s} τ_{n} (θ_{d}) - τ_{pd}) \\ = sinc (- P - L_{h} + 1 - i + j - \frac{f_{s} n δ cos (θ_{d}) + 2 d}{c}) \end{matrix}

(7)

where

i = 1, \dots, L_{h}

and

j = 1, \dots, L

. Combining the samples from the N sensors, we get a vector of length

N L_{h}

\begin{matrix} x (t) & = {[\begin{matrix} x_{0} (t) & x_{1} (t) & x_{N - 1} (t) \end{matrix}]}^{T} \\ = G (θ_{d}, d) s (t) \end{matrix}

(8)

where

G (θ_{d}, d)

is a matrix of size

N L_{h} \times L

G (θ_{d}, d) = [\begin{matrix} G_{0} (θ_{d}, d) \\ G_{1} (θ_{d}, d) \\ ⋮ \\ G_{N - 1} (θ_{d}, d) \end{matrix}] .

(9)

The signal

x (t)

is affected by the array’s geometry, which is represented by a secondary term. This is similar to the structure observed in frequency domain signal models. Therefore, the steering vector can be considered as the counterpart to

G (θ_{d}, d)

in the frequency domain. This shows a direct relationship between time-domain signal processing and its frequency-domain equivalent through the array geometry.

3. Feedback Beamforming

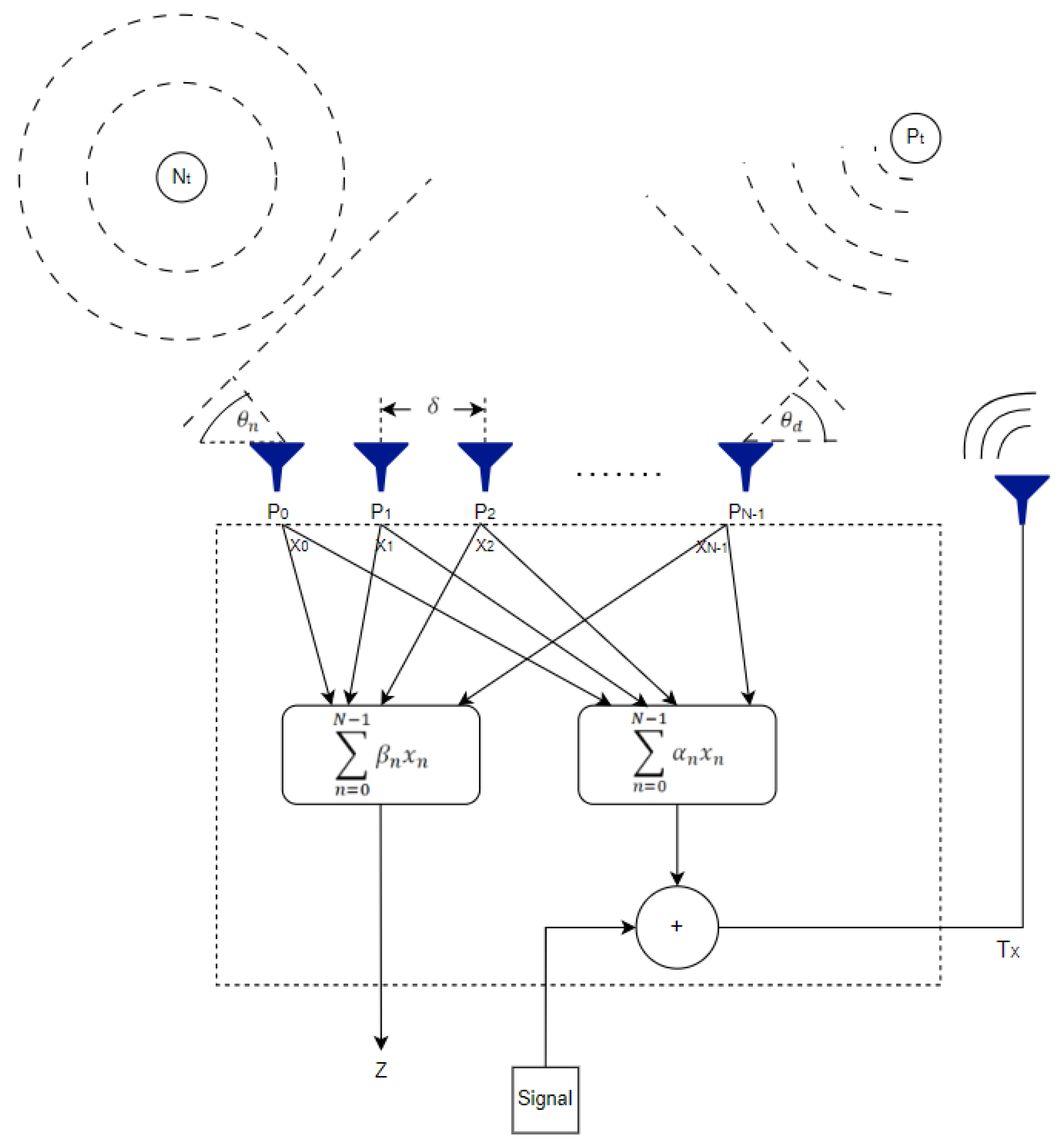
This section discusses the Feedback-Based Beamformer (FB) architecture used for spatial signal processing. The FB architecture is similar to an IIR-like filter and uses a feedback loop to re-transmit the signal S, which is synthesized from the weighted aggregation of sensor samples. This feedback loop creates a dynamic spatial processing environment, making it a novel approach for spatial signal processing. The details of this architecture are discussed in [13]. The architecture combines data collected by sensors and processes it through two weighted sums, called

α

and

β

. In the time domain,

L_{h}

consecutive time samples are taken from each of the N sensors.

α

and

β

are vectors with dimensions of

N L_{h}

. These samples may contain both desired signals and unwanted noise or interference from different directions. The output of the system is denoted as

z (t)

and is created using a weighted vector called

β

. The re-transmitted signal is a combination of the original source signal and an additional weighted sum using the vector

α

. To demonstrate the presence of interference in this setup, Figure 2 introduces a noise source,

N_{t}

, placed at an angle

θ_{n}

relative to the array’s broadside. This noise is irrelevant to both the target signal and the array itself. This configuration highlights the ability of the FB architecture to handle complicated signal environments by utilizing spatial feedback loops for improved signal processing.

Extending the signal model in (1) to the FB architecture and considering the noiseless case, the signal measured at the nth sensor is as follows:

x_{n} (t) = g_{c} [s (t - τ_{pd} - f_{s} τ_{n}) + \sum_{m = 0}^{N - 1} α_{m} x_{m} (t - τ_{pd} - f_{s} τ_{n})] .

(10)

Using Shannon’s sampling theorem, the measured signal can be written as:

x_{n} (t) \approx g_{c} [\sum_{l = - P}^{P + L_{h}} s (t - l) sinc (l - τ_{pd} - f_{s} τ_{n}) + \sum_{m = 0}^{N - 1} α_{m} x_{m} (t - l) sinc (l - τ_{pd} - f_{s} τ_{n})] .

(11)

Simplifying the expression above, (11) can be rewritten as:

x_{n} (t) = g_{c} \{\sum_{l = - P}^{P + L_{h}} sinc (l - τ_{pd} - f_{s} τ_{n}) [s (t - l) + \sum_{m = 0}^{N - 1} α_{m} x_{m} (t - l)]\} .

(12)

Combining both (6) and (12), results in:

x_{n} (t) = g_{c} G_{n} (θ_{d}, d) [s (t) + i_{l} α^{T} x (t)]

(13)

where

i_{l}

is the lth column of the

L \times L

identity matrix

I_{l}

, and

α

is a vector of length

N L_{h}

consisting of the weights for all the samples. Unifying all the sensors together, we obtain

x (t) = g_{c} G (θ_{d}, d) [s (t) + i_{l} α^{T} x (t)] .

(14)

The above can be simplified to

\begin{matrix} x (t) [1 - g_{c} α^{T} G (θ_{d}, d) i_{l}] = g_{c} G (θ_{d}, d) s (t) . \end{matrix}

(15)

Thus, the relation between the input signal and the sensors’ samples is given by

x (t) = \frac{g_{c} G (θ_{d}, d) s (t)}{1 - g_{c} α^{T} G (θ_{d}, d) i_{l}} .

(16)

In principal, any element of the input vector signal

s (t)

can be considered as the desired signal. Moreover, based on the proposed feedback beamforming architecture, the output of the beamformer can be represented as

z (t) = β^{T} x (t)

. Therefore, the relationship between the input signal and FB output can be expressed as follows:

H_{β, α} \overset{Δ}{=} \frac{z}{s} = \frac{g_{c} β^{T} G (θ_{d}, d) i_{l}}{1 - g_{c} α^{T} G (θ_{d}, d) i_{l}} .

(17)

After analyzing both the time-domain response and the frequency-domain response outlined in [13], it is apparent that they are closely related. The steering vector utilized in the frequency domain is similar to the construct

G (θ_{d}, d) i_{l}

in the time domain. Additionally, the phase shift component

e^{- j ϕ}

in the frequency domain is comparable to fine-tuning the interpolation matrix

G (θ_{d}, d)

in the time domain by adjusting the propagation delay associated with the target’s range estimation. Thus, this adjustment shows the alignment between time-domain processing and its frequency-domain counterpart through manipulation of the coefficient interpolation matrix.

4. Finding the Optimal Weights

The optimal selection of the beamformer weights is a crucial factor in its performance. Unfortunately, even slight deviations from optimal weights may significantly impact the beamformer efficacy, a concept that will be further explored in subsequent sections. Compared to a conventional beamformer (CB), the unique aspect of the feedback beamformer is the introduction of spatial feedback through the retransmitted signal. This retransmission adds a layer of complexity and potential for enhanced performance by incorporating additional system information, as detailed in [13]. The efficacy of the FB hinges on the precise estimation of both the DOA,

θ_{d}

) and the target’s range

(d)

. The methodology for assessing these estimations’ accuracy is the application of the Cramér-Rao Bound (CRB), leveraging the Fisher Information Matrix (FIM) for this purpose. Given that the analysis and development of the beamformer’s response are conducted within the time domain, we utilize the time-domain FIM for evaluating the performance potential of the FB system.

The

(m, n)

th FIM element is given by [26]

\begin{matrix} {[J (ζ)]}_{m, n} = {|\frac{\partial z (ζ)}{\partial ζ_{m}}|}^{T} R^{- 1} (ζ) |\frac{\partial z (ζ)}{\partial ζ_{n}}| + \frac{1}{2} tr [R^{- 1} (ζ) \frac{\partial R (ζ)}{\partial ζ_{m}} R^{- 1} (ζ) \frac{\partial R (ζ)}{\partial ζ_{n}}] \end{matrix}

(18)

where

ζ = [θ_{d}, d]

represents the vector of parameters, and

tr (\cdot)

denotes the trace operation on a matrix. The variables

m, n \in 1, 2

are used to specify the parameters being estimated, and

R (ζ)

represents the

N \times N

noise covariance matrix. Assuming the presence of white noise, which is statistically independent of the parameter vector

ζ

, and given that

z (t)

is scalar, the expression (17) can be simplified as

{[J (ζ)]}_{m, n} = |\frac{\partial z (ζ)}{\partial ζ_{m}}| |\frac{\partial z (ζ)}{\partial ζ_{n}}| .

(19)

The above derivatives yield the following main diagonal elements:

\begin{matrix} J_{θ_{d} θ_{d}} & = \frac{f_{1}^{2}}{{[1 - g_{c} α^{T} G^{T} (θ_{d}, d) i_{l}]}^{4}} \end{matrix}

(20)

\begin{matrix} J_{d d} & = \frac{f_{2}^{2}}{{[1 - g_{c} α^{T} G^{T} (θ_{d}, d) i_{l}]}^{4}} \end{matrix}

(21)

where

f_{1}

and

f_{2}

are functions of the parameter set

α

β

G (θ_{d}, d)

and its partial derivatives. A detailed proof of (20) is given in the Appendix. To obtain the optimal estimate, it is required to maximize the diagonal elements of the FIM,

J_{θ_{d} θ_{d}}

and

J_{d d}

. This maximization is done by minimizing the denominator

|1 - g_{c} α^{T} G (θ_{d}, d) i_{l}|

The optimal weight

α

can be written as:

α_{opt}^{T} = \frac{1}{{\hat{g}}_{c}} i_{l}^{T} G^{T} (θ_{d}, d) {[G (θ_{d}, d) G^{T} (θ_{d}, d)]}^{- 1}

(22)

where

{\hat{g}}_{c}

is the channel gain estimate. Additionally, the output weight is

β = α_{opt}

. The optimal beamformer weights vector contains the exact values for the DOA and the target range, which, in practice, are unknown. Thus, the optimal weights, considering both the DOA estimate

{\hat{θ}}_{d}

and the range estimate

\hat{d}

, are

α_{opt}^{T} = β_{opt}^{T} = \frac{1}{{\hat{g}}_{c}} i_{l}^{T} G^{T} ({\hat{θ}}_{d}, \hat{d}) {[G ({\hat{θ}}_{d}, \hat{d}) G^{T} ({\hat{θ}}_{d}, \hat{d})]}^{- 1} .

(23)

Substituting (23) into (17) yields the optimal beamformer time response:

\begin{matrix} H_{β_{opt}, α_{opt}} & = \frac{r i_{l}^{T} G^{T} ({\hat{θ}}_{d}, \hat{d}) {[G ({\hat{θ}}_{d}, \hat{d}) G^{T} ({\hat{θ}}_{d}, \hat{d})]}^{- 1} G (θ_{d}, d) i_{l}}{1 - r i_{l}^{T} G^{T} ({\hat{θ}}_{d}, \hat{d}) {[G ({\hat{θ}}_{d}, \hat{d}) G^{T} ({\hat{θ}}_{d}, \hat{d})]}^{- 1} G (θ_{d}, d) i_{l}} \end{matrix}

(24)

where

r = \frac{g_{c}}{{\hat{g}}_{c}}

is the channel gain error.

5. Beamformer Evaluation

To assess the beamformer’s efficacy, it is essential to consider a range of parameters, both architecture-specific (such as M and

δ

) and target-specific (like the DOA and the target’s distance from the array). This section aims to examine the FB response, as detailed in (24), and evaluate its performance using key metrics such as sidelobe level reduction, directivity factor (DF), and beamwidth. These metrics are standard for evaluating the performance of ULA beamformers. The FB’s performance metrics will be benchmarked against those of conventional ULA beamformers, including the delay-and-sum (DS) and the maximum DF beamformers, which lack the FB’s feedback mechanism. This comparative analysis will highlight the FB’s advancements and its potential impact.

5.1. Mainlobe and Sidelobe Attenuation

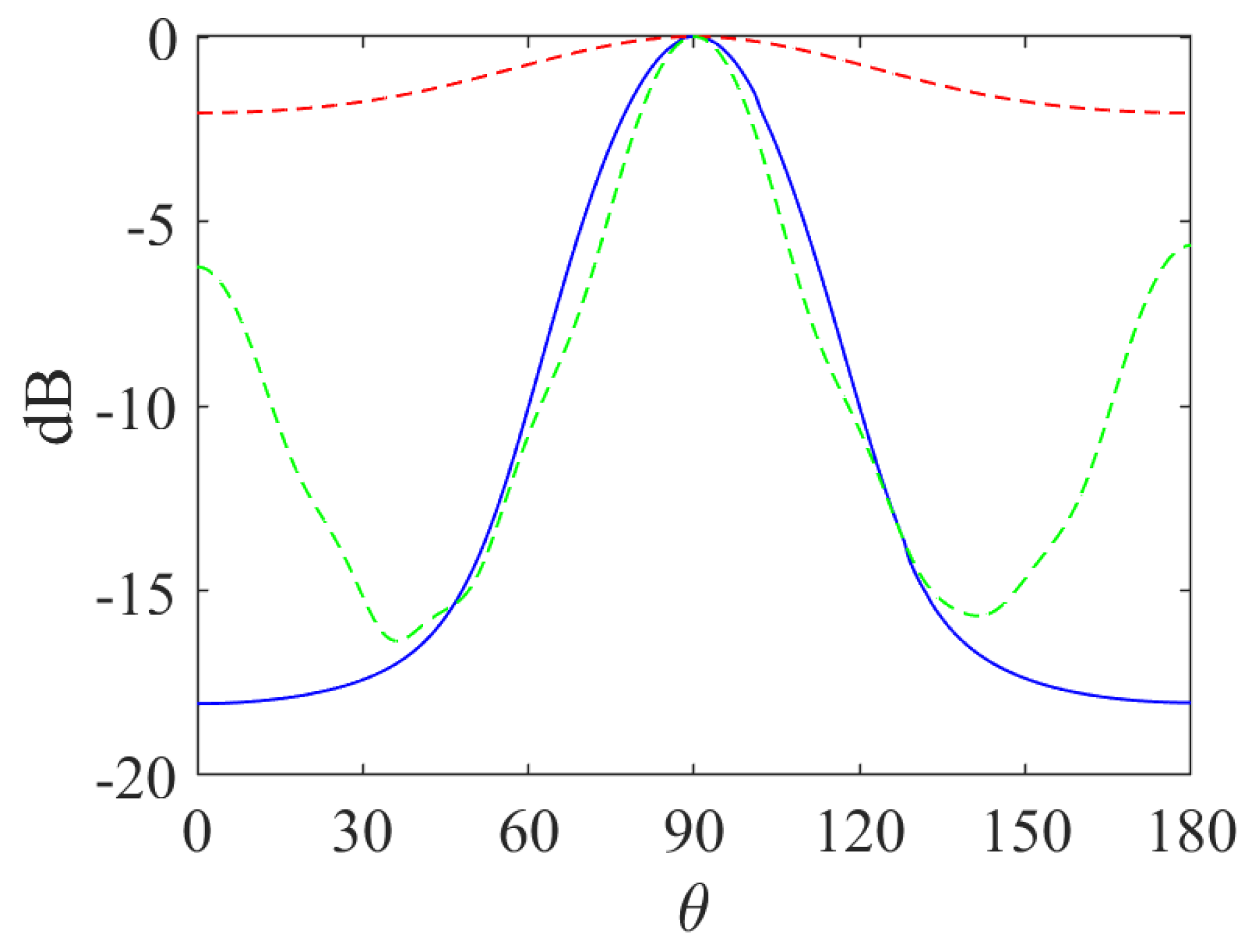
The accuracy of a beamformer is determined by the width of its center lobe and the height of its side lobes. The behavior of a proposed feedback beamformer, compared to DS and maximum DF beamformers, is shown in Figure 3 depending on

θ

. As demonstrated in Figure 3, the feedback beamformer has a narrower mainlobe compared to the DS beamformer, and is almost as narrow as the maximum DF beamformer. This indicates that the beamformer filter is spatially effective, nearly as much as a beamformer explicitly designed for that purpose. Additionally, the feedback beamformer has better attenuation compared to the DS beamformer. Moreover, while the distortionless maximum DF beamformer is designed to have a narrow beamwidth, it comes at the cost of high sidelobes. The feedback beamformer closely matches the mainlobe beamwidth, while having much better sidelobe attenuation.

5.2. Directivity Factor

The directivity factor (DF) is an important quality factor of the beamformer. It refers to the level of directionality of the beamformer and is measured by the ratio between the beamformer gain in a specific direction and the average gain in all directions. In the time domain, it is defined as [24]

D [α, β, c o s (θ_{d}), d] = \frac{| B (α, β, c o s (θ_{d}), d) |^{2}}{\frac{1}{2} \int_{0}^{π} {| B (α, β, c o s (θ_{d}), d) |}^{2} s i n (θ) d θ} .

(25)

As explained and developed in [27], the DF of a generic ULA is

D = 2 \frac{N δ}{λ}

(26)

for large values of N and

λ ≫ δ

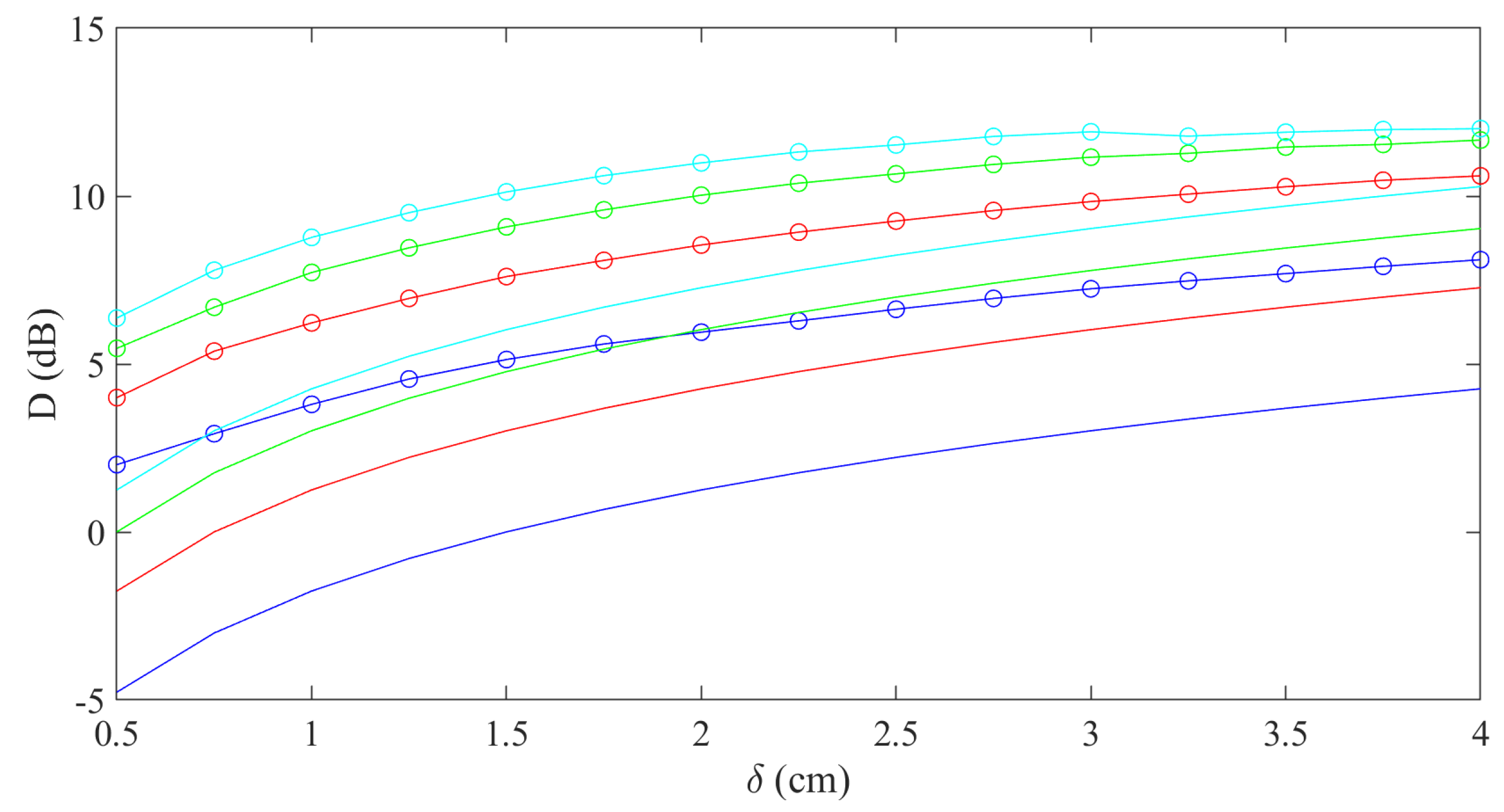
Simulating the DF for both the feedback beamformer architecture and generic ULA, and plotting the result as a function of

δ

, we show in Figure 4 that the DF was significantly improved. In addition, it can be seen from Figure 4 that when the number of sensors is increased or the distance between sensors is increased, the DF of both cases increases as well due to better spatial understanding.

5.3. Range Error Influence

While in CB, the target’s DOA is the only important parameter, in our design, the range is estimated to get the target’s position more accurately. We considered the perfect estimation of the target’s range for the sake of equal comparison between our architecture and CB. Estimating the target’s range can increase the level of accuracy of a target to a specific location instead of a particular direction.

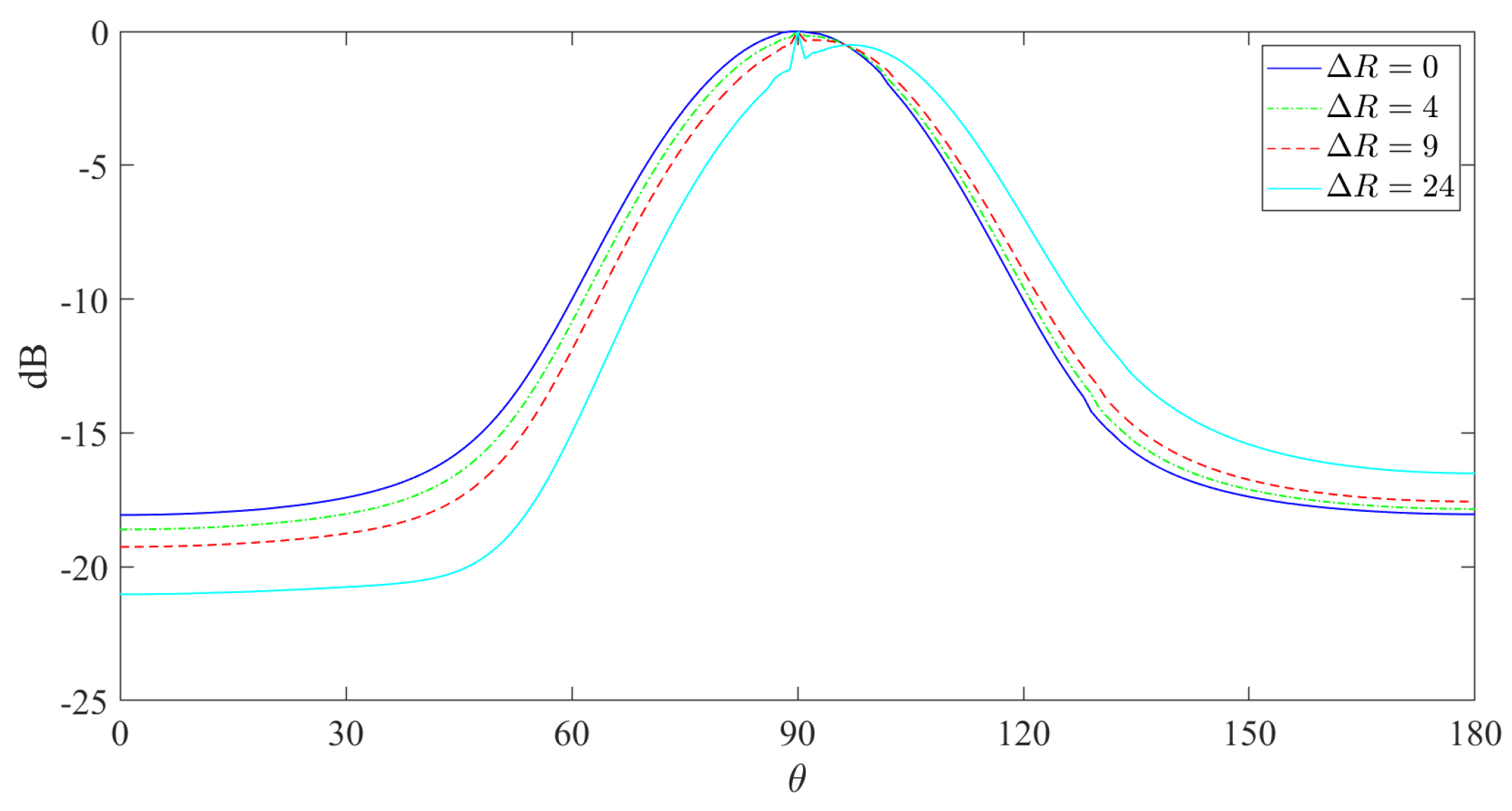
To check the influence of the target’s range misestimation, we simulate the proposed beamformer with different range errors as a function of

θ

in Figure 5. It can be seen that the range estimation error can change the beamformer performance by way of shifting the mainlobe direction and different attenuation on both sides of the mainlobe. As opposed to the range error influence in the frequency domain [13], the time-domain implementation is significantly less sensitive regarding the range error. This robustness can be seen in a way that in the time domain, range estimation error negligibly affects the mainlobe position. In contrast, small changes in the frequency domain can shift the position of the mainlobe by tens of degrees. In [13], this estimation error was addressed by adding another feedback beamformer. The minor effect of the estimation error in the time domain eliminates the use of an additional beamformer, which results in less hardware and a smaller footprint, which are critical considerations.

6. Time Domain vs. Frequency Domain Feedback Beamforming

To thoroughly investigate the proposed filter, we compare the proposed beamformer and the frequency domain beamformer [13]. Some common comparison measures include beamformer fidelity, the system’s robustness, and the computational complexity [28]. Additional parameters according to which a comparison is made between time-frequency domain implementations are the number of sensors used for the desired output, SNR, sampling frequency, data storage, and processing requirements, as well as area consideration for implementing the hardware.

6.1. Calculation Complexity

Time-domain spatial filters offer distinct advantages over their frequency-domain counterparts, notably in computational efficiency. A significant benefit of time-domain processing, as demonstrated in the filter design outlined above (24), is its lower computational complexity relative to an analogous design in the frequency domain. Specifically, the most computationally intensive operation in the time-domain design is given by:

G^{T} ({\hat{θ}}_{d}, \hat{d}) {[G ({\hat{θ}}_{d}, \hat{d}) G^{T} ({\hat{θ}}_{d}, \hat{d})]}^{- 1} G (θ_{d}, d) .

This operation underscores the efficiency of time-domain designs in handling spatial filtering tasks, where the focus is on minimizing the processing load without compromising the accuracy or effectiveness of the filtering process.

The above matrix multiplications require approximately

3 N^{2} L_{h}^{3}

multiplications and the same number of additions, where

N ≫ 1

and

L \approx L_{h}

. In the frequency-domain design, as defined and developed in [13], the beamformer is

H = \frac{g β^{H} d e^{- j ϕ}}{1 - g α^{H} d e^{- j ϕ}} = \frac{g \frac{e^{j \hat{ϕ}} {\hat{d}}^{H}}{\hat{g} | | \hat{d} {| |}^{2}} d e^{- j ϕ}}{1 - g \frac{e^{j \hat{ϕ}} {\hat{d}}^{H}}{\hat{g} | | \hat{d} {| |}^{2}} d e^{- j ϕ}} .

(27)

One must take into consideration the transform of each sensor signal to the frequency domain using the fast Fourier transform (FFT) and then use the inverse FFT. Considering each time frame contains

L_{h}

samples, each sensor requires

L_{h} {log}_{2} L_{h}

operations. The FFT requires

N L_{h} {log}_{2} L_{h}

operations. The most expensive operation in the filter design (27) is the multiplication of the steering vector by itself, which requires

4 N L_{h}

multiplications and the same number of additions, where the factor 4 is due to the fact that the frequency-domain design deals with complex numbers. The frequency-domain design requires approximately

4 N^{2} L_{h}^{2} {log}_{2} L_{h}

multiplications and a similar number of additions. The above frequency domain’s complexity calculation assumes that

L_{h}

is an integer power of two. Otherwise, due to the FFT algorithm, zero padding must be added to each frame, which increases the computational complexity even more.

6.2. Execution Time

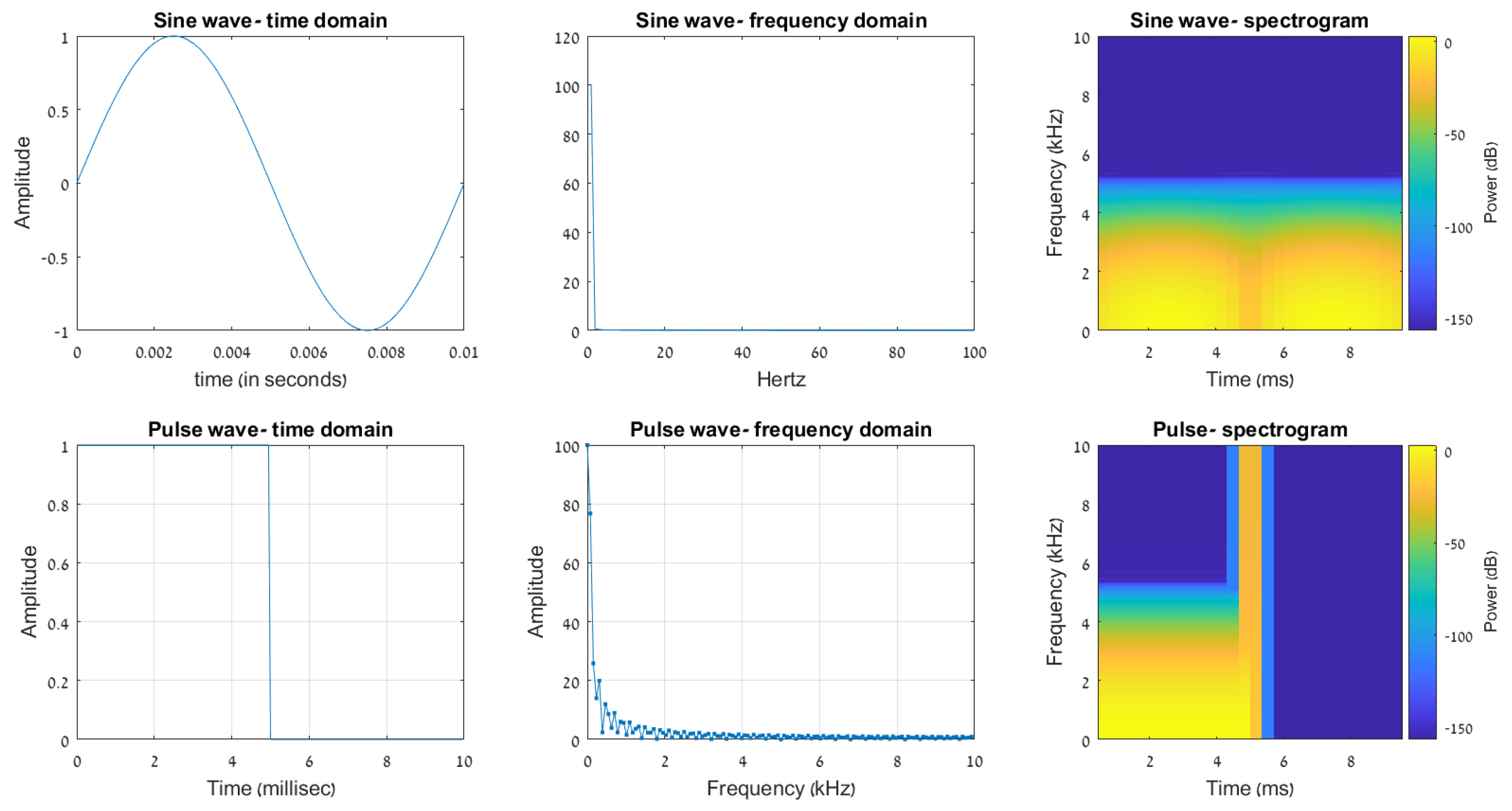
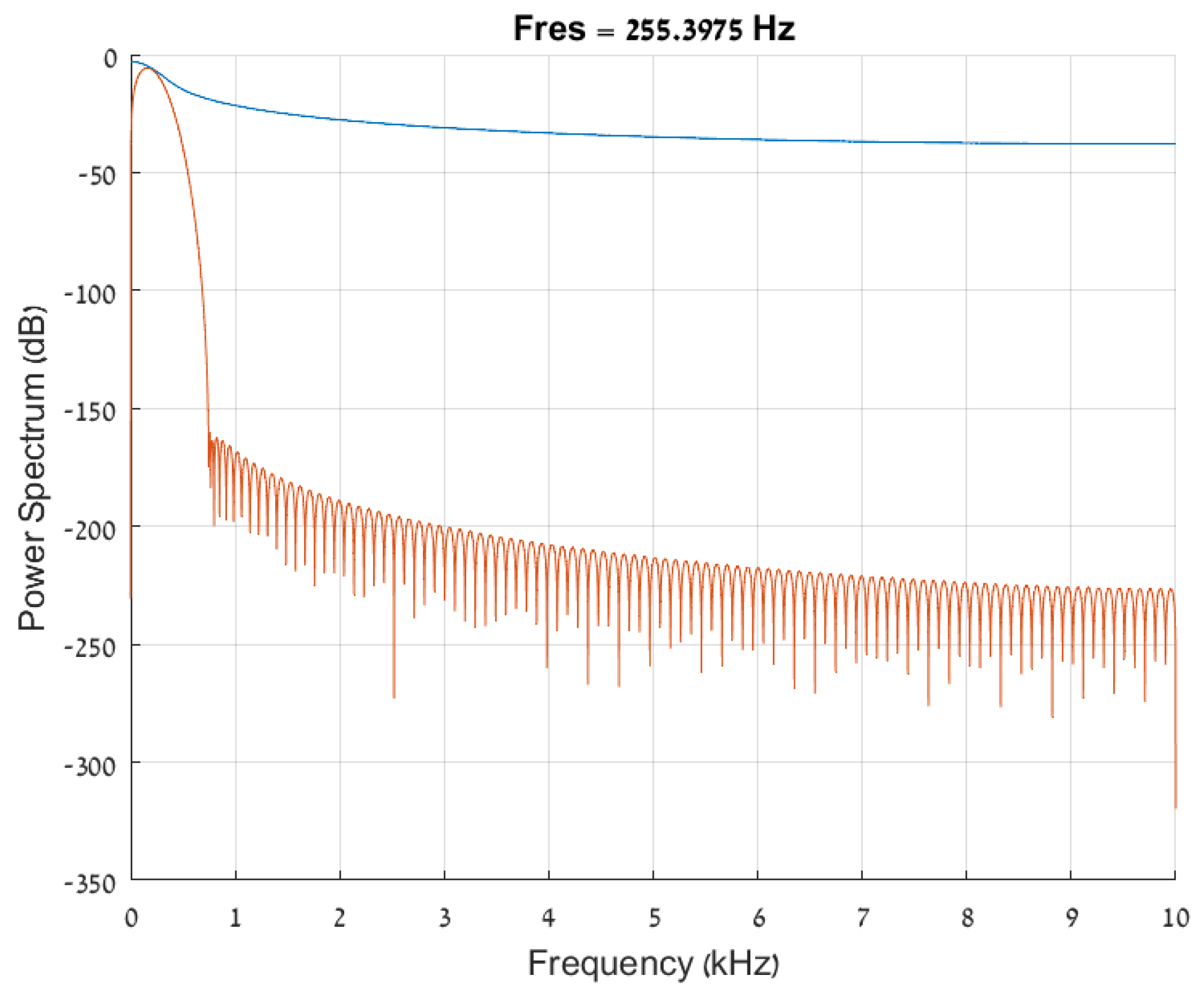
Radar processing systems are based on pulse signals rather than continuous-wave (CW) stimuli. Although CW signals simplify the analysis of a system, they are hardly feasible to implement, waste a significant part of the system’s power, and, therefore, are barely used. Moreover, CW radar systems rarely measure distance, which is our primary goal. One main drawback when using pulse-based signals is the known fact that pulse signals, which are finite in the time domain, contain high frequencies. A practical pulse signal contains many more frequencies than a CW signal, which includes, in theory, only one frequency. Each of the frequencies is considered in the steering vector in the frequency domain, increasing the execution time of such a beamformer. Figure 6 and Figure 7 demonstrate the differences from the time domain to the power spectrum between CW and pulse signal. As can be seen in the figures, the frequencies that must be considered are in the orders of magnitudes larger in pulse-based signal, in comparison to sine wave signal. While in the sine wave, just the sine frequency is a reasonable power, for the pulse-based signal, the power is quite the same with increasing frequency.

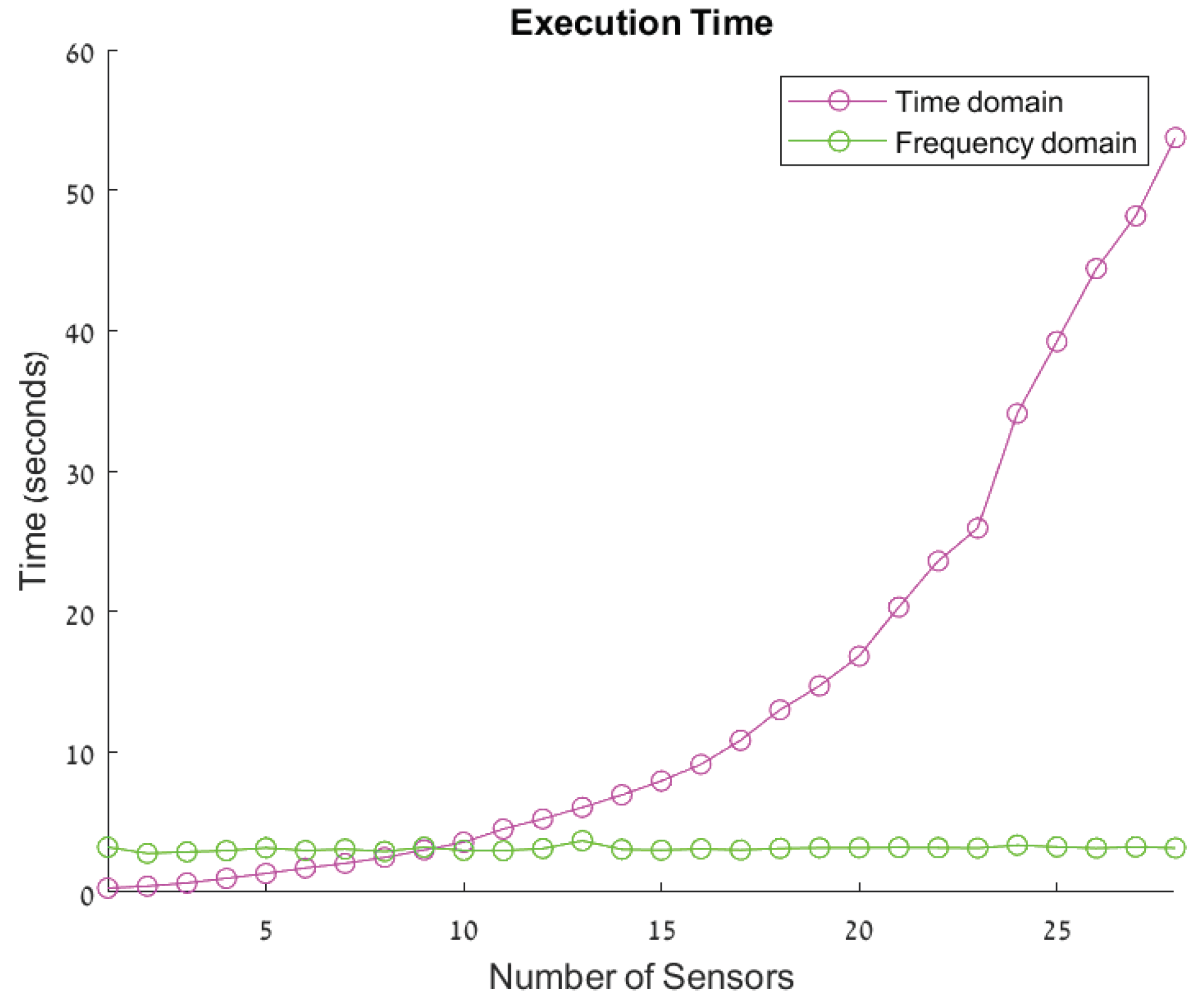
This fact directly results from the execution time of the frequency domain beamformer implementation. In [13], the beamformer computational complexity does not increase with the number of sensors. To authenticate this claim, we show in Figure 8 the execution time of the feedback beamformer in both the time and frequency domains as a function of the array size. In can be seen from Figure 8 for a small number of sensors (up to 10 sensors) the time domain has better execution time. In addition, one can see that the frequency domain calculation time is in the scale of seconds, which is not feasible in real-time systems. The exponential increase in calculation time in the time domain is due to the growth of (9), and the samples must be taken at each interval.

7. Conclusions

We have introduced a closed-form solution for a time-domain feedback-based beamformer, laying the groundwork for its future application and development. The feedback architecture demonstrated notable enhancements over traditional beamforming techniques, such as delay-and-sum and maximum directivity factor beamformers, while also confirming its equivalence to frequency-domain approaches. We conducted an in-depth analysis of how range estimation errors influence the performance of the beamformer, revealing that the time-domain implementation offers superior robustness to these errors compared to its frequency-domain counterpart. The comparative study on computational complexity and execution time between time- and frequency-domain beamformers indicates that the choice between these implementations depends on specific use-case scenarios, particularly the number of sensors and the volume of sampled data. Notably, our time-domain beamformer exhibits improved execution times with a limited number of sensors, especially in applications utilizing pulse-based signals common in radar systems. This feature is crucial for real-time applications where execution speed is critical.

Future research directions for the time-domain FB will explore its application to ultra-wideband (UWB) signals, examining how pulse signals influence the results presented in this study and identifying specific conditions under which these effects are most pronounced. Another area of interest involves extending the current findings to scenarios involving non-stationary or multiple targets, enhancing the beamformer’s applicability to dynamic environments. Additionally, the proposed implementation holds potential for broader applications across various spatial array processing tasks, suggesting its versatility in the field. A particularly promising avenue involves refining the design of feedback beamforming to enhance adaptive beamforming techniques. This includes dynamically adjusting the

α

and

β

coefficients within iterative processes to achieve improved performance compared to the static beamforming approach detailed in this research.

Author Contributions

Conceptualization, Z.H. and I.C.; methodology, Z.H. and I.C; writing—original draft preparation, Z.H.; writing—review and editing, I.C.; visualization, Z.H.; supervision, I.C.; project administration, I.C. All authors have read and agreed to the published version of the manuscript.

Funding

This research was supported by the Israel Science Foundation (grant no. 1449/23) and the Pazy Research Foundation.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Abbreviations

The following abbreviations are used in this manuscript:

CB	conventional beamformer
CRB	Cramér-Rao Bound
CW	continuous-wave
DF	directivity factor
DOA	direction of arrival
DS	Delay-and-Sum
FB	feedback beamformer
FFT	fast Fourier transform
FIM	Fisher Information Matrix
IIR	infinite impulse response
ULA	uniform linear array
UWB	Ultra-wideband

Appendix A. FIM Calculation

A full proof of the FIM main diagonal elements is presented, yielding (20). Combining (16) and

z (t) = β^{T} x (t)

, we calculate the spatial derivatives,

\frac{\partial z (t)}{\partial θ_{d}}

and

\frac{\partial z (t)}{\partial d}

\begin{matrix} \frac{\partial z (t)}{\partial θ_{d}} = & \frac{\partial}{\partial θ_{d}} \frac{g_{c} β^{T} G (θ_{d}, d) s (t)}{1 - g_{c} α^{T} G (θ_{d}, d) i_{l}} \\ = & \frac{g_{c} β^{T} \frac{\partial}{\partial θ_{d}} G (θ_{d}, d) s (t) [1 - g_{c} α^{T} G (θ_{d}, d) i_{l}]}{{[1 - g_{c} α^{T} G (θ_{d}, d) i_{l}]}^{2}} \\ + \frac{g_{c} α^{T} \frac{\partial}{\partial θ_{d}} G (θ_{d}, d) i_{l} g_{c} β^{T} G (θ_{d}, d) s (t)}{{[1 - g_{c} α^{T} G (θ_{d}, d) i_{l}]}^{2}} \end{matrix}

(A1)

and

\begin{matrix} \frac{\partial z (t)}{\partial d} = & \frac{g_{c} β^{T} \frac{\partial}{\partial d} G (θ_{d}, d) s (t) [1 - g_{c} α^{T} G (θ_{d}, d) i_{l}]}{{[1 - g_{c} α^{T} G (θ_{d}, d) i_{l}]}^{2}} \\ + \frac{g_{c} α^{T} \frac{\partial}{\partial d} G (θ_{d}, d) i_{l} g_{c} β^{T} G (θ_{d}, d) s (t)}{{[1 - g_{c} α^{T} G (θ_{d}, d) i_{l}]}^{2}} . \end{matrix}

(A2)

Recall that derivative a matrix with a scalar is the derivative of each element, the partial derivatives of

G_{i j}

, can be written as

\frac{\partial G_{i j}}{\partial θ_{d}} = \frac{\partial}{\partial θ_{d}} sinc [- P - L_{h} + 1 - i + j - \frac{f_{s} δ cos (θ_{d}) + 2 d}{c}] .

(A3)

Defining

A = - P - L_{h} + 1 - i + j

B = f_{s} δ

and

D = 2 d

, we get

\begin{matrix} \frac{\partial}{\partial θ_{d}} sinc [A - \frac{B cos (θ_{d}) + D}{c}] \\ = & \frac{π B cos [\frac{π}{c} (c A - B cos (θ_{d}) - D)] sin (θ_{d}) [c A - B cos (θ_{d}) - D]}{π {[c A - B cos (θ_{d}) - D]}^{2}} \\ + \frac{c B sin [\frac{π}{c} (c A - B cos (θ_{d}) - D)] sin (θ_{d})}{π {[c A - B cos (θ_{d}) - D]}^{2}} . \end{matrix}

(A4)

Denoting

F = c A - B c o s (θ_{d}) - D

, we have

\frac{\partial}{\partial θ_{d}} sinc [A - \frac{B cos (θ_{d}) + D}{c}] = \frac{π B cos (\frac{π}{c} F) sin (θ_{d}) F - c B sin (\frac{π}{c} F) sin (θ_{d})}{π F^{2}} .

(A5)

Since

F \approx c

we can conclude that

cos (\frac{π}{c} F) = - 1

and

sin (\frac{π}{c} F) = 0

. In conclusion, the spatial derivative with respect to

θ_{d}

is given by

\frac{\partial G_{i j}}{\partial θ_{d}} = - \frac{π B sin (θ_{d}) F}{π F^{2}} = - \frac{B sin (θ_{d})}{F} .

(A6)

In the same way for large

\frac{\partial G_{i j}}{\partial d}

, we get for

A = - P - L_{h} + 1 - i + j

B = f_{s} δ

and

F = c A - B cos (θ_{d}) - 2 R

that

\frac{\partial G_{i j}}{\partial d} = \frac{- 2 π cos (\frac{π F}{c}) F + 2 D sin (\frac{π F}{c})}{π F^{2}} = - \frac{2 π F}{π F^{2}} = - \frac{2}{F}

(A7)

where

f_{1}

and

f_{2}

are the numerators of

\frac{\partial z (t)}{\partial θ_{d}}

and

\frac{\partial z (t)}{\partial d}

, respectively.

References

Geng, Z.; Deng, H.; Himed, B. Adaptive radar beamforming for interference mitigation in radar-wireless spectrum sharing. IEEE Signal Processing Letters 2014, 22, 484–488. [Google Scholar] [CrossRef]
Blomberg, A.E.A.; Austeng, A.; Hansen, R.E.; Synnes, S.A.V. Improving sonar performance in shallow water using adaptive beamforming. IEEE Journal of Oceanic Engineering 2013, 38, 297–307. [Google Scholar] [CrossRef]
Allen, G.E.; Evans, B.L. Real-time sonar beamforming on workstations using process networks and POSIX threads. IEEE Transactions on Signal Processing 2000, 48, 921–926. [Google Scholar] [CrossRef]
Lin, Z.; Lin, M.; Wang, J.B.; Huang, Y.; Zhu, W.P. Robust secure beamforming for 5G cellular networks coexisting with satellite networks. IEEE Journal on Selected Areas in Communications 2018, 36, 932–945. [Google Scholar] [CrossRef]
Phan, A.H.; Tuan, H.D.; Kha, H.H. Space-time beamforming for multiuser wireless relay networks. In Proceedings of the 2011 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP). IEEE; 2011; pp. 2836–2839. [Google Scholar]
Paulraj, A.J.; Papadias, C.B. Space-time processing for wireless communications. IEEE signal processing magazine 1997, 14, 49–83. [Google Scholar] [CrossRef]
Schuler, K.; Younis, M.; Lenz, R.; Wiesbeck, W. Array design for automotive digital beamforming radar system. In Proceedings of the IEEE International Radar Conference, 2005. IEEE, 2005, pp. 435–440.
Harter, M.; Hildebrandt, J.; Ziroff, A.; Zwick, T. Self-calibration of a 3-D-digital beamforming radar system for automotive applications with installation behind automotive covers. IEEE Transactions on Microwave Theory and Techniques 2016, 64, 2994–3000. [Google Scholar] [CrossRef]
Bond, E.J.; Li, X.; Hagness, S.C.; Van Veen, B.D. Microwave imaging via space-time beamforming for early detection of breast cancer. IEEE Transactions on Antennas and Propagation 2003, 51, 1690–1705. [Google Scholar] [CrossRef]
Byrne, D.; Craddock, I.J. Time-domain wideband adaptive beamforming for radar breast imaging. IEEE Transactions on Antennas and Propagation 2015, 63, 1725–1735. [Google Scholar] [CrossRef]
Van Veen, B.D.; Buckley, K.M. Beamforming: A versatile approach to spatial filtering. IEEE assp magazine 1988, 5, 4–24. [Google Scholar] [CrossRef] [PubMed]
Chernyakova, T.; Eldar, Y.C. Fourier-domain beamforming: the path to compressed ultrasound imaging. IEEE transactions on ultrasonics, ferroelectrics, and frequency control 2014, 61, 1252–1267. [Google Scholar] [CrossRef]
Karo, I.Y.; Dvorkind, T.G.; Cohen, I. Source localization with feedback beamforming. IEEE Transactions on Signal Processing 2020, 69, 631–640. [Google Scholar] [CrossRef]
Dougherty, R. Advanced time-domain beamforming techniques. In Proceedings of the 10th AIAA/CEAS Aeroacoustics Conference; 2004; p. 2955. [Google Scholar]
Buchris, Y.; Cohen, I.; Benesty, J. On the design of time-domain differential microphone arrays. Applied Acoustics 2019, 148, 212–222. [Google Scholar] [CrossRef]
Shubair, R.M.; Hakam, A. Adaptive beamforming using variable step-size LMS algorithm with novel ULA array configuration. In Proceedings of the 2013 15th IEEE International Conference on Communication Technology. IEEE; 2013; pp. 650–654. [Google Scholar]
Ye, Z.; Dai, J.; Xu, X.; Wu, X. DOA estimation for uniform linear array with mutual coupling. IEEE Transactions on Aerospace and Electronic Systems 2009, 45, 280–288. [Google Scholar]
Liao, B.; Chan, S.C. Adaptive beamforming for uniform linear arrays with unknown mutual coupling. IEEE Antennas and Wireless Propagation Letters 2012, 11, 464–467. [Google Scholar] [CrossRef]
Ioannides, P.; Balanis, C.A. Uniform circular and rectangular arrays for adaptive beamforming applications. IEEE Antennas and Wireless Propagation Letters 2005, 4, 351–354. [Google Scholar] [CrossRef]
Tsai, J.A.; Buehrer, R.M.; Woerner, B.D. BER performance of a uniform circular array versus a uniform linear array in a mobile radio environment. IEEE Transactions on Wireless Communications 2004, 3, 695–700. [Google Scholar] [CrossRef]
Ioannides, P.; Balanis, C.A. Uniform circular arrays for smart antennas. IEEE Antennas and propagation magazine 2005, 47, 192–206. [Google Scholar] [CrossRef]
Wu, X.; Yang, X.; Ma, S.; Zhou, B.; Yang, G. Hybrid channel estimation for UPA-assisted millimeter-wave massive MIMO IoT systems. IEEE Internet of Things Journal 2021, 9, 2829–2842. [Google Scholar] [CrossRef]
Song, J.; Choi, J.; Love, D.J. Common codebook millimeter wave beam design: Designing beams for both sounding and communication with uniform planar arrays. IEEE Transactions on Communications 2017, 65, 1859–1872. [Google Scholar] [CrossRef]
Benesty, J.; Cohen, I.; Chen, J. Fundamentals of signal enhancement and array signal processing; John Wiley & Sons, 2017.
Shannon, C.E. Communication in the presence of noise. Proceedings of the IRE 1949, 37, 10–21. [Google Scholar] [CrossRef]
Zeira, A.; Nehorai, A. Frequency domain Cramer-Rao bound for Gaussian processes. IEEE transactions on acoustics, speech, and signal processing 1990, 38, 1063–1066. [Google Scholar] [CrossRef]
SV, H. Radio and Microwave Wireless Systems.
Bao, C. Performance of time domain and time-frequency domain adaptive beamformers with moving sound sources. In Proceedings of the INTER-NOISE and NOISE-CON Congress and Conference Proceedings. Institute of Noise Control Engineering. 2014, Vol. 249, pp. 3727–3734.

Figure 1. Uniform linear array.

Figure 2. Proposed beamformer structure. The goal is to spatially localize the target

P_{t}

by re-transmitting the signal.

Figure 2. Proposed beamformer structure. The goal is to spatially localize the target

P_{t}

by re-transmitting the signal.

Figure 3. Feedback beamformer response (blue line), compared to known ULA beamformers, DS (dashed red line) and maximum DF (dashed green line) for

θ_{d} = 90^{\circ}

and

r = 0.6

Figure 3. Feedback beamformer response (blue line), compared to known ULA beamformers, DS (dashed red line) and maximum DF (dashed green line) for

θ_{d} = 90^{\circ}

and

r = 0.6

Figure 4. Directivity factor as a function of

δ

for the feedback beamformer (lines with circles), compared to DF for a generic ULA (25) (solid lines) for a signal wave with frequency carrier of 1GHz,

r = 0.6

θ_{d} = 45^{\circ}

. DF is tested for several values of N: N=10 (blue lines), N=20 (red lines), N=30 (green lines) and N=40 (light blue lines).

Figure 4. Directivity factor as a function of

δ

for the feedback beamformer (lines with circles), compared to DF for a generic ULA (25) (solid lines) for a signal wave with frequency carrier of 1GHz,

r = 0.6

θ_{d} = 45^{\circ}

. DF is tested for several values of N: N=10 (blue lines), N=20 (red lines), N=30 (green lines) and N=40 (light blue lines).

Figure 5. Effect of incorrect estimation of the target’s range for

θ_{d} = 90^{\circ}

and

r = 0.6

Figure 5. Effect of incorrect estimation of the target’s range for

θ_{d} = 90^{\circ}

and

r = 0.6

Figure 6. Sine and pulse wave characteristics.

Figure 7. Power spectrum of both pulse wave (blue line) and sine wave(red line) in the same sampling frequency.

Figure 8. Execution time of the beamformer output for both time and frequency domain, for the case when 10K frequencies are considered.

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Feedback Beamforming in the Time Domain

Abstract

1. Introduction

2. Signal Model

3. Feedback Beamforming

4. Finding the Optimal Weights

5. Beamformer Evaluation

5.1. Mainlobe and Sidelobe Attenuation

5.2. Directivity Factor

5.3. Range Error Influence

6. Time Domain vs. Frequency Domain Feedback Beamforming

6.1. Calculation Complexity

6.2. Execution Time

7. Conclusions

Author Contributions

Funding

Institutional Review Board Statement

Informed Consent Statement

Abbreviations

Appendix A. FIM Calculation

References

MDPI Initiatives

Important Links

Subscribe