Preprint
Article
The Quantum Ratio
Altmetrics
Downloads
88
Views
25
Comments
0
A peer-reviewed article of this preprint also exists.
This version is not peer-reviewed
Submitted:
22 February 2024
Posted:
26 February 2024
You are already at the latest version
Alerts
Abstract
The concept of {\it quantum ratio} emerged in the recent efforts to
understand how Newton's equations appear for the center of mass (CM) of an isolated macroscopic body at finite body-temperatures, as the first approximation to quantum-mechanical equations.
It is defined as $Q\equiv R_q/L_0$, where the quantum fluctuation range $R_q$ is the spatial extension of the pure-state CM wave function, whereas $L_0$ stands for the body's linear size (the space support of the internal, bound-state wave function). The two cases $R_q /L_0 \lesssim 1$ or $R_q/ L_0 \gg 1$, roughly correspond to the body's CM behaving classically or quantum mechanically, respectively. In the present note we elaborate more on this concept, illustrating it in several examples. An important notion following from introduction of the quantum ratio is that the elementary particles (thus the electron and the photon) are quantum mechanical, even when the environment-induced decoherence turns them into a mixed state. Decoherence and classical state should not be identified. This simple observation, further illustrationed by the consideration of a few atomic or molecular processes, may have significant implications on the way quantum mechanics works in biological systems.
Keywords:
Subject: Physical Sciences - Quantum Science and Technology
1. Introduction: the quantum ratio
The concept of quantum ratio emerged during the efforts to understand the conditions under which the center of mass (CM) of an isolated macroscopic body possesses a unique classical trajectory. It is defined as
where is the quantum fluctuation range of the CM of the body under consideration, and is the body’s (linear) size. The criterion proposed to tell whether the body behaves quantum mechanically or classically is [1]
or
respectively.
Let us assume that the total wave function of the body has a factorized form,
where is the CM wave function, the N-body bound state is described by the internal wave function . are the internal positions of the component atoms or molecules, is the CM position and (). In the case of a macroscopic body N can be as large as etc.
1.1. The size of the body
is determined by . A possible definition of is
but the detailed definition is not important here. is the spatial support (extension) of the internal wave function describing the bound state 1. It is the (linear) size of the body. Even though might somewhat depend on the body temperature T (the average internal excitation energy) it is well defined even in the limit. It represents the extension of the ground-state wave function of the bound state describing the body.
For an atom the definition (1.5) gives correctly the outmost orbit in the electronic configuration. varies from Å to hundreds of Å for atoms and molecules. The atomic nuclei (composed of protons and neutrons) which are bound more strongly by short-range nuclear forces, have smaller size of the order of Fermi cm. As for mesoscopic to macroscopic bodies varies vastly, depending on their composition, types of the forces which bind them and their particular molecular or crystalline structures. For the earth (the radius) km. An exception is the case of the elementary particles: they have . This has a simple implication, according to (1.2) having , the elementary particles are quantum mechanical. One might argue that the length scales (i.e., small or large) are relative concepts in physics: at distance much larger than , any body looks pointlike. More generally, changing the scales of distances or energies, physics might look similar. A more rigorous formulation of this idea (the scale invariance) is that of the renormalization group in relativistic quantum field theories in four dimensions (e.g., theories of the fundamental interactions [2,3,4,5]), or in lower dimensional models of critical phenomena [6].
Scale invariance holds if the system possesses no fixed length scale 2. From the point of view of the theory of the fundamental interactions, the absence of a fixed length scale means that physics at low energies does not depend on the ultraviolet cutoff we need to introduce to regularize (and renormalize) the theory because of the ultraviolet divergences present. In other words, the theory is of renormalizable type, that is, a quantum field theory without any a priori mass (or length) parameter. For the questions of interest in the present work, however, it is important, and we do know, that the world we live in has definite length scales, such as Bohr’s radius, and the size of the atomic nuclei. In other words, the terms such as microscopic (from elementary particles, nuclei, atoms, to molecules) and macroscopic (much larger than these) have a well-defined, concrete meaning. These fixed sizes (or length scales) characterizing our world are set by the fundamental constants of Nature (ℏ, e, c) and by the parameters in the theory of the fundamental (strong and electroweak) interactions [2,3,4,5], namely, the quark and lepton masses, W and Z masses. See Section 2.1 more about this.
1.2. Quantum range
The quantum fluctuation range is determined by . In principle, it is just the (spatial) extension of the pure-state wave function describing the CM of the body. But it is a much more complex quantity than : it depends on many factors. In quantum mechanics (QM) there is no a priori upper limit to 3. Take for instance the wave function of a free particle, . It might be thought that the normalization condition necessarily sets a finite quantum fluctuation range, but it is not so. As is well known (Weyl’s criterion), a particle can be in a state arbitrarily close to a plane-wave state,
i.e., in a momentum eigenstate, which has .
Given a body, will in general depend on the internal structures, excitation modes and on its body-temperature. These cause the self-induced (or thermal) decoherence, due to the emission of photons which carry away information, and seriously reduce . If the body is not isolated, its is severely affected by the environment-induced decoherence [9,10,11,12,13,14], on the surrounding temperature, flux, etc. also depends on the external electromagnetic fields, which may split the wave packets as in the Stern-Gerlach set-up, or on possible quantum-mechanical correlations (entanglement) among distant particles. may depend also on time.
An important question concerns the width of the wave packet of the CM of an isolated (microscopic or macroscopic) particle, . It should not be confused with . Being the spread of a single-particle wave function, is a measure of the quantum fluctuation range
but can be much larger than in general.
As for the relation between and , corresponds to the uncertainty of the CM position of the body. For a macroscopic body, an experimentalist who is capable to measure and determine its size with some precision, will certainly be able to measure the CM position R with
Nevertheless, such a relation neither holds necessarily nor is required in general. A macroscopic body, especially at exceedingly low temperatures near , may well be in a state of position uncertainty (the width of the wave packet)
Such a system is seen, by using (1.7), to have , so is quantum mechanical. Many attempts to realize macroscopic quantum states experimentally, bringing the system temperatures down to close to , have been made recently [15,16,17,18,19,20,21,22,23,24,25,26].
Vice versa, a well-defined CM position (1.8) set up at time , does not in itself tell whether the system will behave quantum-mechanically or classically.
A free wave packet of an atom or molecule with the initial position uncertainty , will quickly diffuse (the diffusion rate depends on the mass) and will acquire See Table 1 taken from [1]. In the Stern-Gerlach set-up, with an inhomogeneous magnetic field, the (transverse) wave packet of an atom or a molecule with spin will be spilt in two or more wave packets, which can get separated even by a macroscopic distance (), such that , (see Section 2.3 for more about it).
On the other hand, a macroscopic body does not diffuse (see Table 1). Its CM wave packet does not split under an inhomogeneous magnetic field, either [1]. Therefore, if the CM position of a macroscopic body is measured with precision (1.8) at time , the relation () is maintained in time. Such a body evolves classically, with a well-defined trajectory, obeying Newton’s equations [1].
1.3. The microscopic degrees of freedom inside a macroscopic body are quantum mechanical
The present discussion on the quantum ratio is concerned with the question how classical behavior for the CM of a macroscopic body emerges from QM. An important fact to be kept in mind is the following. Even if a macroscopic (or a mesoscopic) body, as a whole, might behave classically, due to environment-induced or self-induced (or thermal) decoherence and due to its large mass [1], the internal microscopic degrees of freedom, the electrons, the atomic nuclei, and the photons, remain quantum mechanical (see Section 2.1, Section 2.2, Section 3). All sorts of quantum-mechanical processes (e.g., tunnelling) continue to be active inside the body, even if various decoherence effects may be significant. These quantum phenomena constitute the essence of the physics of polymers and of general macromolecules, therefore of biology. They hold the key to the answers to many questions in biology, genetics and in neuroscience, unanswered today (see for instance [27,28]). The consideration of the present note has nothing to add, directly, to these questions. See however a few more related general comments below, in Section 3.
2. The quantum ratio illustrated
In this section the quantum ratio will be illustrated in several examples.
2.1. Elementary particles
The elementary particles known today (as of the year 2024) are the quarks, leptons (electron, muon, lepton), the three types of neutrinos, and the gauge bosons (the gluons, W, Z bosons and the photon), with masses listed below.
Table 2.
The quark masses in MeV/; the errors not indicated. 1 MeV g
| (u) | (d) | (s) | (c) | (b) | (t) |
Table 3.
The lepton masses. The e, and masses given in MeV.
| (e) | () | () | ; eV |
Table 4.
Gauge bosons and their masses
| photon | gluons | (GeV) | Z (GeV) |
| 0 | 0 |
The fact that the processes involving these particles are very accurately described by the local quantum field theory up to the energy range of TeV, means that
In future, these elementary particles might well turn out to be made of some constituents unknown today, bound by some new forces yet to be discovered. For the present-day physics their size can be taken to be 4
The elementary particles are quantum mechanical. This notion is generally taken for granted by physicists, even if no justification is (was) known, as such. Here, as we are enquiring whether certain “particle", be it an atom, molecule, macromolecule, a piece of crystal, etc., behaves quantum-mechanically or classically, and under which conditions, it perhaps makes sense to ask whether or why an elementary particle is quantum mechanical 5. Introduction of the criterion of quantum ratio offers an immediate (affirmative) answer to the first question, and explains the second. By definition the elementary particles have no internal structures, hence no internal excitations. There is no sense in talking about their body-temperature or thermal decoherence. The observation that the elementary particles are quantum mechanical in the light of quantum ratio (2.1), (2.2), might sound new, but it is not really so. Actually, it reflects the common understanding matured around 1970 in high-energy physics community (e.g., ’t Hooft, Cargese lecture [30]) that the law of Nature at the microscopic level is expressed by a renormalizable, relativistic local gauge theory (a quantum field theory) of the elementary particles. Such a theory describes pointlike particles () 6. The scale or dilatation invariance of this type of theories is broken by the necessity of introducing an ultraviolet cutoff, a mass scale , to regularize, renormalize and define a finite theory (quantum anomaly). Remarkably, the scale invariance is restored by the introduction of the renormalized coupling constants, defined conveniently at some reference mass scale , and giving them an appropriate dependence (the renormalization-group equations). See e.g., Coleman’s 1971 Erice lecture [31]. The fixed length or mass scales of our world, mentioned in Section 1.1, concern the infrared fate of such dilatation invariance. These fixed scales can be, ultimately, traced to (i) the vacuum expectation value of the Higgs scalar field in the Glashow-Weinberg-Salam electroweak theory and (ii) the mass scale dynamically generated by the strong interactions (Quantum Chromodynamics). They break the scale invariance. All fixed length scales from the microscopic to macroscopic world we live in follow from them and from some dimensionless coupling constants in the theory 7.
2.2. Hadrons and Atomic nuclei
The atomic nuclei, together with various hadrons (the mesons and baryons), are the smallest composite particles known today. Until around 1960, the mesons (, K, ...) and baryons (p, n,...) used to be part of the list of “elementary particles", together with leptons. As the theory of the strong interactions (the quark model, and subsequently, the quantum chromodynamics, a nonAbelian gauge theory of quarks and gluons) was established around 1974 - 1980, they were replaced by the quarks and gluons, as more fundamental constituents of Nature.
The atomic nuclei are bound states of the nucleons, i.e., protons (p) and neutrons (n). They are bound by the strong interactions and their size is of the order of
where A is the mass number. The Coulombic wave functions in the atoms and molecules have extension () of the order of , thus
The atomic nuclei are quantum mechanical.
To say that the atomic nuclei are quantum mechanical because of the atomic extension (2.4), is however certainly too reductive. The atomic nuclei indeed may appear without being bound in atoms. For instance the particle is the nucleus of the helium atom, but may come out of a metastable nucleus through the decay, and propagate as a free particle. It possesses the size of the order of (2.3), much larger than the typical size of an elementary particles, (2.1), but still for the processes typically involving the distance scales much larger than 1 fm, it behaves as a pointlike particle, i.e., quantum mechanically, just as any elementary particle. Similarly for the proton, the nucleus of the hydrogen atom, with fm.
2.3. Stern-Gerlach experiment
The next smallest composite particles known in Nature are the atoms. They are Coulombic composite states made of the electrons moving around the positively charged atomic nuclei, almost pointlike (at the atomic scales) and times heavier than the electron.
Let us consider the well-known Stern-Gerlach process of atoms with a magnetic moment in an inhomogeneous magnetic field. To be concrete, we take as an example the very original Stern-Gerlach experiment with the silver atom [32], , with mass and size,
Having the electronic configuration and the global quantum number 8,
the magnetic moment of the atom is dominated by the spin of the outmost electron,
where g is the gyromagnetic ratio of the electron.
The question is whether the silver atom, which is certainly a quantum-mechanical bound state of 47 electrons, 47 protons and 51 neutrons and with mass times that of the hydrogen atom, behaves as a whole (i.e., its CM) as a QM particle with spin or a classical particle of magnetic moment .
The beam of is sent into the region, long cm, of an inhomogeneous magnetic field, , , as it proceeds in the e.g., direction. The beam width, which reflects the apertures of the two slits used to prepare the well collimated beam, is about mm wide 9. After passing the region of the magnetic field, the image of the atoms on the glass screen shows two bands clearly separated about mm in the direction of . In other words, at the end of the region with the magnetic field, the atom is described by a split wave packet of the form,
with the centers of the two subpackets and at and , respectively, where mm. The spatial support of the wave function can be taken as about that size. It follows that
the atom, as a whole, is behaving perfectly as a quantum-mechanical particle.
Actually, the fact that the wave packets are divided in two by an inhomogeneous magnetic field does not necessarily mean that the system is in a pure state of the form (2.8). The wave function of the form (2.8) corresponds to a 100% polarized beam, where all incident atoms are in the same spin state
If the beam is partially polarized or unpolarized, the spin state is described by a density matrix . The pure state (2.10) corresponds to the density matrix
whereas a general mixed state is described by a generic, Hermitian matrix with
In an unpolarized beam, .
What the Stern-Gerlach experiment measures is the relative frequency that the atom arriving at the screen happens to have spin or spin . Let
be the projection operators on the spin up (down) states; the relative intensities of the upper and lower blots on the screen are, according to QM,
The prediction about the relative intensities of the two narrow atomic image bands from the wave function (2.8) and from the density matrix, (2.14) is in general indistinguishable, as is well known. In other words, what the Stern-Gerlach experiment has shown is not whether the atom is in a pure state of the form, (2.8), or in a generic (spin-) mixed state, (2.14), but that the silver atom is a quantum-mechanical particle.
Indeed, the prediction for a classical particle is qualitatively different. Each atom, if classical, would move depending on the orientation of its magnetic moment, tracing a well-defined trajectory,
It would arrive at some generic point on the screen. If the initial orientation of the magnetic moment is random, after many classical atoms have arrived they would leave a continuous band of atomic images, instead of two narrow, well separated bands, as has been experimentally observed and as QM predicts.
Vice versa, if the orientation of the magnetic moment / spin is fixed (and the same) for all incident atoms, the classical atoms will produce only one narrow band, whereas QM atoms will leave two separate image bands. These considerations clearly tell that the concepts of mixed state and classical particle should be distinguished. We extend these discussions further in Section 3, taking into account also the effects of environment-induced decoherence, as well as the large spin limit, and their relations to the classical limit, (2.15).
2.4. Atomic and molecular interferometry
Many beautiful experiments exhibiting the quantum-mechanical feature (wave character) of atoms and molecules have been performed (or proposed), by using various types of interferometers [33,34,35,36,37,38,39,40,41,42]. One of the most powerful approaches uses the Talbot-Lau interferometry [33,36,37,38,39].
The essential part of all these experiments makes use of the so-called Talbot effect [43]. In a typical setting, an atomic or molecular beam, passing through the first slit is sent to the diffraction grating ( in Figure 1), consisting of many slit apertures set with period d. After the passage of the diffraction grating, the wave function of the atom or molecule, which originated from a point source, has the form,
where is the (transverse) wave packet of the atom (molecule) which has passed through the i-th slit. Just behind the diffraction grating, the distribution of the atom (molecule) has a modulation such as in Figure 2, each peak corresponding to the position of a slit opening.
The coherent components of the wave function, (2.16), corresponding to different paths shown in Figure 1, interfere constructively or destructively, depending on the vertical position on the imaging screen, set at a distance from the diffraction grating. In the so-called near-field diffraction - interference effects, the intensity modulation behind the diffraction grating (Figure 2) is reproduced (self-imaging) on the screen [33,36,37,38,39,43], when takes definite values, related to the Talbot length 10,
as shown in Figure 1. The details of the calculation on the sum over paths can be found in [36]. By introducing the geometrical magnification factors, ; , the sum over the different paths of Figure 1 is shown to give, for instance at , the intensity pattern behind the diffraction grating reproduced at , with an enlarged period, . For , instead, the same intensity pattern appears but shifted by a half period, .
In the Talbot-Lau interferometer, which is a variation of the above, the imaging screen is replaced by a vertically (i.e., in the direction) movable transmission-scanning grating, with an appropriate period . See Figure 3. This way, the occurrence of the interference fringes - the Talbot self-imaging - is converted to the total transmission rate of the molecules (atoms) which varies periodically as a function of the vertical () position of the scanning grating as a whole. Another advantage of the Talbot-Lau interferometer is the possibility of introducing the incoherent source beam hitting the first grating. Even though the coherence sum over paths is relevant only for the atoms (or the molecules) which have originated from a definite source slit, the use of an incoherent source can increase the total counts after the third, transmission grating, improving significantly the statistics of the experiments.
For the purpose of discussing the quantum-fluctuation range and the quantum ratio, these details of the set-up are not really fundamental. We need simply to know the transverse, spatial extension of the wave function, (2.16). This in turn can be taken as the height of the diffraction grating , H, of Figure 3. The detection of the Talbot effect or Talbot-Lau fringe visibility, is a proof that the transverse wave packets in (2.16) are indeed in coherent superposition: i.e., that it is a pure state. We thus take the quantum fluctuation range in Table 5 from the experimental total height H of the diffraction grating , Figure 3.
A large quantum ratio implied by such a quantum range (and their size) is certainly an indication that these atoms and molecules are quantum mechanical, even though such an observation does not supersede the direct evidence of quantum coherence and interference effects presented in [33,36,37,38,39].
2.4.1. On the “matter wave"
A familiar word used in the articles on the atomic and molecular interferometry [34,35,36,37,38,39,40,41,42] is “matter wave". It might appear to summarize well the characteristic feature of quantum-mechanics: “wave-particle duality". Actually, such an expression is more likely to obscure the essential quantum mechanical features of these processes, rather than clarifying them. It appears to imply that the beams of atoms or molecules somehow behave as a sort of wave: that is not quite an accurate description of the processes studied in [34,35,36,37,38,39,40,41,42].
The wave-particle duality of de Broglie, the core concept of quantum mechanics, refers to the property of each single quantum-mechanical particle, and not to any unspecified collective motion of particles in the beam 11. This point was demonstrated experimentally by Tonomura et. al.[44] in a double-slit electron interferometry experiment à la Young, with exemplary clarity.
Exactly the same phenomena occur in any atomic or molecular interferometry. For each single incident atom or molecule, it amounts to the position measurement at the third, imaging screen. For each incident particle, the result for the exact final vertical position at is not known: it cannot be predicted, in accordance with QM. Only after the data with many incident particles are collected, one observes the interference effect reflecting the coherence among the components of the extended wave function, (2.16), in accordance with the QM laws.
From the data given in [34,35,36,37,38,39,40,41,42] it is not difficult to verify that the average distance between the successive atoms (or the molecules), as compared to the size of their longitudinal wave-packet (which can be deduced from the momentum uncertainty ), is many orders of magnitudes larger. For instance, in the case of the sodium-atom experiment [39], their ratio is about . In the case of the [38] this ratio seems to be even greater. The atoms or molecules do arrive one by one.
As the correlation among the atoms or molecules in the beam is negligible (as it should be), and the position of each final atom/molecule is apparently random, the resulting interference fringes such as manifested in the Talbot (or the Talbot-Lau) interferometers, is all the more surprising and interesting. What these experiments show goes much deeper into the heart of QM, than the words, “matter wave" or “wave-particle duality", might suggest.
3. Decoherence versus classicality
The atomic and molecular experiments discussed in Section 2.3, Section 2.4 are all performed in a high-quality vacuum [32,33,34,35,36,37,38,39,40,41,42]. This is necessary, lest the scattering of the atom or molecule under study with the environment particles, e.g., air molecules, destroy their pure quantum-state nature and let them lose the ability of exhibiting typical quantum phenomena such as diffraction, coherent superposition, and interferences. These processes are known as the environment-induced decoherence [9,10,11,12,13,14]. Under environment-induced decoherence the object under consideration becomes a mixture. Diffraction, coherent superposition, and interference phenomena typical of pure quantum states get lost.
But it does not necessarily mean that the system becomes classical. Being in a mixed state is necessary for the system to behave classically, but is in general not sufficient [1]. Unfortunately, there seems to be a widespread and inappropriate identification in the literature of these two concepts: mixed (decohered) states and classical states. Consider the free electron. Its decoherence rate / time, has been studied under various types of environments [9,10,11,12,13,14]. For instance, in the atmosphere at 1 atm pressure, a free electron decoheres in s [11]. But when it interacts subsequently with other systems, it does so quantum mechanically, not as a classical particle. Once it comes out of the region with “environment", it emerges as a free particle, a pure quantum state. The same can be said of the photon (as of any other elementary particle). A related remark may be made about the cosmic rays. The gamma ray (photons), neutrinos, protons, etc., which are produced in hot and dense interiors of stars, once out, travel in cosmic space (a good approximation of vacuum) as free, quantum particles in pure states. In the experiment of [38], molecules are excited by a laser beam, before they enter the interferometry. When the average temperature of the molecules exceeds 3000K, the Talbot-Lau interference fringe signals are found to disappear, showing that the molecules became mixed states, in agreement with the decoherence theory 12. The quantum fluctuation range becomes of the order of the diffraction grating period, d. This value is given in Table 5. But this does not mean that the molecules have become classical: what one can conclude from [38] is that the thermal decoherence renders the molecule incoherent, mixed state. Below we consider two more test cases where the difference among the pure state, decohered mixed state, and the classical state, is seen very clearly. These considerations can have far-reaching consequences. For instance, they may indicate a way out of the “no-go" verdict for the relevance of quantum mechanics in the brain dynamics [12]. They may be fundamental in all microscopic processes underlying biological systems (see Section 1.3) [27,28].
3.1. Stern-Gerlach set-up, decoherence and classical limit
The original Stern-Gerlach (SG) process was discussed already (Section 2.3). What the experimental result shows is that the silver atom behaves as a quantum-mechanical particle, either in a pure or (spin-) mixed state.
Here we discuss the SG process again, in more detail, in three different regimes, (i) a pure QM process; (ii) the environmental decoherence (an incoherent, mixed state); and (iii) for a classical particle. The main aim of this discussion is to hilight the differences between these different physics situations as sharply as possible.
3.1.1. Pure QM state
For definiteness let us take the incident atom with spin directed in a definite, but generic, direction, , i.e.,
where
and describes the wave packet of the atom, moving towards the direction, before entering the region with an inhomogeneous magnetic field . The Hamiltonian is given by
and the time evolution of the system is described by the Schrödinger equation
where the total energy is conserved.
After the atom enters the inhomogeneous field , the upper and lower spin components of the wave function split, so let us write
The upper and down-spin components satisfy the Schrödinger equation 13
We assume that the wave function , before entering the region with the magnetic field, is a compact wave packet (e.g., a Gaussian with width a), moving towards the direction.
From (3.7) and their complex conjugates, the Ehrenfest theorems for spin-up and spin-down components follow separately,
where , etc. Namely, for a sufficiently compact initial wave packet, , the expectation values of and in the up and down components follow respectively the classical trajectories of a spin-up or spin-down particle. At the end of the region with the magnetic field 14 it is described as a split wave packet of the form, (2.8). Even though the two subpackets might be well separated by a macroscopic distance , they are still in coherent superposition. Its pure-state nature can be verified by reconverging them by using a second magnetic field of opposite gradients, and studying their interferences (the quantum eraser).
A variational solution of (3.7) in the case of a linear potential, , is given in Appendix A. The splitting of the wavepacket is illustrated in Figure 4 (a).
3.1.2. Environment-induced decoherence
Let us now consider the SG process (3.1)-(3.4) again, but this time in a poor vacuum, e.g., in the presence of non-negligible background. The decoherence of a well separated split wave packet as (2.8) due to the interactions with the environment particles has been the subject of intense study [9,10,11,12,13,14]. The upshot of the results of these investigations is that the environment-induced decoherence causes the pure state (2.8) to become a mixed state at , described by a diagonal density matrix
where is the decoherence rate [9,10,11,12,13,14] and is the de Broglie wavelength of the environment particles. The density matrix (3.10) means that each atom is now either near or near . The prediction for the SG experiment is however the same as the case of spin-mixed state (partially polarized source atoms), (2.14): it cannot be distinguished from the prediction for the relative intensities of the two image bands, in the case of the pure state. Actually, the study of the effects of the environment particles on any given quantum process is a complex, and highly nontrivial problem, as it involves many factors, such as the density and flux of these particles, the pressure, the average temperature, kinds of the particles present and the type of interactions, etc. [9,10,11,12,13,14]. A simple statement such as (3.10) might sound as an oversimplification.
Without going into the detailed features of the environment, we may nevertheless attempt to clarify the basic conditions under which the result such as (3.10) can be considered reliable. Following [11], we introduce the decoherence time , as a typical timescale over which the decoherence takes place. Also the dissipation time may be considered, as a timescale in which the loss of the energy, momentum of the atom under study due to the interactions with the environmental particles, become significant 15. We need to consider also a typical quantum diffusion time, , and finally, the transition time, , the interval o f time the atom spends between the source slit to the image screen (or anyway the final, reference position in the direction of motion).
First of all, we assume that the velocity of the incident atom, its mass, and the size of the whole apparatus are such that the free quantum diffusion (the spreading of the wave packets) is negligible, during the process under study. Furthermore, the environment is assumed to be sufficiently weak so that the effects of energy loss, the momentum transfer, etc. can also be neglected to a good approximation. As shown in [9,10,11,12,13,14], the loss of the phase coherence is a much more rapid process than the dynamical effects affecting the motion of the particle considered.
In other words, we consider the time scales
The first inequality tells that the motion of the wave packets is much slower than the typical decoherence time. Consider the atom at some point, where it is described by a split wave packet of the form (2.8), with their centers separated by
where a is the size of the original wavepacket. We may then treat such an atom as if it were at rest, and take into account the rapid decoherence processes studied in [9,10,11,12,13,14] first (a sort of Born-Oppenheimer approximation). Furthermore, let us also take the environment particles with a typical de Broglie wavelength such that
the environment particle can resolve between the split wave packets, but not the interior of each of the subpackets, or
In conclusion, under the conditions (3.11)-(3.13), each of the split wave packets proceeds just as in the pure case (no environment) reviewed in Sec. (2.10), whose average position and momentum (i.e., the expectation values) obey Newton’s equations, (3.8), (3.9). Each of the subpackets describes a quantum particle, in a (position) mixed state, that is, either near or . After leaving the region of the SG magnets, it is just a (pure-state) wave packet or . The two possibilities no longer interfere, in contrast to the pure split wave packet studied in Sec. (2.10). See Figure 4 (b).
Needless to say, if any of the conditions (3.11)-(3.13) are violated, the motion of the atom would be very different. For instance, would mean a totally random motion for the atom. Even in such a case, though, the effects of the environment-induced decoherence/disturbance are quite distinct from the motion of a classical particle, with a unique, smooth trajectory, discussed below.
3.1.3. Classical (or quantum?) particle
A classical particle, with the magnetic moment directed towards
is described by Newton’s equation, (2.15). The way the unique trajectory for a classical particle emerges from quantum mechanics has been discussed in [1], where the magnetic moment is an expectation value
taken in the internal bound-state wave function and and denote the intrinsic magnetic moment and one due to the orbital motion of the i-th constituent atom (molecule); . Clearly, in general, the considerations made in Section 3.1.1 and Section 3.1.2 for a spin atom, with a doubly split wave packet, cannot be generalized simply to (or compared with) a classical body (3.15) with .
Nevertheless, logically, one cannot exclude particular systems (e,g, a magnetized metal piece) with all spins directed in the same direction, for instance. One might thus wonder how a quantum-mechanical particle of spin S behaves under an inhomogeneous magnetic field, in the large spin limit, , .
The question is whether the conditions, discussed in [1], for the emergence of classical mechanics (with a unique trajectory) for a macroscopic body (see also Section 5 below), are sufficient, or whether some extra condition or a mechanism is needed to suppress possible, wide spreading of the wave function into many subpackets (see Figure 5) under an inhomogeneous magnetic field.
The answer is simple but somewhat unexpected. Consider the state of a spin S directed towards a direction, ,
Assuming that the magnetic field (and its gradients) is in the z direction, we need to express as a superposition of the eigenstates of ,
The expansion coefficients are known 16:
where are binomial coefficients, . By using Stiring’s formula, one finds at large N and k with fixed, the distribution in various ,
with
The saddle-point approximation, valid at , gives
and thus
in the ( fixed) limit. The narrow peak position corresponds (see (3.17)) to
Thus a large spin () quantum particle with spin directed towards , in a Stern-Gerlach setting with an inhomogeneous magnetic field, , moves along a single trajectory of a classical particle with , instead of spreading over a wide range of split subpacket trajectories covering ! See Figure 5 and Figure 6.
3.2. Tunnelling molecule
As another example, let us consider a toy version of an atom (or a molecule) of mass m moving in the z direction with momentum , but with a split wave packet in the transverse () plane,
where and are narrow (free) wave packets centered at and , respectively. This is somewhat analogous to the wave function of the silver atom (2.8) or of the molecule (2.16). Actually, we take also for the longitudinal wave function a wave packet, , by considering a linear superposition of the plane waves with momentum p narrowly distributed around . For instance a Gaussian distribution in p, , yields a Gaussian longitudinal wave packet in z of width . At times much smaller than the characteristic diffusion time 19, the particle is approximately described by the wave function,
Assume that such a particle is incident from (), moves towards right (increasing z), and hits a potential barrier (Figure 7),
whose height is above the energy of the particle, approximately given by the longitudinal kinetic energy, . As the longitudinal and transverse motions are factorized, the relative frequencies (probabilities) 20 of finding the particle on both sides of the barrier (barrier penetration and reflection) at large t can be calculated by the standard one-dimensional QM. The answer is well known: the tunnelling frequency is given, in the semi-classical approximation, by
(). The particle on the right of the barrier is described by the wave function
where c is the transmission coefficient of (3.27). The transverse, coherent superposition of the two components (sub wavepackets), (3.24), remains intact. See Figure 7.
Now reconsider the whole process, with the region left of the barrier () immersed in air 21. The precise decoherence rate depends on several parameters, but the incident particles get decohered in a very short time in general, as in (3.10) [9,10,11,12,13,14]. The particle at the left of the barrier 22 is now a mixture: each atom (molecule) is either near or in the transverse plane. But when it hits the potential barrier it will tunnel through it, with the relative frequencies (3.27), and will emerge on the other side of the barrier as a free particle. It has the wave function, (3.28), with replaced by , with relative frequency , and by , with frequency ). It is a statistical mixture, but each is a pure quantum mechanical particle. See Figure 8.
Our discussion above assumes that the air molecules (the environment particles) are just energetic enough (their de Broglie wave length small enough) to resolve the transverse split wave packets (see (3.10)), but are at the same time much less energetic than the longitudinal kinetic energy and that their flux is sufficiently small. In writing (3.28) we assumed that the effects of the environment particles on the longitudinal wave packet are small, even though the tunnel frequency may be somewhat modified, as it is very sensitive to its energy.
Obviously, in a much warmer and denser environment the effects of the scatterings on our molecule would be more severe, and the tunnelling rate would become considerably smaller. Even then, our atom (or molecule) remains quantum mechanical 23.
4. Abstract concept of “particle of mass m"
It is customary to consider an otherwise unspecified “particle of mass m", to discuss model systems, both in quantum mechanics and in classical mechanics. We will see that the consideration based on such an abstract concept of a particle cannot be used to discriminate classical objects from quantum mechanical systems, or as a way to explain the emergence of classical mechanics from QM.
Let us consider a particle of mass m, moving in a harmonic-oscillator potential
The coherent state is defined by where a is the annihilation operator. Its well-known solution, in the coordinate representation, is just the Gaussian wave packet 24
with
The Schrödinger time evolution can be expressed as the time variation of the center of mass and its mean momentum,
while the wave packet shape and size (4.4) remain unchanged in time. This looks exactly like the motion of a classical oscillator of mass m and size D!
It is sometimes thought that such a behavior of the coherent states carries the key to understand the emergence of classical mechanics from QM. There are however reasons to believe that this may not be quite the correct way of reasoning.
In order to see that such an identification/analogy cannot be pushed too far, consider the quenching, i.e., turning off the oscillator potential suddenly, setting , at . The particle starts moving freely, with the initial condition, .
The problem is that there is no way to tell what happens at . A quantum mechanical particle would diffuse, with the rate depending on mass, as in Table 1. A classical particle does not diffuse. The expression “a particle of mass m" does not tell if it is a quantum or a classical particle, and what the true size of the body, (unrelated to D) is.
Note that by describing this body as a “particle", one has tacitly assumed that its physical size is irrelevant (i.e., ) to the model harmonic-oscillator problem. But the physical size of the particle, , does matter. If its (unspecified) size were truly zero, it would be quantum mechanical, as . The lesson one draws from this discussion is that a model system based on an abstract “particle" concept, in which the information about is lacking, cannot be used to study the emergence of classical physics from quantum mechanics. Allowing for the decoherence effects, and selecting particular class of the mixed states as privileged ones by introducing some criteria, may not lead to a satisfactory understanding of how classical physics emerges from QM.
5. Discussion
An immediate implication of the introduction of the concept of quantum ratio is that the elementary particles are quantum mechanical. This is so even if under certain conditions such as envirornment-induced decoherence, they may be reduced to mixed states. They remain quantum mechanical. The distinction between the concept of mixed (quantum) states and classical states is essential. As the electron and photon are elementary particles they remain quantum mechanical even in warm and dense environment of biological systems.
We have studied the quantum ratio of some larger particles, atoms and molecules, via examination of various interferometry experiments, which indeed show that these particles behave quantum-mechanically, in the vacuum.
We discussed extensively in Section 3 several real and model examples involving atoms, molecules and elementary particles, to highlight the reasons why the environment-induced decoherence [9,10,11,12,13,14], in itself, does not make the particle affected classical, as often stated or assumed tacitly.
Though in a slightly different context, the so-called negative-result experiments or null measurements [48,49] tell us a similar story. There, the exclusion of some of the possible experimental outcomes (a non-measurement), by use of an intentionally biased measurement set-up, implies the loss of the original superposition of states. But the predicted state of the system is still perfectly a quantum-mechanical one, though it now lives in a more restricted region of the Hilbert space. See [45] for a recent review and for a careful re-examination of the interpretation of these negative-result experiments.
All these discussions lead us naturally back to the recurrent theme in quantum mechanics: mixed state versus pure quantum states. As is widely acknowledged, there are no differences of principle. As famously noted by Schrödinger, a complete knowledge of the total, closed system (its wave function, the pure state vector) does not necessarily mean the same for a part of the system ().
Only in exceptional situations in which the interactions and correlations between the subsystem of our interest (“local", A) and the rest of the world (“rest", ) can be neglected, and therefore the total wave function has a factorized form
can we describe the local system A in terms of a wave function. Whenever the factorization (5.1) fails, system A is a mixture, described by a density matrix.
The quantum measurement is a process in which the factorized state (5.1), where is the quantum state of interest, and the measurement device is part of , is brought into an entangled state, triggered by a spacetime pointlike interaction event [7,45,46].
Even a macroscopic system can be brought to the pure-state form as in (5.1), at sufficiently low temperatures. At any system is in its quantum mechanical ground state. See [15,16,17,18,19,20,21,22,23,24,25,26] for the efforts to realize such macroscopic quantum states experimentally by going to very low temperatures.
Vice versa, classical equation of motion describes the CM of a macroscopic body at finite temperatures. When three conditions
- (i)
- that for macroscopic motions (i.e., ) the Heisenberg relation does not limit the simultaneous determination - the initial condition - for the position and momentum;
- (ii)
- the lack of quantum diffusion, due to a large mass (a large number of atoms and molecules composing the body); and
- (iii)
- a finite body temperature, implying the thermal decoherence and mixed-state nature of the body,
are met, the CM of a body has a unique trajectory [1]. Newton’s equations for it follow from the Ehrenfest theorem. If the quantum fluctuation range is not larger than the size of the body, i.e., , then such a trajectory can be regarded as the classical trajectory of that body.
To summarize, introduction of the quantum ratio is an attempt to go beyond the familiar ideas on the emergence of classical physics from QM, such as the large action, semiclassical limit (or ) and Bohr’s correspondence principle, or the environment-induced decoherence [9,10,11,12,13,14]. Clearly, there is no sharp boundary between where or when QM or Classical mechanics describes a given system more appropriately. The quantum ratio is a proposal for an approximate, but simple, universal criterion for characterizing the two kinds of physical systems: quantum () and classical ().
Acknowledgments
We thank Francesco Cappuzzello, Giovanni Casini, Marco Matone, Pietro Menotti and Arkady Vainshtein for discussions. The work by KK is supported by the INFN special-initiative project grant GAST (Gauge and String Theories).
Appendix A. Variational solution for the SG wavepackets
The Schrödinger equation (3.7) can be solved by separation of the variables,
As the motions in x and y directions are free ones, we shall focus on
We recall Dirac’s variational principle [50]. Consider the effective action
The variation with respect to and
i.e., requiring the effective action to be stationary against arbitrary variations of the normalized wave function, which vanish at , is equivalent to the exact Schrödinger equation 25.
An important property, which follows immediately, is that orthogonal superpositions of variational trial eigenstates of the Hamiltonian evolve independently, without interfering with each other. Let be the sum of the two orthogonal spin-up and spin-down eigenstates of
in the Stern-Gerlach set-up (with ). Then, the effective action becomes a sum of two independent terms, and , which can be varied separately.
We choose the following normalized Gaussian trial wave functions, which are suitable for the effectively one-dimensional problem of particles with mass m and the magnetic moment moving in a magnetic field , transverse to the beam direction (i.e., ):
where are the variational-parametric functions. describe the momentum and position of the wave packet, and the quantum diffusion. Substituting this into (A2) yields
Independent variations with respect to give
Note that in the magnetic field of linear inhomogenuity under consideration, the center of the wave packet moves as a classical particle, and the diffusion effects are the same as for a free wave packet.
The solution of Equations (A7)-(A8) is:
where , and set the initial conditions at . The diffusion of the wave packet, , is the same as in the free case as we noted already. We understand this as due to the fact that in the linear field the force is constant and the same for each part inside the wave packets, . The effect of quantum diffusion is negligible for , where is the initial wave packet size.
References
- K. Konishi, “Newton’s equations from quantum mechanics for a macroscopic body in the vacuum", Int. Journ. Mod. Phys. A 38 (2023) 2350080 [arXiv:2209.07318 [quant-ph]]. [CrossRef]
- S. Weinberg, “A model of Leptons", Phys. Rev. Lett. 19, 1264 (1967). [CrossRef]
- A . Salam “Weak and electromagnetic interactions," in “Elementary Particle Theory”, ed. N. Svartholm, Almqvist Forlag AB, 367 (1968). [CrossRef]
- S .L . Glashow, J . Iliopoulos and L . Maiani (1970), “Weak Interactions with Lepton-Hadron Symmetry," Phys. Rev. D 2, 1285 (1970). [CrossRef]
- H. Fritzsch, M. Gell-Mann, H. Leutwyler, "Advantages of the color octet gluon picture", Physics Letters 47 B (1973), 365. [CrossRef]
- K. G. Wilson, “The Renormalization Group and Critical Phenomena", Rev. Mod. Phys. 55, 583 (1983). [CrossRef]
- K. Konishi, “Quantum fluctuations, particles and entanglement: a discussion towards the solution of the quantum measurement problems,” Int. Journ. Mod. Phys. A 37 (2022) 2250113 [arXiv:2111.14723 [quant-ph]]. [CrossRef]
- R. Jackiw, “Delta-Function Potentials in Two- and Three-Dimensional Quantum Mechanics", Bég Memorial Volume, eds. A. Ali and P. Hoodbhoy (Singapore: World Scientific) (1991). [CrossRef]
- E. Joos and H. D. Zeh, “The emergence of classical properties through interaction with the environment", Z. Phys. B 59, 223-243 (1985). [CrossRef]
- W. H. Zurek, “Decoherence and the Transition from Quantum to Classical", Physics Today 44, 10, 36 (1991). [CrossRef]
- M. Tegmark, “Apparent wave function collapse caused by scattering,” Found. Phys. Lett. 6, 571 (1993) [arXiv:gr-qc/9310032 [gr-qc]]. [CrossRef]
- M. Tegmark, “Importance of quantum decoherence in brain processes", Phys. Rev. E 61 (2000) 4194. [CrossRef]
- E. Joos, H. D. Zeh, C. Kiefer, D. Giulini, J. Kupsch, I. O. Stamatescu, “Decoherence and the Appearance of a Classical World in Quantum Theory", Springer, 2002.
- W. H. Zurek, “Decoherence, einselection, and the quantum origins of the classical,” Rev. Mod. Phys. 75, 715-775 (2003) [arXiv:quant-ph/0105127 [quant-ph]]. [CrossRef]
- A. J. Leggett, “Macroscopic Quantum Systems and the Quantum Theory of Measurement", Suppl. of the Progress of Theoretical Physics, 69 (1980) 80. [CrossRef]
- J.-M. Courty, A. Heidmann, and M. Pinard, “Quantum limits of cold damping with optomechanical coupling", Eur. Phys. J. D 17, 399–408 (2001). [CrossRef]
- A. D. Armour, M. P. Blencowe, K. C. Schwab, “Entanglement and decoherence of a Micromechanical Resonator via Coupling to a Cooper-Pair Box", Phys. Rev. Lett. 88 (2002), 148301. [CrossRef]
- R. G. Knobel, A. N. Cleland, “Nanometer-scale displacement sensing using a single electron transistor", Nature, 424 (2003) 17.
- M. D. LaHaye, O. Buu, B. Camarota, K. C. Schwab, “Approaching the Quantum Limit of a Nanomechanical Resonator", Science 304, 74–77 (2004). [CrossRef]
- A. N. Cleland, M. R. Geller, “Superconducting Qubit Storage and Entanglement with Nanomechanical Resonators", Phys. Rev. Lett. 93 (2004) 070501. [CrossRef]
- I. Martin, A. Shnirman, L. Tian, P. Zoller, “Ground-state cooling of mechanical resonators", Phys. Rev. B 69, 125339 (2004). [CrossRef]
- D. Kleckner, D. Bouwmeester, “Sub-kelvin optical cooling of a micromechanical resonator", Nature, 444 2 (2006).
- C. A. Regal, J. D. Teufel, K. W. Lehnert, “Measuring nanomechanical motion with a microwave cavity interferometer", Macmillan Publishers Limited (2008). [CrossRef]
- A. Schliesser, R. Rivière, ,G. Anetsberger, O. Arcizetandt, J. Kippenberg, “Resolved-sideband cooling of a micromechanical oscillator", Macmillan Publishers Limited (2008). [CrossRef]
- B. Abbott et al. [LIGO Scientific], “Observation of a kilogram-scale oscillator near its quantum ground state,” New J. Phys. 11, 073032 (2009). [CrossRef]
- A. D. O’Connell, et. al., “Quantum ground state and single-photon control of a mechanical resonator", Nature, 464 (7289) (2010) 697.
- Y. Kim, et. al., “Quantum Biology: An Update and Perspective", Quantum Reports 3, 80 (2021), number: 1 Publisher: Multidisciplinary Digital Publishing Institute. [CrossRef]
- G. Di. Pietra, V. Vedral and C. Marletto, “Temporal witnesses of non-classicality in a macroscopic biological system", arXiv:2306.12799v1 [quant-ph] 22 Jun 2023. [CrossRef]
- R. L. Workman et.al, (Particle Data Group), Prog. Theor. Exp. Phys. 2022 083C01 (2022) and 2023 update.
- G. ’t Hooft, “Why Do We Need Local Gauge Invariance in Theories With Vector Particles? An Introduction,” NATO Sci. Ser. B 59, 101-115 (1980). [CrossRef]
- S. Coleman, “Dilatations" (1971), in “Aspect of Symmetry - selected Erice Lectures" Cambridge University Press (1985).
- W. Gerlach and O. Stern “Der experimentelle Nachweis der Richtungsquantelung im Magnetfeld", Zeitschrift für Physik. 9 (1) (1922) 349. [CrossRef]
- D. W. Keith, C. R. Ekstrom, Q. A. Turchette, D. E. Prichard, “An interferometer for Atoms", Phys. Rev. Lett. 66 (1991) 2693. [CrossRef]
- C. Brand, S. Troyer, C. Knobloch, O. Cheshinovsky, M. A. Arndt, “Single, double and triple-slit diffraction of molecular matter waves", arXiv:2108.06565v2 [quant-ph], 2021. [CrossRef]
- M. Arndt, O. Nairz, J. Vos-Andreae, C. Keller, G. van der Zouw, A. Zeilinger, “Wave-particle duality of C60 molecules", Nature 401 (1999) 680.
- B. Brezger, M. Arndt and A. Zeilinger, “Concepts for near-field interferometers with large molecules", J. Opt. B: Quantum Semiclass. Opt. 5 (2003) S82–S89. [CrossRef]
- B. Brezger, L. Hackermüller, S. Uttenthaler, J. Petschinka, M. Arndt, and A. Zeilinger “Matter-Wave Interferometer for Large Molecules" Phys. Rev. Lett. 88.100404 (2002). [CrossRef]
- L. Hackermüller, K. Hornberger, B. Brezger, A. Zeilinger, M. Arndt, “Decoherence of matter waves by thermal emission of radiation", Nature, 427, (2004) 711. arXiv:quant-ph/0402146.
- M. S. Chapman, C. R. Ekstrom, T. D. Hammond, J. Schmiedmayer, B. E. Tannian, S. Wehinger, and D. E. Pritchard, “Near-field imaging of atom diffraction gratings: The atomic Talbot effect", Phys. Rev. A, 51 (1995), R14-R17. [CrossRef]
- S. Nowak, Ch. Kurtsiefer, T. Pfau, and C. David, "High-order Talbot fringes for atomic matter waves," Opt. Lett. 22, 1430 (1997). [CrossRef]
- J. F. Clauser and S. Li, “Talbot-vonLau atom interferometry with cold slow potassium", Phys. Rev. A 49 (1994), R2213. [CrossRef]
- J. Bateman, S. Nimmrichter, K. Hornberger, H. Ulbricht, “Near-field interferometry of a free-falling nanoparticle from a point-like source", Nature communications, 5, Article number: 4788 (2014).
- H.F. Talbot, Esq. F.R.S. (1836) LXXVI. “Facts relating to optical science. No. IV", The London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science, 9:56, 401-407. [CrossRef]
- A. Tonomura, J. Endo, T. Matsuda, T. Kawasaki and H. Ezawa, “Dimonstration of single-electron buildup of interference pattern", American Journal of Physics 57, 117 (1989).
- K. Konishi, “On the negative-result experiments in quantum mechanics,” [arXiv:2310.01955 [quant-ph]. [CrossRef]
- K. Konishi, “Quantum fluctuations, particles and entanglement: solving the quantum measurement problems,” J. Phys. Conf. Ser. 2533, no.1, 012009 (2023) [arXiv:2302.08892 [quant-ph]]. [CrossRef]
- K. Hansen and E. E. B. Campbell, “Thermal radiation from small particles", Phys. Rev. E 58 (1998), 5477. [CrossRef]
- M. Renninger, “Messungen ohne Störung des Meßobjekts", Zeitschrift für Physik, 158 417 (1960).
- A. C. Elitzur, L. Vaidman, “Quantum mechanical interaction-free measurements", Foundations of Physics. 23 (7): 987 (1993). [CrossRef]
- R. Jackiw and A. Kerman, “Time-dependent variational principle and the effective action", Phys. Lett. 71A (1979) 158. [CrossRef]
- T. Blum and H. T. Elze, “Semiquantum Chaos in the Double-Well", Phys. Rev. E 53 3123 (1996). [CrossRef]
- H. T. Elze, “Quantum Decoherence, Entropy and Thermalization in Strong Interactions at High Energy", Nucl. Phys. B 436 213 (1995); “Entropy, Quantum Decoherence and Pointer States in Scalar “Parton” Fields", Phys. Lett. B 369 295 (1996).
| 1 | A macroscopic body, and from some scales upwards, might well be described as a classical bound state, due to gravitational or electromagnetic forces, but their size is always well defined. |
| 2 | Nonrelativistic quantum mechanics, having only ℏ with the dimension of an action as the fundamental constant in its formulation, shares this property [7]. The so-called quantum nonlocality is one of its consequences. However in specific problems, the masses and the potential break explicitly the scale invariance in general. For a class of the potentials, such as the delta-function or potentials in space dimensions, the system possesses an exact scale invariance [8]. |
| 3 | This is another consequence of the fact that QM laws contain no fundamental constant with the dimension of a length. |
| 4 | Virtual emission and absorption of a particle of mass m gives a physical “size", , known as the Compton length, to any quantum-mechanical particle. This should however be distinguished from the size defined as the extension of its internal wave function. |
| 5 | Any quantum particle such as electron behaves “classically" under certain conditions (the Ehrenfest theorem), e.g., when it is well localized, and free or under homogeneous electromagnetic field, and within the diffusion time. This is however not what we mean by a classical particle. |
| 6 | Quantum gravity or string theory effects, possibly relevant near the Planckian energies , does contain a length scale . It is beyond the scope of the present work to consider if and how these affect the discussion of quantum or classical physics at larger distances ( cm) we are concerned with here. |
| 7 | For instance, the nuclear size is typically of the order of the pion Compton length, , and . The proton and neutron masses ( MeV/) are mainly given by the strong-ineraction effects, . The Bohr radius is . |
| 8 |
indicates the zero angular momentum-spin () closed shell of the Kripton electronic configuration describing the first 36 electrons. |
| 9 | The transverse wave packet size of the atom can be taken to be of this order. The silver atom, having the mass roughly 100 times that of the hydrogen atom, has the diffusion time of the order of sec (see Table 1), so that the diffusion during the travel of cm is entirely negligible. |
| 10 |
d is the period of the slits in the diffraction grating, and is the de Broglie wavelength (p is the longitudinal momentum) of the atom or molecule. |
| 11 | |
| 12 | |
| 13 |
is the Bohr magneton. We recall the well-known fact that the gyromagnetic ratio of the electron and the spin magnitude approximately cancel. |
| 14 | We assume that the transit time of the whole process and the mass of the atom, are such that the free quantum diffusion of the wave packets is negligible. See also Appendix A. |
| 15 | Unlike [11], however, we shall not consider , the typical timescale of the internal motion of the object under study. Roughly speaking the size (the space support of the internal wave function) we introduced in defining the quantum ratio, (1.1), corresponds to it (). Quantum-classical criteria suggested by [11] might appear to have some similarity with (1.2), (1.3). However, the former seems to leave unanswered questions such as “what happens to a quantum particle (), at ?" This is precisely the sort of question which we are trying to address here. |
| 16 | To get (3.18), consider (3.16) as a direct product state of N spin particles, all oriented in the same direction, (3.2). Collecting terms with a fixed k (the number of spin-up particles) gives (3.18). |
| 17 | If the value is understood as due to the large number of spin particles composing it (see the previous footnote), the spike (3.21), (3.22) can be understood as due to the accumulation of an enormous number of microstates giving . |
| 18 | Of course this does not mean that the classical limit necessarily requires or implies . |
| 19 | The exact answer has the Gaussian width in the exponent replaced as , and the overall wave function multiplied by . These are the standard diffusion effects of a free Gaussian wave packet of width . Also, if the longitudinal wave packet and the transverse subwave packets are taken to be of a similar size, then the free diffusion of the transverse wave packets (hence t-dependence of ) can also be neglected. |
| 20 | It was proposed in [7,46] to use “(normalized) relative frequency" instead of the word “probability". The traditional probabilistic Born rule places the human intervention as the central element of its formulation, and distorts the way quantum-mechanical laws (the laws of Nature!) look. To the authors’ view, this was the origin of innumerable puzzles, apparent contradictions and conundrums entertained in the past. See [7,46] for a new perspective and a more natural understanding of the QM laws. |
| 21 | Or, as in the experiments [38], the incident molecules may get bombarded by laser beams, get excited, and emit photons, before they reach the potential barrier. |
| 22 | We assume that the environment particles (air molecules) have energy much less than the barrier height, so that they are confined in the region left of the barrier. |
| 23 | The situation is reminiscent of the particle track in a Wilson chamber. is scattered by atoms, ionizing them on the way, but traces roughly a straight trajectory. When it arrives at the end of the chamber, it is just the same particle. It has not become classical. |
| 24 | The position and momentum of the center of the wave packet are
|
| 25 |
Figure 1.
The Talbot effect. The intensity modulation of the molecules immediately after the passage of the diffraction grating , Figure 2, is reproduced, due to the sum over paths, at an imaging plane placed at definite distances , related to the Talbot length (2.17), from .
Figure 1.
The Talbot effect. The intensity modulation of the molecules immediately after the passage of the diffraction grating , Figure 2, is reproduced, due to the sum over paths, at an imaging plane placed at definite distances , related to the Talbot length (2.17), from .
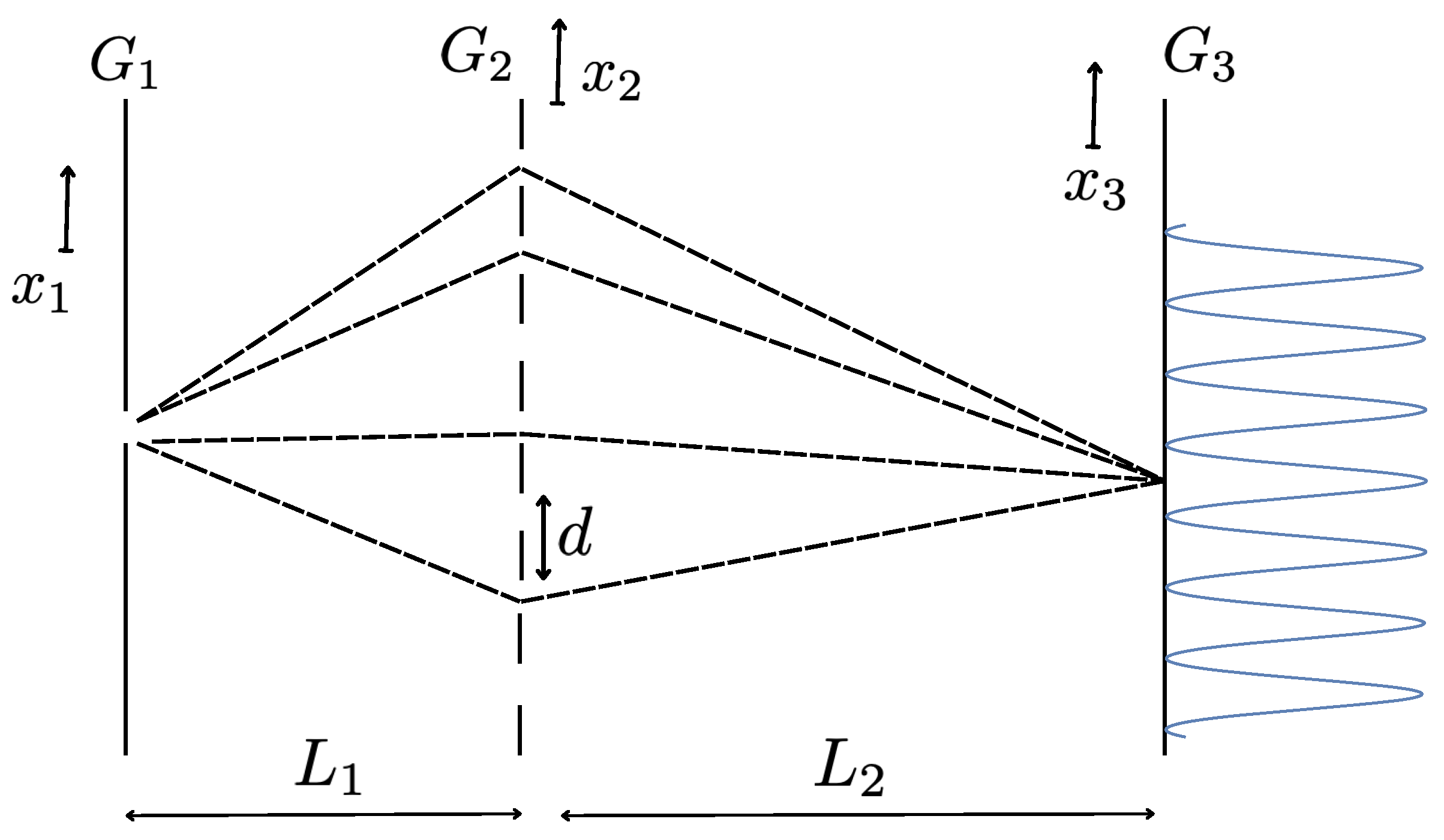
Figure 2.
The intensity pattern of the atom (or molecule) behind the diffraction grating . Each peak corresponds to a slit opening.
Figure 2.
The intensity pattern of the atom (or molecule) behind the diffraction grating . Each peak corresponds to a slit opening.
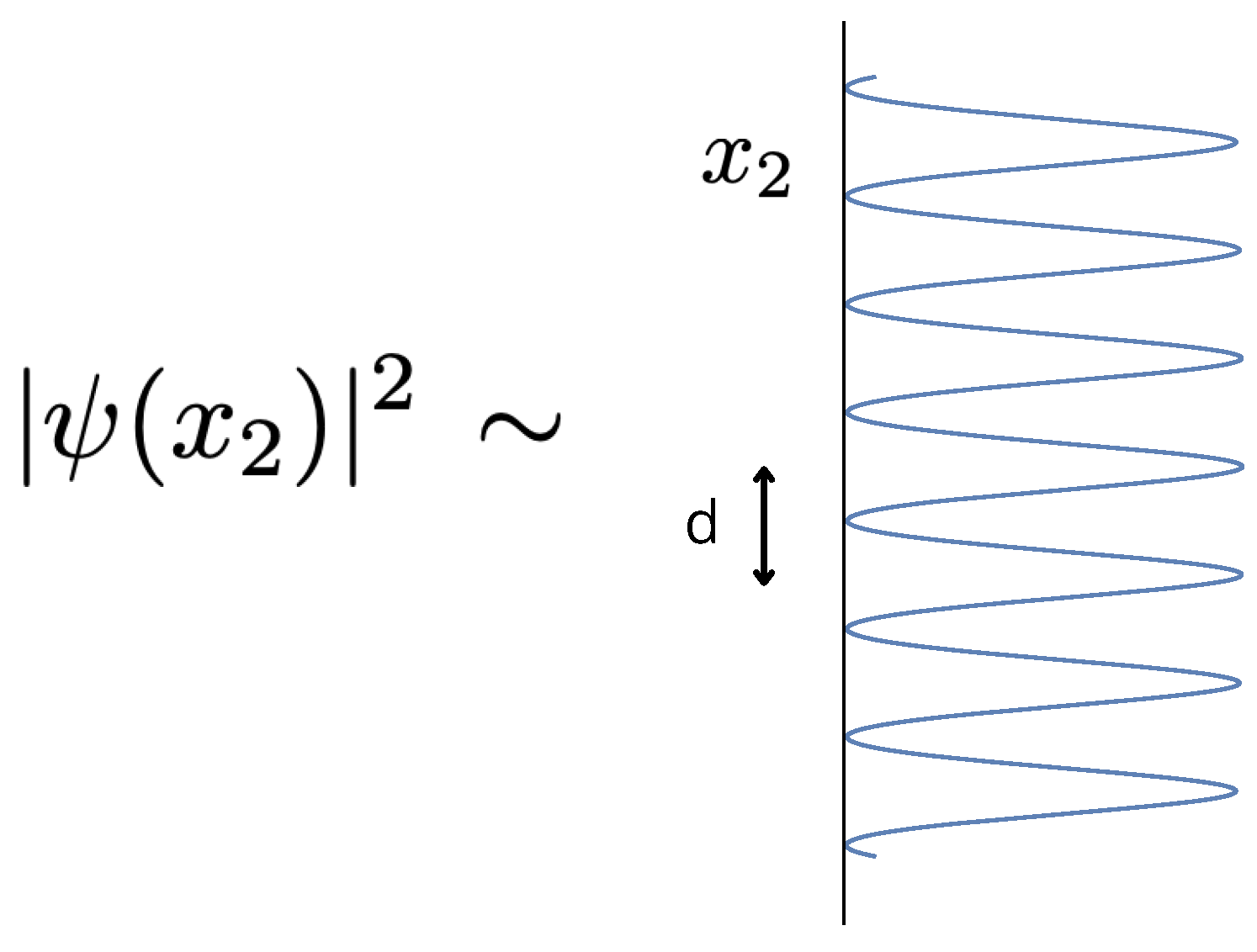
Figure 3.
Talbot-Lau interferometer. is the diffraction grating. Thick lines are the slit openings. is a transmission-scanning grating movable vertically. are the source slits.
Figure 3.
Talbot-Lau interferometer. is the diffraction grating. Thick lines are the slit openings. is a transmission-scanning grating movable vertically. are the source slits.
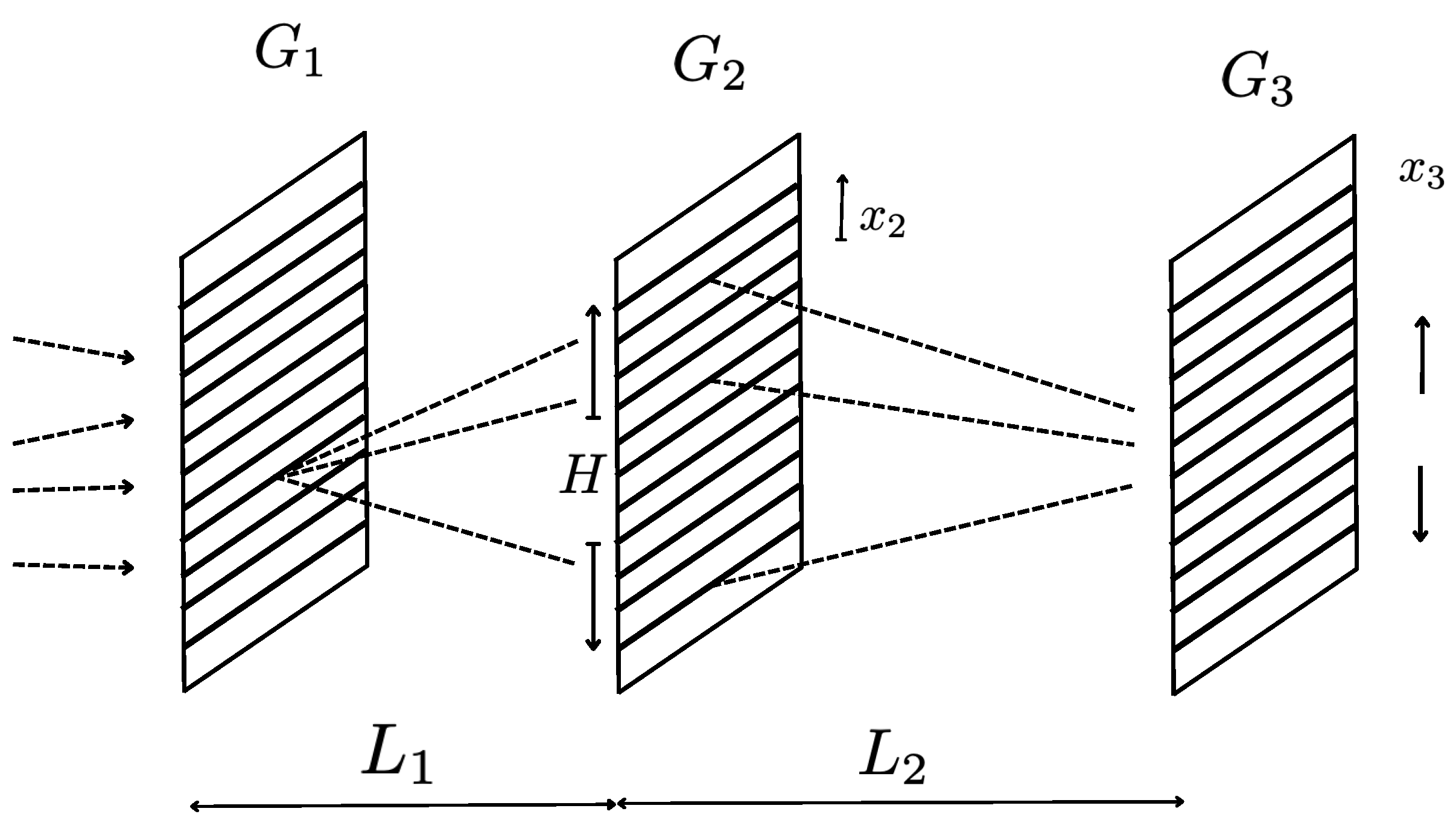
Figure 4.
The spin-up and spin-down sub wavepackets of the silver atom evolve independently under the Schrödinger equation, both in the vacuum (Figure (a), pure state) and in a weak environment (3.11)-(3.13) (Figure (b)), where the decoherence is represented by an unknown, to-be-averaged-over, relative phase between and . Figure (c) represents a unique classical trajectory.
Figure 4.
The spin-up and spin-down sub wavepackets of the silver atom evolve independently under the Schrödinger equation, both in the vacuum (Figure (a), pure state) and in a weak environment (3.11)-(3.13) (Figure (b)), where the decoherence is represented by an unknown, to-be-averaged-over, relative phase between and . Figure (c) represents a unique classical trajectory.
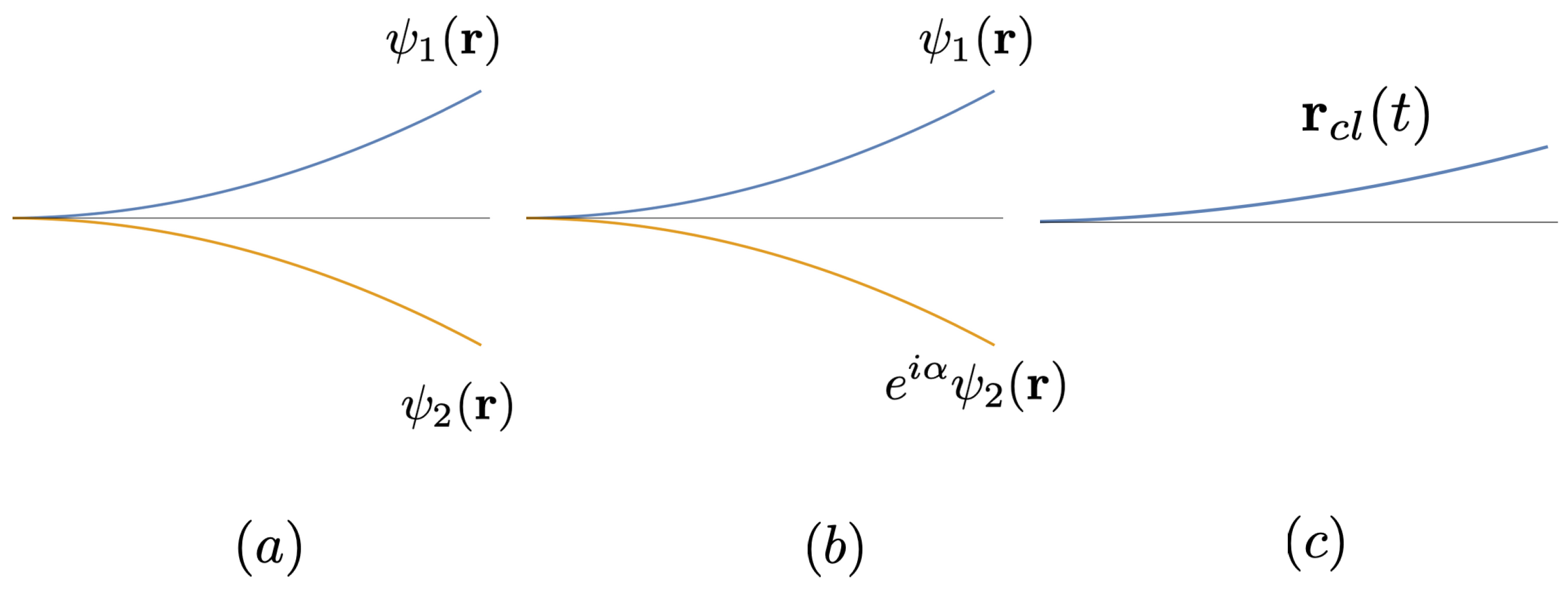
Figure 5.
The distribution in k, i.e., in possible values of , , for a spin particle in the state (3.16), with (center) and (right).
Figure 5.
The distribution in k, i.e., in possible values of , , for a spin particle in the state (3.16), with (center) and (right).
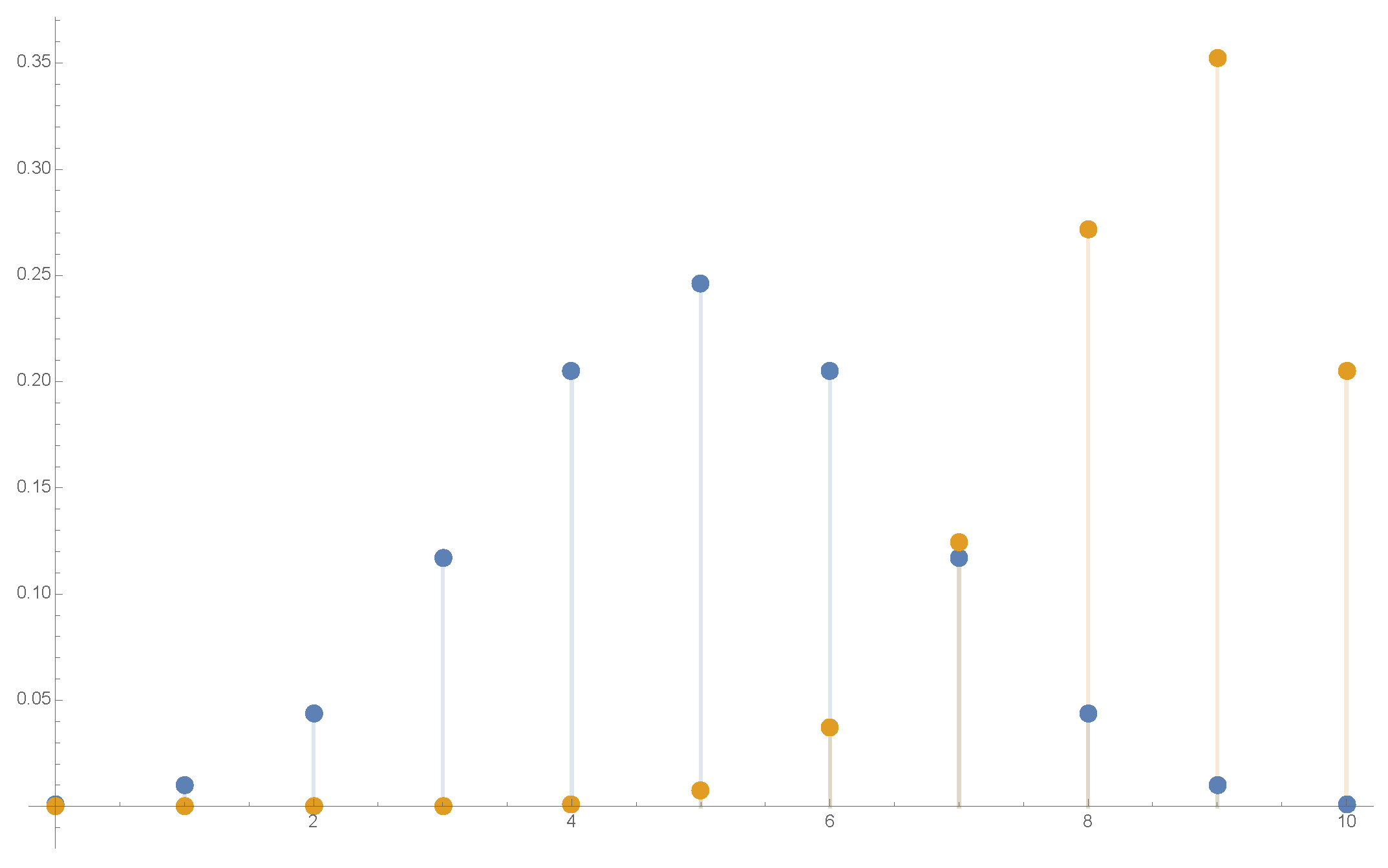
Figure 6.
The distribution in possible values of , for a spin particle in the state (3.16), with (center) and (right). The particle starts looking like classical.
Figure 6.
The distribution in possible values of , for a spin particle in the state (3.16), with (center) and (right). The particle starts looking like classical.
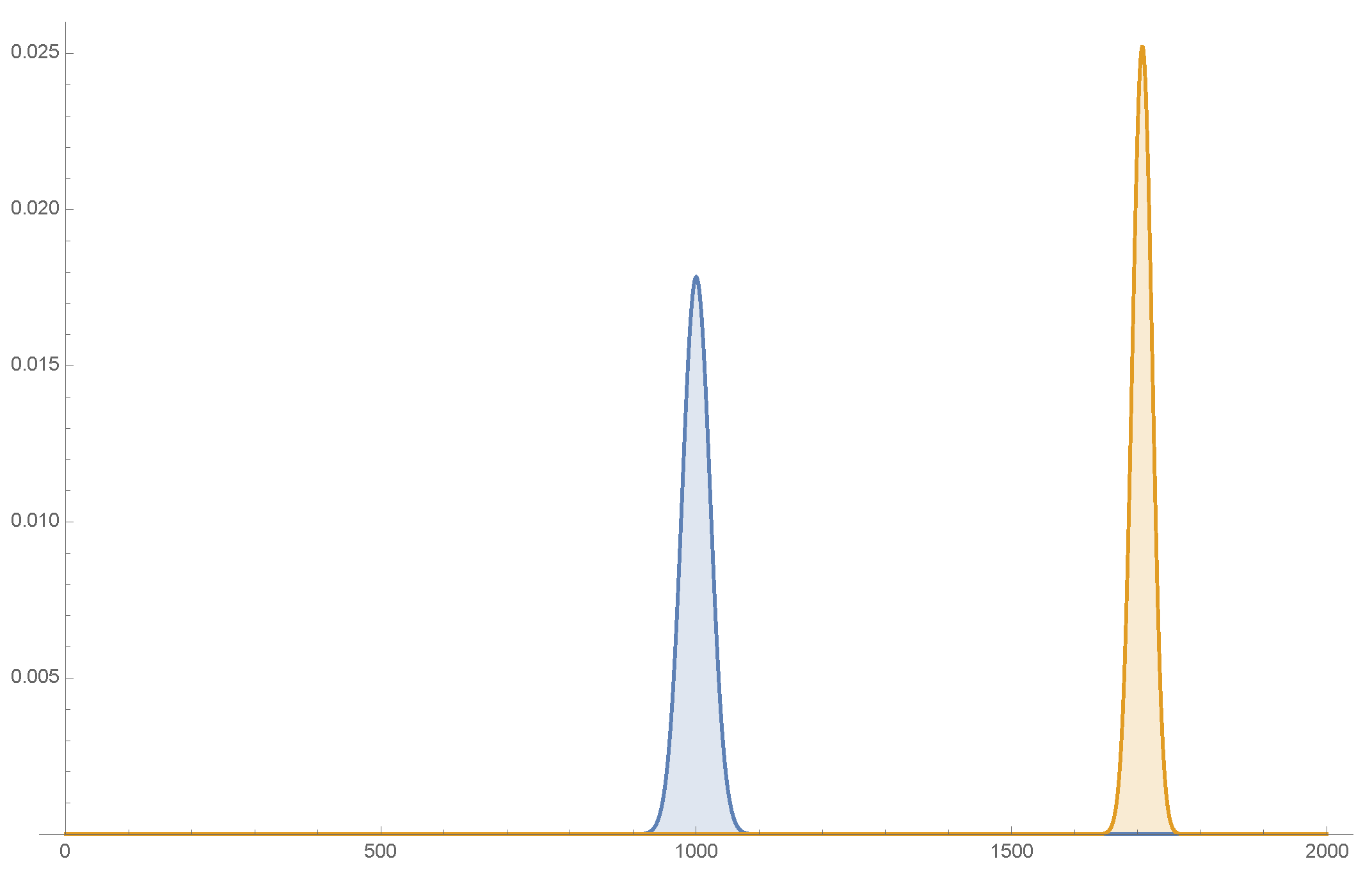
Figure 7.
On the left figure (A), an atom (molecule) arrives from and moves towards the potential barrier at (independent of x and y). It is described by a wave packet (split in the transverse direction as in (3.24)). The wave function of the particle at , shown in the right part (B), contains both the reflected and transmitted waves. The coherent superposition of the two sub wavepackets in the plane remains intact.
Figure 7.
On the left figure (A), an atom (molecule) arrives from and moves towards the potential barrier at (independent of x and y). It is described by a wave packet (split in the transverse direction as in (3.24)). The wave function of the particle at , shown in the right part (B), contains both the reflected and transmitted waves. The coherent superposition of the two sub wavepackets in the plane remains intact.

Figure 8.
On the left figure (A), an atom (molecule) arrives from and moves towards the potential barrier at , as in Figure 7. But in contrast to the process in the vacuum in Figure 7, this time the half space on the left of the potential barrier contains air. The molecule is now in a mixed state due to the environment-induced decoherence. Its (transverse) position density matrix became diagonal: it is either near or near . The wave function of the particle at , shown in the right part (B), contains still a small transmitted wave as well as the reflected wave, however without coherent superposition of two transverse wave packets.
Figure 8.
On the left figure (A), an atom (molecule) arrives from and moves towards the potential barrier at , as in Figure 7. But in contrast to the process in the vacuum in Figure 7, this time the half space on the left of the potential barrier contains air. The molecule is now in a mixed state due to the environment-induced decoherence. Its (transverse) position density matrix became diagonal: it is either near or near . The wave function of the particle at , shown in the right part (B), contains still a small transmitted wave as well as the reflected wave, however without coherent superposition of two transverse wave packets.
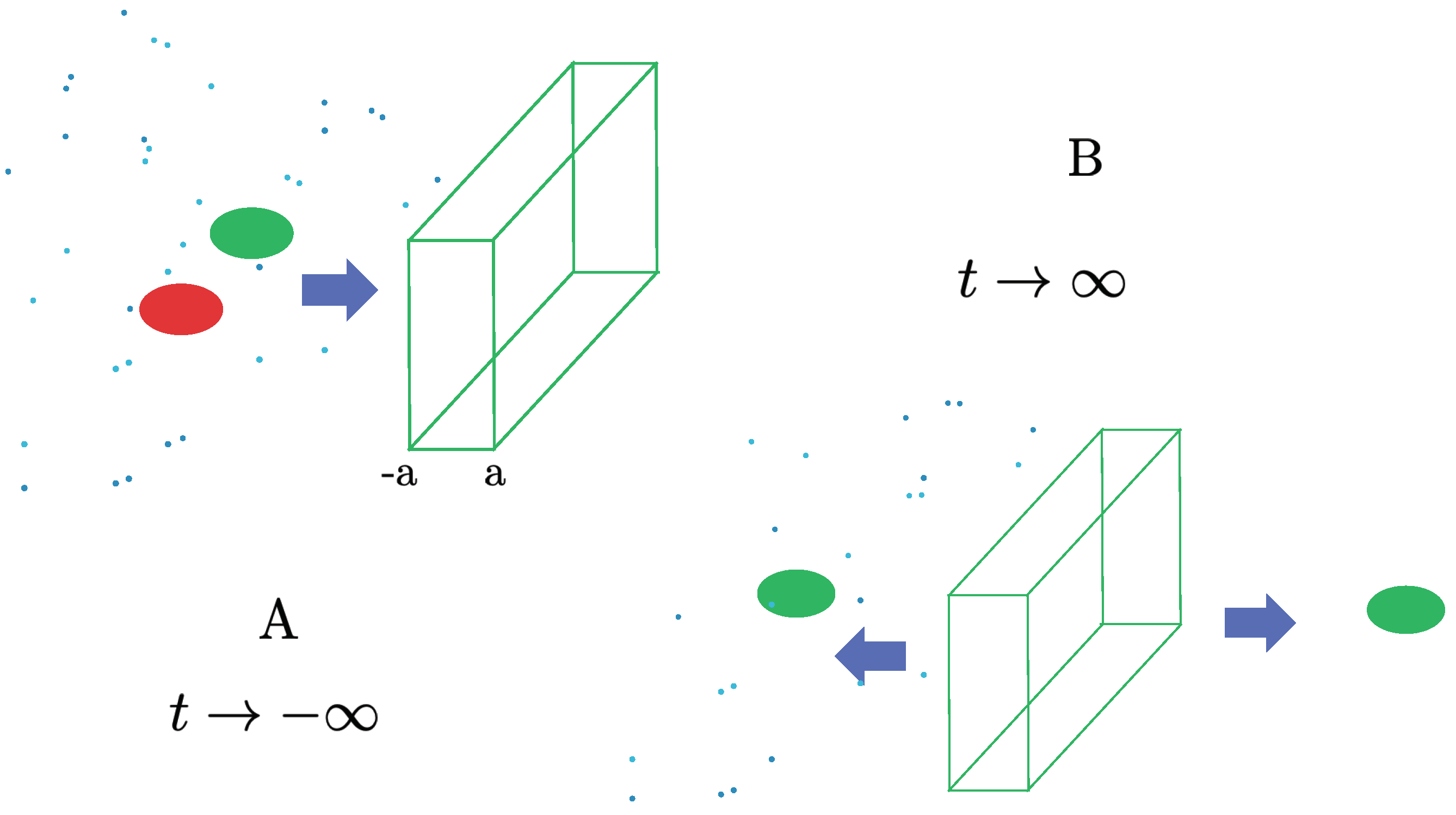
Table 1.
Diffusion time of the free wave packet for different particles. Conventionally, we take the initial wave packet size of , and define the diffusion time as needed for doubling its size. For a macroscopic particle of , the doubling time, , exceeds the age of the universe.
Table 1.
Diffusion time of the free wave packet for different particles. Conventionally, we take the initial wave packet size of , and define the diffusion time as needed for doubling its size. For a macroscopic particle of , the doubling time, , exceeds the age of the universe.
| particle | mass (in g) | diffusion time (in s) |
| electron | ||
| hydrogen atom | ||
| fullerene | ||
| a stone of | 1 |
Table 5.
The size (), the quantum fluctuation range () and the quantum ratio of atoms and molecules in various experiments. The mass is in atomic unit (); is given in Angström (Å); is in . In all cases, the momentum of the atom (molecule), their masses, the size of the whole experimental apparatus, thus the time interval involved, are such that the quantum diffusion of their (transverse) wave packets are negligible.
Table 5.
The size (), the quantum fluctuation range () and the quantum ratio of atoms and molecules in various experiments. The mass is in atomic unit (); is given in Angström (Å); is in . In all cases, the momentum of the atom (molecule), their masses, the size of the whole experimental apparatus, thus the time interval involved, are such that the quantum diffusion of their (transverse) wave packets are negligible.
| Particle | mass | Q | Exp | Miscl | ||
| 108 | [32] | Stern-Gerlach | ||||
| 23 | [39] | |||||
| 840 | 16 | [36,37,38] | ||||
| 840 | [38] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
MDPI Initiatives
Important Links
© 2024 MDPI (Basel, Switzerland) unless otherwise stated







