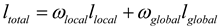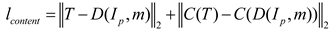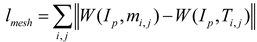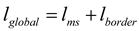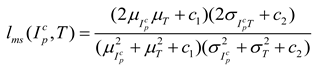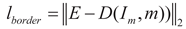Prerpints.org logo
Preprint
Article

Rectification for Stitched Images with Deformable Meshes and Residual Networks

Altmetrics

Downloads

73

Views

27

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

27 February 2024

Posted:

28 February 2024

You are already at the latest version

Alerts
Abstract
Image stitching is a crucial aspect of image processing. However, factors like perspective and environment often lead to irregular shapes in stitched images. Cropping or completion methods typically result in substantial loss of information. This paper proposes a method for rectifying irregularly images into rectangles using deformable meshes and residual networks. The method utilizes a convolutional neural network to quantify rigid structures of images. Choosing the most suitable mesh structure based on the extraction results, offering options such as triangular, rectangular, and hexagonal. Subsequently, the irregularly image, predefined mesh structure, and predicted mesh structure are input into a wide residual neural network for regression. The loss function comprises local and global, aimed at minimizing the loss of image information within the mesh and global target. This method not only significantly reduces information loss during rectification but also adapting to different images with various rigid structures. Validation on the DIR-D dataset shows this method outperforms state-of-the-art methods in image rectification.
Keywords: 
Subject: Computer Science and Mathematics  -   Computer Vision and Graphics

1. Introduction

With the rapid development of image stitching and image fusion technologies, methods for obtaining multi-view or even global perspectives through multiple single viewpoints have been widely applied in human production and daily life [1,2,3,4,5]. For instance, the extensive use of technologies such as panoramic images, autonomous driving, and virtual reality (VR) enables precise remote observation of scenes by individuals [6,7,8,9]. However, in the process of stitching multiple single-view images, it is necessary to align the overlapping regions of different images by adjusting their positions, angles, and local distortions [10,11]. This often results in irregular boundaries in non-overlapping regions, making it challenging for individuals to adapt and prone to misjudgments when observing panoramic images [12].
One approach to addressing irregular boundaries directly involves the use of smaller rectangular boxes for cropping images [13,14]. However, this method may result in the loss of a significant amount of information, contradicting the original purpose of image stitching, which aims to expand the field of view [15,16]. Additionally, image completion can be employed to predict missing portions of an image and restore its integrity to some extent [17,18]. Nevertheless, its limitations are evident, particularly in cases where the missing portions contain complex structures or highly personalized information, making it challenging for image completion to accurately predict the missing areas [19,20,21,22]. This limitation renders image completion unsuitable for applications in fields with high security requirements, such as autonomous driving and industrial production monitoring [23].
To address the challenges posed by image cropping and image completion, Zhu proposed adjusting the stitched image by computing a perspective transformation matrix to make it closer to a rectangular shape [24]. However, this method often relies on the estimation of the geometric structures in specific regions of the image, such as lines or corners. Some approaches suggest transforming local quadrilateral mesh regions on the stitched image to make the overall image more rectangular [25,26,27,28,29]. Building upon the aforementioned research, He proposed optimizing the preservation of line meshes and deforming the rigid structures within the mesh [30]. Li improved the preservation term from line meshes to geodesic lines [31]. However, the applicability of this method is restricted due to the common occurrence of curved ground lines in panoramic images. Some researchers introduced Seam Carving, an algorithmic approach that alters the size of an image by carving or inserting pixels in different parts of the image, thereby transforming irregular images into rectangular forms [32,33,34,35,36]. Meanwhile, Lang proposed DRIS (Deep Rectagling for Image Stitching), employing a residual progressive regression strategy for fully convolutional network prediction of mesh deformations [37]. Based on the predicted mesh, irregular images are corrected. This method partially addresses the challenges of flexible structural distortions for image rectification and computational acceleration. Moreover, the approach utilizes a residual progressive regression strategy for fully convolutional network prediction of mesh deformations and subsequent correction of irregular images. However, DRIS still faces certain challenges. For instance, its loss function focuses solely on the situation within the initial mesh, without considering global information for further adjustments. This limitation results in deformation errors in panoramic information. Additionally, the method concentrates on horizontal and vertical objectives within the mesh, making it prone to deformation errors when correcting targets in other scale directions [38,39]. Currently, there is relatively limited research on image rectification, and achieving image rectification while ensuring minimal loss of information remains a challenging task [40,41,42,43,44].
To address the aforementioned challenges, this study proposes a deep learning-based image rectification algorithm named RIS-DMRN (Rectification for Image Stitching with Deformable Mesh and Residual Network). The algorithm defines a deformable target mesh for irregularly stitched images, which can be predicted during model training. The selection of the deformable mesh shape is based on the judgment of the current image's rigid structure by a convolutional neural network, offering three options: triangle, rectangle, and regular hexagon. Once the mesh shape is determined, the prediction network generates an initial predicted mesh based on the input irregular image and its mask matrix. The training process employs a width residual network to predict the initial mesh by content-aware processing of irregularly stitched images. Subsequently, the input irregular image, predicted initial mesh, and predefined target mesh are collectively input into the width residual neural network for rectification regression. The loss function of the width residual network comprises local and global. The local loss function controls the deformation loss of targets within the mesh, while the global-related loss function helps avoid global information loss during the deformation process. In comparison to existing methods, this approach utilizes a deformable mesh as the initial mesh, allowing for more versatile directional movement during mesh restoration and achieving better correction effects for targets within irregular images, as illustrated in the comparative results against various methods (Figure 1). Additionally, the introduction of local and global-related loss functions significantly mitigates the drawbacks of traditional methods that focus only on partial regions, enhancing the overall coherence during the deformation recovery process and preserving content more effectively after image rectification.

2. Materials and Methods

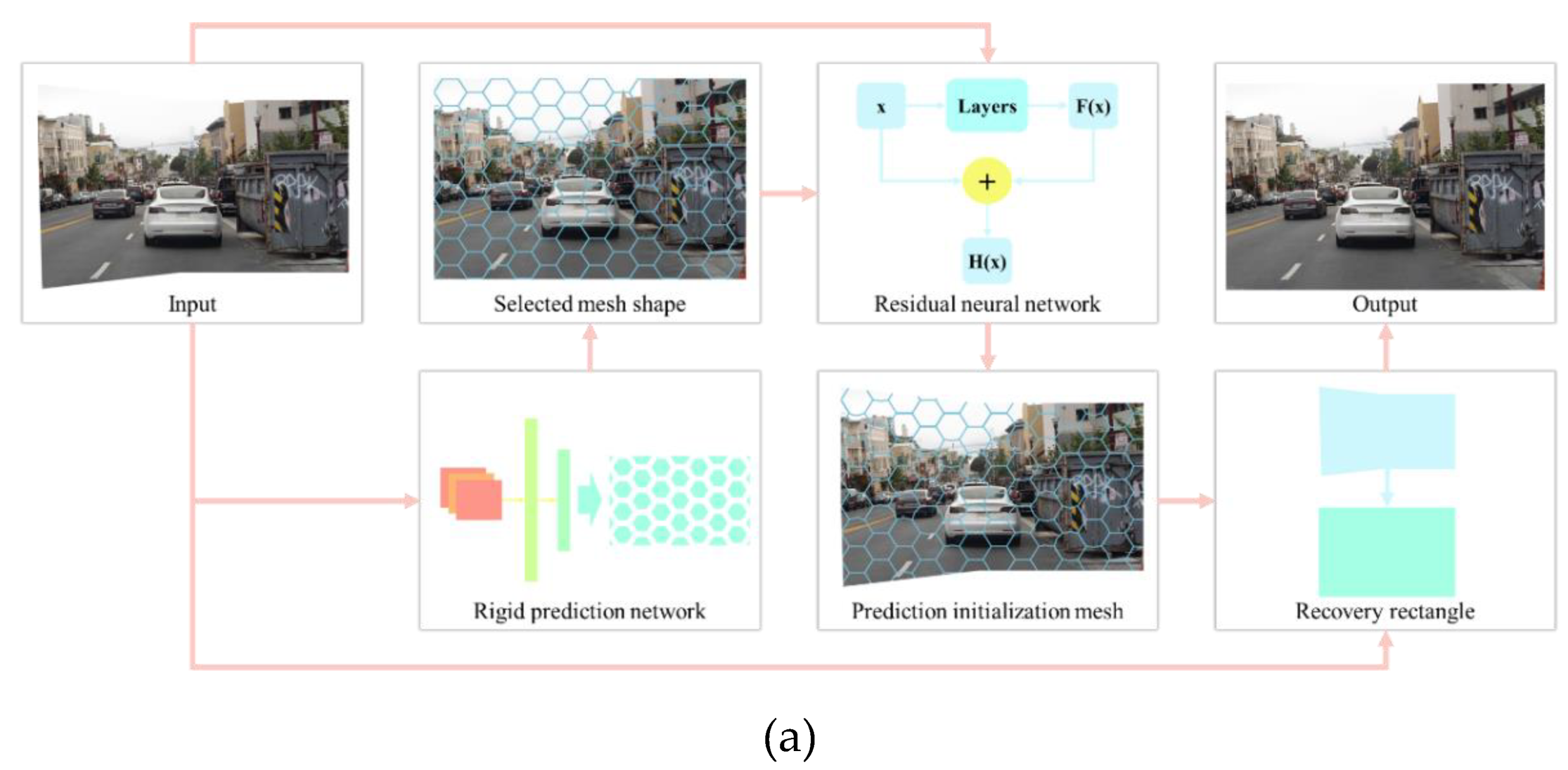
This paper proposes a deformable mesh structure for the initial prediction of irregular images, enhancing its adaptability in various spatial scene structures. In light of this mesh structure, the paper establishes two methods for mesh application. One approach involves predicting the rigid structure of the input image through a simple convolutional neural network. Based on the prediction results, the most suitable mesh shape for the image is selected (Figure 2(a)). Subsequently, the input image and the chosen mesh shape are input into a width residual network for initializing mesh prediction. Finally, the predicted initial mesh and the input irregular image are jointly used for image rectification regression, resulting in the output image.
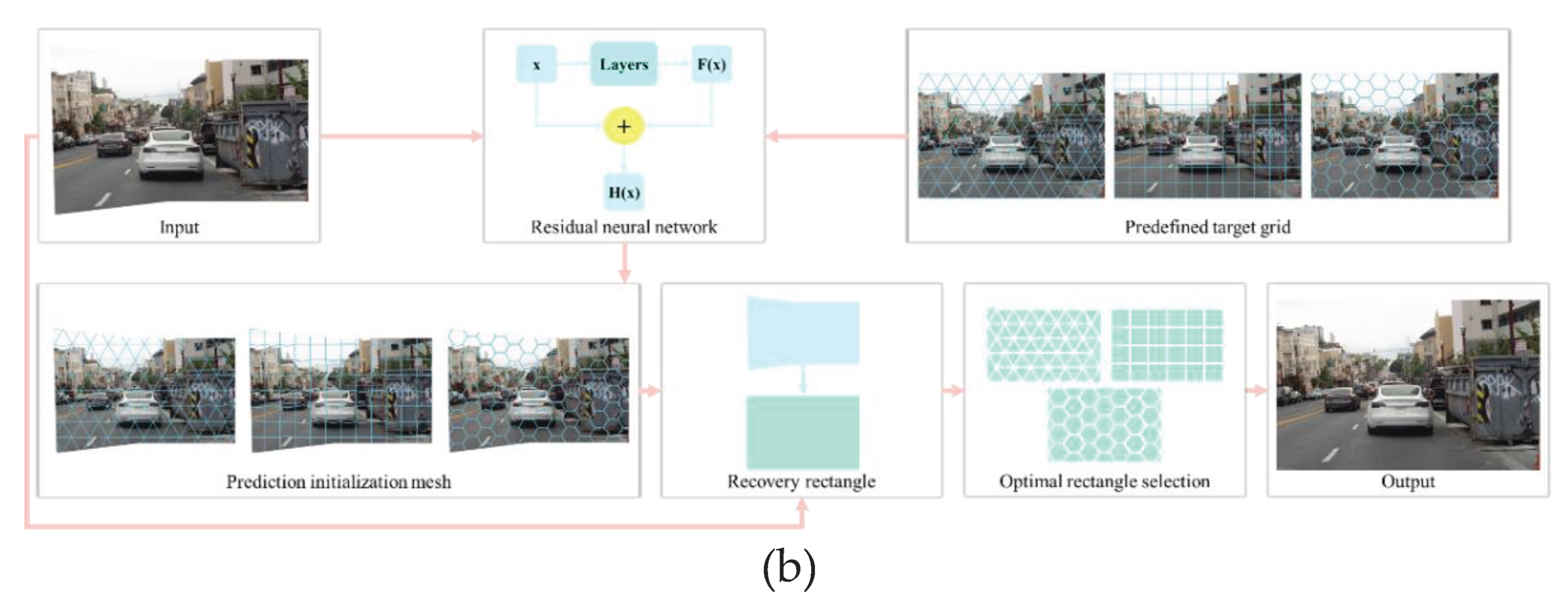
Another option is to input the input image and predefined target meshes for all shapes into a width residual neural network to generate initial mesh predictions (Figure 2(b)). Subsequently, image rectification regression is performed with the input image. The optimization is then based on the regression loss of the rectified image, selecting the one with the minimum information loss as the final output image.

2.1. Deformable mesh

This paper introduces deformable meshes to meet the application demands in different scenarios. Traditional rectangles exhibit weaker generalization capabilities when dealing with complex scenes. Therefore, the paper introduces two additional mesh models: hexagonal and triangular meshes. Hexagonal meshes have more uniform relationships between adjacent pixels, with each hexagon having six neighbors with equal adjacency properties. This provides better spatial consistency for image rectification. For example, during the image interpolation process, hexagonal meshes can offer smoother and more natural transitions. Moreover, hexagonal meshes closely resemble the shapes of many objects and structures found in the natural world, such as beehives and crystal structures [45]. Therefore, they may provide a more natural representation of images related to natural landscapes. Triangular meshes, on the other hand, excel in realistically reconstructing the shapes in images, especially when the images contain curves and surfaces [46]. The use of triangular meshes allows for better adaptation to irregular image regions, enabling more flexible shape approximation and, consequently, a more accurate capture of details in the images.
Simultaneously, this paper proposes two operational modes for the deformable meshes: speed-oriented and quality-oriented. In the speed-oriented mode, the input image undergoes detection of rigid structures within irregular images using a simple recognition network. Based on the detected structure count and orientation, the mesh shape that best fits the threshold is directly selected. Currently available mesh shapes include triangles, rectangles, hexagons, and more. In the quality-oriented mode, each mesh shape conducts residual regression predictions on the input image, generating a rectified image. Ultimately, the optimal output is selected based on the loss values of the rectified images, choosing the one with a relatively superior rectification effect.

2.2. Network Architecture

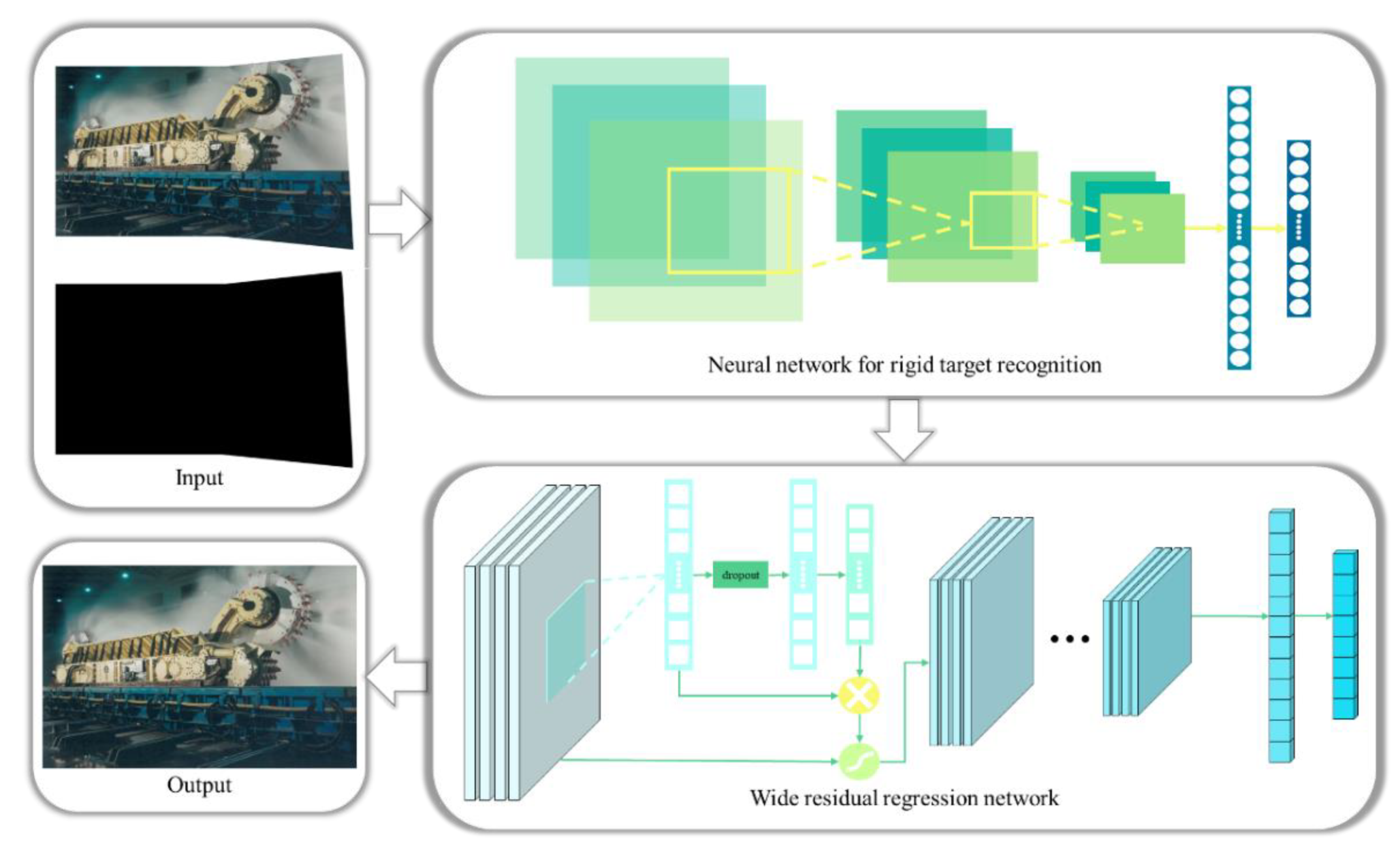
The network architecture proposed in RIS-DMRN consists of two components (Figure 3): the rigid target recognition network and the width residual regression network [47]. The input comprises irregularly stitched images and their stitching mask matrix. The input image is initially processed by a simple recognition convolutional neural network to detect the quantity and orientation of rigid structures. Based on the detection results, the most suitable mesh shape is chosen for rectification. For instance, if there are predominantly horizontal or vertical rigid structures in the image, a preference is given to selecting a rectangular mesh. In the case of a higher prevalence of curved surfaces or curved structures, a triangular mesh is chosen. If the quantities of vertical rigid structures and curved structures are comparable, a hexagonal mesh is selected for image rectification.
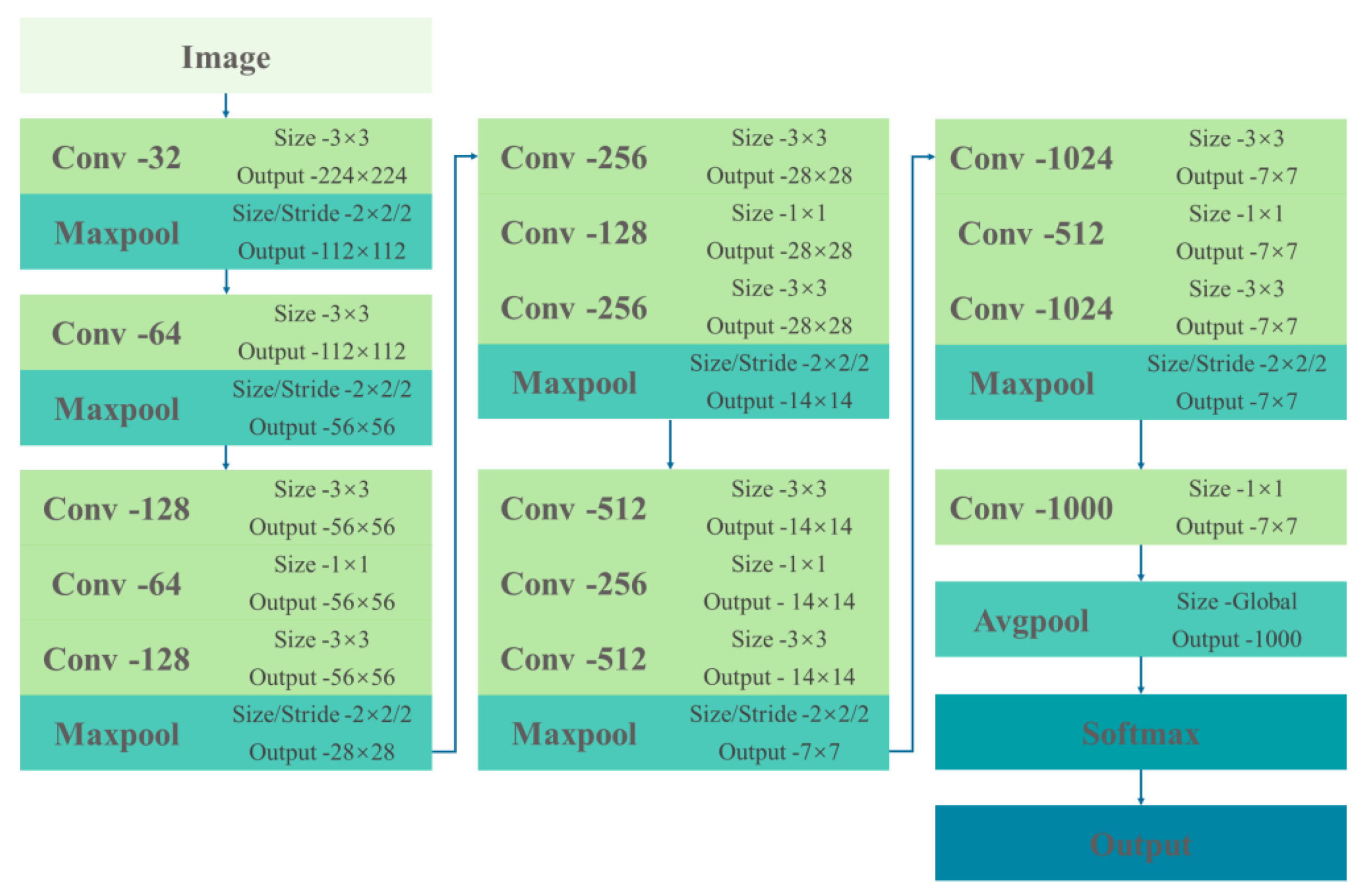
The main structure for rigid structure detection in this paper is a convolutional neural network (Figure 4), with input images resized to a unified 448×448. The CNN consists of 6 convolutional blocks, each composed of various combinations of 3×3 convolutional kernels, 1×1 convolutional kernels, and 2×2 max-pooling layers with a stride of 2. After extracting image features into a 1000-dimensional 7×7 feature vector, a 1000-dimensional vector is generated through average pooling. This vector is then input into Softmax for rigid structure detection. The network also incorporates normalization and dropout operations, although they are not explicitly shown in the diagram.
Once the mesh shape is determined, the irregularly stitched image and its mask matrix are fed into the Wide Residual Neural Network (Wide ResNet) for the rectification process. The choice of Wide ResNet as the recovery prediction network for image rectification is motivated by its ability to enhance feature dimensions in each residual block through increased channel numbers. This augmentation enables the network to capture richer feature representations, playing a crucial role in the recovery of content items after mesh transformation and minimizing the loss in rectified content. Moreover, due to significant internal variations within the meshes during the rectification process, some meshes experience a gradual decrease in gradients during the backward propagation of model training, leading to convergence challenges. The introduction of wider residual blocks in the Wide ResNet facilitates easier gradient flow, mitigating the issue of gradient vanishing during training [48,49].
The architecture of the Wide ResNet employed in RIS-DMRN consists of four residual convolutional blocks followed by an average pooling layer (Table 1). In the network, 'k' represents the multiplier for the convolutional kernels in the original module, ' N ' indicates the number of residual modules in that layer, and ' B (3,3) ' signifies each residual module consisting of two 3×3 convolutional layers. After feature extraction through the residual network, a simple fully convolutional structure is utilized as a mesh motion regressor to predict the horizontal and vertical movements of each vertex based on the regular mesh, facilitating the output of the rectified image.

2.3. Loss function

The loss function of the proposed RIS-DMRN consists of two components: the local loss function and the global loss function. The calculation is formulated as follows Equation (1):
Preprints 99972 i001
Where ω l o c a l and ω g l o b a l represent the weights assigned to the local loss and global loss, respectively. The local loss l l o c a l and global loss l g l o b a l contribute to the overall loss, and the weights control the balance between preserving local details and maintaining global context during the rectification process.

2.3.1. Local loss

The content loss term in the RIS-DMRN consists of two components: content loss and mesh loss. The content loss term, represented by Equation (2), involves the comparison between the predicted mesh (m) applied to the input irregular image ( I p ) and the warped version of the irregular image ( D ( I p , m ) ) using the bending operation. Additionally, the content loss incorporates the difference between the predicted mesh and the ground truth mesh (T). The function C, denoting the 'conv4' convolutional layer in the width recognition network, plays a role in shaping the content loss term. This formulation aims to ensure that the rectified image aligns closely with both the original irregular content and the ground truth mesh structure.
Preprints 99972 i002
For the mesh loss term in RIS-DMRN, the formula can be expressed as Equation (3):
Preprints 99972 i003
Where l m e s h represents the mesh loss term, i and j are indices within the mesh, m i , j is the predicted mesh by the model, T i , j is the ground truth label mesh, and W is the mesh generation function. This loss term aims to encourage the model to better learn and preserve the mesh structure of the image by comparing the differences between the predicted mesh by the model and the true label mesh.

2.3.2. Global loss

The global loss term in RIS-DMRN proposed in this paper consists of two components: global structural loss term and boundary loss term, expressed as shown in Equation (4):
Preprints 99972 i004
The computation of the global structural loss term is expressed as Equation (5), where I p c represents the irregular image cropped based on the mask matrix, μ I p c is the mean of I p c , μ_T is the mean of T, σ I p c 2 is the variance of I p c , σ T 2 is the variance of T, and σ I p c T is the covariance between I p c and T. Constants c 1 and c 2 are constants used to stabilize the formula.
Preprints 99972 i005
The expression for the boundary loss term is given by Equation (6), where I m represents the mask matrix of the original irregular image, and E represents the target template of an all-ones matrix. The boundary loss adjusts based on the 0/1 mask matrix of the irregular stitched image, with an all-ones matrix as the true target, gradually approaching the rectangularization.
Preprints 99972 i006

3. Results

The experimental implementation of the RIS-DMRN algorithm in this study was conducted on the following workstation configuration: Processor (CPU): Intel Core i9-13900HX (2.2 GHz, 6 cores, 12 threads), Memory (RAM): 16GB DDR4 2400MHz, Graphics Card (GPU): NVIDIA GeForce GTX 4070 Ti (8GB GDDR5X). The algorithm was implemented using Python 3.6 + TensorFlow 1.13.1 for program design. Due to the limited availability of publicly accessible datasets for image rectification research, this study conducted validation on the DIR-D dataset [37]. Following the consistent approach outlined in the paper [37], RIS-DMRN set the batch size to 8 during the training process, initialized the learning rate to 1×10-3, and performed exponential decay on the learning rate every 50 epochs. The parameters ω l o c a l and ω g l o b a l were set to 0.7 and 0.3, respectively, aiming to preserve detailed content while simultaneously focusing on the global shape changes. After experimenting with this paper, this combination is found t to be the better choice.

3.1. Quantitative comparison of image rectification

The algorithm proposed in this paper was primarily tested on 300 samples selected from the DIR-D dataset. A quantitative comparison was performed against mainstream rectification methods, and the results are presented in Table 1. The term "Initialization" denotes the initial state of the freshly stitched image without image rectification processing. The quantification metrics include the average values of SSIM, PSNR, and FID within the samples for comparison [50,51,52].
It is evident that compared to the RPIW [30] and DRIS [37], the proposed RIS-DMRN outperforms in all metrics (Table 2). Additionally, it surpasses traditional seam carving and image completion. This superiority is attributed to the configurations in the loss functions of the deep learning rectification algorithm, which includes the design of content loss and mesh loss. These designs minimize the deformation of target content within the image during rectification, resulting in a more effective image rectification. In comparison to DRIS, the global structure loss term and boundary loss term in RIS-DMRN better preserve global information. Preserving global information is crucial for the algorithm to better understand the contextual relationships of objects in the image. This understanding is vital for interpreting the relative positions, sizes, and interrelationships of objects. Additionally, global information contributes to maintaining consistency between different regions of the image, ensuring that the algorithm produces coherent output throughout the entire image, especially in tasks like image rectification [53,54,55]. Simultaneously, it can be observed that using a hexagon as the initial mesh shape yields slightly better results than traditional rectangular meshes (Table 2). This improvement is attributed to hexagons having more rigid directional choices and better shape adjacency relationships. While hexagons may increase the computational time to some extent compared to rectangles, they often produce superior results.
Consistent with the settings in the paper [37], this study also acknowledges that there may be differences in quantitative measurements when objects undergo slight positional variations in the generated rectangular results. Although the visual perception may still appear very natural in such cases, it could weaken the persuasiveness of quantitative experiments. Therefore, this study also incorporates BIQUE [56] and NIQE [57] as "no-reference" evaluation metrics (Table 3). These two evaluation methods are no-reference image quality assessment metrics, dedicated to quantifying the quality of images without the need for any additional reference data [58,59,60,61]. It is noteworthy that RIS-DMRN produces higher quality results under these blind image quality evaluation metrics. This indicates that the proposed method not only excels in preserving global information but also achieves significant improvements in overall image quality.

3.2. Qualitative comparison of image rectification

To visually demonstrate the effectiveness of RIS-DMRN in image rectification, this study divided the test set into two parts—one with more global contextual information and the other with more local detailed information. The algorithm was tested on both sets, and the results were compared qualitatively (Figure 5). Specifically, the study showcases the effects of different input irregular images, image completion results, RIS-DMRN processed images, and ground truth label images in scenes where global correlations are more prominent, such as natural landscapes.
It is evident that image completion can fully rectify the image into a rectangle (Figure 5), but it relies heavily on pixel-level adjustments based on context, making it overly dependent on surrounding information. This dependency may lead to inaccurate filling of missing parts, resulting in generated images that appear unrealistic or unnatural, and may even cause a certain degree of decrease in image clarity [62,63,64,65]. In contrast, the rectangular images generated by RIS-DMRN closely resemble the real label images. RIS-DMRN performs well in maintaining the global rigidity or curvature of target objects in the image, attempting to preserve the original appearance without introducing local barrel or pincushion distortions.
In scenarios with dense local information, this study compares the results of image completion and RIS-DMRN processing when dealing with irregular images (Figure 6). It is observed that image completion methods often lead to deformations in local rigid structures during the rectification process. Moreover, when addressing the boundaries of missing regions, noticeable boundary effects are common, as image completion methods need to ensure smooth transitions between the filled area and the surrounding region, leading to prominent boundary artifacts [2,66,67]. In addition, this article also presents other qualitative comparison results, as shown in Appendix A Figure A1 and Figure A2.
RIS-DMRN, with its finer mesh design, can control the loss and deformation of local information within a certain range. This ensures that local shape changes do not excessively impact the deformation of adjacent meshes, guaranteeing the preservation of local information during the rectification process. Additionally, constraints in different mesh directions in RIS-DMRN allow it to adapt to various deformations of rigid and curved structures, enabling a better fit to the original shape of the image during the deformation process.

3.3. Impact of Deformable Mesh and Loss Functions on Image Rectification

In accordance with practical application requirements, this study designed three types of deformable meshes—triangle, rectangle, and regular hexagon—for predicting the rectification of irregular images. For the input size of the dataset at 512×384, a uniform mesh resolution of 16×12 was employed for rectification prediction. In terms of loss functions, both local and global loss terms were designed for regression prediction. Taking a random selection of 300 images from the test set of the DIR-D dataset as an example, the study tested the quantitative metrics for image rectification under different method combinations (Table 4). In the table, "𝒲" indicates the inclusion of the current mesh shape or loss function in the combination.
When combining local and global loss terms on the basis of using a rectangular mesh, the overall rectification regression performance is poorer. Comparatively, the absence of the local loss term has a more significant impact on rectification. This is because the global loss term introduces substantial stretching and bending during the regression process, while the local loss term predicts the regression of rigid or curved structures based on the actual content within the mesh. If only the global loss term is used, the rectification may result in severe deformation within local structures, as they are not adequately repaired.
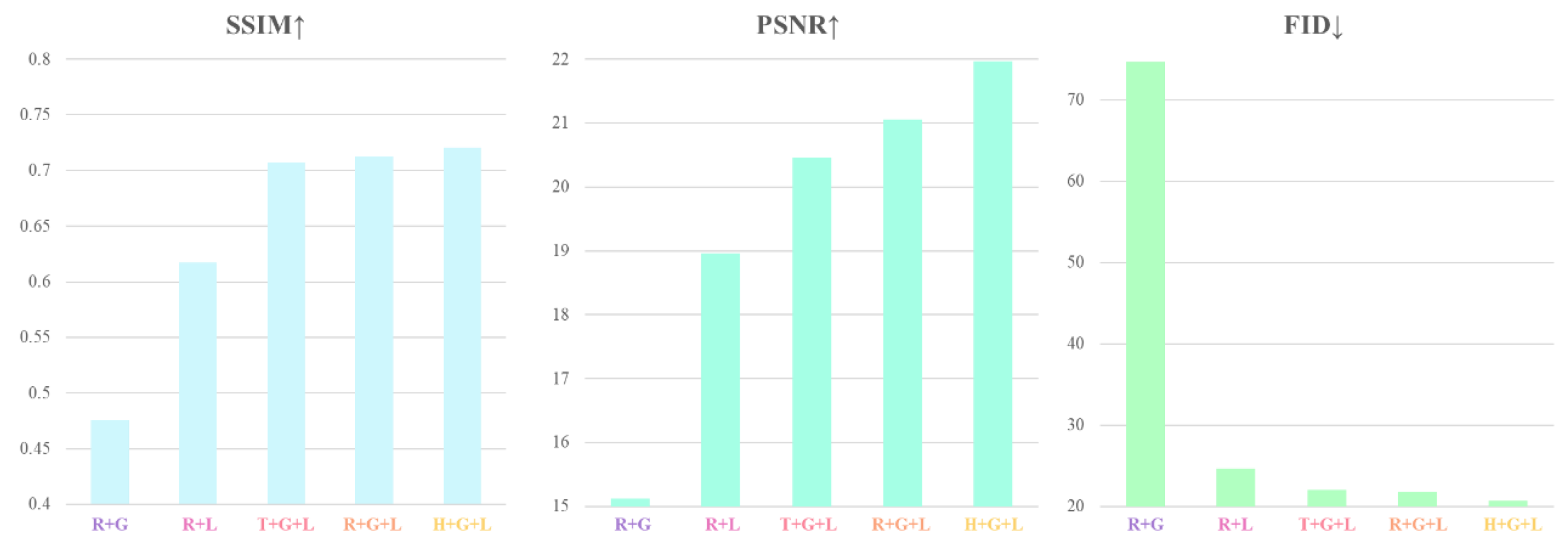
The figures provide a more intuitive sense of the image loss resulting from different combinations, offering a direct visual representation of the changes in evaluation metrics under various combinations (Figure 7). In terms of the overall rectification performance with deformable meshes, it can be observed that the hexagon performs the best, followed by the rectangular mesh, while the triangular mesh exhibits a poorer rectification effect. This is because the hexagonal mesh has better adaptability compared to other meshes; it can effectively cover and adapt to various irregular contours, thereby enhancing the performance of the regression model [68,69].
Simultaneously, the hexagonal mesh can more compactly cover the image area, reducing redundancy. It can decrease edge effects when handling image boundaries, reducing the likelihood of extensive deformation at the image edges and thereby improving representation efficiency [70]. In contrast, rectangular meshes may require more mesh points to represent the same image area, resulting in larger input dimensions [71]. Although triangular meshes, compared to rectangular meshes, can better adapt to irregular shapes and exhibit greater flexibility in handling complex image structures [72,73], the special interpolation between triangular meshes and the relationships between neighboring triangles may result in the need for more mesh points to represent the same image area, thus increasing redundancy [74]. Additionally, when dealing with image boundaries, triangular meshes may encounter issues of discontinuity or lack of smoothness at the borders.

4. Discussion

This paper proposes a method for rectifying irregularly stitched images using deformable meshes and residual networks. The approach involves predicting initial mesh models for irregular images using three types of shapes: triangles, rectangles, and regular hexagons. The selection of different meshes can dynamically adjust based on the requirements of predicting rigid structures or actual image content. The predicted mesh model, predefined mesh model, and irregular input image are jointly input into a width residual network for rectification regression. The loss function comprises local and global loss terms, ensuring that the loss of image information within the mesh and global contextual information is minimized. The final output rectifies the irregularly stitched image into a rectangularized image.
Although the algorithm proposed in this paper has made progress, there is still room for further improvement and optimization. One aspect that could be enhanced is the optimization of computational complexity. Currently, when constructing non-traditional rectangular meshes such as triangular or hexagonal meshes, the calculations tend to become more complex. For instance, calculating the relative positions or distances between adjacent cells might involve more intricate geometric operations. Additionally, the vertex coordinates and connectivity of triangular and hexagonal meshes are more complex compared to rectangular meshes, typically requiring more storage to represent the same area. Furthermore, using neural network structures to handle non-rectangular meshes in deep learning networks may require more parameters and more complex processing layers, potentially leading to reduced training and inference speeds. In the future, the paper will continue to research and improve efficiency in these areas.

5. Conclusions

This paper proposes a method for rectifying irregularly images into rectangles using deformable meshes and residual networks. The method utilizes a convolutional neural network to quantify rigid structures of images. Choosing the most suitable mesh structure based on the extraction results, offering options such as triangular, rectangular, and hexagonal. Subsequently, the irregularly image, predefined mesh structure, and predicted mesh structure are input into a wide residual neural network for regression.

Author Contributions

Conceptualization, Yingbo Fan and Shanjun Mao; Data curation, Yingbo Fan; Formal analysis, Wu Zheng and Li Ben; Funding acquisition, Shanjun Mao; Methodology, Yingbo Fan; Project administration, Shanjun Mao; Resources, Yingbo Fan; Software, Yingbo Fan; Supervision, Shanjun Mao; Validation, Yingbo Fan, Li Mei and Kang Jitong; Visualization, Shanjun Mao; Writing – original draft, Yingbo Fan; Writing – review & editing, Yingbo Fan.

Funding

This research was funded by the National Key R&D Program for the 14th Five-Year Plan (Prevention and Control of Major Natural Disasters and Public Security), grant number SQ2022YFC3000083”.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

Not applicable.

Acknowledgments

We would like to express our gratitude to many colleagues at Beijing LongRuan Technology Co., Ltd. for their extensive assistance in providing data and hardware support for this experiment.

Conflicts of Interest

Not applicable.

Appendix A

Preprints 99972 g0a1
Figure A1. Randomly selected stitched images for testing the RIS-DMRN in this paper.
Figure A1. Randomly selected stitched images for testing the RIS-DMRN in this paper.
Preprints 99972 g0a1
Preprints 99972 g0a2
Figure A2. Randomly selected stitched images for testing the RIS-DMRN in this paper.
Figure A2. Randomly selected stitched images for testing the RIS-DMRN in this paper.
Preprints 99972 g0a2

References

  1. Lin, M.X.; Xu, G.; Ren, X.N.; Xu, K.; Ieee. Cylindrical Panoramic Image Stitching Method Based On Multi-cameras. In Proceedings of the IEEE International Conference on Cyber Technology in Automation, Control, and Intelligent Systems (CYBER), Shenyang, PEOPLES R CHINA, Jun 09-12, 2015; pp. 1091-1096.
  2. Yang, L.; Liu, G.H.; Shi, Z.Y. Research on Suppression Algorithms of the Ringing Effect caused by Blind Image Restoration. In Proceedings of the Fifth International Conference on Instrumentation & Measurement, Computer, Communication, and Control (IMCCC), Qinhuangdao, PEOPLES R CHINA, Sep 18-20, 2015; pp. 1264-1267.
  3. Zou, C.M.; Wu, P.; Xu, Z.Q. Research on Seamless Image Stitching based on Depth Map. In Proceedings of the 6th International Conference on Pattern Recognition Applications and Methods (ICPRAM), Porto, PORTUGAL, Feb 24-26, 2017; pp. 341–350. [Google Scholar]
  4. Bai, Z.W.; Li, Y.; Chen, X.H.; Yi, T.T.; Wei, W.; Wozniak, M.; Damasevicius, R. Real-Time Video Stitching for Mine Surveillance Using a Hybrid Image Registration Method. Electronics 2020, 9. [Google Scholar] [CrossRef]
  5. Gao, H.; Huang, Z.Q.; Yang, H.P.; Zhang, X.B.; Cen, C. Research on Improved Multi-Channel Image Stitching Technology Based on Fast Algorithms. Electronics 2023, 12. [Google Scholar] [CrossRef]
  6. Zhu, L.; Wang, W.; Liu, Y.; Lai, S.M.; Li, J.; Ieee. A virtual reality video stitching system based on mirror pyramids. In Proceedings of the 7th International Conference on Virtual Reality and Visualization (ICVRV), Zhengzhou, PEOPLES R CHINA, Oct 21-22, 2017; pp. 288–293. [Google Scholar]
  7. Madhusudana, P.C.; Soundararajan, R. Subjective and Objective Quality Assessment of Stitched Images for Virtual Reality. Ieee Transactions on Image Processing 2019, 28. [Google Scholar] [CrossRef]
  8. Wang, L.; Yu, W.; Li, B. Multi-scenes Image Stitching Based on Autonomous Driving. In Proceedings of the 4th IEEE Information Technology, Networking, Electronic and Automation Control Conference (ITNEC), Electr Network, Jun 12-14, 2020; pp. 694–698. [Google Scholar]
  9. Kinzig, C.; Cortés, I.; Fernández, C.; Lauer, M.; Ieee. Real-time Seamless Image Stitching in Autonomous Driving. In Proceedings of the 25th International Conference of Information Fusion (FUSION), Linkoping, SWEDEN, Jul 04-07, 2022. [Google Scholar]
  10. Yuan, T.; Li, X.M. Optimal Local Warp Model for Image Stitching. In Proceedings of the 9th International Congress on Image and Signal Processing, BioMedical Engineering and Informatics (CISP-BMEI), Datong, PEOPLES R CHINA, Oct 15-17, 2016; pp. 369–373. [Google Scholar]
  11. Liao, T.L.; Li, N. Single-Perspective Warps in Natural Image Stitching. Ieee Transactions on Image Processing 2020, 29, 724–735. [Google Scholar] [CrossRef]
  12. Chang, C.-H.; Sato, Y.; Chuang, Y.-Y. Shape-preserving half-projective warps for image stitching. In Proceedings of the Proceedings of the IEEE conference on computer vision and pattern recognition; 2014; pp. 3254–3261. [Google Scholar]
  13. Kurilin, I.V.; Safonov, I.V.; Rychagov, M.N.; Lee, H.; Kim, S.H. High-performance automatic cropping and deskew of multiple objects on scanned images. In Proceedings of the Conference on Image Quality and System Performance XI (IQSP), San Francisco, CA, Feb 03-05, 2014. [Google Scholar]
  14. Shi, J.Y.; Dang, J.; Zuo, R.Z. Bridge damage cropping-and-stitching segmentation using fully convolutional network based on images from UAVs. In Proceedings of the 10th International Conference on Bridge Maintenance, Safety and Management (IABMAS), Electr Network, Apr 11-18, 2021; pp. 264–270. [Google Scholar]
  15. Liu, H.J.; Lee, S.H. Stitching of Video Sequences for Weed Mapping. In Proceedings of the 11th International Conference on Intelligent Information Hiding and Multimedia Signal Processing (IIH-MSP), Adelaide, AUSTRALIA, Sep 23-25, 2015; pp. 441–444. [Google Scholar]
  16. Cui, J.G.; Liu, M.; Zhang, Z.T.; Yang, S.Q.; Ning, J.F. Robust UAV Thermal Infrared Remote Sensing Images Stitching Via Overlap-Prior-Based Global Similarity Prior Model. Ieee Journal of Selected Topics in Applied Earth Observations and Remote Sensing 2021, 14, 270–282. [Google Scholar] [CrossRef]
  17. Zarif, S.; Faye, I.; Rohaya, D. Image Completion: Survey and Comparative Study. International Journal of Pattern Recognition and Artificial Intelligence 2015, 29. [Google Scholar] [CrossRef]
  18. Sari, I.N.; Du, W.W. Structure-Texture Consistent Painting Completion for Artworks. Ieee Access 2023, 11, 27369–27381. [Google Scholar] [CrossRef]
  19. Wu, H.; Miao, Z.J.; Wang, Y.; Chen, J.Y.; Ma, C.; Zhou, T.Y. Image completion with multi-image based on entropy reduction. Neurocomputing 2015, 159, 157–171. [Google Scholar] [CrossRef]
  20. Xu, S.Z.; Zhu, Q.; Wang, J. Generative image completion with image-to-image translation. Neural Computing & Applications 2020, 32, 7333–7345. [Google Scholar] [CrossRef]
  21. Kapoor, N.; Lynch, E.A.; Lacson, R.; Flash, M.J.E.; Guenette, J.P.; Desai, S.P.; Eappen, S.; Khorasani, R. Predictors of Completion of Clinically Necessary Radiologist Recommended Follow- Up Imaging: Assessment Using an Automated Closed- Loop Communication and Tracking Tool. American Journal of Roentgenology 2023, 220, 429–440. [Google Scholar] [CrossRef] [PubMed]
  22. Xu, J.W.; Li, F.; Shao, C.C.; Li, X.L. Face Completion Based on Symmetry Awareness with Conditional GAN. Symmetry-Basel 2023, 15. [Google Scholar] [CrossRef]
  23. Wang, H.T.; Guo, E.T.; Chen, F.; Chen, P.P. Depth Completion in Autonomous Driving: Adaptive Spatial Feature Fusion and Semi-Quantitative Visualization. Applied Sciences-Basel 2023, 13. [Google Scholar] [CrossRef]
  24. Zhu, S.D.; Zhang, Y.Z.; Zhang, J.; Hu, H.; Zhang, Y.Z. ISGTA: an effective approach for multi-image stitching based on gradual transformation matrix. Signal Image and Video Processing 2023, 17, 3811–3820. [Google Scholar] [CrossRef]
  25. Mishiba, K.; Ikehara, M.; Yoshitome, T.; Ieee. CONTENT ASPECT RATIO PRESERVING MESH-BASED IMAGE RESIZING. In Proceedings of the 19th IEEE International Conference on Image Processing (ICIP), Lake Buena Vista, Lake Buena Vista, FL, Sep 30-Oct 03, 2012; pp. 865–868. [Google Scholar]
  26. Mishiba, K.; Ikehara, M.; Yoshitome, T. Content Aware Image Resizing with Constraint of Object Aspect Ratio Preservation. Ieice Transactions on Information and Systems 2013, E96D, 2427–2436. [Google Scholar] [CrossRef]
  27. Li, C.; Guo, B.L.; Guo, X.X.; Zhi, Y.P. Real-Time UAV Imagery Stitching Based on Grid-Based Motion Statistics. In Proceedings of the 3rd Annual International Conference on Information System and Artificial Intelligence (ISAI), Suzhou, PEOPLES R CHINA, Jun 22-24, 2018. [Google Scholar]
  28. Liu, S.G.; Chai, Q.P. Shape-Optimizing and Illumination-Smoothing Image Stitching. Ieee Transactions on Multimedia 2019, 21, 690–703. [Google Scholar] [CrossRef]
  29. Wang, J.L.; Ma, M.X.; Yan, S.; Zhang, J. Image stitching using double features-based global similarity constraint and improved seam-cutting. Multimedia Tools and Applications 2023. [Google Scholar] [CrossRef]
  30. He, K.M.; Chang, H.W.; Sun, J. Rectangling Panoramic Images via Warping. Acm Transactions on Graphics 2013, 32. [Google Scholar] [CrossRef]
  31. Li, D.P.; He, K.M.; Sun, J.; Zhou, K.; Ieee. A Geodesic-Preserving Method for Image Warping. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Boston, MA, Jun 07-12, 2015; pp. 213–221. [Google Scholar]
  32. Il Koo, H.; Kuk, J.G.; Cho, N.I.; Ieee. ELIMINATING STRUCTURE MISALIGNMENTS USING ROBUST MATCHING AND IMAGE EDITING BASED ON SEAM CARVING. In Proceedings of the 16th IEEE International Conference on Image Processing, Cairo, EGYPT, Nov 07-10, 2009; pp. 209–212. [Google Scholar]
  33. Conger, D.D.; Kumar, M.; Radha, H. Multi-seam carving via seamlets. In Proceedings of the Conference on Image Processing: Algorithms and Systems IX, San Francisco, CA, Jan 24-25, 2011. [Google Scholar]
  34. Kim, H.K.; Lee, K.W.; Jung, J.Y.; Jung, S.W.; Ko, S.J. A Content-Aware Image Stitching Algorithm for Mobile Multimedia Devices. Ieee Transactions on Consumer Electronics 2011, 57, 1875–1882. [Google Scholar] [CrossRef]
  35. Ryu, S.J.; Lee, H.Y.; Lee, H.K. Detecting Trace of Seam Carving for Forensic Analysis. Ieice Transactions on Information and Systems 2014, E97D, 1304–1311. [Google Scholar] [CrossRef]
  36. Ye, J.Y.; Shi, Y.Q. A Hybrid Feature Model for Seam Carving Detection. In Proceedings of the 16th International Workshop on Digital Forensics and Watermarking (IWDW), Otto Guericke Univ, Dept Comp Sci, Adv Multimedia & Secur Lab, Magdeburg, GERMANY, Aug 23-25, 2017; pp. 77–89. [Google Scholar]
  37. Nie, L.; Lin, C.Y.; Liao, K.; Liu, S.C.; Zhao, Y.; Ieee Comp, S.O.C. Deep Rectangling for Image Stitching: A Learning Baseline. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), New Orleans, LA, Jun 18-24, 2022; pp. 5730–5738. [Google Scholar]
  38. Cai, X.X.; Jiang, B.N.; Liao, G.J. Adaptive grid generation based on the least-squares finite-element method. Computers & Mathematics with Applications 2004, 48, 1077–1085. [Google Scholar] [CrossRef]
  39. Liao, G.J.; Xue, J.X. Moving meshes by the deformation method. Journal of Computational and Applied Mathematics 2006, 195, 83–92. [Google Scholar] [CrossRef]
  40. Priest, A.N.; De Vita, E.; Thomas, D.L.; Ordidge, R.J. EPI distortion correction from a simultaneously acquired distortion map using TRAIL. Journal of Magnetic Resonance Imaging 2006, 23, 597–603. [Google Scholar] [CrossRef]
  41. Kiryu, S.; Inoue, Y.; Masutani, Y.; Haishi, T.; Yoshikawa, K.; Watanabe, M.; Ohtomo, K. Distortion correction in whole-body imaging of live mice using a 1-Tesla compact magnetic resonance imaging system. Japanese Journal of Radiology 2011, 29, 353–360. [Google Scholar] [CrossRef] [PubMed]
  42. Andersson, J.L.R.; Sotiropoulos, S.N. An integrated approach to correction for off-resonance effects and subject movement in diffusion MR imaging. Neuroimage 2016, 125, 1063–1078. [Google Scholar] [CrossRef]
  43. Talat, R.; Muzammal, M.; Shan, R. A decentralised approach to scene completion using distributed feature hashgram. Multimedia Tools and Applications 2020, 79, 9799–9817. [Google Scholar] [CrossRef]
  44. Wang, Z.H.; Tang, Z.J.; Huang, J.K.; Li, J.D. A real-time correction and stitching algorithm for underwater fisheye images. Signal Image and Video Processing 2022, 16, 1783–1791. [Google Scholar] [CrossRef]
  45. Yao, X.C.; Yu, G.J.; Li, G.Q.; Yan, S.; Zhao, L.; Zhu, D.H. HexTile: A Hexagonal DGGS-Based Map Tile Algorithm for Visualizing Big Remote Sensing Data in Spark. Isprs International Journal of Geo-Information 2023, 12. [Google Scholar] [CrossRef]
  46. Zeng, W.B.; Deng, Q.Y.; Zhao, X.Y.; Li, D.H.; Min, X.R. A method for stitching remote sensing images with Delaunay triangle feature constraints. Geocarto International 2023, 38. [Google Scholar] [CrossRef]
  47. Li, Y.Q.; Luo, T.; Yip, N.K. Towards an Understanding of Residual Networks Using Neural Tangent Hierarchy (NTH). Csiam Transactions on Applied Mathematics 2022, 3, 692–760. [Google Scholar] [CrossRef]
  48. Shi, J.; Li, Z.; Ying, S.H.; Wang, C.F.; Liu, Q.P.; Zhang, Q.; Yan, P.K. MR Image Super-Resolution via Wide Residual Networks With Fixed Skip Connection. Ieee Journal of Biomedical and Health Informatics 2019, 23, 1129–1140. [Google Scholar] [CrossRef]
  49. Chen, Z.Y.; Wang, Y.H.; Wu, J.; Deng, C.; Jiang, W.X. Wide Residual Relation Network-Based Intelligent Fault Diagnosis of Rotating Machines with Small Samples. Sensors 2022, 22. [Google Scholar] [CrossRef] [PubMed]
  50. Qureshi, H.S.; Khan, M.M.; Hafiz, R.; Cho, Y.; Cha, J. Quantitative quality assessment of stitched panoramic images. Iet Image Processing 2012, 6, 1348–1358. [Google Scholar] [CrossRef]
  51. Hensel, M.; Ramsauer, H.; Unterthiner, T.; Nessler, B.; Hochreiter, S. GANs Trained by a Two Time-Scale Update Rule Converge to a Local Nash Equilibrium. In Proceedings of the 31st Annual Conference on Neural Information Processing Systems (NIPS), Long Beach, CA, Dec 04-09, 2017. [Google Scholar]
  52. Wang, Z.B.; Yang, Z.K. Seam elimination based on Curvelet for image stitching. Soft Computing 2019, 23, 5065–5080. [Google Scholar] [CrossRef]
  53. Jenkinson, M.; Bannister, P.; Brady, M.; Smith, S. Improved optimization for the robust and accurate linear registration and motion correction of brain images. Neuroimage 2002, 17, 825–841. [Google Scholar] [CrossRef]
  54. Cheng, M.-M.; Zhang, G.-X.; Mitra, N.J.; Huang, X.; Hu, S.-M.; Ieee. Global Contrast based Salient Region Detection. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Colorado Springs, CO, 2011 Jun 20-25, 2011; pp. 409–416. [Google Scholar]
  55. Zhang, Y.; Wang, T.; Zheng, T.J.; Zhang, Y.S.; Li, L.; Yu, Y.; Li, L. On-Orbit Geometric Calibration and Performance Validation of the GaoFen-14 Stereo Mapping Satellite. Remote Sensing 2023, 15. [Google Scholar] [CrossRef]
  56. Venkatanath, N.; Praneeth, D.; Bh, M.C.; Channappayya, S.S.; Medasani, S.S.; Ieee. BLIND IMAGE QUALITY EVALUATION USING PERCEPTION BASED FEATURES. In Proceedings of the 21st National Conference on Communications (NCC), Indian Inst Technol, Bombay, INDIA, Feb 27-Mar 01, 2015. [Google Scholar]
  57. Mittal, A.; Soundararajan, R.; Bovik, A.C. Making a "Completely Blind" Image Quality Analyzer. Ieee Signal Processing Letters 2013, 20, 209–212. [Google Scholar] [CrossRef]
  58. Mittal, A.; Saad, M.A.; Bovik, A.C. Zero Shot Prediction of Video Quality using Intrinsic Video Statistics. In Proceedings of the Conference on Human Vision and Electronic Imaging XIX, San Francisco, CA, Feb 03-06, 2014. [Google Scholar]
  59. Sang, Q.B.; Wu, X.J.; Li, C.F.; Bovik, A.C. Blind image quality assessment using a reciprocal singular value curve. Signal Processing-Image Communication 2014, 29, 1149–1157. [Google Scholar] [CrossRef]
  60. Shao, F.; Li, K.M.; Lin, W.S.; Jiang, G.Y.; Yu, M.; Dai, Q.H. Full-Reference Quality Assessment of Stereoscopic Images by Learning Binocular Receptive Field Properties. Ieee Transactions on Image Processing 2015, 24, 2971–2983. [Google Scholar] [CrossRef]
  61. Yao, J.C.; Liu, G.Z. Improved SSIM IQA of contrast distortion based on the contrast sensitivity characteristics of HVS. Iet Image Processing 2018, 12, 872–879. [Google Scholar] [CrossRef]
  62. Chen, Q.C.; Li, G.Y.; Xie, L.; Xiao, Q.G.; Xiao, M. Image completion via texture direction analysis. Journal of Modern Optics 2019, 66, 1880–1888. [Google Scholar] [CrossRef]
  63. Alotaibi, A. Deep Generative Adversarial Networks for Image-to-Image Translation: A Review. Symmetry-Basel 2020, 12. [Google Scholar] [CrossRef]
  64. Ao, J.Y.; Ke, Q.H.; Ehinger, K.A. Image amodal completion: A survey. Computer Vision and Image Understanding 2023, 229. [Google Scholar] [CrossRef]
  65. Saleh, K.; Szénási, S.; Vámossy, Z. Generative Adversarial Network for Overcoming Occlusion in Images: A Survey. Algorithms 2023, 16. [Google Scholar] [CrossRef]
  66. Chen, L.C.; Papandreou, G.; Kokkinos, I.; Murphy, K.; Yuille, A.L. DeepLab: Semantic Image Segmentation with Deep Convolutional Nets, Atrous Convolution, and Fully Connected CRFs. Ieee Transactions on Pattern Analysis and Machine Intelligence 2018, 40, 834–848. [Google Scholar] [CrossRef]
  67. Wang, F.; Liu, Q.X.; Hu, D.X.; Wang, Y.C.; Zheng, T.R. Research of the image restoration algorithm based on boundary pre-processing in the space domain and fast computing in the frequency domain. In Proceedings of the 5th Symposium on Novel Optoelectronic Detection Technology and Application, Xian, PEOPLES R CHINA, Oct 24-26, 2018. [Google Scholar]
  68. Nagy, B. Calculating distance with neighborhood sequences in the hexagonal grid. In Combinatorial Image Analysis, Proceedings; Klette, R., Zunic, J., Eds.; Lecture Notes in Computer Science; 2004; Volume 3322, pp. 98–109. [Google Scholar]
  69. Varghese, P.; Saroja, G.A.S. Biologically Inspired Hexagonal Image Structure for Computer Vision. In Proceedings of the 3rd International Conference on Advances in Information Communication Technology and Computing (AICTC), Bikaner, INDIA, Dec 20-21, 2021; pp. 487–496. [Google Scholar]
  70. Linnér, E.; Strand, R.; Ieee. Comparison of Restoration Quality on Square and Hexagonal Grids using Normalized Convolution. In Proceedings of the 21st International Conference on Pattern Recognition (ICPR), Univ Tsukuba, Tsukuba, JAPAN, Nov 11-15, 2012; pp. 3046–3049. [Google Scholar]
  71. Mostafa, K.; Chiang, J.Y.; Tsai, W.C.; Her, I. Fuzzy Noise Removal and Edge Detection on Hexagonal Image. Journal of the Chinese Society of Mechanical Engineers 2017, 38, 659–667. [Google Scholar]
  72. Fang, T.Z.; Hu, Z.G.; Jin, W.K. Progressive transmission of single-resolution mesh image. Electronics Letters 2004, 40, 984–986. [Google Scholar] [CrossRef]
  73. Lizier, M.A.S.; Siqueira, M.F.; Daniels, J., II; Silva, C.T.; Gustavo Nonato, L. Template-based quadrilateral mesh generation from imaging data. Visual Computer 2011, 27, 887–903. [Google Scholar] [CrossRef]
  74. Phan, T.D.K. A triangle mesh-based corner detection algorithm for catadioptric images. Imaging Science Journal 2018, 66, 220–230. [Google Scholar] [CrossRef]
Preprints 99972 g001
Figure 1. Comparison of rectification methods for irregular image stitching.
Figure 1. Comparison of rectification methods for irregular image stitching.
Preprints 99972 g001
Preprints 99972 g002aPreprints 99972 g002b
Figure 2. Image rectification with different mesh shape selection modes. (a) Selecting a mesh shape based on the image. Predicting the most suitable mesh shape for an input image through a convolutional neural network. Subsequently, the predicted initial mesh based on this shape and the predefined mesh are jointly input into a residual network for image rectification. (b) Selecting all mesh shapes for loss comparisons. Applying all mesh shapes to the input image and jointly inputting them into a residual network for rectification. The rectified image with the lowest loss is selected as the final output.
Figure 2. Image rectification with different mesh shape selection modes. (a) Selecting a mesh shape based on the image. Predicting the most suitable mesh shape for an input image through a convolutional neural network. Subsequently, the predicted initial mesh based on this shape and the predefined mesh are jointly input into a residual network for image rectification. (b) Selecting all mesh shapes for loss comparisons. Applying all mesh shapes to the input image and jointly inputting them into a residual network for rectification. The rectified image with the lowest loss is selected as the final output.
Preprints 99972 g002aPreprints 99972 g002b
Preprints 99972 g003
Figure 3. Schematic structure of width residual neural network.
Figure 3. Schematic structure of width residual neural network.
Preprints 99972 g003
Preprints 99972 g004
Figure 4. Neural networks for target detection in rigid structures.
Figure 4. Neural networks for target detection in rigid structures.
Preprints 99972 g004
Preprints 99972 g005
Figure 5. Rectification effect of different irregular images under images with more global correlation information. 'Reference' in the figure represents the experimental result of image completion.
Figure 5. Rectification effect of different irregular images under images with more global correlation information. 'Reference' in the figure represents the experimental result of image completion.
Preprints 99972 g005
Preprints 99972 g006
Figure 6. Rectification effect of different irregular images under images with more local structural information.
Figure 6. Rectification effect of different irregular images under images with more local structural information.
Preprints 99972 g006
Preprints 99972 g007
Figure 7. Trends of evaluation indexes under different combinations of loss functions and mesh shapes. The chart displays from left to right, with the vertical axis indicating SSIM, PSNR, and FID values respectively, while the horizontal axis represents different combinations of mesh shapes and loss functions. Higher SSIM and PSNR values indicate better image rectification effects, and a lower FID value suggests superior image rectification performance.
Figure 7. Trends of evaluation indexes under different combinations of loss functions and mesh shapes. The chart displays from left to right, with the vertical axis indicating SSIM, PSNR, and FID values respectively, while the horizontal axis represents different combinations of mesh shapes and loss functions. Higher SSIM and PSNR values indicate better image rectification effects, and a lower FID value suggests superior image rectification performance.
Preprints 99972 g007
Table 1. Schematic structure of width residual neural network. In the table, 'k' represents the multiplier for the convolutional kernels in the original module, ' N ' indicates the number of residual modules in that layer, and ' B (3,3) ' signifies each residual module consisting of two 3×3 convolutional layers. the image undergoes processing through a mean pooling layer, resulting in the final output image.
Table 1. Schematic structure of width residual neural network. In the table, 'k' represents the multiplier for the convolutional kernels in the original module, ' N ' indicates the number of residual modules in that layer, and ' B (3,3) ' signifies each residual module consisting of two 3×3 convolutional layers. the image undergoes processing through a mean pooling layer, resulting in the final output image.
Type Block type = B(3,3) Output
conv1 [3×3, 16] 32×32
conv2 3 × 3 ,   16 × k 3 × 3 ,   16 × k × N 32×32
conv3 3 × 3 ,   16 × k 3 × 3 ,   16 × k × N 16×16
conv4 3 × 3 ,   16 × k 3 × 3 ,   16 × k × N 8×8
avgpool [8×8] 1×1
Table 2. Quantization comparison of image rectification on DIR-D. Structural Similarity Index (SSIM), Peak Signal-to-Noise Ratio (PSNR), and Fréchet Inception Distance (FID) are employed to assess image quality from different perspectives. SSIM measures the structural similarity between two images, considering brightness, contrast, and structure. And SSIM values range from -1 to 1, with 1 indicating identical images. PSNR compares original and processed images by measuring signal-to-noise strength. Higher PSNR values in decibels (dB) indicate better image quality. FID primarily assesses dissimilarity between generated and real images in terms of distribution. Lower FID values indicate greater similarity in latent space.
Table 2. Quantization comparison of image rectification on DIR-D. Structural Similarity Index (SSIM), Peak Signal-to-Noise Ratio (PSNR), and Fréchet Inception Distance (FID) are employed to assess image quality from different perspectives. SSIM measures the structural similarity between two images, considering brightness, contrast, and structure. And SSIM values range from -1 to 1, with 1 indicating identical images. PSNR compares original and processed images by measuring signal-to-noise strength. Higher PSNR values in decibels (dB) indicate better image quality. FID primarily assesses dissimilarity between generated and real images in terms of distribution. Lower FID values indicate greater similarity in latent space.
Method SSIM ↑ PSNR ↑ FID ↓
Reference 0.3354 11.42 43.57
RPIW [30] 0.3805 15.03 37.51
DRIS [37] 0.7173 21.57 21.26
Ours 0.7234 22.65 20.05
Table 3. Quantitative comparison of non-referenced assessment indicators. Blind Image Quality Evaluator (BIQUE) and Natural Image Quality Evaluator (NIQE) are "no-reference" metrics designed to assess image quality without an original reference image. BIQUE estimates image quality by considering local contrast, structural information, and global color and brightness variations. NIQE focuses on natural images, assessing quality through the analysis of statistical features such as gradients, luminance, and color distribution.
Table 3. Quantitative comparison of non-referenced assessment indicators. Blind Image Quality Evaluator (BIQUE) and Natural Image Quality Evaluator (NIQE) are "no-reference" metrics designed to assess image quality without an original reference image. BIQUE estimates image quality by considering local contrast, structural information, and global color and brightness variations. NIQE focuses on natural images, assessing quality through the analysis of statistical features such as gradients, luminance, and color distribution.
Method BIQUE ↓ NIQE ↓
RPIW [30] 14.045 16.927
DRIS [37] 13.796 16.421
Label 11.017 14.763
Ours 13.562 16.027
Table 4. Influence of different loss functions and mesh shapes on image rectification. SSIM, PSNR, and FID are utilized as components in various combinations. The symbol " 𝒲 " denotes the inclusion of the current grid shape or loss function in the combination. The 'model' column represents different combinations, where L stands for 'Localized loss', G for 'Global loss', T for 'Triangle', R for 'Rectangle', and H for 'Hexagon'. Various colors are employed in the table for clear correspondence with the combination methods illustrated in Figure 7.
Table 4. Influence of different loss functions and mesh shapes on image rectification. SSIM, PSNR, and FID are utilized as components in various combinations. The symbol " 𝒲 " denotes the inclusion of the current grid shape or loss function in the combination. The 'model' column represents different combinations, where L stands for 'Localized loss', G for 'Global loss', T for 'Triangle', R for 'Rectangle', and H for 'Hexagon'. Various colors are employed in the table for clear correspondence with the combination methods illustrated in Figure 7.
Loss function Mesh shape Model Quantitative index
Localized loss Global loss Triangle Rectangle Hexagon color SSIM ↑ PSNR ↑ FID ↓
W W W R+G 0.4753 15.12 74.68
W W W R+L 0.6169 18.96 24.70
W W W W W T+G+L 0.7071 20.46 22.02
W W W W W R+G+L 0.7126 21.05 21.74
W W W W W H+G+L 0.7203 21.97 20.68
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated