Preprint
Article
Bipartite (P_6,C_6 )-Free Graphs, Recognition and Optimization Problems
This version is not peer-reviewed.
Submitted:
26 February 2024
Posted:
27 February 2024
You are already at the latest version
A peer-reviewed article of this preprint also exists.
Abstract
The canonical decomposition of a bipartite graph is a new decompositionmethod that involves three operators, parallel, series and K+S. The class of weak bisblit graphs is totally decomposable with respect of these operators, and the class of bicographs is totally decomposable with respect of parallel and series operators. We prove in this paper that the class of bipartite (P_6,C_6)-free graphs is exactly the class of bipartite graphs that are totally decomposable with respect of parallel and K+S operators. We simplify the recognition algorithm of weak-bisplit graphs to adepte with bipartite (P_6,C_6)-free graphs. As a result of this adapted algorithm, we prsent efficient solutions in this class of graphs for two optimization graph problems, the first is the maximm balanced bi-clique problem and the the second is the maximum independent set problem.
Keywords:
Subject:
Computer Science and Mathematics - Discrete Mathematics and Combinatorics1. Introduction
All graphs under consideration are undirected and simple. A graph is called bipartite if the vertex set can be partitioned into two sets that called the black vertices and that called the white vertices such that . So a bipartite graph will be referred as . This property makes bipartite graphs useful in various practical applications, including: recommender systems [18], social networks [13], and information retrieval [10]. A bipartite graph is called complete or bi-clique if . A complete bipartite graph with and is referred as . A is a tree for which there is only one vertex of degree three and three other vertices of degree one such that the distance from to those vertices are respectively and . for example is . We can remark that every connected component in a bipartite -free graph is either a chordless path or a chordless cycle. Fouquet et al. in [5] presented a decomposition method concerning bipartite graphs, called canonical decomposition, which is based on three operators, series, parallel and , and proved that the class of graphs that are totally decomposable with respect of this three operators of decomposition is the class of bipartite -free graphs which is called the class of weak bisplit graphs since it is considered as bipartite analogue of split graphs. Obviously, the class of weak bisplit graphs is a natural generalization of the class of bipartite -free graphs and this last is a natural generalizationof the class of bipartite -free graphs which is studied by Lozin in [17]. Giakoumakis et. al. in [15] defined the class of bicographs as bipartite analogue of cographs. It is proved in [15] that the class of bicographs is exactly the class of bipartite-free graphs and is the class of totally decomposable graphs with respect of parallel and series decompositions.We prove in this work that the class of bipartite -free graphs is the class of totally decomposable graphs with respect of parallel and decompositions. As a result of this fact, the class of bipartite -free graphs can be recognized in linear time using the recognition algorithm of weak bisplit graphs presented in [16] or the recognition algorithm of -free graphs presented in [12]. But since these two algorithms contain several redundant cases when projected to bipartite -free graphs, we propose a simplification of these two algorithms to adapt only the class of bipartite -free graphs. As a result of this adapted algorithm, we prsent efficient solutions in this class of graphs for two optimization graph problems, the first is the maximm balanced bi-clique problem and the the second is the maximum independent set problem.
Figure 1.
The configuration and .
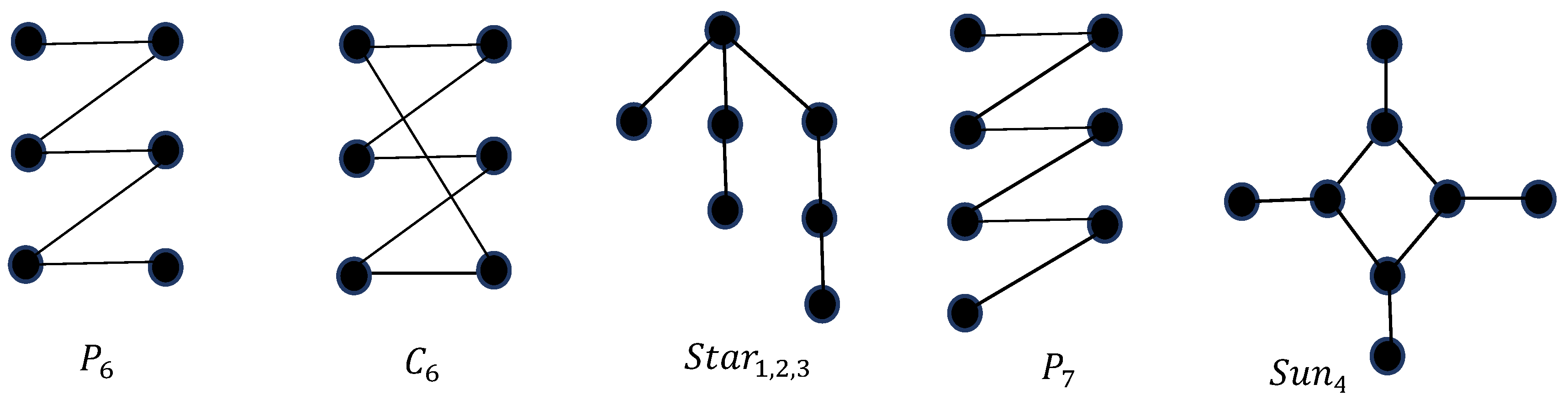
2. Notation and Terminology
For a graph , we use to represent its vertices and to represent its edges. The number is represented by and the number is represented by . If the two vertex sets and in a bipartite graph are both non-empty, the graph is referred to as bi-chromatic, otherwise it is monochromatic. The bi-complement of a bipartite graph is defined as . The set of neighbors of a vertex in is represented by and the number is referred to as the degree of and represented by . A vertex is considered isolated if and is considered universal if when or when . A is the complement of . A subset of vertices of is called independent set if there is no edge between any two vertices of . The sub-graph induced by a subset of vertices of is represented by . A graph is considered -free, where is a set of graphs, if for any subset , that is there is no sub-graph of isomorphic to a graph in . Decomposition of graphs according to predefined operators is a powerful method for obtaining efficient solutions of a big number of graph problems. The reader can found a survey on graph decomposition methods and their uses in [11]. In this direction, Fouquet et al. in [5] presented a decomposition method concerning bipartite graphs, which is based on three operators: decomposing a bipartite graph into connected components, decomposing the bi-complement of a bipartite graph into connected components, and decomposing a bipartite graph into components. Our recognition algorithm of bipartite -free graphs depends mainly on this method of decomposition, so to introduce our algorithm we need to present an overview of this method.
Definition 1 [5].
A bipartite graph such that is a graph if the vertex set contains an isolated vertex or there is a partition of into two sets: a bi-clique and an independent set .
Property 1 [5].
A bipartite graph with is a -graph if and only if can be partitioned into two sets and , such that for every black vertex and for every white vertex and for every white vertex and for every black vertex .
We denote by the ordered pair to represent the partition of the vertex set of a -graph and we called it a -partition of .
Property 2 [5].
In a bipartite graph that does not contain universal or isolated vertices, either is a -graph or, for any partition of the black vertices or white vertices into two sets and , there is an induced in with vertices in both and .
Corollary 1 [5].
If a graph is not a -graph, then every vertex , is a vertex of some .
Theorem 1 provides a method for decomposing a graph of type .
Theorem 1 [5].
A bipartite graph is a -graph if and only if there exists a unique partition of , such that the following conditions are hold:
- For every , .
- For every , the sets and form a -partition of .
- For every the sub-graph is not a -graph.
The partition of the vertex set is called the -decomposition of the graph , and each set is referred to as a -component of .
According to Theorem 1, the arrangement of components in a -decomposition is important. Specifically, let be the -decomposition of , if a black vertex , then for every white vertex where , , and for every white vertex where , . Similarly, if a white vertex , then for every black vertex where , , and for every black vertex where , .
The canonical decomposition of a bipartite graph is a new decomposition method defined in [5] as following:
- Decompose into its -components if is a -graph, this decomposition is called -decomposition and is denoted by .
- Decompose into the connected components of if is not connected graph, this decomposition is called parallel decomposition and is denoted by .
- Decompose into the connected components of if is not connected graph, this decomposition is called series decomposition and is denoted by .
- If cannot be decomposed in , parallel or series decomposition then is called indecomposable graph or prime graph.
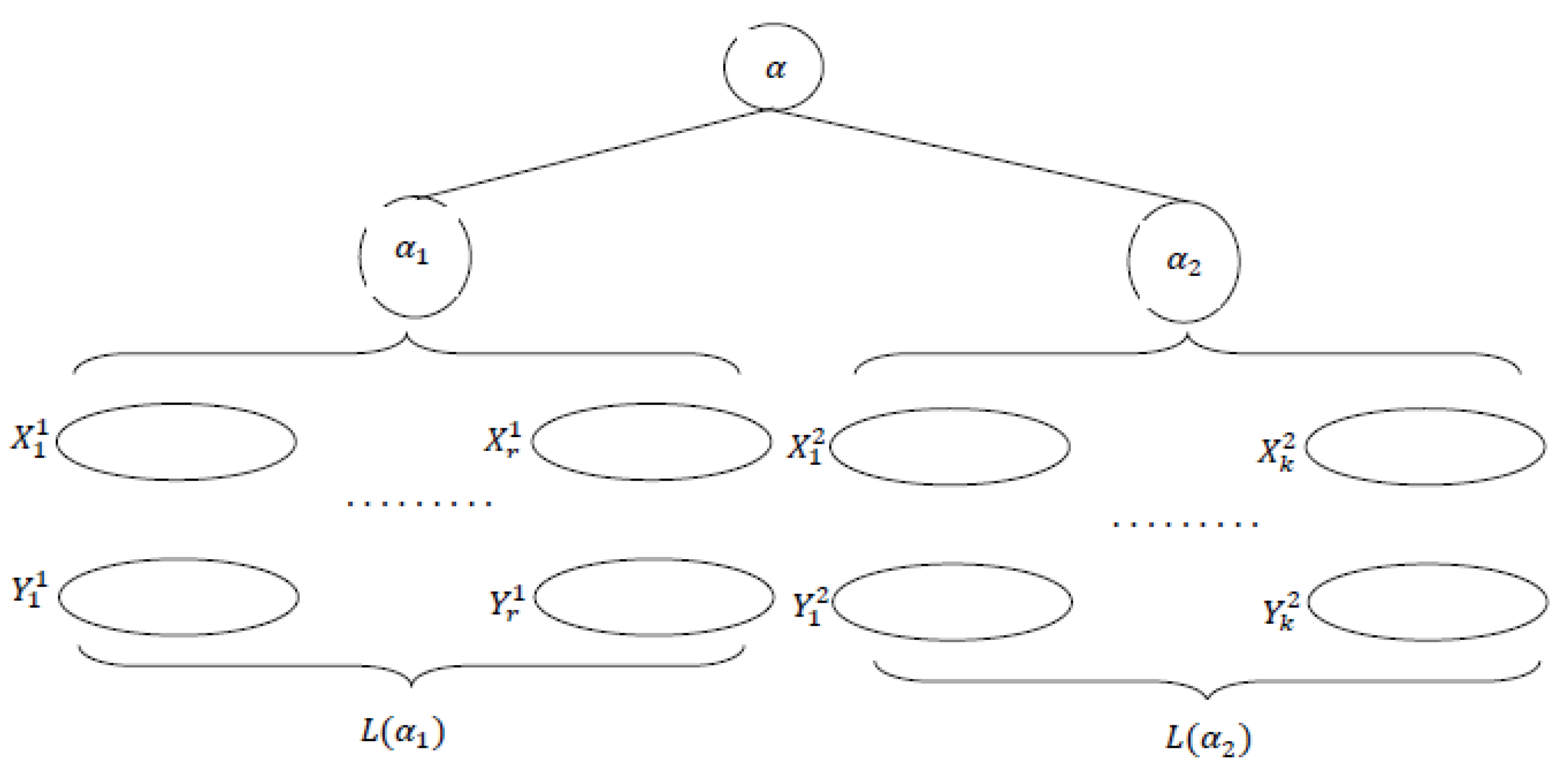
It has been proven in [5] that no matter the order in which the operator of decomposition is applied (series decomposition, parallel decomposition, or -decomposition), the set of indecomposable graphs obtained is unique. This also creates a unique tree (up to isomorphism) associated with this decomposition known as the canonical decomposition tree. The internal nodes of the tree are labeled by the type of decomposition applied, and the leaves correspond to indecomposable graphs. Figure 2 shows an illustration of a bipartite graph and its canonical decomposition tree.
The canonical decomposition tree of a bipartite graph resulting in order from the -decomposition, parallel decomposition, and series decomposition procedure has several properties outlined below. The terms vertex node, son, parent, and grandparent are used in their conventional sense. If is an internal node then is the sub-graph induced by the set of vertices nodes having as their least common grandparent.
- 1)
- The tree consists of 3 types of internal nodes: parallel denoted by , series nodes denoted by , and-nodes.
- 2)
- Two consecutive internal nodes cannot have the same label.
- 3)
- An internal node labeled or cannot have a son that is a vertex node . Otherwise, would be either an isolated or a universal vertex in . By the definition of a -graph, would be a -graph.
- 4)
- The parent of a vertex node is always labeled (consequence of 3).
- 5)
- If is a bi-chromatic graph, then for any -node , must also be bi-chromatic. Otherwise, if there is a node labelled and is a monochromatic graph then the parent of say would have isolated or universal vertices so would be a -graph, a contradiction with 2.
- 6)
- The sons of a -node are ordered according to the -decomposition.
- 7)
- Let be a-node and are respectively the first and last sons of . If the parent of say is a -node then, cannot be a white vertex node and cannot be a black vertex node. Otherwise, by Property 1, and are isolated vertices in , since is a -node, and are also isolated vertices in , so must be a -node, a contradiction with 2.
- 8)
- If the parent of a -node is labeled and are respectively the first and last sons of then cannot be a black vertex node and cannot be a white vertex node. Similar to 7.
3. Recognition Algorithm of Bipartite -free Graphs
The following Theorem is the key of our recognition algorithm for bipartite -free graphs.
Theorem 2.
A bipartite graph is -free if and only if every connected sub-graph of is a -graph.
Proof.
Suppose that is a bipartite graph -free. Let be a connected sub-graph of which is not a -graph. By Corollary 1, contains a say . Since is a connected sub-graph of and is -free graph, there is a vertex in that connects and . Suppose without loss of generality that is a black vertex such that . Since is not -graph, the vertex is not universal, so there is a white vertex such that . Since is connected there is a path in that connects the vertex w and the path . But now the set forms a or a , a contradiction.
The inverse is clear since a or a is connected and contains a , so it is not a -graph. □
Theorem 2 states that the class of bipartite -free graphs is the smallest class closed under parallel and -decomposition. So the canonical decomposition tree of a bipartite -free graph consists only of -nodes or -nodes. Our recognition algorithm builds a decomposition tree with or labeled internal nodes if the input graph is -free otherwise a failure message.This building was influenced by the cographs recognition method proposed by Corneil, et al in [2]. Moreover, this algorithm greatly simplifies two recognition algorithms when projected on bipartite -free graphs. The first is for weak bisplit graphs presented in [16] and the second for bipartite -free graphs presented in [12], where both these two algorithms need to examine more than twenty cases in order to confirm that the input graph is -free or not, while, as we will see, our algorithm needs to examine only two cases that are presented below in Theorem 3 and in Theorem 4. The algorithm begins with an empty graph and gradually adds vertices, ensuring that the resulting sub-graphs remain -free. The initial bipartite graph is considered -free if all vertices can be added successfully in this manner. The principal step of the algorithm takes into considerationthe decomposition tree of a -free bipartite graph , a vertex , and a set of edges denoted by , and produces the decomposition tree of the resulting graph if it remains -free, or stops otherwise. The algorithm considers the connections of to other vertices in using a marking procedure. We can assume without loss of generality that is a white vertex and the graph is a bi-chromatic graph.
3.1. Marking Procedure
The Marking procedure, used in [2], takes into consideration the neighbors of the vertex in the graph to mark the nodes of , the decomposition tree of .

At the end of the marking procedure on tree , a node can have three possible states: marked by, marked by , or marked by . If a node is marked by , it means that is total for , that is, is connected to all black vertices in . If it is marked by , it means that is partial for , that is, is connected to some but not all black vertices in . If it is marked by , it means that is independent of , that is, it is not connected to any black vertex in . If a node is a vertex node, it can either be marked by or marked by . By Theorem 2, the marking procedure focuses only on -nodes and -nodes, ignoring the -nodes that must be unavailable. For the graph to be considered bipartite-free, it must meet a necessary condition.
Lemma 1.
If two internal nodes in the tree are marked by , and is a -free bipartite graph, then one of these two nodes must be a grandparent of the other.
Proof.
Suppose that and are two internal nodes marked by then and are partial with respect to . Let be the least common grandparent of and . We denote by and to be respectively the son of containing and the son of containing. Since and are sub-graphs of and then and are partial with respect to . Assume that is labeled , then and are connected sub-graphs of . Thus there is an induced path in (resp. in ) such that is adjacent to and not adjacent to (resp. to and not to ). The set forms a , a contradiction.
Assume that is labeled . By Corollary 1, (resp.) contains a that is partial with respect to . Let (resp. ) be a in (resp. in such that is adjacent to and not adjacent to (resp. to and not to ). Then the set forms a , a contradiction. □
By lemma 1, the nodes in that are marked by are arranged in a single path that starts from the lowest node marked by and goes up to the root. The lowest node marked by is referred to as . It is assumed that the conditions of Lemma 1 are met and that is known. The following notations are introduced:
- Given two internal nodes and such that is a grandparent of , the unique son of that contains is denoted as .
- For an internal node , which is either or one of its grandparents, the set of sons of that are marked by is denoted as , and the set of sons that are marked by is denoted as .
- If has a label , considering the ordering of the sons of , the set of sons of marked by and located before is denoted as , and the set of sons marked by and located after is denoted as . The set of sons of marked by and located before is denoted as , and the set of sons marked by and located after is denoted as .
So, a node labeled which is a grandparent of splits its sons into at most three categories: , , and the son that contains,. If is labeled , its sons can be divided into at most five sets: , , , , and . Meanwhile, the sons of are split into two non-empty categories: , and .
Definition 2.
If is a grandparent of in , then is considered incompatible -node if it has at least one son marked by (i.e. . If is a -node, it is considered incompatible before if it has at least one son marked by located before (i.e. ) . If is a -node, it is considered incompatible after if it has at least one son marked by located after (i.e. ).
3.2. Building the tree
We assume that the necessary condition of Lemma 1 has been verified and all nodes that are marked by are known and are arranged in a single path that starts from the lowest marked node and goes up to the root of . In order to build , we examine the label of and the presence of incompatible marked nodes.When is -node and since it is the lowest node marked by , we can divide its group of sons into a maximum of four consecutive subsets, namely , , , where:
includes the first group of consecutive sons of that are either a group of white vertices nodes or total with respect to .
includes the first group of consecutive sons of that are not part of and either a group of white vertices nodes or not related to .
includes the first group of consecutive sons of that are not part of nor of and either a group of white vertices nodes or total with respect to .
represents the remaining sons of .
Note that, as a result of this division of the sons of when its label is , and cannot be together monochromatic graphs.
Lemma 2.
Assume that is a -node. If is a bipartite -free graph then the following conditions are hold:
- 1)
- has no neighbor in .
- 2)
- If is empty then is a monochromatic graph or a complete bipartite graph.
Proof.
Suppose that is not empty, otherwise we are done. Let’s show that has no neighbor in . Since is not empty then and are both non empty. Let such that is adjacent to . Now, contains two adjacent vertices such that is not adjacent to otherwise . Let be two black vertices of and respectively. By construction, there is a white vertex such that is adjacent to and is not adjacent to . But now the set forms a , a contradiction.
Let’s show now that the condition 2 must be hold. Suppose that is not empty then is also non empty.
Claim 1.
Every element of is a vertex node.
Proof.
Suppose that is an element of that is an internal node. Then is a -node, thus it contains a say . Let , then the set forms a , a contradiction. ■
Claim 2.
contains a white vertex.
Proof.
Suppose that does not contain any white vertex then contains an element that is an internal node, a contradiction with claim 1. ■
Let be two vertices of such that . Suppose that is neither a monochromatic graph nor a complete bipartite graph. Then contains the vertices such that is adjacent to and is independent of . Consequently forms a , a contradiction.□
Theorem 3.
Assume that there is no incompatible grandparent of . is a bipartite - free graph if and only if one of either
- 1)
- is a -node or
- 2)
- is a -node and Lemma 2 is hold.
Proof.
The if part of the Theorem has been proved in lemma 2. We will describe the building of for the only if part. The building of when i s a-node is described in Figure 3.a. If consists of a unique son then this son will be a son of the node labeled . Suppose that is a -node. If is empty, then we insert in as a new son of . The building of when is a monochromatic graph or a complete bipartite graph is described also in Figure 3b In this case, if ] is a monochromatic graph then . □
Lemma 3.
Assume that is a bipartite -free graph. If there is an incompatible grandparent of then the following condition are holds:
- 1)
- is a -incompatible node after .
- 2)
- is the unique incompatible grandparent of .
- 3)
- The set consists of black vertices nodes located exactly after .
Proof.
Suppose that is an incompatible grandparent of of type . Then there exists two adjacent vertices in an element of . Since induces a connected graph, it contains an induced say such that is adjacent to and is independent of . But now forms a , a contradiction.
If is a -incompatible node before α, then contains a black vertex independent of . By Corollary 1, contains a say such that is adjacent to and is independent of . The set forms a , a contradiction. Consequently is a -incompatible node after . Let’s consider to be the highest incompatible grandparent of and let .
Claim.
There is no grandparent of containing a white vertex total for .
Proof.
Let be a grandparent of and is a white vertex of total for . Let be an induced of such that is adjacent to and independent of . Then the set forms a , a contradiction. ■
By this claim, if is a -incompatible node after then the set consists of black vertices nodes located exactly after . Moreover, for every grandparent of labeled and located between and , is the last son of , otherwise contains a white vertex total for , a contradiction, thus cannot be incompatible. Therefore, is the unique incompatible grandparent of . □
Theorem 4.
Assume that is the unique -incompatible grandparent after and the set consists of black vertices nodes located exactly after . is a bipartite -free graph if and only if one of the following conditions is hold:
- 1)
- is a -node.
- 2)
- is a -node such that is an empty set.
Proof.
Suppose that is a -node and let . Suppose that is non empty. By lemma 2, is a monochromatic graph or a complete bipartite graph. In the two cases cannot be a monochromatic graph otherwise is empty. Thus contains two adjacent vertices . Let be a black vertex of . Since is a connected graph then there is a white vertex say in the last son of , but now forms a , a contradiction.
For the only if part, we describe the building of .When is a -node, the building of is illustrated in Figure 4.a. If the set is a unique son then this son must be labeled . In this case, we delete the node and the element will be a son of . The building of when the condition 2 is hold is illustrated in Figure 4b If is a unique son, then this son is either a node labeled or a black vertex node. In this case, we delete the node , and the element will be a son of .□
3.3. Recognition Algorithm
The recognition algorithm of bipartite -free graphs is given by Algorithm 2, where the procedure of the step Build-tree is presented in Algorithm 3.

3.4. Complexity
Our aim is to demonstrate that recognizing a bipartite graph , which does not contain or , can be accomplished in time complexity. Since the principal step of our algorithm is the step Build-tree, we will demonstrate the linearity of our algorithmby showing that this step requires only operations, where is the degree of the node in .
It is evident that the step 1 runs within time, as only a maximum of nodes are marked. Furthermore, we can assume that for every node in the tree , the set of its sons that are marked by , by or by has been calculated. So find the set requires also operations. Suppose that . We can check whether one of the two nodes of is a grandparent of the other as following: Choose an element of and start to mark the parent of this element, then mark the parent of parent and so on until the other element of is marked or until the root of is marked. For the last case, that is, if the root of has been marked, we repeat this process for the other element of . By this manner, we can also determine the node , the lowest node marked by and the grandparent . Obviously, this process can be done in mark operations.
It remain analysis the time complexity of the function . This requires to verify the necessary conditions in Theorem 3 or in Theorem 4. Therefore we need to compute all required sets for building the tree . If has label , then the computation of the set and the set is straightforward. Suppose has label . We can compute the sets , , ,and as following: First, we compute by traversing the set of sons of from left to right. In this manner, will be the first nodes that are either a set of white vertices or nodes marked by , we continue by this traversing until a son of marked by has been found. The remaining sons of marked by must belong to since is independent of according to Lemma 2. To compute , we choose a son of (let’s call it ) from the remaining nodes marked by and we traverse the set of sons of starting from in left and right directions, from left until a son of marked by has been found and from right also until a son of marked by has been found or until the last son from right has been found. We continue by this traversing as long as every son is either a white vertex node or is a node marked by . As long as the set has been computed, the sets can be computed immediately. The remaining sons of form the set which must be independent of This computation requires time complexity.
Finally, we need to determine if the node , which its label is , is incompatible after or not and check whether the set is a set of black vertices nodes located exactly after . This two conditions can be achieved together as following: Since is known as a grandparent of , the son is identified. Now, we can traverse the sons of starting from the first son located exactly after and determine whether any one of these sons is a white vertex node or not. In addition, we must traverse the sons of starting from the first son located exactly before to determine if the set is empty or not. This traverse also requires time complexity.
we leave to the reader to verify that the step Build-tree that correspond to insert in the tree takes a constant time in all cases.
Since testing whether is a bipartite -free or not can be done within time complexity, it is clear that recognition of bipartite -free graph algorithm runs in time complexity.
4. Optimization Problems
We believe that the canonical decomposition tree for bipartite -free graph can be used to find efficient solutions for several optimization graph problems because of the simple structure of this tree.In this paper, we limit ourselves to show that the canonical decomposition tree of a bipartite graph -free can be used to solve in polynomial time the maximal balanced bi-clique problem and in linear time the maximum independent set problem. In the conclusion part of this paper, we talk about some potential use for this result and consider it as a subject for further study.
Let be the canonical decomposition tree for a bipartite -free graph . To present our solutions of the above two problems, we need to covert to a binary tree as following:
Visit the nodes of in depth first search
Let be an internal visited node and are the sons of .If then the left son of is and the right son becomes a new son that has the same label as with sons .
4.1. Maximum balanced bi-clique problem
A sub-graph of a bipartite graph is called balanced bi-clique if is a bi-clique and . The balanced bi-clique problem is to compute a balanced bi-clique in of maximum size. This problem is important in many different fields of study. It has numerous practical uses in very large-scale integration (VLSI), such as the design of defect-tolerant devices [1,7], programmable logic array folding [14]. Balanced bi-clique problem is NP-complete for a general bipartite graph [9], and there are very few works dedicated to obtaining an exact maximum balanced bi-clique, aside from the work [6] where it is proposed two exact algorithms to find a maximum balanced bi-clique for small dense and large sparse bipartite graphs respectively. The majority of known techniques for determining a maximum balanced bi-clique are heuristic algorithms, see for example, [8,19].
We propose in this work an time complexity algorithm to compute a maximum balanced bi-clique in a bipartite -free graph using its canonical decomposition binary tree . The idea of our solution is to compute all possible bi-cliques in , that are maximal with respect to set inclusion, then find among them the one that contains a maximum balanced bi-clique. A bi-clique is maximal with respect to set inclusion if there is no bi-clique in that contains . The structure of when is a bipartite -free graph and the definition of operation allow us to achieve this computation by a post order traversal of and associating for each internal node all possible maximal bi-cliques in (with respect to set inclusion) through the two sets ofmaximal bi-cliques associated with the left son and the right son of .The set of maximal bi-cliques associated with denoted by and the set of maximal bi-cliques associated with denoted by . We suppose that for every bi-clique , is a set of black vertices and is a set of white vertices. In addition, we suppose that the members of are arranged from left to right according to their appearance in the sub-tree . Likewise, we suppose that the members of are arranged from left to right according to their appearance in the sub-tree . This supposition is done directly according to the arrangement of sons for every -node in . The reader can verify simply the truth of computation used in the algorithm Balanced Bi-clique for the set of maximal bi-cliques according to the definition of -node and the definition of -node. Figure 5 can help to imagine this computation.

The number of bi-cliques computed for each internal node is at most . Since contains node, the algorithm Balanced Bi-clique has a time complexity .
4.2. Maximum independent set problem
A subset of the vertex set in a graph is called independent set if any two vertices in are not adjacent. The maximum independent set problem is to compute an independent set in of maximum size. This problem is NP-complete for general graphs [9], but it can be solved in time complexity for a general bipartite graph [4]. This time complexity can improved to for bipartite -free graph using its canonical binary decomposition tree.. The idea of our solution results from the structure of -graph as following: Let be a -partition of the vertex set . By Property 1, every black vertex of is connected to every white vertex of and every white vertex of is independent to every black vertex of . So, the maximum independent set in is either the maximum independent set in or the maximum independent set in or the independent set formed by the union of white vertices of and black vertices of . This remark proves the correctness of the following algorithm. Note that if is not connected then the maximum independent set in is equal to the union of the maximum independent sets in its connected components.

Since contains node, the algorithm maximum independent set has a time complexity .
Conclusion
we have showed in this paper that bipartite -free graphs can be recognized in linear time. Using this result, we solved two optimization graph problems in this class of graphs, the first is the maximm balanced bi-clique problem and the the second is the maximum independent set problem. An additional potential using of the canonical decomposition tree of bipartite -free graph is to solve the problem P| prec. | Cmax : Suppose there are tasks with a unit execution time, and their order is constrained by a directed acyclic graph. Additionally, there are machines of the same type. The goal is to discover a schedule that minimizes the makespan, which is the time when the final task in the graph finishes its execution. It is proved in [3] that this problem is NP-complete even if the precedence constraints form a bipartite graph of depth one. We conjecture that this problem can be solved in polynomial time for bipartite -free graph.
References
- A. Al-Yamani, S. Ramsundar, and D. K. Pradhan. A defect tolerance scheme for nanotechnology circuits. IEEE Transactions on Circuits and Systems I: Regular Papers, 54(11):2402–2409, 2007. [CrossRef]
- D. G. Corneil, Y. Perl, L.K. Stewart, A linear recognition algorithm for cographs. SIAM Journal of Computing, Vol.14, No 4, November, 926-934. 1985. [CrossRef]
- E. BAMPIS, The Complexity of short schedules for UET bipartite graphs, RAIRO Oper. Res. 33 367-370. (1999). [CrossRef]
- H. Alt, N. Blum, K. Mehlhorn, M. Paul, Computing a maximum cardinality matching in bipartite graphs in time , Inform. Process. Lett. 37, 237–240 (1991). [CrossRef]
- J.L. Fouquet, V. Giakoumakis, J.M. Vanherpe, Bipartite graphs totally decomposable by canonical decomposition, Internat. J. Foundations Comput. Sci. 10(4) 513–533. (1999). [CrossRef]
- L. Chen, C. Liu, R. Zhou, J. Xu, J. Li. Efficient Exact Algorithms for Maximum Balanced Biclique Search in Bipartite Graphs, SIGMOD ’21: Proceedings of the 2021 International Conference on Management of Data, June 2021Pages 248–260 18. [CrossRef]
- M. B. Tahoori. Application-independent defect tolerance of reconfigurable Nano architectures. ACM Journal on Emerging Technologies in Computing Systems (JETC), 2(3):197–218, 2006. [CrossRef]
- M. Li, J.-K. Hao, and Q. Wu. General swap based multiple neighborhood adaptive search for the maximum balanced biclique problem. Computers & Operations Research, 119:104922, 2020. [CrossRef]
- M.R. GAREY and D. S. JOHNSON, Computers and Intractability, A Guide to the Theory of NP-completeness, Mathematical Series. Freeman, San Francisco, CA, 1979.
- P. Biró, & Fleiner, T..Recent advances in matching algorithms. European Journal of Operational Research, 294(3), 745-769. (2022).
- R. Quaddoura, K. Mansour, Classical graphs decomposition and their totally decomposable graphs, IJCSNS International Journal of Computer Science and Network Security, VOL.10 No.1, January 2010. 20 January.
- R. Quaddoura, Linear time recognition of bipartite Star123-free graphs, The international Arab Journal of Information Technology, Vol. 3, No. 3, July (2006).
- R. Wang, Y. Wu, X. Hu, & J. Liu, Bipartite graph neural networks for social recommendation. Information Sciences, 572, 396-409 (2021).
- S. Ravi and E. L. Lloyd. The complexity of near-optimal programmable logic array folding. SIAM Journal on Computing, 17(4):696–710, 1988. [CrossRef]
- V. Giakoumakis, J.-M. Vanherpe, Bi-complement reducible graphs, Adv. Appl. Math. 18 (1997) 389– 402. [CrossRef]
- V. Giakoumakis, J.M. Vanherpe, Linear time recognition and optimization for weak bisplit graphs, bi—cographs and bipartite P6-free graphs, International Journal of Foundation of Computer Science, Vol. 14, No. 1,107-136(2003). [CrossRef]
- V.V. Lozin, E-free bipartite graphs, Discrete Anal. Oper. Res. Ser. 1 7(1) (2000) 49–66 (in Russian).
- X. Chakraborty, A Kumar. & G. Tomar, A survey on bipartite graph based recommender systems. Information, Processing & Management, 58(6), 102536. (2021).
- Y. Zhou and J.-K. Hao. Tabu search with graph reduction for finding maximum balanced bicliques in bipartite graphs. Engineering Applications of Artificial Intelligence, 77:86 – 97, 2019. [CrossRef]
Figure 2.
An example of bipartite graph and the canonical decomposition tree .
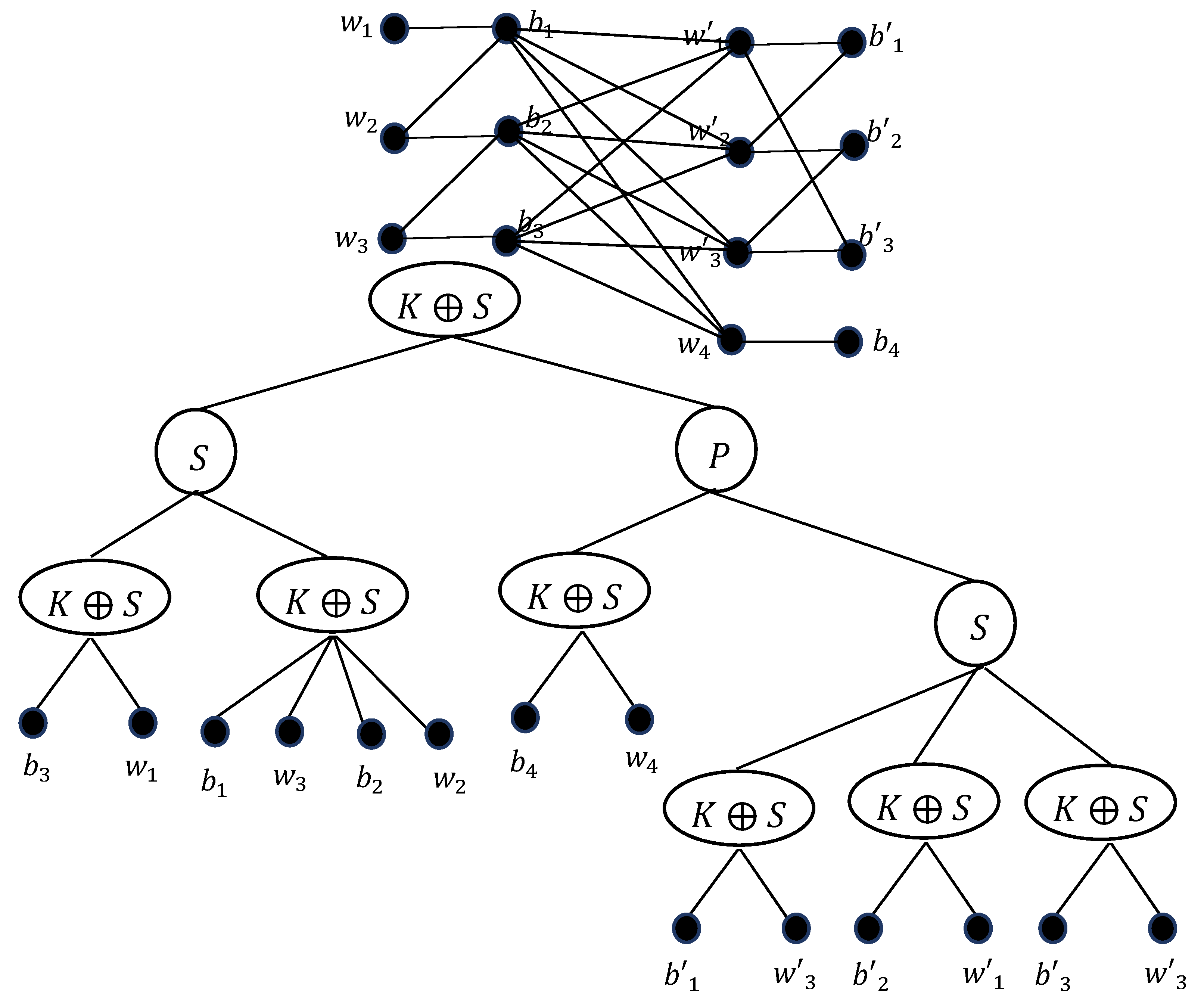
Figure 3.
Building of when there is no incompatible grandparent of .
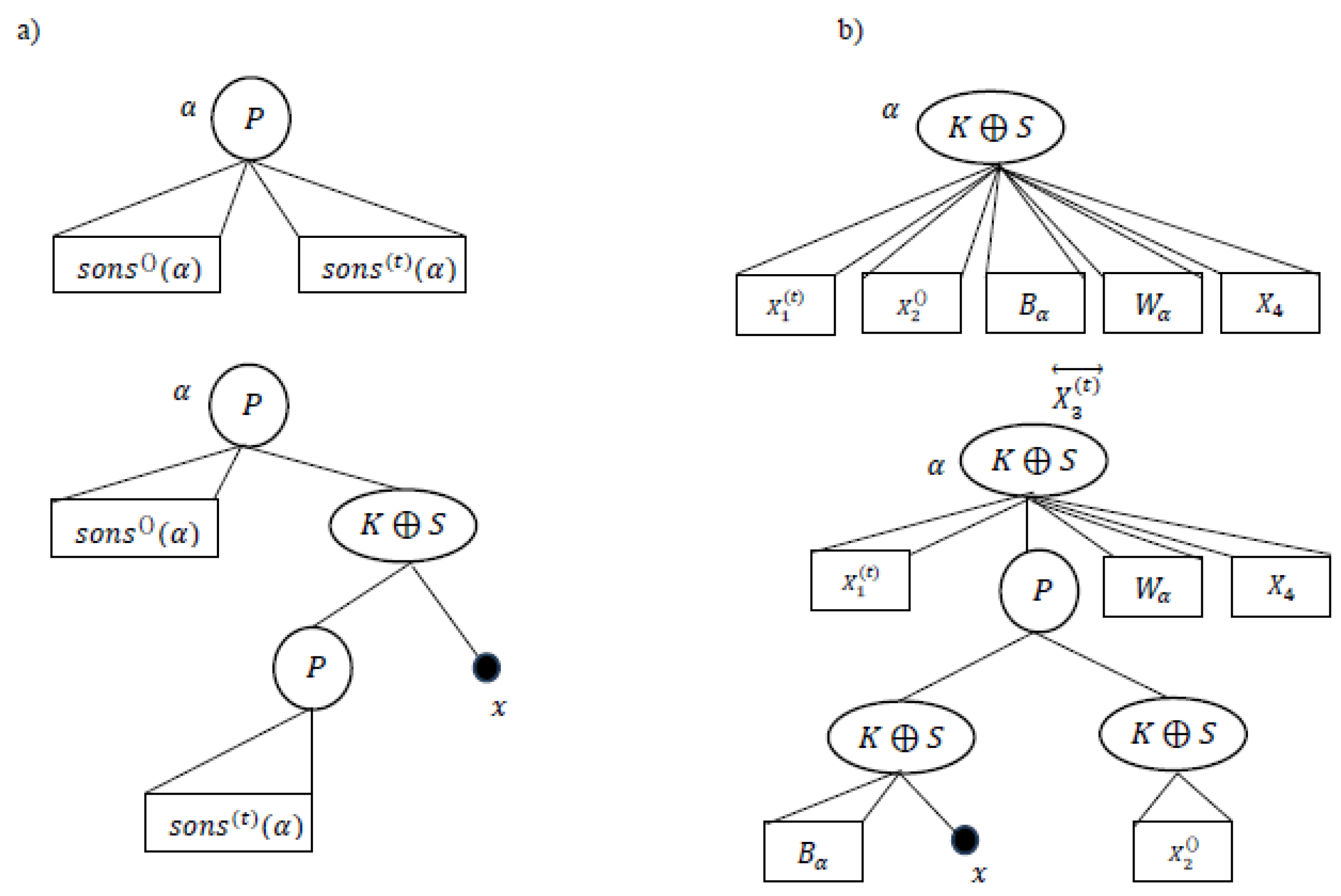
Figure 4.
Building of when the unique -incompatible grandparent of exist.
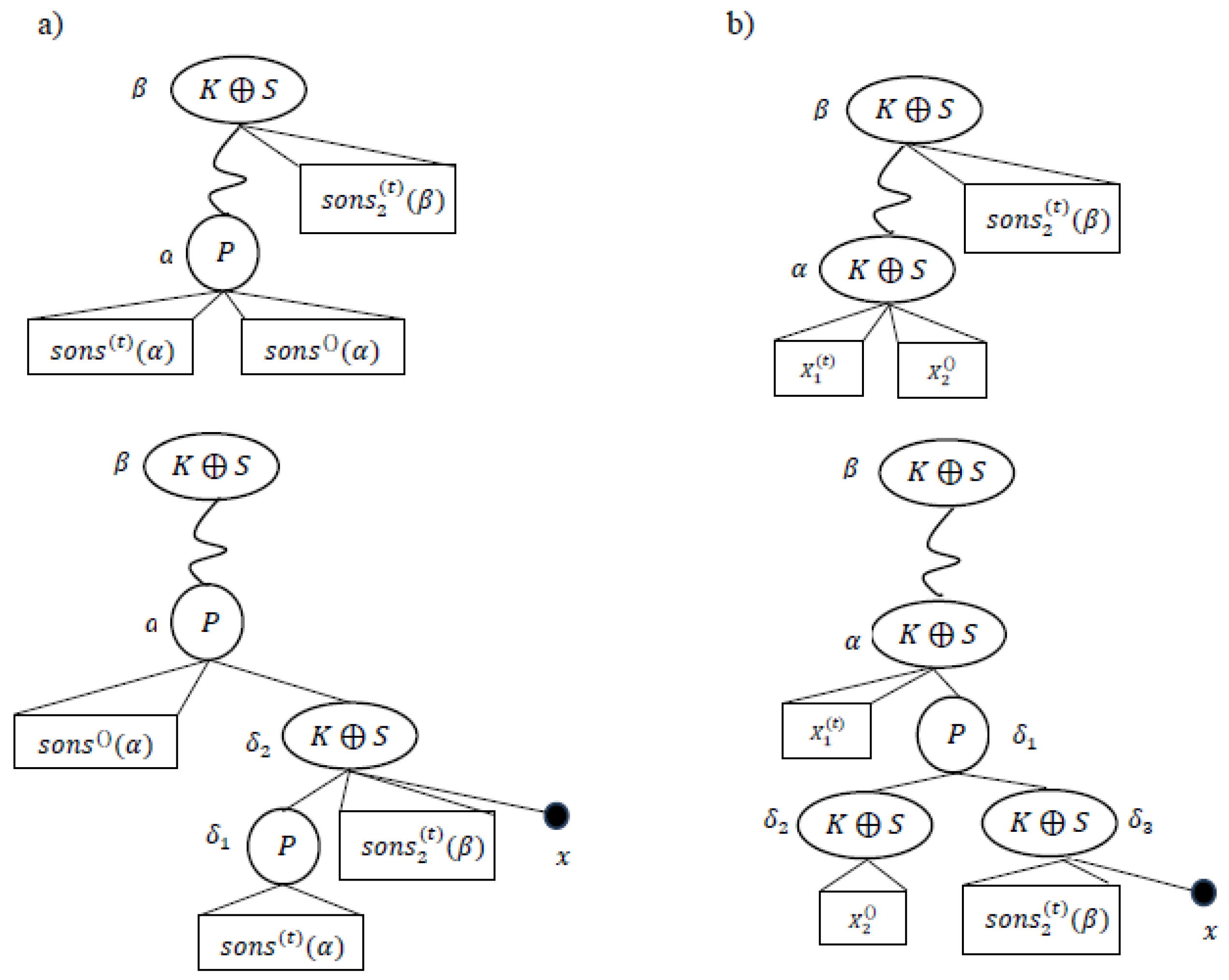
Figure 5.
A node and the sets of all maximal bi-cliques associated with its sons.
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Alerts
MDPI Initiatives
Important Links
© 2025 MDPI (Basel, Switzerland) unless otherwise stated





