Preprint
Article
Dynamic 3D Point Cloud Driven Autonomous Hierarchical Path Planning for Quadruped Robots
Altmetrics
Downloads
131
Views
54
Comments
0
A peer-reviewed article of this preprint also exists.
This version is not peer-reviewed
Submitted:
28 February 2024
Posted:
29 February 2024
You are already at the latest version
Alerts
Abstract
Aiming at effectively generating safe and reliable motion paths for quadruped robots, a hierar-chical path planning approach driven by dynamic 3D point cloud is proposed in this article. The developed path planning model is essentially constituted of two layers: global path planning layer and local path planning layer. At the global path planning layer, a new method is proposed for calculating terrain potential field based on point cloud height segmentation. Variable step size is employed to improve the path smoothness. At the local path planning layer, a real-time prediction method for potential collision area and a strategy for temporary target point selection is developed. Quadruped robot experiments were carried out in an outdoor complex environment. The experi-mental results verified that, for global path planning, the smoothness of the path is improved and the complexity of the passing ground is reduced. The effective step size is increased by a maxi-mum of 13.4 times, and the number of iterations is decreased by up to 1/6, compared with the traditional fixed step size planning algorithm. For local path planning, the path length is short-ened by 20%, more efficient dynamic obstacle avoidance and more stable velocity planning are achieved by using the improved dynamic window approach (DWA).
Keywords:
Subject: Computer Science and Mathematics - Robotics
1. Introduction
In recent years, quadruped robots, due to their excellent motion flexibility and terrain adaptability, have been extensively developed to play important roles in many fields, such as military, disaster relief, and factory inspection, etc [1,2,3]. Path planning is a crucial component of the quadruped robot to accomplish the above tasks. It is usually separated into two steps: 1) global path planning using a known environment map; 2) local path planning using real-time perception of the local environment. Currently, numerous algorithms have been proposed to plan safe and reliable path for wheeled robots and quadrotor unmanned aerial vehicles (UAV) [4,5,6,7]. However, the inherent limitations of these algorithms are: 1) the absence of performance validation in real environment point cloud map; 2) scale difficulties in path smoothness calculation; 3) the lack of evaluation of the velocity of dynamic obstacle and future trajectory for dynamic obstacle avoidance. Furthermore, for the quadruped robot platform, the limitations of these algorithms are apparent in the lack of terrain complexity evaluation, which results in risk of unstable robot motion. Therefore, a hierarchical path planning approach for quadruped robots with PSO-based 3D APF and improved DWA is proposed in this article to break through the inherent limitations of existing path planning methods for quadruped robots and boost the autonomous adaptation of quadruped robots to complex environments.
1.1. Global Path Planning
The existing global path planning algorithms can be grouped into two classes: heuristic algorithms (rapidly random-exploring tree, D*, A*, APF, etc.) and intelligence algorithms (artificial neural network, genetic algorithm, particle swarm optimization, reinforcement learning, etc.). A search tree with the starting point as the root node is constructed by the rapidly random-exploring tree-based algorithms [8,9,10] and the feasible path is found by the single-query algorithm. However, these algorithms are computationally expensive and difficult to construct optimal smooth paths in a point cloud map. The D*-based and A*-based algorithms [5,11,12,13] incorporate the heuristic function into the Dijkstra algorithm [6] to plan optimal paths in 2D space. However, these algorithms suffer from the "dimensional disaster" in 3D space, resulting in extremely inefficient planning. The artificial neural network-based algorithms [14,15,16,17,18] explicitly render the configuration space and the robot state-space into an array of locally connected neurons. This array is then trained with various methods, resulting in a path that connects the present state of the robot with the target state. However, these algorithms suffer from a challenging training process. The genetic algorithms [19,20] and PSO-based algorithms [21,22] represent alternative solutions of the optimization function as individuals of a population, and evolve the population according to the fitness value of the individuals to select a more suitable population. However, the terrain complexity is not considered in the optimization objective function of these algorithms, which makes them not applicable to quadruped robots. The reinforcement learning-based algorithms [23,24,25,26] utilize environmental spatio-temporal information and set a reward structure to maximize the value function to plan optimal paths. However, when the point cloud map is used as the input, the reward becomes sparse, which increases the training times of these algorithms and decreases planning efficiency.
The APF-based algorithms [27,28] simulate repulsive and attractive fields to plan the direction of robot moti1.2on, which are the general and easy-to-implement frame for global path planning. However, traditional APF algorithms suffer from fixed repulsive and attractive force coefficients, which cause robots fail to reach the target point and stop when there are obstacles near the target point, and even oscillate when the robots fall into the minimum trap of the local potential field. For upgrading the traditional APF, the PSO-based APF algorithms [29,30] are proposed to optimize the repulsive and attractive force coefficients. The fitness function of PSO includes two indicators: distance to the target and path smoothness. However, the efficiency global planning is severely limited by the fixed step size used in these methods. Moreover, the absence of a path complexity indicator makes these algorithms limited in applications to quadruped robots. In [31], obstacles are approximated as regular geometric shapes and projected onto a 2D plane. The fitness function is calculated as the linear sum of the iteration number of particles and the difference in steering angle of the neighboring path points. However, as the number of optimization iterations rises, the significant of difference in magnitude between different optimization indicators will lead to a tendency to update the particle’s position and velocity during the optimization process. In [32,33], opposition-based learning (OBL) is introduced to improve the inertia weight and step size to prevent the precocity of PSO. However, a problem arises with slow convergence or even non-convergence, resulting in low planning efficiency. In [34], the tangent vector, which is based on the information about obstacles, is added into APF model as an auxiliary force in the obstacle avoidance process. However, the tangent vector is challenging to be estimated in real complex environment.
1.2. Local Path Planning
The existing local path planning algorithms mainly include Behavior Decomposition (BD), Cased Learning (CL), and Dynamic Window Approach (DWA). The BD-based algorithms [35,36] decompose the path planning into independent units, i.e. behavioral primitives, which collaborate to accomplish the entire moving task. However, due to the limited weight and space of quadruped robots, it is difficult to carry numerous sensors and actuators. An intelligent typical case-based reasoning for path planning is proposed in the CL-based algorithms [37,38]. The path is planned based on current empirical knowledge and road network information. The reliability of such algorithms is difficult to assess as they rely on empirical knowledge.
The DWA-based approaches [39,40] have attracted the attention of a wide range of researchers. The DWA strategy aims to select the optimal combination of velocity in the dynamic velocity window by minimizing the evaluation function. In [41,42], the evaluation functions of these approaches are calculated only based on the static environmental information, making them unsuitable for planning in dynamic environments. An improved DWA approach for quadruped robots is proposed in [43], where the emergency obstacle avoidance goal and the nearest obstacle are distinguished to achieve segmentation design of collision probability coefficients for static and dynamic obstacles. However, dynamic obstacles are only evaluated in terms of the position impact, while the potential risk of collision caused by the influence of dynamic obstacles in velocity impact is ignored. In [44,45], arc-shaped obstacles are gridded, and concave obstacles are made convex in order to prevent the robot from becoming trapped in the obstacle. The evaluation function is adaptively updated according to the robot’s safety threshold, obstacles, and environment information. The influence of the dynamic obstacles’ state on the efficiency and stability of planning are ignored in these algorithms. In addition, convex processing of the environment is not applicable in complex real-world environment and the tiny grid size reduces the efficiency of local path planning.
In summary, traditional path planning algorithms for quadruped robots are facing the following issues:
- (1)
- The environment map composed of idealized regular geometry is used as the input of the algorithm, which cannot effectively plan the path in the real complex environment.
- (2)
- The planning efficiency is limited due to the fixed step used by PSO-based APF algorithms. The terrain complexity is ignored in the evaluation function of the fitness function, which poses a risk of planning an unreliable path. The calculation of the terrain potential field is ignored in the 3D APF algorithms, resulting in the inability of the quadruped robot torso to maintain an appropriate height from the ground.
- (3)
- The influence of the velocity of dynamic obstacle is ignored in the local path planning algorithm, which decreases the efficiency and stability of the local planning.
- (4)
- The optimal velocity planning based on DWA algorithm is limited in solving velocity due to the vast amount of the point cloud.
To solve the above problems, a hierarchical path planning method consisting of PSO-based 3D APF and improved DWA is proposed in this article. The PSO-based 3D APF algorithm is utilized for global path planning, while a point cloud height segmentation-based calculation method for terrain potential field, and a DEM-based terrain complexity calculation method are proposed. An improved DWA algorithm is employed for local path planning. The velocity of dynamic obstacles is mapped to their distance from the robot, which are used to predict the potential collision area. Then, a strategy for temporary target point selection is proposed. Finally, CUDA is used to accelerate the solution velocity in path planning.
The main contributions of our approach are as follows:
- (1)
- The neighborhood points of the quadruped robot torso are segmented into the obstacle points and terrain points. Using a static environment point cloud map to plan the global path, the spatial shape feature and data distribution feature are preserved well, which helps the robot to choose the optimal path.
- (2)
- The terrain potential field is introduced into APF to restrict the distance between the torso and the ground to ensure that the torso remains within a stable operating altitude range, thereby guaranteeing the reliability of path planning.
- (3)
- The terrain complexity is integrated into the fitness function to enhance the reliability of global path planning. The method of calculating path smoothness is improved to overcome the scale problem.
- (4)
- A method of predicting the potential collision area is proposed to enhance the efficiency and stability during dynamic obstacle avoidance. The calculation of optimal velocity combination is accelerated by CUDA.
The outline of this article is as follows: Section 2 presents the methodology framework of the proposed hierarchical path planning method. Section 3 illustrates the map pre-processing: 1) point cloud processing; 2) point cloud height segmentation. The approach proposed for global and local path planning is discussed in Section 4 and 5, respectively. In Section 6, experimental details are illustrated and results are analyzed. Section 7 concludes the article highlighting and future research direction.
2. Methodology Framework
The overall framework of the developed hierarchical path planning is illustrated in Figure 1. Global path planning and local path planning are conducted separately. An offline planning mode is adopted in the global path planning, and a static environment point cloud map is utilized as input. The point cloud is segmented into obstacle points and terrain points based on height and distance to the robot. The terrain points are utilized to calculate the terrain potential field. Thus, the total potential field is the sum of obstacles, the target point and the terrain potential field. The global path points will be planned in the direction of the fastest decreasing potential field gradient with the 3D APF algorithm. In this case, the force parameters of the potential field and the step size will be optimized by PSO algorithm.
An online planning mode with the real-time environment point cloud is utilized as input in the local path planning. The global path points are refined and selected as temporary target points for local path planning based on the strategy for temporary target point selection. A pedestrian tracking algorithm is utilized to predict the potential collision area. The velocity of dynamic obstacles is mapped to its distance from the robot in the evaluation function of the improved DWA algorithm. The optimal velocity combination which solution is accelerated by CUDA is planned by the improved DWA algorithm.
3. MAP Pre-processing
3.1. Environment Point Cloud Processing
The environment point cloud map consists of static environment point cloud map generated by the algorithm [46] and the real-time local environment perception [47,48]. The static environment map is used in global path planning. The following sequence are applied to crop the raw environment map and reduce noise:
- ●
- A voxel filter with leaf size is applied to reduce the size of point;
- ●
- A Statistical-Outlier-Removal (SOR) filter with a neighborhood radius of and a neighborhood point number of is utilized to reduce outliers;
- ●
- A passthrough filter is used to crop the raw environment map along specified dimension.
The real-time local environment perception is used in local path planning. The above processing sequence are also applied to real-time local environment information first, and then the scope of the point cloud of local environment is cropped to reduce unnecessary calculations in local path planning by the following sequence:
- ●
- The point cloud at the depth limit representing influence range of obstacles is cropped during local path planning;
- ●
- The point cloud at the height is cropped to remove the ceiling points;
- ●
- The algorithm in [47] is used to track the motion state of dynamic obstacles.
The motion state of dynamic obstacles is denoted by , where and represent the position and velocity of the dynamic obstacle ().
This section may be divided by subheadings. It should provide a concise and precise description of the experimental results, their interpretation, as well as the experimental conclusions that can be drawn.
3.2. Height Segmentation of the Point Cloud
The purpose of the point cloud segmentation is to obtain the terrain and obstacle points in the neighborhood point cloud. The segmentation schematic diagram is shown in Figure 2. The neighborhood points of the robot are defined as points in the sphere with a radius of . The sphere is concentric with the mass center of the robot torso. The obstacle points and terrain points are denoted by and , respectively. The obstacle points are defined as points within height form to in the sphere. The terrain points are defined as points within a cylinder with a radius of and a height from to . Attractive and repulsive forces are exerted on the robot by the terrain points, depending on the height of the point, to keep the robot body at a proper height. The detailed calculation is described in Section 4.
4. Global Path Planning with PSO-based 3D APF
In this Section, firstly, the basic form of attractive and repulsive potential field calculation for 3D APF are illustrated and the corresponding potential fields are calculated. Then, the parameters to be optimized in 3D APF is illustrated. Finally, the fitness function, each indicator and the proposed terrain complexity and improved path smoothness calculation method are introduced. The framework of the designed PSO-based 3D APF is shown in Figure 3.
4.1. 3D APF with Terrain Potential Field
Referring to the traditional APF algorithm, attractive and repulsive potential field functions of the 3D APF can be expressed as the following form.
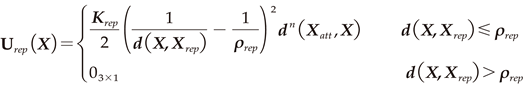
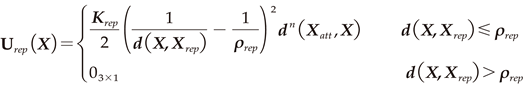
where is the position of the mass center of the quadruped robot torso. and are the positions of the object exerting attractive and object exerting repulsive force, respectively. and are the distance gain coefficient of the attractive and repulsive potential field, respectively. The input of are two vectors. The euclidean distance of the input vectors is represented by the scalar of , while the direction of is from latter vector to former vector. is the influence range of the obstacle on the robot in the directions. is the index factor of repulsive potential field.
According to Eq.1, the attractive potential field of the target point can be expressed as
where is the distance gain coefficient of the attractive potential field of the target point. is the position of the target point.
According to Eq.2, the repulsive potential field of the obstacle point cloud can be expressed as
where is the distance gain coefficient of the repulsive potential field of the obstacle point. is the position of the obstacle point. are the obstacle points in the neighborhood. is the influence range of the obstacle on the robot in the directions.
During the iterative planning process, the quadruped robot torso is subject to the repulsive force exerted by each obstacle point in the neighborhood. This article superimposes the repulsive potential field of each obstacle point, and takes the average value as the repulsive potential field of obstacle points in the neighborhood. Therefore, the repulsive potential field of the obstacle points can be expressed as:
where is the number of obstacle points in the neighborhood.
During the motion of the quadruped robot, the height of the mass center of the torso from the ground should be kept within an appropriate range. The minimum and maximum height threshold are represented by and , respectively. is the height of the mass center of robot torso. When >, the attractive terrain point will attract the robot. Similarly, when <, the repulsive terrain point will repulse the robot. According to the point cloud height segmentation, the terrain point cloud exerts two forces on the robot torso at the same time. The attractive force is generated by the attract point , while the repulsive force is generated by the repulsive force point . The attractive potential field and the repulsive potential field can be expressed as:
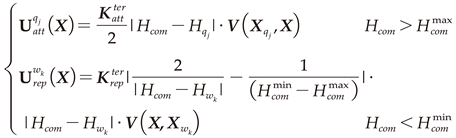
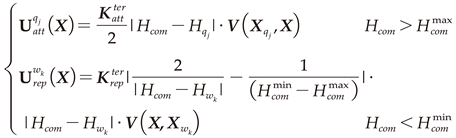
Similar to the Eq 5, the authors superimpose the attractive potential field and the repulsive potential field generated by the terrain points, and takes the average value as the attractive potential field and the repulsive potential field generated by the ground:
where and are the size of attractive terrain points and repulsive terrain points, respectively. is the th, , point in attractive terrain points, and is the th, , point in repulsive terrain points. and are the heights of the th attractive terrain points and the th repulsive terrain points, respectively. Their positions are denoted by and , respectively. is the unit direction vector of the mass center of robot torso and the terrain point. The direction is from the terrain point to the mass center of robot torso when the terrain point is repulsive, otherwise, the direction of is opposite. is the distance gain coefficient of the potential field of attractive terrain points, while is the distance gain coefficient of the potential field of repulsive points. Therefore, the total potential field generated by the static environment point cloud can be expressed as
According to the classical APF principle, the robot moves in the direction of downward potential energy. The moving direction can be represented by a unit vector as follows.
4.2. PSO-based Optimization of APF
During global path planning, the potential field parameters and step planned need to be updated dynamically. The PSO algorithm is utilized to optimize these parameters adaptively. PSO is a population-based stochastic optimization algorithm whose particles are represented as potentially optimal solutions in a D-dimensional search space. The th particle’s position is defined as and its velocity is denoted by . The position and velocity of particles are updated as
where is the inertial weight, and are the individual and group learning factors which satisfy the condition . , are random factors. is the position with the best fitness for the th particle so far; is the position with the best fitness for all particles in current iteration.
4.3. Fitness Function
To overcome the limitations of the classical APF, the PSO algorithm is utilized to optimize the attractive and repulsive parameters. In order to improve the effectiveness of this method in quadruped robot, a new fitness function is designed in this article, which includes an terrain complexity evaluation.
The fitness function is composed of three evaluation indicators: the distance from the robot to the target point, path smoothness and terrain complexity, which can be expressed as
where represents the fitness function of the th particle. is the number of iterations. , and are the distance indicator, path smoothness indicator, and terrain complexity indicator, respectively. , and are the position of the robot in th, th and th iteration, respectively. , and are the weight coefficients of each indicator respectively. The distance indicator is calculated from the Euclidean distance between the robot’s torso and target point.
To improve the efficiency of global path planning, a dynamic step size is designed and implemented in our method. In traditional methods, path smoothness is represented as the angle between neighboring steps, easily resulting in scaling problems when using dynamic programming steps. To solve this problem, we use the ratio of the valid move length to the actual move length as the path smoothness. The improved path smoothness indicator can be expressed as
The terrain complexity is determined by its roughness and undulation. For calculating terrain complexity, the mass center of the robot’s torso is taken as the starting point, and the point cloud is cropped in a rectangular region with a vertical length of , a horizontal length of , and a height of , in direction. The rectangular region is shown in the Figure 4a. In the rectangular area, the height difference between the point cloud (blue) and the robot torso is distributed in m. The raw point cloud is represented by a digital elevation model (DEM) composed of regular grids. The DEM grids are shown in Figure 4b. The terrain complexity is expressed as the average of the roughness and undulation of DEM grids. As shown in Figure 4c, a DEM grid denoted by and its neighborhood DEM grids denoted by are selected. For convenience, the height of each DEM grid is also denoted by . The roughness is defined as the sum of the absolute value of the height difference between the grid and its neighborhood grids. The roughness can be calculated by Eq.13.
where is the size of DEM in the rectangular region and is the index of DEMs. The undulation is defined as the sum of the absolute value of maximum height difference between the grid and its neighborhood grids. The undulation can be calculated by Eq.14.
Therefore, the terrain complexity can be calculated by Eq.15.
where and are the weighting coefficients of the roughness and undulation, respectively.
5. Local Path Planning with Improved DWA
In this Section, the method for predicting potential collision areas is first illustrated. Then, the strategy for selecting temporary target points is introduced. Finally, the related evaluation function is constructed, which takes the effect of the velocity of dynamic obstacles into consideration. Overall framework of the improved DWA is shown in Figure 5.
5.1. Potential Collision Area Prediction
The schematic diagram of potential collision area prediction is shown in Figure 6. Firstly, the safe range is utilized to determine whether dynamic obstacle affects local path planning. When the distance between the robot and dynamic obstacle is less than the safe range, the collection of future path points of dynamic obstacle denoted by in a prediction period will be predicted according to the motion state of dynamic obstacle. The future path points are predicted dynamically in real-time. This means that the path points will be predicted at each moment based on the current position of the dynamic obstacle, assuming that it moves at a constant velocity.
Therefore, track point prediction can be expressed as
where and are the position and velocity of the dynamic obstacle in the world coordinate system at the current moment, respectively; the symbol represents rounding; is the number of future path points. The collection of future path points of dynamic obstacle can be expressed as
where is the future path point of the dynamic obstacle.
The risk area is generated with the future path point of the dynamic obstacle as the center, which means that when the robot is within the risk area, there will be a risk of collision with the dynamic obstacle. The radius of the risk area is . When the global path point is located in the risk area, it is considered as a potential collision point. is the index of all potential collision points in the global path point. A virtual obstacle with the same height as the risk area and a radius is added at each potential collision point. The function of virtual obstacles is to help the robot avoid potential collision areas as much as possible, but it could not completely exclude the robot from entering.
5.2. Strategy for Temporary Target Point Selection
An important concept of hierarchical path planning is that the local path planning requires to be guided by global path points. Thus, in local path planning, the temporary target points are selected from the global path points. Firstly, the global path points outputted by the PSO-based 3D APF algorithm are refined. Then, a strategy for temporary target point selection is designed. The refinement of global path points is achieved through linear interpolation between neighboring path points. is the number of interpolations. represents the refined global path points.
The temporary target points are selected according to Figure 7. is the index of the temporary target point in global path points. Firstly, the current temporary target point denoted by is initialized to be the starting point of the robot denote by . Then, it is determined whether the current temporary target point is within the potential collision areas using the method developed in Section 5.1. If the temporary target point is not within the potential collision areas, it is needed to further determine whether the robot reaches the temporary target point. If the robot does not reach the current temporary target point, the index of current temporary target point will be returned, otherwise, the returned index can be expressed as
where is the number of refined global path point
If the temporary target point is in the potential collision areas, a suitable temporary target point is searched in with the index value greater than . Moreover, the index of suitable temporary target point is the smallest. is the distance from the suitable point to the potential collision area, which should be greater than the collision range denoted by .
5.3. Evaluation Function
It can be seen from the above analysis that there are three types of obstacles in the environment, namely static, dynamic, and virtual obstacles. The impact of virtual obstacles on the evaluation calculation is similar to that of static obstacles. The different is that the position of virtual obstacles changes with the motion state of the dynamic obstacle. The DWA algorithm is improved by mapping the velocity of dynamic obstacles to its distance from the robot. The evaluation function is represented as follows
where , and , are the weighting factor of each evaluation indicator. and are the linear and angular velocity, respectively. These parameters are selected from the dynamic velocity window expressed in Section 6. is the distance of the robot to the temporary target point, and is the velocity of the robot. is the shortest distance from the robot to the obstacles. The distance from the robot to the dynamic obstacle is denoted as
where represents the velocity of dynamic obstacle, which is the adjustment factor of the actual distance between the robot and the dynamic obstacle. Based on the minimization of the evaluation function with the dynamic velocity window, the optimal velocity combination can be returned as the desired command for robot motion.
6. Experimental Results and Discussion
6.1. Experimental platform and setup
A commercial quadruped robot (Y10, YOBTICS) is utilized as the experimental platform, as shown in Figure 8. For environment reconstruction and dynamic obstacles tracking, a 3D camera (ZED2) with an IMU sensor is mounted on the front of the robot. For real-time performance, A single-board computer (UP Squared Board) and an embedded system-on-module (Nvidia Xaiver NX) are mounted on the back of the robot’s torso. Nvidia Xaiver NX is utilized to reconstruct static environment, generate real-time point cloud and track dynamic obstacles. UP Squared Board is utilized to plan both global and local paths. The communication method between Nvidia Xaiver NX and UP Squared Board depends on ROS (Robot Operation System). The desired control commands generated by local path planning are transformed to the robot control board via LCM (Lightweight Communications and Marshalling).
The experimental environment is shown in Figure 9. The shape of the experimental environment is equivalent to a rectangle with a length of 10m and a width of 7m. The rectangle-shaped experimental area is shown in Figure 9a. Bricks are used to augment the complexity of the terrain. There are 4 brick piles stacked on the terrain, as shown in the Figure 9b. The maximum height of the brick piles is between 0.11m and 0.17m.
This article utilizes the point cloud generated by the 3D camera to create a static environment point cloud map. The process of constructing the static environment point cloud map is shown in the Figure 10. The raw static environment point cloud map with 25,9162 points is shown in Figure 10a. The origin of the world coordinate system is selected as the initial camera position when constructing the map.
As discussed in Section 3, the map needs to be filtered to reduce the noise and the number of point clouds. The pre-processing flow is as follows:
- ●
- The passthrough filter is applied to crop the map in artificially set directions and ranges, only the point cloud within the scope of the test site is kept. The passthrough filter parameters are set to: ,,.
- ●
- A voxel filter with leaf size is utilized to reduce the size of point;
- ●
- A statistical-Outlier-Removal filter with the number to reduce outliers of neighborhood points within a radius is utilized to reduce outliers
The number of point clouds contained in the pre-processed map reduced from 159,162 to 33,945, as shown in Figure 10b.
6.2. Results and Discussion for PSO-based 3D APF in Global Path Planning
The range of parameters to be optimized of PSO-based 3D APF is shown in Table 1. The fixed parameters of PSO algorithm and global path planning is shown in Table 2. The population size of PSO is 100. According to the characteristics of quadruped robot motion, the vertical distance from the torso to terrain points is set to m.
The initial position of the robot in the world coordinate system is set to . Two target destinations in the world coordinate system are set in our experiment: and . In the experiment on evaluating terrain complexity, the weight factors of the roughness and undulation are set as β1= β2=1. Four sets of weight parameters of the fitness function are applied to each target point, which are set to [1, 0, 0], [1, 5, 0], [1, 0, 50], and [1, 5, 50], respectively.
The path planning process is visualized by utilizing ROS and RViz (Robot Visualization). The results of global path planning with the target point and are shown in Figure 11.
The average and maximum values of path smoothness and terrain complexity are utilized as metrics to compare the performance of global path planning with different parameter settings. The quantitative comparison of PSO-based 3D APF performance under different parameter settings is shown in Table 3. It is obvious that when the parameter is set to , the average and maximum values of the smoothness of global path is the smallest. Likewise, when the parameter is set to , the average and maximum values of the terrain complexity are the smallest. Undeniably, setting the parameters simultaneously to and achieves only the best performance in path smoothness with the target . While the rest is sub-best, but pretty close to the best performance. The biggest difference between the sub-best and best performance is within . It is believed that the reason is that the designed fitness function needs to adaptively balance each indicator. By comparing the performance of different parameter settings, the path smoothness can be improved by the proposed fitness function to guide the robot to pass over the low complexity terrain.
To compare the result (planning efficiency and path smoothness) of our method with that of the method in reference [30], the weight parameters of the fitness function are set to . In reference [30], a fixed step is used for PSO. The efficiency of planning is reflected in the number of PSO iterations, with fewer iterations indicating higher efficiency. The effective step ratio is used as an overall gauge for the path smoothness. The effective step ratio is calculated as follows
where is the number of iterations. is the linear distance between the initial position and the target point. is the fixed step.
Obviously, a larger effective step ratio means that the global path is closer to a straight line, which also represents a smoother global path. The step variation is shown in Figure 12. The step is adaptively adjusted between 0.1 and 0.5 m. The effective step ratio is calculated by using the average of steps in all iterations. The fixed step is set to 5 sets of values from 0.1 to 0.5m. The effective step ratio is shown in Table 4. As can be seen from the table, our method obtains higher effective step ratio with a maximum improvement of 9/0.67≈13.4 times, and an average improvement of (9/0.67+3.2/0.43)/2≈10.4 times. Furthermore, our method requires fewer iterations, resulting in a maximum improvement of 121/21≈5.8 times, and an average improvement of (121/21+103/20)/2≈5.5 times. Experimental results illustrate that our method can improve both path planning efficiency and path smoothness.
The height of global path points above the ground is used as the metric to evaluate the path reliability. The ground height is represented by the average height of the terrain point cloud in the neighborhood. The global path planning is repeated 5 times to check the height difference. It can be seen from Figure 13 that, the height of the robot torso from the ground is maintained within the range m, comparable to the maximum height of the attractive point and the minimum height of the repulsive point. Thus, the validity and rationality of the method for constraining the height of the torso using terrain point potential field is verified.
6.3. Results and Discussion for Improved DWA in Local Path Planning
Firstly, on the basis of traditional DWA algorithms, this article proposes a method of potential collision area prediction and a strategy for temporary target point selection. In the evaluation function of the improved DWA, the velocity of the dynamic obstacle is mapped to its distance from the robot to improve the efficiency and stability of the robot's dynamic obstacle avoidance. Then, our improved DWA is compared with the traditional DWA algorithm in reference [30]. Since our improved DWA algorithm focuses on dynamic obstacle avoidance, we emphatically compare the efficiency of dynamic obstacle avoidance and the stability of velocity planning between the two algorithms. Finally, the computational scale of the optimal velocity solution is briefly introduced, and the solution velocity is accelerated by CUDA.
The velocity window is essentially a space of achievable velocities that are determined by the robot's current motion state and motion parameters within a given time interval. According to the kinematic and dynamic constrains of our quadruped robot, the motion parameters of the quadruped robot are listed in Table 5. In the following experiment, the time interval is set to 0.1s.
In the local velocity planning experiment, the dynamic obstacle tracking is applied to detect the position and velocity of dynamic obstacles. Potential collision areas are predicted, and temporary target points are selected by setting two dynamic obstacles, obs-1 and obs-2. The effective range of dynamic obstacles is set to m. At each tracking output time, assuming that dynamic obstacles move in a straight line at a constant velocity, the path points in the future time seconds are predicted based on the position and velocity of dynamic obstacles. With the path points of the dynamic obstacles as the center, a risk area with a radius m is generated. The virtual obstacles are added with a radius m. The predicted results of the potential collision region are shown in Figure 14a. The potential collision area will be applied to the temporary target point selection and evaluation function. The local path planning results of the improved DWA and traditional DWA algorithms are shown in Figure 14b. The performance evaluation of the Z-axis linear velocity has been ignored. The efficiency of dynamic obstacle avoidance is expressed as the length of the locally planned path. The stability of the velocity planning is determined by calculating the average of the velocity variance across all iteration windows, each with a size set to 10.
The velocity planning results of the improved DWA method and the traditional DWA method are shown in Figure 15. Based on the results of velocity planning, the stability and efficiency of the two methods are compared in this article. The stability of dynamic obstacle avoidance can be assessed by calculating the average variance of velocity within a given iteration window. The stability of velocity planning increases as the mean value decreases. The size of the iteration window is set to 10. It means that the variance within the iteration window is calculated for every 10 adjacent combinations of iteration velocity. The efficiency of dynamic obstacle avoidance is expressed is represented by the length of the local path planning. The results of local path planning are shown in Table 6. The stability of the torso's X and Y-axis velocities, and the planned angular velocities around the Z axis, are compared in this table. Additionally, the combined velocity variance is also analyzed. The combined velocity is defined as the sum of the velocities along the X, Y and Z axes. It can be observed from the table that the variance of the improved DWA algorithm in each velocity component and the combined velocity is smaller, with a minimum improvement ratio of 2.6 times. This suggests that the improved algorithm can effectively improve the velocity stability during dynamic obstacle avoidance. Similarly, the planned path length during dynamic obstacle avoidance is effectively reduced with a reduction ratio of more than 20%.
Taking the 3D point cloud of the actual environment as the input of path planning algorithm, is the biggest different between our work and most other path planning work. When the 3D point cloud is combined with velocity information, millions of calculations are generated. This makes it difficult for the algorithm to achieve good real-time performance when calculating the expected velocity required for the robot to move at the next moment. To this point, CUDA is employed instead of traditional CPU to accelerate the calculation velocity in our article. One velocity combination within the velocity window corresponds to one CUDA thread running independently. Information of point cloud, velocity combination, robot's current position, target point position, and dynamic obstacles are utilized as input for each thread calculation. In each thread, a score is calculated for each velocity combination, and an array of scores is returned with the evaluation function. Finally, the score array is sorted to obtain the index of velocity combination corresponding to the highest score. In actual deployment, the block size of the CUDA kernel function is set to 128, and the grid size is set to 6. The memory size occupied by the kernel function during operation is about 300MB. The calculation time of the evaluation function before and after CUDA acceleration is compared by the experiment. The cost time of evaluation function calculation with CUDA and CPU is shown in Figure 16.
7. Conclusions
Path planning is an essential procedure for robots to move autonomously in complicated dynamic environments. For quadruped robots, most of the proposed global path planning methods lack terrain complexity assessment, while the local path planning methods do not fully consider practical factors like dynamic obstacle moving velocity. In this paper, a 3D point cloud driven hierarchical path planning method has been developed for quadruped robots, which consists of PSO-based 3D APF for global path planning and improved DWA for local path planning. The main contributing results are as follows:
- In global path planning, the authors improve the calculation method of path smoothness to make it suitable for variable step optimization. Compared with the traditional APF method using fixed step size, the dynamic step planning method we proposed is more effective in terms of the number of iterations and the step rate to achieve the optimum performance, effectively enhancing planning efficiency.
- In global path planning, a terrain complexity calculation method based on digital elevation model is proposed, and terrain complexity evaluation is designed in the PSO fitness function. Compared with the PSO evaluation function that does not evaluate terrain characteristics, the developed algorithm is more efficient in complex environments. It is more advantageous for robots to plan movements on complex terrain than on flat roads.
- In the local path planning, the authors introduce potential collision area prediction, temporary target point selection strategy and the velocity of dynamic obstacle mapping to the improved DWA algorithm. Compared with traditional DWA, the improved DWA algorithm has higher planning efficiency and velocity stability.
- CUDA is applied to solve the optimal velocity. In edge computing devices, the solution velocity is increased by 600 times compared to the traditional CPU solution, meeting the requirements for real-time deployment.
The limitations of this work include: 1) the environment map is created by the binocular camera with a hole problem, which makes the algorithm treat the hole as a passable area; 2) due to the low tracking accuracy and robustness of dynamic obstacles, the potential collision area prediction accuracy is low, while the algorithm to determine the location and velocity of dynamic obstacles are also affected; 3) the selection of optimal velocity depends on the solution of hardware, which increases the hardware requirement. In the next step, multi-beam LIDAR will be used to construct static environment maps. In addition, pedestrian trajectory intention analysis and velocity constraints will be added to dynamic obstacle tracking to reduce the computational scale of velocity planning solutions.
Author Contributions
Conceptualization, Q.Z. and J.S.; methodology, R.L.; software, L.W.; validation, J.H., R.L. and L.W.; resources, Y.T.; data curation, Q.Z.; writing—original draft preparation, J.S.; writing—review and editing, Q.Z.; visualization, R.L.; supervision, J.H.; project administration, Y.T.; funding acquisition, R.L. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Key Research and Development Project of Hubei Province under grant 2022BAA056.
Institutional Review Board Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Kim T-J, So B, Kwon O, Park S, editors. The energy minimization algorithm using foot rotation for hydraulic actuated quadruped walking robot with redundancy. ISR 2010 (41st International Symposium on Robotics) and ROBOTIK 2010 (6th German Conference on Robotics); 2010: VDE.
- Delmerico J, Mintchev S, Giusti A, Gromov B, Melo K, Horvat T, et al. The current state and future outlook of rescue robotics. Journal of Field Robotics. 2019;36(7):1171-91. [CrossRef]
- Xu RW, Hsieh KC, Chan UH, Cheang HU, Shi WK, Hon CT, editors. Analytical review on developing progress of the quadruped robot industry and gaits research. 2022 8th International Conference on Automation, Robotics and Applications (ICARA); 2022: IEEE.
- Wang C, Meng L, She S, Mitchell IM, Li T, Tung F, et al., editors. Autonomous mobile robot navigation in uneven and unstructured indoor environments. 2017 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS); 2017: IEEE.
- Tang G, Tang C, Claramunt C, Hu X, Zhou P. Geometric A-star algorithm: An improved A-star algorithm for AGV path planning in a port environment. IEEE access. 2021;9:59196-210. [CrossRef]
- Liu L-s, Lin J-f, Yao J-x, He D-w, Zheng J-s, Huang J, et al. Path planning for smart car based on Dijkstra algorithm and dynamic window approach. Wireless Communications and Mobile Computing. 2021;2021:1-12. [CrossRef]
- Almurib HA, Nathan PT, Kumar TN, editors. Control and path planning of quadrotor aerial vehicles for search and rescue. SICE Annual Conference 2011; 2011: IEEE.
- Zhang H, Wang Y, Zheng J, Yu J. Path planning of industrial robot based on improved RRT algorithm in complex environments. IEEE Access. 2018;6:53296-306. [CrossRef]
- Wang J, Chi W, Li C, Wang C, Meng MQ-H. Neural RRT*: Learning-based optimal path planning. IEEE Transactions on Automation Science and Engineering. 2020;17(4):1748-58.
- Wang H, Li G, Hou J, Chen L, Hu N. A path planning method for underground intelligent vehicles based on an improved RRT* algorithm. Electronics. 2022;11(3):294. [CrossRef]
- Guruji AK, Agarwal H, Parsediya D. Time-efficient A* algorithm for robot path planning. Procedia Technology. 2016;23:144-9. [CrossRef]
- Raheem FA, Hameed UI. Path planning algorithm using D* heuristic method based on PSO in dynamic environment. American Scientific Research Journal for Engineering, Technology, and Sciences. 2018;49(1):257-71.
- Zhu X, Yan B, Yue Y. Path planning and collision avoidance in unknown environments for USVs based on an improved D* lite. Applied Sciences. 2021;11(17):7863. [CrossRef]
- Yu J, Su Y, Liao Y. The path planning of mobile robot by neural networks and hierarchical reinforcement learning. Frontiers in Neurorobotics. 2020;14:63. [CrossRef]
- Sung I, Choi B, Nielsen P. On the training of a neural network for online path planning with offline path planning algorithms. International Journal of Information Management. 2021;57:102142. [CrossRef]
- Sun Y, Ran X, Zhang G, Xu H, Wang X. AUV 3D path planning based on the improved hierarchical deep Q network. Journal of marine science and engineering. 2020;8(2):145. [CrossRef]
- Qureshi AH, Miao Y, Simeonov A, Yip MC. Motion planning networks: Bridging the gap between learning-based and classical motion planners. IEEE Transactions on Robotics. 2020;37(1):48-66. [CrossRef]
- Li Q, Gama F, Ribeiro A, Prorok A, editors. Graph neural networks for decentralized multi-robot path planning. 2020 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS); 2020: IEEE.
- Wu J, Bin D, Feng X, Wen Z, Zhang Y. GA based adaptive singularity-robust path planning of space robot for on-orbit detection. complexity. 2018;2018. [CrossRef]
- Lamini C, Benhlima S, Elbekri A. Genetic algorithm based approach for autonomous mobile robot path planning. Procedia Computer Science. 2018;127:180-9. [CrossRef]
- Song B, Wang Z, Zou L. An improved PSO algorithm for smooth path planning of mobile robots using continuous high-degree Bezier curve. Applied Soft Computing. 2021;100:106960. [CrossRef]
- Krell E, Sheta A, Balasubramanian APR, King SA. Collision-free autonomous robot navigation in unknown environments utilizing PSO for path planning. Journal of Artificial Intelligence and Soft Computing Research. 2019;9(4):267-82. [CrossRef]
- Yao Q, Zheng Z, Qi L, Yuan H, Guo X, Zhao M, et al. Path planning method with improved artificial potential field—a reinforcement learning perspective. IEEE access. 2020;8:135513-23. [CrossRef]
- Lei X, Zhang Z, Dong P. Dynamic path planning of unknown environment based on deep reinforcement learning. Journal of Robotics. 2018;2018. [CrossRef]
- Chen C, Chen X-Q, Ma F, Zeng X-J, Wang J. A knowledge-free path planning approach for smart ships based on reinforcement learning. Ocean Engineering. 2019;189:106299. [CrossRef]
- Bae H, Kim G, Kim J, Qian D, Lee S. Multi-robot path planning method using reinforcement learning. Applied sciences. 2019;9(15):3057. [CrossRef]
- Chen Y-b, Luo G-c, Mei Y-s, Yu J-q, Su X-l. UAV path planning using artificial potential field method updated by optimal control theory. International Journal of Systems Science. 2016;47(6):1407-20. [CrossRef]
- Agirrebeitia J, Avilés R, De Bustos IF, Ajuria G. A new APF strategy for path planning in environments with obstacles. Mechanism and Machine Theory. 2005;40(6):645-58. [CrossRef]
- Raheem FA, Badr MM. Development of Modified path planning algorithm using artificial potential field (APF) based on PSO for factors optimization. American Scientific Research Journal for Engineering, Technology, and Sciences (ASRJETS). 2017;37(1):316-28.
- Lin Z, Yue M, Chen G, Sun J. Path planning of mobile robot with PSO-based APF and fuzzy-based DWA subject to moving obstacles. Transactions of the Institute of Measurement and Control. 2022;44(1):121-32. [CrossRef]
- Girija S, Joshi A. Fast hybrid PSO-APF algorithm for path planning in obstacle rich environment. IFAC-PapersOnLine. 2019;52(29):25-30. [CrossRef]
- Wang Z, Li G, Ren J. Dynamic path planning for unmanned surface vehicle in complex offshore areas based on hybrid algorithm. Computer Communications. 2021;166:49-56. [CrossRef]
- Shin Y, Kim E. Hybrid path planning using positioning risk and artificial potential fields. Aerospace Science and Technology. 2021;112:106640. [CrossRef]
- Zhou Z, Wang J, Zhu Z, Yang D, Wu J. Tangent navigated robot path planning strategy using particle swarm optimized artificial potential field. Optik. 2018;158:639-51. [CrossRef]
- Whitbrook AM, Aickelin U, Garibaldi JM. Idiotypic immune networks in mobile-robot control. IEEE Transactions on Systems, Man, and Cybernetics, Part B (Cybernetics). 2007;37(6):1581-98. [CrossRef]
- Fernandez-Leon JA, Acosta GG, Mayosky MA. Behavioral control through evolutionary neurocontrollers for autonomous mobile robot navigation. Robotics and Autonomous Systems. 2009;57(4):411-9. [CrossRef]
- Marefat M, Britanik J. Case-based process planning using an object-oriented model representation. Robotics and Computer-Integrated Manufacturing. 1997;13(3):229-51. [CrossRef]
- Abdelwahed MF, Mohamed AE, Saleh MA. Solving the motion planning problem using learning experience through case-based reasoning and machine learning algorithms. Ain Shams Engineering Journal. 2020;11(1):133-42. [CrossRef]
- Li X, Hu X, Wang Z, Du Z, editors. Path planning based on combinaion of improved A-STAR algorithm and DWA algorithm. 2020 2nd International Conference on Artificial Intelligence and Advanced Manufacture (AIAM); 2020: IEEE.
- Cai JC, Wan MF, Huang ZL, Liu Z, editors. An Improved DWA Path Planning Algorithm Integrating Global JPS Strategy. 2022 2nd International Conference on Computer, Control and Robotics (ICCCR); 2022: IEEE.
- Zhang F, Li N, Xue T, Zhu Y, Yuan R, Fu Y, editors. An improved dynamic window approach integrated global path planning. 2019 IEEE International Conference on Robotics and Biomimetics (ROBIO); 2019: IEEE.
- Wang J, Wu S, Li H, Zou J, editors. Path planning combining improved rapidly-exploring random trees with dynamic window approach in ROS. 2018 13th IEEE Conference on Industrial Electronics and Applications (ICIEA); 2018: IEEE.
- Chen Z, Wang Z, Wu M, Chen H, Zhang W, editors. Improved dynamic window approach for dynamic obstacle avoidance of quadruped robots. IECON 2020 The 46th Annual Conference of the IEEE Industrial Electronics Society; 2020: IEEE.
- Tianyu L, Ruixin Y, Guangrui W, Lei S, editors. Local path planning algorithm for blind-guiding robot based on improved DWA algorithm. 2019 Chinese Control And Decision Conference (CCDC); 2019: IEEE.
- Bai X, Jiang H, Cui J, Lu K, Chen P, Zhang M. UAV Path Planning Based on Improved A ∗ and DWA Algorithms. International journal of aerospace engineering. 2021;2021:1-12. [CrossRef]
- Xue G, Wei J, Li R, Cheng J. LeGO-LOAM-SC: An Improved Simultaneous Localization and Mapping Method Fusing LeGO-LOAM and Scan Context for Underground Coalmine. Sensors. 2022;22(2):520. [CrossRef]
- Asvadi A, Girao P, Peixoto P, Nunes U, editors. 3D object tracking using RGB and LIDAR data. 2016 IEEE 19th International Conference on Intelligent Transportation Systems (ITSC); 2016: IEEE.
- Eppenberger T, Cesari G, Dymczyk M, Siegwart R, Dubé R, editors. Leveraging stereo-camera data for real-time dynamic obstacle detection and tracking. 2020 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS); 2020: IEEE.
Figure 1.
The developed hierarchical path planning method.
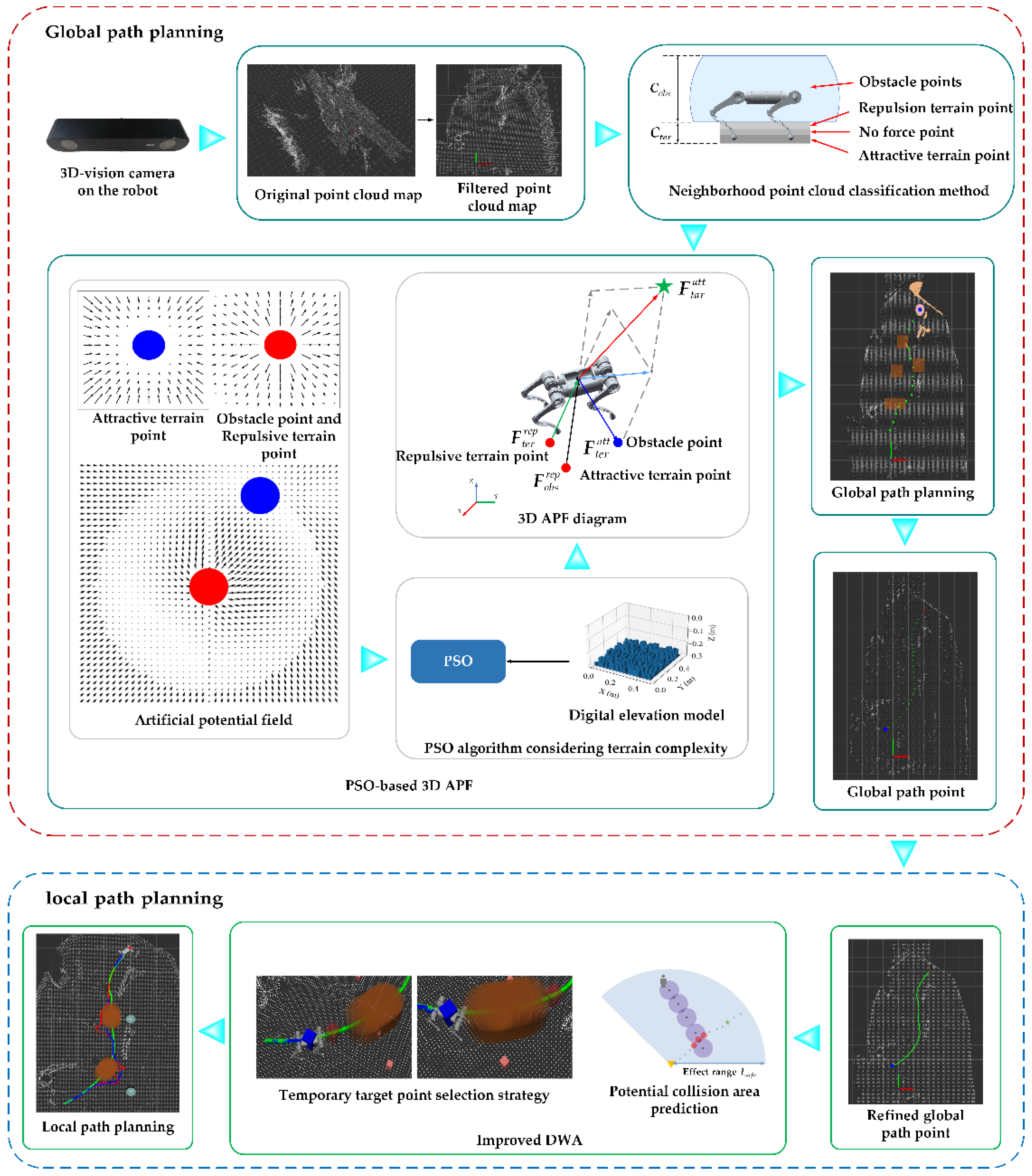
Figure 2.
Neighborhood point cloud classification.
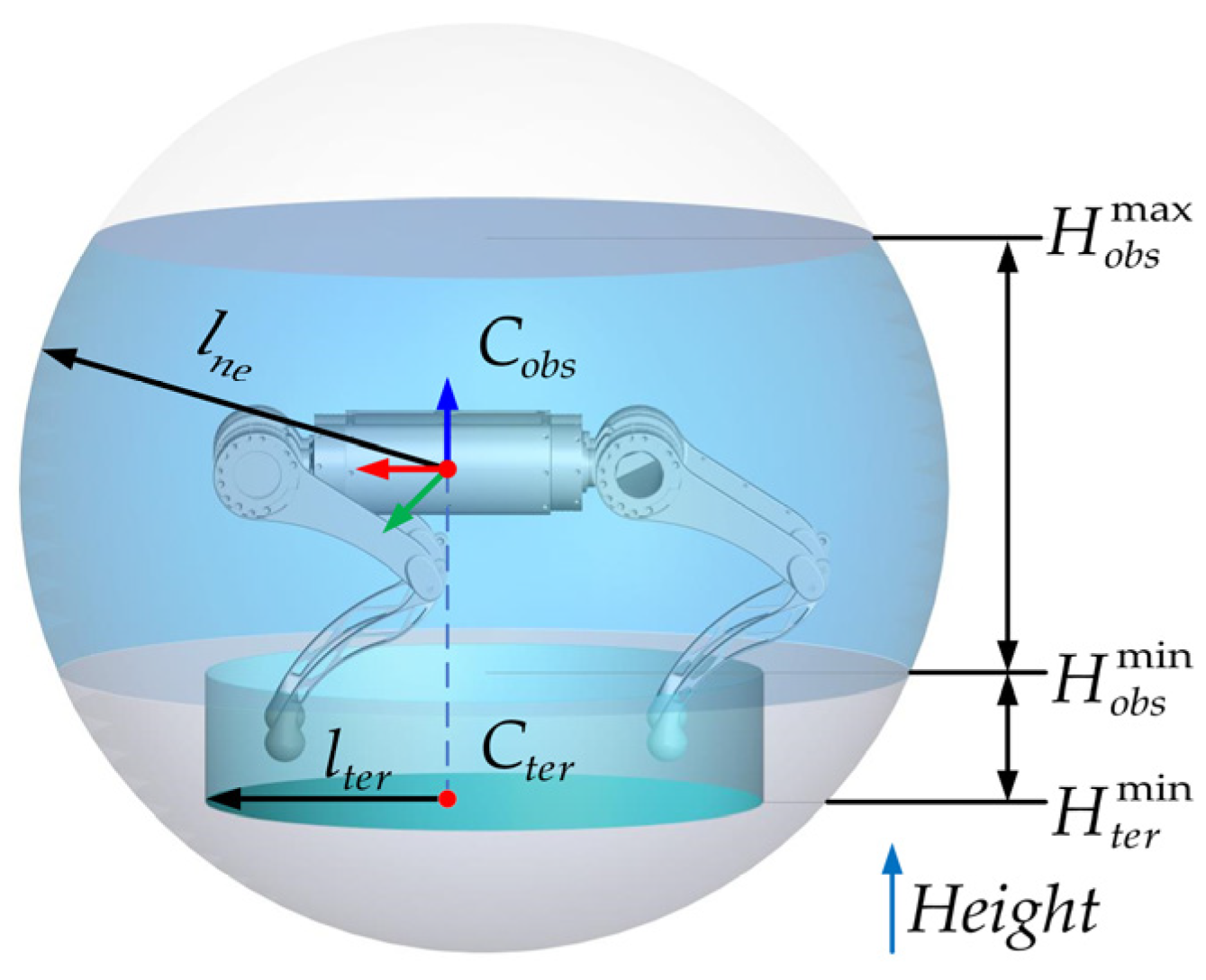
Figure 3.
The designed PSO-based 3D APF.
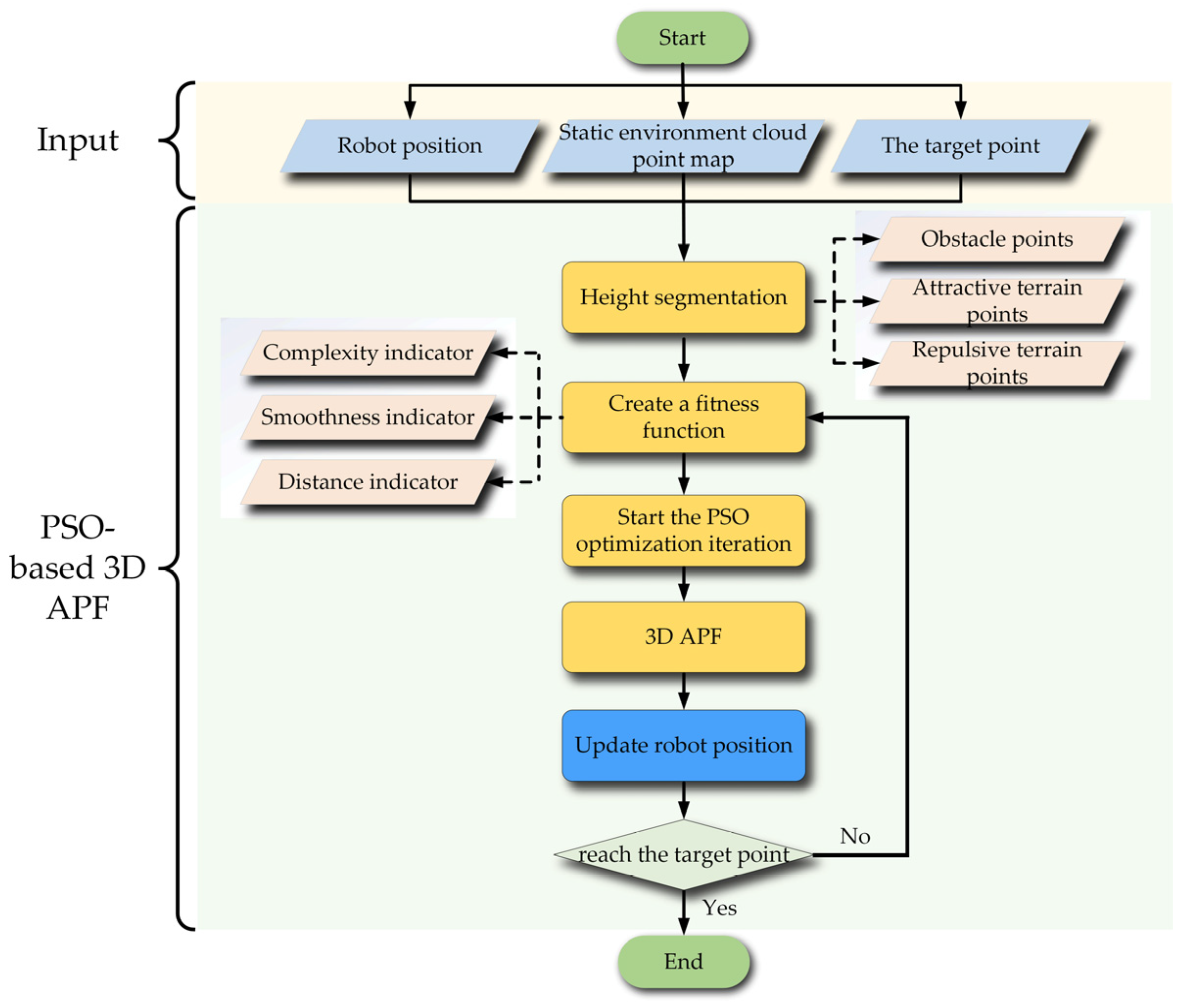
Figure 4.
The terrain complexity calculation. (a) the rectangular region (within the yellow area); (b) the regular grid of digital elevation model; (c) the DEM grid; (d) and (e) the calculation results of roughness and undulation on the simulated point cloud.
Figure 4.
The terrain complexity calculation. (a) the rectangular region (within the yellow area); (b) the regular grid of digital elevation model; (c) the DEM grid; (d) and (e) the calculation results of roughness and undulation on the simulated point cloud.
Figure 5.
The improved DWA.
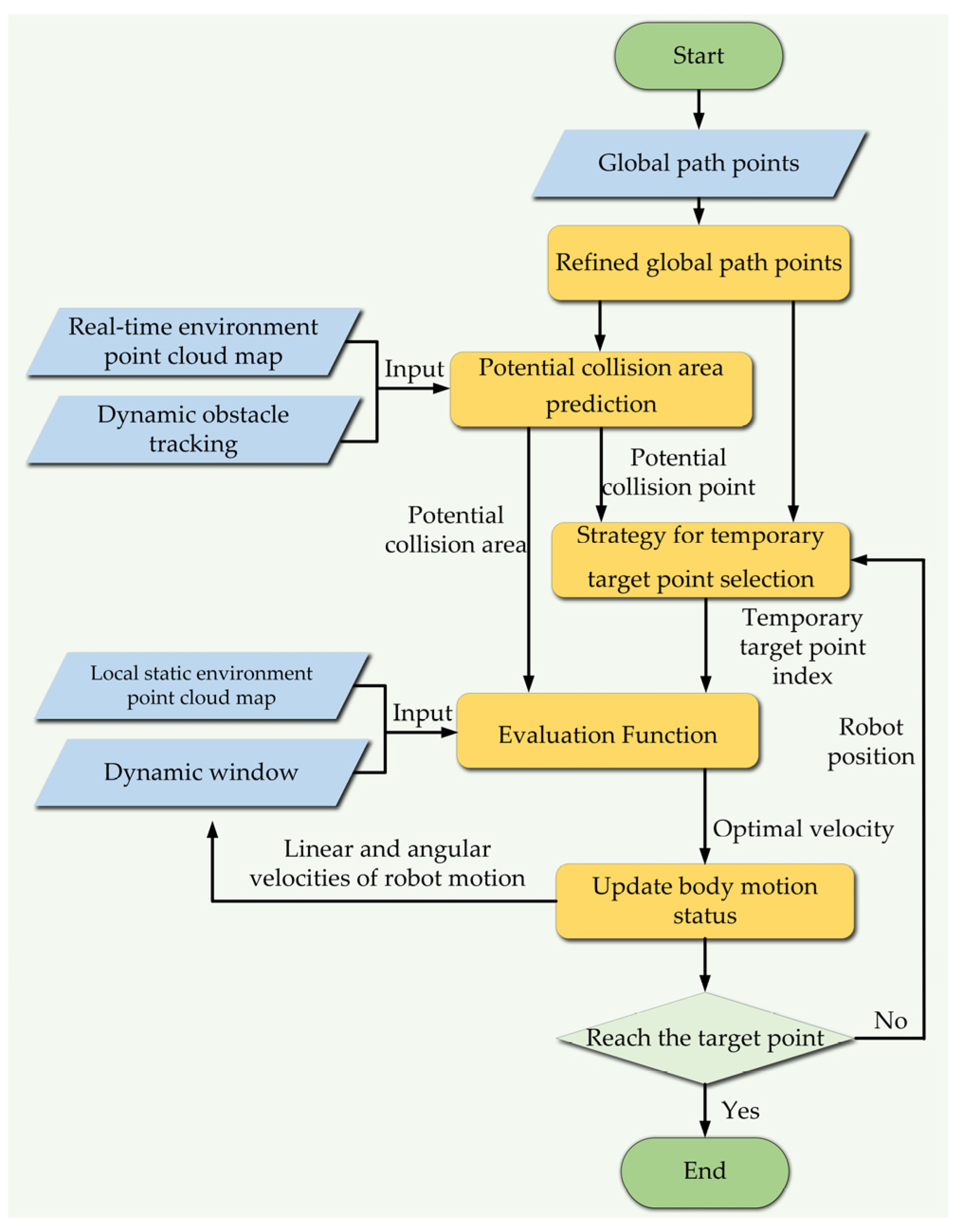
Figure 6.
Prediction of potential collision area (red area).
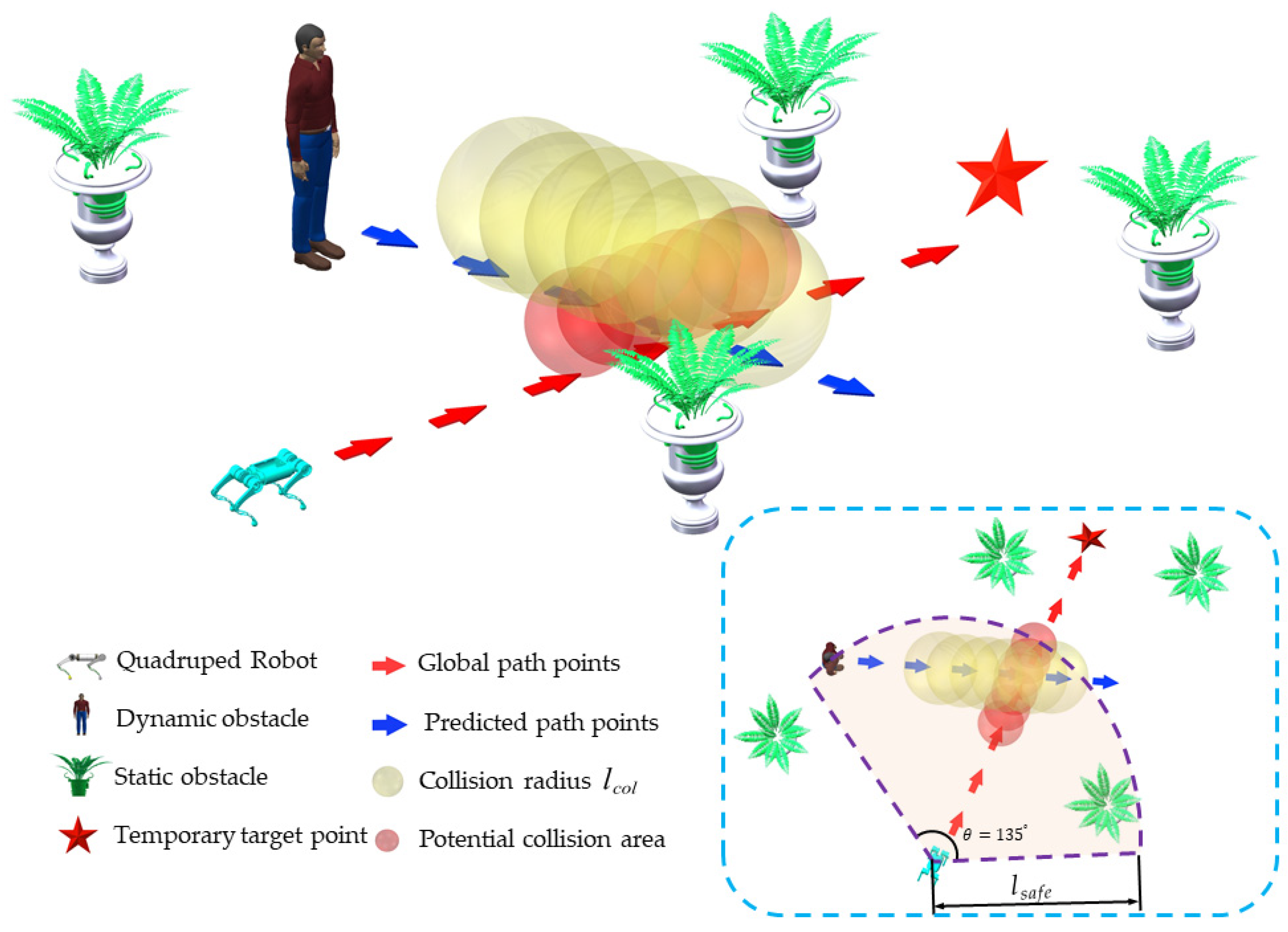
Figure 7.
The selection strategy of temporary target points.
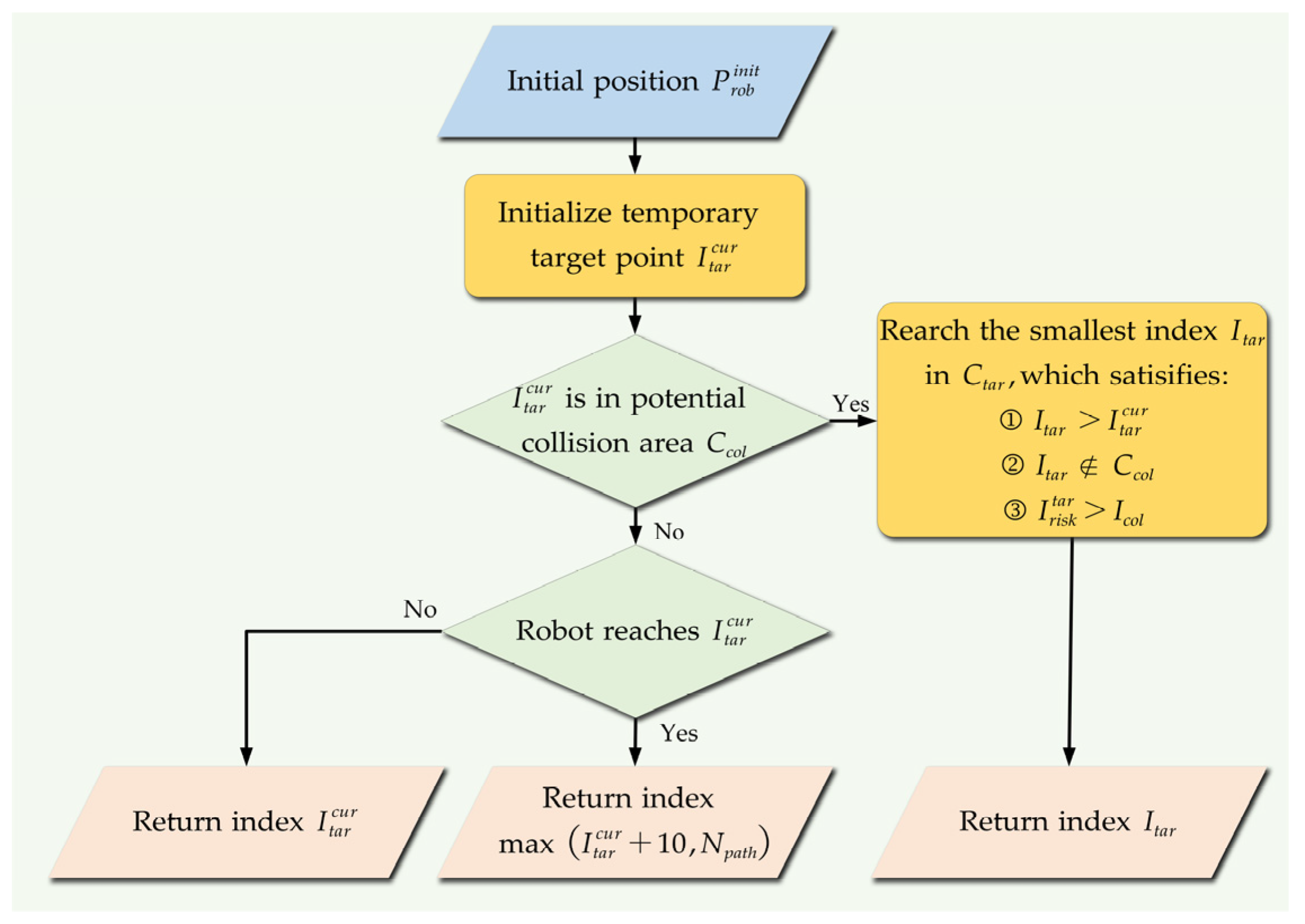
Figure 8.
Experimental setup.

Figure 9.
Static environment setup. (a) the rectangle-shaped environmental area with 4 brick piles; (b) the height of each brick pile.
Figure 9.
Static environment setup. (a) the rectangle-shaped environmental area with 4 brick piles; (b) the height of each brick pile.

Figure 10.
Static environment point cloud map. (a) the raw point cloud map; (b) the filtered map; (c) the process of constructing the map.
Figure 10.
Static environment point cloud map. (a) the raw point cloud map; (b) the filtered map; (c) the process of constructing the map.

Figure 11.
The results of global path planning with target and .
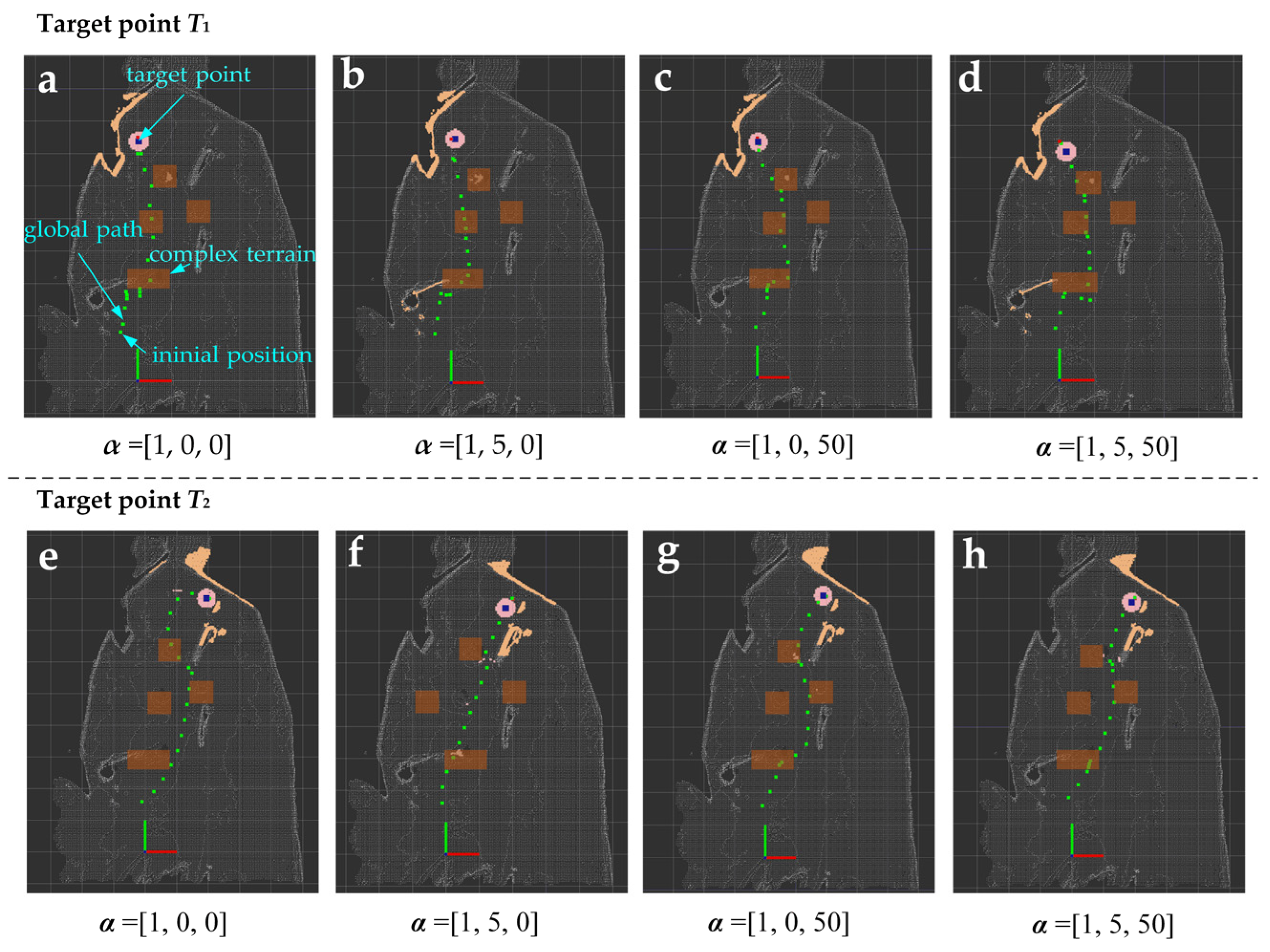
Figure 12.
Variation in step after being optimized by PSO.
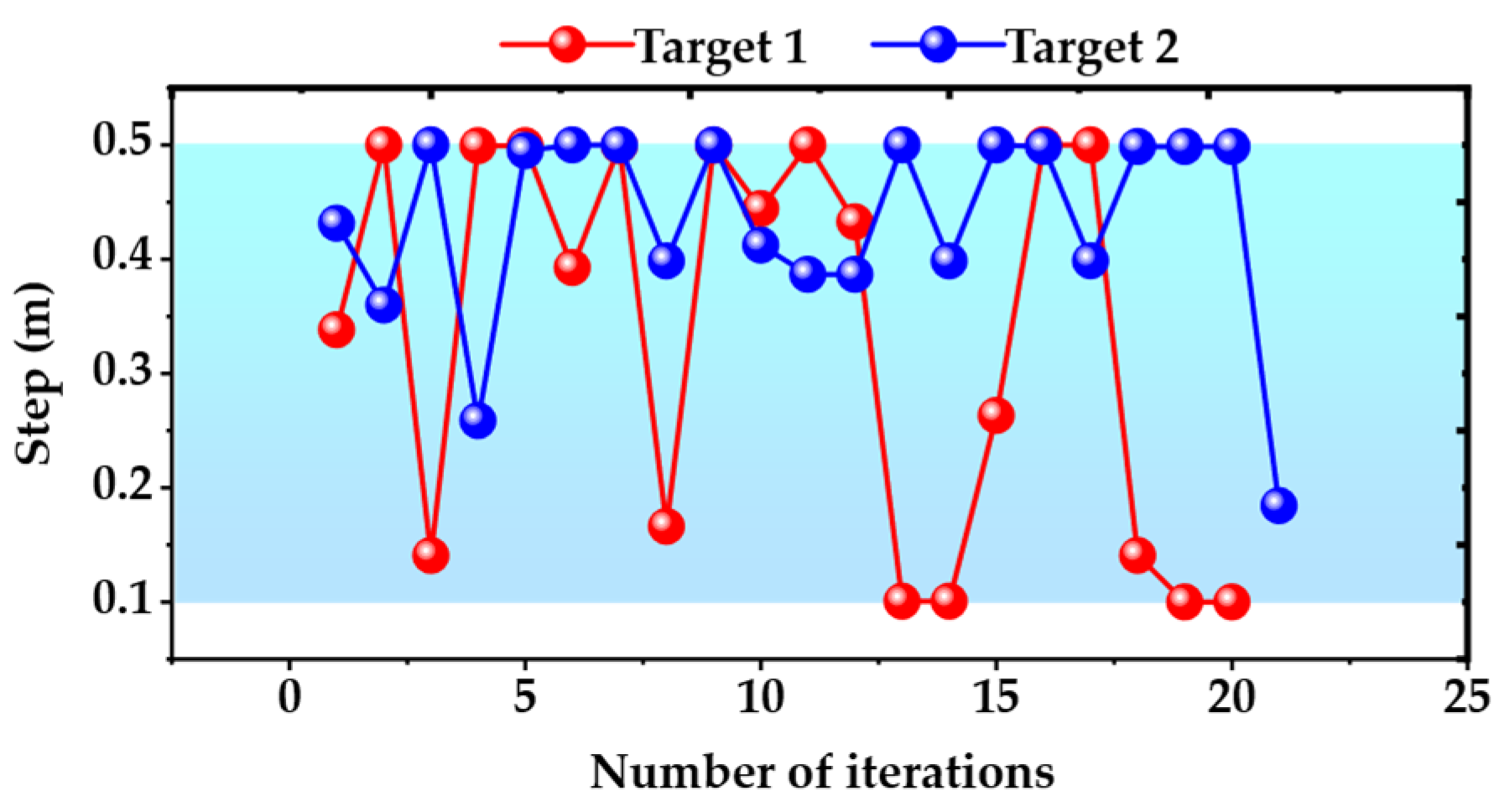
Figure 13.
The height difference between the path points and the ground.
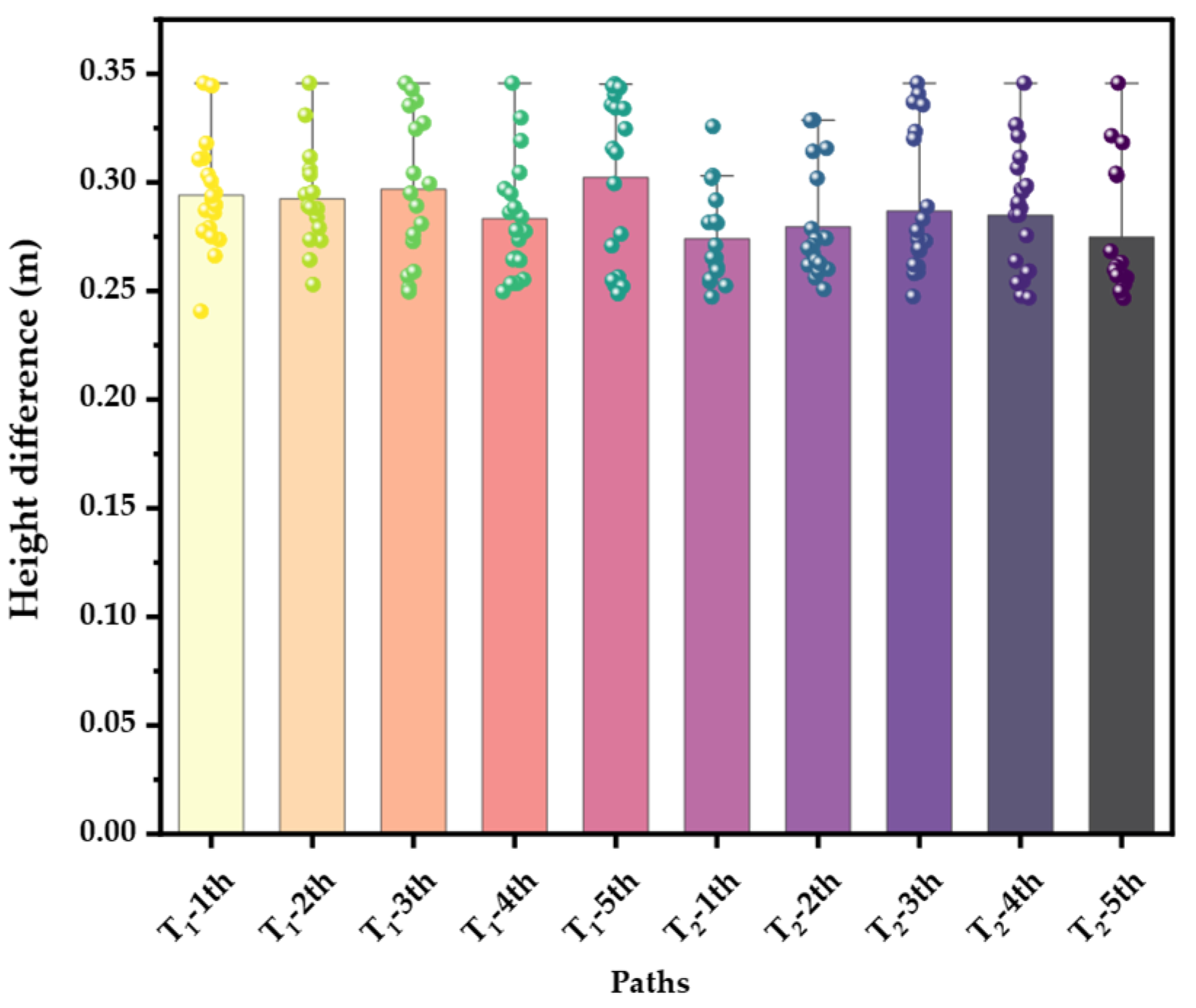
Figure 14.
Dynamic obstacle avoidance. (a) potential collision area prediction; (b) the local path planning results of the improved DWA and traditional DWA algorithm. The green paths represent the refined global path points. The red and blue paths represent the planning results of the improved DWA and traditional DWA algorithms, respectively. The paths in the cyan box are the dynamic obstacle avoidance process.
Figure 14.
Dynamic obstacle avoidance. (a) potential collision area prediction; (b) the local path planning results of the improved DWA and traditional DWA algorithm. The green paths represent the refined global path points. The red and blue paths represent the planning results of the improved DWA and traditional DWA algorithms, respectively. The paths in the cyan box are the dynamic obstacle avoidance process.

Figure 15.
The velocity planning results of the improved DWA and traditional DWA algorithm. Only the linear velocity of the body in X and Y directions, and the angular velocity around Z axis are compared. (a), (b), and (c) are for obstacle 1; (d), (e), and (f) are for obstacle 2.
Figure 15.
The velocity planning results of the improved DWA and traditional DWA algorithm. Only the linear velocity of the body in X and Y directions, and the angular velocity around Z axis are compared. (a), (b), and (c) are for obstacle 1; (d), (e), and (f) are for obstacle 2.
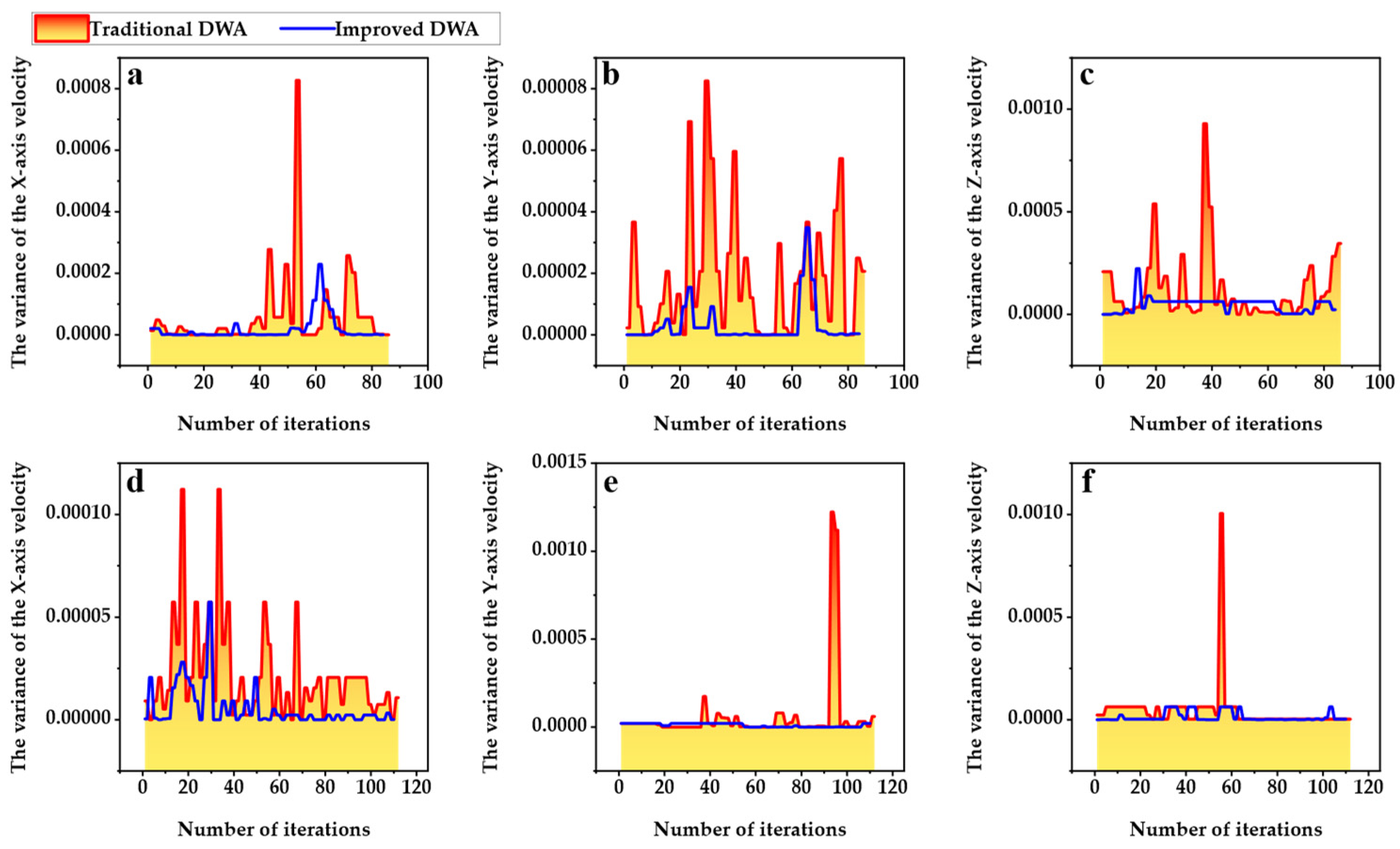
Figure 16.
The cost time of evaluation function calculation with CUDA and CPU.
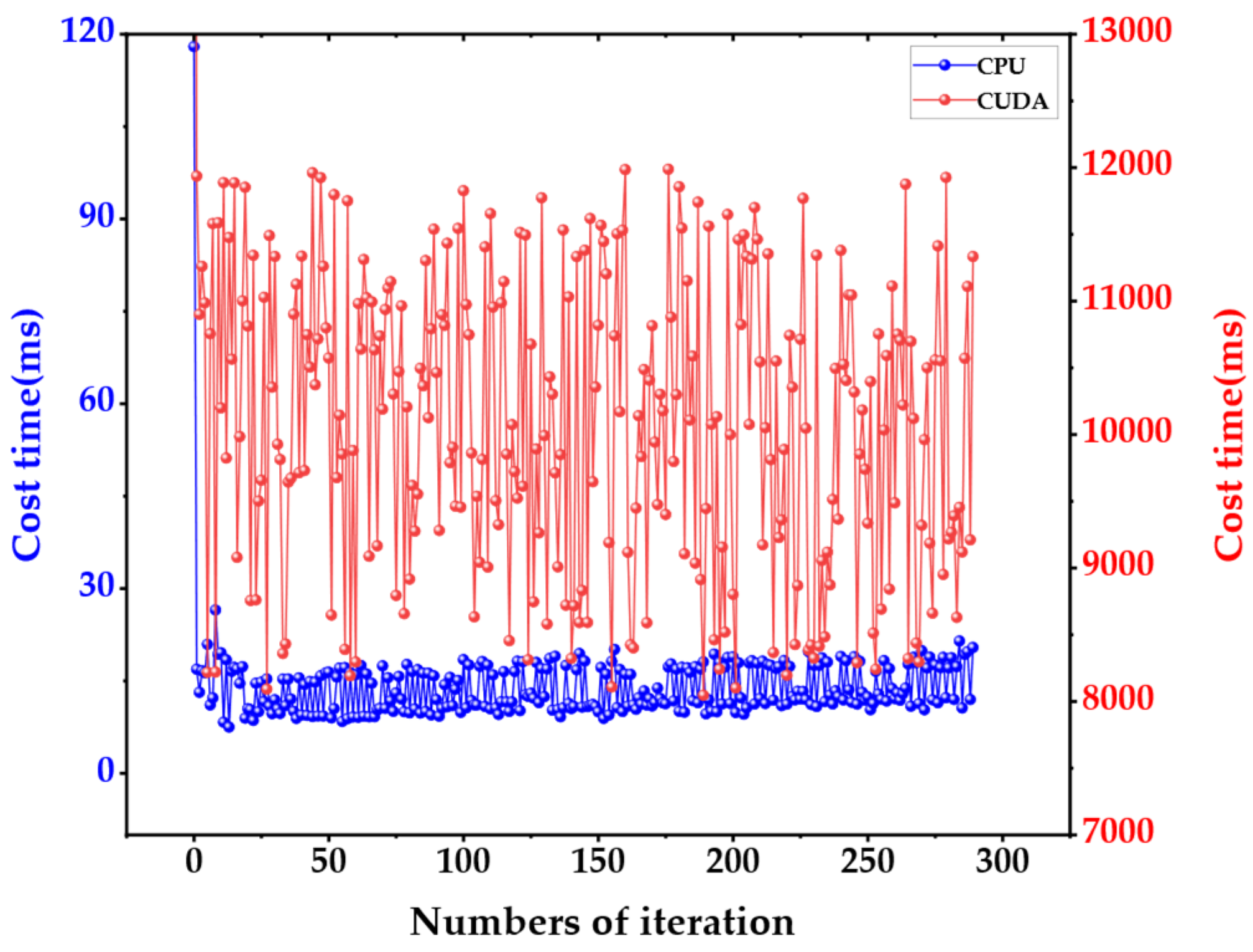
Table 1.
The range of parameters to be optimized of PSO-based 3D APF.
| Symbol | Range | Symbol | Range |
|---|---|---|---|
| n | |||
| step |
Table 2.
The fixed parameters of PSO algorithm and global path planning.
| Symbol | Value | Symbol | Value |
|---|---|---|---|
| 0.6 | 1.2m | ||
| 1.49455 | -0.12m | ||
| 1.49455 | -0.5m | ||
| 1.5m | -0.25m | ||
| 0.3m | -0.35m |
Table 3.
Quantitative comparison of PSO-based 3D APF performance under different parameters settings.
Table 3.
Quantitative comparison of PSO-based 3D APF performance under different parameters settings.
| Target | [α1, α2, α3] | Path Smoothness | Terrain Complexity | Number of iterations |
||
|---|---|---|---|---|---|---|
| Mean | Max | Mean | Max | |||
| [1, 0, 0] | 0.08286 | 0.31429 | 0.01125 | 0.02898 | 16 | |
| [1, 5, 0] | 0.02225 | 0.08126 | 0.00915 | 0.02359 | 16 | |
| [1, 0, 50] | 0.04948 | 0.29854 | 0.00612 | 0.01385 | 19 | |
| [1, 5, 50] | 0.01696 | 0.06698 | 0.00627 | 0.01456 | 20 | |
| [1, 0, 0] | 0.08444 | 0.48541 | 0.0096 | 0.02268 | 17 | |
| [1, 5, 0] | 0.00894 | 0.09857 | 0.01114 | 0.02531 | 19 | |
| [1, 0, 50] | 0.05536 | 0.41764 | 0.00562 | 0.01366 | 21 | |
| [1, 5, 50] | 0.00985 | 0.11690 | 0.00639 | 0.01646 | 21 | |
Table 4.
The effective step ratio
| Target | Step | iter | σ | |
|---|---|---|---|---|
| Fixed step (reference [30]) |
0.1 | 103 | 1.41 | |
| 0.2 | 43 | 2.31 | ||
| 0.3 | 32 | 1.67 | ||
| 0.4 | 27 | 1.25 | ||
| 0.5 | 30 | 0.67 | ||
| Dynamic step(this article) | Varies in [0.1~0.5] | 20 | 9 | |
| Fixed step (reference [30]) |
0.1 | 121 | 1.36 | |
| 0.2 | 51 | 2.19 | ||
| 0.3 | 37 | 1.64 | ||
| 0.4 | 32 | 1.21 | ||
| 0.5 | 47 | 0.43 | ||
| Dynamic step(this article) | Varies in [0.1~0.5] | 21 | 3.2 |
Table 5.
The motion parameters of the quadruped robot.
| Symbol | Representation | Value |
|---|---|---|
| Minimum linear velocity (X-Y-Z) | m/s | |
| Maximum linear velocity (X-Y-Z) | m/s | |
| Maximum linear acceleration (X-Y-Z) | 0.3 m/s2 | |
| Minimum angular velocity (Z) | -0.5235 rad/s | |
| Maximum angular velocity (Z) | 0.5235 rad/s | |
| Maximum angular acceleration (Z) | 0.5235 rad/s2 |
Table 6.
The comparative results of the improved DWA and traditional algorithms. The field All represents the velocity variance of the combined velocity containing the Z-axis linear velocity.
Table 6.
The comparative results of the improved DWA and traditional algorithms. The field All represents the velocity variance of the combined velocity containing the Z-axis linear velocity.
| Mean of velocity variance | Path length(m) | ||||
|---|---|---|---|---|---|
| X-axis | Y-axis | Yaw | All | ||
| traditional-obs1 | 2.514 | ||||
| improved-obs1 | 2.021 | ||||
| traditional-obs2 | 2.327 | ||||
| improved-obs2 | 1.834 | ||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
MDPI Initiatives
Important Links
© 2024 MDPI (Basel, Switzerland) unless otherwise stated








