Prerpints.org logo
Preprint
Article

Influence of Specimen Size on Compressive Strength of Wood

Altmetrics

Downloads

88

Views

57

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

29 February 2024

Posted:

01 March 2024

You are already at the latest version

Alerts
Abstract
This study investigates the impact of specimen size on the mechanical properties of wood, specifically focusing on compression strength, elastic modulus, and Poisson's ratio. Compression tests were conducted using three different specimen sizes (20mm×20mm×30mm, 40mm×40mm×60mm, 60mm×90mm×90mm) in the longitudinal, radial, and tangential directions. Mechanical parameters, failure mechanisms, load-displacement curves, and stress-strain relationships were systematically analyzed for each size. The study also evaluated the influence of specimen size on the accuracy of finite element numerical simulations by utilizing the obtained mechanical parameters. The results reveal a significant correlation between compressive strength and specimen size, indicating a decrease in compressive strength with increasing specimen size. Conversely, elastic modulus and Poisson's ratio exhibit less sensitivity to variations in specimen size. Notably, parameters derived from small-sized specimens (20mm×20mm×30mm) exhibited substantial errors, while those obtained from medium-sized (40mm×40mm×60mm) and large-sized specimens (60mm×90mm×90mm) demonstrated greater reliability, providing precise results in finite element numerical simulations.
Keywords: 
Subject: Engineering  -   Civil Engineering

1. Introduction

In recent years, escalating concerns about environmental sustainability have spurred increased interest in sustainable materials for structural applications. The choice of structural materials significantly influences the global environment, particularly in terms of the greenhouse effect. 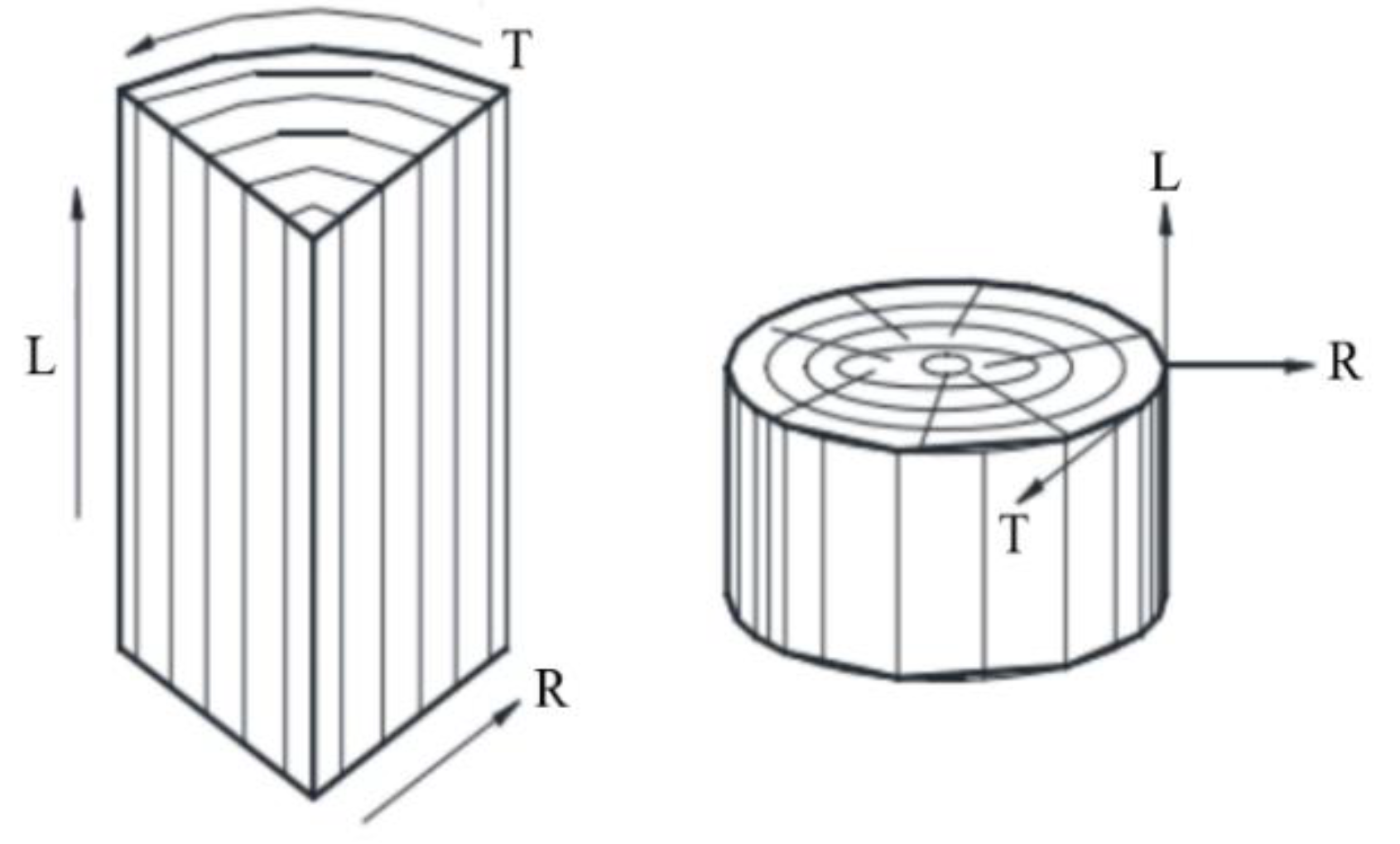Wood, with its ability to absorb carbon dioxide from the atmosphere, is increasingly recognized as a natural and eco-friendly building material within the construction industry [1]. However, unlike isotropic materials such as steel, wood exhibits anisotropic properties in the longitudinal (L), radial (R), and tangential (T) directions [2]. This characteristic necessitates the consideration of a greater number of physical and mechanical parameters during numerical simulations, calculations, and analysis. Consequently, the exploration of wood’s mechanical properties, the development of strength criteria, and the establishment of constitutive models have garnered attention from numerous researchers [3,4]. Despite extensive research on the mechanical behavior of wood, the fundamental step of acquiring basic physical and mechanical properties remains crucial [5]. Wood, influenced by its growth patterns, is inherently porous and non-uniform. Various physical and mechanical properties of wood are susceptible to change due to factors such as tree species, age, distance from the heartwood, and the direction of applied force [6]. Therefore, obtaining accurate physical and mechanical parameters for wood is of significant importance for a deeper understanding and rational utilization of this versatile material.
In the Chinese standard, the acquisition of compressive strength and physical-mechanical parameters of wood predominantly adheres to established technical regulations [7,8,9]. These regulations prescribe the use of test specimens with dimensions of 30mm×20mm×20mm. It is noteworthy that researchers both in China and internationally have employed varying specimen sizes in their studies on wood structures. For instance, Mascia N. T. et al. [10] utilized 5mm×5mm×5mm specimens to investigate the influence of the elastic modulus on the mechanical properties of wood. Li L. et al. [11] employed specimens measuring 21mm×14mm×14mm to determine the radial and tangential elastic modulus of pine wood. In the examination of the bending performance of glued laminated timber beams reinforced with FRP, specimens sized at 100mm×35mm×35mm were utilized to obtain the compressive performance parameters of wood. Yang Na et al. [12] conducted axial compressive tests on red pine wood using prism specimens measuring 40mm×20mm×20mm to determine the elastic constants of red pine wood while exploring non-linear constitutive models for wood under compression. Additionally, Yue Kong et al. [13] investigated the influence of temperature on wood compressive strength using specimens sized at 60mm×20mm×20mm. While researchers domestically and internationally have employed diverse specimen sizes in their experiments and research, the current standard specimen size of 30mm×20mm×20mm, as specified by testing methods and technical regulations, may not adequately consider the influence of growth patterns and annual ring variations. It is known that the compressive strength of concrete changes based on specimen sizes and shapes [14]. Although the influence of specimen size on the compressive strength of concrete has been extensively studied [15,16,17,18,19], the mechanical parameter, such as the compressive strength of wood, influenced by specimen sizes, has not been thoroughly investigated. Issues related to strength in different directions concerning the growth ring in the cross-section have garnered attention [20,21,22,23,24]. 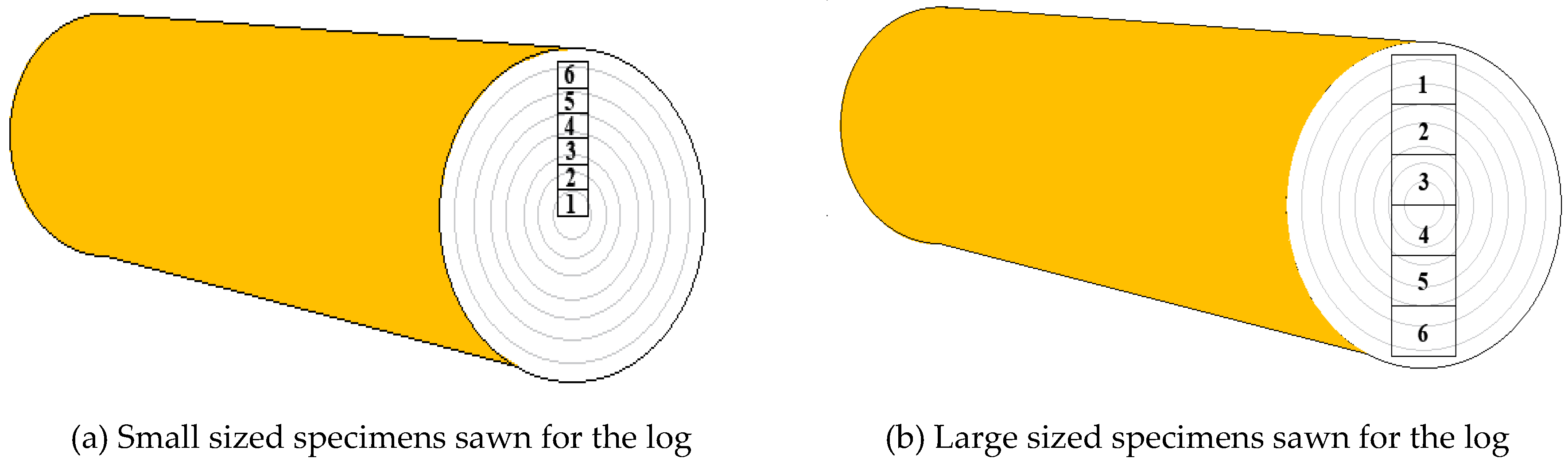Figure 1 illustrates that the dimensions of the specimen’s cross-sectional side, when sawn along the lag, are approximately the same as the width of one annual ring, as shown in Figure 1(a). Conversely, if the specimens are sawn in the manner, the dimension of the cross-sectional side is approximately the same as the width of 2-3 annual rings, as shown in Figure 1(b). Evidently, the size of the compression specimens will also impact the compressive strength parameter values of the wood.
To address these concerns, this experiment aims to investigate the impact of specimen size on the compressive strength parameter of wood. The objective is to discern variations in the mechanical properties of wood obtained from specimens of different sizes and to understand how specimen size influences the mechanical parameters of wood. To establish a comprehensive understanding of the relationship between specimen size and wood mechanical properties, a constitutive model expressing the stress-strain relationship was developed based on the experimental data. Subsequently, finite element numerical simulations were employed to further explore the influence of specimen size on the compressive strength parameter of wood. The outcomes of these experiments and simulations provide insights into the significance of considering specimen size when evaluating the physical and mechanical parameters of wood. The results suggest that specimen size indeed impacts the compressive strength parameters of wood, indicating the potential presence of size effects.

2. Test Program

2.1. Experimental Design

To investigate the influence of specimen size on the compressive strength of wood, three sets of experiments were meticulously planned. Each set focused on assessing the impact of specimen size on the longitudinal, radial, and tangential compressive strength of camphor wood, with all specimens sourced from the same origin. The camphor wood was precisely sawn following the diagram in Figure 2 and subsequently subjected to oven drying to achieve the required moisture content for testing, set at 12%, which was designed according to ASTM D143-09[7] and Hoffmeyer [8].
According to GB/T 1935-2009 [8] and GB/T 1939-2009 [9], basic specimens measuring 20mm×20mm×30mm (small-sized specimens) were obtained in the longitudinal, radial, and tangential directions. Subsequently, specimens of sizes 40mm×40mm×60mm (medium-sized specimens) and 60mm × 90mm × 90mm (large-sized specimens) were procured, maintaining a proportional ratio of 1:2:3 in dimensions. Six specimens were prepared for each direction and size, resulting in a total of 54 specimens.

2.2. Loading and Measurement Plan

The compressive strength tests were carried out utilizing a 30-ton universal testing machine, applying a loading rate of 2mm/min [22]. Axial load and displacement were monitored using pressure sensors and displacement gauges. Strain gauges were affixed to both the axial and lateral surfaces of the specimens in the longitudinal, radial, and tangential directions to record strain during testing, as shown in Figure 3. This data was collected to explore how specimen size influences parameters such as wood elastic modulus and Poisson’s ratio.

3. Experimental Results

3.1. Experimental Phenomenon

The compressive strength experiments unveiled the influence of specimen size on failure patterns in the longitudinal, radial, and tangential directions. In longitudinal tests, both small-sized (20mm × 20mm × 30mm) and medium-sized (40mm × 40mm × 60mm) specimens displayed transverse cracks in the central part under increasing load, followed by lateral movement before ultimate failure. Large-sized specimens (60mm × 90mm × 90mm) exhibited the formation of two diagonal cracks that intersected, resulting in vertical cracks at the intersection point, leading to ultimate failure.
Radial tests with small-sized specimens showed failure due to fiber misalignment, resulting in cracks perpendicular to the radial direction and shear failure. Medium-sized and large-sized specimens primarily developed cracks perpendicular to the growth rings, leading to a typical compression failure mode.
In the tangential compressive strength tests, all three specimen sizes encountered failure at the growth ring boundary in the specimen center. Initially, small cracks emerged, and as the load increased, these cracks propagated along the growth rings, causing the specimen to break into blocks. Larger specimens exhibited a more pronounced block formation, with an increased number of blocks displaying a buckling state. Moreover, significant variations in failure modes were observed based on specimen direction. In longitudinal specimens, fine transverse cracks initially formed perpendicular to the grain direction. These cracks gradually expanded as the load increased, spanning the entire surface and leading to failure, as shown in Figure 4. Conversely, radial specimens exhibited an initial formation of small cracks perpendicular to the growth rings, which expanded into larger cracks spanning the entire surface with increased displacement, resulting in specimen separation and failure, as shown in Figure 5. Tangential specimens demonstrated a distinct failure mode compared to the other two directions. The first crack formed along the growth rings, followed by the gradual formation of second and third cracks along the growth rings. These cracks progressively separated into individual blocks, and ultimately, failure occurred as each block buckled, as shown in Figure 6.

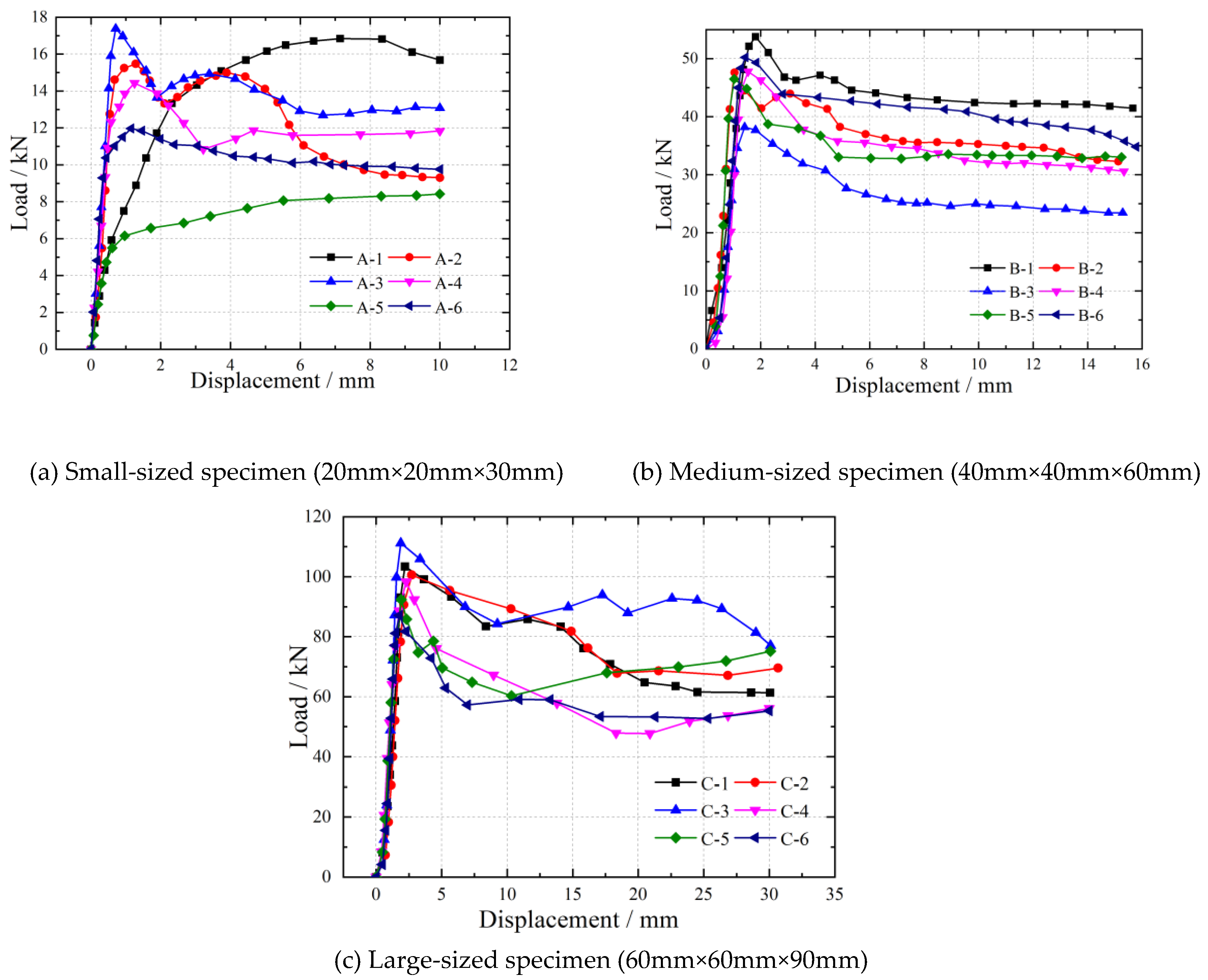
3.2. Load-Displacement Curve

The load-displacement relationship curves for wood specimens in the longitudinal, radial, and tangential directions have been obtained and presented in Figure 7 (longitudinal load-displacement curve), Figure 8 (radial load-displacement curve), and Figure 9 (tangential load-displacement curve).
Distinct characteristics are evident in the load-displacement relationship curves for the longitudinal, radial, and tangential specimens. Notably, the longitudinal compression specimen’s load-displacement curve deviates significantly from those of the radial and tangential specimens. The load-displacement relationship curve for the longitudinal compression specimen can be roughly divided into three stages. In the initial loading stage, it demonstrates linear elastic behavior with a steep slope, indicating a substantial linear increase in load with displacement. As the load continues to rise, a degree of nonlinearity becomes apparent, accompanied by the development of small cracks in the specimen, and the curve’s slope gradually decreases. Subsequently, the ultimate load is reached, initiating a descending stage. Due to wood’s relatively high residual strength, the curve can still maintain a horizontal or slowly decreasing trend.
For the tangential and radial compression specimens, the load-displacement curves also exhibit three distinct stages. Initially, there is an initial linear elastic stage characterized by a steep slope, indicating a significant increase in load with displacement. Following the elastic stage, a plastic development stage is observed, where the load increases at a slower rate with displacement, and the curve slope during this stage is smaller compared to the initial elastic stage. Finally, a strengthening stage follows, where the slope of the curve increases compared to the plastic stage, suggesting that the material is becoming stronger as the load is applied. However, beyond a certain point, the load suddenly decreases after reaching the peak load.
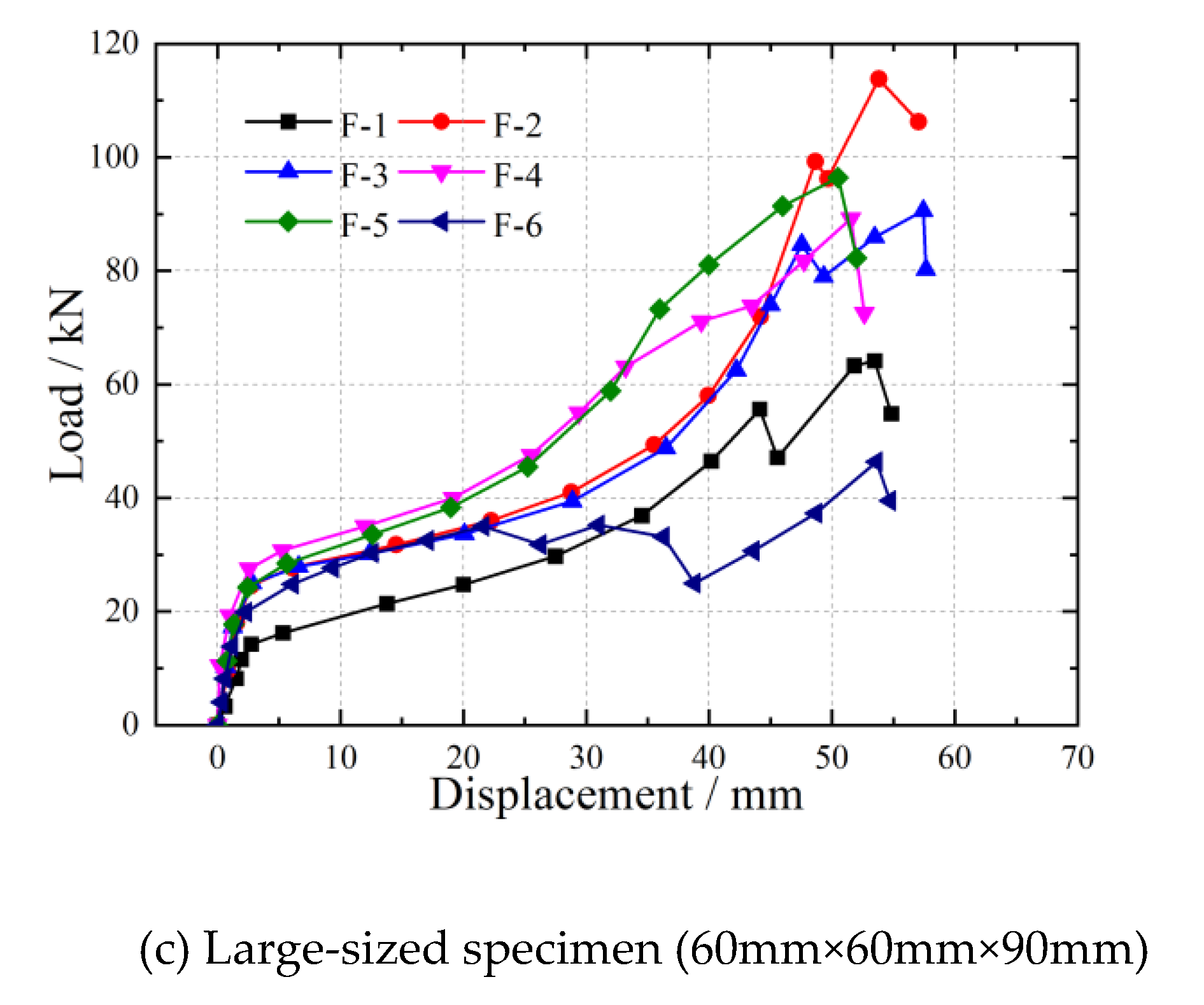
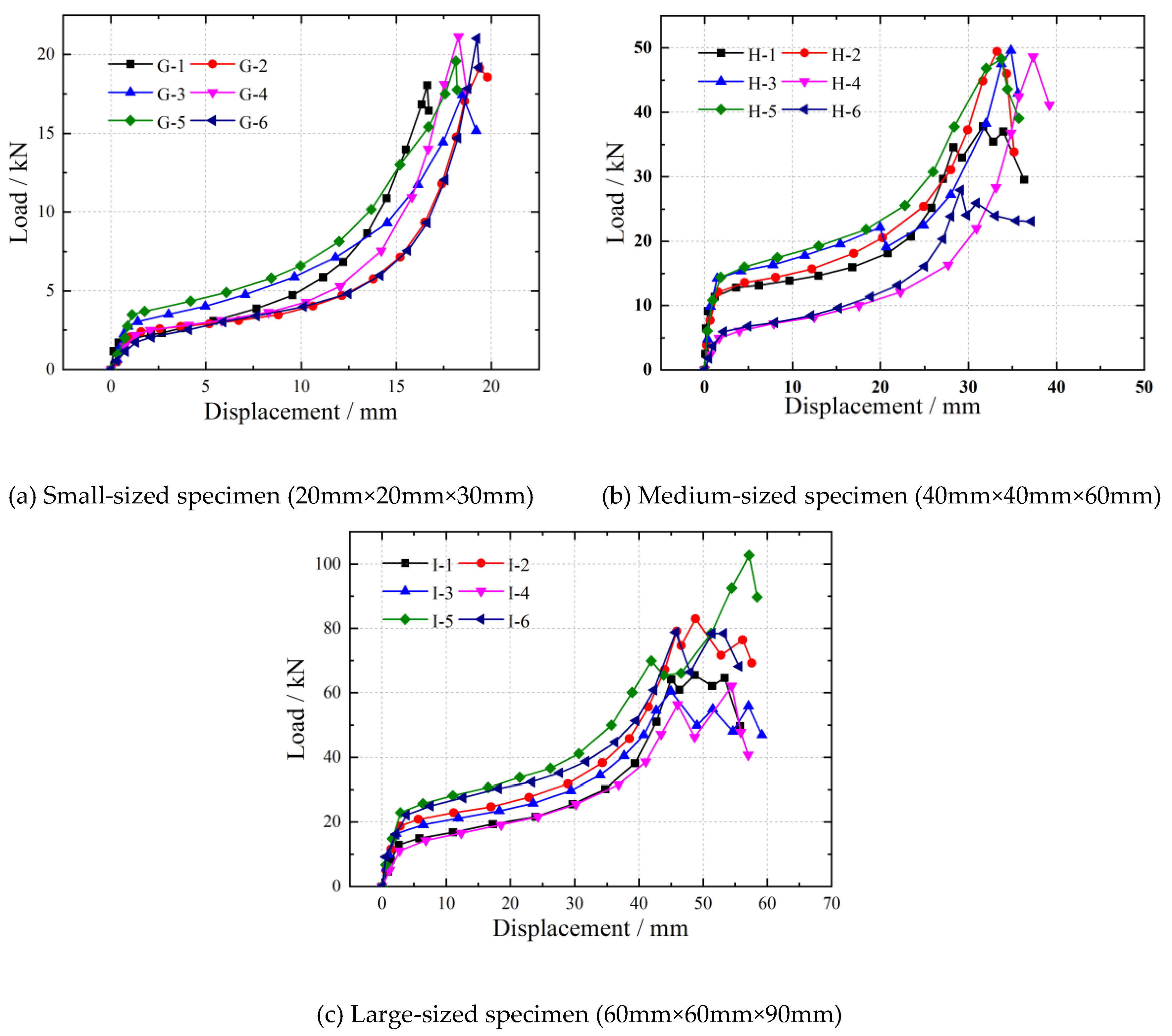
Upon analyzing the load-displacement curves of longitudinal and radial specimens of different sizes, it becomes apparent that conducting compression tests using small and large specimens results in more scattered load-displacement curves compared to tests with medium-sized specimens. The load-displacement curves for tangential compression tests of different sizes show that the curves tend to be consistent for small, medium, and large specimens, with medium-sized specimens showing a slight degree of variability, although not very pronounced. This variation may be attributed to individual differences in the specimens. However, considering the load-displacement curve characteristics in all three directions, the specimen size has an impact on the load-displacement relationship curves in compression strength tests, with the load-displacement curves obtained from medium-sized specimens being relatively reasonable.

3.3. Compressive Strength

Based on the experimental tests, data regarding the longitudinal, radial, and tangential compression strength parameters of wood specimens with varying sizes have been compiled. This data encompasses measurements of compressive strength, elastic modulus, and Poisson’s ratio. The organized data is presented in Table 1, Table 2 and Table 3, respectively.
Table 1 provides information on the average compressive strength values for longitudinal wood, revealing a noticeable decrease as specimen size increases. Furthermore, the data variability suggests that larger specimens exhibit smaller coefficients of variation, indicating that the longitudinal compressive strength values obtained from larger specimens are more stable and reliable than those from smaller specimens. The elastic modulus also shows a trend of decreasing values with increasing specimen size. However, the impact of specimen size on Poisson’s ratios μLT and μRT is not very pronounced.

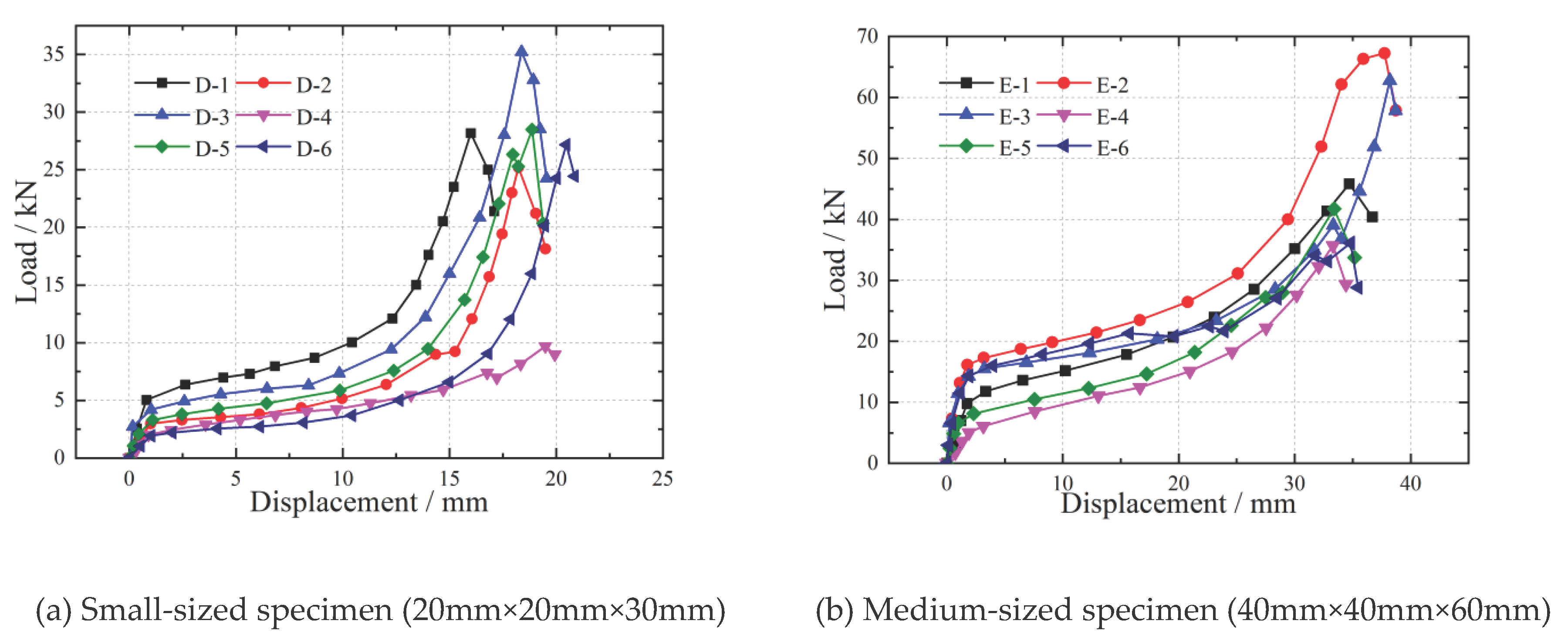
3.4. Stress-Strain Curve

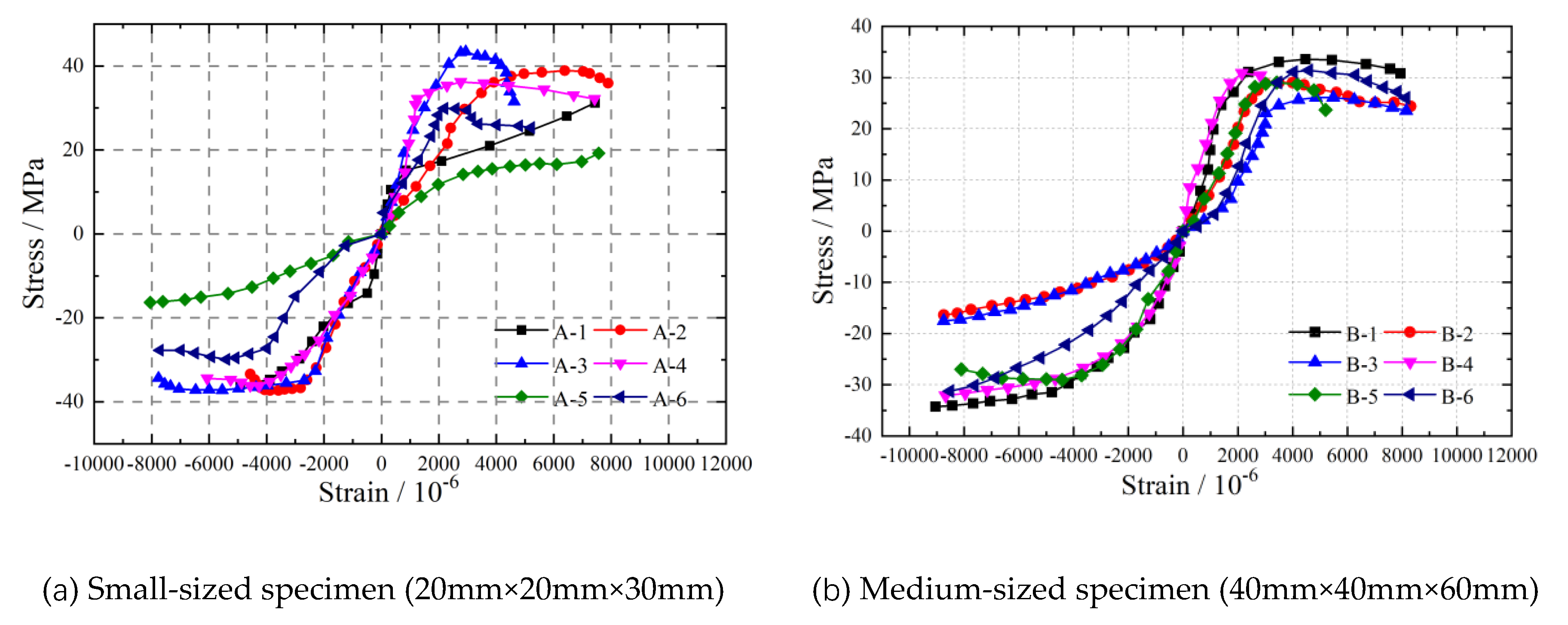
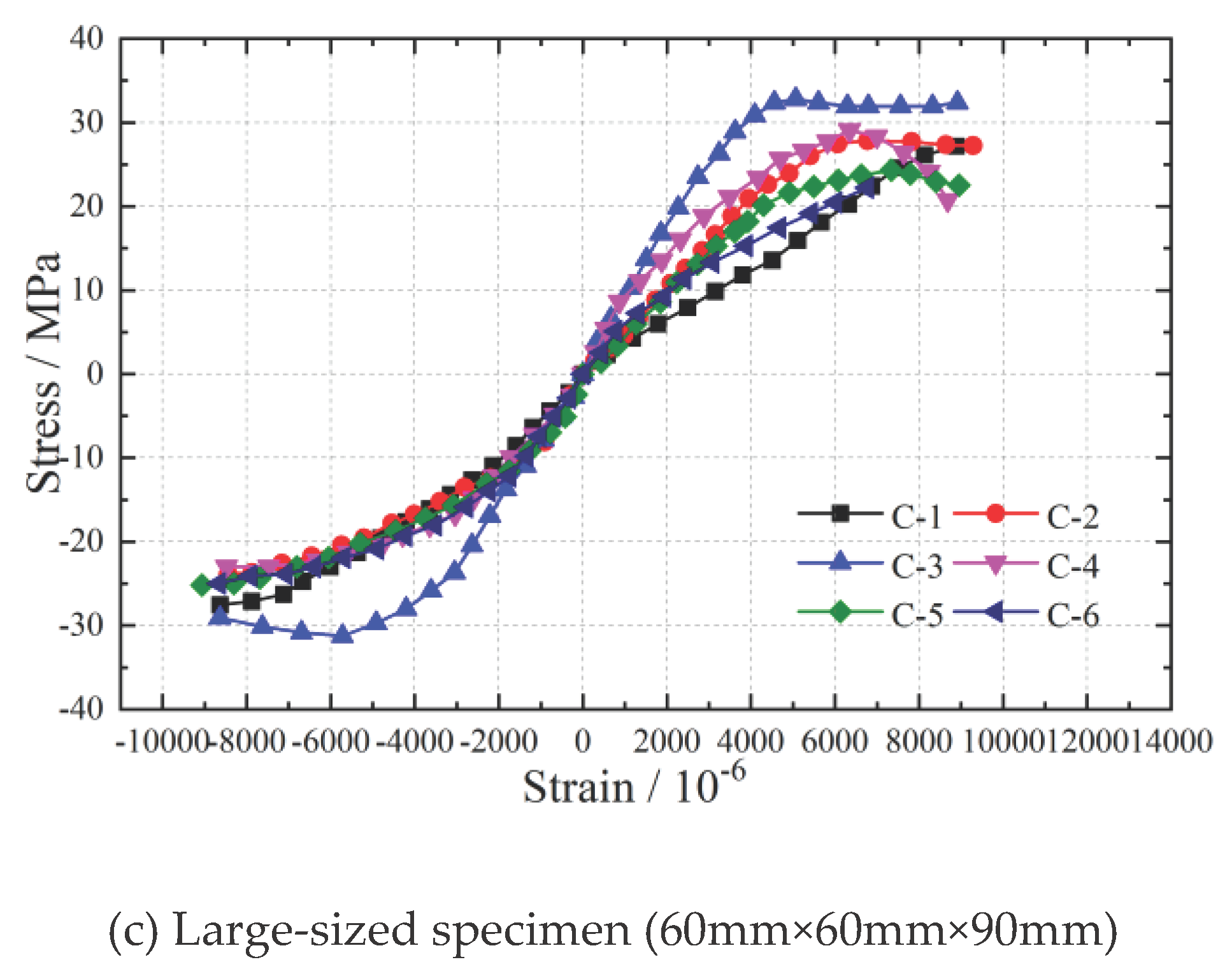
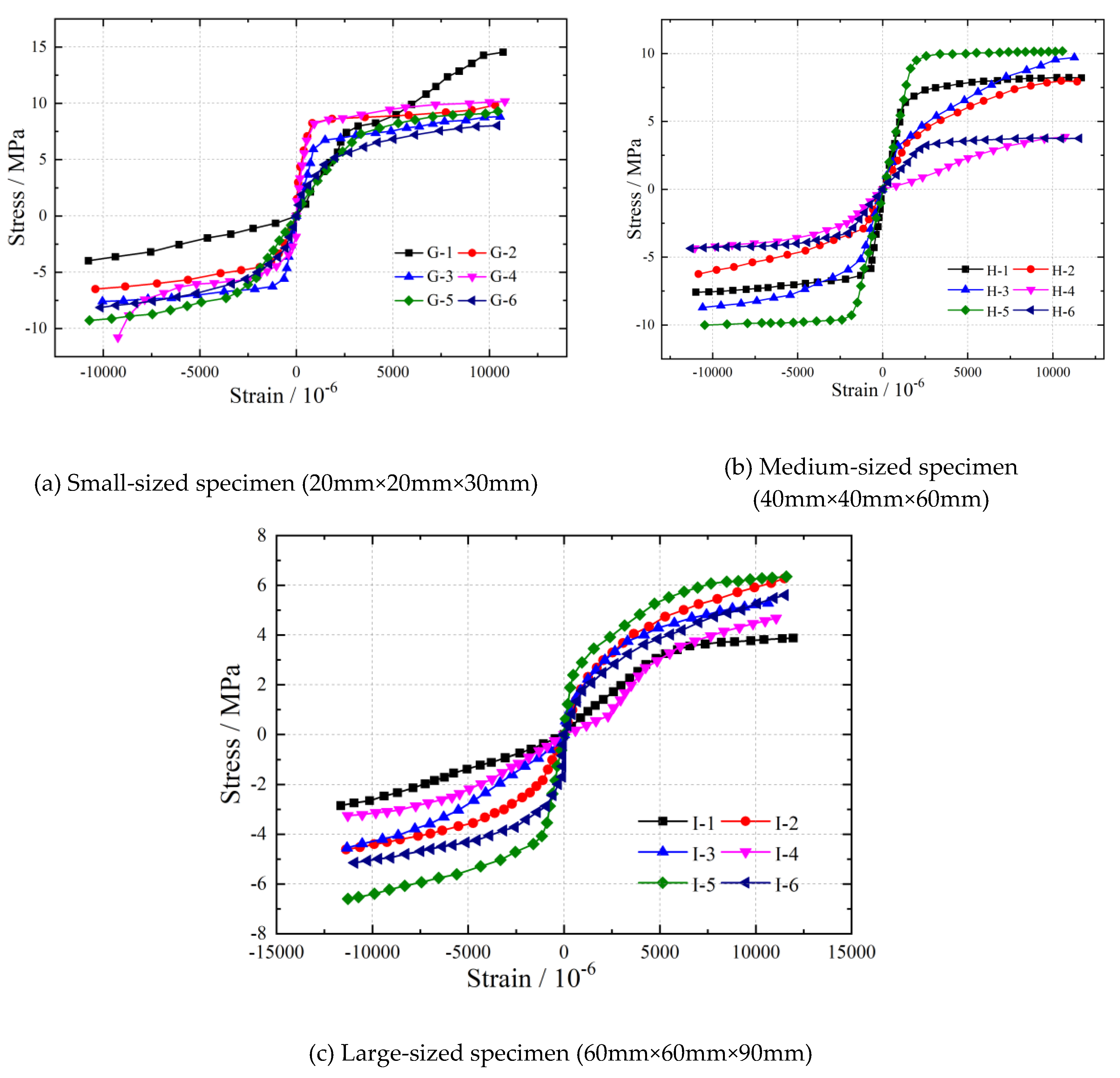
Figure 10, Figure 11 and Figure 12 depict stress-strain relationship curves for specimens of different sizes in the longitudinal, radial, and chord directions. These curves highlight similar trends in the stress-strain behavior of wood specimens in these three directions. Initially, in the elastic phase, all curves exhibit a linear increase in stress with strain. However, as the specimen’s transition into the plastic phase, the stress-strain relationship becomes nonlinear. The stress-strain curves for longitudinal compression, as shown in Figure 10, indicate that as the specimen size increases, the stress-strain curves of all six specimens gradually converge. This convergence suggests that smaller specimens yield more variable experimental results. Similarly, the stress-strain relationships for radial and tangential compression, as presented in Figure 11 and Figure 12, demonstrate comparable trends. This observation emphasizes that specimen size plays a role in influencing the establishment of stress-strain relationships (constitutive models) for wood under compression.
Preprints 100191 g010aPreprints 100191 g010b
Figure 10. Stress-strain curve of longitudinal specimens.
Figure 10. Stress-strain curve of longitudinal specimens.
Preprints 100191 g010aPreprints 100191 g010b
Preprints 100191 g011
Figure 11. Stress-strain curve of radial specimens.
Figure 11. Stress-strain curve of radial specimens.
Preprints 100191 g011
Preprints 100191 g012
Figure 12. Stress-strain curve of tangential specimens.
Figure 12. Stress-strain curve of tangential specimens.
Preprints 100191 g012
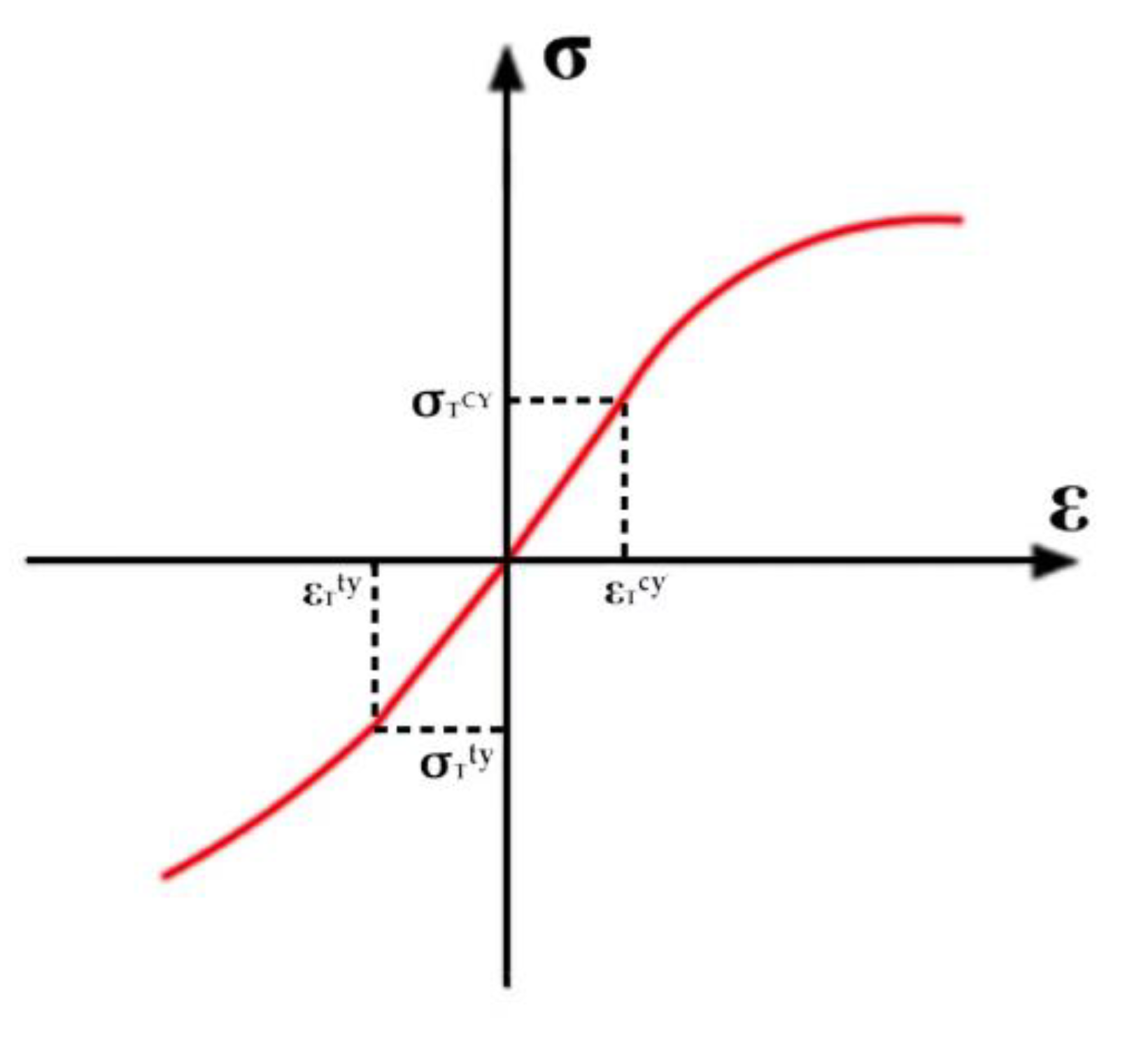
Preprints 100191 g013
Figure 13. Simplified stress-strain curve.
Figure 13. Simplified stress-strain curve.
Preprints 100191 g013
Table 4. Coefficient of the stress-strain curve of longitudinal compression specimens.
Table 4. Coefficient of the stress-strain curve of longitudinal compression specimens.
Coefficient Specimen size
Small-sized Medium-sized Large-sized
a 1 8168.2 1478.7 3572.6
b 1 1578.1 395.2 566.4
c 1 4.0 -7.1 -2.5
a 2 1197.7 913.9 791.3
b 2 -1.4 -0.9 -0.3
a 3 1745.2 1017.1 630.5
b 3 0.3 0.4 0.1
b 4 424.5 666.3 686.6
c 2 15.8 8.8 -0.1
εTty (×10−6) -1020 -1160 -870
εTcy (×10−6) 1140 2010 1120
Table 5. Coefficient of the stress-strain curve of radial compression specimens.
Table 5. Coefficient of the stress-strain curve of radial compression specimens.
Coefficient Specimen size
Small-sized Medium-sized Large-sized
a 1 401.2 491.2 195.9
b 1 158.4 77.1 51.3
c 1 -5.1 -3.2 -2.9
a 2 906.3 494.2 303.9
b 2 -0.9 -0.6 -1.0
a 3 529.3 233.3 213.6
b 3 3.1 0.6 1.1
b 4 -1598.4 -1709.1 -928.0
c 2 170.1 190.4 110.7
εTty (×10−6) 6.6 3.3 1.9
εTcy (×10−6) -560 -630 -730
Table 6. Coefficient of the stress-strain curve of tangential compression specimens.
Table 6. Coefficient of the stress-strain curve of tangential compression specimens.
Coefficient Specimen size
Small-sized Medium-sized Large-sized
a 1 310.4 376.8 289.9
b 1 77.3 64.4 56.9
c 1 -3.0 -3.8 -1.2
a 2 373.6 254.8 159.1
b 2 -0.6 -0.4 -0.3
a 3 600.6 184.1 158.6
b 3 0.8 0.6 -0.3
b 4 -1475.3 -4590.2 -418.6
c 2 166.1 202.5 80.3
εTty (×10-6) 3.8 3.3 1.0
εTcy (×10-6) -800 -720 -850

4. Finite Element Analysis

4.1. Finite Element Model

To illustrate the impact of specimen size on obtaining effective compression strength parameters, finite element numerical simulations were conducted using ABAQUS software. Longitudinal, radial, and tangential specimens of three different sizes were modeled in the simulations. The finite element models employed 8-node solid C3D8R elements for meshing, and isotropic elastic constitutive models were applied in the elastic phase. Input physical properties from experiments and established stress-strain relationships (constitutive models) were used to define the material behavior. In the plastic phase, Hill’s yield criterion was utilized to simulate anisotropic mechanical behavior once the internal stresses exceeded material strength [18]. Furthermore, to ensure consistent results with the experiments, the displacement in the finite element models was simulated to match the experimental displacements.

4.2. Finite Element Analysis of Results

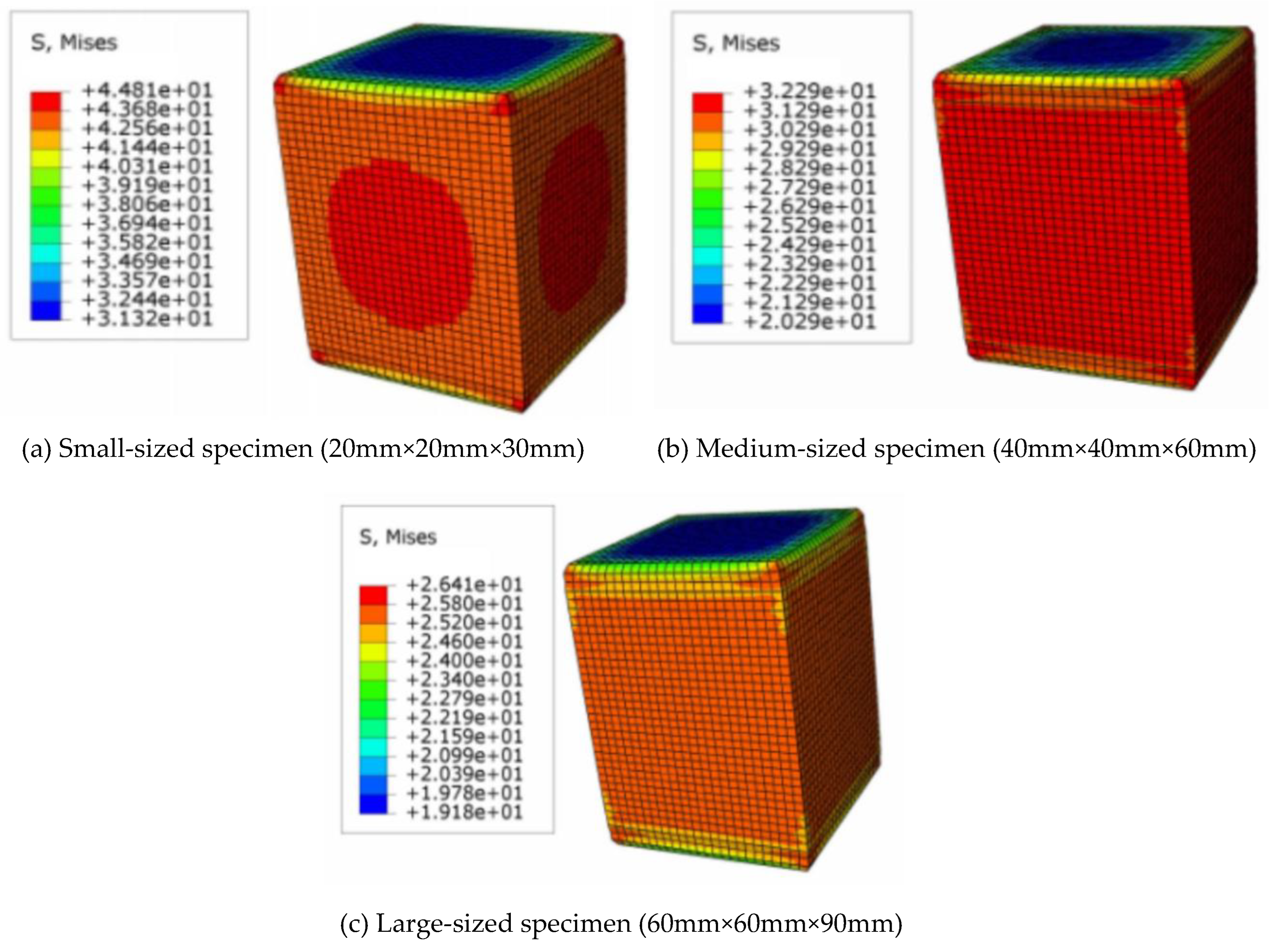
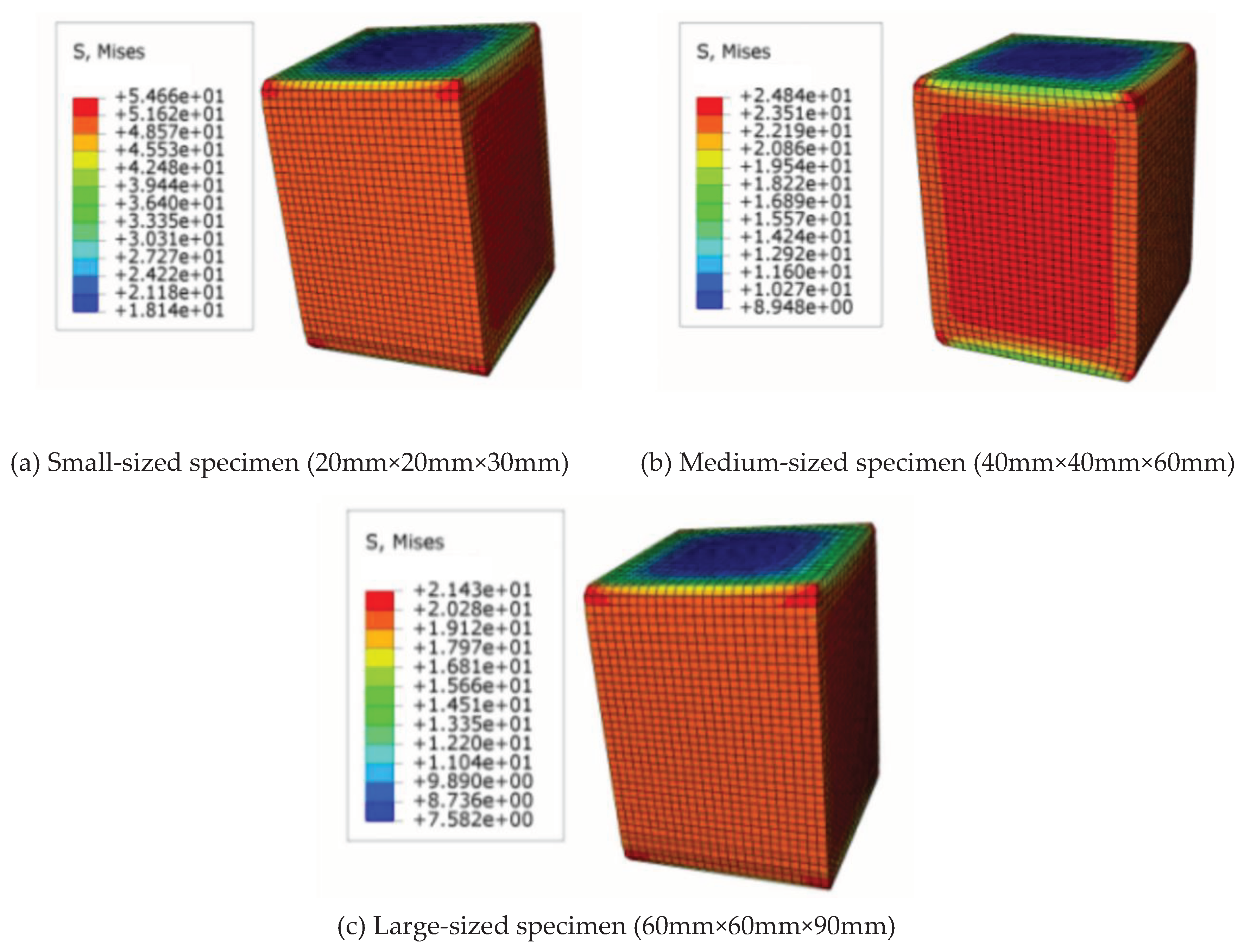
The finite element numerical simulations utilized a computational approach to derive stress results for specimens of varying sizes in the longitudinal, radial, and tangential directions. These computational results, closely aligned with the experimental findings, were significant in understanding the stress behavior of the wood specimens. Stress distribution maps for these specimens are shown in Figure 14 and Figure 15.
Table 7 indicates the results of stress of numerical simulation compare with the results of stress of tests. As shown in Table 7, the discrepancy between stress values obtained through numerical simulations and experimental measurements increases as specimen size decreases, with errors exceeding 15%, and tangential errors reaching 22.7%. Moderate-sized specimens and large-sized specimens exhibit good agreement between numerical simulation results and experimental data, with errors below 10%. In the case of moderate-sized specimens, the error is 9.1% for longitudinal specimens and less than 3% for radial and tangential specimens. The numerical simulation analysis also demonstrates that specimen size influences the accuracy of obtaining accurate mechanical properties for wood under compression. Small specimen sizes can result in significant errors.
In conclusion, the comparison between numerical simulations and experimental results underscores the significance of specimen size in compression strength testing for wood. The data strongly supports the recommendation of utilizing moderate-sized (40mm×40mm×60mm) and large-sized specimens (60mm×60mm×90mm) to achieve more accurate physical properties and constitutive models.

5. Conclusions

Through a series of compression tests on wood specimens in the longitudinal, radial, and tangential directions, this study aimed to establish comprehensive compression strength parameters and stress-strain relationships (constitutive models) for specimens of varying sizes. Following the experiments, finite element numerical simulations were employed to complement the experimental findings. The main conclusions are as follows:
  • The size of the wood specimens has a significant impact on obtaining reasonable and effective compression strength parameters, with the longitudinal specimens being the most affected. The use of the moderate-sized specimens proposed in this paper (40mm×40mm×60mm) and large-sized specimens (60mm×60mm×90mm) provides more reasonable compression strength parameters.
  • It is suggested that the specimen size can be the moderate-sized specimens proposed in this paper (40mm×40mm×60mm). While the current test methods and technical specifications use small-sized specimens (20mm×20mm×30mm) which only reflect the mechanical properties of wood within a single growth ring, leading to significant variability.
  • Using moderate-sized (40mm×40mm×60mm) camphorwood specimens, mechanical properties for longitudinal, radial, and tangential compression strength, stress-strain relationships (constitutive models) can be used in numerical simulations for camphorwood components and structures, providing more accurate computational results.

Author Contributions

Investigation, Writing—Data curation, C.Z.; Conceptualization, Investigation, Methodology & Writing D.L.; Conceptualization, Investigation, Writing—reviewing & editing, C.Z.; Experiment, Data curation, Y.W.; Investigation, Writing—reviewing & editing Y.L. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by the Sichuan Science and Technology Program (Grant No. 2019YJ0437), and National Natural Science Foundation of China (Grant No. 51868013, 51508482).

Data Availability Statement

The data presented in this study are available on request from the corresponding author. The data are not publicly available due to [Fund Requirements].

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Z. Li, M. He, X. Wang, et al. Seismic performance assessment of steel frame infilled with prefabricated wood shear walls. J Constr Steel Res. 140 (2018) 62-73. [CrossRef]
  2. J. Thamboo, S. Navaratnam, Poologanathan, Corradi. Experimental investigation of timber samples under triaxial compression condition. J Build Eng. 57 (2022) 104891. [CrossRef]
  3. M. Gharib, A. Hassanieh, H. Valipour, M A. Bradford. Three-dimensional constitutive modelling of arbitrarily orientated timber based on continuum damage mechanics. Finite Elem Anal Des. 135 (2017) 79-90. [CrossRef]
  4. H. Valipour, N. Khorsandnia, K. Crews, et al. A simple strategy for constitutive modelling of timber. Constr Build Mater. 53 (2014) 138-148. [CrossRef]
  5. M. Oudjene, M. Khelifa. Finite element modelling of wooden structures at large deformations and brittle failure prediction. Mater Design. 30 (2009) 4081–4087. [CrossRef]
  6. André, R. Kliger, L. Asp. Compression failure mechanism in small scale timber specimens. Constr Build Mater. 50 (2014) 130-139. [CrossRef]
  7. GB/T 1935-2009.Method of testing in compressive strength parallel to grain of wood. Ministry of Construction of the People’s Republic of China.
  8. GB/T 1939-2009.Method of testing in compressive strength perpendicular to grain of wood. Ministry of Construction of the People’s Republic of China.
  9. GB/T 50005-2017.Standard for Design of Timber Structure. Ministry of Housing and Urban-Rural Development of the People’s Republic of China.
  10. N T. Mascia, L. Vanalli. Evaluation of the coefficients of mutual influence of wood through off-axis compression tests. Constr Build Mater. 30 (2014) 522-528. [CrossRef]
  11. L. Li, M. Gong, Y H. Chui, et al. Measurement of the elastic parameters of densified balsam fir wood in the radial-tangential plane using a digital image correlation (DIC) method. J Mater Sci. 48 (2013) 7728–7735. [CrossRef]
  12. N. Yang, L. Zhang, S. Qin. A nonlinear constitutive model for characterizing wood under compressive load and its test verification. China Civil Engineering Journal. 50(4) (2017) 80-88.
  13. K. Yue, W. Liu, X. Cheng, et al. Experimental study on parallel-to-grain compressive strength of structural Douglas fir wood exposed to elevated temperatures. Journal of Huazhong University of science and technology (Natural science edition). 47(08) (2019) 44-49.
  14. H, F. H F. Gonnerman. Effect of size and shape of test specimen on compressive strength of concrete. 25 (2) (1925) 237-250.
  15. M. Issa, A. Issa, M. A, M. Islam, A. Chudnovsky. Size effects in concrete fracture-partⅡ: analysis of test results. Int J Fracture. 102(1) (2013) 5-42. [CrossRef]
  16. S T. Yi, E I. Yang, J C. Choi. Effect of specimen sizes, specimen shapes, and placement directions on compressive strength of concrete. Nucl Eng Des. 236(2) (1925) 115-127. [CrossRef]
  17. Y. Che, S. Ban, J. Cui, G. Chen, Y. Song. Effect of Specimen Shape and Size on Compressive Strength of Concrete. International Conference on Structures and Building Materials. 163-167 (2011) 375-1379. [CrossRef]
  18. M. Sandemir. Effect of specimen size and shape on compressive strength of concrete containing fly ash application of genetic programming for design. Mater Design.56 (2014) 297-304. [CrossRef]
  19. A. Abdullah. Effects of specimen sizes and loading rates on compressive strength of concrete. Matr Today Proc 46 (2021) 1783-1786. [CrossRef]
  20. S T. Akter, E. Serrano, T K. Bader. Numerical modelling of wood under combined loading of compression perpendicular to the grain and rolling shear. Eng Struct. 244 (2021) 112800. [CrossRef]
  21. E F. Rodrigues, C. De, V A. Araujo, et al. Influence of growth rings position of wood on the determination of its shear strength parallel to grain. J Mater res technol. 24 (2023) 9765-9779. [CrossRef]
  22. K Yue, X Li, X K Jiao, et al. Strength grading of Chinese poplar wood for structural use following thermal modification. Polymer Testing,123 (2023) 108032. [CrossRef]
  23. Y. Chen, C. Zhang. Stability analysis of pultruded basalt fiber-reinforced polymer (BFRP) tube under axial compression. Compos. Struct. 2024, 327, 117660. [CrossRef]
  24. C. Zhang; Y. Chen; Dou, M. Axial Compression Behaviour and Modelling of Pultruded Basalt-Fibre-Reinforced Polymer (BFRP) Tubes. Buildings 2023, 13, 1397. [CrossRef]
Preprints 100191 g001
Figure 1. Compressive strength specimens sawn form the log.
Figure 1. Compressive strength specimens sawn form the log.
Preprints 100191 g001
Preprints 100191 g002
Figure 2. Sawing of wood.
Figure 2. Sawing of wood.
Preprints 100191 g002
Preprints 100191 g003
Figure 3. Sticking of strain gauge.
Figure 3. Sticking of strain gauge.
Preprints 100191 g003
Preprints 100191 g004
Figure 4. Failure process of longitudinal specimens.
Figure 4. Failure process of longitudinal specimens.
Preprints 100191 g004
Preprints 100191 g005
Figure 5. Failure process of radial specimens.
Figure 5. Failure process of radial specimens.
Preprints 100191 g005
Preprints 100191 g006
Figure 6. Failure process of tangential specimens.
Figure 6. Failure process of tangential specimens.
Preprints 100191 g006
Preprints 100191 g007
Figure 7. Load-displacement curve of longitudinal specimens.
Figure 7. Load-displacement curve of longitudinal specimens.
Preprints 100191 g007
Preprints 100191 g008aPreprints 100191 g008b
Figure 8. Load-displacement curve of radial specimens.
Figure 8. Load-displacement curve of radial specimens.
Preprints 100191 g008aPreprints 100191 g008b
Preprints 100191 g009
Figure 9. Load-displacement curve of tangential specimens.
Figure 9. Load-displacement curve of tangential specimens.
Preprints 100191 g009
Preprints 100191 g014
Figure 14. Stress nephogram of radial specimens.
Figure 14. Stress nephogram of radial specimens.
Preprints 100191 g014
Preprints 100191 g015
Figure 15. Stress nephogram of longitudinal specimens.
Figure 15. Stress nephogram of longitudinal specimens.
Preprints 100191 g015
Table 1. Longitudinal compressive strength parameters.
Table 1. Longitudinal compressive strength parameters.
Specimen size Compressive strength/MPa Average compressive strength/MPa Elastic modulus
Small-sized 16.43 29.93 33.40
(0.281)		 E/MPa 11600
35.80 36.08 μLT 0.48
38.68 43.45 μLT 0.44
Medium-sized 23.88 29.05 29.59
(0.109)		 E/MPa 11010
29.86 31.39 μLT 0.49
29.76 33.61 μLT 0.48
Large-sized 24.19 25.66 27.48
(0.085)		 E/MPa 10040
27.48 27.94 μLT 0.48
28.72 30.89 μLT 0.42
Table 2. Radial compressive strength parameters.
Table 2. Radial compressive strength parameters.
Specimen size Compressive strength/MPa Average compressive strength/MPa Elastic modulus
Small-sized 4.88 5.18 6.03
(0.376)		 E/MPa 2390
6.85 5.43 μLT 0.65
8.73 5.13 μRT 0.11
Medium-sized 3.14 5.09 7.05
(0.382)		 E/MPa 2470
6.13 8.93 μRT 0.63
8.95 10.08 μRT 0.11
Large-sized 3.95 5.52 6.27
(0.212)		 E/MPa 2110
6.74 6.82 μRT 0.67
6.94 7.65 μRT 0.13
Table 3. Tangential compressive strength parameters.
Table 3. Tangential compressive strength parameters.
Specimen size Compressive strength/MPa Average compressive strength/MPa Elastic modulus
Small-sized 4.28 4.33 5.80
(0.296)		 E/MPa 1200
5.18 5.43 μTL 0.08
6.85 8.75 μTL 0.34
Medium-sized 3.11 3.73 6.57
(0.389)		 E/MPa 1380
7.11 7.57 μTL 0.06
8.89 8.99 μTL 0.37
Large-sized 3.06 3.58 4.81
(0.279)		 E/MPa 1220
4.54 5.19 μTL 0.06
6.16 6.35 μTL 0.35
Table 7. The results of stress of numerical simulation compare with the results of stress of tests.
Table 7. The results of stress of numerical simulation compare with the results of stress of tests.
Specimen Specimen direction Numerical simulation of maximum stress/MPa Test maximum stress/MPa Error
Small size longitudinal 44.81 38.60 16.1%
radial 54.66 65.80 17.0%
tangential 34.46 44.60 22.7%
Medium size longitudinal 32.29 29.60 9.1%
radial 24.84 25.36 2.1%
tangential 24.25 23.63 2.6%
Large size longitudinal 26.41 27.90 5.3%
radial 21.43 23.50 8.8%
tangential 22.80 21.78 4.7%
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated