Investigating the Impact of Topology and Physical Impairments on the Capacity of an Optical Backbone Network

Preprint

Article

Investigating the Impact of Topology and Physical Impairments on the Capacity of an Optical Backbone Network

Altmetrics

Downloads

Views

Comments

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

29 February 2024

Posted:

01 March 2024

You are already at the latest version

Alerts

Abstract

Optical backbone networks constitute the fundamental infrastructure employed today by network operators to deliver services to users. As network capacity is a key factor influencing optical network performance, it is important to understand how topological and physical properties impact its behavior and to have the capability to estimate its value. In this context, we propose here a method to evaluate the network capacity that relies on the optical reach to account for physical layer aspects, in conjunction with constrained routing techniques for traffic routing. As this type of routing can lead to traffic blocking, particularly due to the limitation on the number of wavelengths per fiber, we also propose a fiber assignment algorithm designed to deal with this problem. We apply this method to a set of randomly generated networks using a modified Waxman model, and for a network with 60 nodes, in a scenario without blocking, we obtain capacities of about 2.5 Pbit/s for a symbol rate of 64 Gbaud and about 5 Pbit/s for a symbol rate of 128 Gbaud. Remarkably, this duplication in the total network capacity is achieved by an increase in the total fiber length of only about 51%.

Keywords:

Subject: Engineering - Telecommunications

1. Introduction

In recent years, there has been an enormous growth in telecommunications traffic due to the surge of applications and services that require high bandwidth and generate large amounts of data, such as video streaming services, social media platforms, cloud computing, and the adoption of emerging technologies such as 5G, artificial intelligence, etc. This evolving landscape requires the use of very high-speed telecommunications networks like optical networks [1].

Optical networks are communication infrastructures that utilize light for transmission, processing, and routing information and rely on optical fibers as their transmission medium. These networks vary in terms of distance and capacity, falling into several tiers: 1) Backbone networks, span extensive geographic distances and offer huge capacities (in the order of dozens of Tbit/s); 2) Metro networks, cover cities or metropolitan areas, handling data transmission in the range of hundreds of Gbit/s; 3) Access networks, also known as ‘last-mile networks,’ encompass small areas, connecting end-users to the network providers and delivering data rates on the order of a few Gbit/s.

WDM (Wavelength Division Multiplexing) is a fundamental technology in the optical networking field, as it enables the transmission of large amounts of data across long distances. It works by simultaneously transmitting multiple optical signals, often referred to as optical channels, through a single optical fiber, with each channel utilizing its own wavelength. The number of channels transmitted per fiber depends on both the spacing between wavelengths and the WDM signal bandwidth, which in turn is limited by the bandwidth of the optical amplifiers used to compensate the fiber losses. The most commonly used optical amplifier is the EDFA (Erbium-Doped Fiber Amplifier), which utilizing standard technology can provide an amplification bandwidth of approximately 4800 GHz, although more advanced solutions can achieve values up to 6000 GHz. Therefore, for a typical channel spacing of 50 GHz, the first solution can support up to 96 channels, while the second one can accommodate up to 120 channels [2].

Network capacity is an important performance feature of optical networks. This capacity can be defined as the maximum amount of data that the entire network can handle per unit of time, and it is closely related to channel capacity. The concept of channel capacity was introduced by Claude Shannon in 1948 [3]. This refers to the maximum data rate at which the information can be reliably transmitted through a noisy channel without errors. The fundamental assumptions behind this definition are that the noise is additive, white, and Gaussian (AWGN) and that the channel is linear, i.e., the capacity always increases with increasing signal power. However, the last assumption does not hold for optical fiber channels, which are non-linear by nature. This behavior implies that the optical channel capacity does not grow indefinitely; instead, it is limited and reaches a maximum value as the transmitted signal power increases [4,5,6].

When estimating the capacity of an optical network, one must necessarily consider the optical channel capacity. However, the problem is more complex than that, as it is necessary to also consider topological aspects, traffic demands, routing, as well as wavelength and modulation assignments. In other words, this capacity estimation can be viewed as a multilayer problem, in the sense that it requires taking into account not only physical layer properties, but also network layer aspects. Furthermore, for an optimized design it would be paramount to have a clear understanding of how these different aspects correlate with the network capacity. For that purpose, it is convenient to have available a large number of network topologies, which can be obtained using, for example, generative graph models [7].

The problem of estimating the optical channel capacity has been the focus of many studies. Some rely on accurate numerical simulations [6], while others offer detailed analytical models based on either the Gaussian noise (GN) model [8,9,10] or a regular perturbation model [11]. More recently, the topic of optical network capacity has also received some attention. In [12], the authors presented an algorithm to maximize the capacity of an optical network in the presence of physical layer impairments. The algorithm was based on an integer linear program (ILP) and was designed with the goal of optimizing routing, wavelength assignment, modulation format, and launched power allocation. An alternative approach for capacity estimation using a heuristic algorithm for routing and wavelength assignment instead of the ILP was provided in [13]. To understand how network topology characteristics influence network capacity [14] proposed a new generative graph model. This model is based on the classical Barabási-Albert model, which has been properly modified to incorporate physical layer aspects. The published results showed that it can maximize the network capacity in comparison with classical models. Recently, a framework was also proposed to study the relationship between various topological parameters and network performance metrics, including network capacity [15]. That framework provided valuable insights into the key parameters that affect network capacity.

Apart from the last work, which relies on dynamic routing, all the other referred studies on network capacity used static routing with no channel blocking. However, since the number of optical channels per optical fiber is limited, it makes sense to also use a constraint routing approach, as this limitation can lead to blocking under certain conditions. Another topic that deserves consideration is studying how the symbol rate (also referred to as baud rate) impacts network capacity. In fact, there has been considerable research aiming at increasing the symbol rate within optical networks. Currently, commercial deployments typically operate between 60-90 Gbaud, while field trials have reached 130 Gbaud [16], and laboratory demonstrations have achieved symbol rates of 200 Gbaud [17].

This paper is focused on the topic of capacity in optical backbone networks and examines how different network and physical layer parameters influence its value, giving special emphasis to symbol rate. We present an alternative approach to evaluate the capacity of optical networks that uses a constrained routing algorithm to account for the limitations in the number of optical channels and use the metric optical reach, which measures the maximum distance an optical channel can effectively propagate, to describe the impact of the physical layer. Furthermore, a strategy to address the blocking caused by insufficient spectral resources (wavelengths) by adding additional optical fibers is also proposed. The paper’s results are obtained across hundreds of network topologies generated using the modified Waxman method.

The rest of the paper is organized as follows: Section 2 reviews the concept of channel and introduces the necessary background to determine optical reach. Section 3 defines the method used to generate random networks. Section 4 introduces a suitable approach to compute the optical network capacity taking into account the constraints due to the limited number of optical channels per fiber, while Section 5 describes a strategy to overcome blocking by adding more fibers per link. Section 6 provides some simulation results and finally, Section 7 summarizes and concludes the paper.

2. Optical Channel Capacity

An optical channel can be seen as a communication pathway through which information is transmitted in the optical domain from a sender to a receiver, utilizing an optical fiber as a transmission medium. This channel is characterized by its carrier frequency denoted as

ν_{c}

(or carrier wavelength

λ_{c})

and occupied bandwidth, denoted as

B_{c h}

. The minimum bandwidth that guarantees a signal transmission over the channel without inter-symbol interference is defined by the Nyquist criterion and is equal to the symbol rate

R_{s}

[4]. The capacity of an optical channel is defined as the maximum data rate at which the information can be effectively transmitted through the channel. This capacity is typically expressed in bit/s. This capacity can be calculated using Shannon’s theory [3], under the assumption that the noise sources present in these channels are modelled as AWGN sources, giving [6]

C_{c h} = 2 R_{s} \log_{2} (1 + S N R) [b i t / s]

(1)

where

S N R

is the signal-to-noise ratio at the receiver side computed for a channel bandwidth equal to

R_{s}

, given by

S N R = \frac{P_{c h}}{N_{0} R_{s}}

(2)

where

P_{c h}

is the average optical power per channel in watt, and

N_{0}

is the noise power spectral density (PSD) in watt/Hz. Note that the factor 2 in (1) stems from the fact that the optical fiber channel supports two optical channels with orthogonal polarizations, commonly referred to as polarization multiplexed (PM) optical channels.

One important noise source in optical communications systems is the amplified spontaneous emission (ASE) noise. This noise is generated inside of optical amplifiers simultaneously with signal amplification and can be effectively described by a random optical field with statistical properties like those of AWGN noise [6]. Optical amplifiers are used to compensate for the optical fiber losses. To achieve this, optical amplifiers, typically EDFAs, are placed at discrete intervals along an optical link, with each amplifier exactly compensating the loss incurred by each fiber span. For a link of length

L

composed of

N_{s}

identical spans, the span length is

L_{s} = L / N_{s}

, while the span attenuation is

A_{s} = α L_{s}

, where α is the fiber attenuation coefficient in dB/km. Typically,

α

is approximately 0.2 dB/km, within the 1550-nm wavelength region, denoted as C-band. The PSD of the ASE noise at the end of a chain of

N_{s}

amplifiers, spaced by fiber spans of length

L_{s},

is given by

N_{a s e} = N_{a s e, 1} N_{s} = h ν_{c} f_{n} (a_{s} - 1) N_{s}

(3)

where

N_{a s e, 1}

is the ASE per span,

h

is the Planck’s constant (in joule-second)

, f_{n}

is the noise figure (

f_{n} = 10^{F_{n} / 10}

, with

F_{n}

in dB), and

a_{s} = 10^{A_{s} / 10}

Another significant noise source is nonlinear interference (NLI) resulting from the Kerr effect in optical fibers. The Kerr effect refers to the dependence of the refractive index of the fiber on the transmitted signal power. This characteristic makes the optical fiber channel intrinsically non-linear and, in this sense, different from other transmission media used for information transfer that have a linear behavior. Interestingly, it has been demonstrated in [18] through simulations and experiments that the impact of NLI noise on WDM links, supported in dispersion uncompensated fibers, can also be modeled as additive Gaussian noise. Furthermore, it was shown in [9] that under specific conditions, such as the Nyquist limit, the white noise assumption leads to quite accurate results. Note that, such limit is achieved when all the WDM channels have a rectangular spectral width and a frequency spacing equal to

R_{s}

. This permits us to characterize the NLI noise also as an AWGN process with power spectral density of

N_{n l i}

. As the ASE and NLI noises are assumed to be uncorrelated their power spectral densities simply add, resulting in

N_{0} = N_{a s e} + N_{n l i}

. In these circumstances, the signal-to-noise ratio of an optical channel can be described as

S N R = \frac{P_{c h}}{(N_{a s e} + N_{n l i}) R_{s}}

(4)

where

P_{c h}

denotes the launched average optical power per channel.

A rigorous characterization of

N_{n l i}

is not an easy task, and many studies have been published on this topic (see, for example [18,19]). Fortunately, some closed-form approximations have also been published [8,18], which simplifies the evaluation of

N_{n l i}

. One of these approximations, which is based on the white noise assumption, allows to write the PSD of the NLI at the end of a fiber link with

N_{s}

spans in the following way:

N_{n l i} = μ_{n} N_{s} P_{c h}^{3}

(5)

where

μ_{n}

is the NLI coefficient per span given by

{μ_{n} \approx {\overset{´}{μ}}_{n} \frac{1}{{R_{s}}^{3}} = (\frac{2}{3})}^{3} γ^{2} L_{e f} \frac{l n (π^{2} |β_{2}| L_{e f} B_{W D M}^{2})}{π | β_{2} |} \frac{1}{{R_{s}}^{3}} .

(6)

In the last equation, one can identify parameters related with the optical fiber, such as

γ

, the fiber nonlinear coefficient in

W^{- 1} {k m}^{- 1}

β_{2},

the fiber dispersion in

{p s}^{- 2} {k m}^{- 1}

and

L_{e f}

, the span effective length in km. Additionally, there are parameters related with the signal, such as

B_{W D M}

, the optical bandwidth of the WDM signal in Hz, assumed to be composed of

N_{c h}

channels spaced by

{Δ ν}_{c h}

, in such a way that

B_{W D M} = N_{c h} {Δ ν}_{c h}

. In addition, the span effective length is given as

L_{e f} = (1 - \exp (- 2 a_{N} L_{s})) / (2 α_{N})

(7)

where

L_{s}

is the span length and

a_{N}

is the fibre attenuation coefficient in Np/km, i,e.

α_{N} = α_{d B / k m} / 20 \log_{10} e

. Using (4), (5) and (6), one arrives to

S N R = \frac{P_{c h}}{(N_{a s e, 1} + μ_{n} P_{c h}^{3}) {N_{s} R}_{s}} .

(8)

From (8) one can derive the following equation for the optimum launch power [9]

P_{c h}^{o p t} = R_{s} \sqrt[3]{\frac{N_{a s e, 1}}{2 \overset{´}{μ_{n}}}} .

(9)

The maximum channel capacity can be determined by inserting (8) and (9), into (1), giving

C_{c h} = 2 R_{s} \log_{2} (1 + \frac{L_{s}}{3 L} \sqrt[3]{\frac{4}{{\overset{´}{μ}}_{n} N_{a s e, 1}^{2}}}) .

(10)

From (9) and (10) we can see that:

1): $P_{c h}^{o p t}$ depends on ASE and NLI noise and varies linearly with the symbol rate. For the parameters given in Table 1 we arrive to $P_{c h}^{o p t} = 0.89 d B m$ for $R_{s} = 64 G b a u d$ , and $P_{c h}^{o p t}$ =3.89 dBm for $R_{s} = 128 G b a u d .$
2): The channel capacity increases linearly with the symbol rate and decreases linearly with the total link length.

The optical reach, also denoted as transmission reach, is an important parameter used in the context of this work to describe the impact of the physical layer on the performance of an optical channel. The optical reach is defined here as the maximum length of an optical channel for which a certain value of the capacity can be met. As this length can be viewed as the total link length

L

, one can use (10) to obtain the optical reach for various capacity values. Assuming, as seen before, that for the 64 Gbaud case,

L

is a multiple of the span length, Table 2 shows the optical reach obtained using (10) for different values of the Shannon channel capacities. Furthermore, in the case of 128 Gbaud, we considered a 10% reach reduction compared to the previous scenario, to address additional limitations not taken into account in the formulation that leads to (10) (see [19]). Although, these capacity values can be seen as upper bounds, it is worth noting that a recent field trial reported an 800 Gb/s transmission over a distance of 6600 km for a symbol rate of 120 Gbaud [20], which is not far from the values of the reach given in Table 2 for that bit rate.

3. Network Topology Model

In an abstract way, an optical network can be described as an undirected graph

G (V, E),

with

V = {v_{1}, \dots, v_{N}

} denoting a set of nodes and

E = {e_{1}, \dots, e_{K}

} denoting a set of links, where

N = |V|

is the number of nodes and

K = |E|

is the number of links. In transparent optical networks all node functionalities take place in optical domain, and the nodes are built upon reconfigurable optical add-drop multiplexers (ROADMs). Meanwhile, an optical link represents a physical interconnection between two nodes, implemented using optical fibers and optical amplifiers. In bidirectional links, some fibers are used in one direction and others (typically the same number) in the opposite direction. Each optical fiber supports WDM signals, meaning it carries a specific number of optical channels.

Besides

N

and

K

, other important parameters are the node degree

δ (G)

, the network diameter

d i a m (G)

, and the edge connectivity

λ (G)

δ (G)

defines the number of links connected to a node,

d i a m (G)

is the length of the longest shortest path between any two nodes, while

λ (G)

represents the maximum number of link-disjoint paths between two nodes. The

λ

-connectivity is a measure of a network’s resilience against link failures, making it a key parameter in designing protection paths in optical networks.

To have a clear understanding of how different topological parameters impact network capacity, it is paramount to have available large numbers of network topologies, which can be obtained from a set of random graphs designed to describe adequately the characteristics of real-world optical networks. Erdős-Rényi and Waxman models are widely used to generate random networks. The last model works by randomly placing nodes in a two-dimensional space with specific coordinates and connecting them with links based on a probability function determined by the distance between those nodes. In the Waxman model, the probability that node

i

establishes a link to node

j

is given by [7]:

P (i, j) = β \exp \frac{- d (i, j)}{L_{w} α}

(11)

where

d (i, j)

is the Euclidean distance between the nodes,

L_{w}

is the maximum distance between any two nodes, and

α

and

β

are parameters in the range of 0 to 1.

In contrast, the first model does not reference node positions, and the links are added with a uniform probability. Assigning the nodes positions in space makes the Waxman model better suited for describing realistic optical networks. However, the Waxman model cannot generate

λ

-connected graphs, which is a significant limitation in the context of optical backbone networks, where survivability is a primordial feature. To overcome such a limitation, one uses in this work the modified Waxman model [7].

The modified Waxman model is designed to generate optical backbone networks survivable to single link failures, conceived as interconnected sets of subnetworks. In this sense, the two-dimensional space is divided into a set of regions where nodes are randomly placed in the first part of the process. In the subsequent steps, nodes are interconnected within each region and then across different regions according to the Waxman probability, subject to certain constrains in terms of node degree and

λ

-connectivity. For exemplification purposes, Figure 1 shows a generated graph with

N = 10

K = 20

, which gives an average node degree of

< δ > = 2 K / N = 4 .

Two distinct subnetworks

S_{1}

and

S_{2}

are clearly identified within the graph with

S_{1} = \{0, 1, 2, 3\}

and

S_{2} = \{5, 7, 8, 9\}

. Furthermore,

λ (G) =

3, with this value being determined by calculating the minimum number of links that need to be removed to disconnect the graph.

To ensure that the generated graphs accurately mimic real optical backbone networks it is important to compare certain statistics. In [7], it is demonstrated that the node degree distribution of these networks follows a Poisson distribution. Figure 2 shows that the node degrees of the random graphs generated by the modified Waxman model closely approximate the Poisson statistics seen in real networks.

4. Constrained Routing and Network Capacity

Network capacity, also known as throughput, can be defined as the maximum amount of data that a network can handle per unit of time. This capacity depends on various network properties such as the physical and logical topology (traffic profile), optical reach, link capacity, node structure, routing, and wavelength assignment, etc. Physical topology describes the interconnection pattern of nodes and typically is known in advance. Nodes are considered simultaneously as the source and destination of traffic. A starting point in the network capacity evaluation is the definition of the traffic demand profile. This profile is defined by the traffic matrix

T = [t_{s, d}

], where each entry

t_{s, d}

represents a traffic demand, or in other terms, the volume of traffic flowing from a source node

s

to a destination node

d

, with

s, d \in V

. In this analysis, it is assumed that the traffic profile is uniform and equal among all node pairs, which corresponds to

t_{s, d} = \{\begin{matrix} 1 & s \neq d \\ 0 & s = d \end{matrix}

(12)

Note that this traffic profile describes a full-mesh logical topology, in the sense that each node is logically connected to every other node within the network [21]. Another important point in the network capacity evaluation is the link characterization. The link

(i, j) \in E

can be described by two attributes: 1) length

l_{i, j}

; 2) capacity

c_{i, j}

determined by the number of optical channels

N_{c h}

available in the links, given by

c_{i, j} = N_{c h}

. As already seen, this number is limited by the bandwidth

B_{W D M}

and the symbol rate

R_{s} .

For each traffic demand, it is necessary to find a path in the physical topology between each pair of nodes. This process is known as routing. Since there are multiple paths between each pair of nodes, the objective is to determine the shortest path using a heuristic like the Dijkstra’s algorithm. The shortest path corresponds to the one that minimizes the total path length, defined as the sum of the lengths of all the links traversed by the path. However, in this case the routing is constrained by the capacity

c_{i, j}

leading to the concept of constrained routing (CR) problem [22]. The objective of this problem is to maximize the number of allocated traffic demands while minimizing the blocking ratio in a network with limited link capacity. The input parameters include the weighted graph

G (V, E)

, with the link

(i, j) \in E

, being characterized by

l_{i, j}

and

c_{i, j}

, and the traffic matrix

T = [t_{s, d}]

, while the output parameters include the list of blocked traffic demands

B = [b_{s, d}]

and the list of established paths

Ρ = [π_{s, d}]

, with the path

π_{s, d}

having the length

l (π_{s, d}) = \sum_{i, j} l_{i, j}

Furthermore, we assume that each path

π_{s, d}

(also denoted as lightpath) computed using the CR approach is physically established using an optical channel with a specific wavelength, which is computed in this work using a first-fit heuristic [23]. In other words, a channel

k = (s, d)

, defined as

k = \{π_{k}, λ_{k}\} \in S

has an associated path

π_{k}

and wavelength

λ_{k}

, and belongs to the set of optical channels required to implement a logical full mesh topology

S = \{1, 2, \dots, N (N - 1)\}

. In the process of assigning wavelengths to the optical channels, which occurs during the routing process, it must be assured that all the optical channels that traverse the same link are assigned different wavelengths, as otherwise there would be interference between the channels. That means that there can be different channels using the same wavelength, as long as there are no common links in their paths.

The algorithm, denoted as Algorithm 1, used for solving this problem can be described as follows:

1)

Compute the shortest paths:

Run the Dijkstra’s algorithm to find the shortest path between each source-destination node pair in the network ( $π_{s, d}$ ), considering the total path length $l (π_{s, d})$ as the metric that defines that computation.

2)

Order the traffic demands:

Apply a specific sorting strategy (e.g., shortest-first, longest-first, largest-first) to order traffic demands $t_{s, d}$ . If the order is “shortest” the traffic demands are sorted by path length in ascending order, while for the “longest” order the traffic demands are sorted by path length in descending order. Furthermore, if the order is “largest” the traffic demands are sorted by their value in descending order.

3)

Route the demand, update link loads and assign a wavelength:

For each traffic demand $t_{s, d}$ , in accordance with the order established in Step 2, route it through $π_{s, d}$ , updating the load (number of demands routed through the link) of each link in $π_{s, d}$ , and assign a wavelength $λ_{k}$ to that optical channel (a wavelength being represented by an integer between 1 and $N_{c h}$ ).

4)

Blocking:

If, in Step 3, a link (or more than one) in $π_{s, d}$ doesn’t have enough residual capacity (which is defined as the difference between the link capacity and its load) or if a wavelength that fits all links of the path doesn’t exist (respecting the principle that two optical channels with the same wavelength cannot exist on the same link), then the traffic demand $t_{s, d}$ is blocked.

5)

Remove links and determine alternative shortest paths:

After routing each traffic demand, remove all the links that have residual capacity zero from the weighted graph.
With the updated topology, determine new shortest paths, as in Step 1, so that alternative paths are found for the remaining traffic demands.
Go to Step 3, to route the next traffic demand.

To compute the total network capacity, one can apply the concepts of channel capacity introduced in Section 2, which can be written as [14]

C_{n e t} = \sum_{k \in S} C_{c h, k}

(13)

where

C_{c h, k}

is the capacity of channel

k

, which according to (11) and (13) becomes:

C_{c h, k} = 2 R_{s} \log_{2} (1 + {S N R}_{k})

(14)

with

{S N R}_{k}

being the

S N R

of channel

k

. The

{S N R}_{k}

can be readily evaluated using (4), assuming that the optical nodes (ROADMs) are ideal and, as a result, do not affect the calculations. In this context, the number of spans for optical channel

k

is denoted as

n_{s, k} = ⌊L_{k} / L_{s}⌋

, with

L_{k}

representing the length of path

π_{k}

. To avoid calculating the

{S N R}_{k}

and reduce the computation time, we can take advantage of the analysis undertaken in Section 2 and use the optical reach to obtain the channel’s capacities. For instance, by knowing the lengths of the different paths and utilizing the data from Table 1, we can obtain the capacities of the different channels for a span length of 80 km and two values of the symbol rate (64 Gbaud and 128 Gbaud) (see Table 2). These capacities are referred to as Shannon capacities because the reach values are obtained using the Shannon theory.

An additional important metric for network analysis is the network-wide average channel capacity, defined as [24]

{\bar{C}}_{c h} = \sum_{k \in S} C_{c h, k} / \sum_{k \in S} γ_{k}

(15)

where

γ_{k}

denotes the expected utilization ratio of channel

k

. For the sake of simplicity, it is assumed that

γ_{k} = 1

for all channels. As a result, the sum in the denominator of (15) equals the total number of paths in the network, which for a full-mesh logical topology, amounts to

N (N - 1) .

With this simplification, the network capacity for a full-mesh logical topology reduces to

C_{n e t} = {\bar{C}}_{c h} \times N (N - 1) \times (1 - \bar{B})

(16)

where

\bar{B}

is the average blocking ratio obtained as

\bar{B} = \sum_{k \in S} b_{k} / (N (N - 1) .

(17)

5. Unconstrained Routing and Fiber Assignment

Optical backbone networks are typically designed to avoid blocking of traffic demands. Blocking occurs when there is insufficient capacity to accommodate all the incoming traffic demands at a particular node or link. In the previous analysis, blocking occurred due to the limited number of optical channels and their corresponding wavelengths on each link. This limitation arises, namely, from bandwidth constraints of the optical amplifiers, which, in this work, are assumed to be operating in the C-band. To address the blocking problem in optical backbone networks, one can utilize optical amplifiers that operate in other bands different from the C-band, such as the L-band and the S-band. Nevertheless, this solution has some drawbacks: one can refer, for example, to the technical difficulties associated with building optical amplifiers to operate in the S-band, and the need to add band multiplexer/ demultiplexers to separate the different bands for individual amplification, which can significantly increase the transmission losses.

A more straightforward solution for increasing the overall capacity of an optical backbone network is to add more optical fibers per link. However, this can be a costly and complex solution, particularly when extensive upgrades are required. Nonetheless, in common scenarios where network operators own dark fibers, lighting additional fibers emerges as a viable and cost-effective solution. This study will explore this approach as a means of overcoming blocking. To achieve this objective a fiber-assignment algorithm, designated as Algorithm 2, will be proposed. The input parameters of this algorithm are also a weighted graph

G (V, E),

as in Algorithm 1, but now with

c_{i, j} = \infty

, the traffic matrix

T = [t_{s, d}

] and the maximum number of available optical channels per fiber

N_{m a x} = N_{c h}

. On the other hand, the output parameters comprise the list of established paths

Ρ = [π_{s, d}]

with the path

π_{s, d}

having the length

l (π_{s, d})

, as in the Algorithm 1, and an

N \times N

matrix with the number of optical fibers per link,

N F = [{n f}_{i, j}]

, where

{n f}_{i, j}

is the number of optical fibers in the link

(i, j) .

The first part of the algorithm is equivalent to Steps 1-3 of Algorithm 1, but now using an unconstrained routing strategy, which permits obtaining the list

Ρ

, and an

N \times N

matrix with the wavelengths in each link,

W = [w_{i, j}]

, where

w_{i, j}

is the list of all the wavelengths

λ_{k}

present in the link

(i, j)

w_{i, j} = [λ_{k}]

. Subsequently, the next steps of the algorithm are the following:

4)

Assign fibers when there is no traffic in a link:

If there is no traffic in that link but the link does exist in the network’s physical topology, set ${n f}_{i, j} = 1$

5)

Assign fibers when there is traffic in a link:

Set ${n f}_{i, j} = m a x (n u m_r e p_w_{i, j})$ , where $n u m_r e p_w_{i, j}$ is the number of repeated wavelengths in $w_{i, j}$ , $\forall (i, j) \in E$

Note that in this context, where unconstrained routing is being done, the number of wavelengths in each link does not have a limit, so the value attributed to a given

λ_{k}

is any natural number (and not bounded by

N_{m a x}

, as in Algorithm 1). To determine the number of fibers needed in each link, the maximum number of “repeated wavelengths” in that link needs to be determined. A wavelength is considered a “repeated wavelength” when its value modulo

N_{m a x}

(the modulo operation referring to the remainder of a division) is equal to that of another wavelength also present in that link. For instance, if

N_{m a x}

is 75, then wavelengths 1 and 76 are “repeated” because 76 modulo 75 equals 1. This implies that both wavelengths would occupy the same channel in a link, hence they are “repeated”. This concept is crucial in determining the number of fibers needed for a link, ensuring that each “repeated” wavelength has its own fiber. Finding the maximum count of “repeated wavelengths” will ensure that there are enough fibers to accommodate all the wavelengths, thus assuring that there are no channels with the same wavelength on the same fiber.

By knowing the length

l (π_{s, d})

of all the paths belonging to

Ρ

, it is possible to compute the capacity of the optical channel corresponding to those paths using the values of the reach given in Table 2 and consequently computing the average channel capacity using (15) and total network capacity using (16) with

\bar{B} = 0

. To assess the network performance in the present scenario, it is also necessary to account for the network cost. For simplification purpose, we assume that the transponders cost can be neglected in comparison with fiber cost, which seems to be a reasonable assumption for optical backbone network [25]. In this case the network cost is given as

Λ_{n e t} = \sum_{i, j} l_{i, j} \times {n f}_{i, j} .

(18)

6. Results and Discussion

To investigate the dependence of network capacity on network parameters, five sets, each comprising 200 graphs, were obtained using the modified Waxman model described in Section 3, with the number of nodes varying from 20 to 60 in increments of 10. All the graphs were generated assuming a bi-dimensional plane with dimension 1000×1000 km and Waxman parameters

α = β = 0.4

, as well as an average node degree varying randomly from 2 to 4. These sets of random networks were used in both routing scenarios described previously, i.e., constrained routing (Section 5) and unconstrained routing with fiber assignment (Section 6).

In the first scenario, the routing was performed considering a full-mesh logical topology described by the traffic profile (12), using Algorithm 1 and the shortest-first sorting strategy. The study was undertaken for two symbol rate values, 64 Gbaud and 128 Gbaud, considering the optical reach values provided in Table 2, and one fiber pair per link, with each fiber being used in a communication direction. Furthermore, the number of optical channels per fiber was limited to 75 for 64 Gbaud and 37 for 128 Gbaud. This limitation arises from the fixed bandwidth of 4800 GHz in optical amplifiers, inherently leading to blocking as the number of traffic demands increases.

The values of the computed total network capacity are depicted in Figure 3 using boxplots. A boxplot is a way of illustrating the statistical distribution of a data set and include the median, the interquartile range, and both the minimum and the maximum values of the set. The boxplots in Figure 3 also show outliers, represented as small circles, to describe data samples, that differ significantly from the rest of the data set.

It can be seen from Figure 3 that using a symbol rate of 128 Gbaud makes it possible to achieve a higher total network capacity in comparison to the 64 Gbaud case, although the extent of the improvement tends to decrease as the number of nodes increases. Comparing the median capacity values between the sets of generated graphs, transmission at 128 Gbaud results in an improvement over the transmission at 64 Gbaud of approximately: 34%, 24%, 19%, 17% and 16%, for the respective sets of graphs, listed in ascending order of number of nodes. The average improvement across all sets is around 22%. The decrease in performance improvement verified in networks with more nodes can be explained by the slight increase in the blocking probability, which, for example, for the case of 60 nodes, rises from 0.6 to 0.7 as the symbol rates goes from 64 Gbaud to 128 Gbaud, as can be seen in Figure 4. The improvement in the networks’ capacity, coupled with the simultaneous reduction in the number of wavelengths, which are halved, represents an important advantage in utilizing 128 Gbaud compared to 64 Gaud.

The previous analysis deals with the constrained routing of traffic demands due to the limited number of optical channels per link. As can be seen, this leads to blocking, which increases with the size of the network, as shown in Figure 4. This figure depicts both the number of blocked traffic demands and the blocking probability, which is obtained by dividing the number of blocked traffic demands by

N \times (N - 1)

. To address the blocking problem, one can enhance the link capacity by adding more optical fibers, following the strategy outlined in Algorithm 2. As a result, the network achieves an unconstrained total capacity, determined only by the load of the traffic demands, without any imposed constraint. This capacity is shown in Figure 5 also using boxplots.

The first conclusion we can draw from this figure is that the total capacity increases approximately in a quadratic manner with the number of nodes (

~ N^{2})

. Another noteworthy aspect is the huge capacities achieved in this scenario, which corresponds to about 2.5 Pbit/s for 60 node networks and a symbol rate of 64 Gbaud (see Figure 5a). It can also be referred that the total network capacity median values for a 30-node network (

~

660 Tbit/s) are similar to the values reported in [14] (Figure 9) for the 30-node CONUS topology generated using the Erdős-Rényi model. As expected, Figure 5b shows a twofold increase in the total capacity, when the symbol rate is set at 128 Gbaud.

According to what is expected, the significant increase in capacity comes at the cost of a substantial rise in network cost, which translates into the increase of the optical fiber length to be deployed. Figure 6 shows the total fiber cost, expressed in terms of the total fiber length, as a function of the number of nodes. This figure shows a law of variation of the cost as a function of the number of nodes similar to the one of the capacity referred above. A prominent conclusion we can draw from Figure 6 is that when the symbol rate increases from 64 Gbaud to 128 Gbaud, the total fiber cost increases by about 51%, while the total network capacity value doubles, as seen previously.

7. Conclusions

In this paper the problem of assessing the impact of topological and physical impairments on the capacity of optical backbone networks was investigated.

The capacity was defined using Shannon’s theory, and the impact of the physical layer was studied using the optical reach, which was computed, considering both linear and non-linear noise terms, for two values of the symbol rate: 64 Gbaud and 128 Gbaud. To explore the influence of topological characteristics we used a modified Waxman model to generate random networks that mimic real optical backbone networks, ensuring an edge connectivity greater than or equal to 2.

The paper also proposed a constrained routing and wavelength assignment algorithm to deal with the fact that the number of optical channels/wavelengths per link is limited, which inevitably results in traffic blocking as the number of demands increases. Given that traffic blocking is not acceptable in optical backbone networks, we also devised a strategy to overcome it by adding more optical fibers per link, albeit at the expense of increasing the network cost.

The total network capacity was evaluated for a set of generated random networks considering a full-mesh logical topology. The results showed that although the capacity increases with the number of nodes, the rate of increase tends to diminish due to the rising of the blocking ratio. By moving from a symbol rate of 64 Gbaud to 128 Gbaud one observes an improvement in median total capacity of about 34% for

N =

20 and 16% for

N = 60

. The reduction in improvement is also explained by the rising of blocking ratio. With proper fiber assignment one can see a substantial increase in the total capacity. For a network with

N = 60

, median values of about 2.5 Pbit/s can be achieved for a symbol rate of 64 Gbaud, and about 5 Pbit/s for a symbol rate of 128 Gbaud. Remarkably, this duplication in the total network capacity is achieved by an increase in the total fiber length of only about 51%.

Funding

This research received no external funding.

Data Availability Statement

Not applicable.

Conflicts of Interest

The authors declare no conflicts of interest.

References

Winzer, P.J.; Neilson, D.T. From Scaling Disparities to Integrated Parallelism: A Decathlon for a Decade. J. Lightw.Technol. 2017, 35, 1099–1115. [Google Scholar] [CrossRef]
Deng, N.; Zong, L.; Jiang, H.; Duan, Y.; Zhang, K. Challenges and Enabling Technologies for Multi-Band WDM Optical Networks. J. Lightw. Technol. 2022, 40, 3385–3394. [Google Scholar] [CrossRef]
Shannon, C.E. A Mathematical Theory of Communication. The Bell System Technical J. 1948, 27, 379–423. [Google Scholar] [CrossRef]
Essiambre, R.-J.; Tkach, R.W. Capacity Trends and Limits of Optical Communication Networks. Proceedings of the IEEE 2012, 100, 1035–1055. [Google Scholar] [CrossRef]
Mitra, P.P.; Stark, J.B. Nonlinear limits to the information capacity of optical fiber communications. Nature 2001, 411, 1027–1030. [Google Scholar] [CrossRef] [PubMed]
Essiambre, R.-J.; Kramer, G.; Winzer, P.J.; Foschini, G.J.; Goebel, B. Capacity limits of optical fiber networks. J. Lightw.Technol. 2010, 28, 662–701. [Google Scholar] [CrossRef]
Pavan, C.; Morais, R.M.; Rocha, J.R.F.; Pinto, A.N. Generating Realistic Optical Transport Network Topologies. J. Opt. Commun. Netw. 2010, 2, 80–90. [Google Scholar] [CrossRef]
Bosco, G.; Poggiolini, P.; Carena, A.; Curri, V.; Forghieri, F. Analytical results on channel capacity in uncompensated optical links with coherent detection. Opt. Express 2011, 19, B438–B449. [Google Scholar] [CrossRef] [PubMed]
Poggiolini, P.; Bosco, G.; Carena, A.; Curri, V.; Jiang, Y.; Forghieri, F. The GN-Model of Fiber Non-Linear Propagation and its Applications. J. Lightw.Technol. 2014, 32, 694–721. [Google Scholar] [CrossRef]
Bayvel, P.; Maher, R.; Xu, T.; Liga, G.; Shevchenko, N.A.; Lavery, D.; Alvarado, A.; Killey, R.I. Maximizing the optical network capacity. Phil. Trans. R. Soc A. 2016, 374, 2014044. [Google Scholar] [CrossRef]
Mocozzi, A.; Essiambre, R.-J. Nonlinear Shannon Limit in Pseudolinear Coherent Systems. J. Lightw.Technol. 2012, 30, 2011–2024. [Google Scholar] [CrossRef]
Ives, D.J.; Bayvel, P.; Savory, S.J. Routing, Modulation, Spectrum and Launch Power Assignment to Maximize the Traffic Throughput of a Nonlinear Optical Mesh Network. Photon. Netw. Commun. 2015, 29, 244–256. [Google Scholar] [CrossRef]
Vincent, R.J.; Ives, D.J.; Savory, S.J. Scalable Capacity Estimation for Nonlinear Elastic All-Optical Core Networks. J. Lightw.Technol. 2019, 37, 5380–5391. [Google Scholar] [CrossRef]
Matzner, R.; Semrau, D.; Luo, R.; Zervas, G.; Bayvel, P. Making intelligent topology design choices: understanding structural and physical property performance implications in optical networks. J. Opt. Commun. Netw. 2021, 13, D53–D67. [Google Scholar] [CrossRef]
Higashimori, K.; Tanaka, T.; Inuzuka, F.; Ohara, T.; Inoue, T. Key physical topology features for optical backbone networks via a multilayer correlation. J. Opt. Commun. Netw. 2023, 15, B23–B32. [Google Scholar] [CrossRef]
Pittalà, F.; Braun, R.-P.; Böcherer, G.; Schulte, P.; Schaedler, M.; Bettelli, S.; Calabrò, S.; Kuschnerov, M.; Gladisch, A.; Westphal, F.-J.; et al. 1.71 Tb/s Single-Channel and 56.51 Tb/s DWDM Transmission Over 96.5 km Field-Deployed SSMF. IEEE Photonics Techn. Lett. 2022, 34, 157–160. [Google Scholar] [CrossRef]
Chen, X.; Raybon, G.; Che, D.; Cho, J.; Kim, K.W. Transmission of 200-GBaud PDM Probabilistically Shaped 64-QAM Signals Modulated via a 100-GHz Thin-film LiNbO3 I/Q Modulator. In Proceedings of the Optical Fiber Communications Conference, Washington DC, USA, 6-11 June 2021. Paper F3C.5. [Google Scholar]
Carena, A.; Curri, V.; Bosco, G.; Poggiolini, P.; Forghieri, F. Modeling of the Impact of Nonlinear Propagation Effects in Uncompensated Optical Coherent Transmission Links. J. Lightw.Technol. 2012, 30, 1524–1539. [Google Scholar] [CrossRef]
Poggiolini, P.; Jiang, Y.; Carena, A.; Bosco, G.; Forghieri, F. Analytical results on system maximum reach increase through symbol rate optimization. In Proceedings of the Optical Fiber Communications Conference, Los Angeles, USA, 22-26 March 2015. Paper Th3D. [Google Scholar]
GEN120+ Coherent Trials and Deployments. Available online: https://cignal.ai/2023/11/gen120-coherent-trials-and-deployments/ (accessed on 16 January 2024).
Pires, J.J.O.; O´Mahony, M.; Parnis, N.; Jones, E. Scaling limitations in full-mesh WDM ring networks using arrayed-waveguide grating OADMs. Electronics Letters 1999, 35, 73–75. [Google Scholar] [CrossRef]
Kuipers, F.; Korkmaz, T.; Krunz, M.; Mieghem, P.V. An Overview of Constraint-Based Path Selection Algorithms for QoS Routing. IEEE Comm. Mag. 2003, 40, 50–55. [Google Scholar] [CrossRef]
Zang, H.; Jue, J.P.; Mukherjee, B. A Review of Routing and Wavelength Assignment Approaches for Wavelength-Routed Optical WDM Networks. Opti. Netw. Mag. 2000, 47–60. [Google Scholar]
Souza, A.; Correia, B.; Costa, N.; Pedro, J.; Pires, J. Accurate and scalable quality of transmission estimation for wideband opti-672 cal systems. In Proceedings of the IEEE International Workshop on Computer-Aided Modeling Analysis and Design of Communication Links and Networks, 25–27 October 2021. [Google Scholar]
Çetinkaya, E.K.; Alenazi, M.J.F.; Cheng, Y.; Peck, A.M.; Sterbenz, P.G. A comparative analysis of geometric graph models for modelling backbone networks. Optical Switch. and Networ. 2014, 14, 95–106. [Google Scholar] [CrossRef]

Figure 1. Network topology generated by the modified Waxman model with N = 10, K = 20 and λ(G)=3.

Figure 2. Average node degree frequency and Poisson distribution for random graphs generated with the modified Waxman model: (a)

N = 50

and

< δ > = 6.52

; (b)

N = 100

and

< δ > = 6.0

Figure 2. Average node degree frequency and Poisson distribution for random graphs generated with the modified Waxman model: (a)

N = 50

and

< δ > = 6.52

; (b)

N = 100

and

< δ > = 6.0

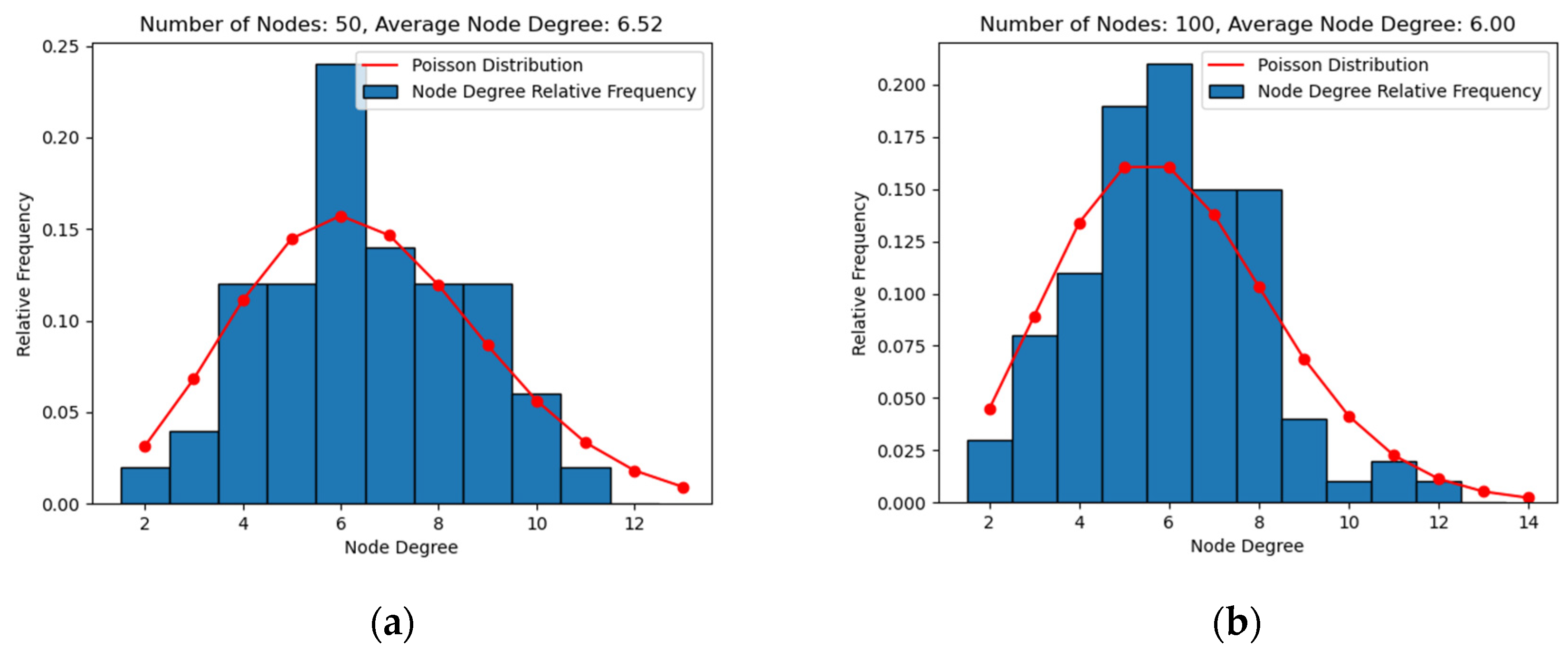
Figure 3. Total network capacity in the case of constrained routing: (a) 75 channels, 64 Gbaud; (b) 37 channels, 128 Gbaud.

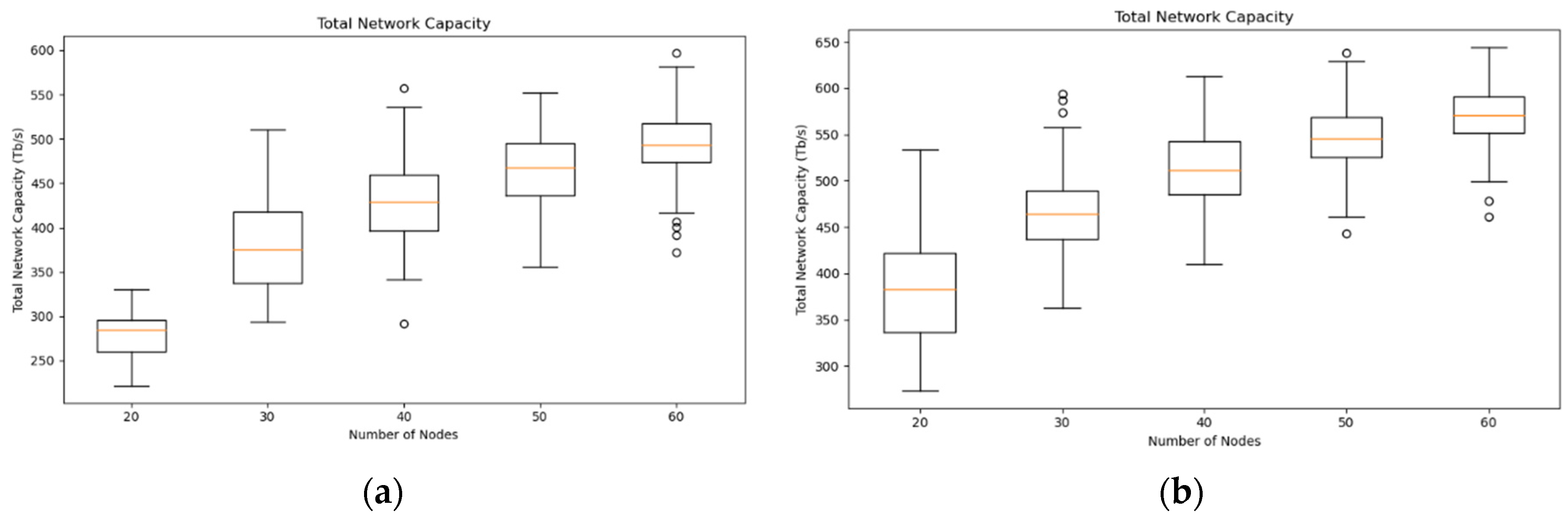
Figure 4. Average number of traffic demands and average blocking probability as a function of the number of nodes (average across each set). (a) 75 channels, 64 Gbaud; (b) 37 channels, 128 Gbaud.

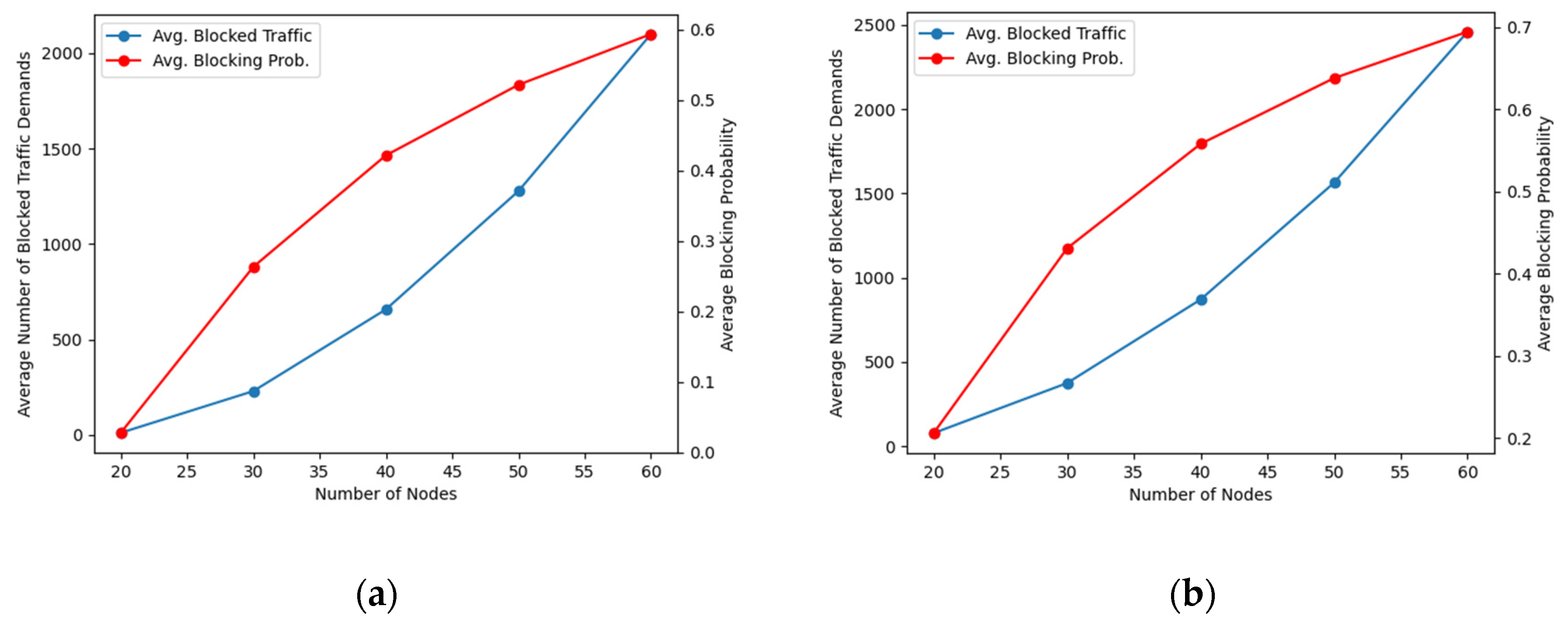
Figure 5. Total network capacity in the case of unconstrained routing: (a) 64 Gbaud; (b) 128 Gbaud.

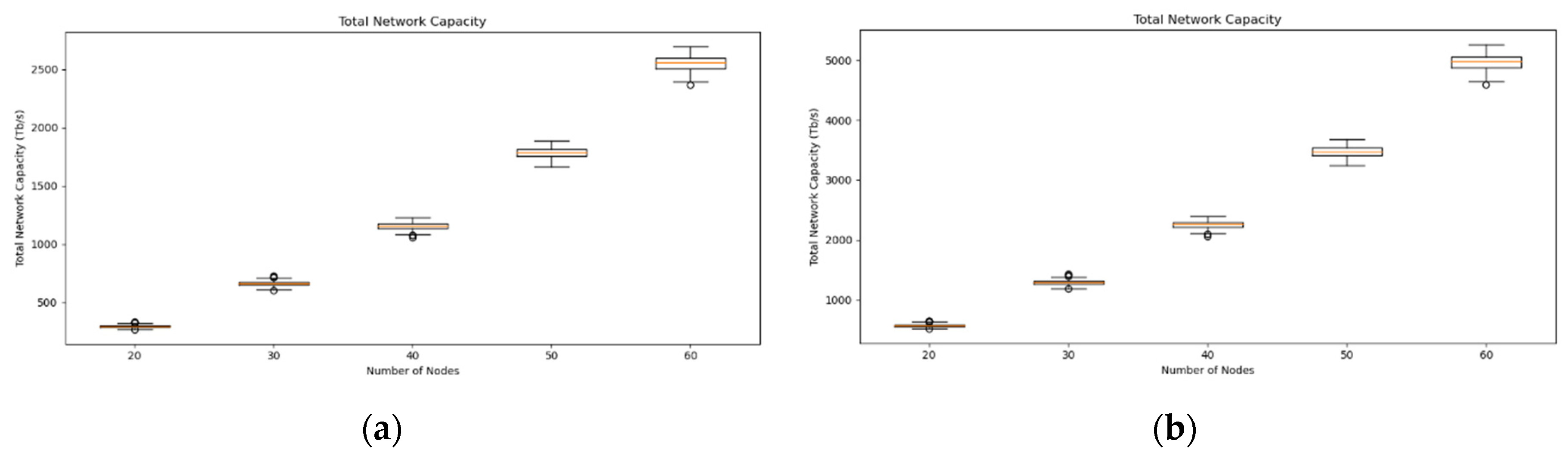
Figure 6. Total fiber length (average across each set). (a) 64 Gbaud; (b) 128 Gbaud.

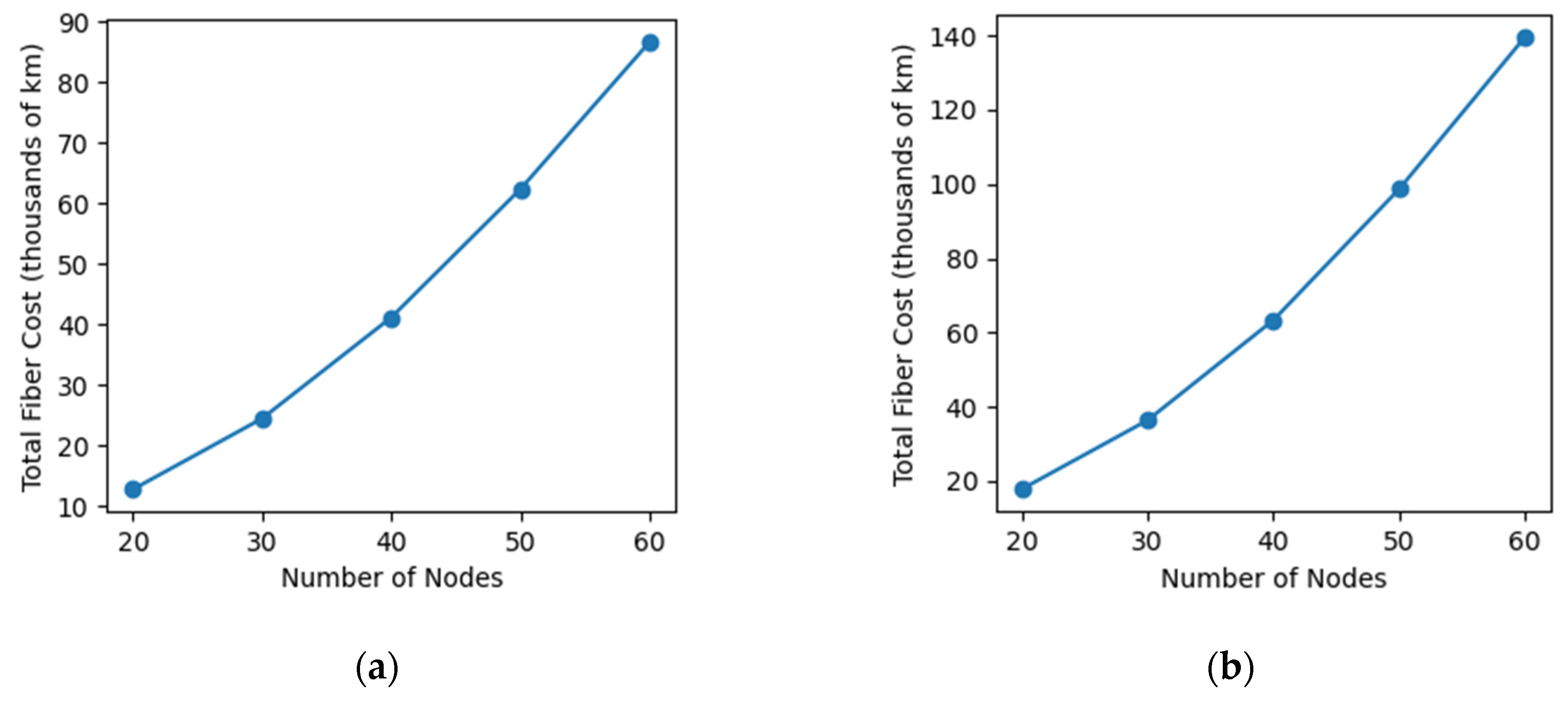
Table 1. Optical fiber and system parameters.

Parameter	Symbol	Value
Fiber Attenuation Coefficient	$α$	$0.22 d B / k m$
Fiber Dispersion Parameter	$β_{2}$	$- 21.7 {p s}^{2} {k m}^{- 1}$
Fiber Nonlinear Coefficient	$γ$	$1.27 W^{- 1} {k m}^{- 1}$
Carrier Frequency	$ν_{c}$	$193.41 T H z$
Carrier Wavelength	$λ_{c}$	$1550 n m$
Span length	$L_{s}$	$80 k m$
EDFA noise figure	$F_{n}$	$5 d B$
Symbol rate	$R_{s}$	$64 G b a u d$ , 128 Gbaud
Channel Spacing	${Δ ν}_{c h}$	$64 G H z$ , 128 GHz
Number of Channels	$N_{c h}$	$75$ , 37
WDM bandwidth	$B_{W D M}$	$4800 T H$ z

Table 2. Optical reach values for two symbol rates.

Reach (km) 64 Gbaud	Capacity (Gb/s) 64 Gbaud	Reach (km) 128 Gbaud	Capacity (Gb/s) 128 Gbaud
23120	200	20808	400
11120	300	10008	600
5840	400	5256	800
3280	500	2952	1000
1760	600	1584	1200
1040	700	936	1400
560	800	504	1600
320	900	288	1800
160	1000	144	2000
80	1100	72	2200

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Investigating the Impact of Topology and Physical Impairments on the Capacity of an Optical Backbone Network

Abstract

1. Introduction

2. Optical Channel Capacity

3. Network Topology Model

4. Constrained Routing and Network Capacity

5. Unconstrained Routing and Fiber Assignment

6. Results and Discussion

7. Conclusions

Funding

Data Availability Statement

Conflicts of Interest

References

MDPI Initiatives

Important Links

Subscribe