Prerpints.org logo
Preprint
Article

Improvement of Phased Antenna Array Applied in Focused Microwave Breast Hyperthermia

Altmetrics

Downloads

128

Views

33

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

29 February 2024

Posted:

04 March 2024

You are already at the latest version

Alerts
Abstract
Focused microwave breast hyperthermia (FMBH) employs a phased antenna array to perform beamforming that can focus microwave energy at targeted breast tumors. Selective heating of the tumor endows the hyperthermia treatment with high accuracy and low side effects. The effect of FMBH is highly dependent on the applied phased antenna array. This work investigates the effect of polarizations of antenna elements on the microwave focusing results by simulations. We explore two kinds of antenna arrays with the same number of elements using different digital realistic human breast phantoms. The first array has all the elements’ polarization in the vertical plane of the breast while the second array has half elements’ polarization in the vertical plane and the other half in the transverse plane, i.e., cross polarization. In total 96 sets of different simulations are performed, and the results show that the second array leads to a better focusing effect in dense breasts than the first array. This work is very meaningful for the potential improvement of the antenna array for FMBH, which is of great significance for the future clinical applications of FMBH. The antenna array with cross polarization can also be applied in micro-wave imaging and sensing for biomedical applications.
Keywords: 
Subject: Engineering  -   Bioengineering

1. Introduction

As an emerging cancer treatment technology, hyperthermia has attracted many research interests and can be used as a potential alternative method for breast cancer treatment [1,2,3,4,5]. The hyperthermia technique heats up the tumor and increases the temperature in the tumor to above 42 °C to destroy the tumor cells [6]. It has become the focus of more and more laboratory and clinical researches in the past 30 years [7,8,9,10,11,12,13,14]. The current clinically applicable mechanism of microwave hyperthermia is to insert a thin metallic probe into the human breast and directly transfer microwave energy to the tumor, which is an invasive treatment method [12,13,14].
Focused microwave breast hyperthermia (FMBH) is a new technique for noninvasive and effective breast cancer treatment. FMBH requires the use of microwave phased array antennas (or applicators) to generate a focused beam at the tumor, which can enable selective and accurate heating of the tumor [15,16,17,18,19]. Therefore, the undesired burning of surrounding normal tissues can be largely avoided, so as to reduce potential side effects [20,21,22,23,24,25].
Due to the complicated tissue composition, human breasts are usually highly heterogeneous in terms of dielectric constant and conductivity distribution. An optimization algorithm is commonly needed in FMBH to optimize the excitation phase/amplitude of each individual element of the antenna array [26,27]. In some special scenarios, however, desired focusing at a breast tumor may not be obtainable by a specific antenna array. This means microwave energy in some other parts of the breast is also very high, which can induce unwanted damage of normal tissues. Thus, it is meaningful to exploit novel approaches to improve the focusing performance.
To explore new antenna array configurations for FMBH, we conduct a computational study in this work to investigate the effect of polarization of the antenna array on the microwave focusing results. Two antenna arrays shown in Figure 1 are investigated. The array 1 has all the elements’ polarization within the vertical planes, i.e., the planes passing the z axis. The array 2 has half of the elements’ polarization within the vertical plane and the other half elements’ polarization within the horizontal plane, i.e., the xy plane, which can be considered as cross polarization. We use six digital realistic human breast phantoms to do simulations to compare the performances of the two arrays. In each breast phantom, we put a tumor at eight different locations to test the generalization of the two arrays, which leads to 48 different simulation models. For each simulation model, both the two arrays are tested and the antenna excitation phase/amplitude for each case is optimized to perform beamforming at the tumor. Simulation results indicate that the two arrays have largely the same focusing effects for fatty breast phantoms, while the array 2 outperforms the array 1 for establishing focused fields in dense breast phantoms. In other words, the cross-polarized antenna array 2 is more suitable for focusing in highly heterogeneous breast phantoms. We also use some modified breast models to further verify this conclusion. This finding is very useful for future advancement and clinical applications of the FMBH technique. The cross-polarization configuration may be also meaningful for biomedical microwave imaging and sensing for dealing with highly heterogeneous environment.
As compared to our previous work [27], this work is fundamentally different since two antenna arrays are studied and the focusing results are compared. To the best of the authors’ knowledge, this is the first work that systematically studies the effects of polarization on FMBH and proposes a cross-polarized antenna array for better focusing performance in dense breasts. This work clearly shows that antenna polarization is a critical factor needs to be considered in the array design for FMBH. Another novelty of this work is that we apply modified breast models to demonstrate that the array 2 performs better in a more heterogeneous breast model.

2. Materials and Methods

2.1. Design of Antenna Array

The simulation setup and the two studied antenna arrays are given in Figure 1. Each antenna array or applicator is a bowl-shaped array and composed of 26 patch antennas, as shown in Figure 2(a). The antennas are arranged in three layers, with 12 on the top layer, 10 in the middle and 4 on the bottom layer. These antennas are evenly distributed on a bowl-shaped surface around a digital realistic human breast phantom (to be described in the Section IIA). The radiated field of the antenna is polarized along the x axis in Figure 2(a). The operating frequency of the antenna is 2.45 GHz [28], which is an ISM frequency suitable for medical applications. It is reported that 2.45 GHz can result in penetration depth larger than 5 cm in human breasts.
In the array 1, all the antennas are placed vertically, and the polarizations are within the vertical planes. In the array 2, half of the antennas are placed vertically while the other half are placed horizontally, meaning half of the antennas’ polarization are within the horizontal plane. In addition, each two adjacent antennas’ polarizations are orthogonal to each other in the array 2. This work mainly investigates the effect of polarization.
Oil with a dielectric constant of 2.6 is used as the microwave coupling fluid and fill into the gap between the antenna array and the breast phantom [29]. The coupling medium can obviously enhance the impedance matching between the antennas and the breast phantom, which improves the microwave transmission efficiency [30]. This is very meaningful since microwave power efficiency of the antenna array is a crucial figure of merit for FMBH.
The substrate of the patch antennas has a permittivity of 10.2, which can reduce the antenna size [31,32,33]. The geometry parameters of the antenna are optimized via CST Microwave Studio. The breast phantom is present when conducting the optimization. The final obtained return loss of some antennas is shown in Figures 2(b) and (c). It is seen that the antennas have good impedance matching at 2.45 GHz.
Generally, more antenna elements offer more degrees of freedom, which can produce better focusing effects for tumors in the breast with complex structures [28]. However, the focusing effect and the overall array size also need to be balanced. This is because a bigger antenna array (antennas distributed on a bigger bowl) may lead to a bigger focusing spot. Thus, using 26 patch antennas is a tradeoff solution.
The realization of the FMBH method requires a multi-channel microwave source with tunable phase and amplitude for each channel. The microwave source can output either continuous wave or pulsed wave signals, which are both suitable for FMBH [15,16]. Ideal focusing condition requires that the microwave power density at the tumor is higher than that of healthy tissues at other locations. In such a situation, the tumor is selectively heated to 42 °C after several mins’ irradiation and malignant cells undergo apoptosis [3,4], while the normal tissues still maintain normal temperature.

2.2. Digital Realistic Human Breast Phantoms

In view of the vast discrepancies among the parameters of the breasts, including sizes, shapes, and tissue compositions, we apply six digital realistic human breast phantoms to compare the focusing effects of the two arrays. As showcased in Figure 3, the six breast phantoms can be classified into four categories [34], namely mostly fatty (class 1), scattered fibroglandular (class 2), heterogeneously dense (class 3), and very dense (class 4). They are defined according to the amount of glandular tissues in the breast [27,35]. As observed from Figure 3, the class 1 phantom has the least glandular tissues while the class 4 phantom has the most glandular tissues. The first phantom in Figure 3(a) belongs to class 1, the second phantom in Figure 3(b) belongs to class 2, the third to fifth phantoms in Figures 3(c)-(e) belong to class 3, and the last phantom in Figure 3(f) belongs to class 4. Each phantom is tested for eight times and a 1-cm-diameter tumor is embedded at a randomly chosen location in the phantom in each case, as depicted in Figure 3. Thus, there are in total 48 different scenarios to study.

2.3. Optimization Algorithm for Microwave Focusing

Due to the need to achieve precise microwave focusing at a tumor in a highly inhomogeneous environment such as human breasts, there is no simple analytical method to calculate the excitation phase/amplitude of the antenna array. An optimization algorithm must be used to perform multiple iterations to obtain the optimal phase/amplitude. In each iteration, the microwave power deposition in the breast phantom is obtained through some monitoring or guidance mechanism. In experiments or clinical scenarios, the power density distribution in the breast can be detected by methods such as MRI [36], ultrasound imaging [37] and thermoacoustic imaging [38]. In the current simulation study, we just need to record the power distribution in the breast phantom in CST software.
In this work, we use an optimization algorithm called differential evolution (DE) [39,40] to implement the searching for the optimal phase/amplitude. This algorithm has been well demonstrated in some previous works [27,40,41]. It has been found that the excitation phase imposes a much larger impact on the focusing effect than the excitation amplitude. Therefore, only phase is optimized in this work and all the amplitude is set to uniform.
In order to realize the DE algorithm, a fitness function needs to be defined as the evaluation criterion for each iteration step. We adopt the fitness function as
Q ratio = Q tumor Q healthy
where the power density Q is calculated by
Q = σ | E ⇀ tot | 2 = σ | ∑ i = 1 26 e j φ i E ⇀ i | 2
where Q is the microwave power density in W/m3, σ is the electrical conductivity of the breast tissues, φi denotes the excitation phase of the ith antenna, Ei is the electric field in the breast phantom solely contributed by the ith antenna, and Etot is the total electric field (a complex number) in the breast phantom contributed by all the 26 antennas. Qtumor is the average microwave power density in the tumor, and Qhealthy is the maximum microwave power density in healthy tissues.
In each step of iterative optimization, the phase of each individual antenna is adjusted by the optimization algorithm. The algorithm uses the microwave focusing results (i.e., microwave power distribution) of the previous steps as feedback information for the next iteration to maximize the fitness function in Equation (1). In this way, the value of the fitness function is gradually increased, which means that the hot spots in the healthy tissue region are gradually eliminated. Once the fitness function reaches a desired value, an acceptable focused microwave field is achieved and the iteration is terminated. This algorithm has been proven to be superior to the particle swarm optimization.

2.4. Procedure of Computational Study

First, we conduct the microwave simulation of the complex breast phantom by CST software [42]. A total of 26 sets of CST simulations are performed using a breast phantom containing a tumor. In each set of simulation, only one antenna is radiating while the excitation signal of the rest 25 antennas is set to 0. Then the electric field in the entire breast due to the ith radiating antenna is recorded, which is Ei in Equation (2). This process is repeated for 26 times and in total 26 sets of electric field distributions are obtained.
Second, we employ the DE algorithm to optimize the fitness function and the excitation phase. The initial phase of the antennas can be set to 0 or arbitrary value. In each iteration, we calculate Q by Equation (2) using the excitation phase of all the 26 antennas (φ1 to φ26) in the current iteration. It should be noted that although the 26 sets of electric fields are obtained individually, they can be used to synthesize the total electric field as the 26 antennas were radiating together. Then we use Equation (1) to determine whether an acceptable focus has been achieved. If not, the DE algorithm yields a new set of excitation phase and the iterative optimization is continued. Generally, Qratio > 1 is a desired result of the optimization, which means the power in the healthy tissues does not exceed that in the tumor. However, such a desired condition may not be obtainable in some cases. Thus, a more practical goal is to optimize Qratio until its value becomes convergent.
In this work, we set the maximum number of iterations to be 100, which is because Qratio of most of the studied cases can no longer be increased after 100 iterations. In other words, the optimization process becomes convergent and more iterations are not needed. Then the optimization process is terminated. The value of the final Qratio and corresponding excitation phase can be obtained [26].

3. Results

3.1. Focusing Results Using Original Breast Phantoms

We then compare the focusing effects of the two antenna arrays. The simulated microwave power density distributions of all the 96 studied cases are shown in Figure 4, Figure 5, Figure 6, Figure 7, Figure 8 and Figure 9. Each figure has 8 sets of subfigures and each set has three subfigures representing the conductivity distribution, power density distribution using the array 1 and power distribution using the array 2. To be specific, the first and fourth columns of each figure of Figure 4, Figure 5, Figure 6, Figure 7, Figure 8 and Figure 9 display the sagittal plane view of the conductivity distribution of the breast phantom with a tumor, the second and fifth columns give the corresponding power density for the array 1, and the third and sixth columns present the corresponding power density for the array 2. The circular bright spot in the conductivity distribution is the tumor, which has the highest conductivity among all the tissues. It can be seen that both the arrays can render good microwave-focused fields at the tumor for most of the 48 studied cases. Some parts of the skin can also absorb high microwave power due to its high conductivity. But some measures can be taken to cool down the skin to avoid burning in it.

3.2. Quantitative Comparison

In order to quantitatively evaluate the focusing effect, the ratio of the fitness function Qratio of the two arrays defined in Equation (1) is provided in Figure 10. For most of the cases, Qratio is greater than 0.7. For those conditions with Qratio < 0.7, the maximum power density in the healthy tissue probably occur around the tumor, which is acceptable for the treatment purpose of FMBH.
For a more intuitive and generalized comparison, the Qratio of the same breast phantom with different tumor locations are averaged to obtain Qavgratio1 and Qavgratio2. Then a new ratio defined in (3) is obtained.
Q ratio 21 = Q avgratio 2 Q avgratio 1
The results of Equation (3) of the six breast phantoms are plotted in Figure 11. It is straightforward that the focusing effect of the array 2 is better than that of the array 1 for the three class 3 phantoms and the class 4 phantom since Qratio21 > 1. The improvement is greater than 20%. For the class 1 and class 2 phantoms, the focusing effects of the two arrays are comparable. As a result, we can reach a conclusion that the array 2 outperforms the array 1 in terms of focusing effect for FMBH in dense breasts, while the two arrays perform equally well for FMBH in fatty breasts. Furthermore, the advantage of array 2 in terms of microwave focusing is more obvious in denser breasts or breasts with higher inhomogeneity. This implies that the microwave focusing effect can be enhanced to a certain extent by simply using an antenna array embracing orthogonal polarizations without adjusting the antenna structure or increasing the number of antennas. Orthogonal polarization tends to offer more flexibility in microwave focusing and leads to a better focused field, especially in dense breasts.

3.3. Focusing Results Using Modified Breast Models

We perform further studies to compare the two arrays. We use the class 4 phantom with a tumor as the case in Figure 9(d) and modify the tissue properties in it. As shown in Figure 12 (a), the original model is named as Model 1. The permittivity as well as conductivity of the healthy breast tissues in the phantoms in Figures 12 (b) and (c) are reduced to 70% and 30%, respectively, of those in the Model 1, which are referred to as Model 2 and Model 3. The dielectric property of the tumor is not changed. The three models are investigated by the two arrays and the microwave power distributions after 100 iterations are shown in Figures 12(d)-(i), with (d)-(f) for the array 1 and (g)-(i) for the array 2.
The corresponding Qratio results are shown in Figure 13. It can be observed that as the permittivity and conductivity of the healthy tissues decrease, the Qratio of the two arrays gradually increases, meaning that the focusing effect becomes better. At the same time, the increase in the focusing effect of the array 2 is relatively smaller than that of the array 1. Moreover, for the densest breast Model 1, the focusing effect of the array 2 is better than that of the array 1. For the Model 3 that is nearly a fatty breast, the array 1 performs better than the array 2. For the Model 2, the two arrays lead to largely the same focusing effect. These results further prove that the array 2 is more favorable for establishing a good focused microwave field in a dense breast.
This finding is also valuable to microwave imaging or sensing applications based on antenna arrays. For most of the microwave imaging or inverse scattering techniques, antennas are configured with the same polarizations around the sample under test [43,44]. However, exploring imaging applying dual polarization or cross polarization can offer the possibility of extracting more information and acquiring higher image quality of the target. In addition, Figure 13 implies that a cross-polarized antenna array is favorable for imaging highly inhomogeneous objects like the dense breasts.

4. Conclusions

To summarize, we propose a cross-polarized antenna array to improve the microwave focusing in breast hyperthermia. Six real breast phantoms with different densities and different tumor positions are used to conduct numerical simulations to compare the focusing effect of two antenna arrays. The complete process and data comparison are presented in details. The simulated power density distribution indicates that the arrangement of the antenna array 2 can obviously improve the focusing quality in heterogeneously dense and very dense breast phantoms. This computational research is of great significance for improving the performance of FMBH and the microwave imaging/sensing technique.

Author Contributions

Conceptualization, X.W. and X.W.; methodology, Z.X. and K.Y.; writing—original draft preparation, X.W.; writing—review and editing, Z.G. and X.W.; supervision, X.W. and Y.C. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by the National Natural Science Foundation of China, grant number 61971287 and in part by the Open Project of State Key Laboratory of Millimeter Waves, grant number K202207.

Data Availability Statement

Data are available upon request.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. F. Bai, P. Liu, and L. X. Xu. Recent advances in thermal treatment techniques and thermally induced immune responses against cancer. IEEE Trans. Biomed. Eng. 2014, 61, 1497–1505. [CrossRef]
  2. J. van der Zee. Heating the patient: A promising approach. Ann. Oncol. 2002, 13, 1173–1184. [CrossRef] [PubMed]
  3. J. Mendecki et al. Microwave-induced hyperthermia in cancer treatment: Apparatus and preliminary results. Int. J. Radiat. Oncol. Biol. Phys. 1978, 4, 1095–1103. [CrossRef]
  4. N. Saniei. Hyperthermia and cancer treatment. Heat Transf. Eng. 2009, 30, 915–917. [CrossRef]
  5. K. Kim, T. Seo, K. Sim, and Y. Kwon. Magnetic nanoparticle-assisted microwave hyperthermia using an active integrated heat applicator. IEEE Trans. Microw. Theory Techn. 2016, 64, 2184–2197. [CrossRef]
  6. M. H. Falk and R. D. Issels. Hyperthermia in oncology. Int. J. Hyperthermia 2001, 17, 1–18. [CrossRef]
  7. C. A. Perez et al. Quality assurance problems in clinical hyperthermia and their impact on therapeutic outcome: a report by the Radiation Therapy Oncology Group. Int. J. Radiat. Oncol. Biol. Phys. 1989, 16, 551–558. [CrossRef]
  8. D. G. Frew, J. M. Dobson, S. P. Stenning, and N. M. Bleehen. Response of 145 spontaneous canine head and neck tumours to radiation versus radiation plus microwave hyperthermia: results of a randomized phase III clinical study. Int. J. Hyperthermia 1995, 11, 217–230. [CrossRef]
  9. P. Cherukuri, E. S. Glazer, and S. A. Curley. Targeted hyperthermia using metal nanoparticles. Adv. Drug Deliv. Rev. 2010, 62, 339–345. [CrossRef]
  10. N. R. Datta et al. Local hyperthermia combined with radiotherapy and-/or chemotherapy: Recent advances and promises for the future. Cancer Treat. Rev. 2015, 41, 742–753. [CrossRef]
  11. J. Beik et al. Nanotechnology in hyperthermia cancer therapy: From fundamental principles to advanced applications. J. Control Release 2016, 235, 205–221. [CrossRef]
  12. J. Torres-Reveron, H. C. Tomasiewicz, A. Shetty, N. M. Amankulor, and V. L. Chiang. Stereotactic laser induced thermotherapy (LITT): a novel treatment for brain lesions regrowing after radiosurgery. J. Neurooncol. 2013, 113, 495–503. [CrossRef]
  13. T. J. Vogl et al. Thermal ablation of colorectal lung metastases: retrospective comparison among laser-induced thermotherapy, radiofrequency ablation, and microwave ablation. AJR. Am. J. Roentgenol. 2016, 207, 1340–1349. [CrossRef]
  14. J. C. Nielsen et al. Radiofrequency ablation as initial therapy in paroxysmal atrial fibrillation. N. Engl. J. Med. 2012, 367, 1587–1595. [CrossRef]
  15. J. Stang, M. Haynes, P. Carson, and M. Moghaddam. A preclinical system prototype for focused microwave thermal therapy of the breast. IEEE Trans. Biomed. Eng. 2012, 59, 2431–2438. [CrossRef]
  16. P. T. Nguyen, A. Abbosh, and S. Crozier. Microwave hyperthermia for breast cancer treatment using electromagnetic and thermal focusing tested on realistic breast models and antenna arrays. IEEE Trans. Antennas Propag. 2015, 63, 4426–4434. [CrossRef]
  17. P. T. Nguyen, A. M. Abbosh, and S. Crozier. 3-D focused microwave hyperthermia for breast cancer treatment with experimental validation. IEEE Trans. Antennas Propag. 2017, 65, 3489–350. [CrossRef]
  18. G. G. Bellizzi, L. Crocco, G. M. Battaglia, and T. Isernia. Multi-frequency constrained SAR focusing for patient specific hyperthermia treatment. IEEE J. Electromagn., RF Microw. Med. Biol. 2017, 1, 74–80. [CrossRef]
  19. P. Takook, M. Persson, and H. D. Trefná. Performance evaluation of hyperthermia applicators to heat deep-seated brain tumors. IEEE J. Electromagn., RF Microw. Med. Biol. 2018, 2, 18–24. [CrossRef]
  20. K. R. Mahmoud and A. M. Montaser. Design of multiresonance flexible antenna array applicator for breast cancer hyperthermia treatment. IEEE Access 2022, 10, 93338–93352. [CrossRef]
  21. P. T. Nguyen, A. Abbosh and S. Crozier. Three-dimensional microwave hyperthermia for breast cancer treatment in a realistic environment using particle swarm optimization. IEEE Trans. Biomed. Eng. 2017, 64, 1335–1344. [CrossRef] [PubMed]
  22. X. He, W. Geyi and S. Wang. A Hexagonal focused array for microwave hyperthermia: Optimal design and experiment. IEEE Trans. Antennas Propag. 2016, 15, 56–59. [CrossRef]
  23. D. A. M. Iero, L. Crocco and T. Isernia. Thermal and microwave constrained focusing for patient-specific breast cancer hyperthermia: A robustness assessment. IEEE Trans. Antennas Propag. 2014, 62, 814–821. [CrossRef]
  24. D. Brizi et al. A Radiating system for low-frequency highly focused hyperthermia with magnetic nanoparticles. IEEE J. Electromagn., RF Microw. Med. Biol. 2020, 4109-116. [CrossRef]
  25. H. P. Kok et al. Heating technology for malignant tumors: a review. Int. J. Hyperthermia 2020, 37, 711–741. [CrossRef]
  26. L. Xu and X. Wang. Comparison of two optimization algorithms for focused microwave breast cancer hyperthermia. in 2018 International Applied Computational Electromagnetics Society (ACES) Symposium, Beijing, China, July 29−Aug. 1, 2018. [CrossRef]
  27. L. Xu and X. Wang. Focused microwave breast hyperthermia monitored by thermoacoustic imaging: A computational feasibility study applying realistic breast phantoms. IEEE J. Electromagn., RF Microw. Med. Biol. 2020, 4, 81–88. [CrossRef]
  28. J. Li, L. Xu, and X. Wang. A computational study on number of elements in antenna array for focused microwave breast hyperthermia. in 2019 IEEE MTTS International Microwave Biomedical Conference (IMBioC), Nanjing, China, 2019, pp. 1–3. [CrossRef]
  29. K. Nemez, A. Baran, M. Asefi, and J. LoVetri. Modeling error and calibration techniques for a faceted metallic chamber for magnetic field microwave imaging. IEEE Trans. Microw. Theory Techn. 2017, 65, 4347–4356. [CrossRef]
  30. D. Wu, L. Huang, M. Jiang, and H. Jiang. Contrast agents for photoacoustic and thermoacoustic imaging: A review. Int. J. Mol. Sci. 2014, 15, 23616–23639. [CrossRef] [PubMed]
  31. M. E. Bialkowski. Ultra wideband microwave system with novel image reconstruction strategies for breast cancer detection. The 40th European Microwave Conference, Paris, France, 2010, pp. 537-540.
  32. E. Razzicchia et al. Metasurface-enhanced antennas for microwave brain imaging. Diagnostics 2021, 11, 424. [CrossRef]
  33. Z. Xi, X. Wang, K. Ye, and X. Wang. Performance evaluation of focused microwave brain hyperthermia guided by microwave-induced thermoacoustic tomography. IEEE J. Electromagn., RF Microw. Med. Biol. 2023, 7, 383–391. [CrossRef]
  34. X. Wang, T. Qin, R. S. Witte, and H. Xin. Computational feasibility study of contrast-enhanced thermoacoustic imaging for breast cancer detection using realistic numerical breast phantoms. IEEE Trans. Microw. Theory Techn. 2015, 63, 1489–1501. [CrossRef]
  35. E. Zastrow et al. Database of 3D grid-based numerical breast phantoms for use in computational electromagnetics simulations. Univ. Wisconsin–Madison, Madison, WI, USA, 2007. [Online]. Available online: http://uwcem.ece.wisc.edu/MRIdatabase/ (accessed on 1 November 2023).
  36. R. Sinkus et al. Potential of MRI and ultrasound radiation force in elastography: applications to diagnosis and therapy. Proc. IEEE 2008, 96, 490–499. [CrossRef]
  37. M. Pernot, M. Tanter, J. Bercoff, K. R. Waters, and M. Fink. Temperature estimation using ultrasonic spatial compound imaging. IEEE Trans. Ultrason., Ferroelectr., Freq. Control 2004, 51, 606–615. [CrossRef]
  38. B. Wang, Y. Sun, Z. Wang, and X. Wang. Three-dimensional microwave-induced thermoacoustic imaging based on compressive sensing using an analytically constructed dictionary. IEEE Trans. Microw. Theory Techn. 2020, 68, 377–386. [CrossRef]
  39. K. Price and R. Storn. Differential evolution—a simple and efficient heuristic for global optimization over continuous spaces. J. Global Optim. 1997, 11, 341–359. [CrossRef]
  40. G. Cappiello et al. Differential evolution optimization of the SAR distribution. IEEE Trans. Biomed. Eng. 2017, 64, 1875–1885. [CrossRef]
  41. J. Li et al. A preclinical system prototype for focused microwave breast hyperthermia guided by compressive thermoacoustic tomography. IEEE Trans. Biomed. Eng. 2021, 68, 2289–2300. [CrossRef]
  42. CST Users’ Manuals, CST GmbH. [Online]. Available online: www.cst.com (accessed on 1 November 2023).
  43. K. Xu, Z. Qian, Y. Zhong, J. Su, H. Gao, and W. Li. Learning-assisted inversion for solving nonlinear inverse scattering problem. IEEE Trans. Microw. Theory Techn. 2023, 71, 2384–2395. [CrossRef]
  44. M. Ostadrahimi, A. Zakaria, J. LoVetri, and L. Shafai. A Near-field dual polarized (TE–TM) microwave imaging system. IEEE Trans. Microw. Theory Techn. 2013, 61, 1376–1384. [CrossRef]
Preprints 100231 g001
Figure 1. Configurations of the two studied antenna arrays: (a) Array 1; (b) Array 2 (cross polarization).
Figure 1. Configurations of the two studied antenna arrays: (a) Array 1; (b) Array 2 (cross polarization).
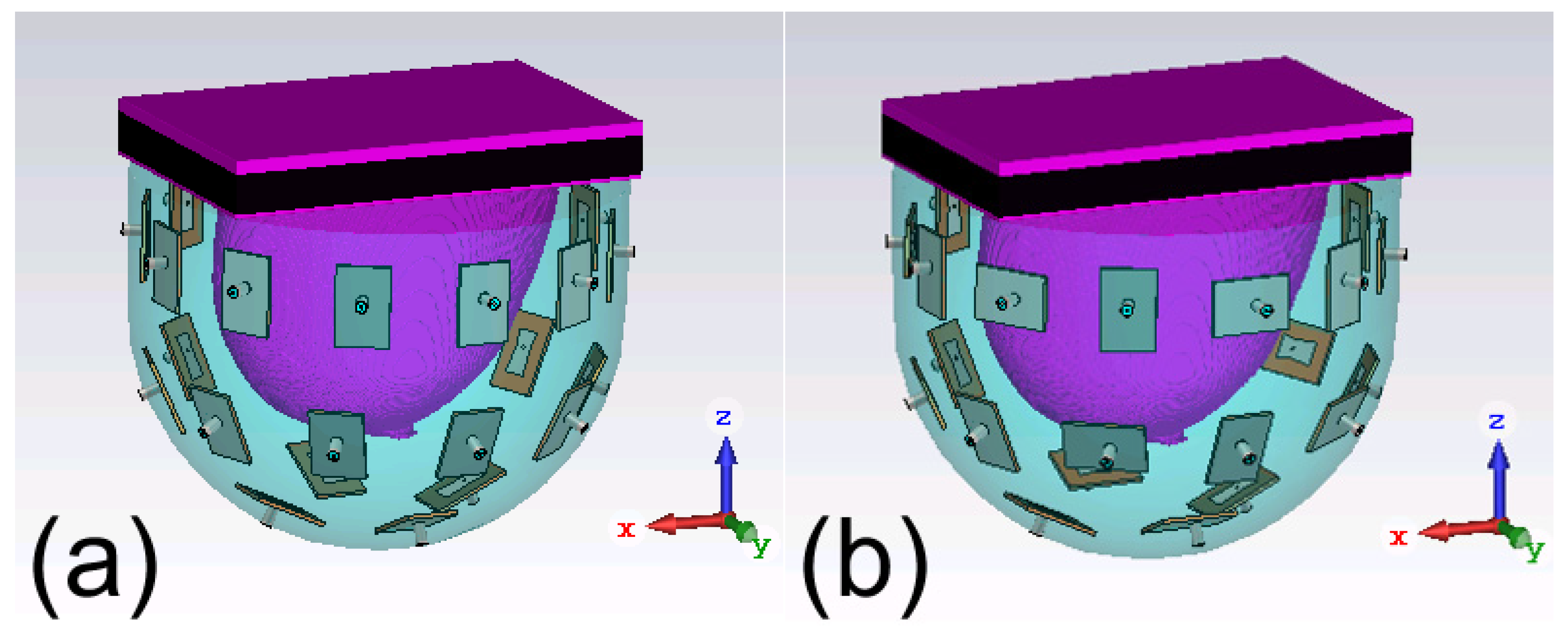
Preprints 100231 g001
Preprints 100231 g002
Figure 2. Details of the antenna: (a) The structure of the patch antenna; (b) Simulated return loss of typical 3 patch antennas in the array 1 with the breast phantom present; (c) Simulated return loss of typical 3 patch antennas in the array 2 with the breast phantom present.
Figure 2. Details of the antenna: (a) The structure of the patch antenna; (b) Simulated return loss of typical 3 patch antennas in the array 1 with the breast phantom present; (c) Simulated return loss of typical 3 patch antennas in the array 2 with the breast phantom present.
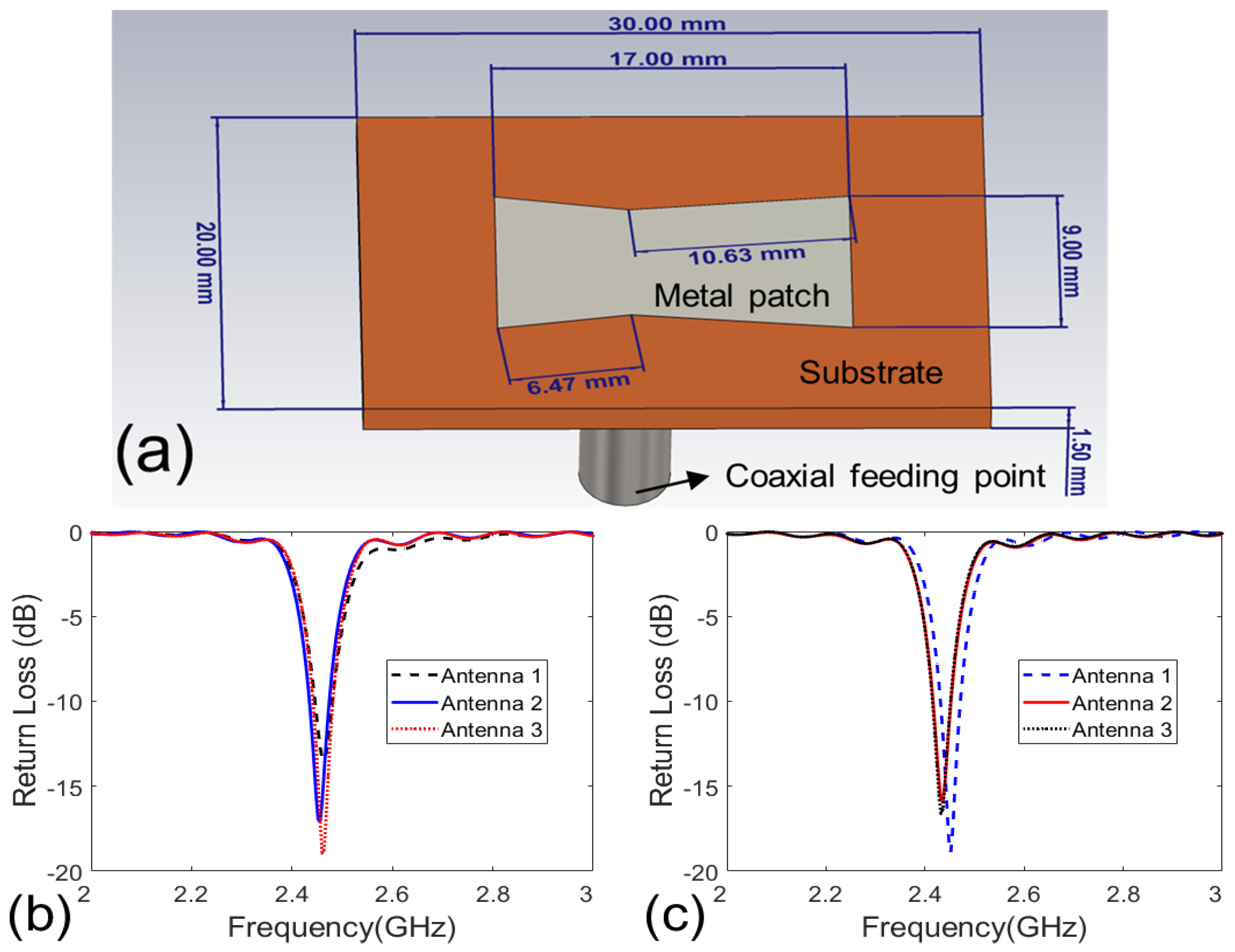
Preprints 100231 g002
Preprints 100231 g003
Figure 3. Six breast phantoms with tumors: (a) Class 1; (b) Class 2; (c) Class 3 A; (d) Class 3 B; (e) Class 3 C; (f) Class 4. The small blue balls represent the tumors and the complicated structures in purple are mainly the breast glandular tissues.
Figure 3. Six breast phantoms with tumors: (a) Class 1; (b) Class 2; (c) Class 3 A; (d) Class 3 B; (e) Class 3 C; (f) Class 4. The small blue balls represent the tumors and the complicated structures in purple are mainly the breast glandular tissues.
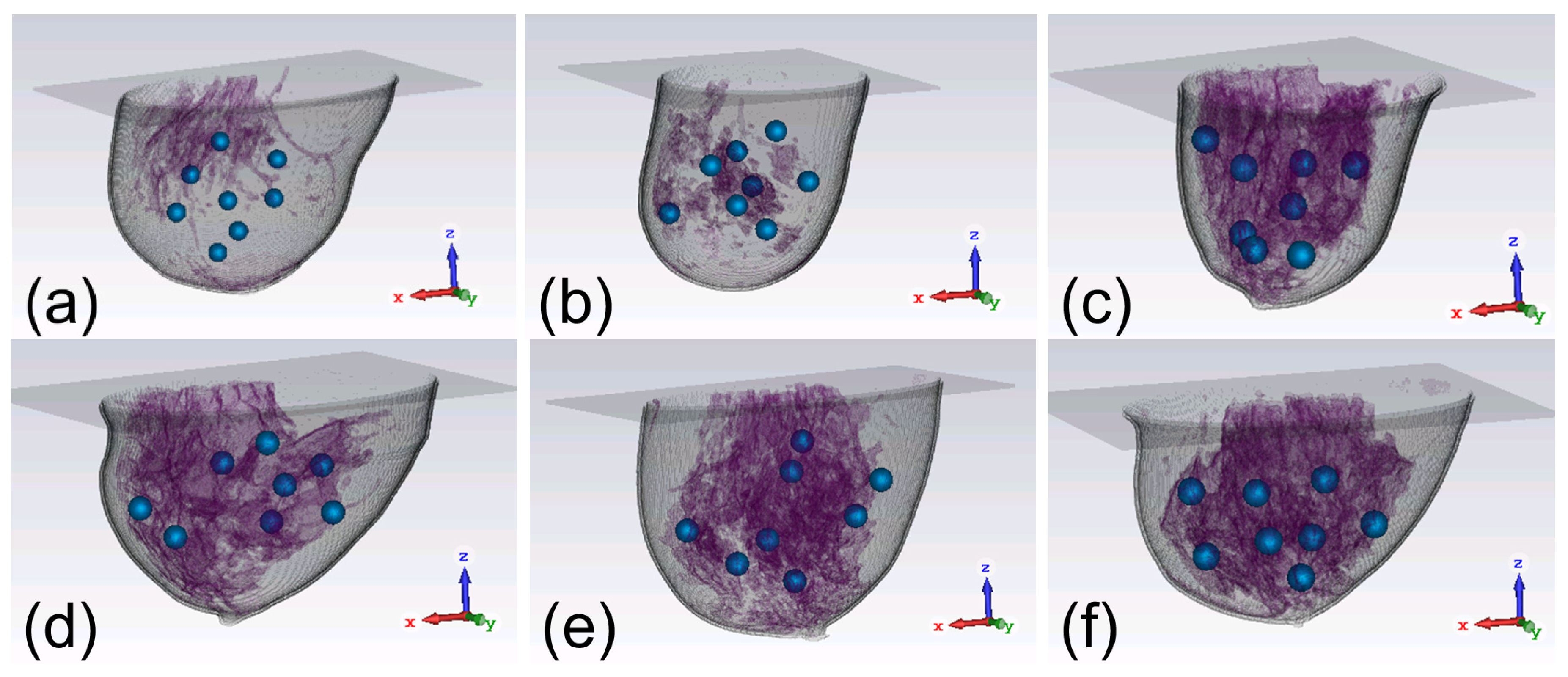
Preprints 100231 g003
Preprints 100231 g004
Figure 4. (a)-(h) Conductivity distribution of Class 1 A breast model with 8 different tumor positions; (i)-(p) The power density distribution of antenna array 1; (q)-(x) The power density distribution of antenna array 2.
Figure 4. (a)-(h) Conductivity distribution of Class 1 A breast model with 8 different tumor positions; (i)-(p) The power density distribution of antenna array 1; (q)-(x) The power density distribution of antenna array 2.
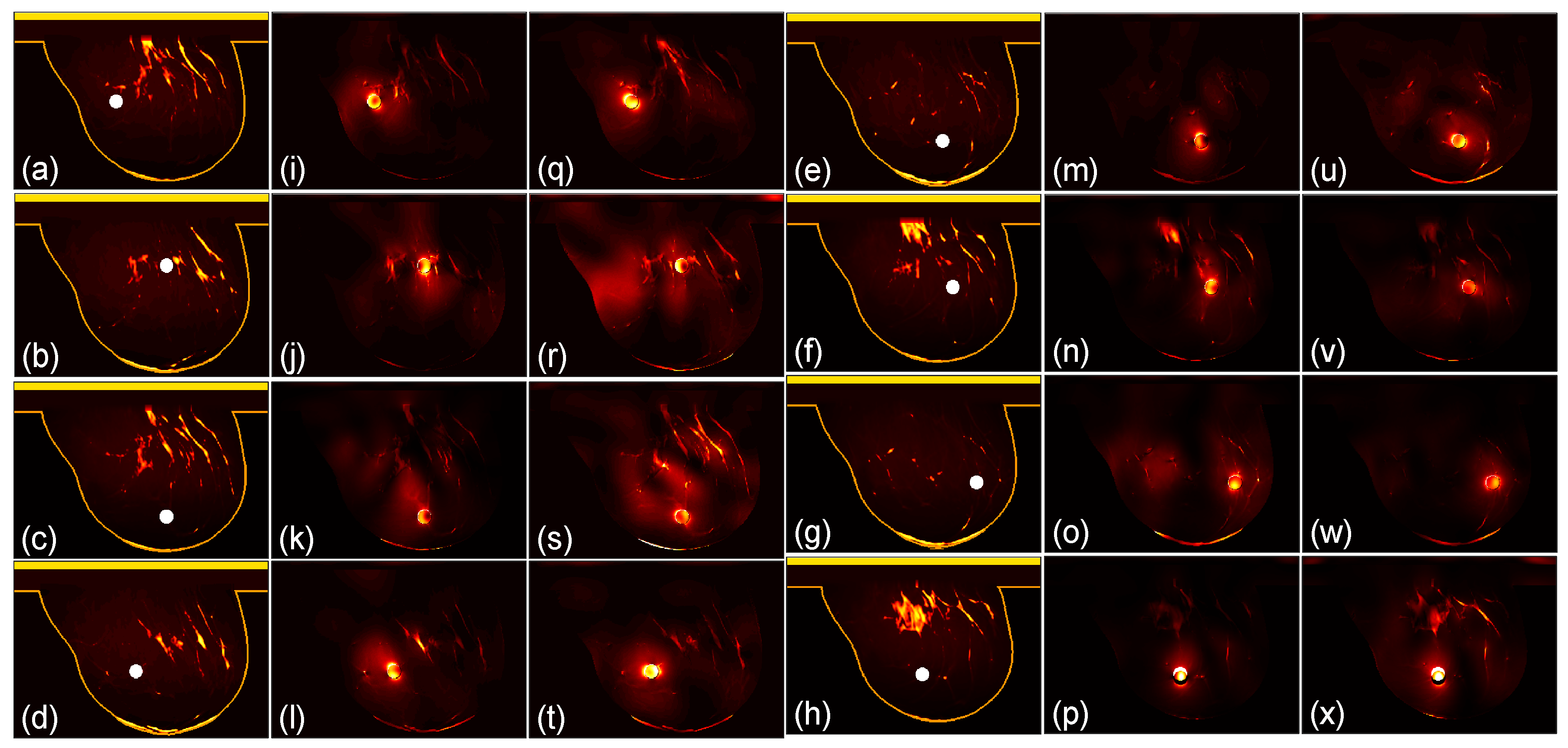
Preprints 100231 g004
Preprints 100231 g005
Figure 5. (a)-(h) Conductivity distribution of Class 2 A breast model with 8 different tumor positions; (i)-(p) The power density distribution of antenna array 1; (q)-(x) The power density distribution of antenna array 2.
Figure 5. (a)-(h) Conductivity distribution of Class 2 A breast model with 8 different tumor positions; (i)-(p) The power density distribution of antenna array 1; (q)-(x) The power density distribution of antenna array 2.
Preprints 100231 g005
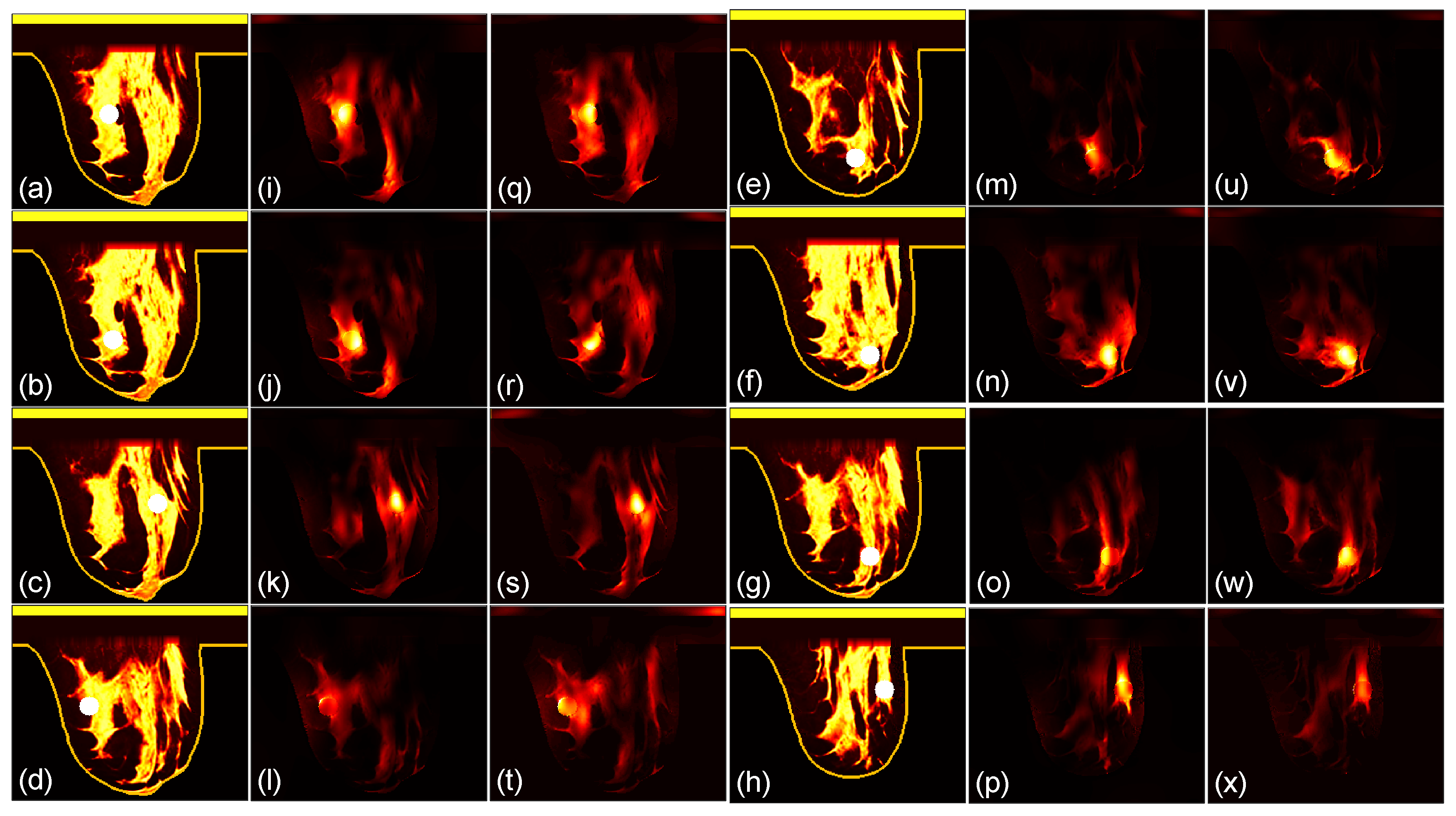
Preprints 100231 g006
Figure 6. (a)-(h) Conductivity distribution of Class 3 A breast model with 8 different tumor positions; (i)-(p) The power density distribution of antenna array 1; (q)-(x) The power density distribution of antenna array 2.
Figure 6. (a)-(h) Conductivity distribution of Class 3 A breast model with 8 different tumor positions; (i)-(p) The power density distribution of antenna array 1; (q)-(x) The power density distribution of antenna array 2.
Preprints 100231 g006
Preprints 100231 g007
Figure 7. (a)-(h) Conductivity distribution of Class 3 B breast model with 8 different tumor positions; (i)-(p) The power density distribution of antenna array 1; (q)-(x) The power density distribution of antenna array 2.
Figure 7. (a)-(h) Conductivity distribution of Class 3 B breast model with 8 different tumor positions; (i)-(p) The power density distribution of antenna array 1; (q)-(x) The power density distribution of antenna array 2.
Preprints 100231 g007
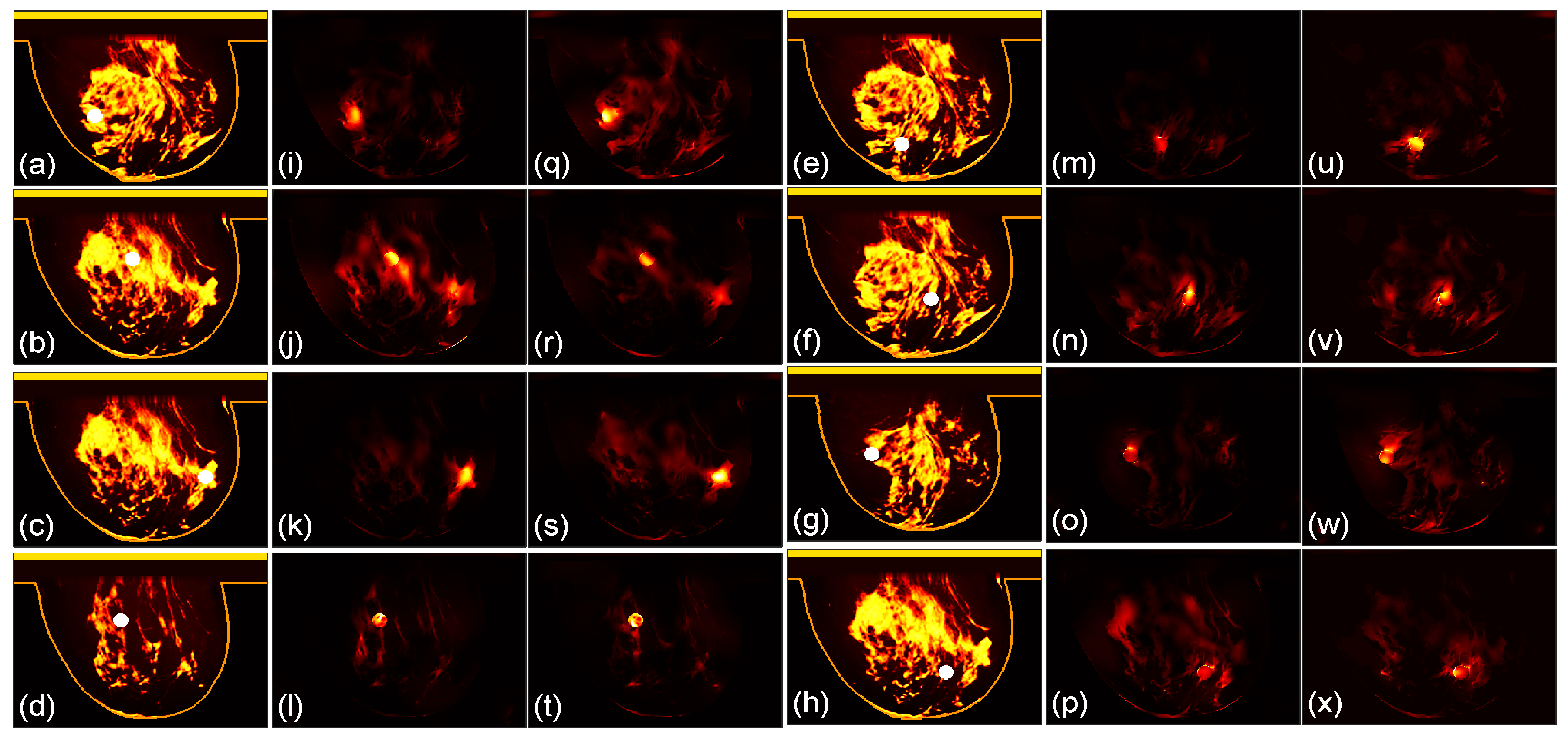
Preprints 100231 g008
Figure 8. (a)-(h) Conductivity distribution of Class 3 C breast model with 8 different tumor positions; (i)-(p) The power density distribution of antenna array 1; (q)-(x) The power density distribution of antenna array 2.
Figure 8. (a)-(h) Conductivity distribution of Class 3 C breast model with 8 different tumor positions; (i)-(p) The power density distribution of antenna array 1; (q)-(x) The power density distribution of antenna array 2.
Preprints 100231 g008
Preprints 100231 g009
Figure 9. (a)-(h) Conductivity distribution of Class 4 A breast model with 8 different tumor positions; (i)-(p) The power density distribution of antenna array 1; (q)-(x) The power density distribution of antenna array 2.
Figure 9. (a)-(h) Conductivity distribution of Class 4 A breast model with 8 different tumor positions; (i)-(p) The power density distribution of antenna array 1; (q)-(x) The power density distribution of antenna array 2.
Preprints 100231 g009
Preprints 100231 g010
Figure 10. The value of Qratio of the focusing results of all the 48 models by the two arrays.
Figure 10. The value of Qratio of the focusing results of all the 48 models by the two arrays.
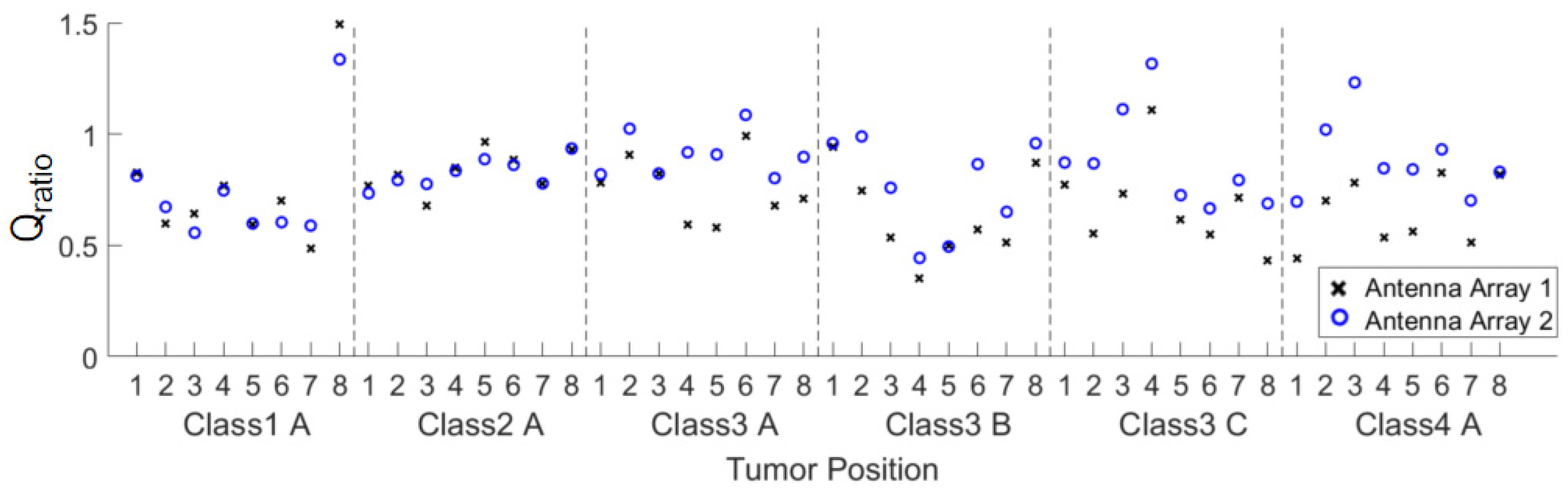
Preprints 100231 g010
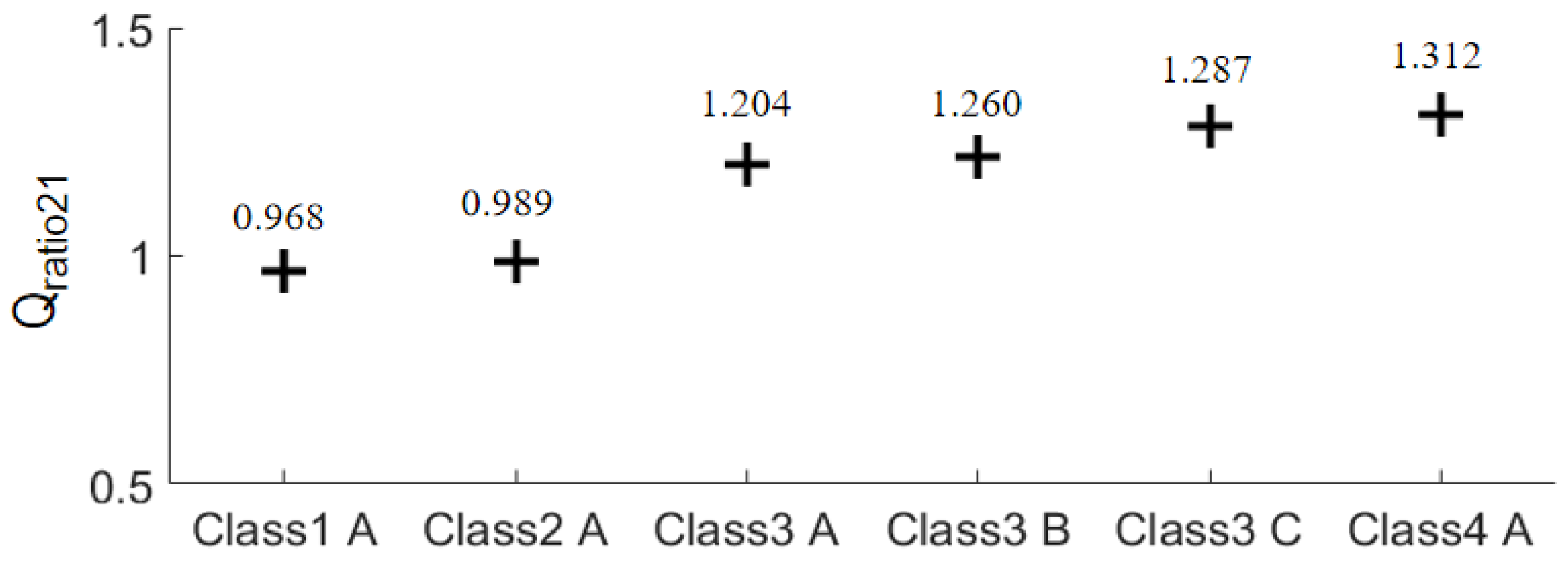
Preprints 100231 g011
Figure 11. Comparison of the averaged Qratio21 of the focusing results of the two arrays in the six breast phantoms.
Figure 11. Comparison of the averaged Qratio21 of the focusing results of the two arrays in the six breast phantoms.
Preprints 100231 g011
Preprints 100231 g012
Figure 12. (a)-(c) Conductivity distribution of the modified breast Model 1, Model 2 and Model 3, which are based on the class 4 phantom in Figure 9(d); (d)-(f) The power density distribution using antenna array 1; (g)-(i) The power density distribution using antenna array 2.
Figure 12. (a)-(c) Conductivity distribution of the modified breast Model 1, Model 2 and Model 3, which are based on the class 4 phantom in Figure 9(d); (d)-(f) The power density distribution using antenna array 1; (g)-(i) The power density distribution using antenna array 2.
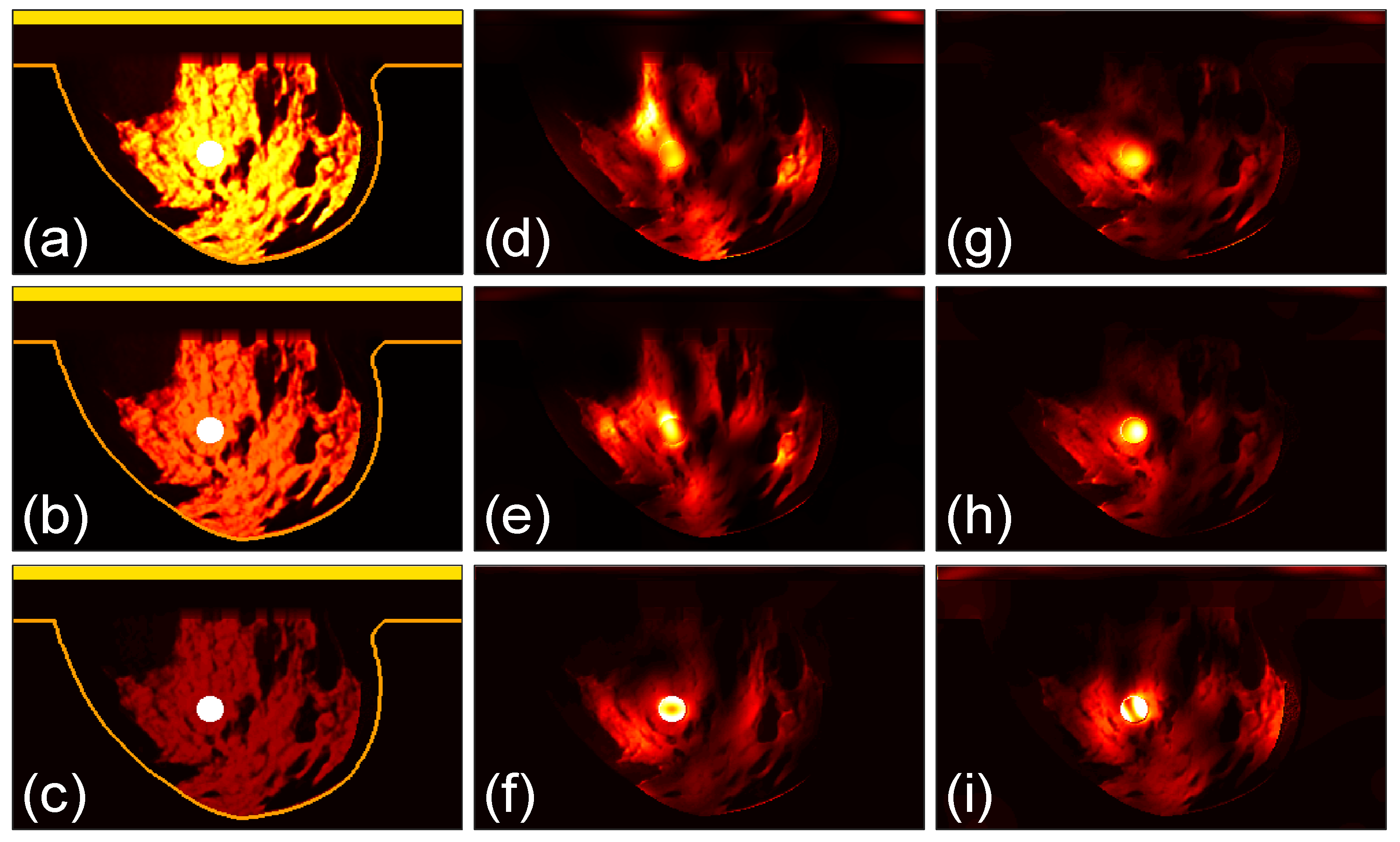
Preprints 100231 g012
Preprints 100231 g013
Figure 13. The focusing results using the modified breast models in Figure. 12.
Figure 13. The focusing results using the modified breast models in Figure. 12.
Preprints 100231 g013
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated