Preprint

Article

Environmental Factors Affecting Requirements for Wind Power Stations

Altmetrics

Downloads

Views

Comments

This version is not peer-reviewed

Submitted:

29 February 2024

Posted:

01 March 2024

You are already at the latest version

Alerts

Abstract

The paper presents modelling of relationships between wind velocity distributions observed in Poland and technical requirements for wind power stations design. The wind velocities distributions for various locations in Poland are determined, and expressed in Weibull distribution parameters. Theoretical computations concerning the dependence of wind power station as function of wind speed and aire physical properties are presented. Conclusions important for design of power stations fitted to atmospheric conditions in Poland are given. Wind power plants have been an important source of electricity generation for many years.Wind power modelling with the use of wind speed is used to improve the accuracy of forecasts and analyses of the power production of wind farms.

Keywords:

Subject: Environmental and Earth Sciences - Sustainable Science and Technology

1. Introduction

The energy policy and environmental policy of European Union (EU) for years have an impact on the renewable energy [1,2]. The renewable energy sources are a starting point of many debates between European politics, representatives of energy companies, scientists and consumers [3,4,5]. According to findings of European Parliament, by 2030 the renewable energy sources must make at least 40% of energy consumed within EU, which leads to reduction of the greenhouse gases even up to 55% in comparison to 1990. Internal law regulations of UE members strongly underline a need of acceleration of the energy market structure transformation [6,7].

In 2023 in Germany 55 percent of electric energy have been created by renewable energy sources. A majority of such production had in-land wind turbines. All wind turbines, both in-land and seashore, made up 31.1% of the produced electric energy [8]. In the same year, Portugal generated even greater amounts of electric energy coming form renewable energy sources: up to 61%, a quarter of which came from the wind energy. Noticeable, just a year before (in 2022) the amount of renewable energy sources in total production of electric energy in Portugal was 49% [9].

According to PSE (Polskie Sieci Elektroenergetyczne – Polish Electricity Networks) data, the dominant amount of coal energy in 2023 has been reduced to 63%, amount of renewable energy sources has been increased to 27% and the amount of gas energy was 10%. The total power of all installed wind farms was 9428.3MW (end of December, 2023). Moreover, Polish seashore wind turbines are currently being developed, a power of which should achieve 5.9MW by 2030 and 11MW by 2040. Energy Policy of Poland by 2040 defines building and development of seashore wind farms as a strategical direction of the energy market transformation, which enforces the energetical safety and excites the economic development of Poland [10].

For years, one may observe a progression of design and technology used in the wind turbines, both seashore and in-land. For instance, the Dutch start-up company TouchWind proposes a concept of single-bladed wind turbines Mono. The advantages of such concept are, amongst others, lower mass and wide range of wind speed when the turbine works effectively. Furtherly, the manufacturing cost of such turbine may be even 30% - 50% of similar value for typical, 3-bladed wind turbine. The latter has been achieved due to simplicity of both the rotor and its base [11].

At the end of 2020, Vestas company introduced the V155-3.3MW wind turbine, as a variation of 4MW platform, developed to utilize weak and ultra-weak wind. Similarly, the version V155-3,6MW has been modernized and technically optimized to extend the possibility of application. Such turbine is aimed on offer to location where the dominant wind speed is low – including India, USA and a lot of countries in Europe and Latin America [12].

The Norwegian start-up World Wide Wind started the testing of the prototype of the floating wind turbine, equipped with a pair of contra-rotating, vertical axis rotors. The power of the prototype is only 30 kW. The electric generator is located on the bottom – below the water surface – as a stabilizer and a contra-balance. The rotor blades move along a 3-dimensional curves and additional supports increase the efficiency of wind energy capturing. The concept allows on reduction of the distance between adjacent turbines within the wind farm even up to 50%. [13].

Moreover, at Northwester 2 wind farm the MHI Vestas company had installed a prototype of the turbine with the power of 9.5MW, rotor dimension of 174 m and blade length of 85 m.

Another prototype, developed by GE Renewable Energy, is Haliade-X wind turbine with the output power of 12MW. It is estimated that for wind conditions typical for the German part of the Northern Sea the outcome of electric energy may reach up to 67GWh per year. This turbine may be compared to Cypress – another turbines family produced by GE Renewable Energy. The Cypress is the in-land wind turbine with the power of 5.3MW and rotor diameter of approximately 160 m. Its prototype has been installed in Wieringermeer (Holland) and started the operational phase in February, 2019 [14,15].

Also Siemens Gamesa developed an offshore wind turbine, with the power of 14MW. According to the producer, the rotor diameter achieves 222 m, blades length is 108 m and hub weight is 500 tons. The same Siemens Gamesa company develops a concept of energy storage, that utilize wind turbines and volcanic stones heated up to 600 Celcius degrees using the energy collected by the wind turbine. The heated stones are stored in the isolated sarcophagus and may be cooled when the wind turbine is off. At this time the vapor is produced to power the turbine [16].

An example of different approach are Polish wind turbines VENTUS Power Generator [17,18]. Such turbine is designed as extremaly small device used by a single household. The company offers 3-bladed HAWT turbines that create the Y-type family: Ventus 500W, Ventus 1000W and Ventus 2000W. The design is based on the FD family developed in Canada, but the tail shape and blades airfoil have been implemented to shift the optimum efficiency point to the wind speeds between 4.5m/s and 6.5m/s – which are the most common values that appear in Poland. A key factor during the optimization was low noise and mass, as well as high reliability [19,20].

2. Materials and Methods

In general, the energy generated by the wind turbine depends obviously on: wind velocity, turbine efficiency (as a function of wind velocity).

The wind velocity may be described with the velocity magnitude and the wind direction – however a vast majority of wind turbines is designed to enable all possible directions. In other words, the turbine efficiency should be independent from the wind direction. This feature is achieved by enabling a rotation along the vertical mast (in case of HAWT, horizontal axis wind turbines, which make up a vast majority of wind turbines utilized in Poland) or simply by axial symmetry of the turbine (in case of VAWT, vertical axis wind turbines – Savonius-type, Darrieus-type etc.). Eventually, the wind turbine energy is a function of its efficiency and the wind velocity magnitude.

The probability of the wind maximum speed can be approximated using a simple, single-equation Gumbel distribution [21,22,23]:

F (V_{k}) = e x p \{- e x p [- α (V_{k} - U)]\}

(1)

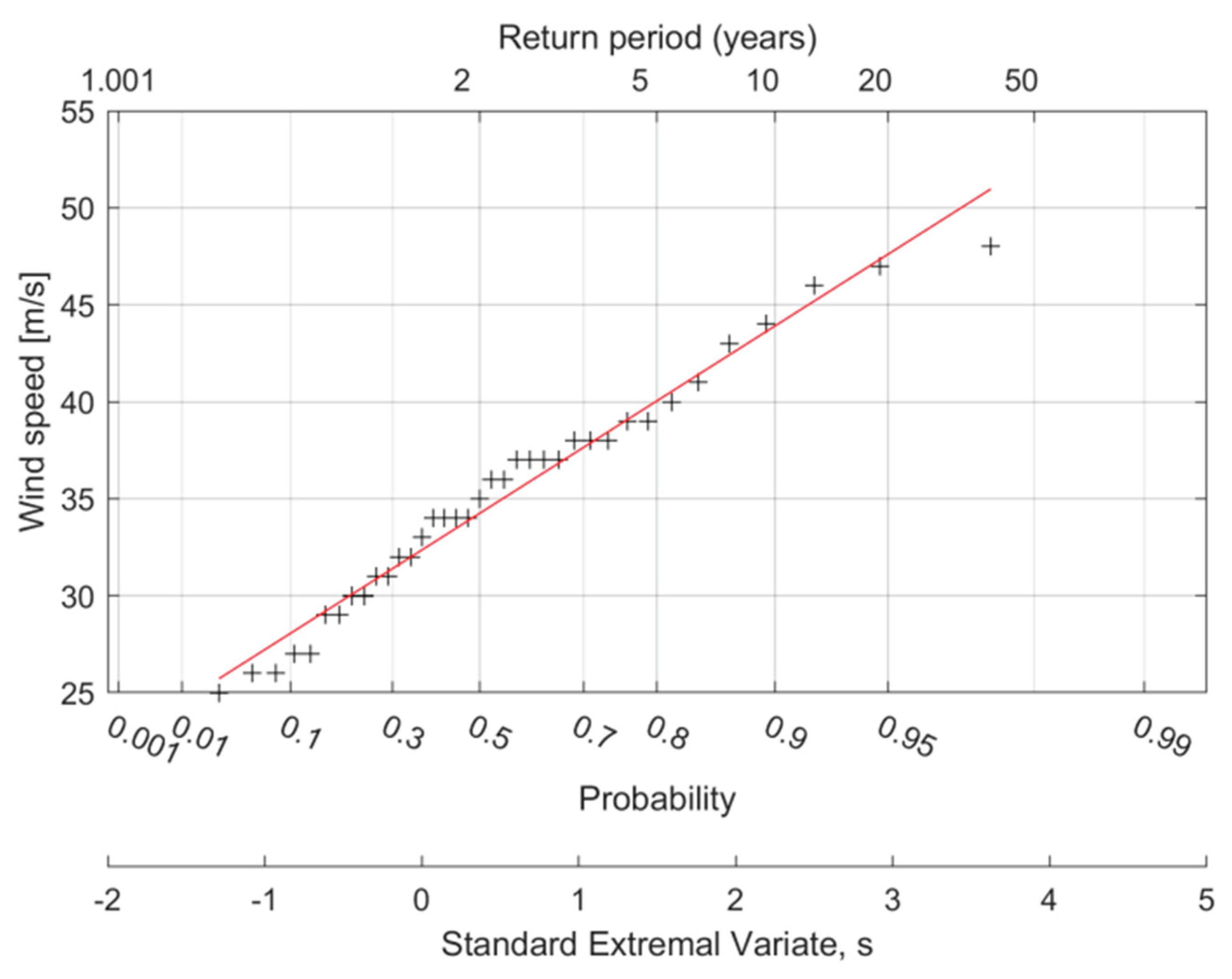
According to [1], the parameters of Gumbel distribution presented in Figure 1 are: U=32.4, 1/a=5.14. As it has been presented, this fitting works well for the maximum wind speed below 47m/s, which covers about 95% of all cases.

The relation presented above shows the maximum speed independently from the direction. Meteorological data processed and presented by Żurański and Jaśpińska in [21] showed clearly that in the whole lowland part of Poland the strongest winds come from the western direction. The dynamic pressure of eastern and southern winds can be reduced even twice. On the other hand, the maximum wind speed is crucial in terms of the wind turbine strength, but not so in terms of assessment its energy. Clearly, each turbine works when the wind speed is in respective threshold – above the lowest wind speed, which may move the turbine’s rotor and below the maximum allowable speed, determined by the blades’ strength. It is thus needed to know the distribution of the wind speed probability density. For years, the researchers agree that such distribution may be well defined using the Weibull distribution [26,27] – despite its limitations, e.g. purely empirical basis, which leads to omission of physical relations that determine the wind speed [28]. As a result of abovementioned limitations, some new statistical models have been developed to improve the fitting of the wind speed parent data, including the Offset Elliptical Normal (OEN) model applied in [28], or a combination of three models (Kappa distribution, Wakeby distribution and Burr-Generalized Extreme Value distribution) proposed in [29]. Results of such studies promise a better overall accuracy of the parent data fitting, than the Weibull distribution. On the other hand, the novel approach is a tool which has not been widely utilized yet, thus using the well-known Weibull distribution allows us to employ previously generated data.

3. Results

3.1. The Weibull Distribution

In the Weibull distribution, the probability of given wind speed can be expressed with the formula:

f (V) = \frac{k}{c} {(\frac{V}{c})}^{k - 1} \cdot e x p (- {(\frac{V}{c})}^{k})

(2)

where:

k – shape parameter;

c – scale parameter;

V – wind speed.

Clearly, the parameters of the Weibull distribution vary with the geographical position and the height above the ground. Data gathered for 6 different meteorological station across Poland have been analyzed and estimated using Weibull distribution in [30] – see Błąd! Nie można odnaleźć źródła odwołania., Figure 2, Figure 3. One may easily observe that the shape parameter ranges slightly, from 1.9 to 2.4 in all covered locations and heights above the ground. Meanwhile the scale parameter varies in much wider range, from about 3.7 to almost 10, and its values increase significantly with the increment of height. It confirms the known fact that the wind speed increases with the height, and this relation is commonly described using Hellman’s exponential law [31,32]:

\frac{V_{1}}{V_{2}} = {(\frac{H_{1}}{H_{2}})}^{α}

(3)

Data presented in Table 1 have been achieved by fitting the Hellman’s law to the parent data from two different heights.

The density of probability of the wind speed plotted for all covered heights have been presented in Figure 4. Firstly, one may observe a significant impact of the height on the variation of f(V). For the lowest value, H=10 m, clearly a variation of maximum probability of the maximum wind speed can be observed. For Lębork and Zielona Góra stations this probability equals about 0.25, while for Łeba station - 0.15 only. On the other hand, the most probable wind speed in Łeba is higher and equals about 5 m/s, while for other stations (except Suwałki) this speed is about 3 m/s. It should be noted, however, that the greatest discrepancies of the plots are visible for the height of 10 m, which can be explained by strong impact of the terrain roughness. As the height increases to 60 m and eventually to 160 m, the plots of probability density get closer to each other – except one for Łeba station, where still the most probable wind speed is higher, and the probability of higher values of the wind speed is significantly increased. This is understandable as Łeba lies on the coast of Baltic Sea and a proximity of the open terrain has greater impact than mezoscale distribution – which can be deduced by simple comparison of results achieved for Łeba and Lębork stations, which are distanced by about 30 km only. In contrary, the lowest value of wind speed dominant has been observed in Wrocław, which lies in the mesoscale region with slightly lower mean speeds – see winds’ map in Figure 3.

The distribution function of the Weibull distribution equals:

F (V; c, k) = 1 - e^{- {(\frac{V}{c})}^{k}}, V \geq 0

(4)

3.2. Power Depending on Wind

A knowledge about the wind speed is crucial to determine the power of wind that flows through a known cross-section (in this particular case – through the disc of the wind turbine, which frontal area is denoted as

A_{T}

). The power may be calculated as:

P_{w i n d} = \frac{1}{2} \dot{m} \cdot V^{2} = \frac{1}{2} ρ \cdot A_{T} \cdot V^{3}

(5)

The abovementioned formula describes the power that is supplied to the wind turbine. However, it is impossible to consume all the wind power, as if the efficiency were equal to 100%. It is clearly impossible to achieve, as the power consumed by the wind turbine is related to the reduction in flow speed in front of the rotor and behind it. Thus, such efficiency would require that the flow speed shortly behind the rotor is equal to zero. Such a situation can be easily compared with the Carnot heat cycle, where the efficiency is related to the difference in temperatures.

The efficiency of the wind turbine is defined as the Betz coefficient – named after the German engineer, Albert Betz, who introduced this fundamental equation in 1919 and published shortly after in [33]:

C_{P} = \frac{P_{t u r b i n e}}{P_{w i n d}}

(6)

According to Betz, the efficiency of the wind turbine can be assessed using the Rankine – Froude actuator disk theory, which defines the flow through a rotor as a unifor8m, single-dimensional, axisymmetric and steady flow. Obviously the rotor is simplified to the infinitely thin disc, with no hub nor blades; consequently no torque is introduced in this model. The diameter and speed of the flow varies with the distance from the rotor.

This simple model allows us to determine the force acting on the flow due to rotor presence [34]:

F = m \frac{d V}{d t} = \dot{m} \cdot ∆ V = ρ {\cdot A}_{T} \cdot V (V_{1} - V_{2})

(7)

Where: index “1” refers to the cross section far in front of the rotor disc (upstream), index “2” – far behind it (downstream) and parameters with no index refers to the disc position.

The power is equal to:

P_{t u r b i n e} = F \frac{d x}{d t} = F V

(8)

and consequently:

P_{t u r b i n e} = ρ {\cdot A}_{T} \cdot V^{2} (V_{1} - V_{2})

(9)

On the other hand, the power can be expressed as the rate of change in kinetic energy (from upstream position to the downstream one):

P_{t u r b i n e} = \frac{∆ E}{∆ t} = \frac{\frac{1}{2} m V_{1}^{2} - \frac{1}{2} m V_{2}^{2}}{∆ t} = \frac{1}{2} \dot{m} (V_{1}^{2} - V_{2}^{2})

(10)

As we compare both forms of the power and include the mass flow rate

\dot{m = ρ S V}

P_{t u r b i n e} = \frac{1}{2} ρ {\cdot A}_{T} \cdot V (V_{1}^{2} - V_{2}^{2}) = ρ {\cdot A}_{T} \cdot V^{2} (V_{1} - V_{2})

(11)

Eventually, if we eliminate air density and disc area and include the reduced multiplication formula, we get:

\frac{1}{2} (V_{1}^{2} - V_{2}^{2}) = \frac{1}{2} (V_{1} - V_{2}) (V_{1} + V_{2}) = V (V_{1} - V_{2})

(12)

Eventually we may see that the velocity of the flow in the rotor disc plane is equal to arithmetic mean of velocities upstream and downstream – as long as air density

ρ

, rotor disc area

S

, velocity in the rotor disc

V

and velocity reduction

(V_{1} - V_{2})

are not equal to 0.

V = \frac{1}{2} (V_{1} + V_{2})

(13)

The latter equation allows us to rewite the formula defining the turbine power:

P_{t u r b i n e} = ρ {\cdot A}_{T} \cdot V^{2} (V_{1} - V_{2}) = \frac{1}{4} ρ {\cdot A}_{T} \cdot {(V_{1} + V_{2})}^{2} (V_{1} - V_{2})

(14)

Let us implement the “interference factor” as a ratio of velocities downstream and upstream:

μ = \frac{V_{2}}{V_{1}}

(15)

Then the extractable turbine power may be expressed with the equation:

P_{t u r b i n e} = \frac{1}{4} ρ {\cdot A}_{T} \cdot {V_{1}}^{3} \cdot (1 - μ^{2}) (1 + μ)

(16)

The abovementioned equation shows clearly that the power of the wind turbine is proportional to the cube of the upstream flow speed V₁ – which is simply the incoming wind speed. It also is, intuitively, proportional to the rotor area and is somehow dependent on the interference factor μ.

As we developed the formulae describing both wind power and extractable power of the turbine, we may eventually calculate the Betz coefficient, i.e. the turbine efficiency:

C_{P} = \frac{P_{t u r b i n e}}{P_{w i n d}} = \frac{\frac{1}{4} ρ \cdot A_{T} \cdot {V_{1}}^{3} \cdot (1 - μ^{2}) (1 + μ)}{\frac{1}{2} ρ \cdot A_{T} \cdot V^{3}}

(17)

Eventually the Betz coefficient is dependent (in direct way) only on the interference factor:

C_{P} = (1 - μ^{2}) (1 + μ)

(18)

The

C_{P} (μ)

function is a third-order parabola with a single local maximum in the range of

μ

between 0 and 1. The optimum value of the interference factor

μ

can be found by simple differentiation and solving the equation:

\frac{d C_{P}}{d μ} = 0

(19)

The derivative of Betz coefficient is thus equal to:

\frac{d C_{P}}{d μ} = \frac{1}{2} (1 - 3 μ) (1 + μ) = 0

(20)

This equation has clearly two possible solutions:

(1 - 3 μ) = 0 (1 + μ) = 0

(21)

but the latter one is a trivial solution

μ = - 1

, which leads to non-physical condition:

V_{2} = - V_{1}

(22)

The other solution gives us, however, the optimum value of the interference factor:

μ_{o p t} = \frac{1}{3}

(23)

which means that

{(V_{2})}_{o p t} = \frac{1}{3} V_{1}

– so the flow speed behind the turbine disc should be three times lower than the wind speed.

If we substitute this value to Błąd! Nie można odnaleźć źródła odwołania. we may easily check that the maximum value of the Betz coefficient is equal to 16/27=59.26%. This value is referred as Betz Limit or Betz Criterion and – despite it was formulated over a century ago, it remains valid for all types of wind turbines. On the other hand, it is only a theoretical maximum value, which not includes air flow friction, blades roughness and all other energy losses. Modern wind turbines reaches lower practical values of maximum efficiency, around 40% [34].

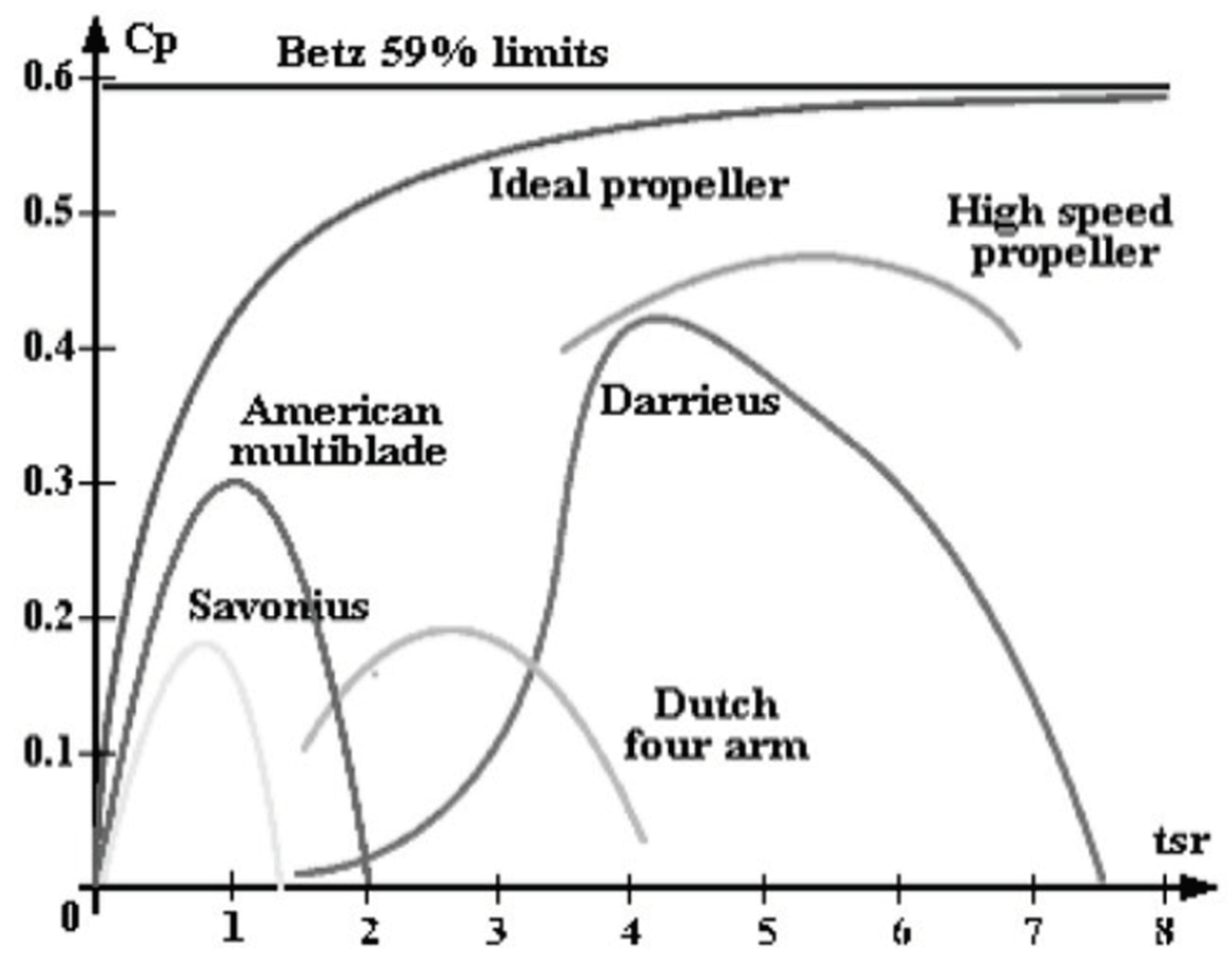
The maximum efficiency can be achieved only in one, specific conditions – depending, amongst others, on the turbine configuration. It can be easily spotted in Figure 5, where the C_p has been presented in the range of tip speed ratio. The latter parameter defines the linear speed of the blade’s tip related to the wind speed:

t s r = \frac{b l a d e ’ s t i p s p e e d}{w i n d s p e e d} = \frac{ω R}{V}

(24)

On the other hand, the tip speed ratio is the nondimensional coefficient, which defines the turbine operating point, but is not measured directly. The TSR depends on wind speed and revolutions speed of the turbine, which is also affected by the wind speed and turbine settings (like blades pitch angle). Thus it is convenient to analyse the C_p plotted directly versus wind speed – see Figure 5. Clearly the Betz coefficient has its maximum for the wind speed of about 8m/s in the presented example – but it depends on the turbine settings. In practical applications, two control strategy are typically implemented [36]: blade pitch control, stall control.

Both strategies are aimed at ensuring the safety of the turbine if the limit wind speed (upper cut-off speed) is exceeded. In first case, the blades pitch is reduced by a hydraulic actuator or an electric stepper motor, to reduce lift coefficient which powers the rotor’s revolution. Meanwhile stall-controlled turbines use passive control systems, i.e. the blades’ geometry is designed to direct the wake behind one blade towards another one, if the wind speed achieves its limit. Eventually, the power output versus wind speed gives a well-known power curve (Figure 6).

The turbine should operate with the highest efficiency as the wind speed increases to the nominal/rated value. In this case the power output becomes maximum from the generator’s point of view, thus it should not be further increased [37,38]. Pitch-controlled turbines maintain the constant level of the power, while stall-controlled ones are designed such that the rotor efficiency “collapses” at high wind speeds. Due to the blade design, this behavior is intrinsic, and no active control systems are required to achieve the aerodynamic efficiency reduction [36] (Figure 7).

It should be underlined that the power of the wind turbine is related to the cube of wind velocity, which in line is dependent on the height above the ground – see Błąd! Nie można odnaleźć źródła odwołania.. Eventually the power ratio is equal to the height above the ground in the power of

3 α

\frac{P_{1}}{P_{2}} = {(\frac{V_{1}}{V_{2}})}^{3} = {(\frac{H_{1}}{H_{2}})}^{3 α}

(25)

While the mean value of the wind speed, or rather its most probable values are determinable in the mesoscale, the exponent α is strongly dependent on the surroundings of the wind turbine, as it modifies the shear layer of the wind. This effect can be compared with the impact of the surface roughness on the boundary layer thickness, when the fluid flows along this surface. To determine the exponent α, it is convenient to define some categories of the terrain: it is clearly expected that in the clear area, like a seashore, the shear layer will be much thinner than in densely populated cities. In Poland (as in other EU countries) the terrain categories and respective exponents are proposed by architectural standard PN-EN 1991-1-4:2008 with its national annex [32]. The categories have been summarized in Table 2, as well as wind power ratios: between 160m and 60m, between 60m and 10m.

It can be clearly seen that the power of the wind turbine located at 60m is nearly 2 times higher than in 10m (in case of an open terrain) and even 3.63 times higher in case of densely populated area – however placing the high wind turbine in such terrain is not likely due to formal prohibitions. Further increase of the height to 160 m can bring further growth in power, from 1.38 to about 2 times. It should be, however, strongly reminded that only the height is changed in this analysis and the rotor area remains the same. In practice the rotor diameter is increased with the hub height, to maximize the disc area.

It should be noted that the energy should be integrated along the height, since the wind speed alters along it, and thus is not constant on the rotor disc area. Omitting this is, however, reasonable and a difference due to this simplification is about 5% [26].

The air density typically may be calculated using the Clapeyron’s ideal gas law, assuming that the air is dry. However, if the air humidity is significant, it can be also included. The air density is then given by the equation:

ρ = \frac{p_{a t m}}{r_{d r y} \cdot (T + 273.15)} - \frac{R H \cdot a \cdot e^{(\frac{b T}{T + c})}}{r_{d r y} \cdot (T + 273.15)} + \frac{R H \cdot a \cdot e^{(\frac{b T}{T + c})}}{r_{v a p} \cdot (T + 273.15)}

(26)

As it has been presented in Figure 8, the air density is strongly related with the temperature, and in a smaller part with the humidity (especially in higher temperatures) and pressure.

It should be again underlined that the Weibull distribution of the daily-averaged wind speed still is an approximation, which omits some observation. For instance, the measurements of wind speed during the year showed that in most meteorological stations in Poland the highest wind speed values have been achieved during the winter – from December to March. Meanwhile, the lowest values have been recorded in July and August [39]. Furthermore, the daily variation of the wind speed is also clearly observable. Koźmiński and Michalska in [39] have compared the measurement taken at 7:00 a.m., 1:00 p.m. and 9:00 p.m. – see Table 2. According to that, the greatest wind speed has been observed around noon – especially in the spring, from March to May. In the morning the wind is significantly weaker and in the evening – the weakest. The monthly variation of wind speed is the greatest in February, March and September, while in January, May and June the variation coefficient decays (Table 3).

4. Conclusions and Discussion

As the wind speed and the turbine efficiency (Betz coefficient) are known and determined mathematically, one may utilize them as an input for the calculation of the wind power. According to [5], the power of the wind turbine energy may be determined by multiplication of the Betz coefficient and the probability density function of the wind speed (estimated above).

P_{t u r b i n e} = \int_{V l o w e r c u t - o f f}^{V u p p e r c u t - o f f} f (V) \cdot C_{P} (V) d V

(27)

On the other hand, such an equation has no analytic solution, but it can be solved numerically. That approach gives the wind power density defined using parameters of the Weibull distribution:

W P D = 0.5 \cdot ρ \cdot c^{3} (1 + \frac{3}{k})

(28)

Values of the wind power density calculated for 6 meteorological stations across Poland, discussed above, have been presented in Table 3. Clearly it is seen that the greatest values are obtained for the greatest height of 160 m. It may be mathematically expressed that the scale parameter of the Weibull distribution is roughly 1.75 times to 2.5 times greater than for the height of 10 m. As the power density is related to the cube of scale parameter, it is clear that the ratio of WPD on these heights will range from about 5 to about 15. Obviously, such increment is caused by strong vertical gradient of the wind speed, which is expressed by the scale parameter.

Calculation presented in Table 4 has been performed with an assumption that the air density is 1.225kg/m³, according to the International Standard Atmosphere (ISA) – which reflects the pressure of 101325Pa and temperature of 15°C.

Clearly one may observe that the greatest values of the wind power density are observed in northern stations (over 1000 W/m²) – especially in Łeba station, which had more uniform distribution of the wind speed probability. In this case the power density of over 1400 W/m² has been noted. In contrary, the least power density has been observed in Wrocław – in the south-western part of Poland, where the most probable wind speed is the lowest, as it has been presented in the wind map – Figure 3 and on the plots of wind speed probability distributions – Figure 4.

It is clear that even subtle differences in the wind speed distribution have crucial impact on the wind power density – the least value of such parameter (taking into account only the height of 160 m), achieved in Wrocław, makes up only 60% of the greatest one – calculated for Łeba. Thus it is clear that the statistical estimation of the wind speed probability, including the vertical gradient of the wind speed (described mathematically eg. using Hellman’s law) may foresee significant changes in the wind power density, that eventually determine an efficiency of any wind turbine installed in a given localization.

The primary task of modelling wind power as a function of wind speed is to improve the accuracy of forecasts and analyses of wind farm power production. Analyses and forecasts of electricity production in existing and planned wind power plants are the basis of investments in these energy sources. In addition, it is important to reproduce historical data to make more accurate forecasts and analyses.

Wind turbine designers strive to increase the efficiency of wind turbines and ensure continuity of operation, even in adverse weather conditions. Computer simulations are very often used in engineering calculations. They allow you to model the operation of turbines in terms of aerodynamics, acoustics or construction. Correctly defined boundary conditions, e.g. wind speeds, are a prerequisite for a properly prepared computer simulation.

Author Contributions

Conceptualization, P.R., O.O., K.T. and A.W.; methodology, P.R., O.O. and K.T.; software, O.O., P.R., A.W. and K.T.; validation, P.R. and O.O.; formal analysis, P.R., O.O. and K.T.; investigation, P.R., A.W. and O.O.; data curation, P.R., O.O., K.T. and A.W.; writing—original draft preparation, P.R., O.O. and K.T.; writing—review and editing, O.O., P.R. and K.T.; visualization, P.R., A.W., O.O. and K.T.; supervision, P.R., O.O. and K.T. All authors have read and agreed to the published version of the manuscript.

Funding

Financing by Bialystok University of Technology under the project WZ/WIZ-INZ/4/2022 (Olga Orynycz) research conducted in part during cooperation stays in Łukasiewicz Institute of Aviation, Warsaw 2023 r.

Conflicts of Interest

The authors declare no conflicts of interest.

References

Schislyaeva, E.; Evgrafova, I.; Butakova, N.; Mishalchenko, Y. The EU - Russia - Turkey energy triangle: legal and economic conditions of gas transportation via the TurkStream pipeline. Transportation Research Procedia 2022, 63, 1984–1990. [Google Scholar] [CrossRef]
Bembenek, M.; Kotsyubynsky, V.; Boychuk, V.; Rachiy, B.; Budzulyak, I.; Kowalski, Ł.; Ropyak, L. Effect of Synthesis Conditions on Capacitive Properties of Porous Carbon Derived from Hemp Bast Fiber. Energies 2022, 15, 8761. [Google Scholar] [CrossRef]
Lotko, W.; Smigins, R.; Tziourtzioumis, D.; Górska, M. Environmental Aspects of a Common Rail Diesel Engine Fuelled with Biodiesel/Diesel Blends. Advances in Science and Technology Research Journal 2022, 16, 192–201. [Google Scholar] [CrossRef]
Kurczyński, D.; Łagowski, P.; Wcisło, G. Experimental study into the effect of the second-generation BBuE biofuel use on the diesel engine parameters and exhaust composition. Fuel 2021, 284, 118982. [Google Scholar] [CrossRef]
Waluś, K.J.; Warguła, Ł. Experimental research on kinematic features of agricultural tractor movement on asphalt pavement. Available online: https://www.matec-conferences.org/articles/matecconf/pdf/2022/04/matecconf_mms2020_05005.pdf (accessed on 19 February 2024).
Peng, B.; Streimikiene, D.; Agnusdei, G.P.; Balezentis, T. Is sustainable energy development ensured in the EU agriculture? Structural shifts and the energy-related greenhouse gas emission intensity. Journal of Cleaner Production 2024, 141325. [Google Scholar] [CrossRef]
Ovaere, M.; Proost, S. Cost-effective reduction of fossil energy use in the European transport sector: An assessment of the Fit for 55 Package. Energy Policy 2022, 168, 113085. [Google Scholar] [CrossRef]
GlobEnergia. Germany produced more than 50% of electricity from RES in 2023! Available online: https://globenergia.pl/niemcy-wyprodukowali-ponad-50-energii-elektrycznej-z-oze-w-2023/ (accessed on 19 February 2024).
GlobEnergia. Portugal with record share of RES in electricity generation! Available online: https://globenergia.pl/portugalia-z-rekordowym-udzialem-oze-w-generacji-pradu/ (accessed on 19 February 2024).
GlobEnergia. Wind in sails for offshore wind farms in Poland! Available online: https://globenergia.pl/wiatr-w-zagle-dla-morskich-elektrowni-wiatrowych-w-polsce/ (accessed on 19 February 2024).
TouchWind. Consortium starts demonstration project into positive wake effects of TouchWind’s floating wind turbine. Available online: https://touchwind.org/news/consortium-starts-demonstration-project-into-positive-wake-effects-of-touchwinds-floating-wind-turbine/ (accessed on 19 February 2024).
Vestas. Wind Turbine Product Portfolio. Available online: https://us.vestas.com/en-us/products (accessed on 19 February 2024).
Tests to Begin on a Counter-Rotating Floating Offshore Wind Turbine Concept. Available online: https://maritime-executive.com/article/tests-to-begin-on-a-counter-rotating-floating-offshore-wind-turbine-concept (accessed on 19 February 2024).
GE Renewable Energy. Haliade-X offshore wind turbine. Available online: https://www.ge.com/renewableenergy/wind-energy/offshore-wind/haliade-x-offshore-turbine (accessed on 19 February 2024).
GE Renewable Energy. Cypress Onshore Wind Turbine Platform. Available online: https://www.ge.com/renewableenergy/wind-energy/onshore-wind/cypress-platform (accessed on 19 February 2024).
Siemens Gamesa. SG 14-222 DD: The winds of change have never been stronger. Available online: https://www.siemensgamesa.com/products-and-services/offshore/wind-turbine-sg-14-222-dd (accessed on 19 February 2024).
VENTUS Power Generator. Products & Services. Available online: https://ventus.group/products-services (accessed on 19 February 2024).
EnVentus platform variants. Available online: https://www.vestas.com/en/products/enventus-platform (accessed on 19 February 2024).
Polish wind power plants. Available online: https://generatory-wiatrowe.pl/produkty/polskie-elektrownie-wiatrowe/ (accessed on 19 February 2024).
Bošnjaković, M.; Katinić, M.; Santa, R.; Marić, D. Wind Turbine Technology Trends. Appl. Sci. 2022, 12, 8653. [Google Scholar] [CrossRef]
Żurański, J.A.; Jaśpińska, B. Directional analysis of extreme wind speeds in Poland. Journal of Wind Engineering and Industrial Aerodynamics 1996, 66, 13–20. [Google Scholar] [CrossRef]
Simiu, E. , Scanlan, R.H. Wind Effects on Structures: An Introduction to Wind Engineering, 2nd ed.; John Wiley and Sons: New York, USA, 1986. [Google Scholar]
Gumbel, E. J. . Statistics of Extremes, 1st ed.; Columbia University Press: New York Chichester, West Sussex, 1958. [Google Scholar] [CrossRef]
Chmielewski, T.; Bońkowski, A.P. Wind as a natural hazard in Poland. Natural Hazards and Earth System Sciences 2023, 23, 3839–3844. [Google Scholar] [CrossRef]
Lorenc, H. Maksymalne prędkości wiatru w Polsce, 1st ed. Instytut Meteorologii i Gospodarki Wodnej: Warszawa, Polska, 2012, pp. 5–94. Available online: https://bibliotekanauki.pl/books/2049055 (accessed on 19 February 2024).
Belu, R. Assessment and Analysis of Offshore Wind Energy Potential. Available online: https://www.intechopen.com/chapters/74556 (accessed on 19 February 2024).
Wei, J.; Hulio, Z.H.; Rashid, H. Site specific assessment of wind characteristics and determination of wind loads effects on wind turbine components and energy generation. International Journal of Energy Sector Management 2018, 12, 341–363. [Google Scholar] [CrossRef]
Harris, R.I.; Cook, N.J. The parent wind speed distribution: Why Weibull. Journal of Wind Engineering & Industrial Aerodynamics 2014, 131, 72–87. [Google Scholar] [CrossRef]
Jung, C.; Schindler, D.; Laible, J.; Buchholz, A. Introducing a system of wind speed distributions for modeling properties of wind speed regimes around the world. Energy Conversion and Management 2017, 144, 181–192. [Google Scholar] [CrossRef]
Kowalik-Pilarska, E. Wind speed parameters estimation for Poland as a result of mezoscale modelling. Available online: http://www.phd4gen.pl/wp-content/uploads/2021/06/22_06_2021_EKP_UZ3.pdf (accessed on 19 February 2024).
Banuelos-Ruedas, F.; Camacho, C.A.; Rios-Marcuello, S. Methodologies Used in the Extrapolation of Wind Speed Data at Different Heights and Its Impact in the Wind Energy Resource Assessment in a Region. Available online: https://www.intechopen.com/chapters/17121 (accessed on 19 February 2024). [CrossRef]
PN-EN 1991-1-4 2005 Oddziaływania na konstukcje. Oddziaływania wiatru. Available online: https://www.studocu.com/pl/document/wojskowa-akademia-techniczna/konstrukcje-betonowe/pn-en-1991-1-4-2005-oddzialywania-na-konstukcje-oddzialywania-wiatru/25166081 (accessed on 19 February 2024).
Betz, A. Wind-Energie und ihre Ausnutzung durch Windmühlen; Vandenhoeck und Ruprecht: Göttingen, Germany, 1926. [Google Scholar]
Ragheb, M.; Ragheb, A.M. Wind Turbines Theory - The Betz Equation and Optimal Rotor Tip Speed Ratio. Available online: https://cdn.intechopen.com/pdfs/16242/InTechWind_turbines_theory_the_betz_equation_and_optimal_rotor_tip_speed_ratio.pdf (accessed on 19 February 2024).
Santiago, G.; Hernandez, W.; Costa De Araujo, A.C.; Rosa, M.; González, M. Application of product development process (PDP) in the construction of vertical axis wind turbine with movable blades. Available online: https://www.academia.edu/42937714/Application_of_product_development_process_PDP_in_the_construction_of_vertical_axis_wind_turbine_with_movable_blades (accessed on 19 February 2024).
Mihet-Popa, L.; Groza, V. Dynamic modeling, simulation and control strategies for 2 MW wind generating systems. International Review of Modelling and Simulation 2010, 3, 1410–1418. [Google Scholar]
Heier, S. Grid Integration of Wind Energy: Onshore and Offshore Conversion Systems, 1st ed.; John Wiley and Sons: New York, USA, 1998. [Google Scholar]
Hansen, L.H.; Helle, L.; Blaabjerg, F.; Ritchie, E.; Munk-Nielsen, S.; Binder, H.; Sorensen, P.; Bak-Jensen, B. Conceptual survey of generators and power electronics for wind turbines. Riso-r-1205(EN), Riso National Laboratory, Roskilde, 2001. Available online: https://www.osti.gov/etdeweb/biblio/20262554 (accessed on 19 February 2024).
Koźmiński, C.; Michalska, B. Characterization of wind speed and calms in Poland. Acta Agrophysica 2002, 78, 111–132. Available online: https://agro.icm.edu.pl/agro/element/bwmeta1.element.agro-article-18ec9a36-3a7d-4f1d-8490-7a7ed28bfc05 (accessed on 19 February 2024).

Figure 1. Probability of maximum wind speed in Poland [24,25].

Figure 2. Meteorological stations included in assessment of Weibull distribution of the wind speed [30].

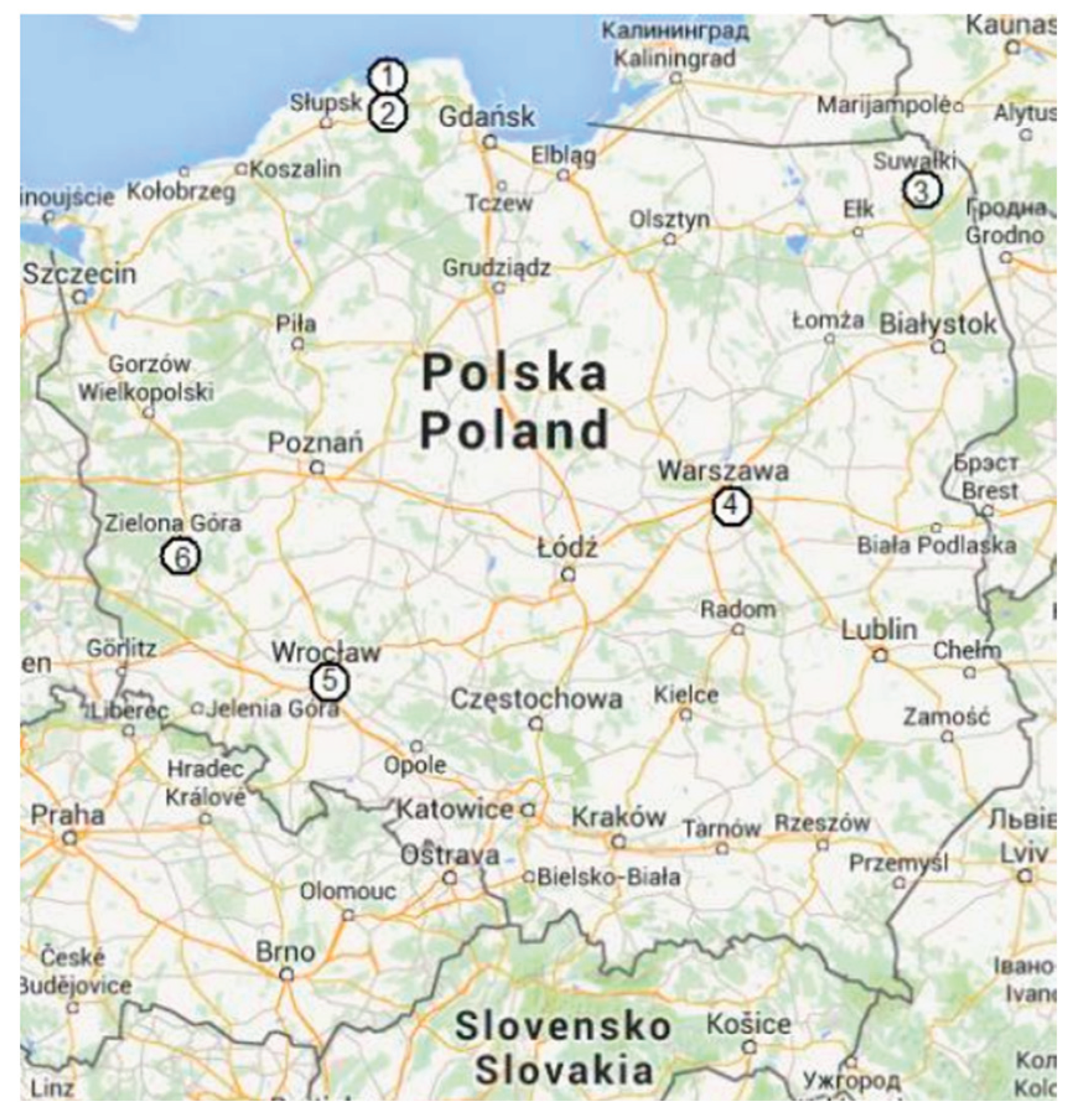
Figure 3. 10-minute mean values of the wind speed (measured at the height of 10 m) in various locations in Poland.

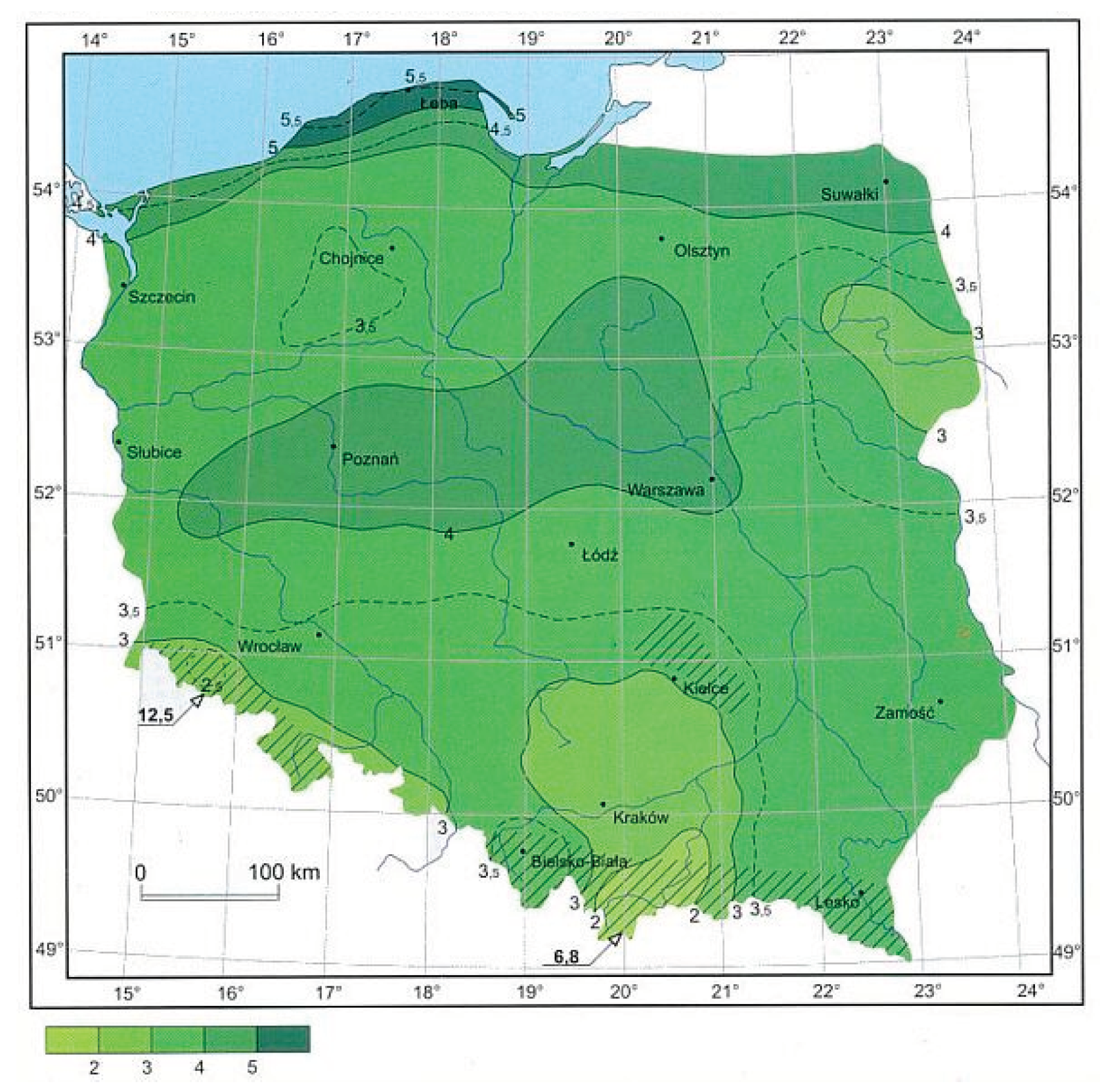
Figure 4. The density of probability of the wind speed: (a) H=10m; (b) H=60m; (c) H=160m.

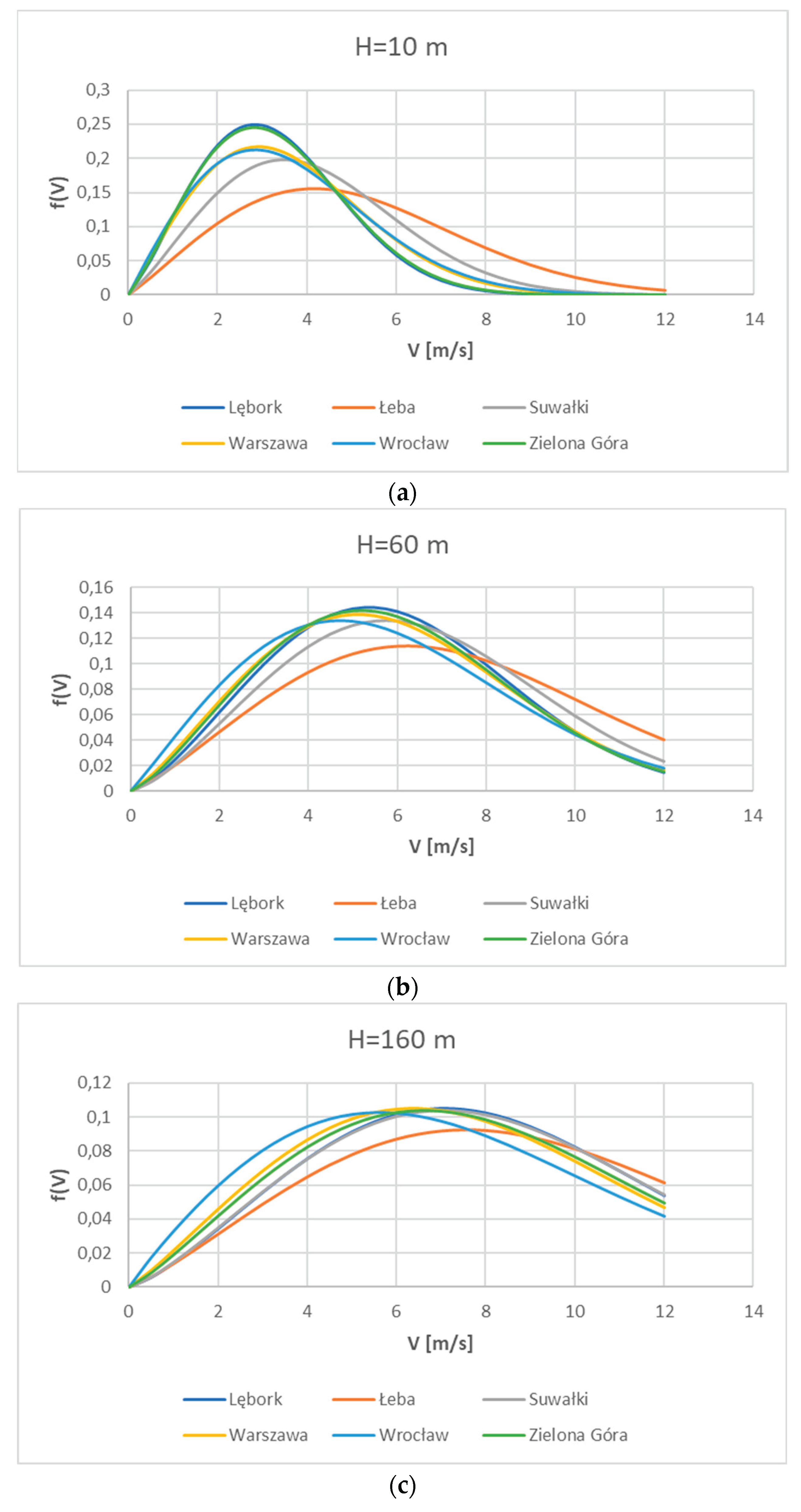
Figure 5. The power coefficient as a function of tip speed ratio [34,35].

Figure 6. Power coefficient of the exemplary 2MW wind turbine, as a function of the wind speed [36].

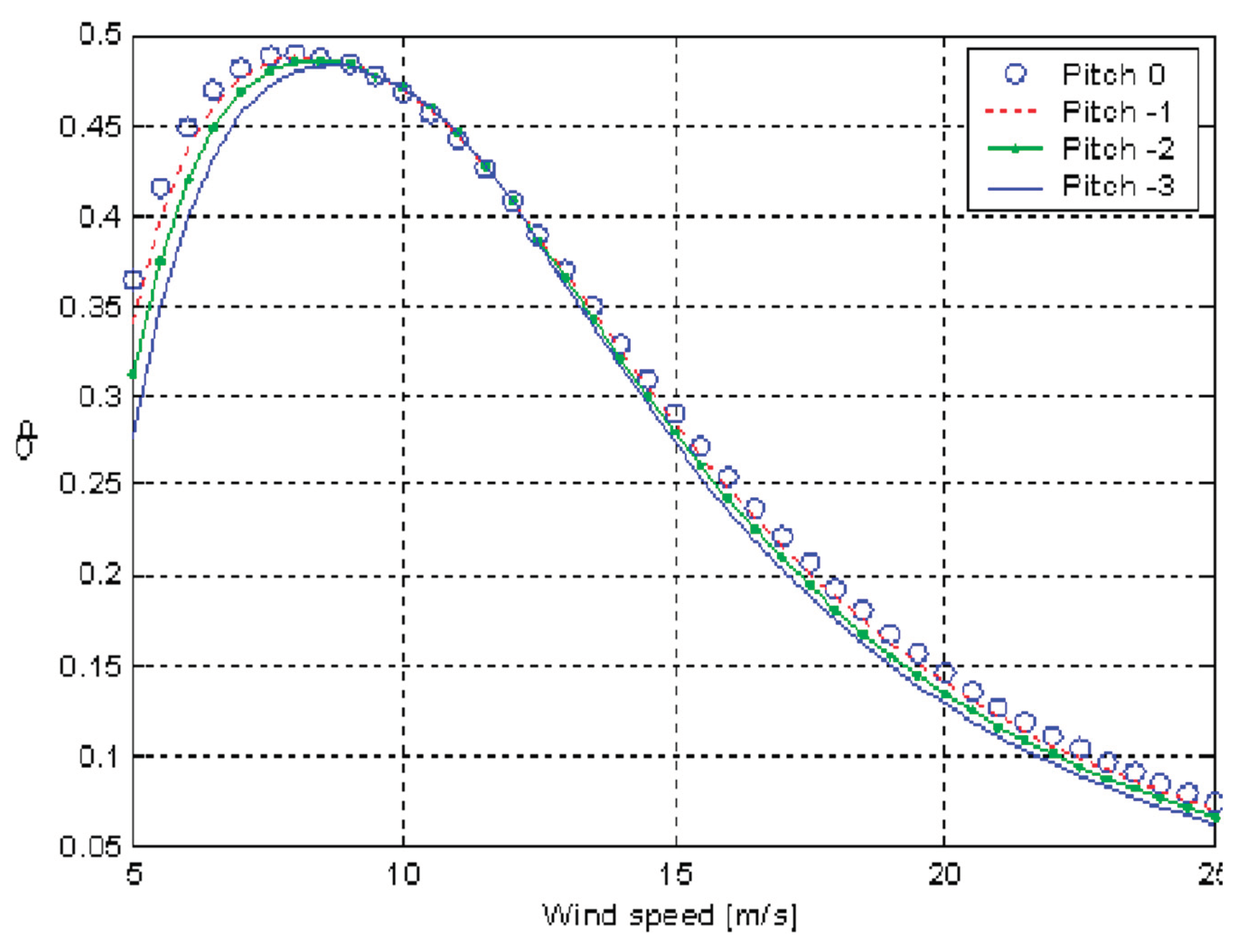
Figure 7. Exemplary power curve for pitch-controlled and stall-controlled wind turbines [36].

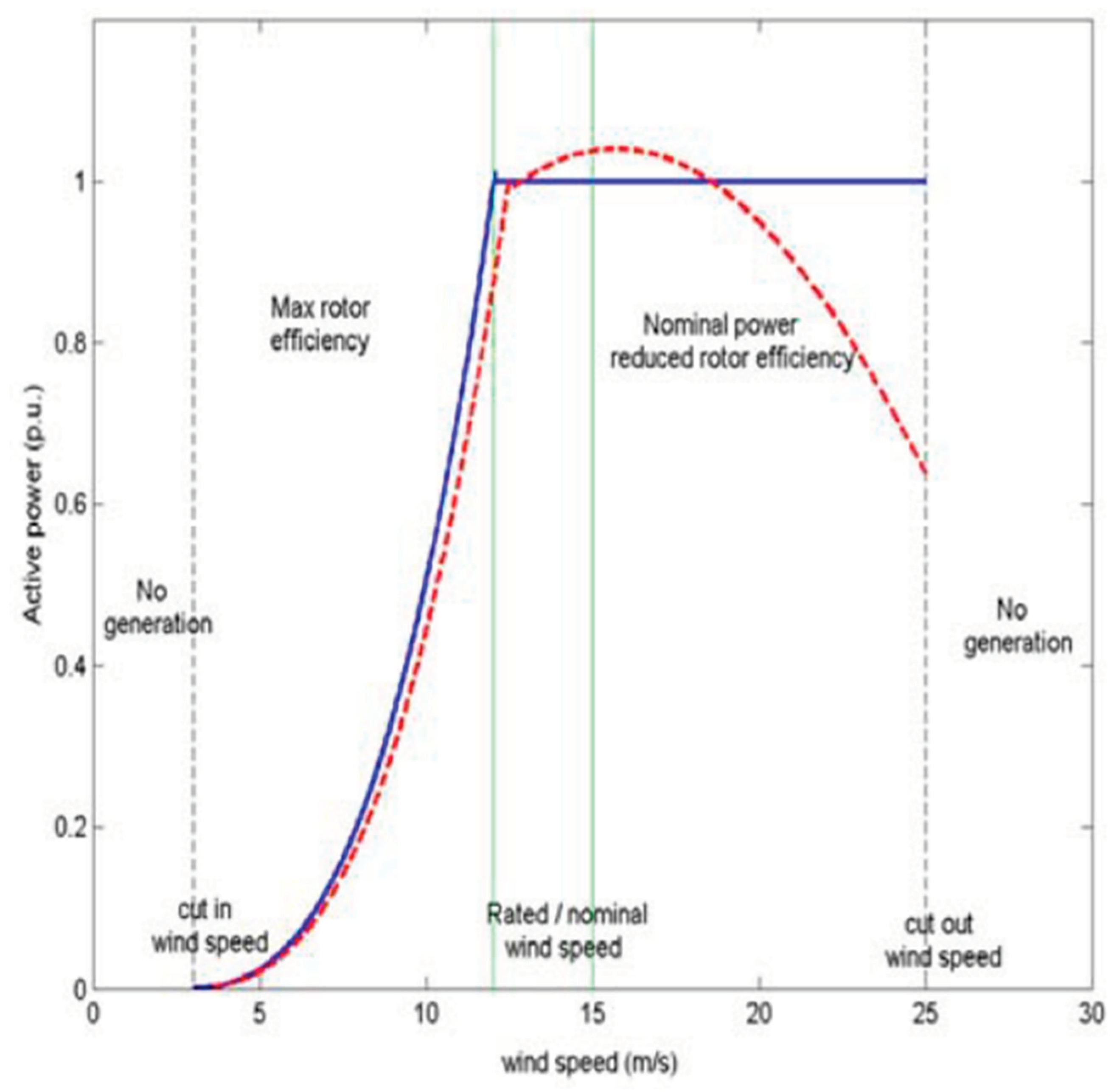
Figure 8. Air density as a function of temperature, pressure and humidity.

Table 1. Parameters of Weibull distribution of wind speed probability in various stations in Poland [27].

No	Area	Shape parameter k			Scale parameter c
		H=10 m	H=60 m	H=160 m	H=10 m	H=60 m	H=160 m
1	Lębork	2.22367	2.38800	2.31024	3.69743	6.73439	9.02310
2	Łeba	2.09544	2.23580	2.20473	5.66472	8.11317	9.94361
3	Suwałki	2.18803	2.37893	2.28595	4.60317	7.23649	9.06978
4	Warszawa	2.06053	2.23177	2.13516	4.01736	6.67782	8.55266
5	Wrocław	1.98781	2.05001	1.92884	4.0324	6.52111	8.18830
6	Zielona Góra	2.19040	2.29967	2.17879	3.72479	6.66344	8.75553

Table 2. Impact of the height on the wind turbine power, depending on the terrain category.

Terrain class	Terrain	alpha	P160/P60	P60/P10
0	Sea and coastal area exposed to the open sea	0.11	1.38	1.81
I	Lakes or area with negligible vegetation and without obstacles	0.13	1.47	2.01
II	area with a low vegetation, such as grass and isolated obstacles (trees, buildings) with separations of at least 20 obstacle heights	0.17	1.65	2.49
III	area with regular cover of vegetation or buildings or with isolated obstacles with separation of max. 20 obstacle heights (e.g. Villages, suburbia, permanent forest)	0.19	1.75	2.78
IV	area in which at least 15% of the surface is covered with buildings and their average height exceeds 15m	0.24	2.03	3.63

Table 3. Average wind speed in Poland (in [m/s]) versus day-time and year-time.

Season	Month	7:00 a.m.	1:00 p.m.	9:00 p.m
Spring	March – May	2.8	4.3	2.5
Summer	June – August	2.4	3.8	1.8
Autumn	September – November	2.5	3.8	2.5
Winter	December – February	3.3	3.9	3.3
Yearly average		2.7	3.9	2.5

Table 4. Wind power density.

Area	H=10 m	H=60 m	H=160 m
Lębork	72.8	422.4	1035.0
Łeba	270.9	766.5	1422.6
Suwałki	141.8	525.2	1057.4
Warszawa	97.6	427.9	922.2
Wrocław	100.8	418.7	859.9
Zielona Góra	75.1	417.9	977.9

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.