An Attitude Adaptive Integral Sliding Mode Control Algorithm with Feedforward Compensation Disturbance Observer for Microsatellites to Track High-Speed Moving Targets

Gaze tracking of high-speed moving targets is a novel application mode for low Earth orbit microsatellites. In this mode, small satellites are equipped with high-resolution narrow-field-of-view video cameras for stable gaze-tracking imaging of high-speed moving targets. This paper proposes a high-precision attitude adaptive integral sliding mode control method with a feedforward compensation disturbance observer to enhance the capability of a microsatellite attitude control system for gaze tracking of high-speed moving targets. Specifically, first, we present the attitude control system model for microsatellites and the calculation method for the desired attitude of target tracking based on image feedback. Then, an adaptive integral sliding mode attitude control algorithm with a feedforward compensation disturbance observer, which meets the requirements of high-precision tracking control, is designed. The developed algorithm utilizes the disturbance observer to observe the friction torque of the flywheel and compensates for it through feedforward control. It also employs the adaptive integral sliding mode control algorithm to reduce the impact of uncertain disturbances, decrease the steady-state error of the system, and enhance the attitude control precision. Simulation experiments demonstrated that the designed disturbance observer can successfully observe the frictional disturbance torque of the flywheel. The attitude Euler angle control precision for high-speed moving target tracking reached 0.009°, and the angular velocity control precision reached 0.005°/s, validating the effectiveness of the proposed approach.

Keywords:

Subject: Engineering - Aerospace Engineering

1. Introduction

Video microsatellites offer continuous target observation, which, coupled with short development cycles and low costs, makes microsatellites widely applicable. Gaze tracking of targets is a primary operational mode for video microsatellites [1,2]. However, for high-precision target gaze under high resolution and narrow field of view, the attitude control precision of microsatellites has strict requirements. Furthermore, given that video microsatellites operate in low Earth orbit, external disturbances significantly influence the satellite [3]. In addition, the internal actuation mechanism within the satellite is subject to interference from frictional forces [4], and the satellite's moment of inertia may also vary over time [5]. This is particularly the case for microsatellites, which feature a relatively low moment of inertia. These factors substantially impact the attitude control precision of microsatellites, sometimes leading to spacecraft control failures [6]. Overcoming the effects of these disturbances is a major challenge in satellite attitude tracking control.

Currently, two main approaches address the impact of disturbances on spacecraft attitude control [7,8,9,10]. The first one compensates for disturbance torques through precise modeling or establishing observers. For instance, a method based on event-triggered anti-disturbance attitude control [11] addressed the rigid spacecraft facing attitude control challenges under multiple disturbances. This method categorizes disturbances into uncertain model disturbances and norm-bounded equivalent disturbances. It designs a disturbance observer to estimate the disturbances, ensuring the convergence of the attitude control system to a small invariant set. In [12], the authors proposed a composite attitude stabilization scheme for spacecraft based on dual disturbance observers and high-precision nonsingular terminal sliding mode control. This scheme considers flywheel dynamics and multiple disturbances, compensating for estimated disturbances and mitigating the impact of estimation errors through a composite nonsingular terminal sliding mode attitude controller. It should be noted that existing external disturbance observers often assume that external disturbances remain constant or change slowly. Thus, in [13], a new disturbance observer was designed to ensure the convergence of attitude and angular velocity to a small range under arbitrary disturbance conditions.

The second approach involves designing robust controllers with superior performance and achieving attitude control while sacrificing a certain degree of precision. Among various control algorithms, sliding mode variable structure control is a typical robust control algorithm. However, the robustness of sliding mode variable structure control relies on the controller continuously changing structures near zero, leading to the chattering problem. Hence, to reduce chattering, scholars worldwide have proposed various methods, such as the boundary layer method [14], high-order sliding mode control [15,16], and control methods based on the convergence law [17,18,19,20,21,22]. In [23], a spacecraft attitude-tracking control problem was studied using an adaptive integral sliding mode fault-tolerant control strategy. Furthermore, incorporating adaptive laws, a modified fault-tolerant control scheme was proposed to compensate for actuator faults and system uncertainties, including external disturbances and inertia uncertainties. In [24], the authors combined integral sliding mode with an adaptive law based on barrier functions to address external disturbances and inertia uncertainties a rigid spacecraft faces. This method suppresses disturbances and inertia uncertainties while ensuring the rigid spacecraft system is initially near the sliding mode surface, enhancing system robustness.

This paper synthesizes the above two approaches and proposes an adaptive integral sliding mode controller with a feedforward compensation disturbance observer. Specifically, a disturbance observer was designed to estimate the friction torque for the flywheel’s frictional disturbance torque. Disturbance compensation for the friction torque was achieved through feedforward control, reducing the upper bound of total disturbances. Secondly, an adaptive integral sliding mode controller was developed for external uncertain disturbances. The adaptive law adjusts the switching gain according to the magnitude of disturbances, reducing the chattering amplitude of the control torque.

The remainder of this paper is organized as follows: Section 2 presents the calculation method for the desired attitude of target tracking based on image feedback and describes the reaction wheel and microsatellite attitude models. Section 3 derives the feedforward compensation disturbance observer and adaptive integral sliding mode variable structure controller. Section 4 introduces the simulation experiments and analysis, while Section 5 concludes this work.

2. Attitude Control System Model

2.1. Calculation of Desired Attitude for Target Tracking Based on Image Feedback

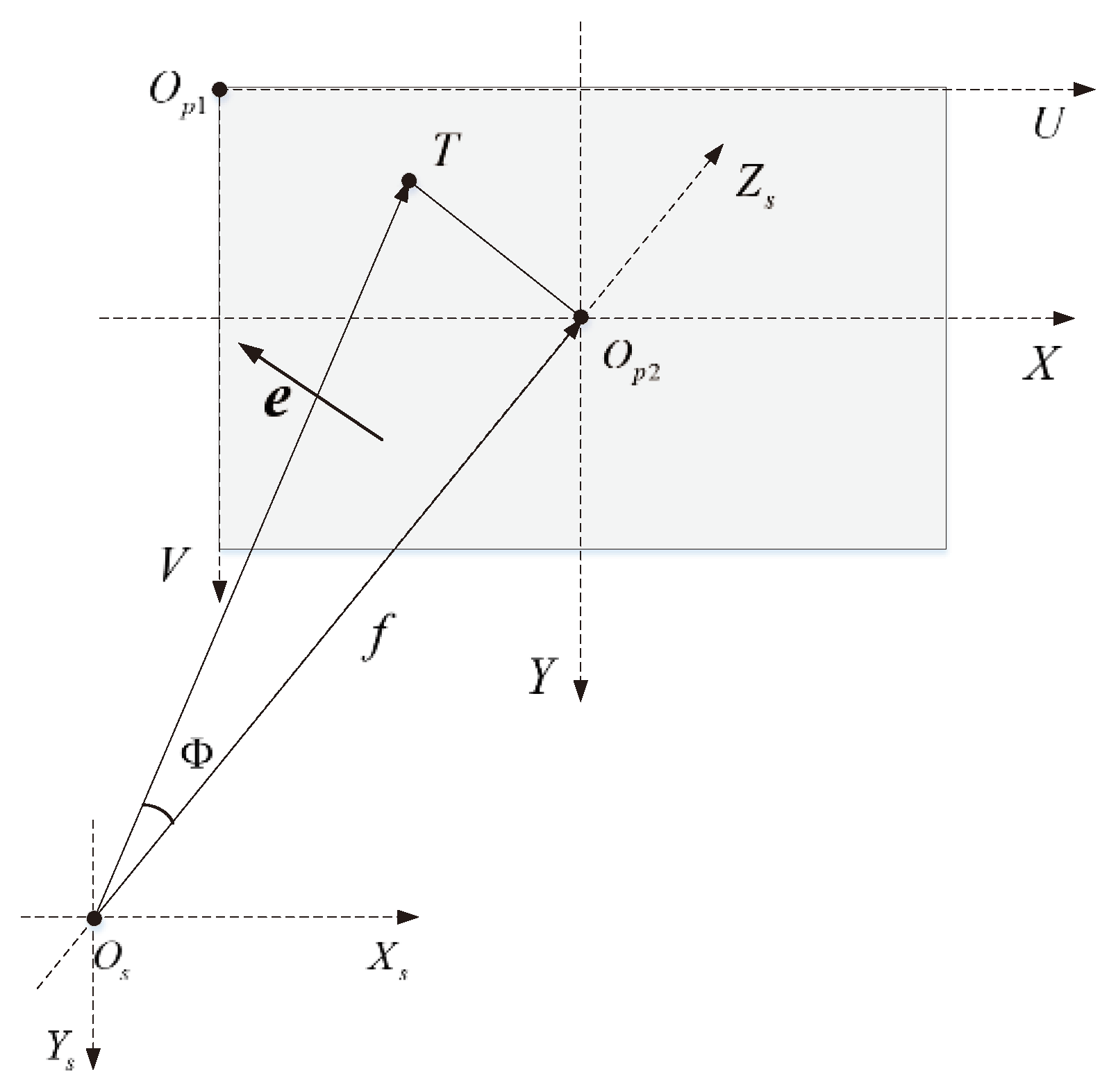
For attitude tracking control based on image feedback, the first step involves solving for the angle

Φ

between the satellite camera's optical axis direction and the satellite's target direction, as depicted in Figure 1. According to the parameter definition of Euler axis/angle attitude, this angle represents the Euler rotation angle between the current attitude and the desired attitude, and the normal to face

O_{s} T O_{p 2}

is the Euler axis

\vec{e}

. However, only the target coordinates

(\begin{matrix} u & v \end{matrix})

in the detector plane can be obtained through the camera payload. Therefore, solving the desired attitude for target tracking is transformed into determining the Euler rotation angle

Φ

and Euler axis

\vec{e}

based on

(\begin{matrix} u & v \end{matrix})

In the detector plane coordinate system

O_{p 1} - U V

and

O_{p 2} - X Y

the coordinates of the target image point T are

(\begin{matrix} u & v \end{matrix})

and

(\begin{matrix} x_{t} & y_{t} \end{matrix})

, respectively. Their relationship is given by:

\{\begin{matrix} x_{t} = (u - \frac{n}{2}) d x \\ y_{t} = (v - \frac{m}{2}) d y \end{matrix}

(1)

where

n

and

m

are the number of detector pixels in the horizontal and vertical directions, and

d x

and

d y

are the physical dimensions of a single pixel in the horizontal and vertical directions, respectively.

Based on their geometric relationship, we have:

Φ = \arctan (\frac{\sqrt{x_{t}^{2} + y_{t}^{2}}}{f})

(2)

\vec{e} = \frac{\vec{O_{s} T} \times \vec{O_{s} O_{p 2}}}{‖\vec{O_{s} T} \times \vec{O_{s} O_{p 2}}‖}

(3)

According to the relationship between attitude quaternion and Euler axis/angle, the error quaternion between the current attitude and the desired attitude is:

q_{e} = [\begin{matrix} q_{e 0} \\ q_{e v} \end{matrix}] = {[\begin{matrix} \cos \frac{Φ}{2} & e_{x} \sin \frac{Φ}{2} & e_{y} \sin \frac{Φ}{2} & e_{z} \sin \frac{Φ}{2} \end{matrix}]}^{T}

(4)

The desired angular velocity when tracking the target is related to the target's velocity on the detector plane. At this point, the target is considered to be in the center of the detector's field of view. Therefore, the desired angular velocity is:

ω_{c} = \frac{\sqrt{{\dot{x}}_{i} + {\dot{y}}_{i}}}{f} = \frac{\sqrt{\dot{u} d x + \dot{v} d y}}{f}

(5)

The direction of angular velocity is perpendicular to

\vec{O_{s} O_{p 2}}

and the linear velocity direction.

2.2. Reaction Wheel Model

Moving target tracking requires the microsatellite detector's optical axis to constantly align with the target, imposing high demands on control precision. Among various actuation mechanisms, the reaction wheel can continuously output high-precision torque, making it suitable for high-precision attitude control of satellites. Therefore, this paper designs an attitude controller using the reaction wheel as the actuation mechanism. Next, we present the configuration and mathematical model of the reaction wheel system.

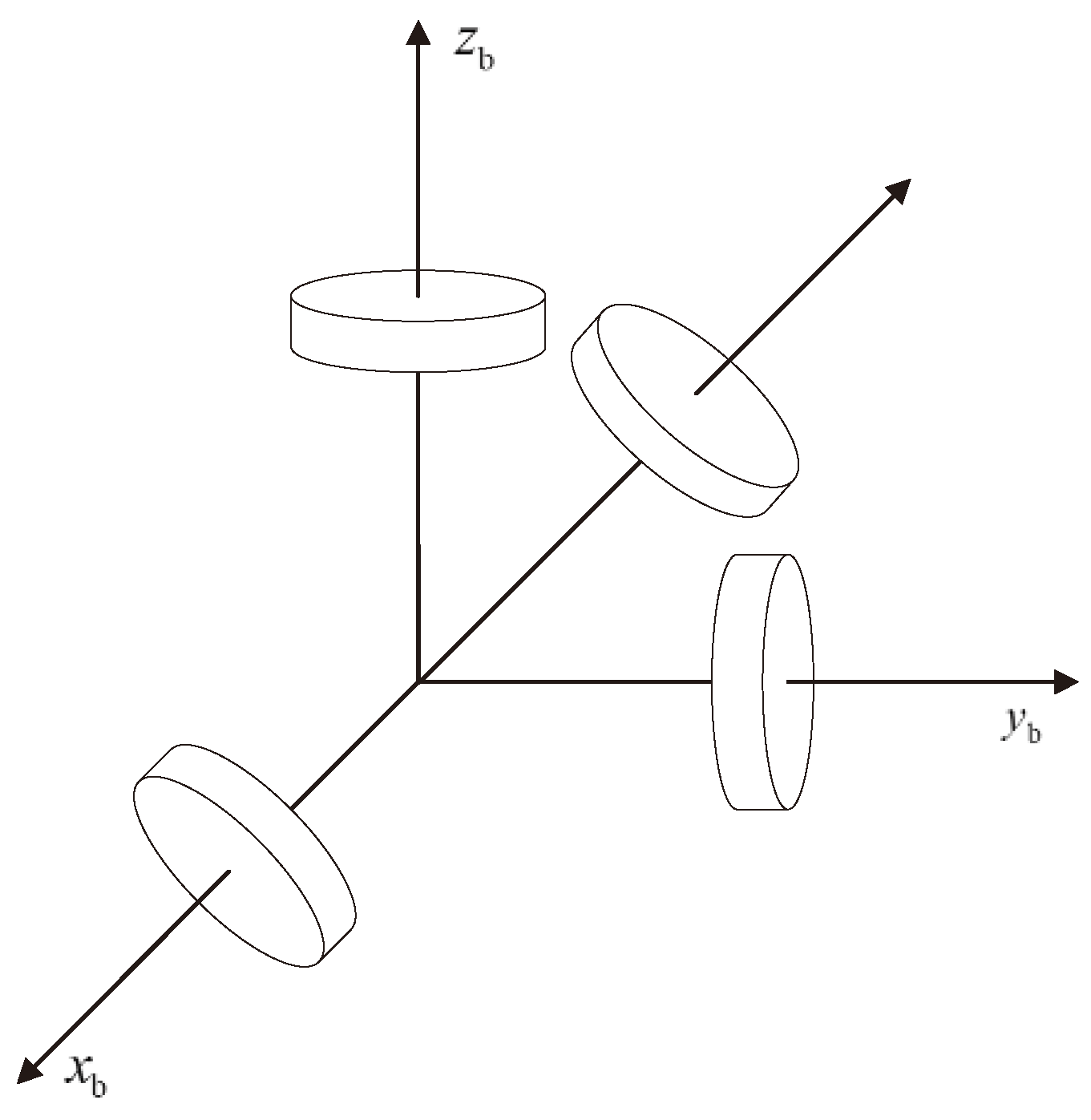
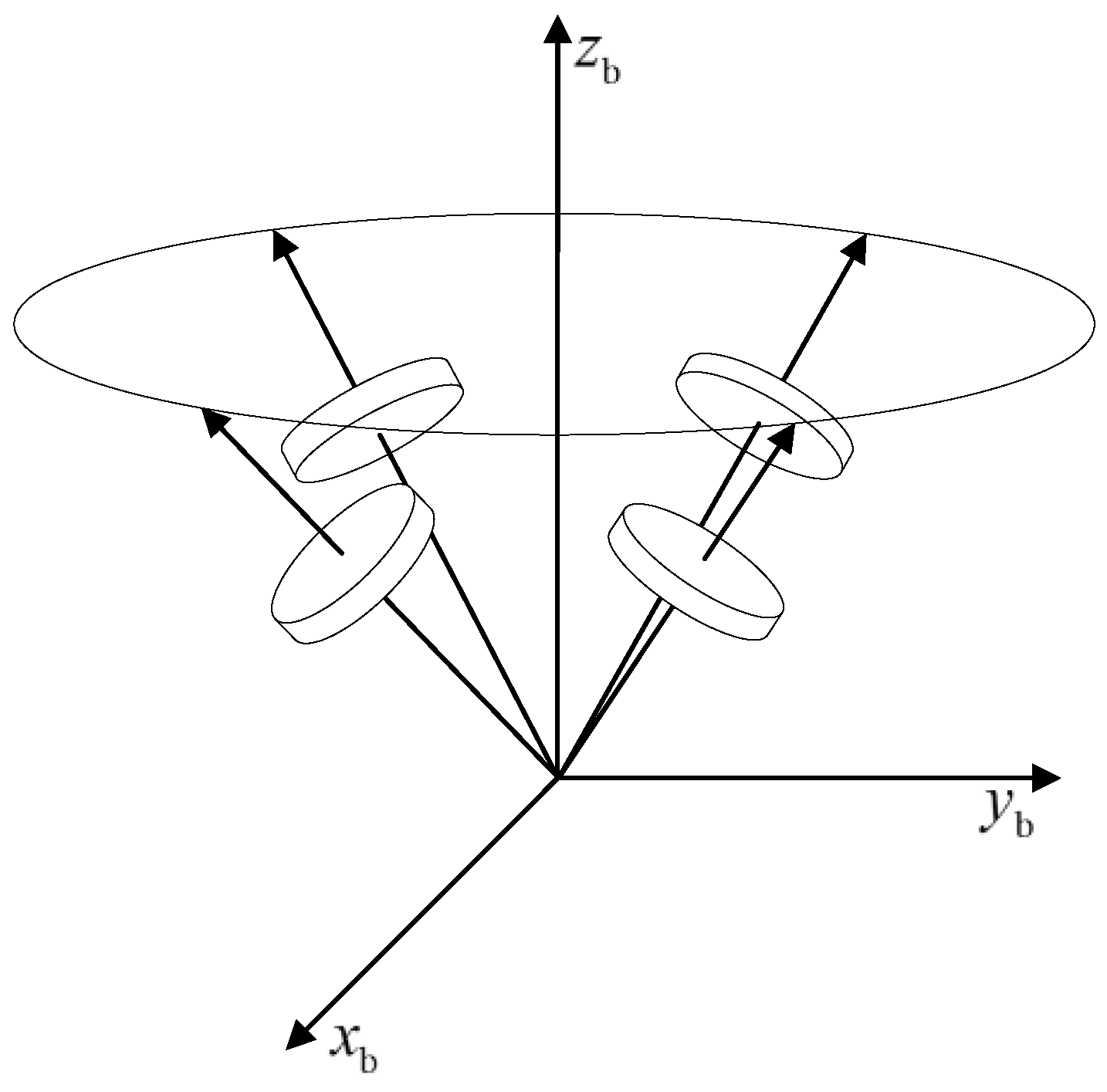
In reaction wheel systems, common configurations include the three orthogonal configurations, one oblique configuration, and the four skewed configurations, as illustrated in Figure 2 and Figure 3. The three orthogonal and one oblique configurations comprise four reaction wheels, with three wheels orthogonally mounted along the three axes of the satellite's body coordinate system and one wheel obliquely mounted. The oblique axis is generally inclined at an angle equal to the satellite's body coordinate system axes. Besides, the four-skewed configuration has all four wheels inclined and serving as backups to each other.

Theoretically, it can be proven that the oblique configuration has certain advantages in terms of power consumption, maximum output torque, reliability, and adaptability compared to the orthogonal configuration. However, the oblique configuration has a noticeable impact on the overall design of the satellite, especially on the layout and structure, as it requires the installation of reaction wheel brackets, adding weight to the satellite. Moreover, the internal space utilization efficiency is not high, posing a significant drawback for microsatellites. Therefore, this paper adopts the reaction wheel system's three orthogonal and one oblique configuration.

Let the angular momentum of the oblique wheel be

h_{4}

, represented in the body coordinate system as:

h_{4} = {(h_{4 x}, h_{4 y}, h_{4 z})}^{T}

(6)

The components satisfy

h_{4 x}^{2} + h_{4 y}^{2} + h_{4 z}^{2} = h_{4}^{2}

, and since the three components are equal in magnitude:

h_{4 x} = h_{4 y} = h_{4 z} = \frac{1}{\sqrt{3}} h_{4}

(7)

The angle between the oblique axis and each coordinate axis is then given by:

β = \cos^{- 1} (\frac{1}{\sqrt{3}}) = {54.74}^{\circ}

(8)

Let the array of angular momenta for the reaction wheels be

h_{w} = {[\begin{matrix} h_{1} & h_{2} & h_{3} & h_{4} \end{matrix}]}^{T}

, and the total angular momentum of the reaction wheel system in the satellite body coordinate system be

h

. The relationship between them is expressed as:

h = C h_{w}

(9)

where

C

is the mounting matrix for the reaction wheel system.

For the three orthogonal and one oblique configuration,

C = [\begin{array}{l} \begin{matrix} 1 & 0 & 0 & \frac{\sqrt{3}}{3} \end{matrix} \\ \begin{matrix} 0 & 1 & 0 & \frac{\sqrt{3}}{3} \end{matrix} \\ \begin{matrix} 0 & 0 & 1 & \frac{\sqrt{3}}{3} \end{matrix} \end{array}]

(10)

The primary control effect of a reaction wheel on the microsatellite is the reaction torque of the wheel. According to Newton's third law, the reaction torque

T_{0}

exerted by the wheel on the satellite is equal in magnitude but opposite in direction to the torque

T_{1}

applied by the motor on the wheel. Combining the angular momentum theorem:

T_{0} = - T_{1} = - (T_{w o} - T_{w f}) = - C J_{w} {\dot{Ω}}_{w}

(11)

where

T_{w o}

is the electromagnetic torque on the reaction wheel,

T_{w f}

is the frictional disturbance torque on the reaction wheel,

J_{w}

is the rotational inertia of the reaction wheel, and

Ω_{w}

is the angular velocity of the reaction wheel.

Operating under torque mode, the reaction wheel follows that

T_{0} - T_{w f}

is proportional to the commanded torque. This paper adopts the Stribeck friction model to simulate the frictional disturbance torque on the reaction wheel.

For a single reaction wheel, when the wheel is at rest:

T_{w f} = \{\begin{cases} T_{\max} T_{w o} > T_{\max} \\ T_{w o} - T_{\max} \leq T_{w o} \leq T_{\max} \\ - T_{\max} T_{w o} < - T_{\max} \end{cases}

(12)

When the wheel is rotating:

T_{w f} = k_{υ} Ω_{w} + [T_{c} + (T_{\max} - T_{c}) e^{- μ |Ω_{w}|}] sgn (Ω_{w})

(13)

where

T_{\max}

is the maximum static friction torque,

k_{υ}

is the viscous friction coefficient,

T_{c}

is the Coulomb friction torque, and

μ

is the empirical coefficient.

2.3. Microsatellite Attitude Model

Using quaternions to express satellite attitude kinematics equations avoids singularity issues and simplifies the calculation process by only involving matrix multiplication operations without complex trigonometric calculations. Therefore, this paper models the kinematic characteristics of the satellite using the attitude kinematics equations based on the attitude quaternion

q = {[\begin{matrix} q_{0} & q_{1} & q_{2} & q_{3} \end{matrix}]}^{T} = {[\begin{matrix} q_{0} & q_{v} \end{matrix}]}^{T}

The satellite attitude kinematics model based on the attitude quaternion is given by:

\{{\dot{q}}_{v} = \frac{1}{2} (q_{v}^{\times} + q_{0} I_{3}) ω_{bi}

(14)

where

q_{v}^{\times} = [\begin{matrix} 0 & - q_{3} & q_{2} \\ q_{3} & 0 & - q_{1} \\ - q_{2} & q_{1} & 0 \end{matrix}]

is the cross product antisymmetric skew-symmetric matrix of

q_{v}

, and

ω_{bi}

is the angular velocity vector of the satellite relative to the inertial coordinate system in the body coordinate system.

The object studied is a microsatellite, generally treated as a rigid body. The dynamics model for the attitude of the microsatellite is given by:

J {\dot{ω}}_{bi} + ω_{bi} \times (J ω_{bi} + C h_{w}) = - C \frac{d h_{w}}{d t} + T

(15)

where

J

is the rotational inertia matrix of the microsatellite and

T

is the external torque applied at the satellite's center of mass.

3. High-Precision Attitude Adaptive Integral Sliding Mode - Tracking Control Algorithm Based on Feedforward Compensation Disturbance Observer

3.1. Design of Feedforward Compensation Disturbance Observer

Focusing on the frictional torque of the flywheel, this paper employs the disturbance observer approach to estimate the frictional torque and compensate for it through feedforward control. Based on the previously presented flywheel torque model, the disturbance observer is designed as follows:

\{\begin{cases} {\dot{\hat{Ω}}}_{w} = \frac{1}{J_{w}} (T_{w o} - {\hat{T}}_{w f}) + L_{1} (Ω_{w} - {\hat{Ω}}_{w}) \\ {\dot{\hat{T}}}_{w f} = L_{2} (Ω_{w} - {\hat{Ω}}_{w}) \end{cases}

(16)

where

{\hat{Ω}}_{w}

and

{\hat{T}}_{w f}

are the estimated values of the flywheel angular velocity

Ω_{w}

and frictional disturbance torque

T_{w f}

, respectively.

Utilizing the disturbance observer mentioned above and choosing suitable

L_{1}

and

L_{2}

ensures that as

t \to + \infty

, and thus the estimated errors for flywheel angular velocity and frictional disturbance torque tend to be zero.

The estimation error of the observer is defined as:

\{\begin{cases} Ω_{w e} = Ω_{w} - {\hat{Ω}}_{w} \\ T_{w f e} = T_{w f} - {\hat{T}}_{w f} \end{cases}

(17)

Taking the derivative of both sides of the above equation concerning time:

\{\begin{cases} {\dot{Ω}}_{w e} = {\dot{Ω}}_{w} - {\dot{\hat{Ω}}}_{w} \\ {\dot{T}}_{w f e} = {\dot{T}}_{w f} - {\dot{\hat{T}}}_{w f} \end{cases}

(18)

Substituting the observer model and flywheel torque model into the equation, we obtain:

\{\begin{cases} {\dot{Ω}}_{w e} = - \frac{T_{w f e}}{J_{w}} + L_{1} Ω_{w e} \\ {\dot{T}}_{w f e} = L_{2} Ω_{w e} \end{cases}

(19)

Organizing the above equation into matrix form:

[\begin{matrix} {\dot{Ω}}_{w e} \\ {\dot{T}}_{w f e} \end{matrix}] = [\begin{matrix} L_{1} & - \frac{1}{J_{w}} \\ L_{2} & 0 \end{matrix}] [\begin{matrix} Ω_{w e} \\ T_{w f e} \end{matrix}]

(20)

The characteristic equation of the observer is then given by:

λ^{2} - L_{1} λ + \frac{L_{2}}{J_{w}} = 0

(21)

Ensuring

L_{1} < 0

and

L_{2} > 0

, the characteristic equation guarantees that all roots of the equation fall on the left half of space s. For any initial values, as time

t \to + \infty

, the estimated errors for flywheel angular velocity and frictional disturbance torque satisfy

Ω_{w e} \to 0

and

T_{w f e} \to 0

3.2. Design of Adaptive Integral Sliding Mode Variable Structure Controller

This section proposes an adaptive global integral sliding mode control algorithm for external disturbance torque. By designing an adaptive law, this controller can dynamically adjust the gain based on the magnitude of external disturbances, thereby reducing chattering amplitude. Specifically, to prevent excessive adaptation of the adaptive law, a global integral sliding mode vector is adopted, as presented in Eq. (22). This structure ensures the system's initial state is already on the sliding surface

S = 0

, eliminating the approaching phase.

S = ω_{e} + \int_{0}^{t} (k_{P} ω_{e} + k_{I} q_{e v}) d τ - ω_{e} (0)

(22)

where

k_{P} > 0

and

k_{I} > 0

When on the sliding surface, the system's state eventually stabilizes at the origin. Combining the sliding mode vector with the kinematic and dynamic models of the microsatellite, we get:

J \dot{S} = T_{0} + T_{f} + k_{P} J ω_{e} + k_{I} J q_{e v} - Γ (\cdot)

(23)

where

Γ (\cdot) = J (C_{o}^{b} {\dot{ω}}_{d} - ω_{e}^{\times} C_{o}^{b} ω_{d}) + ω_{b}^{\times} (J ω_{b} + C J_{w} Ω_{w})

Combining Eqs. (22) and (23), the sliding mode variable structure controller is:

u^{'} = - k sgn (S) - k_{P} J ω_{e} - k_{I} J q_{e v} + Γ (\cdot)

(24)

The fundamental idea is to continuously transform the control structure so the system remains on the sliding surface

S = 0

, allowing the system error to converge to zero. The term

- k sgn (S)

in the controller is the root cause of chattering in the sliding mode variable structure control and is also the factor that imparts robustness to external disturbances. Besides, the magnitude of the switching gain

k

determines the chattering amplitude, and stability is achieved only when the chattering amplitude exceeds the disturbance upper limit.

In a traditional sliding mode variable structure control, the parameter

k

is fixed, often chosen to be large to ensure stability, thus increasing the chattering amplitude. Adaptive sliding mode variable structure control adjusts the value of

k

in real-time through the adaptive law, precisely meeting the stability requirements of the system. Based on the analysis above, the adaptive law is designed as follows:

\hat{k} = ε {\int_{0}^{t} ‖S‖}_{\infty} d τ

(25)

where

\hat{k}

is the adaptive switching gain and

ε > 0

From the structure of the adaptive law presented above, it is clear that the adaptation does not originate directly from external disturbance torque but adjusts the gain's magnitude based on how far the sliding mode vector

S

deviates from zero. That is, the gain is increased whenever

S

is non-zero until

S

converges to zero.

Considering Eqs. (16), (24), and (25), the adaptive integral sliding mode controller can be designed as:

u = - ε {\int_{0}^{t} ‖S‖}_{\infty} d τ sgn (S) - k_{P} J ω_{e} - k_{I} J q_{e} + Γ (\cdot) + {\hat{T}}_{w f}

(26)

Next, we proceed to prove the stability of this controller.

Proof. Taking the Lyapunov function as:

V = \frac{1}{2} S^{T} J S + \frac{1}{2} {(\hat{k} - \bar{k})}^{2}

(27)

where

\bar{k}

is the final value that satisfies the switching gain required for control

\bar{k} > {‖T_{f}‖}_{\infty}

\dot{V} = S^{T} J \dot{S} + (\hat{k} - \bar{k}) \dot{\hat{k}} = S^{T} (T_{0} + T_{f} + k_{P} J ω_{e} + k_{I} J q_{e} - Γ (\cdot)) + (\hat{k} - \bar{k}) \dot{\hat{k}}

(28)

Substituting the designed controller and adaptive law into Eq. (28), we get:

\begin{matrix} \dot{V} & = S^{T} (- \hat{k} sgn (S) + {\hat{T}}_{w f} - T_{w f} + T_{f}) + (\hat{k} - \bar{k}) {‖S‖}_{1} \\ = \hat{k} ({‖S‖}_{1} - S^{T} sgn (S)) + (S^{T} T_{f} - \bar{k} {‖S‖}_{1}) + ({\hat{T}}_{w f} - T_{w f}) \\ = (S^{T} T_{f} - \bar{k} {‖S‖}_{1}) + ({\hat{T}}_{w f} - T_{w f}) \end{matrix}

(29)

As time progresses,

{\hat{T}}_{w f} - T_{w f}

will eventually tend to zero. Therefore:

\lim_{t \to \infty} \dot{V} = (S^{T} T_{f} - \bar{k} {‖S‖}_{1}) < ({‖T_{f}‖}_{\infty} - \bar{k}) {‖S‖}_{1} < 0

(30)

So, the system will eventually remain on the sliding surface

S = 0

, and the system state on the sliding surface will eventually stabilize to zero. □

Although this paper reduces chattering amplitude by designing the adaptive law, the controller still exhibits noticeable chattering due to the non-continuous function

sgn (S)

. Thus, a saturation function

sat (S)

inspired by the boundary layer method is introduced to overcome this drawback Therefore, the final design of the controller is:

u_{1} = - ε {\int_{0}^{t} ‖S‖}_{\infty} d τ sat (S) - k_{P} J ω_{e} - k_{I} J q_{e} + Γ (\cdot) + {\hat{T}}_{w f}

(31)

4. Simulation Results and Analysis

The following simulations involve moving target tracking using a semi-physical ground real-time simulation system for microsatellites. The system comprises an electric satellite, a real-time simulation machine, and ground measurement software, as depicted in Figure 4. The electric satellite is composed and configured to mimic the real conditions of satellites in orbit, enabling the physical simulation of microsatellites. The real-time simulation machine facilitates the simulation of satellite orbital operations, environmental conditions, and target scenarios. The ground measurement software monitors and controls the satellite's state.

The simulation conditions were set as follows. The satellite operates in a circular orbit at an altitude of 500 km from the Earth's surface, with an inclination angle

i = 30^{o}

, right ascension of the ascending node

Ω = 0^{o}

, and the initial ground projection geographical coordinates of the target point are

(9.9727 ° N, 150.5970 E)

, with an altitude of 12 km, flying North at a speed of 0.8 Ma.

The moment of inertia for the microsatellite's rotation was given by:

J = [\begin{matrix} 4 & 0 & 0 \\ 0 & 6 & 0 \\ 0 & 0 & 5 \end{matrix}] (kg \cdot m^{2})

External environmental disturbance torque was configured as:

d = [\begin{matrix} 3 \sin (10 t) - 6 \\ 3 \sin (10 t) - 5 \\ 3 \sin (10 t) + 2 \end{matrix}] \times 10^{- 4} (N \cdot m)

The controller parameters were set as

k_{P} = 0.4

k_{I} = 0.1

ε = 1.5

, and

δ = 0.01

. The disturbance observer parameters were set as

L_{1} = - 1

and

L_{2} = 0.03

. Table 1 reports the performance parameters of the flywheel.

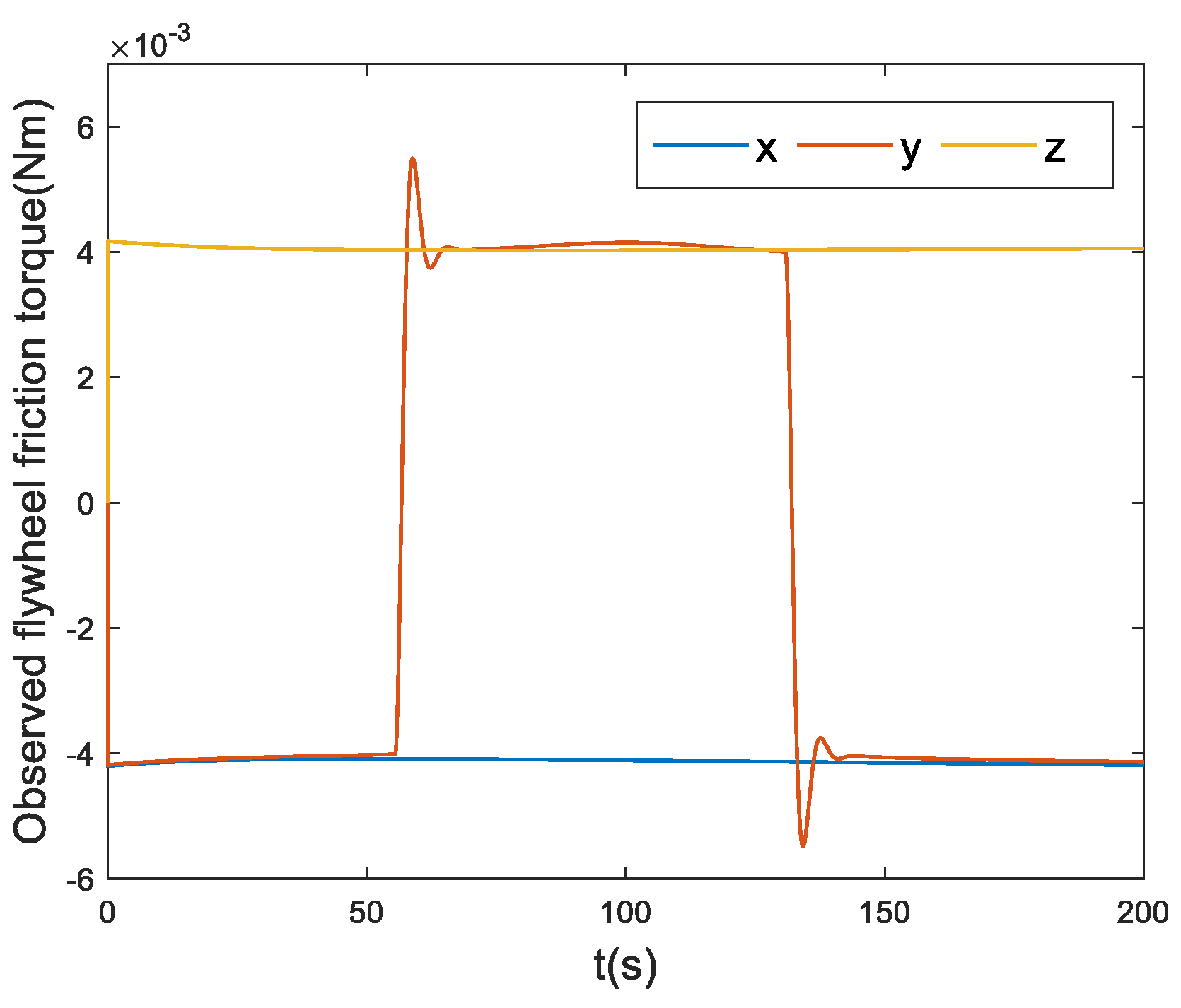
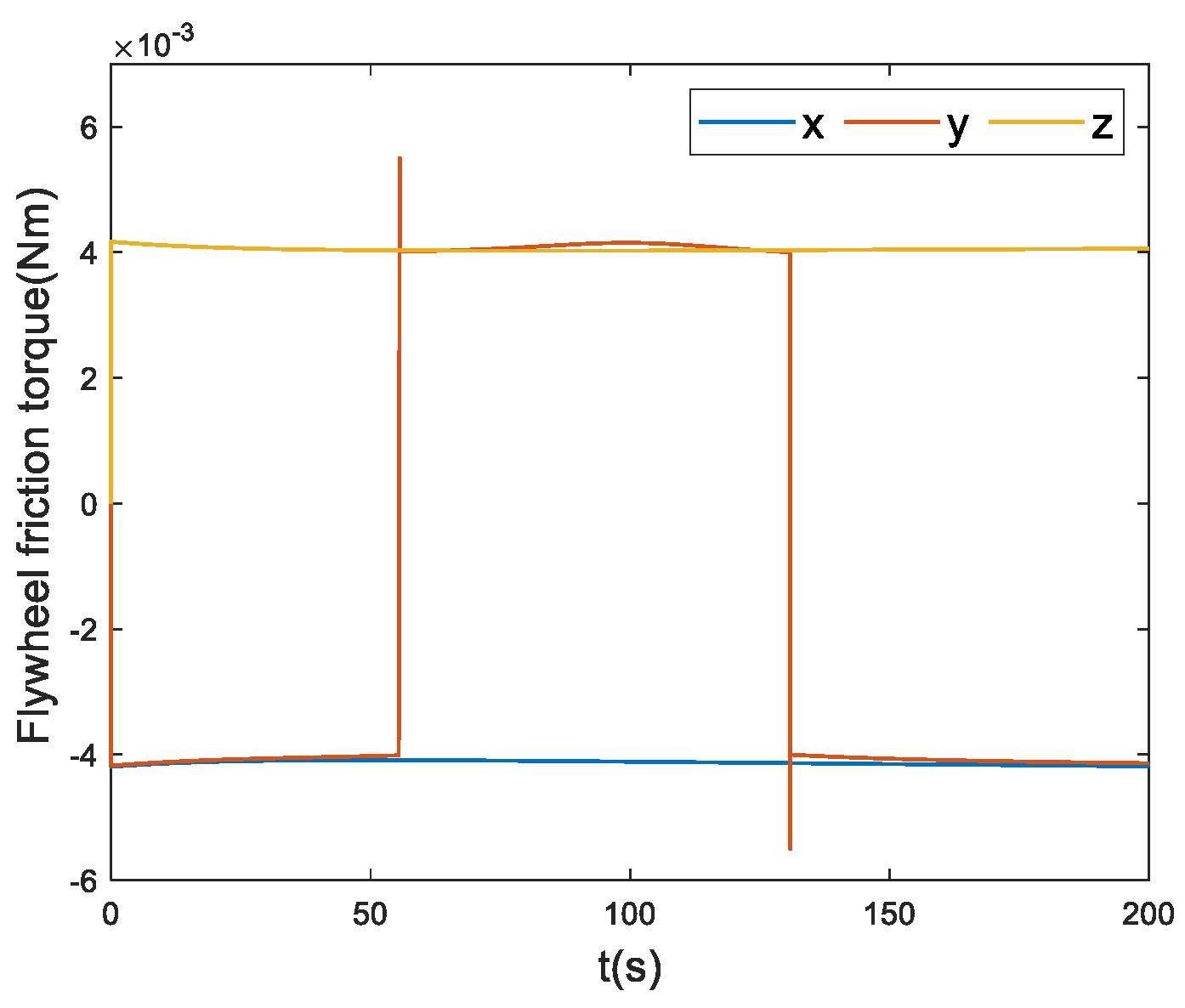
Utilizing the method presented in Section 3 provides the quaternion error and desired angular velocity between the current attitude and the desired attitude. The designed controller was then used to track the desired attitude. In this simulation, first, the effectiveness of the disturbance observer was examined, with the corresponding results illustrated in Figure 5 and Figure 6. Figure 5 presents the actual friction torque values generated by the flywheel, and Figure 6 displays the observed flywheel friction torque values obtained by the disturbance observer. Figure 5 highlights that the flywheel experienced zero speed at 56s and 132s, resulting in a sudden change in frictional force. Comparing the two figures, it is evident that the designed disturbance observer successfully observed the frictional disturbance torque of the flywheel, albeit with a slight deviation at the zero-speed crossings.

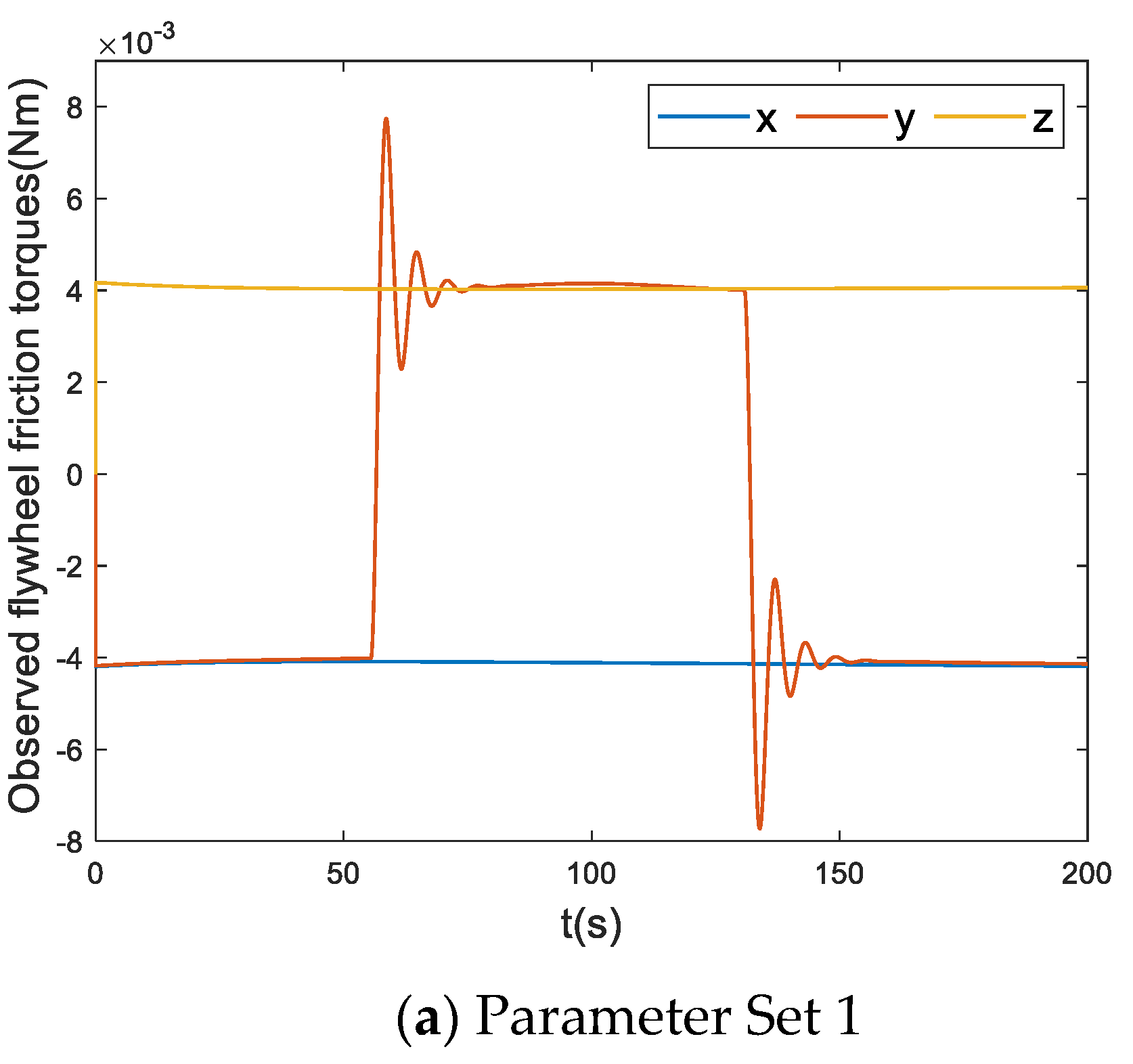
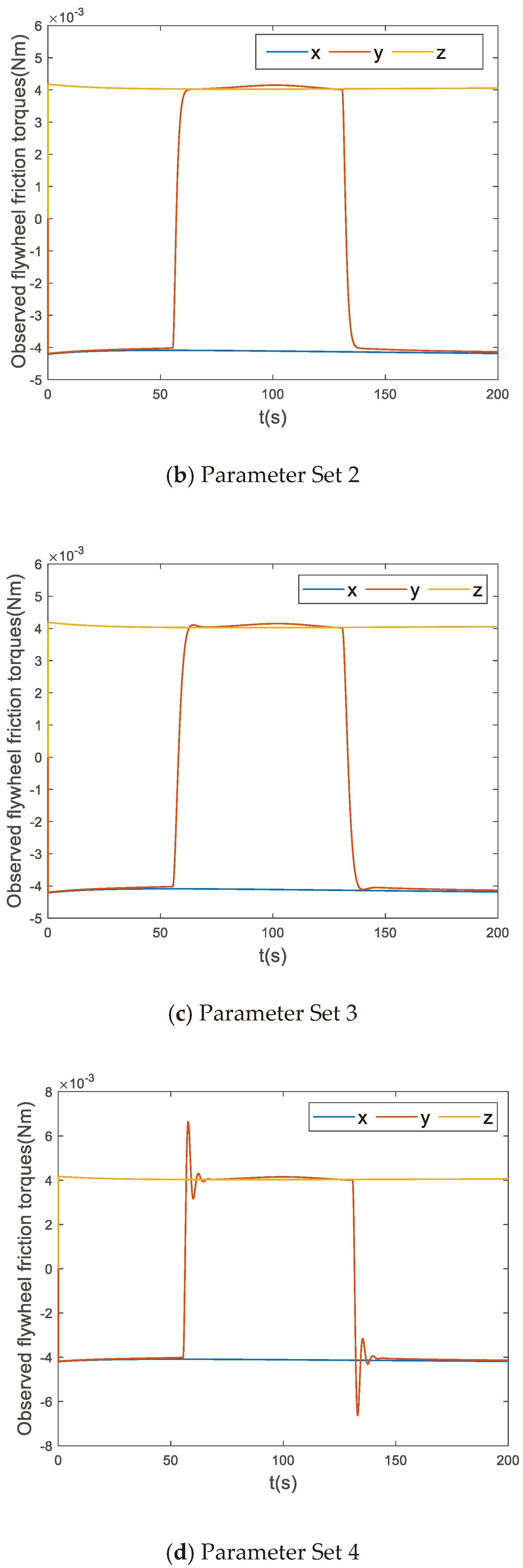
Four additional parameter combinations were simulated to demonstrate the impact of parameters

L_{1}

and

L_{2}

on the disturbance observer. Table 2 reports the four data sets, and the corresponding simulation results are depicted in Figure 7.

Figure 7(a) and (b) reveal that as the parameter

L_{1}

increased, the observer became less sensitive to abrupt changes in frictional force. Similarly, Figure 7(c) and (d) highlight that as the parameter

L_{2}

decreased, the observer became less sensitive to abrupt changes in frictional force. In practical applications, a reasonable choice of observer parameters is crucial. Indeed, if

|L_{2} / L_{1}|

is too large, the observer becomes overly sensitive to sudden changes in frictional force, leading to oscillations in observed values at the point of frictional force transition, thereby affecting subsequent observations. Conversely, if

|L_{2} / L_{1}|

is too small, the observer may fail to detect abrupt changes in frictional force.

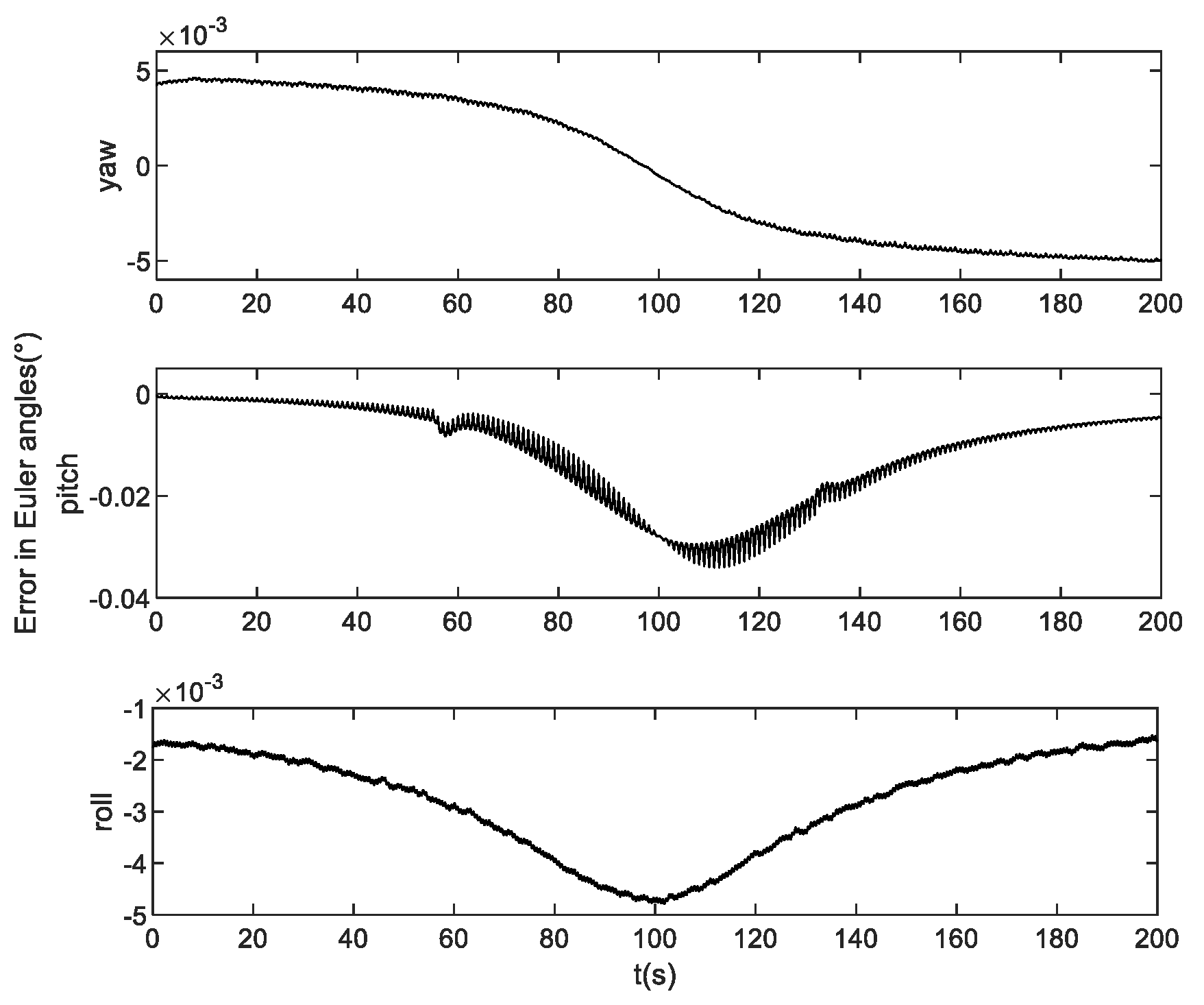
Next, the tracking performance of the controller was examined. For clarity, the quaternion attitude was converted to Euler angles. The simulation results are illustrated in Figure 8, Figure 9 and Figure 10.

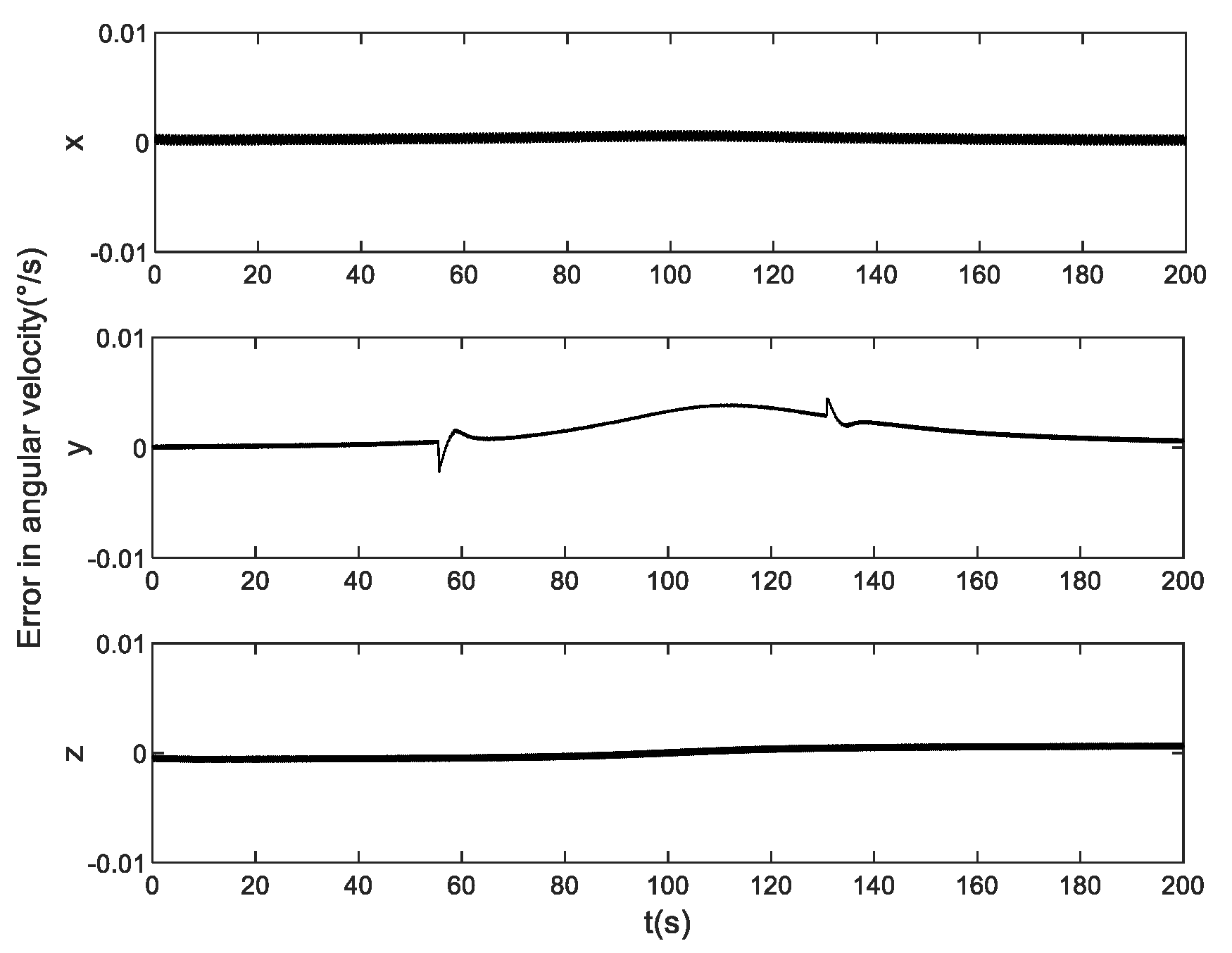
Figure 8 infers that the satellite achieved high accuracy in yaw and roll angles while the pitch angle accuracy was slightly lower. Specifically, the yaw accuracy was 0.0012°, roll accuracy was 0.0011° and pitch accuracy was 0.009°. Figure 9 demonstrates that the satellite's angular velocity control accuracy was high, with errors in all three axes maintained within 0.005°/s. The lowest accuracy in satellite attitude was observed around 110s, primarily because the satellite is closest to the target point at this time, resulting in rapid changes in satellite attitude. The deviation between attitudes at the previous and subsequent instants is significant within one control cycle, preventing complete convergence to zero. This gives rise to a certain level of attitude control error.

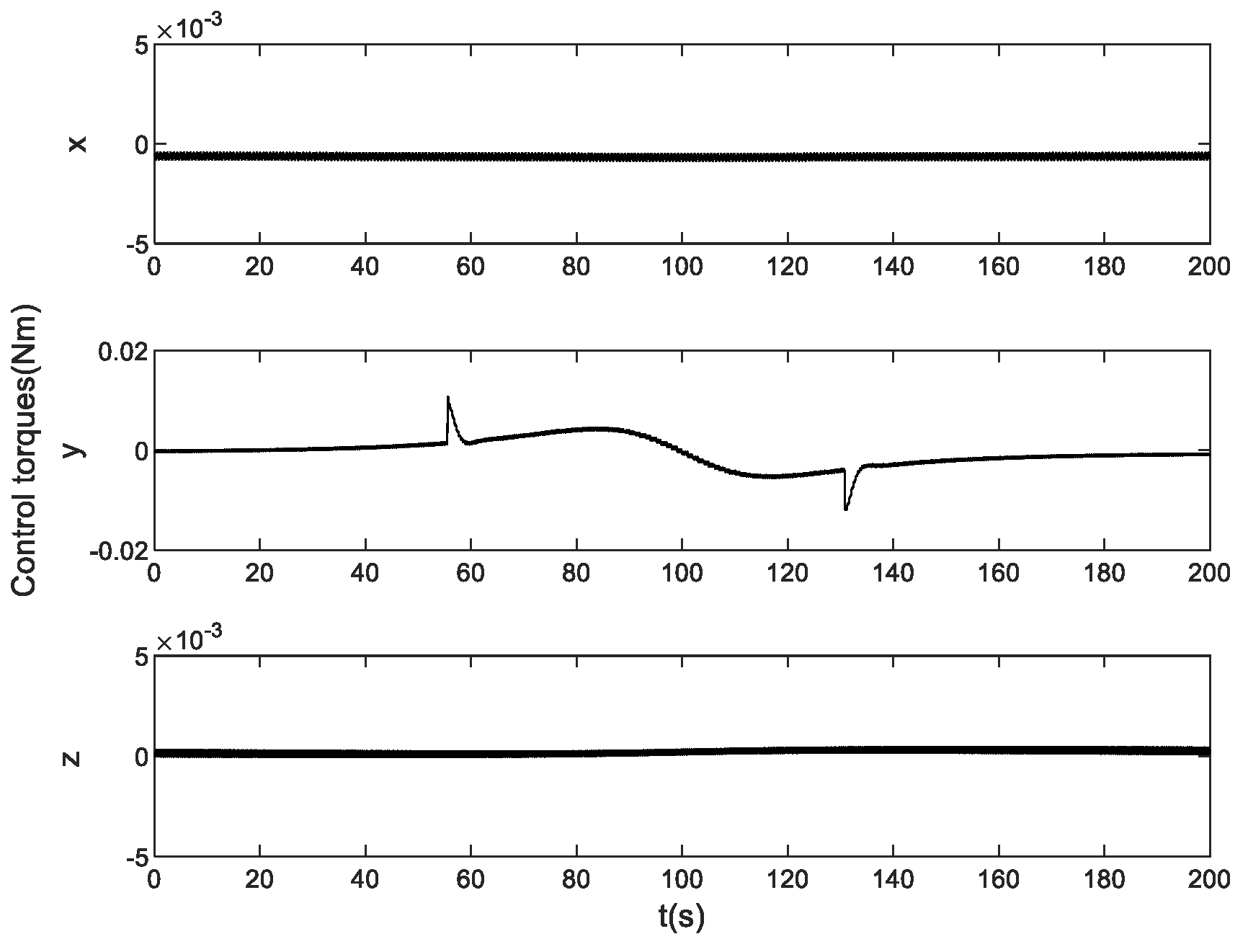
Figure 10 illustrates the variation of satellite control torques in the entire process. The x-axis- and z-axis torques were almost zero, while the y-axis direction had significant torque between 60s and 140s. The satellite's attitude changed relatively quickly during this interval, calling for a large control torque. A sudden torque transition occurred around the 60s and 130s, which is evident in Figure 8 and Figure 9. This is attributed to the zero crossing of the flywheel's speed, where the flywheel friction torque transitions from moving friction to static friction and then back to moving friction, as indicated in the performance analysis of the disturbance observer.

5. Conclusions

This paper proposes an adaptive integral sliding mode variable structure attitude controller based on feedforward compensation disturbance observer to address the challenge of stable tracking of high-speed moving targets by low Earth orbit microsatellites under conditions of high-resolution narrow-field-of-view. The proposed method improved the precision of microsatellite tracking and gaze attitude control for high-speed moving targets.

Overall, the following conclusions are drawn through simulation verification:

The designed disturbance observer can accurately estimate the flywheel's friction torque. Specifically, a larger parameter $L_{1}$ and a smaller parameter $L_{2}$ make the observer less sensitive to abrupt changes in frictional force.
Under the simulation conditions of this paper, with the existence of flywheel friction torque and external disturbance torque, the designed controller ensures Euler angle precision of 0.009° and angular velocity control accuracy of 0.005°/s during the process of tracking high-speed moving targets validating the effectiveness of the proposed algorithm.

Author Contributions

Formal analysis, Yurong Liao; Investigation, Xinyan Yang and Zhaoming Li; Software, Lei Li; Validation, Zhaoming Li.

Funding

This research received no external funding.

Data Availability Statement

The data presented in this study is available on request from the corresponding author.

Conflicts of Interest

The authors declare no conflicts of interest.

References

AF Pei, Wenjing.” Staring Imaging Attitude Tracking Control Laws for Video Satellites Based on Image Information by Hyperbolic Tangent Fuzzy Sliding Mode Control” Computational Intelligence and Neuroscience. [CrossRef]
Huang, XW, Dong, ZY, Zhang, K, Zhang, F and Zhang, LH Approximation-Free Attitude Fault-Tolerant Tracking Control of Rigid Spacecraft with Global Stability and Appointed Accuracy. IEEE Transactions on Aerospace and Electronic Systems. [CrossRef]
Zhang Gaowang, S. Qiu, and F. Wang. "Adaptive Fuzzy Fault-Tolerant Control of Flexible Spacecraft with Rotating Appendages." International Journal of Fuzzy Systems, 25.1(2023):326-337. [CrossRef]
Wu, Shunan, et al. "Robust attitude maneuver control of spacecraft with reaction wheel low-speed friction compensation." Aerospace Science & Technology, 2015:213-218. [CrossRef]
Fan, Shaoyan, et al. "Quick-response attitude takeover control using multiple servicing spacecraft based on inertia properties identification." Advances in Space Research: The Official Journal of the Committee on Space Research(COSPAR) (2022). [CrossRef]
Yu, Xiang, et al. "Antidisturbance Controllability Analysis and Enhanced Antidisturbance Controller Design with Application to Flexible Spacecraft." IEEE Transactions on Aerospace and Electronic Systems 57-5(2021). [CrossRef]
He, Tongfu, and Z. Wu. "Iterative Learning Disturbance Observer Based Attitude Stabilization of Flexible Spacecraft Subject to Complex Disturbances and Measurement Noises." IEEE/CAA Journal of Automatica Sinica 008.009(2021):P.1576-1587. [CrossRef]
He, Tongfu, and Z. Wu. "Neural network disturbance observer with extended weight matrix for spacecraft disturbance attenuation." Aerospace Science and Technology, Jul.(2022):126. [CrossRef]
Chen, Zhaoyue, H. Zhang, and B. Xiao. " Appointed-time nonsingular sliding mode control of spacecraft attitude stabilization." IET Control Theory and Applications. [CrossRef]
Xiao, B, Wu, XW, Cao, L and Hu, XX Prescribed Time Attitude Tracking Control of Spacecraft with Arbitrary Disturbance. IEEE Transactions on Aerospace and Electronic Systems. [CrossRef]
Cao, Lei Ding, Zhengtao. "Event-triggered anti-disturbance attitude control for rigid spacecrafts with multiple disturbances." International Journal of Robust and Nonlinear Control, 31.2(2021). [CrossRef]
Qiao, Jianzhong, et al. "Composite Nonsingular Terminal Sliding Mode Attitude Controller for Spacecraft with Actuator Dynamics Under Matched and Mismatched Disturbances." IEEE Transactions on Industrial Informatics, (2020). [CrossRef]
Xiao, Bing, L. Cao, and D. Ran. "Attitude Exponential Stabilization Control of Rigid Bodies via Disturbance Observer." IEEE Transactions on Systems, Man, and Cybernetics: Systems PP.99(2019):1-9. [CrossRef]
Eshghi, Samira, and R. Varatharajoo. "Singularity-Free Integral-Augmented Sliding Mode Control for Combined Energy and Attitude Control System." Advances in Space Research 59.2(2016):631-644. [CrossRef]
Van, Mien. "Higher-order terminal sliding mode controller for fault accommodation of Lipschitz second-order nonlinear systems using fuzzy neural network." Applied Soft Computing 104.4(2021):107186. [CrossRef]
Mazare, Mahmood, M. Taghizadeh, and P. Ghaf-Ghanbari. "Fault-tolerant control based on adaptive super-twisting nonsingular integral-type terminal sliding mode for a delta parallel robot." Journal of the Brazilian Society of Mechanical Sciences and Engineering 42.8(2020):1-15. [CrossRef]
Yang, YX, Chen, M, Peng, KX and Yu, M. Adaptive Sliding Mode Fault-tolerant Control for Attitude Tracking of Spacecraft with Actuator Faults. International Journal of Control Automation and Systems. [CrossRef]
Lu K, Xia Y, Zhu Z, et al. Sliding mode attitude tracking of rigid spacecraft with disturbances. Journal of the Franklin Institute, 2012, 349(2):413-440. [CrossRef]
Gao S, Jing Y, Liu X, et al. Finite-time attitude-tracking control for rigid spacecraft with actuator failures and saturation constraints. International Journal of Robust and Nonlinear Control, 2019, 30(2). [CrossRef]
Wu Y D, Wu S F, Gong D R, et al. Spacecraft Attitude Maneuver Using Fast Terminal Sliding Mode Control Based on Variable Exponential Reaching Law. International Conference on Aerospace System Science and Engineering. Springer, Singapore, 2019. [CrossRef]
Wang C, Xia H, Wang Y, et al. Discrete-time Sliding Mode Control with Adaptive Reaching Law via Implicit Euler Method. International Journal of Control, Automation, and Systems, 2023. [CrossRef]
Ma H, Xiong Z, Li Y, et al. Sliding Mode Control for Uncertain Discrete-Time Systems Using an Adaptive Reaching Law. IEEE Transactions on Circuits and Systems II: Express Briefs, 2020. [CrossRef]
Wang Z, Li Q, Li S. Adaptive Integral-Type Terminal Sliding Mode Fault Tolerant Control for Spacecraft Attitude Tracking. IEEE Access, 2019:35195-35207. [CrossRef]
Wang, Jie, Y. S. Hu, and W. Ji. "Barrier Function-Based Adaptive Integral Sliding Mode Finite-time Attitude Control for Rigid Spacecraft." Nonlinear Dynamics :1-16. [CrossRef]

Figure 1. Relationship between the optical axis direction for target imaging and the satellite’s target direction.

Figure 2. Three orthogonal and one oblique configuration of reaction wheels.

Figure 3. Four skewed configurations of reaction wheels.

Figure 4. Semi-physical ground real-time simulation system for microsatellites.

Figure 5. Flywheel friction torque.

Figure 6. Observed flywheel friction torque.

Figure 7. Observed flywheel friction torques under various parameter sets:(a) Parameter Set 1;(b) Parameter Set 2; (c) Parameter Set 3; (d) Parameter Set 4.

Figure 8. Euler angle error of attitude tracking.

Figure 9. Angular velocity error of attitude tracking.

Figure 10. Control torque of attitude tracking.

Table 1. Flywheel performance parameters.

Parameter	Value
Maximum torque $/ (Nm)$	0.4
Maximum angular velocity ${Ω (rad s^{- 1})}_{m a x}$	±5000
Moment of inertia $J_{w} / (kg m^{2})$	0.025
Viscous friction coefficient $k_{υ}$	0.0000318
Coulomb friction torque $T_{c} / (Nm)$	0.0040
Maximum static friction torque ${T (Nm)}_{m a x}$	0.0055
Empirical coefficient $μ$	2
Maximum torque $/ (Nm)$	0.4
Maximum angular velocity ${Ω (rad s^{- 1})}_{m a x}$	±5000
Moment of inertia $J_{w} / (kg m^{2})$	0.025

Table 2. Disturbance observer parameters.

	Set 1	Set 2	Set 3	Set 4
$L_{1}$	-0.5	-2	-1	-1
$L_{2}$	0.03	0.03	0.01	0.06

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

An Attitude Adaptive Integral Sliding Mode Control Algorithm with Feedforward Compensation Disturbance Observer for Microsatellites to Track High-Speed Moving Targets

Abstract

1. Introduction

2. Attitude Control System Model

2.1. Calculation of Desired Attitude for Target Tracking Based on Image Feedback

2.2. Reaction Wheel Model

2.3. Microsatellite Attitude Model

3. High-Precision Attitude Adaptive Integral Sliding Mode - Tracking Control Algorithm Based on Feedforward Compensation Disturbance Observer

3.1. Design of Feedforward Compensation Disturbance Observer

3.2. Design of Adaptive Integral Sliding Mode Variable Structure Controller

4. Simulation Results and Analysis

5. Conclusions

Author Contributions

Funding

Data Availability Statement

Conflicts of Interest

References

MDPI Initiatives

Important Links

Subscribe