An Autonomous Tow Truck Algorithm for Engineless Aircraft Taxiing

The aviation industry has proposed multiple solutions to reduce fuel consumption, air pollution and noise at airports, one of which involves deploying electric trucks for aircraft towing between the stand and the runway. However, the introduction of tow trucks results in increased surface traffic, posing challenges from the perspective of Air Traffic Controller's (ATCO). Various solutions involving automated planning and execution have been proposed, but many are constrained by their inability to manage multiple active runways simultaneously, and their failure to account for tow truck battery state-of-charge during assignments. This paper presents a novel system for taxi operations that employs autonomous tow trucks to enhance ground operations and address deficiencies in existing approaches. The system focuses on identifying conflict-free solutions that minimize taxi-related delays and route length while maximising the efficient use of the tow trucks. The algorithm operates at a strategic level and uses a centralised approach. It has the capacity to cater for multiple active runways and considers factors such as tow truck battery state-of-charge and availability of charging stations. Furthermore, the proposed algorithm is capable of scheduling and routing tow trucks for aircraft taxiing without generating traffic conflicts.

Keywords:

Subject: Engineering - Aerospace Engineering

1. Introduction

Currently, taxiing operations contribute to high fuel consumption, emissions, and economic costs for airlines and airports. In 2022, the average duration of the taxi-out and taxi-in phases of flight was 10.2% and 5.1%, respectively, of the duration of intra-European flights [1]. Furthermore, the annual fuel consumption during taxiing is approximately five million tonnes [2]. The issue is worsened by the fact that aircraft engines are optimised for high-altitude cruise operations, leading to inefficiencies while taxiing, particularly in high-traffic airports like Dallas/Fort Worth International Airport. In 2008, 18% of ground operation fuel at DFW was consumed by stop-and-go situations, primarily caused by congestion [3]. Similarly, at Heathrow airport in 2011, taxi operations were responsible for generating 56% of the total NOx emissions [4].

Taxiing is a significant contributor of pollution and noise at airports [5]. The European Commission has recognised these effects and set strict targets for emission reduction through initiatives such as “Flight Path 2050” [6] and the European Green Deal [7]. Carbon neutrality for all taxiing procedures will be required by 2050. Besides environmental impact, taxiing also has an economic impact on airlines due to the associated fuel costs, which constitute a substantial portion of airlines’ operating expenses [8,9,10]. Inefficient taxi operations cause delays and affect air traffic efficiency, incurring additional costs for airlines and airports.

To address the challenge of reducing emissions during the taxi phase, the aviation industry is considering two main technologies [3]: electric motors installed in the landing gear (such as Wheel Tug [11] and Electric Green Taxiing System [12]) and tow trucks (such as TaxiBot [13]). Tow trucks, although not adding to the weight of the aircraft, may increase surface traffic and Air Traffic Controller (ATCO) workload, potentially leading to congestion.

The rest of this paper is organised as follows. Section II explores previous work to identify the strengths and limitations of solutions proposed in different contexts. Section III describes the airport modelling and model assumptions considered in this work and gives an overview of the algorithm. Section IV defines the performance metrics and test scenarios, and then presents and discusses the results. Finally, Section V outlines the key conclusions of this paper and highlights areas for future research.

2. Literature Review

The solutions proposed in the literature follow two main optimisation strategies: centralised and decentralised [14]. With centralized optimization, a central ‘authority’ coordinates and makes decisions for all ground movements. This strategy aims to find the global optimum, however, it requires a comprehensive knowledge of all the vehicles on the airport’s surface [15,16]. In contrast, decentralised (multi-agent) optimisation, such as the approach adopted by Udluft [17], distributes the decision-making authority among various agents, including individual aircraft, tow trucks and taxiway or runway intersections. However, this approach typically identifies only local optima.

The SAFETug project [18,19], carried out by NASA, proposed a fully autonomous taxiing system – including a surface scheduler, an automated route planning system and a Human Machine Interface (HMI) – which can assist ATC, pilots and ground crew during tow truck-based taxi operations, by making tactical decisions to ensure safe and efficient procedures. The system is based on the Floyd-Warshall All-Pairs Shortest Path Optimiser (SPO) and has been tested at Dallas/Fort Worth International Airport. The project, as opposed to the other works discussed in this section, focuses almost completely on technical aspects such as the appearance of the HMI and the state-of-the-art of the tow trucks and of the obstacle detection technology. While the work addresses issues such as the logistical challenges associated with autonomous engines-off taxiing, the precision of navigation of the autonomous tow trucks and the situation awareness of ATCOs, it does not offer solutions for the reduction of the delays caused by the introduction of the tow trucks, or for an efficient route planning of the vehicles in high traffic scenarios.

Vemula et al. [20] consider the problem of path planning in the presence of dynamic obstacles, employing the concept of adaptive dimensionality to enhance computational efficiency. Their approach strategically incorporates the time dimension only within regions of the environment prone to potential collisions, while planning in a low-dimensional state-space elsewhere. However, their solution, based on A* (a SPO algorithm), is constrained as it exclusively proposes path alterations, neglecting the possibility of postponed departures.

Gawrilow et al. [21] proposed a routing algorithm based on Dijkstra for Automated Guided Vehicles (AGVs) in an automated logistics system. Notably, this algorithm prioritises conflict avoidance, deadlocks and livelocks during route computation rather than solely during execution. Whilst efficient in generating conflict-free routes, the algorithm exhibits vulnerability to significant system disruptions, such as substantial delays or severe congestion.

More recently, Zhang et al. [22] proposed a multi-objective optimization method for aircraft taxiing on an airport surface, considering both environment constraints of the airport and aircraft conflicts. The method employs a multi-objective Genetic Algorithms (GAs) and aims to achieve a Pareto-optimized taxiing scheme in terms of taxiing time, fuel consumption, and pollutant emissions. The algorithm offers two distinct taxiing schemes: one prioritising time savings and another emphasising fuel savings. However, the optimisation process primarily focuses on reducing aircraft waiting time during taxiing when a potential conflicts arise, rerouting affected aircraft when two or more need to cross the same taxiway or intersection. Notably, other solutions, such as postponing aircraft departures, are not considered within this framework.

The use of Mixed Integer Linear Programming (MILP) for solving a multiple route taxi scheduling problem was proposed by Montoya et al. [23]. The proposed MILP model aims to minimise the total operational cost of taxi operations, considering taxi times and delays. Notably, the model can determine when arrivals should use the perimeter taxiway, thereby mitigating conflicts with departing aircraft and reducing taxi time and delays. However, the paper does not consider any other factors, such as the fuel consumption, which may increase when aircraft use the perimeter taxiway instead of a central taxiway.

Adacher et al. [24] proposed a graph-based approach to scheduling surface movements, employing an autonomous multi-agent framework to address air traffic congestion in real-time. Their method models air traffic using a graph, partitioned in different sectors, with each sector managed by a decision agent. These agents control traffic within their sector and imposes real-time aircraft schedules to adhere to timetables and capacity constraints. In the event of predicted congestion, aircraft scheduling is recalculated and verified until the capacity constraints are met and congestion is resolved. Two different SPOs (Generalized Dijkstra and Bidirectional Search) are implemented for each aircraft involved in congestion. However, a limitation of this work is that once a conflict arises, both aircraft are already in motion, making it difficult to delay or reroute them due to limited alternative paths. This limitation may lead to knock-on effects, increasing the number of conflicts in the surrounding environment.

Li et al. [25] employ a directed graph model to discretise the layout of a fictitious airport, introducing a multi-factor constrained optimization scheme for aircraft taxiing paths based on the Dijkstra algorithm. They consider various factors such as the runway changes, aircraft conflicts and engine failure during taxiing. The taxi path is determined by analysing these factors on path selection, which in turn determines the weight of the graph’s edges. However, the algorithm overlooks aspects such as taxi time, fuel consumption, and taxi delays when optimising routes, making it more suitable for real-time (tactical) decision-making rather than strategic decisions.

Ibrahim et al. [26] introduces a Genetic Algorithm (GA) for robot path planning in a dynamic environment. Each gene in a chromosome of this system encodes information about subsequent robot location, with the total number of genes determined by the minimum steps needed to reach the final location. The algorithm identifies optimal paths for robots while avoiding static and dynamic obstacles. However, in the context of robots, there are no constraints on the direction of movement. Translating this unrestricted movement to an airport setting, where aircraft and tow truck directions are confined by the taxiway and runway network, could pose significant challenges.

After analysing the solutions described in the literature, several limitations were identified as follows:

Some studies allow solutions with potential vehicle conflicts during the strategic planning phase in order to speed-up the results;
Many tow truck-based taxiing solutions focus solely on identifying conflict-free routes and schedules, neglecting efficient allocation of tow trucks, such as minimising taxi delays or maximising fuel savings;
Existing performance metrics are often limited to taxi delays and number of potential vehicle conflicts. Additional metrics, such as fuel consumption and fuel savings, could highlight the potential environmental benefits of tow trucks;
The taxiing solutions presented are typically tested on single airport layouts. This does not guarantee their applicability to airports of varying sizes and layouts;
Performance evaluations of taxiing algorithms are frequently conducted using a single medium-level traffic scenario. This approach, while useful for initial testing, fails to assess the system’s robustness across different traffic levels;
Performance evaluations commonly employ a fixed number of tow trucks, discarding potential variation in tow truck numbers;
State-of-charge of tow truck batteries is often overlooked during scheduling. This approach potentially skews the tow truck performance and underestimates the number of tow trucks required for taxi operations.

This work primarily focuses on utilising tow trucks for taxi operations, and introduces a fully autonomous scheduling and routing algorithm. This novel algorithm has the ability to assign tow trucks and determine conflict-free routes, eliminating the necessity for ATCO input. As a result, this automation significantly enhances the overall efficiency and effectiveness of taxi operations. Operating at a strategic level, the algorithm pre-establishes all routes, adjusts aircraft schedules, and sets tow truck schedules before taxi operations commence. Moreover, it adopts a centralised approach, where the algorithm is executed on a single computer, acting as a ‘central authority’ to identify conflict-free routes for all vehicle movements.

Moreover, the algorithm offers the flexibility to prioritise either taxi delays or fuel consumption, depending on the chosen approach: Time-Wise Approach or the Fuel-Wise Approach. Additionally, it can be configured to assign tow trucks to aircraft using either Static Allocation, requiring them to be parked in a depot, or Dynamic Allocation, allowing assignment from any location within the airport. Importantly, the algorithm’s scalability and the adaptability to diverse taxiing environments are ensured through rigorous testing across various scenarios. The test outcomes confirm that the algorithm’s solutions remain conflict-free, even under conditions of high traffic volumes.

3. Description of Algorithm

The algorithm’s primary objective is to determine conflict-free taxi routes for multiple aircraft and to allocate electric tow trucks to these aircraft to minimise fuel consumption. In addition, the algorithm aims to reduce the aircraft taxi delays and maximize the utilisation of the available tow truck fleet. To achieve this, the algorithm is divided into two main parts. Firstly, the Flight Dispatcher sub-module assigns conflict-free routes to each aircraft, adjusting their schedules within specified boundaries if no route is identified. Secondly, the Tug Dispatcher sub-module allocates tow trucks to the aircraft, identifying conflict-free tow truck routes and generating a tow truck schedule. A control flow diagram of the algorithm is shown in Figure 1.

3.1. Airport Modelling and Assumptions

The efficiency of the airport’s taxi operations relies heavily on the flight schedules, which dictate the timing of arrivals and departures. Each departing aircraft are assigned a planned Off-Block Time (OBT), indicating when they should leave their parking position to begin taxiing towards a runway. However, actual departures may occur later than the planned OBT due to various factors such as cargo and passenger loading delays or deliberate pilot decisions to wait before taxiing. Similarly, arriving aircraft have a planned Time of Arrival (TOA), specifying when they are expected to land. Upon landing, aircraft are expected to promptly vacate the runway without delay to avoid disrupting subsequent arrivals and departures. Any delay in runway vacation may lead to complications, potentially necessitating go-arounds for following landing aircraft.

Implementing autonomous electric tow trucks for taxi operations requires the establishment of multiple depots within the aerodrome. These depots act as parking and recharging hubs for the tow trucks. Currently, most airports do not utilise electric tow trucks and hence no tow truck depots are designated. In view of this, for this study, the locations of the depots were manually defined for each airport that was considered. The selection criteria for depot locations included the absence of other facilities in the selected location, easy connectivity to nearby taxiways and service roads, and proximity to one or more aprons. Each tow truck depot is linked to the airport’s road network via one or more connections, designated as service roads, which were manually defined.

The number of parking slots available per depot is a design choice and can vary from one airfield to another. To ensure an adequate number of free charging points, the total number of parking slots, denoted as (

S_{b}

), at each depot

b

is given by:

S_{b} = 1.5 \times (R / B)

(1)

where:

R

is the total number of tow trucks, and

B

is the total number of depots in the airfield.

Using this equation, the total number of charging points is always greater than the number of tow trucks and scales in proportion to the size of the tow truck fleet.

Furthermore, a simplifying assumption of the work is that each runway has a fixed take-off point (ToP) and a fixed landing point (LEP) 1.

The airport environment is represented as a directed graph that connects the airport’s roads, stands and tow truck depots. The graph consists of nodes and edges, where nodes denote relevant points such as aircraft stands, Taxi Out Points (ToPs), Landing End Points (LEPs), tow truck depots, and road intersections (i.e. runways, taxiways or service roads). Edges, connecting pairs of nodes symbolises the airport’s roads. An edge between two nodes indicate a physical connection via a road. Figure 2. shows a graphical depiction of Malta International Airport (MLA) together with the corresponding directed graph. All graph edges are deemed bi-directional.

In this work, time is discretised into uniform time intervals known as Time Windows, each lasting 10 seconds. No acceleration or deceleration is modelled for the vehicle’s motion. It is assumed that the vehicles, including aircraft and tow trucks, are either stationary (i.e. with a velocity of 0 m/s) or travelling at a constant speed. The Average Vehicle Velocity (

v_{a v}

) is set to 10 m/s (19.4 Knots), a value within the typical range of aircraft taxi speeds [27].

To ensure safety and avoid conflicts between vehicles, including aircraft and tow trucks, several rules and minimum separation distances are enforced. To this effect, taxiways and runways do not allow simultaneous bi-directional traffic flow of aircraft. Additionally, a minimum separation distance between two taxiing aircraft is mandated to prevent potential hazards. This distance cannot be less than 50 meters due to aircraft jet blast and ideally should range between 100 meters and 300 meters, depending on the aircraft type [28] In this work, a conflict is defined as occurring when the geometric centres of two vehicles, at least one of which is either an aircraft or a tow truck towing an aircraft, come closer than 200 m. To implement this, circular buffer areas (

A_{b}

) with a radius of 100 m (defined as Buffer Distance,

d_{b}

) centred on each vehicle’s geometrical centre, are defined. A conflict is registered if the circular buffer areas of two vehicles intersect. However, when both vehicles are unloaded tow trucks (i.e. not towing aircraft), no minimum separation distance is imposed. Therefore, tow trucks are permitted to cross each other’s path or travel alongside each other on all the types of airport roads, including service roads. Thus, conflicts between tow trucks are assumed to be non-existent, and the circular buffer area is not applicable in such cases. These rules are applicable regardless of whether the vehicles are travelling in opposite directions or in the same direction with one vehicle trailing another.

3.2. Flight Dispatcher

The Flight Dispatcher sub-module utilises the Dijkstra Shortest Path Optimisation (SPO) technique to determine conflict-free routes for each aircraft in the flight schedule, aiming to minimise their delays. For each aircraft, denoted by

a

, the Flight Dispatcher assigns a path consisting of nodes and edges, connecting its initial position, denoted as

n_{s t}^{a}

, to its final position,

n_{e n d}^{a}

, along with a designated start time for taxiing

t_{a s}

For departing aircraft,

n_{s t}^{a}

corresponds to the aircraft stand assigned by a predefined flight schedule, while

n_{e n d}^{a}

aligns with one of the Takeoff Points (ToPs). Conversely, for arriving aircraft,

n_{s t}^{a}

corresponds to one of the Landing Entry Points (LEPs), while

n_{e n d}^{a}

aligns with the aircraft stand assigned in the flight schedule.

To maintain conflict-free paths, the Flight Dispatcher assesses each path for potential traffic conflicts and adjusts the path if a conflict is anticipated. For this work, two strategies have been incorporated to address predicted traffic conflicts. For the first strategy, the conflict is resolved by modifying the aircraft’s taxi path, while the second strategy involves adjusting the start time for taxiing. Both strategies can resolve identified conflicts but may result in delays to the aircraft’s arrival time at the intended end point. Additionally, a combination of these strategies is feasible and has been implemented accordingly.

To achieve this objective, the Flight Dispatcher aims to minimise the Total Delay

Δ t_{d t o t}

for each aircraft, which is calculated follows:

Δ t_{d t o t} = Δ t_{d s} + Δ t_{d t}

(2)

where

Δ t_{d s}

is the delay experienced by an aircraft while waiting next to the runway (for arrivals) or at the stand (for departures) and

Δ t_{d t}

is the delay accumulated by an aircraft during taxiing.

The module calculates a flight’s

Δ t_{d t o t}

for all the LEPs (in case of arrival) or all the ToPs (in the case of departures), to determine the appropriate runway for aircraft landing on or takeoff. Aircraft are analysed sequentially, based on their arrival or departure time in the flight schedule, and solutions are explored for each LEP (for arrivals) or each ToP (for departures), as follows:

$n_{s t}^{a}$ and $n_{e n d}^{a}$ are input to the module Path Finder, which finds the ideal (i.e. shortest) path and the ideal (i.e. shortest) taxi distance. This distance is then divided by $v_{a v}$ to find an ideal taxi time $Δ t_{i t}$ ;
The module attempts to find a conflict-free solution. First, the ideal path is forwarded to the Conflict Detector module. This module checks if the path is conflict-free; produces a Vehicle Occupation Table (VOT), which stores all the time windows during which the edges of the path are occupied by the vehicle; and, if potential conflicts are detected, stores them in the Edges in Conflict List (ECL), which contains a list of edges that need to be excluded from the next iteration of Path Finder;
If potential conflicts are detected, Path Finder calculates a new path, excluding the edges listed in ECL, and the feasibility of the path – indicating whether the module found a feasible path (i.e. $n_{s t}^{a}$ and $n_{e n d}^{a}$ are connected by a number of edges) – is checked. If the path is not feasible, the solution is discarded and the process restarts with an incremented $Δ t_{d s}$ (see point 5.); otherwise, the feasible path is sent again to the Conflict Detector to check for the presence of conflicts. This process is repeated until a conflict-free path is identified or, as mentioned, until the path is flagged as not feasible. In case a conflict-free path is found, the module calculates and stores $Δ t_{d t o t}$ of the current iteration;
$Δ t_{d s}$ is incremented by a time interval equal to 10 s (i.e. with the same duration of a time window) and the process is repeated from point 2. for a new iteration;
New solutions are calculated until the $Δ t_{d s}$ of a new solution is greater than or equal to the $Δ t_{d t o t}$ of any solution, in which case the search for solutions is stopped for the analysed runway. The whole process is repeated for the next runway until all the LEPs (in case of an arrival) or all the ToPs (in case of a departure) are analysed;
In case no conflict-free solutions are found (meaning that all of the solutions are discarded because the corresponding paths are considered to be unfeasible), the whole set of solutions is marked as unfeasible and the algorithm stops the calculations for the selected simulation;
The solution with the lowest $Δ t_{d t o t}$ is selected and the VOT of the selected solution is appended to the Global Occupation Table (GOT), which represents the combination of all the VOTs of the selected solutions of the previously analysed aircraft; therefore, when the first aircraft is analysed, the GOT is empty.

3.3. Tug Dispatcher

The Tug Dispatcher sub-module manages the assignment of tow truck to each flight, determining conflict-free routes for each tow truck from its position to the aircraft’s starting node, and from the aircraft’s end node to each tow truck depot. It also assigns a depot to a tow truck upon completing its towing mission and updates the status of assigned tow trucks and their destination depots.

The Tug Dispatcher aims to optimise the utilisation of available tow trucks, minimising reliance on conventional engine-driven taxiing for aircraft. It generates conflict-free routes for tow trucks that don’t interfere with routes calculated by the Flight Dispatcher. Additionally, it ensures a balanced workload among tow trucks, allowing for recharging in depots when their battery level drops below a set threshold. As explained in Section II, the Tug Dispatcher operates in two allocation modes: Static Allocation and Dynamic Allocation.

To achieve these objectives, the Tug Dispatcher assesses each aircraft sequentially, utilising sub-modules such as the Tug Paths Generator to generate conflict-free routes, the Tug Selector to assign a tow truck to a flight, and the Tug Status Updater to update the status of the assigned tow trucks and their destination depots.

The aim of the Tug Paths Generator is to produce conflict-free routes for tow trucks, ensuring timely arrival at aircraft or return to a depot. To accomplish this, the module operates twice for each flight: first, to identify viable paths from each tow truck to the aircraft’s attachment node (

n_{s t}^{a}

), and second, to find feasible paths from the aircraft’s detachment node (

n_{e n d}^{a}

) to the depots. While its operation resembles that of the Flight Dispatcher; adaptations are made to tailor the process to the unique requirements of tow truck dispatching.

The Tug Selector module plays a critical role in assigning tow trucks to aircraft and determining the depot to which the tow truck returns after its taxi mission. It evaluates various tow truck parameters, such as battery level and utilisation time, along with depot availability. In the case of Static Allocation, where tow trucks are assigned from depots, availability is determined by whether a tow truck is parked and sufficiently charged. However, under Dynamic Allocation, where tow trucks can be assigned from anywhere in the airport, availability extends to tow trucks not parked in depots. In either scenario, a tow truck must be unloaded, possess sufficient battery charge and by without any ongoing mission to be considered for assignment.

After a tow truck is assigned to an aircraft, the Tug Status Updater module takes over, ensuring that the tow truck’s status, including its battery charge, assigned depot, and assigned aircraft, is updated for all time windows. Subsequently, the Tug Dispatcher proceeds to the next flight in the schedule, initiating the entire process.

Static and Dynamic Allocation of Tow Trucks

The algorithm employs two distinct types of tow truck allocations: Static Allocation and Dynamic Allocation. In the case of Static Allocation, a tow truck needs to be parked in a depot to be eligible for assignment to an aircraft. After completing its mission, it must return to the same or different depot. Conversely, Dynamic Allocation allows a tow truck to be assigned to an aircraft from any location within the airport. Once the towing operation concludes, the tow truck either returns to a depot or it is reassigned to a new mission. Reassignment can also take place while the tow truck is en route to a depot.

2.: Tow Trucks Allocation Criteria

To determine which tow truck should be allocated to an aircraft, the system first eliminates unavailable tow trucks, namely those already assigned to another mission or lacking sufficient battery charge. A minimum battery charge threshold ensures successful towing of an aircraft to its destination and is selected based on the typical expected duration of a single towing mission. In this study, an arbitrary value of 20% was selected for this purpose. In the event no trucks meet the required battery charge, the aircraft is permitted to taxi using its own engines, following conventional procedures. On the other hand, if at least one tow truck meets the battery charge criteria, the algorithm selects one based on the following three criteria, prioritised in the following order:

Availability of a conflict-free route from the tow truck’s location to the aircraft’s $n_{s t}$ that permits the tow truck to reach the aircraft exactly at the $t_{a s}$ of the aircraft;
If multiple tow trucks meet the first criterion, the tow truck with the lowest associated Total Mission Cost (given by Eq. (3)) is chosen;
If more than one tow truck has the lowest associated cost as defined in the second criterion, the tow truck with the least utilisation time is selected to ensure a fair distribution of missions between the tow trucks.

Finally, if multiple tow trucks meet all the three criteria, an arbitrary tow truck is assigned to the aircraft.

The Total Mission Cost (

c_{t o t}^{r}

) for each tow truck

r

, is computed as follows:

c_{t o t}^{r} = c_{t o w}^{r} + c_{t o w . m a x} - \frac{c_{t o w . m a x}}{(b_{m a x} - b_{m i n})} \times (b_{r} - b_{m i n})

(3)

where:

c_{t o w}^{r}

is the time that

r

needs to complete the towing mission,

c_{t o w . m a x}

is the maximum

c_{t o w}^{r}

over all the tow trucks,

b_{m a x}

is the maximum battery charge, equal to 100%,

b_{m i n}

is the minimum allowed battery charge, equal to 20%, and

b_{r}

is the battery charge of

r

3.: Time-Wise and Fuel-Wise Approach

If no tow trucks meet the first criterion of Section 2. (i.e. availability of a conflict-free route for any tow truck), the Tug Dispatcher adopts one of the following two approaches to proceed:

-: Time-Wise Approach: In this approach, no tow trucks are assigned to the flight, and the aircraft is permitted to taxi with its own engines.

Fuel-Wise Approach: Alternatively, if the Fuel-Wise Approach is chosen, the algorithm seeks to delay the

t_{a s}

of the aircraft by up to a maximum of 10 minutes. It then recalculates the aircraft schedule to determine if, under these adjusted conditions, (a) the aircraft route remains feasible (it should not be in conflict with the routes of the subsequent flights), and (b) at least one tow truck becomes available to satisfy the first criterion. If both conditions are met, the algorithm updates the aircraft schedule and assigns it a tow truck. However, if either conditions is not met, the aircraft is instructed to taxi with its own engines.

4.: Depot Allocation Criteria

After the towing phase, the algorithm determines the destination depot for a tow truck based on three criteria:

A conflict-free route exists from the final position of the assigned aircraft, $n_{e n d}^{a}$ , to the depot under consideration.
The depot under consideration has at least one available parking slot at the time the tow truck is scheduled to arrive.
The time required to return to the depot under consideration is shorter than the time needed to return to any other depot.

If no depots satisfy the first two criteria, no tow truck is assigned to the flight, and the aircraft is instructed to taxi with its own engines. Additionally, any potential update of the aircraft schedule with the Fuel-Wise Approach is cancelled.

This method of depot allocation is employed in both Static Allocation and Dynamic Allocation scenarios. However, in the case of Dynamic Allocation, during the final phase of its mission, the tow truck becomes available for a new assignment. Consequently, its route to the depot may be adjusted to redirect towards another aircraft.

5.: Battery Discharge Rates

The battery levels of all tow trucks are initially all set to 100%. The rates of battery discharge and recharge are assumed to be constant and are updated in the Tug Status Updater based on the following three parameters, which were arbitrarily selected for this study:

The Higher Battery Discharging Rate ( $r_{b d h}$ ) is the battery discharge rate applied when the tow truck is in motion and loaded and is set equal to 2%/minute.
The Lower Battery Discharging Rate ( $r_{b d l}$ ) is the battery discharge rate applied when the tow truck is in motion and unloaded and is set equal to 1%/minute.
The Battery Charging Rate ( $r_{b c}$ ) is the recharge rate applied when the tow truck is at a charging point in a depot and is set equal to 2%/minute.

When a tow truck is stationary (but not connected into a charging point), its battery discharge rate is assumed to be negligible.

4. Testing and Results

In this section, the methodology and approach adopted to evaluate the performance of the algorithm are presented. Additionally, a comprehensive analysis of the results obtained from the testing process is provided.

In the testing all of the flight schedules were randomly generated (i.e. not based on historic data) with an equal number of arrivals and departures per schedule and all of the flights are simulated.

4.1. Performance Metrics

One of the primary objectives of the testing is to quantify the average total delay and the percentage of delayed aircraft to ensure that, following the introduction of tow trucks, taxi operations adhere to the flight schedule timings. The Average Total Delay (

Δ t_{d t o t}^{a v g}

, %) represents the average accumulated delay

Δ t_{d t o t}

experienced by all aircraft, accounting for both towed and self-taxiing instances, compared to their ideal taxi time. The Delayed Aircraft (

D A

, %) metric denotes the percentage of aircraft whose start time is delayed (i.e.

Δ t_{d s} > 0

In the case of the of tow trucks, testing should enable the prediction of the expected utilisation of the tow truck fleet across various levels of airport traffic and determine the necessary quantity of tow trucks required to manage the anticipated ground traffic levels. Therefore, it is important to quantify the percentage of aircraft that are towed rather than taxiing using their own engines and the amount of fuel saved during the tow truck operations. Additionally, to measure tow truck usage accurately, testing should assess the duration for which tow trucks are active throughout the simulation. The Towed Aircraft (

T A

, %) metric represents the percentage of aircraft that are towed. The Average Fuel Savings (

Δ F_{s}^{a v g}

, kg) is defined as the average fuel saved per aircraft when tow truck-based taxiing is used. Fuel consumption for a taxiing aircraft is calculated using a model developed by Khadilkar et al. [29], while the fuel consumption of a towed aircraft is assumed to be equal to zero. Finally, the Average Tow Trucks Utilisation Time (

Δ t_{r u}^{a v g}

, %) denotes the average duration for which each tow truck is active, expressed as a percentage of the total simulation time.

4.2. Airport Selection

An important aspect of the testing phase is to ensure that the algorithm can be fine-tuned and effectively implemented across airports of varying sizes and geometries. In practice, while the algorithm may perform well at a large airport with an extensive network of taxiways, its efficacy may not translate to a smaller airport characterised by frequent bottlenecks and a higher likelihood of conflicts even with low levels of traffic. On the other hand, if the algorithm is only tested for small or medium-sized airports, its scalability of the solutions will remain uncertain. For these reasons, the algorithm was tested at four airports with different sizes and geometries as follows:

-: Malta International Airport (MLA): Relatively small in size.
-: Ben Gurion Airport (TLV): Medium-sized, featuring a unique layout of the runways.
-: Toulouse–Blagnac Airport (TLS): Medium-sized, with a classic layout of runways.

Dallas/Fort Worth International Airport (DFW): One of the busiest airport in the world [30].

4.3. Test Scenarios

A set of six scenarios, each of which includes a number of simulations defined by various combinations of simulation settings, was used to assess the performance of the algorithm. The parameters which were used in different scenarios and the number of simulations for each scenario are shown in Table 1.

4.4. Test Results

Results for Test Scenario 1

Figure 3 illustrates the average total delay,

Δ t_{d t o t}^{a v g}

(%), for various traffic levels at each airport for Test Scenario 1. It can be noted that, for each airport, there is a gradual increase of

Δ t_{d t o t}^{a v g}

, which eventually escalates significantly with higher traffic volumes. It can be noted that the trend observed at each airport is influenced by the size and geometry. Due to MLA's confined size, values significantly increase when traffic volume exceeds 30 aircraft per hour. TLS features two active runways and a simpler geometry compared to TLV, which has only one active runway at a time and a complex layout. This results in shorter average delays for TLS and a smaller percentage of delayed aircraft for the same volume of traffic. The values of

Δ t_{d t o t}^{a v g}

(%) are expressed as percentage and compared to the ideal taxi route, highlighting a progressive increase in the impact of delays for MLA. Conversely, at DFW,

Δ t_{d t o t}^{a v g}

(%) is negligible up to 50 aircraft an hour, and then gradually increasing up to a maximum of 20%.

Figure 4 shows the percentage delayed aircraft,

D A

(%), for various traffic levels at each airport for Test Scenario 1. The values exhibit a gradual increase with higher level of traffic, initially rising moderately before escalating sharply. However, the trend observed at each airport depends on the airport’s size and geometry. For instance, in the case of MLA, the small dimensions of the airport lead to a significant increase in values for traffic levels exceeding 30 aircraft per hour. Conversely, TLV features a complex geometry with multiple taxiways crossing the runways, and operates only one active runway at a time. In contrast, TLS features a simpler geometry and accommodates two active runways, resulting in lower average start delays and a smaller percentage of delayed aircraft compared to TLV for similar traffic levels.

2.: Results for Test Scenario 2

Figure 5 shows the percentage number of towed aircraft,

T A

(%), for various percentages of tow trucks at each airport for Test Scenario 2. Initially, both percentages increase with an increasing proportion of tow trucks but eventually levels off. Notably, when the percentage of tow trucks exceeds approximately 30%, over 90% of the traffic is managed by the tow trucks. Consequently, only 10% or less of the aircraft need to taxi using their main engines. Moreover, there is no substantial improvement observed when the percentage of tow trucks is increased beyond 30%.

As expected, the trend of the average fuel savings,

Δ F_{s}^{a v g}

(kg), observed for various percentages of tow trucks at each airport for Test Scenario 2 and shown in Figure 6, correlates strongly with the number of towed aircraft

T A

(%). Specifically, when the percentage of tow trucks surpasses approximately 30%, there is minimal additional improvement in fuel savings. Notably, the fuel saved at MLA is significantly lower compared to the other airports. This discrepancy is likely attributed to the limited length of its taxiway infrastructure, as fuel savings are directly proportional to route length. Consequently, this suggests that tow truck-based taxiing yields greater benefits at larger airports with extensive taxiway networks.

Figure 7 shows the average tow truck utilisation time,

Δ t_{r u}^{a v g}

(%), for various percentages of tow trucks at each airport for Test Scenario 2. It is notable that

Δ t_{r u}^{a v g}

(%) steadily decreases for all airports as the percentage of tow trucks increases. Interestingly, the results are relatively consistent across all airports, suggesting that different airport geometries and sizes have minimal impact on this metric. Determining the optimal number of tow trucks is critical for efficient aircraft towing operations. Sufficient tow trucks must be available to tow as many aircraft as possible, while avoiding an excessive number of tow trucks to prevent them from being left idle and maximise their utilisation. Interestingly,

Δ t_{r u}^{a v g}

(%) never exceeds 50% for any airport. One possible reasons for this is the occasional need for tow trucks to recharge their batteries. Since the tow truck utilisation time is calculated as a percentage of the total simulation time, if a tow truck spends a significant amount of time recharging, the value of this metric decreases. This clearly shows the importance of battery performance in tow truck-based electric taxi operations. In addition to utilising fast-charging tow trucks, the utilisation value can be enhanced by employing Dynamic Allocation (tested in Test Scenario 4), which assigns tow trucks not only when they are parked in a depot, but also while they are returning to a depot after completing a previous mission.

3.: Results for Test Scenario 3

Figure 8 shows

T A

(%) shows the percentage number of towed aircraft,

T A

(%), for various percentages of tow trucks at each airport for Test Scenario 3. Similar to Test Scenario 2 (shown in Figure 5), the percentage initially increases with a rise in the percentage of tow trucks, but eventually levels off. Notably, when the percentage of tow trucks surpasses approximately 30%, over 90% of the traffic is managed by the tow trucks, resulting in only 10% or less of aircraft needing to taxi using their main engines. Consequently, the percentage of towed aircraft does not exhibit a significant increase beyond this threshold. The higher values observed for this metric in Test Scenario 3, compared to the outcomes of Test Scenario 2, could be attributed to the utilisation of the Fuel-Wise Approach. With this approach, the algorithm prioritises maximising the number of towed aircraft, even at the expense of taxi delays. This strategic adjustment results in higher percentage of towed aircraft compared to Test Scenario 2.

Figure 9 and Figure 10 illustrate the trend of the average fuel savings,

Δ F_{s}^{a v g}

(kg), and the average total delay,

Δ t_{d t o t}^{a v g}

(s), respectively, observed for various percentages of tow trucks at each airport for Test Scenario 3. These results are closely related to the towing time

T A

(%). Indeed, for a percentage of tow trucks exceeding approximately 30%, fuel savings do not significantly improve, while delays do not increase any further. However,

Δ F_{s}^{a v g}

(kg) in this case is slightly higher for each airport (for instance, 20 kg on average for a traffic level of 30 aircraft per hour) than the fuel savings obtained in Test Scenario 2 (shown in Figure 6). On the other hand,

Δ t_{d t o t}^{a v g}

(s), which is represented by including the values obtained with 0% tow trucks in Test Scenario 1 (shown in Figure 3) increases with the percentage of tow trucks and levels off when the percentage of tow trucks exceeds 30%. This outcome was expected, as Test Scenario 2 was conducted using the Time-Wise Approach, whereas Test Scenario 3 employed the Fuel-Wise Approach, prioritising fuel savings over time delays.

Figure 11 displays the average tow trucks utilisation time,

Δ t_{r u}^{a v g}

(%), for various percentages of tow trucks at each airport for Test Scenario 3. As expected,

Δ t_{r u}^{a v g}

(%) steadily decreases at all airports as the percentage of tow trucks increases. When compared to Test Scenario 2 (shown in Figure 7),

Δ t_{r u}^{a v g}

(%) exhibits slightly higher values. However, even in this case, it never exceeds 50%, reaffirming the significance of battery performance for tow truck utilisation. Furthermore, the need for better management of tow trucks is evident and employing Dynamic Allocation could be a valuable approach to improve this metric.

4.: Results for Test Scenario 4

Figure 12 shows the percentage of towed aircraft,

T A

(%), for various percentages of tow trucks at each airport for Test Scenario 4. Initially, the values of the metric increase as the percentage of tow trucks rises, but eventually stabilise for a percentage of tow trucks exceeding approximately 30%, similar to what was observed in the previous two scenarios. However, in this instance, the values are slightly higher than those observed in Test Scenario 3 (refer to Figure 8), and significantly higher than those ones observed in Test Scenario 2 (as shown in Figure 5). This is attributed to the enhanced efficiency of the algorithm when employing the Dynamic Allocation approach to assign tow trucks.

Figure 13 depicts the trend of the average fuel savings,

Δ F_{s}^{a v g}

(kg), observed for various percentages of tow trucks at each airport for Test Scenario 4. Similar to the previous metric

Δ F_{s}^{a v g}

does not significantly change for a percentage of tow trucks over 30%. However, in this instance,

Δ F_{s}^{a v g}

is slightly higher than the values recorded for Test Scenario 2 (shown in Figure 6) and similar to the values obtained in Test Scenario 3 (shown in Figure 9). This outcome underscores the superior performance of the Dynamic Allocation approach compared to Static Allocation when assigning tow trucks. With the Dynamic Allocation approach, the tow trucks are not required to return to a depot after each mission before being allocated to a new one. Consequently, they can complete a higher number of missions during the simulation, leading to increased average fuel savings.

Figure 14 illustrates the average tow trucks utilisation time,

Δ t_{r u}^{a v g}

(%), for different percentages of tow trucks at each airport for Test Scenario 4. Consistent with the trend observed in the previous two scenarios (as seen in Figure 7 and Figure 11),

Δ t_{r u}^{a v g}

steadily decreases at all airports as the percentage of tow trucks increases. However,

Δ t_{r u}^{a v g}

exhibits higher values, exceeding 50%, when compared to the previous two cases. Nevertheless,

Δ t_{r u}^{a v g}

never surpasses 60%, reaffirming the significance of battery performance in tow truck utilisation.

5.: Results for Test Scenario 5

Figure 15 displays the percentage towed aircraft,

T A

(%), for different percentages of tow trucks at each airport for Test Scenario 5. Initially, the percentage shows a correlation with the number of tow trucks, but gradually levels out, similar to the trend observed in Test Scenarios 2-4. When the proportion of tow trucks reaches around 30%, they can handle 90% (or more) of the traffic, indicating that only 10% (or fewer) of aircraft must taxi using their primary engines. Notably, for all percentages of tow trucks, the values of this metric for Test Scenario 5 are the highest among Test Scenarios 2-5. This improvement can be attributed to the combined use of the Fuel-Wise Approach, in which the algorithm prioritises maximising the number of towed aircraft at the expense of taxi delays), and the Dynamic Allocation, where tow trucks are not required to return to a depot after each mission before being allocated to a new one. This approach allows each tow truck to complete a higher number of missions during the simulation, leading to improved overall performance.

Figure 16 and Figure 17 present the results of the average fuel savings,

Δ F_{s}^{a v g}

(kg) and average total delay,

Δ t_{d t o t}^{a v g}

(s), respectively, observed for different percentages of tow trucks at each airport for Test Scenario 5. These metrics are closely related to

T A

(%). For a percentage of tow trucks exceeding approximately 30%,

Δ F_{s}^{a v g}

remains relatively stable, whereas the delays

Δ t_{d t o t}^{a v g}

does not significantly increase. This indicates that fuel savings do not significantly improve beyond this threshold, and delays do not increase accordingly.

However,

Δ F_{s}^{a v g}

in this scenario is slightly higher for each airport compared to the fuel savings obtained in Test Scenarios 2-4, likely due to the combined use of the Fuel-Wise Approach and Dynamic Allocation. On the other hand,

Δ t_{d t o t}^{a v g}

, which is represented by including the values obtained with 0% tow trucks in Test Scenario 1, as displayed in Figure 3, increases with the percentage of tow trucks and its values are comparable to the ones of Test Scenario 3 (shown in Figure 10). This result was expected as, while Test Scenario 2 was carried out using the Time-Wise Approach, Test Scenarios 3 and 5 were carried out using the Fuel-Wise Approach, thus favouring fuel savings over delays.

Figure 18 illustrates the average tow trucks utilisation time,

Δ t_{r u}^{a v g}

(%), for different percentages of tow trucks at each airport for Test Scenario 5. Consistent with the preceding three scenarios,

Δ t_{r u}^{a v g}

steadily decreases as the percentage of tow trucks increases. However, when compared to Test Scenarios 2-3,

Δ t_{r u}^{a v g}

exhibits higher values, surpassing 50%, and slightly higher values when compared to Test Scenario 4. Nevertheless, the figure never exceeds 60%, highlighting once again the critical importance of battery performance for tow truck usage.

6.: Results for Test Scenario 6

The purpose of Test Scenario 6 was to evaluate the relationship between tow truck performance and battery performance. This scenario was tested in TLS for 40 aircraft per hour and a percentage of tow trucks equal to 20%. As shown in Table 2, for lower discharge rates,

T A

(%),

Δ F_{s}^{a v g}

(kg) and

Δ t_{r u}^{a v g}

(%) have higher values. Particularly,

T A

exceeds 80%, indicating a consistent improvement in tow truck performance compared to the base scenario (i.e. nominal values of

r_{b d h}

and

r_{b d l}

). On the other hand, an increase in discharge rates results in a sharp decline in the value of the metrics. This decline may occur because the tow trucks are frequently not assigned to the aircraft due to their low battery level. Large variations in the metrics for relatively small percentage changes in discharge rates underscores the importance of battery performance for tow truck operations and for determining the appropriate number of tow trucks to deploy to meet demand corresponding to various traffic levels.

5. Conclusions and Future Work

5.1. Conclusions

This work introduced an algorithm aimed at automating and optimising taxi operations using autonomous electric tow trucks. Operating at a strategic level, the algorithm generates conflict-free routes for both aircraft and tow trucks whilst achieving multiple objectives; reducing taxi-related delays and fuel consumption whilst maximising the utilisation of tow trucks for taxi operations. Furthermore, the algorithm can be fine-tuned to target specific performance aspects. To facilitate engineless taxi operations, an appropriate airport environment was established, followed by the design and implementation of the algorithm. Numerous simulations were conducted for various algorithm configurations and test scenarios, leading to several performance metrics being defined. The results indicate that the algorithm effectively limits delays in relation to the flight schedule, even under high traffic volumes, optimally utilises tow trucks, and maximises fuel savings. Moreover, further improvements in performance aspects are expected through adequate tuning.

The algorithm consistently delivered conflict-free solutions, even under conditions of high traffic volumes. Test results show that approximately 70% of flights necessitated short delays of up to 3 minutes to ensure sufficient traffic separation at all times. Moreover, a tow truck fleet comprising 30% of the hourly aircraft traffic effectively towed over 90% of these aircraft. This finding offers valuable insight into determining the appropriate number of tow truck for different traffic levels and airport types. Additionally, it could be utilised during the design phaes to compare the required investment with the anticipated fuel savings.

Furthermore, the results of the tests underscore the scalability of the algorithm, its adaptability to diverse taxiing environments, and its resilience to unforeseen circumstances. This is evidenced by the extensive array of tests conducted, encompassing four airports with significantly different sizes and geometries, varying number of active runways at each airport, diverse rates of aircraft per hour, and different ratios of tow trucks to aircraft per hour. Additionally, the number of charging points per depot was adjusted in accordance with the number of tow trucks, further highlighting the algorithm’s robustness.

5.2. Potential Areas of Future Work

The proposed algorithm provides strategic solutions by pre-computing route and tug assignments. In practice, this approach may prove insufficient due to the inherent uncertainty in taxi operations, which can disrupt the predictions made by the strategic algorithm. Therefore, future efforts should prioritise the incorporation of tactical solutions alongside the strategic ones, enabling a real-time responsiveness to unexpected events.

Additionally, this work updated the tow truck battery discharge and recharge rates based on three predetermined parameters and were assumed to be constant. In the future, a more sophisticated battery charging and discharging model could be implemented. Furthermore, testing the algorithm with varying battery parameters would offer insights into their impact on performance, facilitating a more comprehensive understanding of the algorithm’s capabilities.

Nomenclature

OBT	=	Off-Block Time (-)
TOA	=	Time of Arrival (-)
$S_{b}$	=	number of parking slots at a depot (-)
$R$	=	total number of tow trucks (-)
$B$	=	total number of depots (-)
ToP	=	Takeoff Point (-)
LEP	=	Landing Point (-)
$v_{a v}$	=	Average Vehicle Velocity (m/s)
$A_{b}$	=	Buffer Area (m²)
$d_{b}$	=	Buffer Distance (m)
$a$	=	aircraft (-)
$n_{s t}^{a}$	=	$a$ (-)
$n_{e n d}^{a}$	=	$a$ (-)
$t_{a s}$	=	time to start taxiing
$Δ t_{d t o t}$	=	Total Delay (s)
$Δ t_{d s}$	=	delay experienced by an aircraft while waiting (s)
$Δ t_{d t}$	=	delay accumulated by an aircraft while taxiing (s)
$Δ t_{i t}$	=	ideal taxi time (s)
VOT	=	Vehicle Occupation Table (-)
ECL	=	Edges in Conflict List (-)
GOT	=	Global Occupation Table (-)
$c_{t o t}^{r}$	=	Total Mission Cost (s)
$r$	=	tow truck (-)
$c_{t o w}^{r}$	=	$r$ needs to complete the mission (-)
$c_{t o w . m a x}$	=	$maximum c_{t o w}^{r}$ over all the tow trucks (s)
$b_{m a x}$	=	maximum battery charge (%)
$b_{m i n}$	=	minimum allowed battery charge (%)
$b_{r}$	=	$r$ (%)
$r_{b d h}$	=	Higher Battery Discharging Rate (%)
$r_{b d l}$	=	Lower Battery Discharging Rate (%)
$r_{b c}$	=	Battery Charging Rate (%)
$Δ t_{d t o t}^{a v g}$	=	Average Total Delay (s)
$D A$	=	Delayed Aircraft (%)
$T A$	=	Towed Aircraft (%)
$Δ F_{s}^{a v g}$	=	Average Fuel Savings (kg)
$Δ t_{r u}^{a v g}$	=	Average Tow Trucks Utilisation Time (%)

Notes

1	In practice, the exact takeoff/landing point depends on multiple factors such as: the takeoff/landing distance required; wind speed and direction; runway conditions; etc.

References

"www.eurocontrol.int," Eurocontrol, 10 March 2023. [Online]. Available: https://www.eurocontrol.int/publication/eurocontrol-data-snapshot-40-taxi-times#:~:text=Typically%2C%20flying%20from%20one%20of,time%20of%20over%2020%20minutes. [Accessed 12 May 2023].
M. Zhang, Q. Huang, S. Liu and H. Li, "Assessment Method of Fuel Consumption and Emissions of Aircraft during Taxiing on Airport Surface under Given Meteorological Conditions," College of Civil Aviation, Nanjing University of Aeronautics and Astronautics, Nanjing, China, 2019.
T. Nikoleris, G. Gupta and M. Kistler, "Detailed estimation of fuel consumption and emissions during aircraft taxi operations at Dallas/Fort Worth International Airport," Transportation Research Part D, Elsevier, 2011.
N. Dzikus, J. Fuchte, A. Lau and V. Gollnick, "Potential for Fuel Reduction through Electric Taxiing," in 11th AIAA Aviat. Technol. Integr. Oper. Conf., 2011.
E. Fleuti and S. Maraini, "Taxi-Emissions at Zurich Airport," 2017.
"op.europa.eu," European Commission, 2011. [Online]. Available: https://op.europa.eu/en/publication-detail/-/publication/296a9bd7-fef9-4ae8-82c4-a21ff48be673. [Accessed 15 March 2023].
"ec.europa.eu," European Commission, 2020. [Online]. Available: https://ec.europa.eu/clima/policies/transport/aviation_en. [Accessed 15 March 2023].
"www.iata.org," International Air Transport Association, December 2022. [Online]. Available: https://www.iata.org/en/iata-repository/pressroom/fact-sheets/fact-sheet---fuel/. [Accessed 4 April 2023].
"www.fitchratings.com," Fitch Ratings, 25 February 2022. [Online]. Available: https://www.fitchratings.com/research/corporate-finance/oil-price-shock-is-a-material-risk-for-us-european-airlines-25-02-2022. [Accessed 4 April 2023].
"www.statista.com," Statista, 2023. [Online]. Available: https://www.statista.com/statistics/591285/aviation-industry-fuel-cost/. [Accessed 4 April 2023].
WheelTug, [Online]. Available: https://www.wheeltug.com/. [Accessed 15 March 2023].
"tec.ieee.org," IEEE TRansportation Electrification Community, 2014. [Online]. Available: https://tec.ieee.org/newsletter/march-april-2014/electric-green-taxiing-system-egts-for-aircraft. [Accessed 15 March 2023].
"TaxiBot," 2020. [Online]. Available: https://www.taxibot-international.com/. [Accessed 15 March 2023].
P. H. Abreu and E. Oliveira, "Comparing a Centralized and Decentralized Multi-Agent Approaches to Air Traffic Control," 2014.
Y. J. Chiang, J. T. Klotowski, C. Lee and J. S. B. Mitchell, "Geometric algorithms for conflict detection/resolution in air traffic management," in 36th IEEE Conference on Decision and Control, San Diego, California, USA, 2004.
X. Wang, H. Peng, J. Liu, X. Dong, X. Zhao and C. Lu, "Optimal control based coordinated taxiing path planning and tracking for multiple carrier aircraft on flight deck," Defence Technology, February 2022.
H. Udluft, "Decentralization in Air Transportation," Delft, Netherland, 2017.
R. Morris, M. L. Chang, R. Archer, E. V. I. Cross, S. Thompson, J. L. Franke, R. C. Garrett, W. Malik, K. McGuire and G. Hermann, "Self-Driving Aircraft Towing Vehicles: A Preliminary Report," Austin, Texas, USA, 2015.
R. Morris, M. L. Chang, R. Archer, E. V. Cross II, S. Thompson, J. Franke, R. C. Garrett, C. Pasareanu, W. Malik and G. Hemann, "SafeTug Semi-Autonomous Aircraft Towing Vehicles," NASA, 2016.
Vemula, K. Muelling and J. Oh, "Path Planning in Dynamic Environments with Adaptive Dimensionality," Robotics Institute, Carnegie Mellon University, Pittsburgh, Pennsylvania, USA, 2016.
E. Gawrilow, E. Köhler, R. H. Möhring and B. Stenzel, "Dynamic Routing of Automated Guided Vehicles in Real-time," Institut für Mathematik, Technische Universität Berlin, Berlin, Germany, 2007.
M. Zhang, Q. Huang and H. Li, "Multi-Objective Optimization of Aircraft Taxiing on the Airport Surface with Consideration to Taxiing Conflicts and the Airport Environment," College of Civil Aviation, Nanjing University of Aeronautics and Astronautics, Nanjing, China, 2019.
J. Montoya, W. Zachary, S. Rathinam and W. Malik, "A Mixed Integer Linear Program for Solving a Multiple Route Taxi Scheduling Problem," NASA Ames Research Center, Moffett Field, California, USA, 2010.
L. Adacher, M. Flamini and E. Romano, "Rerouting Algorithms Solving the Air Traffic Congestion," Università degli studi Roma Tre, Rome, Italy, 2017.
L. Li and G. Jiawei, "Research on aircraft taxiing path optimization based on digraph model and Dijkstra algorithm," in IOP Conference Series Materials Science and Engineering, 2021.
M. F. Ibrahim, A. Z. A. Bakar and A. Hussain, "Genetic Algorithm-based Robot Path Planning," Department of Electrical, Electronics and Systems Engineering, Universiti Kebangsaan Malaysia, Bangi, Selangor, Malaysia, 2009.
R. Jordan, M. A. Ishutkina and T. G. Reynolds, "A Statistical Learning Approach to the Modeling of Aircraft Taxi TIme," in Digital Avionics Systems Conference, Salt Lake City, Utah, USA, 2010.
L. Yang, Y. Suwan, K. Han, J. Haddad and H. M., "Fundamental diagrams of airport surface traffic: Models and applications," Transportation Research Part B: Methodological, 2017.
H. Khadilkar and H. Balakrishnan, "Estimation of Aircraft Taxi-out Fuel Burn using Flight Data Recorder Archives," Massachusetts Institute of Technology, Cambridge, Massachusetts, USA, 2011.
"ACI World," Airports Council International, 2022. [Online]. Available: https://aci.aero/2022/04/11/the-top-10-busiest-airports-in-the-world-revealed/. [Accessed 27 April 2023].

Figure 1. Control flow of the algorithm.

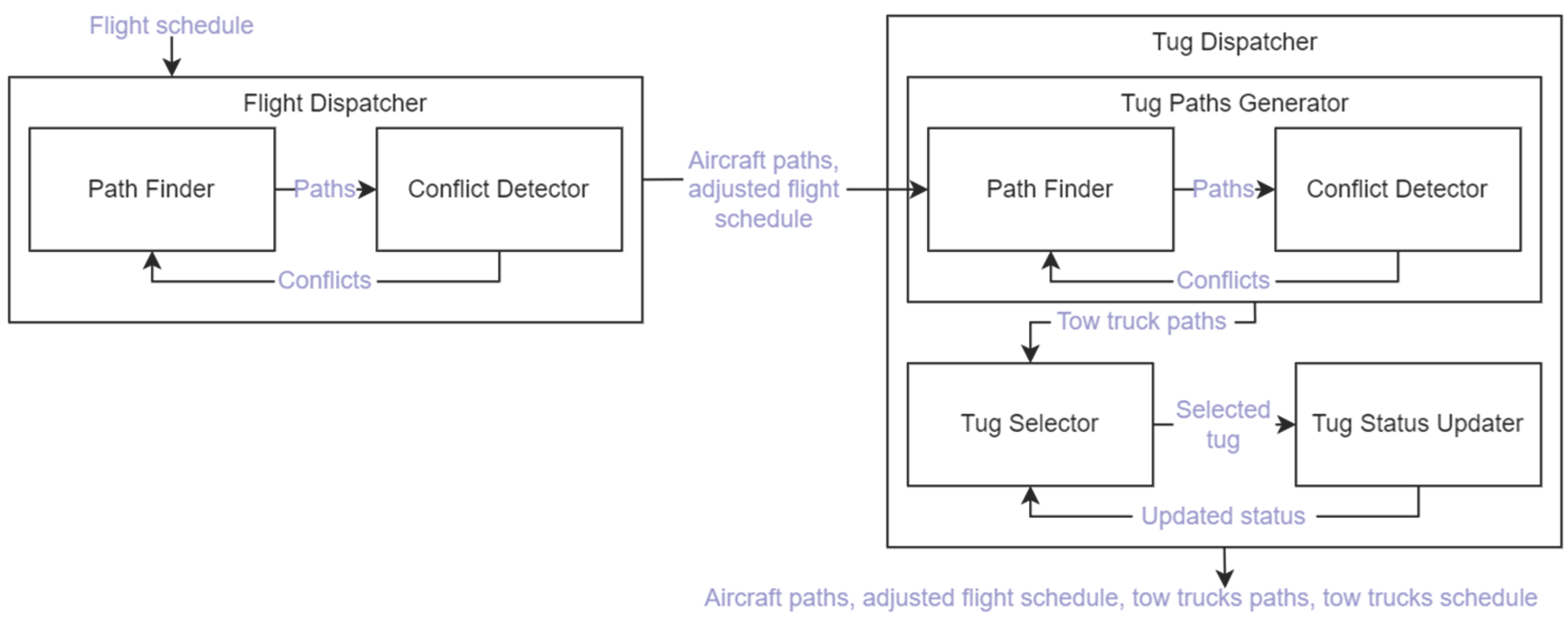
Figure 2. Directed graph for Malta International Airport (MLA) superimposed on MLA graphical representation. The thickness of the lines represents the runways (thickest), taxiways (medium thickness) and service roads (thinnest). The blue nodes represent the aircraft stands, the red nodes mark the ToPs/LEPs and the yellow nodes show the position of the tow truck depots.

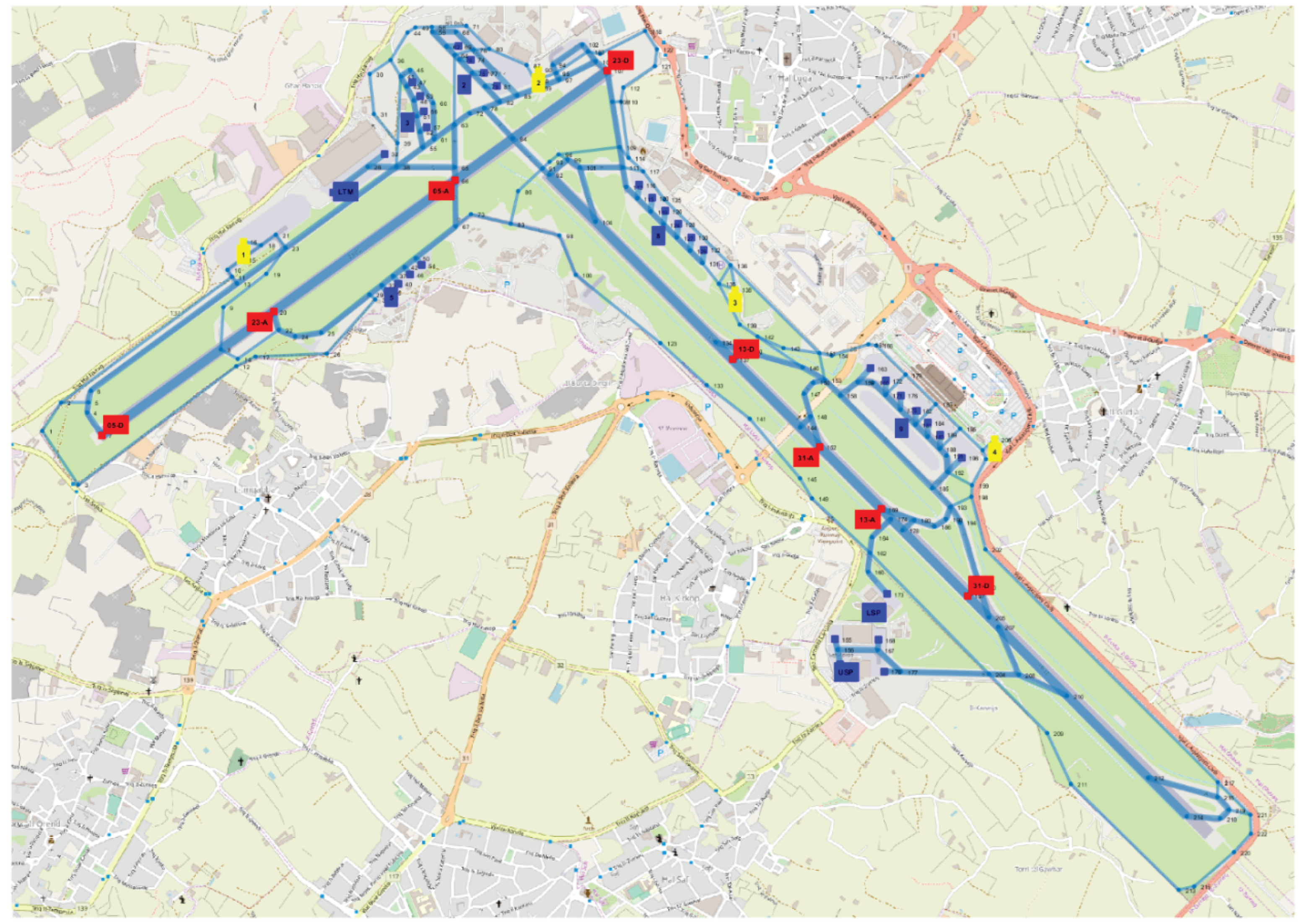
Figure 3. Average Total Delay, Δt_dtot^avg (%) in Test Scenario 1.

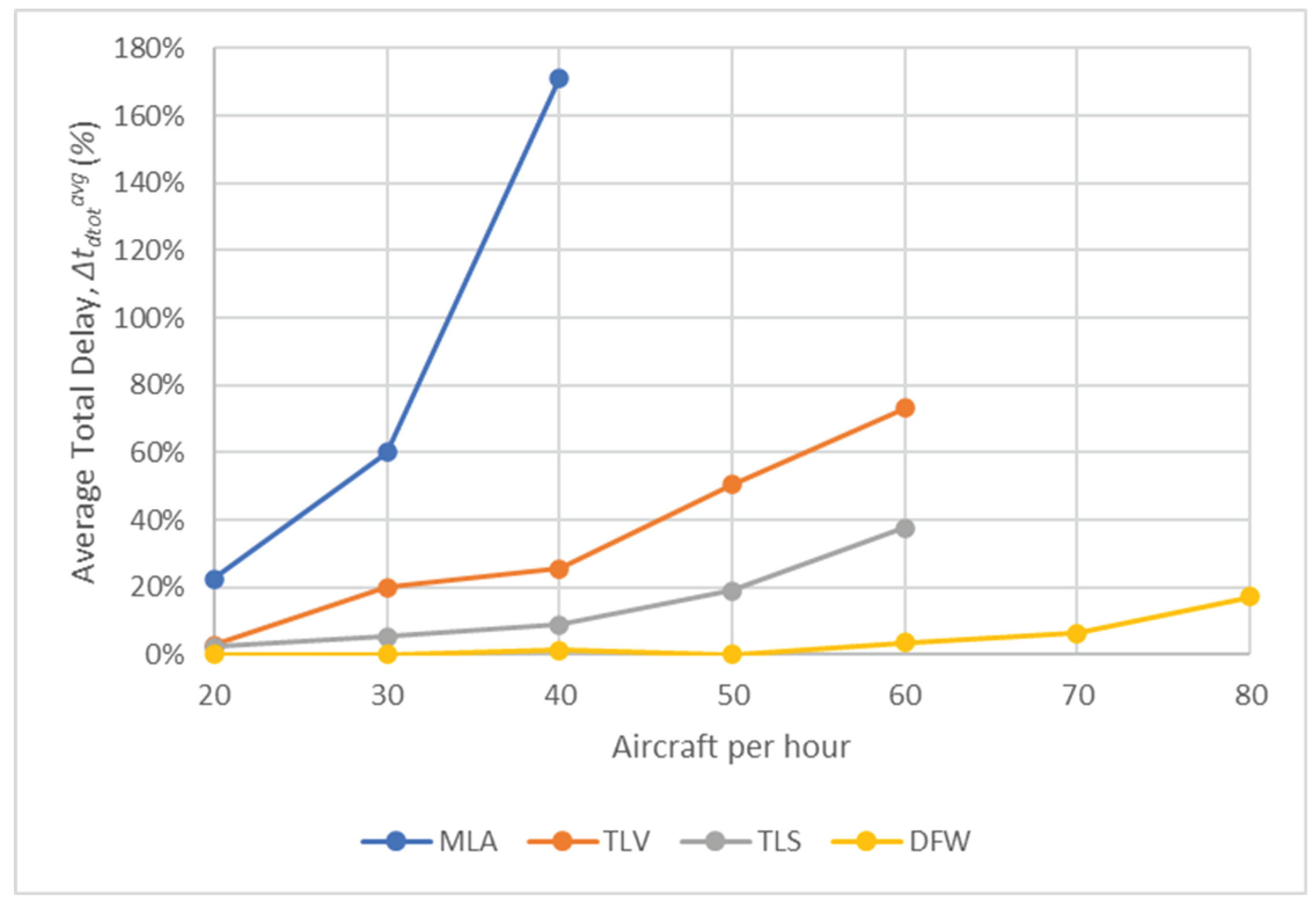
Figure 4. Delayed Aircraft, DA (%) in Test Scenario 1.

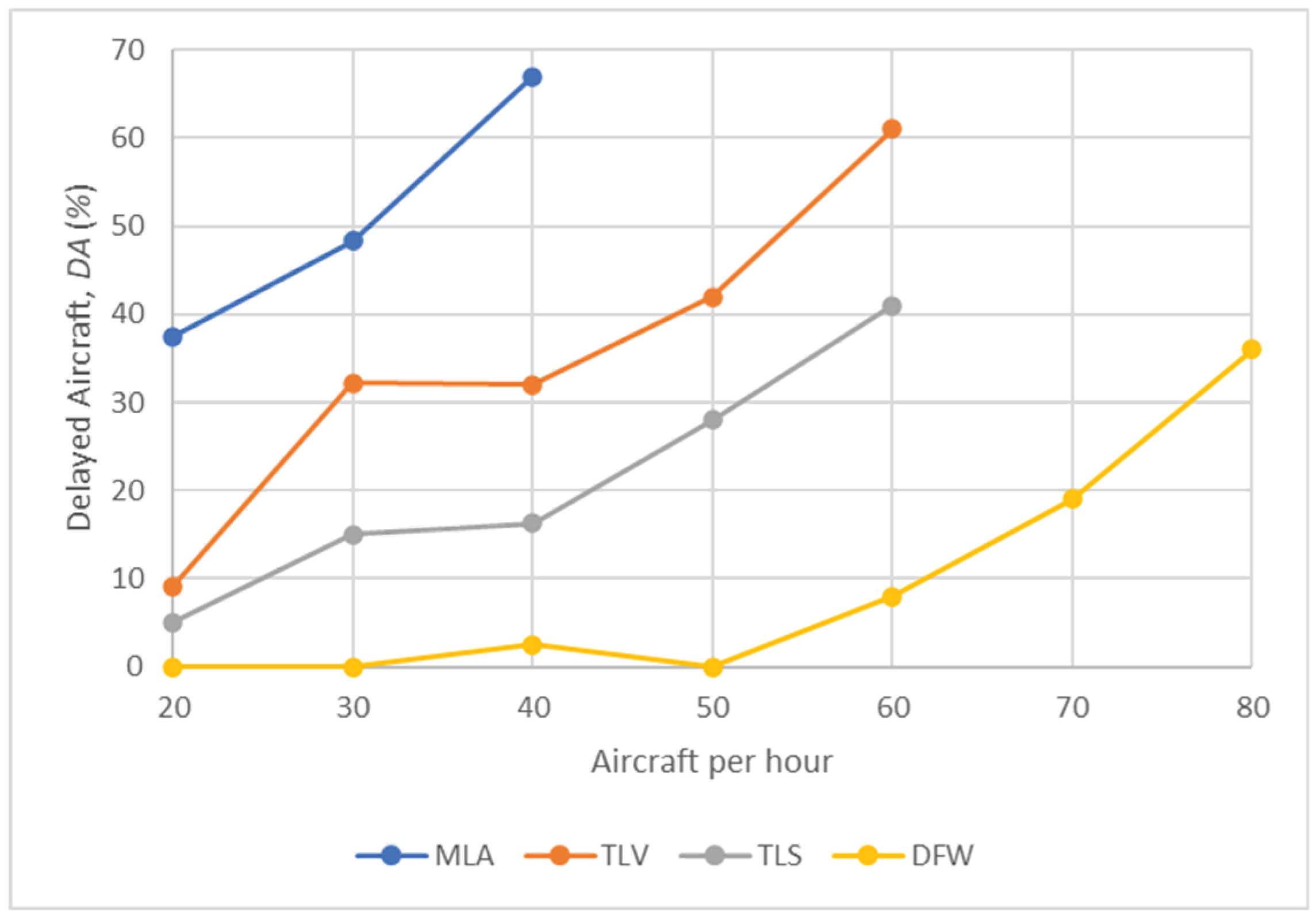
Figure 5. Towed Aircraft, TA (%) in Test Scenario 2.

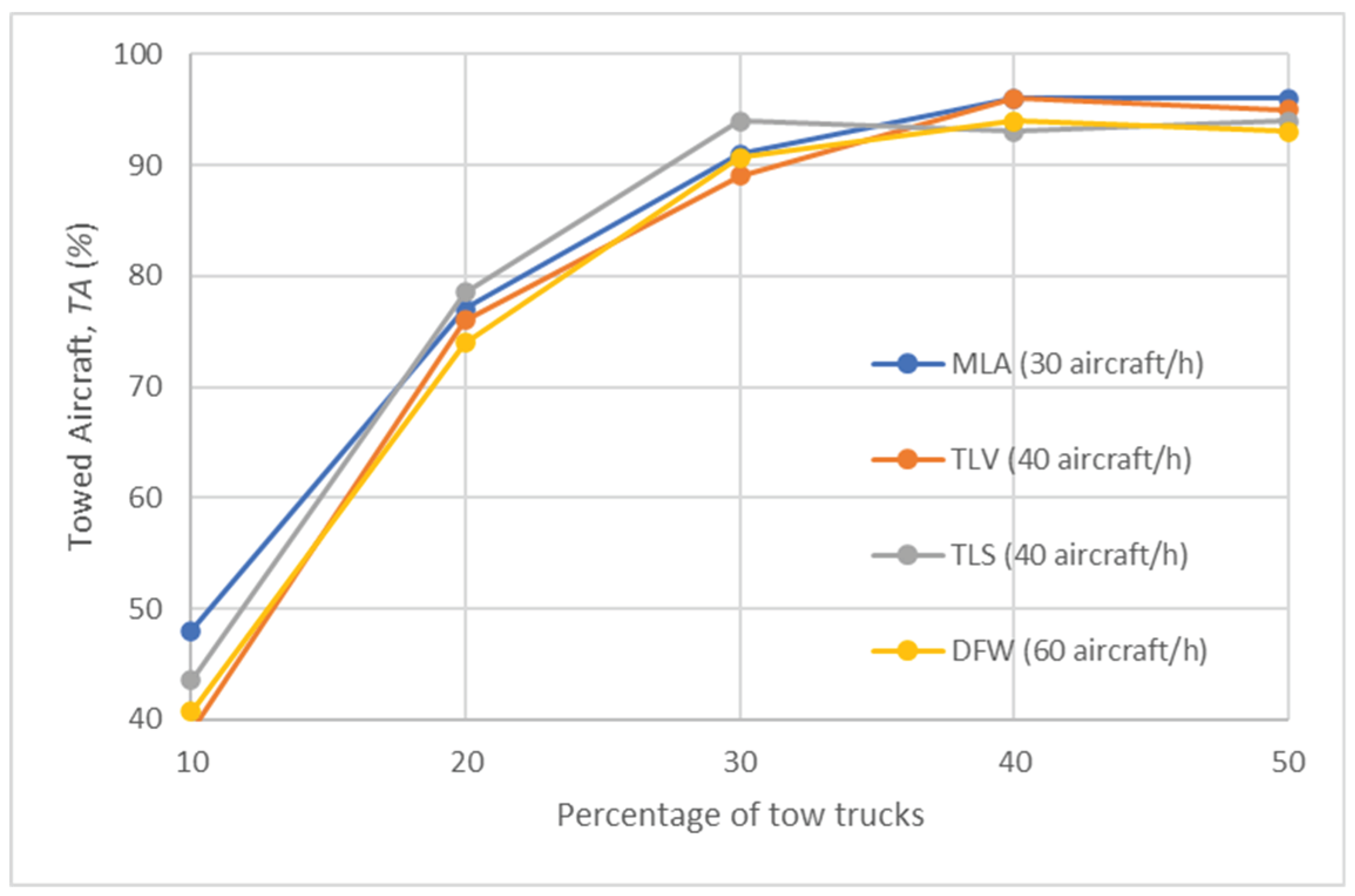
Figure 6. Average Fuel Savings, ΔF_s^avg (kg) in Test Scenario 2.

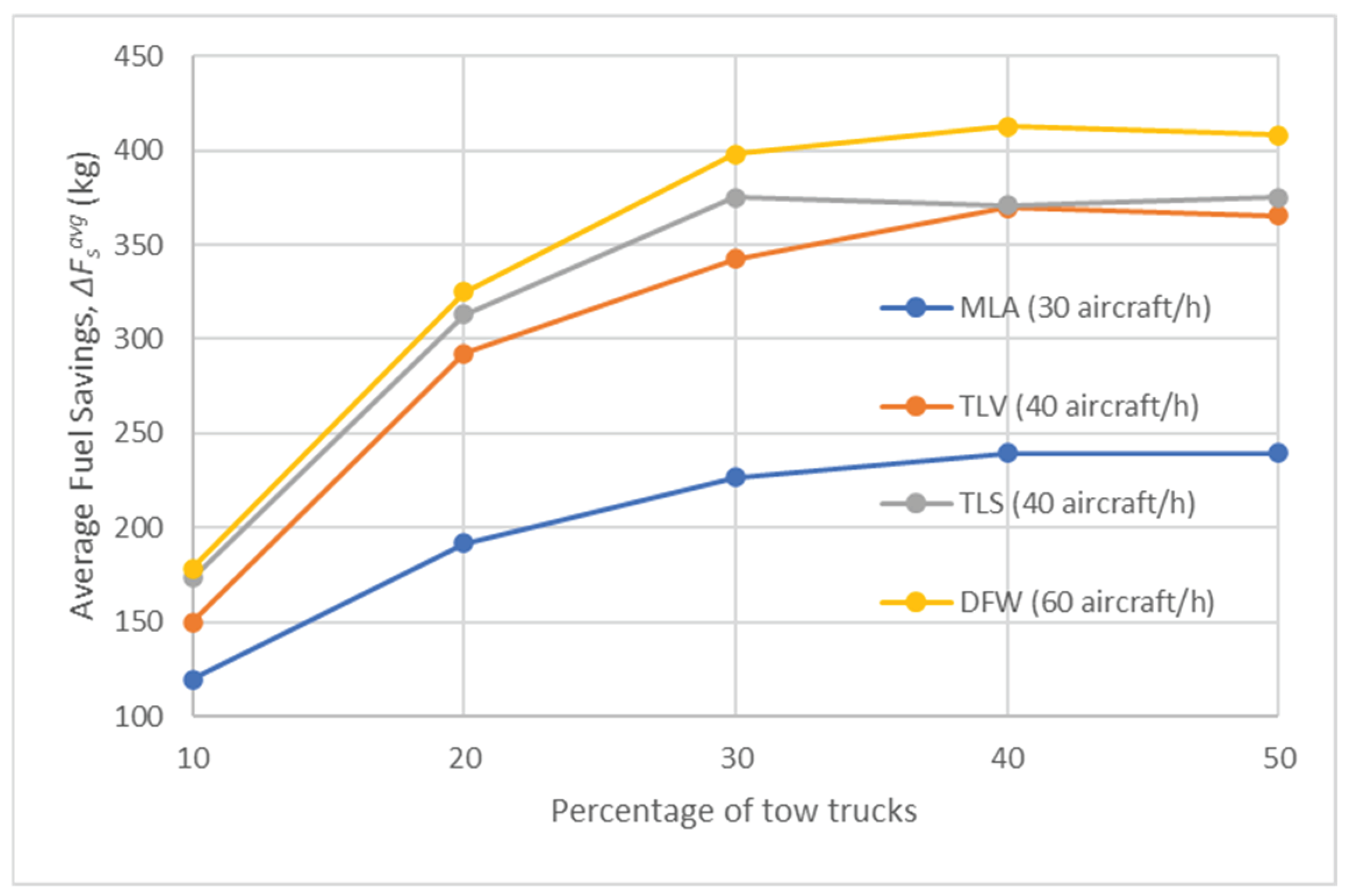
Figure 7. Tow Truck Utilisation Time, Δt_ru^avg (%) in Test Scenario 2.

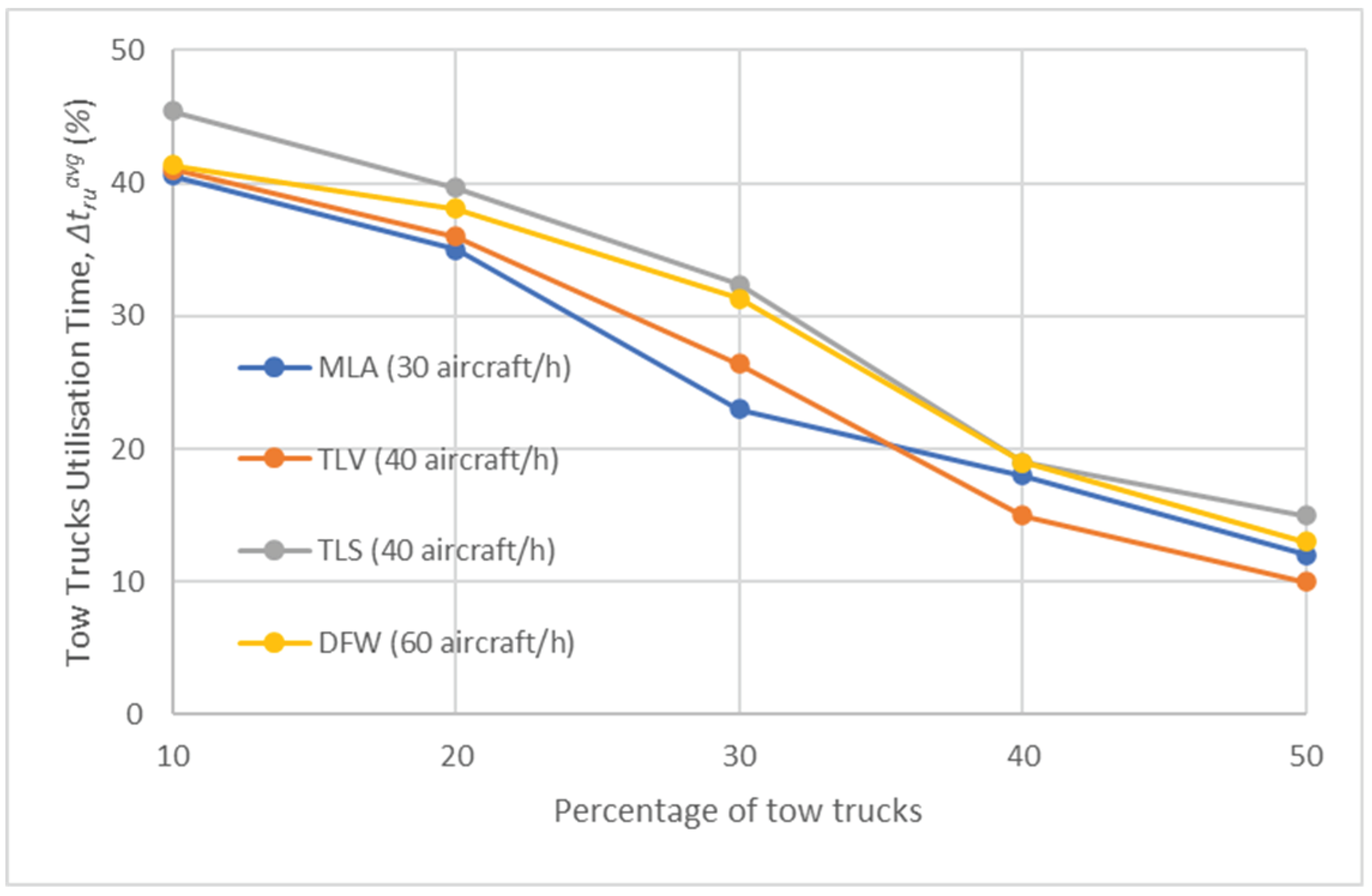
Figure 8. Towed Aircraft, TA (%) in Test Scenario 3.

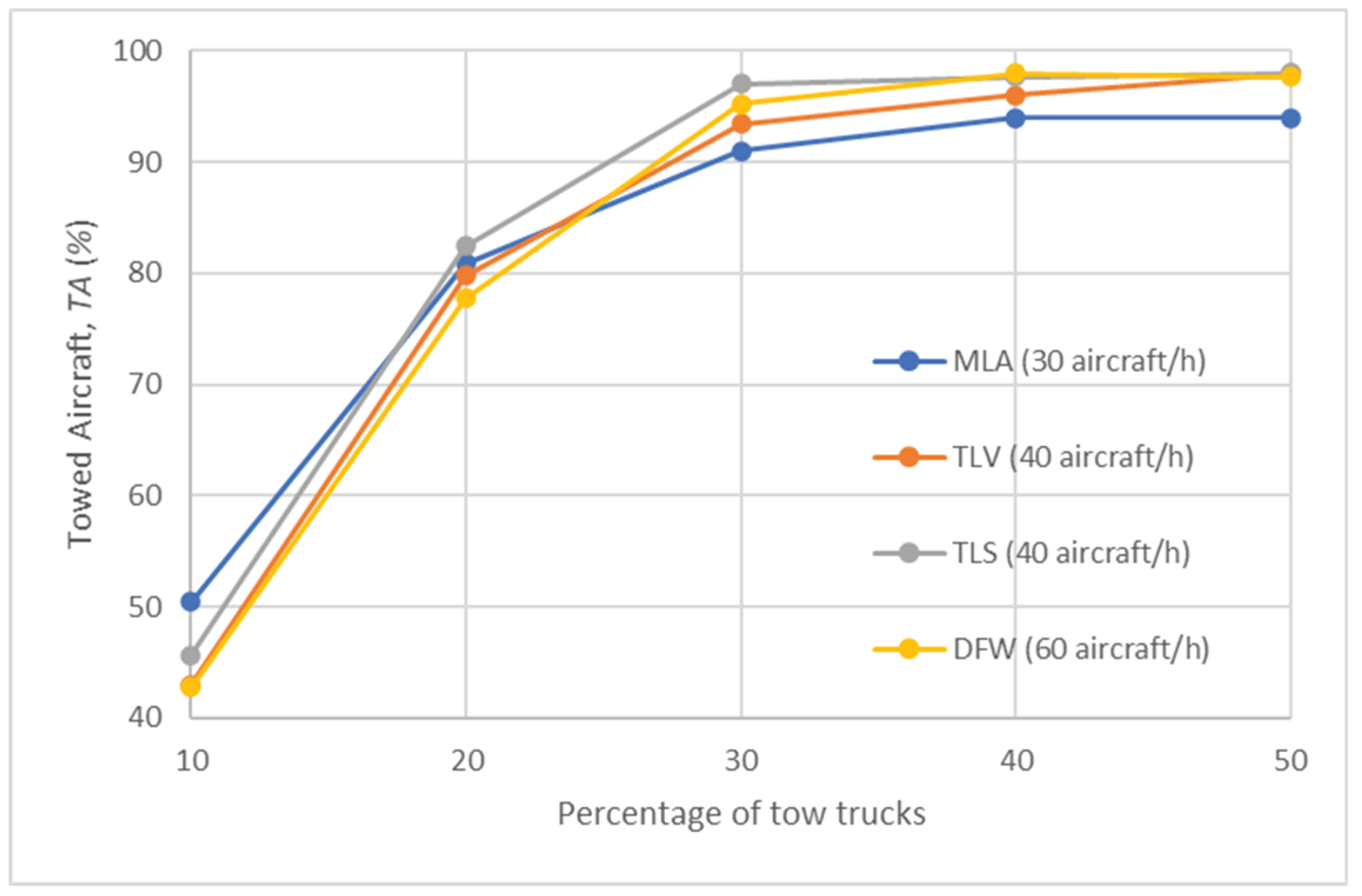
Figure 9. Average Fuel Savings, ΔF_s^avg (kg) in Test Scenario 3.

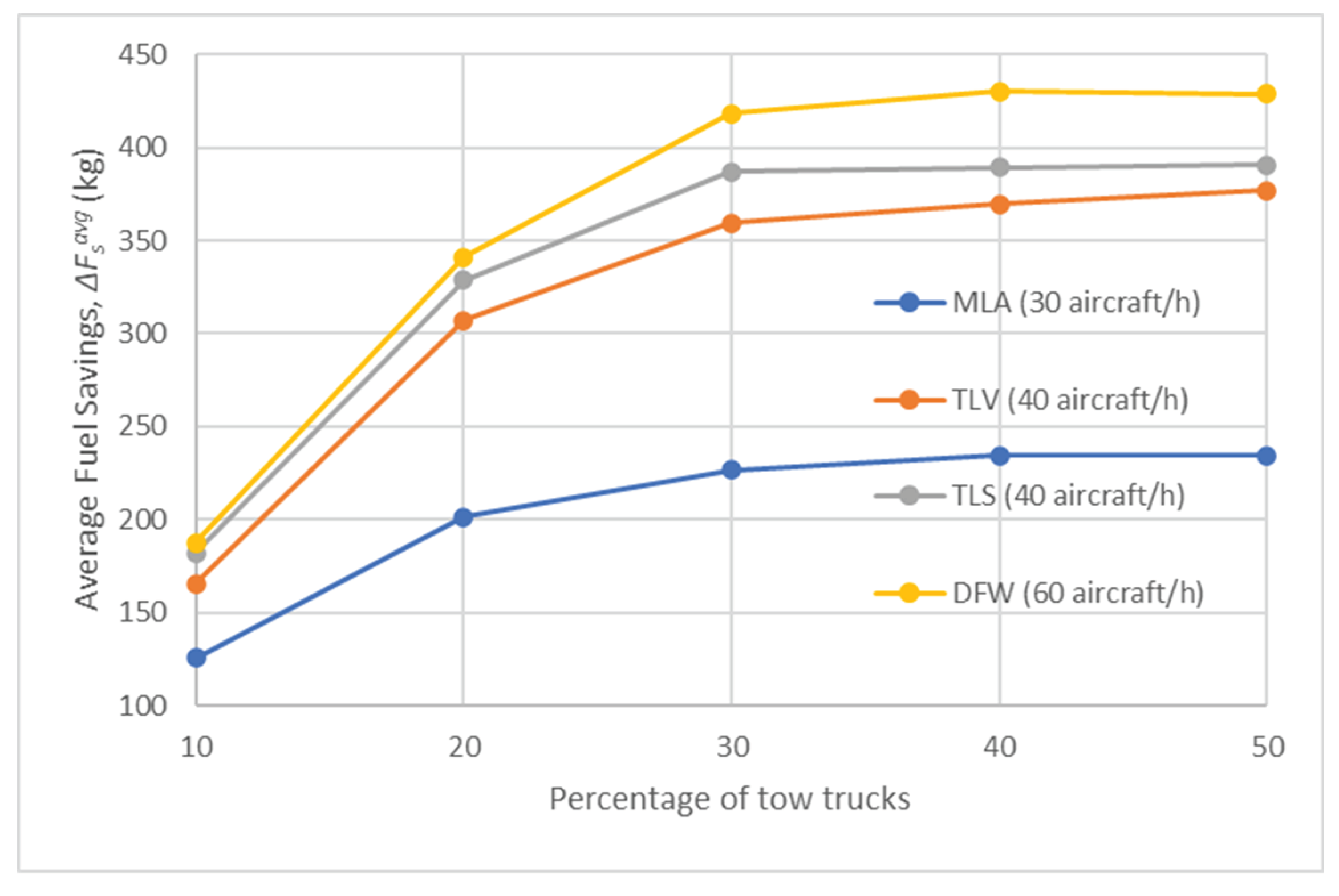
Figure 10. Average Total Time Delay, Δt_dtot^avg (s) in Test Scenario 3.

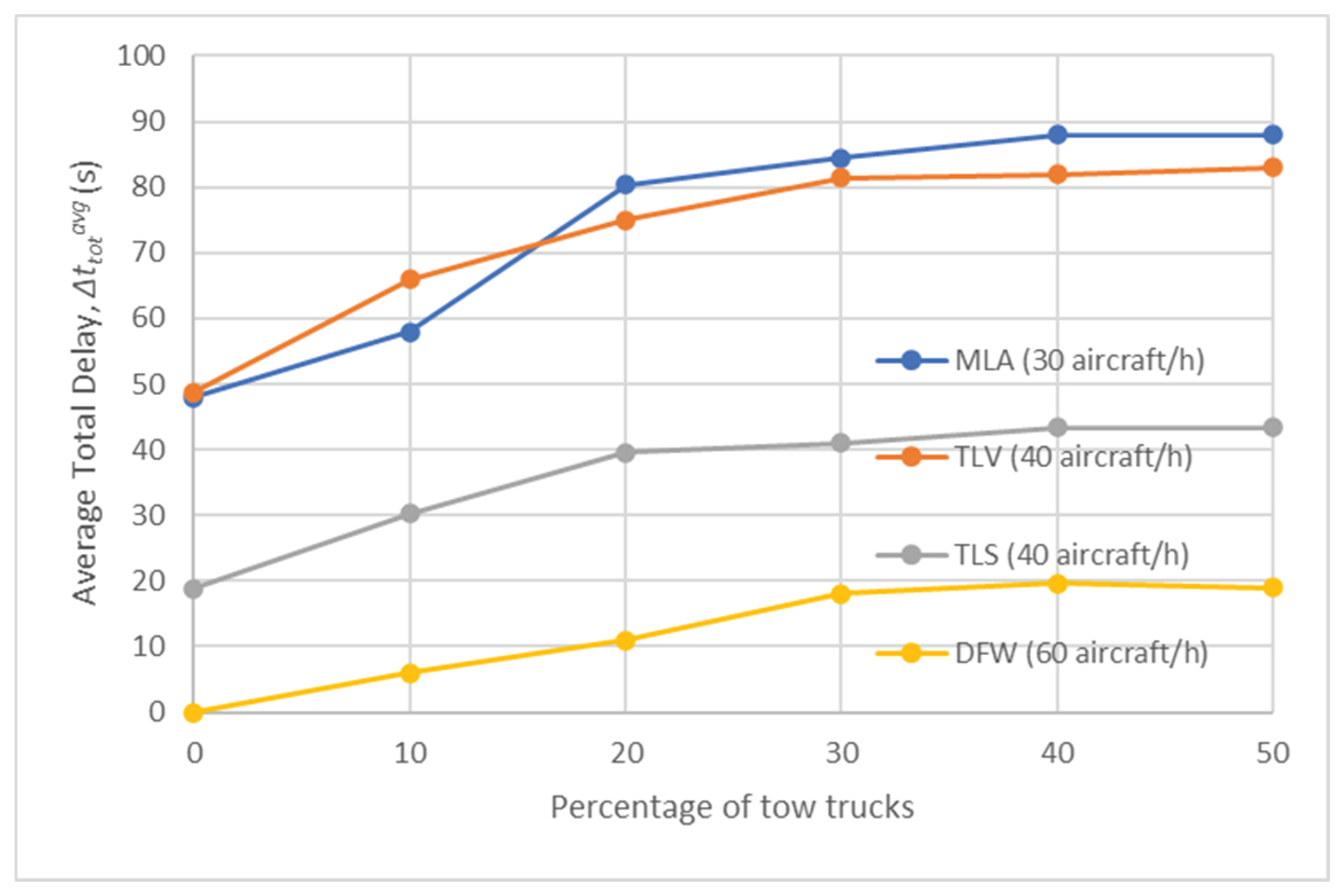
Figure 11. Tow Truck Utilisation Time, Δt_ru^avg (%) in Test Scenario 3.

Figure 12. Towed Aircraft, TA (%) in Test Scenario 4.

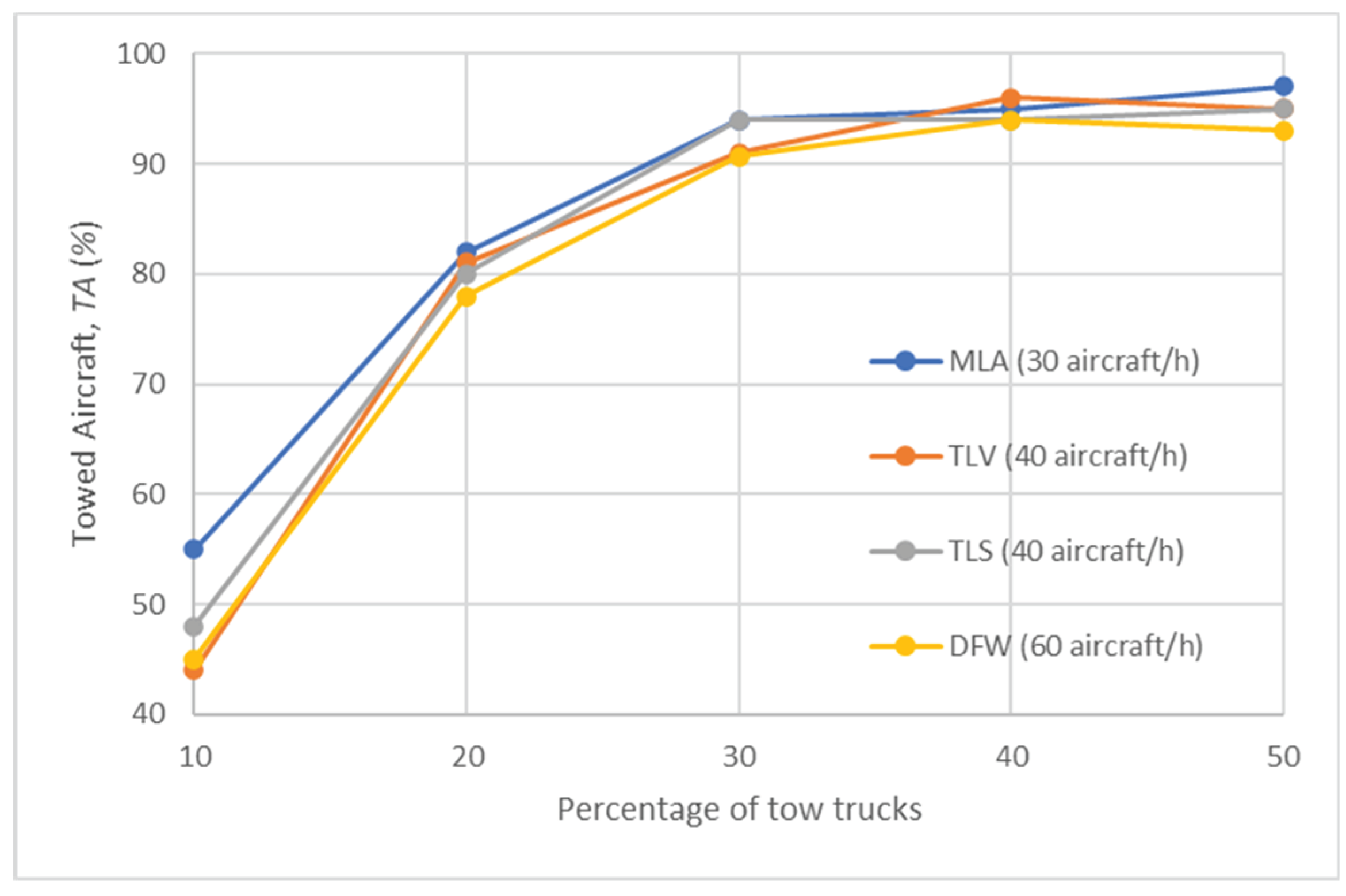
Figure 13. Average Fuel Savings, ΔF_s^avg (kg) in Test Scenario 4.

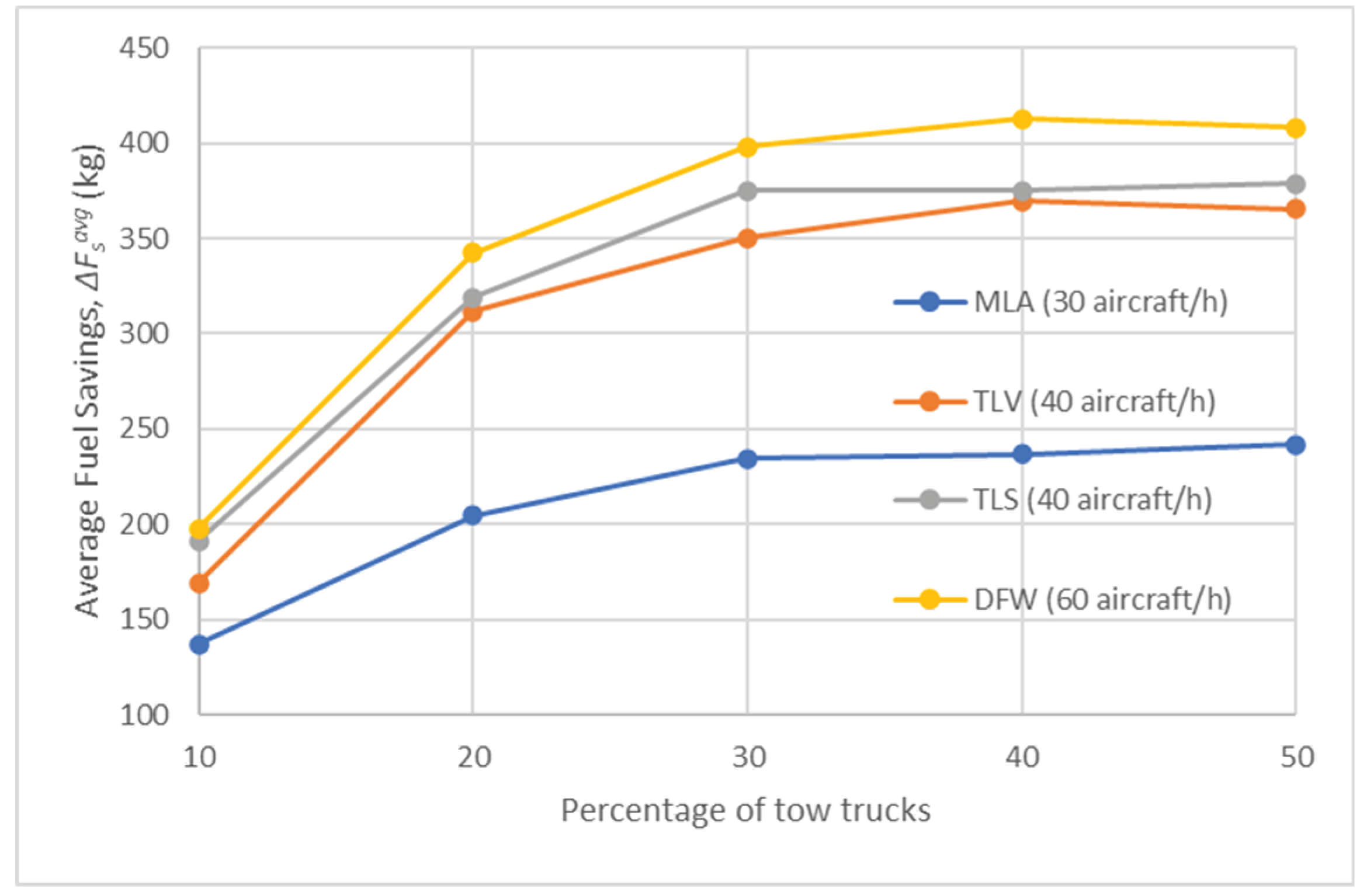
Figure 14. Tow Truck Utilisation Time, Δt_ru^avg (%) in Test Scenario 4.

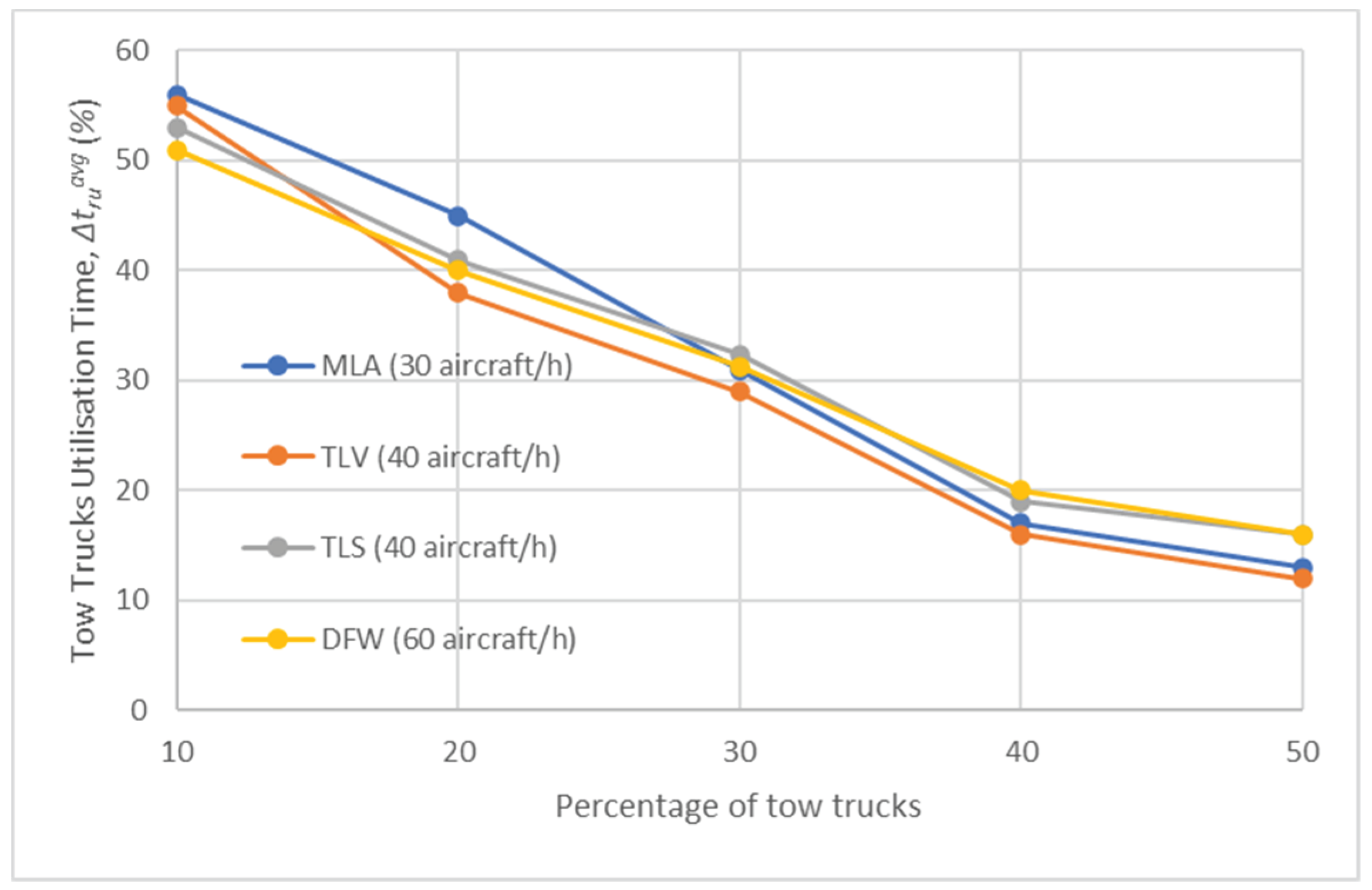
Figure 15. Towed Aircraft, TA (%) in Test Scenario 5.

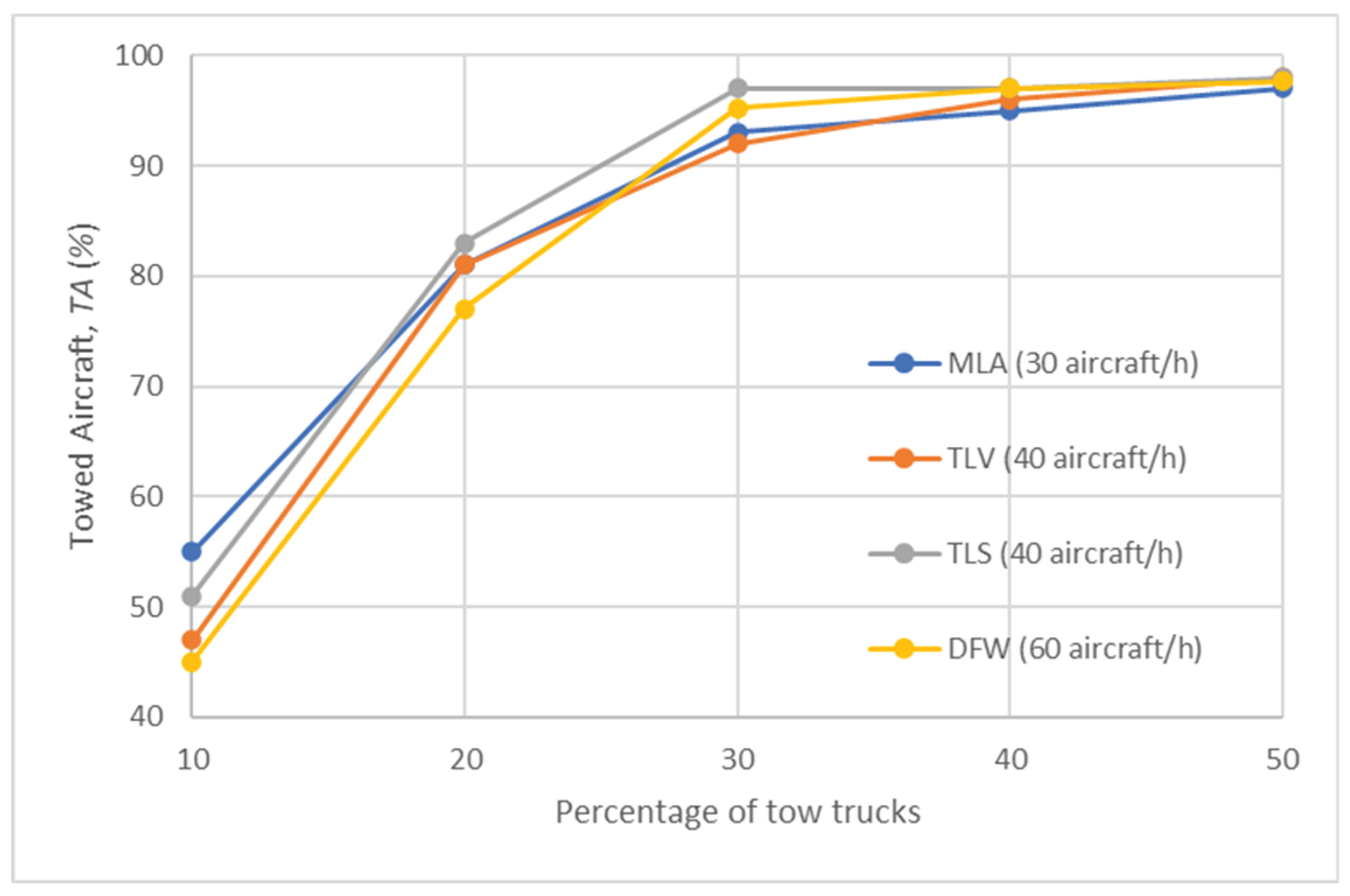
Figure 16. Average Fuel Savings, ΔF_s^avg (kg) in Test Scenario 5.

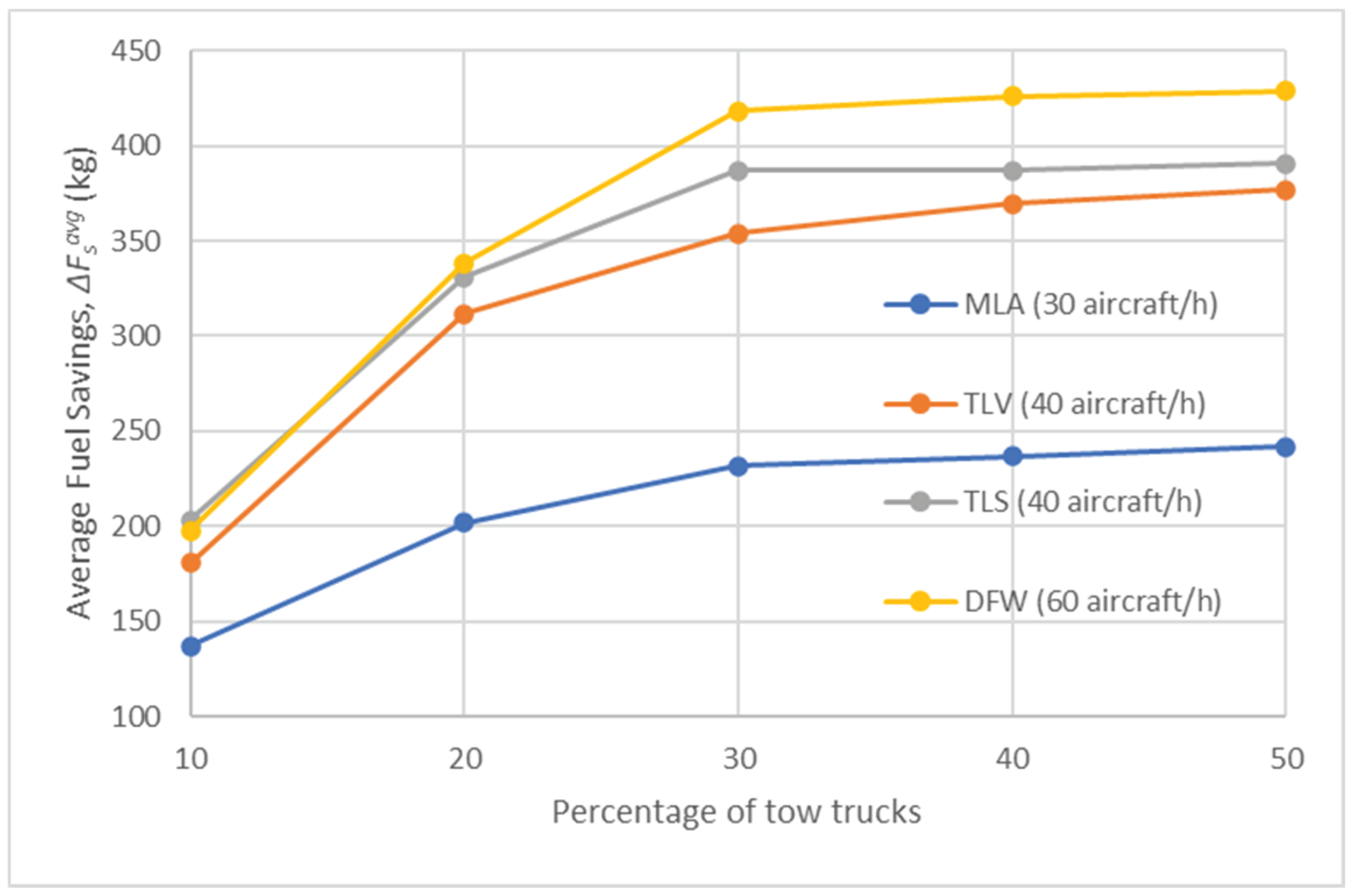
Figure 17. Average Total Time Delay, Δt_dtot^avg (s) in Test Scenario 5.

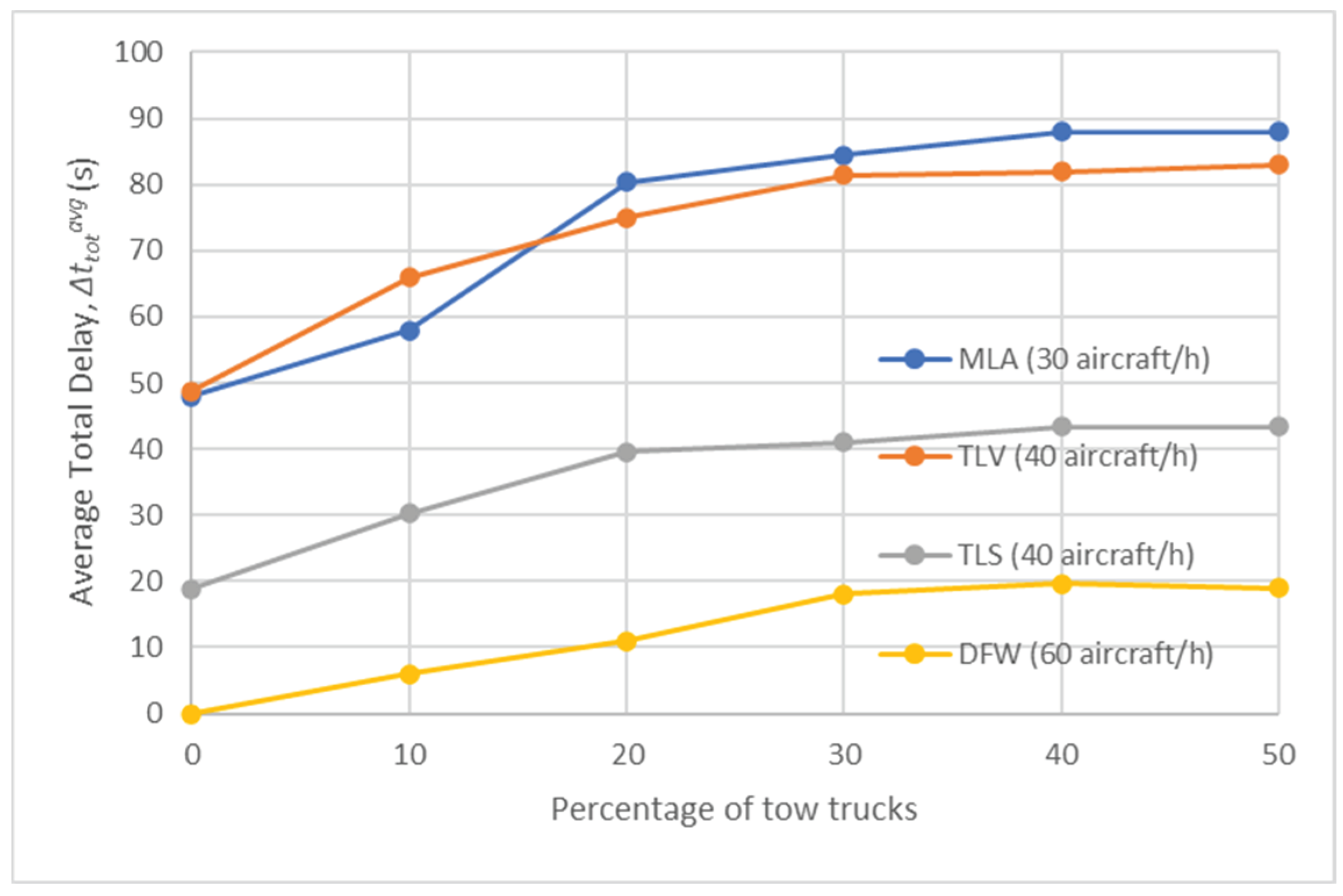
Figure 18. Tow Truck Utilisation Time, Δt_ru^avg (%) in Test Scenario 5.

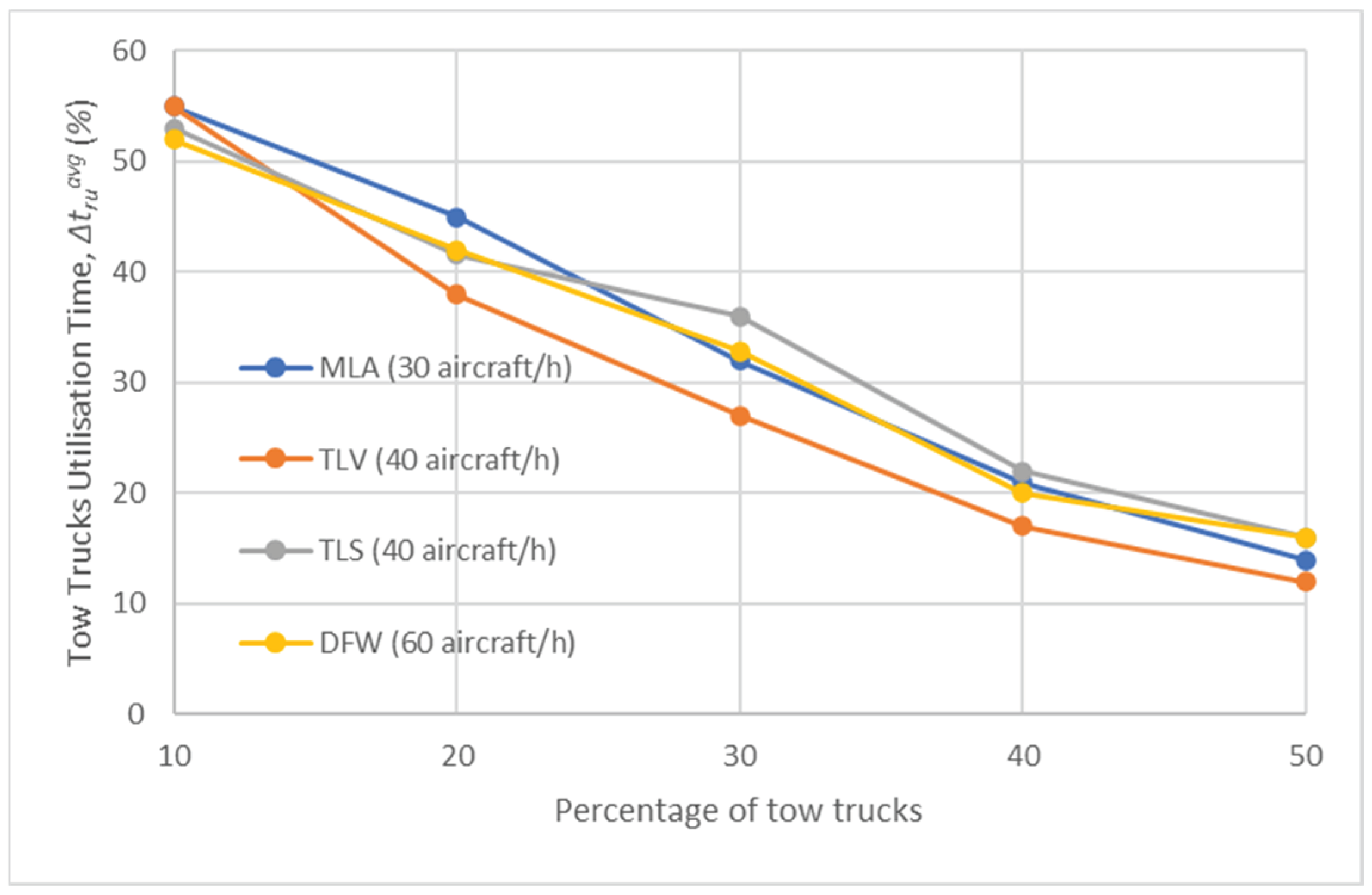
Table 1. Overview of the test scenarios.

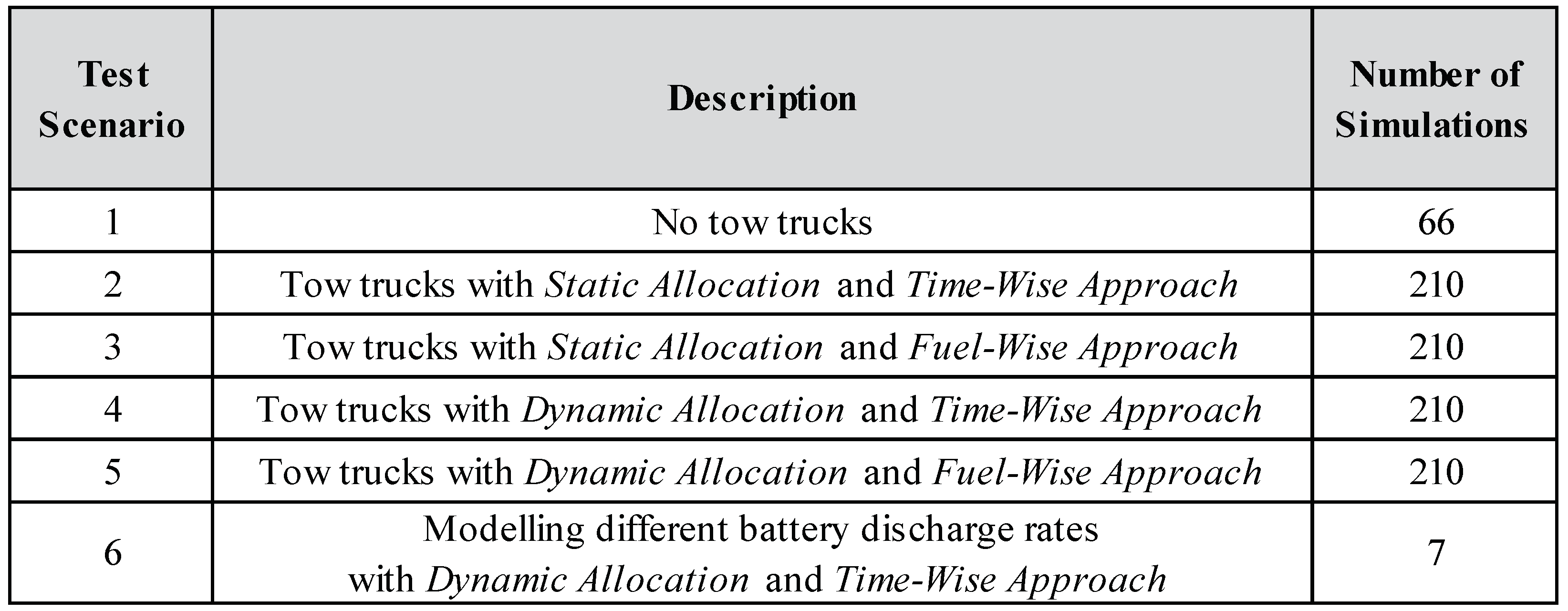Table 2. Relationship between tow truck performance and battery performance in Test Scenario 6.

Discharge rates percentage variation (%/min)	r_bdh (%/min)	r_bdl (%/min)	TA (%)	ΔF_s^avg (kg)	Δt_ru^avg (%)
-0.75	1.25	0.25	85	337	45
-0.50	1.50	0.50	83	329	44
-0.25	1.75	0.75	82	325	42
0	2.00	1.00	78	315	40
+0.25	2.25	1.25	75	305	39
+0.50	2.50	1.50	72	288	37
+0.75	2.75	1.75	65	258	31
+1.00	3.00	2.00	55	221	27

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer