Minkowskian Approach to the Pseudorange Navigation Equations

Preprint

Article

Minkowskian Approach to the Pseudorange Navigation Equations

Altmetrics

Downloads

Views

Comments

A peer-reviewed article of this preprint also exists.

Ramón Serrano Montesinos^*,

Juan Antonio Morales-Lladosa

Ramón Serrano Montesinos^*,

Juan Antonio Morales-Lladosa

This version is not peer-reviewed

Submitted:

01 March 2024

Posted:

04 March 2024

You are already at the latest version

Alerts

Abstract

Our starting point is the covariant coordinate transformation equation of a relativistic positioning system in Minkowski space-time, which maps the receiver’s emission coordinates (proper times broadcast by the emitters) to its coordinates in some inertial reference frame. Bancroft’s analytical (closed-form) solution to the basic pseudorange navigation equations with four emitters is recovered and the subjacent elements are geometrically interpreted. The case of four static beacons is analized as a clarifying situation.

Keywords:

Subject: Physical Sciences - Other

1. Introduction

In the context of Global Navigation Satellite Systems (GNSS), a modern approach is that of relativistic positioning. The foundations of the theory of Relativistic Positioning Systems (RPS) were laid down some time ago, for a genesis and perspectives please refer to [1,2].

In any space-time, a RPS can be thought of as a set of four emitters A

(A = 1, 2, 3, 4)

of world-lines

γ_{A} (τ^{A})

, broadcasting their respective proper times

τ^{A}

by means of electromagnetic signals. In a RPS, the basic observable is the set of four proper times

{τ^{A}}

received at an event x by the user. These are the user’s emission coordinates (refer to [3] for a detailed analysis). The four space

T \equiv [τ^{1}] [τ^{2}] [τ^{3}] [τ^{4}] \approx R^{4}

is called the grid of the positioning system. For generalities on this concept and RPS constructions in two and three dimensions see [4,5,6]. Similar constructions apply to locate an emitter from a given set of coplanar receivers [7,8].

The set of four emission events

{γ_{A} (τ^{A})}

at the emission times

{τ^{A}}

received at the event x is known as the configuration of the emitters for the event x. Suppose the four world-lines

γ_{A} (τ^{A})

are known in an inertial coordinate system

{x^{α}} (α = 0, 1, 2, 3)

. In Minkowski space-time, the location problem consists in finding the transformation between the user’s emission coordinates and its coordinates in that inertial coordinate system, by solving the following algebraic system of four non-linear equations (called the null propagation equations):

{(x - γ_{A})}^{2} = 0, A = 1, 2, 3, 4,

(1)

where x and

γ_{A} = O γ_{A} (τ^{A})

are respectively the user and the emitters position four-vectors with respect to the origin O of

{x^{α}}

. The solution to (1), mapping the user’s emission coordinates to its inertial coordinates, is what we may call the RPS coordinate transformation or the RPS solution [9,10].

In the traditional approach to GNSS, one of the basic observables is the pseudorange, which is the apparent range (distance) between the emitter and the user as inferred from the travelling time of the signal. Neglecting gravitational, atmospheric and instrumental effects, this apparent distance differs from the Euclidean geometric distance at the time of signal emission due to synchronisation errors between emitter and user clocks (clock biases or offsets). With at least four pseudorange measurements, the receiver can estimate its position and clock bias by solving the corresponding navigation equations. In practice, this estimation is the result of a multilateration problem which is solved by iterative methods (least squares algorithms) [11,12]. Analytical or closed-form solutions are usually brought in as an initial (approximate) estimation [13]. This work is concerned only with analytical solutions, leaving aside the treatment of any source of errors due to measurement uncertainties, for which further estimation and statistical analysis is necessary (see [8,14] for an analysis in the context of source localization).

The main purpose of this paper is to bring the (non-relativistic) theoretical foundations of current GNSSs closer to the RPS approach, by recovering from the RPS coordinate transformation equation [9,10] one of the classical solutions to the problem which is still in use today: Bancroft’s closed-form solution (with four emitters) [15]. Abel and Chaffee [16,17] used Lorentzian geometry in their interpretion of the Bancroft algorithm, providing conditions for the existence and unicity of solutions. Bancroft’s solution has been recently considered in [18,19]. However, Bancroft’s characteristic elements in terms of the RPS geometric ones have not been sufficiently interpreted up to now.

We begin by explaining the notation (Section 2), we then briefly review the RPS solution (Section 3) and express Bancroft’s solution using a relativistic notation (Section 4). Next, by choosing a specific value for the subsidiary vector

ξ

, we recover Bancroft’s solution from the RPS solution (Section 5) and provide proofs of the results in Section 6. Section 7 contains a positioning example to illustrate the correspondence between both solutions for four static emitters, and Section 8 contains constructions of the characteristic regions for this static situation. Section 9 extends these constructions considering some of the satellites as receivers. Finally, we set out our conclusions in Section 10.

Some preliminary results of this work have been communicated at the congress Mathematical Modelling in Engineering and Human Behaviour 2023 [20].

2. Notation

The main sign conventions and notation adopted in this paper are:

(i) g is the Minkowski space-time metric, with signature

(-, +, +, +)

. We use units in which the speed of light in vacuum is

c = 1

(ii)

η

is the metric volume element of g, defined by

η_{α β γ δ} = - \sqrt{- \det g} ϵ_{α β γ δ}

, where

ϵ_{α β γ δ}

stands for the Levi-Civita permutation symbol,

ϵ_{0123} = 1

. The Hodge dual operator associated to

η

is denoted by an asterisk ∗. For instance, in index notation (where summing over repeated indices is understood), if

x, y, z

are space-time vectors, one has

{[* (x \land y \land z)]}_{α} = η_{α β γ δ} x^{β} y^{γ} z^{δ},

(2)

where ∧ stands for the wedge or exterior product (defined by the antisymmetrized tensor product of antisymmetric tensors).

(iii)

i ()

denotes the interior or contracted product, that is, if x is a vector and T a covariant 2-tensor, one has

{[i (x) T]}_{ν} = x^{μ} T_{μ ν}

(contracting the first left tensor index). If k is another space-time vector, then we have the following properties

\begin{matrix} i (k) * (x \land y) = & - * (k \land x \land y), \end{matrix}

(3)

\begin{matrix} i (k) * (x \land y \land z) = & * (k \land x \land y \land z) . \end{matrix}

(4)

(iv) In terms of matrices, a contravariant space-time vector is represented by a column and a covariant vector by a row. In index notation, the interior or contracted (or scalar) product of a column vector (

x^{α}

) and a row vector (

y_{β}

) is the contraction

i (x) y = x \cdot y = x^{α} y_{α}

. A column vector (

x^{α}

) is converted into a row vector (

x_{α}

) with the metric:

x_{α} = g_{α β} x^{β}

. A matrix M acts on a column vector x yielding another column vector

M x

and on a row vector y yielding another row vector

y M

3. The RPS Solution in Minkowski Space-Time

In this section we present a brief compendium of relativistic positioning in flat space-time. For more explanations and details please refer to [9,10].

As detailed in [9], the set of equations (1) can be conveniently solved by referring both the user’s position x and three of the emitters, say

{γ_{1}, γ_{2}, γ_{3}}

, to the fourth one,

γ_{4}

\begin{matrix} y & = x - γ_{4}, \end{matrix}

(5)

\begin{matrix} e_{a} & = γ_{a} - γ_{4}, a = 1, 2, 3, \end{matrix}

(6)

and separating (1) into a quadratic equation

\begin{matrix} y^{2} = 0, \end{matrix}

(7)

and a system of three linear equations

\begin{matrix} e_{a} \cdot y = Ω_{a}, a = 1, 2, 3, \end{matrix}

(8)

where

Ω_{a} = \frac{1}{2} {(e_{a})}^{2}

are the world-function scalars associated with the three pairs of events (

γ_{a}, γ_{4}

) at emission times.

Here we consider only regular emitter configurations, that is, when the four emission events

{γ_{A} (τ^{A})}

determine a 3-plane

Γ

. According to [9], a regular emitter configuration is an emission/reception configuration iff all the relative emitter positions are space-like, that is,

{(e_{a})}^{2} > 0, {(e_{a} - e_{b})}^{2} > 0 .

(9)

These conditions express that the vectors defined by

m_{A} = x - γ_{A},

are null (1) and are all future (past) oriented,

m_{A} \cdot m_{B} < 0, A \neq B

. The bounds imposed by conditions (9) are called the shadows that the emitters produce to each other. The null vectors

m_{A}

and

m_{B}

become collinear (

m_{A} \cdot m_{B} = 0

) at the mutual shadows produced by

γ_{A}

and

γ_{B}

. The precise definition of the shadow that a world-line produces to another world-line was given in [21] (see also [22]).

Furthermore,

{γ_{A} (τ^{A})}

is an emission (reception) configuration iff, in addition to (9), the null vector y is future (past) oriented. These conditions allow to interpret the solutions of the null propagations equations (1) as emission solutions.

The general solution to the underdetermined system (8) is of the form:

\begin{matrix} y = y_{*} + λ χ, \end{matrix}

(10)

where

y_{*}

is a particular solution to the system,

λ

is a real parameter and

\begin{matrix} χ = * (e_{1} \land e_{2} \land e_{3}) = * ((γ_{1} - γ_{4}) \land (γ_{2} - γ_{4}) \land (γ_{3} - γ_{4})) \end{matrix}

(11)

the configuration vector of the RPS, which is orthogonal to the configuration 3-plane

Γ

. A regular emitter configuration (at x) is said to be space-like, light-like or time-like if

χ^{2} < 0

χ^{2} = 0

χ^{2} > 0

, respectively, at x. The regions defined by these conditions are respectively denoted as

C_{s}

C_{l}

and

C_{t}

. In Section 8.1 and Section 8.2 we analysis these regions for the case of four static emitters.

The particular solution

y_{*}

is found by bringing in a subsidiary vector

ξ

such that

ξ \cdot χ \neq 0

(that is, transversal to the emitter configuration) and otherwise arbitrary:

y_{*} = \frac{1}{ξ \cdot χ} i (ξ) H,

(12)

where H is the configuration bivector,

H = Ω_{1} E^{1} + Ω_{2} E^{2} + Ω_{3} E^{3},

(13)

with

\begin{matrix} E^{1} = * (e_{2} \land e_{3}), E^{2} = * (e_{3} \land e_{1}), E^{3} = * (e_{1} \land e_{2}) . \end{matrix}

(14)

Then

y_{*}

is orthogonal to

ξ

i (ξ) y_{*} = 0

. Quantities

Ω_{a}

, H and

χ

are intrinsically related to the configuration of the emitters at x, and are independent of the origin of the inertial chart

{x^{α}}

The general solution x to the null propagation equations (1) is obtained by introducing (10) in the main quadratic Equation (7),

\begin{matrix} χ^{2} λ^{2} + 2 (y_{*} \cdot χ) λ + y_{*}^{2} = 0, \end{matrix}

(15)

and solving for

λ

. This prodcedure gives:

\begin{matrix} x = γ_{4} + y_{*} + λ χ, \end{matrix}

(16)

with

\begin{matrix} λ = - \frac{y_{*}^{2}}{(y_{*} \cdot χ) + \hat{ϵ} \sqrt{Δ}}, \end{matrix}

(17)

where

Δ = {(y_{*} \cdot χ)}^{2} - y_{*}^{2} χ^{2},

(18)

and

\hat{ϵ}

is the orientation of the positioning system at the event x. The orientation

\hat{ϵ}

is defined as the sign of the Jacobian determinant of the coordinate transformation

τ^{A} (x^{α})

from inertial to emission coordinates, that is

\hat{ϵ} = s g n [* (d τ^{1} \land d τ^{2} \land d τ^{3} \land d τ^{4})],

(19)

with

d τ^{A} = \frac{\partial τ^{A}}{\partial x^{α}} d x^{α}

. In [9] the orientation is expressed as

\hat{ϵ} = s g n (χ \cdot y)

and is determined by the configuration of the emitters as seen by the user, which is analysed in [10] in connection with the bifurcation problem as follows.

Depending on the causal character of the configuration vector

χ

and assuming the coordinate condition

χ \cdot y \neq 0

, we distinguish three situations (see Figure 3, Figure 4 and Figure Figure 5 in [10]):

(i): If $χ$ is time-like, there is only one emission solution P, the other ( $P^{'}$ ) is a reception solution (the events P and $P^{'}$ are on opposite sides of the configuration hyperplane $Γ$ ). In this case, the sign of $\hat{ϵ}$ can be determined from the sole standard emission data ${γ_{A} (τ^{A}), {τ^{A}}}$ .
(ii): If $χ$ is light-like, there is only one valid emission solution (the other solution is degenerate). The sign of $\hat{ϵ}$ can be determined from ${γ_{A} (τ^{A}), {τ^{A}}}$ .
(iii): If $χ$ is space-like, there are two valid emission solutions: in order to determine the sign of $\hat{ϵ}$ , additional observational information is necessary (relative positions of emitters on the user’s celestial sphere).

In practical GPS applications, there is generally no bifurcation problem because the valid solution is always the one that is closest to the Earth radius. Nevertheless, bifurcation is inherent to any time-like emitter configuration and therefore acquires importance in positioning situations beyond the proximity of the Earth.

On the other hand, the sign of

Δ

determines the causal character of the 2-plane generated by {

y_{*}, χ

}. It is negative when the plane is space-like, zero when light-like and positive when time-like. From (5) and (16), this plane is the same generated by {

y, χ

}. Since y is light-like, this 2-plane is non space-like and therefore

Δ \geq 0

. Moreover,

s g n (Δ) = s g n [{(χ \cdot y)}^{2}]

. Consequently, the events where

Δ = 0

are those where the Jacobian determinant of

τ^{A} (x^{α})

vanishes (

\hat{ϵ} = 0

); these events form the border which separates two (the front and back) coordinate domains, where

\hat{ϵ}

takes opposite values [10].

4. Bancroft’s Solution

As mentioned earlier, we aim to bring the traditional GNSS approach closer to the RPS formalism. In this section we express Bancroft’s solution using the RPS notation. In fact, Bancroft’s solution, despite being based on non-relativistic concepts, incorporates four-vectors and a Minkowski-like scalar product. Nevertheless, it calls for a reinterpretation of those concepts on relativistic terms.

Bancroft first defines the user’s spatial coordinates,

\vec{x}

, and those of the n satellites,

{\vec{s}}_{i}

(for our purposes,

1 \leq i \leq n = 4

). Then he introduces the pseudorange measurements

t_{i}

made by the user with respect to each of the satellites:

\begin{matrix} t_{i} = d (\vec{x}, \vec{s_{i}}) + b, \end{matrix}

(20)

where

d (\vec{x}, \vec{s_{i}}) = \sqrt{{(x - s_{i}^{x})}^{2} + {(y - s_{i}^{y})}^{2} + {(z - s_{i}^{z})}^{2}}

is the Euclidean distance between the ith satellite and the user and b what he calls the user clock’s offset.

Reinterpreting (20) as a past light-cone equation (with the user at its vertex), we identify

t_{i}

with the coordinate time component, with respect to some inertial coordinate system

{x^{α}}

, of the world-line of the ith emitter:

t_{i} ⟷ γ_{i}^{t},

and the clock’s offset b, with the inertial time coordinate of the user’s position four-vector x:

b ⟷ t .

Bancroft now defines the four-vectors

a_{i}

, which we identify as the (position vectors of the) emitters’ world-lines:

a_{i} = (t_{i}, \vec{s_{i}}) ⟷ γ_{i} = (γ_{i}^{t}, \vec{γ_{i}}), i = 1, 2, 3, 4 .

He introduces a scalar product between four-vectors

〈 a, b 〉

, which is equivalent to the scalar product in Minkowski space-time,

a \cdot b \equiv g (a, b)

, with metric signature

(-, +, +, +)

Bancroft’s solution vector

y_{1, 2} = (- b_{1, 2}, {\vec{x}}_{1, 2})

can be readily identified with the user’s position four-vector x of the RPS.

These correspondences are summarized in Table 1. Now we are ready to write down the navigation equations solved by Bancroft, using the RPS notation. These are none other than Equations (1):

{(x - γ_{i})}^{2} = x^{2} - 2 γ_{i} \cdot x + γ_{i}^{2} = 0,

(21)

with

i = 1, 2, 3, 4

This system of four equations can be rewritten with the help of the following scalar:

ρ = \frac{1}{2} x^{2},

(22)

row vectors:

\begin{matrix} 1 = (\begin{matrix} 1 & 1 & 1 & 1 \end{matrix}), r = (\begin{matrix} r_{1} & r_{2} & r_{3} & r_{4} \end{matrix}), \end{matrix}

(23)

where

r_{i} = \frac{1}{2} γ_{i}^{2},

(24)

and the following matrix:

A = (γ_{1} γ_{2} γ_{3} γ_{4}),

(25)

where

γ_{i}

are considered column vectors. The system (21) reads:

\begin{matrix} ρ 1 - i (x) A + r & = 0, \end{matrix}

or equivalently, provided that

A

is invertible:

x = ρ u + v,

(26)

where

\begin{matrix} u = 1 A^{- 1}, v = r A^{- 1} . \end{matrix}

(27)

Squaring (26) and substituting

x^{2} = 2 ρ

E ρ^{2} + 2 F ρ + G = 0,

(28)

where

\begin{matrix} E = u^{2}, F = u \cdot v - 1, G = v^{2} . \end{matrix}

(29)

Equation (26) is Bancroft’s solution to the location problem, where u and v are known from the emitters’ trajectories

γ_{i}

, and

ρ

is obtained by solving equation (28). Here we can distinguish the case where

E = 0

(which, as we will see, corresponds to a light-like configuration of the emitters):

\begin{matrix} E = 0 \Rightarrow ρ = - \frac{G}{2 F}, \end{matrix}

(30)

and the cases where

E \neq 0

(which correspond to time-like and space-like emitter configurations):

\begin{matrix} E \neq 0 \Rightarrow ρ = & \frac{- F \pm \sqrt{F^{2} - E G}}{E} . \end{matrix}

(31)

Bancroft does not make this distinction and implicitly assumes

E \neq 0

, his solution being Equation (26) with

ρ

as in (31). The following expression can be used for any value of E:

ρ = - \frac{G}{F \pm \sqrt{F^{2} - E G}} .

(32)

5. Recovering Bancroft’s Solution from the RPS Solution

In this section, the quantities E, F and G, used to express Bancroft’s solution, are related to the geometric elements of the RPS statement of the location problem. The subjacent correspondence is achieved using exterior calculus in Lorentzian geometry (Minkowski space-time). For clarity, the steps of this calculation are grouped into propositions, proof of which is given in Section 6.

Proposition 1.

Let

A = (γ_{1} γ_{2} γ_{3} γ_{4})

be a matrix whose columns are the emitters’ world-lines

γ_{i}

. The inverse of

A

is given by:

A^{- 1} = {[d e t (A)]}^{- 1} (\begin{matrix} \begin{matrix} Γ^{1} \\ Γ^{2} \\ Γ^{3} \\ Γ^{4} \end{matrix} \end{matrix}),

(33)

the matrix entries now being row vectors

\begin{matrix} Γ^{1} & = - * (γ_{2} \land γ_{3} \land γ_{4}), Γ^{2} = * (γ_{1} \land γ_{3} \land γ_{4}), \\ Γ^{3} & = - * (γ_{1} \land γ_{2} \land γ_{4}), Γ^{4} = * (γ_{1} \land γ_{2} \land γ_{3}), \end{matrix}

(34)

and where

d e t (A) = - * (γ_{1} \land γ_{2} \land γ_{3} \land γ_{4})

(35)

is the determinant of

A

On the other hand, for

χ

and H we have:

Proposition 2.

The configuration vector χ and the bivector H of a RPS can be written as:

χ = \sum_{i = 1}^{4} Γ^{i},

(36)

and

\begin{matrix} H = & Ω_{1} * (γ_{2} \land γ_{3}) + Ω_{2} * (γ_{3} \land γ_{1}) + Ω_{3} * (γ_{1} \land γ_{2}) \\ + (Ω_{3} - Ω_{1}) * (γ_{2} \land γ_{4}) + (Ω_{2} - Ω_{3}) * (γ_{1} \land γ_{4}) + (Ω_{1} - Ω_{2}) * (γ_{3} \land γ_{4}), \end{matrix}

(37)

respectively.

Notice that

{Θ^{i}}

, with

Θ^{i} = {[d e t (A)]}^{- 1} Γ^{i},

(38)

is the dual basis of

{γ_{i}}

, that is,

Θ^{i} (γ_{j}) = δ_{j}^{i}

. Now we can write u and v according to (27):

\begin{matrix} u & = {[d e t (A)]}^{- 1} \sum_{i = 1}^{4} Γ^{i} = \sum_{i = 1}^{4} Θ^{i}, \end{matrix}

(39)

\begin{matrix} v & = {[d e t (A)]}^{- 1} \sum_{i = 1}^{4} r_{i} Γ^{i} = \sum_{i = 1}^{4} r_{i} Θ^{i}, \end{matrix}

(40)

and the configuration vector

χ

can now be written as

χ = d e t (A) u .

(41)

With

E, F

and G defined as in (29), we can state the next proposition.

Proposition 3.

Setting

ξ = γ_{4}

, (i) the particular solution

y_{*}

and the discriminant Δ can be written as

\begin{matrix} y_{*} & = v + r_{4} u - γ_{4}, \end{matrix}

(42)

\begin{matrix} Δ & = {[d e t (A)]}^{2} [F^{2} - E G], \end{matrix}

(43)

and (ii) the RPS solution is expressed as

\begin{matrix} x = v + & ρ u, \end{matrix}

(44)

where u and v are given by (39) and (40), and

\begin{matrix} ρ = & - \frac{G}{F + \hat{ϵ} μ \sqrt{F^{2} - E G}}, \end{matrix}

(45)

which is Equation (32), that is, Bancroft’s solution extended to any emitter configurations, with

μ = s g n (d e t (A))

and

\hat{ϵ}

the orientation of the RPS at x.

On the other hand, from (41) and (42) we can write Bancroft’s scalars E, F and G, given by (29), explictly in terms of the RPS variables.

\begin{matrix} E = & {[d e t (A)]}^{- 2} χ^{2}, \\ F = & {[d e t (A)]}^{- 1} (y_{*} \cdot χ - \frac{r_{4}}{d e t (A)} χ^{2}), \end{matrix}

(46)

\begin{matrix} G = & {(y_{*} - \frac{r_{4}}{d e t (A)} χ + γ_{4})}^{2} = {(y_{*} - \frac{r_{4}}{d e t (A)} χ)}^{2} . \end{matrix}

(47)

In Equation (47) we have used

γ_{4} \cdot y_{*} \propto H (γ_{4}, γ_{4}) = 0

i (γ_{4}) u = 1

and

γ_{4}^{2} = 2 r_{4}

Equation (46) says that the sign of E provides the causal character of the emitter configuration for x. Therefore,

E = 0 \Leftrightarrow χ^{2} = 0

, corresponds to light-like emitter configurations, which are not covered by Bancroft’s solution. In contrast, Equations (16)-(18) and their transcription using Bancroft’s notation (Equations (44) and (45)) are valid for any emitter configuration.

6. Proof of the Propositions

Proposition 1 (proof)

Since

A^{- 1}

is defined in terms of row vectors and

A

in terms of column vectors, the matrix product

A^{- 1} A

is straightforward. In index notation, the only non-vanishing entries of

{[A^{- 1} A]}_{β}^{α}

are:

\begin{matrix} {[A^{- 1} A]}_{0}^{0} & = {[A^{- 1} A]}_{1}^{1} = {[A^{- 1} A]}_{2}^{2} = {[A^{- 1} A]}_{3}^{3} \\ = - \frac{1}{d e t (A)} i (γ_{1}) * (γ_{2} \land γ_{3} \land γ_{4}) = - \frac{1}{d e t (A)} * (γ_{1} \land γ_{2} \land γ_{3} \land γ_{4}) = 1, \end{matrix}

(48)

where in the last two steps we have taken into account (4) and (35).

Proposition 2 (proof)

To obtain Equation (36), we write out (11) explicitly,

χ = - * (γ_{2} \land γ_{3} \land γ_{4}) + * (γ_{1} \land γ_{3} \land γ_{4}) - * (γ_{1} \land γ_{2} \land γ_{4}) + * (γ_{1} \land γ_{2} \land γ_{3}) = \sum_{i = 1}^{4} Γ^{i} .

And to obtain (37), we write (13) explicitly taking into account (14). The quantities

χ

and H only depend on the relative positions between pairs of emitters at the emission times.

Proposition 3 (proof)

To derive Equation (42), we start by writing out the right-hand side of

y_{*}

using (12). Setting

ξ = γ_{4}

and calculating the contraction

ξ \cdot χ

using (41), we obtain:

\begin{matrix} γ_{4} \cdot χ & = & d e t (A) i (γ_{4}) u = d e t (A) i (γ_{4}) \sum_{i = 1}^{4} Θ^{i} = d e t (A), \end{matrix}

since

i (γ_{4}) Θ^{i} = δ_{4}^{i}

. From (3) and (37) we get:

\begin{matrix} i (γ_{4}) H = - Ω_{1} * (γ_{2} \land γ_{3} \land γ_{4}) + Ω_{2} * (γ_{1} \land γ_{3} \land γ_{4}) - Ω_{3} * (γ_{1} \land γ_{2} \land γ_{4}) = \sum_{a = 1}^{3} Ω_{a} Γ^{a} . \end{matrix}

Then, the particular solution

y_{*}

is written as

\begin{matrix} y_{*} = & \frac{1}{γ_{4} \cdot χ} i (γ_{4}) H = {[d e t (A)]}^{- 1} \sum_{a = 1}^{3} Ω_{a} Γ^{a} = \sum_{a = 1}^{3} Ω_{a} Θ^{a}, \end{matrix}

(49)

where, using (6) and (24), the world-function scalars

Ω_{a} = \frac{1}{2} {(e_{a})}^{2}

can be expressed as:

\begin{matrix} Ω_{a} = r_{a} + r_{4} - γ_{a} \cdot γ_{4} (a = 1, 2, 3) . \end{matrix}

(50)

Now, substituing (50) in (49) and using (39) and ():

\begin{matrix} y_{*} = & \sum_{a = 1}^{3} Ω_{a} Θ^{a} = \sum_{a = 1}^{3} (r_{a} + r_{4} - γ_{a} \cdot γ_{4}) Θ^{a} = \sum_{a = 1}^{3} r_{a} Θ^{a} + r_{4} \sum_{a = 1}^{3} Θ^{a} - \sum_{a = 1}^{3} (γ_{a} \cdot γ_{4}) Θ^{a} \\ = & v - r_{4} Θ^{4} + r_{4} (u - Θ^{4}) - \sum_{a = 1}^{3} (γ_{a} \cdot γ_{4}) Θ^{a} = v + r_{4} u - 2 r_{4} Θ^{4} - \sum_{a = 1}^{3} (γ_{a} \cdot γ_{4}) Θ^{a} \\ = & v + r_{4} u - g (γ_{4}), \end{matrix}

where, in the last step, we have taken into account that

2 r_{4} = γ_{4}^{2}

and that

g (γ_{4}) = \sum_{i = 1}^{4} (γ_{i} \cdot γ_{4}) Θ^{i},

is the one-form metrically equivalent to

γ_{4}

On the other hand, to obtain (43), noting that, from (39) and (40),

γ_{4} \cdot u = 1, γ_{4} \cdot v = r_{4},

and from the definitions (29) and using (41) and (42):

χ^{2} = {[d e t (A)]}^{2} E, y_{*}^{2} = G + r_{4}^{2} E + 2 r_{4} F, y_{*} \cdot χ = d e t (A) [r_{4} E + F] .

Then

Δ = {(y_{*} \cdot χ)}^{2} - y_{*}^{2} χ^{2} = {[d e t (A)]}^{2} [F^{2} - E G] .

Substituting the above expressions in (16) and taking into account that

χ = d e t (A) u

, we obtain (44) with

ρ = r_{4} - \frac{G + r_{4}^{2} E + 2 r_{4} F}{r_{4} E + F + \hat{ϵ} μ \sqrt{F^{2} - E G}},

where

μ = s g n (d e t (A))

. To obtain (45), multiply the denominator by

r_{4} E + F - \hat{ϵ} μ \sqrt{F^{2} - E G}

and simplify the expression.

7. Four Static Emitters: Solutions

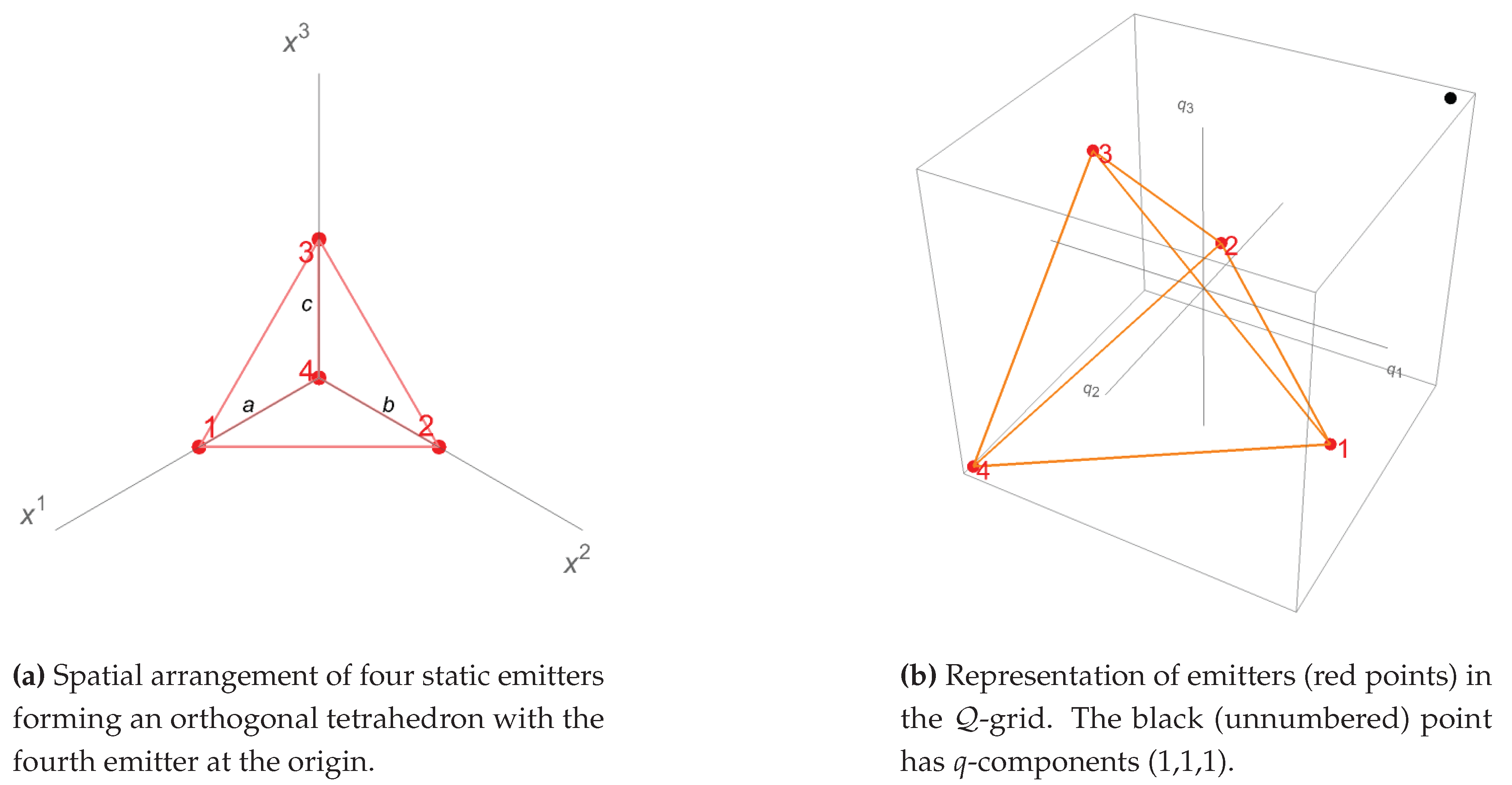
To illustrate the correspondence between the RPS and Bancroft’s solution, in this section we use both approaches to solve the location problem for the case of four static emitters. This is a simple but clarifying example to gain insight into the RPS terminology. For any given time t measured by an inertial observer of unit velocity

e_{0}

(

e_{0}^{2} = - 1, {[e_{0}]}^{α} = (1, 0, 0, 0)

), we choose the simple spatial arrangement of an orthogonal tetrahedron as shown in Figure 1, where the reference emitter

γ_{4}

is at the origin of the observer’s (spatial) coordinate system

{x^{1}, x^{2}, x^{3}}

The essential simplification that the static situation provides is the possibility to synchronize the emitters’ clocks at a given common (initial) instant. The respective proper times then become synchronized for ever, which allows to represent the static case in 3-dimensional diagrams. We will come back to this point in Section 8.

Figure 1. Representation of emitters when

a = b = c = 1

Figure 1. Representation of emitters when

a = b = c = 1

7.1. Emitters’ World-Lines and Emission/Reception Conditions

As the emitters’ clocks are synchronized at

x^{0} = 0

taking

τ^{1} = τ^{2} = τ^{3} = τ^{4} = 0

, the emitters’ world-lines, expressed with respect to an inertial reference frame

{x^{α}}

, can be easily written down in the case of static emitters:

\begin{matrix} γ_{1} (τ^{1}) = τ^{1} e_{0} + d_{1}, γ_{2} (τ^{2}) = τ^{2} e_{0} + d_{2}, γ_{3} (τ^{3}) = τ^{3} e_{0} + d_{3}, γ_{4} (τ^{4}) = τ^{4} e_{0}, \end{matrix}

(51)

where

d_{a}

are the position vectors, with respect to the fourth emitter, of the other three emitters:

\begin{matrix} d_{1} = (0, a, 0, 0), d_{2} = (0, 0, b, 0), d_{3} = (0, 0, 0, c), \end{matrix}

(52)

with

{a, b, c}

real constants and where we have switched to component notation, the first component being the coordinate time

x^{0}

. We can now write the position vector of the referred emitters with respect to the reference emitter:

\begin{matrix} e_{1} = T_{1} e_{0} + d_{1}, e_{2} = T_{2} e_{0} + d_{2}, e_{3} = T_{3} e_{0} + d_{3}, \end{matrix}

(53)

where

T_{a} \equiv τ^{a} - τ^{4}

. Then, substituting (53) in (11), we obtain the covariant components of the configuration vector

χ

\begin{matrix} {[χ]}_{α} = a b c (- 1, q_{1}, q_{2}, q_{3}), \end{matrix}

(54)

where

q_{1} = \frac{T_{1}}{a}, q_{2} = \frac{T_{2}}{b}, q_{3} = \frac{T_{3}}{c} .

The Cartesian product

Q \equiv [q_{1}] [q_{2}] [q_{3}] \approx R^{3}

is included in the grid

T

of the positioning system and will be called the

Q

-grid (quotient grid) according to the meaning of the triads

(q_{1}, q_{2}, q_{3}) \in Q

given below. Figure 1 shows the emitters’ arrangement in the

Q

-grid (see Equations (76) and (77)).

According to (9), the emission/reception conditions are written as

| q_{a} | < 1, | a q_{1} - b q_{2} | < \sqrt{a^{2} + b^{2}}, | a q_{1} - b q_{3} | < \sqrt{a^{2} + c^{2}}, | b q_{2} - c q_{3} | < \sqrt{b^{2} + c^{2}},

(55)

and the emission condition as

a b c λ > 0,

(56)

with

λ

given by (17) in terms of

y_{*}, χ

and

\hat{ϵ}

7.2. Computing the RPS Quantities

To compute the particular solution

y_{*}

(12), we begin by setting

ξ = γ_{4} = τ^{4} e_{0}

ξ \cdot χ = - a b c τ^{4} .

(57)

To obtain

H = Ω_{a} E^{a}

, we calculate the world-function scalars

Ω_{a} = \frac{1}{2} {(e_{a})}^{2}

from (53):

\begin{matrix} Ω_{1} = \frac{1}{2} (a^{2} - T_{1}^{2}), Ω_{2} = \frac{1}{2} (b^{2} - T_{2}^{2}), Ω_{3} = \frac{1}{2} (c^{2} - T_{3}^{2}), \end{matrix}

(58)

and the bivectors

E^{a}

from (14) substituing (53):

\begin{matrix} E^{1} = & * (T_{2} e_{0} \land d_{3}) - * (T_{3} e_{0} \land d_{2}) + * (d_{2} \land d_{3}), \\ E^{2} = & * (T_{3} e_{0} \land d_{1}) - * (T_{1} e_{0} \land d_{3}) - * (d_{1} \land d_{3}), \\ E^{3} = & * (T_{1} e_{0} \land d_{2}) - * (T_{2} e_{0} \land d_{1}) + * (d_{1} \land d_{2}) . \end{matrix}

(59)

Computing the contractions

i (ξ = γ_{4}) E^{a}

using (3):

i (τ^{4} e_{0}) E^{1} = (0, - τ^{4} b c, 0, 0), i (τ^{4} e_{0}) E^{2} = (0, 0, - τ^{4} a c, 0), i (τ^{4} e_{0}) E^{3} = (0, 0, 0, - τ^{4} a b),

yields the covariant components of the particular solution

y_{*}

from (12)-(14), using (57) and (58):

{[y_{*}]}_{α} = \frac{1}{2} (0, a (1 - q_{1}^{2}), b (1 - q_{2}^{2}), c (1 - q_{3}^{2})) .

(60)

To obtain the user’s inertial coordinates from (16), we need the following to calculate

λ

from (17):

\begin{matrix} y_{*} \cdot χ = & \frac{1}{2} a b c [a q_{1} (1 - q_{1}^{2}) + b q_{2} (1 - q_{2}^{2}) + c q_{3} (1 - q_{3}^{2})], \end{matrix}

(61)

\begin{matrix} y_{*}^{2} = & \frac{1}{4} [a^{2} {(1 - q_{1}^{2})}^{2} + b^{2} {(1 - q_{2}^{2})}^{2} + c^{2} {(1 - q_{3}^{2})}^{2}], \end{matrix}

(62)

\begin{matrix} χ^{2} = & a^{2} b^{2} c^{2} (- 1 + q_{1}^{2} + q_{2}^{2} + q_{3}^{2}), \end{matrix}

(63)

as it follows from (54) and (60). Then, by substitution in (18),

\begin{matrix} Δ = & {(y_{*} \cdot χ)}^{2} - y_{*}^{2} χ^{2} \\ = & \frac{1}{4} a^{2} b^{2} c^{2} [2 a b q_{1} q_{2} (1 - q_{1}^{2}) (1 - q_{2}^{2}) + 2 a c q_{1} q_{3} (1 - q_{1}^{2}) (1 - q_{3}^{2}) + 2 b c q_{2} q_{3} (1 - q_{2}^{2}) (1 - q_{3}^{2}) \\ + a^{2} {(1 - q_{1}^{2})}^{2} (1 - q_{2}^{2} - q_{3}^{2}) + b^{2} {(1 - q_{2}^{2})}^{2} (1 - q_{1}^{2} - q_{3}^{2}) + c^{2} {(1 - q_{3}^{2})}^{2} (1 - q_{1}^{2} - q_{2}^{2})] . \end{matrix}

(64)

Notice that

Δ

is an even symmetric function,

Δ (q_{1}, q_{2}, q_{3}) = Δ (- q_{1}, - q_{2}, - q_{3})

, which is symmetric about the origin. With these quantities we can express the coordinate transformation

x^{α} (τ^{A})

using (16)-(18).

7.3. Interpretation of the RPS Solution

In order to remark the essential properties of the RPS solution, let us consider the inertial coordinate location of those users whose emission coordinates satisfy the restrictions

q_{1} = q_{2} = q

and

q_{3} = \pm q

. Then, expressions (60)-(64) simplify and their substitution in (16) gives:

\begin{matrix} x^{α} (τ + a q, τ + b q, τ \pm c q, τ) = (τ, 0, 0, 0) + \frac{1}{2} (1 - q^{2}) (0, a, b, c) + λ a b c (1, q, q, \pm q), \end{matrix}

(65)

with

τ^{4} \equiv τ

, that is,

γ_{4} (τ) = τ e_{0}

, and

\begin{matrix} λ (q, q, \pm q) = - \frac{(1 - q^{2}) (a^{2} + b^{2} + c^{2})}{2 a b c [(a + b \pm c) q + \hat{ϵ} ν \sqrt{q^{2} {(a + b \pm c)}^{2} + (1 - 3 q^{2}) (a^{2} + b^{2} + c^{2})}]}, \end{matrix}

(66)

where

ν \equiv s g n (a b c) = s g n (χ^{0}) .

Then (65) will be an emission solution iff, in addition to (55) and

Δ \geq 0

, Equation (56) holds, with

λ

given by (66), that is,

(a + b \pm c) q + \hat{ϵ} ν \sqrt{q^{2} {(a + b \pm c)}^{2} + (1 - 3 q^{2}) (a^{2} + b^{2} + c^{2})} < 0 .

(67)

Table 2 shows the result assuming

q_{1} = q_{2} = q_{3} = q

for different values of q, where for the sake of clarity we have taken

a = b = c = 1

and thus

Δ (q, q, q) = \frac{3}{4} {(1 - q^{2})}^{2}

(i): For $q = 0$ , the emitter configuration is space-like at $x^{α} = (τ + \frac{\sqrt{3}}{2}, \frac{1}{2}, \frac{1}{2}, \frac{1}{2})$ , which is the sole emission solution (with $\hat{ϵ} = - 1$ ). The solution with $\hat{ϵ} = 1$ is a reception solution.
(ii): For $q = - \sqrt{\frac{1}{3}}$ , the emitter configuration is light-like at $x^{α} = (τ + \frac{1}{2 \sqrt{3}}, \frac{1}{6}, \frac{1}{6}, \frac{1}{6})$ , which is the sole emission solution (with $\hat{ϵ} = - 1$ ). The solution with $\hat{ϵ} = 1$ is degenerate.
(iii): For $q = - \sqrt{\frac{2}{3}}$ , the emitter configuration is time-like at

$x_{\mp}^{α} = (τ + \frac{\sqrt{2} \mp 1}{2 \sqrt{3}}, \frac{1}{6} (\pm \sqrt{2} - 1), \frac{1}{6} (\pm \sqrt{2} - 1), \frac{1}{6} (\pm \sqrt{2} - 1)),$

both being emission solutions (with $\hat{ϵ} = \mp 1$ ); $x_{-} (x_{+})$ is in the front (back) emission coordinate domain.

Similarly, Table 3 shows the result assuming

q_{1} = q_{2} = q

and

q_{3} = - q

for different values of q, where again we have taken

a = b = c = 1

and thus

Δ (q, q, - q) = \frac{1}{4} {(1 - q^{2})}^{2} (3 - 8 q^{2})

7.4. Computing Bancroft’s Quantities

In order to relate the RPS and Bancroft’s expression of the solution to the location problem, we begin by writing the matrix

A

given by (25), whose columns are the emitters’ world-lines (51):

A = (τ^{1} e_{0} + d_{1}; τ^{2} e_{0} + d_{2}; τ^{3} e_{0} + d_{3}; τ^{4} e_{0}) .

(68)

In component notation:

A = (\begin{matrix} τ^{1} & τ^{2} & τ^{3} & τ^{4} \\ a & 0 & 0 & 0 \\ 0 & b & 0 & 0 \\ 0 & 0 & c & 0 \end{matrix}) .

(69)

To calculate

A^{- 1}

, we verify that:

\begin{matrix} d e t (A) = & - * (γ_{1} \land γ_{2} \land γ_{3} \land γ_{4}) \\ = & - * [(τ^{1} e_{0} + d_{1}) \land (τ^{2} e_{0} + d_{2}) \land (τ^{3} e_{0} + d_{3}) \land τ^{4} e_{0}] \\ = & - τ^{4} * (d_{1} \land d_{2} \land d_{3} \land e_{0}) = τ^{4} a b c η_{0123} = - τ^{4} a b c, \end{matrix}

(70)

and that the row vectors (1-forms)

Γ^{i}

, appearing in (33) and given by (34), are expressed as:

\begin{matrix} Γ^{1} = & - b c τ^{4} θ^{1}, Γ^{2} = - a c τ^{4} θ^{2}, Γ^{3} = - a b τ^{4} θ^{3}, \\ Γ^{4} = & - a b c θ^{0} + b c τ^{1} θ^{1} + a c τ^{2} θ^{2} + a b τ^{3} θ^{3}, \end{matrix}

(71)

where

{θ^{0}, θ^{1}, θ^{2}, θ^{3}}

is the dual basis of the inertial cartesian basis.

Now we can write

A^{- 1}

A^{- 1} = (\begin{matrix} 0 & \frac{1}{a} & 0 & 0 \\ 0 & 0 & \frac{1}{b} & 0 \\ 0 & 0 & 0 & \frac{1}{c} \\ \frac{1}{τ^{4}} & - \frac{τ^{1}}{τ^{4} a} & - \frac{τ^{2}}{τ^{4} b} & - \frac{τ^{3}}{τ^{4} c} \end{matrix}),

(72)

and then compute the vector u and verify (41):

\begin{matrix} {[u]}_{α} = & {[d e t (A)]}^{- 1} \sum_{i = 1}^{4} Γ^{i} = (\frac{1}{τ^{4}}, \frac{1}{a} (1 - \frac{τ^{1}}{τ^{4}}), \frac{1}{b} (1 - \frac{τ^{2}}{τ^{4}}), \frac{1}{c} (1 - \frac{τ^{3}}{τ^{4}})) \\ = & \frac{1}{τ^{4}} (1, - q_{1}, - q_{2}, - q_{3}) = \frac{1}{d e t (A)} {[χ]}_{α} . \end{matrix}

(73)

The vector v is obtained from (40), by substitution of (70), (71) and (24) with

r_{1} = \frac{1}{2} (a^{2} - {(τ^{1})}^{2}), r_{2} = \frac{1}{2} (b^{2} - {(τ^{2})}^{2}), r_{3} = \frac{1}{2} (c^{2} - {(τ^{3})}^{2}), r_{4} = - \frac{1}{2} {(τ^{4})}^{2} .

(74)

After simplification, it results:

{[v]}_{α} = \frac{1}{2} (- τ^{4}, a - τ^{1} q_{1}, b - τ^{2} q_{2}, c - τ^{3} q_{3}) .

(75)

We can substitute (73)-(75) and

γ_{4} = τ^{4} e_{0}

in Equation (42) and check that it is satisfied.

To compute the user’s coordinates from Bancroft’s solution (26), with

ρ

as in (31) or (32), we need the following expressions for E, F and G, which follow from (73) and (75) by scalar product:

\begin{matrix} E = & u^{2} = \frac{1}{{(τ^{4})}^{2}} (- 1 + q_{1}^{2} + q_{2}^{2} + q_{3}^{2}) . \end{matrix}

\begin{matrix} F = & u \cdot v - 1 = - \frac{1}{2} [1 + \frac{q_{1}}{τ^{4}} (a - τ^{1} q_{1}) + \frac{q_{2}}{τ^{4}} (b - τ^{2} q_{2}) + \frac{q_{3}}{τ^{4}} (c - τ^{3} q_{3})] . \end{matrix}

\begin{matrix} G = & v^{2} = \frac{1}{4} [- {(τ^{4})}^{2} + {(a - τ^{1} q_{1})}^{2} + {(b - τ^{2} q_{2})}^{2} + {(c - τ^{3} q_{3})}^{2}] . \end{matrix}

Notice that Bancroft’s quantities E, F and G involve the emission coordinates

{τ^{A}}

in addition to

{q_{1}, q_{2}, q_{3}}

. In contrast, the RPS quantities

χ^{2}, y_{*}^{2}

and

χ \cdot y_{*}

are polynomial functions only of the

{q_{a}}

variables. This property simplifies the representation of the RPS regions in the

Q

-grid, which is carried out in the next section.

8. Four Static Emitters: Representations

In this section we continue with the preceding example. The characteristic regions of the RPS solution are represented both in Cartesian and in emission coordinates.

8.1. Representations in Cartesian Coordinates

Figure 2 shows, for a given

x^{0}

value (inertial instant), the emission configuration regions

C_{s}

(space-like),

C_{l}

(light-like) and

C_{t}

(time-like) which are colored in green, red and blue, respectively. The

C_{t}

region is the union of two disjoint regions, denoted by

C_{t}

-front and

C_{t}

-back, separated by the 3-surface

Δ (x^{0}, x^{1}, x^{2}, x^{3}) = 0

, which is shown in black. This 3-surface, where the Jacobian determinant of

τ^{A} (x^{α})

vanishes, is the border between the front (

C_{s} \cup C_{l} \cup C_{t}

-front) and the back (

C_{t}

-back) coordinate domains. The union of both disjoint domains is called the emission coordinate region

C

[9,10].

Figure 2. Representation of the emission configuration regions for a RPS with four static emitters (when

a = b = c = 1

). The emission configuration regions

C_{s}

(space-like),

C_{l}

(light-like) and

C_{t}

(time-like) are colored in green, red and blue, respectively. The 3-surface where

Δ

vanishes is shown in black.

Figure 2. Representation of the emission configuration regions for a RPS with four static emitters (when

a = b = c = 1

). The emission configuration regions

C_{s}

(space-like),

C_{l}

(light-like) and

C_{t}

(time-like) are colored in green, red and blue, respectively. The 3-surface where

Δ

vanishes is shown in black.

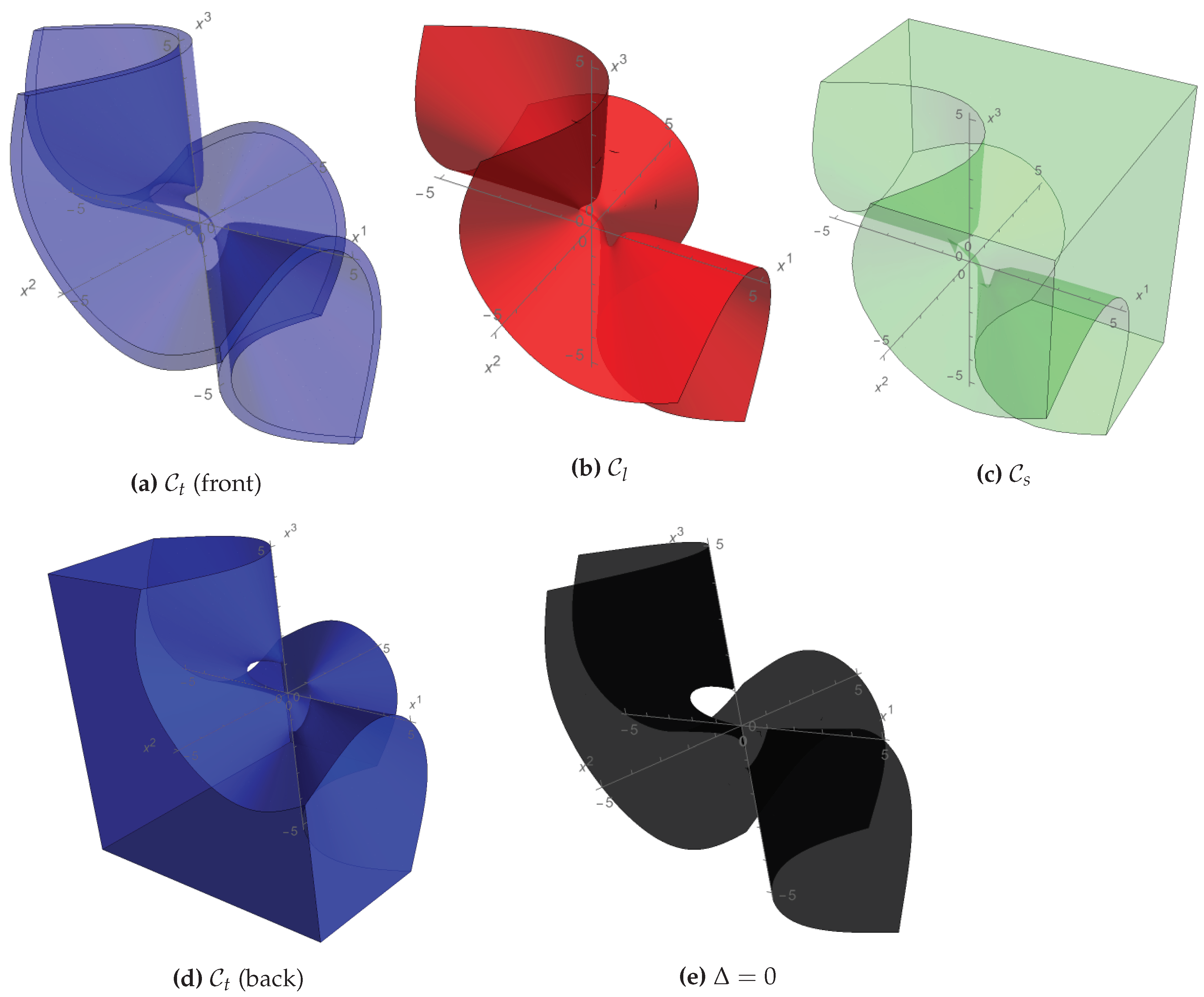
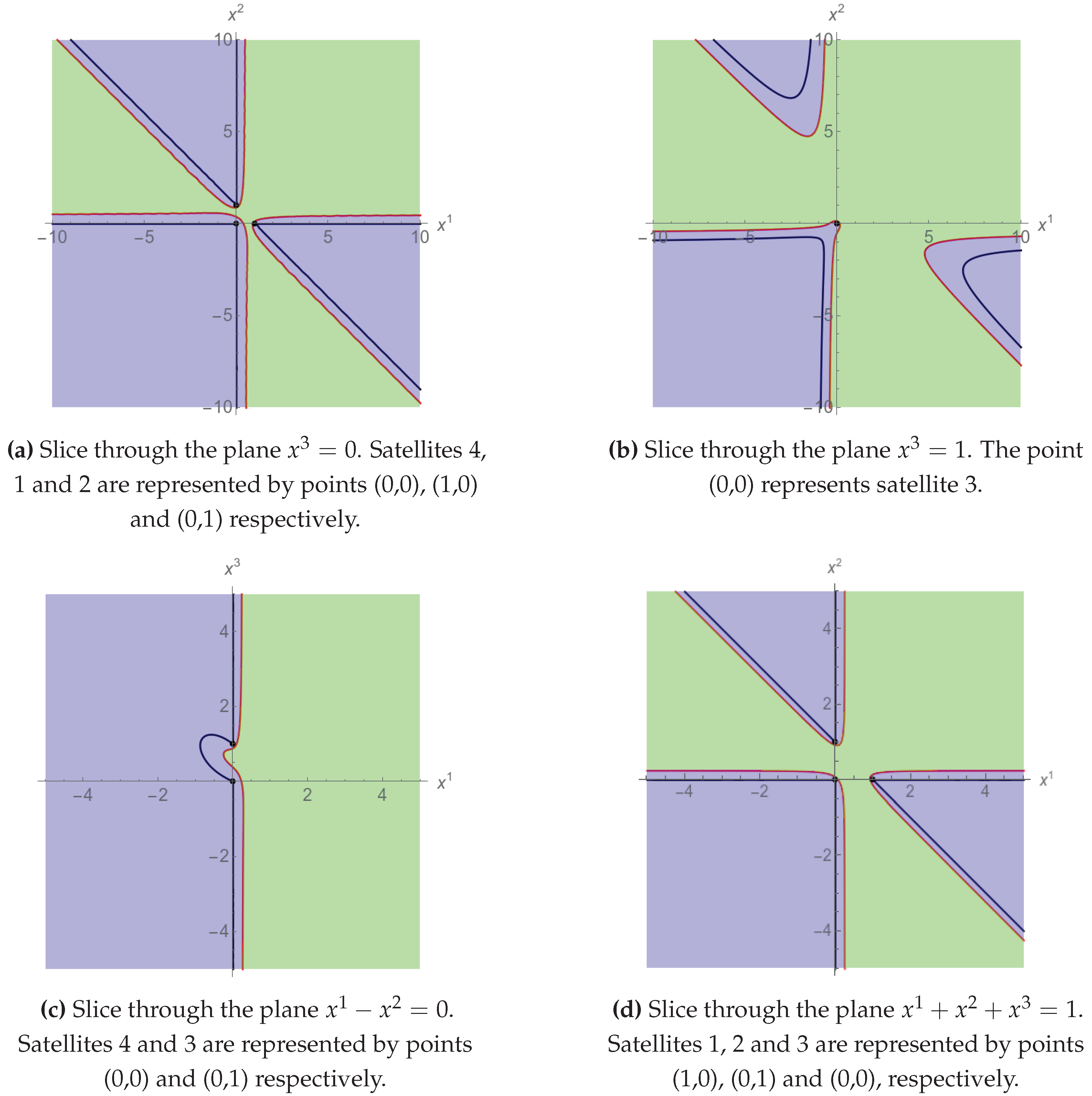
Figure 3 includes two dimensional slices of the emission configuration regions shown in Figure 2. The black points represent the satellite trajectories. The intersection with

Δ = 0

is also represented.

Figure 3. Slices of the emission configuration regions (shown in Figure 2) through different 2-planes. Black points represent the satellites.

8.2. Representations in the $Q$ -Grid

Since the emitters’ trajectories

{γ_{A}}

in inertial coordinates are known from (51), we can obtain their positions

S_{A}

in the

Q

-grid, as well as their trajectories

γ_{A}

in the grid

T

. For

a = b = c = 1

we have

\begin{matrix} S_{1} = & (1, 1 - \sqrt{2}, 1 - \sqrt{2}), S_{2} = (1 - \sqrt{2}, 1, 1 - \sqrt{2}), \end{matrix}

(76)

\begin{matrix} S_{3} = & (1 - \sqrt{2}, 1 - \sqrt{2}, 1), S_{4} = (- 1, - 1, - 1), \end{matrix}

(77)

and

\begin{matrix} γ_{1} = & (1 + τ, 1 - \sqrt{2} + τ, 1 - \sqrt{2} + τ, τ), γ_{2} = (1 - \sqrt{2} + τ, 1 + τ, 1 - \sqrt{2} + τ, τ), \\ γ_{3} = & (1 - \sqrt{2} + τ, 1 - \sqrt{2} + τ, 1 + τ, τ), γ_{4} = (- 1 + τ, - 1 + τ, - 1 + τ, τ), with τ = τ^{4}, \end{matrix}

which are straight lines in the direction defined by

(1, 1, 1, 1) \in T

. In other words, the (parallel) emitter world-lines are represented as parallel lines in the grid

T

along the direction defined by the main bisectrix. Each

γ_{A}

is represented by the corresponding point

S_{A}

in the quotient grid

Q

. Figure 1 is a representation of the emitters in the

Q

-grid.

The boundary of the emission/reception conditions (55) defines twelve 2-planes in the

Q

-grid, which are denoted by

S_{A B}

A \neq B

S_{A B}

is the representation in the

Q

-grid of the shadow that satellite A produces to satellite B. Concretely, for

a = b = c = 1

we have,

\begin{matrix} S_{12} : q_{1} - q_{2} = \sqrt{2}, & S_{13} : q_{1} - q_{3} = \sqrt{2}, & S_{14} : q_{1} = 1, \\ S_{21} : q_{1} - q_{2} = - \sqrt{2}, & S_{23} : q_{2} - q_{3} = \sqrt{2}, & S_{24} : q_{2} = 1, \\ S_{31} : q_{1} - q_{3} = - \sqrt{2}, & S_{32} : q_{2} - q_{3} = - \sqrt{2}, & S_{34} : q_{3} = 1, \\ S_{41} : q_{1} = - 1, & S_{42} : q_{2} = - 1, & S_{43} : q_{3} = - 1 . \end{matrix}

(78)

Figure 4 contains representations in the

Q

-grid for

a = b = c = 1

. Figure 4 represents the convex polyhedron formed by pieces of the twelve satellite shadows (78). It has

12 = 6 + 6

faces (six squares with side length

\sqrt{2}

and six rhomboids with side lengths

\sqrt{2}

and

2 (\sqrt{2} - 1)

), that is, a dodecahedron, which we may call the shadow-dodecahedron

D

. The fourteen vertices of

D

are, apart from

S_{4}

and

- S_{4}

, the following points:

\begin{matrix} V_{1} = (1, 1, 1 - \sqrt{2}), & V_{2} = (1, 1 - \sqrt{2}, 1), & V_{3} = (1 - \sqrt{2}, 1, 1), \\ V_{4} = (1, 1 - \sqrt{2}, 1 - \sqrt{2}), & V_{5} = (1 - \sqrt{2}, 1, 1 - \sqrt{2}), & V_{6} = (1 - \sqrt{2}, 1 - \sqrt{2}, 1) \end{matrix}

and their opposites. The interior of

D

contains the

Q

-grid points that satisfy the emission/reception conditions (55). Figure 4 shows the surface of vanishing Jacobian determinant of the coordinate transformation

τ^{A} (x^{α})

, equivalently

Δ (q_{1}, q_{2}, q_{3}) = 0

, in the

Q

-grid. This surface is strictly confined inside

D

. The interior of this surface satisfies

Δ (q_{1}, q_{2}, q_{3}) > 0

and corresponds to solutions of the null propagation equations. The region inside

D

satisfying

Δ (q_{1}, q_{2}, q_{3}) < 0

does not represent any physical region in the

Q

-grid.

Figure 4. Representation of the surface

Δ (q_{1}, q_{2}, q_{3}) = 0

in the

Q

-grid region where the emission/reception conditions are satisfied (with

a = b = c = 1

), which is bounded by

D

Figure 4. Representation of the surface

Δ (q_{1}, q_{2}, q_{3}) = 0

in the

Q

-grid region where the emission/reception conditions are satisfied (with

a = b = c = 1

), which is bounded by

D

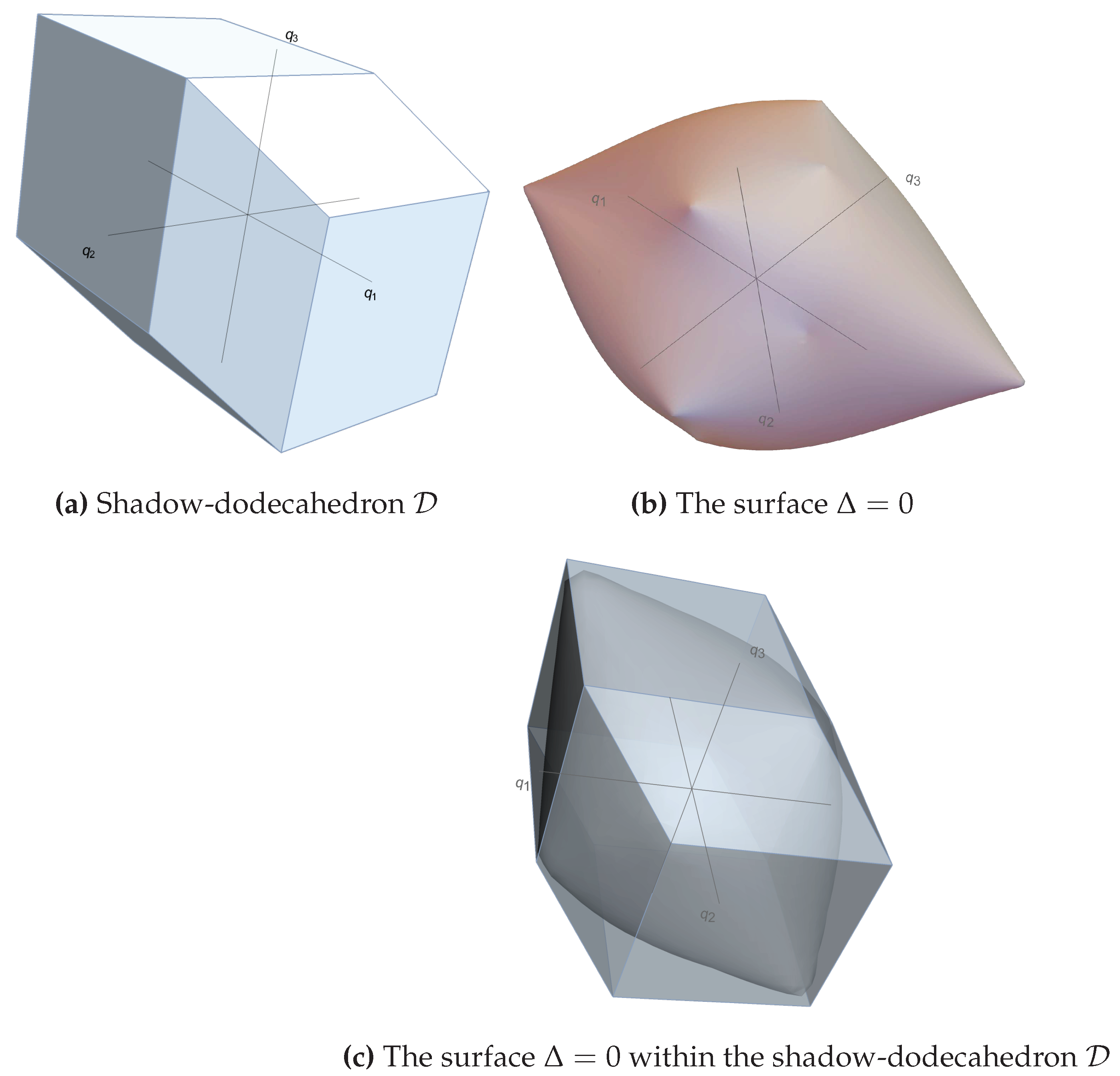
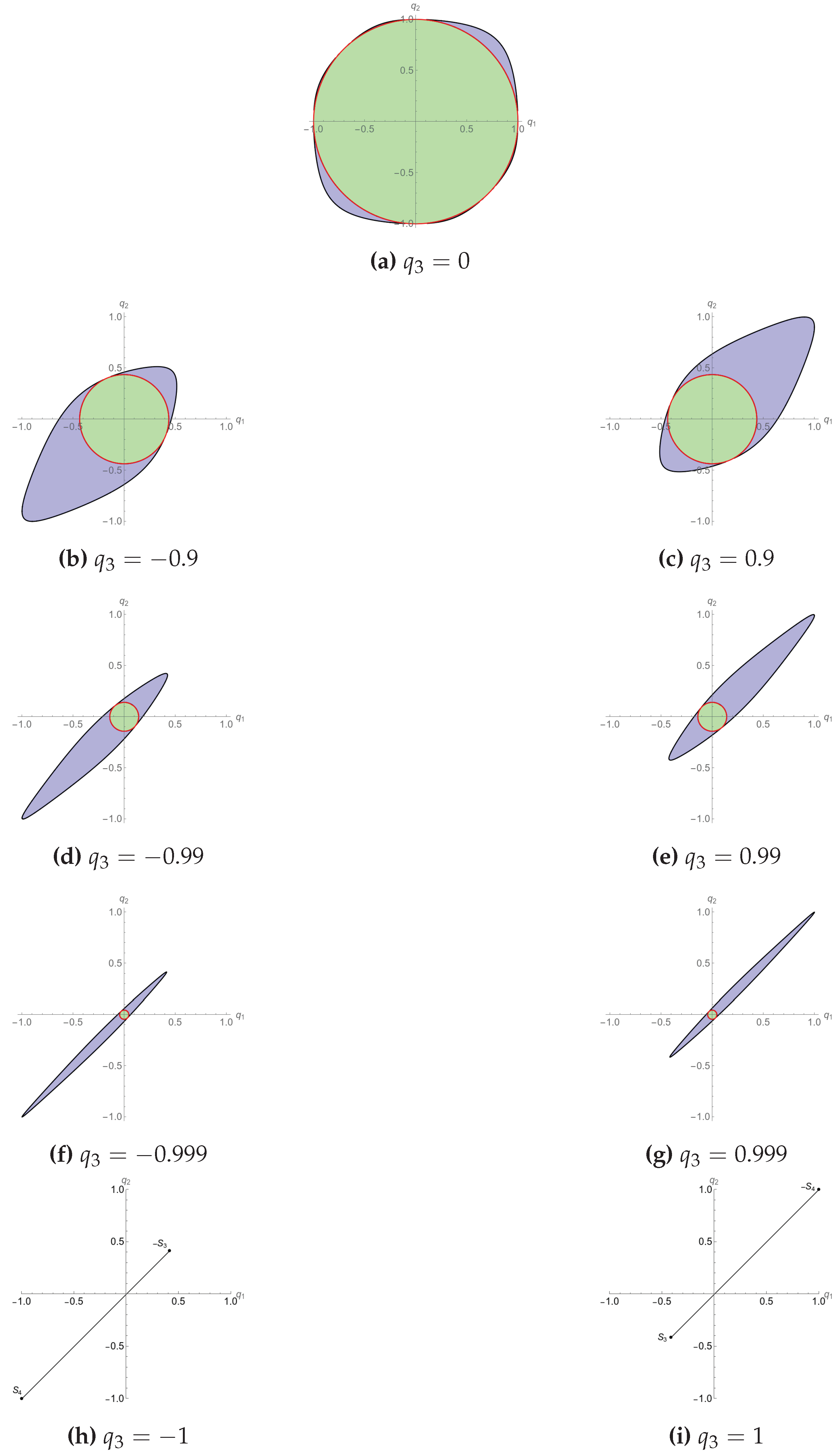
Figure 5 shows two dimensional slices of the configuration regions in the

Q

-grid, applying the emission/reception conditions (55) for

a = b = c = 1

. The colors green, red and blue are used for the space-like, light-like or time-like character of the configuration, respectively. The black lines are different slices of the 2-surface

Δ (q_{1}, q_{2}, q_{3}) = 0

. For clarity, the intersections with the shadow-dodecahedron are not shown.

Figure 5. Representation of the emitter configuration regions in the

Q

-grid for different values of

q_{3}

when

a = b = c = 1

. The colors green, red and blue are used for the space-like, light-like or time-like character of the configuration, respectively. The black lines are different level cuts of the 2-surface

Δ (q_{1}, q_{2}, q_{3}) = 0

. For

q_{3} = - 1

(

q_{3} = 1

) the points shown are

S_{4}

and

- S_{3}

(

S_{3}

and

- S_{4}

), with

S_{3}

and

S_{4}

the third and fourth satellite, respectively, given by (77).

Figure 5. Representation of the emitter configuration regions in the

Q

-grid for different values of

q_{3}

when

a = b = c = 1

. The colors green, red and blue are used for the space-like, light-like or time-like character of the configuration, respectively. The black lines are different level cuts of the 2-surface

Δ (q_{1}, q_{2}, q_{3}) = 0

. For

q_{3} = - 1

(

q_{3} = 1

) the points shown are

S_{4}

and

- S_{3}

(

S_{3}

and

- S_{4}

), with

S_{3}

and

S_{4}

the third and fourth satellite, respectively, given by (77).

9. Emission-Reception Conditions and Grid Regions

Figure 1b, Figure 4 and Figure 5 provide representations in the

Q

-grid of the standard positioning data and the elements derived from these data. In this section, we use the

Q

-grid representations to obtain further information about other regions where solutions to the null propagation equations (1) exist, without imposing all of the emission/reception conditions (55). We analyze a mixture of emission and reception conditions that apply to other location systems [1,2] based on null coordinates such as reception or radar coordinates. For an analysis of the notion of a location system (physical realization of a coordinate system) see [5] and previous references quoted therein.

Figure 6 shows the surfaces in the

Q

-grid defined by

Δ (q_{1}, q_{2}, q_{3}) = 0

, in whose interior there is a solution to the null propagation equations. There exist fifteen disjoint regions satisfying

Δ > 0

. The exterior of this surface (

Δ < 0

) has no physical meaning. The interior (

Δ > 0

) is the

Q

-grid representation of the solutions to the null propagation equations and is disjointly divided in fifteen regions. Only one region contains the origin and is divided in two subregions where all the emission/reception conditions are satisfied (see Figure 4). Among the fourteen remaining regions eight satisfy only three emission/reception conditions (each one is confined by three pairs of parallel planes). The other six satisfy only two emission/reception conditions (each one is confined by two pairs of parallel planes).

Table 4 shows the signs of the products

m_{A} \cdot m_{B}

(

A \neq B

) and the related regions.The emission or reception character of a

τ^{A}

-coordinate is denoted by e or r respectively.

The results of this section may be compared with those presented in [7,8] regarding the 2D localization of a source with three receivers. In particular, there is an interesting similarity between the surface of vanishing Jacobian (Fig. Figure 6) and the Kummer surface represented in Figure 4 of [8]. The surface shown in Figure 6 has a total of thirty-two singular points, eight of them on the central piece and twenty-four on the tube-like pieces, each of these points connecting the different pieces that make up the surface. In addition to

S_{A}

and

- S_{A}

, the surface has the following singular points:

\begin{matrix} N_{1} = (- 1, 1, 1), & N_{2} = (1, - 1, 1), & N_{3} = (1, 1, - 1), \\ N_{4} = (1, 1 - \sqrt{2}, 1 + \sqrt{2}), & N_{5} = (1 - \sqrt{2}, 1, 1 + \sqrt{2}), & N_{6} = (1 - \sqrt{2}, 1 + \sqrt{2}, 1), \\ N_{7} = (1, 1 + \sqrt{2}, 1 - \sqrt{2}), & N_{8} = (1 + \sqrt{2}, 1, 1 - \sqrt{2}), & N_{9} = (1 + \sqrt{2}, 1 - \sqrt{2}, 1), \\ N_{10} = (1, 1 + \sqrt{2}, 1 + \sqrt{2}), & N_{11} = (1 + \sqrt{2}, 1, 1 + \sqrt{2}), & N_{12} = (1 + \sqrt{2}, 1 + \sqrt{2}, 1), \end{matrix}

and their opposites. Of these singular points, only

S_{4}

and

- S_{4}

are also vertices of

D

Figure 7 shows the cuts of the surface

Δ (q_{1}, q_{2}, q_{3}) = 0

with the different planes

q_{3} = c o n s t a n t

. Similar cuts are obtained for constant values of

q_{1}

q_{2}

10. Conclusions

The RPS approach to GNSSs is grounded in the fundamental principles of relativity on which, one might think, navigation systems should be based. Current GNSSs rely on a posteriori corrections for (special) relativistic effects (and for gravitational, atmospheric and instrumental effects). In this paper we have deduced a classical solution to the navigation equations, Bancroft’s solution, which is still in use today, within a relativistic framework. In fact, Bancroft’s closed-form solution is suitable for this purpose, since it already incorporates four-vectors and a Minkowski scalar product, although it still presumes a universal time and a deviation from it (the clock offset). We have recovered Bancroft’s solution from the RPS solution using the language of relativity: contravariant (column) and covariant (row) vectors, their inner (scalar) product and their exterior algebra.

The characteristic elements of a RPS (emission and configuration regions, front and back coordinate domains, shadows produced by the satellites to each other, etc.) have been exemplified for the static situation. These regions are represented both in the physical and in the grid space of the RPS, by introducing an appropiate quotienting procedure. This kind of representation has been tentatively studied for other location systems for which not all the emission/reception conditions are assumed. However, to deal with general location systems, the RPS terminology should be appropriately adapted.

All of this with the hope of bringing the traditional GNSS approach closer to the framework of Relativity Theory, a worthwhile task, if only from a scientific perspective.

[custom]

Author Contributions

Both authors contributed equally to develop the idea of the manuscript and have read and agreed to the published version of the manuscript.

Funding

We would like to thank the support from the Spanish Ministerio de Ciencia, Innovación y Universidades, Projects PID2019-109753GB-C21/AEI/10.13039/501100011033 and PID2019-109753GB-C22/AEI/10.13039/501100011033 and from the Conselleria d’Educació, Universitats i Ocupació, Generalitat Valenciana, Project CIAICO/2022/252.

Institutional Review Board Statement

Not applicable

Informed Consent Statement

Not applicable

Data Availability Statement

Not applicable

Acknowledgments

We would like to thank the /Universe/ Editorial Office at MDPI for the invitation to submit this manuscript free of charge.

Conflicts of Interest

The authors declare no conflict of interest.

References

Coll, B. Relativistic positioning systems: perspectives and prospects. Acta Futura 2013, 7, 35–47. [Google Scholar] [CrossRef]
Coll, B. Epistemic Relativity: An Experimental Approach to Physics; Springer International Publishing, 2019; pp. 291–315. [CrossRef]
Coll, B.; Pozo, J.M. Relativistic positioning systems: the emission coordinates. Classical and Quantum Gravity 2006, 23, 7395. [Google Scholar] [CrossRef]
Pozo, J. Constructions in 3D (I) and (II); Talks delivered at the School on Relativistic Coordinates, Reference and Positioning Systems (University of Salamanca, Spain), 2005.
Coll, B.; Ferrando, J.J.; Morales, J.A. Two-dimensional approach to relativistic positioning systems. Phys. Rev. D 2006, 73, 084017. [Google Scholar] [CrossRef]
Coll, B.; Ferrando, J.J.; Morales, J.A. Positioning with stationary emitters in a two-dimensional space-time. Phys. Rev. D 2006, 74, 104003. [Google Scholar] [CrossRef]
Compagnoni, M.; Notari, R.; Antonacci, F.; Sarti, A. A comprehensive analysis of the geometry of TDOA maps in localization problems. Inverse Problems 2014, 30, 035004. [Google Scholar] [CrossRef]
Compagnoni, M.; Notari, R.; Ruggiu, A.A.; Antonacci, F.; Sarti, A. The Algebro-geometric Study of Range Maps. Journal of Nonlinear Science 2017, 27, 99–157. [Google Scholar] [CrossRef]
Coll, B.; Ferrando, J.J.; Morales-Lladosa, J.A. Positioning systems in Minkowski spacetime: from emission to inertial coordinates. Classical and Quantum Gravity 2010, 27, 065013. [Google Scholar] [CrossRef]
Coll, B.; Ferrando, J.J.; Morales-Lladosa, J.A. Positioning systems in Minkowski space-time: Bifurcation problem and observational data. Phys. Rev. D 2012, 86, 084036. [Google Scholar] [CrossRef]
Strang, G.; Borre, K. Linear Algebra, Geodesy, and GPS; Wellesley-Cambridge Press, 1997. [Google Scholar]
Closas, P.; Gusi-Amigo, A. Direct Position Estimation of GNSS Receivers: Analyzing main results, architectures, enhancements, and challenges. IEEE Signal Processing Magazine 2017, 34, 72–84. [Google Scholar] [CrossRef]
Vincent, F.; Vilà-Valls, J.; Besson, O.; Medina, D.; Chaumette, E. Doppler-aided positioning in GNSS receivers - A performance analysis. Signal Processing 2020, 176, 107713. [Google Scholar] [CrossRef]
Compagnoni, M.; Notari, R.; Antonacci, F.; Sarti, A. On the statistical model of source localization based on Range Difference measurements. Journal of the Franklin Institute 2017, 354, 7183–7214. [Google Scholar] [CrossRef]
Bancroft, S. An Algebraic Solution of the GPS Equations. IEEE Transactions on Aerospace and Electronic Systems 1985, AES-21, 59–59. [Google Scholar] [CrossRef]
Abel, J.; Chaffee, J. Existence and uniqueness of GPS solutions. IEEE Transactions on Aerospace and Electronic Systems 1991, 27, 952–956. [Google Scholar] [CrossRef]
Chaffee, J.; Abel, J. On the exact solutions of pseudorange equations. IEEE Transactions on Aerospace and Electronic Systems 1994, 30, 1021–1030. [Google Scholar] [CrossRef]
Ruggiero, M.L.; Tartaglia, A.; Casalino, L. Geometric definition of emission coordinates. Advances in Space Research 2022, 69, 4221–4227. [Google Scholar] [CrossRef]
Feng, J.C.; Hejda, F.; Carloni, S. Relativistic location algorithm in curved spacetime. Phys. Rev. D 2022, 106, 044034. [Google Scholar] [CrossRef]
Serrano Montesinos, R.; Morales-Lladosa, J.A. Bancroft’s GPS navigation solution: relativistic interpretation; I.U. de Matemática Multidisciplinar, Universitat Politècnica de València, 2023; pp. 150–157.
Coll, B.; Pozo, J.M. General Causal Properties of Emission Coordinates. Preprint (private communication). 2006. [Google Scholar]
Coll, B.; Ferrando, J.J.; Morales-Lladosa, J.A. Newtonian and relativistic emission coordinates. Phys. Rev. D 2009, 80, 064038. [Google Scholar] [CrossRef]

Figure 6. Representation of the surface

Δ (q_{1}, q_{2}, q_{3}) = 0

in the

Q

-grid for

a = b = c = 1

. The closed piece at the centre is represented in Figure 4.

Figure 6. Representation of the surface

Δ (q_{1}, q_{2}, q_{3}) = 0

in the

Q

-grid for

a = b = c = 1

. The closed piece at the centre is represented in Figure 4.

Figure 7. Representation in the

Q

-grid of the level lines

Δ (q_{1}, q_{2}, q_{3} = k) = 0

for different values of k and with

a = b = c = 1

. The points in Figure 7 and Figure 7 are singular points.

Figure 7. Representation in the

Q

-grid of the level lines

Δ (q_{1}, q_{2}, q_{3} = k) = 0

for different values of k and with

a = b = c = 1

. The points in Figure 7 and Figure 7 are singular points.

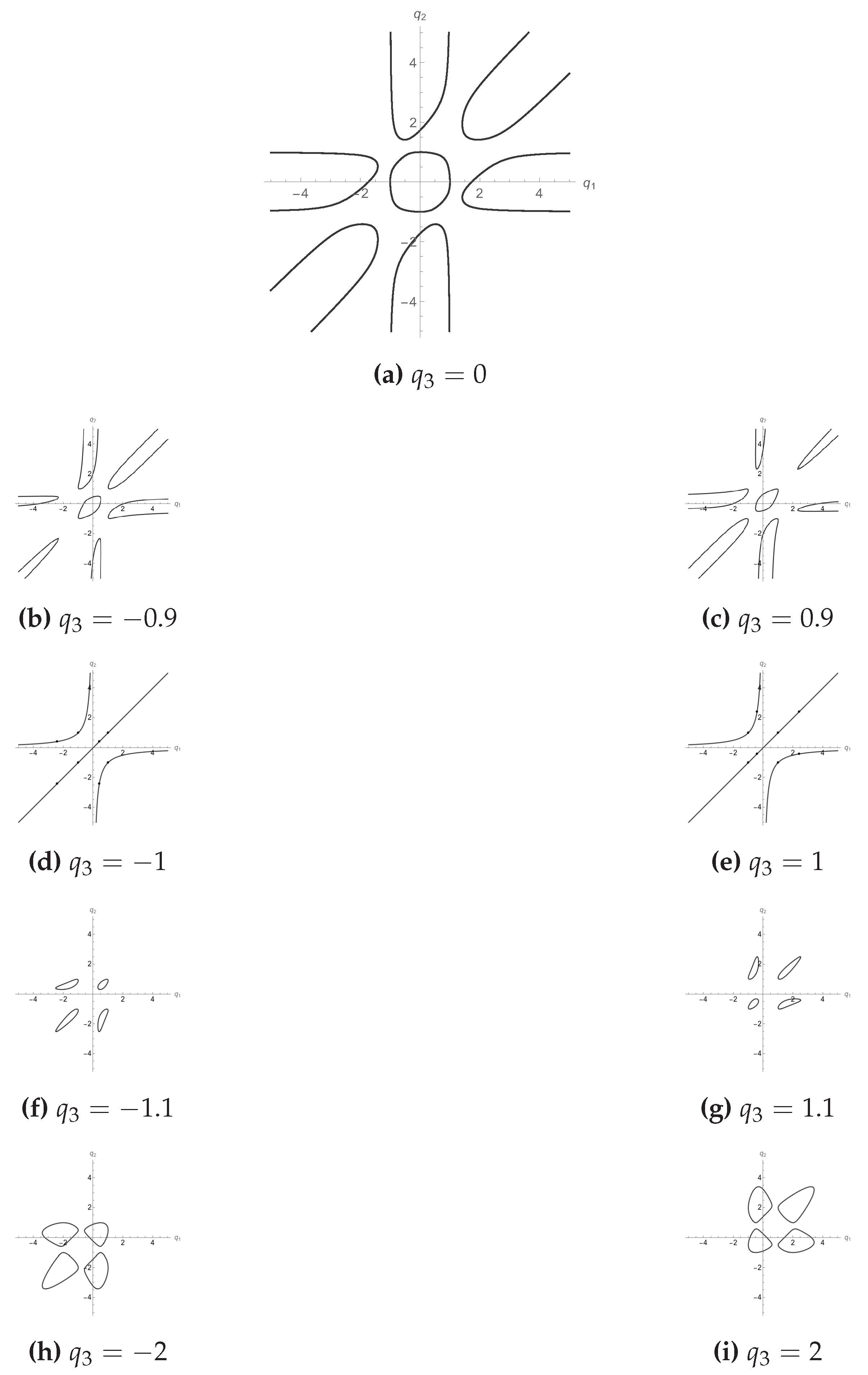
Table 1. This is a table caption. Tables should be placed in the main text near to the first time they are cited.

Bancroft		RPS
pseudorange	$t_{i}$	$γ_{i}^{t}$	emitter coordinate time
data vector	$a_{i}$	$γ_{i}$	emitter worldline
clock offset	b	t	user coordinate time
solution vector	$y_{1, 2}$	x	user position four-vector

Table 2. RPS solution for users with

q_{1} = q_{2} = q_{3} \equiv q

and

τ^{4} \equiv τ

Table 2. RPS solution for users with

q_{1} = q_{2} = q_{3} \equiv q

and

τ^{4} \equiv τ

q	$χ^{2}$	$Δ$	$x^{0}$	$x^{1} = x^{2} = x^{3}$	Emission solutions
0	$- 1$	$\frac{3}{4}$	$τ - \frac{\sqrt{3}}{2} \hat{ϵ}$	$\frac{1}{2}$	$\hat{ϵ} = - 1$ One emission solution
$- \sqrt{\frac{1}{3}}$	0	$\frac{1}{3}$	$τ + \frac{1}{\sqrt{3} (1 - \hat{ϵ})}$	$\frac{1}{6}$	$\hat{ϵ} = - 1$ One emission solution
$- \sqrt{\frac{2}{3}}$	1	$\frac{1}{12}$	$τ + \frac{\sqrt{2} + \hat{ϵ}}{2 \sqrt{3}}$	$- \frac{1}{6} (1 + \sqrt{2} \hat{ϵ})$	$\hat{ϵ} = - 1$ , $\hat{ϵ} = 1$ Two emission solutions

Table 3. RPS solution for users with

q_{1} = q_{2} = q

q_{3} = - q

and

τ^{4} \equiv τ

Table 3. RPS solution for users with

q_{1} = q_{2} = q

q_{3} = - q

and

τ^{4} \equiv τ

q	$χ^{2}$	$Δ$	$x^{0}$	$x^{1} = x^{2}$	Emission solutions
				$x^{3}$
0	$- 1$	$\frac{3}{4}$	$τ - \frac{\sqrt{3}}{2} \hat{ϵ}$	$\frac{1}{2}$	$\hat{ϵ} = - 1$
				$\frac{1}{2}$	One emission solution
$- \sqrt{\frac{1}{3}}$	0	$\frac{1}{27}$	$τ + \frac{\sqrt{3}}{2}$	$- \frac{1}{6}$	$\hat{ϵ} = - 1$
				$\frac{5}{6}$	One emission solution
$- \sqrt{\frac{6}{17}}$	$\frac{1}{17}$	$\frac{363}{19652}$	$τ + \frac{11}{2} \sqrt{\frac{3}{17}} (\sqrt{2} + \hat{ϵ})$	$\frac{11}{34} [1 - 3 (2 + \sqrt{2} \hat{ϵ})]$	$\hat{ϵ} = - 1$ , $\hat{ϵ} = 1$
				$\frac{11}{34} [1 + 3 (2 + \sqrt{2} \hat{ϵ})]$	Two emission solutions

Table 4. Regions according to the sign of the products

m_{A} \cdot m_{B}

(

A \neq B

). The emission or reception character of a

τ^{A}

-coordinate is denoted by e or r, respectively. The subregions

{e e e e}

and

{r r r r}

form one region containing the origin (closed piece at the center of Figure 6). The other fourteen regions correspond to the fourteen tube-like pieces emerging fom the central piece in Figure 6.

Table 4. Regions according to the sign of the products

m_{A} \cdot m_{B}

(

A \neq B

). The emission or reception character of a

τ^{A}

-coordinate is denoted by e or r, respectively. The subregions

{e e e e}

and

{r r r r}

form one region containing the origin (closed piece at the center of Figure 6). The other fourteen regions correspond to the fourteen tube-like pieces emerging fom the central piece in Figure 6.

$m_{1} \cdot m_{2}$	$m_{1} \cdot m_{3}$	$m_{1} \cdot m_{4}$	$m_{2} \cdot m_{3}$	$m_{2} \cdot m_{4}$	$m_{3} \cdot m_{4}$	Character
−	−	−	−	−	−	${e e e e}, {r r r r}$
−	−	+	−	+	+	${e e e r}$ , ${r r r e}$
−	+	−	+	−	+	${e e r e}$ , ${r r e r}$
+	−	−	+	+	−	${e r e e}$ , ${r e r r}$
+	+	+	−	−	−	${r e e e}$ , ${e r r r}$
−	+	+	+	+	−	${e e r r}$ , ${r r e e}$
+	−	+	+	−	+	${e r e r}$ , ${r e r e}$
+	+	−	−	+	+	${e r r e}$ , ${r e e r}$

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Minkowskian Approach to the Pseudorange Navigation Equations

Abstract

1. Introduction

2. Notation

3. The RPS Solution in Minkowski Space-Time

4. Bancroft’s Solution

5. Recovering Bancroft’s Solution from the RPS Solution

6. Proof of the Propositions

Proposition 1 (proof)

Proposition 2 (proof)

Proposition 3 (proof)

7. Four Static Emitters: Solutions

7.1. Emitters’ World-Lines and Emission/Reception Conditions

7.2. Computing the RPS Quantities

7.3. Interpretation of the RPS Solution

7.4. Computing Bancroft’s Quantities

8. Four Static Emitters: Representations

8.1. Representations in Cartesian Coordinates

8.2. Representations in the Q -Grid

9. Emission-Reception Conditions and Grid Regions

10. Conclusions

Author Contributions

Funding

Institutional Review Board Statement

Informed Consent Statement

Data Availability Statement

Acknowledgments

Conflicts of Interest

References

MDPI Initiatives

Important Links

Subscribe

8.2. Representations in the $Q$ -Grid