Prerpints.org logo
Preprint
Article

The Effect of Noncommutative Phase-Space, Local and Nonlocal Potentials on the Current Density in the Context of Minimal Uncertainty in Momentum

Altmetrics

Downloads

97

Views

43

Comments

0

This version is not peer-reviewed

Submitted:

02 March 2024

Posted:

04 March 2024

You are already at the latest version

Alerts
Abstract
In this article, we investigate both the Schrödinger and continuity equations in the presence of nonlocal potential that arising from electron-electron interaction and local one in the context of minimal uncertainty in momentum within commutative and noncommutative frameworks. Furthermore, the Frahn–Lemmer potential type is used. Interestingly, the combined effects of both the phase-space noncommutativity and nonlocality on the current density while considering a minimal uncertainty in momentum are examined. We find that the current density, as conventionally defined, does not fulfil the condition of current conservation, thus, a new definition of the current density that encompasses the aforementioned contributions is given. Thereafter, it is shown that the computed current using the new definition of the current density satisfies the current conservation. Noting that using both the ★ product and linear Bopp-Shift, the noncommutativity is inserted.
Keywords: 
Subject: Physical Sciences  -   Theoretical Physics

I. Introduction

In contemporary nanotechnology advancement, the study of transport properties pertaining to nanodevices has garnered escalating significance. Consequently, exploring the dynamics of currents within nanodevices and how the current densities provide information about the heat dissipation proves to be a captivating subject of understand [1]. Also, in the QCD theory, color charges of the quarks and gluons [2,3] are always conserved. Therefore, for this color charges current, there established a continuity equation (CE) in terms of the gluon field strength tensor, which is a second order field tensor characterizing the gluon interaction between quarks. However, generally, many physical quantities are often or always conserved, consequently, to delve into their respective conservation laws, it becomes necessary to arrive at their respective CEs. In quantum mechanics, the CE is a fundamental principle that describes the conservation of probability density. It relates the flow of probability density, represented by the wave function, to the rate of change of probability density at a given point in space. The importance of the CE lies in its connection to several fundamental concepts. The CE is not an approximation, but it stands as a fundamental physical equation elucidating core principles, wherein it captures the kinematic dimension of symmetry and serves as a valuable supplementary relation. It is always possible to derive the CE from the equations of motion. It can be expressed in the differential form by the divergence theorem or in the integral form, and will be significant once it is applied to conserved quantities. The CE delineates the transport of a physical quantity, so, for a quantity x which can flow or move, ρ x will be its volume density, the manner this quantity flows is described by its flux, denoted J → x . At steady state, ∂ t ρ x = 0 , the divergence of current density has to be zero in order to satisfy current conservation. The divergence of current density ∇ → · J → x represents the rate at which x is lost from the surrounding volume. The relationship between these quantities is in the equation ∂ t ρ x r → , t = − ∇ → · J → x r → , t . However, in this work, we extract the CE for a particle experiencing nonlocal and local potentials in the context of minimal uncertainty in momentum (MUM) for the cases of commutative and noncommutative (NC) frameworks. So, in quantum mechanics, a nonlocal potential (NLP) refers to a type of potential energy function that depends on the positions of particles over a range of distances, rather than just their local positions. Unlike local potentials, which only consider the interactions between particles at the same spatial point, NLPs take into account the influence of particles across a broader spatial region. These NLPs play a crucial role in describing various physical phenomena, such as the study of entanglement, and the behavior of particles in complex environments and systems with long-range interactions. Their inclusion in quantum mechanical models allows for a more accurate and comprehensive understanding of the behavior and properties of quantum systems. Moreover, the NLP can be present, in descriptions of systems in atomic physics, condensed matter physics and quantum optics [4,5,6]. Here, we are interested in a NLP, which can appear in nuclear reactions [7]. Note that there are some types of nonlocality, including the Feshbach nonlocality, Pauli nonlocality, Perey-Buck nonlocality, Bell nonlocality, etc. It is worth noting that these different types of nonlocality arise in distinct physical contexts and have specific manifestations and implications within their respective fields of study. However, the NLP and the CE are related through the conservation of probability where the NLP is introduced into the quantum system, it affects the behavior of the wave function and the associated probability density. It refers to a potential energy term that depends on the values of the wave function at different points in space, rather than just the local value at a given point. The presence of NLP modifies the dynamics of the system and can lead to nonlocal effects. This means that the properties of the wave function and the associated probabilities are influenced not only by the local conditions but also by the wave function values at distant points in space.
Moreover, the Schrödinger equation in the presence of NLP has been the subject of many studies over several years (see, e.g., Refs. [8,9,10]). For instance, within the scattering theories concerning nucleons and nuclei [11], the NLP arises from the exchange interaction occurring between the nucleons [12]. In the transport properties calculations for nano-devices using the DFT and Green’s function theory [13,14]. Furthermore, the nuclear optical potential that characterizes the interaction between colliding nuclei also exhibits nonlocal behavior. [15,16,17]. So far, the NLP has generally been treated as minor in numerous nuclear structure and reaction calculations, and approximation techniques have been incorporated it into the local potential model to accurately account for its effects [18,19,20].
On the other side, obviously, the NC geometry is very important in both quantum mechanics and quantum field theory. The investigations on NC geometry have become an issue of considerable interest over the past few decades. NC geometry is highly influential in many areas of high-energy physics and modern physics including quantum physics [21,22], string theories [23], standard model [24], quantum field theory [25,26], cosmology, black holes and gravity [27,28]. It has been shown that the NC phase-space (NCPS) is very interesting for understanding phenomena at tiny distances and at very high-energy ranges. Also, it is worth noting that different types of phase-space noncommutativity have been considered (see Refs. [29,30,31,32] for an overview). The transition between the commutative setting and the NC one, or vice versa, involves four essential methods: (i) Moyal–Weyl product (★product) instead of the ordinary product for actions and physical systems functions, (ii) Weyl–Wigner maps, which utilize the ordinary product alongside Weyl operators. (iii) Bopp-shift transformations, and (iv) Seiberg–Witten maps. These methods have been extensively discussed in the literature (check, e.g., [33,34,35,36,37] and references therein). In this study, we adopt a combination of the ★product and Bopp-shift to address the research objectives.
As previously stated, we take our problem in question to the MUM context, there we test the combined effects of MUM, noncommutativity and nonlocality on both Schrödinger and continuity equations. Therefore, the concept of minimal uncertainty plays an essential role in understanding the particles behavior. The Heisenberg uncertainty principle asserts that one cannot accurately determine both the exact position and momentum of a particle simultaneously. However, the principle also implies that there exists a lower limit to the uncertainty in these measurements. This lower limit is known as the Minimal Uncertainty in Position (MUP) and Minimal Uncertainty in Momentum (MUM). The MUP signifies the minimum uncertainty achievable when determining the position of a particle, while the MUM represents the minimum uncertainty attainable in measuring its momentum. These limitations have profound implications on our comprehension of quantum systems and underscore the intrinsic probabilistic nature of particles at the quantum level. Numerous studies have explored the integration of NC geometry with either MUP or MUM, as evident from the literature (e.g., [38,39,40]).
This study aims to examine the impacts of NLP and MUM on the CE within the NC setting. Additionally, motivated by the goal of gaining a deeper understanding of the nonlocality phenomena, we undertake this research. The plane of the paper is outlined as follows. In Sec. II, a concise review of both NC geometry and MUM is provided. In Sec. III, for the commutative phase-space, both the Schrödinger and continuity equations are investigated in the presence of local and nonlocal potentials. Moving on to Sec. IV, we present the Schrödinger and continuity equations for both nonlocal and local potentials in the context of MUM all inside NC setting. Note that the nonlocal FLP is used in commutative and NC cases. Sec. V, is devoted to the conclusion and supplementary remarks.

II. Noncommutative Geometry and Minimal Uncertainty in Momentum

In this part of our study, we provide a brief explanation of the NC geometry and MUM. So, at the string scale, i.e. very tiny scale, the coordinates of position no longer commute neither do the momenta, which means, the order of operators matters when carrying out calculations. Consider now the operators of coordinates and momentum in NCPS x i n c and p j n c , respectively, then, in a d-dimensional NCPS, the deformed commutation relations are given as follows:
x μ n c , x ν n c = i Θ μ ν , p μ n c , p ν n c = i η μ ν , x μ n c , p ν n c = i ℏ ˜ δ μ ν , ( μ , ν = 1 , . . d ) ,
with Θ μ ν , η μ ν stand for constant antisymmetric d × d matrices and δ μ ν is the identity matrix. The effective Planck constant, i.e. deformed ℏ, is defined as
ℏ ˜ = ℏ A B + ξ , with ξ = Tr [ Θ η ] 4 A B ℏ 2 ,
where ξ ≪ 1 is the consistency condition in quantum mechanics, and is expected to be usually satisfied once the NC parameters be of the 2nd order. Now, x i n c and p i n c can be presented in terms of the commutative ones x i and p j in ordinary quantum mechanics through the following Bopp-shift [37]
x μ n c = A x μ − Θ μ ν 2 A ℏ p ν , and p μ n c = B p μ + η μ ν 2 B ℏ x ν ,
where A = 1 − Θ η 8 ℏ 2 and B = 1 A , which are scaling constants and are usually considered A = B = 1 to the 1st order of Θ and η . As a consequence Equations (3) and (2) become
x μ n c = x μ − Θ μ ν 2 ℏ p ν , p μ n c = p μ + η μ ν 2 ℏ x ν and ℏ ˜ = ℏ 1 + ξ A = B = 1 .
As long as the system in question is three-dimensional, we use the following NC algebra
x j n c , x k n c = i 2 ϵ j k l Θ l , p j n c , p k n c = i 2 ϵ j k l η l , x j n c , p k n c = i ℏ 1 + Θ η 4 ℏ 2 δ j k , ( j , k , l = 1 , 2 , 3 ) ,
with Θ l = 0 , 0 , Θ , η l = 0 , 0 , η where Θ , η are real-valued NC parameters with [ Θ ] = L 2 and [ η ] = M 2 L 2 T − 2 , and ϵ j k l is the Levi-Civita permutation tensor. Note that the NC parameters are assumed to be extremely small. Now, the three-dimensional Bopp-shift is given as follows
x i n c = x i − ϵ i j k 4 ℏ Θ k p j , and p i n c = p i + ϵ i j k 4 ℏ η k x j .
In NC quantum mechanics, use the ★product instead of usual product, merely makes our quantum mechanical system a NC one. Also, if H x , p is the usual Hamiltonian operator, then its corresponding Schrödinger equation commonly be
H x , p ★ ψ x , p = E ψ x , p .
The ★product between two arbitrary functions F x , p and G x , p from R D in phase-space is defined as [35]
F ★ G x , p = exp [ i 2 Θ a b ∂ x a ∂ x b + i 2 η a b ∂ p a ∂ p b ] F x a , p a G x b , p b = F x , p G x , p + ∑ n = 1 1 n ! i 2 n Θ a 1 b 1 . . . Θ a n b n ∂ a 1 x . . . ∂ a n x F ( x , p ) ∂ b 1 x . . . ∂ b n x G ( x , p ) + ∑ n = 1 1 n ! i 2 n η a 1 b 1 . . . η a n b n ∂ a 1 p . . . ∂ a n p F ( x , p ) ∂ b 1 p . . . ∂ b n p G ( x , p ) ,
with F x , p and G x , p supposed to be infinitely differentiable. But once consider only the NC space case, the definition (8) turns to [41]
F ★ G x = exp [ i 2 Θ a b ∂ x a ∂ x b ] F x a G x b = F ( x ) G ( x ) + ∑ n = 1 1 n ! i 2 n Θ a 1 b 1 . . . Θ a n b n ∂ a 1 . . . ∂ a n F ( x ) ∂ b 1 . . . ∂ b n G ( x ) .
At classical level, the theories of NC field for low-energy fields where E 2 1 / Θ are completely reduced to their commutative versions by means of the nature of ★product.
However, this remains a classical result and even in low-energy scenarios, quantum corrections consistently reveal the effects of NCy parameters. Knowing that in quantum mechanics, terms involving NCy parameters can always be approached as perturbations. If let Θ = η = 0 , the NC algebra simplifies to the standard commutative one, consequently the canonical commutation relations transform to
x j , x k = p j , p k = 0 , x j , p k = i ℏ δ j k , ( j , k = 1 , . . 3 ) .
In our calculations, we make use the following properties of ★product:
1.
The ★-product under the integral sign
∫ f ★ g x d 4 x = ∫ g ★ f x d 4 x = ∫ f g x d 4 x .
2.
The Complex conjugation
f x ★ g x * = g * x ★ f * x .
Now, the minimal uncertainty in momentum and position can be generalized to be GUP in QM as follows [40,42]
▵ x ▵ p ≥ ℏ 2 1 + α ˜ ▵ x 2 + β ˜ ▵ p 2 + γ ˜ in 1 D ,
where α ˜ , β ˜ and γ ˜ = α ˜ x 2 + β ˜ p 2 are positive small and independent of Δ x and Δ p parameters. Noting that equation (13) can be derived by using the following relations
x ˜ j , p ˜ k = − i ℏ δ j k 1 + α ˜ r 2 + β ˜ p 2 with r 2 = ∑ k = 1 3 x k 2 ; p 2 = ∑ k = 1 3 p k 2 .
So, by assuming α ˜ = 0 in the equations (13) and (14), we have only quantum mechanics with MUP. Conversely, putting β ˜ = 0 in the equations (13) and (14), yields only quantum mechanics with MUM. Note that, α ˜ and β ˜ are respectively the parameters of MUM and MUP, determined from a fundamental theory [43,44]. Besides, to explore certain experimental findings concerning bounds on GUP parameters, check Refs. [45,46]. We recover the Heisenberg uncertainty principle at low energy, i.e., energy much smaller than the Planck mass when α ˜ = β ˜ = γ ˜ = 0 in equation (13). As examples of researches in the context of MUM and MUP, check [47,48].
Now, the canonical commutation relations (10) in the presence of MUM become
x ˜ j , x ˜ k = 0 ; p ˜ j , p ˜ k ≠ 0 , x ˜ j , p ˜ k = − i ℏ δ j k 1 + α ˜ r 2 with 0 ≤ α ˜ ≤ 1 .
Here is the MUM representation of the operators x ˜ j and p ˜ i that adheres to (15) [42]:
x ˜ i ψ x = x i ψ x and p ˜ i ψ x = ℏ i 1 + α ˜ r 2 ∂ i ψ x = 1 + α ˜ r 2 p i ψ x .
Then, the modified scalar product using the condition of symmetricity of the coordinates and momenta operators can be given as
φ ∣ ψ = ∫ d D x → 1 + α ˜ r 2 1 + D 2 φ × x → ψ x → .
Note that when study NC quantum mechanical systems in the context of MUM (or even MUP), one need to modify the Schrödinger equation to NC one thereafter substitute the momentum operator with the modified one, i.e. p → ⟶ p → ˜ .

III. Schrödinger and Continuity Equations in Commutative Case

A. Schrödinger Equation with NLP in the Context of MUM

In the presence of local potential V L r → and NLP V N L r → , r → ′ , the time-dependent integro-differential Schrödinger equation is given as follows
p → 2 2 m + V L r → ψ r → , t + ∫ V N L r → , r → ′ ψ r → ′ , t d r → ′ = i ℏ ∂ ∂ t ψ r → , t .
Note that we consider the general case of the local potential for which it may be complex. Knowing that the idea behind use a complex potential was introduced long ago for absorption in nuclear scattering as part of a phenomenological model [49,50]. The model involving a complex potential, often termed the optical model, is used also in various other fields, including nanotransport, molecular and atomic physics, and more to describe inelastic losses. The term containing V N L accounts for the nonlocal interactions between particles, where the NLP depends on both the position r → of the particle being considered and the position r → ′ of the interacting particle. Exactly, the integral term represents the integration of the NLP over all possible positions r → ′ of the interacting particles. It captures the cumulative effect of the nonlocal interactions on the quantum state ψ of the system. The both potentials depict the scattering as follows:
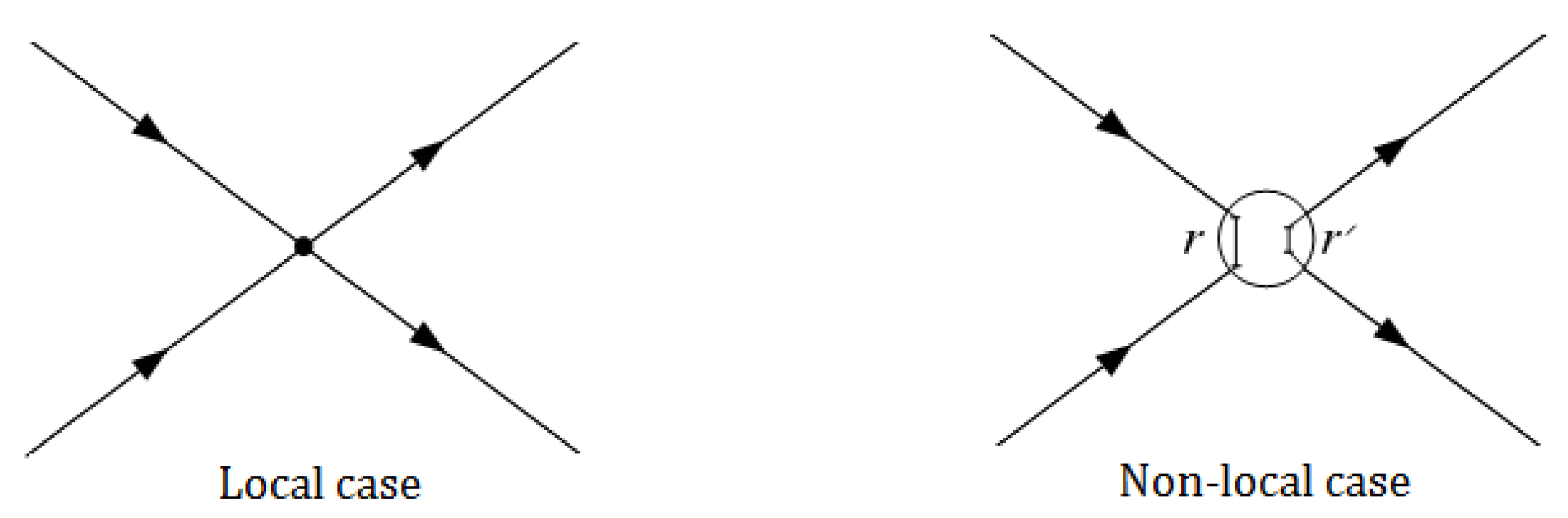
Preprints 100404 g001
Figure 1. A schematic representation of both local and nonlocal potentials.
Figure 1. A schematic representation of both local and nonlocal potentials.
Preprints 100404 g001
Here the local potential is when r = r ′ and the nonlocal one expresses two extra distances where r → is the relative distance between two in-coming particles; and r → ′ is the relative distance between two out-going particles. The form of the NLP operating on a wave function [51] is as follows
∫ V N L r → , r → ′ ψ r → ′ , t d r → ′ = ∫ V N L r → , r → + s → ψ r → + s → , t d s → ,
where r → ′ = r → + s → , with d r → ′ = d s → . Note that the kernel function V N L r → , r → ′ is symmetric in r → and r → ′ [52], i.e., V N L r → , r → ′ = V N L r → ′ , r → . Then by using the series expansion of ψ r → + s → = ( 1 + s → ∂ ∂ r → + s → 2 2 ∂ 2 ∂ r → 2 + s → 3 3 ! ∂ 3 ∂ r → 3 + . . ) ψ r → = e i ℏ s → · p → ψ r → , one obtains
∫ V N L r → , r → ′ ψ r → ′ , t d r → ′ = ∫ V N L r → , r → + s → e i ℏ s → · p → d s → ψ r → , t ,
then
∫ V N L r → , r → + s → e i ℏ s → · p → d s → ψ r → , t = ∫ d s e i s → · p → 2 ℏ V N L r → − s → 2 , r → + s → 2 e i s → · p → 2 ℏ ψ r → , t = V N L r → , p → ψ r → , t .
Thus, equation (18) simply takes the following form
p → 2 2 m + V L r → + V N L r → , p → ψ r → , t = i ℏ ∂ ∂ t ψ r → , t .
Now, the Frahn-Lemmer potential (FLP), which is separable, can be defined as [11,53]
V N L r → , r → ′ = U 1 2 r → + r → ′ Y r → − r → ′ ,
where Y , U represent the width and the local average value of the nonlocality respectively, also note that the form (23) is similar to those used in local optical model calculations [11]. We consider U 1 2 r → + r → ′ ≈ V 0 , and Y is taken as a Gaussian function as
Y r → − r → ′ = 1 π β 2 3 2 e − r → − r → ′ 2 β 2 ,
which is normalized, i.e., ∫ Y r → − r → ′ d r → ′ = 1 . Consequently, equation (23) becomes
V N L r → , r → ′ = V 0 π β 2 3 2 e − r → − r → ′ 2 β 2 ,
with β , V 0 are the nonlocality range, which is usually 0.85 fm and the depth of the nuclear potential says Wood–Saxon function type, respectively.
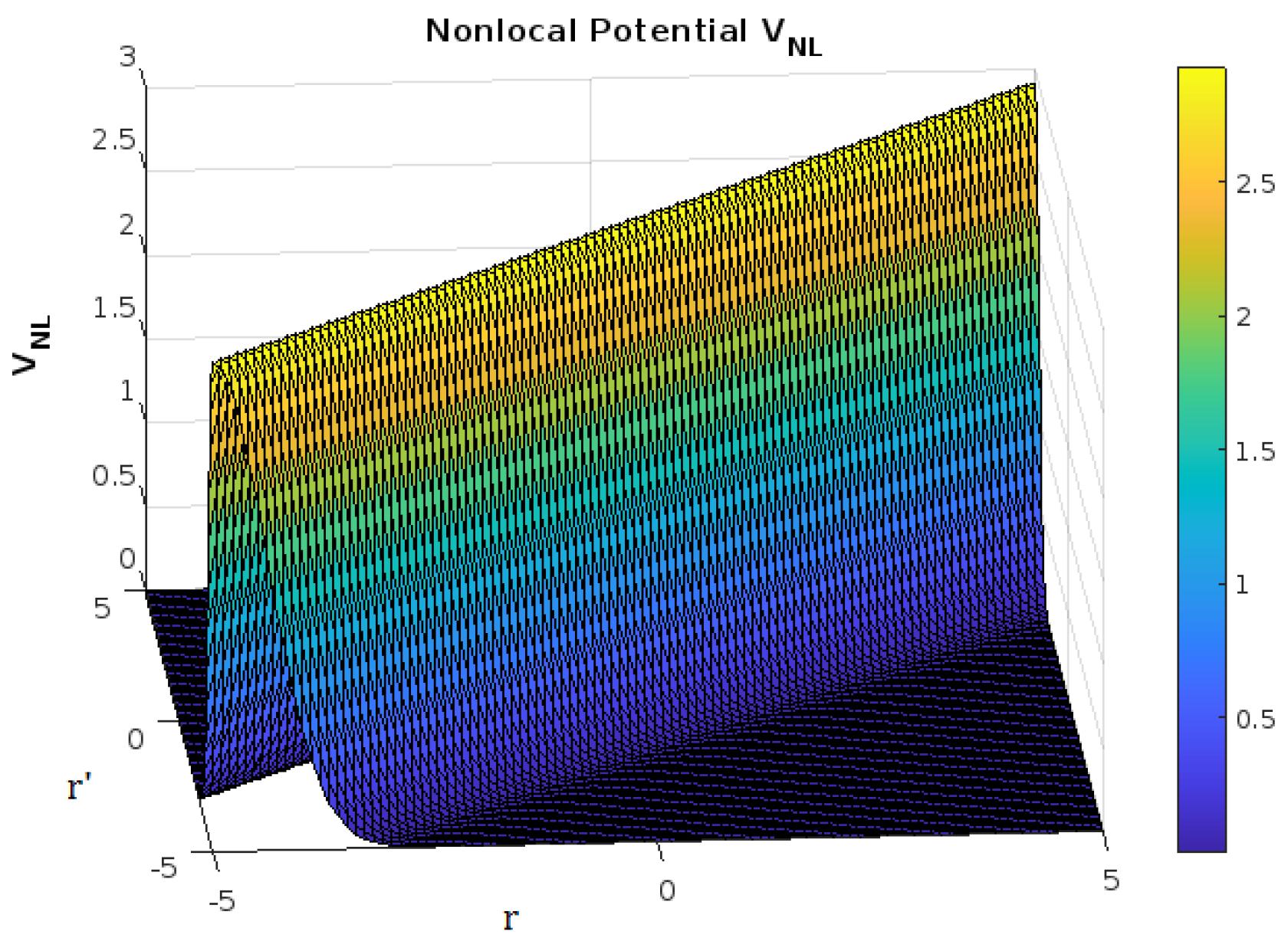
Preprints 100404 g002
Figure 2. Plot of NLP against r → and r → ′ according to Eqution (25), where β = 0.85 fm and V 0 = 10 in arbitrary units.
Figure 2. Plot of NLP against r → and r → ′ according to Eqution (25), where β = 0.85 fm and V 0 = 10 in arbitrary units.
Preprints 100404 g002
Once the range parameter is very small, the NLP tends to V 0 δ r → − r → ′ . Thereafter, by putting equation (25) into equation (18), we obtain
p → 2 2 m + V L r → ψ r → , t + V 0 π β 2 3 2 ∫ e − r → − r → ′ 2 β 2 ψ r → ′ , t d r → ′ = i ℏ ∂ ∂ t ψ r → , t .
By using equation (21), we have
V N L r → , p → = ∫ d s e i sp 2 ℏ V 0 π β 2 3 2 e − r → − s → 2 − r → − s → 2 2 β 2 e i sp 2 ℏ = V 0 π β 2 3 2 ∫ d s e − s → 2 β 2 + i ℏ s → · p → ,
then, through the integral ∫ − ∞ + ∞ e − A 2 s 2 + B s d s = π A e B → 2 4 A 2 , where A = 1 β , B → = i ℏ p → , equation (26) becomes
p → 2 2 m + V L r → ψ r → , t + V 0 e − p → 2 β 2 4 ℏ 2 ψ r → , t = i ℏ ∂ ∂ t ψ r → , t .
Now, by using equation (16), the Schrödinger equation with FLP and in the context of MUM is given as follows
1 + α ˜ r 2 2 p → 2 2 m + V L r → ψ r → , t + V 0 e − 1 + α ˜ r 2 2 p → 2 β 2 4 ℏ 2 ψ r → , t = i ℏ ∂ ∂ t ψ r → , t .
Note that once wanting to solve the equation (29), we use the Fourier transform to switch for the momentum representation, i.e. P representation, there the calculations shall be simple, noting that the equation will be considered time-independently. Thus, with p → = ℏ k → , equation (29) turns to
1 + α ˜ r 2 2 ℏ k → 2 2 m + V L + V 0 e − 1 + α ˜ r 2 2 ℏ k → 2 β 2 4 ℏ 2 = E .
By way of illustration, we consider V L = 0 , then we have
1 + α ˜ r 2 2 ℏ k → 2 2 m + V 0 e − 1 + α ˜ r 2 2 ℏ k → 2 β 2 4 ℏ 2 = E .
Now, as long as β is small, then we have the following series expansion
e − 1 + α ˜ r 2 2 p → 2 β 2 4 ℏ 2 = 1 − 1 + α ˜ r 2 2 p → 2 β 2 4 ℏ 2 + O β 4 ,
so that equation (31) becomes
E − V 0 = 1 + α ˜ r 2 2 ℏ k → 2 1 2 m − V 0 β 2 4 ℏ 2 .
The above relation (33) exhibits the relation between the nuclear potential and the momentum. For V 0 = 0 , we have
E = 1 + α ˜ r 2 2 ℏ k → 2 2 m .
For a best and profound understanding of the behavior of the energy, we report on some numerical results for the energy in (33) and show the different effects on it. However, E were plotted for the values of ℏ k → 2 = ℏ = 1 and V 0 = 1 in Figures 3–5.
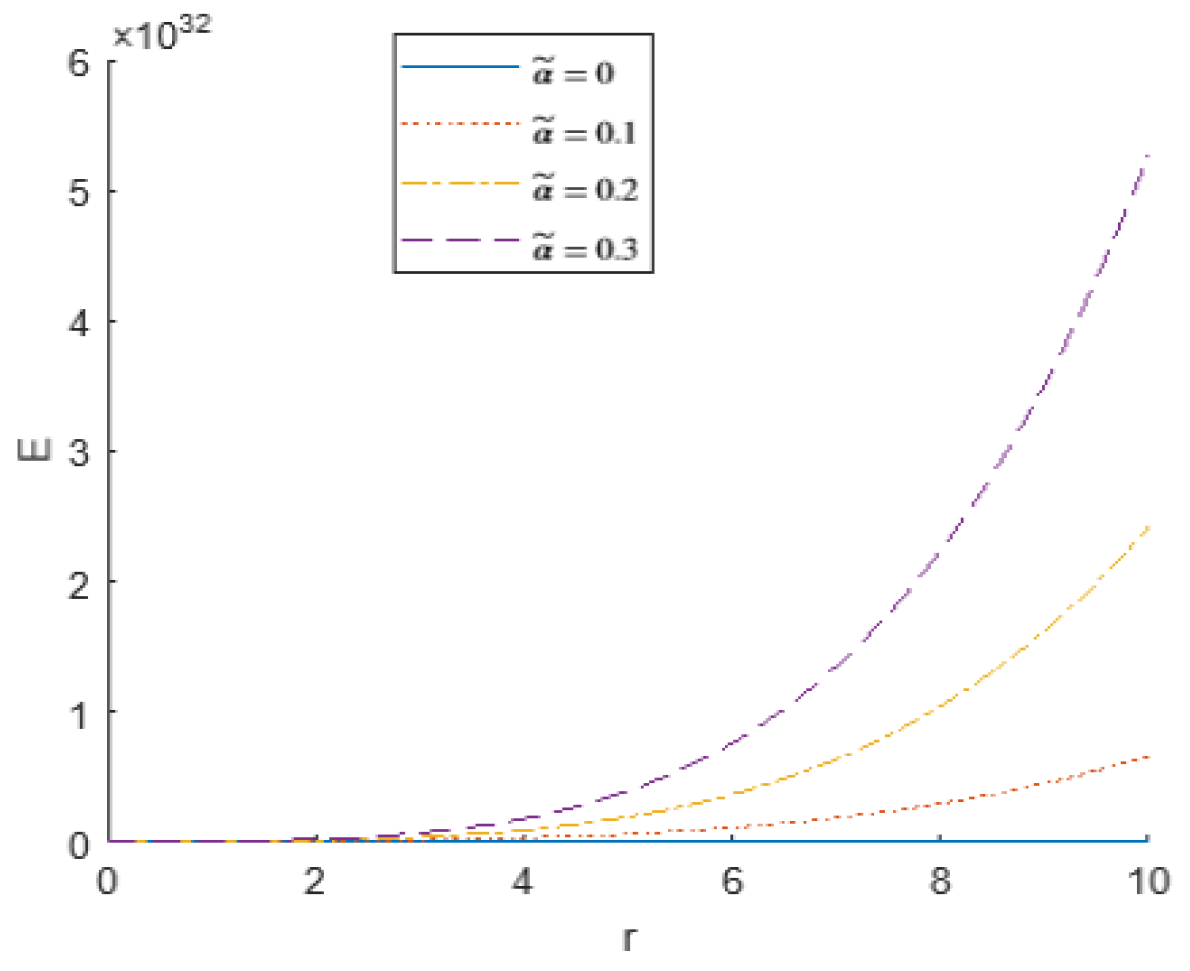
Preprints 100404 g003
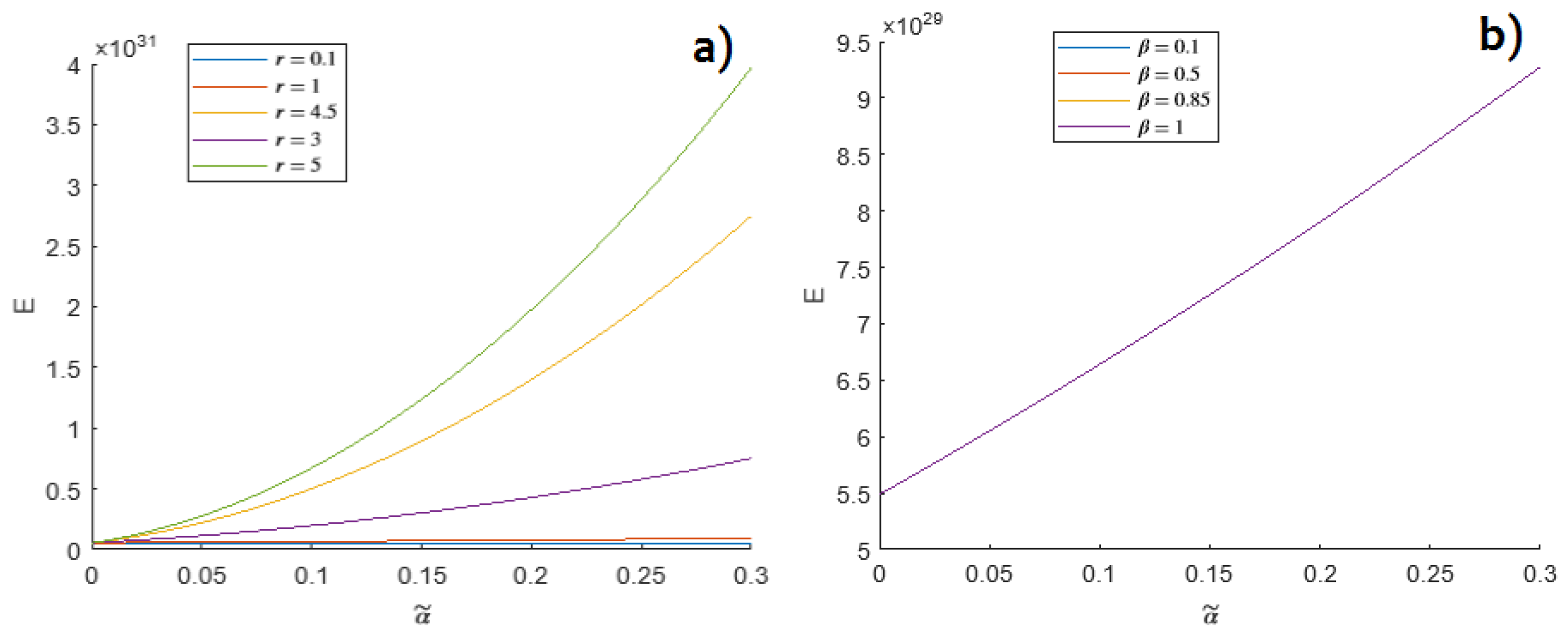
Figure 3. E vs. r for values of α ˜ , i.e. α ˜ = 0,0.1,0.2,0.3. And β = 0.85 fm.
Figure 3. E vs. r for values of α ˜ , i.e. α ˜ = 0,0.1,0.2,0.3. And β = 0.85 fm.
Preprints 100404 g003
Preprints 100404 g004
Figure 4. E as a function of α ˜ . a) The variation of energy is for different values of r, i.e. r=0.1, 1, 3, 4.5, 5, and fixed β = 0.85 fm; b) the variation is for different values of β and fixed r=1.
Figure 4. E as a function of α ˜ . a) The variation of energy is for different values of r, i.e. r=0.1, 1, 3, 4.5, 5, and fixed β = 0.85 fm; b) the variation is for different values of β and fixed r=1.
Preprints 100404 g004

B. Continuity Equation with NLP in the Context of MUM

In the presence of both local and nonlocal potentials, the Schrödinger equation in the context of MUM is written as follows
i ℏ ∂ ∂ t ψ r → , t = − 1 + α ˜ r 2 2 ℏ 2 2 m ∇ → 2 ψ r → , t + ∫ V N L r → , r → ′ ψ r → ′ , t d r → ′ + V L r → ψ r → , t ,
the complex conjugate of equation (35) is given as
− i ℏ ∂ ∂ t ψ † r → , t = − 1 + α ˜ r 2 2 ℏ 2 2 m ∇ → 2 ψ † r → , t + ∫ V N L * r → , r → ′ ψ † r → ′ , t d r → ′ + V L * r → ψ † r → , t .
Here * and † stand for the complex conjugations. Then, the continuity equation bu using equations (35) and (36) is
i ℏ ∂ ∂ t ψ † ψ = − ℏ 2 2 m 1 + α ˜ r 2 2 ∇ → 2 ψ † ∇ → ψ − ψ ∇ → ψ † + ∫ ψ † V N L r → , r → ′ ψ r → ′ , t − ψ V N L * r → , r → ′ ψ † r → ′ , t d r → ′ + ψ † V L ψ − ψ V L * ψ † ,
which may be contracted as
∂ ρ ∂ t + ∇ → · J → ˜ + ρ N L + ρ L = 0 .
Note that the obtained continuity equation (38) comprises new quantities, which are the local density ρ L and the nonlocal density ρ N L , where
ρ = ψ † ψ = ψ 2 , ρ L = 1 i ℏ ψ V L * ψ † − ψ † V L ψ , J → ˜ = 1 + α ˜ r 2 2 ℏ 2 i m ψ † ∇ → ψ − ψ ∇ → ψ † , ρ N L = 1 i ℏ ∫ ψ V N L * r → , r → ′ ψ † r → ′ , t − ψ † V N L r → , r → ′ ψ r → ′ , t d r → ′ .
Once the local potential is Hermitian and real-valued, ρ L vanishes, then its symmetry is maintained. In this case, the results is similar to that of Ref. [7] provided that α ˜ ⟶ 0 . Then, in the steady state, i.e. ∂ ∂ t ρ = 0 , equation (38) becomes
∇ → J → ˜ + ρ N L = 0 .
Besides, if the NLP is a real diagonal matrix, then the quantity ρ N L will vanish. The deformed current density vector J → ˜ is conserved since ∇ → J → ˜ = 0 and it appears that MUM does not affect the current conservation. However, in presence of NLP, the quantity ρ N L is nonzero (also if ρ L is nonzero), therefore ∇ → J → ˜ ≠ 0 , consequently, the current obtained from the current density is not conserved. Hence, it becomes necessary to modify the conventional definition of current density to encompass the contribution of ρ N L and ρ L arising from the nonlocal and local potentials. We define the new current density with nonlocal and local potentials as
J → t o t = J → ˜ + J → N L + J → L ,
where J → N L , J → L are the nonlocal and local current density vectors (merely named according to the local and nonlocal potentials), defined as
J → N L = − ∇ → χ N L r → , J → L = − ∇ → φ L r → ,
with χ N L r → , φ L r → defined through the following set of Poisson equation
∇ → 2 χ N L + ρ N L = 0 , ∇ → 2 φ L + ρ L = 0 .
Now, by solving each Poisson equation (43) with proper boundary conditions, we can define J → N L and J → L . Then, it is obvious now that the new defined current density satisfies ∇ → J → t o t = 0 , therefore the calculated current from the current density satisfies the current conservation.
Once the considered interactions are absent, the continuity equation takes the following deformed form
i ℏ ∂ ∂ t ψ 2 + 1 + α ˜ r 2 2 ℏ 2 2 m ∇ → ψ † ∇ → ψ − ψ ∇ → ψ † = 0 .
Besides, in the limit of α ˜ ⟶ 0 , the equation (44) takes its conventional known form in the literature as follows
i ℏ ∂ ∂ t ψ 2 + ℏ 2 2 m ∇ → ψ † ∇ → ψ − ψ ∇ → ψ † = 0 .

IV. Schrödinger and Continuity Equations in Noncommutative Case

A. Noncommutative Schrödinger Equation with NLP in the Context of MUM

We start with implementing the space noncommutativity in equation (18) through the ★product, thus the Schrödinger equation with local and nonlocal potentials in NC space is given as follows
p → 2 2 m ψ r → , t + ∫ V N L r → , r → ′ ★ ψ r → ′ , t d r → ′ + V L r → ★ ψ r → , t = i ℏ ∂ ∂ t ψ r → , t ,
note that as shown in equation (11), the ★product under the integral sign become ordinary product. If V L r → ∝ B r , with B represents the magnetic field, and using equation (9) the third term in the right side of equation (46) becomes
V L r → ★ ψ r → , t = V L r → ψ r → , t + i Θ a b ∂ a V L r → ∂ b ψ r → , t + 0 Θ 2 .
Now, we implement the phase noncommutativity by the linking p → ⟶ p → n c using the Bopp-shift (6), so we have
p → n c 2 2 m ψ + ∫ V N L r → , r → ′ ψ r → ′ , t d r → ′ + V L ψ + i Θ a b ∂ a V L ∂ b ψ = i ℏ ∂ ∂ t ψ ,
where
p → n c 2 = p → 2 − 2 ℏ L → · η → + O η 2 ,
with L → = r → × p → is the angular momentum. So, by substituting equation (49) in (48), we get
i ℏ ∂ ψ ∂ t = p → 2 2 m ψ + ∫ V N L r → , r → ′ ψ r → ′ , t d r → ′ − L → · η → m ℏ ψ + V L ψ + i Θ a b ∂ a V L ∂ b ψ .
So, the Schrödinger equation with FLP and a local potential in NCPS is given by
i ℏ ∂ ψ ∂ t = p → 2 2 m ψ + V 0 e − p → 2 − 2 ℏ L → · η → β 2 4 ℏ 2 ψ − L → · η → m ℏ ψ + V L ψ + i Θ a b ∂ a V L ∂ b ψ .
Using equation (16), the equation (50) is linked to MUM, thereafter we have
i ℏ ∂ ψ ∂ t = − 1 + α ˜ r 2 2 ℏ 2 ∇ → 2 2 m ψ + V 0 e − 1 + α ˜ r 2 2 p → 2 − 2 ℏ L → · η → β 2 4 ℏ 2 ψ − L → · η → m ℏ ψ + V L ψ + i Θ a b ∂ a V L ∂ b ψ ,
then, as long as β is small, we have
e − 1 + α ˜ r 2 2 p → 2 − 2 ℏ L → · η → β 2 4 ℏ 2 = 1 − 1 + α ˜ r 2 2 p → 2 β 2 4 ℏ 2 + L → · η → β 2 2 ℏ 3 .
So, using the result of (53) we rewrite equation (52) to have
i ℏ ∂ ψ ∂ t = − 1 + α ˜ r 2 2 ℏ 2 ∇ → 2 2 m − L → · η → m ℏ + V L + i Θ a b ∂ a V L ∂ b + V 0 1 − 1 + α ˜ r 2 2 p → 2 β 2 4 ℏ 2 + L → · η → β 2 2 ℏ 3 ψ .
The equation (54) is the NC Schrödinger equation with nonlocal and local potentials in the context of MUM. As we can note, the noncommutativity in space affected the local part, while the noncommutativity in phase affected the nonlocal part.

B. Noncommutative Continuity Equation with NLP in the Context of MUM

The NC Schrödinger equation with nonlocal and local potentials in the context of MUM is given by
i ℏ ∂ ψ ∂ t = − 1 + α ˜ r 2 2 ℏ 2 2 m ∇ → 2 ψ + ∫ V N L r → , r → ′ ψ r → ′ , t d r → ′ − L → · η → m ℏ ψ + V L ψ + i Θ a b ∂ a V L ∂ b ψ ,
and its complex conjugate is given as follows
− i ℏ ∂ ψ † ∂ t = − 1 + α ˜ r 2 2 ℏ 2 2 m ∇ → 2 ψ † + ∫ V N L * r → , r → ′ ψ † r → ′ , t d r → ′ − L → · η → m ℏ ψ † + V L * ψ † − i Θ a b ∂ a V L * ∂ b ψ † .
So, from the equations (55) and (56), we obtain the following continuity equation
i ℏ ∂ ∂ t ψ † ψ = − 1 + α ˜ r 2 2 ℏ 2 2 m ∇ → 2 ψ † ∇ → ψ − ψ ∇ → ψ † + ∫ ψ † r → , r → ′ V N L r → , r → ′ ψ r → ′ , t − ψ V N L * r → , r → ′ ψ † r → ′ , t d r → ′ + ψ † V L ψ − ψ V L * ψ † + 1 m ℏ ψ L → · η → ψ † − ψ † L → · η → ψ + i Θ a b ψ † ∂ a V L ∂ b ψ + ψ ∂ a V L * ∂ b ψ † ,
which is contracting as follows
∂ ρ ∂ t + ∇ → J → ˜ + ρ N L + ρ L n c + T n c = 0 .
The equation (57) is recognized as a deformed continuity equation whose separate terms are given as
ρ = J 0 = ψ † ψ = ψ 2 , T n c = 1 i m ℏ 2 ψ † L → · η → ψ − ψ L → · η → ψ † , J → ˜ = 1 + α ˜ r 2 2 ℏ 2 i m ψ † ∇ → ψ − ψ ∇ → ψ † , ρ L n c = 1 i ℏ ψ V L * ψ † − ψ † V L ψ − 1 ℏ Θ a b ψ † ∂ a V L ∂ b ψ + ψ ∂ a V L * ∂ b ψ † , ρ N L = 1 i ℏ ∫ ψ V N L * r → , r → ′ ψ † r → ′ , t − ψ † V N L r → , r → ′ ψ r → ′ , t d r → ′ .
Now, it is obvious that the current from current density in the NC setting does not adhere to the current conservation. However, the effect of the NLP on the continuity equation arises as nonlocal quantity of density type, as well as for the local potential. Note that the presence of the quantities that explicitly related to the NC parameters is due to the considered effects of the noncommutativity in our considered system. Exactly, the effect of the space noncommutativity is on the local quantity, while the effect of the phase noncommutativity is on the newly result quantity, namely T n c . On the other hand, we see MUM affects only the form of the current density, yielding a deformed current density, i.e. J → ˜ . Once the local potential is zero, the local density along with its NC correction vanish. To be more precise, by comparing the continuity equation in both NC and commutative cases, it becomes clear that the NC effect is obvious in the quantity from local potential, while the effect vanishes for the quantity from NLP, also it is shown that the NC effect violates the conservation of the continuity equation. Now, we alter the formulation of the density current to achieve the conservation within the NC setting. Thus, supposing that the local potential is real then ρ L n c vanishes, evenly, when the NLP is a real diagonal matrix, ρ N L disappears. But, the current obtained from J → ˜ will not adhere to conservation due to the NC correction T n c . This leads to understanding that while ρ N L and ρ L are zero or nonzero, as a result, T n c will violate the current conservation, as well as the symmetry will not be maintained in the NC setting. Therefore, we adjust the ordinary definition of the current density to encompass the contribution of ρ N L , ρ L n c and T n c , so in the steady state, i.e. ∂ ρ ∂ t = 0 , equation (58) becomes
∇ → J → ˜ + ρ N L + ρ L n c + T n c = 0 .
Thereafter, we implement the following substitution
J → ˜ + J → n c → J → n c , w i t h T n c = ∇ → J → n c ,
with the condition ∇ → T n c = 0 . We define the new deformed current density with the nonlocal and local potentials as follows
J → t o t n c = J → n c + J → N L + J → L n c ,
where J → L n c , J → N L are the NC local current and nonlocal current densities, which are defined as
J → N L = − ∇ → χ N L , J → L n c = − ∇ → φ L n c ,
where χ N L , φ L n c determined using the following set of Poisson equation
∇ → 2 χ N L + ρ N L = 0 , ∇ → 2 φ L n c + ρ L n c = 0 .
By solving each Poisson equation in (64) through the proper boundary conditions, we find J → N L and J → L n c . Then the newly defined deformed current density satisfies ∇ → J → t o t n c = 0 , therefore, the calculated NC current from this current density will satisfy the current conservation.

V. Conclusions

Our research centered around the combination of three interesting subjects in theoretical physics: the NLP, NC Schrödinger equation and MUM formalism of quantum mechanics. However, we conducted a comprehensive examination of how local and nonlocal potentials, along with the MUM, affect the Schrödinger equation within both NC and commutative frameworks. As a result, we derived continuity equations to account for these effects. Exactly, the presence of the local and nonlocal potentials in our quantum system led to the emergence of local and nonlocal quantities of density type, while MUM affected explicitly the current density. In the commutative case, the local and nonlocal potentials affect the behavior of the wave function at distant points, leading to local and nonlocal effects in the flow of probability. Then the continuity equation, in this case, captures these influences and ensures the conservation of probability density in the system. But, in the NC case, the conservation of probability density was found to be violated, which means that the phase-space noncommutativity is unsuitable for the current conservation under the considered non-trivial contributions. Accordingly, a new definition of the current density including the local, nonlocal, MUM and NC contributions is given. Then, the obtained current based on the new definition of the current density satisfies the current conservation. Furthermore, in the limits of Θ → 0 , η → 0 and α ˜ → 0 , both the deformed Schrödinger and continuity equations converge to those of ordinary quantum mechanics, affirming the compatibility and reducibility of our findings. Besides, the outcomes of our study provide valuable insights that can be extended to investigate the Klein paradox in the system under consideration, or maybe test its invariance under the CPT symmetry and Lorentz symmetry violation.

Funding

This research received no external funding.

Conflicts of Interest

The author declares no conflict of interest.

References

  1. Michael, G, et al. Heat conduction in molecular transport junctions. Phys. Rev. B 75, 155312. [CrossRef]
  2. Nayak, G.C. General form of the color potential produced by color charges of the quark. J. High Energ. Phys. 2013, 1 (2013). [CrossRef]
  3. Nayak, G.C. General form of color charge of the quark. Eur. Phys. J. C, 73, 2442 (2013). [CrossRef]
  4. Mott, N. F., Massey, H. S. The Theory of Atomic Collisions, (Oxford Univ. Press, London). (1965).
  5. Baseia, B., Nussenzveig, H. M. Semiclassical theory of laser transmission loss. Optica Acta: International Journal of Optics, 31(1), 39(1984). [CrossRef]
  6. Balantekin, A.B, et al. Green’s function for nonlocal potentials. J. Phys. G: Nucl. Part. Phys. 24(11), 2087 (1998). [CrossRef]
  7. Li, C, et al. Definition of current density in the presence of a non-local potential. Nanotechnology. 19, 15, 155401 (2008). [CrossRef]
  8. Reeves, M., Owen, L. W. Solution of a Schroedinger equation with a nonlocal potential. J. Comput. Phys. 4(4), 572 (1969). [CrossRef]
  9. Pattanayak, D. N. Wolf, E.Scattering states and bound states as solutions of the schrödinger equation with nonlocal boundary conditions. Phys. Rev. D, 13(4), 913 (1976). [CrossRef]
  10. Kidun, O., et al. Scattering and bound-state problems with non-local potentials: application of the variable-phase approach. J. Phys. A: Math. Gen. 35, 9413 (2002). [CrossRef]
  11. Perey, F., Buck, B. A Non-Local Potential Model for the Scattering of Neutrons by Nuclei. Nucl. Phys, 32, 353 (1962). [CrossRef]
  12. Fetter, A.L., Walecka, J.D. Quantum Theory of Many-Particle Systems. McGraw-Hill, New York. (1971).
  13. Balantekin, A.B., et al. Green’s Function for Nonlocal Potentials. J. Phys. G: Nucl. Part. Phys, 24, 2087 (1998). [CrossRef]
  14. Taylor, J., et al. Initio Modeling of Quantum Transport Properties of Molecular Electronic Devices. Phys. Rev. B, 63, 245407 (2001). [CrossRef]
  15. Deltuva, A. Three-body direct nuclear reactions: Nonlocal optical potential. Phys. Rev. C, 79(2), 021602 (2009). [CrossRef]
  16. Jaghoub, M. I., et al. Exploration of the energy dependence of proton nonlocal optical potentials. Physical Review C, 98(2), 024609 (2018). [CrossRef]
  17. Deltuva, A., Jurčiukonis, D. Nonlocal optical potential with core excitation in Be10(d,p)11 Be and Be11(p,d)10 Be reactions. Phys. Lett. B, 840, 137867 (2023). [CrossRef]
  18. Coz, M., Arnold, L. G., & MacKellar, A. D. Nonlocal potentials and their local equivalents. Ann. Phys. 59(1), 219 (1970). [CrossRef]
  19. De Forest. Jr, T. Equivalence of local and non-local potentials and the perey effect. Nucl. Phys. A, 163(1), 237 (1971). [CrossRef]
  20. Lassaut, M., Mau, N. V. l-Dependent local potentials equivalent to a non-local potential. Nucl. Phys. A, 518(3), 441(1990). https://doi.org/10.1016/0375-9474(90)90139-D. [CrossRef]
  21. Madore, J.: An introduction to noncommutative geometry. In: H. Gausterer, L. Pittner, H. Grosse, (eds) Geometry and Quantum Physics. Lecture Notes in Physics, vol 543. (Springer, Berlin, Heidelberg, 2000). [CrossRef]
  22. Haouam, I. Two-dimensional Pauli equation in noncommutative phase-space. Ukr. J. Phys.66(9), 771 (2021). [CrossRef]
  23. Seiberg. N., Witten. E, String theory and noncommutative geometry. J. High Energy Phys. 1999(09), 032 (1999). [CrossRef]
  24. Calmet, X., Jurčo, B., Schupp, P. et al. The standard model on non-commutative space-time. Eur. Phys. J. C 23, 363 (2002). [CrossRef]
  25. Haouam, I. On the Fisk-Tait equation for spin-3/2 fermions interacting with an external magnetic field in noncommutative space-time. J. Phys. Stud. 24, 1801 (2020). [CrossRef]
  26. Grosse, H., Klim£ík, C. & Prešnajder, P. On finite 4D quantum field theory in non-commutative geometry. Commun.Math. Phys. 180, 429 (1996). [CrossRef]
  27. Moffat, J. W. Noncommutative quantum gravity. Phys. Lett. B, 491(3-4), 345 (2000). [CrossRef]
  28. Spallucci, E., Smailagic, A., & Nicolini, P. Non-commutative geometry inspired higher-dimensional charged black holes. Phys. Lett. B, 670(4-5), 449 (2009). [CrossRef]
  29. Haouam, I. Dirac oscillator in dynamical noncommutative space. Acta. Polytech.61(6), 689 (2021). [CrossRef]
  30. Haouam, I. Analytical solution of (2+1) dimensional Dirac equation in time-dependent noncommutative phase-space. Acta. Polytech. 60(2), 111 (2020). [CrossRef]
  31. Haouam, I., Hassanabadi, H. Exact solution of (2+1)-dimensional noncommutative Pauli equation in a time-dependent background. Int. J. Theor. Phys. 61, 215 (2022). [CrossRef]
  32. Haouam, I., Alavi, S.A. Dynamical noncommutative graphene. Int. J. Mod. Phys. A. 37(10), 2250054 (2022). [CrossRef]
  33. Haouam, I. Solutions of Noncommutative Two-Dimensional Position–Dependent Mass Dirac Equation in the Presence of Rashba Spin-Orbit Interaction by Using the Nikiforov–Uvarov Method. Int. J. Theor. Phys. 62, 111 (2023). [CrossRef]
  34. Chaichian., M., et al. Hydrogen Atom Spectrum and the Lamb Shift in Noncommutative QED. Phys. Rev. Lett. 86, 2716 (2001). [CrossRef]
  35. Haouam, I. On the noncommutative geometry in quantum mechanics. J. Phys. Stud. 24(2), 2002 (2020). [CrossRef]
  36. Gouba, L. A comparative review of four formulations of noncommutative quantum mechanics. Int. J. Mod. Phys. A, 31, 1630025 (2016). [CrossRef]
  37. Haouam, I. On the three-dimensional Pauli equation in noncommutative phase-space. Acta Polytech. 61(1), 230 (2021). [CrossRef]
  38. Hassanabadi, H. et al. Noncommutative phase space Schrödinger equation with minimal length. Adv. High Energy Phys. 2014, article ID 459345, 6 (2014). [CrossRef]
  39. Dossa, F.A et al. Non-commutative phase space Landau problem in the presence of a minimal length. Vestnik KRAUNC. Fiz.-mat. nauki. 33(4), 188 (2020). [CrossRef]
  40. Haouam, I. Foldy–Wouthuysen Transformation of Noncommutative Dirac Equation in the Presence of Minimal Uncertainty in Momentum. Few-Body. Syst. 64, 9 (2023). [CrossRef]
  41. Haouam, I. The non-relativistic limit of the DKP equation in non-commutative phase-space. Symmetry. 11, 223 (2019). [CrossRef]
  42. Zarei, M., Mirza, B. Minimal uncertainty in momentum: the effects of IR gravity on quantum mechanics. Phys. Rev. D, 79, 125007 (2009). [CrossRef]
  43. Chang, L. N., et al. Exact solution of the harmonic oscillator in arbitrary dimensions with minimal length uncertainty relations. Physical Review D, 65(12), 125027 (2002). [CrossRef]
  44. Brau, F., Buisseret, F. Minimal length uncertainty relation and gravitational quantum well. Physical Review D, 74 (3), article ID 036002, 5 (2006). [CrossRef]
  45. Nairz. O., et al. Experimental verification of the Heisenberg uncertainty principle for fullerene molecules. Phys. Rev. A. 65, 032109 (2002). [CrossRef]
  46. Stetsko, M. M. Corrections to the ns levels of the hydrogen atom in deformed space with minimal length. Phys.Rev. A. 74(6), 062105 (2006). [CrossRef]
  47. Das, S., Vagenas, E. C. Universality of quantum gravity corrections. Phys. Rev. Lett. 101(22), 221301 (2008). [CrossRef]
  48. Kempf, A. On quantum field theory with nonzero minimal uncertainties in positions and momenta, J. Math. Phys. 38, 1347 (1997). [CrossRef]
  49. Feshbach. H, et al. Model for Nuclear Reactions with Neutrons. Phys. Rev. 96, 448 (1954). [CrossRef]
  50. Schiff, L. I. Quantum Mechanics (New York: McGraw-Hill), 1968.
  51. Horiuchi, H. A Semi-Classical Treatment of Non-Local Potentials. Progress of Theoretical Physics, 64, 184 (1980). [CrossRef]
  52. Peierls, R., Mau, N. V. Local approximation to a non-local potential. Nuclear Physics A, 343, 1 (1980). [CrossRef]
  53. Frahn, W.E,. Lemmer, R.H. Velocity-Dependent Nuclear Interaction. Il Nuovo Cimento, 6, 1221 (1957). [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated