Dynamic Coalition Formation Among IoT Service Providers: A Systematic Exploration of IoT Dynamics Using an Agent-Based Model

Preprint

Article

Dynamic Coalition Formation Among IoT Service Providers: A Systematic Exploration of IoT Dynamics Using an Agent-Based Model

Altmetrics

Downloads

Views

Comments

A peer-reviewed article of this preprint also exists.

Joshua Shakya^*,Morgan Chopin,

Leila Merghem-Boulahia

Joshua Shakya^*,Morgan Chopin,

Leila Merghem-Boulahia

This version is not peer-reviewed

Submitted:

01 March 2024

Posted:

04 March 2024

You are already at the latest version

Alerts

Abstract

This paper introduces an Agent-Based Model (ABM) for investigating the dynamics of the Internet of Things (IoT) ecosystem, specifically focusing on dynamic coalition formation among IoT Service Providers (SPs). Extending our prior work in 5G network modeling, the ABM captures intricate interactions among device, network operator, SP, and customer agents, offering a versatile framework for studying IoT ecosystem dynamics. The simulation portrays the adaptive nature of collaborations, providing insights into the role of dynamic coalition formation in shaping the collaborative landscape of IoT.

Keywords:

Subject: Computer Science and Mathematics - Other

1. Introduction

The Internet of Things (IoT) [1,2] is a revolutionary paradigm that intertwines the physical and digital realms through interconnected devices. In this network, devices seamlessly communicate, generating vast streams of data that encapsulate the pulse of our interconnected world. The IoT ecosystem involves not only device interactions but also critical roles played by mobile network operators (MNOs) and IoT Service Providers (SPs). MNOs, as the backbone of IoT networks, manage infrastructure for seamless communication among devices, ensuring reliability, scalability, and security. SPs contribute significantly by offering specialized applications, analytics, and value-added services [3] built upon the foundation of IoT-generated data.

Despite the transformative potential and applications of IoT, the escalating complexity of its dynamics presents formidable challenges. There is a noticeable gap in existing literature, with comprehensive studies examining dynamics and interactions between entities within the IoT landscape lacking. While certain works address specific aspects of IoT dynamics [4], they often fall short of encompassing the full spectrum of interactions among key players. The relationships among devices, MNOs, and SPs play a pivotal role in shaping the IoT ecosystem, necessitating a nuanced approach that current research efforts have yet to thoroughly explore.

To address the existing gap in IoT literature, we advocate for an agent-based methodology [5], a robust approach involving the construction of a dynamic model that encapsulates the roles and interactions of entities within the IoT ecosystem. Agents, representing devices, MNOs, SPs,and more, authentically emulate real-world behaviors and collaborations, thereby enabling a nuanced exploration of IoT’s inherent complexity. This approach stands out from traditional methods by allowing for a meticulous examination of relationships and dynamics that might be overlooked in broader scopes. Furthermore, its adaptability and scalability make it well-suited to accommodate the evolving nature of the IoT landscape.

As a use-case implementation within the model, the effectiveness of the agent-based framework in simulating dynamic coalition formation among SPs within the IoT ecosystem is demonstrated. While prior research, exemplified by [20], has predominantly examined SP coalition formation through a pricing perspective and utilized bundling strategies to attract more customers and increase revenue, it often overlooked the complexities of large-scale collaboration scenarios. These scenarios entail numerous SPs engaging in multiple collaborations, competitions, and overlapping coalitions. To address this gap, our work delves into the dynamics of strategic collaborations, adaptive behaviors, and decision-making processes among SPs, uncovering insights crucial for optimizing collective profits in the IoT landscape. By integrating real-world use cases, our model showcases its versatility in capturing and analyzing the nuanced collaborative dynamics inherent in the evolving IoT ecosystem, thus enhancing its practical relevance and applicability.

1.1. Related Works

In the context of IoT, significant research efforts have been dedicated to exploring various aspects such as architectural considerations [6,7], device interactions [8], and resource allocation and optimization strategies [9]. Additionally, the utilization of ABM for IoT systems has gained recognition, with numerous papers [10,11] employing this approach to dissect and analyze IoT dynamics. Notably, ABM has been applied in diverse IoT use cases, ranging from smart waste monitoring [12] to self-adaptive and self-organizing applications [13]. Furthermore, a comprehensive survey [14] extensively explores the potential of ABM in the context of 5G networks, highlighting its effectiveness in understanding and analyzing the dynamics of next-generation telecommunications systems. This research forms a robust foundation for extending ABM methodologies to address the complexities and challenges of the broader IoT ecosystem. Although the ABM model was primarily focused on network slicing scenarios [15,16], it still holds great potential for IoT networks, given its versatility.

While dynamic coalition formation has been extensively studied in various domains, ranging from applications in small cell networks [17] to smart grids [18], its exploration within IoT networks has garnered significant interest. Specifically, coalition formation mechanisms have been tailored for IoT device coalitions [19], aiming at optimizing energy and resource utilization in IoT environments. Despite this progress, the establishment of coalitions among SPs remains a relatively underexplored area, with limited existing literature. Notably, a few studies have initiated investigations into this emerging topic, focusing on strategies such as bundling [20,21] and their implications for fostering collaborative arrangements among SPs. This evolving research direction holds promise for optimizing service delivery, enhancing resource utilization, and fostering collaborative innovation within the dynamic IoT ecosystem.

1.2. Contributions

In summary, the key contributions of our work are as follows:

Proposal of an adaptable and scalable Agent-Based Model for the IoT Ecosystem: The paper introduces a comprehensive model for the IoT ecosystem, which includes diverse entities such as devices, MNOs, SPs, and customers. This model ensures adaptability and scalability, effectively accommodating the dynamic nature of the IoT landscape. It serves as a practical and effective tool for researchers and practitioners seeking a systematic understanding of the multifaceted interactions shaping the future of IoT.
Demonstration of Model’s Versatility through a Practical Use-Case: Another key contribution of the paper lies in its practical demonstration of the proposed agent-based model through a focused use-case scenario. Specifically, the paper explores the dynamic formation of coalitions among IoT SPs—a critical aspect of the IoT ecosystem often overlooked in existing literature. Through this use-case scenario, the paper not only showcases the versatility and effectiveness of the agent-based approach but also provides valuable insights into optimizing collaborative strategies and maximizing collective profits within the IoT ecosystem. By bridging the gap between theoretical frameworks and real-world applications, the paper contributes to a deeper understanding of the collaborative dynamics shaping the future of IoT.

2. An Agent-Based Modelization for IoT

This section delves into the technical details of the ABM, purposefully designed to dissect the dynamics within the IoT ecosystem. Building upon prior work in modeling 5G networks with an agent-based approach [15,16], the model has been adapted to fit the specific characteristics of the IoT ecosystem. This evolution demonstrates the flexibility of the modeling framework to address diverse network architectures and underscores its adaptability to different technological paradigms. Functioning as a precision instrument, our proposed ABM IoT model comprises four key entities:

Device agents ( $A_{D}$ ): These agents represent the myriad of IoT devices within the ecosystem, each equipped with specific functionalities and capabilities tailored to their intended purposes.
Mobile network operator agents ( $A_{M}$ ): Responsible for managing and orchestrating the communication infrastructure, these agents oversee the transmission of data between devices and SPs within the network.
Service Provider agents ( $A_{S P}$ ): These entities offer a range of services and solutions to customers with different needs and preferences, by leveraging the data provided by device agents.
Customer agents ( $A_{C}$ ): Representing the end-users and consumers of IoT services, these agents interact with SPs to access and utilize the offerings provided by the ecosystem.

Each entity is defined by a unique set of attributes that delineate their functionalities within the ecosystem. Interactions among these entities, governed by predefined rules, intricately shape the evolution of the IoT landscape. Additionally, the model incorporates dynamic coalition formation, introducing supplementary rules dictating the collaborative behaviors of SPs.

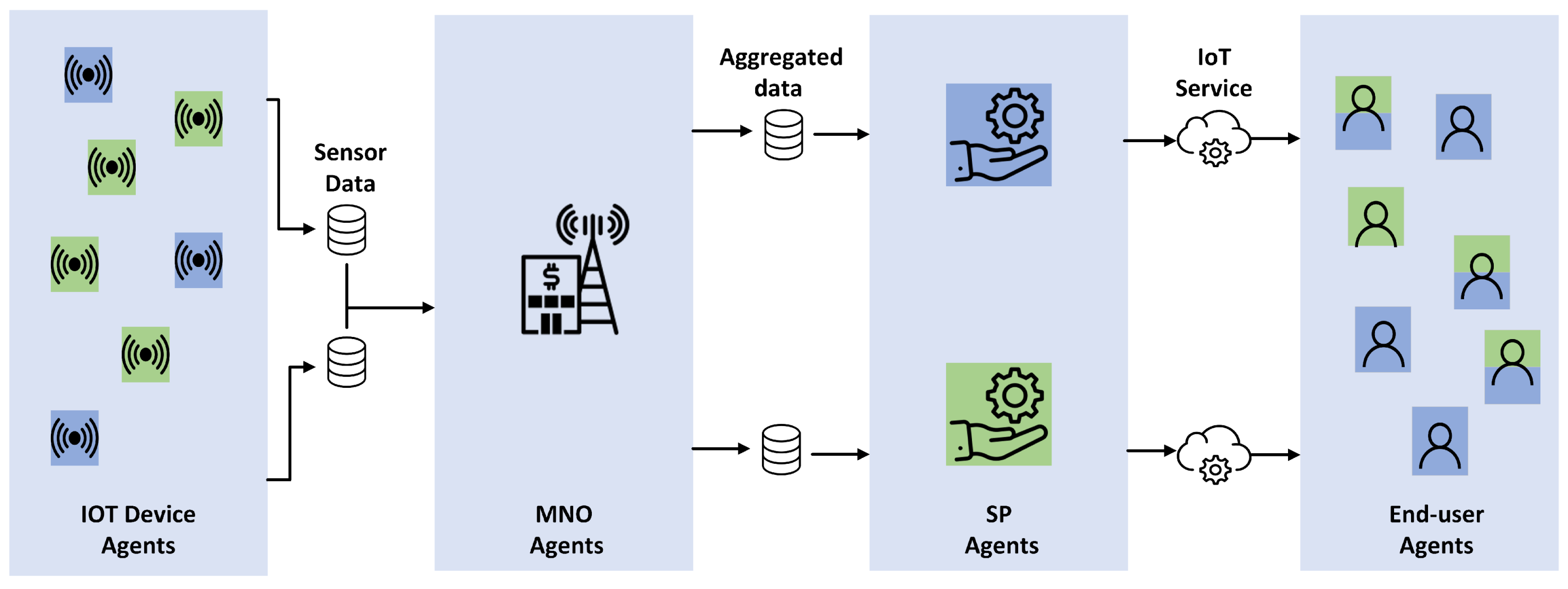
Figure 1 presents a detailed schematic of the IoT ecosystem, showcasing the interactions among its core components. At the center of the ecosystem, various IoT devices generate extensive data streams, which are efficiently aggregated and managed by the MNO agent. SP agents play a crucial role by strategically acquiring sensor data from the MNO and utilizing advanced processing techniques to offer a wide range of IoT services. Customers within the IoT ecosystem interact dynamically with the SPs, subscribing to the services that best align with their preferences and objectives. Importantly, customers may have varied needs and requirements, often necessitating the utilization of multiple services offered by different SPs. This dynamic demand for diverse services encourages collaboration and partnership among the SPs, leading to the formation of coalitions or alliances aimed at delivering comprehensive solutions to the users. While the figure illustrates data flow in one direction, it is important to note that there is significant interplay between the components in both directions. For instance, the preferences of customers can influence SP behavior and the selection of IoT devices, while feedback from SPs can shape the development and deployment of IoT devices. This reciprocal interaction contributes to the dynamic nature of the ecosystem and underscores the importance of considering multidirectional relationships. Overall, the figure provides a holistic representation of the IoT ecosystem, highlighting the interconnectedness of its key components and the collaborative dynamics that drive innovation and value creation within the ecosystem.

To provide an overview of the system dynamics, Algorithm 1 outlines the computational process. It commences with IoT device agents generating and transmitting data to their respective MNO agents. These MNO agents process and distribute the data to selected SP agents. Subsequently, customer agents select SPs based on their preferences and subscribe to them. SP agents then execute the Multi-Agent Dynamic Coalition Formation (MA-DCF) algorithm (see Section 3) to evaluate their coalition status and offer both standalone and collaborative services. Finally, customers benefit from the services provided by the selected providers, thereby completing the iterative cycle. This orchestrated approach ensures efficient data flow, subscription processes, and service provision within the IoT landscape, catering to the diverse needs of both customers and SPs.

Algorithm 1 High-level Orchestrator Algorithm for IoT Ecosystem Dynamics

1:: while true do
2:: for all IoT Device Agents $A_{D_{i}}$ do
3:: GenerateData( $A_{D_{i}}$ )
4:: $A_{M_{i}} \leftarrow$ SelectMNO( $A_{D_{i}}$ ) ▹ Assigns the MNO associated with $A_{D_{i}}$
5:: TransmitData( $A_{D_{i}}$ , $A_{M_{i}}$ )
6:: end for
7:: for all Mobile Network Operator Agents $A_{M_{i}}$ do
8:: ReceiveData( $A_{M_{i}}$ )
9:: $S e l e c t e d S e r v i c e P r o v i d e r s \leftarrow$ SelectServiceProviders( $A_{M_{i}}$ ) ▹ Selects the SPs contracted by $A_{M_{i}}$
10:: for all $S e l e c t e d S e r v i c e P r o v i d e r s$ $A_{S P_{k}}$ do
11:: TransmitData( $A_{M_{i}}$ , $A_{S P_{k}}$ )
12:: end for
13:: end for
14:: for all Customer Agents $A_{C_{j}}$ do
15:: $S e l e c t e d S e r v i c e P r o v i d e r s \leftarrow$ SelectServiceProviders( $A_{C_{j}}$ ) ▹ Customer’s preferred SPs
16:: for all $A_{S P_{k}}$ in $S e l e c t e d S e r v i c e P r o v i d e r s$ do
17:: Subscribe( $A_{C_{j}}$ , $A_{S P_{k}}$ )
18:: end for
19:: end for
20:: for all SP Agents $A_{S P_{i}}$ do
21:: MA-DCF( $A_{S P_{i}}$ ) ▹ See Section 3
22:: if $A_{S P_{i}}$ is part of a coalition then
23:: OfferCollaborativeService( $A_{S P_{i}}$ )
24:: end if
25:: OfferStandaloneService( $A_{S P_{i}}$ )
26:: end for
27:: for all Customer Agents $A_{C_{j}}$ do
28:: BenefitFromServices( $A_{C_{j}}$ )
29:: end for
30:: end while

3. Simulation of A Practical Use-Case: Multi Agent—Dynamic Coalition Formation (MA-DCF)

Coalitions in multi-agent systems, particularly within the IoT landscape, represent collaborative alliances formed by independent entities. These entities, often agents, pool their resources and expertise to collectively address challenges or capitalize on opportunities that may surpass individual capacities. Coalition formation involves strategic decision-making, where agents evaluate potential partners based on shared goals, complementary capabilities, and mutual benefits.

To unravel the intricacies of this dynamic coalition formation, we delve into the variables that govern the decision-making process and the evolving dynamics within this landscape.

$A_{SP} = {A_{{SP}_{0}}, \dots, A_{{SP}_{n}}}$ : Denotes the set of service provider agents in the system.
$C = {C_{0}, \dots, C_{n}}$ : Represents all coalitions formed among service provider agents, where each coalition $C_{c} \subseteq A_{SP}$ .
$B e n e f i t (C_{c}, t) \in [0, 1]$ : Represents the normalized benefit associated with coalition $C_{c}$ at time step t, indicating the overall advantage or gain obtained from the collaboration within that coalition.
$C o s t (C_{c}, C_{c^{'}}, t) \in [0, 1]$ : Denotes the normalized cost associated with coalition $C_{c}$ at time step t, including the joining cost and, if applicable, the leaving cost if the agent needs to exit coalition $C_{c^{'}}$ at time step t.
$U t i l i t y (C_{c}, C_{c^{'}}, t) \in [- 1, 1]$ : Represents the utility derived from coalition $C_{c}$ at time step t, calculated based on the difference between its benefit and the cost incurred to form the coalition, reflecting the overall satisfaction and effectiveness of collaboration within the coalition.

3.1. Core Matrices Guiding Multi-Agent Coalition Dynamics

In our simulation framework, we utilize four key matrices to capture various aspects of collaboration and compatibility among SPs within coalitions:

Data Sharing Matrix ( $D$ ): Represents the sharing of IoT devices between pairs of SPs at time step t, where $D_{i j} (t) \in [0, 1]$ signifies the level of data sharing capability between SPs $A_{S P_{i}}$ and $A_{S P_{j}}$ .
Service Compatibility Matrix ( $S$ ): Reflects co-subscription rates between pairs of SPs at time step t, with $S_{i j} (t) \in [0, 1]$ incrementally increasing based on customer co-subscriptions, indicating a higher level of collaborative potential and compatibility between the involved providers.
Resource Sharing Matrix ( $R$ ): Represents the intersection of assigned tasks between SPs at time step t, with $R_{i j} (t) \in [0, 1]$ values dynamically adjusted to signify high compatibility if two providers are engaged in identical computation tasks, indicating task redundancy.
Joining Cost Matrix ( $X$ ): Evaluates the cost of a SP joining a coalition with existing members at time step t, considering factors such as technological alignment and strategic fit. This matrix facilitates informed decision-making regarding coalition expansion or restructuring, where $X_{i j} (t) \in [0, 1]$ .

Matrices

D_{i j} (t)

S_{i j} (t)

, and

R_{i j} (t)

play pivotal roles in shaping coalition dynamics among SPs

A_{S P_{i}}

and

A_{S P_{j}}

at time step t. These matrices, representing data sharing, service compatibility, and resource sharing respectively, range from 0 to 1, denoting absence to high levels of capability or compatibility. As our simulation progresses, these matrices evolve dynamically, mirroring shifts in compatibility between SPs. For instance,

S_{i j} (t)

responds to changing customer co-subscriptions, while

D_{i j} (t)

reflects the utilization of shared IoT devices, reducing redundant data purchases. Meanwhile,

R_{i j} (t)

identifies task redundancy, optimizing resource utilization. Finally, the joining cost matrix

X_{i j} (t)

assesses the feasibility and cost of integrating members into a coalition based on technological alignment and strategic fit.

3.2. Benefit, Cost and Utility of Coalitions

Understanding the benefit, cost, and utility of coalitions is crucial for guiding strategic decision-making among SP agents. These metrics provide insights into the advantages and challenges associated with collaboration, ultimately influencing the formation and evolution of coalitions.

3.2.1. Normalized Benefit of Coalition

In our analysis, coalition benefit (

B e n e f i t (C_{c}, t)

) serves as a critical metric for assessing the overall advantage derived from collaboration within a specific coalition

C_{c}

at time step t. The benefit is calculated using the formula:

B e n e f i t (C_{c}, t) = \frac{2}{3 | C_{c} | (| C_{c} | - 1)} (\sum_{i, j \in C_{c} : i < j} D_{i j} (t) + \sum_{i, j \in C_{c} : i < j} S_{i j} (t) + \sum_{i, j \in C_{c} : i < j} R_{i j} (t))

(1)

Here,

| C_{c} |

denotes the number of agents within the coalition

C_{c}

, and

D_{i j} (t)

S_{i j} (t)

, and

R_{i j} (t)

represent the values in the data sharing, service compatibility, and resource sharing matrices, respectively, between SPs

A_{S P_{i}}

and

A_{S P_{j}}

within the coalition at time step t. The term

\frac{2}{3 | C_{c} | (| C | - 1)}

is utilized to normalize the benefit value between 0 and 1, ensuring standardized scaling across different coalition sizes and numbers of matrices. The factor of

\frac{1}{2} (| C_{c} | (| C_{c} | - 1))

accounts for the total number of pairwise combinations within the coalition. Since there are three matrices (data sharing, service compatibility, and resource sharing) contributing to the benefit calculation, the factor of 3 is included to balance the influence of each matrix.

3.2.2. Normalized Cost of Coalition

The normalized cost associated with a coalition at time step t, denoted as

C o s t (C_{c}, C_{c^{'}}, t)

, comprises two components: the joining cost and the leaving cost. If a SP must exit an existing coalition before potentially joining another coalition, the leaving cost

C o s t_{Leave} (C_{c^{'}}, t)

is considered, where

C_{c^{'}}

represents the coalition the SP intends to leave.

C o s t (C_{c}, C_{c^{'}}, t) = \frac{1}{2} (C o s t_{Join} (C_{c}, t) + C o s t_{Leave} (C_{c^{'}}, t))

(2)

The join cost (

C o s t_{Join} (C_{c}, t)

) represents the expense associated with a SP

A_{S P_{i}}

joining a coalition

C_{c}

. The value in the joining cost matrix

X_{i j} (t)

signifies the expense for SP

A_{{SP}_{i}}

to join a coalition

C_{c}

containing member

A_{{SP}_{j}}

and time step t. By summing over all current coalition members

A_{{SP}_{j}}

within

C_{c}

except

A_{{SP}_{i}}

, the formulation accounts for the joining costs associated with each existing member. It is calculated as:

C o s t_{Join} (C_{c}, t) = \frac{1}{| C_{c} | - 1} \sum_{j \in C_{c}, j \neq i} X_{i j} (t)

(3)

C_{c^{'}} \neq \emptyset

, the leaving cost function involves two terms. The first term is denoted by

f (δ (t))

, where

δ (t)

represents the duration of the coalition. It is modeled as a sigmoid function that converges towards 1 as the duration of the coalition increases, capturing the increasing complexity and costliness of disengagement over time. Mathematically, the sigmoid function can be defined as:

f (δ (t)) = \frac{1}{1 + e^{- α (δ (t) - β)}}

(4)

Here,

α

and

β

are parameters determining the shape of the sigmoid function.

Additionally, in the second term,

| C_{c^{'}} |

denotes the number of SP agents within the coalition, and

| A_{SP} |

determines the total number of SP agents. As the coalition size grows, the leaving cost proportionally increases, reflecting the heightened intricacies and dependencies inherent in larger coalitions. Thus, the leaving cost dynamically adjusts based on both the temporal and structural dimensions of coalition dynamics.

The leaving cost function is mathematically represented as:

C o s t_{Leave} (C_{c^{'}}, t) = f (δ (t)) \cdot \frac{| C_{c^{'}} |}{| A_{SP} |}

(5)

It’s important to note that if

C_{c^{'}}

is empty, the leaving cost becomes 0.

3.2.3. Utility of Coalition

The utility of a coalition at time step t, denoted as

U t i l i t y (C_{c}, C_{c^{'}}, t)

, signifies the net gain achieved by engaging in the coalition

C_{c}

after accounting for associated costs, including potential impacts of departing from another coalition

C_{c^{'}}

. It is calculated as the difference between the benefit (

B e n e f i t (C_{c}, t)

) accrued from collaboration within

C_{c}

and the total cost (

C o s t (C_{c}, C_{c^{'}}, t)

) incurred to maintain membership in

C_{c}

, while also considering the potential cost of leaving

C_{c^{'}}

U t i l i t y (C_{c}, C_{c^{'}}, t) = B e n e f i t (C_{c}, t) - C o s t (C_{c}, C_{c^{'}}, t)

(6)

The utility of coalition

U t i l i t y (C_{c}, C_{c^{'}}, t)

is constrained within the range

- 1 \leq U t i l i t y (C_{c}, C_{c^{'}}, t) \leq 1

, ensuring a normalized utility metric that offers a standardized measure of the net gain obtained from coalition participation. A positive utility value (

U t i l i t y (C_{c}, C_{c^{'}}, t) > 0

) signifies a favorable inclination towards joining

C_{c}

, even after contemplating the potential cost of leaving

C_{c^{'}}

. Conversely, a zero or negative utility value (

U t i l i t y (C_{c}, C_{c^{'}}, t) \leq 0

) suggests that the incurred costs surpass the benefits, indicating a less desirable scenario for coalition participation.

3.3. Strategic Decision-Making

In the strategic decision-making process of SP agents, two critical elements drive their behavior: the commencement of coalition formation and the subsequent determination of whether to accept or decline coalition requests.

3.3.1. Initiation of Coalition Formation

Each SP agent assesses its neighboring agents using various compatibility metrics, such as data sharing capabilities, service compatibility, and resource sharing potential, represented by matrices

D

S

, and

R

respectively. The compatibility between SP agents

A_{S P_{i}}

and

A_{S P_{j}}

at time step t is determined by the function:

C o m p a t i b i l i t y (A_{S P_{i}}, A_{S P_{j}}, t) = \{\begin{matrix} 1, & if D_{i j} (t) > θ_{D} or S_{i j} (t) > θ_{S} or R_{i j} (t) > θ_{R} \\ 0, & otherwise \end{matrix}

(7)

where

θ_{D}

θ_{S}

, and

θ_{R}

are predefined thresholds. If the compatibility score between two SP agents exceeds any of the thresholds in the matrices, they are considered suitable partners for coalition formation.

To determine the compatible neighbors for a given SP agent

A_{S P_{i}}

at time step t, the algorithm iterates through all neighboring agents

A_{S P_{j}}

and evaluates their compatibility using the Compatibility function. The set of compatible neighbors, denoted by

C o m p a t i b l e N e i g h b o r s (A_{S P_{i}}, t)

, is defined as:

C o m p a t i b l e N e i g h b o r s (A_{S P_{i}}, t) = {A_{S P_{j}} ∣ C o m p a t i b i l i t y (A_{S P_{i}}, A_{S P_{j}}, t) = 1}

(8)

After assessing compatibility with neighboring agents, the SP agent forms a potential coalition by including itself and its compatible neighbors. If all members of this potential coalition accept the request, a new coalition is established. Mathematically, the decision to form a coalition, denoted by

C o a l i t i o n F o r m a t i o n (P o t e n t i a l C o a l i t i o n, t)

, is determined by:

C o a l i t i o n F o r m a t i o n (P o t e n t i a l C o a l i t i o n, t) = \{\begin{matrix} 1, & if \forall A_{S P_{j}} \in P o t e n t i a l C o a l i t i o n, \\ A c c e p t a n c e (A_{S P_{j}}, P o t e n t i a l C o a l i t i o n, t) = 1 \\ 0, & otherwise \end{matrix}

(9)

where

P o t e n t i a l C o a l i t i o n = {A_{S P_{i}}} \cup C o m p a t i b l e N e i g h b o r s (A_{S P_{i}}, t)

. The binary variable

A c c e p t a n c e (A_{S P_{j}}, P o t e n t i a l C o a l i t i o n, t)

indicates whether SP agent

A_{S P_{j}}

accepts the coalition request. This equation ensures that a new coalition is formed only if all potential members accept the coalition request.

3.3.2. Acceptance or Rejection of Coalition Requests

When a SP

A_{{SP}_{i}}

receives a request for coalition formation, it can either accept or reject it. Let

B u d g e t (A_{{SP}_{i}})

be the budget of

A_{{SP}_{i}}

, representing the total number of coalitions it can join, and

C o a l i t i o n s (A_{{SP}_{i}}, t)

be the current coalitions of

A_{{SP}_{i}}

. If the current number of coalitions

| C o a l i t i o n s (A_{{SP}_{i}}, t) |

is less than the budget, the SP accepts the request directly.

When the number of coalitions formed by SP

A_{{SP}_{i}}

reaches its budget

B u d g e t (A_{{SP}_{i}})

, the SP must carefully evaluate new coalition requests. In such cases,

A_{{SP}_{i}}

calculates the utility of the potential coalition by considering the cost of leaving one of its current coalitions

C_{c^{'}}

at time t. Afterward, it selects the maximum utility among and assesses whether this maximum utility is greater than 0. A utility greater than 0 signifies that leaving a coalition to join the new request would be beneficial.

The acceptance decision is determined by the following condition:

A c c e p t a n c e (A_{{SP}_{i}}, C_{c}, t) = \{\begin{matrix} 1, & if (| C o a l i t i o n s (A_{{SP}_{i}}, t) | < B u d g e t (A_{{SP}_{i}})) or \\ (| C o a l i t i o n s (A_{{SP}_{i}}, t) | = B u d g e t (A_{{SP}_{i}}) and \\ max_{C_{c^{'}} \in C o a l i t i o n s (A_{{SP}_{i}}, t)} U t i l i t y (C_{c}, C_{c^{'}}, t) > 0) \\ 0, & otherwise \end{matrix}

(10)

Here,

{max}_{C_{c^{'}} \in C o a l i t i o n s (A_{{SP}_{i}}, t)} U t i l i t y (C_{c}, C_{c^{'}}, t)

represents the maximum utility obtained by evaluating the utility function for the coalition request

C_{c}

with respect to each existing coalition

C_{c^{'}}

at time t. If the maximum utility is greater than 0, the SP accepts the coalition request; otherwise, it rejects it.

3.4. Coalition and Individual Payoffs

Two critical metrics play significant roles in evaluating the effectiveness of our MA-DCF algorithm: coalition payoff and individual payoff. Coalition payoff reflects the collective benefit accrued from collaboration within formed coalitions, providing a measure of the overall success in achieving shared objectives and maximizing mutual gains. On the other hand, individual payoff assesses the net benefit obtained by individual SP agents participating in coalitions, capturing the effectiveness of their strategic decisions and the impact on their individual objectives and resources.

3.4.1. Coalition Payoff

Coalition payoff represents the cumulative benefit derived from collaboration within a formed coalition at a specific time step t. Unlike the normalized benefit, coalition payoff does not involve normalization and provides a raw measure of the total advantage obtained from coalition participation. Mathematically, the coalition payoff (

P a y o f f (C_{c}, t)

) at time step t is calculated as the sum of contributions from various factors such as data sharing (

D_{i j}

), service compatibility (

S_{i j}

), and resource sharing (

R_{i j}

) between all pairs of service provider (SP) agents

A_{S P_{i}}

and

A_{S P_{j}}

within the coalition

C_{c}

P a y o f f (C_{c}, t) = (\sum_{i, j \in C_{c} : i < j} D_{i j} (t) + \sum_{i, j \in C_{c} : i < j} S_{i j} (t) + \sum_{i, j \in C_{c} : i < j} R_{i j} (t))

(11)

3.4.2. Individual Payoff

The individual payoff refers to the net benefit received by a specific SP agent within a formed coalition, considering its contribution to the coalition’s overall payoff. It can be conceptualized as the difference between the coalition payoff with the individual SP (

P a y o f f (C_{c}, t)

) and the coalition payoff without the individual SP (

P a y o f f (C_{c} ∖ {A_{{SP}_{i}}}, t)

). Mathematically, the individual payoff (

I n d i v i d u a l P a y o f f (A_{{SP}_{i}}, C_{c}, t)

) for SP agent

A_{{SP}_{i}}

within coalition

C_{c}

at time step t can be expressed as:

I n d i v i d u a l P a y o f f (A_{{SP}_{i}}, C_{c}, t) = P a y o f f (C_{c}, t) - P a y o f f (C_{c} ∖ {A_{{SP}_{i}}}, t)

(12)

4. Results

In the instantiation of our ABM for the IoT ecosystem, we meticulously define the parameters to reflect a realistic and dynamic simulation. The number of IoT Device Agents (

A_{D}

) is set at 1000, representing a diverse range of devices contributing to the IoT landscape. Mobile Network Operator Agents (

A_{M}

) are limited to 1, capturing the presence of a single operator managing the network infrastructure. SP Agents (

A_{S P}

) are introduced with a count of 10, signifying a competitive yet collaborative environment with a variety of service offerings. Customer Agents (

A_{C}

) are initialized to 500, representing the end-users engaging with the IoT services. Each SP Agent’s budget, reflecting the maximum number of coalitions it can join, ranges from 1 to 5. This allocation, detailed in Table 1, signifies varying levels of strategic flexibility and collaboration potential within our simulated IoT ecosystem.

To initiate the simulation, we assume there are no existing coalitions among the SPs. Each SP operates independently, offering services separately to the IoT ecosystem. Therefore, the maximum number of coalitions (

| C |

) is initially set to 10, aligning with the number of SPs. This setup reflects the starting point, where SPs function individually without collaborative arrangements. Additionally, customers are subscribed to one or more SPs, with a higher probability of subscribing to a complementary SP, modeled using normal and mixed normal distribution.

The matrices representing capabilities and compatibilities between SPs within a coalition—

D

(data sharing),

S

(service compatibility), and

R

(resource sharing)— are initialized with random real numbers taken from the interval

[0, 1]

. The matrices are given in Table 2. The initialization process is based on various factors, including the instantiation of SPs, and customers’ initial subscription behavior. These matrices serve as the foundation for modeling the collaborative relationships between SPs within a coalition, and their values will evolve over time as the simulation progresses. Additionally, there is matrix

X

, which represents the cost for an SP to join a coalition considering all the members.

The simulation progresses through discrete time steps

t = 1, 2, 3, . . ., T

, where T represents the total number of time steps defined. Each time step captures the actions and interactions among agents within the IoT ecosystem, including coalition formation, customer subscriptions, and resource exchange.

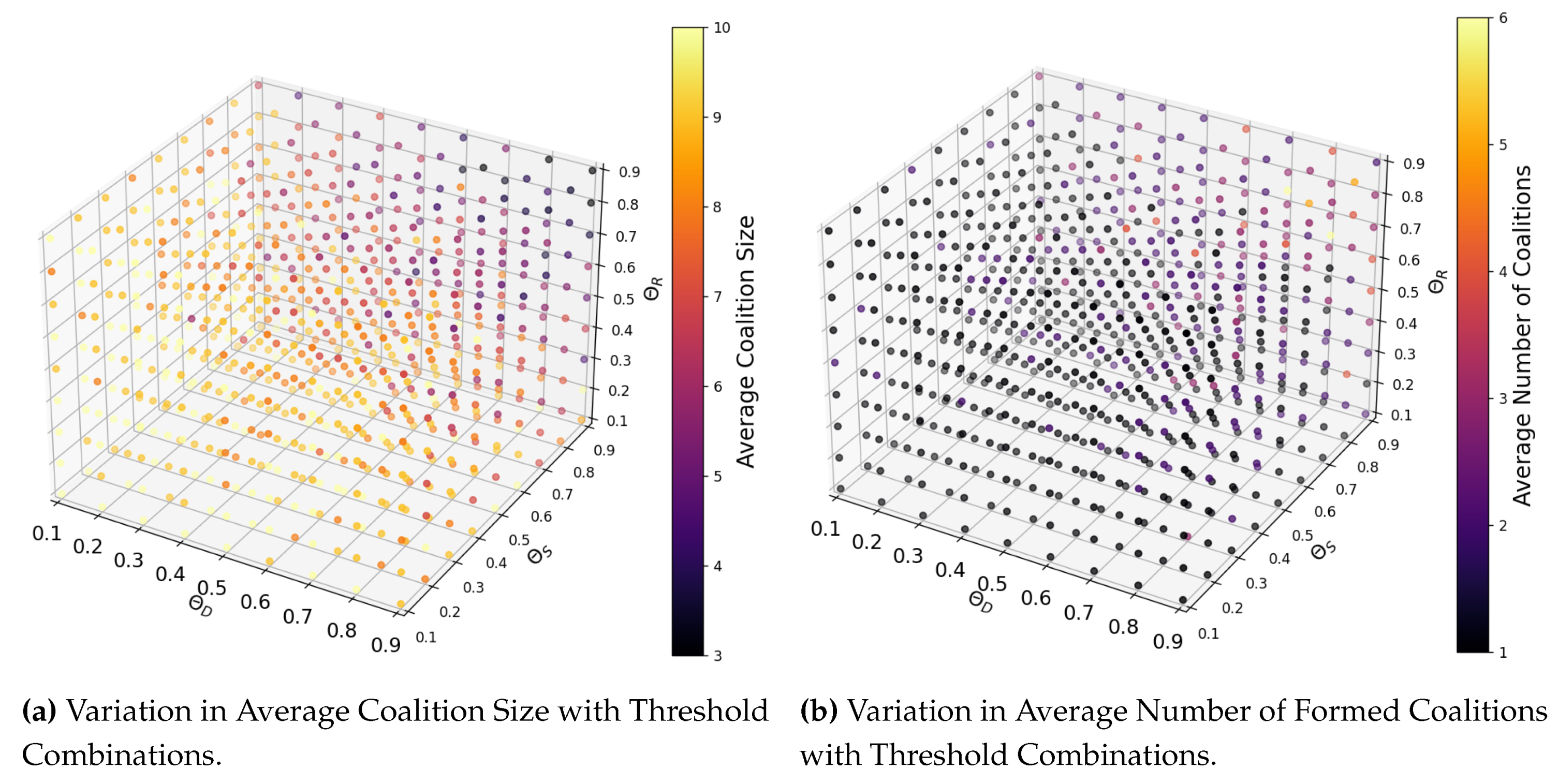
4.1. Sensitivity Analysis of Key Threshold Variables in MA-DCF

The size and number of coalitions within the MA-DCF exhibit sensitivity to variations in threshold values

θ_{D}

θ_{S}

, and

θ_{R}

. In our experimental setup, these thresholds are set within the range of 0.1 to 0.9 to elucidate their impact. Lower threshold values relax compatibility constraints, resulting in fewer but larger coalitions as SP agents find it easier to meet the relaxed compatibility criteria. Conversely, higher threshold values impose stricter compatibility requirements, leading to the formation of many smaller and more exclusive coalitions. This nuanced relationship is illustrated in Figure 2a, showing how different combinations of threshold values correspond to varying average coalition sizes, and Figure 2b, which depicts the corresponding number of coalitions formed. Therefore, precise calibration of threshold values is essential for shaping both the size and number of coalitions within the IoT ecosystem, ensuring that formed coalitions effectively leverage synergies and resources while maintaining compatibility among participating agents.

In our experimental setup, we opted for threshold values of 0.9 across all three metrics. This choice was motivated by the objective of striking a balance between fostering collaboration among SPs and maintaining compatibility standards. A higher threshold, ensures that only highly compatible SPs are eligible for coalition formation, thereby promoting synergy and mutual benefit within the formed coalitions.

4.2. Performance Assessment of MA-DCF

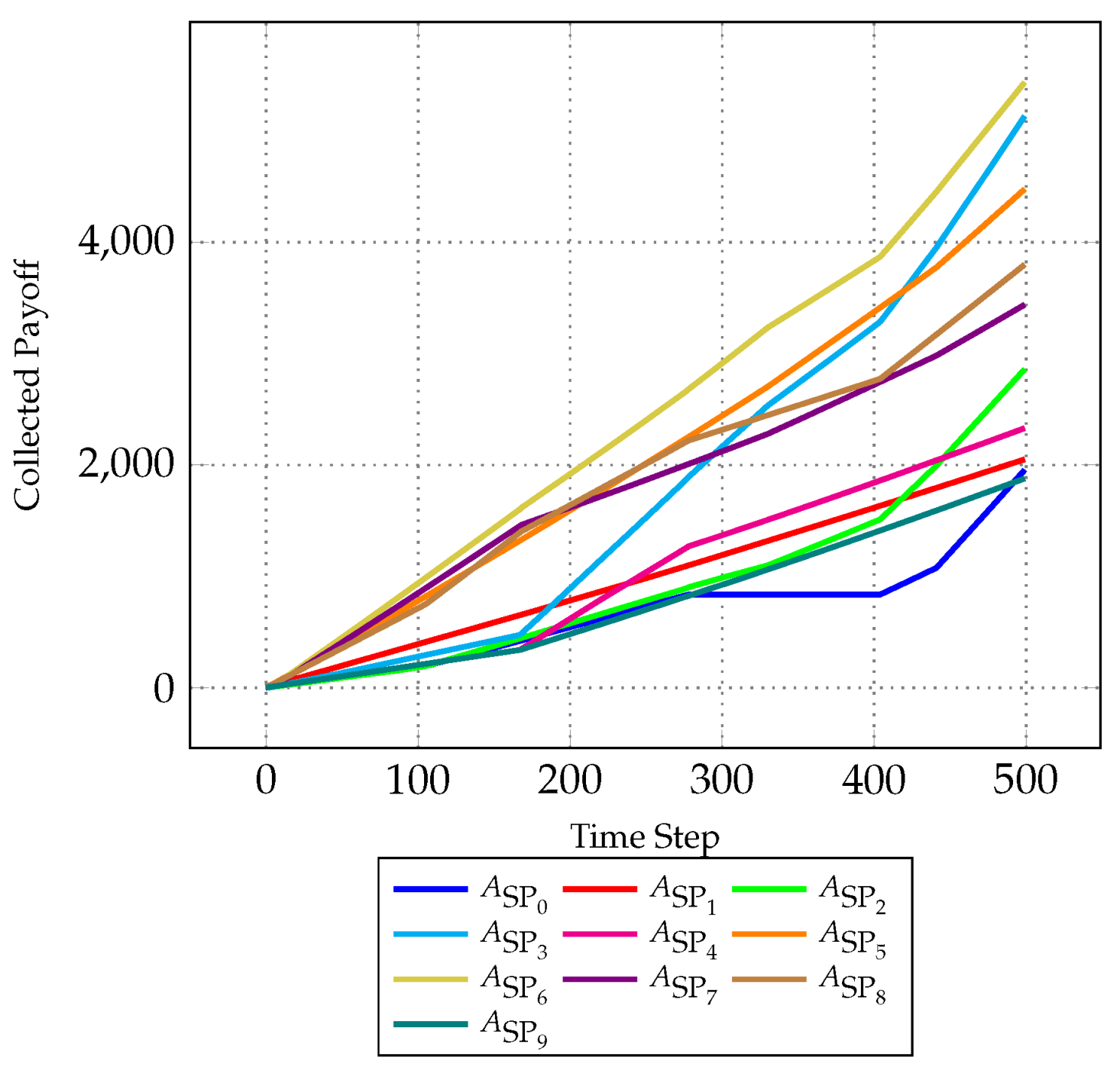
Figure 3 presents a comprehensive evaluation of the MA-DCF model’s performance, focusing on the aggregated collected payoff of individual SPs over successive time steps. The collected payoff of SP

A_{{SP}_{i}}

at time step t is obtained by summing the individual payoffs (Refer to equation 12) for all coalitions

C_{c}

in which

A_{{SP}_{i}}

is participating at each time step t:

\sum_{C_{c} \in C o a l i t i o n s (A_{{SP}_{i}}, t)} I n d i v i d u a l P a y o f f (A_{{SP}_{i}}, C_{c}, t)

(13)

Each SP’s payoff trajectory is depicted with a distinct line plot, enabling a granular analysis of their performance dynamics. The x-axis delineates time progression, offering a temporal context for assessing SP behavior, while the y-axis quantifies accumulated payoffs, reflecting the efficacy of coalition formations and strategic decisions.

A rigorous analysis of this figure is imperative for evaluating the efficacy of the MA-DCF model. For instance, sustained upward trends in the collected payoff of certain SPs, such as

A_{{S P}_{6}}

, may signify successful coalition formations or strategic alliances yielding favorable outcomes. Conversely, fluctuations or stagnation in payoff trajectories, like for SPs

A_{{S P}_{0}}

, may indicate challenges or inefficiencies in coalition dynamics, potentially necessitating further investigation into underlying factors such as negotiation strategies, or coalition stability. Comparative analysis across SPs facilitates the identification of performance disparities and strategic behaviors, informing refinements to the model and coalition formation strategies. This analysis can uncover the impact of factors such as SP budget allocations, resource availability, and strategic decision-making on coalition dynamics and overall performance.

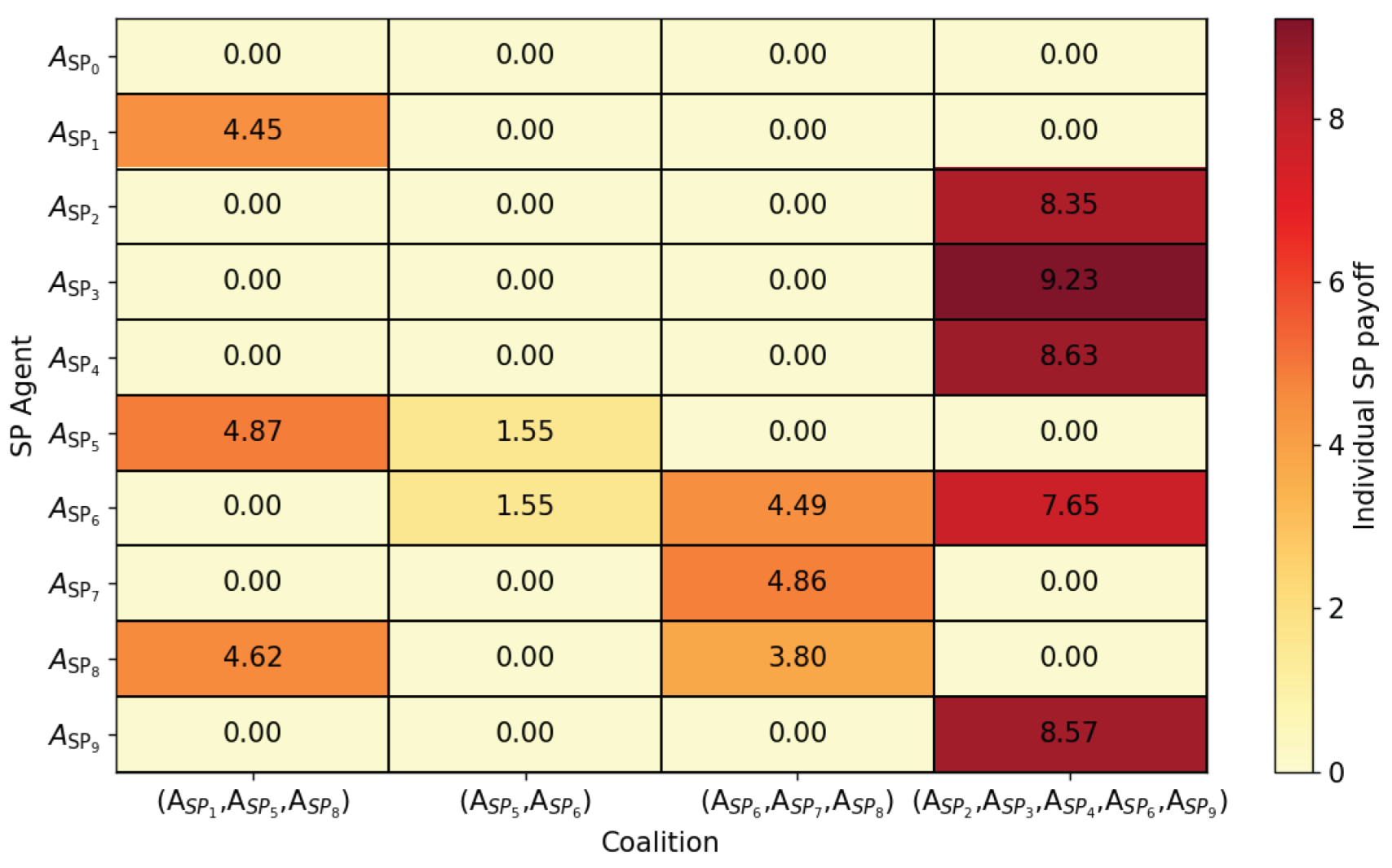
Figure 4 sheds light on the individual payoffs attained by each SP agent through participation in dynamic coalitions at a specific time step. By visually mapping the distribution of payoffs across different SP agents and coalition configurations, valuable insights can be gleaned regarding the efficacy of coalition formations. Additionally, it offers insights into the equitable distribution of payoffs among SP agents, facilitating the design of fair and sustainable coalition structures. Consider the analysis focused on the last coalition,

(A_{{SP}_{2}}, A_{{SP}_{3}}, A_{{SP}_{4}}, A_{{SP}_{6}}, A_{{SP}_{9}})

. Here, SP agent

A_{{SP}_{3}}

emerges as the primary beneficiary, garnering the highest payoff due to its substantial contributions to the coalition’s objectives. Conversely, SP agent

A_{{SP}_{6}}

receives a notably lower payoff, underscoring variations in engagement levels and contributions among coalition members. It’s worth noting that non-member SP agents receive a payoff of 0.0, indicative of their exclusion from coalition activities.

4.3. Comparative Analysis of MA-DCF: Performance Benchmarking

This analysis benchmarks the performance of the presented MA-DCF model against established baselines. By contrasting its strategic decision-making and compatibility matching with alternative scenarios, valuable insights are gained into its effectiveness and suitability for various applications.

The static coalition baseline represents a fixed partnership approach where coalitions remain unchanged throughout the process. While offering stability, it lacks the dynamic adaptations to resource availability and changing requirements inherent to the proposed model.
The non-overlapping coalition baseline restricts SPs to single memberships, ensuring clear responsibilities and minimizing conflict. However, this approach might limit resource sharing and adaptability when tasks require diverse skillsets or resources scattered across multiple SPs.
The random coalition baseline establishes a benchmark for improvement. Despite the potential for occasional compatibility through chance, this approach lacks strategic direction and is likely to underperform the proposed model.

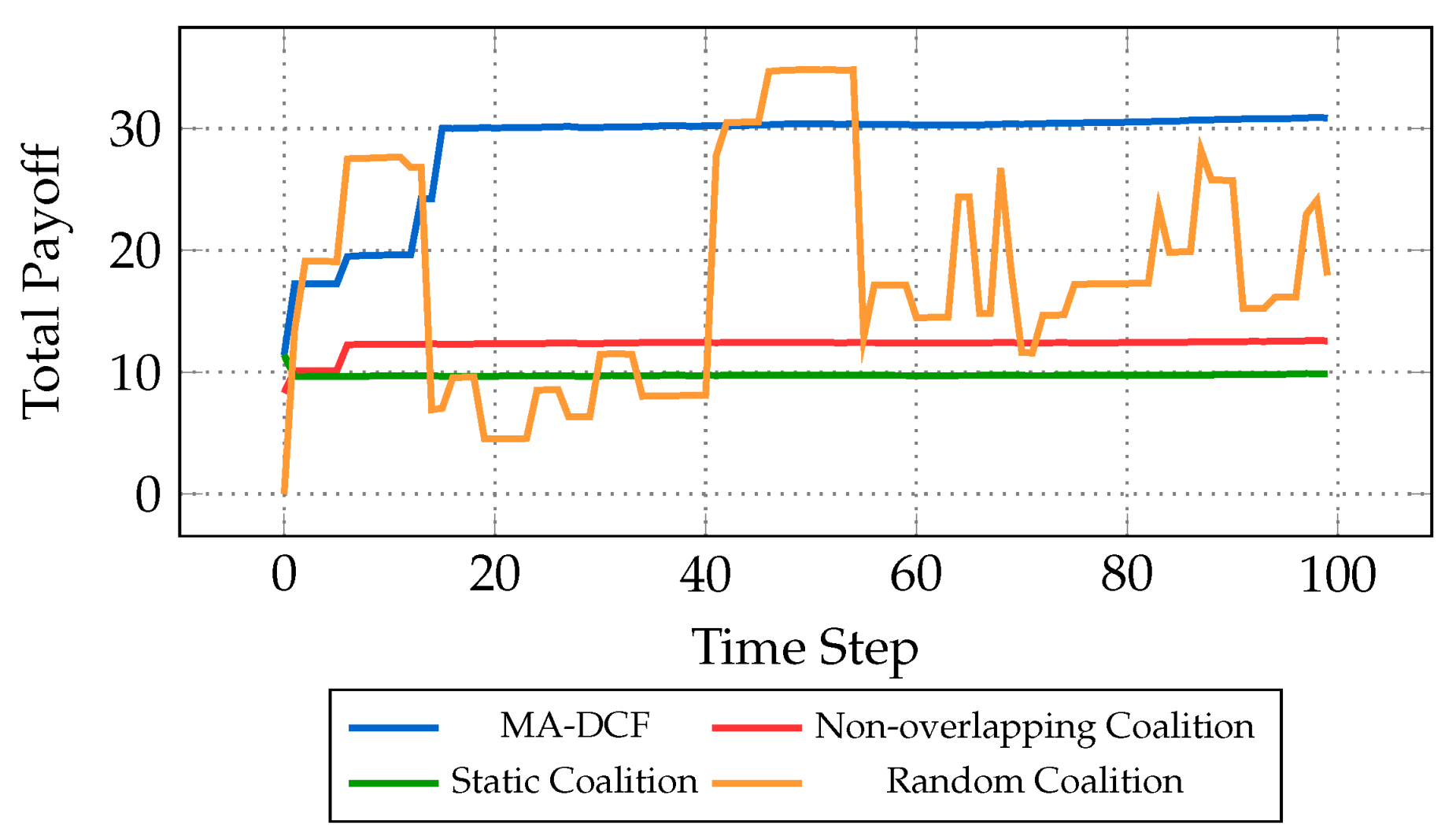
Figure 5 serves as a visual depiction of the temporal evolution of total payoff using different coalition formation strategies . The total payoff at each time step, denoted as

\sum_{C_{c} \in C} Payoff (C_{c}, t)

, where C represents the coalitions formed using each approach, is analyzed across four distinct coalition formation strategies: MA-DCF, Static coalition formation baseline, Non-overlapping coalition formation baseline, and Random coalition formation baseline. By iteratively optimizing coalition compositions based on agent preferences and environmental factors, MA-DCF ensures adaptability and responsiveness to evolving conditions. Conversely, the Static coalition baseline predefines coalition structures without accounting for changing dynamics, potentially leading to suboptimal outcomes in volatile environments. The Non-overlapping coalition baseline focuses on selecting the best coalition for each agent individually, aiming to maximize individual payoffs. However, this approach may inadvertently overlook opportunities for multiple collaborations among agents, thereby limiting the potential for synergistic partnerships and collective gain. By restricting agents to single coalitions, the Non-overlapping Coalition baseline may fail to exploit complementary skills and resources across different coalition configurations, leading to suboptimal overall performance. On the other hand, the Random coalition baseline randomly selects coalitions, offering little strategic insight and resulting in unpredictable performance. This approach, while occasionally yielding favorable outcomes, lacks strategic foresight and stability, rendering its performance unpredictable and unsuitable for robust decision-making processes.

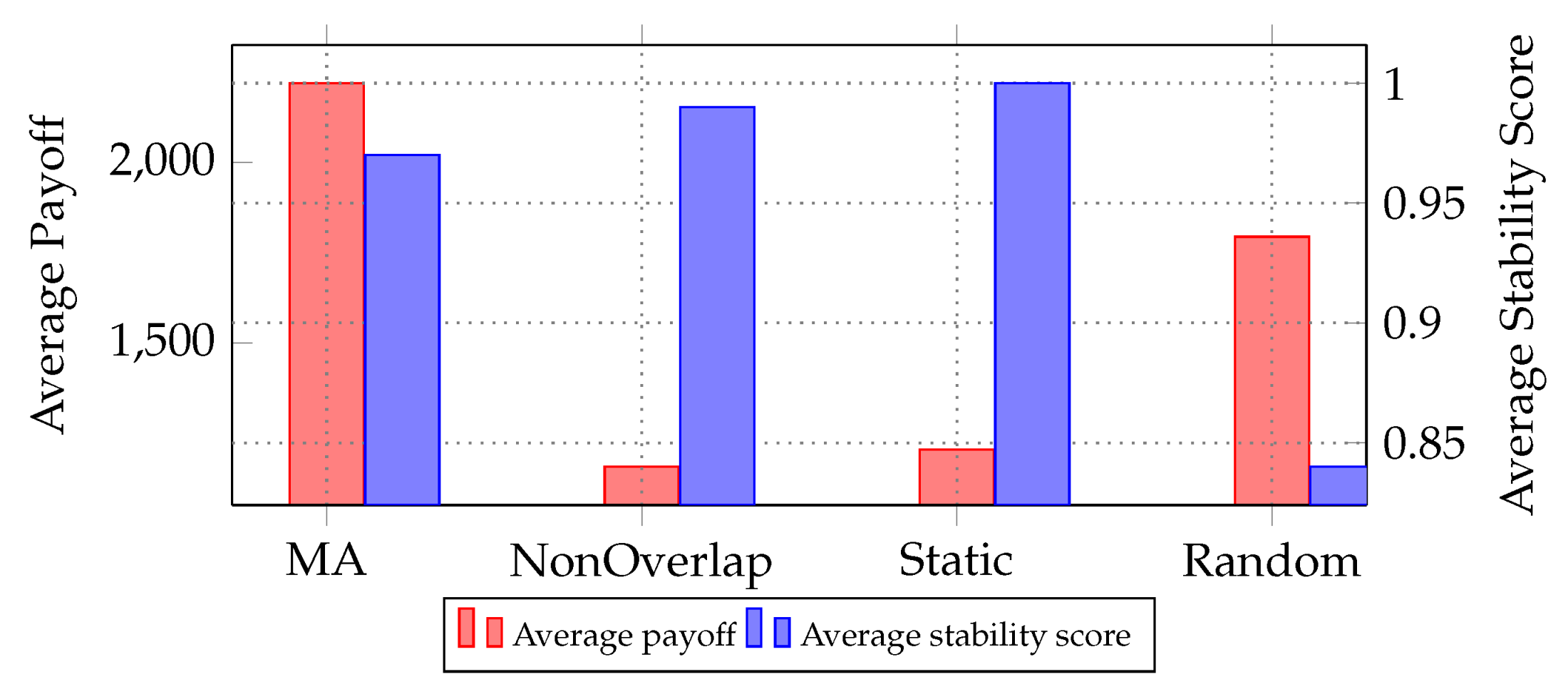
Figure 6 further delves into the comparison between the four coalition formation strategies, providing a deeper analysis of their performance and stability. This detailed analysis is derived from a comprehensive simulation comprising 10 runs, each spanning 100 time steps. The average payoff, depicted on the left y-axis, represents the payoff (Refer to equation 11) amassed by coalitions formed using each approach after 100 time steps, averaged across the 10 runs. It can be calculated as:

\frac{1}{N} \sum_{i = 1}^{N} \sum_{t = 1}^{T} \sum_{C_{c} \in C} P a y o f f (C_{c}, t)

(14)

where N is the number of runs, T is the number of time steps, and C represents the set of coalitions formed using each approach at time step t.

On the right y-axis, the stability metric is introduced to evaluate the consistency and resilience of coalition formations over time. This metric, calculated as the average stability using Jaccard’s index [22] between two consecutive time steps in each run, provides deeper insights into the dynamics of coalition structures. It can be computed as:

\frac{1}{N} \sum_{i = 1}^{N} \frac{1}{T - 1} \sum_{t = 2}^{T} J (C_{i, t - 1}, C_{i, t})

(15)

where

J (C_{i, t - 1}, C_{i, t})

denotes the Jaccard’s index between coalition structures at time steps

t - 1

and t in the current iteration.

Notably, the MA-DCF approach emerges as the most promising, yielding the highest average payoff after 100 time steps. This underscores its efficacy in orchestrating dynamic coalitions to maximize collective gains. Conversely, the Non Overlap baseline exhibits the lowest average payoff, reflecting its limited capability to foster collaboration among agents. Meanwhile, both the Random and Static coalition baselines present mixed outcomes, with their respective payoffs fluctuating inconsistently. Delving into stability, the Static approach demonstrates remarkable stability, maintaining a consistent coalition structure throughout the simulation. In contrast, the Random baseline displays the lowest stability, characterized by frequent coalition reconfigurations that could potentially incur additional costs. Notably, the MA-DCF approach, along with the Static baseline, demonstrates respectable stability, suggesting their reliability in dynamic environments. Taking into consideration all factors, the MA-DCF approach emerges as the superior choice in terms of both profitability and stability compared to the alternatives provided.

5. Conclusions

In summary, our Agent-Based Model (ABM) serves as a powerful tool for dissecting the intricate dynamics within the Internet of Things (IoT) ecosystem. By integrating dynamic coalition formation among Service Providers (SPs), the model adeptly captures the adaptive nature inherent in collaborations amidst the evolving IoT landscape. This adaptability empowers SPs to strategically navigate coalition formations based on mutual benefits, offering invaluable insights into the complex interplay of collaborative strategies within the IoT domain. Notably, our research has yielded compelling results, demonstrating the efficiency of our Multi-Agent Dynamic Coalition Formation (MA-DCF) algorithm over three baseline coalition formation algorithms in terms of both payoff and stability. This empirical validation not only reinforces the efficacy of our approach in optimizing outcomes within the IoT ecosystem but also solidifies the model’s foundational role in comprehensively assessing both present and future states of IoT interactions.

Looking ahead, our study underscores several key technical avenues for further exploration. Firstly, a deeper dive into subscriber behavior analysis is essential to unravel the impact of coalition formations on consumer preferences, adoption patterns, and loyalty dynamics across diverse coalition structures. This involves employing advanced data analytics techniques and behavioral modeling methodologies to glean insights into the complex interplay between coalition strategies and subscriber behavior within the IoT ecosystem. Additionally, a more granular exploration of market dynamics modeling holds immense potential for uncovering the interplay of factors such as pricing strategies, competitive dynamics, and the influx of new market entrants, all of which are significantly influenced by coalition formations over time. Complementing these avenues, an examination of the effects of coalitions on service quality metrics—ranging from network reliability and data security to customer support—will be pivotal in ensuring the longevity and trustworthiness of IoT services. By directing our research efforts along these technical trajectories, we can deepen our understanding of coalition dynamics within the IoT ecosystem and develop informed strategies that drive the field towards greater resilience and innovation.

References

Rose, K., Eldridge, S., & Chapin, L The internet of things: An overview. The internet society (ISOC). 2015; 80, 1–50.
Li, S., Xu, L. D., & Zhao, S. The internet of things: a survey. Information systems frontiers. 2015; 17, 243–259. [CrossRef]
Khanna, A., & Kaur, S. Internet of things (IoT), applications and challenges: a comprehensive review. Wireless Personal Communications. 2020, 114, 1687–1762. [CrossRef]
J. Kim and J. -W. Lee, "OpenIoT: An open service framework for the Internet of Things," 2014 IEEE World Forum on Internet of Things (WF-IoT), Seoul, Korea (South), 2014, pp. 89-93. [CrossRef]
Siebers, P. O., & Aickelin, U. Introduction to multi-agent simulation. In Encyclopedia of decision making and decision support technologies (pp. 554-564). IGI Global. 2008. [CrossRef]
Krčo, S., Pokrić, B., Carrez, F. Designing IoT architecture (S): A European perspective. In 2014 IEEE world forum on internet of things (WF-IoT) (pp. 79-84). IEEE. 2014. [CrossRef]
Soumyalatha, S. G. H. Study of IoT: understanding IoT architecture, applications, issues and challenges. In 1st International Conference on Innovations in Computing & Net-working (ICICN16), CSE, RRCE. International Journal of Advanced Networking & Applications (Vol. 478). 2016. [Google Scholar]
Mahalank, S. N., Malagund, K. B., & Banakar, R. M. Device to device interaction analysis in IoT based Smart Traffic Management System: An experimental approach. In 2016 Symposium on Colossal Data Analysis and Networking (CDAN) (pp. 1-6). IEEE. 2016. [CrossRef]
Sangaiah, A. K., Hosseinabadi, A. A. R., Shareh, M. B., Bozorgi Rad, S. Y., Zolfagharian, A., & Chilamkurti, N. IoT resource allocation and optimization based on heuristic algorithm. Sensors. 2020; 20, 539. [CrossRef]
Kaminski, N. J., Murphy, M., & Marchetti, N. Agent-based modeling of an IoT network. In 2016 IEEE international symposium on systems engineering (ISSE) (pp. 1-7). IEEE. 2016. [CrossRef]
Butt, M. M., Dey, I., Dzaferagic, M., Murphy, M., Kaminski, N., & Marchetti, N. Agent-based modeling for distributed decision support in an IoT network. IEEE Internet of Things Journal. 2020; 7, 6919–6931. [CrossRef]
Likotiko, E. D., Nyambo, D., & Mwangoka, J. Multi-agent based IoT smart waste monitoring and collection architecture. arXiv, 2017; arXiv:1711.03966.
do Nascimento, N. M., & de Lucena, C. J. P. Fiot: An agent-based framework for self-adaptive and self-organizing applications based on the internet of things. Information Sciences. 2017; 378, 1661–176. [CrossRef]
Shakya, J., Ghribi, C., & Merghem-Boulahia, L. Agent-based modeling and simulation for 5G and beyond networks: A comprehensive survey. Simulation Modelling Practice and Theory. 2023; 102855. [CrossRef]
Shakya, J., Ghribi, C., Chopin, M., & Merghem-Boulahia, L. (2023, January). Agent-based Simulation for Placement and Pricing of 5G Network Slices. In 2023 IEEE 20th Consumer Communications & Networking Conference (CCNC) (pp. 883-884). IEEE.
Shakya, J., Ghribi, C., Chopin, M., & Merghem-Boulahia, L. (2023, January). Agent-based Simulation for Placement and Pricing of 5G Network Slices. In 2023 IEEE 20th Consumer Communications & Networking Conference (CCNC) (pp. 883-884). IEEE.
Guruacharya, S., Niyato, D., Bennis, M., & Kim, D. I. Dynamic coalition formation for network MIMO in small cell networks. IEEE Transactions on Wireless Communications. 2013, 12(10), 5360–5372. [CrossRef]
Mondal, A., & Misra, S. Dynamic coalition formation in a smart grid: A game theoretic approach. In 2013 ieee international conference on communications workshops (icc) (pp. 1067-1071). IEEE. 2013. [CrossRef]
Tsiropoulou, E. E., Paruchuri, S. T., & Baras, J. S. nterest, energy and physical-aware coalition formation and resource allocation in smart IoT applications. In 2017 51st Annual conference on information sciences and systems (CISS) (pp. 1-6). IEEE. 2017. [CrossRef]
Niyato, D., Hoang, D. T., Luong, N. C., Wang, P., Kim, D. I., & Han, Z. Smart data pricing models for the internet of things: a bundling strategy approach. IEEE Network. 2016; 30, 18–25. [CrossRef]
Alsheikh, M. A., Hoang, D. T., Niyato, D., Leong, D., Wang, P., & Han, Z. Optimal pricing of Internet of Things: A machine learning approach. IEEE Journal on Selected Areas in Communications. 2020; 38, 669–684. [CrossRef]
Real, R., & Vargas, J. MThe probabilistic basis of Jaccard’s index of similarity. Systematic biology. 1996; 45, 380–385. [CrossRef]

Figure 1. Schematic representation of the IoT ecosystem.

Figure 2. Impact of Threshold Values on Coalition Dynamics.

Figure 3. Evolution of collected individual payoff of each SP over time.

Figure 4. Heatmap illustrating individual SP payoffs from coalitions at the final simulation time step t = 500.

Figure 5. Temporal Evolution of Total Payoff Utilizing Different Coalition Formation Strategies.

Figure 6. Comparison of average payoff and stability score for each approach over 10 iterations, each comprising 100 steps.

Table 1. Budget allocation for Service Providers.

Service Provider (A_{SP_i})	A_SP₀	A_SP₁	A_SP₂	A_SP₃	A_SP₄	A_SP₅	A_SP₆	A_SP₇	A_SP₈	A_SP₉
Budget (A_{SP_i})	2	3	2	4	4	2	4	5	4	3

Table 2. Initial State of Matrices: Data Sharing (

D

), Service Compatibility (

S

), Resource Sharing (

R

), and Joining Cost (

X

) at simulation time step t=0.

Table 2. Initial State of Matrices: Data Sharing (

D

), Service Compatibility (

S

), Resource Sharing (

R

), and Joining Cost (

X

) at simulation time step t=0.

$D = [\begin{matrix} 0.0 & 0.5 & 0.9 & 0.1 & 0.6 & 0.4 & 0.8 & 0.4 & 0.2 & 0.3 \\ 0.5 & 0.0 & 0.7 & 0.8 & 0.5 & 0.4 & 0.4 & 0.6 & 0.3 & 0.1 \\ 0.9 & 0.7 & 0.0 & 0.1 & 0.3 & 0.2 & 0.7 & 0.6 & 0.1 & 0.3 \\ 0.1 & 0.8 & 0.1 & 0.0 & 0.7 & 0.0 & 0.9 & 0.1 & 0.5 & 0.7 \\ 0.6 & 0.5 & 0.3 & 0.7 & 0.0 & 0.3 & 0.6 & 0.2 & 0.8 & 0.4 \\ 0.4 & 0.4 & 0.2 & 0.0 & 0.3 & 0.0 & 0.1 & 0.4 & 0.4 & 0.5 \\ 0.8 & 0.4 & 0.7 & 0.9 & 0.6 & 0.1 & 0.0 & 0.9 & 0.2 & 0.1 \\ 0.4 & 0.6 & 0.6 & 0.1 & 0.2 & 0.4 & 0.9 & 0.0 & 0.7 & 0.9 \\ 0.2 & 0.3 & 0.1 & 0.5 & 0.8 & 0.4 & 0.2 & 0.7 & 0.0 & 0.8 \\ 0.3 & 0.1 & 0.3 & 0.7 & 0.4 & 0.5 & 0.1 & 0.9 & 0.8 & 0.0 \end{matrix}]$	$S = [\begin{matrix} 0.0 & 0.1 & 0.6 & 0.8 & 0.9 & 0.7 & 0.2 & 0.4 & 0.8 & 0.7 \\ 0.1 & 0.0 & 0.1 & 0.1 & 0.9 & 0.9 & 0.4 & 0.5 & 1.0 & 0.9 \\ 0.6 & 0.1 & 0.0 & 0.9 & 0.2 & 0.3 & 0.8 & 0.1 & 0.6 & 0.8 \\ 0.8 & 0.1 & 0.9 & 0.0 & 0.4 & 0.0 & 0.5 & 0.2 & 0.2 & 0.9 \\ 0.9 & 0.9 & 0.2 & 0.4 & 0.0 & 0.3 & 0.0 & 0.2 & 0.2 & 1.0 \\ 0.7 & 0.9 & 0.3 & 0.0 & 0.3 & 0.0 & 1.0 & 0.3 & 1.0 & 0.2 \\ 0.2 & 0.4 & 0.8 & 0.5 & 0.0 & 1.0 & 0.0 & 0.9 & 0.4 & 0.6 \\ 0.4 & 0.5 & 0.1 & 0.2 & 0.2 & 0.3 & 0.9 & 0.0 & 0.1 & 0.4 \\ 0.8 & 1.0 & 0.6 & 0.2 & 0.2 & 1.0 & 0.4 & 0.1 & 0.0 & 0.1 \\ 0.7 & 0.9 & 0.8 & 0.9 & 1.0 & 0.2 & 0.6 & 0.4 & 0.1 & 0.0 \end{matrix}]$
$R = [\begin{matrix} 0.0 & 0.3 & 0.3 & 0.5 & 0.2 & 0.7 & 0.0 & 0.4 & 0.2 & 0.4 \\ 0.3 & 0.0 & 0.2 & 0.5 & 0.8 & 1.0 & 0.8 & 0.6 & 0.3 & 0.8 \\ 0.3 & 0.2 & 0.0 & 0.8 & 0.6 & 0.1 & 0.2 & 0.0 & 0.8 & 0.3 \\ 0.5 & 0.5 & 0.8 & 0.0 & 0.7 & 0.1 & 0.7 & 0.2 & 0.5 & 0.6 \\ 0.2 & 0.8 & 0.6 & 0.7 & 0.0 & 0.6 & 0.5 & 0.8 & 0.3 & 0.6 \\ 0.7 & 1.0 & 0.1 & 0.1 & 0.6 & 0.0 & 0.2 & 0.9 & 1.0 & 0.7 \\ 0.0 & 0.8 & 0.2 & 0.7 & 0.5 & 0.2 & 0.0 & 0.6 & 0.7 & 0.3 \\ 0.4 & 0.6 & 0.0 & 0.2 & 0.8 & 0.9 & 0.6 & 0.0 & 1.0 & 0.5 \\ 0.2 & 0.3 & 0.8 & 0.5 & 0.3 & 1.0 & 0.7 & 1.0 & 0.0 & 0.8 \\ 0.4 & 0.8 & 0.3 & 0.6 & 0.6 & 0.7 & 0.3 & 0.5 & 0.8 & 0.0 \end{matrix}]$	$X = [\begin{matrix} 0.0 & 0.1 & 0.8 & 0.9 & 0.4 & 0.3 & 0.5 & 0.4 & 0.1 & 0.1 \\ 0.1 & 0.0 & 0.0 & 0.5 & 0.9 & 0.3 & 0.6 & 0.0 & 0.4 & 0.1 \\ 0.8 & 0.0 & 0.0 & 0.9 & 0.7 & 0.1 & 0.1 & 0.4 & 0.6 & 0.4 \\ 0.9 & 0.5 & 0.9 & 0.0 & 0.0 & 0.6 & 0.2 & 0.3 & 0.6 & 0.7 \\ 0.4 & 0.9 & 0.7 & 0.0 & 0.0 & 1.0 & 1.0 & 0.2 & 0.3 & 0.5 \\ 0.3 & 0.3 & 0.1 & 0.6 & 1.0 & 0.0 & 0.5 & 0.0 & 0.4 & 0.6 \\ 0.5 & 0.6 & 0.1 & 0.2 & 1.0 & 0.5 & 0.0 & 1.0 & 0.1 & 0.1 \\ 0.4 & 0.0 & 0.4 & 0.3 & 0.2 & 0.0 & 1.0 & 0.0 & 0.9 & 0.4 \\ 0.1 & 0.4 & 0.6 & 0.6 & 0.3 & 0.4 & 0.1 & 0.9 & 0.0 & 0.1 \\ 0.1 & 0.1 & 0.4 & 0.7 & 0.5 & 0.6 & 0.1 & 0.4 & 0.1 & 0.0 \end{matrix}]$

D = [\begin{matrix} 0.0 & 0.5 & 0.9 & 0.1 & 0.6 & 0.4 & 0.8 & 0.4 & 0.2 & 0.3 \\ 0.5 & 0.0 & 0.7 & 0.8 & 0.5 & 0.4 & 0.4 & 0.6 & 0.3 & 0.1 \\ 0.9 & 0.7 & 0.0 & 0.1 & 0.3 & 0.2 & 0.7 & 0.6 & 0.1 & 0.3 \\ 0.1 & 0.8 & 0.1 & 0.0 & 0.7 & 0.0 & 0.9 & 0.1 & 0.5 & 0.7 \\ 0.6 & 0.5 & 0.3 & 0.7 & 0.0 & 0.3 & 0.6 & 0.2 & 0.8 & 0.4 \\ 0.4 & 0.4 & 0.2 & 0.0 & 0.3 & 0.0 & 0.1 & 0.4 & 0.4 & 0.5 \\ 0.8 & 0.4 & 0.7 & 0.9 & 0.6 & 0.1 & 0.0 & 0.9 & 0.2 & 0.1 \\ 0.4 & 0.6 & 0.6 & 0.1 & 0.2 & 0.4 & 0.9 & 0.0 & 0.7 & 0.9 \\ 0.2 & 0.3 & 0.1 & 0.5 & 0.8 & 0.4 & 0.2 & 0.7 & 0.0 & 0.8 \\ 0.3 & 0.1 & 0.3 & 0.7 & 0.4 & 0.5 & 0.1 & 0.9 & 0.8 & 0.0 \end{matrix}]

S = [\begin{matrix} 0.0 & 0.1 & 0.6 & 0.8 & 0.9 & 0.7 & 0.2 & 0.4 & 0.8 & 0.7 \\ 0.1 & 0.0 & 0.1 & 0.1 & 0.9 & 0.9 & 0.4 & 0.5 & 1.0 & 0.9 \\ 0.6 & 0.1 & 0.0 & 0.9 & 0.2 & 0.3 & 0.8 & 0.1 & 0.6 & 0.8 \\ 0.8 & 0.1 & 0.9 & 0.0 & 0.4 & 0.0 & 0.5 & 0.2 & 0.2 & 0.9 \\ 0.9 & 0.9 & 0.2 & 0.4 & 0.0 & 0.3 & 0.0 & 0.2 & 0.2 & 1.0 \\ 0.7 & 0.9 & 0.3 & 0.0 & 0.3 & 0.0 & 1.0 & 0.3 & 1.0 & 0.2 \\ 0.2 & 0.4 & 0.8 & 0.5 & 0.0 & 1.0 & 0.0 & 0.9 & 0.4 & 0.6 \\ 0.4 & 0.5 & 0.1 & 0.2 & 0.2 & 0.3 & 0.9 & 0.0 & 0.1 & 0.4 \\ 0.8 & 1.0 & 0.6 & 0.2 & 0.2 & 1.0 & 0.4 & 0.1 & 0.0 & 0.1 \\ 0.7 & 0.9 & 0.8 & 0.9 & 1.0 & 0.2 & 0.6 & 0.4 & 0.1 & 0.0 \end{matrix}]

R = [\begin{matrix} 0.0 & 0.3 & 0.3 & 0.5 & 0.2 & 0.7 & 0.0 & 0.4 & 0.2 & 0.4 \\ 0.3 & 0.0 & 0.2 & 0.5 & 0.8 & 1.0 & 0.8 & 0.6 & 0.3 & 0.8 \\ 0.3 & 0.2 & 0.0 & 0.8 & 0.6 & 0.1 & 0.2 & 0.0 & 0.8 & 0.3 \\ 0.5 & 0.5 & 0.8 & 0.0 & 0.7 & 0.1 & 0.7 & 0.2 & 0.5 & 0.6 \\ 0.2 & 0.8 & 0.6 & 0.7 & 0.0 & 0.6 & 0.5 & 0.8 & 0.3 & 0.6 \\ 0.7 & 1.0 & 0.1 & 0.1 & 0.6 & 0.0 & 0.2 & 0.9 & 1.0 & 0.7 \\ 0.0 & 0.8 & 0.2 & 0.7 & 0.5 & 0.2 & 0.0 & 0.6 & 0.7 & 0.3 \\ 0.4 & 0.6 & 0.0 & 0.2 & 0.8 & 0.9 & 0.6 & 0.0 & 1.0 & 0.5 \\ 0.2 & 0.3 & 0.8 & 0.5 & 0.3 & 1.0 & 0.7 & 1.0 & 0.0 & 0.8 \\ 0.4 & 0.8 & 0.3 & 0.6 & 0.6 & 0.7 & 0.3 & 0.5 & 0.8 & 0.0 \end{matrix}]

X = [\begin{matrix} 0.0 & 0.1 & 0.8 & 0.9 & 0.4 & 0.3 & 0.5 & 0.4 & 0.1 & 0.1 \\ 0.1 & 0.0 & 0.0 & 0.5 & 0.9 & 0.3 & 0.6 & 0.0 & 0.4 & 0.1 \\ 0.8 & 0.0 & 0.0 & 0.9 & 0.7 & 0.1 & 0.1 & 0.4 & 0.6 & 0.4 \\ 0.9 & 0.5 & 0.9 & 0.0 & 0.0 & 0.6 & 0.2 & 0.3 & 0.6 & 0.7 \\ 0.4 & 0.9 & 0.7 & 0.0 & 0.0 & 1.0 & 1.0 & 0.2 & 0.3 & 0.5 \\ 0.3 & 0.3 & 0.1 & 0.6 & 1.0 & 0.0 & 0.5 & 0.0 & 0.4 & 0.6 \\ 0.5 & 0.6 & 0.1 & 0.2 & 1.0 & 0.5 & 0.0 & 1.0 & 0.1 & 0.1 \\ 0.4 & 0.0 & 0.4 & 0.3 & 0.2 & 0.0 & 1.0 & 0.0 & 0.9 & 0.4 \\ 0.1 & 0.4 & 0.6 & 0.6 & 0.3 & 0.4 & 0.1 & 0.9 & 0.0 & 0.1 \\ 0.1 & 0.1 & 0.4 & 0.7 & 0.5 & 0.6 & 0.1 & 0.4 & 0.1 & 0.0 \end{matrix}]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Dynamic Coalition Formation Among IoT Service Providers: A Systematic Exploration of IoT Dynamics Using an Agent-Based Model

Abstract

1. Introduction

1.1. Related Works

1.2. Contributions

2. An Agent-Based Modelization for IoT

3. Simulation of A Practical Use-Case: Multi Agent—Dynamic Coalition Formation (MA-DCF)

3.1. Core Matrices Guiding Multi-Agent Coalition Dynamics

3.2. Benefit, Cost and Utility of Coalitions

3.2.1. Normalized Benefit of Coalition

3.2.2. Normalized Cost of Coalition

3.2.3. Utility of Coalition

3.3. Strategic Decision-Making

3.3.1. Initiation of Coalition Formation

3.3.2. Acceptance or Rejection of Coalition Requests

3.4. Coalition and Individual Payoffs

3.4.1. Coalition Payoff

3.4.2. Individual Payoff

4. Results

4.1. Sensitivity Analysis of Key Threshold Variables in MA-DCF

4.2. Performance Assessment of MA-DCF

4.3. Comparative Analysis of MA-DCF: Performance Benchmarking

5. Conclusions

References

MDPI Initiatives

Important Links

Subscribe