Submitted:
22 February 2024
Posted:
04 March 2024
You are already at the latest version
Abstract
Keywords:
1. Introduction
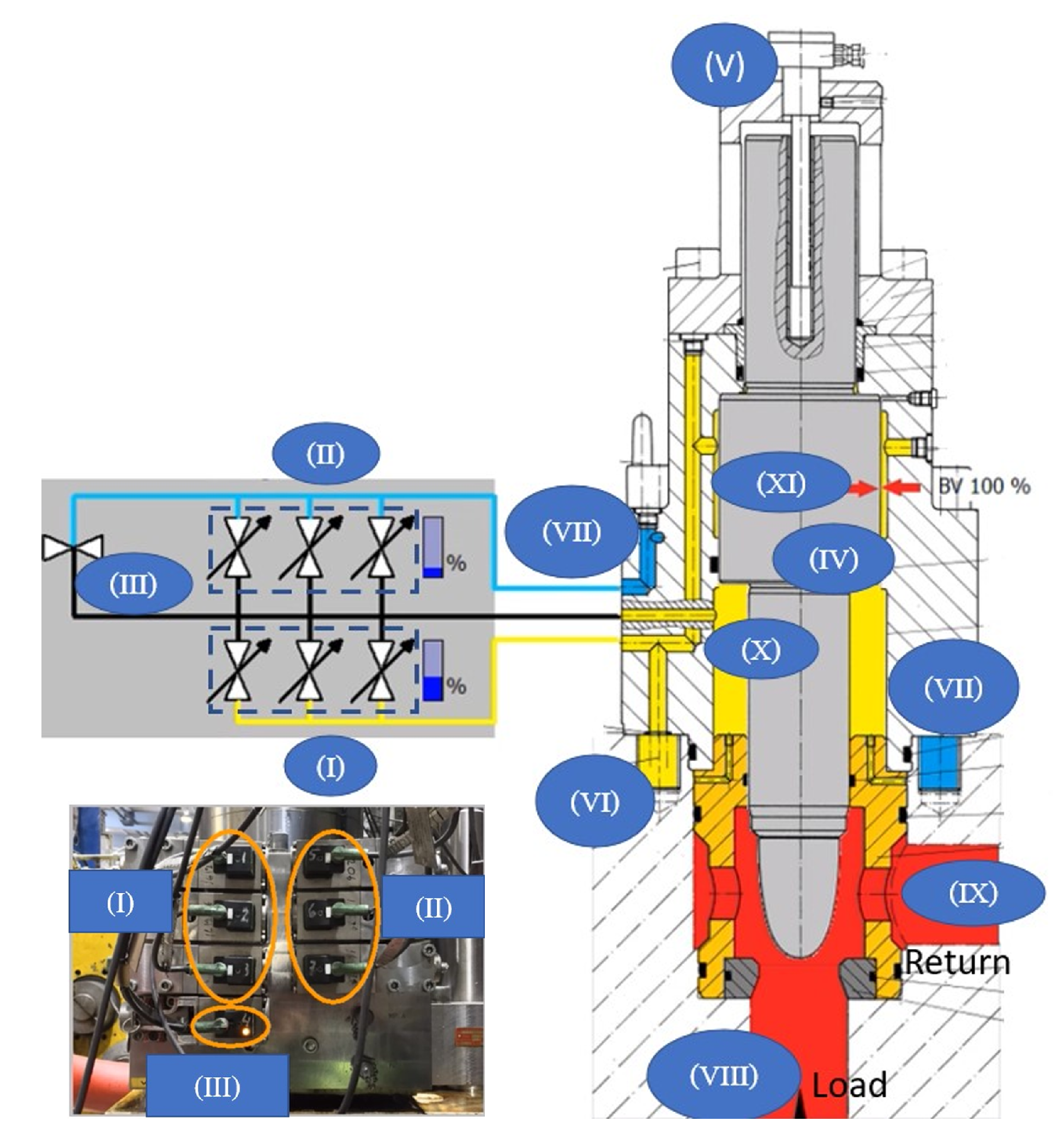
2. Device and Operating
3. Modeling
3.1. Physical Model
- 1
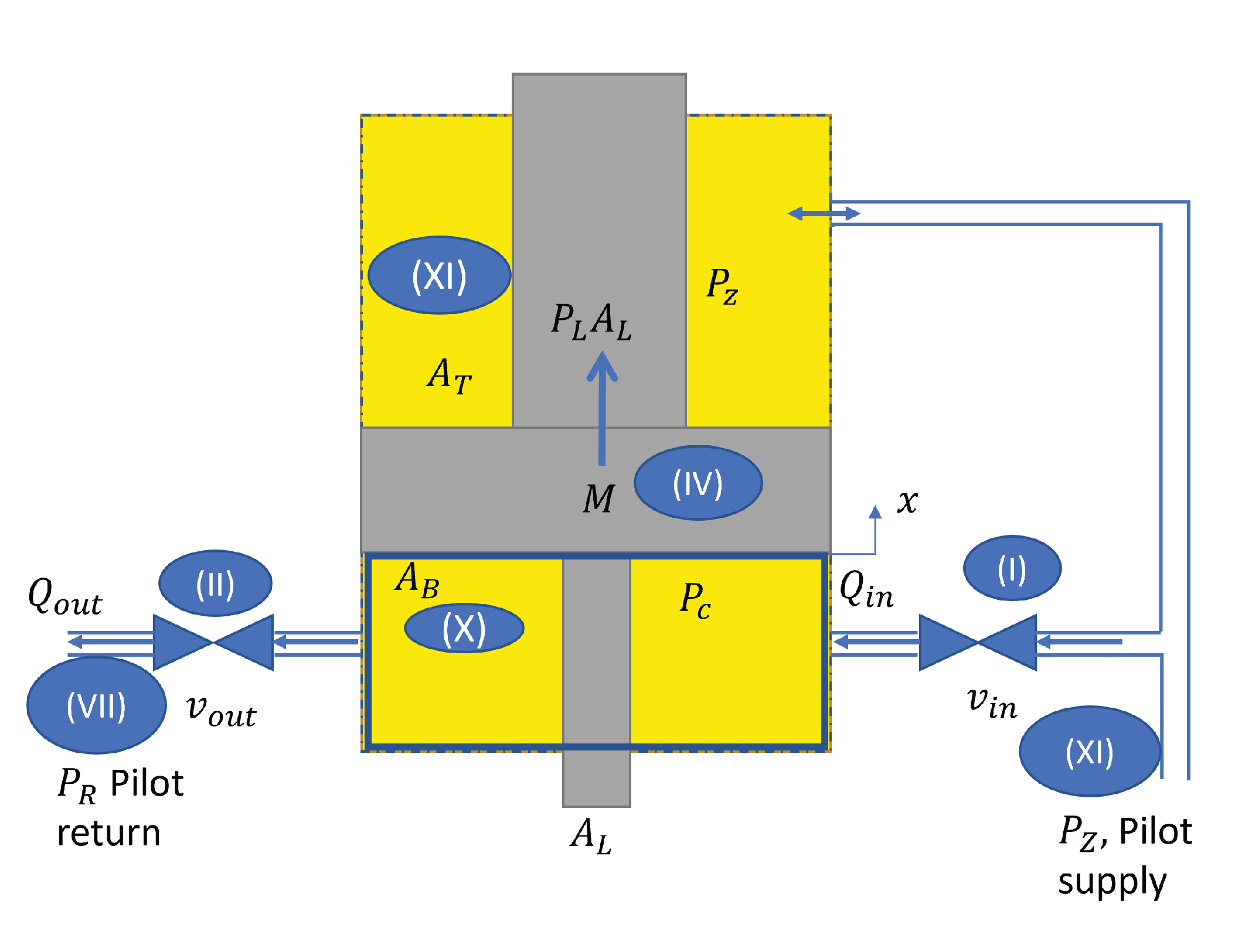
- Pilot valve model (I and II): These pilot valves consist of a solenoid, its armature, and a pre-loaded spring. Equations (3.6) and (3.7) in [11] describe a third-order coupled system, which, in this case, is the dynamics of the armature and the electrical circuit of the coil. We assumed that the time-constants of the armature’s motion are much smaller than those of the spindle’s motion. Therefore, we neglect the inductance of the coil’s circuit, the linear momentum, the viscous force, the flow forces acting on the armature, and the induced electromagnetic force from the armature’s motion. The last is allowed because the electromagnetic force to the armature is greater; as such, we obtainfor valve i, where corresponds to the m pilot valves of Group (I), and to the n of Group (II). In this case, (see Figure 1); is the spring rate of the spring; is the armature position; is the magnetic coupling coefficient, which provides the constant of proportionality for the electromagnetic force; is the maximum supplied voltage applied to the coil; is the resistance of the electrical circuit of the coil; is the supplied voltage with respect to its maximum value applied to the coil; and is the pre-load force acting on the armature by the spring when . By setting for , we obtainwhere . assumes as the offset of , which is assumed to be the same for all i (see Figure 3b).
- 2
- Volumetric flow rate of the pilot valves (I and II): we use the standard equation (4.1) in [11] for describing the flow (which assumes the fluid to be incompressible with a high Reynold number (i.e. laminar flow)). As such, we obtainwhere is the discharge coefficient; is the discharge flow area when assuming a rectangular section, which depends on the voltage applied to the coil of the pilot valve i; and is the fluid density and is the pressure drop across the valve, which is for , and for . We substitute j by subindexing for , as well as by subindexing for .
- 3
- The deformable volume (X) of the main valve is chosen as the control volume, as indicated by the solid blue line in Figure 2. The change in the control volume is understood as a function of the spindle’s position. For an incompressible fluid, the continuity Equation (5.5) in [32] becomeswhere is the cross-sectional area of the lower chamber subtracting , which is assumed to be constant along x; is the derivative of the spindle’s position; and is the volumetric flow rate of valve i (see Figure 1 and Figure 2).
- 4
-
The spindle (IV) equation of motion of the main valve determines the motion of the main valve’s spindle, which iswhen or , and where M is the main valve’s spindle mass, and B is the viscous drag coefficient. For a marginally stable valve, as the one under study, there is no spring; hence, no term is proportional to x. is the coefficient of the Coulomb friction, and is the force exerted by the flow going from (VIII) to (IX) in Figure 1. An analysis of the flow forces allows for the term to appear in the equation. is the force given by the main valve’s spindle mass. We assumed that the Coulomb friction term can be neglected in contrast to and due to a difference of 3–5 orders of magnitude when assuming friction between steel and rubber, i.e., the seal’s material. Furthermore, as we had values of (c.f. scale of Figure 3 (c) and (d)) and (c.f. Figure 2), we thus obtained , as well as . The flow forces can be described bywhich can be obtained after deriving and linearizing with respect to x and (see (4.20) in [11]), where is the flow gain coefficient, is the pressure-flow coefficient, is the flow force gain, and is the pressure flow force. Considering the control volume, as illustrated in Figure 4–21 by dashed lines and the dimension given in (4.122) in [11], as well as the operating conditions of the hydraulic valve under study, we consider to be negligible in contrast to and . This was performed because there was a difference of two orders of magnitude. More information about how to derive the expression of the coefficients in (6) can be found in Chapter 4, more specifically in Section 4.3 and Section 4.6, in [11]. Finally, we obtained the main valve’s spindle equation of motion, which is
- 5
-
Approximation of in the main valve (X): Since is not measured, it is derived from (3) and (4). Furthermore, assuming that the pilot parallel valves are identical, and knowing that is applied to all of the coils of pilot valves (I) and to (II) (see Figure 1 and (4)), we obtainwhere and . For , we use the auxiliary functionand, for , we usewhich are derived from (3). We approximate and by a Taylor series in around the operating point , which is the equilibrium point of (7). By performing this, keeping the linear terms, and substituting these in (8), we obtainwhereIn the above, is the first derivative of , which is evaluated at , is the one of , , and .
- 6
-
We approximate the auxiliary function by a Taylor series in and around and , respectively, where . We keep the linear terms and (13) is approximated bywherewhere , is the derivative of with respect to , and is the derivative of with respect to . Indeed, both are evaluated at . The sign of each of the parameters is specified explicitly in (15), and this is performed in accordance with the physics of the device described in (1-13). is positive or negative depending on . Notice that (14) is a non-linear input–output model and linear in the parameters. The non-linearities are related to , , , and . These terms are obtained from the square root in and the product in (3).
3.2. Parameter Estimation
3.3. Model Validation
4. Results and Discussion
4.1. Physical Model
| Description | ||||
|---|---|---|---|---|
| -1.16 | -1.24 | -0.99 | ||
| - | - | |||
| - | ||||
| MSE training | ||||
| MSE test |
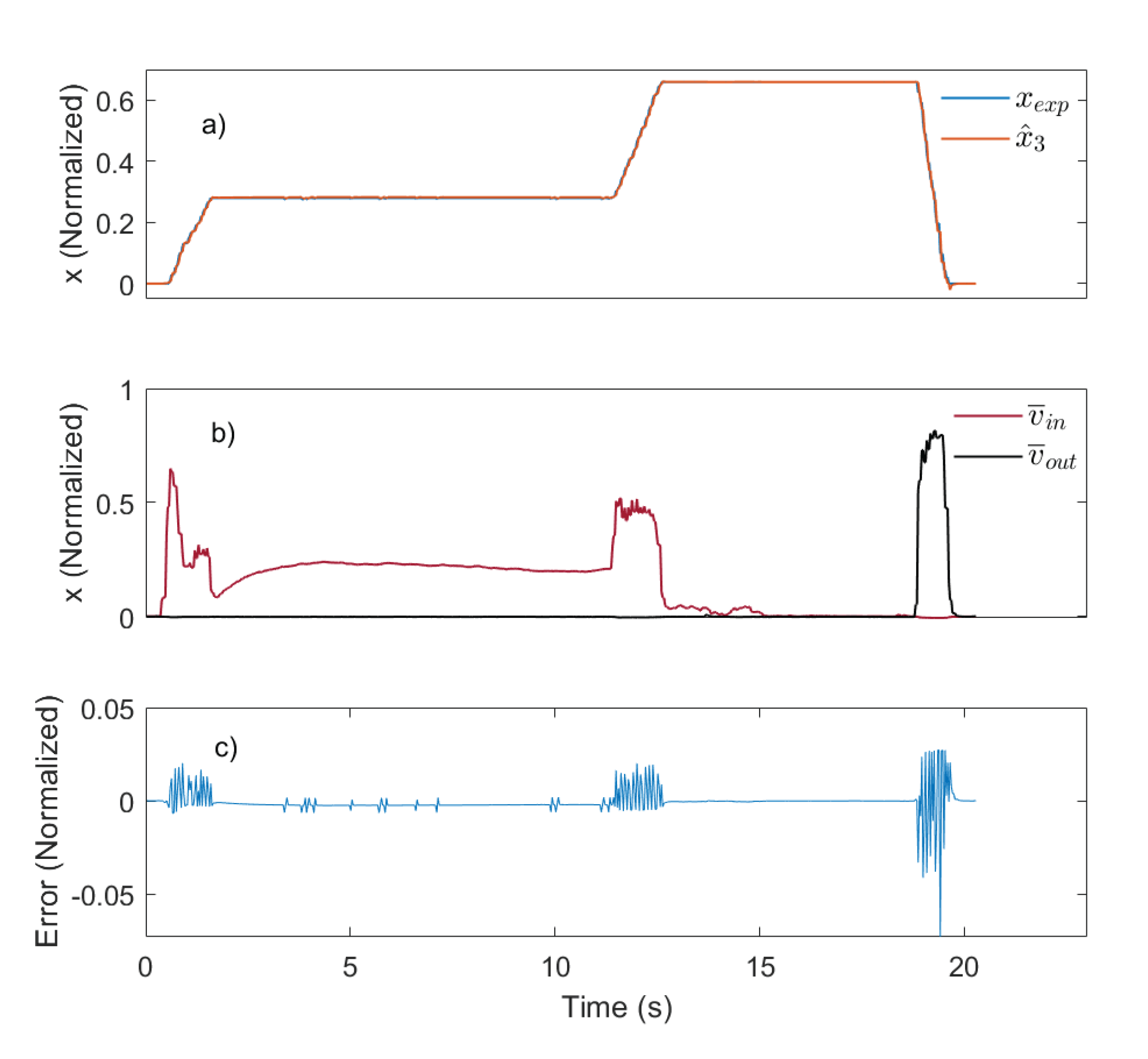
4.2. Modeling Errors
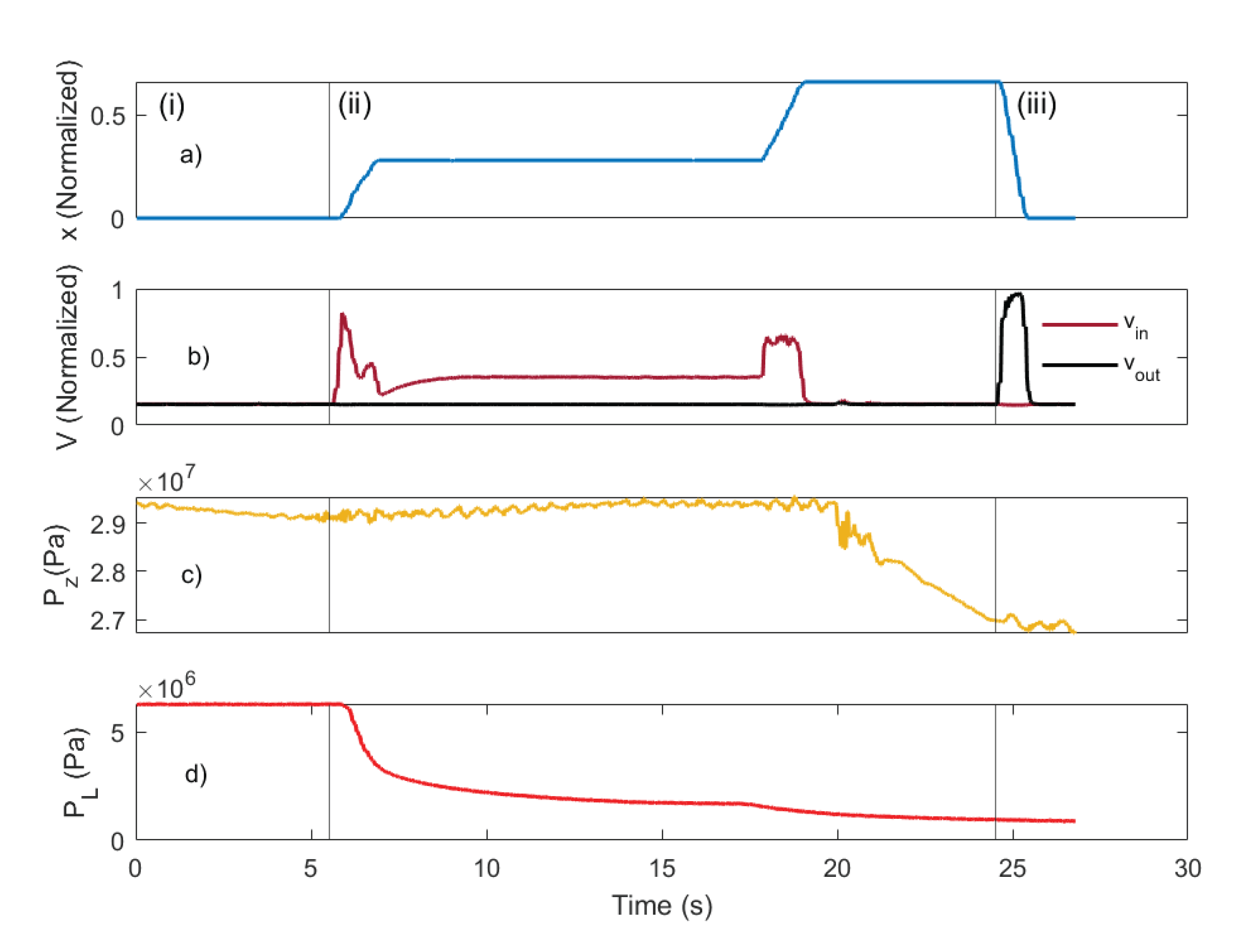
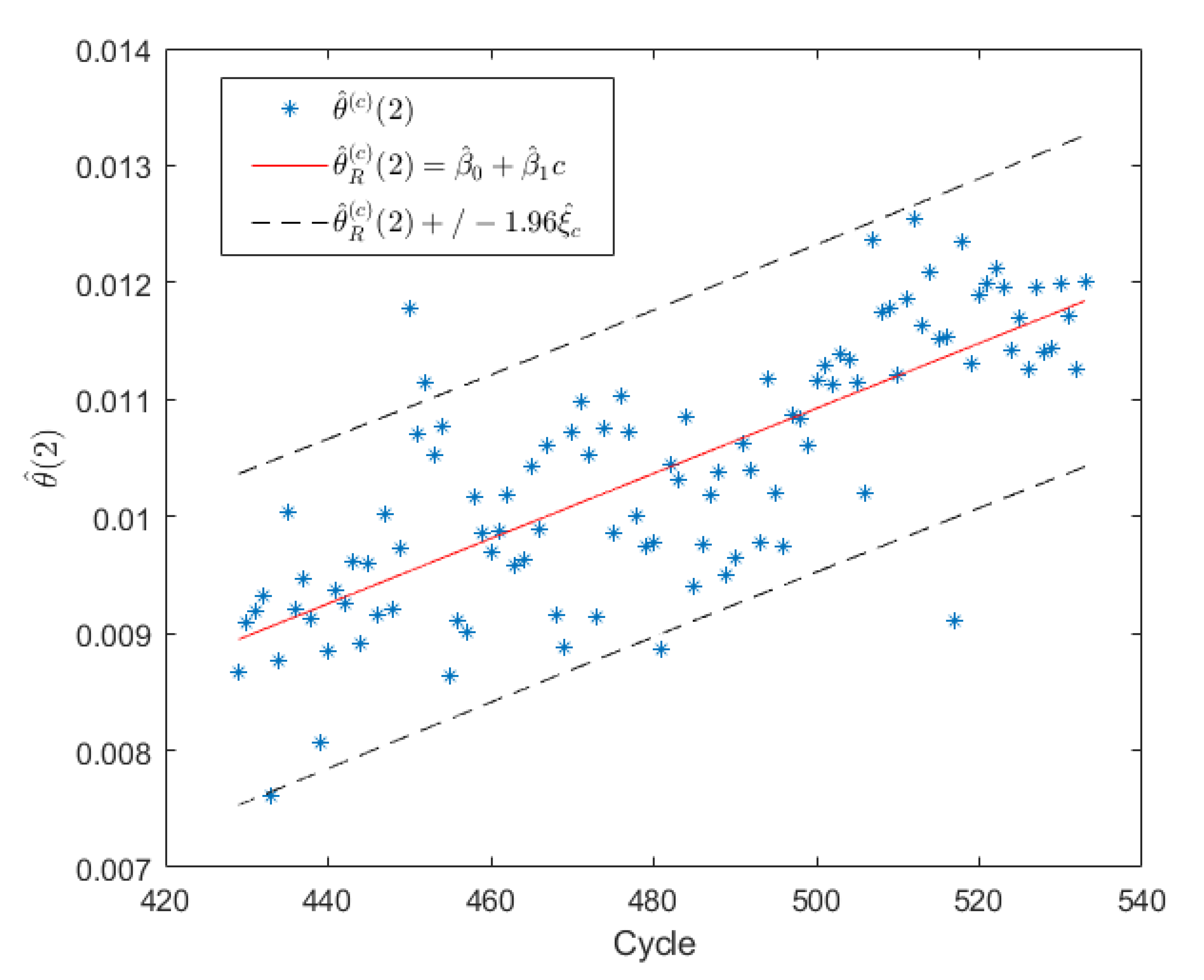
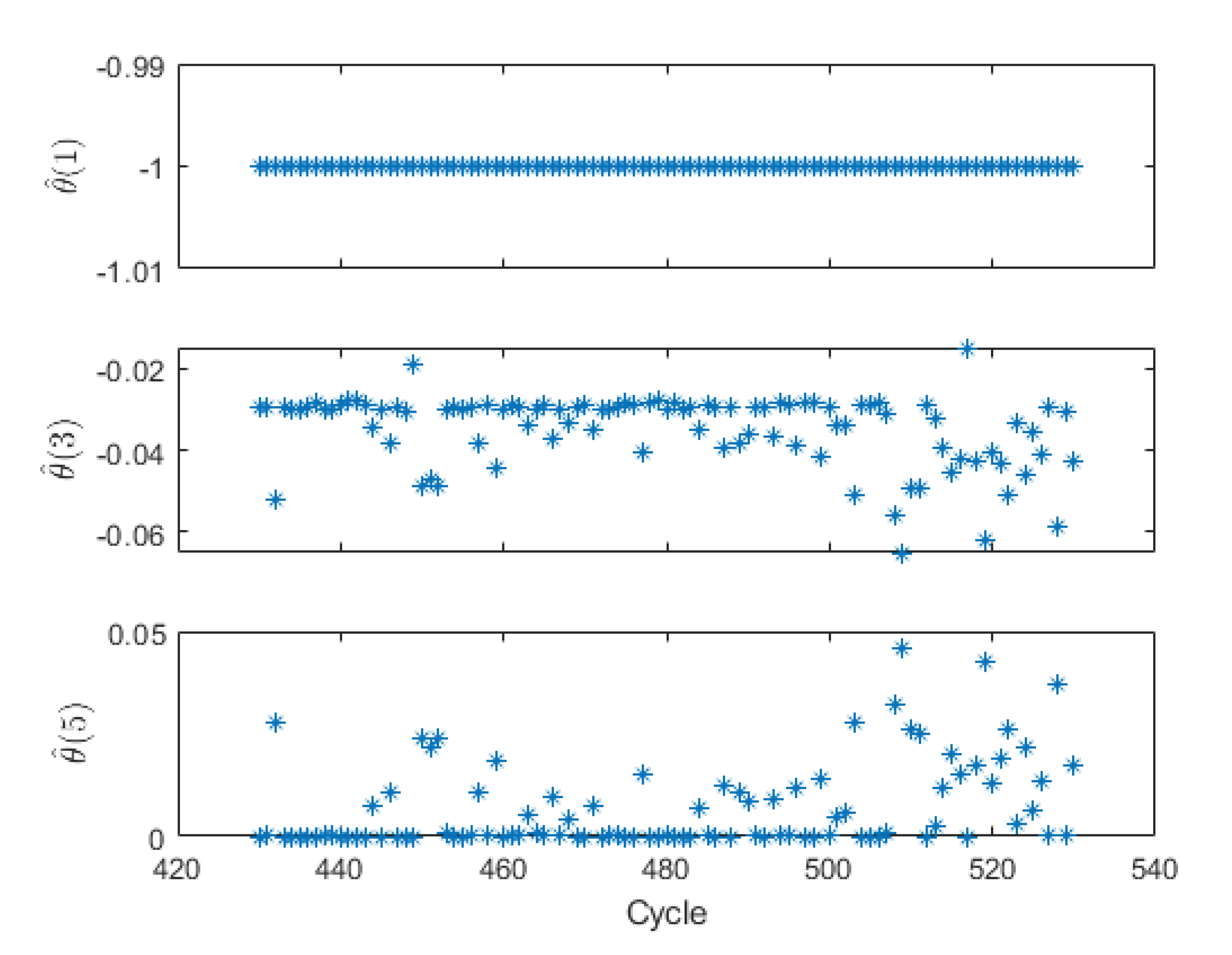
4.3. Aging
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Tao, F.; Zhang, H.; Liu, A.; Nee, A.Y. Digital twin in industry: State-of-the-art. IEEE Transactions on industrial informatics 2018, 15, 2405–2415. [Google Scholar] [CrossRef]
- Wright, L.; Davidson, S. How to tell the difference between a model and a digital twin. Advanced Modeling and Simulation in Engineering Sciences 2020, 7, 1–13. [Google Scholar] [CrossRef]
- Roy, R.B.; Mishra, D.; Pal, S.K.; Chakravarty, T.; Panda, S.; Chandra, M.G.; Pal, A.; Misra, P.; Chakravarty, D.; Misra, S. Digital twin: current scenario and a case study on a manufacturing process. The International Journal of Advanced Manufacturing Technology 2020, 107, 3691–3714. [Google Scholar] [CrossRef]
- He, B.; Bai, K.J. Digital twin-based sustainable intelligent manufacturing: A review. Advances in Manufacturing 2021, 9, 1–21. [Google Scholar] [CrossRef]
- Rituraj, R.; Scheidl, R. Towards digital twin development of counterbalance valves: Modelling and experimental investigation. Mechanical Systems and Signal Processing 2023, 188, 110049. [Google Scholar] [CrossRef]
- Xiang, F.; Zhi, Z.; Jiang, G. Digital twins technolgy and its data fusion in iron and steel product life cycle. 2018 IEEE 15th international conference on networking, sensing and control (ICNSC). IEEE. 2018; pp. 1–5. [Google Scholar]
- Karandaev, A.S.; Gasiyarov, V.R.; Radionov, A.A.; Loginov, B.M. Development of digital models of interconnected electrical profiles for rolling–drawing wire mills. Machines 2021, 9, 54. [Google Scholar] [CrossRef]
- Gasiyarova, O.A.; Karandaev, A.S.; Erdakov, I.N.; Loginov, B.M.; Khramshin, V.R. Developing digital observer of angular gaps in rolling stand mechatronic system. Machines 2022, 10, 141. [Google Scholar] [CrossRef]
- Gonzalez, O.B.; Rönnow, D. Time series modelling of a radial-axial ring rolling system. International Journal of Modelling, Identification and Control 2023, 43, 13–25. [Google Scholar] [CrossRef]
- Gonzalez, O.B.; Rönnow, D. A Study of OBF-ARMAX Performance for Modelling of a Mechanical System Excited by a Low Frequency Signal for Condition Monitoring. European Workshop on Advanced Control and Diagnosis. Springer, 2022; pp. 73–82. [Google Scholar]
- Manring, N.D.; Fales, R.C. Hydraulic control systems; John Wiley & Sons, 2019.
- Han, M.; Liu, Y.; Wu, D.; Tan, H.; Li, C. Numerical analysis and optimisation of the flow forces in a water hydraulic proportional cartridge valve for injection system. Ieee Access 2018, 6, 10392–10401. [Google Scholar] [CrossRef]
- Liu, Z.; Li, L.; Yue, D.; Wei, L.; Liu, C.; Zuo, X. Dynamic Performance Improvement of Solenoid Screw-In Cartridge Valve Using a New Hybrid Voltage Control. Machines 2022, 10, 106. [Google Scholar] [CrossRef]
- Xu, B.; Shen, J.; Liu, S.; Su, Q.; Zhang, J. Research and development of electro-hydraulic control valves oriented to industry 4.0: a review. Chinese Journal of Mechanical Engineering 2020, 33, 1–20. [Google Scholar] [CrossRef]
- Tamburrano, P.; Plummer, A.R.; Distaso, E.; Amirante, R. A review of electro-hydraulic servovalve research and development. International Journal of Fluid Power 2018, 1–23. [Google Scholar] [CrossRef]
- Liu, S.; Yao, B. Energy-saving control of single-rod hydraulic cylinders with programmable valves and improved working mode selection. SAE Transactions 2002, 51–61. [Google Scholar]
- Liu, S.; Yao, B. Adaptive robust control of programmable valves with manufacturer supplied flow mapping only. 2004 43rd IEEE Conference on Decision and Control (CDC)(IEEE Cat. No. 04CH37601). IEEE, 2004; 1, pp. 1117–1122. [Google Scholar]
- Liu, S.; Yao, B. On-board system identification of systems with unknown input nonlinearity and system parameters. ASME International Mechanical Engineering Congress and Exposition 2005, 42169, 1079–1085. [Google Scholar]
- Liu, S.; Yao, B. Automated onboard modeling of cartridge valve flow mapping. IEEE/ASME transactions on mechatronics 2006, 11, 381–388. [Google Scholar]
- Lu, L.; Yao, B.; Liu, Z. Energy saving control of a hydraulic manipulator using five cartridge valves and one accumulator. IFAC Proceedings Volumes 2013, 46, 84–90. [Google Scholar] [CrossRef]
- Xu, B.; Ding, R.; Zhang, J.; Su, Q. Modeling and dynamic characteristics analysis on a three-stage fast-response and large-flow directional valve. Energy conversion and management 2014, 79, 187–199. [Google Scholar] [CrossRef]
- Yue, D.; Li, L.; Wei, L.; Liu, Z.; Liu, C.; Zuo, X. Effects of pulse voltage duration on open–close dynamic characteristics of solenoid screw-In cartridge valves. Processes 2021, 9, 1722. [Google Scholar] [CrossRef]
- Han, M.; Liu, Y.; Zheng, K.; Ding, Y.; Wu, D. Investigation on the modeling and dynamic characteristics of a fast-response and large-flow water hydraulic proportional cartridge valve. Proceedings of the Institution of Mechanical Engineers, Part C: Journal of Mechanical Engineering Science 2020, 234, 4415–4432. [Google Scholar] [CrossRef]
- Ljung, L. System identification. In Signal analysis and prediction; Springer, 1998; pp. 163–173. [Google Scholar]
- Zhang, J.; Lu, Z.; Xu, B.; Su, Q. Investigation on the dynamic characteristics and control accuracy of a novel proportional directional valve with independently controlled pilot stage. ISA transactions 2019, 93, 218–230. [Google Scholar] [CrossRef]
- Li, C.; Lyu, L.; Helian, B.; Chen, Z.; Yao, B. Precision motion control of an independent metering hydraulic system with nonlinear flow modeling and compensation. IEEE Transactions on Industrial Electronics 2021, 69, 7088–7098. [Google Scholar] [CrossRef]
- Lu, Z.; Zhang, J.; Xu, B.; Wang, D.; Su, Q.; Qian, J.; Yang, G.; Pan, M. Deadzone compensation control based on detection of micro flow rate in pilot stage of proportional directional valve. ISA transactions 2019, 94, 234–245. [Google Scholar] [CrossRef]
- Li, Y.; Wang, Q. Adaptive robust tracking control of a proportional pressure-reducing valve with dead zone and hysteresis. Transactions of the Institute of Measurement and Control 2018, 40, 2151–2166. [Google Scholar] [CrossRef]
- Folgheraiter, M. A combined B-spline-neural-network and ARX model for online identification of nonlinear dynamic actuation systems. Neurocomputing 2016, 175, 433–442. [Google Scholar] [CrossRef]
- Tørdal, S.S.; Klausen, A.; Bak, M.K. Experimental system identification and black box modeling of hydraulic directional control valve. 2015. [Google Scholar]
- Kilic, E.; Dolen, M.; Koku, A.B.; Caliskan, H.; Balkan, T. Accurate pressure prediction of a servo-valve controlled hydraulic system. Mechatronics 2012, 22, 997–1014. [Google Scholar] [CrossRef]
- Munson, B.R.; Okiishi, T.H.; Huebsch, W.W.; Rothmayer, A.P. Fluid mechanics; Wiley Singapore, 2013. [Google Scholar]
- Atkinson, K. An introduction to numerical analysis; John wiley & sons, 1991.
- Boyd, S.P.; Vandenberghe, L. Convex optimization; Cambridge university press, 2004.
- Grant, M.; Boyd, S.; Ye, Y. CVX: Matlab software for disciplined convex programming, 2009.
- Grant, M.C.; Boyd, S.P. Graph implementations for nonsmooth convex programs. Recent advances in learning and control. Springer, 2008; pp. 95–110. [Google Scholar]
- Stoica, P.; Söderström, T. System identification. In Prentice-Hall International; 1989. [Google Scholar]
- Wasserman, L. All of statistics: a concise course in statistical inference. Springer, 2004; Volume 26. [Google Scholar]
| Parameter | Units |
|---|---|
| , , , |
| M | |
|---|---|
| B | |
| 0.95-0.97 | |
| 1000 | |
| Interval | ||
|---|---|---|
| -0.99 | ||
| 0.01 - 0.6 |
| Description | |||||
|---|---|---|---|---|---|
| (a) | |||||
| (b) | |||||
| (c) | |||||
| (d) | |||||
| (e) | |||||
| (f) | |||||
| (g) | Euler Forward method | ||||
| (h) | Approx. (9) and (10) | - | |||
| (i) | Approx. (12) | ||||
| (j) | Approx. (9), (10), and (12) | - | |||
| (k) | Compressibility | ||||
| Total |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).





