Introducing the Framework of a "Dynamic" Higher Dimensional Spacetime. How Time behaves in It. Similarities with Quantum Mechanical and Relativistic Behaviour.

Preprint

Hypothesis

Introducing the Framework of a "Dynamic" Higher Dimensional Spacetime. How Time behaves in It. Similarities with Quantum Mechanical and Relativistic Behaviour.

Altmetrics

Downloads

117

Views

342

Comments

A peer-reviewed article of this preprint also exists.

Georgios Alamanos^*

This version is not peer-reviewed

Submitted:

29 February 2024

Posted:

04 March 2024

You are already at the latest version

Alerts

Abstract

The aim of the present work is to explore a different non-traditional approach to higher dimensional spacetime which differs from the usual approaches such as large extra space dimensions, warped extra space dimensions and multiple extra time dimensions. This approach will be referred to as "Dynamic" higher dimensional spacetime. By this term will be introduced a new kind of higher dimensional spacetime (more than the usual 3+1 dimensions), which behaves dynamically in the sense that time is not a fixed dimension but is the extra plus one dimension to the spatial dimensions of the phenomenon we are studying. For a higher dimensional phenomenon, the lower dimensional time will behave as space and the new time will be a plus one dimension, meaning if we study a 3-dimensional phenomenon then time is the usual 4th dimension but if we are studying a 4-dimensional phenomenon then its time will be an extra 5th dimension and for this phenomenon the 4th dimension will behave as space. All spatial dimensions are indistinguishable from each other and behave in the exact same way, which means that the important parameter is not the dimension we are studying (for example the 4th or the 5th) but the number of dimensions in which a phenomenon can interact and how higher dimensional phenomena interact with lower ones. This non-traditional approach to higher dimensional spacetime may appear confusing at first but will become clearer in the rest of the paper. For this reason, we will first associate the time dimension with propagation relative to space dimensions and change orthogonal to them in order to give the reader a better intuition. Following that, we will describe how higher - dimensional phenomena would appear to us, the 3 - dimensional observer and try to set some guidelines on how we should mathematically model higher - dimensional phenomena in order for us to make accurate predictions of their behaviour. Then we will express the general framework of a "Dynamic" higher - dimensional spacetime and turn our gaze to 4+1 – dimensional phenomena. We will explore how a mass term arises for 4 – dimensional waves by generalizing the frequency – speed – wavelength relation of 3D waves and give a basic description on a possible way to describe a 4+1 – dimensional disturbance in a scalar Energy Field in order to make accurate predictions on our 3+1 dimensional plane. In this framework we will derive the Klein – Gordon equation by generalizing the wave equation and ignoring all lower than 4+1 - dimensional disturbances and compere our mass term findings with the Klein – Gordon equation mass term and with results from gravity – induced quantum interference experiments. Lastly, we will describe how a "Dynamic" 5 - dimensional spacetime would appear in a 3D observer and examine whether our findings are compatible with quantum mechanics and the special theory of relativity.

Keywords:

Subject: Physical Sciences - Theoretical Physics

1. Introduction

In physics there have been many attempts to describe higher dimensions in a meaningful framework with the purpose of acquiring a more complete and unifying understanding of the fundamental forces of nature or developing more powerful tools for problem solving. In 1921 Theodor Kaluza presented a classical extension of general relativity to 5 dimensions in order to combine Einstein Field Equations with Maxwell’s Equations. In 1926 Oskar Klein in order to give a quantum interpretation to Kaluza’s classical 5 - dimensional theory, made the hypothesis of a curled up and microscopic 5^th dimension creating what is now known as Kaluza–Klein theory. Since then, many new theories have been proposed involving extra dimensions including large extra space dimensions, warped extra space dimensions and multiple extra time dimensions. All these theories even though they promise solutions to unanswered physical problems and possess great mathematical beauty, they experience many problems. The warped extra space dimensional theories require a great number of extra dimensions (26 in bosonic string theory, 10 is superstring theory and 11 in M-theory) which are all spatial except one time dimension. Large extra space dimensional theories that rely on geometry have difficulties with quantization. Multiple extra time dimensions are infamous for chaotic behaviors. These are only some of the many problems. So, the question that comes in mind is: can there be a simpler approach to higher dimensional physics which explains our reality without so many warped extra dimensions and why time is treated differently to space?

In the present work we will explore a different non-traditional approach to higher dimensional spacetime which diverges from the usual approaches in the way time is treated. In our approach, time is not a fixed dimension which is experienced in the same way for all other dimensions, which are spatial. We model time by making it “dynamical” in nature, in the sense that it is neither fixed nor the same for different dimensional phenomena. Our time will always be the plus one dimension to the spatial dimensions our phenomena interact. For a phenomenon that propagates and interact in 3 dimensions, time is the 4^th dimension. For a phenomenon that propagates and interact in 4 dimensions, time will be an extra 5th dimension and for this phenomenon the 4th dimension will behave as space together with the other 3 spatial dimensions of the lower dimensional phenomena. A phenomenon can not propagate nor interact in the 1^st, 2^nd, 4^th and 5^th dimensions, it must interact in the correct order (1^st, 2^nd, 3^rd, 4^th). This may seem to invoke a hierarchy to dimensions, but this hierarchy applies only for time. All spatial dimensions are indistinguishable from each other and behave in the exact same way (no spatial dimension is more important or different than the other). The important parameter is not the dimension we are studying (for example the 4th or the 5th) but the number of dimensions. In such an approach time for one phenomenon can act as space for a higher dimensional one. This may appear confusing at first and may seem prone to chaotic behaviors like a multiple extra time dimensional theory, but when a set of rules is applied to such a “Dynamic” multi-dimensional spacetime some beautiful results may arise and possibly many similarities with special relativity and quantum mechanical behaviours.

In the following sections we will try to clarify some characteristics that a time dimension has and try to generalize them. Following that, we will describe how higher - dimensional phenomena would appear to us, the 3 - dimensional observer and try to set some guidelines on how we should mathematically model higher - dimensional phenomena in order for us to make accurate predictions of their behavior. Then we will express the general framework of a “Dynamic” higher - dimensional spacetime and turn our gaze to 4+1 – dimensional phenomena. We will explore how a mass term arises for 4 – dimensional waves by generalizing the frequency – speed – wavelength relation of 3D waves and give a basic description on a possible way to describe a 4+1 – dimensional disturbance in a scalar Energy Field in order to make accurate predictions on our 3+1 dimensional plane. In this framework we will derive the Klein – Gordon equation by generalizing the wave equation and ignoring all lower than 4+1 - dimensional disturbances and compere our mass term findings with the Klein – Gordon equation mass term and with results from gravity – induced quantum interference experiments. Lastly, we will describe how a “Dynamic” 5 - dimensional spacetime would appear in a 3D observer and examine whether our findings are compatible with quantum mechanics and the special theory of relativity.

The purpose of this work is not to present a new equation of physics or to solve a physical problem but to introduce a new framework, that of a “Dynamic” higher dimensional spacetime, examine its behaviour, whether it is compatible with our physical reality and investigate if such a higher dimensional spacetime is suitable for further study. For this reason, our results will be general and we will focus more on finding similarities with our physical reality.

2. Characteristics of a Time Dimension and the Core Idea of “Dynamic Time”

The core idea of a “Dynamic” higher dimensional spacetime, or “Dynamic time” in general can be better understood by examining the effects that a time dimension has on a periodic function.

We start with the usual 3 - dimensional wave of the form:

Ψ = A \sin (ω t - k_{x} x - k_{y} y - k_{z} z)

(1)

where

\vec{k}

[\begin{matrix} k_{x} \\ k_{y} \\ k_{z} \end{matrix}]

\frac{ω}{\sqrt{({k_{x}}^{2} + {k_{y}}^{2} + {k_{z}}^{2})}}

u

-: A is the amplitude of the wave (of what is not really important here since we focus on making general conclusions)
-: ω is the angular frequency and is defined as ω = 2π/T (T is the period of the wave and f = 1/T is the frequency)
-: $\vec{k}$ is the wave vector. The direction of the wave-vector specifies the spatial direction in which the wave travels
-: $u$ is the velocity of the wave

In such a wave the time dimension (symbolized by t) is vital for performing two functions:

(1): It propagates the wave (or more accurately the wave front) in space with speed $u$ in the direction of $\vec{k}$ .
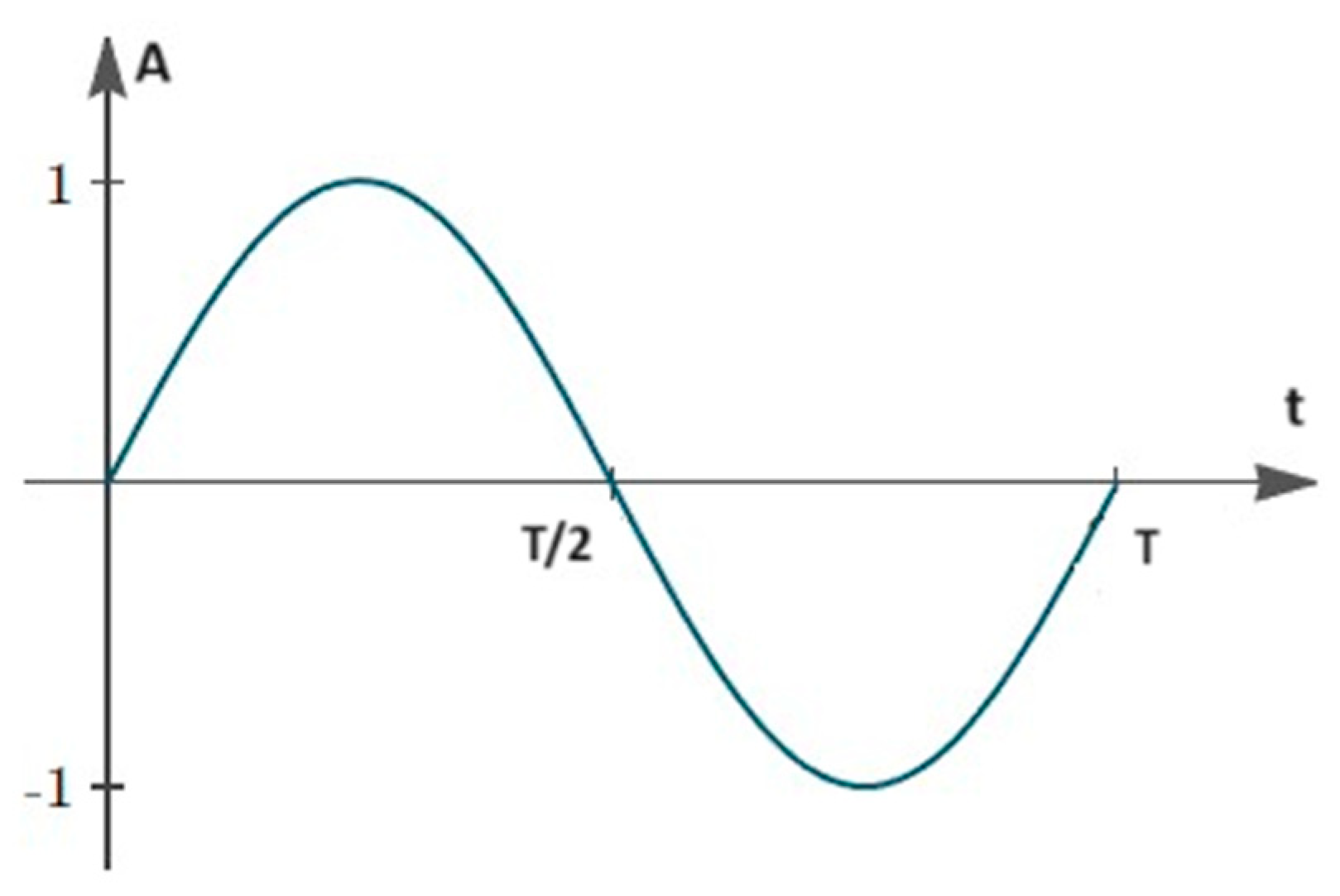
(2): If we focus on a specific point in space (for example $\vec{x}$ = ( $\begin{matrix} x_{1}, & y_{1}, & z_{1} \end{matrix})$ ), the amplitude A of that point oscillates with time with frequency f = ω/2π.

Figure 1. How the Amplitude of a 3-dimensional wave changes with time (Max Amplitude = 1, T = period of the wave) for a specific point in space

\vec{x}

= (

\begin{matrix} x_{1}, & y_{1}, & z_{1} \end{matrix})

Figure 1. How the Amplitude of a 3-dimensional wave changes with time (Max Amplitude = 1, T = period of the wave) for a specific point in space

\vec{x}

= (

\begin{matrix} x_{1}, & y_{1}, & z_{1} \end{matrix})

Those two properties of time can help us draw conclusions on how waves with same frequencies but different phases interact, how waves with different frequencies interact, how waves coming from different sources interact and how interference patterns arise.

Every wave function corresponds to a wave equation which typically takes the form:

\frac{\partial^{2} φ}{{\partial t}^{2}} = u^{2} (\frac{\partial^{2} φ}{{\partial x}^{2}} + \frac{\partial^{2} φ}{{\partial y}^{2}} + \frac{\partial^{2} φ}{{\partial z}^{2}})

(2)

(what φ represents is not important here)

The link between the two is the equation:

u = f * λ

(3)

(λ is the wavelength of the wave)

k = 2π/λ

which help us draw all the conclusions above and helps us deduce interference patterns for points in space by only knowing the spatial geometry of the sources and the phase difference between them. A more detailed explanation of this will be given in the following section where we will try to find a working framework in which our model can work.

Now we want to generalize the two characteristic functions that time for a 3 - dimensional wave performs, mentioned above, together with a relationship such as (3) which describes the rate of transmition for a wave of the form (1). That rate of transmition is the link which connects time and space.

In the framework we want to explore, if there was a 4^th dimensional wave with time as the 5^th dimension (treating the time dimension of a 3D wave as space) how would the above characteristics of time apply to that new wave?

We will start with the first one, which concerns the propagation of the wave (or more accurately the wave front) in space with some speed

u

in some direction of the wave vector.

Now our space is 4 dimensional (3 - dimensional time is part of our spatial dimensions now) and all space dimensions are equivalent and treated the exact same way.

This means that our new wave vector

\vec{k'}

must be 4 dimensional and have the form

\vec{k'} = [\begin{matrix} k_{t} \\ k_{x} \\ \begin{matrix} k_{y} \\ k_{z} \end{matrix} \end{matrix}]

If the speed or more accurately the rate of transmition of that wave is

u'

then the angular frequency of that wave would be ω

'

u' * k'

\vec{k'}

now has a 4 - dimensional direction, which means that the rate of transmition of that wave

\vec{u'}

will also have a 4 - dimensional direction.

If we take the magnitude

| \vec{u'} |

of the rate of transmition of all waves, no matter their dimensionality, be equal to the same number c, which is equal to the speed of light for the 3 - dimensional wave, then a 4 - dimensional wave would have to always move to 3 dimensional space at a speed less than the speed of light and the more its 3D speed components are, the less its speed will be in the 4^th dimension.

A 3D observer would perceive such a wave as a wave which changes its internal structure (the way it is composed and behaves) as it propagates through space. Also, such an observer would measure its speed in 3D space always less than that of light and the more its speed in 3D space is the lower the rate it changes its internal structure.

From now on when we refer to a 4+1 - dimensional wave we will use the term rate of transmition instead of speed, because speed is usually associated with 3D time and may cause unnecessary misunderstandings. The term speed will instead be used from now on when we refer to the components of the vector

\vec{u'}

in 3D space.

At this point the readers can see a clear association with the theory of special relativity and may even question why we don’t go in further detail by using 4-vectors or even 5-vectors in order to give our theory a solid mathematical foundation. The reason for this will become clearer in the following section where we will try to mathematically model a “dynamic” time dimension. This comes at the expense of not substantiating our theory and is the precise reason this paper will focus more on finding similarities with our physical reality and give general results.

There is a debate among theoretical physicists whether Minkowski’s approach of making time equivalent to space thus using 4-vectors and quadratic forms is the correct approach or time is fundamentally different to space. In our framework, even though time is clearly different to space, 4-vectors and metric tensors such as Minkowski’s metric may still be very useful in describing the behavior of 4+1 or higher dimensional phenomena precisely because of the fact that for such a phenomenon our time (4^th dimension) behaves as space. Later in this paper when we study how mass arises for 4+1 dimensional waves this will become more intuitive.

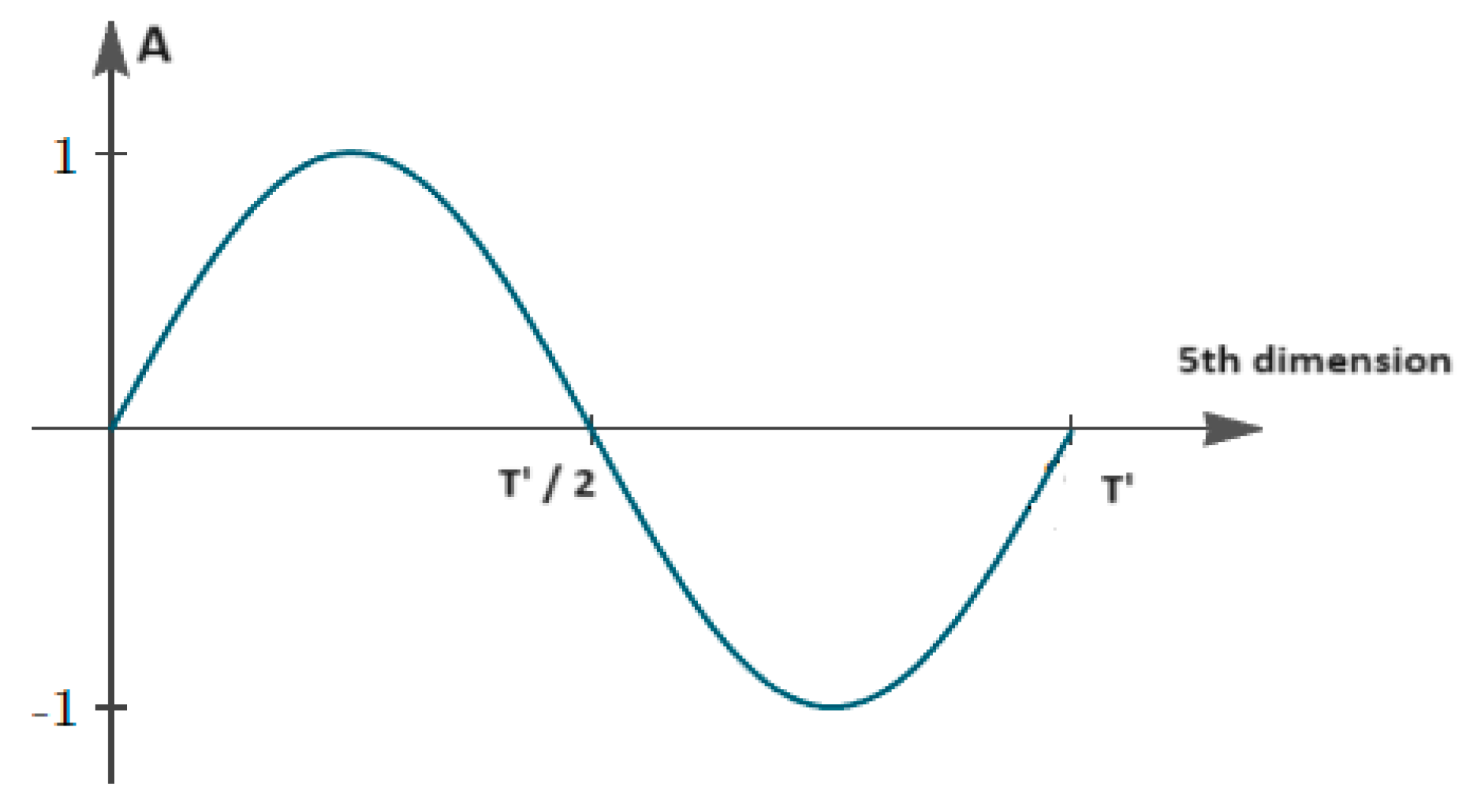
Continuing with the second characteristic function of time mentioned above, for a 4 - dimensional wave, we now turn our attention on a specific point in 4D space

\vec{x'}

= (

x_{1}, y_{1}, z_{1}, t_{1}

). If the 4^th dimension is treated as space, then at any such point the amplitude A of the 4th dimensional wave will oscillate in the 5^th dimension with frequency f

'

= ω

'

/2π

Figure 2. How the Amplitude of a 4-dimensional wave changes in the 5th dimansion (Max Amplitude = 1, T´ = period of the wave in the 5th dimansion) for a specific point in 4D space

\vec{x'}

= (

x_{1}, y_{1}, z_{1}, t_{1}

Figure 2. How the Amplitude of a 4-dimensional wave changes in the 5th dimansion (Max Amplitude = 1, T´ = period of the wave in the 5th dimansion) for a specific point in 4D space

\vec{x'}

= (

x_{1}, y_{1}, z_{1}, t_{1}

This means that for a specific point in space and time, as a 3D observer perceives them, a 4 - dimensional wave would seem to possess many values of A which cannot be known in advance since the observer doesn’t have access to the 5^th dimension. Regardless, the effects of the interactions that occur from 4 - dimensional waves would not seem totally chaotic to the observer since 4 dimensional waves obey the rules mentioned in this section. That means the observer could be able to derive correlations between interactions and model them appropriately but always in a probabilistic way, as the information from the propagation of these waves to the 5^th dimension will be unknown and unobtainable.

Now the readers can see a clear association with quantum mechanics, though they may not be entirely convinced. More information will be given in the following sections which will provide them with more similarities and explore the need of complex numbers, which are essential both in our model and in quantum mechanics.

At the current point of this paper, it is important that some points are cleared out. All spatial and time dimensions form a continuum and a wave must propagate in a way that this continuity is not violated. Since we modeled our waves, or our phenomena in general to always propagate with the same rate of transmition our framework does not allow faster than light communication or the transmition of energy or information in a non-local way, at least in scales larger than those that quantum mechanical uncertainty principles allow. A 4 - dimensional observer would not have access to all space and time, the same way a 3 - dimensional observer does not have access, information and cannot influence all of space at the same time.

3. Mathematical Framework for a “Dynamic” Multidimensional Space-Time. The Need for Complex Numbers

Throughout the years there have been many debates about how time differs from space and whether it should be treated differently. Today we most commonly use the mathematical model of 4-dimensional spacetime and general relativity, which fuses the 3 spatial dimensions with the time dimension in a single four-dimensional continuum and which makes use of metric tensors (such as Minkowski’s metric) to represent geometric structures and define notions such as time, distance, volume, curvature and separation of the future and the past. Though this model is extremely useful and we will use some of its features in our calculations in Section 5, we will not generally take its approach because time in our framework is dynamic and changes from one phenomenon to another. Maybe a metric tensor of rank 3 and dimension 5 could be used to make the mathematical model of spacetime, as used in general relativity, compatible with our theory but this would be very complicated and much beyond the scope of this paper.

From the very first moment we try to mathematically model a dynamic spacetime, in the sense that we explained above, problems start to arise.

All different dimensions, time and spatial, have to be orthogonal to each other. Time has to do both with change and motion relative to the spatial dimensions, so how can we model change and motion that happens orthogonally to our understanding of time (since we are the 3 - dimensional observer). More specifically, is it possible for a 3D observer to describe changes that happen in the same moment in time (4^th dimension), like the Amplitude oscillation mentioned in the previous section? If the magnitude

| \vec{u'} |

of the vector of the rate of transmition for 4 dimensional phenomena is always equal to the same number (the magnitude of the speed of light) can this help us at least make some presumptions on how 4 dimensional phenomena interact?

In order to answer these questions and start giving our dynamic spacetime a mathematical foundation, we once again turn to the 3 - dimensional wave of the form given in (1) and we ask a different question which may give us some insight in our problem. Can we model some aspects of the interactions and interferences of 3 dimensional waves without the need of time, only by using space?

Not surprisingly the answer is yes. If these waves all travel with the same speed (

u

) and all obey the equation:

u

= f

*

λ, then we can make predictions about the Amplitude of the wave on a specific point in space in correlation with its Amplitude on another point in space and also make predictions about interference patterns if we know the geometry of the sources and the relative phases of the waves. This is where complex numbers come into play.

We can describe a wave of the form (1):

\begin{array}{l} Ψ = A \sin (ω t - k_{x} x - k_{y} y - k_{z} z) \\ = A \sin (ω t - \vec{k} \vec{r}), where \vec{r} = [\begin{matrix} x \\ y \\ z \end{matrix}] \end{array}

as the real part of a complex wavefunction of the form:

Ψ = Re [A e^{i (ω t - \vec{k} \vec{r} - \frac{π}{2})}]

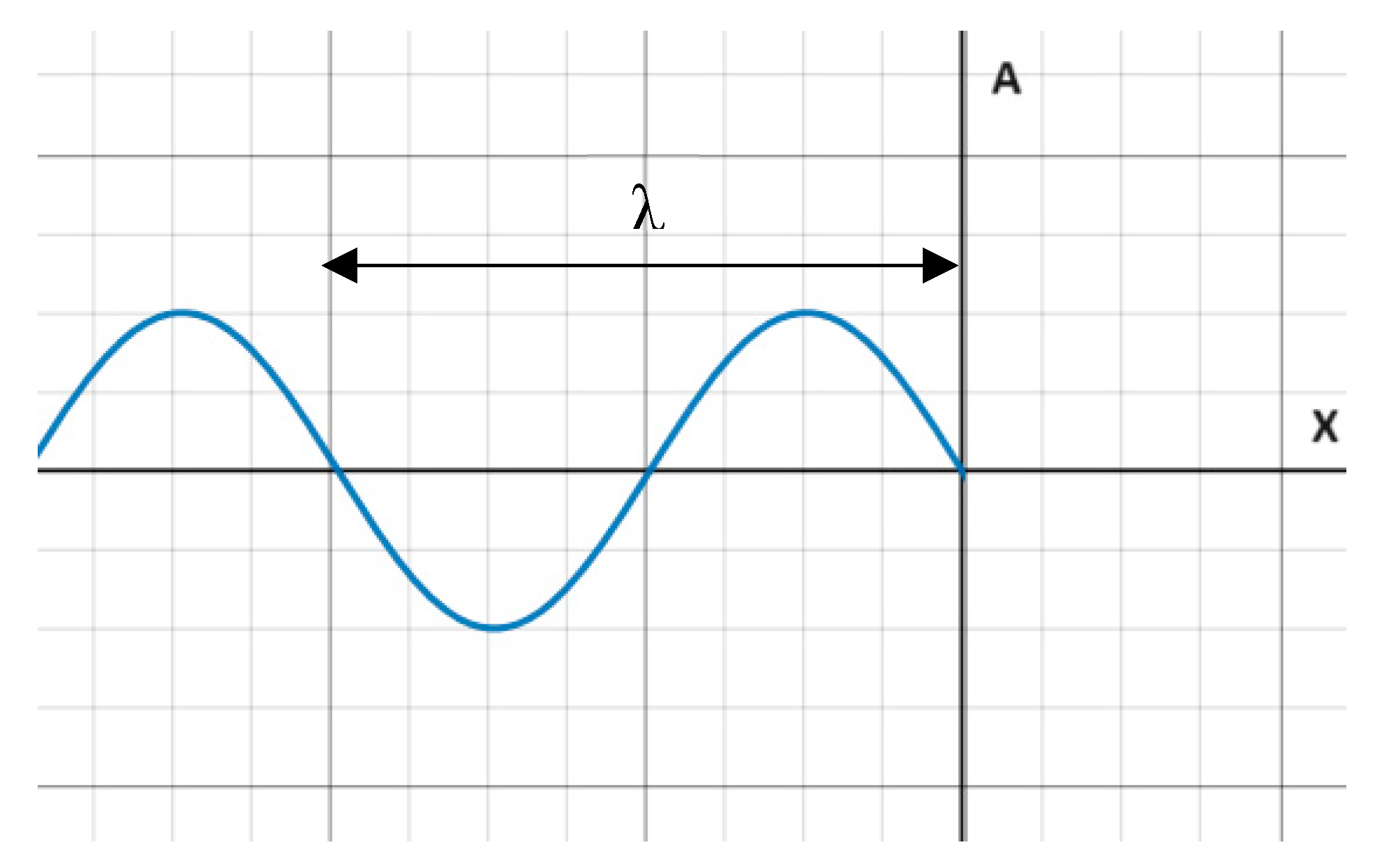
Now imagine a wave of this form propagating in the positive x direction at speed

u

(

u

_y=

u

_z=0)

At time t = t_o the wavefront is in position x₀ = 0

Figure 3. A wave of the form (1) propagating in the positive x direction. At t=t₀ its wavefront is at x₀ = 0.

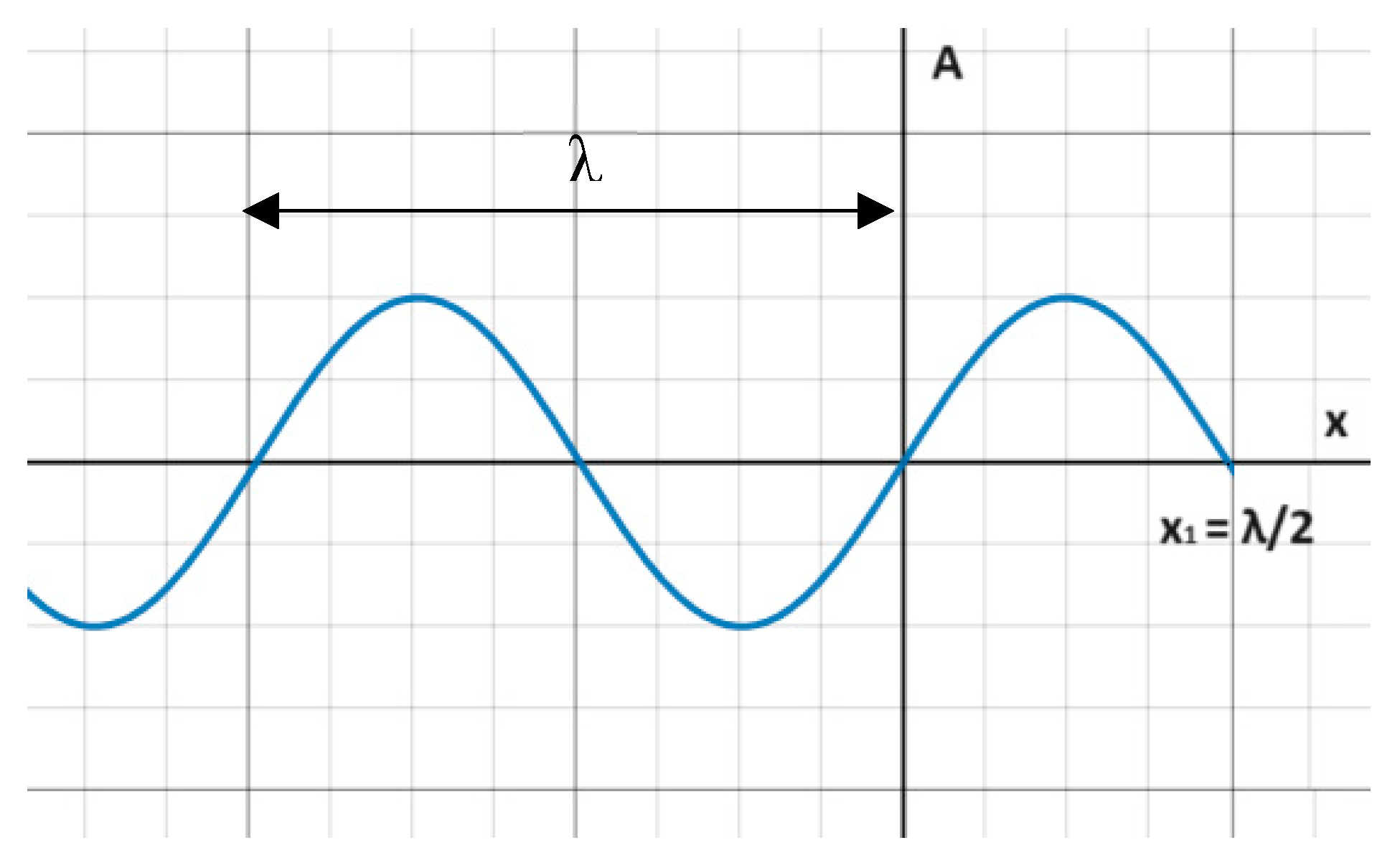
At a later time t=t₁ its wavefront is at position x₁ = λ/2

Figure 4. A wave of the form (1) propagating in the positive x direction. At t = t₁ its wavefront is at x₁ = λ/2.

The two points in space (x₀ and x₁) will always be at a phase difference Δφ = π at any point in time.

This information about the phase difference can be derived for any number of points that the wave passes through simply by knowing the spatial separation between the points and the wavelength λ.

If we measure the Amplitude (A₁) of the wave in one point in space we can know the amplitude (A₂) of another point at distance dx from the first point by multiplying it with a phase factor in the form:

A_{2} = Re [\frac{A}{A_{1}} e^{i d x * \frac{2 π}{λ}}], i = \sqrt{- 1 (imaginary unit)}

This is nothing new for us (the 3D observer), but if we wanted to explain or give a meaningful representation of a wave to an observer who doesn’t understand and can’t measure time, complex numbers and correlations with other measurable aspects of the wave, would actually be the only viable solution since the 3 - dimensional wave always changes its Amplitude at any point due to its propagation. If we measure its Amplitude at one point and then want to measure its amplitude at another point, we must account for the change that the wave undertook in the time we had to move from the first point to the next. If an observer can’t measure time, then the only solution is to make correlations between observables. One correlation for the spatial difference

\propto

e^{i * d x * \frac{2 π}{λ}}

and another correlation to account for the speed difference between the wave and the observer who made the two measurements ∝

e^{i * 2 π \frac{u}{λ} * \frac{d x}{d u}}

2 π \frac{u}{λ} \to 2 π f (u is the speed of the wave)

\frac{d x}{d u} \to dt (d u is the speed difference between the wave and the observer)

)

This could also be expressed by us without using complex numbers. Nevertheless, because a 3D wave is oscillating both in space and in time, for two different points (x₁, y₁, z₁, t₁) and (x₂, y₂, z₂, t₂), making precise correlations about the Amplitude in different times is impossible without any information about the time separation t₂-t₁.

Taking that into account, the observer who can’t understand and measure time would have to make use of complex functions and associate them with observables which the observer can measure and understand such as wavelength λ or energy (if the energy of a wave is proportional to its frequency which is the case for electromagnetic radiation – photons and free fundamental particles). In fact, energy being a scalar, is a very useful quantity for making correlations and this is why in later sections we will try to describe what would happen to an energy field in a “Dynamic” spacetime. Also, such waves can not be entirely described only by spatial functions (for example

\sin (\vec{k} \vec{r})

). Using the complex plane gives us a necessary extra degree of freedom, essential for our correlations.

In a more complex (realistic) scenario with waves being superpositions of many pure frequency waves and also if the act of measurement requires some sort of interference of the wave measured with another wave or apparatus that itself is 3 - dimensional, the observer would not be able to have the complete picture and some information would be lost to him. Nevertheless, that observer would still be able to calculate possible results probabilistically.

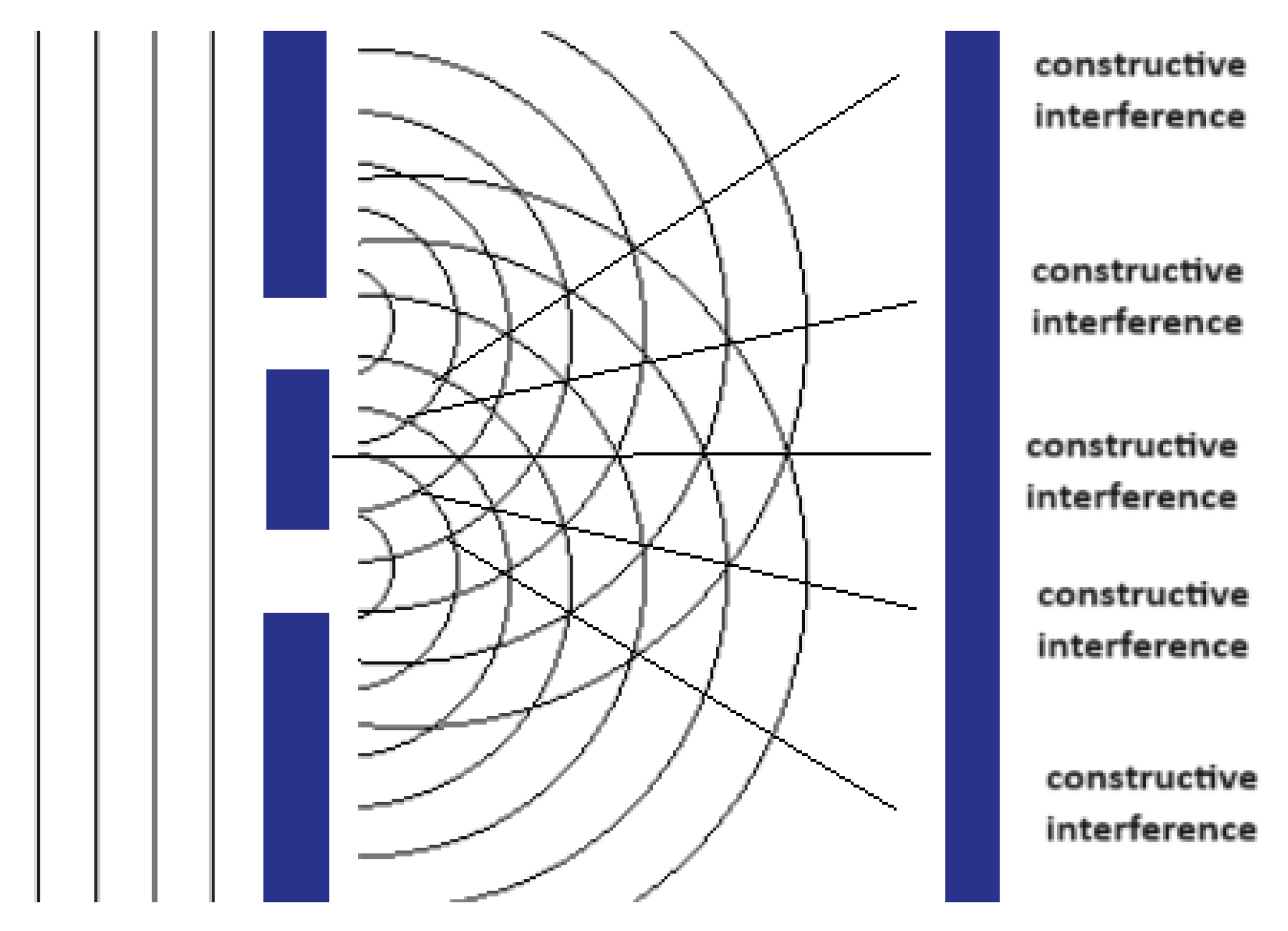
In addition to the relations mentioned above, we can also make predictions about interference patterns of waves and derive equations about the intensities of those interferences only by knowing the geometry of the sources and their phase differences. For example in the case of the double slit experiment for light, we know that the Amplitude of the interference pattern for any point on the screen is analogous to

e^{i φ (r 1)}

e^{i φ (r 2)}

, where

r 1

r 2

the distances of the slits from the point measured on the screen and

φ (r) \propto

k * r

. This way an observer who can’t measure time would be able to have some information on how the resulting wave behaves only by knowing the geometry of the slits or the sources.

This is where the use of complex numbers becomes apparent. In a classical representation, complex numbers would not be essential since we only need sines and cosines, but for the observer who can’t measure nor understand time, their use is vital. Imagine such an observer be located in a point on the screen of a double slit experiment. The observer is oblivious to the concept of our time (4^th dimension) so it would seem to him that the Amplitude of the wave can take many values as mentioned is Section 2. The only way any conclusion or correlation about the wave and its behavior can arise is with the use of complex numbers. Still some information is lost to the observer (like the exact value of the Amplitude because it oscillates with time, which the observer can’t measure or understand) but at least a great portion of the total information of the system would be accessible (for example if there is a constructive or destructive interference like in the double slit experiment for light).

Figure 5. The double slit experiment and how it creates constructive and destructive interferences which have to do with the geometry of the experimental setup.

At this point in the paper the connection between a “Dynamic” spacetime and quantum mechanics may start to become clearer for the reader. Complex numbers are essential for quantum mechanics. Experiments have shown that it is impossible to predict experimental results with real-number quantum theory. Also, the use of complex numbers is apparent in the fact that we can’t derive both Planck-Einstein and deBroglie relations (E = hf and p = h/λ) in quantum mechanics without their use.

Considering all the above and since time in our framework is dynamic and changes from phenomenon to phenomenon, we therefore propose that higher dimensional time is always treated mathematically with the use of the imaginary unit (i =

\sqrt{- 1})

in relation to other measurable quantities for the reference frame of the lower dimensional phenomenon. For example, if we the 3D observer wants to describe a phenomenon which is 4 dimensional in space and has time as the 5^th dimension, treating our time as space, we can only describe it in a way meaningful to us with the use of complex numbers and by making correlations with quantities that we can observe and by preserving some symmetries so that the system is not chaotic (similarly with what we do in quantum mechanics).

In addition, if we consider that imaginary numbers are orthogonal to the real number plane, and that together make the complex plane, which is ideal for expressing rotations, it stands to reason why we may want to make use of them. For the dimensions the observer has access to and can measure (including the observer’s time) the use of vectors is adequate for describing the degrees of freedom that those dimensions represent, but for higher dimensional phenomena which treat the observer’s time as space and have a plus one dimension as time, a different number system is required. The need of making correlations and expressing relations can therefore be described by a complex plane because rotations are a very useful way of expressing them, especially when these relations are periodic. We believe that this may not be mandatory though. The observer’s dimensions can also be expressed with imaginary numbers and the higher dimensional time as real value number or make use of any other combination of different number systems. In the rest of the paper, we will not explore any such combination because we think it would be unnecessarily complicated, but we think that in principle it can be done.

It is important to note at this point that vectors and complex numbers are not representative of the dimensions themselves. They express the relation these dimensions have between them and are used in functions that utilize these relations. In later sections we will briefly explore how specific symmetries of functions can help us express some quantity as the imaginary value of another quality, without meaning this is the general case.

To summarize, if an observer wants to describe a higher dimensional phenomenon in the framework explored by this paper (that of a “Dynamic” spacetime), this is possible only by making correlations and relations between observables (measurable for the observer quantities), which in turn need to be expressed by complex functions.

4. The General Framework for a “Dynamic” Multidimensional Space-Time and How It Behaves

At this point in the paper, we have covered all the basic aspects of what a “Dynamic” multidimensional spacetime is, how it behaves, what it means for time to be “Dynamic” in the sense that it changes from one phenomenon to the other and how time for one phenomenon can be treated as space for another. We have given certain characteristic functions that a time dimension executes and have related time with motion and change relative to space, where all the spatial dimensions are equivalent to each other and behave in the exact same way. Until now we have only used periodic functions, more specifically functions that represent waves, because the key ideas are easier to be explained by examining them.

In this section, we will concentrate the above and try to give a general framework of what a “Dynamic” multidimensional spacetime is.

The “Dynamic” multidimensional spacetime is a field of n dimensions which are all orthogonal to each other. Any disturbance in this field can be described by i of those dimensions. Then we say that this disturbance is i – dimensional. It does not matter which these dimensions are. The thing that matters is the number of these dimensions which represent our space dimensions. Any i – dimensional disturbance behaves in the exact same way from a higher-dimensional frame. This disturbance can move or change relative to other disturbances in the i - plane therefore its time is the i+1 dimension. This means that time is not a fixed dimension for all disturbances and it is not experienced in the same way always. For example, for a disturbance that propagates and interacts in 3 dimensions, time is the 4^th dimension. For a disturbance that propagates and interacts in 4 dimensions, time will be an extra 5th dimension and for this phenomenon the 4^th dimension will behave as space together with the other 3 spatial dimensions of the lower dimensional disturbance. All disturbances are in motion with each other. The way they are transmitted depends on their rate of transmition an how that rate of transmition is distributed in the spatial dimensions (for example u_x, u_y, u_z for the 3 -dimensional wave). The magnitude of that rate of transmition is constant and equal for any - dimensional disturbances. This value of the magnitude depends on the energy density of the region we are studying. By energy density we refer to the total energy in a region of space that is the same dimension as the disturbance we are studying.

The role of the last part is to make the framework of the “Dynamic” multidimensional spacetime compatible with the results and predictions of general relativity. It will not be referenced or taken into account for the rest of the paper because our goal is simply to introduce the idea of a “Dynamic” multidimensional spacetime, explore its behavior and determine if it has any relation with our physical reality making it worth for further study. It is known from the general theory of relativity that curvature determines the motion of objects in spacetime. If we don’t account for curvature it will appear as the force of a field is acting on the object. Because we want to make things as less complicated as possible, we will not take the curvature approach and therefore we mention the possibility of the change of the magnitude of the rate of transmition to provide a possible approach for making our framework compatible with the results of the general theory of relativity.

5. The Behaviour of a Scalar Energy Field in a “Dynamic” 5—Dimensional Spacetime and the Quantity of Mass

In this Section we will make some suggestions on how a Scalar Energy Field should be treated in the framework of a “Dynamic” 5 – dimensional spacetime and examine how this field’s behavior may give rise to some physical phenomena, focusing specifically on the quantity of mass and how it arises. We will focus on 4+1 dimensions because we want to investigate whether our framework is compatible with our physical reality. Taking a more general approach would make matters unnecessarily more complicated and make general assumptions much less clear. We focus on Energy and specifically on an Energy field because of the fundamental place it has on physics and because Energy is a scalar which means it only has one value at every point in space at any moment in time. Also, a scalar field exhibits a very useful behavior in terms of its derivatives. The gradient of a scalar field is a vector field and the divergence of a vector field is a scalar field. The properties of those fields are well known as well as the fact that the curl of the gradient of a scalar field is always zero thus physical reality cannot be explained just with a single scalar field. The fundamental change that takes place in our approach is that time for one phenomenon is experienced as space for another. This may give rise to some unexpected behavior in the way different dimensional phenomena interact making a simple scalar field much more versatile than its classical counterpart. This is the part we want to delve into.

Most commonly when we study a non-classical field in physics, we take the approach of quantum field theory. In quantum field theory the field and its conjugate momentum field are promoted to operators and then canonical commutation relations are imposed on them. Then we find the Lagrangian density

L

of the field and apply the principle of least action 0 = δS = δ

\int d^{4} x L

to determine the field’s equations of motion. If we are considering a field φ with the potential V for the Lagrangian which does not have a minimum at φ = 0 and the true minimum is at φ = ± ν (the true ground states), we say that the symmetry is broken and we rescale the field as φ(x) = ν + η(x) where η(x) are fluctuations of the field about the right-hand minimum ν (considering we take the case where φ = ν). When this procedure of spontaneous symmetry breaking is combined with a gauge invariance, it leads to the appearance of new particles (excitations of fields) some of them massive and some of them massless. The mass term is recognized as a term in the Lagrangian that is quadratic in the field and has the form

A^{2} φ^{2}

for some

A

(

A

∝ m the mass of the particle).

Despite the fact that quantum field theory is one of the most successful theories regarding its results, we will not take its approach for various reasons. As mentioned in Section 3, if a 3 - dimensional observer (such as ourselves) wants to describe a 4 - dimensional phenomenon (whose time is the 5^th dimension), is only able to do so by making relations and correlations with things the observer can measure. These measurable quantities are the operators that quantum mechanics makes use of. Regarding that and since fields in quantum field theory are promoted to operators, we will avoid taking the qft (quantum field theory) approach in fear of missing the bigger picture (one could say that the fields that appear in qft are the measurable quantities of the various interactions that 3-dimensional phenomena have with higher-dimensional phenomena in our 3-dimansional frame). Also, we will not make use of any particular Lagrangian. Instead, one could interpret the principle of least action as the path of least resistance or the least difference of energy density as mentioned in Section 4. As for the mass term and how it arises, we will identify it as a general property that every higher dimensional phenomenon possesses.

We remind the reader that we do not have a complete working mathematical framework for expressing the behavior of a “Dynamic” spacetime and doing so is beyond the scope of this paper which focuses on introducing the general concept and provide similarities of the expected behavior of such a spacetime with our physical reality. Considering that, we will therefore suggest how a scalar Energy field should be treated in our “Dynamic” spacetime and examine if its behavior bears any resemblance to known physical concepts.

We will start with a general relation that was firstly mentioned in Section 2.

A 3-dimesnional wave always obeys these relations:

\vec{k} = [\begin{matrix} k_{x} \\ k_{y} \\ k_{z} \end{matrix}], \frac{ω}{\sqrt{({k_{x}}^{2} + {k_{y}}^{2} + {k_{z}}^{2})}} = u, ω = 2 π * f

u = f * λ, k = 2 π / λ

Focusing on a 4-dimensional wave we must keep in mind the rules we imposed on our “Dynamic” spacetime framework. More specifically for our 4-dimensional wave:

-: Its time is the 5^th dimension (an extra +1 dimension).
-: The 4^th dimension (our time) behaves as space and is indistinguishable from the other 3 spatial dimensions.
-: The magnitude of the rate of transmition of all waves, no matter their dimensionality, is equal to the same number c, which is equal to the speed of light for the 3-dimensional wave.

Taking the above into account we define a new quantity:

A

which is the wave’s angular frequency in the 5^th dimension.

Additionally, since the 4^th dimension (our time) behaves as space and is indistinguishable from the other 3 spatial dimensions we must express it in the same units as the others. As expected, we do that by multiplying 3-dimensional time (4^th dimension) with the speed of light (this applies to all 4^th dimensional time related quantities).

Now we want to generalize the relation:

\frac{ω}{\sqrt{({k_{x}}^{2} + {k_{y}}^{2} + {k_{z}}^{2})}} = u

(4)

making it applicable to a 4-dimensional wave.

The new wave vector

\vec{k'}

must be 4 dimensional and have the form

\vec{k'} = [\begin{matrix} k_{t} \\ k_{x} \\ \begin{matrix} k_{y} \\ k_{z} \end{matrix} \end{matrix}] = [\begin{matrix} \frac{ω}{c} \\ k_{x} \\ \begin{matrix} k_{y} \\ k_{z} \end{matrix} \end{matrix}]

(5)

(ω is the 4-dimensional frequency which is now expressed in units of space)

Also, we want to produce results that make sense in our 3+1 dimensional perspective and are true for all 3+1 dimensional reference frames. This is the reason we will use the Minkowski inner product in order to express the magnitude of this vector so that it is invariant for all 3D observers.

Therefore:

|\vec{k'}| = \sqrt{\frac{ω^{2}}{c^{2}} - {k_{x}}^{2} - {k_{y}}^{2} - {k_{z}}^{2}}

(6)

The magnitude of the rate of transmition is equal to the same number c for waves of any dimensionality

u = c

(7)

Generalizing (4) for the 4-dimensional wave using (5), (6), (7) and the quantity

A

we get:

c = \frac{A}{\sqrt{(\frac{ω^{2}}{c^{2}} - {k_{x}}^{2} - {k_{y}}^{2} - {k_{z}}^{2})}}

(8)

Taking the square of (8) in order to get rid of the square root in the denominator

c^{2} = \frac{A^{2}}{\frac{ω^{2}}{c^{2}} - {k_{x}}^{2} - {k_{y}}^{2} - {k_{z}}^{2}} \to

c^{2} * (\frac{ω^{2}}{c^{2}} - {k_{x}}^{2} - {k_{y}}^{2} - {k_{z}}^{2}) = A^{2} \to

ω^{2} - c^{2} {k_{x}}^{2} - {c^{2} k}_{y}^{2} - {c^{2} k}_{z}^{2} = A^{2} \to

multiplying both sides with

ℏ^{2}

in order to get units of energy we get

({ℏ ω)}^{2} - c^{2} ({{ℏ k}_{x})}^{2} - {{c^{2} (ℏ k}_{y})}^{2} - {{c^{2} (ℏ k}_{z})}^{2} = {(ℏ A)}^{2}

({h f)}^{2} - c^{2} ({p_{x})}^{2} - {{c^{2} (p}_{y})}^{2} - {{c^{2} (p}_{z})}^{2} = {(ℏ A)}^{2}

E^{2} - c^{2} ({p_{x})}^{2} - {{c^{2} (p}_{y})}^{2} - {{c^{2} (p}_{z})}^{2} = {(ℏ A)}^{2}

(9)

For equation (9) we have used the deBroglie relation:

p = h / λ = ℏ k

and the Einstein – Planck equation:

E = h f

which applies to all fundamental particles.

Comparing (9) with the Einstein energy equation:

$E^{2} = {(m c^{2})}^{2} + c^{2} ({p_{x})}^{2} + {{c^{2} (p}_{y})}^{2} + {{c^{2} (p}_{z})}^{2}$

(10)

we find that every 4-dimensional wave that obeys the rules we imposed on our framework for a “Dynamic” spacetime should have a property which behaves like mass and is proportional to the wave’s angular frequency in the 5^th dimension noted by the letter

A

More specifically, by relating the quantity

A

with mass we conclude that:

{(ℏ A)}^{2} = {(m c^{2})}^{2} \to

ℏ A = \pm m c^{2} \to

m = \pm \frac{ℏ A}{c^{2}} or

A = \pm \frac{m c^{2}}{ℏ} \to

\frac{A}{c} = \pm \frac{m c}{ℏ}

which is identical to the mass related component in the Klein – Gordon and Dirac equations:

[\frac{1}{c^{2}} \frac{\partial^{2}}{\partial^{2} t} - \nabla^{2} + {(\frac{m c}{ℏ})}^{2}] Ψ = 0

(Klein–Gordon equation)

γ^{0} \frac{\partial Ψ}{c \partial t} + γ^{1} \frac{\partial Ψ}{\partial x} + γ^{2} \frac{\partial Ψ}{\partial y} + γ^{3} \frac{\partial Ψ}{\partial z} + \frac{m c}{ℏ} i Ψ = 0

(Dirac equation)

Taking everything into account, we are now ready to propose how a scalar Energy field should be treated in the framework of a “Dynamic” 5 – dimensional spacetime.

Since all 4+1 dimensional phenomena exhibit mass and 3+1 dimensional phenomena do not, we should start examining how energy disperses across any direction of any dimension. When doing so we should focus on two factors. Which dimension is considered as time for which interaction and whether the energy difference between any point and its surrounding points is greater than the term

ℏ A

for the interaction that is happening. The term

ℏ A

corresponds to the angular frequency of the interaction on the 5^th dimension and is proportional to mass meaning if the spatial gradient of Energy at any point is greater than the term

ℏ A

for the interaction that is happening then at that point there will be a massive particle.

For this reason, we should start considering more general equations like the Laplace equation, the Wave equation or the Heat equation and start applying them on a 5-dimensional energy field for modeling the energy dispersion. Every single possible way this energy dispersion can happen is what we were referring to the entire paper as interactions. Of course, we cannot just add an extra time term in these equations and demote 3+1 dimensional time t as a spatial dimension which we will include in the spatial gradient terms. If we did so, we would lose track of any possible way that energy could disperse in a 3+1 dimensional way. Combining this with the fact that we as the 3D observer are not able to measure any change in the 5^th dimension (Section 2,3) or measure the exact way energy disperses in it, we are left with very few options.

The answer is given again by what we mentioned in Section 2 and Section 3. The only viable way for a 3D observer to describe and model interactions of a higher dimensional phenomenon is by making relations and correlations with quantities which are measurable to the observer. This can also be applied here together with the use of symmetries.

If we consider for example the case where energy is dispersed in a harmonic way in the 5^th dimension, the solutions describing this dispersion should have a constant 5 – dimensional angular frequency term

A

which does not vary along any point in spacetime. If we consider a solution in the form of a sinusoidal or an exponential function (which is usually the case) any derivative concerning the 5^th dimension will give a term in the form of a constant term times the original function. For instance, let’s consider the wave equation for describing energy dispersion in a 5 - dimensional energy field, which is happening in a harmonic way in the 5^th dimension and we disregard any dispersion term that has 3 spatial dimensions and time as the 4^th dimension as well as any interactions that may occur between the two ways of dispersion. Then the equation takes the form:

Second 5^{th} dimensional derivative term = c^{2} \times (second spatial derivative terms)

(11)

Considering that energy is dispersed in a harmonic way in the 5^th dimension and taking a sinusoidal solution Ψ, the second 5^th dimensional derivative term will be in the form:

{- A}^{2} Ψ

(12)

The second spatial derivative terms will now include 3-dimensional time (4^th dimension) and we will again make use of the Minkowski metric because we want the results to have a physical meaning to us the 3D observer. This means that they will take the form:

(\frac{1}{c^{2}} \frac{\partial^{2}}{\partial^{2} t} - \nabla^{2}) Ψ

(13)

Combining (11), (12) and (13) we get:

{- A}^{2} Ψ = c^{2} \times (\frac{1}{c^{2}} \frac{\partial^{2}}{\partial^{2} t} - \nabla^{2}) Ψ

(\frac{1}{c^{2}} \frac{\partial^{2}}{\partial^{2} t} - \nabla^{2}) Ψ + \frac{A^{2}}{c^{2}} Ψ = 0 \to

which is equal to the Klein – Gordon equation if we consider that:

\frac{A^{2}}{c^{2}} = {(\frac{m c}{ℏ})}^{2} \to

\frac{A}{c} = \pm \frac{m c}{ℏ}

The same result as the one we derived earlier.

In addition, the fact that we equated the 5^th dimensional frequency with a term proportional to the quantity

\frac{m}{ℏ}

means that the interference of 4+1 dimensional waves may produce results that are actually measurable to the 3D observer. This is in accordance with the gravity – induced quantum interference experiment in 1975 by R. Colella, A. Overhauser and S. A. Werner and their results published in Physical Rev. Lett. 34 (1975) 1472, which say that the effects depend on the quantity

{(\frac{m}{ℏ})}^{2}

To sum up, even if we are not able to describe in full detail all the possible ways that energy is dispersed in a “Dynamic” 5 - dimensional Energy Field, we can make use of general known to us equations, correlations with observables and symmetries in order to give an approximate description of the higher – dimensional picture. It is the author’s belief that this is somewhat equivalent to what quantum field theory is doing by making use of different fields, which describe different ways that energy is dispersed and different interactions between all these ways together with symmetries.

At this point it seems appropriate to make a reference to the method often used in physics known as the Wick Rotation. This is a method of finding a solution to a problem in Minkowski space from a solution to a related problem in Euclidean space. It does that by substituting an imaginary-number variable for a real-number variable. It has many uses in physics and especially in quantum mechanics, but the one we should focus our attention to is that it relates static problems in n dimensions to dynamics problems in n − 1 dimensions. This is done by replacing:

-: a function of position in one dimension with a function of i $\times$ time.
-: one quantity which is usually the spring constant k with the quantity of mass.

This is particularly interesting because it may be a way of exploiting certain symmetries in some problems and also shows that by Wick Rotation, we must also replace one physical quantity with another. This may be a possible hint that certain physical quantities are connected to the way energy disperses in certain number of dimensions, which is a clear result to the fact that since the concept of time changes from interaction to interaction a scalar field in a “Dynamic” spacetime may be much more versatile in its behavior than its classical 3 - dimensional counterpart, thus connecting many physical quantities to the same field.

6. How a “Dynamic” 5—Dimensional Spacetime Is Perceived by a 3D Observer. Relations with Quantum Mechanics and Relativity

From all the previous Sections, we have now gathered enough information in order to ascertain how a “Dynamic” 5 - dimensional spacetime would be perceived by us, the 3D observer and if the way it behaves has any resemblance with what we comprehend as our physical reality. This will help us determine whether the framework we have introduced in this paper and the general idea of a “Dynamic” higher - dimensional spacetime are suitable for further study and generally worth considering as an alternative approach to higher dimensional physics.

In our framework, time is not a fixed dimension. We have modeled time by making it “Dynamical” in nature, in the sense that it is neither fixed nor the same for different dimensional phenomena. Time for one phenomenon or interaction can behave as space for another and time is always the +1 dimension to the spatial dimensions we are considering. We have associated time with two characteristic qualities which refer to propagation and change, both relative to other interactions or phenomena. Taking this into consideration together with the fact that we perceive 3 spatial and one time dimension we will therefore try to examine how 4 + 1 dimensional phenomena would be perceived by us, by summarizing all the key points made in previous Sections. We will refer to the possible ways that Energy disperses with the term interactions as we did in Section 5. However, one can consider any possible interaction with any possible field. What is important here is that we treat spacetime with the same framework.

In Section 5, we demonstrated that any 4 + 1 dimensional phenomenon or interaction would have a property which is corresponding to mass. In addition, since we have modeled our framework in such a way that the magnitude of the rate of transmition of all waves, no matter their dimensionality, be equal to the same number c, which is equal to the speed of light for the 3 - dimensional wave (Section 2), then a 4 + 1 dimensional interaction would have to always move to 3 - dimensional space at a speed less than the speed of light. Also, the more its 3D speed components are, the less its speed will be in the 4th dimension, meaning the lesser the rate in which it changes its internal state will be. This implies that 4 + 1 dimensional interactions would appear to the 3D observer as having mass and as obeying the rules of special relativity, making the use of Minkowski or other types of metrics essential for the 3D observer in order to properly describe the behavior of such an interaction. However, any 3 + 1 interaction would not exhibit mass and would always have to move with the speed of light. A disturbance that is produced by such an interaction would not be able to change its internal state, as the internal state would be perceived by the 3D observer, if it is not acted upon by any other interaction. The 3D observer would be able to perfectly model such interactions and how they propagate, nevertheless it would not be possible for the observer to perfectly model the way 3 + 1 interactions interfere with higher – dimensional ones. Considering all the above, this picture relates strongly to the results of the special theory of relativity.

We now turn our gaze on how 4 + 1 dimensional interactions would be modeled by the 3D observer. The problem that the 3D observer has with the 5^th dimension is that the observer can not directly measure it and does not comprehend how 4 + 1 dimensional interactions behave, since their time is the 5^th dimension and the observer’s time (4^th dimension) acts as another dimension of space for those interactions. In Section 2 and Section 3 we delved into that matter and expressed how the observer could make predictions about their behavior even though the information about the 5^th dimension is lost. We made an analogy with 3D waves and how we would model them if we had no information about the 4^th dimension. We concluded that for 4 + 1 dimensional interactions there would be some quantities that the 3D observer could measure like momentum, wavelength, energy and others and the observer would have to use those quantities in order to make correlations between different states of the interaction in different points in the 4 – dimensional plane. This is analogous to our understanding of quantum mechanics. In quantum mechanics, physical quantities are expressed by operators. Applying an operator is equivalent to making a measurement and it changes the value of the system because it requires an interaction. Before a measurement all we can know is the probability of an outcome and the expectation values of a quantity. We also use those operators and the possible values they can take together with the multiple states that correspond to each of these values and the probability of them occurring in order to make predictions about how our system will evolve through time or space (3+1 dimensions) and make possible correlation between observables and states. Our results are always probabilistic, but we can calculate how these probabilities change with space and time together with the possible effects interactions can have.

Taking the above into account we see that a 3D observer would perceive a “Dynamic” 5 - dimensional spacetime very similarly with what we perceive as our physical reality. The fact that it is compatible with both quantum mechanics and the special theory of relativity is a strong indication that our framework is indeed suitable for further study and has the potential of producing significant results.

We also think that our framework could be used in relating certain physical quantities with others, similarly with what happens in Wick Rotation. It is often the case in Partial Differential Equations (PDEs) that for some solution

u

(x,t) of the PDE, we can define a coarse – grained quantity as a functional (for example

\int_{V}^{} u d x

\int_{V}^{} u_{x} d x

) which maps the solution to the real numbers. Usually, these functionals represent quantities of physical interest and physicists use them in order to get useful information about the system without having to derive every single detail about how the system behaves. Since in our framework time is not a fixed dimension for every interaction or phenomenon, a simple field is much more versatile than its classical counterpart in how its gradient or divergence produces results and that could in principle produce many functionals from the same field, which could have physical significance in our 3+1 dimensional plane. Some of those quantities could be orthogonal to each other because every dimension is orthogonal to each other and integrating for example a 3+1 dimensional interaction solution term and a 4+1 dimensional interaction solution term could produce this orthogonality. This could lead to quantities being expressed as imaginary representations of other quantities in certain situations (for example a → scalar term

\times

\times

b), similar to what happens in Wick Rotation, or lead to Pythagorean like relations like the famous

E^{2} = {(m c^{2})}^{2} + ({p c)}^{2}

. Two such quantities may be mass and electric charge, but this is just a speculation which is indicated by the fact that 4+1 dimensional interaction solutions exhibit mass and the most prominent 3+1 dimensional phenomenon is light which has no mass and is an electromagnetic wave.

7. Conclusion and Recommendations for Future Research

In summary this paper has introduced the framework of a “Dynamic” higher - dimensional spacetime, where time is “dynamical” in nature, in the sense that it is neither fixed nor the same for different dimensional phenomena meaning that time for a lower dimensional phenomenon can behave as space for a higher – dimensional one. In order to describe such a framework, we first associated a time dimension with two characteristic functions: propagation relative to space dimensions and change orthogonal to space dimensions. This was done in pursuance of giving a basic intuition on how time for one phenomenon can behave as space for a higher dimensional one and why time is modelled to be the +1 dimension to the spatial dimensions we are studying. Following that, we described how higher - dimensional phenomena would appear to us, the 3D observer and tried to set some guidelines on how we should mathematically model higher - dimensional phenomena in order for us to make accurate predictions of their behaviour, underlining the need for imaginary numbers in the process. Then we expressed the general framework of a “Dynamic” higher - dimensional spacetime and turned our gaze to 5 – dimensional phenomena. Then we associated the frequency term of a 5 – dimensional wave with the quantity of mass by generalizing the frequency – speed – wavelength relation of 3D waves. Next, we argued the importance of studying a scalar Energy Field and gave a basic description on a possible way to describe a 5 – dimensional disturbance in such a filed in order to make accurate predictions on the 3+1 dimensional plane. By generalizing the wave equation and ignoring all lower than 5 - dimensional disturbances we derived the Klein – Gordon equation and compered our mass term findings with the gravity – induced quantum interference experiment in 1975 and found that both results are in accordance. Lastly, we described how a “Dynamic” 5 - dimensional spacetime would appear in a 3D observer and concluded that it is compatible with both quantum mechanics and the special theory of relativity. Considering all the above, we conclude that our framework exhibits a behaviour that has a remarkable relation with our physical reality and produces results similar with some of our greatest physical theories. Therefore, we believe that it is suitable for further study, should be considered as viable framework for higher - dimensional physics and has the potential of producing significant results. Of course, it is not a complete mathematical framework and much more work needs to be done in order to make it complete. Some fields that are possible candidates for further study in order to better understand and model our framework are:

-: Better examination of the results of quantum mechanics, quantum field theory and special relativity in order to investigate if they are all compatible with our framework or if there are contradictions. This will validate the use of our framework further.
-: Developing a full mathematical model of how a field is transformed when we take its derivatives, how the gradient, the divergence or the curl of that field behaves when we apply them on higher dimensions in the framework of a “Dynamic” higher - dimensional spacetime. What are the interaction terms with lower dimensional aspects of the field and how the one affects the other.
-: The connection between time and entropy and how that connection affects interactions in our 3+1 dimensional plane when higher dimensional phenomena are present. The effects that entropy increase of a 4+1 dimensional plane has on local entropy in a region of the 3+1 dimensional plane. Possible link on how complexity emerges.
-: Studying whether our model is compatible with the general theory of relativity. This can be done either by introducing curvature or by making the value of the magnitude of the rate of transmition for any – dimensional disturbance depend on the energy density of the region we are studying (Section 4).
-: Modeling the motion of a disturbance of any – dimensionality as the path of least resistance or the least difference of energy density as mentioned in Section 4 in order to examine if the results are in accordance with the principle of least action for quantum particles and the principle of least time for light.

Author Contributions

The concept of a “Dynamic” higher - dimensional spacetime, as described in this paper, its core idea and the framework in which behaves are attributed to the author alone. The same is true for the for the writing of this paper and all its results.

Notification

For any use, sharing, adaptation, distribution and reproduction in any media or format, appropriate credit must be given to the author. This applies to this paper, the concept of a “Dynamic” higher - dimensional spacetime, as described in this paper, its core idea and the framework in which behaves.

References

R. Colella, A. W. Overhauser, S. A. Werner, Observation of Gravitationally Induced Quantum Interference, Phys. Rev. Lett. 34, 1472, June 1975. [CrossRef]
Griffiths, D. J. Introduction to Quantum Mechanics 2^nd ed., Upper Saddle River, NJ: Pearson, 2005.
Arfken, G. B. and H. J. Weber. Mathematical Methods for Physicists, 4^th ed., New York: Academic Press, 1995.
J.J. Sakurai, J. Napolitano, Modern Quantum Mechanics, 2^nd ed., Boston: Addison-Wesley, 2010.
Dirac, P. A. M. Quantum Mechanics 4^th ed., London : Oxford University Press, 1958.
Feynman R. P. and A. R. Hibbs. Quantum Mechanics and Path Integrals, New York: McGraw-Hill, 1965.
Newton, R. G. Scattering Theory of Waves and Particles, 2^nd ed., New York: McGraw-Hill, 1982.
M.Peskin and D.Schroder, An Introduction to Quantum Field Theory, Perseus Books, 1995.
S.Coleman, Quantum Field Theory, World Scientific, 2019.
Gregory L. Naber, The Geometry of Minkowski Spacetime: An Introduction to the Mathematics of the Special Theory of Relativity. Springer-Verlag, 1992.
Wick, G. C.. “Properties of Bethe-Salpeter Wave Functions”. Physical Review. 96 (4): 1124–1134, (1954). [CrossRef]
Komissarov S.S., General Relativity MATH3443, 2009.
Morse P. M. and H. Feshbach, Methods of Theoretical Physics (2 vols.), New York: McGraw-Hill, 1982.
Jackson J. D., Classical Electrodynamics, 2^nd ed. New York: Wiley, 1964.
Wesson, Paul S., Space–Time–Matter, Modern Kaluza–Klein Theory, Singapore: World Scientific 1999.

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Introducing the Framework of a "Dynamic" Higher Dimensional Spacetime. How Time behaves in It. Similarities with Quantum Mechanical and Relativistic Behaviour.

Abstract

1. Introduction

2. Characteristics of a Time Dimension and the Core Idea of “Dynamic Time”

3. Mathematical Framework for a “Dynamic” Multidimensional Space-Time. The Need for Complex Numbers

4. The General Framework for a “Dynamic” Multidimensional Space-Time and How It Behaves

5. The Behaviour of a Scalar Energy Field in a “Dynamic” 5—Dimensional Spacetime and the Quantity of Mass

6. How a “Dynamic” 5—Dimensional Spacetime Is Perceived by a 3D Observer. Relations with Quantum Mechanics and Relativity

7. Conclusion and Recommendations for Future Research

Author Contributions

Notification

References

MDPI Initiatives

Important Links

Subscribe