Prerpints.org logo
Preprint
Article

FBGS Strain–Optic Behavior with Different Polymeric Coatings Subject to Transverse Strain

This version is not peer-reviewed.

Submitted:

01 March 2024

Posted:

04 March 2024

You are already at the latest version

A peer-reviewed article of this preprint also exists.

Abstract
This research work has been based on a previous study by the authors that characterized the behavior of a polyimide-coated FBG sensor in a structural monitoring system. Sensors applied to structural health monitoring are affected in the presence of a state of multidirectional strains simultaneously. The previous study observed the influence of transverse strain (ε_y) while keeping longitudinal strain constant (ε_x), where the direction x is the direction of the optical fiber. The present study developed an experimental methodology which has consisted of carrying out a campaign of biaxial tests on cruciform specimens with three embedded FBG sensors coated with polyimide, acrylate and ORMOCER®. Applying the Strain–Optic Theory as reference, a comparison of the results obtained with the different coatings has been studied. This experimental work has done it possible to study the influence of transverse strain (ε_y) in the longitudinal measurement of each of the FBG sensor and the influence of the coating material. Finally, the calibration procedure as well as the strain sensitivity factor K for each sensor has been defined.
Keywords: 
Subject: 
Chemistry and Materials Science  -   Materials Science and Technology

1. Introduction

Composite materials have established themselves as an alternative to metal materials in the construction of structures in multiple areas [1]. In the aerospace industry, composite materials are primarily used for constructing aerostructures, particularly in the case of aircraft. They exceed 50% of the structural weight of a modern aircraft [2,3,4,5]. In other industries, such as naval [9,10,11] and transport [12,13,14,15,16], the use of composite materials is more limited. This is due to factors such as the recycling of materials made from thermoset resins [17,18] and the absence of high-speed manufacturing processes. However, the use of composite materials is trending upwards. The use of composite materials in structures is generally linked to the design of lightweight and optimized structures, a key factor in the aerospace sector and important in other sectors. Applied design philosophies have evolved over the last few decades, moving from structures designed for safe living to structures designed for certain failure, to finally arrive at structures that can withstand damage, the latter philosophy being the one that is applied when you want to build a structurally optimized component. The philosophy of tolerance to harm is based on two key pillars:
-
Know and quantify the properties of the material, such as: maximum allowable defect size or speed and propagation of the defect, among others. Both fields have been exhaustively studied in recent years for the specific case of composite materials [19,20,21].
-
Have an inspection and maintenance policy that is capable of detecting the fault before it reaches a critical size [22,23].
Normally, maintenance policy was based on a schedule of inspections and preventive actions; although current trends in sectors such as aerospace, wind or railways tend to replace this with maintenance on condition which allows you to reduce costs significantly. One of the keys to maintenance on condition [24] it is the sensorization of the equipment to be maintained, which allows us to know their real situation at all times and to act specifically when necessary. The sensorization of structures is known as SHM (Structural Health Monitoring) [25,26]. Its objectives are to detect the levels of stress of the structure, the possible occurrence of failures, the reduction of its life to fatigue or the appearance of overloads, among others [27,28,29]. One of the most widely used monitoring technologies is fiber optic sensors in Bragg gratings (FBGS). They offer several interesting advantages over extensometry technologies: small dimensions, ability to be embedded, simplicity in cabling due to their multiplexability, stability in thermal and load monitoring during the structural life and insensitivity to electromagnetic interference, among others [30,31,32,33,34]. The use of FBGS in structures necessitates a comprehensive understanding of the sensor's behavior and its response to various variables, including temperature, humidity, dynamic loads, and the occurrence of loads and/or strains in multiple directions. This last aspect has been studied by multiple authors and was the subject of an experimental study by the same authors of this article [35,36,37,38,39]. Have an inspection and maintenance policy that is capable of detecting the fault before it reaches a critical size. Typically, the most commonly used coatings are: polyimide, acrylate and ORMOCER® [40,41,42,43]. The importance and influence of the coating on the response of an FBGS sensor lies in the very function it performs, which is to protect the core and the coating from exposure to moisture and abrasion on its surface, preventing the appearance of micro cracks and premature damage to the optical fiber, as well as guaranteeing the phenomenon of reflection according to the Snell Theory. According to Nath et al [44], polyimide coatings have the advantage of being resistant to elevated temperatures up to 300ºC and providing reliable results when embedded. In contrast, polyimide is sensitive to humidity. As for acrylate, it is the coating that best protects fiber optics and is immune to humidity, but they are usually critical at temperatures from 100ºC [44]. The first acrylate coatings consisted of one layer, but due to problems of attenuation induced by microcurvatures or shear retardation, they became two layers. Gloge [45] He elaborated on this study by stating that the losses produced by microcurvatures are minimized by using an inner (primary) and an outer (secondary) coating with an elastic modulus ratio ten times higher than the secondary versus the primary. In recent years, the ORMOCER® coating formed by the combination of ceramic and metal has been used. It has a high elastic modulus, is not affected by humidity, provides better radiation protection and is very stable at temperatures above 200ºC [46,47,48].
There are different studies on the influence of coating on embedded FBGS. For example, Pak et al [49] and Sirkis et al [50] observed that the thickness and shear modulus of the coating influences the shear–induced strain in the sensor. Roberts et al [51] concluded that the use of brittle materials as a coating leads to the formation of cracks at low load levels. Other research has studied how bonding between the sensor and the host material influences depending on the type of coating material and bonding agent to improve adhesion [44,52]. The most recent studies on coatings are focused on temperature measurement with FBGS. Mishra et al [53] conducted experiments with different coatings to study how temperature sensitivity varies from the coefficient of thermal expansion. The study comparing coatings is noteworthy for the results obtained at cryogenic temperatures. Sampath et al [54] performed a comparison of coatings on composite materials under cryogenic conditions for the measurement of temperature and strains, with and without coating, the results of which conclude that the coated sensors have a sensitivity of 48pm/ºC, ten times higher than that of an uncoated FBGS. The use of metallic coatings such as gold and silver has demonstrated a marked improvement in sensor sensitivity to high temperature gradients, with a delay response of 300ms compared to the bare sensor [55]. It is of interest to mention the study contributed by Weisbrich et al [56] on shrinkage tests. It analyzes the influence on the output signals of distributed FBGS (Rayleigh type) in concrete structures with the same coatings studied in the present work, whose results show that the ORMOCER® coating is the one with the least strain losses (< 2%), followed by the polyimide and acrylate coating (< 4 %).
The need to study the influence of transverse strain on the response of the FBGS is justified by some researchers in the scientific community such as R. M. Measures [57] or in the Review by Luyckx et al [58]. This work investigates the generation of multiaxial states of strain in a cruciform specimen made of carbon fiber reinforced composite material under different load cases. Three FBG sensors located in the central area of the specimen have been embedded with three types of coating material: polyimide, acrylate and ORMOCER®. In a previous study, we examined the impact of transverse strain on longitudinal strain measurement for an embedded polyimide-coated FBGS. In this work, a non–negligible measurement error was observed in the tests caused by transverse strain transmitted to the sensor, and K (strain sensitivity factor) was calculated by a proceeding of a uniaxial characterization [39]. In the present work, a campaign of similar biaxial tests has been done, keeping the longitudinal strain constant and varying the transverse strain, taking as a measurement reference a strain gauge rosette installed in the central area. The tests consisted of four cases of longitudinal strain (500 μ ε , 1000 μ ε , 1500 μ ε and 2000 μ ε ), simultaneously varying the transverse strain between 0 μ ε and 4000 μ ε in steps of 500 μ ε and keeping the longitudinal strain constant, leaving a time pause in each step to stabilize the sensor. We have applied the equations of Kim et al [59] correspondent of the Strain–Optic Theory, for an isotropic sensor a constant temperature. These strain values correspond to those common in composite structures for naval, aeronautics and space use. In addition to calculating for each sensor the influence of transverse strain on the sensor response by analyzing ∆ λ B (variation of the Bragg wavelength) it has been observed how the mechanical behavior of the coating material affects the results.

2. Materials and Methods

2.1. Coating Material of FBGS

In this work, three FBG sensors with a different coating have been installed: polyimide, acrylate and ORMOCER®, from the manufacturer FBGS for the sensors with polyimide and ORMOCER® coating, and the School of Aeronautical and Space Engineering of the Polytechnic University of Madrid for the acrylate coated sensor. These sensors are the most widely used in the monitoring of strains and temperature applied to structures. They are characterized by being isotropic and single mode FBGS (Table 1). The three sensors have been embedded in the cruciform specimen in the plane of symmetry and installed in the central zone of the specimen (Figure 1 and Table 2). A single exit of the wiring has been left through one of the arms of the specimen, which when placed in the jaws of the triaxial testing machine has ensured that the bending radius is greater than 30mm, to avoid significant losses in the induced light intensity. Table 3 compares the initial values of each sensor measured by our interrogator in vacuum before it is embedded in the specimen and after the curing process in a forced air circulation oven. A variation in wavelengths is observed due to residual stresses originating in a circulation oven curing process, decreasing ≈ 500pm in the polyimide and acrylate sensors, and from ≈ 250pm in ORMOCER®.

2.2. Experimental Setup

The cruciform specimens used in this work are made with CFRPs (Carbon Fiber Reinforced Plastics) by using a unidirectional tape ref. UD UTC–200 and an epoxy resin ref. Ampreg–26 with slow hardener Gurit, whose mechanical properties have been experimentally obtained in the Composite Materials Laboratory of the National Institute of Aerospace Technology (INTA), according to ASTM–D3039, ASTM–D3518, ASTM–D2344 and ASTM–D695 [60,61,62,63]. The design of the cruciform specimen has been based on previous research [64,65]; see Figure 2 with dimensions in mm. The manufacturing or lamination process used has been wet, using a lamination sequence [0º/90º]10s. The curing process consisted of applying a vacuum bag at a pressure of 930mbar at a temperature of 20ºC for 24 hours. After curing, an autoclave post–curing process was carried out at a temperature of 50ºC with a ramp of 3ºC/min, maintaining the temperature at 50ºC ± 5ºC for 16 hours, being its glass transition temperature T g = 73.9ºC. The FBGS sensors used (with polyimide, acrylate and ORMOCER® coating) they have been installed in the plane of symmetry of the specimens in the direction of the fiber of the composite laminate, in the central area of the specimens, in a non–aligned manner and at a distance between them, according to the Figure 1. Finally, a sensor output terminal has been left that coincides with one of the arms of the cruciform specimen, with connectors to be installed in the optical interrogator of make and model HBM SI405. Table 4 shows the physical properties of fiber optics and Figure 3 shows the parts that make up a FBGS.
The testing setup consists of a Microtest triaxial machine; model EM6/50/FR/SCM for biaxial tests, using four actuators in the horizontal plane (Figure 4). This machine is located in the Testing Laboratory of Continuous Media Mechanics of the University of Castilla – La Mancha. Additionally, a strain gauge rosette has been installed on one side and in the central zone of the specimens (Figure 4) to measure strains. The rosette is connected to the extensometry data acquisition system PCD-300B from KYOWA™ and is measured using a microscope from Vision ENGINEERING Ltd. and Quadra-Check® 200 from METRONICS®. The deviation from the orientation of the X and Y axes of the cruciform specimens is approximately 0° 8'.The Optical Interrogator used HBM SI405 it has four channels, three of which are used in this work. The output signals obtained from the interrogator during the test have been recorded to the computer by means of software Micron Optics ENLIGHT version 1.18.8.0 – 32 bits with a sample rate of 5Hz.

2.3. Strain–Optic Theory

According to reference [59] and applying the equations to an isotropic sensor, it can be determined that the variation of the average ( Δ s n a v g ) and differential ( Δ s n d i f f ) refractive coefficient of the study grating is as follows:
Δ s n a v g = − n 0 3 2 p 12 ε 1 + p 11 + p 12 ε 2 + ε 3 2
Δ s n d i f f = − n 0 3 p 11 − p 12 4   ε 2 − ε 3 2 + γ 23 2
where n 0 is the index of refraction initial, ε i   is strain field with index 1to3 (the index 1 correspond to the optical fiber direction and the index 2–3 are oriented plane perpendicular to the sensor direction), the term ( ε 2 − ε 3 2 + γ 23 2 ) is the maximum shear strain in the sensor in the plane perpendicular to the sensor axis, and p 11 and p 12 the Pockel constants of the sensor, for an isotropic sensor, tested at a constant temperature. In the previous equations, the variations in the refractive coefficients in the sensor have been considered without taking into account the residual strains, typical of the curing of the matrix, since they are always present during the tests. Considering a straight Bragg sensor and using the equations of Kim et al [59] the normalized variation of the mean and differential Bragg wavelength variation of the two components is expressed as:
Δ s λ B , a v g λ B 0 = ε 1 + Δ n a v g n 0 = 1 − n 0 2 2 p 12 ε 1 − n 0 2 4 ( p 11 + p 12 ) ( ε 2 + ε 3 )
Δ s λ B , d i f f λ B 0 − n 0 2 p 11 − p 12 4   ε 2 − ε 3 2 + γ 23 2
According to these equations, it can be observed that for a strain in the transverse direction to the fiber, keeping the strain constant in the longitudinal direction to the fiber, two effects happen. First, there is a displacement of the two components p → and   q → (displacement vectors perpendicular to the fiber direction) reducing the wavelengths of both. Second, you should see a splitting in the peaks due to the presence of transverse forces. The splitting of peaks should be minimal since there is no cut and the strains in the transverse plane of the fiber are similar. Additionally, the term   n 0 2 p 11 − p 12 4 < 1 − n 0 2 2 p 12 .
It is very important to note that the strains exposed in this section are those seen on the surface of the fiber, and not those observed in laminate in general. Strain gauges measure the strain in the walls of the specimen, but this strain is not the one that the fiber sees and suffers, and a transformation function is necessary that relates the strains in the sheet in which the fiber is located and the strains experienced by the fiber. In the case of Van Steenkiste et al [66] they take the cross-section of the fiber as if it were an inclusion and then apply the equations of Lekhnitskii [67].

3. Experimental Results

3.1. Testing Plan

From these tests, the behavior of the FBGS in a state of biaxial strain is obtained, analyzing the transverse influence on the output signals of the sensor, as well as the influence of the different coatings on the results. For this purpose, the cruciform specimens have been tested biaxial, with a longitudinal strain ( ε x ) constant for values of 500 μ ε , 1000 μ ε , 1500 μ ε and 2000 μ ε . For each longitudinal strain state, the transverse strain ( ε y ) has been varied in steps of 500 μ ε . The transverse strain has taken values from 0 μ ε to 4000 μ ε , keeping a 2 minutes break for each step. During the tests, an average temperature of 18.5ºC was recorded with constant humidity values. The loads have been applied at a speed of 0.5 m m   m i n − 1 (load and unload). The test plan has consisted on six biaxial tests for each longitudinal strain value (Figure 5).
To obtain K (strain sensitivity factor) of each of the FBGS, the standard procedure is through a uniaxial test in the direction of the FBGS. In this work, uniaxial tests have been performed on the same cruciform specimen, carrying out a loading and unloading up to 2000 μ ε in the arms where the optical fiber is installed, leaving the two arms perpendicular to them free. The results obtained are as shown in the following illustrations from the slope of the linear interpolation.
Using the equations in section 2.3 and defining the following values for different parameters ( p 11 = 0.113 ;   p 12 = 0.252 ;   n 0 = 1.449 ;   ν s = 0.16 ) and a Bragg wavelength of λ B 0 = 1535 nm , it can be determined that:
Δ λ B ≃ 1.2 ε 1
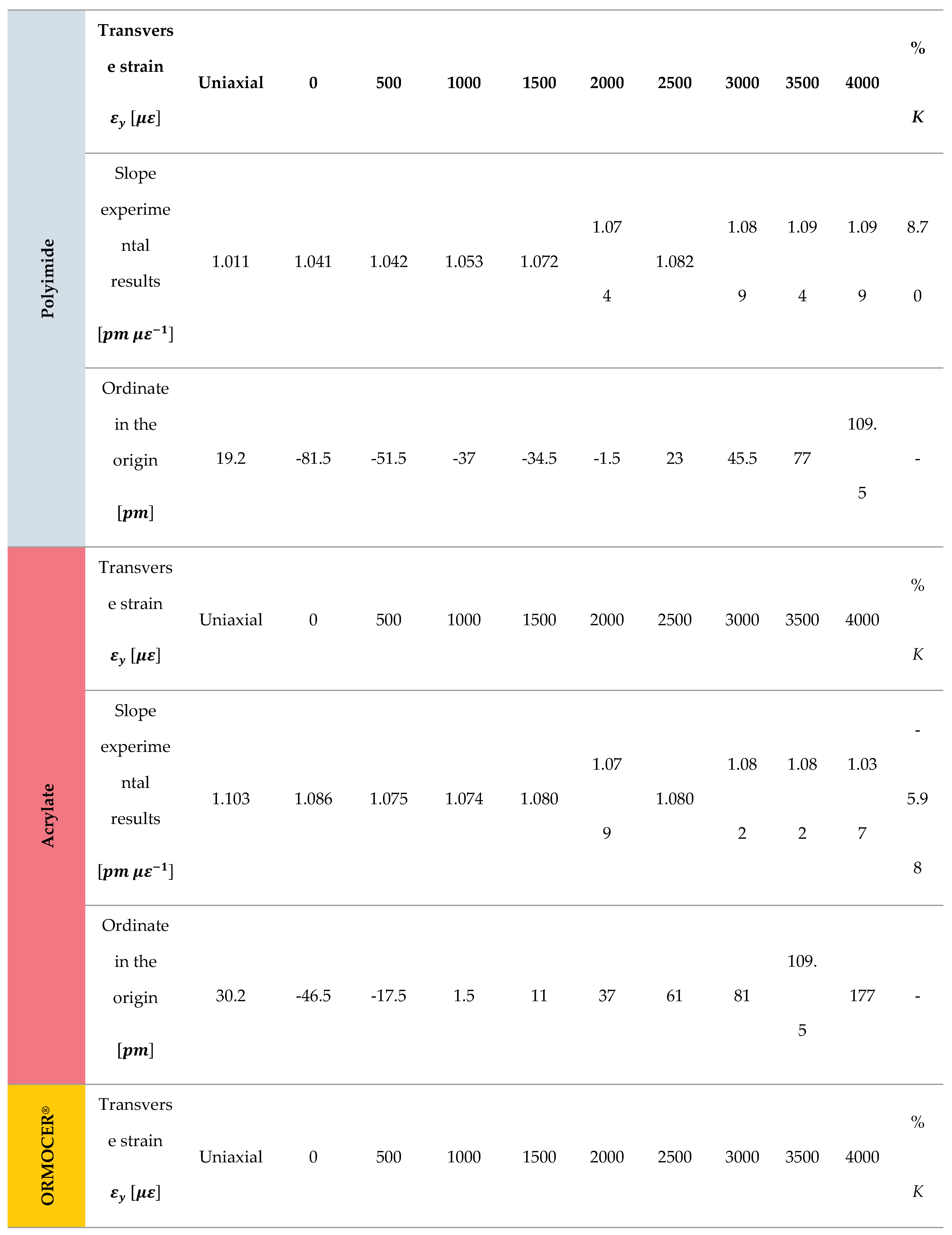
From Table 7, the K strain sensitivity factor values for each coating are obtained ( K P o l y i m i d e = 1.011 ± 0.020 p m μ ε − 1 ; K A c r y l a t e = 1.103 ± 0.020 p m μ ε − 1 and K O R M O C E R ® = 1.154 ± 0.020 p m μ ε − 1 ), being values lower than the value theoretical (1.2 p m μ ε − 1 ).
This data makes a lot of sense since ORMOCER® has greater rigidity than acrylate. Acrylate is higher than polyimide. The differences between the theoretical and experimental slopes are due to two reasons. First, the coating, not being completely rigid, causes a strain gradient between the optical fiber and the material around it. Secondly, the strain measured in the tested specimens was carried out by means of the strain gauge installed on the surface of the central area of these specimens. The strain of the specimen on its surface ( ε ∞ ) it is different from that experienced by the fiber on its outer surface   ( ε s ) . There would therefore be a strain gradient between the walls of the fiber coating and the specimen strain and a strain gradient between the outer walls of the coating and the surface of the fiber optic (cladding).
In the experimental tests conducted in this study, the longitudinal strain ε x has been constant while the transverse strain ε y has been varied by different values (see Figure 5). The strain field is transmitted to the optical fiber; ε 1 ≈ ε x ,   ε 2 ≈ ε y   and the component in the direction perpendicular ( ε 3 )   to ε 1   and ε 2 will be affected by Poisson effects. Under these conditions, the factor   Δ λ B / λ B for a ε 1 constant would be a decreasing function for an increase of   ε 2 , contrary to the experimental results obtained. It is possible that the transverse strain of the specimens is not transmitted to the FBG sensor, as in the case of strain gauges. Therefore, caution should be exercised when using fiber optics to measure strains in a biaxial strain state.

3.2. Biaxial Tests

The Figure 7 show the performance of the three sensors installed for each coating for the different values of transverse strain. Doing a qualitative analysis, it has observed for constant values of ε x (500 μ ε , 1000 μ ε , 1500 μ ε and 2000 μ ε ) sensor responses ( ∆ λ B ) they are not constant with an increasing output values. This phenomenon confirms the influence and dependence of the transverse strain ( ε y ) response. The curves would be horizontal if the FBG sensor had only longitudinal strain   ( ε x ) . Also observed with respect to our first study [39], the dependence of the type of coating material on the response of the sensor, with differences in wavelength variation values observed ( ∆ λ B ), as well as in the response in the download phase. In addition, as in our first study [39], when longitudinal strain   ( ε x ) increases from 500 μ ε to 2000 μ ε , the wavelength variation ( ∆ λ B )   increases proportionately. In all graphs, the strain states are observed a delay between the loads and unload curves. It is possible that this phenomenon is related with the mechanical properties of the coating material (Table 1), called hysteresis. The Figure 7 shows the wavelength increment obtained respect to the initial point of the curves for zero transverse strain.
The Table 5 exposes the average values of dependence on the sensor's output signals ( ∆ λ B ) of the accumulated transverse strains for load and unload longitudinal strain states. It is noted that for the tests with longitudinal stain values of 500 μ ε , the influence is high with values around of 46% for the polyimide coating and 30% for the acrylate and ORMOCER® coatings. It is noted a significant difference between values of 500 μ ε in the longitudinal direction and 4000 μ ε in the transverse direction (extreme case). The influence is attenuated for the tests with values of 1000 μ ε in the longitudinal direction, taking values around of 20%. The results suggest that high transverse – longitudinal strain states have a significant impact on the behavior of the FBGS and therefore in its measurements.
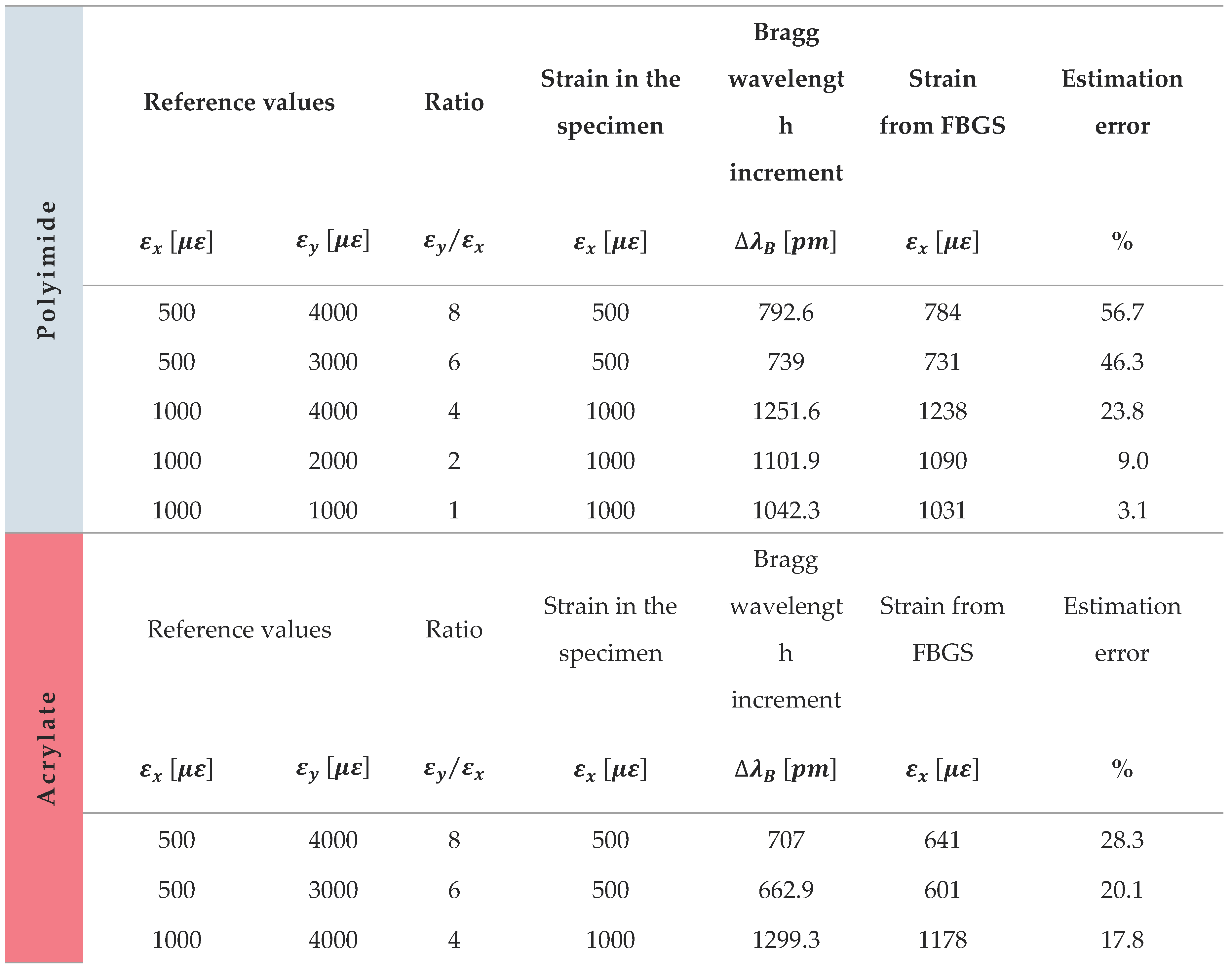
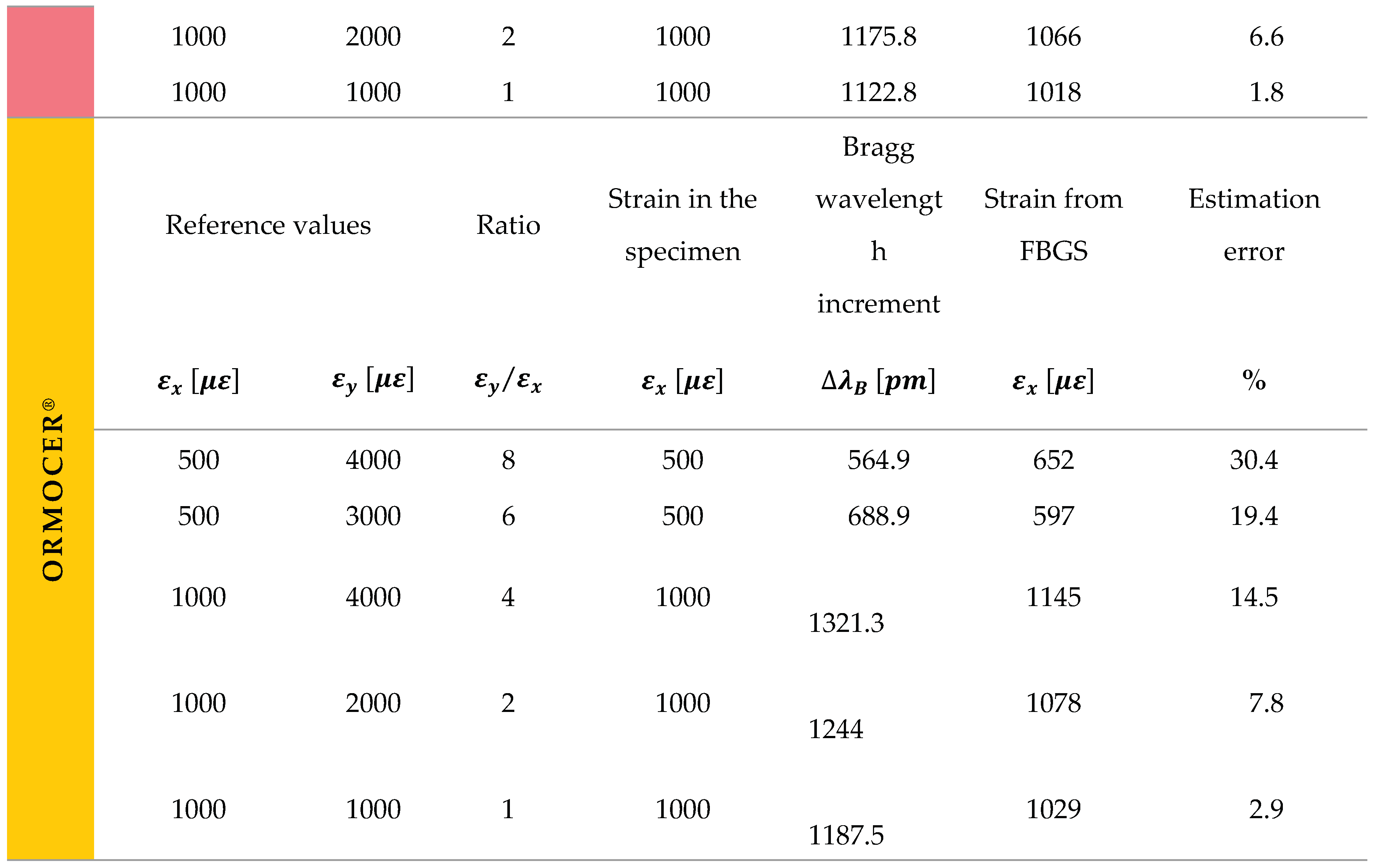
The influence of transverse strain on the behavior of FBG sensors can be quantified. Table 6 shows the longitudinal strain obtained in the FBGS for each strain state and the increase in Bragg wavelength measured by the interrogator, applying the strain sensitivity factor calibrated. It is compared with the strain obtained. For a transverse to longitudinal strain ratio of 8, the error estimated longitudinal strain is around 56% for the polyimide coating and 30% for acrylate and ORMOCER®. The influence of transverse strain on the behavior of FBG sensors can be quantified.
In the following Figure 8, the increase in the Bragg wavelength (this time taking the initial Bragg wavelength as a reference) is represented in the face of the longitudinal strain for each of the tests done and for each type of coating.
From the graph above, we get a linear fit for each value of transverse strain ( ε y ) up to ε y   = 4000 μ ε . Furthermore, the ordinate at the origin provided by the linear fit differs for each transverse strain and demonstrates the important impact of this general strain state on the sensor response. All these values and for each type of coating are listed in Table 7. A negative evolution in % K (strain sensitivity) has been observed to acrylate coating with respect to the other polymers. This value may is justified by its mechanical behavior (see Table 1).
Table 7. K values (strain sensitivity factor) for each transverse strain value fixed and evolution percentage.
Table 7. K values (strain sensitivity factor) for each transverse strain value fixed and evolution percentage.
Preprints 100318 i004
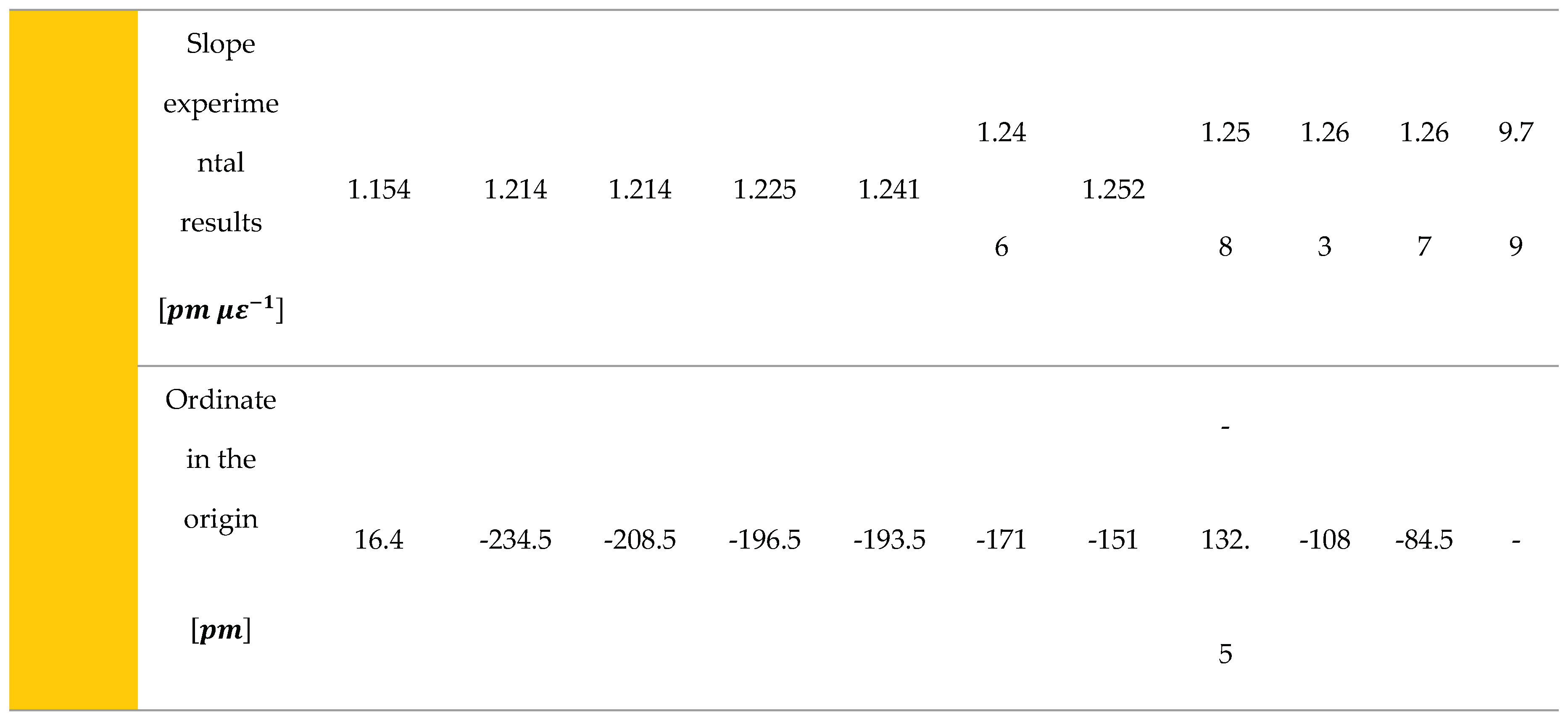
Preprints 100318 i005

4. Conclusions

The aim of this study was to evaluate the effect of transverse strains on the response of a FBGS type sensor, embedded in a cruciform specimen of composite material. The sensors analyzed have different coatings (polyimide, acrylate and ORMOCER®) commonly used in structural monitoring. The characterization of this type of sensor is usually carried out with standard uniaxial stress tests. This type of test allows the relationship between the longitudinal strain in the sensor to be obtained ε x and the physical response of it   ∆ λ B , which is defined through K   of the sensor (strain sensitivity) by applying a linear regression to the experimentally obtained points. This value depends on the sensor coating material and is considered constant for the entire strain field.
In uniaxial tests, the sensor will be subjected to transverse strain ε y which will depend on the longitudinal strain ε x and the Poisson coefficient   μ , and that it will be equal to   ε y = − ε x μ . This transverse strain will have the following characteristics:
-
It will present a fixed value for each longitudinal strain value   ε y = − ε x μ .
-
It will present negative values for each longitudinal strain value   μ > 0 .
-
It will have low proportions   ε y ε x .
The above characteristics do not correspond to the real situation that can be found in a real structure in which it is common, due to complex load states, to have different transverse strain values for the same longitudinal strain value or situations in which the transverse strain may be higher than the longitudinal strain. In laminate composite structures with thin thicknesses, we can assume plane stress hypothesis when are subjected to loads contains in the plane. For this reason, a scientific methodology presented in this article has been carried out to develop different plane stress cases by means of biaxial tests. The results of which have reached the following conclusions:
-
The response of the sensor ∆ λ B to longitudinal ε x strain is significantly influenced by the transverse ε y strain and by the coating material. The influence of transverse strain affects three fundamental parameters of the sensor: the output or response of the sensor ∆ λ B and two derived values such as the sensor's K (strain sensitivity) and the interpreted μ ε value. The influence of transverse strain on the response of the sensor ∆ λ B can reach values of up to 46% increase in the signal with respect to the defined reference state (the one with a ratio   ε y ε x = 0 ). This extreme case is observed in a polyimide coated sensor subjected to a ratio   ε y ε x = 8 . For lower ratios, the influence decreases. It is also observed that the influence on the sensor's output signal is lower in acrylate and ORMOCER® coatings that exhibit very similar behaviors, around 30%.
-
Regarding the magnitudes derived from sensor K (strain sensitivity) and μ ε interpreted, the influence can reach a 10% increase in the most extreme case ( ε y = 4000   μ ε ) for polyimide and ORMOCER® coatings. On the other hand, for the acrylate coating, a decrease of 6% in the sensor's K value (strain sensitivity) is observed. This phenomenon may be due to the mechanical nature of the coating material (Table 1).
-
A significant hysteresis effect has been observed in the loading and unloading cycles in the acrylate coating, being higher than 150pm for one of the cases, which is logical due to the less rigid nature (Table 1) of this polymer.
-
Based on the results obtained, the standardized sensor characterization procedure should be reconsidered, for those sensors working for multiaxial stress states with high ε y ε x ratios where the sensor's K (strain sensitivity) could lead to an erroneous interpretation of the results in terms of interpreted μ ε .
The experimental results have been compared with the Strain–Optic Theory, observing that the increase in the Bragg wavelength recorded follows a trend contrary to the equations of this theory. It is maintained that among the possible causes may be that the strain field is not completely transferred to the FBGS in traction, but is in out of plane compression. In order to analyze and study this phenomenon, and therefore the response of the sensor, it would be of interest to carry out different studies in which states of deformation are applied to compression or equivalent to confirm or discard this hypothesis experimentally.

Acknowledgements

This research is born of the doctoral studies done by Ph. D. student Manuel González–Gallego. The authors thank the collaboration of the University of Castilla – La Mancha and National Institute of Aerospace Technology "Esteban Terradas", in the line of research of structural health monitoring in composite structures with technology type FBGS (Collaboration Agreement published in the BOE, 29th October 2021, No. 259, Sec. III, 131588-131596, Spain). This article has been funded by the Ministerio de Ciencia e Innovación of Spain under the grant PID2021-122491OB-I00, the Junta de Comunidades de Castilla – La Mancha under the grant SBPLY/19/180501/000170, the University of Castilla – La Mancha and National Institute of Aerospace Technology "Esteban Terradas”.

References

  1. Frövel, M. (2006). Sensores de fibra óptica tipo redes de Bragg embebidos en material compuesto para medir deformaciones y temperaturas criogénicas. (Doctoral Thesis). Universidad Politécnica de Madrid. Madrid (España).
  2. Bertrán, G. (2013): Y el A350 XWB voló…. AVION REVUE Internacional, 373, 22-25.
  3. González-Gallego, M. (2014). Comportamiento multiaxial de laminados de material compuesto reforzado con fibra de carbono a partir de ensayos uniaxiales. (Master Thesis). Universidad de Castilla-La Mancha. Ciudad Real (España).
  4. Infographic-A350-Family. Available online: https://www.airbus.com/sites/g/files/jlcbta136/files/2021-10/Infographic-A350-Family (accessed on 07 November 2023).
  5. AERO—Boeing787fromtheGroundUp. Available online: http://www.boeing.com/commercial/aeromagazine/articles/qtr_4_06/article_04_2.html (accessed on 07 November 2023).
  6. Teng, H. et al (2023). Carbon Fiber Composites for Large-Scale Wind Turbine Blades: Applicability Study and Comprehensive Evaluation in China. Marine Science and Engineering, 11, 624, pp. 1-22. [CrossRef]
  7. Leon Mishnaevsky Jr. et al (2023). Materials for Wind Turbine Blades: An Overview. Materials, 10, 1285, pp. 1-24. [CrossRef]
  8. Yentl Swolfs (2017). Perspective for Fibre-Hybrid Composites in Wind Energy Applications. Materials, 10, 1281, pp. 1-17. [CrossRef]
  9. Fiberships-Final_Brochurehttp. Available online: https://www.fibreship.eu/wp-content/uploads/2020/06/Fibreship-Final-BROCHURE.pdf (accessed on 07 November 2023).
  10. M. Saravanan et al (2021). A review on navy ship parts by advanced composite material. Materialstoday: Proceedings, Volume 45, Part 7, pp. 6072-6077. [CrossRef]
  11. A. P. Mouritz et al (2001). Review of advanced composite structures for naval ships and submarines. Composite Structures, Volume 53, Issue 1, pp. 21-42. [CrossRef]
  12. George Edward Street et al (2021). Impact Resistance of Fibre Reinforced Composite Railway Freight Tank Wagons. Journal of Composites Science, 5, 152, pp. 1-22. [CrossRef]
  13. Sakdirat Kaewunruen et al (2017): Composites for Timber-Replacement Bearers in Railway Switches and Crossings. Infrastructures, 2, 13, pp. 1-16.
  14. M. Robinson et al (2017). Application of Composites in rail vehicles. 21st International Conference on Composite Materials, pp. 1-13.
  15. Adil Wazeer et al (2022). Composites for electric vehicles and automotive sector: A review. Green Energy and Intelligent Transportation, 2, 100043, pp. 1-23. [CrossRef]
  16. 16. Gonzalo Marmol et al (2021). Automotive and construction applications of fiber reinforced composites. Fiber Reinforced Composites, 2021, pp. 785-819.
  17. Andrey E. Krauclis et al (2021). Composite Material Recycling Technology-State-of-the-Art and Sustainable Development for the 2020s. Journal of Composites Science, 5, 28, pp. 1-33. [CrossRef]
  18. Beatrice Colombo et al (2021). Recycling of Waste Fiber-Reinforced Plastic Composites: A Patent-Based Analysis. Recycling, 6, 72, pp. 1-18. [CrossRef]
  19. Aniello Smarrazzo et al (2022). Failure Propagation Controlling for Frangible Composite Canister Design. Applied Sciences, 12, 12220, pp. 1-15. [CrossRef]
  20. Aniello Riccio et al (2023). Delamination Effect on the Buckling Behaviour of Carbon-Epoxi Composite Typical Aeronautical Panels. Applied Sciences, 13, 4358, pp. 1-18. [CrossRef]
  21. S. Z. H. Shah et al (2019). Impact resistance and damage tolerance of fiber reinforced composites: A review. Composite Structures, 217, pp. 100-121. [CrossRef]
  22. Matthieu Nicol et al (2023). Automated crack detection in laminated composites by optical flow measurements. Composites Part B: Engineering, Volume 255, pp. [CrossRef]
  23. Josué Pacheco-Chérrez et al (2021). Experimental Detection and Measurement of Crack-Type Damage Features in Composite Thin-Wall Beams Using Modal Analysis. Sensors, 21, 8102, pp. 1-23. [CrossRef]
  24. Wim J. C. Verhagen. et al (2023). Condition-Based Maintenance in Aviation: Chellenges and Opportunities. Aerospace, 10, 762, pp. 1-23.
  25. Güemes, A. et al (2020). Structural Health Monitoring for Advanced Composite Structures: A Review. Journal of Composites Science, 4, 13, pp. 1-15. [CrossRef]
  26. Senthilkumar et al (2020). Nondestructive health monitoring techniques for composite materials: A review. Polymers and Polymer Composites, Vol. 29 (5), pp. 528-540.
  27. Félix Terroba et al (2018). Structural health and usage monitoring of an unmanned turbojet target drone. Structural Health Monitoring, pp. 1-16. [CrossRef]
  28. Fernández-López et al (2017). Sensor integration and data explotation of Structural Health Monitoring Network integrated on a Unmananned Aerial Vehicle (UAV), vol 2, nº 2, pp. 94-99. [CrossRef]
  29. Yingtao Liu et al (2010). Condition based structural health monitoring and prognosis of composite structures under uniaxial and biaxial loading. Journal of Nondestructive Evaluation, 3, 29, pp. 181-188. [CrossRef]
  30. Güemes, A. (2014). Fiber Optics Strain Sensors. NATO-STO Lecture Series, pp. 1-26, STO-EN-AVT-220-03.
  31. Stephen J. Mihailov (2012). Fiber Bragg Grating Sensors for Harsh Environments. Sensors, 12, pp. 1898-1918. [CrossRef]
  32. Ji-Ying Huang et al (2017). FBGs written in specialty fiber for high pressure/high temperature measurement. Optics Express, Vol. 25, nº 15, pp. 17936-17947. [CrossRef]
  33. Bruno da Silva Falcão et al (2023). Strain measurement with multiplexed FBG sensor arrays: An experimental investigation. Heliyon, 9 e18652, pp. 1-15. [CrossRef]
  34. Adriana Morana et al (2022). Radiation Effects on Fiber Bragg Gratings: Vulnerability and Hardening Studies. Sensors, 22, 8175, pp. 1-33. [CrossRef]
  35. Bal, H. K. et al (2010). Fibre Bragg grating transverse strain sensing using reflections at twice the Bragg wavelength. Measurement Science and Technology Vol. 21, 094004. [CrossRef]
  36. Lai, M. et al (2013). On the Effects of the Lateral Strains on the Fiber Bragg Grating Response. Sensors,13, 2631-2644. [CrossRef]
  37. Gouws, A. et al (2020). Transverse strain measurements in polymer-embedded, polarization-maintaining Fiber Bragg Gratings. Engineering Research Express Vol. 2, 045016. [CrossRef]
  38. Wachtarczyk, K. et al (2022). In-Plane Strain Measurement in Composite Structures with Fiber Bragg Grating Written in Side-Hole Elliptical Core Optical Fiber. Materials Vol. 15(1), 77. [CrossRef]
  39. J. L. Martínez Vicente et al (2023). Study of the transverse strain effect on the Fiber Bragg Grating Sensor (FBGS) response with polyimide coating under experimental biaxial tests. Composite Structures, 326 (2023) 117621, pp. 1-12. [CrossRef]
  40. FiSens. Available online: https://fisens.com/sensor-configurator#start (accessed on 10 November 2023).
  41. Smart fibres. Available online: https://www.smartfibres.com/files/pdf/SmartFBG.pdf (accessed on 10 November 2023).
  42. FBGS. Available online: https://fbgs.com/technology/ormocer-coating/ (accessed on 10 November 2023).
  43. Janani, R. et al (2023). From acrylates to silicones: A review of common optical fibre coatings used for normal to harsh environments. Progress in Organic Coatings, 180, 107557. [CrossRef]
  44. Nath, D. K. et al (1991). Polyimide Coated Embedded Optical Fiber Sensors. Structures Sensing and Control, SPIE, vol. 1489, pp. 17-32.
  45. Gloge, D. (1975). Optical-Fiber Packaging and Its Influence on Fiber Straightness and Loss. The Bell System Technical Journal, vol. 54, Issue 2, pp. 245-262, USA. [CrossRef]
  46. Wolter, H. et al (1992). Multifunctional (meth) acrylate alkoxysilanes - A new type of reactive compounds. Mater. Res. Soc. Symp. Proc., vol. 271, pp. 719-724. [CrossRef]
  47. Rose, K. et al (1992). Multifunctional acrylate alkoxysilanes for polymeric materials. Mater. Res. Soc. Symp. Proc., vol. 271, pp. 731-736. [CrossRef]
  48. Schuster, K. et al (2010). Innovative fiber coating systems based on organic modified ceramics. Proc. SPIE, vol. 7598, pp. 75980H-1–75980H-8.
  49. Pak, Y. E. (1992). Longitudinal Shear Transfer in Fiber Optic Sensors. Smart Materials and Structures, vol. 1, pp. 57-62. [CrossRef]
  50. Sirkis, J. S. et al (1993). Longitudinal The Role of Local Interaction Mechanics in Fiber Optic Smart Structures. J. Intell. Mat. Systems & Struct., vol. 4, pp. 260-271.
  51. Roberts, S. S. et al (1991). Mechanical Properties of Composites Materials Containing Embedded Fiber Optic Sensors. Fiber Optic Smart Structures and Skins IV, SPIE, vol. 1588, pp. 326-341.
  52. Paul, C. A. et al (1993). Static Test Study of Composites with Embedded Optical Fibers using Fractional Factorial Methods. Soc. Exper. Mechanism (SEM) Conf., Michigan, USA.
  53. Mishra, V. et al (2016). Improvement in temperature sensitivity of FBG by coating of different materials. Optik 127, pp. 825-828. [CrossRef]
  54. Sampath, U. et al (2018). Polymer-coated FBG sensor for simultaneous temperature and strain monitoring in composite materials under cryogenic conditions. Applied Optics, vol. 57, No. 3, pp. 492-497. [CrossRef]
  55. Yanchao Liu et al (2019). Temperature characteristics of FBG sensors with different coatings for High Temperature Superconductor Application. IEEE 3rd International Electrical and Energy Conference (CIEEC), pp. 1546-1550.
  56. Weisbrich, M. et al (2020). Comparison of different fiber coatings for distributed strain measurement in cementitious matrices. Journal of Sensors and Sensor Systems, 9, pp. 189-197. [CrossRef]
  57. Measures, R. M. (2001). Structural Monitoring with Fiber Optic Technology. Academic Press, USA. [CrossRef]
  58. Luyckx, G. et al (2011). Strain Measurements of Composite Laminates with Embedded Fibre Bragg Gratings: Criticism and Opportunities for Research. Sensors, 11, pp. 384-408. [CrossRef]
  59. Kim, K. (1993). A Model of Embedded Fiber Optic Fabry-Perot Temperature and Strain Sensors. (Doctoral Thesis). Stanford University. Stanford, California (Estados Unidos). [CrossRef]
  60. ASTM D3039/D3039M-08. Standard Test Method for Tensile Properties of Polymer Matrix Composite Materials. ASTM International.
  61. ASTM D3518/D3518M-18. Standard Test Method for In-Plane Shear Response of Polymer Matrix Composite Materials by Tensile Test of a ±45° Laminate. ASTM International.
  62. ASTM D2344/D2344M-22. Standard Test Method for Short-Beam Strength of Polymer Matrix Composite Materials and Their Laminates. ASTM International.
  63. ASTM D695-15. Standard Test Method for Compressive Properties of Rigid Plastics. ASTM International.
  64. Serna, M. C. et al (2011). Failure envelope under biaxial tensile loading for chopped glass-reinforced polyester composites. Composites Science and Technology, Elsevier.
  65. Serna, M.C. et al (2013). Failure strain and stress fields of a chopped glass-reinforced polyester under biaxial loading. Composite Structures, 103, 27-33.
  66. Van Steenkiste, R. J. et al (1997). Strain and Temperature Measurement with Fiber Optic Sensors. Technomic Publishing Company.
  67. Lekhnitskii, S. (1977). Theory of Elasticity of an Anisotropic Body. Moscow: MIR Publishers.
Preprints 100318 g001
Figure 1. FBG sensors installed on the specimen central zone.
Figure 1. FBG sensors installed on the specimen central zone.
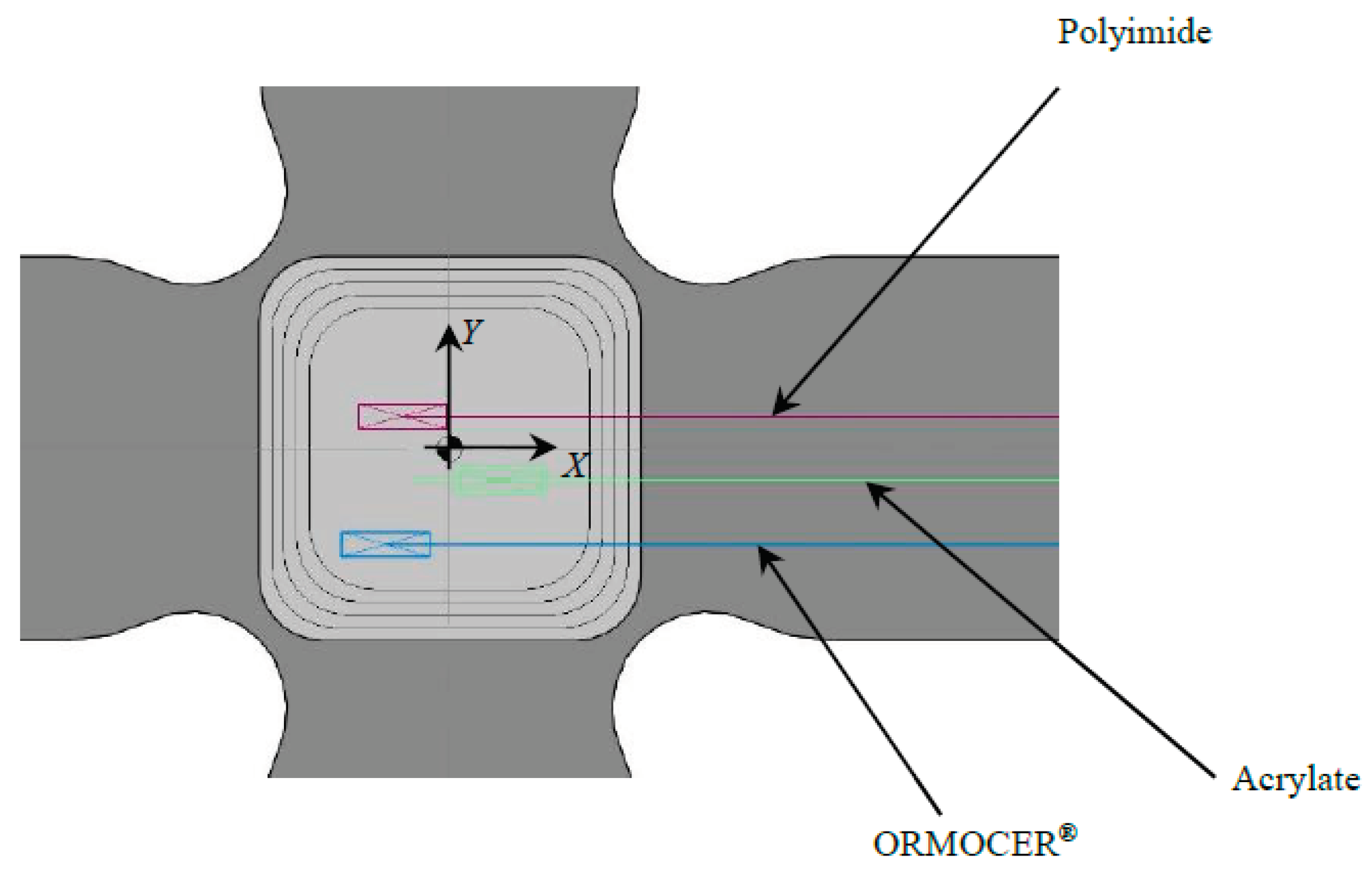
Preprints 100318 g001
Preprints 100318 g002
Figure 2. Specimen dimensions and detail views.
Figure 2. Specimen dimensions and detail views.
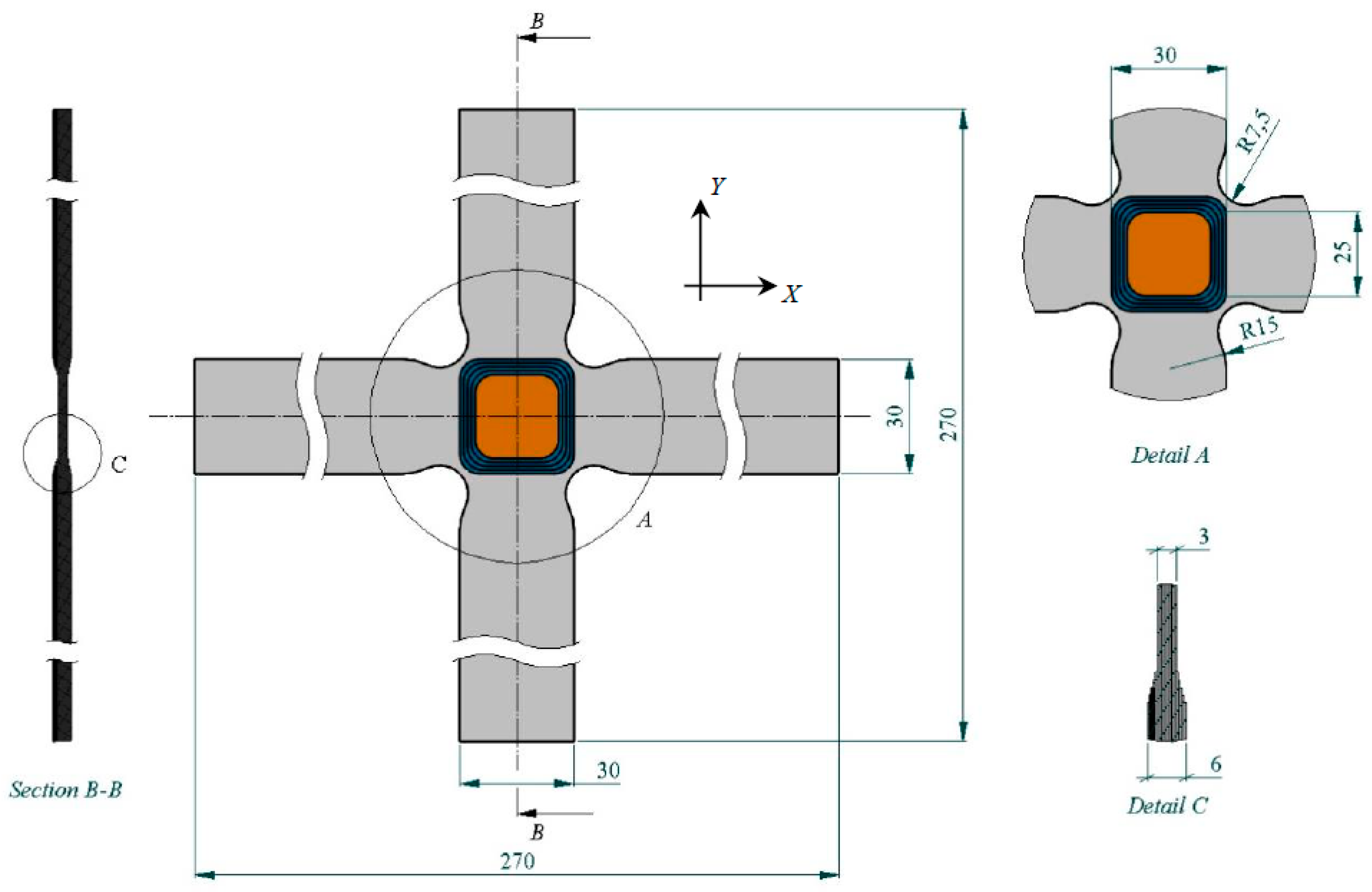
Preprints 100318 g002
Preprints 100318 g003
Figure 3. Parts of the Fiber Bragg Gratings Sensors (FBGS).
Figure 3. Parts of the Fiber Bragg Gratings Sensors (FBGS).
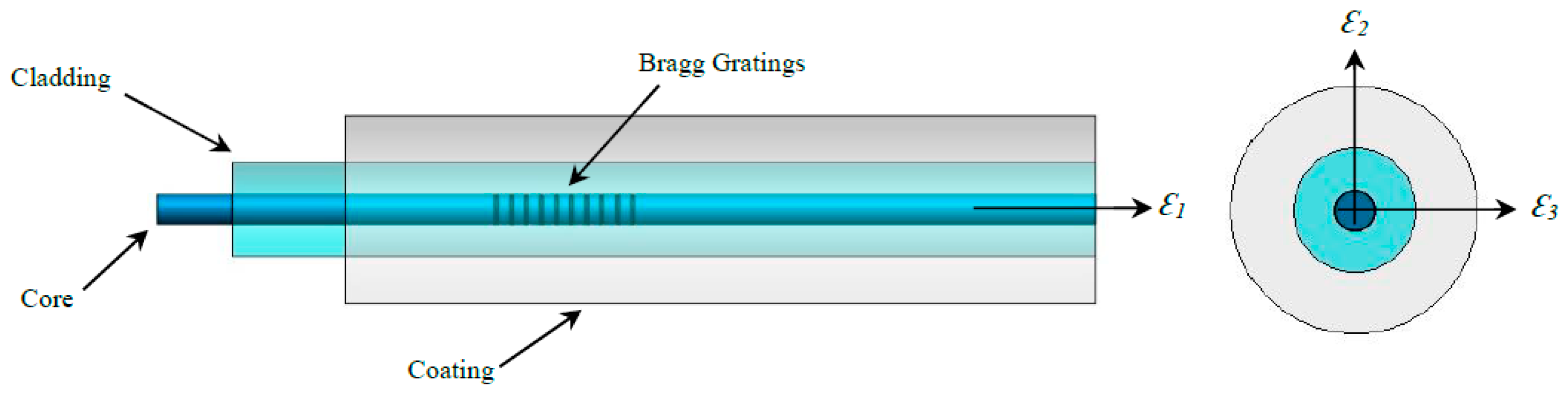
Preprints 100318 g003
Preprints 100318 g004
Figure 4. Biaxial test in the horizontal plane of triaxial machine and cruciform specimen with a strain gauge rosette and FBGS.
Figure 4. Biaxial test in the horizontal plane of triaxial machine and cruciform specimen with a strain gauge rosette and FBGS.
Preprints 100318 g004
Preprints 100318 g005
Figure 5. Biaxial design strain values.
Figure 5. Biaxial design strain values.
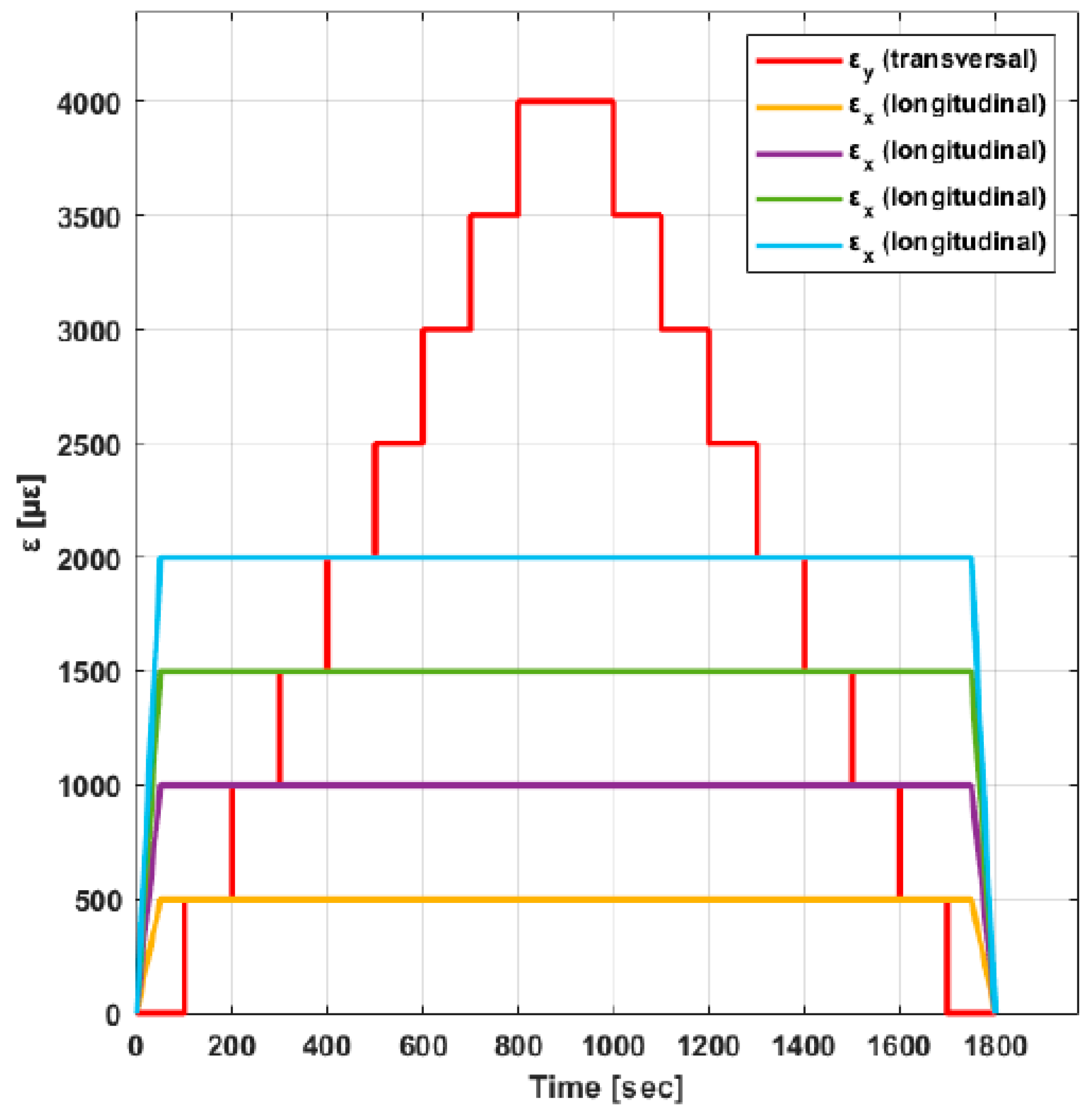
Preprints 100318 g005
Preprints 100318 g006
Figure 6. Bragg wavelength increment versus longitudinal strain for three coatings.
Figure 6. Bragg wavelength increment versus longitudinal strain for three coatings.
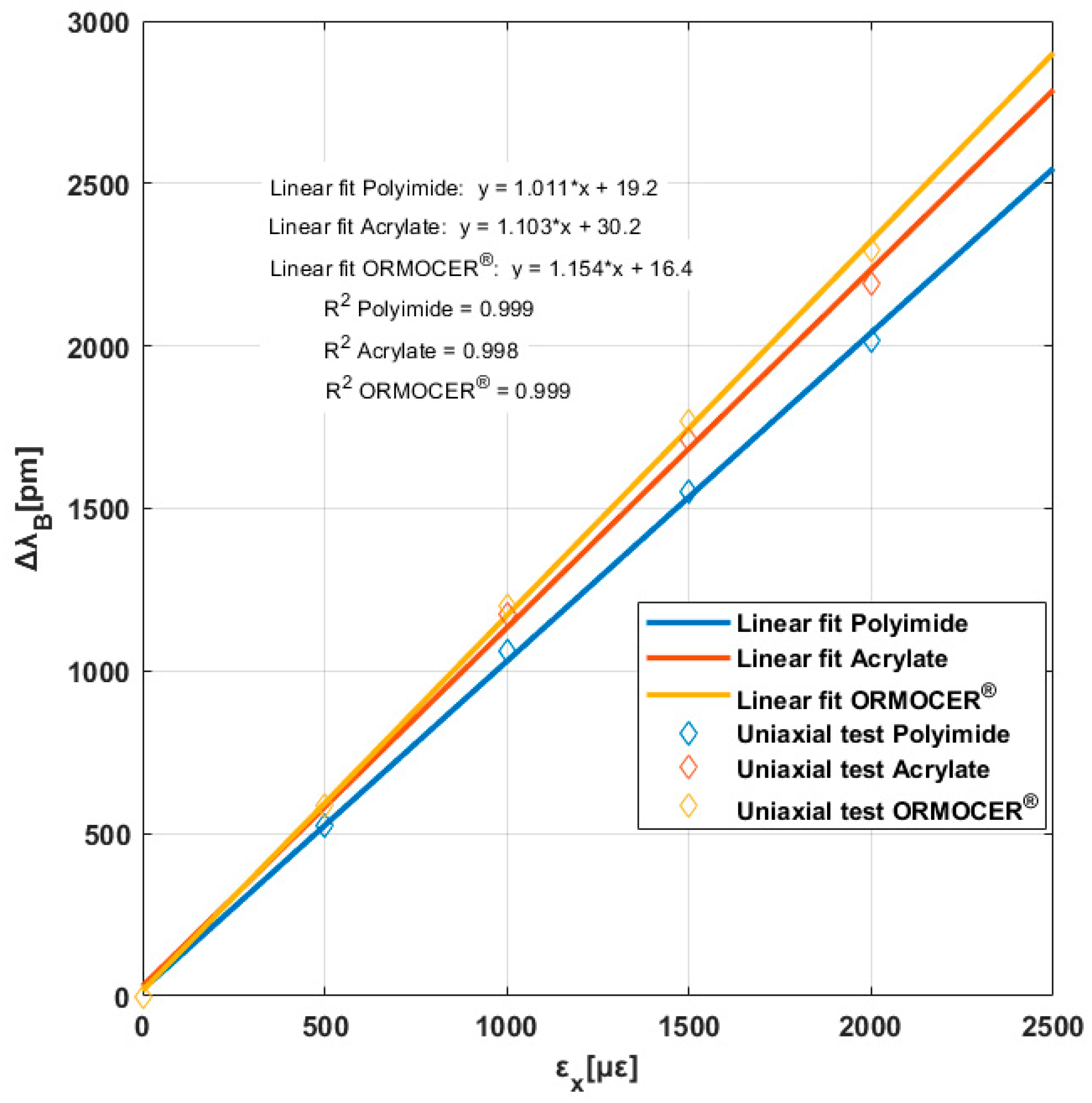
Preprints 100318 g006
Preprints 100318 g007
Figure 7. Evolution of ∆ λ B against ε y for each longitudinal strain state in polyimide, acrylate and ORMOCER® coatings.
Figure 7. Evolution of ∆ λ B against ε y for each longitudinal strain state in polyimide, acrylate and ORMOCER® coatings.
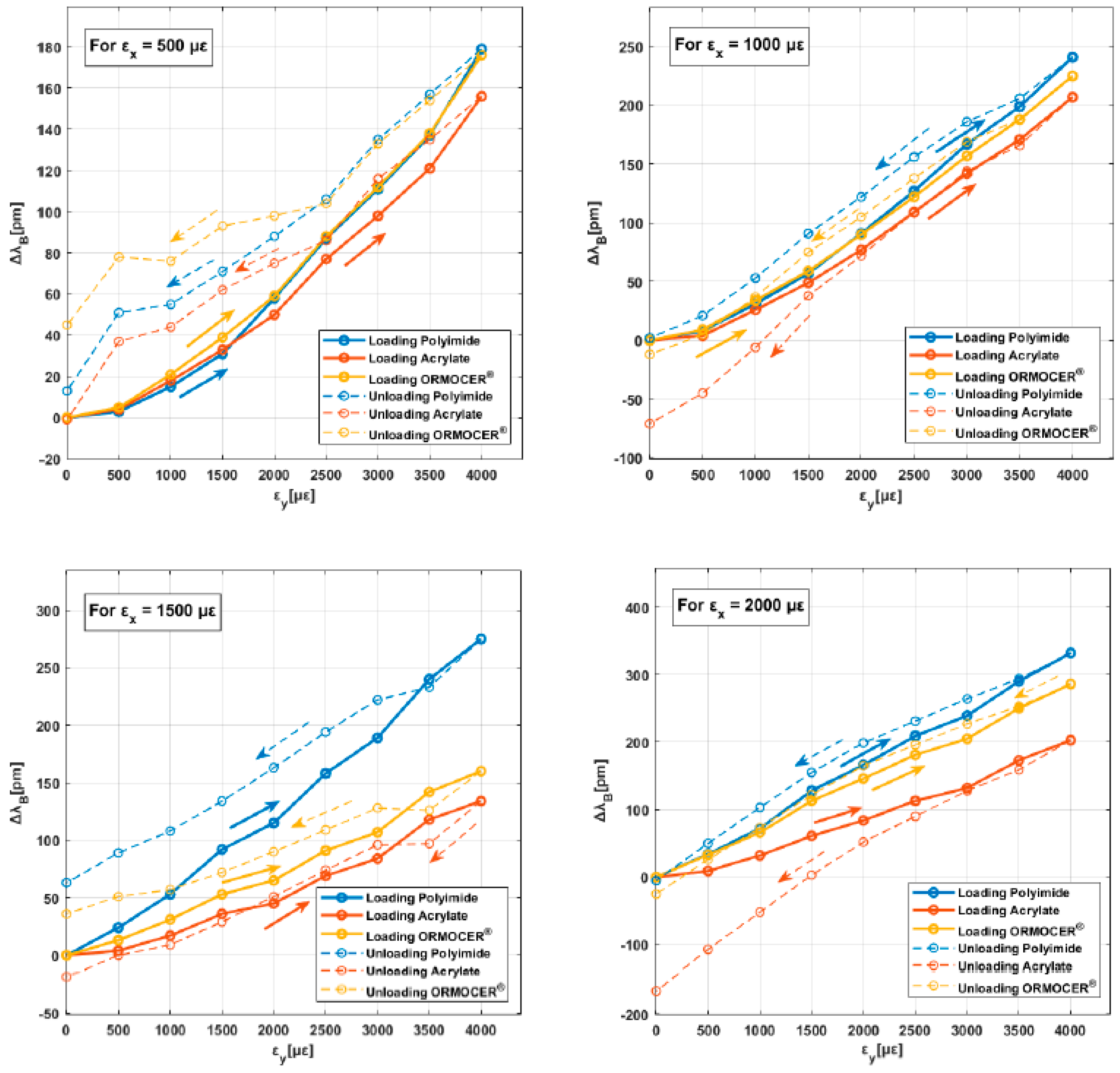
Preprints 100318 g007
Preprints 100318 g008
Figure 8. Average values and linear approximation lines with their slopes for the three coatings obtained biaxial tests.
Figure 8. Average values and linear approximation lines with their slopes for the three coatings obtained biaxial tests.
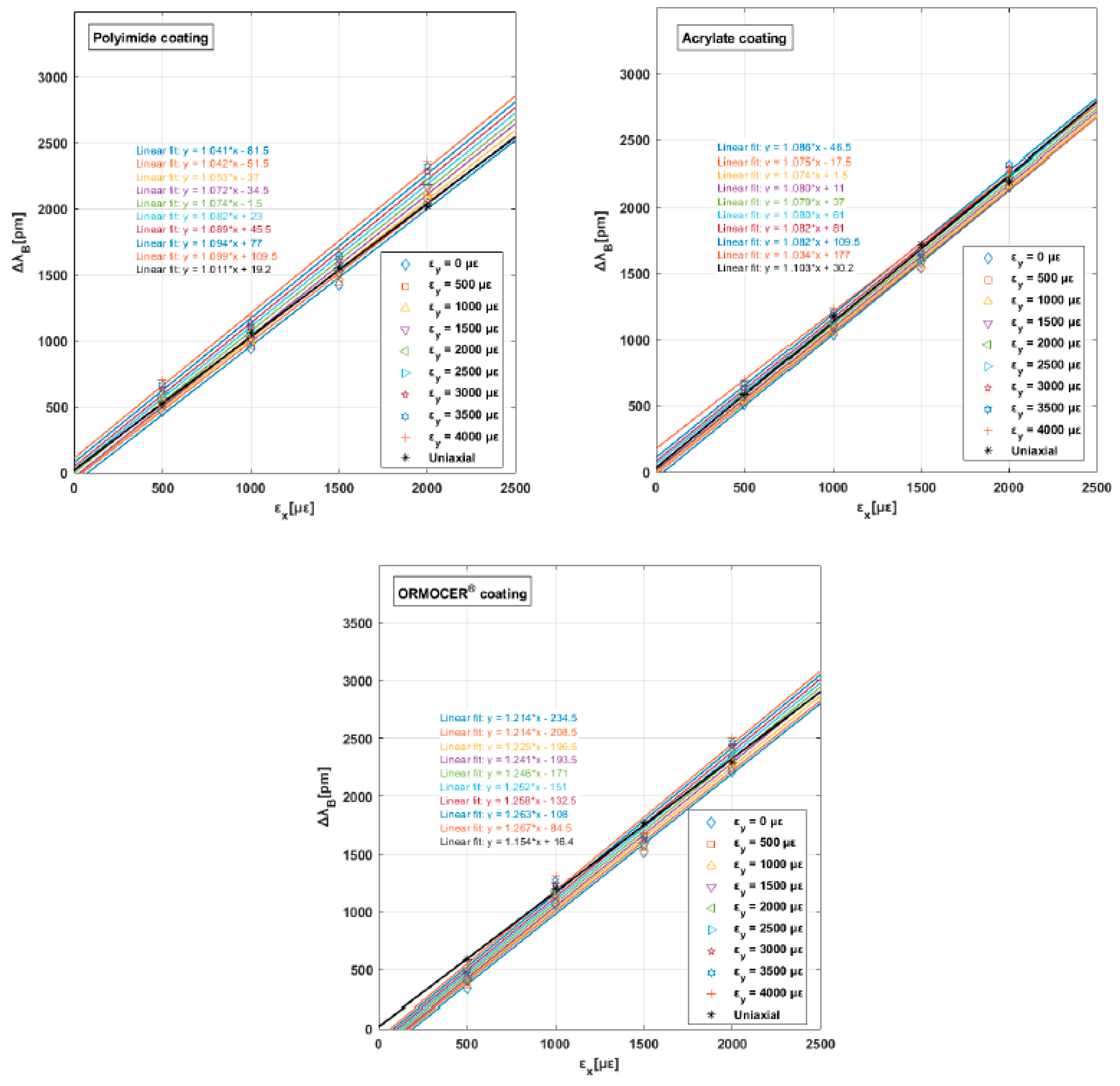
Preprints 100318 g008
Table 1. Physics properties of the polyimide, acrylate and ORMOCER® coatings used in the work [1,42,43].
Table 1. Physics properties of the polyimide, acrylate and ORMOCER® coatings used in the work [1,42,43].
Properties Units Polyimide Acrylate ORMOCER®
Young’s modulus ( E ) G P a 2.40 0.60 2.00
Density g / c m 3 1.43 [1.14–1.20] Not available
Temperature glass transition ° C > 400 ≈ 105 250
Temperature of fusion ° C Not available [160–200] Not available
Vicat Softening Temperature (VST) ° C 220 Not available Not available
Operative range of temperature ° C [-190–350] [-55–85] [-180–200]
Core diameter µ m 9 9 6
Cladding diameter µ m 125 125 125
Coating diameter µ m 160 250 200
Table 2. Absolutes coordinates since zero reference [mm].
Table 2. Absolutes coordinates since zero reference [mm].
Coatings X Y
Polyimide -3.7 2.5
Acrylate 4 -2.5
ORMOCER® -5 -7.5
Table 3. Values of λ B for FBGS with the polyimide, acrylate and ORMOCER® coatings used in the work.
Table 3. Values of λ B for FBGS with the polyimide, acrylate and ORMOCER® coatings used in the work.
Properties Units Polyimide Acrylate ORMOCER®
Pre-installation nm 1535.004 1562.028 1546.816
Post-installation nm 1534.624 1561.634 1546.578
Table 4. Properties FBGS used in this study [1,39].
Table 4. Properties FBGS used in this study [1,39].
Properties Units Values
Young’s modulus ( E s ) G P a 73.1
Poisson’s ratio ( ν s ) 0.16
Shear modulus ( G s ) G P a 31.5
Thermal expansion coefficient ( α s ) 10 − 6 / ° C 0.5
Index of refraction ( n 0 ) 1.449
Pockel constant ( p 11 ) 0.113
Pockel constant ( p 12 ) 0.252
Thermooptic coefficient ( d n 0 d T ) 10 − 5 / ° C 0.83
Table 5. Average percentages of accumulated transverse strains for each longitudinal strain tested.
Table 5. Average percentages of accumulated transverse strains for each longitudinal strain tested.
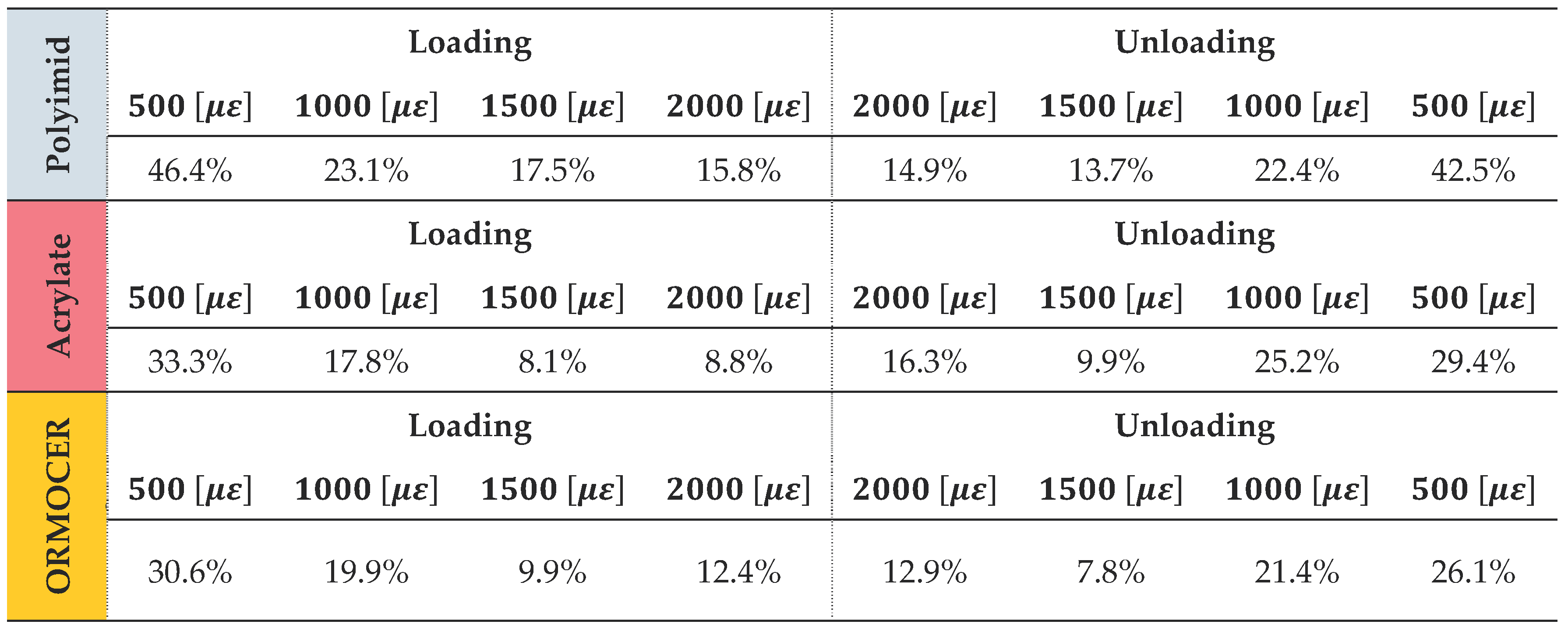
Preprints 100318 i001
Table 6. Experimental values measured in the interrogator with different ratios and coatings.
Table 6. Experimental values measured in the interrogator with different ratios and coatings.
Preprints 100318 i002
Preprints 100318 i003
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Alerts
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2025 MDPI (Basel, Switzerland) unless otherwise stated