Prerpints.org logo
Preprint
Article

Integrating Bayesian Classification into a Mobile App for Enhanced ACL Assessment: “Pivot-Shift Meter App”

Altmetrics

Downloads

102

Views

36

Comments

0

Submitted:

28 February 2024

Posted:

06 March 2024

You are already at the latest version

Alerts
Abstract
ACL instability poses a significant challenge in traumatology and orthopedic medicine, often requiring accurate diagnosis for appropriate treatment. While the pivot-shift test offers a crucial means of assessment, its reliance on subjective interpretation underscores the need for supplementary imaging studies. This study aims to address this limitation by developing a Bayesian classification algorithm tailored for integration into a mobile application. Using the built-in inertial sensors of smartphones, this new approach aims to dynamically evaluate rotational stability during knee examinations. Orthopedic specialists conducted knee evaluations on 52 subjects, with subsequent analysis revealing interesting insights. Intraobserver and interobserver analyses, as measured by ICC, demonstrated strong agreement both in terms of timing between maneuvers (ICC = 0.94) and signal amplitude (ICC = 0.71-0.66). Notably, the Bayesian algorithm successfully classified 95% of joint hypermobility cases, with an additional 7 cases of hyperlaxity identified by the Pivot-Shift Meter (PSM). These findings highlight the practicality and effectiveness of implementing a Bayesian classification algorithm within a mobile application for assessing and categorizing signals captured by smartphone inertial sensors during the pivot-shift test.
Keywords: 
Subject: Computer Science and Mathematics  -   Artificial Intelligence and Machine Learning

1. Introduction

The knee is the largest and most complex joint in the human skeleton, essential for walking, supporting body weight, taking off, and receiving jumps, considered one of the joints most subjected to constant stress for which it has a set of ligaments that give it its biomechanical skill: Anterior cruciate ligament (ACL), posterior cruciate ligament (PCL), medial collateral ligament (MCL) and lateral collateral ligament (LCL), as well as secondary or accessory stabilizers. The anatomy of the ACL is made up of two bundles: the anteromedial (AM) bundle mainly prevents anterior to posterior displacement, while the posterolateral (PL) bundle stretches in extension and prevents rotational instability of the knee. These bundles work synergistically during knee movement, presenting tension during extension and laxity during knee flexion, providing a role as the main stabilizer of the joint. Knee ligament injuries can occur due to a sudden axial load on the knee, combined with valgus stress and rotational force around the tibia. An injury to the ligament complex results in a loss of stability; therefore, an early clinical diagnosis of instability is imperative. [1,2,3,4,5].
To assess the integrity of this structure, imaging techniques and even arthroscopy itself are used. Clinical evaluation includes tests such as the Lachman test, anterior drawer test, and Pivot-Shift (PS) test, considered the "gold standard" for assessing knee rotational function after an injury. There are also scales based on questionnaires from the International Knee Documentation Committee (IKDC) and the Tegner Activity Scale (TAS). However, these are subjective measurements [4,5].
On the other hand, to quantify knee laxity, various systems, such as the KT1000 and KT2000 arthrometers (MED metric Corp., San Diego, CA, USA), have been developed to measure sagittal laxity. However, methods for evaluating rotational laxity involve a range of techniques, including ambulatory devices, instrumented boots, magnetic resonance imaging (MRI), electromagnetic sensors, robotic technology, and navigation systems. While these technological advancements are impressive, it is crucial to consider their practicality, affordability, and comfort when implementing them in a clinical setting. The use of technologies to quantify the pivot maneuver is currently being studied; infrared markers are one of them, as well as the use of sensors like accelerometers to detect the signal generated by the pivot maneuver with the disadvantage of high cost of the hardware [6,7,8,9,10,11,12,13,14,15,16,17].
A study by Tanaka [18] et al. comparing the diagnostic reliability of the quantitative evaluation of the Pivot Shift test, using an electromagnetic measurement system for anterior cruciate ligament deficiency against an accelerometer system (KiRA), an application of Image analysis using external devices, no significant differences were found between these measurements, both measurement methods were able to detect ACL laxity, however, it is important to highlight the need to use additional devices, generating extra cost for the patient [10].
Among the available tests, the PS test stands as the sole clinical evaluation that effectively correlates with knee joint hypermobility. The PS test subjectively assessed pivot change and has been the focus of efforts to quantify bone movements and correlate them with laxity grading. However, it is important to acknowledge that the unrestricted and dynamic nature of the PS maneuver introduces significant kinematic variability, and a need for careful consideration during the evaluation process.
The use of machine learning algorithms to solve problems regarding pattern recognition in medicine seems to be increasing in recent years. Bayesian model averaging linearly mixes the probabilistic predictions of multiple models, each weighted by its posterior probability [19,20,21,22,23,24,25].
To address the limitations of subjective evaluations, Pivot-Shift Meter (PSM) has been developed: a novel mobile application capable of recording signals acquired during the pivot-shift maneuver. This study aims to process the information gathered through the PS maneuver, by the development of filtering algorithms and a Bayesian classifier, to determine the reproducibility of the pivot-shift maneuver between testers based on the acquired signals. Furthermore, we aim to establish an ACL instability/laxity grade using the KT-1000 arthrometer as the gold standard tool.

2. Materials and Methods

2.1. Population

The study sample size for the trial was obtained from 66 volunteer students who participated in a control event held at the School of Medicine and Biomedical Sciences of the Universidad Autónoma de Chihuahua. Delving into the demographics, considering a total population of 156 4th-year medicine alumni, we selected our sample size with a confidence level of 95% and a margin of error of 10%.
Inclusivity was paramount in our participant selection process, encompassing individuals aged between 18 and 37 to construct a well-rounded representation of both young and middle-aged adults. Striving for gender balance, our cohort comprised 34 women and 32 men, acknowledging potential gender-related nuances in the study's outcomes. Prior to enrollment, all participants underwent a thorough informed consent process, affirming their comprehension of the study's objectives, methodologies, and associated risks. As the study focused on healthy individuals, individuals with pre-existing orthopedic conditions, injuries, or any other known health issues were excluded from participation. The study protocol had been approved by the ethics committee of "Christus Muguerza del Parque" hospital.
The evaluation phase was orchestrated by a proficient team of six evaluators, boasting a diverse range of expertise and experience in orthopedic surgery. Comprising two orthopedic surgeons with over 25 years of seasoned practice, complemented by a practitioner with 3 years of experience, and further enhanced by the contribution of three budding orthopedic surgeons with less than 3 years of practice. This diverse panel was entrusted with conducting a meticulous examination, which included the rigorous administration of the Pivot Shift (PS) test, capturing and documenting pertinent data.
Among the initial 66 participants, the data from 52 participants were deemed usable for analysis due to technical errors in data saving or mislabeling of the samples. The excluded data were not included in the subsequent analysis to ensure the accuracy and reliability of the results.

2.2. Measurements

The development of the Pivot-Shift Meter (PSM) application stemmed from a dual focus: firstly, to capture and record the signal generated by the gyroscope in the mobile device; and secondly, to seamlessly store and organize this information in an online database. The initial version of the application was developed using the program MIT App Inventor 2.
The application successfully achieved two key goals:
1)
Signal capture: The PSM application recorded angular velocity (rad/s) data corresponding to the three axes of movement on the mobile device at a sampling rate of 100 Hz, resulting in 500 data points captured in 5 seconds—this high-frequency data acquisition aimed to capture precise and detailed measurements of the pivot-shift maneuver. X-axis data was used because it corresponds best to the movement of the leg when executing the maneuver concerning the position of the cell phone (Figure 1A).
2)
Data storage: The recorded data were securely saved in a database, which was configured to provide a user-friendly experience for the physicians involved in the study. This database facilitated the physician's ability to review and follow up on each case (Figure 2). During the study, the pivot-shift maneuver was performed three consecutive times on each test subject. The mobile device was placed on the anteromedial aspect of the tibia, approximately two fingers away from the tibial tuberosity. To ensure secure placement, the mobile device was connected to a sports-type cellular armband with the PSM application pre-installed, allowing for accurate recording of the maneuver.

2.3. Data Recording in the PSM Application by the Evaluator

  • Patient Data Recording: Patient initials, age, gender, height, and weight. (Figure 2)
  • Placement of the Cell Phone: The cell phone with the PSM application installed is placed on the tibial tuberosity of the patient, securing it approximately two fingers below the patella with an elastic band, ensuring that the device is slightly tilted towards the medial aspect of the tibia. (Figure 1B)
  • Execution of the Pivot Maneuver: The evaluator holds the ankle on the medial side with the hand corresponding to the patient's leg, and with the opposite hand, the posterior part of the leg is held at the level of the tibial head, rotating slightly medially. Subsequently, the leg is flexed until reaching a 90o angle.
  • Results Recording: The evaluators are instructed to perform two maneuvers and save the results obtained with the PSM application. Additionally, the application allows for adding observations, clinical classification according to IKDC criteria, results of digital arthrometry (KT-1000), results of imaging studies, arthroscopic images, and notes with relevant clinical information.
In addition to the PSM data, the KT-1000 arthrometer was used to measure the anteroposterior displacement of the knee joint in millimeters. This measurement provided an assessment of the laxity in the anteromedial (AM) bundle of the ACL. Measurements were performed on both legs of each participant, and the results were compared to determine the degree of injury. The development of the laxity grade table was inspired by the need to provide a comprehensive assessment tool for the resulting data. The objective measurements were obtained through the KT-1000 arthrometer, which indicates the millimeter displacement of the knee joint, and a grading system, “Del Parque” Classification (CDP), which categorizes laxity into grades 1, 2, and 3. In recognizing the importance of identifying cases without significant knee laxity, we introduced an additional grade, grade 0, to the classification table. This grade signifies a stable knee with minimal or no laxity.
With this scale, a knee laxity grade is obtained by measuring both legs of a patient and determining the difference between these results (Table 1). The table ensures consistency in grading PSM data by providing clear criteria for each grade.

2.4. Statistical Analysis

Intraclass Correlation Coefficient (ICC) was used to compare repeatability among the evaluators of the data acquired by the PSM when performing a pivot shift test. MatLab was the software used for this purpose.
ICC is used to find correlations within a single class of data rather than two different classes of data. Is a value that goes from 0 to 1 and acts as a measure of the reliability of the ratings for data that exists in groups of quantitative variables.
From each X signal of each evaluator, characteristics of the signal that agree with the amplitude in radians per second (rad/s) and location in time of each positive peak in centiseconds (cs) were obtained as seen in marks PI-III in Figure 1C and summarized in Table 2.
Characteristic vectors (CV) were formed by data provided by each peak of each signal:
Subject 45: [137.54, 179.86, 156.83] ; [111.00, 267.00, 448.00]
Once this set of samples was arranged, two types of comparisons were made: an intra-observer and an inter-observer.

2.5. Bayesian Classification Algorithm

The main objective was to find the characteristics of the signal that could help to determine a degree of laxity. For this analysis, 28 of the 52 samples were used to maintain similar groups in the number of samples of each grade, composed of maneuvers classified with the KT-1000 in the different grades, from 0 to 3. Once the analysis method was determined, the rest of the maneuvers were analyzed to determine their degree of laxity according to PSM.
The first step of the signal processing was to normalize every signal to values between 0 to 1 to be further analyzed only by its morphologic characteristics.
Next, the area indicated as the “pivot” in Figure 1C, was extracted from each sample, in its normalized values (NV) and its original values (OV).
Characteristics considered for the Bayesian classification algorithm (BCA) were: the standard deviation (SD) from the NV; and the maximum value, range plus average of the signal values, and sum of squares divided by the amount of data in the signal, which were extracted from the OV. With these values, a BCA tree was developed.

3. Results

From the samples obtained, it was identified that the X-axis corresponds best to the movement of the leg when executing the maneuver concerning the position of the cell phone. Thus, it was possible to relate portions of the graph to leg movements. We could identify and relate three sectors: flexion, extension, and "pivot" (Figure 1C).
The intraobserver ICC analysis showed a global average of 0.95 and 0.71 in terms of the time between maneuvers and the maximum amplitude of each one respectively. On the other hand, the interobserver analysis yielded 0.94 and 0.66 allusive to the time and maximum amplitude between each maneuver, respectively. From these correlation results, the samples were grouped into classes determined by the speed of the maneuver reached, and then analyzed each sample to determine the degree of laxity. Initially, 28 participants were classified according to the potential degree of laxity, which was distributed as can be seen in Table 3.
The SD of the pivot part of the signal, turned out to be the characteristic that had the higher weight in the classification algorithm; thus, once the SD of the data of every signal was determined, the cases were classified into different classes, covering a total of 5 groups, from 0 to 4. The first class, 0, is considered unanalyzable with the algorithm since these are samples that did not present characteristics that could be analyzed, which can be seen in Figure 3G. The rest of the samples were distributed as shown in Table 4 and the SD range of each class is shown.
With this first classification by classes carried out, according to the characteristics obtained from the VO, the degrees of laxity from the maneuvers were obtained, which can be seen in Table 5. It was observed that class 1 could not be classified since it does not present a sufficiently high maneuvering speed. Finally, Table 6 shows the results of test subjects who, according to the grade of laxity, are negative tests, it was also determined whether they showed a degree of laxity with PSM. Of these cases, 7 participants had characteristics corresponding to a degree of laxity according to PSM. Three samples were discarded since they lacked the minimum characteristics to be analyzed. With these results and those provided in Table 4, 49 of the 52 samples were analyzed.

4. Discussion

Technological advancements have played a critical role in the development of new medical techniques and treatments, particularly in the field of orthopedics, allowing for less invasive procedures and more effective clinical analysis methods during joint physical examinations. While the pivot-shift test is considered a cornerstone in assessing knee laxity, its clinical application comes with several significant limitations. Performing the test and evaluating the results are subjective tasks prone to errors. This subjectivity is a relevant factor contributing to uncertainty among observers and intra-observers, limiting the reliability of the obtained data. Additionally, the development of tools and the use of technology in clinical settings to optimize diagnosis, prognosis, and medical treatment have revolutionized the concept of healthcare. Inertial sensors like accelerometers and gyroscopes in smartphones offer a novel, convenient, accessible, and comparatively affordable option for diagnosing and quantitatively evaluating ACL injuries in knees. KT-1000 arthrometer can’t be quite compared with the PS maneuver due to the nature of the biomechanics of each maneuver. Nevertheless, in the present study, the Pivot Shift Meter app was able to accurately classify acquired signals, providing quantitative dynamic diagnostic information of rotational instability that the gold standard arthrometer cannot offer.
According to Landis and Kotch criteria, the time in which the maneuvers were performed reached an almost perfect value (>0.8) both in the intra-observer analysis and in the inter-observer analysis, which may be because the evaluators have adapted test after test to achieve three maneuvers in a row within five seconds [26]. Meanwhile, the substantial correlation obtained between the intra-observer analysis, regarding the amplitude in which the peaks were detected, may be because each evaluator has a unique way of executing the maneuver, anatomical factors may influence both the evaluator and the examination subjects, such as height and physical condition. This suggests that a stricter standardization of the pivot maneuver is necessary, desirably given by the same application. As Nicola Lopomo et al. mentions in a systematic review, a generalized pivot change maneuver is still desirable, which was demonstrated with the ICC analysis of the maximum amplitude of each maneuver [11,14,27].
Also, Hoshino et al. described standardized technique improves measurement accuracy, thus, once this standardization is applied, it would be possible to obtain a higher correlation [28].
Regarding the comparison against the KT-1000, a relationship of 19/28 classifiable cases was determined, 67.9%. This relationship was low since 8 cases could not be correctly determined by PSM, belonging to classes 0 and 1. Therefore, there remains a relationship of 19/20 cases, 95%, which would be maintained only by asking the evaluator to repeat the maneuver. On the other hand, the PSM managed to detect 7 extra cases that presented high laxity in both legs, which according to the KT-1000 would pass as very lax patients and not as possible bilateral injuries. These cases require further analysis to determine causes and conclusions.
Compared to other ways to quantify pivot shift test, the approach exposed in the present work has some advantages, highlighting the fact that is very simple to use, as the only other requirement besides the device itself, is a proper way to fix the phone in position; as mentioned before, a simple armband was used for this purpose. Also, this software has no trouble being installed in both commercial operative systems. [6,18,29,30,31,32,33,34,35,36,37,38,39]
Some authors have approached the pivot shift quantification by the use of inertial sensors, especially accelerometers. Vaidya et al. also conducted a study with mobile devices using these sensors. Even when they had satisfactory results, it can be noted that these sensors tend to add more noise to the signal, this is because what they measure (acceleration) depends on more variables since it is of a higher order compared to speed measured by gyroscopes [8,36,37,40,41].
Most authors that approached the quantification of the pivot test through accelerometers seem to agree on a method to interpret a signal acquired by the pivot test with only one morphological characteristic in the graph, which allows them to detect subluxation and reduction of the joint, equivalent to the “pivot” part of the signals acquired in this study [6,18,29,31,36,39]. Nevertheless, this method could be enhanced by the use of machine learning algorithms [42,43,44,45].
Results of initial studies showed a low correlation between intra-observer analysis regarding the amplitude of the pivot shift effect graphed in the application due to the variables presented by each evaluator during the maneuver. This led to the initiation of another current multicenter and international case study in which we aim to analyze, classify, and follow more than 400 tests performed by specialist physicians from five different countries, including Bolivia, Chile, Colombia, Ecuador, and Mexico, using the mobile application PSM on patients with ACL injuries.
The purpose is to optimize the software's adaptability for each user and the motivation behind conducting this study lies in the importance of diagnosing and postoperative monitoring of ACL injuries due to the potential repercussions such as early joint degeneration and knee instability. Therefore, digital arthrometry appears to be the path toward developing precise and numerical evaluation methods for rotational instability, with all the advantages that early diagnosis and classification can provide before any surgical treatment.

5. Conclusions

The development of this innovative software marks a significant stride forward for orthopedists, ushering in a future where only a mobile device is needed, eliminating additional expenses for examiners and patients. This advancement not only introduces new technologies but also enhances the scope of comprehensive care, facilitating timelier diagnoses and more effective treatments tailored to each case. By integrating injury degree classification with specific surgical recommendations for each grade, our aim is to furnish clinicians with a practical tool to discern the most appropriate approach for individual patients. Furthermore, the successful integration of a Bayesian classification algorithm into a mobile application for assessing and classifying signals from inertial sensors within a cellphone during a pivot shift test underscores the potential of technology in clinical evaluations.
In general, the application of technology such as inertial sensors in smartphones and neural networks can serve as valuable tools to enhance the precision and objectivity of clinical evaluations of ACL injuries and other joint conditions. Continued research and refinement of these tools are imperative to ensure their accuracy and utility in clinical practice.
It's crucial to acknowledge that no measurement system is flawless, and there are inherent limitations in its clinical application. One such limitation is the necessity of adhering to standardized pivot maneuver techniques, as variability in technique may impact the accuracy of the measurements obtained.
Further studies are warranted to validate the measurement accuracy of the pivot using the application across different patient populations and clinical scenarios. This will ascertain the application's ability to identify ACL injuries at various stages of the injury and evaluate the utility of inertial sensors in clinical practice.

Funding

This research received no external funding.

Institutional Review Board Statement

The study was conducted in accordance with the Declaration of Helsinki, and approved by the Institutional Review Board of Autonomous University of Chihuahua (UACH) protocol code CI-020-22 date of approval: 07/12/23.

Informed Consent Statement

Informed consent was obtained from all subjects involved in the study.

Data Availability Statement

The dataset used in this study is publicly available online at https://www.ormeds.com.mx and can be accessed freely by any interested party.

Acknowledgments

Special thanks to Ph.D. Irene Leal-Berumen (Leal-Solis), professor investigator of the Universidad Autónoma de Chihuahua for her invaluable support in reviewing this work during its edition, and to B.E. Gabriela Sámano, coordinator of the Biomedical Engineering career at the Universidad Autónoma de Chihuahua for her invaluable contribution in arranging the preparations to make use of the faculty's facilities in order to capture the data for this work.

Conflicts of Interest

The authors declare no conflicts of interest.

References

  1. Hassebrock, J.D.; Gulbrandsen, M.T.; Asprey, W.L.; Makovicka, J.L.; Chhabra, A. Knee ligament anatomy and biomechanics. Sports Med. Arthrosc. Rev. 2020, 28, 80–86. [Google Scholar] [CrossRef]
  2. Dalley, A.F.; Moore, K.L.; Agur, A.M.R. Anatomía con orientación clínica, 9th ed.; 2022.
  3. Latarjet, M.; Liard, A.R. Anatomía Humana 5a edición. Panamericana; 2019, p. 18. [Online]. Available online: https://www.medicapanamericana.com/mx/libro/coleccion-latarjet-anatomia-humana-incluye-version-digital-2-tomos (accessed on 10 January 2023).
  4. Kumar, P.J.; Kumar, A.M.; Professor, A. Healthy Gait: Review of Anatomy and Physiology of Knee Joint. Int. J. Curr. Res. Rev. 2020, 12, 1–8. [Google Scholar] [CrossRef]
  5. Ayala-Mejías, J.; García-Estrada, G.; Pérez-España, L.A. Lesiones del ligamento cruzado anterior. Acta Ortop. Mex. 2014, 28, 57–67. Available online: http://www.scielo.org.mx/scielo.php?script=sci_arttext&pid=S2306-41022014000100012&lng=es&nrm=iso&tlng=es (accessed on 28 February 2023). [PubMed]
  6. Hoshino, Y.; et al. Quantitative evaluation of the pivot shift by image analysis using the iPad. Knee Surg. Sports Traumatol. Arthrosc. 2013, 21, 975–980. [Google Scholar] [CrossRef] [PubMed]
  7. Roessler, P.P.; Schüttler, K.F.; Heyse, T.J.; Wirtz, D.C.; Efe, T. The anterolateral ligament (ALL) and its role in rotational extra-articular stability of the knee joint: a review of anatomy and surgical concepts. Arch. Orthop. Trauma. Surg. 2016, 136, 305–313. [Google Scholar] [CrossRef] [PubMed]
  8. Helfer, L.; et al. Triaxial accelerometer evaluation is correlated with IKDC grade of pivot shift. Knee Surgery, Sports Traumatology, Arthroscopy 2020, 28, 381–388. [Google Scholar] [CrossRef] [PubMed]
  9. Vaidya, R.K.; Yoo, C.W.; Lee, J.; Han, H.S.; Lee, M.C.; Ro, D.H. Quantitative assessment of the pivot shift test with smartphone accelerometer. Knee Surgery, Sports Traumatology, Arthroscopy 2020, 28, 2494–2501. [Google Scholar] [CrossRef]
  10. Napier, R.J.; et al. Is the KiRA Device Useful in Quantifying the Pivot Shift in Anterior Cruciate Ligament–Deficient Knees? Orthop. J. Sports Med. 2021, 9. [Google Scholar] [CrossRef]
  11. Lopomo, N.; Zaffagnini, S.; Bignozzi, S.; Visani, A.; Marcacci, M. Pivot-shift test: Analysis and quantification of knee laxity parameters using a navigation system. Journal of Orthopaedic Research 2010, 28, 164–169. [Google Scholar] [CrossRef]
  12. Kuroda, R.; et al. Quantitative measurement of the pivot shift, reliability, and clinical applications. Knee Surg. Sports Traumatol. Arthrosc. 2012, 20, 686–691. [Google Scholar] [CrossRef]
  13. Zaffagnini, S.; et al. Inertial sensors to quantify the pivot shift test in the treatment of anterior cruciate ligament injury. Joints 2014, 2, 124. [Google Scholar] [CrossRef] [PubMed]
  14. Lopomo, N.; Signorelli, C.; Bonanzinga, T.; Muccioli, G.M.M.; Visani, A.; Zaffagnini, S. Quantitative assessment of pivot-shift using inertial sensors. Knee Surg. Sports Traumatol. Arthrosc. 2012, 20, 713–717. [Google Scholar] [CrossRef] [PubMed]
  15. Berumen-Nafarrate, E.; et al. Clasificación cuantitativa de la maniobra de pivot-shift. Acta Ortop. Mex. 2021, 35, 153–157. [Google Scholar] [CrossRef] [PubMed]
  16. Murase, A.; et al. Comparison of quantitative evaluation between cutaneous and transosseous inertial sensors in anterior cruciate ligament deficient knee: A cadaveric study. J. Orthop. Sci. 2017, 22, 874–879. [Google Scholar] [CrossRef] [PubMed]
  17. Berumen Nafarrate, E.; Manuel Paz, G. Lesiones multiligamentarias de rodilla. Ortho-Tips 2009, 5, 49–58. Available online: http://www.medigraphic.com (accessed on 2 August 2023).
  18. Tanaka, T.; et al. The diagnostic reliability of the quantitative pivot-shift evaluation using an electromagnetic measurement system for anterior cruciate ligament deficiency was superior to those of the accelerometer and iPad image analysis. Knee Surg. Sports Traumatol. Arthrosc. 2018, 26, 2835–2840. [Google Scholar] [CrossRef] [PubMed]
  19. Tack, C. Artificial intelligence and machine learning | applications in musculoskeletal physiotherapy. Musculoskelet. Sci. Pract. 2019, 39, 164–169. [Google Scholar] [CrossRef] [PubMed]
  20. Hamed, M.G.; Akbari, A. Hierarchical Bayesian Classifier Combination. 2018, 113–125. [CrossRef]
  21. Raschka, S.; Mirjalili, V. Python Machine Learning: Machine Learning and Deep Learning with Python, Scikit-Learn, and Tensorflow 2, 3rd ed.; Packt Publishing 2019.
  22. Calin, O. Deep Learning Architectures. 2020. [CrossRef]
  23. Nielsen, M.A. Neural Networks and Deep Learning. Determination Press 2019. [Online]. Available online: http://neuralnetworksanddeeplearning.com (accessed on 7 May 2023).
  24. Paluszek, M.; Thomas, S. Practical MATLAB deep learning: A project-based approach. Practical MATLAB Deep Learning: A Project-Based Approach 2020, 1–252. [CrossRef]
  25. Vaudreuil, N.J.; Rothrauff, B.B.; de Sa, D.; Musahl, V. “The Pivot Shift: Current Experimental Methodology and Clinical Utility for Anterior Cruciate Ligament Rupture and Associated Injury,” Current Reviews in Musculoskeletal Medicine, vol. 12, no. 1. Humana Press Inc., pp. 41–49, Mar. 15, 2019. [CrossRef]
  26. Landis, J.R.; Koch, G.G. The measurement of observer agreement for categorical data. Biometrics 1977, 33, 159–174. [Google Scholar] [CrossRef]
  27. Lopomo, N.; Zaffagnini, S.; Amis, A.A. “Quantifying the pivot shift test: A systematic review,” Knee Surgery, Sports Traumatology, Arthroscopy, vol. 21, no. 4. Springer Verlag, pp. 767–783, Apr. 01, 2013. [CrossRef]
  28. Hoshino, Y.; et al. Standardized pivot shift test improves measurement accuracy. Knee Surg. Sports Traumatol. Arthrosc. 2012, 20, 732–736. [Google Scholar] [CrossRef]
  29. Soudé, G.; et al. Pivot shift intraoperative quantitative assessment using a smartphone accelerometer in ACL deficient knees. J. Exp. Orthop. 2023, 10. [Google Scholar] [CrossRef]
  30. Arilla, F.V.; et al. “Experimental execution of the simulated pivot-shift test: A systematic review of techniques,” Arthroscopy - Journal of Arthroscopic and Related Surgery, vol. 31, no. 12. W.B. Saunders, pp. 2445-2454.e2, Dec. 01, 2015. [CrossRef]
  31. Helfer, L.; et al. Triaxial accelerometer evaluation is correlated with IKDC grade of pivot shift. Knee Surgery, Sports Traumatology, Arthroscopy 2020, 28, 381–388. [Google Scholar] [CrossRef]
  32. Muller, B.; et al. Development of computer tablet software for clinical quantification of lateral knee compartment translation during the pivot shift test. Comput. Methods Biomech. Biomed. Eng. 2016, 19, 217–228. [Google Scholar] [CrossRef]
  33. Zaffagnini, S.; et al. Anatomic Anterior Cruciate Ligament Reconstruction Using Hamstring Tendons Restores Quantitative Pivot Shift. Orthop. J. Sports Med. 2018, 6. [Google Scholar] [CrossRef] [PubMed]
  34. Vaudreuil, N.J.; Rothrauff, B.B.; de Sa, D.; Musahl, V. “The Pivot Shift: Current Experimental Methodology and Clinical Utility for Anterior Cruciate Ligament Rupture and Associated Injury,” Current Reviews in Musculoskeletal Medicine, vol. 12, no. 1. Humana Press Inc., pp. 41–49, Mar. 15, 2019. [CrossRef]
  35. Tisherman, R.T.; Patel, N.K.; Murphy, C.I.; Debski, R.E.; Musahl, V. Mobile application for quantification of the pivot shift examination: Intraoperative usability and utility during real-world deployment. J. ISAKOS 2020, 5, 345–350. [Google Scholar] [CrossRef]
  36. Vaidya, R.K.; Yoo, C.W.; Lee, J.; Han, H.S.; Lee, M.C.; Ro, D.H. Quantitative assessment of the pivot shift test with smartphone accelerometer. Knee Surg. Sports Traumatol. Arthrosc. 2020, 28, 2494–2501. [Google Scholar] [CrossRef] [PubMed]
  37. Nakamura, K.; et al. Evaluation of pivot shift phenomenon while awake and under anaesthesia by different manoeuvres using triaxial accelerometer. Knee Surg. Sports Traumatol. Arthrosc. 2017, 25, 2377–2383. [Google Scholar] [CrossRef] [PubMed]
  38. Berumen-Nafarrate, E.; et al. Interpretación de la Maniobra de Pivote Mediante el uso de Acelerómetros en Pacientes que Acuden a Consulta Ortopédica. Acta Ortopédica Mexicana. [Online]. Available online: https://www.medigraphic.com/cgi-bin/new/resumen.cgi?IDARTICULO=62801 (accessed on 2 August 2023).
  39. Berumen-Nafarrate, E.; et al. Clasificación cuantitativa de la maniobra de pivot-shift. Acta Ortop. Mex. 2021, 35, 153–157. [Google Scholar] [CrossRef] [PubMed]
  40. “Signo del pistón. ¿Una nueva prueba para detectar la inestabilidad anterior de la rodilla?|Enhanced Reader”.
  41. Lerat, J.L.; Moyen, B.; Jenny, J.Y.; Perrier, J.P. A comparison of pre-operative evaluation of anterior knee laxity by dynamic X-rays and by the arthrometer KT 1000. Knee Surg. Sports Traumatol. Arthrosc. 1993, 1, 54–59. [Google Scholar] [CrossRef] [PubMed]
  42. Kunze, K.N.; et al. Application of Machine Learning Algorithms to Predict Clinically Meaningful Improvement After Arthroscopic Anterior Cruciate Ligament Reconstruction. Orthop. J. Sports Med. 2021, 9. [Google Scholar] [CrossRef] [PubMed]
  43. Goebel, R.; Wahlster, W.; Siekmann, J. Lecture Notes in Artificial Intelligence Subseries of Lecture Notes in Computer Science LNAI Series Editors LNAI Founding Series Editor. [Online]. Available online: http://www.springer.com/series/1244.
  44. Rabb, E.; Steckenrider, J.J. Walking Trajectory Estimation Using Multi-Sensor Fusion and a Probabilistic Step Model. Sensors 2023, 23, 6494. [Google Scholar] [CrossRef]
  45. Kim, H.-C.; Ghahramani, Z. Bayesian Classifier Combination. 2012.
Preprints 100142 g001
Figure 1. A) X, Y, and Z axis of movement of gyroscopes integrated in a mobile device. B) Placement of the mobile device: on the anteromedial face of the tibia, two finger widths from the tibial tuberosity and attached with a sports-type cell phone bracelet C) X-axis signal; it can highlight the sequence of the pivot-shift maneuver: a) flexion movement, b) extension movement and c) joint reduction or “pivot”. It is also noticeable that this pattern repeats, giving the clue of the start of the next maneuver.
Figure 1. A) X, Y, and Z axis of movement of gyroscopes integrated in a mobile device. B) Placement of the mobile device: on the anteromedial face of the tibia, two finger widths from the tibial tuberosity and attached with a sports-type cell phone bracelet C) X-axis signal; it can highlight the sequence of the pivot-shift maneuver: a) flexion movement, b) extension movement and c) joint reduction or “pivot”. It is also noticeable that this pattern repeats, giving the clue of the start of the next maneuver.
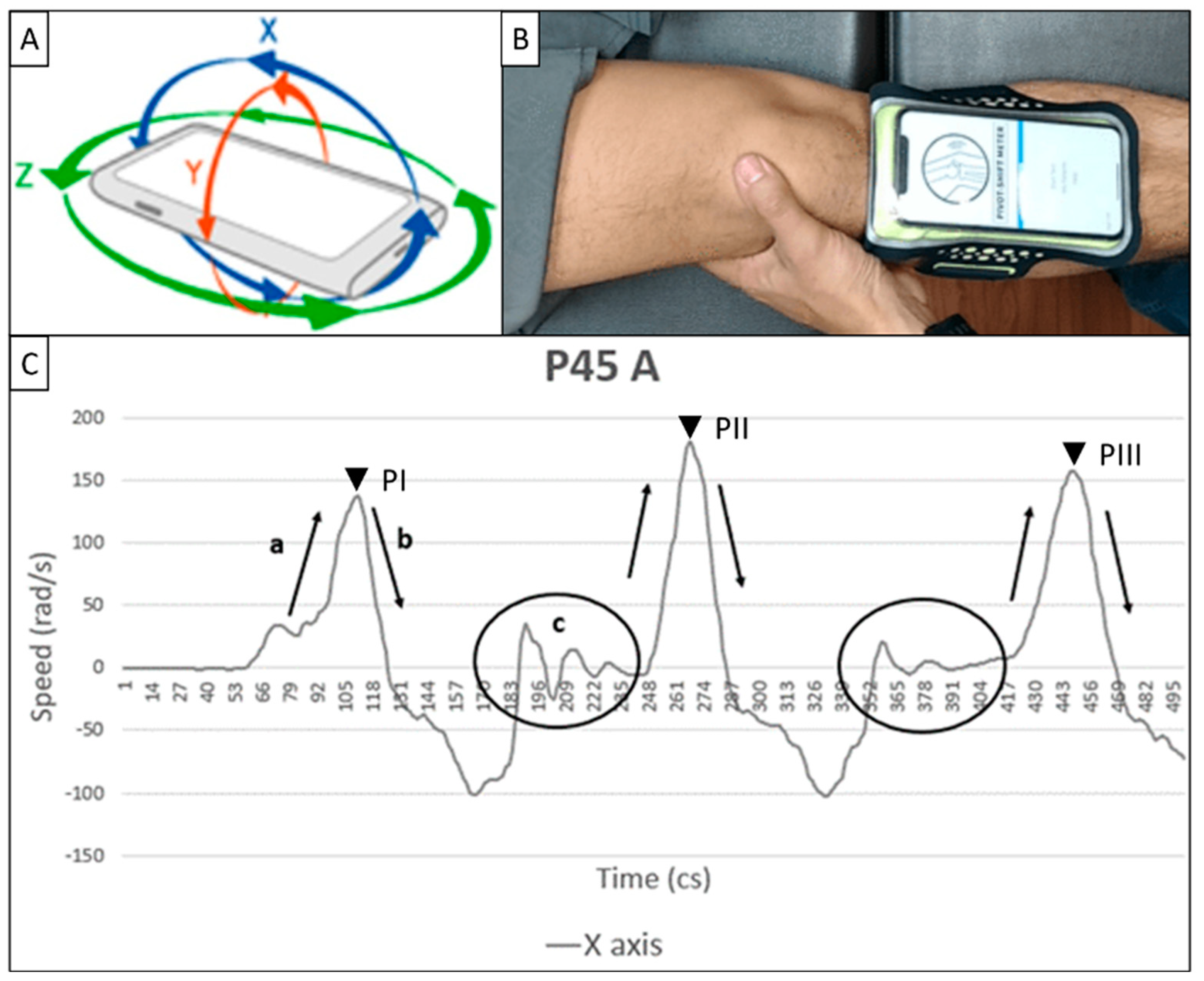
Preprints 100142 g001
Preprints 100142 g002
Figure 2. App Interface for Patient Registration for data base.
Figure 2. App Interface for Patient Registration for data base.
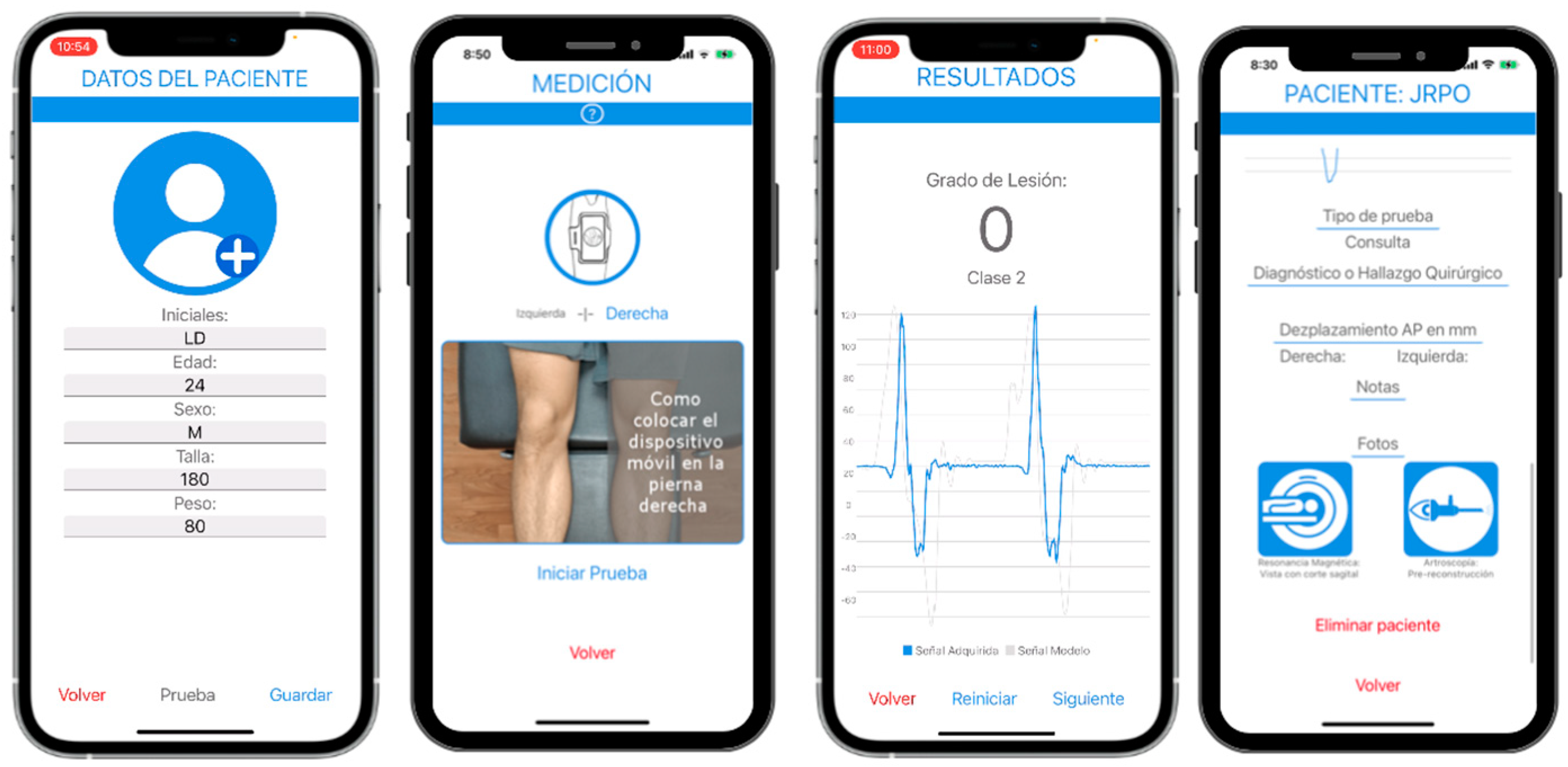
Preprints 100142 g002
Preprints 100142 g003
Figure 3. A-F) Signal processing. After normalizing the signal, it was segmented to obtain the important portion of data, which corresponds to the “pivot” (F). G) Graphic difference between classes: 1, 2, 3, and 4 have a sinusoidal-based waveform, while class 0 has a plateau shape.
Figure 3. A-F) Signal processing. After normalizing the signal, it was segmented to obtain the important portion of data, which corresponds to the “pivot” (F). G) Graphic difference between classes: 1, 2, 3, and 4 have a sinusoidal-based waveform, while class 0 has a plateau shape.
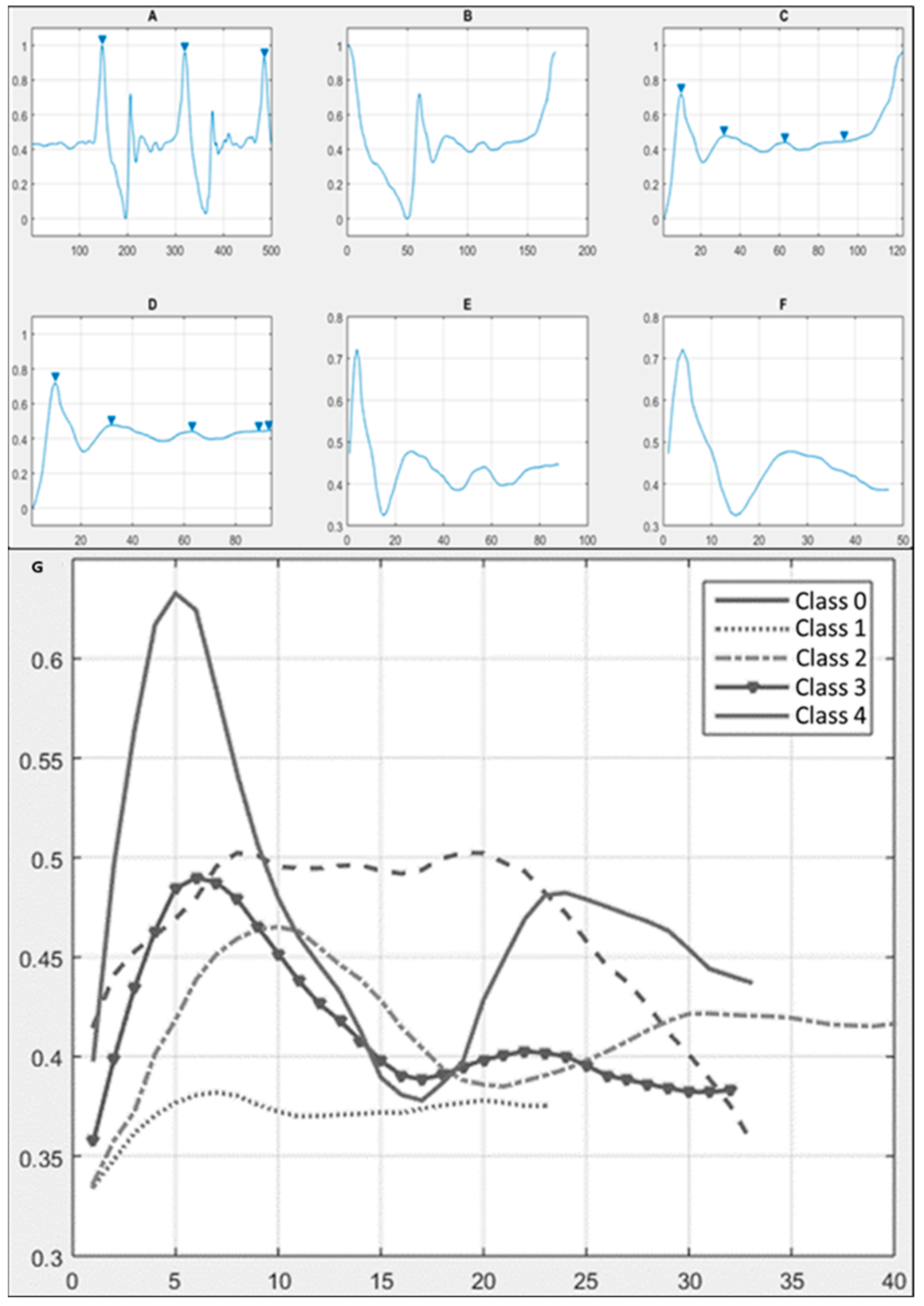
Preprints 100142 g003
Table 1. CDP: Grading System for Knee Laxity Based on Difference in Millimeters Measured by KT-100011.
Table 1. CDP: Grading System for Knee Laxity Based on Difference in Millimeters Measured by KT-100011.
Grade Difference in mm Meaning
0 0 a 2 Almost null laxity
1 3 Low laxity
2 4 a 5 Considerable laxity
3 > 6 High laxity
1 Modified from: Iñigo-Palvovich R., Leal-Contreras C., Pakuts-Sahr A., Tonche-Ramos J.J., Pérez-Fontes A.G., et al. Quo Vadis, Quo Venis. In: Olvera R.G., director. Lesiones Ligamentarias de Rodilla. Dirección de Extensión y Difusión Cultural. Chihuahua; 2021. p. 379-403, table 2-18.
Table 2. Summary of signal characteristics arrangement for the ICC analysis.
Table 2. Summary of signal characteristics arrangement for the ICC analysis.
Evaluator A Evaluator N
Peak 1 Peak 2 Peak 3 Peaks 1, 2, 3
Subject n-1 … …
Subject 45 Time of detection (cs) …
111.00 267.00 448.00
Amplitude (rad/s)
137.54 179.86 156.83
Subject n+1 … …
Table 3. Classification of participants according to their potential degree of laxity.
Table 3. Classification of participants according to their potential degree of laxity.
Grade of Laxity Number of subjects
0 9
1 8
2 9
3 2
Table 4. Distribution of samples in classes according to range of SD.
Table 4. Distribution of samples in classes according to range of SD.
Class Number of subjects SD range
0 5 -
1 3 0 - 0.01999
2 7 0.020 - 0.034
3 6 0.03401 - 0.049
4 7 0.04901 - 1
Table 5. Degrees of laxity present during the PS maneuver.
Table 5. Degrees of laxity present during the PS maneuver.
CLASS 1
Participant CDP Grade Grade PSM
21 0 -
2 2 -
49 2 -
CLASS 2
Participant CDP Grade Grade PSM
1 0 0
12 0 0
53 0 0
8 0 1
10 1 1
20 2 2
23 2 2
CLASS 3
Participant CDP Grade Grade PSM
66 0 0
32 1 1
11 1 1
63 2 2
34 2 2
20 2 2
57 2 2
CLASS 4
Participant CDP Grade Grade PSM
18 1 0
29 0 0
50 1 1
58 1 1
46 3 3
51 3 3
Table 6. Degree of laxity detected with PSM.
Table 6. Degree of laxity detected with PSM.
CLASS 2
Participant Grade PSM KT-1000 max mm of displacement
7 0 2
15 0 3
6 0 4
35 1 5
9 0 6
5 0 7
42 1 7
31 2 9
CLASS 3
Participant Grade PSM KT-1000 max mm of displacement
26 0 2
38 0 4
443 0 4
13 0 5
64 2 6
CLASS 4
Participant Grade PSM KT-1000 max mm of displacement
52 0 3
25 0 4
56 1 4
14 2 5
19 0 5
45 0 5
65 0 7
4 1 7
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated