Prerpints.org logo
Preprint
Article

Surface Thermodynamic Properties of 3D/4D Printing Poly Lactic Acid by Inverse Gas Chromatography

Altmetrics

Downloads

119

Views

30

Comments

0

supplementary.pdf (294.05KB )

This version is not peer-reviewed

Submitted:

02 March 2024

Posted:

04 March 2024

You are already at the latest version

Alerts
Abstract
The poly lactic acid (PLA) is one of the most used bio-derived thermoplastic polymers in 3D and 4D printing applications. The determination of PLA surface properties is of capital importance in 3D/4D printing technology. (1) Background: The surface thermodynamic properties of PLA polymer were determined by using the inverse gas chromatography (IGC) technique at infinite dilution. The determination of the retention volume of polar and non-polar molecules adsorbed on the PLA particles filling the column allowed us to obtain the dispersive, polar, and Lewis’s acid-base surface properties at different temperatures from 40 °C to 100 °C. (2) Methods: the applied surface method was based on our recent model that used the London dispersion equation and the new chromatographic parameter function of the deformation polarizability and the harmonic mean of the ionization energies of the PLA polymer and organic molecules. (3) Results: The application of this new method led to the determination of the dispersive and polar free surface energy of adsorption of molecules on the polymeric material, as well as the glass transition and the Lewis acid-base constants. (4) Conclusions: four interval temperatures were distinguished showing four zones of the variations of the surface properties of PLA as a function of the temperature before and after the glass transition.
Keywords: 
Subject: Chemistry and Materials Science  -   Materials Science and Technology

1. Introduction

Since the first description of three-dimensional (3D) printing in the 1980s, many publications were devoted to the additive manufacturing, also known as 3D printing, which was extremely developed in many applications such as engineering, materials science, physics and astronomy, computer science, chemistry, mathematics, genetics, and molecular biology, varying from biomedical engineering, and precision manufacturing to the aerospace and military industries [1,2,3,4,5,6,7,8,9,10]. In 3D printing, the three-dimensional object is created from a digital model by adding material, typically in successive layers, on the contrary of traditional manufacturing technologies such as machining, grinding, and casting, where molten material is filled in a mold to create a product [1,2,3,4]. Seven classes were distinguished in 3D printing technologies: material extrusion, material jetting, binder jetting, powder bed fusion, directed energy deposition, sheet lamination, and vat photopolymerization [1].
The increasing evolution of the spatial technology of 3D printing led to the fourth-dimensional printing (4D printing) by considering the fourth dimension of time to modulate one or more properties of the 3D printed objects with the help of smart materials that can control the application of any external stimulus implying light, water, self-diagnostic, heating, pressure, and shape-changing effects [1,2,3,4,11,12,13,14,15,16].
One of the most used materials in 3D/4D printing is the poly (lactic acid) (PLA), because of its unique properties such as good appearance, higher transparency, less toxicity, and low thermal expansion that help reduce the internal stresses caused during cooling [17,18,19,20,21]. The PLA, a bio-derived thermoplastic polymer, is a 100% biodegradable polymer with high tensile strength and modulus and easily synthesized from lactic acid obtained from corn, sugarcane, and other biomass. It can be recycled up to 8 times and is compostable at the end of life [1,22].
The highest tensile and flexural strengths of PLA and the use of its composites with bio-derived reinforcements such as flax, hemp, jute, bamboo, and other natural fibres were widely researched for 3D printing to enhance mechanical properties, reduce material and production cost, and improve the sustainability of manufactured products [1,22,23,24,25,26,27,28,29,30,31,32,33,34].
PLA, a biodegradable aliphatic polyester, is produced from renewal resources has received much attention in the research of alternative biodegradable polymers [35,36,37]. This PLA polymer is the most popular polymer in the world and may be processed using standard machines, equipment and technologies for classic polymers [35,38,39]. PLA shows good biocompatibility and physical properties, such as high mechanical strength, thermoplasticity and fabricability [35].
The biodegradable PLA polymer is the most used material worldwide for 3D printing [1,22,23,35], and very solicited in 4D printing technology. PLA is an excellent bio-derived polymer is now used as a shape-memory polymer in 4D printing applications [28,29,30,31,32,33]. The future of 4D printing biocomposites involves multi-disciplinary research to combine design strategies, material properties, stimulus properties, and composite mechanics [1].
The surface properties, the Lewis acid-base parameters, and the dispersive and polar energies of PLA polymer are very important to be determined in many 3D and 4D applications involving the mechanical, adhesion and surface properties. Such properties were not correctly determined in literature.
In this paper, we were interested in determining the surface thermodynamic properties and the various variables of interactions between PLA polymer and other organic molecules. The technique used to study the polymer material was the inverse gas chromatography (IGC) technique at infinite dilution (ID). Our new models [40,41,42,43,44,45,46] were applied to quantify the dispersive and polar interaction energies to understand the behavior of PLA polymer and, therefore, to predict the various superficial thermodynamic properties of this 3D/4D printing material in interaction with organic molecules.
The London dispersive interaction [47] between the solvents and the solid materials was determined by applying the London equation and the notion of polarizabilities and ionization energies of the organic molecules and the polymeric material. This new methodology led to the separation between the dispersive and polar surface free energies of PLA and to the accurate determination of the Lewis enthalpic and entropic acid–base constants, the polar acid and base surface energies, and the glass transition of the PLA polymer.

2. Methods and Materials

In this paper, the inverse gas chromatography (IGC) at infinite dilution (ID) was used to determine the net retention time of organic solvents adsorbed on the solid material [48,49,50,51,52,53,54,55,56,57,58,59,60]. This results in the calculation of the net retention volume V n of the adsorbed probes, and therefore to the values of the free energy of adsorption ∆ G a 0 of organic molecules adsorbed on PLA polymer given by the following equation:
∆ G a 0 T = − R T l n V n + K ( T )
Where T is the absolute temperature, R the perfect constant gas and K ( T ) a constant depending on the temperature and the interaction solvents-PLA
∆ G a 0 ( T ) is expressed at any temperature by the summation of the London dispersive energy ∆ G a d ( T ) and the polar energy ∆ G a s p ( T ) :
∆ G a 0 T = ∆ G a d ( T ) + ∆ G a p ( T )
Many methods and molecular models were used in literature [48,49,50,51,52,53,54,55,56,57,61] to separate the two dispersive and polar contributions of the free energy of adsorption. It was previously showed [40,41,42] that the best method that gave the accurate separation between ∆ G a d ( T ) and ∆ G a p ( T ) was that based on the London dispersion interaction energy given by equation (3):
∆ G a d T = − α 0 S     H 6 3 N 2 4 π ε 0 2 ε S   ε X ε S + ε X α 0 X
Where N is the Avogadro number, ε 0 the dielectric constant of vacuum, α 0 S   and α 0 X the respective deformation polarizabilities of the solid material denoted by S and the organic molecule denoted by X, separated by a distance H , and ε S and ε X their corresponding ionization energies.
By combining equations (1) to (3), equation (4) was obtained:
R T l n V n = α 0 S     H 6 3 N 2 4 π ε 0 2 ε S   ε X ε S + ε X α 0 X − ∆ G a s p T + K T
The chosen interaction parameter P S X was given by equation (5):
P S X = ε S   ε X ε S + ε X α 0 X
For non-polar molecules such as n-alkanes, the representation of R T l n V n of as a function of 3 N 2 4 π ε 0 2 ε S   ε X ε S + ε X α 0 X of adsorbed molecules is given by equation (6):
R T l n V n n o n − p o l a r = A 3 N 2 4 π ε 0 2 P S X n o n − p o l a r − K ( T )
where A is the slope of the non-polar straight line given by:
A = α 0 S     H 6
For a polar molecule adsorbed on PLA polymer, the geometric point representing the polar probe will be located outside the straight line of n-alkanes and the distance between the polar point and this straight line will be equal to ∆ G a p p o l a r of the polar molecule, at chosen temperature.
∆ G a p T ,   p o l a r = R T l n V n   T ,   p o l a r − A 3 N 2 4 π ε 0 2 P S X p o l a r + K ( T )
In the case of linear variations of ∆ G a p T of polar probes as a function of the temperature, it is possible to deduce the specific enthalpy − ∆ H a p and entropy − ∆ S a p of polar probes adsorbed on PLA polymer by using the classic thermodynamic relation (9)):
∆ G a p T = ∆ H a p − T ∆ S a p
The determination of − ∆ H a p and − ∆ S a p of adsorbed polar molecules leads to characterize the Lewis’s acid-base properties of PLA polymer by its enthalpic (KA, KD) and entropic ( ω A , ω D ) acid-base constants using the following relations:
− ∆ H p = K A × D N ′ + K D × A N ′     − ∆ S a p = ω A × D N ′ + ω D × A N ′
where D N ′ and A N ′ are, respectively, the corrected electron donor and acceptor numbers of the polar molecule [62,63].
Experimental results showed that the relations (10) were not always satisfied. In similar cases, other relations (11) were proposed in literature [44,46,64] taking into consideration the amphoteric coupling constants K C C and ω C C of solid materials:
− ∆ H p = K A × D N ′ + K D × A N ′ − K C C × A N ′ × D N ′ − ∆ S a p = ω A × D N ′ + ω D × A N ′ − ω C C × A N ′ × D N ′
Relations (11) can be written as:
a i   K A + K D − b i   K C C = c H i   a i   ω A + ω D − b i   ω C C = c S i  
Where a i , b i , c H i and c S i , relative to the adsorbed polar molecule denoted by i , are known experimental values given by equations (13), whereas, K D , K A , K C C , ω A , ω D and ω C C are the unknown quantities of the problem (12)
a i = D N ′ A N ′ i b i = D N ′ i c H i = − ∆ H p A N ′   i c S i = − ∆ S p A N ′ i  
The unique solution of the system (12) can be obtained if the number n of polar solvents satisfies n ≥ 3 , by using the least squares method. The obtained solution K D ;   K A ;   K C C or ω D ;   ω A ;   ω C C thus minimizing the sum of the squares of the residuals.

Materials

PLA polymer and all organic solvents (highly pure grade (i.e., 99%) were purchased from Sigma-Aldrich. The various non-polar molecules used in this study were n-alkanes (pentane, hexane, heptane, octane, and nonane); acidic: dichloromethane, amphoteric: acetone and toluene; basic solvents: ethyl acetate and tetrahydrofuran (THF). The PLA particles of size between 100 and 250 m, were introduced into a stainless-steel column, which was 30 cm long and had an internal diameter of 5 mm. A mass of 1 g of PLA was used to fill the chromatographic column. The column filled with the sample was conditioned at 120 °C for 12 h to remove any impurities. Helium was used as carrier gas with a flow-rate equal to 25 mL/min. The IGC measurements at infinite dilution were carried out with a DELSI GC 121 FB Chromatograph equipped with a flame ionization detector of high sensitivity. The injector and detector temperatures were maintained at 180 ºC during the experiments. To achieve infinite dilution approach linear condition gas chromatography, 0.1 L of each probe was injected with 1 L Hamilton syringes. In such a way that the interactions between probe molecules can be neglected and only the interactions between the surface of the solid and an isolated probe molecule are important. The column temperatures were 40 to 100 °C, varied in 5 °C steps. Each probe injection was repeated three times, and the average retention time, was used for the calculation of the retention volume. The standard deviation was less than 1% in all measurements.

3. Results

3.1. London Dispersive Component of Surface Energy of PLA

By using the same procedure developed in previous studies [40,41] and by varying the temperature of the chromatographic column containing the PLA particles, IGC technique allowed us to obtain the net retention times of the various solvents adsorbed on the PLA polymer. This led to the net retention volumes of injected probes and therefore the values of R T l n V n of adsorbed organic molecules. The experimental results were given in Table S1 and S2 (Supporting Materials).
The London dispersive component γ s d ( T ) of the surface energy of PLA polymer was obtained by applying the Hamieh thermal model [43,44,45,64,65]. The variation of γ s d ( T ) of PLA polymer as a function of the temperature was plotted on Figure 1.
A non-linear evolution of γ s d ( T ) was observed (Figure 1a) showing an important change in the thermodynamic properties of PLA when the temperature varies. However, three linear variations were distinguished (Figure 1b) characterized by a decrease of γ s d ( T ) in the temperature interval [313.15K, 333.15] given by the equation (14):
γ s d T = − 0.384   T + 165.87
Passing by a minimum of the London dispersive surface energy equal to 35.8 mJ/m2 at T = 343.15 K , followed by an increase variation of γ s d ( T to reach a maximum equal to 56.4 mJ/m2 at T = 363.15 K , with the following straight-line equation (15):
γ s d T = 1.030   T + 317.68
And finally, a decrease characterized by equation (16):
γ s d T = − 1.272   T + 518.31
This interesting result highlighted the possible glass transition temperature of PLA around T g = 343.15 K (70°C) explained by the change in the variations of γ s d ( T ) of PLA before and after T g , when the temperature increases.

3.2. Polar Surface free Energy of PLA polymer

All thermodynamic surface properties of PLA polymer were obtained by using our new method of the harmonic mean of the ionization energies and the deformation polarizability of particles. Table 1 and Table 2 respectively presented the values of deformation polarizability, harmonic mean of the ionization energies and the parameter P P L A − X of the various organic molecules in interaction with the PLA polymer. The Handbook of Physics and Chemistry [66] were used to determine the parameters of the different solvents.
The obtained experimental results (Tables S1 and S2), the values in Table 1 and Table 2 and the equations 2, 4, and 8 allowed us to calculate the polar free surface energy ( − ∆ G a s p T ) of the polar solvents adsorbed on PLA polymer as a function of the temperature T (Table 3).
The results in Table 3 showed an amphoteric behavior of PLA with stronger basic character which is clearly shown by the high values of − ∆ G a s p T of dichloromethane, the most acidic solvent among the five used polar molecules, and then traducing the important interaction energy with PLA. It was observed in Table 3 that the variations of − ∆ G a s p T   for all polar molecules, are not linear. The curves of − ∆ G a s p T of polar solvents adsorbed on PLA in Figure 2 proved this non-linearity against the temperature with a maximum temperature around 343.15 K confirming the presence of the glass temperature of PLA which was previously shown with the variations of London dispersive surface energy γ s d T as a function of the temperature.

3.3. Lewis’s Acid–Base Constants of PLA

The curves of ( − ∆ G a s p T ) of polar molecules drawn in Figure 2 showed four different temperature intervals in which the variations of ( − ∆ G a s p T ) are represented by straight line with an excellent linear regression coefficient equal to 0.9990. The results were given in Table 4 with the different equations.
The values of the polar enthalpy ( − ∆ H a p ) and entropy ( − ∆ S a p ) of the polar molecules adsorbed on PLA polymer were deduced from the equations of ∆ G a s p T in Table 4. The values of these polar thermodynamic parameters were given in Table 5.
Table 5 allowed us to draw on Figure 3 the curves of ( − ∆ H a p ( T ) ) and entropy ( − ∆ S a p ( T ) ) of polar molecules as a function of the temperature
It was observed that the curves of Figure 3 present positive values of polar enthalpy and entropy of polar solvents before and after the glass transition temperature highlighting the adsorption phenomenon, whereas, the desorption was observed during the transition process showing a repulsive interaction around the glass transition.
By using the empirical relation (10) and the results in Table 5 and Figure 3, the Lewis enthalpic and entropic acid–base constants K A , K D ,   ω A , and ω D   of PLA polymer as a function of the temperature with their ratios were given in Table 6.
The results in Table 6 showed that the behavior of the PLA surface is 5.5 times more basic than acidic for a temperature less than 333.15K (Figure 4). The desorption of the polar solvents in the glass transition process led to a neutral surface of the polymer for 333.15 K   <   T   <   343.15 K characterized by negative values of the Lewis acid-base constants K A , K D ,   ω A , and ω D   of PLA. After the glass transition temperature, two zones were distinguished (Figure 4):
-
Stronger amphoteric character of PLA with highest values of the Lewis acid-base constants for 343.15 K < T < 353.15 K
-
Decreasing amphoteric behavior of PLA surface with lowest values of K A , K D ,   ω A , and ω D   of the polymer for T > 353.15 K
Table 6 and Figure 4 clearly showed the stronger basic character of PLA varying with the temperature and decreasing amphoteric behavior for larger temperatures ( T > 353.15 K )

Correction of the acid-base parameters of PLA

The validity of the equations (10) was not always satisfied as was shown by the values of the linear regression coefficients R2 given in Table 6. The correction reported by Hamieh et al. in other papers was applied in this work to give more accurate values of the acid-base constants of PLA polymer. Equations (11) to (13) were used with procedure developed in a recent paper [42]. The corrected results were presented in Table 7.
The comparison between the results in Table 6 and Table 7 showed that the error committed by neglecting the amphoteric constant reaches 25%, however, the tendency of the acid-base behavior of PLA remains the same with two used methods.

3.3. Dispersive and Polar Free Energy of PLA

This new method applied on the PLA polymer using the London dispersion interaction equation resulted in the net separation of the London dispersive free energy ∆ G a d ( T ) and the polar free energy ∆ G a p ( T ) of interaction between the PLA and the adsorbed organic molecules. By using equation (3), it was possible to experimentally determine the values of ∆ G a d ( T ) of all molecules adsorbed on the PLA polymer from the following equation:
∆ G a d T = A 3 N 2 4 π ε 0 2 P S X
Where the values of the parameter A was determined from the experimental results (Table 8).
It was observed that the variations of the parameter A given in Table 7 passed through a minimum corresponding exactly to the glass transition temperature T g = 343.15 K .
The values of ∆ G a d ( T ) of the adsorbed organic molecules were determined (Tables S3 and S4). The obtained results led drawing the variations of ∆ G a d ( T ) also showed a minimum at glass transition as was shown in Figure 5.
The experimental determination of the dispersive ∆ G a d ( T ) and polar ∆ G a p ( T ) energy of interaction allowed us to obtain the total free energy ∆ G a 0 T of organic molecules (Table S5 and Figure S1) that also highlighted the presence of the glass transition

3.4. Average Separation Distance H

Table 8 and equation 7 allowed determining the average separation distance H between PLA surface and the organic molecules as a function of the temperature. The obtained results are given in Table 9. These results showed a slight variation of the separation distance when the temperature varies, but it respects the general tendency observed with the other thermodynamic variables showing a signature at the glass transition temperature reported for H = 8.30 Å (Figure S2). The results in Table 9 and Figure S2 showed a small increase of the separation distance when the temperature increases until the glass transition T < 343.15 K , followed by a slight decrease of H after this temperature. This result confirmed that obtained by the stronger acid-base constants of PLA obtained for T > 343.15 K .

3.4. Lewis Acid-Base Surface Energies of PLA

To determine the acid γ s + and base γ s − surface energy of PLA polymer, Van Oss’s relation was used [67]:
− ∆ G a p X − P o l a r = 2 N a X γ l X − γ s + + γ l X + γ s −
Where γ l X + and γ l X − are the respective acid and base surface energy of the polar molecule X adsorbed on PLA surface with a X the surface area of the adsorbed solvent.
Using the experimental values relative to ethyl acetate (EA) and dichloromethane (CH2Cl2) respectively given by γ E A + = 0 , γ E A − = 19.2   m J / m 2 and γ C H 2 C l 2 + = 5.2   m J / m 2 , γ C H 2 C l 2 − = 0 ; it was possible to determine the values of γ s + and γ s − of PLA polymer by using equations (19):
γ s + = ∆ G a s p T E A 2 4 N 2 a E A 2 γ E A −                                   γ s − = ∆ G a s p T C H 2 C l 2 2 4 N 2 a C H 2 C l 2 2 γ C H 2 C l 2 +  
Whereas, the acid-base (polar) surface energy γ s A B of PLA was obtained from equation (20):
γ s A B = 2 γ s + γ s −
The results were reported in Table 10 and Figure S3. The variations of the acid and base surface energies versus the temperature showed a decrease of these surface energy parameters and then an increase reaching a maximum at the glass transition temperature, followed by a final decrease until T = 373.15 K . An important basic surface energy γ s − of PLA was observed with smaller acidic surface energy.
The results in Table 10 with those relative to the dispersive surface energy of PLA previously obtained in this work, led to the determination of the Lifshitz – Van der Waals (LW) surface energy γ s L W (Table 11) by using equation (21):
γ s L W = γ s d + γ s A B

3.5. Polar Component of the Surface Energy of Polar Molecules

By using the previous results and the equation (22) relating the polar free energy of polar molecules adsorbed on PLA to the polar components of the surface energy of the PLA polymer γ s p and the polar organic molecules γ l p .
− ∆ G a p X = 2 N a X   γ s p γ l p   o r     γ l p = − ∆ G a p X 2 4 N 2 a X 2 γ s p                          
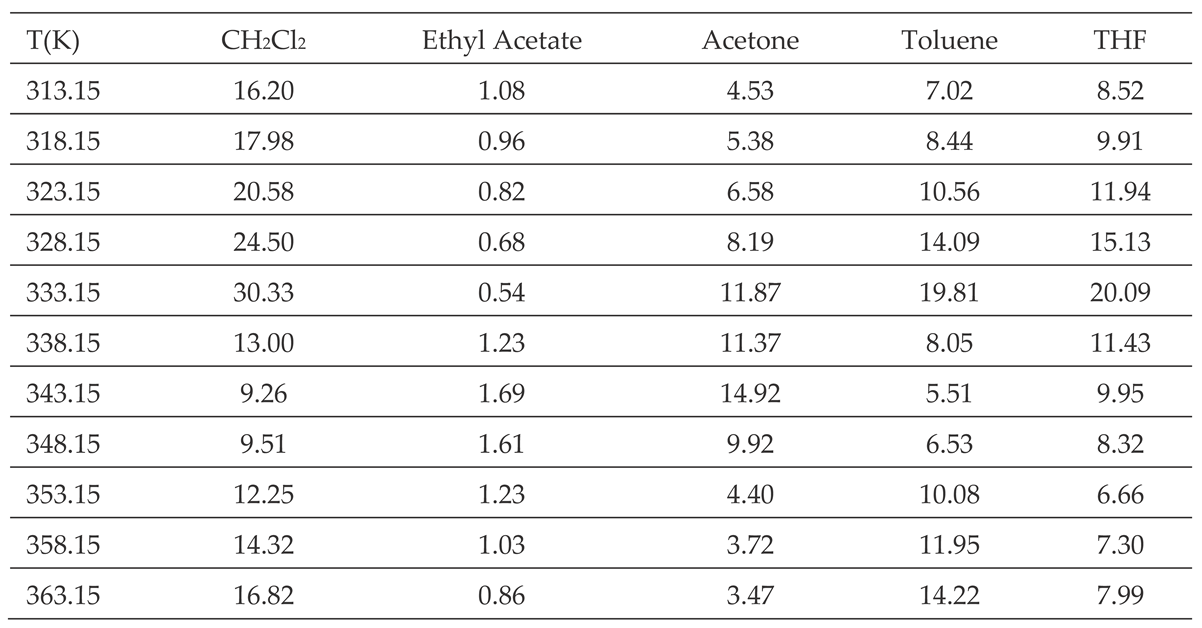
γ l p of polar molecules was directly obtained from equation (22). The results were given in Table 12
Table 12 showed that among all obtained values of the polar components of the surface energy of polar molecules, the stronger γ l p values were obtained with the dichloromethane, the highest acidic solvent used in this study, once again proving the highest Lewis basicity of PLA polymer.

4. Conclusion

Inverse gas chromatography (IGC) at infinite dilution was used to determine the surface thermodynamic properties of the biodegradable poly lactic acid considered as the most interesting material that can be used in 3D and printing applications. The new method used was that based on the London dispersion interaction equation. This equation took into account the polarizability and the harmonic mean of the ionization energies PLA polymer and adsorbed organic solvents. The London dispersive energy of PLA material was determined by using the Hamieh thermal model. The free dispersive and polar energies of adsorbed solvents were obtained by using the new parameter P S X and the net retention volumes of adsorbed probes from chromatographic measurements. The variations of all thermodynamic parameters of interaction of organic molecules adsorbed on PLA highlighted four temperature intervals with linear equations in each interval of temperature. A glass transition temperature of PLA was located at T g = 343.15 K . The presence of this transition phenomenon had an important effect on the non-linearity in the domain of temperature containing the glass transition temperature. This conducted to the strong variation of the enthalpic and entropic acid base constants of PLA as a function of the temperature. A stronger basic character of PLA surface was highlighted before and after the glass transition. A slight variation of the average separation distance between the PLA polymer and the solvents.
The determination of the various components γ s + , γ s − , and γ s A B of acid–base surface energies of PLA allowed us to calculate the Lifshitz – Van der Waals surface energy γ s L W . A dominant basic surface character was shown with a highest value of γ s − of PLA. All these surface parameters confirmed the presence of T g = 343.15 K for the poly lactic acid.
The application of this new method allowed a net separation between the polar and dispersive free energy and also the determination of the polar components of the surface energy of polar solvents adsorbed on PLA polymer. These new findings are very useful and can be directly applied to an accurate determination of the dispersive and polar works of adhesion between the PLA surface and other materials.

Supplementary Materials

The following supporting information can be downloaded at the website of this paper posted on Preprints.org. Table S1. Values of - R T l n V n (in kJ/mol) of the various non-polar solvents adsorbed on PLA polymer as a function of the temperature. Table S2. Values of - R T l n V n (in kJ/mol) of the various polar solvents adsorbed on PLA polymer as a function of the temperature. Table S3. Values of - ∆ G a d ( T ) (kJ/mol) of the various non-polar solvents adsorbed on PLA polymer as a function of the temperature. Table S4. Values of - ∆ G a d ( T ) (kJ/mol) of the various polar solvents adsorbed on PLA polymer as a function of the temperature. Table S5. Values of - ∆ G a 0 ( T ) (kJ/mol) of the various polar solvents adsorbed on PLA polymer as a function of the temperature. Figure S1. Variations the total free energy ∆ G a d ( T ) (kJ/mol) of polar molecules adsorbed on PLA polymer as a function of the temperature. Figure S2. Variations of the average separation distance H (in Å) as a function of the temperature Figure S3. Variations of the polar acid and base surface energies γ s + , γ s − and γ s A B (mJ/m2) of PLA as a function of the temperature.

Funding

This research received no external funding.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

The data presented in this study are available in article and Supplementary Materials.

Conflicts of Interest

The author declares no conflicts of interest.

References

  1. Lakshmi Priya Muthe, Kim Pickering, Christian Gauss, A Review of 3D/4D Printing of Poly-Lactic Acid Composites with Bio-Derived Reinforcements, Composites Part C, Volume 8, 2022, 100271. [CrossRef]
  2. Y. Zhang, Y. Gao, L. Michelin, L. Josien, L. Vidal, G. Schrodj, A. Simon-Masseron, J. Lalevée. Photopolymerization of ceramic/zeolite reinforced photopolymers: Towards 3D/4D printing and gas adsorption applications. Eur. Polym. J. 2022, 179, 111552. [Google Scholar] [CrossRef]
  3. J. Yin, X. Zhao, B. Hu, Q. Zhou, Y. Yu, Y. Zhang, J. Gao, Y. Xu, J. Lalevée. Fabrication of a Novel Fluorescein Embedded Photocomposite Based on Interpenetrating Polymer Network (IPN) and Its Application in 4D Printing. Adv. Mater. Technol. 2024, 9, 2301323. [Google Scholar] [CrossRef]
  4. X. Zheng, H. Lee, T. H. Weisgraber, M. Shusteff, J. Deotte, E. B. Duoss, J. D. Kuntz, M. M. Biener, Q. Ge, J. A. Jackson, S. O. Kucheyev, N. X. Fang, C. M. Spadaccini. Ultraléger, ultra-rigideMétamatériaux mécanique. Science 2014, 344, 1373. [Google Scholar]
  5. J. W. Stansbury, M. J. Idacavage. 3D printing with polymers: Challenges among expanding options and opportunities. Dent. Mater. 2016, 32, 54–64. [Google Scholar] [CrossRef] [PubMed]
  6. M. Shahbazi, H. Jäger, R. Ettelaie, A. Mohammadi, P. Asghartabar Kashi, Multimaterial 3D printing of self-assembling smart thermo-responsive polymers into 4D printed objects: A review. Addit. Manuf. 2023, 71, 103598. [Google Scholar]
  7. C. Hull. Apparatus for production of three-dimensional objects by stereothography. United States Patent No. 4575330, 1986. [Google Scholar]
  8. B. Jian, F. Demoly, Y. Zhang, H. J. Qi, J.-C. André, S. Gomes. Origami-Based Design for 4D Printing of 3D Support-Free Hollow Structures. Engineering 2022, 12, 70–82. [Google Scholar] [CrossRef]
  9. Y. Zhang, Y. Xu, A. Simon-Masseron, J. Lalevée. Radical photoinitiation with LEDs and applications in the 3D printing of composites. Chem. Soc. Rev. 2021, 50, 3824. [Google Scholar] [CrossRef] [PubMed]
  10. J. J. Schwartz, A. J. Boydston. Multimaterial actinic spatial control 3D and 4D printing. Nat. Commun. 2019, 10, 791. [Google Scholar] [CrossRef]
  11. G.C. Dumitrescu, I.A. Tanase. 3D Printing – A New Industrial Revolution. Knowl. Horizons. Econ. 2016, 8, 32–39. Available online: https://econpapers.repec.org/article/kh ejournl/v_3a8_3ay_3a2016_3ai_3a1_3ap_3a32-39.htm.
  12. T. Pereira, J.V. Kennedy, J. Potgieter, A comparison of traditional manufacturing vs additive manufacturing, the best method for the job, Procedia Manuf 30 (2019) 11–18. [CrossRef]
  13. N.Z. Nkomo, A review of 4D printing technology and future trends, National University of Science and Technology, Zimbabwe, 2018. Available online: https://www.researchgate.net/publication/328162917%0AA.
  14. X. Li, J. Shang, Z. Wang, Intelligent materials: A review of applications in 4D printing, Assem. Autom. 37 (2017) 170–185. [CrossRef]
  15. S. Tibbits, C. McKnelly, C. Olguin, D. Dikovsky, S. Hirsch, 4D printing and universal transformation, ACADIA 2014 - Des. Agency Proc. 34th Annu. Conf. Assoc. Comput. Aided Des. Archit, 2014-Octob (2014) 539–548.
  16. F. Momeni, S. M.Mehdi Hassani.N, X. Liu, J. Ni, A review of 4D printing, Mater. Des. 122 (2017) 42–79. [CrossRef]
  17. Nor Amira Izzati Ayob , Nurul Fazita Mohammad Rawi, Azniwati Abd Aziz, Baharin Azahari and Mohamad Haafiz Mohamad Kassim. "The properties of 3D printed poly (lactic acid) (PLA)/poly (butylene-adipate-terephthalate) (PBAT) blend and oil palm empty fruit bunch (EFB) reinforced PLA/PBAT composites used in fused deposition modelling (FDM) 3D printing" Physical Sciences Reviews, vol. 8, no. 12, 2023, pp. 5135-5151. [CrossRef]
  18. Cardoso, PHM, Coutinho, RRTP, Drummond, FR, da Conceição, MdoN, Thiré, RMdaSM. Evaluation of printing parameters on porosity and mechanical properties of 3D printed PLA/PBAT blend parts. Macromol Symp 2020;394:1–12. [CrossRef]
  19. Liu, Z, Wang, Y, Wu, B, Cui, C, Guo, Y, Yan, C. A critical review of fused deposition modeling 3D printing technology in manufacturing polylactic acid parts. Int J Adv Manuf Technol 2019;102:2877–89. [CrossRef]
  20. Iwata, T. Biodegradable and bio-based polymers: future prospects of eco-friendly plastics. Angew Chem Int Ed 2015;54:3210–5. [CrossRef]
  21. Farah, S, Anderson, DG, Langer, R. Physical and mechanical properties of PLA, and their functions in widespread applications — a comprehensive review. Adv Drug Deliv Rev 2016;107:367–92. [CrossRef]
  22. [80] A. Pappu, K.L. Pickering, V.K. Thakur, Manufacturing and characterization of sustainable hybrid composites using sisal and hemp fibres as reinforcement of poly (lactic acid) via injection moulding, Ind. Crops Prod. 137 (2019) 260–269. [CrossRef]
  23. A.V. Wijk, I.V. Wijk, 3D printing with biomaterials: Towards a sustainable and circular economy, IOS Press, 2015. [CrossRef]
  24. S.P. Dubey, V.K. Thakur, S. Krishnaswamy, H.A. Abhyankar, V. Marchante, J. L. Brighton, Progress in environmental-friendly polymer nanocomposite material from PLA: Synthesis, processing and applications, Vacuum 146 (2017) 655–663. [CrossRef]
  25. S. Wickramasinghe, T. Do, P. Tran, FDM-Based 3D printing of polymer and associated composite: A review on mechanical properties, defects and treatments, Polymers (Basel) 12 (2020) 1–42. [CrossRef]
  26. T. Mukherjee, N. Kao, PLA Based Biopolymer Reinforced with Natural Fibre: A Review, J. Polym. Environ. 19 (2011) 714–725. [CrossRef]
  27. M. Murariu, P. Dubois, PLA composites, From production to properties, Adv. Drug Deliv. Rev. 107 (2016) 17–46. [CrossRef]
  28. A.S. Getme, B. Patel, A review: Bio-fiber’s as reinforcement in composites of polylactic acid (PLA), Mater. Today Proc 26 (2019) 2116–2122. 2116–2122. [CrossRef]
  29. X. Wu, W.M. Huang, Y. Zhao, Z. Ding, C. Tang, J. Zhang, Mechanisms of the shape memory effect in polymeric materials, Polymers, 5 (2013) 1169–1202. [CrossRef]
  30. J. Zhou, S. Sheiko, Reversible shape-shifting in polymeric materials, J. Polym. Sci. Part B Polym. Phys. 54 (2016). [CrossRef]
  31. S.K. Leist, D. Gao, R. Chiou, J. Zhou, Investigating the shape memory properties of 4D printed polylactic acid (PLA) and the concept of 4D printing onto nylon fabrics for the creation of smart textiles, Virtual Phys. Prototyp. 12 (2017) 290–300. [CrossRef]
  32. C. Yang, B. Wang, D. Li, X. Tian, Modelling and characterisation for the responsive performance of CF/PLA and CF/PEEK smart materials fabricated by 4D printing, Virtual Phys. Prototyp. 12 (2017) 69–76. [CrossRef]
  33. K. Dogan, S. Boyacioglu, M. Kodal, O. Gokce, G. Ozkoc, Thermally induced shape memory behavior, enzymatic degradation and biocompatibility of PLA/ TPU blends: “Effects of compatibilization, J. Mech. Behav. Biomed. Mater. 71 (2017) 349–361. 2017. [CrossRef]
  34. F.S. Senatov, K.V. Niaza, M.Y. Zadorozhnyy, A.V. Maksimkin, S.D. Kaloshkin, Y. Z. Estrin, Mechanical properties and shape memory effect of 3D-printed PLA- based porous scaffolds, J. Mech. Behav. Biomed. Mater. 57 (2016) 139–148. 2016. [CrossRef]
  35. Mohapatra, AK, Mohanty, S, Nayak, SK. Study of thermo-mechanical and morphological behaviour of biodegradable PLA/PBAT/layered silicate blend nanocomposites. J Polym Environ 2014;22:398–408. [CrossRef]
  36. suji H, Ikada YJ, Blends of aliphatic polyesters. II. Hydrolysis of solution-cast blends from poly(L-lactide) and poly(E-caprolactone) in phosphate-buffered solution, (1998) J Appl Polym Sci, 67, 405–415. [CrossRef]
  37. Perego G, Cella GD, Bastioli C, Effect of molecular weight and crystallinity on poly(lactic acid) mechanical properties, (1996) J Appl Polym Sci, 59, 37–43. [CrossRef]
  38. Bledzki A, Fabrycy E, Degradable polymers - a technical report (1992), Polimery 37, 343-350. [CrossRef]
  39. Garlotta D, A Literature Review of Poly(Lactic Acid, (2001) J Polym Env, 9, 63–84. [CrossRef]
  40. T. Hamieh, New Progress on London Dispersive Energy, Polar Surface Interactions, and Lewis’s Acid–Base Properties of Solid Surfaces, Molecules 29 (5), 949. [CrossRef]
  41. T. Hamieh, London Dispersive and Lewis Acid-Base Surface Energy of 2D Single-Crystalline and Polycrystalline Covalent Organic Frameworks, Crystals 2024, 14(2), 148. [CrossRef]
  42. T. Hamieh, Inverse Gas Chromatography to Characterize the Surface Properties of Solid Materials, Chem. Mater. 2024, 2024. [CrossRef]
  43. Hamieh, T. Study of the temperature effect on the surface area of model organic molecules, the dispersive surface energy and the surface properties of solids by inverse gas chromatography. J. Chromatogr. A 2020, 1627, 461372. [Google Scholar] [CrossRef] [PubMed]
  44. Hamieh, T. New Methodology to Study the Dispersive Component of the Surface Energy and Acid–Base Properties of Silica Particles by Inverse Gas Chromatography at Infinite Dilution. J. Chromatogr. Sci. 2021, 60, 126–142. [Google Scholar] [CrossRef] [PubMed]
  45. Hamieh, T. New physicochemical methodology for the determination of the surface thermodynamic properties of solid particles. Appliedchem 2023, 3, 229–255. [Google Scholar] [CrossRef]
  46. Hamieh, T.; Ahmad, A.A.; Roques-Carmes, T.; Toufaily, J. New approach to determine the surface and interface thermodynamic properties of H-β-zeolite/rhodium catalysts by inverse gas chromatography at infinite dilution. Sci. Rep. 2020, 10, 20894. [Google Scholar] [CrossRef] [PubMed]
  47. London, F. The general theory of molecular forces. Trans. Faraday Soc. 1937, 33, 8–26. [Google Scholar] [CrossRef]
  48. Saint-Flour, C.; Papirer, E. Gas-solid chromatography. A method of measuring surface free energy characteristics of short carbon fibers. 1. Through adsorption isotherms. Ind. Eng. Chem. Prod. Res. Dev. 1982, 21, 337–341. [Google Scholar] [CrossRef]
  49. Saint-Flour, C.; Papirer, E. Gas-solid chromatography: Method of measuring surface free energy characteristics of short fibers. 2. Through retention volumes measured near zero surface coverage. Ind. Eng. Chem. Prod. Res. Dev. 1982, 21, 666–669. [Google Scholar] [CrossRef]
  50. Saint-Flour, C.; Papirer, E. Gas-solid chromatography: A quick method of estimating surface free energy variations induced by the treatment of short glass fibers. J. Colloid Interface Sci. 1983, 91, 69–75. [Google Scholar] [CrossRef]
  51. Schultz, J.; Lavielle, L.; Martin, C. The role of the interface in carbon fibre-epoxy composites. J. Adhes. 1987, 23, 45–60. [Google Scholar] [CrossRef]
  52. Donnet, J.-B.; Park, S.; Balard, H. Evaluation of specific interactions of solid surfaces by inverse gas chromatography. Chromatographia 1991, 31, 434–440. [Google Scholar] [CrossRef]
  53. Brendlé, E.E.; Papirer, E. A new topological index for molecular probes used in inverse gas chromatography for the surface nanorugosity evaluation, 2. Application for the Evaluation of the Solid Surface Specific Interaction Potential. J. Colloid Interface Sci. 1997, 194, 217–224. [Google Scholar] [CrossRef] [PubMed]
  54. Brendlé, E.E.; Papirer, E. A new topological index for molecular probes used in inverse gas chromatography for the surface nanorugosity evaluation, 1. Method of Evaluation. J. Colloid Interface Sci. 1997, 194, 207–216. [Google Scholar] [CrossRef] [PubMed]
  55. Sawyer, D.T.; Brookman, D.J. Thermodynamically based gas chromatographic retention index for organic molecules using salt-modified aluminas and porous silica beads. Anal. Chem. 1968, 40, 1847–1850. [Google Scholar] [CrossRef]
  56. Chehimi, M.M.; Pigois-Landureau, E. Determination of acid–base properties of solid materials by inverse gas chromatography at infinite dilution. A novel empirical method based on the dispersive contribution to the heat of vaporization of probes. J. Mater. Chem. 1994, 4, 741–745. [Google Scholar] [CrossRef]
  57. Donnet, J.-B.; Ridaoui, H.; Balard, H.; Barthel, H.; Gottschalk-Gaudig, T. Evolution of the surface polar character of pyrogenic silicas, with their grafting ratios by dimethylchlorosilane, studied by microcalorimetry. J. Colloid Interface Sci. 2008, 325, 101–106. [Google Scholar] [CrossRef] [PubMed]
  58. Jagiełło, J.; Ligner, G.; Papirer, E. Characterization of silicas by inverse gas chromatography at finite concentration: Determination of the adsorption energy distribution function. J. Colloid Interface Sci. 1990, 137, 128–136. [Google Scholar] [CrossRef]
  59. Rückriem, M.; Inayat, A.; Enke, D.; Gläser, R.; Einicke, W.-D.; Rockmann, R. Inverse gas chromatography for determining the dispersive surface energy of porous silica. Colloids Surfaces A Physicochem. Eng. Asp. 2010, 357, 21–26. [Google Scholar] [CrossRef]
  60. Bauer, F.; Meyer, R.; Czihal, S.; Bertmer, M.; Decker, U.; Naumov, S.; Uhlig, H.; Steinhart, M.; Enke, D. Functionalization of porous siliceous materials, Part 2: Surface characterization by inverse gas chromatography. J. Chromatogr. A 2019, 1603, 297–310. [Google Scholar] [CrossRef] [PubMed]
  61. Hamieh, T.; Schultz, J. New approach to characterise physicochemical properties of solid substrates by inverse gas chromatography at infinite dilution. J. Chromatogr. A. 2002, 969(1-2), 17-47. [CrossRef]
  62. Gutmann, V. The Donor-Acceptor Approach to Molecular Interactions; Plenum: New York, NY, USA, 1978. [Google Scholar]
  63. Riddle, F.L.; Fowkes, F.M. Spectral shifts in acid-base chemistry. Van der Waals contributions to acceptor numbers, Spectral shifts in acid-base chemistry. 1. van der Waals contributions to acceptor numbers. J. Am. Chem. Soc. 1990, 112, 3259–3264. [Google Scholar] [CrossRef]
  64. Hamieh, T.; Rageul-Lescouet, M.; Nardin, M.; Haidara, H.; Schultz, J. Study of acid-base interactions between some metallic oxides and model organic molecules. Colloids Surfaces A Physicochem. Eng. Asp. 1997, 125, 155–161. [Google Scholar] [CrossRef]
  65. Hamieh, T.; Schultz, J. Study of the adsorption of n-alkanes on polyethylene surface—State equations, molecule areas and covered surface fraction. Comptes Rendus L'acad. Sci. Sér. IIb 1996, 323, 281–289. [Google Scholar]
  66. Lide, D.R. (Ed.) CRC Handbook of Chemistry and Physics, 87th ed.; Internet Version 2007; Taylor and Francis: Boca Raton, FL, USA, 2007. [Google Scholar]
  67. Van Oss, C.J.; Good, R.J.; Chaudhury, M.K. Additive and nonadditive surface tension components and the interpretation of contact angles. Langmuir 1988, 4, 884–891. [Google Scholar] [CrossRef]
Preprints 100428 g001
Figure 1. Evolution of γ s d   ( m J / m 2 ) of PLA polymer as a function of the temperature T (K) by using the thermal model.
Figure 1. Evolution of γ s d   ( m J / m 2 ) of PLA polymer as a function of the temperature T (K) by using the thermal model.
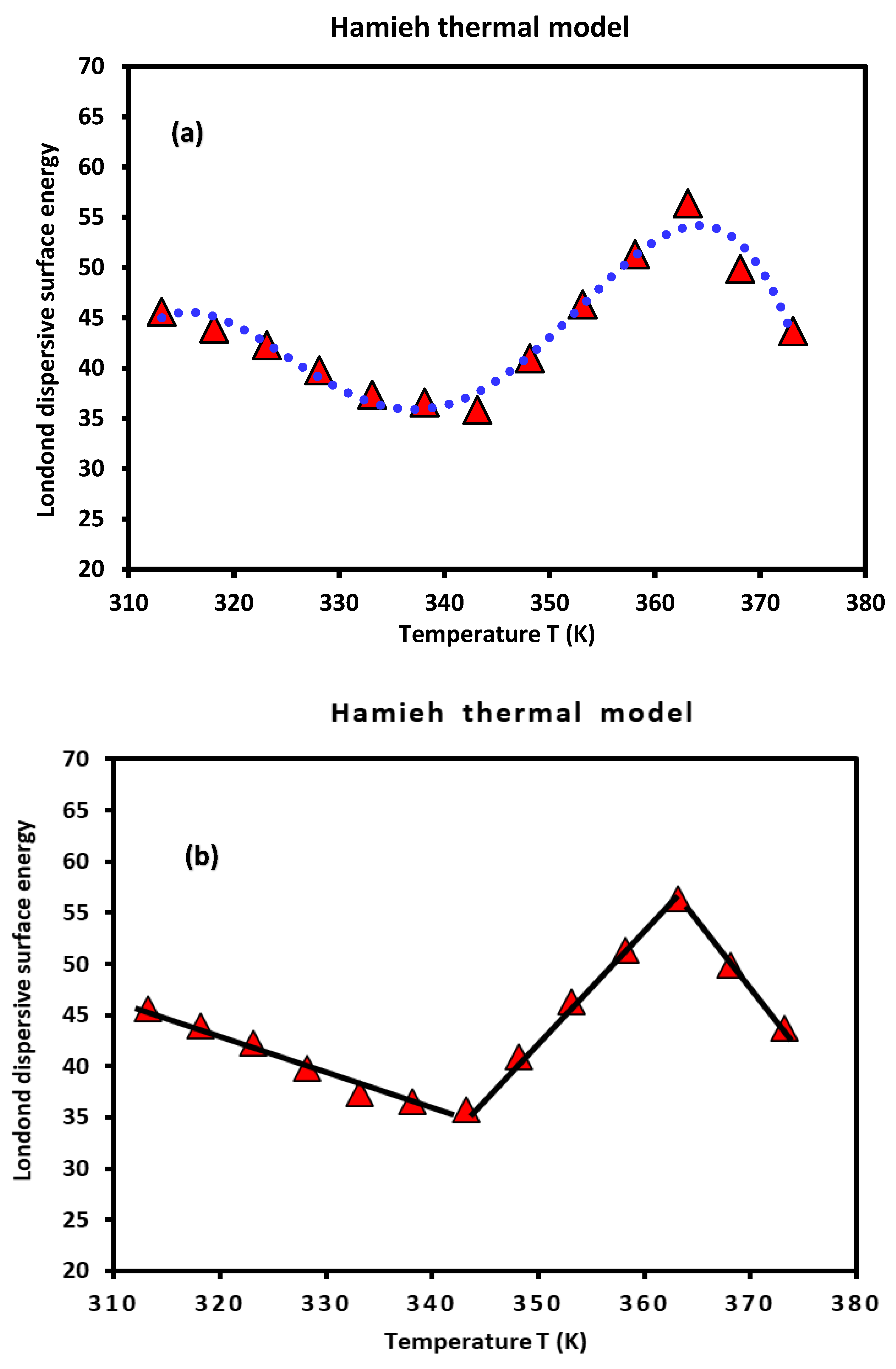
Preprints 100428 g001
Preprints 100428 g002
Figure 2. Variations of the polar free surface energy ( − ∆ G a s p T ) of polar solvents adsorbed on PLA polymer as a function of the temperature.
Figure 2. Variations of the polar free surface energy ( − ∆ G a s p T ) of polar solvents adsorbed on PLA polymer as a function of the temperature.
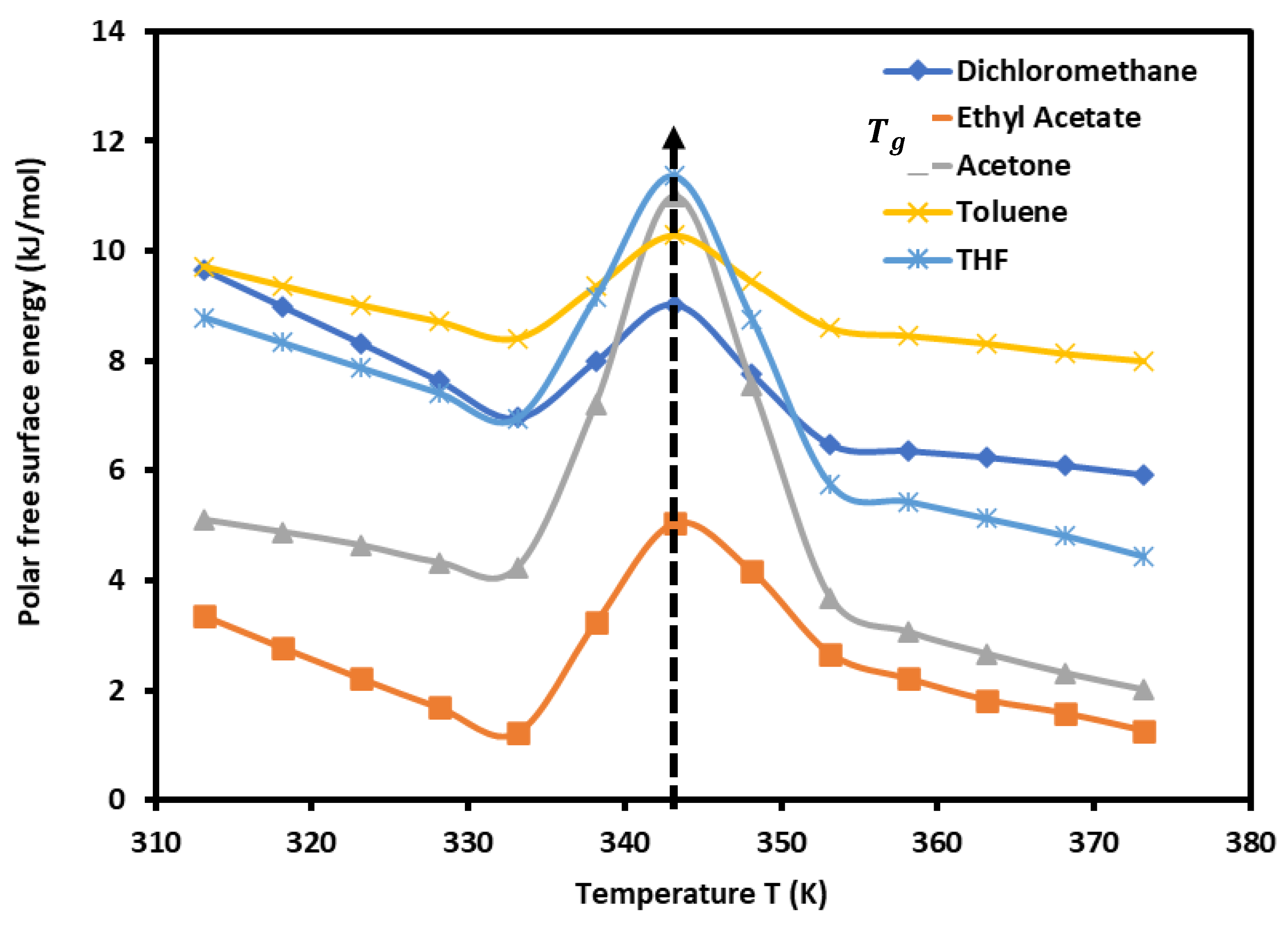
Preprints 100428 g002
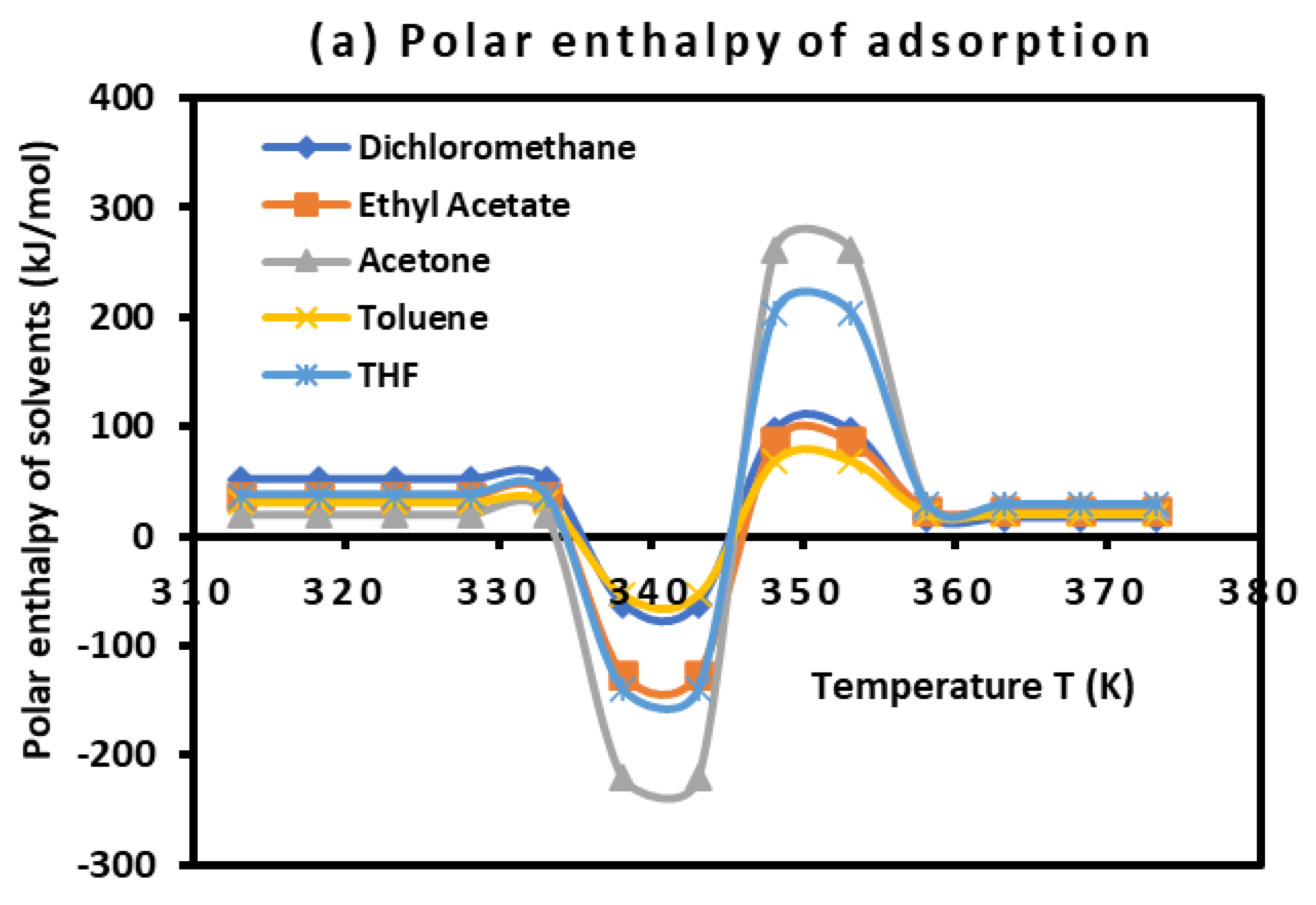
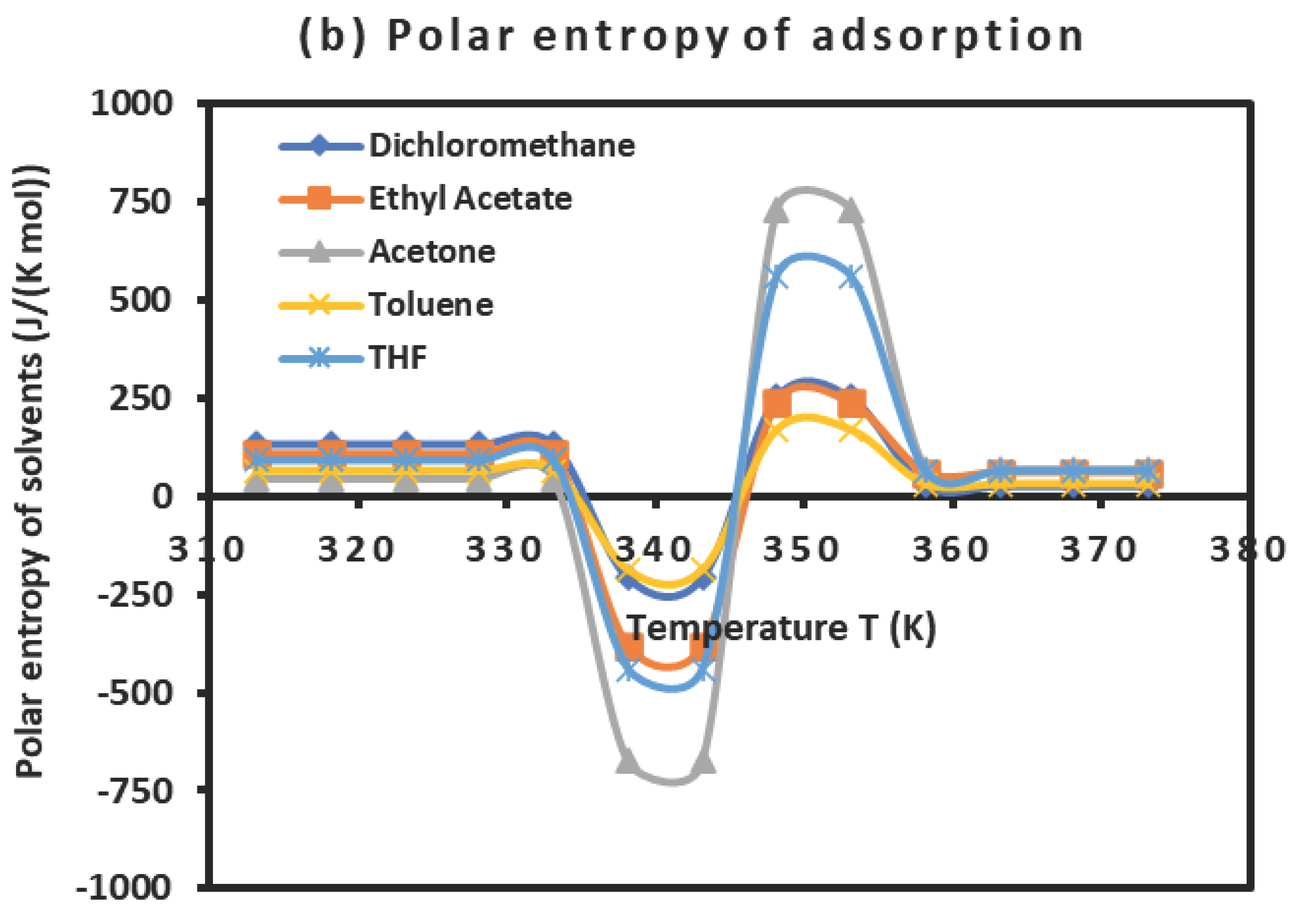
Preprints 100428 g003aPreprints 100428 g003b
Figure 3. Variations of ( − ∆ H a p ( T ) ) (a) and entropy ( − ∆ S a p ( T ) ) (b) of polar molecules adsorbed on PLA polymer as a function of the temperature.
Figure 3. Variations of ( − ∆ H a p ( T ) ) (a) and entropy ( − ∆ S a p ( T ) ) (b) of polar molecules adsorbed on PLA polymer as a function of the temperature.
Preprints 100428 g003aPreprints 100428 g003b
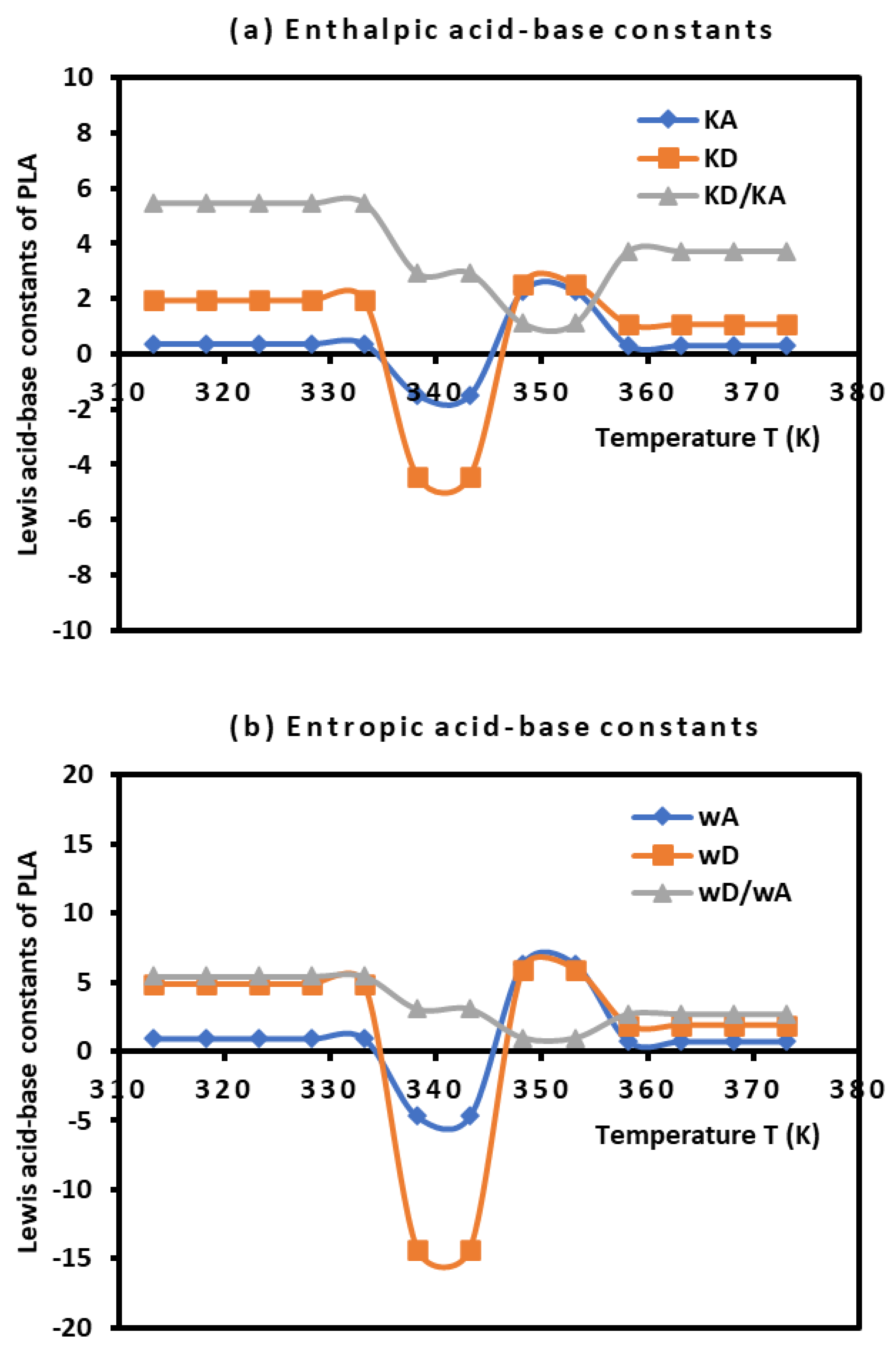
Preprints 100428 g004
Figure 4. Variations of the Lewis enthalpic acid–base constants K A and K D (a) and the Lewis entropic acid base constants ω A and ω D   (b) as a function of the temperature.
Figure 4. Variations of the Lewis enthalpic acid–base constants K A and K D (a) and the Lewis entropic acid base constants ω A and ω D   (b) as a function of the temperature.
Preprints 100428 g004
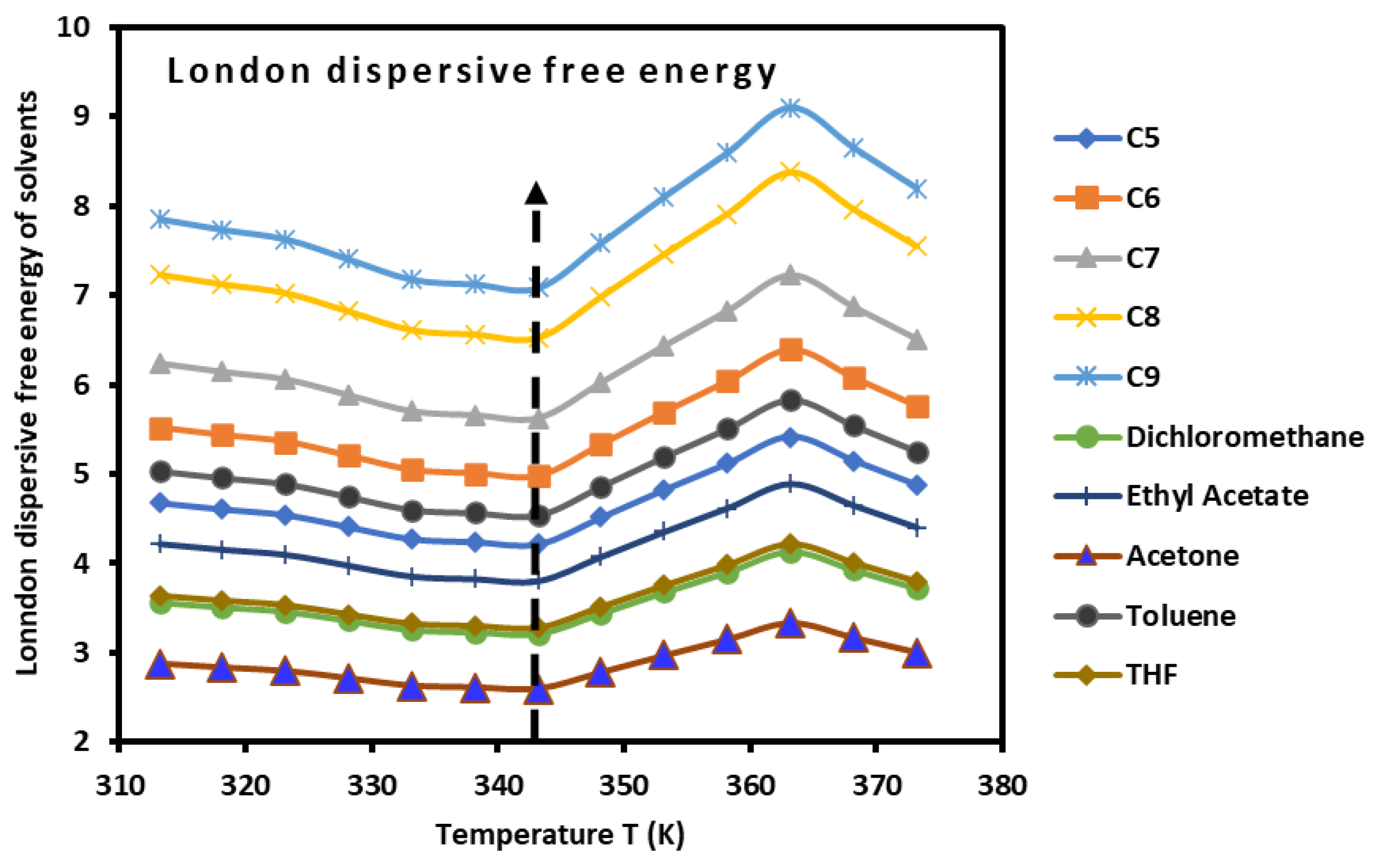
Preprints 100428 g005
Figure 5. Variations the London dispersive free energy ∆ G a d ( T ) (kJ/mol) of polar molecules adsorbed on PLA polymer as a function of the temperature.
Figure 5. Variations the London dispersive free energy ∆ G a d ( T ) (kJ/mol) of polar molecules adsorbed on PLA polymer as a function of the temperature.
Preprints 100428 g005
Table 1. Values of deformation polarizability α 0 (respectively in 10−30 m3 and in 10−40 C m2/V) and ionization energy ε (in eV) of the various organic molecules and PLA polymer.
Table 1. Values of deformation polarizability α 0 (respectively in 10−30 m3 and in 10−40 C m2/V) and ionization energy ε (in eV) of the various organic molecules and PLA polymer.
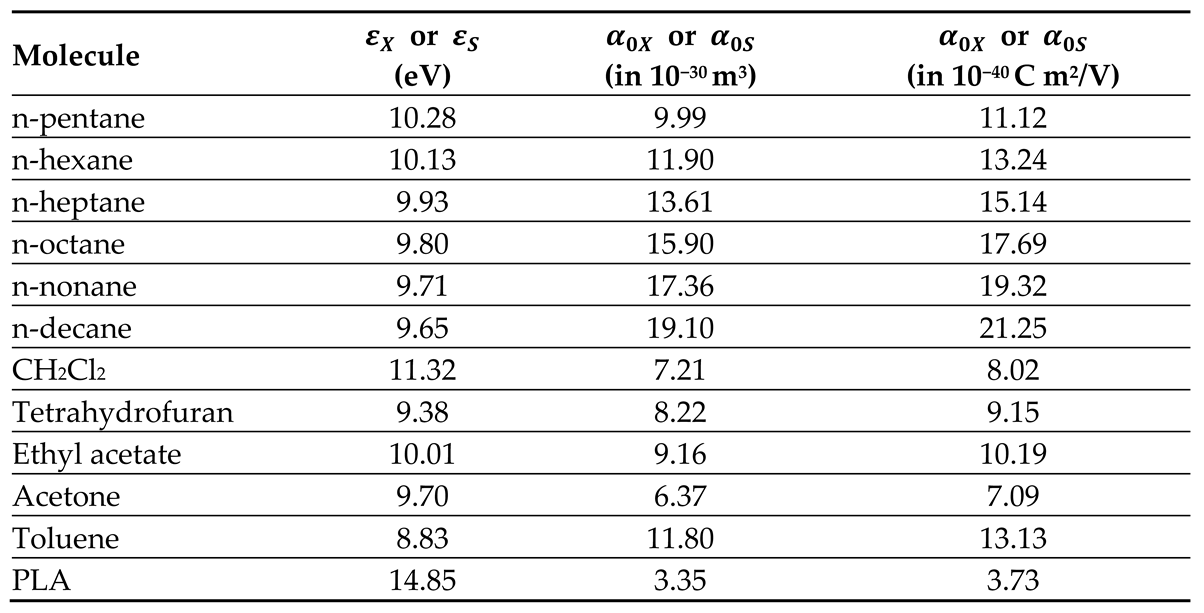Preprints 100428 i001
Table 2. Values of the harmonic mean of the ionization energies of PLA particles and organic solvents (in 10−19 J) and the parameter 3 N 2 4 π ε 0 2 P P L A − X (in 10−15 SI unit) for the various organic molecules.
Table 2. Values of the harmonic mean of the ionization energies of PLA particles and organic solvents (in 10−19 J) and the parameter 3 N 2 4 π ε 0 2 P P L A − X (in 10−15 SI unit) for the various organic molecules.
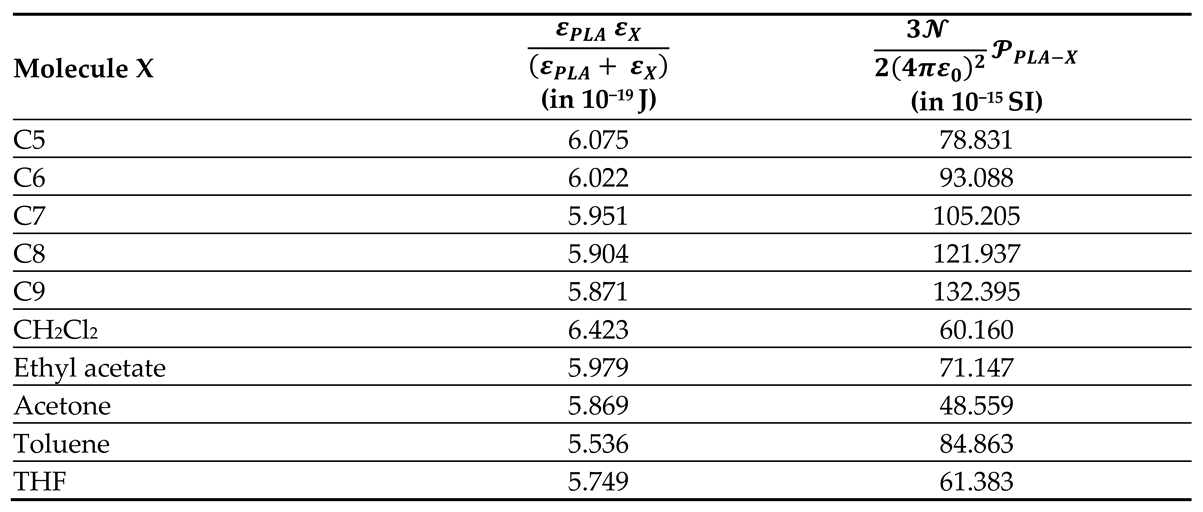Preprints 100428 i002
Table 3. Values of − ∆ G a p T (in kJ/mol) of polar molecules adsorbed on PLA.
Table 3. Values of − ∆ G a p T (in kJ/mol) of polar molecules adsorbed on PLA.
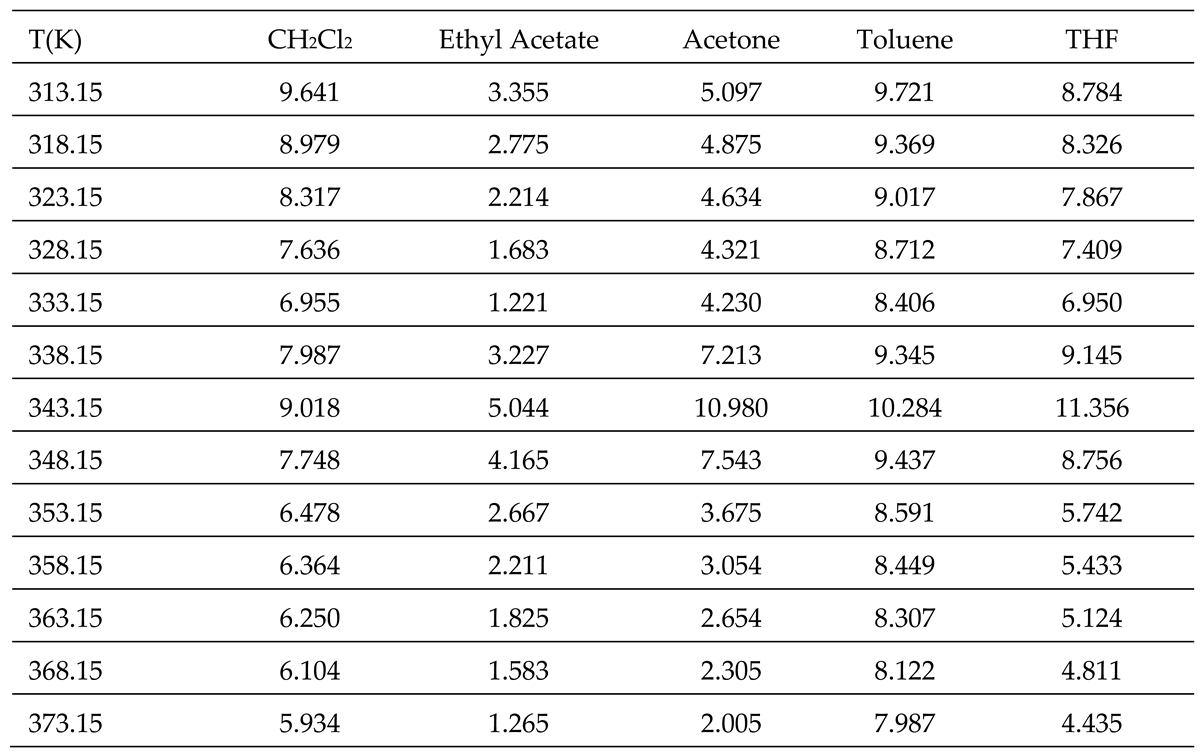Preprints 100428 i003
Table 4. Equations of − ∆ G a s p ( T ) of the polar solvents adsorbed on PLA for the different temperature intervals.
Table 4. Equations of − ∆ G a s p ( T ) of the polar solvents adsorbed on PLA for the different temperature intervals.
Preprints 100428 i004
Table 5. Values of polar enthalpy ( − ∆ H a p   i n   k J   m o l − 1 ) and entropy ( − ∆ S a p i n   J   K − 1 m o l − 1 ) of polar probes adsorbed on PLA.
Table 5. Values of polar enthalpy ( − ∆ H a p   i n   k J   m o l − 1 ) and entropy ( − ∆ S a p i n   J   K − 1 m o l − 1 ) of polar probes adsorbed on PLA.
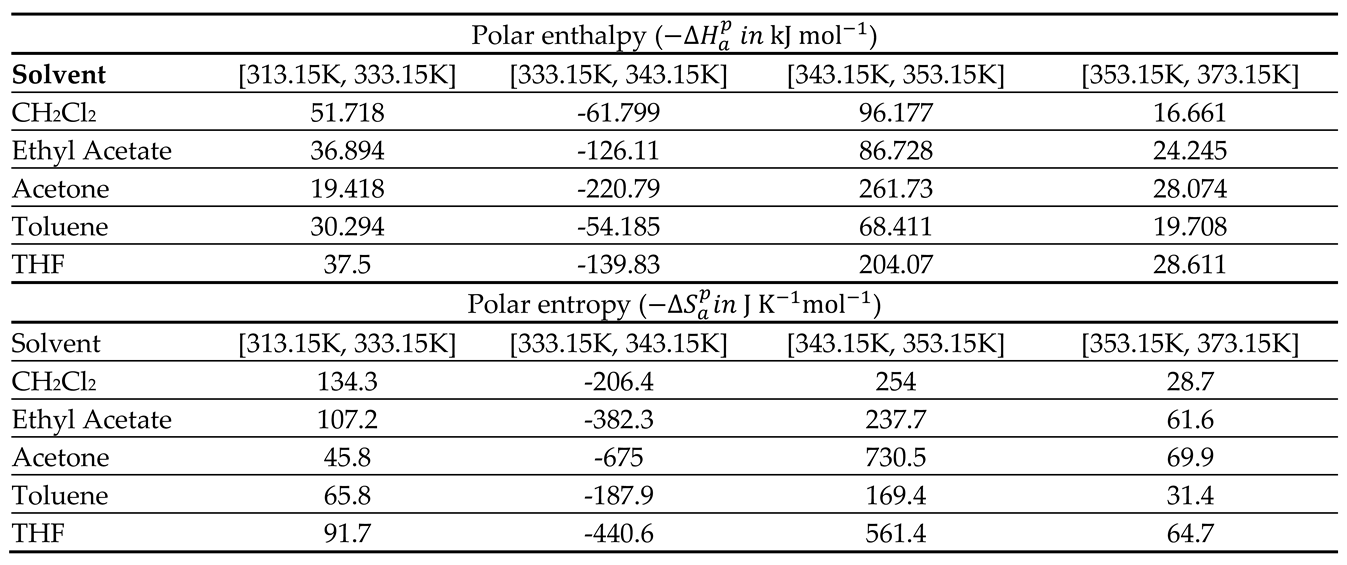Preprints 100428 i005
Table 6. Values of the enthalpic acid–base constants K A and K D   (unitless), the entropic acid base constants ω A and ω D   (unitless), the acid–base ratios of PLA, and the linear regression coefficients.
Table 6. Values of the enthalpic acid–base constants K A and K D   (unitless), the entropic acid base constants ω A and ω D   (unitless), the acid–base ratios of PLA, and the linear regression coefficients.
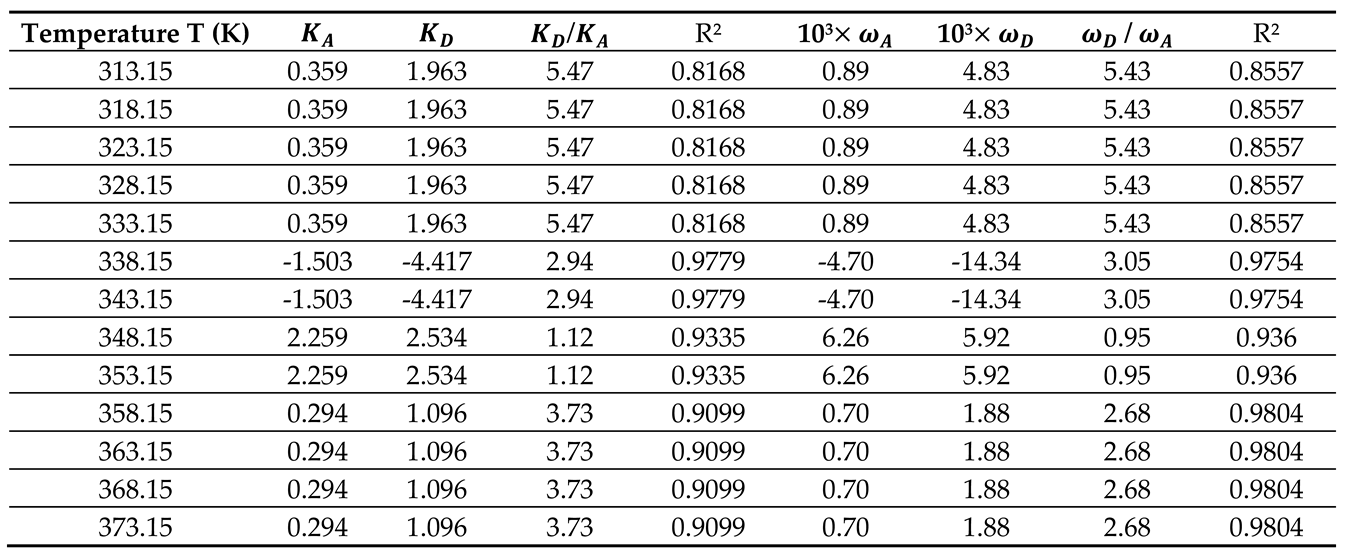Preprints 100428 i006
Table 7. Values of the corrected acid–base constants K A , K D ,     K C C , ω A , ω D , ω C C and the acid–base ratios of PLA.
Table 7. Values of the corrected acid–base constants K A , K D ,     K C C , ω A , ω D , ω C C and the acid–base ratios of PLA.
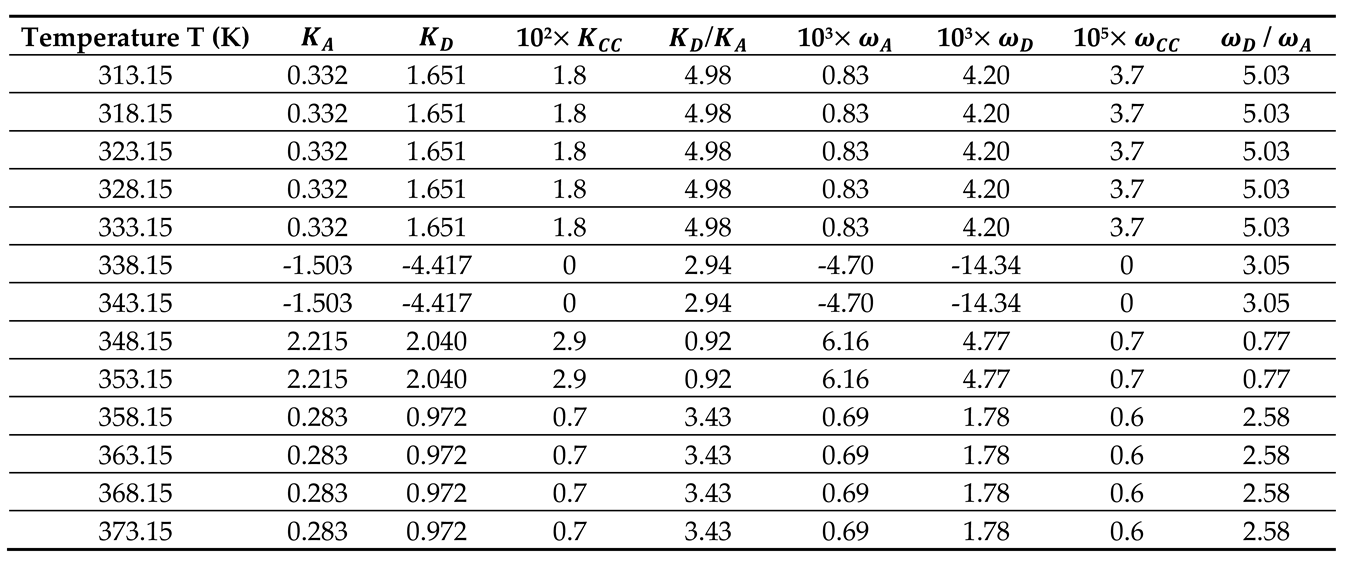Preprints 100428 i007
Table 8. Values of the parameter A as a function of the temperature.
Table 8. Values of the parameter A as a function of the temperature.
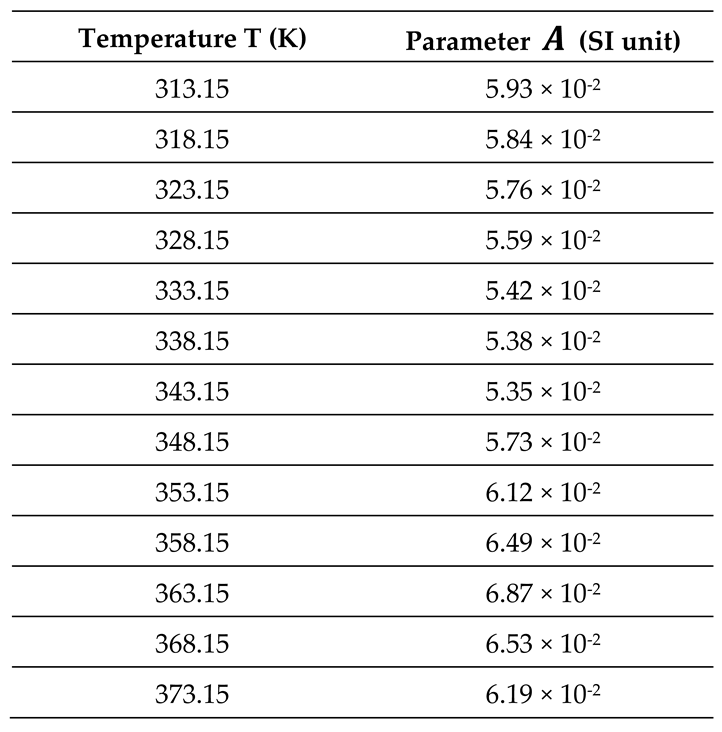Preprints 100428 i008
Table 9. Values of the average separation distance H (in Å) as a function of the temperature.
Table 9. Values of the average separation distance H (in Å) as a function of the temperature.
Temperature T (K) Separation distance H (in Å)
313.15 8.16
318.15 8.18
323.15 8.20
328.15 8.24
333.15 8.29
338.15 8.30
343.15 8.30
348.15 8.21
353.15 8.12
358.15 8.04
363.15 7.97
368.15 8.03
373.15 8.10
Table 10. Values of the polar acid and base surface energies γ s + , γ s − and γ s A B (mJ/m2) of PLA as a function of the temperature.
Table 10. Values of the polar acid and base surface energies γ s + , γ s − and γ s A B (mJ/m2) of PLA as a function of the temperature.
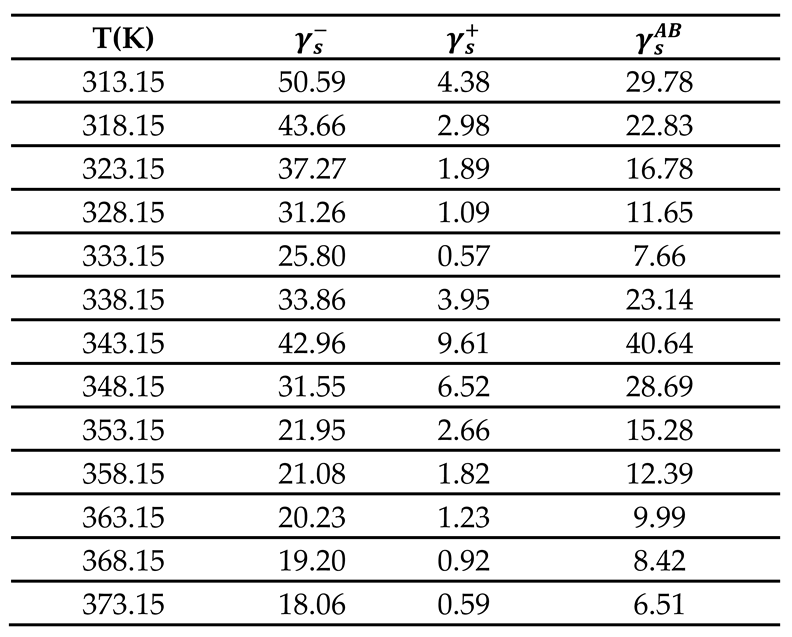Preprints 100428 i009
Table 11. Values of the polar acid and base surface energies γ s + , γ s − and γ s A B (mJ/m2) of PLA as a function of the temperature.
Table 11. Values of the polar acid and base surface energies γ s + , γ s − and γ s A B (mJ/m2) of PLA as a function of the temperature.
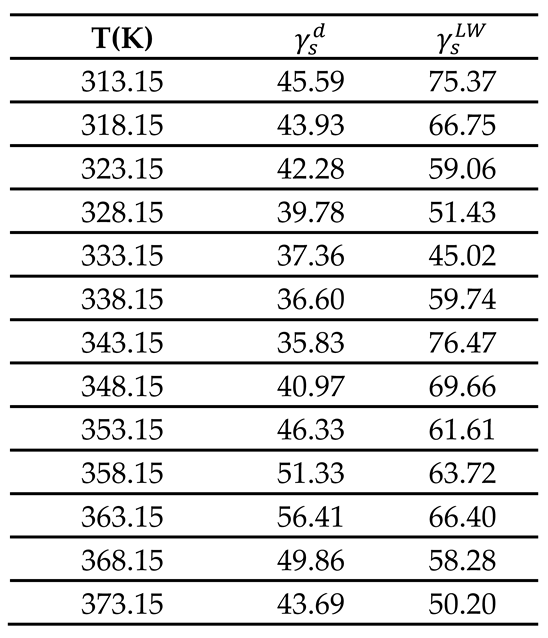Preprints 100428 i010
Table 12. Values of γ l p (mJ/m2) of polar molecules adsorbed on PLA.
Table 12. Values of γ l p (mJ/m2) of polar molecules adsorbed on PLA.
Preprints 100428 i011Preprints 100428 i012
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated