Kinematics of Balls and Light Versus the Theory of Special Relativity

Preprint

Article

Kinematics of Balls and Light Versus the Theory of Special Relativity

Altmetrics

Downloads

193

Views

107

Comments

Filip Dambi^*

This version is not peer-reviewed

Submitted:

31 May 2024

Posted:

03 June 2024

Read the latest preprint version here

Alerts

Abstract

The study of the emission, propagation, and reflection of balls in Newtonian mechanics, applying the laws of conservation of momentum and energy when the mass of the balls converges to zero, concludes that the kinematics of light are like those of massless balls. The kinematics of light explain why the speed of light is the constant c in each inertial frame in which the light source and reflective mirror are at rest, why the laws of physics have the same form in each inertial frame, and why any light experiment in an inertial frame cannot prove the motion of that inertial frame. The following law of mechanics governs the kinematics of balls and electromagnetic radiation: Each inertial frame drags at its velocity the balls and electromagnetic radiation emitted by bodies at rest in that inertial frame. The theory of special relativity misapplies the symmetry observed in phenomena to two inertial frames; therefore, it duplicates a physical phenomenon from one inertial frame, which is considered stationary, into another. There are multiple issues rooted in Lorentz's and Einstein's transformations. For example, transformations offer the speed of light at the constant c in the moving and opposite directions of the inertial frame. At the same time, it is variable in any other direction, converging to infinity. Time contraction in the moving direction of the inertial frame is different from time dilation in the opposite direction. It requires a ruler and time synchronization in each direction. There are no length contractions in Lorentz's and Einstein's transformations to support the fundamental concept of length contraction in special relativity. With these unacceptable conclusions, the theory of special relativity is self-negating.

Keywords:

Subject: Physical Sciences - Theoretical Physics

1. Introduction

The kinematics of balls are independent of their mass. However, their kinetics depend on it because the energy consumed to change their states is proportional to their mass. Suppose that a carrier moves balls with different masses from rest to a velocity

v

. The carrier consumes energy for itself and different energy for each ball according to its mass. At the velocity

v

, the carrier and balls continue traveling independently from one another and without consuming energy. The energy that the carrier consumes to reach velocity

v

is stored proportionally in the carrier and each ball in the form of momentum according to the carrier and balls' mass. At the limit when the mass of the balls converges to zero, hypothetical massless balls have the same velocity

v

without consuming energy and without having momentum.

Suppose that the carrier has a hypothetical source that emits balls of different masses at a velocity

V

when the carrier is at velocity

v

. The balls with mass or that are massless will have the same velocity given by the vector sum of velocity

v

and

V

. Therefore, it is rational to compare the kinematics of light with those of massless balls, whose velocity depends on the source velocity

v

and emitted velocity

V

. We call this dependency the dragging of balls emitted at velocity

V

by the source velocity

v

. For light, we have the dragging of light emitted at velocity

c

of electromagnetic nature by the source velocity

v

of mechanical nature. The law of dragging balls and electromagnetic radiation emitted by bodies is based on this simple understanding of the Newtonian laws of mechanics.

2. Kinematics of Balls

2.1. Balls Brought from Rest to a Velocity $v$

A constant force

F

acts on a ball of mass

m

with a constant acceleration

a

in a straight line of length

d

from rest to a speed

v

. In time

t

, while the speed of the ball increases from zero to

v

, the inertial force

F_{i}

of the ball acts with the same magnitude in the opposite direction of force

F

, which changes its state. The energy

E

consumed to overcome

F_{i}

is given by the mechanical work created by the force

F

L = F \times d = m \times a \times (1 / 2) \times a \times t^{2} = (1 / 2) m v^{2}

. While the ball is moved from rest to speed

v

, it gains energy

E

stored in its momentum

P = m v

, which opposes any force that would change its new state. Indeed, the integral of momentum

P = m v

, as a linear function with a constant slope

m

and variable speed from zero to

v

, gives the energy gained by the ball of

(1 / 2) m v^{2} = E

. The ball continues to travel at velocity

v

when the force

F

stops.

Suppose that a carrier with balls of different masses stops at velocity

v

. In that case, all balls continue traveling independently from the carrier and one another with velocity

v

, regardless of their mass, including hypothetical massless ones. Differently from balls with mass, the massless balls travel from rest to speed

v

without energy consumption,

E = 0

, without a force,

F = 0

, to act upon them, and without momentum after that,

P = 0

. Massless balls need a carrier that only consumes energy for itself.

2.2. Elastic Collision of Two Balls Moving in Opposite Directions

In the absolute frame, two balls, one of mass

m_{1}

traveling at velocity

v_{1}

and another of mass

m_{2}

traveling at velocity

v_{2}

, are engaged in a frontal elastic collision, as in Figure 1. The velocities of the balls after collision are

v_{1}^{'}

and

v_{2}^{'}

, respectively. The equations for the law of conservation of momentum and the energy of the balls before and after collision are

m_{1} v_{1} + m_{2} v_{2} = m_{1} v_{1}^{'} + m_{2} v_{2}^{'}, a n d

(1)

\frac{1}{2} m_{1} v_{1}^{2} + \frac{1}{2} m_{2} v_{2}^{2} = \frac{1}{2} m_{1} v_{1}^{' 2} + \frac{1}{2} m_{2} v_{2}^{' 2}

(2)

The two equations yield the solution for speeds

v_{1}^{'} = \frac{m_{1} - m_{2}}{m_{1} + m_{2}} v_{1} + \frac{2 m_{2}}{m_{1} + m_{2}} v_{2}

and

v_{2}^{'} = \frac{2 m_{1}}{m_{1} + m_{2}} v_{1} + \frac{m_{2} - m_{1}}{m_{1} + m_{2}} v_{2} .

m_{1} ≫ m_{2}

, the simplified solutions are

v_{1}^{'} ≅ v_{1}

and

v_{2}^{'} ≅ 2 v_{1} - v_{2}

, which are given with approximations. The solutions are offered without considering the directions of velocities

v_{1}^{'}

and

v_{2}^{'}

. For

m_{1} ≫ m_{2}

, the directions of

v_{1}^{'}

and

v_{2}^{'}

are as shown in Figure 1. If we consider that the direction of

v_{1}

is positive, then the direction of

v_{2}

is negative, and the directions of

v_{1}^{'}

and

v_{2}^{'}

are positive. Therefore, the simplified solutions with approximations are

v_{1}^{'} ≅ v_{1}

and

v_{2}^{'} ≅ v_{2} + 2 v_{1}

. At the limit when

m_{2}

is zero/massless, the simplified solutions are

v_{1}^{'} = v_{1}

and

v_{2}^{'} = v_{2} + 2 v_{1}

When the ball of mass

m_{1}

travels in the opposite direction, the simplified solutions for massless balls are

v_{1}^{'} = v_{1}

and

v_{2}^{'} = v_{2} - 2 v_{1}

, considering the same positive direction.

Nevertheless, massless balls respect the equation for the law of conservation of momentum

m_{1} v_{1} = m_{1} v_{1}^{'}

and the equation for the law of conservation of energy

\frac{1}{2} m_{1} v_{1}^{2} = \frac{1}{2} m_{1} v_{1}^{' 2}

. According to these two simplified laws, there is no energy consumption to change the state of massless balls, and massless balls do not have momentum.

A rigid wall can replace the ball of mass

m_{1}

to study the reflection of balls with mass

m_{2}

or without mass in any direction. The solution

v_{2}^{'} = v_{2} + 2 v_{1}

is given in the frame at absolute rest. In the wall inertial frame, the incident relative speed of the massless ball with respect to the wall is

v_{i i} = v_{2} + v_{i}

, where

v_{i}

is the speed of the wall;

v_{i} = v_{1}

in the case of Figure 1. In the wall inertial frame, the speed of the reflected massless ball is

v_{r i} = v_{i i} = v_{2} + v_{i}

; velocities

v_{r i}

and

v_{i i}

are in opposite directions in the case of Figure 1. In the frame at absolute rest, the speed of the reflected massless balls is

v_{2}^{'} = v_{r i} + v_{r}

, where

v_{r}

is the speed of the wall in the direction of the reflected massless ball;

v_{r} = v_{1}

in the case of Figure 1. The expression

v_{2}^{'} = v_{r i} + v_{r}

, where

v_{r i} = v_{2} + v_{i}

, yields the equation

v_{2}^{'} = v_{2} + v_{i} + v_{r}

(3)

Equation (3) offers the massless balls' speeds in the absolute frame for different wall inclinations. Speeds

v_{i}

and

v_{r}

vary with the inclination of the wall and the incident velocity of the massless balls with the direction of velocity

v_{1}

. Eq. (3) is independent of balls’ mass and applies with approximation to balls with mass in an elastic collision when

m_{1} ≫ m_{2}

. Eq. (3) also applies to the reflection of light by a moving mirror [1,2,3].

2.3. Elastic Reflection of a Ball by a Moving Wall

Figure 2 illustrates in the absolute frame a wall W traveling at velocity

v

and a ball at velocity

V

that hits the wall in an elastic collision; the wall’s mass is much greater than the ball’s mass

m

. The wall reflects the ball at

A_{1}

, which is the instance of point

A

of the moving wall in the absolute frame at collision. In the inertial frame of the wall, the incident and reflected angles are equal only at the point of collision

A_{1}

. One second after the collision, the ball is at point

B_{2}

This section employs Eq. (3),

v_{2}^{'} = v_{2} + v_{i} + v_{r}

, in which the speed of the ball

V

replaces

v_{2}

and the reflected speed of the ball in the absolute frame

V_{r a}

replaces

v_{2}^{'}

V_{r a} = V + v_{i} + v_{r}

(4)

In the absolute frame, the speed of the wall in the opposite direction of the incident ball is

v_{i} = v \cos a

, and the speed of the wall in the direction of the reflected ball is

v_{r} = v \cos b

. Another form of Eq. (4) is

V_{r a} = V + v \cos a + v \cos b

(5)

where angles

a

and

b

are measured counterclockwise from velocity

v

In the absolute frame, the wall moves in one direction, but the wall inclination reflects a ball in multiple directions. The ball’s velocity in the mirror’s inertial frame is

V_{i}

, given by the vector difference of velocity

v

from velocity

V

. The velocity triangle

A_{1} A_{2} B_{2}

applies to the ball at any time. On another scale,

A_{1} A_{2} B_{2}

represents the momentum triangle.

2.4. Emission, Propagation, and Reflection of Balls in the Absolute Frame and an Inertial Frame

Figure 3 illustrates the same ball source and rigid wall at rest in the absolute and inertial frames. The source and wall have the same geometry with respect to each frame's origin.

In the absolute frame

O X Y Z

, the source in origin

O

emits a ball at an “instant” velocity

V_{e}

at an angle

a

from axis

O X

. After a time

t_{1}

, the ball is at point

A

of wall

W

. At point

A

, the ball is reflected in an elastic collision at velocity

V_{r}

and then travels the path

A B

in time

t_{2}

. Velocities

V_{e}

and

V_{r}

have the same magnitude

V

. The ball travels the paths

O A

and

A B

in time

t = t_{1} + t_{2}

at speed

V

. The ball continues traveling in the direction

A B

The inertial frame

O^{'} X^{'} Y^{'} Z^{'}

travels at velocity

v

, and the source is in origin

O^{'}

. Origin

O^{'}

and points

A

and

B

belong to the inertial frame, and their instances in the absolute frame receive a corresponding index. The source at origin

O^{'}

emits a ball at “instant” velocity

V_{e}

in direction

O_{1}^{'} A_{1}

at an angle

a

from axis

O^{'} X^{'}

. The velocity

v

drags the ball from the projected path at emission,

O_{1}^{'} A_{1}

, on the propagation path,

O_{1}^{'} A_{2}

, at velocity

V_{s a}

in the absolute frame, which is given by the vector sum of the emitted velocity

V_{e}

and velocity

v

. The dragging of a ball does not change the direction and magnitude

V

of the emitted velocity

V_{e}

, only its propagation direction to that of

V_{s a}

. At point

O_{2}^{'}

, the ball is at

A_{2}

; it has traveled the path

O_{2}^{'} A_{2}

at velocity

V_{e}

in time

t_{1}

, and the direction

O_{2}^{'} A_{2}

makes an angle

a

from axis

O^{'} X^{'}

. The path

O_{2}^{'} A_{2}

is the path

O^{'} A

in the inertial frame, which is identical to

O A

in the absolute frame. If the source emits other balls between

O_{1}^{'}

and

O_{2}^{'}

, all of these balls are on the path

O_{2}^{'} A_{2}

In the elastic collision at point

A_{2}

, the wall perceives only the magnitude and direction of the emitted ball’s velocity

V_{e}

because the ball and wall have the same velocity

v

. The incident and reflected angle

b

are measured from the normal to the wall at the point of collision to the incident velocity

V_{e}

and reflected velocity

V_{r}

, as in the absolute frame. After reflection, velocity

v

keeps dragging the ball in the same direction and with the same magnitude. Therefore, velocity

v

drags the ball from the projected direction of the reflected velocity

V_{r}

on the propagation path,

A_{2} B_{3}

, at velocity

V_{r a}

, which is given by the vector sum of the reflected velocity

V_{r}

and velocity

v

. The dragging of a ball does not change the direction and magnitude of the reflected velocity

V_{r}

, only its propagation direction. At point

O_{3}^{'}

, the ball is at

B_{3}

, the direction

O_{3}^{'} A_{3}

makes an angle

a

from axis

O^{'} X^{'}

, and the ball has traveled the path

O_{3}^{'} A_{3} = O_{2}^{'} A_{2} = {O_{1}^{'} A_{1} = O}^{'} A

at speed

V

in time

t_{1}

and the path

A_{3} B_{3} = A B

at speed

V

in time

t_{2}

. The path

A_{3} B_{3}

is the path

A B

in the inertial frame, which is identical to that in the absolute frame. At point

O_{3}^{'}

, the ball has traveled the paths

O_{3}^{'} A_{3} = O A

and

A_{3} B_{3} = A B

in time

t = t_{1} + t_{2}

at speed

V

, as in the absolute frame.

Newtonian mechanics based on observations and experiments are rationally understood and formulated in laws that are applicable with the same rational understanding to experiments, phenomena, and the needs of everyday life. However, Newtonian laws say nothing about observations of phenomena.

3. Kinematics of Light

The kinematics of light as a mechanical phenomenon arise from a series of articles [1,2,3,4,5,6,7,8,9,10,11,12] about the emission, propagation, and reflection of light as mechanical phenomena applied to a few fundamental experiments. The reflection of light as a mechanical phenomenon [1,2,3] was the first step, and an experiment on the reflection and emission of light [12], summarized in Appendix A, was the turning point towards the kinematics of light.

The electromagnetic theory offers the kinetics of electromagnetic wave radiation and the speed of light

c

in a vacuum when the source is at rest in the absolute frame. We study the kinematics of light in the natural interactions of electromagnetic radiation with matter, such as at emission from its source, reflection with a mirror, and refraction through a transparent medium in motion.

The speed of light

c

behaves similarly to the speed of a ball

V

in Subsections 2.3. and 2.4.

3.1. Reflection of Light by a Moving Mirror

Unlike References [1] and [2], Figure 4 illustrates the absolute frame in which a mirror

M

travels at velocity

v

and a source

S

of coherent light is at rest.

This section employs Eq. (3),

v_{2}^{'} = v_{2} + v_{i} + v_{r}

, in which the speed

c

of electromagnetic nature replaces

v_{2}

, and the reflected speed of wavefronts

c_{r a}

in the absolute frame replaces

v_{2}^{'}

c_{r a} = c + v_{i} + v_{r}

(6)

In the absolute frame, the speed of the mirror in the opposite direction of incident light is

v_{i} = v \cos a

, and the speed of the mirror in the direction of reflected light is

v_{r} = v \cos b

Another form of Eq. (6) is

c_{r a} = c + v \cos a + v \cos b

(7)

where angles

a

and

b

are measured counterclockwise from velocity

v

In the absolute frame, the mirror moves in one direction, but the mirror's inclination reflects light in multiple directions.

After a second from the instance of the collision at

A_{1}

, the wavefront from

A_{1}

is at

B_{2}

, and the mirror is at

A_{2}

. The wavefronts reflected between

A_{1}

and

A_{2}

travel in the absolute frame in the direction

A_{1} B_{2}

at velocity

c_{r a}

. In the mirror’s inertial frames, the wavefronts travel from

A

B

in the direction

A_{2} B_{2}

, forming a continuous wave of light propagating at velocity

c_{i}

, wavelength

λ_{i}

, period

T_{i}

, and frequency

f_{i}

. Velocity

c_{i}

is given by the vector difference of velocity

v

from velocity

c_{r a}

. A local observer at point

B

perceives this wave of light traveling at speed

c_{r a}

, wavelength

λ_{r a}

, period

T_{r a}

, and frequency

f_{r a}

In References [1] and [2], the source is at rest in the mirror's inertial frame, and the velocity of light is considered independent from the velocity of its source. The wavefronts reflected at point

A

come from one point of the source. In Figure 4, the wavefronts reflected in point

A

of the mirror belong to waves coming from sequential points of the source.

The source may not be at rest; therefore, the source's speed of light propagation is

c_{s} \neq c

in the absolute frame. In this case, the mirror may also perceive the source’s velocity. References [6] and [7] consider this situation.

3.2. Emission, Propagation, and Reflection of Light as Mechanical Phenomena in the Absolute Frame and an Inertial Frame

Unlike the Newtonian laws, we employ the expressions “observer in the absolute frame” and “observer in an inertial frame”, meaning that the observer is hypothetical and knows/oversees the phenomena in that frame. These terms may be eliminated and state how the phenomena are to be consistent with mechanics. However, the expression “local observer” must remain. A local observer perceives the phenomena through light coming directly from a source or being reflected by objects from the observer’s frame or others, as well as partially reflected wavefronts of light traveling in a transparent medium, such as air. In a vacuum, a beam of light is invisible, except when it comes directly to the human eye. Furthermore, the human eye observes only the light emitted from a source and its reflection in a mirror, not their light propagation. Therefore, the phenomena of physics are perceived by a local observer differently from reality, as given by the Newtonian laws. Nevertheless, we may know reality better by applying the Newtonian laws and local observation of light.

The study of the emission, propagation, and reflection of light is based on that of balls, as described in Subsection 2.4. Velocity

v

of a mechanical nature is the same as that for balls with mass or massless balls. The emitted velocity

c

, as defined by Maxwell’s equations, replaces the emitted velocity

V

of balls.

Figure 5 illustrates the same light source and reflective mirror at rest in the absolute and inertial frames. The source and mirror have the same geometry with respect to each frame's origin.

In the absolute frame

O X Y Z

, the source at origin

O

emits a wavefront at velocity

c_{e}

at an angle

a

from axis

O X

. After a time

t_{1}

, the wavefront is at point

A

of the mirror

M

. At point

A

, the wavefront is reflected at velocity

c_{r}

, then travels the path

A B

in time

t_{2}

. Velocities

c_{e}

and

c_{r}

have the same magnitude

c

. The light travels the paths

O A

and

A B

in time

t = t_{1} + t_{2}

at speed

c

, wavelength

λ

, period

T

, and frequency

f

The inertial frame

O^{'} X^{'} Y^{'} Z^{'}

travels at velocity

v

, and the source is at origin

O^{'}

. Origin

O^{'}

and points

A

and

B

belong to the inertial frame, and their instances in the absolute frame receive a corresponding index. The source at origin

O^{'}

emits a wavefront at velocity

c_{e}

in direction

O_{1}^{'} A_{1}

at an angle

a

from axis

O^{'} X^{'}

. Velocity

v

drags the wavefront from the projected path at emission,

O_{1}^{'} A_{1}

, on the propagation path,

O_{1}^{'} A_{2}

, at velocity

c_{s a}

, which is given by the vector sum of the emitted velocity

c_{e}

and source velocity

v

. The dragging of the wavefront does not change the direction and magnitude of its emitted velocity

c_{e}

, only its propagation direction to that of

c_{s a}

. At point

O_{2}^{'}

, the wavefront is at

A_{2}

; it has traveled the path

O_{2}^{'} A_{2}

at speed

c

in time

t_{1}

, and the direction

O_{2}^{'} A_{2}

makes an angle

a

from axis

O^{'} X^{'}

. The emitted wavefronts between

O_{1}^{'}

and

O_{2}^{'}

are on the path

O_{2}^{'} A_{2}

At point

A_{2}

of reflection, the mirror perceives only the magnitude and direction of the emitted velocity

c_{e}

because the wavefront and mirror have the same velocity

v

. The incident and reflected angle

b

are measured from the normal to the mirror at the collision point to the incident velocity

c_{e}

and reflected velocity

c_{r}

. After reflection, velocity

v

keeps dragging the wavefront in the same direction and with the same magnitude. Therefore, the velocity

v

drags the wavefront from the projected direction of reflected velocity

c_{r}

on the propagation path,

A_{2} B_{3}

, at velocity

c_{r a}

, given by the vector sum of reflected velocity

c_{r}

and velocity

v

. The dragging of the wavefront does not change the direction and magnitude of its reflected velocity

c_{r}

, only its propagation direction. At point

O_{3}^{'}

, the wavefront emitted from

O_{1}^{'}

is at

B_{3}

, the direction

O_{3}^{'} A_{3}

makes an angle

a

from axis

O^{'} X^{'}

, and the wavefront has traveled the path

O_{3}^{'} A_{3} = O_{2}^{'} A_{2} = O_{1}^{'} A_{1} = O^{'} A

at speed

c

in time

t_{1}

and the path

A_{3} B_{3} = A B

at speed

c

in time

t_{2}

. The path

A_{3} B_{3}

is the path

A B

in the inertial frame, which is identical to that in the absolute frame. At point

O_{3}^{'}

, the light has traveled the paths

O_{3}^{'} A_{3} = O A

and

A_{3} B_{3} = A B

in time

t = t_{1} + t_{2}

at speed

c

, wavelength

λ

, period

T

, and frequency

f

, as in the absolute frame.

We can conclude the following:

A source at rest in the absolute frame emits waves of light that are uniformly distributed in space in all directions at speed

c

, as defined by Maxwell’s equations, with wavelength

λ

, period

T

, and frequency

f

. A source in motion emits uniform wavefronts of light in the absolute frame in all directions independent of the source at speed

c

. The source velocity drags each of the emitted wavefronts such that the waves are uniformly distributed in the space of the source’s inertial frame and travel at speed

c

with wavelength

λ

, period

T

, and frequency

f

, as in the absolute frame.

In a source’s inertial frame, a mirror at rest perceives only the emitted directions of wavefronts, which are reflected accordingly. The source velocity continues to drag each reflected wavefront so that the waves travel in the source's inertial frame at the same

c

λ

T

, and

f

In each inertial frame, the law of dragging applies to balls, with or without mass, and light emitted by bodies at rest belonging to that inertial frame. It works in the background of each inertial frame. It acts on balls and electromagnetic radiation emitted by bodies of each inertial frame, making phenomena similar to those in the absolute frame. Therefore, the dragging explains and confirms the principle of relativity, according to which no experiment in an inertial frame can prove its motion. It explains that the laws of physics have the same form in each inertial frame and that the speed of electromagnetic radiation is the constant

c

in the absolute and each inertial frame when the source and reflected mirror are at rest in those frames.

For theoretical studies, it is convenient to compare physical phenomena from inertial frames only with the frame at absolute rest, which is a hypothetical inertial frame at zero speed. The kinematics of phenomena in each inertial frame are like those in the frame at absolute rest. Therefore, each inertial frame can be considered a local frame at absolute rest for phenomena belonging to that inertial frame. To study interactions between physical systems belonging to two inertial frames, one can be considered a stationary/local frame at absolute rest in which another frame travels at the relative velocity between the two frames.

3.3. Experiments and Observations that Support the Kinematics of Light as a Mechanical Phenomenon

The kinematics of light as a mechanical phenomenon explain experiments and local observations that supported special relativity due to insufficient and incorrect understanding.

3.3.1. Michelson‒Morley Experiment

Light travels through a transparent medium at a specific constant speed independent of the source speed. Michelson and Morley [13] considered their experiment in the fixed ether. Therefore, the speed of light emitted by a source and reflected by a mirror has the same magnitude in the hypothetical ether at rest in the absolute frame regardless of whether the source and mirror are at rest or in motion. In the ether theory, the speed of light is limited by ether. The Michelson‒Morley experiment predicts a fringe shift, which is not confirmed by the zero fringe shift of the experimental results.

Differently, the kinematics of light demonstrate that in an inertial frame where a source of light and a mirror are at rest, the speed of light is the constant

c

of electromagnetic nature, as in Maxwell’s equations. Therefore, the kinematics of light predict zero fringe shift for the Michelson‒Morley experiment, which is in agreement with the experimental results.

3.3.2. Experiment Performed at CERN, Geneva

The emission, propagation, and reflection of light in inertial frames [4] explain the experiment performed at CERN, Geneva, in 1964 [14] without rejecting Ritz’s ballistic theory [15]. Figure 6 illustrates the phenomenon in a simplistic approach.

When a boson

B

of mass

m

accelerates at a mechanical speed

v

near the constant speed of light

c

, it decays into a particle

A

of mass

m

and one massless photon. At speed

v

, particle

A

changes its direction, and the photon moves freely at speed

v

. Bosons are only carriers that give photons their mechanical speed

v

near the constant speed of light

c

. Bosons are not sources of light to give photons the speed

c

of electromagnetic nature on top of speed

v

of mechanical nature. This experiment confirms the dragging of light by the source velocity.

3.3.3. Observation of a Star in the Universe

Figure 7(a) illustrates the observation of a star in the Universe according to the kinematics of light as a mechanical phenomenon. Suppose that a star at point

A_{1}

and Earth at point

B_{1}

travel at velocity

v

. At the initial instance, the star emits a wavefront of light in the direction

A_{1} B_{1}

at the emitted speed

c

After a time, the star travels the path

A_{1} A_{2}

and Earth travels the path

B_{1} B_{2}

, which are of equal length

L_{1}

. Velocity

v

drags the wavefront emitted in the direction

A_{1} B_{1}

along

A_{1} B_{2}

. At

B_{2}

, a local observer perceives the wavefront coming from

A_{2}

. Therefore, the star is seen at its actual location.

Figure 7(b) illustrates the observation of a star in the Universe according to the hypothesis that the speed of light is independent of the motion of the source. Suppose that a star at point

A_{1}

and Earth at point

B_{1}

travel at velocity

v

. At the initial instance, the star emits a wavefront of light in the direction

A_{1} B_{3}

at the emitted speed

c

After a time, the star travels the path

A_{1} A_{3}

and Earth travels the path

B_{1} B_{3}

, which are of equal length

L_{2}

. The wavefront emitted in the direction

A_{1} B_{3}

reaches point

B_{3}

, where a local observer perceives the wavefront coming from

A_{1}

. Therefore, the star is observed at the initial location, not its actual one, which means that the hypothesis of the constancy of the speed of light creates irregularities that are unobserved by astronomers. These irregularities differ from those that de Sitter incorrectly predicted [16,17].

3.3.4. Observation of a Star’s Orbit

The emission of light as a mechanical phenomenon [4] applies to observing a star’s orbit [5]. Figure 8 depicts an actual star orbit of radius

R

in the plane of the paper and an imaginary circle of radius

O A^{'}

with its plane parallel to the front of the paper's plane. The distance

d = O O_{s}

is perpendicular to the orbit and imaginary circle planes. An observer at rest is at point

O

. The observed star orbit of radius

R_{O}

is centered at

O_{s}

. The view is from the back-right of the observer to gain a clear image of the actual and observed orbits.

The distances in each set of (

A A^{'}, A^{''} O, E E^{'}, E^{''} O, \dots)

and (

A O, E O, . . .

), including all other similar distances corresponding to points

B, C, D, F, G

, and

H,

are equal.

Some waves emitted from the star in motion are dragged by the star velocity

v

at the emission point through different paths to the local observer

O

. At point

A

, the star emits a wavefront of light at velocity

c

in the direction

A A'

, and this wavefront is dragged by velocity

v

along the path

A O

at the propagation velocity

c_{p}

. At point

O

, the observer sees the wavefront coming from point

A''

at speed

c

. At point

E

, the star emits a wavefront of light at velocity

c

in the direction

E E^{'} = A A'

, and this wavefront is dragged by velocity

v

along the path

E O = A O

at the propagation velocity

c_{p}

. At point

O

, the observer sees the wavefront coming from point

E''

at speed

c

along the path

E^{''} O = A'' O

. The same observation occurs for each point of the circular orbit.

Points

A, B, C, D, E, F, G

, and

H

give the corresponding points

A'', B'', C'', D'', E'', F'', G''

, and

H''

, which form the observed orbit with the center at

O_{s}

for this particular case. The local observer sees the star’s orbit rotated and with a larger diameter than that of the actual orbit. The speed of light from any point of the observed orbit to the observer is the constant

c

. Therefore, no time irregularities exist to reject Ritz’s ballistic theory [15], as de Sitter predicted [16,17]. Observing the star’s orbit supports the kinematics of light as a mechanical phenomenon.

This study is an example of a star-orbiting phenomenon being observed as an enlarged orbit by a local observer at rest. In this case, the observed orbital speed is higher than speed

v

3.3.5. Miller Experiment

The emission, propagation, and reflection of light as mechanical phenomena explain the Michelson‒Morley experiment, with an interferometer arm length of 32 m instead of 11 m, while employing sunlight as a source [8,9] in Miller’s experiment [18] at the Cleveland Laboratory in 1924; the fringe shift is on the order of

10^{- 8}

[8,9].

Miller mainly employed light from local sources in his experiments. The kinematics of light [4] predict zero fringe shift for any location and altitude on Earth’s inertial frame. Reference [4] explains the experiments with local sources at the Cleveland Laboratory in 1924. On Mount Wilson, at a high altitude, where experiments were performed with local sources, the fringe shifts of 0.08 in 1921 and 0.088 in 1925 remain unexplained.

In Reference [8], the author incorrectly considered that the experiments at Mount Wilson employed sunlight, which explains the fringe shifts of 0.08 and 0.088. The mistake was caught later in the review process [9].

3.3.6. Majorana Experiment

Majorana’s experiment [19] in Earth’s inertial frame employs a fixed light source. The light travels through three stages, each consisting of one movable and one fixed mirror, and it enters a Michelson interferometer with unequal-length arms. The movable mirrors are fixed on a rotational disk in both directions. When the disk is at rest, a fringe image is observable. When the disk is rotated from the maximum speed of one direction to another, a shift of 0.71 fringes is observed [19]. Like the Michelson interferometer, Majorana’s experimental device remains an outstanding contribution to the physics of light despite changes in the interpretation of the experiment over time. Majorana misunderstood the phenomenon within the device and the significance of the fringe shift observed at the experimental time, explaining the fringe shift favorably to special relativity. The reflection of light as a mechanical phenomenon [1,2,4] applied to the Majorana experiment [10] shows that the speed of light changes after each stage, causing the fringe shift in the Michelson interferometer. Reference [10] approximates rotational mirrors as inertial frames and derives a shift of 0.27 fringes. However, the observed shift of 0.71 fringes confirms the kinematics of light as a mechanical phenomenon and rejects the constancy of light propagation.

3.3.7. Airy Experiment

Aside from interactions of the emission and reflection of light with matter, another example is the refraction of light when it travels from one medium to another at rest according to Snell’s law. Airy’s experiment is an example of the dragging of light by a moving medium. Observing the star γ Draconis, Airy [20] expected to adjust the telescope’s inclination after introducing a tube with water along its axis, but that was unnecessary. Considering the dragging of light by the moving water and the experimental results, we obtained the Fresnel dragging coefficient

1 - \frac{1}{n_{1}^{2}}

from a mechanical perspective [11], where

n_{1}

is the medium’s refraction index.

3.4. Galilean Transformation

We study Galilean transformation for light as in mechanics, where physical phenomena are as they are and without observations.

When extended to infinity, all inertial frames overlap. The phenomenon in an inertial frame is shared instantly in any other inertial frame. The inertial frame in which a phenomenon is to be shared is considered to be at relative rest/in a stationary frame.

The Galilean transformation depicts how the physical phenomenon of light emission is shared instantly from a stationary frame in an inertial frame. Figure 9 depicts a stationary frame

O X Y Z

in which an inertial frame

O^{'} X^{'} Y^{'} Z^{'}

travels at relative velocity

v

along the

O X

axis, and the planes

O X Y

and

O^{'} X^{'} Y^{'}

coincide.

The kinematics of light prove that a stationary frame/frame at relative rest can be considered a local frame at absolute rest; we do not assume this fact.

Origins

O

and

O^{'}

coincide at the initial instance when the source belonging to origin

O

of the stationary frame emits a spherical wavefront of light formed by individual waves' wavefronts. After a time

t

, the spherical wavefront of light has its center at

O

, and the origin of the inertial frame

O^{'}

is at a distance

v t

from

O

. The Galilean transformation offers the coordinates of each wave's wavefront on the spherical wavefront. Figure 9 shows the wave wavefronts at points

A

B

C

, and

D

on the circular wavefront in plane

O X Y

at time

t

and their coordinates in plane

O^{'} X^{'} Y^{'}

The Galilean transformation, in its simplest form, consists of four equations that are applicable to the wavefront of each wave in a spherical wavefront:

x^{'} = x - v t, y^{'} = y, z^{'} = z, a n d t^{'} = t

(8)

The wave wavefront emitted in direction

O B

at the initial instance travels in this direction at all times, and it is at all times on this spherical wavefront, which enlarges continuously. This wave wavefront travels length

O^{'} B

in the inertial frame at the propagation speed

c^{'}

. The vector difference of vector

c

and vector

v

gives velocity

c^{'},

which is illustrated at points

O

and

B

. This wave wavefront travels at the same angles

a

and

a^{'}

and speed

c^{'}

for any other instance of the spherical wavefront. Angles

a

and

a^{'}

and speed

c^{'}

are different for any other point of the spherical wavefront. The speed of wave wavefronts varies from 2.999,700,000E+08 for

a = 0 °

to 3.000,000,015E+08 for

a = 90 °

and to 3.000,300,000E+08 for

a = 180 °

. The density of the wave increases from

a = 0 °

a = 90 °

in the inertial frame's space.

Figure 9 and the Galilean transformation apply to a hypothetical ball source when the source emits a spherical ball front and the speed of balls

V > v

In Figure 9, the physical phenomenon consists of the source and spherical wavefront and belongs to the stationary frame. The source, which has its coordinate

x^{'} = - v t

, and the spherical wavefront do not belong to the inertial frame. A phenomenon in an inertial frame is unique in the Universe, independent of any other inertial frame, and instantly shared in any other inertial frame through its coordinates but not duplicated. There are no transformations of phenomena from the stationary frame to the inertial frame to undergo changes that may or may not affect the laws of physics of those phenomena. The term "transformation" may be inappropriately used. A better wording may be "Galilean coordinates”.

4. Einsteinian Theory of Special Relativity

4.1. Einstein's Suggestions

In the first paragraph on page one of his manuscript “On the electrodynamics of moving bodies”, [21] Einstein says: “It is known that Maxwell’s electrodynamics—as usually understood at the present time—when applied to moving bodies, leads to asymmetries which do not appear to be inherent in the phenomena. Take, for example, the reciprocal electrodynamic action of a magnet and a conductor. The observable phenomenon here depends only on the relative motion of the conductor and the magnet, whereas the customary view draws a sharp distinction between the two cases in which either the one or the other of these bodies is in motion. For if the magnet is in motion and the conductor at rest, there arises in the neighborhood of the magnet an electric field with a certain definite energy, producing a current at the places where parts of the conductor are situated. But if the magnet is stationary and the conductor in motion, no electric field arises in the neighborhood of the magnet. In the conductor, however, we find an electromotive force, to which in itself there is no corresponding energy, but which gives rise—assuming equality of relative motion in the two cases discussed—to electric currents of the same path and intensity as those produced by the electric forces in the former case.”

Einstein considers his example asymmetric because when the magnet is at rest, no electric field arises in the moving conductor, and still, the reciprocal phenomena occur. He may suggest that observations are enough to accept reciprocal phenomena even if an electromagnetic quantity, such as an electric field, does not arise. Therefore, there is no need to understand physical phenomena rationally.

Appendix B shows that in Einstein’s example, when the magnet is at rest, an electromotive force (emf) is created in the conductor in motion, making the conductor an electrical source; therefore, an electric field arises. Thus, Maxwell’s electrodynamics applied to moving bodies lead to symmetries; each physical quantity involved in a phenomenon arises, and the phenomena can be rationally explainable.

However, can we apply the symmetry of phenomena observed and understood as an equilibrium in reciprocity between two inertial frames? What physical similarities can be among the reciprocal and symmetrical phenomena between the magnet and conductor given by Einstein, or any other symmetrical phenomena, and the phenomenon between two inertial frames, if there is one?

The example has the magnet and conductor in proximity, and they have reciprocal electromagnetic properties. None of these characteristics apply to a stationary and inertial frame to support special relativity. The origins of the two frames depart from one another and are in proximity for a relatively short time. Frames, including the absolute frame, are hypothetical entities. These simple tools help us study and understand physical phenomena. They have no physical properties to transform/duplicate a physical system from one frame to another, not even for observations.

Symmetry applied to two inertial frames, the main idea in special relativity, creates duplications. It is unrealistic and leads to irrational conclusions, as will be discussed further.

From “Examples of this sort, together with the unsuccessful attempts to discover any motion of the earth relatively to the 'light medium'”, Einstein concludes with three suggestions in the second paragraph of page 1:

1. “… the phenomena of electrodynamics as well as of mechanics possess no properties corresponding to the idea of absolute rest.”

Einstein rejected the idea of absolute rest, but an inertial frame considered stationary is a local frame at absolute rest for another inertial frame. The stationary frame was a convenient choice to present his transformational understanding of a phenomenon between two inertial frames.

2. “… the same laws of electrodynamics and optics will be valid for all frames of reference for which the equations of mechanics hold good.”

The equations/laws of mechanics are valid for the phenomena belonging to an inertial frame, not for the coordinates of phenomena in another inertial frame. Still, opposite to the second suggestion, special relativity forces the laws of electrodynamics and optics to hold good to coordinate observations for which mechanics do not hold good.

3. “… light is always propagated in a vacuum with a definite velocity

c

, which is independent of the state of motion of the emitting body.”

In a stationary frame/local frame at absolute rest, without considering the dragging of light, the waves emitted from a source at rest travel at velocity

c

and are uniformly distributed in the frame of the source and the stationary frame. However, when the source is in motion at velocity

v

, the waves travel in the source’s inertial frame at speeds different from

c

, are not uniformly distributed in space, and are deformed. Therefore, there are differences in wave propagation in a stationary frame according to the motion states of the sources.

Without understanding the physical phenomenon of his example and missing details from the above suggestions, Einstein chose to make hypotheses based on observations, elevating them to postulates.

4.2. Einstein's Postulates

From the three suggestions, Einstein formulates two postulates:

“The laws by which the states of physical systems undergo change are not affected, whether these changes of state be referred to the one or the other of two systems of co-ordinates in uniform translatory motion.”
“Any ray of light moves in the “stationary” system of co-ordinates with the determined velocity c, whether the ray be emitted by a stationary or by a moving body.”

A phenomenon in a stationary frame is independent of each other’s inertial frame. It is shared instantly through the coordinates in each other’s inertial frame. By sharing, the states of physical systems do not undergo changes to affect their laws of physics or not. The Galilean transformation describes how the coordinates of a phenomenon from a stationary frame are in an inertial frame. The first postulate forces the coordinates of the Galilean transformation to obey the same form of laws of physics as that applied in the stationary frame; this creates a fictive duplication of a phenomenon from a stationary frame into an inertial frame. The first postulate includes the phenomena of electrodynamics, optics, and mechanics in physical systems (see also Suggestion 2 of Subsection 4.1.). However, practically, this is applied to observing light.

The second postulate indicates that the details of Suggestion 3 of Subsection 4.1. were not considered in Einstein’s time.

Einstein applies his transformation when the source belongs to the stationary or inertial frame. When the source belongs to the inertial frame, there is no need for Einstein’s transformation; the phenomenon is already there. For clarity, we consider that the light source belongs to the stationary frame. If the source belongs to the inertial frame, then this frame is considered stationary. Therefore, Einstein’s transformation has one direction from stationary to the inertial frame. Einstein presents a transformation identical to the well-known Lorentz transformation [22].

4.3. The Lorentz Transformation and Einstein Transformation

Figure 10 depicts a stationary frame

O X Y Z

in which an inertial frame

O^{'} X^{'} Y^{'} Z^{'}

travels at relative velocity

v

along the

O X

axis, and the planes

O X Y

and

O^{'} X^{'} Y^{'}

coincide. Origins

O

and

O^{'}

coincide at the initial instance when a light source belonging to the origin

O

emits waves of light in all directions. After a time

t

, the spherical wavefront of light is on a circle in the plane

O X Y

with the center at

O

, and origin

O^{'}

is at distance

v t

from

O

The conclusion from observations and the Michelson‒Morley experiment was that the speed of light has the constant

c

in each inertial frame. FitzGerald [23], with no explanation of the Michelson‒Morley experiment at his time, wrote: “I would suggest that almost the only hypothesis that can reconcile this opposition is that the length of material bodies changes, according as they are moving through the ether or across it, by an amount depending on the square of the ratio of their velocity to that of light.”

With his transformation, Lorentz presents how the coordinates of the points belonging to the circular wavefront of light from the stationary frame are in the inertial frame. He applied his transformation along the axis

O^{'} X^{'}

, keeping the constancy of light in both directions.

Lorentz’s transformation consists of four equations that are applicable to each point of the circular wavefront in plane

O^{'} X^{'} Y^{'}

when changes in time occur along the axis

O^{'} X^{'}

in both directions, and it can be written as

x_{γ}^{'} = γ (x - v t), y^{'} = y, z^{'} = z, a n d t_{γ}^{'} = γ (t - \frac{v x}{c^{2}}),

(9)

where

γ = \frac{1}{\sqrt{1 - \frac{v^{2}}{c^{2}}}}

is the Lorentz factor, which is comparable to the square of the ratio of the velocity

v

and

c

suggested by FitzGerald.

Substituting

x = c t

at point

A

x^{'} = x - v t = (c - v) t

is the absolute coordinate in the inertial frame as in the Galilean transformation, and

t^{'} = t - \frac{v x}{c^{2}} = t - \frac{v c t}{c^{2}} = t - \frac{v}{c} t = \frac{c - v}{c} t = \frac{x^{'}}{c}

is the hypothetical contracted time

t

\frac{v}{c} t

given by Lorentz, in which the wavefront travels the length

x^{'}

at speed

c

x_{γ}^{'} = γ x^{'}

t_{γ}^{'} = γ t^{'}

, and then

\frac{x_{γ}^{'}}{t_{γ}^{'}} = \frac{x^{'}}{t^{'}} = c

, which verifies the constancy of light. Because

γ > 1

for

v \neq 0

, the length

x_{γ}^{'} = γ x^{'}

is longer than

x^{'}

, and point

A

shifts right to

A_{γ}

Substituting

x = - c t

at point

D

x^{'} = - x - v t = - (c + v) t

is the absolute coordinate in the inertial frame as in the Galilean transformation, and

t^{'} = t - \frac{v x}{c^{2}} = t + \frac{v c t}{c^{2}} = t + \frac{v}{c} t = \frac{c + v}{c} t = \frac{- x^{'}}{c}

is the hypothetical dilated time

t

\frac{v}{c} t

given by Lorentz in which the wavefront travels the length

x^{'}

at speed

c

x_{γ}^{'} = γ x^{'}

t_{γ}^{'} = γ t^{'}

, and then

\frac{x_{γ}^{'}}{t_{γ}^{'}} = \frac{x^{'}}{t^{'}} = - c

, which verifies the constancy of light. Because

γ > 1

for

v \neq 0

, the length

x_{γ}^{'} = γ x^{'}

is longer than

x^{'}

, and point

D

shifts left to

D_{γ}

Note that the times

t^{'} = \frac{c - v}{c} t

in the direction

O^{'} X^{'}

and

t^{'} = \frac{c + v}{c} t

in the opposite direction enforce different relative times in the two directions. The shift/dilation creates a duplicated image that is different from the spherical coordinates of the stationary frame. These are reasons to reject Lorentz’s transformation and special relativity. Factor

γ

can be ignored without affecting the constancy of the speed of light. With or without

γ

, the first postulate creates a fictive duplication, but the shift/dilation makes the duplication more evident. Eliminating factor

γ

, the set in Eq. (9) becomes

x^{'} = x - v t, y^{'} = y, z' = z, a n d t^{'} = t - \frac{v x}{c^{2}}

(10)

The following numerical calculation employs the lengths offered by Lorentz’s transformation, which all are absolute, for the hypothetical time

t^{'}

, considering the set in Eq. (10). Employing the set in Eq. (9), the numerical calculations are slightly different, but the conclusions are the same.

Distance

O B

is the radius

R

of the spherical wavefront in the stationary frame. At time

t

and for an angle

a

, we can calculate

R = c t

y = R \sin a

x^{'} = R \cos a - v t

, and

t^{'} = \frac{x^{'}}{c}

⇒

t^{'} = \frac{R \cos a - v t}{c}

. In triangle

O^{'} B E

, the radius is

R^{'} = \sqrt{x^{' 2} + y^{2}}

. The speed along

R^{'}

for the hypothetical time

t^{'}

given by Lorentz in which the wavefront travels length

O^{'} B

and corresponding coordinate length

x^{'}

c^{'} = \frac{R^{'}}{t^{'}}

Table 1 offers the numerical calculation for the

x^{'}

and

c^{'}

functions of angle

a

at time

t = 1

Table 1 confirms that Lorentz's transformation maintains the constancy of the speed of light for the waves in the direction

O^{'} X^{'}

and the opposite direction. These results are in contradiction concerning the speeds of all other wave directions, which vary and converge to infinity. The second postulate asserts the constancy of the speed of light in the inertial frame, regardless of its direction, while the transformation drastically concludes otherwise.

Lorentz’s transformation keeps

x^{'}

for any point on the spherical wavefront as absolute lengths, adjusting their corresponding times

t^{'}

. The factor

γ

gives only length dilations to

x^{'}

of all points on the spherical wavefront. Therefore, the concept of length contractions is non-existent in Lorentz’s and Einstein’s transformations and is incorrect in special relativity.

The conclusions from the above two paragraphs show that special relativity is self-negating.

4.4. Discussions

1. Is it reasonable to observe the spherical coordinates with their center at origin

O^{'}

and to keep the speed of light a constant along the axis

O^{'} X^{'}

in both directions to have a theory based on experimental observations without understanding the physical phenomena of those experiments? Furthermore, is it reasonable to force the spherical coordinates and their observation to have the same physical laws as those in the stationary frame? This approach, which Einstein chose, leads to an irrational world. Newtonian mechanics' fundamental difference from special relativity is that the laws present the phenomena as they are, rationally understood by themselves, and not accepted by observations, hypotheses or postulates. In mechanics, the dragging of balls and electromagnetic radiation created by bodies explain even the principle of relativity.

2. What natural phenomena can transform each wave from the stationary frame in its unique form, as Lorentz’s transformation requires in Figure 10? We can consider other mathematical transformations, such as by ignoring Lorentz’s factor

γ a s i n S u b s e c t i o n 4.3 .

, by allowing the speed of light to be constant along each wave in the inertial frame, or by allowing the time to be constant instead of the speed of light, to explain the Michelson‒Morley experiment [24]. Could there be a phenomenon for each of these particular hypothetical mathematical transformations, and which one would be correct? There are no such phenomena. If we try these transformations, we obtain a theory with irrational conclusions for each, as for special relativity.

3. The manuscripts, presentation, and teaching of special relativity are focused on observation. Is Lorentz’s transformation not applicable when there is no light or when a phenomenon is too far to be observable? Observation depends on the perception of light by the human eye. Paragraph one of Subsection 3.2. describes the limitations of observation with the human eye. Suppose a source that emits waves of light in a vacuum in all directions. We see only the wave that travels directly to our eyes; all other waves are invisible. No light waves are observed at the source location. If the source emits waves in a medium such as air, the particles of the medium reflect some waves, and our eyes may have a limited, deformed, and delayed observation. This discussion raises questions about the validity of time synchronization in special relativity.

4. According to special relativity, in an inertial frame, we need a ruler identical to that of the stationary frame to measure the length of phenomena that occur in our frame. We must also have two rulers with different scales to measure the lengths

O^{'} x^{'}

transformed from the stationary frame according to

x^{'}

positive or negative, without mention of any other direction. The use of multiple rulers is unacceptable. The same conclusion applies to multiple synchronized clocks.

5. Suppose that the inertial frame also has a source at its origin. When the origins coincide, each source emits a spherical wavefront of light. Considering factor

γ

, imagine the confusion of an observer in the inertial frame observing two different spherical wavefronts with the center at

O^{'}

6. When we observe a star, as in the example in Subsection 3.4.4., which involves astronomical distances, we see the star in an enlarged orbit without irregularities, but our observation does not change the actual orbit. There is no need to mention other observations close to our eyes that we know are not factual. The observations are explainable through the laws of physics. However, we must distinguish between the phenomena and how our eyes observe them. Therefore, we cannot rely only on observations. Special relativity talks about observation, but it does not consider that our eyes perceive only the direction of waves emitted by the source and reflected by mirrors, not necessarily the direction of waves’ propagation. Therefore, this is another fact that was not understood at that time.

7. Lorentz struggled to explain the Michelson‒Morley experiment because, at his time, the law of dragging of light was not understood or accepted. W. Ritz offered the ballistic theory of light [15], which is similar to the concept of dragging of light. However, de Sitter’s observations of binary stars [16,17] rejected it. With the same transformation as Lorentz's [22], Einstein's theory set physics on the wrong path. Time

t^{'} = t - \frac{v}{c} t

for point

A

in the direction

O^{'} X^{'}

is different from time

t^{'} = t + \frac{v}{c} t

for point

D

in the opposite direction. The two different times cannot explain the Michelson‒Morley experiment. Considering the wave that travels at the aberration angle with a speed

c^{'}

converging to infinity, as indicated in Table 1, the experimental explanation is excluded.

8. Figure 10 illustrates a case when the origins

O

and

O^{'}

coincide at the initial instance. However, when the source emits wavefronts at an initial instance, the origin

O^{'}

may be far away from

O

. In this case, there are times when the spherical wavefront does not include origin

O^{'}

, there is a time when the spherical wavefront is at origin

O^{'}

, and there are times when the spherical wavefront includes origin

O^{'}

. How is the initial spherical wavefront observed at

O^{'}

at different times? Do we force the coordinates of the spherical wavefront to be observed according to Lorentz transformation with its center at

O^{'}

at any time?

9. Suppose that the light source is a ball source and emits balls of equal mass in all directions at a speed

V

higher than the speed of the inertial frame

v

. As for light, the Galilean transformation gives the coordinates of the spherical ball front in the inertial frame at a time

t

as they are. Mechanics do not and cannot force the coordinates of the spherical ball front to have its center at

O^{'}

; or, in Einstein’s words, the equations of mechanics do not hold good in this case. Still, special relativity does not respect Suggestion 2 of Section 4.1. Thus, this is a reason to reject special relativity.

10. The first postulate indicates that physical systems from the stationary frame change when transformed/duplicated into the inertial frame. A physical system mentioned in the first postulate may have a source that creates a spherical wavefront. However, it may contain bodies, living beings, and observers involved in a phenomenon. Considering that the origin of an inertial frame can be at any point of that inertial frame, imagine what duplicating the physical systems from a stationary frame means in all other inertial frames. Moreover, each inertial frame, arbitrarily, may be stationary; therefore, all physical systems from each inertial frame are transformed/duplicated in all other inertial frames. All of these duplications are irrational and not observed at the scale of the Universe or the local scale.

11. In a stationary frame, as in Figure 10, the origin

O^{'}

of the inertial frame may travel through a few consecutive points of axis

O X

. Suppose that a phenomenon arises in the stationary frame when the origin

O^{'}

coincides with each consecutive point. Each of these phenomena is transformed at the origin

O^{'}

. Imagine all of these phenomena involving bodies and living beings at

O^{'}

. Note that Galilean coordinates do not eliminate collisions between phenomena of different inertial frames. However, these collisions are rational, understandable, and explicable.

12. This discussion focuses on the propagation of light waves in the stationary frame, the observed phenomena in the inertial frame, and the hypothetical Lorentz phenomenon in the inertial frame.

In , when origins coincide, the source of light emits waves of light at speed

c

, wavelength

λ

, period

T

, and frequency

f

. Wave propagation is undisturbed by and observed differently in the inertial frame. When the initial wavefront arrives at point

A

at time

t

, the length

O A

c t = c^{'} t + v t

⇒

t = \frac{c^{'}}{c} t + \frac{v}{c} t

⇒

t = \frac{c - v}{c} t + \frac{v}{c} t

, which can be written as

\frac{t}{T} = \frac{c - v}{c} \frac{t}{T} + \frac{v}{c} \frac{t}{T}

. The terms

\frac{t}{T}

\frac{c - v}{c} \frac{t}{T}

, and

\frac{v}{c} \frac{t}{T}

are the numbers of waves with period

T

and wavelength

λ

on paths

O A

O^{'} A

, and

O O^{'}

, respectively.

In the particular details of Figure 10, light travels the fraction

\frac{c - v}{c} λ

of a wavelength in time

T

. This means that in the inertial frame, light travels one wavelength

λ^{'} = λ

at period

T^{'} = \frac{c}{c - v} T

, frequency

f^{'} = \frac{c - v}{c} f

, and speed

c^{'} = c - v

, which is the observed wave propagation offered by the Doppler effect. The number of wavelengths

λ

comprising

x^{'} = O^{'} A

\frac{c - v}{c} \frac{t}{T}

In the direction

O^{'} D

, light travels the length

λ + \frac{v}{c} λ = \frac{c + v}{c} λ

in time

T

and one wavelength

λ^{'} = λ

at period

T^{'} = \frac{c}{c + v} T

, frequency

f^{'} = \frac{c + v}{c} f

, and speed

c^{'} = c + v

, which is the observed wave propagation offered by the Doppler effect. The number of wavelengths comprising

x^{'} = O^{'} D

\frac{c + v}{c} \frac{t}{T}

According to Lorentz’s transformation, in the particular details of Figure 10, light travels the fraction

\frac{c - v}{c} λ

of a wavelength in time

t^{'} = \frac{c - v}{c} T

. This means that in the inertial frame, light travels one wavelength

λ^{'} = λ

at period

T^{'} = t^{'} + \frac{v}{c} T = \frac{c - v}{c} T + \frac{v}{c} T

⇒

T^{'} = T

, frequency

f^{'} = f

, and speed

c^{'} = c

, as in the stationary frame. However, the number of wavelengths comprising

x^{'} = O^{'} A

\frac{c - v}{c} \frac{t}{T}

, which gives the absolute length

O^{'} A

In the direction

O^{'} D,

light travels at wavelength

λ^{'} = λ

at period

T^{'} = t^{'} - \frac{v}{c} T = \frac{c + v}{c} T - \frac{v}{c} T

⇒

T^{'} = T

, frequency

f^{'} = f

, and speed

c^{'} = c

. The number of wavelengths comprising

x^{'} = O^{'} D

\frac{c + v}{c} \frac{t}{T}

, which gives the absolute length

O^{'} D

. In the stationary frame, Lorentz’s transformation forces light to travel at speed

c + v

in the direction

O^{'} X^{'}

and at speed

c - v

in the opposite direction.

From this discussion, we understand the difference between the Doppler effect and the incorrectness of Lorentz's transformation, resulting in speed

c^{'}

converging to infinity. Therefore, any mathematical modeling of Lorentz's transformation in space does not reflect reality.

5. Conclusions

Lorentz's and Einstein's transformations are based on observations and duplicate physical phenomena from the stationary to the inertial frame.

The transformations give a constant speed of light in the moving and opposite directions of the inertial frame. At the same time, it is variable in any other direction, converging to infinity. However, special relativity claims that it is the same for all directions.

Time contraction in the moving direction of the inertial frame is different from time dilation in the opposite direction. It requires a ruler and time synchronization in both directions as well as in any other direction.

There are no length contractions in Lorentz's and Einstein's transformations to support the fundamental concept of length contraction in special relativity.

With the above unacceptable conclusions, the theory of special relativity rejects itself.

The saga of special relativity started with FitzGerald’s statement that the length of material bodies changes, which was based on a misunderstanding of the Michelson‒Morley experiment. Lorentz continued it with his transformation, Einstein did so with an entire theory, and many others followed. Special relativity should not have been written and accepted.

Special relativity focuses on observations of phenomena instead of how phenomena are, as mechanics do. Differently from the two approaches, the kinematics of light present how the phenomena are, as in mechanics, and how a local observer perceives them, which helps us to understand reality.

The kinematics of light as a mechanical phenomenon are derived from the laws of mechanics, which are self-evident and need no explanations. The mechanical law of dragging extends to electromagnetic radiation. The kinematics of light explain why the speed of light is a constant

c

in each inertial frame in which the light source and reflective mirror are at rest, why the laws of physics have the same form in each inertial frame, and why any light experiment in an inertial frame cannot prove the motion of that inertial frame.

Matter creates light, and the kinematics of light as a mechanical phenomenon naturally present light in its interaction with matter through emission and reflection [1,2,3,4,5,6,7,8,9,10] and refraction [11]. Light and any other electromagnetic radiation that consists of an electromagnetic field can be considered massless matter/fields and included in mechanics.

The following law of mechanics governs the kinematics of balls and electromagnetic radiation: Each inertial frame drags at its velocity the balls and electromagnetic radiation emitted by bodies at rest in that inertial frame.

Acknowledgments

I am grateful to the person who set me on the right path and inspired me to study the emission, propagation, and reflection of light as mechanical phenomena.

Appendix A

Michelson derived the fringe shift in his interferometer by employing the ether theory. The Michelson‒Morley experiment [13] is expected to give a

0.40

fringe shift. The experimental result is less than the theoretical one by enough to consider it a failure. By employing the ether theory, References 1 and 2 derive the fringe shift for a particular geometry of the Michelson‒Morley experiment in which the beam splitter makes an angle of

45 °

with the source rays, one opaque mirror is perpendicular to the source rays, and another is parallel to them. In this case, the expected fringe shift is also

0.40

References 1 and 2 present the reflection of light as a mechanical phenomenon and derive the speed of light reflected by a moving mirror for any angle measured from velocity

v

of the mirror to velocity

c

of incident light and for any inclination of the mirror; the light source is at rest in the inertial frame of the mirror. The speed of light is considered independent of the light source, as in the ether theory. In this setting, the particular geometry predicts a zero fringe shift, and the geometry of the Michelson‒Morley experiment predicts a

0.40 \times 10^{- 4}

fringe shift. These theoretical results satisfy the experimental ones. To confirm or reject this conclusion, we looked for another interferometer.

Figure 11 illustrates this interferometer at rest in an inertial frame at velocity

v

[12]. The light source splits on beam splitter

M_{1}

. The transmitted rays travel from

M_{1}

to opaque mirrors

M_{2}

and

M_{3}

, beam splitter

M_{4}

, and screen

S c

. The reflected rays travel from

M_{1}

to beam splitter

M_{4}

and then to screen

S c

. All four mirrors make a 45° angle with the incoming rays.

The theoretical fringe shift derived in steps of

90 °

210

[12]; this predicted high fringe shift leaves no uncertainty about the experimental result of a zero fringe shift. Therefore, the combination of light reflection as a mechanical phenomenon, which is incorrect in the ether theory, and the speed of light considered independent of the source speed, as in the ether theory, is incompatible. If we apply only the ether theory to this interferometer, the theoretical fringe shift is zero according to the experimental results.

Figure 11. Schematic of the interferometer.

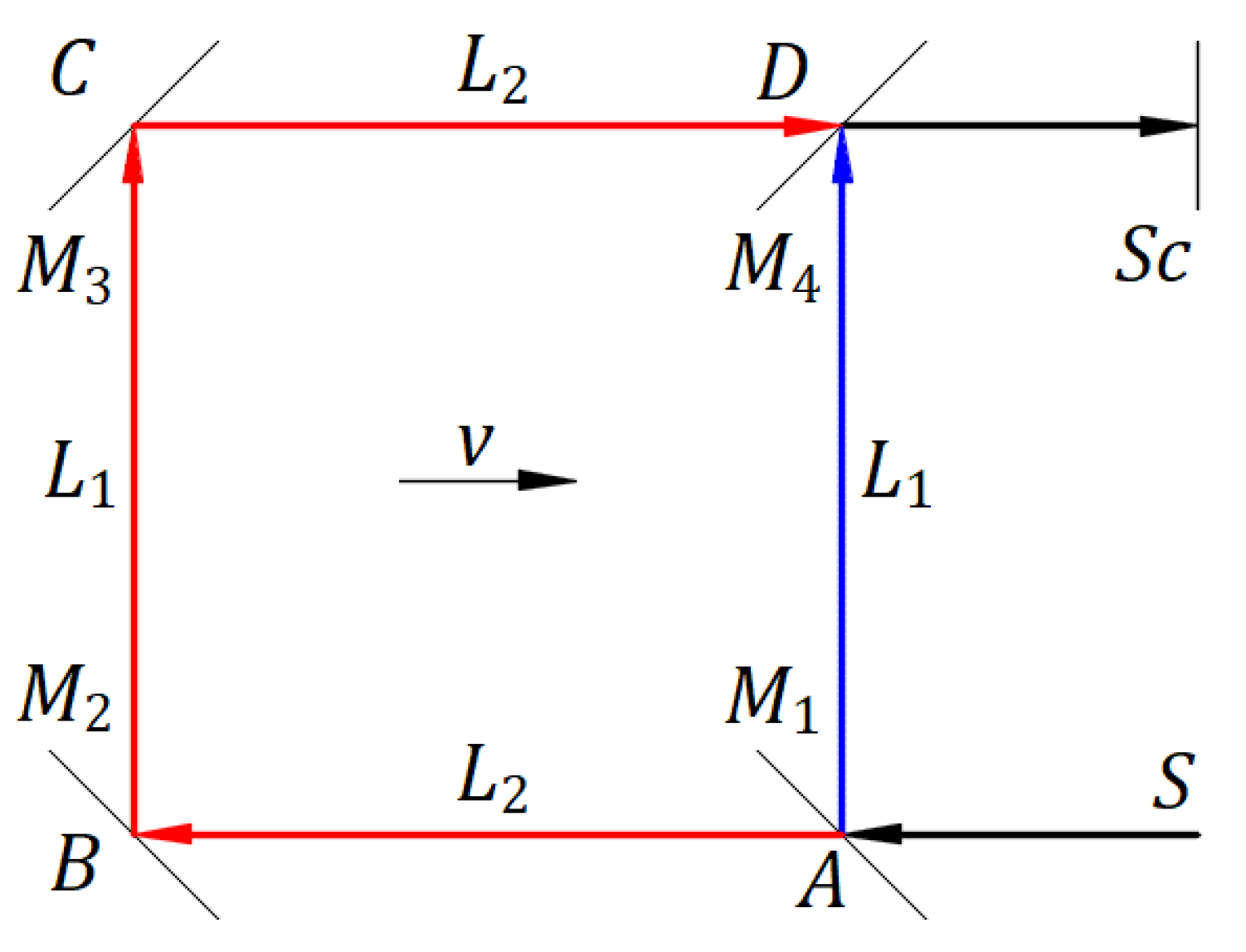
The ether theory and the combination of the two hypotheses predict theoretical results that are inconsistent with the experimental results. This conclusion leads us to consider the emission and reflection of light as mechanical phenomena. The kinematics of light as a mechanical phenomenon explain the Michelson‒Morley experiment and others, as presented in this article.

Appendix B

In the magnetic field

B

of a fixed magnet, Lorentz’s electromagnetic force is given by the cross product

F_{e m} = \pm q v \times B

, where

v

is the velocity of a positive or negative electrical charge

q

with respect to the fixed magnetic field

B

. When the electrical charge

q

is at rest, and the magnet is in motion at velocity

- v

, the velocity of the charge at rest relative to the moving magnetic field

B

v

. Considering the velocity

v

of the electrical charge

q

in motion or relative to the moving magnetic field

B

when the electrical charge

q

is at rest, Lorentz’s electromagnetic force keeps the same form,

F_{e m} = \pm q v \times B

The expression

q v

has the units of

(a m p e r e \times s e c o n d) \times (m e t e r / s e c o n d) = a m p e r e \times m e t e r

, which, in physical quantities, means

l e n g t h \times c u r r e n t = l I,

that is, the total electrical charge in a conductor of length

l

through which a constant current

I

flows. Therefore, when the magnet is fixed, Lorentz’s force becomes

F_{e m} = l I \times B

, where

I

is the current vector with the direction of positive charge flow. Lorentz’s electromagnetic force is

F_{e m} = l (B \times I)

when the magnet is in motion and the conductor is fixed.

Lorentz’s right-hand rule and Fleming’s right-hand and left-hand rules are replaced with the following rule derived from the cross product of

F_{e m}

for perpendicular vectors: The movable quantity rotated in the short direction over the fixed quantity yields the direction of Lorentz’s force.

Figure 12(a) shows a magnet with its magnetic field

B

perpendicular to and toward the paper plane and a conductor that can be connected to an electric current source. The magnet and conductor are in equilibrium when they are at rest relative to each other, and no current flows through the conductor.

Suppose that the magnet is fixed, and the conductor, which has a degree of horizontal freedom in both directions, connects to the source. The source electric field

E

forces the current

I

to flow through the conductor in the direction from top to bottom. The interaction between the magnetic field

B

and the current

I

produces an electromagnetic force

F_{e m}

of reciprocal repulsion between the conductor and magnet. Lorentz’s electromagnetic force is

F_{e m} = l I \times B

. In this case,

I

of the movable conductor rotated in the short direction over

B

of the fixed magnet gives the direction of reciprocal repulsive electromagnetic force

F_{e m}

that moves the conductor to the right in another state of equilibrium.

Suppose that the conductor is fixed, and the magnet has a degree of horizontal freedom in both directions. Connecting the conductor to the source, the source electric field

E

forces the current

I

to flow through the conductor in the direction from top to bottom. The interaction between the magnetic field

B

and the current

I

produces an electromagnetic force

F_{e m}

of reciprocal repulsion between the conductor and magnet. Lorentz’s electromagnetic force is

F_{e m} = B \times l I

. In this case,

B

of the movable magnet rotated in the short direction over

I

of the fixed conductor offers the direction of reciprocal repulsive electromagnetic force

F_{e m}

that moves the magnet to the left in another state of equilibrium.

Figure 12. (a) Charged conductor in a magnet’s magnetic field. (b) Moving a conductor or magnet when they are in proximity.

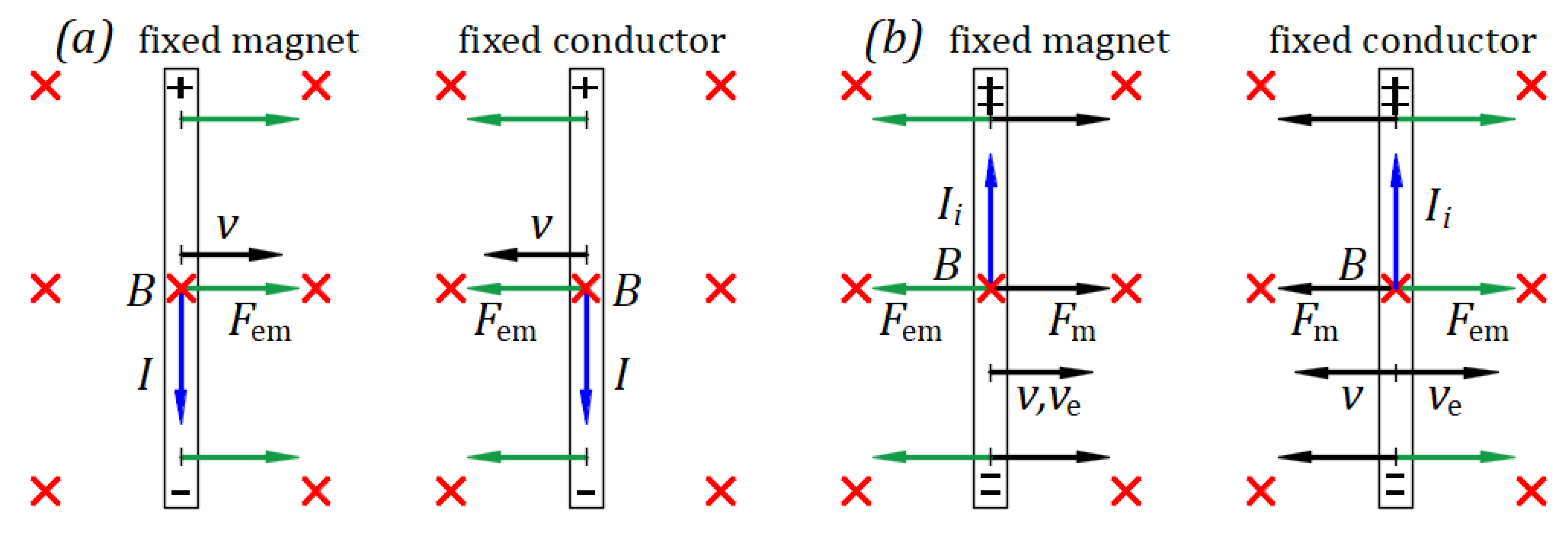
Figure 12(b) illustrates Einstein’s example. A magnet at rest or in motion does not create an electric field without a conductor. The magnet and conductor must be in proximity, and one must be in motion. An electric field arises in a conductor at rest in the neighborhood of a moving magnet, and, opposing to Einstein’s understanding, an electric field also arises in a moving conductor in the neighborhood of a magnet at rest, resulting in a reciprocal and symmetric phenomenon.

Suppose that the magnet is fixed. The conductor connected to a galvanometer is forced to move to the right by a mechanical force

F_{m}

at a velocity

v

, which is the velocity of electrons

v_{e}

from within the conductor. Lorentz’s electromagnetic force for negative electrical charges is

F_{e m} = - q v_{e} \times B

. The magnetic field

B

forces the moving electrons at velocity

v_{e}

to the bottom end of the conductor, and the top end becomes positively charged, creating an electromotive force (emf) within the conductor. The conductor acts as a source, and the induced electric field

E_{i}

creates the induced current

I_{i}

flowing through the galvanometer from the top positive end to the bottom negative end of the conductor. The arising of an electromotive force (emf) and induced electric field

E_{i}

that generates the induced current

I_{i}

was not understood at Einstein’s time.

The interaction of the magnetic field

B

and the current

I_{i}

produces an electromagnetic force

F_{e m} =

l I_{i} \times B

I_{i}

of the movable conductor rotated in the short direction over

B

of the fixed magnet yields the direction of electromagnetic force of reciprocal attraction

F_{e m}

that opposes

F_{m}

. As long as

F_{m}

moves the conductor at velocity

v

, the induced current

I_{i}

flows through the galvanometer. When the mechanical force stops, the system arrives at a state of equilibrium with the conductor at rest.

Suppose that the conductor connected to a galvanometer is fixed. The magnet is forced to move to the left by a mechanical force

F_{m}

at a velocity

- v

that opposes the velocity of electrons

v_{e}

relative to the magnet from within the conductor. Because the velocity

v_{e}

relative to the magnet is velocity

v

, Lorentz’s electromagnetic force for negative electrical charges has the same form,

F_{e m} = - q v_{e} \times B

. Therefore, the induction phenomenon is like that for the fixed magnet, and the conductor is forced to move. The magnetic field

B

forces the moving electrons at velocity

v_{e}

to the bottom end of the conductor, and the top end becomes positively charged, creating an electromotive force (emf) within the conductor. The conductor acts as a source, and its induced electric field

E_{i}

creates the induced current

I_{i}

flowing through the galvanometer from the top positive end to the bottom negative end of the conductor.

The interaction of the magnetic field

B

with the current

I_{i}

produces an electromagnetic force

F_{e m} =

B \times l I_{i}

B

of the movable magnet rotated in the short direction over

I_{i}

of the fixed conductor gives the direction of the electromagnetic force of reciprocal attraction

F_{e m}

that opposes

F_{m}

. As long as

F_{m}

moves the magnet at velocity

- v

, the induced current

I_{i}

flows through the galvanometer. The system reaches equilibrium with the magnet at rest when mechanical force stops.

References

Filipescu, F.D. Reflection of Light as a Mechanical Phenomenon Applied to a Particular Michelson Interferometer. Preprints 2020, 2020090032. [Google Scholar] [CrossRef]
Filipescu, F.D. Opposing hypotheses of the reflection of light applied to the Michelson interferometer with a particular geometry. Phys. Essays 2021, 34, 3–268. [Google Scholar] [CrossRef]
Filipescu, F.D. Opposing hypotheses of the reflection of light applied to the Michelson interferometer. Phys. Essays 2021, 34, 3–389. [Google Scholar] [CrossRef]
Filipescu, F.D. Emission, propagation, and reflection of light as mechanical phenomena in inertial frames. Phys. Essays 2021, 34, 587–590. [Google Scholar] [CrossRef]
Filipescu, F.D. Observation of a star orbit based on the emission and propagation of light as mechanical phenomena. Phys. Essays 2022, 35, 2–111. [Google Scholar]
Filipescu, F.D. Emission, propagation, and reflection of light as mechanical phenomena. Preprints 2022, 2022040061. [Google Scholar] [CrossRef]
Filipescu, F.D. Emission, propagation, and reflection of light as mechanical phenomena: General considerations. Phys. Essays 2022, 35, 3–266. [Google Scholar] [CrossRef]
Filipescu, F.D. Reflection of light as a mechanical phenomenon applied to the Michelson interferometer with sunlight as a source. Preprints 2022, 2022080472. [Google Scholar] [CrossRef]
Filipescu, F.D. Reflection of light as a mechanical phenomenon applied to the Michelson interferometer with sunlight as a source. Phys. Essays 2023, 36, 2–223. [Google Scholar] [CrossRef]
Filipescu, F.D. Emission, propagation, and reflection of light as mechanical phenomena applied to the Majorana experiment. Phys. Essays 2023, 36, 4–361. [Google Scholar] [CrossRef]
Filipescu, F.D. Airy’s experiment and the dragging of light by a moving medium. Phys. Essays 2023, 36, 3–274. [Google Scholar] [CrossRef]
Filipescu, F.D. Experiment on the reflection and emission of light. Phys. Essays 2024, 37, 1–64. [Google Scholar] [CrossRef]
Michelson, A.A. , Morley, E.W. On the relative motion of the earth and the luminiferous ether. Am. J. Sci. 1887, 34(203), 333–345. [Google Scholar] [CrossRef]
Alvager, T. , Farley, F.J.M., Kjellman, J., and Wallin, L. Test of the second postulate of special relativity in the GeV region. Phys. Lett. A. 1964, 12, 260–262. [Google Scholar] [CrossRef]
Ritz, W. Recherches critiques sur l’Électrodynamique Générale. Ann. Chim. Phys. 1908, 13, 145. [Google Scholar]
Bibcode: 1932JMaPh..11..218H. English translation: Critical Researches on General Electrodynamics http://www.shadetreephysics.com/crit/1908a.
De Sitter, W. A proof of the constancy of the velocity of light. Proc. R. Neth. Acad. Arts and Sci. 1913, 15(II), 1297–1298. [Google Scholar]
De Sitter, W. On the constancy of the velocity of light. Proc. R.Neth. Acad. Arts and Sci. 1913, 16, 395–396. [Google Scholar]
Miller, D.C. Ether-Drift Experiments at Mount Wilson. Proc. Natl. Acad. Sci. U. S. A. 1925, 11, 306–314. [Google Scholar] [CrossRef]
Majorana, Q. On The Second Postulate of the Theory of Relativity: An Experimental Demonstration of the Constancy of the Velocity of Light Reflected by a Moving Mirror. Phys. Rev. 1918, 11, 411. [Google Scholar] [CrossRef]
G. B. Airy. On a supposed alteration in the amount of Astronomical Aberration of Light, produced by the passage of the Light through a considerable thickness of Refracting Medium. Proc. R. Soc. Lond. 1871, 20, 35.
Einstein, A. Zur Elektrodynamik bewegter Körper. AdP 1905 322 (10): 891921. https://doi.org/10.1002/andp.19053221004. English translation: https://www.fourmilab.ch/etexts/einstein/specrel/specrel.pdf. [CrossRef]
Lorentz, H.A. Electromagnetic phenomena in a system moving with any velocity smaller than that of light. KNAW, Proceedings, 6, 1903-1904, Amsterdam, 1904, pp. 809-831. English translation: http://www.orgonelab.org/EtherDrift/Lorentz1904.pdf.
FitzGerald, G.F. Letters to the editor. 1889. https://www.science.org/doi/10.1126/science.ns-13.328.390.a.
N. Bărbulescu, Physics foundations of Einsteinian relativity, St. & Enc. ed.: Bucharest, Romania 1975, pp. 74-77.

Figure 1. Elastic collision of two balls moving in opposite directions.

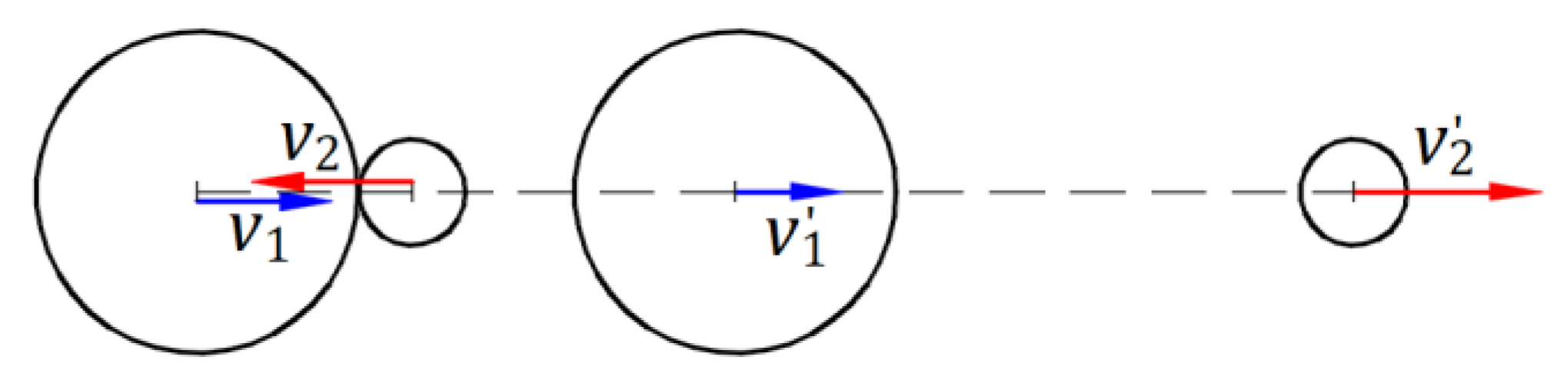
Figure 2. Elastic reflection of a ball by a moving wall.

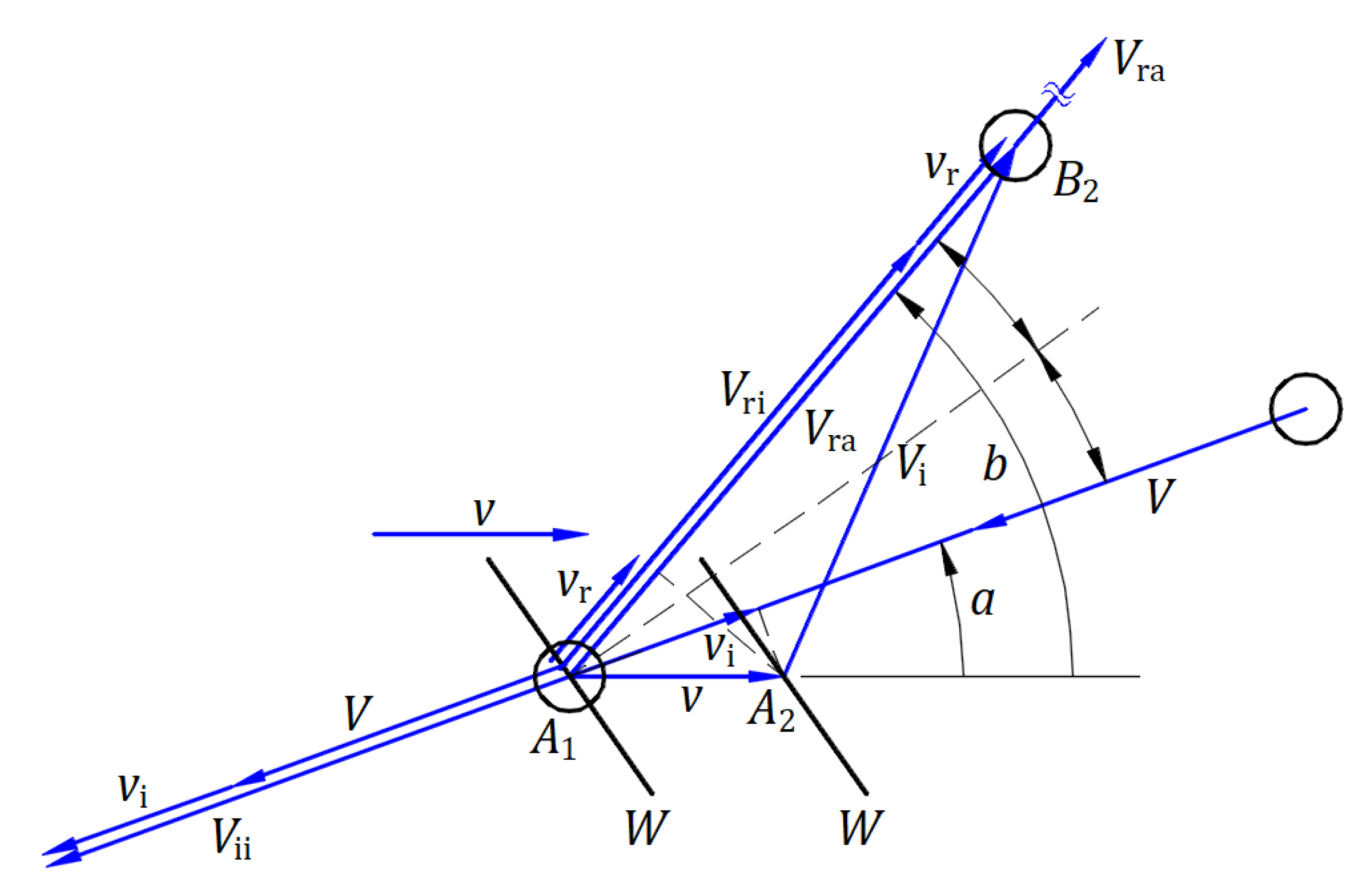
Figure 3. Emission, propagation, and reflection of balls in the absolute frame and an inertial frame.

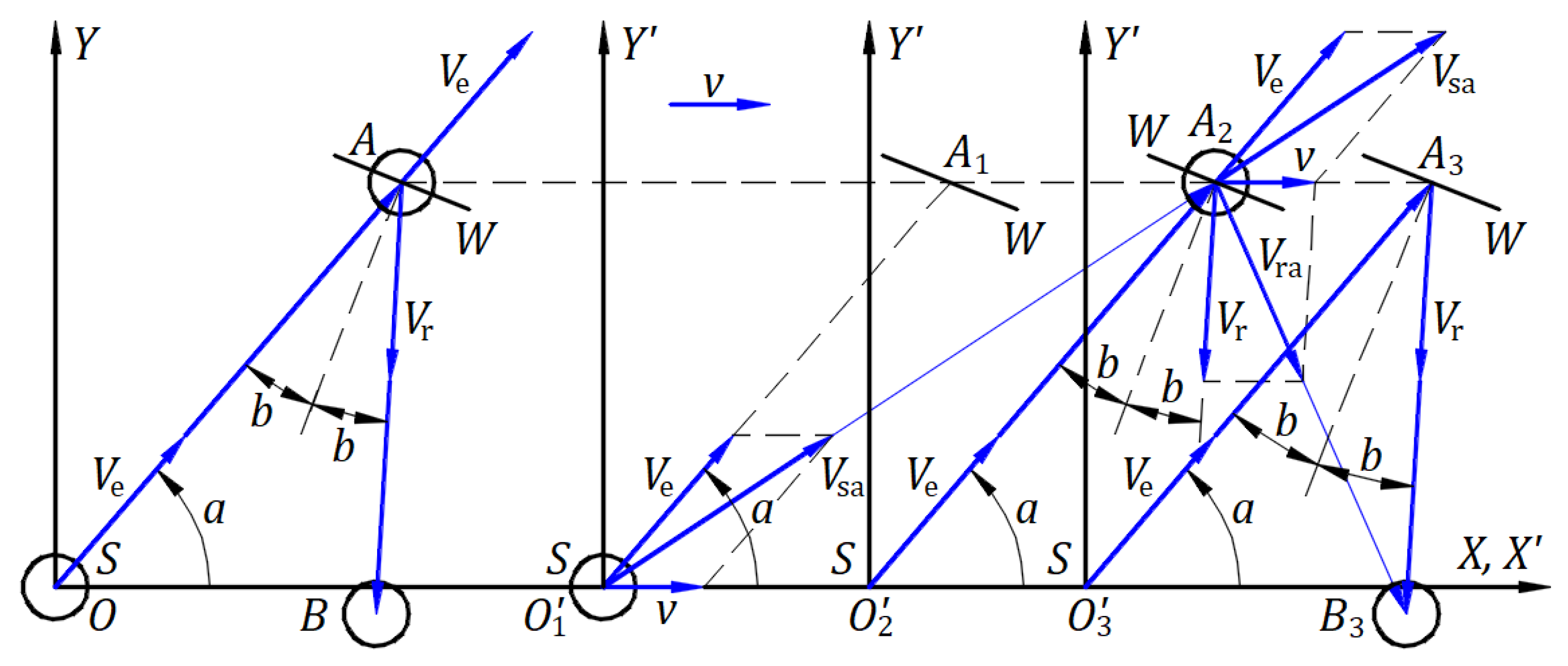
Figure 4. Reflection of light by a moving mirror.

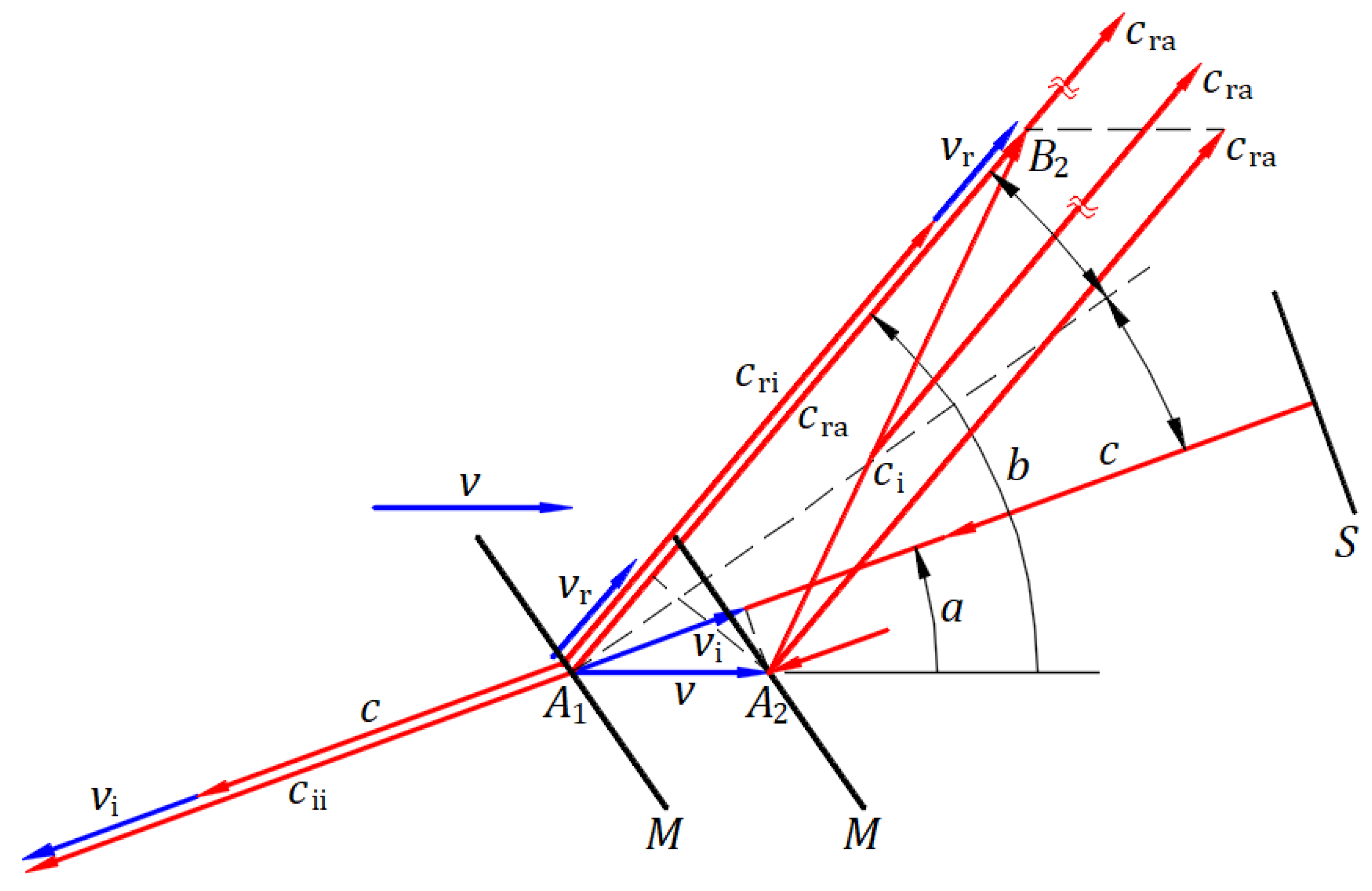
Figure 5. Emission, propagation, and reflection of light in the absolute frame and an inertial frame.

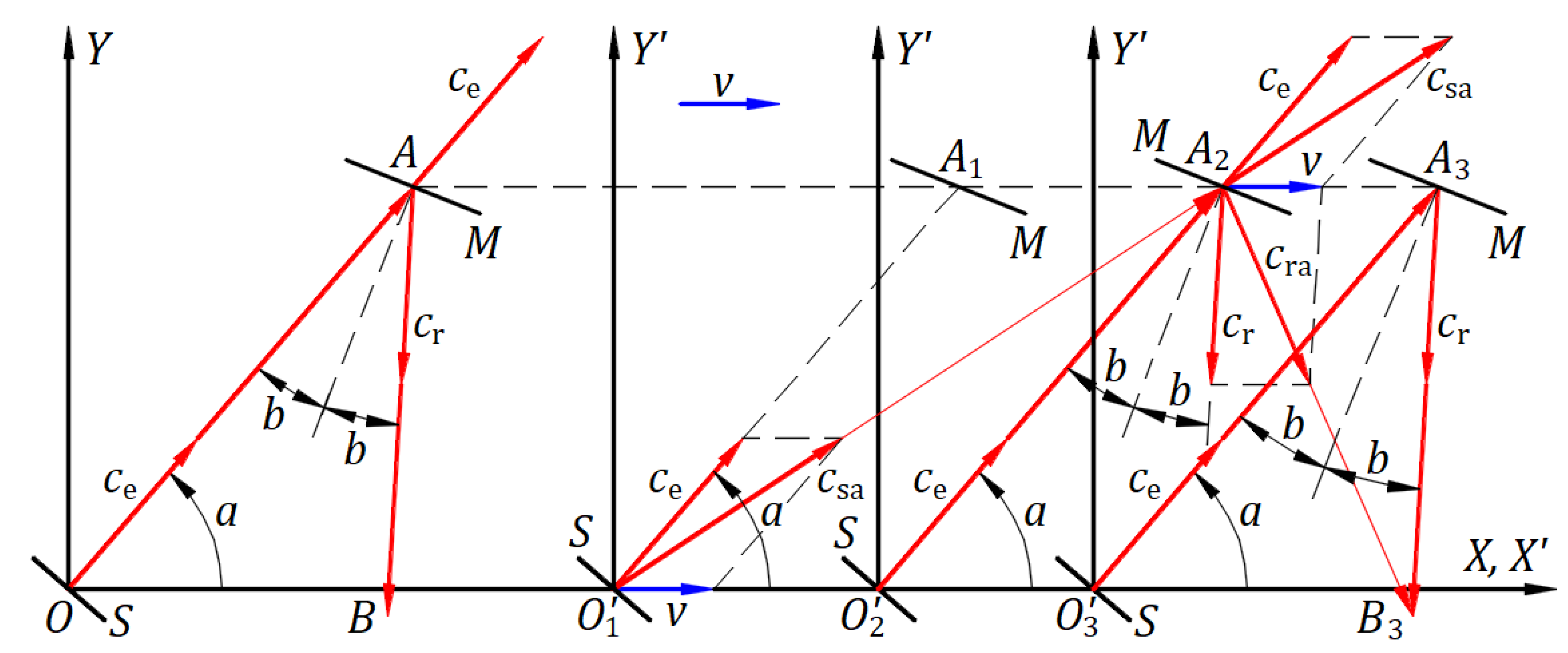
Figure 6. A boson as a carrier decaying at mechanical speed

v

near the speed of light

c

Figure 6. A boson as a carrier decaying at mechanical speed

v

near the speed of light

c

Figure 7. Observation of a star in the Universe considering (a) the dragging of light and (b) the constancy of light.

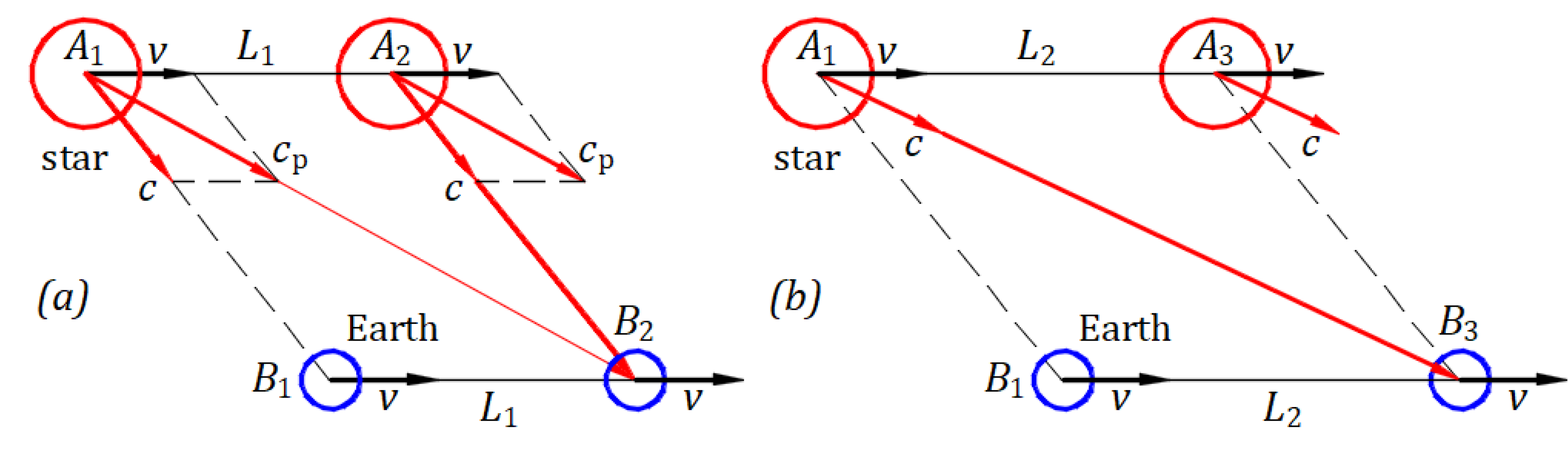
Figure 8. Observation of a star’s orbit.

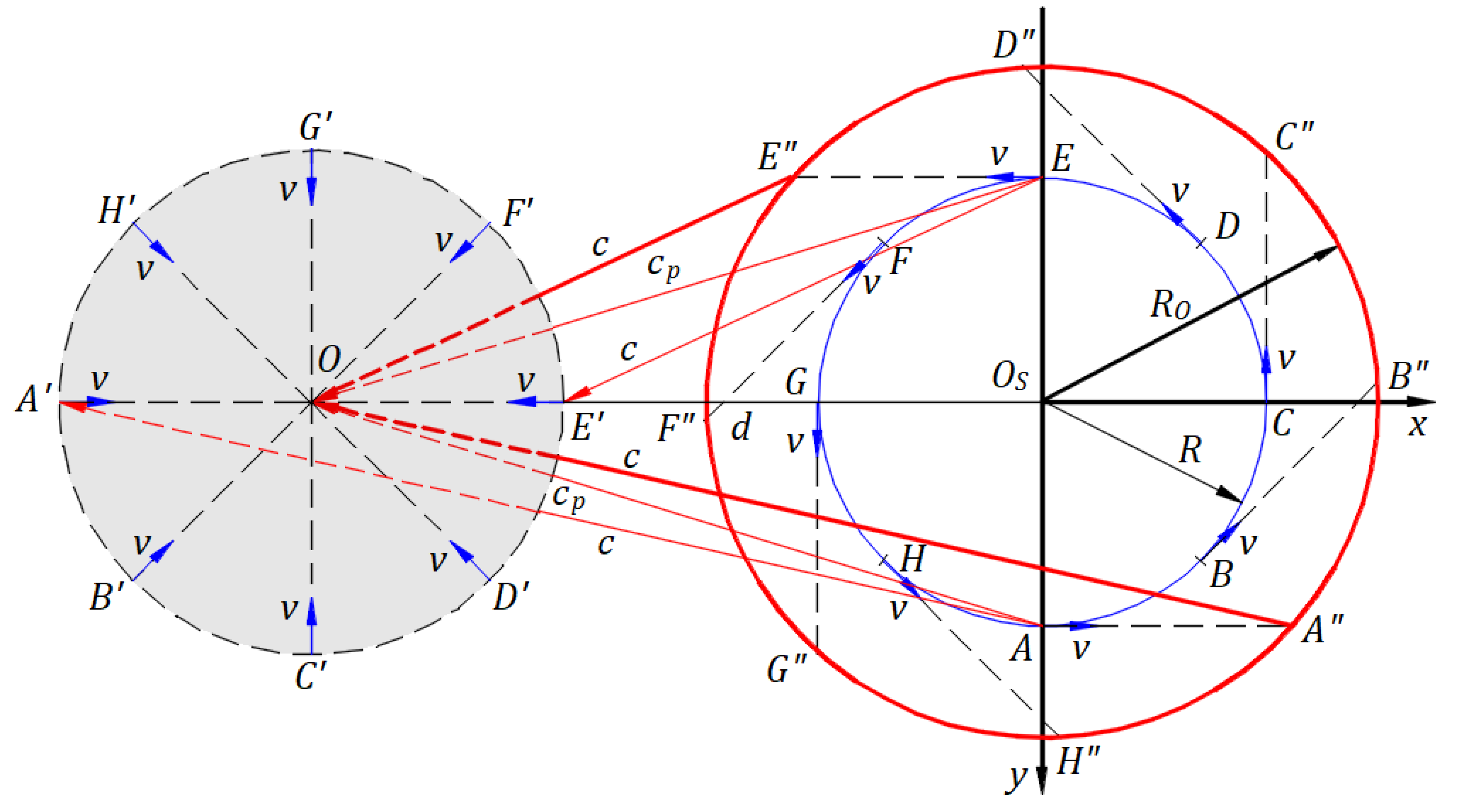
Figure 9. Galilean coordinates of a spherical light wavefront from a stationary frame shared in an inertial frame.

Figure 10. Lorentz’s transformation applied to a circular wavefront of light from a stationary frame to an inertial frame.

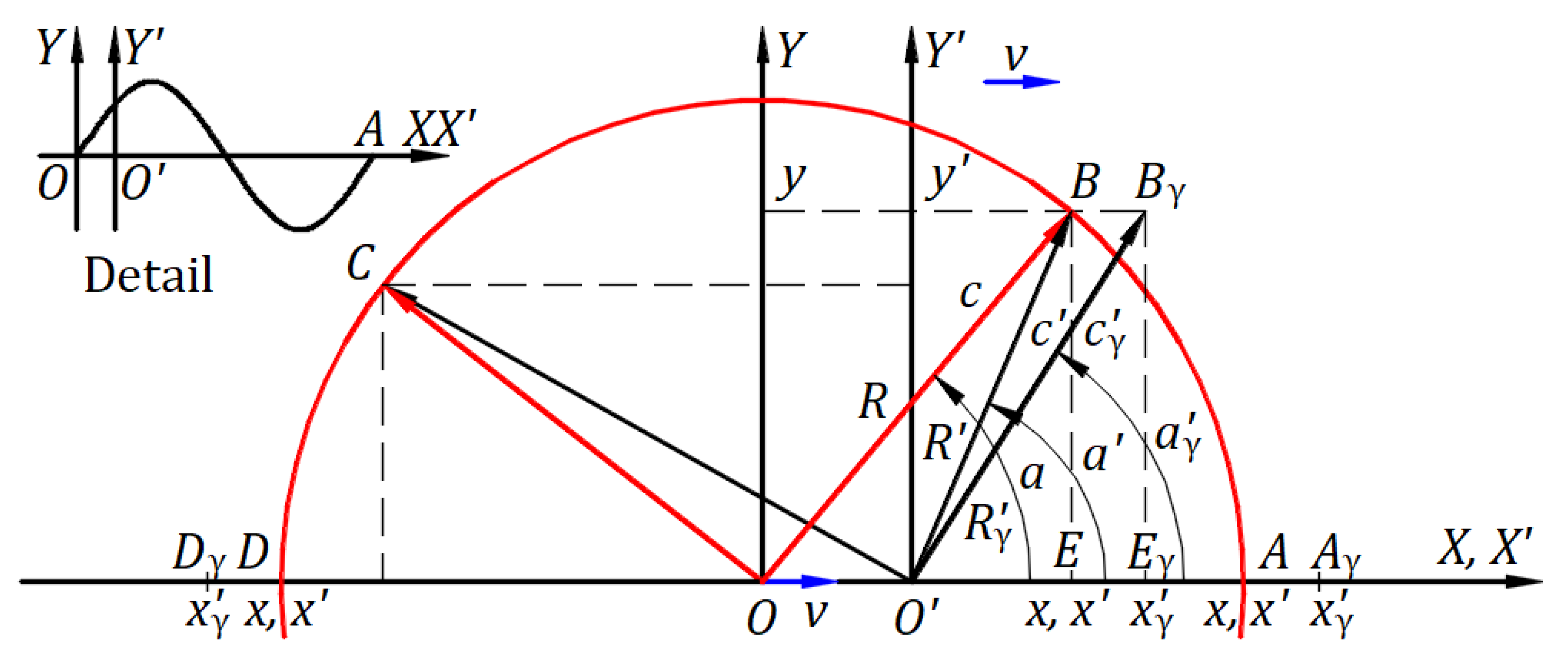
Table 1. Numerical calculation for the

x^{'}

and

c^{'}

functions of angle

a

at time

t = 1

Table 1. Numerical calculation for the

x^{'}

and

c^{'}

functions of angle

a

at time

t = 1

$a$ [°]	0	88
$x'$ [m]	2.99970000000000E+08	1.04398490107503E+07
$c^{'}$ [m/s]	3.00000000000000E+08	8.62078429116235E+09
89.99	89.9942704220391	89.9942704220392
2.23598772940828E+04	2.41565430769697E-07	–2.24728864850476E-07
4.02506676112310E+12	3.72569863424722E+23	–4.00482597595470E+23
90	92	180
–2.99999999999816E+04	–1.04998490107502E+07	–3.00030000000000E+08
–3.00000001500184E+12	–8.57158178682134E+09	–3.00000000000000E+08

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Kinematics of Balls and Light Versus the Theory of Special Relativity

Abstract

1. Introduction

2. Kinematics of Balls

2.1. Balls Brought from Rest to a Velocity v

2.2. Elastic Collision of Two Balls Moving in Opposite Directions

2.3. Elastic Reflection of a Ball by a Moving Wall

2.4. Emission, Propagation, and Reflection of Balls in the Absolute Frame and an Inertial Frame

3. Kinematics of Light

3.1. Reflection of Light by a Moving Mirror

3.2. Emission, Propagation, and Reflection of Light as Mechanical Phenomena in the Absolute Frame and an Inertial Frame

3.3. Experiments and Observations that Support the Kinematics of Light as a Mechanical Phenomenon

3.3.1. Michelson‒Morley Experiment

3.3.2. Experiment Performed at CERN, Geneva

3.3.3. Observation of a Star in the Universe

3.3.4. Observation of a Star’s Orbit

3.3.5. Miller Experiment

3.3.6. Majorana Experiment

3.3.7. Airy Experiment

3.4. Galilean Transformation

4. Einsteinian Theory of Special Relativity

4.1. Einstein's Suggestions

4.2. Einstein's Postulates

4.3. The Lorentz Transformation and Einstein Transformation

4.4. Discussions

5. Conclusions

Acknowledgments

Appendix A

Appendix B

References

MDPI Initiatives

Important Links

Subscribe

2.1. Balls Brought from Rest to a Velocity $v$