Preprint

Article

A Novel Hybrid Approach to the Diagnosis of Simultaneous Imbalance and Shaft-Bow in a Jeffcott Rotor-Bearing System.

Altmetrics

Downloads

Views

Comments

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

04 March 2024

Posted:

05 March 2024

You are already at the latest version

Alerts

Abstract

Ensuring optimal performance and reliability in rotor-bearing systems is crucial for industrial applications. Imbalance and shaft bow in these systems can lead to decreased efficiency and increased vibrations. Early detection and mitigation of a rotor’s faults are essential, and model-based fault identification has gained much attention in the manufacturing industry for years. Over the past two decades, however, the development of fault diagnosis rules with data-driven and artificial intelligence (AI) has become a trend, and in the foreseeable future, AI combined with big data will become mainstream. Nevertheless, the critical role of rotating machinery in manufacturing introduces a challenge, as the availability of fault data is often insufficient. This limitation renders the establishment of diagnostic rules using data-driven methods and AI technologies impractical. In light of these challenges, this study proposes a novel hybrid approach, that combines a physical model with machine learning (ML) techniques for the diagnosis of multi-faults (imbalance and shaft-bow demonstrated) in a Jeffcott rotor. To overcome the lack of real-world faulted, labeled datasets, a physics-based Jeffcott rotor model is first derived and then used to generate abundant fault datasets for ML. Subsequently, simulated data are employed for the training of an artificial neural network (ANN), enabling the network to learn from and analyze the vast array of generated data. The results prove that a well-trained feed-forward neural network (FNN) can accurately isolate and diagnose the imbalance and shaft-bow faults using the simulated data and the real data from the Jeffcott rotor experiment. These physics-based and ML approaches prove effective particularly for multi-fault, offering new possibilities for advanced rotor system monitoring and maintenance strategies in industrial applications.

Keywords:

Subject: Engineering - Mechanical Engineering

1. Introduction

Rotating machines find widespread utilization across diverse domains, encompassing manufacturing sectors, wind energy generation, aviation propulsion systems, electric motor assemblies, marine propulsion systems, and mining equipment, owing to their notable attributes of elevated efficacy and robustness. Within the framework of Industry 5.0, a significant transformation is observed, wherein the convergence of cutting-edge technologies and the promotion of sustainable practices in the manufacturing sector are emphasized. In this context, the utilization of rotating machines assumes a crucial and prominent role. Advancements in cutting-edge technologies in the field of material sciences have led to the development of rotating machines that are both faster and lighter while also being capable of withstanding prolonged periods of operation. Numerous operational irregularities, including but not limited to mass unbalance, bowed shafts, cracked shafts, misalignment, elevated temperatures, quick acceleration, and frequent load fluctuations, all contribute to reduced efficiency and premature mechanical breakdown. Consequently, these issues result in unplanned periods of inactivity and financial detriment. Hence, ensuring the efficient maintenance and accurate fault detection of rotating machines holds significant significance in achieving the objectives of Industry 5.0, where the convergence of efficiency, sustainability, and productivity is emphasized [1].

The vibration fluctuations, which are highly sensitive to both minor structural variation and changes in the operational process, are the basis for problem monitoring and diagnostics in rotating equipment. Any fault that occurs in a rotor will alter its vibrational behavior, and the degree of this impact depends largely on the various fault types. Given this, vibration-based diagnostics (VBD) has gained popularity and is often used in practice to diagnose a variety of rotor faults [2]. Walker et al. [3] reviewed the recent advances in the VBD and prognosis of rotors with eight common problems. The diagnosis of the machine must be carried out as accurately as possible because rotating machinery plays the main role in all industry applications. As a result, an efficient approach to diagnosing defects in rotating machinery is required. Approaches for fault diagnosis can be broadly divided into three categories: (1) physic-based or model-based; (2) data-driven; and (3) the combination of the first two categories is called the hybrid method.

Data-driven approaches utilize statistical theories or artificial intelligence (AI) algorithms to process the collected data, especially fault data, for fault diagnosis [4]. In recent years, data-driven approaches have become promising with the advancement of signal processing techniques such as empirical mode decomposition (EMD), Hilbert-Huang transforms (HHT) [5,6,7], and wavelet transforms [8,9,10]. In the foreseeable future, data-driven methodologies combined with artificial intelligence (AI) technology will remain well-liked and fruitful. Given the progress in the field of vibration analysis, there is an increasing interest in the application of AI techniques for fault diagnosis in rotating machinery. The integration of AI approaches has gained significant recognition and traction in both academic and industrial circles, presenting a promising avenue for addressing industrial challenges. Walker et al. [11] proposed automating the localization of unbalanced faults using ANN techniques. Mohamed et al. [12] propose a method for diagnosing faults in rotating machinery using frequency domain vibration analysis and neural network (NN) pattern classification. A variety of unbalanced types have been localized with high precision on a dynamic rotor test rig by ANN, providing benefits in the form of reduced sensors. Liu et al. [13] provided a comprehensive analysis of AI-based research and development for rotating machinery fault diagnostics, encompassing both theoretical and practical standpoints. Aneesh et al. [14] recently presented a comprehensive review of the role of AI in rotor fault diagnosis. They discussed the difference between traditional machine learning (ML) and deep learning approaches.

The availability of enough accurate data for network training is a need for the success of data-driven techniques. However, industrial plant rotor systems always have insufficient run-to-failure datasets. In that regard, model-based techniques for fault identification originating from physical models of rotor systems (complete or partial) have been offered for years.

The model-based method involves deriving the mathematical model of the rotor system from the dynamic theory and then inputting the operation data into the mathematical model to calculate the system’s defects and deterioration trends [15]. Using model-based techniques, numerous studies have detected rotor faults with success. Edward et al. [16] used model-based identification in the frequency domain to identify unbalance on a test rig. Bachschmid and Pennacchi [17] used experimental validation to support model-based methods for fault location, severity assessment, and fault classification. To assess the accuracy of the accomplished identification, they developed a new qualitative index termed residual. On several test rigs and actual machines, this approach has been experimentally proven (see references) [18,19,20] for a variety of problems, including unbalances, rotor permanent bows, rotor rubs, coupling misalignments, cracks, looseness, and rotor stiffness asymmetries. Sekhar [21] applied this methodology to concurrently identify instances of unbalance and cracking within a rotor-bearing system. Jain and Kundra [22] employed model-based techniques to detect unbalance and cracks, with experimental validation of unbalance identification conducted on a test rig. Sinha et al. [23] conducted an estimation of the unbalance and misalignment of a flexible rotating machine based on a single run-down procedure. The authors illustrated their approach by employing empirical data. In their comprehensive study, Lees et al. [2]. provided a thorough analysis of the application of model-based rotating machine identification. They discussed various methods for deriving foundation models from operational data and subsequently updating them. Additionally, they extended various models derived for rotor problems and their use in fault identification. Jalan and Mohanty used an experimental model-based method to identify unbalance and misalignment in a rotor-bearing system [24]. However, there are numerous applications for this technique conducted by the work group [25,26,27], which has made significant contributions to the field of rotor fault identification using a model-based method. In a very recent study, Lin et al. [28] derived a novel model-based approach in which model parameters like bearing constants and initial unbalances are identified in the first phase and progressive unbalances based on daily operational data are used to identify them in the second phase. The unbalance can therefore be monitored online and in real-time. In general, the model-based method yields the most accurate results, which are consistent with physical theory; however, model derivation and verification are extremely time-consuming and must be performed by rotors specialists.

Rotating machines exhibit several forms of defects throughout their distinct components. When examining faults in rotors, there exist eight widely acknowledged categories, namely: imbalance, misalignment, cracks in blades and shafts, bearing faults, fluid-induced instability, shaft bow, rub, and looseness [29]. Imbalance and shaft bow are prevalent rotor problems that can lead to excessive synchronous or asynchronous vibration [30]. The predominant source of vibration in a rotor system is attributed to imbalance. Vibration stemming from rotor imbalance represents the most prevalent malfunction observed in rotor systems [11]. Conceptually, imbalance can be understood as a state in which vibrations, forces, or motions are transmitted to the bearings due to centrifugal forces generated by the rotor’s imperfect center of mass alignment with its rotation centerline [31].

Numerous ongoing studies on imbalance in rotating machinery have been done and span a wide range of topics, such as unbalance-misalignment [32], unbalance diagnostics [33], modeling methodologies to help with unbalance prediction, and lab-based experimental investigation. There are a number of comprehensive literature studies, including those by Edward et al. [34], Randall [35], and Walker et al. [36], that outline the range of unbalance prediction research.

Moreover, the shaft bow refers to the deviation from the perfect alignment of the geometrical axis of the rotor shaft. This phenomenon is often attributed to factors such as heat gradients experienced during the initiation and cessation of thermal turbo-turbines, material creep, manufacturing discrepancies, and other contributing factors. Depending on the amount and location of the bend, a shaft-bow causes an excessive amount of vibration in a machine [37]. Numerous scholarly studies have been conducted to discern the impacts of shaft-bows in rotating machinery, assess their dynamic properties, and implement suitable corrective measures [30]. The impact of residual rotor bow on rotor vibrations was examined in a seminal study conducted by Nicholas et al. [38,39].

The researchers studied how residual shaft bow affects the imbalance response in a simplified rotor model. They examined different combinations of bow and imbalance to understand their interaction. Additionally, they proposed three distinct balancing methods based on their findings. Flack et al. [40] employed a transfer matrix technique to forecast the imbalance response of a Jeffcott rotor subjected to bowing. The rotor was affixed to various fluid film bearings, and the outcomes were subsequently contrasted with prior experimental investigations. Shiau et al. [41] investigated the impact of residual shaft bow on the dynamic response of a simply supported single disk rotor. Their study systematically examined the interplay of factors such as disk skew, mass imbalances, and the positioning of the disk between the bearings. Ehrich et al. [42] examined the impact of the rotor bow and unbalance concerning the operating speed relative to the critical speed. Rao et al. [43] scrutinized a warped Jeffcott rotor model across diverse scenarios of a bow, revealing instances of self-balancing and phase jumping. The study conducted by Kang et al. [44] examined a sophisticated model of a geared rotor system featuring viscoelastic supports. The researchers investigated the impact of gear eccentricity, transmission error, and residual rotor bow on the system.

The significance of identifying residual shaft bows and investigating their impact on more intricate rotors was demonstrated by the aforementioned theoretical and experimental research. Pennacchi et al. [45] employed statistical techniques to quantitatively evaluate the precision of identifying a generator rotor afflicted by a thermal bow. Using short-bearing theory, Shen et al. [46] presented a nonlinear analysis of a rub-impact rotor-bearing system with nonlinear oil-film forces. Darpe et al. [47], investigated the effects of residual shaft bow on the dynamics of a cracked rotor and Song et al. [48] examined the effects of residual rotor bow on the rotor’s longitudinal responses. During this investigation, numerical simulations and experiments were employed, and the principal component analysis method was utilized to identify rotor faults. Rossner et al. [49] devised a method for autonomous model-based monitoring of an unstable bow curve using the Ritz technique.

Any bow in the shaft system will result in synchronous shaft motion, which introduces vibrations just like the unbalance does [50]. The machine will react roughly as follows if the bow is present during the run-up. If an imbalance existed, the vibration amplitude would rise with a steady machine speed. If the bow is a result of shaft-rub or another non-uniform heating process, for instance, the vibration amplitude and phase will significantly change over time. The simultaneous existence of both will superimpose the response, making it difficult to identify each fault simply from the vibration response. These two conditions are essentially the same, and only the location distinguishes them. Therefore, identifying these two types of flaws, also called multiple faults, is an important task.

Apart from that, a few published papers and simulations have identified multiple faults simultaneously. Srinivas et al. [51] employed ANN and wavelet transform to categorize a rotor system that experienced both shaft bow and imbalance. This was achieved by monitoring the vibrations in the transverse and axial directions. Rezazadeh et al. [52] presented recent research where they used a combination of WTS (wavelet transform spectrum) with LSTM (long short-term memory) and SVM (Support Vector Machine) to detect imbalances and shaft bows in rotor systems.

The present research posits a novel approach for the identification of multiple faults, employing a hybrid methodology that combines physical modeling with machine learning (ML) techniques. Even though model-based approaches have been used to diagnose and anticipate rotor defects for many years, there are drawbacks, including the need for lengthy model creation and a lack of self-adaptability to aging machinery. Therefore, with the aid of modern signal processing, hybrid methods that make use of AI techniques and physical modeling have appeared. An exemplar in this domain is the work of Huang et al. [53,54], who adeptly introduced the concept of a hybrid approach incorporating a neural network (NN) alongside physical modeling. Djeziri et al. [55] used a hybrid method for fault prognosis based on the physical model, data clustering, and the geolocation principle to predict the remaining useful life (RUL) for wind turbine systems. Recently, Wilhelm et al. [56] reviewed hybrid approaches for fault detection and diagnosis (FDD) that combine data-driven analysis with physics-based and knowledge-based models to overcome a lack of data to increase FDD accuracy. Moreover, Fang et al. [57] present a fault diagnosis and prognosis based on a hybrid approach that combines structural and data-driven techniques.

The purpose of this study is to create a hybrid approach based on a physical model to diagnose multiple faults in rotor-bearing systems. The essence of this innovative method can be elaborated as follows:

Establish the physical and mathematical model to derive the Jeffcott rotor model and identify the model parameters, including imbalance and shaft-bow characteristics.
After parameter identification, the physical model can be used to generate sufficient sets of simulated data for ANN-supervised training, which helps to produce a more reliable model. A trained ANN can be integrated into a Jeffcott rotor monitoring system for online diagnosis of imbalance and shaft-bow fault components using simulated and experimental data from Jeffcott rotor experiments.

The remainder of this paper’s structure may be summed up as follows: In Section 2, the physical model of a Jeffcott rotor subjected to imbalance and shaft-bow is described, and Section 3 introduces the hybrid methodology employed in the present study. Numerical analysis and experimental verification is given Section 4. Finally, in Section 5, concluding remarks are drawn to justify the effectiveness of this approach.

2. Physical Model of Jeffcott Rotor with Simultaneous Imbalance and Shaft-Bow

The schematic design adopted a purely physics-based approach. This design, as elucidated in Figure 1, provides a visual representation of the Jeffcott rotor systems consisting of an imbalance and shaft-bow with a rigid disc, supported by two simple bearings. It is assumed that the shaft-bearing possesses only stiffness K and possible damping B. Here O stands for the center of rotation axis, C for the disk’s geometry center, and e the distance of the rotor’s imbalance away of the geometric center, Ω represents the rotational speed, s represents the residual shaft-bow, m represents an imbalance mass, θ represents the shaft-bow angle, and α represents the imbalance angle, both reference to a key-phasor (KP).

The rotor imbalance is commonly specified by a term of U=me with a unit of g·mm or kg·m. The acceleration of the imbalance mass at point A can be calculated, based on fundamental dynamics, to be.

{\overset{⇀}{a}}_{A} = \ddot{u} \vec{i} + \ddot{v} \vec{j} - Ω^{2} [e \cdot \cos (Ω t + α) \vec{i} + e \cdot \sin (Ω t + α) \vec{j}]

(1)

where

\vec{i}

and

\vec{j}

respectively denote the unit vector in X and Y direction.

The inertia force resulting from the imbalanced mass can be represented by

- m {\overset{⇀}{a}}_{A} = [- m \ddot{u} + m e Ω^{2} (\cos Ω t + α)] \vec{i} + [- m \ddot{v} + m e Ω^{2} (\sin Ω t + α)] \vec{j}

(2)

The equation of motion (EOM) for the Jeffcott rotor with simultaneous imbalance and shaft-bow can be obtained by using Newton’s second law.

Σ F_{u} = M \ddot{u}

(3)

Σ F_{v} = M \ddot{v}

(4)

Subsequently, the EOMs subject to imbalance and residual shaft-bow, in X and Y directions, are summarized as

(M + m) \ddot{u} + B_{x} \dot{u} + K_{x} u = K_{x} s \cos (Ω t + θ) + m e Ω^{2} \cos (Ω t + α)

(5)

(M + m) \ddot{v} + B_{y} \dot{v} + K_{y} v = K_{y} s \cos (Ω t + θ) + m e Ω^{2} \cos (Ω t + α)

(6)

Or, in terms of vibration nominal forms as:

\ddot{u} + 2 ζ_{x} ω_{n x} \dot{u} + {ω_{n x}}^{2} u = s {ω_{n x}}^{2} \cos (Ω t + θ) + \frac{U}{M_{T}} Ω^{2} \cos (Ω t + α)

(7)

\ddot{v} + 2 ζ_{y} ω_{n y} \dot{v} + {ω_{n y}}^{2} v = s {ω_{n y}}^{2} \cos (Ω t + θ) + \frac{U}{M_{T}} Ω^{2} \cos (Ω t + α)

(8)

where M, B, and K respectively represent the mass, damping.

M_{T} = M + m \approx M

denotes the total mass of the rotor.

ω_{n i} = \sqrt{K_{i} / M_{T}}

and

ζ_{i} = C_{i} / 2 \sqrt{K_{i} M_{T}}, i = x, y

represent the system’s natural frequency and damping ratio in X and Y directions, respectively.

The right-hand side terms in Equations (7) and (8) describe the excitation forces caused by shaft-bow and imbalance, respectively. The vibrational responses of u and v due to shaft- bow and imbalance can be separately solved and superimposed for the total responses. Nonetheless, identifying the rotor’s imbalance (U,α) and shaft-bow (s,θ) from the total responses is a backward process and non-linear functions of α and θ and there exists non-unique solutions. That is the difficulty in almost of all cases of multi-fault diagnosis.

Let us first solve the responses due to these two types of faults, separately, and introduce the idea of combining the physical modeling and machining learning techniques for multi-fault diagnosis. The EOM of u due to bow alone is.

{\ddot{u}}_{b} + 2 ζ_{x} ω_{n x} {\dot{u}}_{b} + {ω_{n x}}^{2} u_{b} = s {ω_{n x}}^{2} \cos (Ω t + θ)

(9)

where the subscript b represents the term “bow”. The solution of Equation (9) can be readily obtained from any standard textbook on vibrations [58].

u_{b} = s \cdot A_{x} \cos (Ω t + θ - λ_{x})

(10)

where A_x is the amplification factor, and it can be expressed as follows:

A_{x} = \frac{1}{\sqrt{{(1 - {τ_{x}}^{2})}^{2} + {(2 ζ_{x} τ_{x})}^{2}}}

(11)

τ_{x} = \frac{Ω}{ω_{n x}}

(12)

λ_{x} = \tan^{- 1} \frac{2 ζ_{x} τ_{x}}{1 - {τ_{x}}^{2}}

(13)

τ is the speed ratio and λ is the response phase lag.

In most cases,

m < < M

. Thus,

M_{T} \approx M

and similarly the EOM caused by imbalance can be written as:

{\ddot{u}}_{u} + 2 ζ_{x} ω_{n x} {\dot{u}}_{u} + {ω_{n x}}^{2} u_{u} = \frac{U}{M} Ω^{2} \cos (Ω t + α)

(14)

The subscript u represents a state of unbalance. Similarly, the response due to the imbalance can be solved to be

u_{u} = \frac{U \cdot τ_{x}^{2}}{M} A_{x} \cos (Ω t + α - λ_{x})

(15)

Via superposition, the response in the X and Y directions can be expressed as follows:

u (t) = A_{x} [\frac{U τ_{x}^{2}}{M} \cos (Ω t + α - λ_{x}) + s \cos (Ω t + θ - λ_{x})]

(16)

v (t) = A_{y} [\frac{U τ_{y}^{2}}{M} \sin (Ω t + α - λ_{y}) + s \sin (Ω t + θ - λ_{y})]

(17)

The responses of Equations (16) and (17) can be further rearranged in terms of

\cos (Ω t)

and

\sin (Ω t)

components as follows:

u (t) = f_{1} \cos (Ω t) + f_{2} \sin (Ω t)

(18)

v (t) = f_{3} \cos (Ω t) + f_{4} \sin (Ω t)

(19)

where f₁, f₂, f₃, and f₄ are the defined four features as functions of the four-fault variables U, α, s, and θ as

\begin{array}{l} f_{1} = A_{x} [\frac{U τ_{x}^{2}}{M} \cos (α - λ_{x}) + s \cos (θ - λ_{x})] \\ f_{2} = - A_{x} [\frac{U τ_{x}^{2}}{M} \sin (α - λ_{x}) + s \sin (θ - λ_{x})] \\ f_{3} = A_{y} [\frac{U τ_{y}^{2}}{M} \sin (α - λ_{y}) + s \sin (θ - λ_{y})] \\ f_{4} = A_{y} [\frac{U τ_{y}^{2}}{M} \cos (α - λ_{y}) + s \cos (θ - λ_{y})] \end{array}

(20–23)

Or, in terms of the feature vector:

f_{4 \times 1} = {f_{1}, f_{2}, f_{3}, f_{4}}^{T}

(24)

The fault variables associated with imbalance and shaft-bow can be written as a fault vector,

m_{4 \times 1} = {U, α, s, θ}^{T}

(25)

and the subject of diagnosis is to identify Equation (25) from the data of Equation (24), by calculations of measurements. It is apparent that due to multi-variable and nonlinearity the solution is non-unique. ANN provides a robust alternative to solve this type of problem.

Note that the features shown in (20-23) are not only functions of the fault variables but also functions of system variables such as speed ratio τ and damping ratio λ The damping has been found minor effects on the response, but the speed ratio has significant impact on the diagnosis accuracy and will be discussed in Section 4.

3. Hybrid Methodology

In this study, the authors propose a comprehensive approach for establishing a real-time imbalance and shaft-bow diagnosis system for the rotor system and demonstrate a Jeffcott rotor-bearing system as the application. This approach combines mathematical modeling techniques with ML-based prediction methods to enable accurate and timely detection of multiple faults in the system. The ability to assess the onset of faults is a crucial aspect of both physics-based and machine-learning approaches to analyzing the overall system.

ML techniques are increasingly being used to diagnose faults in rotating machinery by analyzing data from sensors on the machinery. These models can learn to detect patterns that indicate faults and classify the type and severity of the problem, which helps maintenance teams diagnose issues earlier and prevent costly downtime. To overcome this challenge, a novel hybrid approach is to be developed. This approach combines machine learning techniques with expert knowledge and physical models to augment the limited fault data.

Data-driven methodologies leverage statistical theories and artificial intelligence (AI) algorithms to analyze gathered data, particularly fault data, to facilitate fault diagnosis. However, the efficacy of data-driven techniques is contingent upon the availability of a substantial amount of accurately labeled data for network training. Notably, industrial plant rotor systems frequently encounter challenges in acquiring sufficient labelled datasets. Addressing this data constraint, the physical model employs a knowledge-based approach, presenting a viable alternative to overcome the lack of relevant data.

Nevertheless, it is imperative to acknowledge the limitations of a data-driven approach, particularly in scenarios involving multiple faults, where its reliability may be compromised. In such instances, utilizing a physical model to generate fault data for ANN training emerges as a more dependable solution, enhancing the robustness of the overall diagnostic process.

Two steps were involved in this process: model construction and real-time diagnosis as shown in Figure 2. The model construction phase involved a combination of physical modeling and ML techniques. By using a physical model, one can generate sufficient sets of simulated data for ANN-supervised training, which helps to produce a more reliable model to diagnose imbalance and shaft-bow in a Jeffcott rotor-bearing system. Following that, the derived model is implemented into a real rotor system for real-time diagnosis, as displayed in phase 2. In this phase, cases with two different residual bows plus various imbalance combinations are tested to acquire the real response features from an experimental setup of a rotor rig. Note that in the designed scenarios the bow was made only at two values, s=0.5 mm run at 1600 rpm and 3200 rpm and s=4 mm run at 680 rpm due to the difficulty of bending the shaft to reach a small, permanent bow. Moreover, in the s=4 mm bow case, the rotor can be run only at very low speed due to safety concerns.

The real response features (f₁, f₂, f₃, and f₄) are then calculated from the measured response of the rotor rig and fed into the trained FNN for the instant fault components identification i.e., m^T= {U, α, s, θ}. By combining phase-1 and phase-2, this hybrid approach can overcome the limitations of data availability and provide accurate diagnosis model for imbalance and bow faults in rotating machinery.

To achieve this goal, we employed the most common ML-based approaches used for rotor fault diagnosis, which are ANNs. ANNs can learn to classify different types of faults based on vibration, current, or acoustic data from sensors on the machinery. In particular, ANNs can be utilized to diagnose imbalance and shaft bow in rotating machinery, which is a common problem that can lead to excessive vibrations, reduced machine performance, and even catastrophic failure.

Among various types of ANNs, we have tested various types such as Feed-forward neural networks (FNN), RNN, LSTM and found their difference in accuracy is almost non-differentiable. Hence, FNN is selected for its simple structure and computational efficiency. In FNN, the information flows in one direction, from the input layer through one or more hidden layers to the output layer. By training the FNN with historical data from the rotor system, it can learn the underlying patterns and relationships between various system parameters and the occurrence of multiple faults. This enables FNN to make predictions about future fault events based on real-time sensor data.

Here is how machine learning approach can be used to diagnose multiple faults in a Jeffcott rotor machine:

Figure 3. ML approach to diagnosing multiple faults in a Jeffcott roto-bearing system.

Acquiring data: The physical model is used to generate the datasets randomly. Nevertheless, the training set can be generated from measured data as much as one need. It is notable that these imbalance and shaft-bow components, m^T= {U, α, s, θ}, are randomly inputs to the physical model, and the response features components at the disk centre after forwarding calculation, are the output, i.e., Equation (24).
Data preparation: The generated datasets will be considered raw data for further processing by supervised training. The simulated inputs/outputs are reversed during the network training. The response components, f^T, i.e., 4 parameters are used for input to the ANN, and the 4 parameters i.e., m^T are used for the target.
ANN architecture: An appropriate model needs to be selected and configured for the problem at hand. Typically, a feedforward neural network (FNN) with one or more hidden layers is used. There are several parameters in each model that were varied to arrive at the best model parameter for each case. The proposed framework is modeled in MATLAB software.
Model Training: In the present study, the FNN is trained with a single hidden layer architecture with a varying number of nodes by using 10,000 datasets, which are randomly generated from a physical model. The first 70 percent of the datasets are utilized for training, the second 15 percent are used for validation, and the final 15 percent are used for testing.
Model Testing: To rigorously evaluate the FNN model’s performance, we employed root mean squared error (RMSE) to evaluate the closer alignment between the randomly generated (so-called real data) and the estimated values. A lower RMSE value signifies better accuracy and model performance. The formula of RMSE is:

$R M S E = \sqrt{\frac{1}{n} \sum_{i = 1}^{n} {(y_{i} - {\hat{y}}_{i})}^{2}}$

(26)

where $y_{i}$ denotes the real value for the i^th point, ${\hat{y}}_{i}$ denotes the estimated value, and n denotes the number of data points.
Diagnosis: The trained FNN is tested using simulated and real data acquired from the experimental setup of the Jeffcott rotor to diagnose the multi-fault components, i.e., U, α, s, and θ. Based on the output of the FNN, the machine operator can monitor the growth of imbalances and shaft-bow to take necessary actions.

4. Numerical analysis and Experimental Verification

4.1. Numerical Analysis Using Simulated Data

Detecting imbalance and shaft-bow in Jeffcott rotor systems is an immensely significant task within numerous industrial domains. To tackle this challenge, employing an ANN model has proven to be highly effective. The investigation commenced by employing a FNN that comprised multiple hidden layers, an input layer, and an output layer, all lacking feedback connections or loops [59].

In the context of diagnosing multiple faults, the input layer adeptly receives the vibration signals or response components originating from the horizontal and vertical directions of the Jeffcott rotor system. Subsequently, these signals are skillfully processed by the neurons residing within the concealed layers, which judiciously employ activation functions like the tan-sigmoid function or the rectified linear unit (ReLU) function. The outcome obtained from the hidden layer is then skillfully mapped to the ultimate output through the neurons residing within the output layer. It is worth noting that the output layer typically employs a linear transfer function, such as the purelin transfer function, to carry out this mapping process.

To train the FNN, 10,000 datasets are randomly generated, and 70% of them are used for training, 15% for validation, and the last 15% for testing. The Levenberg-Marquardt backpropagation (LM) training algorithm, specifically the trainlm training function in MATLAB, was employed to train the network. To determine the most suitable number of hidden nodes, a trial-and-error approach was employed, as there is no precise method to select this parameter based solely on the number of inputs and outputs. However, in many ANN applications, including FNNs applied to the rotor system, a single hidden layer has been proven sufficient [51,60]. Once the FNN is trained, it can be used to accurately detect and diagnose imbalance and shaft-bow in the Jeffcott rotor system based on the input vibration signals.

To examine the performance of the models, networks were trained with 10, 20, 30, 40, 50, and 60 hidden nodes and the results of the study revealed that a single hidden layer with 40 nodes had the lowest RMSE as shown in Figure 4. The error drops rapidly and reaches the minimum at the configuration of 40 nodes. The errors of the testing set were reported in Table 1 in terms of (U_x, U_y, s_x, s_y) rather than (U, s, α, θ), because the phase angle values (α and θ), did not align accurately because of their periodic nature. This change was made to mitigate concerns regarding potentially misleading outcomes. In Table 1, the least errors for four components all occur at 40-node number.

During the investigation of the performance of FNN using simulated data, this study proposed a variety of faults conditions so that the diagnosis accuracy can be observed and compared. Different fault combinations are classified as imbalance dominating, shaft-bow dominant, and equal. As imbalance dominates, U values range from 0.6 to 0.9 kg·m and s from 0.5 to 0.1 mm. That denotes the unbalance component is 100 times the shaft-bow component. In contrast, shaft-bow dominance has U from 0.00001 to 0.00002 kg·m and s from 2 to 3 mm, opposing the imbalance scenario. U and s parameters vary from 0.002 to 0.003 kg·m and 2 to 3 mm, respectively, in the equal case.

In addition, the effects of imbalance and shaft-bow vary differently with rotational speed. The FNN performance under three different operational range, said sub-critical speed (τ < 1), near-critical speed (τ ≈ 1), and trans-critical speed (τ > 1), are also investigated. RMSE is used as the metric for performance evaluation in each scenario, and the lower RMSE values indicate better performance or closer alignment with the FNN predictions.

The data illustrated in Table 2 demonstrates the performance of FNN across various fault dominations under different speeds. Let us first look at the third column of imbalance dominant case and it is observed the estimated error sum of FNN being the least (bold face) as running at near-critical speed τ ≈ 1, then τ > 1 and τ < 1. The identification error sum of shaft-bow, however, exhibits no significant difference at different speed ranges. As to the cases of shaft-bow dominant, there was no significant difference in imbalance and bow estimation errors under various speeds. When these two faults are of equal weight, the least estimation errors for imbalance and shaft-bow happen at different speed regions. The imbalance is the best identified at τ > 1, yet bow identification shows the least error as the rotor runs at τ < 1.

From the results shown above, it can be concluded that the imbalance is better diagnosed at higher speeds, τ ≈ 1 or τ > 1, but the shaft-bow is better at lower speed, τ < 1. This conclusion can be well explained and verified from the frequency response of these two types of fault as shown in Figure 5. In this figure, it is clearly seen the imbalance response significantly magnified at higher speed, but the shaft-bow response, to the opposite, diminishes with speed increasing. In words, shaft-bow dominates at sub-critical speeds and imbalance takes over after critical speed. Both reach the maximum response at near critical speed.

Moreover, it is noteworthy, from Table 2, that the equal scenario case exhibits much smaller RMSE than the others for both imbalance and shaft bow. It means that FNN diagnoses simultaneous imbalance and shaft-bow would be the most accurate when shaft-bow and imbalance are not unduly dominant.

4.2. Experimental Verification and Real-time Diagnosis

The Bently experimental rig, depicted in Figure 6, is used for the rotor fault experiment, and consists of a motor attached to a single disk rotor. The motor runs counterclockwise as viewed from the motor side. The rotor shaft is upheld by simple, identical bearings with unknown stiffness. The diameter of the rotor shaft is 10mm. A disk of 75mm in diameter and 800 g in mass are mounted on the rotor shaft by radial screws. There are 16 tapped holes symmetrically placed on each side of the disk with flat faces at e=30mm to attach any desired amount of imbalance mass. The Memstec Glory Laser types of sensors CD3S-30 and CD3S-50 were precisely positioned on the corresponding disk along the X and Y axes, which are positioned at an angular separation of 90 degrees. After installation, the sensors were integrated into the power supply system to ensure a reliable and uninterrupted power source to ease the measurement operation.

The rotor in the present study encounters flexible support conditions, where the stiffness and damping coefficients are determined by a combination of the shaft and bearing components in the rotor system, as shown in Figure 7. The support stiffness consists of a combination of K_s (shaft stiffness) and K_b (bearing stiffness). It is important to acknowledge that the mass of the shaft, m_s, cannot be ignored and it must be lumped to a certain fraction to the mass of the disk, M_d. To determine the amount of shaft mass to be lumped with the disk mass, calculations can be carried out using an equivalent system. This entails establishing an equivalent system by analyzing the total kinetic energy (KE) of the shaft under the assumption of vibration at the static deflection mode.

Subsequently, the effective mass of the shaft should be lumped onto the disk is 0.48 m_s. Additionally, the mass of the disk (M_d) is increased by 0.48m_s. Therefore, the value of M_eq would be 0.96 kg.

The system’s overall stiffness is determined by the series connection of the shaft and the bearings as shown in Figure 7. The stiffness of the shaft under simple supports can be easily calculated to be K_s=(48EI/L³). Nonetheless, the bearing stiffness K_b is difficult to calculate, theoretically, therefore, a practical approach is used to run the rotor experimentally to identify its critical speed (ω_cr), which was found to be 2300 rpm for the present case. The identified system critical speed

ω_{c r} = \sqrt{K_{e q} / M_{e q}}

can be reversely used to evaluate the bearing stiffness K_b.

The critical speeds associated with X and Y vibrations for an asymmetric rotor are different. However, the asymmetry in the rotor rig is too small to be differentiable in the vibration measurement. While evaluating the critical speeds, it was assumed that the first recorded critical speed pertains to the Y direction. Additionally, it was noted that the critical speed in the X direction, as referenced in prior research [61], is approximately 5% greater than in the Y direction.

The damping ratios in the X and Y directions of the rotor can be calculated using the logarithmic decrement from the measured transient response as shown in Figure 8. The transient response curves in X and Y sensors were recorded after shutting down the motor from a steady operation. The values obtained for ζ_x and ζ_y are 0.5% and 0.47%, respectively. Table 3 illustrates model parameters of the rotor-bearing system of test rig.

The experimental rotor is connected to a computer, enabling the acquisition of data via sensors, which is then analyzed using LabVIEW software. The rotor’s vibration signals were recorded by the sensors located on the rotor disk, measuring the vibrations in both the X and Y axes. Figure 9 demonstrates one example of recorded sensors’ response, in which the red-colored dots represent the key-phasor pulses in X and Y. The response phase angle φ is defined as the angular displacement in degrees from the key-phasor pulse to the first positive peak of vibration amplitude. From Figure 9, the estimated value of φ_x is roughly 110⁰, whereas φ_y approximately 200⁰, with φ_y lagging behind the X probe sensor by 90⁰. This phase difference somewhat verifies the correctness of the data sequences as the Y sensor is precisely positioned 90⁰ behind the X sensor.

The vibration responses from the sensors’ outputs can be expressed as:

\begin{array}{l} u (t) = A_{x} \cos (Ω t - φ_{x}) = A_{x} \cos (φ_{x}) \cos (Ω t) + A_{x} \sin (φ_{x}) \sin (Ω t) \\ v (t) = A_{y} \cos (Ω t - φ_{y}) = A_{y} \cos (φ_{y}) \cos (Ω t) + A_{y} \sin (φ_{y}) \sin (Ω t) \end{array}

(27)

where the vibration amplitudes and phases in the X and Y directions can be obtained from Figure 9. The four feature responses (f₁, f₂, f₃, and f₄) from the experimental study can be assessed using the equations shown above as well as Equations (20)–(23). This response can be fed into a trained FNN implemented into the monitoring system for real-time fault component (U, α, s, θ) diagnosis.

The disk illustrated in Figure 10a, features 16 holes with an angular separation of 22.5° between each hole, facilitating the determination of the imbalance phase angle α measured from the key-phasor. The formation of a small permanent shaft bow is difficult to control because it needs to heat and bend the shaft to reach the plastic deformation region. Therefore, only two shaft bows were employed in the study, each with residual bows of 0.5 mm and 4 mm as shown in Figure 11. These shafts were installed on the rotor kit and varied in mass imbalance values on the disk before initiating rotor operation.

The operational parameters were deliberately set at 1600 rpm and 3200 rpm, corresponding to the sub-critical (τ=0.69) and trans-critical speeds (τ=1.39), respectively, given an initial bow of 0.5 mm. In the interest of safety protocols, the machinery was deliberately operated at a speed far below the critical threshold during the initial bow phase of 4 mm. This experimental validation is used to determine FNN capability in identifying fault components related to imbalance and shaft-bow (U, α, s, θ). However, the real fault component was employed at four different values while maintaining s constant to estimate the fault components by FNN.A detailed comparison between the experiment’s real data and the FNN’s estimated value is given in Table 4, Table 5 and Table 6. Each table illustrates four scenarios of imbalance and shaft-bow combinations: case-1 reveals two fault angles in the same quadrant with a difference, case-2 demonstrates the two fault angles in phase, case-3 depicts faults almost in anti-phase and case-4 demonstrates two faults are almost perpendicular to each other, i.e., almost 90 degrees difference.

In the following tables, the diagnosed errors are expressed in two types: First, in terms of fault amplitude percentage error and the phase difference, as shown in column 5. Columns 6 and 7 are, however, express the errors in terms of in-line and vertical amplitude error percentage ΔU_//, Δs_// and ΔU_⊥_,Δs_⊥. The error in-line with the fault vector indicates the amplitude error, however, the vertical component can be viewed as direction error. Based on the results presented in Table 4, it can be observed that, under sub-critical speed running and the amplitude error of concern, the imbalance and shaft-bow errors both exhibit the lowest value as they are in phase. The biggest errors of the two faults occur in case 4, in which the two faults are perpendicular to each other. Note that the maximum and minimum errors in tables are respectively highlighted in red and green. Table 5 shows similar cases as Table 4 except the rotor is running at a trans-critical speed of 3200 rpm. It is observed that the least error for imbalance happens in case 4 and the least bow error occurs in case 3. A peculiar feature in Table 5 is observed, in which the shaft bow exhibits significant error up to 38% for all cases except case 3, where two faults in anti-phase. It is explainable that bow response diminishes at high speed such that the identification process generates larger errors. Table 6 illustrates the case of the s=4mm at a very slow running speed. Under such a condition, the overall imbalance errors are bigger because that the bow strongly dominates the response, such that imbalance response becomes a fraction of the total one and it generates a larger error during data fitting process. The least imbalance error happens in an anti-phase situation. The overall shaft bow errors are small except for case 4.

However, an observable error disparity, related to imbalance and shaft-bow, becomes apparent when the rotor is rotating over the critical speed, particularly above 3200 rpm. Investigating the vibration patterns caused by imbalance and shaft-bow faults suggests that a smaller discrepancy in inaccuracy occurs for the imbalance when the frequency ratio surpasses one, which is observed at 3200 rpm as shown in Figure 5. Upon further examination, it is evident that the imbalance error at 3200 rpm exceeds the prediction based on theoretical explanation. The variation is caused by various practical engineering issues that can impact the results, adding complexities beyond the reduced theoretical models.

For s = 4mm at 650 rpm in this state, the rotor’s frequency ratio is lower than the critical speed. Figure 5 shows that when the frequency ratio is smaller than one, the system’s behavior indicates that the response is mostly influenced by the shaft-bow amplitude. This crucial finding suggests that in specific circumstances, the influence of shaft bow on the system’s behavior is greater than that of imbalance. The small discrepancy in the error margins indicates that both types of faults have a substantial role in the observed vibrations, despite their theoretical differences. The consistent error gaps highlight the complex relationship between imbalance and shaft-bow effects on the system’s dynamic behavior. It shows a situation where both causes have similar effects, and their combined impact is seen in the total inaccuracy in the system’s response.

As seen, the more significant disparities between actual and diagnosed faults are prominently observed in all experiments, unlike the scenarios of using simulated data, in which very high accuracy has been achieved. Larger error may be attributed to several reasons. For instance, there have been existing imbalance and bow before intentionally added trial weight and notable clearance between shaft and bearing is apparently not fit for the simple-support assumption. All of these would generate vibration noises and deviate the diagnosis accuracy in the experimental works.

In essence, this research demonstrates the efficacy of the combined physical model and machine learning approach in identifying multiple faults. The integration of the physical model ensures an accurate representation of the Jeffcott rotor system, while the FNN provides efficient and reliable diagnosis capabilities. This research can open new possibilities for advanced rotor system diagnosis and maintenance strategies in various industrial applications.

5. Conclusion

This study proposes a novel hybrid approach that combines model-based and ML approaches to investigate imbalance and shaft-bow monitoring for Jeffcott rotor-bearing systems in online settings. Initially, the physical model of the Jeffcott rotor system involves the development of a mathematical model to determine rotor parameters, generating a substantial amount of simulated fault data for the ANN model. The validated physical model serves as the basis for generating a significant volume of simulated data (10,000 datasets), which is subsequently employed to train ML models such as FNN. This dataset serves the purpose of training, validating, and testing the models, ensuring their effectiveness in diagnosing multiple faults. However, the FNN with 40 nodes exhibits the lowest RMSE, indicating better performance. After that, FNN encompassed diverse conditions, including varying fault dominations and frequency ratios. In these diverse conditions, using the simulated datasets, the FNN consistently demonstrated exceptional performance, particularly when the imbalance and shaft bow did not dominate each other. Moreover, to achieve higher diagnosis accuracy in shaft-bow, the rotor better runs at low speed but, to the opposite, at higher speed for imbalance diagnosis.

The combinations of fault components (U, α, s, θ) were applied to the Jeffcott rotor experiment, and the experimental data were obtained and fed into the trained FNN for instant diagnosis. The FNN effectively identified and quantified faults within the system. The results show that both the imbalance and bow exhibit the lowest diagnosis error as these two faults are in-phase under sub-critical running. At trans-critical speed, the imbalance remains the least error; however, the bow error significantly increases because the bow response rapidly diminishes.

These findings highlight the superiority of the hybrid approach and its potential for enhancing the precision and reliability of imbalance and shaft bow diagnosis in rotor systems. The integration of the physical model ensures an accurate representation of the rotating system, while the machine-learning-based approach provides efficient and reliable diagnosis and monitoring capabilities. The hybrid approach proves effective in identifying multiple faults, specifically imbalances and shaft-bow issues, addressing challenges faced by conventional diagnostic techniques. Consequently, this study opens new possibilities for advanced rotor system monitoring and maintenance strategies in various industrial applications.

Author Contributions

Conceptualization and methodology, S.-C.H.; validation, M.N.; formal analysis and software, S.O.; writing—original draft preparation, M.N.; writing—review and editing, S.-C.H. All authors have read and agreed to the published version of the manuscript.

Acknowledgments

The authors are very grateful to Taiwan’s National Science and Technology Council (NSTC) for the support of this research under Project No. NSTC 112-2221-E-131-020.

Conflicts of Interest

The authors declare no conflicts of interest.

References

Misbah, I.; Lee, C.; Keung, K. Fault Diagnosis in Rotating Machines Based on Transfer Learning: literature review. Knowledge-Based Systems, 2023: p. 111158. [CrossRef]
Lees, A.; Sinha, J.; Friswell, M. Model-based identification of rotating machines. Mechanical Systems and Signal Processing, 2009. 23(6): p. 1884-1893. [CrossRef]
Walker, R.; Perinpanayagam, S.; Jennions, I.K. Rotordynamic faults: recent advances in diagnosis and prognosis. International Journal of Rotating Machinery, 2013. [CrossRef]
Zhao, X. Data-driven fault detection, isolation and identification of rotating machinery: With applications to pumps and gearboxes. 2012. [CrossRef]
Wu, T.; Chung, Y. Misalignment diagnosis of rotating machinery through vibration analysis via the hybrid EEMD and EMD approach. Smart Materials and Structures, 2009. 18(9): p. 095004. [CrossRef]
Lin, L.; Chu, F. HHT-based AE characteristics of natural fatigue cracks in rotating shafts. Mechanical Systems and Signal Processing, 2012. 26: p. 181-189. [CrossRef]
Yu, Y.; Junsheng, C. A roller bearing fault diagnosis method based on EMD energy entropy and ANN. Journal of sound and vibration, 2006. 294(1-2): p. 269-277. [CrossRef]
Al-Badour, F.; Sunar, M.; Cheded, L. Vibration analysis of rotating machinery using time–frequency analysis and wavelet techniques. Mechanical Systems and Signal Processing, 2011. 25(6): p. 2083-2101. [CrossRef]
Ocak, H.; Loparo, K.A.; Discenzo, F.M. Online tracking of bearing wear using wavelet packet decomposition and probabilistic modeling: A method for bearing prognostics. Journal of sound and vibration, 2007. 302(4-5): p. 951-961. [CrossRef]
Zou, J.; Chen, J.; Pu, Y. Wavelet time-frequency analysis of torsional vibrations in rotor system with a transverse crack. Computers & structures, 2004. 82(15-16): p. 1181-1187. [CrossRef]
Walker, R. et al., Unbalance localization through machine nonlinearities using an artificial neural network approach. Mechanism and Machine Theory, 2014. 75: p. 54-66. [CrossRef]
Mohamed, K.A.-H.; Hassaan, G.A.; Hegazy, A.A.-H. Artificial neural network based intelligent fault identification of rotating machinery. Technology, 2016. 2(2): p. 26-39. [CrossRef]
Liu, R. et al., Artificial intelligence for fault diagnosis of rotating machinery: A review. Mechanical Systems and Signal Processing, 2018. 108: p. 33-47. [CrossRef]
Nath, A.G.; Udmale, S.S.; Singh, S.K. Role of artificial intelligence in rotor fault diagnosis: A comprehensive review. Artificial Intelligence Review, 2021. 54(4): p. 2609-2668. [CrossRef]
Xue, S.; Howard, I. Torsional vibration signal analysis as a diagnostic tool for planetary gear fault detection. Mechanical Systems and Signal Processing, 2018. 100: p. 706-728. [CrossRef]
Edwards, S.; Lees, A.; Friswell, M. Estimating rotor unbalance from a single run-down, in IMeche Conference Transactions. 2000, Professional Engineering Publishing;. p. 323-334.
Bachschmid, N.; Pennacchi, P. Accuracy of fault detection in real rotating machinery using model based diagnostic techniques. JSME International Journal Series C Mechanical Systems, Machine Elements and Manufacturing, 2003. 46(3): p. 1026-1034. [CrossRef]
Bachschmid, N. et al., Identification and simulation of faults in rotor systems: experimental results. Euro Diname, 1999. 99: p. 3-11.
Audebert, S., et al., Identification of transverse cracks in rotors systems, in Proceedings of the 8th International Symposium on Transport Phenomena and Dynamics of Rotating Machinery (ISROMAC-8). 2000. p. 1065-1072.
Bachschmid, N.; Pennacchi, P.; Audebert, S. Some results in model-based transverse crack identification in rotor systems. CIT Informacion Tecnologica, 2001. 12(5): p. 25-32.
Sekhar, A. Identification of unbalance and crack acting simultaneously in a rotor system: Modal expansion versus reduced basis dynamic expansion. Journal of Vibration and Control, 2005. 11(9): p. 1125-1145. [CrossRef]
Jain, J.; Kundra, T. Model based online diagnosis of unbalance and transverse fatigue crack in rotor systems. Mechanics Research Communications, 2004. 31(5): p. 557-568. [CrossRef]
Sinha, J.K.; Lees, A.; Friswell, M. Estimating unbalance and misalignment of a flexible rotating machine from a single run-down. Journal of Sound and Vibration, 2004. 272(3-5): p. 967-989. [CrossRef]
Jalan, A.K.; Mohanty, A. Model based fault diagnosis of a rotor–bearing system for misalignment and unbalance under steady-state condition. Journal of sound and vibration, 2009. 327(3-5): p. 604-622. [CrossRef]
Pennacchi, P.; Vania, A. Diagnosis and model based identification of a coupling misalignment. Shock and Vibration, 2005. 12(4): p. 293-308. [CrossRef]
Bachschmid, N.; Pennacchi, P.; Vania, A. Identification of multiple faults in rotor systems. Journal of sound and vibration, 2002. 254(2): p. 327-366. [CrossRef]
Pennacchi, P. et al., Use of modal representation for the supporting structure in model-based fault identification of large rotating machinery: part 1—theoretical remarks. Mechanical Systems and Signal Processing, 2006. 20(3): p. 662-681. [CrossRef]
Lin, C.-L. et al., A novel model-based unbalance monitoring and prognostics for rotor-bearing systems. Advances in Mechanical Engineering, 2023. 15(1): p. 16878132221148019. [CrossRef]
Bently, D.E.; Hatch’Charles, T. Fundamentals of rotating machinery diagnostics. Mechanical Engineering-CIME, 2003. 125(12): p. 53-54.
Gavalas, I. et al. On the quality of stability and bifurcation sets in rotors with permanent shaft bow on nonlinear supports. International Journal of Non-Linear Mechanics, 2023: p. 104563. [CrossRef]
Diouf, P.; Herbert, W. Understanding rotor balance for electric motors. Conference Record of 2014 Annual Pulp and Paper Industry Technical Conference, 2014: p. 7-17.
Zhang, J.H. et al., Dynamic analysis of flexible rotor-ball bearings system with unbalance-misalignment-rubbing coupling faults, in Applied Mechanics and Materials. 2012, Trans Tech Publ. p. 448-453. [CrossRef]
Ganeriwala, S.N.; Schwarz, B.; Richardson, M.H. Operating deflection shapes detect unbalance in rotating equipment. Sound and Vibration, 2009. 43(5): p. 11-13. Available online: http://www.sandv.com/downloads/0905gane.pdf.
Edwards, S.; Lees, A.W.; Friswell, M.I. Fault diagnosis of rotating machinery. Shock and vibration digest, 1998. 30(1): p. 4-13. [CrossRef]
Randall, R.B. State of the art in monitoring rotating machinery-part 1. Sound and vibration, 2004. 38(3): p. 14-21.
Walker, R.; Perinpanayagam, S.; Jennions, I.K. Physics-based simulation for health management of rotating machinery. 2011. Available online: http://dspace.lib.cranfield.ac.uk/handle/1826/8453.
Mogal, S.; Lalwani, D. Fault diagnosis of bent shaft in rotor bearing system. Journal of Mechanical Science and Technology, 2017. 31(1): p. 1-4. [CrossRef]
Nicholas, J.; Gunter, E.; Allaire, P. Effect of residual shaft bow on unbalance response and balancing of a single mass flexible rotor—Part I: Unbalance response. 1976. [CrossRef]
Nicholas, J.; Gunter, E.; Allaire, P. Effect of residual shaft bow on unbalance response and balancing of a single mass flexible rotor—Part II: balancing. 1976. [CrossRef]
Flack, R.; Rooke, J. A theoretical-experimental comparison of the synchronous response of a bowed rotor in five different sets of fluid film bearings. Journal of Sound and Vibration, 1980. 73(4): p. 505-517. [CrossRef]
Shiau, T.N.; Lee, E.K. The residual shaft bow effect on dynamic response of a simply supported rotor with disk skew and mass unbalances. 1989. [CrossRef]
Ehrich, F.F. Handbook of rotordynamics. (No Title), 1992.
Rao, J. A note on Jeffcott warped rotor. Mechanism and Machine Theory, 2001. 36(5): p. 563-575. [CrossRef]
Kang, C. et al., Dynamic analysis of gear-rotor system with viscoelastic supports under residual shaft bow effect. Mechanism and Machine Theory, 2011. 46(3): p. 264-275. [CrossRef]
Pennacchi, P.; Vania, A. Accuracy in the identification of a generator thermal bow. Journal of Sound and Vibration, 2004. 274(1-2): p. 273-295. [CrossRef]
Shen, X.; Jia, J.; Zhao, M. Nonlinear analysis of a rub-impact rotor-bearing system with initial permanent rotor bow. Archive of Applied Mechanics, 2008. 78: p. 225-240. [CrossRef]
Darpe, A.; Gupta, K.; Chawla, A. Dynamics of a bowed rotor with a transverse surface crack. Journal of Sound and Vibration, 2006. 296(4-5): p. 888-907. [CrossRef]
Song, G. et al., Theoretical–experimental study on a rotor with a residual shaft bow. Mechanism and Machine Theory, 2013. 63: p. 50-58. [CrossRef]
Rossner, M.;Thuemmel, T.; Ulbrich, H. Inclusion of unsteady bow in a model-based monitoring system for rotors. in Proceedings of the 9th IFToMM International Conference on Rotor Dynamics. 2015. Springer.
Tong, X.; Palazzolo, A.; Suh, J. A Review of the Rotordynamic Thermally Induced Synchronous Instability (Morton) Effect. Applied Mechanics Reviews, 2017. 69(6). [CrossRef]
Srinivas, H.; Srinivasan, K.; Umesh, K. Application of artificial neural network and wavelet transform for vibration analysis of combined faults of unbalances and shaft bow. Adv. Theor. Appl. Mech, 2010. 3(4): p. 159-176.
Rezazadeh, N. et al. Classification of Unbalanced and Bowed Rotors under Uncertainty Using Wavelet Time Scattering, LSTM, and SVM. Applied Sciences, 2023. 13(12): p. 6861. [CrossRef]
Huang, S.-C.; Lin, C.-L.; Najibullah, M. Identification of A Turbine Rotor Unbalance Using A Hybrid Approach International Congress on Sound and Vibration 2022.
Huang, S.-C.N.M. Unbalance Monitoring of an Overhung Rotor Using a Physics-Based and Machine Learning Approach, in 29th International Congress on Sound and Vibration. 2023.
Djeziri, M.A.; Benmoussa, S.; Sanchez, R. Hybrid method for remaining useful life prediction in wind turbine systems. Renewable Energy, 2018. 116: p. 173-187. [CrossRef]
Wilhelm, Y. et al., Overview on hybrid approaches to fault detection and diagnosis: Combining data-driven, physics-based and knowledge-based models. Procedia Cirp, 2021. 99: p. 278-283. [CrossRef]
Fang, X.; Puig, V.; Zhang, S. Fault diagnosis and prognosis using a hybrid approach combining structural analysis and data-driven techniques, in 2021 5th International Conference on Control and Fault-Tolerant Systems (SysTol). 2021, IEEE. p. 145-150. [CrossRef]
Rao, S.S. Mechanical vibrations fifth edition. 2011.
Razavi, S.; Tolson, B.A. A new formulation for feedforward neural networks. IEEE Transactions on neural networks, 2011. 22(10): p. 1588-1598. [CrossRef]
Najibullah, M.; Lin, C.-L.; Huang, S.-C. Effect of Different Training Algorithms in Artificial Neural Networks on the Rotor Unbalance Diagnosis, in 2022 IET International Conference on Engineering Technologies and Applications (IET-ICETA). 2022. p. 1-2. [CrossRef]
Alsaleh, A.; Sedighi, H.M.; Ouakad, H.M. Experimental and theoretical investigations of the lateral vibrations of an unbalanced Jeffcott rotor. Frontiers of Structural and Civil Engineering, 2020. 14: p. 1024-1032. [CrossRef]

Figure 1. Schematic diagram of Jeffcott rotor with simultaneous imbalance and shaft-bow.

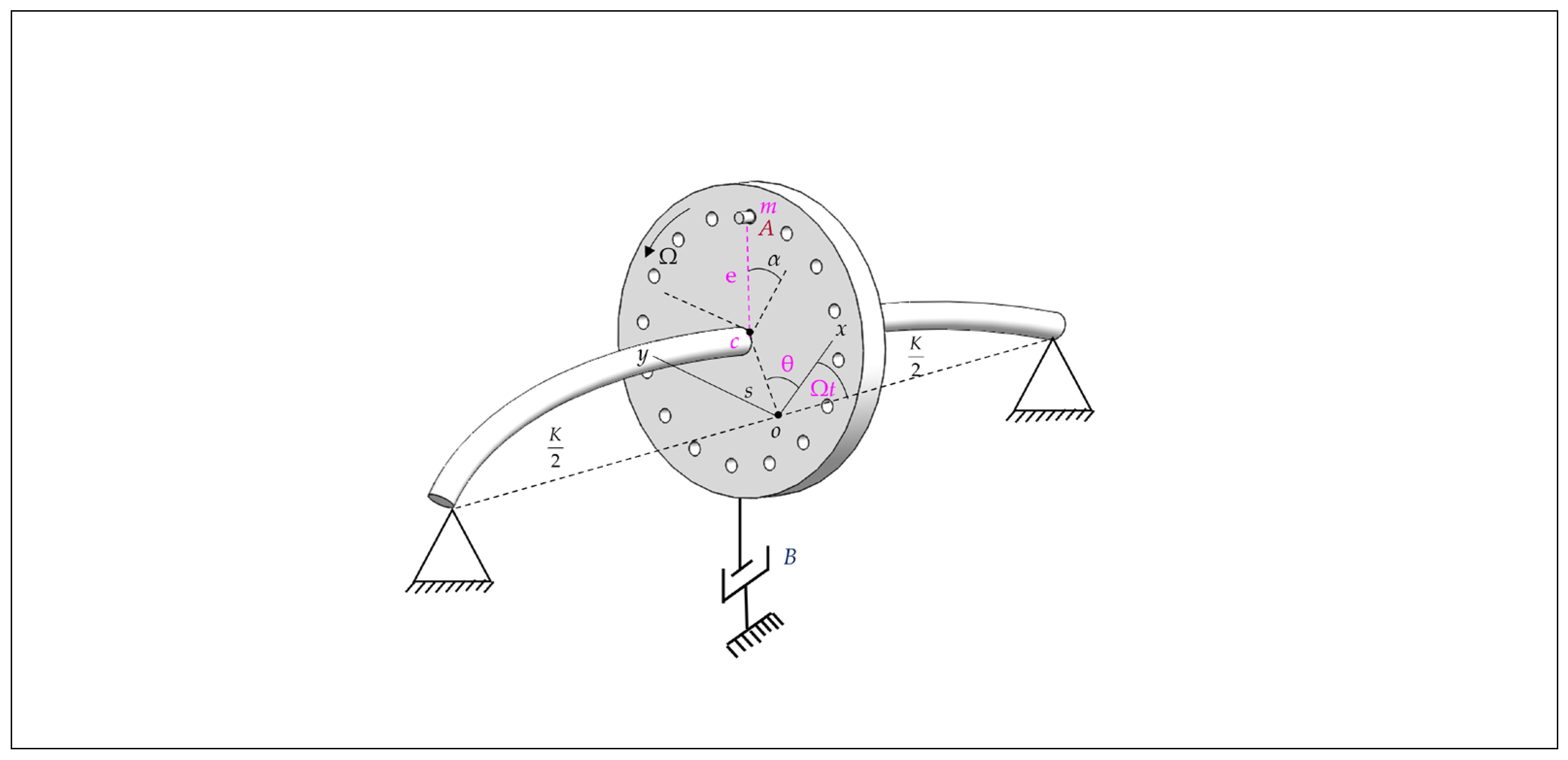
Figure 2. A novel hybrid approach methodology for real-time imbalance and shaft-bow diagnosis.

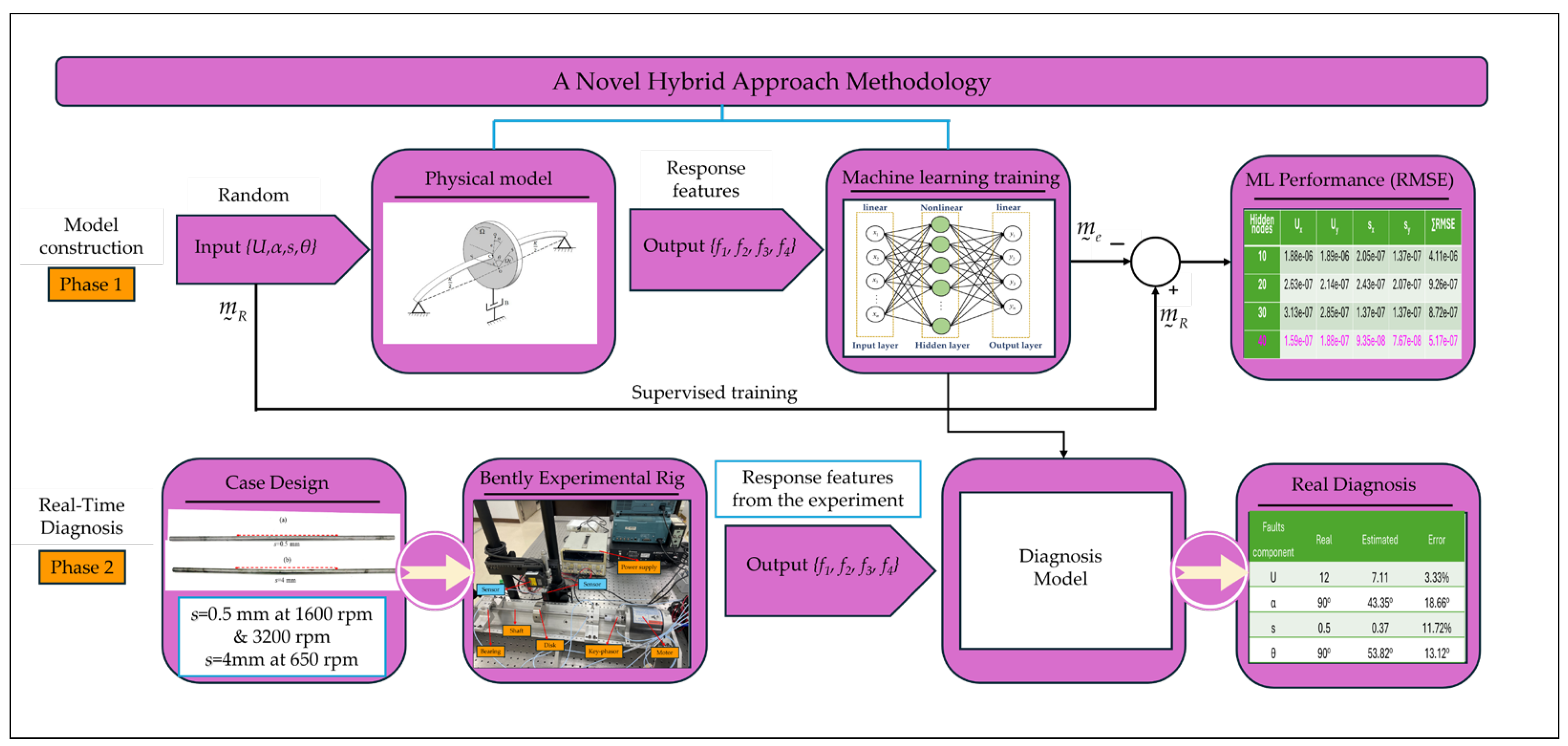
Figure 4. Comparison of different hidden nodes.

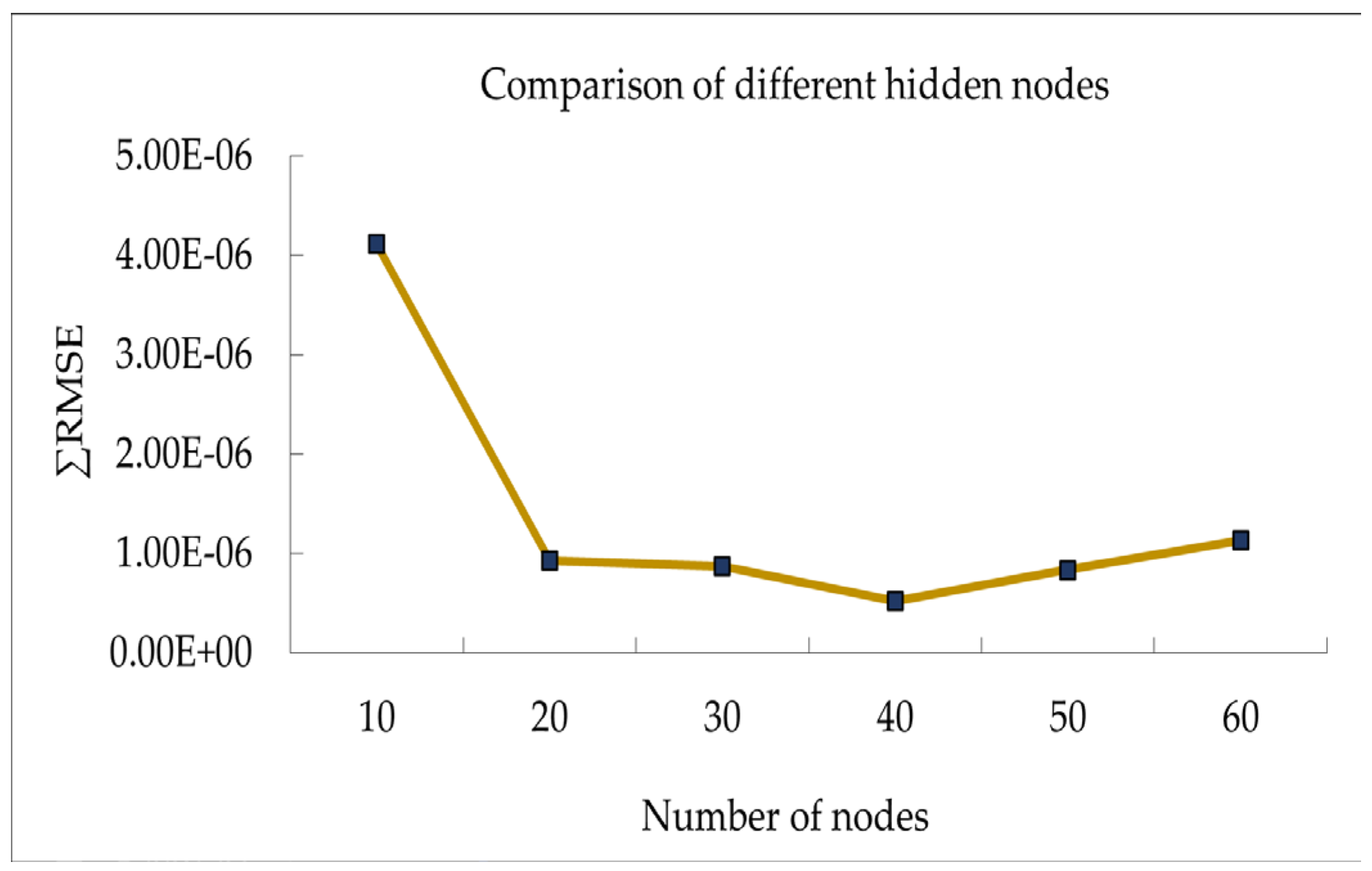
Figure 5. Frequency responses of imbalance and shaft-bow.

Figure 6. The rotor experiment platform.

Figure 7. Analogy of the Jeffcott rotor to an equivalent 1-D discrete system.

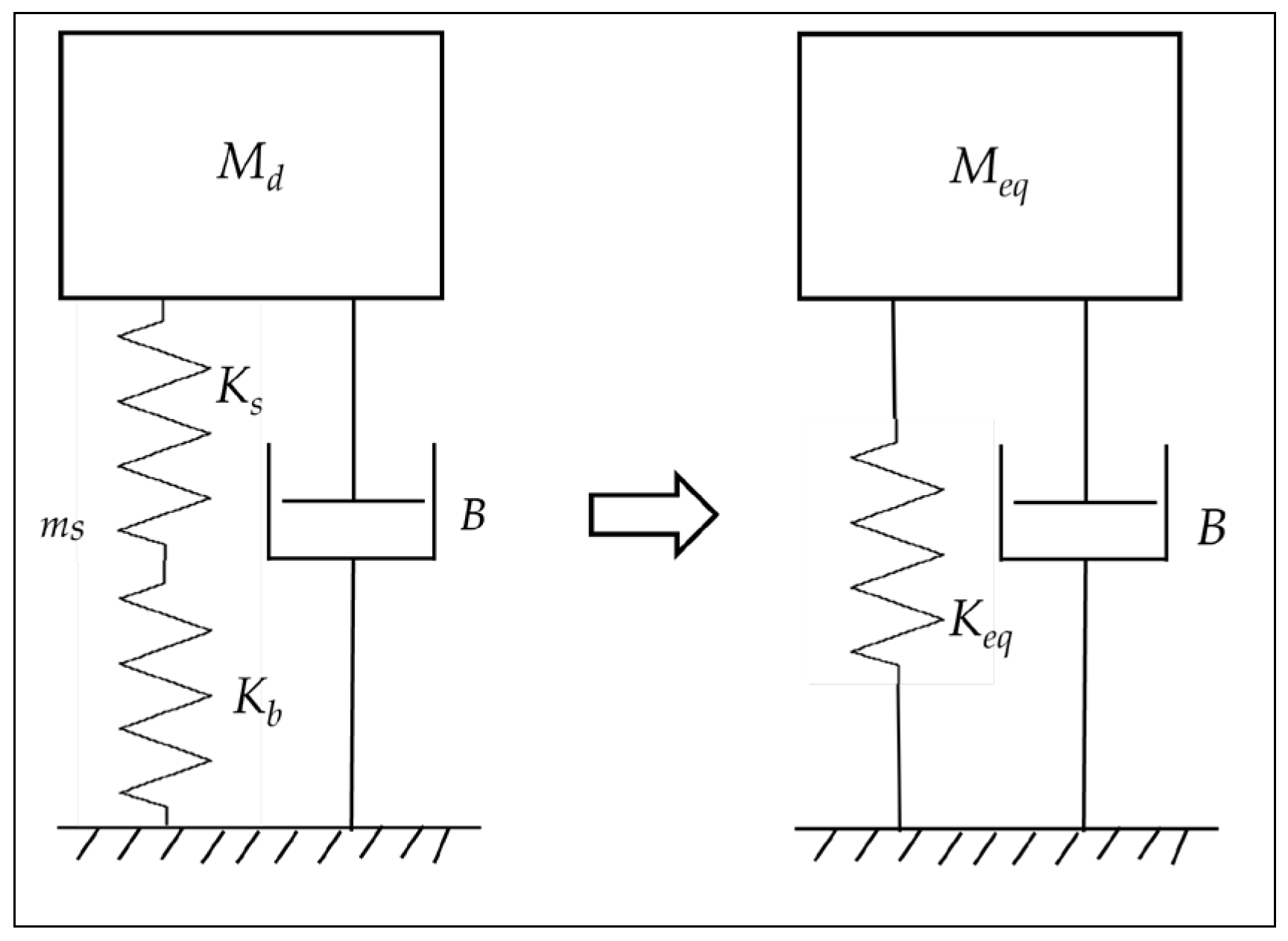
Figure 8. Transient response for damping evaluation.

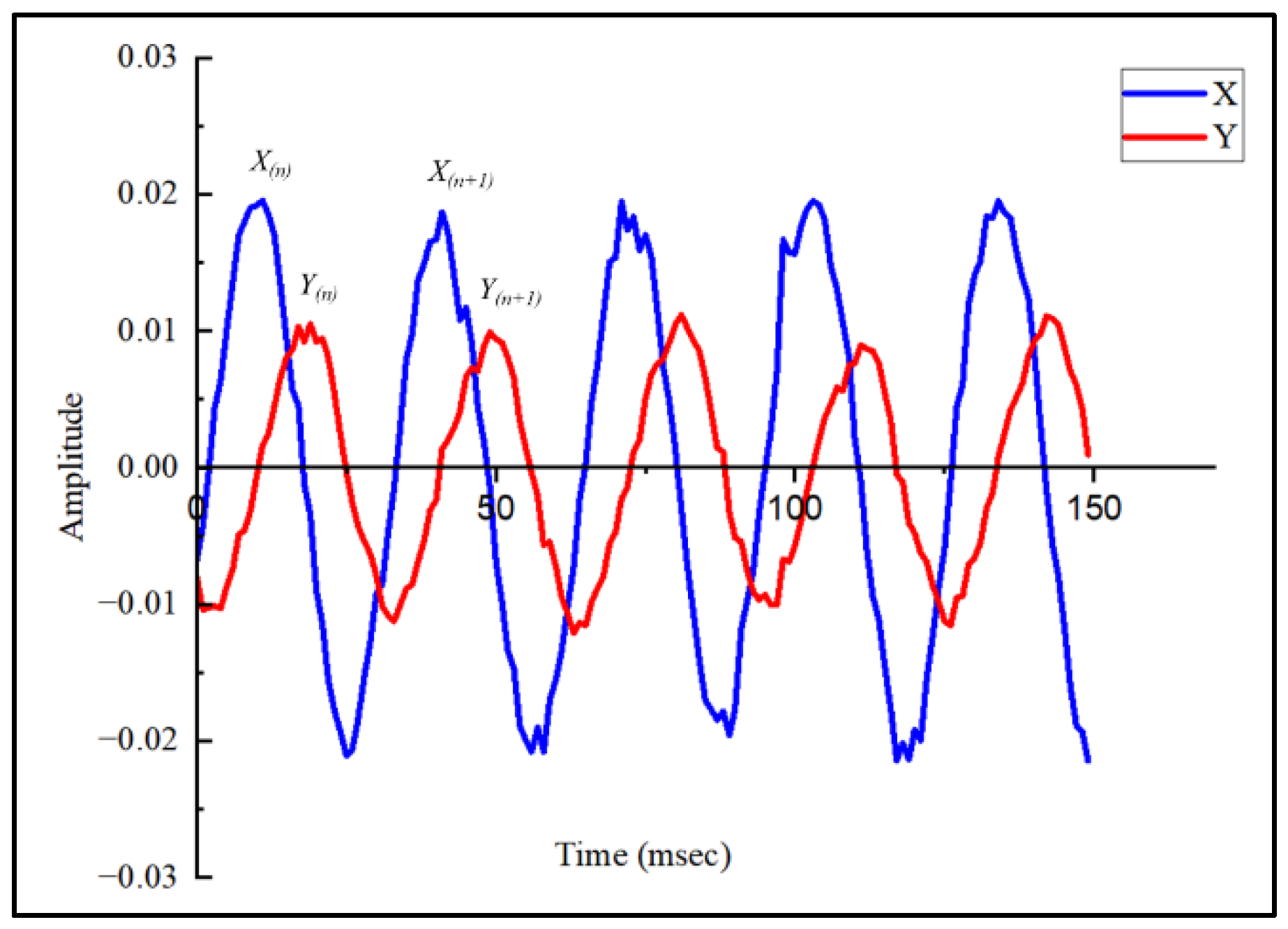
Figure 9. Phase angle and amplitude from the measured sensors’ responses.

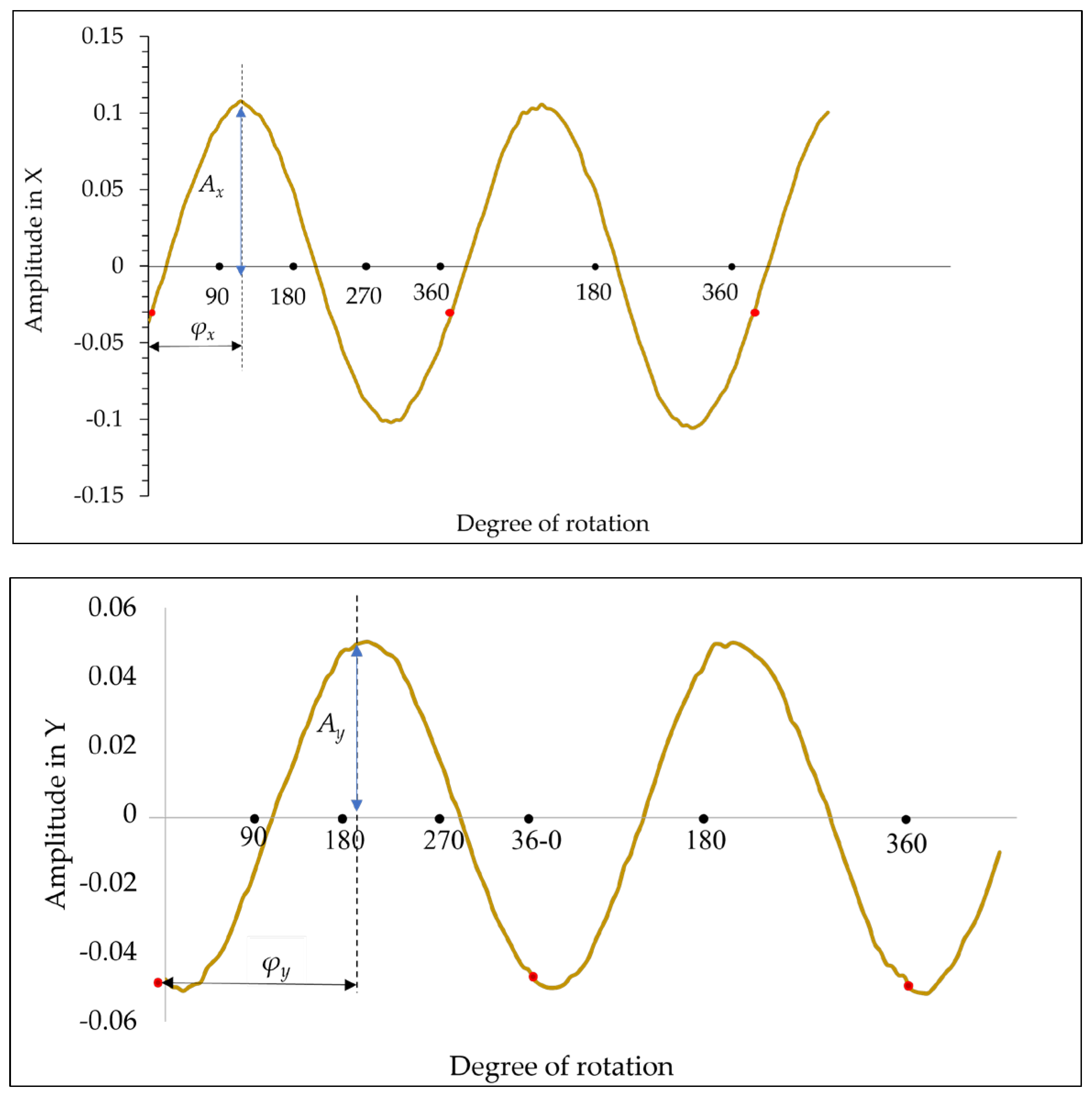
Figure 10. a) rotating disk with 16 holes (b) the variation of mass imbalance.

Figure 11. a) shaft bow with s= 0.5 mm (b) shaft-bow with s=4 mm.

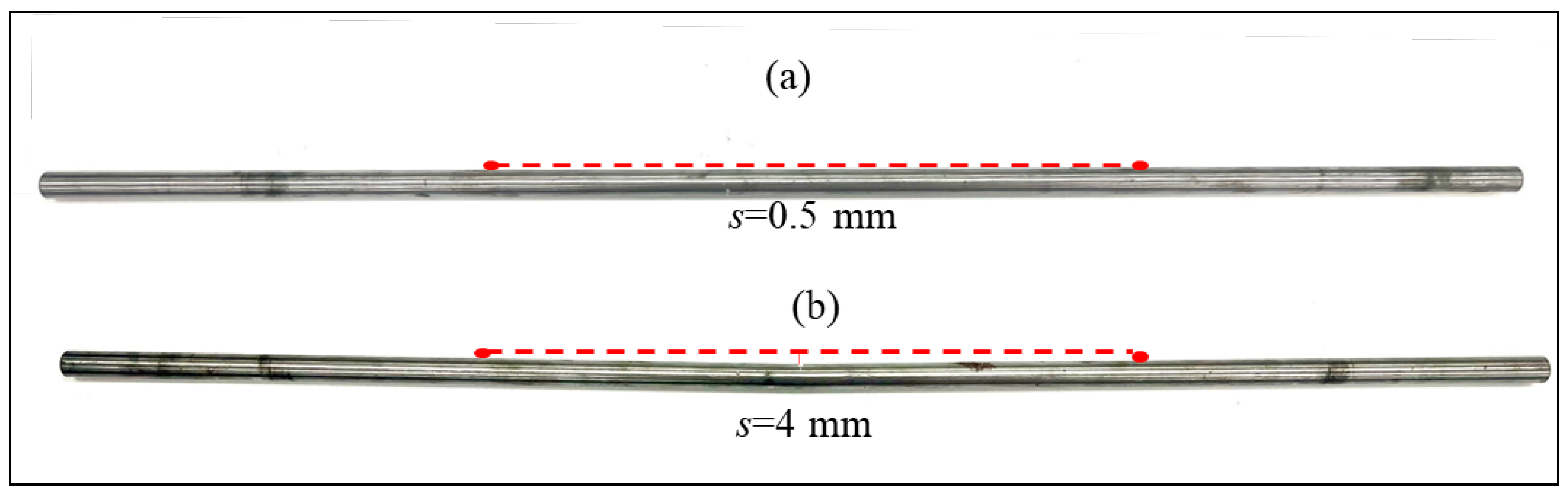
Table 1. RMSE in terms of imbalance and shaft-bow components of different node-number.

Hidden nodes	U_x	U_y	s_x	s_y	∑RMSE
10	1.88e-06	1.89e-06	2.05e-07	1.37e-07	4.11e-06
20	2.63e-07	2.14e-07	2.43e-07	2.07e-07	9.26e-07
30	3.13e-07	2.85e-07	1.37e-07	1.37e-07	8.72e-07
40	1.59e-07	1.88e-07	9.35e-08	7.67e-08	5.17e-07
50	2.18e-07	2.73e-07	1.57e-07	1.87e-07	8.34e-07
60	4.59e-07	4.34e-07	1.17e-07	1.18e-07	1.13e-06

Table 2. Comparison of RMSE values for fault components under different speed ratios.

	Fault components	Imbalance dominant	Shaft-bow dominant	Equal
τ < 1
	U_x	0.0323	0.3101	4.69e-05
	U_y	0.0581	0.3140	6.01e-05
	s_x	0.2924	0.0147	1.37e-05
	s_y	0.3398	0.0215	1.66e-05
τ ≈ 1
	U_x	0.0200	0.2937	3.96e-06
	U_y	0.0200	0.3295	6.87e-06
	s_x	0.3031	0.0238	3.31e-05
	s_y	0.2727	0.0146	6.67e-05
τ > 1
	U_x	0.0288	0.3557	6.59e-06
	U_y	0.0315	0.3008	3.11e-06
	s_x	0.3459	0.0105	4.07e-05
	s_y	0.2873	0.0221	6.99e-05

Table 3. Estimated model parameters of the rotor-bearing system of the test rig.

C	M_eq (kg)	ζ	K_s (kN/m)	K_b (kN/m)	K_eq (kN/m)	ω_n (rad/s)
Y	0.96	0.47%	96.908	108.92	51.282	230.1
X	0.96	0.5%	96.908	135.72	56.538	241.6

Table 4. Diagnosis error percentage at 1600 rpm (τ=0.69) for initial bow 0.5mm.

Case	Faults	Real	Diagnosed	Error	Comp	Error%
1 (same quadrant)	U	6	7.03	17.2%	ΔU_//	17.0
	α	45^o	48.80^o	3.08^o	ΔU_⊥	6.3
	s	0.5	0.36	28.0%	Δs_//	-28.4
	θ	60^o	53.95^o	6.05^o	Δs_⊥	-7.6
2 (in-phase)	U	12	12.29	2.4%	ΔU_//	-0.6
	α	90^o	76.14^o	13.86^o	ΔU_⊥	-24.5
	s	0.5	0.58	16.0%	Δs_//	14.6
	θ	90^o	81.16^o	8.84^o	Δs_⊥	-17.8
3 (anti-phase)	U	24	21.28	11.3%	ΔU_//	-13.1
	α	225^o	213.63^o	11.37^o	ΔU_⊥	-17.5
	s	0.5	0.39	22.0%	Δs_//	-22.3
	θ	30^o	35.28^o	5.28^o	Δs_⊥	7.2
4 (perpendicular)	U	30	38.24	27.5%	ΔU_//	22.9
	α	67.5^o	82.88^o	15.38^o	ΔU_⊥	33.8
	s	0.5	0.35	30.0%	Δs_//	-30.0
	θ	150^o	147.87^o	2.13^o	Δs_⊥	-2.6

Table 5. Diagnosis error percentage at 3200 rpm(τ=1.39) for initial bow 0.5mm.

Number	Faults	Real	Diagnosed	Error	Comp	Error%
1 (same quadrant)	U	6	4.4	26.7%	ΔU_//	-27.7
	α	45^o	35.24^o	9.76^o	ΔU_⊥	12.4
	s	0.5	0.69	38.0%	Δs_//	36.5
	θ	60^o	54.41^o	8.59^o	Δs_⊥	20.6
2 (in-phase)	U	12	13..34	11.2%	ΔU_//	10.3
	α	90^o	97.24^o	7.24 ^o	ΔU_⊥	14.0
	s	0.5	0.31	38.0%	Δs_//	-38.4
	θ	90^o	96.18^o	6.18.^o	Δs_⊥	6.7
3 (anti-phase)	U	24	26.72	11.3%	ΔU_//	2.8
	α	225^o	202.39^o	22.61^o	ΔU_⊥	42.8
	s	0.5	0.54	8.0%	Δs_//	5.9
	θ	30^o	18.68^o	11.32^o	Δs_⊥	21.2
4 (perpendicular)	U	30	28.41	5.3%	ΔU_//	-7.0
	α	67.5^o	56.53^o	10.97^o	ΔU_⊥	18.0
	s	0.5	0.31	38.0%	Δs_//	-39.0
	θ	150^o	139.88^o	10.12^o	Δs_⊥	10.9

Table 6. Diagnosis error percentage at 650 rpm (τ=0.28) for initial bow 4mm.

Number	Faults	Real	Diagnosed	Error	Comp	Error%
1 (same quadrant)	U	6	5.12	14.7%	ΔU_//	-15.9
	α	45^o	54.71^o	9.71^o	ΔU_⊥	14.4
	s	4.0	4.17	4.2%	Δs_//	0.8
	θ	60^o	74.84^o	14.84^o	Δs_⊥	26.7
2 (in-phase)	U	12	14.86	23.8%	ΔU_//	11.7
	α	90^o	64.39^o	25.61^o	ΔU_⊥	53.5
	s	4.0	4.27	6.8%	Δs_//	-4.7
	θ	90^o	116.83^o	26.83^o	Δs_⊥	48.2
3 (anti-phase)	U	24	30.28	26.0%	ΔU_//	24.3
	α	225^o	215.06^o	9.94^o	ΔU_⊥	21.8
	s	4.0	3.72	7.0%	Δs_//	-7.1
	θ	30^o	32.71^o	2.71^o	Δs_⊥	4.4
4 (perpendicular)	U	30	32.16	7.2%	ΔU_//	-5.2
	α	67.5^o	39.63^o	27.87^o	ΔU_⊥	50.1
	s	4.0	3.0	25.0%	Δs_//	-29.7
	θ	150^o	169.19^o	19.9^o	Δs_⊥	25.4

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.