Prerpints.org logo
Preprint
Article

New Model and Finite Element Analysis of the Anti-extrusion Strength of Backfill Drilling Pipelines

Altmetrics

Downloads

67

Views

16

Comments

0

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

06 March 2024

Posted:

06 March 2024

You are already at the latest version

Alerts
Abstract
Currently, in some domestic and foreign mines, the backfill drilling pipeline experience a rupture phenomenon even when the wear degree is low. This results in a delay in production due to the filling becoming 'sick'. This paper presents, for the first time, the damage mechanism from a mechanical perspective and re-derives the anti-extrusion strength model of the backfill drilling pipeline. We investigate the influence of law on the anti-extrusion strength of pipelines from the perspective of stratum and cement ring. We then verify the theoretical and simulation results through engineering examples. The results demonstrate that the Mises stress criterion is a suitable modification principle for the anti-extrusion strength model of the backfill drilling pipeline. The anti-extrusion strength of the pipeline is related to the elastic modulus and Poisson's ratio of the stratum, and the thickness of the cement ring. It is negatively affected by the depth of the stratum. For hard strata, a cement ring with a smaller elastic modulus is suitable, while for soft stratum, a cement ring with a larger elastic modulus is recommended. When the missing angle of the cement ring is less than 60°, the stress concentration factor increases up to 2.2. The stress unloading capacity of the cement ring ranges from 32.7% to 37.8%, and optimal performance of the cement ring is achieved when it has high strength and low rigidity. The backfill filling pipeline of a copper mine abroad was destroyed due to external extrusion force exceeding its anti-extrusion strength value. The modified pipeline anti-extrusion strength model is 18.2% higher than the casing API strength value. This finding can inform the design of the backfill filling pipeline for China's kilometer-deep wells in the future.
Keywords: 
Subject: Engineering  -   Mining and Mineral Processing

1. Introduction

Due to the gradual depletion of shallow mineral resources, deep mining has become an inevitable trend in the development of mineral resources in China [1,2]. Deep mining faces a unique mining environment characterized by high stress, high well temperature, and high well depth. The backfill mining method can effectively maintain the surrounding rock, reduce rock movement, and better control regional ground pressure. Therefore, it is an effective method for safely and efficiently mining deep mineral deposits [3,4,5]. The backfill drilling pipeline is a critical component of the entire filling system, acting as the ‘throat’ of the operation. Its safety is paramount as it directly impacts the smoothness of the filling process [6,7].
Current research on the damage caused by backfill drilling pipelines primarily focuses on pipeline wear [8,9,10,11]. Levy [12] conducted experimental research demonstrating that the shape and size of filler slurry particles have a significant impact on pipeline wear. Sharp and irregular particles cause four times more wear on pipelines than spherical particles. Creber et al. [13] found that the erosion rate increases with particle size. Qiao et al. [14] used Fluent software to investigate the effect of roughness on pipeline erosion rate under mortar action. They found that the pipeline structure had the highest erosion rate at a roughness of 0.3% under the same sand content and water flow conditions. Wang et al. [15] used a discrete phase model to simulate the flow of slurry in variable diameter bends. They found that the inlet and outlet pipe diameter ratio had the most severe impact on pipeline erosion. The wear condition of the variable diameter pipe fluctuated greatly with changes in pipeline factors when its length was below 80 mm.
Research on pipeline damage mostly exists in oil pipelines. According to Rodriguez et al. [16], the inner wall of the pipeline bears the greatest pressure, and its stress value is highly correlated with the Poisson’s ratio of the formation. The stress value of the pipeline increased by 66% when the Poisson’s ratio changed from 0.1 to 0.5. Medjo et al. [17] conducted experiments that demonstrate how cracks are caused by environmental factors. They found that the stress intensity factor at the crack tip increases with internal pressure, leading to crack propagation when it reaches a critical value. This confirms the effectiveness of fracture mechanics theory in predicting pipeline failure resistance. Liu [18] analyzed the damage to oil pipelines caused by formation creep pressure.
The research presented above suggests that there is limited information available on the damage caused by mining filling pipelines, and wear does indeed pose a threat to the safety of the backfill drilling pipelines. Notably, fractures have been observed in the backfill drilling bimetallic composite pipes of a foreign copper mine and a domestic iron mine within less than a year of production, as shown in Figure 1. It is worth noting that the drilling depth of both mines did not exceed 1000 m, and the degree of pipeline wear was very low. Although wear can reduce the wall thickness of a pipeline and accelerate the process of pipeline rupture, it is not the main factor that induces pipeline rupture. The stress state of the pipeline should also be considered, as even a pipeline with low wear can still rupture under a large load.
This article draws on research results from petroleum pipelines [19], tunnels, and other engineering projects [20,21,22,23]. It combines the basic principles of elastic mechanics and material mechanics to reveal their failure mechanisms from a mechanical perspective. The article derives the anti-extrusion strength model of the backfill drilling pipeline. The article explores the influence of stratum and cement ring parameters on the anti-extrusion strength of backfill drilling pipelines through finite element analysis. The rationality of the theoretical model and finite element analysis is verified through engineering cases of backfill drilling pipeline damage in foreign mines. This finding can inform the design of the backfill filling pipeline for China’s kilometer-deep wells in the future.

2. Modification of the Mechanical Model for the Anti-Extrusion Strength of Backfill Drilling Pipelines

Steel pipes can fail in two ways: elastic instability failure and plastic yield failure. Elastic instability failure is more likely to occur when the diameter to thickness ratio is greater than 32, which is not typically the case for mine backfill drilling pipelines. This article focuses on correcting the anti-extrusion strength of backfill filling pipeline with regards to plastic yield failure.

2.1. API Yield Strength Model

Assuming that the pipeline conforms to the basic assumptions of elasticity, namely an ideal pipeline with uniform wall thickness, infinite length, and small deformation [24]. When the external extrusion force causes the stress generated on the pipeline to reach or exceed the yield strength limit of the pipeline, it is considered that the pipeline has begun to undergo plastic deformation, and the safety factor is relatively low. When the pipeline undergoes plastic deformation, the stress can be solved according to the Lame formula under uniform external load [25], that is:
σ r = P r 2 2 r 2 2 − r 1 2 [ 1 − ( r 1 r ) 2 ]
σ θ = P r 2 2 r 2 2 − r 1 2 [ 1 + ( r 1 r ) 2 ]
When the circumferential stress on the inner wall of the pipeline is equal to or exceeds the minimum yield strength of the pipeline itself, it indicates that the pipeline has begun to yield and collapse. Using σ to denote the minimum yield strength value of the pipeline, i.e., σ instead of σθ, the pipe yield strength model (i.e., the API model) can be expressed as follows when the pipe undergoes yield crushing:
P = 2 σ [ D t − 1 ( D t ) 2 ]
In Equations (1) to (3) above: σ r is the radial stress; σ θ is the circumferential stress, P is the anti-extrusion strength of the pipeline, r2 is the outer radius of the pipeline, r1 is the inner radius of the pipeline, r is the distance from any point on the pipeline wall to the pipeline axis, σ is yield strength of the pipeline, D is the outer diameter of the pipeline, t is the wall thickness of the pipeline.

2.2. Modification of the Anti-Extrusion Strength of Backfill Drilling Pipelines

The backfill drilling system consists of the stratum, pipeline, and cementing ring between the stratum and pipeline, as shown in Figure 2. In actual working conditions, the system is subjected to significant formation pressure σ, as shown in Figure 2. The shape of the tube in space also belongs to axisymmetric problems, so stress can be solved according to formula (1). Formula (3) represents the yield strength model of pipelines under ideal conditions. This model has been widely used for designing pipelines in various fields. However, only the circumferential stress of the pipeline σ θ , is utilized in this formula. To make a more reasonable judgment, the most commonly used failure criterion for metallic materials is the application of the fourth strength theory of material mechanics [26] (Mises’s stress criterion), as shown in formula (4). If the equivalent Mises stress inside the pipeline exceeds the pipeline’s yield strength after being subjected to stratum pressure, it is considered a failure. The pipeline can ensure safety when   ≤   .
σ s = ( σ r − σ θ ) 2 + ( σ r − σ z ) 2 + ( σ z − σ θ ) 2 2
In the formula: σ s is the equivalent Mises stress value, MPa, σ r is the radial stress value, MPa, σ θ Is the radial stress value, MPa, σ z is the axial stress value, where σ z = μ ( σ r + σ θ ) , MPa, μ Poisson’s ratio for pipelines, σ t is the yield strength value of the pipeline, MPa.
Formula (1) shows that the maximum value of σ θ is on the inner wall of the pipeline, while the maximum value of σ θ is on the outer wall of the pipeline and is numerically significant. σ θ is greater than σ r . Thus, the maximum effective stress occurs on the inner wall of the pipeline, causing it to reach the yield condition first with σ r =0. To obtain the revised yield extrusion strength model for the pipeline, substitute σ θ and σ z into formula (4) and organize accordingly:
P t = σ t ( 1 − r 1 2 r 2 2 ) 2 1 − μ + μ 2
In the formula: P t is the anti-extrusion strength of the pipeline, MPa, r1 is the inner radius of the pipeline, mm, r2 is the outer radius of the pipeline, mm, μ Poisson’s ratio for pipelines, σ t is the yield strength value of the pipeline, MPa.
After production and processing, the backfill drilling pipeline is not an ideal round pipe. Factors such as pipeline non-roundness, uneven pipeline wall thickness, and residual stress must be considered in calculations to ensure pipeline safety. Scholars [27] have conducted extensive research on non-circularity, wall thickness unevenness, and residual stress. The pipeline’s anti-extrusion strength test obtained a calculation model for the influence of out-of-roundness defects, uneven wall thickness defects, and residual stress on the pipeline’s anti-extrusion strength.
P e = P t ( 1 − e )
P ε = P t ( 1 − ε 2 )
P σ u = P t ( 1 − σ u σ t )
In the formula: P e is the anti-extrusion strength value considering the non-circularity of the pipeline, MPa; P ε is the anti-extrusion strength value considering the non-uniformity of pipeline wall thickness, MPa, P σ u is the anti-extrusion strength value considering residual stress in the pipeline, MPa, e is the out of roundness of the pipeline, %. ε is the unevenness of pipeline wall thickness, %; σ u is the residual stress of the pipeline, MPa.
Taking into account the Mises stress intensity criterion and the out of roundness e and wall thickness unevenness of the pipeline ε, and residual stress σ u , the final revised anti-extrusion strength model of the backfill drilling pipeline is:
P = σ t ( 1 − σ u σ t ) ( 1 − ε 2 ) ( 1 − e ) ( 1 − r 1 2 r 2 2 ) 2 1 − μ + μ 2

3. Finite Element Analysis of Backfill Drilling Pipelines

To investigate the influence of the actual environment on the strength of the mine backfill drilling pipelines, finite element analysis is carried out for the parameters of the stratum and the cement ring, and the damage state of the pipe can be judged by comparing the value of the Mises stress of the pipe and the yield strength, or by comparing the value of the external extrusion force of the pipe and the value of the pipe’s resistance to anti-extrusion strength.

3.1. Modeling Process

This study analyzes the idea: through the establishment of a finite element model, the establishment of the contact surface between the pipe and the cement ring, through the extraction of the contact stress as the actual external extrusion force suffered by the pipeline, through the comparison of the external extrusion force with the anti-extrusion strength of the pipeline and the pipeline’s mises stress value with the pipeline’s yield strength value, as a way to analyze the effect of the parameters of the cement ring, the stratum on the value of the pipeline’s resistance to anti-extrusion strength of the regularity.
The pipeline is a bimetallic composite pipe, with an outer layer of Q235 and an inner layer of high chromium wear-resistant alloy steel. The specific material properties are shown in Table 1.
Based on the analysis above, the force problem of the filling system can be simplified as a plane strain problem. This model applies uniform stress in the x and y directions σ. A contact surface is established between the pipeline, cement ring, and stratum. The external extrusion force of the pipeline is P1, and the external extrusion force of the cement ring is P2. Analyzing Mises stress ( σ s ) inside pipelines by changing formation and cement ring parameters. The study investigates the variation of external squeezing force.

3.2. The Influence of Stratum Parameters on the Anti-Extrusion Strength of Pipelines

The selection of Stratum parameters includes the elastic modulus (Ed), Poisson’s ratio(μd), cement ring thickness (d), and ground stress ( σ d ) as variables. Due to the large number of factor level designs, it is not possible to comprehensively display stress nephogram at each level. However, upon comparison, it was found that the nephogram patterns at each level are similar. Therefore, only one stress nephogram is displayed for each factor as a reference. Polar coordinates are used to compare the stress distribution of each factor at each level.

3.2.1. Finite Element Analysis of Elastic Modulus of Strata

The Ed is set at a level of 10GPa to 70GPa. Figure 3 and Figure 4 display the results of the finite element analysis. As shown in the figure, the σ s ,   P1, P2 of the pipeline are equal in the circumferential direction, σ s decreases from the inside out and reaches its maximum value at the inner wall of the pipeline. This result is consistent with the analytical solution of the Lame formula, which predicts that the pipeline will first experience yield failure in the inner layer. The σ s ,   P1, P2 of pipeline gradually decrease as the strata’s Ed increases, with a maximum reduction amplitude of about 45.3% (without a cement ring) and 69.7% (with a cement ring). However, the reduction amplitude gradually slows down. This indicates that the Ed elastic modulus and stiffness are directly proportional to its ability to resist distant ground stresses and provide an ‘iron tube’ protective effect. The protective effect on the pipeline is stronger when the strata has a larger elastic modulus.
Upon comparison of the data, it was discovered that while the presence or absence of a cement ring cannot entirely eliminate stress on the pipeline, the presence of a cement ring results in an average decrease of 32.7% in σ s ,   P1, P2. This can be attributed to the fact that, in general, the elastic modulus and stiffness of the cement ring are smaller than that of the strata, but its deformation ability is stronger. When distant stress is transmitted to the cement ring through the formation, the cement ring absorbs a portion of the force through deformation, resulting in a decrease in the force transmitted to the pipeline. This suggests that the cement ring has a stress-relieving effect and provides some protection to the pipeline.

3.2.2. Finite Element Analysis of Poisson’s Ratio of Strata

The μd is set at a level of 0.1–0.45, and the results of the finite element model are shown in Figure 5 and Figure 6. As shown in the figure, the σ s ,   P1, P2 of the pipeline are equal in the circumferential direction, σ s gradually decreases radially from the inside out and reaches its maximum value at the inner wall of the pipeline, which is consistent with the elastic modulus law of the strata. The σ s ,   P1, P2 of pipeline all decrease gradually with the increase of μd, and the maximum decrease is about 16.7% (without cemented ring) and 8.9% (with cemented ring), which is a small decrease. This indicates that the larger μd is, the stronger the protection of the pipe is, but from the polar plot, it can be found that the difference in the value of annular stress at each level is small, indicating that this protection is not significant. Both σ s and P1 of the pipeline are reduced by 37.8% on average when there is a cement ring present. This indicates that the cement ring has a stress unloading effect and provides some protection to the pipe.

3.2.3. Finite Element Analysis of Geological Stress of Strata

The σ d is set at the level of 18MPa–1MPa, and the finite element modeling results are shown in Figure 7 and Figure 8. From the figure, it can be seen that the σ s ,   P1, P2 of the pipeline are equal in the circumferential direction, σ s gradually decreases radially from the inside out and reaches its maximum value at the inner wall of the pipeline, which is consistent with the elastic modulus law of the strata. The σ s ,   P1, P2 of the pipeline all increase with the increase of σ d , and the maximum increase is about 239.8% (without cemented ring) and 238.8% (with cemented ring). This result is also consistent with the general rule that the value of strata stress is proportional to the depth of the strata, i.e., the deeper the depth of the strata, the greater the ground stress. However, it should be noted that the pipeline stress value increases exponentially according to the strata depth, even though the stress value decreases by 37.3% in the case of cemented ring, the final pipeline stress value still increases exponentially. This indicates that when mining deep wells, it is important to focus on the value of ground stress due to the depth of the strata to determine the mechanical parameters of the pipeline in order to ensure the safety of the pipeline.

3.3. The Influence of Cement Ring Parameters on the Anti-Extrusion Strength of Pipelines

The selection of cement ring parameters includes the elastic modulus (Ec), Poisson’s ratio(μc), cement ring thickness(d), and cement ring missing(α) angle as variables. Due to the large number of factor level designs, it is not possible to comprehensively display stress nephogram at each level. However, upon comparison, it was found that the nephogram patterns at each level are similar. Therefore, only one stress nephogram is displayed for each factor as a reference. Polar coordinates are used to compare the stress distribution of each factor at each level.

3.2.1. Finite Element Analysis of Elastic Modulus of Cement Ring

The Ec is set at a level of 5 MPa–0 MPa, and the finite element modeling results are shown in Figure 9. From the figure, it can be seen that the σ s ,   P1, P2 of the pipeline are equal in the circumferential direction, σ s gradually decreases radially from the inside out and reaches its maximum value at the inner wall of the pipeline, which is consistent with the previous law. In this study, the stratum Ed is set to 30 GPa, and it is obvious from Figure 9b–d that when Ec < Ed, the σ s , P1, P2 of pipeline all increase with the increase of Ec, and when Ec > Ed, the pipeline’s   σ s , P1, P2 all gradually decrease with the increase of Ec.
It is commonly believed that a larger Ec provides a stronger protective effect on the pipeline. However, our findings differ from this view. From an energy perspective, when Ec < Ed, the stress in the distance generates energy by transmitting force and doing work on the cement ring. However, the cement ring’s smaller elastic modulus allows it to absorb some energy through its own deformation, while the remaining energy is transmitted to the pipeline. This results in a reduction of both the energy transmitted to the pipeline and the force exerted on it. Conversely, when Ec > Ed, the cement ring cannot absorb as much energy transmitted from the formation due to its larger Ec. As a result, the energy received by the pipeline increases. Based on the analysis above, it can be concluded that to enhance the anti-extrusion strength of the pipeline, the elastic modulus of the cement ring should be appropriately reduced when the local layer is relatively hard (Ec < Ed), and increased when the local layer is relatively soft (Ec > Ed). In general, materials with high strength can better withstand damage, while those with low stiffness can more easily deform. Therefore, if the cement ring possesses both high strength and low stiffness, it can significantly enhance the pipeline’s resistance to extrusion. However, such materials are uncommon and require further research and development.

3.2.2. Finite Element Analysis of Poisson’s Ratios of Cement Ring

The μc is set at the level of 0.1–0.4, and the results of the finite element model are shown in Figure 10. From the figure, it can be seen that the σ s ,   P1, P2 of the pipeline are equal in the circumferential direction, σ s gradually decreases radially from the inside out and reaches its maximum value at the inner wall of the pipeline, which is consistent with the previous law. It can be found through the polar plot that the difference between σ s and P1 of the pipeline at each level is small. Combined with the line graphs, it can be seen that the σ s ,   P1, P2 of pipeline all increase slightly with the increase of μc, with a maximum increase of 5.9%. This indicates that the change of μc has a small degree of influence on the stress of the pipeline, and its protective effect on the pipeline is basically negligible.

3.2.3. Finite Element Analysis of Thicknesses of Cement Ring

The d is set at the level of 10–70mm, and the finite element model results are shown in Figure 11. As shown in the figure, it can be seen that the σ s ,   P1, P2 of the pipeline are equal in the circumferential direction, σ s gradually decreases radially from the inside out and reaches its maximum value at the inner wall of the pipeline, which is consistent with the previous law. The σ s ,   P1, P2 of pipeline all decrease with increasing d, with a maximum increase of 30.9%. This can be explained as: the increase in cement ring d causes the deformation degree of the cement ring in the thickness direction to increase after receiving the force transmitted by the strata, that is, the “consumption and absorption” force increases, and the force transmitted to the pipeline decreases. This indicates that increasing the thickness of the cement ring has a certain protective effect on the pipeline.

3.2.4. Finite Element Analysis of Missing Angle of Cement Ring

In cementing, it is usually difficult to quantify the quality of cementing. This study characterizes the quality of cementing by setting the angle of missing cement rings. The d is set at the level of 15°–80°, and the finite element model results are shown in Figure 12. From the nephogram, it can be seen that the σ s ,   P1, P2 of the pipeline vary in the circumferential direction, with the maximum stress occurring at the center of the missing angle of the cement ring, σ s gradually decreases radially from the inside out and reaches its maximum value at the inner wall of the pipeline. According to the polar coordinate diagram, the stress value gradually increases in the 0°–90 ° and 180°–270° directions of the pipeline, but reaches its maximum at 90°. Due to its symmetrical structure, the other half exhibits the same pattern. When the cement ring is missing, it can lead to stress concentration at the missing location. Comparing the σ s values at 270° and 90°, it can be seen that σ s increases from 118MPa to a value of 257MPa, and the stress concentration factor is 2.2, which is enough to show that there is a significant effect on the stress of the pipe when the cement ring is missing.
The line graph shows that when 15° < α < 60°, the σ s ,   P1, P2 of the pipeline all increase with α, with a maximum increase of 64.9%. When 60° < α < 180°, the σ s ,   P1, P2 of the pipeline all decrease with increasing α, with a maximum decrease of 74.1%. This is different from our usual understanding, which usually assumes that the larger α is, the larger the stress value is. This can be explained by the fact that when the missing angle is small, the stress inside the pipe increases sharply, and as the angle increases, this stress concentration will reach its maximum value and not increase after that. This suggests that when cementing, there is a need to strictly ensure that the cement ring is defective, with the most unfavorable case being that smaller defects (less than 60°) are not allowed in the cement ring.

4. Engineering Case Verification

Taking a foreign copper mine as an engineering case, bimetallic composite pipes were used for backfill drilling pipelines. The damage location of the borehole in the mine is 680m, and the uniform stress value at this location is calculated to be 41MPa, indicating damage to the inner layer of the pipeline. Based on this, numerical simulation analysis was conducted, and the results are shown in Figure 13. The parameters of the model are shown in Table 1.
According to Figure 13, it can be seen that the results of this nephogram have a similar pattern with the previous numerical simulation results, i.e., σ s ,   P1, P2 are equal in the annulus upward, and the value of σ s in the radial direction becomes smaller from the inside outward, and there is a maximum value at the inner wall. In Figure 13(a), the value of σ s at the inner wall of the pipe is 227.53 MPa, which has exceeded the yield strength value of the inner layer of the pipe of 205 MPa, while the maximum value of σ s at the outer layer of the pipe is 211.27 MPa, which has not exceeded the yield strength value of the outer layer of the pipe of 235 MPa, and therefore the pipe has already been damaged by yielding at the inner wall.
According to Figure 13(b), it can be seen that the external squeezing force P1 of the pipe is 47.46 MPa, and according to the literature, σ u σ t is generally between 0.15–0.2, and 0.2 is taken in this case, and the out-of-roundness e of the pipe is taken as 0.5%, the unevenness of the wall thickness ε is taken as 10%, and the Poisson’s ratio of the inner pipeline is taken as 0.27, which is substituting into the API strength (2) and the modified anti-extrusion strength model (9), respectively. obtained and compared with the numerical simulation results, the results are shown in the following table:
According to Table 2, it can be seen that the value of API strength of the pipeline is 18.2% higher than the value of modified anti-extrusion strength, which indicates that the API value is too large, and when the strength of the pipeline is designed, the pipeline will be ruptured due to the design value is too low. According to the numerical simulation results, the actual external extrusion force of the pipeline in this mine is 27.9% higher than the API strength value and 51.1% higher than the modified anti-extrusion strength, which indicates that the pipeline sizing parameters in this mine cannot be applied to the geostress environment in which it is located. The modified anti-extrusion strength model in this study can provide theoretical guidance for the design of pipeline parameters.

4. Discussion

This study focuses on the use and rupture of backfill drilling bimetallic composite pipes in foreign mines. By deriving mechanical formulas, the mechanical failure mechanism of pipes is preliminarily explored and analyzed. Due to the limited mechanical analysis of deep well filling pipelines both domestically and internationally, there are certain limitations in the analysis:
(1) The formula derivation in this article is under ideal conditions, where the pressure at which the pipeline is located is uniform, while in reality, the pressure in most strata is non-uniform, resulting in certain errors in the calculation results.
(2) Theoretical analysis lacks support from indoor experiments. The pipeline should be subjected to triaxial compression tests indoors to simulate the actual compression environment of the pipeline in the formation and verify the rationality of the theoretical analysis.
Despite the limitations mentioned above, the mechanical analysis and exploration conducted in this study based on engineering cases have preliminarily and for the first time revealed the mechanical extrusion mechanism of deep backfill drilling pipelines under non wear damage, providing theoretical support for further in-depth and accurate analysis.

5. Conclusion

Based on the knowledge of elastic mechanics and material mechanics, combined with numerical simulation, theoretical analysis and engineering example means, the mechanical damage of mine backfill drilling pipeline was analyzed, and the conclusions obtained are as follows:
Based on the API yield strength model, the pipe anti-extrusion strength model was modified by considering the pipe out-of-roundness defects, wall thickness unevenness defects, and residual stress factors, and combining with the fourth strength criterion.
(2) Through the finite element analysis results, increase the stratum elastic modulus, Poisson’s ratio on the pipeline has a protective effect, and the role of the stratum elastic modulus is much larger than the stratum Poisson’s ratio. In the deeper stratum depth, the existence of larger ground stress makes the pipeline stress value increase exponentially, which has unfavorable effects on the pipeline.
(3) Cement ring has certain stress unloading effect, the average stress unloading degree 32.7–37.8%. Increasing the thickness of the cement ring will have a protective effect on both pipes, and the Poisson’s ratio of the cement ring has a basically negligible protective effect on the pipes. In hard strata, reducing the elastic modulus of cement ring appropriately, and in soft strata, increasing the elastic modulus of cement ring appropriately both have protective effect on the pipeline. Selection of high strength and low stiffness cement ring materials can improve the crush strength of the pipe. When the missing angle of cement ring < 60°, the stress concentration factor is as high as 2.2, and the stress concentration effect is reduced when it exceeds 60°.
(4) Through the API strength model, modified anti-extrusion strength model and finite element analysis results, the API crush strength value of the pipeline is 18.2% higher than the modified anti-extrusion strength value, and at the same time, it is verified that the inner layer of the pipeline rupture in a foreign mine filling borehole is due to its own low design of the anti-extrusion strength value. The modified anti-extrusion strength model in this study can provide theoretical guidance for the design of pipeline parameters.

Author Contributions

LH conducted indoor experimental design and analysis, W HJ conducted theoretical analysis, L CK established a model. All authors read and approved the final manuscript.

Funding

This work was supported by the Key Program of National Natural Science Foundation of China (Grant No. 51834001); Key Program of National Natural Science Foundation of China (Grant No. 52130404).

Ethics Approval and Consent to Participate

This research does not involve any ethical issues and all participants have agreed.

Consent for Publication

All participants in the paper have agreed to publish.

Availability of Data and Materials

The datasets used and/or analyzed during the current study are available from the corresponding author on reasonable request.

Competing Interests

The authors declare that they have no competing interests.

References

  1. Xie, H.P.; Gao, F.; JU, Y. Research and exploration of deep rock mass mechanics. J. Rock Mech. Eng. 2015, 34, 2161–2178. [Google Scholar]
  2. Wang, L.M.; Luo, Y.K.; Yin, S.H.; Zhou, G.M.; Liao, W.S.; Li, Z.K. Exploration of Strengthening Fluidized Leaching Process of Deep Ground Metal Mines and Geothermal Collaborative Mining. J. Eng. Sci. 2022, 44, 1694–1708. [Google Scholar]
  3. Cai, M.F.; Tan, W.H.; Wu, X.H.; Zhang, L.P. The Current Situation and Development Strategy of Deep Intelligent Mining in Metal Mines. Chin. J. Nonferrous Met. 2021, 31, 3409–3421. [Google Scholar]
  4. Cheng, H.Y.; Wu, A.X.; Wu, S.C.; Zhu, J.Q.; Li, H.; Liu, J.; Niu, Y.H. Research Status and Development Trends of Solid Waste Filling in Metal Mines. J. Eng. Sci. 2022, 44, 11–25. [Google Scholar]
  5. Wu, A.X.; Wang, Y.; Wang, H.J. The current situation and trend of paste filling technology. Met. Mines 2016, 7, 1–9. [Google Scholar]
  6. Zheng, B.K.; Zhang, P.Q.; Yin, X.Y.; Wang, Y.S. Research on Pressure Regulating Technology of Deep Well Low Power Line Filling Pipeline. Min. Technol. 2019, 1, 31–33. [Google Scholar]
  7. Zhang, J.F.; Dong, K.F.; Chen, Y.; Wang, S.M. Application of Multi process Drilling Technology in Vertical Filling `Drilling. Well Constr. Technol. 2023, 44, 8–14. [Google Scholar]
  8. Qi, W.; Guo, M.C.; Tan, Y.Y.; Zhang, C.Y. Analysis of Gravity Transportation Parameters and Study on Wear Law of Filling Pipeline in Daye Iron Mine. Min. Res. Dev. 2021, 41, 164–169. [Google Scholar]
  9. Jose, W.; Calderon, H.; Amilton, S. Hydraulic convey of iron ore slurry pipeline wear and ore particle degradation in function of pumping time. Wear 2020, 450, 203272. [Google Scholar]
  10. Jones, M.; Llewellyn, R.J. Erosion–corrosion assessment of materials for use in the resources industry. Wear 2009, 267, 2003–2009. [Google Scholar] [CrossRef]
  11. Buchan, A.J.; Spearing, A.J.S. The effect of corrosion on the wear rate of steel pipelines conveying backfill slurry. J. South. Afr. Inst. Min. Metall. 1994, 94, 37–45. [Google Scholar]
  12. Levy, A.V.; Pauline, C. The effects of erodent composition and shape on the erosion of steel. Wear 1983, 89, 151–162. [Google Scholar] [CrossRef]
  13. Creber, K.J. Experimental and In-Situ Investigation into Pipeline Wear in Mine Backfill Distribution Systems; Montreal: McGill University, 2016. [Google Scholar]
  14. Qiao, Z.W.; Liu, Z.; Zhang, X.T.; Zhang, H.X.; Li, Z.J.; Li, D. The influence of roughness on the mechanical characteristics and erosion of cylindrical structures under the action of water and sand flow. J. Shandong Univ. Sci. Technol. (Nat. Sci. Ed. ) 2021, 40, 44–49. [Google Scholar]
  15. Wang, Z.C.; Chen, Y.; Sun, J.; Xia, H.C. Analysis of erosion and wear of variable diameter pipes by filling slurry. J. Shandong Univ. Sci. Technol. (Nat. Sci. Ed. ) 2022, 41, 39–46. [Google Scholar]
  16. Rodriguez, W.J.; Fleckenstein, W.W.; Eustes, A.W. Simulation of Collapse Loads on Cemented Casing, Using Finite Element Analysis. J. Pet. Technol. 2003, 56, 59–61. [Google Scholar]
  17. Medjo, B.; Rakin, M.; Gubeljak, b. Failure resistance of drilling rig casing pipes with an axial crack. Eng. Fail. Anal. 2015, 58, 429–435. [Google Scholar] [CrossRef]
  18. Liu, Q.J. Analysis of casing damage mechanism and research on treatment measures. Petrochem. Technol. 2021, 28, 35–39. [Google Scholar]
  19. Han, H.; Yin, S.; Hen, Z.C. Estimate of in-situ stress and geomechanically parameters for Duvernay Formation based on borehole deformation data. J. Pet. Sci. Eng. 2021, 196, 107994. [Google Scholar] [CrossRef]
  20. Gao, F. Peak Study on the distribution law of ground stress and its influence on the stability of surrounding rock of roadway; China University of Mining and Technology: Beijing, 2009. [Google Scholar]
  21. Mo, P.; Marshall, A.M.; Yu, H. Elastic-plastic solutions for expanding cavities embedded in two different cohesive-frictional materials, International. J. Numer. Anal. Methods Geomech. 2014, 38, 961–970. [Google Scholar] [CrossRef]
  22. Guo, K.Y.; Wang, J.E. The failure mechanism and anti-deformation design of vertical shafts affected by mining. Coal Sci. Technol. 2020, 48, 179–184. [Google Scholar]
  23. Li, C.; Hou, S.; Liu, Y. Analysis on the crown convergence deformation of surrounding rock for double-shield TBM tunnel based on advance borehole monitoring and inversion analysis. Tunn. Undergr. Space Technol. 2020, 103, 103513. [Google Scholar] [CrossRef]
  24. Xu, Z.L. Linear elasticity; Higher Education Press: Beijing, 2016. [Google Scholar]
  25. Hu, H.X.; Yao, Y.P.; Luo, T.; Jin, X.F. The plane strain strength formula based on the Lade Duncan criterion. Rock Soil Mech. 2022, 43, 389–396. [Google Scholar]
  26. Yang, Y.; Zhang, Y. Research on residual stress of domestically produced high anti extrusion casing. Pet. Spec. Pipe 1998, 46–49. [Google Scholar]
  27. Huang, Y.; Lin, H.Z.; Du, C.C. Relative Error Analysis of Strength Calculation for Thin walled Cylinders. J. Chang. Univ. 2019, 29, 10–13+45. [Google Scholar]
Preprints 100706 g001
Figure 1. Schematic diagram of backfill drilling pipeline rupture: (A) A foreign copper mine filled with drilling and salvaged fragments; (B) Cracking diagram of backfill drilling pipeline in a domestic iron mine.
Figure 1. Schematic diagram of backfill drilling pipeline rupture: (A) A foreign copper mine filled with drilling and salvaged fragments; (B) Cracking diagram of backfill drilling pipeline in a domestic iron mine.
Preprints 100706 g001
Preprints 100706 g002
Figure 2. Schematic diagram of backfill drilling system.
Figure 2. Schematic diagram of backfill drilling system.
Preprints 100706 g002
Preprints 100706 g003
Figure 3. Numerical simulation results under different elastic moduli of strata (without cement ring): (a) σ s   and P1 nephogram(Ed = 10GPa) (b) σ s comparison analysis results (c) P1 comparison analysis results (d) Ed and σ s , P1 relationship diagram.
Figure 3. Numerical simulation results under different elastic moduli of strata (without cement ring): (a) σ s   and P1 nephogram(Ed = 10GPa) (b) σ s comparison analysis results (c) P1 comparison analysis results (d) Ed and σ s , P1 relationship diagram.
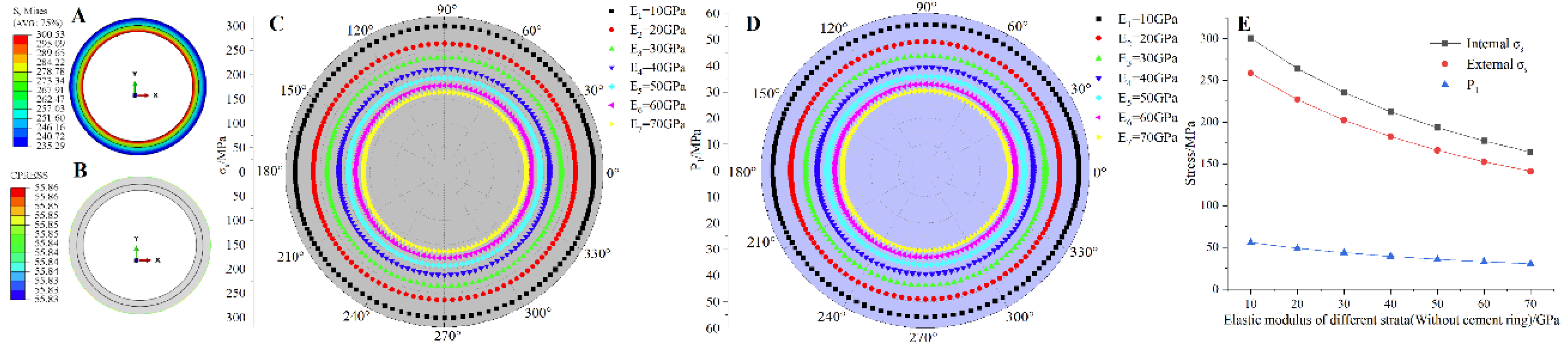
Preprints 100706 g003
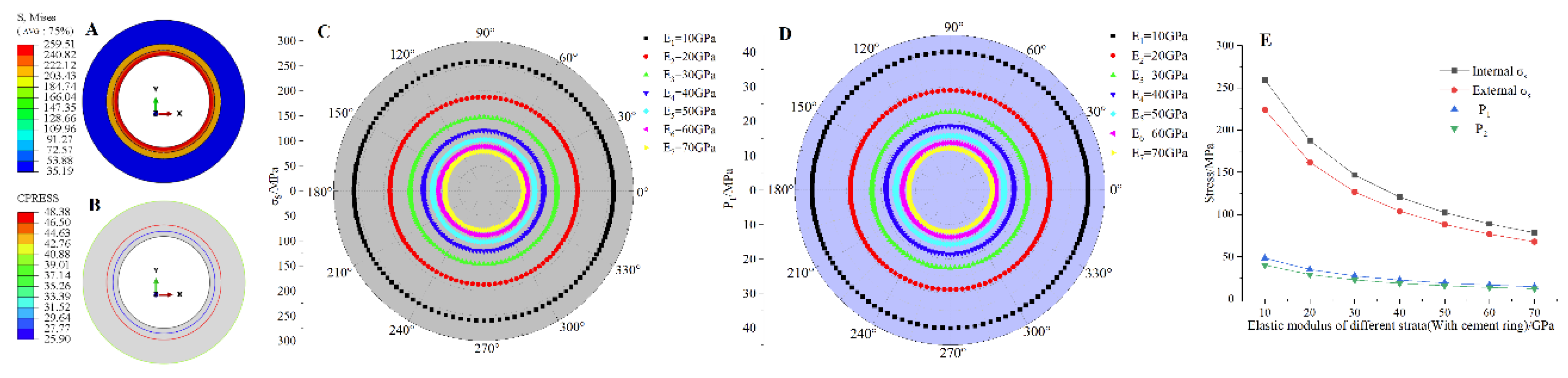
Preprints 100706 g004
Figure 4. Numerical simulation results under different elastic moduli of strata (with cement ring): (a) σ s   and P1 nephogram(Ed = 10GPa) (b) σ s comparison analysis results (c) P1 comparison analysis results (d) Ed and σ s , P1, P2 relationship diagram.
Figure 4. Numerical simulation results under different elastic moduli of strata (with cement ring): (a) σ s   and P1 nephogram(Ed = 10GPa) (b) σ s comparison analysis results (c) P1 comparison analysis results (d) Ed and σ s , P1, P2 relationship diagram.
Preprints 100706 g004
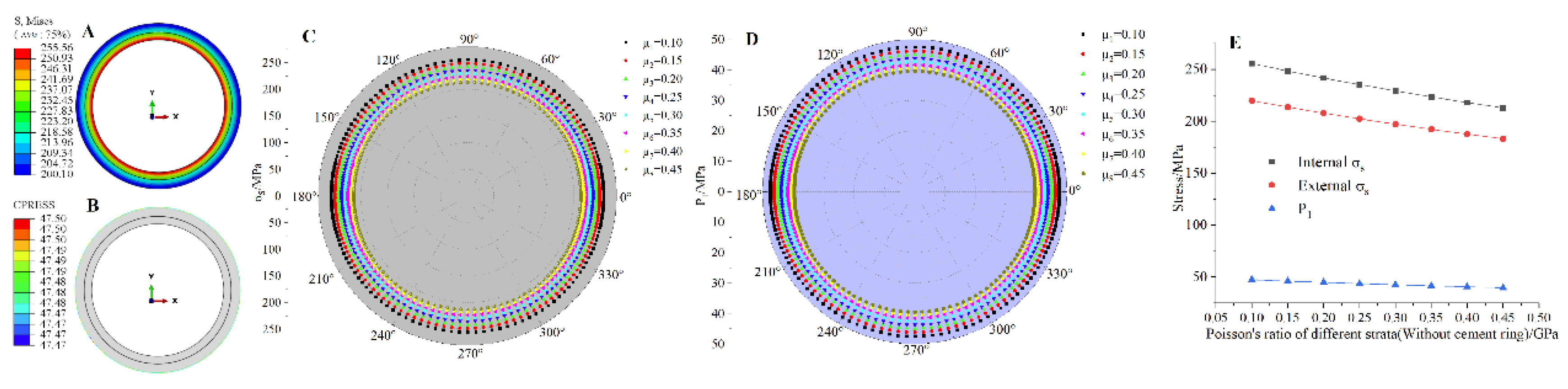
Preprints 100706 g005
Figure 5. Numerical simulation results under different Poisson’s ratios of strata (without cement ring): (a) σ s   and P1 nephogram(μd =0.1) (b) σ s comparison analysis results (c) P1 comparison analysis results (d) μd and σ s , P1 relationship diagram.
Figure 5. Numerical simulation results under different Poisson’s ratios of strata (without cement ring): (a) σ s   and P1 nephogram(μd =0.1) (b) σ s comparison analysis results (c) P1 comparison analysis results (d) μd and σ s , P1 relationship diagram.
Preprints 100706 g005
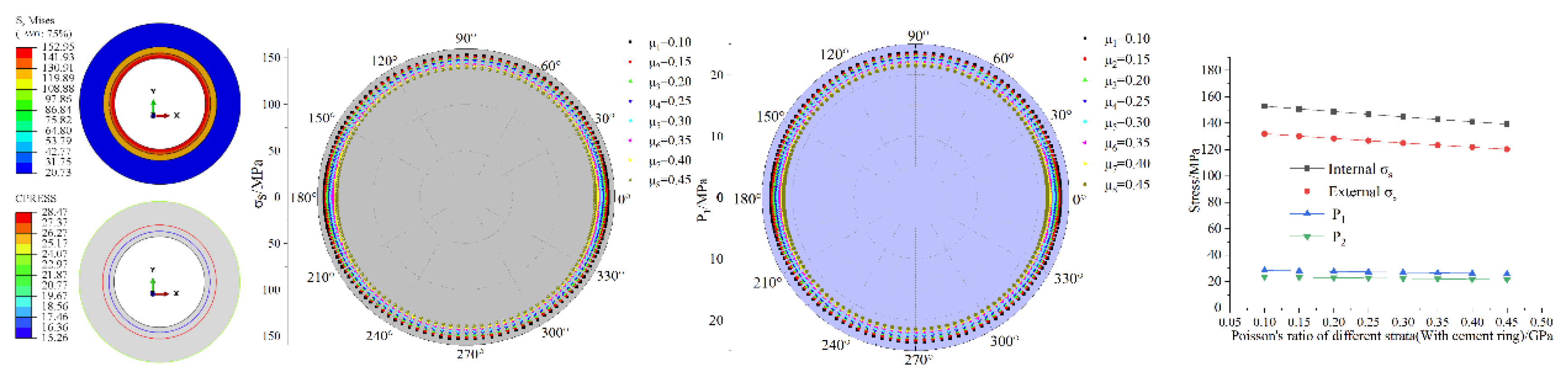
Preprints 100706 g006
Figure 6. Numerical simulation results under different Poisson’s ratios of strata (with cement ring): (a) σ s   and P1 nephogram(μd =0.1) (b) σ s comparison analysis results (c) P1 comparison analysis results (d) μd and σ s , P1, P2 relationship diagram.
Figure 6. Numerical simulation results under different Poisson’s ratios of strata (with cement ring): (a) σ s   and P1 nephogram(μd =0.1) (b) σ s comparison analysis results (c) P1 comparison analysis results (d) μd and σ s , P1, P2 relationship diagram.
Preprints 100706 g006
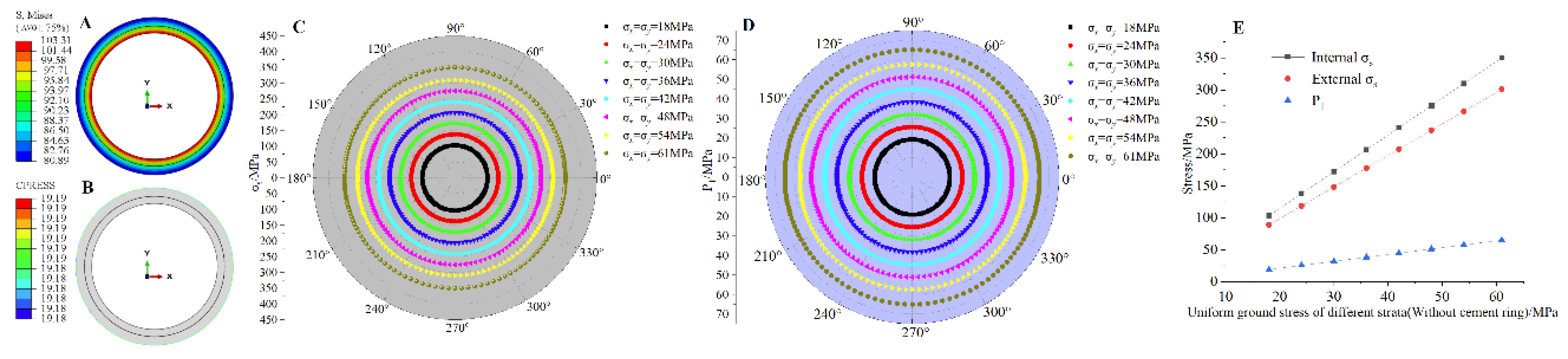
Preprints 100706 g007
Figure 7. Numerical simulation results under different geological stresses of strata (without cement ring): (a) σ s   and P1 nephogram(   =   1 8MPa) (b) σ s comparison analysis results (c) P1 comparison analysis results (d) σ d and σ s , P1 relationship diagram.
Figure 7. Numerical simulation results under different geological stresses of strata (without cement ring): (a) σ s   and P1 nephogram(   =   1 8MPa) (b) σ s comparison analysis results (c) P1 comparison analysis results (d) σ d and σ s , P1 relationship diagram.
Preprints 100706 g007
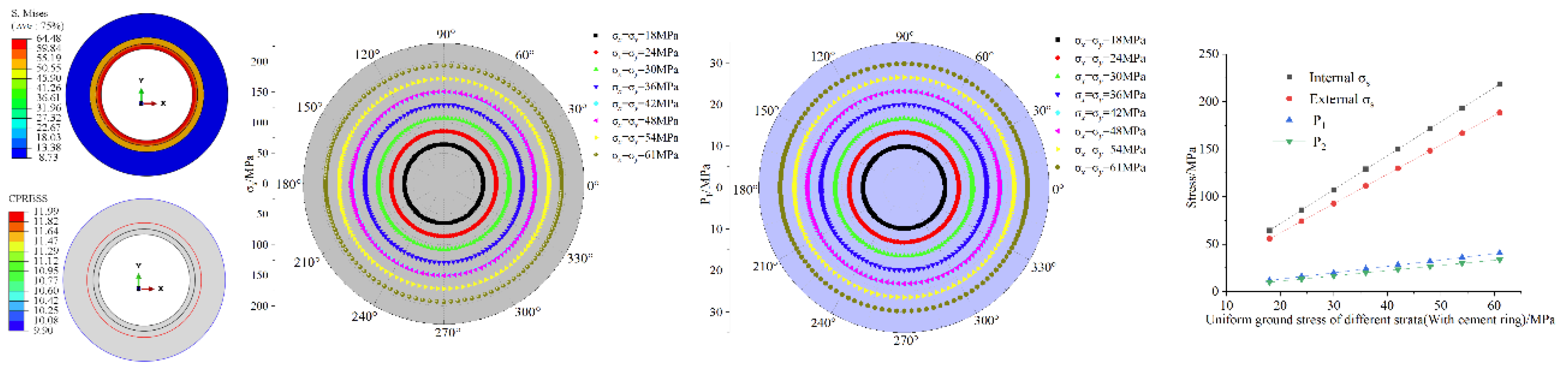
Preprints 100706 g008
Figure 8. Numerical simulation results under different ground stresses of strata (with cement ring): (a) σ s   and P1 nephogram( σ d =18MPa) (b) σ s comparison analysis results (c) P1 comparison analysis results (d) σ d and σ s , P1, P2 relationship diagram.
Figure 8. Numerical simulation results under different ground stresses of strata (with cement ring): (a) σ s   and P1 nephogram( σ d =18MPa) (b) σ s comparison analysis results (c) P1 comparison analysis results (d) σ d and σ s , P1, P2 relationship diagram.
Preprints 100706 g008
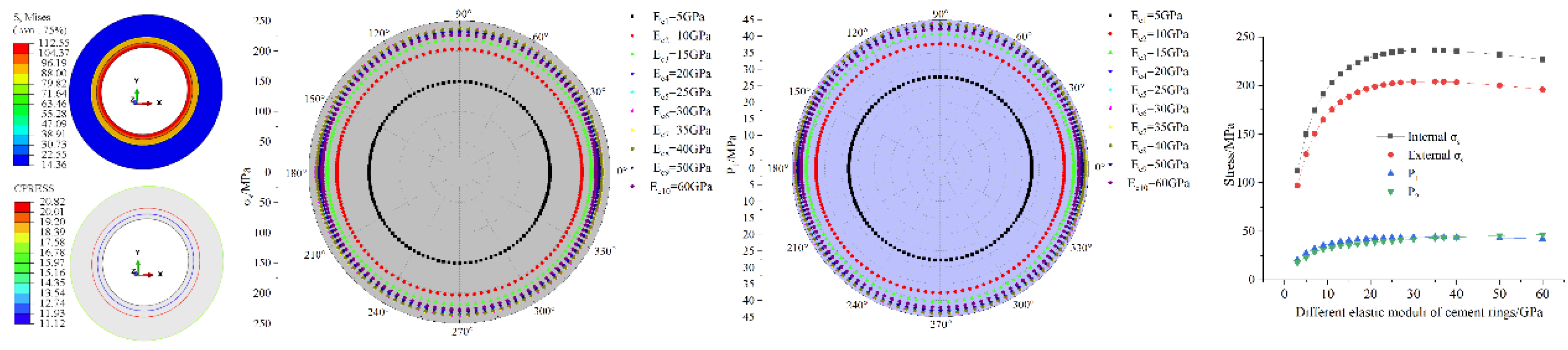
Preprints 100706 g009
Figure 9. Numerical simulation results under different elastic moduli of cement rings: (a) σ s   and P1 nephogram(Ec =5GPa) (b) σ s comparison analysis results (c) P1 comparison analysis results (d) Ec and σ s , P1, P2 relationship diagram.
Figure 9. Numerical simulation results under different elastic moduli of cement rings: (a) σ s   and P1 nephogram(Ec =5GPa) (b) σ s comparison analysis results (c) P1 comparison analysis results (d) Ec and σ s , P1, P2 relationship diagram.
Preprints 100706 g009
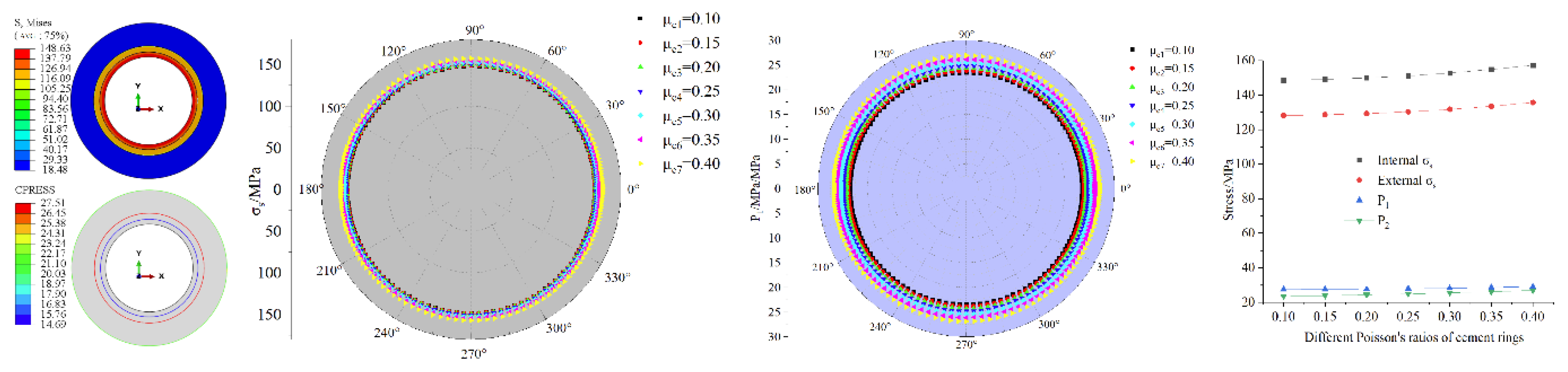
Preprints 100706 g010
Figure 10. Numerical simulation results under different Poisson’s ratios of cement rings: (a) σ s   and P1 nephogram(μc =0.1) (b) σ s comparison analysis results (c) P1 comparison analysis results (d) μc and σ s , P1, P2 relationship diagram.
Figure 10. Numerical simulation results under different Poisson’s ratios of cement rings: (a) σ s   and P1 nephogram(μc =0.1) (b) σ s comparison analysis results (c) P1 comparison analysis results (d) μc and σ s , P1, P2 relationship diagram.
Preprints 100706 g010
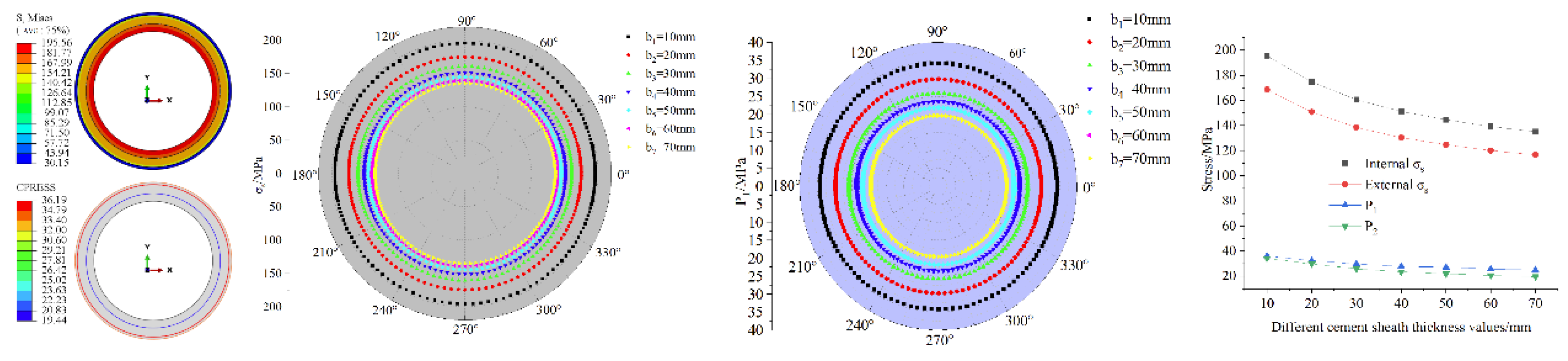
Preprints 100706 g011
Figure 11. Numerical simulation results under different thicknesses of cement rings: (a) σ s   and P1 nephogram(d =10mm) (b) σ s comparison analysis results (c) P1 comparison analysis results (d) d and σ s , P1, P2 relationship diagram.
Figure 11. Numerical simulation results under different thicknesses of cement rings: (a) σ s   and P1 nephogram(d =10mm) (b) σ s comparison analysis results (c) P1 comparison analysis results (d) d and σ s , P1, P2 relationship diagram.
Preprints 100706 g011
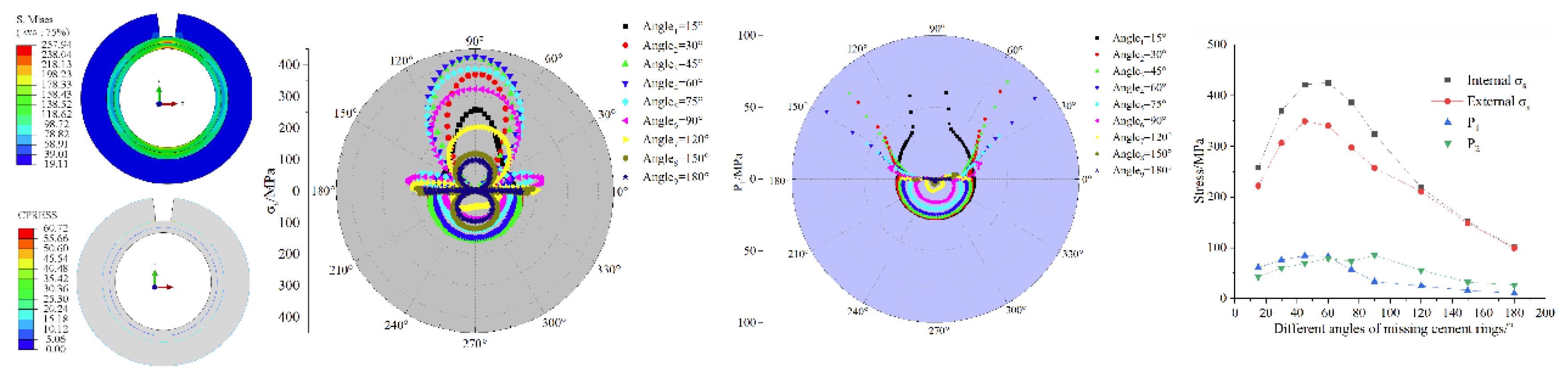
Preprints 100706 g012
Figure 12. Numerical simulation results under different angles of missing of cement rings: (a) σ s   and P1 nephogram(α =15°) (b) σ s comparison analysis results (c) P1 comparison analysis results (d) α and σ s , P1, P2 relationship diagram.
Figure 12. Numerical simulation results under different angles of missing of cement rings: (a) σ s   and P1 nephogram(α =15°) (b) σ s comparison analysis results (c) P1 comparison analysis results (d) α and σ s , P1, P2 relationship diagram.
Preprints 100706 g012
Preprints 100706 g013
Figure 13. Numerical simulation results of a copper mine pipeline abroad: (a) σ s   nephogram (b) P1 nephogram.
Figure 13. Numerical simulation results of a copper mine pipeline abroad: (a) σ s   nephogram (b) P1 nephogram.
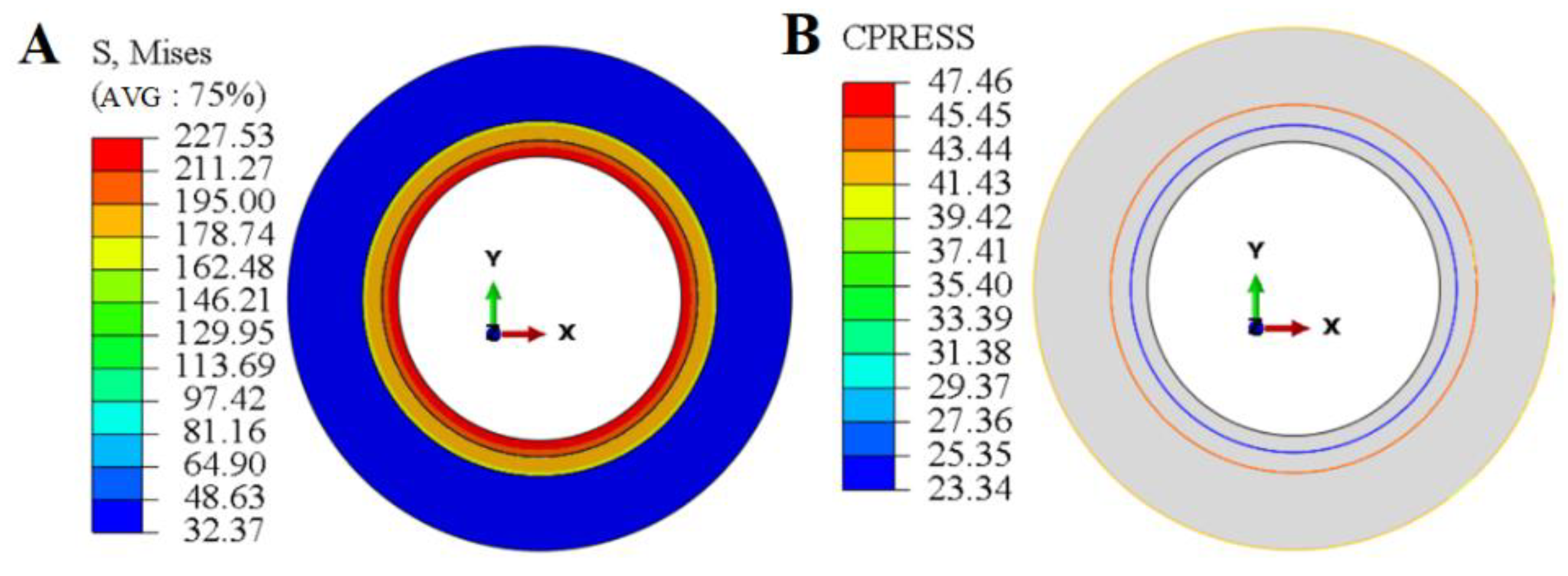
Preprints 100706 g013
Table 1. Material parameters of strata, cement rings, pipelines.
Table 1. Material parameters of strata, cement rings, pipelines.
Medium Size/mm Density/
g/cm−3 		Elastic Modulus/GPa Poisson’s Ratio Yield Strength/MPa Friction Angle/°
Strata 2000 × 2000 2.7 30 0.25 - 40
Cement rings φ310 × t46 1.7 15 0.2 - 25
External pipeline φ219 × t12 7.85 206 0.30 235 -
Internal pipeline φ195 × t10 7.85 210 0.27 205 -
Table 2. Comparison results of pipeline anti-extrusion strength.
Table 2. Comparison results of pipeline anti-extrusion strength.
Typology API strength modified anti-extrusion strength external squeezing force P1
Strength value/MPa 37.1 31.4 47.5
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated