Prerpints.org logo
Preprint
Article

Deterministic chaos models-based Gaussian noise generator

Altmetrics

Downloads

120

Views

38

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

06 March 2024

Posted:

07 March 2024

You are already at the latest version

Alerts
Abstract
The abilities of quantitative description of noise are restricted due to its origin and only the statistical and spectral analysis methods can be applied while an exact time evolution cannot be defined or predicted. It emphasizes the challenges faced in many applications including communication systems where noise can play, on one hand, a vital role impacting signal-to-noise ratio but possessing, on the other hand, unique properties such as infinite entropy (infinite information capacity), exponentially decaying correlation function and so on. Despite the deterministic nature of chaotic systems, the predictability of chaotic signals is limited for a short time window putting them close to random noise. In this article, we propose and experimentally verify an approach to achieve Gaussian-distributed chaotic signals by processing the outputs of chaotic systems. The mathematical criteria, on which the main idea of the study is based on, is the Central Limit Theorem which states that the sum of a large number of independent random variables with similar variances approaches a Gaussian distribution. The study involves more than 40 mostly three-dimensional continuous-time chaotic systems (Chua’s, Lorenz’s, Sprott’s, memristor-based, etc.) whose output signals are analyzed according to criteria that encompass the probability density functions of a chaotic signal itself and its envelope and phase, statistical and entropy-based metrics such as skewness, kurtosis, and entropy power. We found that two chaotic signals of Chua’s and Lorenz’s systems exhibited superior performance across the chosen metrics. Furthermore, our focus extended to determining the minimum number of independent chaotic signals necessary to yield a Gaussian-distributed combined signal. The analytic and experimental results indicate that the sum of at least three non-Gaussian chaotic signals closely approximates Gaussian distribution. It allows generation of reproducible Gaussian-distributed deterministic chaos by modeling simple chaotic systems.
Keywords: 
Subject: Engineering  -   Electrical and Electronic Engineering

1. Introduction

Chaos theory has radically revolutionized our understanding of the potential for complex, unpredictable behavior within seemingly simple deterministic systems. This phenomenon, known as chaos, arises in nonlinear systems and is characterized by extreme sensitivity to initial conditions, often leading to the iconic “butterfly effect”. Chaotic dynamics are remarkably pervasive, manifesting in diverse domains such as social, biological, and technical systems [1,2,3,4,5,6].
Security threads and challenges prompt scientists to research how chaotic signals are suitable to resolve these issues. Numerous applications have been proposed including secure and covert communication, pseudo-random number generator (PRNG) and cryptography [7,8,9,10,11,12,13,14]. Despite the diverse applications, varying advantages and drawbacks in each of these scopes, in all of them, chaotic systems are used as sources of entropy, a fundamental property crucial for security applications.
Chaos generator, present in both hardware and software implementation, produces time series that either mask information-bearing signals or undergo postprocessing for various cryptographic purposes. Chaotic trajectories form strange attractors in phase space, which, in contradiction to limit cycle that represents regular behavior, has fractional or fractal dimension [1]. There are several variants of fractal dimension, generally measuring the average closeness, density, and distribution of points on chaotic attractors in phase space. Chaos sources are categorized into two groups including continuous time and discrete maps systems. Due to differences in attractor properties, the trajectories of a chaotic system exhibit different statistics reflected in their probability density functions (PDFs). Chaos applications necessitate a high-quality entropy source, emphasizing the necessity to maximize the entropy of chaotic signals. Statistical analyses have been proposed by Yong Wang et al. to increase the quality of chaos for the same purpose as in this paper [15]. Concerning PDF, the most necessary is a number with uniform PDF and Gaussian distributed signals with bell-shaped PDF. The first requirement is common in cryptography, the second is useful in communication. Both of them maximize uncertainty of range-limited and variance-limited signals, respectively [16].
A two-dimensional discrete-time white Gaussian noise generator was proposed in [17]. To obtain an independent time series with a Gaussian probability density function, a special transformation was used on the tent map. A similar approach to the same tent map demonstrated the efficiency of the transformation method [18].
The Gaussian distribution is not the sole target widely sought in signal processing. Contributions in this direction also focus on achieving a uniform probability density. In paper [19] it is proved that the folding sums of chaotic trajectories, bounded within a given interval by modulus operation, tend to approach uniformity. It is worth noting, that certain discrete chaotic systems yield series with a uniform probability density function without requirement of additional transformations [20,21,22,23,24,25].
Significant achievements have been attained in the realm of optical chaos generators [26,27,28,29,30,31]. Wideband optical chaos exhibits a heightened propensity for Gaussian-distributed probability density functions. This characteristic has prompted suggestions for harnessing optical chaos generators as high-quality, ultra-fast entropy sources [28,29]. A recently reported experimental technique focuses on generating a Gaussian-invariant distribution [32]. Such sources hold potential for diverse applications spanning communication [33,34], random number generation [26,27] and cryptography [30,35].
Covert communication, originally designed to conceal and render the transmission undetectable, is now being harnessed for commercial and private applications to provide physical-level protection. In contrast to conventional communication, where Gaussian white noise diminishes the signal-to-noise ratio, covert communication employs it as a countermeasure against eavesdroppers. Thermal noise is utilized to randomize the transmitted signal in a Gaussian-distributed spread spectrum [36]. Additionally, extending this concept, the utilization of artificially generated Gaussian-distributed noise has been proposed across diverse scenarios [37,38,39,40].
Despite hundreds of chaotic systems have been designed and studied, little of them can produce Gaussian-distributed signals. Therefore, finding an approach for obtaining the most complex chaotic signal based on simple and well-studied nonlinear systems is important. In this paper, we study the statistical properties of some chaotic signals to find out how much of them are necessary to form a Gaussian-distributed waveform with the following experimental implementation and achievement verification that allow an implementation of ”deterministic noise” generators.
The manuscript is organized as follows. In section 2, we describe the quality metrics used to evaluate and compare chaotic signals. The properties of time series produced by mathematic models of Chua’s circuit and Lorenz system are studied in section 3. Experimental verification of the results is provided by the section 4. The discussion and conclusion are presented in section 5. The appendix presents the result of computing statistical properties of more than 40 continuous-time chaotic systems found in literature.

2. Materials and Methods

2.1. Central Limit Theorem

The central limit theorem (CLT) relates to probability theory and explains why Gaussian noise is widespread in nature. For identically distributed independent samples, the standardized sample mean tends towards the standard normal distribution even if the original variables themselves are not normally distributed. There are several variants of CLT. In its common Lindeberg-Lévy form the CLT is following [41,42]:
Theorem 1.
Suppose { X 1 , ⋯ , X n } is a sequence of independent and identically distributed random variables with expectation E [ X i ] = μ and variance Var [ X i ] = σ 2 < ∞ . Then as n approaches infinity, the random variables n ( 1 n ∑ i = 1 n X i − μ ) converge in distribution to a normal N ( 0 , σ 2 ) .
The CLT shows a way to obtain a variable with Gaussian-like distribution from several others by summation ones. The key condition for particular components is their limited variance which chaotic signals satisfy due to existence of their attractors in bounded phase space. The question is to find how many independent chaotic signals are necessary and which criteria the resulting signal should meet to be considered Gaussian-like. Therefore, the following consideration of the basic distributions will give a possibility to develop an algorithm for testing of chaotic signals.

2.2. Basic Distribitions

As a reference signal, we chose white Gaussian noise whose statistical properties can be described by three basic distributions which are the PDF of the shape, envelope and phase of the signal.
The term ”Gaussian noise” or ”Gaussian signal” refers to a normal or bell-shaped probability density function of this signal. Such signals can be either random noise or information-bearing. A Gaussian variable has following PDF
p ( x ) = 1 2 π σ e − ( x − μ ) 2 2 σ 2 ,
where σ – standard deviation; μ – mathematical expectation or mean.
The envelope of white noise has Rayleigh distribution
p ( x , σ ) = x σ 2 e − x 2 2 σ 2 ,
where σ – standard deviation of the gaussian distribution (1).
Uniform distribution describes the phase of signal
p ( ϕ ) = 1 2 π ,
where 0 ≤ ϕ ≤ 2 π .

2.3. Measures of Similarity of Probability Density Functions

To evaluate similarity of any signal to WGN, the normality tests that includes computing of skewness and excess kurtosis are conventionally utilized [43].
Skewness is a measure of the asymmetry of PDF around its mean and is defined as the normalized third central moment of signal
μ ˜ 3 = E x − μ σ 3 ,
where E – expectation operator.
Excess kurtosis is the metric of the height and sharpness of PDF, relative to that of a standard bell curve
μ ˜ 4 = E x − μ σ 4 − 3 .
For WGN both skewness and excess kurtosis are equal to zero.
It is worth noting, that if a signal exhibits a symmetric distribution with zero excess kurtosis, it by no means guarantees that its probability density function is normal. There are non-Gaussian distributions with μ ˜ 3 = 0 and μ ˜ 4 = 0 [44,45]. Therefore, at least, a graphical analysis is necessary to confidently assert the normality of the distribution, or confirmation through more sophisticated tests.
The envelope and phase of a signal can be found by using Hilbert transform [46]. For a given function x ( t ) , Hilbert transform is given as
x ^ ( t ) = H x ( t ) = 1 π ∫ − ∞ ∞ x ( t ) t − τ d τ .
Then the envelope and phase of x ( t ) are
a ( t ) = x 2 ( t ) + x ^ 2 ( t ) ,
ϕ ( t ) = arctan x ^ ( t ) x ( t ) .
If x ( t ) is WGN, the envelope a ( t ) has Rayleigh PDF (2), and phase ϕ ( t ) has a uniform PDF (3).
The informational properties of signals can be assessed by their differential entropy. For a variable x with a probability density function p ( x ) , the differential entropy is given by
h = − ∫ − ∞ ∞ p ( x ) log p ( x ) d x .
The Gaussian distribution (1) attains the maximum differential entropy, which, for μ = 0 and variance σ 2 is equal
h g = 1 2 ln 2 π e σ 2 .
For any other signal with the same variance σ 2 , the differential entropy h ( x ) does not exceed the value given in (10), i.e., h ( x ) ≤ h g ( x ) .
Entropy power, a concept pioneered by Shannon [47], allows us to compare the probability density functions of a signal and Gaussian noise:
k 1 = e 2 h 2 π e , 0 ≤ k 1 ≤ 1 ,
where h – entropy of signal.
The entropy power of a distribution coincides with the variance of a Gaussian distribution possessing an identical entropy.
To compare two arbitrary PDFs we used entropy power ratio, mathematically defined as follows for distributions p 1 ( x ) and p 2 ( x ) bearing entropies h 1 and h 2 , respectively:
k 1 ( h 2 ) k 1 ( h 1 ) = e 2 Δ h ,
where Δ h = h 1 − h 2 – the difference between differential entropies of two distributions.
To restrict the value of ratio (12) into interval 0 ≤ k 1 ≤ 1 the following expression can be applied:
k = e − 2 | Δ h | .
The entropy power (13) increases when the difference between entropies of distributions becomes smaller.
To evaluate the similarity of probability density functions of amplitude and phase with reference distributions, we utilize the entropy power relative to these baseline distributions. Thus, the entropy power of the envelope of the signal is determined as:
k 2 = e − 2 | h e − h R | ,
where h e – entropy of the envelope of signal; h R = 1 + ln σ 2 + γ 2 – entropy of Rayleigh PDF (2) [44]; γ ≈ 0.577 – Euler-Mascheroni constant.
The entropy power for evaluating the similarity of phase distribution of signal and uniform one would be determined as:
k 3 = e − 2 | h p h − h u | ,
where h p h – entropy of phase of signal; h u = ln 2 π – entropy of uniform PDF (3) [44].

3. Properties of Sums of Chaotic Signals

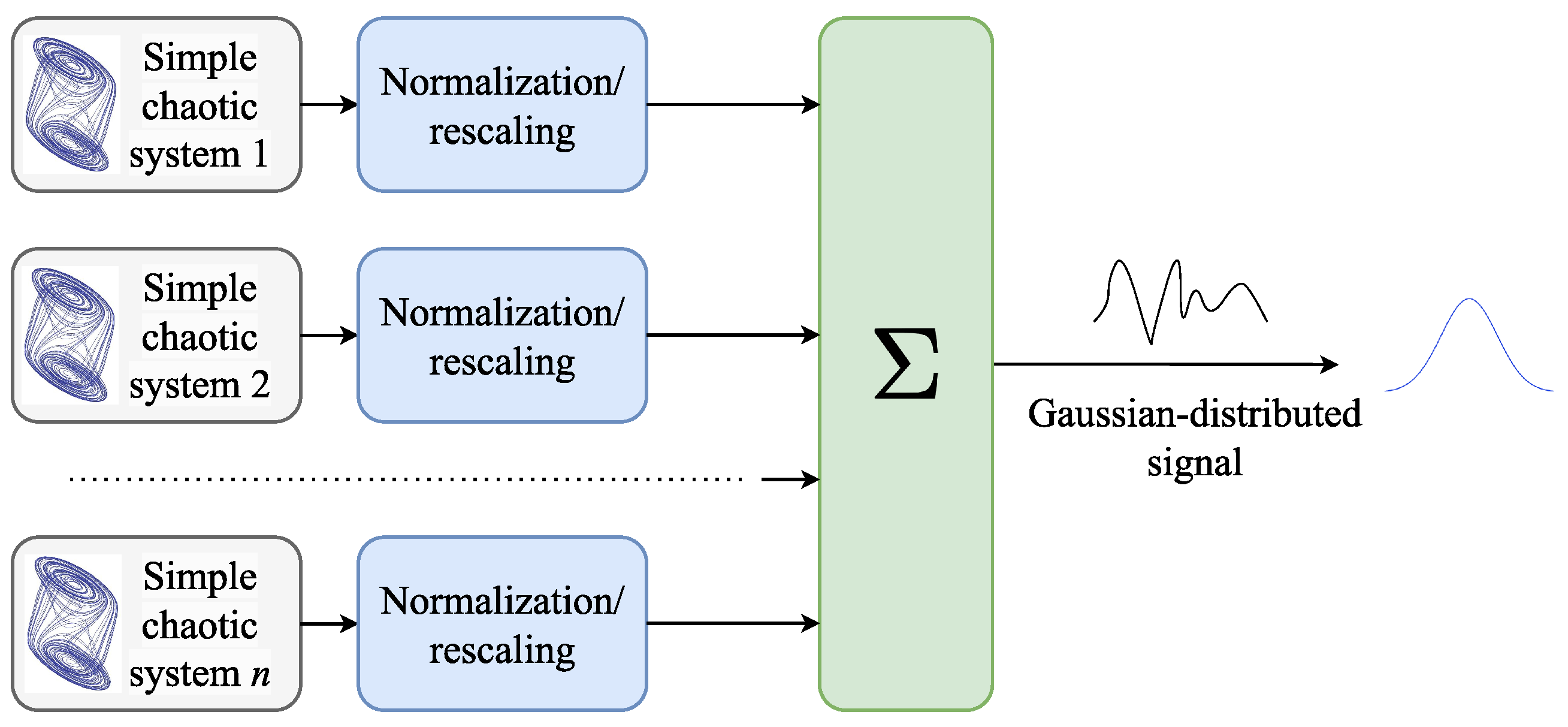
The approach for generating a Gaussian-distributed chaotic signal is schematically illustrated in Figure 1. Selected chaotic outputs undergo normalization, followed by summation, to achieve a transformation from their original probability density function to a Gaussian PDF. The normalization step may be omitted depending on the properties of the original chaotic signals and the desired variance of the resulting sum.
There are lots of different nonlinear systems exhibiting chaotic behavior. We investigated more than 40 mostly three-dimensional chaotic systems through computing PDFs, skewness, excess kurtosis, and entropy power of their output signals. Before estimation of the mentioned in the algorithm characteristic, each chaotic signal was centered around its zero mean and normalized to have unit variance. The results show that the majority of the studied chaotic systems exhibit characteristics that are far from being considered Gaussian-like signals.
The obtained results for the variety of chaotic systems appear in the Appendix, and a detailed description of the algorithm is analytically and experimentally demonstrated below with examples from two widely used and extensively studied systems: Chua and Lorenz. They were specifically chosen since their signals, among all examined, possess the most favorable parameters to serve as a platform for generating deterministic chaotic Gaussian signals.

3.1. Chua’s Circuit

The Chua’s circuit is one of the most well-known systems that generate deterministic chaos and can be easily implemented as an electrical circuit [48]. Moreover, various types of nonlinearities can be utilized in this circuit [49,50].
The mathematical model of Chua’s circuit in dimensionless form is a system of three differential equation
x ˙ = α ( y − x − f ( x ) ) y ˙ = x − y + z z ˙ = − β y
where x, y, z – output variables; α , β – parameters of the model; f ( x ) = m 2 x + 0.5 ( ( m 0 − m 1 ) ( | x + a 1 | − | x − a 1 | ) + ( m 1 − m 2 ) ( | x + a 2 | − | x − a 2 | ) ) – nonlinear function, a 1 = 1 , a 2 = 6.88 , m 0 = − 1.238 , m 1 = − 0.6665 , m 2 = 500 . The connection between the circuit’s and the model’s parameters can be found in [48,51].
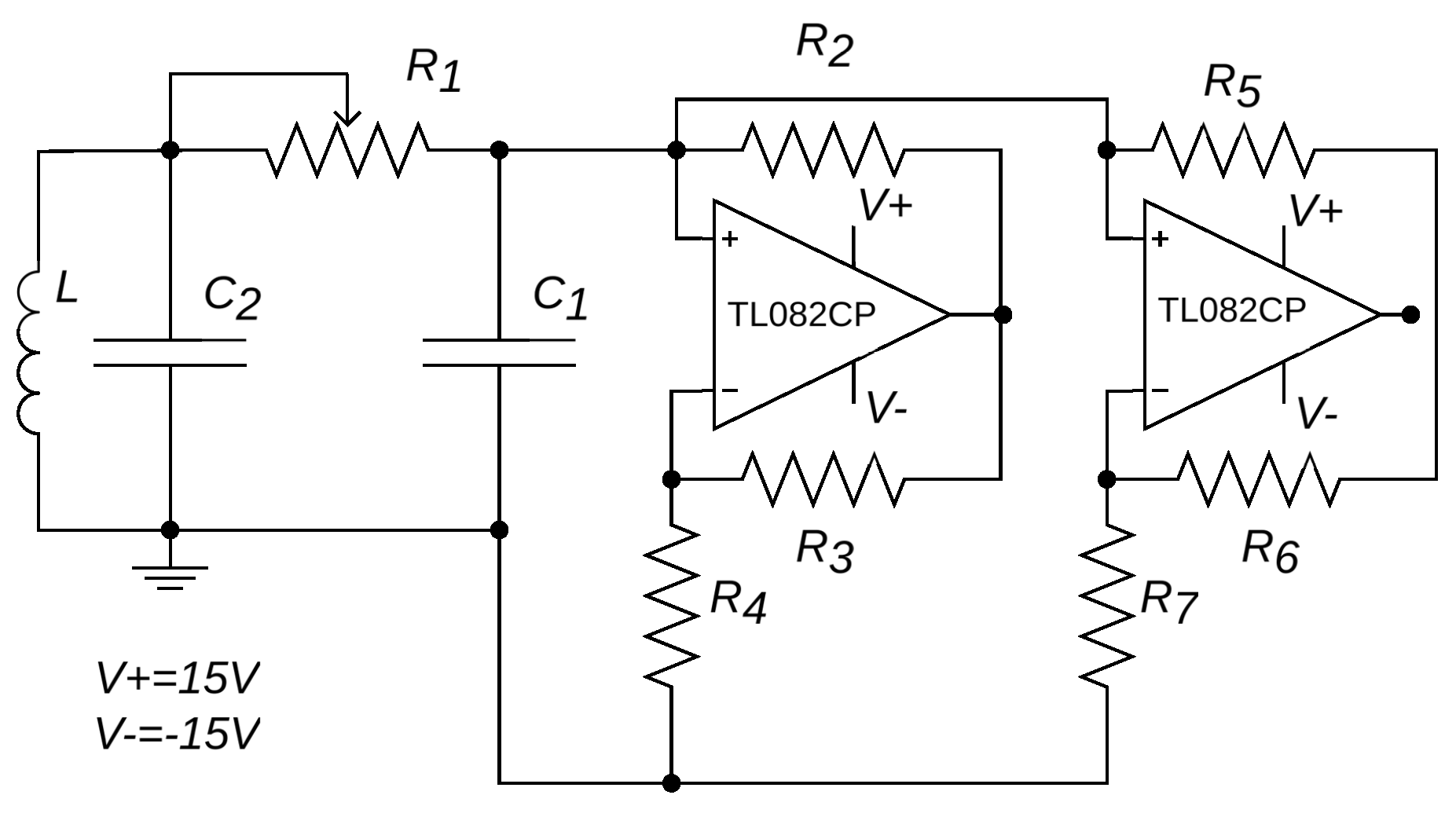
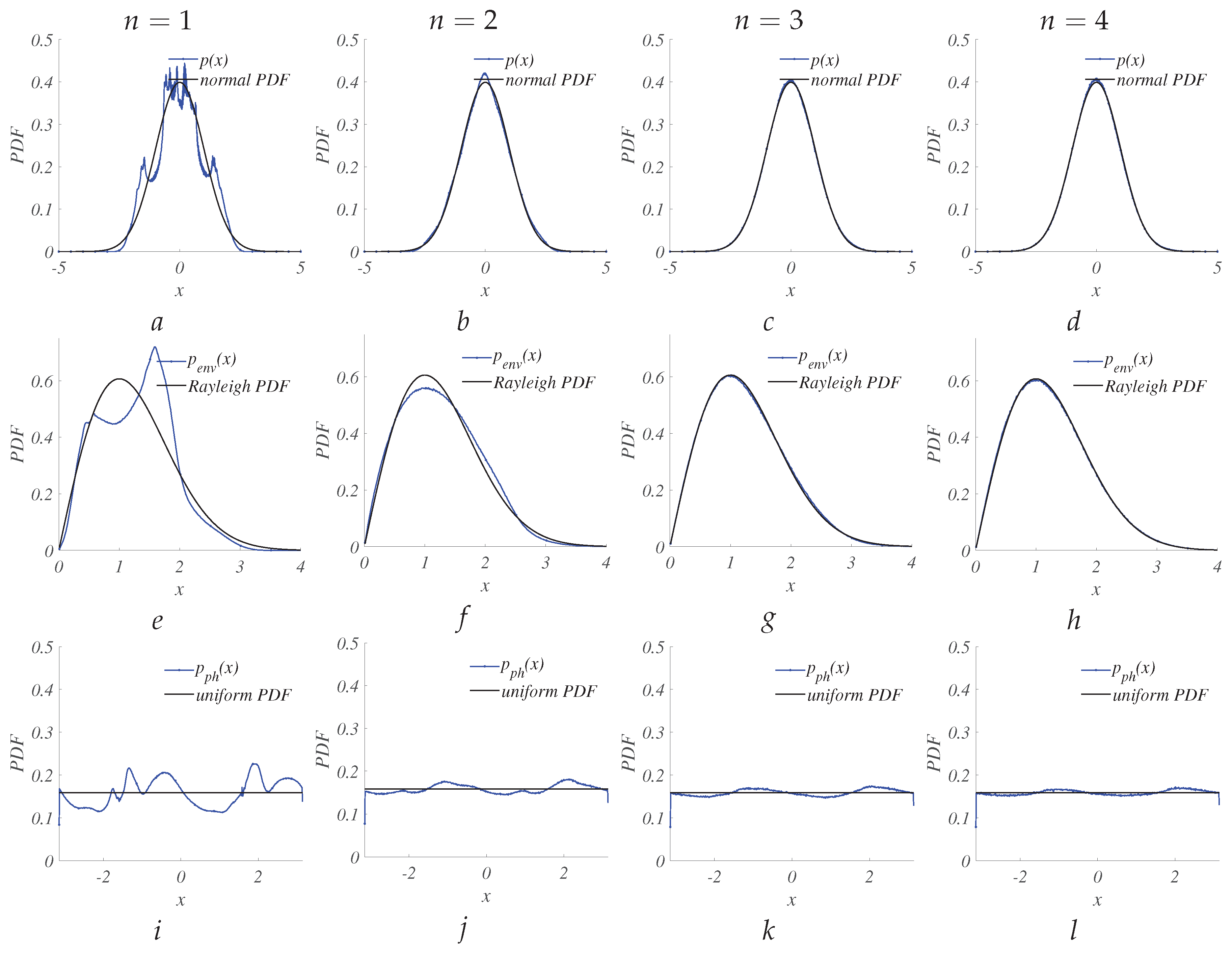
We studied Chua’s circuit with the piecewise linear characteristic of the nonlinear part which provides various dynamical modes including a single or double-scroll chaotic attractor. As shown in Figure 2, the circuit encompasses inductance, two capacitors, and nonlinearity implemented on two operational amplifiers [51].
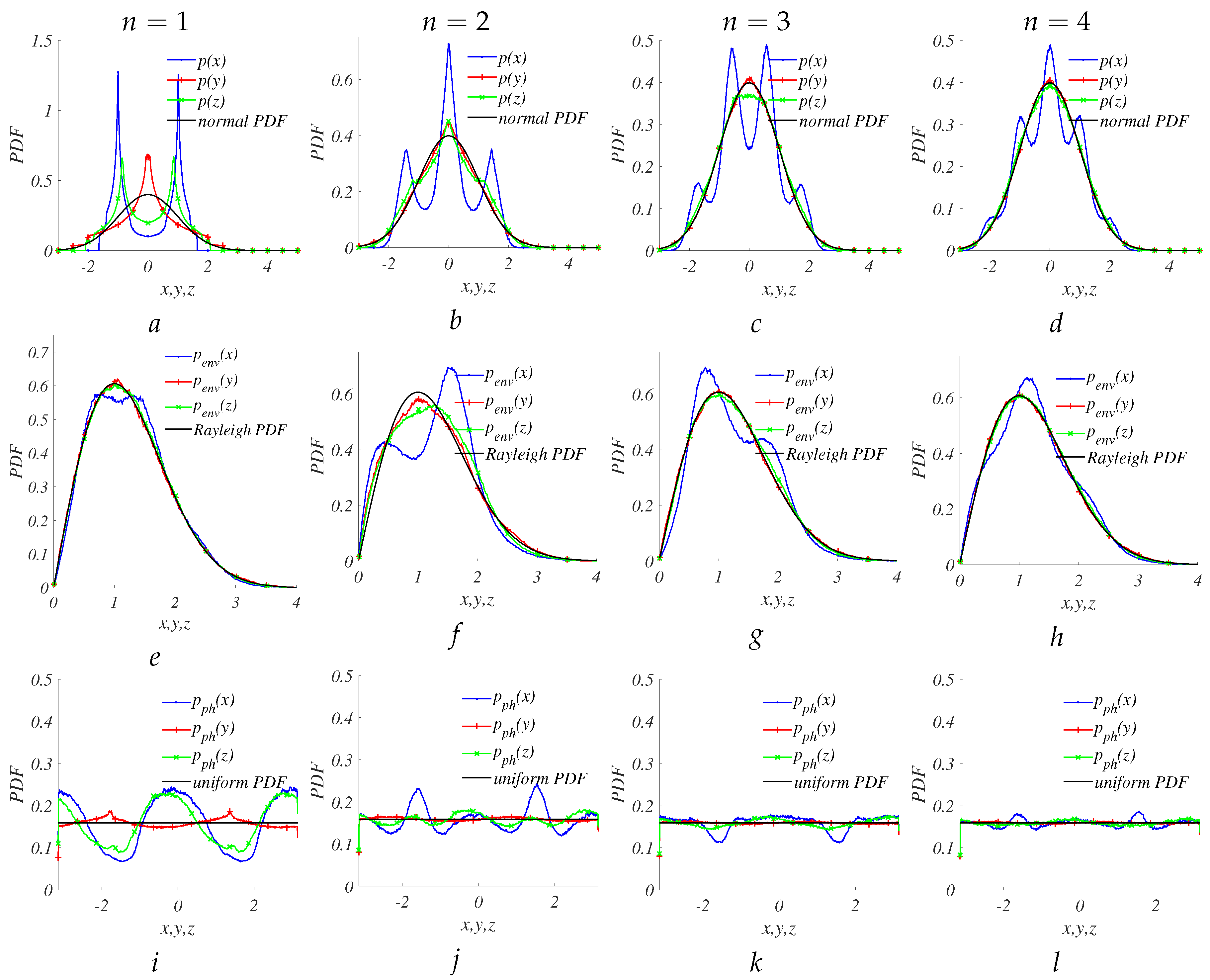
When α = 10 , β = 14.6 , the circuit operates in double-scroll mode and all the outputs possess a symmetric PDF with skewness close to zero. The y output produces low excess kurtosis μ ˜ 4 = 0.1421 , which also has the highest entropy power k 1 = 0.9039 , k 2 = 0.9756 , and k 3 = 0.998 . Nevertheless, there are distinct visual differences between PDFs of chaotic and basic distributions which can be seen on Figure 3a,e,i and numerically from Table 1.
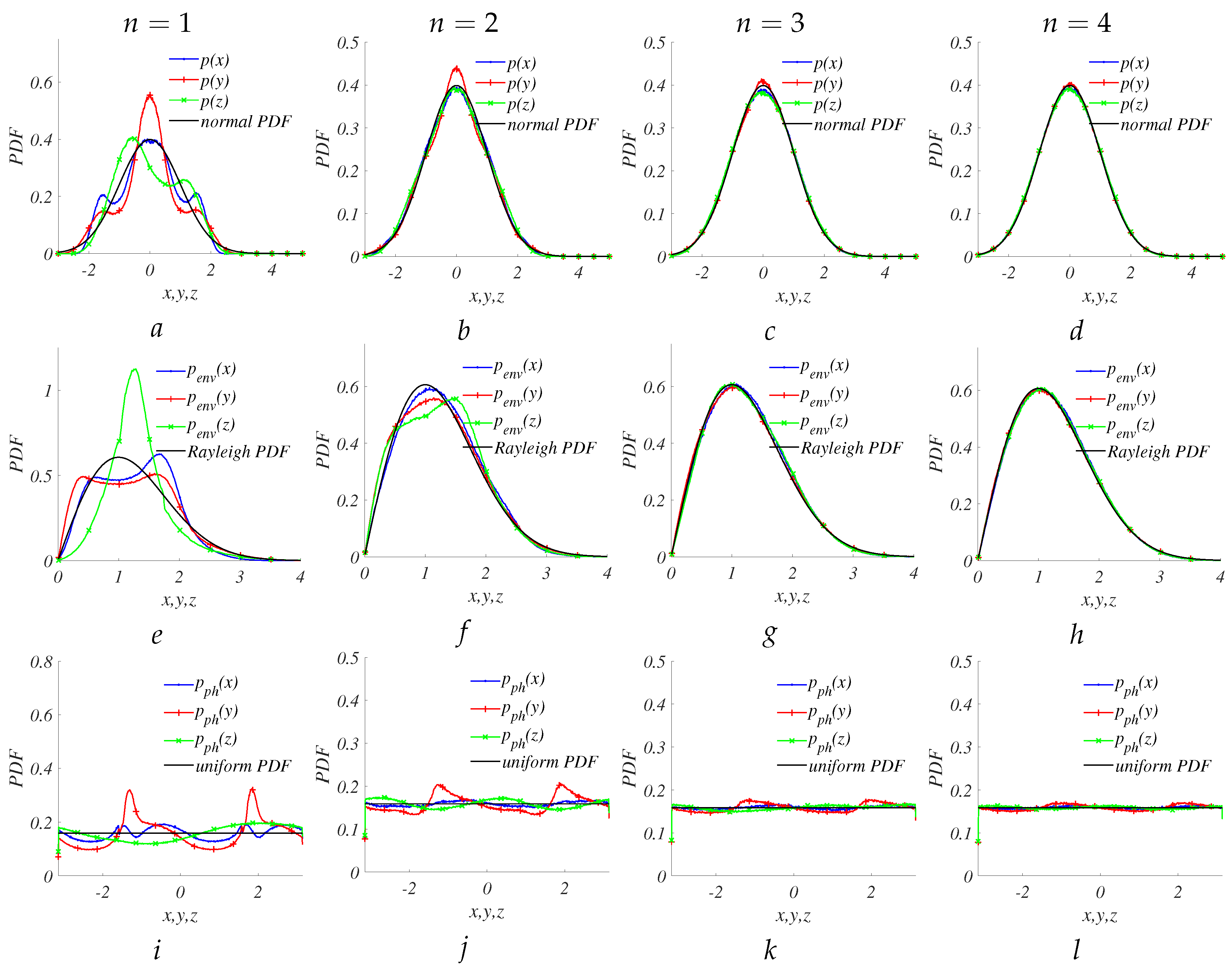
The Central Limit Theorem states that the summation of two or more chaotic signals yields a PDF of the sum that exhibits a greater resemblance to a Gaussian PDF compared to that of a single signal. The evolution of PDFs when the number n of independent chaotic signals in sum increases is shown in Figure 3. To minimize the number of chaotic signal in the sum, it is efficient to use the variable y. When only three independent outputs of y are added, the PDF of the sum, along with its envelope and phase, closely resemble the basic ones, i.e., normal, Rayleigh, and uniform PDFs. The entropy powers of the sum k 1 , k 2 , k 3 exceed 0.99 .
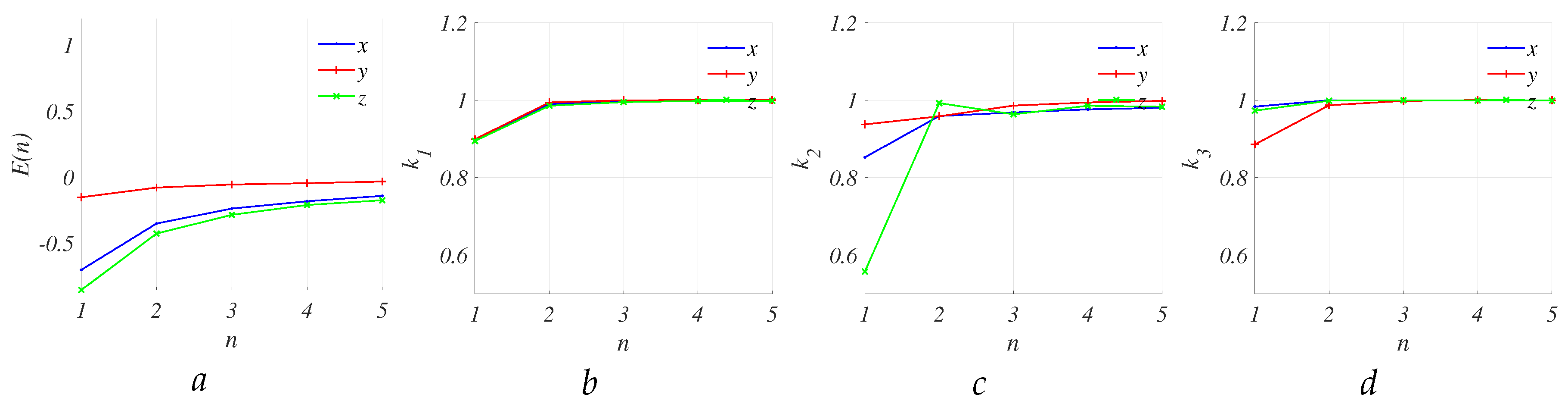
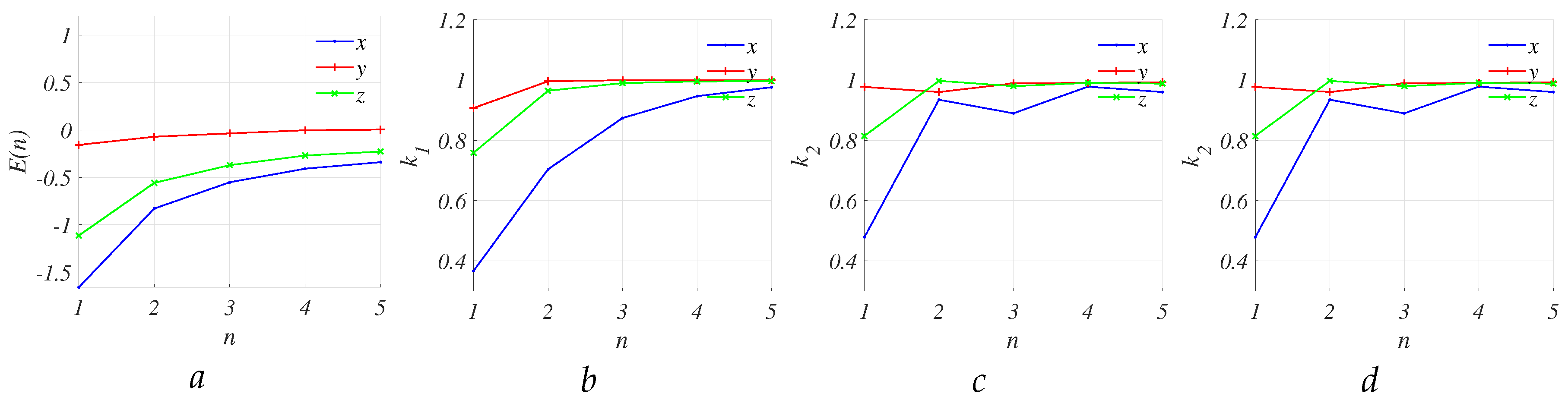
The quality metrics of the sum of signals are contingent upon the number of signals incorporated, as illustrated in Figure 4. The excess kurtosis decreases to zero, and all entropy powers converge to 1 with an increasing value of n. This suggests that achieving chaos resembling Gaussian noise necessitates the addition of a minimum of three original chaotic signals from Chua’s circuit.
A change of circuit parameters with preservation of chaotic double-scroll mode causes significant changes in quality metrics, particularly, excess kurtosis and entropy power. For example, when α = 9.273 , β = 16.8 , a = 1587 Chua’s circuit has following metrics: E = − 0.9334 , k 1 = 0.8739 , k 2 = 0.5006 and k 3 = 0.999 which are quite different from ones mentioned above. This result suggests that the PDFs of signals are sensitive to the parameters of chaotic system.

3.2. Lorenz System

While the previously considered Chua’s circuit is one of the simplest in both as an analytical model and experimental implementation, Lorenz system is the well-known and extensively investigated source of deterministic chaos such as the system was originally developed to model atmospheric convection in meteorology and allows describing of different atmospheric phenomena [52]. Lorenz system is usually applicable in its mathematical representation (a system of three differential equations with nonlinearity (17)) that found widespread use in diverse fields such as physics, engineering, biology, economics, and even art. 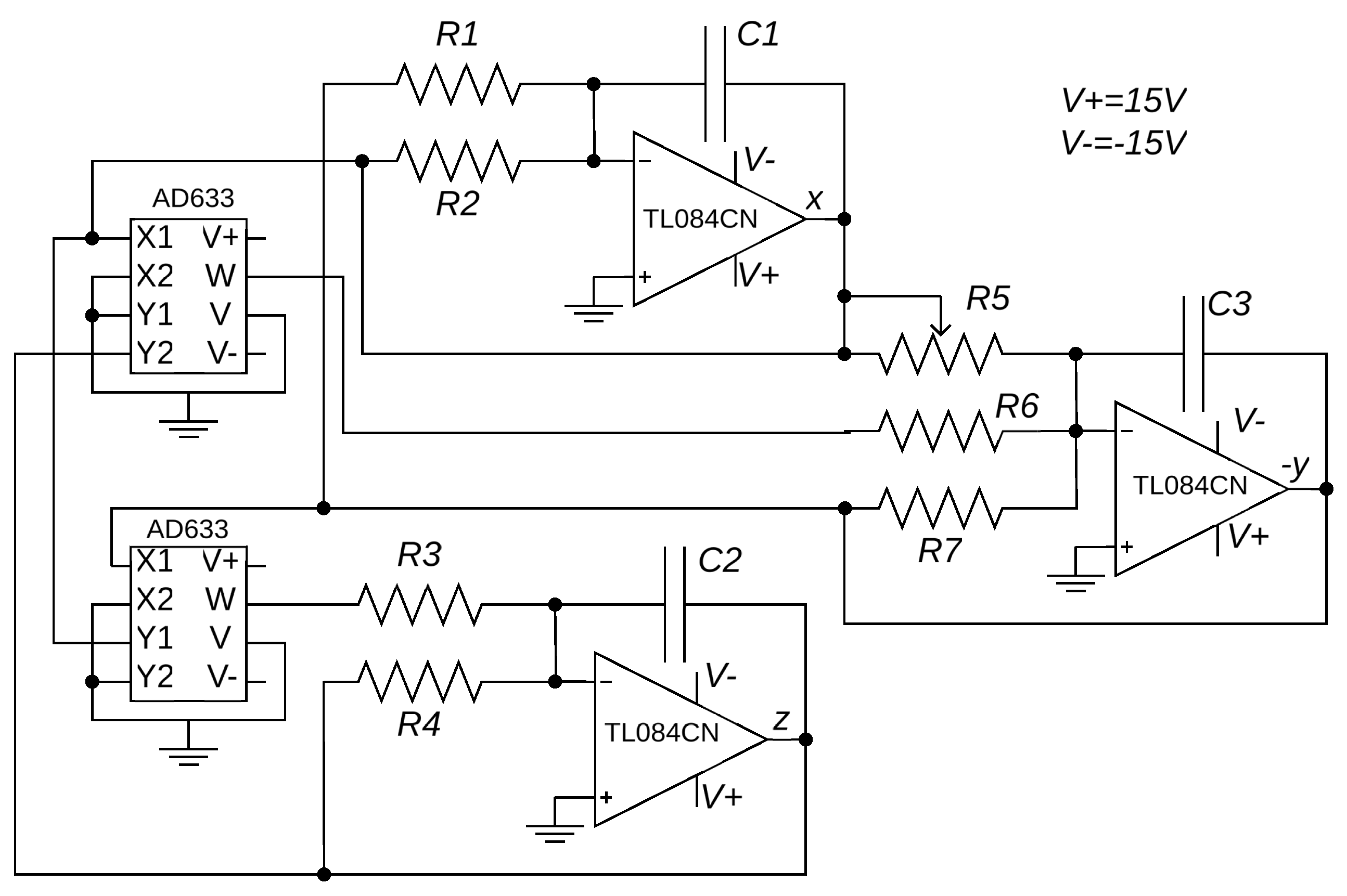However, its hardware implementation is inherently more complex than Chua’s circuit due to involvement of analog multipliers (Figure 5) [53].
x ˙ = σ ( y − x ) y ˙ = ( r − z ) x − y z ˙ = x y − b z
where x, y, z – system variables; σ = 10 , r = 28 , b = 8 3 – parameters.
We simulated the system (17) with two different values of the parameter r: r = 28 and r = 60 keeping other parameters constant. The statistic parameters of Lorenz system is shown in Table 2. Two of the three outputs in the Lorenz system, namely x and y, exhibit symmetric PDFs. Similarly to the Chua’s circuit, the results indicate a significant impact of model parameters on the appearance and characteristics of the PDFs of the output signals. For the investigated parameter values, the signal most resembling Gaussian noise is y with σ = 10 , r = 28 , and b = 8 3 , featuring coefficients μ ˜ 4 = − 0.1573 , k 1 = 0.9013 , k 2 = 0.9368 , and k 3 = 0.8877 .
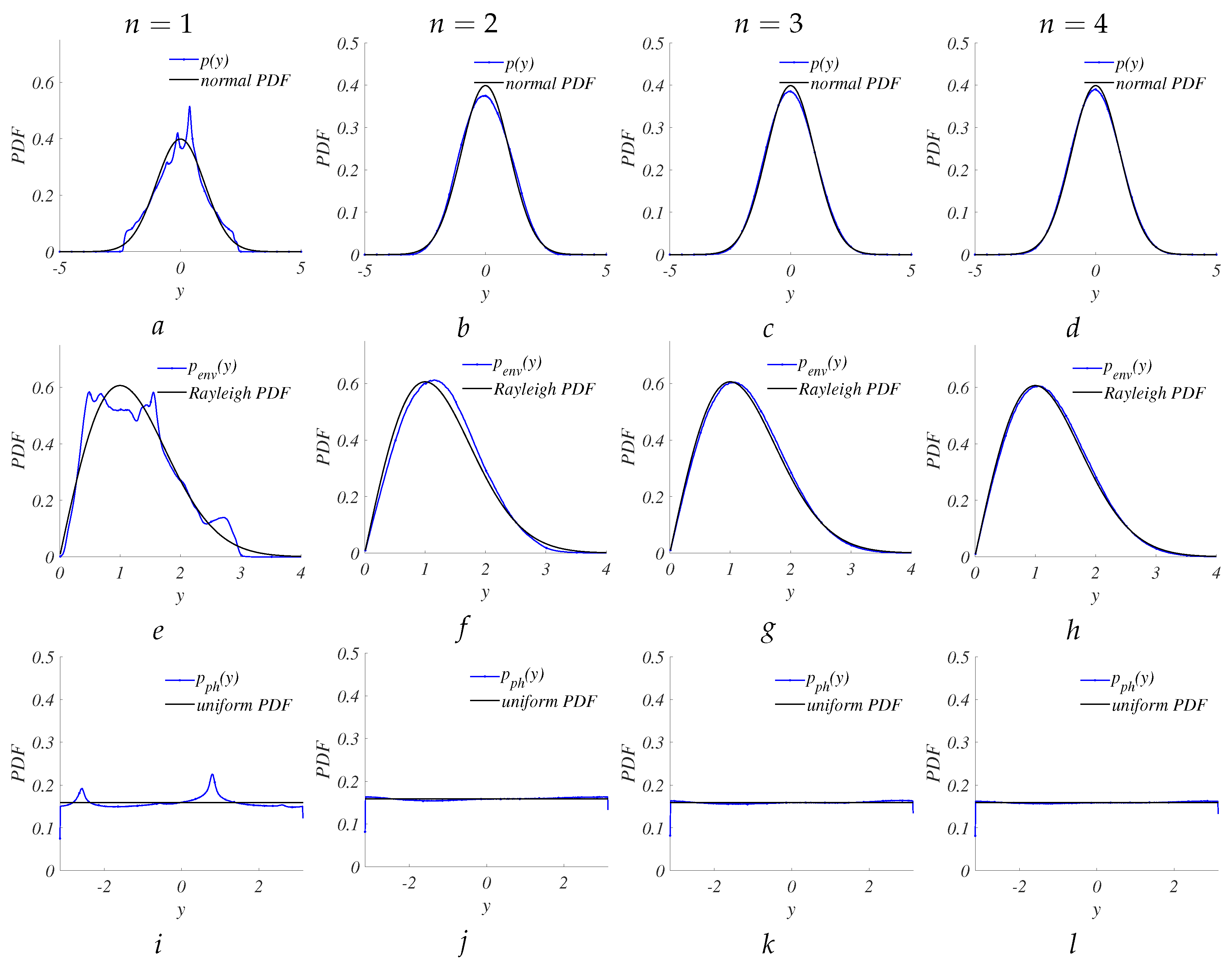
The original histograms of normalized output signals from the Lorenz system are shown in Figure 6. Despite the asymmetry in the output signal z, combining all three outputs can yield a normal PDF when summing only 3-4 signals. The relationship between the excess kurtosis coefficient and entropy powers for different n is presented in Figure 7 and confirms this conclusion.
The entropy power values ( k 1 , k 2 , k 3 ) for the sum of three and four y variables exceeded 0.98 and 0.99, respectively. Furthermore, a comparison of PDFs in Figure when n = 4 suggests no significant discrepancies between the PDFs of the sum and the basic PDFs.
Analyses of Chua’s circuit and Lorenz system reveal that the summation of chaotic non-Gaussian signals proves to be an effective method for obtaining deterministic chaotic Gaussian signals.

4. Experimental Verification

4.1. Experiment with Chua’s Circuit

The following results were obtained for the Chua circuit with a piecewise-linear nonlinear element implemented using operational amplifiers TL082CP, as depicted in Figure 2. Four circuits were assembled with slightly different parameters. The parameter difference was provided be the used components feature – the used capacitors C 1 = 100 μ F and C 2 = 10 μ F , as well as inductor L = 18 m H have tolerance ± 5 % . The parameters of nonlinear element were as R 2 , R 3 = 220 O h m , R 4 = 2.2 k O h m , R 5 , R 6 = 22 k O h m , R 7 = 3.3 k O h m .
Additionally, a potentiometer was utilized as the resistance R 1 = 1580 O h m whose value could be adjusted with increment ± 100 O h m to change the chaotic circuit behavior. The voltages across the capacitors C 2 , corresponding to the variable y in the model of circuit, were recorded and processed for further analysis. The set of signal records (50 samples of voltages across the capacitors C 2 ) was performed where each record contained 2 ∗ 10 6 sweep points.
The experimental results have confirmed the theoretical assumptions and analytical outcomes. As depicted in Figure 8, increasing the number of chaotic systems, rapidly drives the distribution of their summed signals towards a normal distribution. This observation extends to the envelope and phase of the signal, where Rayleigh and uniform distributions were observed, respectively.

4.2. Experiment with Lorenz System

The experimental investigation was performed using a simplified electronic realization of the Lorenz oscillator, constructed in accordance with the specifications outlined in [53,54] and circuit in Figure 5. We used analog multiplier AD633 and operational amplifier TL084CN. The others circuit elements were following: R 1 , R 2 = 100 k O h m , R 3 , R 6 = 10 k O h m , R 7 = 1 M O h m with tolerance 5% and R 4 = 370 O h m with tolerance 0.5%. The variable resistor R 5 allows tuning of the parameter r and was set R 5 = 35.72 k O h m .
Four circuits were assembled on a breadboard, and the appropriate oscillograms were recorded. Subsequently, they were subjected to the suggested set of tests. The probability density functions of the normalized output x from the electronic circuit of Lorenz system are illustrated in Figure 9. A comparison between Figure 6 and Figure 9 reveals a good agreement between analytic and experimental results.

5. Discussion and Conclusions

The results underscore a promising approach for generating deterministic Gaussian-like signals using an optimal number of chaotic systems. The PDFs of the original chaotic signals exhibit essential deviations from a normal distribution, indicating their inherently lower information capacity compared to fully random Gaussian noise. This observation prompts the need to establish criteria for selecting chaotic systems to achieve Gaussian signal formation through summation chaotic signals. It requires an optimization process to minimize the number of independent simple chaotic signals. The performed analysis demonstrates that adherence to the following guidelines significantly enhances the likelihood of successful chaotic system and signal selection:
  • Prioritize signals possessing symmetric probability density functions.
  • Minimize the excess kurtosis of the selected signals, ideally aiming for μ ˜ 4 < 1 .
  • Ensure that all three entropy powers ( k 1 , k 2 , k 3 ) of the original chaotic signal surpass the value 0.85 .
While strict adherence to these guidelines does not ensure Gaussian signal achievement, however, it substantially increases the probability of generating a Gaussian chaotic signal with desired entropy coefficients k 1 , k 2 , k 3 > 0.95 by summing merely three or four independent chaotic signals.
It is crucial to underscore that chaotic signals are generated by deterministic systems, rendering their summation equally deterministic. This underscores the capability of simple summation to yield intricate, noise-mimicking chaotic signals that retain their deterministic nature. The most innovative aspect of this method emphasizes the possibility of attributing the output voltage and current of random chaotic circuits to a well known signal as the Gaussian noise, whose properties are well-known and exploitable in many applications. The possibility of obtaining a Gaussian like signal description allows the opportunity to design and model chaotic circuits’ output voltage, preserving all the general properties of the Gaussian distribution. Moreover, since many chaotic circuits do not show output’s signals linked to Gaussian noise, this method allows widening the field of investigation even to those circuits that apparently do not have these properties. It is also considerable that more than 40 chaotic systems have been evaluated that have led to the confirmation of this theory, confirming the validity of this method.
Output signals, obtained with this process, hold considerable value across a variety of applications, including generating deterministic Gaussian noise, electronic warfare systems, coherent and/or covert communication systems, radars, statistical modeling, machine learning, cryptography and more.
The possibility of obtaining a pseudo-random number generator through the simple sum of chaotic signals, predisposes this method to a wide usability, bypassing any possible complication of chaotic signal processing. All the possible applications mentioned have the support of both hardware and software implementation of chaotic circuits, with the addition in this case, of greater properties and guidelines that can be exploited during the implementation guaranteed by the traceability to Gaussian noise. Since the main aim is to give more known laws to circuits that in certain conditions are dominated by chaos, other aspects and elaborations of the output signals of the proposed chaotic circuits are also being investigated, which could lead back to the properties of a Gaussian pseudo noise. Future investigations will be aimed at trying to reconstruct more and more well-known properties of apparently chaotic signals, trying to make it easier to implement the chosen application.

Author Contributions

Conceptualization, S.H.; methodology, S.H., and D.A.; software, S.H., E.S., and J.S.; validation, V.B. and F.C.; formal analysis, all authors; investigation, S.H., D.V., E.S., and J.S.; resources, V.B. and F.C.; data curation, S.H. and D.V.; writing—original draft preparation, all authors; visualization, all authors; supervision, V.B. and F.C.; project administration, V.B. and F.C. All authors have read and agreed to the published version of the manuscript.

Conflicts of Interest

The authors declare no conflict of interest.

Appendix A

Table 1,Table 2, and Table A1 present the results of passing the suggested algorithm tests, including skewness μ ˜ 3 , excess kurtosis μ ˜ 4 , and entropy power for the signal k 1 , its envelope k 2 , and phase k 3 . The initial conditions for the majority of chaotic systems were randomly selected from the interval (0, 1). In cases where the chaotic mode demonstrates dependence on the initial condition, the specific values are indicated in Table A1. Signals suitable for summation are highlighted in green, while those that successfully passed the suggested algorithm’s tests are highlighted in blue.
Table A1. Statistical properties of signals of chaotic systems.
Table A1. Statistical properties of signals of chaotic systems.
Bhalekar and Gejji [55]
x ˙ = − 2.677 x − y 2 x -0.4940 -0.3912 0.8739 0.5924 0.9420
y ˙ = 10 ( z − y ) y -0.0029 -0.2152 0.9362 0.7205 0.7675
z ˙ = − 27.3 y − z + x y z -0.0029 -0.0071 0.9586 0.9157 0.6919
Chen and Lee [56]
x ˙ = − y z + 5 x x -0.0009 -1.3013 0.7086 0.2180 0.9371
y ˙ = x z − 10 y y 0.0027 -0.7711 0.9037 0.3269 0.8813
z ˙ = 1 3 x y − 3.8 z z 0.4027 -0.6617 0.7847 0.5387 0.9838
Cheng et al. [57]
x ˙ = y x 0.0042 -0.7241 0.8544 0.7317 0.9969
y ˙ = − 0.2 y − ( 0.25 x sin x ) ( 10 cos 2 t + 0.1 ) y 0.0002 -0.6388 0.9540 0.7494 0.9792
Colpitts chaotic oscillator [58,59]
x ˙ = 1 C 1 ( z − β f ( x ) ) x -1.3378 1.5271 0.5924 0.7753 0.7510
y ˙ = 1 C 2 ( 1 R e ( v e − y ) − z − f ( x ) ) y -0.9897 0.0021 0.4836 0.6179 0.9102
z ˙ = 1 L ( v c e − x − r L z + y ) z 1.0142 0.3489 0.6171 0.9408 0.8144
where C 1 = 15 * 10 − 9 ; C 2 = 9.7 * 10 − 9 ; L = 30 * 10 − 6 ; v e = 2 ; R e = 400 ;
β = 300 ; v c e = 7 ; r L = 40 ; f ( x ) = 0 , x ≤ 0.75 , x − 0.75 200 , x > 0.75 . .
Dong et al., [60], [ x 0 , y 0 , z 0 ] = [ 0.78 , 0.52 , 0.30 ]
x ˙ = a 1 x − a 2 x 2 − a 3 ( y + z ) x 1.3143 15.2455 0.1413 0.2982 0.7632
y ˙ = − b 1 y − b 2 z + b 3 x y -1.5546 1.4611 0.1139 0.6076 0.7315
z ˙ = c 1 ( z − c 2 ) ( x − c 3 ) z 1.6361 1.9200 0.0925 0.6168 0.7312
where a 1 = 0.09 , a 2 = 0.05 , a 3 = 0.15 , b − 1 = 0.06 , b 2 = 0.085 , b 3 = 0.07 ,
b 4 = 0.07 , c 1 = 0.1 , c 2 = 0.041 , 0.042
Flux controlled memristor [61]
x ˙ = 1 C 1 [ y − x R − r x ] x -0.0145 3.7663 0.6712 0.8624 0.9455
y ˙ = 1 C 2 [ x − y R − z ] y -0.0000 0.3748 0.8951 0.8874 0.9883
z ˙ = y L z 0.0017 0.2822 0.8733 0.8835 0.9959
w ˙ = − x ζ w -0.0916 -1.8739 0.1006 0.3087 0.6974
where ζ = 8200 * 47 e − 9 ; R = 2000 ; C 1 = 6.8 e − 9 ; C 2 = 68 e − 9 ; L = 18 e − 3 ;
α = − 0.667 e − 3 ; β = 0.029 e − 3 ; r = − α + 3 β y 2 .
Genesio and Tesi [62,63]
x ˙ = y x 0.1377 -1.1867 0.6227 0.2463 0.9980
y ˙ = z y 0.3478 -1.2245 0.5156 0.1004 0.9931
z ˙ = − a x − b y − c z + x 2 z 0.1864 -1.1514 0.6580 0.2095 0.9697
where a = 6 ; b = 2.92 ; c = 1.2 .
Li et al. [64]
x ˙ = − 16 x + 20 y z x -0.0051 -0.2485 0.7872 0.8415 0.8433
y ˙ = 10 y − 6 x z y -0.0003 -0.6939 0.8603 0.7182 0.9157
z ˙ = − 5 z + 18 y 2 z -0.0980 -0.9221 0.8613 0.7934 0.9360
Li and Sprott [65]
x ˙ = y z x 0.0023 -0.2196 0.8567 0.9277 0.8624
y ˙ = 1 − z 2 y -0.2622 0.1621 0.9575 0.9152 0.9130
z ˙ = x + y z z 0.0094 0.3070 0.9607 0.5493 0.8597
Liu and Chen [66]
x ˙ = 1.5 x − y z x 0.0132 0.9226 0.9241 0.9580 0.7826
y ˙ = − 10 y + x z y -0.0007 11.7760 0.3050 0.9763 0.5337
z ˙ = − 4 z + x y z -0.0449 5.0172 0.5013 0.8873 0.7990
Lü and Chen [67]
x ˙ = 36 ( y − x ) x -0.0002 -0.4949 0.9266 0.8457 0.8685
y ˙ = − x z + 20 y y -0.0006 -0.3236 0.9422 0.9108 0.8483
z ˙ = x y − 3 z z 0.2535 -0.3539 0.9408 0.7114 0.9495
Lü et al. [68,69]
x ˙ = 0.4 x − y z x 0.0113 0.2948 0.9342 0.8041 0.5401
y ˙ = − 12 y + x z y -0.1063 41.3350 0.0006 0.1884 0.0019
z ˙ = − 5 z + x y z -0.0601 23.7057 0.0011 0.6488 0.0110
Memristive circuit [12,70]
x ˙ = y x -0.8235 0.0391 0.7455 0.6689 0.9496
y ˙ = − 1 3 [ x + 1.52 ( z 2 − 1 ) y ] y 0.4986 0.5598 0.8316 0.9146 0.8807
z ˙ = − y − 0.6 z + y z z -0.8277 -0.2585 0.6046 0.4188 0.9038
Özoǧuz et al. [71]
x ˙ = y x 0.0039 -0.8260 0.8818 0.8230 0.9784
y ˙ = z y -0.0032 -0.6363 0.9356 0.7480 0.9489
z ˙ = − 0.25 ( y + z ) − a f ( x ) z -0.0048 -1.0010 0.8591 0.6947 0.9769
where f ( x ) = ∑ j = − 3 5 ( − 1 ) j − 1 tanh k ( x − 2 j ) .
Qi et al. [72]
x ˙ = 14 ( y − x ) + 4 y z x -0.0313 0.6421 0.9562 0.8812 0.9000
y ˙ = − x + 16 y − x z y 0.0158 0.9269 0.9554 0.9238 0.9044
z ˙ = − 43 z + x y z 0.0375 4.1904 0.7527 0.8528 0.9239
Ring oscillating systems [73]
x ˙ = α ( M f ( z ) − x ) x -0.0003 -0.7734 0.8992 0.7333 0.9900
y ˙ = 4 π 2 ( x − z ) y 0.0012 -0.5155 0.9619 0.9643 0.9762
z ˙ = y − β z z 0.0014 -1.1498 0.7992 0.7124 0.9259
where α = 2.1 ; β = 1.38 ; M = 5 ; f ( z ) = | z + 1 | − | z − 1 | + 0.5 ( | z − 4 | − | z + 4 | ) .
Rössler [74]
x ˙ = − y − z x 0.2261 -0.7120 0.8709 0.5620 0.9958
y ˙ = x + 0.2 y y -0.1768 -0.8174 0.8565 0.5895 0.9958
z ˙ = 0.2 + z ( x − 6.5 ) z 5.3359 31.4457 0.0007 0.1869 0.4920
Sprott [75], system A
x ˙ = y x 0.4457 0.1407 0.7233 0.8802 0.9472
y ˙ = − x + y z y 0.0004 0.6015 0.9336 0.8052 0.8718
z ˙ = 1 − y 2 z -0.0003 -0.7692 0.9357 0.5446 0.9792
Sprott [75], system B
x ˙ = y z x -0.0854 0.6461 0.9488 0.9882 0.8560
y ˙ = x − y y -0.0859 -0.4976 0.9265 0.7967 0.9309
z ˙ = 1 − x y z 0.0550 1.0485 0.9573 0.9551 0.9124
Sprott [75], system C
x ˙ = y z x -0.0285 -0.1891 0.9670 0.9618 0.9479
y ˙ = x − y y -0.0333 -0.9804 0.8582 0.8341 0.9715
z ˙ = 1 − x 2 z -0.6070 3.6133 0.8816 0.6143 0.9590
Sprott [75], system D, [ x 0 , y 0 , z 0 ] = [ 0.05 , 0.05 , 0.05 ]
x ˙ = − y x -1.4687 1.7451 0.5122 0.9302 0.8719
y ˙ = x + z y -0.2164 0.4422 0.8908 0.9015 0.9176
z ˙ = x z + 3 y 2 z 1.4479 1.8039 0.5215 0.8628 0.9014
Sprott [75], system E
x ˙ = y z x 0.4423 0.7410 0.8625 0.6111 0.8678
y ˙ = x 2 − y y 7.8746 203.4464 0.2325 0.4360 0.8765
z ˙ = 1 − 4 x z -0.2077 -1.1366 0.7000 0.3984 0.9822
Sprott [75], system F, [ x 0 , y 0 , z 0 ] = [ 0.3196 , 0.4268 , 0.5159 ]
x ˙ = y + z x -0.2414 -0.3601 0.9374 0.8712 0.9195
y ˙ = − x + 0.5 y y -0.7451 -0.4105 0.6865 0.8476 0.9080
z ˙ = x 2 − z z 1.5488 1.9861 0.3528 0.7115 0.8282
Sprott [75], system G, [ x 0 , y 0 , z 0 ] = [ 1.0755 , 0.0291 , 0.0274 ]
x ˙ = 0.4 x + z x -0.4155 -0.4738 0.7584 0.6293 0.8725
y ˙ = x z − y y -1.3171 1.9318 0.5137 0.7544 0.8240
z ˙ = − x + y z -0.2177 -0.4342 0.8068 0.8614 0.9355
Sprott [75], system H, [ x 0 , y 0 , z 0 ] = [ 0.9767 , − 0.6578 , 0.1281 ]
x ˙ = − y + z 2 x -0.9067 1.0592 0.8259 0.8943 0.9268
y ˙ = x + 0.5 y y 0.8846 0.1870 0.7236 0.8897 0.9088
z ˙ = x − z z -0.2380 -0.3583 0.9374 0.8753 0.9163
Sprott [75], system I, [ x 0 , y 0 , z 0 ] = [ 0.05 , 0.05 , 0.05 ]
x ˙ = − 0.2 y x -0.6289 -0.6397 0.5727 0.5888 0.9878
y ˙ = x + z y -0.4225 -0.8321 0.7032 0.3328 0.9710
z ˙ = x + y 2 − z z -0.1394 0.1985 0.7051 0.8696 0.8300
Sprott [75], system J
x ˙ = − 2 z x 0.6591 -0.5538 0.6268 0.6359 0.9792
y ˙ = − 2 y + z y -0.4453 -0.7307 0.7934 0.5190 0.9716
z ˙ = − x + y + y 2 z -0.7874 -0.2111 0.7026 0.5675 0.9482
Sprott [75], system K
x ˙ = x y − z x -0.6564 -0.1459 0.8233 0.5426 0.9263
y ˙ = x − y y -0.1882 -0.8507 0.8653 0.5430 0.9624
z ˙ = x + 0.3 z z 0.9667 0.1361 0.5752 0.6775 0.9612
Sprott [75], system L, [ x 0 , y 0 , z 0 ] = [ − 7.3474 , 30.4894 , − 5.4293 ]
x ˙ = y + 3.9 z x -0.4581 -1.0074 0.6298 0.2881 0.9741
y ˙ = 0.9 x 2 − y y 0.6651 -0.4800 0.6865 0.7803 0.9235
z ˙ = 1 − x z -0.4601 -0.4952 0.6950 0.6331 0.9728
Sprott [75], system M, [ x 0 , y 0 , z 0 ] = [ − 1.6768 , − 0.8718 , 1.4698 ]
x ˙ = − z x 0.1887 -1.0776 0.6689 0.4527 0.9901
y ˙ = − x 2 − y y -1.0221 0.2497 0.5754 0.7964 0.8224
z ˙ = 1.7 + 1.7 x + y z -0.6044 -0.7847 0.6011 0.2816 0.9553
Sprott [75], system N
x ˙ = − 2 y x -0.6613 -0.5537 0.6247 0.6483 0.9790
y ˙ = x z 2 y -0.7877 -0.2074 0.7006 0.5577 0.9483
z ˙ = 1 + y − 2 z z -0.4452 -0.7278 0.7912 0.5151 0.9716
Sprott [75], system O, [ x 0 , y 0 , z 0 ] = [ − 0.4120 , − 0.5758 , − 0.7232 ]
x ˙ = y x -0.1672 -0.9803 0.7362 0.4725 0.9929
y ˙ = x − z y -0.3632 -1.1061 0.5690 0.2467 0.9963
z ˙ = x + x z + 2.7 y z -0.0199 -1.1439 0.7198 0.2928 0.9920
Sprott [75], system P, [ x 0 , y 0 , z 0 ] = [ − 0.0115 , 0.5545 , − 0.2078 ]
x ˙ = 2.7 y + z x 0.9197 0.1877 0.7137 0.9358 0.9261
y ˙ = − x + y 2 y -0.2534 -0.5963 0.8894 0.8862 0.9202
z ˙ = x + y z 0.7941 -0.1643 0.7097 0.8449 0.8992
Sprott [75], system Q
x ˙ = − z x -0.4461 -0.1058 0.8224 0.8859 0.9232
y ˙ = x − y y -0.3738 -0.6333 0.7944 0.7859 0.9237
z ˙ = 3.1 x + y 2 + 0.5 z z 0.6820 0.1400 0.7650 0.8623 0.9857
Sprott [75], system R
x ˙ = 0.9 − y x -0.4423 -0.4140 0.8797 0.6456 0.9681
y ˙ = 0.4 + z y 0.8124 0.9527 0.8116 0.5035 0.8950
z ˙ = x y − z z -1.9040 6.0313 0.4899 0.7703 0.6918
Sprott [75], system S
x ˙ = − x − 4 y x -0.5469 -0.5727 0.7623 0.6349 0.9775
y ˙ = x + z 2 y 0.5628 -0.4412 0.7384 0.8145 0.9541
z ˙ = 1 + x z -0.4298 -0.7253 0.7986 0.7416 0.9527
Wu and Wang [76], [ x 0 , y 0 , z 0 ] = [ 0 , 0 , 0 ]
0.2 x + y x -0.3147 -1.0386 0.7434 0.3887 0.9940
− 1 3 ( x − z 2 y ) y 0.4113 -0.7459 0.8099 0.4452 0.9695
− 0.4 y − 0.4 z + y z z -1.0675 0.0421 0.3894 0.6262 0.9119
Zhang et al. [77]
x ˙ = y x -0.0022 -0.4024 0.8803 0.7467 0.9745
y ˙ = − x − ( − 1 + z + 2 z 2 ) y y 0.0166 -0.1566 0.9239 0.6519 0.9363
z ˙ = − 2 z + ( 0.5 + z + 2 z 2 ) y 2 z 1.8648 2.9939 0.2449 0.7947 0.8099

References

  1. Moon, F.C. Chaotic and fractal dynamics: Introduction for applied scientists and engineers; John Wiley & Sons, 2008. [Google Scholar]
  2. Kiel, L.D.; Elliott, E.W. Chaos theory in the social sciences: Foundations and applications. University of Michigan Press, 1997. [Google Scholar]
  3. Turner, J.R.; Baker, R.M. Complexity Theory: An Overview with Potential Applications for the Social Sciences. Systems 2019, 7. [Google Scholar] [CrossRef]
  4. Scharf, Y. A chaotic outlook on biological systems. Chaos, Solitons & Fractals 2017, 95, 42–47. [Google Scholar] [CrossRef]
  5. Fernández-Díaz, A. Overview and Perspectives of Chaos Theory and Its Applications in Economics. Mathematics 2023, 12, 92. [Google Scholar] [CrossRef]
  6. Biswas, H.R.; Hasan, M.M.; Bala, S.K. Chaos theory and its applications in our real life. Barishal University Journal Part 2018, 1, 123–140. [Google Scholar]
  7. Vasyuta, K.; Zots, F.; Zakharchenko, I. Building the air defense covert information and measuring system based on orthogonal chaotic signals. Innovative Technologies and Scientific Solutions for Industries 2019, pp. 33–43. [CrossRef]
  8. Macovei, C.; Răducanu, M.; Datcu, O. Image encryption algorithm using wavelet packets and multiple chaotic maps. 2020 International Symposium on Electronics and Telecommunications (ISETC), 2020, pp. 1–4. [CrossRef]
  9. Kushnir, M.; Vovchuk, D.; Haliuk, S.; Ivaniuk, P.; Politanskyi, R. Approaches to Building a Chaotic Communication System. In Data-Centric Business and Applications: ICT Systems-Theory, Radio-Electronics, Information Technologies and Cybersecurity; Springer International Publishing: Cham, 2021; Volume 5, pp. 207–227. [Google Scholar] [CrossRef]
  10. Kocarev, L.; Lian, S. Chaos-based cryptography: Theory, algorithms and applications; Vol. 354, Springer Science & Business Media, 2011. [CrossRef]
  11. Cang, S.; Kang, Z.; Wang, Z. Pseudo-random number generator based on a generalized conservative Sprott-A system. Nonlinear Dynamics 2021, 104, 827–844. [Google Scholar] [CrossRef]
  12. Haliuk, S.; Krulikovskyi, O.; Vovchuk, D.; Corinto, F. Memristive Structure-Based Chaotic System for PRNG. Symmetry 2022, 14. [Google Scholar] [CrossRef]
  13. Kushnir, M.; Haliuk, S.; Rusyn, V.; Kosovan, H.; Vovchuk, D. Computer modeling of information properties of deterministic chaos. CHAOS 2014 - Proceedings: 7th Chaotic Modeling and Simulation International Conference, 2019, p. 265 – 276.
  14. Kushnir, M.; Ivaniuk, P.; Vovchuk, D.; Galiuk, S. Information security of the chaotic communication systems. CHAOS 2015 - 8th Chaotic Modeling and Simulation International Conference, Proceedings, 2015, p. 441 – 452.
  15. Wang, Y.; Liu, Z.; Zhang, L.Y.; Pareschi, F.; Setti, G.; Chen, G. From chaos to pseudorandomness: A case study on the 2-D coupled map lattice. IEEE Transactions on Cybernetics 2023, 53, 1324–1334. [Google Scholar] [CrossRef]
  16. Cover, T.; Thomas, J.A. Elements of information theory; Wiley-Interscience: Hoboken, NJ, USA, 2006. [Google Scholar]
  17. Eisencraft, M.; Monteiro, L.H.A.; Soriano, D.C. White Gaussian Chaos. IEEE Communications Letters 2017, 21, 1719–1722. [Google Scholar] [CrossRef]
  18. Mliki, E.; Hasanzadeh, N.; Nazarimehr, F.; Akgul, A.; Boubaker, O.; Jafari, S. Some New Chaotic Maps With Application in Stochastic. In Recent Advances in Chaotic Systems and Synchronization; Boubaker, O.; Jafari, S., Eds.; Emerging Methodologies and Applications in Modelling, Academic Press, 2019; pp. 165–185. [CrossRef]
  19. Rovatti, R.; Setti, G.; Callegari, S. Limit properties of folded sums of chaotic trajectories. IEEE Transactions on Circuits and Systems I: Fundamental Theory and Applications 2002, 49, 1736–1744. [Google Scholar] [CrossRef]
  20. Kilias, T.; Kristina Kelber, A.M.; Schwarz, W. Electronic chaos generators—design and applications. International Journal of Electronics 1995, 79, 737–753. [Google Scholar] [CrossRef]
  21. Liu, J.d.; Kai, Y.; Wang, S.h. Coupled Chaotic Tent Map Lattices System with Uniform Distribution. 2010 2nd International Conference on E-business and Information System Security, 2010, pp. 1–5. [CrossRef]
  22. Li, P.; Li, Z.; Halang, W.A.; Chen, G. A stream cipher based on a spatiotemporal chaotic system. Chaos, Solitons & Fractals 2007, 32, 1867–1876. [Google Scholar]
  23. Espinel, A.; Taralova, I.; Lozi, R. New alternate ring-coupled map for multi-random number generation. Journal of Nonlinear Systems and Applications 2013, pp. 64–69.
  24. Haliuk, S.; Krulikovskyi, O.; Politanskyi, L. Analysis of time series generated by Tratas chaotic system. Herald of Khmelnytskyi National University 2017, 251, 187–192. [Google Scholar]
  25. Haliuk, S.; Krulikovskyi, O.; Politanskyi, L.; Corinto, F. Circuit implementation of Lozi ring-coupled map. 2017 4th International Scientific-Practical Conference Problems of Infocommunications. Science and Technology (PIC S&T). IEEE, 2017, pp. 249–252. [CrossRef]
  26. Naruse, M.; Kim, S.J.; Aono, M.; Hori, H.; Ohtsu, M. Chaotic oscillation and random-number generation based on nanoscale optical-energy transfer. Scientific Reports 2014, 4, 6039. [Google Scholar] [CrossRef] [PubMed]
  27. Elsonbaty, A.; Hegazy, S.F.; Obayya, S.S.A. Numerical analysis of ultrafast physical random number generator using dual-channel optical chaos. Optical Engineering 2016, 55, 094105–094105. [Google Scholar] [CrossRef]
  28. Yoshiya, K.; Terashima, Y.; Kanno, K.; Uchida, A. Entropy evaluation of white chaos generated by optical heterodyne for certifying physical random number generators. Opt. Express 2020, 28, 3686–3698. [Google Scholar] [CrossRef] [PubMed]
  29. Kawaguchi, Y.; Okuma, T.; Kanno, K.; Uchida, A. Entropy rate of chaos in an optically injected semiconductor laser for physical random number generation. Opt. Express 2021, 29, 2442–2457. [Google Scholar] [CrossRef] [PubMed]
  30. Baby, H.T.; Sujatha, B.R. Optical Chaos KEY generator for Cryptosystems. Journal of Physics: Conference Series 2021, 1767, 012046. [Google Scholar] [CrossRef]
  31. Nguyen, N.; Kaddoum, G.; Pareschi, F.; Rovatti, R.; Setti, G. A fully CMOS true random number generator based on hidden attractor hyperchaotic system. Nonlinear Dynamics 2020, 102, 2887–2904. [Google Scholar] [CrossRef]
  32. Guo, Y.; Li, H.; Wang, Y.; Meng, X.; Zhao, T.; Guo, X. Chaos with Gaussian invariant distribution by quantum-noise random phase feedback. arxiv 2023, arXiv:physics.optics/2306.06912. [Google Scholar] [CrossRef]
  33. Fadil, E.; Abass, A.; Tahhan, S. Secure WDM-free space optical communication system based optical chaotic. Optical and Quantum Electronics 2022, 54, 477. [Google Scholar] [CrossRef]
  34. Wang, L.; Mao, X.; Wang, A.; Wang, Y.; Gao, Z.; Li, S.; Yan, L. Scheme of coherent optical chaos communication. Optics Letters 2020, 45, 4762–4765. [Google Scholar] [CrossRef]
  35. Liu, B.C.; Xie, Y.Y.; Zhang, Y.S.; Ye, Y.C.; Song, T.T.; Liao, X.F.; Liu, Y. ARM-Embedded Implementation of a Novel Color Image Encryption and Transmission System Based on Optical Chaos. IEEE Photonics Journal 2020, 12, 1–17. [Google Scholar] [CrossRef]
  36. Shakeel, I.; Hilliard, J.; Zhang, W.; Rice, M. Gaussian-Distributed Spread-Spectrum for Covert Communications. Sensors 2023, 23. [Google Scholar] [CrossRef]
  37. Negi, R.; Goel, S. Secret communication using artificial noise. VTC-2005-Fall. 2005 IEEE 62nd Vehicular Technology Conference, 2005., 2005, Vol. 3, pp. 1906–1910. [CrossRef]
  38. Zhou, X.; McKay, M.R. Secure Transmission With Artificial Noise Over Fading Channels: Achievable Rate and Optimal Power Allocation. IEEE Transactions on Vehicular Technology 2010, 59, 3831–3842. [Google Scholar] [CrossRef]
  39. Nguyen, L.L.; Nguyen, T.T.; Fiche, A.; Gautier, R.; Ta, H.Q. Hiding Messages in Secure Connection Transmissions with Full-Duplex Overt Receiver. Sensors 2022, 22. [Google Scholar] [CrossRef]
  40. Yang, W.; Lu, X.; Yan, S.; Shu, F.; Li, Z. Age of Information for Short-Packet Covert Communication. IEEE Wireless Communications Letters 2021, 10, 1890–1894. [Google Scholar] [CrossRef]
  41. Anderson, D.F.; Seppäläinen, T.; Valkó, B. Introduction to probability; Cambridge University Press, 2017.
  42. Athreya, K.B.; Lahiri, S.N. Measure theory and probability theory; Vol. 19, Springer, 2006.
  43. Thode, H.C. Testing for Normality, 1st ed.; Statistics: Textbooks and Monographs 164, Marcel Dekker, 2002. [Google Scholar]
  44. Michalowicz, J.V.; Nichols, J.M.; Bucholtz, F. Handbook of differential entropy; Crc Press, 2013.
  45. Krasil’nikov, A.I. Class of non-Gaussian distributions with zero skewness and kurtosis. Radioelectronics and Communications Systems 2013, 56, 312–320. [Google Scholar] [CrossRef]
  46. Kschischang, F.R. The hilbert transform 2006.
  47. Shannon, C.E. A mathematical theory of communication. The Bell system technical journal 1948, 27, 379–423. [Google Scholar] [CrossRef]
  48. Matsumoto, T.; Chua, L.; Komuro, M. The double scroll. IEEE Transactions on Circuits and Systems 1985, 32, 797–818. [Google Scholar] [CrossRef]
  49. Zhong, G.Q. Implementation of Chua’s circuit with a cubic nonlinearity. IEEE Transactions on Circuits and Systems I: Fundamental Theory and Applications 1994, 41, 934–941. [Google Scholar] [CrossRef]
  50. Shi, Z.; Ran, L. Tunnel diode based Chua’s circuit. Proceedings of the IEEE 6th Circuits and Systems Symposium on Emerging Technologies: Frontiers of Mobile and Wireless Communication (IEEE Cat. No.04EX710), 2004, Vol. 1, pp. 217–220 Vol.1. [CrossRef]
  51. Kennedy, M.P. Robust op amp realization of Chua’s circuit. Frequenz 1992, 46, 66–80. [Google Scholar] [CrossRef]
  52. Lorenz, E.N. Deterministic nonperiodic flow. Journal of the atmospheric sciences 1963, 20, 130–141. [Google Scholar] [CrossRef]
  53. Pappu, C.S.; Flores, B.C.; Debroux, P.S.; Boehm, J.E. An Electronic Implementation of Lorenz Chaotic Oscillator Synchronization for Bistatic Radar Applications. IEEE Transactions on Aerospace and Electronic Systems 2017, 53, 2001–2013. [Google Scholar] [CrossRef]
  54. Horowitz, P. Build a Lorenz attractor. Harvard Univ., Cambridge, MA, USA. [Online].
  55. Bhalekar, S.; Daftardar-Gejji, V. A new chaotic dynamical system and its synchronization. Proceedings of the international conference on mathematical sciences in honor of Prof. AM Mathai, 2011, pp. 3–5.
  56. Chen, H.K.; Lee, C.I. Anti-control of chaos in rigid body motion. Chaos, Solitons & Fractals 2004, 21, 957–965. [Google Scholar] [CrossRef]
  57. Cheng, G.; Li, D.; Yao, Y.; Gui, R. Multi-scroll chaotic attractors with multi-wing via oscillatory potential wells. Chaos, Solitons & Fractals 2023, 174, 113837. [Google Scholar] [CrossRef]
  58. Dmitriev, A.; Panas, A. Dynamic Chaos: New Data Carrying Media for Communication Systems, 2002.
  59. Semenov, A. Reviewing the mathemetical models and electrical circuits of deterministic chaos transistor oscillators. 2016 International Siberian Conference on Control and Communications (SIBCON), 2016, pp. 1–6. [CrossRef]
  60. Dong, G.; Du, R.; Tian, L.; Jia, Q. A novel 3D autonomous system with different multilayer chaotic attractors. Physics Letters A 2009, 373, 3838–3845. [Google Scholar] [CrossRef]
  61. Muthuswamy, B. Implementing memristor based chaotic circuits. International Journal of Bifurcation and Chaos 2010, 20, 1335–1350. [Google Scholar] [CrossRef]
  62. Genesio, R.; Tesi, A. Harmonic balance methods for the analysis of chaotic dynamics in nonlinear systems. Automatica 1992, 28, 531–548. [Google Scholar] [CrossRef]
  63. Park, J.H. Synchronization of Genesio chaotic system via backstepping approach. Chaos, Solitons & Fractals 2006, 27, 1369–1375. [Google Scholar] [CrossRef]
  64. Li, C.; Li, H.; Tong, Y. Analysis of a novel three-dimensional chaotic system. Optik 2013, 124, 1516–1522. [Google Scholar] [CrossRef]
  65. Li, C.; Sprott, J.C. Variable-boostable chaotic flows. Optik 2016, 127, 10389–10398. [Google Scholar] [CrossRef]
  66. Liu, W.; Chen, G. A new chaotic system and its generation. International Journal of Bifurcation and Chaos 2003, 13, 261–267. [Google Scholar] [CrossRef]
  67. LÜ, J.; Chen, G. A new chaotic attractor coined. International Journal of Bifurcation and Chaos 2002, 12, 659–661. [Google Scholar] [CrossRef]
  68. Lü, J.; Chen, G.; Cheng, D. A new chaotic system and beyond: The generalized lorenz-like system. International Journal of Bifurcation and Chaos 2004, 14, 1507–1537. [Google Scholar] [CrossRef]
  69. Huang, J.; Xiao, T.J. Chaos synchronizations of chaotic systems via active nonlinear control. Journal of Physics: Conference Series 2008, 96, 012177. [Google Scholar] [CrossRef]
  70. Muthuswamy, B.; Chua, L.O. Simplest chaotic circuit. International Journal of Bifurcation and Chaos 2010, 20, 1567–1580. [Google Scholar] [CrossRef]
  71. Özoguz, S.; Elwakil, A.; Salama, K.N. N-scroll chaos generator using nonlinear transconductor. Electronics Letters 2002, 38, 1. [Google Scholar] [CrossRef]
  72. Qi, G.; Chen, G.; van Wyk, M.A.; van Wyk, B.J.; Zhang, Y. A four-wing chaotic attractor generated from a new 3-D quadratic autonomous system. Chaos, Solitons & Fractals 2008, 38, 705–721. [Google Scholar] [CrossRef]
  73. Haliuk, S.; Kushnir, M.; Politanskyi, L.; Politanskyi, R. Synchronization of chaotic systems and signal filtration in the communication channel. Eastern-European Journal of Enterprise Technologies 2012, 1, 20–24. [Google Scholar] [CrossRef]
  74. Rössler, O.E. An equation for continuous chaos. Physics Letters A 1976, 57, 397–398. [Google Scholar] [CrossRef]
  75. Sprott, J.C. Some simple chaotic flows. Physical review E 1994, 50, R647. [Google Scholar] [CrossRef] [PubMed]
  76. Wu, R.; Wang, C. A New Simple Chaotic Circuit Based on Memristor. International Journal of Bifurcation and Chaos 2016, 26, 1650145. [Google Scholar] [CrossRef]
  77. Zhang, X.; Tian, Z.; Li, J.; Cui, Z. A Simple Parallel Chaotic Circuit Based on Memristor. Entropy 2021, 23. [Google Scholar] [CrossRef] [PubMed]
Preprints 100739 g001
Figure 1. Schematic representation of the suggested algorithm for forming of Gaussian-distributed signal. Simple chaotic systems with different initial conditions and/or system’s parameters suffer normalization (an optional stage depending on the conditions) and are added in the summation block. The number of chaotic systems (n) can vary until the output signal successfully passes the suggested algorithm’s tests, resulting in the achievement of the Gaussian-distributed signal.
Figure 1. Schematic representation of the suggested algorithm for forming of Gaussian-distributed signal. Simple chaotic systems with different initial conditions and/or system’s parameters suffer normalization (an optional stage depending on the conditions) and are added in the summation block. The number of chaotic systems (n) can vary until the output signal successfully passes the suggested algorithm’s tests, resulting in the achievement of the Gaussian-distributed signal.
Preprints 100739 g001
Preprints 100739 g002
Figure 2. Chua’s circuit
Figure 2. Chua’s circuit
Preprints 100739 g002
Preprints 100739 g003
Figure 3. The PDFs of sum of n chaotic signals generated by Chua’s circuit: PDF signals (a-d), PDF envelope of signals (e-h), PDF of phase of signals (i-l)
Figure 3. The PDFs of sum of n chaotic signals generated by Chua’s circuit: PDF signals (a-d), PDF envelope of signals (e-h), PDF of phase of signals (i-l)
Preprints 100739 g003
Preprints 100739 g004
Figure 4. Quality metrics of sum of n signals x, z generated by Chua’s circuit for different n: excess kurtosis (a), entropy power of the amplitude of signals (b), entropy power of the envelope of signals (c) and entropy power of phase of signals (d)
Figure 4. Quality metrics of sum of n signals x, z generated by Chua’s circuit for different n: excess kurtosis (a), entropy power of the amplitude of signals (b), entropy power of the envelope of signals (c) and entropy power of phase of signals (d)
Preprints 100739 g004
Preprints 100739 g005
Figure 5. Electronic implementation of Lorenz system [53]
Figure 5. Electronic implementation of Lorenz system [53]
Preprints 100739 g005
Preprints 100739 g006
Figure 6. The PDFs of sum of n chaotic signals generated by Lorenz circuit: PDF signals (a-d), PDF envelope of signals (e-h), PDF of phase of signals (i-l)
Figure 6. The PDFs of sum of n chaotic signals generated by Lorenz circuit: PDF signals (a-d), PDF envelope of signals (e-h), PDF of phase of signals (i-l)
Preprints 100739 g006
Preprints 100739 g007
Figure 7. Quality metrics of sum of n signals x, y, z generated by Lorenz circuit for different n: excess kurtosis (a), entropy power of the amplitude of signals (b), entropy power of the envelope of signals (c) and entropy power of phase of signals (d)
Figure 7. Quality metrics of sum of n signals x, y, z generated by Lorenz circuit for different n: excess kurtosis (a), entropy power of the amplitude of signals (b), entropy power of the envelope of signals (c) and entropy power of phase of signals (d)
Preprints 100739 g007
Preprints 100739 g008
Figure 8. The experimental PDFs of sum of n chaotic signals generated by prototype of Chua’s circuit: PDF signals (a-d), PDF envelope of signals (e-h), PDF of phase of signals (i-l)
Figure 8. The experimental PDFs of sum of n chaotic signals generated by prototype of Chua’s circuit: PDF signals (a-d), PDF envelope of signals (e-h), PDF of phase of signals (i-l)
Preprints 100739 g008
Preprints 100739 g009
Figure 9. The experimental PDFs of sum of n chaotic signals generated by prototype of Lorenz circuit: PDF signals (a-d), PDF envelope of signals (e-h), PDF of phase of signals (i-l)
Figure 9. The experimental PDFs of sum of n chaotic signals generated by prototype of Lorenz circuit: PDF signals (a-d), PDF envelope of signals (e-h), PDF of phase of signals (i-l)
Preprints 100739 g009
Table 1. Statistical properties of signals of Chua’s circuit.
Table 1. Statistical properties of signals of Chua’s circuit.
Chaotic system Output
variable		 μ ˜ 3 μ ˜ 4 k 1 k 2 k 3
Chua’s circuit [48]
x ˙ = 10 ( y − x − f ( x ) ) x -0.0116 -1.6609 0.3626 0.4754 0.8435
y ˙ = x − y + z y -0.0028 -0.1421 0.9039 0.9756 0.9980
z ˙ = − 14.6 y z 0.0084 -1.1152 0.7541 0.8128 0.9056
where
f ( x ) = m 2 x + 0.5 ( ( m 0 − m 1 ) ( | x + a 1 | − | x − a 1 | ) + ( m 1 − m 2 ) ( | x + a 2 | − | x − a 2 | ) ) ;
a 1 = 1 ; a 2 = 6.88 ; m 0 = − 1.238 ; m 1 = − 0.6665 ; m 2 = 500
Pairwise sum of two signals
x 1 + x 2 0.0033 -0.8287 0.7040 0.9349 0.9696
y 1 + y 2 0.0029 -0.0717 0.9961 0.9604 0.9989
z 1 + z 2 -0.0007 -0.5581 0.9648 0.9976 0.9965
Pairwise sum of three signals
x 1 + x 2 + x 3 -0.0059 -0.5519 0.8741 0.8897 0.9873
y 1 + y 2 + y 3 0.0015 -0.0367 0.9996 0.9893 0.9986
z 1 + z 2 + z 3 0.0089 -0.3715 0.9901 0.9798 0.9987
Pairwise sum of four signals
x 1 + x 2 + x 3 + x 4 -0.0090 -0.4088 0.9467 0.9783 0.9982
y 1 + y 2 + y 3 + y 4 0.0009 -0.0034 0.9998 0.9908 0.9985
z 1 + z 2 + z 3 + z 4 0.0105 -0.2700 0.9955 0.9907 0.9994
Experiment with Chua’s circuit
y 1 y -0.0518 -0.4249 0.9437 0.9381 0.9950
y 1 + y 2 0.0339 -0.3837 0.9897 0.9192 0.9986
y 1 + y 2 + y 3 0.0511 -0.2393 0.9962 0.9629 0.9986
y 1 + y 2 + y 3 + y 4 0.0420 -0.1846 0.9979 0.9720 0.9985
Chua’s circuit [48]
x ˙ = 9.273 ( y − x − f ( x ) ) x -0.0763 -1.4807 0.5463 0.6532 0.9087
y ˙ = x − y + z y -0.0070 -0.9334 0.8739 0.5006 0.9989
z ˙ = − 16.8 y − 0.0042 z z 0.0465 -0.8164 0.8676 0.8860 0.9808
where
f ( x ) = m 2 x + 0.5 ( ( m 0 − m 1 ) ( | x + a 1 | − | x − a 1 | ) + ( m 1 − m 2 ) ( | x + a 2 | − | x − a 2 | ) ) ;
a 1 = 1 ; a 2 = 6.88 ; m 0 = − 1.238 ; m 1 = − 0.6665 ; m 2 = 500 .
Table 2. Statistical properties of signals of Lorenz systems.
Table 2. Statistical properties of signals of Lorenz systems.
Chaotic system Output
variable		 3 4 k 1 k 2 k 3
Lorenz [52]
x ˙ = 10 ( y − x ) x 0.0003 -0.7093 0.8989 0.8535 0.9830
y ˙ = ( 28 − z ) x − y y 0.0005 -0.1573 0.9013 0.9368 0.8877
z ˙ = x y − 8 3 z 0.2023 -0.8499 0.8974 0.5618 0.9731
Pairwise sum of two signals
x 1 + x 2 -0.0102 -0.3529 0.9893 0.9587 0.9995
y 1 + y 2 -0.0103 -0.0801 0.9938 0.9580 0.9865
z 1 + z 2 0.0014 -0.4291 0.9852 0.9921 0.9983
Pairwise sum of three signals
x 1 + x 2 + x 3 -0.0053 -0.2393 0.9966 0.9677 0.9989
y 1 + y 2 + y 3 -0.0059 -0.0570 0.9993 0.9857 0.9978
z 1 + z 2 + z 3 0.0397 -0.2867 0.9946 0.9631 0.9994
Pairwise sum of four signals
x 1 + x 2 + x 3 + x 4 -0.0031 -0.1840 0.9981 0.9759 0.9987
y 1 + y 2 + y 3 + y 4 -0.0040 -0.0468 0.9997 0.9937 0.9999
x 1 + x 2 + x 3 + x 4 0.0002 -0.2122 0.9975 0.9852 0.9987
Experiment with Lorenz system
x 1 x 0.0131 -0.5906 0.9292 0.8454 0.9606
x 1 + x 2 0.0150 -0.1978 0.9937 0.9995 0.9976
x 1 + x 2 + x 3 0.0204 -0.0523 0.9989 0.9996 0.9993
x 1 + x 2 + x 3 + x 4 0.0246 0.0499 0.9995 0.9886 0.9996
Lorenz [52]
x ˙ = 10 ( y − x ) x -0.0034 -0.9328 0.8961 0.7523 0.9649
y ˙ = ( 60 − z ) x − y y -0.0038 -0.3519 0.9801 0.9247 0.8355
z ˙ = x y − 8 3 z z 0.0821 -0.4826 0.9736 0.7515 0.9786
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated